The Federal Reserve Board eagle logo links to home page

Rise of the Machines: Algorithmic Trading in the Foreign Exchange Market

Alain Chaboud, Benjamin Chiquoine, Erik Hjalmarsson, Clara Vega1

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

We study the impact that algorithmic trading, computers directly interfacing at high frequency with trading platforms, has had on price discovery and volatility in the foreign exchange market. Our dataset represents a majority of global interdealer trading in three major currency pairs in 2006 and 2007. Importantly, it contains precise observations of the size and the direction of the computer-generated and human-generated trades each minute. The empirical analysis provides several important insights. First, we find evidence that algorithmic trades tend to be correlated, suggesting that the algorithmic strategies used in the market are not as diverse as those used by non-algorithmic traders. Second, we find that, despite the apparent correlation of algorithmic trades, there is no evident causal relationship between algorithmic trading and increased exchange rate volatility. If anything, the presence of more algorithmic trading is associated with lower volatility. Third, we show that even though some algorithmic traders appear to restrict their activity in the minute following macroeconomic data releases, algorithmic traders increase their provision of liquidity over the hour following each release. Fourth, we find that non-algorithmic order flow accounts for a larger share of the variance in exchange rate returns than does algorithmic order flow. Fifth, we find evidence that supports the recent literature that proposes to depart from the prevalent assumption that liquidity providers in limit order books are passive.

Keywords: Algorithmic trading, volatility, liquidity provision, private information

JEL classification:F3, G12, G14, G15

 

1   Introduction

The use of algorithmic trading, where computer algorithms directly manage the trading process at high frequency, has become common in major financial markets in recent years, beginning in the U.S. equity market more than 15 years ago. There has been widespread interest in understanding the potential impact of algorithmic trading on market dynamics, as some analysts have highlighted the potential for improved liquidity and more efficient price discovery while others have expressed concern that it may be a source of increased volatility and reduced liquidity, particularly in times of market stress. A number of articles and opinion pieces on the topic have recently appeared in the press, with most decrying practices used by some algorithmic traders in the equity market, and there have been calls for regulatory agencies in the United States and Europe to begin investigations.2 Despite this interest, there has been very little formal empirical research on algorithmic trading, primarily because of a lack of data where algorithmic trades are clearly identified. A notable exception is a recent paper by Hendershott, Jones, and Menkveld (2007), who get around the data constraint by using the flow of electronic messages on the NYSE as a proxy for algorithmic trading. They conclude that algorithmic trading on the NYSE, contrary to the pessimists' concerns, likely causes an improvement in market liquidity.3 In the foreign exchange market, there has been no formal empirical research on the subject. The adoption of algorithmic trading in the foreign exchange market is a far more recent phenomenon than in the equity market, as the two major interdealer electronic trading platforms only began to allow algorithmic trades a few years ago. Growth in algorithmic trading has been very rapid, however, and a majority of foreign exchange transactions in the interdealer market currently involve at least one algorithmic counterparty.

In algorithmic trading (AT), computers directly interface with trading platforms, placing orders without immediate human intervention. The computers observe market data and possibly other information at very high frequency, and, based on a built-in algorithm, send back trading instructions, often within milliseconds. A variety of algorithms are used: for example, some look for arbitrage opportunities, including small discrepancies in the exchange rates between three currencies; some seek optimal execution of large orders at the minimum cost; and some seek to implement longer-term trading strategies in search of profits. Among the most recent developments in algorithmic trading, some algorithms now automatically read and interpret economic data releases, generating trading orders before economists have begun to read the first line.

The extreme speed of execution that AT allows and the potential that algorithmic trades may be highly correlated, perhaps as many institutions use similar algorithms, have been cited as reasons for concerns that AT may generate large price swings and market instability. On the other hand, the fact that some algorithms aim for optimal execution at a minimal price impact may be expected to lower volatility. In this paper, we investigate whether algorithmic ("computer") trades and non-algorithmic ("human") trades have different effects on the foreign exchange market. We first ask whether the presence of computer trades causes higher or lower volatility and whether computers increase or reduce liquidity during periods of market stress. We then study the relative importance of human and computer trades in the process of price discovery and re-visit the assumption that liquidity providers are "uninformed."

We formally investigate these issues using a novel dataset consisting of two years (2006 and 2007) of minute-by-minute trading data from EBS in three currency pairs: the euro-dollar, dollar-yen, and euro-yen. The data represent the vast majority of global spot interdealer transactions in these exchange rates. An important feature of the data is that the volume and direction of human and computer trades each minute are explicitly identified, allowing us to measure their respective impacts.

We first show some evidence that computer trades are more highly correlated with each other than human trades, suggesting that the strategies used by computers are not as diverse as those used by humans. But the high correlation of computer trades does not necessarily translate into higher volatility. In fact, we find next that there is no evident causal relationship between AT and increased market volatility. If anything, the presence of more algorithmic trading appears to lead to lower market volatility, although the economic magnitude of the effect is small. In order to account for the potential endogeneity of algorithmic trading with regards to volatility, we instrument for the actual level of algorithmic trading with the installed capacity for algorithmic trading in the EBS system at a given time.

Next, we study the relative provision of market liquidity by computers and humans at the times of the most influential U.S. macroeconomic data release, the nonfarm payroll report. We find that, as a share of total market-making activity, computers tend to pull back slightly at the precise time of the release but then increase their presence in the following hour. This result suggests that computers do provide liquidity during periods of market stress.

Finally, we estimate return-order flow dynamics using a structural VAR framework in the tradition of Hasbrouck (1991a). The VAR estimation provides two important insights. First, we find that human order flow accounts for much of the long-run variance in exchange rate returns in the euro-dollar and dollar-yen exchange rate markets, i.e., humans appear to be the " informed" traders in these markets. In contrast, in the euro-yen exchange rate market, computers and humans appear to be equally " informed." In this cross-rate, we believe that computers have a clear advantage over humans in detecting and reacting more quickly to triangular arbitrage opportunities, where the euro-yen price is briefly out of line with prices in the euro-dollar and dollar-yen markets. Second, we find that, on average, computers or humans that trade on a price posted by a computer do not impact prices quite as much as they do when they trade on a price posted by a human. One possible interpretation of this result is that computers tend to place limit orders more strategically than humans do. This empirical evidence supports the literature that proposes to depart from the prevalent assumption that liquidity providers in limit order books are passive.4

The paper proceeds as follows. In Section 2 we introduce the EBS exchange rate data, describing the evolution over time of algorithmic trading and the pattern of interaction between human and algorithmic traders. In Section 3 we study the correlation of algorithmic trades. In Section 4 we analyze the relationship between algorithmic trading and exchange rate volatility. In Section 5 we discuss the provision of liquidity by computers and humans at the time of a major data release. In Section 6 we report the results of the high-frequency VAR analysis. We conclude in Section 7. Some robustness results are presented in the Appendix.

2   Data description

Today, two electronic platforms process the vast majority of global interdealer spot trading in the major currency pairs, one offered by Reuters, and one offered by EBS.5 These platforms, which are both electronic limit order books, have become essential utilities for the foreign exchange market. Importantly, trading in each major currency pair has over time become very highly concentrated on only one of the two systems. Of the most traded currency pairs, the top two, euro-dollar and dollar-yen, trade primarily on EBS, while the third, sterling-dollar, trades primarily on Reuters. As a result, the reference price at any moment for, say, spot euro-dollar, is the current price on the EBS system, and all dealers across the globe base their customer and derivative quotes on that price. EBS controls the network and each of the terminals on which the trading is conducted. Traders can enter trading instructions manually, using an EBS keyboard, or, upon approval by EBS, via a computer directly interfacing with the system. The type of trader (human or computer) behind each trading instruction is recorded by EBS, allowing for our study.6

We have access to AT data from EBS from 2003 through 2007. We focus on the sample from 2006 and 2007, because, as we will show, algorithmic trades were a very small portion of total trades in the earlier years. In addition to the full 2006-2007 sample, we also consider a sub-sample covering the months of September, October, and November of 2007, when algorithmic trading played an even more important role than earlier in the sample.7 We study the three most-traded currency pairs on the EBS system: euro-dollar, dollar-yen, and euro-yen.

The quote data, at the one-second frequency, consist of the highest bid quote and the lowest ask quote on the EBS system in these currency pairs, from which we construct one-second mid-quote series and compute one-minute exchange rate returns; all the quotes are executable and therefore represent the true price at that moment. The transactions data are at the one-minute frequency and provide detailed information on the volume and direction of trades that can be attributed to computers and humans in each currency pair. Specifically, the transactions volume data are broken down into categories specifying the "maker" and "taker" of the trades (i.e., human or computer), and the direction of the trades (i.e., buy or sell the base currency), for a total of eight different combinations. That is, the first transaction category may specify, say, the minute-by-minute volume of trade that results from a human taker buying the base currency by "hitting" a quote posted by a human maker. We would record this activity as the human-human buy volume, with the aggressor (taker) of the trade buying the base currency. The human-human sell volume is defined analogously, as are the other six buy and sell volumes that arise from the remaining combinations of computers and humans acting as makers and takers.

From these eight types of buy and sell volumes, we can construct, for each minute, trading volume and order flow measures for each of the four possible pairs of human and computer makers and takers: human-maker/human-taker $ (HH)$, computer-maker/human-taker $ (CH)$, human-maker/computer-taker $ (HC)$, and computer-maker/computer-taker $ (CC)$.8 That is, the sum of the buy and sell volumes for each pair gives the volume of trade attributable to that particular combination of maker and taker (which we symbolize as, $ Vol(HH)$ or $ Vol(HC)$, for example). The difference between the buy and sell volume for each pair gives us the order flow attributable to that maker-taker combination (which we symbolize simply as $ HH$ or $ HC$, for example). The sum of the four volumes, $ Vol(HH+CH+HC+CC)$, gives the total volume of trade in the market. The sum of the four order flows, $ HH+CH+HC+CC$, gives the total (market-wide) order flow.9 Throughout the paper, we will use the expression " order flow" to refer both to the market-wide order flow and to the order flows from other possible decompositions, with the distinction clearly indicated. Importantly, the data allow us to consider order flow broken down by the type of trader who initiated the trade, human-taker order flow $ (HH+CH)$ and computer-taker order flow $ (HC+CC)$.

The main goal of this paper is to analyze the effect algorithmic trading has on price discovery and volatility in the foreign exchange market. In our exchange rate data as in other financial data, the net of signed trades from the point of view of the takers (the market-wide order flow) is highly positively correlated with exchange rate returns, so that the takers are considered to be more " informed" than the makers. Thus, in our analysis of the relative effects of human and computer trades in the market, we consider prominently the order flow decomposition into human-taker order flow and computer-taker order flow. However, we also consider two other decompositions in our work. We consider the most disaggregated decomposition of order flow $ (HH,CH,HC,CC)$, as this decomposition allows us to study whether the liquidity suppliers, who are traditionally assumed to be " uninformed", are posting quotes strategically. This situation is more likely to arise in our data, which comes from a pure limit order book market, than in data from a hybrid market like the NYSE, because, as Parlour and Seppi (2008) point out, the distinction between liquidity supply and liquidity demand in limit order books is blurry.10 We also decompose the data by maker type (human or computer) in order to study whether computers or humans are providing liquidity during the release of public information, which are periods of high exchange rate volatility and, often, market stress.

In our analysis, we exclude data collected from Friday 17:00 through Sunday 17:00 New York time from our sample, as activity on the system during these " non-standard" hours is minimal and not encouraged by the foreign exchange community. We also drop certain holidays and days of unusually light volume: December 24-December 26, December 31-January 2, Good Friday, Easter Monday, Memorial Day, Labor Day, Thanksgiving and the following day, and July 4 (or, if this is on a weekend, the day on which the U.S. Independence Day holiday is observed).

We show summary statistics for the one-minute returns and order flow data in Table 1. This table contains a number of noteworthy features. First, order flow, whether in total, broken down by human and computer takers, or broken down into the 4 possible pairs of makers and takers, is serially positively correlated, which is consistent with some informed trading models. For example, Easley and O'Hara (1987) model a situation where sequences of large purchases (sales) arise when insiders with positive (negative) signals are present in the market. He and Wang (1995) also show that insiders with good (bad) news tend to buy (sell) repeatedly until their private information is revealed in the prices. The positive serial correlation in order flow is also consistent with strategic order splitting, i.e. a trader willing to buy for informational or non-informational reasons and splitting his order to reduce market impact. Second, the standard deviations of the various order flows differ by exchange rates, by type of taker and across maker/taker pairs. These differences will be important in the interpretation of the upcoming VAR analysis and variance decompositions.

We show in Figure 1, from 2003 through 2007 for our three major currency pairs, the fraction of trading volume where at least one of the two counterparties was an algorithmic trader, i.e. $ Vol(CH+HC+CC)$ as a fraction of total volume.11 From its beginning in 2003, the fraction of trading volume involving AT grew by the end of 2007 to near 60% for euro-dollar, and dollar-yen trading, and to about 80% for euro-yen. Figure 2 shows, for our three currency pairs, the evolution over time of the four different possible types of trades (i.e. $ Vol(HH)$, $ Vol(CH)$, $ Vol(HC)$, and $ Vol(CC),$ as fractions of the total volume). By the end of 2007, in the euro-dollar and dollar-yen markets, human to human trades, in black, accounted for slightly less than half of the volume, and computer to computer trades, in green, for about ten to fifteen percent. In euro-dollar and dollar-yen, we note that $ Vol(HC)$ and $ Vol(CH)$ are about equal to each other, i.e. computers " take" prices posted by humans, in red, about as often as humans take prices posted by market-making computers, in blue. The story is different for the cross-rate, the euro-yen currency pair. By the end of 2007, there were more computer to computer trades than human to human trades. But the most common type of trade was computers trading on prices posted by humans. We believe this reflects computers taking advantage of short-lived triangular arbitrage opportunities, where prices set in the euro-dollar and dollar-yen markets are very briefly out of line with the euro-yen cross rate. In interpreting our results later in the paper, we will keep in mind that trading volume is largest in the euro-dollar and dollar-yen markets, and that price discovery happens mostly in those markets, not in the cross-rate. Our conclusions based on the euro-dollar and dollar-yen markets will then be more easily generalized than those based on the euro-yen market. Table 2 tabulates the averages of the volume fractions shown in Figures 1 and 2, both for the full 2006-2007 sample and the shorter three-month sub-sample.

3  How Correlated Are Algorithmic Trades and Strategies?

We first investigate the proposition that computers tend to have trading strategies that are more correlated than those of humans. Since the outset of the financial turmoil in the summer of 2007, articles in the financial press have suggested that AT programs tend to be similarly designed, leading them to take the same side of the market in times of high volatility and potentially exaggerating market movements.12

One such instance may have happened on August 16, 2007, a day of very high volatility in the dollar-yen market. On that day, the Japanese yen appreciated sharply against the U.S. dollar around 6:00 a.m. and 12:00 p.m. (NY time), as shown in Figure 3. The figure also shows, for each 30-minute interval in the day, computer-taker order flow $ (HC$ $ +CC)$ in the top panel and human-taker order flow $ (HH+CH)$ in the lower panel. The two sharp exchange rate movements mentioned happened when computers, as a group, aggressively sold dollars and bought yen. We note that computers, during these episodes, mainly traded with humans, not with other computers. Human order flow at those times was, in contrast, quite small, even though the overall trading volume initiated by humans (not shown) was well above that initiated by computers (human takers were therefore selling and buying dollars in almost equal amounts). The " taking" orders generated by computers during those time intervals were far more correlated than the taking orders generated by humans. After 12:00 p.m., human traders, as a whole, then began to buy dollars fairly aggressively, and the appreciation of the yen against the dollar was partially reversed. This is only a single example, of course, but it leads us to ask how correlated computer trades and strategies have tended to be overall.

We do not know precisely the exact mix of the various strategies used by algorithmic traders on EBS. Traders keep the information about their own strategies confidential, including, to some extent, from EBS, and EBS also keeps what they know confidential.13 However, one can get a general sense of the market and of the strategies in conversations with market participants. About half of the algorithmic trading volume on EBS is believed to come from what is often known as the " professional trading community," which primarily refers to hedge funds and commodity trading advisors (CTAs). These participants, until very recently, could not trade manually on EBS, so all their trades were algorithmic. Some hedge funds and CTAs seek to exploit short-lived arbitrage opportunities, including triangular arbitrage, often accessing several trading platforms. Others implement lower-frequency strategies, often grouped under the statistical arbitrage appellation, including carry trades, momentum trades, and strategies spanning several asset classes. Only a very small fraction of the trading volume in our sample period is believed to have been generated by algorithms designed to quickly react to data releases. The other half (approximately) of the algorithmic trading volume comes from foreign exchange dealing banks, the only participants allowed on the EBS system until 2003. Some of the banks' algorithmic trading is clearly related to activity on their own customer-to-dealer platforms, to automate hedging activity, and to minimizing the impact of the execution of large orders. But a sizable fraction is believed to be proprietary trading implemented algorithmically, likely using a mix of strategies similar to those employed by hedge funds and CTAs. Overall, market participants generally believe that the mix of algorithmic strategies used in the foreign exchange market differs from that seen in the equity market, where optimal execution algorithms are thought to be relatively more prevalent.

The August 16, 2007 episode shown above was widely viewed as the result of a sudden unwinding of the yen-carry trade, with hedge funds and proprietary trading desks at banks rushing to close risky positions and buying yen to pay back low-interest loans. The evidence in this case raises the possibility that many algorithmic traders were using fairly similar carry trade and momentum strategies at the time, leading to the high correlation of algorithmic orders and to sharp exchange rate movements. Of course, this is only one episode in our two-year sample. Furthermore, episodes of very sharp appreciation of the yen due to the rapid unwinding of yen carry trades have occurred on several occasions since the late 1990s, some obviously before algorithmic trading was allowed in the market. The sharp move of the yen in October 1998, including a 1-day appreciation of the yen against the dollar of about 7 percent, is the best-known example of such an episode. Next, we investigate whether there is evidence that, over the entire sample, the strategies used by algorithmic traders have tended to be more correlated than those used by human traders.

If computers and humans are indifferent between taking or making liquidity at a given point in time, then we should observe that computers and humans trade with each other in proportion to their relative presence in the market. If, on the other hand, computers tend to have more homogeneous trading strategies, we should observe computers trading less among themselves and more with humans. At the extreme, if all computers used the very same algorithms and had the exact same speed of execution, we would observe no trading volume among computers. Therefore, the fraction of trades conducted between computers contains information on how correlated their strategies are.14

To investigate the proposition that computers tend to have trading strategies that are more correlated than those of humans we pursue the following approach.We first consider a simple benchmark model that assumes random and independent matching of traders. This model allows us to determine the theoretical probabilities of the four possible trades: Human-maker/human-taker, computer-maker/human-taker, human-maker/computer-taker and computer-maker/computer-taker. We then make inferences regarding the diversity of computer trading strategies based on how the trading pairs we observe compare to those the benchmark model predicts.

In the benchmark model there are$ H_{m}$ potential human-makers (the number of humans that are standing ready to provide liquidity), $ H_{t}$ potential human-takers, $ C_{m}$ potential computer-makers, and $ C_{t}$ potential computer-takers. For a given period of time, the probability of a computer providing liquidity to a trader is equal to $ Prob(computer-make)=\frac{C_{m}}{C_{m}+H_{m}}$, which we label for simplicity as $ \alpha_{m}$, and the probability of a computer taking liquidity from the market is $ Prob(computer-take)=\frac{C_{t}}{C_{t}+H_{t}}=\alpha_{t}$. The remaining makers and takers are humans, in proportions $ (1-\alpha_{m})$ and $ (1-\alpha_{t})$, respectively. Assuming that these events are independent, the probabilities of the four possible trades, human-maker/human-taker, computer-maker/human-taker, human-maker/computer-taker and computer-maker/computer taker, are:

 

$\displaystyle Prob(HH)$$\displaystyle =(1-\alpha_{m})(1-\alpha_{t})$
$\displaystyle Prob(HC)$$\displaystyle =(1-\alpha_{m})\alpha_{t}$
$\displaystyle Prob(CH)$$\displaystyle =\alpha_{m}(1-\alpha_{t})$
$\displaystyle Prob(CC)$$\displaystyle =\alpha_{m}\alpha_{t}.$

These probabilities yield the following identity,

 

$\displaystyle Prob(HH)\times Prob(CC)\equiv Prob(HC)\times Prob(CH), $

which can be re-written as,

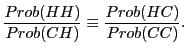
$\displaystyle \frac{Prob(HH)}{Prob(CH)}\equiv\frac{Prob(HC)}{Prob(CC)}. $

We label the first ratio, $ RH\equiv\frac{Prob(HH)}{Prob(CH)}$, the " human-taker" ratio and the second ratio, $ RC\equiv\frac{Prob(HC)}{Prob(CC)}$, the " computer-taker" ratio. In a world with more human traders (both makers and takers) than computer traders, each of these ratios will be greater than one, because $ Prob(HH)>$ $ Prob(CH)$ and $ Prob(HC)>Prob(CC)$ i.e., computers take liquidity more from humans than from other computers, and humans take liquidity more from humans than from computers. However, under the baseline assumptions of our random-matching model, the identity shown above states that the ratio of ratios, $ R\equiv\frac{RC}{RH}$, will be equal to one. In other words, humans will take liquidity from other humans in a similar proportion that computers take liquidity from humans.

Turning to the data, under the assumption that potential human-takers are randomly matched with potential human-makers, i.e., that the probability of a human-maker/human-taker trade is equal to the one predicted by our model, $ Prob(HH)=\frac{H_{m}\times H_{t}}{(H_{m}+C_{m})\times(H_{t}+C_{t})}$ , we can now derive implications from observations of $ R$, our ratio of ratios. In particular, finding $ R>1$ must imply that algorithmic strategies are more correlated than what our random matching model implies. In other words, for $ R>1$ we must observe that either computers trade with each other less than expected ( $ Prob(CC)<\frac{C_{m}\times C_{t}}{(H_{m}+C_{m})\times(H_{t}+C_{t} )}$ ) or that computers trade with humans more than expected (either $ Prob(CH)>\frac{C_{m}\times H_{t}}{(H_{m}+C_{m})\times(H_{t}+C_{t})} $ or $ Prob(HC)>\frac{H_{m}\times C_{t}}{(H_{m}+C_{m})\times(H_{t}+C_{t})}$ ).

Our dataset allows us to estimate an ex-post proxy for $ R$. Namely, for each trading day we estimate $ \widehat{RH}=\frac{Vol\left( HH\right) }{Vol\left( CH\right) }$ and $ \widehat{RC}=\frac{Vol\left( HC\right) }{Vol\left( CC\right) }$ , where $ Vol\left( HH\right) $ is the daily trading volume between human makers and human takers, and so forth. In Table 3 we show the mean of the daily ratio of ratios, $ \widehat{R}=\frac{\widehat{RC} }{\widehat{RH}},$ for each currency pair for the full sample and the three-month sub-sample. In contrast to the above theoretical prediction that $ R\equiv\frac{RC}{RH}=1$, we find that for all currency pairs $ \widehat{R}$ is statistically greater than one. This result is very robust: in euro-dollar, all daily observations of $ \widehat{R}$ are above one, and only a very small fraction of the daily observations are below one for the other currency pairs. The results thus show that computers do not trade with each other as much as random matching would predict. We take this as evidence that algorithmic strategies are likely less diverse than the trading strategies used by human traders.

This finding, combined with the observed growth in algorithmic trading over time, may raise some concerns about the impact of AT on volatility in the foreign exchange market. As mentioned previously, some analysts have pointed to the possible danger of having many algorithmic traders take the same side of the market at the same moment. However, it is not a foregone conclusion that a high correlation of algorithmic strategies should necessarily lead to higher volatility or large swings in exchange rates. Both the high correlation of trading strategies and the widespread use of de-stabilizing strategies may need to be present to cause higher volatility. For instance, if many algorithmic traders use similar triangular arbitrage strategies, the high correlation of those strategies should have little impact on volatility, and may even lower volatility as it improves the efficiency of the price discovery process. Strategies designed to minimize the price impact of trades should also, a priori, not be expected to increase volatility. In contrast, if the high correlation reflects a large number of algorithmic traders using the same carry trade or momentum strategies, as in the August 2007 example shown at the beginning of this section, then there may be some reasons for concern. However, as noted earlier, episodes of sharp movements in exchange rates similar to that example have occurred in the past on several occasions, including well before the introduction of algorithmic trading in the foreign exchange market, suggesting that such episodes are a result of the dramatic unwinding of certain trading strategies, regardless of whether these strategies are implemented through algorithmic trading or not. In the next section, we explicitly investigate the relationship between the presence of algorithmic trading and market volatility.

4  The impact of algorithmic trading on volatility

In this section, we study whether the presence of algorithmic trading is associated with disruptive market behavior in the form of increased volatility. In particular, taking into account the potential endogeneity of algorithmic trading activity, we test for a causal relationship between the fraction of daily algorithmic trading relative to the overall daily volume, and daily realized volatility.

4.1  A first look

We first take an informal look at the data. Figure 4 shows monthly observations of annualized realized volatility (based on 1-minute returns) and of the fraction of algorithmic trading (the fraction of total trading volume involving at least one computer trader) for each of our currency pairs. As discussed earlier, there is a clear upward trend in the fraction of AT in the three currency pairs over 2006 and 2007. Realized volatility in euro-dollar, dollar-yen, and euro-yen declines slightly until mid-2007, and then rises in the second half of 2007, particularly sharply in the yen exchange rates, as the financial crisis begins.

In Figure 5, we study whether days with high market volatility are also days with a higher-than-usual fraction of algorithmic trading, and vice-versa. Using daily observations, we first sort the data into increasing deciles of realized volatility (the decile means are shown as bars in the graphs on the left).15 We then calculate the mean fraction of AT for the days in each of these deciles (shown as lines in the same graphs). To account for the sharp upward trend in algorithmic participation over our sample, the daily fraction of algorithmic trading is normalized: we divide it by a $ 20$-day moving average centered on the chosen observation (a moving average from day $ t-10$ through day $ t+10$, excluding day $ t$). Next, we repeat the exercise, now sorting the daily data into increasing deciles of the normalized fraction of AT (the decile means are shown as bars in the graphs on the right) and calculating mean realized volatility for the days in each of these deciles (shown as lines in the same graphs). The results in Figure 5 (both the graphs on the left and the graphs on the right) show little or no relationship between the level of realized volatility on a particular day and the normalized fraction of AT on that same day. The highest decile in the euro-dollar currency pair may be the only possible exception, with a slight uptick evident in both volatility and AT activity. Finally, we note that, in untabulated results, for each of the three currency pairs, not one of the top 10 days in realized volatility is associated with a top ten day in the share of (normalized) AT.

The simple analysis in Figure 5 does not point to any substantial systematic link between AT activity and volatility. However, this analysis ignores the possible, and likely, endogeneity of algorithmic activity with regards to volatility, and therefore does not address the question of whether there is a causal relationship between algorithmic trading and volatility. In the remainder of this section, we attempt to answer this question through an instrumental variable analysis.

4.2  Identification

The main challenge in identifying a causal relationship between algorithmic trading and volatility is the potential endogeneity of algorithmic trading. That is, although one may conjecture that algorithmic trading impacts volatility, it is also plausible that algorithmic trading activity may be a function of the level of volatility. For instance, highly volatile markets may present comparative advantages to automated trading algorithms relative to human traders, which might increase the fraction of algorithmic trading during volatile periods. In contrast, however, one could also argue that a high level of volatility might reduce the informativeness of historical price patterns on which some trading algorithms are likely to base their decisions, and thus reduce the effectiveness of the algorithms and lead them to trade less. Thus, one can not easily determine in what direction the bias will go in an OLS regression of volatility on the fraction of algorithmic trading. To deal with the endogeneity issue, we adopt an instrumental variable (IV) approach as outlined below.

We are interested in estimating the following regression equation,

$\displaystyle RV_{it}=\alpha_{i}+\beta_{i}AT_{it}+\gamma_{i}^{\prime}\tau_{it}+\sum _{k=1}^{22}\delta_{i}RV_{it-k}+\epsilon_{it},$ (1)

where $ i=1,2,3$ represents currency pairs and $ t=1,...,T$, represents time. $ RV_{it}$ is (log) realized daily volatility, $ AT_{it}$ is the fraction of algorithmic trading at time $ t$ in currency pair $ i$, $ \tau_{it}$ is either a time trend or a set of time dummies that control for secular trends in the data, and $ \epsilon_{it}$ is an error term that is assumed to be uncorrelated with $ RV_{it-k}$, $ k\geq1$, but not necessarily with $ AT_{it}$. The large number of lags of volatility, which covers the business days of the past month, is included to control for the strong serial correlation in volatility (e.g. Andersen, Bollerslev, Diebold, and Labys, 2003 and Bollerslev and Wright, 2000). The exact definitions of $ RV_{it}$, $ AT_{it}$, and $ \tau_{it}$ are given below.

The main focus of interest is the parameter $ \beta_{i}$, which measures the impact of algorithmic trading on volatility in currency pair $ i$. However, since $ AT_{it}$ and $ \epsilon_{it}$ may be correlated, due to the potential endogeneity discussed above, the OLS estimator of $ \beta_{i}$ may be biased. In order to obtain an unbiased estimate, we will therefore consider an instrumental variable approach. Formally, we need to find a variable, or set of variables, $ z_{it}$, that is uncorrelated with $ \epsilon_{it}$ (validity of the instrument) and correlated with $ AT_{it}$ (relevance of the instrument).

The instrument we propose to use is the fraction of trading floors equipped to trade algorithmically on EBS relative to the total number of trading floors linked to the EBS system.16 That is, in order to place algorithmic trades on EBS, a special user interface is required, and the total number of trading floors with such user interfaces thus provides a measure of the overall algorithmic trading " capacity" in the market. The ratio of these algorithmic trading floors to the total number of trading floors provides a measure of the potential fraction of algorithmic trading. Since setting up an algorithmic trading operation likely takes several months, the number of trading floors of each type is clearly exogenous with regards to daily market volatility; the fraction of AT trading floors is therefore a valid instrument. In addition, it is positively correlated with the fraction of algorithmic trading, and it provides a relevant instrument as seen from the tests for weak instruments discussed below.

Under the breakdown provided by EBS, there are three types of trading floors linked to the EBS system: purely algorithmic trading floors, purely manual trading floors, and dual trading floors, those equipped to handle both manual and algorithmic trades. We consider two natural instrumental variables: the fraction of pure AT trading floors over the total number of trading floors (including pure AT, manual, and dual ones), and the fraction of the sum of pure AT and dual trading floors over the total number. Since it is not obvious which variable is the better instrument, we use both simultaneously.17

The data on AT trading floors are provided on a monthly basis, whereas the data on realized volatility and algorithmic trading are sampled on a daily frequency. We therefore transform the trading floor data to daily data by repeating the monthly value each day of the month. Although this leads to a dataset of two years of daily data, the number of daily observations (498) overstates the effective number of observations, since the coefficient on AT participation will be identified from monthly variations in the instrumental variables. Transforming the instruments to a daily frequency is, however, more efficient than transforming all data to a monthly frequency, since the daily data help to identify the monthly shifts.

The instrumental variable regressions are estimated using Limited Information Maximum Likelihood (LIML), and we test for weak instruments by comparing the first stage $ F-$statistic for the excluded instruments to the critical values of Stock and Yogo's (2005) test of weak instruments. We use LIML rather than two-stage least squares since Stock and Yogo (2005) show that the former is much less sensitive to weak instruments than the latter (see also Stock et al., 2002).

4.3  Variable definitions

4.3.1  Realized Volatility

Volatility is measured as the daily realized volatility obtained from one minute returns; that is, the volatility measure is equal to the square root of the daily sum of squared one minute log-price changes. The use of realized volatility, based on high-frequency intra-daily returns, as an estimate of ex-post volatility is now well established and generally considered the most precise and robust way of measuring volatility. Although many older studies relied on five minute returns in order to avoid contamination by market microstructure noise (e.g. Andersen et al., 2001), recent work shows that sampling at the one-minute frequency, or even higher frequencies, does not lead to biases in liquid markets (see, for instance, the results for liquid stocks in Bandi and Russel, 2006, and the study by Chaboud et al., 2007, who explicitly examine EBS data on the euro-dollar exchange rate during 2005 and finds that sampling frequencies upwards of once every 20 seconds does not lead to noticeable biases). Here, we restrict ourselves to using minute-by-minute data.18 Following the common conventions in the literature on volatility modelling (e.g. Andersen, Bollerslev, Diebold, and Labys, 2003), the realized volatility is log-transformed to obtain a more well behaved time-series.

4.3.2  Algorithmic trading

We consider two measures of the fraction of algorithmic trading, $ AT_{it}$, in a given currency pair: the computer-participation fraction and the computer-taker fraction. The first is simply the percent of the overall trading volume that includes an algorithmic trader as either a maker or a taker $ (Vol(CH+HC+CC))$; that is, the percent of trading volume where a computer is involved in at least one side of the trade. In addition, we also consider an alternative measure defined as the fraction of overall trading volume that is due to a computer-taker $ (Vol(HC+CC))$.

4.3.3  Time controls

As seen in Figure 4, there is a clear secular trend in the computer-participation fraction,19 which is not present in realized volatility. Euro-dollar, dollar-yen, and euro-yen volatility is trending down at the beginning of the period and starts to trend up in the summer of 2007. In order to control for the trend in algorithmic trading in the regression, we include either a " linear quarterly" time trend or a full set of year-quarter dummies, one for each year-quarter pair in the data (8 dummies). That is, the linear quarterly time trend stays constant within each quarter and increases by the same amount each quarter, whereas the year-quarter dummies allows for a more flexible trend specification that can shift in arbitrary fashion from year-quarter to year-quarter. Both secular trend specifications are thus fixed within each quarter. This restriction is imposed in order to preserve the identification coming from the monthly instrumental variables. Using monthly, or finer, time dummies would eliminate the variation in the instrument and render the model unidentified. Although it is theoretically possible to include a monthly time trend, this would lead to very weak identification empirically.

4.4  Empirical results

The regression results are presented in Table 4. We present OLS and LIML-IV results, with either the quarterly trend or the year-quarter dummies included. We show in Panels A and B the results for the computer-participation volume, and in Panels C and D the results for computer-taker volume. We report results for the sample starting in January 2006 and ending in December 2007. In order to save space, we only show the estimates of the coefficients in front of the fraction of algorithmic trading volume variables.

The OLS results, which are likely to be biased due to the aforementioned endogeneity issues, show a fairly clear pattern of a positive correlation between volatility and AT participation, with several positive and statistically significant coefficients. The $ R^{2}s$ are fairly large, reflecting the strong serial correlation in realized volatility, which is picked up by the lagged regressors. There are also no systematic differences between the quarterly trend and quarterly dummies specifications.

Turning to the more interesting IV results, which control for the endogeneity bias, the coefficient estimates change fairly dramatically. All point estimates are now negative and some of them are statistically significant. Thus, if there is a causal relationship between the fraction of algorithmic trading and the level of volatility, all evidence suggests that it is negative, such that increased AT participation lowers the volatility in the market. The stark difference between the IV and OLS results shows the importance of controlling for endogeneity when estimating the causal effect of AT on volatility; the opposite conclusion would have been reached if one ignored the endogeneity issue. The evidence of a statistically significant relationship is fairly weak, however, with most coefficients statistically indistinguishable from zero. The more restrictive quarterly trend specification suggests a significant relationship for the euro-dollar and dollar-yen, but this no longer holds if one allows for year-quarter dummies.

To the extent that the estimated coefficients are statistically significant, it is important to discuss the economic magnitude of the estimated relationship between AT and volatility. The regression is run with log volatility rather than actual volatility, which makes it a little less straightforward to interpret the size of the coefficients. However, some back-of-the-envelope calculations can provide a rough idea. Suppose that the coefficient on computer participation is about -0.01, which is in line with the coefficient estimates for the euro-dollar. The average monthly shift in computer participation in the euro-dollar is about 1.5 percentage points and the average log-volatility in the euro-dollar is about $ 3.76$ (with returns calculated in basis points), which implies an annualized volatility of about $ 6.82$ percent. Increasing the computer participation fraction by 1.5 percentage points decreases log-volatility by 0.015 and results in an annualized volatility of about 6.72. Thus, a typical change in computer participation might change volatility by about a tenth of a percentage point in annualized terms, a small effect.

The first stage $ F-$statistics for the excluded instruments in the IV regressions are also reported in Panels B and D. Stock and Yogo (2005) show that this $ F-$statistic can be used to test for weak instruments. Rejection of the null of weak instruments indicates that standard inference on the IV-estimated coefficients can be performed, whereas a failure to reject indicates possible size distortions in the tests of the LIML coefficients. The critical values of Stock and Yogo (2005) are designed such that they indicate a maximal actual size for a nominal sized five percent test on the coefficient. Thus, in the case considered here with two excluded instruments and one endogenous regressor, a value greater than $ 8.68$ for this $ F-$statistic indicates that the maximal size of a nominal 5 percent test will be no greater than 10 percent, which might be deemed acceptable; a value greater than 5.33 for the $ F-$statistic indicates a maximal size of 15 percent for a nominal 5 percent test. In general, the larger the $ F-$statistic, the stronger the instruments. As is evident from the table, there are no signs of weak instruments in the specification with a quarterly trend. There are, however, signs of weak instruments in the case with year-quarter dummies, for the euro-yen. This is not too surprising given that the instruments only change on a monthly frequency, and the year-quarter dummies therefore put a great deal of strain on the identification mechanism. Importantly, though, the results for the two major currency pairs are robust to any weak-instrument problems and the reported coefficients and standard errors are unbiased.

To sum up, the evidence of any causal effect of algorithmic trading on volatility is not strong, but what evidence there is points fairly consistently towards a negative relationship. There is thus no systematic statistical evidence to back the often-voiced opinion that AT leads to increased levels of market volatility. If anything, the contrary appears to be true.


5  Who provides liquidity during the release of public announcements?

In the previous section we discuss one of the major concerns regarding algorithmic trading, namely, whether AT causes exchange rate volatility. We now examine another major concern, whether AT improves or reduces liquidity during stress periods, when it is arguably needed the most. To answer this question, we cannot simply regress computer-maker volume, a proxy for liquidity provided by computers, on exchange rate volatility, a proxy for stress periods, because, as we discussed in the previous section, algorithmic volume and volatility are endogenous variables. In contrast to the previous section we do not estimate an IV regression, as there are no obvious instruments for volatility.20 Instead, we follow the event study literature and compare the liquidity provision by humans and computers during U.S. nonfarm payroll announcements, a period of exogenously heightened volatility, to the liquidity provision by both types of agents during non-announcement days. This comparison will help us determine who provides relatively more liquidity during stress periods. We note that, when we consider liquidity provision by humans and computers following other important macroeconomic news announcements, the results are qualitatively similar. However, we focus in this section on the nonfarm payroll announcement only, as it routinely generates the highest volatility of all US macroeconomic announcements.21

We consider two liquidity provision estimates: a one-minute estimate and a one-hour estimate. The one-minute estimate is calculated using volume observations from 8:30 a.m. to 8.31 a.m. ET (when U.S. nonfarm payroll is released), while the one-hour estimate is calculated using observations from 8:25 am to 9:24 am ET. We define the one-minute (one-hour) liquidity provision by humans, $ LH$, as the sum of human-maker volume, $ Vol(HH+HC)$, divided by total volume during that period, and the one-minute (one-hour) liquidity provision by computers, $ LC$, as the sum of computer-maker volume, $ Vol(CC+CH)$, divided by total volume during that period. Similar to the liquidity provision measures, we define the one-minute volatility as the squared 1-minute return from 8:30 a.m. to 8.31 a.m. ET and the one-hour volatility as the sum of squared 1-minute returns from 8:25 am to 9:24 am ET.

To compare liquidity provision by humans and computers during announcement times to liquidity provision during (more tranquil) non-announcement times, we could estimate the average liquidity provision during announcement times and compare it to the average liquidity provision during non-announcement times, with both means taken over the entire sample period. However, as we discussed previously, exchange rate trading volumes and the shares of liquidity provision by humans and computers exhibit clear trends over our sample, making the comparison of the two different means problematic. Alternatively, and this is the methodology we follow, on each announcement day we estimate the ratio of liquidity provision on that day relative to the liquidity provision on days surrounding the announcement. This amounts to using a non-parametric approach to detrend the data. The time series of these ratios will be stationary, and we can then test the hypothesis that the ratio is greater than one. Specifically, we divide the one-minute (one-hour) liquidity provision by humans, $ LH_{a}$, and computers, $ LC_{a}$, estimated on announcement day $ t$ by the one-minute (one-hour) liquidity provision by humans, $ LH_{n}$, and computers, $ LC_{n}$, respectively, estimated during the surrounding non-announcement day period, defined as 10 business days before and after a nonfarm payroll release date $ t$. The liquidity provision measures on the non-announcement days are calculated in the same manner as on the announcement days, using data only for the periods 8:30 a.m. to 8.31 a.m. ET or 8:25 am to 9:24 am ET, for the one-minute and one-hour measures, respectively.22 We follow the same procedure with our one-minute and one-hour volatility estimates.

Consistent with previous studies, we show in Table 5 Panel A that the one-hour volatility on nonfarm payroll announcement days is 3 to 6 times larger than during non-announcement days. The one-minute volatility is 15 to 30 times larger during announcement days compared to non-announcement days. As expected, given the fact that we focus on a U.S. data release, the volatility increase is smaller in the cross-rate, the euro-yen exchange rate, than in the euro-dollar and yen-dollar exchange rates. Focusing on the statistically significant estimates, we show in Table 5 Panel B that, as a share of total volume, human-maker volume tends to increase during the minute of the announcement (the one-minute ratio $ \frac{LH_{a}}{LH_{n}}$ is greater than one), while computer-maker volume tends to decrease (the one-minute ratio $ \frac{LC_{a}}{LC_{n}}$ is less than one). Interestingly, this pattern is reversed when we focus on the one-hour volume estimates for the euro-dollar and euro-yen exchange rate markets. In relative terms, computers do not increase their provision of liquidity as much as humans do during the minute following the announcement. However, computers increase their provision of liquidity relatively more than humans do over the entire hour following the announcement, a period when market volatility remains quite elevated.

We note that, over our sample period, the U.S. nonfarm payroll data releases were clearly the most anticipated and most influential U.S. macroeconomic data releases. They often generated a large initial sharp movement in exchange rates, followed by an extended period of volatility. The behavior of computer traders observed in the first minute could reflect the fact that many algorithms are not designed to react to the sharp, almost discrete, moves in exchange rates that often come at the precise moment of the data release. Some algorithmic traders may then prefer to pull back from the market a few seconds before 8:30 a.m. ET on days of nonfarm payroll announcements, resuming trading once the risk of a sharp initial price movement has passed. But the data show that algorithmic traders, as a whole, do not shrink back from providing liquidity during the extended period of volatility that follows the data releases.

6   Price Discovery

In the previous three sections, we analyze questions that are primarily motivated by practical concerns regarding algorithmic trading, such as whether computer traders induce volatility or reduce liquidity. In this section we turn to questions that are driven more by the market microstructure literature, but that also lead to interesting practical insights regarding the effects and nature of algorithmic trading. In particular, we study price discovery within a vector autoregressive framework, which enables us to evaluate to what extent humans or computers represent the "informed" traders in the market. Our findings reveal several interesting features regarding the impact of algorithmic trades and the order placement behavior of computer traders.

6.1  Who are the "informed" traders, humans or computers?

We first investigate whether human or computer trades have a more " permanent" impact on prices. To this end, we estimate return-order flow dynamics in a structural vector autoregressive (VAR) framework in the tradition of Hasbrouck (1991a), where returns are contemporaneously affected by order flow, but order flow is not contemporaneously affected by returns. Similar to Hasbrouck's (1996) decomposition of program and nonprogram order flow, we decompose order flow into two components: human-taker $ \left( OF^{\left( ht\right) }=HH+CH\right) $ and computer-taker $ \left( OF^{\left( ct\right) }=HC+CC\right) $, and thus we estimate for each currency $ i$ one return equation and two order flow equations. In light of Evans and Lyons (2008) findings, we estimate the structural VAR with U.S. macroeconomic news surprises as exogenous variables that affect both returns and order flow. Specifically, we estimate the following system of equations for each currency $ i$,

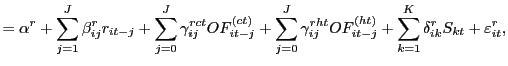$\displaystyle r_{it}$$\displaystyle =\alpha^{r}+\sum_{j=1}^{J}\beta_{ij}^{r}r_{it-j}+\sum_{j=0} ^{J}\gamma_{ij}^{rct}OF_{it-j}^{\left( ct\right) }+\sum_{j=0}^{J}\gamma _{ij}^{rht}OF_{it-j}^{\left( ht\right) }+\sum_{k=1}^{K}\delta_{ik}^{r} S_{kt}+\varepsilon_{it}^{r},$ (2)
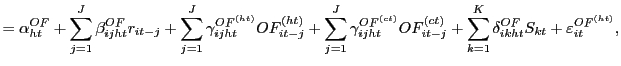$\displaystyle OF_{it}^{\left( ht\right) }$$\displaystyle =\alpha_{ht}^{OF}+\sum_{j=1}^{J}\beta _{ijht}^{OF}r_{it-j}+\sum_{j=1}^{J}\gamma_{ijht}^{OF^{(ht)}}OF_{it-j}^{\left( ht\right) }+\sum_{j=1}^{J}\gamma_{ijht}^{OF^{(ct)}}OF_{it-j}^{\left( ct\right) }+\sum_{k=1}^{K}\delta_{ikht}^{OF}S_{kt}+\varepsilon_{it} ^{OF^{\left( ht\right) }},$    
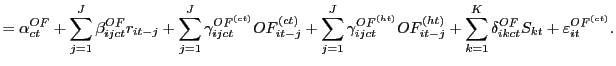$\displaystyle OF_{it}^{\left( ct\right) }$$\displaystyle =\alpha_{ct}^{OF}+\sum_{j=1}^{J}\beta _{ijct}^{OF}r_{it-j}+\sum_{j=1}^{J}\gamma_{ijct}^{OF^{(ct)}}OF_{it-j}^{\left( ct\right) }+\sum_{j=1}^{J}\gamma_{ijct}^{OF^{(ht)}}OF_{it-j}^{\left( ht\right) }+\sum_{k=1}^{K}\delta_{ikct}^{OF}S_{kt}+\varepsilon_{it} ^{OF^{\left( ct\right) }}.$    

Here $ r_{it}$ is the 1-minute exchange rate return for currency $ i$ at time $ t$; $ OF_{it}^{ht}$ is the currency $ i$ human-taker order flow at time $ t$; $ OF_{it}^{ct}$ is the currency $ i$ computer-taker order flow at time $ t$; and $ S_{kt}$ is the macroeconomic news announcement surprise for announcement $ k$ at time $ t$ defined as the difference between the announcement realization and its corresponding market expectation. We use Bloomberg's real-time data on the expectations and realizations of $ K=28$ U.S. macroeconomic fundamentals to calculate $ S_{kt}$. The $ 28$ announcements we consider are similar to those in Andersen et al. (2003, 2007) and Pasquariello and Vega (2007).23 Since units of measurement vary across macroeconomic variables, we standardize the resulting surprises by dividing each of them by their sample standard deviation. Economic theory suggests that we should also include foreign macroeconomic news announcements in equation (2). However, previous studies find that exchange rates do not respond much to non-U.S. macroeconomic announcements, even at high frequencies (e.g. Andersen et al., 2003), so we expect the omitted variable bias in our specification to be small.

The underlying economic model is based on continuous time, and we thus estimate the VAR using the highest sample frequency available to us, minute-by-minute data. The estimation period is restricted to the $ 2006-2007$ sample, and the total number of observations for each currency pair is $ 717,120$ in the full sample and $ 89,280$ in the three-month sub-sample (September, October and November of 2007). In both samples, 20 lags are included in the estimated VARs, i.e. $ J=20$.

Our specification in equation (2) does not allow human-taker order flow to contemporaneously affect computer-taker order flow or vice-versa. The advantage of this approach is that we can estimate the impulse response functions without giving more importance to a particular type of order flow, i.e., we do not need to assume a particular ordering of the human-taker and computer-taker order flow in the VAR. The disadvantage is that the human-taker and computer-taker order flow shocks may not be orthogonal. However, in our estimation this does not appear to be a problem, as our residuals are found to be approximately orthogonal (the correlation between the human-taker and computer-taker equation residuals are -0.001, -0.1 and -0.1 for the euro-dollar, yen-dollar, and euro-yen exchange rates respectively). As a robustness check, we also estimate the VAR with two different orderings. We first assume human-taker order flow affects computer-taker order flow contemporaneously, and then assume the opposite ordering. This latter approach allows us to compute upper and lower bound impulse responses. These results are presented in the Appendix, and show that the results presented here are not sensitive to alternative identification schemes in the VAR.

Before considering the impulse response functions and the variance decompositions, we briefly summarize the main lessons from the estimated coefficients in the VAR. Focusing on the return equation, we find that minute-by-minute returns tend to be negatively serially correlated, with the coefficient on the first own lag varying between -0.08 and -0.15; there is thus some evidence of mean reversion in the exchange rates at these high frequencies, which is a well-know empirical finding. Both order flows are significant predictors of returns. The price impact of the lagged order flows range from around 4 to 18 basis points per billion units of order flow (denominated in the base currency), as compared to a range of approximately 28-100 basis points in the contemporaneous order flow. As theory would predict, we find that U.S. macroeconomic news announcements affect less the euro-yen exchange rate (i.e., the $ R^{2}$ of regressing the euro-yen exchange rate on macroeconomic news surprises and restricting the sample to announcement-only observations is 23%) than the euro-dollar and dollar-yen exchange rates (i.e., the $ R^{2}$s of an announcement-only sample are 60% and 59%, respectively). However, U.S. macroeconomic news announcements still have an effect on the cross-rate to the extent that the U.S. economy is more or less correlated with the Japanese or the Euro-area economy.

Focusing on the order-flow equations, we find that the first own lag in both order flow equations is always highly significant, and typically around $ 0.1$ for all currency pairs. There is thus a sizeable first-order autocorrelation in the human-taker and computer-taker order flows. The coefficients on the first order cross-lags in the order flow regressions are most often substantially smaller than the coefficient on the own lag and vary in signs. Lagged returns have a small but positive impact on order flow, suggestive of a form of trend chasing by both computers and humans in their order placement.

We note that despite the strongly significant estimates that are recorded in the VAR estimations, the amount of variation in the order flow and return variables that is captured by their lagged values is very limited. The $ R^{2} $ for the estimated equations with only lagged variables are typically around three to ten percent for the order flow equations, and between one and three percent for the return equations. This can be compared to an $ R^{2} $ of 20 to 30 percent when one includes contemporaneous order flow.

6.2  Impulse Response Function and Variance Decomposition Results

As originally suggested by Hasbrouck (1991b), we use the impulse response functions to assess the price impact of various order flow types, and the variance decompositions to measure the relative importance of the variables driving foreign exchange returns. In Table 6 Panel A, we show the results from the impulse response analysis based on the estimation of equation (2), using the full sample for 2006-2007 and the three-month sub-sample, when the size of the shock is the same across the different types of order flow: a one billion base currency shock to order flow. We also show the results when the size of the shock varies according to the average size shock: a one standard deviation base currency shock to order flow (Table 6 Panel B). We show both the short-run (instantaneous) impulse responses, the long-run cumulative responses, and the difference between the two responses. The long-run statistics are calculated after 30-minutes, at which point the cumulative impulse responses have converged and can thus be interpreted as the long-run total impact of the shock. All the responses are measured in basis points. The standard errors reported in the tables are calculated by bootstrapping, using 200 repetitions.

Starting with a hypothetical shock of one billion base currency order flow, the results in Table 6 Panel A, show that the immediate response of prices to human-taker order flow is often larger than the immediate response to computer-taker order flow. This may partially be attributed to the fact that some of the algorithmic trading is used for the optimal execution of large orders at a minimum cost. Algorithmic trades appear to be successful in that endeavor, with computers likely breaking up the larger orders and timing the smaller trades to minimize the impact on prices. We emphasize, though, that the differences in price impact, which range from 1 to 8 basis points, are not very large in economic terms. Furthermore, we find that the result can be reversed in the long-run and in the three-month sub-sample. For example, the euro-dollar human-taker price impact is larger than the computer-taker price impact in the short-run, but the opposite is true in the long-run and in the three-month sub-sample.

In contrast to these results, the response to a hypothetical one standard deviation shock to the different order flows (Table 6 Panel B) consistently shows that in the euro-dollar and dollar-yen markets, humans have a bigger impact on prices than computers and the differences are relatively large. For example, a one standard deviation shock to human-taker order flow in the yen-dollar exchange rate market has an average long-run effect of 0.9 basis points compared to an average effect of 0.3 basis points for computer-taker order flow. Interestingly, the difference in price impact in the cross-rate, the euro-yen exchange rate, is very small. In this market, computers have a clear advantage over humans in detecting and reacting more quickly to triangular arbitrage opportunities so that a large proportion of algorithmic trading contributes to more efficient price discovery. It is then not so surprising that in this market computers and humans, on average, appear to be equally "informed."

In Table 7 we report the fraction of the total (long-run) variance in returns that can be attributed to innovations in human-taker order flow and computer-taker order flow.24 Following Hasbrouck (1991b), we interpret this variance decomposition as a summary measure of the informativeness of trades, and thus, in the current context, a comparison of the relative informativeness of the different types of order flow. Consistent with the results from the impulse response functions based on a one standard deviation shock to order flow, we find that in the euro-dollar and dollar-yen exchange rate markets human-taker order flow explains much more of the total variance in returns than computer-taker order flow. Specifically, human-taker order flow explains about 30 percent of the total variance in returns compared to only 4 percent explained by computer-taker order flow.

The fact that human-taker order flow explains a bigger portion of total variance in returns is not surprising because human-taker volume is about 75 percent of total volume in these two markets in the full sample period and about 65 percent of total volume in the three-month sub-sample (see Table 2). Moreover large buy (sell) orders tend to be human-taker orders, i.e. we show in Table 1 that the standard deviation of human-taker order flow is twice as big as that of the computer-taker order flow. But, do computers tend to contribute " disproportionately" little to the long-run variance in returns relative to their trading volume? To answer this question we do a back-of-the-envelope calculation. We compute the relative share of the explained variance that is due to computer-taker order flow as the percent of total variation in returns explained by computer-taker order flow divided by the percent of total variation in returns explained jointly by both human-taker and computer-taker order flow. For example, this relative share is $ 14\%=100\times\frac{4.74}{34}$ (Table 7) in the euro-dollar market. We can then compare this relative share to the fraction of overall trading volume that is due to computer-taker volume, which we show in Table 2. In the full 2006-2007 sample for the euro-dollar and the dollar-yen currency pairs, the fraction of volume due to computer-takers is about twice as large as the fraction of the explained long-run variance that is due to computer-taker order flow. In the euro-yen, the fractions are approximately equal. These results are fairly similar in the three-month sub-sample, although the fraction of explained variance has increased somewhat compared to the volume fraction. Thus, in the two major currency pairs, there is evidence that computer-taker order flow contributes relatively less to the variation in returns than one would infer from just looking at the proportion of computer-taker volume.

6.3  Are liquidity providers "uninformed"?

We now turn to examine whether liquidity providers post quotes strategically. To this end we augment equation (2) and decompose order flow into four components. Specifically, we estimate the following system of equations for each currency $ i,$

$\displaystyle r_{it}$$\displaystyle =\alpha^{r}+\sum_{j=1}^{J}\beta_{ij}^{r}r_{it-j}+\sum_{l=1}^{L} \sum_{j=0}^{J}\gamma_{ij}^{rl}OF_{it-j}^{\left( l\right) }+\sum_{k=1} ^{K}\delta_{ik}^{r}S_{kt}+\varepsilon_{it}^{r},$ (3)
$\displaystyle OF_{it}^{\left( l\right) }$$\displaystyle =\alpha_{l}^{OF}+\sum_{j=1}^{J}\beta _{ijl}^{OF}r_{it-j}+\sum_{l=1}^{L}\sum_{j=1}^{J}\gamma_{ijl}^{OF^{(l)} }OF_{it-j}^{\left( l\right) }+\sum_{k=1}^{K}\delta_{ikl}^{OF}S_{kt} +\varepsilon_{it}^{OF^{\left( l\right) }}.$    

where $ r_{it}$ is the 1-minute exchange rate return for currency $ i$ at time $ t$; $ L=4$, $ OF_{it}^{\left( 1\right) }=OF_{it}^{HH}$ is the currency $ i$ human-maker/human-taker order flow at time $ t$; $ OF_{it}^{\left( 2\right) }=OF_{it}^{CH}$ is the currency $ i$ computer-maker/human-taker order flow at time $ t$; $ OF_{it}^{\left( 3\right) }=OF_{it}^{HC}$ is the currency $ i$ human-maker/computer-taker order flow at time $ t$; $ OF_{it}^{\left( 4\right) }=OF_{it}^{CC}$ is the currency $ i$ computer-maker/computer-taker order flow at time $ t$; $ S_{kt}$ is the macroeconomic news announcement surprise for announcement $ k$ at time $ t$.25

In addition to identifying whether traders, on average, have a more permanent impact on prices when trading with humans than with computers, this specification also allows us to observe the effect order flow has on prices when, for instance, no party has a speed advantage, i.e. both parties are humans or both parties are computers, and when either the maker has a speed advantage, $ CH$, or the taker has a speed advantage, $ HC$. This distinction may be particularly useful when analyzing the cross-rate, where computers likely have a clear advantage over humans in detecting short-lived triangular arbitrage opportunities.

Starting with a hypothetical shock of one billion base currency order flow, the results in Table 8 Panel A show that there is no clear pattern in which order flow impacts prices the most. However, the dynamics of the VAR system help reveal an interesting finding: There is a consistent and often large short-run over-reaction to $ CC$ and $ CH$ shocks. That is, as seen in Table 8, the short run response to a $ CC$ or $ CH$ order flow shock is always larger than the long-run response, and sometimes substantially so. The euro-dollar in the sample covering September, October, and November of 2007 provides an extreme case where the initial reaction to a one billion dollar $ CC$ shock is a 22 basis point move, but the long-run cumulative reaction is just 6 basis points. Interestingly, the opposite pattern is true for the $ HH$ order flow shocks, where there is always an initial under-reaction in returns. To the extent that an over-reaction of prices to order flow is suggestive of the presence of liquidity traders, these impulse response patterns suggest that computers provide liquidity when the probability of trading with an informed trader is low.26

The response to a hypothetical one standard deviation shock to the different order flows consistently shows that $ HH$ order flow has a bigger impact on prices than $ CC$ order flow (Table 8 Panel B) and that the differences are large. In particular, a one standard deviation shock to $ HH$ order flow has an average long-run effect of 0.6 basis points across currencies compared to a one standard deviation shock to $ CC$ order flow, which has an average effect of 0.1 basis points. Interestingly, we observe that when humans trade with other humans they influence prices more than when they trade with computers (the impact of $ HH$ on prices is bigger than the impact of $ CH$ on prices), and when computers trade with other computers they influence prices less than when they trade with humans (the impact of $ CC$ on prices is smaller than the impact of $ HC$ on prices). Our interpretation is that computers provide liquidity more strategically than humans, so that the counterparty cannot affect prices as much. This interpretation is consistent with the over-reaction of prices to $ CC$ and $ CH $ order flow described above: Computers appear to provide liquidity when adverse selection costs are low. This finding relates to the literature that proposes to depart from the prevalent assumption that liquidity providers in limit order books are passive.27

We also find that the price response to order flow varies across currencies as these markets differ along several dimensions. Trading volume is largest in the euro-dollar and dollar-yen markets, compared to the euro-yen market, and price discovery clearly happens mostly in the two largest markets. In the cross-rate market, the euro-yen, computers have a speed advantage over humans in profiting from triangular arbitrage opportunities, where prices set in the euro-dollar and dollar-yen markets are very briefly out of line with the euro-yen rate. Consistent with this speed advantage we observe that human-maker/computer-taker order flow has a larger price impact in the cross-rate market than in the other two markets.

In addition to the impulse response functions, we also report the long-run forecast variance decomposition of returns in Table 9 for both the full sample and the three-month sub-sample. Consistent with the impulse response functions to a one standard deviation shock to order flow, the $ HH$ order flow makes up the dominant part of the variance share in the euro-dollar and dollar-yen exchange rate markets. In the last three months of the sample, this share has generally decreased. The share of variance in returns that can be attributed to the $ CC$ order flow is surprisingly small, especially in the latter sub-sample, given that this category of trades represents a sizeable fraction of overall volume of trade during the last months of 2007, as seen in Table 2. The mixed order flow ($ CH$ and $ HC$ order flow) typically contributes with about the same share to the explained variance in the euro-dollar and dollar-yen exchange rate markets. In contrast, in the euro-yen exchange rate market $ HC$ order flow makes up the dominant part of the variance share, which is consistent with our discussion of computers taking advantage of triangular arbitrage opportunities in this market.

Overall, about $ 15$ to $ 35$ percent of the total variation in returns can be attributed to shocks to the four order flows. However, in most currency pairs, very little of this ultimate long-run price discovery that occurs via order flow does so via the $ CC$ order flow. Similar to Table 7, we also report in Table 9 the fraction of the explained share of the return variance that can be attributed to the different order flow combinations. Comparing these to the fraction of overall volume that is due to these combinations of computers and humans, reported in Table 2, gives an idea of whether the different order flow combinations contribute proportionately to the variance in returns. It is clear that $ CC$ order flow tends to contribute disproportionately little to the long-run variance of returns, and that $ HH$ order flow often contributes disproportionately much.

7  Conclusion

Using highly-detailed high-frequency trading data for three major exchange rates over 2006 and 2007, we analyze the impact of the growth of algorithmic trading on the spot interdealer foreign exchange market. We focus on the following questions: (i) Are the algorithms underlying the computer-generated trades similar enough to result in highly correlated strategies, which some fear may cause disruptive market behavior? (ii) Does algorithmic trading increase volatility in the market, perhaps as a result of the previous concern? (iii) Do algorithmic traders improve or reduce market liquidity at times of market stress? (iv) Are human or computer traders the more " informed" traders in the market, i.e. who has the most impact on price discovery? (v) Is there evidence in this market that the liquidity providers (the " makers") and not just the liquidity " takers", are informed, and do computer makers post orders more strategically than human makers?

The first three questions directly address concerns that have been raised recently in the financial press, especially in conjunction with the current crisis, while the last two questions relate more to the empirical market microstructure literature on price discovery and order placement. Together, the analysis of these questions brings new and interesting results to the table, both from a practical and academic perspective, in an area where almost no formal research has been available.

Our empirical results provide evidence that algorithmic trades are more correlated than non-algorithmic trades, suggesting that the trading strategies used by the computer traders are less diverse than those of their human counterparts. Although this may cause some concerns regarding the disruptive potential of computer-generated trades, we do not find evidence of a positive causal relationship between the proportion of algorithmic trading in the market and the level of volatility; if anything, the evidence points towards a negative relationship, suggesting that the presence of algorithmic trading reduces volatility. As for the provision of market liquidity, we find evidence that, compared to non-algorithmic traders, algorithmic traders reduce their share of liquidity provision in the minute following major data announcements, when the probability of a price jump is very high. However, they increase their share of liquidity provision to the market over the entire hour following these announcements, which is almost always a period of elevated volatility. This empirical evidence thus suggests that computers do provide liquidity during periods of market stress.

To address the last two questions (price discovery and order placement), we use a high-frequency VAR framework in the tradition of Hasbrouck (1991a). We find that non-algorithmic trades account for a substantially larger share of the price movements in the euro-dollar and yen-dollar exchange rate markets than would be expected given the sizable fraction of algorithmic trades. Non-algorithmic traders are the " informed" traders in these two markets, driving price discovery. In the cross-rate, the euro-yen exchange rate market, we find that computers and humans are equally " informed," likely because of the large proportion of algorithmic trades dedicated to search for triangular arbitrage opportunities. Finally, we find that, on average, computer takers or human takers that trade on prices posted by computers do not impact prices as much as they do when they trade on prices posted by humans. One interpretation of this result is that computers place limit orders more strategically than humans do. This finding dovetails with the literature on limit order books that relaxes the common modeling assumption that liquidity providers are passive.

Overall, this study therefore provides essentially no evidence to bolster the widespread concerns about the effect of algorithmic trading on the functioning of financial markets. The lesson we take from our analysis of algorithmic trading in the interdealer foreign exchange market is that it is more how algorithmic trading is used and what it is predominantly designed to achieve that determines its impact on the market, and not primarily whether or not the order flow reaching the market is generated at high frequency by computers. In the global interdealer foreign exchange market, the rapid growth of algorithmic trading has not come at the cost of lower market quality, at least not in the data we have seen so far. Given the constant search for execution speed in financial markets and the increasing availability of algorithmic trading technology, it is likely that, absent regulatory intervention, the share of algorithmic trading across most financial markets will continue to grow. Our study offers hope that the growing presence of algorithmic trading will not have a negative impact on global financial markets.

Appendix: Robustness check of the VAR results

The impulse responses and variance decompositions in the above VAR analyses are derived under the assumption that there are no contemporaneous interactions between the different order flow components. This identifying assumption is appealing because it treats the order flow components symmetrically and ensures that the results are not driven by the ordering of the order flows in the VAR. On the other hand, it cannot be ruled out that one order flow component affects another one contemporaneously within the one-minute timespan over which each observation is sampled. If this is the case, the VAR specification that we use above would be too restrictive and the resulting impulse responses and variance decompositions would likely be biased. As discussed above, given the fairly low correlation that we observe in the VAR residuals for the different order flow equations, this does not appear to be a major concern, but since these correlations are not identical to zero it is still possible that other identification schemes would lead to different conclusions.

In this section we therefore perform a comprehensive robustness check of the VAR results by calculating upper and lower bounds on the impulse responses and variance decompositions. In particular, we consider all possible orderings of the order flows in the VARs, while imposing a triangular structure. That is, we still assume that returns are ordered last in the VAR and are thus affected contemporaneously by all order flow components, but we then consider all possible orderings for the different order flows. In the case where we split order flow into human and computer order flow, this results in just two different specifications--one where computer order flow affects human order flow contemporaneously but contemporaneous human order flow has no impact on computer order flow, and the opposite specification where human order flow affects computer order flow contemporaneously. In the case with four different order flows, there are 24 different orderings, when one allows for all possible triangular identification schemes, only imposing that returns are ordered last. From each of these specifications, we calculate impulse responses and variance decompositions. The minimum and maximum of these over all specifications are reported in Tables A1 and A2 for the two order flow case and in Tables A3 and A4 in the four order flow case.

Starting with the simpler case with order flow split up into human or computer order flow, Tables A1 and A2 confirm our conjecture that the low correlation in the VAR residuals render the VAR specification very robust to the ordering of the order flows. The min-max intervals shown in the two tables are generally very tight and all of our earlier qualitative conclusions that we draw from our preferred structural VAR specification holds also under these alternative orderings.

Turning to the VAR analysis with four separate order flow, the number of possible orderings increases dramatically to 24. This large number of possible specifications inevitably results in wider min-max intervals, even though the correlations in the VAR residuals are generally small. In order to usefully interpret these results, we check whether our main qualitative conclusions from our preferred structural specification analyzed above also holds up, in a min-max sense, under all possible orderings. Our first main result in the above analysis was that there is an initial over-reaction to $ CC$ and $ CH$ shocks and an initial under-reaction to $ HH$ shocks. As seen in Table A3, these findings are mostly supported by the min-max results as well. The only exceptions recorded are for the euro-yen cross rate, where the under-reaction to $ CC$ and $ CH$ shocks is also much weaker in the original results in Table 8. It is also evident from Table A3, Panel B, that the min-max results support the finding that a one standard deviation shock to $ HH$ has a substantially bigger impact on returns than a $ CC$ shock. In addition, Table A3, Panel B, also shows that the impact of the $ HH$ shock tends to be larger than the $ CH$ impact, and the $ CC$ impact tends to be smaller than the $ HC$ impact. Finally, the results in Table A3 also mostly support the finding that the reactions to $ HC$ order flow are greater in the euro-yen cross currency than in the two main currency pairs, although some overlap is seen for the one standard deviation shock in Panel B.

Table A4 shows the corresponding min-max results for the variance decomposition. Again, our main conclusions are mostly supported in a min-max sense. $ HH$ makes up the largest share of the explained variance in the two main currency pairs in the full sample, although in the three-month sub-sample there is some overlap between the min-max intervals for the $ HH$ order flow and the $ HC$ order flow. $ CC$ always contributes a very small share of the explained variance and $ HC$ always contributes a fairly substantial share in the cross currency.

In summary, these robustness checks show that our main VAR used for examining price discovery (equation (2)), using human and computer order flows, is not particularly sensitive to the exact identification scheme that is used. The results presented in Tables 6 and 7 thus appear to be robust to alternative orderings in the VAR. Our second VAR specification (equation (3)), which we use to analyze strategic liquidity provision, is a little more sensitive to the exact identification scheme used, but the min-max results are still overall very supportive of our main conclusions.

Table A1

Min-max impulse responses from the VAR specification with human-taker and computer-taker order flow. The table shows the minimum and maximum triangular impulse responses for returns as a result of shocks to the human-taker order flow $ (HH+CH)$ or computer-taker $ (CC+HC)$ order flow, denoted H-taker and C-taker in the table headings, respectively. In Panel A we show the return response, in basis points, to a one-billion base-currency shock to one of the order flows. In Panel B we show the return response, in basis points, to a one standard deviation shock to one of the order flows. We show the results for the full 2006-2007 sample and for the three-month sub-sample, which only uses data from September, October, and November of 2007. For each currency pair we show the short-run (immediate) response of returns; the corresponding cumulative long-run response of returns, calculated as the cumulative impact of the shock after 30 minutes; and the difference between the cumulative long-run response in returns minus the immediate response of returns, i.e., we provide the extent of over-reaction or under-reaction to an order flow shock. There are a total of $ 717,120$ minute-by-minute observations in the full two-year sample and $ 89,280$ observations in the three-month sub-sample.

Table A1, Panel A: One billion base-currency shock

  Full 2006-2007
sample: H-taker		Full 2006-2007
sample: C		 3-month sub-sample: H-taker3-month sub-sample: C -taker
USD/EUR: Short run $ [28.05,28.06]$ $ [26.84,26.94]$ $ [23.11,23.20]$ $ [24.89,25.22]$
USD/EUR: Long run $ [27.85,27.87]$ $ [32.26,32.35]$ $ [24.06,24.16]$ $ [31.04,31.38]$
USD/EUR: Difference $ [-0.20,-0.20]$ $ [5.42,5.42]$ $ [0.94,0.96]$ $ [6.14,6.16]$
JPY/USD: Short run $ [44.96,46.76]$ $ [28.92,39.81]$ $ [44.99,48.02]$ $ [33.45,44.88]$
JPY/USD: Long run $ [45.50,47.50]$ $ [33.21,44.27]$ $ [46.80,49.54]$ $ [28.83,40.63]$
JPY/USD: Difference $ [0.54,0.74]$ $ [4.29,4.46]$ $ [1.52,1.81]$ $ [-4.62,-4.25]$
JPY/EUR: Short run $ [90.18,99.32]$ $ [90.50,102.71]$ $ [109.04,124.02]$ $ [101.74,115.52]$
JPY/EUR: Long run $ [98.30,108.07]$ $ [96.57,109.85]$ $ [116.54,132.53]$ $ [108.54,123.26]$
JPY/EUR: Difference $ [8.12,8.75]$ $ [6.07,7.14]$ $ [7.50,8.51]$ $ [6.79,7.74]$

Table A1, Panel B: One standard deviation shock

  Full 2006-2007 sample: H-takerFull 2006-2007 sample: C-taker 3-month sub-sample: H-taker3-month sub-sample: C-taker
USD/EUR: Short run $ [0.6613,0.6616]$ $ [0.2630,0.2639]$ $ [0.6023,0.6045]$ $ [0.3139,0.3180]$
USD/EUR: Long run $ [0.6566,0.6570]$ $ [0.3161,0.3170]$ $ [0.6269,0.6296]$ $ [0.3914,0.3957]$
USD/EUR: Difference $ [-0.0047,-0.0046]$ $ [0.0531,0.0531]$ $ [0.0246,0.0251]$ $ [0.0775,0.0777]$
JPY/USD: Short run $ [0.8370,0.8660]$ $ [0.2375,0.3251]$ $ [0.9594,1.0158]$ $ [0.3798,0.5056]$
JPY/USD: Long run $ [0.8470,0.8796]$ $ [0.2727,0.3616]$ $ [0.9980,1.0480]$ $ [0.3274,0.4577]$
JPY/USD: Difference $ [0.0100,0.0137]$ $ [0.0352,0.0364]$ $ [0.0322,0.0386]$ $ [-0.0524,-0.0479] $
JPY/EUR: Short run $ [0.5060,0.5541]$ $ [0.4318,0.4874]$ $ [0.6671,0.7532]$ $ [0.6725,0.7581]$
JPY/EUR: Long run $ [0.5515,0.6030]$ $ [0.4608,0.5213]$ $ [0.7130,0.8049]$ $ [0.7174,0.8089]$
JPY/EUR: Difference $ [0.0455,0.0488]$ $ [0.0289,0.0339]$ $ [0.0459,0.0517]$ $ [0.0449,0.0508]$

Table A2

Min-max variance decompositions from the VAR specification with human-taker and computer-taker order flow. The table shows the minimum and maximum triangular long-run variance decomposition of returns, expressed in percent and calculated at the 30 minute horizon. That is, the table shows the proportion of the long-run variation in returns that can be attributed to shocks to the human-taker order flow $ (HH+CH)$ and the computer-taker $ (CC+HC)$ order flow, denoted H-taker and C-taker in the table headings, respectively. For each currency pair we show the actual variance decomposition, and the proportion of the $ explained$ variance in returns that can be attributed to each order flow type. That is, we re-scale the variance decompositions so that they add up to 100 percent. We show results for the full 2006-2007 sample and for the three-month sub-sample, which only uses data from September, October, and November of 2007. There are a total of $ 717,120$ minute-by-minute observations in the full two-year sample and $ 89,280$ observations in the three-month sub-sample.

  Full 2006-2007 sample: H-takerFull 2006-2007 sample: C-taker3-month sub-sample: H-taker3-month sub-sample: C-taker
USD/EUR: Variance decomposition $ [29.25,29.28]$ $ [4.71,4.74]$ $ [25.78,25.96]$ $ [7.08,7.26]$
USD/EUR: Proportion of explained share $ [86.04,86.14]$ $ [13.86,13.96]$ $ [78.02,78.58]$ $ [21.42,21.98]$
JPY/USD: Variance decomposition $ [27.71,29.67]$ $ [2.31,4.28]$ $ [26.03,29.19]$ $ [4.21,7.37]$
JPY/USD: Proportion of explained share $ [86.63,92.77]$ $ [7.23,13.37]$ $ [77.94,87.40]$ $ [12.60,22.06]$
JPY/EUR: Variance decomposition $ [10.15,12.16]$ $ [7.37,9.39]$ $ [9.94,12.67]$ $ [10.15,12.88]$
JPY/EUR: Proportion of explained share $ [51.93,62.27]$ $ [37.73,48.07]$ $ [43.55,55.53]$ $ [44.47,56.45]$

Table A3

Min-max impulse responses from the VAR specification with all four human/computer-maker/taker order flow combinations. The table shows the minimum and maximum triangular impulse responses for returns as a result of shocks to the human-maker/human-taker order flow $ (HH)$, computer-maker/human-taker order flow $ (CH)$, human-maker/computer-taker order flow $ (HC)$, or computer-maker/computer-taker order flow $ (CC)$, denoted in obvious notation in the table headings. The results are based on estimation of equation (3), using minute-by-minute data. In Panel A we show the return response, in basis points, to a one-billion base-currency shock to one of the order flows. In Panel B we show the return response, in basis points, to a one standard deviation shock to one of the order flows. We report the results for the full 2006-2007 sample and for the three-month sub-sample, which only uses data from September, October, and November of 2007. For each currency pair we show the short-run (immediate) response of returns; the corresponding cumulative long-run response of returns, calculated as the cumulative impact of the shock after 30 minutes; and the difference between the cumulative long-run response in returns minus the immediate response of returns, i.e., we provide the extent of over-reaction or under-reaction to an order flow shock. There are a total of $ 717,120$ minute-by-minute observations in the full two-year sample and $ 89,280$ observations in the three-month sub-sample.

Table A3, Panel A: One billion base-currency shock

  Full 2006-2007 sample: H-maker/H-takerFull 2006-2007 sample: C-maker/H-takerFull 2006-2007 sample: H-maker/H-takerFull 2006-2007 sample: C-maker/C-taker3-month sub-sample: H-maker/H-taker3-month sub-sample: C-maker/H-taker3-month sub-sample: H-maker/C-taker3-month sub-sample: C-maker/C-taker
USD/EUR: Short run [27.33,33.32] [18.63,53.71] [15.26,45.85] [20.49,52.41] [20.21,27.69] [17.49,47.57] [17.01,42.58] [12.66,38.58]
USD/EUR: Long run [29.89,34.83] [8.21,46.56] [22.08,50.08] [12.17,47.64] [24.08,30.77] [7.50,42.68] [25.64,49.51] [-4.72,26.10]
USD/EUR: Difference [1.05,2.88] [-10.48,-7.05] [2.69,7.20] [-9.13,-3.56] [2.26,4.55] [-10.15,-4.71] [4.31,9.43] [-17.81,-11.64]
JPY/USD: Short run[43.11,51.88] [39.54,95.65] [19.41,60.20] [51.93,83.64] [41.51,54.04] [40.20,94.60] [23.08,64.84] [61.16,89.94]
JPY/USD: Long run[46.68,54.24] [29.22,89.09] [25.02,63.23] [43.96,77.69] [46.49,57.52] [36.14,90.68] [19.96,59.37] [44.83,71.65]
JPY/USD: Difference[2.25,3.71] [-10.42,-6.47] [1.75,5.81] [-8.45,-4.72] [3.48,4.98] [-7.41,-1.59] [-7.05,-2.82] [-18.43,-15.85]
JPY/EUR: Short run [102.33,123.80] [30.23,132.09] [78.32,121.12] [99.99,113.19] [138.95,178.40] [30.01,147.48] [90.10,137.21] [86.01,101.70]
JPY/EUR: Long run [115.86,137.80] [25.52,136.33] [84.82,129.72] [91.10,105.26] [159.08,198.13] [20.15,146.71] [96.18,144.85] [86.58,102.72]
JPY/EUR: Difference [13.37,14.59] [-4.75,4.27] [6.14,8.73] [-8.89,-7.87] [18.60,21.43] [-9.86,-0.77] [4.46,7.81] [0.53,1.67]

Table A3, Panel B: One standard deviation shock

  Full 2006-2007 sample: H-maker/H-takerFull 2006-2007 sample: C-maker/H-takerFull 2006-2007 sample: H-maker/H-takerFull 2006-2007 sample: C-maker/C-taker3-month sub-sample: H-maker/H-taker3-month sub-sample: C-maker/H-taker3-month sub-sample: H-maker/C-taker3-month sub-sample: C-maker/C-taker
USD/EUR: Short run[0.4906,0.6497] [0.1545,0.4421] [0.1276,0.3793] [0.0551,0.1454] [0.3895,0.5839] [0.1739,0.4644] [0.1823,0.4469] [0.0481,0.1498
USD/EUR: Long run[0.5365,0.6791] [0.0681,0.3832] [0.1847,0.4143] [0.0327,0.1321] [0.4641,0.6489] [0.0746,0.4164] [0.2747,0.5157] [-0.0179,0.1014]
USD/EUR: Difference[0.0202,0.0537] [-0.0868,-0.0580] [0.0214,0.0609] [-0.0246,-0.0099] [0.0468,0.0919] [-0.1008,-0.0460] [0.0432,0.1029] [-0.0677,-0.0452]
JPY/USD: Short run[0.6273,0.8020] [0.2540,0.5984] [0.1395,0.4108] [0.1244,0.2043] [0.6484,0.9038] [0.3427,0.7866] [0.2224,0.5924] [0.2306,0.3453]
JPY/USD: Long run[0.6793,0.8384] [0.1877,0.5574] [0.1799,0.4315] [0.1053,0.1898] ]0.7261,0.9619] [0.3080,0.7540] [0.1923,0.5424] [0.1690,0.2751]
JPY/USD: Difference[0.0347,0.0547] [-0.0669,-0.0405] [0.0118,0.0418] [-0.0203,-0.0116] [0.0581,0.0777] [-0.0576,-0.0143] [-0.0633,-0.0272] [-0.0708,-0.0597]
JPY/EUR: Short run[0.4281,0.5356] [0.0847,0.3515] [0.3459,0.5018] [0.1549,0.1755] [0.5595,0.7502] [0.1084,0.5103] [0.5330,0.7700] [0.2191,0.2590]
JPY/EUR: Long run[0.4847,0.5963] [0.0715,0.3628] [0.3746,0.5374] [0.1412,0.1632] [0.6405,0.8332] [0.0728,0.5076] [0.5690,0.8128] [0.2206,0.2616]
JPY/EUR: Difference[0.0565,0.0620] [-0.0133,0.0114] [0.0250,0.0362] [-0.0138,-0.0122] [0.0775,0.0884] [-0.0356,-0.0027] [0.0244,0.0466] [0.0014,0.0043]

Table A4

Min-max variance decompositions from the VAR specification with all four human/computer-maker/taker order flow combinations. The table shows the minimum and maximum triangular long-run variance decomposition of returns, expressed in percent and calculated at the 30 minute horizon. That is, the table shows the proportion of the long-run variation in returns that can be attributed to shocks to the human-maker/human-taker order flow (HH), computer-maker/human-taker order flow (CH), human-maker/computer-taker order flow (HC), and computer-maker/computer-taker order flow (CC), denoted in obvious notation in the table headings. We show the actual variance decomposition, and the proportions of the explained variance in returns that can be attributed to each order flow type. That is, we re-scale the variance decompositions so that they add up to 100 percent. We present results for the full 2006-2007 sample and for the three-month sub-sample, which only uses data from September, October, and November of 2007. There are a total of 717,120 minute-by-minute observations in the full two-year sample and 89,280 observations in the three-month sub-sample.

  Full 2006-2007 sample: H-maker/H-takerFull 2006-2007 sample: C-maker/H-takerFull 2006-2007 sample: H-maker/C-takerFull 2006-2007 sample: C-maker/C-taker 3-month sub-sample: H-maker/H-taker 3-month sub-sample: C-maker/H-taker3-month sub-sample: H-maker/C-taker3-month sub-sample: C-maker/C-taker
USD/EUR: Variance decomp.[16.15, 28.28] [1.64, 13.06] [1.16, 9.71] [0.21, 1.42] [10.90, 24.29] [2.22, 15.27] [2.50, 14.24] [0.23, 1.63]
USD/EUR: Proportion[7.42, 83.05] [4.80, 38.36] [3.42, 28.51] [0.63, 4.17] [32.50, 72.41] [6.61, 45.52] [7.46, 42.43] [0.69, 4.85]
JPY/USD: Variance decomp.[15.61, 25.47] [2.57, 14.16] [0.85, 6.77] [0.61, 1.65] [12.00, 23.18] [3.34, 17.45] [1.51, 10.04] [1.52, 3.40]
JPY/USD: Proportion[48.22, 78.70] [7.94, 43.74] [2.64, 20.92] [1.90, 5.10] [35.04, 67.65] [9.74, 50.94] [4.40, 29.29] [4.44,9.91]
JPY/EUR: Variance decomp.[7.29, 11.38] [0.29, 4.89] [4.73, 9.95] [0.95, 1.22] [7.02, 12.58] [0.29, 5.83] [6.41, 13.31] [1.07, 1.50]
JPY/EUR: Proportion[37.25, 58.18] [1.49, 24.98] [24.19, 50.87] [4.87, 6.24] [30.40, 54.54] [1.26, 25.27] [27.79, 57.67] [4.66, 6.49]

References

Albuquerque, R., and Miao, J., 2008, Advanced Information and Asset Prices, Working Paper Boston University.

Andersen, T.G., and T. Bollerslev, 1998, Deutsche Mark-Dollar Volatility: Intraday activity patterns, macroeconomic announcements, and longer run dependencies, Journal of Finance 53, 219-265.

Andersen, T.G., T. Bollerslev, F.X. Diebold, and H. Ebens, 2001. The distribution of realized stock return volatility, Journal of Financial Economics 61, 43-76.

Andersen, T.G., T. Bollerslev, F.X. Diebold, and P. Labys, 2003. Modeling and Forecasting Realized Volatility, Econometrica 71, 579-625.

Andersen, T.G., T. Bollerslev, F.X. Diebold, and C. Vega, 2003. Micro Effects of Macro Announcements: Real-Time Price Discovery in Foreign Exchange, American Economic Review 93, 38-62.

Andersen, T.G., T. Bollerslev, F.X. Diebold, and C. Vega, 2007. Real-time price discovery in global stock, bond, and foreign exchange markets, Journal of International Economics 73, 251-277.

Angel, J., 1992, Limit versus Market Orders, working paper, Georgetown University.

Bandi, F.M., and J.R. Russel, 2006. Separating microstructure noise from volatility, Journal of Financial Economics 79, 655-692.

Berger, D.W., A.P. Chaboud, S.V. Chernenko, E. Howorka, and J.H. Wright, 2008. Order Flow and Exchange Rate Dynamics in Electronic Brokerage System Data, Journal of International Economics 75, 93-109.

Biais, B., Hillion, P., and Spatt, C., 1995, An empirical analysis of the limit order book and the order flow in the Paris Bourse, Journal of Finance, 50, 1655-1689.

Bollerslev T., and J.H. Wright, 2000. Semiparametric estimation of long-memory volatility dependencies: The role of high-frequency data, Journal of Econometrics 98, 81-106.

Bloomfield, R., M. O'Hara and G. Saar, 2005, The " Make or Take" Decision in an Electronic Market: Evidence on the Evolution of Liquidity, Journal of Financial Economics 75, 165-199.

Chaboud, A., B. Chiquoine, E. Hjalmarsson, and M. Loretan, 2007. Frequency of Observation and the Estimation of Integrated Volatility in Deep and Liquid Markets, Journal of Empirical Finance, Forthcoming.

Chakravarty, S., and C. Holden, 1995, An Integrated Model of Market and Limit Orders, Journal of Financial Intermediation 4, 213-241.

Easley, D., and O'Hara, M., 1987, Price, trade size, and information in securities markets, Journal of Financial Economics, 19, 69-90.

Evans, M., and R. Lyons, 2002. Order Flow and Exchange Rate Dynamics, Journal of Political Economy 110, 170-180.

Evans, M., and R. Lyons, 2008. How is Macro News Transmitted to Exchange Rates?, Journal of Financial Economics 88, 26-50.

Goettler, R., C. Parlour and U. Rajan, 2007, Microstructure effects and asset pricing, working paper, UC Berkeley.

Harris, L., 1998, Optimal Dynamic Order Submission Strategies in Some Stylized Trading Problems, Financial Markets, Institutions & Instruments 7, 1-76.

Hasbrouck, J., 1991a. Measuring the information content of stock trades, Journal of Finance 46, 179-207.

Hasbrouck, J., 1991b. The summary informativeness of stock trades: An econometric analysis, Review of Financial Studies 4, 571-595.

Hasbrouck, J., 1996. Order characteristics and stock price evolution: An application to program trading, Journal of Financial Economics 41, 129-149.

He, H., and J. Wang, 1995, Differential information and dynamic behavior of stock trading volume, Review of Financial Studies, 8, 919-972.

Hendershott, T., C.M. Jones, and A.J. Menkveld, 2007. Does algorithmic trading improve liquidity?, working paper, University of California, Berkeley.

Kaniel, R., and H. Liu, 2006, So What Orders do Informed Traders Use?, Journal of Business 79, 1867-1913.

Kumar, P., and D. Seppi, 1994, Limit and Market Orders with Optimizing Traders, working paper, Carnegie Mellon University.

Madhavan, A., Richardson, M., and Roomans, M., 1997, Why do security prices change? A transaction-level analysis of NYSE stocks, Review of Financial Studies, 10, 1035-1064.

Milgrom, P., and Stokey, N., 1982, Information, trade and common knowledge, Journal of Economic Theory, 26, 17-27.

Parlour, Christine, and Seppi, Duane, 2008, Limit Order Markets: A Survey, Handbook of Financial Intermediation & Banking, ed. A.W.A. Boot and A.V. Thakor, forthcoming.

Pasquariello, Paolo, and Vega, Clara, 2007, Informed and Strategic Order Flow in the Bond Markets, Review of Financial Studies, 20, 1975-2019.

Stock, J.H., J.H. Wright, and M. Yogo, 2005. A Survey of Weak Instruments and Weak Identification in Generalized Method of Moments, Journal of Business and Economic Statistics, 20, 518-529.

Stock, J.H., and M. Yogo, 2005. Testing for Weak Instruments in Linear IV Regression, in D.W.K. Andrews and J.H. Stock, eds., Identification and Inference for Econometric Models: Essays in Honor of Thomas Rothenberg, Cambridge: Cambridge University Press, 80-108.

Stoffman, Noah, 2007. Who Trades With Whom? Individuals, Institutions, and Returns. Unpublished Manuscript.

Table 1

Summary statistics for the one-minute return and order flow data. The mean and standard deviation, as well as the first-order autocorrelation, $ \rho$, are shown for each variable and currency pair. The returns are expressed in basis points and the order flows in millions of the base currency. The summary statistics are given for both the full 2006-2007 sample, as well as for the three-month sub-sample, which only uses observations from September, October, and November of 2007. The first two rows for each currency show the summary statistics for returns and the total market-wide order flow. The following two rows give the results for the order flows broken down into human-takers and computer-takers and the last four rows show the results for the order flow decomposed into each maker-taker pair. There are a total of 717, 120 observations in the full two-year sample and $ 89,280$ observations in the three-month sub sample. We show the statistical significance of the first order autocorrelation. The $ ^{***}$, $ ^{**}$, and $ ^{*}$ represent significance at the 1, 5, and 10 percent level, respectively.

  Full 2006-2007 Sample: MeanFull 2006-2007 Sample: Std. dev. Full 2006-2007 Sample: $ \rho$3-month sub sample: Mean 3-month sub sample: Std. dev. 3-month sub sample: $ \rho$
USD/EUR: Returns$ 0.0030$ $ 1.2398$ $ -0.005^{\ast\ast\ast}$ $ 0.0080$ $ 1.2057$ $ 0.007^{\ast\ast}$
USD/EUR: Total order flow $ \left( HH+CH+HC+CC\right) $$ 0.0315 $ $ 25.9455$ $ 0.150^{\ast\ast\ast}$ $ -0.0937$ $ 29.7065$ $ 0.174^{\ast\ast\ast}$
USD/EUR: H-taker $ \left( HH+CH\right) $$ 0.0413$ $ 23.977$ $ 0.155^{\ast\ast\ast}$ $ -0.0796$ $ 26.8096$ $ 0.189^{\ast\ast\ast}$
USD/EUR: C-taker $ \left( HC+CC\right) $$ -0.0099$ $ 9.9363$ $ 0.127^{\ast\ast\ast}$ $ -0.0140$ $ 12.8900$ $ 0.115^{\ast\ast\ast}$
USD/EUR: H-maker/H-taker $ \left( HH\right) $$ 0.1425$ $ 19.9614$ $ 0.177^{\ast\ast\ast}$ $ 0.0327$ $ 21.9211$ $ 0.209^{\ast\ast\ast}$
USD/EUR: C-maker/H-taker $ \left( CH\right) $$ -0.1012$ $ 8.8970$ $ 0.166^{\ast\ast\ast}$ $ -0.1123$ $ 10.7649$ $ 0.215^{\ast\ast\ast}$
USD/EUR: H-maker/C-taker $ \left( HC\right) $$ 0.0123$ $ 8.9232$ $ 0.152^{\ast\ast\ast}$ $ 0.0483$ $ 11.5856$ $ 0.150^{\ast\ast\ast}$
USD/EUR: C-maker/C-taker $ \left( CC\right) $$ -0.0222$ $ 2.7939$ $ 0.053^{\ast\ast\ast}$ $ -0.0623$ $ 3.9477$ $ 0.072^{\ast\ast\ast}$
JPY/USD: Returns$ -0.0007$ $ 1.6038$ $ -0.010^{\ast\ast\ast}$ $ -0.0045$ $ 1.9110$ $ 0.007^{\ast\ast}$
JPY/USD: Total order flow $ \left( HH+CH+HC+CC\right) $$ 0.1061 $ $ 20.0980$ $ 0.189^{\ast\ast\ast}$ $ -0.3439$ $ 23.6359$ $ 0.211^{\ast\ast\ast}$
JPY/USD: H-taker $ \left( HH+CH\right) $$ 0.0853$ $ 19.1127$ $ 0.190^{\ast\ast\ast}$ $ -0.2088$ $ 22.0344$ $ 0.204^{\ast\ast\ast}$
JPY/USD: C-taker $ \left( HC+CC\right) $  $ 8.3941$ $ 0.170^{\ast\ast\ast}$ $ -0.1351$ $ 11.5877$ $ 0.158^{\ast\ast\ast}$
JPY/USD: H-maker/H-taker $ \left( HH\right) $$ 0.1037$ $ 15.9972$ $ 0.209^{\ast\ast\ast}$ $ -0.1203$ $ 17.4612$ $ 0.226^{\ast\ast\ast}$
JPY/USD: C-maker/H-taker $ \left( CH\right) $$ -0.0184$ $ 6.9030$ $ 0.172^{\ast\ast\ast}$ $ -0.0885$ $ 9.1773$ $ 0.162^{\ast\ast\ast}$
JPY/USD: H-maker/C-taker $ \left( HC\right) $$ 0.0198$ $ 7.5686$ $ 0.198^{\ast\ast\ast}$ $ -0.0901$ $ 10.1673$ $ 0.191^{\ast\ast\ast}$
JPY/USD: C-maker/C-taker $ \left( CC\right) $$ 0.0011$ $ 2.4556$ $ 0.032^{\ast\ast\ast}$ $ -0.045$ $ 3.8751$ $ 0.026^{\ast\ast\ast}$
JPY/EUR: Returns$ 0.0024$ $ 1.5976$ $ -0.053^{\ast\ast\ast}$ $ 0.0036$ $ 2.1398$ $ -0.017^{\ast\ast\ast}$
JPY/EUR: Total order flow $ -0.0648$ $ 7.0941$ $ 0.152^{\ast\ast\ast}$ $ -0.1574$ $ 8.5978 $ $ 0.147^{\ast\ast\ast}$
JPY/EUR: H-taker $ \left( HH+CH\right) $$ -0.0497$ $ 5.7006$ $ 0.150^{\ast\ast\ast}$ $ -0.1216$ $ 6.2074$ $ 0.125^{\ast\ast\ast}$
JPY/EUR: C-taker $ \left( HC+CC\right) $$ -0.0151$ $ 4.8409$ $ 0.146^{\ast\ast\ast}$ $ -0.0358$ $ 6.7000$ $ 0.131^{\ast\ast\ast}$
JPY/EUR: H-maker/H-taker $ \left( HH\right) $$ -0.0172$ $ 4.4203$ $ 0.159^{\ast\ast\ast}$ $ -0.0600$ $ 4.3106$ $ 0.157^{\ast\ast\ast}$
JPY/EUR: C-maker/H-taker $ \left( CH\right) $$ -0.0325$ $ 2.8912$ $ 0.129^{\ast\ast\ast}$ $ -0.0616$ $ 3.7197$ $ 0.092^{\ast\ast\ast}$
JPY/EUR: H-maker/C-taker $ \left( HC\right) $$ -0.0095$ $ 4.5331$ $ 0.173^{\ast\ast\ast}$ $ -0.0264$ $ 6.0968$ $ 0.161^{\ast\ast\ast}$
JPY/EUR: C-maker/C-taker $ \left( CC\right) $$ -0.0056$ $ 1.5558$ $ 0.023^{\ast\ast\ast}$ $ -0.0095$ $ 2.5621$ $ -0.001$

Table 2

Summary statistics for the fractions of trade volume attributable to different trader combinations. The table shows the fraction of the total volume of trade that is attributable to different combinations of makers and takers. Results for the full 2006-2007 sample as well as for the three-month sub-sample, which only uses data from September, October, and November of 2007, are shown. We show the average of the daily fractions, calculated by summing up across all minutes within a day, and the standard deviations of those daily fractions. For each currency, the first row shows the fraction of the total volume of trade where a computer was involved on at least one side of the trade (i.e. as a maker or a taker). The second row shows the fraction of the total volume where a human acted as a taker, the third row shows the fraction of the total volume where a computer acted as a taker, and the following four rows shows the fractions broken down by each maker-taker pair.

  Full 2006-2007 Sample: MeanFull 2006-2007 Sample: Std. dev.3-month sub sample: Mean3-month sub sample: Std. dev.
USD/EUR: C-participation $ \left( Vol\left( CH+HC+CC\right) \right) $$ 0.4163$ $ 0.1135$ $ 0.5386$ $ 0.0355$
USD/EUR: H-taker $ \left( Vol\left( CH+HH\right) \right) $$ 0.7810$ $ 0.0791$ $ 0.6864$ $ 0.0331$
USD/EUR: C-taker $ \left( Vol\left( HC+CC\right) \right) $$ 0.2190$ $ 0.0791$ $ 0.3136$ $ 0.0331$
USD/EUR: H-maker/H-taker $ \left( Vol\left( HH\right) \right) $$ 0.5837$ $ 0.1135$ $ 0.4614$ $ 0.0355$
USD/EUR: C-maker/H-taker $ \left( Vol\left( CH\right) \right) $$ 0.1973$ $ 0.0398$ $ 0.2251$ $ 0.0144$
USD/EUR: H-maker/C-taker $ \left( Vol\left( HC\right) \right) $$ 0.1710$ $ 0.0514$ $ 0.2304$ $ 0.0205$
USD/EUR: C-maker/C-taker $ \left( Vol\left( CC\right) \right) $$ 0.0480$ $ 0.0290$ $ 0.0831$ $ 0.0150$
JPY/USD: C-participation $ \left( Vol\left( CH+HC+CC\right) \right) $$ 0.4242$ $ 0.1065$ $ 0.5652$ $ 0.0364$
JPY/USD: H-taker $ \left( Vol\left( CH+HH\right) \right) $$ 0.7585$ $ 0.0805$ $ 0.6461$ $ 0.0311$
JPY/USD: C-taker $ \left( Vol\left( HC+CC\right) \right) $$ 0.2415$ $ 0.0805$ $ 0.3539$ $ 0.0311$
JPY/USD: H-maker/H-taker $ \left( Vol\left( HH\right) \right) $$ 0.5758$ $ 0.1065$ $ 0.4348$ $ 0.0364$
JPY/USD: C-maker/H-taker $ \left( Vol\left( CH\right) \right) $$ 0.1827$ $ 0.0304$ $ 0.2114$ $ 0.0126$
JPY/USD: H-maker/C-taker $ \left( Vol\left( HC\right) \right) $$ 0.1860$ $ 0.0498$ $ 0.2486$ $ 0.0154$
JPY/USD: C-maker/C-taker $ \left( Vol\left( CC\right) \right) $$ 0.0555$ $ 0.0321$ $ 0.1052$ $ 0.0193$
JPY/EUR: C-involved $ \left( Vol\left( CH+HC+CC\right) \right) $$ 0.6186$ $ 0.1154$ $ 0.7907$ $ 0.0410$
JPY/EUR: H-taker $ \left( Vol\left( CH+HH\right) \right) $$ 0.5557$ $ 0.1018$ $ 0.4037$ $ 0.0467$
JPY/EUR: C-taker $ \left( Vol\left( HC+CC\right) \right) $$ 0.4443$ $ 0.1018$ $ 0.5963$ $ 0.0467$
JPY/EUR: H-maker/H-taker $ \left( Vol\left( HH\right) \right) $$ 0.3814$ $ 0.1154$ $ 0.2093$ $ 0.0410$
JPY/EUR: C-maker/H-taker $ \left( Vol\left( CH\right) \right) $$ 0.1743$ $ 0.0360$ $ 0.1944$ $ 0.0164$
JPY/EUR: H-maker/C-taker $ \left( Vol\left( HC\right) \right) $$ 0.3337$ $ 0.0473$ $ 0.3734$ $ 0.0193$
JPY/EUR: C-maker/C-taker $ \left( Vol\left( CC\right) \right) $$ 0.1106$ $ 0.0673$ $ 0.2229$ $ 0.0464$

Table 3

Estimates of the ratio $ R=RC/RH$. The table reports the mean estimates of the ratio $ R=RC/RH$, where $ RC=Vol(HC)/Vol(CC)$ and $ RH=Vol(HH)/Vol(CH)$. $ Vol(HH) $ is the daily trading volume between human-makers and human-takers, $ Vol(HC) $ is the daily trading volume between human-makers and computer-takers, $ Vol( CH) $ is the daily trading volume between computer-makers and human-takers, and $ Vol(CC) $ is the daily trading volume between computer-makers and computer-takers. We report the mean of the daily ratio $ R$ and the standard errors are shown in parantheses below the estimate. We also show the number of days that had a ratio that was less than one. We report the results for the full 2006-2007 sample and the three-month sub-sample, which only uses data from September, October, and November of 2007. The $ ^{***}$, $ ^{**}$, and $ ^{*}$ represent a statistically significant deviation from one at the 1, 5, and 10 percent level, respectively.

 Full 2006-2007 sample3-month sub sample
USD/EUR: Mean of daily $ R=\left. RC\right/ RH$ $ 1.4463^{\ast \ast\ast}$ $ 1.3721^{\ast\ast\ast }$
USD/EUR: Standard Error$ (0.0063)$ $ (0.0099)$
USD/EUR: No. of days with $ R<1$0 0
USD/EUR: No. of obs498 62
JPY/USD: Mean of daily $ R=\left. RC\right/ RH$ $ 1.2619^{\ast \ast\ast}$ $ 1.1719^{\ast\ast\ast }$
JPY/USD: Standard Error$ (0.0074)$ $ (0.0142)$
JPY/USD: No. of days with $ R<1$15 4
JPY/USD: No. of obs498 62
JPY/EUR: Mean of daily $ R=\left. RC\right/ RH$ $ 1.6886^{\ast \ast\ast}$ $ 1.6242^{\ast\ast\ast }$
JPY/EUR: Standard Error$ (0.0154)$ $ (0.0250)$
JPY/EUR: No. of days with $ R<1$4 0
JPY/EUR: No. of obs498 62

Table 4

Regressions of realized volatility on the fraction of algorithmic trading. The table shows the results from estimating the relationship between daily realized volatility and the fraction of algorithmic trading, using daily data from 2006 and 2007. Robust standard errors are given in parentheses below the coefficient estimates. The left hand side of the table shows the results with a quarterly time trend included in the regressions and the right hand side of the table shows the results with year-quarter time dummies (i.e., eight time dummies, one for each quarter in the two years of data) included in the regressions. Panels A and B show the results when the fraction of algorithmic trading is measured as the fraction of the total trade volume that has a computer involved on at least one side of the trade (i.e. as a maker or a taker). Panels C and D show the results when only the fraction of volume with computer taking is used. In addition to the fraction of algorithmic trading and the control(s) for secular trends, 22 lags of volatility are also included in every specification. In all cases, only the coefficient on the fraction of algorithmic trading is displayed. Panels A and C show the results from a standard OLS estimation, along with the $ R^2$. Panels B and D show the results from the IV specification estimated with Limited Information Maximum Likelihood (LIML). In Panels B and D, the Stock and Yogo (2005) $ F-$test of weak instruments are also shown. The critical values for Stock and Yogo's (2005) F-test are designed such that they indicate a maximal actual size for a nominal sized five percent test on the coefficient in the LIML estimation. Thus, in order for the actual size of the LIML test to be no greater than 10% (15%), the F-statistic should exceed 8.68 (5.33). There are a total of $ 498$ daily observations in the data. The $ ^{***}$, $ ^{**}$, and $ ^{*}$ represent significance at the 1, 5, and 10 percent level, respectively.

 With quarterly time trend: USD/EURWith quarterly time trend: JPY/USDWith quarterly time trend: JPY/EURWith year-quarter time dummies: USD/EURWith year-quarter time dummies: JPY/USDWith year-quarter time dummies: JPY/EUR
Panel A. Fraction of volume with any computer participation, OLS estimation - Coeff. on AT$ 0.0029$$ (0.0024)$ $ 0.0018$$ (0.0021)$ $ 0.0034^{\ast\ast \ast}$$ (0.0012)$ $ 0.0078^{\ast\ast\ast}$$ (0.0027)$ $ -0.0030$$ (0.0024)$ $ 0.0065^{\ast\ast\ast}$$ (0.0016)$
Panel A. Fraction of volume with any computer participation, OLS estimation - $ R^{2}\left( \%\right) $$ 53.44\%$ $ 61.13\%$ $ 71.90\%$ $ 56.73\%$ $ 62.57\%$ $ 73.33\%$
Panel B. Fraction of volume with any computer participation, IV estimation - Coeff. on AT $ -0.0121^{\ast}$$ (0.0062)$ $ -0.0186^{\ast\ast}$$ (0.0089)$ $ -0.0022$$ (0.0039)$ $ -0.0078$$ (0.0061)$ $ -0.0101$$ (0.0069)$ $ -0.0128$$ (0.0175)$
Panel B. Fraction of volume with any computer participation, IV estimation - F-Stat$ 29.58$ $ 19.46$ $ 32.18$ $ 38.17$ $ 20.89$ $ 2.25$
Panel C. Fraction of volume with computer-taking, OLS estimation - Coeff. on AT$ 0.0037$$ (0.0036)$ $ -0.0027$$ (0.0024)$ $ 0.0015$$ (0.0012)$ $ 0.0094^{\ast\ast}$$ (0.0038)$ $ -0.0034$$ (0.0027)$ $ 0.0032^{\ast\ast}$$ (0.0016)$
Panel C. Fraction of volume with computer-taking, OLS estimation -$ R^{2}\left( \%\right) $$ 53.39\%$ $ 61.17\%$ $ 71.56\%$ $ 56.43\%$ $ 62.55\%$ $ 72.66\%$
Panel D. Fraction of volume with computer-taking, IV estimation - Coeff. on AT $ -0.0160^{\ast\ast}$$ (0.0080)$ $ -0.0215^{\ast\ast}$$ (0.0109)$ $ -0.0007$$ (0.0028)$ $ -0.0072$$ (0.0070)$ $ -0.0122$$ (0.0082)$ $ -0.0182$$ (0.0291)$
Panel D. Fraction of volume with computer-taking, IV estimation - F-Stat$ 39.99$ $ 17.63$ $ 64.81$ $ 55.45$ $ 21.20$ $ 1.04$

Table 5

We report the mean ratio of the exchange rate volatility (Panel A) and liquidity provision by humans and by computers (Panel B) estimated during announcement days relative to that estimated during non-announcement days. The one-hour measure is estimated using observations from 8:25 am to 9:24 am ET and the one-minute measure is estimated using 8:30 am to 8:31 am ET observations. Announcement days are defined as nonfarm payroll announcement days and non-announcement days are defined as 10 business days before and after the nonfarm payroll announcement. In each panel, we report the chi-squared and p-value of the Wald test that the ratio is equal to 1. In Panel C we report the chi-squared and p-value of the Wald test that the liquidity provision of humans during announcement days relative to non-announcement days is similar to the liquidity provision of computers. The statistics are estimated using data in the full sample from 2006 to 2007 and there are 23 observations (April 6, 2007 nonfarm payroll announcement is missing because it falls on Good Friday, when trading in the foreign exchange market is limited). Human liquidity provision, , is defined as the sum of human-maker/human-taker volume plus human-maker/human-taker volume divided by total volume. Computer liquidity provision, , is defined as the sum of computer-maker/computer-taker volume plus computer-maker/human-taker volume divided by total volume. The ***,** and * represent significance at the 1, 5, and 10 percent level, respectively.

  USD/EUR: HourUSD/EUR: MinuteJPY/USD: HourJPY/USD: MinuteJPY/EUR: HourJPY/EUR: Minute
Panel A: Volatility - $ \frac{\sigma_{a}}{\sigma_{n}}$ $ 6.236^{\ast\ast\ast}$ $ 21.704^{\ast\ast\ast}$ $ 5.595^{\ast\ast\ast}$ $ 24.812^{\ast\ast\ast}$ $ 3.697^{\ast\ast\ast}$ $ 14.403^{\ast\ast}$
Panel A: Volatility - $ \chi^{2}$ $ \left( H_{0}:\sigma_{a}=\sigma_{n}\right) $$ 69.86$ $ 18.76$ $ 33.34$ $ 15.45$ $ 19.37$ $ 5.96$
Panel A: Volatility - p-value$ 0.0000$ $ 0.0003$ $ 0.0000$ $ 0.0008$ $ 0.0002$ $ 0.0235$
Panel B: Liquidity Provision - Liquidity provision by humans, $ \frac{LH_{a}}{LH_{n}}$ $ 0.964^{\ast\ast\ast}$ $ 1.062^{\ast\ast\ast}$ $ 1.023$ $ 1.183^{\ast\ast\ast}$ $ 0.888^{\ast\ast\ast}$ $ 0.980 $
Panel B: Liquidity Provision - Liquidity provision by computers, $ \frac{LC_{a}}{LC_{n}}$ $ 1.132^{\ast\ast\ast}$ $ 0.871^{\ast\ast\ast}$ $ 0.974$ $ 0.652^{\ast\ast\ast}$ $ 1.227^{\ast\ast\ast}$ $ 1.151 $
Panel B: Liquidity Provision - $ \chi^{2}$ $ \left( H_{0}:LH_{a}=LH_{n}{\footnotesize or} LC_{a}=LC_{n}\right) $ $ 16.56$ $ 9.04$ $ 2.71$ $ 31.91$ $ 25.19$ $ 0.5$
Panel B: Liquidity Provision - p-value$ 0.0005$ $ 0.0067$ $ 0.1143$ 0 $ 0.0001$ $ 0.487$
Panel C: Comparison of Liquidity Provision between Humans and Computers - $ \frac{LH_{a}}{LH_{n}}-\frac{LC_{a}}{LC_{n}}$ $ -0.168^{\ast\ast\ast}$ $ 0.191^{\ast\ast}$ $ 0.049$ $ 0.532^{\ast \ast\ast}$ $ -0.339^{\ast\ast\ast}$ $ -0.171$
Panel C: Comparison of Liquidity Provision between Humans and Computers - $ \chi^{2}$ $ \left( H_{0}:\frac{LH_{a}}{LH_{n}} =\frac{LC_{a}}{LC_{n}}\right) $ $ 19.24$ $ 5.91$ $ 1.50$ $ 36.07$ $ 25.21$ $ 0.66$
Panel C: Comparison of Liquidity Provision between Humans and Computers - p-value$ 0.0003$ $ 0.0241$ $ 0.2339$ $ 0.0000$ $ 0.0001$ $ 0.4245$

Table 6

Impulse responses from the VAR specification with human-taker and computer-taker order flow. The table shows the impulse responses for returns as a result of shocks to the human-taker order flow $ (HH+CH)$ or computer-taker $ (CC+HC)$ order flow, denoted H-taker and C-taker in the table headings, respectively. The results are based on estimation of equation (2), using minute-by-minute data. In Panel A we show the return response, in basis points, to a one-billion base-currency shock to one of the order flows. In Panel B we show the return response, in basis points, to a one standard deviation shock to one of the order flows. We show the results for the full 2006-2007 sample and for the three-month sub-sample, which only uses data from September, October, and November of 2007. For each currency pair we show the short-run (immediate) response of returns; the corresponding cumulative long-run response of returns, calculated as the cumulative impact of the shock after 30 minutes; and the difference between the cumulative long-run response in returns minus the immediate response of returns, i.e., we provide the extent of over-reaction or under-reaction to an order flow shock. There are a total of 717, 120 minute-by-minute observations in the full two-year sample and 89, 280 observations in the three-month sub-sample. We show in parenthesis the standard errors of the difference between the short-run and long-run response. These standard errors are calculated by bootstrapping, using 200 repetitions.

Table 6, Panel A: One billion base-currency shock

  Full 2006-2007 sample: H-takerFull 2006-2007 sample: C -taker 3-month sub-sample: H-taker3-month sub-sample: C -taker
USD/EUR: Short run$ 28.06$ $ 26.94$ $ 23.20$ $ 25.22$
USD/EUR: Long run$ 27.87$ $ 32.35$ $ 24.16$ $ 31.38$
USD/EUR: Difference$ -0.20$$ \left( 0.29\right) $ $ 5.42$$ \left( 0.67\right) $ $ 0.96$$ \left( 0.72\right) $ $ 6.16$$ \left( 1.36\right) $
JPY/USD: Short run$ 46.77$ $ 39.81$ $ 48.02$ $ 44.89$
JPY/USD: Long run$ 47.50$ $ 44.27$ $ 49.54$ $ 40.63$
JPY/USD: Difference$ 0.74$$ \left( 0.48\right) $ $ 4.46$$ \left( 1.08\right) $ $ 1.52$$ \left( 1.36\right) $ $ -4.26$$ \left( 2.35\right) $
JPY/EUR: Short run$ 99.32$ $ 102.71$ $ 124.02$ $ 115.52$
JPY/EUR: Long run$ 108.07$ $ 109.85$ $ 132.53$ $ 123.26$
JPY/EUR: Difference$ 8.75$ $ \left( 1.50\right) $ $ 7.14$$ \left( 1.67\right) $ $ 8.51$$ \left( 4.79\right) $ $ 7.74$$ \left( 4.76\right) $

Table 6, Panel B: One standard deviation shock

  Full 2006-2007 sample: H-takerFull 2006-2007 sample: C -taker 3-month sub-sample: H-taker3-month sub-sample: C -taker
USD/EUR: Short run$ 0.6617$ $ 0.2639$ $ 0.6045$ $ 0.3181$
USD/EUR: Long run$ 0.6570$ $ 0.3170$ $ 0.6296$ $ 0.3957$
USD/EUR: Difference$ -0.0046$ $ \left( 0.0068\right) $ $ 0.0531$$ \left( 0.0065\right) $ $ 0.0251$$ \left( 0.0189\right) $ $ 0.0777 $$ \left( 0.0172\right) $
JPY/USD: Short run$ 0.8706$ $ 0.3269$ $ 1.0241$ $ 0.5098$
JPY/USD: Long run$ 0.8843$ $ 0.3635$ $ 1.0565$ $ 0.4614$
JPY/USD: Difference$ 0.0137$$ \left( 0.0090\right) $ $ 0.0366$$ \left( 0.0089\right) $ $ 0.0324$$ \left( 0.0289\right) $ $ -0.0483 $$ \left( 0.0267\right) $
JPY/EUR: Short run$ 0.5572$ $ 0.4901$ $ 0.7587$ $ 0.7636$
JPY/EUR: Long run$ 0.6063$ $ 0.5242$ $ 0.8108$ $ 0.8148$
JPY/EUR: Difference$ 0.0491$$ \left( 0.0085\right) $ $ 0.0341$$ \left( 0.0080\right) $ $ 0.0520$$ \left( 0.0294\right) $ $ 0.0512$$ \left( 0.0314\right) $

Table 7

Variance decompositions from the VAR specification with human-taker and computer-taker order flow. The table provides the long-run variance decomposition of returns, expressed in percent and calculated at the 30 minute horizon, based on estimation of equation (2), using minute-by-minute data. That is, the table shows the proportion of the long-run variation in returns that can be attributed to shocks to the human-taker order flow and the computer-taker order flow, denoted H-taker and C-taker in the table headings, respectively. For each currency pair we show the actual variance decomposition, and the proportion of the variance in returns that can be attributed to each order flow type. That is, we re-scale the variance decompositions so that they add up to 100 percent. We show results for the full 2006-2007 sample and for the three-month sub-sample, which only uses data from September, October, and November of 2007. There are a total of minute-by-minute observations in the full two-year sample and observations in the three-month sub-sample. We show in parenthesis the standard errors calculated by bootstrapping, using 200 repetitions.


  Full 2006-2007 sample: H-takerFull 2006-2007 sample: C-taker3-month sub-sample: H-taker3-month sub-sample: C-taker
USD/EUR: Variance decomposition$ 29.27$$ \left( 0.95\right) $ $ 4.74$$ \left( 0.19\right) $ $ 25.92$$ \left( 0.79\right) $ $ 7.25$$ \left( 0.42\right) $
USD/EUR: Proportion of explained share$ 86.06$$ \left( 2.79\right) $ $ 13.94$$ \left( 0.56\right) $ $ 78.14$$ \left( 2.38\right) $ $ 21.86$$ \left( 1.27\right) $
JPY/USD: Variance decomposition$ 29.31$$ \left( 0.35\right) $ $ 4.22$$ \left( 0.11\right) $ $ 28.59$$ \left( 0.50\right) $ $ 7.22$$ \left( 0.33\right) $
JPY/USD: Proportion of explained share$ 87.41$$ \left( 1.04\right) $ $ 12.59$$ \left( 0.33\right) $ $ 79.84$$ \left( 1.40\right) $ $ 20.16$$ \left( 0.92\right) $
JPY/EUR: Variance decomposition$ 12.03$$ \left( 0.21\right) $ $ 9.28$$ \left( 0.20\right) $ $ 12.47$$ \left( 0.38\right) $ $ 12.67$$ \left( 0.38\right) $
JPY/EUR: Proportion of explained share$ 56.45$$ \left( 0.99\right) $ $ 43.55$$ \left( 0.94\right) $ $ 49.60$$ \left( 1.51\right) $ $ 50.40$$ \left( 1.51\right) $

Table 8

Impulse responses from the VAR specification with all four human/computer-maker/taker order flow combinations. The table shows the impulse responses for returns as a result of shocks to the human-maker/human-taker order flow $ (HH)$, computer-maker/human-taker order flow $ (CH)$, human-maker/computer-taker order flow $ (HC)$, or computer-maker/computer-taker order flow $ (CC)$, denoted in obvious notation in the table headings. The results are based on estimation of equation (3), using minute-by-minute data. In Panel A we show the return response, in basis points, to a one-billion base-currency shock to one of the order flows. In Panel B we show the return response, in basis points, to a one standard deviation shock to one of the order flows. We report the results for the full 2006-2007 sample and for the three-month sub-sample, which only uses data from September, October, and November of 2007. For each currency pair we show the short-run (immediate) response of returns; the corresponding cumulative long-run response of returns, calculated as the cumulative impact of the shock after 30 minutes; and the difference between the cumulative long-run response in returns minus the immediate response of returns, i.e., we provide the extent of over-reaction or under-reaction to an order flow shock. There are a total of 717, 120 minute-by-minute observations in the full two-year sample and 89, 280 observations in the three-month sub-sample. We show in parenthesis the standard errors of the difference between the short-run and the long-run response. These standard errors are calculated by bootstrapping, using 200 repetitions.

Table 8, Panel A: One billion base-currency shock

  Full 2006-2007 sample: H-maker/H-takerFull 2006-2007 sample: C-maker/H-takerFull 2006-2007 sample: H-maker/C-takerFull 2006-2007 sample: C-maker/C-taker3-month sub-sample: H-maker/H-taker3-month sub-sample: C-maker/H-taker 3-month sub-sample: H-maker/C-taker3-month sub-sample: C-maker/C-taker
USD/EUR: Short run$ 27.64$ $ 29.66$ $ 26.57$ $ 32.19$ $ 20.58$ $ 30.94$ $ 28.94$ $ 21.74$
USD/EUR: Long run$ 30.13$ $ 20.47$ $ 29.89$ $ 24.92$ $ 24.18$ $ 23.35$ $ 34.64$ $ 5.94$
USD/EUR: Difference$ 2.49$$ \left( 0.35\right) $ $ -9.19$$ \left( 0.88\right) $ $ 3.32$$ \left( 0.83\right) $ $ -7.26$$ \left( 2.42\right) $ $ 3.60$$ \left( 0.97\right) $ $ -7.59$$ \left( 2.03\right) $ $ 5.70$$ \left( 1.79\right) $ $ -15.80$$ \left( 4.64\right) $
JPY/USD: Short run$ 43.48$ $ 58.94$ $ 40.34$ $ 61.57$ $ 41.96$ $ 64.63$ $ 46.08$ $ 67.65$
JPY/USD: Long run$ 47.01$ $ 49.53$ $ 42.61$ $ 54.37$ $ 46.83$ $ 57.24$ $ 40.33$ $ 51.81$
JPY/USD: Difference$ 3.53$$ \left( 0.59\right) $ $ -9.41$$ \left( 1.57\right) $ $ 2.27$$ \left( 1.30\right) $ $ -7.20$$ \left( 3.38\right) $ $ 4.87$$ \left( 1.62\right) $ $ -7.39$$ \left( 3.43\right) $ $ -5.75$$ \left( 2.89\right) $ $ -15.85$$ \left( 7.39\right) $
JPY/EUR: Short run$ 102.61$ $ 92.16$ $ 100.91$ $ 102.04$ $ 139.33$ $ 103.92$ $ 114.01$ $ 94.47$
JPY/EUR: Long run$ 116.12$ $ 91.24$ $ 107.18$ $ 93.41$ $ 159.46$ $ 96.85$ $ 118.47$ $ 95.20$
JPY/EUR: Difference$ 13.51$$ \left( 1.98\right) $ $ -0.92$$ \left( 3.18\right) $ $ 6.27$$ \left( 1.94\right) $ $ -8.63$$ \left( 4.98\right) $ $ 20.13$$ \left( 7.25\right) $ $ -7.07$$ \left( 9.35\right) $ $ 4.46$$ \left( 5.78\right) $ $ 0.74$$ \left( 10.70\right) $

Table 8, Panel B: One standard deviation shock

  USD/EUR: Full 2006-2007 sample: H-maker/H-takerUSD/EUR: Full 2006-2007 sample: C-maker/H-takerUSD/EUR: Full 2006-2007 sample: H-maker/C-takerUSD/EUR: Full 2006-2007 sample: C-maker/C-takerUSD/EUR: 3-month sub-sample: H-maker/H-takerUSD/EUR: 3-month sub-sample: C-maker/H-takerUSD/EUR: 3-month sub-sample: H-maker/C-takerUSD/EUR: 3-month sub-sample: C-maker/C-taker
USD/EUR: Short run$ 0.5389$ $ 0.2575$ $ 0.2318$ $ 0.0893$ $ 0.4342$ $ 0.3211$ $ 0.3228$ $ 0.0845$
USD/EUR: Long run$ 0.5875$ $ 0.1777$ $ 0.2608$ $ 0.0692$ $ 0.5101$ $ 0.2424$ $ 0.3864$ $ 0.0231$
USD/EUR: Difference$ 0.0486$$ \left( 0.0069\right) $ $ -0.0798$$ \left( 0.0076\right) $ $ 0.0290$$ \left( 0.0072\right) $ $ -0.0202$$ \left( 0.0067\right) $ $ 0.0760$$ \left( 0.0203\right) $ $ -0.0788$$ \left( 0.0211\right) $ $ 0.0636$$ \left( 0.0200\right) $ $ -0.0614$$ \left( 0.0180\right) $
JPY/USD: Short run$ 0.6721$ $ 0.3968$ $ 0.2962$ $ 0.1506$ $ 0.7019$ $ 0.5801$ $ 0.4544$ $ 0.2607$
JPY/USD: Long run$ 0.7267$ $ 0.3334$ $ 0.3129$ $ 0.1330$ $ 0.7834$ $ 0.5137$ $ 0.3976$ $ 0.1997$
JPY/USD: Difference$ 0.0546$$ \left( 0.0091\right) $ $ -0.0634$$ \left( 0.0106\right) $ $ 0.0167$$ \left( 0.0096\right) $ $ -0.0176$$ \left( 0.0083\right) $ $ 0.0815$$ \left( 0.0274\right) $ $ -0.0663$$ \left( 0.0307\right) $ $ -0.0567$$ \left( 0.0284\right) $ $ -0.0611$$ \left( 0.0284\right) $
JPY/EUR: Short run$ 0.4440$ $ 0.2629$ $ 0.4481$ $ 0.1583$ $ 0.5859$ $ 0.3829$ $ 0.6809$ $ 0.2409$
JPY/EUR: Long run$ 0.5024$ $ 0.2603$ $ 0.4760$ $ 0.1449$ $ 0.6706$ $ 0.3568$ $ 0.7076$ $ 0.2428$
JPY/EUR: Difference$ 0.0584$$ \left( 0.0086\right) $ $ -0.0026$$ \left( 0.0091\right) $ $ 0.0279$ $ \left( 0.0086\right) $ $ -0.0134$$ \left( 0.0077\right) $ $ 0.0847$$ \left( 0.0306\right) $ $ -0.0260$$ \left( 0.0344\right) $ $ 0.0266$$ \left( 0.0345\right) $ $ 0.0019$$ \left( 0.0273\right) $

Table 9

Variance decompositions from the VAR specification with all four human/computer-maker/taker order flow combinations. The table provides the long-run variance decomposition of returns, expressed in percent and calculated at the 30 minute horizon, based on estimation of equation (3), using minute-by-minute data. That is, the table shows the proportion of the long-run variation in returns that can be attributed to shocks to the human-maker/human-taker order flow $ (HH)$, computer-maker/human-taker order flow $ (CH)$, human-maker/computer-taker order flow $ (HC)$, and computer-maker/computer-taker order flow $ (CC)$, denoted in obvious notation in the table headings. We show the actual variance decomposition, and the proportions of the $ explained$ variance in returns that can be attributed to each order flow type. That is, we re-scale the variance decompositions so that they add up to 100 percent. We present results for the full 2006-2007 sample and for the three-month sub-sample, which only uses data from September, October, and November of 2007. There are a total of 717, 120 minute-by-minute observations in the full two-year sample and $ 89,280$ observations in the three-month sub-sample. We show in parenthesis the standard errors, which are calculated by bootstrapping, using 200 repetitions.


  Full 2006-2007 sample: H-maker/H-takerFull 2006-2007 sample: C-maker/H-takerFull 2006-2007 sample: H-maker/C-takerFull 2006-2007 sample: C-maker/C-taker3-month sub-sample: H-maker/H-taker3-month sub-sample: C-maker/H-taker3-month sub-sample: H-maker/C-taker3-month sub-sample: C-maker/C-taker
USD/EUR: Variance decomp.$ 20.71$ $ \left( 0.89\right) $ $ 4.73$$ \left( 0.24\right) $ $ 3.89$$ \left( 0.21\right) $ $ 0.58$$ \left( 0.04\right) $ $ 14.19$$ \left( 0.75\right) $ $ 7.68$$ \left( 0.48\right) $ $ 7.86$$ \left( 0.43\right) $ $ 0.59$$ \left( 0.09\right) $
USD/EUR: Proportion$ 69.24$$ \left( 2.98\right) $ $ 15.81$$ \left( 0.80\right) $ $ 13.01$$ \left( 0.70\right) $ $ 1.94 $$ \left( 0.13\right) $ $ 46.80$$ \left( 2.47\right) $ $ 25.33$$ \left( 1.58\right) $ $ 25.92$$ \left( 1.42\right) $ $ 1.95$$ \left( 0.30\right) $
JPY/USD: Variance decomp.$ 18.62$$ \left( 0.33\right) $ $ 6.48$$ \left( 0.15\right) $ $ 3.70$$ \left( 0.11\right) $ $ 0.93$$ \left( 0.04\right) $ $ 14.47$$ \left( 0.46\right) $ $ 9.78$$ \left( 0.41\right) $ $ 6.12$$ \left( 0.31\right) $ $ 2.00$$ \left( 0.13\right) $
JPY/USD: Proportion$ 62.63$$ \left( 1.11\right) $ $ 21.80$$ \left( 0.50\right) $ $ 12.45$$ \left( 0.37\right) $ $ 3.13 $$ \left( 0.13\right) $ $ 44.70$$ \left( 0.29\right) $$ \left( 1.42\right) $ $ 30.21$$ \left( 1.27\right) $ $ 18.91$$ \left( 0.96\right) $ $ 6.18$$ \left( 0.40\right) $
JPY/EUR: Variance decomp.$ 7.84$$ \left( 0.16\right) $ $ 2.74$$ \left( 0.12\right) $ $ 7.94$$ \left( 0.19\right) $ $ 0.99$$ \left( 0.06\right) $ $ 7.72$ $ 3.32$$ \left( 0.20\right) $ $ 10.47$$ \left( 0.42\right) $ $ 1.30$$ \left( 0.11\right) $
JPY/EUR: Proportion$ 40.18$$ \left( 0.82\right) $ $ 14.04$$ \left( 0.61\right) $ $ 40.70$$ \left( 0.97\right) $ $ 5.07 $$ \left( 0.31\right) $ $ 33.84$$ \left( 1.27\right) $ $ 14.56$$ \left( 0.88\right) $ $ 45.90$$ \left( 1.84\right) $ $ 5.70$$ \left( 0.48\right) $

Figure 1: 50-Day moving averages of participation rates of algorithmic traders

Figure 1: There is 1 panel on figure 1, which is a line graph with 3 lines. The x-axis shows time, from January 2003 through the end of 2007. The y-axis shows the percent algorithmic participation, as a fraction of total trading volume. The graphs shows data for our 3 currency pairs, in 50-day moving averages of daily values. All begin near zero in late 2003 and rise gradually over time. JPY-EUR rises the fastest, to near 80% by late 2007. USD-EUR and JPY-USD rise to near 60% by late 2007.

Figure 2: 50-day Moving Averages of Participation Rates Broken Down into Four Maker-Taker Pairs

Figure 2: There are 3 panels on figure 2, each a line graph with 4 lines. The x-axis shows time, from January 2003 through the end of 2007. The y-axis shows the percent algorithmic participation for the four possible types of trades (HH, CC, HC, CH), each as a fraction of total trading volume. Data are 50-day moving averages of daily values. In the top two panels (EUR-USD and JPY-USD), HH trades declines from near 100% in late 2003 to about 40% by late 2007. CC trades rise slowly from zero to about 10%. HC and CH trades rise about evenly, from zero to about 20 percent each. The pattern is different for JPY-EUR, in the lower panel. There, HH trades decline from 100% in 2003 to near 20% in late 2007. HC trades rise from zero to about 40% by late 2007, while CH trades rise to about 20%. CC trades rise from zero to near 20%.

Figure 3: Dollar-Yen market on August 16, 2007

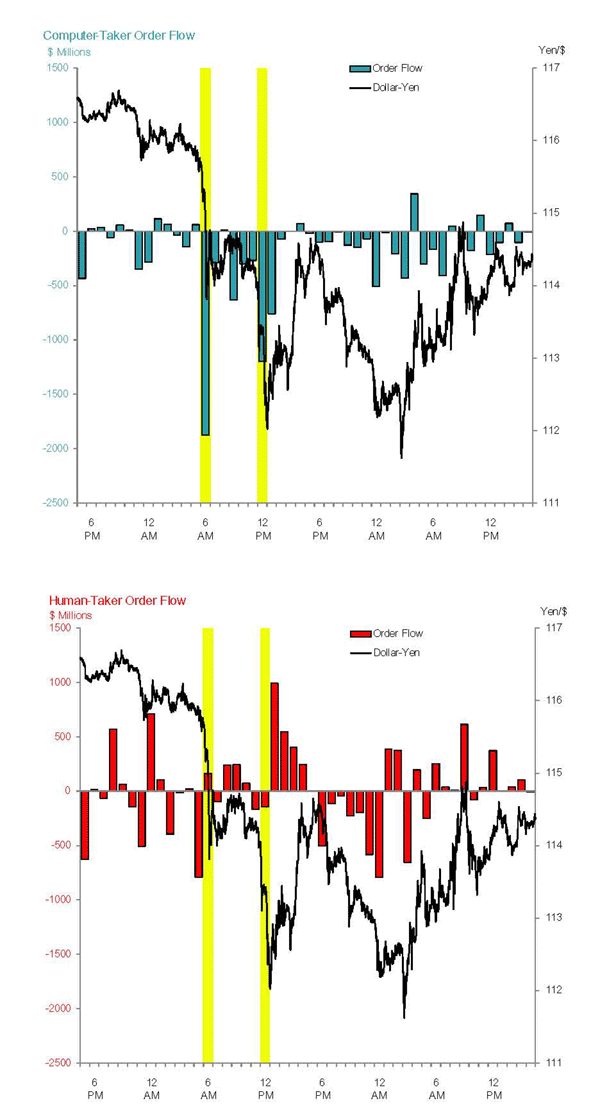
Figure 3: There are two panels on figure 3. In each panel, the x-axis shows time, hourly from 5 p.m. New York time on August 15, 2007 until 5 p.m. on August 17, 2007. On each panel, the y-axis shows order flow, in millions of dollars, computer-taker order flow in the top panel, human-taker order flow in the lower panel. Both panels show the dollar-yen exchange rate at a five-minute frequency, as a line. The top panel shows computer-taker order flow as bars, one per hour, the lower panel shows human-taker order flow as bars, one per hour. The top panel reveals that large appreciations of the yen, near 6 a.m. and 12 p.m., occur when computer-taker order flow is large and negative. In contrast, the lower panel shows that, at those times, human-taker order flow is near zero.

Figure 4: Volatility and Algorithmic Market Participation

Figure 4: There are three similar panels in Figure 4, one for each currency pair. In each, the x-axis shows months for 2006 and 2007, the y-axis on the left shows percent algorithmic participation, the left axis on the right shows annualized realized volatility expressed as a percent of the price. In each panel, algorithmic participation, shown as monthly bars, rises gradually over time. In each panel, realized volatility, shown monthly, declines slightly from the beginning of 2000 through mid 2007, and then generally rises until the end of 2007. The increase in volatility in late 2007 is smallest for euro-dollar.

*Daily realized volatility is based on 1-minute returns. We show monthly observations
**Share of algorithmic trading is at a monthly frequency

Figure 5: Deciles of Realized Volatility and AT Participation

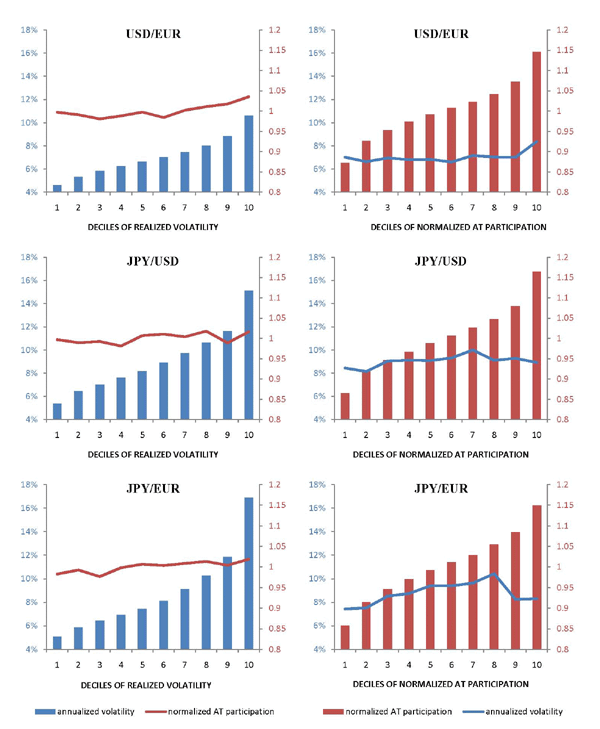
Figure 5: There are six panels in Figure 5, two for each currency pair. In all panels, the x-axis is indexed 1 through 10, showing deciles from one particular sort of the data, the left y-axis shows annualized realized volatility, expressed as a percent of the price, ranging from 4% to 18%, and the right axis shows normalized AT participation, ranging from 0.8 to 1.2. The three left panels, one for each currency pair, show, as bars, increasing deciles of realized volatility and, as lines, the corresponding normalized AT participation. The lines remain almost flat across the deciles, except for a slight increase for the highest deciles in euro-dollar. The three right panels, one for each currency pair, show, as bars, the increasing deciles of normalized AT participation and, as lines, the corresponding realized volatility. The lines generally remain flat across the deciles.

Footnotes

1.  Chaboud, Hjalmarsson, and Vega are with the Division of International Finance, Federal Reserve Board, Mail Stop 20, Washington, DC 20551, USA. Chiquoine is with the Investment Fund for Foundations, 97 Mount Auburn Street, Cambridge MA 02138, USA. Please address comments to the authors via e-mail at alain.p.chaboud@frb.gov, bchiquoine@tiff.org, erik.hjalmarsson@frb.gov and clara.vega@frb.gov. We are grateful to Terrence Hendershott and Albert Menkveld for their valuable insights, to EBS/ICAP for providing the data, and to Nicholas Klagge and James S. Hebden for their excellent research assistance. We also benefited from the comments of Gordon Bodnar, Charles Jones, Luis Marques, Dagfinn Rime, Alec Schmidt, John Schoen, Noah Stoffman, and of participants in the Spring 2009 Market Microstructure NBER conference, San Francisco AEA 2009 meetings, the SAIS International Economics Seminar, the SITE 2009 conference at Stanford, and the Barcelona EEA 2009 meetings. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

2.  See, for instance, " Rewarding Bad Actors," by Paul Krugman, New York Times, August 3, 2009, " High-Frequency Trading Grows, Shrouded in Secrecy," Time, August 5, 2009, and " Don't Set Speed Limits on Trading," by Arthur Levitt Jr., Wall Street Journal, August 18, 2009. Return to text

3.  We also note a paper by Hasbrouck (1996) on program trading, where he analyzes 3 months of data where program trades can be separately identified from other trades. He concludes that both types of orders have an approximately equivalent impact on prices. Algorithmic trading is not exactly equivalent to program trading, though it is a close cousin. In principle, a program trade could be generated by a trader's computer and then the trade conducted manually by a human trader. Our definition of AT refers to the direct interaction of a trader's computer with an electronic trading platform, that is the automated placement of a trade order on the platform.  Return to text

4.  For example, Chakravarty and Holden (1995), Kumar and Seppi (1994), Kaniel and Liu (2006), and Goettler, Parlour and Rajan (2007) allow informed investors to use both limit and market orders. Bloomfield, O'Hara and Saar (2005) argue that informed traders are natural liquidity providers, and Angel (1994) and Harris (1998) show that informed investors can optimally use limit orders when private information is sufficiently persistent. Return to text

5.  EBS has been part of the ICAP group since 2006. Return to text

6.  EBS uses the name " automated interface" (AI) to describe trading activity directly generated by a computer, activity we call AT. Return to text

7.  We do not use December 2007 in the sub-sample to avoid the influence of year-end effects.  Return to text

8.  The naming convention for " maker" and " taker" reflects the fact that the " maker" posts quotes before the " taker" chooses to trade at that price. Posting quotes is, of course, the traditional role of the market-" maker." Return to text

9.  There is a very high correlation in this market between trading volume per unit of time and the number of transactions per unit of time, and the ratio between the two does not vary much over our sample. Order flow measures based on amounts transacted and those based on number of trades are therefore very similar. Return to text

10.  Parlour and Seppi (2008) note that in a limit order book investors with active trading motives, some of which are " informed" traders, may choose to post limit orders that are more aggresive than those a disinterested liquidity provider would use but less aggresive than market orders. Return to text

11.  The data in Figures 1 and 2 are 50-day moving averages of daily values, highlighting the broad trends over time. Return to text

12.  See, for instance, " Algorithmic Trades Produce Snowball Effects on Volatility," Financial Times, December 5, 2008. Return to text

13.  EBS requires that new algorithmic traders on its system first test their algorithms in simulated conditions. EBS then routinely monitors the trading practices of its customers. A high number of excessively short-lived quotes (flashing) is discouraged, as is a very low ratio of trades to quotes. Return to text

14.  Stoffman (2007) uses a similar method to estimate how correlated individual investor strategies are compared to institutional investor strategies. Return to text

15.  With 498 daily observations, the first 9 deciles each include 50 observations, and the highest decile contains 48 observations. Return to text

16.  More precisely, we actually observe a time series of the number of EBS " deal codes" of each type over our sample period. Generally speaking, EBS assigns a deal code to each trading floor equipped with at least one of its terminals, and records whether they are equipped to trade algorithmically or not. These data are confidential. Return to text

17.  Regressions not reported here show that using the fraction of pure AT trading floors as a single instrument gives qualitatively similar results to those presented below based on both instruments. Using the fraction of the sum of both pure and dual AT trading floors as a single instrument also leads to the same qualititative conclusion, but with more signs of weak instruments. Return to text

18.  Using realized volatility based on five-minute returns leads to results that are very similar to those reported below for the one-minute returns, and the qualitative conclusions are identical. Return to text

19.  The same is true for the computer-taker fraction, not shown in the figure. Return to text

20.  One could consider macroeconomic news announcements as potential instruments for volatility. However, macroeconomic news announcements are exogeneous variables that cause both foreign exchange rate volatility and liquidity changes. Since we cannot assume that the effect macroeconomic news announcements have on liquidity is only due to the effect macroeconomic news announcements have on volatility, the exclusion restriction required by IV estimation is violated. Return to text

21.  Andersen and Bollerslev (1998), among others, refer to the nonfarm payroll report as the " king" of announcements, because of the significant sensitivity of most asset markets to its release. Return to text

22.  For simplicity, we label the 10 business days before and after the nonfarm payroll announcement as non-announcement days. However, during this 20-day period there are both days with no macroeconomic news and days with news. For instance, every Thursday, including the day before the monthly nonfarm payroll number is released, initial jobless claims are released. Thus, our estimation will likely be biased towards not finding statistically different behavior across the two periods. As we show in Table 5, volatility is, on average, much lower during this 20-day period than on nonfarm payroll days, and therefore the period still serves as a good benchmark.  Return to text

23.  Our list of U.S. macroeconomic news announcements is the same as the list of announcements in Andersen et al. (2007) and Pasquariello and Vega (2007) with the addition of three announcements: unemployment rate, core PPI and core CPI. Andersen et al. (2007) and Pasquariello and Vega (2007) use International Money Market Services (MMS) data on the expectations of U.S. macroeconomic fundamentals. In contrast, we use Bloomberg data because the MMS data are no longer available after 2003. Bloomberg provides survey data similar to those MMS previously provided. Return to text

24.  The variance decompositions are virtually identical in the short- and long-run and thus we only show the long-run decomposition results. Return to text

25.  In the Appendix, we analyze the robustness of this structural VAR by also estimating impulse responses and variance decompositions from all possible triangular identification schemes, only imposing that returns are ordered last in the VAR. Return to text

26.  Dynamic learning models with informed and uninformed investors predict that prices will temporarily over-react to uninformed order flow and under-react to informed order flow (e.g., Albuquerque and Miao, 2008). We note that the over- and under-reaction of prices to a particular type of order flow is different from the over- and under-reaction of prices to public news, which are both considered a sign of market inefficiency. Order flow types are not public knowledge, so that agents cannot trade on this information. Return to text

27.  For example, Chakravarty and Holden (1995), Kumar and Seppi (1994), Kaniel and Liu (2006), and Goettler, Parlour and Rajan (2007) allow informed investors to use both limit and market orders. Bloomfield, O'Hara and Saar (2005) argue that informed traders are natural liquidity providers and Angel (1994) and Harris (1998) show that informed investors can optimally use limit orders when private information is sufficiently persistent. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: November 3, 2009