The Federal Reserve Board eagle logo links to home page

Characteristic-Based Mean-Variance Portfolio Choice

Erik Hjalmarsson and Peter Manchev1

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

We study empirical mean-variance optimization when the portfolio weights are restricted to be direct functions of underlying stock characteristics such as value and momentum. The closed-form solution to the portfolio weights estimator shows that the portfolio problem in this case reduces to a mean-variance analysis of assets with returns given by single-characteristic strategies (e.g., momentum or value). In an empirical application to international stock return indexes, we show that the direct approach to estimating portfolio weights clearly beats a naive regression-based approach that models the conditional mean. However, a portfolio based on equal weights of the single-characteristic strategies performs about as well, and sometimes better, than the direct estimation approach, highlighting again the difficulties in beating the equal-weighted case in mean-variance analysis. The empirical results also highlight the potential for `stock-picking' in international indexes, using characteristics such as value and momentum, with the characteristic-based portfolios obtaining Sharpe ratios approximately three times larger than the world market.

Keywords: Mean-variance analysis, momentum strategies, portfolio choice, stock characteristics, value strategies

JEL classification: C22, C23, G11, G15

 

1   Introduction

The theoretical portfolio choice literature provides seemingly clear prescriptions for asset allocations, subject to preferences and return distributions. However, given the difficulties of estimating either conditional or unconditional moments of asset returns, the practical applicability of modern portfolio choice theory has typically been limited to simple and small-dimensional cases. Perhaps the strongest case in point is the difficulty of practically implementing the traditional mean-variance analysis of Markowitz (1952), where it is very challenging to obtain useful estimates of the variance-covariance matrix for any sizeable number of assets. Although the focus in the mean-variance literature has typically been on the difficulties in estimating the covariance matrix2, the vast empirical literature on the cross-section of stock returns also shows that conditional expected returns are likely to vary across stocks (e.g. Fama and French (1992, 1996, 1998)). Explicitly taking into account these cross-sectional differences in expected returns adds extra complexity to the problem.

In order to avoid the difficulties in estimating the conditional moments of the return distribution, some recent studies have suggested methods for directly estimating the portfolio weights, which are the ultimate object of interest (e.g. Brandt (1999), Aït-Sahalia and Brandt (2001), Brandt and Santa-Clara (2006), and Brandt et al. (Forthcoming)). Brandt et al. (BSCV, hereafter), in particular, study large-scale portfolio choice problems where asset returns are functions of individual stock characteristics such as value, momentum, and size. Assuming that the portfolio weights are (linear) functions of the portfolio characteristics, they show how the weights can be estimated for arbitrary utility functions. This leads to a tightly parameterized problem, where the parameter space only increases with the number of stock characteristics, rather than the number of assets.

This paper builds upon the idea of directly modeling portfolio weights. We first show how the weights in a mean-variance optimization problem can be directly estimated as functions of the underlying stock characteristics, such as value and momentum. The mean-variance formulation offers a closed-form solution to the portfolio weights estimator and thus permits a deeper understanding of the mechanics of the portfolio weights estimator. This is in contrast to BSCV, who work with general utility functions, rather than a mean-variance setup, and express their weight estimators as extremum estimators without closed-form solutions, which makes it harder to fully comprehend the properties of these estimators.

The closed-form solution shows how the direct parameterization of the weights reduces the original mean-variance problem with $ n$ assets to a much smaller $ k-$dimensional mean-variance problem, where $ k$ is the number of stock characteristics. Specifically, the direct estimator of the portfolio weights, expressed in terms of the stock characteristics, turns out to be the sample-efficient solution to a different, and much smaller, mean-variance problem where the new set of `assets' is made up of portfolios of the original assets with weights that are proportional to the (standardized) values of a given single stock characteristic (e.g. momentum). This is an interesting finding since the original motivation for parameterizing and directly estimating portfolio weights is to avoid the poor (out-of-sample) properties of sample-efficient solutions. However, by drastically reducing the dimension of the problem, the primary drawbacks of the sample-efficient mean-variance solution are avoided. By specifying a simple conditional CAPM framework for the returns process, we also compare the directly parameterized portfolio weights estimator to a naive weight estimator based solely on the conditional expected returns, and show that the former reduces to the latter if one imposes the assumption that the covariance matrix of the idiosyncratic innovations to returns is diagonal and homoskedastic.

We consider an empirical application to international stock index returns. In particular, we analyze the monthly returns on MSCI indexes for 18 developed markets, and use three different characteristics: the book-to-market value, the dividend-price ratio, and momentum. We focus on international index returns since the cross-section of these has been studied relatively less than for individual stock returns. In addition, it is interesting to see how powerful these methods of cross-sectional stock picking are when applied to a fairly small number of indexes rather than a vast number of individual stocks, where the scope for cross-sectional variation in the stock characteristics is obviously much greater.

The empirical analysis shows that the approach of directly parameterizing the portfolio weights as functions of the stock characteristics delivers clearly superior results compared to the simple baseline strategy, which only uses a prediction of the conditional mean in the portfolio choice. The portfolio with directly estimated weights also performs extremely well in absolute terms, delivering Sharpe ratios around one, which is almost three times greater than that of the market portfolio, and with a world CAPM beta that is indistinguishable from zero. These results hold in out-of-sample exercises, and the in-sample and out-of-sample results are, in fact, very close. There is thus ample scope for characteristic-based `stock-picking' in international return indexes, even though the cross-section is only made up of 18 assets.

Since the direct parameterization of the weights reduces the portfolio problem to a mean-variance analysis of single-characteristic strategies (e.g. pure value and momentum portfolios), the equal-weighted portfolio of these single-characteristic strategies provides another natural comparison to the directly-estimated portfolio. Our empirical analysis shows that the results for the portfolio with directly-estimated weights are very close to those of this equal-weighted portfolio. This finding appears to partly reflect the fact that the optimal weights on these single-characteristic portfolios are sometimes close to the equal-weighted case, but also partly the fact that it is difficult, even in small-dimensional settings, to beat the equal-weighted portfolio. This result also relates to recent work by Asness et al. (2009), who show the benefits of combining momentum and value strategies in a simple equal-weighted manner; as seen in the current paper, the optimal combination is, in fact, very close to the equal-weighted one.

The rest of the paper is organized as follows. Section 2 outlines the basic CAPM framework in which the portfolio choice estimators are analyzed, and derives the direct estimator of the portfolio weights. Section 3 presents the empirical results, and Section 4 concludes.

2   Modeling framework

In this section, we specify the returns process and detail the specification and estimation of the investor's portfolio choice problem. The direct estimation of portfolio weights, based on stock characteristics, avoids the need to explicitly model the returns process. However, an explicit returns specification allows for the derivation of the theoretically optimal portfolio weights, and hence a better understanding of the functioning and (dis-) advantages of the empirical portfolio weight estimators. In addition, the returns equation will form the basis for a naive `plug-in' regression-based approach to portfolio choice, which will serve as a useful comparison to the directly estimated strategies. The returns specification is kept deliberately simple in order to facilitate the subsequent analytics; the purpose of the paper is not to validate this model, but rather, use it as a basic framework for understanding and motivating our estimation procedures.

2.1   The returns generating process

It is assumed that the returns satisfy a conditional CAPM model, which, given the subsequent empirical application, will be interpreted as an international world CAPM. Let $ r_{i,t+1},$ $ i=1,...,n$, $ t=1,...,T$, be the excess returns on asset, or country index, $ i$, from period $ t$ to $ t+1,$ and let $ x_{i,t}$ be the corresponding $ k\times1$ vector of predictor variables, such as value and momentum. The (world) market excess returns are denoted $ r_{t+1}^{m}$ and the individual excess returns $ r_{i,t+1}$ are assumed to satisfy,

$\displaystyle r_{i,t+1}=\beta_{i}r_{t+1}^{m}+\theta^{\prime}x_{i,t}+u_{i,t+1}.$ (1)

That is, the returns on asset $ i$ are a function of both the contemporaneous market factor and the lagged predictor variable $ x_{i,t}$. Thus, $ \beta_{i}$ represents the CAPM beta for asset $ i$, after controlling for the idiosyncratic predictability in the returns. The innovations $ u_{i,t}$ are assumed to be $ iid$ and normally distributed with mean zero and variance-covariance matrix $ \Sigma$. Throughout the study, we will focus on the case where $ x_{i,t}$ is mean zero in the cross-section, and thus represents deviations from a cross-sectional mean.

This returns specification captures the stylized facts that the market-based CAPM model will explain a significant proportion of the cross-section of expected stock-returns, and that conditioning variables such as value and momentum have cross-sectional predictive power for future returns. For the data used in the current paper, country-by-country estimates of the unconditional version of the CAPM (see Table 1), with $ x_{i,t}$ excluded but with intercepts included, show that the individual intercepts in these regressions tend not to be statistically significantly different from zero, and that the $ R^{2}$ of the regressions typically range from 30 to 50 percent, providing some validation of the CAPM model.

A common slope coefficient $ \theta$, across all $ i$, for the predictive part of the model is imposed. Although this may be hard to defend from a theoretical view point, from a modeling parsimony aspect it is quite natural and frequently done (see Hjalmarsson (Forthcoming) for an extensive discussion on this pooling assumption). Equation (1) is estimated by pooling the data across $ i$ and using least squares.

In the subsequent analysis, it will be useful to write the returns model in matrix form, as follows,

$\displaystyle \mathbf{r}_{t+1}=\mathbf{\beta}r_{t+1}^{m}+\mathbf{x}_{t}\theta+\mathbf{u} _{t+1},$ (2)

where $ \mathbf{r}_{t+1}$ is the $ n\times1$ vector of country returns at time $ t$, $ \mathbf{\beta}$ is the $ n\times1$ vector of CAPM betas, and $ \mathbf{x}_{t}$ is the $ n\times k$ matrix of asset characteristics. The expected returns, conditional on $ \mathbf{x}_{t}$, at time $ t$ are thus

$\displaystyle \mathbf{\mu}_{t}=\mathbf{\beta}E_{t}\left[ r_{t+1}^{m}\right] +\mathbf{x} _{t}\theta\mathbf{.}$ (3)

2.2   Portfolio choice

2.2.1   The investor's problem and the benchmark portfolio weights

We consider a mean-variance investor who pursues zero-cost strategies. The zero-cost restriction is imposed because it is natural to think of the return characteristics as deviations from a cross-sectional average, where an above (below) average ranking indicates an above (below) average expected return. In addition, it will also be assumed that the portfolios are market neutral in the sense that $ \mathbf{\omega}^{\prime}\mathbf{\beta}=0$, where $ \mathbf{\omega}$ is the $ n\times1$ vector of portfolio weights. This restriction is imposed in order to eliminate the effects of the expected market returns, $ E_{t}\left[ r_{t+1}^{m}\right] $, in the portfolio choice, and thus avoid explicitly modeling this conditional mean. Since the CAPM betas are all fairly similar, as seen in the application below, we will not attempt to actually enforce this constraint in the empirical portfolios, but take it as given. That is, it is assumed that the zero-cost constraint $ \mathbf{\omega }^{\prime}\mathbf{1}=0$, where $ \mathbf{1}$ is an $ n\times1$ vector of ones, implies that the market-neutral constraint $ \mathbf{\omega}^{\prime }\mathbf{\beta}=0$ is satisfied. This would obviously hold if $ \beta_{i} \equiv\beta$ for all $ i$, but will also be approximately satisfied in most situations where the $ \beta_{i}s$ do not exhibit too much cross-sectional variation.3

Thus, the mean-variance investor maximizes expected utility according to

$\displaystyle \max_{\omega_{t}}\mathbf{\omega}_{t}^{\prime}\mathbf{\mu}_{t}-\frac{\gamma} {2}\mathbf{\omega}_{t}^{\prime}\mathbf{\Sigma\omega}_{t},$ s.t. $\displaystyle \mathbf{\omega}_{t}^{\prime}\mathbf{1}=0$, (4)

where $ \gamma$ can be interpreted as the coefficient of relative risk aversion and $ \mathbf{\omega}_{t}\mathbf{=}\left( \omega_{1,t},...,\omega _{n,t}\right) $ are the portfolio weights. The solution to the investor's problem, assuming that $ \beta_{i}\equiv\beta$, follows from straightforward calculations and is given by

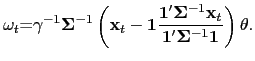
$\displaystyle \mathbf{\mathbf{\omega}}_{t}\mathbf{=}\gamma^{-1}\mathbf{\mathbf{\Sigma}} ^{-1}\left( \mathbf{x}_{t}-\mathbf{\mathbf{1}}\frac{\mathbf{1}^{\prime }\mathbf{\mathbf{\Sigma}}^{-1}\mathbf{x}_{t}}{\mathbf{1}^{\prime }\mathbf{\mathbf{\Sigma}}^{-1}\mathbf{\mathbf{1}}}\right) \theta.$ (5)

In the special case that $ \mathbf{\mathbf{\Sigma=}}\sigma^{2}I$, and provided that $ \mathbf{\mathbf{x}}_{t}$ is cross-sectionally demeaned (i.e., $ \mathbf{1}^{\prime}\mathbf{x}_{t}=0$), the weights simplify to

$\displaystyle \mathbf{\mathbf{\omega}}_{t}\mathbf{\mathbf{=}}\gamma^{-1}\sigma ^{-2}\mathbf{x}_{t}\theta.$ (6)

Equation (6) thus provides the solution to the investor's problem when only the mean aspects of the returns are taken into account and the covariance structure is completely ignored. Estimating equation (1) gives an estimate of $ \theta$ and the pooled sample standard deviation of the residuals from equation (1) provides an estimate of $ \sigma$. Given the difficulties of estimating large scale covariance matrices, we restrict our empirical attention to this special case with $ \Sigma=\sigma^{2}I$, and the weights $ \mathbf{\mathbf{\hat{\omega}}}_{t}\mathbf{\mathbf{=}}\gamma ^{-1}\hat{\sigma}^{-2}\mathbf{x}_{t}\hat{\theta}$ will serve as the benchmark strategy against which the direct estimation approach, described below, is compared.

2.2.2   Direct estimation of the portfolio weights

As shown above, in the special case with $ \Sigma=\sigma^{2}I$, and assuming that $ \mathbf{x}_{t}$ is cross-sectionally demeaned, the portfolio weights, up to a multiplicative constant, are given by $ \mathbf{x}_{t}\theta$. In the spirit of BSCV, we can therefore consider a procedure that directly estimates the weights, or rather estimates $ \theta$, from a portfolio choice perspective, rather than a pure return predictability perspective. That is, consider the following sample analogue of the investor's problem:

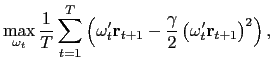
$\displaystyle \max_{\omega_{t}}\frac{1}{T}\sum_{t=1}^{T}\left( \mathbf{\omega}_{t}^{\prime }\mathbf{r}_{t+1}-\frac{\gamma}{2}\left( \mathbf{\omega}_{t}^{\prime }\mathbf{r}_{t+1}\right) ^{2}\right) ,$ (7)

Substitute in the weights $ \mathbf{\mathbf{\omega}}_{t}=\mathbf{x}_{t}\theta$, and we get the following estimation problem,

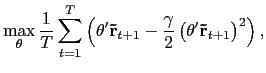
$\displaystyle \max_{\theta}\frac{1}{T}\sum_{t=1}^{T}\left( \theta^{\prime}\mathbf{\tilde {r}}_{t+1}-\frac{\gamma}{2}\left( \theta^{\prime}\mathbf{\tilde{r}} _{t+1}\right) ^{2}\right) ,$ (8)

where $ \mathbf{\tilde{r}}_{t+1}\equiv\mathbf{x}_{t}^{\prime}\mathbf{r}_{t+1}$ . The first order conditions are given by

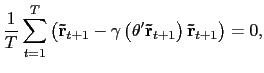
$\displaystyle \frac{1}{T}\sum_{t=1}^{T}\left( \mathbf{\tilde{r}}_{t+1}-\gamma\left( \theta^{\prime}\mathbf{\tilde{r}}_{t+1}\right) \mathbf{\tilde{r}} _{t+1}\right) =0,$ (9)

and the estimator of $ \theta$ is given by,

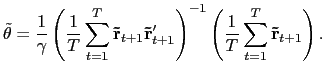
$\displaystyle \tilde{\theta}=\frac{1}{\gamma}\left( \frac{1}{T}\sum_{t=1}^{T} \mathbf{\tilde{r}}_{t+1}\mathbf{\tilde{r}}_{t+1}^{\prime}\right) ^{-1}\left( \frac{1}{T}\sum_{t=1}^{T}\mathbf{\tilde{r}}_{t+1}\right) .$ (10)

Several features of $ \tilde{\theta}$ are worth pointing out. First, $ \tilde{\theta}$ is proportional to the OLS regression coefficient in a regression of ones on $ \mathbf{\tilde{r}}_{t}$ and the variance-covariance matrix of $ \tilde{\theta}$ is therefore given by the standard formula for OLS regressions (see also Britten-Jones (1999)).4 $ ^{\text{,}}$5 Second, note that within the framework of the current simple conditional CAPM, the optimal weights are generally proportional to $ \mathbf{\mathbf{\Sigma}}^{-1}\left( \mathbf{x} _{t}-\mathbf{\mathbf{1}}\frac{\mathbf{1}^{\prime}\mathbf{\mathbf{\Sigma}} ^{-1}\mathbf{x}_{t}}{\mathbf{1}^{\prime}\mathbf{\mathbf{\Sigma}} ^{-1}\mathbf{\mathbf{1}}}\right) \theta$ , rather than $ \mathbf{x}_{t}\theta$. Thus, by restricting the weights to be proportional to $ \mathbf{x}_{t}\theta$, the optimal weights will in general not lie in the range of the weights obtained via $ \tilde{\theta}$. That is, even though the above procedure for choosing the weights should dominate the naive regression-based approach, it will in general not be able to recover the theoretically optimal weights.

Further, and most interestingly, from the above derivations and the results in Britten-Jones (1999) it follows that the estimator $ \tilde{\theta}$ is proportional to the sample mean-variance efficient portfolio weights for the $ k$ assets with return vector $ \mathbf{\tilde{r}}_{t+1}$. This makes good intuitive sense. The estimated weights are equal to $ \mathbf{\mathbf{\tilde {\omega}}}_{t}\mathbf{\mathbf{=}x}_{t}\tilde{\theta}=\tilde{\theta} _{1}\mathbf{x}_{t,1}+...+\tilde{\theta}_{k}\mathbf{x}_{t,k}$ , with weight $ i$ given by $ \tilde{\omega}_{t,i}=\tilde{\theta}_{1}x_{i,t,1}+...+\tilde{\theta }_{k}x_{i,t,k}$ . The return on this portfolio is $ \mathbf{\tilde{\omega}} _{t}^{\prime}\mathbf{r}_{t+1}\mathbf{=}\tilde{\theta}_{1}\mathbf{x} _{t,1}^{\prime}\mathbf{r}_{t+1}+...+\tilde{\theta}_{k}\mathbf{x}_{t,k} ^{\prime}\mathbf{r}_{t+1}\mathbf{=}\tilde{\theta}_{1}\tilde{r}_{t+1,1} +...+\tilde{\theta}_{k}\tilde{r}_{t+1,k}$ , and the components of $ \tilde{\theta}$ thus provide the portfolio weights on the `assets' in the vector $ \mathbf{\tilde{r}}_{t}$. Thus, by forcing the estimated weights to be of the form $ \mathbf{x}_{t}\theta$, and directly solving for the optimal value of $ \theta$, the general mean-variance problem described by equation (4) is reduced to the problem of finding the sample efficient solution for the assets with returns $ \mathbf{\tilde{r}}_{t+1}=\left( \tilde {r}_{t+1,1},...,\tilde{r}_{t+1,k}\right) $ , where asset $ j=1,...,k$ represents a portfolio of the underlying assets with weights given by the characteristic $ \mathbf{x}_{j,t}$.

It is also interesting to compare $ \tilde{\theta}$ to the regression-based estimate $ \hat{\theta}$. Assuming that $ \beta_{i}=\beta$ for all $ i$, the pooled OLS estimate of $ \theta$ in equation (1) is given by

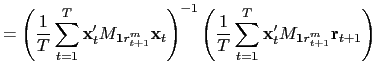
$\displaystyle \hat{\theta}$ $\displaystyle =\left( \frac{1}{T}\sum_{t=1}^{T}\mathbf{x}_{t}^{\prime }M_{\mathbf{1}r_{t+1}^{m}}\mathbf{x}_{t}\right) ^{-1}\left( \frac{1}{T} \sum_{t=1}^{T}\mathbf{x}_{t}^{\prime}M_{\mathbf{1}r_{t+1}^{m}}\mathbf{r} _{t+1}\right)$ (11)
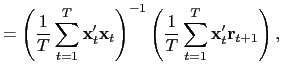
  $\displaystyle =\left( \frac{1}{T}\sum_{t=1}^{T}\mathbf{x}_{t}^{\prime}\mathbf{x} _{t}\right) ^{-1}\left( \frac{1}{T}\sum_{t=1}^{T}\mathbf{x}_{t}^{\prime }\mathbf{r}_{t+1}\right) ,$ (12)

where

$\displaystyle \mathbf{x}_{t}^{\prime}M_{\mathbf{1}r_{t+1}^{m}}=\mathbf{x}_{t}^{\prime }\left( I_{n}-\left( \mathbf{1}r_{t+1}^{m}\right) \left( \left( \mathbf{1}r_{t+1}^{m}\right) ^{\prime}\left( \mathbf{1}r_{t+1}^{m}\right) \right) \left( \mathbf{1}r_{t+1}^{m}\right) ^{\prime}\right) =\mathbf{x}_{t}^{\prime},$ (13)

provided that $ \mathbf{x}_{t}$ is cross-sectionally demeaned. That is, if one imposes a common beta, and $ \mathbf{x}_{t}$ is cross-sectionally demeaned, the effects of the market factor disappear. Write the estimator $ \tilde{\theta}$ as,

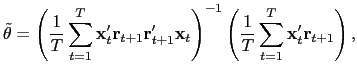
$\displaystyle \tilde{\theta}=\left( \frac{1}{T}\sum_{t=1}^{T}\mathbf{x}_{t}^{\prime }\mathbf{r}_{t+1}\mathbf{r}_{t+1}^{\prime}\mathbf{x}_{t}\right) ^{-1}\left( \frac{1}{T}\sum_{t=1}^{T}\mathbf{x}_{t}^{\prime}\mathbf{r}_{t+1}\right) ,$ (14)

and it is easy to see that $ \hat{\theta}$, up to a constant of scale, is a special case of $ \tilde{\theta}$ where one has imposed the assumption that the returns $ \mathbf{r}_{t+1}$ are homoskedastic with a diagonal covariance matrix and independent of $ \mathbf{x}_{t}$. The regression-based estimate $ \hat{\theta}$ therefore only takes into account the covariance structure in $ \mathbf{x}_{t}$, but ignores the one in $ \mathbf{r}_{t+1}$.

These derivations shed some additional light on the work by BSCV, by explicitly deriving the closed form solutions for the directly estimated weights. BSCV, who work with general utility functions rather than a mean-variance setup, express their weight estimators as extremum estimators without closed-form solutions, which makes it harder to fully comprehend the properties of these estimators. In particular, the formulas above, which obviously are restricted to the mean-variance case, highlight the fact that by adopting the approach of parameterizing the weights as (linear) functions of the stock characteristics, the portfolio problem is reduced to a mean-variance analysis of assets with returns given by the single-characteristic strategies. This result also highlights the possibility for further improving upon the approach by using techniques developed for making mean-variance analysis both more robust or more flexible, such as estimating the covariance matrix (i.e., the denominator in $ \tilde{\theta}$) using a shrinkage estimator, or allowing for time-variation in the covariance matrix by fitting, for instance, a multivariate GARCH model. With the availability of high-frequency data, and the low dimension of the problem, one might also consider using realized covariance matrices that allow for more timely estimates of the variance-covariance structure of the relevant returns. In the current study, we do not pursue these extensions, however, but find that also in the basic setup the procedure tends to work very well.

3   Empirical results for international portfolio choice

3.1  Data and preliminary results

3.1.1   Data description

The data are obtained from the MSCI database and consist of total returns for stock market indexes in 18 developed markets. In addition, the MSCI world index is used as a proxy for the world market return.6 The data are on a monthly frequency and span the period December 1974 through December 2008. All returns are expressed in U.S. dollars as excess returns over the 1-month U.S. T-bill rate. In order to form the initial parameter estimates, the earliest starting date for measuring portfolio performance is January 1980, and portfolio results for the periods 1980-2008 and 1999-2008 are provided, where the latter period is used to evaluate the more recent performance of the strategies over the last ten years.

Three separate characteristics are considered: the book-to-market value (BM), the dividend-price ratio (DP), and the cumulative returns over the past $ t-12$ to $ t-1$ months (MOM). The first two variables obviously represent measures of value and the last one is a measure of momentum, or auto-correlation, in returns. For individual stocks, momentum is often captured by the cumulative returns over the past $ t-12$ to $ t-2$ months, excluding the most recent month's return, since short-term return reversals in individual stocks are recorded at the monthly level (e.g. Lo and MacKinlay (1990), Jegadeesh (1990), and Jegadeesh and Titman (1995)). Since there are no such return reversals evident in index returns (e.g. Patro and Wu (2004)), we use the above definition of momentum.

The list of countries is shown in Table 1, along with country-by-country OLS estimates from an unconditional world CAPM model, where the individual country (excess) returns are regressed on the world market index. As is seen, the CAPM betas are all fairly similar and none of the intercepts are statistically significantly different from zero at the five percent level. The basic assumptions underlying the model of the paper thus seem to be reasonably satisfied. It should be stressed again, however, that equation (1) merely serves as a simple framework for the analysis of characteristic-based portfolio policies; the aim of the paper is not to examine whether equation (1) is, in fact, an adequate representation of international stock returns.

For each cross-section, i.e., each time-period $ t$, the characteristics are demeaned and rank-standardized. In particular, at each time $ t$, the cross-section of each stock characteristic takes on equidistant values between -1 and 1, where, for instance, the standardized characteristic for the stock with the lowest book-to-market value is assigned -1 and the stock with highest value +1. The cross-section demeaning is performed since we are interested in ranking stocks in the cross-section, rather than in the time-series, and the zero-cost strategies naturally leads to this demeaning in any case. The rank-standardization is performed to avoid outliers leading to large positions in single assets; Asness et al. (2009) pursue a similar approach.

3.1.2   Single-characteristic portfolios

As pointed out previously in the paper, the portfolio strategies analyzed here can be thought of as weighted combinations of simple strategies that use portfolio weights identical to the values of a given single standardized characteristic. That is, these simple strategies represent, for instance, the pure value strategy using the standardized values of the book-to-market variable as portfolio weights in each period. Although the primary interest of the current study is on the optimal combination of such simple portfolios, it is nevertheless interesting to first study the return characteristics of these underlying building blocks for the composite strategies. Since there are no parameters to estimate in order to implement these strategies, the results are comparable to the out-of-sample results for the combined strategies below. In order to set the scale for these zero-cost strategies, it is simply assumed that one dollar is allocated to the short part of the portfolio and one dollar to the long part; the rank-standardization leads to a permutation of the same values for the characteristics in each cross-section, so this merely sets the scale of the portfolio and does not lead to any `timing' of the portfolio.

Table 2 shows the statistics for the single-characteristic strategies for the full examination period 1980-2008, as well as for the more recent 1999-2008 sub-sample, along with the statistics for the world market portfolio. Starting with the results for the 1980-2008 sample, it appears that all three characteristics, momentum, book-to-market value, and the dividend-price ratio, contain information on the cross-section of expected returns. The long-short portfolios based on these characteristics all deliver returns that are virtually uncorrelated with the world market (the world CAPM beta is never significant) and with positive CAPM alphas that are all statistically significant at the 10 percent level. However, only the portfolio strategy based on momentum delivers a Sharpe ratio that is markedly greater (0.60) than that of the world market portfolio (0.35). The Sharpe ratio for the book-to-market strategy is somewhat smaller (0.31) than the market's and the Sharpe ratio for the dividend-price ratio strategy is virtually identical to the market's (0.36). Apart from the leptokurtosis in momentum, the characteristic-based portfolios have less left-skewness and thinner tails than the market. The bottom rows of Panel A also show the correlation between the returns on the various strategies. As might be expected, momentum is fairly strongly negatively correlated with the two value measures, which are positively correlated with each other.

In the more recent sub-sample from 1999-2008, which spans a very difficult time period for stock investments, the market portfolio delivered an average negative return of about two percent. The momentum and dividend-price ratio strategies both resulted in Sharpe ratios of around 0.2, and only the book-to-market strategy delivered a somewhat sizeable Sharpe ratio of about 0.5.

3.2   Empirical results

3.2.1   Empirical implementation

We analyze the empirical performance of the zero-cost characteristic-based strategies outlined previously in the paper. That is, if $ \mathbf{x} _{t}=\left[ \mathbf{x}_{1t}\text{ }\cdots\text{ }\mathbf{x}_{kt}\right] $ denote the $ n\times k$ matrix of standardized stock characteristics at time $ t$, the portfolio weights $ \mathbf{\omega}_{t}$ are proportional to $ \mathbf{x}_{t}\theta$, for some $ \theta$. In particular, we consider three different `estimates' of the parameter $ \theta$: (i) the regression-based estimate, denoted $ \hat{\theta}$, which is obtained from the estimation of equation (1) and effectively ignores the covariance structure of the returns and focuses only on the conditional mean; (ii) the estimate of $ \theta$ resulting from the direct estimation of the weights in equation (10), denoted $ \tilde{\theta}$, which solves the sample analogue of the investor's problem subject to the restriction of a portfolio policy linear in the characteristics; and (iii) a scheme that sets all components in $ \theta$ equal, which can be seen as a portfolio strategy that takes equal positions in each of the single-characteristic portfolios. The equal weighted scheme thus provides a benchmark for the two data driven approaches and can be seen as an analogue to the usual equal-weighted portfolio that is typically used to evaluate the success of mean-variance analysis (e.g., DeMiguel, Garlappi, and Uppal (2007)).

For the regression-based $ \hat{\theta}$, the final weights are given by $ \mathbf{\omega}_{t}=\gamma^{-1}\hat{\sigma}^{-2}\mathbf{x}_{t}\hat{\theta}$ , where $ \hat{\sigma}$ is the pooled sample standard deviation of the residuals from the regression equation (1), and $ \gamma$ is formally the coefficient of relative risk aversion. For the directly-estimated $ \tilde{\theta}$, $ \gamma$ is already part of the estimator and the weights are simply given by $ \mathbf{\omega}_{t}=\mathbf{x}_{t}\tilde{\theta}$. In order to fix the scale in the equal-weighted portfolio, we set each of the individual components of $ \theta$ equal to the average of the components of $ \tilde{\theta}$ in the full-sample estimate. Since this merely sets the scale of the weights, using the full-sample estimate does not lead to any look-ahead bias in the portfolio evaluation, but provides results that are easy to compare.

Changing $ \gamma$ merely scales up or down the mean and volatility of the returns on the portfolio, but leaves the Sharpe ratio unaffected. For the purposes here, choosing $ \gamma$ is therefore primarily a matter of choosing a convenient scale in which to express the results. We set $ \gamma=5$, which is in line with many previous studies.

Given that the portfolio weights can be scaled up or down arbitrarily (as long as the scaling constant is identical in all periods), it is the relative size of the components in $ \theta$ that is of primary interest. In the result tables, we therefore report estimates of $ \theta$ that have been standardized such that the sum of the components in $ \theta$ add up to unity. Each component of $ \theta$ can therefore be interpreted as the relative weight given to the corresponding stock characteristic.

We present both `in-sample' and `out-of-sample' results for the portfolio strategies. That is, the estimates of $ \theta$ used to calculate the portfolio weights are either obtained using the full sample or are recursively updated using only information available at the time of the portfolio formation. From a practical portfolio management perspective, the latter approach is clearly the relevant one, but comparison with the in-sample results show how much the performance of the portfolio strategies deteriorates due to poor estimates in a real-time setting. In order to form the initial estimates of $ \theta$, the earliest starting date for measuring portfolio performance is January 1980.

We consider two different combinations of characteristics: (i) momentum and book-to-market value, and (ii) momentum, book-to-market value, and the dividend-price ratio. In general, book-to-market is considered a better measure of value than the dividend-price ratio (although this is only weakly supported by the results in Table 2), and the combination with both value measures included can be seen as a test of whether the dividend-price ratio contributes any extra information over and above that of the book-to-market value.

BSCV provide an in-depth analysis of transaction costs in their related setup and show that their portfolio results and conclusions remain fairly unchanged when transaction costs are taken into account. Since there is little reason to believe that these findings would not apply to the current analysis as well, we keep the empirical application simple and omit the effects of transaction costs.

3.2.2   Portfolio results

Table 3 shows the results for the multi-characteristic portfolio choice strategies, for the full 1980-2008 period (Panel A), and the recent 1999-2008 sub-sample (Panel B). Summary statistics for the portfolio returns for the different combinations of characteristics and estimation approaches are shown, for both out-of-sample and in-sample exercises. In addition, the estimates of the parameters determining the portfolio choices are also provided. The out-of-sample results are formed by using parameter estimates for the portfolio choice that are recursively updated, based on all available data up till that period. In the tables, the average estimates over the evaluation period are shown. The `in-sample' estimates that are shown, and used to form the in-sample portfolios, are defined as follows. For the 1980-2008 evaluation period (Panel A), the in-sample estimates are obtained from using the entire data set from 1974-2008. For the 1999-2008 sub-sample (Panel B), the in-sample estimates represent the estimates using data only from the actual portfolio formation period; i.e. from 1999 to 2008. We adopt this approach to make the most use of the data in the long sample and to investigate whether the parameters have changed much over time by using a shorter in-sample period in the recent sub-sample. $ t-$statistics for the full-sample estimates are shown in parentheses below the point estimates.

Starting with the full 1980-2008 sample in Table 3, Panel A, several interesting results stand out. First, during this sample period, the multi-characteristic portfolios always outperform the single-characteristic portfolios, regardless of the way the weights are obtained; the virtues of diversification are thus clearly present also in zero-cost characteristic-based portfolios. This is true both for the out-of-sample and in-sample exercises. In general, the Sharpe ratios are upwards of one in value, which is almost three times the market Sharpe ratio. Second, the portfolios based on the direct-weight-estimation approach (denoted Dir. in the tables) substantially outperform the portfolios using naive regression-based weights (denoted Reg.), with Sharpe ratios that are about 25 percent larger. Third, the equal-weighted portfolios (denoted EW) always perform better than the regression-based ones in terms of Sharpe ratios, and very similarly to the portfolios with directly estimated weights. One interpretation is thus that even with as few as two or three effective assets over which to choose, it is difficult to beat an equal weighted portfolio in a mean-variance setup. This need not only be due to poor estimates of the variance-covariance matrix and mean parameters as such, which is typically the case in large-scale mean-variance analysis, but likely also reflects changes over time in these parameters. However, the strong performance of the equal-weighted portfolio also partly reflects the fact that, at least in the portfolios based on just momentum and book-to-market value, the equal-weighting scheme is in fact very close to the optimal in-sample scheme. This result also helps explain the strong findings by Asness et al. (2009), who explicitly analyze the benefits of combining momentum and value portfolios and always consider the equal-weighted case. As seen here, the equal weighting is, in fact, very close to the in-sample optimal weights.

In terms of higher moments, the equal-weigthed portfolios have the thinnest tails, and the regression-based ones by far the heaviest. The regression-based weights also lead to more left-skewness than the two other approaches. Further, for all strategies the CAPM betas are very close to zero in absolute value and none of the $ t-$statistics are significant, whereas the CAPM alphas are all highly statistically significant. Finally, the in-sample and out-of-sample results are very similar for the direct-estimation approach, highlighting the robustness of the method. The regression-based approach does surprisingly well in-sample, suggesting that part of the gains from the direct-estimation approach are due to stable estimates over time. This is confirmed by Figure 1, which shows the recursive estimates of $ \theta$, from both the regression-based approach and the direct-estimation approach. The estimates are standardized to add up to one in each period, and it is clear that the directly-estimated parameters remain much more stable over the sample period than the regression-based ones.

The estimates of the parameters governing the portfolio choice are also of interest and reveal the differences between the regression-based and direct-optimization approaches. The regression-based weights always put a very large weight on momentum (around 60 to 70 percent), which is the strategy that delivers by far the highest mean in Panel A, Table 2, and subsequently smaller weights on the other characteristic(s). This is not surprising since the regression weights effectively only take into account the expected returns. The direct-optimization weights, on the other hand, put a much larger weight on the valuation characteristics, since the returns on the portfolios formed on the book-to-market or the dividend-price ratio are negatively correlated with the momentum returns and thus reduce the variance in the combined portfolio. As seen from the full-sample weight estimates, the characteristics typically enter with statistically significant coefficients into the portfolio choice. The only exception is the dividend-price ratio in the regression-based three-characteristic portfolio; all other estimates are significant at the 10 percent level, and the momentum and book-to-market value are always highly significant. Although the dividend-price ratio shows up as statistically significant in the directly-estimated portfolio weights, its impact on the performance characteristics is slightly negative out-of-sample. Adding the dividend-price ratio to the equal-weighted portfolio does reduce the kurtosis and increase the right-skewness somewhat, without much effect on the Sharpe ratio.

Panel B of Table 3 reports the portfolio results for the most recent 10-year episode from 1999 to 2008, which covers both the extremely tumultuous times in international stock markets due to the recent credit crisis as well as the sharp decline in stock markets at the start of the millennium. Qualitatively, the results are very similar to those for the full sample, with the direct-optimization approach clearly outperforming the regression-based approach in terms of Sharpe ratios. The overall performances of all the strategies are much weaker than in the full sample, reflecting the weak results seen in Table 2 for the single-characteristic strategies. Compared to the performance of the market index, however, the characteristic-based strategies perform very well: The equal-weighted strategy in all three characteristics delivers an annual mean return of 11% with a 16% annual volatility, whereas the market returned an average of -2% during the same period with a similar volatility.

The out-of-sample and in-sample results are again fairly similar for the directly-estimated weights, which is somewhat striking given that the in-sample results only use data from 1999-2008, whereas the out-of-sample results use data recursively all the way back to 1974. Given the short sample period, it is not surprising that many of the estimated parameters are not statistically significant. The equal weighted portfolio again performs very well and, in fact, dominates the directly estimated portfolio strategy along all dimensions in the out-of-sample results. During this sample period, adding the dividend-price ratio to the portfolios also substantially reduces the kurtosis, while marginally increasing the Sharpe ratio.

4    Conclusion

We study the empirical implementation of mean-variance portfolio choice when the distribution of the cross-section of returns can, at least partially, be described by characteristics such as value and momentum. Following the work of Brandt et al. (Forthcoming), we analyze a method that directly parameterizes the portfolio weights as a function of these underlying characteristics. In the mean-variance case, this allows for a closed form solution of the parameters governing the portfolio choice, which provides for additional insights into the mechanics of this approach for obtaining portfolio weights. In particular, it turns out that the direct estimator of the portfolio weights is the sample-efficient solution to the mean-variance problem where the set of assets is made up of portfolios based on individual stock characteristics, which is typically of a much smaller dimension.

In an empirical application, we study long-short portfolio choice in international MSCI indexes for 18 developed markets, using three different characteristics: book-to-market, the dividend price-ratio, and momentum. The results for the directly-estimated portfolio weights are compared to a naive regression-based approach, which effectively only considers the conditional mean returns when assigning weights, as well as to an equal-weighted scheme in the characteristic-based portfolios.

The empirical results highlight several important findings. First, the benefits from combining several characteristics are clear, and the improvement in portfolio performance is substantial compared to the single-characteristic strategies. Second, using the direct-estimation approach generally outperforms the naive regression-based approach by a wide margin. Third, there is also evidence that a simple equal-weigthed characteristic-based portfolio does almost as well, and sometimes better, than the direct-estimation approach.

The paper highlights the strong and robust performance that is achieved by parameterizing portfolio weights directly as functions of underlying characteristics, as opposed to methods where the distribution of returns is modelled and estimated in an intermediate step. However, the results of the paper also suggest that much of the strong performance that is seen derives simply from the diversification benefits of combining several strategies, such as value and momentum, rather than the optimal choice of the weights put on each strategy.

References

Aït-Sahalia Y., and M.W. Brandt. "Variable Selection for Portfolio Choice." Journal of Finance, 56 (2001), 1297-1351.

Asness, C.S., T.J. Moskowitz, and L. Pedersen. "Value and Momentum Everywhere." Working Paper, Stern School of Business, New York University (2009).

Brandt, M.W. "Estimating Portfolio and Consumption Choice: A Conditional Euler Equations Approach." Journal of Finance, 54 (1999), 1609-1645.

Brandt, M.W, and P. Santa-Clara. "Dynamic Portfolio Selection by Augmenting the Asset Space." Journal of Finance, 61 (2006), 2187-2217.

Brandt, M.W, P. Santa-Clara, and R. Valkanov. "Parametric Portfolio Policies: Exploiting Characteristics in the Cross-Section of Equity Returns." Review of Financial Studies, (Forthcoming).

Britten-Jones, M. "The Sampling Error in Estimates of Mean-Variance Efficient Portfolio Weights." Journal of Finance, 54 (1999), 655-671.

DeMiguel, V., L. Garlappi, F.J. Nogales, and R. Uppal. "A Generalized Approach to Portfolio Optimization: Improving Performance by Constraining Portfolio Norms." Working Paper, London Business School (2007).

DeMiguel, V., L. Garlappi, and R. Uppal. "Optimal versus Naive Diversification: How Inefficient Is the 1/N Portfolio Strategy." Working Paper, London Business School (2007).

Fama, E.F., and K.R. French. "The Cross-Section of Expected Stock Returns." Journal of Finance, 47 (1992), 427-465.

Fama, E.F., and K.R. French. "Multifactor Explanations of Asset Pricing Anomalies." Journal of Finance, 51 (1996), 55-84.

Fama, E.F., and K.R. French. "Value versus Growth: The International Evidence." Journal of Finance, 53 (1998), 1975-1999.

Hjalmarsson, E., "Predicting Global Stock Returns." Journal of Financial and Quantitative Analysis, (Forthcoming).

Jegadeesh, N. "Evidence of Predictable Behavior of Security Returns." Journal of Finance, 45 (1990), 881-898.

Jegadeesh, N., and S. Titman. "Overreaction, Delayed Reaction, and Contrarian Profits." Review of Financial Studies, 8 (1995), 973-993.

Lo, A.W., and A.C. ManKinlay. "When Are Contrarian Profits Due to Stock Market Overreaction?" Review of Financial Studies, 3 (1990), 175-205.

Markowitz, H.M. "Portfolio Selection." Journal of Finance, 7 (1952), 77-91.

Newey, W.K., D. McFadden. "Large Sample Estimation and Hypothesis Testing," in Engle, R.F., and D.L. McFadden, eds., Handbook of Econometrics, Vol. IV (North-Holland, Amsterdam) (1994), 2111-2245.

Patro. D.K., and Y. Wu. "Predictability of Short-Horizon Returns in International Equity Markets." Journal of Empirical Finance, 11 (2004), 553-584.

Table 1

Estimates of the unconditional CAPM for individual countries. This table reports country-by-country estimates from regressing individual country excess returns on the world market excess returns and a constant. The first two columns report the estimate and $ t-$statistic for the intercept, respectively, and the following two columns report the estimated CAPM beta and corresponding $ t-$statistic. The final column shows the $ R^2$ of the regression. The sample spans the period from December 1974 to December 2008, for a total of 409 monthly observations.

>
Country $ \alpha_{i}$ $ t_{\alpha_{i}}$$ \beta_{i}$ $ t_{\beta_{i}}$$ R_{i}^{2}$
Australia2.740.850.9715.450.37
Austria0.390.110.7110.180.20
Belgium1.320.490.9818.730.46
Canada0.480.211.0122.440.55
Denmark3.661.400.8015.540.37
France2.380.871.1020.520.51
Germany1.400.511.0218.830.47
Hong Kong7.231.611.1412.850.29
Italy0.160.040.9413.040.29
Japan-0.67-0.251.0519.400.48
Netherlands3.771.911.0426.760.64
Norway0.390.111.1716.310.40
Singapore1.800.471.1515.350.37
Spain0.210.070.9715.500.37
Sweden3.911.241.1418.480.46
Switzerland3.161.420.8719.860.49
U.K.3.421.281.0920.630.51
U.S.A.1.100.820.8933.960.74

Table 2

Annualized performance statistics for the single-characteristic portfolios. The table reports summary statistics for the excess returns on the pure momentum (MOM), book-to-market (BM), and dividend-price ratio (DP) portfolios, as well as for the MSCI world index (Market) portfolio. The scale of the characteristic-based portfolios is set such that one dollar is allocated to the short part of the portfolio and one dollar to the long part of the portfolio in each period. Panel A reports the results for the full 1980-2008 sample and Panel B reports the results for the 1999-2008 sub-sample. The first five rows report the annualized mean, standard deviation, skewness, kurtosis, and Sharpe ratio for the excess returns on each portfolio. The following four rows report the annualized world CAPM alpha and beta, with t-statistics in parentheses below the point estimates. The final rows in the table show the correlation between the excess returns on the portfolios.

Table 2, Panel A: January 1980 - December 2008

  MOM BM DP Market
Mean 8.331 3.323 3.608 5.258
Std. dev. 13.889 10.815 9.942 14.886
Skewness -0.259 0.257 -0.187 -0.749
Kurtosis 5.299 4.777 3.849 4.921
Sharpe ratio 0.600 0.307 0.363 0.353
Alpha 8.118 3.639 3.638  
Alpha T-Stat (3.130) (1.806) (1.957)  
Beta 0.041 -0.060 -0.006  
Beta T-Stat (0.808) (-1.547) (-0.159)  

Table 2, Panel A: Correlation Matrix: January 1980-December 2008

  MOM BM DP Market
MOM 1.000 -0.614 -0.428 0.043
BM   1.000 0.609 -0.083
DP     1.000 -0.009
Market       1.000

Table 2, Panel B: January 1999-December 2008

  MOM BM DP Market
Mean 2.320 4.774 1.644 -1.977
Std. dev. 10.575 8.617 7.877 15.306
Skewness 0.099 0.511 -0.063 -0.957
Kurtosis 3.801 7.219 3.888 5.006
Sharpe ratio 0.219 0.554 0.209 -0.129
Alpha 1.961 4.968 1.891  
Alpha T-Stat (0.605) (1.843) (0.779)  
Beta -0.181 0.098 0.125  
Beta T-Stat (-2.956) (1.925) (2.719)  

Table 2, Panel B: Correlation Matrix: January 1999-December 2008

  MOM BM DP Market
MOM 1.000 -0.400 -0.468 -0.263
BM   1.000 0.431 0.174
DP     1.000 0.243
Market       1.000

Table 3

Annualized performance statistics for the multi-characteristic portfolios. The table reports summary statistics for the excess returns on the momentum and book-to-market (MOM,BM) portfolios, and the momentum, book-to-market, and dividend-price ratio (MOM,BM,DP) portfolios, with . Panel A reports the results for the full 1980-2008 sample and Panel B reports the results for the 1999-2008 sub-sample. The columns labeled Reg., Dir., and EW, show the results for the portfolios based on regression-based, direct-optimization, and equal-weighted estimates of , respectively. The top part of the table shows the out-of-sample results, using recursively updated estimates of , and the bottom part of the table shows the in-sample results. The first five rows in each section report the annualized mean, standard deviation, skewness, kurtosis, and Sharpe ratio for the excess returns on each portfolio. The following four rows report the annualized CAPM alpha and beta, with statistics in parentheses below the point estimates. The final rows show the estimates of . For the out-of-sample results, the average estimate of used over the portfolio evaluation period is shown and for the in-sample results, the full-sample estimates are shown with statistics in parentheses below; in the 1980-2008 evaluation period, the in-sample estimates use data for the full 1974-2008 sample, and for the 1999-2008 evaluation period, the in-sample estimates only use data from the 1999-2008 period.

Table 3, Panel A: Out of Sample Results: January 1980 - December 2008

  MOM, BM : Reg. MOM, BM : Dir. MOM, BM : EW MOM, BM, DP: Reg. MOM, BM, DP:Dir. MOM, BM, DP:EW
Mean 21.404 22.666 20.157 21.334 22.959 19.630
Std. dev. 28.510 22.501 19.371 28.275 23.036 19.794
Skewness -0.236 0.178 0.017 -0.202 0.149 0.220
Kurtosis 5.689 4.330 3.776 5.715 4.534 3.490
Sharpe ratio 0.751 1.007 1.041 0.754 0.997 0.992
Alpha 21.032 22.748 20.336 20.901 22.710 19.802
Alpha T-Stat (3.949) (5.408) (5.618) (3.958) (5.276) (5.353)
Beta 0.071 -0.016 -0.034 0.082 0.047 -0.033
Beta T-Stat (0.687) (-0.191) (-0.487) (0.807) (0.570) (-0.458)
Weight-MOM 0.653 0.478 0.500 0.646 0.463 0.333
Weight-BM 0.347 0.522 0.500 0.346 0.401 0.333
Weight-DP       0.008 0.137 0.333

Table 3, Panel A: In Sample Results: January 1980 - December 2008

  MOM, BM : Reg. MOM, BM : Dir. MOM, BM : EW MOM, BM, DP: Reg. MOM, BM, DP:Dir. MOM, BM, DP:EW
Mean 21.932 19.822 20.157 22.860 21.654 19.630
Std. dev. 24.236 18.970 19.371 23.964 19.894 19.794
Skewness -0.142 0.044 0.017 -0.191 0.085 0.220
Kurtosis 4.163 3.743 3.776 4.299 3.833 3.490
Sharpe ratio 0.905 1.045 1.041 0.954 1.088 0.992
Alpha 21.852 20.037 20.336 22.734 21.737 19.802
Alpha T-Stat (4.824) (5.653) (5.618) (5.075) (5.846) (5.353)
Beta 0.015 -0.041 -0.034 0.024 -0.016 -0.033
Beta T-Stat (0.173) (-0.596) (-0.487) (0.276) (-0.219) (-0.458)
Weight-MOM 0.643 0.481 0.500 0.596 0.445 0.333
Weight-MOM T-Stat (5.768) (5.689)   (5.746) (5.869)  
Weight-BM 0.357 0.519 0.500 0.279 0.347 0.333
Weight-BM T-Stat (3.207) (4.815)   (2.443) (3.037)  
Weight-DP       0.126 0.207 0.333
Weight-DP T-Stat       (1.124) (1.914)  

Table 3, Panel B: Out of Sample Results: January 1999 - December 2008

  MOM, BM : Reg. MOM, BM : Dir. MOM, BM : EW MOM, BM, DP:Reg. MOM, BM, DP:Dir. MOM, BM, DP:EW
Mean 10.264 11.989 12.270 9.717 10.835 11.240
Std. dev. 21.204 18.580 18.402 20.191 17.244 16.052
Skewness -0.077 -0.171 -0.160 -0.032 0.012 0.228
Kurtosis 4.268 4.571 4.203 3.863 3.826 3.731
Sharpe ratio 0.484 0.645 0.667 0.481 0.628 0.700
Alpha 9.747 11.766 11.985 9.283 10.712 11.346
Alpha T-Stat (1.473) (2.001) (2.064) (1.467) (1.958) (2.227)
Beta -0.262 -0.113 -0.144 -0.220 -0.062 0.054
Beta T-Stat (-2.090) (-1.018) (-1.310) (-1.837) (-0.600) (0.557)
Weight-MOM 0.622 0.478 0.500 0.582 0.443 0.333
Weight-BM 0.378 0.522 0.500 0.300 0.351 0.333
Weight-DP       0.118 0.206 0.333

Table 3, Panel B: In Sample Results: January 1999 - December 2008

  MOM, BM : Reg. MOM, BM : Dir. MOM, BM : EW MOM, BM, DP:Reg. MOM, BM, DP:Dir. MOM, BM, DP:EW
Mean 11.392 10.591 12.270 11.719 11.011 11.240
Std. dev. 15.638 14.452 18.402 15.915 14.725 16.052
Skewness 0.119 -0.021 -0.160 0.207 0.087 0.228
Kurtosis 4.947 4.461 4.203 5.190 4.348 3.731
Sharpe ratio 0.728 0.733 0.667 0.736 0.748 0.700
Alpha 11.445 10.553 11.985 11.845 11.018 11.346
Alpha T-Stat (2.304) (2.298) (2.064) (2.346) (2.355) (2.227)
Beta 0.027 -0.019 -0.144 0.063 0.004 0.054
Beta T-Stat (0.288) (-0.218) (-1.310) (0.665) (0.043) (0.557)
Weight-MOM 0.317 0.376 0.500 0.291 0.360 0.333
Weight-MOM T-Stat (0.980) (1.607)   (1.002) (1.664)  
Weight-BM 0.683 0.624 0.500 0.589 0.501 0.333
Weight-BM T-Stat (2.116) (2.210)   (1.999) (1.945)  
Weight-DP       0.120 0.139 0.333
Weight-DP T-Stat       (0.408) (0.469)  

Figure 1. Recursive Estimates of θ

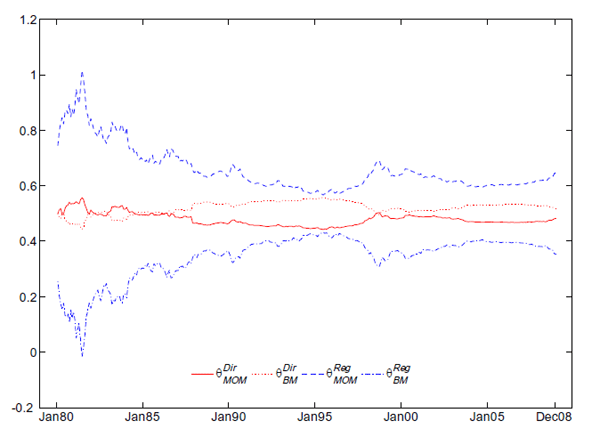
Figure 1 shows recursive estimates of the theta parameters for momentum and book-to-market, with the first estimate using data up till January 1980, and the last one using data up till December 2008. Both the regression based estimates from equation (1) as well as the direct estimates from equation (10) are shown. The graph shows that the directly estimated parameters are much more stable over time than the regression based parameters.

The figure shows the standardized recursive estimates of θ from either the estimation of the regression equation (1), denoted $\displaystyle \theta_{MOM}^{\operatorname{Re}g} $ and $\displaystyle \theta_{BM}^{\operatorname{Re}g} $, or from the direct estimation of the weights in equation (10), denoted $\displaystyle \theta_{MOM}^{Dir} $ and $\displaystyle \theta_{BM}^{Dir} $. Data from December 1974 up till the date in the graph are used to form each estimate.

Footnotes

1.  Both authors are with the Division of International Finance at the Federal Reserve Board, Mail Stop 20, Washington, DC 20551, USA. Helpful comments have been provided by Lennart Hjalmarsson and Randi Hjalmarsson. Corresponding author: Erik Hjalmarsson. Tel.: +1-202-452-2426; fax: +1-202-263-4850; email: [email protected]. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System.  Return to text

2.  For recent work on this topic, see, for instance, DeMiguel, Garlappi, and Uppal (2007), and DeMiguel, Garlappi, Nogales, and Uppal (2007). Return to text

3.  The general case where the $ \beta_{i}s$ differ across $ i$, and the constraint $ \mathbf{\omega}^{\prime}\mathbf{\beta}=0$ is explicitly imposed, can easily be solved for and implemented using estimates of the $ \beta_{i}s$ obtained from estimating equation (1). However, empirical results not presented in the paper clearly show that the subsequent portfolio weights often tend to differ substantially from the ones that do not impose the zero-beta constraint, even though the unconstrained solution typically has a beta that is very close to zero empirically. This follows because in order to exactly satisfy the zero-beta constraint in-sample, the weights might have to shift substantially. Since correlations and betas move over time, and there is thus no guarantee that the out-of-sample portfolio will have a beta closer to zero if the constraint is imposed, there seems little point in pursuing this constraint. Return to text

4.  Alternatively, by noting that $ \tilde{\theta}$ is an extremum estimator, the asymptotic covariance matrix could be derived in the ususal fashion (c.f. Newey and Mcfadden (1994)). Return to text

5.  Note that the relative size of the components in $ \tilde{\theta}$ is not affected by whether the demeaned or non-demeaned squared returns are used as penalty in equation (7), as discussed in Britten-Jones (1999). Return to text

6.  The MSCI world index is a market capitalization weighted index intended to capture the equity market performance of developed markets, which makes it a suitable benchmark for the analysis here. As of June 2007, the MSCI world index consisted of the 18 country indexes in Table 1, plus Finland, Greece, Ireland, New Zealand, and Portugal. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: November 3, 2009