
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 984, November 2009 --- Screen Reader
Version*
Portfolio Inertia and the Equity Premium 1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We develop a DSGE model in which aggregate shocks induce endogenous movements in risk. The key feature of our model is that households rebalance their financial portfolio allocations infrequently, as they face a fixed cost of transferring cash across accounts. We show that the model can account for the mean returns on equity and the risk-free rate, and generates countercyclical movements in the equity premium that help explain the response of stock prices to monetary shocks. The model is consistent with empirical evidence documenting that unanticipated changes in monetary policy have important effects on equity prices through changes in risk.
Keywords: Limited financial market participation, infrequent portfolio adjustment, equity premium
JEL classification: E32, E44
1 Introduction
Monetary policy primarily affects the macroeconomy through its effect on financial markets. In standard monetary models, this interaction between the financial and real sides of the economy occurs through short-term interest rates, as changes in monetary policy affect the conditional mean of the short-term interest rate which in turn influences macroeconomic variables such as output, employment, and inflation. These models, however, abstract from another channel through which monetary policy affects financial markets and the macroeconomy. In these models, there is little or no role for monetary policy to influence the conditional variances of variables or the perceived riskiness of the economy.3 In contrast, [Bernanke and Kuttner 2005] provide evidence that monetary policy does affect risk, suggesting that standard monetary models are potentially missing an important channel through which monetary shocks propagate from the financial to the real economy. They show that, while an unanticipated easing of monetary policy lowers real short-term interest rates, it also has a significant effect on equity returns occurring through a reduction in the equity premium.
In this paper, we develop a DSGE model in which monetary policy affects the economy through the standard interest rate channel and through its effect on economic risk. The key feature of the model is that asset and goods markets are segmented, because it is costly for households to transfer funds between these markets. Accordingly, they may only infrequently update their desired allocation of cash between a checking account devoted to purchasing goods and a brokerage account used for financial transactions. The optimal decision by an individual household to rebalance their cash holdings is a state-dependent one, reflecting that doing so involves paying a fixed cost in the presence of uncertainty. Households are heterogenous in this fixed cost, and only those households that rebalance their portfolios during the current period matter for determining asset prices. Because the fraction of these household changes over time in response to both real and monetary shocks, risk in the economy is both time-varying and endogenous.
We show that the model, unlike standard monetary models, generates countercyclical movements in the equity premium and in particular, a reduction in the equity premium resulting from an easing of monetary policy. For reasonable calibrations of the model, the reduction in the equity premium is an important determinant of the response of stock prices to a monetary policy shock.
We also examine the model's ability to account for the mean returns on equity and the risk-free rate. As shown by [Mehra and Prescott 1985], standard representative agent models with power utility have difficulty quantitatively accounting for these moments. For reasonable calibrations of monetary and technology shocks, our model is able to match the observed means on equity and risk-free rates with a power utility function that implies constant relative risk aversion equal to two. We show that to match these moments, the average fraction of households that reallocates funds across markets can not be too large. For a constant relative risk aversion of two, the average fraction of rebalancers in a quarter must range between roughly 10 to 20 percent. Underlying this average fraction of rebalancing, there is a considerable degree of heterogeneity, with some households rebalancing every period and another fraction rarely rebalancing away from their initial allocation.
Recent microdata on household finance provides strong support for infrequent portfolio rebalancing. For instance, in two recent papers, [Calvet et al. 2009a] and [Calvet et al. 2009b] document that, while there is little rebalancing of the financial portfolios of stockholders by the average household, there is a great deal of heterogeneity at the micro level with some households rebalancing these portfolios very frequently. In addition, using information on asset holdings from the PSID, [Bilias et al. 2008] and [Brunnermeier and Nagel 2008] provide evidence that household portfolio allocation display substantial inertia. Surveys conducted by the Investment Company Institute (ICI) and the Securities Industry Association (SIA) also suggest that households rebalance their portfolios infrequently. For instance, in 2004, the median number of total equity transactions for an individual was four. In addition, sixty percent of equity investors did not conduct any equity transactions during 2004. Finally, in a 2005 survey, the ICI reports that more than two-thirds of the time the proceeds from the sales of stocks by households are fully reinvested.4
Our model is most closely related to and builds on the analysis of [Alvarez et al. 2009]. They introduce endogenously segmented markets into an otherwise standard cash-in-advance economy and show how changes in monetary policy can induce fluctuations in risk. However, our model differs from theirs in two important respects. First, we incorporate production and equity returns. Second and more importantly, in their model, risk is endogenous, because the fraction of households that participates in financial markets is state-dependent. In our model, it is costly to reallocate cash between the asset and goods markets from a household's initial allocation. In other words, endogenous asset segmentation occurs along an intensive margin in our model rather than an extensive margin. This distinction is important, because we show that for reasonable calibrations the endogenous participation model can not match the average equity premium and monetary policy shocks have no effect on the equity premium.5
Our paper is also related to portfolio choice models that emphasize infrequent adjustment. In this literature, the paper most closely related to ours is [Abel et al. 2007].6 They also model infrequent adjustment of cash between a transaction account used to purchase goods and another account used to purchase financial assets. Their framework differs from ours, since they do not consider the role of monetary policy and use a partial equilibrium framework in which returns are exogenous. However, they show that infrequent portfolio adjustment can arise due to rational inattention on the part of households.7
The rest of this paper proceeds as follows. The next section describes the model and its calibration. Section 3 presents the results, emphasizing the model's ability to match unconditional moments such as the mean returns on equity and a risk-free asset as well as the conditional responses of these variables to a monetary policy shock. Section 4 concludes and discusses directions for future research.
2 The Model
The model builds on the cash-in-advance economy of [Alvarez et al. 2009], which we extend to incorporate equity prices. Our approach differs from theirs, since we emphasize that time-varying risk is driven by costly portfolio rebalancing of financial accounts rather than limited participation in financial markets.
The economy is populated by a large number of households, firms, and a government sector. Trade occurs in financial and goods markets in separate locations so that they are segmented from each other. After choosing an initial non-state contingent plan that allocates funds across asset and goods markets, households must pay a fixed cost to make state contingent transfers between these markets. This fixed cost is constant over time but varies across households. We refer to a household's cash balances in the goods market as her checking account, and her cash balances in the asset market as her brokerage account. An active household is one that pays her fixed cost and rebalances cash across these two accounts, and an inactive household does not.
There are two sources of uncertainty in our economy -- aggregate
shocks to technology,
![]() , and money growth,
, and money growth, ![]() . We let
. We let
![]() index the aggregate event in period
index the aggregate event in period ![]() , and
, and
![]() denote the state,
which consists of the aggregate shocks that have occurred through
period
denote the state,
which consists of the aggregate shocks that have occurred through
period ![]() .
.
2.1 Firms
There is large number of perfectly competitive firms, which each
have access to the following technology for converting capital,
![]() , and labor,
, and labor, ![]() ,
into output,
,
into output, ![]() at dates
at dates ![]() :
:
| (1) |
The variable
![]() is an aggregate technology shock
which follows a first-order autoregressive process:
is an aggregate technology shock
which follows a first-order autoregressive process:
| (2) |
where
![]() for all
for all
![]() .
.
Capital does not depreciate, and there exists no technology for increasing or decreasing its magnitude. We adopt the normalization that the aggregate stock of capital is equal to one. Labor is supplied inelastically by households, and its supply is normalized to one.
Firm production begins at date 1. Following
[Boldrin et al. 1997], we assume that firms have a one-period
planning horizon. To operate capital in period ![]() , a firm must purchase it at the end of period
, a firm must purchase it at the end of period ![]() from those firms operating during period
from those firms operating during period ![]() .
To do so, a firm issues equity
.
To do so, a firm issues equity ![]() at dates
at dates
![]() , and purchases capital subject to its
financing constraint,
, and purchases capital subject to its
financing constraint,
| (3) |
where
![]() denotes the price of capital.
denotes the price of capital.
A firm derives revenue from its sale of output,
![]() , and the sale of its
capital stock,
, and the sale of its
capital stock,
![]() , at the end of period
, at the end of period
![]() . A firm's expenses include its
obligations on equity,
. A firm's expenses include its
obligations on equity,
![]() , and payments to
to labor,
, and payments to
to labor,
![]() . A firm's net revenues,
. A firm's net revenues,
![]() , including its expenses, must be
greater than zero in each state so that:
, including its expenses, must be
greater than zero in each state so that:
| (4) |
The firm's problem at date ![]() is to maximize
is to maximize
![]() across states of nature by choice
of
across states of nature by choice
of ![]() and
and
![]() subject to (1) and (3). This problem
implies that the financing constraint (3) is satisfied as
a strict equality in equilibrium. The equilibrium real wage,
subject to (1) and (3). This problem
implies that the financing constraint (3) is satisfied as
a strict equality in equilibrium. The equilibrium real wage,
![]() is given by:
is given by:
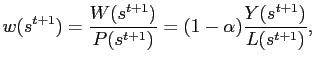
|
(5) |
Linear homogeneity of the firm's objective, together with the weak
inequality in equation (4) imply that
![]() for all
for all ![]() so that:
so that:
![$\displaystyle 1+r^{e}(s^{t+1})= \frac{1+R^{e}(s^{t+1})}{\pi(s^{t+1})} =\frac{\left[ \alpha\frac{Y(s^{t+1})}{K(s^{t})}+p_{k}(s^{t+1})\right] } {p_{k}(s^{t} )}.$](img40.gif)
|
(6) |
In the above,
![]() denotes the real price of capital and
denotes the real price of capital and
![]() is
the economy's inflation rate.
is
the economy's inflation rate.
2.2 Households
There are a large number of households of type ![]() , which denotes a household's fixed cost of making
state contingent transfers from a brokerage account to a checking
account. This cost is constant across time but differs across
household types according to the probability density function
, which denotes a household's fixed cost of making
state contingent transfers from a brokerage account to a checking
account. This cost is constant across time but differs across
household types according to the probability density function
![]() .
.
2.2.1 Brokerage Account
At date 0, a household learns her type and engages in an initial
round of trade in the asset market, as goods markets do not open
until date 1. With initial asset holdings,
![]() in her brokerage account
at date 0, the household purchases equity,
in her brokerage account
at date 0, the household purchases equity,
![]() , issued by the firms and a
complete set of one-period contingent claims,
, issued by the firms and a
complete set of one-period contingent claims,
![]() , issued by the government.
Accordingly, the flow of funds in a household's brokerage account
at date 0 is given by:
, issued by the government.
Accordingly, the flow of funds in a household's brokerage account
at date 0 is given by:
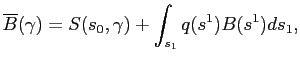
|
(7) |
where ![]() is the price of the bond in state,
is the price of the bond in state,
![]() .
.
For dates ![]() , a household's brokerage account
evolves according to:
, a household's brokerage account
evolves according to:
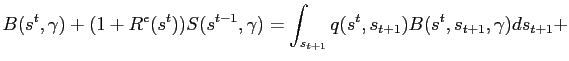
|
||
| (8) |
where ![]() is a non-state contingent transfer
of funds from a household's brokerage account to checking account
at date
is a non-state contingent transfer
of funds from a household's brokerage account to checking account
at date ![]() chosen at date 0 after a household learns
her type. A household can alter this initial transfer plan by
choosing
chosen at date 0 after a household learns
her type. A household can alter this initial transfer plan by
choosing
![]() , which requires paying
the fixed cost
, which requires paying
the fixed cost ![]() . Accordingly,
. Accordingly,
![]() is an indicator variable
equal to one if a household opts to pay her fixed cost and make a
state-contingent transfer and equal to zero if a household does
not.
is an indicator variable
equal to one if a household opts to pay her fixed cost and make a
state-contingent transfer and equal to zero if a household does
not.
We view the fixed cost, ![]() , as reflecting
cognitive costs associated with collecting and processing
information necesssary to recompute the optimal portfolio
allocation in response to shocks. Our approach is similar to
[Gabaix and Laibson 2001] and [Bacchetta and van Wincoop 2009];
however, we emphasize that the decision to reoptimize portfolio
holdings is state dependent rather than time dependent. Our
approach also shares similarities with [Reis 2006], who derives
inattentive behavior on the part of households who infrequently
adjust their consumption and saving plans using a rational
inattentive framework.
, as reflecting
cognitive costs associated with collecting and processing
information necesssary to recompute the optimal portfolio
allocation in response to shocks. Our approach is similar to
[Gabaix and Laibson 2001] and [Bacchetta and van Wincoop 2009];
however, we emphasize that the decision to reoptimize portfolio
holdings is state dependent rather than time dependent. Our
approach also shares similarities with [Reis 2006], who derives
inattentive behavior on the part of households who infrequently
adjust their consumption and saving plans using a rational
inattentive framework.
The key assumption we make about a household's initial
allocation scheme, ![]() , is that it is
non-state contingent. In principle, a household could choose a
time-varying, non-state contingent plan at date 0 and would do so
if the model allowed for finite-lived agents with life-cycle
considerations.8 For example, a household born with low
initial assets would save some of her wage income by setting up a
plan that at first transferred a fixed amount of funds from her
checking account to her brokerage account. However, the household
would also set up her transfer scheme to reverse this flow at her
expected retirement date, when cash transfers from her brokerage to
her checking account become her primary source of cash for
consumption. While including financial planning over a household's
life cycle would be more realistic, we abstract from such
considerations to keep the analysis tractable and simply focus on
the non-state contingent nature of
, is that it is
non-state contingent. In principle, a household could choose a
time-varying, non-state contingent plan at date 0 and would do so
if the model allowed for finite-lived agents with life-cycle
considerations.8 For example, a household born with low
initial assets would save some of her wage income by setting up a
plan that at first transferred a fixed amount of funds from her
checking account to her brokerage account. However, the household
would also set up her transfer scheme to reverse this flow at her
expected retirement date, when cash transfers from her brokerage to
her checking account become her primary source of cash for
consumption. While including financial planning over a household's
life cycle would be more realistic, we abstract from such
considerations to keep the analysis tractable and simply focus on
the non-state contingent nature of ![]() . By
incorporating this initial portfolio decision and a fixed cost of
altering it in response to shocks, our model is broadly consistent
with the micro evidence that many households adjust their portfolio
decisions very infrequently.9
. By
incorporating this initial portfolio decision and a fixed cost of
altering it in response to shocks, our model is broadly consistent
with the micro evidence that many households adjust their portfolio
decisions very infrequently.9
2.2.2 Checking Account
For ![]() , a household purchases goods for
consumption,
, a household purchases goods for
consumption,
![]() , and works in the labor
market. To purchase goods in period
, and works in the labor
market. To purchase goods in period ![]() , a household
uses cash in her checking account:
, a household
uses cash in her checking account:
| (9) |
At the beginning of period ![]() , a household has
, a household has
![]() dollars in her checking
account with which to purchase goods. A household also receives
cash from her non-state contingent transfer plan and
dollars in her checking
account with which to purchase goods. A household also receives
cash from her non-state contingent transfer plan and
![]() dollars from her
brokerage account, if she chooses to incur the fixed cost and
transfer additional funds.10
dollars from her
brokerage account, if she chooses to incur the fixed cost and
transfer additional funds.10
Each household inelastically supplies her labor to the economy's
firms. With a household's labor supply normalized to one, a
household earns real wage income, ![]() . This
wage income is received at the end of the period so it can not be
used for current consumption. Accordingly, a household cash in its
checking account at the end of period
. This
wage income is received at the end of the period so it can not be
used for current consumption. Accordingly, a household cash in its
checking account at the end of period ![]() is given
by:
is given
by:
| (10) |
We have abstracted from the possibility that a household may want to save extra cash in their checking and/or brokerage accounts since equations (8) and (9) always bind. Since incorporating occasionally binding constraints greatly complicates the analysis, we address it in the appendix and in [Gust and López-Salido 2009]. As discussed there, the main results of our analysis are robust to this possibility.
A household's problem is to choose ![]() and
and
![]()
![]() to maximize:
to maximize:
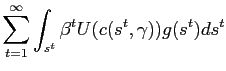
|
(11) |
subject to equations (7)-(10), taking prices
and initial holdings of money, bonds, and stocks as given. In
equation (11), the
function ![]() denotes the probability distribution
over history
denotes the probability distribution
over history ![]() .
.
2.2.3 Endogenous Participation
If households are not able to set up the initial, non-state
contingent transfer plan, the model is similar to the endogenous
participation framework of [Alvarez et al. 2009]. In this
case, asset markets are completely segmented from goods markets for
agents who do not transfer
![]() between them. We call this
version of the model, the "endogenous participation model'',
because the decision to transfer funds from asset to the goods
market determines whether a household participates in financial
markets. In contrast, in the "endogenous rebalancing'' model, the
decision to transfer funds
between them. We call this
version of the model, the "endogenous participation model'',
because the decision to transfer funds from asset to the goods
market determines whether a household participates in financial
markets. In contrast, in the "endogenous rebalancing'' model, the
decision to transfer funds
![]() at date
at date ![]() amounts to a rebalancing of cash from a household's initial
allocation chosen at date 0.
amounts to a rebalancing of cash from a household's initial
allocation chosen at date 0.
2.3 The Government
The government issues the economy's one-period state-contingent
bonds and controls the economy's money stock, ![]() . Its budget constraints at date 0 is
. Its budget constraints at date 0 is
![]() where
where ![]() is given, and at dates
is given, and at dates ![]() , its budget constraint is:
, its budget constraint is:
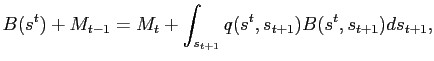
|
(12) |
with ![]() given. The government injects
cash into the economy via a first-order autoregressive process for
money growth,
given. The government injects
cash into the economy via a first-order autoregressive process for
money growth,
![]() :
:
| (13) |
where
![]() , and
, and
![]() for all
for all ![]() .
.
2.4 Market Clearing
The economy's resource constraint is:
![$\displaystyle Y(s^{t}) = \int^{\infty}_{0} \left[ c(s^{t},\gamma)+\gamma z(s^{t},\gamma) \right] f(\gamma)d\gamma,$](img95.gif)
|
(14) |
while market clearing in factor markets requires
![]() and
and
![]() . In asset markets, for stock and
bond markets to clear at dates
. In asset markets, for stock and
bond markets to clear at dates ![]() we have:
we have:
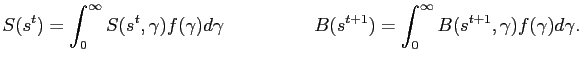
|
At date 0, we also have
![]() .
For
.
For ![]() , beginning of the period cash
holdings satisfy:
, beginning of the period cash
holdings satisfy:
![$\displaystyle \int^{\infty}_{0} \left\{ M(s^{t-1},\gamma)+P(s^{t})[x(s^{t},\gamma )+\gamma]z(s^{t},\gamma) + P(s^{t})A(\gamma) \right\} f(\gamma)d\gamma= M_{t},$](img102.gif)
|
(15) |
where the presence of the fixed cost reflects it is paid using cash from the brokerage account.
An equilibrium is a collection of asset prices,
![]() ,
wages, and goods prices, which together with money, bonds, stocks,
and allocations,
,
wages, and goods prices, which together with money, bonds, stocks,
and allocations,
![]()
![]() satisfying
the household's optimization problem. These prices together with
the allocations
satisfying
the household's optimization problem. These prices together with
the allocations
![]() satisfies the firm's optimization problem. Finally, the government
budget constraint holds and the resource constraint along with the
market clearing conditions for capital, labor, bonds, stocks, and
money are all satisfied.
satisfies the firm's optimization problem. Finally, the government
budget constraint holds and the resource constraint along with the
market clearing conditions for capital, labor, bonds, stocks, and
money are all satisfied.
2.5 Equilibrium Characterization
We now characterize equilibrium consumption and transfers of
households. We then discuss the link between the consumption of
households that actively rebalance their portfolios (i.e., choose
![]() ) and equity returns.
) and equity returns.
2.5.1 Consumption and Transfers
We begin by characterizing a household's consumption conditional
on her choice of paying the fixed cost of making a state dependent
transfer (i.e., her choice of
![]() ). To do so, we use the fact
that market clearing of factor markets implies that
). To do so, we use the fact
that market clearing of factor markets implies that
![]() exp
exp![]() . In addition, we can determine the economy's
price level and inflation rate by substituting equations (9) and (14) into the money
market clearing condition to write:
. In addition, we can determine the economy's
price level and inflation rate by substituting equations (9) and (14) into the money
market clearing condition to write:
| (16) |
With these expressions, we can show that the consumption of an
inactive household (i.e., one that sets
![]() ) is given by:
) is given by:
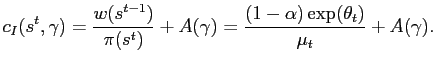
|
(17) |
From this expression, we can see that inflation is distortionary, since, all else equal, it reduces the consumption of inactive households. Accordingly, an unanticipated increase in money that raises inflation will induce the marginal household to pay her fixed cost and become active. Although the consumption of inactive households rises due to an increase in wages following an unexpected technological improvement, the benefits of being active are even greater, reflecting that active consumption is also boosted by higher capital income. Thus, a technology shock will also boost the number of active households.
There is perfect risk-sharing amongst active households, and
following [Alvarez et al. 2002], we assume that the initial
asset holdings,
![]() , of the households
implies:
, of the households
implies:
| (18) |
Accordingly, the consumption of active households is independent of
![]() . To further characterize, the
consumption of active and inactive households, we need to determine
. To further characterize, the
consumption of active and inactive households, we need to determine
![]() . A household's choice of
. A household's choice of
![]() satisfies:
satisfies:
![$\displaystyle \sum_{t=1}^{\infty} \int_{s^{t}} \beta^{t} \left[ U^{\prime}(c_{A} (s^{t}))-U^{\prime}(c_{I}(s^{t},\gamma))\right] (1-z(s^{t},\gamma ))g(s^{t})ds^{t}=0.$](img119.gif)
|
(19) |
This latter condition states that in states of the world in which a
household is inactive (i.e.,
![]() ), the household chooses
), the household chooses
![]() to equate her expected discounted
value of marginal utility of its consumption to the expected
discounted value of the marginal utility of consumption of the
active households. Accordingly, the non-state contingent transfer
plan provides some consumption insurance to households with
relatively large fixed costs of rebalancing their portfolio
allocation. Such households will choose
to equate her expected discounted
value of marginal utility of its consumption to the expected
discounted value of the marginal utility of consumption of the
active households. Accordingly, the non-state contingent transfer
plan provides some consumption insurance to households with
relatively large fixed costs of rebalancing their portfolio
allocation. Such households will choose
![]() to compensate for their
infrequent access to capital income derived from equity markets.
to compensate for their
infrequent access to capital income derived from equity markets.
While equation (19) places
restrictions on the choice of ![]() for most
households, this condition is irrelevant for a household that is
active in each state of the world. In this case, a household's
choice of
for most
households, this condition is irrelevant for a household that is
active in each state of the world. In this case, a household's
choice of ![]() is redundant, since she can
use
is redundant, since she can
use
![]() to achieve her desired level
of consumption.
to achieve her desired level
of consumption.
We now characterize a household's decision for
![]() given optimal decisions for
given optimal decisions for
![]() ,
,
![]() , and
, and ![]() . A household will choose to be active if
. A household will choose to be active if
![]() where
where
![]() is defined by:
is defined by:
| (20) |
and inactive otherwise. Equation (20) implies that
there is a marginal household with fixed cost
![]() whose net gain of
rebalancing is equal to the cost of transferring funds across the
two markets. The net gain,
whose net gain of
rebalancing is equal to the cost of transferring funds across the
two markets. The net gain,
![]() , is simply the difference in the level of utility from being
active as opposed to inactive. The net cost of making the
state-contingent transfer comprises the fee
, is simply the difference in the level of utility from being
active as opposed to inactive. The net cost of making the
state-contingent transfer comprises the fee ![]() and the amount transferred by the household, since
and the amount transferred by the household, since
![]() . In our
context, the fixed cost of rebalancing leads to a state-dependent
rule determining the fraction of households that reoptimize their
portfolio allocations. With this rule, the resource constraint can
be rewritten as:
. In our
context, the fixed cost of rebalancing leads to a state-dependent
rule determining the fraction of households that reoptimize their
portfolio allocations. With this rule, the resource constraint can
be rewritten as:
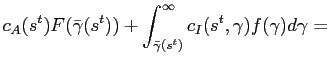 exp
exp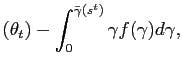
|
(21) |
where ![]() is the cumulative distribution
function for
is the cumulative distribution
function for ![]() .
.
2.5.2 Consumption of Rebalancers and the Equity Premium
The asset pricing kernel in the economy depends on the consumption of the rebalancers and is given by:
![$\displaystyle m(s^{t+1}) = \beta\frac{U^{\prime}[c_{A}(s^{t+1})]}{U^{\prime}[c_{A}(s^{t})]}.$](img141.gif)
|
(22) |
This pricing kernel is the state-contingent price of a security
expressed in consumption units and normalized by the probabilities
of the state. This pricing kernel can be used to determine the real
risk-free rate (![]() ) as well as the real return on
equity (
) as well as the real return on
equity (![]() ). These returns are given by:
). These returns are given by:
![$\displaystyle [1+r^{f}(s^{t})]^{-1} = \int_{s_{t+1}} m(s^{t},s_{t+1}) g(s_{t+1}\vert s^{t}) ds_{t+1},$](img144.gif)
|
(23) |
![$\displaystyle 1 = \int_{s_{t+1}} m(s^{t},s_{t+1}) [1+r^{e}(s^{t},s_{t+1})] g(s_{t+1} \vert s^{t})ds_{t+1},$](img145.gif)
|
(24) |
where
![]() denotes
the probability of state
denotes
the probability of state ![]() conditional on state
conditional on state
![]() . From equation (25) in the firm's
problem, the equilibrium real return on equity is given by:
. From equation (25) in the firm's
problem, the equilibrium real return on equity is given by:
![$\displaystyle 1+r^{e}(s^{t+1})=\frac{\left[ \alpha\hspace{0.05cm} \text{exp}(\theta _{t+1})+p_{k}(s^{t+1})\right] } {p_{k}(s^{t})}.$](img149.gif)
|
(25) |
Using these two equations, we can then define the equity premium in our economy as:
![$\displaystyle \frac{ \text{E}_{t}[1+r^{e}_{t+1}]}{1+r^{f}_{t}}= 1 - \text{cov}_{t}\left( m_{t+1},1+r^{e}_{t+1}\right) ,$](img150.gif)
|
(26) |
where for convenience we have switched notation to express both the
expected return on equity and the covariance between the pricing
kernel and the return on equity, which are both conditional on the
state of the world at date ![]() .
.
2.6 Parameter Values and Numerical Solution
A household's per-period preferences are given by:
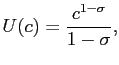 |
(27) |
where ![]() is the coefficient of constant
relative risk aversion, which is set equal to 2 based on the survey of the literature in [Hall 2008]. The discount
factor,
is the coefficient of constant
relative risk aversion, which is set equal to 2 based on the survey of the literature in [Hall 2008]. The discount
factor,
![]() , is chosen to be consistent with
a quarterly model, while the economy's capital share,
, is chosen to be consistent with
a quarterly model, while the economy's capital share, ![]() , is 0.36.
, is 0.36.
For the distribution of the fixed cost, ![]() , we assume that there is some small positive mass
of households with zero fixed costs and choose the remaining
distribution,
, we assume that there is some small positive mass
of households with zero fixed costs and choose the remaining
distribution, ![]() , to be log-normal so that
, to be log-normal so that
![]() . We set
. We set
![]() ,
,
![]() , and
, and
![]() , which imply that, on
average, about 9 percent of households rebalance their portfolios
in a quarter with some households rebalancing frequently and a
large mass of households rarely rebalancing. As discussed in the
introduction, such a calibration is broadly in line with the the
micro evidence from the household finance literature discussed in
the introduction.
, which imply that, on
average, about 9 percent of households rebalance their portfolios
in a quarter with some households rebalancing frequently and a
large mass of households rarely rebalancing. As discussed in the
introduction, such a calibration is broadly in line with the the
micro evidence from the household finance literature discussed in
the introduction.
In the model, absent the small average transaction cost, the
aggregate consumption process corresponds to the technology shock.
Therefore, we calibrated the parameters governing the process for
technology based on the time series properties of aggregate
consumption. We set
![]() and chose
and chose
![]() so that the standard
deviation for annualized consumption growth is slightly higher than
3 percent, consistent with annual data on U.S. consumption over
1890-1993 from [Campbell 1999]. For the money growth process, we
used quarterly data on M2 over the sample period 1959:Q1-2009:Q2
and estimated
so that the standard
deviation for annualized consumption growth is slightly higher than
3 percent, consistent with annual data on U.S. consumption over
1890-1993 from [Campbell 1999]. For the money growth process, we
used quarterly data on M2 over the sample period 1959:Q1-2009:Q2
and estimated
![]() and
and
![]() . We set
. We set
![]() so that average, annualized
money growth rate is 2%.
so that average, annualized
money growth rate is 2%.
The model is solved numerically using a global algorithm. We use
Newton-Cotes quadrature to approximate the expectations associated
with the normally-distributed technology and monetary shocks. As
discussed in [Judd 1999], the stochastic difference equation
implied by equations (24) and (25) can then be
used to determine the price of equity using linear Fredholm
integral equations (Type 2). The function ![]() is approximated by solving the recursive
representation of equation (19) exactly at a
finite number of points and then using splines to approximate the
function elsewhere.
is approximated by solving the recursive
representation of equation (19) exactly at a
finite number of points and then using splines to approximate the
function elsewhere.
3 Results
Before discussing the model's implications for monetary policy and the equity premium, it is helpful to characterize the non-stochastic steady state of the model.
3.1 Deterministic Steady State
In a deterministic environment with average money growth equal to 2% and output equal to unity, the endogenous rebalancing model reduces to a representative agent economy. This model only becomes interesting in the presence of uncertainty; nevertheless, it is useful to compare its deterministic steady state with the version of the model with endogenous participation.
In the non-stochastic steady state of the endogenous rebalancing
model, all households will have the same level of consumption.
According to equation (19), a household
that chooses to be inactive obtains the same level of consumption
as an active household. An inactive household can obtain such a
level of consumption by choosing her initial plan such that
![]() ,
where
,
where ![]() takes on the same value across all
inactive households. With consumption the same across households,
all households with
takes on the same value across all
inactive households. With consumption the same across households,
all households with ![]() will never
rebalance their portfolios, and the households with
will never
rebalance their portfolios, and the households with ![]() will be indifferent between rebalancing or using
the non-state contingent transfer,
will be indifferent between rebalancing or using
the non-state contingent transfer, ![]() .
.
In the non-stochastic steady state of the endogenous
participation model (i.e.,
![]() for all
for all ![]() ), the consumption of active households exceeds the
consumption of inactive households, who only receive
), the consumption of active households exceeds the
consumption of inactive households, who only receive
![]() . By choosing to
be inactive, these agents do not receive the capital income
associated with participating in the stock market. Accordingly,
without a much larger fixed cost, there is a strong incentive for
all households to participate in financial markets.
. By choosing to
be inactive, these agents do not receive the capital income
associated with participating in the stock market. Accordingly,
without a much larger fixed cost, there is a strong incentive for
all households to participate in financial markets.
3.2 Endogenous Rebalancing and the Equity Premium
Figure 1
shows the sample averages for the risk-free rate and the equity
premium (see the black dot labeled "U.S. Data'') taken from
[Guvenen 2009]. We also report 5% confidence ellipse, based on his
estimates. The figure also shows the average equity premium and
risk-free rate in the endogenous rebalancing model using the
benchmark calibration with ![]() . This
calibration leads to an average equity premium of about 7% and a
risk-free rate of 1.5%.
. This
calibration leads to an average equity premium of about 7% and a
risk-free rate of 1.5%.
Moving from southeast to northwest along the blue line with
circles, each point reports the equity premium and risk-free rate
for different values of
![]() , which leads to a different
average fraction of rebalancers. There are two basic results that
can be evinced from this line. First, decreasing the average
fraction of rebalancers (by increasing
, which leads to a different
average fraction of rebalancers. There are two basic results that
can be evinced from this line. First, decreasing the average
fraction of rebalancers (by increasing
![]() ) produces a rise in the equity
premium and fall in the risk-free rate. Second, if the fraction of
household rebalancers lies between roughly 8% and 13%, then the
model lies within the 95% confidence region.11
) produces a rise in the equity
premium and fall in the risk-free rate. Second, if the fraction of
household rebalancers lies between roughly 8% and 13%, then the
model lies within the 95% confidence region.11
The green line with squares in Figure 1 shows the
results if we vary ![]() in the endogenous
rebalancing model. Raising the coefficient of relative risk
aversion has a similar effect on the equity premium and risk-free
rate as lowering the average fraction of rebalancers via
in the endogenous
rebalancing model. Raising the coefficient of relative risk
aversion has a similar effect on the equity premium and risk-free
rate as lowering the average fraction of rebalancers via
![]() . As the coefficient of relative
risk aversion increases, the mean equity premium rises and the
risk-free rate falls. For values of
. As the coefficient of relative
risk aversion increases, the mean equity premium rises and the
risk-free rate falls. For values of ![]() between
1 and 2.5, the combination of mean returns on equity and the
risk-free asset lies within the 95% confidence region. For
comparison purposes, the magenta line with triangles in the
southeast corner of the figure shows the results for the
representative agent economy. In this model, as in [Mehra and
Prescott 1985], the only way to match the observed equity premium
is to increase the coefficient of relative risk aversion to a high
level.
between
1 and 2.5, the combination of mean returns on equity and the
risk-free asset lies within the 95% confidence region. For
comparison purposes, the magenta line with triangles in the
southeast corner of the figure shows the results for the
representative agent economy. In this model, as in [Mehra and
Prescott 1985], the only way to match the observed equity premium
is to increase the coefficient of relative risk aversion to a high
level.
The red line with diamonds shows the mean of the equity premium
and risk-free rate for the endogenous participation model of
[Alvarez et al. 2009] for different values of
![]() . With the benchmark value of
. With the benchmark value of
![]() , the participation rate
is close to 1, the average equity premium is zero, and the real
interest rate is about 4 percent. Raising
, the participation rate
is close to 1, the average equity premium is zero, and the real
interest rate is about 4 percent. Raising
![]() lowers the average participation
rate in financial markets; however, there is little change in the
average equity premium and real rate. Even if the participation
rate is as low as 15% (
lowers the average participation
rate in financial markets; however, there is little change in the
average equity premium and real rate. Even if the participation
rate is as low as 15% (
![]() ), the average equity
premium and real rate lie well outside the ellipse.
), the average equity
premium and real rate lie well outside the ellipse.
With
![]() in the benchmark
calibration of the endogenous rebalancing model, the average
household rebalancing cost is relatively small - less than 0.2
percent of average household consumption. In contrast, in the
endogenous participation model, large values of
in the benchmark
calibration of the endogenous rebalancing model, the average
household rebalancing cost is relatively small - less than 0.2
percent of average household consumption. In contrast, in the
endogenous participation model, large values of
![]() are necessary to induce
reasonable rates of stock market participation. For example, a
value of
are necessary to induce
reasonable rates of stock market participation. For example, a
value of
![]() implies that the average
participation rate is 40%, and the average participation cost is
more than 15% of average consumption.
implies that the average
participation rate is 40%, and the average participation cost is
more than 15% of average consumption.
Since the only difference between the endogenous rebalancing and
participation models is the presence of the non-state contingent
transfer plan ![]() , Figure 1 demonstrates the
critical role that this variable plays in the analysis. The top
panel of Figure 2 also shows that
the demand for this transfer plan is increasing in a household's
fixed cost. The function is increasing, because a household with a
higher fixed cost anticipates that she will rebalance her portfolio
allocation less frequently and therefore demand a larger value of
, Figure 1 demonstrates the
critical role that this variable plays in the analysis. The top
panel of Figure 2 also shows that
the demand for this transfer plan is increasing in a household's
fixed cost. The function is increasing, because a household with a
higher fixed cost anticipates that she will rebalance her portfolio
allocation less frequently and therefore demand a larger value of
![]() to help ensure against consumption
losses.
to help ensure against consumption
losses.
The transfer plan helps account for the level of the equity premium by driving up the volatility of active consumption. The middle panel of Figure 2 shows the standard deviation of consumption for different types of households in the endogenous rebalancing model. The consumption volatility of a household that frequently rebalances is about 4 times greater than a household that keeps its portfolio unchanged from her initial plan. This higher volatility of consumption for active households leads to a higher positive covariance between the return on equity and active consumption growth, which then translates into a higher average equity premium via expression (26).
The implication of the model regarding the consumption volatility of different household types appears to be in line with recent evidence provided by [Parker and Vissing-Jorgensen 2009]. Using data from the Consumer Expenditure (CEX) Survey, they found that the consumption of `high-consumption' households is more exposed to fluctuations in aggregate consumption (and income) than that of low-consumption households. In particular, they found that the exposure to changes in aggregate consumption growth of households in the top 10 percent of the consumption distribution is about five times that of households in the bottom 80 percent.
The lower panel of Figure 2 indicates that
active households have a higher level of consumption than inactive
households. In effect, households that rebalance more frequently
are trading off higher consumption volatility against a higher
level of consumption. The consumption of active households is more
volatile than the consumption of inactive households, because the
two aggregate shocks only affect the consumption of the latter type
of household through changes in labor income, while active
households experience fluctuations in both labor and capital
income. Later, we develop the intuition of this result more
formally using a version of the model in which ![]() is assumed to be the same for all households.
is assumed to be the same for all households.
3.3 Monetary Policy and Equity Prices
In the endogenous rebalancing model, monetary policy shocks can induce important fluctuations in equity prices and the equity premium. In this section, we investigate this relationship and compare our model's implications to the estimates of [Bernanke and Kuttner 2005].
Using high-frequency data on the federal funds rate, [Bernanke and Kuttner 2005] construct a measure of unanticipated changes in monetary policy. They find that a broad index of stock prices registers a gain of 1 percent in reaction to a 25 basis point easing of the federal funds rate. [Bernanke and Kuttner 2005] then use monthly data with a structural VAR to decompose the response of stock prices into three components: changes in current and expected future dividends, changes in current and expected future real interest rates, and changes in expected future excess equity returns or equity premia. While an unanticipated easing lowers interest rates, they conclude that an important channel in which increases in stock prices occur is through changes in equity premia or the perceived riskiness of stocks.
To compare the model's implications to their empirical results,
we compute impulse response functions. Since the model is
nonlinear, it is important to define how we construct these impulse
responses. Follow the discussion in [Hamilton 1994], we define the
impulse response of variable, ![]() , at date
, at date
![]() to a monetary innovation that occurs at
date
to a monetary innovation that occurs at
date ![]() as:
as:
| (28) |
Thus, an impulse response is defined as the revision in
expectations after a shock that occurs at date ![]() .
For log-linear models, equation (28) simplifies to
the usual analytical representation in which (up to a scaling
factor) the model's linear coefficients characterize the impulse
response function.
.
For log-linear models, equation (28) simplifies to
the usual analytical representation in which (up to a scaling
factor) the model's linear coefficients characterize the impulse
response function.
Figure 3 shows the impulse response of different economic variables to a decline in money growth. In the endogenous rebalancing model (the solid black line), the nominal interest rate increases 50 basis points on impact, and the real rate increase about 1 percentage point. Thus, as in the limited participation models of [Lucas 1990], [Fuerst 1992], and [Alvarez et al. 2002], the economy displays a liquidity effect. Moreover, the effect is persistent, as interest rates gradually fall back to their pre-shocked level. In line with [Bernanke and Kuttner 2005], equity prices fall about 1 percent on impact, with much of the decline reflecting a higher equity premium. On impact, the equity premium rises more than 1 percentage point, and its response mirrors that of equity prices.12
To understand why the model generates a sharp rise in the equity premium, the bottom left panel of Figure 3 shows the response of consumption of active households (rebalancers). The monetary contraction has no effect on output but has an important redistributive effect. It raises the consumption of non-active households, whose real money balances available for consumption increase, and lowers the consumption of those that choose to rebalance. This redistributive effect provides households with less incentive to rebalance their portfolios, which reduces the degree of risk-sharing amongst active households and helps push up the equity premium.
The blue dashed line shows the effects of the same increase in money growth in the endogenous participation model of [Alvarez et al. 2009]. This model does not generate a liquidity effect and there is very little movement in the equity premium. Accordingly, variation along the intensive margin (i.e., the frequency of rebalancing between checking and brokerage accounts) appears to be a more fruitful way of generating movements in the equity prices than the extensive margin (i.e., the number of financial market participants).
3.4 Understanding the Mechanism
To understand how endogenous changes in the number of
rebalancers can induce time-varying movements in risk, it is
helpful, for illustrative purposes, to assume that
![]()
![]() where
where ![]() is
given and that
is
given and that ![]() is distributed according to a
continuous, uniform distribution with
is distributed according to a
continuous, uniform distribution with
![]() . Under these
conditions, the model has a unique and closed form solution when
. Under these
conditions, the model has a unique and closed form solution when
![]() . In particular, equation (20) can be
rewritten as:
. In particular, equation (20) can be
rewritten as:
| (29) |
and the resource constraint can be rewritten as:
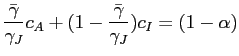 exp
exp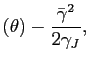
|
(30) |
where
![]() .13Equation (29) characterizes
the marginal household's decision to rebalance its portfolio (i.e.,
the type
.13Equation (29) characterizes
the marginal household's decision to rebalance its portfolio (i.e.,
the type
![]() household). We call the
schedule of the combination of values of
household). We call the
schedule of the combination of values of
![]() and
and ![]() the MR
curve in reference to the marginal rebalancer. The top panel of
Figure 4 shows
that this curve is a parabola with a minimum occurring at
the MR
curve in reference to the marginal rebalancer. The top panel of
Figure 4 shows
that this curve is a parabola with a minimum occurring at
![]() . For
. For
![]() , the state-contingent
transfer of an active household (i.e.,
, the state-contingent
transfer of an active household (i.e.,
![]() ) is positive, as is the cost
of transferring funds. A rise in the consumption of active
households, all else equal, makes it more attractive to make the
state contingent transfer, and thus for
) is positive, as is the cost
of transferring funds. A rise in the consumption of active
households, all else equal, makes it more attractive to make the
state contingent transfer, and thus for
![]() , the MR schedule is
increasing.
, the MR schedule is
increasing.
The second equation represents the combination of values of
![]() and
and
![]() that satisfy goods market
clearing, and can be used to express the fraction of rebalancers
(i.e.,
that satisfy goods market
clearing, and can be used to express the fraction of rebalancers
(i.e.,
![]() ) as a
function of their consumption. We call this schedule the GM curve
for goods market clearing. For
) as a
function of their consumption. We call this schedule the GM curve
for goods market clearing. For
![]() where
where
![]() , the top
panel of Figure 4 shows that this
curve is downward sloping. This reflects that an increase in
, the top
panel of Figure 4 shows that this
curve is downward sloping. This reflects that an increase in
![]() raises the average level of
transaction costs in the economy, reducing real resources, and
lowering the consumption of rebalancers.
raises the average level of
transaction costs in the economy, reducing real resources, and
lowering the consumption of rebalancers.
Figure 4 displays the equilibrium in the endogenous rebalancing model as the
intersection of these two curves. In the endogenous rebalancing
model, this intersection occurs at a point in which
![]() , though consumption of a
rebalancer is not much higher than the consumption of a
non-rebalancer, reflecting
, though consumption of a
rebalancer is not much higher than the consumption of a
non-rebalancer, reflecting ![]() . In contrast,
the bottom panel of Figure 4 shows that the
equilibrium in the endogenous participation model (
. In contrast,
the bottom panel of Figure 4 shows that the
equilibrium in the endogenous participation model (![]() ) occurs at a point in which active consumption is much
higher than inactive consumption (given by the vertex of the
parabola). The equilibrium financial market participation rate
shown in the bottom panel is also much higher than the rate of
rebalancing that occurs in equilibrium in the top panel.
) occurs at a point in which active consumption is much
higher than inactive consumption (given by the vertex of the
parabola). The equilibrium financial market participation rate
shown in the bottom panel is also much higher than the rate of
rebalancing that occurs in equilibrium in the top panel.
3.4.1 Technology Shocks
This difference in the equilibrium positions of the two
economies has important implications for the volatility of the
consumption of active households and therefore the equity premium.
To demonstrate this using our illustrative example, the upper panel
of Figure 5
displays the effects of a deterministic increase in technology on
the equilibrium allocations implied by equations (29) and (30). An increase in
technology shifts the GM curve upward and to the right, as the
economy's resources expand. The MR curve shifts to the right, as
the wage income of non-rebalancers rises. This boosts the
consumption of non-rebalancers from ![]() to
to
![]() .
.
With the initial equilibrium occurring near the minimum of the parabola, there is a large increase in the consumption of rebalancers that exceeds both the increase in non-rebalancer consumption and technology. This large increase reflects that the technology shock, by raising the return on equity, also involves a redistribution away from non-rebalancers to rebalancers. While this redistribution occurs in the endogenous participation model, its effects on active consumption are modest, given that the initial equilibrium is at a point at which the MR curve is relatively steep. Accordingly, Figure 5 demonstrates that active consumption in the endogenous rebalancing model will be considerably more volatile than active consumption in the participation model.
3.4.2 Monetary Policy Shocks
To understand why a monetary contraction induces an increase in
the equity premium, it is helpful to consider the effect of a
deterministic change in money growth on the GM and MR schedules.
The lower panel of Figure 5 shows the
effects of a small decrease in the money growth rate. This decrease
shifts the GM curve to the left, since the consumption of
rebalancers falls for a fixed
![]() . In addition, higher
consumption of the non-rebalancers (which occurs at the minimum of
the parabola) shifts the MR curve downward and to the right,
implying that the benefit to making the state-contingent transfer
has gone down. Hence, the deterministic fall in money growth leads
to an equilibrium with both lower consumption of active rebalancers
and a smaller fraction of rebalancers.
. In addition, higher
consumption of the non-rebalancers (which occurs at the minimum of
the parabola) shifts the MR curve downward and to the right,
implying that the benefit to making the state-contingent transfer
has gone down. Hence, the deterministic fall in money growth leads
to an equilibrium with both lower consumption of active rebalancers
and a smaller fraction of rebalancers.
With the decrease in money growth occurring from an initial equilibrium close to the minimum of the parabola, a small monetary contraction may induce a relatively large fall in the consumption of rebalancers. However, this effect diminishes as the monetary shock becomes larger, reflecting the concavity of the MR schedule. Near the initial equilibrium, small declines in monetary growth induce relatively large decreases in consumption, while larger declines have a proportionately smaller effect on consumption.
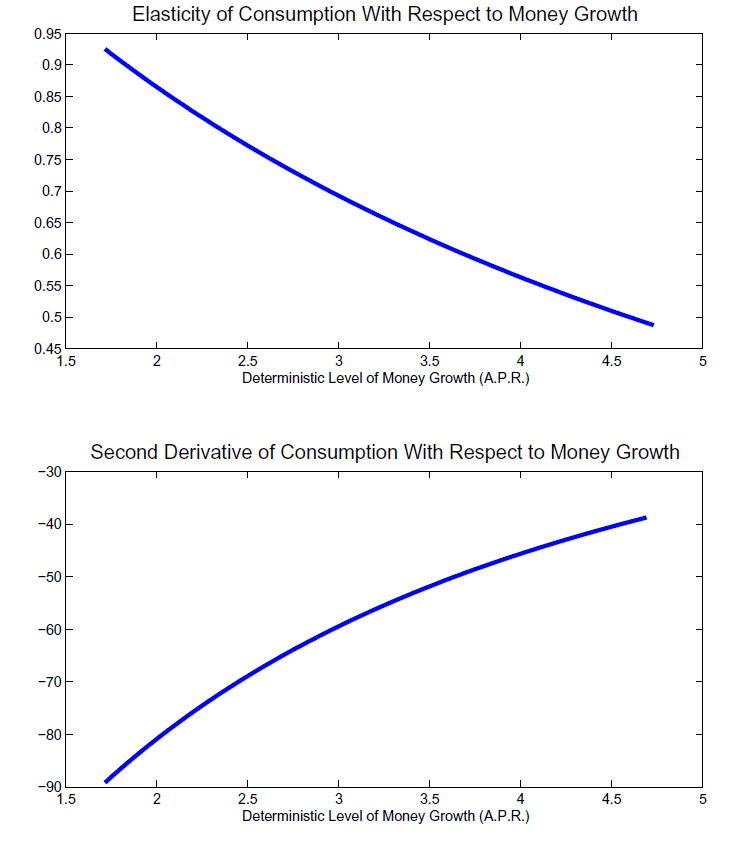
Building on this analysis, the top two panels of Figure 6 show the first
and second derivatives of the logarithm of active consumption with
respect to the logarithm of money growth. The top panel shows that
the first derivative (i.e.,
![]() ) is
positive and decreasing, reflecting that higher money growth boosts
active consumption but by progressively less. The middle panel
shows that the second derivative is a large, negative number,
reflecting the high degree of concavity of active consumption. In
addition, the second derivative is increasing in money growth,
implying that larger increases in money growth have a
proportionately smaller effect on risk.
) is
positive and decreasing, reflecting that higher money growth boosts
active consumption but by progressively less. The middle panel
shows that the second derivative is a large, negative number,
reflecting the high degree of concavity of active consumption. In
addition, the second derivative is increasing in money growth,
implying that larger increases in money growth have a
proportionately smaller effect on risk.
This nonlinearity drives the endogenous fluctuations in risk in our model. An increase in money growth reduces the sensitivity of active consumption to expected future changes in money growth, as the fraction of active rebalancers increases. Thus, for higher rates of money growth, active consumption growth becomes less volatile and its covariance with the return on equity diminishes, leading to a decline in the equity premium.
4 Conclusions
We have developed a dynamic stochastic general equilibrium model in which aggregate shocks affect the economy through movements in risk. Our model is an extension of a neoclassical framework in which asset and goods markets are segmented from each other. We view this model as the next link in the chain beginning with [Lucas 1990] and recently extended by [Alvarez et al. 2002]. We depart from the former in two important respects. First, we explicitly model a production economy with equity returns. Second, we emphasize endogenous asset segmentation along an intensive margin (i.e., portfolio rebalancing decision) rather than along an extensive margin (i.e., participation decision). Through this mechanism, we are able to account for the average excess returns on equity, countercyclical movements in risk, and, in line with the evidence of [Bernanke and Kuttner 2005], a monetary easing can lead to a decline in the equity premium.
A natural extension of this paper will be to incorporate endogenous capital and labor supply considerations to examine whether the model can account for key features of both asset prices and business cycles.
References
Abel, A. B., J. C. Eberly, and S. Panageas (2007). Optimal Inattention to the Stock Market and Information Costs and Transaction Costs. mimeo, Wharton School of the University of Pennsylvania.
Alvarez, F., A. Atkeson, and P. Kehoe (2007). If Exchange Rates are Random Walks, Then Almost Everything we Say About Monetary Policy is Wrong. American Economic Review 97, 339-345.
Alvarez, F., A. Atkeson, and P. Kehoe (2009). Time-Varying Risk, Interest Rates, and Exchange Rates in General Equilibrium.The Review of Economic Studies. forthcoming.
Alvarez, F., A. Atkeson, and P. J. Kehoe (2002). Money, Interest Rates, and Exchange Rates with Endogenously Segmented Markets. Journal of Political Economy 110, 73-112.
Ameriks, J. and S. P. Zeldes (2004). How Do Household Portfolio Shares Vary with Age? mimeo, Columbia University.
Bacchetta, P. and E. van Wincoop (2009). Infrequent Portfolio Decisions: A Solution to the Forward Discount Puzzle. American Economic Review. Forthcoming.
Bernanke, B. and K. Kuttner (2005). What Explains the Stock Market’s Reaction to Federal Reserve Policy? Journal of Finance LX, 1221-1257.
Bilias, Y., D. Georgarakos, and M. Haliassos (2008). Portfolio Inertia and Stock Market Fluctuations. CFS Working Paper 2006/4. Revised July 2008.
Boldrin, M., L. J. Christiano, and J. D. Fisher (1997). Habit Persistence and Asset Returns in an Exchange Economy. Macroeconomic Dynamics 1, 312-332.
Bonaparte, Y. and R. Cooper (2009). Costly Portfolio Adjustment. National Bureau of Economic Research Working Paper 15227.
Brunnermeier, M. and S. Nagel (2008). Do Wealth Fluctuations Generate Time-Varying Risk Aversion? Micro-Evidence from Individuals Asset Allocation. American Economic Review 98, 713-736.
Calvet, L. E., J. Y. Campbell, and P. Sodini (2009a). Fight or Flight? Portfolio Rebalancing by Individual Investors. Quarterly Journal of Economics 124, 301-348.
Calvet, L. E., J. Y. Campbell, and P. Sodini (2009b). Measuring the Financial Sophistication of Households. American Economic Review 99, 393-398.
Campbell, J. Y. (1999). Asset Prices, Consumption, and the Business Cycle. In J. B. Taylor and M. Woodford (Eds.), Handbook of Macroeconomics. North-Holland, Amsterdam.
Fuerst, T. S. (1992). Liquidity, Loanable Funds, and Real Activity. Journal of Monetary Economics 29, 3-24.
Gabaix, X. and D. Laibson (2001). The 6D Bias and the Equity-Premium Puzzle. In B. Bernanke and J. Rotemberg (Eds.), NBER Macroeconomics Annual. MIT Press.
Gomes, F. and A. Michaelides (2006). Asset Pricing with Limited Risk Sharing and Heterogeneous Agents. mimeo, London School of Economics.
Gust, C. and D. López-Salido (2009). Monetary Policy, Velocity, and the Equity Premium. Centre for Economic Policy Research Discussion Paper No. 7388.
Guvenen, F. (2005). A Parsimonious Macroeconomic Model for Asset Pricing: Habit Formation or Cross-sectional Heterogeneity? mimeo, University of Rochester.
Guvenen, F. (2009). A Parsimonious Macroeconomic Model for Asset Pricing. Econometrica. forthcoming.
Hall, R. (2008). Sources and Mechanisms of Cyclical Fluctuations in the Labor Market. mimeo, Stanford University.
Hamilton, J. D. (1994). Time Series Analysis. Princeton, NJ: Princeton University Press.
Judd, K. L. (1999). Numerical Methods in Economics. Cambridge, MA: The MIT Press.
Lucas, R. E. (1990). Liquidity and Interest Rates. Journal of Economic Theory 50, 237-264.
Lynch, A. (1996). Decision Frequency and Synchronization Across Agents: Implications for Aggregate Consumption and Equity Returns. Journal of Finance LI, 1479–-1497.
Marshall, D. and N. Parekh (1999). Can Costs of Consumption Adjustment Explain Asset Pricing Puzzles? Journal of Finance LIV, 623-654.
Mehra, R. and E. Prescott (1985). The Equity Premium Puzzle. Journal of Monetary Economics 15, 145-166.
Parker, J. and A. Vissing-Jorgensen (2009). Who Bears Aggrgate Fluctuations and How? American Economic Review 99, 399-405.
Polkovnichenko, V. (2004). Limited Stock Market Participation and the Equity Premium. Finance Research Letters 1, 24-34.
Reis, R. (2006). Inattentive Consumers. Journal of Monetary Economics 53, 1761-1800.
Souleles, N. S. (2003). Household Portfolio Choice, Transactions Costs, and Hedging Motives. mimeo, University of Pennsylvania.
Vissing-Jorgensen, A. (2002). Towards an Explanation of Household Portfolio Choice Heterogeneity: Non-Financial Income Participation Costs Structures. National Bureau of Economic Research Working Paper 8884.
Vissing-Jorgensen, A. (2003). Perspectives on Behavioral Finance: Does ‘Irrationality’ Disappear with Wealth? Evidence from Expectations and Actions. In M. Gertler and K. Rogoff (Eds.), NBER Macroeconomics Annual. MIT Press.
Figure 1: Endogenous Rebalancing and the Equity Premium
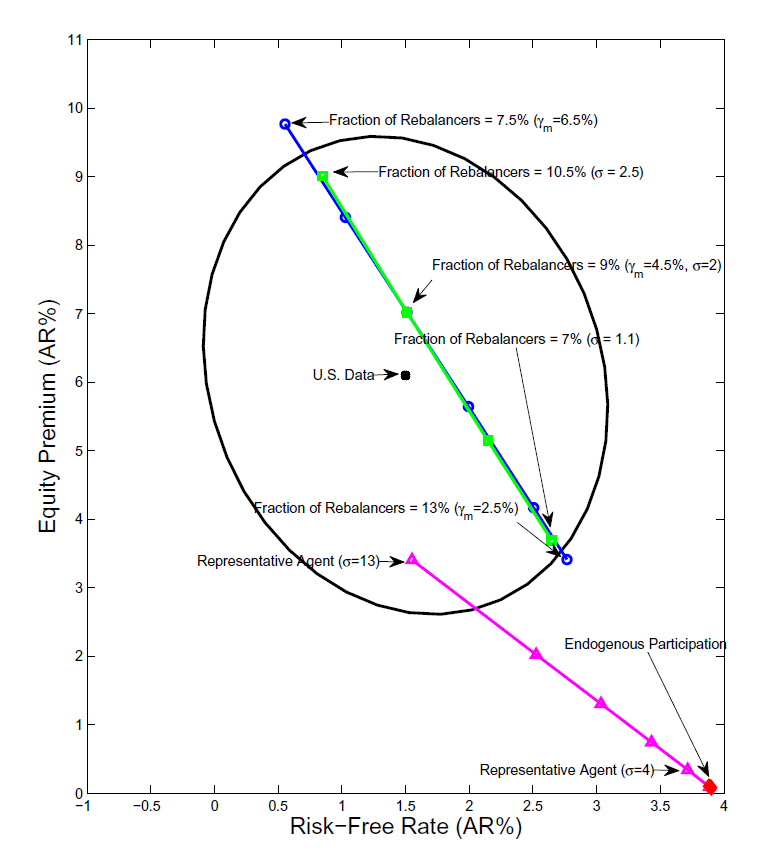
Figure 2: The Non-State Contingent Transfer Plan and Consumption Across Households
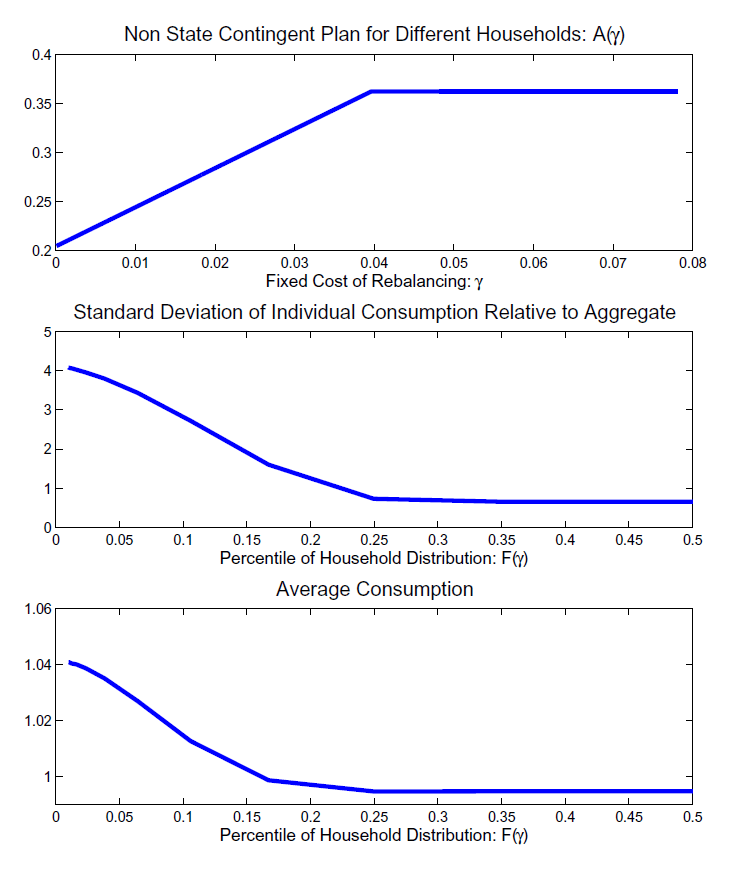
Figure 3: Impulse Response to a Contractionary Monetary Shock (Deviation from Date 0 Expectation of a Variable)
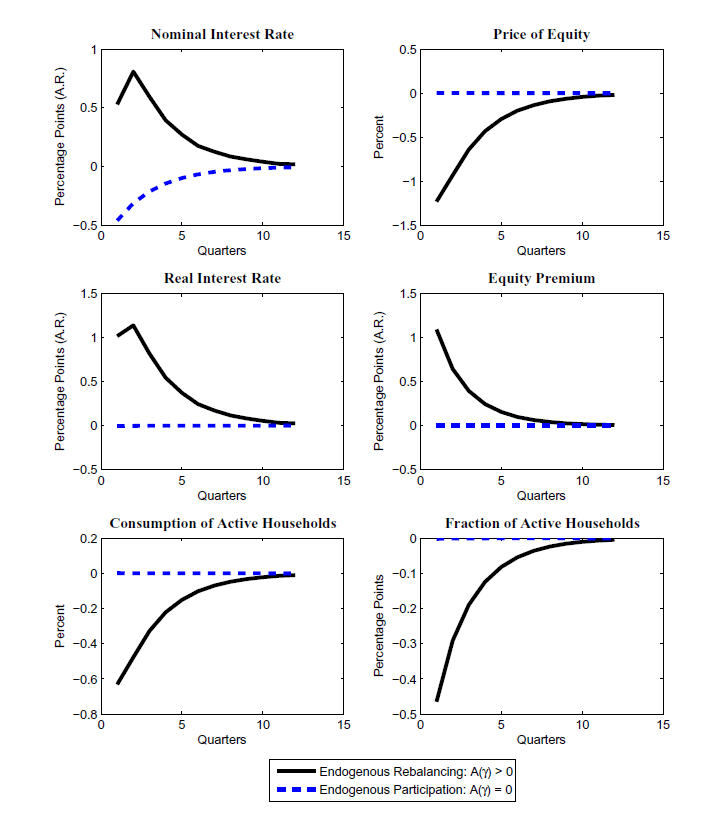
Figure 4: Equilibrium in the Two Models
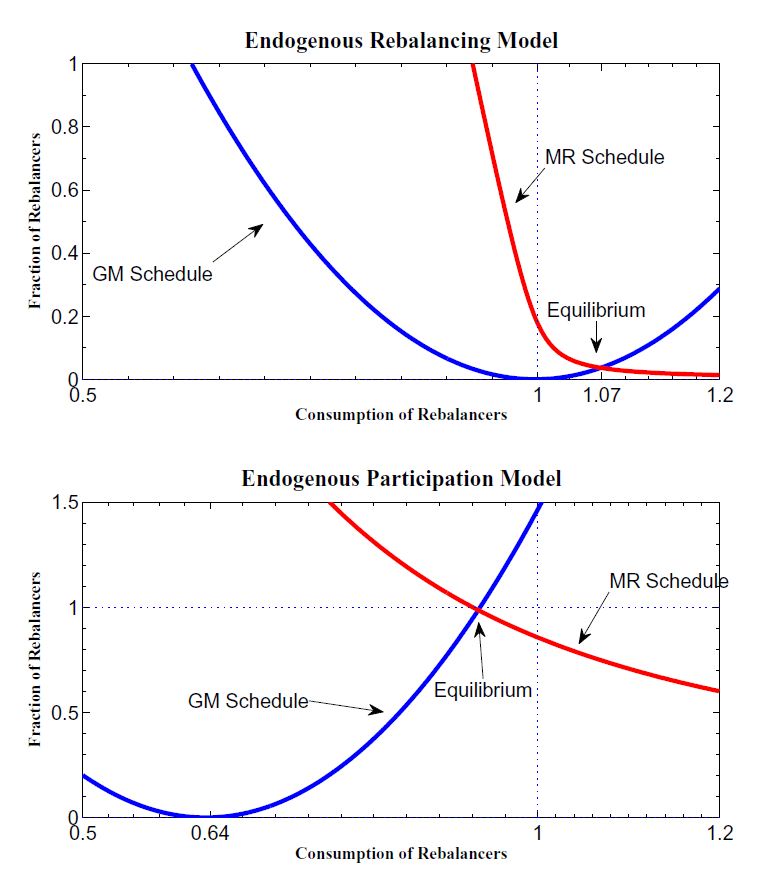
Figure 5: Deterministic Changes in the Rebalancing Model
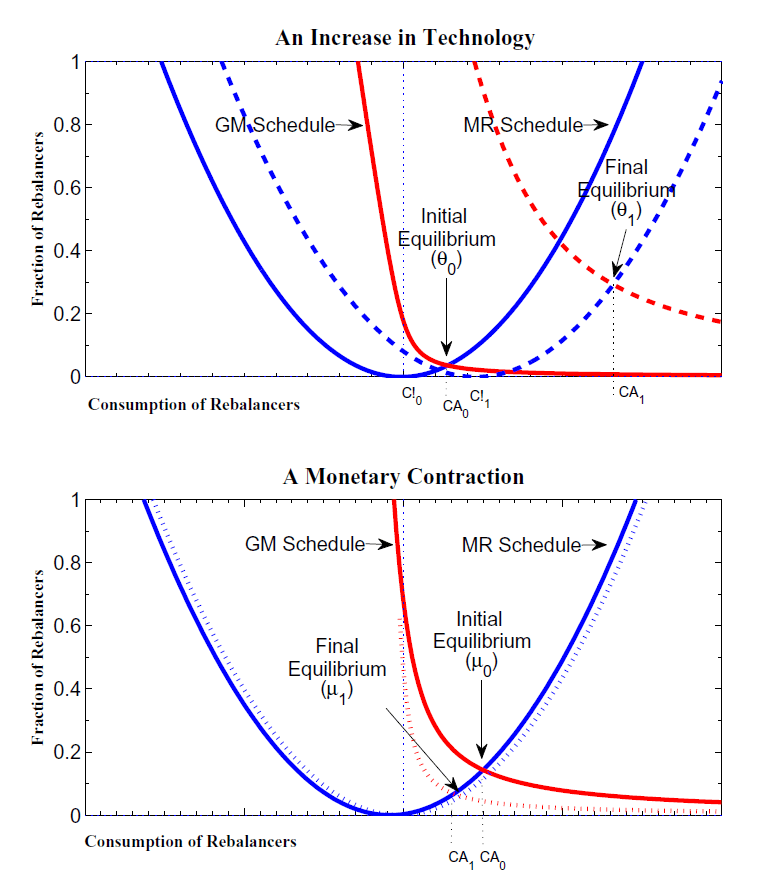
Figure 6: The Shape of Active Consumption
Appendix
In this appendix, we briefly describe how the model is modified to
incorporate occasionally binding cash constraints for households.
We then compare selected model statistics for the endogenous
rebalancing model to the endogenous participation model when these
constraints only bind occasionally. [Gust and López-Salido
2009] provide a more detailed treatment of this version of the
model and its implications. To incorporate the possibility that a
household may choose to save cash in its brokerage account, we
denote
![]() as cash saved for transactions
next period and rewrite a household's flow of funds in her
brokerage account at date 0 as:
as cash saved for transactions
next period and rewrite a household's flow of funds in her
brokerage account at date 0 as:
|
(A.1) |
A household's flow of funds in her brokerage account at future dates is given by:
| (A.2) | |||
![$\displaystyle \hspace{1cm} \int_{s_{t+1}}q(s^{t},s_{t+1})B(s^{t},s_{t+1},\gamma )ds_{t+1} + P(s^t)[x(s^{t},\gamma )+ \gamma ]z(s^{t},\gamma ).$](img239.gif)
|
Each household will choose not to store excess cash in its
brokerage account if the nominal interest rate, ![]() , is positive, where the nominal interest rate is given
by:
, is positive, where the nominal interest rate is given
by:
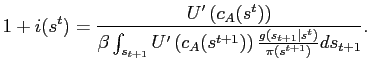
|
(A.3) |
If the nominal interest rate reaches its zero lower bound (ZLB),
then households may carry excess cash in their brokerage accounts.
In this case, the ZLB constraint can be used to determine an
equilibrium value for
![]() ,
,
![]() , as each household faces the
same first order condition regarding its choice of
, as each household faces the
same first order condition regarding its choice of
![]() . A household may also choose
to save extra cash in her checking account as a form of
precautionary savings. In this case, we can rewrite a household's
evolution of cash in her checking account as:
. A household may also choose
to save extra cash in her checking account as a form of
precautionary savings. In this case, we can rewrite a household's
evolution of cash in her checking account as:
| (A.4) |
where
![]() denotes excess cash used for
future consumption instead of consumption today. Thus, a
household's cash in her checking account at the end of period
denotes excess cash used for
future consumption instead of consumption today. Thus, a
household's cash in her checking account at the end of period
![]() is given by:
is given by:
| (A.5) |
A household will not carry excess cash in its checking account if:
![$\displaystyle \frac{U'\left(c_A(s^t)\right) z(s^t,\gamma) + U'\left(c_I(s^t,\gamma)\right) \left(1-z(s^t,\gamma))\right)}{\beta \int_{s_{t+1}} \left[ U'\left(c_A(s^{t+1})\right) z(s^{t+1},\gamma) + U'\left(c_I(s^{t+1},\gamma)\right) \left(1-z(s^{t+1},\gamma)\right) \right] \frac{g(s_{t+1}\vert s^t)}{\pi(s^{t+1})} ds_{t+1}} > 1.$](img249.gif)
|
(A.6) |
This condition states that in states of the world in which
consumption is low relative to expected discounted future
consumption a household will not save excess cash but use it for
consumption today. However, this condition can be violated in
states of the world in which a household's consumption today is
high. In that case, equation (A.6) will
hold as a strict equality and can be used to determine a
household's excess cash,
![]() . For a household that
always rebalances, equation (A.6)
simplifies to
. For a household that
always rebalances, equation (A.6)
simplifies to
![]() , and for such a household
carrying excess cash in their checking account is irrelevant.
, and for such a household
carrying excess cash in their checking account is irrelevant.
In equation (A.6), the consumption of an inactive household needs to reflect that she may hold excess cash in her checking account:
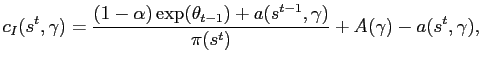
|
(A.7) |
while consumption of active households still satisfies equation (18), which equates consumption across active households. In equilibrium, inflation now must reflect that velocity is non-constant so that
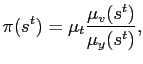
|
(5.9) |
where
![]() ,
,
![]() ,
and
,
and
![$\displaystyle V(s^t) \equiv \frac{P(s^t)Y(s^t)}{M_t} = \frac{Y(s^t)}{Y(s^t) + \sum^{J}_{j=1} \left[ a(s^{t},\gamma_j )+ N(s^{t},\gamma_j ) \right]f(\gamma_j)}.$](img256.gif)
|
(5.10) |
The expression for velocity implies that in states of the world in
which all households do not store excess cash, velocity will be a
constant equal to unity. However, velocity will be less than one in
states in which one or more household chooses to hold excess cash.
In the above expression for velocity, we have modified the
distribution of household types, ![]() so that it
is discrete where
so that it
is discrete where
![]() .14 This
assumption reflects that with each household potentially holding
excess cash, there are as many state variables in the model as
household types. Accordingly, we use a discrete distribution of
types to help avoid the "curse of dimensionality''. With a
discrete number of household types, there is not necessarily a
marginal household satisfying equation (20). Instead, a
household with type
.14 This
assumption reflects that with each household potentially holding
excess cash, there are as many state variables in the model as
household types. Accordingly, we use a discrete distribution of
types to help avoid the "curse of dimensionality''. With a
discrete number of household types, there is not necessarily a
marginal household satisfying equation (20). Instead, a
household with type ![]() will choose to be
active if:
will choose to be
active if:
| (5.11) |
and inactive otherwise. The second column of Table 1 shows selected
statistics from the endogenous rebalancing model with three types
of households: one that always rebalances (
![]() ), another that frequently
rebalances (
), another that frequently
rebalances (
![]() ), and a type that rarely
rebalances (
), and a type that rarely
rebalances (
![]() ).15 These three types are
distributed so that there are a large mass of households who rarely
rebalance (
).15 These three types are
distributed so that there are a large mass of households who rarely
rebalance (
![]() ), a moderate mass of
frequent rebalancers (
), a moderate mass of
frequent rebalancers (
![]() ), and a smaller mass of
households that always rebalance (
), and a smaller mass of
households that always rebalance (
![]() ). As shown in Table 1, this
calibration implies that 20 percent of households rebalance their
portfolios in a quarter and as discussed in the introduction is
broadly in line with the micro evidence from the household finance
literature that provides strong support for infrequent portfolio
rebalancing.
). As shown in Table 1, this
calibration implies that 20 percent of households rebalance their
portfolios in a quarter and as discussed in the introduction is
broadly in line with the micro evidence from the household finance
literature that provides strong support for infrequent portfolio
rebalancing.
While the average fraction of households that
rebalance in a quarter is somewhat higher than when the households
are distributed log-normally, the average equity premium and
average risk-free rate at 5.4% and and 0.7%, respectively, are well
within the confidence ellipse shown in Figure 1. Households that
never rebalance (![]() ) and households that rarely
rebalance (
) and households that rarely
rebalance (![]() ) do not hold excess cash in
their checking accounts. Households that frequently rebalance
(
) do not hold excess cash in
their checking accounts. Households that frequently rebalance
(![]() ) hold excess cash in their checking
accounts less than 1% of the time. In contrast, the ZLB constraint
binds about 15% of the time, resulting in households occasionally
carrying excess cash in their brokerage accounts. Still, the
results for the average equity premium and risk-free rate are quite
similar to the results for the version of the model in which the
ZLB constraint is ignored. Gust and López-Salido (2009) also
show that the response of equity prices, the equity premium, and
nominal interest rates after a monetary shock is qualitatively
similar in this version of the model to those discussed in Figure
3. In
particular, there is still a liquidity effect and a relatively
large decrease (increase) in the equity premium following a
monetary injection (contraction). Gust and López-Salido
(2009) also emphasize the procyclical movements in velocity shown in
Table 1, which
occurs because demand for liquidity surges in very bad states of
the world. In such states, there is heightened risk, and
precautionary savings drive down the economy's nominal rate to its
lower bound.
) hold excess cash in their checking
accounts less than 1% of the time. In contrast, the ZLB constraint
binds about 15% of the time, resulting in households occasionally
carrying excess cash in their brokerage accounts. Still, the
results for the average equity premium and risk-free rate are quite
similar to the results for the version of the model in which the
ZLB constraint is ignored. Gust and López-Salido (2009) also
show that the response of equity prices, the equity premium, and
nominal interest rates after a monetary shock is qualitatively
similar in this version of the model to those discussed in Figure
3. In
particular, there is still a liquidity effect and a relatively
large decrease (increase) in the equity premium following a
monetary injection (contraction). Gust and López-Salido
(2009) also emphasize the procyclical movements in velocity shown in
Table 1, which
occurs because demand for liquidity surges in very bad states of
the world. In such states, there is heightened risk, and
precautionary savings drive down the economy's nominal rate to its
lower bound.
Table 1: Statistics from Model Economies
Note: The equity premium, the real rate, and the standard deviation of consumption are expressed at an annual percentage rate.
| Endogenous Rebalancing | Endogenous Participation | Representative Agent | |
|---|---|---|---|
|
| 5.4 | 0.5 | 0.4 |
| 0.7 | 3.7 | 3.7 | |
|
| 3.4 | 3.8 | 3.5 |
|
| 1.08 | 1.75 | 1 |
|
| 3.8 | 1.09 | 1 |
| Percent of Active Types | 20.0 | 28.8 | 100 |
| Average Fixed Cost (% of GDP) | 0.26 | 8.8 | 0 |
| 0.23 | 0 | 0 | |
| Percent of Time at ZLB | 15.7 | 0 | 0 |
| Percent of Time
| 0.2 | 0 | 0 |
| Percent of Time
| 0.0 | 0 | 0 |
|
| 0.25 | 0 | 0 |
|
| 0.35 | 0 | 0 |
Footnotes
1. We thank Orazio Attanasio, Gianluca Benigno, Martin Bodenstein, V.V. Chari, John Driscoll, Mike Dotsey, Luca Guerrieri, Pat Kehoe, Narayana Kocherlakota, Sylvain Leduc, Andy Levin, Ricardo Nunes, Victor Rios-Rull, Harald Uhlig, Annette Vissing-Jørgensen, Mike Woodford, and seminar participants at the Bank of Spain, Federal Reserve Board, Georgetown University, International Monetary Fund, and the Federal Reserve Banks of Minneapolis and San Francisco for useful comments. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
2.Corresponding Author: Christopher Gust. Email: [email protected], [email protected]. Return to text
3. See [Alvarez et al. 2007] for an extended discussion of this point. In a companion paper, [Alvarez et al. 2009] argue that the evidence on the relationship between interest rates and exchange rates is consistent with movements in these variables that are driven mainly by changes in conditional variances. Return to text
4. See, Figure F.7, "Disposition of Proceeds from most recent sale of individual stocks", in ICI 2005. Return to text
5. [Polkovnichenko 2004], [], [], and [Gomes and Michaelides 2006] also show that it is difficult to match the equity premium in a model with endogenous stock market participation. [Guvenen 2005] considers a model in which stock market participation is fixed exogenously and shows that this feature in addition to heterogeneity in preferences can help account for the average equity premium. Return to text
6. Also, see [Lynch 1996], [Marshall and Parekh 1999], [Gabaix and Laibson 2001], and more recently, [Bacchetta and van Wincoop 2009] and [Bonaparte and Cooper 2009]. Return to text
7. See also [Reis 2006], who uses a rational inattentive framework to explain the excess sensitivity of consumption to past information and its excess smoothness to permanent income shocks. Return to text
8. The non-state contingent plan would also need to be time-varying if we incorporated deterministic growth in technology. It is relatively straightforward to do so, and incorporating growth in this way would not alter our conclusions. Return to text
9. See, for example, [Souleles 2003] and [Ameriks and Zeldes 2004]. Return to text
10. A household can reoptimize by setting
![]() , thereby transferring
additional cash from her checking to brokerage account. Similarly,
a household is free to choose
, thereby transferring
additional cash from her checking to brokerage account. Similarly,
a household is free to choose
![]() . Return to text
. Return to text
11. For the version of the model
discussed in the appendix, which uses a discrete distribution over
![]() , we find a somewhat higher range of
between 18% to 24% for the average fraction of rebalancers. See
Table 1 in the
appendix. Return to text
, we find a somewhat higher range of
between 18% to 24% for the average fraction of rebalancers. See
Table 1 in the
appendix. Return to text
12. The increase in stock prices also reflects the decline in real rates. Dividends in our model are simply a function of technology and do not change in response to the monetary innovation. Return to text
13. Given our assumptions, the equations
determining the equilibrium are static, and we simplify our
notation, ignoring that these variables depend on ![]() . Return to text
. Return to text
14. To derive the expression for velocity, we used the resource constraint, a household's cash constraint in her checking account, and the money market clearing condition modified to incorporate excess cash holdings by households. Return to text
15. For this calibration, we also assumed that the technology and monetary shock are governed by finite-state, symmetric Markov chains that are designed to well approximate AR(1) processes. See [Gust and López-Salido 2009] for details. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text