
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 985, December 2009 --- Screen Reader
Version*
Executive Compensation and Earnings Management Under Moral Hazard1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper analyzes executive compensation in a setting where managers may take a costly action to manipulate corporate performance, and whether managers do so is stochastic. We examine how the opportunity to manipulate affects the optimal pay contract, and establish necessary and sufficient conditions under which earnings management occurs. Our model provides a set of implications on the role earnings management plays in driving the time-series and cross-sectional variation of executive compensation. In addition, the model's predictions regarding the changes of earnings management and executive pay in response to corporate governance legislation are consistent with empirical observations.
Keywords: Earnings management, executive compensation, optimal contract, corporate governance
JEL classification: D82, D86, G38, J31
1 Introduction
The lack of adequate and accurate information in financial markets has played a significant role in enlarging the current economic downturn.3 In particular, Lehman Brothers announced that its capital position was "strong" just days before it filed for bankruptcy. The mortgage giants Freddie Mac, and to a lesser extent Fannie Mae, were found to be playing games with their accounting and ultimately led to the largest-ever financial rescue until then.4 Executive pay structures' role in the financial meltdown has also raised increased academic attention and regulatory scrutiny.5 The primary role of financial reporting to provide executives with a credible means of communicating their private information on firms' performance often become entangled with executives' desire to maximize their own compensation. Such motives give rise to the phenomenon of earnings management, defined as intentional manipulation of reported earnings by knowingly choosing accounting methods and estimates that do not accurately reflect the firm's underlying fundamentals. This paper analyzes the implication of earnings management for executive compensation contracts, and sheds light on regulation and reform of pay practices.
We depart from the existing literature in that the manager in the model may take a costly action to distort the firm's reported performance in order to maximize his compensation, and whether the manager has such an opportunity is stochastic. The principal takes into account the possibility of manipulation but fails to perfectly infer the value of true earnings, because of the uncertainty about the manager's ability to manipulate. In the same spirit as Dye (1988), in our setting the Revelation Principle is not applicable, because the message space is limited to a single-dimensional signal while the privately-informed agent receives multiple dimensions of information. The stochastic opportunity to manipulate breaks down the direct mapping between actual earnings and reported earnings, obscuring the true performance under the optimal contract.
A key insight of our model is that an increase in the possibility of manipulation actually calls for executive pay to be more responsive to reported performance. In our optimal contracting model, the potential to artificially inflate performance serves as insurance for managers against a low compensation payoff and thus weakens incentives to exert costly effort. A more high-powered compensation scheme is therefore necessary to incentivize effort when earnings management is possible. In a closely related paper, Goldman and Slezak (2006) also consider an agency problem in which compensation structure is determined so as to strike a balance between effort and manipulation. They allow market participants to correctly gauge the manager's reporting choice and predict that the pay-performance sensitivity is lower than it would be in the absence of possibility of manipulation. In sharp contrast, we analyze an environment where earnings management is not fully unraveled by a rational and sophisticated principal, and produce the opposite implication.
Our simple model of manipulation helps understand the time series and cross sectional variation of executive pay structure. In the time-series data, companies' management of earnings and the use of performance-based compensation both trended upwards since the late 1980s until the passage of the Sarbanes-Oxley Act (SOX) (Hall and Liebman 1998; Murphy 1999; Brown 2001; Bartov et al. 2002; Lopez and Rees 2002; Cohen et al. 2005). Gao and Shrieves (2002) and Bergstresser and Philippon (2006) also provide evidence that firms with a higher level of earnings management are the firms with more incentive pay in the cross section. While the positive association between misreporting and incentive pay has been mostly interpreted as evidence of suboptimality, we show that it could be consistent with optimal contracting and need not reflect inefficiency. Another direct and testable implication of our model is that the use of performance pay is more intensive in the industries with more opportunities for manipulation. For example, by virtue of having more intangible assets, managers in the financial sector have more leeway in financial reporting and more opportunities for managerial manipulation than those in the traditional manufacturing sector. The observation that pay-for-performance is substantially strong in financial industry lends support to our model.
This paper also provides implications for the change of compensation structure in response to tightened corporate governance legislation. We model the cost managers incur when manipulating earnings as a policy parameter. This manipulation cost can represent a collection of parameters influenced by monitoring technology and regulatory mechanisms, including the probability of detection, the amount of penalty upon detection, and the cost involved in manipulating financial reports. The manipulation cost may vary according to the effectiveness of regulation, or in the cross section according to the strength of internal control systems over financial reporting. When the manipulation cost increases due to more stringent corporate governance, in an environment where managerial effort positively influences output, the manager has stronger incentives to exert productive effort in order to avoid unfavorably high manipulation costs in financial reporting. As a result, less monetary incentive is required in the compensation contract to motivate effort. This implication is compatible with the empirical finding that firms responded to the additional liabilities SOX imposed on executives by reducing the proportion of incentive compensation (Cohen et al. 2004 and Narayanan and Seyhun 2005). Similar to our argument, a recent paper by Agrawal and Nasser (2009) finds empirically that blockholders and incentive pay are substitutes. Another implication derived from the model is that earnings management is less widespread in a more litigious corporate governance environment. Cohen et al. (2005) and Narayanan and Seyhun (2005) present evidence that earnings management diminished abruptly after the passage of SOX.
A final feature of the model that deserves mention is the identification of the condition for earnings management to emerge under the optimal contract. The paper shows that earnings management arises, at least in part, due to the substitutability of financial manipulation for managerial effort in enhancing reported performance and hence executive pay. If the manipulation cost is small compared to the manager's cost of expending effort, it becomes prohibitively difficult to elicit the truth while maintaining managerial incentives to put forth effort, and earnings management emerges endogenously under the optimal contract. A similar tradeoff is also discussed in Goldman and Slezak (2006), and our result is complementary to theirs. The substitutability of earnings management and productive effort in enhancing executive pay illustrated in the model adds new perspectives to the ongoing debate on regulation of managerial compensation: the aforementioned conflict presents a tradeoff between weakened firm-wide efficiency versus improved economy-wide efficiency. On one hand, restrictions like pay cuts or caps on executive compensation make it more difficult to induce effort and hence weaken corporate performance by adding additional constraints to the compensation design problem. On the other hand, the model suggests that regulation can be optimal from an efficiency viewpoint. Suppose that companies inflating their performance show seemingly stronger financial statements than honest firms, and therefore attract more capital from investors. Restrictions on executive compensation discourage manipulation and are likely to improve capital allocation across firms, helping direct the resources in the economy to the most efficient use.
In the contracting literature with manipulation, Hertzberg (2004) and Peng and Roell (2009) analyze the interplay of short-term and long-term incentives with a central focus on asset price efficiency. Abstracting away from market efficiency, our focus on costly manipulation in an agency model has antecedents in Lacker and Weinberg (1989), which examines optimal contracts under costly state falsification. Lacker and Weinberg (1989) investigate the main properties of optimal no-falsification contracts. A recent paper by Edmans et al. (2009) further derives a dynamic compensation contract that implements truthful reporting. Among the papers that deliver earnings management in the equilibrium, Crocker and Slemrod (2007) considers an alternative environment where the Revelation Principle can be applied and actual earnings can be unambiguously recovered by inverting the reporting function. However, in our problem the principal faces uncertainty over whether earnings management occurs. There is a second dimension of private information the manager possesses in our model, and hence the reporting function is no longer invertible. Similar to Crocker and Slemrod (2007), Goldman and Slezak (2006) also consider an equilibrium in which the firm's performance is adjusted to fully correct for the bias in the manipulated reports. Our results differ with respect to how pay-performance sensitivities vary with the potential for manipulation and the change of public policies.
The rest of the paper proceeds as follows. Section 2 lays out the principal-agent model. Section 3 shows general results and relevant properties of the optimal compensation contract with manipulation. Section 4 illustrates model implications for analysis and interpretations of empirical observations. Section 5 presents concluding remarks.
2 Model
2.1 Assumptions
A risk-neutral principal (shareholders) hires a risk-averse
agent (manager) for one period. The utility function of the manager
is represented by a strictly increasing and strictly concave
function ![]() . The firm's earnings are stochastic
and influenced by the manager's effort. The unobserved effort level
of the manager,
. The firm's earnings are stochastic
and influenced by the manager's effort. The unobserved effort level
of the manager, ![]() , can take two values, low
, can take two values, low
![]() and high
and high ![]() , that is,
, that is,
![]() where
where ![]() .
The manager incurs disutility from exerting effort, denoted by the
cost function
.
The manager incurs disutility from exerting effort, denoted by the
cost function ![]() . In particular, high effort is
associated with a cost of
. In particular, high effort is
associated with a cost of ![]() , while low
effort involves no cost:
, while low
effort involves no cost: ![]() . Earnings
. Earnings ![]() take two possible values,
, where
take two possible values,
, where ![]() .
Let
.
Let ![]() be the probability that earnings are
equal to
be the probability that earnings are
equal to ![]()
![]() when the effort is
when the effort is ![]() , where
, where
![]() with
with
![]() .
.
Figure 1. Model Timeline
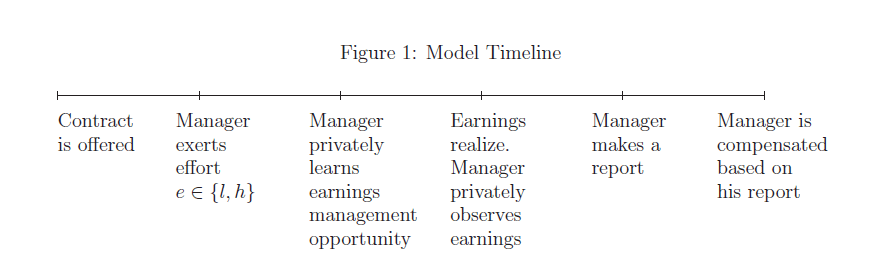
The timeline of Figure 1 chronicles the
sequence of events in the model. After the manager accepts the
take-it-or-leave-it contract offered by the principal, he decides
whether to exert managerial effort. After exerting effort, the
manager also privately learns whether he has an opportunity to
manage earnings. With probability ![]() , he has
discretion over how much earnings to report.6 With probability
, he has
discretion over how much earnings to report.6 With probability
![]() , the manager is prohibited from
manipulating earnings.7 Then the manager privately observes
the earnings and makes an earnings announcement.
, the manager is prohibited from
manipulating earnings.7 Then the manager privately observes
the earnings and makes an earnings announcement.
If the manager produces an inaccurate report, the manager incurs
a personal cost, denoted by
![]() . Reporting honestly incurs no
cost, that is,
. Reporting honestly incurs no
cost, that is, ![]() .8 When the manager
overstates earnings, there is a positive cost
.8 When the manager
overstates earnings, there is a positive cost
![]() . The cost of manipulating
earnings includes the costs involved in preventing auditors from
reporting a discrepancy in the earnings report, the expected
reputation damage, and the expected penalties imposed through legal
and market systems in case of being caught. We also assume that
there is no cost associated with underreporting, and we will see
that there is no incentive to understate earnings in this model. We
define that earnings management occurs when the reported earnings
differ from true earnings. More specifically, earnings management
emerges in this environment if the manager announces that high
earnings
. The cost of manipulating
earnings includes the costs involved in preventing auditors from
reporting a discrepancy in the earnings report, the expected
reputation damage, and the expected penalties imposed through legal
and market systems in case of being caught. We also assume that
there is no cost associated with underreporting, and we will see
that there is no incentive to understate earnings in this model. We
define that earnings management occurs when the reported earnings
differ from true earnings. More specifically, earnings management
emerges in this environment if the manager announces that high
earnings ![]() have been achieved when the actual
realization of earnings is low
have been achieved when the actual
realization of earnings is low ![]() .9
.9
One alternative to this formulation is to assume that the
manager can choose the possibility of having discretion to
manipulate (i.e, a level of ![]() ) subject to an
increasing and convex cost function
) subject to an
increasing and convex cost function
![]() . Manipulation is costless
when the manipulation opportunity realizes.
. Manipulation is costless
when the manipulation opportunity realizes. ![]() is
then interpreted as the policy parameter that is determined by
either an internal governance mechanism or an external regulatory
agency. Under this alternative, model results do not change but the
model solution becomes cumbersome; therefore we choose the current
formulation.
is
then interpreted as the policy parameter that is determined by
either an internal governance mechanism or an external regulatory
agency. Under this alternative, model results do not change but the
model solution becomes cumbersome; therefore we choose the current
formulation.
As the contract must be designed based on mutually observed
variables, the manager's compensation must be based on his report.
As long as the manager's reported earnings fall in the set
![]() , the principal cannot directly
detect whether the manager has misstated earnings and must pay the
manager before the revelation of underlying true performance. It is
also assumed that the manager is essential to the operation of the
firm, so the contract must be such that the manager (weakly)
prefers to work for the principal regardless of whether he obtains
the opportunity to engage in earnings management.
, the principal cannot directly
detect whether the manager has misstated earnings and must pay the
manager before the revelation of underlying true performance. It is
also assumed that the manager is essential to the operation of the
firm, so the contract must be such that the manager (weakly)
prefers to work for the principal regardless of whether he obtains
the opportunity to engage in earnings management.
One key feature of our framework is that shareholders are uncertain about whether earnings reports are inflated. If all managers were able to exaggerate the firm's performance and the degree of manipulation was homogeneous,10 a rational principal would correctly infer the true state of the firm. In reality, however, the degree of reporting discretion available varies with economic situations, and managers are not all equally versed in manipulating financial records.11 Shareholders are therefore often faced with a significant degree of information asymmetry as to whether financial results are biased. In the model the stochastic opportunity to manipulate earnings breaks down a direct mapping between reported earnings and actual earnings, and adds an additional noise in financial reports that principal cannot perfectly filter out. Due to the additional uncertainty, the principal fails to make perfect inferences as to whether earnings management occurs, and earnings management is not fully unraveled in the equilibrium.12 We show in the next section that manipulation uncertainty has systematic impact on the characteristics of the optimal incentive contract.
2.2 Setup
The contract between the risk-neutral principal and the
risk-averse manager includes a set of wages contingent on the
reports, which can be alternatively characterized as a set of
contingent utilities. The utility level corresponding to
compensation level ![]() ,
,
![]() , is denoted as
, is denoted as
![]() . Let
. Let
![]() . Then
. Then ![]() is the cost to the principal of providing the agent
with utility
is the cost to the principal of providing the agent
with utility ![]() . Since
. Since ![]() is a
strictly increasing and strictly concave function,
is a
strictly increasing and strictly concave function, ![]() is a strictly increasing and strictly convex
function.
is a strictly increasing and strictly convex
function.
The model presented in this section places restrictions on the ability of the manager to communicate the truth. That is, the manager observes multiple dimensions of information, including the value of earnings and the realization of misreporting opportunity. However, he is only permitted to communicate a single-dimensional signal, which is an earnings announcement. Communication is restricted in that the manager cannot communicate the full dimensionality of his private information because of a limited message space, and hence the Revelation Principle is not applicable. As a result, the reporting function is not invertible, and true earnings cannot be unambiguously backed out from the reports.
In this environment, the contract must not only induce effort but also control for the manager's reporting incentive. As in the standard principal-agent model, the principal in our model is the residual claimant, and hence entitled to the firm's terminal value (i.e, true earnings net of managerial compensation). The one-step departure from the standard model here is that the principal in this model does not observe the earnings when he has to compensate the manager. In this paper, we assume that the difference in expected earnings is large enough that the principal always wants to implement high effort.
The objective of the manager is to maximize his utility by
choosing a level of effort and a reporting strategy represented by
![]() , subject to the contract he is offered.
The manager's utility is of the form
, subject to the contract he is offered.
The manager's utility is of the form
![]() .
.
The principal chooses the utility values ![]() ,
,
![]() , and recommended reporting
choice
, and recommended reporting
choice ![]() for each realization of earnings that
minimize the expected cost of inducing effort. Formally, the
optimal contract solves
for each realization of earnings that
minimize the expected cost of inducing effort. Formally, the
optimal contract solves
![\begin{displaymath} \begin{array}[c]{rl} \displaystyle\mathop{\min}_{u_{H}, u_{L}, R(H), R(L)} & \ E [ V (u) \vert h]\ & = x [ p_{h} V(u_{R(H)})+(1-p_{h}) V(u_{R(L)})] + (1-x) [p_{h} V(u_{H} )+(1-p_{h})V(u_{L})] \end{array}\end{displaymath}](img53.gif)
subject to
![$\displaystyle h = \mathop{\arg \max}_{e \in\{l,h \}} E [U(e, R(y))]=\mathop{\arg \max}_{e \in\{l,h \}} x E[ u_{R(y)}-\phi(R(y)-y)-a(e)]+(1-x) E [ u_{y}-a(e) ].$](img54.gif) |
(1) |
| (2) |
The objective function is the expected cost for the principal to
motivate effort. The first term is the cost to the principal of
implementing effort when the manager has an opportunity to
misreport, and the second term is the cost if he does not have such
an opportunity. The first constraint is the incentive constraint
for the manager's choice of effort--here, we assume that the
principal wants to induce high effort. The second is the
participation constraint, where ![]() is the
manager's outside option. In addition to these constraints, when
the manager has an opportunity to misstate earnings, the principal
faces another constraint. As the reporting decision has been
necessarily delegated to the manager, the "recommended reporting
strategy" has to be voluntarily followed by the manager:
is the
manager's outside option. In addition to these constraints, when
the manager has an opportunity to misstate earnings, the principal
faces another constraint. As the reporting decision has been
necessarily delegated to the manager, the "recommended reporting
strategy" has to be voluntarily followed by the manager:
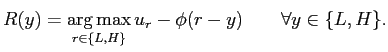 |
(3) |
This incentive constraint captures the inapplicability of the Revelation Principle in this setting: the manager is merely allowed to convey his private information on both true earnings and manipulation opportunity using only one single-dimensional signal and must report a mixture of these two in the earnings report.13
The optimal contract includes a set of utility promises
![]() and the recommended action
and the recommended action
![]() . Following the convention, we
assume that the principal wants to induce high effort, that is,
. Following the convention, we
assume that the principal wants to induce high effort, that is,
![]() . There are
. There are ![]() possible
reporting strategies the manager may take:
possible
reporting strategies the manager may take:
Strategy 1: Report truthfully, that is,
![]() .
.
Strategy 2: Report high earnings no matter which level of
earnings is realized, that is,
![]() .
.
Strategy 3: Report low earnings no matter which level of
earnings is realized, that is,
![]() .
.
Strategy 4: Report high earnings if low earnings are realized
and report low earnings if high earnings are realized, that is,
![]() .
.
It is straightforward to see that strategy ![]() cannot be achieved without sacrificing effort, and strategy
cannot be achieved without sacrificing effort, and strategy
![]() is not possible to implement. The
contracting problem is solved by characterizing the optimal payment
schedule that implements high effort as well as each of strategy
is not possible to implement. The
contracting problem is solved by characterizing the optimal payment
schedule that implements high effort as well as each of strategy
![]() and strategy
and strategy ![]() , and then
calculating the cost the principal incurs. The recommended
reporting choice is the strategy that enables the principal to
motivate high effort at the least cost, and the set of utility
promises associated with the recommended reporting choice is the
compensation schedule in the optimal contract.
, and then
calculating the cost the principal incurs. The recommended
reporting choice is the strategy that enables the principal to
motivate high effort at the least cost, and the set of utility
promises associated with the recommended reporting choice is the
compensation schedule in the optimal contract.
Below we will see that in some situations it is impossible to satisfy (1) and (3) simultaneously with a truthful report. In such a case, the principal has to endure a falsified report if he wants to implement high effort.
3 Equilibrium Reporting Strategy
Figure 2
summarizes the main results.14 The optimal contract is described
as the curve ![]() . It depicts how the wedge between
promised utilities assigned to reports of high and low earnings
varies with different values of manipulation cost
. It depicts how the wedge between
promised utilities assigned to reports of high and low earnings
varies with different values of manipulation cost ![]() .
.
In Figure 2,
the inequality (4) is
represented by the shaded area below the
![]() line. The inequality (5) is
represented by the area above the horizontal line at
line. The inequality (5) is
represented by the area above the horizontal line at
![]() . For
. For
![]() , we can see that
these areas do not overlap: If the cost of manipulating earnings is
small compared to the cost of exerting effort, it is impracticable
to implement truthful reporting. A sharp conflict arises between
the desire of the principal to implement high effort and motivate
truthful reporting, as performance pay generates incentives not
only to produce earnings but also to manipulate it. The low-output
manager will choose to report honestly when the payoff
differential, that is, the difference between the payoff following
high and low reported earnings, is sufficiently small, in
particular, smaller than the cost of manipulation. However, the
agent will exert high effort only if the compensation wedge is
sufficiently large compared to the cost of effort. The conflict
makes it impossible to motivate effort while obtaining truthful
reporting in this case, and the manager will always falsify the
report when he has a chance to do so. Earnings management thus
emerges under the optimal contract.
, we can see that
these areas do not overlap: If the cost of manipulating earnings is
small compared to the cost of exerting effort, it is impracticable
to implement truthful reporting. A sharp conflict arises between
the desire of the principal to implement high effort and motivate
truthful reporting, as performance pay generates incentives not
only to produce earnings but also to manipulate it. The low-output
manager will choose to report honestly when the payoff
differential, that is, the difference between the payoff following
high and low reported earnings, is sufficiently small, in
particular, smaller than the cost of manipulation. However, the
agent will exert high effort only if the compensation wedge is
sufficiently large compared to the cost of effort. The conflict
makes it impossible to motivate effort while obtaining truthful
reporting in this case, and the manager will always falsify the
report when he has a chance to do so. Earnings management thus
emerges under the optimal contract.
Figure 2. Main Results
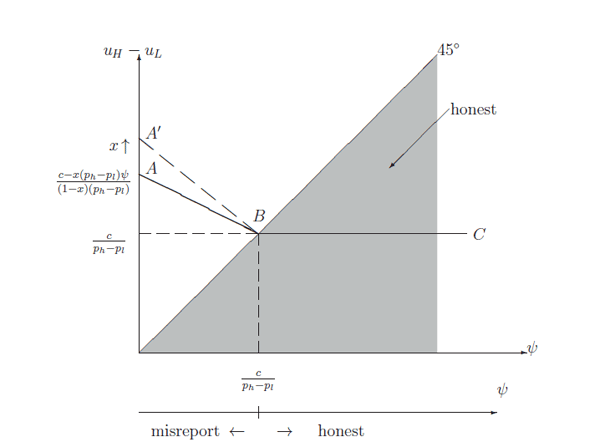
In this figure, ψ is the manipulation cost, c is the cost of exerting high effort, x; is the probabilty of having the mainpulation opportunity in one period, ph and pl represent the probability of achieving high earnings given high effort and low effort, and uH and uL represent the promised utilites for high report and low report respectively.
Proof: Incentive compatibility constraint on truthful reporting 3 is
Combining these two, we obtain
| (4) |
Incentive compatibility constraint on exerting high effort (1) is
which implies
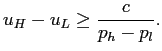 |
(5) |
If
![]() , incentive
constraints on reporting choice (4) and effort
decision (5) cannot be
satisfied simultaneously, therefore truthful reporting is not
feasible.
, incentive
constraints on reporting choice (4) and effort
decision (5) cannot be
satisfied simultaneously, therefore truthful reporting is not
feasible.
Now if the cost of misstating earnings is large compared to the cost of exerting effort, it is relatively easy to motivate truthful earnings reports, and honest reporting becomes implementable. When truth-telling strategy is feasible to implement, it is always in the principal's best interest to achieve truthful reporting. The reason is that although manipulation is personally costly to the manager, since the principal must design a compensation contract that meets the manager's participation constraint, the cost of manipulation undertaken by the manager is ultimately borne by the principal.
Proof: As described in the previous section, there are
two possible reporting strategies the principal can implement: One
strategy is reporting truthfully, that is,
![]() , and the other choice is
to report honestly if high earnings are realized and overstate
earnings when low earnings are realized, that is,
, and the other choice is
to report honestly if high earnings are realized and overstate
earnings when low earnings are realized, that is,
![]() .
.
If
![]() and the principal
implements truthful reporting, the incentive compatibility
constraint on effort decision (5) will
be binding, and hence the truthful-reporting constraint (4) will
be automatically satisfied. Suppose that the incentive
compatibility constraint on effort decision (5) is
not binding. Then a small reduction in
and the principal
implements truthful reporting, the incentive compatibility
constraint on effort decision (5) will
be binding, and hence the truthful-reporting constraint (4) will
be automatically satisfied. Suppose that the incentive
compatibility constraint on effort decision (5) is
not binding. Then a small reduction in ![]() and an
increase in
and an
increase in ![]() that just keep the participation
constraint (2) satisfied
will still satisfy the incentive constraint (5).
This change will reduce the objective function value--therefore, it
causes a contradiction.
that just keep the participation
constraint (2) satisfied
will still satisfy the incentive constraint (5).
This change will reduce the objective function value--therefore, it
causes a contradiction.
We can then solve for ![]() and
and ![]() as follows:
as follows:
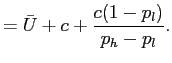 |
||
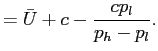 |
If
![]() and the principal
implements the alternative strategy,
and the principal
implements the alternative strategy,
![]() . The incentive
compatibility constraint on reporting choice (3) becomes
. The incentive
compatibility constraint on reporting choice (3) becomes
Combining these two, we obtain
| (6) |
The incentive compatibility constraint on effort decision (1) in this case becomes
![\begin{displaymath} \begin{array}[c]{l} x [p_{h} (u_{H} -c) +(1-p_{h}) (u_{H}-\psi-c)]+(1-x) [p_{h} (u_{H} - c)+(1-p_{h}) (u_{L}-c)]\ \ge x [p_{l} u_{H} +(1-p_{l}) (u_{H} -\psi)]+(1-x) [p_{l} u_{H}+(1-p_{l}) u_{L}], \end{array}\end{displaymath}](img116.gif)
which can be simplified as
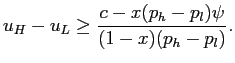
|
(7) |
As
![]() , the
right-hand-side is
, the
right-hand-side is
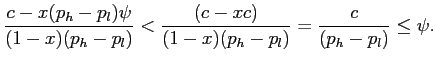
Thus if the incentive compatibility constraint on reporting choice (6) is binding, (7) is automatically satisfied. Suppose that the incentive constraint on reporting choice (6) is not binding. Then a small reduction in ![]() and
an increase in
and
an increase in ![]() that just keep the
participation constraint (2) satisfied will
still satisfy the incentive constraint (6). This change
will reduce the objective function value--therefore, it causes a
contradiction. Hence, the incentive compatibility constraint on
reporting decision (6) is binding
under the optimal contract.
that just keep the
participation constraint (2) satisfied will
still satisfy the incentive constraint (6). This change
will reduce the objective function value--therefore, it causes a
contradiction. Hence, the incentive compatibility constraint on
reporting decision (6) is binding
under the optimal contract.
We can solve for ![]() and
and ![]() as follows
as follows
Compared to the case with the alternative reporting strategy,
implementing truthful-reporting strategy requires a lower
![]() and a higher
and a higher ![]() ,
and hence makes the utility promises more equalized. Given the
convex cost of providing utilities, it incurs a lower cost to
induce effort with truth-telling strategy. Truthful reporting is
the optimal recommended strategy in this case.
,
and hence makes the utility promises more equalized. Given the
convex cost of providing utilities, it incurs a lower cost to
induce effort with truth-telling strategy. Truthful reporting is
the optimal recommended strategy in this case.
When does earnings management occur? The following proposition establishes the necessary and sufficient condition for earnings management to emerge under the optimal contract.
Proof: Straightforward from Lemma 1 and Lemma 2.
Here, the optimal contract is fully characterized, and the condition for earnings management to take place is derived explicitly. We turn to discuss some comparative static results that have clear empirical implications in the next section.
4 Optimal Contract
4.1 Manipulation Opportunities and Incentive Pay
In Figure 2,
the line ![]() shifts to
shifts to
![]() as
as ![]() increases.
Suppose that
increases.
Suppose that ![]() becomes greater and so the manager is
more likely to be able to manipulate earnings. The manager enjoys a
higher chance of having discretion to overstate earnings in case
low state occurs, which reduces the manager's incentive to exert
effort under any given compensation schemes. A larger reward for
high earnings reports is thus required to incentivize effort, and
executive compensation consequently involves more performance
pay.
becomes greater and so the manager is
more likely to be able to manipulate earnings. The manager enjoys a
higher chance of having discretion to overstate earnings in case
low state occurs, which reduces the manager's incentive to exert
effort under any given compensation schemes. A larger reward for
high earnings reports is thus required to incentivize effort, and
executive compensation consequently involves more performance
pay.
Proof: When
![]() holds, truth-telling
is not feasible to implement. The principal implements the
alternative strategy,
holds, truth-telling
is not feasible to implement. The principal implements the
alternative strategy,
![]() . As in Lemma 2, the incentive
compatibility constraint on reporting choice
. As in Lemma 2, the incentive
compatibility constraint on reporting choice
The incentive compatibility constraint on effort decision becomes
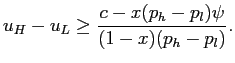
From Lemma 2, it must be
binding in the optimal contract when
![]() , and consequently
the incentive compatibility constraint on reporting choice is
automatically satisfied. We thus have
, and consequently
the incentive compatibility constraint on reporting choice is
automatically satisfied. We thus have
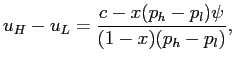
|
(8) |
which can be rewritten as follows:
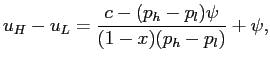
and the right-hand-side is increasing in ![]() .
.
Compared to a situation in the absence of opportunities to
manage earnings (![]() ), in a case where it is possible
(
), in a case where it is possible
(![]() ) and not too costly to manipulate
earnings (
) and not too costly to manipulate
earnings (
![]() ), it is optimal for
the shareholders to provide stronger monetary incentives to
executives through the compensation packages they offer. When
), it is optimal for
the shareholders to provide stronger monetary incentives to
executives through the compensation packages they offer. When
![]() , the index for the likelihood of earnings
management holding corporate productivity constant, rises, the
model predicts an executive compensation structure that is more
responsive to performance.15 Within firms, Aggarwal and Samwick
(2003) report that managers with divisional responsibilities have
lower pay-performance sensitivities than chief executives. They
attribute the substantial incentives of the top management team to
a less precise individual-specific signal of effort than those of
the managers with lower managerial responsibilities. Our
explanation for the magnified pay-for-performance, that is,
executives' manipulation opportunities, is different, but the two
mechanisms may co-exist.
, the index for the likelihood of earnings
management holding corporate productivity constant, rises, the
model predicts an executive compensation structure that is more
responsive to performance.15 Within firms, Aggarwal and Samwick
(2003) report that managers with divisional responsibilities have
lower pay-performance sensitivities than chief executives. They
attribute the substantial incentives of the top management team to
a less precise individual-specific signal of effort than those of
the managers with lower managerial responsibilities. Our
explanation for the magnified pay-for-performance, that is,
executives' manipulation opportunities, is different, but the two
mechanisms may co-exist.
Our model predicts a varying degree of optimal performance pay across firms and industries. For example, management in the financial sector is better able to manipulate financial records than that in the manufacturing sector, due to a larger fraction of the firm's assets being intangible. A more intensive use of performance pay is required in the financial industry to incentivize managerial effort.
4.2 Governance Policies and Incentives
We interpret the cost of manipulation as a policy parameter, influenced by public policies and internal governance. This analysis shows that changes of corporate governance or accounting standards can influence the optimal structure of executive pay in the economy. Our model also has implications for how pay practices vary across firms with the effectiveness of corporate governance or the strength of internal control systems.
If the manipulation cost is sufficiently large due to stringent
governance policies (
![]() ), the equilibrium
compensation wedge is as in the standard moral hazard model when
manipulation is not possible:
), the equilibrium
compensation wedge is as in the standard moral hazard model when
manipulation is not possible:
![]() . In Figure
2 is represented by a horizontal
line
. In Figure
2 is represented by a horizontal
line ![]() . In weaker governance systems (i.e.,
. In weaker governance systems (i.e.,
![]() ), the equilibrium
compensation differential is a function of the manipulation cost,
and is greater than in a sufficiently strong regulatory environment
(
), the equilibrium
compensation differential is a function of the manipulation cost,
and is greater than in a sufficiently strong regulatory environment
(
![]() ). The compensation
differential is represented by a downward-sloping line
). The compensation
differential is represented by a downward-sloping line ![]() in Figure 2 in this case.
The following proposition states the comparative static results
when the manager's cost of manipulation is insufficient to prevent
earnings management.
in Figure 2 in this case.
The following proposition states the comparative static results
when the manager's cost of manipulation is insufficient to prevent
earnings management.
Proof: As in Proposition 2, (8) holds, and the
right-hand-side of (8) is decreasing
in ![]() .
.
Suppose that misstating earnings becomes more costly to the
manager. Then, if the low outcome realizes and the manager has an
opportunity to misreport, he will over-report but this
overstatement of earnings is more costly. The manager has more
incentives to avoid the unfavorably high manipulation cost in the
case of low state, and this works as an additional incentive for
the manager to work hard. Thus, the principal does not have to
provide as much monetary incentive (that is,
![]() ) to satisfy the incentive
compatibility constraint (1).
) to satisfy the incentive
compatibility constraint (1).
It is also worth pointing out that in this framework, firms with more stringent corporate governance and hence fewer opportunities to manage earnings have weaker incentives in compensation contracts but more dispersion in the compensation that is paid out; whereas firms with poor corporate governance and hence greater opportunities to manage earnings provide stronger incentives in pay structures, but there is little variation in the level of compensation paid to the executives because their reported earnings cluster at the high end. As a result, all else equal, the firm with ineffective corporate governance is associated with an excessive executive pay.16
4.3 Prevalence of Manipulation
Because of the intrinsic substitutability between manipulation and effort, the opportunities for manipulation exacerbate the agency problem. The following proposition illustrates that any change in disutility from putting forth effort not only affects the manager's effort decision, but also has a considerable impact on the equilibrium financial reporting strategy.
Proof: Suppose that in each industry there are different
firms, each of which is run by a manager with a different level of
manipulation cost ![]() . Then
. Then
![]() represents the
threshold level of manipulation cost below which the manager
manipulates earnings, and hence the percentage of managers with
represents the
threshold level of manipulation cost below which the manager
manipulates earnings, and hence the percentage of managers with
![]() is the percentage of
managers potentially engaging in earnings management in the
industry. When spending effort is more costly to the manager, or to
put it in another way, when it is more difficult to monitor effort
in one industry, the threshold
is the percentage of
managers potentially engaging in earnings management in the
industry. When spending effort is more costly to the manager, or to
put it in another way, when it is more difficult to monitor effort
in one industry, the threshold ![]() to achieve
truthful reports rises, resulting in a larger fraction of managers
with a manipulation cost below the threshold level and therefore a
higher prevalence of earnings management in the industry.
to achieve
truthful reports rises, resulting in a larger fraction of managers
with a manipulation cost below the threshold level and therefore a
higher prevalence of earnings management in the industry.
Notice that when it is more difficult to monitor productive effort, it also becomes more difficult to induce truthful reports. The substitutability of earnings management for productive effort in improving reported earnings and hence the compensation aggravates the incentive problems.
In addition, a change of corporate governance will also affect
the equilibrium prevalence of earnings management in the economy.
In a representative economy, when the manipulation cost increases
from
![]() to
to
![]() due to public
policy changes, the equilibrium reporting strategy under the
optimal contract changes from manipulation (in low states) to
truth-telling. When incorporating heterogeneity in
due to public
policy changes, the equilibrium reporting strategy under the
optimal contract changes from manipulation (in low states) to
truth-telling. When incorporating heterogeneity in ![]() among firms, Proposition 5 states that
regulatory reforms that increase manipulation costs reduce earnings
management.
among firms, Proposition 5 states that
regulatory reforms that increase manipulation costs reduce earnings
management.
Proof: In an economy where the cost of spending effort
![]() is firm or industry specific, the
threshold level of
is firm or industry specific, the
threshold level of ![]() below which truthful
reports are produced is
below which truthful
reports are produced is
![]() . Only the managers with a
level of disutility incurred from putting effort less than the
threshold level report truthfully. If
. Only the managers with a
level of disutility incurred from putting effort less than the
threshold level report truthfully. If ![]() grows,
the percentage of honest managers increases accordingly, and
earnings management becomes less prevalent in the economy.
grows,
the percentage of honest managers increases accordingly, and
earnings management becomes less prevalent in the economy.
4.4 Business Cycle Implications
A final implication of our model concerns possible business
cycle properties of manipulation and incentive pay. It is
reasonable to think that the likelihood of success given high
effort and benefit of managerial effort, that is, ![]() and
and
![]() , vary with the aggregate
state of the economy. The following proposition uses comparative
statics of
, vary with the aggregate
state of the economy. The following proposition uses comparative
statics of
![]() to show that manipulation and
incentive pay are countercyclical if the benefit of managerial
effort is greater during booms than recessions.
to show that manipulation and
incentive pay are countercyclical if the benefit of managerial
effort is greater during booms than recessions.
Proof: As in Proposition 4, the percentage
of managers with
![]() is
the percentage of managers potentially engaging in earnings
management in the industry.
is
the percentage of managers potentially engaging in earnings
management in the industry. ![]() increases
when
increases
when
![]() decreases.
decreases.
Recall that from (8),
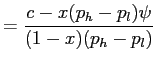
|
||
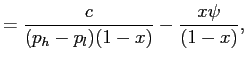
|
and the right-hand-side is decreasing in
![]() .
.
5 Equilibrium Effort Level
In our benchmark model, we assumed that the difference between high and low earnings is large enough that the principal always wants to implement high effort. In this section we study the condition under which it is in the principal's best interest to motivate effort. The expected wealth of the risk-neutral principal is the terminal value of the firm, i.e., the expected true earnings net of managerial compensation. If the principal chooses to induce high effort, the expected compensation paid out is
| (11) |
The first term is the expected compensation if the manager has the opportunity to manipulate and hence always reports high earnings. The second term in (11) is the expected wage if the manager does not have the manipulation opportunity and truthfully reports earnings.
If the principal decides to give up on managerial effort, the principal will assign
The expected compensation paid to the manager in this case is thus
![]() , where
, where ![]() is
defined in Section 2 as the cost to the principal of providing the
manager with utility
is
defined in Section 2 as the cost to the principal of providing the
manager with utility ![]() ,
,
![]() .
.
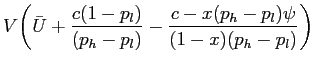
|
(12) | |
![$\displaystyle \displaystyle \frac{1}{(1-x)(1-p_{h})} \bigg\{(p_{h}-p_{l})(H-L) -[(1-p_{h})x +p_{h}] V \bigg(\bar U + \frac{c(1-p_{l})}{(p_{h}-p_{l})} \bigg) +V(\bar U) \bigg \}.$](img214.gif)
|
Proof: If high effort generates higher expected wealth for the principal, the following condition holds.
| (13) |
The left-hand-side is the expected firm value given high effort,
and the right-hand-side is that given low effort. Substituting the
expressions of ![]() and
and ![]() ,
that is, (9) and (10), into (13) yields (12).
,
that is, (9) and (10), into (13) yields (12).
Because the manipulation cost increases the equilibrium cost of inducing effort but does not change the benefit of effort, there is a point from which the cost of inducing high effort outweighs the benefit.
Proof: Since
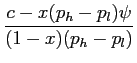 is decreasing in
is decreasing in ![]() and
and ![]() is a strictly increasing function, the
left-hand-side of (12)
is increasing in
is a strictly increasing function, the
left-hand-side of (12)
is increasing in ![]() . The right-hand-side of
(12) is independent
of
. The right-hand-side of
(12) is independent
of ![]() . Therefore, (12) holds for
. Therefore, (12) holds for
![]() , where
, where
![]() satisfies
satisfies
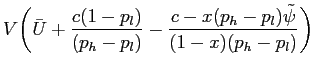
|
||
![$\displaystyle \displaystyle \frac{1}{(1-x)(1-p_{h})} \{(p_{h}-p_{l})(H-L) -[(1-p_{h})x +p_{h}] V(\bar U + \frac{c(1-p_{l})}{(p_{h}-p_{l})}) +V(\bar U) \}.$](img229.gif)
|
Although manipulation is personally costly to the manager, the
principal ultimately bears the manipulation cost, as the principal
must offer a compensation schedule that satisfies the participation
constraint. Hence a high effort accompanied by earnings management
becomes exceedingly costly when the manipulation cost increases.
All else equal, earnings management and high effort will be a part
of optimal contracting if the manipulation cost is sufficiently
small (i.e.,
![]() ); otherwise, the
principal chooses to relinquish productive effort and induce
truthful reporting by providing the manager with the reservation
utility
); otherwise, the
principal chooses to relinquish productive effort and induce
truthful reporting by providing the manager with the reservation
utility ![]() in all states.
in all states.
In our model when ![]() increases from
increases from
![]() to
to
![]() , the equilibrium effort
level moves from high
, the equilibrium effort
level moves from high ![]() to low
to low ![]() . The pay-for-performance sensitivity decreases from
positive to zero accordingly. When manipulation is exceedingly
costly due to regulatory reforms, the principal may prevent
earnings management by reducing pay-for-performance and
relinquishing managerial effort.
. The pay-for-performance sensitivity decreases from
positive to zero accordingly. When manipulation is exceedingly
costly due to regulatory reforms, the principal may prevent
earnings management by reducing pay-for-performance and
relinquishing managerial effort.
6 Comparison with Goldman and Slezak (2006)
In the literature on manipulation, Goldman and Slezak (2006)
(referred to as GS in this section) is closest to ours. Contrary to
ours, they show that optimal pay-performance sensitivities in
compensation contracts decrease with the possibility of
manipulation, and that tightened regulatory policies
increase the pay-for-performance sensitivity and the extent
of manipulation. In analyzing the effect of opportunities to
manipulate on compensation contracts, we derive the opposite
results to theirs. One key difference between GS and ours is that
the Revelation Principle holds in their setting, while it does not
in ours. Aside from this, it turns out that some differences in
model setting generate the different results. In this section we
modify our specification and study a special case of our model, in
order to make the comparison with GS transparent. First, we
introduce a "monitoring technology" in our model, following
specifications in GS. Comparisons of this specification with our
benchmark model in Section 2 and GS model are examined. Second, we
consider the case ![]() and show our model
contains their result in this case.
and show our model
contains their result in this case.
6.1 Monitoring Technology
In addition to the effects of incentive contracts, GS also
considers a monitoring technology that can detect manipulation ex
post with some probability, and the manager is fined only if
detected. Following their notation, we let
![]() denote the probability that the
manager is caught manipulating. If manipulation is detected, the
manager must pay an amount of financial penalties
denote the probability that the
manager is caught manipulating. If manipulation is detected, the
manager must pay an amount of financial penalties ![]() :
: ![]() and
and ![]() .
.
Now the manager's utility when he exerts high effort and overstates low earnings (when manipulation opportunity is available) is
which can be rewritten as
Recall that in our benchmark model the manager incurs a cost when
manipulating reports ![]() . An interpretation of
. An interpretation of
![]() in this setting is the expected
financial penalties:
in this setting is the expected
financial penalties:
![]() . With this transformation, a
model with monitoring technology is reduced to our benchmark model.
. With this transformation, a
model with monitoring technology is reduced to our benchmark model.
6.2 Discussion of Improved Monitoring
When the external regulatory agency increases the expected penalty for manipulation, this increases the pay-for-performance sensitivity in GS. The reason is that higher expected penalty reduces the need for compensation contracts to control manipulation, and the principal hence focuses more on effort and raises pay for performance. As a result, manipulation becomes more pronounced after regulatory reforms. However, with similar modelling approach of regulatory technology, our model yields the opposite implications for incentive pay and manipulation: because incentives to overstate earnings are strong when performance is weak, under tightened governance schemes, managers have stronger incentives to work in order to avoid paying the increased manipulation cost in low states. Less monetary incentive is needed in compensation contracts to motivate effort, and manipulation is consequently less pervasive.
The key difference is that the manager in GS chooses the extent of manipulation before observing the actual output, and so reporting incentive is independent of the true state of the firm. Our mechanism that stronger governance rewards managerial effort, which builds upon the state-dependency of reporting incentives, is thus absent in their model.
Our model feature that earnings management behavior varies with true earnings is motivated by the empirical literature on misreporting patterns. It is well documented that managers inflate earnings to avoid reporting losses and declines, and to meet analysts' expectations and some pre-specified targets (Holthausen et al. 1995, Dechow and Skinner 2000, and Myers et al. 2007). For example, Burgstahler and Dichev [1997] estimate that 8-12 percent of the firms with small pre-managed earnings decreases manipulate earnings to achieve earnings increases, and 30-44 percent of the firms with small pre-managed losses manage earnings to create positive earnings. In our model the manager only manipulates earnings when true earnings are low; therefore governance reforms that increase the manipulation cost, which only incurs in low states, generate additional incentives for effort. Pay-for-performance is thus weaker in the optimal contract in our setting.
6.3 Manipulation Opportunity and Effort Level
Another striking difference between GS and ours is the opposite
result on how manipulation opportunities affect incentive pay in
the optimal contract. One way to reconcile our findings is to
consider a special case in our model: the opportunity to manipulate
is always available (i.e., ![]() ). Opportunities
to inflate earnings significantly undermine the manager's incentive
to exert effort. In this case it becomes prohibitively expensive to
induce effort: Line
). Opportunities
to inflate earnings significantly undermine the manager's incentive
to exert effort. In this case it becomes prohibitively expensive to
induce effort: Line
![]() in Figure 2 shoots to
infinity. The principal will pay the manager a fixed compensation
regardless of reported earnings, and the manager exerts low effort
under the optimal contract.
in Figure 2 shoots to
infinity. The principal will pay the manager a fixed compensation
regardless of reported earnings, and the manager exerts low effort
under the optimal contract.
Therefore, increasing ![]() from
from
![]() to
to ![]() leads to a
reduction in the pay-performance sensitivity in our model. This
result shares the same spirit as in GS that as the tendency to
manipulate goes up, the cost of inducing managerial effort
increases and the principal responds by lowering the
pay-for-performance so as to induce less effort. A result similar
to GS thus emerges from a special case of our model.
leads to a
reduction in the pay-performance sensitivity in our model. This
result shares the same spirit as in GS that as the tendency to
manipulate goes up, the cost of inducing managerial effort
increases and the principal responds by lowering the
pay-for-performance so as to induce less effort. A result similar
to GS thus emerges from a special case of our model.
7 Empirical Implications
The model results illustrated in this paper are useful in classifying the endogeneity of earnings management in executive compensation design and thus help understand some stylized facts of earnings management and executive compensation. In particular, the model yields implications for the role earnings management plays in accounting for the time-series and cross-sectional variation of executive pay practices. The results also have predictions for the impact of corporate governance changes on the structure of executive compensation and the prevalence of earnings management. The empirical findings discussed below lend support to our model.
7.1 Positive Link Between Earnings Management Practice and Executive Compensation Structure
The model has a clear empirical implication described by Proposition 2: executive pay needs to be more sensitive to performance as earnings management becomes more pronounced. A positive correlation between manipulation and incentive pay has been observed in both time series and cross section. Many have interpreted it as being evidence of inefficiency: manipulation is a suboptimal, unintended consequence of incentives. Our model suggests that it can be consistent with optimal contracting and need not reflect inefficiency.
It is worth noting that in the literature on manipulation, Goldman and Slezak (2006) produce a reduced pay-performance sensitivity due to precise discounting of overstated performance, and they relate their result to the low sensitivity of compensation to firm value reported by Jensen and Murphy (1990) and Murphy (1999).17 Contrast to theirs, shareholders in our framework cannot perfectly gauge the true performance, and our model yields the opposite implication for optimal pay structure. We further cite direct empirical evidence on the relationship between earnings management and executive pay in both time series and cross section.
7.1.1 Time-Series Trends in Earnings Management and Executive Compensation
As indicated by Figure 3 from Cohen et al.
(2005), the research documenting the trend in earnings management
over time indicates that firms' management of earnings grew
steadily from the late 1980s until the passage of the
Sarbanes-Oxley Act (Brown 2001; Bartov et al. 2002; Lopez and Rees
2001; Cohen et al. 2005). 18 Meanwhile, one of the striking
developments in the American economy since the 1990s has been the
enormous increase in performance-based executive compensation (See
Figure ![]() from Cohen et al. (2004)). Hall and
Liebman (1998) show that the median exposure of CEO wealth to firm
value tripled during the 1990s, when stock options replaced base
salaries as the single largest component of compensation. The
comovement between the two time series supports the model
implication that there is a predictable link between the
pervasiveness of earnings management and the use of
performance-based compensation.
from Cohen et al. (2004)). Hall and
Liebman (1998) show that the median exposure of CEO wealth to firm
value tripled during the 1990s, when stock options replaced base
salaries as the single largest component of compensation. The
comovement between the two time series supports the model
implication that there is a predictable link between the
pervasiveness of earnings management and the use of
performance-based compensation.
Figure 3. Trends in Earnings Management 1987-2003 (Source: Cohen et al. 2005)
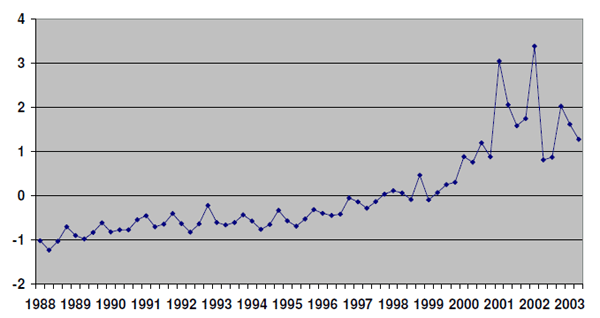
This figure plots EM-SCORE, the metric in Cohen et al (2005) for earnings managmement over the 1987-2003 sample period. EM_SCORE is obtained by performing a principal factor analysis of the different earnings management metrics, including three measures of discretionary accruals (the absolute value of discretionary accruals estimated using the modified Jones, the modified Jones model controlling for performance and the modified Jones model controlling for both performance and growth, respectively); the ratio of the absolute values of total accruals and cash flow from operations; the ratio of the change in accounts receivables to the change in sales; the ratio of the change in inventory to the change in sales; and the frequency of negative special items.
7.1.2 Cross-sectional Studies on Earnings Management and Executive Compensation
This model prediction also fits well with the cross-sectional pattern of earnings management and executive compensation found in the data. Gao and Shrieves (2002) utilize ExecuComp and CRSP database, covering 1,200 firms over the period 1992 to 2000. They show that earnings management intensity, as measured by the absolute value of discretionary accruals scaled by asset size, is related to managerial compensation contracts. They find that the amounts of stock options and bonuses, and the incentive intensity of stock options, are positively related to earnings management intensity, whereas salaries are negatively related. Bergstresser and Philippon (2006) use the COMPUSTAT and the ExecuComp datasets from the 1990s and find evidence that companies with higher levels of earnings management are the companies with more "incentivized" CEOs -- those whose overall compensation is more sensitive to company share prices.
While the conventional wisdom tends to attribute managerial manipulation to incentives in executive compensation, our model suggests that the underlying causality is rather subtle: the possibility of manipulation actually requires executive pay to be more sensitive to the possibly biased reports. Our analysis complements the existing view in an interesting and plausible way.
7.2 Influence of Changes in Corporate Governance on Compensation Structure and Earnings Management
The Sarbanes-Oxley Act of 2002 (SOX) was a regulatory reaction to a number of high-profile corporate accounting scandals, including those affecting Enron, Tyco, and WorldCom. SOX aims to improve the reliability of corporate disclosures by modifying the governance, the reporting, and the disclosure rules for public companies. One of the requirements introduced by SOX is that CEOs and CFOs must certify the veracity of their financial statements (Section 302). SOX also penalizes fraud by requiring the return of incentive-based compensation and profits from stock sales in the event of earnings restatements (Section 304).
The parameter of policy interest is the manipulation cost managers incur when cooking the books, which reflects corporate governance environment determined by regulatory authorities. The policy implications derived by Proposition 3 and Proposition 6 predict that when corporate governance policy becomes more stringent, as is the case with the passage of SOX, executive compensation will be less responsive to performance, and earnings management will be less widespread in the economy.
Cohen et al. (2004) report that the ratio of incentive
compensation to fixed salary declined significantly subsequent to
the passage of SOX (post-SOX period), suggesting an increase in
base salary as compared to incentive compensation (See Figure
![]() from Cohen et al (2004)). Narayanan and
Seyhun (2005) also show that the average grant size steadily
declined since the passage of SOX, and the total number of options
granted showed a downward trend in the post-SOX period. In
addition, Bayer and Burhop (2008) study a major shift in legal
rules of corporate governance in Germany and document a significant
decrease in pay-performance sensitivities of executive pay after
the reform.
from Cohen et al (2004)). Narayanan and
Seyhun (2005) also show that the average grant size steadily
declined since the passage of SOX, and the total number of options
granted showed a downward trend in the post-SOX period. In
addition, Bayer and Burhop (2008) study a major shift in legal
rules of corporate governance in Germany and document a significant
decrease in pay-performance sensitivities of executive pay after
the reform.
To examine the level of earnings management surrounding the passage of SOX, Cohen et al. (2005) use a modified cross-sectional Jones model and find that earnings management reversed abruptly after the passage of SOX (See Figure 3). Narayanan and Seyhun (2005) analyze managerial influencing of grant date stock prices based on a database of over 569,000 option grants reported to the SEC by insiders, and their results suggest that managerial influencing of stock prices was still prevalent after SOX, but it diminished in magnitude.
8 Conclusion
In this paper, we model the shareholder-manager relationship to study the implications of earnings management for executive compensation and analyze the responses of compensation schemes to corporate governance reforms. Consistent with data, we show that equilibrium pay-performance sensitivities actually increase with manipulation of corporate performance. Goldman and Slezak (2006) produce the opposite results and suggest a reduction in pay-performance sensitivities in the presence of manipulation. In contrast to their signal-jamming model, shareholders in our framework are faced with information asymmetry as to whether financial reports are biased and cannot perfectly gauge the true performance. As earnings management incentive depends on the true state of the firm in our model, the opportunity to manipulate financial records undermines the incentives to work, a more high powered compensation contract is therefore required to incentivize effort.
On a somewhat related note, there is a widely-held view that earnings management is an unintended consequence of incentive pay. In this paper, we present a model that draws a layered portrait of the underlying causality and suggests that the positive association between manipulation and incentives can be consistent with optimal contracting: Additional incentives are necessary in executive pay because of the presence of potential for manipulation, in spite that they lead to manipulation as a side effect. Our approach enhances our understanding of determinants of optimal pay-performance sensitivities and complements the existing view in an interesting and plausible way.
In addition, our model suggests that pay-performance sensitivities decrease in response to regulatory reforms and governance policies. Because incentives to overstate earnings are strong when performance is weak, tightened governance schemes generate additional incentives for effort in order to avoid paying the increased manipulation cost in low states. Less monetary incentive is needed in compensation contracts to motivate effort, and manipulation is consequently less pervasive. Empirical results on the effects of Sarbanes-Oxley Act lend support to our model.
Finally, it should be noted that the model developed here may be useful for studying the issues of how incentives and pay vary across firms. It it natural to think that managerial manipulation of financial data incurs a larger personal cost in the firms with more effective internal corporate governance. One way to further test the model implications is to check indicators of strong governance, such as the proportion of independent directors, efficiency of internal audit and frequency of BOD meetings, and explore whether they are associated with less incentive pay in managerial compensation contracts.
Bibliography
Agrawal, A. and Nasser, T. 2009. "Blockholders on Boards and CEO Compensation, Turnover and Firm Valuation ," University of Alabama Working Paper.
Arya, A., Glover, J., Sunder, S., 1998. "Earnings Management and the Revelation Principle," Review of Accounting Studies, 3, 7-34.
Arya, A., Glover, J., Sunder, S., 2003. "Are Unmanaged Earnings Always Better for Shareholders?" Accounting Horizons, 17, 111-116.
Aggarwal, R. K., Samwick, A. A., 2003. "Performance Incentives within Firms: The Effect of Managerial Responsibility," The Journal of Finance, 58, 1613-1650.
Bartov, E., Givoly, D., Hayn, C., 2002. "The Rewards to Meeting or Beating Earnings Expectations," Journal of Accounting and Economics, 33, 173-204.
Bayer, C., Burhop, C., 2008. "Corporate Governance and Incentive Contracts: Historical Evidence from a Legal Reform," Working paper.
Bergstresser, D., Philippon, T., 2006. "CEO Incentives and Earnings Management," Journal of Financial Economics, 80, 511-529.
Brown, L. D., 2001. "A Temporal Analysis of Earnings Surprises: Profits versus Losses," Journal of Accounting Research, 39, 221-241.
Burgstahler, D. and Dichev, I. 1997. "Earnings Management to Avoid Earnings Decreases and Losses," Journal of Accounting and Economics, 24, 99-126.
Burns, N., Kedia, S. 2006. "The Impact of Performance-based Compensation on Misreporting," Journal of Financial Economics, 79, 511-529.
Cohen, D., Dey, A., Lys, T., 2004. "The Sarbanes Oxley Act of 2002: Implications for Compensation Structure and Risk-Taking Incentives of CEOs," Working Paper, New York University, University of Chicago, and Northwestern University.
Cohen, D., Dey, A., Lys, T., 2005. "Trends in Earnings Management and Informativeness of Earnings Announcements in the Pre- and Post-Sarbanes Oxley Periods," Working Paper, New York University, University of Chicago, and Northwestern University.
Crocker, K., Slemrod, J., 2007. "The Economics of Earnings Manipulation and Managerial Compensation," The RAND Journal of Economics, 38, 698-713.
Dechow, P. and Skinner, D. 2000. "Earnings Management: Reconciling the Views of Accounting Academics, Practitioners, and Regulators," Accounting Horizons 14, 235-250.
Dye, R., 1988. "Earnings Management in An Overlapping Generations Model," Journal of Accounting Research, 26, 195-226.
Edmans, A., Gabaix, X. Sadzik, T., Sannikov, Y., 2009. "Dynamic Incentive Accounts," NBER Working paper.
Efendi, J., Srivastava, A., Swanson, E., 2005. "Why do corporate managers misstate financial statements? The role of option compensation and other factors," Journal of Financial Economics, 85, 667-708.
Evans III, J., Sridhar, S. S., 1996. "Multiple Control Systems, Accrual Accounting, and Earnings Management," Journal of Accounting Research, 34, 45-65.
Gabaix, X., Landier, A., 2006. "Why Has CEO Pay Increased So Much?" Working Paper, Princeton University and New York University.
Gao, P., Shrieves, R., 2002. "Earnings Management and Executive Compensation: A Case of Overdose of Option and Underdose of Salary?" Working Paper, Northwestern University and University of Tennessee.
Gaver, J., Gaver, K., Austin, J., 1995. "Additional Evidence on Bonus Plans and Income Management" Journal of Accounting and Economics 19, 3-28.
Goldman, E., Slezak, S.L., 2006. "An Equilibrium Model of Incentive Contracts in the Presence of Information Manipulation" Journal of Financial Economics 80, 603-626.
Hall, B. J., Liebman, J. B., 1998. "Are CEOs Really Paid Like Bureaucrats?" The Quarterly Journal of Economics, 113, 653-691.
Healy, P. M., Wahlen, J. M., 1999. "A Review of the Earnings Management Literature and Its Implications for Standard Setting," Accounting Horizons, 13, 365-383.
Holmstrom, B., 1979. "Moral Hazard and Observability," Bell Journal of Economics, 10, 74-91.
Holthausen, R., Larcker, D., Sloan, R., 1995. "Annual bonus schemes and the manipulation of earnings," Journal of Accounting and Economics 19, 29-74.
Ittner, C. D., Larcker, D. F., Rajan, M. V., 1997. "The Choice of Performance Measures in Annual Bonus Contracts," The Accounting Review, 72, 231-255.
Jensen, M. C., Murphy, K. J., 1990. "Performance Pay and Top-Management Incentives," Journal of Political Economy, 98, 225-264.
Jones, J. J., 1991. "Earnings Management During Import Relief Investigations," Journal of Accounting Research, 29, 193-228.
Kedia, S., Philippon, T., 2007. "The Economics of Fraudulent Accounting," Review of Financial Studies, forthcoming.
Lacker, J. M., Weinberg, J. A., 1989. "Optimal Contract under Costly State Falsification," Journal of Political Economy, 97, 1345-62.
Lambert, R., 2001. "Contracting Theory and Accounting," Journal of Accounting and Economics, 32, 3-87.
Lopez, T., Rees, L., 2002. "The Effect of Beating and Missing
Analysts![]() ¯ Forecasts on the
Information Content of Unexpected Earnings," Journal of
Accounting, Auditing, and Finance, 17, 155-184.
¯ Forecasts on the
Information Content of Unexpected Earnings," Journal of
Accounting, Auditing, and Finance, 17, 155-184.
Peng, L. and Roell, A., 2008. "Manipulation and Equity-based Compensation," American Economic Review: Papers and Proceedings, 98:2, 285-290.
Peng, L. and Roell, A., 2009. "Managerial Incentives and Stock Price Manipulation," Working Paper, Baruch College/CUNY and Columbia University.
Matsumoto, D. A., 2002. "Management's Incentives to Avoid Negative Earnings Surprises," The Accounting Review, 77, 483-514.
Myers, J. N., Myers, L. A., and Skinner, D. J. 2007. "Earnings Momentum and Earnings Management," Journal of Accounting, Auditing and Finance, 2007, 22, 249-284.
Murphy, K. J., 1999. "Executive Compensation," In Handbook of Labor Economics Volume 3b, ed. Orley C. Ashenfelter and David Card, 2485-2563. Amsterdam: Elsevier.
Narayanan, M. P., Seyhun, H. N., 2005. "Effect of Sarbanes-Oxley Act on the Influencing of Executive Compensation," Working Paper, University of Michigan.
Palmrose, Z., Richardson, V. J., Scholz, S., 2004. "Determinants of Market Reactions to Restatement Announcement," Journal of Accounting and Economics, 37, 59-89.
Turner, L., Dietrich, J. R., Anderson, K., Bailey, A. J., 2001. "Accounting Restatements," Unpublished working paper, Office of Economic Analysis, United States Securities and Exchange Commission.
Verrecchia, R. E., 1983. "Discretionary Disclosure," Journal of Accounting and Economics, 5, 179-194.
Wu, M., 2001. "Earnings Restatements: A Capital Market Perspective," Unpublished dissertation, New York University.
Footnotes
1. I gratefully acknowledge Eric Young and Chris Otrok for their inspiration and unwavering support. A special debt of gratitude is owed to Toshi Mukoyama for meticulous guidance, and to Mark Carey for invaluable help. I am also greatly indebted to Alex Edmans, Maxim Engers, Rick Green, Zhiguo He, Nathan Larson, Leo Martinez, Ned Prescott, Adriano Rampini, John Weinberg, Stan Zin, and seminar participants at Boston University, Carnegie Mellon University, Cornell University, Darden School of Business, Federal Reserve Board of Governors, Federal Reserve Bank of Cleveland, Federal Reserve Bank of Richmond, Georgetown University, INSEAD, Peking University, University of Chicago Booth School of Business, University of Maryland, University of Virginia, Wharton School of Business, World Bank, and Tsinghua University for their helpful comments and suggestions. The views expressed herein are the author's and do not necessarily reflect the opinions of the Board of Governors of the Federal Reserve System. Return to text
2. Contact: Division of International Finance, Board of Governors of the Federal Reserve, Mail Stop 44, 20th Street and Constitution Avenue, Washington, DC 20551. [email protected]. (202)452-2343. Return to text
3. In a recent article entitled "Capitalist Fools", Joe Stiglitz listed "faking the numbers" as one of five major causes of the economic crisis in 2008. Return to text
4. Morgan Stanley determined that accounting tactics, while legal, enabled Freddie Mac, and to a lesser extent Fannie Mae, to overstate the value of their reserves. Both companies also pushed losses into the future by sharply curtailing their repurchases of soured mortgages out of the securitizations they guaranteed. "Fannie Mae and Freddie Mac were `playing games with their accounting' to meet reserve requirements, prompting the government to seize control of the companies," U.S. Senator Richard Shelby said (Bloomberg [September 9, 2008]). In the case of AIG, PricewaterhouseCoopers prompted an announcement about material accounting weaknesses related to the valuation of AIG's derivatives holdings. Prosecutors insisted that five former executives from the American International Group deliberately mounted a fraud to manipulate its financial statements, after a string of AIG scandals early this decade."Accounting flaws at American International Group significantly understated the insurance giant's losses on complex financial instruments linked to mortgages and corporate debt." (The New York Times [February 12, 2008]). Return to text
5. While the widely-accepted view that executive compensation was a main contributing factor to the financial crisis is calling for regulation and reforms of pay practices, a recent paper by Fahlenbrach and Stulz (2009) finds no evidence that bank performance during the credit crisis of 2008 is related to CEO incentives. Return to text
6. This analysis does not make a distinction between earnings management and fraud. While the accounting choices that explicitly violate Generally Accepted Accounting Principles (GAAP) clearly constitute both earnings management and fraud, according to the SEC, systematic choices made within the boundaries of GAAP can constitute earnings management as long as they are used to obscure the true performance of a firm and will lead to adverse consequences for the firm in the same way as fraud.
Following this notion, there is no economic difference between fraud and earnings management in the model: in both cases the reported number is different from the true amount, and the manager bears costs for such behavior. Return to text
7. In an economy where there are a large
number of such shareholders and managers, ![]() represents the fraction of managers who are able to manipulate
earnings. Return to text
represents the fraction of managers who are able to manipulate
earnings. Return to text
8. There are two frictions in the model
that restrain earnings management: earnings management opportunity
that realizes with probability ![]() and the cost
involved in misstating earnings
and the cost
involved in misstating earnings ![]() . This model can
be also considered with only one friction: the cost of manipulation
with a simple stochastic structure. The manipulation cost now in
the model follows a binary distribution with two possible
realizations
. This model can
be also considered with only one friction: the cost of manipulation
with a simple stochastic structure. The manipulation cost now in
the model follows a binary distribution with two possible
realizations ![]() and
and ![]() . Return to text
. Return to text
9. This paper has a central focus on upward manipulation. The reason to focus on misreporting on upside is that overstatement of earnings is more widespread than understatement in the data and more problematic in general. Empirical work on SEC enforcement actions aimed at violations of Generally Accepted Accounting Principles suggests that over-reporting is the more frequent source of firm-wide financial misrepresentation (Feroz et al. [1991]). The average amount of restated earnings is hugely negative, and over 75% of restating firms restated their earnings downwards, indicating that managers have a strong drive to appear more productive than they actually are. Return to text
10. An environment where the opportunity to manipulate reports realizes with certainty while the size of manipulation is stochastic would be essentially identical to the current model. Return to text
11. Here, whether the manager has the opportunity of managing earnings is assumed to be a random event, and the outcome is the manager's private information. Generally Accepted Accounting Principles (GAAP) provide guidelines on how to record and summarize each type of economic transaction, and hence define the accounting latitude available to senior management in financial reporting. In practice, certain economic activities, those where there is no hard-and-fast rule for which accounting method to use, lead to more discretion than others. In any particular period, economic transactions of this type may or may not take place. By virtue of being closer to the operations process, only the manager knows the extent of these activities and hence the degree of reporting latitude available. Return to text
12. In capturing the additional source of uncertainty on both shareholders and managers, we do not model detection technology in this framework. There is a vast literature on costly state verification, which is an element we do not consider in this paper. In the current environment, the inability of the principal to implement a contract contingent on detection of manipulation reflects enforcement frictions observed in reality, such as imperfect auditing, inadequate and delayed SEC investigations, and CEO departure before detection and liquidation. Return to text
13. If the Revelation Principle applied, we would have two truth-telling incentive constraints, one for the earnings and another for the realization of manipulation opportunity. Return to text
14. The figure only describes
![]() . The level of
. The level of ![]() and
and ![]() are pinned down by the
participation constraint(2). Return to text
are pinned down by the
participation constraint(2). Return to text
15. It is worth pointing out that the principal in the model compensates the manager with utility promises contingent on earnings reports, and a larger utility differential does not necessarily translate into a larger wage difference. In this model, incentive compatibility constraint on effort choice (1) determines utility differential between high and low reports, and participation constraint (2) pins down the exact levels of promised utilities
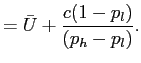 |
(9) | |
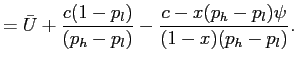
|
(10) |
Since ![]() is independent of
is independent of ![]() or
or ![]() , the change of
, the change of
![]() is solely due to the change of
is solely due to the change of
![]() . It is straightforward to map utility
wedge into wage differential in this case. Return to text
. It is straightforward to map utility
wedge into wage differential in this case. Return to text
16. Gabaix and Landier (2006) report evidence that a one standard deviation deterioration in their measure of corporate governance quality at the firm level implies a 5.2% increase in CEO compensation. Return to text
17. Our result is also different from Peng and Roell (2009) in that their equilibrium compensation contract increases the sensitivity of pay to the stock market value only as a result of an reduction in the elasticity of prices to the manager's reports. Return to text
18. In this strand of the literature, one of the most common metrics used to detect earnings management is the magnitude of discretionary accruals, which proxies for the discretion used by managers to achieve their financial reporting goals. A commonly used approach is Jones (1991) model of accruals, which estimates discretionary accruals as the residual from a regression of total accruals on lagged firm size, the change in firm sales, and gross property plant and equipment scaled by total firm assets. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text