
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1000, June 2010 --- Screen Reader
Version*
Interpreting Investment-Specific Technology Shocks**
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Investment-specific technology (IST) shocks are often interpreted as multi-factor productivity (MFP) shocks in a separate investment-producing sector. However, this interpretation is strictly valid only when some stringent conditions are satisfied. Some of these conditions are at odds with the data. Using a two-sector model whose calibration is based on the U.S. Input-Output Tables, we consider the implications of relaxing several of these conditions. In particular, we show how the effects of IST shocks in a one-sector model differ from those of MFP shocks to an investment-producing sector of a two-sector model. Importantly, with a menu of shocks drawn from recent empirical studies, MFP shocks induce a positive short-run correlation between consumption and investment consistent with U.S. data, while IST shocks do not.
Keywords: DSGE models, multi-factor productivity shocks, investment-specific technology shocks
JEL classification: E13, E32
1 Introduction
In post-WWII U.S. data, the relative price of equipment investment has a downward trend and varies over the cycle. In a pair of highly influential papers, Greenwood, Hercowitz and Krusell (1997, 2000)--hereafter GHK--showed how a modified one-sector model can be used to analyze these regularities. They introduced an investment-specific technology (IST) shock to distinguish equipment investment from other final-use categories.1 In particular, when allocated to equipment investment, the single and undifferentiated good yields more or less installed capital depending on the level of IST, but when allocated to other uses it remains unchanged. Over the last decade, IST shocks have become a leading candidate explanation for post-war business cycle fluctuations.2 This paper is about the interpretation of IST shocks.
GHK point the way to an interpretation. They show that their one-sector model is a special case of a model with two sectors, one that produces a good used only for equipment investment and another that produces a good used for both consumption and structures investment. Under certain conditions, an IST shock to equipment investment in their one-sector model is equivalent for aggregate variables to a multi-factor productivity (MFP) shock to equipment production in the two-sector model. This "aggregate eqivalence" (AE) result provides a basis for interpreting the IST shock as an MFP shock.
It may come as no surprise that the GHK conditions for AE are quite restrictive and that some of them are clearly at odds with the data. They entail a production structure that differs significantly from the one implied by the U.S. Input-Output (IO) Tables. In addition, capital is perfectly mobile between sectors. Furthermore, there are no costs of adjusting investment.
We investigate the effects of reasonable departures from the GHK conditions for AE. We use a model with two production sectors calibrated to the U.S. IO Tables and other sectoral statistics.3 In this model, MFP increases in the machinery-producing sector have effects that are qualitatively different from IST increases in a one-sector model, even though the models are calibrated to match the same aggregate features whenever possible. One important difference is that with MFP shocks, consumption is boosted at all horizons, while with IST shocks consumption is reduced initially.4
Our two-sector model has some similarities to the one posited by GHK to support their interpretation. Both models have two production sectors and the same three final goods (equipment investment, consumption, and structures investment).
However, we extend the GHK model in three ways. The first
extension is that the outputs of both production sectors are used
in "assembling"all three final goods. The two production
sectors are the machinery (![]() ) sector and its
complement, the non-machinery (
) sector and its
complement, the non-machinery (![]() ) sector. For
example, equipment investment is assembled using machines from the
) sector. For
example, equipment investment is assembled using machines from the
![]() sector and distribution services from the
sector and distribution services from the
![]() sector. Thus, the structure of our economy
differs from that in GHK except in the limiting case of "complete
specialization in assembly"in which
sector. Thus, the structure of our economy
differs from that in GHK except in the limiting case of "complete
specialization in assembly"in which ![]() output is used
only in the assembly of equipment and
output is used
only in the assembly of equipment and ![]() output is used
only in the assembly of consumption and structures. In this
limiting case, the machinery sector could just as well be referred
to as the equipment sector, as it is in GHK.
output is used
only in the assembly of consumption and structures. In this
limiting case, the machinery sector could just as well be referred
to as the equipment sector, as it is in GHK.
The other two extensions are additions of two types of real rigidities. First, as has become common in dynamic stochastic general equilibrium (DSGE) models, we allow for costs of changing investment.5 This extension enables us to consider conditions for equivalence under alternative specifications of these costs. Second, we allow for costs of adapting capital suitable for one sector for use in the other. This extension makes it possible for us to consider the case in which capital stocks are predetermined not only at the aggregate level but also at the sectoral level. Of course, others have considered this case, but to our knowledge none of them have explored the implications for the interpretation of IST shocks.
We derive conditions for AE in our extended model. These conditions can be divided into two distinct sets. Under one set of conditions there is two-sector equivalence (TE): in a two-sector model, IST shocks and sectoral MFP shocks are equivalent. The first condition is that there is "partial specialization"in assembly under which assembly of consumption and structures investment uses only non-machinery output and assembly of equipment is Cobb-Douglas in both outputs. The limiting case of partial specialization is "complete specialization"in which equipment investment assembly uses only machinery output. This case is important because both GHK and the other DSGE literature that relates IST shocks to MFP shocks focus on it almost exclusively. The second condition is that investment adjustment costs are suitably specified as explained below. These conditions are sufficient for TE and are necessary for TE to first order.
Under a second set of conditions, aggregation is possible: a two-sector model can be reduced to a one-sector model for the determination of aggregate variables. First, there are no costs adapting capital used in one sector for use in the other. Second, the two sectoral production functions are identical up to a multiplicative productivity factor. The combined third and fourth conditions are that both depreciation rates and investment adjustment-cost functions are the same for all inherited stocks of a given type of capital.6 We can show that these conditions are sufficient for aggregation, that the third and fourth conditions are necessary, and that each of the first two conditions is necessary given the other.7
Following the empirical validation for the importance of IST shocks provided by Fisher (2006) and Smets and Wouters (2007), a growing number of papers that attempt to estimate DSGE models have included IST shocks and found them to be a major driver of business cycle fluctuations. However, these studies struggle with the problem that if IST shocks are prominent, they cause the unconditional correlation between investment and consumption to be counterfactually negative. For example, Justiniano and Primiceri (2008) found that IST shocks are the most important drivers of business cycle fluctuations in U.S. output and hours. Using a one-sector model, they show the comovement between investment and consumption to be positive in the data, but negative in the model. MFP shocks in the machinery sector, while sharing many features with IST shocks, have the potential to resolve this incongruence.
A good overview of the literature on comovement is provided by Christiano and Fitzgerald (1998). Recent contributions by Christiano et al. (2008) and Jaimovich and Rebelo (2009) point respectively to consumption habits in combination with investment adjustment costs and to departures from utility functions that are additively separable in consumption and leisure as mechanisms to generate comovement, even in the face of IST shocks. We abstract from consumption habits; although we allow for investment adjustment costs, our two-sector model does not rely on such costs to generate comovement. Furthermore, at no point do we depart from preferences that are consistent with a balanced growth path.
In the final part of the paper we conduct a Monte Carlo experiment. We hypothesize that taking the two-sector model as data-generating process, the estimated one-sector model would still imply negative comovement between consumption and investment. The results of the experiment support this hypothesis and confirm that the one- and two-sector models have dramatically different implications for the correlation of consumption and investment even for the small size of the estimation sample typically used in a macro-econometric context.
2 The Model
Our approach to the analysis of productivity changes is a combination of the growth-accounting approach based on industrial breakdowns--in the style of Solow (1957) and Griliches and Jorgenson (1966) --and the DSGE approach based on final-use breakdowns. We use a closed-economy model with a representative household and a production structure with three central features: two production sectors, three final goods, and two types of capital. We refer to "production sectors"rather than "industries"because the former terminology is more common in the literature on IST shocks.
2.1 Production Sectors
We analyze productivity developments in two production sectors
which we call the machinery (![]() ) sector and the
non-machinery (
) sector and the
non-machinery (![]() ) sector. Both sectors comprise
perfectly competitive firms. Consider the representative firm in
sector
) sector. Both sectors comprise
perfectly competitive firms. Consider the representative firm in
sector ![]() (where
(where
![]() in period
in period ![]() .
It hires labor (
.
It hires labor (![]() ) from households at a wage
) from households at a wage
![]() that is same for both
sectors because labor is perfectly mobile between sectors. It also
rents two types of capital from households: equipment capital (
that is same for both
sectors because labor is perfectly mobile between sectors. It also
rents two types of capital from households: equipment capital (
![]() ) and structures capital
) and structures capital
![]() at rentals (
at rentals (
![]() and
and
![]() ) that are sector-specific because
it is costly to reallocate capital. The firm minimizes the unit
cost of producing a given number of physical units of its sector's
output (
) that are sector-specific because
it is costly to reallocate capital. The firm minimizes the unit
cost of producing a given number of physical units of its sector's
output (![]() ) subject to a sector-specific
Cobb-Douglas production function
) subject to a sector-specific
Cobb-Douglas production function
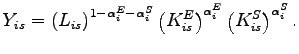 |
(1) |
The factor shares for the two types of capital are
![]() and
and
![]() .
.
There is a multi-factor productivity (MFP) shock
![]() which determines the
efficiency units generated by physical machinery output (
which determines the
efficiency units generated by physical machinery output (
![]() . For example, for
computers
. For example, for
computers ![]() can be thought as the number of
computers produced, and
can be thought as the number of
computers produced, and
![]() as the computing power generated
by these computers. Accounting separately for physical and
efficiency units facilitates comparison of MFP shocks with IST
shocks.
as the computing power generated
by these computers. Accounting separately for physical and
efficiency units facilitates comparison of MFP shocks with IST
shocks.
Since it is competitive and there are constant returns to scale,
the firm ends up selling at a price equal to unit cost. Let
![]() represent the factor cost of a unit of
physical output
represent the factor cost of a unit of
physical output ![]() 8
8
We assume
that the ![]() good is the numeraire, so
good is the numeraire, so ![]() . The factor cost of a physical unit of machinery is
. The factor cost of a physical unit of machinery is
![]() and the cost of an efficiency unit of
machinery is
and the cost of an efficiency unit of
machinery is
![]() so that
so that
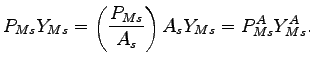 |
(2) |
2.2 Final Goods
There are three final goods: a consumption good (![]() ) and two investment goods, one (
) and two investment goods, one (![]() )
used for gross investment in
)
used for gross investment in ![]() capital stocks and
the other (
capital stocks and
the other (![]() ) used for gross investment in
) used for gross investment in
![]() capital stocks. These goods are assembled
by perfectly competitive final goods firms that use as inputs the
outputs of the two production sectors, and these final goods are
measured in efficiency units. When we find it expedient for the
exposition, we us an upper bar to denote final goods measured in
physical units.
capital stocks. These goods are assembled
by perfectly competitive final goods firms that use as inputs the
outputs of the two production sectors, and these final goods are
measured in efficiency units. When we find it expedient for the
exposition, we us an upper bar to denote final goods measured in
physical units.
The assembly function for ![]() is a constant
elasticity of substitution (CES) function of the two consumption
inputs, efficiency units of
is a constant
elasticity of substitution (CES) function of the two consumption
inputs, efficiency units of ![]() goods (
goods (
![]() ) along with
) along with ![]() goods (
goods (![]() ):
):
![$\displaystyle C_{s}=\left[ \phi_{M}^{C}\left( \frac{A_{s} C_{Ms}}{\phi_{M}^{C}}\right) ^{\frac{\sigma_{C}-1}{\sigma_{C}}}+\phi_{N}^{C}\left( \frac{C_{Ns}}{\phi _{N}^{C}}\right) ^{\frac{\sigma_{C}-1}{\sigma_{C}}}\right] ^{\frac {\sigma_{C}}{\sigma_{C}-1}},$](img50.gif) |
(3) |
where
![]() and
and
![]() are the weights for
are the weights for ![]() and
and ![]() goods, and
goods, and
![]() is the elasticity of substitution
between
is the elasticity of substitution
between ![]() and
and ![]() goods in the
assembly of
goods in the
assembly of ![]() .
.
The assembly functions for ![]() and
and
![]() are CES functions of the two
investment inputs, efficiency units of
are CES functions of the two
investment inputs, efficiency units of ![]() goods (
goods (
![]() ,
,
![]() ) along with
) along with ![]() goods (
goods (
![]() ,
,
![]() ):
):
![$\displaystyle J_{s}^{E}=\left[ \phi_{M}^{E}\left( \frac{A_{s} I_{Ms}^{E}}{\phi_{M}^{E} }\right) ^{\frac{\sigma_{E}-1}{\sigma_{E}}}+\phi_{N}^{E}\left( \frac {I_{Ns}^{E}}{\phi_{N}^{E}}\right) ^{\frac{\sigma_{E}-1}{\sigma E}}\right] ^{\frac{\sigma_{E}}{\sigma_{E}-1}},$](img67.gif) |
(4) |
![$\displaystyle J_{s}^{S}=\left[ \phi_{M}^{S}\left( \frac{A_{s}I_{Ms}^{S}}{\phi_{M}^{S} }\right) ^{\frac{\sigma_{S}-1}{\sigma_{S}}}+\phi_{N}^{S}\left( \frac {I_{Ns}^{S}}{\phi_{N}^{S}}\right) ^{\frac{\sigma_{S}-1}{\sigma_{S}}}\right] ^{\frac{\sigma_{S}}{\sigma_{S}-1}},$](img68.gif) |
(5) |
where
![]() and
and
![]() are the weights given to
are the weights given to
![]() and
and ![]() goods, and
goods, and
![]() and
and
![]() are the elasticities of
substitution between
are the elasticities of
substitution between ![]() and
and ![]() goods.
goods.
The assembly firms minimize the unit cost of producing
efficiency units of consumption, equipment, and structures.9 Because
they are perfectly competitive, firms end up selling final goods at
prices that are equal to these costs and that are indicated by
![]() ,
,
![]() , and
, and
![]() . We assume that the assembly
functions for both
. We assume that the assembly
functions for both ![]() and
and ![]() are
are ![]() -intensive relative to the
function for
-intensive relative to the
function for ![]() .
.
There is an investment-specific technology (IST) shock
![]() which further enhances
the efficiency of
which further enhances
the efficiency of ![]() , equipment assembled
using
, equipment assembled
using ![]() and
and ![]() inputs. The final
total amount of equipment efficiency units is given by
inputs. The final
total amount of equipment efficiency units is given by
![]() and the all-in unit cost is
and the all-in unit cost is
![]() so that
so that
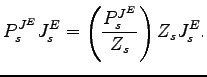 |
(6) |
For example, the expression
![]() and
and
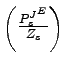 in the model are analogous to the measures of computer output and
the price of computer output in the NIPA.
in the model are analogous to the measures of computer output and
the price of computer output in the NIPA.
We sometimes refer to the case of "partial specialization"in
assembly. Under partial specialization, the assembly functions for
![]() and
and ![]() depend only on
the
depend only on
the ![]() good:
good:
| (7) |
and the assembly function for total efficiency units of equipment
investment,
![]() , is Cobb-Douglas:
, is Cobb-Douglas:
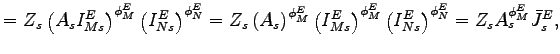 |
||
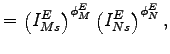 |
(8) |
where
![]() incorporates the enhancements
coming from
incorporates the enhancements
coming from ![]() as well as from
as well as from ![]() and where
and where
![]() represents equipment
investment in "physical units" (number of computers). Therefore,
represents equipment
investment in "physical units" (number of computers). Therefore,
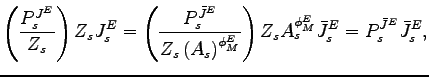 |
(9) |
where
![]() is the cost of a unit of
is the cost of a unit of
![]() and
and
![]() is the cost of a unit
of
is the cost of a unit
of
![]()
Partial specialization has the case of "complete
specialization"as a limit. Under complete specialization, the
assembly function for equipment investment depends only on the
![]() good
good
![]() and all machinery output is used for equipment investment so
that
and all machinery output is used for equipment investment so
that
| (10) |
The complete specialization case is important because, beginning
with GHK, the literature that relates IST shocks to MFP shocks
focuses almost exclusively on this case. For this reason, we assume
complete specialization
![]() in our
baseline case.
in our
baseline case.
2.3 Tastes and Constraints
In period ![]() , the representative household supplies
a fixed amount of labor
, the representative household supplies
a fixed amount of labor ![]() and maximizes the
intertemporal utility function
and maximizes the
intertemporal utility function
 |
(11) |
where ![]() is a consumption preference shock. The
household also chooses holdings of a single bond (
is a consumption preference shock. The
household also chooses holdings of a single bond (![]() ) denominated in the
) denominated in the ![]() good (the
numeraire good for the model). In addition, for each of the four
inherited capital stocks (
good (the
numeraire good for the model). In addition, for each of the four
inherited capital stocks (
![]() , and
, and
![]() )
)![]() the
household decides how much to adapt to obtain the four capital
stocks rented out for use in production (
the
household decides how much to adapt to obtain the four capital
stocks rented out for use in production (
![]() , and
, and
![]() ) as well as the fractions (
) as well as the fractions (
![]() , and
, and
![]() ) of investment of the two types (
) of investment of the two types (
![]() or
or ![]() ) to
be added to the four capital stocks. The distinction between
capital inherited from the previous period, the
) to
be added to the four capital stocks. The distinction between
capital inherited from the previous period, the
![]() stocks, and capital used in
production, the
stocks, and capital used in
production, the
![]() stocks, allows us to nest in the
same model the case in which capital is predetermined only at the
aggregate level and the case in which capital is
predetermined also at the sectoral level.
stocks, allows us to nest in the
same model the case in which capital is predetermined only at the
aggregate level and the case in which capital is
predetermined also at the sectoral level.
The household is subject to period budget constraints. In each period, factor income plus income from bonds held in the previous period must be at least enough to cover purchases of final goods (consumption goods and the two types of investment goods), as well as bonds:
| (12) |
where
![]() ,
,
![]() ,
,
![]() ,
,
![]() are the rental rates for the
capital stocks used in production. The term
are the rental rates for the
capital stocks used in production. The term
![]() is the gross return on bonds.
is the gross return on bonds.
The household is subject to technological constraints when
allocating capital. It inherits four capital stocks from the
previous period. Inherited capital suited for one sector can be
adapted for use in the other sector before being rented out, but
only by incurring increasing marginal costs. For example, inherited
equipment capital (
![]() ) suited for the
) suited for the ![]() sector can be adapted for use in the
sector can be adapted for use in the ![]() sector (
sector (
![]() . Therefore, the capital of type
. Therefore, the capital of type
![]() actually available for production in
sector
actually available for production in
sector ![]() in period
in period ![]() depends on
how much has been adapted for production in that sector:
depends on
how much has been adapted for production in that sector:
![$\displaystyle =D_{Ms}^{h}\left[ 1-\frac{\omega^{h}}{2}\left( \frac{K_{Ms}^{h}}{D_{Ms}^{h}}-1\right) ^{2}\right]$](img151.gif) |
||
![$\displaystyle + D_{Ns}^{h}\left[ 1-\frac{\omega^{h}}{2}\left( \frac{K_{Ns}^{h}} {D_{Ns}^{h}}-1\right) ^{2}\right] , \,\,\, h \in\{E,S\}.$](img152.gif) |
(13) |
Here, we restrict our attention to two special cases: the case in
which capital can be adapted at no cost (
![]() so that capital is
predetermined only at the aggregate level, and the case in which
the marginal cost of adapting capital becomes prohibitive (
so that capital is
predetermined only at the aggregate level, and the case in which
the marginal cost of adapting capital becomes prohibitive (
![]() so that capital
is predetermined at the sectoral level as well.
so that capital
is predetermined at the sectoral level as well.
The household is also subject to technological constraints when
accumulating capital. The accumulation equations for structures
capital are more straightforward, so we consider them first. Let
![]() represent the amount of
represent the amount of
![]() capital available for production in sector
capital available for production in sector
![]() in period
in period ![]() without
incurring any costs of adaptation:
without
incurring any costs of adaptation:
![$\displaystyle \begin{tabular}[c]{c} $D_{is}^{S}=\left( 1-\delta^{S}\right) K_{is-1}^{S}+j_{is-1}^{S}J_{s-1} ^{S}-\frac{\nu_{0}^{S}}{2}j_{is-1}^{S}J_{s-1}^{S}\left( \frac{j_{is-1} ^{S}J_{s-1}^{S}}{j_{is-2}^{S}J_{s-2}^{S}}-1\right) ^{2},\,\,\,\,i\in\{M,N\},$ \end{tabular}$](img159.gif) |
(14) |
where
![]() is the proportion of total
structures investment in period
is the proportion of total
structures investment in period ![]() that is added to
the structures capital suitable for sector
that is added to
the structures capital suitable for sector ![]() in that
period.
in that
period.
![]() has three components represented
by the three terms on the right hand side of equation (14). The first is the amount of
has three components represented
by the three terms on the right hand side of equation (14). The first is the amount of ![]() capital
actually used in production in sector
capital
actually used in production in sector ![]() in period
in period
![]() remaining after depreciation. The second
is the amount of
remaining after depreciation. The second
is the amount of ![]() investment added to structures
capital suitable for sector
investment added to structures
capital suitable for sector ![]() in period
in period
![]() . The third represents the adjustment
costs incurred if the
. The third represents the adjustment
costs incurred if the ![]() investment in a given type
of capital in period
investment in a given type
of capital in period ![]() differs from that in
period
differs from that in
period ![]() . It is important to note that while the
IST shock
. It is important to note that while the
IST shock ![]() does not enter the accumulation
equations for structures capital by assumption, the MFP shock
does not enter the accumulation
equations for structures capital by assumption, the MFP shock
![]() does enter through
does enter through ![]() except in the case of complete specialization in
assembly in which
except in the case of complete specialization in
assembly in which
![]() .
.
The accumulation equations for equipment capital are less
straightforward because of the distinction between physical units
and efficiency units. Let
![]() represent the amount of
represent the amount of
![]() capital available for production in sector
capital available for production in sector
![]() in period
in period ![]() without
incurring any costs of adaptation:
without
incurring any costs of adaptation:
![$\displaystyle +\frac{\nu_{0}^{E}}{2}\left( Z_{s-1}\right) ^{\nu_{1}^{E}}j_{is-1} ^{E}J_{s-1}^{E}\left[ \left( \frac{Z_{s-1}}{Z_{s-2}}\right) ^{\nu_{2}^{E} }\frac{j_{is-1}^{E}J_{s-1}^{E}}{j_{is-2}^{E}J_{s-2}^{E}}-1\right] ^{2},\,\,\,\,i\in\{M,N\},$](img183.gif) |
(15) |
where
![]() is the proportion of total
equipment investment that is devoted to accumulation of structures
capital suited for sector
is the proportion of total
equipment investment that is devoted to accumulation of structures
capital suited for sector ![]() in period
in period
![]() , and where the parameters
, and where the parameters
![]() and
and
![]() can take on the values of one or
zero.10 Like
can take on the values of one or
zero.10 Like
![]() has three components.
The first components of
has three components.
The first components of
![]() and
and
![]() are completely analogous. The
second component of
are completely analogous. The
second component of
![]() is the amount of investment in
equipment capital suited for sector
is the amount of investment in
equipment capital suited for sector ![]() measured in
efficiency units. It reflects the increase in the efficiency of the
machinery input resulting from the MFP shock
measured in
efficiency units. It reflects the increase in the efficiency of the
machinery input resulting from the MFP shock ![]() which is imbedded in
which is imbedded in ![]() and the
increase in efficiency resulting from the IST shock
and the
increase in efficiency resulting from the IST shock ![]() . The third component represents investment adjustment
costs. If
. The third component represents investment adjustment
costs. If
![]() , then adjustment
costs apply to efficiency units no matter whether
, then adjustment
costs apply to efficiency units no matter whether ![]() or
or ![]() is the source of increased
efficiency. We consider the implication of zero values for either
is the source of increased
efficiency. We consider the implication of zero values for either
![]() or
or
![]() or both below.
or both below.
It is instructive to consider the case of Cobb-Douglas assembly
for equipment in which
![]() is given by
is given by
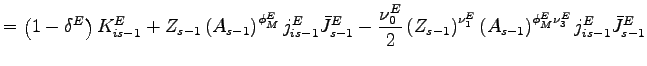 |
||
![$\displaystyle \times\left[ \left( \frac{Z_{s-1}}{Z_{s-2}}\right) ^{\nu_{2}^{E}}\left( \frac{A_{s-1}}{A_{s-2}}\right) ^{\phi_{M}^{E}\nu_{4}^{E}}\frac{j_{is-1} ^{E}\bar{J}_{s-1}^{E}}{j_{is-2}^{E}\bar{J}_{s-2}^{E}}-1\right] ^{2} ,\,\,\,\,i\in\{M,N\},$](img209.gif) |
(16) |
where we have introduced the parameter
![]() and
and
![]() for ease of exposition. The
first component of
for ease of exposition. The
first component of
![]() is the same as in the general
case. The second component, investment in sector
is the same as in the general
case. The second component, investment in sector ![]() measured in efficiency units (computing power), can be expressed as
the product of two terms, an efficiency enhancement term
measured in efficiency units (computing power), can be expressed as
the product of two terms, an efficiency enhancement term
![]() and investment measured in "physical units"
and investment measured in "physical units"
![]() (where
(where
![]() is defined in
Equation 8). For the third component,
investment adjustment costs, there are two versions that are
consistent in the sense that whenever
is defined in
Equation 8). For the third component,
investment adjustment costs, there are two versions that are
consistent in the sense that whenever ![]() and
and
![]() appear in the accumulation equations, they
appear together in the same function (
appear in the accumulation equations, they
appear together in the same function (
![]() ).
First, if
).
First, if
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , then adjustment costs depend on efficiency units. Second,
if
, then adjustment costs depend on efficiency units. Second,
if
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() then adjustment costs depend on physical units. In a third
version where
then adjustment costs depend on physical units. In a third
version where
![]()
![]()
![]()
![]()
![]()
![]()
![]() but
but
![]() , the two efficiency factors
, the two efficiency factors
![]() and
and ![]() do not always
appear together in the same function. This last version is of
interest because papers that attempt to capture the importance of
IST shocks for the business cycle routinely incorporate investment
adjustment costs that include some efficiency enhancements but not
others.11 At least to us, it is not obvious how investment
adjustment costs should be modeled.
do not always
appear together in the same function. This last version is of
interest because papers that attempt to capture the importance of
IST shocks for the business cycle routinely incorporate investment
adjustment costs that include some efficiency enhancements but not
others.11 At least to us, it is not obvious how investment
adjustment costs should be modeled.
The final household constraint is that for each type of investment good the proportions of the total amount added to the two capital stocks of the same type must sum to one:
2.4 Market Clearing
Market clearing requires that the outputs of the production sectors must be used up in the assembly of final goods:
that labor demand equal labor supply,
| (17) |
and that the bond be in zero net supply
| (18) |
The conditions that firms' demands for
![]() and
and
![]() equal households' supplies are
imposed implicitly by using the same symbol for both.
equal households' supplies are
imposed implicitly by using the same symbol for both.
3 Equivalence
Under certain conditions, the aggregate effects of an MFP shock in the machinery sector of our model with two production sectors can be reproduced by an IST shock to equipment investment in a one-sector model. In this sense, the two shocks display "aggregate equivalence (AE)"12 . Table 1 defines some additional aggregate variables, and Table 2 describes the one-sector model.
In this section we interpret and extend the conditions for AE. We observe that the conditions can be divided into two distinct sets. Under one set, there is two-sector equivalence; that is, IST shocks and MFP shocks are equivalent in a two-sector model with different production functions in the two sectors. Under the other, aggregation is possible; that is, a two-sector model can be reduced to a one-sector model for the determination of aggregate variables. Previous discussions of AE assume that (using our terminology) assembly is completely specialized and that investment adjustment is costless. We extend the conditions for AE in two ways. First, we show that specialization in assembly of consumption and structures is necessary for AE but specialization of assembly of equipment is not. Second, we identify conditions under which there is AE when there are costs of adjusting investment.
This section also contains simulation results for a calibration that includes adjustment costs for investment and satisfies the extended conditions for AE. We use these results as a benchmark against which to compare results for calibrations that do not satisfy these conditions.
3.1 Conditions for Aggregate Equivalence in the Extended Model
Here we state conditions for aggregate equivalence (AE) in our
extended model.13Throughout our discussion we maintain two standard
assumptions. Production functions exhibit constant returns to
scale, and adjustment costs are homogeneous of degree zero in
current and lagged investment. Sketches of proofs of our assertions
can be found in section A of the
appendix. The conditions can be divided into two distinct sets
denoted ![]() and
and ![]() . The conditions in
set
. The conditions in
set ![]() are sufficient for "two-sector
equivalence" (TE). By TE, we mean that in a model with two distinct
production sectors
are sufficient for "two-sector
equivalence" (TE). By TE, we mean that in a model with two distinct
production sectors ![]() and
and ![]() possibly with different production functions, an MFP shock
(
possibly with different production functions, an MFP shock
(![]() ) that raises output in the
) that raises output in the ![]() sector by a given percentage has the same sectoral and aggregate
effects as a pair of IST shocks (
sector by a given percentage has the same sectoral and aggregate
effects as a pair of IST shocks (![]() ) that push up the
effectiveness of equipment investment in both sectors by that given
percentage. These conditions are also necessary for TE to
first-order. The set c
) that push up the
effectiveness of equipment investment in both sectors by that given
percentage. These conditions are also necessary for TE to
first-order. The set c![]() onditions are
onditions are
A-1. Assembly of both consumption and structures investment is specialized in non-machinery output.14 Even though it is standard to assume specialization in assembly in DSGE models, in fact the outputs of several sectors are often used in the assembly goods for final uses. In particular, the final-use equipment investment as it appears in the NIPA is a combination of machinery with transportation and distribution services.
A-2. Assembly of equipment investment is a Cobb-Douglas function of machinery and non-machinery outputs with a limiting case in which it is specialized in machinery output.
A-3. If there are adjustment costs for equipment investment, MFP shocks and IST shocks enter the costs combined in the same function wherever they appear.
Greenwood, Hercowitz, and Krusell ( 1997) and Oulton (2007) assume that (using our terminology) assembly is completely specialized and that investment adjustment is costless. Under these assumptions, our conditions for TE are met, but the assumptions are unnecessarily restrictive.
The conditions in set B are sufficient for aggregation,
that is, for the existence of a model with one production sector
that yields the same values for aggregate variables as a model with
distinct ![]() and
and ![]() production
sectors:
production
sectors:
B-1. The production functions forand
are identical up to a multiplicative factor.
B-2. Inherited stocks of both equipment and structures capital are costlessly adaptable for renting out to either production sector.15
B-3. Depreciation rates for equipment stocks are identical for theand
sectors. The same is true for structures stocks.
B-4. Any investment adjustment costs for equipment are identical in theand
sectors. The same is true for structures stocks.
If the conditions for TE (set A) and for aggregation (set B) are met, then there is AE whether or not investment adjustment costs are present.16 We have not found earlier statements of sufficient conditions for aggregation of capital accumulation equations when adjustment costs are present, our B-4.
We can draw conclusions about the necessity of some of the conditions in Set B:
- Depreciation rates must be identical.
- Investment adjustment costs must be identical.
- If capital is costlessly adaptable, production functions must be identical.
- If production functions are identical, capital must be costlessly adaptable.
In fact, we conjecture, but have not yet shown, that all of the conditions in set B are necessary for aggregation.
3.2 Calibration Ensuring Equivalence
Table 3 summarizes
the parameter choices for the simulation that illustrates aggregate
equivalence (AE) between IST and MFP shocks under our extended
conditions for aggregation equivalence. To facilitate comparisons
with previous work on IST shocks, we adhere to the parameter
choices of Greenwood, Hercowitz, and Krusell (1997) whenever possible.17 Accordingly, the output share of equipment in both the ![]() and
and ![]() sectors is 17% and
the share of structures is 13%. The parameters governing the
assembly functions are set so that there is complete
specialization: consumption and structures investment are assembled
using inputs from the
sectors is 17% and
the share of structures is 13%. The parameters governing the
assembly functions are set so that there is complete
specialization: consumption and structures investment are assembled
using inputs from the ![]() sector only, while
equipment investment is assembled using inputs from the
sector only, while
equipment investment is assembled using inputs from the ![]() sector only.18 The
depreciation rates for equipment and structures capital are 12.4%
per quarter and 5.6% per quarter respectively. The discount factor
is set at 0.99, consistent with an annualized real interest rate of
4%. The intertemporal substitution elasticity for consumption is
taken to be 1.
sector only.18 The
depreciation rates for equipment and structures capital are 12.4%
per quarter and 5.6% per quarter respectively. The discount factor
is set at 0.99, consistent with an annualized real interest rate of
4%. The intertemporal substitution elasticity for consumption is
taken to be 1.
There is one major departure from GHK: there are adjustment
costs for investment in accord with recent common practice. The
parameters governing adjustment costs for both types of investment
(
![]() and
and
![]() ) are set to 0.5. Adjustment
costs are assumed to depend on efficiency units (
) are set to 0.5. Adjustment
costs are assumed to depend on efficiency units (
![]() ).
).
3.3 A Numerical Illustration
Figures 1 and 2 show the effects of two distinct shocks in the
baseline model. The solid lines relate to a permanent shock to ![]() , the level of investment-specific
technology. In this case, we could have cut off the model's
sectoral details following Greenwood, Hercowitz, and Krusell (1997), and have
simply obtained the aggregate responses from a canonical one-sector
RBC model augmented with an IST shock in the capital accumulation
equation as described in Table 2. The dashed lines relate instead to a
permanent MFP shock in the
, the level of investment-specific
technology. In this case, we could have cut off the model's
sectoral details following Greenwood, Hercowitz, and Krusell (1997), and have
simply obtained the aggregate responses from a canonical one-sector
RBC model augmented with an IST shock in the capital accumulation
equation as described in Table 2. The dashed lines relate instead to a
permanent MFP shock in the ![]() sector.
sector.
In all the figures presented, the sizes of the shocks are
normalized so that aggregate output (in quality-adjusted units at
constant prices) increases by 1 percent in the long run.19 For this calibration, the
(quality-adjusted) relative price of equipment investment (
![]() ) mirrors the
path of the shocks, as shown in the bottom right panel of
Figure 1.20
) mirrors the
path of the shocks, as shown in the bottom right panel of
Figure 1.20
As implied by the calibration, ![]() -sector goods
are used to assemble equipment investment only. The baseline
calibration also implies that these shocks will produce equal
effects on the aggregate variables as shown in Figure 1 since the requirements for AE between IST shocks
and MFP shocks in the machinery sector (discussed above) are
satisfied.
-sector goods
are used to assemble equipment investment only. The baseline
calibration also implies that these shocks will produce equal
effects on the aggregate variables as shown in Figure 1 since the requirements for AE between IST shocks
and MFP shocks in the machinery sector (discussed above) are
satisfied.
The capital accumulation process adds persistence to the effects of the shocks so that output takes a considerable number of quarters to approach its new steady-state level. The top two panels in the figure show the output response, but focus on different horizons so as to depict both the medium- and long-run effects.
Both shocks make it possible to produce efficiency units of
equipment investment with smaller amounts of factor inputs,
regardless of which sector receives the investment. Taking account
of investment adjustment costs has significant implications. Were
it not for these costs, the substitution effect associated with the
shocks would be so strong as to cause an immediate buildup of the
equipment and structures capital stocks in the ![]() sector. Recall that under the conditions for aggregate equivalence
capital is costlessly adaptable for use in different sectors.
Therefore, labor and both kinds of capital inputs would be
transferred immediately away from the
sector. Recall that under the conditions for aggregate equivalence
capital is costlessly adaptable for use in different sectors.
Therefore, labor and both kinds of capital inputs would be
transferred immediately away from the ![]() sector and
into the
sector and
into the ![]() sector. Without investment adjustment
costs, consumption would drop on impact, and then increase as
higher production in the
sector. Without investment adjustment
costs, consumption would drop on impact, and then increase as
higher production in the ![]() sector would push up the
equipment capital stock in the
sector would push up the
equipment capital stock in the ![]() sector. However,
with quadratic adjustment costs in investment, it becomes costly to
ramp up equipment investment, reducing the incentive to transfer
factor inputs across sectors. Instead of spiking up, aggregate
investment follows a hump shape. Accordingly, consumption declines
more gradually.
sector. However,
with quadratic adjustment costs in investment, it becomes costly to
ramp up equipment investment, reducing the incentive to transfer
factor inputs across sectors. Instead of spiking up, aggregate
investment follows a hump shape. Accordingly, consumption declines
more gradually.
The consumption share of output takes a long time to recover as
shown in Figure 2. According to the
baseline calibration, ![]() -sector goods are the sole
input in the assembly of consumption. First,
-sector goods are the sole
input in the assembly of consumption. First, ![]() -sector output goes down, as factor inputs are moved to the
sector that received the shock. Then, part of
-sector output goes down, as factor inputs are moved to the
sector that received the shock. Then, part of ![]() -sector output is devoted to pushing up the
-sector output is devoted to pushing up the ![]() sector's stock of structures.
sector's stock of structures.
4 Departures from Aggregate Equivalence
The simulations in Figure 3 illustrate that the effects of an IST shock in a one-sector model and those of an MFP shock in the machinery sector of a two-sector model can differ substantially when there are departures from the conditions for aggregate equivalence summarized in Section 3.1.
4.1 Adjustment Costs and Aggregate Equivalence
The first comparison shown in Figure 3 involves the solid and dotted lines. As in
Figure 1, the solid lines show the
effects on aggregate variables of an IST (or a machinery-sector
MFP) shock when the conditions for aggregate equivalence are met.
One of the conditions for aggregate equivalence in Section 3.1 is that adjustment costs depend on
either efficiency units only (as is the case with the solid line)
or physical units only. The dotted lines show the effects of a
machinery-sector MFP shock when all of the conditions for aggregate
equivalence are met except that adjustment costs depend on a
mixture of units as in some recent formulations.21 In
particular,
![]() is set equal to 0 but
is set equal to 0 but
![]() ,
,
![]() , and
, and
![]() are left equal to 1. Specifying
adjustment costs in this alternative way temporarily lowers the
cost of adjustment relative to the specification that reflects only
efficiency units. The difference is largest in the first period.
The first comparison confirms that the specification of investment
adjustment costs can, by itself, break aggregate equivalence.
are left equal to 1. Specifying
adjustment costs in this alternative way temporarily lowers the
cost of adjustment relative to the specification that reflects only
efficiency units. The difference is largest in the first period.
The first comparison confirms that the specification of investment
adjustment costs can, by itself, break aggregate equivalence.
4.2 Alternative Calibration
The second comparison in Figure 3 involves the solid and dashed lines. The dashed lines show results for a machinery-sector MFP shock under the alternative calibration reported in Table 2. The alternative calibration departs from the baseline calibration in three essential ways as described below. In order to highlight the importance of these departures, aggregate factor shares are kept the same as in the baseline calibration.
- Predetermined capital stocks
By setting
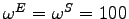 capital stocks
become predetermined in each sector as well as at the aggregate
level.
capital stocks
become predetermined in each sector as well as at the aggregate
level. - Sector-specific production functions
Following Greenwood, Hercowitz, and Krusell (1997), the baseline calibration implies identical production functions across sectors. However, for the three factor inputs in the model, U.S. data imply different input intensities across the machinery and non-machinery sectors (the
 and
and  sectors in the
model).
sectors in the
model).To differentiate the intensities of factor inputs across sectors, we used the following restrictions: a) while allowing variation across sectors, we kept the aggregate factor input intensities the same as in Greenwood, Hercowitz, and Krusell (1997); b) factor payments are equalized across sectors, making the factors' shares of sectoral output proportional to the sectoral stocks of capital (since production functions are Cobb-Douglas); c) factor input intensities are equal regardless of where the output of a sector is used.
We combined data for the net capital stock of private nonresidential fixed assets from the U.S. Bureau of Economic Analysis, with data from the Input-Output Bridge Table for Private Equipment and Software. The first data set contains data on the size of equipment and non-equipment capital stocks by sector. The second data set allowed us to ascertain the commodity composition of private equipment and software. Finally, we used BEA data to establish a sector's value added output. We focused on the year 2004, the latest available at the time of writing, but similar sector-specific production functions would be implied by older vintages of data.
Our calculations show that the machinery-producing sector is less intensive in structures and labor than the aggregate economy, but more intensive in equipment capital. For the machinery sector, the share of structures is 11 percent, the labor share 46 percent, and the share of equipment capital the remaining 43 percent (thus,
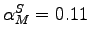 ,
,
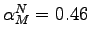 ,
,
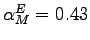 ). For the
non-machinery sector the share of structures is 13 percent, the
share of labor 72 percent, and the share of equipment capital 15
percent.
). For the
non-machinery sector the share of structures is 13 percent, the
share of labor 72 percent, and the share of equipment capital 15
percent. - Incomplete specialization
The baseline calibration assumes complete specialization in the assembly of investment and consumption goods. Equipment investment is assembled using output from the
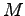 sector only.
In contrast, structures investment and consumption goods are
assembled using output from the
sector only.
In contrast, structures investment and consumption goods are
assembled using output from the 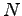 sector only. This
complete specialization does not reflect the composition of final
goods revealed in the Input-Output Bridge Tables that link final
uses in the NIPA to sectors (industries) in the U.S. Input-Output
Tables. For example, according to the data for 2004, wholesale and
retail services (part of our non-machinery sector) are important
inputs not only for consumption but also for equipment investment,
accounting for 15 percent of the total output of private equipment
and software.22 Furthermore,
electric and electronic products are used in the assembly of
consumption, accounting for 4 percent of the total.23
sector only. This
complete specialization does not reflect the composition of final
goods revealed in the Input-Output Bridge Tables that link final
uses in the NIPA to sectors (industries) in the U.S. Input-Output
Tables. For example, according to the data for 2004, wholesale and
retail services (part of our non-machinery sector) are important
inputs not only for consumption but also for equipment investment,
accounting for 15 percent of the total output of private equipment
and software.22 Furthermore,
electric and electronic products are used in the assembly of
consumption, accounting for 4 percent of the total.23The model captures the commingling implied by the bridge tables through assembly functions that specify how inputs from the
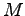 and
and 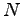 sectors are
combined to obtain consumption, structures investment, and
equipment investment. In the alternative calibration used to
generate the dashed lines in Figure 3, the
share parameters for the assembly functions are set as follows: the
shares for equipment investment are
sectors are
combined to obtain consumption, structures investment, and
equipment investment. In the alternative calibration used to
generate the dashed lines in Figure 3, the
share parameters for the assembly functions are set as follows: the
shares for equipment investment are
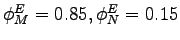 and the
shares for consumption and structures investment are
and the
shares for consumption and structures investment are
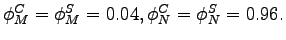 We assume that in each of the final-good assembly functions the
elasticity of substitution between inputs from the
We assume that in each of the final-good assembly functions the
elasticity of substitution between inputs from the 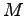 and
and 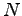 sectors is 0.5 (i.e.,
sectors is 0.5 (i.e.,
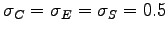 ). This
relatively low substitution elasticity seems appropriate given that
the assembly functions capture the commingling of inputs as
different as electronic equipment on one side and wholesale,
retail, and transportation services on the other.
). This
relatively low substitution elasticity seems appropriate given that
the assembly functions capture the commingling of inputs as
different as electronic equipment on one side and wholesale,
retail, and transportation services on the other.
4.3 The Effects of MFP Shocks Under the Alternative Calibration
The size of the MFP shock hitting the ![]() sector
shown in Figure 3 was chosen again to
bring about a permanent 1 percent increase in aggregate output.
sector
shown in Figure 3 was chosen again to
bring about a permanent 1 percent increase in aggregate output.
Some key differences between the IST and MFP shocks can be
captured by decomposing the responses of consumption into
substitution and wealth effects. The bottom left panels of the
figure show the Hicksian decomposition laid out by King (1991) for
general equilibrium models. For this decomposition the change in
utility ![]() is computed in the following
way:
is computed in the following
way:
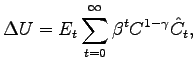 |
(19) |
where a caret symbol denotes a variable in log deviation from its
steady state. The wealth effect on consumption is given by the
change in consumption that would yield the same change in utility
as that generated by the shock, while the real interest rate is
kept constant at its steady state value. Accordingly, the Euler
equation for consumption for the model implies that the wealth
effect on consumption
![]() is constant over time and
equal to:
is constant over time and
equal to:
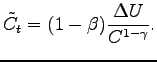
|
(20) |
The substitution effect is the path of consumption that would
induce no change in utility in reaction to the interest rate
changes induced by the shock. Accordingly, the substitution effect
on consumption,
![]() , is the path of that
solves the system:
, is the path of that
solves the system:
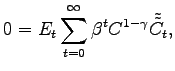 |
(21) | |
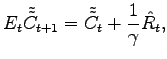 |
(22) |
where
![]() is expressed as the difference
of the interest rate from its steady state value. Simple algebraic
manipulations yield the result that
is expressed as the difference
of the interest rate from its steady state value. Simple algebraic
manipulations yield the result that
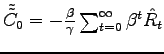 , which allows one to solve for the full path of the substitution
effect by combining knowledge of
, which allows one to solve for the full path of the substitution
effect by combining knowledge of
![]() with Equation (22) above.
with Equation (22) above.
A common feature among changes implied by the alternative
calibration is a reduction in the magnitude of the substitution
effect on consumption associated with the MFP shock. With capital
predetermined at the sectoral level, more of the factor inputs
remain temporarily locked up in the ![]() sector,
reducing the substitution effect associated with the MFP shock.24 This reduction
dampens the response of consumption, as its composition is
intensive in the output of the
sector,
reducing the substitution effect associated with the MFP shock.24 This reduction
dampens the response of consumption, as its composition is
intensive in the output of the ![]() sector. Similarly,
structures and equipment capital take longer to shift back and
forth across sectors, making the response of aggregate investment
more subdued.
sector. Similarly,
structures and equipment capital take longer to shift back and
forth across sectors, making the response of aggregate investment
more subdued.
Under the alternative calibration, with sector-specific
production functions, the making of ![]() -sector goods
used in equipment investment is more intensive in equipment capital
relative to the aggregate. This feature contributes to the
reduction in the substitution effect on consumption coming from the
MFP shock relative to the IST shock. Accordingly,
-sector goods
used in equipment investment is more intensive in equipment capital
relative to the aggregate. This feature contributes to the
reduction in the substitution effect on consumption coming from the
MFP shock relative to the IST shock. Accordingly, ![]() -sector output and investment increase by less at first.
-sector output and investment increase by less at first.
Finally, the incomplete specialization in the assembly of
equipment investment not only reduces the magnitude of the
substitution effect but also boosts the wealth effect. Relaxing the
assumption of complete sectoral specialization implies that the MFP
shock in the ![]() sector acquires a direct effect on
consumption through the assembly function.
sector acquires a direct effect on
consumption through the assembly function.
Altogether, the weaker substitution effect and stronger wealth effect lead to a uniform rise in consumption in reaction to the MFP shock (while consumption temporarily falls for the IST shock) and a corresponding reduction in the rise of investment relative to the effects of the IST shock. The cumulative effect of the departures from the baseline calibration is to generate qualitative differences between the responses to IST and MFP shocks as can be seen by comparing the dashed and dotted lines in Figure 3. While in the case of an IST shock in the one-sector model, consumption falls initially, the response of the two-sector model to the MFP shock in the machinery sector is such that consumption never falls. Similarly, aggregate investment shows protracted differences, with the response to the IST shock in the one-sector model being persistently more pronounced than the response to the MFP shock in the two-sector model.
Finally, this alternative calibration also causes a decoupling of the responses of the relative price of investment and the size of the MFP shock. As can be seen in the bottom right panel of Figure 3, the relative price of investment ceases to be the mirror image of the unit-root process for the MFP shock in the two-sector model. The initial drop in the relative price of investment is not as pronounced as the long-run drop due to elevated demand for equipment investment. Under this scenario, using the relative price of investment to back out the size of IST shocks would be inappropriate.
4.4 Isolating the Role of Incomplete Specialization
While all of the departures from the baseline aggregate
calibration are important in reversing the conditional correlation
between consumption and investment implied by MFP shocks in the
machinery sector, a key role is played by incomplete sectoral
specialization in the production of final
goods.25 Figure 4 compares again the effects of an IST shock in a
one-sector model with an MFP shock in a two-sector model. The solid
lines denoting the effects of the IST shock replicate what is also
shown in Figure 1. The calibration
used in constructing the effects of the MFP shock in the ![]() sector departs from the aggregate
equivalence calibration summarized in Table 3 only insofar as it allows for
incomplete sectoral specialization in the production of final
goods, as described in Section 4.2. With the baseline calibration
for investment adjustment costs, this change alone is sufficient to
reverse the short-term correlation between investment and
consumption.
sector departs from the aggregate
equivalence calibration summarized in Table 3 only insofar as it allows for
incomplete sectoral specialization in the production of final
goods, as described in Section 4.2. With the baseline calibration
for investment adjustment costs, this change alone is sufficient to
reverse the short-term correlation between investment and
consumption.
5 Sensitivity Analysis: Investment Adjustment Costs
High adjustment costs for investment, by slowing adjustment, have the potential to dampen the negative correlation between consumption and investment following IST and sector-specific MFP shocks. To investigate the importance of investment adjustment costs in preventing consumption from falling after a sector-specific MFP shock, Figure 5 presents simulations that abstract from such costs.
The solid line shows again the effects of an IST shock in a
one-sector model as in Figure 1. We
depart from the calibration described in Table 3 only insofar as we eliminate the
investment adjustment costs by setting
![]() . As investment can
now jump on impact, the negative correlation between consumption
and investment becomes stronger.
. As investment can
now jump on impact, the negative correlation between consumption
and investment becomes stronger.
The dashed lines show the effects of an MFP shock. The only departure from the calibration used in Figure 3 and summarized in Table 4 is again the elimination of investment adjustment costs. Even without investment adjustment costs, consumption never falls in reaction to an MFP shock in the equipment-producing sector.
The dotted line in the figure reproduces the effects of the MFP shock shown in Figure 4 in that the calibration departs from the one shown in Table 3 by allowing for incomplete specialization. Furthermore, investment adjustment costs are turned off. The dotted line shows that consumption turns negative on impact. This simulation substantiates that incomplete specialization plays an important quantitative role in reducing the negative correlation between consumption and investment following shocks to the equipment-producing sector. However, incomplete specialization alone cannot reverse the initial negative correlation between consumption and investment without adjustment costs. Furthermore, the simulation confirms that no single departure from the conditions for aggregate equivalence--by itself--can account for the positive comovement between investment and consumption conditional on sector-specific MFP shocks.
6 Investigating the Correlation Between Consumption and Investment
As illustrated above, in a one-sector model a permanent increase
in the level of the IST shock, ![]() would
initially boost investment while compressing consumption.
Conversely, in a two-sector model with our alternative calibration,
the corresponding increase in the MFP shock specific to the
machinery sector,
would
initially boost investment while compressing consumption.
Conversely, in a two-sector model with our alternative calibration,
the corresponding increase in the MFP shock specific to the
machinery sector, ![]() would imply positive
conditional comovement between consumption and investment.
Economy-wide MFP shocks imply positive conditional comovement of
consumption and investment in both the one-sector and two-sector
models. Thus, such MFP shocks, if important enough, could account
for the unconditional positive correlation between consumption and
investment observed for the United States.
would imply positive
conditional comovement between consumption and investment.
Economy-wide MFP shocks imply positive conditional comovement of
consumption and investment in both the one-sector and two-sector
models. Thus, such MFP shocks, if important enough, could account
for the unconditional positive correlation between consumption and
investment observed for the United States.
We investigate this possibility using the empirical evidence provided by Fisher (2006), who separately identified economy-wide MFP shocks, productivity shocks specific to the machinery sector (equipment in Fisher's terminology), and other shocks. Fisher (2006) augmented the long-run identification scheme of Gali (1999) so as two distinguish between two kinds of productivity shocks. All productivity shocks are identified by the assumption that they are the only ones to affect the level of labor productivity in the long run. Technology shocks that are specific to the machinery sector are separated out from aggregate MFP shocks by the assumption that they are the only ones to affect the relative price of machinery in the long run. As noted by Fisher (2006), the sector-specific productivity shocks could be interpreted either as IST shocks in a one-sector model, or MFP shocks specific to the machinery sector in a two-sector model such as ours.
We calibrate the relative importance of the two types of productivity shocks by matching the variance decomposition for output at business cycle frequencies estimated by Fisher (2006). Accordingly, overall MFP shocks account for 35 percent of the variation of output, and machinery-specific MFP (or IST shocks in the one-sector model) the remaining 65 percent. When we match these statistics, the unconditional correlation between consumption and investment at business-cycle frequencies is -0.19 for the one-sector model and 0.16 for the two-sector model. Similar correlations obtain in the model for the unfiltered quarterly growth rates of consumption and investment: -0.17 for the one-sector model and 0.17 for the two-sector model. Using U.S. data, we estimate the level correlation between consumption and investment at 0.68 and the correlation between the growth rates at 0.20.26 The two-sector model matches the sign of the level correlation and is strikingly close to the data for the correlation of the growth rates.
While the one-sector model is not able to deliver a positive correlation between consumption and investment with plausibly calibrated machinery-sector shocks and aggregate MFP shocks, it is still possible that the one-sector misspecification bias might imply a different shock decomposition that could reproduce the correlations observed in the data. To investigate this possibility we performed a Monte Carlo exercise. In the exercise, the two-sector model is the data-generating process. The model was used to generate 100 replications of a sample containing 200 observations, the typical size of an estimation sample using aggregate time-series data for the United States. The data-generating process was calibrated to match Fisher's estimates for the relative importance of the two technology shocks. Even though the data-generating process excluded consumption shocks, we considered them at the estimation stage as a way for the one-sector model to reconcile the positive correlation between consumption and investment implied by data-generating process. For each sample we used a maximum likelihood estimator to estimate the standard deviations for both the overall MFP shock and the IST (or sector-specific MFP) shock as well as the standard deviation and AR(1) persistence parameter for the consumption shock. We performed the estimation for both the one-sector model and the two-sector model keeping all other parameters as set in tables 1 and 2 respectively. The levels of consumption and investment were the two observed variables.
Figure 6 shows the sampling distributions for the correlation between consumption and investment at business cycle frequencies implied by the Monte Carlo experiment. As is evident from the figure, even allowing for misspecification bias in the relative importance of the sector-specific technology shock and the consumption shock, the one-sector model still implies a negative correlation between consumption and investment. The distribution of correlations between consumption and investment for the two-sector model serves for comparison. Interestingly, the correlations are tightly clustered around the pseudo-true value (denoted by the vertical line in the figure) implied by the data-generating process. Such tight clustering confirms that the two-sector model and one-sector model have observationally different implications for the correlation between consumption and investment.27
7 Conclusion
In post-WWII U.S. data, the relative price of equipment investment trends downward and varies over the cycle. As a parsimonious way of allowing for these regularities, Greenwood, Hercowitz, and Krusell (1997) add an investment-specific technology shock to an otherwise standard one-sector model. Increases in this shock enhance the efficiency of the single homogeneous output when it is used for equipment investment but not otherwise. Greenwood, Hercowitz, and Krusell (2000) and several others provide empirical support for the view that IST shocks are important for explaining the cyclical behavior of aggregate variables.
The conventional interpretation of IST shocks is based on "aggregate equivalence"results. Under stringent conditions, IST shocks in a one-sector model have the same effects on aggregate variables as MFP shocks in a two-sector model. Revisiting these conditions, we extend them to take account of adjustment costs for investment and the sectoral composition of final goods.
We present impulse responses for two calibrations of our two-sector model. One is a "baseline calibration"with adjustment costs for investment that satisfies our extended conditions for aggregate equivalence. The other is an "alternative calibration"with three important departures. The first is that capital stocks are predetermined at the sectoral level. The second and third departures reflect the input-output data: sectoral production functions have different factor intensities, and assembly functions reflect incomplete specialization. We compare the effects of a positive IST shock under the baseline calibration with those of a positive machinery-sector MFP shock under the alternative calibration. There is a striking qualitative difference between the results: in the first several periods, investment rises and consumption falls with the IST shock, but investment and consumption both rise with the MFP shock. If investment adjustment costs are present, incomplete specialization in assembly is sufficient by itself to generate the difference in results.
In sum, our results have at least two important implications. First, a two-sector model seems better suited than a one-sector model for distinguishing empirically among alternative sources of economic fluctuations, even if the focus is on aggregate time series. Second, while IST shocks may be of interest in their own right, the structure of the U.S. economy seems to be such that interpreting them as stand-ins for sector-specific MFP shocks can be misleading.
References
Christiano, L. J. and T. J. Fitzgerald (1998). The business cycle: It's still a puzzle. Economic Perspectives, Federal Reserve Bank of Chicago, 56-83. Federal Reserve Bank of Minneapolis: Staff Report 200.
Christiano, L. J., C. Ilut, R. Motto, and M. Rostagno (2008). Monetary policy and stock market boom-bust cycle. European Central Bank, Working Paper Series 955.
Christiano, L. J., R. Motto, and M. Rostagno (2007). Shocks, structures or monetary policies? the euro area and us after 2001. Journal of Economic Dynamics and Control 32(8), 2476-2506.
Edge, R., M. T. Kiley, and J.-P. Laforte (2008). Natural rate measures in an estimated dsge model of the u.s. economy. Journal of Economic Dynamics and Control 32, 2512-2535.
Fisher, J. (2006). The dynamic effects of neutral and investment-specific technology shocks. Journal of Political Economy 114(3), 413-452.
Gali, J. (1999). Technology, employment, and the business cycle: Do technology shocks explain aggregate fluctuations? American Economic Review 89, 249-271.
Greenwood, J., Z. Hercowitz, and P. Krusell (1997). Long-run implications of investment-specific technological change. American Economic Review 87, 342-362.
Greenwood, J., Z. Hercowitz, and P. Krusell (2000). The role of investment-specific technological change in the business cycle. European Economic Review 44, 91-115.
Greenwood, J. and P. Krusell (2007). Growth accounting with investment-specific technological progress: A discussion of two approaches. Journal of Monetary Economics 54(4), 1300-1310.
Griliches, Z. and D. W. Jorgenson (1966). Sources of measured productivity change: Capital input. The American Economic Review 56(1/2), 50-61.
Hornstein, A. and J. Praschnik (1997). Intermediate inputs and sectoral comovement in the business cycle. Journal of Monetary Economics 40(3), 573-595.
Jaimovich, N. and S. Rebelo (2009). Can news about the future drive the business cycle? American Economic Review 99(4), 1097-1118.
Justiniano, A. and G. Primiceri (2008). The time varying volatility of macroeconomic fluctuations. American Economic Review 98(3), 604-641.
King, R. (1991). Value and capital in the equilibrium business cycle program. In L. McKenzie and S. Zamagni (Eds.), Value and Capital Fifty Years Later. London: MacMillan Limited Press.
Long, J. B. and C. Plosser (1983). Real business cycles. Journal of Political Economy 91(1), 179-197.
Oulton, N. (2007). Investment-specific technological change and growth accounting. Journal of Monetary Economics 54, 1290-99.
Smets, F. and R. Wouters (2007). Shocks and frictions in us business cycles: A bayesian dsge approach. American Economic Review 97(3), 586-606.
Solow, R. (1957). Technical change and the aggregate production function. Review of Economics and Statistics 39(3), 312-320.
Swanson, E. T. (2006). The relative price and relative productivity channels for aggregate fluctuations. Contributions to Macroeconomics 6(1).
Table 1. Aggregation Equations
|
|
|
Table 2. One-Sector Model Under Assumptions for Aggregate Equivalence
| Utility maximization problem of households | 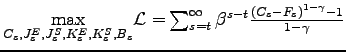 |
|---|---|
| Utility maximization problem of households, subject to the constraints: | ![$ K^{E}_{s} = \left( 1-\delta^{E} \right) K^{E}_{s-1}+Z_{s-1}A_{s-1} ^{\phi^{E}_{M}}\bar{J}^{E}_{s-1}-\frac{\nu^{E}_{0} }{2}Z_{s-1}A_{s-1} ^{\phi^{E}_{M}}\bar{J}^{E}_{s-1}\left[ \left( \frac{Z_{s-1}}{Z_{s-2}}\right) \left( \frac{A_{s-1}}{A_{s-2}}\right) ^{\phi^{E}_{M}}\frac{\bar{J}^{E}_{s-1} }{\bar{J}^{E}_{s-2}}-1\right] ^{2} $](img340.gif) 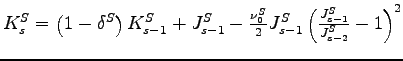 |
| Cost minimization problem of firms | |
| Cost minimization problem of firms, subject to the constraint | |
| Equilibrium Conditions |
All markets are
assumed to be competitive. Recall that
![]() represents equipment
investment in physical units. We left both shocks
represents equipment
investment in physical units. We left both shocks ![]() and
and ![]() in the description of the model to
underscore their equivalence for aggregate variables.
in the description of the model to
underscore their equivalence for aggregate variables.
Table 3a. Model Calibration for Baseline Experiment: Utility Function
| Parameter | Determines |
|---|---|
| Intertemporal
consumption elast.
|
|
| Discount factor |
Table 3b. Model Calibration for Baseline Experiment: Depreciation Rates
| Parameter | Determines |
|---|---|
|
|
Equipment capital |
| Structures capital |
Table 3c. Model Calibration for Baseline Experiment: Adjustment Costs
| Parameter | Determines |
|---|---|
|
|
M, N Equipment Capital |
|
|
M, N Equipment Investment |
|
|
M, N Equipment Investment |
| M, N Structures Capital | |
| M, N Structures Investment |
Table 3d. Model Calibration for Baseline Experiment: M Goods Production
| Parameter | Determines |
|---|---|
|
|
Labor share |
|
|
Structures share |
| Equipment share |
Table 3e. Model Calibration for Baseline Experiment: N Goods Production
| Parameter | Determines |
|---|---|
|
|
Labor share |
|
|
Structures share |
| Equipment share |
Table 3f. Model Calibration for Baseline Experiment: Consumption Assembly
| Parameter | Determines |
|---|---|
|
|
M goods intensity |
| N goods intensity |
Table 3g. Model Calibration for Baseline Experiment: Assembly of Equipment Investment
| Parameter | Determines |
|---|---|
|
|
M goods intensity |
| N goods intensity |
Table 3h. Model Calibration for Baseline Experiment: Assembly of Structures Investment
| Parameter | Determines |
|---|---|
|
|
M goods intensity |
| N goods intensity |
Table 4a. Alternative Calibration: Changes Relative to Baseline: Adjustment Costs*
| Parameter | Determines |
|---|---|
|
|
M, N Equipment Capital |
| M, N Structures Capital |
*For ease of comparison with Table 3, this table only reports the parameters that vary from the baseline calibration.
Table 4b. Alternative Calibration: Changes Relative to Baseline: M Goods Production*
| Parameter | Determines |
|---|---|
|
|
Labor share |
|
|
Structures share |
| Equipment share |
*For ease of comparison with Table 3, this table only reports the parameters that vary from the baseline calibration.
Table 4c. Alternative Calibration: Changes Relative to Baseline: N Goods Production*
| Parameter | Determines |
|---|---|
|
|
Labor share |
|
|
Structures share |
| Equipment share |
*For ease of comparison with Table 3, this table only reports the parameters that vary from the baseline calibration.
Table 4d. Alternative Calibration: Changes Relative to Baseline: Consumption Assembly*
| Parameter | Determines |
|---|---|
|
|
M goods intensity |
|
|
Substitution elast. for M and N goods |
| N goods intensity |
*For ease of comparison with Table 3, this table only reports the parameters that vary from the baseline calibration.
Table 4e. Alternative Calibration: Changes Relative to Baseline: Assembly of Equipment Investment*
| Parameter | Determines |
|---|---|
|
|
M goods intensity |
|
|
Substitution elast. for M and N goods |
| N goods intensity |
*For ease of comparison with Table 3, this table only reports the parameters that vary from the baseline calibration.
Table 4f. Alternative Calibration: Changes Relative to Baseline: Assembly of Structures Investment*
| Parameter | Determines |
|---|---|
|
|
M goods intensity |
|
|
Substitution elast. for M and N goods |
| N goods intensity |
*For ease of comparison with Table 3, this table only reports the parameters that vary from the baseline calibration.
Figure 1. Equivalent IST and MFP Shocks Under Baseline Calibration
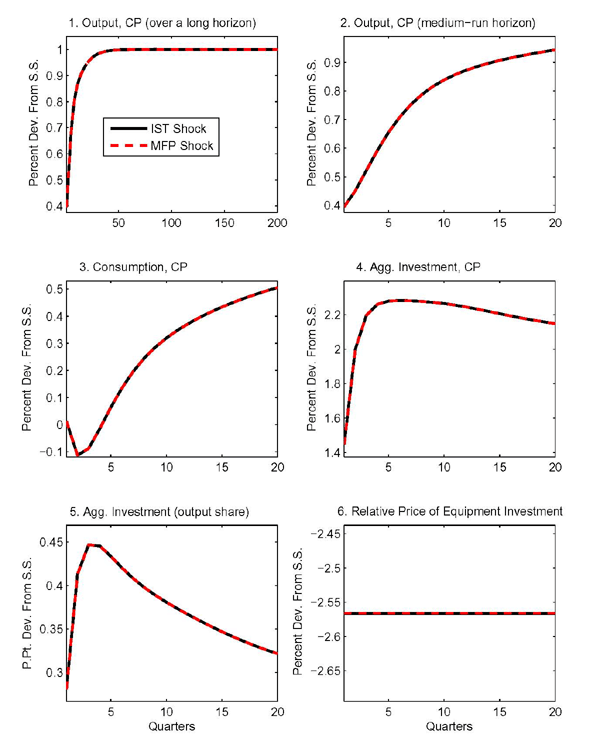
Figure 2. Equivalent IST and MFP Shocks Under Baseline Calibration (Sectoral Details)
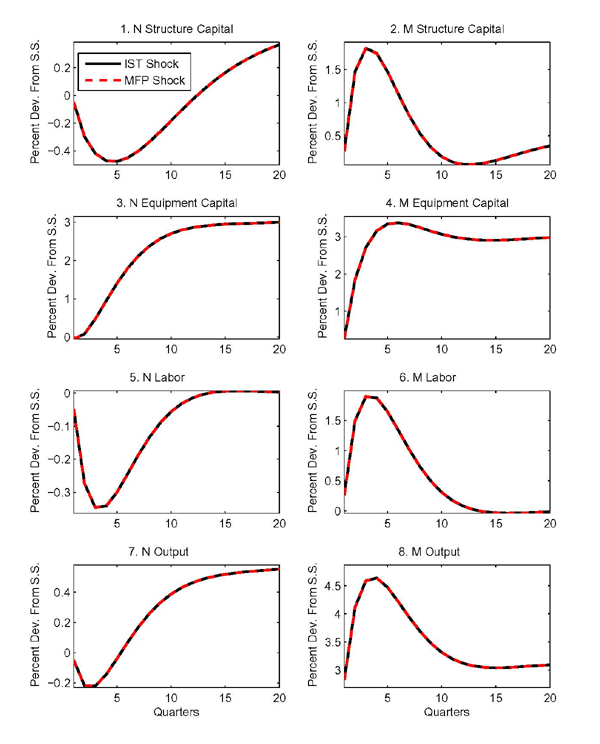 Figure 3. Cummulative Effects of Departures from Baseline Calibration
Figure 3. Cummulative Effects of Departures from Baseline Calibration
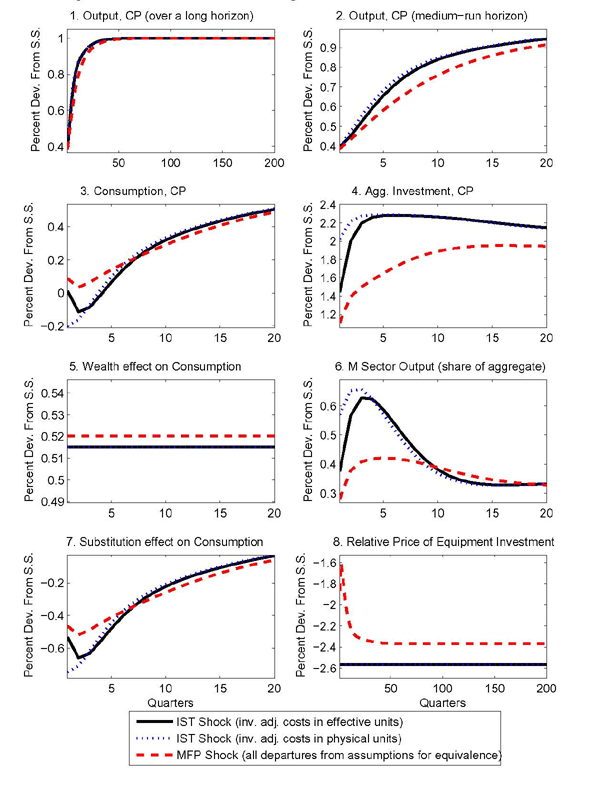
Figure 4. IST Under Baseline Calibration and MFP Shocks With Incomplete Specialization in Assembly
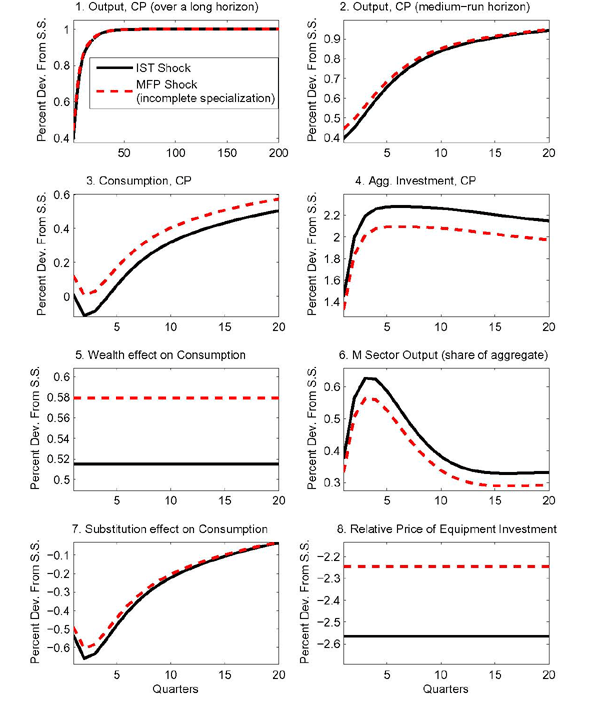
Figure 5. Sensitiviety Analysis: No Investment Adjustment Costs
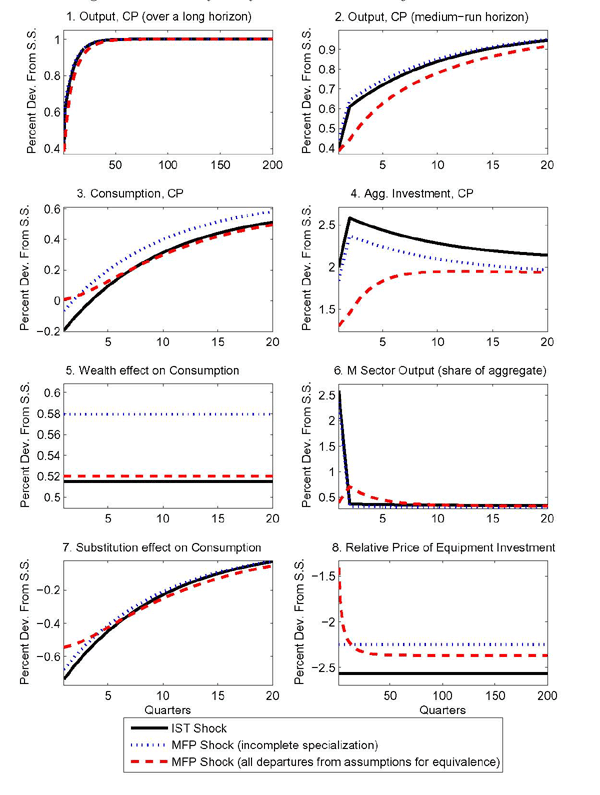
Figure 6. Probability Density Functions: Correlation Between Consumption and Investment at Business Cycle Frequencies
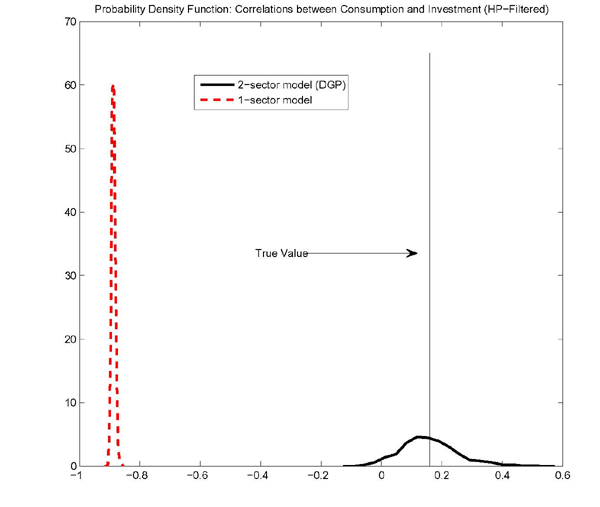
A Equivalence Between MFP Shocks in the M Sector of a Two-Sector Model and IST Shocks in a One-Sector Model
In this section of the appendix, we sketch proofs of some of the assertions in section 3.1
A.1 Aggregate Equivalence of IST and MFP Shocks in a Two-Sector Model (TE)
A.1.1 Sufficiency of the Set A Conditions for TE
The equations of the model can be written in a form such that
when the set A conditions are imposed ![]() and
and
![]() always enter together in the form
always enter together in the form
![]() .
For example, Equation 16 repeated here for
convenience
.
For example, Equation 16 repeated here for
convenience
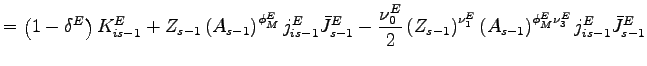 |
||
![$\displaystyle \times\left[ \left( \frac{Z_{s-1}}{Z_{s-2}}\right) ^{\nu_{2}^{E}}\left( \frac{A_{s-1}}{A_{s-2}}\right) ^{\phi_{M}^{E}\nu_{4}^{E}}\frac{j_{is-1} ^{E}\bar{J}_{s-1}^{E}}{j_{is-2}^{E}\bar{J}_{s-2}^{E}}-1\right] ^{2} ,\,\,\,\,i\in\{M,N\},$](img403.gif) |
satisfies the set A conditions either when
![]() , or when
, or when
![]() . Conclude
that for any change in
. Conclude
that for any change in ![]() there is an offsetting
change in
there is an offsetting
change in ![]() that leaves the equilibrium values of
all variables unchanged.
that leaves the equilibrium values of
all variables unchanged.
A.1.2 Necessity of Set A Conditions for TE to First Order
Linearize the unrestricted equations of the model around a
steady state. The combinations of shocks that yield equivalent
outcomes are obtained by setting the changes for all the endogenous
variables equal to zero for all periods. Consider an arbitrary
sequence of changes in the MFP shock ![]() ,
,
![]()
![]() Confirm that the
zero-change equilibrium conditions can be satisfied only if terms
in changes in
Confirm that the
zero-change equilibrium conditions can be satisfied only if terms
in changes in ![]() and terms in changes in
and terms in changes in
![]() always appear together in the same
linear combination. The necessity of condition
always appear together in the same
linear combination. The necessity of condition ![]() -
-![]() is established by noting that if
is established by noting that if
![]() -
-![]() is not met,
is not met, ![]() enters the assembly function for at least consumption or structures
investment but
enters the assembly function for at least consumption or structures
investment but ![]() does not enter either. That
does not enter either. That
![]() -
-![]() and
and ![]() -
-![]() are necessary is established by showing
that a single linear combination of changes in
are necessary is established by showing
that a single linear combination of changes in ![]() and changes in
and changes in ![]() would not
satisfy some set of equations. For
would not
satisfy some set of equations. For ![]() -
-![]() the set comprises the equipment assembly function and the
first-order conditions for cost minimization in equipment assembly
(not included in paper). For
the set comprises the equipment assembly function and the
first-order conditions for cost minimization in equipment assembly
(not included in paper). For ![]() -
-![]() the set comprises the equipment assembly function and the
accumulation equations for equipment capital stocks.
the set comprises the equipment assembly function and the
accumulation equations for equipment capital stocks.
A.2 Equivalent Aggregate Outcomes in Two-Sector and One-Sector Models
A.2.1 Sufficiency of Set B Conditions for Aggregation
As stated in the text, GHK and Oulten have shown that conditions B-1 through B-3 are sufficient for aggregation in models without investment adjustment costs. If condition B-4 is imposed, sectoral capital stocks, investment flows, and capital accumulation equations can be aggregated to yield
![$\displaystyle \begin{tabular}[c]{l} $K_{s}^{j}=K_{Ms}^{j}+K_{Ns}^{j},$\\ $J_{s}^{j}=J_{Ms}^{j}+J_{Ns}^{j},$\\ $D_{s}^{S}=\left( 1-\delta^{S}\right) K_{s-1}^{S}+J_{s-1}^{S}-\frac{\nu^{S} }{2}J_{s-1}^{S}\left( \frac{J_{s-1}^{S}}{J_{s-2}^{S}}-1\right) ^{2},$\\ $D_{s}^{E}=\left( 1-\delta^{E}\right) K_{s-1}^{E}+Z_{s-1}\left( A_{s-1}\right) ^{\phi_{M}^{E}}J_{is-1}^{E}$\\ $\ \ \ \ \ \ \ \ \ -\frac{\nu_{0}^{E}}{2}\left[ Z_{s-1}\left( A_{s-1} \right) ^{\phi_{M}^{E}}\right] ^{\nu^{E}}J_{s-1}^{E}\left[ \left( \frac{Z_{s-1}\left( A_{s-1}\right) ^{\phi_{M}^{E}}}{Z_{s-2}\left( A_{s-2}\right) ^{\phi_{M}^{E}}}\right) ^{\nu^{E}}\frac{J_{s-1}^{E}} {J_{s-2}^{E}}-1\right] ^{2},$ \end{tabular}$](img429.gif) |
(23) |
where
![]() and
and ![]() is
equal to either zero or one.
is
equal to either zero or one.
A.2.2 Necessity of Set B Conditions for Aggregation
It is evident that aggregation is not possible if depreciation rates and adjustment costs are not identical. For aggregation to be possible the production possibility curve (PPC) for the two production sectors must be a straight line. It is well known that in the standard two-sector model if capital is costlessly adaptable the PPC is concave to the origin unless production functions are identical. Also, if production functions are identical, the PPC is concave to the origin unless capital is costlessly adaptable.
B Additional Simulation Results
The discussion in the main body of the paper omitted to consider in isolation two departures from our baseline calibration. The effects of relaxing perfect capital mobility across sectors and of varying the factor intensities across sectors are illustrated below.
In Figure 7, the solid lines
reproduce the responses to the IST shock from Figure 1. Instead, the dashed lines show the economy's
response to an MFP shock in the ![]() sector when
relaxing only the assumption of perfect capital mobility across
sectors in every period. Perfect capital mobility, as argued
before, is necessary to represent our two-sector model as an
aggregate one-sector model. To produce the responses shown by the
dashed lines, we set the parameters governing the capital
adjustment costs
sector when
relaxing only the assumption of perfect capital mobility across
sectors in every period. Perfect capital mobility, as argued
before, is necessary to represent our two-sector model as an
aggregate one-sector model. To produce the responses shown by the
dashed lines, we set the parameters governing the capital
adjustment costs
![]() and
and
![]() both equal to 100. This
parametrization implies that sectoral capital allocations only move
with a delay of one period. Thus capital stocks are not only
predetermined at the aggregate level, but also at the sectoral
level.
both equal to 100. This
parametrization implies that sectoral capital allocations only move
with a delay of one period. Thus capital stocks are not only
predetermined at the aggregate level, but also at the sectoral
level.
The size of the MFP shock hitting the ![]() sector
was again chosen to bring about a permanent 1 percent increase in
aggregate output. While the wealth effect on consumption is
identical for the two shocks in Figure 7, the negative substitution effect is reduced in
magnitude when the sectoral capital stocks are predetermined.
sector
was again chosen to bring about a permanent 1 percent increase in
aggregate output. While the wealth effect on consumption is
identical for the two shocks in Figure 7, the negative substitution effect is reduced in
magnitude when the sectoral capital stocks are predetermined.
Figure 8 shows the responses to an IST shock in the aggregate model (replicating, for ease of comparison, what is also shown in figures 1 and 7), as well as the responses to an MFP shock in the machinery sector of a two-sector model that allows for sector-specific production functions (the only difference relative to the baseline calibration). Again, the magnitude of the MFP shock is chosen to match the 1 percent long-run increase in aggregate output for the IST shock.
The figure shows persistent differences in the responses of
consumption and investment. As under the alternative calibration
the making of ![]() -sector goods used in equipment
investment is more intensive in equipment capital relative to the
aggregate, the substitution effect on consumption coming from the
MFP shock is not as strong initially relative to the IST shock.
Accordingly,
-sector goods used in equipment
investment is more intensive in equipment capital relative to the
aggregate, the substitution effect on consumption coming from the
MFP shock is not as strong initially relative to the IST shock.
Accordingly, ![]() -sector output increases by less, at
first. However, eventually more resources need to be devoted to the
-sector output increases by less, at
first. However, eventually more resources need to be devoted to the
![]() sector to maintain the larger stock of
equipment capital implied by the alternative calibration, and the
MFP shock in the investment sector leads to a larger long-run
increase in equipment investment and a smaller long-run increase in
consumption. Consequently, the wealth effect on consumption is
smaller for the MFP shock than for the IST shock.
sector to maintain the larger stock of
equipment capital implied by the alternative calibration, and the
MFP shock in the investment sector leads to a larger long-run
increase in equipment investment and a smaller long-run increase in
consumption. Consequently, the wealth effect on consumption is
smaller for the MFP shock than for the IST shock.
Figure 7. IST Under Baseline Calibration and MFP Shock With Capital Stocks Predetermined in Each Sector
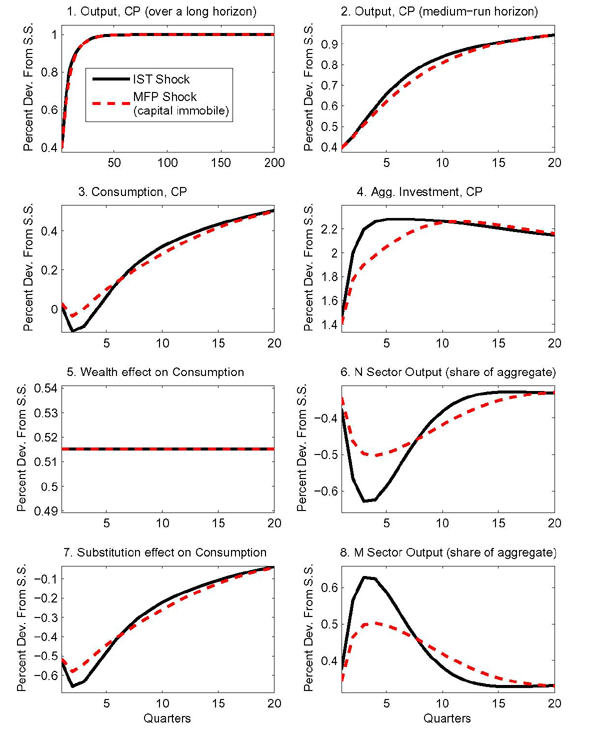
Figure 8. IST Under Baseline Calibration and MFP Shocks With Sector-Specific Production Functions
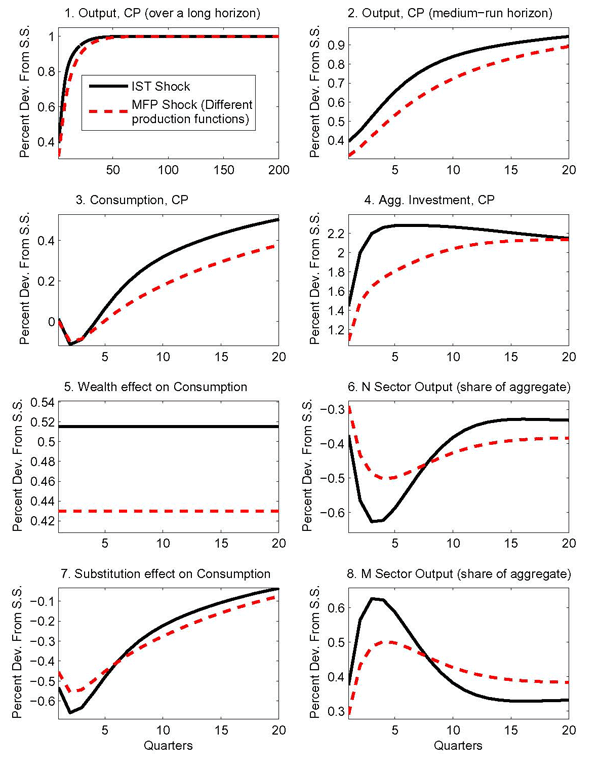
Footnotes
** Affiliation and contact information: Luca Guerrieri, Federal Reserve Board, telephone (202) 452 2550, email [email protected]; Dale Henderson, Georgetown University, email [email protected]; Jinill Kim, Federal Reserve Board, telephone (202) 452 2981, email [email protected]. Return to text
*** The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. Throughout this paper, we used the term "equipment"investment to refer to what is called "Equipment and Software"investment in the NIPA tables. Return to text
2. For example, see Greenwood, Hercowitz, and Krusell (2000), Fisher (2006), Smets and Wouters (2007), and Justiniano and Primiceri (2008). Return to text
3. One of the first papers to emphasize the importance of the input-output structure for the business cycle is Long and Plosser (1983). More recent contributions include Hornstein and Praschnik (1997) and Edge, Kiley, and Laforte (2008). Return to text
4. In related work, Swanson (2006) showed that MFP shocks at the sectoral level in a multi-sector model can lead to di�erent aggregate implications from those of MFP shocks in a one-sector model. Return to text
5. Investment adjustment costs are not a part of the model developed by Greenwood, Hercowitz, and Krusell (1997), but are a common ingredient of models developed subsequently that also incorporate IST shocks. Return to text
6. There are two other standard assumptions. Production functions exhibit constant returns to scale, and investment adjustment costs are homogeneous of degree zero in current and lagged investment. As is well known, if the model economy is to have a balanced steady-state growth path, the production functions must be Cobb-Douglas. Return to text
7. We conjecture, but have not yet shown, that the four conditions are jointly necessary. Return to text
8. For example, ![]() is the multiplier in the Lagrangian expression (
is the multiplier in the Lagrangian expression (
![]() ) used to the minimize costs
of producing a given physical quantity
) used to the minimize costs
of producing a given physical quantity ![]() :
:
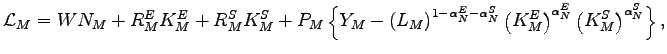 |
where time subscripts have been omitted for simplicity. Return to text
9. For
example, ![]() , is the multiplier in the
Lagrangian expression (
, is the multiplier in the
Lagrangian expression (
![]() ) used to the minimize
costs of producing a given quantity
) used to the minimize
costs of producing a given quantity ![]() :
:
![$\displaystyle \mathcal{L}_{J^{E}}=P_{M}I_{M}^{E}+I_{N}^{E}+P^{J^{E}}\left\{ J^{E}-\left[ \phi _{M}^{E}\left( \frac{A_sI_{M}^{E}}{\phi _{M}^{E}}\right) ^{\frac{\sigma _{E}-1}{\sigma _{E}}}+\phi _{N}^{E}\left( \frac{I_{N}^{E}}{\phi _{N}^{E}}\right) ^{\frac{\sigma _{E}-1}{\sigma E}}\right] ^{\frac{\sigma _{E}}{\sigma _{E}-1}}\right\},$](img80.gif) |
where time subscripts have been omitted for simplicity. Return to text
10. For simplicity we assume that depreciation rates (
![]() and
and
![]() ) and investment adjustment-cost
parameters (
) and investment adjustment-cost
parameters (
![]() and
and
![]() ) may differ between types of
capital but are the same across sectors of use. Return to text
) may differ between types of
capital but are the same across sectors of use. Return to text
11. See, for example, Smets and Wouters (2007) and Christiano, Motto, and Rostagno (2007). Return to text
12. Greenwood, Hercowitz, and Krusell (1997) and Greenwood, Hercowitz, and Krusell (2000) state sufficient conditions for AE in the case with Cobb-Douglas production functions, complete specialization in assembly, and no adjustment costs for investment. Oulton (2007) extends the GHK analysis to the case with general constant returns to scale (CRTS) production functions; Greenwood and Krusell (2007) provides further discussion. Return to text
13. We conjecture, but have not yet shown, that the four conditions are jointly necessary. Return to text
14. We conjecture, but have not yet shown, that the four conditions are jointly necessary. Return to text
15. Instead of assuming that is costlessly adaptable, Greenwood, Hercowitz, and Krusell (2000) assume that firms can move between sectors at will. Return to text
16. Greenwood, Hercowitz, and Krusell (2000) and Oulton (2007) have shown that in the absence of investment adjustment costs, conditions B-1 through B-3 are sufficient for aggregation. Return to text
17. For simplicity, we abstract from trend growth as well as capital and labor taxes, while Greenwood, Hercowitz, and Krusell (1997) incorporate them in their model. Return to text
18. The substitution elasticities between inputs in assembly become irrelevant under complete specialization. Return to text
19. In
multi-sector models there are multiple ways of aggregating sectoral
outputs depending, for instance, on which good is chosen as the
numeraire. We focus on a measure of aggregate output that sums
sectoral outputs at constant prices after adjusting for quality.
This measure is defined as
![]() . This approach can be shown to be first-order equivalent to a
Tornqvist, chain-weighted index. Return to text
. This approach can be shown to be first-order equivalent to a
Tornqvist, chain-weighted index. Return to text
20. Growth accounting exercises that exploit the tight short-run relationship between the relative price of equipment investment and the size of technology shocks in constructing technology shock series might be intermingling technology shocks with demands shifts. For example, see Greenwood, Hercowitz, and Krusell (1997). Return to text
21. See, for example, Smets and Wouters (2007) and Christiano, Motto, and Rostagno (2007). Return to text
22. There are bridge tables for consumption as well as equipment and software investment but not for structures investment. We assume that the sectoral composition of structures investment is the same as that of consumption. Return to text
23. The machinery sector encompasses two components. The first component is the BEA definition of "Equipment and Software"Investment, after excluding the Transportation, Wholesale, and Retail Margins. The second component is the inputs from the following five BEA "industries"that are used in consumption: (334) Computer and Electronic Products; (335) Electrical equipment, appliances, and components; (513) Broadcasting and telecommunications; (514) Information and data processing services; and (5412OP) Miscellaneous professional, scientific and technical services. Return to text
24. Only with much higher input substitution elasticities would there be an incentive to shift so much labor to the sector as to lower the output of the sector. Return to text
25. Appendix B isolates the role of capital being predetermined at the sectoral level and of sector-specific production functions in distancing the effects of MFP shocks in the machinery sector from those of IST shocks in a one-sector model. Return to text
26. Both correlations reported were constructed with data from Table 1.1.6 of the National Income and Product Accounts for the period between 1947:q1 and 2009:q2. Return to text
27. Similar results apply for the sampling distribution of the correlation between the growth rate of consumption and investment. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text