
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1001, June 2010 --- Screen Reader
Version*
Imperfect Credibility and the Zero Lower Bound on the Nominal Interest Rate**
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
When the nominal interest rate reaches its zero lower bound, credibility is crucial for conducting forward guidance. We determine optimal policy in a New Keynesian model when the central bank has imperfect credibility and cannot set the nominal interest rate below zero. In our model, an announcement of a low interest rate for an extended period does not necessarily reflect high credibility. Even if the central bank does not face a temptation to act discretionarily in the current period, policy commitments should not be postponed. In reality, central banks are often reluctant to allow a recovery path with output and inflation temporarily above target. From the perspective of our model such a policy reflects a low degree of credibility. We find increased forecast uncertainty in inflation and the output gap at the zero lower bound while interest rate uncertainty is reduced. Furthermore, misalignments between announced interest rate paths and market expectations are found to be best explained by lack of credibility.
Keywords: Monetary policy, zero interest rate bound, commitment, liquidity trap
JEL classification: C61, E31, E52
1 Introduction
When the nominal interest rate reaches zero, the central bank faces a time inconsistency problem. Initially, a promise to keep the nominal interest rate low for an extended period will raise inflation expectations, lower current and future real interest rates, and thus stimulate current output. However, once the economy has emerged from the recession, honoring the earlier promise of low interest rates overstimulates the economy leading to elevated inflation and a positive output gap. Therefore, a central bank whose announced promises for the interest rate path are perceived as not credible cannot provide effective forward guidance and the economy goes through a deeper recession than otherwise. Whereas commitment always matters for the conduct of monetary policy, the negative effects of low credibility are particularly painful at the zero bound.1
Academics and policymakers alike deem central bank credibility pivotal for the conduct of monetary policy as documented in Blinder (2000). However, recent episodes of zero (or very low) interest rates suggest that the credibility of central banks in industrialized economies is imperfect. For example in 1999/2000, the Bank of Japan never followed the prescription of the optimal policy under full commitment. After instituting a zero interest rate policy in February 1999, it raised interest rates in March 2000 although the economy was still weak and inflation was negative.
We analyze the optimal monetary policy in a standard New Keynesian model when the central bank has imperfect credibility and the nominal interest rate is constrained to be non-negative. The central bank can promise a policy plan, however, in the future it may obtain the opportunity to discard its earlier promises and re-optimize. This framework captures the fact that in practice central banks have an intermediate degree of credibility. Besides being more realistic than the two extremes of full commitment and full discretion, our model of imperfect credibility allows us to address the following questions. How does the possibility of future renouncements influence current policies and promises? What are the economic consequences of policy renouncements? How does the temptation to default evolve over time?
First, as private agents' expectations reflect the possibility of future policy renouncements under imperfect credibility, the central bank resorts to an even more extreme promise about keeping the interest rate at zero than under full commitment. Hence, the mere announcement to keep the interest rate low for an extended period is not necessarily a sign of credibility. Second, re-optimization does not prompt an immediate exit from the zero bound unless the economy has sufficiently recovered. However, the new policy promises to raise the interest rate earlier in order to moderate the post-recession boom. And third, policy renouncements are most valuable when the economy is about to emerge from the zero lower bound regime. At this stage, the benefits from forward guidance have been reaped whereas the welfare costs of elevated inflation and higher output gap have not yet materialized.
Our results support the view expressed in Walsh (2009) that central banks operate under imperfect commitment and have not followed the prescriptions of the optimal monetary policy under full commitment as derived in the New Keynesian model. Federal Reserve officials have stated publicly that promising to keep both inflation and the output gap above target is currently not considered, i.e., they do not intend to follow the optimal policy prescription of the New Keynesian model. While there may be other interpretations of such statements, our model establishes a theoretical link to central bank credibility and suggests that it is low.2
Furthermore, when the Swedish Riksbank lowered its path for the repo-rate in April 2009, market expectations decoupled from the announced repo-rate path, thus raising doubts about the credibility of the Riksbank - see Svensson (2009, 2010). Through the lens of our model, such misalignments between the announced interest rate path and market expectations more likely stem from imperfect credibility rather than increased forecast uncertainty. Whereas uncertainty about inflation and the output gap rises, the forecast for the interest rate becomes less uncertain at the zero bound. Our model also provides insight why central banks, in particular the Federal Reserve System, have come under unprecedented political pressure in the aftermath of the 2008 financial crisis. Even without changes in the political environment, the temptation to re-optimize a policy path is substantially larger in a recession with the interest rate at zero than in stable economic times.
Our work is related to Adam and Billi (2006, 2007) and Nakov (2008) who analyze stochastic economies imposing the zero lower bound as an occasionally binding constraint. These authors focus on the extreme cases of full commitment and full discretion. Schaumburg and Tambalotti (2007) examine imperfect commitment but abstract from the zero lower bound.3 Since the zero lower bound introduces pronounced non-linearities, closed form solutions as described in Schaumburg and Tambalotti (2007) are not available. Instead, we use the imperfect credibility setting with global methods proposed in Debortoli and Nunes (2010).
Benhabib et al. (2001, 2002) show that once the zero lower bound on the nominal interest rate is taken into account, active interest rate feedback rules can lead to liquidity traps and multiple equilibria. Schmitt-Grohé and Uribe (2007) follow a different strategy by analyzing simple rules in stochastic economies and checking ex-post that the zero lower bound constraint is not violated too often. In this paper, we do not focus on interest rate rules nor on multiple equilibria.
Other authors opted to examine the zero lower bound constraint in a perfect foresight setting, e.g., Eggertsson and Woodford (2003), Jung et al. (2005), Levin et al. (2009) and Bodenstein et al. (2009).4 This modeling approach allows for analyzing more complex models. However, under perfect foresight agents do not take into account the possibility of future shocks when forming their expectations. In our setting of imperfect credibility, the uncertainty about future shocks and the possibility of policy renouncements crucially shape agents' expectations and impact the policy plans of the central bank. Thus, global methods that can handle occasionally binding constraints need to be employed.
2 The Model
The model consists of two building blocks: the private sector and the monetary authority. The behavior of the private sector is given by a standard New Keneysian model as described among others in Yun (1996), Clarida et al. (1999), and Woodford (2003). The central bank attempts to maximize the welfare of the representative household but faces two limitations. First, the central bank's single tool is the nominal interest rate on one-period, non-contingent debt which cannot fall below zero (zero lower bound). Second, the central bank's commitment to earlier plans is revoked with a known and fixed probability (imperfect credibility).
2.1 Private Sector
The optimization problems of households and firms imply the well-known linear aggregate demand and supply relationships
| (1) | |
| (2) |
where ![]() is a cost push shock
is a cost push shock
| (3) |
and ![]() is a demand shock
is a demand shock
| (4) |
![]() denotes the inflation rate,
denotes the inflation rate,
![]() is the output gap, and
is the output gap, and ![]() is the nominal interest rate on one period
non-contingent debt.5 Policymakers do not tax money holdings
and thus the nominal interest rate is bounded from below.6As
is the nominal interest rate on one period
non-contingent debt.5 Policymakers do not tax money holdings
and thus the nominal interest rate is bounded from below.6As
![]() is expressed in deviation from the
steady state interest rate (with zero steady state inflation), this
condition reads as follows
is expressed in deviation from the
steady state interest rate (with zero steady state inflation), this
condition reads as follows
| (5) |
where ![]() is the value of the nominal interest
rate in steady state. For later use, we also define the level of
the nominal interest rate
is the value of the nominal interest
rate in steady state. For later use, we also define the level of
the nominal interest rate
![]() .
.
The discount factor is denoted by
![]() and the slope of
the Phillips curve is
and the slope of
the Phillips curve is
![]() .
. ![]() is the probability with which a firm
cannot adjust its price,
is the probability with which a firm
cannot adjust its price, ![]() is the intertemporal
elasticity of substitution of the household,
is the intertemporal
elasticity of substitution of the household, ![]() measures the elasticity of a firm's real marginal cost
with respect to its own output level, and
measures the elasticity of a firm's real marginal cost
with respect to its own output level, and ![]() is
the elasticity of substitution between the varieties produced by
the monopolistic competitors.
is
the elasticity of substitution between the varieties produced by
the monopolistic competitors.
2.2 Monetary Policy
The monetary authority minimizes the present discounted value of
its period objective function subject to the constraints (1) - (5) using the one-period nominal interest rate as its sole policy
instrument. The period utility function ![]() is of the
quadratic form
is of the
quadratic form
| (6) |
Following the derivations in Woodford (2003), we
assume
![]() .
.
As in Roberds (1987), Schaumburg and Tambalotti (2007), adn Debortoli and Nunes (2010), the policymaker has imperfect
credibility. At the beginning of each time period, a realization of
the random variable ![]() is drawn with
is drawn with
![]() and the probability
distribution
and the probability
distribution
![\begin{displaymath} p\left( x\right) =\left\{ \begin{array}[c]{c} \text{ \ \ }\eta\text{\ \ \ \ \ \ \ \ \ \ \ if }x=C\ 1-\eta\text{ \ \ \ \ \ \ \ if }x=D \end{array}\right. \end{displaymath}](img30.gif)
with
![]() .
.
In the event ![]() , the policymaker follows her
previously announced policy path, whereas she reneges on her
earlier promises if
, the policymaker follows her
previously announced policy path, whereas she reneges on her
earlier promises if ![]() . Thus, a policymaker's
promises made in time
. Thus, a policymaker's
promises made in time ![]() about the future path of the
nominal interest rate will be implemented in period
about the future path of the
nominal interest rate will be implemented in period ![]() with probability
with probability ![]() .
.
If ![]() , policy promises are always kept and
the policymaker is referred to as fully committed or perfectly
credible. If
, policy promises are always kept and
the policymaker is referred to as fully committed or perfectly
credible. If ![]() , the policymaker acts under full
discretion. Adam and Billi (2006, 2007) analyze the optimal monetary policy under the
zero bound constraint in a fully stochastic environment for these
two cases.7 The intermediate cases, with
, the policymaker acts under full
discretion. Adam and Billi (2006, 2007) analyze the optimal monetary policy under the
zero bound constraint in a fully stochastic environment for these
two cases.7 The intermediate cases, with
![]() , correspond to
imperfect credibility and have not been previously analyzed.
, correspond to
imperfect credibility and have not been previously analyzed.
Assuming the default event to be stochastic rather than an endogenous decision is a simplification analogous to the Calvo pricing model. This setup allows us to solve a nonlinear stochastic model with global methods, which may become infeasible with more complex imperfect credibility settings. More importantly, the credibility setting modeled here allows us to address our goals: examining the interaction between the anticipation of future policy re-optimizations and commitments, and analyzing the effects of policy renouncements and the welfare effects of doing so. These issues cannot be addressed in either the full commitment or the discretion framework.
Under imperfect credibility, the optimization problem of the policymaker is stated as
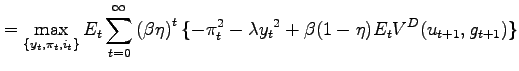 |
(7) | |
where variables evaluated under default carry the superscript D.
The objective function contains two parts. The first term in the
summation refers to future nodes in which current promises are
kept. The possibility of future re-optimizations causes such
histories to be discounted at the rate ![]() .
Second, at any point in time, current promises are discarded with
probability
.
Second, at any point in time, current promises are discarded with
probability ![]() and a new policy is formulated.
The value obtained by the monetary authority in that case is
summarized in the function
and a new policy is formulated.
The value obtained by the monetary authority in that case is
summarized in the function ![]() . The
expectation terms in the constraints also reflect the uncertainty
about future policy renouncements.
. The
expectation terms in the constraints also reflect the uncertainty
about future policy renouncements.
2.3 Equilibrium and Solution
The current problem can be recast into the recursive formulation of Marcet and Marimon (2009). After rearranging terms, the problem can be written as
| (8) | ||
where
![]() are the
Lagrange multipliers associated with the aggregate supply and
demand constraints,
are the
Lagrange multipliers associated with the aggregate supply and
demand constraints,
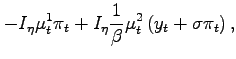 |
(9) |
and ![]() is an indicator function satisfying
is an indicator function satisfying
![\begin{displaymath} I_{\eta}=\left\{ \begin{array}[c]{c} 0\text{ \ \ \ \ if }\eta=0\ 1\text{ \ \ \ \ if }\eta\neq0. \end{array}\right. \end{displaymath}](img77.gif)
It follows from Marcet and Marimon (2009) and Debortoli and Nunes (2010) that the optimal policy and the value
functions are time invariant if the state space is enlarged to
contain the lagged Lagrange multipliers
![]() . The multipliers
summarize previous promises, with the case of non-binding promises
corresponding to the multipliers being zero.8 Since the
multipliers are not physical state variables, only commitment
impedes the monetary authority from ignoring previous promises,
reflecting the time inconsistent nature of the problem. In fact,
resetting the Lagrange multipliers to zero is optimal, and occurs
in equilibrium when the monetary authority is allowed to do so.
Definition 1 specifies the
equilibrium concept.
. The multipliers
summarize previous promises, with the case of non-binding promises
corresponding to the multipliers being zero.8 Since the
multipliers are not physical state variables, only commitment
impedes the monetary authority from ignoring previous promises,
reflecting the time inconsistent nature of the problem. In fact,
resetting the Lagrange multipliers to zero is optimal, and occurs
in equilibrium when the monetary authority is allowed to do so.
Definition 1 specifies the
equilibrium concept.
Definition 1 The equilibrium with imperfect commitment satisfies the following conditions:
- Given
 and
the value
and
the value  , the path
, the path
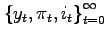 solves
problem (7).
solves
problem (7). - The value function
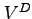 is such that
is such that
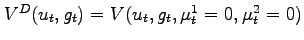 and
and 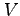 is defined by equation (8).
is defined by equation (8). - Denote the optimal policy functions as
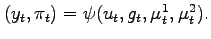 The pair
The pair
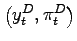 satisfies the condition
satisfies the condition
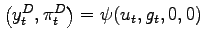 .
.
First, definition requires optimality given the constraints. The
second part defines the value of default ![]() to
be the continuation value without binding promises, i.e., the
lagged Lagrange multipliers are at zero. The two value functions
would not coincide if policy objectives are not consensual.9 The
third part requires the policy functions that private agents expect
to be implemented under default
to
be the continuation value without binding promises, i.e., the
lagged Lagrange multipliers are at zero. The two value functions
would not coincide if policy objectives are not consensual.9 The
third part requires the policy functions that private agents expect
to be implemented under default
![]() to be
consistent with the optimal policy functions implemented when there
are no promises to be honored.
to be
consistent with the optimal policy functions implemented when there
are no promises to be honored.
The solution of equation (8) is not
standard, as both the value function ![]() and the
policy functions under default are unknown. In addition, the
solution requires maximizing with respect to the controls and
minimizing with respect to the Lagrange multipliers. In the
numerical algorithm, we approximate the value function directly. As
in Debortoli and Nunes (2010), we make use of Definition 1 to
employ a numerical procedure with one fixed point only. The
numerical algorithm is described in detail in Appendix A.2.
and the
policy functions under default are unknown. In addition, the
solution requires maximizing with respect to the controls and
minimizing with respect to the Lagrange multipliers. In the
numerical algorithm, we approximate the value function directly. As
in Debortoli and Nunes (2010), we make use of Definition 1 to
employ a numerical procedure with one fixed point only. The
numerical algorithm is described in detail in Appendix A.2.
The two model features that dictate the use of global methods are the presence of the occasionally binding zero bound constraint and the possibility of policy renouncements. Most of the literature on monetary policy at the zero bound assumes perfect foresight. Whereas this approach allows for a simplified treatment of the binding constraint, it inhibits studying the link between monetary policy and household expectations about future policy renouncements. By construction, households do not anticipate policy changes under perfect foresight.
3 Results
The parameterization of our model is summarized in Table 1.
To facilitate comparison with the work of Adam and Billi (2006, 2007) and Woodford (2003), we opted not to deviate from these authors'
parameter choices. The one parameter in our analysis for which
there is almost no guidance provided in the literature is
![]() , the probability with which the
policymaker will honor her previous promises. One can also measure
the credibility level by the expected time before a policy
renouncement occurs
, the probability with which the
policymaker will honor her previous promises. One can also measure
the credibility level by the expected time before a policy
renouncement occurs
![]() . Throughout our discussion,
we show results for the cases described in Table 2.
. Throughout our discussion,
we show results for the cases described in Table 2.
Table 1: Parameterization
| Parameter | Value | Economic Meaning |
|---|---|---|
β | 0.9913 | discount factor |
υ | 0.66 | prob. of no price change |
σ | 6.25 | interest rate sensitivity consumption |
ω | 0.47 | elasticity of firms' marginal cost |
θ | 7.66 | price elasticity of demand |
κ | 0.024 | slope of Phillips curve |
λ | 0.003 | weight on output in utility function |
ρu | 0 | persistence cost push shock |
σu | 0.154 | std. cost push shock |
ρg | 0.8 | persistence demand shock |
σg | 1.524 | std. demand shock |
Depending on the long-run inflation target, previous research suggests that the nominal interest rate reaches the zero bound with low probability.10 However, once the economy is at the zero bound, additional shocks have amplified consequences on economic activity. In the New Keynesian model, demand shocks are considered to be more volatile and persistent than cost-push shocks and therefore play a more important role when focusing on zero bound issues.11 Furthermore, for a large demand shock that pushes the interest rate to zero, the economy experiences key characteristics of a liquidity trap with both output and inflation dropping. By contrast, for a cost-push shock to lower the interest rate, inflation drops but output rises.
Table 2: Imperfect Credibility Cases
| p(x=C)=η | α=1/1-η | economic meaning |
|---|---|---|
0 | 1 | full discretion |
0.5 | 2 | loose commitment |
0.75 | 4 | loose commitment |
1 | ∞ | full commitment |
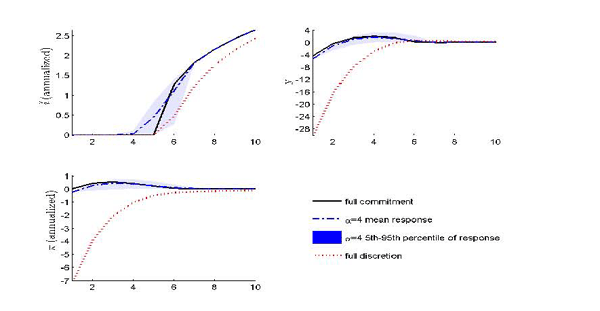
3.1 Credibility and Cost-Push Shocks
To illustrate the effects of imperfect credibility in a simple
example, we first examine the familiar response to a cost-push
shock. Figure 1 plots the
responses of the nominal interest rate in levels
![]() , the output gap
, the output gap ![]() , and the inflation rate
, and the inflation rate ![]() to a
negative i.i.d. cost push shock (i.e.,
to a
negative i.i.d. cost push shock (i.e.,
![]() , and
, and
![]()
![]() ). Under full discretion, the
economy experiences price deflation and an expansion in output. In
the second period, the cost-push shock vanishes and inflation and
output are back to target.12 This is not the case with full
commitment. The monetary authority promises to keep the interest
rate below its long-run value, thus causing persistent inflation
and elevated output. Consequently, the initial impact of the shock
is dampened.
). Under full discretion, the
economy experiences price deflation and an expansion in output. In
the second period, the cost-push shock vanishes and inflation and
output are back to target.12 This is not the case with full
commitment. The monetary authority promises to keep the interest
rate below its long-run value, thus causing persistent inflation
and elevated output. Consequently, the initial impact of the shock
is dampened.
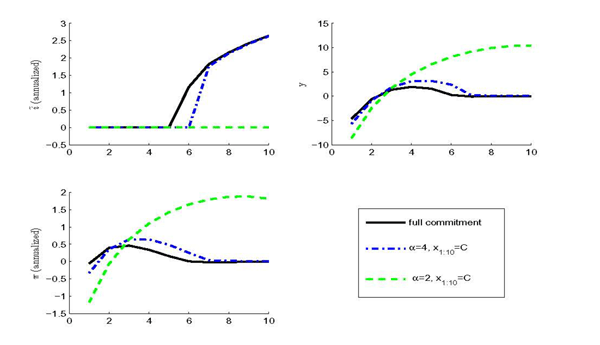
Figure 1: Cost-Push Shock Under Imperfect Credibility
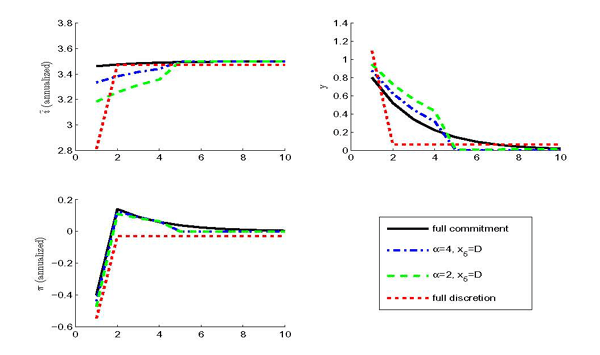
Notes: The figure plots the response to a negative cost-push shock. The shocks are initialized at εu,1=-σu,εg,1=0, and (εu,t,εg,t=0∀≥2. For the imperfect commitment cases (α=2 and α=4), the figure plots the specific history with x5=D, xt=C∀≠5.
For the imperfect credibility settings with ![]() and
and ![]() , Figure 1 considers the
specific history in which the monetary authority reneges in period
5 only (
, Figure 1 considers the
specific history in which the monetary authority reneges in period
5 only (
![]()
![]() ). Until period 4, the output
gap and inflation are kept above target, honoring the monetary
authority's past promises. In period 5, policy is re-optimized and
it is feasible to bring output and inflation back to target. Since
private agents are aware of the possibility of such future policy
renouncements, the task of the central bank is adversely affected:
in the first period the central bank does not stabilize the economy
as effectively as under full commitment.
). Until period 4, the output
gap and inflation are kept above target, honoring the monetary
authority's past promises. In period 5, policy is re-optimized and
it is feasible to bring output and inflation back to target. Since
private agents are aware of the possibility of such future policy
renouncements, the task of the central bank is adversely affected:
in the first period the central bank does not stabilize the economy
as effectively as under full commitment.
3.2 Credibility at the Zero Lower Bound
When the nominal interest rate reaches zero in response to a large contractionary demand shock, monetary policy faces a dilemma. To mitigate the impact of the shock the central bank has to promise to keep the interest rate low for an extended period in order to allow inflation and the output gap to rise above their target values in the future. However, once the economy enters the phase of elevated inflation and a positive output gap, the central bank faces the temptation to renege on its earlier promise and to raise the interest rate. Under imperfect credibility, the monetary authority will not deliver on its earlier promises and will raise the interest rate path if it obtains the chance to do so. Thus, the ability of such a central bank to ease the recession may be greatly diminished.
To illustrate how policy promises and renouncements chosen under
limited credibility affect the path of the economy, we analyze the
impulse response functions after a large and persistent contraction
in aggregate demand that pushes the nominal interest rate to zero.
More specifically, across experiments we set ![]() ,
, ![]() , and (
, and (
![]()
![]() . However, we consider
different specific histories of
. However, we consider
different specific histories of ![]() . Initially,
the lagged Lagrange multipliers are at zero, i.e.,
. Initially,
the lagged Lagrange multipliers are at zero, i.e.,
![]() .
.
3.2.1 Promises
If the central bank has limited credibility, private agents
correctly incorporate the possibility of future re-optimizations
when forming expectations. The monetary authority tries to
influence the expectations of the private sector by adjusting its
announced policy. Figure 2
plots the optimal plan announced by the central bank without policy
renouncements (![]()
![]() ) for different levels of
credibility (
) for different levels of
credibility (![]() ,
, ![]() , and
full commitment). The lower the credibility of the monetary
authority is, the more extreme its promises are. The policymaker
with
, and
full commitment). The lower the credibility of the monetary
authority is, the more extreme its promises are. The policymaker
with ![]() promises to keep the interest rate
at zero over the entire horizon plotted, whereas the policymaker
with
promises to keep the interest rate
at zero over the entire horizon plotted, whereas the policymaker
with ![]() promises to keep the interest rate
at zero for 6 periods. Hence, the announcement that the interest
rate is planned to be at zero for a long period should not be
necessarily understood as a signal of high credibility. In a purely
forward looking model, such inference is correct only when
comparing the extreme cases of full commitment and
discretion.13
promises to keep the interest rate
at zero for 6 periods. Hence, the announcement that the interest
rate is planned to be at zero for a long period should not be
necessarily understood as a signal of high credibility. In a purely
forward looking model, such inference is correct only when
comparing the extreme cases of full commitment and
discretion.13
Figure 2: Imperfect Credibilty and the Zero Lower Bound - Extreme Promises
Notes: the figure plots the
transition dynamics in response to a negative and large demand
shock causing the interest rate to reach its zero lower bound. The
shocks are initialized at
![]() , and
, and
![]()
![]() . For the imperfect commitment
cases (
. For the imperfect commitment
cases (![]() and
and ![]() ), the
figure plots the specific history with
), the
figure plots the specific history with ![]()
![]() .
.
However, the central bank may have to deliver on its promises.
At the optimum, the policymaker equates the expected benefits from
a promise to keep the interest rate low with the expected costs of
having to deliver on these promises (the cost of not defaulting).
If a policymaker does not get a chance to revisit an extreme
promise, the low interest rate fuels a sizable and persistent boom
with increased inflation, as seen in particular for the case of
![]() .
.
3.2.2 Renouncements
While a policymaker in default ignores all past promises, the
new policies depend on the state of the economy at the time of
re-optimization. If the economy is still sufficiently deep in
recession, the central bank will keep the interest rate at zero
under its new policy. The left panel in Figure 3
confirms this claim for ![]() when a policy
renouncement occurs in period 2 (
when a policy
renouncement occurs in period 2 (![]() and
and
![]()
![]() ) or period 3 (
) or period 3 (![]() and
and ![]()
![]() ). One could therefore infer
that in times of a deep recession, policy commitments are not
relevant: the interest rate will be at zero irrespective of policy
renouncements. However, such inference is misguided. The promise of
a low interest rate is made because of its positive effects
throughout the entire recession. If the interest rate policy is
reformulated in the midst of the recession, the incentive to keep
the interest rate low is reduced. In fact, if policy renouncements
occur in the early phase of the recession, the economy exits the
zero bound earlier. Commitment is important well before the central
bank faces the temptation to start economic tightening.
). One could therefore infer
that in times of a deep recession, policy commitments are not
relevant: the interest rate will be at zero irrespective of policy
renouncements. However, such inference is misguided. The promise of
a low interest rate is made because of its positive effects
throughout the entire recession. If the interest rate policy is
reformulated in the midst of the recession, the incentive to keep
the interest rate low is reduced. In fact, if policy renouncements
occur in the early phase of the recession, the economy exits the
zero bound earlier. Commitment is important well before the central
bank faces the temptation to start economic tightening.
Figure 3: Imperfect Credibility and the Zero Lower Bound - Reneging on Promises
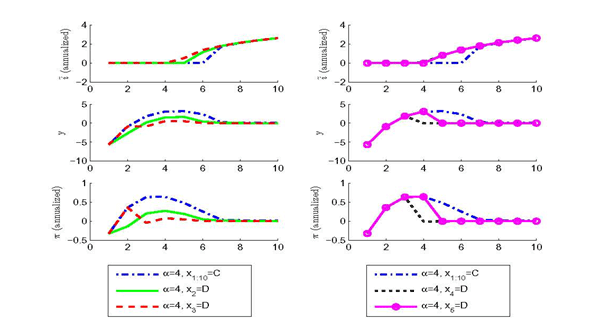
Notes: the figure plots the
transition dynamics in response to a negative and large demand
shock causing the interest rate to reach its zero lower bound. The
shocks are initialized at
![]() , and
, and
![]()
![]() . All cases refer to imperfect
credibility with
. All cases refer to imperfect
credibility with ![]() . The dot-dashed line in
both panels refers to the specific history
. The dot-dashed line in
both panels refers to the specific history
![]() . The remaining lines in
the figure plot a specific history
. The remaining lines in
the figure plot a specific history ![]()
![]() , with
, with
![]() .
.
While the economy is on its recovery path, the interest rate may
still be zero due to earlier commitments. As depicted in the right
panel of Figure 3,
the central bank raises the interest rate immediately if a default
occurs in this phase. For defaults in period 4 (![]() ,
, ![]()
![]() ) or 5 (
) or 5 (![]() ,
, ![]()
![]() ), such action puts an end
to the policy of elevated inflation and output gap previously
promised and brings both variables closer to target.
), such action puts an end
to the policy of elevated inflation and output gap previously
promised and brings both variables closer to target.
Once the economy has exited from the zero bound, it is
immaterial whether new commitments are made after a policy
renouncement. After exiting from the zero lower bound, commitments
hardly have additional value with respect to the demand shocks.
Figure 4 shows that after
a default in period 6, the projected path with ![]()
![]() and the path with
and the path with
![]()
![]() overlap.14
overlap.14
Figure 4: Imperfect Credibility and the Zero Lower Bound - After Reneging on Promises
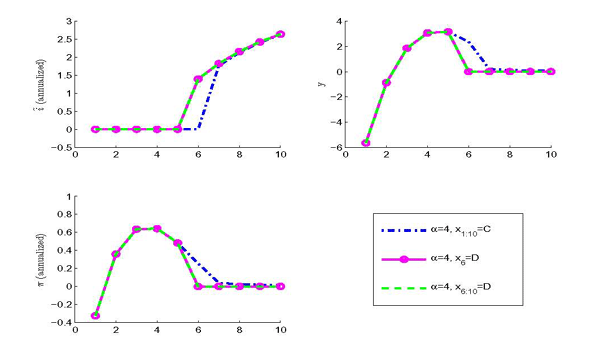
Notes: the figure plots the
transition dynamics in response to a negative and large demand
shock causing the interest rate to reach its zero lower bound. The
shocks are initialized at
![]() , and
, and
![]()
![]() . All cases refer to imperfect
credibility with
. All cases refer to imperfect
credibility with ![]() . The first line plots the
specific history
. The first line plots the
specific history ![]()
![]() ; the
second line plots the specific history
; the
second line plots the specific history ![]()
![]() ; the third line plots the
specific history
; the third line plots the
specific history
![]() .
.
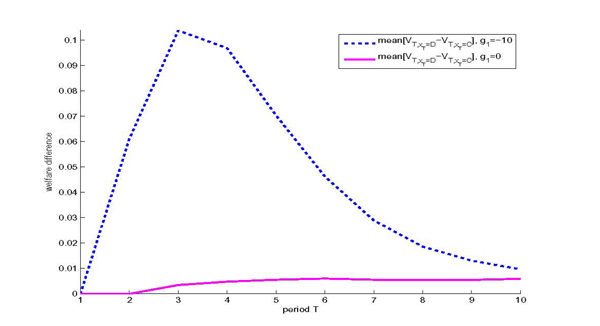
3.2.3 Temptation and Welfare
The exact nature of the time inconsistency problem faced by the
central bank is illustrated by a welfare analysis in Figure 5. We plot the
welfare gain from a random default in period T relative to staying
committed,
![]() .
.
![]() is the present discounted value
of the central bank's utility from T onwards with realization
is the present discounted value
of the central bank's utility from T onwards with realization
![]() .15 In period 1, the economy
experiences a large contractionary demand shock,
.15 In period 1, the economy
experiences a large contractionary demand shock, ![]() , that pushes the interest rate down to zero.
Afterwards no cost-push or demand shocks realize. In all periods
prior to period T, the policymaker is assumed to honor her
promises.
, that pushes the interest rate down to zero.
Afterwards no cost-push or demand shocks realize. In all periods
prior to period T, the policymaker is assumed to honor her
promises.
Figure 5: Welfare Gains from Default
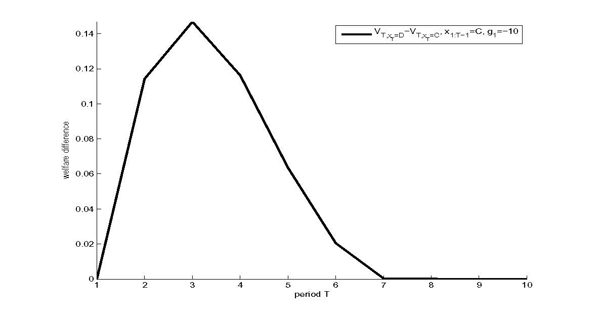
Notes: the figure plots the
period ![]() expectation of the gain in discounted
welfare due to a default in period
expectation of the gain in discounted
welfare due to a default in period ![]() , for the
case of imperfect credibility with
, for the
case of imperfect credibility with ![]() and
the specific histories
and
the specific histories ![]()
![]() . The shocks are initialized
at
. The shocks are initialized
at
![]() , and
, and
![]()
![]() .
.
The temptation to renege is the highest in period 3. Revisiting Figure 3 reveals that defaulting in period 3 avoids the costly overshooting of inflation and the output gap. The economy is stabilized more effectively if the opportunity to re-optimize occurs in this period rather than any other.
3.3 Distribution of Responses
To highlight specific features of our model, the impulse
response functions shown so far have been based on specific
histories for ![]() ,
,
![]() , and
, and
![]() . For the next two
experiments, we analyze more generally the distribution of impulse
responses at the zero bound.
. For the next two
experiments, we analyze more generally the distribution of impulse
responses at the zero bound.
First Experiment We first restrict attention to histories
with ![]() and
and
![]()
![]() , and
, and ![]() and
and
![]()
![]() , but allow for all possible
histories of
, but allow for all possible
histories of ![]() . Figure 6 shows
the mean impulse response under imperfect credibility with
. Figure 6 shows
the mean impulse response under imperfect credibility with
![]() surrounded by the impulse response
functions lying between the 5th and 95th percentiles, the shaded area. The figure also displays
the impulse responses when the policymaker has full commitment or
acts under full discretion, respectively. As we still condition on
a specific history for the demand and cost-push shocks, there is no
uncertainty about the impulse responses under full commitment and
full discretion.
surrounded by the impulse response
functions lying between the 5th and 95th percentiles, the shaded area. The figure also displays
the impulse responses when the policymaker has full commitment or
acts under full discretion, respectively. As we still condition on
a specific history for the demand and cost-push shocks, there is no
uncertainty about the impulse responses under full commitment and
full discretion.
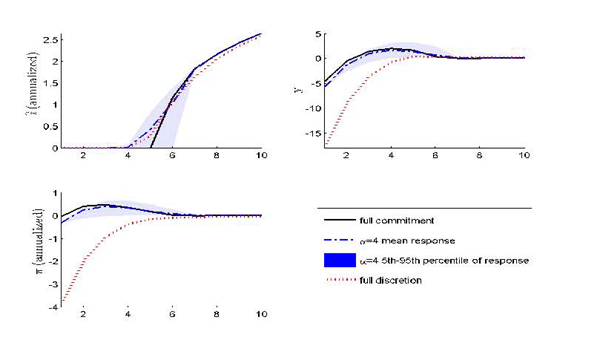
Figure 6: Distribution of Impulse Response Functions - Default Uncertainty Only
Notes: the figure plots the
transition dynamics in response to a negative and large demand
shock causing the interest rate to reach its zero lower bound. The
shocks are initialized at
![]() , and
, and
![]()
![]() . The mean and selected
percentiles are computed from simulated histories of the commitment
shock (i.e.
. The mean and selected
percentiles are computed from simulated histories of the commitment
shock (i.e.
![]() ). For the full commitment
and full discretion cases, there is no uncertainty with regard to
). For the full commitment
and full discretion cases, there is no uncertainty with regard to
![]() shocks, and therefore any percentile
coincides with the mean.
shocks, and therefore any percentile
coincides with the mean.
For the mean response under imperfect credibility, the economy exits the zero bound earlier than both under full commitment and full discretion.16 Nevertheless, the output gap and inflation rise above target before returning to it for the mean response under limited credibility as is the case under full commitment. However, this mean response is surrounded by considerable uncertainty. The shaded area spanned by the 5th and 95th percentile responses covers the special cases depicted in Figures 2 through 4. These scenarios showed that imperfect credibility may lead to large and persistent positive or negative deviations of the output gap and inflation from their long-run target values.
For histories with many default events, the impulse response
functions replicate the qualitative features of the economy under
full discretion. However, for our benchmark calibration of
![]() , the economy does not perform as
poorly as the economy under full discretion, in which the
policymaker re-optimizes every period. Thus, being somewhat
committed but defaulting in many periods by chance, is different
from being known to have no commitment at all.
, the economy does not perform as
poorly as the economy under full discretion, in which the
policymaker re-optimizes every period. Thus, being somewhat
committed but defaulting in many periods by chance, is different
from being known to have no commitment at all.
Second Experiment We consider all possible histories for
![]() ,
,
![]() , and
, and
![]() for
for ![]() . For the initial period,
. For the initial period, ![]() , however,
we distinguish two cases. In the first case, the economy
experiences a large negative demand shock that pushes the nominal
interest rate to zero, i.e.,
, however,
we distinguish two cases. In the first case, the economy
experiences a large negative demand shock that pushes the nominal
interest rate to zero, i.e., ![]() ,
,
![]() , whereas for the second case we
initialize the economy at
, whereas for the second case we
initialize the economy at ![]() ,
, ![]() .
.
Figure 7 plots the
interquantile range between the 95th percentile
response and the 5th percentile response when
policymakers act under full commitment, imperfect credibility
(![]() ), and full discretion. The dashed
lines depict the interquantile ranges when the economy is initially
at the zero bound (
), and full discretion. The dashed
lines depict the interquantile ranges when the economy is initially
at the zero bound (![]() ) and the solid
lines depict the case when the economy is initialized at
) and the solid
lines depict the case when the economy is initialized at
![]() .
.
The economy experiences higher uncertainty about the future
paths of the output gap and the inflation rate as measured by the
interquantile range when the economy is initially at the zero lower
bound. Monetary policy can no longer counteract shocks as
effectively as it can when the interest rate is positive. The
resulting increase in the economy's sensitivity to shocks
translates into (temporarily) increased uncertainty about the
output gap and the inflation rate. As the nominal interest rate is
the predominant shock absorber when the interest rate is positive,
the uncertainty about the future path of the nominal interest rate
is lower when the economy is initially at the zero bound.17 For
periods further in the future, the interquantile ranges for the two
cases (![]() and
and ![]() )
converge as it is less likely for the zero bound to remain binding
for the case with
)
converge as it is less likely for the zero bound to remain binding
for the case with ![]() once the initial
demand shock has sufficiently receded.
once the initial
demand shock has sufficiently receded.
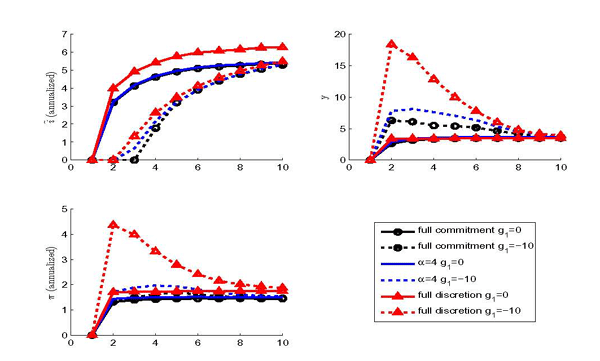
Figure 7: Forecast Uncertainty - Interquantile Range
Notes: the figure plots the
difference between the 95th and 5th percentiles in several
scenarios. In all simulations, the shocks
![]() are drawn from their respective distributions. For the cases
reported with the solid lines, the simulations are initialized at
are drawn from their respective distributions. For the cases
reported with the solid lines, the simulations are initialized at
![]() . For the cases reported with
the dashed lines, the simulations are initialized at
. For the cases reported with
the dashed lines, the simulations are initialized at
![]() , which causes the interest
rate to reach its zero lower bound. For the full commitment and
full discretion cases, there is no uncertainty with regard to
, which causes the interest
rate to reach its zero lower bound. For the full commitment and
full discretion cases, there is no uncertainty with regard to
![]() shocks.
shocks.
Policy commitment is especially important when the economy is at
the zero bound. For an interest rate of zero, the interquantile
ranges for inflation and the output gap are substantially higher in
an economy with imperfect credibility compared to an economy with
full commitment. Doubts about the commitment of the central bank
impinge upon the ability to use interest rate announcements for
forward guidance.18 By contrast, for ![]() , there is little difference regarding the
interquantile ranges for the two policy regimes away from the zero
bound. In the 2008/2009 recession, markets have experienced
increased volatility and uncertainty in the inflation and output
outlook. Our findings suggest that part of this uncertainty is a
consequence of the zero lower bound and low credibility.
, there is little difference regarding the
interquantile ranges for the two policy regimes away from the zero
bound. In the 2008/2009 recession, markets have experienced
increased volatility and uncertainty in the inflation and output
outlook. Our findings suggest that part of this uncertainty is a
consequence of the zero lower bound and low credibility.
4 Credibility and Times of Crisis
Actions by politicians, central bank officials, and financial markets during the sharp world-wide downturn in economic activity 2008/2009 have created doubt about how much credibility central banks actually have. In this section, we provide examples of such actions and interpret them through the lens of our model.
4.1 Credibility and Increased Uncertainty
A central bank's interest rate forecast can be misaligned with market expectations either because of credibility problems or because of large forecast uncertainty. Our framework can distinguish between these two competing explanations. The recent experience of the Swedish Riksbank provides an interesting application of our model along this dimension. Since February 2007, the Riksbank has published its intended path for the repo-rate, the short-term interest rate used by the Riksbank to achieve its policy goals.19
Figure 8 plots the repo-rate path and market expectations before and after the February 11 and April 21 2009 meetings. On February 11, the interest rate was reduced by 100 basis points to 1%. At this date, the new repo-rate path and market expectations were aligned. At the April 21 meeting, the repo-rate was reduced further and approached the effective lower bound.20 This time, the repo-rate path and market expectations decoupled, as market expectations suggested much faster tightening. These patterns are also present at other dates (not displayed); market expectations are not aligned with the repo-rate path only in periods of very low interest rates.
Figure 8: Low Credibility and Market Expectations
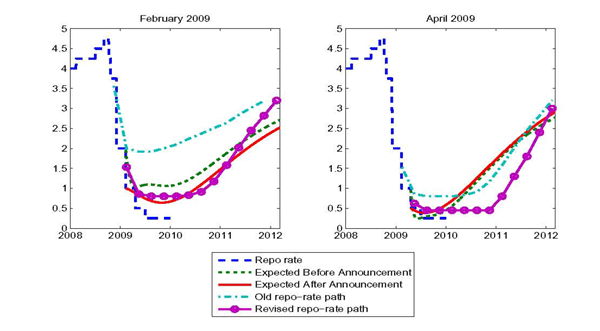
Notes: the figure plots the Riksbank's revised forecast of the repo-rate path as announced in February and April 2009 in the left and right panels, respectively, along with the old forecast, the historical path, and the market expectation of the path both preceding and following each announcement.
Market expectations and the repo-rate path could differ significantly because of increased forecast uncertainty about the interest rate. However, as highlighted in our discussion of Figure 7, the zero lower bound does not introduce additional uncertainty in the interest rate path. From the perspective of our model, the explanation seems to be imperfect credibility.
As discussed earlier, if the central bank reneges on past promises, the interest rate is raised earlier. Furthermore, a central bank with imperfect credibility attempts to correct agents' expectations by making even more extreme promises of low interest rates. The dynamics of market expectations and the repo-rate path in Figure 8 are largely consistent with the case in which the interest rate path announced by the central bank ignores policy renouncements while market expectations do not.21
4.2 Central Bank Statements
Kohn (2009b) states: "To be sure, we have not followed the theoretical prescription of promising to keep rates low enough for long enough to create a period of above-normal inflation." Similar statements can be found in Kohn (2009a) and Bernanke (2009).22 The intention of U.S. policymakers not to follow the recommendations of the optimal policy under full commitment, casts doubt on the credibility of the Federal Reserve under the assumption that the New Keynesian model applies.
Current Federal Reserve policy simultaneously promises to keep the interest rate low and to prevent inflation from rising. As pointed out by Walsh (2009), such policies are inconsistent with the optimal policy under full commitment. However, these two policies are not mutually exclusive under imperfect credibility. It is because of its imperfect credibility that the central bank makes an even more extreme promise to leave the interest rate low (see Figure 2). At the same time, the policymaker knows that with positive probability the policy path will be re-optimized to avoid the rise in inflation (see Figure 3).
Rather than by appealing to specific histories, we could
interpret the above statements by referring to the average path of
the economy. In this case, a policy that avoids an expected rise of
inflation above target as suggested inKohn (2009b) indicates very low commitment. Figure 9 plots the mean
impulse responses to a large contractionary demand shock that
pushes the interest rate to the zero bound for different degrees of
policy credibility. The mean response does not entail a significant
rise of the output gap and inflation above their long-run target
levels for
![]() .
.
Figure 9: Average Recovery Path for Different Commitment Levels
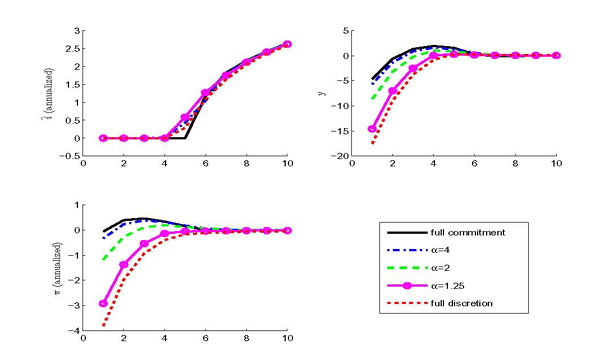
Notes: the figure plots the
mean transition dynamics in response to a negative and large demand
shock causing the interest rate to reach its zero lower bound. The
shocks are initialized at
![]() , and
, and
![]()
![]() . All histories regarding the
commitment shock are considered (i.e.
. All histories regarding the
commitment shock are considered (i.e.
![]() ) for the computation of the
means. For the full commitment and full discretion cases, there is
no uncertainty with regard to
) for the computation of the
means. For the full commitment and full discretion cases, there is
no uncertainty with regard to ![]() shocks.
shocks.
Kohn (2009b) continues: "The arguments in favor of such a policy hinge on a clear understanding on the part of the public that the central bank will tolerate increased inflation only temporarily - say, for a few years once the economy has recovered - before returning to the original inflation target in the long term. In standard theoretical model environments, long-run inflation expectations are perfectly anchored. In reality, however, the anchoring of inflation expectations has been a hard-won achievement of monetary policy over the past few decades, and we should not take this stability for granted. Models are by their nature only a stylized representation of reality, and a policy of achieving "temporarily" higher inflation over the medium term would run the risk of altering inflation expectations beyond the horizon that is desirable. Were that to happen, the costs of bringing expectations back to their current anchored state might be quite high." Thus, policymakers seem to be very much aware how fragile their credibility is.23 To justify their opposition against the theoretical recommendation derived from the New Keynesian model, policymakers seem to emphasize fear of losing control over inflation expectations. However, such fears can also be rationalized in our model. Although long-run inflation expectations are well-anchored in our model for any degree of credibility, inflation can be hard to control in the medium-run if credibility is low.
A related possibility is that central banks favor models in which a large fraction of agents are backward looking or employ learning mechanisms. Nevertheless insofar as some agents are forward looking, such features dampen the post-recession inflation but do not eliminate it. However, central bank statements dismiss the idea of above normal inflation and output altogether rather than claiming that these effects are of small magnitude. Furthermore, the private sector choosing to dismiss announcements and engaging in backward looking behavior may be a consequence of low central bank credibility.24
4.3 Political Pressure
Since the beginning of the 2008/2009 recession, the Federal Reserve System has encountered unprecedented attacks on its independence. Federal Reserve Chairman Ben Bernanke himself said in a Time Magazine article honoring him as "Person of the Year 2009": "It is true that the Federal Reserve faces a lot of political pressure and is unpopular in many circles." Suggestions for how to curb the power of the Fed have ranged from stripping it of its regulatory powers, changing the selection procedures of the president of the New York Fed, to having its monetary policy decisions audited by the Government Accountability Office.25 In reaction to these developments, Goodfriend (2010) has laid out a detailed plan to ensure that the Federal Reserve remains a strongly independent institution.
Why has the political pressure on the Federal Reserve
intensified so much during this crisis, although credibility and
central bank independence are perceived to be important building
blocks in mitigating the effects of the downturn, e.g., see Walsh (2009)? One possible answer is provided in
Figure 10.
We plot the difference between the value of staying committed in
period T,
![]() , and the value of defaulting
in period T,
, and the value of defaulting
in period T,
![]() , both for an economy that has
been hit by a large negative demand shock (
, both for an economy that has
been hit by a large negative demand shock (![]() ) and an economy that is initialized at
) and an economy that is initialized at ![]() .26 Although commitment is extremely
important in times of crisis, this is also the time when commitment
is under attack. In Figure 10, the temptation
to default on earlier promises is significantly higher at every
point in time when the economy is in a severe recession compared to
the case of
.26 Although commitment is extremely
important in times of crisis, this is also the time when commitment
is under attack. In Figure 10, the temptation
to default on earlier promises is significantly higher at every
point in time when the economy is in a severe recession compared to
the case of ![]() .
.
Figure 10: Pressure to Default
Notes: the figure plots the
mean period ![]() expectation of the gain in discounted
welfare due to a default in period
expectation of the gain in discounted
welfare due to a default in period ![]() , in
simulations of imperfect credibility with
, in
simulations of imperfect credibility with ![]() .
In all simulations, the shocks
.
In all simulations, the shocks
![]() are drawn from their respective distributions. For the cases
represented by the dotted line and the solid line, simulations are
initialized at
are drawn from their respective distributions. For the cases
represented by the dotted line and the solid line, simulations are
initialized at
![]() and
and
![]() , respectively.
, respectively.
Admittedly, much of the public criticism of the Federal Reserve has focused on issues other than the future path of the Federal Funds rate. Nevertheless, many legislative suggestions coming out of Congress could directly or indirectly have an impact on the conduct of monetary policy in the future.27
5 Sensitivity Analysis
In this section, we conduct two robustness exercises with respect to partial price indexation and the intertemporal elasticity of substitution.
5.1 Indexation
Galí and Gertler (1999) and several other empirical
studies have found that inflation dynamics are also affected by
backward looking behavior. Hence, this section considers a hybrid
Phillips curve with partial indexation. A firm ![]() that is not allowed to optimally reset its price in the current
period adjusts the price mechanically by:
that is not allowed to optimally reset its price in the current
period adjusts the price mechanically by:
| (10) |
Appendix A.1 describes the Phillips curve, the objective function, and the solution method with indexation. Introducing indexation significantly complicates the solution method. First, lagged inflation increases the number of state variables to 5. Second, inflation can now be used strategically to influence future decisions. The central bank anticipates future decisions and understands that, although it cannot commit to future actions, it can affect future decisions through the inflation process. In the solution procedure, this strategic interaction means that both the level and the derivative of the policy function need to be accounted for.
Figure 11 repeats the
exercise shown in Figure 6 for an
indexation parameter ![]() equal to 0.14.28 The
qualitative features pointed out earlier remain unchanged.
Quantitatively, price indexation reinforces the problems posed by
the zero bound constraint. Indexation is particularly painful for a
discretionary central bank because the central bank already cannot
control expectations and now price indexation adds momentum.
equal to 0.14.28 The
qualitative features pointed out earlier remain unchanged.
Quantitatively, price indexation reinforces the problems posed by
the zero bound constraint. Indexation is particularly painful for a
discretionary central bank because the central bank already cannot
control expectations and now price indexation adds momentum.
Figure 11: Distribution of Impulse Response Functions - Default Uncertainty Only - Indexation
Notes: see notes to figure 6. The indexation
parameter is
![]()
Both with and without price indexation, a central bank with high credibility promises and implements an interest rate path that supports a post-recession boom with elevated inflation and a positive output gap. A monetary authority that acts under full discretion does not allow inflation and the output gap to exceed their target levels. In contrast to Figure 6, the observed interest rate under full discretion never lies above the interest rate under full commitment when prices are partially indexed. Thus, a low observed interest rate does not reveal high credibility. The committed policymaker can avoid a deep recession and still implement a higher path of the interest rate because her commitments are conditional on future economic outcomes. If an additional shock occurred, the central bank would adjust the promised interest rate path in accordance with its credible and fully state contingent plan.29 Unable to make highly credible state contingent promises, a monetary authority with low credibility falls into a deep recession to which partial indexation adds momentum. As a result, the observed interest rate path remains below the interest rate path shown under full commitment.
The incentives and effects of renouncements under imperfect credibility cannot be inferred by simply comparing the full commitment and full discretion case. Although the interest rate path under full discretion is kept below the path under full commitment, a renouncement under imperfect credibility still implies higher interest rates than promised earlier.
5.2 Intertemporal Elasticity of Substitution
Our baseline value for the intertemporal elasticity of
substitution (![]() ) has been 6.25. In line with the
literature, a high value of
) has been 6.25. In line with the
literature, a high value of ![]() is supposed
to capture interest rate sensitive demand for investment that is
not modeled explicitly. However, a literal interpretation of our
model requires a lower value of
is supposed
to capture interest rate sensitive demand for investment that is
not modeled explicitly. However, a literal interpretation of our
model requires a lower value of ![]() . Figure 12 plots the
distribution of impulse response functions with default uncertainty
only for
. Figure 12 plots the
distribution of impulse response functions with default uncertainty
only for
![]() and
and
![]() .30 As stated in equation
(2), the demand
shock
.30 As stated in equation
(2), the demand
shock ![]() affects aggregate demand equally
irrespective of the value of
affects aggregate demand equally
irrespective of the value of ![]() .31
.31
For lower values of ![]() the uncertainty
stemming from imperfect credibility increases considerably. In
period 4, the interquantile range for inflation roughly doubles.
Furthermore, the central bank does not manage to stabilize the
economy as effectively. The recession is more pronounced and both
inflation and output rise higher above target during the
post-recession boom. With a lower value of
the uncertainty
stemming from imperfect credibility increases considerably. In
period 4, the interquantile range for inflation roughly doubles.
Furthermore, the central bank does not manage to stabilize the
economy as effectively. The recession is more pronounced and both
inflation and output rise higher above target during the
post-recession boom. With a lower value of ![]() ,
the nominal interest rate must be adjusted more aggressively in
order to affect the path of the economy.
,
the nominal interest rate must be adjusted more aggressively in
order to affect the path of the economy.
6 Conclusion
When the interest rate reaches zero, central bank credibility and the public's perception thereof are crucial for the conduct of monetary policy. Whereas credibility matters always for monetary policy, its importance is augmented at the zero lower bound. In reality, central banks have some credibility, but they typically do not operate under full commitment. Central banks announce and describe future policies to influence current economic decisions, but markets realize that not all promises will necessarily be delivered. To address these issues, we analyzed the optimal monetary policy at the zero bound in a setting that allows for imperfect credibility.
Our work could be extended in several dimensions. Considering more complex models and imperfect credibility settings is desirable. For instance, central banks have also used unconventional measures to affect the economy and interest rate spreads at the zero lower bound. While incorporating such features is certainly interesting, we believe it is necessary to first understand the effects of imperfect credibility on conventional monetary policy. In addition, the solution of our model is already intricate and incorporating additional features may be infeasible.
Figure 12: Impulse Response Functions - Default Uncertainty Only - Sensitivity to σ
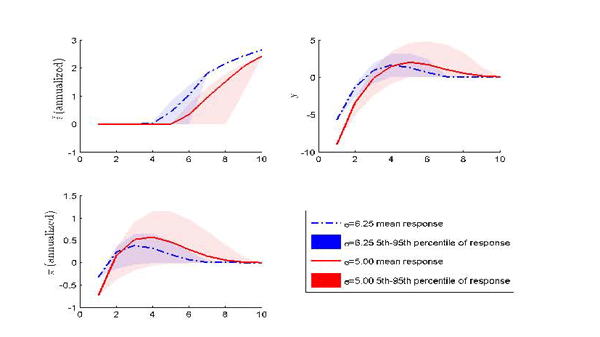
Notes: see notes to figure 6. The
intertemporal elasticity of substitution (![]() )
is set to 6.25 and 5.00.
)
is set to 6.25 and 5.00.
References
Adam, K., Billi, R., 2006. Optimal monetary policy under commitment with a zero bound on
nominal interest rates. Journal of Money, Credit and Banking 38 (7), 1877-1905.
Adam, K., Billi, R., 2007. Discretionary monetary policy and the zero lower bound on nominal interest rates. Journal of Monetary Economics 54 (3), 728-752.
Barro, R. J., Gordon, D. B., 1983. A positive theory of monetary policy in a natural rate model. Journal of Political Economy 91 (4), 589-610.
Benhabib, J., Schmitt-Grohe, S., Uribe, M., 2001. The perils of taylor rules. Journal of Economic Theory 96 (1-2), 40-69.
Benhabib, J., Schmitt-Grohe, S., Uribe, M., 2002. Avoiding liquidity traps. Journal of Political Economy 110 (3), 535-563.
Bernanke, B., 2009. Semiannual monetary policy report to the congress. Testimony Chairman Ben S. Bernanke Semiannual Monetary Policy Report to the Congress Before the Committee on Financial Services, U.S. House of Representatives, Washington, D.C. http://www.federalreserve.gov/newsevents/testimony/bernanke20090721a.htm.
Billi, R., 2009. Optimal inflation for the U.S. economy. Federal Reserve Bank of Kansas City Working Papers RWP 07-03.
Blinder, A., 2000. Central bank credibility: Why do we care? How do we build it? American Economic Review 90 (5), 1421-1431.
Bodenstein, M., Erceg, C., Guerrieri, L., 2009. The effects of foreign shocks when interest rates are at zero. International Finance Discussion Papers 983.
Brock, W., Hommes, C., 1997. A rational route to randomness. Econometrica 65, 1059-1160.
Calvo, G., 1983. Staggered prices in a utility maximizing framework. Journal of Monetary Economics 12 (3), 383-398.
Clarida, R., Galí, J., Gertler, M., 1999. The science of monetary policy: A new Keynesian perspective. Journal of Economic Literature 37 (4), 1661-1707.
Debortoli, D., Nunes, R., 2006. Political disagreement, lack of commitment and the level of debt. Universitat Pompeu Fabra. Manuscript.
Debortoli, D., Nunes, R., 2010. Fiscal policy under loose commitment. Journal of Economic Theory (Forthcoming).
Eggertsson, G. B., 2006. Was the new deal contractionary? Federal Reserve Bank of New York Staff Report 264.
Eggertsson, G. B., Woodford, M., 2003. The zero bound on interest rates and optimal monetary policy. Brookings Papers on Economic Activity 34 (1), 139-233.
Evans, G., Ramey, G., 1992. Expectation calculation and macroeconomic dynamics. American Economic Review 82, 207-224.
Galí, J., Gertler, M., 1999. Inflation dynamics: A structural econometric analysis. Journal of Monetary Economics 44 (2), 195-222.
Goodfriend, M., 2000. Overcoming the zero bound on interest rate policy. Journal of Money, Credit, and Banking 32, 1007-1035.
Goodfriend, M., 2010. Central banking in the credit turmoil: An assessment of federal reserve practice. Journal of Monetary Economics forthcoming.
Jung, T., Teranishi, Y., Watanabe, T., 2005. Zero bound on nominal interest rates and optimal monetary policy. Journal of Money, Credit, and Banking 37 (5), 813-836.
Kohn, D., 2009a. Central bank exit policies. At the Cato Institute's Shadow Open Market Committee Metting, Washington, D.C. http://www.federalreserve.gov/newsevents/speech/kohn20091009a.htm.
Kohn, D., 2009b. Monetary policy research and the financial crisis: Strengths and shortcomings. At the Federal Reserve Conference on Key Developments in Monetary Policy, Washington, D.C. http://www.federalreserve.gov/newsevents/speech/kohn20091009a.htm.
Kydland, F. E., Prescott, E. C., 1977. Rules rather than discretion: The inconsistency of optimal plans. Journal of Political Economy 85 (3), 473-91.
Levin, A., Lopez-Salido, D., Nelson, E., Yun, T., 2009. Limitations on the effectiveness of forward guidance at the zero lower bound. Federal Reserve Board. Manuscript.
Linde, J., Hebden, J., Svensson, L., 2010. Optimal monetary policy in the hybrid New Keynesian model under the zero lower bound. Manuscript.
Marcet, A., Marimon, R., 2009. Recursive contracts. Universitat Pompeu Fabra. Working Paper.
Mishkin, F., 2009. Is monetary policy effective during financial crises? American Economic Review, Papers and Proceedings 99, 573-577.
Nakov, A., 2008. Optimal and simple monetary policy rules with zero floor on the nominal interest rate. International Journal of Central Banking 4 (2), 73-127.
Reifschneider, D., Williams, J., 2000. Three lessons for monetary policy in a low inflation era. Journal of Money, Credit, and Banking 32, 936-966.
Roberds, W., 1987. Models of policy under stochastic replanning. International Economic Review 28 (3), 731-755.
Sargent, T. J., Fand, D., Goldfeld, S., 1973. Rational expectations, the real rate of interest, and the natural rate of unemployment. Brookings Papers on Economic Activity 1973 (2), 429-480.
Schaumburg, E., Tambalotti, A., 2007. An investigation of the gains from commitment in monetary policy. Journal of Monetary Economics 54 (2), 302-324.
Schmitt-Grohé, S., Uribe, M., 2007. Optimal simple and implementable monetary and fiscal rules. Journal of Monetary Economics 54 (6), 1702-1725.
Svensson, L., 2009. Transparency under flexible inflation targeting: Experiences and challenges. Sveriges Riksbank Economic Review 1, 5-44.
Svensson, L., 2010. Policy expectations and policy evaluations: The role of transparency and communication. Sveriges Riksbank Economic Review forthcoming.
Tobin, J., 1972. The wage-price mechanism: Overview of the conference. In: Eckstein, O. (Ed.), The Econometrics of Price Determination Conference. Washington D.C. Federal Reserve System, pp. 5-15.
Walsh, C., 2009. Using monetary policy to stabilize economic activity. UC Santa Cruz, manuscript.
Williams, J., 2010. Heeding daedalus: Optimal inflation and the zero lower bound. Brookings Papers on Economic Activity forthcoming.
Woodford, M., 2003. Interest and Prices: Foundations of a Theory of Monetary Policy. Princeton University Press.
Yun, T., 1996. Nominal price rigidity, money supply endogeneity and business cycles. Journal of Monetary Economics 37 (2), 345-370.
A Appendix: Model Solution
This appendix provides the mathematical details behind our solution approach and discusses our computational implementation.
A.1 The model with Indexation
The Phillips curve with indexation is given by
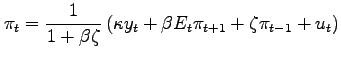 |
(11) |
while the aggregate demand curve remains unchanged. As in (), the per period utility function is assumed to be
| (12) |
Following Marcet and marimom (2009), the problem of the monetary authority written in its Lagrangian form is given by
| (13) | ||
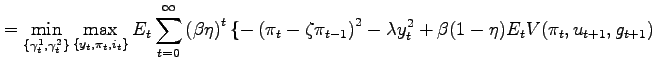 |
||
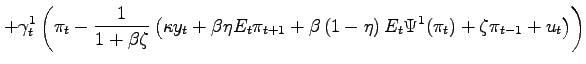 |
||
Note, the value
![]() depends on the
state of the shocks and past inflation. The policy functions under
discretion are:
depends on the
state of the shocks and past inflation. The policy functions under
discretion are:
| (14) | ||
| (15) |
For convenience we adopt the short notation:
| (16) | ||
| (17) |
Without (partial) indexation, the value ![]() and policy
functions
and policy
functions
![]() do not depend on past
inflation.
do not depend on past
inflation.
Rewriting the Lagrangean
| (18) | ||
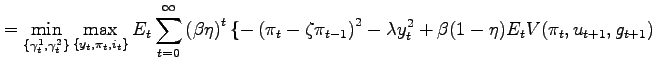 |
||
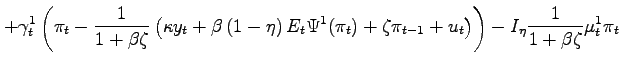 |
||
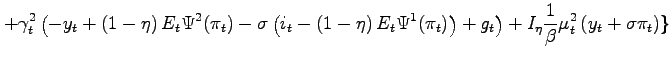 |
||
where
![]() if
if ![]() , and
, and
![]() if
if ![]() . The
value function can be written recursively as:
. The
value function can be written recursively as:
| (19) | ||
where
| (20) | |
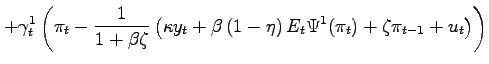 |
|
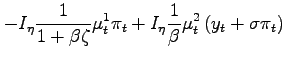 |
A.2 Solution Algorithm
We use value function iteration to solve the Bellman equation
(19). The number
of collocation nodes that span the state space
![]()
![]() is
is ![]() .
The solution algorithm is as follows:
.
The solution algorithm is as follows:
- Make initial guesses for
 ,
, 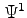 , and
, and 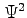 at the collocation
nodes. The solutions of models that do not impose the zero lower
bound or do not have indexation can be used as the starting guesses
for models with these features.
at the collocation
nodes. The solutions of models that do not impose the zero lower
bound or do not have indexation can be used as the starting guesses
for models with these features. -
Construct multivariate tensor product spline approximations of
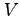 ,
, 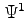 , and
, and
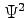 . Update
. Update 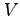 to
to
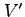 by solving the
by solving the 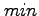
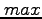 problem at each collocation node. In
practice, we solve a minimization problem over all state variables
subject to nonlinear constraints that correspond to the first order
conditions of the maximization problem. Expectations of
problem at each collocation node. In
practice, we solve a minimization problem over all state variables
subject to nonlinear constraints that correspond to the first order
conditions of the maximization problem. Expectations of 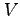 ,
, 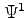 , and
, and 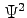 are
approximated using 9 Gauss-Hermite quadrature nodes.
are
approximated using 9 Gauss-Hermite quadrature nodes. - Update
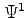 and
and 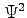 to
to
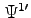 and
and
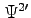 using the arguments
using the arguments
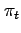 and
and 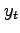 of the
of the
 problem,
respectively.
problem,
respectively. - Repeat steps 2 and 3 until
![$ \max\left[ \left\vert V^{\prime}-V\right\vert _{\max},\left\vert \Psi^{1\prime}-\Psi^{1}\right\vert _{\max}{\normalsize ,}\left\vert \Psi^{2\prime}-\Psi^{2}\right\vert _{\max }\right] <$](img355.gif)
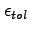 where
where
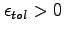 and
and
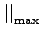 indicates
the maximum absolute norm.
indicates
the maximum absolute norm.
The choice of collocation nodes requires some experimentation.
We concentrate the nodes where the splines exhibit more curvature.
Additionally, the location of the nodes is guided by the
distribution of values
![]() that are
encountered in simulations, such that we do not evaluate the
functions far outside of the grid of collocation nodes.
that are
encountered in simulations, such that we do not evaluate the
functions far outside of the grid of collocation nodes.
Footnotes
** We are grateful to David Kjellberg and Lars Svensson for sharing their data. We are also grateful to Tack Yun and seminar participants at the Federal Reserve Board and Georgetown University for helpful comments. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
*** Contact information: Martin Bodenstein: phone (202) 452 3796, [email protected]; James Hebden: phone (202) 452 3159, [email protected]; Ricardo Nunes: phone (202) 452 2337, [email protected]. Return to text
1. Following the seminal papers by Kydland and Prescott (1977) and Barro and Gordon (1983) the literature has taken two different approaches to tackle optimal policy problems - commitment and no commitment. Return to text
2. Details of statements by Federal Reserve officials are provided in section 4. Admittedly, the reluctance of policymakers to follow the prescriptions of the New Keynesian model may reflect general uncertainty about the right model. Return to text
3. The imperfect commitment setting with stochastic replanning was first proposed in Roberds (1987). Return to text
4. Lindé et al. (2010) propose a different method to impose the zero lower bound in perfect foresight simulations by adding anticipated shocks to the instrument rule. Return to text
5. The representative household in this economy chooses consumption, leisure, money and bond holdings subject to her budget constraint. Firms are monopolistic competitors and set nominal prices. The nominal price contracts are modeled as in Calvo (1983) and Yun (1996), i.e., each period only a fixed fraction of firms is allowed to re-optimize their prices. We follow the literature in using the linear equations that are obtained from log-linearizing the nonlinear equations around the model's deterministic steady state. Although such an approach removes possibly interesting nonlinearities, it facilitates our computations and the comparisons with earlier work on the zero bound constraint and/or optimal monetary policy. See also the discussion in Section 2.1 in Adam and Billi (2006). Return to text
6. Goodfriend (2000) proposes three options to overcome the zero bound on interest rate policy: a carry tax on money, open market operations in long bonds, and monetary transfers. Our choice to not include into our analysis these and other policies, such as fiscal stimulus and credit easing policies, should not be interpreted as us passing judgement on the effectiveness of these policies. The purpose of our paper is to shed light on the effectiveness of forward guidance through short term interest rates. Return to text
7. Nakov (2008) performs a similar analysis but includes instrument and targeting rules. Return to text
8. In the case of full discretion, the
lagged Lagrange multipliers are neither zero nor a state variable.
This case is covered in the general formulation by the inclusion of
the indicator function ![]() in equation (9). Return to text
in equation (9). Return to text
9. This case is analyzed in Debortoli and Nunes (2006) who consider two political parties with different utility functions. In such a situation, the continuation value function depends on which party gains power. Return to text
10. See Reifschneider and Williams (2000), Schmitt-Grohé and Uribe (2007, Billi (2009), and most recently Williams (2010). Return to text
11. In our framework, small aggregate demand shocks can be completely offset by adjusting the nominal interest rate, as long as the interest rate is sufficiently positive. Return to text
12. As we solve for the model using global methods rather than linear methods, the long-run responses do not return to zero in the presence of an occasionally binding constraint due to precautionary motives. Return to text
13. As shown in Section 5, the observed interest rate may be lower under full discretion than under full commitment for a given demand shock if inflation is not purely forward looking due to price indexation. Return to text
14. In creating Figure 4, we set
![]()
![]() . Furthermore, no shocks to
demand and costs realize after period 1. If the economy experiences
additional shocks after exiting the zero bound, new commitments can
be important. Return to text
. Furthermore, no shocks to
demand and costs realize after period 1. If the economy experiences
additional shocks after exiting the zero bound, new commitments can
be important. Return to text
15. For a fixed default probability
![]() , the central bank achieves higher
utility in a given period when re-optimization occurs. In equation
(9)
the last two terms make the problem recursive but are not welfare
relevant. In the computations we consider only the welfare relevant
terms, which would be equivalent to computing the discounted sum of
the period utility function in equation (6). Return to text
, the central bank achieves higher
utility in a given period when re-optimization occurs. In equation
(9)
the last two terms make the problem recursive but are not welfare
relevant. In the computations we consider only the welfare relevant
terms, which would be equivalent to computing the discounted sum of
the period utility function in equation (6). Return to text
16. Our results remain largely unaffected when replacing the mean by the median of the impulse responses. Return to text
17. Among others, Eggertsson (2006) and Bodenstein et al. (2009) have pointed out the increased sensitivity of the economy to additional shocks once the policy interest rate has reached zero. However, as most authors have abstained from employing global methods in solving their models, earlier work does not show the rise in uncertainty explicitly. Return to text
18. Under full discretion the increase in uncertainty is most pronounced. As the monetary authority re-optimizes every period, no forward guidance can be provided. Return to text
19. Svensson (2009, 2010) provides a discussion of this data and draws connections to credibility and forecast targeting. Return to text
20. For reasons not considered in the model, central banks are often reluctant to set interest rates exactly at zero and operate with a positive lower bound. Return to text
21. While central banks may not take into account policy renouncements in their forecasts, it is arguable whether in practice central banks change their forecasts to more extreme paths in order to correct expectations. Our model identifies the incentive to make a more extreme promise, where the only cost is that such promises may need to be fulfilled. Other costs that may occur in practice affect our results quantitatively but not qualitatively. Return to text
22. Presenting the semiannual monetary policy report in July 2009, Federal Reserve Chairman Bernanke stated: "In light of the substantial economic slack and limited inflation pressures, monetary policy remains focused on fostering economic recovery. Accordingly, as I mentioned earlier, the FOMC believes that a highly accommodative stance of monetary policy will be appropriate for an extended period. However, we also believe that it is important to assure the public and the markets that the extraordinary policy measures we have taken in response to the financial crisis and the recession can be withdrawn in a smooth and timely manner as needed, thereby avoiding the risk that policy stimulus could lead to a future rise in inflation. The FOMC has been devoting considerable attention to issues relating to its exit strategy, and we are confident that we have the necessary tools to implement that strategy when appropriate." Return to text
23. See also former Fed Governor Mishkin in Mishkin (2009). Return to text
24. Evans and Ramey (1992), Brock and Hommes (1997) and the literature that followed model private agents as choosing among different predictors based on their performance and availability. If the central bank disseminates and produces credible forecasts, then a larger fraction of private agents is likely to form rational expectations (see the discussions in Tobin (1972) and Sargent et al. (1973)). Return to text
25. Under a draft bill released by the Chairman of the Senate Committee on Banking, Housing, and Urban Affairs, Chris Dodd, future presidents of the New York Fed would be appointed by the White House and approved by the Senate. The following web site provides links to news stories that report on these attacks, see http://freerisk.org/wiki/index.php/Reform_of_the_Federal_Reserve. Return to text
26. In Figure 10, the two groups
of economies experience the same innovations and default shocks (
![]() ). Return to text
). Return to text
27. Additional political pressure stems from the large fiscal deficit that has accumulated since 2009. Financial market commentators have pushed the notion that higher interest rates may be needed soon to curb inflation fears. Return to text
28. For values of
![]() the solution algorithm
does not converge for all cases. For high values of
the solution algorithm
does not converge for all cases. For high values of ![]() and low credibility the recession and the deflation can
be quite severe, creating convergence problems in the algorithm. Adam and Billi (2007) also report similar
issues. Return to text
and low credibility the recession and the deflation can
be quite severe, creating convergence problems in the algorithm. Adam and Billi (2007) also report similar
issues. Return to text
29. This reasoning is supported by the fact that under perfect foresight and partial indexation, a fully committed central bank implements an interest rate path that lies below the path implemented by a policymaker acting with full discretion. Return to text
30. For values of
![]() the solution algorithm
does not converge for all cases. For low values of
the solution algorithm
does not converge for all cases. For low values of ![]() , the nominal interest rate may stay at zero for a very
extended period in a deep recession, preventing our algorithm from
converging. To circumvent this problem, one could reduce
, the nominal interest rate may stay at zero for a very
extended period in a deep recession, preventing our algorithm from
converging. To circumvent this problem, one could reduce
![]() and consider alternative
calibrations. We opted to leave all the other parameters unchanged
to facilitate comparisons. Return to
text
and consider alternative
calibrations. We opted to leave all the other parameters unchanged
to facilitate comparisons. Return to
text
31. If ![]() was multiplied by
was multiplied by
![]() , the effective shock to the economy
would be reduced for a lower values of
, the effective shock to the economy
would be reduced for a lower values of ![]() ; doing
so would also imply re-calibrating
; doing
so would also imply re-calibrating
![]() and the initial shock
and the initial shock ![]() . Return to text
. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text