
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1004 - Technical Appendix, July 2010 --- Screen Reader
Version*
Technical Appendix for: Input and Output Inventories in General Equilibrium
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
A: Summary of the Model Equations
The model equations
Below, we summarize the equations that describe the equilibrium in our model:
(1) |
|
(2) |
|
(3) |
|
(4) |
|
(5) |
|
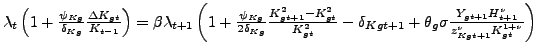 |
(6) |
(7) |
|
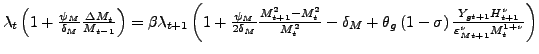 |
(8) |
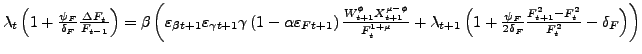 |
(9) |
(10) |
|
(11) |
|
(12) |
|
(13) |
|
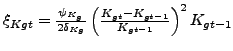 |
(14) |
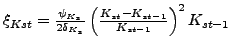 |
(15) |
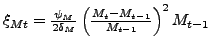 |
(16) |
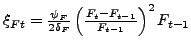 |
(17) |
(18) |
|
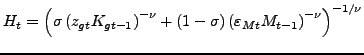 |
(19) |
(20) |
|
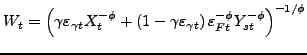 |
(21) |
(22) |
The stochastic processes for the shocks are described in the main
text. The term ![]() in the first equation denotes
the total adjustment costs. The term
in the first equation denotes
the total adjustment costs. The term ![]() denotes the marginal utility of one unit of goods' wealth. The term
denotes the marginal utility of one unit of goods' wealth. The term
![]() determine the marginal utility of
one unit of services. We can thus interpret
determine the marginal utility of
one unit of services. We can thus interpret
![]() as the price of goods in
terms of services.
as the price of goods in
terms of services.
The steady state
The first-order conditions for fixed capital in the goods sector
and input inventories imply that in the steady state, the
capital-to-output ratio in the goods sector,
![]() , and the
input-inventories-to-output ratio,
, and the
input-inventories-to-output ratio, ![]() ,
can be written as
,
can be written as
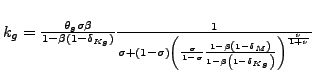 |
(23) |
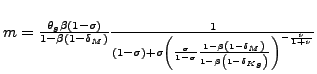 |
(24) |
These conditions state that the capital-to-output ratio and the
input-inventory-to-output ratio are increasing in their relative
weights in production, ![]() and
and ![]() , respectively. At the same time, the different factor
intensities depend on the degree of substitutability. When the
ratios in large parentheses are larger than one (a condition that
holds in the data since input inventories are much smaller than
capital), then capital is decreasing in
, respectively. At the same time, the different factor
intensities depend on the degree of substitutability. When the
ratios in large parentheses are larger than one (a condition that
holds in the data since input inventories are much smaller than
capital), then capital is decreasing in ![]() and input
inventories are increasing in
and input
inventories are increasing in ![]() .
.
The optimality conditions for goods consumption and output inventories imply:
 |
(25) |
where
![]() and
and ![]() .
The ratio of consumption to output inventories is increasing in
.
The ratio of consumption to output inventories is increasing in
![]() while it is decreasing (increasing) in
while it is decreasing (increasing) in
![]() when the term in parentheses is larger
(smaller) than one. Using the linear homogeneity of the CES
aggregators and the first-order conditions for
when the term in parentheses is larger
(smaller) than one. Using the linear homogeneity of the CES
aggregators and the first-order conditions for ![]()
![]() , and
, and ![]() , we derive
the following expression for
, we derive
the following expression for
![]() :
:
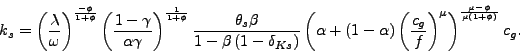 |
(26) |
This equation says that capital in the services sector is higher
when the relative price of goods in terms of services
![]() is low, when the
weight to services in utility,
is low, when the
weight to services in utility, ![]() , is high, or
when the production function for services is capital intensive
(
, is high, or
when the production function for services is capital intensive
(![]() high). Using the first-order
conditions for labor and the linear homogeneity of the production
functions, the relative price of goods is:
high). Using the first-order
conditions for labor and the linear homogeneity of the production
functions, the relative price of goods is:
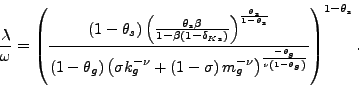 |
(27) |
Finally, the market-clearing condition for the goods sector is
(28) |
For given parameter values, equations 23 to 28 above can be
jointly solved for ![]()
![]()
![]()
![]() ,
, ![]() and
and
![]() . The first-order conditions for
. The first-order conditions for
![]()
![]() , and
, and
![]() , together with the production functions,
can be solved for
, together with the production functions,
can be solved for
![]() and
and
![]() . (Details for all the derivations are
given below.)
. (Details for all the derivations are
given below.)
Matching steady-state ratios through
choices of
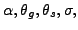 and
and
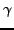
For each estimated value of ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and
![]() , and given calibrated values for
, and given calibrated values for
![]() ,
, ![]() , and
, and
![]() , our estimation procedure aims at
exactly matching the following steady state ratios that we take to
be the average values obtained from the data (denoted with a
bar):
, our estimation procedure aims at
exactly matching the following steady state ratios that we take to
be the average values obtained from the data (denoted with a
bar):
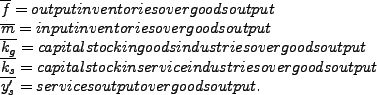
where
![]() measures services output in units of goods output.
measures services output in units of goods output.
Given ![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and ![]() simple algebra
shows that there is a unique set of values of
simple algebra
shows that there is a unique set of values of
![]() that satisfies the five ratios above. These values are obtained as
follows. Given the
that satisfies the five ratios above. These values are obtained as
follows. Given the
![]() ratios, we obtain
ratios, we obtain
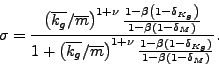 |
(29) |
From the
![]() ratio, we
derive
ratio, we
derive
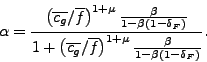 |
(30) |
The formula for ![]() can be used to derive
can be used to derive
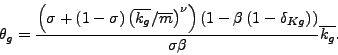 |
(31) |
Finally, we need to choose ![]() and
and ![]() to match the values of
to match the values of ![]() and
and
![]() From the formula for
From the formula for
![]() we derive an
expression for
we derive an
expression for ![]()
(32) |
Last, we need to obtain ![]() . Using the expressions
for
. Using the expressions
for ![]() and
and
![]() above, we obtain
above, we obtain
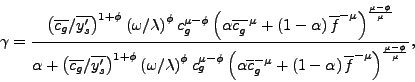 |
(33) |
where
![]() can be calculated from
expression 27 above.
can be calculated from
expression 27 above.
Summarizing:
(1) for given observed values in
the data of ![]()
![]()
![]()
![]()
![]() and
and
![]() ; and
(2) for any possible combination
of
; and
(2) for any possible combination
of
![]() the values of
the values of ![]()
![]()
![]()
![]() and
and
![]() that satisfy expressions 29 to 33 are consistent
with the the steady-state values of the ratios
that satisfy expressions 29 to 33 are consistent
with the the steady-state values of the ratios ![]()
![]()
![]()
![]()
![]() and
and
![]() .
.
Calculating steady-state hours, output, and prices
The optimal labor supply schedules satisfy
(34) |
|
(35) |
From the first-order conditions for ![]() and
and
![]() after some algebra, we obtain the
following formula:
after some algebra, we obtain the
following formula:
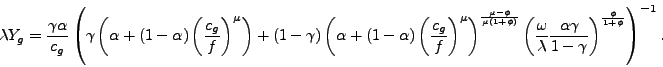 |
(36) |
By the same token, we find that:
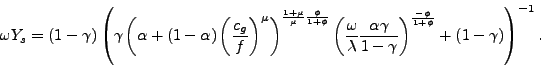 |
(37) |
From the production functions, we know that:
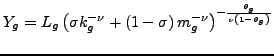 |
(38) |
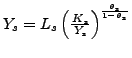 |
(39) |
Equations 34 through 39 can be then be
solved for ![]()
![]()
![]()
![]()
![]() and
and
![]() using a non-linear equation solver.
using a non-linear equation solver.
B: Data
Most of the data come from the national income and product accounts (NIPA) produced by the U.S. Bureau of Economic Analysis (BEA) and obtained from Haver Analytics. All NIPA data are quarterly and real data are in chain-weighted $2000. Table B.1 lists the variable names, Haver mnemonics, and variable descriptions. Our model and data exclude government spending. We used the Tornquist approximation for chain-weighted data when constructing the actual model-consistent data, as recommended by Whelan (2002). For simplicity, the formulas in this appendix abstract from the notational details associated with chain weighting.
The NIPA data classify output by sectors called goods
(![]() ), structures (
), structures (![]() ), and
services (
), and
services (![]() ):
):
In contrast, inventory investment, ![]() , is
classified by industry (goods inventories include the agriculture,
mining, and manufacturing industries; structures inventories
include the construction industry; and the services sector includes
utilities and trade). Thus, the NIPA output and inventory data do
not correspond to the inventory-based sectors of our model
definitions of goods and services.
, is
classified by industry (goods inventories include the agriculture,
mining, and manufacturing industries; structures inventories
include the construction industry; and the services sector includes
utilities and trade). Thus, the NIPA output and inventory data do
not correspond to the inventory-based sectors of our model
definitions of goods and services.
To obtain model-consistent data, we condense the three NIPA sectors into two by redefining and combining the NIPA sector variables as follows. First, write the components of private domestic aggregate output as
where ![]() is net exports and government
spending is excluded. Household consumption of structures
(
is net exports and government
spending is excluded. Household consumption of structures
(![]() ) does not exist because construction of
residential structures is investment, which we assume is installed
in the services sector. Household consumption of services,
) does not exist because construction of
residential structures is investment, which we assume is installed
in the services sector. Household consumption of services,
![]() , includes two components,
distinguished by a second subscript indicating the appropriate
model sector to which the services consumption data should belong.
Thus,
, includes two components,
distinguished by a second subscript indicating the appropriate
model sector to which the services consumption data should belong.
Thus, ![]() represents the consumption of services
from industries that distribute goods (utilities and trade), which
we redefine as goods consumption. Also,
represents the consumption of services
from industries that distribute goods (utilities and trade), which
we redefine as goods consumption. Also, ![]() includes
the service flow from housing.
includes
the service flow from housing.
Given these definitions, model-consistent goods output is
and model-consistent services output as
Following Cooley and Prescott (1995), we include net exports in investment because there is no foreign sector in the model; instead, net exports are viewed as the net claims of foreigners on the domestic capital stock. The remainder of this appendix explains how each of the relevant variables is defined and constructed.
Consumption
NIPA consumption data are classified by thetype of good consumed by households:
In this equation, goods consumption includes nondurables
(![]() ) plus durables (
) plus durables (![]() );
consumption of services (
);
consumption of services (![]() ) includes the service flow
obtained from housing. Theoretically, it would be preferable to
construct the service flow from other consumer durable goods
besides housing, rather than use actual expenditures, but this is
not done in the NIPA data (except for automobile leasing, which is
implicitly a service yield). Because we are ultimately trying to
explain the volatility, and the change in volatility, of actual GDP
data, we use the raw NIPA data instead.
) includes the service flow
obtained from housing. Theoretically, it would be preferable to
construct the service flow from other consumer durable goods
besides housing, rather than use actual expenditures, but this is
not done in the NIPA data (except for automobile leasing, which is
implicitly a service yield). Because we are ultimately trying to
explain the volatility, and the change in volatility, of actual GDP
data, we use the raw NIPA data instead.
To construct model-consistent consumption data, we must
reclassify a portion of the NIPA services consumption data
(![]() ) as goods consumption because the
industries associated with those services are in the model's goods
sector. The NIPA consumption data treat energy consumption (such as
electricity) as a service. However, because this household energy
service is output attributed to the utilities industry, which holds
inventories, it belongs in the model's goods sector.4 So, we
must define household energy (
) as goods consumption because the
industries associated with those services are in the model's goods
sector. The NIPA consumption data treat energy consumption (such as
electricity) as a service. However, because this household energy
service is output attributed to the utilities industry, which holds
inventories, it belongs in the model's goods sector.4 So, we
must define household energy (![]() ) consumption
services as model-consistent goods consumption,
) consumption
services as model-consistent goods consumption,
![]() .
.
Table B.1: Variable Names and Data Definitions
| Variable | Mnemonic | Description |
|---|---|---|
| C | Consumption | |
| CN | Consumption of nondurable goods | |
| CD | Consumption of durable goods | |
| CS | Consumption of services | |
| CSE | Consumption of energy services | |
| F | Fixed investment, total | |
| FR | Fixed investment, residential | |
| FN | Fixed investment, nonresidential | |
| M | Imports | |
| JC | Consumption chain-weighted price index | |
| JCS | Consumption of services chain-weighted price index | |
| JCSE | Consumption of energy services chain-weighted price index | |
| SF | Farm inventories | |
| SNM | Manufacturing inventories | |
| SNW | Wholesale trade inventories | |
| SNR | Retail trade inventories | |
| SNO2 | Other inventories, SIC (fixed-weight $1996) | |
| SNB | Mining, utilities, and construction inventories | |
| SNT | Other inventories, NAICS | |
| RES513 | Inventory chain-weighted residual | |
| X | Exports |
Note: These Haver mnemonics are for the nominal data; the real data have an 'H' added at eh end and, unless otherwise noted, are in chain-weighted $2000.
Thus, model-consistent data (denoted by a double tilde) for domestic services consumption are
and model-consistent data for domestic goods consumption are
Because the underlying NIPA data are based on the type of good
consumed, ![]() and
and ![]() already
contain the output of the retail-trade industry and any output of
the wholesale-trade industry that is classified as consumption
(i.e., a final sale to consumers rather than an intermediate input
into retail trade or manufacturing).5
already
contain the output of the retail-trade industry and any output of
the wholesale-trade industry that is classified as consumption
(i.e., a final sale to consumers rather than an intermediate input
into retail trade or manufacturing).5
Investment
Capital is a good, so it follows that investment is output of the goods sector. However, our model has two sectors that each accumulates a sector-specific capital stock, so the model requires classification of investment data by the type of sector (or industry) in which the capital is installed. Although the NIPA data do not classify investment by the sector in which it is installed, the BEA provides other annual data source on investment by industry that does, and we use this source to divide total fixed non-residential investment into sector-specific domestic investment.6
Before dividing investment into sectors, we first add net
exports to the sum of nonresidential
![]() and residential
and residential
![]() fixed investment, as
advocated by Cooley and Prescott (1995):
fixed investment, as
advocated by Cooley and Prescott (1995):
where
![]() . We are forced by the data
to combine the net exports of the two sectors here, rather than
keeping net exports of goods and net exports of services separate
in constructing
. We are forced by the data
to combine the net exports of the two sectors here, rather than
keeping net exports of goods and net exports of services separate
in constructing ![]() and
and ![]() . During
the second half the sample, net exports of goods become negative
and large in absolute value so that
. During
the second half the sample, net exports of goods become negative
and large in absolute value so that
![]() ; net exports
of services are positive but relatively small. From a theoretical
perspective, it may also be preferable to use
; net exports
of services are positive but relatively small. From a theoretical
perspective, it may also be preferable to use ![]() because it is not clear that the net claims of foreigners defined
by
because it is not clear that the net claims of foreigners defined
by ![]() and
and ![]() map directly
to the measures of
map directly
to the measures of ![]() and
and ![]() , or even to the sectoral components of the installed
U.S. capital stock. In any case, by including net exports in
investment the data reflect the influences of foreign trade
(exports and imports), which changed during the data sample, on
inventory investment in the econometric model, albeit in a
reduced-form manner. Residential investment is netted out before
the following calculations because it is classified as capital
installed entirely in the services sector, and will be added back
in later.
, or even to the sectoral components of the installed
U.S. capital stock. In any case, by including net exports in
investment the data reflect the influences of foreign trade
(exports and imports), which changed during the data sample, on
inventory investment in the econometric model, albeit in a
reduced-form manner. Residential investment is netted out before
the following calculations because it is classified as capital
installed entirely in the services sector, and will be added back
in later.
Next, the share of non-residential fixed investment for the
goods sector includes data for the seven inventory-holding
industries: agriculture, mining, utilities, construction,
manufacturing, wholesale trade, and retail trade. Using annual BEA
data on investment by industry (denoted by a double hat), the share
(![]() ) of goods investment is
) of goods investment is
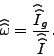
The "real estate and rental and leasing" industry, which is classified as a service industry by the BEA, rents and leases capital to the rest of the economy, a practice that has increased in frequency over time and now represents a large fraction of total capital services in production (especially for structures). Because these data do not identify the sector to which the real estate industry leases its capital, we apply the seven-industry share above to partition real estate and rental and leasing industry investment into both of the two sectors. Finally, these annual share data are interpolated to obtain a quarterly frequency.
Using the constructed shares of investment by sector, foreign-trade adjusted goods-sector investment is
and foreign-trade adjusted services-sector investment is
In each case, the interpolated investment share data is applied to the actual quarterly data on domestic, non-residential fixed investment.
Inventories
According to the NIPA definitions, each output sector is associated with at least one inventory-holding industry,
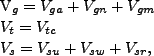
with industries defined as agriculture (![]() ), mining
(
), mining
(![]() ), manufacturing (
), manufacturing (![]() ),
construction (
),
construction (![]() ), utilities (
), utilities (![]() ),
wholesale trade (
),
wholesale trade (![]() ), and retail trade (
), and retail trade (![]() ).
Thus, to construct model-consistent inventories, we redefine the
goods sector as the holder of all inventories:
).
Thus, to construct model-consistent inventories, we redefine the
goods sector as the holder of all inventories:
as discussed in the main text, the services sector holds no
inventories (
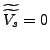 ) by
assumption.7
) by
assumption.7
We further divide total inventories into two types,
where ![]() denotes input and
denotes input and ![]() denotes
output. Economic theory provides no clear categorical definition of
input and output inventories in general equilibrium. We view goods
as being produced and distributed along a supply and distribution
chain, so one (but not the only) logical definition of output
inventories for our model is simply the last link of the chain,
which is the retail industry:
denotes
output. Economic theory provides no clear categorical definition of
input and output inventories in general equilibrium. We view goods
as being produced and distributed along a supply and distribution
chain, so one (but not the only) logical definition of output
inventories for our model is simply the last link of the chain,
which is the retail industry:
In this case, input inventories are
In general, all non-retail inventory stocks can be considered
inputs into production along the supply chain. According to the
Census of Construction, ![]() certainly is input
inventory (raw materials) and does not include unsold finished
structures. In actuality, some fraction of the remaining stocks may
be sold directly to consumers, and hence should be classified as
output inventories, but we assume this fraction is small.
certainly is input
inventory (raw materials) and does not include unsold finished
structures. In actuality, some fraction of the remaining stocks may
be sold directly to consumers, and hence should be classified as
output inventories, but we assume this fraction is small.
To obtain a long time series of inventory data, we combine
non-farm stocks constructed under two different industry
classifications: SIC (1947-1997) and NAICS (1987-present).8 At this
high level of industry definition, the manufacturing, wholesale,
and retail inventory data are generally consistent across industry
classification schemes, so we splice these data series without
further manipulation. The inventories for all remaining industries
(![]() ), however, are defined as follows:
), however, are defined as follows:
where ![]() denotes "other" industries in each
classification system; MUC denotes mining, utilities, and
construction. CW denotes the chain-weighted residual for real data
(real data on an SIC basis are in fixed-weight $1996, and thus have
no residual). In splicing the data, we use the SIC stocks through
1997, and then use the growth rates of the NAICS from 1997 on to
extend the SIC data.
denotes "other" industries in each
classification system; MUC denotes mining, utilities, and
construction. CW denotes the chain-weighted residual for real data
(real data on an SIC basis are in fixed-weight $1996, and thus have
no residual). In splicing the data, we use the SIC stocks through
1997, and then use the growth rates of the NAICS from 1997 on to
extend the SIC data.
Unfortunately, unlike the NIPA consumption and investment data, it is impossible to identify separately the foreign and domestic components of NIPA inventory stocks from existing data. Rather than make ad hoc adjustments, we use the actual inventory data as published.
Consumption Prices
The prices of goods and services consumption are constructed
analogously to the respective quantities of consumption. Let
![]() be the nominal expenditure weight for
energy services, and
be the nominal expenditure weight for
energy services, and
![]() be the nominal
expenditure weight for model-consistent (non-energy) services.
Then, having calculated the appropriate Tornquist index on the
data, the model-consistent price of services consumption is
be the nominal
expenditure weight for model-consistent (non-energy) services.
Then, having calculated the appropriate Tornquist index on the
data, the model-consistent price of services consumption is
Likewise, let
![]() be the nominal expenditure
weight for model-consistent services, and
be the nominal expenditure
weight for model-consistent services, and
![]() be the nominal
expenditure weight for model-consistent goods. Then the
model-consistent price of goods consumption is
be the nominal
expenditure weight for model-consistent goods. Then the
model-consistent price of goods consumption is
The ratio of the consumption prices,
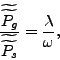
equals the ratio of Lagrange multipliers from the model's first-order conditions.
C: Another Look at Output Inventories in the Utility Function
In this appendix, we illustrate the result that there exists a
functional equivalence between entering output inventories in the
utility function and an alternative formulation that motivates
output inventories using the argument that they reduce shopping
costs. To keep the notation simple, we abstract from endogenous
labor supply, from consumption of services and from capital and
input inventories, and consider the problem of a planner that has
to allocate an exogenous stream of goods ![]() to
either consumption or finished good inventories. Consider the
following two alternative models.
to
either consumption or finished good inventories. Consider the
following two alternative models.
Problem 1. In the first formulation, the planner's problem is:

where utility ![]() depends on the goods purchased
depends on the goods purchased
![]() and the stock of inventories
and the stock of inventories
![]() . This is essentially the barebones
formulation and notation of our model in the main text.
. This is essentially the barebones
formulation and notation of our model in the main text.
Problem 2. In the second formulation, the problem is:
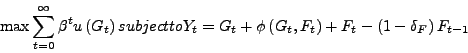
where the term in the budget constraint
![]() denotes the
real resource cost of purchasing goods, which is assumed to be a
decreasing function of the amount of output inventories
denotes the
real resource cost of purchasing goods, which is assumed to be a
decreasing function of the amount of output inventories ![]() available and an increasing function of the amount of
goods consumed
available and an increasing function of the amount of
goods consumed ![]() .
.
Following Feenstra (1986) the two problems are equivalent if
![]() , and
, and
![]() .
We therefore interpret
.
We therefore interpret ![]() as gross consumption
including both net consumption
as gross consumption
including both net consumption ![]() and shopping
costs
and shopping
costs
![]() Feenstra
focused on justifying the inclusion of money in the utility
function and to show the condition for equivalence between that
model and one in which liquidity costs are introduced in the budget
Our cases is isophorphiic to his, once money balances are replaced
with finished good inventories.
Feenstra
focused on justifying the inclusion of money in the utility
function and to show the condition for equivalence between that
model and one in which liquidity costs are introduced in the budget
Our cases is isophorphiic to his, once money balances are replaced
with finished good inventories.
Consider our momentary utility function and budget constraint in the paper. Abstracting from services, endogenous labor and capital and input inventories, it reads as
subject to
This utility function and budget constraint yield the same first-order conditions and equilibrium conditions of a model where momentary utility is given by:
and the budget constraint is
We can find ![]() by setting
by setting
![]() , solving for
, solving for ![]() and it in
and it in
![]() This yields:
This yields:
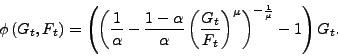
One can easily verify that the two problems yield the same first order conditions. The result also holds when one allows for consumption of services and leisure in the utility function, provided they enter utility in an additively separable way, so that the optimality condition with respect to consumption and inventories are not affected. Additive separability of leisure has been assumed from the outset. Approximate additive separability of consumption of services is suggested by our empirical estimates.
Of course, what differs across models is the structural
interpretation of the parameters. In our model, ![]() measures the relative weight in utility of goods
consumption relative to finished good inventories. In the
transaction cost model,
measures the relative weight in utility of goods
consumption relative to finished good inventories. In the
transaction cost model, ![]() measures the size of
the transaction cost: the higher
measures the size of
the transaction cost: the higher ![]() the lower the
transaction cost (in the limiting case of
the lower the
transaction cost (in the limiting case of ![]() there are no transaction costs for purchasing goods,
there are no transaction costs for purchasing goods, ![]() and no inventories are held in equilibrium, just like
in our model). In our model,
and no inventories are held in equilibrium, just like
in our model). In our model, ![]() measures the
elasticity of substitution between
measures the
elasticity of substitution between ![]() and
and
![]() In the transaction cost model,
In the transaction cost model,
![]() measures the way in which more
inventories of finished goods reduce or increase the shopping cost
of obtaining a given amount of consumption goods. In particular, a
higher estimate of
measures the way in which more
inventories of finished goods reduce or increase the shopping cost
of obtaining a given amount of consumption goods. In particular, a
higher estimate of ![]() in the transaction cost
model implies: (1) lower average transaction
costs on average;
(2) a more convex transaction
cost function itself.
in the transaction cost
model implies: (1) lower average transaction
costs on average;
(2) a more convex transaction
cost function itself.
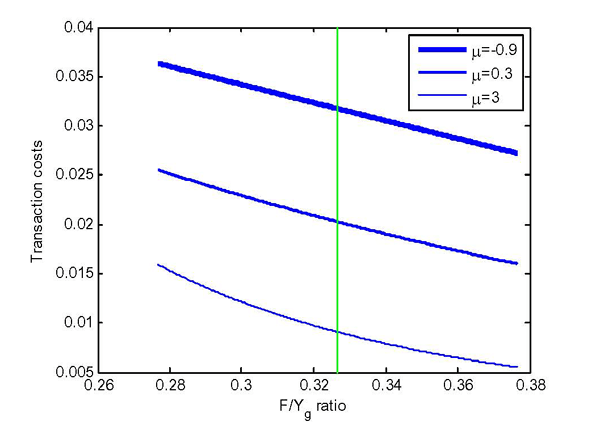
Below, we plot how our estimates of ![]() (.3) and
(.3) and
![]() (.9668) map in the resulting
(.9668) map in the resulting
![]() function. We also assume that
function. We also assume that
![]() is at its steady state value and that
measured consumption in the data corresponds to net consumption
is at its steady state value and that
measured consumption in the data corresponds to net consumption
![]() As can be seen in the figure, the
transaction cost function is decreasing (and convex) in
As can be seen in the figure, the
transaction cost function is decreasing (and convex) in ![]() . At our estimates (given the calibrated value for
. At our estimates (given the calibrated value for
![]() ), the function implies transaction
costs equal to 2% of total goods output (see the figure below). The
other two lines plot the transaction cost function under the
assumption that
), the function implies transaction
costs equal to 2% of total goods output (see the figure below). The
other two lines plot the transaction cost function under the
assumption that ![]() and
and ![]() respectively.
respectively.
Figure C.1: Estimates of μ (.3) and α (.9668) Map in the Resulting φ Function
D: A Model of Input Inventories with Usage Only
Here we sketch a version of the model in the paper where we allow for a treatment of input inventories that ignores their convenience service but models explicitly their usage.
Assume that (1) only input inventories that are "used up"' augment society's ability to produce more; and that (2) the usage of inventories depends upon the beginning of period stock. This specification leads to a gross production function of the form:
where
![]() is the
utilization rate of inventories, so that
is the
utilization rate of inventories, so that
![]() is the amount of
inventories that are used (and used up) in production. We assume
that higher utilization of the stock
is the amount of
inventories that are used (and used up) in production. We assume
that higher utilization of the stock ![]() leads to a
higher depreciation in a convex fashion, and that depreciation rate
and utilization rate are equal in a neighborhood of the steady
state. These considerations lead us to write a "depreciation
function" for inventories as follows:
leads to a
higher depreciation in a convex fashion, and that depreciation rate
and utilization rate are equal in a neighborhood of the steady
state. These considerations lead us to write a "depreciation
function" for inventories as follows:
where: ![]() is a fixed component of the
depreciation rate unrelated to usage and reflecting wastage and/or
linear holding costs;
is a fixed component of the
depreciation rate unrelated to usage and reflecting wastage and/or
linear holding costs; ![]() captures the usage of
materials (proportional to the stock); and the term
captures the usage of
materials (proportional to the stock); and the term ![]() describes the additional component of wastage that
depends upon utilization in a convex fashion: this component
reflects the idea that, at the margin, a higher or faster usage
might provoke collateral damage to the remaining parts of the stock
that are not directly used in production. Namely, we assume that
describes the additional component of wastage that
depends upon utilization in a convex fashion: this component
reflects the idea that, at the margin, a higher or faster usage
might provoke collateral damage to the remaining parts of the stock
that are not directly used in production. Namely, we assume that
![]() , where
, where
![]() . The
function
. The
function ![]() is convex in
is convex in ![]() and
is normalized so that it equals zero when
and
is normalized so that it equals zero when ![]() equals the optimal, steady-state choice
equals the optimal, steady-state choice ![]() 9 The
assumption of convexity has two appealing properties: first, it
allows us to solve the model using standard perturbation methods;
second, it captures the idea that, at the margin, a higher
utilization rate leads to a higher depreciation. This is reflected
in the functional form of
9 The
assumption of convexity has two appealing properties: first, it
allows us to solve the model using standard perturbation methods;
second, it captures the idea that, at the margin, a higher
utilization rate leads to a higher depreciation. This is reflected
in the functional form of ![]() . The good's
sector resource constraint is now:
. The good's
sector resource constraint is now:
(40) |
This equations illustrates how, at the optimal utilization rate, the total "depreciation" of the stock of inventories is now larger, since usage "subtracts" from the stock of inventories that can be carried into next period.
The optimality condition for accumulation of ![]() (previously equation 8 in Appendix A)
becomes now:
(previously equation 8 in Appendix A)
becomes now:
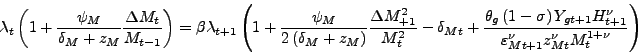 |
(41) |
where
![]() . The equation for
the optimal usage of inventories (which implicitly pins down the
optimal value of
. The equation for
the optimal usage of inventories (which implicitly pins down the
optimal value of ![]() ) satisfies:
) satisfies:
| (42) |
Relative to the baseline model spelled out in Appendix A, this
new model features one additional equation (equation 42 above) and one
additional endogenous variable (![]() ).
).
Footnotes
1. Matteo Iacoviello, Division of International Finance, Federal Reserve Board, 20th and C St. NW, Washington, DC 20551. Email: [email protected]. Return to text
2. Fabio Schiantarelli, Boston College, Department of Economics, 140 Commonwealth Avenue, Chestnut Hill, MA 02467. Tel: (617) 552-4512. Fax: (617) 552-2308. Email: [email protected]. Return to text
3. Scott Schuh, Federal Reserve Bank of Boston, Research Department, 600 Atlantic Ave., Boston, MA 02210. Tel: (617) 973-3941. Fax: (617) 619-7541. Email: [email protected]. Return to text
4. We assume that all types of energy are measurable goods distributed (a task of the model goods sector) to consumers. In this regard, electric and natural gas utility firms are similar to firms specializing in wholesale and retail trade, which distribute finished goods from their producers to their final consumers. Return to text
5. One way to think of the different
types of "goods" is in terms of their depreciation rates:
![]() ,
where subscript
,
where subscript ![]() denotes housing services and
denotes housing services and
![]() denotes other services (that is, not a
flow from a durable stock). Return to
text
denotes other services (that is, not a
flow from a durable stock). Return to
text
6. These data can be obtained from http://bea.gov/. Return to text
7. The NIPA make this same assumption, equating output and final sales in both the structures and services sectors, and associating all inventory investment with the goods sector. Return to text
8. Farm, or agricultural, inventory stocks on a consistent industry classification are already available for the full sample period (1947-present). Return to text
9. The assumption of convexity has two
appealing properties: first, it allows us to solve the model using
standard perturbation methods; second, and most importantly, it
captures the idea that, at the margin, a higher utilization rate
leads to a higher depreciation. Note that there are some analogies
with the way we write down the utilization function for fixed
capital. For fixed capital, we assume that the optimal (steady
state) utilization rate of capital is unity, and normalize the
utilization function so that no resources are wasted at the optimal
utilization rate. Instead, here we normalize the function
![]() so that the optimal steady state
utilization rate is less than unity. Return to text
so that the optimal steady state
utilization rate is less than unity. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text