
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1004, July 2010 --- Screen Reader
Version*
Input and Output Inventories in General Equilibrium1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We build and estimate a two-sector (goods and services) dynamic stochastic general equilibrium model with two types of inventories: materials (input) inventories facilitate the production of finished goods, while finished goods (output) inventories yield utility services. The model is estimated using Bayesian methods. The estimated model replicates the volatility and cyclicality of inventory investment and inventory-to-target ratios. Although inventories are an important element of the model's propagation mechanism, shocks to inventory efficiency or management are not an important source of business cycles. When the model is estimated over two subperiods (pre and post 1984), changes in the volatility of inventory shocks or in structural parameters associated with inventories, such as the input inventory to output ratio, play a small role in reducing the volatility of output.
Keywords: Inventories, business cycles, output volatility, Bayesian estimation, great moderation
JEL classification: E22, E32, E37
1. Introduction
Macroeconomists recognize that inventories play an important role in business cycle fluctuations, but constructing macroeconomic models that explain this role successfully has been an elusive task. Early Real Business Cycle (RBC) models, such as Kydland and Prescott (1982), treated inventories as a factor of production. However, Christiano (1988) showed that RBC models with aggregate inventories cannot explain the volatility and procyclicality of inventory investment without including a more complex information structure and restrictions on the timing of agents' decisions. Moreover, Christiano and Fitzgerald (1989) concluded, "the study of aggregate phenomena can safely abstract from inventory speculation."Nevertheless, the recent empirical literature continues to affirm the conventional view of inventories as propagating business cycle fluctuations. For example, McConnell and Perez-Quiros (2000), among others, argue that structural changes in inventory behavior are an important reason for the decline in the volatility of U.S. GDP since the early 1980s.
We re-examine the role of inventories in business cycle fluctuations by developing and estimating a dynamic stochastic general equilibrium (DSGE) model rich enough to explain essential elements of inventory behavior. To confront the data, the model requires four extensions over existing models with inventories: 1) two sectors, goods and services, differentiated by whether they hold inventories; 2) a disaggregation of inventories into two distinct types, input and output inventories; 3) several modern DSGE features, which have been shown to be necessary to fit the data; and 4) multiple shocks, which provide a diverse array of economically interpretable sources of stochastic variation. Because these extensions increase the complexity of the model, we abstract from other potentially important features -- variable markups, nominal rigidities, intermediate goods with input-output relationships, and nonconvexities -- that others have incorporated in equilibrium models of inventory behavior.5
Studying inventories in an equilibrium framework motivates a natural sectoral decomposition. Because inventories are goods mostly held by the firms that produce goods, our model contains a goods-producing sector that holds inventories and a service-producing sector that does not hold inventories. This inventory-based sector decomposition yields a broader goods sector than in prior studies that distinguished goods from services because the model includes in the good sector also industries that distribute goods (wholesale and retail trade plus utilities).6
Our model disaggregates inventories into input (materials and
work-in-progress) and output (finished goods) stocks, as suggested
by the stage-of-fabrication approach employed in Humphreys, Maccini
and Schuh (2001) in a partial equilibrium model.7 This distinction is
strongly supported by the data because the cyclical properties of
input and output inventories differ. We define output inventories
(![]() ) as stocks held by retailers for final sale;
all other stocks are input inventories (
) as stocks held by retailers for final sale;
all other stocks are input inventories (![]() ). By these
definitions, input inventories empirically are more volatile and
procyclical than output inventories. Perhaps more importantly, the
ratios of each inventory type to its steady-state target exhibit
very different cyclical behavior. Relative to output of goods,
input inventories (
). By these
definitions, input inventories empirically are more volatile and
procyclical than output inventories. Perhaps more importantly, the
ratios of each inventory type to its steady-state target exhibit
very different cyclical behavior. Relative to output of goods,
input inventories (![]() ) are very
countercyclical. However, we find that relative to the consumption
of goods, output inventories (
) are very
countercyclical. However, we find that relative to the consumption
of goods, output inventories (![]() ) are mildly
procyclical.
) are mildly
procyclical.
In our model setup, we motivate the holding of input and output inventories differently. Input inventories enter as a factor in the production of value added, but only in the goods-producing sector. Holding input inventories is assumed to facilitate production by minimizing resource costs involved in procuring input materials, guarding against stockouts, and allowing for batch production. This approach follows the tradition of earlier DSGE models, such as Kydland and Prescott (1982) and Christiano (1988), as well as the work of Ramey (1989).
Output inventories pose a different specification challenge. Much of the earlier inventory literature deals with partial-equilibrium analyses of the inventory-holding problem. Typically, a firm is assumed either to hold output inventories to avoid lost sales or stockouts (Kahn 1987) or to "facilitate" sales (Bils and Kahn 2000). Following Kahn, McConnell and Perez-Quiros (2002), we assume that output inventories provide a convenience yield to the consumer and enter the consumers' utility function directly. The convenience yield may reflect the reduction in shopping cost associated, for instance, with less frequent stockouts and with the provision of variety or of other consumer benefits associated with the underlying retailing services. Indeed, under some simplifying assumptions, we can show that the model with output inventories in the utility function is equivalent to a model in which inventories appear in the budget constraint because they affect shopping costs, but do not enter the utility function.8
We acknowledge that our modeling shortcuts are taken in order to obtain a relatively simple, estimable model. Moving forward, it will be important to take to the data inventory models with different and arguably deeper microfoundations for inventory demand. Fisher and Hornstein (2000), for instance, develop a dynamic general equilibrium model with retail inventories and fixed ordering costs that generate (S,s) policies for inventory demand. Khan and Thomas (2007) also rely on ordering costs to motivate inventories and find that a version of the model driven by a single technology shock can reproduce the cyclical properties exhibited by total inventories. Wen (2009) develops, instead, a model of input and output inventories where firms hold inventories because of a stock-out avoidance motive and production lags in the face of idiosyncratic demand and technology shocks and he shows that his model can match important features of the data. However, we believe that the estimation - as opposed to calibration, as in the papers above - of a simple model such as ours is a useful contribution. To the best of our knowledge, in fact, all estimated modern DSGE models have ignored inventories, either by leaving them out of the model, or subsuming them within other forms of capital. Our estimation approach delivers some new insights into the dynamics of inventories and into their role in business cycle fluctuations and, to that extent, it leaves one hopeful that further progress can be made in taking even more richly specified models to the data.
Our setup includes several important features now standard in estimated DSGE models, such as adjustment costs on all capital stocks (including inventories) and variable utilization of capital. We also allow for nonzero inventory depreciation (or, equivalently, an inventory holding cost that is proportional to the total stock). This is a relatively novel feature in the inventory literature, except in models of inventories with highly perishable goods (Pindyck 1994). We allow nonzero depreciation because it is theoretically plausible and essential to fit the data. The model incorporates six shocks. We include two (correlated) sector-specific technology shocks and one demand-type shock to the discount rate. A fourth shock captures shifts in preferences between goods and services. Lastly, we introduce two inventory-specific shocks that create roles for unobserved changes in inventory technologies or preferences to influence the model. While multiple shocks are not common in general equilibrium models of inventory behavior, we find it appealing to work with both technology and preference shocks on the one hand, and inventory shocks on the other, because our interest is not just in understanding how inventories propagate aggregate shocks, but also in whether shocks that affect inventories more directly spill over to other sectors of the economy.
We estimate the model using Bayesian methods. The estimated model fits the data well. Parameter estimates are consistent with the theory and are relatively precise. The estimated model replicates the volatility and procyclicality of inventory investment, and the qualitative differences in the observed cyclicality of the two inventory to target ratios. In particular, the model captures the countercyclicality of the input inventory to output ratio and the relatively acyclicality of the output inventory to consumption ratio. We also find that inventory shocks do explain some of the variation in investment and consumption, but little of the variation in aggregate output. Input inventory shocks (that increase the contribution of inventories to production) reduce inventory demand, and raise business investment and, with some delay, total output. Output inventory shocks instead move preferences away from output inventories and towards consumption goods, thus proxying for a classic demand shock. However, the effects on the aggregate economy are not large. Altogether, the results are consistent with the conventional view that inventories are an important part of the propagation mechanism, but in and of themselves are not an important source of macroeconomic fluctuations.
The estimation results shed light on inventory behavior over the business cycle. We find that the elasticity of substitution between input inventories and fixed capital in the production function is much smaller than unity. In contrast, the elasticity of substitution between consumption and output inventories in the utility function is closer to unity. Adjustment costs on fixed capital are large, while adjustment costs on inventory stocks are small and relatively insignificant. However, estimated depreciation rates for inventories, which might also reflect holding costs, are sizeable. Nonzero depreciation rates for inventories, together with fixed capital adjustment costs, are crucial in explaining the absolute and relative volatility of inventory investment and their role in the propagation mechanism.
Finally, we provide the first analysis of the Great Moderation based on an estimated DSGE model with independent roles for input and output inventories. By estimating the model over the sub-periods 1960-1983 and 1984-2007, we account for the notable changes in the steady-state values of the inventory-to-target ratios and for the relatively greater importance of the service sector since 1984. We find that most of the decline in aggregate output volatility is attributable to the lower volatility of shocks, which occurred primarily in the goods-sector technology shock.9 The volatility of the input-inventory technology shock also declined, but this decline only accounts for a very small reduction in the volatility of aggregate output or goods output. We also find that structural changes in the parameters account for a smaller fraction of the reduction in aggregate output volatility. The reduced ratio of input inventories to goods output observed in the data is associated with a decrease in goods-sector output and GDP volatility, but the size of the decrease is small.
2 The Model
2.1 Motivating Inventories
To motivate why input inventories (materials for short) are held, we follow the literature that treats them as a factor of production alongside labor and fixed capital, following a tradition going back to Kydland and Prescott (1982), Christiano (1988) and Ramey (1989). This approach assumes that the stock of inventories facilitates production - over and above their usage - by minimizing the cost of procuring input materials, by guarding against stockouts that would reduce productivity, and by allowing batch production. 10 In the Kydland and Prescott and Christiano's models, the production function should be interpreted as a value added (gross output minus materials used) production function. As a factor aiding the production of value added, one can think of inventory stocks as a type of capital, which are characterized by adjustment and holding costs and subject to physical depreciation.11 In Section 6, we also consider a version of the model in which we explicitly model the usage of materials and abstract from their convenience yield.
In modeling output inventories, we follow Kahn, McConnell and Perez-Quiros (2002) who assume that output inventories provide convenience services to the consumer and include them directly in the utility function. The convenience yield may reflect the reduction in shopping cost associated, for instance, with less frequent stockouts and with the provision of variety or of other consumer benefits associated with the underlying retailing services. Indeed, under some simplifying assumptions, we can show that the model with output inventories in the utility function is equivalent to a model in which inventories appear in the budget constraint because they affect shopping costs, but do not enter the utility function. Feenstra (1986) proves the equivalence, under some (mild) conditions, between including consumption and money in the utility function; and including only consumption, but with liquidity/shopping costs - increasing in consumption and decreasing in money balances - appearing in the budget constraint. Feenstra's result suggests that our model with output inventories in the utility function, could be reinterpreted as a model having only consumption in the utility function, but having shopping costs in the budget constraint that are decreasing in output inventories. When the utility function is additively separable in consumption of goods and output inventories, on the one hand, and consumption of services, on the other, we can derive analytically the form of the shopping cost function. We discuss all this more fully in Section 6.
Our representative agent, perfectly competitive approach to output inventories abstracts from the decentralized problem of inventory holding by retailers (or by final good producers) that is common in partial-equilibrium analyses of inventories. To address this issue properly, one should model explicitly the relationship between individual consumers and retailers (or final good producers) in an imperfectly competitive setting. We leave this important task for future research in the context of a model that also allows for input-output (supply-chain) relationships, which are equally important to the decentralized problem. We also avoid modeling stockouts of output or input inventories explicitly and abstract from the presence of fixed ordering costs. We are aware that our modeling choices for both input and output inventories are shortcuts taken in order to obtain a relatively simple estimable model. The judgement whether they are useful ones will partly depend upon the ability of our model to explain the movement of inventories over the business cycle.
2.2 Preferences
The household chooses consumption of goods ![]() , services
, services ![]() output inventories
output inventories
![]() and hours in the goods sector
and hours in the goods sector ![]() and services sector
and services sector ![]() to maximize the
following objective function:
to maximize the
following objective function: 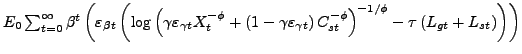 ,
,
where ![]() is a CES
bundle of goods and output inventories, and is defined as
is a CES
bundle of goods and output inventories, and is defined as
| (2.1) |
where ![]() ,
, ![]() , and
, and ![]() . In this formulation,
. In this formulation, ![]() is the inverse elasticity of substitution between the
consumption of final goods and output inventories. Similarly,
is the inverse elasticity of substitution between the
consumption of final goods and output inventories. Similarly,
![]() is the inverse elasticity of
substitution between services and the bundle of goods
(consumption-output inventories). Utility is linear in leisure,
following Hansen (1985) and Rogerson (1988), which both assume that
the economy is populated by a large number of identical households
that agree on an efficient contract that allocates individuals
either to full-time work or to zero hours.
is the inverse elasticity of
substitution between services and the bundle of goods
(consumption-output inventories). Utility is linear in leisure,
following Hansen (1985) and Rogerson (1988), which both assume that
the economy is populated by a large number of identical households
that agree on an efficient contract that allocates individuals
either to full-time work or to zero hours.
We allow for three shocks to impact the intertemporal and
intratemporal margins of the household. The shock
![]() affects preferences for
goods, services, and leisure today versus tomorrow. The shock
affects preferences for
goods, services, and leisure today versus tomorrow. The shock
![]() affects the relative
preference between goods and services.12 Finally, the shock
affects the relative
preference between goods and services.12 Finally, the shock
![]() affects the preference
between the consumption of goods and output inventories: this shock
is meant to capture the reduced-form impact on utility of temporary
movements in the "technology" to produce output inventories
occurring in the storage of physical goods
affects the preference
between the consumption of goods and output inventories: this shock
is meant to capture the reduced-form impact on utility of temporary
movements in the "technology" to produce output inventories
occurring in the storage of physical goods![]() Low-frequency evolution in the storage and retailing technology
(such as the emergence of megastores like Walmart, Internet
shopping, and other key retail developments, especially since the
early 1980s) might also be reflected in changes in structural
parameters such as
Low-frequency evolution in the storage and retailing technology
(such as the emergence of megastores like Walmart, Internet
shopping, and other key retail developments, especially since the
early 1980s) might also be reflected in changes in structural
parameters such as ![]() and
and ![]() or in the volatility of the inventory specific shock
or in the volatility of the inventory specific shock
![]() . Changes in
. Changes in ![]() and
and ![]() will affect the ratio between
output inventories and consumption. It is difficult to explicitly
model these trends, but, at least, we will allow for discrete
changes in the parameters by estimating the model separately for
different subperiods (pre and post 1984).
will affect the ratio between
output inventories and consumption. It is difficult to explicitly
model these trends, but, at least, we will allow for discrete
changes in the parameters by estimating the model separately for
different subperiods (pre and post 1984).
2.3 Technology
Following Christiano (1988), value added in the goods sector is
a Cobb-Douglas function in labor ![]() , and a CES
aggregate of services from fixed capital and input
inventories,
, and a CES
aggregate of services from fixed capital and input
inventories,
| (2.2) |
where ![]() and
and ![]() . In equation
(2.2)
,
. In equation
(2.2)
,
![]() is the end-of-period
is the end-of-period ![]() capital in the goods sector (plant, equipment, and structures),
capital in the goods sector (plant, equipment, and structures),
![]() is the time-varying utilization rate of
is the time-varying utilization rate of
![]() , and
, and ![]() is the
end-of-period
is the
end-of-period ![]() stock of input inventories. Here,
stock of input inventories. Here,
![]() measures the inverse elasticity of
substitution between fixed capital and input inventories. If
measures the inverse elasticity of
substitution between fixed capital and input inventories. If
![]() then fixed capital and input
inventories will be defined here as complements; if
then fixed capital and input
inventories will be defined here as complements; if
![]() then input inventories and
capital are substitutes.
then input inventories and
capital are substitutes.
The production function above does not explicitly feature the usage of materials as one of its arguments. Equation (2.2) describes a value added (gross output minus materials used) production function, once materials used have been maximized out. So long as materials can be produced from gross output using a one-for-one technology, our model generates the same optimality conditions for primary inputs as a model that treats materials used as an additional factor of production in the production function of gross output.13
We allow for two disturbances in the goods sector technology:
![]() is a technology shock, while
is a technology shock, while
![]() is a shock that affects the
productive efficiency of input inventories, so that
is a shock that affects the
productive efficiency of input inventories, so that
![]() is input inventories
in efficiency units.
is input inventories
in efficiency units.
![]() captures, in a reduced-form
way, the impact on production efficiency of changes in the input
inventory technology. The (low frequency) evolution over time of
new methods of inventory management like just-in-time production or
flexible manufacturing system, which are characterized by elaborate
supply and distribution chains, may be reflected in changes in the
volatility of
captures, in a reduced-form
way, the impact on production efficiency of changes in the input
inventory technology. The (low frequency) evolution over time of
new methods of inventory management like just-in-time production or
flexible manufacturing system, which are characterized by elaborate
supply and distribution chains, may be reflected in changes in the
volatility of
![]() , in the weight of input
inventories in the CES aggregate,
, in the weight of input
inventories in the CES aggregate, ![]() , and
in the parameter governing the elasticity of substitution,
, and
in the parameter governing the elasticity of substitution,
![]() or, more generally, in the ratio between
the stock of input inventories and goods output.
or, more generally, in the ratio between
the stock of input inventories and goods output.
Production in the services sector is modeled by a Cobb-Douglas
production function only for labor ![]() and
capital services:
and
capital services:
| (2.3) |
where ![]() is the end-of-period
is the end-of-period ![]() capital in the service sector and
capital in the service sector and ![]() is the
time-varying utilization rate of
is the
time-varying utilization rate of ![]() . The
empirical fact that service-producing firms do not hold inventories
motivates our model's different specification of the
services-production technology. We also allow for a technology
disturbance,
. The
empirical fact that service-producing firms do not hold inventories
motivates our model's different specification of the
services-production technology. We also allow for a technology
disturbance, ![]() , in the services sector.
, in the services sector.
2.4. Resource Constraints
Output from the goods sector provides consumption goods, new fixed investment in both sectors, and investment in output and input inventories. Output from the services sector provides services to the consumer. The resource constraints for the goods and service sectors are, respectively,
| (2.4) |
and
| (2.5) |
The capital depreciation rates in both sectors,
![]() and
and
![]() , are
increasing functions of the respective utilization rates. The
inventory depreciation rates,
, are
increasing functions of the respective utilization rates. The
inventory depreciation rates, ![]() and
and
![]() , are fixed and possibly capture
inventory holding costs as well. Adjustment costs (denoted by
, are fixed and possibly capture
inventory holding costs as well. Adjustment costs (denoted by
![]() ) are quadratic and given by the
expression:
) are quadratic and given by the
expression:
| (2.6) |
for
![]() . It is
straightforward to show, log-linearizing around the steady state,
that the elasticity of capital (investment) with respect to its
shadow price is
. It is
straightforward to show, log-linearizing around the steady state,
that the elasticity of capital (investment) with respect to its
shadow price is
![]() (
(
![]() ). For the utilization function,
we choose a parameterization such that the marginal cost of
utilization equals the marginal product of capital in steady state.
The time
). For the utilization function,
we choose a parameterization such that the marginal cost of
utilization equals the marginal product of capital in steady state.
The time ![]() depreciation rate of
depreciation rate of ![]() ,
defined as
,
defined as ![]() (with
(with ![]() ), is given by
), is given by
| (2.7) |
The parameter ![]() determines the curvature
of the capital-utilization function, where
determines the curvature
of the capital-utilization function, where
![]() is a normalization that guarantees that steady-state utilization is
unity.
is a normalization that guarantees that steady-state utilization is
unity.
2.5. Shocks
The shocks ![]()
![]()
![]()
![]()
![]() and
and ![]() follow AR(1) stationary processes in logs:
follow AR(1) stationary processes in logs:
| (2.8) |
| (2.9) |
| (2.10) |
| (2.11) |
| (2.12) |
| (2.13) |
The innovations ![]()
![]()
![]()
![]()
![]() ,
,![]() and
and ![]() are serially uncorrelated with zero means and standard
deviations given by
are serially uncorrelated with zero means and standard
deviations given by ![]()
![]()
![]()
![]()
![]() ,
,![]() and
and ![]() . In
addition, we allow for correlation between the two technology
innovations,
. In
addition, we allow for correlation between the two technology
innovations, ![]() and
and ![]() .
.
2.6. Optimality Conditions and Steady State
Because the two welfare theorems apply, we solve the model as a planner's problem. The first-order conditions are standard and reported in the technical appendix, along with a full characterization of the steady state. The model's optimality conditions, together with the market-clearing conditions and the laws of motion for the shocks, can be used to obtain a linear approximation around the steady state for the decision rules of the model variables, given the initial conditions and the realizations of the shocks. Given the model's structural parameters, the solution takes the form of a state-space econometric model that links the behavior of the endogenous variables to a vector of partially unobservable state variables that includes the six autoregressive shocks.
In our econometric application, we use observed deviations from the steady state of six variables, namely, the output of goods and services, the stock of input inventories and output inventories, the relative price of goods, and total fixed investment to estimate the model's parameters and the properties of the shocks. We will also require that the estimated parameters match the steady-state ratios of the model (proxied by their average values). Before describing the estimation procedure (Section 4), Section 3 maps the model variables into their data counterparts.
2.7. Inventory Management Techniques and Steady-State Ratios
Two of the model's steady-state ratios are worth highlighting.
The steady-state ratios of input inventories to goods output,
![]() , and output inventories to goods
consumption,
, and output inventories to goods
consumption, ![]() , are:
, are:
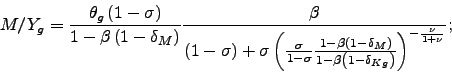
|
(2.14) |
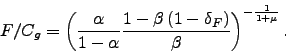
|
(2.15) |
These ratios are structural analogues of the reduced-form "inventory-target" ratios that have played a central role in the
inventory literature, which has usually taken a partial equilibrium
approach to modeling inventories. The literature has primarily
focused on output inventories, ![]() , and
, and ![]() is normally represented as the "sales" of a firm(s) -
hence the "inventory-sales" ratio or target.
is normally represented as the "sales" of a firm(s) -
hence the "inventory-sales" ratio or target.
Changes in inventory-target ratios figure prominently in analyses of the data and hypotheses about improvements in inventory management techniques, as explained in the next section. Here we simply highlight the ways such techniques might be manifested through the theoretical model. Because the model does not explicitly incorporate inventory management techniques, changes in such techniques mostly likely would appear as changes in the structural parameters that determine the inventory-target ratios.
The input inventory-target ratio, ![]() ,
depends on three production function parameters that might reflect
the current state of inventory management (
,
depends on three production function parameters that might reflect
the current state of inventory management (![]()
![]()
![]() ), as well
as two depreciation rates (
), as well
as two depreciation rates (![]()
![]() ). The ratio is increasing in
the relative weight of inventories in the non-labor input to
production (
). The ratio is increasing in
the relative weight of inventories in the non-labor input to
production (![]() ) and in the non-labor share of
inputs in production (
) and in the non-labor share of
inputs in production (![]() ). Thus, new
production techniques that economize on inventories, such as
changes in delivery lags or ordering procedures for material
inputs, may contribute to a lower ratio. The target ratio is also
likely to be increasing in the degree of complementarity between
inventories and fixed capital (
). Thus, new
production techniques that economize on inventories, such as
changes in delivery lags or ordering procedures for material
inputs, may contribute to a lower ratio. The target ratio is also
likely to be increasing in the degree of complementarity between
inventories and fixed capital (![]() ).14
Investment in new types of capital associated with inventory
management techniques might reduce this complementarity. Finally,
the ratio is decreasing in inventory depreciation,
).14
Investment in new types of capital associated with inventory
management techniques might reduce this complementarity. Finally,
the ratio is decreasing in inventory depreciation, ![]() although this parameter is unlikely to be
directly related to inventory management techniques.
although this parameter is unlikely to be
directly related to inventory management techniques.
The output inventory target-ratio, ![]() ,
depends on two utility function parameters (
,
depends on two utility function parameters (![]()
![]() ) and one depreciation rate (
) and one depreciation rate (![]() ). The ratio is increasing in the relative weight
of inventories in the goods aggregator
). The ratio is increasing in the relative weight
of inventories in the goods aggregator ![]() . It
is also increasing in the degree of complementarity between
consumption and inventories (
. It
is also increasing in the degree of complementarity between
consumption and inventories (![]() ) when the term
in parenthesis in equation
(2.15) is
greater than one - a result that holds in our baseline
estimates.15
) when the term
in parenthesis in equation
(2.15) is
greater than one - a result that holds in our baseline
estimates.15
3. Data
3.1. Sector and Inventory Definitions
To obtain model-consistent data, we divide the economy into two sectors according to the inventory-holding behavior of their industries: 1) the "goods" sector, which holds inventories; and 2) the "services" sector, which does not hold inventories (at least none as measured by statistical agencies). 16 The goods sector includes seven industries: agriculture, mining, utilities, construction, manufacturing, and wholesale and retail trade. All other private-sector industries are in the services sector.17
Table 1 depicts our sectoral classification, compares it with the National Income and Product Accounts (NIPA) classification, and reports output shares in 2000. The goods sector accounts for a larger share of output than the NIPA goods sector (35.9 percent versus 21.2 percent). Nevertheless, under our definition, the services sector accounts for about three-fifths of private output (59.1 percent versus 40.9 percent for private goods), which excludes government but include foreign trade. However, the private goods sector becomes even larger after adjusting for foreign trade and the leasing of capital, as explained in the next subsection.
Our goods sector is larger than the NIPA good sector (and larger than conventional wisdom would suggest) because it includes the utilities, wholesale trade, and retail trade industries - all of which hold measured inventories. Reclassification of these NIPA-based "services" (utilities and trade) as "goods" can be motivated by assuming that the "service" provided - distributing goods from their producers to the final destination (consumers or firms) - can be internalized in a model of a representative goods producer which makes and distributes goods. Nevertheless, separate treatment of the production and distribution of goods may be preferable in future research that incorporates multiple stages of processing in the goods sector.
NIPA inventories are classified as input (![]() )
or output (
)
or output (![]() ) stocks following the
stage-of-fabrication perspective advanced by Humphreys, Maccini,
and Schuh (2001). Generally speaking, most goods production follows
an input-output structure in which the output of one industry
becomes an input to the next industry situated along a supply or
distribution chain - raw materials, then work-in-process, and
finally finished goods. Table 2 depicts this
inventory classification scheme by industry, along with inventory
shares in 2000. Inventory-holding industries appear in approximate
order according to their location in the stages of fabrication;
industries tending to producing raw materials are listed first, and
industries tending to producing finished goods listed last.
) stocks following the
stage-of-fabrication perspective advanced by Humphreys, Maccini,
and Schuh (2001). Generally speaking, most goods production follows
an input-output structure in which the output of one industry
becomes an input to the next industry situated along a supply or
distribution chain - raw materials, then work-in-process, and
finally finished goods. Table 2 depicts this
inventory classification scheme by industry, along with inventory
shares in 2000. Inventory-holding industries appear in approximate
order according to their location in the stages of fabrication;
industries tending to producing raw materials are listed first, and
industries tending to producing finished goods listed last.
Prior research focuses on stage-of-fabrication inventories only
within manufacturing. However, manufacturing only accounts for 31
percent of all inventories, so a decision must be made on how to
classify the remaining 69 percent. We define ![]() as retail inventories because they represent the most finished
stage of goods in supply and distribution chains. By this
definition, output inventories account for about one-fourth of all
stocks (26.6 percent), hence input inventories account for the
about three-fourths (73.4 percent).18
as retail inventories because they represent the most finished
stage of goods in supply and distribution chains. By this
definition, output inventories account for about one-fourth of all
stocks (26.6 percent), hence input inventories account for the
about three-fourths (73.4 percent).18
Our empirical definition of ![]() yields a smaller
role for output inventories than they play within manufacturing.
Within manufacturing, output (finished goods) inventories account
for about 36 percent of all manufacturing inventories (11.1 percent
out of 31.1 percent). In addition, our empirical definition of
input inventories is heavily oriented toward work-in-process
inventories (54.5 percent), whereas these types of inventories
account for only about 29 percent of all manufacturing stocks (8.9
percent out of 31.1 percent). Thus, one should not necessarily
expect the stylized facts for stage-of-fabrication inventories in
our model to be the same as for stage-of-fabrication inventories in
manufacturing.
yields a smaller
role for output inventories than they play within manufacturing.
Within manufacturing, output (finished goods) inventories account
for about 36 percent of all manufacturing inventories (11.1 percent
out of 31.1 percent). In addition, our empirical definition of
input inventories is heavily oriented toward work-in-process
inventories (54.5 percent), whereas these types of inventories
account for only about 29 percent of all manufacturing stocks (8.9
percent out of 31.1 percent). Thus, one should not necessarily
expect the stylized facts for stage-of-fabrication inventories in
our model to be the same as for stage-of-fabrication inventories in
manufacturing.
3.2. Data Construction
We use NIPA data and identities to construct data for the econometric work. For simplicity, we suppress the notational details associated with chain-weighted aggregation in the equations below describing the data construction.19 The output and investment data are constructed as follows:
where ![]() is nonresidential fixed investment,
is nonresidential fixed investment,
![]() is residential fixed investment,
is residential fixed investment,
![]() is net exports, and
is net exports, and ![]() is the share of capital installed in the goods sector;
NIPA data on
is the share of capital installed in the goods sector;
NIPA data on ![]() and
and ![]() are
modified slightly to match the sectoral definitions of the model.
In estimating the model we account for the fact that NIPA output
does not include inventory depreciation, whereas model output does:
we thus subtract inventory depreciation from model output of goods,
are
modified slightly to match the sectoral definitions of the model.
In estimating the model we account for the fact that NIPA output
does not include inventory depreciation, whereas model output does:
we thus subtract inventory depreciation from model output of goods,
![]() , in order to obtain measured goods
output,
, in order to obtain measured goods
output, ![]() . GDP is the Tornqvist index of
measured output in the two sectors.
. GDP is the Tornqvist index of
measured output in the two sectors.
All data represent value added ("output" for short) of the private economy, which excludes government spending. We include net exports as part of investment in order to match objects in the our closed economy model with the data that refer to an open economy, following the suggestion of Cooley and Prescott (1995), the approach of Hayashi and Prescott (2002), and Conesa, Kehoe and Ruhl (2007), among the others.20Another advantage of including net exports in our definition of output is that our sample includes a period in which the U.S. moved from being a net exporter (before 1984) to running a significant trade deficit (since 1984): omitting net exports from our definition of goods could significantly bias our assessment of the trends in the inventory-output ratios.
Because the model and NIPA sectoral definitions differ, the standard NIPA consumption, investment, and inventory data require three adjustments to obtain model-consistent variables. First, consumption of energy services (such as gas and electricity) is reclassified as consumption of goods (energy) produced by the utilities industry. Second, non-NIPA investment-by-industry data are used to obtain measures of investment (capital installed) in each sector, which is not available in the NIPA data. A substantial proportion of investment occurs in the "real estate, rental and leasing" industry, which is in the services sector, but much of this capital actually is leased back to the goods sector. Thus, a portion of real estate and leasing investment is reclassified as goods investment. And third, inventory data from two industrial classification schemes - the old SIC system and the newer NAICS system - are spliced to obtain consistent time-series data for the entire sample.
3.3. Output and Investment Data
Figure 1 plots the raw data in real terms (normalized to 100 in 1960). As the figure illustrates, the series have grown at different real rates over the sample period. In particular, output in the services sector has grown faster than in the goods sector, and input inventories have grown much slower than output inventories, especially since the early 1980s. Figure 2 plots each variable in nominal terms as a share of total output. The ratios of total consumption-to-output and total investment-to-output are roughly constant, except for the slight downward trend in the investment-to-output ratio during the second half of the sample due to the decline in net exports.
However, the nominal ratios in each sector are not roughly constant. 21The most noticeable sector-level trends are the opposing trends in consumption (an upward drift in the share of services consumption, from 30 percent to 50 percent, and a downward drift in the share of goods consumption of the reverse magnitude), and the different trends in inventory stocks (downward drift in the ratio of input inventories and upward drift in the ratio of output inventories). Similarly, the ratio of investment-to-output in goods is declining while that ratio in services is roughly constant. These changing shares of goods and services have been extensively discussed in the literature and reflect the slow reallocation of resources from manufacturing to services, a process often referred to as "structural change" and well documented at least since Kuznets (1957).
The sector-level trends in the data pose a challenge in terms of modeling choices. Standard one-sector models of the business cycle rely on an important property of U.S. macroeconomic aggregates: the nominal shares of total consumption and investment in total GDP have been roughly constant over the post-world-war II period. The plain-vanilla one-sector model, indeed, features "balanced growth" : output, consumption and investment all grow at about the same rate, and the decentralized equilibrium features constant relative prices across output, consumption and investment (Whelan, 2003). Extensions of the one-sector model to a multi-sector framework allow for balanced growth even if the real variables are growing at different rates over time, so long as preferences and technology satisfy specific functional forms.22 In these extensions, although there is no balanced growth in the traditional sense, it is possible to find a transformation of the model variables that will render them stationary. This transformation, loosely speaking, is admissible insofar as variables grow at different rates in real terms, but relative prices adjust in a way that expenditure shares remain constant. Hence a necessary condition for balanced growth both in one-sector and multi-sector models is that nominal ratios are approximately constant over time. Our framework, however, features a finer level of disaggregation than typical multi-sector models. In particular, it divides consumption into two categories (goods and services) and investment into three categories (business investment, input inventory investment, and output inventory investment). The discipline of a model obeying the balanced growth property would require the shares of Figure 2 to be stationary, but they are not. Jointly modeling of the trend and the cycle would be fascinating, but the data appear to reject balanced growth at the level of disaggregation that we propose in the model. Thus, we use standard filtering techniques to remove the trends from each variable prior to estimation.
3.4. Inventory Data and the Inventory Management Hypotheses
Figure 3 (top panel) plots the inventory-target ratios of the
model, ![]() and
and ![]() .23 A striking fact is that input and
output inventory-target ratios exhibit opposite trends over the
full sample. The input inventory ratio (
.23 A striking fact is that input and
output inventory-target ratios exhibit opposite trends over the
full sample. The input inventory ratio (![]() )
declined by about one-third (from about 1.5 to 1.0) and the output
inventory ratio (
)
declined by about one-third (from about 1.5 to 1.0) and the output
inventory ratio (![]() ) increased by 50 percent
(from about 0.35 to 0.5). Because input inventories account for
most of the inventory stock (73.4 percent, from Table 2), the aggregate
inventory-target ratio,
) increased by 50 percent
(from about 0.35 to 0.5). Because input inventories account for
most of the inventory stock (73.4 percent, from Table 2), the aggregate
inventory-target ratio,
![]() (or relative to
(or relative to
![]() ), declined.
), declined.
The prevailing view in the literature is that a decline in
![]() or
or ![]() likely resulted from improvements in inventory
management and production techniques, such as "Just-in-Time"
production, "Flexible Manufacturing Systems", and "Material
Resources Planning." 24 Ramey and Vine (2004) rightly point
out the importance of measuring inventory-target ratios with
numerator (inventory) and denominator (target) measuring the same
sectors of the economy (which our model does), but conclude that
doing so yields trends less supportive of the conventional view.
Alternatively, holding fewer inventories relative to sales would be
possible if the volatility of demand declined, as predicted by
stockout avoidance models such as Kahn (1987). Because the decline
in the input inventory-target ratio occurred at about the same time
that GDP volatility declined - the "Great Moderation" - a
connection between these two events is a natural hypothesis to
evaluate.
likely resulted from improvements in inventory
management and production techniques, such as "Just-in-Time"
production, "Flexible Manufacturing Systems", and "Material
Resources Planning." 24 Ramey and Vine (2004) rightly point
out the importance of measuring inventory-target ratios with
numerator (inventory) and denominator (target) measuring the same
sectors of the economy (which our model does), but conclude that
doing so yields trends less supportive of the conventional view.
Alternatively, holding fewer inventories relative to sales would be
possible if the volatility of demand declined, as predicted by
stockout avoidance models such as Kahn (1987). Because the decline
in the input inventory-target ratio occurred at about the same time
that GDP volatility declined - the "Great Moderation" - a
connection between these two events is a natural hypothesis to
evaluate.
In contrast, the literature offers little or no explanation for
a rising inventory-target ratio, such as output (retail)
inventories rising relative to their target
![]() . Perhaps this
oversight occurred because inventories in the retail industry are
not examined much in the literature, but for some reason much less
attention has been devoted to explaining this phenomenon and its
implications for the aggregate economy. By separating inventories
into input and output components, we highlight the need to
understand the economic factors behind the trend increase in output
inventories. The output inventory-target ratio leveled off in the
1990s, much later than the break for the input inventory-target
ratio. This fact may reflect an effect of inventory management
occurring later than for input inventories, but the evidence for
this hypothesis is less clear and warrants additional
investigation. Finally, a rising output inventory-target ratio may
be consistent with a love-for-variety story, in which firms are
required to keep a larger, more diverse stock of finished goods to
satisfy greater demand for variety coming from an increase in the
number of types of goods produced.
. Perhaps this
oversight occurred because inventories in the retail industry are
not examined much in the literature, but for some reason much less
attention has been devoted to explaining this phenomenon and its
implications for the aggregate economy. By separating inventories
into input and output components, we highlight the need to
understand the economic factors behind the trend increase in output
inventories. The output inventory-target ratio leveled off in the
1990s, much later than the break for the input inventory-target
ratio. This fact may reflect an effect of inventory management
occurring later than for input inventories, but the evidence for
this hypothesis is less clear and warrants additional
investigation. Finally, a rising output inventory-target ratio may
be consistent with a love-for-variety story, in which firms are
required to keep a larger, more diverse stock of finished goods to
satisfy greater demand for variety coming from an increase in the
number of types of goods produced.
3.5. Cyclical Properties
For all of the reasons described earlier about the complexity of the sectoral trends, and following the common procedure in the inventory literature, we detrended all data used in the econometric work with a conventional bandpass filter.25 By all measures, output in the goods sector is much more variable than output in the service sector. For our definition of the goods sector (first column of Table 1), output fluctuations in the goods sector account for 76 percent of the variance of aggregate output in real terms. By comparison, the growth rate of goods output in the narrower, more volatile NIPA definition of goods (second column of Table 1, not including the construction industry) accounts for 89 percent of the variance of real GDP growth, according to Irvine and Schuh (2005b). Our goods sector accounts for less of aggregate output variance because it includes relatively less volatile industries, such as wholesale and retail trade.
Moving to inventories, the middle panel of Figure 3 shows how inventory-target ratios exhibit markedly different cyclical properties. On average, the output-inventory ratio is roughly acyclical (the correlation with goods output is 0.10), as can be seen by the lack of consistent movement during recessions (shaded regions). Although the output-inventory ratio shot up during the 1973-75 recession, it has not done so during other recessions. In contrast, the input-inventory ratio is very countercyclical (the correlation with goods output is -0.89), as can be seen by its consistent increase during recessions. Thus, the existence of countercyclical inventory-target ratios for manufacturing output inventories, as emphasized by Bils and Kahn (2000), is not evident for all inventories. This result suggests that successful theories of aggregate inventory behavior must be comprehensive enough to explain heterogenous behavior among different types of stocks.
Another key fact, seen in the bottom panel of Figure 3, is that input-inventory investment is much more volatile than output-inventory investment (the ratio of variances is about 2), when both investment series are normalized by total output. This relative volatility is comparable to the analogous variance ratios observed within manufacturing (Blinder and Maccini 1991). However, the relative volatility of the two types of inventory investment has declined dramatically, from a ratio of 4.6 in the early sample (1960-1983) to a ratio of 2.5 since then. The volatility of input-inventory investment fell while the volatility of output-inventory investment remained about constant. Both types of inventory investment are procyclical over the full sample, but input-inventory investment is more procyclical than output-inventory investment (the correlation with goods output is 0.62 for input inventories and 0.42 for output inventories). The procyclicality of output-inventory investment decreased from 0.44 in the early sample (1960-1983) to 0.25 since then, but the cyclical correlation of input-inventory investment has remained relatively stable.
In sum, the distinctly different cyclical properties of input- and output-inventory investment provide additional motivation for disaggregating inventories. Thus, theoretical models that allow different inventory-target adjustments and volatility across stocks are likely to have an advantage in explaining and understanding aggregate inventory behavior.
4.1. Model Estimation
4.1. Overview
We use observations on the following variables: (1) output from the goods sector; (2) output from the service sector; (3) the stock of input inventories; (4) the stock of output inventories; (5) total fixed investment; (6) the relative price of goods to services. We estimate the model for the full sample from 1960:1-2007:4. We also estimate the model for the two subperiods: 1960:1-1983:4 and 1984:1-2007:4. The breakpoint corresponds to point estimates of when the Great Moderation began, as indicated in McConnell and Perez-Quiros (2000).
We use Bayesian techniques to estimate the structural
parameters. For given values of the parameters, the solution to our
linearized model takes the form of a state-space econometric model,
and the Kalman filter enables to evaluate the likelihood of the
observable variables as follows: ![]() , where
, where
![]() is the vector collecting all the
model parameters and
is the vector collecting all the
model parameters and ![]() is the vector of
observable variables. We combine the information observed in the
data with prior information on the model parameters to construct
the posterior density function:
is the vector of
observable variables. We combine the information observed in the
data with prior information on the model parameters to construct
the posterior density function:
| (4.1) |
Specifically, we first calculate the posterior mode of the parameters using a numerical optimization procedure. Then we generate 250,000 draws from the posterior mode using the Metropolis-Hastings algorithm to obtain the posterior distribution. The mean of the posterior distribution is used to compute impulse response functions, variance decompositions, and moments of the estimated model.
4.2. Prior Distributions
We keep some parameters fixed during our estimation exercise.
More specifically, we set the quarterly discount factor at
0.99, implying an annual interest rate of
4 percent. We also calibrate the depreciation
rates for fixed capital, which we set at
![]() . 26 Once
these values are set, 29 remaining parameters need
to be estimated. We partition these into three groups:
. 26 Once
these values are set, 29 remaining parameters need
to be estimated. We partition these into three groups:
- The autocorrelation parameters (
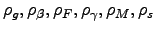 ), standard deviations of the innovation disturbances (
), standard deviations of the innovation disturbances (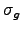 ,
,
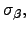
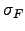 ,
,
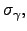
 ,
, 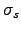 ), and the
correlation between the innovations in the goods-sector technology
and the services-sector technology (
), and the
correlation between the innovations in the goods-sector technology
and the services-sector technology (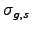 ).
). - The adjustment cost parameters (
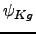 ,
,
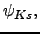
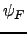 , and
, and
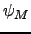 ), and the parameters characterizing
the curvature of the utilization functions for fixed capital
(
), and the parameters characterizing
the curvature of the utilization functions for fixed capital
(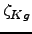 ,
, 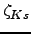 ).
). - The inventory depreciation rates (
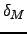 and
and
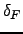 ), the elasticities of
substitution (
), the elasticities of
substitution (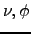 ,
, 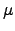 ), the
labor shares (
), the
labor shares (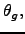
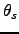 ),
the weight of services in utility (
),
the weight of services in utility (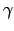 ), the
weight of input inventories in the CES capital aggregator
(
), the
weight of input inventories in the CES capital aggregator
(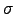 ), and the weight (
), and the weight (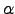 ) on consumption in the goods-bundle aggregator. This
third group of parameters affects not only the model's dynamics,
but also the steady-state values of fixed capital and input- and
output-inventory stocks relative to output, as well as the relative
size of the service versus the goods sector. For our sample (and
for the two subsamples), the average values of these ratios are
reported in Table 3. One can show
that, for each combination of
) on consumption in the goods-bundle aggregator. This
third group of parameters affects not only the model's dynamics,
but also the steady-state values of fixed capital and input- and
output-inventory stocks relative to output, as well as the relative
size of the service versus the goods sector. For our sample (and
for the two subsamples), the average values of these ratios are
reported in Table 3. One can show
that, for each combination of 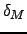 ,
,
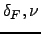 ,
, 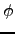 ,
,
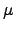 , it is possible to determine a unique
set of values for
, it is possible to determine a unique
set of values for
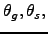
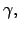
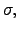 and
and 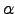 that
are consistent with these five ratios.27 Accordingly, in the
estimation of the model, for each value of
that
are consistent with these five ratios.27 Accordingly, in the
estimation of the model, for each value of 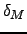 ,
,
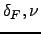 ,
, 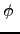 and
and
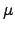 , we set
, we set
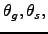
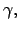
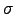 and
and 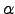 to the
values that match the ratios. Intuitively, we let the likelihood
function use information on the behavior around the steady state of
our observables to determine values for the depreciation rates,
to the
values that match the ratios. Intuitively, we let the likelihood
function use information on the behavior around the steady state of
our observables to determine values for the depreciation rates,
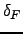 and
and 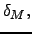 and the elasticity of substitution in the CES aggregates in the
production and utility functions,
and the elasticity of substitution in the CES aggregates in the
production and utility functions, 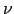 ,
,
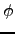 , and
, and 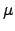 (in addition to
the autocorrelation, adjustment costs, and utilization function
parameters). We then use the ratios reported in Table 3 to recover
the remaining parameters. This procedure also enables us to account
for the changes in the ratios over the sample period: when we
estimate the model separately for the two subsamples, we use the
average values of the relevant ratios in each period.28
(in addition to
the autocorrelation, adjustment costs, and utilization function
parameters). We then use the ratios reported in Table 3 to recover
the remaining parameters. This procedure also enables us to account
for the changes in the ratios over the sample period: when we
estimate the model separately for the two subsamples, we use the
average values of the relevant ratios in each period.28
Our prior distributions are summarized in the first three
columns of Table 4. For the
parameters measuring adjustment costs ![]() we
specify a beta prior over
we
specify a beta prior over
![]() with mean equal to
0.5: this value corresponds to a prior mean of unity for the
elasticity of investment to its shadow price. For the curvature of
the utilization function, we choose a beta prior over
with mean equal to
0.5: this value corresponds to a prior mean of unity for the
elasticity of investment to its shadow price. For the curvature of
the utilization function, we choose a beta prior over
![]() with mean equal to
0.5. For the elasticity of substitution between services and the
goods bundle, between consumption and output inventories, and
between input inventories and capital, we select priors centered
around two thirds. In other words, our prior goes slightly in favor
of complementarity.
with mean equal to
0.5. For the elasticity of substitution between services and the
goods bundle, between consumption and output inventories, and
between input inventories and capital, we select priors centered
around two thirds. In other words, our prior goes slightly in favor
of complementarity.
The existing literature and the NIPA offer little guidance in
choosing the inventory depreciation rates, ![]() and
and ![]() . An assumption in
line with the procedures used in the NIPA would be that inventories
do not depreciate. Yet inventories are subject to various forms of
"shrinkage," such as obsolescence, perishability, wear and tear,
and breakage, in addition to incurring holding costs, so that the
depreciation parameter may well be larger than the rate set for
fixed capital. For instance, on a quarterly basis, Ramey (1989)
reports inventory holding and storage costs of 4 percent, while
Khan and Thomas (2007) set these costs at 3 percent. We balance
NIPA and other studies and choose a prior mean for the depreciation
rates equal to 0.02.
. An assumption in
line with the procedures used in the NIPA would be that inventories
do not depreciate. Yet inventories are subject to various forms of
"shrinkage," such as obsolescence, perishability, wear and tear,
and breakage, in addition to incurring holding costs, so that the
depreciation parameter may well be larger than the rate set for
fixed capital. For instance, on a quarterly basis, Ramey (1989)
reports inventory holding and storage costs of 4 percent, while
Khan and Thomas (2007) set these costs at 3 percent. We balance
NIPA and other studies and choose a prior mean for the depreciation
rates equal to 0.02.
The autoregressive coefficients of the exogenous shocks have
beta prior distributions, as in Smets and Wouters (2003), centered
at 0.75. The standard deviations of the shocks
are assigned a diffuse inverse gamma distribution prior. The
correlation between ![]() and
and ![]() is assumed to be normal and is centered around
0.50. The choices of the mean of the prior
distribution for the standard deviation of the technology and
preference shocks are in the ballpark of the findings in the
literature. Preliminary estimation attempts also suggested a higher
standard deviation for the input inventory shock relative to the
output inventory shock.
is assumed to be normal and is centered around
0.50. The choices of the mean of the prior
distribution for the standard deviation of the technology and
preference shocks are in the ballpark of the findings in the
literature. Preliminary estimation attempts also suggested a higher
standard deviation for the input inventory shock relative to the
output inventory shock.
5. Estimation results
5.1. Full sample
Parameter Estimates. We begin by discussing the estimates for the entire sample. Table 4 reports the mean and the 5th and 95th percentiles of the posterior distribution of the parameters obtained through the Metropolis-Hastings algorithm. Table 5 reports the implied share parameters that match the target steady-state ratios of the model.29
All shocks are estimated to be quite persistent, with the autoregressive parameters ranging from 0.86 to 0.94. The standard deviation of the shocks ranges from 0.33% (for the output-inventory shock) to 10.34% (for the input-inventory shock): the quantitative relevance of each shock will be discussed below in the variance-decomposition exercise.
The elasticity of substitution between ![]() and
and
![]() (the inverse of
(the inverse of ![]() ) equals
0.28. The elasticity of substitution between
) equals
0.28. The elasticity of substitution between
![]() and
and ![]() (the inverse of
(the inverse of
![]() ) equals 0.77, and is
not significantly different from unity. Similarly, the elasticity
of substitution between services and the CES aggregator for
consumption of goods and output inventories (the inverse of
) equals 0.77, and is
not significantly different from unity. Similarly, the elasticity
of substitution between services and the CES aggregator for
consumption of goods and output inventories (the inverse of
![]() ) is close to one.
) is close to one.
Estimates of the inventory adjustment-cost parameters,
![]() and
and ![]() , are
close to zero, while the bigger values of
, are
close to zero, while the bigger values of
![]() and
and ![]() indicate larger adjustment costs for fixed capital.
At the posterior mean, the estimated values imply an elasticity of
investment to the user cost equal to
indicate larger adjustment costs for fixed capital.
At the posterior mean, the estimated values imply an elasticity of
investment to the user cost equal to ![]() in the goods
sector, and equal to
in the goods
sector, and equal to ![]() in the service
sector.30 These different elasticities confirm
that input inventories and fixed capital are indeed distinguished
by having different degrees of adjustment costs.
in the service
sector.30 These different elasticities confirm
that input inventories and fixed capital are indeed distinguished
by having different degrees of adjustment costs.
Another important difference between inventories and fixed
capital emerges from the estimated depreciation rates. The
depreciation rate for ![]() is 2.2
percent, about the same as capital, but the depreciation rate for
is 2.2
percent, about the same as capital, but the depreciation rate for
![]() is 8.1 percent, much
larger: as we will show below, the nonzero depreciation rates are a
key feature of the model in generating large and positive responses
of inventories to productivity shocks. Finally, estimates of the
convexity of the utilization function suggest little role for
variable utilization in the goods sector, where input inventories
enter the production function alongside fixed capital and offer an
additional margin of factor adjustment in response to shocks.
Conversely, capital utilization plays a more important role in the
service sector, where inventories do not appear in the production
function.
is 8.1 percent, much
larger: as we will show below, the nonzero depreciation rates are a
key feature of the model in generating large and positive responses
of inventories to productivity shocks. Finally, estimates of the
convexity of the utilization function suggest little role for
variable utilization in the goods sector, where input inventories
enter the production function alongside fixed capital and offer an
additional margin of factor adjustment in response to shocks.
Conversely, capital utilization plays a more important role in the
service sector, where inventories do not appear in the production
function.
Impulse Responses and Variance Decompositions. Figure 4 presents the model impulse responses to the estimated shocks. In Table 6 , we report asymptotic variance decompositions. Both in Figure 4 and in Table 6, we choose an orthogonalization scheme that orders the goods technology before the services technology shock. As a result, any variation in the responses due to the correlation between the goods and the services shock is attributed to the goods technology disturbance.
The first row plots the responses to a positive goods technology shock. 31 This disturbance is fundamental in generating comovement of quantities in our model, and accounts for a large fraction of the fluctuations in economic activity. In response to the shock, consumption, business investment and both types of inventory investment all rise. The goods shock spills over to the service sector (over and above the effect caused by the correlation of the shocks) because it facilitates the production of fixed capital that is then used in the service sector. The goods technology shock also accounts for a non-negligible fraction of the fluctuations in both types of inventory investment - around 11-12 percent of their asymptotic variance. The responses of output and input inventory investment are, as a proportion of the respective stocks, larger than the one for fixed investment, relative to the fixed capital stock. For instance, the impact response of input inventories relative to business investment is two-thirds as big, when both variables are scaled by goods output. However, since the stock of business capital is about ten times larger than the stock of input inventories, the response of input inventories is between six and seven times larger than that of business investment, when both variables are scaled by their own steady-state stock. This is not surprising, since fixed capital is more costly to adjust. In this sense, inventories are an important part of the propagation mechanism, even if inventory investment counts for a small fraction of average output.
The second row shows the responses to a discount factor shock: this shock moves consumption and investment in opposite directions, and creates negative comovement between the output of each sector. It also contributes to fluctuations of input inventories - about 20 percent of the total variance.
The third row shows responses to a shock that shifts preferences away from output inventories towards goods consumption. The mechanics of this disturbance have the classic implications of a demand shock. Consumption of goods increases; inventories of finished goods fall; following the increase in demand, with a modest lag, the output of the goods sector increases while output of the service sector is only marginally affected (because the estimated elasticity of substitution implies an approximate separability in utility between goods and services). This preference-based shock accounts for a large share (about 80 percent) of the variance in output-inventory investment.
The fourth row shows the response to a shock that shifts preferences away from services and towards goods. While this shock, which basically reflects shifts in the composition of demand, accounts only for a small fraction of GDP fluctuations, it accounts for a quarter of the variance of output in the service sector. It also accounts for about half of the total variance of sectoral hours, because the shock causes a reallocation of labor from one sector to the other.
The fifth row plots the response to a positive shock to the efficiency of input inventories. This shock captures a large fraction (about two-thirds) of the variance in input-inventory investment. More efficient management of input inventories reduces their usage, increases the demand for fixed capital, and raises consumption (immediately) and output (with a slight delay). The shock also accounts for around 10 percent of the variance of fixed investment.
The last row plots responses to a technology shock in the service sector. While it is obviously important in explaining output of services, the effects of the shock in this sector transmit only marginally to the rest of the economy, since the services sector does not produce capital.
The literature has often looked at the cyclical properties of the inventory-target ratios, so Figure 5 reports the impulse responses of GDP and the inventory-target ratios to the four disturbances -- goods technology shock, discount factor shock, output-inventory shock, and input-inventory shock -- that cause most of the variation in GDP and inventories. Following the goods technology shock, the input-inventory target ratio is strongly countercyclical, as in the data. Input inventories rise, but, since business capital is costly to adjust, input inventories -- which are complementary to business capital -- do not rise enough, so that their ratio to GDP falls. The output inventory-target ratio is almost acyclical (as in the data), since the household prefers to maintain a relatively constant balance of output inventories to consumption. The second row plots the dynamics following the discount factor shock: since input inventories falls less than output, the input inventory to GDP ratio rises, again generating countercyclical behavior of the input inventory to target ratio. The third and fourth row plot the responses to the inventory-specific shocks. While these shocks are central to reproducing the volatility of inventory investment observed in the data, they mostly affect the inventory-target ratios through their effects on the numerators, without having large effects on output or consumption. In other words, inventory-specific shocks help fit the volatility of inventory investment, but they do not influence the cyclical properties of the inventory-target ratios, which are mostly driven by the aggregate productivity shocks.
We conclude this subsection with a note of caution. It is conceivable that our inventory shocks, which explain a large fraction of the volatility of both inventory types, mask an important endogenous propagation mechanism. We are however skeptical about this possibility. Our results suggest that inventory "innovations" are unlikely to be the driving forces of business cycles: this happens mostly because output inventory shocks generate substitution away from output inventories into consumption, so that their net effect on total output is small; and because input inventory shocks generate substitution away from input inventories into business investment, so that their net effect on total output is small. As a consequence, while the inventory shocks might have important consequences in terms of sectoral reallocation, they are not per se a driving force of business cycle fluctuations.
A Comparison between the Model and the Data. Figure 6 offers a check of the model's ability to reproduce key features of the data. We compare the model responses with the impulse responses from a VAR (with two lags) in the same variables. To enable a proper comparison, we use a Choleski ordering for both the VAR and the DSGE model, by ordering and orthogonalizing the DSGE model reduced form as in the VAR. As the Figure shows, most of the model's impulse responses lie within the 95% credible sets constructed from the reference VAR, thus suggesting that the model fits the data reasonably well, except perhaps for its inability to match some of the hump-shaped responses of variables to shocks. It should be borne in mind that the model is dominated by the VAR in terms of statistical fit. The log data density of our model is 4,073; the log data densities for unconstrained VAR models in the same observables range from 4,059 (for a VAR with one lag) to 4,331 (for a VAR with four lags). The VAR with two lags of Figure 6 has a log data density of 4,217. We use such VAR as a benchmark for our DSGE model, since it attains a higher posterior probability than our model.32 We also note that the inferior performance of the DSGE model is consistent with the findings of other papers where small-scale DSGE models without bells and whistles are compared with richly parameterized VAR models.33
In the first two columns of Table 8, we focus on some unconditional correlations in the data, and compare these with those of our estimated model. The central message is that our model accounts well for the volatility and comovement of the key model variables. In particular, the model simultaneously accounts for the volatility and procyclicality of inventory investment.34 It successfully mimics the greater volatility of input-inventory investment and its higher degree of procyclicality as compared to output-inventory investment. This result is true whether we look at the correlation between inventory investment and goods output, or the connection between changes in inventory investment and the change in GDP. Moreover, the model can reproduce the countercyclicality of the input-inventory target ratio, although not its magnitude, and the relative acyclicality of the output-inventory target ratio. Finally, the model successfully reproduces the relative volatilities of all types of investment.
To better gain insights into how our model achieves these results, it is useful to think of a reference model without inventory depreciation: this model is closer to Christiano's (1988) model with inventories as a factor of production. With this assumption, the model's ability to explain the behavior of inventories worsens. Figure 7 illustrates this result. With no inventory depreciation, the response of fixed investment is essentially the same as in the unrestricted model, but the responses of both types of inventory investment are essentially zero. The positive response of inventories - relative to this counterfactual - in our estimated model enhances the amplification mechanism of a given productivity shock: the impact response of GDP rises from 0.6 to 0.7 percent.
This counterfactual exercise shows that positive depreciation is an essential feature to fit the volatilities of inventory investment. Differential adjustment costs (greater for fixed capital) are also important: in their absence, the volatility of business investment would be implausibly large (we do not report this experiment to avoid cluttering the figure). Absent depreciation, output inventories would be smooth due to standard consumption smoothing reasons. The intuition as to why input inventories become less volatile than fixed capital, if they do not depreciate, can be most easily provided when there are no adjustment costs. In this case, input inventories would respond to a productivity shock less than capital because these shocks have a larger effect on the marginal return to fixed capital. This occurs because a productivity shock has the same effect, percentage-wise, on the marginal return to fixed capital and inventories. When the depreciation rate on inventories is zero, and fixed capital must be compensated for the higher depreciation rate with a higher return, the absolute effect of a shock to the marginal return to capital is much greater in absolute value. As a result, capital would be more responsive to productivity shocks than input inventories. The bottom two panels of Figure 7 suggest that this effect is not undone by allowing for greater adjustment costs for capital at our estimated parameter values.
5.2. Subsamples
Parameter Estimates. We re-estimate the model (with the same priors) over the
subperiods 1960:1-1983:4 and 1984:1-2007:4. We allow
![]()
![]()
![]() and
and ![]() to
differ across subsamples to match the different sample means for
the share of services in the economy and for the investment and the
inventory ratios relative to goods output (reported in Table 3). This
exercise allows us to investigate what lies at the root of the
decline in output volatility since 1984, and what role, if any,
inventories may have played in this regard. We should make clear,
however, that our approach can only address a subset of the
explanations of the Great Moderation that have been put forward in
the literature. For instance, we cannot properly address the role
of changes in policies in reducing output volatility.
to
differ across subsamples to match the different sample means for
the share of services in the economy and for the investment and the
inventory ratios relative to goods output (reported in Table 3). This
exercise allows us to investigate what lies at the root of the
decline in output volatility since 1984, and what role, if any,
inventories may have played in this regard. We should make clear,
however, that our approach can only address a subset of the
explanations of the Great Moderation that have been put forward in
the literature. For instance, we cannot properly address the role
of changes in policies in reducing output volatility.
Table 7 reports the
results of the subsample estimation. With few exceptions, the
full-sample parameter estimates lie between those for the two
subsamples. Regarding the structure of the economy, some
results are worth emphasizing. First, the depreciation rate for
output inventories, ![]() , is smaller in the second
part of the sample, as it goes from 5.6 to
4.6 percent. Second, output inventories and
consumption become less substitutable (
, is smaller in the second
part of the sample, as it goes from 5.6 to
4.6 percent. Second, output inventories and
consumption become less substitutable (![]() increases). Third, the utilization function for capital in the
service sector becomes more convex (
increases). Third, the utilization function for capital in the
service sector becomes more convex (![]() rises). Fourth, capital in the goods (service) sector becomes less
(more) costly to adjust in the second period.
rises). Fourth, capital in the goods (service) sector becomes less
(more) costly to adjust in the second period.
It is difficult to provide exhaustive explanations for the
changes in these "deep" parameters of the model. Potential
reasons for the lower estimate of the depreciation rate ![]() might be a change in the inventory mix or better
inventory management in general. It is not clear how to interpret
the change in adjustment costs for fixed capital, although the
higher costs in the service sector might reflect:
(1) the increased weight of
innovative investment in the second subperiod and the greater
associated costs in terms of learning and disruption; or
(2) higher sector (or firm)
specificity of capital goods.
might be a change in the inventory mix or better
inventory management in general. It is not clear how to interpret
the change in adjustment costs for fixed capital, although the
higher costs in the service sector might reflect:
(1) the increased weight of
innovative investment in the second subperiod and the greater
associated costs in terms of learning and disruption; or
(2) higher sector (or firm)
specificity of capital goods.
We also find important changes in the parameters measuring the stochastic processes for technology and preferences. The most important result is that the volatility of general technology shocks in the goods and service sectors falls. They also become less correlated with each other. There is also a decrease in the volatility of the input-inventory shock, consistent with the idea that new methods of inventory management adopted since the early 1980s have made it easier to control the level of input inventories in efficiency units. However the decrease is not large.
Standard Deviations, Correlations and Variance Decompositions. Table 8 shows that, across the two subperiods, the model can reproduce the volatility decline in most macroeconomic aggregates. For instance, in our data, the standard deviation of detrended GDP falls by 0.77 percentage points between the 1960-1983 and 1984-2007 subperiods (from 1.89 to 1.12 percent). Our subsample estimates match the volatility decline, showing a reduction in the standard deviation of GDP of 0.76 percentage points. Our model also captures the decrease in the volatility of input inventories but not the one of output inventories. The model can also account for the reduced procyclicality of output inventory investment after 1983.
Table 9 shows how, in the second subperiod, output (input) inventory movements depend more (less) on their own innovations. As for the other variables, a larger fraction of the volatility in economic activity is due to demand-preference shocks: in the second part of the sample, the share of GDP variance that can be accounted for by discount rate shocks rises from about 15 percent to about 40 percent.
5.3. The role of Inventories in the Great Moderation
Prompted by the preceding results, a natural question is to what extent the reduced volatility of economic activity is due to a reduction in the volatility of the shocks -- the "good luck" hypothesis -- or to a change in the economy's structure. To answer this question, we partition the factors that can affect the implied volatility of the model variables into the following three sets:
- Parameters that are estimated without using information on the steady-state ratios. This parameter set includes the autocorrelation of the shocks, the inventory depreciation rates, the elasticities of substitution, the adjustment costs, and the capital utilization parameters.
- Parameters that are determined using steady-state information.
When we estimate the model across subsamples, we choose values of
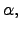
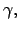
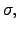
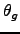 , and
, and 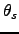 that match the values of the ratios of input
inventories to output and capital investment to output, plus the
share of services in GDP, for each subperiod, conditional on the
depreciation rates and the elasticities of substitution.
that match the values of the ratios of input
inventories to output and capital investment to output, plus the
share of services in GDP, for each subperiod, conditional on the
depreciation rates and the elasticities of substitution. - Parameters that measure the unconditional volatility of the shocks.
Table 10 breaks down how the three sets of parameters above contribute to the reduction in volatility captured by the model. Using the estimates obtained from the 1960-1983 sample as a reference point, we change one estimated parameter at a time, setting it to the value estimated for the 1984-2007 sample. This way, we can approximately measure each parameter's contribution to the change in volatility. The main result is that most of the reduction in GDP volatility is attributable to the reduction in the volatility of the underlying shocks -- especially of the technology shock in the goods sector. This is consistent with the conclusions reached by Stock and Watson (2003) and Justiniano and Primiceri (2008). By themselves, smaller shocks can explain a reduction in GDP volatility of 0.52 percentage points (as measured by the standard deviation), compared to an estimated total decline of 0.76 percentage points. Most of the remainder is attributable to larger capacity-utilization costs, as well as the increased importance (share) of services in the economy. The latter, for instance, accounts for a quarter in the reduction in GDP volatility.
What about the role inventories may have played in the Great
Moderation? There is a reduction in the volatility of
input-inventory shocks, but it is small and it accounts only for
about 0.01 percentage points of the total reduction
in volatility of GDP and goods output. We also consider the effect
of changes in ![]()
![]()
![]()
![]() , and
, and
![]() implied by the changes in the
steady-state ratios. Consider, for instance, the consequences of
setting
implied by the changes in the
steady-state ratios. Consider, for instance, the consequences of
setting
![]() equal to its post-1984
average value, while keeping all the other ratios and parameters -
except
equal to its post-1984
average value, while keeping all the other ratios and parameters -
except ![]()
![]()
![]()
![]() , and
, and ![]() - at the pre-1984 level: the decline in
- at the pre-1984 level: the decline in
![]() is likely to be an indicator
of better inventory control methods such as "just-in-time" or "flexible manufacturing systems." Such decline accounts for
approximately 0.04 percentage points of the decrease in
the volatility of GDP and 0.09 percentage
points of the decrease in the volatility of output of the goods
sector.
is likely to be an indicator
of better inventory control methods such as "just-in-time" or "flexible manufacturing systems." Such decline accounts for
approximately 0.04 percentage points of the decrease in
the volatility of GDP and 0.09 percentage
points of the decrease in the volatility of output of the goods
sector.
To summarize, our estimated model suggests that reductions in the volatility of the model's technological shocks account for most of the reduction in GDP volatility -- a result generally consistent with the "good luck" hypothesis. Structural changes in the model's parameters have contributed to the reduction in GDP volatility by a smaller amount, working primarily through parameter changes that reduced the volatility of fixed investment. There is only a small role for inventory investment in the Great Moderation, associated with the decrease in the input inventories to output ratio. This conclusion is consistent with Khan and Thomas (2007), who consider how aggregate volatility changes in a general equilibrium model following a decrease in fixed ordering costs; and with Wen (2009), who shows that a decrease in idiosyncratic uncertainty and information frictions, which in turn reduces the level of inventories held by firms, does not lead to a decline in aggregate volatility.
6. Input and Output Inventories: More on Motivation and Extensions
In this section we return to the arguments we have used to motivate the holding of inventories. We first explore in more detail the equivalence of the choice of introducing inventories in the utility function with the choice of including them in the budget constraint on the basis of the assumption that they affect shopping costs. We then provide a different model for input inventories that focuses on the notion that inventories are "used up" during the production process.
6.1. he Role of Inventories in Reducing Shopping Costs
Our formulation that treats output inventories as a good
entering the utility function is convenient, simple and has
interesting empirical properties. For example, it can rationalize
why the ratio between output inventories and consumption is
essentially acyclical, since the consumer (absent large
fluctuations in the user cost of holding inventories) prefers to
hold a relatively constant ratio of ![]() over
over
![]() over time. However, one might feel
uncomfortable about putting output inventories in the utility
function, when what output inventories really do is to make the
consumer life easier by reducing shopping costs. This argument
means that output inventories should essentially affect the
consumer through the budget constraint, rather than the utility
function. We can show that -- at least for an empirically relevant,
simpler version of the utility function -- our model is equivalent
to a model where output inventories do not enter the utility
function at all, but affect the consumer via the budget constraint
by affecting the cost of purchasing goods. The argument follows
Feenstra (1986) who discusses the functional equivalence of
including money in the utility function or liquidity costs in the
budget constraint. These liquidity costs are decreasing in
inventories and increasing in goods consumption and the functional
form of the shopping cost function can be explicitly derived.
Assume a unit elasticity of substitution between services and good
consumption, as suggested by our estimates. In this case our
utility function becomes:
over time. However, one might feel
uncomfortable about putting output inventories in the utility
function, when what output inventories really do is to make the
consumer life easier by reducing shopping costs. This argument
means that output inventories should essentially affect the
consumer through the budget constraint, rather than the utility
function. We can show that -- at least for an empirically relevant,
simpler version of the utility function -- our model is equivalent
to a model where output inventories do not enter the utility
function at all, but affect the consumer via the budget constraint
by affecting the cost of purchasing goods. The argument follows
Feenstra (1986) who discusses the functional equivalence of
including money in the utility function or liquidity costs in the
budget constraint. These liquidity costs are decreasing in
inventories and increasing in goods consumption and the functional
form of the shopping cost function can be explicitly derived.
Assume a unit elasticity of substitution between services and good
consumption, as suggested by our estimates. In this case our
utility function becomes:
![]()
with ![]() still equal to
still equal to
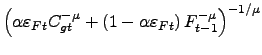 . It can be shown that this model yields the same equilibrium
conditions as a model where inventories do not appear in the
utility function, and the latter is written as:35
. It can be shown that this model yields the same equilibrium
conditions as a model where inventories do not appear in the
utility function, and the latter is written as:35
![]() ,
,
where ![]() denotes goods consumption net of shopping costs, so that
denotes goods consumption net of shopping costs, so that
![]() The term
The term
![]() denotes the
shopping cost function that appears an additional argument in the
budget constraint, equation (2.4), and can be
shown to take the following form:
denotes the
shopping cost function that appears an additional argument in the
budget constraint, equation (2.4), and can be
shown to take the following form:
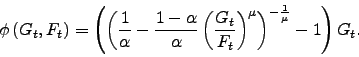
|
(6.1) |
At our model estimates for ![]()
![]() (and given the steady-state ratios implied by the data),
the function
(and given the steady-state ratios implied by the data),
the function
![]() is decreasing
and convex in the stock of output inventories. Moreover, one can
estimate the transaction costs to be equal to approximately
2 percent of total goods output, which seems
a reasonable number.
is decreasing
and convex in the stock of output inventories. Moreover, one can
estimate the transaction costs to be equal to approximately
2 percent of total goods output, which seems
a reasonable number.
6.2. A "Usage Only" Model of Input Inventories
As we mentioned above, our model allows for a convenience yield of holding a larger stock of input inventories in producing value added. This convenience yield accrues in production over and above the usage of inventories, which is maximized out in deriving the value added production function. In other words, by focusing on value added (gross output minus materials used), one pushes the material usage decision in the background, but does not abstract from it.
In this section we outline and analyze an alternative model with no additional convenience yield and that focuses on the usage of material in producing gross output.36 This model is based on the following assumptions: (1) Only inventories that are "used up" augment society's ability to produce more gross output; (2) The usage of inventories depends upon the beginning of period stock. These considerations lead to a production function for gross output of the form:
| (6.2) |
where ![]() denotes the utilization rate of
inventories, so that the term
denotes the utilization rate of
inventories, so that the term ![]() denotes
inventories used in production. We also assume that higher
utilization of inventories leads to a greater wastage, and hence,
to higher depreciation in a convex fashion. As a result, the total
"depreciation rate" for inventories is now the sum of three
parts:
denotes
inventories used in production. We also assume that higher
utilization of inventories leads to a greater wastage, and hence,
to higher depreciation in a convex fashion. As a result, the total
"depreciation rate" for inventories is now the sum of three
parts:
| (6.3) |
where ![]() is a fixed component of the
depreciation rate unrelated to usage and reflecting wastage and/or
linear holding costs; the term
is a fixed component of the
depreciation rate unrelated to usage and reflecting wastage and/or
linear holding costs; the term ![]() captures the
usage of materials (proportional to the stock), and the term
captures the
usage of materials (proportional to the stock), and the term
![]() describes the additional component of
wastage that depends upon utilization in a convex fashion: this
component reflects the idea that, at the margin, a higher or faster
usage might provoke collateral damage to the remaining parts of the
stock that are not directly used in production. Namely, we assume
that
describes the additional component of
wastage that depends upon utilization in a convex fashion: this
component reflects the idea that, at the margin, a higher or faster
usage might provoke collateral damage to the remaining parts of the
stock that are not directly used in production. Namely, we assume
that
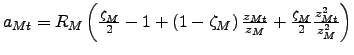 , where
, where
![]() . The
function
. The
function ![]() is convex in
is convex in ![]() and
is normalized so that it equals zero when
and
is normalized so that it equals zero when ![]() equals the optimal, steady-state choice
equals the optimal, steady-state choice ![]() . 37 In
absence of direct estimates of the fraction of the stock of input
inventories that is used in production, we set the steady-state,
optimal utilization rate at 20 percent when taking the model to the
data. The resource constraint is now:
. 37 In
absence of direct estimates of the fraction of the stock of input
inventories that is used in production, we set the steady-state,
optimal utilization rate at 20 percent when taking the model to the
data. The resource constraint is now:
where ![]() denotes total adjustment costs. Value
added in the goods sector is then obtained by subtracting materials
used,
denotes total adjustment costs. Value
added in the goods sector is then obtained by subtracting materials
used, ![]() from gross output,
from gross output, ![]() .
.
We then estimate the model using the same priors of our baseline
model (we estimate an additional parameter, ![]() which measures the convexity of the utilization
function). Table 11 reports the estimates. Figure 8 compares the impulse responses to a
technology shock in the goods sector between the baseline model and
the usage only model. The overall conclusion is that the two models
yield similar impulse response functions and, more in general, have
very similar implications for the business cycle properties of the
variables of interest. One interesting difference is that the "usage only" model generates a high steady-state return on the
stock of inventories - this happens because it implies a higher
depreciation rate on the stock of inventories that is used in
production -, thus enhancing somewhat the response of inventories
to productivity shocks. While valuable and yielding some
interesting results, this model is based on a set of assumptions
that some would regard more stringent that those of our preferred
model. Specifically, materials purchased in the period cannot be
used immediately in production. Moreover, the assumption that
greater use leads to greater depreciation in a convex fashion may
be questioned.
which measures the convexity of the utilization
function). Table 11 reports the estimates. Figure 8 compares the impulse responses to a
technology shock in the goods sector between the baseline model and
the usage only model. The overall conclusion is that the two models
yield similar impulse response functions and, more in general, have
very similar implications for the business cycle properties of the
variables of interest. One interesting difference is that the "usage only" model generates a high steady-state return on the
stock of inventories - this happens because it implies a higher
depreciation rate on the stock of inventories that is used in
production -, thus enhancing somewhat the response of inventories
to productivity shocks. While valuable and yielding some
interesting results, this model is based on a set of assumptions
that some would regard more stringent that those of our preferred
model. Specifically, materials purchased in the period cannot be
used immediately in production. Moreover, the assumption that
greater use leads to greater depreciation in a convex fashion may
be questioned.
7. Conclusions
The most important lesson of this paper is that an estimated DSGE model can incorporate inventories and fit the data reasonably well with plausible and interesting estimates of structural parameters that help characterize the role of input and output inventories. Each type of inventory investment plays a logically different role in the model and exhibits different degrees of volatility and procyclicality. The model can replicate the observed volatility and cyclicality of both input and output inventory investment, and particularly the fact that input-inventory investment is more volatile and procyclical than output-inventory investment. Moreover, the model can reproduce the countercyclicality of the input-inventory target ratio, and the relative acyclicality of the output-inventory target ratio. This finding represents a step forward relative to previous attempts to model inventories in DSGE models, especially given our model's ability to fit the data. Thus, our model provides a new, more expansive, and data-consistent framework for analyzing the cyclical properties of inventories.
When estimated across two subperiods, 1960-1983 and 1984-2007, the model captures the volatility reduction observed in aggregate variables, as well as the decline in procyclicality of output-inventory investment. However, the model suggests that the bulk of the Great Moderation is explained primarily by a reduction in the volatility of the technology shock in the goods sector (and of the discount rate shock). The reduction in the volatility of inventory shocks accounts for only a small portion of the decrease in output volatility. Nevertheless, the model's framework identifies several dimensions along which the economy's structure changed in an economically important manner, and contributed to the reduction in GDP volatility. Some of these structural changes are related to inventory behavior and influence the propagation role inventories play in the macroeconomy, but, at best, they have only played a minor role in accounting for the reduced volatility of output.
These conclusions are based on an estimated two-sector general equilibrium model that includes novel features such as the distinction between goods-producing and the services-producing sectors according to their inventory-holding behavior, and the distinction between input and output inventories. Non-zero inventory depreciation, which in the model provides an incentive to adjust inventories more in response to shocks, is another novel feature that is empirically important.
Despite the additional complexity, our model precludes an examination of certain aspects of inventory behavior that may be important to understanding business cycle fluctuations. First, we eschewed a richer examination of the stage-of-fabrication structure within the goods sector. For example, classifying inventories into only two types abstracts from the supply and distribution chains that pervade the actual input-output structure of the goods sector and probably play a vital role in the propagation of shocks. A second issue is that the model is silent on how markup variations and nominal features matter for inventory behavior and business cycles. Some inventory research examines how markup variation or interest rate policies influence inventory behavior. However, this work with nominal rigidities generally has not incorporated the inventory distinction in a general equilibrium setting that we have advanced here. Third, we have sidestepped the micro-founded motivation for firms' holding of finished goods (output inventories): by focusing on the value of output inventories to households through utility and concentrating on the social planner's solution, we have not taken up a more detailed examination of the determinants of a firm's decision to hold output inventories in a market environment. We plan to address these issues in future work, and we hope that others will too.
Bibliography
Ahmed, Shaghil, Andrew Levin, and Beth Anne Wilson. (2004) "Recent U.S. Macroeconomic Stability: Good Policies, Good Practices, or Good Luck?" Review of Economics and Statistics, 86(3), August, 824-832.
An, Sungbae, and Frank Schorfheide (2007) "Bayesian analysis of DSGE models" , Econometric Reviews, 26(2), 113-172
Arias, Andres, Gary D. Hansen, and Lee E. Ohanian. (2006) "Why Have Business Cycle Fluctuations Become Less Volatile?" National Bureau of Economic Research (Cambridge, MA), Working Paper No. 12079, March.
Baxter, Marianne and Robert G. King. (1999) "Measuring Business Cycles: Approximate Band-Pass Filters for Economic Time Series." Review of Economics and Statistics, 81(4), November, 575-593.
Bils, Mark and James A. Kahn. (2000) "What Inventory Behavior Tells Us about Business Cycles." American Economic Review, 90(3), June, 458-481.
Bivin, David. (1993) "The Influence of Inventories on Output and Prices: A Stage of Fabrication Approach." Journal of Macroeconomics, 15 (4), Fall, 627-651.
Blanchard, Olivier and John Simon. (2001) "The Long and Large Decline in U.S. Output Volatility." Brookings Papers on Economic Activity, 2001:1, 135-164.
Blinder, Alan S. and Louis J. Maccini. (1991) "Taking Stock: A Critical Assessment of Recent Research on Inventories." Journal of Economic Perspectives, 5(1), Winter, 73-96.
Boileau, Martin and Marc-Andre Letendre.(2009) "Inventory, Sticky Prices and the Persistence of Output and Inflation." Applied Economics, 1-14.
Chang, Yongsung, Andreas Hornstein, and Pierre-Daniel G. Sarte. (2009) "On the Employment Effects of Productivity Shocks: The Role of Inventories, Demand Elasticity, and Sticky Prices." Journal of Monetary Economics, 56, 328-343.
Chirinko, Robert S. (1993) "Business Fixed Investment Spending: Modeling Strategies, Empirical Results, and Policy Implications." Journal of Economic Literature, 31(4), December, 1875-1911.
Christiano, Lawrence J. (1988) "Why Does Inventory Investment Fluctuate So Much?" Journal of Monetary Economics, 21(2/3), March-May, 247-280.
Christiano, Lawrence J. and Terry J. Fitzgerald. (1989) "The Magnitude of the Speculative Motive for Holding Inventories in a Real Business Cycle Model." Federal Reserve Bank of Minneapolis Discussion Paper No. 10, January.
Coen-Pirani, Daniele. (2004) "Markups, Aggregation, and Inventory Adjustment." American Economic Review, 94(5), December, 1328-1353.
Conesa, Juan Carlos, Timothy J. Kehoe, and Kim J. Ruhl (2007) " Modeling Great Depressions: The Depression in Finland in the 1990s" in Timothy J. Kehoe and Edward C. Prescott, eds., Great Depressions of the Twentieth Century, Federal Reserve Bank of Minneapolis.
Cooley, Thomas and Edward Prescott. (1995), "Economic growth and business cycles" , in Cooley, T. (ed.), Frontiers of Business Cycle Research, Princeton University Press: Princeton, 1-38.
Cooper, Russell and John C. Haltiwanger. (1990) "Inventories and the Propagation of Sectoral Shocks." American Economic Review, 80(1), March, 170-190.
Davis, Steven J., and James A. Kahn. (2008). "Interpreting the Great Moderation: Changes in the Volatility of Economic Activity at the Macro and Micro Levels," Journal of Economic Perspectives, 22(4), Fall, 155-80.
Del Negro, Marco, and Frank Schorfheide. (2004). "Priors from General Equilibrium Models for VARs." International Economic Review, 45(2), 643-73.
Del Negro, Marco and Frank Schorfheide (2008), "Forming Priors for DSGE Models (and How it Affects the Assessment of Nominal Rigidities)." Journal of Monetary Economics, 55(7), October, 1191-1208.
Doan, Thomas (2004), Rats Manual, Version 6, Estima, Evanston, IL.
Feenstra, Robert C. (1986) "Functional Equivalence between Liquidity Costs and the Utility of Money," Journal of Monetary Economics, 17(2), March, 271-291.
Feldstein, Martin S. and Alan Auerbach. (1976) "Inventory Behavior in Durable-Goods Manufacturing: The Target-Adjustment Model." Brookings Papers on Economic Activity, 1976:2, 351-396.
Fisher, Jonas D. M. and Andreas Hornstein. (2000) "(S,s) Inventory Policies in General Equilibrium." Review of Economic Studies, 67(1), January, 117-145.
Gomme, Paul, and Peter Rupert. (2007). "Theory, Measurement and Calibration of Macroeconomic Models." Journal of Monetary Economics, 54(2), March, 460-497.
Greenwood, Jeremy, Zvi Hercowitz, and Per Krusell. (2000) "The Role of Investment-Specific Technological Change in the Business Cycle." European Economic Review, 44(1), January, 91-115.
Hansen, Gary D. (1985) "Indivisible Labor and the Business Cycle." Journal of Monetary Economics , 16(3), November, 309-327.
Hayashi, Fumio, and Edward C. Prescott. (2002) "The 1990s in Japan: A Lost Decade." Review of Economic Dynamics, 5 (January), 206-35.
Hornstein, Andreas and Pierre-Daniel Sarte. (2001) "Sticky Prices and Inventories: Production Smoothing Reconsidered." Federal Reserve Bank of Richmond Working Paper No. 01-6, March.
Huang, Kevin X. D. and Zheng Liu. (2001) "Production Chains and General Equilibrium Aggregate Dynamics." Journal of Monetary Economics, 48(2), October, 437-462.
Humphreys, Brad R., Louis J. Maccini, and Scott Schuh. (2001) "Input and Output Inventories." Journal of Monetary Economics, 47(2), April, 347-375.
Husted, Steven and Tryphon Kollintzas. (1987) "Linear Rational Expectations Equilibrium Laws of Motion for Selected U.S. Raw Material Imports." International Economic Review, October, 28(3), 651-70.
Irvine, F. Owen and Scott Schuh. (2005a) "The Roles of Comovement and Inventory Investment in the Reduction of Output Volatility." Federal Reserve Bank of Boston Working Paper No. 05-09, July.
Irvine, F. Owen and Scott Schuh. (2005b) "Inventory Investment and Output Volatility." International Journal of Production Economics, 93-94(0), January, Special Issue, 75-86.
Jung, Yongseung and Tack Yun. (2006) "Monetary Policy Shocks, Inventory Dynamics, and Price-Setting Behavior." Federal Reserve Bank of San Francisco Working Paper 2006-02, August.
Justiniano, Alejandro and Giorgio E. Primiceri (2008) "The Time-Varying Volatility of Macroeconomic Fluctuations," American Economic Review, 98(3), 604-41, June.
Kahn, James A. (1987) "Inventories and the Volatility of Production." American Economic Review , 77(4), September, 667-679.
Kahn, James A. and Margaret M. McConnell. (2005) "Making Sense of Inventory-Sales Ratios." Unpublished working paper, Federal Reserve Bank of New York, August.
Kahn, James A., Margaret M. McConnell, and Gabriel Perez-Quiros. (2002) "On the Causes of the Increased Stability of the U.S. Economy." Economic Policy Review, 8(1), Federal Reserve Bank of New York, May, 183-202.
Khan, Aubhik, and Julia K. Thomas. (2007) "Inventories and the Business Cycle: An Equilibrium Analysis of (S, s) Policies." American Economic Review, 97(4), September, 1165-88.
Kimura, Takeshi, and Kyosuke Shiotani. (2009) "Stabilized Business Cycles with Increased Output Volatility at High Frequencies," Journal of the Japanese and International Economies, 23(1), March, 1-19..
Kongsamut, Piyabha, Sergio Rebelo and Danyang Xie. (2001) "Beyond Balanced Growth," Review of Economic Studies, 68(4), October, 869-82.
Kuznets, Simon. (1957) "Quantitative Aspects of the Economic Growth of Nations II: Industrial Distribution of National Product and Labor Force." Economic Development and Cultural Change V (4, supplement), 3-111.
Kydland, Finn E. and Edward C. Prescott. (1982) "Time to Build and Aggregate Fluctuations." Econometrica, 50(6), November, 1345-1370.
Leduc, Sylvain and Keith Sill. (2006) "Monetary Policy, Oil Shocks, and TFP: Accounting for the Decline in U.S. Volatility." Board of Governors of the Federal Reserve System, International Finance Discussion Paper No. 873.
Lee, Donghoon and Kenneth I. Wolpin. (2006) "Intersectoral Labor Mobility and the Growth of the Service Sector." Econometrica, 74(1), January, 1-46.
Lovell, Michael C. (1961) "Manufacturers' Inventories, Sales Expectations, and the Acceleration Principle." Econometrica, 29(3), July, 293-314.
Maccini, Louis J. and Adrian Pagan. (2007) "Exploring the Role of Inventories in Business Cycles." Unpublished working paper, John Hopkins University.
Marquis, Milton and Bharat Trehan. (2005a) "Accounting for the Secular `Decline' of U.S. Manufacturing." Federal Reserve Bank of San Francisco Working Papers in Applied Economic Theory and Econometrics No. 2005-18, September.
Marquis, Milton and Bharat Trehan. (2005b) "On Using Relative Prices to Measure Capital-specific Technological Progress." Federal Reserve Bank of San Francisco Working Papers in Applied Economic Theory and Econometrics No. 2005-02.
McConnell, Margaret M. and Gabriel Perez-Quiros. (2000) "Output Fluctuations in the United States: What Has Changed Since the Early 1980s?" American Economic Review, 90(5), December, 1464-1476.
Pindyck, Robert S. (1994) "Inventories and the Short-Run Dynamics of Commodity Prices." RAND Journal of Economics, 25(1), Spring, 141-159.
Ramey, Valerie A. (1989) "Inventories as Factors of Production and Economic Fluctuations." American Economic Review, 79(3), June, 338-354.
Ramey, Valerie A. and Daniel J. Vine. (2004) "Why Do Real and Nominal Inventory-Sales Ratios Have Different Trends?" Journal of Money, Credit, and Banking, 36(5), October, 959-963.
Rogerson, Richard. (1988) "Indivisible Labor, Lotteries and Equilibrium." Journal of Monetary Economics, 21(1), January, 3-16.
Rossana, Robert J. (1990) "Interrelated Demands for Buffer Stocks and Productive Inputs: Estimates for Two-Digit Manufacturing Industries." Review of Economics and Statistics, 72(1), February, 19-29.
Schorfheide, Frank (2000). "Loss Function-Based Evaluation of DSGE Models," Journal of Applied Econometrics, 15(6), 645-670.
Stock, James H. and Mark W. Watson. (2003) "Has the Business Cycle Changed and Why?" In NBER Macroeconomics Annual 2002, edited by Mark Gertler and Kenneth Rogoff, 159-218. Cambridge and London: MIT Press.
Stock, James R. and Douglas Lambert. (2001), Strategic Logistics Management, 4th Ed., McGraw-Hill Irwin.
Smets, Frank and Raf Wouters. (2003) "An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area." Journal of the European Economic Association , 1(5), September, 1123-1175.
Smets, Frank, and Raf Wouters. 2007. "Shocks and Frictions in U.S. Business Cycles." American Economic Review, 97(3): 586-606.
Wen, Yi. (2005a) "The Multiplier: A General equilibrium Analysis of Multi-Stage-Fabrication Economy with Inventories." Federal Reserve Bank of St. Louis Working Paper No. 2005-046A, June.
Wen, Yi. (2005b) "Understanding the Inventory Cycle." Journal of Monetary Economics, 52 (8), November, 1533-1555.
Wen, Yi. (2009) "Input and Output Inventory Dynamics." Federal Reserve Bank of St. Louis Working Paper No. 2008-008B, February.
Whelan, Karl. (2002) "A Guide to U.S. Chain Aggregated NIPA Data." Review of Income and Wealth , 48(2), June, 217-233.
Whelan, Karl. (2003) "A Two-Sector Approach to Modeling U.S. NIPA Data." Journal of Money, Credit, and Banking, 35(4), August, 627-656.
Table 1a: Sector Definitions and Output Shares
NAICS Industries | GDP Share (%) |
|---|---|
Agriculture |
1.0 |
Mining |
1.2 |
Manufacturing |
14.5 |
Construction |
4.4 |
Utilities |
1.9 |
Wholesale Trade |
6.0 |
Retail Trade |
6.7 |
Transportation |
3.1 |
Information |
4.7 |
FIREL |
19.7 |
Services, business |
11.6 |
Education & Health |
6.9 |
Leisure |
3.6 |
Other services |
2.3 |
Government |
12.3 |
Table 1b: Sector Definitions and Output Shares - Sectors (%)
Model | NIPA |
|---|---|
Goods (35.9) [Excluding government (40.1)] |
Goods (21.2) |
Services (51.8) [Excluding government (59.1)] |
Services (78.8) |
Government (12.3) |
Notes: FIREL denotes Finance, Insurance, Real Estate, and Leasing.
Table 2: Inventory Stock Definitions and Shares
Model Inventories: Input & Output | Model Inventories: Stage-of-Fabrication | NIPA Inventories (NAICS): Industry | 2000 Share (in percent) |
|---|---|---|---|
Input (73.4%) | Raw Materials (18.9%) | Agriculture | 8.6 |
Input (73.4%) | Raw Materials (18.9%) | Mining, utilities, construction (MUC) | 2.9 |
Input (73.4%) | Raw Materials (18.9%) | Mining, utilities, construction (MUC): Mining | n.a. |
Input (73.4%) | Raw Materials (18.9%) | Mining, utilities, construction (MUC): Utilities | n.a. |
Input (73.4%) | Raw Materials (18.9%) | Mining, utilities, construction (MUC): Construction | n.a. |
Input (73.4%) | Raw Materials (18.9%) | Other | 7.4 |
Input (73.4%) | Work-in-process (54.5%) | Manufacturing | 31.1 |
Input (73.4%) | Work-in-process (54.5%) | Materials and supplies | 11.0 |
Input (73.4%) | Work-in-process (54.5%) | Materials and supplies: Work-in-process | 8.9 |
Input (73.4%) | Work-in-process (54.5%) | Materials and supplies: Finished goods | 11.1 |
Input (73.4%) | Work-in-process (54.5%) | Materials and supplies: Wholesale trade | 23.4 |
OUtput (26.6%) | Finished goods (26.6%) | Retail trade | 26.6 |
Table 3: Target Steady-State Ratios of the Model
| Full sample | 1960-1983 | 1984-2007 | |
|---|---|---|---|
| 0.34 | 0.30 | 0.36 | |
| 1.16 | 1.37 | 1.07 | |
| 4.59 | 5.26 | 4.29 | |
| 9.32 | 8.22 | 9.82 | |
| | 0.81 | 0.54 | 0.88 |
Notes: Output is expressed in quarterly units. The last row is
the ratio of nominal output of services over nominal output of the
goods sector. The capital output ratios are calculated from the
investment-to-output ratios, assuming depreciation rates of
![]() and
and
![]() .
.
Table 4: Prior Distributions and Parameter Estimates, Full Sample
| Prior: Mean | Prior: Distribution | Prior: St.dev. | Full Sample: Mean | Full Sample: 5% | Full Sample: 95% | |
|---|---|---|---|---|---|---|
| 0.020 | beta | 0.01 | 0.081 | 0.055 | 0.110 | |
| 0.020 | beta | 0.01 | 0.022 | 0.013 | 0.032 | |
| 1.500 | norm | 0.5 | 1.30 | 0.88 | 1.74 | |
| 1.500 | norm | 0.5 | 3.60 | 3.09 | 4.13 | |
| 1.500 | norm | 0.5 | 1.03 | 1.01 | 1.07 | |
| | 0.500 | beta | 0.2 | 0.03 | 0.02 | 0.04 |
| | 0.500 | beta | 0.2 | 0.20 | 0.14 | 0.35 |
| | 0.500 | beta | 0.2 | 0.47 | 0.28 | 0.65 |
| | 0.500 | beta | 0.2 | 0.02 | 0.01 | 0.04 |
| 0.750 | beta | 0.1 | 0.86 | 0.83 | 0.90 | |
| | 0.750 | beta | 0.1 | 0.93 | 0.90 | 0.96 |
| 0.750 | beta | 0.1 | 0.92 | 0.86 | 0.96 | |
| | 0.750 | beta | 0.1 | 0.86 | 0.80 | 0.91 |
| 0.750 | beta | 0.1 | 0.94 | 0.91 | 0.96 | |
| 0.750 | beta | 0.1 | 0.94 | 0.91 | 0.96 | |
| | 0.500 | beta | 0.2 | 0.95 | 0.89 | 0.99 |
| | 0.500 | beta | 0.2 | 0.80 | 0.62 | 0.94 |
| 0.025 | invg | Inf | 1.49% | 1.29% | 1.72% | |
| | 0.025 | invg | Inf | 3.80% | 2.57% | 5.59% |
| 0.01 | invg | Inf | 0.33% | 0.25% | 0.42% | |
| | 0.01 | invg | Inf | 0.65% | 0.54% | 0.80% |
| 0.05 | invg | Inf | 10.34% | 8.00% | 13.18 | |
| 0.025 | invg | Inf | 1.52% | 1.21% | 1.92% | |
| 0.50 | norm | 0.25 | 0.72 | 0.65 | 0.78 |
Table 5: Values of the Share Parameters Implied by the Estimation Results
| Full sample | 1960-1983 | 1984-2007 | |
|---|---|---|---|
| 0.9668 | 0.9768 | 0.9788 | |
| 0.4710 | 0.5686 | 0.4407 | |
| 0.9926 | 0.9843 | 0.9856 | |
| 0.1665 | 0.1934 | 0.1570 | |
| 0.3268 | 0.4408 | 0.3237 |
Table 6: Variance Decompositions of the Model, Full Sample
| | | |||||
|---|---|---|---|---|---|---|
| | 65.9 | 28.4 | 2.1 | 2.3 | 1.3 | 0.001 |
| | 1.1 | 0.4 | 0.01 | 26.4 | 0.1 | 72.0 |
| 30.3 | 60.5 | 0.1 | 0.3 | 8.9 | 0.0 | |
| | 11.3 | 3.7 | 83.4 | 0.4 | 1.3 | 0.0 |
| | 12.4 | 21.3 | 0.1 | 0.0 | 66.2 | 0.0 |
| | 64.6 | 10.8 | 5.6 | 13.4 | 5.6 | 0.01 |
| 66.3 | 26.0 | 1.4 | 0.01 | 0.8 | 5.5 |
Notes: For each variable, the columns indicate the fractions of the total variance explained by each shock. Variables with a hat are scaled by their steady-state value. Variables with a tilde are scaled by steady-state goods output.
Table 7: Parameter Estimates, Subsamples
| Prior | Prior | Prior | 1960-1983: Mean | 1960-1983: 5% | 1960-1983: 95% | 1984-2007: Mean | 1984-2007: 5% | 1984-2007: 95% | |
|---|---|---|---|---|---|---|---|---|---|
| 0.020 | beta | 0.01 | 0.056 | 0.033 | 0.082 | 0.046 | 0.023 | 0.074 | |
| 0.020 | beta | 0.01 | 0.022 | 0.013 | 0.034 | 0.022 | 0.013 | 0.035 | |
| 1.500 | norm | 0.5 | 1.13 | 0.64 | 1.62 | 1.40 | 0.79 | 2.03 | |
| 1.500 | norm | 0.5 | 3.13 | 2.57 | 3.70 | 3.08 | 2.67 | 3.56 | |
| 1.500 | norm | 0.5 | 0.93 | 0.82 | 0.98 | 1.16 | 1.07 | 1.31 | |
| | 0.500 | beta | 0.2 | 0.02 | 0.01 | 0.03 | 0.04 | 0.02 | 0.06 |
| | 0.500 | beta | 0.2 | 0.27 | 0.15 | 0.60 | 0.16 | 0.09 | 0.29 |
| | 0.500 | beta | 0.2 | 0.50 | 0.23 | 0.77 | 0.61 | 0.30 | 0.84 |
| | 0.500 | beta | 0.2 | 0.04 | 0.02 | 0.06 | 0.02 | 0.01 | 0.04 |
| 0.750 | beta | 0.1 | 0.84 | 0.79 | 0.89 | 0.92 | 0.86 | 0.98 | |
| | 0.750 | beta | 0.1 | 0.93 | 0.89 | 0.95 | 0.92 | 0.87 | 0.95 |
| 0.750 | beta | 0.1 | 0.95 | 0.90 | 0.98 | 0.94 | 0.89 | 0.97 | |
| | 0.750 | beta | 0.1 | 0.85 | 0.76 | 0.92 | 0.88 | 0.81 | 0.95 |
| 0.750 | beta | 0.1 | 0.95 | 0.92 | 0.97 | 0.97 | 0.95 | 0.98 | |
| 0.750 | beta | 0.1 | 0.94 | 0.90 | 0.97 | 0.95 | 0.93 | 0.98 | |
| | 0.500 | beta | 0.2 | 0.91 | 0.80 | 0.98 | 0.90 | 0.79 | 0.98 |
| | 0.500 | beta | 0.2 | 0.37 | 0.17 | 0.57 | 0.88 | 0.74 | 0.97 |
| 0.025 | invg | Inf | 1.91% | 1.59% | 2.28% | 1.51% | 1.03% | 2.63% | |
| | 0.025 | invg | Inf | 3.83% | 2.47% | 5.63% | 3.17% | 1.91% | 4.85% |
| 0.01 | invg | Inf | 0.38% | 0.28% | 0.50% | 0.47% | 0.33% | 0.62% | |
| | 0.01 | invg | Inf | 0.51% | 0.40% | 0.67% | 0.78% | 0.58% | 1.13% |
| 0.05 | invg | Inf | 14.1% | 10.5% | 18.9% | 12.8% | 9.4% | 16.4% | |
| 0.025 | invg | Inf | 1.70% | 1.31% | 2.26% | 1.49% | 1.15% | 1.96% | |
| 0.50 | norm | 0.25 | 0.72 | 0.61 | 0.81 | 0.44 | 0.29 | 0.59 |
Table 8 - Panel A: Properties of the Estimated Model Correlations and Standard Deviations - Standard Deviations
| Variable | Full Sample: Model: 5% | Full Sample: Model: Median | Full Sample: Model: 95% | Full Sample: Data | 1960-1983: Model: 5% | 1960-1983: Model: Median | 1960-1983: Model: 95% | 1960-1983: Data | 1984-2007: Model: 5% | 1984-2007: Model: Median | 1984-2007: Model: 95% | 1984-2007: Data |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| 1.22% | 1.57% | 2.08% | 1.56% | 1.43% | 1.95% | 2.65% | 1.89% | 0.82% | 1.19% | 1.72% | 1.12% |
| | 1.93% | 2.41% | 3.10% | 2.52% | 2.01% | 2.70% | 3.56% | 3.04% | 1.41% | 1.96% | 2.70% | 1.86% |
| | 0.78% | 1.07% | 1.57% | 0.66% | 0.80% | 1.18% | 1.82% | 0.76% | 0.54% | 0.82% | 1.25% | 0.53% |
| | 1.06% | 1.39% | 1.83% | 1.18% | 1.02% | 1.46% | 2.01% | 1.33% | 0.80% | 1.14% | 1.62% | 1.01% |
| | 0.38% | 0.44% | 0.51% | 0.38% | 0.42% | 0.51% | 0.66% | 0.41% | 0.39% | 0.52% | 0.68% | 0.33% |
| | 0.66% | 0.78% | 0.92% | 0.68% | 0.69% | 0.89% | 1.14% | 0.70% | 0.53% | 0.68% | 0.87% | 0.65 |
Table 8 - Panel B: Properties of the Estimated Model: Correlations and Standard Deviations - Correlations
| Variable | Full Sample: Model: 5% | Full Sample: Model: Median | Full Sample: Model: 95% | Full Sample: Data | 1960-1983: Model: 5% | 1960-1983: Model: Median | 1960-1983: Model: 95% | 1960-1983: Data | 1984-2007: Model: 5% | 1984-2007: Model: Median | 1984-2007: Model: 95% | 1984-2007: Data |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| | 0.14 | 0.31 | 0.46 | 0.38 | 0.10 | 0.38 | 0.10 | 0.38 | 0.61 | 0.44 | -0.07 | 0.25 |
| | 0.28 | 0.49 | 0.65 | 0.62 | 0.12 | 0.50 | 0.12 | 0.50 | 0.72 | 0.63 | 0.16 | 0.62 |
| | 0.34 | 0.46 | 0.56 | 0.39 | 0.34 | 0.53 | 0.34 | 0.53 | 0.66 | 0.43 | 0.15 | 0.36 |
| | 0.44 | 0.55 | 0.66 | 0.51 | 0.40 | 0.56 | 0.40 | 0.56 | 0.69 | 0.53 | 0.39 | 0.45 |
| | 0.62 | 0.70 | 0.77 | 0.61 | 0.60 | 0.72 | 0.60 | 0.72 | 0.81 | 0.62 | 0.51 | 0.56 |
| | -0.24 | 0.11 | 0.46 | 0.13 | -0.41 | 0.11 | -0.41 | 0.11 | 0.57 | 0.14 | -0.58 | 0.07 |
| | -0.56 | -0.23 | 0.21 | -0.85 | -0.81 | -0.46 | -0.81 | -0.46 | 0.04 | -0.90 | -0.73 | -0.72 |
| | 0.14 | 0.44 | 0.69 | 0.67 | 0.17 | 0.53 | 0.17 | 0.53 | 0.77 | 0.75 | -0.24 | 0.49 |
Table 9 - Panel A: Variance Decompositions, Subsamples - 1960 - 1983
| | | |||||
|---|---|---|---|---|---|---|
| | 79.0 | 17.9 | 1.8 | 0.7 | 0.6 | 0.001 |
| | 12.3 | 0.8 | 0.0 | 38.6 | 1.5 | 46.8 |
| 43.9 | 40.7 | 0.1 | 1.2 | 14.1 | 0.002 | |
| | 12.7 | 4.7 | 81.0 | 0.1 | 1.5 | 0.0 |
| | 17.4 | 19.7 | 0.1 | 0.0 | 62.8 | 0.0 |
| | 69.0 | 7.3 | 5.1 | 7.4 | 11.2 | 0.03 |
| 81.6 | 14.9 | 1.3 | 0.1 | 0.4 | 1.6 |
Table 9 - Panel B: Variance Decompositions, Subsamples - 1984-2007
| | | |||||
|---|---|---|---|---|---|---|
| | 49.4 | 41.9 | 3.7 | 3.7 | 1.2 | 0.02 |
| | 1.3 | 0.3 | 0.2 | 30.8 | 0.1 | 67.3 |
| 21.2 | 68.7 | 0.1 | 0.1 | 9.9 | 0.0 | |
| | 2.3 | 3.7 | 93.6 | 0.1 | 0.3 | 0.001 |
| | 7.9 | 30.7 | 0.1 | 0.01 | 61.3 | 0.0 |
| | 65.9 | 6.6 | 8.3 | 12.8 | 6.2 | 0.2 |
| 51.5 | 39.0 | 2.5 | 0.1 | 0.8 | 6.2 |
Table 10 - Accounting for the Decline in Volatility
| Parameter | Value: 1960-1983 | Value: 1984-2007 | Contribution to change: ( | Contribution to change: ( | Contribution to change: ( | Contribution to change: ( |
|---|---|---|---|---|---|---|
| 0.056 | 0.046 | 0.00 | 0.00 | 0.01 | -0.01 | |
| 0.022 | 0.022 | -0.01 | -0.02 | 0.00 | -0.01 | |
| 1.13 | 1.40 | -0.01 | -0.02 | 0.00 | -0.01 | |
| 3.13 | 3.08 | 0.00 | -0.01 | 0.00 | 0.00 | |
| 0.93 | 1.16 | 0.02 | -0.03 | -0.01 | -0.05 | |
| | 0.02 | 0.04 | 0.00 | -0.01 | 0.01 | 0.01 |
| | 0.27 | 0.16 | 0.21 | 0.36 | 0.00 | 0.42 |
| | 0.50 | 0.61 | -0.08 | -0.13 | -0.01 | -0.16 |
| | 0.04 | 0.02 | 0.03 | 0.06 | 0.00 | 0.00 |
| | 0.91 | 0.90 | -0.02 | -0.02 | -0.01 | -0.01 |
| | 0.37 | 0.88 | -0.16 | -0.12 | -0.24 | -0.13 |
| All estimated parameters | 0.06 | 0.19 | -0.27 | 0.14 | ||
| 0.30 | 0.36 | 0.01 | 0.01 | 0.00 | -0.01 | |
| 1.37 | 1.07 | -0.04 | -0.09 | 0.01 | -0.04 | |
| | 13.48 | 14.11 | 0.06 | 0.09 | -0.04 | 0.00 |
| | 0.54 | 0.88 | -0.20 | 0.00 | 0.01 | 0.00 |
| All steady-state parameters | -0.16 | 0.04 | -0.01 | -0.06 | ||
| 1.91% | 1.51% | -0.29 | -0.40 | -0.05 | -0.10 | |
| 0.38% | 0.47% | 0.01 | 0.02 | 0.01 | 0.00 | |
| 14.13% | 12.77% | -0.01 | -0.01 | -0.01 | -0.01 | |
| All shocks | -0.52 | -0.64 | -0.06 | -0.25 | ||
| All parameters and shocks | -0.76 | -0.73 | -0.35 | -0.30 |
Notes: Columns 2 and 3 indicate the estimated value of the parameter in the first column in each subsample. In the last four columns, we take the period 1960-1983 as the baseline period and change each parameter to its 1984-2004 value to account for its contribution to reducing volatility. The columns indicate, for each variable, the change in the standard deviation (times 100) due to the change in that parameter.
Table 11: Prior Distributions and Parameter Estimates of the Model with Usage of Inventories
| Prior: Mean | Prior: Distrib. | Prior: St.dev. | Usage Model: Mean | Usage Model: 5% | Usage Model: 95% | Baseline Model: Mean | |
|---|---|---|---|---|---|---|---|
| 0.020 | beta | 0.01 | 0.078 | 0.053 | 0.106 | 0.081 | |
| 0.020 | beta | 0.01 | 0.009 | 0.003 | 0.018 | 0.022 | |
| 1.500 | norm | 0.5 | 1.33 | 0.91 | 1.76 | 1.30 | |
| 1.500 | norm | 0.5 | 4.20 | 3.75 | 4.61 | 3.60 | |
| 1.500 | norm | 0.5 | 1.01 | 0.86 | 1.17 | 1.03 | |
| | 0.500 | beta | 0.2 | 0.02 | 0.01 | 0.04 | 0.03 |
| | 0.500 | beta | 0.2 | 0.27 | 0.19 | 0.36 | 0.20 |
| | 0.500 | beta | 0.2 | 0.51 | 0.39 | 0.65 | 0.47 |
| | 0.500 | beta | 0.2 | 0.08 | 0.05 | 0.11 | 0.02 |
| 0.750 | beta | 0.1 | 0.83 | 0.79 | 0.87 | 0.86 | |
| | 0.750 | beta | 0.1 | 0.97 | 0.95 | 0.98 | 0.93 |
| 0.750 | beta | 0.1 | 0.94 | 0.91 | 0.97 | 0.92 | |
| | 0.750 | beta | 0.1 | 0.84 | 0.78 | 0.89 | 0.86 |
| 0.750 | beta | 0.1 | 0.95 | 0.93 | 0.97 | 0.94 | |
| 0.750 | beta | 0.1 | 0.95 | 0.92 | 0.97 | 0.94 | |
| | 0.500 | beta | 0.2 | 0.98 | 0.96 | 1.00 | 0.95 |
| | 0.500 | beta | 0.2 | 0.13 | 0.06 | 0.20 | 0.80 |
| | 0.500 | beta | 0.2 | 0.25 | 0.14 | 0.41 | |
| 0.025 | invg | Inf | 1.49% | 1.29% | 1.70% | 1.49% | |
| | 0.025 | invg | Inf | 8.95% | 5.82% | 13.50% | 3.80% |
| 0.01 | invg | Inf | 0.35% | 0.27% | 0.45% | 0.33% | |
| | 0.01 | invg | Inf | 0.66% | 0.52% | 0.86% | 0.65% |
| 0.05 | invg | Inf | 6.68% | 5.52% | 8.06% | 10.34% | |
| 0.025 | invg | Inf | 1.34% | 1.06% | 1.72% | 1.52% | |
| 0.50 | norm | 0.25 | 0.49 | 0.39 | 0.59 | 0.72 |
Figure 1. Data by Sector
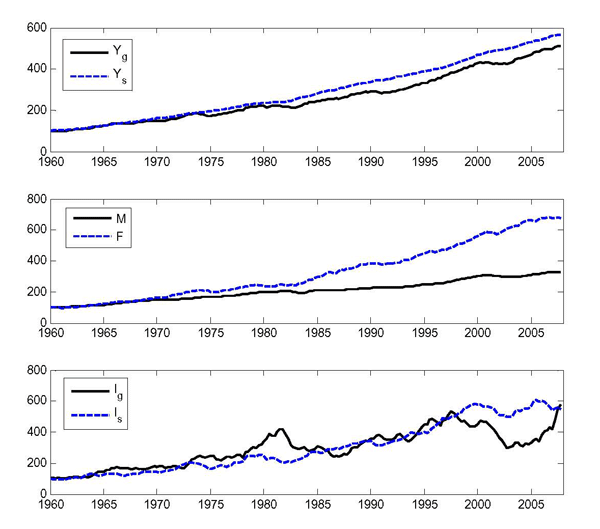
Notes: All series are normalized to 100 in the initial period.
Figure 2. Nominal Shares of Total Output
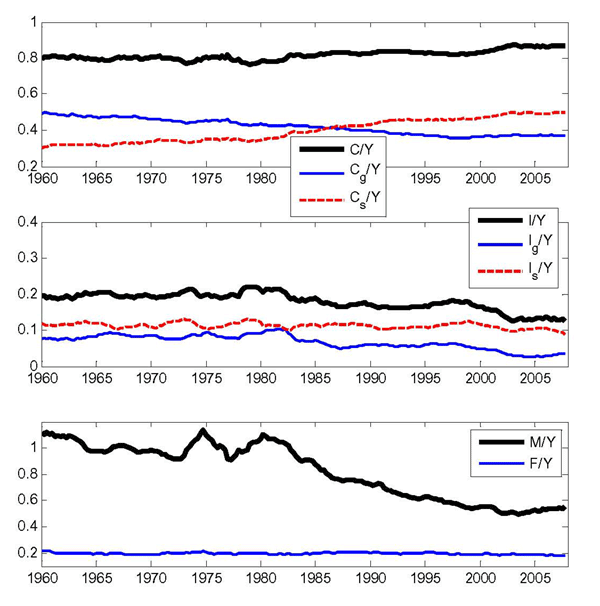
Notes Y denotes total output. Numerators and denominator are all expressed in nominal terms.
Figure 3. Inventory Target Ratios and Inventory Investment
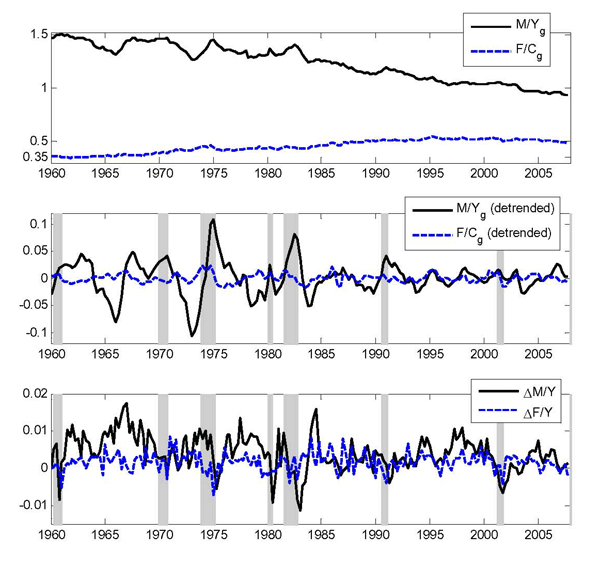
Notes: Shaded Areas Indicate NBER Recession Dates.
Figure 4. Impulse Responses of the Estimated Model
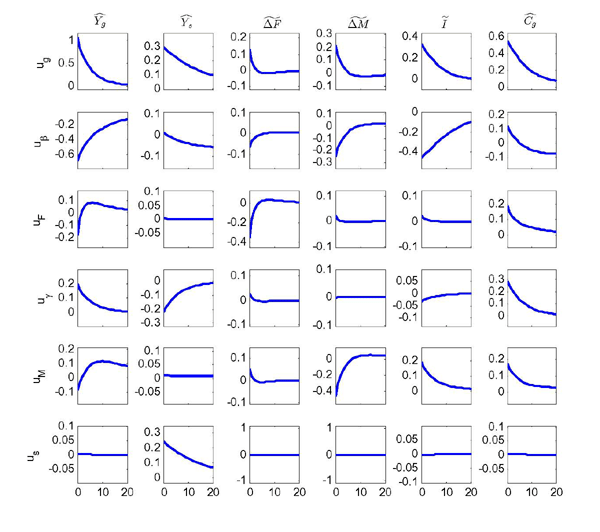
Notes: Each row shows the impulse responses to an estimated one-standard-deviation shock. X-axis: Time horizon. Y-axis: Deviation from baseline, multiplied by 100.
Variable with a hat are scaled by their steady state value. Variables with a tilde are scaled by steady state output in the goods sector.
Figure 5. Impulse Responses of the Estimated Model to Selected Shocks GDP and Inventory-to-Target Ratios
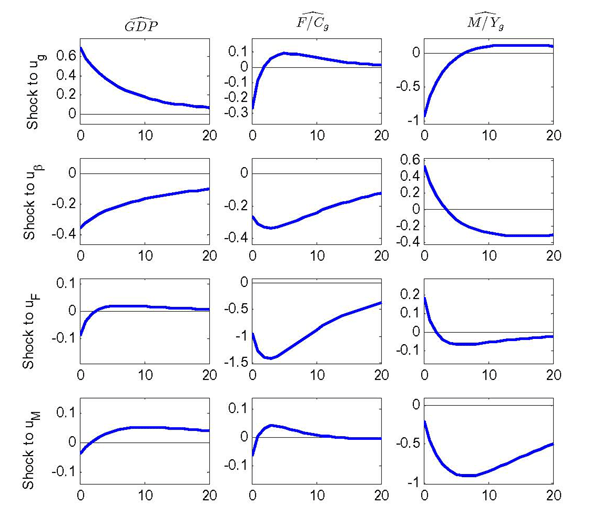
Notes: Each row shows the impulse responses to an estimated one-standard-deviation shock. X-axis: Time horizon. Y-axis: Deviation from baseline, multiplied by one hundred.
Figure 6. Orthogonalized Impulse Responses of the Estimated Model, Comparison with VAR
Note: Impulse responses from Bayesian VAR with two lags (dashed lines correspond to the median and the 95% posterior bands); and impulse responses based on the reduced form representation of the DSGE model (solid lines). Both sets of impulse responses have been orthogonalized in the same way. The posterior of the VAR is obtained multiplying the likelihood function by the Jeffrey�s prior, as in Doan (2004). Our results are nearly identical using normal-diffuse prior instead of the Jeffrey�s prior.
Figure 7. Impulse Responses to a Positive Technology Shock in the Goods Sector
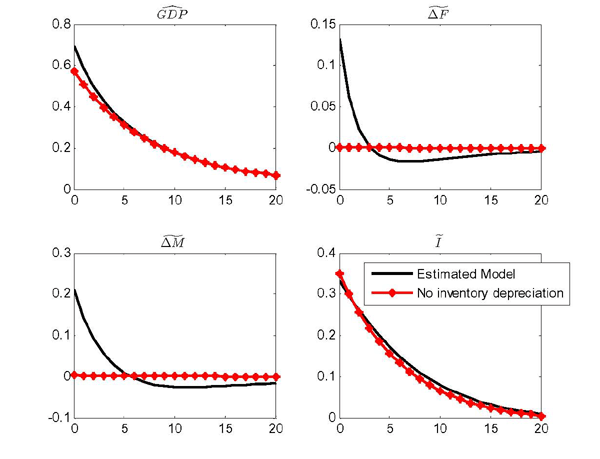
Notes: Responses to an estimated one-standard-deviation technology shock in the goods sector. X-axis: Horizon in quarters. Y-axis: Deviation from baseline, multiplied by 100. Output is scaled by its steady-state value. Inventory investment and fixed investment are scaled by steady-state output in the goods sector, so that their impulse responses measure the growth contribution to goods output.
Figure 8. Impulse Responses to a Positive Technology Shock in the Goods Sector Baseline Model and Model with Inventory Usage
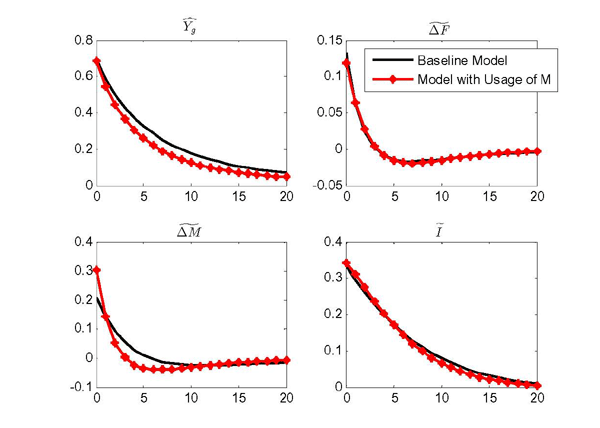
Notes: X-axis: Time horizon. Y-axis: Deviation from baseline, multiplied by one hundred.
Footnotes
1. We would like to thank David DeRemer and Massimo Giovannini for invaluable research assistance and very useful discussions. We are also grateful to Susanto Basu, Martin Eichenbaum, Fabià Gumbau-Brisa, Andreas Hornstein, Michel Juillard, Michael Kumhof, Lou Maccini, Julio Rotemberg, Paul Willen, and various seminar participants for very useful suggestions. We thank Elizabeth Murry and Tyler Williams for expert editorial assistance. A technical appendix is available at http://www.federalreserve.gov/pubs/ifdp/2010/1004/default.htm. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System, the Federal Reserve Bank of Boston, or of any other person associated with the Federal Reserve System. Return to text
2. Matteo Iacoviello, Division of International Finance, Federal Reserve Board, 20th and C St. NW, Washington, DC 20551. Email: [email protected]. Return to text
3. Fabio Schiantarelli, Boston College, Department of Economics, 140 Commonwealth Avenue, Chestnut Hill, MA 02467. Email: [email protected]. Return to text
4. Scott Schuh, Federal Reserve Bank of Boston, Research Department, 600 Atlantic Ave., Boston, MA 02210. Email: [email protected]. Return to text
5. Papers that incorporate variable markups include Bils and Kahn (2000), Hornstein and Sarte (2001), Boileau and Letendre (2009), Coen-Pirani (2004), Jung and Yun (2006), and Chang, Hornstein, and Sarte (2009). General equilibrium models with intermediate goods and supply-chain relationships include Huang and Liu (2001) and Wen (2005a). Fisher and Hornstein (2000) and Khan and Thomas (2007) study (S,s) policies for retail inventories and intermediate goods inventories respectively, while Wen (2009) develops a model of inventories based on a precautionary stockout-avoidance motive. Return to text
6. Marquis and Trehan (2005a) define goods as manufacturing firms, while Lee and Wolpin (2006) use the NIPA definition (agriculture, mining, construction, and manufacturing). For multi-sector consumption/investment models, see Greenwood, Hercowitz, and Krusell (2000); Whelan (2003); and Marquis and Trehan (2005b). Return to text
7. The importance of stage-of-fabrication inventories dates back to Lovell (1961) and Feldstein and Auerbach (1976). More recent models include Husted and Kollintzas (1987), Bivin (1993), Ramey (1989), and Rossana (1990). Cooper and Haltiwanger (1990) and Maccini and Pagan (2007) examine the linkages between firms created through inventories playing different input and output roles in production. Return to text
8. The argument follows Feenstra (1986) who discusses the functional equivalence of including money in the utility function or liquidity costs in the budget constraint. Return to text
9. This result is consistent with other aggregate analyses of the Great Moderation. See the VAR-based analyses of Blanchard and Simon (2001); Stock and Watson (2003); and Ahmed, Levin, and Wilson (2004). See also Khan and Thomas (2007) and Maccini and Pagan (2007) for analyses based on structural models with inventories. Arias, Hansen, and Ohanian (2006) use a calibrated RBC model without inventories, and Leduc and Sill (2006) use an equilibrium model to assess the quantitative importance of monetary policy. Return to text
10. Humphreys, Maccini, and Schuh (2001) and Maccini and Pagan (2007) argue that it is important to model the delivery and usage of input materials in gross production together with the holding of input inventories. However, absent input-output (supply-chain) relationships among firms, a representative-firm approach cannot admit deliveries of raw materials produced by an upstream supplier. Return to text
11. If holding costs are proportional to the stock, then the inventory depreciation rate will include both physical wastage and the resource cost of holding inventories. Inventory carrying costs have a long history in the operations management literature. See for instance the book by Stock and Lambert (2001). Return to text
12. For the model to admit a solution, a
necessary condition is that
![]() never exceeds
unity for each possible realization of
never exceeds
unity for each possible realization of
![]() . Even though we
assume that
. Even though we
assume that ![]()
![]() has an unbounded
support, empirically its standard deviation turns out to be rather
small, so that this condition is always satisfied in
practice. Return to text
has an unbounded
support, empirically its standard deviation turns out to be rather
small, so that this condition is always satisfied in
practice. Return to text
13. We are assuming here absence of delivery lags or time to build considerations. As pointed out by one referee, delivery lags or time-to-build delays would invalidate this result. Return to text
14. This will be true if the term in the larger parenthesis in the denominator is greater than one, which is almost certainly the case in practice since capital has a much larger weight in production. Return to text
15. The papers by Kimura and Shiotani (2009) and Maccini and Pagan (2007) interpret changes in inventory-target ratios as evidence of changes in inventory management techniques, and attempt to map these techniques into particular parameters of a linear-quadratic inventory model. Return to text
16. Given our reliance on inventory holding as the defining characteristic of sectors, we could label the sectors "inventory holding" and "non-inventory holding" but we opted for "goods" and "services" because this nomenclature is simpler and more traditional. Return to text
17. See the technical appendix for details on data sources, variable definitions, and data construction. Return to text
18. A reasonable case can be made for output inventories to include manufacturing finished goods and perhaps wholesale inventories. However, no clear theoretical (or empirical) justification exists for any particular alternative classification. For instance, wholesale inventories include construction material supplies, and manufacturing-output inventories contain goods that do not enter the consumer's utility function. Moreover, each industry's inventory investment exhibits different cyclical and trend characteristics, and the correlation of inventory investment between industries is low. Return to text
19. All real data are in chain-weighted 2000 dollars. When constructing the actual real chain-weighted data, we use the Tornquist index approximation to the Fisher ideal chain index as recommended by Whelan (2002). Return to text
20. Our approach is particularly close to Hayashi and Prescott (2002). As discussed in Conesa, Kehoe and Ruhl (2007), all solutions to the problem of matching a closed economy model with the data have a degree of arbitrariness. In a previous version of the paper, imports were included in consumption and investment, but export were omitted as a component of demand. As one referee pointed out, this may lead to misleading conclusions on the behavior of the input inventory to output ratio. Fortunately, our conclusions concerning the qualitative behavior of this ratio, as well as the quantitative findings of the model, are not sensitive to this choice. Return to text
21. In real terms, the ratio of investment to output has trended upwards during the sample. However, the relative price of investment has fallen, so the nominal ratio of output to investment has remained approximately constant. Return to text
22. Kongsamut, Rebelo and Xie (2001) and Gomme and Rupert (2007) discuss the restrictions on preferences and technology that are required for balanced growth in multisector models. These restrictions call for production functions and consumption aggregators to be Cobb-Douglas. Return to text
23. Although ![]() is
consistent with traditional practice in the inventory literature,
such as Lovell (1961) and Feldstein and Auerbach (1976),
is
consistent with traditional practice in the inventory literature,
such as Lovell (1961) and Feldstein and Auerbach (1976),
![]() differs from the traditional
inventory-to-sales ratio specified by microeconomic models of the
firm. In the model, the "sales" measure most analogous to that
used in the inventory literature is final goods sales,
differs from the traditional
inventory-to-sales ratio specified by microeconomic models of the
firm. In the model, the "sales" measure most analogous to that
used in the inventory literature is final goods sales, ![]() . Empirically, however, the choice of the scale
variable for inventories does not alter the qualitative properties
of inventory-target ratios. Return to
text
. Empirically, however, the choice of the scale
variable for inventories does not alter the qualitative properties
of inventory-target ratios. Return to
text
24. For examples, see McConnell and Perez-Quiros (2000), Blanchard and Simon (2001), Humphreys, Maccini, and Schuh (2001), Kahn, McConnell, and Perez-Quiros (2002), Kahn and McConnell (2005), Maccini and Pagan (2007), Davis and Kahn (2008), and Kimura and Shiotani (2009). Many authors note that the decline in the inventory-target ratio centers on durable goods manufacturing in the 1980s, when most new technologies were adopted. Return to text
25. A trend is removed from the variables in logs, using the band-pass filter of Baxter and King (1999) that isolates frequencies between 3 and 32 quarters. Linear quadratic detrending and first-differencing are also common in the literature, but these techniques tend to yield similar cyclical properties in the detrended data. Wen (2005b) shows that the cyclical properties of detrended inventory investment are sensitive to the cyclical frequency. Business cycle frequencies like ours yield procyclical inventory investment, whereas higher frequencies (2-3 quarters) yield countercyclical inventory investment. Return to text
26. In the data, the service sector has a higher proportion of structures in its total capital stock than the goods sector does. Because structures generally have lower depreciation rates than equipment, we also estimated a model with a smaller depreciation rate of capital in the service sector, obtaining similar results. Return to text
27. See the technical appendix for additional details. Return to text
28. Essentially, we are constructing
degenerate, non-independent priors for a set of parameters
![]() with the goal of matching five first moments of the data that are
excluded from the likelihood function (that is, they are not used
as part of our estimation exercise). Put differently, these
parameters can be more easily identified from steady state
relationships among the variables rather than from the dynamics of
the data. Del Negro and Schorfheide (2008) provide and describe a
more general approach for forming priors for steady-state related
parameters that allows for the steady-state to be measured with
error: we implicitly rule measurement error out. Return to text
with the goal of matching five first moments of the data that are
excluded from the likelihood function (that is, they are not used
as part of our estimation exercise). Put differently, these
parameters can be more easily identified from steady state
relationships among the variables rather than from the dynamics of
the data. Del Negro and Schorfheide (2008) provide and describe a
more general approach for forming priors for steady-state related
parameters that allows for the steady-state to be measured with
error: we implicitly rule measurement error out. Return to text
29. An important issue concerns the convergence of the simulated draws from the posterior distribution of the parameters. We fine tune our estimation algorithm in order to obtain acceptance rates around 35 percent, and check for convergence using the cumulative sum of the draws statistics. Although convergence typically obtains within 50,000 iterations, we set the draws to 250,000 and calculate the statistics based on the last 75 percent of the draws. Return to text
30. One can interpret ![]() as the inverse elasticity of each type of investment to
its shadow price. Our numbers are slightly higher than
microeconometric findings based on estimates of investment
equations (see Chirinko, 1993). Return
to text
as the inverse elasticity of each type of investment to
its shadow price. Our numbers are slightly higher than
microeconometric findings based on estimates of investment
equations (see Chirinko, 1993). Return
to text
31. To facilitate comparison across all
investment categories, we scale the response of inventory
investment and business investment by steady-state goods output
(rather than by their own steady state values). This way, the
vertical axis measures the percent growth contribution of each
investment category to the response of goods output. Note that in
the figures and in the tables the measure of ![]() is net of inventory depreciation. Return to text
is net of inventory depreciation. Return to text
32. Our data span from 1960Q1 to 2007Q4. To compare likelihoods, we estimate both the DSGE and VAR model over the sample 1965Q1-2007Q4. The marginal likelihood of the DSGE model is computed using the Laplace approximation around the posterior mode. The observations from 1960Q1 to 1964Q4 are used as a training sample to construct a diffuse prior for the VAR model as in Smets and Wouters (2007). Return to text
33. See for instance the discussion in
Schorfheide (2000). Del Negro and Schorfheide (2004) propose the
so-called DSGE-VAR approach as a way to compare the DSGE model
against a VAR model: under this approach, one interprets the DSGE
model as a set of restrictions on the VAR, so that the DSGE model
induces a prior for the VAR coefficients. The summary measure of
the relative fit of the DSGE model is an estimated hyperparameter (
![]() ) measuring the optimal
weight (ranging from zero to infinity) of the DSGE model based
prior for the VAR model. We find that the (hybrid) model that
attains the highest marginal likelihood features a small value of
) measuring the optimal
weight (ranging from zero to infinity) of the DSGE model based
prior for the VAR model. We find that the (hybrid) model that
attains the highest marginal likelihood features a small value of
![]() , equal to
, equal to ![]() For this reason, we use the unrestricted VAR (that
corresponds to
For this reason, we use the unrestricted VAR (that
corresponds to ![]() ) to compare model and
data. Return to text
) to compare model and
data. Return to text
34. In Christiano (1988), it was necessary to rely on a more complex information structure in order to account for these two features of the data. He assumes that, at the time hours and capital decisions are made, firms observe the shocks with noise. Inventory and consumption decisions are, instead, made with full knowledge of the shocks. When there is no signal-extraction problem, his model can generate enough inventory-investment variability, but at the cost of a negative correlation between the change in inventory investment and output growth. Return to text
35. The technical appendix discusses this equivalence in more detail. Return to text
36. Our technical appendix contains more complete details on this model. Return to text
37. The assumption of convexity has two
appealing properties: first, it allows us to solve the model using
standard perturbation methods; second, and most importantly, it
captures the idea that, at the margin, a higher utilization rate
leads to a higher depreciation. Note that there are some analogies
with the way we write down the utilization function for fixed
capital. For fixed capital, we assume that the optimal (steady
state) utilization rate of capital is unity, and normalize the
utilization function so that no resources are wasted at the optimal
utilization rate. Instead, here we normalize the function
![]() so that the optimal steady state
utilization rate is less than unity. Return to text
so that the optimal steady state
utilization rate is less than unity. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text