
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1005, September 2010 --- Screen Reader
Version*
The Information Content of High-Frequency Data for Estimating Equity Return Models and Forecasting Risk
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We demonstrate that the parameters controlling skewness and kurtosis in popular equity return models estimated at daily frequency can be obtained almost as precisely as if volatility is observable by simply incorporating the strong information content of realized volatility measures extracted from high-frequency data. For this purpose, we introduce asymptotically exact volatility measurement equations in state space form and propose a Bayesian estimation approach. Our highly efficient estimates lead in turn to substantial gains for forecasting various risk measures at horizons ranging from a few days to a few months ahead when taking also into account parameter uncertainty. As a practical rule of thumb, we find that two years of high frequency data often suffice to obtain the same level of precision as twenty years of daily data, thereby making our approach particularly useful in finance applications where only short data samples are available or economically meaningful to use. Moreover, we find that compared to model inference without high-frequency data, our approach largely eliminates underestimation of risk during bad times or overestimation of risk during good times. We assess the attainable improvements in VaR forecast accuracy on simulated data and provide an empirical illustration on stock returns during the financial crisis of 2007-2008.
Keywords: Equity return models, parameter uncertainty, Bayesian estimation, MCMC, high-frequency data, jump-robust volatility measures, value at risk, forecasting
JEL classification: C11, C13, C14, C15, C22, C53, C80, G17
1 Introduction
Modeling equity returns is central to risk management, derivatives pricing, portfolio choice, and asset pricing in general. Continuous time jump-diffusion models succeeding those pioneered by Merton (1969) and Black and Scholes (1973) are now commonplace. Typically, the inherent time-varying and stochastic nature of continuous market activity is represented by a combination of persistent and non-persistent latent stochastic volatility factors. The pronounced asymmetric return-volatility relation in equities, known also as leverage or volatility feedback effects, is captured by correlated return and volatility innovations. Sudden price revisions due to news and other market surprises give rise to jumps in returns, while the often abrupt changes in the level of market activity and risk has justified the introduction of jumps in volatility. The latent nature of volatility in such rich models, however, poses serious challenges for reliable inference based solely on daily or monthly return series, even the longest existing ones. It is thus critical to develop estimation methods exploiting relevant additional information that could help reduce the severe parameter and volatility estimation uncertainty.
Two different approaches have emerged to improve estimation
efficiency in this regard. The first approach relies on the cross
section of option prices over time.2 However, as pointed out
by Eraker, Johannes, and Polson (2003), it is unclear whether the
inclusion of option price data leads to decrease or increase of
parameter uncertainty given that the risk premia embedded in option
prices introduce additional parameters, which are typically
difficult to estimate. The second and seemingly more viable
approach avoids such complications by exclusively relying on daily
realized volatility measures extracted from nowadays ubiquitous
high-frequency intraday return data.3![]() 4 Our paper contributes to this second
line of research by utilizing high-frequency realized volatility
measures within a standard Bayesian Markov Chain Monte Carlo (MCMC)
estimation framework of popular equity return models. In
particular, we take explicitly into account the resulting
substantial reduction in parameter uncertainty and are able to show
sizeable economic gains when forecasting risk.
4 Our paper contributes to this second
line of research by utilizing high-frequency realized volatility
measures within a standard Bayesian Markov Chain Monte Carlo (MCMC)
estimation framework of popular equity return models. In
particular, we take explicitly into account the resulting
substantial reduction in parameter uncertainty and are able to show
sizeable economic gains when forecasting risk.
The most closely related studies to our work such as Alizadeh, Brandt, and Diebold (2002), Barndorff-Nielsen and Shephard (2002), Bollerslev and Zhou (2002), Corradi and Distaso (2006), Todorov (2009) among others have used classical rather than Bayesian estimation methods and have focused on using high-frequency volatility measures for assessing the goodness of fit of alternative model specifications without explicitly analyzing the economic value of reducing parameter uncertainty. These studies have largely ruled out the simplest known single factor stochastic volatility models with Poisson jumps in returns in favor of more complex specifications including one or more extra features such as a second stochastic volatility factor, pronounced non-linearities, jumps both in returns and volatility (possibly even of infinite activity).5 But rather than reconciling or refining such findings, our main goal is to go a step beyond specification testing and clearly demonstrate the economic gains from harnessing the information content of high-frequency volatility measures regardless of the underlying model.
To this end, we exploit recent advances in jump robust volatility estimation from high-frequency data such as Andersen, Dobrev, and Schaumburg (2009), Barndorff-Nielsen, Shephard, and Winkel (2006), Podolskij and Vetter (2009) and references therein to formally introduce an asymptotically precise volatility measurement equation directly within the standard state-space representation of popular equity return models estimated at daily or lower frequency. Then we adopt a standard Bayesian MCMC estimation framework allowing us to exploit the strong information content of such volatility measurement equation across a wide range of models featuring stochastic volatility, leverage effects, and jumps in returns and volatility. In terms of efficiency, our approach considerably improves on Bayesian estimation methods based on an identical state-space representation at a daily or lower frequency but without a volatility measurement equation such as Eraker, Johannes, and Polson (2003) and Jacquier, Polson, and Rossi (2004), among others.6 In terms of generality, we overcome major limitations of the quasi-maximum likelihood estimation methods for state-space formulations with volatility measurement equation pursued by Barndorff-Nielsen and Shephard (2002) who consider non jump-robust realized volatility measures and Alizadeh, Brandt, and Diebold (2002) who consider non jump-robust and less efficient range-based volatility measures. In particular, our approach incorporates leverage effects and jumps, necessary for modeling equity returns, as well as possibly two (one persistent and one non-persistent) stochastic volatility factors. We also offer an attractive alternative to existing moment-based estimation approaches such as Bollerslev and Zhou (2002), Corradi and Distaso (2006) and Todorov (2009) in terms of more fully exploiting the information content of high frequency volatility measures in various model settings via their state-space formulations. In particular, unlike these studies, the Bayesian estimation approach we propose allows us to easily account for parameter uncertainty and demonstrate the economic gains from using high-frequency volatility measures for model estimation and risk forecasting across a range of popular equity return models. 7
Our main contributions can be summarized as follows. First, we demonstrate theoretically and empirically that the parameters controlling skewness and kurtosis in popular equity return models estimated at daily and monthly frequency can be obtained almost as precisely as if volatility is observable by incorporating the strong information content of realized volatility measures extracted from high-frequency data. In particular, we extend the empirical findings in Alizadeh, Brandt, and Diebold (2002) by showing that not only the parameters controlling volatility of volatility but also those controlling leverage effects can be estimated several times more precisely by exploiting high-frequency volatility measures. Second, we show that our highly efficient estimates lead in turn to substantial gains for forecasting various risk measures at horizons ranging from a few days to a few months ahead when taking also into account parameter uncertainty. In fact, our approach not only reduces the root mean square prediction error but also shrinks and almost eliminates the forecast bias, which inevitably arises from the pronounced nonlinearities in the involved transformation of parameter and volatility estimates. As a practical rule of thumb we find that two years of high frequency data often suffice to obtain the same level of precision as twenty years of daily data, thereby making our approach particularly useful in finance applications where only short data samples are available or economically meaningful to use. Third, and most important in risk management applications, our simulation results reveal that risk forecasts stemming from traditional model inference on daily data tend to be overly conservative in good times (e.g. overestimating risk by as much as 30%) but they are not conservative enough in bad times (e.g. underestimating risk by as much as 10%). By contrast, risk forecasts based on our approach to exploiting high-frequency data are considerably closer to the truth in both bad and good times. Thanks to incorporating the strong information content of high-frequency volatility measures, we are able to better curb risk taking exactly when needed the most, i.e. early on in times of crisis, while avoiding unnecessary overstatement of risk in normal times. Finally, our findings are robust both across different models and jump-robust volatility measures on high frequency data that we analyze. This allows us to remain largely agnostic about the best suited ones, while making a strong case for the potentially large economic value of our approach to using high-frequency volatility measures in model estimation and risk forecasting or other closely related finance applications such as derivatives pricing.
The rest of the paper is organized as follows. Section 2 introduces our volatility measurement equations in detail. Section 3 incorporates such equations within the state space formulation of popular equity return models and develops appropriate Bayesian estimation methods. Section 4 documents the resulting gains in estimation efficiency and risk forecasting accuracy. Section 5 provides an empirical comparison of Value-at-Risk forecasts on S&P 500 and Google returns during the financial crisis of 2007-2008. Section 6 concludes.
2 Volatility Measurement Equations
Jumps in returns have been recognized as an important feature for continuous-time modeling of equity returns within standard no-arbitrage semimartingale setting. Moreover, recent progress in non-parametric volatility measurement based on high-frequency intraday data has made it possible to separate ex-post the daily continuous part of the volatility process from the daily return variation induced by discontinuities or jumps. Originally pioneered by Barndorff-Nielsen and Shephard (2004), jump-robust volatility estimators with different asymptotic and finite sample properties have been proposed by Andersen, Dobrev, and Schaumburg (2009), Barndorff-Nielsen, Shephard, and Winkel (2006), Podolskij and Vetter (2009) among others. A common feature among these and other high-frequency volatility estimators is that as the intraday sampling frequency increases, the arising measurement error shrinks to zero and converges to a known mixed normal asymptotic distribution.8
For our purposes, suitable asymptotic results of this kind directly imply asymptotically precise measurement equations that formally capture the extent to which the continuous and jump parts of daily total variance become ex-post nearly observable when high frequency intraday data is available. Such separation of the continuous and jump components of volatility can be directly utilized in state space form. In this section, we formally introduce a general form of the jump-robust volatility measurement equations that play a key role in our approach to estimating models in state space form and allow us to tackle considerably more general settings than those considered by Alizadeh, Brandt, and Diebold (2002) and Barndorff-Nielsen and Shephard (2002) in the absence of jump-robust volatility measures nearly a decade ago.
2.1 Jump-robust estimators of diffusive volatility
On a filtered probability space
![]() we
consider an adapted process
we
consider an adapted process
![]() , providing the following
jump-diffusion represention of the evolution of the logarithmic
price of an asset in continuous time:
, providing the following
jump-diffusion represention of the evolution of the logarithmic
price of an asset in continuous time:
| (1) |
Here ![]() is a locally bounded and predictable
process,
is a locally bounded and predictable
process, ![]() is cadlag and bounded away from zero
almost surely, while
is cadlag and bounded away from zero
almost surely, while ![]() is a jump process so that
is a jump process so that
![]() , whenever different from zero,
represents the size of a jump at time
, whenever different from zero,
represents the size of a jump at time ![]() . Without loss
of generality, we restrict attention to finite activity
jumps.9
. Without loss
of generality, we restrict attention to finite activity
jumps.9
For a day of unit length with ![]() discrete
observations of the logarithmic price process
discrete
observations of the logarithmic price process
![]() on
on
![]() we denote the
intraday time intervals and corresponding returns as
we denote the
intraday time intervals and corresponding returns as
![]() and
and
![]() ,
,
![]() . In what follows, we consider
standard continuous record in-fill asymptotics where the time
intervals characterizing the intraday sampling scheme uniformly
shrink towards zero as the sampling frequency
. In what follows, we consider
standard continuous record in-fill asymptotics where the time
intervals characterizing the intraday sampling scheme uniformly
shrink towards zero as the sampling frequency ![]() increases.
increases.
In this setting, the daily quadratic variation (QV) of the
observed process consists of the sum of its continuous and jump
parts,
![]() , and
is estimated consistently by the well established realized
volatility (RV) measure:10
, and
is estimated consistently by the well established realized
volatility (RV) measure:10
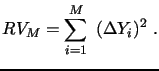 |
(2) |
Our main object of interest, though, is the diffusive part of
the quadratic variation defined as the integrated variance (IV),
![]() . It can be
conveniently estimated by various multipower variation measures
developed by Barndorff-Nielsen and Shephard (2004)
and
Barndorff-Nielsen, Shephard, and Winkel (2006) or
more recent analogous measures based on nearest neighbor truncation
developed by Andersen, Dobrev, and Schaumburg (2009).11In
the case of finite activity jumps, the most efficient multipower
variation measure that allows for an asymptotic mixed normal limit
theory is the realized tripower variation (TV) based on the product
of triplets of adjacent absolute returns:12
. It can be
conveniently estimated by various multipower variation measures
developed by Barndorff-Nielsen and Shephard (2004)
and
Barndorff-Nielsen, Shephard, and Winkel (2006) or
more recent analogous measures based on nearest neighbor truncation
developed by Andersen, Dobrev, and Schaumburg (2009).11In
the case of finite activity jumps, the most efficient multipower
variation measure that allows for an asymptotic mixed normal limit
theory is the realized tripower variation (TV) based on the product
of triplets of adjacent absolute returns:12
| (3) |
The TV estimator is only marginally less efficient than the corresponding MedRV estimator based on (two-sided) nearest neighbor truncation, taking the median instead of the product of triplets of adjacent absolute returns:13
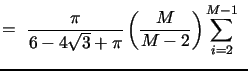 med med |
(4) |
Hence, in our empirical analysis we rely on both TV and MedRV, allowing us to conclude that our main results are not sensitive to the particular jump-robust volatility measures that we use to derive volatility measurement equations. By presenting these equations below in generic form, we are able to abstract from the chosen jump-robust estimators that we are going to utilize in the state space formulation of various models for the sake of reducing parameter and volatility estimation uncertainty.
2.2 Generic asymptotic results and volatility measurement equations
Let
![]() be some jump-robust volatility
estimator applicable in the considered setting such as TV and MedRV
defined above. Then a central limit theorem (CLT) of the following
generic form holds:
be some jump-robust volatility
estimator applicable in the considered setting such as TV and MedRV
defined above. Then a central limit theorem (CLT) of the following
generic form holds:
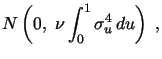 |
(5) |
where ν is a known asymptotic variance factor
depending on the particular estimator (e.g. 3.06 for TV and 2.96
for MedRV), while
![]() is the integrated
quarticity controlling the precision of all such estimators.
Moreover, since the convergence in (5) is
stable, it is possible to apply the delta method to derive feasible
asymptotic results based on any consistent jump-robust estimator
is the integrated
quarticity controlling the precision of all such estimators.
Moreover, since the convergence in (5) is
stable, it is possible to apply the delta method to derive feasible
asymptotic results based on any consistent jump-robust estimator
![]() of
of ![]() .14 In
particular,
.14 In
particular,
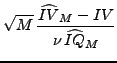 |
(6) |
and
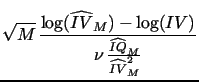 |
(7) |
The log transformation in (7) results in better finite sample approximation than (6), as already noted byBarndorff-Nielsen and Shephard (2005) and Huang and Tauchen (2005). This is especially useful for our purposes as we will focus our subsequent analysis exactly on logarithmic SV models.
In what follows, we denote the feasible estimate of the
asymptotic variance of
![]() implied by (7) as
implied by (7) as
![]() to obtain the following logarithmic volatility measurement
equation that we are going to utilize in the state space
representation of various logarithmic SV models (with leverage
effects and jumps) to improve estimation efficiency:
to obtain the following logarithmic volatility measurement
equation that we are going to utilize in the state space
representation of various logarithmic SV models (with leverage
effects and jumps) to improve estimation efficiency:
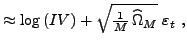 |
(8) |
where
![]() is independent of
the underlying process and the measurement error vanishes as the
intraday sampling frequency M increases. More generally, to make
explicit distinction between different days, we rewrite this key
equation as:
is independent of
the underlying process and the measurement error vanishes as the
intraday sampling frequency M increases. More generally, to make
explicit distinction between different days, we rewrite this key
equation as:
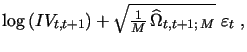 |
(9) |
where
![]() as above, while
as above, while
![]() ,
,![]() , and
, and ![]() stand,
respectively, for the true daily diffusive variance, its available
jump-robust estimate at any sample frequency M,
and the corresponding asymptotic variance on a given day of unit
length represented by the interval
stand,
respectively, for the true daily diffusive variance, its available
jump-robust estimate at any sample frequency M,
and the corresponding asymptotic variance on a given day of unit
length represented by the interval ![]() .
.
We restrict attention to moderate sample frequencies such as two
or five minutes (e.g. ![]() or M=78 over a typical trading day of six and a half hours) in
order to avoid complications arising from various market
microstructure effects that cannot be safely ignored.15Alternatively, for jump-robust
volatility estimation at higher frequencies one can resort to
noise-reduction techniques such as pre-averaging, introduced in the
context of multipower variations by
Podolskij and Vetter (2009).16
or M=78 over a typical trading day of six and a half hours) in
order to avoid complications arising from various market
microstructure effects that cannot be safely ignored.15Alternatively, for jump-robust
volatility estimation at higher frequencies one can resort to
noise-reduction techniques such as pre-averaging, introduced in the
context of multipower variations by
Podolskij and Vetter (2009).16
Quite similarly to the way we obtained equation (9) above, it is possible to single out also the jump part of volatility by using available asymptotic results for the difference between non jump-robust and jump-robust high frequency volatility measures, such as those exploited for moment-based estimation by Todorov (2009). What is important to keep in mind is that any such volatility measurement equations based on high-frequency data similar to (9) do not require knowledge of the exact intraday dynamics of the logarithmic price process. This observation is crucial for our analysis as it allows us to largely abstract from modeling complications due to non-trivial intraday market microstructure effects. Thus, in the next section we focus entirely on the estimation of popular parametric models for equity returns at daily or lower frequencies by directly bringing our generic daily volatility measurement equations based on high-frequency intraday data to the state space form of each model.
3 Equity return models and estimation
With this extra machinery at hand, our goal is to demonstrate the ease and importance of utilizing high-frequency data for more efficient estimation of a broad range of commonly used equity return models. On one side of the spectrum we consider a basic continuous-time diffusion model similar to the setting of Jacquier, Polson, and Rossi (2004) with log-volatility specification, leverage effect and no jumps. On the other side of the spectrum we also study a two-factor logarithmic SV model with leverage effects and compound Poisson jumps in returns. It offers a less restrictive setting than the two-factor models studied by Alizadeh, Brandt, and Diebold (2002) and Bollerslev and Zhou (2002) thanks to incorporating both leverage effects and jumps. Moreover, like the single-factor model, it can still be successfully fitted using information on daily data only, which we use as a natural benchmark for gauging the attainable efficiency gains from our approach to incorporating high-frequency data. Formally, by relying on Bayesian estimation methods, we are able to fully exploit the information content of high frequency volatility measures within the standard state-space form of the models. Hence, we can obtain a clean measure of the incremental value of high-frequency data compared to estimation based on daily data only.
As shown in Das and Sundaram (1999) among others, models with stochastic volatility, leverage effects and jumps allow for skewness and excess kurtosis of returns and make it possible to closely match stylized facts of empirical asset return distributions that have been extensively studied under both physical and risk-neutral measures. For example,Andersen, Benzoni, and Lund (2002) find that adding jumps in returns to single-factor stochastic volatility models can help better fit stock return skewness and kurtosis and better reproduce volatility smiles in option prices. Eraker, Johannes, and Polson (2003) further extend single-factor jump-diffusion models by adding jumps not only in returns but also in volatility, which Broadie, Chernov, and Johannes (2007) show to be important for fitting volatility skewness and kurtosis. Studies of stochastic volatility models with similar findings under risk-neutral measure include Bakshi, Cao, and Chen (1997), Bates (2000), among others. A unified approach using both returns and options data, pursued by Chernov and Ghysels (2000), Eraker (2004) and Jones (2003), has also stressed the importance of properly fitting the conditional skewness and kurtosis of return distributions at various return horizons.
From such broader modeling point of view, it is not our goal to use high-frequency data for the sake of improved specification testing as done, for example, by Alizadeh, Brandt, and Diebold (2002), Bollerslev and Zhou (2002), Corradi and Distaso (2006) and Todorov (2009). Instead, we go a step beyond specification testing and attempt to clearly demonstrate first the efficiency and then the economic gains from harnessing the information content of high-frequency volatility measures regardless of the underlying model.
As our workhorse for analysis, in this section we develop appropriate Bayesian estimation methods that allow us to easily incorporate high frequency volatility measurement equations (such as those presented in the previous section) directly in state space form of any model. In this regard, our estimation approach is closest to Barndorff-Nielsen and Shephard (2002), although they do not allow for jumps and use quasi-maximum likelihood rather than Bayesian estimation methods. By following a Bayesian Markov Chain Monte Carlo (MCMC) approach to estimation, we are able to easily take parameter uncertainty into account and demonstrate that high-frequency information helps greatly increase precision in the parameter estimates governing skewness and kurtosis of returns, which in turn leads to considerably more precise and less biased Value-at-Risk forecasts for multi-day returns. Thus, our study contributes directly to the growing body of evidence that high frequency returns are an important source of information in asset pricing and risk management.
Without loss of generality, here we restrict our exposition to one and two-factor models on opposite sides of the spectrum in terms of complexity. We impose a logarithmic specification for the stochastic volatility components in our models directly in line with Andersen, Bollerslev, Christoffersen, and Diebold (2007) who point out that lognormal/normal mixture models show great appeal in financial risk management in view of the empirically observed near lognormality of realized volatility coupled with the near normality of daily returns standardized by realized volatility.
3.1. One-factor log-SV model with leverage effects
We consider a standard one-factor log-SV model that provides a high level of simplicity and transparency, while it is still rich enough to allow for both skewness and excess kurtosis of asset returns. Our contribution consists in extending the equations of the model in state space form with our extra volatility measurement equation derived in generic form in Section2.2, which is the only difference compared to the standard specification in Jacquier, Polson, and Rossi (2004). It is worth noting that Jones (2003) has studied a similar system of equations with extra measurement equation coming from option implied volatilities. In our model we use high-frequency volatility measures as extra information, which in contrast to implied volatilities allows to theoretically derive the variance of measurement noise and does not require estimation of risk-premia related parameters. In order to facilitate the exposition, we first present the part of our single-factor model identical with Jacquier, Polson, and Rossi (2004). After standard first order Euler discretization as in Kloeden and Platen (1992), or cast directly as a discrete-time model, the system of equations takes the following form:
| = | 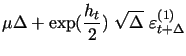 |
(10) | |
| = | (11) |
where ![]() is a
sequence of discrete times,
is a
sequence of discrete times,
![]() are sequences of jointly independent i.i.d.
are sequences of jointly independent i.i.d. ![]() random variables,
random variables,
![]() denotes the logarithmic
asset price or index level at time
denotes the logarithmic
asset price or index level at time ![]() ,
,
![]() is the drift part of the
return process,
is the drift part of the
return process,
![]() defines the speed of mean
reversion17 of the log-volatility process
ht towards its mean
defines the speed of mean
reversion17 of the log-volatility process
ht towards its mean
![]() ,
,
![]() defines the volatility of
volatility parameter,
defines the volatility of
volatility parameter,
![]() defines the typically
negative correlation between returns and volatility increments
known as leverage effect, and finally
defines the typically
negative correlation between returns and volatility increments
known as leverage effect, and finally ![]() is
a discretization parameter. In this paper we consider dynamics at a
daily frequency and fix accordingly
is
a discretization parameter. In this paper we consider dynamics at a
daily frequency and fix accordingly ![]() .18
.18
We next consider a version of the model new to the literature, where the discretized system of equations(10)-(11) is augmented by our additional daily volatility measurement equation based on high-frequency data, given by (9) above for this model as:
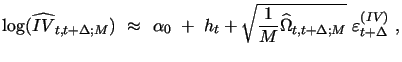 |
(12) |
where
![]() is a
sequence of i.i.d.
is a
sequence of i.i.d. ![]() random variables
independent of
random variables
independent of ![]() for j = 1, 2, while
for j = 1, 2, while
![]() is
some integrated variance measure such as MedRV or TV with
measurement error determined by the sampling frequency
is
some integrated variance measure such as MedRV or TV with
measurement error determined by the sampling frequency ![]() and efficiency
and efficiency
![]() as described
in Section 2.2. Note that both
as described
in Section 2.2. Note that both
![]() and
and
![]() are treated
as daily observations and are directly calculated as functions of
the available high frequency intraday returns at any suitable
sample frequency
are treated
as daily observations and are directly calculated as functions of
the available high frequency intraday returns at any suitable
sample frequency ![]() . As part of the volatility
measurement equation (12)
we also introduce an optional auxiliary parameter
. As part of the volatility
measurement equation (12)
we also introduce an optional auxiliary parameter
![]() , which serves the purpose of
correcting for the discrepancy between the log integrated variance
measures
, which serves the purpose of
correcting for the discrepancy between the log integrated variance
measures
![]() calculated
using open-to-close intraday data and the corresponding
log-variances of close-to-close daily returns represented by
calculated
using open-to-close intraday data and the corresponding
log-variances of close-to-close daily returns represented by
![]() .19 Note, that such correction is not
required, though, if we use open-to-close data for the daily
returns, in which case we simply impose
.19 Note, that such correction is not
required, though, if we use open-to-close data for the daily
returns, in which case we simply impose
![]() . To complete the probabilistic
set-up of the one-factor model, we assume that all random variables
are constructed on a probability space
. To complete the probabilistic
set-up of the one-factor model, we assume that all random variables
are constructed on a probability space ![]() with a given
filtration
with a given
filtration
![]() and all
processes are adapted to the filtration.
and all
processes are adapted to the filtration.
We keep the daily dynamics given by (10) and (11
) in the center
of our analysis, while (12)
serves the sole purpose of incorporating the information content of
high-frequency data without incurring modeling complications due to
market microstructure effects and other features of intraday data
not relevant for modeling of daily returns, as discussed in Section 2.2.
Thus, the use of non-parametric high-frequency volatility measures
![]() designed to be robust to known irregularities of intraday data
gives us an additional degree of freedom to implicitly allow for
high-frequency returns to follow possibly different dynamics from
that of daily returns.
designed to be robust to known irregularities of intraday data
gives us an additional degree of freedom to implicitly allow for
high-frequency returns to follow possibly different dynamics from
that of daily returns.
In order to find the contribution of high frequency information, we consider the above two versions of the model in state space form: (i) the one with daily returns only; (ii) the one including both daily returns and a daily volatility measurement equation from high frequency intraday data. The former is given by the system of equations (10)-(11), while the latter consists of all equations from the "daily only" model augmented by our additional volatility measurement equation (12).
3.2 Two-factor log-SV model with leverage effects and jumps
Alizadeh, Brandt, and Diebold (2002) and Bollerslev and Zhou (2002) provide strong support in favor of two-factor models of foreign exchange rates by utilizing high frequency data as part of non-Bayesian estimation procedures for specifications without leverage effects. Their first factor mimics the long-memory component in volatility, while the second factor has considerably smaller degree of persistence. Bollerslev and Zhou (2002) further find that even in the presence of a second short-memory stochastic volatility factor, it is still important to include also a jump component in the model. Therefore, we consider a two factor log-SV model with compound Poisson jumps in returns. Moreover, we extend the specification by incorporating leverage effects, which allows us to model also the negative correlation between return and volatility innovations typical for equity returns.
Thus, our two-factor logarithmic stochastic volatility model with Poisson jumps in returns represents a very general setting in the current literature. It still allows, though, successful estimation with the use of only daily data, for the sake of comparison to our approach with an extra volatility measurement equation. Similarly to our one-factor specification above, the discretized version of our two-factor model is given by the following set of equations in state space form, where the probabilistic setup and notation are analogous to those of our one-factor model:
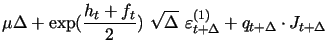 |
(13) | ||
| (14) | |||
| (15) | |||
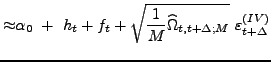 |
(16) |
We assume without loss of generality that
![]() and denote the
persistent and non-persistent volatility factors as ht and ft respectively. Other
than that, the parameters κf and
and denote the
persistent and non-persistent volatility factors as ht and ft respectively. Other
than that, the parameters κf and
![]() governing the short-memory factor
governing the short-memory factor
![]() have similar domain and
interpretation as their counterparts
have similar domain and
interpretation as their counterparts
![]() and
and
![]() for the long-memory factor
for the long-memory factor
![]() . We further assume for
identification purposes
. We further assume for
identification purposes
![]() , since only the total
(unconditional) mean log-volatility is identified in the model.
Also by construction,
, since only the total
(unconditional) mean log-volatility is identified in the model.
Also by construction,
![]() and
and
![]() are
sequences of jointly independent i.i.d.
are
sequences of jointly independent i.i.d. ![]() random
variables. Thus, we allow for leverage effects in both factors,
which is more explicitly seen by defining the innovations specific
to
random
variables. Thus, we allow for leverage effects in both factors,
which is more explicitly seen by defining the innovations specific
to ![]() and
and ![]() as:
as:
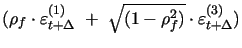 |
(17) | ||
| (18) |
In particualar, the instantaneous covariance matrix between return and volatility innovations is given by:
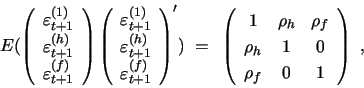 |
where we impose the positive definite restriction
![]() .
.
Our compound Poisson jump specification with normally
distributed jump sizes draws onAndersen, Benzoni, and Lund (2002),
Eraker, Johannes, and Polson (2003), and Johannes and Polson (2002).
In particular, we assume a maximum of one jump per day. The jump
increments in the interval
![]() follow the law of
follow the law of
![]() , where the
jump times
, where the
jump times
![]() are i.i.d.
are i.i.d.
![]() and the jump sizes
and the jump sizes
![]() are i.i.d.
are i.i.d.
![]() . The parameters
. The parameters
![]() and
and
![]() denote respectively the jump
intensity, mean and standard deviation of jump sizes. Since at a
daily frequency the jump intensity parameter
denote respectively the jump
intensity, mean and standard deviation of jump sizes. Since at a
daily frequency the jump intensity parameter ![]() is close to zero, our assumption of maximum one jump
per day is not binding.
is close to zero, our assumption of maximum one jump
per day is not binding.
Most importantly, we extend the state-space form of the model
with our volatility measurement equation (16), which is a
direct counterpart to equation (12)
in the one-factor model and specializes equation (9) given in
general form in section 2.2. Here
the high frequency measure of log integrated variance
![]() is an
estimate of
is an
estimate of
![]() as the total diffusive variance
in the two-factor model. The extra parameter
as the total diffusive variance
in the two-factor model. The extra parameter
![]() serves the same purpose as in the
one-factor model. It provides standard correction for the
discrepancy between log integrated variance measures
serves the same purpose as in the
one-factor model. It provides standard correction for the
discrepancy between log integrated variance measures
![]() calculated using open-to-close intraday data and the log variance
of close-to-close daily returns modeled by
calculated using open-to-close intraday data and the log variance
of close-to-close daily returns modeled by
![]() . For modeling the log variance
of open-to-close daily returns we simply restrict
. For modeling the log variance
of open-to-close daily returns we simply restrict
![]() .
.
In order to find the contribution of high frequency information, similarly to our one-factor model, we consider two versions of the two factor model: (i) the one with only daily returns; (ii) the one including both daily returns and a daily volatility measurement equation from high frequency intraday data. The former is given by the system of equations (13)-(15), while the latter consists of all equations from the "daily" model augmented by our additional volatility measurement equation (16).
3.3. Estimation
3.3.1. Markov chain Monte Carlo methods
We first briefly describe the general principles of Markov chain
Monte Carlo (MCMC) methods, with more detailed exposition in
Chib and Greenberg (1996), Johannes and Polson (2002) and
Jones (1998). Let ![]() denote the vector of
observations,
denote the vector of
observations, ![]() be the vector of latent state
variables and
be the vector of latent state
variables and ![]() be the vector of model
parameters. In Bayesian inference we utilize the prior information
on the parameters to derive the joint posterior distribution for
both parameters and state variables. By the Bayes rule, we
have:
be the vector of model
parameters. In Bayesian inference we utilize the prior information
on the parameters to derive the joint posterior distribution for
both parameters and state variables. By the Bayes rule, we
have:
where
![]() is the likelihood
function of the model,
is the likelihood
function of the model,
![]() is the probability
distribution of state variables conditional on the parameters and
is the probability
distribution of state variables conditional on the parameters and
![]() is the prior probability
distribution on the parameters of the model. Ideally we would like
to know the analytical properties of the joint posterior
distribution of Xand
is the prior probability
distribution on the parameters of the model. Ideally we would like
to know the analytical properties of the joint posterior
distribution of Xand ![]() ,
however, this is hardly feasible. The highly multidimensional joint
posterior distribution is very often too complicated to work with
and analytically intractable and hence even direct simulation from
the joint posterior distribution is hard to perform.
,
however, this is hardly feasible. The highly multidimensional joint
posterior distribution is very often too complicated to work with
and analytically intractable and hence even direct simulation from
the joint posterior distribution is hard to perform.
In the sequel we base our exposition on Jones (2003). The
idea behind MCMC methods is to break the highly dimensional vectors
of latent variables ![]() and parameters
and parameters ![]() into smaller pieces. The Gibbs sampler developed in
Geman and Geman (1984) considers partitioning of
into smaller pieces. The Gibbs sampler developed in
Geman and Geman (1984) considers partitioning of ![]() and
and ![]() into respectively
into respectively ![]() and
and
![]() subvectors
subvectors
![]() and
and
![]() . Then
the Markov chain is constructed by first defining starting values
of the chain
. Then
the Markov chain is constructed by first defining starting values
of the chain ![]() and
and
![]() and then iteratively forming the
chain
and then iteratively forming the
chain
The draws of
![]() are performed for each
are performed for each
![]() and each
and each
![]() by drawing from the
following transition densities:
by drawing from the
following transition densities:
| (19) | |
| (20) |
where
![]() and
and
![]() It can be shown that under mild conditions the chain
It can be shown that under mild conditions the chain
![]() converges to its
invariant distribution
converges to its
invariant distribution
![]() that is by construction a
joint posterior distribution of the model under consideration. The
proof of the Gibbs sampler convergence to invariant distribution,
sufficient conditions and some applications can be found in
Chib and Greenberg (1996).
that is by construction a
joint posterior distribution of the model under consideration. The
proof of the Gibbs sampler convergence to invariant distribution,
sufficient conditions and some applications can be found in
Chib and Greenberg (1996).
The Gibbs sampler algorithm provides a tractable method to draw from multidimensional and complicated distributions only if one can draw from all complete conditional distributions in equations (19) and (20). However, even one-dimensional complete conditional distributions can be in practice difficult if not impossible to draw from. In this case we replace a particular Gibbs sampler step by the Metropolis-Hastings (MH) step in Metropolis, Rosenbluth and Rosenbluth (1953). Chib and Greenberg (1996) provide further details about the MH algorithm. The main building block of our estimation method is based on the Gibbs sampler algorithm with some blocks replaced by MH steps.
After discarding a "burn-in" period of the first N draws, the discrete approximation
![]() of the
joint posterior density
of the
joint posterior density
![]() allows one to compute
various statistics. For example, the sample mean of the posterior
distributions can be taken to obtain parameter estimates for our
models. Likewise, one can estimate statistics of particular
interest in applications such as moment and quantile forecasts for
multi-horizon returns as well as associated risk measures such as
Value-at-Risk (VaR) or any other function of the conditional
multi-horizon return density such as the price of a derivative
contract. Moreover, parameter uncertainty is taken automatically
into account by integrating over the entire joint posterior
distribution of parameters and state variables. This important
property of MCMC estimation methods is especially valuable for our
purposes, as it allows us to show how increasing the precision of
parameter and volatility state estimation (by including our
volatility measurement equations (12)
and (16) gets
translated into more accurate conditional return density forecasts
and moments/quantiles in particular.
allows one to compute
various statistics. For example, the sample mean of the posterior
distributions can be taken to obtain parameter estimates for our
models. Likewise, one can estimate statistics of particular
interest in applications such as moment and quantile forecasts for
multi-horizon returns as well as associated risk measures such as
Value-at-Risk (VaR) or any other function of the conditional
multi-horizon return density such as the price of a derivative
contract. Moreover, parameter uncertainty is taken automatically
into account by integrating over the entire joint posterior
distribution of parameters and state variables. This important
property of MCMC estimation methods is especially valuable for our
purposes, as it allows us to show how increasing the precision of
parameter and volatility state estimation (by including our
volatility measurement equations (12)
and (16) gets
translated into more accurate conditional return density forecasts
and moments/quantiles in particular.
3.3.2. Bayesian MCMC inference for models with high frequency volatility measurement equations
We limit our exposition to describing our MCMC estimation procedure for the two-factor stochastic volatility models from Section (3.2).20 We put special emphasis on how to estimate models including our high-frequency measurement equations by offering a straightforward extension of estimation methods based only on daily returns.
Following the notation from the previous section, we need to
specify the vector of observations ![]() , the vector
of latent state variables
, the vector
of latent state variables ![]() and the vector of
parameters
and the vector of
parameters ![]() along with their appropriate
subdivision in line with the construction of the Gibbs sampler
algorithm. In particular, we define the following vectors, where
"Daily" stays for estimation based only on daily returns
(equations (13)-(15)) and "HF"
stays for estimation incorporating also volatility measures based
on high-frequency intraday data (equations (13)-(16)):
along with their appropriate
subdivision in line with the construction of the Gibbs sampler
algorithm. In particular, we define the following vectors, where
"Daily" stays for estimation based only on daily returns
(equations (13)-(15)) and "HF"
stays for estimation incorporating also volatility measures based
on high-frequency intraday data (equations (13)-(16)):
The partitions of ![]() and
and ![]() are given by
are given by
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
,
![]() ,
,
![]() ,
,
![]() where
where
![]() ,
,
![]() . Thus, we treat each element of
the state vector
. Thus, we treat each element of
the state vector ![]() as a single block. For the vector
of parameters
as a single block. For the vector
of parameters ![]() all elements are treated as a
single block with the exception of
all elements are treated as a
single block with the exception of
![]() and
and
![]() . These parameters are
drawn jointly as in Jacquier, Polson, and Rossi (2004). Finally, the extra parameter
. These parameters are
drawn jointly as in Jacquier, Polson, and Rossi (2004). Finally, the extra parameter
![]() in equation
(16)
appears only in the "HF" model including high frequency
information and is estimated along with the rest of the parameters
or it can be exogenously specified following standard approaches in
the realized volatility literature to obtain variances for the
whole day such as Hansen and Lunde (2005). It is set to
zero when modeling open-to-close daily returns.
in equation
(16)
appears only in the "HF" model including high frequency
information and is estimated along with the rest of the parameters
or it can be exogenously specified following standard approaches in
the realized volatility literature to obtain variances for the
whole day such as Hansen and Lunde (2005). It is set to
zero when modeling open-to-close daily returns.
Having defined above all blocks for the latent state variables
X and parameters ![]() , we
apply the MCMC algorithm based on the Gibbs sampler presented in
Section 3.3.1. Since draws of
all parameters and jump related latent variables are standard in
the literature, we directly refer to Szerszen (2009) for the
imposed prior distributions on the model parameters
, we
apply the MCMC algorithm based on the Gibbs sampler presented in
Section 3.3.1. Since draws of
all parameters and jump related latent variables are standard in
the literature, we directly refer to Szerszen (2009) for the
imposed prior distributions on the model parameters ![]() and all other details.
and all other details.
Here we focus on addressing the fundamental difference between
estimation of the standard "Daily" and our "HF" version of the
model, which differ just by the additional volatility measurement
equation (16) based on
high-frequency data. The information provided by this extra
equation affects only the complete conditional posteriors of the
volatility states ![]() and
and ![]() . In particular, the MCMC update for
. In particular, the MCMC update for ![]() is given by
is given by
for t=1, 2, ..., T, where the second and fourth kernels on the
right hand side are omitted for t=1, while the first, third and
last kernels are omitted for t = T. The MCMC update for the second
factor ![]() is performed analogously.
is performed analogously.
Thus, an inspection of the above update expression reveals that
the only kernel affected by the high frequency information with
![]() is the last one
is the last one
![]() for the
for the ![]() factor and, similarly,
factor and, similarly,
![]() for the
for the ![]() factor. The rest of the kernels are
exactly those coming from inference based on daily returns only,
i.e. with
factor. The rest of the kernels are
exactly those coming from inference based on daily returns only,
i.e. with
![]() , which appear also with
, which appear also with
![]() . This is of key importance for
understanding how the extra information provided by high-frequency
data improves estimation efficiency in our "HF" versus "Daily"
approaches. The extra kernels
. This is of key importance for
understanding how the extra information provided by high-frequency
data improves estimation efficiency in our "HF" versus "Daily"
approaches. The extra kernels
![]() and
and
![]() in the MCMC updates of
in the MCMC updates of ![]() and
and ![]() ,
respectively, are very spiked around the mode for dates with low
values of
,
respectively, are very spiked around the mode for dates with low
values of
![]() in the
volatility measurement equation (16) and, hence,
they are very informative about the latent volatility states. The
attainable precision improvements increase with the sample
frequency
in the
volatility measurement equation (16) and, hence,
they are very informative about the latent volatility states. The
attainable precision improvements increase with the sample
frequency ![]() and depend also on
and depend also on
![]() , being a function
of the underlying volatility paths and the chosen high-frequency
integrated variance and quarticity measures as detailed in Section
2.2.
By contrast, the use of only daily data is equivalent to
artificially setting
, being a function
of the underlying volatility paths and the chosen high-frequency
integrated variance and quarticity measures as detailed in Section
2.2.
By contrast, the use of only daily data is equivalent to
artificially setting
![]() to
infinity in order to suppress the strong information content of
high frequency data provided by our volatility measurement
equation. In what follows, we analyze the gains in estimation
efficiency and risk forecasting accuracy from our "HF" versus
traditional "Daily" estimation as a natural benchmark for
comparison.
to
infinity in order to suppress the strong information content of
high frequency data provided by our volatility measurement
equation. In what follows, we analyze the gains in estimation
efficiency and risk forecasting accuracy from our "HF" versus
traditional "Daily" estimation as a natural benchmark for
comparison.
4 Estimation efficiency and risk forecasting accuracy
The ability to estimate parameters and volatility states more efficiently directly translates into more accurate risk forecasts. Moreover, the highly non-linear nature of the underlying transformation from noisy parameter and volatility estimates to risk forecasts implies reduction not only in the variance but also in the bias of the prediction errors. Our analysis in this section is designed to study the interplay between longer sample size and higher intraday frequency as an additional source of information introduced by our volatility measurement equation for the purpose of reducing estimation uncertainty. We document that even for the longest sample lengths encountered in practice there is a substantial efficiency gain from incorporating the extra information provided by high-frequency volatility measures. Moreover, for key model parameters controlling skewness and kurtosis we find that two or five years of high frequency data would suffice to obtain the same level of precision as twenty years of daily data. This suggests that our approach can be particularly useful in finance applications where only short data samples are available or economically meaningful to use.
It is possible to derive analytical results along these lines in certain more restrictive settings. An instructive example for a canonical log-SV model is given in the appendix. Monte Carlo analysis is the only viable option, though, for models that are not analytically tractable. Hence, we take a Monte Carlo approach to study estimation efficiency and the impact of parameter uncertainty on risk forecasting accuracy. We conduct considerably more thorough and extensive simulations than usual in order to properly document the substantial efficiency gains and improved precision of risk forecasts at horizons of up to a few months ahead regardless of the chosen model when high frequency information is included in the model. Perhaps the most important of our findings is that there is considerable asymmetry between bad and good times when it comes to the attainable improvements in risk forecasting accuracy: in good times we are able to largely eliminate overstatement of risk, while in bad times our approach helps avoid understatement of risk. From a practical point of view, this implies imposing an appropriate larger risk cushion exactly when needed the most, e.g. early on in times of crisis (rather than with a delay), while at the same time avoiding excessive risk cushion requirements in normal times. In this sense, our main purpose in what follows is to document both the efficiency gains for model estimation and forecasting and the implied potentially large economic value of our approach to incorporating the information content of high-frequency volatility measures for model estimation and risk forecasting.
4.1. Monte Carlo setup
In order to set-up the stage for Monte Carlo analysis we first
describe how to draw sample paths consistent with the data
generating process implied by our model specifications. Daily
dynamics of both returns and volatility are based on equations
(10)-(11) and (13)-(15)
respectively for the one-factor and two-factor log-SV models that
we consider. The intraday dynamics is based on a Brownian bridge
connecting consecutive daily sample points and producing valid
integrated variance measures
![]() and
corresponding scaled integrated quarticity measures
and
corresponding scaled integrated quarticity measures
![]() that govern our additional volatility measurement equations in
(12) and (16) as
described in Section 2.2. In
this way, we allow for potentially richer intraday dynamics than
the one at the daily frequency, possibly including also realistic
intraday market-microstructure effects that many novel
high-frequency volatility measures are designed to be robust to
when sampled at two to five minute frequency.21
that govern our additional volatility measurement equations in
(12) and (16) as
described in Section 2.2. In
this way, we allow for potentially richer intraday dynamics than
the one at the daily frequency, possibly including also realistic
intraday market-microstructure effects that many novel
high-frequency volatility measures are designed to be robust to
when sampled at two to five minute frequency.21
We draw 1,000 sample paths for each of the considered one- and two-factor log-SV models. For each sample path we estimate the underlying model parameters using different information sets: (i) daily data only; (ii) daily data with additional high frequency volatility measurements based on 5-minute or 2-minute intraday returns; (iii) the "infeasible" case of perfectly observed volatility.22 In order to study the interplay between additional information coming from more high frequency data and longer sample size in terms of number of days, we consider three sample windows of 2, 5 and 20 years. This gives a total of twelve one-factor and twelve two-factor specifications for the information sets used for model estimation. We estimate all specifications using the Bayesian MCMC methods described in Section 3 with 250,000 draws, where the first 50,000 draws are discarded as the burn-in sample. For the purposes of forecasting conditional return moments and quantiles, based on the obtained 200,000 draws of the posterior distribution of parameters and volatility states, we approximate multi-period conditional density forecasts by a cloud of 25,000,000 points. We then compare moments and quantiles of the obtained conditional density forecasts for the two different estimation procedures that we consider, depending on whether a daily volatility measurement equation based on high-frequency data is used or not.
4.2. Efficiency gains in parameter and volatility estimation
In Tables 1 and 2 we report parameter estimates, bias and root mean squared error (RMSE) of volatility related parameters governing equations (11) and (14)-(15) for our one-factor and two-factor specifications respectively. The true parameter values in each table represent our estimates on S&P 500 daily futures returns for the period October 2, 1985 - February 26, 2009.
For the one-factor model (Table 1) we attain up to few times
better precision when using high frequency data compared to only
daily data for estimating the parameters governing skewness and
kurtosis. This translates into RMSE reduction of as much as 70%. In
particular, we find that the information content of high-frequency
volatility measures improves the most the estimation efficiency of
the volatility of volatility parameter ![]() and
the leverage effect parameter
and
the leverage effect parameter ![]() in the
model.23 Moreover, the gains are consistent
across different sample lengths, even for the longest ones
typically encountered in practice such as 20 years, when daily
estimation is more likely to produce satisfactory results. As a
practical rule of thumb we find that two years of high frequency
data often suffice to obtain the same level of precision for these
parameters as twenty years of daily data. At the same time, a
comparison between the attainable improvement by switching from
daily to 5-minute estimation and any further increase in the
intraday sample frequency from 5 to 2 minutes and beyond (up to the
infeasible case of perfectly known volatility) reveals a rapid
decrease in the additional efficiency gains that can be obtained.
We also observe a substantial RMSE reduction for the parameter
governing persistence of volatility
in the
model.23 Moreover, the gains are consistent
across different sample lengths, even for the longest ones
typically encountered in practice such as 20 years, when daily
estimation is more likely to produce satisfactory results. As a
practical rule of thumb we find that two years of high frequency
data often suffice to obtain the same level of precision for these
parameters as twenty years of daily data. At the same time, a
comparison between the attainable improvement by switching from
daily to 5-minute estimation and any further increase in the
intraday sample frequency from 5 to 2 minutes and beyond (up to the
infeasible case of perfectly known volatility) reveals a rapid
decrease in the additional efficiency gains that can be obtained.
We also observe a substantial RMSE reduction for the parameter
governing persistence of volatility ![]() for
the shortest sample sizes, while still dominating the estimation
efficiency with only daily data across all sample sizes.
for
the shortest sample sizes, while still dominating the estimation
efficiency with only daily data across all sample sizes.
For the richer two-factor log-SV model (Table 2) these
substantial efficiency gains from incorporating high-frequency
volatility measures naturally get even larger. Moreover, a somewhat
larger part of the gains is due to bias reduction. It is important
to note that here skewness and kurtosis are driven not only by a
persistent volatility factor but also by a second non-persistent
factor. For the non-persistent factor we find that the gains from
incorporating high frequency information are more pronounced than
those from increasing the yearly sample length. We do not find such
evidence for the persistent factor, where both sources of
information play an important role in parameter estimation. This
implies bigger efficiency gains from incorporating high frequency
information for the parameters ![]() and
and
![]() governing skewness and kurtosis
arising from the non-persistent factor
governing skewness and kurtosis
arising from the non-persistent factor ![]() . The
reduction of parameter uncertainty for the persistent factor
. The
reduction of parameter uncertainty for the persistent factor
![]() is somewhat smaller but still very
visible.
is somewhat smaller but still very
visible.
The quality of risk forecasts depends not only on the degree of
parameter uncertainty but also on the degree of volatility
estimation uncertainty. In particular, it is important to assess
the impact of incorporating additional high frequency information
on the accuracy of estimation of terminal volatility states as they
play important role in forecasting risk. In Table 3 we report mean
estimates, bias and RMSE for the terminal volatility states
![]() and
and ![]() of the
two-factor log-SV model. Thus, we conclude that our volatility
measurement equation helps in estimating better not only model
parameters but also latent volatility states. Considerable
efficiency gains are obtained mainly for the persistent volatility
factor, while for the non-persistent factor we still observe slight
improvements. Similarly to parameter estimates, our findings for
volatility states are consistent across all considered sample
sizes. Moreover, the biggest efficiency gains take place when
moving from estimation based only on daily data to estimation
incorporating our volatility measurement equation based on 5-minute
returns. Further increase of the intraday sample frequency from
5-minutes to 2-minutes leads to additional efficiency gains of much
smaller magnitude. Overall, for the estimation of volatility states
adding high frequency information has somewhat bigger importance
than increasing the yearly sample length. This plays a major role
especially for short-term risk forecasting.
of the
two-factor log-SV model. Thus, we conclude that our volatility
measurement equation helps in estimating better not only model
parameters but also latent volatility states. Considerable
efficiency gains are obtained mainly for the persistent volatility
factor, while for the non-persistent factor we still observe slight
improvements. Similarly to parameter estimates, our findings for
volatility states are consistent across all considered sample
sizes. Moreover, the biggest efficiency gains take place when
moving from estimation based only on daily data to estimation
incorporating our volatility measurement equation based on 5-minute
returns. Further increase of the intraday sample frequency from
5-minutes to 2-minutes leads to additional efficiency gains of much
smaller magnitude. Overall, for the estimation of volatility states
adding high frequency information has somewhat bigger importance
than increasing the yearly sample length. This plays a major role
especially for short-term risk forecasting.
4.3. Precision improvements in risk forecasting accuracy
The documented substantial decrease in parameter and volatility estimation uncertainty implies non-trivial improvements in the accuracy of forecasts of conditional return moments and quantiles. We compare forecasts resulting from inference based on daily data to those utilizing 5-minute high frequency volatility measures. We restrict attention to the 5-minute frequency in accordance with our finding that it offers essentially the bulk of the attainable improvements based on our volatility measurement equation. We perform our analysis incorporating parameter and volatility estimation uncertainty for all three considered sample lengths of 2, 5 and 20 years.
In Tables 4 and 5 we report forecasts of conditional return moments respectively for one-factor and two-factor models. In Tables 6 and 7 we also report forecasts of conditional return quantiles. The considered forecast horizons are 1, 5, 10 and 20 days ahead and are presented in separate panels in each table. These forecast horizons are of primary interest in many finance applications.
Our main finding is that our more efficient parameter and state estimates incorporating the strong information content of high-frequency volatility measures translate into equally better conditional return density forecasts not only in terms of RMSE but also in terms of bias. The bias reduction is due to the pronounced non-linearities in the underlying transformation of parameters and state variables. The main message from our analysis summarized in Tables 4-7 is that for any model, any estimation sample length, and across all forecast horizons of interest, the forecasts incorporating the extra information from our volatility measurement equation clearly dominate those based only on daily data. Moreover, these results strengthen our rule of thumb that model specifications estimated with two years of high frequency data perform at least as good as the same model specifications estimated with twenty years of daily data, which in turn are considerably outperformed if estimated on twenty years of high-frequency data.
4.4. Forecast error reductions in good versus bad times
From risk management perspective it is important to know how the improvements in risk forecasting accuracy vary across good and bad times. To this end, in Table 8 we report relative errors of forecasts of the 0.01 and 0.05 conditional return quantiles at horizons of one (panel A), five (panel B), ten (panel C) and twenty (panel D) days ahead. The reported relative errors are calculated across 1,000 Monte Carlo replications as the mean of the percentage difference between a forecast based on parameter and state estimates and the forecast based on the corresponding true values. The results are sorted by the rank order of the true quantile forecasts from low (representing bad times) to high (representing good times), as indicated in the first column. In our model this is equivalent to sorting by terminal volatility state from high (representing bad times) to low (representing good times). Each three rows reported for ranks 1 (low) to 5 (high) of the true quantile forecasts contain results for three different sample lengths T equal to 2 years, 5 years and 20 years (as given in the second column), taking parameter and volatility estimation uncertainty into account. For each quantile and forecast horizon we report results for the two alternative Bayesian estimation procedures in adjacent column pairs: either with (right column denoted "HF 5-min") or without (left column denoted "Daily only") augmenting the underlying state-space formulation with our daily volatility measurement equation based on high frequency intraday data.
As a graphical summary of the results reported in Table 8, Figure 1 plots the one-percent VaR (top graph) and five-percent VaR (bottom graph) relative forecast errors at a five-day horizon as a function of the rank order of the underlying true forecasts from low (representing bad times) to high (representing good times). The resulting VaR forecast errors without utilizing our high-frequency volatility measures are plotted as a solid line (denoted "Daily"), while those incorporating the information content of intraday data for the latent daily volatility are plotted as a dashed line (denoted "HF 5-min"). The reported relative errors of conditional return quantile forecasts can be interpreted also as the percentage overestimation or understimation of the implied capital charge for market risk based on one-percent (quantile 0.01) and five-percent (quantile 0.05) VaR.
Both Table 8 and Figure 1 reveal that risk forecasts stemming from traditional model inference on daily data tend to be overly conservative in good times (e.g. overestimating risk by as much as 30%) but they are not conservative enough in bad times (e.g. underestimating risk by as much as 10%). By contrast, risk forecasts based on our approach to exploiting high-frequency data are considerably closer to the truth in both bad and good times.
Leaving the reported magnitudes aside, this result is very intuitive as the use of volatility measures based on high frequency data allows for considerably faster and more precise incorporation of major changes in the current volatility level compared to daily data alone. For example, in bad times when volatility goes up it should take a longer sequence of daily returns alone than in conjunction with high-frequency volatility measures to deliver volatility state estimates that are not downward biased. Similarly, in good times when volatility goes down it should take longer for daily data alone than in conjunction with high-frequency volatility measures to produce volatility state estimates that are not upward biased. Thus, the observed differences between the risk forecast errors in bad versus good times (Table 8 and Figure 1) are completely in line with the asymmetric increase in volatility state uncertainty, coupled also with higher parameter uncertainty (see Section 4.2 above), characterizing traditional daily estimation in comparison to the proposed approach utilizing also high-frequency data. In sum, thanks to incorporating the strong information content of high-frequency volatility measures, we are able to better curb risk taking exactly when needed the most, i.e. early on in times of crisis, while avoiding unnecessary overstatement of risk in normal times.
5 Empirical Illustration
Conditional return quantile forecasts play important role in risk management as they represent value-at-risk (VaR) forecasts. A key testable implication from our analysis in the previous section is that during bad times, e.g. early on in times of crisis, VaR forecast time-series based on our approach to exploiting high-frequency data will tend to "cross from above" the VaR forecast time-series stemming from traditional model inference on daily data. This is because, as explained above, the daily-based VaR forecasts are downward biased in bad times (when risk is elevated) and upward biased in good times (when risk is minimal), while our HF-based VaR forecasts are considerably closer to the truth in both bad and good times.
In order to test the empirical validity of this important risk management implication, we study the dynamics of five-day ahead VaR forecasts for S&P 500 and Google returns throughout the financial crisis of 2007-2008. Our goal is to illustrate the potentially large economic value from the proposed approach to incorporating the information content of high-frequency volatility measures. It is beyond the scope of this paper, though, to run a horse race between many viable alternative VaR forecasting techniques. We limit ourselves strictly to evaluating the empirical validity of our main testable implication with regard to HF-based versus daily-based VaR forecasts in the context of popular equity return models such as the fairly general two-factor log-SV model with jumps analyzed in the previous sections.
5.1. Data and estimation
In our empirical illustration we consider S&P 500 daily futures returns for the period October 2, 1985 - February 26, 2009 and Google daily equity returns for the period August 30, 2004 - July 31, 2009.24 We exclude from each series holidays and shortened trading days. Our high-frequency measurement equation is constructed from five-minute intraday returns following the procedures given in section 2.2, while model estimation and forecasting is conducted as detailed in sections 3 and 4. We study the dynamics of five-day ahead VaR forecasts for the last 120 business weeks in each sample, both of which cover the financial crisis of 2007-2008. To produce each forecast we re-estimate our two-factor log-SV model with all available data going back to the beginning of each sample. Thus, the sample for S&P 500 roughly corresponds to 20 years of data in our Monte Carlo study (Section 4). The sample for Google, on the other hand, represents 2-5 years of data and cannot be extended further back as it starts ten days after Google's IPO.
5.2 Forecasting risk throughout the 2007-2008 financial crisis
On Figures 2 and 3 we plot one-percent (top graph) and five-percent (bottom graph) VaR forecasts without overlapping at five-day horizon for S&P 500 futures returns (Figure 2) and Google equity returns (Figure 3) based on a two-factor log-SV model with jumps in returns. The model is estimated at a daily discretization interval by Bayesian MCMC methods either without or with augmenting the underlying state-space formulation with our daily volatility measurement equation based on high frequency intraday data. The resulting VaR forecasts without utilizing high-frequency volatility measures are plotted as a solid line (denoted "VaR with daily data"), those incorporating the information content of intraday data for the latent daily volatility are plotted as a dashed line (denoted "VaR with HF 5-min data"), while the corresponding actual observed returns are plotted as vertical bars (denoted "Return realizations").
As clearly seen from the graphs, the VaR forecasts with HF 5-min data seemingly correctly predict more risk and "cross from above" the VaR forecasts with daily data exactly around major turmoil events during the financial crisis of 2007-2008. These include the Bear Sterns turmoil in July 2007, the Countrywide turmoil in January 2008, the Fannie Mae and Freddie Mac turmoil in July 2008, and most notably, the Lehman Brothers collapse followed by the TARP Legislation turmoil in October 2008. The gap between the two alternative VaR forecasts around these events implies sizeable underestimation of risk by the traditional approach based on daily data. This is more pronounced for Google in line with the fact that individual stocks tend to be more risky than stock indices. At the same time, before the summer of 2007 and on many occasions afterwards the VaR forecasts with HF 5-min data predict a bit less risk than the VaR forecasts with daily data. Nonetheless, the number of incurred violations (given by the number of times the return realizations, plotted as vertical bars, go below the VaR forecasts) remains completely in line with the expected number of violations at the 1% and 5% VaR levels across 120 (non-overlapping) forecasts.
Overall, the observed dynamics of VaR forecasts for S&P 500 and Google returns throughout the financial crisis of 2007-2008 is in striking agreement with the key testable implication from our analysis in the previous sections. We obtain strong empirical support that not only in theory but also in important real-world examples our approach to incorporating the information content of high frequency volatility measures can help better curb risk taking exactly when needed the most, i.e. early on in times of crisis, while avoiding unnecessary overstatement of risk in normal times.
6 Conclusion
In this paper, we have developed a method for estimating popular equity return models relying not only on daily returns but also on nowadays ubiquitous high-frequency intraday return data. The essence of our approach is to borrow asymptotic results from the growing realized volatility literature and cast them as precise volatility measurement equations directly within the standard state-space representation of popular equity return models estimated at daily frequency. In this way, we avoid specifying explicitly the intraday return dynamics, while considerably improving estimation efficiency of such models at daily or monthly frequency. In particular, we utilize daily returns along with high-frequency jump-robust realized volatility measures within a standard Bayesian MCMC estimation framework. This allows us to take explicitly into account the resulting substantial reduction in parameter uncertainty. Thus, we are able to show sizeable economic gains when forecasting risk, compared to inference based on the more limited information provided by daily returns alone.
In this way, we depart from previous studies geared primarily towards specification testing that have focused on the use of such high-frequency volatility measures in classical rather than Bayesian estimation procedures. Instead, we demonstrate that across a variety of equity return models estimated at daily frequency the parameters controlling skewness and kurtosis can be obtained almost as precisely as if volatility is observable by incorporating the strong information content of realized volatility measures extracted from high-frequency data. In particular, we show that not only the parameters controlling volatility of volatility but also those controlling leverage effects can be estimated several times more precisely by exploiting high-frequency volatility measures. Furthermore, we show that our highly efficient estimates lead in turn to substantial gains for forecasting various risk measures at horizons ranging from a few days to a few months ahead when taking also into account parameter uncertainty. In fact, our approach not only reduces the root mean square prediction error but also shrinks and almost eliminates the forecast bias, which inevitably arises from the pronounced nonlinearities in the involved transformation of parameter and volatility estimates. As a practical rule of thumb we find that two years of high frequency data often suffice to obtain the same level of precision as twenty years of daily data, thereby making our approach particularly useful in finance applications where only short data samples are available or economically meaningful to use. Last, but perhaps most important in risk management applications, we find that risk forecasts based on our approach to exploiting high-frequency data are considerably closer to the truth in both bad and good times relative to those stemming from traditional model inference on daily data, which we find can overestimate risk by as much as 30% in good times or underestimate it by as much as 10% in bad times. We support our findings both with extensive simulations and an empirical illustration on VaR forecasts for S&P500 and Google returns during the financial crisis of 2007-2008. Thanks to incorporating the strong information content of high-frequency volatility measures, we are able to better curb risk taking exactly when needed the most, i.e. early on in times of crisis (rather than with a delay), while avoiding unnecessary overstatement of risk in normal times. Qualitatively, our findings are robust both across different models and jump-robust volatility measures on high frequency data that we analyze.
In view of the documented substantial precision gains in forecasting risk of equity returns, the estimation approach we propose can directly add value in different areas of risk management and asset pricing. Beyond equity returns, the method can be applied also to other financial data such as foreign exchange rates, bonds and interest rates. It can be easily geared also towards model specification testing. More generally, we establish a promising and tractable way to incorporate additional sources of information, such as alternative high frequency volatility measures, into models in state space form.
A Analytical Results In Toy Model: A Motivating Example
In this paper we introduce asymptotically exact volatility measurement equations in state space form and propose a Bayesian MCMC estimation approach that we use to demonstrate the efficiency gains when estimating key parameters in various popular SV models. Although our expressions for the complete conditional posteriors given in section 3.3.2 provide an intuitive explanation where the documented efficiency gains are coming from, it is useful to provide some extra analytical support for the obtained results also by using classical estimation methods in a suitable "toy model".
To this end,
here we restrict attention on estimating the kurtosis parameter
![]() in the following simplified
log-SV model in state space form augmented with a volatility
measurement equation based on high-frequency
data:
in the following simplified
log-SV model in state space form augmented with a volatility
measurement equation based on high-frequency
data:
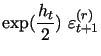 |
(21) | ||
| (22) | |||
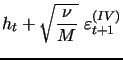 |
(23) |
where all error
terms are i.i.d. Gaussian. Note that equations (21)-(22) represent a
canonical log-SV model for daily returns (and log-variances)
extensively studied in the literature, see e.g. Taylor (1986),
Nelson (1988), Harvey, Ruiz, and Shephard (1994), Ruiz (1994),
Andersen and Sorensen (1996), Francq and Zakoïan (2006), among
others.25 Without loss of generality, the
log-variance process is zero mean with persistence controlled by
![]() . Equation
(23)
represents our volatility measurement equation based on
high-frequency intraday data in its simplest form (for implicitly
assumed Brownian intraday dynamics), where
. Equation
(23)
represents our volatility measurement equation based on
high-frequency intraday data in its simplest form (for implicitly
assumed Brownian intraday dynamics), where ![]() is the intraday sample frequency and
is the intraday sample frequency and ![]() is an efficiency factor depending on the chosen
volatility measure
is an efficiency factor depending on the chosen
volatility measure
![]() as detailed in section
2.2.
as detailed in section
2.2.
As usual, it is
convenient to substitute the return measurement equation in this
canonical log-SV model with the one obtained after taking the
logarithm of squared returns (without incurring any information
loss when the distribution of
![]() is
symmetric):
is
symmetric):
| (24) | |||
| (25) | |||
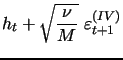 |
(26) |
It is
convenient to further simplify notation by redefining the
measurements and their errors as
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
This yields the following representation of the model in state
space form:
.
This yields the following representation of the model in state
space form:
| (27) | |||
| (28) | |||
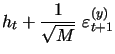 |
(29) |
In what
follows, we study the efficiency of estimating ![]() taking
taking ![]() as given in the
following two specifications: (i) Standard "Daily" given by the
first two equations (27)-(28);
(ii) Augmented "Daily + HF" given by the full system (27)-(29).
Intuitively, it is clear that the relative difference in the
precision of the two measurement equations (27)
and (29) determines the
attainable efficiency gains from using both measurement equations
in the proposed "Daily + HF" specification as opposed to using
only the first measurement equation in the standard "Daily"
specification. Clearly, increasing the sample frequency
as given in the
following two specifications: (i) Standard "Daily" given by the
first two equations (27)-(28);
(ii) Augmented "Daily + HF" given by the full system (27)-(29).
Intuitively, it is clear that the relative difference in the
precision of the two measurement equations (27)
and (29) determines the
attainable efficiency gains from using both measurement equations
in the proposed "Daily + HF" specification as opposed to using
only the first measurement equation in the standard "Daily"
specification. Clearly, increasing the sample frequency ![]() improves the precision of the additional volatility
measurement equation (29)
and in the limit as
improves the precision of the additional volatility
measurement equation (29)
and in the limit as
![]() it yields perfect
measurements of the volatility states. This means that the maximum
attainable efficiency in the case of perfectly observed volatility
states can be closely achieved by increasing the sample frequency
it yields perfect
measurements of the volatility states. This means that the maximum
attainable efficiency in the case of perfectly observed volatility
states can be closely achieved by increasing the sample frequency
![]() sufficiently.
sufficiently.
A GMM
estimation approach provides a straightforward formalization of
these intuitive observations. Let
![]() and
and
![]() denote the known second and fourth unconditional moments of the
two measurement error terms. Consider the following two moment
conditions:
denote the known second and fourth unconditional moments of the
two measurement error terms. Consider the following two moment
conditions:
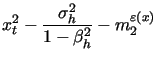 |
(30) | ||
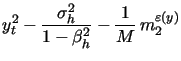 |
(31) |
It is easy to confirm that these are valid moments:
| 0 | (32) | ||
| 0 | (33) |
The corresponding variance of each moment and the covariance between them is given by:
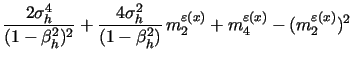 |
(34) | ||
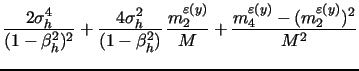 |
(35) | ||
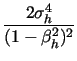 |
(36) |
Note that the
unconditional second moment of the log-variance process is given by
![$ m^{h}_{2}=\mathbb{E}[h_t^2]=\frac{\sigma_h^2}{(1-\beta_h^2)}$](img317.gif) .
Hence, the above variance and covariance expressions take the
following form:
.
Hence, the above variance and covariance expressions take the
following form:
| (37) | |||
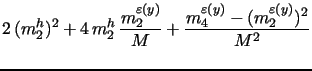 |
(38) | ||
| (39) |
The resulting optimal GMM weighting matrix is given by:
![\begin{displaymath}\left( \begin{array}{cc} \mathbb{V}[g_{1}] & \mathbb{C}[g_{1},g_{2}] \ \mathbb{C}[g_{1},g_{2}] & \mathbb{V}[g_{2}] \ \end{array}\right)^{-1}\end{displaymath}](img327.gif) |
![$\displaystyle \frac{1}{\mathbb{V}[g_{1}] \, \mathbb{V}[g_{2}] - \mathbb{C}[g_{1},g_{2}]^{2}} \, \left( \begin{array}{cc} \mathbb{V}[g_{2}] & -\mathbb{C}[g_{1},g_{2}] \ -\mathbb{C}[g_{1},g_{2}] & \mathbb{V}[g_{1}] \ \end{array} \right)$](img329.gif) |
(40) |
It follows that
the ratio between the variance of an estimator of ![]() based on the first moment condition ("Daily"
specification) and the variance of the optimal GMM estimator of
based on the first moment condition ("Daily"
specification) and the variance of the optimal GMM estimator of
![]() combining both moment conditions
("Daily + HF" specification) is given by:
combining both moment conditions
("Daily + HF" specification) is given by:
![$\displaystyle \frac{\mathbb{V}[g_{1}]}{\left(\frac{\mathbb{V}[g_{1}]+\mathbb{V}[g_{2}]-2 \, \mathbb{C}[g_{1},g_{2}]}{\mathbb{V}[g_{1}] \, \mathbb{V}[g_{2}]-\mathbb{C}[g_{1},g_{2}]^2} \right)^{-1}} = 1+\frac{\left( \frac{\mathbb{V}[g_{1}]}{\mathbb{C}[g_{1},g_{2}]}- 1 \right)^{2}}{\frac{\mathbb{V}[g_{1}]}{\mathbb{C}[g_{1},g_{2}]} \, \frac{\mathbb{V}[g_{2}]}{\mathbb{C}[g_{1},g_{2}]}-1}$](img332.gif) |
(41) | ||
![$\displaystyle 1 + \frac{ 2 \, \frac{m^{\varepsilon{(x)}}_{2}}{m^{h}_{2}} + \frac{1}{2} \, [\frac{m^{\varepsilon{(x)}}_{4}}{(m^{h}_{2})^2}-(\frac{m^{\varepsilon{(x)}}_{2}}{m^{h}_{2}})^2] }{1 + \left( \frac{2}{M} \, \frac{m^{\varepsilon{(y)}}_{2}}{m^{h}_{2}} + \frac{1}{2M^2}[\frac{m^{\varepsilon{(y)}}_{4}}{(m^{h}_{2})^2}-(\frac{m^{\varepsilon{(y)}}_{2}}{m^{h}_{2}})^2] \right ) \, \left( 1 + 2 \, \frac{m^{\varepsilon{(x)}}_{2}}{m^{h}_{2}} + \frac{1}{2} \, [\frac{m^{\varepsilon{(x)}}_{4}}{(m^{h}_{2})^2}-(\frac{m^{\varepsilon{(x)}}_{2}}{m^{h}_{2}})^2] \right)}$](img334.gif) |
(42) |
Expressed in
this form, the variance reduction factor is a function of the
variance of each measurement error relative to the variance of the
state variable and, hence, the intraday sample frequency
![]() affecting the precision of the second
measurement equation based on high-frequency intraday
data.
affecting the precision of the second
measurement equation based on high-frequency intraday
data.
Two important
conclusions follow. First, as
![]() this variance reduction
factor approaches
this variance reduction
factor approaches
![$\displaystyle 1 + 2 \, \frac{m^{\varepsilon{(x)}}_{2}}{m^{h}_{2}} + \frac{1}{2} \, [\frac{m^{\varepsilon{(x)}}_{4}}{(m^{h}_{2})^2}-(\frac{m^{\varepsilon{(x)}}_{2}}{m^{h}_{2}})^2] = \frac{\mathbb{V}[g_{1}]}{\mathbb{C}[g_{1},g_{2}]} \equiv \frac{\mathbb{V}[g_{1}]}{\lim_{M \rightarrow \infty}\mathbb{V}[g_{2}]} ~ ,$](img337.gif) |
(43) |
which means
that the Hausman principle applies in the limit, in the sense that
when volatility is perfectly observed in the second measurement
equation then it alone achieves minimum variance, i.e. maximum
efficiency of the estimator. Second, for values of ![]() typically used in empirical work such as
typically used in empirical work such as ![]() (five-minute returns) and
(five-minute returns) and ![]() (two-minute
returns), the above variance reduction factor (42) is
very close to its limiting value (43) for
(two-minute
returns), the above variance reduction factor (42) is
very close to its limiting value (43) for
![]() since the denominator
in (42) would be close
to unity.
since the denominator
in (42) would be close
to unity.
This proves
analytically in the considered simplified setting that augmenting
the state space form of the model with a volatility measurement
equation based on high frequency data yields an estimator with
several times smaller variance compared to the one without a
volatility measurement equation. For typical values of ![]() in the order of 100 the variance reduction factor is fairly
close to its limiting value (43). In particular,
based on the derived formulas it is easy to see that for parameter
values in the neighborhood of those used in prior studies of the
same model (see for example Ruiz (1994) or Andersen and Sorensen
(1997)) implies variance reduction factor somewhere in the range 5
to 30 times, which roughly translates into 2 to 5 times smaller
standard deviation. This is quite in line with the RMSE reduction
documented in our Monte Carlo study for popular non-analytically
tractable models for which we propose Baysian MCMC estimation
methods with the added benefit of more fully exploiting information
via the model state space form.
in the order of 100 the variance reduction factor is fairly
close to its limiting value (43). In particular,
based on the derived formulas it is easy to see that for parameter
values in the neighborhood of those used in prior studies of the
same model (see for example Ruiz (1994) or Andersen and Sorensen
(1997)) implies variance reduction factor somewhere in the range 5
to 30 times, which roughly translates into 2 to 5 times smaller
standard deviation. This is quite in line with the RMSE reduction
documented in our Monte Carlo study for popular non-analytically
tractable models for which we propose Baysian MCMC estimation
methods with the added benefit of more fully exploiting information
via the model state space form.
B Figures and Tables
Table 1a. Parameter Estimates for a One-Factor log-SV Model With Leverage Effects - Panel A: κh= 0.0163
For select model parameters we report the mean, bias, and RMSE of the estimates obtained across 1,000 Monte Carlo replications. The state-space form of the model is as follows:
![]()
![]()
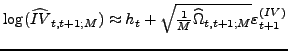
Columns represent results for alternative estimation procedures depending on weather our volatility measurement equation based on high-frequency log integrated variance measures log(![]() ) is used (HF 5-min with M=78; HF 2-min with M=195) or not (daily only), as well as for the infeasible case of perfect observability (known volatility). The rows in each block contain results for different yearly sample lengths (2, 5, or 20 years).
) is used (HF 5-min with M=78; HF 2-min with M=195) or not (daily only), as well as for the infeasible case of perfect observability (known volatility). The rows in each block contain results for different yearly sample lengths (2, 5, or 20 years).
| Sample Length T (years) | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN = 2 | 0.0249 | 0.0176 | 0.0174 | 0.0173 |
| MEAN = 5 | 0.0188 | 0.0171 | 0.0171 | 0.0171 |
| MEAN = 20 | 0.0168 | 0.0165 | 0.0165 | 0.0165 |
| BIAS = 2 | 0.0086 | 0.0014 | 0.0011 | 0.0010 |
| BIAS = 5 | 0.0025 | 0.0009 | 0.0009 | 0.0008 |
| BIAS = 20 | 0.0006 | 0.0002 | 0.0002 | 0.0002 |
| RMSE = 2 | 0.0309 | 0.0092 | 0.0090 | 0.0089 |
| RMSE = 5 | 0.0071 | 0.0050 | 0.0049 | 0.0048 |
| RMSE = 20 | 0.0028 | 0.0021 | 0.0021 | 0.0021 |
Table 1b. Parameter Estimates for a One-Factor log-SV Model With Leverage Effects - Panel B: σh= 0.1648
| Sample Length T (years) | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN = 2 | 0.1739 | 0.1655 | 0.1647 | 0.1649 |
| MEAN = 5 | 0.1694 | 0.1649 | 0.1650 | 0.1649 |
| MEAN = 20 | 0.1653 | 0.1647 | 0.1647 | 0.1647 |
| BIAS = 2 | 0.0091 | 0.0007 | 0.0000 | 0.0001 |
| BIAS = 5 | 0.0046 | 0.0002 | 0.0002 | 0.0001 |
| BIAS = 20 | 0.0005 | -0.0001 | 0.0000 | 0.0000 |
| RMSE = 2 | 0.0260 | 0.0087 | 0.0069 | 0.0047 |
| RMSE = 5 | 0.0183 | 0.0058 | 0.0045 | 0.0030 |
| RMSE = 20 | 0.0100 | 0.0028 | 0.0023 | 0.0015 |
Table 1c. Parameter Estimates for a One-Factor log-SV Model With Leverage Effects - Panel C: θh= 9.4243
| Sample Length T (years) | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN =2 | -9.4024 | -9.4837 | -9.5006 | -9.5067 |
| MEAN = 5 | -9.4481 | -9.4468 | -9.4478 | -9.4467 |
| MEAN = 20 | -9.4308 | -9.4299 | -9.4297 | -9.4295 |
| BIAS = 2 | 0.0219 | -0.0594 | -0.0764 | -0.0825 |
| BIAS = 5 | -0.0239 | -0.0225 | -0.0235 | -0.0224 |
| BIAS = 20 | -0.0065 | -0.0057 | -0.0054 | -0.0053 |
| RMSE = 2 | 0.9659 | 0.8943 | 0.8897 | 0.8720 |
| RMSE = 5 | 0.3026 | 0.2906 | 0.2917 | 0.2911 |
| RMSE = 20 | 0.1416 | 0.1390 | 0.1395 | 0.1398 |
Table 1d. Parameter Estimates for a One-Factor log-SV Model With Leverage Effects - Panel D: ρh= 0.6716
| Sample Length T (years) | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN =2 | -0.5840 | -0.6618 | -0.6651 | -0.6679 |
| MEAN = 5 | -0.6360 | -0.6668 | -0.6683 | -0.6704 |
| MEAN = 20 | -0.6599 | -0.6709 | -0.6703 | -0.6706 |
| BIAS = 2 | 0.0875 | 0.0098 | 0.0065 | 0.0037 |
| BIAS = 5 | 0.0355 | 0.0047 | 0.0032 | 0.0012 |
| BIAS = 20 | 0.0116 | 0.0006 | 0.0012 | 0.0010 |
| RMSE = 2 | 0.1383 | 0.0395 | 0.0321 | 0.0210 |
| RMSE = 5 | 0.0776 | 0.0247 | 0.0214 | 0.0140 |
| RMSE = 20 | 0.0392 | 0.0132 | 0.0110 | 0.0073 |
Table 2a. Parameter Estimates for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel A: κh= 0.0130
For select model parameters we report the mean, bias, and RMSE of the estimates obtained across 1,000 Monte Carlo replications. The state-space form of the model is as follows:
![]()
![]()
![]()
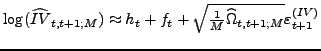
Columns represent results for alternative estimation procedures depending on weather our volatility measurement equation based on high-frequency log integrated variance measures log(![]() ) is used (HF 5-min with M=78; HF 2-min with M=195) or not (daily only), as well as for the infeasible case of perfect observability (known volatility). The rows in each block contain results for different yearly sample lengths (2, 5, or 20 years).
) is used (HF 5-min with M=78; HF 2-min with M=195) or not (daily only), as well as for the infeasible case of perfect observability (known volatility). The rows in each block contain results for different yearly sample lengths (2, 5, or 20 years).
| Sample Length T (years) | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN = 2 | 0.0254 | 0.0203 | 0.0202 | 0.0154 |
| MEAN = 5 | 0.0195 | 0.0157 | 0.0156 | 0.0142 |
| MEAN = 20 | 0.0150 | 0.0136 | 0.0136 | 0.0134 |
| BIAS = 2 | 0.0124 | 0.0073 | 0.0072 | 0.0024 |
| BIAS = 5 | 0.0065 | 0.0027 | 0.0026 | 0.0012 |
| BIAS = 20 | 0.0020 | 0.0006 | 0.0006 | 0.0004 |
| RMSE = 2 | 0.0206 | 0.0156 | 0.0156 | 0.0101 |
| RMSE = 5 | 0.0121 | 0.0079 | 0.0079 | 0.0059 |
| RMSE = 20 | 0.0042 | 0.0027 | 0.0027 | 0.0025 |
Table 2b. Parameter Estimates for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel B: κf= 0.6724
| Sample Length T (years) | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN = 2 | 0.9868 | 0.7011 | 0.6930 | 0.6750 |
| MEAN = 5 | 0.9146 | 0.6870 | 0.6774 | 0.6719 |
| MEAN = 20 | 0.7303 | 0.6810 | 0.6742 | 0.6721 |
| BIAS = 2 | 0.3144 | 0.0287 | 0.0206 | 0.0026 |
| BIAS = 5 | 0.2422 | 0.0146 | 0.0050 | -0.0005 |
| BIAS = 20 | 0.0579 | 0.0086 | 0.0018 | -0.0003 |
| RMSE = 2 | 0.3794 | 0.0866 | 0.0775 | 0.0424 |
| RMSE = 5 | 0.3400 | 0.0512 | 0.0444 | 0.0275 |
| RMSE = 20 | 0.2444 | 0.0260 | 0.0231 | 0.0131 |
Table 2c. Parameter Estimates for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel C: σh= 0.1320
| Sample Length T (years) | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN = 2 | 0.1553 | 0.1426 | 0.1421 | 0.1321 |
| MEAN = 5 | 0.1507 | 0.1367 | 0.1362 | 0.1322 |
| MEAN = 20 | 0.1400 | 0.1333 | 0.1329 | 0.1320 |
| BIAS = 2 | 0.0233 | 0.0106 | 0.0101 | 0.0001 |
| BIAS = 5 | 0.0187 | 0.0047 | 0.0042 | 0.0002 |
| BIAS = 20 | 0.0080 | 0.0013 | 0.0009 | 0.0000 |
| RMSE = 2 | 0.0338 | 0.0208 | 0.0205 | 0.0042 |
| RMSE = 5 | 0.0285 | 0.0143 | 0.0139 | 0.0026 |
| RMSE = 20 | 0.0154 | 0.0072 | 0.0070 | 0.0013 |
Table 2d. Parameter Estimates for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel D: σf= 0.3876
| Sample Length T (years) | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN = 2 | 0.1685 | 0.3818 | 0.3795 | 0.3862 |
| MEAN = 5 | 0.1752 | 0.3883 | 0.3849 | 0.3864 |
| MEAN = 20 | 0.2643 | 0.3919 | 0.3879 | 0.3872 |
| BIAS = 2 | -0.2191 | -0.0058 | -0.0081 | -0.0014 |
| BIAS = 5 | -0.2124 | 0.0007 | -0.0027 | -0.0012 |
| BIAS = 20 | -0.1233 | 0.0043 | 0.0003 | -0.0004 |
| RMSE = 2 | 0.2203 | 0.0196 | 0.0184 | 0.0121 |
| RMSE = 5 | 0.2159 | 0.0118 | 0.0117 | 0.0081 |
| RMSE = 20 | 0.1423 | 0.0075 | 0.0056 | 0.0039 |
Table 2e. Parameter Estimates for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel E: ρh= 0.2831
| Sample Length T (years) | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN = 2 | -0.2225 | -0.2615 | -0.2610 | -0.2802 |
| MEAN = 5 | -0.2509 | -0.2769 | -0.2755 | -0.2815 |
| MEAN = 20 | -0.2669 | -0.2849 | -0.2824 | -0.2824 |
| BIAS = 2 | 0.0606 | 0.0216 | 0.0221 | 0.0029 |
| BIAS = 5 | 0.0322 | 0.0062 | 0.0076 | 0.0016 |
| BIAS = 20 | 0.0162 | -0.0018 | 0.0007 | 0.0007 |
| RMSE = 2 | 0.1965 | 0.1316 | 0.1276 | 0.0411 |
| RMSE = 5 | 0.1376 | 0.0864 | 0.0857 | 0.0256 |
| RMSE = 20 | 0.0774 | 0.0461 | 0.0453 | 0.0121 |
Table 2f. Parameter Estimates for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel F: ρf= 0.1109
| Sample Length T (years) | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN = 2 | -0.1443 | -0.1130 | -0.1172 | -0.1095 |
| MEAN = 5 | -0.1739 | -0.1096 | -0.1116 | -0.1105 |
| MEAN = 20 | -0.1712 | -0.1104 | -0.1112 | -0.1098 |
| BIAS = 2 | -0.0334 | -0.0021 | -0.0063 | 0.0014 |
| BIAS = 5 | -0.0630 | 0.0013 | -0.0007 | 0.0004 |
| BIAS = 20 | -0.0603 | 0.0005 | -0.0003 | 0.0011 |
| RMSE = 2 | 0.2543 | 0.0628 | 0.0613 | 0.0439 |
| RMSE = 5 | 0.2305 | 0.0399 | 0.0375 | 0.0292 |
| RMSE = 20 | 0.1185 | 0.0190 | 0.0178 | 0.0143 |
Table 3a. Volatility State Estimates for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel A: hr : E[hr] = -9.8998
We report the mean, bias, and RMSE of the terminal volatility state estimates obtained across 1,000 Monte Carlo replications. The state-space form of the model is as follows:
![]()
![]()
![]()
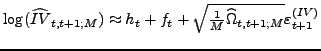
Columns represent results for alternative estimation procedures depending on weather our volatility measurement equation based on high-frequency log integrated variance measures log(![]() ) is used (HF 5-min with M=78; HF 2-min with M=195) or not (daily only), as well as for the infeasible case of perfect observability (known volatility). The rows in each block contain results for different yearly sample lengths (2, 5, or 20 years).
) is used (HF 5-min with M=78; HF 2-min with M=195) or not (daily only), as well as for the infeasible case of perfect observability (known volatility). The rows in each block contain results for different yearly sample lengths (2, 5, or 20 years).
Sample Length | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN = 2 | -9.8259 | -9.8616 | -9.8560 | -9.9200 |
| MEAN = 5 | -9.8631 | -9.9379 | -9.9238 | -9.8467 |
| MEAN = 20 | -9.9611 | -9.9978 | -9.9893 | -9.9037 |
| BIAS = 2 | 0.0030 | -0.0326 | -0.0270 | 0.0000 |
| BIAS = 5 | 0.0520 | -0.0229 | -0.0087 | 0.0000 |
| BIAS = 20 | 0.0255 | -0.0112 | -0.0027 | 0.0000 |
| RMSE = 2 | 0.4748 | 0.3049 | 0.2958 | 0.0000 |
| RMSE = 5 | 0.4687 | 0.3116 | 0.2997 | 0.0000 |
| RMSE = 20 | 0.4491 | 0.2736 | 0.2662 | 0.0000 |
Table 3b. Volatility State Estimates for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel B: fr : E[fr] = 0
Sample Length | Daily Only | HF 5-min | HF 2-min | Known Volatility |
|---|---|---|---|---|
| MEAN = 2 | 0.0017 | 0.0014 | -0.0013 | -0.0065 |
| MEAN = 5 | -0.0028 | -0.0170 | -0.0172 | -0.0084 |
| MEAN = 20 | -0.0042 | -0.0028 | -0.0029 | 0.0013 |
| BIAS = 2 | 0.0207 | 0.0204 | 0.0177 | 0.0000 |
| BIAS = 5 | 0.0299 | 0.0157 | 0.0155 | 0.0000 |
| BIAS = 20 | 0.0184 | 0.0199 | 0.0197 | 0.0000 |
| RMSE = 2 | 0.4207 | 0.4075 | 0.4070 | 0.0000 |
| RMSE = 5 | 0.4343 | 0.4197 | 0.4189 | 0.0000 |
| RMSE = 20 | 0.3980 | 0.3813 | 0.3800 | 0.0000 |
Table 4a. Forecasts of Conditional Return Moments at Horizons of One, Five, Ten and Twenty Days Ahead for a One-Factor log-SV Model with Leverage Effects - Panel A: 1-Day Horizon
We report the mean, bias and RMSE of forecasts of the conditional return mean, standard deviation, skewness and kurtosis at horizons of one (panel A), five (panel B), ten (panel C) and twenty (panel D) days ahead, obtained across 1,000 Monte Carlo replications. Each three rows reported for the mean, bias and RMSE of these moment forecasts contain results for three different sample lengths T equal to 2, 5 and 20 years (as indicated in the second column), taking parameter and volatility estimation uncertainty into account. For each moment and forecast horizon we report results for two alternative Bayesian estimation procedures in adjacent column pairs: either without (left column denoted "Daily only") or with (right column denoted "HF 5-min") augmenting the underlying state-space formulation with a daily volatility measurement equation based on high frequency intraday daya, as proposed in this paper.
| T (years) | Mean Forecast Daily Only | Mean Forecast HF 5-min | StdDev Forecast Daily Only | StdDev Forecast HF 5-min | Skewness Forecast Daily Only | Skewness Forecast HF 5-min | Kurtosis Forecast Daily Only | Kurtosis Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | 0.0001 | 0.0001 | 0.0089 | 0.0085 | 0.0004 | 0.0001 | 3.6083 | 3.0767 |
| MEAN = 5 | 0.0001 | 0.0001 | 0.0090 | 0.0087 | 0.0000 | 0.0000 | 3.5487 | 3.0757 |
| MEAN = 20 | 0.0001 | 0.0001 | 0.0088 | 0.0087 | 0.0000 | 0.0000 | 3.5070 | 3.0752 |
| BIAS = 2 | 0.0000 | 0.0000 | 0.0004 | 0.0000 | 0.0003 | 0.0001 | 0.6141 | 0.0826 |
| BIAS = 5 | 0.0000 | 0.0000 | 0.0003 | 0.0000 | 0.0000 | 0.0001 | 0.5546 | 0.0815 |
| BIAS = 20 | 0.0000 | 0.0000 | 0.0001 | -0.0001 | 0.0000 | 0.0000 | 0.5129 | 0.0811 |
| RMSE = 2 | 0.0003 | 0.0003 | 0.0019 | 0.0008 | 0.0023 | 0.0008 | 0.6347 | 0.0831 |
| RMSE = 5 | 0.0002 | 0.0002 | 0.0018 | 0.0008 | 0.0011 | 0.0007 | 0.5671 | 0.0818 |
| RMSE = 20 | 0.0001 | 0.0001 | 0.0018 | 0.0008 | 0.0009 | 0.0007 | 0.5214 | 0.0812 |
Table 4b. Forecasts of Conditional Return Moments at Horizons of One, Five, Ten and Twenty Days Ahead for a One-Factor log-SV Model with Leverage Effects - Panel B: 5-Day Horizon
| T (years) | Mean Forecast Daily Only | Mean Forecast HF 5-min | StdDev Forecast Daily Only | StdDev Forecast HF 5-min | Skewness Forecast Daily Only | Skewness Forecast HF 5-min | Kurtosis Forecast Daily Only | Kurtosis Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | 0.0009 | 0.0008 | 0.0238 | 0.0228 | -0.0747 | -0.0728 | 3.3648 | 3.1203 |
| MEAN = 5 | 0.0009 | 0.0009 | 0.0239 | 0.0232 | -0.0756 | -0.0729 | 3.3232 | 3.1185 |
| MEAN = 20 | 0.0010 | 0.0010 | 0.0235 | 0.0231 | -0.0761 | -0.0733 | 3.2938 | 3.1175 |
| BIAS = 2 | -0.0001 | -0.0002 | 0.0011 | 0.0001 | -0.0020 | -0.0001 | 0.2857 | 0.0411 |
| BIAS = 5 | -0.0001 | -0.0001 | 0.0008 | 0.0001 | -0.0030 | -0.0003 | 0.2442 | 0.0396 |
| BIAS = 20 | 0.0000 | 0.0000 | 0.0002 | -0.0002 | -0.0036 | -0.0008 | 0.2149 | 0.0386 |
| RMSE = 2 | 0.0024 | 0.0022 | 0.0050 | 0.0021 | 0.0352 | 0.0108 | 0.3032 | 0.0441 |
| RMSE = 5 | 0.0015 | 0.0014 | 0.0047 | 0.0020 | 0.0234 | 0.0072 | 0.2534 | 0.0408 |
| RMSE = 20 | 0.0007 | 0.0007 | 0.0047 | 0.0020 | 0.0125 | 0.0037 | 0.2204 | 0.0390 |
Table 4c. Forecasts of Conditional Return Moments at Horizons of One, Five, Ten and Twenty Days Ahead for a One-Factor log-SV Model with Leverage Effects - Panel C: 10-Day Horizon
| T (years) | Mean Forecast Daily Only | Mean Forecast | StdDev Forecast Daily Only | StdDev Forecast HF 5-min | Skewness Forecast Daily Only | Skewness Forecast HF 5-min | Kurtosis Forecast Daily Only | Kurtosis Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | 0.0017 | 0.0015 | 0.0327 | 0.0313 | -0.0953 | -0.0929 | 3.3719 | 3.1644 |
| MEAN = 5 | 0.0017 | 0.0016 | 0.0328 | 0.0318 | -0.0957 | -0.0926 | 3.3232 | 3.1614 |
| MEAN = 20 | 0.0018 | 0.0018 | 0.0322 | 0.0317 | -0.0959 | -0.0929 | 3.2909 | 3.1598 |
| BIAS = 2 | -0.0002 | -0.0004 | 0.0016 | 0.0002 | -0.0032 | -0.0008 | 0.2449 | 0.0374 |
| BIAS = 5 | -0.0001 | -0.0003 | 0.0012 | 0.0002 | -0.0038 | -0.0007 | 0.1966 | 0.0349 |
| BIAS = 20 | 0.0000 | 0.0000 | 0.0003 | -0.0002 | -0.0041 | -0.0011 | 0.1643 | 0.0332 |
| RMSE = 2 | 0.0045 | 0.0042 | 0.0067 | 0.0029 | 0.0453 | 0.0141 | 0.2717 | 0.0457 |
| RMSE = 5 | 0.0027 | 0.0026 | 0.0063 | 0.0027 | 0.0297 | 0.0093 | 0.2092 | 0.0384 |
| RMSE = 20 | 0.0013 | 0.0013 | 0.0062 | 0.0027 | 0.0154 | 0.0047 | 0.1708 | 0.0343 |
Table 4d. Forecasts of Conditional Return Moments at Horizons of One, Five, Ten and Twenty Days Ahead for a One-Factor log-SV Model with Leverage Effects - Panel D: 20-Day Horizon
| T (years) | Mean Forecast Daily Only | Mean Forecast HF 5-min | StdDev Forecast Daily Only | StdDev Forecast HF 5-min | Skewness Forecast Daily Only | Skewness Forecast HF 5-min | Kurtosis Forecast Daily Only | Kurtosis Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | 0.0031 | 0.0027 | 0.0451 | 0.0433 | -0.1375 | -0.1347 | 3.5016 | 3.2777 |
| MEAN = 5 | 0.0031 | 0.0029 | 0.0451 | 0.0438 | -0.1370 | -0.1335 | 3.4183 | 3.2694 |
| MEAN = 20 | 0.0034 | 0.0034 | 0.0441 | 0.0434 | -0.1364 | -0.1334 | 3.3711 | 3.2646 |
| BIAS = 2 | -0.0003 | -0.0007 | 0.0024 | 0.0006 | -0.0051 | -0.0022 | 0.2698 | 0.0460 |
| BIAS = 5 | -0.0003 | -0.0005 | 0.0017 | 0.0004 | -0.0049 | -0.0014 | 0.1879 | 0.0390 |
| BIAS = 20 | 0.0000 | 0.0000 | 0.0004 | -0.0002 | -0.0045 | -0.0015 | 0.1410 | 0.0345 |
| RMSE = 2 | 0.0082 | 0.0077 | 0.0091 | 0.0042 | 0.0669 | 0.0219 | 0.3366 | 0.0760 |
| RMSE = 5 | 0.0050 | 0.0048 | 0.0084 | 0.0037 | 0.0429 | 0.0142 | 0.2169 | 0.0539 |
| RMSE = 20 | 0.0025 | 0.0023 | 0.0079 | 0.0035 | 0.0214 | 0.0071 | 0.1525 | 0.0387 |
Table 5a. Forecasts of Conditional Return Moments at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel A: 1-Day Horizon
We report the mean, bias and RMSE of forecasts of the conditional return mean, standard deviation, skewness and kurtosis at horizons of one (panel A), five (panel B), ten (panel C) and twenty (panel D) days ahead, obtained across 1,000 Monte Carlo replications. Each three rows reported for the mean, bias and RMSE of these moment forecasts contain results for three different sample lengths T equal to 2, 5 and 20 years (as indicated in the second column), taking parameter and volatility estimation uncertainty into account. For each moment and forecast horizon we report results for two alternative Bayesian estimation procedures in adjacent column pairs: either without (left column denoted "Daily only") or with (right column denoted "HF 5-min") augmenting the underlying state-space formulation with a daily volatility measurement equation based on high frequency intraday daya, as proposed in this paper.
| T (years) | Mean Forecast Daily Only | Mean Forecast HF 5-min | StdDev Forecast Daily Only | StdDev Forecast HF 5-min | Skewness Forecast Daily Only | Skewness Forecast HF 5-min | Kurtosis Forecast Daily Only | Kurtosis Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | 0.0005 | 0.0005 | 0.0099 | 0.0098 | -0.5831 | -0.6173 | 92.9059 | 96.2450 |
| MEAN = 5 | 0.0006 | 0.0005 | 0.0097 | 0.0095 | -0.5923 | -0.6520 | 90.2971 | 102.7384 |
| MEAN = 20 | 0.0006 | 0.0006 | 0.0095 | 0.0094 | -0.6382 | -0.6956 | 98.1776 | 110.3568 |
| BIAS = 2 | 0.0000 | 0.0000 | 0.0000 | -0.0001 | 0.0501 | 0.0158 | -6.8173 | -3.4781 |
| BIAS = 5 | 0.0000 | 0.0000 | 0.0002 | 0.0000 | 0.0824 | 0.0226 | -17.8110 | -5.3698 |
| BIAS = 20 | 0.0000 | 0.0000 | 0.0001 | 0.0000 | 0.0871 | 0.0297 | -19.4314 | -7.2521 |
| RMSE = 2 | 0.0003 | 0.0003 | 0.0020 | 0.0012 | 0.3128 | 0.2007 | 114.2795 | 36.3367 |
| RMSE = 5 | 0.0002 | 0.0002 | 0.0017 | 0.0012 | 0.3042 | 0.1981 | 60.8291 | 39.1525 |
| RMSE = 20 | 0.0001 | 0.0001 | 0.0015 | 0.0010 | 0.3085 | 0.1924 | 64.5270 | 37.8032 |
Table 5b. Forecasts of Conditional Return Moments at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel B: 5-Day Horizon
| T (years) | Mean Forecast Daily Only | Mean Forecast HF 5-min | StdDev Forecast Daily Only | StdDev Forecast HF 5-min | Skewness Forecast Daily Only | Skewness Forecast HF 5-min | Kurtosis Forecast Daily Only | Kurtosis Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | 0.0038 | 0.0038 | 0.0264 | 0.0261 | -0.2473 | -0.2722 | 17.1562 | 15.8092 |
| MEAN = 5 | 0.0039 | 0.0038 | 0.0258 | 0.0253 | -0.2617 | -0.2840 | 15.0475 | 16.6968 |
| MEAN = 20 | 0.0040 | 0.0039 | 0.0251 | 0.0249 | -0.2800 | -0.2973 | 16.1293 | 17.7012 |
| BIAS = 2 | -0.0001 | -0.0001 | 0.0002 | 0.0000 | 0.0286 | 0.0036 | 0.9160 | -0.4310 |
| BIAS = 5 | -0.0001 | -0.0001 | 0.0005 | -0.0001 | 0.0287 | 0.0066 | -2.3048 | -0.6776 |
| BIAS = 20 | 0.0000 | -0.0001 | 0.0002 | 0.0000 | 0.0257 | 0.0084 | -2.5075 | -0.9356 |
| RMSE = 2 | 0.0022 | 0.0020 | 0.0052 | 0.0031 | 0.1766 | 0.0621 | 51.3547 | 4.9173 |
| RMSE = 5 | 0.0013 | 0.0012 | 0.0044 | 0.0030 | 0.1009 | 0.0642 | 8.1963 | 5.2467 |
| RMSE = 20 | 0.0006 | 0.0006 | 0.0039 | 0.0025 | 0.1001 | 0.0589 | 8.6529 | 5.0507 |
Table 5c. Forecasts of Conditional Return Moments at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel C: 10-Day Horizon
| T (years) | Mean Forecast Daily Only | Mean Forecast HF 5-min | StdDev Forecast Daily Only | StdDev Forecast HF 5-min | Skewness Forecast Daily Only | Skewness Forecast HF 5-min | Kurtosis Forecast Daily Only | Kurtosis Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | 0.0071 | 0.0071 | 0.0362 | 0.0358 | -0.1987 | -0.2149 | 10.8792 | 9.6985 |
| MEAN = 5 | 0.0072 | 0.0071 | 0.0353 | 0.0346 | -0.2070 | -0.2220 | 9.3137 | 10.1363 |
| MEAN = 20 | 0.0073 | 0.0072 | 0.0344 | 0.0341 | -0.2198 | -0.2306 | 9.8631 | 10.6367 |
| BIAS = 2 | -0.0002 | -0.0003 | 0.0005 | 0.0001 | 0.0169 | 0.0007 | 1.0048 | -0.1759 |
| BIAS = 5 | -0.0001 | -0.0003 | 0.0007 | 0.0000 | 0.0184 | 0.0036 | -1.1204 | -0.3090 |
| BIAS = 20 | 0.0000 | -0.0001 | 0.0003 | 0.0000 | 0.0158 | 0.0050 | -1.2186 | -0.4450 |
| RMSE = 2 | 0.0040 | 0.0037 | 0.0069 | 0.0042 | 0.0986 | 0.0443 | 35.4541 | 2.5309 |
| RMSE = 5 | 0.0024 | 0.0022 | 0.0059 | 0.0040 | 0.0710 | 0.0436 | 4.1702 | 2.6744 |
| RMSE = 20 | 0.0012 | 0.0011 | 0.0051 | 0.0032 | 0.0679 | 0.0395 | 4.3685 | 2.5495 |
Table 5d. Forecasts of Conditional Return Moments at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel D: 20-Day Horizon
| T (years) | Mean Forecast Daily Only | Mean Forecast HF 5-min | StdDev Forecast Daily Only | StdDev Forecast HF 5-min | Skewness Forecast Daily Only | Skewness Forecast HF 5-min | Kurtosis Forecast Daily Only | Kurtosis Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | 0.0132 | 0.0130 | 0.0498 | 0.0492 | -0.1718 | -0.1811 | 7.0727 | 6.5231 |
| MEAN = 5 | 0.0133 | 0.0130 | 0.0484 | 0.0474 | -0.1765 | -0.1848 | 6.3465 | 6.7111 |
| MEAN = 20 | 0.0136 | 0.0133 | 0.0470 | 0.0466 | -0.1842 | -0.1892 | 6.5902 | 6.9316 |
| BIAS = 2 | -0.0004 | -0.0005 | 0.0010 | 0.0004 | 0.0073 | -0.0021 | 0.5331 | -0.0166 |
| BIAS = 5 | -0.0002 | -0.0005 | 0.0010 | 0.0001 | 0.0084 | 0.0003 | -0.4614 | -0.1021 |
| BIAS = 20 | 0.0000 | -0.0002 | 0.0004 | 0.0000 | 0.0070 | 0.0019 | -0.5289 | -0.1875 |
| RMSE = 2 | 0.0074 | 0.0067 | 0.0092 | 0.0058 | 0.0729 | 0.0353 | 14.6681 | 1.2715 |
| RMSE = 5 | 0.0044 | 0.0041 | 0.0077 | 0.0052 | 0.0515 | 0.0298 | 2.0322 | 1.3205 |
| RMSE = 20 | 0.0022 | 0.0020 | 0.0065 | 0.0041 | 0.0432 | 0.0252 | 2.0915 | 1.2267 |
Table 6a. Forecasts of Conditional Return Quantiles at Horizons of One, Five, Ten and Twenty Days Ahead for a One-Factor log-SV Model With Leverage Effects - Panel A: 1-Day Horizon
We report the mean, bias and RMSE of forecasts of the conditional return quantiles at horizons of one (panel A), five (panel B), ten (panel C) and twenty (panel D) days ahead, obtained across 1,000 Monte Carlo replications. Each three rows reported for the mean, bias and RMSE of these quantile forecasts contain results for three different sample lengths T equal to 2, 5 and 20 years (as indicated in the second column), taking parameter and volatility estimation uncertainty into account. For each moment and forecast horizon we report results for two alternative Bayesian estimation procedures in adjacent column pairs: either without (left column denoted "Daily only") or with (right column denoted "HF 5-min") augmenting the underlying state-space formulation with a daily volatility measurement equation based on high frequency intraday daya, as proposed in this paper.
| T (years) | Quantile 0.01 Forecast Daily Only | Quantile 0.01 Forecast HF 5-min | Quantile 0.05 Forecast Daily Only | Quantile 0.05 Forecast HF 5-min | Quantile 0.95 Forecast Daily Only | Quantile 0.95 Forecast HF 5-min | Quantile 0.99 Forecast Daily Only | Quantile 0.99 Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | -0.0215 | -0.0199 | -0.0144 | -0.0139 | 0.0146 | 0.0141 | 0.0218 | 0.0201 |
| MEAN = 5 | -0.0217 | -0.0202 | -0.0146 | -0.0142 | 0.0148 | 0.0144 | 0.0220 | 0.0205 |
| MEAN = 20 | -0.0213 | -0.0202 | -0.0143 | -0.0141 | 0.0146 | 0.0144 | 0.0215 | 0.0205 |
| BIAS = 2 | -0.0018 | -0.0002 | -0.0005 | 0.0000 | 0.0005 | -0.0001 | 0.0018 | 0.0001 |
| BIAS = 5 | -0.0017 | -0.0002 | -0.0004 | 0.0000 | 0.0004 | 0.0000 | 0.0016 | 0.0002 |
| BIAS = 20 | -0.0011 | 0.0000 | -0.0001 | 0.0001 | 0.0001 | -0.0001 | 0.0011 | 0.0000 |
| RMSE = 2 | 0.0048 | 0.0019 | 0.0032 | 0.0014 | 0.0031 | 0.0014 | 0.0048 | 0.0019 |
| RMSE = 5 | 0.0046 | 0.0018 | 0.0030 | 0.0013 | 0.0030 | 0.0013 | 0.0046 | 0.0018 |
| RMSE = 20 | 0.0044 | 0.0018 | 0.0030 | 0.0013 | 0.0030 | 0.0013 | 0.0044 | 0.0018 |
Table 6b. Forecasts of Conditional Return Quantiles at Horizons of One, Five, Ten and Twenty Days Ahead for a One-Factor log-SV Model With Leverage Effects - Panel B: 5-Day Horizon
| T (years) | Quantile 0.01 Forecast Daily Only | Quantile 0.01 Forecast HF 5-min | Quantile 0.05 Forecast Daily Only | Quantile 0.05 Forecast HF 5-min | Quantile 0.95 Forecast Daily Only | Quantile 0.95 Forecast HF 5-min | Quantile 0.99 Forecast Daily Only | Quantile 0.99 Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | -0.0571 | -0.0539 | -0.0384 | -0.0371 | 0.0394 | 0.0378 | 0.0566 | 0.0532 |
| MEAN = 5 | -0.0574 | -0.0548 | -0.0387 | -0.0376 | 0.0397 | 0.0385 | 0.0568 | 0.0541 |
| MEAN = 20 | -0.0562 | -0.0545 | -0.0379 | -0.0374 | 0.0390 | 0.0385 | 0.0558 | 0.0541 |
| BIAS = 2 | -0.0038 | -0.0006 | -0.0017 | -0.0003 | 0.0015 | -0.0001 | 0.0036 | 0.0002 |
| BIAS = 5 | -0.0032 | -0.0005 | -0.0013 | -0.0002 | 0.0012 | 0.0000 | 0.0030 | 0.0002 |
| BIAS = 20 | -0.0015 | 0.0002 | -0.0003 | 0.0003 | 0.0003 | -0.0003 | 0.0015 | -0.0002 |
| RMSE = 2 | 0.0128 | 0.0056 | 0.0088 | 0.0042 | 0.0082 | 0.0040 | 0.0119 | 0.0052 |
| RMSE = 5 | 0.0118 | 0.0050 | 0.0080 | 0.0036 | 0.0078 | 0.0035 | 0.0113 | 0.0047 |
| RMSE = 20 | 0.0113 | 0.0049 | 0.0078 | 0.0035 | 0.0076 | 0.0034 | 0.0108 | 0.0047 |
Table 6c. Forecasts of Conditional Return Quantiles at Horizons of One, Five, Ten and Twenty Days Ahead for a One-Factor log-SV Model With Leverage Effects - Panel C: 10-Day Horizon
| T (years) | Quantile 0.01 Forecast Daily Only | Quantile 0.01 Forecast HF 5-min | Quantile 0.05 Forecast Daily Only | Quantile 0.05 Forecast HF 5-min | Quantile 0.95 Forecast Daily Only | Quantile 0.95 Forecast HF 5-min | Quantile 0.99 Forecast Daily Only | Quantile 0.99 Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | -0.0785 | -0.0745 | -0.0525 | -0.0507 | 0.0544 | 0.0522 | 0.0777 | 0.0733 |
| MEAN = 5 | -0.0787 | -0.0754 | -0.0528 | -0.0514 | 0.0547 | 0.0530 | 0.0779 | 0.0745 |
| MEAN = 20 | -0.0768 | -0.0748 | -0.0516 | -0.0509 | 0.0538 | 0.0530 | 0.0763 | 0.0744 |
| BIAS = 2 | -0.0053 | -0.0012 | -0.0026 | -0.0007 | 0.0022 | 0.0000 | 0.0048 | 0.0004 |
| BIAS = 5 | -0.0041 | -0.0008 | -0.0019 | -0.0005 | 0.0016 | 0.0000 | 0.0037 | 0.0003 |
| BIAS = 20 | -0.0017 | 0.0002 | -0.0004 | 0.0003 | 0.0004 | -0.0004 | 0.0017 | -0.0003 |
| RMSE = 2 | 0.0179 | 0.0085 | 0.0124 | 0.0066 | 0.0113 | 0.0059 | 0.0162 | 0.0075 |
| RMSE = 5 | 0.0160 | 0.0072 | 0.0109 | 0.0053 | 0.0106 | 0.0050 | 0.0151 | 0.0066 |
| RMSE = 20 | 0.0151 | 0.0066 | 0.0104 | 0.0047 | 0.0100 | 0.0045 | 0.0142 | 0.0062 |
Table 6d. Forecasts of Conditional Return Quantiles at Horizons of One, Five, Ten and Twenty Days Ahead for a One-Factor log-SV Model With Leverage Effects - Panel D: 20-Day Horizon
| T (years) | Quantile 0.01 Forecast Daily Only | Quantile 0.01 Forecast HF 5-min | Quantile 0.05 Forecast Daily Only | Quantile 0.05 Forecast HF 5-min | Quantile 0.95 Forecast Daily Only | Quantile 0.95 Forecast HF 5-min | Quantile 0.99 Forecast Daily Only | Quantile 0.99 Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | -0.1092 | -0.1041 | -0.0720 | -0.0697 | 0.0754 | 0.0723 | 0.1075 | 0.1016 |
| MEAN = 5 | -0.1089 | -0.1048 | -0.0720 | -0.0702 | 0.0754 | 0.0732 | 0.1070 | 0.1028 |
| MEAN = 20 | -0.1058 | -0.1035 | -0.0701 | -0.0692 | 0.0741 | 0.0731 | 0.1047 | 0.1024 |
| BIAS = 2 | -0.0078 | -0.0026 | -0.0040 | -0.0017 | 0.0034 | 0.0003 | 0.0069 | 0.0011 |
| BIAS = 5 | -0.0057 | -0.0016 | -0.0028 | -0.0010 | 0.0023 | 0.0001 | 0.0049 | 0.0006 |
| BIAS = 20 | -0.0020 | 0.0003 | -0.0005 | 0.0004 | 0.0005 | -0.0004 | 0.0019 | -0.0003 |
| RMSE = 2 | 0.0258 | 0.0140 | 0.0182 | 0.0111 | 0.0159 | 0.0094 | 0.0223 | 0.0114 |
| RMSE = 5 | 0.0219 | 0.0109 | 0.0150 | 0.0082 | 0.0143 | 0.0073 | 0.0202 | 0.0094 |
| RMSE = 20 | 0.0197 | 0.0089 | 0.0136 | 0.0064 | 0.0128 | 0.0059 | 0.0181 | 0.0081 |
Table 7a. Forecasts of Conditional Return Quantiles at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel A: 1-Day Horizon
We report the mean, bias and RMSE of forecasts of the conditional return quantiles at horizons of one (panel A), five (panel B), ten (panel C) and twenty (panel D) days ahead, obtained across 1,000 Monte Carlo replications. Each three rows reported for the mean, bias and RMSE of these quantile forecasts contain results for three different sample lengths T equal to 2, 5 and 20 years (as indicated in the second column), taking parameter and volatility estimation uncertainty into account. For each moment and forecast horizon we report results for two alternative Bayesian estimation procedures in adjacent column pairs: either without (left column denoted "Daily only") or with (right column denoted "HF 5-min") augmenting the underlying state-space formulation with a daily volatility measurement equation based on high frequency intraday daya, as proposed in this paper.
| T (years) | Quantile 0.01 Forecast Daily Only | Quantile 0.01 Forecast HF 5-min | Quantile 0.05 Forecast Daily Only | Quantile 0.05 Forecast HF 5-min | Quantile 0.95 Forecast Daily Only | Quantile 0.95 Forecast HF 5-min | Quantile 0.99 Forecast Daily Only | Quantile 0.99 Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | -0.0211 | -0.0207 | -0.0133 | -0.0131 | 0.0144 | 0.0142 | 0.0221 | 0.0217 |
| MEAN = 5 | -0.0205 | -0.0198 | -0.0129 | -0.0125 | 0.0141 | 0.0136 | 0.0216 | 0.0208 |
| MEAN = 20 | -0.0199 | -0.0193 | -0.0124 | -0.0122 | 0.0136 | 0.0134 | 0.0210 | 0.0204 |
| BIAS = 2 | -0.0008 | -0.0003 | -0.0001 | 0.0001 | 0.0001 | -0.0001 | 0.0007 | 0.0003 |
| BIAS = 5 | -0.0011 | -0.0004 | -0.0004 | 0.0000 | 0.0003 | -0.0001 | 0.0011 | 0.0003 |
| BIAS = 20 | -0.0011 | -0.0005 | -0.0002 | 0.0000 | 0.0002 | 0.0000 | 0.0011 | 0.0005 |
| RMSE = 2 | 0.0058 | 0.0034 | 0.0037 | 0.0022 | 0.0037 | 0.0022 | 0.0058 | 0.0034 |
| RMSE = 5 | 0.0050 | 0.0033 | 0.0032 | 0.0022 | 0.0032 | 0.0022 | 0.0050 | 0.0034 |
| RMSE = 20 | 0.0045 | 0.0028 | 0.0029 | 0.0018 | 0.0029 | 0.0018 | 0.0045 | 0.0028 |
Table 7b. Forecasts of Conditional Return Quantiles at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel B: 5-Day Horizon
| T (years) | Quantile 0.01 Forecast Daily Only | Quantile 0.01 Forecast HF 5-min | Quantile 0.05 Forecast Daily Only | Quantile 0.05 Forecast HF 5-min | Quantile 0.95 Forecast Daily Only | Quantile 0.95 Forecast HF 5-min | Quantile 0.99 Forecast Daily Only | Quantile 0.99 Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | -0.0618 | -0.0605 | -0.0352 | -0.0348 | 0.0420 | 0.0414 | 0.0650 | 0.0633 |
| MEAN = 5 | -0.0603 | -0.0582 | -0.0342 | -0.0332 | 0.0410 | 0.0398 | 0.0635 | 0.0611 |
| MEAN = 20 | -0.0585 | -0.0570 | -0.0328 | -0.0323 | 0.0397 | 0.0391 | 0.0617 | 0.0600 |
| BIAS = 2 | -0.0023 | -0.0010 | -0.0005 | -0.0001 | 0.0005 | -0.0002 | 0.0024 | 0.0006 |
| BIAS = 5 | -0.0029 | -0.0009 | -0.0011 | -0.0001 | 0.0010 | -0.0002 | 0.0030 | 0.0006 |
| BIAS = 20 | -0.0024 | -0.0009 | -0.0007 | -0.0002 | 0.0007 | 0.0000 | 0.0025 | 0.0008 |
| RMSE = 2 | 0.0139 | 0.0082 | 0.0098 | 0.0062 | 0.0098 | 0.0061 | 0.0138 | 0.0082 |
| RMSE = 5 | 0.0120 | 0.0078 | 0.0086 | 0.0058 | 0.0084 | 0.0059 | 0.0118 | 0.0079 |
| RMSE = 20 | 0.0104 | 0.0064 | 0.0076 | 0.0048 | 0.0074 | 0.0047 | 0.0104 | 0.0065 |
Table 7c. Forecasts of Conditional Return Quantiles at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel C: 10-Day Horizon
| T (years) | Quantile 0.01 Forecast Daily Only | Quantile 0.01 Forecast HF 5-min | Quantile 0.05 Forecast Daily Only | Quantile 0.05 Forecast HF 5-min | Quantile 0.95 Forecast Daily Only | Quantile 0.95 Forecast HF 5-min | Quantile 0.99 Forecast Daily Only | Quantile 0.99 Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | -0.0897 | -0.0885 | -0.0481 | -0.0475 | 0.0608 | 0.0598 | 0.0963 | 0.0945 |
| MEAN = 5 | -0.0875 | -0.0857 | -0.0466 | -0.0453 | 0.0593 | 0.0576 | 0.0942 | 0.0918 |
| MEAN = 20 | -0.0854 | -0.0845 | -0.0446 | -0.0439 | 0.0576 | 0.0566 | 0.0921 | 0.0907 |
| BIAS = 2 | -0.0023 | -0.0011 | -0.0011 | -0.0005 | 0.0009 | -0.0001 | 0.0024 | 0.0006 |
| BIAS = 5 | -0.0024 | -0.0006 | -0.0017 | -0.0003 | 0.0015 | -0.0002 | 0.0026 | 0.0001 |
| BIAS = 20 | -0.0013 | -0.0004 | -0.0010 | -0.0003 | 0.0010 | 0.0000 | 0.0016 | 0.0003 |
| RMSE = 2 | 0.0165 | 0.0100 | 0.0132 | 0.0087 | 0.0132 | 0.0085 | 0.0166 | 0.0101 |
| RMSE = 5 | 0.0133 | 0.0088 | 0.0115 | 0.0077 | 0.0112 | 0.0079 | 0.0133 | 0.0093 |
| RMSE = 20 | 0.0108 | 0.0069 | 0.0100 | 0.0063 | 0.0098 | 0.0062 | 0.0111 | 0.0072 |
Table 7d. Forecasts of Conditional Return Quantiles at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel D: 20-Day Horizon
| T (years) | Quantile 0.01 Forecast Daily Only | Quantile 0.01 Forecast HF 5-min | Quantile 0.05 Forecast Daily Only | Quantile 0.05 Forecast HF 5-min | Quantile 0.95 Forecast Daily Only | Quantile 0.95 Forecast HF 5-min | Quantile 0.99 Forecast Daily Only | Quantile 0.99 Forecast HF 5-min |
|---|---|---|---|---|---|---|---|---|
| MEAN = 2 | -0.1224 | -0.1208 | -0.0656 | -0.0647 | 0.0889 | 0.0875 | 0.1388 | 0.1366 |
| MEAN = 5 | -0.1189 | -0.1169 | -0.0632 | -0.0616 | 0.0867 | 0.0844 | 0.1355 | 0.1327 |
| MEAN = 20 | -0.1158 | -0.1151 | -0.0605 | -0.0597 | 0.0844 | 0.0831 | 0.1327 | 0.1314 |
| BIAS = 2 | -0.0039 | -0.0023 | -0.0022 | -0.0013 | 0.0017 | 0.0003 | 0.0034 | 0.0012 |
| BIAS = 5 | -0.0030 | -0.0010 | -0.0024 | -0.0007 | 0.0020 | -0.0003 | 0.0027 | -0.0001 |
| BIAS = 20 | -0.0012 | -0.0004 | -0.0013 | -0.0005 | 0.0013 | 0.0000 | 0.0012 | -0.0001 |
| RMSE = 2 | 0.0219 | 0.0143 | 0.0179 | 0.0125 | 0.0178 | 0.0122 | 0.0214 | 0.0138 |
| RMSE = 5 | 0.0169 | 0.0114 | 0.0149 | 0.0101 | 0.0145 | 0.0105 | 0.0162 | 0.0117 |
| RMSE = 20 | 0.0130 | 0.0084 | 0.0126 | 0.0079 | 0.0123 | 0.0079 | 0.0128 | 0.0085 |
Table 8a. Relative Errors of Conditional Return Quantile Forecasts Sorted by Rank Order of the Underlying True Forecasts at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel A: 1-Day Horizon
We report relative errors of forecasts of the 0.01 and 0.05 conditional return quantiles at horizons of one (panel A), five (panel B), ten (panel C) and twenty (panel D) days ahead, calculated across 1,000 Monte Carlo replications as the mean of the percentage difference between a forecast based on parameter and state estimates and the forecast based on teh corresponding true values. The results are sorted by the rank order of the true quantile forecasts from low (representing bad times) to high (representing good times), as indicated in the first column. Each three rows reported for ranks 1 (low) to 5 (high) of the true quantile forecasts contain results for three different sample lengths T equal to 2 years, 5 years and 20 years (as given in the second column) taking parameter and volatility estimation uncertainty into account. For each quantile and forecast horizon we report results for two alternative Bayesian estimation procedures in adjacent column pairs: either without (left column denoted "Daily only") or with (right column denoted "HF 5-min") augmenting the underlying state-space formulation with a daily volatility measurement equation based on high frequency intraday data, as proposed in this paper. The reported relative errors of conditional return quantile forecasts can be interpreted also as the percentage overestimation or underestimation of the implied capital charge for market risk based on one-percent (quantile 0.01) and five-percent (quantile 0.05) VaR.
| True Forecast Rank (quintiles) | Quantile 0.01 Forecast Error Daily Only | Quantile 0.01 Forecast Error HF 5-min | Quantile 0.05 Forecast Error Daily Only | Quantile 0.05 Forecast Error HF 5-min |
|---|---|---|---|---|
| 1st (Low) = 2 | -6.49% | -2.45% | -9.18% | -4.75% |
| 1st (Low) = 5 | -6.67% | -4.03% | -9.31% | -6.27% |
| 1st (Low) = 20 | -4.14% | -1.49% | -7.56% | -3.79% |
| 2nd = 2 | -1.83% | -1.09% | -4.84% | -3.26% |
| 2nd = 5 | 0.81% | 1.01% | -1.82% | -1.20% |
| 2nd = 20 | -0.25% | -0.58% | -4.17% | -2.95% |
| 3rd = 2 | 7.88% | 4.67% | 5.02% | 2.53% |
| 3rd = 5 | 11.19% | 4.27% | 8.29% | 1.93% |
| 3rd = 20 | 7.61% | 4.67% | 2.64% | 2.24% |
| 4th = 2 | 15.20% | 6.75% | 12.15% | 4.37% |
| 4th = 5 | 20.04% | 9.40% | 17.02% | 7.05% |
| 4th = 20 | 17.81% | 8.47% | 14.69% | 6.22% |
| 5th (High) = 2 | 30.80% | 11.24% | 27.24% | 8.81% |
| 5th (High) = 5 | 30.95% | 11.75% | 27.66% | 9.26% |
| 5th (High) = 20 | 37.23% | 12.91% | 32.52% | 10.56% |
Table 8b. Relative Errors of Conditional Return Quantile Forecasts Sorted by Rank Order of the Underlying True Forecasts at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel B: 5-Day Horizon
| True Forecast Rank (quintiles) | Quantile 0.01 Forecast Error Daily Only | Quantile 0.01 Forecast Error HF 5-min | Quantile 0.05 Forecast Error Daily Only | Quantile 0.05 Forecast Error HF 5-min |
|---|---|---|---|---|
| 1st (Low) = 2 | -4.58% | -1.64% | -7.91% | -3.30% |
| 1st (Low) = 5 | -5.69% | -3.58% | -9.00% | -5.33% |
| 1st (Low) = 20 | -4.26% | -1.93% | -7.57% | -3.61% |
| 2nd = 2 | -0.57% | -0.61% | -4.01% | -2.35% |
| 2nd = 5 | 1.38% | 0.87% | -1.24% | -0.35% |
| 2nd = 20 | -0.48% | -0.88% | -3.98% | -2.66% |
| 3rd = 2 | 6.88% | 3.87% | 5.33% | 3.23% |
| 3rd = 5 | 9.31% | 3.23% | 8.51% | 2.40% |
| 3rd = 20 | 5.97% | 3.29% | 3.71% | 2.71% |
| 4th = 2 | 11.87% | 5.25% | 12.19% | 4.98% |
| 4th = 5 | 15.53% | 6.58% | 17.36% | 7.36% |
| 4th = 20 | 13.82% | 6.36% | 14.73% | 6.80% |
| 5th (High) = 2 | 19.70% | 6.51% | 28.48% | 8.99% |
| 5th (High) = 5 | 20.28% | 7.60% | 29.71% | 9.75% |
| 5th (High) = 20 | 22.04% | 7.29% | 35.70% | 11.92% |
Table 8c. Relative Errors of Conditional Return Quantile Forecasts Sorted by Rank Order of the Underlying True Forecasts at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel C: 10-Day Horizon
| True Forecast Rank (quintiles) | Quantile 0.01 Forecast Error Daily Only | Quantile 0.01 Forecast Error HF 5-min | Quantile 0.05 Forecast Error Daily Only | Quantile 0.05 Forecast Error HF 5-min |
|---|---|---|---|---|
| 1st (Low) = 2 | -2.96% | -0.56% | -6.45% | -2.02% |
| 1st (Low) = 5 | -4.74% | -2.81% | -8.37% | -4.51% |
| 1st (Low) = 20 | -3.95% | -1.79% | -7.42% | -3.50% |
| 2nd = 2 | 0.84% | 0.13% | -3.01% | -1.66% |
| 2nd = 5 | 1.82% | 1.09% | -0.68% | 0.12% |
| 2nd = 20 | -0.22% | -0.57% | -3.76% | -2.53% |
| 3rd = 2 | 6.09% | 3.46% | 5.56% | 3.56% |
| 3rd = 5 | 7.42% | 2.71% | 8.40% | 2.49% |
| 3rd = 20 | 4.68% | 2.52% | 3.56% | 2.77% |
| 4th = 2 | 8.17% | 3.47% | 11.88% | 5.05% |
| 4th = 5 | 9.53% | 3.85% | 16.39% | 6.53% |
| 4th = 20 | 6.75% | 2.87% | 14.47% | 6.74% |
| 5th (High) = 2 | 6.55% | 1.76% | 27.54% | 8.12% |
| 5th (High) = 5 | 5.51% | 1.45% | 29.46% | 9.63% |
| 5th (High) = 20 | 5.45% | 1.38% | 35.05% | 11.81% |
Table 8d. Relative Errors of Conditional Return Quantile Forecasts Sorted by Rank Order of the Underlying True Forecasts at Horizons of One, Five, Ten and Twenty Days Ahead for a Two-Factor log-SV Model With Leverage Effects and Jumps - Panel D: 20-Day Horizon
| True Forecast Rank (quintiles) | Quantile 0.01 Forecast Error Daily Only | Quantile 0.01 Forecast Error HF 5-min | Quantile 0.05 Forecast Error Daily Only | Quantile 0.05 Forecast Error HF 5-min |
|---|---|---|---|---|
| 1st (Low) = 2 | -0.46% | 1.66% | -3.80% | 0.39% |
| 1st (Low) = 5 | -3.70% | -1.61% | -7.22% | -3.08% |
| 1st (Low) = 20 | -3.99% | -1.76% | -7.19% | -3.28% |
| 2nd = 2 | 2.16% | 0.97% | -1.30% | -0.45% |
| 2nd = 5 | 2.06% | 1.35% | 0.20% | 0.87% |
| 2nd = 20 | -0.46% | -0.57% | -3.52% | -2.26% |
| 3rd = 2 | 5.82% | 3.51% | 5.79% | 4.00% |
| 3rd = 5 | 6.38% | 2.37% | 7.95% | 2.56% |
| 3rd = 20 | 3.46% | 2.03% | 3.06% | 2.41% |
| 4th = 2 | 6.58% | 2.80% | 10.86% | 4.78% |
| 4th = 5 | 7.37% | 2.75% | 14.84% | 6.01% |
| 4th = 20 | 5.21% | 2.28% | 13.27% | 6.41% |
| 5th (High) = 2 | 5.33% | 1.12% | 23.39% | 5.83% |
| 5th (High) = 5 | 4.59% | 1.12% | 25.11% | 7.22% |
| 5th (High) = 20 | 4.52% | 1.20% | 29.98% | 10.18% |
Figure 1a. Relative Error Plots for Five Day VaR Forecasts Against the Rank Order of the Underlying True Forecasts for a Two-Factor log-SV Model with Leverage Effects and Jumps - Panel A: One-Percent VaR
We plot one-percent VaR (top graph) and five-percent VaR (bottom graph) relative forecast errors at a five-day horizon as a function of the rank order of the underlying true forecasts from low (representing bad times) to high (representing good times). The errors are calculated as the mean of the percentage difference between a forecast based on parameter and state estimates and the forecast based on the corresponding true values across 1,000 Monte Carlo replications. The model is estimated at a daily discretization interval by Bayesian MCMC methods either without or with augmenting the underlying state-space formulation with a daily volatility measurement equation based on high frequency intraday data, as proposed in this paper. The resulting VaR forecast errors without utilizing high-frequency volatility measures are plotted as a solid line (denoted "Daily"), while those incorporating the information content of intraday data for the latent daily volatility are plotted as a dashed line (denoted "HF 5-min").
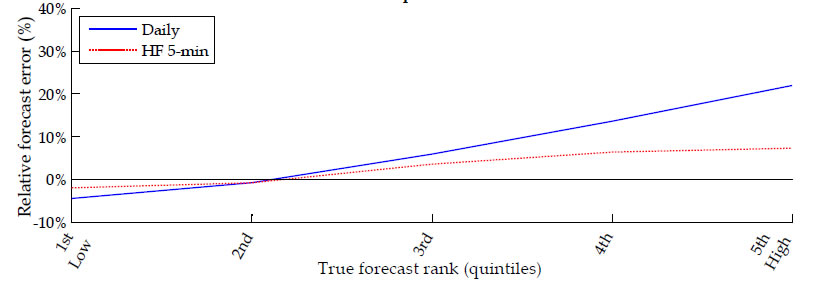
Data for Figure 1a
| True forecast rank (quintiles) | Relative forecast error (%): Daily | Relative forecast error (%): HF - 5min |
|---|---|---|
| 1st (Low) | -0.044362036 | -0.019643889 |
| 2nd | -0.007584341 | -0.007699671 |
| 3rd | 0.059182094 | 0.035794718 |
| 4th | 0.136136396 | 0.064015411 |
| 5th (High) | 0.219711314 | 0.073151988 |
Figure 1b. Relative Error Plots for Five Day VaR Forecasts Against the Rank Order of the Underlying True Forecasts for a Two-Factor log-SV Model with Leverage Effects and Jumps - Panel B: Five-Percent VaR
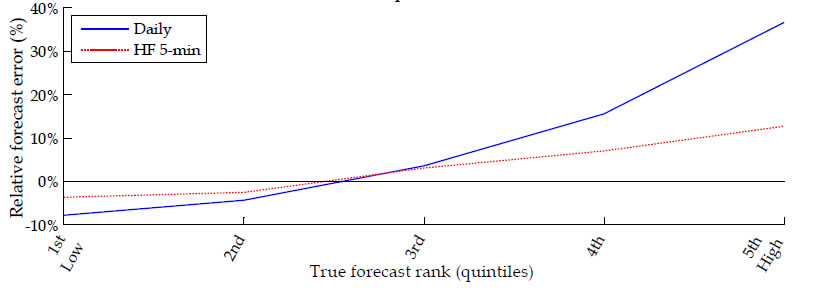
Data for Figure 1b
| True forecast rank (quintiles) | Relative forecast error (%): Daily | Relative forecast error (%): HF - 5min |
|---|---|---|
| 1st (Low) | -0.077766914 | -0.036523759 |
| 2nd | -0.043354677 | -0.025340385 |
| 3rd | 0.036029901 | 0.03095886 |
| 4th | 0.155750262 | 0.070243545 |
| 5th (High) | 0.366354523 | 0.127143196 |
Figure 2a. One-Percent and Five-Percent VaR Forecasts for S&P 500 Returns During the Financial Crisis of 2008 - Panel A: S&P500: One-Percent VaR Forecasts vs Return Realizations
We plot one-percent (top graph) and five-percent (bottom graph) VaR forecasts at five-day horizon without overlapping for S&P 500 futures returns based on a two-factor log-SV model with jumps in returns. The model is estimated at a daily discretization interval by Bayesian MCMC methods either without or with augmenting the underlying state-space formulation with a daily volatility measurement equation based on high frequency intraday data, as proposed in this paper. The resulting VaR forecasts without utilizing high-frequency volatility measures are plotted as a solid line (denoted "VaR with daily data"), those incorporating the information content of intraday data for the latent daily volatility are plotted as a dashed line (denoted "VaR with HF 5-min data"), while the corresponding actual observed returns are plotted as vertical bars (denoted "Return realizations"). The VaR analysis is for the period July 6, 2006 - February 19, 2009 and involves re-estimating the model on each date with all past data going back to October 2, 1985.
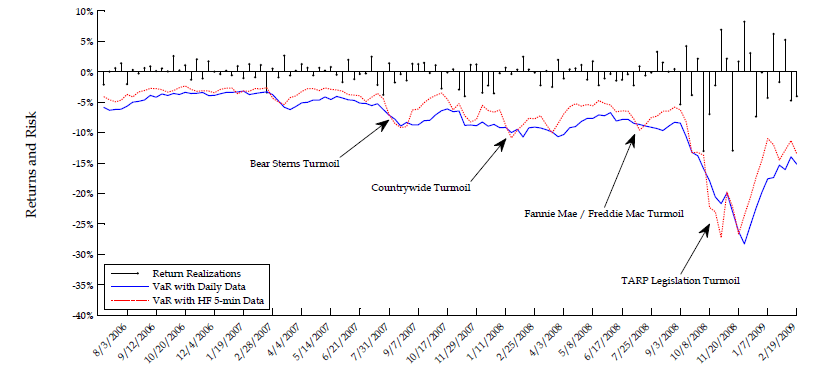
Data for Figure 2a
| Date | Return realizations | VaR with Daily Data | VaR with HF 5-min Data |
|---|---|---|---|
| 7/6/2006 | -0.021028658 | -0.058354993 | -0.040880908 |
| 7/13/2006 | 0.0002985 | -0.063276173 | -0.045981084 |
| 7/20/2006 | 0.005995453 | -0.061884614 | -0.049345546 |
| 7/27/2006 | 0.013826267 | -0.061529118 | -0.046783855 |
| 8/3/2006 | -0.020380651 | -0.056617636 | -0.037249001 |
| 8/10/2006 | 0.002985708 | -0.049889923 | -0.041360293 |
| 8/17/2006 | -0.002936084 | -0.048639369 | -0.033110622 |
| 8/24/2006 | 0.006082311 | -0.046390561 | -0.030840003 |
| 8/31/2006 | 0.008777795 | -0.038717845 | -0.027370733 |
| 9/12/2006 | 0.001076277 | -0.041888812 | -0.027724509 |
| 9/19/2006 | 0.005424237 | -0.036500292 | -0.029530379 |
| 9/26/2006 | 0.000455655 | -0.038943405 | -0.033491773 |
| 10/3/2006 | 0.025563652 | -0.035551145 | -0.03084032 |
| 10/13/2006 | 0.002186266 | -0.037331091 | -0.026096652 |
| 10/20/2006 | 0.010666821 | -0.033767778 | -0.023183769 |
| 10/27/2006 | -0.013051164 | -0.035760615 | -0.028962763 |
| 11/3/2006 | 0.020415073 | -0.035329668 | -0.03208778 |
| 11/15/2006 | -0.011136092 | -0.033999389 | -0.031110484 |
| 11/27/2006 | 0.017047302 | -0.039080556 | -0.03143396 |
| 12/4/2006 | 0.000231079 | -0.038922426 | -0.03454576 |
| 12/11/2006 | -0.003810793 | -0.036251255 | -0.02908869 |
| 12/18/2006 | 0.001671998 | -0.033983025 | -0.02681531 |
| 12/28/2006 | -0.005810005 | -0.033833843 | -0.026652611 |
| 1/9/2007 | 0.009149005 | -0.033150867 | -0.036081919 |
| 1/19/2007 | -0.010537553 | -0.031705885 | -0.031355531 |
| 1/26/2007 | 0.012442309 | -0.037499307 | -0.032058792 |
| 2/2/2007 | -0.008900854 | -0.035723519 | -0.027658291 |
| 2/9/2007 | 0.011070781 | -0.034195022 | -0.028241692 |
| 2/21/2007 | -0.034108465 | -0.032953484 | -0.026058382 |
| 2/28/2007 | 0.005044509 | -0.037442184 | -0.043369065 |
| 3/7/2007 | -0.009179933 | -0.047917253 | -0.049495276 |
| 3/14/2007 | 0.026640444 | -0.058251588 | -0.053827347 |
| 3/21/2007 | -0.006218807 | -0.062120884 | -0.042521608 |
| 3/28/2007 | 0.001633388 | -0.057061555 | -0.039617096 |
| 4/4/2007 | 0.012576361 | -0.051050499 | -0.032325887 |
| 4/16/2007 | 0.00649928 | -0.050104348 | -0.027849764 |
| 4/23/2007 | -0.005967186 | -0.046371209 | -0.027598299 |
| 4/30/2007 | 0.006420796 | -0.046670557 | -0.031026011 |
| 5/7/2007 | 0.001821889 | -0.041368795 | -0.026426279 |
| 5/14/2007 | 0.007882463 | -0.045594407 | -0.028839613 |
| 5/21/2007 | -0.004992987 | -0.040463601 | -0.029868569 |
| 5/31/2007 | -0.017033157 | -0.043162262 | -0.031916787 |
| 6/7/2007 | 0.019481775 | -0.046105467 | -0.03758524 |
| 6/14/2007 | -0.012044948 | -0.046939456 | -0.038269887 |
| 6/21/2007 | -0.003637861 | -0.051674656 | -0.039650486 |
| 6/28/2007 | -0.002924697 | -0.052039055 | -0.048991559 |
| 7/10/2007 | 0.024657993 | -0.055681501 | -0.04187649 |
| 7/17/2007 | -0.021405943 | -0.052523123 | -0.035515194 |
| 7/24/2007 | -0.037888616 | -0.062063433 | -0.044206861 |
| 7/31/2007 | 0.013906806 | -0.071289541 | -0.070600814 |
| 8/7/2007 | -0.017758229 | -0.077929261 | -0.084997957 |
| 8/14/2007 | -0.003978958 | -0.089217711 | -0.091490373 |
| 8/21/2007 | -0.014313181 | -0.083145618 | -0.090162185 |
| 8/28/2007 | 0.012972821 | -0.087252777 | -0.062907484 |
| 9/7/2007 | 0.01269826 | -0.087196434 | -0.061293298 |
| 9/14/2007 | 0.014611479 | -0.080419313 | -0.050847246 |
| 9/21/2007 | -0.002245915 | -0.079679831 | -0.043585695 |
| 9/28/2007 | 0.010664554 | -0.07062842 | -0.038845622 |
| 10/10/2007 | -0.027562083 | -0.063984333 | -0.034805427 |
| 10/17/2007 | -0.0012691 | -0.061019522 | -0.045034564 |
| 10/24/2007 | 0.004214256 | -0.065663017 | -0.062604247 |
| 10/31/2007 | -0.029243358 | -0.064409158 | -0.052426926 |
| 11/7/2007 | -0.040277488 | -0.088085468 | -0.07245921 |
| 11/19/2007 | 0.011386573 | -0.087428659 | -0.082498138 |
| 11/29/2007 | 0.011945248 | -0.088611207 | -0.078103387 |
| 12/6/2007 | -0.034428395 | -0.082486368 | -0.055244957 |
| 12/13/2007 | -0.022719678 | -0.089467011 | -0.063543313 |
| 12/20/2007 | -0.035459643 | -0.086409467 | -0.0665176 |
| 1/4/2008 | -0.002472982 | -0.091964082 | -0.062812815 |
| 1/11/2008 | 0.006498449 | -0.091384666 | -0.087865723 |
| 1/23/2008 | -0.003690539 | -0.099891811 | -0.108709886 |
| 1/30/2008 | 0.003495859 | -0.094581549 | -0.095916622 |
| 2/6/2008 | 0.024731476 | -0.10702698 | -0.086861502 |
| 2/13/2008 | 0.003806349 | -0.092040974 | -0.076336988 |
| 2/25/2008 | -0.001256297 | -0.09097011 | -0.077173087 |
| 3/3/2008 | -0.022233248 | -0.092322218 | -0.072116155 |
| 3/10/2008 | 0.001199936 | -0.095246334 | -0.087210121 |
| 3/17/2008 | -0.024996128 | -0.098944273 | -0.100315779 |
| 3/27/2008 | 0.019582043 | -0.106644235 | -0.085056756 |
| 4/3/2008 | -0.01121951 | -0.103127375 | -0.069269308 |
| 4/10/2008 | 0.003867569 | -0.091965357 | -0.05780333 |
| 4/17/2008 | 0.005606252 | -0.090062344 | -0.05233434 |
| 4/24/2008 | 0.011197778 | -0.08170718 | -0.056396855 |
| 5/1/2008 | -0.012904529 | -0.076706467 | -0.053740133 |
| 5/8/2008 | 0.017370422 | -0.076585105 | -0.055856555 |
| 5/15/2008 | -0.022169409 | -0.07091638 | -0.047216528 |
| 5/22/2008 | -0.010976158 | -0.072222071 | -0.052047082 |
| 6/3/2008 | -0.003566638 | -0.067013199 | -0.05460051 |
| 6/10/2008 | -0.014616831 | -0.080875113 | -0.065817359 |
| 6/17/2008 | -0.013333458 | -0.078432725 | -0.064417869 |
| 6/24/2008 | -0.004174814 | -0.078075812 | -0.064519754 |
| 7/1/2008 | -0.022414413 | -0.084672646 | -0.077352025 |
| 7/11/2008 | 0.008795266 | -0.086598576 | -0.095774252 |
| 7/18/2008 | -0.006144491 | -0.0891376 | -0.087044047 |
| 7/25/2008 | -0.001475145 | -0.091116752 | -0.075220649 |
| 8/1/2008 | 0.032704598 | -0.093361881 | -0.072899273 |
| 8/8/2008 | 0.015115477 | -0.096612175 | -0.064660446 |
| 8/15/2008 | 0.00011369 | -0.089364517 | -0.064505429 |
| 8/22/2008 | 0.00437628 | -0.082932311 | -0.058110806 |
| 9/3/2008 | -0.053588732 | -0.084479521 | -0.062530825 |
| 9/10/2008 | 0.04205589 | -0.106542993 | -0.082233201 |
| 9/17/2008 | -0.038459985 | -0.132339495 | -0.132886983 |
| 9/24/2008 | 0.021430814 | -0.138118641 | -0.132452809 |
| 10/1/2008 | -0.130329787 | -0.15954977 | -0.137126082 |
| 10/8/2008 | -0.069658653 | -0.178970281 | -0.222918123 |
| 10/20/2008 | -0.022405417 | -0.205551366 | -0.230021133 |
| 10/27/2008 | 0.068862906 | -0.216705657 | -0.272510318 |
| 11/3/2008 | 0.021408141 | -0.199235821 | -0.19763746 |
| 11/13/2008 | -0.129586497 | -0.230814732 | -0.22260837 |
| 11/20/2008 | 0.016733026 | -0.26223121 | -0.266579191 |
| 12/2/2008 | 0.082203837 | -0.282939101 | -0.235805567 |
| 12/9/2008 | 0.030653125 | -0.252929116 | -0.207096307 |
| 12/16/2008 | -0.073723328 | -0.22403058 | -0.173736248 |
| 12/23/2008 | -0.00116701 | -0.198086085 | -0.145274776 |
| 1/7/2009 | -0.042953418 | -0.175894699 | -0.109668521 |
| 1/14/2009 | 0.062060449 | -0.173725342 | -0.119970703 |
| 1/26/2009 | -0.017011713 | -0.153318276 | -0.14494977 |
| 2/2/2009 | 0.052214571 | -0.160735257 | -0.128847495 |
| 2/9/2009 | -0.047197964 | -0.139724151 | -0.113104647 |
| 2/19/2009 | -0.040058079 | -0.152029652 | -0.134870876 |
Figure 2b. One-Percent and Five-Percent VaR Forecasts for S&P 500 Returns During the Financial Crisis of 2008 - Panel B: S&P500: Five-Percent VaR Forecasts vs Return Realizations
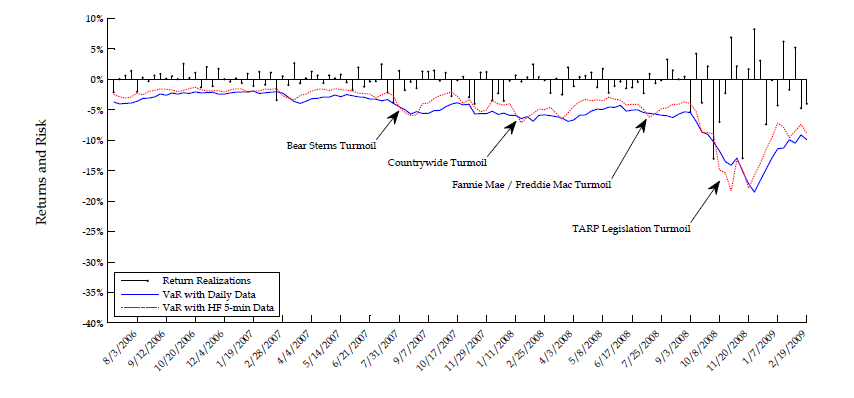
Data for Figure 2b
| Date | Return realizations | VaR with Daily Data | VaR with HF 5-min Data |
|---|---|---|---|
| 7/6/2006 | -0.021028658 | -0.037003789 | -0.025019458 |
| 7/13/2006 | 0.0002985 | -0.040409896 | -0.028486502 |
| 7/20/2006 | 0.005995453 | -0.039335487 | -0.030782536 |
| 7/27/2006 | 0.013826267 | -0.039013501 | -0.029009674 |
| 8/3/2006 | -0.020380651 | -0.036023684 | -0.02258446 |
| 8/10/2006 | 0.002985708 | -0.031346655 | -0.025308254 |
| 8/17/2006 | -0.002936084 | -0.030672514 | -0.019766529 |
| 8/24/2006 | 0.006082311 | -0.028944763 | -0.018225887 |
| 8/31/2006 | 0.008777795 | -0.023928186 | -0.015876054 |
| 9/12/2006 | 0.001076277 | -0.026083687 | -0.01617954 |
| 9/19/2006 | 0.005424237 | -0.022367677 | -0.017380704 |
| 9/26/2006 | 0.000455655 | -0.024176207 | -0.020036268 |
| 10/3/2006 | 0.025563652 | -0.021955148 | -0.018258164 |
| 10/13/2006 | 0.002186266 | -0.023071042 | -0.015052675 |
| 10/20/2006 | 0.010666821 | -0.020567605 | -0.013072155 |
| 10/27/2006 | -0.013051164 | -0.022098072 | -0.016948052 |
| 11/3/2006 | 0.020415073 | -0.021830733 | -0.019089042 |
| 11/15/2006 | -0.011136092 | -0.020919789 | -0.018402035 |
| 11/27/2006 | 0.017047302 | -0.024312922 | -0.018645095 |
| 12/4/2006 | 0.000231079 | -0.024161072 | -0.020720395 |
| 12/11/2006 | -0.003810793 | -0.022196103 | -0.017051686 |
| 12/18/2006 | 0.001671998 | -0.020809044 | -0.015529107 |
| 12/28/2006 | -0.005810005 | -0.020704192 | -0.015423223 |
| 1/9/2007 | 0.009149005 | -0.020255189 | -0.021785989 |
| 1/19/2007 | -0.010537553 | -0.019287062 | -0.018603088 |
| 1/26/2007 | 0.012442309 | -0.023209655 | -0.019110409 |
| 2/2/2007 | -0.008900854 | -0.021965771 | -0.016088279 |
| 2/9/2007 | 0.011070781 | -0.021021529 | -0.016491827 |
| 2/21/2007 | -0.034108465 | -0.020369594 | -0.015019301 |
| 2/28/2007 | 0.005044509 | -0.022459652 | -0.026670376 |
| 3/7/2007 | -0.009179933 | -0.029384338 | -0.030836539 |
| 3/14/2007 | 0.026640444 | -0.036392808 | -0.033761636 |
| 3/21/2007 | -0.006218807 | -0.039499175 | -0.026074977 |
| 3/28/2007 | 0.001633388 | -0.036034863 | -0.024076067 |
| 4/4/2007 | 0.012576361 | -0.03174223 | -0.019174102 |
| 4/16/2007 | 0.00649928 | -0.031067298 | -0.016169753 |
| 4/23/2007 | -0.005967186 | -0.029003167 | -0.016025628 |
| 4/30/2007 | 0.006420796 | -0.029115239 | -0.018346844 |
| 5/7/2007 | 0.001821889 | -0.025689445 | -0.015202779 |
| 5/14/2007 | 0.007882463 | -0.028421846 | -0.016816259 |
| 5/21/2007 | -0.004992987 | -0.024927798 | -0.017524257 |
| 5/31/2007 | -0.017033157 | -0.026840006 | -0.018914442 |
| 6/7/2007 | 0.019481775 | -0.028774758 | -0.022732145 |
| 6/14/2007 | -0.012044948 | -0.029440061 | -0.023190146 |
| 6/21/2007 | -0.003637861 | -0.032412033 | -0.024099157 |
| 6/28/2007 | -0.002924697 | -0.032627534 | -0.030432614 |
| 7/10/2007 | 0.024657993 | -0.035053945 | -0.025627691 |
| 7/17/2007 | -0.021405943 | -0.033200598 | -0.021318368 |
| 7/24/2007 | -0.037888616 | -0.039364342 | -0.027211486 |
| 7/31/2007 | 0.013906806 | -0.044840451 | -0.045052449 |
| 8/7/2007 | -0.017758229 | -0.049924156 | -0.054800247 |
| 8/14/2007 | -0.003978958 | -0.056877192 | -0.059278532 |
| 8/21/2007 | -0.014313181 | -0.052979188 | -0.058350002 |
| 8/28/2007 | 0.012972821 | -0.056042108 | -0.039871529 |
| 9/7/2007 | 0.01269826 | -0.055904676 | -0.038761152 |
| 9/14/2007 | 0.014611479 | -0.051433768 | -0.031648875 |
| 9/21/2007 | -0.002245915 | -0.05089807 | -0.026761126 |
| 9/28/2007 | 0.010664554 | -0.04483332 | -0.02355157 |
| 10/10/2007 | -0.027562083 | -0.04061068 | -0.020836051 |
| 10/17/2007 | -0.0012691 | -0.038374402 | -0.027776497 |
| 10/24/2007 | 0.004214256 | -0.041916903 | -0.039608661 |
| 10/31/2007 | -0.029243358 | -0.040736781 | -0.032681341 |
| 11/7/2007 | -0.040277488 | -0.056850594 | -0.046278029 |
| 11/19/2007 | 0.011386573 | -0.056182098 | -0.053183576 |
| 11/29/2007 | 0.011945248 | -0.056369486 | -0.050150015 |
| 12/6/2007 | -0.034428395 | -0.052290773 | -0.034606352 |
| 12/13/2007 | -0.022719678 | -0.057493435 | -0.04027053 |
| 12/20/2007 | -0.035459643 | -0.055352594 | -0.042274057 |
| 1/4/2008 | -0.002472982 | -0.059146113 | -0.039768756 |
| 1/11/2008 | 0.006498449 | -0.059010209 | -0.056706098 |
| 1/23/2008 | -0.003690539 | -0.064537449 | -0.071001985 |
| 1/30/2008 | 0.003495859 | -0.06104215 | -0.06230428 |
| 2/6/2008 | 0.024731476 | -0.068852157 | -0.056051618 |
| 2/13/2008 | 0.003806349 | -0.059036629 | -0.048885081 |
| 2/25/2008 | -0.001256297 | -0.05823312 | -0.04950801 |
| 3/3/2008 | -0.022233248 | -0.059689715 | -0.046012932 |
| 3/10/2008 | 0.001199936 | -0.061277327 | -0.056231395 |
| 3/17/2008 | -0.024996128 | -0.063769483 | -0.065230462 |
| 3/27/2008 | 0.019582043 | -0.069006346 | -0.054886441 |
| 4/3/2008 | -0.01121951 | -0.066536382 | -0.044144878 |
| 4/10/2008 | 0.003867569 | -0.058932737 | -0.036401801 |
| 4/17/2008 | 0.005606252 | -0.058405968 | -0.032705368 |
| 4/24/2008 | 0.011197778 | -0.051977666 | -0.035366776 |
| 5/1/2008 | -0.012904529 | -0.048845446 | -0.033612151 |
| 5/8/2008 | 0.017370422 | -0.04932064 | -0.035050031 |
| 5/15/2008 | -0.022169409 | -0.045539438 | -0.029202632 |
| 5/22/2008 | -0.010976158 | -0.045955277 | -0.032466802 |
| 6/3/2008 | -0.003566638 | -0.042677298 | -0.034192668 |
| 6/10/2008 | -0.014616831 | -0.05232706 | -0.041795101 |
| 6/17/2008 | -0.013333458 | -0.050358173 | -0.040909858 |
| 6/24/2008 | -0.004174814 | -0.05010078 | -0.040993049 |
| 7/1/2008 | -0.022414413 | -0.054635945 | -0.049676327 |
| 7/11/2008 | 0.008795266 | -0.055894092 | -0.062213764 |
| 7/18/2008 | -0.006144491 | -0.057027782 | -0.056212795 |
| 7/25/2008 | -0.001475145 | -0.058794902 | -0.048285719 |
| 8/1/2008 | 0.032704598 | -0.059795825 | -0.046647051 |
| 8/8/2008 | 0.015115477 | -0.06260059 | -0.041049749 |
| 8/15/2008 | 0.00011369 | -0.057178855 | -0.040953792 |
| 8/22/2008 | 0.00437628 | -0.053268377 | -0.036625006 |
| 9/3/2008 | -0.053588732 | -0.054427576 | -0.039619988 |
| 9/10/2008 | 0.04205589 | -0.069058822 | -0.052951376 |
| 9/17/2008 | -0.038459985 | -0.08641889 | -0.087408758 |
| 9/24/2008 | 0.021430814 | -0.090462036 | -0.087144181 |
| 10/1/2008 | -0.130329787 | -0.102989509 | -0.090360834 |
| 10/8/2008 | -0.069658653 | -0.117581124 | -0.148947961 |
| 10/20/2008 | -0.022405417 | -0.135016154 | -0.153571958 |
| 10/27/2008 | 0.068862906 | -0.141151654 | -0.182970538 |
| 11/3/2008 | 0.021408141 | -0.129169193 | -0.131659495 |
| 11/13/2008 | -0.129586497 | -0.151665437 | -0.148507596 |
| 11/20/2008 | 0.016733026 | -0.171409397 | -0.178759268 |
| 12/2/2008 | 0.082203837 | -0.18510684 | -0.157636853 |
| 12/9/2008 | 0.030653125 | -0.166313611 | -0.138154572 |
| 12/16/2008 | -0.073723328 | -0.14779301 | -0.115070486 |
| 12/23/2008 | -0.00116701 | -0.129247884 | -0.095847161 |
| 1/7/2009 | -0.042953418 | -0.113999093 | -0.071689773 |
| 1/14/2009 | 0.062060449 | -0.112669956 | -0.078628804 |
| 1/26/2009 | -0.017011713 | -0.099006229 | -0.09562326 |
| 2/2/2009 | 0.052214571 | -0.104815497 | -0.084699746 |
| 2/9/2009 | -0.047197964 | -0.09118027 | -0.073896961 |
| 2/19/2009 | -0.040058079 | -0.099028346 | -0.088729223 |
Figure 3a. One-Percent and Five-Percent VaR Forecasts for Google Returns During the Financial Crisis of 2008 - Panel A: Google: One-Percent VaR Forecasts vs Return Realizations
We plot one-percent (top graph) and five-percent (bottom graph) VaR forecasts at five-day horizon without overlapping for Google returns based on a two-factor log-SV model with jumps in returns. The model is estimated at a daily discretization interval by Bayesian MCMC methods either without or with augmenting the underlying state-space formulation with a daily volatility measurement equation based on high frequency intraday data, as proposed in this paper. The resulting VaR forecasts without utilizing high-frequency volatility measures are plotted as a solid line (denoted "VaR with daily data"), those incorporating the information content of intraday data for the latent daily volatility are plotted as a dashed line (denoted "VaR with HF 5-min data"), while the corresponding actual observed returns are plotted as vertical bars (denoted "Return realizations"). The VaR analysis is for the period December 8, 2006 - July 24, 2009 and involves re-estimating the model on each date with all past data going back to August 30, 2004 (ten days after Google's IPO).
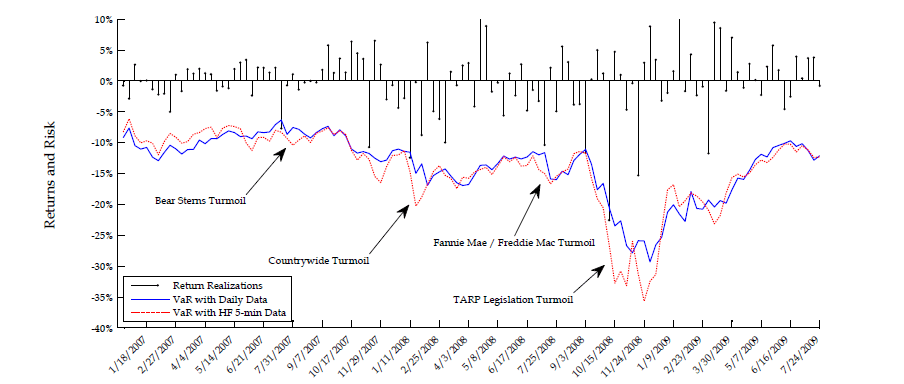
Data for Figure 3a
| Date | Return realizations | VaR with Daily Data | VaR with HF 5-min Data |
|---|---|---|---|
| 12/8/2006 | -0.007592846 | -0.091956615 | -0.082753276 |
| 12/15/2006 | -0.028836421 | -0.076254965 | -0.061354757 |
| 12/27/2006 | 0.026395946 | -0.104800931 | -0.088771705 |
| 1/8/2007 | -0.000298878 | -0.110392696 | -0.100476985 |
| 1/18/2007 | 0.000548216 | -0.107729875 | -0.096903295 |
| 1/25/2007 | -0.013541943 | -0.123463659 | -0.100843629 |
| 2/1/2007 | -0.022036827 | -0.129186874 | -0.119755857 |
| 2/8/2007 | -0.020792353 | -0.116042695 | -0.098549502 |
| 2/15/2007 | -0.050171209 | -0.104239637 | -0.085082971 |
| 2/27/2007 | 0.009879154 | -0.110206272 | -0.091332461 |
| 3/7/2007 | -0.016702011 | -0.118469872 | -0.100904396 |
| 3/14/2007 | 0.018862017 | -0.111231696 | -0.098361243 |
| 3/21/2007 | 0.011694511 | -0.11085735 | -0.086333079 |
| 3/28/2007 | 0.01942558 | -0.09579236 | -0.083700707 |
| 4/4/2007 | 0.012481721 | -0.101651706 | -0.077275693 |
| 4/16/2007 | 0.010753412 | -0.093554306 | -0.074933922 |
| 4/23/2007 | -0.016020033 | -0.093693676 | -0.091423022 |
| 4/30/2007 | -0.009117989 | -0.086688711 | -0.076499207 |
| 5/7/2007 | -0.011840445 | -0.081092399 | -0.072273056 |
| 5/14/2007 | 0.019037367 | -0.083699575 | -0.073951869 |
| 5/21/2007 | 0.029651783 | -0.09016205 | -0.077316642 |
| 5/31/2007 | 0.033974193 | -0.089341759 | -0.100135708 |
| 6/7/2007 | -0.023673116 | -0.093741735 | -0.112877726 |
| 6/14/2007 | 0.02170541 | -0.082527628 | -0.091764035 |
| 6/21/2007 | 0.021034766 | -0.083775923 | -0.091256598 |
| 6/28/2007 | 0.013274909 | -0.082627959 | -0.097648109 |
| 7/10/2007 | 0.02125851 | -0.070762247 | -0.08004136 |
| 7/17/2007 | -0.07707329 | -0.063435192 | -0.08303277 |
| 7/24/2007 | -0.007270309 | -0.086579092 | -0.093348624 |
| 7/31/2007 | 0.010694246 | -0.075415212 | -0.10417482 |
| 8/7/2007 | -0.014209154 | -0.078455577 | -0.095619696 |
| 8/14/2007 | -0.002708414 | -0.086275551 | -0.089131472 |
| 8/21/2007 | -0.000157806 | -0.092306215 | -0.099694143 |
| 8/28/2007 | -0.002586612 | -0.083671525 | -0.084545046 |
| 9/7/2007 | 0.01788062 | -0.077493836 | -0.08125593 |
| 9/14/2007 | 0.057574944 | -0.073535657 | -0.075619338 |
| 9/21/2007 | 0.012976425 | -0.088650376 | -0.086825239 |
| 9/28/2007 | 0.0362804 | -0.079102029 | -0.080765828 |
| 10/10/2007 | 0.013566261 | -0.08876078 | -0.086531901 |
| 10/17/2007 | 0.063628884 | -0.110337934 | -0.112164498 |
| 10/24/2007 | 0.044599164 | -0.117009833 | -0.128300722 |
| 10/31/2007 | 0.035491376 | -0.114492841 | -0.117574603 |
| 11/7/2007 | -0.107376449 | -0.117403098 | -0.126953383 |
| 11/19/2007 | 0.06483664 | -0.125257459 | -0.154938481 |
| 11/29/2007 | 0.026302956 | -0.130892167 | -0.164629136 |
| 12/6/2007 | -0.029998276 | -0.128206088 | -0.138832638 |
| 12/13/2007 | -0.006887781 | -0.113064484 | -0.120532847 |
| 12/20/2007 | -0.04372489 | -0.110427118 | -0.120099291 |
| 1/4/2008 | -0.027956843 | -0.114024859 | -0.113072096 |
| 1/11/2008 | -0.124490329 | -0.115394783 | -0.147124591 |
| 1/23/2008 | -0.002110201 | -0.149666753 | -0.202705495 |
| 1/30/2008 | -0.087659044 | -0.134378213 | -0.188222691 |
| 2/6/2008 | 0.061987757 | -0.169122496 | -0.167136843 |
| 2/13/2008 | -0.049085184 | -0.153269416 | -0.146787905 |
| 2/25/2008 | -0.061643569 | -0.147421827 | -0.137341492 |
| 3/3/2008 | -0.099805535 | -0.142552479 | -0.152894022 |
| 3/10/2008 | 0.014751476 | -0.15430509 | -0.158005256 |
| 3/17/2008 | -0.007224216 | -0.164977258 | -0.174433991 |
| 3/27/2008 | 0.024832327 | -0.169348047 | -0.155844083 |
| 4/3/2008 | 0.028689184 | -0.167734639 | -0.157727943 |
| 4/10/2008 | -0.041350658 | -0.152743208 | -0.147774835 |
| 4/17/2008 | 0.187959466 | -0.13671118 | -0.143459604 |
| 4/24/2008 | 0.088614766 | -0.136153902 | -0.139982292 |
| 5/1/2008 | -0.017539982 | -0.143683203 | -0.151594978 |
| 5/8/2008 | -0.002921918 | -0.133678857 | -0.137835166 |
| 5/15/2008 | -0.056182818 | -0.121607463 | -0.122944699 |
| 5/22/2008 | 0.011896038 | -0.126554948 | -0.130885176 |
| 6/3/2008 | -0.023610437 | -0.123426704 | -0.124026447 |
| 6/10/2008 | 0.026900666 | -0.126323076 | -0.138108833 |
| 6/17/2008 | -0.048174669 | -0.123210399 | -0.136913238 |
| 6/24/2008 | -0.014743833 | -0.114537619 | -0.121378612 |
| 7/1/2008 | -0.032665606 | -0.119667795 | -0.143588157 |
| 7/11/2008 | -0.103633975 | -0.116251661 | -0.150074016 |
| 7/18/2008 | 0.021189062 | -0.158735185 | -0.166724557 |
| 7/25/2008 | -0.049256978 | -0.160072337 | -0.154480434 |
| 8/1/2008 | 0.055642308 | -0.146240035 | -0.147609676 |
| 8/8/2008 | 0.030442487 | -0.15183232 | -0.142595826 |
| 8/15/2008 | -0.038517109 | -0.128805777 | -0.117773498 |
| 8/22/2008 | -0.037682994 | -0.119009151 | -0.11418315 |
| 9/3/2008 | -0.116664527 | -0.110996679 | -0.117232251 |
| 9/10/2008 | 0.002421608 | -0.134980378 | -0.158004335 |
| 9/17/2008 | 0.049647722 | -0.176117205 | -0.190827979 |
| 9/24/2008 | 0.012100668 | -0.1659836 | -0.205466891 |
| 10/3/2008 | -0.225582952 | -0.204170009 | -0.26395574 |
| 10/15/2008 | 0.047031841 | -0.234769889 | -0.327657487 |
| 10/22/2008 | 0.009616199 | -0.226564496 | -0.307786543 |
| 10/29/2008 | -0.046607581 | -0.266956883 | -0.331548792 |
| 11/5/2008 | -0.003835535 | -0.278320974 | -0.259929317 |
| 11/17/2008 | -0.153059827 | -0.258763238 | -0.312868677 |
| 11/24/2008 | 0.029231102 | -0.259076328 | -0.356635829 |
| 12/4/2008 | 0.088214449 | -0.293072435 | -0.324500635 |
| 12/11/2008 | 0.034044238 | -0.265553304 | -0.313485264 |
| 12/18/2008 | -0.032073004 | -0.253080075 | -0.239400072 |
| 12/30/2008 | -0.019429075 | -0.212476075 | -0.176443394 |
| 1/9/2009 | 0.01561053 | -0.200567333 | -0.167844593 |
| 1/21/2009 | 0.140563014 | -0.215362338 | -0.203794317 |
| 1/28/2009 | -0.01655272 | -0.227590534 | -0.193942265 |
| 2/4/2009 | 0.042954933 | -0.179133711 | -0.181636608 |
| 2/11/2009 | -0.023283804 | -0.206543625 | -0.186379399 |
| 2/23/2009 | -0.009310601 | -0.207668064 | -0.19597204 |
| 3/2/2009 | -0.117498403 | -0.192890651 | -0.209747111 |
| 3/9/2009 | 0.094297013 | -0.204156839 | -0.231375816 |
| 3/16/2009 | 0.08543408 | -0.193794692 | -0.217951631 |
| 3/23/2009 | -0.016041344 | -0.198112623 | -0.181781715 |
| 3/30/2009 | 0.070051871 | -0.176373335 | -0.156459732 |
| 4/6/2009 | 0.013971961 | -0.15738741 | -0.151037621 |
| 4/16/2009 | -0.011147178 | -0.159459499 | -0.15567272 |
| 4/23/2009 | 0.027606777 | -0.144746151 | -0.149104762 |
| 4/30/2009 | 0.001287977 | -0.127090942 | -0.135837772 |
| 5/7/2009 | -0.022782645 | -0.118870666 | -0.128044189 |
| 5/14/2009 | 0.023047611 | -0.123253885 | -0.132270528 |
| 5/21/2009 | 0.057441484 | -0.108111555 | -0.123942988 |
| 6/2/2009 | 0.017251189 | -0.104394955 | -0.111721997 |
| 6/9/2009 | -0.045763802 | -0.101041346 | -0.102101391 |
| 6/16/2009 | -0.025533198 | -0.097004942 | -0.10260244 |
| 6/23/2009 | 0.039197955 | -0.106067769 | -0.115055914 |
| 6/30/2009 | 0.004057586 | -0.101649295 | -0.104973126 |
| 7/10/2009 | 0.036910149 | -0.112545531 | -0.111743795 |
| 7/17/2009 | 0.037859123 | -0.128402378 | -0.124103685 |
| 7/24/2009 | -0.007999324 | -0.121139982 | -0.123036889 |
Figure 3b. One-Percent and Five-Percent VaR Forecasts for Google Returns During the Financial Crisis of 2008 - Panel B: Google: Five-Percent VaR Forecasts vs Return Realizations
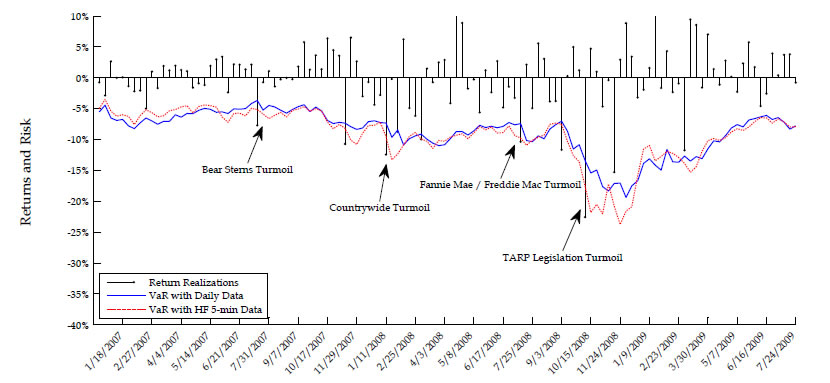
Data for Figure 3b
| Date | Return realizations | VaR with Daily Data | VaR with HF 5-min Data |
|---|---|---|---|
| 12/8/2006 | -0.007592846 | -0.055329142 | -0.049712205 |
| 12/15/2006 | -0.028836421 | -0.0445386 | -0.035132481 |
| 12/27/2006 | 0.026395946 | -0.065258291 | -0.054146418 |
| 1/8/2007 | -0.000298878 | -0.069123564 | -0.06227489 |
| 1/18/2007 | 0.000548216 | -0.067503588 | -0.059915915 |
| 1/25/2007 | -0.013541943 | -0.07808082 | -0.062655591 |
| 2/1/2007 | -0.022036827 | -0.082379619 | -0.075740537 |
| 2/8/2007 | -0.020792353 | -0.073074672 | -0.061276076 |
| 2/15/2007 | -0.050171209 | -0.065175336 | -0.05202972 |
| 2/27/2007 | 0.009879154 | -0.069970888 | -0.056648135 |
| 3/7/2007 | -0.016702011 | -0.075451044 | -0.063254361 |
| 3/14/2007 | 0.018862017 | -0.070604364 | -0.061609751 |
| 3/21/2007 | 0.011694511 | -0.070534575 | -0.053358747 |
| 3/28/2007 | 0.01942558 | -0.060052472 | -0.05164094 |
| 4/4/2007 | 0.012481721 | -0.063900182 | -0.047082583 |
| 4/16/2007 | 0.010753412 | -0.057827796 | -0.045350097 |
| 4/23/2007 | -0.016020033 | -0.05813358 | -0.056996159 |
| 4/30/2007 | -0.009117989 | -0.052889197 | -0.046693121 |
| 5/7/2007 | -0.011840445 | -0.049593565 | -0.044053003 |
| 5/14/2007 | 0.019037367 | -0.051175039 | -0.045231273 |
| 5/21/2007 | 0.029651783 | -0.055945631 | -0.047672067 |
| 5/31/2007 | 0.033974193 | -0.055217751 | -0.06345777 |
| 6/7/2007 | -0.023673116 | -0.058021474 | -0.072208872 |
| 6/14/2007 | 0.02170541 | -0.050330203 | -0.057785575 |
| 6/21/2007 | 0.021034766 | -0.051059708 | -0.057404454 |
| 6/28/2007 | 0.013274909 | -0.050051663 | -0.061866794 |
| 7/10/2007 | 0.02125851 | -0.041926174 | -0.049588768 |
| 7/17/2007 | -0.07707329 | -0.036733017 | -0.051466751 |
| 7/24/2007 | -0.007270309 | -0.052321673 | -0.058756901 |
| 7/31/2007 | 0.010694246 | -0.044930966 | -0.066288975 |
| 8/7/2007 | -0.014209154 | -0.04737044 | -0.060594402 |
| 8/14/2007 | -0.002708414 | -0.052638744 | -0.056115313 |
| 8/21/2007 | -0.000157806 | -0.057391026 | -0.063473724 |
| 8/28/2007 | -0.002586612 | -0.051454016 | -0.052917546 |
| 9/7/2007 | 0.01788062 | -0.046922744 | -0.050693695 |
| 9/14/2007 | 0.057574944 | -0.043712442 | -0.046758328 |
| 9/21/2007 | 0.012976425 | -0.054939567 | -0.054315534 |
| 9/28/2007 | 0.0362804 | -0.047537239 | -0.050103844 |
| 10/10/2007 | 0.013566261 | -0.05387602 | -0.053977731 |
| 10/17/2007 | 0.063628884 | -0.06924459 | -0.071822459 |
| 10/24/2007 | 0.044599164 | -0.074122823 | -0.082818697 |
| 10/31/2007 | 0.035491376 | -0.072254537 | -0.075496943 |
| 11/7/2007 | -0.107376449 | -0.073573074 | -0.081868903 |
| 11/19/2007 | 0.06483664 | -0.079458838 | -0.101218533 |
| 11/29/2007 | 0.026302956 | -0.083714051 | -0.108060995 |
| 12/6/2007 | -0.029998276 | -0.08147282 | -0.089983173 |
| 12/13/2007 | -0.006887781 | -0.071114744 | -0.0773715 |
| 12/20/2007 | -0.04372489 | -0.069642894 | -0.076968081 |
| 1/4/2008 | -0.027956843 | -0.07246983 | -0.072187436 |
| 1/11/2008 | -0.124490329 | -0.073450827 | -0.095344964 |
| 1/23/2008 | -0.002110201 | -0.096473176 | -0.132948478 |
| 1/30/2008 | -0.087659044 | -0.084825628 | -0.123347397 |
| 2/6/2008 | 0.061987757 | -0.108656557 | -0.108898106 |
| 2/13/2008 | -0.049085184 | -0.098732732 | -0.094786127 |
| 2/25/2008 | -0.061643569 | -0.094238727 | -0.088655031 |
| 3/3/2008 | -0.099805535 | -0.091249415 | -0.09932636 |
| 3/10/2008 | 0.014751476 | -0.099584211 | -0.102835049 |
| 3/17/2008 | -0.007224216 | -0.105901511 | -0.114274384 |
| 3/27/2008 | 0.024832327 | -0.109981687 | -0.101576154 |
| 4/3/2008 | 0.028689184 | -0.108607817 | -0.102822714 |
| 4/10/2008 | -0.041350658 | -0.098523985 | -0.09599949 |
| 4/17/2008 | 0.187959466 | -0.087205173 | -0.093193611 |
| 4/24/2008 | 0.088614766 | -0.087044388 | -0.090760954 |
| 5/1/2008 | -0.017539982 | -0.092799784 | -0.098698526 |
| 5/8/2008 | -0.002921918 | -0.086004193 | -0.089261619 |
| 5/15/2008 | -0.056182818 | -0.077009372 | -0.079035033 |
| 5/22/2008 | 0.011896038 | -0.080677598 | -0.084445299 |
| 6/3/2008 | -0.023610437 | -0.078543919 | -0.079750452 |
| 6/10/2008 | 0.026900666 | -0.081025949 | -0.089515091 |
| 6/17/2008 | -0.048174669 | -0.078773973 | -0.088750538 |
| 6/24/2008 | -0.014743833 | -0.072524318 | -0.078092064 |
| 7/1/2008 | -0.032665606 | -0.076276531 | -0.093438742 |
| 7/11/2008 | -0.103633975 | -0.07427321 | -0.09778439 |
| 7/18/2008 | 0.021189062 | -0.10174464 | -0.109349097 |
| 7/25/2008 | -0.049256978 | -0.103513112 | -0.101114995 |
| 8/1/2008 | 0.055642308 | -0.094118655 | -0.096298188 |
| 8/8/2008 | 0.030442487 | -0.098815524 | -0.092804663 |
| 8/15/2008 | -0.038517109 | -0.083126497 | -0.075536567 |
| 8/22/2008 | -0.037682994 | -0.075945026 | -0.073309362 |
| 9/3/2008 | -0.116664527 | -0.070394777 | -0.075371191 |
| 9/10/2008 | 0.002421608 | -0.086720203 | -0.103221702 |
| 9/17/2008 | 0.049647722 | -0.115465204 | -0.126047677 |
| 9/24/2008 | 0.012100668 | -0.108510276 | -0.135924957 |
| 10/3/2008 | -0.225582952 | -0.134032942 | -0.175224519 |
| 10/15/2008 | 0.047031841 | -0.154171125 | -0.218030209 |
| 10/22/2008 | 0.009616199 | -0.149551026 | -0.205011233 |
| 10/29/2008 | -0.046607581 | -0.176267103 | -0.220373118 |
| 11/5/2008 | -0.003835535 | -0.183431414 | -0.172044466 |
| 11/17/2008 | -0.153059827 | -0.171106578 | -0.208058425 |
| 11/24/2008 | 0.029231102 | -0.170671201 | -0.23754697 |
| 12/4/2008 | 0.088214449 | -0.193768278 | -0.216004497 |
| 12/11/2008 | 0.034044238 | -0.175025088 | -0.20894141 |
| 12/18/2008 | -0.032073004 | -0.166883208 | -0.158360623 |
| 12/30/2008 | -0.019429075 | -0.13868581 | -0.115509048 |
| 1/9/2009 | 0.01561053 | -0.131316752 | -0.109837017 |
| 1/21/2009 | 0.140563014 | -0.141560229 | -0.13461005 |
| 1/28/2009 | -0.01655272 | -0.149636889 | -0.127618368 |
| 2/4/2009 | 0.042954933 | -0.116049958 | -0.119229459 |
| 2/11/2009 | -0.023283804 | -0.136163364 | -0.122436105 |
| 2/23/2009 | -0.009310601 | -0.136891436 | -0.129052124 |
| 3/2/2009 | -0.117498403 | -0.126785015 | -0.138743427 |
| 3/9/2009 | 0.094297013 | -0.134988996 | -0.153077651 |
| 3/16/2009 | 0.08543408 | -0.127742694 | -0.143986661 |
| 3/23/2009 | -0.016041344 | -0.131131509 | -0.119155545 |
| 3/30/2009 | 0.070051871 | -0.114936866 | -0.101950509 |
| 4/6/2009 | 0.013971961 | -0.102169303 | -0.098267808 |
| 4/16/2009 | -0.011147178 | -0.103787434 | -0.101556876 |
| 4/23/2009 | 0.027606777 | -0.093745497 | -0.096978189 |
| 4/30/2009 | 0.001287977 | -0.081354185 | -0.087841357 |
| 5/7/2009 | -0.022782645 | -0.075884945 | -0.082508169 |
| 5/14/2009 | 0.023047611 | -0.079502159 | -0.085426937 |
| 5/21/2009 | 0.057441484 | -0.068455381 | -0.079696407 |
| 6/2/2009 | 0.017251189 | -0.066174554 | -0.071187894 |
| 6/9/2009 | -0.045763802 | -0.063406748 | -0.064467249 |
| 6/16/2009 | -0.025533198 | -0.06096979 | -0.064973856 |
| 6/23/2009 | 0.039197955 | -0.067605313 | -0.073683294 |
| 6/30/2009 | 0.004057586 | -0.064528258 | -0.066599906 |
| 7/10/2009 | 0.036910149 | -0.072078411 | -0.071420393 |
| 7/17/2009 | 0.037859123 | -0.083214816 | -0.079844582 |
| 7/24/2009 | -0.007999324 | -0.077900284 | -0.079034879 |
References
Aït-Sahalia, Y. and J. Jacod (2007). Volatility estimators for discretely sampled lévy processes. Ann. Stat. 35 (1), 355–392.
Alizadeh, S., M. Brandt, and F. Diebold (2002). Range-based estimation of stochastic volatility models. The Journal of Finance 57 (3).
Andersen, T. G., L. Benzoni, and J. Lund (2002). An empirical investigation of continuous-time equity return models. Journal of Finance 57 (3), 1239–1284.
Andersen, T. G., T. Bollerslev, P. Christoffersen, and F. X. Diebold (2007). Practical volatility and correlation modeling for financial market risk management. In The Risks of Financial Institutions, NBER Chapters, pp. 513–548. National Bureau of Economic Research, Inc.
Andersen, T. G., T. Bollerslev, and F. X. Diebold (2009). Parametric and nonparametric volatility measurement. North Holland. In Handbook of Financial Econometrics, Yacine Aït-Sahalia, Lars P. Hansen, and Jose A. Scheinkman (Eds.).
Andersen, T. G., T. Bollerslev, F. X. Diebold, and H. Ebens (2001). The distribution of realized stock return volatility. Journal of Financial Economics 61 (1), 43–76.
Andersen, T. G., T. Bollerslev, and D. Dobrev (2007). No-arbitrage semi-martingale restrictions for continuous-time volatility models subject to leverage effects, jumps and i.i.d. noise: Theory and testable distributional implications. Journal of Econometrics 138 (1), 125–80.
Andersen, T. G., D. P. Dobrev, and E. Schaumburg (2009). Jump-robust volatility estimation using nearest neighbor truncation. NBER Working Paper (15533).
Bakshi, G., C. Cao, and Z. Chen (1997). Empirical performance of alternative option pricing models. The Journal of Finance 52 (5), 2003–2049.
Bandi, F. M. and R. Reno (2009). Nonparametric stochastic volatility. Global COE Hi-Stat Discussion Paper Series gd08-035, Institute of Economic Research, Hitotsubashi University.
Bandi, F. M. and J. R. Russell (2007). Volatility. Elsevier Science, New York. in Handbook of Financial Engineering, V. Linetski and J. Birge (Eds.).
Barndorff-Nielsen, O. E. and N. Shephard (2002). Econometric analysis of realised volatility and its use in estimating stochastic volatility models. Journal of the Royal Statistical Society, Series B 64, 253–280.
Barndorff-Nielsen, O. E. and N. Shephard (2004). Power and bipower variation with stochastic volatility and jumps. Journal of Financial Econometrics 2 (1), 1–37.
Barndorff-Nielsen, O. E. and N. Shephard (2005). How accurate is the asymptotic approximation to the distribution of realised volatility? In D. W. K. Andrews and J. H. Stock (Eds.), Identification and Inference for Econometric Models. A Festschrift in Honour of T.J. Rothenberg, pp. 306–331. Cambridge: Cambridge University Press.
Barndorff-Nielsen, O. E. and N. Shephard (2007). Variation, Jumps, Market Frictions and High Frequency Data in Fnancial Econometrics. Cambridge University Press. In Advances in Economics and Econometrics. Theory and Applications, Ninth World Congress, R. Blundell, T. Persson, and W. Newey (Eds.).
Barndorff-Nielsen, O. E., N. Shephard, and M. Winkel (2006). Limit theorems for multipower variation in the presence of jumps. Stochastic Processes and Their Applications 116, 796–806.
Bates, D. S. (2000). Post-’87 crash fears in the s&p 500 futures option market. Journal of Econometrics 94 (1-2), 181–238.
Black, F. and M. Scholes (1973). The pricing of options and corporate liabilities. Journal of Political Economy 81, 637–659.
Bollerslev, T. and H. Zhou (2002). Estimating stochastic volatility diffusion using conditional moments of integrated volatility. Journal of Econometrics 109, 33–65.
Broadie, M., M. Chernov, and M. Johannes (2007). Model specification and risk premia: Evidence from futures options. Journal of Finance 62 (3), 1453–1490.
Chernov, M., A. Gallant, E. Ghysels, and G. Tauchen (2003). Alternative models for stock price dynamics. Journal of Econometrics 116, 225–257.
Chernov, M. and E. Ghysels (2000). A study towards a unified approach to the joint estimation of objective and risk neutral measures for the purpose of option valuation. Journal of Financial Economics 56, 407–458.
Chib, S. and E. Greenberg (1996). Markov chain monte carlo simulation methods in econometrics. Econometric Theory 12 (3), 409–431.
Christensen, K., R. Oomen, and M. Podolskij (2008). Realized quantile-based estimation of integrated variance. Working paper.
Corradi, V. and W. Distaso (2006). Semiparametric comparison of stochastic volatility models via realized measures. Review of Economic Studies 73, 635–667.
Corsi, F., D. Pirino, and R. Renò (2008). Volatility forecasting: The jumps do matter. SSRN Working Paper.
Das, S. R. and R. K. Sundaram (1999). Of smiles and smirks: A term structure perspective. The Journal of Financial and Quantitative Analysis 34 (2), 211–239.
Eraker, B. (2004). Do stock prices and volatility jump? reconciling evidence from spot and option prices. The Journal of Finance 59 (3), 1367–1403.
Eraker, B., M. Johannes, and N. Polson (2003). The impact of jumps in volatility and returns. The Journal of Finance 58 (3), 1269–1300.
Fleming, J., C. Kirby, and B. Ostdiek (2003, March). The economic value of volatility timing using "realized" volatility. Journal of Financial Economics 67 (3), 473–509.
Hansen, P. R. and A. Lunde (2005). A realized variance for the whole day based on intermittent high-frequency data. Journal of Financial Econometrics 3 (4), 525–554.
Huang, X. and G. Tauchen (2005). The relative contribution of jumps to total price variance. Journal of Financial Econometrics 3 (4), 456–99.
Jacquier, E., N. Polson, and P. Rossi (2004). Bayesian analysis of stochastic volatility models with fat-tails and correlated errors. Journal of Econometrics 122, 185–212.
Johannes, M. and N. Polson (2002). Mcmc methods for financial econometrics. In Handbook of Financial Econometrics. North-Holland. Forthcoming.
Jones, C. (1998). Bayesian estimation of continuous-time finance models. Working Paper.
Jones, C. (2003). The dynamics of stochastic volatility: evidence from underlying and options market. Journal of Econometrics 116, 181–224.
Mancini, C. (2006). Estimating the integrated volatility in stochastic volatility models with levy type jumps. Working paper, University of Firenze.
McAleer, M. and M. C. Medeiros (2008). Realized volatility: A review. Econometric Reviews 27 (1-3), 10–45.
Merton, R. C. (1969). Lifetime portfolio selection under uncertainty: The continuous-time case. The Review of Economics and Statistics 51 (3), 247–257.
Pan, J. (2002). The jump-risk premia implicit in options: evidence from an integrated time-series study. Journal of Financial Economics 63 (1), 3–50.
Podolskij, M. and M. Vetter (2009). Bipower-type estimation in a noisy diffusion setting. Stochastic Processes Appl. 119 (9), 2803–2831.
Szerszen, P. (2009). Bayesian analysis of stochastic volatility models with lévy jumps: application to risk analysis. Board of Governors of the Federal Reserve System Working Paper, 40
Todorov, V. (2009). Estimation of continuous-time stochastic volatility models with jumps using high-frequency data. Journal of Econometrics 148 (2), 131–148.
Footnotes
1. Dobrislav Dobrev: Federal Reserve
Board of Governors, [email protected]
Pawel Szerszen: Federal Reserve Board of Governors,
[email protected]We are grateful to Torben Andersen, Federico Bandi, Luca Benzoni,
Neil Ericsson, Michael Gordy, Erik Hjalmarsson, Michael Johannes,
Matthew Pritsker, and Viktor Todorov for helpful discussions and
comments. We also thank conference participants at the 2010
International Risk Management Conference, the 30th International
Symposium on Forecasting, the 16th International Conference on
Computing in Economics and Finance, as well as seminar participants
at the Federal Reserve Board, Johns Hopkins University, the Office
of the Comptroller of the Currency, and University of Maryland for
their feedback. Excellent research assistance has been provided by
Patrick Mason as well as Erica Reisman and Raymond Zhong. Any
errors or omissions are our sole responsibility.
The views in this paper are solely those of the authors and should
not be interpreted as reflecting the views of the Board of
Governors of the Federal Reserve System or of any other person
associated with the Federal Reserve System. Return to text
2. See for example, Chernov and Ghysels (2000), [#!Pan-JumpRiskPremia::2002!#], and Eraker (2004) among others. Return to text
3. Recent surveys of the realized volatility literature include Andersen, Bollserslev, and Diebold (2009), Bandi and Russell (2007), Barndorff-Nielsen and Shephard (2007), McAleer and Medeiros (2008). Return to text
4. Thorough empirical evidence pointing more broadly towards the value of realized volatility for modeling equity returns can be found in Andersen, Bollerslev, Diebold, and Ebens (2001). Return to text
5. Results in the same spirit have been obtained also in studies based solely on daily returns or in combination with options data such as Broadie, Chernov, and Johannes (2007). Other non-parametric studies based on high-frequency data include Andersen, Bollerslev, and Dobrev (2007), Bandi and Reno (2009). Return to text
6. Cf. Andersen, Benzoni, and Lund (2002) and Chernov, Gallant, Ghysels, and Tauchen (2003). Return to text
7. As such, our results add to the growing body of evidence showing the economic value of high-frequency realized volatility measures in finance applications, e.g. Fleming, Kirby, and Ostdiek (2003) among others. Return to text
8. The rate of convergence is typically square-root. It is slower for high-frequency volatility measures that are robust also to market microstructure noise, empirically found to matter at sample frequencies higher than a few minutes. Return to text
9. Our subsequent analysis remains valid to the extent that the utilized asymptotic results are unaffected by jumps of possibly infinite activity (but still finite variation). Return to text
10. For recent surveys of the realized volatility literature see, e.g., Andersen, Bollserslev, and Diebold (2009), Bandi and Russell (2007), Barndorff-Nielsen and Shephard (2007), McAleer and Medeiros (2008). Return to text
11. Other approaches that involve potentially delicate threshold or bandwidth choices include the truncated RV of Mancini (2006) and Aït-Sahalia and Jacod (2007), the truncated bipower variation of Corsi, Pirino, and Renò (2008), as well as the quantile RV estimator of Christensen, Oomen, and Podolskij (2008). Return to text
12. The scaling factor ![]() is defined as
is defined as
![]() ,
,
![]() . Return to text
. Return to text
13. The asymptotic variance factor for TV is 3.06 as opposed to 2.96 for MedRV. Also by design, MedRV is somewhat more robust than TV not only to jumps but also to the occurrence of "zero" returns in finite samples. Return to text
14. Without loss of generality, in our
empirical analysis we focus on the popular realized quad-power
quarticity estimator
QQ![]() of Barndorff-Nielsen and Shephard (2004) as well
as the slightly more efficient (and robust to both jumps and zero
returns) median realized quarticity estimator
MedRQM
of Barndorff-Nielsen and Shephard (2004) as well
as the slightly more efficient (and robust to both jumps and zero
returns) median realized quarticity estimator
MedRQM![]() med
med![]() , of Andersen, Dobrev, and Schaumburg (2009). Return to text
, of Andersen, Dobrev, and Schaumburg (2009). Return to text
15. Volatility measures obtained at higher frequencies can incur biases due to market imperfections such as bid-ask bounce effects, stale quotes, price discreteness, and intraday patterns. Return to text
16. The extra robustness comes at the cost of lower convergence rate that can be easily accommodated by our generic volatility measurement equation (9) by changing the power of M accordingly. Return to text
17. As usual, we restrict
![]() to satisfy standard stationarity
conditions for
to satisfy standard stationarity
conditions for ![]() . Return to text
. Return to text
18. As noted by Eraker, Johannes, and Polson (2003), the discretization bias for daily data is not significant. Return to text
19. This is a standard correction of realized volatility measures as given in more detail, for example, by Hansen and Lunde (2005). Return to text
20. One-factor models can be viewed as a
special case by restricting ![]() for all
for all
![]() , omitting the parameters
, omitting the parameters
![]() for the f factor and imposing the constraint
for the f factor and imposing the constraint
![]() in the instantaneous correlation
matrix. Return to text
in the instantaneous correlation
matrix. Return to text
21. In particular, in our analysis we focus on the MedRV estimator of Andersen, Dobrev, and Schaumburg (2009) and the tri-power variation measure of Barndorff-Nielsen, Shephard, and Winkel (2006). We report results only for the former as the results obtained for the latter are in the same spirit. Return to text
22. In the one-factor model the case of perfectly observed volatility can be viewed as the limiting case of our volatility measurement equation when the intraday sample frequency grows to infinity. In the two-factor model, though, the volatility measurement equation provides information only about the sum of the two volatility factors without separating them as in the infeasible case of full observability. Return to text
23. In this sense, our results extend those obtained by Alizadeh, Brandt, and Diebold (2002) in a considerably more restrictive range-based analysis of a model without leverage effects. Return to text
24. The data for S&P 500 is provided by Tick Data, while the data for Google is from NYSE TAQ. Return to text
25. Comprehensive surveys of the literature on SV models and estimation include Andersen, Bollserslev, and Diebold (2009), Ghysels, Harvey and Renault (1996), Shephard (1996), Taylor (1994), among others. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text