The Federal Reserve Board eagle logo links to home page

U.S. International Equity Investment and Past and Prospective Returns**

Stephanie E. Curcurua, Charles P. Thomasa, Francis E. Warnockb,c,d,e, and Jon Wongswanf

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

Counter to extant stylized facts, using newly available data on country allocations in U.S. investors' foreign equity portfolios we find that (i) U.S. investors do not exhibit returns-chasing behavior, but, consistent with partial portfolio rebalancing, tend to sell past winners; and (ii) U.S. investors increase portfolio weights on a country's equity market just prior to its strong performance, behavior inconsistent with an informational disadvantage. Over the past two decades, U.S. investors' foreign equity portfolios outperformed a value-weighted foreign benchmark by 160 basis points per year.

Keywords: Momentum, contrarian, portfolio performance measures, international returns

JEL classification: G11, G12, F21

A wave of research in the 1990s--the seminal works are Henning Bohn and Linda L. Tesar (1996) (henceforth BT) and Michael J. Brennan and H. Henry Cao (1997) (henceforth BC)--established three stylized facts that characterized the relationship between U.S. international investment and returns: U.S. investors chase returns, do not rebalance their international portfolios, and are at an informational disadvantage when they venture abroad. These stylized facts still inform the literature; for example, the theoretical models in Massimo Guidolin (2005), Rui Albuquerque, Gregory H. Bauer, and Martin Schneider (2007), and Bernard Dumas, Karen K. Lewis, and Emilio Osambela (2010) are designed to incorporate some of these relationships between U.S. investment and returns. The seminal BC and BT results continue to resonate with researchers because similar, updated bilateral flows data and similar empirical techniques produce similar results. Using flows data, U.S. investors still appear to chase returns and not rebalance their international portfolios. And, consistent with an informational disadvantage, flows into a country's equity market are still related to the contemporaneous returns in that market.

However, the theories in BT and BC concern portfolio adjustments, not bilateral flows. Portfolio holdings data were not available--such data did not exist in the 1990s--so both studies relied on data on international capital flows. But the link from changes in asset demands (i.e., portfolio adjustments) to bilateral flows is not straightforward. In particular, as discussed in BC, changes in wealth could confound such analysis. Consider a situation in which domestic investors experience an increase in wealth and allocate some of it to all markets (i.e., there are positive bilateral flows to each market), but in the process reduce the portfolio weights of some markets. If prior returns were high in a particular market, bilateral flows-based analysis would characterize that as returns-chasing behavior, regardless of whether the portfolio allocation to that country increased or decreased. BC tried to control for this by including a benchmark domestic returns series in empirical tests, but acknowledged that this was an imperfect fix.

Portfolio data and portfolio-based techniques, both better suited to address the relationship between international investment and returns, are now available. We revisit the analyses of BC and BT using monthly estimates of bilateral portfolio positions between the U.S. and over 40 foreign countries--data maintained by the Federal Reserve--and the portfolio-based techniques of Mark Grinblatt, Sheriden Titman, and Russ Wermers (1995), B. Espen Eckbo and David C. Smith (1998), and Wayne E. Ferson and Kenneth Khang (2002). Our results are almost completely counter to the extant stylized facts. We do not find evidence that U.S. investors chase returns; rather, they appear to engage in a type of partial rebalancing by selling past winners. We do not find that U.S. investors are necessarily at an informational disadvantage; rather, they shift into markets just prior to their strong abnormal returns. Taken together, our analysis suggests that foreign equities are a very attractive asset class for U.S. investors: On average, U.S. investors' foreign equity portfolio outperformed a value-weighted foreign benchmark by 160 basis points per year over the past two decades.

The paper proceeds as follows. In the next section we discuss the seminal works and present updated flows-based results that are consistent with their findings. In Section II we explore the relationship between U.S. portfolios and past returns before directly examining whether U.S. investors are at an informational disadvantage in foreign markets. Section III compares the performance of U.S. investors' foreign equity portfolios with value-weighted benchmarks. In Section IV we discuss some implications of our findings for theorists, empiricists, and policymakers. Section V concludes.


I.  The Existing Stylized Facts

The stylized facts that characterize the relationship between U.S. international investment and returns come from the seminal BC and BT papers, which were written at a time of limited data availability. Recognizing the limitations, BT tested a theory of portfolio reallocations using the then-available bilateral flows data. Specifically, the authors test for a portfolio rebalancing effect by examining the relationship between bilateral flows and contemporaneous foreign returns (in excess of the rest of the portfolio's returns). In this setup, a negative relationship between flows and contemporaneous returns would be consistent with portfolio rebalancing; when returns in a country were high, U.S. investors would sell that country's equities (i.e., bilateral flows to that country would be negative) to prevent an increased allocation to that country. However, BT found that for many countries the relationship is positive, indicative of a lack of rebalancing. BT also test a returns-chasing hypothesis by examining the relationship between bilateral flows and past (expected or actual) returns. For many countries the relationship was positive, indicative of returns-chasing. BC estimated similar regressions, although in their model a positive relationship between flows and contemporaneous returns would be evidence of an information disadvantage; U.S. investors with poor information about a country would purchase its equity market when its price increased. Similar to BT, BC found a positive relationship between bilateral flows and contemporaneous returns, indicative of poor information on the part of U.S. investors.

BT- and BC-like regression analysis performed today, either with data from the time periods they studied or with updated data, produces results similar to the seminal findings. We replicate the BT analysis using the original January 1981 to November 1994 time period and the original 22 foreign markets (Table 1 columns 1-3). Results from bilateral regressions of U.S. net purchases in foreign equity market i (scaled by the lagged size of the foreign portfolio) on expected excess returns in market i (returns in excess of a one-month eurodollar rate) are in column 1. As in BT, excess returns are forecasted using an information set consisting of lagged values of the following: world returns, U.S. excess dividend yield, U.S. term structure, and the foreign country's excess return and dividend yield. In the BT's reported baseline results, 7 (or 11, depending on the scale factor for flows) out of 22 coefficients on expected returns were positive and significant. In our replication exercise, 7 of 22 coefficients are positive and significant. In column (4) we re-estimate using updated data from January 1990 to December 2008; results are similar, with 8 of the 22 coefficients on expected returns positive and significant. For contemporaneous returns updated data produce even stronger results; the correlation between bilateral flows and contemporaneous returns ($ \rho$0) is positive and significant for 10 countries over the BT period and for 15 countries in the updated sample (columns 2 and 5). Finally, the correlation between flows and lagged returns ($ \rho$1) is positive and significant for 6 countries using the old sample, 13 in the updated samples (columns 3 and 6). The stylized facts continue to inform the literature in part because similar flows-based data and techniques would lead to similar conclusions today (see, for example, Albuquerque, Bauer, and Schneider 2009).


II.  A Reassessment of Returns Chasing and Informational Disadvantages in U.S. International Equity Portfolios

The theories in BT and BC are fundamentally about changes in asset demands. The mapping from changes in asset demands to bilateral flows is straightforward if wealth is constant. But financial wealth is not constant (Figure 1). A more direct test of the theories requires data on portfolio allocations. We describe such data next, and then employ portfolio-based techniques to re-examine the relationship between international investment and past and prospective returns.

A.  The Portfolio Data

A portfolio-based study of U.S. investors' trading style is made possible by the Carol C. Bertaut and Ralph W. Tryon (2007) estimates of the monthly bilateral positions of U.S. investors in the equities of a large set of foreign countries. The country-level dataset includes, for example, a monthly time series of U.S. holdings of German equities (as well the U.S. holdings of equities in many other foreign countries).

Bertaut and Tryon (2007) form the data by combining high-quality low frequency readings on positions, built from security-level benchmark surveys, with higher frequency (monthly) flow data. In the process of combining positions and flows data, the reported flow data is adjusted to alleviate the well-known financial center bias; in the reported flow data, because of the U.S. government's data collection methodology far too many flows are attributed to financial centers like the United Kingdom (see, among others Warnock and Chad Cleaver 2003). Specifically, Bertaut and Tryon (2007) form monthly bilateral positions by starting with an initial position as given by a benchmark survey, forming naïve monthly positions until the next benchmark survey by using flow data and valuation adjustments (from, for foreign equity markets, MSCI indexes), and then adjusting the estimates to eliminate the financial center bias and other wedges between flows-based estimates and survey-based readings.1

The resulting dataset is entirely consistent with officially reported data on U.S. holdings of foreign equities published in U.S. Treasury's annual benchmark surveys and in BEA's U.S. international investment position presentation, as well as with data in both the Philip R. Lane and Gian Maria Milesi-Ferretti (2007) dataset and the IMF's Coordinated Portfolio Investment Survey (CPIS). In fact, an earlier version of the Bertaut Tryon dataset formed the basis for the official U.S. entries in the CPIS for 2002, a year in which the United States did not conduct a benchmark asset survey.2 Aggregate Bertaut and Tryon (2007) data--that is, aggregate foreign positions in U.S. securities and aggregate (not bilateral) U.S. positions in foreign securities--have been used in Curcuru, Tomas Dvorak, and Warnock (2008, 2010) and Curcuru, Thomas, and Warnock (2009) to show that (i) previous estimates of the differential between returns on U.S. investors' foreign portfolios and returns on foreigners' U.S. positions were biased upward and (ii) foreigners' U.S. portfolio returns were reduced by ill-timed switching between U.S. bonds and U.S. equities, whereas U.S. investors' foreign returns were not degraded by switching between asset classes.

The bilateral holdings data provide the country weights in U.S. investors' portfolios. Armed with these weights, and assuming that within each country the market (as represented by MSCI firms) is held, the (unhedged) dollar returns earned by U.S. investors on their foreign equity portfolios can be computed.

B.  The Relationship Between Portfolio Reallocations and Past Returns

Portfolio weights and returns enable an examination of the relationship between portfolio reallocations and past returns using well-established portfolio-based techniques. To test for momentum and portfolio rebalancing, we use the Grinblatt, Titman, and Wermers (1995) momentum statistics to measure the degree to which U.S. investors actively change their portfolio holdings in the direction of previous country-level stock returns. The statistics are computed as follows. Specifically, define Xi,t as the active change in the weight of country i in U.S. investors' foreign portfolio at time t:

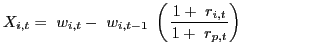$\displaystyle X_{i,t}=\ w_{i,t}-\ w_{i,t-1\ }\left( \left. \frac {1+\ r_{i,t}}{1+\ r_{p,t}}\right) \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ (1)

where ri,,t is the return on country i equities from period t-1 to t; rp,t is the return on U.S. investors' foreign portfolio, defined as $ r_{p,t}=\ \ \sum^{Nt}_{i=1} {w_{i,t-1}r_{i,t}}\ $ ; and wi,t is the weight of country i at time t in U.S. investors' portfolio. If investors follow a buy-and-hold strategy, Xi,t would equal zero. There are three momentum measures:

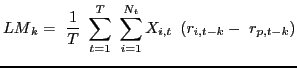$\displaystyle {LM}_{k}=\ \frac{1}{T}\ \sum^{T}_{t=1}{\ \sum^{N_{t}} _{i=1}{X_{i,t}}}\ \left( r_{i,t-k}-\ r_{p,t-k}\right)$ (2)
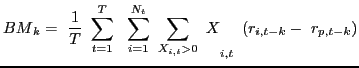$\displaystyle {BM}_{k}=\ \frac{1}{T}\ \sum^{T}_{t=1}{\ \ \sum^{N_{t} }_{i=1}{{\ \sum_{X_{i,t}>0}{\ }X}_{i,t}}}\ \left( r_{i,t-k}-\ r_{p,t-k} \right)$ (3)
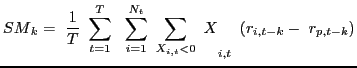$\displaystyle {SM}_{k}=\ \frac{1}{T}\ \sum^{T}_{t=1}{\ \ \sum^{N_{t} }_{i=1}{{\ \sum_{X_{i,t}<0}{\ }X}_{i,t}}}\ \left( r_{i,t-k}-\ r_{p,t-k} \right)$ (4)

where Nt is the number of countries held in the portfolio at time t and k is the number of periods the returns are lagged. A significant, positive LM measure indicates a momentum trading strategy: U.S. investors on average increased the weights on countries whose equities performed well (relative to the other markets) k periods ago. A significantly negative value of LM would be evidence of contrarian trading, which is consistent with a portfolio balancing effect. The two additional momentum statistics isolate trading when investors increase country weights (the BM measure) from when they decrease country weights (the SM measure).

The results are in Table 2. The LM measure is sometimes positive, sometimes negative, but never statistically significant, indicating that when U.S. investors venture abroad, their trading strategy can be characterized as neither momentum following nor contrarian. The BM and SM lines show results when we split the sample into instances in which U.S. investors increased the portfolio weight on country i (BM Buy Only) and instances when they decreased the weight on country i (SM Sell Only). There is again very little evidence of momentum trading; the coefficients on the BM statistic are usually (but not always) positive, indicating that U.S. investors moved into markets that recently performed well, but the statistic is significant in only two of nine cases. In contrast, there is strong evidence that U.S. investors can be characterized as contrarian when selling; the SM (Sell Only) coefficient is negative for all samples and lags, significantly so in eight of nine cases. In their international equity portfolios U.S. investors sell past winners--consistent with a partial portfolio rebalancing effect--and this behavior is apparent in both developed and emerging markets.3,4

C.  The Relationship between Portfolio Reallocations and Future Returns

The conditional weight-based measure (CWM)--a portfolio-based measure developed by Grinblatt and Titman (1993), Eckbo and Smith (1998), and Ferson and Khang (2002) that is based on an estimate of the sum of the covariances between changes in portfolio weights and future abnormal returns--is a direct measure of the relationship between portfolio reallocations and prospective returns. The CWM is used in the literature as a gauge of private information or an informational advantage. Under time-varying expected returns, a risk-averse investor with non-increasing absolute risk aversion would move into (out of) a market when private information indicates a positive (negative) abnormal return relative to that predicted using public information, and in this case the estimate of the sum of the conditional covariances between changes in portfolio weight and future abnormal returns would be positive.

CWM is set up as follows. Define the estimate of the sum of the conditional covariances as

$\displaystyle \sum^{N_{t}}_{i=1}{Co\nu(w_{i,t}},\ r_{i,\ t+1}\left\vert {\Omega}_{\mathrm{t}}\right) \mathrm{=\ }\sum^{N_{t}}_{i=1}{E}\left[ {(w}_{i,t}-\ w^{b}_{i,t}\right) \left( r_{i,t+1}-\ E\left( r_{i,t+1} \mathrel{\left\vert\vphantom{r_{i,t+1} {\Omega }_{{\rm t}}}\right.\kern-\nulldelimiterspace}{\Omega }_{\mathrm{t} }\right) \right) \left\vert {\Omega}_{\mathrm{t}}\right] \mathrm{\ }$ (5)

where $ w^{b}_{i,t}$ is the benchmark weight of country i at time t. Let the benchmark be a buy-and-hold weight of lag k defined as

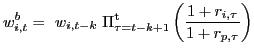$\displaystyle w^{b}_{i,t}=\ w_{i,t-k\ }{\Pi}^{\mathrm{t}}_{\tau =t-k+1}\left( \frac{1+r_{i,\tau}}{1+r_{p,\tau}}\right)$ (6)

Estimate the conditional portfolio weight-based measure via GMM:

$\displaystyle e_{i,t+1}=\ r_{i,t+1}-\ {{\mathbf{b}}}^{{\mathbf{\ }/} }_{{\mathbf{i}}}{{\mathbf{Z}}}_{{\mathbf{t}}}{\mathbf{\ }}$ (7)
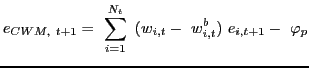$\displaystyle e_{CWM,\ t+1}=\ \sum^{N_{t}}_{i=1}{\ (w_{i,t}} -\ w^{b}_{i,t})\ e_{i,t+1}-\ {\varphi}_{p}$ (8)

Equation (7) is an N vector of errors from estimating a linear function of future excess returns on information variables when N is the maximum value of Nt for the full sample. Zt, a subset of $ {{\mathbf{\Omega}}}_{{\mathbf{t}}}$, arepublic information variables. We use three variables to proxy for public information: lagged changes in the short-term interest rate (U.S. Treasury three-month yield); lagged changes in term structure spread (U.S. Treasury 10-year yield minus U.S. Treasury 3-month yield); and lagged world excess returns.5 Each error in equation (7) can be interpreted as an abnormal return. Equation (8) is the error from estimating an average of the conditional covariances between changes in portfolio weights and future abnormal returns. $ \varphi$p is the average conditional weight measure across the full sample. We set up the following system of moment conditions

$\displaystyle g_{t}=\ \left[ \genfrac{}{}{0pt}{}{ \begin{array}[c]{c} {{\mathbf{e}}}_{{\mathbf{i}}{\mathbf{\ }}}\cdot{\mathbf{Z}}\\ {\mathbf{\ }} \end{array} }{{{\mathbf{e}}}_{{\mathbf{C}WM}}\cdot{\mathbf{Z}}} \right] \ \ $ (9)

The vector of sample moment conditions g is a NL+L vector, where L is the number of information variables, and the parameters are N vectors of L by 1 (bi) and the scalar $ \varphi$p . Because the starting date in our dataset varies by country, we follow Ravi Bansal and Magnus Dahlquist (2000) and define an indicator variable Ii,t that denotes data availability for a country i at time t. As long as Ii,t is independent of the error terms from equations (7) and (8)--for example, missing data are not all in periods with abnormally high excess returns--the indicator variable can be used to in effect fill in missing values with zeros. The augmented set of moments conditions is

$\displaystyle g_{t}=\ \left[ \genfrac{}{}{0pt}{}{ \begin{array}[c]{c} {{\mathbf{e}}}_{{\mathbf{i}}{\mathbf{\ }}}\cdot{\mathbf{Z}}\cdot I_{i,t}\\ {\mathbf{\ }} \end{array} }{{{\mathbf{e}}}_{{\mathbf{C}WM}}\cdot{\mathbf{Z}}} \right] \ $ (10)

Table 3 shows estimates of the average conditional portfolio weight measure, $ \varphi$p, estimated from the system of equations (7) and (8) against one-, two-, and three-month benchmark buy-and-hold strategies (k=1, 2, 3, respectively). In the All Foreign Countries sample and for Advanced Economies, the CWM statistic is positive and significant for all lags. U.S. investors realize positive excess returns over a strategy that prohibits trading within their foreign portfolios for one, two or three months; that is, they reallocate into markets just prior to positive abnormal returns. For emerging markets, the evidence is less compelling; CWM statistic is positive and large in magnitude, but is statistically significant only for k=2.

The positive and significant estimate of the sum of the conditional covariances between changes in portfolio weights (for the full sample and Advanced Economies) and future abnormal returns can be interpreted as evidence of trading expertise from private information. Overall, the main conclusion from the CWM analysis is that U.S. investors switch into markets prior to abnormally strong returns, although the evidence from their emerging market portfolios is somewhat weaker.

D.  What Drives the Results: Data or Techniques?

Relative to the seminal papers, our analysis differs along two dimensions. First, our data differ not only because they are portfolio reallocations (consistent with theory) but also because they correct a severe financial center bias in the as-reported bilateral flows data (Warnock and Cleaver 2003). Second, the portfolio data enable the use of alternative portfolio-based techniques; the main difference there is that each country is examined in conjunction with the rest of the portfolio, not in isolation as in bilateral flows-based analysis.

To determine what is driving our results, we rerun our analysis retaining the original country-by-country techniques but using two alternative sets of data. First, we use "restated" bilateral flows. Restated flows are not as-reported, but rather are consistent with the Bertaut and Tryon (2007) dataset in that the financial center bias has been eliminated. Original empirical techniques using restated bilateral flows (as opposed to TIC-reported bilateral flows) produce results very similar to, if not stronger than, the results in the seminal papers (Table 4, columns 1-3). Correcting for financial center biases does not yield results that differ from the old stylized facts. Next, we conduct the same bilateral analysis but using portfolio reallocations (our X variable from equation 1). Doing so results in many fewer positive and significant estimates (columns 4-6).

Relative to the seminal results, our results appear to be driven by the use of portfolio reallocations instead of flows. This, in turn, suggests that the main problem with flows data is that they do not account for changes in the size of (and reallocations within) U.S. portfolios. Indeed, the correlation between flows and portfolio reallocations is quite low. If the mapping from portfolio reallocations to flows were perfect, the correlation would be one. But across the 43 markets in our study, the correlation averages 0.28 and is less than 0.5 for all but five countries. There is a link from portfolio reallocations to flows, but it is not straightforward in theory and is not tight in the data.


III.  Unconditional Portfolio Performance

Results from the 1990s suggested that U.S. investors' foreign portfolios earned less than the value-weighted benchmark; see, for example, evidence in BT. In contrast, updated data indicates that in almost every year since 1990 U.S. investors' foreign portfolio beat a value-weighted benchmark, constructed using MSCI market capitalization weights for the 43 countries in our sample (Figure 2). The higher mean returns did not come at the expense of higher volatility. Compared to the value-weighted foreign portfolio, U.S. investors' foreign equity portfolio earned higher returns (0.21 percent monthly excess returns vs. 0.08 for the value-weighted portfolio) with less volatility (4.7 vs. 4.9) for a significantly higher Sharpe ratio (Table 5). Relative performance within the set of developed countries is similar, with U.S. investors' portfolios earning higher returns with less volatility, producing a significantly greater Sharpe ratio (4.1 vs. 1.3). In emerging markets, U.S. investors earned higher returns (0.82 percent per month vs. 0.71 percent) but with slightly higher volatility (7.5 vs. 7.2). The unconditional performance of U.S. investors' international equity portfolios has been quite good.


IV.  Implications

An obvious implication of our results is that theoretical models of international portfolio choice should not be explicitly designed to produce returns-chasing behavior, as some have in the past (Guidolin, 2005; Albuquerque, Bauer, and Schneider 2007). Returns-chasing can arise naturally from a rich model, such as in Victoria Hnatkovska (2010), but theorists should hesitate before treating returns-chasing as a stylized fact a model should be designed to produce.6

Somewhat more subtle but perhaps equally important is that theoretical international macro models that incorporate international portfolio choice, which have recently become more prevalent (e.g., Cedric Tille and Eric van Wincoop 2008, 2010; Michael B. Devereux and Alan Sutherland 2010, forthcoming; Hnatkovska 2010), must take seriously the fact that fluctuations in financial wealth are important. Tille and van Wincoop (2010) stress the role of portfolio growth, but, following Aart Kraay and Jaume Ventura (2000, 2003), portfolio growth in their model is essentially net national savings (net capital flows). Just as the empirical capital flows literature has begun to focus on gross instead of net flows (Fernando A. Broner et al 2010; Kristin J. Forbes and Warnock 2010), theorists must recognize that substantial variations in financial wealth can confound some of the facts around which models are being built.

Our analysis also suggests that empiricists should refrain from attaching labels like herding behavior and returns-chasing when the basis for the analysis is flows data. For example, Ken Miyajima and Huanhuan Zheng (2010), part of the IMF's October 2010 Global Financial Stability Report, examines the relationship between (proprietary) bilateral flows and returns, and reports that investors chase returns and exhibit herding. We find the exact opposite results using portfolio data. In our view, if the concept concerns portfolio adjustments, portfolio rather than flows data should be employed.7

Many empirical studies have found that foreigners perform poorly when investing in countries ranging from Indonesia (Dvorak, 2005) and Korea (Hyuk Choe, Bong-Chan Kho, and Stulz, 2005) to Germany (Harald Hau, 2001), so our finding that U.S. investors reallocate into markets just prior to strong returns might appear puzzling. However, recall that our analysis concerns country picking, not within-country timing and execution. Moreover, our results are not inconsistent with empirical work on the predictability of equity prices, especially for one market relative to another. Ferson and Harvey (1993) find some predictability of international equity returns, Kenneth Kasa (1992) finds mean reversion (and, hence, some predictability) in two-country equity portfolios, and Anthony J. Richards (1995) and Ronald Balvers, Yangru Wu, and Erik Gilliland (2000) find that country-specific returns relative to a world index exhibit mean reversion, suggesting that the contrarian strategy of Werner F. M. DeBondt and Richard H. Thaler (1985) and Richards (1997) might be profitable. Thus, both partial rebalancing--the selling of equity markets that performed well in the recent past--and switching into markets that subsequently have high abnormal returns are consistent with the literature on the predictability of international equity market returns. While it may well be difficult for a foreigner to time a market, some skill at timing reallocations between markets is plausible and consistent with both theory and our results.


V.  Conclusion

Many of the stylized facts regarding U.S. investment abroad came out of an era when appropriate data were not available. Many of the seminal results relied on bilateral capital flows data, when the theories called for data on portfolio reallocations. Theory had progressed enough so that researchers knew what relationships should be examined, but appropriate data did not exist. A limitation of flows-based analysis is that it can be confounded by wealth effects. Portfolio-based techniques are consistent with theories of international portfolio choice and are not subject to this limitation.

Using portfolio-based data and techniques, we find evidence that contradicts long-standing stylized facts. U.S. investors do not chase past returns, nor do they refrain from rebalancing their international portfolios. Rather, they sell past winners, a form of partial rebalancing. U.S. investors do not appear to be at an informational disadvantage when they venture abroad. Rather, consistent with having superior information, there is a positive relationship between portfolio reallocations and future returns; U.S. investors increase portfolio weights on a country's equity market just prior to its strong performance. Our results indicate that U.S. investors beat the value-weighted foreign benchmark by an average of 162 basis points per year from 1990-2008.

Our analysis suggests researchers and policymakers should be cautious when using flow data to examine portfolio behavior. Best is to use portfolio data. In cases in which flows data must be used, controlling for changes in wealth is vital.


References

Albuquerque, Rui, Gregory H. Bauer, and Martin Schneider. 2007. "International Equity Flows and Returns: A Quantitative Equilibrium Approach." Review of Economic Studies, 74(1): 1-30.

Albuquerque, Rui, Gregory H. Bauer, and Martin Schneider. 2009. "Global Private Information in International Equity Markets."Journal of Financial Economics, 94(1): 18-46.

Ammer, John, Sara B. Holland, David C. Smith, and Francis E. Warnock. 2006. "Look at Me Now: What Attracts U.S. Shareholders." NBER Working Paper 12500.

Ang, Andrew, and Geert Bekaert. 2007. "Stock Return Predictability: Is It There?" Review of Financial Studies, 20: 651-707.

Balvers, Ronald, Yangru Wu, and Erik Gilliland. 2000. "Mean Reversion across National Stock Markets and Parametric Contrarian Investment Strategies." Journal of Finance, 55(2): 745-772.

Bansal Ravi, and Magnus Dahlquist. 2000. The Forward Premium Puzzle: Different Tales from Developed and Emerging Economies." Journal of International Economics,51: 115-144.

Bekaert, Geert, and Campbell R. Harvey. 1997. "Emerging Equity Market Volatility." Journal of Financial Economics, 43: 29-77.

Bekaert, Geert, Campbell R. Harvey and Christian Lundblad. 2007. "Liquidity and Expected Returns: Lessons from Emerging Markets." Review of Financial Studies, 20: 1783-1831.

Bertaut, Carol C., and Ralph W. Tryon. 2007. "Monthly Estimates of U.S. Cross-Border Securities Positions." FRB International Finance Discussion Paper No. 910.

Bohn, Henning, and Linda L. Tesar. 1996. "U.S. Equity Investment in Foreign Markets: Portfolio Rebalancing or Returns Chasing?" American Economic Review, 86(2): 77-81.

Brennan, Michael J., and H. Henry Cao. 1997. "International Portfolio Investment Flows." Journal of Finance, 52: 1851-1880.

Broner, Fernando A., Tatiana Didier, Aitor Erce, and Sergio L. Schmukler. 2010. `Gross Capital Flows: Dynamics and Crises." http://www.crei.cat/people/broner/BDES.pdf.

Campbell, John Y., and Motohiro Yogo. 2006. "Efficient Tests of Stock Return Predictability." Journal of Financial Economics, 81: 27-60.

Choe, Hyuk, Bong-Chan Kho, and Rene M. Stulz. 2005. "Do Domestic Investors Have an Edge? The Trading Experience of Foreign Investors in Korea." Review of Financial Studies, 18(3): 795-829.

Curcuru, Stephanie E., Tomas Dvorak, and Francis E. Warnock. 2008. "Cross-Border Returns Differentials." Quarterly Journal of Economics, 123(4): 1495-1530.

Curcuru, Stephanie E., Tomas Dvorak, and Francis E. Warnock. 2010. "The Decomposition of the U.S. External Returns Differential."Journal of International Economics, 80: 22-32.

Curcuru, Stephanie E., Charles P. Thomas, and Francis E. Warnock. 2009. "Current Account Sustainability and Relative Reliability." In NBER International Seminar on Macroeconomics 2008, ed. J. Frankel and C. Pissarides, 67-109. Chicago: University of Chicago Press.

Curcuru, Stephanie E., Charles P. Thomas, Francis E. Warnock, and Jon Wongswan. 2010. "What Influences U.S. International Equity Investment: Equity or Currency Returns?" http://faculty.darden.virginia.edu/warnockf/papers/CTWW2__EquityCurrency.pdf.

DeBondt , Werner F. M., and Richard H. Thaler. 1985. "Does the Stock Market Overreact?" Journal of Finance, 40: 793-805.

Devereux, Michael B., and Alan Sutherland. 2010. "Valuation Effects and the Dynamics of Net External Assets." Journal of International Economics, 80: 129-143.

Devereux, Michael B., and Alan Sutherland. Forthcoming. "Country Portfolios in Open Economy Macro Models." Journal of the European Economic Association.

Dumas, Bernard, Karen K. Lewis, and Emilio Osambela. 2010. "Differences of Opinion and International Equity Markets." SSRN Working Paper 1570168.

Dvorak, Tomas. 2005. "Do Domestic Investors Have an Information Advantage? Evidence from Indonesia." Journal of Finance, 60: 817-839.

Eckbo, B. Espen, and David C. Smith. 1998. "The Conditional Performance of Insider Trades." Journal of Finance, 53(2): 467-498.

Ferson, Wayne E., and Campbell R. Harvey. 1993. "The Risk and Predictability of International Equity Returns." Review of Financial Studies, 6: 527-566.

Ferson, Wayne E., and Kenneth Khang. 2002. "Conditional Performance Measurement Using Portfolio Weights: Evidence for Pension Funds." Journal of Financial Economics, 65: 249-282.

Ferson, Wayne E., Sergei Sarkissian, and Timothy T. Simin. 2003. "Spurious Regressions in Financial Economics?" Journal of Finance, 58: 1393-1413.

Forbes, Kristin J., and Francis E. Warnock. 2010. "Capital Flow Waves: Surges, Stops, Flight and Retrenchment." http://www.nber.org/confer/2010/GFCs10/Forbes_Warnock.pdf.

Griever, William L., Gary A. Lee, and Francis E. Warnock. 2001. "The U.S. System for Measuring Cross-Border Investment in Securities: A Primer with Discussion of Recent Developments." Federal Reserve Bulletin, 87: 633-650.

Grinblatt, Mark, and Sheriden Titman. 1993. "Performance Measurement without Benchmarks: An Examination of Mutual Fund Returns." Journal of Business, 60: 97-112.

Grinblatt, Mark, Sheriden Titman, and Russ Wermers. 1995. "Momentum Investment Strategies, Portfolio Performance, and Herding: A Study of Mutual Fund Behavior." American Economic Review, 85(5): 1088-1105.

Guidolin, Massimo. 2005. "Home Bias and High Turnover in an Overlapping-generations Model with Learning." Review of International Economics, 13(4): 725-56.

Harvey, Campbell R. 1991. "The World Price of Covariance Risk." Journal of Finance, 46: 111-157.

Hau, Harald. 2001. "Location Matters: An Examination of Trading Profits." Journal of Finance, 56(5): 1951-1983.

Hnatkovska, Viktoria. 2010. "Home Bias and High Turnover: Dynamic Portfolio Choice with Incomplete Markets." Journal of International Economics, 80: 113-128.

Kaminsky, Graciela, Richard K. Lyons, and Sergio L. Schmukler. 2004. "Managers, Investors, and Crises: Investment Strategies of Mutual Funds." Journal of International Economics, 64(1): 113-134.

Kasa, Kenneth. 1992. "Common Stochastic Trends in International Stock Markets." Journal of Monetary Economics, 29: 95-124.

Kraay, Aart, and Ventura, Jaume. 2000. "Current Accounts in Debtor and Creditor Countries." Quarterly Journal of Economics, 95: 1137-1166.

Kraay, Aart, and Ventura, Jaume. 2003. "Current Accounts in the Long and Short Run." NBER Macroeconomics Annual 2002, 17: 65-112.

Lane, Philip R., and Gian Maria Milesi-Ferretti. 2007. "The External Wealth of Nations Mark II: Revised and Extended Estimates of Foreign Assets and Liabilities, 1970-2004." Journal of International Economics, 73: 223-250.

Miyajima, Ken, and Huanhuan Zheng. 2010. "Analyzing Portfolio Inflows to Emerging and Selected Advanced Markets." In Global Financial Stability Report IMF (Annex 1.3), October.

Newey, Whitney K., and Kenneth D. West. 1987. "A Simple, Positive Semi-definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix." Econometrica,55:703-708.

Richards, Anthony J. 1995. "Comovements in National Stock Market Returns: Evidence of Predictability, but not Cointegration." Journal of Monetary Economics, 36: 631-654.

Richards, Anthony J. 1997. "Winner-loser Reversals in National Stock Market Indices: Can They Be Explained?" Journal of Finance, 52(5): 2129-2144.

Tille, Cedric, and Eric van Wincoop. 2008. "International Capital Flows under Dispersed Information: Theory and Evidence." NBER Working Paper 14390.

Tille, Cedric, and Eric van Wincoop. 2010. "International Capital Flows." Journal of International Economics, 80: 157-175.

Warnock, Francis E., and Chad Cleaver. 2003. "Financial Centers and the Geography of Capital Flows." International Finance, 6(1): 27-59.

Table 1: The Relationship between Reported TIC Flows and Returns

 1981-1994: b1 (1)1981-1994: $ \rho$0 (2)1981-1994: $ \rho$1 (3)1990-2008: b1 (4)1990-2008: $ \rho$0 (5)1990-2008: $ \rho$1 (6)
Australia0.20-0.020.040.280.17**0.23**
Austria-0.02-0.09-0.040.000.020.13*
Belgium0.04-0.05-0.100.01-0.130.00
Canada3.33**0.17**0.18**0.83**0.30**0.22**
Denmark-0.02-0.130.040.090.000.04
Finland0.27**0.26**0.130.060.27**0.09
France0.330.11-0.080.530.040.12*
Germany1.250.13*0.15*0.040.16**0.10
Hong Kong0.710.20**0.010.180.18**0.02
Ireland-0.060.090.140.14**-0.100.07
Italy0.420.15*0.06-0.160.12*0.00
Japan17.52**0.20**0.072.77**0.40**0.34**
Netherlands0.730.13*0.030.97**0.02-0.05
Norway0.160.00-0.090.010.13*0.11*
Singapore0.34**0.100.050.030.12*0.19**
Spain0.800.13*0.07-0.040.21**0.07
Sweden1.03**0.080.060.94**0.26**0.27**
Switzerland0.47-0.010.16**0.410.090.14**
UK7.36**-0.02-0.105.13**0.12*0.14**
Mexico2.340.24**0.19**1.05**0.23**0.16**
Malaysia0.22**0.30**0.26**0.12**0.21**0.21**
South Africa-0.01-0.260.37**0.040.18**0.13**

For expected returns, b1 coefficients are from bilateral regressions of the form $ {{NP}_{i,t}}/{W_{t-1}}=\ b_{0}+b_{1}E_{t-1}\left[ R_{i,t}\right] +{\varepsilon}_{\mathrm{t}}\ $ , where NPi,t is reported U.S. net purchases of country i equities, Wt-1 is the lagged foreign portfolio, and $ E_{t-1}\left[ R_{i,t}\right] $ is the expected returns (in excess of a one-month T-bill rate) in market i forecasted using lagged information variables (world return, U.S. excess dividend yield, U.S. term structure, and country i's excess return and dividend yield). Correlations between net purchases and contemporaneous and lagged returns denoted by $ \rho$0 and $ \rho$1, respectively. Monthly data over 1981-1994 and 1990-2008. ** and * denote statistical significance at the 5 and 10 percent levels, respectively.

Table 2: The Relationship between Reallocations and Past Returns - Foreign Equity Holdings (January 1990 through December 2008)

 Lag 1Lag 2Lag 3
All Foreign Countries: LM (Buy and Sell)0.005, (0.144)-0.169, (0.152)-0.179, (0.146)
All Foreign Countries: BM (Buy Only)0.159, (0.123)0.064, (0.114)0.036, (0.103)
All Foreign Countries: SM (Sell Only)-0.154**, (0.056)-0.232**, (0.065)-0.215**, (0.065)
Advanced Economies: LM (Buy and Sell)-0.072, (0.140)-0.226, (0.145)-0.237, (0.152)
Advanced Economies: BM (Buy Only)0.044, (0.123)-0.056, (0.103)-0.099, (0.109)
Advanced Economies: SM (Sell Only)-0.116**, (0.058)-0.170**, (0.064)-0.138**, (0.067)
Emerging Markets: LM (Buy and Sell)0.589, (0.381)-0.198, (0.428)0.104, (0.373)
Emerging Markets: BM (Buy Only)0.685**, (0.258)0.258, (0.317)0.528**, (0.263)
Emerging Markets: SM (Sell Only)-0.096, (0.183)-0.456**, (0.189)-0.425**, (0.174)

The LM, BM, and SM statistic are defined in the text. Lag 1, Lag 2, and Lag 3 correspond to the measure of momentum based on returns lagged 1, 2, and 3 months, respectively. In this and all tables "Advanced Economies" are the 24 countries in our sample designated as such by the IMF as of 2000: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Greece, Hong Kong, Ireland, Israel, Italy, Japan, Korea, Netherlands, Norway, Portugal, Singapore, Spain, Sweden, Switzerland, Taiwan, and United Kingdom. The other 19 countries in our sample are "Emerging Markets": Argentina, Brazil, Chile, China, Columbia, Czech Republic, Hungary, Indonesia, India, Mexico, Malaysia, Peru, Philippines, Pakistan, Poland, Russia, Thailand, Turkey, and South Africa. Newey and West (1987) standard errors are in parentheses. ** and * denote statistical significance at the 5 and 10 percent levels, respectively.

Table 3: The Relationship Between Reallocations and Future Returns - Foreign Equity Holdings (January 1990 Through December 2008)

 k=1k=2k=3
All Foreign Countries0.369**, (0.147)0.649**, (0.211)0.735**, (0.274)
Advanced Economies0.268*, (0.141)0.519**, (0.201)0.591**, (0.276)
Emerging Markets0.457, (0.382)1.122**, (0.575)1.148, (0.747)

GMM estimates of $ \varphi$p for the following system:
$\displaystyle e_{i,t+1}=\ r_{i,t+1}-\ {{\mathbf{b}}}^{{\mathbf{\ }/}}_{{\mathbf{i}} }{{\mathbf{Z}}}_{{\mathbf{t}}} $
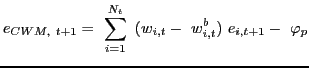
$\displaystyle e_{CWM,\ t+1}=\ \sum^{N_{t}}_{i=1}{\ (w_{i,t}}-\ w^{b}_{i,t})\ e_{i,t+1} -\ {\varphi}_{p} $

where ri,t+1 is the vector of portfolio excess returns in month t+1 , bi is the matrix of coefficients from regressing ri,t+1 on the instruments, Zt (including a constant), and the parameter $ \varphi$p is the average conditional covariance.Newey and West (1987) standard errors are in parentheses.
** and * denote statistical significance at the 5 and 10 percent levels, respectively.

Table 4: Restated Flows, Reallocations, and Returns

 Restated Flows: b1 (1)Restated Flows: $ \rho$0 (2)Restated Flows: $ \rho$1 (3)Portfolio Reallocations: b1 (4)Portfolio Reallocations: $ \rho$0(5)Portfolio Reallocations: $ \rho$1 (6)
Australia0.44*0.21**0.27**-0.120.21-0.89
Austria0.020.15**0.19**0.010.02-0.02
Belgium-0.20-0.38-0.10-0.32-0.720.34**
Canada1.11**0.30**0.22**1.01*0.230.27
Denmark0.00-0.040.00-0.110.11-0.15
Finland0.17**0.29**0.18**0.110.09-0.16
France1.34-0.040.00-2.37-5.070.21
Germany0.900.18**0.15**5.01**10.51**-0.11
Hong Kong0.170.14**-0.030.130.10-0.15
Ireland-0.04-0.23-0.12-0.18-0.18-0.06
Italy-0.270.13**0.06-0.48-0.01-0.30
Japan1.360.38**0.33**0.161.09-0.64
Netherlands1.54**-0.01-0.05-0.272.23**-0.76
Norway0.08*0.18**0.16**0.050.000.02
Singapore0.030.110.16**0.030.030.00
Spain-0.070.13*-0.01-0.35-0.150.12
Sweden0.53*0.11*0.13*0.200.340.03
Switzerland0.300.000.01-1.84-1.570.66
UK3.05-0.010.01-2.09-0.60-0.14
Mexico1.13**0.22**0.14**0.84**1.40**-0.12
Malaysia0.10**0.21**0.19**0.11**0.030.02
South Africa0.12**0.19**0.15**-0.03-0.050.00

The relationship between restated TIC flows (restated U.S. net purchases of country i equities as a share of the lagged foreign portfolio) or, alternatively, active portfolio reallocations (our Xi,t variable) and expected, contemporaneous, and lagged returns. Definitions for b1 , $ \rho$0, and $ \rho$1 are in Table 1. Data are monthly from January 1990 to December 2008. ** and * denote statistical significance at the 5 and 10 percent levels, respectively.

Table 5: Unconditional Performance of U.S. Investors' Foreign Portfolios

 Value-Weighted BenchmarkU.S. Investors' Foreign Portfolio
Foreign Countries: Mean0.0790.214
Foreign Countries: Std Dev4.9394.731
Foreign Countries: Sharpe Ratio (%)1.5924.521
Foreign Countries: Chi-squared: Sharpe Ratio 3.470*, [0.063]
Developed Markets: Mean0.0620.187
Developed Markets: Std Dev4.8814.602
Developed Markets: Sharpe Ratio (%)1.2554.069
Developed Markets: Chi-squared: Sharpe Ratio
 3.439*, [0.064]
Emerging Markets: Mean0.7140.820
Emerging Markets: Std Dev7.1857.536
Emerging Markets: Sharpe Ratio (%)9.93110.878
Emerging Markets: Chi-squared: Sharpe Ratio 0.296, [0.586]

Means, standard deviations, and Sharpe ratios (mean divided by standard deviation) for portfolios of foreign equities. Returns are in excess of a one-month Eurodollar interest rate and are expressed in monthly percentage points. Value-weighted benchmarks are portfolios based on MSCI market capitalization weights. U.S. investors' portfolios are based on U.S. investors' holdings. The Chi-squared: Sharpe Ratio is a test statistic for the null hypothesis that Sharpe ratios in the two columns are equal. Sample period is January 1990 through December 2008. Asymptotic p-values computed from Newey and West (1987) standard errors are in brackets. * Statistically significant at the 10 percent level.

Figure 1: U.S. Financial Wealth

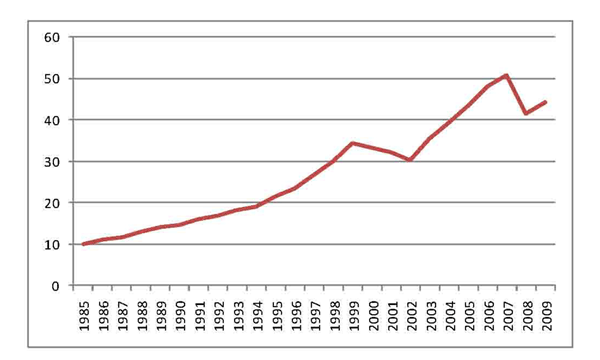
Data for Figure 1 immediately follows

Total financial assets of households and nonprofit organizations (line L.100 from the Federal Reserve's Flow of Funds dataset) in trillions of U.S. dollars from 1985 to 2009.

Data for Figure 1

YearTrillions of U.S. Dollars
19859951.8
198611069.8
198711726.1
198812859.1
198914184.4
199014549.5
199116106
199216950.2
199318226.4
199418902.1
199521502.6
199623398.4
199726707.9
199830041.4
199934479.5
200033350.6
200132210.1
200230236.3
200335336.1
200439217.5
200543306.2
200648089
200750662.8
200841431.4
200944260.2

Figure 2: Comparison of Portfolio Returns

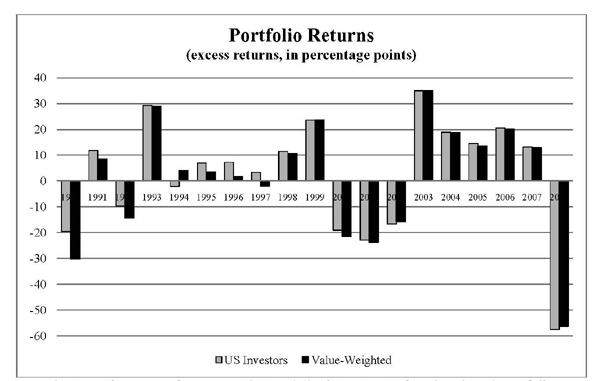
Data for Figure 2 immediately follows

Annual returns (in excess of a one-month Eurodollar interest rate) for a benchmark portfolio based on MSCI market capitalization weights (Value-Weighted) and a portfolio based on U.S. investors' holdings (U.S. Investors).

Data for Figure 2

YearValue-WeightedUS Investors
1990-30.14490675-19.54040449
19918.6184110511.87509998
1992-14.23542697-9.630033626
199328.8971648529.23032376
19944.033962302-2.101346998
19953.5174814716.982062278
19961.7823427687.327249932
1997-2.0308123913.364128188
199810.6064599311.53475594
199923.7059554223.51960089
2000-21.40721564-19.06469928
2001-23.61155109-22.8767787
2002-15.77587591-16.64332505
200334.9925884735.01601597
200418.7189744318.8936716
200513.4508969114.62528952
200620.1037372520.54082515
200712.9651592213.17032026
2008-56.2641253-57.46245609

Footnotes

**  Curcuru: Board of Governors of the Federal Reserve System, Washington DC 20551, [email protected]. Thomas: Board of Governors of the Federal Reserve System, Washington DC 20551, [email protected]. Warnock: Darden Business School, University of Virginia, Charlottesville, VA 22906-6550, and National Bureau of Economic Research, [email protected]. Wongswan: Phatra Securities Public Company Limited, Bangkok 10310 Thailand, [email protected]. We thank the referees, Galina Hale, Assaf Razin, Giorgio Valente, and participants in seminars and conferences including BIS, Clemson University, De Nederlandsche Bank, ECB-JIE, Federal Reserve Bank of Dallas, Federal Reserve Board, Georgetown University, Hong Kong Monetary Authority, Universiteit van Amsterdam, University of Oregon, and University of Virginia. James Albertus provided excellent research assistance. Warnock thanks the Darden School Foundation for generous support and the Asian Institute of Management for its hospitality. Also released as NBER Working Paper 16677. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Federal Reserve Bank of Dallas, the Board of Governors of the Federal Reserve System, or of any other person associated with the Federal Reserve System. Return to text

a Board of Governors of the Federal Reserve System  Return to text

b Darden Graduate School of Business, University of Virginia  Return to text

c Institute for International Integration Studies, Trinity College Dublin  Return to text

d Globalization and Monetary Policy Institute, Federal Reserve Bank of Dallas  Return to text

e National Bureau of Economic Research  Return to text

f Phatra Securities Public Company Limited  Return to text

1.  Bertaut and Tryon (2007) includes a detailed discussion of the methodology. Return to text

2.  While the Bertaut and Tryon (2007) dataset is the best currently available for monthly U.S. investment in foreign equities, in the future such data could be improved in two ways. First, more frequent measurements of positions might become available; the less time between measurements of positions, the more accurate are the interim estimates. In recent years, the surveys have been annual, but in mid-2011 collection of monthly data on aggregate positions by country will commence, which could improve the accuracy of interim holdings estimates. Second, monthly estimates could become more accurate by incorporating more direct measures of the returns U.S. investors earn in foreign markets. No such returns series currently exist, but someone covered under the International Investment Act of 1987 could, in theory, construct them. For now, we must rely on publicly available returns indices. Fortunately, within countries, MSCI indices seem to be representative of U.S. investment; MSCI firms represent almost 80 percent of U.S. investors' foreign equity investment, and an examination of U.S. holdings in over 12,000 foreign firms as of a point in time (December 1997) showed that the correlation between weights in the MSCI World Ex US Index and U.S. investors' foreign equity portfolios is quite high at 0.77 (John Ammer et al. 2006). Return to text

3.  At first glance, our contrarian when selling results appear to contrast with Graciela Kaminsky, Richard K. Lyons, and Sergio L. Schmukler (2004), who find that 13 Latin American mutual funds exhibit momentum trading over the period from 1993 - 1999. However, most of their evidence pertains to LM (Buy and Sell) at a zero lag; we do not analyze contemporaneous momentum statistics because it is impossible to disentangle true momentum trading (reallocations following price changes) from price pressure (price reacting to reallocations). Moreover, Kaminsky, Lyons, and Schmukler (2004) do not compute BM and SM statistics, so our studies are not directly comparable. Return to text

4.  One caveat about time series data on portfolios is that they include stock swaps that arise from international mergers and acquisitions and can induce jumps in Xi,t that are not related to trading (William L. Griever, Gary A. Lee, and Warnock 2001). There is no ideal way to deal with stock swaps, so we reestimated (2), (3), and (4) omitting acquisitions via stock swaps. Excluding stock swaps, the overall LM statistic remains insignificant in all cases, BM is positive and significant in 4 out of 9 cases, and in 7 of 9 cases the SM statistic is negative and significant. Excluding stock swaps, the weight of evidence still indicates that U.S. investors sell past winners. Return to text

5.  These information variables have been found to have robust predictive power for aggregate country-level returns (Campbell R. Harvey, 1991; Ferson and Harvey, 1993; and Geert Bekaert and Harvey, 1997). We also experimented with lagged local excess returns, but found that including this variable does not change our results. We do not use the local or global dividend yield. Ferson, Sergei Sarkisssian, and Timothy T. Simin (2003) illustrate that returns prediction regressions with persistent variables such as the dividend yield tend to over-reject the null hypothesis of no predictability. Moreover, John Y. Campbell and Motohiro Yogo (2006), who account for this bias in a study of the U.S. market, and Andrew Ang and Bekaert (2007) and Bekaert, Harvey, and Christian Lundblad (2007), who use Monte Carlo simulations for a range of emerging and developed markets, find no predictive power for the dividend yield. Return to text

6.  Even in models rich enough to deliver a clear prediction about the relationship between flows and returns (e.g., Dumas, Lewis, and Osambela 2010), focusing on changes in portfolio weights rather than flows might be more appropriate. Return to text

7.  To be exact, our results concern the foreign portfolio. It is plausible that returns-chasing could be absent in the foreign portfolio but present in the global portfolio, which includes domestic holdings. However, there is also no evidence of returns-chasing in U.S. investors' global equity portfolios (Curcuru et al. 2010). Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: March 10, 2011