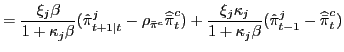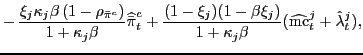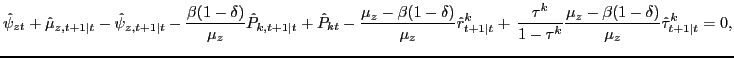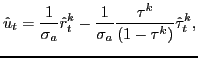Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1023, July 2011 --- Screen Reader
Version*
Optimal Monetary Policy in an Operational Medium-Sized DSGE Model1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We show how to construct optimal policy projections in Ramses, the Riksbank's open-economy medium-sized DSGE model for forecasting and policy analysis. Bayesian estimation of the parameters of the model indicates that they are relatively invariant to alternative policy assumptions and supports our view that the model parameters may be regarded as unaffected by the monetary policy specification. We discuss how monetary policy, and in particular the choice of output gap measure, affects the transmission of shocks. Finally, we use the model to assess the recent Great Recession in the world economy and how its impact on the economic development in Sweden depends on the conduct of monetary policy. This provides an illustration on how Rames incoporates large international spillover effects.
Keywords: Optimal monetary policy, instrument rules, optimal policy projections, open-economy DSGE models
JEL classification: E52, E58
1. Introduction
We study optimal monetary policy in Ramses, the main model used at Sveriges Riksbank for forecasting and policy analysis. Ramses is an estimated small open-economy dynamic stochastic general equilibrium (DSGE) model, developed by Adolfson, Laséen, Lindé, and Villani (ALLV) [4] and [3].
By optimal monetary policy we mean policy that minimizes an intertemporal loss function. The intertemporal loss function is a discounted sum of expected future period losses. We choose a quadratic period loss function that corresponds to flexible inflation targeting and is the weighted sum of three terms: the squared inflation gap between 4-quarter CPI inflation and the inflation target, the squared output gap between output and potential output, and the squared quarterly change in the Riksbank's instrument rate, the repo rate. We interpret such a loss function as consistent with flexible inflation targeting and the Riksbank's mandate, which implies that monetary policy is directed towards stabilizing both inflation around an inflation target of 2 percent and resource utilization around a normal level ([37]).2
A fundamental assumption in our analysis is that Ramses is a structural model whose parameters are invariant to the changes in monetary policy we consider. We estimate the model parameters with Bayesian techniques under different assumptions about the conduct of monetary policy. First, as in ALLV [3], we estimate the model under the assumption that the Riksbank has followed a simple instrument rule during the inflation-targeting period which started in 1993:1.3 Second, we estimate the model under the assumption that the Riksbank has minimized an intertemporal loss function during the inflation-targeting period. The estimates of the instrument-rule and loss-function parameters provide benchmarks for the subsequent policy analysis. A finding in the empirical analysis is that whether past policy of the Riksbank until 2007:3 (the end of the sample used) is better explained as following a simple instrument rule or minimizing a loss function depends on whether the simple instrument rule and the optimal policy rule has a white-noise policy shock (control error) or not. Without a shock in both rules, we find that optimal policy fits the data equally well as the simple instrument rule. With a shock in both rules, there is a clear improvement in the empirical fit of both rules. Furthermore, the simple instrument rule has a slight empirical advantage relative to optimal policy. Hence, for the particular sample period in question, with policy shocks the simple instrument rule offers a slightly better characterization of monetary policy. Our results are hence slightly different than those reported by Wolden Bache, Brubakk, and Maih [38] on Norwegian data, which stems from the fact that they do not allow for a control error in their analysis.
One contribution of our paper is to provide a detailed analysis
of how to do optimal policy projections in an estimated
linear-quadratic model with forward-looking variables, extending on
previous analysis by Svensson [29] and Svensson and Tetlow [35]. A
key issue for a flexible inflation-targeting central bank is which
measure of resource utilization to stabilize. We use the output gap
as measure of resource utilization and study alternative
definitions of potential output and the output gap, in order to
make an assessment to what extent the formulation of the output gap
in the loss function affects the conduct of monetary policy and
propagation of shocks. More precisely, we report results from three
alternative concepts of output gaps (
![]() ), deviations
of actual (log) output (
), deviations
of actual (log) output (![]() ) from potential (log)
output (
) from potential (log)
output (
![]() ), in the loss function. One
concept of output gap is the trend output gap where
potential output is the trend output level, which is growing
stochastically due to the unit-root stochastic technology shock in
the model. A second concept is the unconditional output gap,
where potential output is unconditional potential output, which is
defined as the hypothetical output level that would exist if the
economy would have had flexible prices and wages for a long time
and would have been subject to a subset of the same shocks as the
actual economy. Unconditional potential output therefore presumes
different levels of the predetermined variables, including the
capital stock, from those in the actual economy. A third concept is
the conditional output gap, where potential output is
conditional potential output, which is defined as the hypothetical
output level that would arise if prices and wages suddenly become
flexible in the current period and are expected to remain flexible
in the future. Conditional potential output therefore depends on
the existing current predetermined variables, including the current
capital stock.
), in the loss function. One
concept of output gap is the trend output gap where
potential output is the trend output level, which is growing
stochastically due to the unit-root stochastic technology shock in
the model. A second concept is the unconditional output gap,
where potential output is unconditional potential output, which is
defined as the hypothetical output level that would exist if the
economy would have had flexible prices and wages for a long time
and would have been subject to a subset of the same shocks as the
actual economy. Unconditional potential output therefore presumes
different levels of the predetermined variables, including the
capital stock, from those in the actual economy. A third concept is
the conditional output gap, where potential output is
conditional potential output, which is defined as the hypothetical
output level that would arise if prices and wages suddenly become
flexible in the current period and are expected to remain flexible
in the future. Conditional potential output therefore depends on
the existing current predetermined variables, including the current
capital stock.
To illustrate how the policy maker's choice of output measure can influence the transmission of shocks we study impulse response functions to a persistent but stationary technology shock. According to the estimated model, shocks to total factor productivity is a dominant driver of business cycles in Sweden. In addition to its economic importance, this shock is also particularly interesting to study since it affects the various output gaps differently. Conditional and unconditional potential output increases when a positive stationary technology shock hits the economy, whereas trend output by definition is independent of such shocks and only depends on permanent (unit-root) technology shocks.
With that analysis in hand, we report and discuss optimal policy projections for Sweden using data up to and including 2008:2. We use the model to interpret the economic development in Sweden just at the time when the world economy fell into a deep recession due to the collapse in the financial markets. We choose this period to highlight the sensitivity of the Swedish economy to foreign shocks. We show projections for the estimated instrument rule and for optimal policy with different output gaps in the loss function, which create different trade-offs for the central bank in stabilizing inflation and output.
The paper is organized as follows: Section 2 presents Ramses in more general modeling terms. Section 3 discusses the data and priors used in the estimation and presents estimation results for the various specifications of the model and policy. Section 4 presents and discusses impulse response functions to a technology shock with different output gaps in the loss function. Section 5 discusses how to construct optimal policy projections, and analyzes alternative projections for a policymaker during the recent Great Recession. Finally, Section 6 presents a summary and some conclusions. Appendices A-B contain a detailed specification of Ramses and some other technical details.
2. The Model
Ramses is a small open-economy DSGE model developed in a series of papers by ALLV [4] and [3]. The model economy consists of households, domestic goods firms, importing consumption and importing investment firms, exporting firms, a government, a central bank, and an exogenous foreign economy. Within each manufacturing sector there is a continuum of firms that each produces a differentiated good and sets prices according to an indexation variant of the Calvo model. Domestic as well as global production grows with technology that contains a stochastic unit-root, see Altig et al. [8].
In what follows we provide the optimization problems of the different firms and the households, and describe the behavior of the central bank. The log-linear approximation of the model is presented in appendix A.
2.1 Domestic Goods Firms
The domestic goods firms produce their goods using capital and labor inputs, and sell them to a retailer which transforms the intermediate products into a homogenous final good that in turn is sold to the households.
The final domestic good is a composite of a continuum of
differentiated intermediate goods, each supplied by a different
firm. Output, ![]() , of the final domestic good is
produced with the constant elasticity of substitution (CES)
function
, of the final domestic good is
produced with the constant elasticity of substitution (CES)
function
![$\displaystyle Y_{t}=\left[ \overset{1}{\underset{0}{\int}}\left( Y_{it}\right) ^{\frac {1}{\lambda_{t}^{d}}}di\right] ^{\lambda_{t}^{d}}, \hspace{0.5cm} 1\leq\lambda_{t}^{d}<\infty,$](img6.gif) |
(2.1) |
where ![]() ,
,
![]() , is the input of intermediate
good
, is the input of intermediate
good ![]() and
and
![]() is a stochastic process that
determines the time-varying flexible-price markup in the domestic
goods market. The production of the intermediate good
is a stochastic process that
determines the time-varying flexible-price markup in the domestic
goods market. The production of the intermediate good ![]() by intermediate-good firm
by intermediate-good firm ![]() is given by
is given by
| (2.2) |
where ![]() is a unit-root technology shock common
to the domestic and foreign economies,
is a unit-root technology shock common
to the domestic and foreign economies,
![]() is a domestic covariance
stationary technology shock,
is a domestic covariance
stationary technology shock, ![]() the capital
stock and
the capital
stock and ![]() denotes homogeneous labor hired by
the
denotes homogeneous labor hired by
the ![]() firm. A fixed cost
firm. A fixed cost ![]() is included in the production function. We set this
parameter so that profits are zero in steady state, following
Christiano et al. [11].
is included in the production function. We set this
parameter so that profits are zero in steady state, following
Christiano et al. [11].
We allow for working capital by assuming that a fraction
![]() of the intermediate firms' wage bill has
to be financed in advance through loans from a financial
intermediary. Cost minimization yields the following nominal
marginal cost for intermediate firm
of the intermediate firms' wage bill has
to be financed in advance through loans from a financial
intermediary. Cost minimization yields the following nominal
marginal cost for intermediate firm ![]() :
:
![$\displaystyle \mathrm{MC}_{it}^{d}=\frac{1}{(1-\alpha)^{1-\alpha}}\frac{1}{\alpha^{\alpha} }(R_{t}^{k})^{\alpha}\left[ W_{t}(1+\nu(R_{t-1}-1))\right] ^{1-\alpha} \frac{1}{z_{t}{}^{1-\alpha}}\frac{1}{\epsilon_{t}},$](img22.gif) |
(2.3) |
where ![]() is the gross nominal rental rate
per unit of capital,
is the gross nominal rental rate
per unit of capital, ![]() the gross nominal
(economy wide) interest rate, and
the gross nominal
(economy wide) interest rate, and ![]() the
nominal wage rate per unit of aggregate, homogeneous, labor
the
nominal wage rate per unit of aggregate, homogeneous, labor
![]() .
.
Each of the domestic goods firms is subject to price stickiness
through an indexation variant of the Calvo [10] model. Each
intermediate firm faces in any period a probability ![]() that it can reoptimize its price. The reoptimized
price is denoted
that it can reoptimize its price. The reoptimized
price is denoted
![]() . For the firms that are not
allowed to reoptimize their price, we adopt an indexation scheme
with partial indexation to the current inflation target,
. For the firms that are not
allowed to reoptimize their price, we adopt an indexation scheme
with partial indexation to the current inflation target,
![]() , since there is a
perceived (time-varying) CPI inflation target in the model , and
partial indexation to last period's inflation rate in order to
allow for a lagged pricing term in the Phillips curve
, since there is a
perceived (time-varying) CPI inflation target in the model , and
partial indexation to last period's inflation rate in order to
allow for a lagged pricing term in the Phillips curve
| (2.4) |
where ![]() is the price level,
is the price level,
![]() is gross
inflation in the domestic sector, and
is gross
inflation in the domestic sector, and
![]() is an indexation parameter. The
different firms maximize profits taking into account that there
might not be a chance to optimally change the price in the future.
Firm
is an indexation parameter. The
different firms maximize profits taking into account that there
might not be a chance to optimally change the price in the future.
Firm ![]() therefore faces the following optimization
problem when setting its price
therefore faces the following optimization
problem when setting its price
![\begin{displaymath}\begin{array}[c]{c} \underset{P_{t}^{d,new}}{\max\hspace{0.5cm}}\text{E}_{t} \underset{s=0}{\overset{\infty}{\sum}}\left( \beta\xi_{d}\right) ^{s}\upsilon_{t+s}[(\left( \pi_{t}^{d}\pi_{t+1}^{d}...\pi_{t+s-1}^{d}\right) ^{\kappa_{d}}\left( \bar{\pi}_{t+1}^{c}\bar{\pi}_{t+2}^{c}...\bar{\pi} _{t+s}^{c}\right) ^{1-\kappa_{d}}P_{t}^{d,new})Y_{i,t+s}\\ -\mathrm{MC}_{i,t+s}^{d}(Y_{i,t+s}+z_{t+s}\phi^{j})], \end{array}\end{displaymath}](img35.gif) |
(2.5) |
where the firm is using the stochastic household discount factor
![]() to make profits conditional upon utility
to make profits conditional upon utility![]()
![]() is the discount factor, and
is the discount factor, and
![]() the marginal utility of the
households' nominal income in period
the marginal utility of the
households' nominal income in period ![]() , which is
exogenous to the intermediate firms.
, which is
exogenous to the intermediate firms.
2.2 Importing and Exporting Firms
The importing consumption and importing investment firms buy a
homogenous good at price
![]() in the world market, and convert
it into a differentiated good through a brand naming technology.
The exporting firms buy the (homogenous) domestic final good at
price
in the world market, and convert
it into a differentiated good through a brand naming technology.
The exporting firms buy the (homogenous) domestic final good at
price ![]() and turn this into a differentiated
export good through the same type of brand naming. The nominal
marginal cost of the importing and exporting firms are thus
and turn this into a differentiated
export good through the same type of brand naming. The nominal
marginal cost of the importing and exporting firms are thus
![]() and
and
![]() , respectively, where
, respectively, where
![]() is the nominal exchange rate (domestic
currency per unit of foreign currency). The differentiated import
and export goods are subsequently aggregated by an import
consumption, import investment and export packer, respectively, so
that the final import consumption, import investment, and export
good is each a CES composite according to the following:
is the nominal exchange rate (domestic
currency per unit of foreign currency). The differentiated import
and export goods are subsequently aggregated by an import
consumption, import investment and export packer, respectively, so
that the final import consumption, import investment, and export
good is each a CES composite according to the following:
![$\displaystyle C_{t}^{m}=\left[ \overset{1}{\underset{0}{\int}}\left( C_{it}^{m}\right) ^{\frac{1}{\lambda_{t}^{_{mc}}}}di\right] ^{\lambda_{t}^{_{mc}}},$](img46.gif) ![$\displaystyle I_{t}^{m}=\left[ \overset{1}{\underset{0}{\int}}\left( I_{it} ^{m}\right) ^{\frac{1}{\lambda_{t}^{_{mi}}}}di\right] ^{\lambda_{t}^{mi}},$](img47.gif) ![$\displaystyle X_{t}=\left[ \overset{1}{\underset{0}{\int}}\left( X_{it}\right) ^{\frac{1}{\lambda_{t}^{x}}}di\right] ^{\lambda_{t}^{x}},$](img48.gif) |
(2.6) |
where
![]() for
for
![]() is the
time-varying flexible-price markup in the import consumption
(
is the
time-varying flexible-price markup in the import consumption
(![]() ), import investment (
), import investment (![]() )
and export (
)
and export (![]() ) sector. By assumption the continuum of
consumption and investment importers invoice in the domestic
currency and exporters in the foreign currency. To allow for
short-run incomplete exchange rate pass-through to import as well
as export prices we introduce nominal rigidities in the local
currency price. This is modeled through the same type of Calvo
setup as above. The price setting problems of the importing and
exporting firms are completely analogous to that of the domestic
firms in equation (2.5).4 In
total there are thus four specific Phillips curve relations
determining inflation in the domestic, import consumption, import
investment and export sectors.
) sector. By assumption the continuum of
consumption and investment importers invoice in the domestic
currency and exporters in the foreign currency. To allow for
short-run incomplete exchange rate pass-through to import as well
as export prices we introduce nominal rigidities in the local
currency price. This is modeled through the same type of Calvo
setup as above. The price setting problems of the importing and
exporting firms are completely analogous to that of the domestic
firms in equation (2.5).4 In
total there are thus four specific Phillips curve relations
determining inflation in the domestic, import consumption, import
investment and export sectors.
2.3 Households
There is a continuum of households which attain utility from
consumption, leisure and real cash balances. The preferences of
household ![]() are given by
are given by
E![$\displaystyle _{0}^{j}\sum_{t=0}^{\infty}\beta^{t}\left[ \zeta_{t}^{c}\ln\left( C_{jt}-bC_{j,t-1}\right) -\zeta_{t}^{h}A_{L}\frac{\left( h_{jt}\right) ^{1+\sigma_{L}}}{1+\sigma_{L}}+A_{q}\frac{\left( \frac{Q_{jt}}{z_{t}P_{t} ^{d}}\right) }{1-\sigma_{q}}^{1-\sigma_{q}}\right] ,$](img63.gif) |
(2.7) |
where ![]() ,
, ![]() and
and
![]() denote the
denote the ![]() household's levels of aggregate consumption, labor
supply and real cash holdings, respectively. Consumption is subject
to habit formation through
household's levels of aggregate consumption, labor
supply and real cash holdings, respectively. Consumption is subject
to habit formation through
![]() , such that the household's
marginal utility of consumption is increasing in the quantity of
goods consumed last period.
, such that the household's
marginal utility of consumption is increasing in the quantity of
goods consumed last period.
![]() and
and
![]() are persistent preference
shocks to consumption and labor supply, respectively. Households
consume a basket of domestically produced goods (
are persistent preference
shocks to consumption and labor supply, respectively. Households
consume a basket of domestically produced goods (![]() ) and imported products (
) and imported products (![]() )
which are supplied by the domestic and importing consumption firms,
respectively. Aggregate consumption is assumed to be given by the
following CES function:
)
which are supplied by the domestic and importing consumption firms,
respectively. Aggregate consumption is assumed to be given by the
following CES function:
![$\displaystyle C_{t}=\left[ (1-\omega_{c})^{1/\eta_{c}}(C_{t}^{d})^{(\eta_{c}-1)/\eta_{c} }+\omega_{c}^{1/\eta_{c}}\left( C_{t}^{m}\right) ^{(\eta_{c}-1)/\eta_{c} }\right] ^{\eta_{c}/(\eta_{c}-1)}, $](img73.gif)
where
![]() is the share of imports in
consumption, and
is the share of imports in
consumption, and ![]() is the elasticity of
substitution across consumption goods.
is the elasticity of
substitution across consumption goods.
The households can invest in their stock of capital, save in
domestic bonds and/or foreign bonds and hold cash. The households
invest in a basket of domestic and imported investment goods to
form the capital stock, and decide how much capital to rent to the
domestic firms given costs of adjusting the investment rate. The
households can increase their capital stock by investing in
additional physical capital (![]() ), taking one
period to come in action. The capital accumulation equation is
given by
), taking one
period to come in action. The capital accumulation equation is
given by
| (2.8) |
where
![]() determines the investment adjustment costs through the estimated
parameter
determines the investment adjustment costs through the estimated
parameter
![]() , and
, and
![]() is a stationary
investment-specific technology shock. Total investment is assumed
to be given by a CES aggregate of domestic and imported investment
goods (
is a stationary
investment-specific technology shock. Total investment is assumed
to be given by a CES aggregate of domestic and imported investment
goods (![]() and
and ![]() ,
respectively) according to
,
respectively) according to
![$\displaystyle I_{t}=\left[ (1-\omega_{i})^{1/\eta_{i}}\left( I_{t}^{d}\right) ^{(\eta _{i}-1)/\eta_{i}}+\omega_{i}^{1/\eta_{i}}\left( I_{t}^{m}\right) ^{(\eta _{i}-1)/\eta_{i}}\right] ^{\eta_{i}/(\eta_{i}-1)},$](img83.gif) |
(2.9) |
where
![]() is the share of imports in
investment, and
is the share of imports in
investment, and ![]() is the elasticity of
substitution across investment goods.
is the elasticity of
substitution across investment goods.
Each household is a monopoly supplier of a differentiated labor service which implies that they can set their own wage, see Erceg, Henderson and Levin [16]. After having set their wage, households supply the firms' demand for labor,
![$\displaystyle h_{jt}=\left[ \frac{W_{jt}}{W_{t}}\right] ^{\frac{\lambda_{w}}{1-\lambda _{w}}}H_{t}, $](img86.gif)
at the going wage rate. Each household sells its labor to a firm
which transforms household labor into a homogenous good that is
demanded by each of the domestic goods producing firms. Wage
stickiness is introduced through the Calvo [10] setup, where
household ![]() reoptimizes its nominal wage rate
reoptimizes its nominal wage rate
![]() according to the
following5
according to the
following5
![\begin{displaymath}\begin{array}[c]{c} \underset{W_{jt}^{new}}{\max}\hspace{0.5cm}\text{E}_{t}\sum_{s=0}^{\infty }\left( \beta\xi_{w}\right) ^{s}[-\zeta_{t+s}^{h}A_{L}\frac{\left( h_{j,t+s}\right) ^{1+\sigma_{L}}}{1+\sigma_{L}}+\\ \upsilon_{t+s}\frac{\left( 1-\tau_{t+s}^{y}\right) }{\left( 1+\tau _{t+s}^{w}\right) }\left( \left( \pi_{t}^{c}...\pi_{t+s-1}^{c}\right) ^{\kappa_{w}}\left( \bar{\pi}_{t+1}^{c}...\bar{\pi}_{t+s}^{c}\right) ^{\left( 1-\kappa_{w}\right) }\left( \mu_{z,t+1}...\mu_{z,t+s}\right) W_{jt}^{new}\right) h_{j,t+s}], \end{array}\end{displaymath}](img91.gif) |
(2.10) |
where ![]() is the probability that a household
is not allowed to reoptimize its wage,
is the probability that a household
is not allowed to reoptimize its wage,
![]() a labor income tax,
a labor income tax,
![]() a pay-roll tax (paid for
simplicity by the households), and
a pay-roll tax (paid for
simplicity by the households), and
![]() is the growth rate of
the unit-root technology shock.
is the growth rate of
the unit-root technology shock.
The choice between domestic and foreign bond holdings balances into an arbitrage condition pinning down expected exchange rate changes (that is, an uncovered interest rate parity condition). To ensure a well-defined steady-state in the model, we assume that there is premium on the foreign bond holdings which depends on the aggregate net foreign asset position of the domestic households, see, for instance, Schmitt-Grohé and Uribe [24]. Compared to a standard setting the risk premium is allowed to be negatively correlated with the expected change in the exchange rate (that is, the expected depreciation), following the evidence discussed in for example Duarte and Stockman [15]. For a detailed discussion and evaluation of this modification see ALLV [3]. The risk premium is given by:
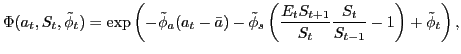 |
(2.11) |
where
![]()
![]() is the net
foreign asset position, and
is the net
foreign asset position, and
![]() is a shock to the risk
premium.
is a shock to the risk
premium.
To clear the final goods market, the foreign bond market, and the loan market for working capital, the following three constraints must hold in equilibrium:
| (2.12) |
| (2.13) |
| (2.14) |
where ![]() is government expenditures,
is government expenditures,
![]() and
and ![]() are
the foreign demand for export goods which follow CES aggregates
with elasticity
are
the foreign demand for export goods which follow CES aggregates
with elasticity ![]() , and
, and
![]() is the monetary
injection by the central bank. When defining the demand for export
goods, we introduce a stationary asymmetric (or foreign) technology
shock
is the monetary
injection by the central bank. When defining the demand for export
goods, we introduce a stationary asymmetric (or foreign) technology
shock
![]() ,
where
,
where
![]() is the permanent technology
level abroad, to allow for temporary differences in permanent
technological progress domestically and abroad.
is the permanent technology
level abroad, to allow for temporary differences in permanent
technological progress domestically and abroad.
2.4 Structural Shocks, Government, Foreign Economy
The structural shock processes in the model are given by the univariate representation
| (2.15) |
where
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() and a hat
denotes the deviation of a log-linearized variable from a
steady-state level (
and a hat
denotes the deviation of a log-linearized variable from a
steady-state level (
![]() for any variable
for any variable
![]() , where
, where ![]() is the
steady-state level).
is the
steady-state level).
![]() and
and
![]() are assumed to be white
noise (that is,
are assumed to be white
noise (that is,
![]()
![]() ).
).
The government spends resources on consuming part of the
domestic good, and collects taxes from the households. The
resulting fiscal surplus/deficit plus the seigniorage are assumed
to be transferred back to the households in a lump sum fashion.
Consequently, there is no government debt. The fiscal policy
variables - taxes on labor income (
![]() ), consumption (
), consumption (
![]() ), and the pay-roll (
), and the pay-roll (
![]() ), together with
(HP-detrended) government expenditures (
), together with
(HP-detrended) government expenditures (
![]() ) - are assumed to follow an
identified VAR model with two lags,
) - are assumed to follow an
identified VAR model with two lags,
| (2.16) |
where
![]() ,
,
![]() ,
,
![]() is a diagonal matrix with standard
deviations and
is a diagonal matrix with standard
deviations and
![]() .
.
Since Sweden is a small open economy we assume that the foreign
economy is exogenous. Foreign inflation,
![]() , output (HP-detrended),
, output (HP-detrended),
![]() and interest rate,
and interest rate,
![]() , are exogenously given by an
identified VAR model with four lags,
, are exogenously given by an
identified VAR model with four lags,
| (2.17) |
where
![]() ,
,
![]()
![]() is a diagonal matrix with
standard deviations and
is a diagonal matrix with
standard deviations and
![]() . Given our assumption of equal substitution elasticities in
foreign consumption and investment, these three variables suffice
to describe the foreign economy in our model setup.
. Given our assumption of equal substitution elasticities in
foreign consumption and investment, these three variables suffice
to describe the foreign economy in our model setup.
2.5 Monetary Policy
Monetary policy is modeled in two different ways. First, we
assume that the central bank minimizes an intertemporal loss
function under commitment. Let the intertemporal loss function in
period ![]() be
be
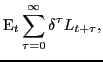 |
(2.18) |
where
![]() is a discount factor,
is a discount factor,
![]() is the period loss that is given by
is the period loss that is given by
| (2.19) |
where the central bank's target variables are; model-consistent
year-over-year CPI inflation rate,
![]() , where
, where ![]() denotes the log of CPI and
denotes the log of CPI and
![]() is the 2 percent inflation
target; a measure of the output gap,
is the 2 percent inflation
target; a measure of the output gap,
![]() ; the first difference of
the instrument rate,
; the first difference of
the instrument rate,
![]() , where
, where ![]() denotes the Riksbank's instrument rate, the repo rate, and
denotes the Riksbank's instrument rate, the repo rate, and
![]() and
and
![]() are nonnegative weights
on output-gap stabilization and instrument-rate smoothing,
respectively.6
are nonnegative weights
on output-gap stabilization and instrument-rate smoothing,
respectively.6
We report results from three alternative concepts of output gaps
(
![]() ) as
measures of resource utilization in the loss function. One concept
of output gap is the trend output gap where potential output
(
) as
measures of resource utilization in the loss function. One concept
of output gap is the trend output gap where potential output
(
![]() ) is the trend output level,
which is growing stochastically due to the unit-root stochastic
technology shock in the model. A second concept is the
unconditional output gap, where potential output is
unconditional potential output, which is defined as the
hypothetical output level that would exist if the economy would
have had flexible prices and wages for a long time and would have
been subject to the same shocks as the actual economy except
mark-up shocks and shocks to taxes which are held constant at their
steady-state levels. Unconditional potential output therefore
presumes different levels of the predetermined variables, including
the capital stock, from those in the actual economy. A third
concept is the conditional output gap, where potential
output is conditional potential output, which is defined as the
hypothetical output level that would arise if prices and wages
suddenly become flexible in the current period and are expected to
remain flexible in the future. Conditional potential output
therefore depends on the existing current predetermined variables,
including the current capital stock. In precise form the three
different concepts of potential output are
) is the trend output level,
which is growing stochastically due to the unit-root stochastic
technology shock in the model. A second concept is the
unconditional output gap, where potential output is
unconditional potential output, which is defined as the
hypothetical output level that would exist if the economy would
have had flexible prices and wages for a long time and would have
been subject to the same shocks as the actual economy except
mark-up shocks and shocks to taxes which are held constant at their
steady-state levels. Unconditional potential output therefore
presumes different levels of the predetermined variables, including
the capital stock, from those in the actual economy. A third
concept is the conditional output gap, where potential
output is conditional potential output, which is defined as the
hypothetical output level that would arise if prices and wages
suddenly become flexible in the current period and are expected to
remain flexible in the future. Conditional potential output
therefore depends on the existing current predetermined variables,
including the current capital stock. In precise form the three
different concepts of potential output are
where ![]() is the unit-root technology shock, the
row vector
is the unit-root technology shock, the
row vector
![]() expresses output as a
function of the predetermined state variables in the flex-price
economy,
expresses output as a
function of the predetermined state variables in the flex-price
economy, ![]() is the vector of predetermined state
variables in Ramses, and
is the vector of predetermined state
variables in Ramses, and ![]() is the state vector
in the economy with flexible prices and wages.
is the state vector
in the economy with flexible prices and wages.
Second, we assume that monetary policy obeys an instrument rule,
following Smets and Wouters [26]. Instead of optimizing an
intertemporal loss function, the central bank is then assumed to
adjust the short term interest rate in response to deviations of
CPI inflation from the perceived inflation target, the trend output
gap (measured as actual minus trend output), the real exchange rate
![]() and the interest rate set in the previous period. The
log-linearized instrument rule follows:
and the interest rate set in the previous period. The
log-linearized instrument rule follows:
| (2.20) | ||
where
![]() (the notation for the
short nominal interest rate in Ramses), and
(the notation for the
short nominal interest rate in Ramses), and
![]() is an uncorrelated monetary
policy shock. Since
is an uncorrelated monetary
policy shock. Since
![]() and
and
![]() are forward-looking variables,
this is an implicit instrument rule (see appendix B.4).7
are forward-looking variables,
this is an implicit instrument rule (see appendix B.4).7
2.6 Model Solution
After log-linearization, Ramses can be written in the following state-space form,
| (2.21) |
Here, ![]() is an
is an ![]() -vector
of predetermined variables in period
-vector
of predetermined variables in period ![]() (where
the period is a quarter);
(where
the period is a quarter); ![]() is an
is an
![]() -vector of forward-looking
variables;
-vector of forward-looking
variables; ![]() is an
is an ![]() -vector
of instruments (the forward-looking variables and the
instruments are the nonpredetermined variables);8
-vector
of instruments (the forward-looking variables and the
instruments are the nonpredetermined variables);8
![]() is an
is an
![]() -vector of i.i.d. shocks with
mean zero and covariance matrix
-vector of i.i.d. shocks with
mean zero and covariance matrix
![]() ;
; ![]() ,
,
![]() , and
, and ![]() , and
, and ![]() are matrices of the appropriate dimension; and, for any
variable
are matrices of the appropriate dimension; and, for any
variable ![]() ,
,
![]() denotes
denotes
![]() , the rational
expectation of
, the rational
expectation of
![]() conditional on information
available in period
conditional on information
available in period ![]() . The variables are measured
as differences from steady-state values; thus their unconditional
means are zero. The elements of the matrices
. The variables are measured
as differences from steady-state values; thus their unconditional
means are zero. The elements of the matrices ![]() ,
,
![]() ,
, ![]() , and
, and ![]() are estimated with Bayesian methods and are considered
fixed and known for the policy simulations. Then the conditions for
certainty equivalence are satisfied. Thus, we abstract from any
consideration of model uncertainty in the formulation of optimal
policy.9
are estimated with Bayesian methods and are considered
fixed and known for the policy simulations. Then the conditions for
certainty equivalence are satisfied. Thus, we abstract from any
consideration of model uncertainty in the formulation of optimal
policy.9
The upper block of (2.21) provides
![]() equations that determine the
equations that determine the
![]() -vector
-vector ![]() in
period
in
period ![]() for given
for given ![]() ,
,
![]() ,
, ![]() and
and
![]()
| (2.22) |
where ![]() and
and ![]() are partitioned
conformably with
are partitioned
conformably with ![]() and
and ![]() as
as
| (2.23) |
The lower block provides ![]() equations that
determine the
equations that
determine the ![]() -vector
-vector ![]() in
period
in
period ![]() for given
for given ![]() ,
, ![]() , and
, and ![]()
| (2.24) |
We hence assume that the
![]() submatrix
submatrix ![]() is nonsingular.10
is nonsingular.10
We assume that the central bank's ![]() -vector
of target variables, measured as the difference from an
-vector
of target variables, measured as the difference from an
![]() -vector
-vector ![]() of
target levels
of
target levels![]()
![]() , can be written as a linear function of the predetermined,
forward-looking, and instrument variables,
, can be written as a linear function of the predetermined,
forward-looking, and instrument variables,
![$\displaystyle Y_{t}=D\left[ \begin{array}[c]{c} X_{t}\\ x_{t}\\ i_{t} \end{array} \right] \equiv\left[ D_{X}\ \ D_{x}\ \ D_{i}\right] \left[ \begin{array}[c]{c} X_{t}\\ x_{t}\\ i_{t} \end{array} \right] ,$](img231.gif) |
(2.25) |
where ![]() is an
is an
![]() matrix and
partitioned conformably with
matrix and
partitioned conformably with ![]() ,
, ![]() , and
, and ![]() . Assuming optimization of
(2.18) under commitment in a
timeless perspective, the resulting intertemporal equilibrium can
then be described by the following difference equations,
. Assuming optimization of
(2.18) under commitment in a
timeless perspective, the resulting intertemporal equilibrium can
then be described by the following difference equations,
| (2.26) | ||
| (2.27) |
for ![]() , where
, where ![]() and
and
![]() are given. This system of
difference equations can be solved with several alternative
algorithms, for instance those developed by Klein [21] and Sims
[25].11 The choice and calculation of the
initial
are given. This system of
difference equations can be solved with several alternative
algorithms, for instance those developed by Klein [21] and Sims
[25].11 The choice and calculation of the
initial ![]() is further discussed in footnote 14 and appendix B.3.
is further discussed in footnote 14 and appendix B.3.
When policy instead is described by the simple instrument rule
in (2.20), there exists ![]() and
and ![]() matrices such that the intertemporal
equilibrium difference equations (2.26) and
(2.27) are still valid but with
matrices such that the intertemporal
equilibrium difference equations (2.26) and
(2.27) are still valid but with ![]() for
for ![]() .
.
3. Estimation
3.1 Data, Prior Distributions, and Calibrated Parameters
We use quarterly Swedish data for the period 1980:1-2007:3 and
estimate the model using a Bayesian approach by placing a prior
distribution on the structural parameters.12![]() 13
13
As in ALLV [3], we include the following ![]() variables among the observable variables: GDP deflator inflation (
variables among the observable variables: GDP deflator inflation (
![]() ), real wage (
), real wage (
![]() ), consumption (
), consumption (![]() ), investment (
), investment (![]() ), real
exchange rate (
), real
exchange rate (
![]() ), short interest rate
(
), short interest rate
(![]() ), hours worked (
), hours worked (![]() ), GDP (
), GDP (![]() ), exports (
), exports (
![]() ), imports (
), imports (
![]() ), CPI inflation (
), CPI inflation (
![]() ), investment-deflator
inflation (
), investment-deflator
inflation (
![]() ), foreign
(trade-weighted) output (
), foreign
(trade-weighted) output (
![]() ), foreign inflation (
), foreign inflation (
![]() ), and foreign interest rate (
), and foreign interest rate (
![]() ). We use first differences of
the quantities and the real wage, since the unit-root technology
shock induces a common stochastic trend in these variables, and
derive the state-space representation for the following vector of
observed variables,
). We use first differences of
the quantities and the real wage, since the unit-root technology
shock induces a common stochastic trend in these variables, and
derive the state-space representation for the following vector of
observed variables,
![$\displaystyle Z_{t}\equiv \begin{array}[c]{l} (\pi_{t}^{d},\Delta\ln(W_{t}/P_{t}),\Delta\ln C_{t},\Delta\ln I_{t} ,\widehat{\tilde{x}}_{t},R_{t},\hat{H}_{t},...\\ \ \Delta\ln Y_{t},\Delta\ln\tilde{X}_{t},\Delta\ln\tilde{M}_{t},\pi _{t}^{\mathrm{cpi}},\pi_{t}^{\mathrm{def},i},\Delta\ln Y_{t}^{\ast},\pi _{t}^{\ast},R_{t}^{\ast})^{\prime}. \end{array}$](img270.gif) |
(3.1) |
The growth rates are computed as quarterly log-differences, while
the inflation and interest-rate series are measured as annualized
quarterly rates. It should be noted that the stationary variables
![]() and
and
![]() are measured as deviations
around the mean and the HP-filtered trend, that is,
are measured as deviations
around the mean and the HP-filtered trend, that is,
![]() and
and
![]() , respectively.14 Finally, all real variables are
measured in per-capita units.
, respectively.14 Finally, all real variables are
measured in per-capita units.
We estimate 13 structural shocks, of which
8 follow AR(1) processes and ![]() are assumed to be i.i.d. (as described in section 2.4). In addition to these, there are
are assumed to be i.i.d. (as described in section 2.4). In addition to these, there are
![]() shocks provided by the exogenous
(pre-estimated) fiscal and foreign VARs, whose parameters are kept
fixed throughout the estimation of the model (uninformative priors
are used for these stochastic processes). The shocks enter in such
a way that there is no stochastic singularity in the likelihood
function.
shocks provided by the exogenous
(pre-estimated) fiscal and foreign VARs, whose parameters are kept
fixed throughout the estimation of the model (uninformative priors
are used for these stochastic processes). The shocks enter in such
a way that there is no stochastic singularity in the likelihood
function.
To compute the likelihood function, the reduced-form solution of the model (2.26-2.27) is transformed into a state-space representation that maps the unobserved state variables into the observed data.15 The posterior mode and Hessian matrix evaluated at the mode is computed by standard numerical optimization routines (see Smets and Wouters [26] and the references there for details).
The parameters we choose to estimate pertain mostly to the
nominal and real frictions in the model and the exogenous shock
processes.16 Table 3.1
shows the assumptions for the prior distribution of the estimated
parameters. For the model with a simple instrument rule, we choose
identical priors for the parameters in the instrument rule before
and after the adoption of an inflation target in 1993:1. For the
model with optimal policy during the inflation-targeting regime, we
use very uninformative priors for the loss-function parameters (
![]() and
and
![]() ), as indicated by the
high standard deviations. As mentioned in the introduction, the
switch from the simple instrument rule to the inflation-targeting
regime in 1993:1 is modelled as unanticipated and expected to last
forever once it has occurred.
), as indicated by the
high standard deviations. As mentioned in the introduction, the
switch from the simple instrument rule to the inflation-targeting
regime in 1993:1 is modelled as unanticipated and expected to last
forever once it has occurred.
Relative to other estimated small open-economy DSGE models (for instance, Justiniano and Preston [17]), the international spillover effects are relatively large due to the inclusion of a worldwide stochastic technology shock. This means that the open-economy aspects are of particular importance in our setting.
3.2 Estimation Results
In table 3.1, we report the prior and estimated posterior distributions. Three posterior distributions are reported. The first, labeled "Simple inst rule", is under the assumption that the Riksbank has followed a simple instrument rule during the inflation-targeting period (see equation (2.20)). The second, labeled "Loss function", is under the assumption that the Riksbank has minimized a quadratic loss function under commitment during the inflation-targeting period, with the output gap in the loss function being the trend output gap (see equation (2.19)). In this case, the optimal policy rule does not include a policy shock. The third, labeled "Loss fn params", only estimates the two parameters in that loss function.17
Table 3.1: Prior and Posterior Distributions
| Parameter | Prior Distribution: Type | Prior Distribution: Mean | Prior Distribution: Std.d/df | Posterior Distribution: Simple Inst Rule: Mode | Posterior Distribution: Simple Inst Rule: Std.d. (Hess.) | Posterior Distribution: Loss Function: Mode | Posterior Distribution: Loss Function: Std.d. | Posterior Distribution: Loss fn Params: Mode | Posterior Distribution: Loss fn Params: Std.d. (Hess.) |
|---|---|---|---|---|---|---|---|---|---|
| Calvo wages | beta | 0.750 | 0.050 | 0.719 | 0.045 | 0.719 | 0.042 | ||
| Calvo domestic prices | beta | 0.750 | 0.050 | 0.712 | 0.039 | 0.737 | 0.043 | ||
| Calvo import cons. prices | beta | 0.750 | 0.050 | 0.868 | 0.018 | 0.859 | 0.016 | ||
| Calvo import inv. prices | beta | 0.750 | 0.050 | 0.933 | 0.010 | 0.929 | 0.011 | ||
| Calvo export prices | beta | 0.750 | 0.050 | 0.898 | 0.019 | 0.889 | 0.025 | ||
| Indexation wages | beta | 0.500 | 0.150 | 0.445 | 0.124 | 0.422 | 0.115 | ||
| Indexation prices | beta | 0.500 | 0.150 | 0.180 | 0.051 | 0.173 | 0.050 | ||
| Markup domestic | truncnormal | 1.200 | 0.050 | 1.192 | 0.049 | 1.176 | 0.050 | ||
| Markup imported cons. | truncnormal | 1.200 | 0.050 | 1.020 | 0.028 | 1.021 | 0.029 | ||
| Markup.imported invest. | truncnormal | 1.200 | 0.050 | 1.137 | 0.051 | 1.154 | 0.049 | ||
| Investment adj. cost | normal | 7.694 | 1.500 | 7.951 | 1.295 | 7.684 | 1.261 | ||
| Habit formation | beta | 0.650 | 0.100 | 0.626 | 0.044 | 0.728 | 0.035 | ||
| Subst. elasticity invest. | invgamma | 1.500 | 4.0 | 1.239 | 0.031 | 1.238 | 0.030 | ||
| Subst. elasticity foreign | invgamma | 1.500 | 4.0 | 1.577 | 0.204 | 1.794 | 0.318 | ||
| Risk premium | invgamma | 0.010 | 2.0 | 0.038 | 0.026 | 0.144 | 0.068 | ||
| UIP modification | beta | 0.500 | 0.15 | 0.493 | 0.067 | 0.488 | 0.029 | ||
| Unit root tech. shock | beta | 0.750 | 0.100 | 0.790 | 0.065 | 0.765 | 0.072 | ||
| Stationary tech. shock | beta | 0.750 | 0.100 | 0.966 | 0.006 | 0.968 | 0.005 | ||
| Invest. spec. tech shock | beta | 0.750 | 0.100 | 0.750 | 0.077 | 0.719 | 0.067 | ||
| Asymmetric tech. shock | beta | 0.750 | 0.100 | 0.852 | 0.059 | 0.885 | 0.041 | ||
| Consumption pref. shock | beta | 0.750 | 0.100 | 0.919 | 0.034 | 0.881 | 0.038 | ||
| Labour supply shock | beta | 0.750 | 0.100 | 0.382 | 0.082 | 0.282 | 0.064 | ||
| Risk premium shock | beta | 0.750 | 0.100 | 0.722 | 0.052 | 0.736 | 0.058 | ||
| Unit root tech. shock | invgamma | 0.200 | 2.0 | 0.127 | 0.025 | 0.201 | 0.039 | ||
| Stationary tech. shock | invgamma | 0.700 | 2.0 | 0.457 | 0.051 | 0.516 | 0.054 | ||
| Invest. spec. tech. shock | invgamma | 0.200 | 2.0 | 0.441 | 0.069 | 0.470 | 0.065 | ||
| Asymmetric tech. shock | invgamma | 0.400 | 2.0 | 0.199 | 0.030 | 0.203 | 0.031 | ||
| Consumption pref. shock | invgamma | 0.200 | 2.0 | 0.177 | 0.035 | 0.192 | 0.031 | ||
| Labour supply shock | invgamma | 1.000 | 2.0 | 0.470 | 0.051 | 0.511 | 0.053 | ||
| Risk premium shock | invgamma | 0.050 | 2.0 | 0.454 | 0.157 | 0.519 | 0.067 | ||
| Domestic markup shock | invgamma | 1.000 | 2.0 | 0.656 | 0.064 | 0.667 | 0.068 | ||
| Imp. cons. markup shock | invgamma | 1.000 | 2.0 | 0.838 | 0.081 | 0.841 | 0.084 | ||
| Imp. invest. markup shock | invgamma | 1.000 | 2.0 | 1.604 | 0.159 | 1.661 | 0.169 | ||
| Export markup shock | invgamma | 1.000 | 2.0 | 0.753 | 0.115 | 0.695 | 0.122 | ||
| Interest rate smoothing | beta | 0.800 | 0.050 | 0.912 | 0.019 | 0.900 | 0.023 | ||
| Inflation response | truncnormal | 1.700 | 0.100 | 1.676 | 0.100 | 1.687 | 0.100 | ||
| Diff. infl response | normal | 0.300 | 0.100 | 0.210 | 0.052 | 0.208 | 0.053 | ||
| Real exch. rate response | normal | 0.000 | 0.050 | -0.042 | 0.032 | -0.053 | 0.036 | ||
| Output response | normal | 0.125 | 0.050 | 0.100 | 0.042 | 0.082 | 0.043 | ||
| Diff. output response | normal | 0.063 | 0.050 | 0.125 | 0.043 | 0.133 | 0.042 | ||
| Monetary policy shock | invgamma | 0.150 | 2.0 | 0.465 | 0.108 | 0.647 | 0.198 | ||
| Inflation target shock | invgamma | 0.050 | 2.0 | 0.372 | 0.061 | 0.360 | 0.059 | ||
| Interest rate smoothing 2 | beta | 0.800 | 0.050 | 0.882 | 0.019 | ||||
| Inflation response 2 | truncnormal | 1.700 | 0.100 | 1.697 | 0.097 | ||||
| Diff. infl response 2 | normal | 0.300 | 0.100 | 0.132 | 0.024 | ||||
| Real exch. rate response 2 | normal | 0.000 | 0.050 | -0.058 | 0.029 | ||||
| Output response 2 | normal | 0.125 | 0.050 | 0.081 | 0.040 | ||||
| Diff. output response 2 | normal | 0.063 | 0.050 | 0.100 | 0.012 | ||||
| Monetary policy shock 2 | invgamma | 0.150 | 2.0 | 0.135 | 0.029 | ||||
| Inflation target shock 2 | invgamma | 0.050 | 2.0 | 0.081 | 0.037 | ||||
| Output stabilization | truncnormal | 0.5 | 100.0 | 1.091 | 0.526 | 1.102 | 0.224 | ||
| Interest rate smoothing | truncnormal | 0.2 | 100.0 | 0.476 | 0.191 | 0.369 | 0.061 | ||
| Log marg likelihood laplace | -2631.56 | -2654.45 | |||||||
There are two important facts to note in the first two posterior
distributions. First, it is clear that the version of the model
where policy is characterized with the simple instrument rule with
an exogenous policy shock is a better characterization of how the
Riksbank has conducted monetary policy during the
inflation-targeting period. The difference between log marginal
likelihoods is almost 23 in favor of the model with
the instrument rule compared to the model with optimal policy. In
terms of Bayesian posterior odds, this is overwhelming evidence
against the loss-function characterization of the Riksbank's past
policy behavior. However, this result crucially depends on the
assumption that the simple instrument rule includes a policy shock
(control error) and that the optimal policy rule does not. If we
follow Wolden Bache, Brubakk, and Maih [38] and treat the two cases
symmetrically by not including a policy shock in the simple rule
during the inflation targeting period, that is, we impose
![]() , then the log marginal
likelihood falls to -2654.5, which is almost the
same as for the optimal policy, implying that optimal policy fits
the data equally well in this case. Alternatively, we can treat the
two cases symmetrically by including a shock in the optimal policy
rule. This improves the fit of optimal policy, but the log marginal
likelihood (-2636.8) is then still lower than the
log marginal likelihood for the simple instrument rule with a
policy shock in table 3.1. Hence, for
the particular sample period in question, with policy shocks in
both rules the simple instrument rule offers a slightly better
characterization of monetary policy. Compared to optimal policy the
Bayesian posterior odds speak clearly in favor of the simple
instrument rule, but in practice we have seen that log marginal
likelihood differences (Laplace approximation) of these magnitudes
do not necessarily generate very large discrepancies in terms of
the forecasting accuracy, see ALLV [3] and Adolfson, Lindé
and Villani [7]. Thus, the improvement in fit relative to optimal
policy is moderate.
, then the log marginal
likelihood falls to -2654.5, which is almost the
same as for the optimal policy, implying that optimal policy fits
the data equally well in this case. Alternatively, we can treat the
two cases symmetrically by including a shock in the optimal policy
rule. This improves the fit of optimal policy, but the log marginal
likelihood (-2636.8) is then still lower than the
log marginal likelihood for the simple instrument rule with a
policy shock in table 3.1. Hence, for
the particular sample period in question, with policy shocks in
both rules the simple instrument rule offers a slightly better
characterization of monetary policy. Compared to optimal policy the
Bayesian posterior odds speak clearly in favor of the simple
instrument rule, but in practice we have seen that log marginal
likelihood differences (Laplace approximation) of these magnitudes
do not necessarily generate very large discrepancies in terms of
the forecasting accuracy, see ALLV [3] and Adolfson, Lindé
and Villani [7]. Thus, the improvement in fit relative to optimal
policy is moderate.
Second, perhaps more relevant for our purpose, the non-policy parameters of the model are fairly invariant to the specification of how monetary policy has been conducted during the inflation-targeting period. This is also true for the non-policy parameters of the model with the simple instrument rule without the policy shock.18
One way to assess the quantitative importance of the parameter differences between the instrument rule and the loss function (columns "Simple inst rule" and "Loss function") is to calibrate all parameters except the coefficients in the loss function to the estimates obtained in the simple rule specification of the model, and then reestimate the coefficients in the loss function conditional on these parameters. If the loss function parameters are similar, we can conjecture that the differences in deep parameters are quantitatively unimportant. The result of this experiment is reported in the last column in table 3.1 labeled "Loss fn params", and, as conjectured, the resulting loss function parameters are very similar to the ones obtained when estimating all parameters jointly. We interpret this result as support for our assumption that the non-policy parameters are unaffected by the alternative assumptions about the conduct of monetary policy we consider below.
In the subsequent analysis we use the posterior-mode estimates
of the non-policy parameters for the model with the simple
instrument rule. In most cases, the model with the simple
instrument rule is also used to generate the (partly) unobserved
state variables. For consistency reasons, the associated estimated
loss function parameters
![]() and
and
![]() are therefore used
in the analysis below.
are therefore used
in the analysis below.
4. Monetary Policy and the Transmission of Shocks
According to the estimated model, shocks to total factor productivity play a dominant role in explaining business cycle variations in Sweden, as these shocks can explain the negative correlation between GDP growth and CPI inflation in our sample. In Adolfson, Laséen, Lindé and Svensson [2], we show that stationary technology shocks are the single most important driver of output fluctuations around trend. To interpret and understand the development of the Swedish economy, it is therefore of key importance to analyze and understand the effects of this type of technology shock.
To illustrate how optimal policy projections are affected by
which output measure the central bank tries to stabilize we
therefore start by looking at impulse response functions to a
stationary technology shock. Although this type of technology shock
(
![]() ) is estimated to be quite
persistent (
) is estimated to be quite
persistent (
![]() ) it does not affect
trend output in the model (which by definition is only influenced
by the permanent technology shock,
) it does not affect
trend output in the model (which by definition is only influenced
by the permanent technology shock, ![]() ). In
contrast, the output level under flexible prices and wages,
flexprice potential output, increases with the shock. Abstracting
from the policy response to the shock this means that the trend-
and flexprice-output gaps, by definition, will behave quite
differently following this shock.
). In
contrast, the output level under flexible prices and wages,
flexprice potential output, increases with the shock. Abstracting
from the policy response to the shock this means that the trend-
and flexprice-output gaps, by definition, will behave quite
differently following this shock.
Figure 4.1 shows impulse response
functions to a positive (one-standard deviation) stationary
technology shock under the instrument rule and under optimal policy
with different output gaps. The plots show deviations from trend,
where by trend we mean the steady state. Output thus equals the
trend output gap. The real interest rate is defined as the
instrument rate less 1-quarter-ahead CPI inflation expectations.
All variables are measured in percent or percent per year. The
impulse occurs in quarter 0. Before quarter 0, the economy is in
the steady state with ![]() and
and
![]() for
for ![]() and
and
![]() and
and ![]() for
for
![]() .
.
Figure 4.1: Impulse responses to a (one-standard deviation) stationary technology shock under optimal policy for different output gaps and under the instrument rule
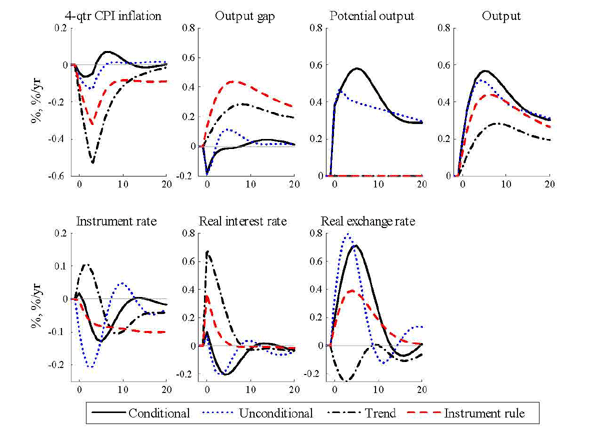
The dashed curves show the impulse responses when policy follows
the instrument rule (which responds to the trend output gap). For
the central bank, the stationary technology shock creates a
trade-off between balancing the induced decline in inflation and
the improvement in the (trend) output gap. Since the shock is very
persistent (
![]() ) this trade-off
will last for many quarters, and it takes time before inflation can
be brought back to target. The instrument rule keeps the nominal
interest rate below the steady state for the 20
periods plotted and longer. The real interest increases and remains
positive for about a year, whereas there is a real depreciation of
the currency. The result is a relatively large positive output gap
and a negative inflation gap between inflation and the target.
These gaps remain for a long time. The instrument rule is obviously
not successful in closing these gaps with the time-period
plotted.
) this trade-off
will last for many quarters, and it takes time before inflation can
be brought back to target. The instrument rule keeps the nominal
interest rate below the steady state for the 20
periods plotted and longer. The real interest increases and remains
positive for about a year, whereas there is a real depreciation of
the currency. The result is a relatively large positive output gap
and a negative inflation gap between inflation and the target.
These gaps remain for a long time. The instrument rule is obviously
not successful in closing these gaps with the time-period
plotted.
The dashed-dotted curves show the responses under optimal policy
when the trend output gap enters the loss function of the central
bank. The weights in the loss function, as for all responses under
optimal policy in this figure, are
![]() , and
, and
![]() , the estimated
weights in table 3.1 when the non-policy
parameters are kept at their posterior mode obtained under the
instrument rule. We see that this optimal policy stabilizes
inflation and the output gap more effectively over time than the
instrument rule, although optimal policy (with the trend output gap
in the loss function) initially allows for a larger fall in CPI
inflation. This requires initially tighter monetary policy than the
instrument-rule, as demonstrated by initially higher nominal and
real interest rates and a real appreciation of the currency.
, the estimated
weights in table 3.1 when the non-policy
parameters are kept at their posterior mode obtained under the
instrument rule. We see that this optimal policy stabilizes
inflation and the output gap more effectively over time than the
instrument rule, although optimal policy (with the trend output gap
in the loss function) initially allows for a larger fall in CPI
inflation. This requires initially tighter monetary policy than the
instrument-rule, as demonstrated by initially higher nominal and
real interest rates and a real appreciation of the currency.
The solid curves show the impulse responses under optimal policy when the output gap in the loss function is the conditional output gap. Hence, potential output plotted in the figure is conditional potential output, and the output gap plotted is the conditional output gap. We see that this optimal policy successfully stabilizes 4-quarter CPI inflation around the inflation target. It also successfully stabilizes the output gap, and we see that the conditional output gap is much smaller than the trend output gap and initially even negative. Due to sticky prices and wages, the stationary technology shock affects potential output quicker than actual output and the flexprice (conditional and unconditional) output gaps are therefore initially negative, whereas the trend output gap is positive. This implies that the interest rate responses will differ depending on which output gap the central bank tries to stabilize. With the flexprice output gap in its loss function, the central bank does not face an unfavorable trade-off between stabilizing inflation and output after a technology shock. Optimal policy takes into account that conditional potential output is high because productivity is temporarily high and therefore allows for more expansionary policy (as shown by lower nominal and real interest rates) and higher actual output than when the trend output gap is the target variable or when the instrument rule is followed. This in effect implies that inflation can be stabilized much quicker than for policy with the trend output gap, even though the weights in the loss function are the same in the two cases.
That the instrument rule is specified in terms of the trend output gap (rather than, for instance, the conditional output gap) is also one of the main reasons why the instrument rule does not bring inflation quickly back to target in this particular situation. Had the rule instead been specified with a stronger inflation response than the estimated one or using a response to the conditional or unconditional output gap, the inefficient trade-off between inflation and output stabilization would be less pronounced.
The dotted curves in figure 4.1 show the
impulse responses when the output gap in the loss function is the
unconditional output gap. Comparing with the impulse responses with
the conditional output gap in the loss function, we see that
potential output levels differ from period ![]() and
onwards. This occurs because the conditional and unconditional
potential output levels are computed from different predetermined
variables (those in the actual sticky-price economy, and those in
the hypothetical economy with flexible prices and wages in the past
and present, respectively). Thus, unconditional potential output is
independent of policy, whereas conditional potential output depends
on policy through the endogenous predetermined variables. When the
shock hits the economy in quarter 0, the two output-gap definitions
will be equal (since the economy by assumption starts out in steady
state in quarter -1, which is the same for both the
actual economy and the hypothetical flexprice economy), but in
quarter
and
onwards. This occurs because the conditional and unconditional
potential output levels are computed from different predetermined
variables (those in the actual sticky-price economy, and those in
the hypothetical economy with flexible prices and wages in the past
and present, respectively). Thus, unconditional potential output is
independent of policy, whereas conditional potential output depends
on policy through the endogenous predetermined variables. When the
shock hits the economy in quarter 0, the two output-gap definitions
will be equal (since the economy by assumption starts out in steady
state in quarter -1, which is the same for both the
actual economy and the hypothetical flexprice economy), but in
quarter ![]() they will diverge. The predetermined
variables in quarter
they will diverge. The predetermined
variables in quarter ![]() in the sticky-price economy
will differ from those in the flexprice economy because the
forward-looking variables and the instrument rate in quarter 0 will
differ between the sticky-price and the flexprice economies. Even
if no new innovations have occurred between quarter 0 and quarter
in the sticky-price economy
will differ from those in the flexprice economy because the
forward-looking variables and the instrument rate in quarter 0 will
differ between the sticky-price and the flexprice economies. Even
if no new innovations have occurred between quarter 0 and quarter
![]() the levels of the predetermined variables
used for computing the two potential output levels will thus
differ. Since actual output and conditional potential output share
the same predetermined variables in each period, we would expect
the conditional output gap will normally be smaller than the
unconditional output gap.
the levels of the predetermined variables
used for computing the two potential output levels will thus
differ. Since actual output and conditional potential output share
the same predetermined variables in each period, we would expect
the conditional output gap will normally be smaller than the
unconditional output gap.
5. Optimal Policy Projections and the Great Recession
Having estimated the model and obtained an understanding of the role of different monetary policy assumptions can play for the propagation of shocks, we now turn to a discussion about how to compute optimal policy projections with the model. We also consider an application to the Great Recession in the world economy that was initiated during 2008.
5.1 Information and Data
To calculate the optimal policy projection for a policy maker in
period(quarter) ![]() we assume the following. The
information set,
we assume the following. The
information set,
![]() , in the beginning of period
, in the beginning of period
![]() , just after the instrument setting for
quarter
, just after the instrument setting for
quarter ![]() has been announced, is specified as
has been announced, is specified as
where ![]() is the
is the ![]() -vector
of observable variables that satisfies the measurement equation,
-vector
of observable variables that satisfies the measurement equation,
![\begin{displaymath} Z_{t}=\bar{D}\left[ \begin{array}[c]{c} X_{t}\ x_{t}\ i_{t} \end{array}\right] +\eta_{t}, \end{displaymath}](img391.gif)
and where ![]() is a given matrix and
is a given matrix and
![]() is an
is an ![]() -vector
of i.i.d. period-
-vector
of i.i.d. period-![]() measurement errors with
distribution
measurement errors with
distribution
![]() .
.
For the monetary-policy decision at the beginning of quarter
![]() , the matrices
, the matrices ![]() ,
, ![]() ,
, ![]() , and
, and ![]() as well as the
state vectors, denoted
as well as the
state vectors, denoted
![]() ,
,
![]() ,
,
![]() , and
, and
![]() for
for
![]() , are formed by the posterior mode
estimates in table 3.1
, are formed by the posterior mode
estimates in table 3.1![]() We also specify the estimate of
We also specify the estimate of ![]() , denoted
, denoted
![]() , as
, as
| (5.1) |
where the estimated shocks
![]() since
since ![]() is not in the information set
is not in the information set
![]() .19
.19
With respect to projections in period ![]() , we
regard the matrices
, we
regard the matrices ![]() ,
, ![]() ,
,
![]() , and
, and ![]() as certain and
known. Then we can rely on certainty equivalence--under which
conditional means of the relevant variables are sufficient for
determining the optimal policy--and compute the optimal projections
accordingly.20
as certain and
known. Then we can rely on certainty equivalence--under which
conditional means of the relevant variables are sufficient for
determining the optimal policy--and compute the optimal projections
accordingly.20
5.2 The Projection Model and Optimal Projections
Let
![]() denote a
projection in period
denote a
projection in period ![]() for any variable
for any variable
![]() , a mean forecast conditional on
information in period
, a mean forecast conditional on
information in period ![]() . The projection
model for the projections
. The projection
model for the projections
![]() in period
in period
![]() is
is
| (5.2) |
![$\displaystyle Y_{t+\tau,t}=D\left[ \begin{array}[c]{c} X_{t+\tau,t}\\ x_{t+\tau,t}\\ i_{t+\tau,t} \end{array} \right]$](img436.gif) |
(5.3) |
for ![]() , where
, where
| (5.4) |
where ![]() is given by (5.1). Thus, we let "" and "
is given by (5.1). Thus, we let "" and "![]()
![]() " in subindices
refer to projections and estimates (rational expectations) in the
beginning of period
" in subindices
refer to projections and estimates (rational expectations) in the
beginning of period ![]() , respectively. The reason
for this separate notation for the projections is that they are
conceptually distinct from the equilibrium rational expectations
and include possible hypothetical projections contemplated by the
central bank during its decision process. The feasible set of
projections for given
, respectively. The reason
for this separate notation for the projections is that they are
conceptually distinct from the equilibrium rational expectations
and include possible hypothetical projections contemplated by the
central bank during its decision process. The feasible set of
projections for given ![]() is the
set of projections that satisfy (5.2)-(5.4).
is the
set of projections that satisfy (5.2)-(5.4).
The policy problem in period ![]() is to determine
the optimal projection in period
is to determine
the optimal projection in period ![]() , denoted
, denoted
![]() .
The optimal projection is the projection that minimizes the
intertemporal loss function,
.
The optimal projection is the projection that minimizes the
intertemporal loss function,
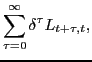 |
(5.5) |
where the period loss,
![]() , is specified as
, is specified as
| (5.6) |
where ![]() is symmetric positive semidefinite matrix
with diagonal (
is symmetric positive semidefinite matrix
with diagonal (![]() ,
,
![]()
![]() )
)![]() . The minimization is subject to the projection
being in the feasible set of projections for given
. The minimization is subject to the projection
being in the feasible set of projections for given ![]() .21
.21
When the policy problem is formulated in terms of projections,
we can allow
![]() , since the above infinite
sum will normally converge also for
, since the above infinite
sum will normally converge also for ![]() . The
optimization is done under commitment in a timeless perspective
(Woodford [39]). The optimization results in a set of first-order
conditions, which combined with the model equations, (2.21), yields a system of difference equations (see
Söderlind [28] and Svensson [30]) that can be solved with
several alternative numerical algorithms (see section 2.6 for references).22
. The
optimization is done under commitment in a timeless perspective
(Woodford [39]). The optimization results in a set of first-order
conditions, which combined with the model equations, (2.21), yields a system of difference equations (see
Söderlind [28] and Svensson [30]) that can be solved with
several alternative numerical algorithms (see section 2.6 for references).22
Under the assumption of optimization under commitment in a timeless perspective, one way to describe the optimal projection is by the following difference equations,
![$\displaystyle \left[ \begin{array}[c]{c} \check{x}_{t+\tau,t}\\ \check{i}_{t+\tau,t} \end{array} \right]$](img459.gif) |
![$\displaystyle =F\left[ \begin{array}[c]{c} \check{X}_{t+\tau,t}\\ \Xi_{t+\tau-1,t} \end{array} \right] ,$](img460.gif) |
(5.7) |
![$\displaystyle \left[ \begin{array}[c]{c} \check{X}_{t+\tau+1,t}\\ \Xi_{t+\tau,t} \end{array} \right]$](img461.gif) |
![$\displaystyle =M\left[ \begin{array}[c]{c} \check{X}_{t+\tau,t}\\ \Xi_{t+\tau-1,t} \end{array} \right] ,$](img462.gif) |
(5.8) |
for ![]() , where
, where
![]() . The matrices
. The matrices
![]() and
and ![]() depend on
depend on
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() , and
, and ![]() , but are independent of
, but are independent of ![]() . The
independence of
. The
independence of ![]() demonstrates the certainty
equivalence of the projections. The
demonstrates the certainty
equivalence of the projections. The ![]() -vector
-vector
![]() consists of the Lagrange
multipliers of the lower block of (5.2), the block determining the projection
of the forward-looking variables. We assume that the optimization
is under commitment in a timeless perspective, so that the initial
Lagrange multiplier,
consists of the Lagrange
multipliers of the lower block of (5.2), the block determining the projection
of the forward-looking variables. We assume that the optimization
is under commitment in a timeless perspective, so that the initial
Lagrange multiplier,
![]() , is non-zero. Commitment is thus
considered having occurred some time in the past, and more
precisely we assume policy has been optimal since the start of the
inflation targeting in 1993:1.23
, is non-zero. Commitment is thus
considered having occurred some time in the past, and more
precisely we assume policy has been optimal since the start of the
inflation targeting in 1993:1.23
5.3 An Application to the Great Recession
Next, we use the model to interpret the future economic development in Sweden for a policy maker standing in 2008:3. This period is especially interesting to analyze since the world economy were just about to enter a deep recession in the following quarters.
Figure 5.1 show projections from Ramses using data up to and including 2008:2, for 10 key variables: foreign output, foreign annualized 1-quarter CPI inflation, foreign interest rate, the real exchange rate, 4-quarter CPI inflation, the output gap, the instrument rate, the real interest rate (the instrument rate less 1-quarter-ahead CPI inflation expectations), output and potential output. The plots show deviations from steady state. The solid vertical line marks 2008:3, which is quarter 0 in the figure. The curves to the left of the line shows the history of actual data up to and including 2008:2, which is quarter -1 in the figure. The state in 2008:2, and its history, is estimated using policy with the instrument rule.
The solid curves to the right of the solid vertical line show the projections for a policy maker following the estimated instrument rule. We see that Ramses' VAR-model for the three foreign variables did not forecast the large drop in the world economy that occurred in the next few quarters after 2008:3, following the turbulence in the financial markets. In reality, world output diminished by almost 4 percent in the next three quarters and world inflation approached 0 percent. Given the VAR-model's counterfactual view of the foreign economy, Ramses projected Swedish CPI inflation to be close to 2 percent and output to be less than 0.5 percent below its trend level. Ex post, we know Swedish GDP decreased by almost 6 percent in the next year and consumer prices actually declined.
We know from VAR evidence that international spillover effects to small open economies are generally large. Lindé [19] shows, using a block exogenity assumption in a VAR model on Swedish data, that foreign shocks account for around 50 percent of the fluctuations around trend in Swedish output and domestic inflation. Can then the substantial drop in the world economy explain the economic development in Sweden during the financial crisis? To analyze this we compute a forecast with Ramses that is conditional upon the decline in foreign output during 2008:4 - 2009:2. After those three quarters the forecast is endogenously determined by the model, which is marked by a dashed vertical line. It is assumed that the agents in the model fully anticipate the path of foreign output during 2008:4 - 2009:2. The expectations in the model are thus consistent with the conditional path of foreign output. We use the method in Laséen and Svensson [18] to calculate how large time-varying intercepts in the VAR equation for foreign output are needed to replicate the drop in foreign output. Foreign inflation and the foreign interest rate is then determined endogenously within the foreign VAR model.
The dashed curves in figure 5.1 show this conditional projection when policy follows the estimated instrument rule. The cumulative drop of about 3.7 percent in world output implies that world inflation drops 1 percent below steady state and that the world interest rate almost hits the zero lower bound. The steady state level of the nominal interest rate in both Sweden and the rest of the world is assumed to be 4.25 percent, and, as stated above, the plots show deviations from steady state. The substantial fall in foreign output implies less demand for Swedish export goods, and domestic output drops below trend by about 1.5 percent. We see that the spillover to Swedish production is approximately 50 percent of the drop in the world economy. However, CPI inflation in Sweden decreases by more than the decline in the world economy. From figure 5.1 we also see that the instrument rule implies that the Swedish interest rate is lowered by about 2 percentage points below its steady state level. Since the foreign interest rate falls by more, this implies that the nominal (not depicted) and real (depicted) exchange rate appreciates, due to the UIP condition in the model. In reality we saw a large flight from the Swedish krona, however.
To account for the large depreciation of the real exchange rate, the model needs risk premium shocks that can capture the deviations from interest rate parity. In reality, substantial declines in investment and exports also occurred. To capture all components in the GDP identity (and thereby describe the entire fall in Swedish GDP), the model additionally requires shocks to investment technology and the export markup. The large fall in foreign output can thus not alone explain all aspects of the development of the Swedish economy during the financial crisis.
There are several reasons for why the model scenario under consideration cannot fully capture the fall in domestic GDP that actually occurred. The scenario above, with a decline in foreign output only, works through the trade and real exchange rate channels of the model. In reality, the recession was created in the financial sector which caused the spread between inter-bank rates and the instrument rate to increase dramatically. As in most DSGE models, Ramses lacks such a financial sector that includes a financing premium which could have further dampened domestic GDP.24 If we would have been able to consider both shocks simultaneously, this would have caused the zero bound on nominal interest rates to bind for Sweden's most important trading partners and in all likelihood also for the Swedish economy. This channel, per se, would have amplified the fall in domestic output even further.
Figure 5.1: Projections in 2008:3 for the instrument rule
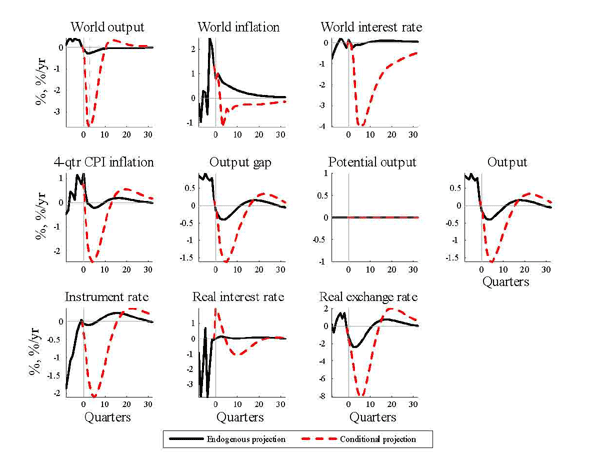
Finally, we assess how the projections during the financial
crisis could have been affected by alternative monetary policies.
Depending on the state of the economy (and thus the current size of
the shocks that persistently die out over the projection horizon),
the policy assumption of which output measure to stabilize can
matter quite a bit for the projections, as shown in section 4. In figure 5.2 we therefore compare projections with the
instrument rule and projections with policy for different output
gaps in the loss function. In all the optimal policy projections in
this figure, we assume commitment in a timeless perspective and
compute the initial vector of Lagrange multipliers for the
equations for the forward-looking variables (![]() ) under the assumption that policy during the
inflation-targeting period has been optimal (see appendix B.3).25 As in figure 5.1 we condition all the projections on the decline
in foreign output during the first three quarters after 2008:3.
) under the assumption that policy during the
inflation-targeting period has been optimal (see appendix B.3).25 As in figure 5.1 we condition all the projections on the decline
in foreign output during the first three quarters after 2008:3.
Figure 5.2: Difference
between unconditional and conditional projections in 2008:3 for
optimal policy with different output gaps (
![]() )
)
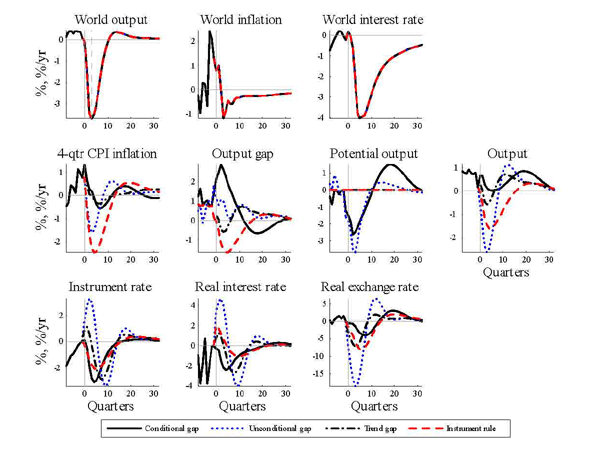
The dashed curves in figure 5.2 reprints the conditional projections from figure 5.1 where policy follows the instrument rule. The solid curves show optimal policy projections with the conditional output gap in the loss function. The dotted curves show the optimal policy projections when the output gap in the loss function is the unconditional output gap (which is computed using equation (C.7) with flexible prices from 1993:1 and onwards to form the state vector under flexible prices). The dashed-dotted curves show the optimal policy projections with the trend output gap in the loss function.
In figure 5.2, we see that 4-quarter CPI-inflation and the output gap falls quite a bit when policy follows the instrument rule. Optimal policy, with the trend output gap in the loss function, is shown with the dash-dotted curves. It is able to stabilize both inflation and the output gap much better. With the instrument rule's slow adjustment of the instrument rate, the real interest rate initially increases because inflation falls so quickly and is then followed by a compensating modest fall in the real interest rate. Optimal policy initially increases the real interest rate less and then lowers the real interest rate substantially. This implies substantially more expansionary policy and succeeds in preventing large falls in both CPI inflation and output. In spite of the non-negligible weight on instrument-rate smoothing, optimal policy allows the instrument rate to first increase and then fall substantially, a much more effective policy than the instrument rule's smooth fall and rise of the instrument rate. It is important to understand that the initial increase in the nominal instrument rate for the loss function with the trend gap is driven by the initial state of the economy. Had the economy been in steady state when the negative foreign demand shocks hit the economy, the instrument rate for the loss function with the trend gap would have been lowered directly.
Optimal policy with the unconditional output gap in the loss function and potential output given by unconditional flexible-price output is shown with the dotted curves. The fall in world output and the other foreign shocks imply a large fall in potential output. Optimal policy results in a small positive output gap. This requires a large fall in output, which requires contractionary monetary policy in the form of a high real interest rate and a real appreciation of the currency. This results in an intermediate fall in CPI-inflation.
Optimal policy with the conditional output gap in the loss function and potential output given by conditional flexible-price output is shown with the solid curves. The shocks from the world economy results in a fall and then a rise in potential output. Optimal policy results in first a positive and then a negative output gap, corresponding to positive output falling to the steady-state level and then rising above. CPI inflation falls modestly below target and then rises above. This requires expansionary monetary policy, with a significant fall in the real interest rate and initially much smaller real appreciation of the currency than the other policies.
Clearly, it matters quite a bit for optimal policy what output gap enters the loss function, with different consequences for the dynamics of output and inflation and the optimal policy response. Some policies result in considerably more output and CPI stabilization than others. Clearly it is important to determine what potential-output definition is the most appropriate.
6. Conclusions
In this paper, we have shown how to construct operational optimal policy projections in the Riksbank's model Ramses, a linear-quadratic open-economy DSGE model. By optimal policy projections we mean projections of the target variables and the instrument rate that minimize a loss function. We have illustrated the use and consequences of different output-gap concepts in the loss function and clarified the difference between output gaps relative to conditional potential output, trend output, and unconditional potential output, where conditional refers to the dependence on existing endogenous predetermined variables, such as the capital stock. When productivity is temporarily high, conditional potential output exceeds trend output. Then optimal policy projections in this case differ substantially depending on whether conditional or trend output gaps enter the loss function.
We have also illustrated how the model interpreted the economic development in Sweden with the Great Recession ahead in 2008:3, using different policy assumptions. We studied the direct impact of the fall in the world economy, but not the financial spillover that must have accounted for a large share of the Swedish output decline. An important challenge ahead for the profession is to develop DSGE models with elaborate financial frictions.
With the tools we have demonstrated, we believe optimal policy projections in Ramses and similar DSGE models can now be applied in real-time policy processes and provide policymakers with useful advice for their decisions--together with the usual input of detailed analysis and estimation of the initial state of the economy, policy simulations with historical policy reaction functions, other forecasting models, judgment, concerns about model uncertainty, and so forth.
Appendix
A. Ramses in Some Detail
This appendix presents the loglinear approximation of the model.
For a more detailed description of the complete model and the
derivation of the loglinear approximation, see ALLV [4]. A hat
denotes the deviation of a loglinearized variable from a
steady-state level (
![]() for any variable
for any variable
![]() , where
, where ![]() is the
steady-state level), and delta denotes the log-difference of a
variable (
is the
steady-state level), and delta denotes the log-difference of a
variable (
![]() for any
variable
for any
variable ![]() ). Since all real variables grow with
the non-stationary technology shock
). Since all real variables grow with
the non-stationary technology shock ![]() , we have
to divide all quantities with the trend level of technology to make
them stationary. We denote the resulting stationary variables by
lower-case letters, that is,
, we have
to divide all quantities with the trend level of technology to make
them stationary. We denote the resulting stationary variables by
lower-case letters, that is,
![]()
![]() (we denote
investment by
(we denote
investment by
![]() to avoid confusion with
the monetary-policy instrument
to avoid confusion with
the monetary-policy instrument ![]() ),
),
![]() (capital-services),
(capital-services),
![]() (physical
capital stock),
(physical
capital stock),
![]() (real
wage).
(real
wage).
Inflation,
![]() in the four sectors of
firms
in the four sectors of
firms
![]() : domestic
(production) (
: domestic
(production) (![]() ), consumer-goods import (
), consumer-goods import (
![]() ), investment-goods import (
), investment-goods import (
![]() ), and export (
), and export (![]() ), is determined from the Phillips curve
), is determined from the Phillips curve
|
(A.1) |
The firms' marginal costs,
![]() , are defined
as
, are defined
as
respectively; where
![]() denotes the effective
nominal interest rate paid by the firms,
denotes the effective
nominal interest rate paid by the firms,
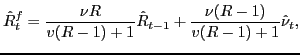
where
![]() is a shock to the fraction of
firms that has to finance their wage bill in advance (throughout we
set
is a shock to the fraction of
firms that has to finance their wage bill in advance (throughout we
set ![]() ). Furthermore,
). Furthermore,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() are relative prices
defined as
are relative prices
defined as
CPI inflation,
![]() , satisfies
, satisfies
The real-wage equation can be written
| 0 | ||
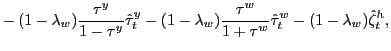 |
where
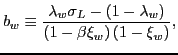
![]() denotes the marginal utility
of income.
denotes the marginal utility
of income.
The Euler equation for consumption expenditures is,
| 0 | ||
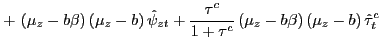 |
||
where
denotes the relative price between consumption and domestically produced goods.
The household's first-order conditions with respect to
investment
![]() , the physical capital
stock
, the physical capital
stock
![]() , and the utilization rate
, and the utilization rate
are, in their loglinearized forms, given by
| (A.2) |
|
(A.3) |
where ![]() is the price of capital goods in
terms of domestic goods,
is the price of capital goods in
terms of domestic goods, ![]() is the depreciation
rate,
is the depreciation
rate,
![]() is a parameter determining the
capital utilization rate (here calibrated so that there is no
variable capital utilization
is a parameter determining the
capital utilization rate (here calibrated so that there is no
variable capital utilization
![]() ) and
) and
![]() denotes the log-linearized
expression for the real rental rate of capital and satisfies
denotes the log-linearized
expression for the real rental rate of capital and satisfies
The loglinearized law of motion for capital is given by
![$\displaystyle \widehat{\bar{k}}_{t+1}=(1-\delta)\frac{1}{\mu_{z}}\widehat{\bar{k}} _{t}-(1-\delta)\frac{1}{\mu_{z}}\hat{\mu}_{zt}+\left[ 1-(1-\delta)\frac {1}{\mu_{z}}\right] \hat{\Upsilon}_{t}+\left[ 1-(1-\delta)\frac{1}{\mu_{z} }\right] \widehat{\tilde{\imath}}_{t}.$](img592.gif)
|
(A.4) |
The output gap satisfies,
| (A.5) |
where
![]() is the steady-state markup.
is the steady-state markup.
By combining the first-order conditions for the holdings of domestic and foreign bonds, we obtain the modified uncovered interest parity (UIP) condition,
| (A.6) |
The real exchange rate,
![]() , satisfies
, satisfies
The loglinearized version of the first-order conditions for
money balances ![]() and cash holdings
and cash holdings
![]() are, respectively,
are, respectively,
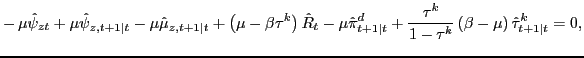
![$\displaystyle \hat{q}_{t}=\frac{1}{\sigma_{q}}\left[ \hat{\zeta}_{t}^{q}+\frac{\tau^{k} }{1-\tau^{k}}\hat{\tau}_{t}^{k}-\hat{\psi}_{zt}-\frac{R}{R-1}\hat{R} _{t-1}\right] ,$](img601.gif)
|
(A.7) |
where ![]() is steady-state money growth and
is steady-state money growth and
![]() is a cash preference
shock, to be specified below.
is a cash preference
shock, to be specified below.
The following aggregate resource constraint must hold in equilibrium
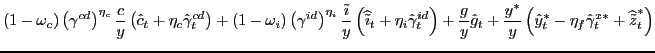
![$\displaystyle =\lambda_{d}[\hat{\varepsilon}_{t}+\alpha(\hat{k}_{t}-\hat{\mu}_{zt})+\left( 1-\alpha\right) \hat{H}_{t}]-\left( 1-\tau^{k}\right) r^{k}\frac{\bar{k} }{y}\frac{1}{\mu_{z}}(\hat{k}_{t}-\widehat{\bar{k}}_{t}); $](img605.gif)
where ![]() ,
, ![]() , and
, and
![]() are elasticities of substitution
between domestic and imported consumer goods, domestic and imported
investment goods, and domestic and foreign goods (in foreign
consumption), respectively;
are elasticities of substitution
between domestic and imported consumer goods, domestic and imported
investment goods, and domestic and foreign goods (in foreign
consumption), respectively; ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are
steady-state levels of consumption, investment, domestic output,
foreign output, government expenditure, and the capital stock,
respectively (when scaled with
are
steady-state levels of consumption, investment, domestic output,
foreign output, government expenditure, and the capital stock,
respectively (when scaled with ![]() , the
technology level);
, the
technology level);
![]() is government expenditure, and
is government expenditure, and
is the relative price between investment and domestically produced goods.
We also need to relate money growth ![]() to
real balances (where real balances
to
real balances (where real balances
![]() are scaled by the technology shock
are scaled by the technology shock ![]() and
and
![]() denote nominal balances) and
domestic inflation,
denote nominal balances) and
domestic inflation,
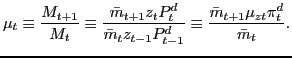
Loglinearizing, we have
| (A.8) |
To clear the loan market, the demand for liquidity from the firms (which are financing their wage bills) must equal the supplied deposits of the households plus the monetary injection by the central bank:
| (A.9) |
where ![]() ,
, ![]() and
and
![]() are steady-state levels of real wages,
real balances, and cash holdings (when scaled by
are steady-state levels of real wages,
real balances, and cash holdings (when scaled by ![]() ),
), ![]() is the steady-state level of hours
worked, and
is the steady-state level of hours
worked, and ![]() is the steady-state inflation of
domestic goods.
is the steady-state inflation of
domestic goods.
The evolution of net foreign assets at the aggregate level satisfies
| (A.10) | ||
![$\displaystyle -\tilde{\imath}^{m}\left[ -\eta_{i}\left( 1-\omega_{i}\right) \left( \gamma^{id}\right) ^{-\left( 1-\eta_{i}\right) }\hat{\gamma}_{t} ^{\mathrm{mi}d}+\widehat{\tilde{\imath}}_{t}\right] +\frac{R}{\pi\mu_{z}} \hat{a}_{t-1};$](img634.gif) |
where ![]() and
and ![]() are
steady-state levels of consumption and investment of imported goods
(when scaled by
are
steady-state levels of consumption and investment of imported goods
(when scaled by ![]() ),
), ![]() is the
steady-state nominal interest-rate level, and
is the
steady-state nominal interest-rate level, and
![]() is a
stationary shock that measures the degree of asymmetry in the
technological level between the domestic economy and the foreign
economy.
is a
stationary shock that measures the degree of asymmetry in the
technological level between the domestic economy and the foreign
economy.
The exogenous shocks of the model are AR(1) given by the representation
where
![]() is i.i.d. and
is i.i.d. and
![]() ,
for
,
for
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and
![]() .
Furthermore, as discussed in ALLV [3], for estimation purposes it
is convenient to rescale the markup shock
.
Furthermore, as discussed in ALLV [3], for estimation purposes it
is convenient to rescale the markup shock
![]()
![]() in the
Phillips curves so as to include the coefficient
in the
Phillips curves so as to include the coefficient
![]() in the markup shock. Then the new coefficient on them in the
Phillips curve is unity. Similarly, we rescale the investment
specific technology shock
in the markup shock. Then the new coefficient on them in the
Phillips curve is unity. Similarly, we rescale the investment
specific technology shock
![]() , the labor supply shock
, the labor supply shock
![]() , and the consumption
preference shock
, and the consumption
preference shock
![]() , so that these shocks enter in
an additive fashion as well.26
, so that these shocks enter in
an additive fashion as well.26
The fiscal policy variables are assumed to be exogenously given
by an identified VAR model with two lags and an uninformative
prior. Let
![]() , where
, where
![]() denotes HP-detrended government
expenditures. The fiscal policy VAR(2)-model is given by
denotes HP-detrended government
expenditures. The fiscal policy VAR(2)-model is given by
| (A.11) |
where
![]()
![]() is a diagonal matrix with the
standard deviations, and
is a diagonal matrix with the
standard deviations, and
![]() .
.
The foreign economy is exogenously given by an identified VAR model with four lags using an uninformative prior,
| (A.12) |
where
![]() , where
, where
![]() and
and
![]() are quarterly foreign inflation
and interest rates, and
are quarterly foreign inflation
and interest rates, and
![]() is foreign output;
is foreign output;
![]()
![]() is a diagonal matrix with the
standard deviations; and
is a diagonal matrix with the
standard deviations; and
![]() .27 When estimating the VAR, we assume
and do not reject that
.27 When estimating the VAR, we assume
and do not reject that ![]() in
in
![]() has the following structure
has the following structure
![\begin{displaymath} \Phi_{0}\equiv\left[ \begin{array}[c]{ccc} 1 & 0 & 0\ 0 & 1 & 0\ -\gamma_{\pi0}^{\ast} & -\gamma_{y0}^{\ast} & 1 \end{array}\right] . \end{displaymath}](img678.gif)
The model can then be written on the form (21), where the specification of the predetermined
variables ![]() , the forward-looking variables
, the forward-looking variables
![]() , the policy instrument
, the policy instrument ![]() , and the shock vector
, and the shock vector
![]() can be found in the
technical appendix [1].
can be found in the
technical appendix [1].
B. Optimal Projections in Some Detail
B.1 Information and Data
First we clarify the information assumptions underlying the
conditional expectation
![]() used in the loss function
used in the loss function
![]() . Let
. Let
![]() where
where
![]() denotes the information set
in period
denotes the information set
in period ![]() . In the standard and simple case when
all variables are observed, we can specify
. In the standard and simple case when
all variables are observed, we can specify
This can be interpreted as information in the beginning of
period ![]() . We can understand this as the agents of
the model (the central bank, the private sector, the fiscal
authority, and the rest of the world) entering the beginning of
period
. We can understand this as the agents of
the model (the central bank, the private sector, the fiscal
authority, and the rest of the world) entering the beginning of
period ![]() with the knowledge of past realizations of
shocks, variables, and instruments,
with the knowledge of past realizations of
shocks, variables, and instruments,
![]() ,...28 Then, at the beginning of period
,...28 Then, at the beginning of period
![]() , the shock
, the shock
![]() is realized and observed,
and
is realized and observed,
and ![]() is determined by (2.22) and observed. We also assume that the agents know
the model, including the matrices
is determined by (2.22) and observed. We also assume that the agents know
the model, including the matrices ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
and
,
and ![]() and the scalar
and the scalar ![]() , so
either
, so
either
![]() or
or ![]() is
sufficient for inferring the other from (2.22),
given that previous realizations are known. Then the central bank
determines, announces, and implements its instrument setting,
is
sufficient for inferring the other from (2.22),
given that previous realizations are known. Then the central bank
determines, announces, and implements its instrument setting,
![]() , which is hence observed by the other
agents. After this, the expectations
, which is hence observed by the other
agents. After this, the expectations ![]() are formed, and
are formed, and ![]() is determined by (2.24).29 In equilibrium, both
is determined by (2.24).29 In equilibrium, both ![]() and
and ![]() will be a function of
will be a function of
![]() and previous realizations of
and previous realizations of
![]() , consistent with this specification of
the information set.
, consistent with this specification of
the information set.
However, Ramses makes more elaborate and realistic information
assumptions as shown in section 5.1. The variables ![]() and
and
![]() include (serially correlated) shocks
and some other unobservable variables for which no data exists.
Furthermore, the elements of
include (serially correlated) shocks
and some other unobservable variables for which no data exists.
Furthermore, the elements of ![]() ,
, ![]() , and
, and ![]() are in many cases quarterly
averages, which have not been realized until the end of quarter
are in many cases quarterly
averages, which have not been realized until the end of quarter
![]() .
.
B.2 Solving for the Optimal Projection
As shown in Svensson [30], the
![]() first-order conditions
for minimizing (2.18) under
commitment subject to (21) can be written
first-order conditions
for minimizing (2.18) under
commitment subject to (21) can be written
![$\displaystyle \bar{A}^{\prime}\left[ \begin{array}[c]{c} \xi_{t+1\vert t}\\ \Xi_{t} \end{array} \right] =\bar{W}\left[ \begin{array}[c]{c} X_{t}\\ x_{t}\\ i_{t} \end{array} \right] +\frac{1}{\delta}\bar{H}^{\prime}\left[ \begin{array}[c]{c} \xi_{t}\\ \Xi_{t-1} \end{array} \right] ,$](img723.gif) |
(B.1) |
where the elements of the ![]() -vector
-vector
![]() are the Lagrange multipliers for
the upper block of (2.21) (the dating of
are the Lagrange multipliers for
the upper block of (2.21) (the dating of
![]() emphasizes that this is a
restriction that applies in period
emphasizes that this is a
restriction that applies in period ![]() ), the
elements of the
), the
elements of the ![]() -vector
-vector ![]() are the Lagrange multipliers for the lower block of (2.21) (the dating of
are the Lagrange multipliers for the lower block of (2.21) (the dating of ![]() emphasizes
that this is restriction that applies in period
emphasizes
that this is restriction that applies in period ![]() ), and the matrices
), and the matrices ![]() ,
, ![]() , and
, and ![]() are defined by
are defined by
| (B.2) |
The first-order conditions can be combined with the
![]() model equations (2.21) to get a system of
model equations (2.21) to get a system of
![]() difference equations
for
difference equations
for ![]() ,
,
![$\displaystyle \left[ \begin{array}[c]{cc} \bar{H} & 0\\ 0 & \bar{A}^{\prime} \end{array} \right] \left[ \begin{tabular}[c]{c} $X_{t+1}$\\ $x_{t+1\vert t}$\\ $i_{t+1\vert t}$\\ \hline $\xi_{t+1\vert t}$\\ $\Xi_{t}$ \end{tabular} \ \right] =\left[ \begin{array}[c]{cc} \bar{A} & 0\\ \bar{W} & \frac{1}{\delta}\bar{H}^{\prime} \end{array} \right] \left[ \begin{tabular}[c]{c} $X_{t}$\\ $x_{t}$\\ $i_{t}$\\ \hline $\xi_{t}$\\ $\Xi_{t-1}$ \end{tabular} \ \right] +\left[ \begin{tabular}[c]{c} $C$\\ $0$\\ \hline $0$\\ $0$ \end{tabular} \ \right] \varepsilon_{t+1}.$](img739.gif) |
(B.3) |
Here, ![]() and
and ![]() are
predetermined variables (
are
predetermined variables (
![]() in total), and
in total), and ![]() ,
, ![]() , and
, and ![]() are
non-predetermined variables (
are
non-predetermined variables (
![]() in total). This system can
be rewritten as
in total). This system can
be rewritten as
![$\displaystyle \left[ \begin{array}[c]{c} \tilde{H}_{11}y_{1,t+1}+\tilde{H}_{12}y_{2,t+1\vert t}\\ \tilde{H}_{21}y_{1,t+1\vert t}+\tilde{H}_{22}y_{2,t+1\vert t} \end{array} \right] =\left[ \begin{array}[c]{cc} \tilde{A}_{11} & \tilde{A}_{12}\\ \tilde{A}_{21} & \tilde{A}_{22} \end{array} \right] \left[ \begin{array}[c]{c} y_{1t}\\ y_{2t} \end{array} \right] +\left[ \begin{array}[c]{c} \tilde{C}\\ 0 \end{array} \right] \varepsilon_{t+1},$](img747.gif) |
(B.4) |
where
![]() is the vector of predetermined variables and
is the vector of predetermined variables and
![]() is the vector of non-predetermined variables. The matrices are
defined as
is the vector of non-predetermined variables. The matrices are
defined as
![\begin{displaymath} \tilde{H}_{11}\equiv\left[ \begin{array}[c]{cc} I & 0\ 0 & A_{22}^{\prime} \end{array}\right] ,\ \ \tilde{H}_{12}\equiv\left[ \begin{array}[c]{ccc} 0 & 0 & 0\ 0 & 0 & A_{12}^{\prime} \end{array}\right] ,\ \ \tilde{H}_{21}\equiv\left[ \begin{array}[c]{cc} 0 & 0\ 0 & A_{21}^{\prime}\ 0 & B_{2}^{\prime} \end{array}\right] ,\ \ \tilde{H}_{22}\equiv\left[ \begin{array}[c]{ccc} H & 0 & 0\ 0 & 0 & A_{11}^{\prime}\ 0 & 0 & B_{1}^{\prime} \end{array}\right] , \end{displaymath}](img750.gif)
![\begin{displaymath} \tilde{A}_{11}\equiv\left[ \begin{array}[c]{cc} A_{11} & 0\ \bar{W}_{xX} & \frac{1}{\delta}H^{\prime} \end{array}\right] ,\ \ \tilde{A}_{12}\equiv\left[ \begin{array}[c]{ccc} A_{12} & B_{1} & 0\ \bar{W}_{xx} & \bar{W}_{xi} & 0 \end{array}\right] ,\ \ \tilde{A}_{21}\equiv\left[ \begin{array}[c]{cc} A_{21} & 0\ \bar{W}_{XX} & 0\ \bar{W}_{iX} & 0 \end{array}\right] , \end{displaymath}](img751.gif)
![\begin{displaymath} \tilde{A}_{22}\equiv\left[ \begin{array}[c]{ccc} A_{22} & B_{2} & 0\ \bar{W}_{Xx} & \bar{W}_{Xi} & \frac{1}{\delta}I\ \bar{W}_{ix} & \bar{W}_{ii} & 0 \end{array}\right] ,\ \ \tilde{C}\equiv\left[ \begin{array}[c]{c} C\ 0 \end{array}\right] . \end{displaymath}](img752.gif)
The solution to (B.4) can be written
| (B.5) | ||
| (B.6) |
for ![]() , where
, where
![]() is given. We note that our assumption that
is given. We note that our assumption that ![]() is
nonsingular implies that
is
nonsingular implies that
![]() is nonsingular.
is nonsingular.
B.3 Determination of the Initial Lagrange Multipliers
As discussed in Svensson [29, Appendix A],30 the value of the
initial Lagrange multiplier,
![]() , is zero, if there is commitment
from scratch in period
, is zero, if there is commitment
from scratch in period ![]() , that is, if any previous
commitment is disregarded. This reflects a time-consistency problem
when there is reoptimization and recommitment in later periods, as
is inherently the case in practical monetary policy. Instead, we
assume that the optimization is under commitment in a timeless
perspective. Then the commitment is considered having occurred some
time in the past, and the initial value of the Lagrange multiplier
satisfies
, that is, if any previous
commitment is disregarded. This reflects a time-consistency problem
when there is reoptimization and recommitment in later periods, as
is inherently the case in practical monetary policy. Instead, we
assume that the optimization is under commitment in a timeless
perspective. Then the commitment is considered having occurred some
time in the past, and the initial value of the Lagrange multiplier
satisfies
| (B.7) |
where
![]() denotes the Lagrange
multiplier of the lower block of (5.2) for the determination of
denotes the Lagrange
multiplier of the lower block of (5.2) for the determination of
![]() in the decision problem in
period
in the decision problem in
period ![]() . The dependence of the optimal policy
projection in period
. The dependence of the optimal policy
projection in period ![]() on this Lagrange multiplier
from the decision problem in the previous period makes the optimal
policy projection depend on previous projections and illustrates
the history dependence of optimal policy under commitment in a
forward-looking model shown in Backus and Driffill [9] and Currie
and Levine [13] and especially examined and emphasized in Woodford
[39].
on this Lagrange multiplier
from the decision problem in the previous period makes the optimal
policy projection depend on previous projections and illustrates
the history dependence of optimal policy under commitment in a
forward-looking model shown in Backus and Driffill [9] and Currie
and Levine [13] and especially examined and emphasized in Woodford
[39].
We now discuss how to compute the initial Lagrange multiplier,
![]() when no explicit optimization
was done in previous periods. In doing so, we assume that past
policy has been optimal.31
when no explicit optimization
was done in previous periods. In doing so, we assume that past
policy has been optimal.31
Note that (5.8) and (B.5) imply that, in real time, the Lagrange multiplier
![]() satisfies
satisfies
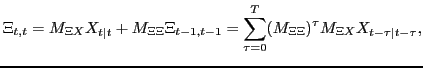
if the commitment occurred from scratch in period ![]() , so
, so
![]() . Here
. Here ![]() is partitioned conformably with
is partitioned conformably with ![]() and
and
![]() so
so
Recall that that ![]() will depend on the weight matrix
will depend on the weight matrix
![]() in the period loss function and hence vary
with the assumed or estimated loss function.
in the period loss function and hence vary
with the assumed or estimated loss function.
Given this, one possible initial value for
![]() is
is
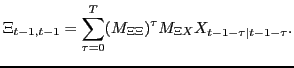 |
(B.8) |
This treats estimated realized
![]() (
(
![]() as resulting from optimal
policy under commitment. The lag
as resulting from optimal
policy under commitment. The lag ![]() may be chosen such
that
may be chosen such
that
![]() is sufficiently
small.
is sufficiently
small.
B.4 Projections with an Arbitrary Instrument Rule
With a constant (that is, time-invariant) arbitrary instrument rule, the instrument rate satisfies
for ![]() , where the
, where the
![]() matrix
matrix
![]() is a given (linear)
instrument rule and partitioned conformably with
is a given (linear)
instrument rule and partitioned conformably with ![]() and
and ![]() .32 If
.32 If
![]() , the instrument rule is an
explicit instrument rule; if
, the instrument rule is an
explicit instrument rule; if
![]() , the instrument rule is an
implicit instrument rule. In the latter case, the instrument
rule is actually an equilibrium condition, in the sense that in a
real-time analogue the instrument rate in period
, the instrument rule is an
implicit instrument rule. In the latter case, the instrument
rule is actually an equilibrium condition, in the sense that in a
real-time analogue the instrument rate in period ![]() and the forward-looking variables in period
and the forward-looking variables in period ![]() would
be simultaneously determined.
would
be simultaneously determined.
An arbitrary more general (linear) policy rule ![]() can be written as
can be written as
| (B.9) |
where the
![]() matrix
matrix
![]() is
partitioned conformably with
is
partitioned conformably with ![]() and
and
![]() and the
and the
![]() matrix
matrix
![]() is
partitioned conformably with
is
partitioned conformably with ![]() ,
, ![]() , and
, and ![]() . This general policy rules
includes explicit, implicit, and forecast-based instrument rules
(in the latter the instrument rate depends on expectations of
future forward-looking variables,
. This general policy rules
includes explicit, implicit, and forecast-based instrument rules
(in the latter the instrument rate depends on expectations of
future forward-looking variables, ![]() ) as well as targeting rules (conditions on
current or expected future target variables). When this general
policy rule is an instrument rule, we require the
) as well as targeting rules (conditions on
current or expected future target variables). When this general
policy rule is an instrument rule, we require the
![]() matrix
matrix ![]() to be nonsingular, so (B.9) determines
to be nonsingular, so (B.9) determines ![]() for
given
for
given ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
The general policy rule can be added to the model equations
(2.21) to form the new system to be solved. With
the notation
![]() ,
the new system can be written
,
the new system can be written
![\begin{displaymath} \left[ \begin{array}[c]{c} X_{t+1}\ \tilde{H}\tilde{x}_{t+1\vert t} \end{array}\right] =\tilde{A}\left[ \begin{array}[c]{c} X_{t}\ \tilde{x}_{t} \end{array}\right] +\left[ \begin{array}[c]{c} C\ 0_{(n_{x}+n_{i})\times n_{\varepsilon}} \end{array}\right] \varepsilon_{t+1}, \end{displaymath}](img815.gif)
where
![\begin{displaymath} \tilde{H}\equiv\left[ \begin{array}[c]{cc} H & 0\ G_{x} & G_{i} \end{array}\right] ,\ \ \tilde{A}\equiv\left[ \begin{array}[c]{ccc} A_{11} & A_{12} & B_{1}\ A_{21} & A_{22} & B_{2}\ f_{X} & f_{x} & f_{i} \end{array}\right] , \end{displaymath}](img817.gif)
where ![]() is partitioned conformably with
is partitioned conformably with
![]() and
and ![]() and
and
![]() is partitioned conformably with
is partitioned conformably with
![]() ,
, ![]() , and
, and
![]() . The corresponding projection model
can then be written
. The corresponding projection model
can then be written
![\begin{displaymath} \left[ \begin{array}[c]{c} X_{t+\tau+1,t}\ \tilde{H}\tilde{x}_{t+\tau+1,t} \end{array}\right] =\tilde{A}\left[ \begin{array}[c]{c} X_{t+\tau,t}\ \tilde{x}_{t+\tau,t} \end{array}\right] , \end{displaymath}](img825.gif)
for ![]() , where
, where
![]() .
.
Then, (under the usual assumption that the policy rule gives
rise to the standard saddlepoint property for the system's
eigenvalues) there exist matrices ![]() and
and
![]() such that the resulting equilibrium
projection satisfies
such that the resulting equilibrium
projection satisfies
for ![]() , where the matrices
, where the matrices ![]() and
and ![]() depend on
depend on ![]() and
and
![]() , and thereby on
, and thereby on ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
and
,
and ![]() .33
.33
C. Flexprice Equilibrium and Alternative Concepts of Potential Output
Under the assumption of flexible prices and wages and an additional equation that determines nominal variables (inflation, the price level, the exchange rate, or some other nominal variable), the flexprice model can be written
![$\displaystyle \left[ \begin{array}[c]{c} X_{t+1}\\ H^{f}x_{t+1\vert t} \end{array} \right] =A^{f}\left[ \begin{array}[c]{c} X_{t}\\ x_{t}\\ i_{t} \end{array} \right] +\left[ \begin{array}[c]{c} C\\ 0_{n_{x}\times n_{\varepsilon}}\\ 0_{n_{i}\times n_{\varepsilon}} \end{array} \right] \varepsilon_{t+1},$](img849.gif) |
(C.1) |
with the same variables ![]() ,
, ![]() , and
, and ![]() and the same i.i.d. shocks
and the same i.i.d. shocks
![]() as in the sticky-price model
but with the new
as in the sticky-price model
but with the new
![]() matrix
matrix ![]() and
and
![]() matrix
matrix
![]() . There are hence
. There are hence ![]() extra equations added to the lower block of the
equations (the block of equations determining the forward-looking
variables), as many equations as the number of policy instruments.
The discussion here is restricted to the case
extra equations added to the lower block of the
equations (the block of equations determining the forward-looking
variables), as many equations as the number of policy instruments.
The discussion here is restricted to the case ![]() (as is Ramses), so only one equation needs to be
added, such as
(as is Ramses), so only one equation needs to be
added, such as
| (C.2) |
In the latter case,
![\begin{displaymath} H^{f}\equiv\left[ \begin{array}[c]{c} H\ 0_{1\times n_{x}} \end{array}\right] ,\ \ A^{f}\equiv\left[ \begin{array}[c]{ccc} A_{11} & A_{12} & B_{1}\ A_{21} & A_{22} & B_{2}\ 0_{1\times n_{X}} & e_{1} & 0 \end{array}\right] , \end{displaymath}](img862.gif)
where ![]() here denotes a row
here denotes a row ![]() -vector with the first element equal to unity and the
other elements equal to zero (reflecting that domestic inflation,
-vector with the first element equal to unity and the
other elements equal to zero (reflecting that domestic inflation,
![]() , is the first
forward-looking variable).
, is the first
forward-looking variable).
The matrix ![]() has been modified so there is no
effect on the endogenous variables of the four time-varying markups
has been modified so there is no
effect on the endogenous variables of the four time-varying markups
![]() ,
,
![]() , since
these time-varying distortions would introduce undesirable
variation in the difference between the (loglinearized) efficient
and flexprice output. This is achieved by setting the corresponding
elements in
, since
these time-varying distortions would introduce undesirable
variation in the difference between the (loglinearized) efficient
and flexprice output. This is achieved by setting the corresponding
elements in ![]() and
and ![]() equal
to zero. With the same argument one may also want to eliminate the
effect on the endogenous variables of time-varying tax rates.
equal
to zero. With the same argument one may also want to eliminate the
effect on the endogenous variables of time-varying tax rates.
Let
![]() and
and ![]() denote the realizations of the
nonpredetermined and predetermined variables, respectively, in a
flexprice equilibrium for
denote the realizations of the
nonpredetermined and predetermined variables, respectively, in a
flexprice equilibrium for
![]() , where
, where ![]() is
some period in the past with given predetermined variables
is
some period in the past with given predetermined variables
![]() from which we compute the
flexprice equilibrium. The flexprice equilibrium is the solution to
the system of difference equations (C.1) for
from which we compute the
flexprice equilibrium. The flexprice equilibrium is the solution to
the system of difference equations (C.1) for
![]() . It can be written
. It can be written
![$\displaystyle \equiv\left[ \begin{array}[c]{c} x_{t}^{f}\\ i_{t}^{f} \end{array} \right] =F^{f}X_{t}^{f}\ \equiv\ \left[ \begin{array}[c]{c} F_{x}^{f}\\ F_{i}^{f} \end{array} \right] X_{t}^{f},$](img878.gif) |
||
for
![]() , where
, where ![]() and
and
![]() are matrices returned by the Klein
[21] algorithm and
are matrices returned by the Klein
[21] algorithm and
![]() . In particular, one
of the elements of
. In particular, one
of the elements of ![]() (and
(and
![]() ) is
) is
![]() , output in the flexprice
equilibrium. We can therefore write flexprice output in period
, output in the flexprice
equilibrium. We can therefore write flexprice output in period
![]() as
as
where the row vector
![]() is the row of the matrix
is the row of the matrix
![]() that corresponds to output.
that corresponds to output.
C.1 Unconditional Potential Output
Consider now a hypothetical flexprice equilibrium that has
lasted forever, the unconditional flexprice equilibrium. The
hypothetical realization of the predetermined variables in period
![]() , denoted
, denoted
![]() , then satisfies
, then satisfies
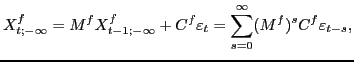
and hence depends on the realizations of the shocks
![]() ,
,
![]() , ... The corresponding
flexprice output is
, ... The corresponding
flexprice output is
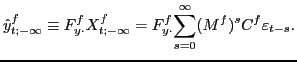 |
(C.3) |
We refer to this output level as unconditional potential output. It hence corresponds to the output level in a hypothetical economy that has always had flexible prices and wages but is subject to the same shocks as the actual economy. It hence has a different capital stock and different realizations of the endogenous both predetermined and nonpredetermined variables compared to the actual economy. It corresponds to the natural rate of output consistent with the definition of the natural rate of interest in Neiss and Nelson [22].
C.2 Conditional Potential Output
Consider also the hypothetical situation in which prices and
wages in the actual economy unexpectedly become flexible in the
current period ![]() and are then expected to remain
flexible forever. The corresponding flexprice output in this
economy is denoted
and are then expected to remain
flexible forever. The corresponding flexprice output in this
economy is denoted
![]() and given by
and given by
| (C.4) |
We refer to this output level as conditional potential output (conditional on prices and wages becoming flexible in the same period and therefore conditional on the existing predetermined variables, including the capital stock). It corresponds to the definition of the natural rate of output presented in Woodford [39, section 5.3.4].
We then realize that we can define
conditional-![]() potential output,
where
potential output,
where
![]() refers to prices and wages
unexpectedly becoming flexible and expected to remain flexible
forever in period
refers to prices and wages
unexpectedly becoming flexible and expected to remain flexible
forever in period ![]() , that is,
, that is, ![]() periods before
periods before ![]() . This concept of potential output
is denoted
. This concept of potential output
is denoted
![]() and is given
by
and is given
by
![$\displaystyle \hat{y}_{t;t-h}^{f}\equiv F_{y\cdot}^{f}X_{t;t-h}^{f}\equiv F_{y\cdot} ^{f}(M^{f}X_{t-1;t-h}^{f}+C^{f}\varepsilon_{t})\equiv F_{y\cdot}^{f} [(M^{f})^{h}X_{t-h}+\sum\limits_{s=0}^{h-1}(M^{f})^{s}C^{f}\varepsilon _{t-s}].$](img907.gif) |
(C.5) |
Conditional-![]() potential output hence depends on the
state of the economy (the predetermined variables) in period
potential output hence depends on the
state of the economy (the predetermined variables) in period
![]() and the shocks from
and the shocks from ![]() to
to ![]() . Conditional-0 potential output is
obviously the same as conditional potential output. Unconditional
potential output is the limit of conditional-
. Conditional-0 potential output is
obviously the same as conditional potential output. Unconditional
potential output is the limit of conditional-![]() potential output when
potential output when ![]() goes to infinity,
goes to infinity,
C.3 Projections of Potential Output
Consider now projections in period ![]() of these
alternative concepts of potential output. The projection in period
of these
alternative concepts of potential output. The projection in period
![]() of unconditional potential output,
of unconditional potential output,
![]() (where
the first subindex,
(where
the first subindex, ![]() , refers to the future
period for which potential output is projected; the second
subindex,
, refers to the future
period for which potential output is projected; the second
subindex, ![]() , indicates that unconditional
potential output is considered; and the third subindex,
, indicates that unconditional
potential output is considered; and the third subindex, ![]() , refers to the period in which the projection is made and
for which information is available), is related to the projection
of the unconditional flexprice predetermined variables,
, refers to the period in which the projection is made and
for which information is available), is related to the projection
of the unconditional flexprice predetermined variables,
![]() , and is given
by
, and is given
by
| (C.6) |
for ![]() , where
, where
![]() denotes the
estimated realization of the unconditional flexprice predetermined
variables in period
denotes the
estimated realization of the unconditional flexprice predetermined
variables in period ![]() conditional on information
available in period
conditional on information
available in period ![]() .
.
Here,
![]() can be estimated
from
can be estimated
from
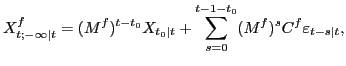 |
(C.7) |
where the unconditional flexprice equilibrium is approximated by a
flexprice equilibrium that starts in a particular period
![]() ,
,
![]() denotes the estimate
conditional on information available in period
denotes the estimate
conditional on information available in period ![]() of the predetermined variables in period
of the predetermined variables in period ![]() ,
and
,
and
![]() denotes the
estimate conditional in information available in period
denotes the
estimate conditional in information available in period ![]() of the realization of the shock in period
of the realization of the shock in period ![]() .
.
The projection in period ![]() of conditional
potential output (that is, conditional-0 potential output),
of conditional
potential output (that is, conditional-0 potential output),
![]() , is
given by
, is
given by
| (C.8) |
for ![]() . Note that the projection of
conditional potential output in period
. Note that the projection of
conditional potential output in period ![]() then
refers to the flexprice output for a flexprice equilibrium that
starts in the future period
then
refers to the flexprice output for a flexprice equilibrium that
starts in the future period ![]() , not in the
current period period
, not in the
current period period ![]() . In the latter case, it
would instead be the projection of conditional-
. In the latter case, it
would instead be the projection of conditional-![]() potential output in period
potential output in period ![]() .
Therefore, the projection of the predetermined variables in period
.
Therefore, the projection of the predetermined variables in period
![]() of the actual economy,
of the actual economy,
![]() , enters in (C.8), not the projection of the
predetermined variables in period
, enters in (C.8), not the projection of the
predetermined variables in period ![]() of the
flexprice equilibrium starting in period
of the
flexprice equilibrium starting in period ![]() ,
,
![]() .
.
The projection in period ![]() of
conditional-
of
conditional-![]() potential output,
potential output,
![]() , is
related to the projection of the conditional-
, is
related to the projection of the conditional-![]() flexprice predetermined variables,
flexprice predetermined variables,
![]() , and is given
by
, and is given
by
| (C.9) |
for ![]() . That is, the projection of the
conditional-
. That is, the projection of the
conditional-![]() predetermined variables in period
predetermined variables in period
![]() enters in (C.9), the predetermined variables in
the flexprice equilibrium that starts
enters in (C.9), the predetermined variables in
the flexprice equilibrium that starts ![]() periods
earlier, in period
periods
earlier, in period ![]() . Furthermore, this
projection is given by
. Furthermore, this
projection is given by
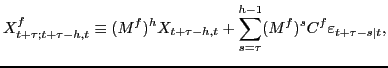
where the summation term is zero when
![]() . Thus, the projection in period
. Thus, the projection in period
![]() of the realization of
conditional-
of the realization of
conditional-![]() potential output in period
potential output in period ![]() ,
,
![]() , depends on
the projection of the predetermined variables in period
, depends on
the projection of the predetermined variables in period ![]() of the actual economy (with sticky prices and
wages),
of the actual economy (with sticky prices and
wages),
![]() , and when
, and when ![]() also on the estimated shocks
also on the estimated shocks
![]() for
for ![]() ,
, ![]() , ...,
, ..., ![]() . (For
. (For
![]() ,
,
![]() ).
).
C.4 Output Gaps
We can then consider several concepts of output gaps: We have
the trend output gap, the gap between actual output and
trend output,
![]() (recall that
(recall that
![]() is the deviation from trend).
For each concept of potential output, we have a corresponding
concept of output gap: The unconditional output gap,
is the deviation from trend).
For each concept of potential output, we have a corresponding
concept of output gap: The unconditional output gap,
the conditional output gap,
and the conditional-![]() output gap,
output gap,
The projections of the different output gaps are then defined in analogy with the projections of the different potential outputs.
References
Adolfson, Malin, Stefan Laséen, Jesper Lindé, and Lars E.O. Svensson (2008a), "Optimal Monetary Policy in an Operational Medium-Sized Model: Technical Appendix," working paper, www.larseosvensson.net.
Adolfson, Malin, Stefan Laséen, Jesper Lindé, and Lars E.O. Svensson (2008b), "Monetary Policy Trade-Offs in an Open-Economy DSGE Model," Sveriges Riksbank Working Paper No. 232, www.riksbank.com.
Adolfson, Malin, Stefan Laséen, Jesper Lindé, and Mattias Villani (2008), "Evaluating an Estimated New Keynesian Small Open Economy Model," Journal of Economic Dynamics and Control 32(8), 2690-2721.
Adolfson, Malin, Stefan Laséen, Jesper Lindé, and Mattias Villani (2007a), "Bayesian Estimation of an Open Economy DSGE Model with Incomplete Pass-Through,", Journal of International Economics 72(2), 481-511.
Adolfson, Malin, Stefan Laséen, Jesper Lindé, and Mattias Villani (2007b), "RAMSES - a New General Equilibrium Model for Monetary Policy Analysis," Sveriges Riksbank Economic Review 2/2007, 5-39, www.riksbank.com.
Adolfson, Malin and Jesper Lindé (![]() ), "Parameter Identification in an Estimated New
Keynesian Open Economy Model", mimeo, Sveriges Riksbank.
), "Parameter Identification in an Estimated New
Keynesian Open Economy Model", mimeo, Sveriges Riksbank.
Adolfson, Malin, Jesper Lindé and Mattias Villani (2007), "Forecasting Performance of an Open Economy DSGE Model", Econometric Reviews 26(2-4), 289-328.
Altig, David, Lawrence Christiano, Martin Eichenbaum and Jesper Lindé (2003), "The Role of Monetary Policy in the Propagation of Technology Shocks," manuscript, Northwestern University.
Backus, David, and John Driffill (1986), "The Consistency of Optimal Policy in Stochastic Rational Expectations Models," CEPR Discussion Paper No. 124.
Calvo, Guillermo (1983), "Staggered Prices in a Utility Maximizing Framework," Journal of Monetary Economics 12, 383-398.
Christiano, Lawrence J., Martin Eichenbaum and Charles Evans (2005), "Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy," Journal of Political Economy 113(1), 1-45.
Christiano, Lawrence J., Mathias Trabandt and Karl Walentin (2011) "Introducing Financial Frictions and Unemployment into a Small Open Economy Model." Sveriges Riksbank Working Paper No. 214, www.riksbank.com.
Currie, David, and Paul Levine (1993), Rules, Reputation and Macroeconomic Policy Coordination, Cambridge University Press.
Del Negro, Marco, Frank Schorfheide, Frank Smets and Raf Wouters (2007), "On the Fit and Forecasting Performance of New Keynesian Models," Journal of Business and Economic Statistics 25(2), 123-143.
Duarte, Margarida, and Alan Stockman (2005), "Rational speculation and exchange rates," Journal of Monetary Economics 52, 3-29.
Erceg, Christopher, Dale Henderson and Andrew Levin, (2000) "Optimal Monetary Policy with Staggered Wage and Price Contracts," Journal of Monetary Economics 46(2), 281-31.
Justiniano, Alejandro and Bruce Preston (2010), "Can Structural Small Open Economy Models Account for the Influence of Foreign Disturbances," Journal of International Economics 81(1), 61-74.
Laséen, Stefan, and Lars E.O. Svensson (2009), "Anticipated Instrument-Rate Paths in Policy Simulations," working paper, www.larseosvensson.net.
Lindé, Jesper (2003), "Monetary Policy Shocks and Business Cycle Fluctuations in a Small Open Economy: Sweden 1986-2002", Sveriges Riksbank Working Paper No. 153, www.riksbank.com.
Levin, Andrew T., Alexei Onatski, John C. Williams, Noah Williams (2005), "Monetary Policy Under Uncertainty in Micro-Founded Macroeconometric Models", in eds. Gertler, Mark and Kenneth Rogoff, NBER Macroeconomics Annual, 229-312.
Klein, Paul (2000), "Using the Generalized Schur Form to Solve a Multivariate Linear Rational Expectations Model," Journal of Economic Dynamics and Control 24, 1405-1423.
Neiss, Katherine S., and Edward Nelson (2003), "The Real Interest Rate Gap as an Inflation Indicator," Macroeconomic Dynamics 7, 239-262.
Onatski, Alexei, and Noah Williams (2003), "Modeling Model Uncertainty," Journal of the European Economic Association 1, 1087-1022.
Schmitt-Grohé, Stephanie and Martín Uribe (2001), "Stabilization Policy and the Cost of Dollarization," Journal of Money, Credit, and Banking 33(2), 482-509
Sims, Christopher A. (2000), "Solving Linear Rational Expectations Models," www.princeton.edu/~sims/.
Smets, Frank and Raf Wouters (2003), "An Estimated Stochastic Dynamic General Equilibrium Model of the Euro Area," Journal of the European Economic Association 1(5), 1123-1175.
Smets, F. and R. Wouters (2007), "Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach," American Economic Review 97(3), 586-606.
Söderlind, Paul (1999), "Solution and Estimation of RE Macromodels with Optimal Policy," European Economic Review 43, 813-823. Related software available at home.tiscalinet.ch/paulsoderlind.
Svensson, Lars E.O. (2005), "Monetary Policy with Judgment: Forecast Targeting," International Journal of Central Banking 1(1), 1-54, www.ijcb.org.
Svensson, Lars E.O. (2007), "Optimization under Commitment and Discretion, the Recursive Saddlepoint Method, and Targeting Rules and Instrument Rules: Lecture Notes," www.larseosvensson.net.
Svensson, Lars E.O. (2010), "Inflation Targeting," in Friedman, Benjamin M., and Michael Woodford, eds., Handbook of Monetary Economics, Volume 3a and 3b, North-Holland, forthcoming.
Svensson, Lars E.O. (2007), "Potential and Efficient Output," research notes.
Svensson, Lars E.O., and Noah Williams (2007a), "Monetary Policy with Model Uncertainty: Distribution Forecast Targeting," working paper, www.larseosvensson.net.
Svensson, Lars E.O., and Noah Williams (2007b), "Bayesian and Adaptive Optimal Policy under Model Uncertainty," working paper, www.larseosvensson.net.
Svensson, Lars E.O., and Robert J. Tetlow (2005), "Optimal Policy Projections," International Journal of Central Banking 1(3), 177-207, www.ijcb.org.
Svensson, Lars E.O., and Michael Woodford (2004), "Indicator Variables for Optimal Policy under Asymmetric Information," Journal of Economic Dynamics and Control 28, 661-690.
Sveriges Riksbank (2010), Monetary Policy in Sweden, www.riksbank.se.
Wolden Bache, Ida, Leif Brubakk, and Junior Maih (2008), "Estimating a DSGE Model for Norway with Optimal Monetary Policy," working paper, Norges Bank.
Woodford, Michael (2003), Interest Rates and Prices, Princeton University Press.
Footnotes
1. We are grateful for helpful comments from Günter Coenen, Lee Ohanian, Frank Smets, and participants in the Second Oslo Workshop on Monetary Policy, the Central Bank Workshop on Macroeconomic Modelling, Oslo, the conference on New Perspectives on Monetary Policy Design, Barcelona, the Lindahl Lectures, Uppsala, the conference on Quantitative Approaches to Monetary Policy in Open Economies, Atlanta, and seminars at the Riksbank and the Institute for International Economic Studies. All remaining errors are ours. The views, analysis, and conclusions in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of those of other members of the Riksbank's staff or executive board, or the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1a. Sveriges Riksbank Return to text
1b. Federal Reserve Board Return to text
1c. Sveriges Riksbank, Stockholm University, CEPR, and NBER Return to text
2. In some simple models, quadratic approximations of the welfare of a representative household results in a similar period loss function (Woodford [39]). Such approximations of household welfare are very model-dependent and reflect the particular distortions assumed in any given model. Household welfare is in any case hardly an operational central-bank objective, although it may be of interest and relevant to examine how household welfare in particular models is affected by central-bank policy. Such an undertaking is beyond the scope of the present paper, though. Return to text
3. The inflation-targeting period is assumed to start 1993:1 (the estimation sample in this paper ends 2007:3). Prior to this period (1986:1-1992:4), the conduct of policy is assumed to be given by a simple instrument rule. The switch to the inflation-targeting regime in 1993:1 is assumed to be completely unanticipated but expected to be permanent once it has occurred. Return to text
4. Total
export demand satisfies
![$ C_{t}^{x}+I_{t}^{x}=\left[ \frac{P_{t}^{x} }{P_{t}^{\ast}}\right] ^{-\eta_{f}}Y_{t}^{\ast}$](img54.gif) , where
, where ![]() and
and ![]() is
demand for consumption and investment goods, respectively;
is
demand for consumption and investment goods, respectively;
![]() the export price;
the export price;
![]() the foreign price level;
the foreign price level;
![]() foreign output and
foreign output and ![]() the elasticity of substitution across foreign
goods
the elasticity of substitution across foreign
goods![]() Return to
text
Return to
text
5. For the
households that are not allowed to reoptimize, the indexation
scheme is
![]() , where
, where
![]() is an indexation
parameter. Return to text
is an indexation
parameter. Return to text
6. We use the 4-quarter CPI difference as a target variable rather than quarterly inflation since the Riksbank and other inflation-targeting central banks normally specify their inflation target as a 12-month rate. Return to text
7. As reported in ALLV [3], the output gap resulting from trend output seems to more closely correspond to the measure of resource utilization that the Riksbank has been responding to historically rather than the unconditional output gap. Del Negro, Schorfheide, Smets, and Wouters [14] report similar results for the US. Return to text
8. A
variable is predetermined if its one-period-ahead prediction error
is an exogenous stochastic process (Klein [21]). For (2.21), the one-period-ahead prediction error of the
predetermined variables is the stochastic vector
![]() . Return to text
. Return to text
9. Onatski and Williams [23] provide a thorough discussion of model uncertainty. Svensson and Williams [33] and [34] show how to compute optimal policies for Markov Jump-Linear-Quadratic systems, which provide a quite flexible way to model most kinds of relevant model uncertainty for monetary policy. Levin, Onatski, Williams and Williams [20] study optimal policy when the central bank faces uncertainty about the true structure of the economy (i.e., they look at the entire posterior distribution of the model parameters). Return to text
10. Without
loss of generality, we assume that the shocks
![]() only enter in the upper
block of (2.21), since any shocks in the lower
block of (2.21) can be redefined as additional
predetermined variables and introduced in the upper
block. Return to text
only enter in the upper
block of (2.21), since any shocks in the lower
block of (2.21) can be redefined as additional
predetermined variables and introduced in the upper
block. Return to text
11. See Svensson [29] and [30] for details of the derivation and the application of the Klein algorithm. Return to text
12. All data are from Statistics Sweden, except the repo rate which is from the Riksbank. The nominal wage is deflated by the GDP deflator. Foreign inflation, output, and interest rate are weighted together across Sweden's 20 largest trading partners in 1991 using weights from the IMF. Return to text
13. In the
data, the ratios of import and export to output are increasing from
about ![]() to
to ![]() and from
and from
![]() to
to ![]() , respectively,
during the sample period. In the model, import and export are
assumed to grow at the same rate as output. We have removed the
excess trend in import and export in the data to make the export
and import shares stationary. For all other variables we use the
actual series (seasonally adjusted with the X12-method, except the
variables in the GDP identity which were seasonally adjusted by
Statistics Sweden). Return to
text
, respectively,
during the sample period. In the model, import and export are
assumed to grow at the same rate as output. We have removed the
excess trend in import and export in the data to make the export
and import shares stationary. For all other variables we use the
actual series (seasonally adjusted with the X12-method, except the
variables in the GDP identity which were seasonally adjusted by
Statistics Sweden). Return to
text
14. The reason why we use a smooth HP-filtered trend for hours per capita, as opposed to a constant mean, is that there is a large and very persistent reduction in hours worked per capita during the recession in the beginning of the 1990s. Neglecting taking this reduction into account implies that the forecasting performance for hours per capita in the model deteriorates significantly, as documented in the forecasting exercises in ALLV [3]. Rather than imposing a discrete shift in hours in a specific time period, we therefore decided to remove a smooth HP trend from the variable. This choice is not particularly important for the parameter estimates, but has some impact on the 2-sided filtered estimates of the unobserved states of the economy. Return to text
15. We use
the Kalman filter to calculate the likelihood function of the
observed variables. The period 1980:1-1985:4 is used to form a
prior on the unobserved state variables in 1985:4, and the period
1986:1-2007:3 is used for inference. During estimation the Lagrange
multipliers, ![]() are updated through the Kalman
filter just as the other state variables. When the instrument rule
is active
are updated through the Kalman
filter just as the other state variables. When the instrument rule
is active ![]() equals zero, and in 1993:1, when
policy (unexpectedly) switches to minimizing the loss function, we
assume commmitment from scratch so that the initial Lagrange
multipliers are zero. Return to text
equals zero, and in 1993:1, when
policy (unexpectedly) switches to minimizing the loss function, we
assume commmitment from scratch so that the initial Lagrange
multipliers are zero. Return to text
16. We
choose to calibrate those parameters that we think are weakly
identified by the variables that we include in the vector of
observed data. These parameters are mostly related to the
steady-state values of the observed variables (that is, the great
ratios: ![]() ,
, ![]() , and
, and ![]() ). The parameters that we calibrate are set as follows:
the money growth
). The parameters that we calibrate are set as follows:
the money growth
![]() ; the discount factor
; the discount factor
![]() ; the steady state growth rate
of productivity
; the steady state growth rate
of productivity
![]() ; the depreciation rate
; the depreciation rate
![]() ; the capital share in
production
; the capital share in
production
![]() ; the share of imports in
consumption and investment
; the share of imports in
consumption and investment
![]() and
and
![]() , respectively; the share of
wage bill financed by loans
, respectively; the share of
wage bill financed by loans ![]() ; the labour
supply elasticity
; the labour
supply elasticity
![]() ; the wage markup
; the wage markup
![]() ; inflation target
persistence
; inflation target
persistence
![]() ; the steady-state tax rates
on labour income and consumption
; the steady-state tax rates
on labour income and consumption
![]() and
and
![]() , respectively; government
expenditures-output ratio
, respectively; government
expenditures-output ratio ![]() ; and the
subsitution elasticity between consumption goods
; and the
subsitution elasticity between consumption goods
![]() . Return to text
. Return to text
17. The estimations are based on allowing the inflation target to be time-varying. The parameter estimates are, however, robust to keeping the inflation target fixed at 2% during the the inflation-targeting period. Return to text
18. It should be noted that data are informative about the parameters as the posteriors are often different, and more concentrated, than the prior distributions. Moreover, Adolfson and Lindé [6] use Monte Carlo methods to study identification in a very similar model, and find that while a few parameters are weakly identified in small samples, all parameters are unbiased and consistent. Return to text
19. Thus,
the estimated/expected shock
![]() and
and
![]() for
for ![]() are zero, whereas the estimated shocks
are zero, whereas the estimated shocks
![]() and
and
![]() for
for ![]() are given by
are given by
![]() and
and
![]() , and are normally nonzero. Return to text
, and are normally nonzero. Return to text
20. It
should be noted that the setup here differs compared to what was
used in, for example, ALLV [3] and [5], which examine forecasts
using an instrument rule. There uncertainty about both parameters,
the current state of the economy, the sequence of future shocks as
well as the measurement errors were allowed for (see Adolfson,
Lindé and Villani [7] for a description). However, this
uncertainty is additive so certainty equivalence holds. Also our
timing convention for the projections differs. In ALLV [3], [5],
and [7] it is assumed that the projections are carried out at the
end of period ![]() (using the estimated instrument rule).
That is,
(using the estimated instrument rule).
That is, ![]() is observed and considered to be known
at the time of the projection in ALLV [3], [5], and
[7]. Return to text
is observed and considered to be known
at the time of the projection in ALLV [3], [5], and
[7]. Return to text
21. Policy projections when monetary policy is characterized by a simple instrument rule are described in appendix B. Return to text
22. As discussed in Woodford [39] and Svensson [30] and [31], optimization under commitment in a timeless perspective allows optimal policy that is consistent over time. Svensson [31] also discusses optimal projections under discretion. Return to text
23. See appendix B.3 for a discussion about alternative methods to calculate the initial Lagrange multipliers. Return to text
24. Christiano, Trabandt and Walentin [12] estimate a similar model to ours extended with financial frictions on Swedish data and find that shocks stemming from the financial sector indeed contributed significantly to the contraction in output during 2008-2009. A variant of their model has recently replaced the version of Ramses we consider in the policy process at the Riksbank. Return to text
25. It should, however, be noted that the results do not change much to setting the Lagrange multipliers to zero. Return to text
26. Although
this is not of any major importance for the baseline estimation of
the model in ALLV [3], it is important when carrying out the
sensitivity analysis there because the effective prior standard
deviation of the shocks changes with the value of the nominal and
real friction parameters. Smets and Wouters [27] adopt the same
strategy. Therefore, to obtain the size of the four truly
fundamental markup shocks, the estimated standard deviations
reported in table ![]() should be divided by
their respective scaling parameter (for instance,
should be divided by
their respective scaling parameter (for instance,
![]() in the case of the domestic markup shock). Return to text
in the case of the domestic markup shock). Return to text
27. The reason why we include foreign output HP-detrended and not in growth rates in the VAR is that the foreign output gap enters the log-linearized model (for instance, in the aggregate resource constraint). This also enables identification of the asymmetric technology shock. Return to text
28. Only the
linear combination
![]() of the shocks
of the shocks
![]() matters, not the individal
shocks
matters, not the individal
shocks
![]() . Return to text
. Return to text
29. More
precisely, the expectations ![]() and
and
![]() are simultaneously
determined. Return to
text
are simultaneously
determined. Return to
text
30. The appendix is availabale at www.larseosvensson.net. Return to text
31. In the working paper version of the paper, we also consider another method which assumes that past policy has been systematic but not necessarily optimal. This method seems less restrictive but is not used in this paper. Return to text
32. For projections with arbitrary time-varying policy rules, see Laséen, and Svensson [18]. Return to text
33. Equivalently, the resulting equilibrium projection
satisfy
![\begin{displaymath} \left[ \begin{array}[c]{c} \check{X}_{t+\tau+1,t}\ \check{x}_{t+\tau+1,t}\ \check{i}_{t+\tau+1,t} \end{array}\right] =\bar{B}\left[ \begin{array}[c]{c} \check{X}_{t+\tau,t}\ \check{x}_{t+\tau,t}\ \check{i}_{t+\tau,t} \end{array}\right] \end{displaymath}](img843.gif)
![$\displaystyle \left[ \begin{array}[c]{c} \check{x}_{t,t}\\ \check{i}_{t,t} \end{array} \right]$](img847.gif)
|
![$\displaystyle =\left[ \begin{array}[c]{c} \bar{B}_{x}\\ \bar{B}_{i} \end{array} \right] \left[ \begin{array}[c]{c} \check{X}_{t-1,t-1}\\ \check{x}_{t-1,t-1}\\ \check{i}_{t-1,,t-1} \end{array} \right] +\left[ \begin{array}[c]{c} \Phi_{xX}\\ \Phi_{iX} \end{array} \right] (X_{t\vert t}-\check{X}_{t,t-1}).$](img848.gif)
|
Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text