
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1038, December 2011--- Screen Reader
Version*
Exports Versus Multinational Production Under Nominal Uncertainty
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper examines how nominal uncertainty affects the choice firms face to serve a foreign market through exports or to produce abroad as a multinational. I develop a two-country, stochastic general equilibrium model in which firms make production and pricing decisions in advance, and I consider its implications on this relative choice. For foreign firms, both exports and multinational production are priced in the destination currency, and this uncertainty has no effect on the relative decision. In the data, U.S. firms set nearly all of their export prices in dollars. Therefore, home firms price exports in their own currency in the model. Home exporters gain an advantage over home multinationals: during a foreign contraction, the foreign exchange rate appreciates, causing exported goods from the home country to be relatively cheaper. This pricing advantage affects exporters non-linearly through demand, which translates to convex profits. As foreign volatility rises, the model implies that the home country should serve the foreign country relatively more through exports. I take this implication to bilateral U.S. data, using inflation volatility as a proxy for nominal volatility. Using sectoral data on sales by majority-owned foreign affiliates matched with U.S. exports, I find that higher inflation volatility is associated with a significantly lower ratio of multinational production to total foreign sales.
Keywords: Multinational production, international trade, nominal uncertainty, proximity-concentration
JEL classification: F12, F23, F41
1 Introduction
Multinational production plays an important role in how firms serve foreign markets. For a typical major trading partner, sales of foreign affiliates of U.S. firms are greater than exports. This paper considers how nominal uncertainty affects the decision firms make between serving the foreign market through multinational production (MP) or exports. There is strong evidence that U.S. export prices are very sticky and are denominated in dollars. Because multinational production is priced in the foreign currency, this creates an important distinction in how foreign nominal uncertainty affects the choice firms make on the margin.
I develop a model with heterogeneous firms and an endogenous decision to export or set up foreign production. Firms set prices and make production-location decisions in advance, so foreign nominal uncertainty affects expected profits. Nominal uncertainty takes the form of a stochastic money growth rate rule. I show that if both exports and multinational production are priced in the destination currency, nominal uncertainty does not affect the choice of how to serve the destination market. If, as in U.S. data, exports are instead priced in dollars, then exporting becomes relatively more attractive for destinations with higher volatility. The intuition is that given a foreign nominal contraction, an exporter with a price stuck in dollars gains a pricing advantage over an equivalent multinational producer whose price is stuck in the foreign currency. This makes expected profits of exporters more convex in foreign volatility.
Recent work demonstrates that nominal uncertainty is important for understanding international transactions. Schoenle (2010) shows that U.S. export prices are more sticky than domestic U.S. prices, with durations of at least one year on average. Gopinath and Rigobon (2008) provide evidence that nearly all such prices are denominated in U.S. dollars. By contrast, production abroad is likely to be denominated in the local currency. This distinction is crucial for understanding how firms react to differences in nominal uncertainty in the model.
The analysis is based on the canonical Helpman, Melitz and Yeaple (2004) framework of trade and multinational production, extended to a stochastic environment. Firms are heterogeneous in productivity, and they face higher fixed costs to produce abroad than to export. Firms with high productivity find it desirable to produce abroad to avoid per-unit transportation costs. Uncertainty plays a role through the non-linear effects of monetary shocks on expected profits, through demand. This in turn affects the extensive margin of firm participation in each market. I first consider the case of foreign firms, who price both their exports and multinational production in the home currency. Here, nominal uncertainty affects neither the extensive nor intensive margin of exporting relative to multinational production. Then I consider the U.S. (home) case, where exports are priced in the home currency and multinational production is priced in the foreign currency. In this case, exporter profits are more convex in foreign nominal volatility. This in turn implies that as volatility rises, multinational production as a fraction of total foreign sales (multinational production plus exports) falls in the model.
I move on to the empirical evidence. Using bilateral data for U.S. exports and sales by foreign affiliates of U.S. multinationals, I examine the impact of inflation volatility on the relative choice. I find that, as predicted by the model, inflation volatility tends to decrease the share of MP relative to exports. Separating the regressions for each major sector, I find that the coefficient on volatility is significant for information, electrical, food, metals, and transportation manufacturing. Other manufacturing sectors have the expected sign, while mining has a positive and insignificant sign. Since mining is a commodity industry where prices tend to be very flexibly spot-priced, this is unsurprising. The results underscore the importance of sectoral heterogeneity in short-term behavior caused in part by the price-setting characteristics of that sector.
Exchange rate volatility has, if anything, the opposite effect. The coefficient on exchange rate volatility tends to be positive but not statistically significant. This suggests that while the mechanism in the model holds for inflation volatility, there may be additional effects from unexplained exchange rate volatility which may be derived from different underlying shocks. The mechanism in my model simply requires that exchange rate volatility caused by the underlying monetary volatility goes in the modeled direction; that is, a foreign nominal contraction leads to a foreign exchange rate appreciation. Since exchange rate volatility can be caused by a multitude of other sources, the empirical results are consistent with the model. I conclude with a discussion of these results and mechanisms by which exchange rate volatility may have different effects from the nominal volatility typically modeled.
This paper contributes to a recent and rapidly growing literature on understanding the effects of various forms of uncertainty in general equilibrium. Most recent work focuses on real uncertainty, including Ramondo and Rappoport (2010), Irarrazabal and Opromolla (2009), Fillat and Garetto (2010), and Ramondo, Rappoport and Ruhl (2010). These papers study either country or firm-specific uncertainty about productivity under flexible prices. In particular, Ramondo et al. (2010) studies the choice of exporting versus multinational production given aggregate uncertainty about country output. They find that the U.S. exports more to countries with more volatile GDP. In a partial equilibrium context, Giovannini (1988) studies the effects of exchange rates on exports given assumptions about the currency of prices set in advance. Goldberg and Kolstad (1995) examine the production-location decision under a combination of exchange rate and demand shocks, with production capacity set in advance and flexible prices. The main results in that paper are driven by firms having some degree of risk aversion. In more recent general equilibrium work, Russ (2007) analyzes the effects of foreign versus domestic nominal uncertainty on multinational production (and by extension, FDI).1 She demonstrates that while either source of volatility translates to exchange rate volatility, foreign volatility encourages multinational production in the foreign market while domestic volatility deters it. All prices are local-currency priced, and firms cannot export.
This paper differs from the literature in two respects. First, I study nominal uncertainty in the form of inflation volatility. Since we observe substantial price stickiness, as noted earlier, it is important to understand how nominal volatility interacts with this stickiness to affects firms' decisions in general equilibrium. Second, the economic mechanism I propose in this paper is distinct, focusing on the asymmetry in the currency denomination of exports compared to multinational production. Thus, differences in foreign volatility change how domestic firms serve the foreign market.
The rest of the paper is organized as follows. Section 2 presents the overall model environment. Section 3 details how foreign firms serve the home market. Section 4 describes how home firms serve the foreign market. Section 5 introduces the data and estimation strategy for testing the model. Section 6 concludes.
2 Model Setup
Consider an economy with two countries, home and foreign (denoted by an asterisk). Each is inhabited by a representative household which maximizes utility over consumption, labor (leisure), and real money holdings. The countries trade a complete set of state-contingent bonds; thus, the model focuses on the implications of uncertainty on firms. That uncertainty takes the form of an exogenous, stochastic money growth rate.
Firms face fixed costs for producing domestically, exporting, and serving foreign markets via multinational production. Exporters face relatively smaller fixed costs but pay per-unit transportation costs, while multinationals avoid transportation costs and pay higher fixed costs. This structure is the basis of Helpman et al. (2004) and a subsequent literature focusing on static determinants of trade and multinational patterns.
To keep the benchmark model as tractable as possible while being consistent with pricing data, prices are set one period in advance. Trade consists of monopolistically competitive intermediate goods and firms have heterogeneous productivities based on a permanent fixed draw from a productivity distribution. Labor is the only input of production.
In the following sections I lay out in more detail the key components of the model, omitting some detail where possible for brevity. The appendix contains the omitted portions.
2.1 Households
Each country is occupied by a
representative household which maximizes the expected discounted
stream of utility ![]() , choosing consumption
, choosing consumption
![]() , labor supplied
, labor supplied ![]() , bond
holdings
, bond
holdings
![]() , and real money balances
, and real money balances
![]() .
. ![]() denotes the state
of the world and its history up to time
denotes the state
of the world and its history up to time ![]() . For
tractability, assume that utility is separable and of the
form:
. For
tractability, assume that utility is separable and of the
form:
![$\displaystyle \max_{C_t,L_t,M_t,B(s^{t+1})} \sum_{t=0}^\infty \beta^t E_t\left[\frac{C_t^{1 - \rho}}{1 - \rho} - \kappa L_t + \chi\ln \left(\frac{M_t}{P_t}\right) \right].$](img8.gif)
|
(1) |
The home household faces a standard budget constraint:
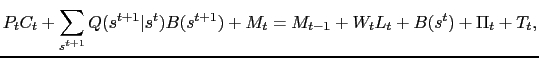
|
where
![]() are the prices of
state-contingent bonds,
are the prices of
state-contingent bonds, ![]() are profits from the
firms households own, and
are profits from the
firms households own, and ![]() are transfers of
seigniorage revenue from changes in the money supply, taken as
given by the representative household. This leads to familiar first
order conditions, shown in the appendix.
are transfers of
seigniorage revenue from changes in the money supply, taken as
given by the representative household. This leads to familiar first
order conditions, shown in the appendix.
The foreign household has an analogous
problem, and the real and nominal exchange rates are solved by
equating the price of state-contingent bonds ![]() and iterating backwards (see , ).
The nominal exchange rate, defined so that an increase represents a
home depreciation, can be expressed as a function entirely of
exogenous variables and parameters (see appendix):
and iterating backwards (see , ).
The nominal exchange rate, defined so that an increase represents a
home depreciation, can be expressed as a function entirely of
exogenous variables and parameters (see appendix):
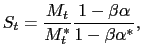
|
where
![$ \alpha \equiv E_t\left[\frac{M_t}{M_{t+1}}\right]$](img15.gif) , the
expected inverse of the money supply growth rate, and
, the
expected inverse of the money supply growth rate, and ![]() is its foreign counterpart. Intuitively, the nominal
exchange rate in any given period depends on the ratio of the money
supplies; an increase in the home currency
is its foreign counterpart. Intuitively, the nominal
exchange rate in any given period depends on the ratio of the money
supplies; an increase in the home currency ![]() leads to
a depreciation (increase in
leads to
a depreciation (increase in ![]() ) of the home
nominal exchange rate. The money growth rate terms are derived from
the real money balance first order condition. As the volatility of
the foreign money growth rate rises, so does
) of the home
nominal exchange rate. The money growth rate terms are derived from
the real money balance first order condition. As the volatility of
the foreign money growth rate rises, so does ![]() . This, all else equal, leads to a higher
. This, all else equal, leads to a higher ![]() (home currency depreciation).2
(home currency depreciation).2
Households consume a basket of domestic and
foreign varieties ![]() through CES aggregation,
with a common elasticity of substitution
through CES aggregation,
with a common elasticity of substitution ![]() :
:
![$\displaystyle C = \left[\int y(i)^{(\theta - 1)/\theta}\, di\right]^{\theta/(\theta - 1)}.$](img23.gif)
|
This implies very standard demand equations for each variety:
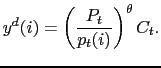
|
(2) |
While there is no explicit home-bias in
preferences over varieties in this setup, transportation costs and
fixed costs will yield lower trade relative to a frictionless
economy. In addition, complete markets and labor entering linearly
in the utility function imply that wages between the two countries
are equalized (
![]() ). Section 2.4 discusses factor
price equalization in more detail.
). Section 2.4 discusses factor
price equalization in more detail.
2.2 Monetary Process
The uncertainty and volatility in the model stem from a stochastic money growth rate rule, found commonly in the literature.3 I assume that the money supply grows at a stochastic log-normal rate with a mean-preserving spread:
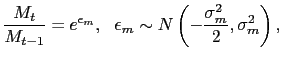
|
with a similar process for the foreign
country. This implies that the inverse of the money growth rate
![]() .4
.4
The comparative static considered in this
paper are changes in the volatility of the foreign money supply,
![]() . Since the paper is focused
on stochastic steady states rather than short-run dynamics
following changes in the money supply, it makes little theoretical
difference to model a money supply growth rate rule as opposed to a
more realistic alternative (e.g. shocks to a Taylor
rule).
. Since the paper is focused
on stochastic steady states rather than short-run dynamics
following changes in the money supply, it makes little theoretical
difference to model a money supply growth rate rule as opposed to a
more realistic alternative (e.g. shocks to a Taylor
rule).
2.3 Intermediate Goods Firms Serving the Local Market
Each country has a potential unit mass of
firms. These firms use one input of production, labor, and their
specific technology ![]() to produce an
intermediate good
to produce an
intermediate good
![]() . To produce for their
local market, firms must pay a per-period fixed cost
. To produce for their
local market, firms must pay a per-period fixed cost ![]() and set their prices in advance of the realization of the
money supply. Firms differ in their productivities
and set their prices in advance of the realization of the
money supply. Firms differ in their productivities ![]() , which completely characterizes the rest of their
decisions. Thus, I omit the variety
, which completely characterizes the rest of their
decisions. Thus, I omit the variety ![]() subscripts
going forward.
subscripts
going forward.
Firms set prices for their local market by solving the following optimization problem:
where
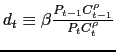 is
the stochastic discount factor of the investors. One can show that
the optimal price choice is then:
is
the stochastic discount factor of the investors. One can show that
the optimal price choice is then:
![$\displaystyle p_t(\phi) = \frac{\theta}{\theta - 1}\frac{1}{\phi}\frac{E_{t-1}\left[d_tW_tP_t^\theta C_t\right]}{E_{t-1}\left[d_tP_t^\theta C_t\right]}.$](img36.gif)
|
Note that if ![]() is
non-stochastic (e.g. if all prices are set in the local currency),
then it may be canceled out of the expectation operators. This
proves crucial in analytically simplifying the expressions for the
foreign country.
is
non-stochastic (e.g. if all prices are set in the local currency),
then it may be canceled out of the expectation operators. This
proves crucial in analytically simplifying the expressions for the
foreign country.
The cutoff of firms serving their own
market is the productivity
![]() above which expected flow profits
exceed the fixed cost:
above which expected flow profits
exceed the fixed cost:
![$\displaystyle E_{t-1}\left[d_t\left(\underbrace{p_{t}(\hat{\phi}_{t})y_{t}(\hat{\phi}_{t})}_{\text{revenue}} - \underbrace{\frac{W_ty_{t}(\hat{\phi}_{t})}{\hat{\phi}_{t}}}_{\text{labor costs}}\right)\right] - E_{t-1}\left[d_t\underbrace{P_tf}_{\text{fixed costs}}\right] = 0.$](img39.gif)
|
Once again, the foreign country has analogous conditions for firms serving its local market.
2.4 A Note on Factor Price Equalization
Factor price equalization holds in the
baseline model because of complete markets and labor entering
linearly in the utility function, as noted by Devereux and Engel (2001). This leads to the first order
conditions
![]() and
and
![]() . Because the real
exchange rate is the ratio of marginal utilities of consumption, it
follows that the nominal exchange rate
. Because the real
exchange rate is the ratio of marginal utilities of consumption, it
follows that the nominal exchange rate
![]() ,
and thus
,
and thus
![]() .
.
One can relax the assumption about complete
markets or the assumption about labor entering linearly. Relaxing
incomplete markets will not provide very large deviations from
factor price equalization, as the exchange rate will follow roughly
similar dynamics (Chari et al. 2002). Labor
entering with an exponent ![]() and
and
![]() , can break factor price
equalization more substantially. Here, the first order conditions
become
, can break factor price
equalization more substantially. Here, the first order conditions
become
![]() . Thus, as more
labor is utilized for a given level of consumption, wages must rise
to compensate households.
. Thus, as more
labor is utilized for a given level of consumption, wages must rise
to compensate households.
While this is certainly a reasonable
assumption, it produces wage dynamics soundly rejected by the data.
Maintaining the assumption of factor price equalization, we have in
logs
![]() . In the
data, the wage-based real exchange rate (from relative unit labor
costs) corresponds to
. In the
data, the wage-based real exchange rate (from relative unit labor
costs) corresponds to
![]() , which is far from
constant, and tracks the nominal exchange rate closely. That is,
, which is far from
constant, and tracks the nominal exchange rate closely. That is,
![]() . With
non-linear labor, the model implies that given a home monetary
expansion, home wages rise more than foreign wages expressed in the
home currency. That is,
. With
non-linear labor, the model implies that given a home monetary
expansion, home wages rise more than foreign wages expressed in the
home currency. That is,
![]() . This
makes nominal wages even more volatile, contrary to the
data.
. This
makes nominal wages even more volatile, contrary to the
data.
3 Foreign Firms Serving the Home Market
Recent empirical evidence by Gopinath and Rigobon (2008) shows that 90% of U.S. imports are priced in dollars. This currency choice is the result of a variety of macroeconomic factors, some of which are the subject of recent work.5 I abstract from this choice and impose it as an assumption for tractability.
Foreign multinationals operating in the home market will also price in the home currency, providing symmetry in the pricing decisions of a foreign exporter and multinational. I consider each pricing decision in turn.6
3.1 Foreign Exporter Price Setting
Consider foreign firms who choose to serve
the foreign market through exports, and denote this price choice
![]() . These firms face per-unit iceberg
transportation costs
. These firms face per-unit iceberg
transportation costs ![]() and per-period fixed
costs
and per-period fixed
costs ![]() paid in advance. The maximization problem
of the firm, omitting firm subscripts, is then:
paid in advance. The maximization problem
of the firm, omitting firm subscripts, is then:
![$\displaystyle \max_{p_{X,t}^*} E_{t-1}\left[d_t^*\left(\tfrac{1}{S_t}p_{X,t}^*y_{X,t}^* - \tau \frac{W_t^*}{\phi}y_{X,t}^*\right)\right].$](img54.gif)
|
Since ![]() is set in the
home currency, this revenue is repatriated with the nominal
exchange rate
is set in the
home currency, this revenue is repatriated with the nominal
exchange rate ![]() . Substituting the demand condition
(2) into the
maximization problem and solving for the optimal price,
. Substituting the demand condition
(2) into the
maximization problem and solving for the optimal price,
![$\displaystyle <tex2html_comment_mark>19 p_{X,t}^*(\phi) = \frac{\theta}{\theta - 1}\frac{1}{\phi}\tau\frac{E_{t-1}\left[d_t^*P_t^\theta C_tW_t^*\right]}{E_{t-1}\left[d_t^*P_t^\theta C_t\tfrac{1}{S_t}\right]}.$](img57.gif)
|
(3) |
3.2 Foreign Multinational Price Setting
Now consider foreign firms who choose to serve the home market via multinational production.7 As mentioned in the previous section, these multinationals set their prices in advance in the home currency, known as local currency pricing (LCP). The maximization problem takes the form:
![$\displaystyle \max_{p_{\textit{MP},t}^*} E_{t-1}\left[d_t^*\tfrac{1}{S_t}\left(p_{\textit{MP},t}^*y_{\textit{MP},t}^* - \frac{W_t}{\phi}y_{\textit{MP},t}^*\right)\right].$](img58.gif)
|
Note the lack of transportation cost
![]() and the the labor cost from home workers
and the the labor cost from home workers
![]() . This yields the following optimal price
choice:
. This yields the following optimal price
choice:
![$\displaystyle p_{\textit{MP},t}^*(\phi) = \frac{\theta}{\theta - 1}\frac{1}{\phi}\frac{E_{t-1}\left[d_t^*P_t^\theta C_t\tfrac{1}{S_t}W_t\right]}{E_{t-1}\left[d_t^*P_t^\theta C_t\tfrac{1}{S_t}\right]}.$](img61.gif)
|
(4) |
As discussed in Section 2.4, factor price
equalization holds in the model. Here, this implies that the ratio
of prices charged by a firm choosing between exporting and MP is
simply
![]() . That is, none of
the expectations play a role in the optimal price choice between MP
and exports. This result is intuitive: with factor price
equalization holding both in expectation and ex-post, firms should
not set different prices except to account for transportation
costs.
. That is, none of
the expectations play a role in the optimal price choice between MP
and exports. This result is intuitive: with factor price
equalization holding both in expectation and ex-post, firms should
not set different prices except to account for transportation
costs.
3.3 Foreign Export Cutoff
Let
![]() be the productivity at
time
be the productivity at
time ![]() above which a foreign firm will enter the
home market. Such a firm will either choose to export or operate in
the home market as a multinational. The marginal firm with
productivity
above which a foreign firm will enter the
home market. Such a firm will either choose to export or operate in
the home market as a multinational. The marginal firm with
productivity
![]() receives zero expected
profit net of the fixed cost of exporting
receives zero expected
profit net of the fixed cost of exporting ![]() . That
is,
. That
is,
![\begin{multline} E_{t-1}\left[d_t^*\left(\underbrace{\frac{1}{S_t}p_{X,t}^*(\hat{\phi}_{X,t}^*)y_{X,t}^*(\hat{\phi}_{X,t}^*)}_{\text{revenue}} - \underbrace{\frac{W_t^*y_{X,t}^*(\hat{\phi}_{X,t}^*)}{\hat{\phi}_{X,t}^*}\tau}_{\text{labor costs}}\right)\right]\ - E_{t-1}\left[d_t^*\underbrace{\frac{1}{S_{t-1}}P_tf_X}_{\text{fixed costs}}\right] = 0 \equiv \xi^*(\hat{\phi}_X^*), \end{multline}](img67.gif)
where again ![]() is the
stochastic discount factor of the foreign firm,
is the
stochastic discount factor of the foreign firm, ![]() is the price of the good paid by home households
(in the home currency),
is the price of the good paid by home households
(in the home currency), ![]() is the demand of the
good at that price, and
is the demand of the
good at that price, and ![]() is the foreign wage.
Define
is the foreign wage.
Define
![]() as the net profit from exporting
for a firm with productivity
as the net profit from exporting
for a firm with productivity ![]() .
.
3.4 Foreign Multinational Cutoff
Now let
![]() be the cutoff
productivity at time
be the cutoff
productivity at time ![]() above which a foreign firm
optimally chooses to serve the home market through multinational
production rather than exporting. It is the productivity at which
expected profits net of fixed costs are equal between the two
methods of serving the foreign market.
above which a foreign firm
optimally chooses to serve the home market through multinational
production rather than exporting. It is the productivity at which
expected profits net of fixed costs are equal between the two
methods of serving the foreign market.
Visually, we can see this in Figure 1. Firms
engage in domestic production if their expected profits exceed the
fixed cost ![]() ; this is where the expected profit line
crosses the x-axis. A foreign firm with productivity higher than
; this is where the expected profit line
crosses the x-axis. A foreign firm with productivity higher than
![]() will produce in the foreign
market. Similarly, a firm will export if its expected profits
exceed the fixed cost
will produce in the foreign
market. Similarly, a firm will export if its expected profits
exceed the fixed cost ![]() . Since exports are subject
to a transportation cost, these profit lines have a flatter slope
and even with the same fixed cost as domestic production, there
would be a higher threshold
. Since exports are subject
to a transportation cost, these profit lines have a flatter slope
and even with the same fixed cost as domestic production, there
would be a higher threshold
![]() to export. Finally, very
productive firms will find it optimal to switch to multinational
production if the expected profit from producing abroad exceeds the
expected profit from exporting; that is, the cutoff
to export. Finally, very
productive firms will find it optimal to switch to multinational
production if the expected profit from producing abroad exceeds the
expected profit from exporting; that is, the cutoff
![]() lies where the
expected profits from exporting
lies where the
expected profits from exporting ![]() and
multinational production
and
multinational production
![]() intersect.
intersect.
Mathematically, this can be expressed as:
![\begin{multline} E_{t-1}\left[d_t^*\frac{1}{S_t}\left(\underbrace{p_{\textit{MP},t}^*(\hat{\phi}_{\textit{MP},t}^*)y_{X,t}^*(\hat{\phi}_{\textit{MP},t}^*)}_{\text{revenue}} - \underbrace{\frac{W_ty_{X,t}^*(\hat{\phi}_{\textit{MP},t}^*)}{\hat{\phi}_{\textit{MP},t}^*}}_{\text{labor costs}}\right)\right]\ - E_{t-1}\left[d_t^*\underbrace{\frac{1}{S_{t-1}}P_tf_X}_{\text{fixed costs}}\right] - \underbrace{\xi^*(\hat{\phi}_{\textit{MP}_t}^*)}_{\text{profit from exporting}} = 0, \end{multline}](img83.gif)
where the first two terms are the expected
profit from MP net of fixed costs. The third term, defined in
5 is the
expected profit from exporting for a firm with productivity
![]() .
.
3.5 Results
Given the pricing structure where both MP
and export prices are set in the home currency, recall that
![]() , and the home
price index
, and the home
price index ![]() is set entirely in advance and is
thus nonstochastic. This yields analytically tractable expressions
of the the home side of the economy in terms of the home money
supply. It can be shown that the relative cutoff is
simply:
is set entirely in advance and is
thus nonstochastic. This yields analytically tractable expressions
of the the home side of the economy in terms of the home money
supply. It can be shown that the relative cutoff is
simply:
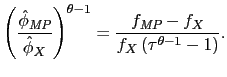
|
Thus, the relative extensive margin is unaffected by nominal uncertainty. The only determinants of the cutoff ratio are exactly those found in Helpman et al. (2004).
An increase in foreign volatility has a negative impact on the foreign producers, while it encourages both exports and multinational production. The intuition is that foreign volatility is good for home producers because a foreign monetary contraction coincides with a foreign currency appreciation, more than compensating the home producers. So both cutoffs fall. But what about actual trade flows and multinational sales? For that, I must be more explicit about the shape of the firm distribution. Proposition 1 demonstrates sufficient conditions under which the export and multinational sales changes are proportional.
Proposition 1
If firm productivity is characterized by a Pareto distribution, exports are priced in the home currency, and factor price equalization holds, then the ratio of foreign multinational sales to exports is unaffected by uncertainty.
Proof. See appendix.
The basic intuition of the proof is that if relative prices are unaffected by nominal volatility, then the relative sales of multinationals and exporters depends only on the mass of firms of each type and the ratio of average productivities. With a Pareto distribution, it can be shown that the ratio of average productivities and ratio of the mass of firms remain constant as volatility changes.
4 Home Firms Serving the Foreign Market
In contrast to foreign firms, U.S. firms set their prices for export overwhelmingly in U.S. dollars. Gopinath and Rigobon (2008) find that 97% of U.S. exports are denominated in dollars. I model this asymmetry in pricing between home and foreign by imposing that home firms serve the foreign market by setting their price in their own currency. Again, I do not model the currency choice explicitly, but we will see that exporters will benefit from having their goods priced in their own currency. While there is less direct evidence of how U.S. multinationals set prices abroad, I treat them as identical to their foreign competitors, pricing in the foreign currency.8
4.1 Home Price Setting
Home multinationals will price analogously to foreign multinationals, with
![$\displaystyle <tex2html_comment_mark>21 p_{\textit{MP},t}(\phi) = \frac{\theta}{\theta - 1}\frac{1}{\phi}\frac{E_{t-1}\left[d_tP_t^{*\theta} C_t^*S_tW_t^*\right]}{E_{t-1}\left[d_tP_t^{*\theta} C_t^*{S_t}\right]}.$](img88.gif)
|
By contrast, home exporters choose their
optimal price in their own currency, which means that foreign
demand for an exported good at home-denominated price ![]() is:
is:
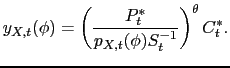
|
(7) |
In other words, changes in the exchange rate fully pass through to the foreign currency price of the good.
The optimal price of the good is:
![$\displaystyle p_{X,t} = \frac{\theta}{\theta - 1}\tau\frac{1}{\phi}\frac{E_{t-1}\left[d_tW_tS_t^\theta P_t^{*\theta}C_t^*\right]}{E_{t-1}\left[d_tS_t^\theta P_t^{*\theta}C_t^*\right]}.$](img91.gif)
|
Now, the ratio of the export and multinational
prices cannot be written simply as the transportation cost
![]() . Furthermore, since the export price
automatically fluctuates in foreign-currency terms with the
exchange rate, the foreign price index
. Furthermore, since the export price
automatically fluctuates in foreign-currency terms with the
exchange rate, the foreign price index ![]() depends
on the exchange rate. As such, it cannot be separated out of
expectation operators. This complicates the analytical solution of
the foreign portion of the model.
depends
on the exchange rate. As such, it cannot be separated out of
expectation operators. This complicates the analytical solution of
the foreign portion of the model.
4.2 Home Export Cutoff
With export prices set in the home
currency, the cutoff productivity
![]() above which home firms serve
the foreign market becomes:
above which home firms serve
the foreign market becomes:
![$\displaystyle E_{t-1}\left[d_t\left(p_{X,t}(\hat{\phi}_{X,t})y_{X,t}(\hat{\phi}_{X,t}) - \tau\frac{W_t}{\hat{\phi}_{X,t}}y_{X,t}(\hat{\phi}_{X,t})\right)\right] - E_{t-1}[d_tS_{t-1}P_t^*f_X] = 0.$](img95.gif)
|
(8) |
The exchange rate plays a role here through the demand condition (7). Substituting demand into (8), one obtains:
![$\displaystyle E_{t-1}\left[d_tS_t^\theta P_t^{*\theta}C_t^*\left(p_{X,t}^{1 - \theta} - \tau\frac{W_t}{\hat{\phi}_{X,t}}p_{X,t}^{-\theta}\right)\right] - E_{t-1}[d_tS_{t-1}P_t^*f_X] = 0 \equiv \xi(\hat{\phi}_X).$](img96.gif)
Note here that expected profits depend on
![]() . This non-linear expression of the
exchange rate is the basis through which nominal uncertainty
affects the extensive margin, despite firms being otherwise risk
neutral.9 The multinational cutoff condition is
simply the home analogue to (6), left to the
appendix.
. This non-linear expression of the
exchange rate is the basis through which nominal uncertainty
affects the extensive margin, despite firms being otherwise risk
neutral.9 The multinational cutoff condition is
simply the home analogue to (6), left to the
appendix.
4.3 A Numerical Illustration
With producer cost pricing, multinational
revenue and export revenue are now affected differently by nominal
volatility. Multinational revenue is a function only of demand
![]() , since the price is set in advance in
the foreign currency. Export revenue varies with the exchange rate
as pass-through to export prices in the foreign currency is
complete.
, since the price is set in advance in
the foreign currency. Export revenue varies with the exchange rate
as pass-through to export prices in the foreign currency is
complete.
Since export prices now vary with the
exchange rate, the price index ![]() becomes
uncertain at date
becomes
uncertain at date ![]() . This substantially
complicates solving the model analytically, so I proceed
numerically by discretizing the state space for the foreign money
supply
. This substantially
complicates solving the model analytically, so I proceed
numerically by discretizing the state space for the foreign money
supply ![]() and computing the stochastic steady
state for various
and computing the stochastic steady
state for various
![]() .
.
To do this, I must calibrate the model
parameters.10 Table 1 outlines the
parameters in the model. Most parameters are very standard; as is
common in the trade literature, I use an elasticity of substitution
between varieties of 5, in the middle of most estimates.11 The
Pareto shape parameter ![]() governing the distribution
of firm productivities is taken to be very close to the elasticity
of substitution, as in Russ (2007).
Iceberg trade costs of 20% are within the range of estimated
tariffs and freight costs. This leaves the fixed costs. I set the
fixed costs of domestic production and export to be the same, as
the focus here is on multinational production.12 I set the fixed
costs of multinational production to be consistent with about 60%
of the value of foreign sales to come from multinational
affiliates, consistent with the average of the data used in Section 5.
governing the distribution
of firm productivities is taken to be very close to the elasticity
of substitution, as in Russ (2007).
Iceberg trade costs of 20% are within the range of estimated
tariffs and freight costs. This leaves the fixed costs. I set the
fixed costs of domestic production and export to be the same, as
the focus here is on multinational production.12 I set the fixed
costs of multinational production to be consistent with about 60%
of the value of foreign sales to come from multinational
affiliates, consistent with the average of the data used in Section 5.
As the variance of the foreign money supply
grows, exporting becomes relatively more attractive compared to
multinational production. Consider an unexpected foreign
contraction. Demand ![]() falls for both
multinational firms and exporters, and the foreign exchange rate
appreciates (
falls for both
multinational firms and exporters, and the foreign exchange rate
appreciates (![]() rises). This makes profits
denominated in the home currency higher for both exporters and
multinationals.13 In addition, the exporter's price,
set in the home currency, becomes relatively cheaper in foreign
currency terms. This stimulates greater demand, and the home
exporter's price is closer to its profit-maximizing point. This
automatic adjustment of the price makes a PCP exporter relatively
better off in the presence of higher foreign uncertainty. This
effect tends to dominate regardless of the correlation between
foreign demand
rises). This makes profits
denominated in the home currency higher for both exporters and
multinationals.13 In addition, the exporter's price,
set in the home currency, becomes relatively cheaper in foreign
currency terms. This stimulates greater demand, and the home
exporter's price is closer to its profit-maximizing point. This
automatic adjustment of the price makes a PCP exporter relatively
better off in the presence of higher foreign uncertainty. This
effect tends to dominate regardless of the correlation between
foreign demand ![]() and the exchange rate
and the exchange rate
![]() , say, from other sources of
shocks.
, say, from other sources of
shocks.
To better understand this, consider first
Figure 2.
It plots the profit of a home exporter against realizations of the
foreign money supply ![]() . Each point represents a
value of the foreign money supply on the discretized grid. Starting
from the median of about 1, the probability of moving one point
left is equal to the probability of moving one point right.
Clearly, exporter profit is convex in the foreign money supply. The
exporter benefits more from foreign contractions than it suffers
from foreign expansions.
. Each point represents a
value of the foreign money supply on the discretized grid. Starting
from the median of about 1, the probability of moving one point
left is equal to the probability of moving one point right.
Clearly, exporter profit is convex in the foreign money supply. The
exporter benefits more from foreign contractions than it suffers
from foreign expansions.
As foreign nominal volatility rises, it increases the likelihood that the firm finds itself further away from the median point. Since the likelihood of a significant foreign contraction increases, this increases the expected profit of an exporter.
A multinational benefits from foreign volatility as well. Yet the multinational does not gain the advantage of having its price automatically lowered in foreign currency terms as a PCP exporter does. Figure 3 shows the relative impact of expected profit for a sample firm as volatility increases. Multinational profit increases slightly, but it is dwarfed by the dramatic increase in expected profit for an exporter.
Expected profit is exactly what determines the extensive margin from (5). As expected profit of a potential exporter rises, it draws in firms from both margins: firms which would otherwise only produce domestically and firms which would otherwise be multinationals. Figure 4 shows the relative impact on the extensive margin for exporters and multinationals. As volatility rises, many multinationals become exporters, reducing their mass. Note that because there are many more exporters, a similar percentage gain in the mass of exporters represents a much larger mass of firms.
In terms of quantity, this translates to a relatively small drop in multinational sales; the lowest productivity multinational firms become exporters, so their total effect is relatively small. For exporters, on the other hand, these new firms are the most productive and translate to a large increase in trade. This can be seen in Figure 5.
Finally, because the effects of volatility may work through additional unmodeled channels, I focus on the fraction of multinational sales as a portion of total foreign sales in Figure 6. In both value and quantity terms, the fraction of foreign sales from multinationals falls as volatility rises. Given the current calibration, going from no volatility to a variance of 0.03 leads to a drop in multinational sales from about 60% to below 50%.
5 Data
I move now to consider evidence based on U.S. exports and U.S. multinational foreign affiliate sales. I use multinational sales data from the BEA for 1999-2007 (the latest year currently available) and match it to export data from the U.S. International Trade Commission. This data exists at the sector, country, year level. Full details of the data used in the regressions are available in Tables 5 and 6 in the appendix.
It is important to keep in mind that both measures are in nominal U.S. dollars. For trade, the Bureau of Labor Statistics does not construct price indices for each export destination. Similarly, there are no multinational sales-specific price indices available by destination country. The analysis in the forthcoming sections will be in terms of nominal ratios, but these may not necessarily correspond to the real goods quantity ratios.
I exclude a small number of countries which experienced currency or debt crises during this time sample.14 Robustness analysis in Section 5.2 shows that the main results of the preferred specification are unaffected by including them.
5.1 Results
There are several measures of volatility one might consider to proxy for the nominal volatility in the model. At its most basic, the model has implications for the money supply growth rate; yet this is a theoretical stand-in for many such nominal demand forces which an economy may face. Since the data on money supplies is lacking for some countries in the sample, it makes sense to consider a more widely available measure: consumer price inflation. In the model, the nominal volatility directly translates to inflation volatility. On the other hand, it also translates into exchange rate volatility; this may seem like the most logical volatility variable, yet because exchange rates are influenced by a large number of other shocks, we will see that inflation can have a very different effect on multinational production compared to exchange rate volatility.
It is reasonable to think that there could be a large number of shocks affecting both exports and multinational sales; it makes sense, then, to consider exports and sales jointly and look for a relative effect. To that end, I estimate the following:
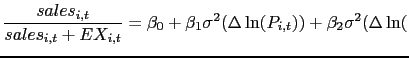 S
S |
(9) |
where ![]() is sales by
foreign affiliates of U.S. multinationals in country
is sales by
foreign affiliates of U.S. multinationals in country ![]() , mapped to the data as total foreign sales of U.S.
affiliates.
, mapped to the data as total foreign sales of U.S.
affiliates. ![]() are total exports to country
are total exports to country
![]() . Both are in current U.S. dollars. Thus,
the dependent variable is the fraction of multinational sales as a
share of multinational sales and exports. The variable of interest
on the right hand side is
. Both are in current U.S. dollars. Thus,
the dependent variable is the fraction of multinational sales as a
share of multinational sales and exports. The variable of interest
on the right hand side is
![]() , the
volatility of the price level in country
, the
volatility of the price level in country ![]() for
year
for
year ![]() .15 The volatility of the nominal
exchange rate is
.15 The volatility of the nominal
exchange rate is
![]() ,
, ![]() consists of a number of country/time specific variables as
controls, and
consists of a number of country/time specific variables as
controls, and
![]() is the regression residual.
Given the limitations of cross-country regressions,
is the regression residual.
Given the limitations of cross-country regressions, ![]() is best considered a conditional correlation,
controlling for other likely determinants of the dependent
variable.
is best considered a conditional correlation,
controlling for other likely determinants of the dependent
variable.
The results pooling available sectors, countries, and years together are presented in Table 2. Each regression has industry-year dummies, which controls for changes in the overall business cycle and the particular characteristics of each industry. There is a robust negative coefficient on inflation volatility. The estimate in column (1) implies that economically, moving one standard deviation to the right in the distribution of inflation volatility implies an 8.7 percentage point reduction in multinational sales as a fraction of total foreign sales.
The regressions include a number of controls in columns 2 and 3. Whether the country is a member of the OECD (generally a developed country status) tends to have a positive impact on the ratio of multinational sales to exports; this is consistent with many explanations, including that developed countries have good institutions which permit horizontal FDI to be more profitable. On the other hand, Mexico and Canada tend to have lower multinational sales relative to exports, but this is not always statistically significant; the sign is consistent with the relatively low transportation costs and tariffs from being members of NAFTA. Distance is significant and of the expected sign; countries further from the U.S. are served relatively more with multinational sales. In column (3), the World Bank's Worldwide Governance Indicator for rule of law has a positive effect, consistent with the notion that good institutions encourage multinationals to produce in the destination country. The effect of per-capita GDP is more mixed; without the rule of law, it is positive but insignificant; with that institutional variable included, it is negative and significant.
Given that the industry dummies do not control for a heterogeneous impact of inflation volatility by sector, I re-run the analysis for each sector individually in Table 3. Here, we see that information, electrical, food, metals, and transportation sectors all have negative and significant coefficients. Chemical manufacturing has a negative coefficient but it is relatively small and statistically insignificant. The outlier is mining, an industry which does not lend itself to horizontal FDI in many cases. Exchange rate volatility is mixed and insignificant in all regressions except information (positive) and food (negative).
5.2 Robustness
I subject the pooled results of Section 5.1 to a series of robustness checks. The results are shown in Table 4. Column 1 reports the results adding back in the crisis countries, showing that the results are not sensitive to those outliers. This provides some evidence that the risk of expropriation is not substantially changing the results. Column 2 includes a number of additional controls, including annual real GDP growth volatility and three gravity-style variables: sharing a common language, being a former colony, and being landlocked. Real GDP volatility has an insignificant, negative coefficient. In this specification, none of the gravity-style explanatory variables are statistically significant. Column 3 instead clusters the errors by industry rather than country, showing that the statistical significance of inflation volatility is not sensitive to this choice.
Columns 4 and 5 report similar regressions with a different dependent variable: the log of the sales/export ratio. This is the measure used by Ramondo et al. (2010) in the context of GDP volatility. Without the crisis countries, I find a positive and insignificant response of inflation volatility, and with the crisis countries the coefficient becomes negative and significant. Exchange rate volatility is positive and significant in the first case but not the second, while real GDP volatility is negative and insignificant in the first case, and positive and insignificant in the second.
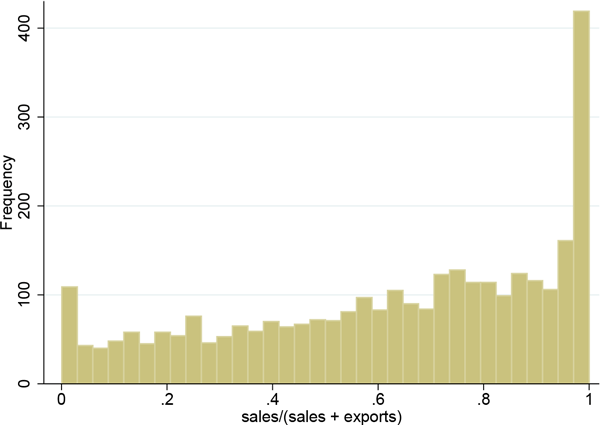
The log ratio puts substantial weight on observations with relatively small multinational sales or relatively small exports. In the data, there are a number of such observations, plotted in Figure 7. Some of these observations in the tails are the result of either zero multinational sales or zero exports; I eliminate them in Figure 8, showing that a substantial proportion remain.16 The log ratio by construction eliminates the extreme points while heavily weighting the near extreme points, making it less suitable for industry-level analysis with a large number of countries. This would only be compounded with more disaggregated data.
5.3 Discussion of Exchange Rate Volatility
The empirical results in Section 5.1 support the model's prediction that increased nominal volatility as measured by inflation volatility should reduce the ratio of multinational sales as a fraction of total foreign sales. Yet the results for exchange rate volatility go in the opposite direction, if anything. The model does imply that nominal volatility affects the firm's choice through the exchange rate, and as inflation volatility rises so should exchange rate volatility. This is not necessarily inconsistent with the empirical evidence.
Eichenbaum and Evans (1995) provide empirical evidence supporting the notion that a contractionary monetary policy shock appreciates the U.S. dollar relative to various foreign currencies.17 While based on U.S. monetary policy, this evidence is consistent with the model's mechanism that a monetary contraction will lead to a nominal exchange rate appreciation.
Exchange rates are not driven by any one shock, however. Another underlying source of exchange rate fluctuations could have the opposite effect on exporting or multinational firms' profits through another channel. Exchange rate volatility may also affect firms if the firm itself is risk averse.18 Because exchange rate volatility is not robustly significant in the preferred specifications, I do not explicitly model the potential effects of risk aversion on this channel. My results do suggest, however, that one should not conflate the nominal volatility of the sort modeled in this paper with nominal exchange rate volatility.
6 Conclusion
International trade theory has recently made significant progress in modeling the endogenous choice of how to serve a foreign market. Yet the standard static considerations are only part of a firm's consideration; this paper contributes to this growing literature by considering how nominal uncertainty affects this choice. This is of particular policy relevance since inflation volatility is commonly seen as something that can be tamed by modern monetary policy.
I show how in a general equilibrium model where exports are priced in the producer's currency and multinational production is priced in the local currency, an increase in foreign nominal volatility decreases the fraction of foreign sales coming from multinational production. Using bilateral, multi-sector trade and multinational sales from the U.S., I find support for this result in the data.
The model predicts that if the country's exports are LCP, then volatility will not matter. As more data becomes available about the activity of multinationals, this can be tested by examining the export and multinational behavior of other countries. Future work should also incorporate vertical production as well as horizontal production, to generate predictions which better match the available trade and multinational sales data. The data suggest that future empirical studies of the effects of volatility on trade or foreign investment should distinguish between exchange rate volatility in general and other forms of uncertainty such as inflation volatility.
A Technical Appendix
A.1 Derivation of 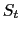
The representative household faces the following budget constraint, written in nominal home currency:
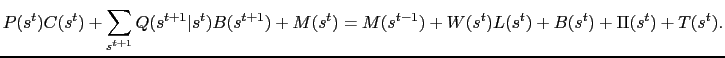
|
where ![]() are profits
from domestic firms and
are profits
from domestic firms and ![]() are lump-sum transfers
of seigniorage revenues from the government. As standard in the
literature,
are lump-sum transfers
of seigniorage revenues from the government. As standard in the
literature, ![]() denotes the state of the world
(including the history up to time
denotes the state of the world
(including the history up to time ![]() ) and is used
to construct a complete set of securities
) and is used
to construct a complete set of securities
![]() .
.
The first order conditions are then very
standard, with Lagrange multiplier
![]() :
:
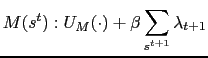
|
||
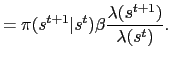
|
The utility function has real money balances in logs, yielding an exact log-linear solution as shown by Obstfeld and Rogoff (1998).
Starting with the ![]() first order condition:
first order condition:
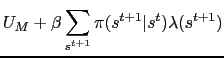
|
||
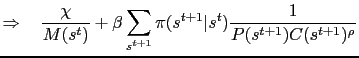
|
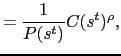 |
|
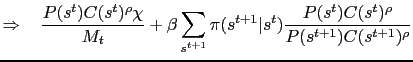
|
||
Following Obstfeld and Rogoff (1998), consider
![$\displaystyle = \frac{\chi P(s^t)C(s^t)^\rho}{M(s^t)} + \sum_{s^{t+1}} \pi(s^{t+1}\vert s^t)\left[\beta\frac{P(s^t)C(s^t)^\rho}{P(s^{t+1})C(s^{t+1})^\rho}\right]$](img147.gif)
|
||
![$\displaystyle = \frac{\chi P(s^t)C(s^t)^\rho}{M(s^t)} + \beta\frac{\chi P(s^t)C(s^t)^\rho}{M(s^t)} \sum_{s^{t+1}}\pi(s^{t+1}\vert s^t)\left[\frac{M(s^t)}{P(s^{t+1})C(s^{t+1})^\rho}\right]$](img148.gif)
|
||
![$\displaystyle = \frac{\chi P(s^t)C(s^t)^\rho}{M(s^t)} + \beta \frac{\chi P(s^t)C(s^t)^\rho}{M(s^t)} \sum_{s^{t+1}}\pi(s^{t+1}\vert s^t)\left[\frac{M(s^t)}{M(s^{t+1})}\frac{M(s^{t+1})}{\chi P(s^{t+1})C(s^{t+1})^\rho}\right].$](img149.gif)
|
A candidate solution is one in which
![]() is a
constant for all
is a
constant for all ![]() . Let
. Let
![$ \alpha \equiv \sum_{s^{t+1}} \pi(s^{t+1}\vert s^t)\left[\frac{M(s^t)}{M(s^{t+1})}\right] = \sum_{s^t}\pi(s^t\vert s^{t-1})\left[\frac{M(s^{t-1})}{M(s^t)}\right]$](img152.gif) . Then,
. Then,
![$\displaystyle = \frac{\chi P(s^t)C(s^t)^\rho}{M(s^t)} + \beta \sum_{s^{t+1}}\pi(s^{t+1}\vert s^t)\left[\frac{M(s^t)}{M(s^{t+1})}\right],$](img154.gif)
|
||
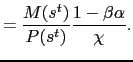
|
The foreign budget constraint is analogous:
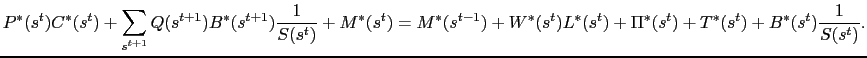
|
The equivalent expression for the same bond
prices ![]() is then:
is then:
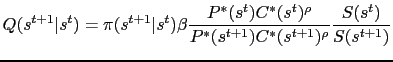
|
With complete markets, the exchange rate is
solved by equating the price of state-contingent bonds
![]() and iterating backward. Chari et al. (2002) provide a detailed derivation
of this. Iterating backwards:
and iterating backward. Chari et al. (2002) provide a detailed derivation
of this. Iterating backwards:
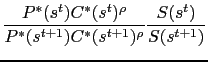
|
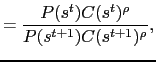
|
|
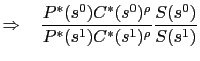
|
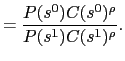
|
Let
![]() , then:
, then:
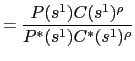
|
||
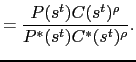
|
This is the standard result that the (nominal)
exchange rate equals the ratio of the marginal utilities of
consumption adjusted by the nominal price indices. With the
expression for
![]() , the exchange rate can be
expressed as a function of exogenous variables:
, the exchange rate can be
expressed as a function of exogenous variables:
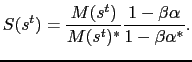
|
With ![]() only being
notationally important for this result, it can be written for the
rest of the analysis to be in terms of subscripts and
expectations.
only being
notationally important for this result, it can be written for the
rest of the analysis to be in terms of subscripts and
expectations.
A.2 Proof of Proposition 1
The weighted-average exporter productivity is
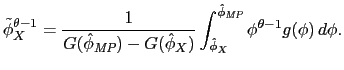
|
(10) |
and the weighted-average multinational productivity is
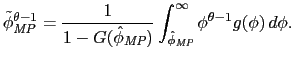
|
The representative exporter charges the following price:
![$\displaystyle \tilde{p}_{X,t} = \frac{\theta}{\theta - 1}\frac{1}{\tilde{\phi}_X}\tau\frac{E_{t-1}[d_tW_tC_t^*]}{E_{t-1}[d_tS_tC_t^*]}.$](img175.gif)
|
Using factor price equalization, one can also express the representative multinational firm price:
![$\displaystyle \tilde{p}_{\textit{MP},t} = \frac{\theta}{\theta - 1}\frac{1}{\tilde{\phi}_{\textit{MP}}}\frac{E_{t-1}[d_tW_tC_t^*]}{E_{t-1}[d_tS_tC_t^*]}.$](img176.gif)
|
Thus, the relative price is simply
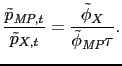
|
Since demand depends only on the price, the ratio of multinational production to exports is simply
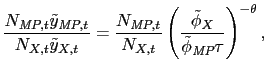
|
where
![]() is the fraction of the
unit mass of home firms which produce abroad, and
is the fraction of the
unit mass of home firms which produce abroad, and ![]() is the fraction which export. To show that nominal
uncertainty does not affect this intensive margin, it is necessary
to demonstrate that the average productivities
is the fraction which export. To show that nominal
uncertainty does not affect this intensive margin, it is necessary
to demonstrate that the average productivities
![]() and
and
![]() are themselves unaffected
by nominal uncertainty. In addition, the ratio of firm masses must
also be unaffected by nominal uncertainty.
are themselves unaffected
by nominal uncertainty. In addition, the ratio of firm masses must
also be unaffected by nominal uncertainty.
To derive expressions for these average
productivities, consider imposing the common assumption that firm
productivities follow a Pareto distribution with parameter
![]() . Previous work, including Helpman et al. (2004), has found that the Pareto
distribution captures well the distribution of firm sizes seen in
the data. Recall that if the minimum productivity of any firm is
normalized to be 1, the PDF of the Pareto distribution is
. Previous work, including Helpman et al. (2004), has found that the Pareto
distribution captures well the distribution of firm sizes seen in
the data. Recall that if the minimum productivity of any firm is
normalized to be 1, the PDF of the Pareto distribution is
![]() and the
corresponding CDF is
and the
corresponding CDF is
![]() .
.
Above we showed that
![]() is a
constant. Let
is a
constant. Let
![]() . Now we seek
to prove that if
. Now we seek
to prove that if ![]() is constant, then
is constant, then
![]() is
also constant.
is
also constant.
As is now common in the literature, it is
straightforward to show that the average multinational productivity
depends only on the elasticity of substitution ![]() , the shape parameter
, the shape parameter ![]() , and the
productivity cutoff
, and the
productivity cutoff
![]() :
:
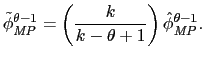
|
Using the definition of the average productivity (10) above, one can also show that:
![$\displaystyle \tilde{\phi}_X^{\theta - 1} = \frac{1}{\hat{\phi}_X^{-k} - \hat{\phi}_{\textit{MP}}^{-k}}\frac{k}{k - \theta + 1}\left[\hat{\phi}_{\textit{MP}}^{\theta - k - 1} - \hat{\phi}_X^{\theta - k - 1}\right].$](img194.gif)
|
Using
![]() with
with
![]() , one can show:
, one can show:
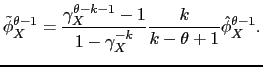
|
Since ![]() is a
constant, this implies that the ratio
is a
constant, this implies that the ratio
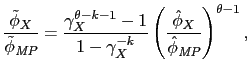
|
is also constant with respect to nominal uncertainty.
Finally, consider the mass of firms engaged in multinational production. This is simply:
and
With
![]() , we have
, we have
![]() and thus:
and thus:
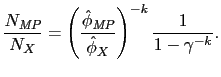
|
That is, nominal uncertainty does not affect
the relative extensive margin
![]() , or
the relative mass of firms
, or
the relative mass of firms
![]() . Thus, it does not
affect the relative intensive margin
. Thus, it does not
affect the relative intensive margin
![]() .
.
A.3 A Note on the Flexible Price Case
It is useful to understand the model's implications under flexible prices for the extensive margin choice between multinational production and exporting. The only decision made in advance is that of whether and how to produce for the foreign market. The cutoff conditions are still a function of expected profits, which could be influenced by any number of shocks. The following proposition demonstrates formally that so long as factor price equalization holds, the relative extensive margin is unaffected by any uncertainty about future consumption, exchange rates, prices, etc.
Proposition 2
With flexible prices and factor price equalization, the relative extensive margin between exports and multinational production is unaffected by uncertainty.
Proof.
With the export price
![]() , the export cutoff becomes:
, the export cutoff becomes:
![$\displaystyle \hat{\phi}_{X,t}^{\theta - 1} = \frac{E_{t-1}[d_tP_t^*S_{t-1}f_X]}{\tau^{1 - \theta}\left(\left(\frac{\theta}{\theta - 1}\right)^{1 - \theta} - \left(\frac{\theta}{\theta - 1}\right)^{-\theta}\right)E_{t-1}\left[d_tS_t^\theta P_t^{*\theta}C_t^*W_t^{1 - \theta}\right]}.$](img209.gif)
|
With flexible prices, the multinational price isand the multinational cutoff becomes:
![$\displaystyle \hat{\phi}_{\textit{MP},t}^{\theta - 1} = \frac{E_{t-1}[d_tP_t^*S_{t-1}(f_{\textit{MP}} - f_X)]}{ \left(\left(\frac{\theta}{\theta - 1}\right)^{1 - \theta} - \left(\frac{\theta}{\theta - 1}\right)^{-\theta}\right) \left(E_{t-1}\left[d_tS_t P_t^{*\theta}C_t^*W_t^{*1 - \theta}\right] - \tau^{1 - \theta}E_{t-1}\left[d_tS_t^\theta P_t^{*\theta}C_t^*W_t^{1 - \theta}\right] \right)}.$](img211.gif) |
More informative is the relative cutoff expression:
![$\displaystyle \left(\frac{\hat{\phi}_{\textit{MP},t}}{\hat{\phi}_{X}}\right)^{\theta - 1} = \frac{f_{\textit{MP}} - f_X}{f_X\left(\tau^{\theta - 1}\frac{E_{t-1}\left[d_tS_tP_t^{*\theta}C_t^*W_t^{*1 - \theta}\right]}{E_{t-1}\left[d_tS_t^\theta P_t^{*\theta}C_t^*W_t^{1 - \theta}\right]} - 1\right)}.$](img212.gif)
|
Here, we can see that the effects of
uncertainty reduce down to a ratio
![$ \frac{E_{t-1}\left[d_tS_tP_t^{*\theta}C_t^*W_t^{*1 - \theta}\right]}{E_{t-1}\left[d_tS_t^\theta P_t^{*\theta}C_t^*W_t^{1 - \theta}\right]}$](img213.gif) . Note that if factor price equalization holds, i.e.
. Note that if factor price equalization holds, i.e.
![]() , then this ratio equals 1.
Then the relative cutoff expression becomes
, then this ratio equals 1.
Then the relative cutoff expression becomes
![]() ,
exactly that found by () in a
deterministic setting. Thus, with flexible prices, any effect of
uncertainty on the relative extensive margin requires factor price
equalization not to hold. This is true regardless of the presence
of other sectors with sticky prices and regardless of the
underlying shock process.
,
exactly that found by () in a
deterministic setting. Thus, with flexible prices, any effect of
uncertainty on the relative extensive margin requires factor price
equalization not to hold. This is true regardless of the presence
of other sectors with sticky prices and regardless of the
underlying shock process.
A.4 Numerical Solution
The model with PCP exports no tractable
analytical solutions for the stochastic steady state. Instead, I
employ numerical techniques to characterize the equilibrium. The
basic procedure is to discretize the exogenous, stochastic variable
(![]() ), and solve the model such that the
pricing, cutoff, and equilibrium conditions hold in every state of
the economy. That is, the expectations are solved by discretizing
the exogenous process with quadrature methods. Since the export
choice and pricing decisions are made one period in advance, the
equilibrium need only be solved for period
), and solve the model such that the
pricing, cutoff, and equilibrium conditions hold in every state of
the economy. That is, the expectations are solved by discretizing
the exogenous process with quadrature methods. Since the export
choice and pricing decisions are made one period in advance, the
equilibrium need only be solved for period ![]() given
conditions in
given
conditions in ![]() .
.
![]() is discretized with
Gaussian quadrature methods using 30 nodes. Then, using numerical
search over
is discretized with
Gaussian quadrature methods using 30 nodes. Then, using numerical
search over
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() , I calculate the other
endogenous variables. The numerical algorithm iterates until the
following equilibrium conditions hold:
, I calculate the other
endogenous variables. The numerical algorithm iterates until the
following equilibrium conditions hold:
- The foreign firm cutoff condition:
![\begin{multline*} E_{t-1}\left[d_t^*P_t^{*\theta} C_t^*\left(p_{t}^*(\hat{\phi}_{t}^*)^{1 - \theta} - \frac{1}{\hat{\phi}_{t}^*}W_t^*p_{t}^*(\hat{\phi}_{t}^*)^{-\theta}\right)\right] - E_{t-1}\left[d_t^*P_t^*f\right] = 0. \end{multline*}](img226.gif)
- The home exporter profit condition, expressed in foreign
terms:19
![\begin{multline*} E_{t-1}\left[d_t^*S_t^{\theta-1} P_t^{*\theta} C_t^*\left(p_{X,t}(\hat{\phi}_{X,t})^{1 - \theta} - \frac{1}{\hat{\phi}_{X,t}}W_t^*S_t\tau p_{X,t}(\hat{\phi}_{X,t})^{-\theta}\right)\right]\ - E_{t-1}\left[d_t^*\frac{S_{t-1}}{S_{t}}P_t^*f_X \right] = 0. \end{multline*}](img229.gif)
- The home multinational production cutoff condition:
- The foreign price condition:
- The exporter price condition:
- The multinational production price condition:
![$\displaystyle p_{\textit{MP},t}(\tilde{\phi}_{\textit{MP}}) = \frac{\theta}{\theta - 1}\frac{1}{\tilde{\phi}_{\textit{MP}}}\frac{E_{t-1}\left[d_t^*P_t^{*\theta}C_t^*W_t^*\right]}{E_{t-1}\left[d_t^*P_t^{*\theta}C_t^*\right]}.$](img233.gif)
![\begin{multline*} E_{t-1}\left[d_t^* P_t^{*\theta} C_t^*\left(p_{\textit{MP},t}(\hat{\phi}_{\textit{MP},t})^{1 - \theta} - \frac{1}{\hat{\phi}_{\textit{MP},t}}W_t^* p_{\textit{MP},t}(\hat{\phi}_{\textit{MP},t})^{-\theta}\right)\right]\ - E_{t-1}\left[d_t^*S_t^{\theta-1} P_t^{*\theta} C_t^*\left(p_{X,t}(\hat{\phi}_{\textit{MP},t})^{1 - \theta} - \frac{1}{\hat{\phi}_{\textit{MP},t}}W_t^*S_t\tau p_{X,t}(\hat{\phi}_{\textit{MP},t})^{-\theta}\right)\right]\ - E_{t-1}\left[d_t^*\frac{S_{t-1}}{S_{t}}P_t^*(f_{\textit{MP}} - f_X)\right] = 0. \end{multline*}](img230.gif)
![$\displaystyle p_{t}^*(\tilde{\phi}) = \frac{\theta}{\theta - 1}\frac{1}{\tilde{\phi}}\frac{E_{t-1}\left[d_t^*P_t^{*\theta}C_t^*W_t^*\right]}{E_{t-1}\left[d_t^*P_t^{*\theta}C_t^*\right]}.$](img231.gif)
|
![$\displaystyle p_{X,t}(\tilde{\phi}_X) = \frac{\theta}{\theta - 1}\frac{\tau}{\tilde{\phi}_X}\frac{E_{t-1}\left[d_t^*P_t^{*\theta}C_t^*S_t^{\theta}W_t^*\right]}{E_{t-1}\left[d_t^*P_t^{*\theta}C_t^*S_t^{\theta-1}\right]}.$](img232.gif)
|
Table 1: Model parameters
| 0.96 | Annual discount rate | |
| 2 | Standard risk-aversion | |
| 5 | Elasticity of substitution | |
| Pareto shape parameter | ||
| 1.2 | 20% iceberg trade cost | |
| 0.035 | Fixed cost of local firms and exporters | |
|
|
1 | 60% of foreign sales from multinationals |
Table 2: The response of trade and multinational sales to inflation volatility
| (1) | (2) | (3) | |
|---|---|---|---|
| Exchange rate volatility | 0.400 (2.325) | 0.173 (1.949) | 0.904 (1.856) |
| Inflation level | 5.622 (6.398) | 11.31** (4.372) | 13.48*** (4.232) |
| OECD | 0.217*** (0.0465) | 0.228*** (0.0614) | 0.199*** (0.0606) |
| U.S. border | -0.188*** (0.0386) | -0.0304 (0.0678) | -0.0195 (0.0776) |
| 0.00436 (0.0236) | -0.0707** (0.0299) | ||
| 0.121** (0.0472) | 0.0908* (0.0503) | ||
| Rule of law index | 0.130** (0.0483) | ||
| Industry-year dummies | yes | yes | yes |
| Observations | 2,881 | 2,857 | 2,857 |
| R-squared | 0.386 | 0.401 | 0.423 |
The dependent variable is sales/(sales + exports). *** p$<$0.01, ** p$<$0.05, * p$<$0.1, standard errors clustered by country in parentheses
Table 3: Total multinational sales as a fraction of total multinational sales and exports, by industry
| Industry | Inflation volatility | Exrate volatility | Obs. |
|---|---|---|---|
| Information | -569.6*** | 17.5* | 338 |
| Manufacturing (chemical) | -157.7 | 3.1 | 353 |
| Manufacturing (computers) | -392.0 | -1.3 | 317 |
| Manufacturing (electrical) | -1468.7** | 3.62 | 301 |
| Manufacturing (food) | -1444.0*** | -5.1** | 334 |
| Manufacturing (machinery) | -413.5 | -0.5 | 325 |
| Manufacturing (metals) | -466.4* | 2.4 | 305 |
| Manufacturing (transportation) | -1296.5** | 3.8 | 305 |
| Mining | 702.9 | 0.5 | 279 |
The dependent variable is sales/(sales + exports). Inflation level, U.S. border, OECD, real GDP per capita, rule of law index, and year dummies included in all regressions. *** p$<$0.01, ** p$<$0.05, * p$<$0.1, clustered by country
Table 4: Robustness exercises of pooled regressions
| (1): sales/(sales + exports) | (2): sales/(sales + exports) | (3): sales/(sales + exports) | (4): 1n(sales/exports) | (5): 1n(sales/exports) | |
|---|---|---|---|---|---|
| Inflation volatility | -459.6*** (157.4) | -608.7*** (221.8) | -608.7*** (160.9) | 811.6 (1,429) | -394.5** (147.8) |
| Exchange rate volatility | 3.345 (4.851) | 1.046 (1.654) | 1.046 (1.179) | 89.56*** (22.17) | 3.435 (4.805) |
| Real GDP volatility | -92.68 (76.69) | -92.68 (56.98) | -433.9 (523.4) | 27.95 (16.86) | |
| Inflation level | 3.483 (5.941) | 10.35** (4.699) | 10.35** (3.280) | 41.99 (38.09) | 1.374 (5.386) |
| OECD | 0.157** (0.0624) | 0.151* (0.0842) | 0.151*** (0.0319) | 0.564 (0.452) | 0.128 (0.0820) |
| U.S. border | -0.0466 (0.0772) | 0.0197 (0.108) | 0.0197 (0.0946) | -1.091* (0.584) | 0.0538 (0.111) |
| -0.0202 (0.0363) | -0.0701** (0.0322) | -0.0701*** (0.0181) | -0.423** (0.209) | -0.0568 (0.0372) | |
| 0.0720 (0.0586) | 0.0987* (0.0548) | 0.0987* (0.0456) | -0.155 (0.367) | 0.0986 (0.0628) | |
| Rule of law index | 0.0532 (0.0506) | 0.136** (0.0544) | 0.136*** (0.0389) | 0.864** (0.329) | 0.116* (0.0582) |
| Common language | -0.0331 (0.0626) | -0.0331 (0.0230) | -0.385 (0.371) | -0.0818 (0.0678) | |
| Former colony | 0.0697 (0.0747) | 0.0697* (0.0344) | 0.456 (0.439) | 0.137 (0.0853) | |
| Landlocked | -0.0319 (0.0716) | -0.0319 (0.0197) | 0.128 (0.297) | -0.0235 (0.0801) | |
| Observations | 3,207 | 2,857 | 2,857 | 2,436 | 3,207 |
| R-squared | 0.382 | 0.432 | 0.432 | 0.554 | 0.395 |
| Industry-year dummies | yes | yes | yes | yes | yes |
| Drop crisis countries | no | yes | yes | yes | no |
| Clustered by | country | country | industry | country | country |
Standard errors in parentheses *** p$<$0.01, ** p$<$0.05, * p$<$0.1
Figure 1: Domestic, export, and FDI cutoffs
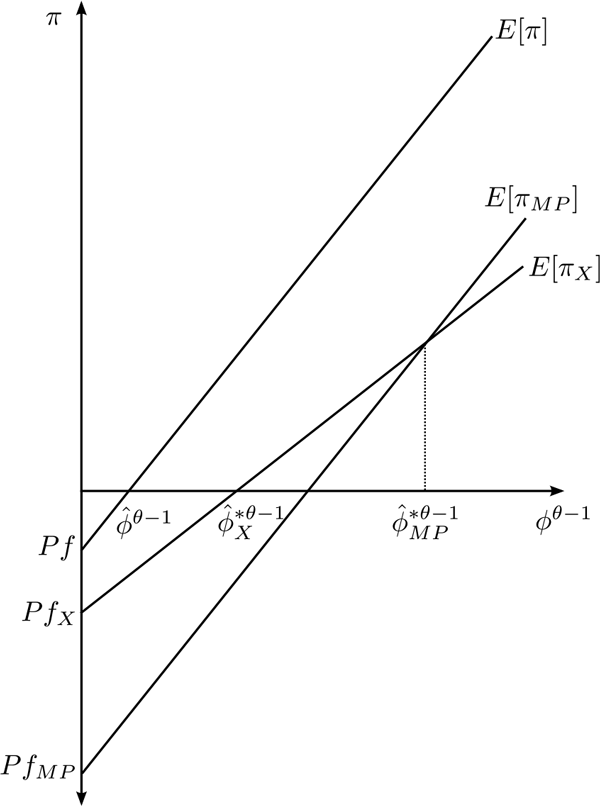
Figure 2: Convexity of the exporter profit function
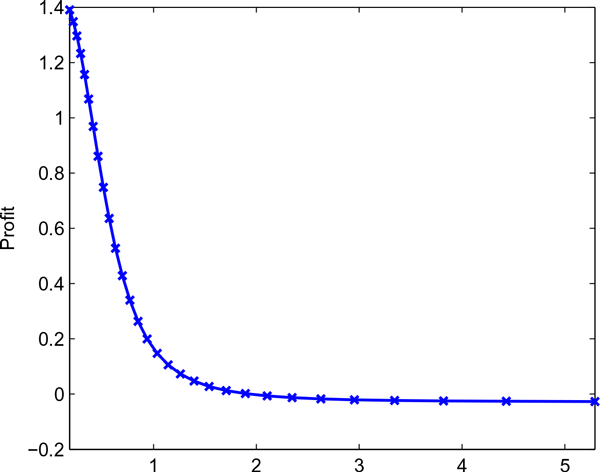
Figure 3: Expected profit for an example firm
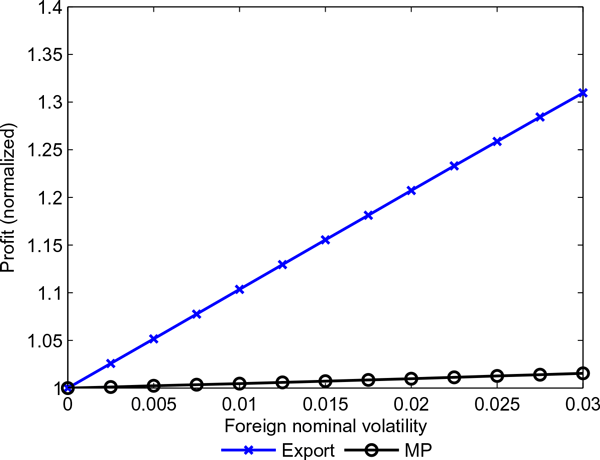
Figure 4: The extensive margin of exporters and multinationals
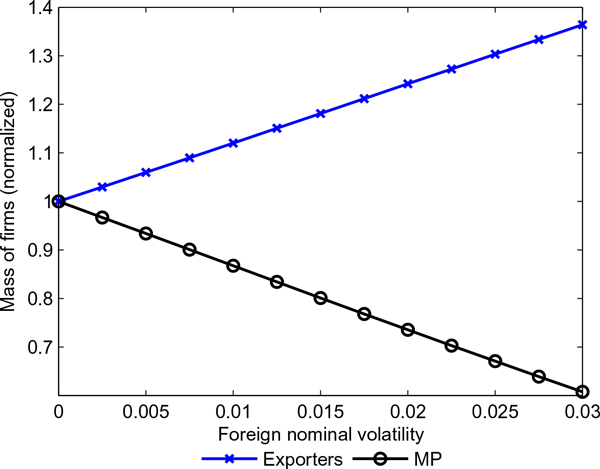
Figure 5: Quantity sales by exporters and multinationals
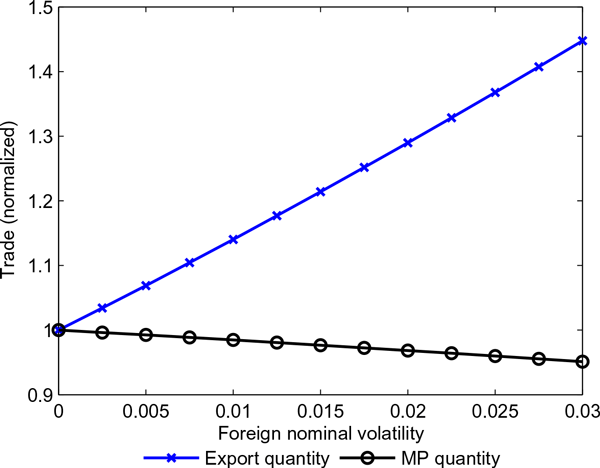
Figure 6: The fraction of total foreign sales from multinationals
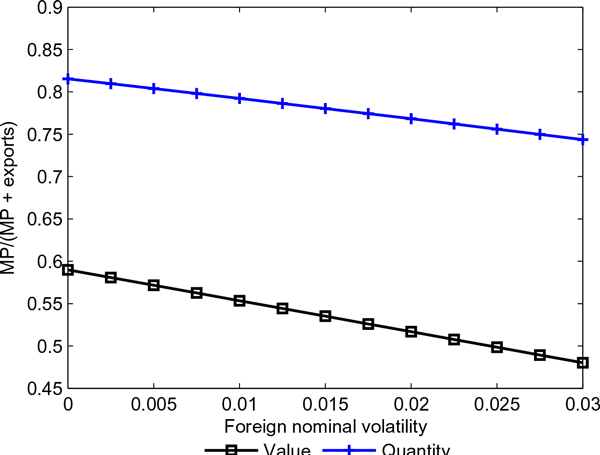
Figure 7: The distribution of multinational sales as a fraction of total foreign sales.
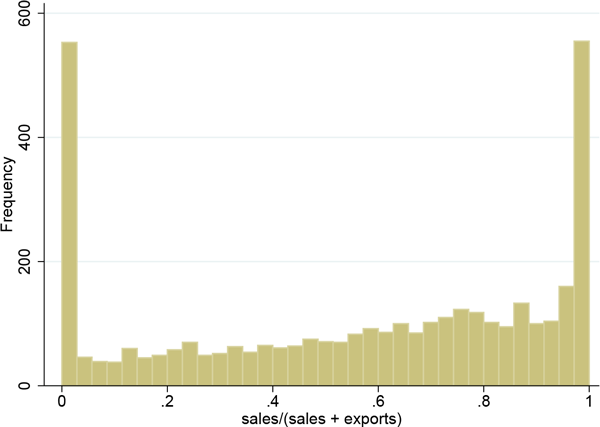
Figure 8: The distribution of multinational sales as a fraction of total foreign sales, for only observations with non-zero sales and non-zero exports
B Data Appendix
B.1 Data Description
Table 5 lists the sources of the variables used in the estimation procedure. Table 6 provide summary statistics for each variable. The full country list is: Argentina, Austria, Barbados, Belgium, Brazil, Canada, Colombia, Costa Rica, Czech Republic, Denmark, Dominican Republic, Ecuador, Egypt, Finland, France, Germany, Greece, Honduras, Hong Kong, Hungary, India, Indonesia, Ireland, Israel, Italy, Japan, Korea, Luxembourg, Malaysia, Mexico, Netherlands, Nigeria, Norway, Panama, Peru, Philippines, Poland, Portugal, Russia, Saudi Arabia, Singapore, South Africa, Spain, Sweden, Switzerland, Thailand, Turkey, United Kingdom, Venezuela. The crisis countries are: Argentina, Turkey, Venezuela, Brazil, and the Dominican Republic.
Table 5: Data Sources
| Variable description | Source |
|---|---|
| Sales by majority-owned foreign affiliates of U.S. multinational firms | Bureau of Economic Analysis |
| Exports by major industry | USITC |
| Inflation (Δ 1n CPI), nominal exchange rate | IMF International Financial Statistics |
| Distance, common language, colony, land-locked | Rose (2005) |
| Rule of law | World Bank World Governance Indicators (WGI) |
| Real GDP, Real GDP per capita | World Bank World Development Indicators (WGI) |
Table 6: Summary Statistics
| Variable | Obs | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|
| sales/(sales + exports) | 3730 | 0.563 | 0.3514721 | 0 | 1 |
| 3142 | 1.001 | 2.539211 | -7.516 | 13.016 | |
| Inflation volatility | 3292 | 4.51E-05 | 1.32E-04 | 5.17E-07 | 1.49E-03 |
| Inflation level | 3292 | 0.004 | 0.0058575 | -0.003 | 0.054 |
| Exchange rate volatility | 3557 | 6.68E-04 | 2.59E-03 | 0.000 | 0.051 |
| Landlocked | 3667 | 0.090 | 0.2865994 | 0 | 1 |
| 3667 | 8.487 | 0.4920865 | 6.981 | 9.154 | |
| U.S. border | 3730 | 0.042 | 0.1995967 | 0 | 1 |
| Common language | 3667 | 0.328 | 0.4695712 | 0 | 1 |
| Colony | 3667 | 0.038 | 0.1923087 | 0 | 1 |
| 3640 | 9.015 | 1.262342 | 5.883 | 11.193 | |
| Real GDP volatility | 3667 | 6.09E-04 | 1.31E-03 | 1.42E-05 | 7.52E-03 |
| Crisis | 3730 | 0.094 | 0.2916364 | 0 | 1 |
| OECD | 3730 | 0.417 | 0.4931105 | 0 | 1 |
| Rule of law | 3730 | 0.660 | 0.9684038 | -1.658 | 1.964 |
References
Bhattarai, Saroj, "Optimal Currency Denomination of Trade: Theory and Quantitative Exploration," 2009. Mimeo, Princeton University.
Cavallari, Lilia, "A Macroeconomic Model of Entry with Exporters and Multinationals," The B.E. Journal of Macroeconomics, September 2007, 7 (1).
__, "Macroeconomic Interdependence with Trade and Multinational Activities," Review of International Economics, 2008, 16 (3), 537-558.
__, "Exports and foreign direct investments in an endogenous-entry model with real and nominal uncertainty," Journal of Macroeconomics, March 2010, 32 (1), 300-313.
Chari, V V, Patrick J Kehoe, and Ellen R McGrattan, "Can sticky price models generate volatile and persistent real exchange rates?," The Review of Economic Studies, July 2002, 69 (240), 533.
Cushman, David O., "Real Exchange Rate Risk, Expectations, and the Level of Direct Investment," The Review of Economics and Statistics, May 1985, 67 (2), 297-308.
Devereux, M.B. and C. Engel, "The Optimal Choice of Exchange Rate Regime: Price-setting Rules and Internationalized Production," in Magnus Blomstrom and Linda S. Goldberg, eds., Topics in Empirical International Economics: A Festschrift in Honor of Robert E. Lipsey, University of Chicago Press, 2001.
Eichenbaum, Martin and Charles L. Evans, "Some Empirical Evidence on the Effects of Shocks to Monetary Policy on Exchange Rates," The Quarterly Journal of Economics, November 1995, 110 (4), 975-1009.
Eichengreen, Barry J., Exorbitant Privilege: The rise and fall of the Dollar and the Future of the International Monetary System, Oxford University Press, 2011.
Engel, Charles, "Equivalence Results for Optimal Pass-Through, Optimal Indexing to Exchange Rates, and Optimal Choice of Currency for Export Pricing," Journal of the European Economic Association, December 2006, 4 (6), 1249-1260.
Fillat, José and Stephania Garetto, "Risk, Returns, and Multinational Production," October 2010. Mimeo.
Giovannini, Alberto, "Exchange rates and traded goods prices," Journal of International Economics, February 1988, 24 (1-2), 45-68.
Goldberg, Linda S. and Charles D. Kolstad, "Foreign Direct Investment, Exchange Rate Variability and Demand Uncertainty," International Economic Review, November 1995, 36 (4), 855-873.
Gopinath, Gita and Roberto Rigobon, "Sticky Borders*," Quarterly Journal of Economics, May 2008, 123 (2), 531-575.
__, Oleg Itskhoki, and Roberto Rigobon, "Currency Choice and Exchange Rate Pass-Through," American Economic Review, March 2010, 100 (1), 304-336.
Helpman, Elhanan, Marc J. Melitz, and Stephen R. Yeaple, "Export versus FDI with Heterogeneous Firms," The American Economic Review, March 2004, 94 (1), 300-316.
Irarrazabal, Alfonso A and Luca David Opromolla, "A Theory of Entry and Exit into Exports Markets," Technical Report, Mimeo, New York University 2009.
Landry, Anthony, "State-dependent pricing, local-currency pricing, and exchange rate passthrough," Journal of Economic Dynamics and Control, 2009, In Press, Corrected Proof.
Obstfeld, Maurice and Kenneth Rogoff, "Risk and Exchange Rates," National Bureau of Economic Research Working Paper Series, August 1998, No. 6694.
Ramondo, Natalia and Veronica Rappoport, "The role of multinational production in a risky environment," Journal of International Economics, July 2010, 81 (2), 240-252.
__, __, and Kim J. Ruhl, "The Proximity-Concentration Tradeoff under Uncertainty," 2010. Mimeo.
Rose, Andrew, "Which International Institutions Promote International Trade?," Review of Internatinal Economics, September 2005, 13 (4), 682-698.
Ruhl, Kim J., "The International Elasticity Puzzle," 2008. Mimeo.
Russ, Katheryn, "The endogeneity of the exchange rate as a determinant of FDI: A model of entry and multinational firms," Journal of International Economics, 2007, 71, 344-372.
Schoenle, Raphael, "International Menu Costs and Price Dynamics," January 2010. Mimeo, Princeton University.
Footnotes
1. In addition, Cavallari (2010) studies real and nominal uncertainty with exports and multinational production in a model without firm heterogeneity and thus without an explicit choice of how to serve the foreign market. See also Cavallari (2008) and Cavallari (2007). Return to text
2. Obstfeld and Rogoff (1998) discuss the effects of relaxing the log-utility assumption over money balances. They also emphasize that this result holds regardless of whether prices are sticky. Return to text
3. e.g. Obstfeld and Rogoff (1998). Return to text
4. For notational simplicity, I abstract from a constant growth rate term, which does not qualitatively affect the results. Return to text
5. See, e.g., Engel (2006), Gopinath, Itskhoki and Rigobon (2010), Bhattarai (2009), and Eichengreen (2011). Devereux and Engel (2001) discuss the effects of LCP and PCP on the optimality of floating versus flexible exchange rate regimes in the context of multinational production. Return to text
6. For a discussion of the implications of flexible prices, see Appendix A.3. Return to text
7. For the purposes of this paper, I restrict firms to either serve the foreign market through MP or exports, but not both. It can be shown that with export prices set in the home currency, foreign firms will never wish to both export and produce abroad. More generally, one can reinterpret "firm" as "product", which is empirically more plausible. Return to text
8. The results will depend on multinational products being priced relatively more in the foreign currency. I assume that all multinationals price in the foreign currency for simplicity. Return to text
9. The stochastic discount factor potentially introduces risk aversion from households into how profits are valued. In practice, this is not a quantitatively important factor. Firms are risk neutral in the sense that they maximize a linear expression of profits, as opposed to partial equilibrium models like Goldberg and Kolstad (1995). Return to text
10. Experimentation with the model parameters reveals that the main qualitative results are not sensitive to the precise parameters chosen. Return to text
11. See Ruhl (2008) for a survey. Return to text
12. These fixed costs imply that 35% of potential entrants export and 90% produce domestically under no uncertainty. Return to text
13. This is also the basic result from Russ (2007), showing that higher foreign volatility is relatively better for home firms over foreign firms in the foreign market. Return to text
14. These countries are Argentina, Turkey, Venezuela, Brazil, and the Dominican Republic. Return to text
15. The CPI measures are monthly, and the variance is taken for each year. The results are generally robust to using lagged values and a quarterly frequency taken over a two year horizon. Return to text
16. Running the pooled regression (3) from Table 2 using only those observations with non-zero exports and non-zero multinational sales, I obtain a point estimate for the effects of inflation volatility on the fraction of multinational production relative to total foreign sales of -196.0 significant at the 10% level. Return to text
17. Landry (2009) provides more recent evidence. Return to text
18. Examples of this include Cushman (1985) and Goldberg and Kolstad (1995). Return to text
19. Note that
![]() and
and
![]() .
Return to text
.
Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text