
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number IFDP 1039, December 2011--- Screen Reader
Version*
Aggregate Hours Worked in OECD Countries: New Measurement and Implications for Business Cycles
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We build a dataset of quarterly hours worked for 14 OECD countries. We document that hours are as volatile as output, that a large fraction of labor adjustment takes place along the intensive margin, and that the volatility of hours relative to output has increased over time. We use these data to reassess the Great Recession and prior recessions. The Great Recession in many countries is a puzzle in that labor wedges are small, while those in the U.S. Great Recession - and those in previous European recessions - are much larger.
Keywords: Hours worked, international business cycles, great recession, labor wedge
JEL classification: E32, F44, J20
1 Introduction
Documenting and assessing cyclical fluctuations in hours worked has been a central focus of business cycle research since at least Kydland and Prescott [1982] and Hansen [1985], and the very different labor market outcomes observed during the 2008-09 recession across countries have generated increased interest in cyclical labor fluctuations. However, the literature typically focuses on the U.S. due to the very limited availability of systematic measures of aggregate hours worked in other countries. Thus, what is known about cyclical changes in labor input and productivity in other countries is largely based on measures of employment, rather than hours worked (see for example Backus, Kehoe, and Kydland, [1995], BKK henceforth).
The fact that international studies of fluctuations omit the intensive labor margin means not only that cross-country comparisons of cyclical changes in labor are limited, but that labor policy analyses are limited as well. Specifically, Hopenhayn and Rogerson's [1993] analyses of hiring and firing costs suggested to many economists that European labor markets provide an excellent opportunity for evaluating and quantifying the impact of these policies, but studies of fluctuations along these lines have thus far been limited because of the lack of data on the intensive margin.
This paper addresses these shortcomings by constructing a new dataset for total hours worked at the quarterly frequency which covers 14 OECD countries and spans the last fifty years. The dataset draws on a variety of international sources, including data from national statistical offices, establishment surveys, and household surveys. There are three contributions. First, this paper provides the most comprehensive, international database of quarterly total hours worked. Second, we document and compare cyclical fluctuations between the U.S. and other countries in total hours and labor productivity, as well as in the labor wedge (the deviation of the marginal product of labor from the marginal rate of substitution between consumption and leisure) and in the productivity wedge (the deviation of output from the combination of capital and labor input). Third, the paper analyzes the Great Recession using these new data.
We construct these measures consistently across countries according to national income and product account principles, with a focus on measuring hours worked, rather than hours paid for. The paper then uses these measures to compare business cycle properties of total hours worked across OECD countries, focusing on three questions: (1) How do accepted business cycle features in OECD countries change when total hours are used as labor input? (2) What fraction of fluctuations in output and labor across countries is accounted for by labor versus productivity wedges? (3) How does the Great Recession in other OECD countries compare to that in the U.S.?
This last question is important, as Ohanian [2010] documents large differences in this recession between the U.S. and other advanced economies. He finds that productivity is close to trend in the US, and that the U.S. Great Recession is due to a very large decline in labor input and a historically large labor wedge. In contrast, the Great Recession in the other G7 countries is the consequence of large productivity declines, with only small employment declines and no labor wedge. Since there is evidence that labor input may have declined considerably through declines in hours per worker in these other countries, we use hours worked to re-assess Ohanian's analysis of the Great Recession, as the small changes in Western European employment may simply reflect large firing costs or other differences in labor markets.1
Our main findings contrast significantly with commonly held views in some cases, and raise significant puzzles in other cases. Specifically, we show that employment is a poor proxy for labor input in many OECD countries, as changes in hours per worker are about as large as changes in employment. We also find that employment-based labor wedges are much too large in Europe, given high European firing costs, while hours-based labor wedges are comparatively too small. Finally, we find that the Great Recession is a substantial puzzle in Europe, as both employment-based and hours-based labor wedges are nearly zero in many European countries. This stands in sharp contrast to labor wedges in the U.S. during the Great Recession, or labor wedges in other European recessions, both of which are an order of magnitude larger.
The paper is organized as follows. Section 2 describes the data sources and the approach we use to construct the hours measures. Section 3 compares standard business cycle features of hours, employment, and productivity across countries. Section 4 uses the business cycle accounting approach developed by Cole and Ohanian [2002], and Chari, Kehoe, and McGrattan [2007], to construct labor and productivity wedges using both employment and hours for recessions since 1960, with a specific focus on assessing the relative importance of these wedges during the Great Recession. Section 5 concludes.
2 Data
We collected national accounts series for nominal output and its
components from the OECD-Economic Outlook and deflate them using
their specific price deflators. Total hours worked (![]() )
is constructed as the product of hours worked per worker
(
)
is constructed as the product of hours worked per worker
(![]() ) and employment (
) and employment (![]() ), normalized
by the size of the population aged 16-64 years (
), normalized
by the size of the population aged 16-64 years (![]() ):
):
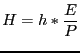 |
(1) |
Labor productivity (![]() ) is the ratio between real
output and total hours worked,
) is the ratio between real
output and total hours worked,
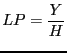 |
(2) |
Employment and population data are from national statistical
offices and the OECD-Economic Outlook database. We next present our
methodology to construct our series for hours per worker
(![]() ), which represents one of the main
contributions of the paper. Appendix A presents country-specific
data sources and details.
), which represents one of the main
contributions of the paper. Appendix A presents country-specific
data sources and details.
2.1 Construction of Hours Per Worker
Official series for quarterly hours worked per worker are typically short and their comparability across countries is problematic, even in advanced OECD economies. In our dataset, only the United States data begins in 1960, while data in many of the other countries start in the mid- to late-1970s. Moreover, the underlying surveys used to construct these series, whether using establishments or labor force surveys, are not uniform across countries and, in some cases, are not consistent in the same country at different dates.
Establishments surveys have been conducted in many countries at a quarterly or even monthly frequency since the 1960s, but they often collect hours paid rather than hours worked. Thus, these survey data do not account for differences across countries in important features of labor contracts such as paid vacation or sick days. In addition, establishment surveys do not sample all sectors of the economy, as the government sector is often omitted.
Labor force surveys tend to be more comprehensive since they directly sample individuals, but they suffer from several shortcomings as well. It is well-known that these surveys present an upward bias for hours worked per worker due to self-reporting. Moreover, there are methodological differences across countries in the construction of these surveys which also affect the concept of working time measured, thus undermining their comparability 2. Finally, in many countries labor force surveys have been conducted only at an annual frequency until very recently.
Given these data limitations, it is not suprising that the literature on international business cycles has focused on employment as the standard measure of labor input. One key contribution of this paper is to provide researchers with a standardized dataset of total hours worked, including both the intensive and the extensive margin.
Our methodology to construct quarterly series of hours per worker consists of three elements. First, we obtain a dataset of hours worked per worker that has been adjusted to take into account cross-country variation in variables such as sick days and holidays, but is available only at annual frequency. Second, we construct a dataset of quarterly indicators for hours worked per worker comprised of the official series extended back in time using information from establishment surveys published by the International Labor Organization (ILO). Third, we adjust our quarterly indicators to ensure that they feature statistical properties of the higher quality annual series. We next discuss the details of our procedure.
The Conference Board and the Groningen Growth and Development Centre (GGDC) have produced estimates of hours worked per worker that are comparable across countries, but are only available annually. These series, which are from their Total Economy Database (TED), are adjusted to reflect most sources of cross-country variation in hours worked, including contracted length of the workweek, statutory holidays, paid vacation and sick days, and days lost due to strikes, and are consistent with NIPA measures of output. The TED dataset covers a large sample of developed and developing countries, in many cases starting as early as 1950, and is currently the benchmark source of data for analysis of long-run changes in total hours worked across countries (see Rogerson [2006], Ohanian et al. [2008], Rogerson and Shimer [2010]).
We construct a dataset of quarterly indicators of hours worked per worker as follows. For all countries in our sample, we collect quarterly series of hours worked per worker that are consistent with the national accounts from national agencies. We refer to these data as the official series. Since these series do not cover the entire sample period, we extend them back to the early 1960s using measures of hours worked per worker collected from ILO and, in a few instances, the OECD Main Economic Indicators (MEI) 3. Although both publications are based on information from establishment surveys, we opted for adopting the ILO series where possible for several reasons. First, the ILO series often measure total hours actually worked,and not just hours paid for. Second, the ILO series cover the non-agricultural sector (i.e. manufacturing, mining and quarrying, construction, commerce, transport and services) whereas the OECD-MEI series typically cover the manufacturing sector only. Third, the ILO series have statistical properties in terms of trend and variability that are closer to the official series.
We extend the official series to the 1960s by estimating a country-specific statistical relationship between the official and the ILO series and then backcasting the official series using the estimated model and the ILO data. To ensure that the estimated OLS coefficients are not affected by extreme values, we remove outliers in the ILO series following the approach of Iglewicz and Hoaglin [1993]. Specifically, weconstruct the modified Z-score test statistic
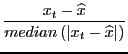
|
(3) |
where ![]() is the first difference of the
logarithm of the ILO series,
is the first difference of the
logarithm of the ILO series,
![]() is the median growth rate, and
is the median growth rate, and
![]() is the median absolute deviation. We then identify as outliers
those observations for which
is the median absolute deviation. We then identify as outliers
those observations for which
![]() that
corresponds to a probability of 0.0005 in a standard normal
distribution, and replace them with an interpolation that uses both
the preceeding and following observations. Notably, our test
statistic identifies at most 4 observations as outliers in each
country.
that
corresponds to a probability of 0.0005 in a standard normal
distribution, and replace them with an interpolation that uses both
the preceeding and following observations. Notably, our test
statistic identifies at most 4 observations as outliers in each
country.
We then estimate an econometric model of the level of the
official series
![]() as a function of a
constant
as a function of a
constant ![]() current and lagged values of the ILO
series
current and lagged values of the ILO
series
![]() , and a
time trend:
, and a
time trend:
| (4) |
We estimate country-specific models using all the observations available for overlapping quarters up to 1984Q4, since there is considerable evidence that the volatility of output declined markedly after 1984 (the Great Moderation). We do not include indicators of activity among the regressors because several economists have documented that the volatility of total hours in the United States has increased relative to the volatility of output over time. Including such indicators would thus impose a fixed relationship between output and labor input that may be strongly at variance with the data.
We select the number of lags ![]() using Akaike and
Schwarz information criteria and perform Lagrange Multiplier tests
on the residuals to test for serial correlation. Overall, this
estimation produced adjusted
using Akaike and
Schwarz information criteria and perform Lagrange Multiplier tests
on the residuals to test for serial correlation. Overall, this
estimation produced adjusted ![]() between 0.55
(in the case of Australia, whose specification does not include a
time trend) and 0.98 (in the case of France and Germany, with a
time trend included only in the specification for Germany).
between 0.55
(in the case of Australia, whose specification does not include a
time trend) and 0.98 (in the case of France and Germany, with a
time trend included only in the specification for Germany).
This estimation is applied to Australia, Canada, France, Germany, Italy, Japan, Norway, and Sweden. Since the official series for Austria, Finland, Ireland, and Korea start after 1982, we use the entire sample to estimate our statistical model for these countries. No estimation is applied to the United States (the BLS series we use begins in 1947) and the United Kingdom (for which only the official series, which starts in 1971, is available). 4
The final step involves adjusting the quarterly indicators of hours worked per worker so that they conform with the annual series obtained from the TED dataset. We follow Denton [1971] as it is commonly implemented by national statistical offices.5 This method minimizes the weighted adjustments imposed on the constructed quarterly indicators subject to the constraint that the sum of the quarterly adjusted series equals the value of the annual TED series:
| (5) |
| (6) |
where ![]() is the annual TED series,
is the annual TED series, ![]() is the quarterly indicators we construct using the official and the
ILO series,
is the quarterly indicators we construct using the official and the
ILO series, ![]() is the adjusted quarterly series that
we will use in our analysis, and
is the adjusted quarterly series that
we will use in our analysis, and
![]() is a wieghting matrix. Note
that using the identity matrix to weight the observations would
evenly distribute the discrepancy between the annual and (the sum
of the) quarterly series across quarterly observations, thus
introducing discrete jumps at the start of each year. Denton shows
that a penalty function based on the difference between the first
difference of the two series
is a wieghting matrix. Note
that using the identity matrix to weight the observations would
evenly distribute the discrepancy between the annual and (the sum
of the) quarterly series across quarterly observations, thus
introducing discrete jumps at the start of each year. Denton shows
that a penalty function based on the difference between the first
difference of the two series
![]() or the proportional first difference of the two series
or the proportional first difference of the two series
![]() does not suffer from this shortcoming.6 These two approaches
yield very similar results and we present results using the
proportional first difference specification. Table 1 shows the
countries and their time periods considered in our sample.
does not suffer from this shortcoming.6 These two approaches
yield very similar results and we present results using the
proportional first difference specification. Table 1 shows the
countries and their time periods considered in our sample.
Table 1. Hours Worked per Worker: Sample
| Australia | 1970-2010 |
|---|---|
| Austria | 1965-2010 |
| Canada | 1960-2010 |
| Finland | 1960-2010 |
| France | 1960-2010 |
| Germany | 1960-2010 |
| Ireland | 1960-2010 |
| Italy | 1960-2010 |
| Japan | 1960-2010 |
| Korea | 1970-2009 |
| Norway | 1960-2010 |
| Sweden | 1975-2010 |
| UK | 1971-2010 |
| U.S. | 1960-2010 |
2.2 Testing the Accuracy of the Methodology
This section tests the quality of the data construction methodology by comparing actual hours in the U.S., Germany, and Japan to constructed hours from these countries. All three of these countries have official data for the early years, as the U.S. data covers the entire period, German data begins in 1970 and Japan's data begins in 1968.
Figure 1 plots the constructed US data together with the
official data. We construct a U.S. series by applying the procedure
presented in Section 2.1. That is, we first collect U.S. hours
worked per worker in the non-agricultural sector for the period
1960Q1-1984Q4 from the ILO and correct for outliers using the
modified Z-score statistics ![]() . We next
estimate a relationship, following equation (4), between the official (BLS) series and the ILO
series over the period 1975Q1-1984Q4. We then use the estimated
coefficients and the ILO series to backcast the official series
from 1974Q4 to 1960Q1. Finally, we adjust this extended series,
that now covers the whole sample 1960Q1-2010Q4, to conform with the
TED annual data using Denton's procedure.
. We next
estimate a relationship, following equation (4), between the official (BLS) series and the ILO
series over the period 1975Q1-1984Q4. We then use the estimated
coefficients and the ILO series to backcast the official series
from 1974Q4 to 1960Q1. Finally, we adjust this extended series,
that now covers the whole sample 1960Q1-2010Q4, to conform with the
TED annual data using Denton's procedure.
Figure 1. Testing the OR [2011] Procedure using U.S. Data
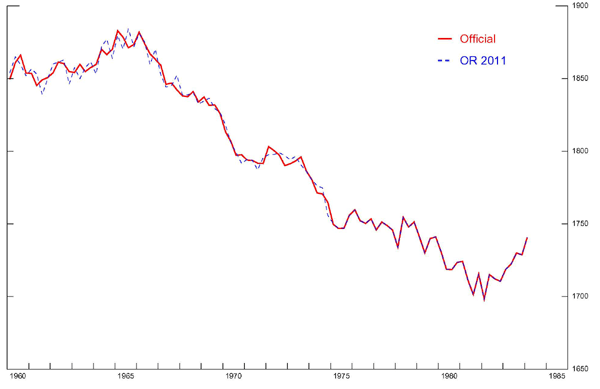
Data for Figure 1
| Dates | or2011 | Official |
|---|---|---|
| 1960Q1 | 1854.04 | 1849.67 |
| 1960Q2 | 1865.14 | 1861.05 |
| 1960Q3 | 1859.66 | 1866.11 |
| 1960Q4 | 1851.94 | 1853.95 |
| 1961Q1 | 1856.74 | 1853.64 |
| 1961Q2 | 1853.24 | 1845.26 |
| 1961Q3 | 1839.07 | 1849.22 |
| 1961Q4 | 1849.82 | 1850.74 |
| 1962Q1 | 1860.24 | 1854.04 |
| 1962Q2 | 1861.3 | 1861.41 |
| 1962Q3 | 1863.01 | 1860.39 |
| 1962Q4 | 1846.23 | 1854.95 |
| 1963Q1 | 1857.66 | 1854.22 |
| 1963Q2 | 1850.03 | 1859.94 |
| 1963Q3 | 1857.57 | 1854.94 |
| 1963Q4 | 1861.53 | 1857.69 |
| 1964Q1 | 1853.28 | 1859.7 |
| 1964Q2 | 1872.11 | 1870.24 |
| 1964Q3 | 1877.13 | 1866.58 |
| 1964Q4 | 1864.16 | 1870.16 |
| 1965Q1 | 1879.73 | 1882.99 |
| 1965Q2 | 1870.43 | 1878.61 |
| 1965Q3 | 1884.22 | 1871.26 |
| 1965Q4 | 1872.19 | 1873.7 |
| 1966Q1 | 1881.2 | 1881.95 |
| 1966Q2 | 1875.33 | 1874.16 |
| 1966Q3 | 1859.79 | 1867.09 |
| 1966Q4 | 1870.3 | 1863.41 |
| 1967Q1 | 1852.87 | 1859.23 |
| 1967Q2 | 1844.23 | 1846.16 |
| 1967Q3 | 1845.38 | 1847.04 |
| 1967Q4 | 1852.41 | 1842.45 |
| 1968Q1 | 1838.94 | 1838.18 |
| 1968Q2 | 1838.79 | 1837.58 |
| 1968Q3 | 1840.63 | 1841.19 |
| 1968Q4 | 1832.65 | 1834.05 |
| 1969Q1 | 1834.56 | 1837.46 |
| 1969Q2 | 1836.54 | 1831.59 |
| 1969Q3 | 1829.43 | 1831.99 |
| 1969Q4 | 1826.55 | 1826.04 |
| 1970Q1 | 1818.38 | 1813.66 |
| 1970Q2 | 1805.84 | 1806.8 |
| 1970Q3 | 1799.41 | 1797.24 |
| 1970Q4 | 1791.76 | 1797.69 |
| 1971Q1 | 1794.45 | 1794.01 |
| 1971Q2 | 1793.89 | 1793.84 |
| 1971Q3 | 1787.24 | 1791.91 |
| 1971Q4 | 1795.94 | 1791.76 |
| 1972Q1 | 1797.64 | 1803.25 |
| 1972Q2 | 1797.77 | 1800.6 |
| 1972Q3 | 1798.96 | 1797.44 |
| 1972Q4 | 1797.1 | 1790.18 |
| 1973Q1 | 1794.19 | 1791.48 |
| 1973Q2 | 1796.57 | 1793.43 |
| 1973Q3 | 1790.65 | 1796.21 |
| 1973Q4 | 1786.13 | 1786.41 |
| 1974Q1 | 1780.56 | 1780.67 |
| 1974Q2 | 1776.27 | 1771.46 |
| 1974Q3 | 1774.85 | 1770.67 |
| 1974Q4 | 1756.08 | 1764.96 |
| 1975Q1 | 1750.24 | 1749.7 |
| 1975Q2 | 1747.03 | 1747 |
| 1975Q3 | 1746.92 | 1747.18 |
| 1975Q4 | 1755.82 | 1756.13 |
| 1976Q1 | 1759.68 | 1759.81 |
| 1976Q2 | 1752.24 | 1752.25 |
| 1976Q3 | 1750.5 | 1750.44 |
| 1976Q4 | 1753.54 | 1753.47 |
| 1977Q1 | 1745.87 | 1745.84 |
| 1977Q2 | 1751.37 | 1751.37 |
| 1977Q3 | 1748.88 | 1748.89 |
| 1977Q4 | 1745.91 | 1745.93 |
| 1978Q1 | 1733.96 | 1733.97 |
| 1978Q2 | 1754.64 | 1754.64 |
| 1978Q3 | 1747.99 | 1747.98 |
| 1978Q4 | 1751.46 | 1751.46 |
| 1979Q1 | 1740.99 | 1740.99 |
| 1979Q2 | 1729.98 | 1729.98 |
| 1979Q3 | 1740.02 | 1740.02 |
| 1979Q4 | 1741.16 | 1741.16 |
| 1980Q1 | 1731.14 | 1731.14 |
| 1980Q2 | 1718.96 | 1718.96 |
| 1980Q3 | 1718.6 | 1718.6 |
| 1980Q4 | 1723.62 | 1723.62 |
| 1981Q1 | 1724.19 | 1724.19 |
| 1981Q2 | 1711.27 | 1711.27 |
| 1981Q3 | 1701.44 | 1701.44 |
| 1981Q4 | 1715.53 | 1715.53 |
| 1982Q1 | 1698.42 | 1698.42 |
| 1982Q2 | 1715.16 | 1715.16 |
| 1982Q3 | 1712.32 | 1712.32 |
| 1982Q4 | 1710.57 | 1710.57 |
| 1983Q1 | 1718.92 | 1718.92 |
| 1983Q2 | 1722.42 | 1722.42 |
| 1983Q3 | 1730.1 | 1730.1 |
| 1983Q4 | 1728.85 | 1728.85 |
| 1984Q1 | 1740.71 | 1740.71 |
This procedure produces constructed hours worked per worker for the US that matches the official hours series very well. Denton's adjustment accurately generates the level of the series while the ILO data largely reproduce the cyclical properties of the series. Table 2 provides additional evidence on the quality of the constructed data by comparing the cyclical properties of the constructed and official US hours series, and also for those in Germany and Japan. Statistics are for three measures: first difference, HP-filter with a smoothing parameter of 1600, and four-quarter changes of the natural logarithm of the hours series.
Table 2. Assessing OR [2011] Procedure (X: Hours per worker constructed following OR [2011] procedure; Y: Official series of hours per worker)
| First Difference | 4-Quarter Changes | HP Residuals | |
|---|---|---|---|
| Std. Deviation (X) Std. Deviation (Y): U.S | 1.2 | 1.1 | 1.1 |
| Std. Deviation (X) Std. Deviation (Y): Germany | 0.9 | 1.0 | 1.0 |
| Std. Deviation (X) Std. Deviation (Y): Japan | 0.8 | 0.9 | 0.9 |
| Correlation (X,Y): U.S. | 0.7 | 0.9 | 0.9 |
| Correlation (X,Y): Germany | 0.9 | 1.0 | 1.0 |
| Correlation (X,Y): Japan | 0.8 | 1.0 | 1.0 |
NB. In all cases, series have been logged and adjusted using Denton [1971] procedure. Regressions are estimated over the sampe 1975-1984. Statistics refer to the following country-specific samples: U.S. (1960Q1-1984Q4), Germany (1970Q1-1984Q4), and Japan (1968Q1-1984Q4).
The standard deviation of the cyclical components of the constructed series for these countries is close to the standard deviation of the official series. The constructed and the official series are also highly correlated. This evidence indicates that our procedure provides an empirically accurate description for the cyclical patterns of hours per worker across these countries.
2.3 Differences Between Fluctuations at the Quarterly and Annual Frequency
Since most business cycle research for the countries presented here is conducted with annual data, it is natural to ask if business cycles have different features when measured with quarterly data. This section presents peak-to-trough statistics for real GDP and total hours worked for both data frequencies. The time period for each analysis is based on data availability which differs across countries.
Table 3. Output and Hours at Trough, Deviations from Peak (Average, All Recessions)
| Output: Quarterly | Output: Annual | Total Hours: Quarterly | Total Hours: Annual | |
|---|---|---|---|---|
| United States | -1.6 | -0.7 | -2.8 | -2.2 |
| France | -0.6 | 0.1 | -1.5 | -1.4 |
| Germany | -0.9 | -0.2 | -4.8 | -3.9 |
| Italy | -1.5 | -0.1 | -2.9 | -2.3 |
| Euro | -1.0 | -0.1 | -3.1 | -2.6 |
| United Kingdom | -4.1 | -2.2 | -4.2 | -4.2 |
Note: For the U.S., recessions refer to NBER dates, excluding the 1960-1961 episode. For other countries, ECRI dates.
Table 3 compares the average peak-to-trough changes in output and total hours worked for all NBER business cycle recession dates for the U.S. at both quarterly and annual frequency. We also include peak-to-trough changes for France, Germany, Italy, their average (Euro), and the UK using ECRI recession dates. This comparison shows that there is considerably more business cycle volatility in the quarterly data. For instance, the average US recession features a decline of 1.6 percent for GDP and 2.8 percent for total hours worked in the quarterly data, whereas these same statistics are only 0.7 percent and 2.2 percent respectively in the annual data. There are also large peak-to-trough differences between these frequencies in the European countries, with a 1 percent decline in real GDP and a 3 percent decline in hours worked in quarterly data for the Euro countries, compared to a roughly unchanged real GDP and a 2.6 percent decline in hours worked at the annual frequency.
These differences in volatility arise because annual data invariably smooths the quarterly variation and because peaks and troughs tend to occur at diffent times during the calendar year. For example, a peak that occurs at the start of a calendar year impacts measurement differently than a peak that occurs at the end of a calendar year.
We also compared fluctuation statistics at the two frequencies using HP filtered data, which allows us to compare differences in co-movement as well. 7 We used the standard smoothing parameter of 1600 for quarterly data and a smoothing parameter of 100 for the annual data, as typically done in the literature (see, for instance, Cooley and Ohanian [1991], and Rogerson and Shimer [2010]). There are considerable differences in the volatilities and correlations between the two frequences in the HP filtered data. In particular, the correlation between total hours and output, among other variables, is significantly lower in the quarterly data than in the annual data. These differences were smaller when we used a smoothing parameter of 10 for the annual data, as recommended by Ravn and Uhlig [2002], although this parameter value has yet to become the benchmark for annual business cycle analysis. In summary, these data suggest that quarterly business cycle measurement differs considerably from annual data.
2.4 Cross-Country Differences in Employment Protection
Before turning to the analysis, we note that these countries have very different labor market institutions and regulations that affect the cost of hiring and firing workers. These regulations are typically called employment protection legislation. Cross-country differences in this legislation differentially impacts the incentives for employers to adjust labor input along the intensive margin compared to the extensive margin. The OECD produces employment protection rankings for OECD countries that measures the strength of these policies, and we summarize the OECD's ranking here [OECD, 2008]. The OECD index is based primarily on (i) the strength of protection of permanent workers against individual dismissal, (ii) the specific requirements for collective worker dismissal, and (iii) regulations on temporary employment contracts.
Several of the European countries studied here have relatively high levels of employment protection. Specifically, Spain ranks 4th highest in protection (out of 40 countries), while France is 6th, Norway 11th, Germany is 13th, and Italy is 15th. At the other end of the distribution, the UK ranks 38th, Canada 39th, and the U.S. has the least amount of employment protection of these 40 countries. These large cross-country differences in employment protection will provide a useful approach in interpreting the findings below.
3 Labor Input and Labor Productivity over the Business Cycle
This section presents standard business cycle facts about labor input, measured as total hours worked per adult, and labor productivity, measured as output per hour, across countries and over time. We also compare these statistics to the corresponding measures constructed with employment rather than hours, as typically done in the literature. Throughout the analysis, these statistics refer to the cyclical component of the data obtained after applying the HP filter with smoothing parameter of 1600 to the logged series 8.
The most striking findings are that labor input is much more volatile than previously considered, that this volatility changes considerably over time, and that hours-based labor productivity is procyclical but, in contrast to employment-based productivity, significantly negatively correlated in some cases with hours worked. Taken together, these facts suggest that employment, which is commonly used in the literature, is a poor proxy for labor input, and that standard international equilibrium models, such as BKK, cannot plausibly account for the observed volatility of hours and the comovement between labor productivity and hours reported here.
3.1 Hours Worked: Volatility and Correlation
Figure 2 presents the standard deviation of total hours worked relative to the standard deviation output for all countries in our dataset over the entire period. Hours worked is almost as volatile as output, as the average of this ratio of standard deviations is about 0.9. There is also substantial variation across countries, ranging from 0.65 in Japan to 1.6 in Norway.
Table 4 shows this volatility separately for the period 1985-2007, often referred to as the "Great Moderation", and the period before that. The table also compares these volatility statistics to the volatility of employment reported in BKK, which is a standard reference in the international business cycle literature.
Figure 2. Volatility of Labor Input (1960-2007)
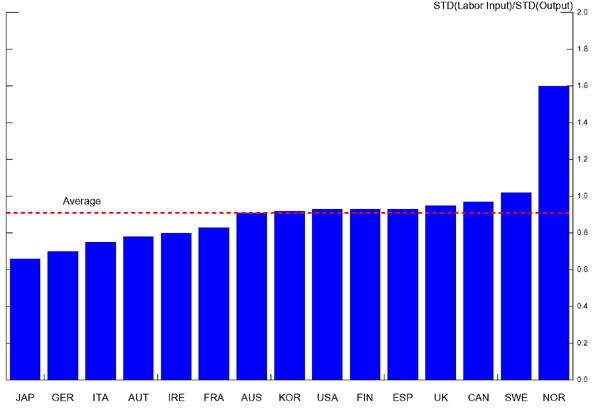
Data for Figure 2
| Country | Volatility | Average |
|---|---|---|
| JAP | 0.66 | 0.91 |
| GER | 0.70 | 0.91 |
| ITA | 0.75 | 0.91 |
| AUT | 0.78 | 0.91 |
| IRE | 0.80 | 0.91 |
| FRA | 0.83 | 0.91 |
| AUS | 0.91 | 0.91 |
| KOR | 0.92 | 0.91 |
| USA | 0.93 | 0.91 |
| FIN | 0.93 | 0.91 |
| ESP | 0.93 | 0.91 |
| UK | 0.95 | 0.91 |
| CAN | 0.97 | 0.91 |
| SWE | 1.02 | 0.91 |
| NOR | 1.60 | 0.91 |
Legend: Average = OECD Mean
Volatility = Standard Deviation (Labor Input)/Standard deviation (Output)
Table 4. Volatility of Labor Input (Standard Deviation Relative to Output)
| Canada | Euro* | Japan | U.S. | OECD Mean | |
|---|---|---|---|---|---|
| BKK [1995] 1970:Q1-1990:Q2: Data (Employment) | 0.86 | 0.53 | 0.36 | 0.68 | 0.64 |
| BKK [1995] 1970:Q1-1990:Q2: Benchmark Model | 0.49 | ||||
| OR [2011] 1960:Q1-1984:Q4: Total Hours | 1.03 | 0.75 | 0.67 | 0.84 | 0.81 |
| OR [2011] 1960:Q1-1984:Q4: Hours per worker | 0.27 | 0.48 | 0.47 | 0.25 | 0.44 |
| OR [2011] 1960:Q1-1984:Q4: Employment | 0.89 | 0.51 | 0.51 | 0.71 | 0.63 |
| OR [2011] 1985:Q1-2007:Q4: Hours | 0.91 | 0.78 | 0.798 | 1.23 | 1.02 |
| OR [2011] 1985:Q1-2007:Q4: Hours Hours per worker | 0.40 | 0.54 | 0.54 | 0.39 | 0.58 |
| OR [2011] 1985:Q1-2007:Q4: Hours Employment | 0.65 | 0.70 | 0.70 | 0.97 | 0.80 |
NB. Statistics refer to reisiduals of the HP-filter. * Euro is the average of France, Germany, and Italy.
Total hours worked in the pre-1984 period are, on average, three-quarters as volatile as output. Moreover, the intensive margin is about as important as the extensive margin, with the standard deviation of hours per worker in the Euro countries and in Japan as large as the standard deviation of employment. These findings contrast not only with volatility statistics based only on employment, but also with the statistics based on U.S. hours data as reported in Hansen [1985], Kydland [1995], Cho and Cooley [1994], and Hall [2009], in which the volatility of hours per worker is less than half of the volatility of employment.9More generally, these results are consistent with the view that different labor market institutions, such as differences in hiring and firing costs and work-sharing arrangements, may significantly affect the extent to which European and Japanese firms adjust labor input along the extensive versus the intensive margin.10
Table 4 also shows that the volatility of total hours worked has increased dramatically during the Great Moderation, when total hours have become as volatile as output. The relevance of this observation is twofold. First, it extends recent findings of Galì and Gambetti [2010] (GG hanceforth) and Galì and Van Rens [2011] (GVR henceforth) for the United States to a broader set of countries, thus warranting a general explanation for why this is the case. Specifically, GG and GVR interpret the U.S. evidence as consistent with an increase in labor market flexibility due to U.S.-specific changes in policies or institutions. Our finding, in contrast, suggests that the Great Moderation requires an explanation that applies to most high income countries.11 Second, this increase in the relative volatility of total hours is at variance with a strong version of the "good luck" interpretation of the Great Moderation (see Stock and Watson [2002]). In particular, a proportional reduction of the variance of all shocks, as proposed by this interpretation, would preserve the ratio of volatilities across variables. While there is evidence that the volatility of consumption and investment have not changed much relative to the volatility of output, this is not the case for hours worked.
We next analyze how labor input covaries with output and how the extensive and intensive margin are related over the cycle. Figure 3 presents the correlation of labor input with output over the entire period (panel a) and in the pre- and post-1984 period (panel b). Total hours are procyclical, but the magnitude of this correlation varies across countries. In particular, labor input is strongly procyclical in Canada, U.K., and U.S., but less so in the Euro countries and in Japan. Moreover, labor input has generally become more correlated with output in the post-1984 period, but this correlation has decreased somewhat in the United States.12
Figure 3. Cyclical Properties of Total Hours Worked (1960-2007)
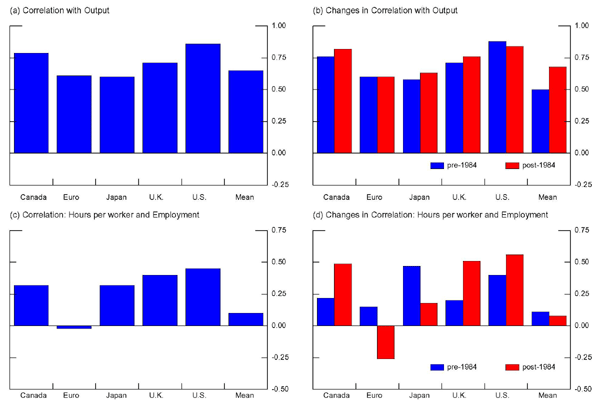
Data for Figure 3
| Country | A | B: Pre-1984 | B: Post-1984 | C | D: Pre-1984 | D: Post-1984 |
|---|---|---|---|---|---|---|
| Canada | 0.786 | 0.760 | 0.824 | 0.322 | 0.223 | 0.487 |
| Euro | 0.610 | 0.603 | 0.597 | -0.017 | 0.148 | -0.258 |
| Japan | 0.603 | 0.582 | 0.634 | 0.317 | 0.466 | 0.183 |
| U.K. | 0.706 | 0.706 | 0.762 | 0.399 | 0.204 | 0.513 |
| U.S. | 0.858 | 0.880 | 0.840 | 0.450 | 0.395 | 0.555 |
| OECD mean | 0.645 | 0.501 | 0.683 | 0.104 | 0.114 | 0.084 |
Legend:
A = Correlation with Output
B = Changes in Correlation with Output
C = Correlation: Hours per Worker and Employment
D = Changes in Correlation: Hours per Worker and Employment
Panels (c) and (d) show that hours per worker and employment are only weakly correlated over the cycle. In particular, this correlation is roughly zero in Euro countries over the whole sample, and has weakened significantly over time, becoming negative after 1984.
These cyclical correlations suggest that labor input is highly synchronized with output fluctuations in Canada, U.K. and U.S., but less so in the Euro countries and Japan. In addition, the adjustment along the intensive and the extensive margin in the United States is almost contemporaneous, whereas in Euro countries it takes place with different leads and lags. This result points to the fact that labor market rigidities, which tend to be higher in the latter group of countries, may significantly affect the timing of adjustment along the two margins.
3.2 Cyclical Labor Productivity
This subsection describes the behavior of labor productivity and how the features of productivity differ depending on whether employment or our measure of hours is used to construct productivity. Figure 4 summarizes the cyclical behavior of productivity over time.
Figure 4. Cyclical Properties of Labor Productivity (1960-2007)
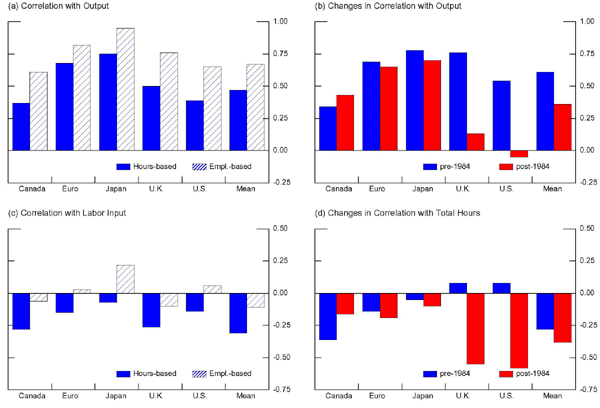
Data for Figure 4
| Country | A: H | A: E | B: pre | B: post | C: H | C: E | D: pre | D: post |
|---|---|---|---|---|---|---|---|---|
| Canada | 0.37 | 0.61 | 0.34 | 0.43 | -0.28 | -0.06 | -0.36 | -0.16 |
| Euro | 0.68 | 0.82 | 0.69 | 0.65 | -0.15 | 0.03 | -0.14 | -0.19 |
| Japan | 0.75 | 0.95 | 0.78 | 0.70 | -0.07 | 0.22 | -0.05 | -0.10 |
| U.K. | 0.50 | 0.76 | 0.76 | 0.13 | -0.26 | -0.10 | 0.08 | -0.55 |
| U.S. | 0.39 | 0.65 | 0.54 | -0.05 | -0.14 | 0.06 | 0.08 | -0.58 |
| OECD Mean | 0.47 | 0.67 | 0.61 | 0.36 | -0.31 | -0.11 | -0.28 | -0.38 |
Legend:
A = Correlation with Output
B = Changes in Correlation with Output
C = Correlations with Labor Input
D = Changes in Correlation with Total Hours
H = Hours-based
E = Employment-based
pre = pre-1984
post= post-1984
The full bars in panel (a) show that labor productivity is generally procyclical between 1960 and 2007, with an average correlation of about 0.5. For comparison, we also show the employment-based measure of labor productivity, which is significantly more procyclical than the hours-based measure. This is particularly the case in Canada and the United States, and to a lesser extent in the United Kingdom. Panel (b) shows how the correlation of the hours-based measure of productivity changed over time. There are important differences across countries, with this correlation falling over time in the U.K. and the U.S., but remaining essentially unchanged in Euro countries and Japan.
Panel (c) shows that the correlation between the hours-based measures of labor productivity and the hours-based measures of labor input (full bars) is negative across countries. This feature of the data is remarkable because it is difficult to reconcile with standard real business cycle theories where the cycle is driven only by productivity shocks. In addition, employment-based labor productivity tends to be much less negatively correlated with employment-based labor input, thus confirming that using employment as a proxy for labor input might distort basic empirical facts.
Panel (d) shows that the hours-based correlation between labor input and labor productivity has declined somewhat in the post-1984 period. While it is well established that labor productivity and hours are only weakly correlated in the U.S., and that this correlation has declined significantly during the Great Moderation (see, for instance, GG and Barnichon [2010]), our evidence suggests that these patterns are common across industrial countries.
3.3 Implications of Hours and Productivity Data for Theory
This analysis indicates that accounting for these data requires models that generate much higher labor input volatility than existing models, and that do not generate a strong correlation between labor and productivity. To see this, note that international real business cycles models, such as BKK reproduce about half of the volatility observed in the data (see top of Table 4). But models that deliver larger labor responses to shocks than BKK, such as Hansen [1985] and Greenwood et al [1988] typically generate a counterfactually high correlation between labor input and labor productivity. 13
These data also have implications for accounting for the Great Moderation. Specifically, several researchers have concluded that the relaxation of borrowing constraints are an important factor in the decline in output volatility (see Campbell and Hercowitz [2006] and Iacoviello and Pavan [2010]). But at the same time, these theories also imply a reduction in the volatility of hours worked, as wealth effects become stronger over time. These data do not support this implication of the borrowing contraint hypothesis.
4 Business Cycle Diagnostics
Cole and Ohanian [2002] and Chari, Kehoe, and McGrattan [2002, 2007] present a diagnostic methodology for broadly evaluating classes of theories of fluctuations. This process has been used implicitly in one form or another by much of the real business cycle literature, including Kydland and Prescott [1982], and in analyses that focus on channels other than productivity, including Hall [1997], Cole and Ohanian [2004], Gali, Gertler, and Lopez-Salido [2007], Shimer [2009, 2010], and Mulligan [2008].
This section uses the new hours data to re-assess diagnostic wedges of this framework. We first construct these wedges using the standard measure of employment as labor input, and then compare them to wedges constructed using the measures of hours worked reported earlier in this paper as the measure of labor input. This process involves using time series data on output, consumption, investment, and labor input to measure wedges from the first order conditions in a parameterized optimal growth model, and then use those wedges as diagnostics for developing theories of fluctuations.
4.1 The Diagnostic Framework
The theoretical framework is given as follows. Preferences are:
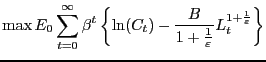
|
(7) |
and the technology, resource constraint and the law of motion for capital are given by:
| (8) |
| (9) |
where the variables are, respectively, per-capita measures of
consumption ![]() , fraction of time devoted to market
activities
, fraction of time devoted to market
activities ![]() , capital stock
, capital stock ![]() real output
real output ![]() investment
investment ![]() and government spending
and government spending ![]() The
variable
The
variable ![]() denotes is productivity parameter and
denotes is productivity parameter and
![]() is the exogenous growth rate of technology,
respectively
is the exogenous growth rate of technology,
respectively![]() All per-capita variables are detrended
at a two percent annual rate.
All per-capita variables are detrended
at a two percent annual rate.
The parameters are chosen as follows. We set ![]() to
to ![]()
![]()
![]() and
and
![]() which represents the Frisch
labor supply elasticity, is 1. Note that the Frisch elasticity is
constant regardless of the steady state level of hours worked.
which represents the Frisch
labor supply elasticity, is 1. Note that the Frisch elasticity is
constant regardless of the steady state level of hours worked.
Typically, this framework is used to construct four deviations, or wedges: (1) a productivity wedge, which is the ratio between output and the Cobb-Douglas aggregator of capital and hours worked (i.e. the Solow Residual), (2) a labor wedge, which is the difference between the marginal rate of substitution between consumption and leisure and the marginal product of labor, (3) a capital market wedge, which is the difference between the intertemporal marginal rate of substitution and the return to capital, and (4) a resource constraint wedge that measures changes in the allocation of output between consumption, investment, and government spending. We will focus on productivity and labor wedges as these are typically the most important quantitatively in terms of accounting for fluctuations. These deviations are given as:
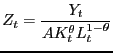
|
(10) |
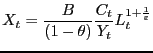
|
(11) |
The wedges are analyzed using HP filtered series for data through the end of 2007. We separately analyze the 2008-09 recession from 2008:1 - through 2009:4, which is the date of the hours trough of the U.S. recession, and allows us to compare our findings to those of Ohanian [2010], who measured these deviations in the U.S. using both hours and employment, but only employment for the other G7 countries (Canada, France, Germany, Italy, Japan, and the United Kingdom).
4.2 Cyclical Features of Labor and Productivity Wedges in OECD Countries: 1960 - 2007
Since the labor supply elasticity plays a key role in shaping the reponse of total hours to changes in wages, we begin by reporting the volatility of the cyclical components of the labor wedge for different values of this parameter. We then compare the volatility and the correlation with output of the labor and productivity wedges constructed using total hours worked and alternatively employment as measures of labor input respectively. We focus on HP filtered logged data to facilitate comparison with existing business cycle studies.14
The analysis will show that the wedges are large, they fluctuate significantly over the business cycle, they differ considerably depending on whether they are measured with total hours or employment, and their properties differ across countries. These findings also identify significant puzzles about the nature of European labor market fluctuations given the size of European firing costs and how those costs affect incentives to adjust between the intensive versus extensive margin.
4.2.1 The Volatility of the Labor Wedge and its Components
Table 5 presents the properties of the detrended labor wedge for
different labor supply elasticities. Standard growth theory, in
which the marginal rate of substitution between consumption and
leisure is always equated to the wage, implies that movements in
the consumption-ouput ratio, ![]() , should be
exactly offset by changes in the labor input component,
, should be
exactly offset by changes in the labor input component,
![]() for the
utility function presented here. Thus, the labor wedge arises when
movements in these variables do not offset each other. The table
also reports statistics on
for the
utility function presented here. Thus, the labor wedge arises when
movements in these variables do not offset each other. The table
also reports statistics on ![]() and labor input.
15
and labor input.
15
Table 5a. Elements of the Labor Wedge: (a) Standard Deviation
| Canada | Euro | Japan | U.K. | U.S. | OECD Mean | |
|---|---|---|---|---|---|---|
| 1960:Q1-2007:Q4: e = 0.5 | 3.65 | 2.90 | 2.75 | 3.91 | 3.91 | 3.97 |
| 1960:Q1-2007:Q4: e = 1.0 | 2.34 | 1.96 | 1.85 | 2.65 | 2.51 | 2.73 |
| 1960:Q1-2007:Q4: e = 2.0 | 1.73 | 1.52 | 1.46 | 2.04 | 1.83 | 2.16 |
| 1960:Q1-2007:Q4: C/Y | 1.71 | 0.93 | 1.22 | 0.99 | 0.72 | 1.34 |
| 1960:Q1-2007:Q4: L | 1.38 | 1.01 | 1.03 | 1.32 | 1.43 | 1.34 |
| 1960:Q1-1984:Q4: e = 1.0 | 2.69 | 2.18 | 1.97 | 2.76 | 2.73 | 2.68 |
| 1960:Q1-1984:Q4: C/Y | 1.07 | 1.08 | 1.49 | 1.14 | 0.89 | 1.43 |
| 1960:Q1-1984:Q4: L | 1.50 | 1.14 | 1.08 | 1.22 | 1.59 | 1.27 |
| 1985:Q1-2007:Q4: e = 1.0 | 1.89 | 1.69 | 1.71 | 2.58 | 2.25 | 2.73 |
| 1985:Q1-2007:Q4: C/Y | 1.27 | 0.74 | 0.81 | 0.78 | 0.48 | 1.21 |
| 1985:Q1-2007:Q4: L | 1.23 | 0.85 | 0.97 | 1.37 | 1.22 | 1.39 |
Table 5b. Elements of the Labor Wedge: (b) Correlation
| Canada | Euro | Japan | U.K. | U.S. | OECD Mean | |
|---|---|---|---|---|---|---|
| 1960:Q1-2007:Q4: C/Y | -0.17 | 0.15 | 0.15 | 0.19 | -0.36 | 0.22 |
| 1960:Q1-2007:Q4: L | 0.91 | 0.89 | 0.81 | 0.94 | 0.97 | 0.87 |
| 1960:Q1-1984:Q4: C/Y | -0.18 | 0.12 | 0.24 | 0.46 | -0.39 | 0.37 |
| 1960:Q1-1984:Q4: L | 0.94 | 0.89 | 0.74 | 0.91 | 0.97 | 0.82 |
| 1985:Q1-2007:Q4: C/Y | -0.17 | 0.21 | -0.06 | -0.07 | -0.32 | 0.08 |
| 1985:Q1-2007:Q4: L | 0.86 | 0.90 | 0.91 | 0.96 | 0.98 | 0.90 |
Note: Statistics refer to the HP-detrended component of the labor wedge for different Frisch labor supply elasticities (e). C/Y is the HP-detrended consumption to output ratio and L is HP-detrended total hours worked.
The table shows that the labor wedge is highly volatile, about
twice as volatile as either ![]() or
or ![]() for the benchmark elasticity of one. The volatility of the
two components,
for the benchmark elasticity of one. The volatility of the
two components, ![]() and
and ![]() is very
similar across countries with the exception of the US, in which
there is relatively much less consumption volatility and much more
labor volatility. The volatility of the labor wedge increases for
lower labor supply elasticities, becoming nearly 50 percent more
volatile for an elasticity of 0.5. Moreover, the volatility of the
labor wedge has declined markedly in both the US and in Euro
countries over time, but has changed very little, on average,
across OECD countries.
is very
similar across countries with the exception of the US, in which
there is relatively much less consumption volatility and much more
labor volatility. The volatility of the labor wedge increases for
lower labor supply elasticities, becoming nearly 50 percent more
volatile for an elasticity of 0.5. Moreover, the volatility of the
labor wedge has declined markedly in both the US and in Euro
countries over time, but has changed very little, on average,
across OECD countries.
The table also shows that the labor wedge is primarily related
to movements in labor, rather than ![]() Specifically, the correlation between the wedge and labor is around
0.9, while its correlation with
Specifically, the correlation between the wedge and labor is around
0.9, while its correlation with ![]() is close to zero
in a number of countries. These findings suggest that competitve
and/or frictionless models of the labor market can account for only
a relatively small fraction of cyclical changes in hours in these
OECD countries. To see this, note that in such a model, changes in
labor input are accounted for entirely by changes in
is close to zero
in a number of countries. These findings suggest that competitve
and/or frictionless models of the labor market can account for only
a relatively small fraction of cyclical changes in hours in these
OECD countries. To see this, note that in such a model, changes in
labor input are accounted for entirely by changes in ![]()
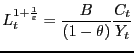
|
(12) |
Thus, the model predicts that the volatility of labor is bounded
above by the volatility of consumption as the Frisch elasticity
becomes infinite. However, labor input is typically more
volatile in these countries than ![]() . This suggests
that research should focus considerably more on the role of labor
market imperfections in understanding fluctuations.
. This suggests
that research should focus considerably more on the role of labor
market imperfections in understanding fluctuations.
4.2.2 Cyclical Propeties of Labor and Productivity Wedges
Table 6a. Properties of the Labor and Productivity Wedges: (a) Standard Deviation Relative to Output
| Canada | Euro | Japan | U.K. | U.S. | OECD Mean | |
|---|---|---|---|---|---|---|
| Hours-based labor wedge | 1.66 | 1.43 | 1.19 | 1.76 | 1.68 | 1.78 |
| Empl.-based labor wedge | 1.38 | 1.11 | 0.74 | 1.31 | 1.35 | 1.47 |
| Hours-based labor productivity wedge | 0.66 | 0.82 | 0.81 | 0.82 | 0.61 | 0.77 |
| Empl.-based productivity wedge | 0.75 | 0.87 | 0.94 | 0.88 | 0.72 | 0.81 |
Table 6b. Properties of the Labor and Productivity Wedges: (b) Cross-Correlation with Output
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|---|---|---|---|
| Canada: Hours-based labor wedge | 0.34 | 0.44 | 0.56 | 0.67 | 0.66 | 0.58 | 0.44 | 0.27 | 0.10 |
| Canada: Empl.-based labor wedge | 0.33 | 0.42 | 0.49 | 0.55 | 0.50 | 0.43 | 0.31 | 0.17 | 0.03 |
| Canada: Hours-based labor productivity wedge | -0.15 | 0.05 | 0.25 | 0.59 | 0.76 | 0.70 | 0.61 | 0.53 | 0.41 |
| Canada: Empl.-based productivity wedge | -0.10 | 0.12 | 0.33 | 0.58 | 0.84 | 0.77 | 0.67 | 0.55 | 0.41 |
| Euro: Hours-based labor wedge | 0.21 | 0.31 | 0.39 | 0.42 | 0.42 | 0.37 | 0.28 | 0.17 | 0.06 |
| Euro: Empl.-based labor wedge | 0.36 | 0.42 | 0.44 | 0.39 | 0.27 | 0.26 | 0.15 | 0.07 | -0.04 |
| Euro: Hours-based labor productivity wedge | -0.04 | 0.14 | 0.36 | 0.57 | 0.88 | 0.68 | 0.54 | 0.39 | 0.22 |
| Euro: Empl.-based productivity wedge | -0.07 | 0.13 | 0.36 | 0.60 | 0.92 | 0.72 | -0.58 | 0.41 | 0.25 |
| U.K.: Hours-based labor wedge | 0.58 | 0.67 | 0.72 | 0.72 | 0.64 | 0.54 | 0.40 | 0.22 | 0.06 |
| U.K.: Empl.-based labor wedge | 0.55 | 0.59 | 0.58 | 0.54 | 0.46 | 0.37 | 0.22 | 0.04 | -0.09 |
| U.K.: Hours-based labor productivity wedge | -0.13 | 0.09 | 0.30 | 0.54 | 0.83 | 0.72 | 0.63 | 0.54 | 0.37 |
| U.K.: Empl.-based productivity wedge | 0.46 | 0.66 | 0.78 | 0.83 | 0.77 | 0.63 | 0.44 | 0.25 | 0.09 |
| U.S.: Hours-based labor wedge | 0.46 | 0.66 | 0.78 | 0.83 | 0.77 | 0.63 | 0.44 | 0.25 | 0.09 |
| U.S.: Empl.-based labor wedge | 0.59 | 0.74 | 0.80 | 0.79 | 0.66 | 0.52 | 0.31 | 0.11 | -0.05 |
| U.S.: Hours-based labor productivity wedge | -0.26 | -0.09 | 0.19 | 0.48 | 0.78 | 0.76 | 0.68 | 0.52 | 0.38 |
| U.S.: Empl.-based productivity wedge | -0.23 | -0.03 | 0.26 | 0.56 | 0.85 | 0.82 | 0.73 | 0.57 | 0.42 |
| OECD: Hours-based labor wedge | 0.29 | 0.39 | 0.46 | 0.49 | 0.46 | 0.40 | 0.30 | 0.18 | 0.07 |
| Mean: Empl.-based labor wedge | 0.40 | 0.44 | 0.45 | 0.42 | 0.32 | 0.28 | 0.17 | 0.08 | -0.03 |
| Mean: Hours-based labor productivity wedge | -0.12 | 0.06 | 0.27 | 0.49 | 0.78 | 0.65 | 0.54 | 0.42 | 0.26 |
| Mean: Empl.-based productivity wedge | -0.14 | 0.06 | 0.29 | 0.52 | 0.84 | 0.67 | 0.57 | 0.43 | 0.28 |
NB. Statistics refer to residuals of the HP-filter (smoothing parameter is 1600).
Table 6 shows the volatility of labor and productivity wedges relative to the volatility of output for both measures of labor input. The most striking finding is that the relative difference in the size of the hours and employment labor wedges are about the same across countries. Specifically, the difference in the Euro countries, in which employment protection is very high, and thus there should be relatively more adjustment along the intensive margin, is 1.43 for the hours labor wedge compared to 1.11 for the employment labor wedge. However, the difference between these wedges in the US, in which there is comparatively little employment protection is 1.68 compared to 1.35, which is almost the same percentage difference as in the Euro countries. The fact that employment protection is much higher in Europe strongly suggests that there should be a significantly larger difference between hours and employment labor wedges in these countries relative to the US.
Table 6 also shows the cross-correlations between the hours-based and employment-based wedges and output between 4 lags and 4 leads. For the US, the labor wedge is procyclical, as the contemporaneous correlation is 0.77 for the hours-based wedge (and 0.66 for the employment based wedge) which means that the wedge between the marginal rate of substitution and the marginal product of labor widens when the economy is below trend, and narrows when the economy is above trend. The labor wedge-output correlations across all lags and leads range between 0.30 to 0.72 for hours and 0.21 to 0.68 for employment. Productivity is strongly contemporaneously procyclical, as the correlation for the two measures of TFP is 0.78 and 0.85, respectively.
The cyclical correlation of the labor wedge with output is not as strong in Europe compared to the US (and also varies considerably across European countries, not shown). The labor wedge in Euro countries is contemporaneoulsy much less procyclical than in the U.S., with a correlation ranging between 0.42 for the hours-based wedge and 0.27 for the employment-based. In contrast, the cyclicality of the labor wedge in the UK is closer to that of the US, where the contemporaneous correlation is 0.64 (hours-based) and 0.46 (employment-based).
The cyclical pattern of the productivity wedge in Europe is very similar to that in the US (and, more generally, very similar across countries in Europe, not shown). The correlation of the hours-based productivity wedge is 0.88 and the correlation for the employment-based productivity wedge is 0.92.
In summary, this analysis suggests that these wedges are larger in Europe than in the US, that the cylical pattern of the labor wedge is quite different in Europe, and that the cyclical pattern of productivity in Europe is similar to that in the US.
4.3 Labor and TFP Wedges in the OECD During the Great Recession
This section reports the labor and productivity wedges for the Great Recession. We pursue this analysis since Ohanian [2010] finds that these wedges - measured using only employment as labor input - differ remarkably between the U.S. and the other advanced countries during the Great Recession. Ohanian documented that the U.S. Great Recession is largely due to a very large decline in labor input associated with an historically large labor wedge, and that productivity is close to trend. In contrast, other G7 countries are virtually the opposite of that in the US, with much smaller employment declines, large productivity declines, and no quantitatively important labor wedge.
Ohanian suggests that these different patterns pose a challenge for the widely held view that all of these recessions were the result of similar banking crises that operated through the same economic channels. But Ohanian's findings are entirely based on employment. The fact that firing costs are higher in several of the other G7 compared to the US suggests that labor input adjustment should have taken place much more on the intensive margin, and that Ohanian's use of employment would generate downard-biased Solow Residuals and upward-biased labor wedges in the European countries.
We therefore reassess this analysis using hours rather than employment. Our main finding is that the this puzzle is perhaps even more striking, as using total hours, which should be a much better measure of labor input given firing costs, does not materially change Ohanian's results.
Table 7 shows output, labor, and labor and productivity wedges across countries for the Great Recession. We first consider Ohanian's comparison of the US to a Western European average of France, Germany, Italy, UK, Austria, Finland, Norway, and Sweden. The table shows that the labor wedge is much larger in the US than in these European countries. Specifically, the US hours-labor wedge is -14.9 percent in 2009:4. In contrast, the hours-based labor wedge is only -2.7 percent on average for the Western European countries studied by Ohanian.
Table 7. Great Recession, Deviation from Peak (US Hours Trough)
| Data: Output | Data: Hours | Data: Empl. | Labor Wedge: Hours | Labor Wedge: Empl. | Productivity Wedge: Hours | Productivity Wedge: Empl. | |
|---|---|---|---|---|---|---|---|
| United States | -7.3 | -8.4 | -6.8 | -14.9 | -11.9 | -1.4 | -2.5 |
| Canada | -8.0 | -4.8 | -2.9 | -4.9 | -1.1 | -5.1 | -6.3 |
| Euro | -8.4 | -2.9 | -1.3 | -2.8 | 0.3 | -6.2 | -7.2 |
| United Kingdom | -9.9 | -.3. | -2.4 | -4.0 | -2.2 | -7.4 | -7.9 |
| Western Europe* | -9.4 | -3.7 | -2.3 | -2.7 | 0.1 | -6.9 | -7.7 |
| Spain | -9.1 | -8.4 | -10.0 | -17.2 | -20.1 | -4.5 | -3.4 |
| Ireland | -18.2 | -15.8 | -12.7 | -23.7 | -18.1 | -9.3 | -11.4 |
| Japan | -8.3 | -4.7 | -0.7 | -5.3 | 2.7 | -5.0 | -7.5 |
| Korea | -2.4 | -5.0 | -1.1 | -9.9 | -2.4 | -0.5 | -3.0 |
* France, Germany, Italy, UK, Austria, Finland, Norway, Sweden.
The European labor wedges are also very small during the Great Recession compared to other postwar recessions in these countries. The average peak-to-trough hours-labor wedge for the above European countries between 1960 and 2007 was about 6 percent, while output fell about 5 percent in these recessions (see Appendix B for details). If this pre-Great Recession relationship between the labor wedge and output also held during the Great Recession, then, given the observed output decline of nearly 11 percent, the European labor wedge would have been around 11 percent, about four times larger than observed.
We next assess the quantitative importance of these labor and productivity wedges using the model economy described and parameterized in section 4.1. We conduct two analyses. First, we feed in the productivity wedges into the model economy from 2007:4 to each country's respective trough in hours worked, and calculates optimal path for labor, output, consumption, and investment relative to their trend values. Second, we replace the productivity wedge with the labor wedge and conduct a symmetric analysis to the previous one.
Not surprisingly, the labor wedge accounts for very little of the Great Recession in Europe. Table 8 shows the percentage of trough output and labor accounted for by the model described in Section 4.1 in response to the labor wedge and the productivity wedge measured in the data, using both employment and hours worked as labor input.
The US hours-labor wedge accounts for almost all of US output, whereas the European hours-labor wedge accounts for only about 10 percent of the drop in European output. In contrast, Table 8 also shows the relative contribution of productivity for the US and Europe. Productivity explains only about 20 percent of the drop in output, and almost none of the drop in hours in the US, whereas productivity accounts on average for almost all of the decline in output and hours in the European countries.
Table 8. Great Recession, Deviation from Peak (Hours Trough)
| Data: Output | Data: Hours | Data: Empl. | Predicted, Model 1: Output | Predicted, Model 1: Hours | Predicted, Model 2: Output | Predicted, Model 2: Hours | Predicted, Model 3: Output | Predicted, Model 3: Hours | Predicted, Model 4: Output | Predicted, Model 4: Hours | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| U.S | -7.3 | -8.4 | -6.8 | -6.8 | -9.8 | -5.1 | -7.5 | -2.0 | -0.3 | -3.5 | -0.6 |
| Canada | -8.0 | -4.8 | -2.9 | -2.2 | -3.1 | -0.5 | -0.7 | -7.0 | -1.6 | -8.7 | -2.0 |
| Euro | -8.4 | -2.9 | -1.3 | -1.2 | -1.8 | 0.1 | 0.1 | 8.6 | -2.0 | -9.9 | -2.3 |
| UK | -9.9 | -3.3 | -2.4 | -1.7 | -2.4 | -0.9 | -1.3 | 10.2 | -2.4 | -10.9 | -2.5 |
| Western Europe* | -9.4 | -3.7 | -2.3 | -1.2 | -1.7 | 0.1 | 0.0 | 9.5 | -2.2 | -10.7 | -2.5 |
| Spain | -9.1 | -8.4 | -10.0 | -8.0 | -11.4 | -9.2 | -13.3 | -6.1 | -1.4 | -4.6 | -1.0 |
| Ireland | -18.2 | -15.8 | -12.7 | -11.4 | -16.4 | -8.1 | -11.9 | -13.3 | -2.8 | -16.2 | -3.5 |
| Japan | -8.3 | -4.7 | -0.7 | -2.3 | -3.3 | 1.2 | 1.6 | -7.0 | -1.5 | -10.4 | -2.3 |
| Korea | -2.4 | -5.0 | -1.1 | -4.5 | -6.2 | -1.0 | -1.4 | -0.8 | -0.1 | -4.3 | -0.8 |
NB. Euro is the average of France, Germany, and Italy. * France, Germany, Italy, U.K., Austria, Finland, Norway, Sweden. ** Model 1=labor wedge, hours; Model 2= labor wedge, employment; Model 3=productivity wedge, hours; Model 4=productivity wedge, employment.
The relevance of these findings is twofold. First, the large differences in the size and importance of labor and productivity wedges during the Great Recession across countries pose a challenge for the common view that the coincident recessions in 2008-2009 were the consequence of very similar banking crises that depressed economies through the same channels. Second, since many researchers and policymakers hold the view that the U.S. Great Recession was generated by a large financial shock, our findings also highlight the need for models in which financial shocks depress labor and output through an increase in the labor wedge. Recent research by Arellano, Bai, and Kehoe [2011], Lopez [2011], and Perri and Quadrini [2011], develop models in which financial shocks depress labor and output by operating through the labor wedge.
Table 8 also shows labor and productivity wedges for some OECD countries that were not analyzed by Ohanian [2010]. In particular, both Spain and Ireland have very large labor wedges. This similarity between the US, Spain, and Ireland suggests a new avenue for understanding cross-country experiences. One possibility relates to the housing market. Specifically, some have argued that in the US, very large housing price declines, coupled with government policies designed to cushion the impact of falling prices on borrowers, including mortgage modification programs, changed the incentives for unemployed individuals to take new jobs or for homeowners to relocate from relatively depressed areas to areas with better job prospects (see Mulligan [2008] and Herkenhoff and Ohanian [2011]).
We present some limited evidence on the relationship between the labor market and housing. Figure 5 shows indicators in housing activity, measured in terms of changes in house prices and in employment in the construction sector, for the US and a number of other countries. It is interesting that the three countries which have large labor wedges - the US, Spain, and Ireland - have also experienced very large correction in housing activities, with marked housing price and employment declines.16 These findings suggest an interesting avenue for future research by developing theories that relate a widening labor wedge to sectoral dislocation in construction.
Figure 5. Housing Sector During the Great Recession
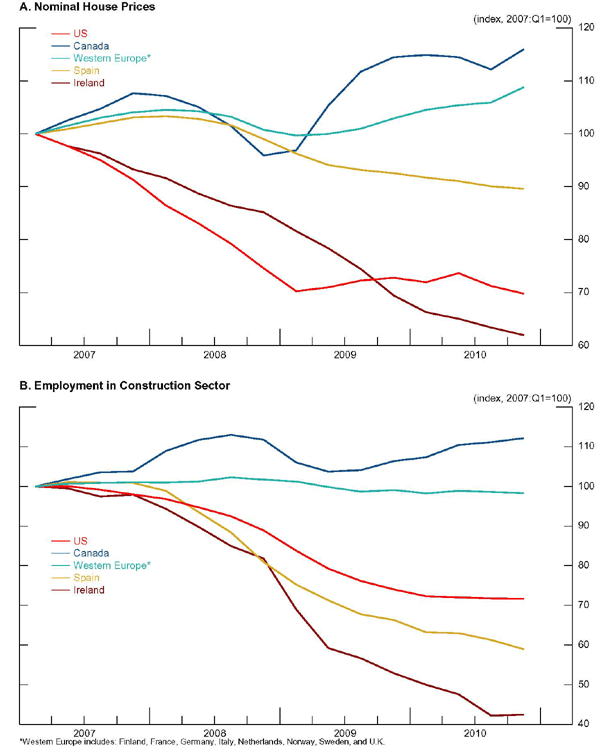
Data for Figure 5
| dates | (A) Nominal House Prices: Canada | (A) Nominal House Prices: Ireland | (A) Nominal House Prices: Spain | (A) Nominal House Prices: US | (A) Nominal House Prices: Western Europe | (B) Employment: Canada | (B) Employment: Ireland | (B) Employment: Spain | (B) Employment: US | (B) Employment: Western Europe |
|---|---|---|---|---|---|---|---|---|---|---|
| 2007Q1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 2007Q2 | 102.56 | 97.64 | 100.9 | 97.67 | 101.53 | 101.86 | 99.51 | 101.07 | 100.03 | 100.63 |
| 2007Q3 | 104.74 | 96.27 | 102.01 | 95.02 | 103.01 | 103.55 | 97.39 | 100.93 | 99.13 | 100.88 |
| 2007Q4 | 107.67 | 93.29 | 103.07 | 91.33 | 104.08 | 103.75 | 97.88 | 100.83 | 98 | 101.03 |
| 2008Q1 | 107.15 | 91.65 | 103.36 | 86.46 | 104.53 | 108.95 | 94.3 | 98.87 | 96.8 | 100.96 |
| 2008Q2 | 105.1 | 88.71 | 102.85 | 83.13 | 104.27 | 111.7 | 89.84 | 93.59 | 94.73 | 101.2 |
| 2008Q3 | 101.5 | 86.43 | 101.66 | 79.24 | 103.24 | 112.96 | 84.94 | 88.39 | 92.49 | 102.25 |
| 2008Q4 | 95.93 | 85.17 | 99.02 | 74.57 | 100.74 | 111.75 | 81.77 | 80.92 | 88.87 | 101.66 |
| 2009Q1 | 96.89 | 81.63 | 96.28 | 70.25 | 99.67 | 106.05 | 68.97 | 75.24 | 83.77 | 101.2 |
| 2009Q2 | 105.35 | 78.38 | 94.09 | 70.98 | 99.97 | 103.67 | 59.23 | 71.25 | 79.22 | 99.82 |
| 2009Q3 | 111.75 | 74.43 | 93.19 | 72.29 | 100.99 | 104.13 | 56.66 | 67.75 | 76.15 | 98.63 |
| 2009Q4 | 114.5 | 69.45 | 92.56 | 72.76 | 102.91 | 106.39 | 52.9 | 66.29 | 74.02 | 99.05 |
| 2010Q1 | 114.91 | 66.26 | 91.71 | 71.94 | 104.55 | 107.32 | 49.98 | 63.24 | 72.32 | 98.23 |
| 2010Q2 | 114.48 | 65.05 | 91.05 | 73.66 | 105.39 | 110.42 | 47.58 | 62.98 | 72.05 | 98.89 |
| 2010Q3 | 112.16 | 63.41 | 90.08 | 71.25 | 105.92 | 111.09 | 42.23 | 61.31 | 71.74 | 98.57 |
| 2010Q4 | 115.97 | 61.94 | 89.62 | 69.78 | 108.79 | 112.16 | 42.47 | 58.97 | 71.66 | 98.31 |
Legend:
Western Europe = Finland, France, Germany, Italy, Netherlands, Norway, Sweden, and U.K.
5 Summary and Conclusions
Labor fluctuations are a central focus of business cycle research, but this research has been limited significantly by the fact that typically only employment, rather than total hours worked, is available for many OECD countries. This paper has constructed quarterly time series of total hours worked for 17 OECD countries, with a focus on constructing hours that are consistent with national income and product account constructs. These hours measures provide new data that can shed light on a number of questions, including changes in the nature and sources of fluctuations over time, how changes in fiscal and monetary policy have impacted fluctuations over time, and how changes in labor market regulations have impacted fluctuations over time.
The results reported here stand in sharp contrast to many common views about cyclical labor market dynamics. Specifically, these new data indicate that employment is a poor proxy for cyclical labor input, and consequently that employment provides a poor measure of productivity, as in many OECD countries about 50 percent of labor adjustment occurs along the intensive margin. Employment fluctuations in much of Western Europe appear to be much too high compared to the US, given much higher hiring and firing costs in Europe. And given the large fluctuations in European hours, employment-based labor wedge fluctuations in Europe appear to be too high, and hours-based labor wedge fluctuations appear to be too low. Our findings also have implications for the international Great Recession. Specifically, there is a common view that the Great Recession across countries was the result of very similar responses to very similar banking crises. The findings presented here contrast with that view, as Western European recessions feature very small labor wedges compared to the US, measured either with employment or hours, and instead feature much larger productivity shocks than the US.
The data presented here will aid future research in addressing these puzzles, with a focus on understanding why the intensive margin adjustment is not larger during European recessions, why labor wedges are so small in many European countries during the Great Recession, and why they are so large in the US.
References
Arellano, C., Bai, Y., Kehoe, P. J., 2011. Financial Markets and Fluctuations in Uncertainty. Research Department Staff Report, Federal Reserve Bank of Minneapolis.
Arias, A., Hansen, G., Ohanian, L.E., 2007. Why Have Business Cycle Fluctuations Become less Volatile? Economic Theory, vol. 32, 1, 43-58.
Backus, D., Kehoe, P., Kydland, F.E., 1992. International Real Business Cycles. Journal of Political Economy, 100(41), 745-775.
Barnichon, R., 2010. Productivity and Unemployment over the Business Cycle. Journal of Monetary Economics, vol. 57, 1013-1025.
Benhabib, J., Rogerson, R., Wright, R., 1991. Homework in Macroeconomics: Household Production and Aggregate Fluctuations. Journal of Political Economy, vol. 99, 6, 1166-87.
Burda, M.C., Hunt, J., 2011. What Explains the German Labor Market Miracle in the Great Recession? NBER Working Paper Series, No. w17187.
Campbell, J.R., Hercowitz, Z., 2005. The Role of Collateralized Household Debt in Macroeconomic Stabilization. NBER Working Papers 11330.
Chari, V. V., Kehoe, P. J., McGrattan, E. R., 2002. Accounting for the Great Depression. American Economic Review, Papers and Proceedings , May 2002, 22-27.
Chari, V. V., Kehoe, P. J., McGrattan, E. R., 2007. Business Cycle Accounting. Econometrica 75(3): 781-836.
Cho, J., Cooley, T. F., 1994. Employment and Hours over the Business Cycle. Journal of Economic Dynamics and Control, vol. 18, 411-432.
Cole, H., Ohanian, L.E., 2002. The U.S. and U.K. Great Depressions Through the Lens of Neoclassical Growth Theory. American Economic Review, vol. 92, 2, 28-32.
Cole, H., Ohanian, L.E., 2004. New Deal Policies and the Persistence of the Great Depression: A General Equilibrium Analysis. Journal of Political Economy, vol. 112, 4, 779-816.
Cooley, T., Ohanian, L.E., 1991. The Cyclical Behavior of Prices. Journal of Monetary Economics, vol. 28, pp. 25-60.
Denton, F.T., 1971. Adjustment of Monthly or Quarterly Series to Annual Totals: An Approach Based on Quadratic Minimization. Journal of the American Statistical Association, vol. 66, 333, 99-102.
The Conference Board Total Economy Database, January 2011, available at http://www.conference-board.org/data/economydatabase/
Fang, L., Rogerson, R., 2009. Policy Analysis in a Matching Model with Intensive and Extensive Margins. International Economic Review, Vol. 50, No. 4, 1153-1168.
Fernandez-Villaverde, J., Ohanian, L.E., 2010. The Spanish Crisis from a Global Perspective", in The Crisis of the Spanish Economy, FEDEA.
Galí, J., Gambetti, L., 2009. On the Sources of the Great Moderation. American Economic Journal: Macroeconomics, 1:1, 26-57.
Galí, J., Gertler, M., Lopez-Salido, D., 2007. Markups, Gaps, and the Welfare Cost of Economic Fluctuations. Review of Economic and Statistics, vol. 89, 44-59.
Galí, J., Van Rens, T., 2010. The Vanishing Procyclicality of Labor Productivity. Unpublished working paper, CREI.
Greenwood, J., Hercowitz, Z., Huffman, G. W., 1988. Investment, Capacity Utilization, and the Real Business Cycle", American Economic Review, 78, 402-17.
Hall, R.E., 1997. Macroeconomic Fluctuations and the Allocation of Time. Journal of Labor Economics, vol. 15, 1, 5223-50.
Hall, R.E., 2009. Reconciling Cyclical Movements in the Marginal Value of Time and the Marginal Product of Labor. Journal of Political Economy, vol. 117, 2, 281-323.
Hansen, G. D., 1985. Indivisible Labor and the Business Cycle. Journal of Monetary Economics, vol 16, 3, 309-27.
Herkenhoff, K.F., Ohanian, L.E., 2011. Labor Market Dysfunction During the Great Recession. NBER working paper 17313.
Hopenhayn, H., Rogerson, R., 1993. Job Turnover and Policy Evaluation: A General Equilibrium Analysis. Journal of Political Economy, vol. 101, 5, 915-38.
Iacoviello, M., Pavan, M., 2011. Housing and Debt Over the Life Cycle and Over the Business Cycle. Boston College Working Papers in Economics 723, Boston College Department of Economics.
Kydland, F, Prescott, E., 1982. Time to Build and Aggregate Fluctuations. Econometrica, 50(6):1,345-70.
OECD 2008, OECD Indicators of Employment Protection, http://www.oecd.org/document/11/0,3746,en_2649_37457_42695243_1_1_1 _37457,00.html
Mulligan, C., 2008. A Depressing Scenario: Mortgage Debt Becomes Unemployment Insurance. NBER Working Paper 14514.
Lopez, J., 2011. Consumption and Labor Income Risk, Aggregation, and Business Cycles. Unpublished working paper, UCLA.
Mortensen, D., Pissarides, C., 1994, Job Creation and Job Destruction in the Theory of Unemployment. Review of Economic Studies, 61(3):397-415.
Ohanian, L.E., 2010. The Economic Crisis from a Neoclassical Perspective. Journal of Economic Perspectives, vol. 24, 4, 45-66.
Ohanian, L.E., Raffo, A., Rogerson, R., 2006. Long-Term Changes in Labor Supply and Taxes: Evidence from OECD Countries 1956-2004. NBER Working Paper Series, No. w12786.
Ohanian, L., Raffo, A., Rogerson, R., 2008. Long-Term Changes in Labor Supply and Taxes: Evidence from OECD Countries 1956-2004. Journal of Monetary Economics, vol. 55, 1353-62.
O'Mahony, M. and M.P. Timmer, 2009. Output, Input and Productivity Measures at Industry Level: the EU-KLEMS Database. Economic Journal, 119(538), F374-F403.
Perri F., Quadrini, V., 2011. International Recessions. Discussion paper, University of Minnesota.
Raffo, A. , 2008. Net Exports, Consumption Volatility, and International Business Cycle Models. Journal of International Economics, vol. 75, 14-29.np
Ravn, M.O., Uhlig, H., 2002. On Adjusting the Hodrick-Prescott Filter for the Frequency of Observations. The Review of Economics and Statistics, Vol. 84, pp. 371-380.
Rogerson, R., 2006. Understanding Differences in Hours Worked. Review of Economic Dynamics, vol. 9, 3, 365-409.
Rogerson R., Shimer, R., 2010. Search in Macroeconomic Models of the Labor Market. Handbook of Labor Economics, Chapter 7, pp. 619-700.
Shimer, R., 2009. Convergence in Macroeconomics: The Labor Wedge. American Economic Journal: Macroeconomics, 1(1): 280-297.
Shimer, R., 2010. Labor Markets and Business Cycles. Princeton University Press.
Stock, J., Watson, M.W., 2002. Has the Business Cycle Changed and Why? NBER Macroeconmics Annual, 2002, ed. M. Gertler and K.S. Rogoff. Cambridge, MA: MIT Press, pp. 159-218.
Footnotes
1. See, for instance, Burda and Hunt [2011]. Return to text
2. For instance, some countries do not include in their questionnaires a distinction between contractual hours and hours not worked because of illness or holidays. Return to text
3. In particular, we used several historical issues of the ILO Bulletin of Labor Statistics and the ILO International Labour Review to import these data into electronic format. We generally used the latest available vintage of data for each series, smoothing breaks due to changes in the survey methodology using interpolation. Return to text
4. Eurostat produces a series of hours worked per worker in Spain which starts in 1995. However, we were not able to find consistent survey data covering the previous years. Thus, we opted to include Spain only in the analysis of the Great Recession. Return to text
5. For instance, the BLS regularly uses this methodology to derive quarterly estimates of U.S. series (e.g. manufacturing output). Return to text
6. For a more articulated discussion on the implications of alternative weighting matrix, see Denton (1971). For a broader discussion about interpolation methods, the reader is invited to check the Handbook of Quarterly National Accounts Compilation. Return to text
7. Correlations and volatilities from HP filtered data are available upon request. Return to text
8. We also reproduced all the tables using the first difference operator, four-quarter changes, and the BP filter. Results are relatively robust to the various filtering procedure and are available upon request. Return to text
9. Incidentally, we note that since we are reporting standard deviations (of HP residuals), the volatility of the intensive and the extensive margin do not sum up to the volatility of total hours worked. When we compute the variance of these series using the first difference operator, for which terms are additive up to a covariance term, we find that the two margins account for nearly 50 percent of the variance of total hours worked. Return to text
10. Recent work by Fang and Rogerson [2010], for instance, shows that, in steady state, higher firing costs induce firms to cut employment and increase hours per worker as, from the perspective of the production function, the two margins are substitute inputs. Return to text
11. Barnichon [2010] argues that lower labor market frictions cannot account for the large increase in hours worked, suggesting that other structural changes might be quantitatively responsible for this change in volatility. Return to text
12. GG also document this observation for the U.S. Return to text
13. The Hansen formulation is commonly used in closed economy settings, while Greenwood et al preferences are commonly used in open economy settings (see Raffo [2008]). Return to text
14. We also construct cyclical wedges using other filters, such as first difference, four-quarter changes, and band-pass. Results are available upon request. Return to text
15. For an analysis of trend changes in the labor wedge and its component, see Ohanian et al. [2008]. Return to text
16. We discount the fact that the Spanish housing price series does not fall as much as those in Ireland and the US, as there are concerns about the measurement of the Spanish housing price series (see Fernandez-Villaverde and Ohanian (2010)). Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text