Missing Import Price Changes and Low Exchange Rate Pass-Through

Etienne Gagnon, Benjamin R. Mandel, and Robert J. Vigfusson

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

A large body of empirical work has found that exchange rate movements have only modest effects on inflation. However, the response of an import price index to exchange rate movements may be underestimated because some import price changes are missed when constructing the index. We investigate downward biases that arise when items experiencing a price change are especially likely to exit or to enter the index. We show that, in theoretical pricing models, entry and exit have different implications for the timing and size of these biases. Using Bureau of Labor Statistics (BLS) microdata, we derive empirical bounds on the magnitude of these biases and construct alternative price indexes that are less subject to selection effects. Our analysis suggests that the biases induced by selective exits and entries are modest over typical forecast horizons. As such, the empirical evidence continues to support the conclusion that exchange rate pass-through to U.S. import prices is low.

Keywords: Exchange rate pass-through, import prices, item replacement

JEL classification: F31, F41, E30, E01, C81

In conducting monetary policy, central bankers are interested in how much exchange rate movements affect the prices of imported goods ("exchange rate pass-through") as fluctuations in these prices can, in turn, affect domestic prices and output. Commonly, exchange rate pass-through is measured by regressing changes in published import price indexes on changes in trade-weighted exchange rate indexes along with other explanatory variables. Using these regressions, researchers have estimated low rates of exchange rate pass-through for the United States. Recent estimates (for example, Campa and Goldberg [2005], and Marazzi and Sheets [2007]) suggest that, following a 10 percent depreciation of the dollar, U.S. import prices increase about 1 percentage point in the contemporaneous quarter and an additional 2 percentage points over the next year, with little if any subsequent increases. These low estimates have led several authors to formulate theories which generate incomplete pass-through.¹

In a recent paper, Nakamura and Steinsson (2011) argue that actual long-run pass-through is substantially higher than these standard estimates because published price indexes are missing price changes associated with item replacement. In their words, "[if] the prices of new products entering the index have already adjusted to exchange rate movements ... [then] the response of these prices to movements in exchange rates ... will be `lost in transit' (i.e., neither picked up by an observed price change of the exiting nor entering product)." They derive an adjustment factor for standard long-run pass-through estimates under specific assumptions regarding the nature of item substitutions and the way firms set prices. They find that measured pass-through is underestimated by a factor of almost two, implying that exchange rate pass-through to U.S. import prices is much more complete in the long run than was previously thought.

Our paper reassesses this conclusion by developing a general framework for understanding how sample exits and sample entries--in conjunction with pricing assumptions--impact measured pass-through, and by proposing and implementing new ways of gauging the biases in standard estimates. Throughout our discussion, we emphasize the implications of item substitutions over the first couple years following an exchange rate shock, as such a short-term horizon is most commonly employed by forecasters and is especially useful for discriminating among theoretical models.² Our conceptual framework captures the possibility that an item whose price is about to change is more likely than others to leave the index (resulting in a "selective exit") and that an item whose price recently changed is more likely than others to join the sample (resulting in a "selective entry"). We demonstrate that the effects of item replacement on measured pass-through crucially depend on the nature of both exits and entries of items. In turn, the magnitude of these effects can be sensitive to pricing assumptions and the time horizon of interest. By contrast, the presence of real rigidities is typically of limited consequences. In presenting these findings, we substantially expand the analysis of Nakamura and Steinsson, who are primarily concerned with the long-run effects of item substitutions and do not explicitly model sample exits.

Our theoretical work explores the implications of selective exits and selective entries under two popular price-setting mechanisms, Calvo and menu-cost, which together span a wide range of pricing behavior relevant for understanding pass-through dynamics. The most consequential situation is when price changes are missed both when items exit the sample and when they enter it. In such a case of selective exits and selective entries, standard pass-through estimates omit a roughly constant fraction of the actual exchange response, a finding that applies to all time horizons and both pricing models. When only exits are subject to a selection bias, the estimation bias as a share of the cumulative response is largest initially, but then falls over time as items that have yet to respond to the exchange rate are brought into the sample. This offsetting effects is largest in the Calvo model due to its relatively slow transmission of shocks. When only entries are subject to a selection bias, measured pass-through is initially unbiased, but a bias then gradually appears as entering items prove insensitive to past exchange rate movements. The bias grows largest in the Calvo model because of its relatively slow pass-through of shocks, which means that item substitutions are likely to take place before pass-through is complete.

In the U.S. import price index, there is about one item replacement for every 5 price changes and as reported by Nakamura and Steinsson (2011) 40 percent of items leave the sample without ever experiencing a price change. The potential for economically important biases in standard pass-through regressions is thus material, provided that many item exits and entries are subject to a selection effect. However, based on a range of empirical exercises, we conclude that the biases induced by selective exits and entries, although a concern and worthy of continued research, do not materially alter the literature's view that pass-through to U.S. import prices is low over typical forecast horizons. To inform our judgement, we first use BLS microdata to derive empirical bounds on the price level response to an exchange rate shock. To do so, we calibrate our Calvo and menu-cost models to match key features of exchange rate movements, item substitutions, and individual price adjustments, then we recover the model-implied correction factors. Our baseline empirical estimate of pass-through to imported finished goods prices after two years is 0.24. After correcting for the most severe case of selective exit and selective entry consistent with the data, our pass-through estimate rises only to 0.28.

We next use BLS microdata to construct alternative price indexes in which the inclusion of newly sampled items in the index is delayed. We formally prove that this delaying procedure can substantially mitigate the selective entry bias over typical forecast horizons in a Calvo model. The intuition is that when entries are selective, added items are too insensitive to past exchange rate movements; simply delaying their entry in the index reduces this selection effect by allowing the distribution of added items to mix. As such, theory predicts that if selective entries were frequent, then these alternative prices should imply higher pass-through rates. However, when we estimate pass-through rates using these alternative price indexes, we do not find any evidence of bias reduction. This result casts further doubt on the empirical relevance of selective entries.

The remainder of the paper is structured as follows. Section 1 describes the sample of items used by the BLS to compute import price inflation and provides an overview of item exits and entries. Section 2 introduces the baseline Calvo and menu-cost models that we use to illustrate the nature of the various biases and to gauge their quantitative importance. Section 3 presents the possible biases associated with selection effects in sample exit and entry. Section 4 explores the empirical relevance of these biases by computing bounds on standard pass-through estimates and by constructing an alternative price index that mitigates these biases. Section 5 concludes.

1 Nature and Occurrence of Item Exits and Entries

Our study focuses on changes to the BLS import price sample, not on changes to the population (universe) of imported items.³ For clarity, we reserve the terms "exit" and "entry" for changes in the composition of the sample. Throughout the presentation of the data and subsequent model-based analysis, we are concerned with the possibility that micro price changes tend to take place just after items exit the sample or shortly before items enter the sample, so that part of the price response to shocks is censored. We define a "selective exit" as the subtraction of an item from the sample that is triggered by its price being about to change, and a "selective entry" as a systematic addition to the sample of an item that recently experienced a price change. By contrast, a "random exit" and a "random entry" are, respectively, the subtraction from and the addition to the sample of an item without regards to its pricing characteristics.

With the above terminology in mind, the remainder of this section provides background information about the construction of the import price indexes used in standard pass-through regressions, emphasizing the nature and occurrence of sample exits and entries, their treatment by the BLS, the potential for selection biases, and their relationship to micro price adjustments.

1.1 The International Price Program

Given identical data to Gopinath and Rigobon (2008) and Nakamura and Steinsson (2011), we rely on their work to convey the details of the BLS' International Price Program (IPP) protocol and sample, as well as on the BLS Handbook of Methods. In brief, import prices are collected through a monthly survey of U.S. establishments. The sample consists of rolling groups of items, each item having a sampling duration of about three years, on average.⁴ The IPP chooses its firms and items based on a proportional-to-size sampling frame with some degree of oversampling of smaller firms and items.⁵ Respondents must provide prices for actual transactions taking place as closely as possible to the first day of the month. In total, we observe the price of approximately 13,000 imported items per month from September 1993 to July 2007. For the purpose of computing our sample statistics, and consistent with previous studies, we carry forward the last reported price to fill in missing values, effectively overwriting IPP price imputations and firm estimates of prices in non-traded periods. We also restrict our sample to U.S. dollar transactions, which account for about 90 percent of all observations.

1.2 Nature of Exits and Entries

BLS price collectors take note when an item exits the sample and assign the retiring item one of the following codes: (1) regular phaseout, (2) accelerated phaseout, (3) sample dropped, (4) refusal, (5) firm out of business, (6) out of scope, not replaced, and (6) out of scope, replaced. Codes (1) through (3) indicate that item exit is driven primarily by the phaseout schedule of the IPP sampling protocol. Codes (4) and (5) describe situations in which price collection is impossible because the survey respondent refuses to respond or ceases to operate, even though the exiting items may continue to be traded in the universe. Codes (6) and (7) are those instances in which price quotes are unavailable because the item ceases to be traded by importers.⁶

The purpose of item phaseouts is to keep the sample representative of the universe of items; the BLS resamples approximately half of its disaggregated product categories every two years and typically plans to retire items five years after their entry. An item may retire early if it is insufficiently traded. We see such exists, given their planned nature, as unlikely to be selective. Contrary to phaseouts, refusals and importers going out of business are not foreseen events. Nevertheless, we view the risk that such exits systematically mask individual price adjustments as relatively modest, as there are several factors unrelated to micro price adjustments that could trigger them. Exits associated with items becoming out of scope likely present the greatest risk of masking price adjustments. For example, an importer could cease to order an item when faced with a price increase eating away its profit margins. The item could also exit because the foreign producer is adjusting the item's effective price through a change in its characteristics. Other situations leading to out-of-scope items may be unrelated to micro price adjustments. For example, the importer may be curtailing the range of varieties it has on offer in order to streamline inventory management.

It is worthwhile to note that exits are not generally accompanied by the simultaneous entry of a newly sampled item. When an item suddenly becomes out of scope, BLS price analysts ask the reporting firm whether it can provide another item that meets the sampling criteria of the exiting item. When it is possible, the BLS may link the price of the entering and exiting items through a one-time quality adjustment, in which case the change in the effective price is properly recorded. However, that is a relatively infrequent practice. In other instances, the firm may provide an alternative item meeting the BLS sampling needs, though that item is recorded as a separate entry. More often, when no item with similar characteristics is available in the same establishment, or when the planned phaseout date is within the next 18 months, the BLS simply waits until the next biennial sample redrawing. The lag between an unplanned exit and the subsequent item entry can thus be fairly long. Even in the case of planned phaseouts, BLS protocol does not necessitate synchronizing exit and entry.⁷

Notwithstanding the fact that exits and entries are staggered, the size of the IPP sample has been roughly constant since 1993 as the gross number of exits has typically been matched by a corresponding number of entries. The BLS uses probability sampling techniques to select establishments within broad strata of items, and then to select product categories within each stratum-establishment combination. A BLS field agent next conducts an interview with the establishment to select specific items. Probability sampling may be used at that stage. In general, special efforts are made to ensure that selected items are traded regularly, which implies that higher-volume items with established price histories are more likely to be selected.

In principle, the BLS's decision to sample a given item from within the universe should be unrelated to the timing of that item's price changes. Indeed, our reading of the BLS methodology is that the risk of selective entries is somewhat low, especially for those items entering the sample through planned sample redrawing. The risk of selective entries is arguably larger for items entering the sample concurrently with or immediately after an unplanned exit when no quality adjustment is made. Our assessment that the risk of selective entries is relatively low stands in contrast with the working assumption in Nakamura and Steinsson (2011) that all entries are selective. For this reason, we will illustrate the magnitude of the bias in our quantitative analysis below under the full range - 0 to 100 percent - of possible selection effects.

1.3 Accounting for Exit and Entry

For a given month , let and be the number of price items exiting and entering the sample, respectively. These items cannot beused in the computation of inflation at month because their price in either month or is missing. For items whose price is available in both month and , let $change\left( t\right)$ and $no\_change(t)$ be the number of observations with a price change and no price change, respectively. We define the exit rate as

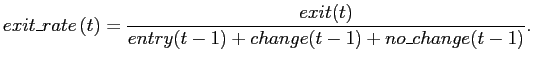
$\displaystyle exit\_rate\left( t\right) =\frac{exit(t)} {entry(t-1)+change(t-1)+no\_change(t-1)}.$

The denominator in the above expression is the number of items whose price was collected in month . The exit rate thus measures the fraction of items present in the sample at the end of month that leaves in the next month. Analogously, the entry rate is measured as

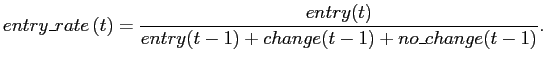
$\displaystyle entry\_rate\left( t\right) =\frac{entry(t)} {entry(t-1)+change(t-1)+no\_change(t-1)}.$

The fourth through seventh columns of table 1 show summary statistics about exits and entries over the period October 1995 to April 2005 for finished goods categories.⁸ For industry groupings, we use the Bureau of Economic Analysis 3-digit Enduse classification to bring descriptions of the microdata closer to the groups of goods commonly used in aggregate pass-through regressions (for instance, Bergin and Feenstra (2009) and Marazzi, et al. (2005)). In aggregating up from unique items in a given month to industry-level statistics, we weight each measure by its importance to overall U.S. import purchases.⁹ We aggregate the measures defined above in two stages: first, by computing unweighted statistics for each Enduse category in each month. Then, we aggregate across categories and time periods using the 2006 import sales value of each Enduse category.¹⁰

The rates of item exits and entries are both approximately 3 percent, indicating that the average size of the IPP sample remained about the same over the course of the sample. However, the steadiness of the overall sample size hides a degree of heterogeneity in exit and entry rates at the Enduse product level. For instance, computers and semiconductors (Enduse 213) had an entry rate of 5.0 percent, nearly twice that of agricultural machinery and equipment (Enduse 212). Certain categories (like computers) expanded over the course of the sample as evidenced by higher entry rates relative to exit rates. Differences in net entries likely reflect the changing trade intensity of certain categories over the course of the sample. Exiting items coded as out of scope, which we see as presenting the highest risk of selective exits, accounted for half (1.5 percentage points) of the total exit rate. Enduse categories with a relatively high share of out-of-scope exits include computers and semiconductors, home entertainment equipment, as well as trucks and buses.

By definition, a selective exit entails a price change concurrent with an item leaving the sample. This pattern suggests that the rate of selective exit should vary over time along with macroeconomic variables triggering price adjustments. Evidence of this phenomenon in scanner data is provided by Broda and Weinstein (2010) in their analysis of barcode creation and destruction over the business cycle. To see if exits of imported goods similarly respond to the exchange rate, the top panel of figure 1 presents the time series of the exit rate restricted to out-of-scope items along with an index of the broad nominal dollar.¹¹ This measure is very close to the "endogenous exit" measure reported in Berger et al. (2009), with the minor difference that we also exclude exits resulting from aggregate refusals and out-of-business. The series is flat at about 1 percent throughout most of the early periods with a transient peak at the beginning of 2000. Then, the out-of-scope rate rises by about 50 basis points in 2003 through 2005. These three prominent features of the time series (i.e., flatness or slight decline early, peak in 2000, and uptick in 2003-5) correspond inversely to the pattern of the broad nominal dollar index, shown in black. The intuition for this relationship is straightforward: as the dollar depreciates, the profitability and viability of a higher proportion of imported items is adversely affected, leading firms to pull the items before the end of their scheduled sample life. We view this evidence as suggestive that exits may, in fact, occur in tandem with price changes.

The occurrence of exits related to factors other than items falling out of scope, which we see as presenting a relatively low risk of selection bias, varies far less systematically with the exchange rate. Rather, the random exit series exhibits the fairly normal pattern of peaks every two years (i.e., the end of 1996, 1998, 2000, 2002, and 2004), which is in line with the biennial shuffling of IPP items. For the most part, the overall entry rate shows a similar pattern with peaks in the middle of the year in 1997, 1999, and so on. Of note, similarly to the out-of-scope exit rate, the rate of overall entry also ticks up towards the end of the sample.

We also note that the timing of the changes in out-of-scope exit rates and, to a lesser extent, in entry rates, does not seem to account for the decline in measured exchange rate pass-through documented in the literature, which has roughly halved since the 1980's. The decrease in pass-through took place primarily in the 1990's, preceding the upticks in exit rates by quite a few years.

1.4 Micro Price Adjustments

As will be made clear in the next section, the quantitative implication of selective exits and selective entries can be sensitive to the nature of the price-setting frictions giving rise to infrequent and lumpy nominal price adjustments. It will be convenient for our discussion to define the observed frequency of individual price changes as

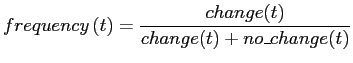$\displaystyle frequency\left( t\right) =\frac{change(t)}{change(t)+no\_change(t)}$ .

The overall weighted incidence of price changes for finished goods is estimated to be 6.2 percent. The analogous statistic for the entire IPP import sample (i.e., additionally including industrial supplies, foods, feeds and beverages) is 15.3 percent.¹² These levels are consistent with the weighted average of 14.1 percent in Nakamura and Steinsson (2011) and the median of 15 percent in Gopinath and Rigobon (2008). The average absolute (nonzero) price change is 6.7 percent for finished goods and 8.0 percent overall, in line with the mean overall estimate of 8.2 percent in Gopinath and Rigobon (2008). Here, again, there is significant dispersion across categories with items belonging to computers and peripherals (Enduse 213) having an average price change of 9.6 percent, compared to 2.0 percent for passenger cars (Enduse 300).

1.5 Other Data Considerations

We conclude the data description by mentioning two additional elements important for the interpretation of the results. First, in any given month, prices are missing for about 40 percent of items in the sample, which could reflect the absence of a transaction or simply reporting issues. Second, nearly half of all observations in the BLS sample refer to items that are traded between affiliates or entities of the same company. Although the BLS prefers that these intra-company transfer prices be market-based or market-influenced, some have expressed concern over whether these prices play the same allocative role as market transactions. Excluding intra-company transfer prices from the sample has a negligible impact on our analysis because intra-firm and market transactions have roughly similar entry rates, exit rates, and frequency of price changes. See Neiman (2010) and Gopinath and Rigobon (2008) for a comparison of intra-firm and market transactions.

2 Pass-Through and Micro Price Adjustments: A Baseline Case

This section introduces the baseline Calvo and menu-cost models that we will use to illustrate the nature of the various selection biases and how they interact with the frequency of prices changes. As we will show, judgement on the quantitative importance of the biases is sensitive to the price-setting mechanism one sees as best representing the data-generating process. Although the Calvo and menu-cost models are only two of the many price-setting mechanisms proposed in the literature, they illustrate the point that the severity of the biases often relates to the frequency of price changes and, more generally, to the speed at which exchange rate movements are passed-through to import prices.

2.1 Economic Environment

We consider the following data-generating process for the change in the price (in logs) of an imported item at period ,

$\begin{displaymath} \Delta p_{it}=\left \{ \begin{array}[c]{cc} 0 & \text{if }\mathcal{I}_{it}^{f}=0\ u_{it}+\beta \Delta x_{t}+\varepsilon_{it} & \text{if }\mathcal{I}_{it}^{f}=1 \end{array}\right. . \end{displaymath}$

Given the opportunity (or decision) to change its price, a firm sets $\Delta p_{it}$ equal to the sum of (a) the amount of price pressure inherited from previous periods, $u_{it}$ , (b) the change in the exchange rate, $\Delta x_{t}$ , and (c) the contribution of a (mean-zero) idiosyncratic factor, $\varepsilon_{it}$ . The occurrence of a price change is marked by the indicator variable $\mathcal{I}_{it}^{f}$ . The price deviation carried to the beginning of the next period is given by

$\begin{displaymath} u_{it+1}=\left \{ \begin{array}[c]{cc} u_{it}+\beta \Delta x_{t}+\varepsilon_{it} & \text{if }\mathcal{I}_{it}^{f}=0\ 0 & \text{if }\mathcal{I}_{it}^{f}=1 \end{array}\right. . \end{displaymath}$

If the firm does not change its price, then the aggregate and idiosyncratic shocks occurring in period are simply added to the amount of price pressure that had already cumulated. If the firm adjusts its price, then the price is set to the optimum and no price pressure is carried into the next period.¹³ The set up so far is quite general and not specific to import prices. One could, for example, interpret $\Delta x_{t}$ as the contribution of aggregate shocks, such as wage inflation, to a firm's reset price. In what follows, we will simply assume that $\Delta x_{t}$ can be represented by an $AR\left( 1\right)$ process,

$\displaystyle \Delta x_{t}=\alpha+\rho \Delta x_{t-1}+\xi_{t},$

with Gaussian innovations, $\xi_{t}$ .

We are ultimately interested in the impact of exchange rate movements on import prices in general. To this end, we define aggregate price inflation as the average change in item prices,

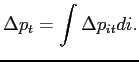
$\displaystyle \Delta p_{t}=\int \Delta p_{it}di.$

Suppose that the econometrician estimates a linear model containing lags of the aggregate variable,

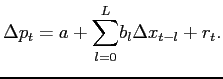
$\displaystyle \Delta p_{t}=a+ {\displaystyle \sum \limits_{l=0}^{L}} b_{l}\Delta x_{t-l}+r_{t}.$

(1)

where $r_{t}$ is an error term. In what follows, we explore how various assumptions about the timing of nominal adjustments impact the estimated regression coefficients.

2.1.1 Calvo Model

In the Calvo model, the decision to change the price is exogenous to the firm. The indicator variable $\mathcal{I}_{it}^{f}$ is a random variable taking the value with constant probability , and 0 with probability . This assumption has strong implications for the dynamic responses of import prices to exchange rate movements. It is convenient to consider the case in which innovations to the exchange rate, $\Delta x_{t}$ , are uncorrelated over time ( $\rho=0$ ), as it allows us to derive analytical expressions for the regression coefficients.

As appendix A shows (in a more general environment), the (plim) linear estimate of $b_{l}$ is

$\displaystyle b_{l}=f\left( 1-f\right) ^{l}\beta.$

(2)

Intuitively, for a movement in the exchange rate periods earlier to impact an item's price today, the firm must be given the opportunity to adjust its price today (probability ) and no price change must have occurred in each of the previous periods (probability in each period). Otherwise, the current price would already reflect $\Delta x_{t-l}$ . The Calvo model provides a textbook example of a geometric lag model in which the coefficient on the explanatory variable decays exponentially with the number of lags. Summing up the (plim) coefficients in the regression, we get

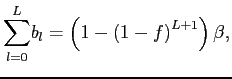
$\displaystyle {\displaystyle \sum \limits_{l=0}^{L}} b_{l}=\left( 1-\left( 1-f\right) ^{L+1}\right) \beta,$

which converges to $\beta$ as $L\rightarrow \infty$ . Thus, although the effects of an exchange rate shock never are passed-through fully to import prices, we can nevertheless approximate $\beta$ (the "long-run" pass-through) as the sum of the regression coefficients with an arbitrary degree of precision.

2.1.2 Menu-Cost Model

In the menu-cost model, the decision t $u_{it}+\beta \Delta x_{t}+\varepsilon_{it}$ o change the price is the result of a cost-benefit analysis performed by the firm. As shown by Sheshinski and Weiss (1977), it is optimal for the firm to keep its price unchanged if the deviation from the reset price, , falls within a certain range. One can show that, to a first-order approximation, this range of inaction is symmetric around the price that sets the price pressure to zero (see Gopinath and Itskhoki, 2010, for a formal derivation). We thus approximate the decision to change the price as

$\begin{displaymath} \mathcal{I}_{it}^{f}=\left \{ \begin{array}[c]{cc} 0 & \text{if }\left \vert u_{it}+\beta \Delta x_{t}+\varepsilon_{it}\right \vert \leq K\ 1 & \text{if }\left \vert u_{it}+\beta \Delta x_{t}+\varepsilon_{it}\right \vert >K \end{array}\right. . \end{displaymath}$

Unfortunately, analytical results are challenging to derive for the menu-cost model unless one is willing to make stringent assumptions (see Danziger (1999) and Gertler and Leahy (2008) for examples). However, the assumptions required for tractability seem less suitable here. Therefore, we will proceed by simulations to illustrate our main points. Note that the decision to change the price now depends on the value of $\beta$ : The larger the pass-through coefficient for a given , the more a shock to the exchange rate is likely to trigger a price adjustment. More generally, the more shocks are large and persistent (and thus associated with relatively large benefit of adjusting the price), the more likely is a firm to change the price immediately. The estimated coefficients in equation 1 are thus sensitive to the particular realization of the shocks in the menu-cost model.

2.2 Calibration of the Models

We first set the mean, standard deviation, and autoregressive coefficient of exchange rate innovations to match the corresponding moment of the broad dollar index computed by the Federal Reserve from January 1995 to March 2010. The standard deviation of monthly (end-of-period) exchange rate movements was 1.5 percent over that period, with no apparent drift. Exchange rate movements were slightly autocorrelated over time ( $\rho=0.19$ ). We report results for $\beta=0.3$ , which is in-line with recent estimates in the literature (e.g., Marazzi et al. (2005), Gopinath, Itskhoki, Rigobon (2010)), but somewhat lower than the consensus value for pass-through in the 1980s (e.g., Goldberg and Knetter (1997)).

The remaining parameters are calibrated to match salient features of individual import price adjustments. As shown by Gopinath and Itskhoki (2010), the median size of individual price changes is rather insensitive to the frequency of price change changes, hovering between 6 and 7 percent. In the case of the Calvo model, we set the probability of a price change equal to a given frequency and calibrate the variance of individual innovations (which is assumed to be Gaussian) to match a median size of price changes of 6.5 percent. In the case of the menu-cost model, we choose the menu cost and the standard deviation of $\varepsilon_{it}$ to match both the median size and the average frequency of price changes. We make the additional assumption that $\varepsilon_{it}$ . is normally distributed with mean zero. The larger is , the less frequent and the larger are the individual price changes. Likewise, the larger is the standard deviation of $\varepsilon_{it}$ , the more frequent and large are individual price changes.

2.3 Impulse Response to an Exchange Rate Movement

Our exercise illustrates the point that the choice of a particular model can have important consequences for the dynamic response of the import price index. Although the Calvo and menu-cost models are calibrated to the same (in steady-state) frequency of price change and the long-run pass-through coefficient, the dynamic transmission of the exchange rate shock is markedly different between the models, with faster rates of pass-through at short horizons in the menu-cost model than in the Calvo model.¹⁴

The response of import price inflation to an exchange rate movement in the Calvo and menu-cost models are shown in the upper, middle, and bottom panels of figure 2 for (steady-state) frequencies of price changes of 5 percent, 20 percent, and 35 percent, respectively. In the case of the Calvo model, the frequency of price changes has a direct impact on the speed at which exchange rate disturbances are transmitted to the import price index. For a relatively low frequency of price changes (upper panel), the exchange rate movement has not yet fully diffused by the end of the forecast horizon, although the impact on import price inflation is rather small. For a frequency of price changes of 20 percent (middle panel), the shock is almost entirely passed-through by the end of the forecast period, with negligible amount of trade price inflation left. Higher frequencies of price changes lead to even faster pass-through. The cumulative response of the import price index in the Calvo model can be seen in the left panels of figure 3 as the sum of the dark, medium, and light bars. For example, when the frequency of price changes is 5 percent, just over 70 percent of the long-run response of the import price index has taken place after two years, leaving almost 30 percent of the price response beyond the forecast horizon. By contrast, the transmission of the exchange rate shock is virtually complete after two years at frequencies of 20 percent or higher.

The speed of pass-through is markedly higher in the menu-cost model at all frequencies (sum of dark, medium, and light bars in right panels of figure 3). Under our low-frequency calibration, there is negligible amount of import price inflation as a result of the shock after a year, even for frequencies as low as 5 percent, well over 90 percent of the long-term response of the price level has already taken place after a year. The speed of transmission is even higher for higher-frequency calibrations, with the bulk of the price level response taking place over just a few months.

3 Selection Effects in Item Exits and Entries

We now expand the baseline model to allow for the exit and entry of items in the index. As was the case earlier, we assume that the universe of items available for purchase is constant over time. Prices are collected at the end of the period after nominal adjustments, exits, and entries have taken place. Items entering or exiting the index thus cannot be used to compute inflation because either their past or current prices are unknown to the statistical agency. Exits occur through two channels. First, items face an exogenous probability of dropping out of the sample every period (the "random exit" channel). These exits do not depend on the behavior of firms and are thus akin to the sample rotation performed by the BLS. Second, some exits are triggered by firms changing their prices (the "selective exit" channel). Conditional on its price being changed in the period, an item faces an exogenous probability of exiting the sample. Such a situation could occur if, for example, price collectors failed to hedonically adjust an item's price after a change in its characteristics, treating instead the old and new prices as unrelated exits and entries. In total, a fraction $s_{t}=d+\left( 1-d\right) ef_{t}$ of items exits the sample every period. Our model is not properly one in which some exits from the index are "endogenous" since the decision to exit is always exogenous to firms. Nevertheless, it has the feature that some exits partly censor the adjustment of the price index.

For convenience, we postulate that exiting items are replaced by an equal number of entering items, which is a rough approximation of the BLS' practice over the past two decades. Entries also occur through two channels. A constant fraction of entering items are drawn at random from the universe of items (the "random entry" channel). The distribution of deviations from the optimal price, $u_{it}$ , is the same as for the entire universe, with some fraction $f_{t}$ of deviations having their price reset during the period. Another fraction of entering items systematically are sampled from price trajectories with a price change in the current period (the "selective entry" channel). Their price already reflects current and past movements in the exchange rate (i.e., $u_{it}=1$ ). Note the symmetry between the selective exit and selective entry channels: They both occur because items experiencing a price change in the current period are more likely to either exit or enter the index.

As was the case earlier, it is convenient to first consider a Calvo model with innovations to the exchange rate. We show in the appendix that the (plim) coefficient on the -th lag of the exchange rate is

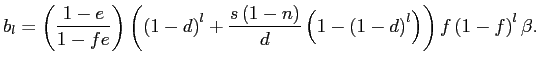
$\displaystyle b_{l}=\left( \frac{1-e}{1-fe}\right) \left( \left( 1-d\right) ^{l} +\frac{s\left( 1-n\right) }{d}\left( 1-\left( 1-d\right) ^{l}\right) \right) f\left( 1-f\right) ^{l}\beta .$

(3)

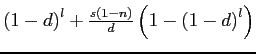The expression in front of $\beta$ is the probability that a price change occurs in period and the previous price change was over periods earlier. Relative to equation 2, the above expression has two new terms , $\frac{1-e}{1-fe}$ and $\left( 1-d\right) ^{l}+\frac{s\left( 1-n\right) }{d}\left( 1-\left( 1-d\right) ^{l}\right)$ , which capture the biases associated with selective exits and selective entries. To gain some intuition about these biases, it is useful to consider four canonical cases. Following our discussion of these canonical cases, we will then relate these cases with the theoretical work in Nakamura and Steinsson (2011).

3.1 All Exits and Entries are Random

When all exits and entries are exogenous (i.e., and ), the (plim) coefficients in the Calvo model with exchange rate innovations are

$\displaystyle b_{l}=f\left( 1-f\right) ^{l}\beta.$

(4)

In short, standard pass-through regressions are unbiased even though, every period, an arbitrary fraction $\left( \text{with }d<1\right)$ of items in the basket is replaced. Intuitively, items in the index have the same distribution of deviations from the optimum price as items in the universe; the only impact of exits and entries is to alter the number of observations usable to compute inflation at any point in time. For the same reason, biases are absent when exchange rate innovations are correlated and in the menu-cost model.

3.2 All Exits and Entries are Selective

Consider now the case when all exits and entries are selective (i.e., and ). This case is related to the well-known "quality-change bias" by which statistical agencies have difficulties accounting for changes in quality from one vintage to the next, so that part or all of an item's effective price adjustment is censored. In our example, the price change is fully censored, the disappearance of the old vintage and the arrival of the new one being recorded as unrelated exits and entries.¹⁵

In the Calvo model with exchange rate innovations, we have

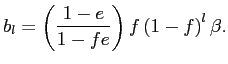
$\displaystyle b_{l}=\left( \frac{1-e}{1-fe}\right) f\left( 1-f\right) ^{l} \beta.$

(5)

All coefficients are downwardly biased by the same factor $\left( 1-e\right) /\left( 1-fe\right)$ relative to the true response. Note that $\hat {f}=\frac{\left( 1-e\right) }{\left( 1-fe\right) }f$ is the frequency of price changes observed by the econometrician so that the estimated coefficients are downwardly biased by a factor $\hat{f}/f$ . This bias can be large even when the exit rate (i.e., ) is low because what crucially matters is the prevalence of exits among price changes rather than among observations in the index.

The left and right panels of figure 3 show the cumulative response of the price index to an exchange rate movement in the Calvo and menu-cost models, respectively, as a share of true long-run pass-through. We tentatively assumed that a quarter of all price changes are accompanied by an exit, a proportion roughly equal to the median across 3-digit Enduse categories of the worse-case probability of exit (0.28) that we estimate later in section 4.2. We leave the other model parameters unchanged relative to the base case described in section 2.2. In addition to , the figure shows the special case (no selective exit), which we will consider shortly. As noted earlier, the censoring of price changes reduces the frequency of price changes observed by the econometrician. For underlying frequencies of 5, 20 and 35 percent in the population of items, the econometrician would report frequencies of about 4, 16, and 29 percent, respectively.

In our calibrated Calvo and menu-cost models, the size of the bias created by selective exit is somewhat large over the forecast horizon at all frequencies considered when the price of entering items has been optimized. For low frequencies of price changes, the bias is roughly equaled to , the probability of an item exit conditional on a price change, which we set to a quarter in the simulations. The bias declines somewhat as we consider higher frequencies, reaching about 20 percent of the long-run response when the underlying frequency is 35 percent.

3.3 All Exits are Selective and all Entries are Random

It can be challenging for price collectors to know if exits are selective or random as they have to press respondents for information about the circumstances in which they take place. Price collectors have some leeway to avoid selection biases in the entry of items in the basket since, in principle, they can design the sampling procedure to randomly select observations from the universe of items. The special case we now consider assumes that all exits are selective while all entries are random (i.e., and ). Although we model the sample exit decision as exogenous to the firm, this case captures the essence of "endogenous exits" problems: Item exits tend to be associated with unobserved price adjustments, so that the price index response to shocks is underestimated.¹⁶ When firms choose the timing of price changes, as in our menu-cost model, exits also tend to be associated with relatively large deviations of individual prices from their optimum.

Starting again with the Calvo model with uncorrelated exchange rate innovations, we have

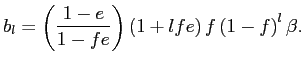
$\displaystyle b_{l}=\left( \frac{1-e}{1-fe}\right) \left( 1+lfe\right) f\left( 1-f\right) ^{l}\beta.$

(6)

The size of the bias depends on the relative strength of two opposite forces. On the one hand, selective exits censor price adjustments, thus dampening the response of the price index to past exchange rate movements. This force is represented by the term $\left( 1-e\right) /\left( 1-fe\right)$ , which we encountered earlier. On the other hand, exits also create opportunities to introduce items whose price has not changed for some time. This possibility subsequently makes the price level more responsive to past exchange rate movements. This second force is captured by . For short lags, the downward bias is the predominant force. In particular, the initial response of the index, $b_{0}=\hat{f}\beta$ , is always downwardly biased. As we increase the number of lags, $\left( 1+lfe\right)$ grows linearly to any arbitrarily large number, so that individual coefficients are systematically upwardly biased at sufficiently long lags. Nevertheless, the cumulative index response remains downwardly biased because the coefficients converge more rapidly to zero.¹⁷

As shown in the left panels of figure 3, assuming that exiting items are replaced by sampling at random from the population () reduces the size of the bias noticeably over the forecast horizon in the Calvo model relative to the case in which entries are selective (). For frequencies of about 20 percent, the estimated two-year cumulative response is nearly the same as the true one. The randomization of entries mitigates the bias from selective exits because some of the entering items have not had a price change in a while, making them responsive to past exchange rate movements. As our figure illustrates, this counterbalancing effect can be quite large, offsetting much of the bias by the end of typical forecast horizons.

The gains from resampling at random are more modest in the menu-cost model (right panels) because pass-through is very rapid. As hinted in equation 6, the counterbalancing effect of random substitutions grows with the number of lags, , but since coefficients are tiny after a small number of lags in the menu-cost model, the ultimate impact on cumulative pass-through is modest.

3.4 All Exits are Random and all Entries are Selective

We next turn our attention to the case in which all exits are random and all entries are selective ( and ). Under these assumptions, the (plim) coefficient on the lag of exchange innovations in our baseline Calvo model is

$\displaystyle b_{l}=\left( 1-s\right) ^{l}f\left( 1-f\right) ^{l}\beta .$

(7)

This expression has a very intuitive interpretation. For a movement in the exchange rate periods ago to contribute to inflation in the current period, one must observe a price change in the current period (probability ) and no price change or substitution in the previous periods (constant probability and , respectively, each period). Price changes and substitutions from period to result in posted prices that already reflect movements in the exchange rate at period . Relative to equation 2, the above expression is downwardly biased by a factor $\left( 1-s\right) ^{l}$ .

A few comments are worth making. First, the nature of the product replacement bias is that items entering the basket systematically are less sensitive to past movements in the exchange rate than items in general. Including entering items in pass-through regressions thus lowers estimated pass-through rates. Second, in the special case of , we have $b_{0}=f\beta$ ; the estimated initial impact of an exchange rate movement on the price index is always unbiased. We also note that the share of the true coefficient correctly measured decays exponentially with the number of lags considered. The importance of the bias as a share of the cumulative response thus grows over time, with estimates of the short-run cumulative response being less biased than estimates of the long-run response.

Third, as stressed by Nakamura and Steinsson (2011), the bias is most important for product categories with very low frequency of price changes. The left panels of figure 4 illustrate the bias over the policy-relevant horizon under Calvo pricing by plotting the cumulative contribution of the coefficients. As seen in the figure, the bias increases in severity with the degree of price stickiness. Only two thirds of the actual cumulative pass-through is correctly estimated at a two-year horizon when the frequency of price changes is 5 percent, and almost one fifth is still missing when the frequency is 20 percent. For a frequency of 35 percent, the econometrician captures more than 95 percent of the true response over the forecast horizon. Under Calvo pricing, only $\left( 1-s\right) ^{l}$ of the contribution of lag to pass-through is correctly estimated. This term typically is decreasing at a slow rate since is small in practice, meaning that the product replacement bias kicks in most strongly when much of the exchange rate response occurs at long lags. Under low frequencies of price changes, the coefficients associated with long lags in the Calvo model account for a substantial share of the long-run price response, so that the product replacement bias can become large over long horizons.

More generally, the size of the bias appears to be related to the speed at which the price index responds to an exchange rate shock. The right panels of figure 4 show the estimated cumulative contribution of the regression coefficients on the various lags of exchange rate movements (the dark-shaded bars), along with the bias left out by the econometrician (the light-shaded bars), under menu-cost pricing. The bias is much less severe than under Calvo pricing. Even for frequencies of price changes as low as 5 percent (upper-left panel), the econometrician captures almost 90 percent of the price index response at the two-year horizon. In the menu-cost model, most of the long-run pass-through occurs in the first few periods following a shock - even at low frequencies - so that the bias does not have time to cumulate to something large.

Finally, our figure depicts the worst-case assumption that all entries are selective (). As noted in section 3.1, there would be no bias if price collectors were replacing exiting items by observations randomly selected from the population (). In the more general case where all exits are random and a fraction of entries are selective, for the Calvo model, we have

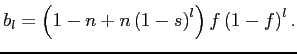
$\displaystyle b_{l}=\left( 1-n+n\left( 1-s\right) ^{l}\right) f\left( 1-f\right) ^{l}.$

Given this expression, we have that long-run pass-through is

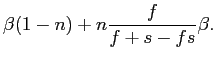
$\displaystyle \beta(1-n)+n\frac{f}{f+s-fs}\beta.$

Departing from the extreme case of can substantially reduce the size of the bias. As a rule of thumb, the reduction in the bias by the end of the forecast horizon is roughly proportional to , so that, for example, setting would roughly halve the area represented by the light bars.

3.5 Comparing our Four Canonical Cases with Product Replacement Bias

Having laid out these four canonical cases, we can now compare our findings with the product replacement bias discussed in Nakamura and Steinsson (2011). 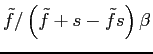Under the assumption of Calvo price setting, if all entries are selective $\left( n=1\right)$ , then, for both the selective exit-selective entry case and the random exit-selective entry case, the long-run pass-through expressions can be written as $\tilde{f}/\left( \tilde{f}+s-\tilde {f}s\right) \beta$ , where $\tilde{f}$ is the observed frequency of price changes. This implied correction factor is the same as the one reported in Nakamura and Steinsson (2011).¹⁸ This long-run pass through expression holds whenever all entries are selective $\left( n=1\right)$ as one can write the regression coefficients as

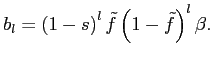
$\displaystyle b_{l}=\left( 1-s\right) ^{l}\tilde{f}\left( 1-\tilde{f}\right) ^{l}\beta.$

The above result that a single expression captures the bias whether exits are selective or random is not a general one, however. As we will now argue, it does not hold (a) when one departs from the knife-edge case in which all entries are selective, (b) when one is interested in correcting the dynamics, or (c) under other models than Calvo.

Departure from the assumption that all entries are selective.

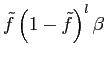Whenever some entries are random (), the long-run pass-through correction factor depends on whether exits are random or selective. To see this, suppose, that all entries are random $\left( n=0\right)$ . If all exits are also random, then the coefficients $b_{l}$ can be expressed as $\tilde{f}\left( 1-\tilde{f}\right) ^{l}\beta$ . In contrast, if all exits are selective, then the coefficients are

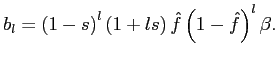
$\displaystyle b_{l}=\left( 1-s\right) ^{l}\left( 1+ls\right) \hat{f}\left( 1-\hat {f}\right) ^{l}\beta.$

The corresponding long-run pass-through corrections are not the same in these two cases. In particular, as we showed above, the long-run correction factor is 1 (i.e. no correction required) for random exit and random entry.

Dynamics.

Although one can correct long-run pass-through estimates using only $\tilde {f}$ and when , it is not possible to do so over any finite horizon in our environment without taking a stand on the selectivity of exit. For example, the measured initial response (i.e., $b_{0}$ ) of the price level to a shock is always $\tilde{f}\beta$ . Whether this is a biased estimate of the true initial response depends on whether $\tilde{f}$ correctly captures the true frequency or not. The value of $\tilde{f}$ is the true frequency when exits are random but not when exits are selective. Thus, $b_{0}$ is unbiased assuming random exit and is biased assuming selective exit. Depending on one's assumptions regarding exit, different correction factors are needed at different horizons.

Other pricing models.

Even when all entries are selective, the connection between long-run pass through in the random exit-selective entry case and the selective exit-selective entry case is specific to the Calvo model. As shown by our comparison of menu-cost and Calvo models, the speed of pass-through is quite important in determining the long-run effects when entry is selective. Models with similar observed frequencies can thus differ in terms of measured long-run pass through. In particular, holding constant the observed frequency, a menu-cost model with selective entry will have a small long-run bias when exits are random and entries are selective but a much larger bias when both exits and entries are selective.

3.6 Robustness to the Presence of Real Rigidities

Gopinath and Itskhoki (2011) find that movements in the exchange rate are passed-through to import prices over more than one price adjustment, consistent with the presence of real rigidities slowing the diffusion of the shock to reset prices. The model adopted so far abstracts from this possibility. However, we show in appendix B that the inclusion of real rigidities has a negligible impact on the theoretical correction factors one should apply to standard pass-through estimates. In particular, we prove that the correction factors for the initial and the long-run responses are independent of real rigidities in the Calvo model, and then show that the factors are overall insensitive to real rigidities at intermediate horizons.

Appendix B also shows that assuming the presence of real rigidities can alter one's judgment regarding the empirical relevance of the Calvo versus the menu-cost models. As we shall see shortly, the empirical impulse response of import prices to an exchange rate movement is consistent with features of both models, in particular the initially rapid response of the index predicted by the menu-cost model, and the continued pass-through over medium-term horizons predicted by the Calvo model. The assumption of real rigidities slows predicted pass-through, which makes it more challenging for the Calvo model to match the initial import price index response to an exchange rate movement.

4 Empirical Relevance of Selective Exits and Entries

In order to assess the impact of selective exits and selective entries on standard estimates of exchange rate pass-through, one needs to form a view on several objects that are not directly observed, namely the type of price-setting frictions giving rise to infrequent nominal adjustments, the extent of price change censoring through exits (), and the prevalence of entries whose prices are relatively unresponsive to past exchange rate movements (). In this section, we first argue that standard estimates of the import price response to exchange rate movements mix features of both the menu-cost and the Calvo models. We next simulate the models to derive bounds on the size of the biases over our forecast horizon. Finally, we present an alternative index construction method to purge standard pass-through estimates of much of the product replacement bias.

4.1 Dynamic Transmission of Exchange Rate Shocks: Data Versus Models

We focus our empirical analysis on finished goods categories, which account for about 60 percent of the total value of U.S. imports. They comprise automotive products, consumer goods, and capital goods. We leave aside fuel and material-intensive goods because the problems associated with selective exits and selective entries appear relatively benign for those categories given that (i) they are relatively homogeneous products, (ii) they tend to be traded between a large number of buyers and sellers, and (iii) their prices can often be readily observed in electronic trading platforms. In fact, the IPP obtains its crude oil import prices from a source outside of the sampling universe we observe for this paper, which altogether precludes an empirical discussion of exit and entry in that important category. Finally, for an economy as large as the United States, exchange rate movements and the price of fuel and material-intensive categories are arguably simultaneously determined to some degree, which raises additional econometric issues.

Our estimation period begins in January 1994 and ends in March 2010. For each three-digit Enduse category (indexed by ), we construct a trade-weighted nominal exchange rate, $NEER_{i,t}$ , and foreign producer price inflation, $\pi_{i,t}^{\ast}$ . We then estimate by ordinary least squares the following equation,

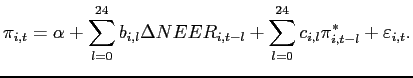
$\displaystyle \pi_{i,t}=\alpha+\sum_{l=0}^{24}b_{i,l}\Delta NEER_{i,t-l}+\sum_{l=0} ^{24}c_{i,l}\pi_{i,t-l}^{\ast}+\varepsilon_{i,t}.$

The number of lags is greater than is typically used in empirical pass-through literature. However, given the simulation results reported earlier, the additional lags seem to be an appropriate choice for robustness. The estimated impulse responses to a 1-percent depreciation of the U.S. dollar are presented in figure 5. The largest responses are found for machinery and equipment categories (Enduse 210, 211, 212, and 215), and, especially, for computers and semi-conductors (Enduse 213). Incidentally, this last category is also one for which the BLS makes special efforts to hedonically adjust prices. By contrast, some categories show little if any pass-through over our two-year horizon, notably automobiles and other vehicles (Enduse 300 and 301), apparel (Enduse 400), and home entertainment equipment (Enduse 412).

To compute a response for finished goods, we aggregate our three-digit category responses using 2006 trade weights. As shown in the lower-left panel, finished goods prices climb more than 0.1 percentage point in the first two months following a 1-percent exchange rate depreciation, another 0.1 percentage point over the remainder the first year, and a more modest 0.05 percentage point over the course of the second year. We obtain a similar response when we regress the index for finished goods on the exchange rate (the dashed line in the lower-left panel).¹⁹ The shape of the impulse response shares aspects of both the menu-cost and Calvo models. The initially rapid response is qualitatively similar to that in the menu-cost model, whereas the ensuing slow but steady increase is more akin to the protracted response in the Calvo model.

Figure 6 directly compares the empirical responses in each three-digit Enduse category to those generated by the Calvo and menu-cost models. The models are calibrated to match category-level statistics as outlined in section 2.2, with the minor difference that we seek to match the observed cumulative rate of pass-though in the last quarter of the forecast horizon rather than some illustrative long-run value. Figure 6 also shows the linear combinations of model responses that minimize the Euclidian distance with the empirical response over the forecast horizon. Again, we find support for both models, with some Enduse categories clearly preferring one model over the other, and others being best represented by a mixture of the two models. On average, each model is attributed about half of the weight. Though the model responses displayed assume no selection effects, this finding is robust to assuming any degree of selective exits or selective entries in the calibration.

4.2 Bounding Standard Pass-Through Estimates

To assess the quantitative importance of selective exits and entries, our next strategy is to derive three sets of bounds on the amount of exchange rate pass-through over the policy horizon. These bounds are related to the canonical cases discussed in sections 3.2 to 3.3, depending on whether we consider, respectively, the largest plausible number of selective exits and entries consistent with the data, the largest plausible number of selective exits in the presence of random entries, or the largest plausible number of selective entries in the presence of random exits.

Our worst case of selective exits assumes that all out-of-scope exits mask a price change. We treat exits for other reasons (as defined in table 1) as random because they typically are planned years in advance by the BLS and thus unlikely to be related to individual pricing decisions. Under these assumptions, we observe the rate of random exit, , and the rate of selective exits, $ef\left( 1-d\right)$ , as they correspond to the rate of out-of-scope and other exits shown in table 1. Knowledge of these rates and of the observed frequency of price changes, $\left( 1-e\right) f/\left( 1-fe\right)$ , is sufficient to identify , , and in the model. Our worst case of selective entries occurs when all items added to the sample experience an unobserved price change upon entry (i.e., ).

Given the sensitivity of biases to price-setting assumptions, we derive our bounds under both Calvo and menu costs. Under Calvo, we compute the correction factors for the estimated cumulative response to an exchange rate movement directly from the analytical expressions for the estimated coefficients, shown in equations 5 to 7. Under menu costs, no such expressions are available, so we compute the corresponding correction factors through simulations. In particular, for each three-digit Enduse category, we select $\sigma_{\varepsilon}$ , , and $\beta$ to match the observed frequency of price changes, the average absolute size of price changes, and the cumulative amount of pass-through by the last quarter of the forecast horizon following a 1-percent depreciation of the dollar. We then apply the correction factors to the estimated responses and aggregate them using 2006 trade shares to derive our bounds on the response of finished goods.

Our worst case of selective exits and entries is shown in the upper-left panel of figure 7. The estimated finished goods price response to a 1-percent depreciation of the dollar is 0.24 percent by the last quarter of the forecast horizon. After correcting for selective exits and selective entries, this figure could be as large as 0.30 percent in the menu-cost model, and 0.32 percent in the Calvo model. The slightly wider bound under Calvo pricing is due to the larger correction for selective entries in that model. If we instead assume that all entries are random (upper-right panel), then the corrected estimate in the last quarter falls to at most 0.26 percent under Calvo, and to at most 0.28 percent under menu costs. The bias is larger under menu costs in this case because the benefits from randomizing entries are largest when pass-through is slow, as in the Calvo model.²⁰Under the worst case of product replacement bias (lower-left panel), the corrected response is very close to the actual response under menu costs, but remains somewhat higher (0.30 percent) than the uncorrected estimate (0.24 percent) by the last quarter of the forecast horizon. Even in this case, the near-term estimate remains relatively precise, however.

Given our earlier evidence that features of both models are present in the data, we derive a fourth set of bounds under what we view as more plausible price-setting assumptions. The three-digit Enduse responses of the Calvo and menu-cost models are first weighted according to the linear combination that provides the best fit of the empirical response, as we did in the previous section, and then aggregated using 2006 trade shares. We posit that all out-of-scope exits correspond to selective exits and selective entries, whereas all other exits are associated with random exits and random entries, so that about half of all exits and entries are selective. The corrected cumulative response under this last set of assumptions is presented in the lower-right panel of figure 7. Following a 1-percent depreciation of the dollar, the corrected cumulative response by the last quarter (0.28 percent) is above the estimated one (0.24 percent). Selective exits and selective entries contribute roughly equally to this difference, as hinted by the special case with only selective entries that is also displayed in the panel.

Summing up, our bound analysis suggests that, even under the stringent assumptions consistent with the microdata, the biases induced by selective exits and selective entries have a limited impact on standard pass-through estimates for finished goods over typical forecast horizons. Given that this conclusion contrasts, at least on the surface, with Nakamura and Steinsson's (2011) assertion that the product replacement bias is quantitatively important, we next discuss how our respective findings can be reconciled.

4.3 Reconciling our Results with Those of Nakamura and Steinsson (2011)

We highlight four differences between our treatment of the product replacement bias and that of Nakamura and Steinsson (2011): the price index of interest, the time horizon of interest, the assumed distribution of heterogeneity in price-setting decisions, and the incidence of selective entries. To facilitate comparisons, we begin by estimating an equation for empirical pass-through that is very similar to equation 1 in their paper,

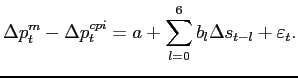
$\displaystyle \Delta p_{t}^{m}-\Delta p_{t}^{cpi}=a+\sum_{l=0}^{6}b_{l}\Delta s_{t-l} +\varepsilon_{t}.$

(8)

We regress the difference between changes in the log of quarterly import prices excluding oil, $\Delta p_{t}^{m}$ , and changes in the log of U.S. CPI excluding food and energy, $\ \Delta p_{t}^{cpi}$ , on a constant as well as the contemporaneous and first lags of the change in log of the Federal Reserve's trade-weighted major currencies real exchange rate index, $\Delta s_{t-l}$ . Our estimation period is from 1995:Q1 to 2010:Q4 and the import price index is the deflator from the National Economic Accounts from the U.S. Bureau of Economic Analysis.

As table 2 shows, our estimated import price response after 6 quarters is 0.41, a figure nearly identical to that reported by Nakamura and Steinsson (0.43). Any substantive difference between our findings below and those of Nakamura and Steinsson (2011) will thus be unrelated to our respective standard pass-through estimates. Table 2 also presents standard pass-through estimates after 6 quarters for two special groups of products, namely finished goods (Enduse categories in the 200s, 300s, and 400s) and material-intensive goods excluding oil (Enduse categories below 200, excluding 100). The rate of pass-through after 6 quarters is much lower for finished goods prices (0.26) than it is for material-intensive goods prices (0.93), highlighting the two groups' sharply different medium-term responses to exchange rate movements. The high pass-through estimate for material-intensive goods is perhaps not surprising given these items' frequent price adjustments, their high commodity content, and the strong relationship between commodity prices and the exchange rate. With pass-through nearly complete after 6 quarters, it is unlikely these items are plagued by severe product replacement biases, further justifying our focus on finished goods in earlier sections.²¹

To facilitate comparison to Nakamura and Steinsson's results, we momentarily assume that the rate of substitution, , and the true pass-through coefficients, $b_{l}$ , are the same for all items in the IPP sample, leaving only the frequency of price changes free to vary across items. The assumption of identical pass-through rates across items in the sample is admittedly unappealing given the evidence presented above for finished goods and material-intensive goods, but it makes the comparison to Nakamura and Steinsson (2011) more direct. The monthly rate of substitution is set to 2.5 percent, a figure in the range of rates reported in table 1.²² For now, we maintain our assumption that items within each 3-digit Enduse categories share the same frequency of price changes (these frequencies are reported in table 1). In addition, to facilitate further comparison with Nakamura and Steinsson's (2011) results, we will calculate the bias-correction factors under the assumption that the data are generated by a Calvo pricing model and that all entries are selective.²³

As in Nakamura and Steinsson (2011), we obtain corrected pass-through estimates by applying a correction factor, $\Lambda$ , to the sum of estimated coefficients after 6 quarters,

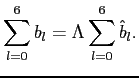
$\displaystyle \sum_{l=0}^{6}b_{l}=\Lambda \sum_{l=0}^{6}\hat{b}_{l} .$

(9)

For long-run pass-through, the correction factor is the following,

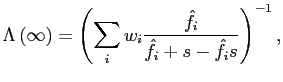
$\displaystyle \Lambda \left( \infty \right) =\left( \sum_{i}w_{i}\frac{\hat{f}_{i}}{\hat {f}_{i}+s-\hat{f}_{i}s}\right) ^{-1},$

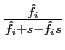$\Lambda \left( \infty \right)$ is the factor we would apply to standard pass-through estimates if our forecast horizon was infinite, an approach close in spirit to that of Nakamura and Steinsson (2011).²⁴ The term $\frac{\hat{f}_{i}}{\hat{f} _{i}+s-\hat{f}_{i}s}$ is the share of long-run pass-through correctly estimated in product category , where $\hat{f}$ is the observed frequency of price changes. Under the assumption of random exit, the observed rate equals the true rate , whereas under the assumption of selective exit, the observed rate is less than the true rate .

In addition, we report correction factors for the cumulated response of the index 6 quarters (i.e., 18 months) after an exchange rate movement. As mentioned earlier, the dynamics of pass-through depend on the assumptions regarding entry. Under the assumption of random exit and selective entry.

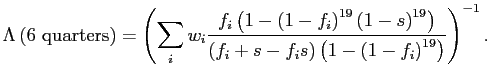
$\displaystyle \Lambda \left( 6\text{ quarters}\right) =\left( \sum_{i}w_{i}\frac {f_{i}\left( 1-\left( 1-f_{i}\right) ^{19}\left( 1-s\right) ^{19}\right) }{\left( f_{i}+s-f_{i}s\right) \left( 1-\left( 1-f_{i}\right) ^{19}\right) }\right) ^{-1}.$

The expression in the weighted sum represents the share of true pass-through correctly estimated after 6 quarters in 3-digit Enduse category . It is obtained by dividing the sum over the first 18 months of the biased coefficients (shown in equation 7) by the corresponding sum of the unbiased coefficients (shown in equation 4). $\Lambda \left( 6\text{ quarters}\right)$ roughly equals the correction factor we would apply to standard pass-through estimates near the end of our two-year horizon. Note that, under the assumption of random exit and selective entry, the correction of the initial response, $\Lambda \left( 0\text{ quarters}\right)$ , equals one. By contrast, under the assumption of selective exit and selective entry, the correction factor at any horizon is the same as $\Lambda \left( \infty \right)$ given above.

Under the assumption of random exit, the choice of either $\Lambda \left( 6\text{ quarters}\right)$ or $\Lambda \left( \infty \right)$ as the correction factor makes a noticeable difference on the resulting corrected pass-through estimates. Our standard estimate for imported goods excluding oil (0.41) rises to 0.47 when we use $\Lambda \left( 6\text{ quarters}\right)$ , and to when we use $\Lambda \left( \infty \right)$ . According to these estimates, the bias in the long-run response is roughly twice as large as the bias in the response after 6 quarters, showing that much of the product replacement bias on long-run estimates falls outside of typical policy horizons. Hence, one important difference between our results and those of Nakamura and Steinsson (2011) is that we use correction factors consistent with different time horizons under the assumption of random entry.

We note that the correction factors for finished goods after six quarters (1.19) and over the long run (1.40) are noticeably larger than for material intensive goods over these horizons (1.10 and 1.13, respectively). The need for a larger correction for finished goods reflects their relatively slow pass-through of exchange rate shocks. In the case of material-intensive goods, the corrected estimates after 6 quarters (1.02) and over the long run (1.04) imply that true pass-through is complete over typical policy horizons.²⁵

Another important difference between our results and those of Nakamura and Steinsson is the treatment of heterogeneity in the frequency of price changes across items. Throughout our paper, we assume that the frequency of price changes is constant within 3-digit Enduse categories, otherwise leaving the frequency free to vary across sectors of activity. This approach may leave some heterogeneity unaccounted for within 3-digit Enduse categories, which would lead us to underestimate the importance of the product replacement bias. By contrast, Nakamura and Steinsson (2011) control for the heterogeneity across firms by assuming that the frequency of price changes is distributed according to a Beta distribution, estimated on observed frequencies. When we adopt their parametrization of the Beta distribution (using and as parameters), our corrected long-run pass-through estimate for imported goods leaps from 0.52 to 0.70, a number in the same range as the one they report (0.67). This large correction is driven by a mass of observations at very low frequencies of price changes. One salient feature of the Beta distribution estimated by Nakamura and Steinsson (2011) is the implication that a third of all observations have a monthly frequency below 2 percent (i.e., with an average duration between price adjustments greater than 4 years), with the density of observations becoming arbitrarily large as the frequency approaches zero. Or, the long-run correction factor is quite sensitive to the presence of very low frequencies because $f/\left( f+s-fs\right)$ converges to zero as approaches zero, making the correction factor arbitrarily large.

To illustrate the sensitivity of the estimated long-run response to the mass of firms updating prices very infrequently, we move all observations with a frequency below 2 percent to a mass point at 2 percent. The correction factor for the long-run response falls from 1.70 to 1.47. This decline in the correction factor should caution us against driving strong conclusions that depend on the very low frequencies of price changes, whose density is difficult to estimate. In particular, the Beta distribution has only two parameters to capture the whole range of variation in the density of frequencies in the sample. It is thus conceivable that some of the very low frequencies implied by the calibration are off the empirical support.

Furthermore, as noted earlier, a severely biased long-run response need not imply a severely biased medium-term response. Under the assumption of random exit, much of the product replacement bias accrues beyond typical policy horizons. In the case of Nakamura and Steinsson's Beta distribution, the correction factor for the 6-quarter response under the assumption of random exit is only 1.17, a number well below that for the long-run response (1.70).

We conclude our comparison by stressing that we see the correction factors derived above as worst cases rather than as base cases. As argued in section 1, we find limited evidence that the BLS methodology is conducive to systematically adding items recently repriced to the IPP sample. The correction factors shrink greatly as we lower the value of the fraction of entries that are selective. The general formula for the correction factor is

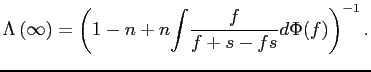
$\displaystyle \Lambda \left( \infty \right) =\left( 1-n+n {\displaystyle \int} \frac{f}{f+s-fs}d\Phi(f)\right) ^{-1}.$

Therefore, if 50 percent of all entries have zero price pressure (i.e. , a figure in line with all forced exits being associated with a selective entry), then the correction factor is only 1.26 under Nakamura and Steinsson's Beta distribution. We also note that our impulse response analysis in section 4.1 suggests that pass-through is faster than implied by Calvo pricing for several Enduse categories, consistent with lower correction factors than derived above whenever some exits are random.

4.4 Reducing Biases Through Delayed Entries

If the estimates were subject solely to a product replacement bias, then one could use a simple trick to remove much of that bias over the policy-relevant horizon. Recall that the product replacement bias arises because entering items systematically are less responsive to past exchange rate movements than items in the universe. Therefore, simply delaying the entry of substitutes into the index should reduce this bias. We show in the appendix that, when all exits are random and all entries are selective, the estimated (plim) coefficients in a Calvo model with an arbitrary -period entry delay are given by

$\begin{displaymath} b_{l}=\left \{ \begin{array}[c]{cc} f\left( 1-f\right) ^{l}\beta & \text{if }l\leq M\ \left( 1-s\right) ^{l-M}f\left( 1-f\right) ^{l}\beta & \text{if }l>M \end{array}\right. . \end{displaymath}$

Delaying entries thus eliminates the product replacement bias for the coefficients associated with the first lags of exchange rate movements. The bias on subsequent lags is also reduced, with $b_{l}$ representing a fraction $\left( 1-s\right) ^{l-M}$ of the true response when entries are delayed by periods, compared to only $\left( 1-s\right) ^{l}$ when there is no entry delay.

The left panels of figure 8 show that delaying entries by 6 months can go a long way in reducing the product replacement bias over the policy-relevant horizon in the Calvo model. The bias at the end of the horizon is negligible when prices are adjusted 20 percent of the time or more. Even at frequencies as low as 5 percent, the prediction over the first year of the forecast suffers little product replacement bias, while the accuracy of the response in the second year is greatly improved. The bias reduction is even larger in the menu-cost model (right panels). Delaying entries by 6 months virtually eliminates the product replacement bias at all frequencies considered. The consistency gains are especially large in the menu-cost model because delaying entries corrects most effectively biases associated with short lags of the exchange rate, which account for the bulk of the price level response.

It turns out that our trick of delaying entries can also mitigate biases in the presence of selective exits. We show in the appendix that, with both selective exits and selective entries that the (plim) regression coefficients under an -period entry delay in the Calvo model are

$\begin{displaymath} b_{l}\left( M\right) =\left \{ \begin{array}[c]{cc} \frac{\left( 1-e\right) }{\left( 1-fe\right) ^{l+1}}f\left( 1-f\right) ^{l}\beta & \text{if }l\leq M\ \frac{\left( 1-e\right) }{\left( 1-fe\right) ^{M+1}}\left( \left( 1-d\right) ^{l-M}+\frac{s\left( 1-n\right) }{d}\left( 1-\left( 1-d\right) ^{l-M}\right) \right) f\left( 1-f\right) ^{l}\beta & \text{if }l>M \end{array}\right. . \end{displaymath}$

We also prove that the bias diminishes as one increases the entry delay given any forecast horizon. As one delays entries by an arbitrary large number of periods, we have

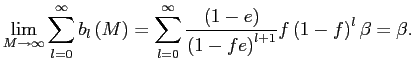
$\displaystyle \lim_{M\rightarrow \infty}\sum_{l=0}^{\infty}b_{l}\left( M\right) =\sum _{l=0}^{\infty}\frac{\left( 1-e\right) }{\left( 1-fe\right) ^{l+1} }f\left( 1-f\right) ^{l}\beta=\beta.$

In short, the estimated long-run pass-through in the Calvo model is unbiased in the limit, a result that holds whether exits are selective, entries are selective, or both. The short-run response remains downward biased in the presence of selective exit, however.

The intuition for why delaying entries can improve pass-through estimates in the presence of selective exits is somewhat subtle. Remember that, for a movement in the exchange rate periods ago to have an impact on the index today, there must have been no price change over the past periods. Delaying entries by periods eliminates observations incorporated into the index in recent periods, leaving only those present in the index for at least periods. Or, these surviving observations are less likely than observations in the universe to have experienced a price change over the past period (since observations with a price change are more likely to have exited), meaning that they are relatively more likely to contribute to inflation today. Under Calvo pricing (left panels of figure 9), it turns out that this selection effect perfectly offsets the downward bias stemming from the censoring of price changes as we consider an arbitrary long entry delay and forecast horizon. Under menu-cost pricing (right panels), the gains are negligible due to the greater mixing of observations.

Our simulations suggest that delaying entries is most effective at reducing biases associated with selective entries over typical forecast horizons, a finding that is robust across pricing mechanisms and degrees of price flexibility. Thus, delaying entries can help us shed light on the empirical importance of selective entries: If estimated pass-through over the forecast horizon increases much after delaying entries, then selective entries may be economically important. By contrast, if estimated pass-through is insensitive to delaying entries, then selective entries may be a marginal phenomenon.

Using the BLS microdata, we have computed price indexes for the Enduse categories belonging to capital goods, automotive products, and consumer goods. We have constructed one index using the methodology introduced in section 1 (i.e., there is no entry delay and missing prices are carried forward). We have also constructed two alternative indexes that implement a 6-month and a 9-month entry delay, respectively. Figure 10 displays the results. As the left-hand column shows, these alternative price indexes are somewhat more volatile than the corresponding published BLS index (the thick black line), especially when entry is delayed. However, estimated pass-through rates are very similar whether we use the published BLS index or our constructed indexes. If selective entry were quantitatively important, then the estimated pass-through rates for the constructed indexes with delayed entry should be noticeably greater than the pass-through rates for the published index or for the constructed index with no delay. Instead, the estimated pass-through rates are very similar. Thus, the available evidence suggests a limited role for selective entry.

5 Concluding Remarks

We have investigated selection biases in standard exchange rate pass-through regressions that arise from missing price changes either due to item exit from or entry into the index. For both Calvo and menu-cost price-setting models, we have shown that these selection effects lower the measured response of an import price index to exchange rate movements over typical policy horizons and that the magnitude of the biases can be sensitive to price-setting assumptions.

In particular, in the presence of both selective exits and selective entries, the import price response is biased downward in both models. Assuming that entering items are sampled randomly from the universe alleviates some of the bias, especially under Calvo pricing. When entries are selective and exits occur at random, the downward bias tends to be small in the menu-cost model over any horizon, whereas the bias slowly grows from being negligible at short horizons to quite large over extended horizons in the Calvo model.

Assessing the quantitative importance of the biases is inherently challenging because selective exits and selective entries are, by their very nature, not observed. Our review of the BLS methodology suggests a moderate risk of such selection effects taking place in practice. We also argue that, under plausible assumptions about nominal price stickiness and the incidence of selective exits and selective entries, the presence of downward biases in standard pass-through regressions, although a concern, does not materially alter the literature's view that pass-through to U.S. import prices is low over typical forecast horizons. Even under our worst-case scenario, our estimated empirical bounds imply that at most about a third of an exchange rate shock is passed through to the price of imported finished goods after two years. Furthermore, our worst-case scenario is likely too severe as our constructed alternative price indexes with delayed item entries suggest a limited role for selective entry.

Although we have focused on import prices, our findings are relevant to the study of any price index subject to selection effects in sample exit and sample entry. The implications of selective exits and selective entries also extend to the measurement of the response of price indexes to aggregate and idiosyncratic shocks other than exchange rate movements.

Future research should aim at better identifying the causes of item exits as well as the characteristics of added items. Currently, the information contained in the IPP database provides useful and suggestive, but ultimately limited, guidance on these aspects.

References

Atkeson, Andrew and Ariel Burstein (2008) "Pricing to Market, Trade Costs, and International Relative Prices," American Economic Review, vol. 98(5), pages 1998-2031.

Berger, David Berger, Jon Faust, John H. Rogers, and Kai Steverson (2009). "Border Prices and Retail Prices," International Finance Discussion Papers 972, Board of Governors of the Federal Reserve System.

Bergin, Paul, and Robert C. Feenstra (2009), "Pass-Through of Exchange Rates and Competition between Floaters and Fixers," Journal of Money, Credit and Banking, vol. 41, pages 35-70.

Bils, Mark (2009). "Do Higher Prices for New Goods Reflect Quality Growth or Inflation?," Quarterly Journal of Economics, Vol. 124(2), pages 637-675.

Bresnahan, Timothy F., and Robert J. Gordon (1997). "The Economics of New Goods," Studies in Income and Wealth, Volume 58, National Bureau of Economic Research.

Broda, Christian, and David E. Weinstein (2010). "Product Creation and Destruction: Evidence and Price Implications," American Economic Review, vol. 100(3), pages 691-723.

Bureau of Labor Statistics. "Handbook of Methods," Washington DC, April 1997.

Bureau of Labor Statistics. "Measurement Issues in the Consumer Price Index," Washington D.C., June 1997, http://www.bls.gov/cpi/cpigm697.htm (last access: March 2010)

Boskin, Michael J., E. Dulberger, R. Gordon, Z. Griliches, and D. Jorgenson (1996). "Toward a More Accurate Measure of the Cost of Living," Final Report to the Senate Finance Committee, December 4.

Campa, José Manuel and Linda S. Goldberg (2005). "Exchange Rate Pass-Through into Import Prices," Review of Economics and Statistics, vol. 87(4), pages 679-690.

Danziger, Leif (1999). "A Dynamic Economy with Costly Price Adjustments," American Economic Review, vol. 89(4), pages 878-901.

Gertler, Mark and John Leahy (2008). "A Phillips Curve with an Ss Foundation," Journal of Political Economy, vol. 116(3), pages 533-572.

Greenlees, John S., and Robert McClelland (2011). "Does Quality Adjustment Matter for Technologically Stable Products? An Application to the CPI for Food," American Economic Review, vol. 101(3), pages 200-205.

Goldberg, Pinelopi and Michael M. Knetter (1997). "Goods Prices and Exchange Rates: What Have We Learned?," Journal of Economic Literature, vol. 35(3), pages 1243-1272.

Gopinath, Gita and Oleg Itskhoki (2010). "Frequency of Price Adjustment and Pass-Through," Quarterly Journal of Economics, Vol. 125(2), pages 675-727.

Gopinath, Gita and Oleg Itskhoki (2011). "In Search of Real Rigidities," NBER Macroeconomics Annual, 2010, vol. 25, , pages 261-309.

Gopinath and Rigobon (2008), "Sticky Borders," Quarterly Journal of Economics, 123(2): 531-75.

Gopinath, Gita, Oleg Itskhoki, and Roberto Rigobon (2010). "Currency Choice and Exchange Rate Pass-Through," American Economic Review, vol. 100(1), pages 304-36.

Gordon, Robert J. (2006). "The Boskin Commission Report: A Retrospective One Decade Later," International Productivity Monitor, vol. 12, pages 7-22.

Gust, Christopher, Sylvain Leduc, and Robert J. Vigfusson (2010). "Trade Integration, Competition, and the Decline in Exchange-Rate Pass-Through," Journal of Monetary Economics, vol. 57(3), pages 309-324.

Marazzi, Mario, Nathan Sheets, Robert J. Vigfusson, Jon Faust, Joseph Gagnon, Jaime Marquez, Robert F. Martin, Trevor Reeve, John Rogers (2005). "Exchange Rate Pass-Through to U.S. Import Prices: Some New Evidence," International Finance Discussion Papers 833, Board of Governors of the Federal Reserve System.

Marazzi, Mario and Nathan Sheets (2007). "Declining Exchange Rate Pass-through to U.S. Import Prices: The Potential Role of Global Factors," Journal of International Money and Finance, vol. 26, pp. 924-47.

Nakamura, Emi, and Jón Steinsson (2011). "Lost in Transit: Product Replacement Bias and Pricing to Market," mimeo, Columbia University.

Neiman, Brent (2010). "Stickiness, Synchronization, and Passthrough in Intrafirm Trade Prices," Journal of Monetary Economics, April 2010.

Sheshinski, Eytan and Yoram Weiss (1977). "Inflation and Costs of Price Adjustment," Review of Economic Studies, vol. 44(2), pages 287-303.

A Regression Coefficients in the Calvo Model

In this appendix, we derive analytical expressions for pass-through coefficients when the data are generated by a Calvo model with selection biases in the exit and entry of items. The environment is as described in section 3 with the extra simplifying assumption that exchange rate innovations are uncorrelated over time. We begin by describing the general case. We then investigate how delaying the entry of items in the index affect the regression coefficients. We finally provide a proof that the bias on the coefficients declines as one delays the entry of items in the index.

A.1 General Case

Let $\mathcal{I}_{it}^{f}$ , $\mathcal{I}_{it}^{d}$ , and $\mathcal{I}_{it}^{e}$ be indicator variables that an item present in the sample at the beginning of period has experienced, respectively, a price change, a random exit, and a selective exit (conditional on a price change and no random exit). For any exiting item, we also define an indicator variable $\mathcal{I}_{it}^{n}$ that the corresponding entry is selective. For convenience, let also $\mathcal{I}_{it}^{s}=\mathcal{I}_{it}^{d}+\left( 1-\mathcal{I}_{it}^{d}\right) \mathcal{I}_{it}^{f}\mathcal{I}_{it}^{e}$ be an indicator variable that an item has exited during the period, either through a random exit (probability ) or a selective exit (probability $\left( 1-d\right) fe$ ).

We first derive an expression for the contemporaneous impact of an exchange rate movement on the price index. Using the covariance approach, we have

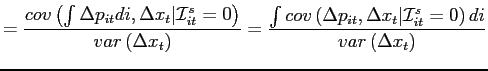
$\displaystyle b_{0}$	$\displaystyle =\frac{cov\left( \int \Delta p_{it}di,\Delta x_{t}\vert\mathcal{I} _{it}^{s}=0\right) }{var\left( \Delta x_{t}\right) }=\frac{\int cov\left( \Delta p_{it},\Delta x_{t}\vert\mathcal{I}_{it}^{s}=0\right) di}{var\left( \Delta x_{t}\right) }$
	$\displaystyle =\frac{cov(u_{it}+\beta \Delta x_{t}+\varepsilon_{it},\Delta x_{t} \vert\mathcal{I}_{it}^{s}=0,\mathcal{I}_{it}^{f}=1)}{var\left( \Delta x_{t}\right) }\Pr \left[ \mathcal{I}_{it}^{f}=1\vert\mathcal{I}_{it}^{s}=0\right]$
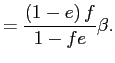	$\displaystyle =\frac{\left( 1-e\right) f}{1-fe}\beta.$

The covariance term is conditioned on $\mathcal{I}_{it}^{s}=0$ because, among observations present in the sample at the beginning of the period, only those that do not exit can be used to compute inflation. These usable observations either had no price change and no exit (probability $\left( 1-d\right) \left( 1-f\right)$ ) or a price change and no exit (probability $\left( 1-d\right) f\left( 1-e\right)$ ). Only the latter observations, which account for a share $\left( 1-e\right) f\left( 1-fe\right)$ of usable observations, can have a nonzero contribution to inflation.

Proceeding similarly with $b_{1}$ ,

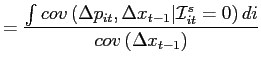
$\displaystyle b_{1}$	$\displaystyle =\frac{\int cov\left( \Delta p_{it},\Delta x_{t-1}\vert\mathcal{I} _{it}^{s}=0\right) di}{cov\left( \Delta x_{t-1}\right) }$
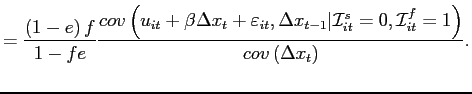
	$\displaystyle =\frac{\left( 1-e\right) f}{1-fe}\frac{cov\left( u_{it}+\beta \Delta x_{t}+\varepsilon_{it},\Delta x_{t-1}\vert\mathcal{I}_{it}^{s}=0,\mathcal{I} _{it}^{f}=1\right) }{cov\left( \Delta x_{t}\right) }.$

Since $\Delta x_{t}$ and $\varepsilon_{it}$ are assumed to be independent of $\Delta x_{t-1}$ , the covariance term is impacted solely through the possible interactions between $\Delta x_{t-1}$ and the cumulated price pressure $u_{it}$ . Conditioning on past realizations of the indicator variables, there are five distinct cases:

$\displaystyle u_{it}=\left \{ \begin{array}[c]{cc} u_{it-1}+\beta \Delta x_{t-1}+\varepsilon_{it-1} & \text{if }\left \{ \mathcal{I}_{it-1}^{s}=0,\mathcal{I}_{it-1}^{f}=0\right \} \\ 0 & \text{if }\left \{ \mathcal{I}_{it-1}^{s}=0,\mathcal{I}_{it-1} ^{f}=1\right \} \\ u_{it-1}+\beta \Delta x_{t-1}+\varepsilon_{it-1} & \text{if }\left \{ \mathcal{I}_{it-1}^{s}=1,\mathcal{I}_{it-1}^{n}=0,\mathcal{I}_{it-1} ^{f}=0\right \} \\ 0 & \text{if }\left \{ \mathcal{I}_{it-1}^{s}=1,\mathcal{I}_{it-1} ^{n}=0,\mathcal{I}_{it-1}^{f}=1\right \} \\ 0 & \text{if }\left \{ \mathcal{I}_{it-1}^{s}=1,\mathcal{I}_{it-1} ^{n}=1\right \} \end{array} \right. .$

(10)

Consequently,

$\displaystyle b_{1}$	$\displaystyle =\frac{\left( 1-e\right) f}{1-fe}\frac{cov\left( \beta \Delta x_{t-1},\Delta x_{t-1}\right) }{cov\left( \Delta x_{t}\right) }\left( \Pr \left[ \mathcal{I}_{it-1}^{s}=0,\mathcal{I}_{it-1}^{f}=0\right] +\Pr \left[ \mathcal{I}_{it-1}^{s}=1,\mathcal{I}_{it-1}^{n}=0,\mathcal{I} _{it-1}^{f}=0\right] \right)$
	$\displaystyle =\frac{\left( 1-e\right) f}{1-fe}\left( 1-f\right) \beta \left( \left( 1-d\right) +\left( d+\left( 1-d\right) fe\right) \left( 1-n\right) \right)$

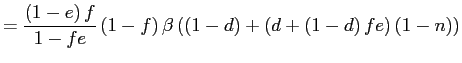
Intuitively, among all observations usable to compute inflation, only those with a price change in the current period (marginal probability $\frac{\left( 1-e\right) f}{1-fe}$ ) and either no price change and no exit in the previous period (marginal probability $\left( 1-d\right) \left( 1-f\right)$ ) or an exit accompanied by no price change (marginal probability $\left( d+\left( 1-d\right) fe\right) \left( 1-n\right) \left( 1-f\right)$ ) have a nonzero contribution of $\Delta x_{t-1}$ to inflation.

The general case with $b_{l}$ is illustrated in the upper panel of figure 11. It shows the various states that are usable in the computation of inflation at each period, along with their associated marginal probability in each period. The arrows indicate the paths through which an exchange rate movement in the period can be reflected as a nonzero price change in period . Observations that have not responded to an exchange rate movement at period can find their way in the index either by having been present in the sample prior to period or by entering the item through a substitution. The marginal probability from period to period associated with the former event (no price change and no exit) is $\left( 1-d\right) \left( 1-f\right)$ for each period. The marginal probability associated with the addition of an item in period whose last price change was prior to period is the product of the probability of having a substitution (probability $d+fr\left( 1-d\right)$ ), a random selection from the universe (probability ), and no price change for periods (probability $\left( 1-f\right) ^{l-k+1}$ ). Summing up across all usable paths, we have

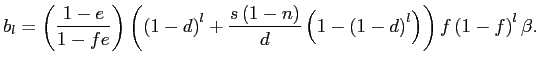
$\displaystyle b_{l}=\left( \frac{1-e}{1-fe}\right) \left( \left( 1-d\right) ^{l} +\frac{s\left( 1-n\right) }{d}\left( 1-\left( 1-d\right) ^{l}\right) \right) f\left( 1-f\right) ^{l}\beta.$

A.2 Delayed Entries

We next assume that the econometrician only uses observations that have been in the sample for more than periods in the computation of inflation. This assumption is made in section 4.4 to argue that delaying the entry of items in the basket can mitigate some of the biases associated with selective exits and entries. We distinguish between two cases: $l\leq M$ and .

The first case is illustrated in the middle panel of figure 11. Because entries are delayed by more periods than the lag of the exchange rate movement considered, all observations used to compute inflation have been continuously in the index since before period . For an exchange rate movement at period to be reflected in a nonzero price change today, we must have had had no price change from period to (marginal probability $\left( 1-f\right) /\left( 1-fe\right)$ ), and a price change at (marginal probability $\left( 1-e\right) f/\left( 1-fe\right)$ ). The resulting coefficient is

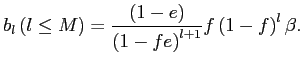
$\displaystyle b_{l}\left( l\leq M\right) =\frac{\left( 1-e\right) }{\left( 1-fe\right) ^{l+1}}f\left( 1-f\right) ^{l}\beta.$

(11)

The case of is illustrated at the bottom of figure 11. It mixes elements of the general case with no delay (upper panel) and the case with $l\leq M$ (middle panel). Prior to period , observations that have not yet responded to the exchange rate movement at period could have found their way in the index either through a substitution or by having been present in the sample before period . From period onward, only observations that are already present in the index at the end of period can be used to compute inflation. Summing up the probabilities over all possible paths and simplifying, we get

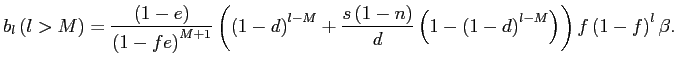
$\displaystyle b_{l}\left( l>M\right) =\frac{\left( 1-e\right) }{\left( 1-fe\right) ^{M+1}}\left( \left( 1-d\right) ^{l-M}+\frac{s\left( 1-n\right) } {d}\left( 1-\left( 1-d\right) ^{l-M}\right) \right) f\left( 1-f\right) ^{l}\beta.$

(12)

A.3 Proof that Biases are Declining in the Entry Delay

We conclude this appendix by showing that delaying the entry of items in the index always improves pass-though estimates. We assume that the number of lags in the regression is at least as large as the forecast horizon, , a condition typically satisfied in standard pass-through regressions. Let $b_{l}\left( M\right)$ be the plim coefficients associated with the -th lag of the exchange rate and an entry delay of periods. The proof proceeds in two steps. We first prove that $b_{l}\left( M+1\right) \geq b_{l}\left( M\right)$ , so that delaying entries by an extra period always (weakly) increases the size of the (plim) regression coefficients. We then show that the cumulative response over any forecast horizon remains bounded above by the true response.

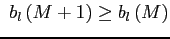
A.3.1 Step 1: $\ b_{l}\left( M+1\right) \geq b_{l}\left( M\right)$

We distinguish between three cases: , , and . When , the plim coefficients are given by equation 11, so that $b_{l}\left( M\right) =b_{l}\left( M+1\right)$ . When , $b_{M+1}\left( M\right)$ is given by equation 12 and $b_{M+1}\left( M+1\right)$ is given by equation 11. For $b_{M+1}\left( M\right) \geq b_{M+1}\left( M\right)$ to be true in this case, we must have

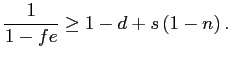
$\displaystyle \frac{1}{1-fe}\geq1-d+s\left( 1-n\right) .$

Note that if the above equation holds for , then it holds for all $n\in \left[ 0,1\right]$ . Imposing and using $s=d+\left( 1-d\right) fe$ , we have

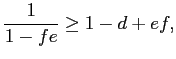
$\displaystyle \frac{1}{1-fe}\geq1-d+ef,$

which is always satisfied. Finally, we want to show that $b_{l}\left( M+1\right) \geq b_{l}\left( M\right)$ when . The plim coefficients are given by equation 12. Note that

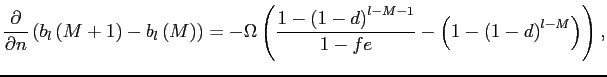
$\displaystyle \frac{\partial}{\partial n}\left( b_{l}\left( M+1\right) -b_{l}\left( M\right) \right) =-\Omega \left( \frac{1-\left( 1-d\right) ^{l-M-1}} {1-fe}-\left( 1-\left( 1-d\right) ^{l-M}\right) \right) ,$

where $\Omega$ is some positive constant. The difference between $b_{l}\left( M+1\right)$ and $b_{l}\left( M\right)$ is thus linear in and either always increasing or always decreasing in . By showing that $b_{l}\left( M+1\right) \geq b_{l}\left( M\right)$ for and , we will prove that the result holds for the worse scenario under either case. Consider first

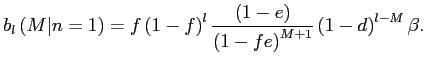
$\displaystyle b_{l}\left( M\vert n=1\right) =f\left( 1-f\right) ^{l}\frac{\left( 1-e\right) }{\left( 1-fe\right) ^{M+1}}\left( 1-d\right) ^{l-M}\beta.$

We have $b_{l}\left( M+1\vert n=1\right) \geq b_{l}\left( M\vert n=1\right)$ if and only if $\left( 1-d\right) ^{l-M-1}\geq \left( 1-fe\right) \left( 1-d\right) ^{l-M}$ , which is always true. Consider next

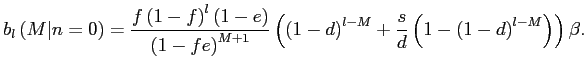
$\displaystyle b_{l}\left( M\vert n=0\right) =\frac{f\left( 1-f\right) ^{l}\left( 1-e\right) }{\left( 1-fe\right) ^{M+1}}\left( \left( 1-d\right) ^{l-M}+\frac{s} {d}\left( 1-\left( 1-d\right) ^{l-M}\right) \right) \beta.$

We have $b_{l}\left( M+1\vert n=0\right) \geq b_{l}\left( M\vert n=0\right)$ if and only if

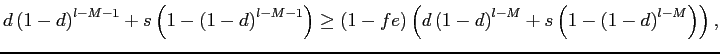
$\displaystyle d\left( 1-d\right) ^{l-M-1}+s\left( 1-\left( 1-d\right) ^{l-M-1}\right) \geq \left( 1-fe\right) \left( d\left( 1-d\right) ^{l-M}+s\left( 1-\left( 1-d\right) ^{l-M}\right) \right) ,$

which can be shown to hold if and only if

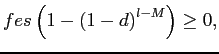
$\displaystyle fes\left( 1-\left( 1-d\right) ^{l-M}\right) \geq0,$

a condition that is always satisfied. Summing up, the individual coefficients are increasing in the entry delay, so that the cumulative pass-through over any forecast horizon also is increasing in the entry delay.

A.3.2 Step 2: Estimated Cumulative Response is Bounded Above by True Response

To complete the proof, we show that the estimated pass-through under delayed entries never exceeds the true pass-through over any forecast horizon. The true pass-through after periods is

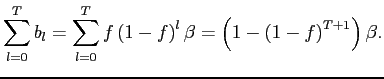
$\displaystyle \sum_{l=0}^{T}b_{l}=\sum_{l=0}^{T}f\left( 1-f\right) ^{l}\beta=\left( 1-\left( 1-f\right) ^{T+1}\right) \beta.$

Because $b_{l}\left( M+1\right) \geq b_{l}\left( M\right)$ , the estimated pass-through is largest when $M\geq T,$ which is associated with

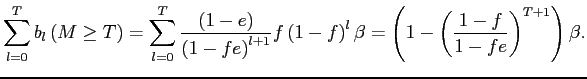
$\displaystyle \sum_{l=0}^{T}b_{l}\left( M\geq T\right) =\sum_{l=0}^{T}\frac{\left( 1-e\right) }{\left( 1-fe\right) ^{l+1}}f\left( 1-f\right) ^{l} \beta=\left( 1-\left( \frac{1-f}{1-fe}\right) ^{T+1}\right) \beta.$

It is immediate that the above expression is bounded above by the unbiased case.

B Real Rigidities

To explore the incidence of real rigidities on our theoretical correction factors, we follow Gopinath and Itskhoki (2011) in adopting a flexible specification for the evolution of the firm's reset price,

$\displaystyle \Delta p_{it}^{\ast}=\left( 1-\alpha \right) \left( \beta \Delta x_{t}+\varepsilon_{it}\right) +\alpha \left( \Delta m_{t}\right) .$

The parameter $\alpha \in \left[ 0,1\right]$ controls the extent of real rigidities by capturing the emphasis placed by the firm on matching movements in the average price of competing importers, $\Delta m_{t}$ , when resetting its price. As was the case earlier, a fraction $\beta$ of exchange rate movements is passed-through to import prices in the long run.

Under Calvo pricing, it is possible to derive expressions for the evolution of the true import price index and for the correction factors in response to a one-time jump in the exchange rate. Abstracting from idiosyncratic disturbances, which have no effect on the index, the initial impact on reset prices is the sum of the direct effect of $\Delta x_{t}$ on $\Delta p_{i,t}^{\ast}$ and of its indirect effect through the change in the price of competing importers,

$\displaystyle \Delta p_{i,t}^{\ast}=\left( 1-\alpha \right) \beta \Delta x_{t}+\alpha \Delta m_{t}.$

The impact in subsequent periods depends only on the evolution of the price of competing importers,

$\displaystyle \Delta p_{i,t+l}^{\ast}=\alpha \Delta m_{t+l}.$

The price of competing importers evolves according to

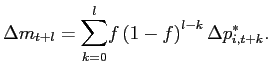
$\displaystyle \Delta m_{t+l}= {\displaystyle \sum \limits_{k=0}^{l}} f\left( 1-f\right) ^{l-k}\Delta p_{i,t+k}^{\ast}.$

(13)

Intuitively, the fraction of firms updating their price in period will take into account $\Delta p_{i,t+l}^{\ast}$ in setting $\Delta p_{i,t+l}$ . Of these firms, a fraction did not update in period and will also take into account $\Delta p_{i,t+l-1}^{\ast}$ . More generally, a fraction $\left( 1-f\right) ^{s}$ of firms updating in period will take into account $\Delta p_{i,t+l-s}^{\ast}$ when setting $\Delta p_{i,t+l}$ .

The above three equations allow us to solve recursively for $\Delta p_{i,t+l}^{\ast}$ and $\Delta m_{t+l}$ . In the initial period,

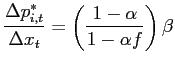
$\displaystyle \frac{\Delta p_{i,t}^{\ast}}{\Delta x_{t}}=\left( \frac{1-\alpha}{1-\alpha f}\right) \beta$

(14)

and

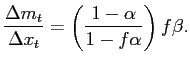
$\displaystyle \frac{\Delta m_{t}}{\Delta x_{t}}=\left( \frac{1-\alpha}{1-f\alpha}\right) f\beta.$

(15)

Subsequently, one can show that

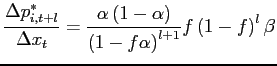
$\displaystyle \frac{\Delta p_{i,t+l}^{\ast}}{\Delta x_{t}}=\frac{\alpha \left( 1-\alpha \right) }{\left( 1-f\alpha \right) ^{l+1}}f\left( 1-f\right) ^{l}\beta$

(16)

and

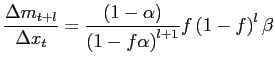
$\displaystyle \frac{\Delta m_{t+l}}{\Delta x_{t}}=\frac{\left( 1-\alpha \right) }{\left( 1-f\alpha \right) ^{l+1}}f\left( 1-f\right) ^{l}\beta$

for . Absent real rigidities ( $\alpha=0$ ), the reset price would initially move by $\beta \Delta x_{t}$ and remain unchanged thereafter. With real rigidities ( $\alpha>0$ ), the reset price moves gradually toward its long-run level so that the response to an exchange rate movement is spread over several price adjustments. The cumulative response of the price of competing importers after period is given by

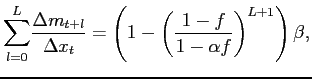
$\displaystyle {\displaystyle \sum \limits_{l=0}^{L}} \frac{\Delta m_{t+l}}{\Delta x_{t}}=\left( 1-\left( \frac{1-f}{1-\alpha f}\right) ^{L+1}\right) \beta ,$

(17)

which implies a slower rate of pass-through than the case with $\alpha=0$ . The cumulative change in the target price is a weighted sum of the long-run change and the cumulative change in the price of competing importers,

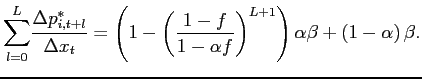
$\displaystyle {\displaystyle \sum \limits_{l=0}^{L}} \frac{\Delta p_{i,t+l}^{\ast}}{\Delta x_{t}}=\left( 1-\left( \frac {1-f}{1-\alpha f}\right) ^{L+1}\right) \alpha \beta+\left( 1-\alpha \right) \beta.$

Using the arguments made in section 3 to derive equation (3), we can express the measured change in the import price index as

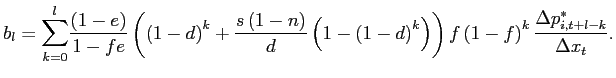
$\displaystyle b_{l}= {\displaystyle \sum \limits_{k=0}^{l}} \frac{\left( 1-e\right) }{1-fe}\left( \left( 1-d\right) ^{k} +\frac{s\left( 1-n\right) }{d}\left( 1-\left( 1-d\right) ^{k}\right) \right) f\left( 1-f\right) ^{k}\frac{\Delta p_{i,t+l-k}^{\ast}}{\Delta x_{t}}.$

(18)

The variable $b_{l}$ corresponds to the (plim) regression coefficient on the -th lag of the exchange rate. The above equation, along with equations (14) and (16), allow us to compute the $b_{l}$ at all lags. To gain intuition about the role of real rigidities, we shall highlight three results.

First, the correction factor on the initial response of the index is independent of the extent of real rigidities. This can be seen by using equations (14), (15), and (18) to write

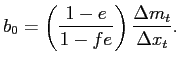
$\displaystyle b_{0}=\left( \frac{1-e}{1-fe}\right) \frac{\Delta m_{t}}{\Delta x_{t}}.$

The inverse of $\left( 1-e\right) /\left( 1-fe\right)$ is the correction factor applicable to the initial response. It does not depend on $\alpha$ . Second, the correction factor for long-run pass-through is also independent of the extent of real rigidities. This can be proven by considering the cumulative sum of $b_{l}$ in equation (18) and taking its limit as the horizon is extended. One can then show that

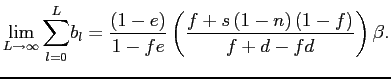
$\displaystyle \lim_{L\rightarrow \infty} {\displaystyle \sum \limits_{l=0}^{L}} b_{l}=\frac{\left( 1-e\right) }{1-fe}\left( \frac{f+s\left( 1-n\right) \left( 1-f\right) }{f+d-fd}\right) \beta.$

The inverse of the expression in front of $\beta$ is the correction factor on long-run pass-through, which is again independent of $\alpha$ . Third, when both exits and entries are selective, then the correction factors are independent of real rigidities at all horizons. In such a case, a constant fraction $\left( 1-e\right) /\left( 1-fe\right)$ of $\Delta m_{t+l}/\Delta x_{t}$ is missed every period.

In the general case, the correction factors on the cumulative index response may depend on $\alpha$ at horizons beyond the initial period but finite. However, we find that these correction factors are rather insensitive to the extent of real rigidities. This aspect is illustrated in figure 12 for a Calvo model with a frequency of price changes of 15 percent and a rate of substitution of 5 percent. The parameter $\alpha$ is set to 0 (no real rigidities) or 0.6 (with real rigidities). The latter value corresponds to the empirical estimate of Gopinath and Itskhoki (2011). The correction factors are identical for the canonical cases in which all exits and entries are either selective (upper-left panel) or random (upper-right panel), as these cases correspond to the absence of a bias and to the censoring of a constant fraction of the index response, respectively. When all exits are selective and all entries are random (lower-left panel) or all exits are random and all entries are selective (lower-right panel), the presence of real rigidities only has a minor impact on the size of the correction factor. This finding is robust to considering smaller or larger frequency of price changes.

Finally, we note that there is often a trade-off in the calibration of the model between the extent of real rigidities and the degree of state-dependence. For several of the three-digit Enduse finished good categories considered in figure 6, we found an initially rapid response of the import price index to an exchange rate movement that was inconsistent with the slow response predicted by the Calvo model. For these categories, the addition of real rigidities to the Calvo model worsens its fit by further slowing the predicted response. As an experiment, we assumed that $\alpha=0.6$ and recomputed the linear combinations of Calvo and menu-cost impulse responses that minimize the Euclidian distance with the empirical response over our forecast horizon. For 9 out of the 16 categories, the weight placed on the menu-cost model rose as we added real rigidities. A strong preference for one model over the other was unchanged for the other categories. This finding cautions against concluding that evidence of real rigidities in the data, notably the pass-through of exchange rate movements over more than one price adjustment, necessarily imply slow pass-through.

Table 1: Exit rate, entry rate, and mean frequency and absolute size of individual price changes in the IPP import price sample

	Enduse Category	Relative Weight	Exit Rate: all reasons	Exit Rate: out-ofscope	Exit Rate: others reasons	Entry Rate	Mean Freq. of Price Changes	Mean Absolute Size of Price Change
Foods, Feeds & Beverages	000 Green coffee, cocoa beans, cane sugar	0.3	2.8	1.1	1.7	3.0	47.0	8.7
Foods, Feeds & Beverages	001 Other agricultural foods	2.8	2.4	0.8	1.5	2.6	21.1	9.4
Foods, Feeds & Beverages	010 Nonagricultural products	1.1	2.2	0.8	1.4	2.4	20.5	7.1
Industrial Supplies and Materials	100 Petroleum & products, excluding gas	16.7	3.6	1.9	1.6	2.5	38.0	11.7
Industrial Supplies and Materials	101 Fuels, n.e.s.-coal & gas	1.8	3.4	2.1	1.2	4.0	55.9	13.4
Industrial Supplies and Materials	110 Paper base stocks	0.2	3.6	1.6	2.0	3.2	36.5	6.1
Industrial Supplies and Materials	111 Newsprint & other paper products	0.7	3.3	1.2	2.0	2.5	19.6	5.0
Industrial Supplies and Materials	120 Agricultural products	0.5	2.2	0.6	1.5	2.1	28.4	7.4
Industrial Supplies and Materials	121 Textile supplies & related materials	0.7	2.6	0.8	1.7	2.5	8.0	6.8
Industrial Supplies and Materials	125 Chemicals, excl. meds., food additives	3.4	2.4	0.7	1.7	2.5	11.2	7.3
Industrial Supplies and Materials	130 Lumber & unfinished building materials	1.1	2.4	0.9	1.5	2.9	33.2	7.7
Industrial Supplies and Materials	131 Building materials, finished	1.0	2.6	0.8	1.8	2.9	10.4	5.7
Industrial Supplies and Materials	140 Steelmaking materials-unmanufactured	0.4	2.4	0.9	1.5	2.0	21.2	7.1
Industrial Supplies and Materials	141 Iron & steel mill products-semifinished	1.3	3.5	1.3	2.1	3.9	15.3	21.4
Industrial Supplies and Materials	142 Major non-Fe metals-crude & semifin.	2.7	3.0	1.4	1.5	2.5	43.4	5.8
Industrial Supplies and Materials	150 Iron & steel products, ex. advanced mfg.	0.5	2.6	0.8	1.9	2.4	9.5	7.1
Industrial Supplies and Materials	151 Iron & steel mfg.-advanced	0.4	2.9	0.7	2.2	2.4	13.2	7.2
Industrial Supplies and Materials	152 Fin. metal shapes & adv. mfg., ex. steel	0.9	2.7	0.6	2.0	2.4	13.3	5.5
Industrial Supplies and Materials	161 Finished	1.5	2.7	1.1	1.6	2.8	7.1	7.9
Capital Goods	210 Oil drilling, mining & const. machinery	1.1	2.5	0.9	1.6	2.9	6.9	6.6
Capital Goods	211 Industrial & service machinery, n.e.c.	6.2	2.5	0.8	1.7	2.5	6.3	6.7
Capital Goods	212 Agricultural machinery & equip.	0.4	2.7	1.2	1.5	3.1	8.9	5.3
Capital Goods	213 Computers, periph. & semiconductors	7.5	3.7	2.2	1.5	5.0	9.7	9.6
Capital Goods	214 Telecommunications equip.	2.3	3.4	1.8	1.6	3.6	5.8	8.9
Capital Goods	215 Business mach. & equip., ex. Computers	0.5	3.3	1.5	1.8	2.5	5.2	6.3
Capital Goods	216 Scientific, hospital & medical machinery	1.5	3.1	1.2	1.9	3.2	4.9	6.9
Automotive	300 Passenger cars, new & used	8.0	2.8	1.6	1.1	3.5	5.3	2.0
Automotive	301 Trucks, buses, & special-purp. vehicles	1.4	2.8	1.9	0.9	3.9	5.8	2.9
Automotive	302 Parts, engines, bodies, & chassis	5.4	2.8	1.2	1.6	3.0	8.0	7.1
Consumer Goods (Ex. Food & Auto.)	400 Apparel, footwear, & household goods	6.6	3.5	1.7	1.8	3.6	3.9	7.6
Consumer Goods (Ex. Food & Auto.)	401 Other consumer nondurables	5.0	2.4	0.8	1.5	2.7	6.0	7.7
Consumer Goods (Ex. Food & Auto.)	410 Household goods	6.1	2.9	1.2	1.7	3.0	4.6	6.2
Consumer Goods (Ex. Food & Auto.)	411 Recreational equip. & materials	2.3	3.2	1.8	1.5	3.1	4.8	5.7
Consumer Goods (Ex. Food & Auto.)	412 Home entertainment equip.	3.1	3.7	2.2	1.5	4.1	5.6	5.8
Consumer Goods (Ex. Food & Auto.)	413 Coins, gems, jewelry, & collectibles	1.3	3.1	1.1	1.9	3.1	6.9	5.9
	500 Imports, N.E.S.	3.5	2.7	0.6	2.1	1.8	5.2	12.5
	Total	100.0	3.0	1.4	1.6	3.1	15.3	8.0

Notes: This table shows, for each 3-digit Enduse category belonging to finished goods, the exit rate and entry rate of items in the IPP import price sample, along with the mean frequency and mean absolute size of individual price changes. These statistics are computed by first applying uniform weights to items within each Enduse-month combination and then averaging the resulting monthly statistics. The sample period is from October 1995 to April 2005. Missing item prices are imputed by their last observed price and used in the computation of the above statistics. The table also shows the relative 2006 import value shares used to aggregate Enduse statistics.

Table 2: Reconciliation of our results with those of Nakamura and Steinsson (2011)

	All goods excluding oil	Finished goods	Material-intensive goods excluding oil
Standard pass-through estimate after 6 quarters: Gagnon, Mandel, and Vigfusson	0.41	0.26	0.93
Standard pass-through estimate after 6 quarters: Nakamura and Steinsson	0.43	n.a.	n.a.
Item frequencies are constant within 3-digit Enduse categories: Case 1: Exits and entries are random; Corrected pass-through (6 quarters)	0.41	0.26	0.93
Item frequencies are constant within 3-digit Enduse categories: Case 1: Exits and entries are random; Corrected pass-through (6 quarters); Correction factor	1.00	1.00	1.00
Item frequencies are constant within 3-digit Enduse categories: Case 1: Exits and entries are random; Corrected pass-through (long-run)	0.41	0.26	0.93
Item frequencies are constant within 3-digit Enduse categories: Case 1: Exits and entries are random; Corrected pass-through (long-run); Correction factor	1.00	1.00	1.00
Item frequencies are constant within 3-digit Enduse categories: Case 2: Exits and entries are selective; Corrected pass-through (6 quarters)	0.55	0.37	1.04
Item frequencies are constant within 3-digit Enduse categories: Case 2: Exits and entries are selective; Corrected pass-through (6 quarters); Correction factor	1.32	1.40	1.12
Item frequencies are constant within 3-digit Enduse categories: Case 2: Exits and entries are selective; Corrected pass-through (long-run)	0.55	0.37	1.04
Item frequencies are constant within 3-digit Enduse categories: Case 2: Exits and entries are selective; Corrected pass-through (long-run); Correction factor	1.32	1.40	1.12
Item frequencies are constant within 3-digit Enduse categories: Case 3: Exits are selective and entries are random; Corrected pass-through (6 quarters)	0.48	0.32	0.96
Item frequencies are constant within 3-digit Enduse categories: Case 3: Exits are selective and entries are random; Corrected pass-through (6 quarters); Correction factor	1.16	1.21	1.04
Item frequencies are constant within 3-digit Enduse categories: Case 3: Exits are selective and entries are random; Corrected pass-through (long-run)	0.45	0.29	0.95
Item frequencies are constant within 3-digit Enduse categories: Case 3: Exits are selective and entries are random; Corrected pass-through (long-run); Correction factor	1.08	1.10	1.02
Item frequencies are constant within 3-digit Enduse categories: Case 4: Exits are random and entries are selective; Corrected pass-through (6 quarters)	0.48	0.31	1.02
Item frequencies are constant within 3-digit Enduse categories: Case 4: Exits are random and entries are selective; Corrected pass-through (6 quarters); Correction factor	1.16	1.19	1.10
Item frequencies are constant within 3-digit Enduse categories: Case 4: Exits are random and entries are selective; Corrected pass-through (long-run)	0.55	0.37	1.04
Item frequencies are constant within 3-digit Enduse categories: Case 4: Exits are random and entries are selective; Corrected pass-through (long-run); Correction factor	1.32	1.40	1.12
Item frequencies follow Beta distribution; All entries are selective; Corrected pass-through (long run)	0.70	n.a.	n.a.
Item frequencies follow Beta distribution; All entries are selective; Corrected pass-through (long run); Correction factor	1.70	n.a.	n.a.
Item frequencies follow Beta distribution; All entries are selective; Corrected pass-through (long-run, no f < 0.02)	0.61	n.a.	n.a.
Item frequencies follow Beta distribution; All entries are selective; Corrected pass-through (long-run, no f < 0.02); Correction factor	1.47	n.a.	n.a.
Addendum: NS' corrected estimates; Corrected pass-through (long run)	0.67	n.a.	n.a.
Addendum: NS' corrected estimates; Corrected pass-through (long run); Correction factor	1.71	n.a.	n.a.

Notes: This table illustrates the sensitivity of the product replacement bias to the time horizon of interest and to the assumed heterogeneity in the frequency of price changes. Standard pass-through estimates after 6 quarters are obtained from an OLS estimation of equation 8. All correction factors assume Calvo pricing and a constant frequency of substitution of 2.5 percent per month, with all exits being random and all entries being selective. The corrected 6-quarter and long-run pass-through estimates are obtained by multiplying the standard pass-through estimate after 6 quarters by a correction factor consistent with a 6-quarter horizon and an infinite horizon, respectively. Two distributions of heterogeneity in the frequency of price changes are considered. The first assumes that the frequency is constant within 3-digit Enduse categories, as reported in Table 1. The second is a Beta distribution with parameters 0.44 and 3.50, as estimated by Nakamura and Steinsson (2011).

Figure 1: Exit rate, entry rate, and the dollar

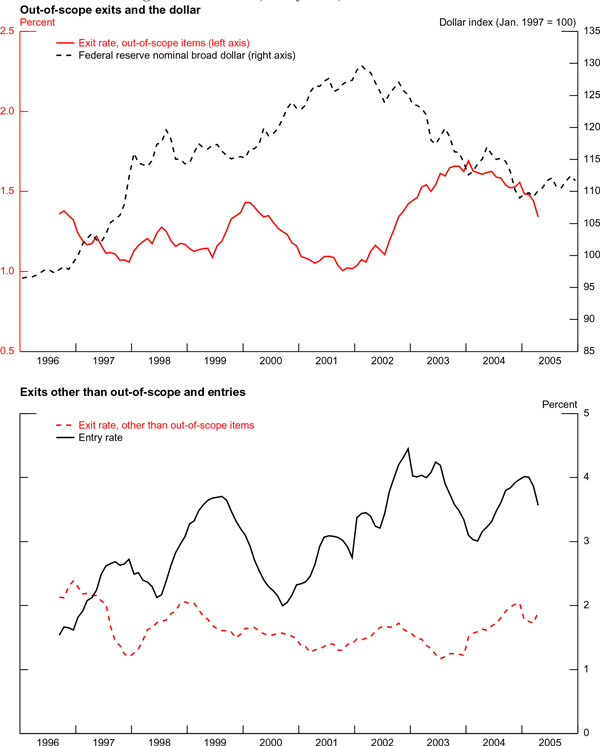
Figure 1: This figure contains two charts. The top chart contains two lines and shows out-of-scope exits and the dollar. The solid red line shows the exit rate for out of scope items across time, while the dashed black line shows an index for the Federal Reserve nominal broad dollar. The red line rises and falls throughout 1996-2005, while the black line largely rises from 1996 to the end of 2001 and then falls from 2001 to 2005.
The bottom chart shows the exit rate excluding out-of-scope as well as the entry rate The dashed red line shows the exit rate, excluding out-of-scope items, and remains largely stable throughout 1996 to 2005. The solid black line shows the entry rate and illustrates cycles of increases in the entry rate followed by corresponding decreases throughout the time period.

Figure 2: Coefficients on lags of the exchange rate in pass-through regressions in baseline Calvo and menu-cost models

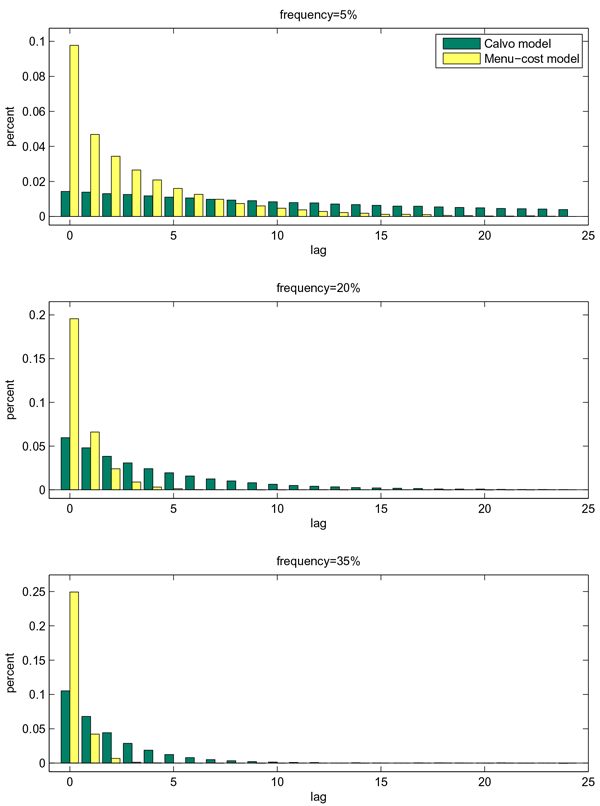
Figure 2: The top chart contains two series of bars corresponding to the coefficients on the lags of the exchange rate in Calvo model (green bars) as well as the Menu-cost model (yellow bars) at a 5% frequency. The chart shows that the Menu-cost model has an initial coefficient value of 0.1% before decaying exponentially with each new lag. The Calvo-model, on the other hand, begins around 0.015% and decays slowly, with an end value of around 0.05% at 24 lags. The middle chart is at a 20% frequency with the bars colored as before. Coefficients of the Menu-cost model are initially 0.2% before decaying exponentially, becoming almost 0% after 5 lags. Coefficients on the Calvo model also decay exponentially but at a much slower rate, beginning around 0.05% and becoming almost zero after 20 lags. The bottom chart is at a 35% frequency. Coefficients on the Menu-cost model begin at 0.25% before decaying rapidly, taking values of almost zero after 2 lags. The Calvo model begins at 0.1% and decays exponentially, reaching nearly zero after 10 lags.

Figure 3: Cumulative contribution of coefficients on lagged exchange rate variables under selective exit (e=0.25)

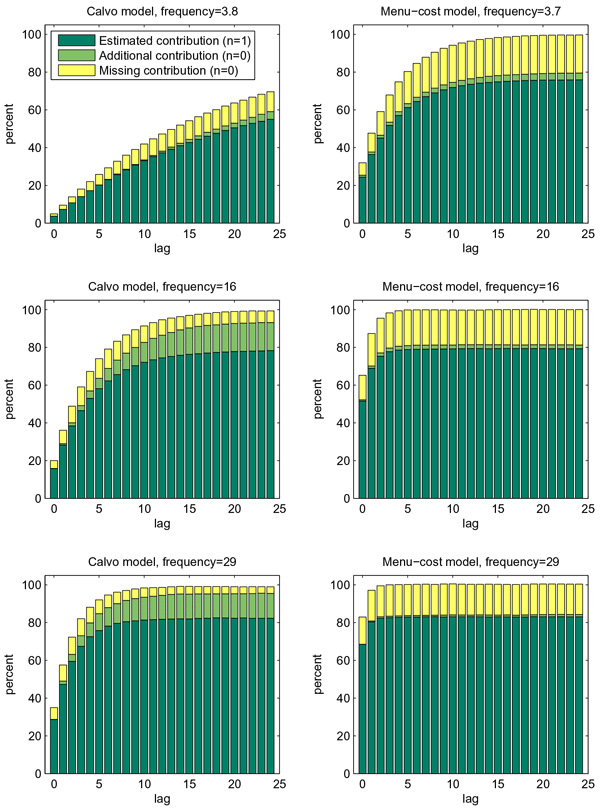
Figure 3: This figure contains six charts comparing the cumulative contribution of coefficients on lagged exchange rate variables under selective exit and similar frequencies for the Calvo (left side) and Menu-cost (right side) models. There are three different series being plotted using three colors in each individual chart: dark green displays the estimated contribution, light green shows additional contribution, and yellow the missing contribution. Beginning with the Calvo model, the top chart is at frequency 3.8 and shows a gradual increase in the cumulative contribution across the lags, beginning at around 5% and ending with almost 70%. The middle Calvo model chart is at frequency 16 and shows a more rapid approach to 100%, beginning near 20% and reaching 90% after 10 lags and nearly 100% after 20. The bottom Calvo chart is at frequency 29 and features a much more rapid rise, beginning at around 35% and reaching 100% after around 10 lags. Moving to the Menu-cost model, the top chart has a frequency of 3.7, beginning around 30% and reaching 100% after 20 lags. The middle chart has a frequency of 16, begins around 65%, and reaches 100% after 5 lags. The bottom chart has a frequency of 29, begins at 85%, and reaches 100% after only 3 lags. Overall, while the Menu-cost model reaches 100% cumulative contribution much more rapidly, the Calvo model results in smaller missing contributions.

Figure 4: Cumulative contribution of coefficients on lagged exchange rate variables in Calvo model under severe product replacement bias (n=1, s=0.05)

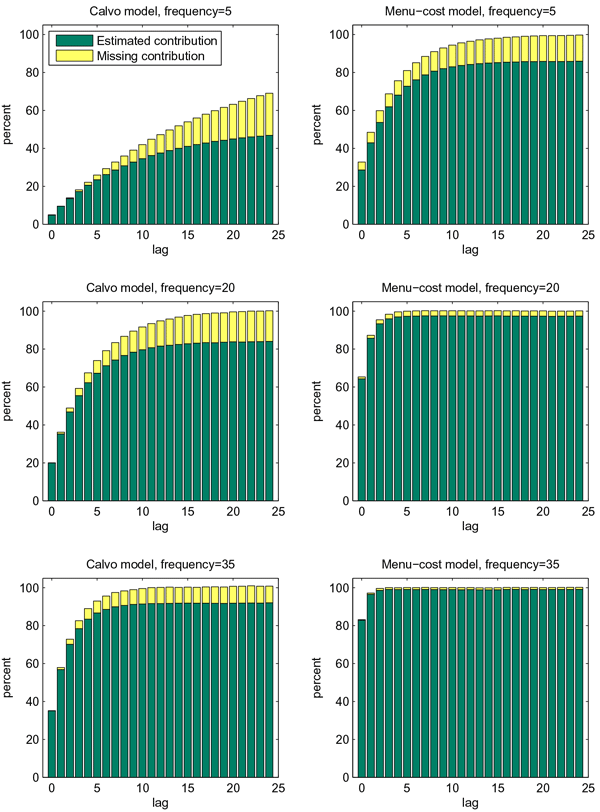
Figure 4: This figure contains six charts comparing the cumulative contribution of coefficients on lagged exchange rate variables in Calvo model under severe product replacement bias for the Calvo (left side) and Menu-Cost (right side) models. There are two different series being plotted in each individual chart: the estimated contribution(green) and the missing contribution (yellow). Beginning with the Calvo model, the top chart is at frequency 5 and shows a gradual increase in the cumulative contribution across the lags, beginning at around 5% and ending with almost 70%. The middle Calvo model chart is at frequency 20 and shows a more rapid approach to 100%, beginning at nearly 20% and reaching 100% after approximately 20 lags. The bottom Calvo chart is at frequency 35 and features a much more rapid rise, beginning at around 35% and reaching 100% after around 10 lags. Moving to the Menu-cost model, the top chart has a frequency of 5, beginning around 30% and reaching 100% after 15 lags. The middle chart has a frequency of 20, begins around 65%, and finishes at 100% after 5 lags. The bottom chart has a frequency of 35, begins at slightly under 85%, and finishes at 100% after only 2 lags. Overall, the Menu-cost model reaches 100% cumulative contribution much more rapidly and also contains less missing contributions than the Calvo model.

Figure 5: Pass-through to imported finished goods prices following a 1-percent depreciation of the dollar (by 3-digit Enduse categories)

Figure 5: This figure contains five charts detailing the pass-through to imported finished goodsâ€™ prices following a 1-percent depreciation of the dollar. The top-left chart has four lines. The solid blue line (Oil drilling, mining, and construction machinery and equipment) has an initial decline before passing through .35% after 24 months. The dotted red line (Industrial and service machinery) begins immediately at 0% before rising to 0.4% at 24 months. The dashed-and-dotted green line (Agricultural machinery and equipment) begins slightly below 0% before gradually reaching 0.45% after 24 months. The dashed magenta line (Computers peripherals and semiconductors) begins at 0% and reaches around 0.65% after 24 months.
The top-right chart has four lines. The solid blue line (Telecommunications equipment) begins at 0% and reaches only 0.15% after 24 months. The dotted red line (Business machinery and equipment except computers) begins immediately at 0% before rising to 0.3% at 24 months. The dashed-and-dotted green line (Scientific and medical machinery) begins at 0% before reaching 0.1% after 2 months and remaining relatively stable through the remaining months of consideration. The dashed magenta line (Passenger cars new and used) begins at 0% and remains relatively unchanged, reaching around 0.05% after 24 months.
The middle-left chart has four lines. The solid blue line (Vehicles designed to transport goods) is relatively stable throughout all 24 months, ending slightly below 0%. The dotted red line (Parts, engines, bodies, and chassis) begins immediately at 0% before rising to 0.22% after 24 months. The dashed-and-dotted green line (Apparel footwear and household goods) is relatively stable throughout all 24 months, ending slightly below 0%.. The dashed magenta line (Other consumer nondurables) begins at 0% and reaches 0.3% after 24 months.
The middle-right chart has four lines. The solid blue line (Household goods) begins at 0% and gradually reaches only 0.2% after 24 months. The dotted red line (Recreational equipment and materials) begins immediately at 0% and gradually reaches 0.2% at 24 months. The dashed-and-dotted green line (Home entertainment equipment) begins at 0%, reaches a maximum of 0.1% at 5 months, then declines until 13 months after the shock, reaching -0.05%, and then reverses for an end value of 0.02% at 24 months. The dashed magenta line (Coins, gems, jewelry, and collectibles) begins at 0% and rises sharply to reach 0.4% at the end of 24 months.
The bottom-left chart has two lines. The dashed red line is an index of the pass-through over 24 months, beginning at zero and gradually reaching 0.25% over the period of consideration. The solid blue line is the weighted response of the different categories and follows the path of index closely.

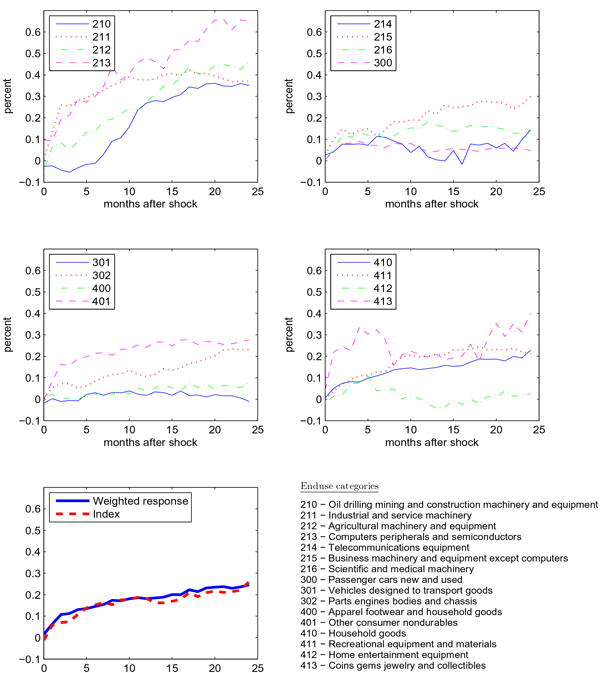
Figure 6: Pass-through to imported finished goods prices following a 1-percent depreciation of the dollar: models versus data

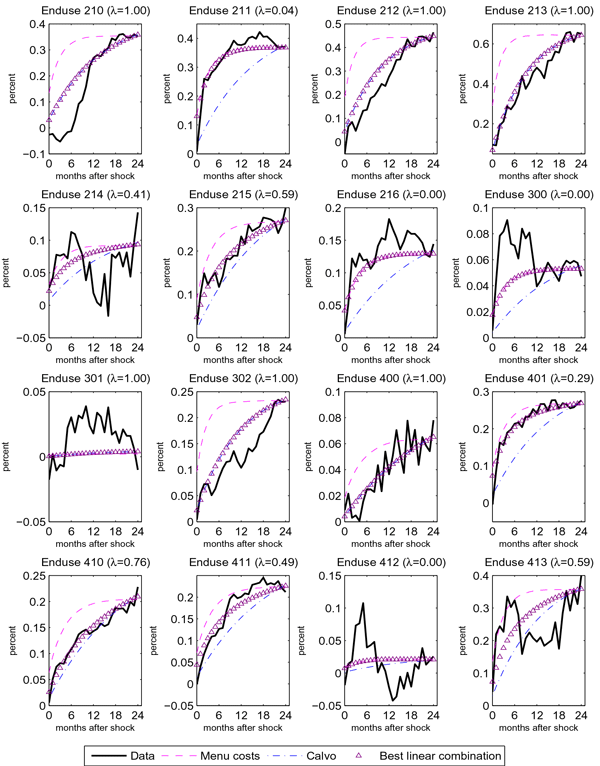
Figure 6: This figure contains sixteen charts detailing the pass-through to imported finished goods prices following a 1-percent depreciation of the dollar. Each chart contains four different lines. The bold line is a series of empirical data. The dashed line contains the results of the Menu Cost model. The line with alternating dashes and dots is the Calvo model. The line composed of triangles contains the best linear combination of thewo models.
The sixteen charts fall into three main groups: those in which the best fitting model is the Calvo model (lambda = 1.00), those in which the Menu cost model is best (lambda = 0), and those in which a linear combination of the two is best (.25<lambda<.75). In the first group we have the following Enduse categories: 210, 212, 213, 301, 302, and 400. In the second group are: 211, 216, 300, and 412. In the last group are: 214, 215, 401, 410, 411, and 413.

Notes: The figure shows the empirical impulse response for three-digit Enduse categories along with calibrated impulse responses in the Calvo and the menu-cost models. The figure also shows the combination of models minimizing over λ IRF_Calvo + (1 - λ) IRF_MC - IRF_data over âˆˆ [0, 1], where is the Euclidian distance and IRF_Calvo, IRF_MC, and IRF_data are the impulse responses in the Calvo model, the menu-cost model, and the data.

Figure 7: Upper bounds on exchange rate pass-through to imported finished goods

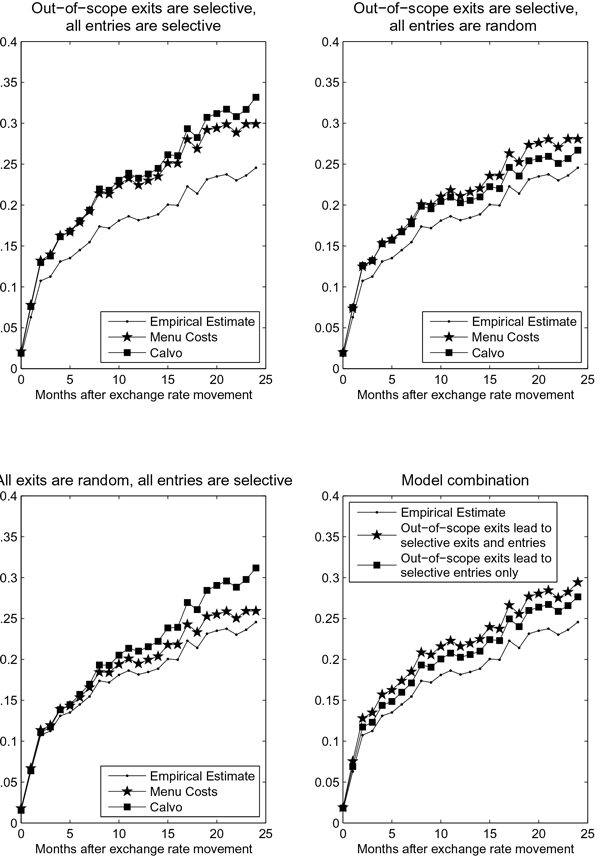
Figure 7: This figure consists of four charts detailing the upper bounds on exchange rate pass-through to imported finished goods. The top-left chart has three lines and describes what happens when out-of-scope exits are selective and all entries are selective. The squared line is the Calvo model, beginning at 0.02 before reaching 0.33 at the end of 24 months. The starred line is the Menu Cost model, beginning at 0.02 and reaching 0.3 at the end of 24 months. The line with dots is the empirical estimate and begins at 0.02 and ends at 0.25 after 24 months.
The top-right chart has three lines and details the situation of selective out-of-scope exits and random entries . The squared line is the Calvo model, beginning at 0.02 before reaching 0.265 at the end of 24 months. The starred line is the Menu Cost model, beginning at 0.02 and reaching 0.275 at the end of 24 months. The dotted line is the empirical estimate and begins at 0.02 and ends at 0.25 after 24 months.
The bottom-left chart has three lines and depicts the upper bounds when all exits are random and all entries are selective. The squared line is the Calvo model, beginning at 0.02 before reaching around 0.315 at the end of 24 months. The starred line is the Menu Cost model, beginning at 0.02 and reaching around 0.255 at the end of 24 months. The dotted line is the empirical estimate, beginning at 0.02 and ending at 0.25 after 24 months.
The bottom-right chart has three lines and details what happens under a combination of the models. The squared line is when out-of-scope exits lead to selective entries only, beginning at 0.02 and ending at around 0.275 after 24 months. The starred line is when out-of-scope exits lead to selective exits and entries, beginning at 0.02 and ending around 0.3 after 24 months. The dotted line is the empirical estimate,beginning at 0.02 and ending at 0.25 after 24 months.

Figure 8: Impact of delaying entries on cumulative contribution of coefficients on lagged exchange rate variables under severe product replacement bias (n=1, s=0.05)

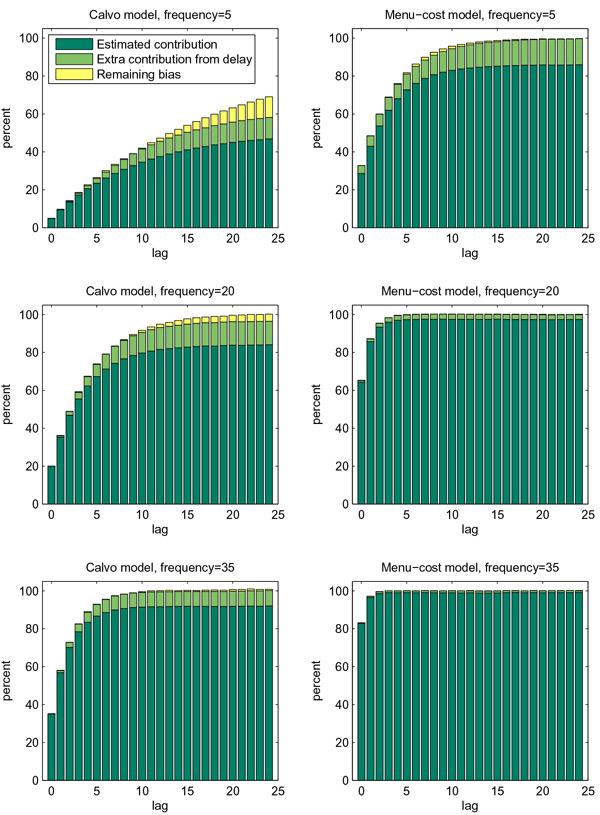
Figure 8: This figure contains six charts comparing the impact of delaying entries upon the cumulative contribution of coefficients on lagged exchange rate variables under severe product replacement bias under similar frequencies for the Calvo (left side) and Menu-cost (right side) models. There are three different series being plotted using three colors in each individual chart: dark green displays the estimated contribution, light green shows extra contribution from delay, and yellow shows the remaining bias. Beginning with the Calvo model, the top chart is at frequency 5 and shows a gradual increase in the cumulative contribution across the lags, beginning around 5% and ending with almost 70%. The middle Calvo model chart is at frequency 20 and shows a more rapid approach to 100%, beginning at nearly 20% and reaching 100% after approximately 20 lags. The bottom Calvo chart is at frequency 35 and features a much more rapid rise, beginning around 35% and reaching 100% after around 10 lags. Moving to the Menu-cost model, the top chart has a frequency of 5, beginning around 30% and reaching 100% after 20 lags. The middle chart has a frequency of 20, beginning around 65% and finishing at 100% after 5 lags. The bottom chart has a frequency of 35beginning at 85% and finishing at 100% after only 3 lags. Overall, the Menu-cost model reaches 100% cumulative contribution much more rapidly than does the Calvo model.

Figure 9: Impact of delaying entries on cumulative contribution of coefficients on lagged exchange rate variables under selective exits and random entries (n=0, e=0.25)

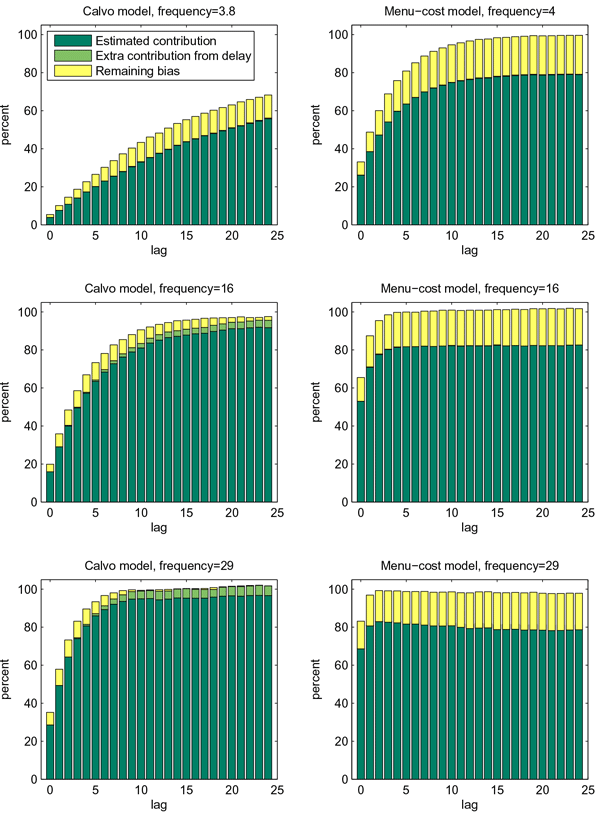
Figure 9: This figure contains six charts comparing the impact of delaying entries upon the cumulative contribution of coefficients on lagged exchange rate variables under selective exits and random entries under similar frequencies for the Calvo (left side) and Menu-cost (right side) models. There are three different series being plotted using three colors in each individual chart: dark green displays the estimated contribution, light green shows extra contribution from delay, and yellow shows the remaining bias. Beginning with the Calvo model, the top chart is at frequency 3.8 and shows a gradual increase in the cumulative contribution across the lags, beginning at around 5% and ending with almost 70%. The middle Calvo model chart is at frequency 16 and shows a more rapid approach to 100%, beginning at nearly 20% and reaching 100% after approximately 20 lags. The bottom Calvo chart is at frequency 29 and features a much more rapid rise, beginning around 35% and reaching around 100% after 10 lags. Moving to the Menu-cost model, the top chart has a frequency of 4, beginning around 30% and reaching 100% after 20 lags. The middle chart has a frequency of 16, beginning around 65% and reaching 100% after 5 lags. The bottom chart has a frequency of 29, beginning at 85% and reaching 100% after only 3 lags. Overall, while the Menu-cost model reaches 100% cumulative contribution much more rapidly and also has more of a remaining bias, the Calvo model contains more extra contributions from delay.

Figure 10: Alternative price indexes and pass-through

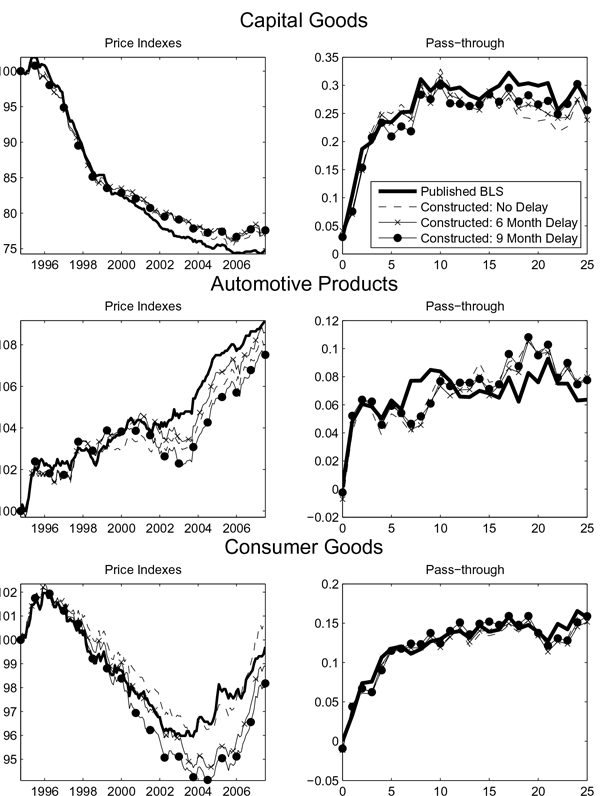
Figure 10: This figure contains six charts and shows the results for constructed alternative price indexes. Each chart contains four lines. The bold line is a series published by the BLS. The dashed line is a constructed series that contains no delay. The crossed line is a constructed series with a 6 month delay. The line with circles is a constructed series with a 9 month delay.
The top row shows the price indexes (left) and pass-through (right) for capital goods. The price indexes all begin at 100 in 1995 and gradually decrease by 2008 to values between 75 and 77, largely following similar paths. As for the pass-through chart, all lines begin at 0.04% at a 0 month lag before ending around 0.25% to 0.275% at the end of 25 lags.
The middle row shows the price indexes (left) and pass-through (right) for automotive products. The price indexes all begin at 100 in 1995 and gradually increase to between 107.5 and 109 in 2007. The four lines of the pass-through chart all begin at 0% after 0 months of lag before ending between 0.06% and 0.08% after a 25 month lag.
The bottom row shows the price indexes (left) and pass-through (right) for consumer goods. The price indexes begin at 100 in 1995, rise to around 102 in 1996, and fall to between 94 and 96.5 in 2004 before rising again to between 98 and 100.5 at the end of 2007. As for the pass-through chart, all four lines begin at 0% after 0 months of lag before rising to around 0.15% after a 25 month lag, largely following a similar path.

Figure 11: Marginal probabilities of observations usable to computed inflation in period ï´ in the Calvo model with iid exchange rate innovations

Figure 11: This figure shows the marginal probabilities in periodsâ€“ t-1 to t of items whose price can be used to compute inflation in period t. The arrows illustrate the various paths through which a movement in the exchange rate in period t-1 could be rejected as a nonzero contribution to inflation in period t. The upper, middle, and lower panels show the case in which observations entering the sample are delayed by 0, M>=l, and M < l period(s), respectively.

Notes: This figure shows the marginal probabilities in periods to of items whose price can be used to compute inflation in period . The arrows illustrate the various paths through which a movement in the exchange rate in period could be reflected as a nonzero contribution to inflation in period . The upper, middle, and lower panels show the case in which observations entering the sample are delayed by 0, $M\geq l$ , and period(s), respectively.

Figure 12: Correction factors for the cumulative index response to an exchange rate shock in a Calvo model with real rigidities

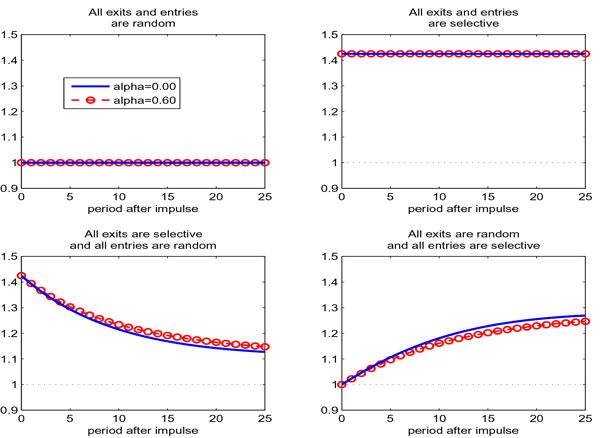
Figure 12: This figure shows the theoretical correction factors one would apply to the cumulative import price index response to a one-time jump in the exchange rate. The model assumes Calvo pricing with an exogenous frequency of price changes of 15 percent and a substitution rate of 5 percent. The real rigidity parameter is set to 0.6. The figure contains four panels showing, on the x axis, the number of periods since the shock (running from 0 to 24 months) and, on the y-axis, the correction factor on standard pass-through estimates. Each panel shows a line for the case with no real rigidities, with real rigidities, and without any bias (that is, a correction factor of one). The upper-left panel shows that the correction factor is trivially 1 when exits and entries are independently of the presence of real rigidities. The upper-right panel shows that the correction factor is also independent of real rigidities at just above 1.4 when both exits and entries are selective. The upper-left panel shows that the correction factor with real rigidities is marginally larger than without real rigidities when exits are selective and entries are random. The upper-left panel shows that the correction factor with real rigidities is marginally larger than without real rigidities when exits are random and entries are selective.

Notes: This figure shows the theoretical correction factors one would apply to the cumulative import price index response to a one-time jump in the exchange rate. The model assumes Calvo pricing with an exogenous frequency of price changes of 15 percent and a substitution rate of 5 percent. The real rigidity parameter is specified as in appendix B.

Footnotes

1. These papers include Atkeson and Burstein (2008), Gopinath, Itskhoki, and Rigobon (2010), Gopinath and Itskhoki (2010), and Gust, Leduc, and Vigfusson (2010). Return to text

2. We focus on the response of import prices over the first two years following an exchange rate movement, which corresponds to the policy horizon of most central banks and international institutions. Near-term horizons are arguably the most relevant when using impulse responses to differentiate among models. For example, the implications of producer and local currency pricing are most stark in the first few years after a shock. Return to text

3. For an introduction to the economics of new goods, see the volume edited by Breshnahan and Gordon (1996). Gordon (2006) and the conference summaries of the Ottawa Group provide overviews of subsequent research. Return to text

4. For a given item, reporting firms typically do not provide a transaction price every month. The BLS imputes an item's missing price by either carrying forward the last reported price or by adjusting it by the average price change for the same firm and product category. Return to text

5. For instance, if there are two items sampled at a firm, one of which has a 90 percent sales share and the other a 10 percent sales share, allocating weights uniformly would over-weight the smaller item. When constructing its aggregate price indexes, BLS corrects for this phenomenon with item-level probability weights. Return to text

6. In some instances, the firm can provide an alternative item that meets BLS sampling needs (called "replaced"), though that new item would still be recorded as a separate entry. Return to text

7. For instance, during biennial sample redrawings, some disaggregate product categories may be retired from further sampling but their items may remain in the index until their planned phaseout. Where outgoing and incoming product groups are dissimilar, the benefit to overlapping their items is unclear. Return to text

8. Incomplete reporting for item discontinuation reasons in the database made available to outside researchers by the IPP truncates our sample at its beginning and end. October 1995 is the first month for which the discontinuation reason field is populated, while the months following April 2005 contain incomplete information about exits. Return to text

9. Doing so assigns the average item frequencies for sampled items and products to those not sampled within the same industry. Return to text

10. An alternative weighting scheme would be to use the BLS product weights, which are akin to annual import values at the Harmonized System 10-digit (HS10) level, spread evenly across items within each product. The end-use weights for a given month would be the sum total of the individual item weights across items and HS10 products within that end-use. However, due to incomplete weight data for petroleum (Enduse 100), that method tends to under-weight those high-frequency products in the aggregate statistics. Otherwise, at the end-use level, the measures are quite similar.
Also, ignoring the BLS probability weights for items and firms within each HS10 product, as we do, does not drastically change the summary statistics. Probability-weighted and unweighted statistics are available upon request. Return to text

11. The exit rates shown in the figure are 12-month moving averages. Return to text

12. Some micro price studies include carried forward prices in their count of price observations (i.e., the denominator of the frequency formula), while others do not. We choose to use such price observations. One benefit of this approach is that the number of usable observations from one month to the next is directly determined by the number of entries and exits. If we instead excluded imputed prices, then our statistics would need to account for the fact that some quotes are inactive. Our decision makes price changes, exits, and entries somewhat less frequent than if imputations were excluded. The broad findings of the paper do not hinge on this methodological choice, however. Return to text

13. Our price-setting rule abstracts from forward-looking concerns, which greatly simplifies the exposition. Monthly exchange rate innovations are only weakly correlated, so our purely backward-looking rule should nevertheless capture central features of micro price adjustments in response to exchange rate movements. Return to text

14. In practice, the frequency of price changes and the degree of exchange rate pass-through appear interrelated. Gopinath and Itskhoki (2010) present evidence that items with relatively low frequencies of price changes tend to be associated with relatively low rates of pass-through. Return to text

15. In principle, mismeasured changes in quality can result in either upward or downward biases, depending on whether the quality change is underestimated (e.g., ignoring improvements in a computer's processing power) or overestimated (e.g., failing to account for the use of lower-quality components). In practice, the quality change bias is associated with a systematic overestimation of inflation (see BLS (1997b) and Bils (2010), among many others). By contrast, in our canonical case with all exits and entries being selective, only a fraction of the aggregate price adjustment is recorded, so that inflation is underestimated when it is positive, and overestimated when it is negative. As a result, the price response to a shock is underestimated, which would not be the case if inflation was mismeasured by a fixed amount every period. Return to text

16. Greenlees and McClelland (2011) offer evidence that exiting food items in the CPI have larger price changes (including zeros) on average than continuing items. They also argue that current CPI techniques may overestimate the extent of quality adjustments for these categories. Return to text

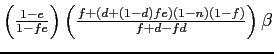17. When all exits are selective and all entries are random, the long-run response of the index is given by $\frac{1-fe-\left( 1-f\right) e^{2}}{1-fe}\beta<\beta$ . The same conclusion applies for the general case, for which the long-run response is $\left( \frac{1-e}{1-fe}\right) \left( \frac{f+\left( d+\left( 1-d\right) fe\right) \left( 1-n\right) \left( 1-f\right) }{f+d-fd}\right) \beta$ . This response is smaller than $\beta$ and increasing in the fraction of entering items randomly sampled from the universe. Randomizing entries thus reduces the downward bias without eliminating it entirely. Return to text

18. We thank Emi Nakamura and Jon Steinsson for pointing out this link in an email correspondence. Return to text

19. Our simple specification does not allow for variation in the magnitude of the response over time, a restriction imposed in part due to the short period over which monthly import price data are available. Taking advantage of the longer time coverage of quarterly series, several authors have documented a decline in pass-through rates in recent decades (e.g., Marazzi et al., 2005), including for finished goods (see Gust et al., 2010). As mentioned earlier, we find little evidence that an increase in the occurrence of selective exits and entries could account for that pattern. Return to text

20. We assume that individual (nonzero) price changes leading to exits have the same distribution as those for items remaining in the sample. Whether this is the case in practice remains an open question. Return to text

21. That said, equation (8) is likely misspecified for material-intensive goods because movements in commodity prices can affect both the exchange rate and material-intensive goods prices. Return to text

22. Allowing the substitution rate to vary across 3-digit Enduse categories based on the entry rates displayed in table 1 has only a minor impact on our findings. Return to text

23. We exclude from our comparisons the possibility that exits are selective and entries are random because Nakamura and Steinsson (2011) do not model the exit decision explicitly. Return to text

24. In particular, when $\Lambda=\Lambda \left( \infty \right)$ , our equation 20 is an implementation of equation 20 in Nakamura and Steinsson (2011) under our distributional assumptions for the frequency of price changes. Return to text

25. We also note that using only 6 lags of quarterly exchange rate movements in the regression would be insufficient to precisely estimate long-run pass-through if the data were truly generated from a Calvo model, even absent any product replacement bias. For import prices excluding oil, 0.79 percent of the true long-run response is realized after 6 quarters, a figure that shrinks to 0.68 when we focus on finished goods. A failure to use a sufficiently large number of lags in the regression would thus be a source of downward bias in the estimation of long-run pass-through. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text