The Federal Reserve Board eagle logo links to home page

Fiscal Consolidation in an Open Economy

Christopher J. Erceg and Jesper Lindè

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

This paper uses a New Keynesian DSGE model of a small open economy to compare how the effects of fiscal consolidation differ depending on whether monetary policy is constrained by currency union membership or by the zero lower bound on policy rates. We show that there are important differences in the impact of fiscal shocks across these monetary regimes that depend both on the duration of the zero lower bound and on features that determine the responsiveness of inflation.

Keywords: Monetary policy, currency union, fiscal policy, zero lower bound constraint, new Keynesian small open economy DSGE Model

JEL classification: E52, E58


1.  Introduction

Given heightened concerns about debt sustainability, many countries are implementing ambitious fiscal consolidation plans in which government spending reductions often play a major role. The usual presumption is that the effects of government spending cuts on output are smaller when a country conducts an independent monetary policy (IMP) than when constrained by membership in a currency union, reflecting that interest rate cuts and currency depreciation appear to dampen the adverse impact on aggregate demand. While econometric analysis (e.g. Ilzetzki, Mendoza and Vegh, 2010) supports this view, it is unclear whether an IMP retains its comparative advantage if constrained by the zero lower bound, especially in light of "closed economy"analysis showing how a liquidity trap can amplify the government spending multiplier.1

This paper uses a New KeynesianDSGE model of a small open economy to compare the effects of a government spending cut under two alternative constraints on monetary policy: currency union (CU) membership and the zero lower bound on interest rates (for an economy with an IMP). Given that adjustment of the policy rate is precluded in both monetary regimes for at least some time, the output effects of fiscal contraction are larger than under an unconstrained IMP. But we show that there are important differences across the two constrained regimes, reflecting that the relative size of the output contraction is highly sensitive to structural features which determine how the real exchange rate and long-term real interest rate respond to the fiscal consolidation. If inflation is fairly sensitive to the output gap (e.g., the Phillips Curve has substantial upward slope), output contracts more deeply under an IMP than a CU if policy rates are constrained from adjusting for a sustained period of roughly two years or more. Importantly, the anchoring of the nominal exchange rate in a CU turns out to be a blessing insofar as it avoids the large appreciation of the real exchange rate that would occur in a persistent liquidity trap, and implies a smaller rise (if any) in long-term real interest rates. By contrast, if the Phillips Curve is very flat, the output contraction under an IMP tends to be smaller than under a CU, reflecting that the real exchange rate depreciates even in a prolonged liquidity trap and long-term real interest rates fall. We conclude by arguing that the responsiveness of inflation during the recent global recession should be highly informative in discriminating between these contrasting predictions of the theory.


2.  A New Keynesian Open Economy Model

Our benchmark model is very similar to the small open economy model of Clarida, Galí, and Gertler (2001).Households consume a domestic and foreign good that are imperfect substitutes. To rationalize Calvo-style price rigidities, the domestic good is assumed to be a comprised of a continuum of differentiated intermediate goods, each of which is produced by a monopolistically competitive firm. The government consumes some of the domestic good and finances itself through lump-sum taxes. The home economy is small in the sense that it does not influence any foreign variables, and financial markets are complete. To save space, we present only the log linearized model in which all variables are expressed as percent or percentage point deviations from their steady state levels, and we omit all foreign variables.

Under anindependent monetary policy, the key equations are given by:

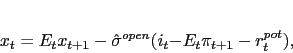
\begin{displaymath} x_{t}=\text{E}_{t}x_{t+1}-\hat{\sigma}^{open}{(i_{t}-}\text{{E}}_{t}{\pi _{t+1}-r_{t}^{pot}),} \end{displaymath} (1)
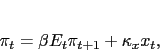
\begin{displaymath} \pi_{t}=\beta\text{E}_{t}\pi_{t+1}+\kappa_{x}{x_{t},} \end{displaymath} (2)
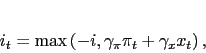
\begin{displaymath} i_{t}=\max\left( -i,\gamma_{\pi}\pi_{t}+\gamma_{x}x_{t}\right) , \end{displaymath} (3)
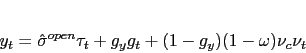
\begin{displaymath} y_{t}=\hat{\sigma}^{open}\tau_{t}+g_{y}g_{t}+(1-g_{y})(1-\omega)\nu_{c}\nu _{t} \end{displaymath} (4)
\begin{displaymath} y_{t}^{pot}=\frac{1}{\phi_{mc}\hat{\sigma}^{open}}[g_{y}{g_{t}}+(1-g_{y} )(1-\omega)\nu_{c}\nu_{t}] \end{displaymath} (5)
\begin{displaymath} \tau_{t}^{pot}=-\frac{1}{\hat{\sigma}^{open}}(1-\frac{1}{\phi_{mc}\hat{\sigma }^{open}})\left[ g_{y}{g_{t}}+(1-g_{y})(1-\omega)\nu_{c}\nu_{t}\right] \end{displaymath} (6)
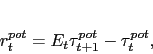
\begin{displaymath} r_{t}^{pot}=\text{E}_{t}\tau_{t+1}^{pot}-\tau_{t}^{pot}{,} \end{displaymath} (7)

where $\hat{\sigma}^{open}$ = $(1-g_{y})$[ $(1-\nu_{c})(1-\omega)^{2}\sigma$ + $\omega(2-\omega)\varepsilon_{P}$] and the superscript `pot' denotes the level that would prevail under completely flexible prices.

As in Clarida et al, the first three equations represent the New Keynesian open economy IS curve, Phillips Curve, and monetary rule, respectively, that jointly determine the output gap ( $x_{t}=y_{t}-y_{t} ^{pot}),$ price inflation ($\pi{_{t}),}$ and the nominal policy rate ($i_{t}),$ with the key difference that equation (3) requires the policy rate to remain above its lower bound ($-i$). Thus, the output gap $x_{t}$ depends inversely on the deviation of the real interest rate ($i_{t} -$E$_{t}\pi_{t+1}$) from the potential real interest rate $r_{t}^{pot}$, with the sensitivity parameter $\hat{\sigma}^{open}$ varying positively with the household's intertemporal elasticity of substitution in consumption $\sigma$ and substitution elasticity $\varepsilon_{P}$ between foreign and domestic goods (the relative weight on the latter rises with trade openness $\omega). $ The Phillips curve slope $\kappa_{x}$ in equation (2) is the product of parameters determining the sensitivity of inflation to marginal cost $\kappa_{mc}$ and of marginal cost to the output gap $\phi_{mc}$, i.e. $\kappa_{x}$ = $\kappa_{mc}\phi_{mc}$. From equation (5), a contraction in government spending $g_{t}$ ($g_{y}$ is the government spending share of steady state output) or negative taste shock $\nu_{t}$ ($\nu_{c}$ is a scaling parameter) reduces potential output $y_{t}^{pot}.$ Even so, both of these exogenous shocks, if negative, cause the the potential terms of trade $\tau_{t}^{pot}$ to depreciate (a rise in $\tau_{t}^{pot}$ in equation 6) because they depress the marginal utility of consumption (noting $\phi_{mc}\hat{\sigma}^{open}$ $>$ $1$). If both shocks follow stationary AR(1)processes, and hence have front-loaded effects, a reduction in government spending or negative taste shock reduces $r_{t}^{pot}$. Finally, the nominal exchange rate $e_{t} $ equals $p_{t}+\tau{_{t}}$ where $p_{t}=p_{t-1}+\pi{_{t}}$.

Given that the form of the equations determining output, inflation, and interest rates is identical to that in a closed economy - as emphasized by Clarida et al - results from extensive closed economy analysis, e.g., Erceg and Lindé (2010a) are directly applicable for assessing the impact of government spending shocks in a liquidity trap.

We next consider how the model is modified for the CU case(largely following the analysis of Corsetti et al. 2011). A CU member takes the nominal exchange rate as fixed, so that the terms of trade $\tau_{t}$ is simply the gap between home and foreign price levels, i.e., $\tau_{t} =-(p_{t}-p_{t}^{\ast})=-p_{t}$.2 Moreover, the home economy is assumed to be small enough that the policy rate is effectively exogenous. Given that equation (4) implies that the output gap is proportional to the terms of trade gap, i.e., $x_{t}=\hat{\sigma}^{open}(\tau_{t}-\tau_{t}^{pot}),$ the price setting equation (2) may be expressed as a second order difference equation in the terms of trade

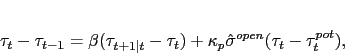
\begin{displaymath} \tau_{t}-\tau_{t-1}=\beta(\tau_{t+1\vert t}-\tau_{t})+\kappa_{p}\hat{\sigma} ^{open}(\tau_{t}-\tau_{t}^{pot}){,} \end{displaymath} (8)

yielding a solution of the form:

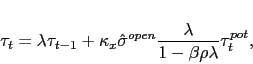
\begin{displaymath} \tau_{t}=\lambda\tau_{t-1}+\kappa_{x}\hat{\sigma}^{open}\frac{\lambda} {1-\beta\rho\lambda}\tau_{t}^{pot}{,} \end{displaymath} (9)

The persistence parameter $\lambda=0.5(a-\sqrt{a^{2}-4/\beta}$ ), where $a=(\frac{1}{\beta})(1+\beta$ + $\kappa_{x}\hat{\sigma}^{open}),$ lies between 0 and unity, and $\rho$ is the persistence of the shock processes (assumed to be the same for the taste shock and government spending). Equation (9) has two important implications. First, because $\lambda>0,$ a contraction in government spending - which raises $\tau_{t}^{pot}$ by equation (6) - moves $\tau_{t}$ in the same direction, implying a depreciation. 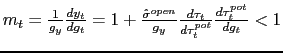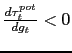Together with equation (4), this implies that the government spending multiplier $m_{t}$ is strictly less than unity, i.e., $m_{t}=\frac{1}{g_{y}}\frac{dy_{t}}{dg_{t}}=1+\frac{\hat{\sigma}^{open}} {g_{y}}\frac{d\tau_{t}}{d\tau_{t}^{pot}}\frac{d\tau_{t}^{pot}}{dg_{t}}<1$ (recalling that $\frac{d\tau_{t}^{pot}}{dg_{t}}<0$)$. $ Second, as $\kappa_{x}\hat{\sigma}^{open}$ becomes very small, $\lambda$ rises toward unity and the coefficient on $\tau_{t}^{pot}$ shrinks, implying very gradual adjustment of the terms of trade to $\tau_{t}^{pot}$ (and hence to a change in government spending); conversely,the terms of trade adjustment is more rapid if $\kappa_{x}\hat{\sigma}^{open}$ is larger. In economic terms, the terms of trade adjusts more quickly if the Phillips Curve slope is higher (high $\kappa_{x})$, or if aggregate demand is relatively sensitive to the terms of trade (high $\hat{\sigma}^{open}).$

2.1.  Simulation Results

The left panel of Figure 1 shows the effects of a 1 percent of baseline GDP cut in government spending under a calibration in which the Phillips Curve parameter relating inflation to marginal cost $\kappa_{mc}$ = $.025$. This calibration is towards the higher side of empirical estimates, while the right panel shows a calibration which sets $\kappa_{mc} $ = $.007$, towards the very low end of empirical estimates. If factors were completely mobile, these calibrations would imply mean price contract durations of about 7 and 12 quarters, respectively, but - as emphasized by an extensive literature (e.g., Altig et al., 2011) - the reduced form slopes could be regarded as consistent with much shorter contract durations under reasonable assumptions about strategic complementarities.3 As seen in the upper panels, the potential terms of trade $\tau_{t}^{pot}$ depreciates (rises) initially, and then dies out slowly at the rate $\rho=0.95.$ This fall in the relative price of domestically-produced goods reflects that the government spending cut boosts home consumption relative to foreign consumption. Moreover, the positive wealth effect reduces potential output $y_{t}^{pot}$ (lower panels). A country with an IMP - if unconstrained by the zero lower bound - could achieve this flexible price allocation simply through a monetary rule (3) that responded very aggressively to inflation and/or the output gap. Under such a rule, the terms of trade $\tau_{t}$ would track $\tau _{t}^{pot}$ exactly, and given that inflation remains unchanged from baseline, both the real and nominal interest rate would decline in line with ${r_{t}^{pot}}$, reflecting that consumption would be expected to fall after its initial rise. Thus, output would track $y_{t}^{pot}$ irrespective of the degree of price stickiness. With the price level constant, the jump in the real exchange rate would be achieved through nominal exchange rate depreciation.

In the CU case, the nominal exchange rate is fixed, so that the government spending cut initially boosts $\tau_{t}^{pot}$ by more than the actual terms of trade $\tau_{t}$ (upper panels)$.$ The negative terms of trade gap $\tau_{t}-\tau_{t}^{pot}$ $-$ which may be regarded as an "overvalued"terms of trade - causes output to fall persistently below potential. The negative output gap causes inflation to fall persistently - implying a progressive depreciation of the terms of trade - and the associated narrowing of the terms of trade gap eventually moves output towards potential. As noted previously, the adjustment process proceeds more quickly with shorter-lived price contracts, which explains why the output contraction in the left panel is smaller and less persistent than in the right panel. In addition, factors that raise the sensitivity $\hat{\sigma}^{open}$ of the output gap to the terms of trade gap - such as a higher trade elasticity $\varepsilon_{p}$ - would also speed-up the adjustment. Importantly, although the terms of trade adjusts sluggishly in line with the price level, it does at least move in the "right direction"for narrowing the output gap. Moreover, as highlighted by Corsetti et al. (2011), the ex ante long-term real interest rate falls in response to a persistent fall in government spending: although inflation declines in the near-term, the terms of trade (and hence the price level) must eventually revert to steady state, implying some rise in long-run expected inflation.

While greater price flexibility cushions the impact of a government spending cut in a CU, more price flexibility - or more generally, a larger Phillips Curve slope $\kappa_{x}$ - can greatly deepen the contraction that occurs under an IMP subject to the zero bound constraint, and imply an output multiplier much larger than in a CU. In this vein, Figure 1 shows the effects of the government spending contraction under an IMP against the backdrop of initial conditions which imply an ten quarter liquidity trap (i.e., a negative taste shock that is scaled to induce a liquidity trap lasting ten quarters in the absence of the fiscal shock). As the government spending shock reduces ${r_{t}^{pot}}$ while the policy rate remains fixed, the output gap would contract even if expected inflation remained constant. However, the output contraction is reinforced by a persistent decline in inflation that is particularly large when price adjustment is relatively rapid (the left panel). Thus, the peak output decline is 1.5 percent under the IMP, compared with 0.8 percent in a CU. Importantly, the large output decline under the IMP reflects two factors. First, long-term ex ante real interest rates rise substantially, in contrast to the decline that occurs in a CU. Second, the rise in the real interest rate under an IMP implies a "perverse"initial appreciation of the terms of trade (as seen in the upper left panel). Thus, although the CU precludes the nominal exchange rate from adjusting, the lack of adjustment better cushions output than the appreciation that occurs under an IMP.

Under more sluggish price adjustment, the multiplier is only 0.7 under an IMP, smaller than the multiplier of 0.9 in a CU. With inflation much less responsive, long-term real interest rates fall under an IMP, allowing a front-loaded terms of trade depreciation to cushion the impact on output. Overall, our results underscore that the same conditions which mitigate the effects of fiscal consolidation in a CU - namely, an upward-sloping Phillips Curve - exacerbate the effects under an IMP constrained by the ZLB; and conversely, a flatter Phillips Curve tends to make an IMP look more attractive, since the real exchange rate can adjust immediately to lessen the bite on aggregate demand.

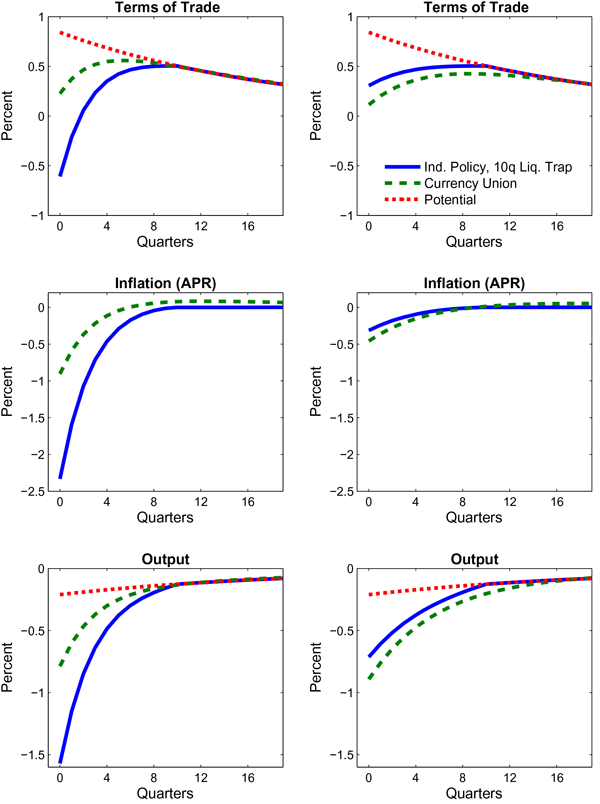
While the results in Figure 1 consider the specific case of a ten quarter liquidity trap, it is natural to ask how long a liquidity trap is required for fiscal consolidation to produce a more contractionary effect under an IMP than a CU. To address this, Figure 2 plots the output response to a 1 percent of GDP contraction under different assumptions about the duration of the liquidity trap under an IMP (generated by appropriately-sized adverse taste shocks). As in Figure 1, the left panel adopts the calibration in which price adjustment is relatively faster, while the right panel assumes that price adjustment is slower. In the former case, the output contraction becomes much more pronounced as the liquidity trap lengthens, with the multiplier in the case of a eight quarter liquidity trap exceeding the multiplier under a CU of 0.8. With a three year liquidity trap, the spending multiplier is nearly 3, as a sharp rise in long-term real interest rates (caused by lower expected inflation) causes a large improvement in the terms of trade (lower panel). In this environment, the anchoring of the long-run price level provided by a CU is very beneficial in insulating the economy from the potential pressures that can arise in a liquidity trap. By contrast, with slower price adjustment, the liquidity trap must last 12 quarters for the multiplier under an IMP to exceed that under a CU; for liquidity traps of less than two years, the front-loaded depreciation of the terms of trade significantly mitigates the effects of the spending cut on output. As the slope of the Phillips Curve becomes flatter, the liquidity trap duration required to produce a larger output downturn than in a CU becomes progressively longer.

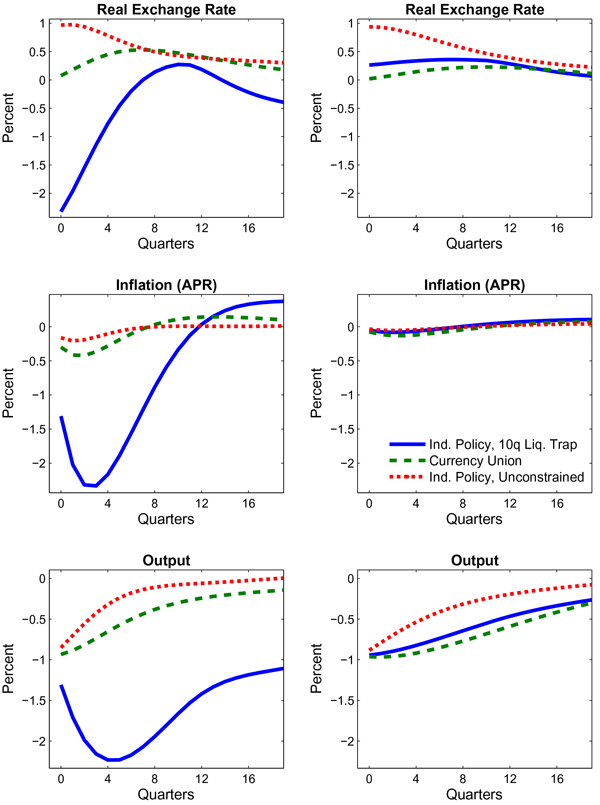
Thus far, our analysis has focused on a simple model that abstracts from an array of empirically-relevant nominal and real frictions. Even so, our key points continue to hold in more realistic open economy settings. Figure 3 shows responses to a 1 percent of GDP fiscal contraction in a larger-scale open economy model used in Erceg and Lindé (2010b) that embeds nominal wage and price rigidities, endogenous capital accumulation, rule-of-thumb consumers, and incomplete exchange rate passthrough in the short-run. The left panel with "faster price adjustment"adopts a calibration of the price and wage contract duration parameters that is broadly representative of the estimates of the slopes of price and wage Phillips Curves based on data prior to the financial crisis; specifically, it adopts the estimate of Altig et al. (2011) of $\kappa_{mc}=0.014.$ The right panel shows estimates under an alternative calibration that imposes an extremely flat price (and wage) Phillips Curve of $\kappa_{mc}=0.002$ .4 The unconstrained IMP follows a Taylor rule, while the constrained policy is derived under the assumption that the liquidity trap lasts ten quarters.

Under the calibration with relatively faster price adjustment, output declines over 2 percent after 4 quarters under the constrained IMP, compared with only about 0.8 percent in a CU. The larger output decline in the former case reflects a larger fall in inflation (middle left panel) - which pushes up long-term real interest rates - and a sizeable real appreciation of the exchange rate. Thus, the fiscal shock is amplified by a sharp contraction in private domestic demand and real net exports. In a CU, the real exchange rate depreciates slightly even in the near-term, and the long-term real interest rate is about constant. By contrast, under very slow price adjustment - the right panel - the effects of fiscal consolidation on output are modestly smaller under a constrained IMP than CU. The smaller output decline under an IMP reflects both a front-loaded exchange rate depreciation and fall in long-term real interest rates (since inflation barely moves, and policy rates fall after two years). For a shorter-lived liquidity trap, the advantages of an IMP are even larger.5


3.  Implications and Open Questions

Conditional on some key structural parameters, including those highlighted above, our modeling framework can potentially help gauge whether the output effects of fiscal consolidation in an economy such as the United Kingdom - where policy rates are constrained by the ZLB -are likely to be larger than in a CU member such as Belgium. But given that even the qualitative answer hinges on factors that determine the responsiveness of inflation, which view does the evidence favor?

There is substantial econometric evidence estimating the sensitivity of price inflation to marginal cost; as noted, the calibration in the left side of Figure 3 seems squarely in line with such evidence. On this basis, fiscal consolidation would have a deeper contractionary impact under an IMP provided that the ZLB was binding for over two years; and the seeming strictures of a CU would in fact ameliorate the output contraction.

However, the resilience of inflation during the recent global recession suggests the possibility that the responsiveness of inflation may be considerably lower than implied by most existing econometric evidence. As seen in the left panel of Figure 3, the 1 percent of GDP fiscal contraction reduces inflation by 2 percentage points. Moreover, under the same calibration of price adjustment, a fall in output of say 6-8 percent or more below its pre-crisis trend path - as was experienced by the United States and Europe during the recession - would cause inflation and one-year ahead expected inflation to fall more than 4 percentage points below the central bank's inflation target if mainly driven by aggregate demand shocks. This implied decline in inflation is much larger than actually occurred either in the United States, where core inflation and market expectations of core inflation remained above 1 percent, or in major economies in Europe.

It is quite conceivable that inflation behavior during the past few years can be rationalized as consistent with econometric evidence based on pre-crisis observations. For example, financial shocks and other shocks may have adversely impacted the supply side of the economy enough to square observed inflation behavior with existing econometric evidence. However, future analysis may well point to a somewhat lower degree of inflation responsiveness. If so, outside of a very prolonged liquidity trap, our analysis would indicate that an economy with an IMP may be somewhat better poised to absorb the effects of fiscal consolidation than a CU, with real exchange rate and interest movements tending to cushion rather than amplify the impact.

Figure 1: Persistent Contraction in Government Spending

Data for Figure 1 immediately follows.

Data for Figure 1 (Fast Price Adjustment)

QuarterIndependent Policy, 10q Liquidity Trap: Terms of Trade - PercentIndependent Policy, 10q Liquidity Trap: Inflation (APR) - Percentage PointsIndependent Policy, 10q Liquidity Trap: Output - PercentCurrency Union: Terms of Trade - PercentCurrency Union: Inflation (APR) - Percentage Points Currency Union: Output - Percent Potential (Flex Price-Wage Economy): Terms of Trade - Percent Potential (Flex Price-Wage Economy): Inflation (APR) - Percentage PointsPotential (Flex Price-Wage Economy): Output - Percent
0-0.608624308-2.332085841-1.5706309350.225978483-0.903913933-0.7881282230.8420520810-0.210513020
1-0.211196814-1.589709976-1.1480128530.373030237-0.588207016-0.6002561750.7999494770-0.199987369
20.05682354-1.072081415-0.8492236690.46534034-0.369240409-0.4662085310.7599520030-0.189988001
30.234815151-0.711966443-0.6372181850.519827835-0.217949983-0.3699974170.7219544030-0.180488601
40.35039465-0.462317998-0.4859849860.54832163-0.113975179-0.3004135980.6858566830-0.171464171
50.422959735-0.290260339-0.3772244640.55908514-0.043054041-0.2495966870.6515638490-0.162890962
60.466181052-0.172885267-0.2980121910.55788460.004802163-0.2120332370.6189856560-0.154746414
70.489761726-0.094322696-0.2391489460.5487375930.036588026-0.1838546470.5880363730-0.147009093
80.500689541-0.043711262-0.1939864350.534437520.057200294-0.1623451740.5586345550-0.139658639
90.504141983-0.013809768-0.1575784900.5169210430.070065907-0.1455971630.5307028270-0.132675707
100.50416004-7.22275E-05-0.1260490900.4975255220.077582084-0.1322694480.5041676860-0.126041921
110.478952038-6.86162E-05-0.1197466350.4771693480.081424693-0.1214180400.4789593010-0.119739825
120.455004436-6.51854E-05-0.1137593030.4564782680.082764321-0.1123774750.4550113360-0.113752834
130.432254214-6.19261E-05-0.1080713380.4358738490.082417677-0.1046776590.4322607690-0.108065192
140.410641504-5.88298E-05-0.1026677710.415635430.080953675-0.0979855910.4106477310-0.102661933
150.390109428-5.58883E-05-0.0975343830.3959434910.078767757-0.0920645120.3901153440-0.097528836
160.370603957-5.30939E-05-0.0926576640.3769099980.076133971-0.0867452770.3706095770-0.092652394
170.352073759-5.04392E-05-0.0880247800.3585996360.07324145-0.0819062820.3520790980-0.088019775
180.334470071-4.79172E-05-0.0836235410.3410446430.070219972-0.0774593880.3344751430-0.083618786
190.317746568-4.55214E-05-0.0794423640.3242551780.06715786-0.0733400540.3177513860-0.079437847

Data for Figure 1 (Slow Price Adjustment)

QuarterIndependent Policy, 10q Liquidity Trap: Terms of Trade - PercentIndependent Policy, 10q Liquidity Trap: Inflation (APR) - Percentage PointsIndependent Policy, 10q Liquidity Trap: Output - PercentCurrency Union: Terms of Trade - PercentCurrency Union: Inflation (APR) - Percentage PointsCurrency Union: Output - PercentPotential (Flex Price-Wage Economy): Terms of Trade - PercentPotential (Flex Price-Wage Economy): Inflation (APR) - Percentage PointsPotential (Flex Price-Wage Economy): Output - Percent
00.306144855-0.314083178-0.7129662370.114383047-0.457532189-0.8927573140.8420520810-0.210513020
10.366238472-0.240374469-0.6066239640.203784208-0.357604641-0.7589370220.7999494770-0.199987369
20.411401577-0.180652418-0.5167801660.272696525-0.275649272-0.6468265550.7599520030-0.189988001
30.444550091-0.132594055-0.4405759490.324842095-0.208582277-0.5528111730.7219544030-0.180488601
40.468122382-0.094289166-0.3756064080.363302605-0.15384204-0.4738828100.6858566830-0.171464171
50.484166017-0.064174541-0.3198389840.390627868-0.109301052-0.4075380140.6515638490-0.162890962
60.494411046-0.040980114-0.2715444540.408926035-0.073192669-0.3516930630.6189856560-0.154746414
70.500332336-0.023685159-0.2292382060.419938588-0.044050211-0.3046133750.5880363730-0.147009093
80.503203102-0.011483064-0.1916297830.425102669-0.020656323-0.2648547970.5586345550-0.139658639
90.504141469-0.003753471-0.1575789720.425602887-0.002000874-0.2312147830.5307028270-0.132675707
100.504151683-4.08557E-05-0.1260569250.4224143740.012754053-0.2026917830.5041676860-0.126041921
110.478944099-3.88129E-05-0.1197540790.4163385560.024303272-0.1784514710.4789593010-0.119739825
120.454996894-3.68722E-05-0.1137663750.4080328850.033222685-0.1577986560.4550113360-0.113752834
130.432247049-3.50286E-05-0.1080780560.3980355330.039989408-0.1401539190.4322607690-0.108065192
140.410634697-3.32772E-05-0.1026741530.3867859080.044998498-0.1250341810.4106477310-0.102661933
150.390102962-3.16133E-05-0.0975404450.3746416950.048576853-0.1120365430.3901153440-0.097528836
160.370597814-3.00327E-05-0.0926634230.3618930010.050994776-0.1008248380.3706095770-0.092652394
170.352067923-2.8531E-05-0.0880302520.3487741050.052475581-0.0911184530.3520790980-0.088019775
180.334464527-2.71045E-05-0.0836287390.335473210.05320358-0.0826830230.3344751430-0.083618786
190.317741301-2.57493E-05-0.0794473020.322140530.053330721-0.0753226950.3177513860-0.079437847

Figure 2: Impact Output Response to Immediate Government Spending Cut With Independent Monetary Policy and in a Currency Union

Data for Figure 2 immediately follows.

Data for Figure 2 (Fast Price Adjustment)

Liquidity Trap DurationIndependent Policy, 10q Liquidity Trap: Terms of Trade - PercentIndependent Policy, 10q Liquidity Trap: Output - PercentCurrency Union: Terms of Trade - PercentCurrency Union: Output - PercentPotential (Flex Price-Wage Economy): Terms of Trade - PercentPotential (Flex Price-Wage Economy): Output - Percent
12-1.841507952-2.7265518180.225978483-0.7881282230.842039311-0.210524993
11-1.132063479-2.0613944170.225978483-0.7881282230.842039311-0.210524993
10-0.608624308-1.5706309350.225978483-0.7881282230.842039311-0.210524993
9-0.222312435-1.2084345820.225978483-0.7881282230.842039311-0.210524993
80.062962371-0.9409680550.225978483-0.7881282230.842039311-0.210524993
70.273876834-0.7432199270.225978483-0.7881282230.842039311-0.210524993
60.430192709-0.5966620710.225978483-0.7881282230.842039311-0.210524993
50.546614312-0.4875080860.225978483-0.7881282230.842039311-0.210524993
40.634180648-0.4054080790.225978483-0.7881282230.842039311-0.210524993
30.70132546-0.3424547810.225978483-0.7881282230.842039311-0.210524993
20.754709258-0.2924034680.225978483-0.7881282230.842039311-0.210524993
10.799908696-0.2500256050.225978483-0.7881282230.842039311-0.210524993
00.842039311-0.2105249930.225978483-0.7881282230.842039311-0.210524993

Data for Figure 2 (Slow Price Adjustment)

Liquidity Trap DurationIndependent Policy, 10q Liquidity Trap: Terms of Trade - PercentIndependent Policy, 10q Liquidity Trap: Output - PercentCurrency Union: Terms of Trade - PercentCurrency Union: Output - PercentPotential (Flex Price-Wage Economy): Terms of Trade - PercentPotential (Flex Price-Wage Economy): Output - Percent
120.114144157-0.8929812920.114383047-0.8927573140.842025354-0.210538079
110.216242858-0.7972561030.114383047-0.8927573140.842025354-0.210538079
100.306144855-0.7129662370.114383047-0.8927573140.842025354-0.210538079
90.385514181-0.6385515410.114383047-0.8927573140.842025354-0.210538079
80.455846623-0.5726096030.114383047-0.8927573140.842025354-0.210538079
70.518501345-0.5138661010.114383047-0.8927573140.842025354-0.210538079
60.57473148-0.4611461330.114383047-0.8927573140.842025354-0.210538079
50.625714584-0.4133456490.114383047-0.8927573140.842025354-0.210538079
40.672584002-0.3694020540.114383047-0.8927573140.842025354-0.210538079
30.716462286-0.3282628720.114383047-0.8927573140.842025354-0.210538079
20.758498047-0.2888511930.114383047-0.8927573140.842025354-0.210538079
10.79990788-0.2500263690.114383047-0.8927573140.842025354-0.210538079
00.842025354-0.2105380790.114383047-0.8927573140.842025354-0.210538079

Figure 3: Persistent Government Spending Cut in Large Model

Data for Figure 3 immediately follows.

Data for Figure 3 (Fast Price Adjustment)

QuarterIndependent Policy, 10q Liquidity Trap: Terms of Trade - PercentIndependent Policy, 10q Liquidity Trap: Inflation (APR) - Percentage PointsIndependent Policy, 10q Liquidity Trap: Output - PercentCurrency Union: Terms of Trade - PercentCurrency Union: Inflation (APR) - Percentage PointsCurrency Union: Output - PercentPotential (Flex Price-Wage Economy): Terms of Trade - PercentPotential (Flex Price-Wage Economy): Inflation (APR) - Percentage PointsPotential (Flex Price-Wage Economy): Output - Percent
0-2.324251977-1.309104459-1.3090808610.075218175-0.30009077-0.9342844980.967674798-0.163001541-0.851520781
1-1.959884008-2.021118801-1.7076618310.179783151-0.416685487-0.8864164010.974439204-0.208154851-0.701779036
2-1.548743944-2.317688974-1.9880602940.285894025-0.422365748-0.8171494370.937207128-0.192116739-0.555503791
3-1.141764712-2.332336391-2.1583041310.378114337-0.366691528-0.7365826010.867683672-0.150600986-0.425536843
4-0.770461104-2.164526115-2.2333602750.449245536-0.282593015-0.6532141570.782379614-0.104349913-0.318747972
5-0.452338476-1.888523564-2.2315093290.497351702-0.191033501-0.5731175460.695413049-0.063893603-0.236630898
6-0.194935025-1.559231168-2.1715688470.523645877-0.104497592-0.5000450260.616211401-0.033248141-0.177008086
70.001101105-1.21630477-2.0710260340.53102563-0.029615522-0.4358719160.549570126-0.012654315-0.135770520
80.139655099-0.887282394-1.9449600280.5230943820.03087847-0.3811083330.496692328-0.000482602-0.108234497
90.227352152-0.590114264-1.8055730690.5035399810.076710569-0.3353611820.4564592310.005541964-0.090023288
100.272217914-0.335286315-1.6622251820.4757696440.109041599-0.2977054430.426557730.00763233-0.077529838
110.263702414-0.127617335-1.5298783410.4427229440.129758102-0.2669598880.4043191770.007596951-0.068069509
120.1855840140.033269303-1.4194851160.4068033290.141003265-0.2418779750.3872530550.006733241-0.059835362
130.0796529170.152149736-1.3333160640.369884050.144884698-0.2212700880.3733230820.005856783-0.051749665
14-0.0299310060.236062328-1.2687934620.3333568150.143308527-0.2040737120.3610359640.005394951-0.043279298
15-0.1307078720.292663374-1.2211936520.2982012070.137900343-0.1893862540.3494120170.00549865-0.034257833
16-0.2175388120.329133339-1.1853567340.2650604010.129983019-0.1764726330.3378944490.006145639-0.024736826
17-0.2895114480.351570889-1.1566516930.2343142020.120589353-0.1647570150.3262380760.007223028-0.014874416
18-0.3478640470.364761519-1.1314152390.206144410.110493837-0.1538056070.3144030190.008585803-0.004860224
19-0.3946810540.372199302-1.1070485970.1805902220.100252896-0.1433054030.3024666930.010093430.005129259

Data for Figure 3 (Fast Price Adjustment)

QuarterIndependent Policy, 10q Liquidity Trap: Terms of Trade - PercentIndependent Policy, 10q Liquidity Trap: Inflation (APR) - Percentage PointsIndependent Policy, 10q Liquidity Trap: Output - PercentCurrency Union: Terms of Trade - PercentCurrency Union: Inflation (APR) - Percentage PointsCurrency Union: Output - PercentPotential (Flex Price-Wage Economy): Terms of Trade - PercentPotential (Flex Price-Wage Economy): Inflation (APR) - Percentage PointsPotential (Flex Price-Wage Economy): Output - Percent
00.262112413-0.052292167-0.9437060500.019090489-0.076104845-0.9625405950.937375096-0.036846745-0.883749316
10.280825388-0.076609991-0.9238101950.048064084-0.115428301-0.9663645630.927933777-0.052792981-0.788800979
20.30103663-0.082924654-0.8962538810.080908877-0.130768261-0.9593491960.898180716-0.056155267-0.697969554
30.319959243-0.07787383-0.8623628050.113743322-0.13065061-0.9428721680.852968154-0.052286404-0.613610635
40.335901059-0.065905678-0.8236038420.144118389-0.12080205-0.9185261560.798060008-0.044585099-0.537259673
50.347907296-0.050017865-0.7813168420.170556628-0.105100659-0.8878343430.738446297-0.035165053-0.469563625
60.355521476-0.032237945-0.7366416260.192244785-0.086192294-0.8521569100.677934165-0.025300514-0.410458796
70.358623733-0.013937574-0.6905210570.208826449-0.065892302-0.8126762810.61917919-0.015723491-0.359398380
80.3573201120.00396059-0.6437282910.220260242-0.045448829-0.7704108930.563867386-0.006821693-0.315555255
90.3518657510.020845561-0.5968972240.226721267-0.025716656-0.7262361970.512933160.001230372-0.277977933
100.3426107820.036325988-0.5505488540.228531404-0.007273044-0.6809047800.466764630.008385403-0.245699286
110.3172190130.050167698-0.5065850240.2261090720.00950413-0.6350631770.4253771720.014667739-0.217805650
120.2833847470.062285951-0.4659061830.2199323630.024382818-0.5892652380.3885502860.020138204-0.193475747
130.2462166350.072696477-0.4287581830.2105115310.037239364-0.5439826660.3559297860.024872547-0.171998170
140.2089900470.081478232-0.3950011040.1983682190.048031697-0.4996134720.3271003230.028948822-0.152774580
150.1737014290.088746181-0.3642900040.1840196450.056779614-0.4564890050.3016340730.032440539-0.135314066
160.1414723650.094632233-0.3361929580.1679665750.063549847-0.4148800220.2791212420.035413437-0.119222629
170.1128404670.09927249-0.3102649030.1506842360.068444443-0.3750021680.2591872940.03792447-0.104190462
180.0879657850.102799237-0.2860908480.1326156070.071591485-0.3370210540.2415008970.040022038-0.089978811
190.06677480.105336327-0.2633083640.1141666370.073137526-0.3010570860.2257757160.041746876-0.076407485

References

Altig, David, Christiano, Lawrence J., Eichenbaum, Martin and Jesper Lindé (2011), "Firm-Specific Capital, Nominal Rigidities and the Business Cycle", Review of Economic Dynamics 14(2), 225-247.

Clarida, Richard, Jordi Galí and Mark Gertler (2001), "Optimal Monetary Policy in Open Versus Closed Economics: An Integrated Approach", American Economic Review Papers and Proceedings 91, 248-252.

Corsetti Giancarlo, Keith Kuester, and Gernot J. Müller (2011), "Floats, Pegs, and the Transmission of Fiscal Policy,"Journal Economía Chilena 14(2), 5-38.

Erceg, Christopher and Jesper Lindé (2010a), "Is There A Fiscal Free Lunch In a Liquidity Trap?", International Finance Discussion Papers No. 1003.

Erceg, Christopher and Jesper Lindé (2010b), "Asymmetric Shocks in a Currency Union with Monetary and Fiscal Handcuffs", NBER International Seminar on Macroeconomics 2010, 95-135.

Ilzetzki, Ethan, Enrique G. Mendoza and Carlos A. Végh (2010), "How Big (Small?) are Fiscal Multipliers?", NBER Working Paper Series No. 16479.

Footnotes

1.  See e.g., Erceg and Lindé (2010a) and the references therein. Return to text

2.  As the real exchange rate is proportional to $\tau_{t}$, we use the terms interchangeably. Return to text

3.  We adopt a standard quarterly calibration by setting the discount factor $\beta=0.995,$ and steady state net inflation $\pi=.005$ so that $i=.01$. We set $\sigma=1$ (log utility)$,$ the capital share $\alpha=0.3,$ the Frisch elasticity of labor supply $\frac{1}{\chi}=0.4,$ the government spending share $g_{y}=0.2,$ and the taste shock parameter $\nu _{c}=0.01\ ($implying $\phi_{mc}$ = $\frac{\chi}{1-\alpha}$+ $\frac{1} {\hat{\sigma}^{open}}$+ $\frac{\alpha}{1-\alpha}$ = 5.1). In the absence of the ZLB, monetary policy completely stabilizes output and inflation (achieved by making $\gamma_{\pi}$ in eq. 3 arbitrarily large). Finally, the open economy parameters $\omega$ = 0.3 and $\varepsilon_{p}$ = 1.5. Return to text

4.  Under "faster price adjustment,"the contract duration parameters for prices and wages are $\xi_{p}=0.86$ and $\xi_{w}=0.82,$ respectively, while $\xi_{p}=0.95$ and $\xi_{w}=0.90$ under "slower price adjustment."The model and calibration of the other parameters are described in Erceg and Lindé (2010b). Return to text

5.  A permanent reduction in government spending would have very similar effects in the larger model to those shown in Figure 3. By contrast, a permanent cut would have no effect on the output gap (even in a liquidity trap) in the stylized model, as the absence of real rigidities allows for strong and immediate crowding-in effects. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: May 23, 2013