
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1049, June 2012 --- Screen Reader
Version*
Exchange Rate Policy and Sovereign Bond Spreads in Developing Countries**
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper empirically analyzes how exchange rate policy affects the issuance and pricing of international bonds for developing countries. We find that countries with less flexible exchange rate regimes pay higher sovereign bond spreads and are less likely to issue bonds. Quantitatively, changing a free-floating regime to a fixed regime decreases the likelihood of bond issuance by 4.6% and increases the bond spread by 1.3% on average. Furthermore, countries with real exchange rate overvaluation have higher bond spreads and higher bond issuance probabilities. Moreover, such positive effects of real exchange rate overvaluation tend to be magnified for countries with fixed exchange rate regimes. Our results suggest that choosing a less flexible exchange rate regime in general leads to higher borrowing costs for developing countries, especially when their currencies are overvalued.
Keywords: Sovereign bond spread, exchange rate regime, overvaluation, debt crisis
JEL classification: E58, F31, F33, F34
1 Introduction
The recent turmoil in the euro zone has disturbed European economies ranging from peripheral to core countries and raises wide spread concerns over the likelihood of sovereign default and the fate of the euro. The relation between exchange rate arrangements and country risk has long been considered an important policy issue. However, the relation has yet to be studied formally in the academic literature. The goal of our paper is to empirically examine how exchange rate policy affects the issuing and pricing of foreign debt for developing countries. This study has potentially useful implications for developed countries, such as those affected by the euro zone debt crisis.
Due to the risk of default,1 developing countries pay a sizable default risk premium on their debt. Moreover, developing countries typically have a large amount of debt denominated in foreign currency. When the foreign debt is denominated in foreign currency, a weaker local currency can exacerbate debt service difficulties through the balance sheet effect and affect the country spread. Hence, exchange rate management plays an important role for developing countries' foreign debt financing. At the same time, the choice of an exchange rate regime remains an elusive part of macroeconomic policy. In this paper, we analyze the impact of exchange rate policy on foreign borrowing using primary bond market data on 42 developing countries. Our main methodology is to estimate a Heckman's sample selection model (Heckman, 1979). In our empirical analysis, we draw on findings in the literature to obtain a reasonable set of control variables and include exchange rate policy as explanatory variables for bond issuance probability and bond spread. We examine the effects of exchange rate policy on the issuance and pricing of international bonds by developing countries.
One measure of a country's exchange rate policy is its exchange rate regime. It remains an open question as to how the choice of an exchange rate regime impacts a country's foreign debt borrowing. First, there are virtually no comprehensive empirical studies on this question.2 Second, whether a country issues a bond and how the bond is priced at issuance are presumably affected by its overall economic performance. However, there is no consensus in the literature as to which exchange rate arrangement promotes a country's economic performance. The impact of exchange rate regimes on economic performance is probably one of the most controversial topics in macroeconomic policies.
Supporters of a flexible exchange rate system argue that countries with hard-pegged currencies are more vulnerable to real shocks, which may adversely affect growth and macro stability. More flexible arrangements can better accommodate shocks and thus reduce the uncertainty in the economy. 3 Based on this argument, a fixed exchange rate regime results in higher default risk in the context of foreign borrowing. Moreover, by eliminating monetary policy as a viable policy instrument, hard pegs may force a government to increase its external liabilities, resulting in higher default risk. Gertler, Gilchrist, and Natalucci (2007) show that fixed exchange rates exacerbate financial crises by tying the hands of the monetary authorities in a financial accelerator framework.4
However, supporters of a fixed exchange rate regime argue that this type of exchange rate arrangement provides policy credibility. For example, pegging the exchange rate may help to impose fiscal discipline on the government. 5 The disciplining effect of a peg may lead to a reduction in the country's default risk. Arellano and Heathcote (2010) show that countries with dollarization face a more favorable borrowing environment because without the monetary policy instrument, these countries value their access to the foreign capital market more and are thus less likely to default. Moreover, supporters of a fixed exchange rate system believe that it fosters a more stable environment and promotes economic growth. As argued in the literature, hard pegs can lead to lower interest rates and eliminate exchange rate volatility, which stimulates investment and international trade, resulting in faster growth. 6 These growth-enhancing effects suggest that a fixed exchange rate regime may be advantageous to a country's foreign borrowing.
As the preceding discussion suggests, determining how a country's exchange rate regime affects its default risk and its foreign debt borrowing is ultimately an empirical issue that can only be elucidated by analyzing the historical evidence.
Our first main finding is that the choice of an exchange rate regime has a significant impact on foreign borrowing by developing countries. Specifically, the less flexible is a country's exchange rate regime, the lower is the likelihood it issues foreign bonds and the higher are the spreads it has to pay. The decrease in the bond issuance probability and the increase in the bond credit spreads are both statistically and economically significant. Changing an exchange rate regime from free-floating to intermediate reduces the bond issuance probability by about 1.5% and increases the average spread by 54 basis points. A further change from an intermediate one to a fixed one decreases the issuance probability by 4 and increases the spread by an additional 34 basis points. Our results, therefore, unambiguously point to the adverse effect of a fixed exchange rate regime on a country's foreign debt financing, which is consistent with the conclusions from Gertler et al. (2007).
Next, we examine the relation between a country's real exchange rate and its sovereign debt borrowing. A country's debt policy may respond to its real exchange rate overvaluation, defined as the difference between the actual real exchange rate and its long-run equilibrium level, for the following reasons.7 First, an overvalued currency reduces a country's trade competitiveness and weakens the macroeconomic fundamentals.8As a result, the default risk may increase, causing an increase in the borrowing costs (Eaton and Gersovitz, 1981). Second, exchange rate overvaluation has been found to be a main cause of currency crises. A vast amount of literature finds that the real exchange rate is overvalued prior to a currency crisis.9 When a country borrows in a foreign currency, its debt liability becomes more costly to serve following the devaluation and hence the default risk rises.10 Lastly, the choice of an exchange rate regime and real exchange rate overvaluation may have a joint impact on the sovereign debt markets. An inflexible exchange rate regime compounds the adverse effects of a real overvaluation because the cost of correcting the exchange rate misalignment is higher for a country with a fixed exchange rate.11 Therefore, a country with an inflexible exchange rate regime is more likely to default on its debt when its currency is overvalued.
Consistent with these arguments, we find that real exchange rate overvaluation in general gives rise to higher bond spreads for developing countries, and this effect is stronger for those with a less flexible exchange rate regime. In our empirical analysis, we use three measures of real exchange rate overvaluation to examine its impact on sovereign bond markets.12 Quantitatively we find that a one-standard-deviation increase in the real exchange rate overvaluation, measured by the percentage deviation of the real effective exchange rate from its 10-year average, increases the spread by 28 basis points on average. Moreover, the increase is magnified by the inflexibility of exchange rate regimes. We show that a one-standard-deviation increase in real exchange rate overvaluation increases the spread by 64 basis points for a country with a fixed exchange rate regime, while the same increase only widens it by 34 basis points for a country under an intermediate regime and 7 basis points for one under a floating regime. The same pattern persists when the other two measures are used.
Our main results hold in a variety of robustness tests that correct for endogeneity and allow for alternative control variables. To address the endogeneity problem for exchange rate regimes and real overvaluation, we conduct a multistage estimation of the Heckman selection model using a set of instrumental variables. We find that controlling for endogeneity does not change our results qualitatively.
Linking explicitly exchange rate policy to bond issuance and pricing is this paper's main contribution to the literature on sovereign default risk in emerging economies. Edwards (1984), Cline (1995), Easton and Rockerbie (1999), and others investigate the determinants of sovereign loan spreads. Eichengreen and Mody (2000) and Kamin and Kleist (1999) analyze bond spreads on the primary markets for developing countries. However, none of these empirical works incorporate the impact of exchange rate policy on sovereign bond pricing and issuance. Edwards (1984) includes nominal exchange rate devaluation as one determinant of spreads, but the impact of devaluation is not significant. We use the real exchange rate overvaluation in our analysis and find it increases spreads significantly.
There are a few empirical analyses and event studies relating exchange rate policy to a country's default risk. Reinhart (2002) examines the linkages between default, currency crises, and sovereign credit rating. She finds that defaults usually follow sharp devaluation or are responses to speculative attacks on exchange rate arrangements. Powell and Sturzenegger (2000) evaluate the relation between the elimination of currency risk through dollarization and country risk, yet their analysis is limited to countries that adopted the U.S. dollar or euro.
This paper also relates to the recent studies on the impact of exchange rate regime and real exchange rate volatility. Levy-Yeyati and Sturzenegger (2003) study the relationship between exchange rate regimes and growth, and find that less flexible exchange rate regimes are associated with slower growth. Broda (2004) finds that countries with flexible regimes are able to buffer terms-of-trade shocks better than those with fixed regimes. Aghion et al. (2009) show some empirical evidence that real exchange rate volatility can affect the long-term productivity growth rate and that the effect depends critically on a country's level of financial development. Our work assesses the impact of exchange rate policy on sovereign default risk, which is another important dimension for developing countries.
In the remainder of the paper, we describe the datasets and our methodology. The main empirical analysis is carried out in Section 3. In Section 4 we summarize the paper and conclude.
2 Data and Methodology
2.1 The Data
The bond data used are from Capital Data's Bondware and contains detailed terms of bonds issued in the primary markets by 42 developing countries between January 1990 and December 2006.13 The Bondware data set contains information on the launch spreads and launch dates of international bonds denominated in dollars issued by developing countries. The launch spread of an issued bond is defined as the difference between its yield and the comparable U.S. Treasury yield. We use the Bondware data at the individual bond level at a monthly frequency. There are a total of 2,653 bond issues in the sample. The list of countries and the total number of bond issues in the sample period are reported in Table 1. Using the primary market data allows us to analyze both the issuing and pricing decisions of developing countries.
Table 1: List of Countries and the Number of Bond Issues
This table lists the names of the 42 countries used and the number of bond issues in the sample.
| Country | # |
|---|---|
| Argentina | 289 |
| Azerbaijan | 2 |
| Bolivia | 1 |
| Brazil | 692 |
| Bulgaria | 3 |
| Chile | 71 |
| China, P. R. | 93 |
| Colombia | 58 |
| Congo, Republic of | 1 |
| Costa Rica | 11 |
| Croatia | 4 |
| Dominican Republic | 8 |
| Ecuador | 5 |
| Egypt | 3 |
| El Salvador | 14 |
| Grenada | 1 |
| Guatemala | 8 |
| India | 60 |
| Indonesia | 107 |
| Jamaica | 20 |
| Jordan | 5 |
| Kazakhstan | 69 |
| Latvia | 1 |
| Malaysia | 54 |
| Mauritius | 7 |
| Mexico | 336 |
| Moldova | 2 |
| Pakistan | 8 |
| Peru | 19 |
| Philippines | 130 |
| Poland | 20 |
| Romania | 5 |
| Russia | 190 |
| South Africa | 22 |
| Sri Lanka | 4 |
| Thailand | 78 |
| Turkey | 97 |
| Ukraine | 36 |
| United Arab Emirates | 32 |
| Uruguay | 30 |
| Venezuela | 56 |
| Vietnam | 1 |
We use the de facto exchange rate regime as a key explanatory variable in our empirical analysis. We employ the monthly classification of the de facto exchange rate regimes constructed by Reinhart and Rogoff (2002) (hereafter, RR), who classify the exchange rate arrangements based on the official exchange rates and parallel market rates. We use the de facto exchange rate regime as opposed to the de jure exchange rate regime because the latter is not a good measure of a country's exchange rate arrangement.14 In most of the analysis, we aggregate the RR exchange rate regime classification into three groups: fixed, intermediate, and free floating. 15 The aggregation of exchange rate regimes is summarized in Table 2.16 In the empirical analysis, we use the following exchange rate regime dummies: FIX (fixed regimes), INT (intermediate regimes), and FLOAT (free floating regimes). FIX (resp., INT or FLOAT) takes the value of 1 when the country is operating under a fixed exchange rate regime (resp., an intermediate or free floating regime) and 0 otherwise.
Table 2: Exchange Rate Regime Classification
Exchange rate regimes are aggregated into three groups: fixed, intermediate, and floating regimes. We use the exchange rate classification from Reinhart and Rogoff (2002).
| Aggregate Class | Reinhart and Rogoff (2002) Classification |
|---|---|
| Fixed (FIX) | (1) No separate legal tender |
| Fixed (FIX) | (2) Pre-announced peg or currency board arrangement |
| Intermediate (INT) | (3) Pre-announced horizontal band that is less than or equal to |
| Intermediate (INT) | (4) De facto peg |
| Intermediate (INT) | (5) Pre-announced crawling peg |
| Intermediate (INT) | (6) Pre-announced crawling band that is less than or equal to |
| Intermediate (INT) | (7) De factor crawling peg |
| Intermediate (INT) | (8) De facto crawling band that is less than or equal to |
| Intermediate (INT) | (9) Pre-announced crawling band that is greater than or equal to |
| Intermediate (INT) | (10) De facto crawling band that is less than or equal to |
| Intermediate (INT) | (11) Moving band that is less than or equal to |
| Floating (FLOAT) | (12) Managed floating |
| Floating (FLOAT) | (13) Freely floating |
Next, we measure real exchange rate overvaluation in three different ways. 17 The first two measures are computed using monthly real effective exchange rates (REER) from the IMF Information Notice System. The REER is a trade-weighted index of multilateral real rates measured by units of foreign goods per domestic goods. The first measure of real exchange rate overvaluation, labeled as ROV1, is the percentage deviation of the REER from its 10-year average. The second measure, ROV2, is the percentage change in the REER over the past five years.18 The third measure, ROV3, is the deviation of the Purchasing Power Parity (PPP) real exchange rate from a certain predicted level. The PPP real exchange rates are retrieved from the Penn World Table (PWT). The predicted level of the PPP real exchange rate is based on the equilibrium concept of Purchasing Power Parity and is adjusted from differences in the relative prices of nontradeables to tradeables attributed to differences in factor endowments (i.e., the "Balassa-Samuelson"effect). 19 Following Dollar (1992) and Aghion et al. (2009), we first perform a pooled ordinary least squares (OLS) regression to obtain the predicted value as an estimate of the equilibrium value of the real exchange rate, and then take the difference between the actual PPP real exchange rate and its predicted value from the OLS regression as the third measure of real exchange rate overvaluation. In the pooled OLS regression, income per capita relative to that of the United States as well as geographical and year dummies are used as proxies for factor endowments.
We draw on the findings in the literature to obtain a comprehensive set of control variables that have been found to be important determinants of bond spreads.20 We use the real interest rate on ten-year U.S. Treasury bond (USRATE) and the U.S. high yield corporate bond spread (HYD) as proxies for the global economic condition. For the domestic economic indicators, we use the GDP growth rate (GDPGR), the GDP per capita in U.S. dollars (GDPPC), the current account as a fraction of GDP (CA2GDP), and inflation (INF). We also include some liquidity and solvency variables, such as total dollar amount and number of bonds issued in the previous year (AMOUNT, ISSUES), the ratio of debt to GNP (DT2GNP), the ratio of debt service to exports (DS2EX), and the ratio of short-term debt to total debt (SHORTDT). In addition, following Eichengreen and Mody (2000) and Dell'Ariccia et al. (2006) we include the residual of credit ratings (RATING) from a regression of the ratings on all macroeconomic control variables. Furthermore, we employ regional dummies for countries in Africa (AFRI) and Latin America (LAT). We collect data on macroeconomic indicators and country-issuer characteristics from the IMF's International Financial Statistics (IFS), the World Bank's World Development Indicators (WDI), the Penn World Table (PWT), Global Development Finance (GDF), and the Federal Reserve Board. All macroeconomic variables are lagged by one year to account for reporting delays and to reduce potential endogeneity problems. A detailed description of the variables and their sources is available in Table A1 in the appendix.
2.2 The Econometric Methodology
Our main econometric model is based on the Heckman sample
selection model. The credit spread of an international bond issued
by a developing country is a measure of its default risk. As in
Eaton and Gersovitz (1981), Edwards (1984), and subsequent studies
in the literature, we assume that the logarithm of the spread is a
linear function of explanatory variables, ![]() , that
affect the default risk. Formally,
, that
affect the default risk. Formally,
| (1) |
where ![]() is a random error term. The explanatory
variables are exchange rate regime dummies, real exchange rate
overvaluation measures, and control variables that summarize the
global economic conditions and country characteristics.
is a random error term. The explanatory
variables are exchange rate regime dummies, real exchange rate
overvaluation measures, and control variables that summarize the
global economic conditions and country characteristics.
Because we only observe the launch spread when a bond is issued,
a sample selection problem arises. When no spread is observed for a
country in a given year, we may assume that the missing spreads are
random occurrences and ignore them; but, if the gaps occur
according to some unknown but systematic selection methods,
estimating Equation (1) alone leads to
biased and inefficient estimates. For example, a country may be
excluded from the international credit markets if its perceived
probability of default exceeds a given level, i.e., if it reaches a
"creditceiling."21Conversely, a country tends to issue
international bonds when the borrowing conditions are favorable and
its need for financing is high. To deal with the sample selection
problem, we create a binary variable for the bond issuance:
![]() equals 1 when we observe a nonzero spread
for a country at time
equals 1 when we observe a nonzero spread
for a country at time ![]() , and zero otherwise. We
assume
, and zero otherwise. We
assume
| (2) |
where ![]() is a set of observed variables that explain
the issuing decision of a country in a given month and
is a set of observed variables that explain
the issuing decision of a country in a given month and ![]() is a random error term. We can think of
is a random error term. We can think of ![]() as the difference between benefit and cost from
issuing bonds. Thus equation (2) indicates that
a bond issue is observed if and only if the benefit exceeds the
cost.
as the difference between benefit and cost from
issuing bonds. Thus equation (2) indicates that
a bond issue is observed if and only if the benefit exceeds the
cost.
The spread equation (1) and the
issuance equation (2) set up a
standard Heckman (1979) sample selection model. We can estimate
equation (25)
as a probit model to determine the issuance probability. Estimating
the probit model requires information on those countries who did
not issue bonds. To address this problem, we record a zero for each
month-country pair for which no bond issuance is observed. The
model can be identified by the exclusion requirement for the
Heckman selection model. In our empirical analysis, the vector of
explanatory variables ![]() in the issuance equation
(2) includes
all the variables in
in the issuance equation
(2) includes
all the variables in ![]() as well as one exclusion
variable that is used for identification. The exclusion variable is
a dummy for January in the bond issuance equation based on the
following logic: countries are less likely to issue new bonds in
January due to the holiday season. However, the January dummy
should not enter the spread equation because whether or not a
particular bond is issued in January should not change the
evaluation of its default risk.
as well as one exclusion
variable that is used for identification. The exclusion variable is
a dummy for January in the bond issuance equation based on the
following logic: countries are less likely to issue new bonds in
January due to the holiday season. However, the January dummy
should not enter the spread equation because whether or not a
particular bond is issued in January should not change the
evaluation of its default risk.
We use the maximum likelihood method to estimate equations
(1) and (2) jointly under
the assumption that the error terms, ![]() and
and
![]() , follow a bivariate normal distribution. The
maximum likelihood method obtains efficient estimates under a
correctly specified model. We also check the results by estimating
the model using Heckman's two-stage method.22 The two
procedures give similar results.
, follow a bivariate normal distribution. The
maximum likelihood method obtains efficient estimates under a
correctly specified model. We also check the results by estimating
the model using Heckman's two-stage method.22 The two
procedures give similar results.
In the empirical analysis, we also quantify the impact of
exchange rate regimes and real overvaluation on the issuing and
pricing of international bonds by calculating the marginal effects.
The marginal effects consist of two components. The first component
captures a direct effect on the mean of
![]() , while the second
component captures an indirect effect because the exchange rate
regime or real overvaluation influences
, while the second
component captures an indirect effect because the exchange rate
regime or real overvaluation influences
![]() indirectly by
affecting the bond issuance decision.
indirectly by
affecting the bond issuance decision.
First, the marginal effect on the bond spread of changing a country's exchange rate regime from FLOAT to INT is given by
|
(3) |
where ![]() is the coefficient of
is the coefficient of
![]() in Equation (1),
in Equation (1),
![]() is the inverse Mill's
ratio, and
is the inverse Mill's
ratio, and
![]() is defined
as the vector of explanatory variables in the bond issuance
equation (2)
with
is defined
as the vector of explanatory variables in the bond issuance
equation (2)
with
![]() and
all the other variables at their mean values.
and
all the other variables at their mean values.
![]() and
and
![]() are
similarly defined with
are
similarly defined with
![]() equal to
equal to
![]() and
and
![]() , respectively. Similarly,
if the exchange rate regime changes from INT to FIX, then the
marginal effect is given by
, respectively. Similarly,
if the exchange rate regime changes from INT to FIX, then the
marginal effect is given by
|
(4) |
where ![]() is the coefficient of
is the coefficient of
![]() in Equation (1).
in Equation (1).
Lastly, the marginal effect of real overvaluation at the sample mean in the observed sample is given by
![\begin{displaymath} \frac{\partial E\left[ \log \left( SPREAD\right) \left\vert BI=1\right. \right] }{\partial ROV}=\alpha _{ROV}-\gamma _{ROV}\rho \sigma _{u}\delta \left( \frac{-\beta \overline{Z}}{\sigma _{v}}\right) , \end{displaymath}](img34.gif)
|
(5) |
where ![]() and
and ![]() denote the coefficients of real exchange rate overvaluation (ROV1,
ROV2, or ROV3) in equations (1)-(2),
denote the coefficients of real exchange rate overvaluation (ROV1,
ROV2, or ROV3) in equations (1)-(2),
![]() , and
, and ![]() is the vector of explanatory
variables in the bond issuance equation (2). The marginal
effect of ROV in a given exchange rate regime is similarly defined.
is the vector of explanatory
variables in the bond issuance equation (2). The marginal
effect of ROV in a given exchange rate regime is similarly defined.
3 Empirical Analysis
In this section we empirically investigate the effects of exchange rate regimes (FIX, INT, or FLOAT) and real exchange rate overvaluation (ROV1-ROV3) on the issuing and pricing of international bonds by developing countries. In the next section we conduct various robustness tests including endogeneity tests.
3.1 Exchange Rate Regimes
We now examine our baseline model that features exchange rate regime dummies (FIX and INT) together with a set of explanatory variables. The estimation result is presented in Table 3. Ignoring the sample selection issue for the time being, we first run a pooled OLS regression using the bond spread as the dependent variable. The regression results are reported in Column (I) of Table 3. We then estimate the Heckman model, as specified in Equations1 and 2, using the full sample including the month-country pairs for which there were no bonds issued. The maximum likelihood estimation result is reported in Column (II) of Table 3.
Table 3 Baseline Model with Exchange Rate Regime
This table presents the regression results regarding the role of the exchange rate regime in affecting launch spreads. Column (I) shows the pooled OLS regression result with (log) spread as the dependent variable. Columns (II) and (III) show the MLE estimation results based on the Heckman sample selection model with (log) spread and (log) amount as the dependent variable, respectively. The t-statistics are shown in parentheses for key variables of exchange rate regimes (FIX and INT). We calculate t-statistics using robust standard errors.34
| OLS (I) Spread | Heckit Model (II) Spread | Heckit Model (II) Issuance | Heckit Model (III) Amount | Heckit Model (III) Issuance | |
|---|---|---|---|---|---|
| FIX | 0.289 (5.455) | 0.291 (5.742) | -0.180 (-2.036) | -0.185 (-2.106) | -0.158 (-1.847) |
| INT | 0.181 (4.012) | 0.199 (4.594) | -0.051 (-0.720) | -0.123 (-1.646) | -0.050 (-0.723) |
| AMOUNT | 0.046 | 0.029 | 0.158 | -0.003 | 0.170 |
| ISSUES | -0.001 | -0.002 | 0.033 | -0.005 | 0.030 |
| RATING | -0.105 | -0.108 | 0.013 | 0.004 | 0.017 |
| USRATE | -0.295 | -0.251 | -0.559 | -1.320 | -0.048 |
| HYD | 0.773 | 0.937 | -1.465 | -1.493 | -1.148 |
| GDPGR | -0.020 | -0.023 | 0.013 | -0.017 | 0.017 |
| GDPPC | -0.088 | -0.095 | 0.038 | 0.033 | 0.028 |
| CA2GDP | 0.032 | 0.028 | 0.044 | -0.023 | 0.045 |
| DT2GNP | 0.004 | 0.005 | -0.004 | 0.003 | -0.003 |
| DS2EX | 0.358 | 0.217 | 0.911 | -1.076 | 0.836 |
| SHORTDT | -0.003 | -0.004 | 0.007 | -0.005 | 0.007 |
| INF | 0.016 | 0.014 | 0.005 | -0.011 | 0.011 |
| AFRI | 0.127 | 0.260 | -0.642 | 0.421 | -0.627 |
| LAC | 0.131 | 0.140 | -0.030 | 0.157 | 0.001 |
| JAN | -0.155 | -0.115 | |||
| CONSTANT | 5.990 | 6.246 | -0.243 | 7.916 | -1.026 |
| No. of bonds | 1824 | 1824 | 2098 | ||
| No. of obs. | 1824 | 4661 | 4935 | ||
| rho | -0.357 | -0.047 | |||
| lambda | -0.192 | -0.041 |
Our results suggest that choosing a less flexible exchange rate regime increases bond spreads. The coefficients on the regime dummies (FIX and INT) are significantly positive and are similar in the OLS regression and the Heckman model. In addition, the estimation result of the Heckman model also shows that hard peggers have lower bond issuance probabilities. Therefore, it is both more difficult and more costly for countries with less-flexible regimes to borrow, suggesting these countries are penalized for not choosing a more-flexible exchange rate arrangement. Further, the coefficient on FIX is significantly higher (lower) than the coefficient on INT in the spread (issuance) equation, implying a monotone relation between the flexibility of the exchange rate arrangement and the bond spread. The results indicate that a country's exchange rate regime impacts foreign borrowing by shifting the demand curve of its international bonds. Specifically, the market is less inclined to demand the bonds of a country that has a less flexible exchange rate regime. As a result, it is less likely to observe an issue and the corresponding decline in demand increases spreads on observed issues.
The impact of the exchange rate regime is not only statistically significant, but also economically significant. To see the latter, we quantify the marginal effect of making a country's exchange rate regime less flexible on the bond spread as shown in equations (3) and (4). In the data, the average spread among the floaters is 319 basis points. From the OLS regression result in Table 3, we can see that changing from a floating exchange rate regime to an intermediate one increases the average spread by 63 (=319*(exp(0.18)-1)) basis points, and changing from an intermediate to fixed regime increases it further by an additional 37 (=319*(exp(0.29-0.18)-1)) basis points. The OLS regression ignores the potential sample selection bias. After we take into account the sample selection issue, the margin effect is slightly smaller. Based on the Heckman model, converting a floating (intermediate) exchange rate regime to an intermediate (floating) one increases the average bond spread by 54 (34) basis points. Thus the direct use of the OLS regression without accounting for the potential sample selection bias tends to slightly overestimate the impact. Using the estimation result of the issuance equation in Table 3, we compute the marginal effect from a change in the exchange rate regime on the bond issuance probability. We find that a country in an intermediate exchange rate regime is 4% less likely to issue a bond if it switches to a fixed regime, but about 1.5% more likely to issue a bond if it becomes a floater. Overall, we find that countries with less flexible exchange rate regimes issue less debt and pay a significantly higher bond spread.
As shown in Table 3, the control variables behave largely as expected. We also find that a higher U.S. real interest rate (USRATE) suppresses incentives of developing countries to issue bonds and at the same time makes spreads narrower.23 A larger high-yield corporate bond spread (HYD) significantly reduces issuance probability and tends to increase the spread. This result confirms the observation that the market requires similar risk premia on high-yield corporate bonds and emerging market country bonds. GDP growth (GDPGR), high GDP per capita (GDPPC), a favorable credit rating (RATING), and a low debt to GNP ratio (DT2GNP) enhance the market demand for international bonds, which increases the issuance probability and decreases the spread. A higher inflation, however, significantly increases the bond spread, but does not affect the likelihood of bond issuance.24 The regional dummies for Africa and Latin America have positive (negative) coefficients in the spread (issuance) equation. The coefficient of current account (CA2GDP) in the spread equation and those of the other two debt indices (DS2EX and SHORTDT) in the issuance equation show signs that are either inconsistent or hard to interpret. This may be due to the collinearity between them and the other macro variables, particularly the debt to GNP ratio, or result from some endogeneity problems. Lastly, the dummy for the January effect significantly reduces the probability of issuing bonds, validating its use as an exclusion variable. The correlation between the error terms in the issuance and spread equations is significantly negative with a value of -0.357. The negative correlation implies that there exist some unobserved factors that simultaneously lead to a higher issuance probability and a lower spread. Thus, these factors should be interpreted as unobserved determinants of demand. Finally, the coefficients of AMOUNT in both spread and issuance equations are significantly positive. This proxies for the supply of bonds (Eichengreen and Mody, 2000). Countries that issued a large amount of bonds in the previous year tend to accumulate an unsatisfied appetite for borrowing and supply additional new issues. The resulting outward shift in the bond supply reduces the bond price and increase the spread.
We also estimate a Heckman selection model for the dollar amount of issuance. In other words, we replace the dependent variable in (1) by the observed amount of individual bonds and use the same set of explanatory variables including the exchange rate regimes for the Heckman model. The result is reported in Column (III) of Table 3. First, all of the coefficients in the issuance equation have the same signs as in Column II, which is expected based on the probit model estimation. Second and more importantly, the result shows how the dollar amount of issuance is linked to the exchange rate regimes as well as global and local economic fundamentals. Most coefficients show signs that are easy to interpret. A country with a less flexible exchange rate regime not only is less likely to issue bonds but also borrows less in dollar amount. Hence combining the estimation results for the bond spread and the issuance amount in Columns (II) and (III) of Table 3, we find the significantly adverse effect of an inflexible exchange rate arrangement on a country's sovereign bond financing in terms of both price and quantity.
3.2 Real Exchange Rate Overvaluation
Next, we investigate the relationship of a country's real exchange rate overvaluation on the bond issuance and pricing. We include measures of real exchange rate overvaluation as well as their interactions with the exchange rate regime dummies in the Heckman model. As stated in Section 2.1, we use three measures of real exchange rate overvaluation (ROV1-ROV3) and report the estimation results in Tables 4A-4C, respectively. Each table contains three columns, Column (I)-Column (III). We first use the real exchange rate overvaluation alone as an explanatory variable in the Heckman selection model and report the result in Column (I). Then we add exchange rare regime dummies as additional explanatory variables (Column II). Lastly, to better identify the joint impact of overvaluation and a regime, we added the interaction terms of the real exchange rate overvaluation and the exchange rate dummies (Column III).25
Table 4A: Model with Exchange Rate Regime and Real Overvaluation (ROV1)
This table presents the regression results based on the Heckman sample selection model regarding the role of exchange rate regimes and exchange rate overvaluation in affecting launch spreads. The t-statistics are shown in parentheses for key variables of exchange rate regimes (ROV1, FIX, INT and their interaction terms). ROV1 is defined as the percentage deviation of the REER from its ten-year average. We calculate t-statistics using robust standard errors.
| Heckit Model (I) Spread | Heckit Model (I) Issuance | Heckit Model (II) Spread | Heckit Model (II) Issuance | Heckit Model (III) Spread | Heckit Model (III) Issuance | |
|---|---|---|---|---|---|---|
| ROV1 | 0.005 (5.750) | 0.006 (4.629) | 0.006 (5.196) | 0.006 (3.896) | ||
| ROV1 | 0.172 | 0.019 | ||||
| ROV1 | (3.984) | (4.958) | ||||
| ROV1 | 0.009 | 0.004 | ||||
| ROV1 | (5.131) | (2.170) | ||||
| ROV1 | 0.006 | 0.003 | ||||
| ROV1 | (4.360) | (0.882) | ||||
| FIX | 0.173 (2.999) | -0.218 (-2.375) | 0.098 (1.440) | -0.421 (-3.766) | ||
| INT | 0.156 (3.682) | -0.048 (-0.658) | 0.172 (3.984) | -0.026 (-0.352) | ||
| AMOUNT | 0.027 | 0.198 | 0.027 | 0.185 | 0.031 | 0.188 |
| ISSUES | -0.001 | 0.026 | -0.002 | 0.027 | -0.003 | 0.026 |
| RATING | -0.097 | 0.031 | -0.096 | 0.019 | -0.097 | 0.026 |
| USRATE | -0.141 | -0.485 | -0.036 | -0.439 | -0.002 | -0.428 |
| HYD | 1.128 | -1.713 | 1.197 | -1.404 | 1.236 | -1.390 |
| GDPGR | -0.024 | -0.001 | -0.022 | 0.007 | -0.025 | 0.004 |
| GDPPC | -0.136 | -0.090 | -0.178 | -0.030 | -0.170 | -0.014 |
| CA2GDP | 0.029 | 0.031 | 0.030 | 0.045 | 0.026 | 0.047 |
| DT2GNP | 0.006 | -0.001 | 0.006 | -0.001 | 0.006 | -0.002 |
| DS2EX | 0.378 | 0.792 | 0.360 | 0.966 | 0.222 | 0.872 |
| SHORTDT | -0.001 | 0.011 | -0.002 | 0.010 | -0.001 | 0.010 |
| INF | 0.016 | 0.011 | 0.011 | 0.004 | 0.012 | 0.002 |
| AFRI | 0.139 | -0.547 | 0.356 | -0.599 | 0.285 | -0.648 |
| LAC | 0.127 | -0.006 | 0.217 | -0.058 | 0.202 | -0.076 |
| JAN | -0.172 | -0.158 | -0.165 | |||
| CONSTANT | 6.253 | 0.475 | 6.344 | -0.068 | 6.243 | -0.152 |
| No. of bonds | 2037 | 1801 | 1801 | |||
| No. of obs. | 4954 | 4398 | 4398 | |||
| rho | -0.176 | -0.342 | -0.340 | |||
| lambda | -0.091 | -0.183 | -0.180 |
Table 4B: Model with Exchange Rate Regime and Real Overvaluation (ROV2)
This table presents the regression results based on the Heckman sample selection model regarding the role of exchange rate regimes and exchange rate overvaluation in affecting launch spreads. The t-statistics are shown in parentheses for key variables of exchange rate regimes (ROV2, FIX, INT and their interaction terms). ROV2 is defined as the percentage change in the REER over the past five years. We calculate t-statistics using robust standard errors.
| Heckit Model (I) Spread | Heckit Model (I) Issuance | Heckit Model (II) Spread | Heckit Model (II) Issuance | Heckit Model (III) Spread | Heckit Model (III) Issuance | |
|---|---|---|---|---|---|---|
| ROV2 | 0.002 (5.627) | 0.002 (1.976) | 0.002 (4.764) | 0.001 (1.119) | ||
| ROV2 | 0.002 | 0.002 | ||||
| ROV2 | (4.165) | (0.904) | ||||
| ROV2 | 0.004 | 0.001 | ||||
| ROV2 | (4.357) | (0.480) | ||||
| ROV2 | -0.000 | 0.001 | ||||
| ROV2 | (-0.300) | (0.461) | ||||
| FIX | 0.229 (4.298) | -0.193 (-2.199) | 0.261 (4.652) | -0.214 (-2.263) | ||
| INT | 0.187 (4.385) | -0.056 (-0.779) | 0.167 (3.781) | -0.050 (-0.688) | ||
| AMOUNT | 0.024 | 0.159 | 0.028 | 0.162 | 0.031 | 0.163 |
| ISSUES | -0.002 | 0.032 | -0.003 | 0.032 | -0.003 | 0.031 |
| RATING | -0.101 | 0.037 | -0.102 | 0.016 | -0.105 | 0.017 |
| USRATE | -0.125 | -0.573 | -0.111 | -0.552 | -0.085 | -0.557 |
| HYD | 1.208 | -1.683 | 1.163 | -1.439 | 1.226 | -1.443 |
| GDPGR | -0.022 | 0.008 | -0.024 | 0.014 | -0.022 | 0.013 |
| GDPPC | -0.096 | -0.030 | -0.137 | 0.025 | -0.157 | 0.030 |
| CA2GDP | 0.029 | 0.033 | 0.028 | 0.044 | 0.025 | 0.045 |
| DT2GNP | 0.006 | -0.003 | 0.006 | -0.003 | 0.006 | -0.003 |
| DS2EX | 0.314 | 0.849 | 0.290 | 0.942 | 0.198 | 0.946 |
| SHORTDT | -0.000 | 0.009 | -0.001 | 0.008 | -0.001 | 0.008 |
| INF | 0.021 | 0.011 | 0.018 | 0.005 | 0.021 | 0.005 |
| AFRI | 0.101 | -0.553 | 0.316 | -0.619 | 0.270 | -0.626 |
| LAC | 0.107 | 0.040 | 0.186 | -0.027 | 0.204 | -0.031 |
| JAN | -0.168 | -0.158 | -0.158 | |||
| CONSTANT | 5.921 | 0.248 | 6.186 | -0.187 | 6.284 | -0.218 |
| No. of bonds | 2060 | 1824 | 1824 | |||
| No. of obs. | 5237 | 4661 | 4661 | |||
| rho | -0.240 | -0.388 | -0.357 | |||
| lambda | -0.125 | -0.209 | -0.190 |
Table 4C: Model with Exchange Rate Regime and Real Overvaluation (ROV3)
This table presents the regression results based on the Heckman sample selection model regarding the role of exchange rate regimes and exchange rate overvaluation in affecting launch spreads. t-statistics are shown in parentheses for key variables of exchange rate regimes (ROV3, FIX, INT and their interaction terms). ROV3 is defined as the deviation from a predicted level of the real exchange rate, which is obtained based on the equilibrium concept of Purchasing Power Parity and is adjusted for the "Balassa-Samuelson" effect. We calculate t-statistics using robust standard errors.
| Heckit Model (I) Spread | Heckit Model (I) Issuance | Heckit Model (II) Spread | Heckit Model (II) Issuance | Heckit Model (III) Spread | Heckit Model (III) Issuance | |
|---|---|---|---|---|---|---|
| ROV3 | 0.004 (0.067) | 0.025 (0.350) | 0.021 (0.304) | 0.018 (0.225) | ||
| ROV3 | 0.923 | 1.156 | ||||
| ROV3 | (5.254) | (4.003) | ||||
| ROV3 | 0.027 | -0.191 | ||||
| ROV3 | (0.384) | (-2.120) | ||||
| ROV3 | -0.148 | 0.649 | ||||
| ROV3 | (-1.016) | (3.191) | ||||
| FIX | 0.281 (5.434) | -0.053 (-0.588) | -0.023 (-0.354) | -0.215 (-2.127) | ||
| INT | 0.168 (3.854) | 0.020 (0.314) | 0.134 (3.170) | -0.065 (-0.961) | ||
| AMOUNT | 0.020 | 0.107 | 0.027 | 0.120 | 0.027 | 0.092 |
| ISSUES | -0.004 | 0.041 | -0.005 | 0.042 | -0.004 | 0.045 |
| RATING | -0.111 | 0.026 | -0.106 | 0.019 | -0.098 | 0.031 |
| USRATE | 0.777 | 0.627 | 0.683 | 0.533 | 0.662 | 0.540 |
| HYD | 2.637 | -0.479 | 2.706 | -0.638 | 2.675 | -0.653 |
| GDPGR | -0.026 | 0.021 | -0.030 | 0.033 | -0.031 | 0.028 |
| CA2GDP | 0.024 | 0.031 | 0.025 | 0.037 | 0.028 | 0.041 |
| DT2GNP | 0.005 | -0.004 | 0.005 | -0.003 | 0.005 | -0.001 |
| DS2EX | 0.235 | 0.887 | 0.297 | 1.001 | 0.271 | 0.816 |
| SHORTDT | -0.005 | 0.005 | -0.005 | 0.005 | -0.004 | 0.005 |
| INF | 0.019 | 0.012 | 0.022 | -0.008 | 0.021 | -0.009 |
| JAN | -0.203 | -0.188 | -0.184 | |||
| CONSTANT | 3.715 | -2.004 | 3.688 | -1.967 | 3.721 | -1.932 |
| No. of bonds | 5272 | 4661 | 4661 | |||
| No. of obs. | 2080 | 1824 | 1824 | |||
| rho | -0.446 | -0.443 | -0.368 | |||
| lambda | -0.249 | -0.248 | -0.201 |
We find that the real exchange rate overvaluation significantly increases both the bond spread and the bond issuance probability. This effect is statistically significant and holds for all three measures of real exchange rate overvaluation, ROV1-ROV3. This result may be due to three factors. First, an overvalued currency makes a country's exports less competitive. Thus real exchange rate overvaluation is usually found to be associated with low economic growth and loss of government revenue.26 Hence, the borrowing country may experience greater difficulty in servicing its debt. When the gain from correcting the exchange rate misalignment is high and cost associated with default is low, default probability increases. Second, a real exchange rate overvaluation is highly likely to be corrected in the form of a currency devaluation or crisis, which increases a country's default risk due to the currency mismatch on the balance sheet. Powell and Sturzenegger (2000), for example, find a strong link between devaluation and default risk. Lastly, because overvaluation may signal good times with the economic prosperity (e.g., due to benign real shocks) and developing countries typically borrow procyclically, a country experiencing real overvaluation tends to borrow more and the increased supply in turn results in a higher bond spread.27
Using the estimation result in Column (I) of Tables 4A-4C, we compute the marginal effect of real exchange rate overvaluation on the spread as specified in equation (5). We find that if the real exchange rate becomes more overvalued by one sample standard deviation, the average bond spread increases by 64, 34, and 7 basis points, respectively, when the real exchange rate overvaluation is measured by ROV1, ROV2, and ROV3, respectively.
The impacts of the real exchange rate overvaluation and the exchange rate regime remain significant when both are included in the regression, as shown in Column (II) of Tables 4A-4C. A fixed or intermediate exchange rate regime has an independent positive effect on the bond spread and an independent negative effect on the bond issuance probability, consistent with the result in Table 3. The coefficients on the regime dummies are slightly lower, but remain a monotone function of the exchange rate flexibility.
Lastly, we investigate the combined effect of real exchange rate
overvaluation and an exchange rate regime. From Column (III) of
Tables 4A-4C, we find that among the three interaction terms,
![]() has the largest and most
significantly positive coefficients in the issuance and spread
equations (except that the coefficient becomes insignificant in the
issuance equation for ROV2). Furthermore, the results of Chi-square
tests show that the coefficients on the interaction term, ROVxFIX,
are statistically and significantly distinct from those on
ROVxFLOAT with p-values equal to 0.0034, 0.0224, and 0.000,
respectively, for the three overvaluation measures. This result
suggests that the effects of the real exchange rate overvaluation
tend to be magnified for countries with fixed exchange rate
regimes. We can think of two possible explanations for these
results. First, when a country has a hard peg or limited exchange
rate flexibility, the real overvaluation tends to be
persistent.28 As a result, servicing foreign debt
can be less costly in domestic currency. Hence, countries with less
flexible exchange rate arrangements are more likely to borrow in
periods of real overvaluation. The increase in the supply of bonds
from countries with fixed exchange rate regimes and real
overvaluation drives down the bond price and results in a higher
bond spread. Second, under a hard peg, the overvaluation has a
larger and more-persistent adverse impact on the economy.29 Debt
becomes rapidly unsustainable and the probability of default
increases. By contrast, owing to the exchange rate flexibility,
nominal devaluation can greatly help to speed up the real exchange
rate realignment for a free-floating regime. Therefore, real
exchange rate overvaluation has the least impact on the bond spread
for countries with free-floating regimes.
has the largest and most
significantly positive coefficients in the issuance and spread
equations (except that the coefficient becomes insignificant in the
issuance equation for ROV2). Furthermore, the results of Chi-square
tests show that the coefficients on the interaction term, ROVxFIX,
are statistically and significantly distinct from those on
ROVxFLOAT with p-values equal to 0.0034, 0.0224, and 0.000,
respectively, for the three overvaluation measures. This result
suggests that the effects of the real exchange rate overvaluation
tend to be magnified for countries with fixed exchange rate
regimes. We can think of two possible explanations for these
results. First, when a country has a hard peg or limited exchange
rate flexibility, the real overvaluation tends to be
persistent.28 As a result, servicing foreign debt
can be less costly in domestic currency. Hence, countries with less
flexible exchange rate arrangements are more likely to borrow in
periods of real overvaluation. The increase in the supply of bonds
from countries with fixed exchange rate regimes and real
overvaluation drives down the bond price and results in a higher
bond spread. Second, under a hard peg, the overvaluation has a
larger and more-persistent adverse impact on the economy.29 Debt
becomes rapidly unsustainable and the probability of default
increases. By contrast, owing to the exchange rate flexibility,
nominal devaluation can greatly help to speed up the real exchange
rate realignment for a free-floating regime. Therefore, real
exchange rate overvaluation has the least impact on the bond spread
for countries with free-floating regimes.
We compute the marginal effect of exchange rate overvaluation to assess the economic significance of their combined effect with the exchange rate regimes. For example, when the exchange rate overvaluation is measured using ROV1 (see Column (III) of Table 4A), we find that a one-standard-deviation rise of ROV1 increases the spread by 86 basis points for a country with a fixed exchange rate regime, while the same rise of ROV1 increases the spread by only 33 and 29 basis points, respectively, if the country is in an intermediate or floating exchange rate regime, respectively. The same pattern persists when the other two measures, ROV2 and ROV3, are used.
In summary, we find that a real exchange rate overvaluation increases both the bond issuance probability and bond spreads, and such effect is strongest when the country has a fixed exchange rate regime.
4 Robustness
In this section we address the potential endogeneity problem associated with exchange rate regimes and real exchange rate overvaluation. We also include more macroeconomic control variables to examine the robustness of our main findings.
First, we add more macroeconomic control variables. We include the debt crisis dummy (DCRISIS), debt rescheduling dummy (DRES), and total reserve to GNI (RES2GNI) as additional regressors. The debt crisis dataset is taken from Reinhart and Rogoff (2008). The debt rescheduling dummy, constructed from GDF, is equal to one (1) if there is a nonzero amount of debt rescheduled for a country and zero otherwise. All of these variables potentially impact the sovereign bond borrowing and pricing. Because of the data availability, there are 40 countries left in the sample when these controls are used.
Column (I) in Table 5A contains the results. A comparison to Table 3 shows that the findings regarding the effect of exchange rate regimes on the issuing and pricing of international bonds are robust after we control for more macroeconomic variables. Both FIX and INT have significantly positive coefficient in the spread equation. The coefficient on FIX in the issuance equation is also negative, although it is not statistically significant. The debt rescheduling dummy, DRES, does not affect the spread nor the issuance probability significantly, but the coefficients are positive. The debt crisis dummy, DCRISIS, significantly reduces the bond issuance probability, implying that a country that is in crisis is more difficult to issue new bonds. The ratio of total reserve to GNI, RES2GNI, decreases both the spread and the likelihood of issuance significantly, which is a very intuitive result.
Next, we address the concerns that the exchange rate regime and real exchange rate overvaluation may be endogenous. In particular, the choice of an exchange rate regime may be a response to a debt crisis or a mechanism to lower borrowing costs.
As a first attempt at fixing the endogeneity issue, we single out observations associated with countries with de facto pegs throughout our sample period (FIXALL) following Levy-Yeyati and Sturzenegger (2003) and include it in the Heckman model (see Columns (I) of Table 5A). As argued by these authors, because this group of countries correspond to economies within long-standing currency unions, it seems reasonable to assume that their original regime choices are independent from their bond issuance and pricing decisions over time. In Columns (I) of Table 5A, the positive impact of a fixed exchange rate regime on the bond spread is significant for this group of countries relative to the rest of the countries in our sample. This presents initial evidence that the main findings in our paper are not severely contaminated by the endogeneity problem.
We next correct for the endogeneity of the exchange rate regime
and real exchange rate overvaluation using a feasible generalized
two-stage IV (2SIV) estimator. We first run a multivariate logit
model of the exchange rate regime choice, ![]() FIX,
INT or FLOAT
FIX,
INT or FLOAT![]() . The multinomial logit model assumes
that the probability of one outcome can be expressed as
follows:
. The multinomial logit model assumes
that the probability of one outcome can be expressed as
follows:
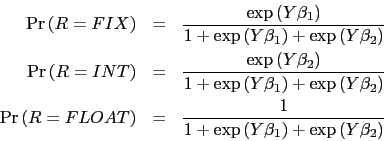
where ![]() is the vector of variables used to explain
the choice of an exchange rate regime, and
is the vector of variables used to explain
the choice of an exchange rate regime, and ![]() 's
are the associated coefficients. The relative probability of
choosing FIX (INT) versus FLOAT is
's
are the associated coefficients. The relative probability of
choosing FIX (INT) versus FLOAT is
![]() (
(
![]() ).
Similarly, to deal with the potential endogeneity problem
associated with real exchange rate overvaluation, we run three OLS
regressions on the variables in the vector
).
Similarly, to deal with the potential endogeneity problem
associated with real exchange rate overvaluation, we run three OLS
regressions on the variables in the vector ![]() to obtain
the fitted values for three measures, ROV1-ROV3. Then we use these
fitted values as well as those for exchange rate regime dummies
from the multinomial logit regression above to estimate the Heckman
model. Table 5A (Column II) and Table 5B report the regression
results.
to obtain
the fitted values for three measures, ROV1-ROV3. Then we use these
fitted values as well as those for exchange rate regime dummies
from the multinomial logit regression above to estimate the Heckman
model. Table 5A (Column II) and Table 5B report the regression
results.
The key goal here is to find suitable instrumental variables for the exchange rate regime and real overvaluation. For the exchange rate regime, following Levy-Yeyati and Sturzenegger (2003), we use the ratio of the country's GDP over the U.S. GDP (SIZE), the geographical area of the country (AREA), an island dummy (ISLAND), the ratio of reserve to monetary base (RESBASE), and a regional exchange rate indicator (REGEXCH) that is equal to the average exchange rate regime of the country's neighbors defined as those under the same IMF department. For the real overvaluation. we use the share of working-age persons in the population (WORKPOP) and a dummy variable for oil-exporting countries (OILEX) as the instrumental variables, as in Prasad et al. (2006) and Eichengreen (2008),
We use these instrumental variables and all of the exogenous regressors in the baseline model to obtain the fitted values for the exchange rate regime and overvaluation based on the auxiliary regressions. Column (I) of Table 5C reports the result of the multinomial logit auxiliary regression of the exchange rate regime over all of the instruments. The coefficients are interpreted as the variation in the relative probability of choosing one regime over a free-floating one. Column (II) shows the estimates of the three OLS regressions for three different measures of real exchange rate overvaluation. Most variables are highly significant and have the expected signs. For the choice of the exchange rate regime, smaller countries tend to be more open and thus are more likely to choose fixed exchange rate regimes. A high initial level of reserves helps a country to overcome the "fear of floating."Finally, the regional exchange rate indicator may indicate explicit or implicit exchange rate coordination among neighboring countries.30 Regarding the OLS regressions for the real overvaluation, a higher share of working-age population reduces the likelihood of real overvaluation.31 Oil-exporting countries are more prone to overvaluation.
Table 5A: Exchange Rate Regime: Endogeneity Correction
This table presents the regression results regarding the role of the exchange rate regime in affecting launch spreads. Column (I) shows the MLE result based on the Heckman sample selection model. Column (II) shows the MLE result from using a feasible generalized two-stage instrumental variable estimator (2SIV) to deal with the potential endogeneity problem associated with an exchange rate regime. The t-statistics are shown in parentheses for key variables of exchange rate regimes (FIX, INT, FIXALL). FIXALL is a dummy variable for countries with de facto pegs throughout our sample period. We also include additional control variables of DRES, DCRISIS and RES2GNI. We calculate t-statistics using robust standard errors.
| Heckit Model (I) Spread | Heckit Model (I) Issuance | Heckit Model (II) Spread | Heckit Model (II) Issuance | |
|---|---|---|---|---|
| FIX | 0.281 (5.487) | -0.099 (-1.043) | 0.335 (5.721) | -0.282 (-2.736) |
| INT | 0.206 (4.847) | -0.031 (-0.422) | 0.292 (4.894) | -0.066 (-0.603) |
| FIXALL | 0.604 (2.830) | -0.386 (-1.363) | ||
| DRES | 0.059 | 0.110 | 0.084 | 0.202 |
| DCRISIS | -0.022 | -0.595 | -0.412 | -0.935 |
| RES2GNI | -0.016 | -0.017 | -0.012 | -0.014 |
| AMOUNT | 0.021 | 0.141 | 0.035 | 0.137 |
| ISSUES | -0.001 | 0.032 | -0.004 | 0.032 |
| RATING | -0.074 | 0.055 | -0.085 | 0.061 |
| USRATE | -0.221 | -0.433 | -0.268 | -0.621 |
| HYD | 0.822 | -1.424 | 0.832 | -1.996 |
| GDPGR | -0.018 | 0.020 | -0.021 | 0.010 |
| GDPPC | -0.036 | 0.130 | -0.039 | 0.114 |
| CA2GDP | 0.037 | 0.049 | 0.030 | 0.041 |
| DT2GNP | 0.006 | -0.001 | 0.006 | -0.001 |
| DS2EX | 0.125 | 0.740 | 0.267 | 0.586 |
| SHORTDT | 0.000 | 0.006 | -0.002 | 0.007 |
| INF | 0.008 | -0.002 | 0.016 | -0.001 |
| AFRI | 0.051 | -0.780 | 0.033 | -0.777 |
| LAC | 0.117 | -0.125 | 0.049 | -0.035 |
| JAN | -0.153 | -0.179 | ||
| CONSTANT | 5.857 | -0.909 | 5.836 | -0.348 |
| No. of bonds | 1822 | 2078 | ||
| No. of obs. | 4542 | 5152 | ||
| rho | -0.248 | -0.198 | ||
| lambda | -0.130 | -0.102 |
Table 5B: Exchange Rate Regime and Overvaluation: Endogeneity Correction
This table presents the regression results from using instrumental variables (IV) to deal with the potential endogeneity problem associated with both exchange rate regime and real overvaluation. Heckit Models (I-III) are for ROV1-ROV3, respectively. The t-statistics are shown in parentheses for key variables of exchange rate regime, overvaluation and their interactions. We also include additional control variables of DRES, DCRISIS, and RES2GNI. We calculate t-statistics using robust standard errors.
| Heckit Model (I) Spread | Heckit Model (I) Issuance | Heckit Model (II) Spread | Heckit Model (II) Issuance | Heckit Model (III) Spread | Heckit Model (III) Issuance | |
|---|---|---|---|---|---|---|
| ROV | 0.037 | 0.070 | 0.013 | 0.008 | 0.967 | 1.234 |
| ROV | (5.967) | (6.981) | (3.160) | (1.525) | (3.236) | (2.814) |
| ROV | 0.022 | 0.029 | 0.006 | -0.010 | -0.109 | 0.116 |
| ROV | (4.512) | (4.056) | (1.417) | (-2.236) | (-0.918) | (0.678) |
| ROV | 0.017 | 0.021 | 0.007 | -0.027 | -0.161 | 0.887 |
| ROV | (3.116) | (2.491) | (1.295) | (-4.619) | (-0.743) | (2.690) |
| FIX | 0.000 (0.000) | -0.723 (-5.678) | 0.109 (1.401) | -0.518 (-4.409) | 0.103 (1.187) | -0.096 (-0.909) |
| INT | 0.240 (3.598) | -0.093 (-0.825) | 0.326 (4.665) | -0.005 (-0.040) | 0.235 (3.483) | 0.027 (0.286) |
| DRES | -0.099 | -0.106 | -0.014 | 0.351 | 0.088 | 0.214 |
| DCRISIS | -0.180 | -0.666 | -0.276 | -1.178 | -0.481 | -0.584 |
| RES2GNI | -0.008 | -0.010 | -0.009 | -0.018 | -0.005 | -0.013 |
| AMOUNT | 0.056 | 0.169 | 0.046 | 0.150 | 0.038 | 0.099 |
| ISSUES | -0.004 | 0.025 | -0.003 | 0.026 | -0.005 | 0.038 |
| RATING | -0.074 | 0.082 | -0.078 | 0.057 | -0.093 | 0.064 |
| USRATE | 0.273 | 0.140 | 0.057 | -0.958 | 0.699 | 0.471 |
| HYD | 1.734 | -0.582 | 1.358 | -2.585 | 2.536 | -0.651 |
| GDPGR | -0.029 | -0.001 | -0.022 | -0.001 | -0.025 | 0.024 |
| GDPPC | -0.337 | -0.277 | -0.141 | 0.309 | ||
| CA2GDP | 0.037 | 0.056 | 0.032 | 0.029 | 0.029 | 0.041 |
| DT2GNP | 0.009 | 0.004 | 0.008 | -0.004 | 0.005 | 0.001 |
| DS2EX | 0.813 | 1.324 | 0.513 | -0.035 | 0.480 | 0.562 |
| SHORTDT | 0.005 | 0.014 | 0.002 | 0.002 | -0.003 | 0.005 |
| INF | 0.012 | -0.002 | 0.024 | -0.006 | 0.021 | 0.003 |
| AFRI | 0.191 | -0.474 | 0.145 | -1.060 | ||
| LAC | 0.145 | 0.044 | 0.103 | -0.135 | ||
| JAN | -0.194 | -0.193 | -0.198 | |||
| CONSTANT | 6.519 | 0.545 | 5.609 | -0.584 | 3.487 | -1.657 |
| No. of bonds | 2078 | 2078 | 2078 | |||
| No. of obs. | 5152 | 5152 | 5152 | |||
| rho | -0.064 | -0.166 | -0.206 | |||
| lambda | -0.032 | -0.085 | -0.107 |
Table 5C: Instruments for Exchange Rate Regime and Overvaluation
Column (I) in this table presents the multinomial logit regression results, which are used to generate the fitted values of exchange rate regimes FIX and INT as their instruments. The dependent variable is the categorical exchange rate class (FIX, INT, or FLOAT). Column (II) presents the OLS regression results, which are used to generate the fitted values of the three exchange rate overvaluation measures (ROV1, ROV2, ROV3), respectively. The explanatory variables include allof the exogenous variables used in Tables 5A and 5B, as well as seven additional variables WORKPOP, OILEX, AREA, ISLAND, REGEXCH, RESBASE, and SIZE as proposed in Levy-Yeyati and Sturzenegger (2003), Prasad, Rajan, and Subrahmanian (2006) and Eichengreen (2008). WORKPOP, obtained from WDI (variable SP.POP.1564.TO.ZS), is the proportion of total population whose ages are between 15 and 64. OILEX is a dummy for oil exporting countries. AREA, obtained from WDI (variable AG.LNK.TOTL.k2) is land area in sq. km. ISLAND is a dummy for countries with no mainland territory. RESBASE, obtained from IMF (line 11/line 14), is the initial ratio of "International Reserves"to "Monetary Base."RESEXCH is the (monthly) average RR exchange rate regime of the region where the regions are defined as those under the same IMF department. SIZE, obtained from WDI (variable NY.GDP.MKTP.CD), is a country's GDP in dollars over U.S. GDP. For simplicity, only the regression coefficients and the corresponding t-statistics for the seven additional variables are reported below. The t-statistics are shown in parentheses, and are calculated using robust standard errors.
| Multinomial Logit (I) FIX | Multinomial Logit (I) INT | OLS (II) ROV1 | OLS (II) ROV2 | OLS (II) ROV3 | |
|---|---|---|---|---|---|
| WORKPOP | -1.047 (-6.334) | -0.332 (-7.266) | 0.101 (0.986) | 1.559 (9.264) | -0.017 (-14.698) |
| OILEX | 4.663 (5.248) | 0.914 (3.434) | 7.251 (11.070) | 5.897 (5.293) | 0.123 (15.505) |
| AREA | -4.804 (-5.051) | 0.429 (10.082) | 0.158 (1.307) | -0.110 (-0.610) | -0.009 (-7.181) |
| ISLAND | -43.560 (-0.061) | -5.453 (-12.170) | 5.528 (5.587) | 6.307 (3.771) | -0.182 (-14.814) |
| REGEXCH | 11.493 (12.086) | 1.717 (8.110) | -4.261 (-7.485) | -0.399 (-0.419) | -0.126 (-18.916) |
| RESBASE | -7.434 (-11.770) | -0.437 (-5.602) | -0.168 (-0.677) | -2.187 (-5.227) | 0.054 (17.612) |
| SIZE | -153.175 (-8.357) | -5.266 (-14.997) | -3.602 (-2.897) | -10.911 (-5.280) | -0.005 (-0.286) |
| No. of obs. | 4816 | 5190 | 5419 | 5458 | |
| pseudo | 0.731 | 0.421 | 0.341 | 0.559 |
Column (II) of Table 5A reports the estimation results using the predicted probabilities of choosing a fixed or intermediate exchange rate regime as the instruments for regime dummies. Our main findings hold after correcting for endogeneity. The coefficients on FIX and INT are still significantly positive in the spread equation and negative in the issuance equation. In general, an inflexible exchange rate regime decreases bond issuing probability and increase bond spreads, which is consistent with our main findings in Section 3.
The estimation results for the real overvaluation after the endogeneity correction are reported in Table 5B. For all three measures of the real overvaluation (ROV1-ROV3), the interaction terms with FIX and INT remain positive and significant with the coefficients in a magnitude similar to those in the baseline model. Moreover, the coefficients of these interaction terms continue to decrease with the flexibility of the regime. We use Chi-square tests to test whether these coefficients are statistically different from each other. The results of Chi-square tests show that the coefficients on the interaction term, ROVxFIX, are statistically and significantly distinct from those on ROVxFLOAT with p-values equal to 0.0000, 0.0347, 0.0033, respectively, for the three overvaluation measures. In addition, the impact of the interaction terms on the bond issuance probability is also robust. Overall, the relation between exchange rate policy and the bond issuing and pricing is robust to the correction of endogeneity for both exchange rate regime and real exchange rate overvaluation.
5 Conclusion
This study is the first empirical work on the impact of exchange rate policy on the issuing and pricing of international bonds. We find that exchange rate policy affects the bond spread in a significant and interlaced way. First, countries with less flexible exchange rate regimes tend to pay higher spreads and are less likely to issue bonds. Second, when the currencies are overvalued, countries tend to issue more debt. But an overvalued real exchange rate has a negative impact on debt sustainability, and thus increases bond spreads, especially for countries in hard peg regimes.
The choice of exchange rate policy is not neutral with respect to the bond issuing and pricing decisions. Attempts to gain credibility in the international market through the use of a pegged exchange rate have gained popularity. Our results emphasize that the choice of a hard peg does not necessarily lead to cheaper borrowing costs, especially if there is a severe risk of currency overvaluation. Overvaluation under hard pegs incites governments to borrow more in the international market; however, foreign investors internalize the risks associated with the overvaluation, increasing borrowing costs.
A few research questions still remain. In particular, one would want to construct a theoretical framework to examine a government's optimal choice in terms of foreign borrowing and default under different exchange rate regimes in a dynamic stochastic general equilibrium model. The empirical findings in this paper show the need to develop new theories that incorporate exchange rate regimes and real exchange rates into the analysis of sovereign default for developing countries. Such analysis also has important policy implications for European countries in the euro zone.
References
Aghion, Philippe, Philippe Bacchetta, Romain Ranciere, and Kenneth Rogoff, 2009, "Exchange Rate Volatility and Productivity Growth: The Role of Financial Development,"Journal of Monetary Economics, Vol. 56, pp. 494-513.
Aguiar, Mark and Gita Gopinath, 2006, "Defaultable Debt, Interest Rates and the Current Account,"Journal of International Economics, Vol. 69, No. 1, pp. 64-83.
Alesina, Alberto and Alexander Wagner, 2003, "Choosing (and Reneging on) Exchange Rate Regimes,"National Bureau of Economics Research, Working Paper 9809.
Arellano, Cristina, 2008, "Default Risk and Income Fluctuations in Emerging Economies,"The American Economic Review, Vol. 98, No. 3, pp. 690-712.
Arellano, Cristina and Jonathan Heathcote, 2010, "Dollarization and Financial Integration,"Journal of Economic Theory, Vol. 145, No. 3 (May), pp. 944-973.
Broda, Christian, 2004, "Terms of Trade and Exchange Rate Regimes in Developing Countries,"Journal of International Economics, Vol. 63, pp. 31-58.
Calvo, Guillermo A. and Carmen M. Reinhart, 2002, "Fear of Floating,"The Quarterly Journal of Economics, Vol. 117, No. 2 (May), pp. 379-408.
Cline, William R., 1995, "International Debt Reexamined,"Chapter 2, Institute for International Economics.
Crespedes, Luis Felipe, Roberto Chang, and Andres Velasco, 2004, "Balance Sheets and Exchange Rate Policy,"The American Economics Review, Vol. 94, No. 4, pp. 1183-1193.
Dell'Ariccia, Giovanni, Isabel Schnabel, and Jeromin Zettelmeyer, 2006, "How Do Official Bailouts Affect the Risk of Investing in Emerging Markets?"Journal of Money, Credit and Banking, Vol. 38, No. 7, pp. 1689-1714.
Dollar, David, 1992, "Outward-Oriented Developing Economies Really Do Grow More Rapidly: Evidence from 95 LDCs, 1976-1985,"Economic Development and Cultural Change , Vol. 40, No. 3 (April), pp. 523-544.
Dornbusch, Rudiger, 2001, "Fewer Monies, Better Monies,"The American Economic Review, Vol. 91, No. 2, pp. 238-242.
Dornbusch, Rudiger, Ilan Goldfajn, and Rodrigo O. Valdes, 1995, "Currency Crises and Collapses,"Brookings Papers on Economic Activity, Vol. 1995, No. 2, pp. 219-293.
Easton, Stephen T. and Duane W. Rockerbie, 1999, "What's in a Default? Lending to LDCs in the Face of Default Risk,"Journal of Development Economics, Vol. 58, pp. 319-332.
Eaton, Jonathan and Mark Gersovitz, 1981, "Debt with Potential Repudiation: Theoretical and Empirical Analysis,"Review of Economics Studies, Vol. 48, No. 2, pp. 289-309.
Edwards, Sebastian, 1984, "LDC Foreign Borrowing and Default Risk: An Empirical Investigation, 1976-80,"The American Economic Review, Vol. 74, No. 4, pp. 726-734.
Edwards, Sebastian, 1988, "Real and Monetary Determinants of Real Exchange Rate Behavior: Theory and Evidence from Developing Countries,"Journal of Development Economics, Vol. 29, pp. 311-341.
Edwards, Sebastian, 1989, "Real Exchange Rates, Devaluations and Adjustment,"Cambridge, MA: MIT Press.
Edwards, Sebastian and Eduardo Levy-Yeyati, 2005, "Flexible Exchange Rates as Shock Absorbers,"European Economic Review, Vol. 77, No.1, pp. 93-106.
Eichengreen, Barry, 2008, "The Real Exchange Rate and Economic Growth,"Commission on Growth and Development, Working Paper No. 4.
Eichengreen, Barry and Ashoka Mody, 2000, "What Explains Changing Spreads on Emerging-Market Debt?"In Capital Flows and the Emerging Economies: Theory, Evidence and Controversies, edited by Sebastian Edwards, pp. 107-134. Chicago and London: The University of Chicago Press.
Eichengreen, Barry, Andrew K. Rose, and C. Wyplosz, 1998, "Speculative Attacks on Pegged Exchange Rates: An Empirical Exploration with Special Reference to the European Monetary System,"in The New Transatlantic Economy, M. Canzoneri and E. Grilli, eds., (New York, NY: Cambridge University Press), pp. 191-228.
Frankel, Jeffrey A. and George Saravelos, 2010, "Are Leading Indicators of Financial Crises Useful for Assessing Country Vulnerability? Evidence from the 2008-09 Global Crisis,"National Bureau of Economics Research, Working Paper No. 16047.
Gertler, Mark, Simon Gilchrist, and Fabio Massimo Natalucci, 2007, "External Constraints on Monetary Policy and the Financial Accelerator,"Journal of Money, Credit and Banking, Vol. 39, No. 2-3, pp. 295-330.
Goldfajn, Ilan and Rodrigo O. Valdes, 1999, "The Aftermath of Appreciations,"The Quarterly Journal of Economics, Vol. 114, No. 1, pp. 229-262.
Giavazzi, Francesco and Marco Pagano, 1988, "The Advantage of Tying One's Hands: EMS Discipline and Central Bank Credibility,"European Economic Review, Vol. 32, No. 5 (June), pp. 1055-1075.
Heckman, James J., 1979, "Sample Selection Bias as a Specification Error,"Econometrica, Vol. 47, No. 1 (January), pp. 153-161.
Hinkle, Lawrence E. and Peter J. Montiel, 1999, "Exchange Rate Misalignment: Concepts and Measurement for Developing Countries,"Chapter 7, Oxford University Press, World Bank.
Jahjah, Samir and Peter J. Montiel, 2003, "Exchange Rate Policy and Debt Crisis in Emerging Economies,"IMF Working Paper 03/60.
Kamin, Steven and Karsten von Kleist, 1999, "The Evolution and Determinants of Emerging Market Credit Spreads in the 1990s,"International Finance Discussion Paper 636. Board of Governors of the Federal Reserve System.
Kaminsky, Graciela, Saul Lizondo, and Carmen M. Reinhart, 1998, "Leading Indicators of Currency Crises,"IMF Staff Papers, Vol. 45, No. 1 (March), pp. 1-48.
Levy-Yeyati, Eduardo and Federico Sturzenegger, 2003, "To Float or to Fix: Evidence on the Impact of Exchange Rate Regimes on Growth,"The American Economic Review , Vol. 93, No. 4 (September), pp. 1173-1193.
Moody's Investors Service, 2003, "Sovereign Bond Defaults, Rating Transitions, and Recoveries (1985-2002),"Global Credit Research Special Comment (February), pp. 1-24.
Obstfeld, Maurice and Alan M. Taylor, 2003, "Sovereign Risk, Credibility and the Gold Standard: 1870-1913 versus 1925-31,"Economic Journal, Vol. 113, No. 487 (April), pp. 241-275.
Powell, Andrew and Federico Sturzenegger, 2000, "Dollarization: The Link between Devaluation and Default Risk,"In Dollarization, Debates and Policy Alternatives edited by Federico Sturzenegger and Eduardo Levy-Yeyati, MIT Press 2003.
Prasad, Eswar, Raghuram Rajan, and Arvind Subramanian, 2006, "Foreign Capital and Economic Growth,"unpublished manuscript, IMF.
Reinhart, Carmen M., 2002, "Default, Currency Crises and Sovereign Credit Ratings,"World Bank Economic Review, Vol. 16, No. 2, pp. 151-170.
Reinhart, Carmen M. and Kenneth S. Rogoff, 2002, "The Modern History of Exchange Rate Arrangements: A Reinterpretation,"National Bureau of Economics Research, Working Paper No. 8963.
Reinhart, Carmen M. and Kenneth S. Rogoff, 2008, "This Time is Different: A Panoramic View of Eight Centuries of Financial Crises,"National Bureau of Economics Research, Working Paper No. 13882.
Rose, Andrew K., 2000, "One Money, One Market? The Effects of Common Currencies on International Trade,"Economic Policy, Vol. 15, No. 30 (April), pp. 7-46.
Rose, Andrew K. and Eric van Wincoop, 2001, "National Money as a Barrier to International Trade: The Real Case for Currency Union,"The American Economic Review, Vol. 91, No. 2, pp. 386-390.
Sachs, Jeffrey D., 1983, "Theoretical Issues in International Borrowing,"National Bureau of Economics Research, Working Paper No. 1189.
Sachs, Jeffrey D. and Daniel Cohen, 1982, "LOC Borrowing with Default Risk,"National Bureau of Economics Research, Working Paper No. 925.
Schneider, Martin and Aaron Tornell, 2004, "Balance Sheet Effects, Bailout Guarantees and Financial Crises,"Review of Economic Studies, Vol. 71, No. 3, pp. 883-913.
Uribe, Martin and Vivian Z. Yue, 2006, "Country Spreads and Emerging Countries: Who Drives Whom?"Journal of International Economics, Vol. 69, No. 1 (June), pp. 6-36.
Yue, Vivian Zhanwei, 2010, "Sovereign Default and Debt Renegotiation,"Journal of International Economics, Vol. 80, No. 2, pp. 176-187.
Appendix: Definition of Variables
Table A1: Variables, Definitions and Sources
| Variable | Definitions and Sources |
|---|---|
| AFRI | Dummy variable for African countries |
| AMOUNT | U.S. $ equivalent amount of bond (Source: Bondware)32 |
| CA2GDP | Current account balance as % of GDP (Source: WDI, variable: BN.CAB.XOKA.GD.ZS ) |
| DCRISIS | Dummy for debt crisis (Source: Reinhart and Rogoff (2008)) |
| DRES | Dummy for debt rescheduling (Source: GDF, series: DT.TXR.DPPG.CD) |
| DS2EX | Total debt service (% of exports) (Source: WDI, variable: DT.TDS.DECT.EX.ZS) |
| DT2GNP | External debt stocks (% of GNI) (Source: WDI, variable: DT.DOD.DECT.GN.ZS) |
| GDPGR | GDP growth rate (Source: WDI, variable: NY.GDP.MKTP.KD.ZG) |
| GDPPC | GDP per capita (current US$) (Source: WDI, variable: NY.GDP.PCAP.CD) |
| HYD | Log of Moody's seasoned Baa corporate bond yield less USRATE (Source: Federal Reserve Board) |
| INF | Inflation, consumer prices (Source: WDI, variable: FP.CPI.TOTL.ZG) |
| ISSUES | Total number of bond issues in a given year (Source: Bondware) |
| LAT | Dummy variable for Latin American countries |
| RATING | Residual from regression of ratings on fundamentals (Source: S&P, Moody's, variable: average of available ratings or only available rating) |
| RES2GNI | Total reserves (% of GNI) (Source: WDI, variable: FI.RES.TOTL.DT.ZS |
| ROV1 | REER Deviation from 10-year average, monthly (Source: IMF) |
| ROV2 | REER 5-year percentage appreciation, monthly (Source: IMF) |
| ROV3 | Exchange rate misalignment measure (Source: PWT)33 |
| SHORTDT | Short-term debt (% of total external debt) (Source: WDI, variable: DT.DOD.DSTC.ZS) |
| SPREAD | Launch spreads in basis point, monthly (Source: Bondware) |
| USRATE | The yield on ten-year U.S. treasury bonds at time of issue (log) (Source: Federal Reserve Board) |
Footnotes
** We are very grateful to two anonymous referees and Pok-sang Lam (the editor) for offering many insightful comments and suggestions that have improved the paper immensely. We would also like to thank Frank Diebold, Charles Engel, Neil Ericsson, Mark Gertler, Martin Uribe, Jenny Xu, and the participants at the IMF Institute Seminar and he Hong Kong Institute for Monetary Research Eighth HKIMR Summer Workshop for their comments. We thank Carmen Reinhart for providing us with the data on crises. The authors are responsible for all errors and omissions. The views expressed in this paper are those of the authors and do not necessarily represent those of the Federal Reserve System or IMF. Return to text
*** Jahjah is at the International Monetary Fund, 700 19th Street, N.W., Washington, D.C. 20431. E-mail: [email protected]. Wei and Yue are at the Board of Governors of the Federal Reserve System, 20 Constitution Avenue Northwest, Washington, D.C. 20551. E-mail: [email protected] and [email protected]. Return to text
1. Reinhart and Rogoff (2008) document 71 default episodes for developing countries from 1975 to 2006. They also provide a "panoramic" analysis of the history of financial crises dating from England's fourteenth-century default to the current United States subprime financial crisis. Return to text
2. Obstfeld and Taylor (2003) study the effect of a gold standard on country borrowing spreads on the London bond market from the 1870s to the 1930s. Arellano and Heathcote (2010) conduct a cross-country regression of sovereign credit ratings on the exchange rate volatility in 1985-2000. Return to text
3. Levy-Yeyati and Sturzenegger (2005) and Broda (2004) provide some empirical evidence that the terms of trade shocks have a larger effect on economic performance in countries with more rigid exchange rate regimes, than in countries with a flexible exchange rate regime. Return to text
4. Gertler, Gilchrist, and Natalucci (2007) focus on the Korean experience during the 1997-1998 financial crisis and quantitatively examine how defending an exchange rate peg may reinforce the financial crisis. Cespedes, Chang, and Velasco (2004) also discuss the role of exchange rate regimes on excerbating financial crisis in a qualitative analysis. Return to text
5. Giavazzi and Pagano (1988) show that a government may choose a particular exchange rate arrangement to buy itself a reputation. Return to text
6. See Dornbusch (2001), Rose (2000), and Rose and van Wincoop (2001). Please see Levy-Yeyati and Stuzenegger (2003) for an extensive review. Return to text
7. It is worthwhile to point out that the degree of overvaluation does not always reflect a deliberate policy choice, whereas the exchange rate regime clearly is a delibrate policy choice. For example, in a floating exchange rate regime with inflation targeting, monetary policy is focused on the goals of inflation (and perhaps output) stabilization, and overvaluation may reflect transitory market forces. In a fixed exchange rate regime, the currency may initially be pegged at an undervalued level, but movements in relative price levels over time may cause it to become overvalued. We are grateful to an anonymous referee for pointing it out. Return to text
8. Aghion et al. (2009) find that countries suffering from real overvaluation experience slower productivity growth. Eichengreen (2008) contains a survey of the literature that documents how a competitive real exchange rate fosters growth and real overvaluation slows growth for developing countries. Return to text
9. See Dornbusch et al. (1995), Edwards (1989), Eichengreen et al. (1998), Kaminsky et al. (1998), Goldfajn and Valdes (1999), and Eichengreen (2008). Return to text
10. Schneider and Tornell (2004) find that balance of payments crises are preceded by lending booms and real appreciation in a model with self-fulfilling crises and balance sheet effects. Return to text
11. Jahjah and Montiel (2003) find that a hard peg increases default likelihood, especially in cases of large exchange rate overvaluation. Return to text
12. Because of a lack of concensus about a well-articulated definition of an equilibrium real exchange rate, there is no universal method to compute exchange rate misalignment or real exchange rate overvalution (Hinkle and Montiel, 1999). This paper is agnostic about the definition of equilibrium real exchange rate and adopts three measures of overvaluation used in the literature for robustness. Return to text
13. There are initially 66 countries covered in the Capital Data's Bondware data during the sample period. Among them, 4 countries are dropped because they have no Reinhart and Rogoff (2002) regime classification, and 20 countries are further dropped from the sample due to the unavailability of some explanatory variables. The number of bond issues by the 24 countries excluded in our analysis is less than one tenth of the total bond issues. Return to text
14. A country may in practice deviate from its announced exchange rate regime. Calvo and Reinhart (2002) and Alesina and Wagner (2003) study the reasons why countries do not follow their de jure exchange rate regimes. Results are similar when we use the IMF de jure or de facto exchange rate regimes. These results, not reported in this paper, are available upon request. Return to text
15. We also repeated the empirical analysis using the exchange rate regimes grouped into either four classes (hard peg, conventional peg, intermediate, and free floating) or two classes (fixed and floating). These alternative grouping ways do not change the results. The estimation results are available upon request. Return to text
16. Two adjustments are made to the RR classification. A free falling regime is defined as one with a monthly inflation rate greater than 40%. Because inflation is one regressor in our empirical analysis, we categorize this group using the secondary classification. We discard the observations in the dual-market regime because no secondary classification is available. Our empirical analysis is robust to the exclusion of these two groups. Return to text
17. Because of a lack of consensus about a well-articulated definition of an equilibrium real exchange rate, there is no universal method to compute exchange rate misalignment or real exchange rate overvalution (Hinkle and Montiel, 1999). This paper is agnostic about the definition of equilibrium real exchange rate. Return to text
18. These two measures are also used in Frankel and Saravelos (2010). Return to text
19. We also measure the exchange rate overvaluation using the difference between log of the real exchange rate and its H-P trend. The results are robust, but not reported in the paper. They are available upon request. Return to text
20. Our baseline specification closely follows those reported in Edwards (1984), Eichengreen and Mody (2000), Dell'Ariccia et al. (2006), etc. We also include control variables that are not in these earlier studies but have been extensively discussed as important determinants of international bond spreads. Return to text
21. See Eaton and Gersovitz (1981), Sachs and Cohen (1982), and Sachs (1983). Return to text
22. The two-stage estimation method of the Heckman model is implemented as follows. In the first stage, equation (2) is estimated as a probit model to determine the probability of a bond issue. Then, the value of Mill's ratio (reflecting the conditional probability of the observation being in the observed sample) is incorporated in an OLS regression of (2) using the observed spreads. Return to text
23. Eichengreen and Moday (2000), Kamin and Keist (1999), and Uribe and Yue (2006) also find that the U.S. real interest rates reduces the contemporaneous country spread. Return to text
24. Reinhart and Rogoff (2008) document the high correlation between high inflation and the occurrence of debt crisis using data that cover a period of over 200 years. Return to text
25. By construction, these interaction terms sum to the measure of the real exchange rate overvaluation. Return to text
26. Prasad et al. (2006), Eichengreen (2008), and Aghion et al. (2009) study the impact of real exchange rate overvaluation on the economic growth. Return to text
27. Arellano (2008), Aguiar and Gopinath (2006), and Yue (2010) document and show the procyclicality of sovereign borrowing in an Eaton-Gersotivz framework. We thank a referee for suggsting this explanation. Return to text
28. Edwards (1988) finds that the autonomous forces that move the real exchange rate back to equilibrium operate very slowly, keeping the country out of equlibrium for a long time. Return to text
29. Edwards and Levy-Yeyati (2005) argue that the adjustment in equilibrium real exchange rate upon a real external shock takes longer in countries with a fixed exchange rate. Return to text
30. See Levy-Yeyati and Sturzenegger (2003) for more details on the multinomial logit model for the exchange rate regime. Return to text
31. Prasad et al. (2006) argue that a rapidly growing labor force should lead to undervaluation due to the pressure on policy makers to maintain a competitive real exchange rate in order to absorb additional workers into employment. Eichengreen (2008) also documents a similar relation between the share of working age population and real overvaluation. Return to text
32. Unless otherwise specified, the explanatory variables are obtained at an annual frequency and are lagged for one year to avoid the simultaneity issue. Return to text
33. This measure is constructed by
following Dollar (1992) and Aghion et al. (2009). Specifically, we
perform the following pooled OLS regression:
![]() , where
, where ![]() is the year dummy. The regression
results are consistent with Aghion et al. (2009):
is the year dummy. The regression
results are consistent with Aghion et al. (2009):
![]() ,
,
![]() ,
,
![]() , and the adjusted
R-square is
, and the adjusted
R-square is ![]() , where
, where ![]() denotes 1%
significance. Return to
text
denotes 1%
significance. Return to
text
34. The superscripts ![]() denote the significance level --
denote the significance level -- ![]() :
significant at 10%;
:
significant at 10%; ![]() : significant at 5%;
: significant at 5%;
![]() : significant at 1%. We use them in all of
the other tables as well. Return to
text
: significant at 1%. We use them in all of
the other tables as well. Return to
text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text
![$\displaystyle \alpha _{INT}+\rho \sigma _{u}\left[ \lambda \left( \frac{-\beta \overline{Z}_{\left( 0,1\right) }}{\sigma _{v}}\right) -\lambda \left( \frac{ -\beta \overline{Z}_{\left( 0,0\right) }}{\sigma _{v}}\right) \right] , \notag$](img18.gif)
![$\displaystyle \alpha _{FIX}-\alpha _{INT}+\rho \sigma _{u}\left[ \lambda \left( \frac{ -\beta \overline{Z}_{\left( 1,0\right) }}{\sigma _{v}}\right) -\lambda \left( \frac{-\beta \overline{Z}_{\left( 0,1\right) }}{\sigma _{v}}\right) \right] , \notag$](img31.gif)