
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1050, June 2012 --- Screen Reader
Version*
Do Oil Prices Help Forecast U.S. Real GDP? The Role of Nonlinearities and Asymmetries
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Abstract: There is a long tradition of using oil prices to forecast U.S. real GDP. It has been suggested that the predictive relationship between the price of oil and one-quarter ahead U.S. real GDP is nonlinear in that (1) oil price increases matter only to the extent that they exceed the maximum oil price in recent years and that (2) oil price decreases do not matter at all. We examine, first, whether the evidence of in-sample predictability in support of this view extends to out-of-sample forecasts. Second, we discuss how to extend this forecasting approach to higher horizons. Third, we compare the resulting class of nonlinear models to alternative economically plausible nonlinear specifications and examine which aspect of the model is most useful for forecasting. We show that the asymmetry embodied in commonly used nonlinear transformations of the price of oil is not helpful for out-of-sample forecasting; more robust and more accurate real GDP forecasts are obtained from symmetric nonlinear models based on the three-year net oil price change. Finally, we quantify the extent to which the 2008 recession could have been forecast using the latter class of time-varying threshold models.
Keywords: Out-of-sample forecast, oil price, real GDP, nonlinearity, asymmetry
JEL classification: C32, C53, Q43
1. Introduction
There has been much interest over the years in the question of whether lagged oil price changes are helpful in forecasting U.S. real GDP growth (see, e.g., Bachmeier, Li and Liu 2008; Kilian and Vigfusson 2011a; Hamilton 2011; Alquist, Kilian and Vigfusson 2012; Ravazzolo and Rothman 2012). Hamilton (2003) made the case that the predictive relationship between oil prices and U.S. real GDP is nonlinear in that (1) oil price increases matter only to the extent that they exceed the maximum oil price in recent years and that (2) oil price decreases do not matter at all. He provided in-sample evidence that including appropriately defined lagged net increases in the nominal price of oil in an autoregression for real GDP growth helps predict U.S. real GDP growth one quarter ahead. This evidence was subsequently confirmed on more recent data by Kilian and Vigfusson (2011b). Evidence of in-sample predictability as documented in these studies, however, need not translate into out-of-sample gains in forecast accuracy, which is the ultimate question of interest to policy makers and applied forecasters. In this paper, we examine how successful the Hamilton model and similar nonlinear models are in reducing out-of-sample prediction mean-squared errors (MSPEs) of U.S. real GDP growth. This question has taken on new urgency following the large fluctuations in the price of oil in recent years. There is interest not only in the question of asymmetries, but also in the notion that increases in the price of oil beyond certain time-varying thresholds may trigger recessions.
In implementing this class of nonlinear and asymmetric forecasting models several potentially important modeling choices arise. One unresolved question is whether such forecasting models should be specified in terms of the nominal price of oil or the real price of oil. A related question is which oil price measure forecasters should rely on. Common choices include the U.S. producer price index for crude oil, the price of West Texas Intermediate (WTI) crude oil, the U.S. refiners' acquisition cost for domestically produced crude oil, for crude oil imports, or for a composite of both. We systematically explore these modeling choices.
A second unresolved question is how to construct forecasts for horizons beyond one quarter. We propose an iterative forecasting method based on a system of equations for oil prices and real GDP, building on the analysis in Kilian and Vigfusson (2011b). Our analysis helps address the additional question of whether it is better to treat the price of oil as exogenous with respect to U.S. real GDP in multi-step ahead forecasting in the interest of greater parsimony or to leave the model unconstrained. We also explore other types of restrictions that have been found helpful in the earlier literature.
Third, we provide a more in-depth analysis of which features of the Hamilton model enhance forecast accuracy. Unlike Mork's (1989) predictive analysis, Hamilton's predictive model combines a specific form of asymmetry with additional nonlinearities not involving asymmetries. It is not clear which aspect of this model is driving its forecast performance. We therefore provide a comparison with several alternative nonlinear forecasting models that do not involve asymmetries. For example, we allow real GDP growth to depend on net changes in the price of oil, defined as the sum of net increases and net decreases in the price of oil, consistent with the behavioral arguments advanced by Hamilton (2003) or to depend on time-varying oil shares, motivated by the analysis of consumer expenditures in Edelstein and Kilian (2009). We also explore model specifications that depend on uncensored deviations from recent oil price peaks and models in which large oil price changes have different effects from small oil price changes (see, e.g., Goldberg 1998; Davis and Kilian 2011). Finally, we consider less restrictive asymmetric models in which net oil price increases and net oil price decreases enter with different weights.
Ours is not the first paper to examine the out-of-sample accuracy of Hamilton's (2003) model. Related work also includes Carlton (2010) and Ravazzolo and Rothman (2012).1 One difference from these studies is that we abstract from real-time data constraints. This simplification is not likely to be crucial for our purposes. Ravazzolo and Rothman (2012) find similar results in recursive regressions for real-time data and for ex-post revised data. A more important difference is that we focus on iterated forecasts rather than direct forecasts of real GDP growth. To the extent that the results in Ravazzolo and Rothman and our results are comparable, we obtain higher accuracy gains using the iterated forecasting method than would be obtained using direct forecasts. This finding is consistent with evidence by Marcellino, Stock, and Watson (2006) that iterated forecasts from multi-equation models often tend to be more accurate than direct forecasts based on single-equation models. Most importantly, however, we explore a much wider range of model specifications and data specifications than earlier studies. For example, Ravazzolo and Rothman explored only one nonlinear regression specification compared with more than one hundred specifications in our analysis. Our analysis not only assesses the out-of-sample forecast accuracy of these nonlinear models, but it sheds light on which aspects of nonlinear forecasting models are most useful.
Within the class of asymmetric nonlinear models, we find only mixed evidence of improvements in forecast accuracy at the one-quarter horizon, but at longer horizons our extension of the three-year net oil price increase model originally proposed by Hamilton (2003) provides more accurate forecasts than many alternative linear and nonlinear forecasting models of U.S. real GDP. We show that this empirical success of the model is due to nonlinear features other than its asymmetry, however. In fact, reductions in the MSPE that are as high or higher than for the three-year net oil price increase model can be obtained based on a model that is based on three-year net oil price changes and involves no asymmetry. This finding is important because to date is has been widely believed that the empirical success of the Hamilton oil price specification derives from its asymmetry. Our results demonstrate that this asymmetry is irrelevant for out-of-sample forecasting, if not harmful. This finding is consistent with the fact that all other asymmetric specifications we consider appear to be inferior to forecasting models that are symmetric in the price of oil.
There also is a second reason to be skeptical of the three-year net oil price increase model. We document that the overall forecasting success of this model appears to be driven by the 2008 recession episode only. There is no evidence that this forecasting model improves on the AR(4) benchmark model for real GDP growth when the evaluation period ends in 2007.Q4, and it is hard to imagine a forecaster would have relied on these models in real time, given their persistent failure during the first seventeen years of the evaluation period. This raises concerns that the model may be overfitting during the financial crisis. Indeed, the out-of-sample accuracy of some nonlinear models during 2008 is too good to be plausible. One explanation is that, under the MSPE metric, overfitting becomes an issue in small samples even when evaluating out-of-sample forecasts.
We show that, in contrast, the symmetric three-year net oil price change model is much more robust across oil price specifications, horizons, and evaluation periods, and produces more plausible forecasts than the corresponding net increase model, alleviating concerns regarding overfitting to some extent. We conclude that the net change specification is preferred over the net increase specification for the purpose of forecasting U.S. real GDP. Even the three-year net oil price change model shows signs of some overfitting, however. For example, it forecasts two spikes in economic activity in the 1990s that did not occur and - like the three-year net oil price increase model - it forecast lower growth in 2005/06 than occurred. These forecast errors are a direct consequence of the estimation procedure choosing model estimates to fit the sharp recession of 1991. After shrinking the model coefficients for the lagged net oil price change by a factor of one half, we find that the model forecasts are much more reasonable during the remaining period of 1992.Q1-2007.Q4. At the same time, this alternative three-year net oil price change model forecasts much smaller recessions in 1991 and 2008.
For example, rather than forecasting one third of the actual decline in cumulative U.S. real GDP growth in 2008 one year in advance, as the original three-year net change model does, or forecasting virtually the entire recession, as the three-year net oil price increase model does, the model after scaling the oil price coefficients in the second equation forecasts about 15% of the observed decline in U.S. real GDP in 2008. This result seems much more economically plausible and is still much larger than the decline implied by linear VAR models, indicating a possible role for threshold nonlinearities in forecasting. It is also in line with forecasts from other nonlinear symmetric specifications such as the gap model. Our analysis of the net change model draws attention to a previously undocumented type of nonlinearity in the predictive relationship between oil prices and the U.S. economy and has important implications for applied forecasters as well as economists interested in modeling the transmission of oil price shocks.
The remainder of the paper is organized as follows. Section 2 reviews the data sources and construction. Section 3 evaluates forecasting success of linear dynamic models. Section 4 evaluates the forecast success of standard nonlinear dynamic models motivated by the analysis of Mork (1989) and Hamilton (1996, 2003). In section 5, we extend the analysis to alternative nonlinear dynamic models. Section 6 contains sensitivity analysis and focuses on the question of how much of the 2008 recession could have been forecast out of sample with the help of nonlinear transformations of the real price of oil. The concluding remarks are in section 7.
2. The Data
All data are quarterly. The sample extends from 1974.Q1 to 2011.Q4. The baseline results are for the U.S. refiners' acquisition cost for imported crude oil, which can be thought of as a proxy for the price of crude oil in global markets. This series is obtained from the U.S. Energy Information Administration (EIA). As discussed in Alquist et al. (2012), this series is the most relevant oil price measure based on standard economic models of the transmission of oil price shocks to the U.S. economy. The case can be made, however, that other oil price series may be more relevant for alternative economic models of the transmission of oil price shocks. In section 6, we therefore discuss how our results are affected by alternative choices for the oil price variable including the U.S. producer price index (PPI) provided by the BLS, the West Texas Intermediate (WTI) price of crude oil and the domestic and composite U.S. refiners' acquisition cost. The latter data are obtained from the EIA) When necessary for the construction of oil price transformations the oil price data have been backcast, as discussed in Baumeister and Kilian (2011). The real price of oil is obtained by deflating the nominal price of oil by the U.S. CPI for all urban consumers. The U.S. CPI data are from the BLS; the real and nominal U.S. GDP data are from the BEA. All macroeconomic data are seasonally adjusted. The data for U.S. crude oil production, crude oil imports and crude oil exports used in constructing the U.S. oil share are from the Monthly Energy Review of the EIA.
3. The Ability of Linear Dynamic Models to Forecast U.S. Real GDP
A natural starting point in thinking about the specification of
nonlinear forecasting models for U.S. real GDP is a linear
VAR(p) model for the real price of oil and for U.S. real GDP
expressed in quarterly percent changes. The general structure of
the model is
![]() , where
, where
![]()
![]() denotes the log of the real price of oil,
denotes the log of the real price of oil, ![]() the log of real GDP,
the log of real GDP, ![]() is the
difference operator,
is the
difference operator, ![]() the regression error, and
the regression error, and
![]() Alternatively, we also consider
Alternatively, we also consider
![]() where
where
![]() denotes the log of the nominal price
of oil. The benchmark model for real GDP growth, relative to which
the forecast performance of all other models will be judged, is the
AR(p) model obtained with
denotes the log of the nominal price
of oil. The benchmark model for real GDP growth, relative to which
the forecast performance of all other models will be judged, is the
AR(p) model obtained with
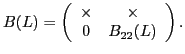
The specification of the components of ![]() marked as
marked as
![]() is irrelevant for this forecasting
model. We determined the most appropriate lag order of this
benchmark model based on a forecast accuracy comparison involving
all combinations of horizons
is irrelevant for this forecasting
model. We determined the most appropriate lag order of this
benchmark model based on a forecast accuracy comparison involving
all combinations of horizons
![]() and lag orders
and lag orders
![]() The AR(4) model for real
GDP growth proved to have the lowest MSPE or about the same MSPE as
the most accurate model at all horizons. The same AR(4) benchmark model
has also been used by Hamilton (2003), Alquist, Kilian and
Vigfusson (2012), and Ravazzolo and Rothman (2012), among others,
facilitating comparisons with existing results in the literature.
The AR(4) model for real
GDP growth proved to have the lowest MSPE or about the same MSPE as
the most accurate model at all horizons. The same AR(4) benchmark model
has also been used by Hamilton (2003), Alquist, Kilian and
Vigfusson (2012), and Ravazzolo and Rothman (2012), among others,
facilitating comparisons with existing results in the literature.
In this section we compare two linear dynamic models to the AR(4) benchmark. One model is the unrestricted VAR(4) model of the form
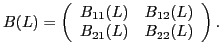
The other is a restricted VAR(4) model of the form
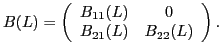
The lag order is chosen to nest the AR(4) model. The
restriction
![]() is implied by the hypothesis
that the price of oil is exogenous with respect to U.S. real GDP.
Although that restriction is not literally true, the predictive
content of U.S. real GDP for the real price of oil, while not zero,
appears to be weak in linear models (see Alquist, Kilian, and
Vigfusson 2012). A natural conjecture is that the added parsimony
from imposing zero feedback from lagged real GDP to the real price
of oil may help reduce the out-of-sample MSPE of cumulative real
GDP growth forecasts.
is implied by the hypothesis
that the price of oil is exogenous with respect to U.S. real GDP.
Although that restriction is not literally true, the predictive
content of U.S. real GDP for the real price of oil, while not zero,
appears to be weak in linear models (see Alquist, Kilian, and
Vigfusson 2012). A natural conjecture is that the added parsimony
from imposing zero feedback from lagged real GDP to the real price
of oil may help reduce the out-of-sample MSPE of cumulative real
GDP growth forecasts.
As in the remainder of the paper, all models are estimated
recursively on data starting in 1974.Q1.The initial estimation
period ends in 1990.Q1, right before the invasion of Kuwait in
August of 1990. The forecast evaluation ends in 2011.Q4. The
maximum length of the recursive sample is restricted by the end of
the data and by the forecast horizon. We evaluate the MSPE of each
model for the cumulative growth rates at horizons
![]() corresponding to
the horizons of interest to policy makers. All results are
expressed as MSPE ratios relative to the benchmark model.2
corresponding to
the horizons of interest to policy makers. All results are
expressed as MSPE ratios relative to the benchmark model.2
The first column of Table 1 shows that, at horizons of three quarters and beyond, including the real price of oil in the autoregressive models may reduce the MSPE for real GDP growth by up to 6% relative to the AR(4) model for real GDP growth. At shorter horizons, the AR(4) benchmark is more accurate by up to 10%. Imposing the restriction that the real price of oil is exogenous, as shown in the second column, marginally reduces the MSPE at some horizons, but the differences are negligible.
Next consider a similar analysis for the nominal price of oil. Although the use of the nominal price of oil in predicting real GDP is not supported by standard economic models, it is useful to explore this alternative approach in light of behavioral arguments in favor of using the nominal price of oil. Table 1 shows that the unrestricted VAR(4) model based on the real price of oil is consistently at least as accurate as the same model based on the nominal price of oil. We conclude that in linear models there are no gains in forecast accuracy from replacing the real price of oil by the nominal price. Imposing exogeneity, as shown in the last column, again makes little difference.
It can be shown that, notwithstanding these differences in MSPEs, the AR(4) and VAR(4) forecasts are generally quite similar. One chief objective in using oil prices to forecast U.S. real GDP is to improve our ability to forecast recessions. Further analysis establishes that neither the AR(4) nor the VAR(4) model is able to forecast the large economic declines of 1990/91, 2001, and 2008/09, however. One possible explanation of this forecast failure is that the VAR model is unable to forecast the real price of oil accurately enough. Put differently, our real GDP forecasts would be more accurate if only we had more accurate forecasts of the real price of oil. Conditioning on realized values of the future price of oil, however, does not greatly improve the forecast accuracy of the linear VAR model for cumulative real GDP growth, so this explanation can be ruled out. An alternative explanation could be that the predictive relationship between the price of oil and domestic macroeconomic aggregates is time-varying. One source of time variation is that the share of oil in U.S. GDP has varied considerably over time. This suggests that we replace the percent change in the real price of oil in the linear VAR model by the percent change in the real price of oil weighted by the time-varying share of oil consumption in U.S. GDP, building on the related analysis in Edelstein and Kilian (2009). Hamilton (2009) reported some success in employing a similar strategy.3 We will examine this approach in section 5. Another source of time variation may be changes in the composition of the underlying oil demand and oil supply shocks, as discussed in Kilian (2009). Finally, yet another potential explanation investigated in section 4 is that the linear forecasting model may be inherently misspecified. Of particular concern is the possibility that nonlinear dynamic regression models may generate more accurate out-of-sample forecasts of cumulative real GDP growth. This latter explanation has received much attention in the literature and is examined in depth in the next section.
4. The Ability of Standard Nonlinear Dynamic Models to Forecast U.S. Real GDP
In this section we examine the forecasting accuracy of a number of nonlinear models motivated by the analysis in Mork (1989) and Hamilton (1996, 2003). Hamilton (2003) suggested that the predictive relationship between oil prices and U.S. real GDP is nonlinear in that (a) oil price increases matter only to the extent that they exceed the maximum oil price in recent years and that (b) oil price decreases do not matter at all. This view was based on the in-sample fit of a single-equation predictive model of the form:
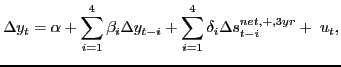
|
(1) |
where ![]() is the regression error,
is the regression error, ![]() denotes the log of the nominal price of oil and
denotes the log of the nominal price of oil and
![]() the corresponding
three-year net increase in the nominal price of oil, defined as
the corresponding
three-year net increase in the nominal price of oil, defined as
![]()
![]() where
where
![]() denotes the highest oil price over
the last three years. More recently, Hamilton (2011) also suggested
that nonlinear predictive models such as model (1) may be useful
for out-of-sample forecasting. We explore this conjecture below. We
consider both one-quarter-ahead forecasts of real GDP growth and
forecasts of the cumulative real GDP growth rate several quarters
ahead. The latter forecasts require a generalization of the
single-equation forecasting approach proposed by Hamilton (2011).
In implementing this approach, there are several potentially
important modeling choices to be made.
denotes the highest oil price over
the last three years. More recently, Hamilton (2011) also suggested
that nonlinear predictive models such as model (1) may be useful
for out-of-sample forecasting. We explore this conjecture below. We
consider both one-quarter-ahead forecasts of real GDP growth and
forecasts of the cumulative real GDP growth rate several quarters
ahead. The latter forecasts require a generalization of the
single-equation forecasting approach proposed by Hamilton (2011).
In implementing this approach, there are several potentially
important modeling choices to be made.
First, even granting the presence of asymmetries in the predictive model, one question is whether the predictive model should be specified as in (1) or rather as:
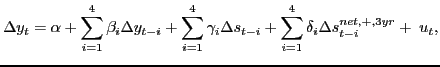
|
(2) |
as in Balke, Brown and Yücel (2002) or Herrera, Lagalo and Wada (2011), for example.
A second point of contention is whether nonlinear forecasting models should be specified in terms of the nominal price of oil or the real price of oil. For linear models, a strong economic case can be made for using the real price of oil. For nonlinear models, the situation is less clear, as noted by Hamilton (2011). Because the argument for using net oil price increases is behavioral, one specification appears as reasonable as the other. Below we therefore will consider models based alternatively on the real price and the nominal price of oil.
A third issue that arises only in constructing iterated forecasts for higher horizons is how to specify the process governing the price of oil. The case can be made that treating this process as exogenous with respect to real GDP might help reduce the out-of-sample MSPE, even if that restriction is incorrect. Below we therefore consider specifications with and without imposing exogeneity.
Tables 2a and 2b allow a systematic investigation of these
issues. We quantify the MSPE reductions associated with the use of
censored oil price variables at horizons
![]() drawing on the
analysis in Kilian and Vigfusson (2011a,b). The main focus is on
the net oil price increase transformation of Hamilton (1996, 2003).
For completeness, we also include results for a percent increase
specification motivated by Mork's (1989) analysis, the
out-of-sample forecasting performance of which has not been
investigated to date. The latter specification involves replacing
negative percent changes in the price of oil by zero, while
retaining positive percent changes in the price of oil. We consider
nonlinear models based on the real price of oil as in Mork (1989)
and Kilian and Vigfusson (2011b) and nonlinear models based on the
nominal price of oil as in Hamilton (1996, 2003). The unrestricted
multivariate nonlinear forecasting model takes the form
drawing on the
analysis in Kilian and Vigfusson (2011a,b). The main focus is on
the net oil price increase transformation of Hamilton (1996, 2003).
For completeness, we also include results for a percent increase
specification motivated by Mork's (1989) analysis, the
out-of-sample forecasting performance of which has not been
investigated to date. The latter specification involves replacing
negative percent changes in the price of oil by zero, while
retaining positive percent changes in the price of oil. We consider
nonlinear models based on the real price of oil as in Mork (1989)
and Kilian and Vigfusson (2011b) and nonlinear models based on the
nominal price of oil as in Hamilton (1996, 2003). The unrestricted
multivariate nonlinear forecasting model takes the form
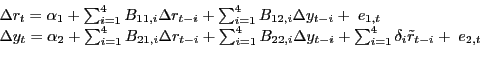
|
(3) |
where ![]() denotes the log of the real price of
oil,
denotes the log of the real price of
oil,
![]() Mork's oil price increase measure is defined as
Mork's oil price increase measure is defined as
![]()
![]() , where
I() is the indicator function. The three-year net oil price
increase measure is defined as
, where
I() is the indicator function. The three-year net oil price
increase measure is defined as
![]() where
where ![]() is the maximum real price of oil
over the most recent three years. The one-year net oil price
increase
is the maximum real price of oil
over the most recent three years. The one-year net oil price
increase
![]() is constructed
similarly based on the largest real price of oil over the most
recent year.
is constructed
similarly based on the largest real price of oil over the most
recent year.
Analogous nonlinear forecasting models may be constructed based
on the nominal price of oil, denoted in logs as ![]()
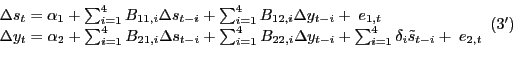
where
![]() In addition, we consider restricted versions of these two models
which impose the hypothesis that the price of oil is exogenous such
that
In addition, we consider restricted versions of these two models
which impose the hypothesis that the price of oil is exogenous such
that
![]() and/ or which restrict
the feedback from lagged percent changes in the price of oil to
real GDP growth such that
and/ or which restrict
the feedback from lagged percent changes in the price of oil to
real GDP growth such that
![]() After imposing the
latter restriction, one-quarter ahead real GDP growth forecasts
only depend on the second equation, so our forecasts are equivalent
to using Hamilton's model (1). For longer
horizons, our models may be viewed as a generalization of model
(1). All 24
models are estimated by least squares, as is standard in the
literature. The nonlinear forecasts are constructed by Monte Carlo
integration based on 10,000 draws (see, e.g., Koop, Pesaran, and
Potter 1996; Kilian and Vigfusson 2011a). For each recursively
estimated multi-equation model we simulate the future path of real
GDP growth conditional on the most recent data by drawing from the
empirical distribution of the reduced-form residuals and iterating
the model forward. Forecasts are computed as averages of the
simulated forecast paths. The estimation and evaluation periods are
the same as in Table 1.
After imposing the
latter restriction, one-quarter ahead real GDP growth forecasts
only depend on the second equation, so our forecasts are equivalent
to using Hamilton's model (1). For longer
horizons, our models may be viewed as a generalization of model
(1). All 24
models are estimated by least squares, as is standard in the
literature. The nonlinear forecasts are constructed by Monte Carlo
integration based on 10,000 draws (see, e.g., Koop, Pesaran, and
Potter 1996; Kilian and Vigfusson 2011a). For each recursively
estimated multi-equation model we simulate the future path of real
GDP growth conditional on the most recent data by drawing from the
empirical distribution of the reduced-form residuals and iterating
the model forward. Forecasts are computed as averages of the
simulated forecast paths. The estimation and evaluation periods are
the same as in Table 1.
Tables 2a and 2b display the MSPE ratios for all 24 models by
horizon. The first result is that no nonlinear model based on
Mork's oil price increase measure yields large or systematic gains
relative to the AR(4) benchmark model
for real GDP growth. In fact, all these models tend to be less
accurate than a linear vector autoregression. Second, among
Hamilton's two net oil price increase specifications, models based
on the three-year net oil price increase are much more accurate
than models based on the one-year net oil price increase. The
latter models improve on the MSPE of the VAR model at all horizons.
Third, imposing the additional restrictions
![]() and
and
![]() reduces the MSPE further.
Most of the gains in accuracy arise from imposing
reduces the MSPE further.
Most of the gains in accuracy arise from imposing
![]() Fourth, there is no
clear ranking between the models based on the real U.S. refiners'
acquisition cost for imported oil and the corresponding models
based on the nominal refiners' acquisition cost. A case in point is
the most restrictive specification for the three-year net oil price
increase model in Table 2b. For example, at the one-year horizon,
the model which combines Hamilton's assumptions with that of
exogenous nominal oil prices and embeds all these assumptions in a
multivariate dynamic framework, yields MSPE reductions of up to 26%
relative to the AR(4) benchmark model
for real GDP growth, whereas the same model for the real price only
reduces the MSPE by 19%. At the one-quarter horizon, however, the
ranking is reversed with an MSPE reduction of 7% for the real price
of oil and an MSPE increase of 2% for the nominal price, and at the
two-year horizon the reduction in the MSPE are 18% and 17%,
respectively.
Fourth, there is no
clear ranking between the models based on the real U.S. refiners'
acquisition cost for imported oil and the corresponding models
based on the nominal refiners' acquisition cost. A case in point is
the most restrictive specification for the three-year net oil price
increase model in Table 2b. For example, at the one-year horizon,
the model which combines Hamilton's assumptions with that of
exogenous nominal oil prices and embeds all these assumptions in a
multivariate dynamic framework, yields MSPE reductions of up to 26%
relative to the AR(4) benchmark model
for real GDP growth, whereas the same model for the real price only
reduces the MSPE by 19%. At the one-quarter horizon, however, the
ranking is reversed with an MSPE reduction of 7% for the real price
of oil and an MSPE increase of 2% for the nominal price, and at the
two-year horizon the reduction in the MSPE are 18% and 17%,
respectively.
5. The Ability of Alternative Nonlinear Dynamic Models to Forecast U.S. Real GDP
The nonlinear specifications in Tables 2a and 2b are a natural starting point, given the prominence of Mork's and Hamilton's work on the predictive relationship between oil prices and one-quarter ahead U.S. real GDP growth, but there are several alternative nonlinear forecasting models that seem equally plausible a priori and deserve closer examination. In this section we contrast the forecasting accuracy of these alternative models with the results in Tables 2a and 2b in an effort to gain a better understanding of what features of Hamilton's model (and its generalizations proposed in this paper) are most helpful in forecasting U.S. real GDP.
It is useful to recall that the net oil price increase specification developed by Hamilton (1996, 2003) involves two quite distinct ideas. One idea is that consumers in oil-importing economies respond to increases in the price of oil only if the price increases to a level that is high relative to the recent highs. The other idea is that consumers do not respond to net decreases in the price of oil, allowing us to omit the net decreases from the model. The poor performance of Mork's model in Tables 2a and 2b suggests that whatever gains in forecast accuracy Hamilton's specification offers are likely to be related more to the first than to the second idea. In fact, his motivation for the net oil price increase measure by construction should equally apply to decreases in the price of oil, suggesting a nonlinear forecasting model that is symmetric in net oil price increases and net oil price decreases. This net-change model may be written as:
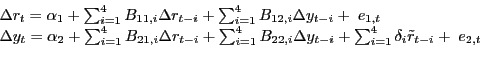
|
(4) |
where
![]()
![]() and
and
![]() In this context,
In this context,
![]() where
where ![]() is the maximum real price of oil
over the most recent three years, refers to the conventional
definition of the three-year net oil price increase discussed
earlier, and
is the maximum real price of oil
over the most recent three years, refers to the conventional
definition of the three-year net oil price increase discussed
earlier, and
![]() where
where
![]() is the minimum real price of oil
over the most recent three years, denotes the corresponding
three-year net oil price decrease. The variables
is the minimum real price of oil
over the most recent three years, denotes the corresponding
three-year net oil price decrease. The variables
![]() and
and
![]() are constructed
analogously based on the largest and smallest real price of oil
over the most recent year.
are constructed
analogously based on the largest and smallest real price of oil
over the most recent year.
A second concern is that the particular form of asymmetry imposed by Hamilton is stronger than that suggested by any of the relevant economic models. Economic models of the asymmetric transmission of oil price shocks such as Hamilton (1988) do not imply that oil price decreases should receive zero weight, only that they may have lower weight under suitable assumptions. This observation suggests that we relax the restriction that net oil price decreases have no effect at all and postulate the asymmetric forecasting model:
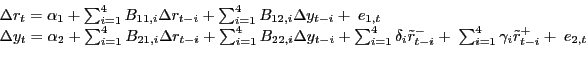
|
(5) |
where either
![]() and
and
![]() or
or
![]() and
and
![]() This
asymmetric net change model allows for weaker forms of
asymmetry in conjunction with the behavioral assumptions invoked by
Hamilton (2011).
This
asymmetric net change model allows for weaker forms of
asymmetry in conjunction with the behavioral assumptions invoked by
Hamilton (2011).
A third conjecture is that what oil consumers respond to is not
the net oil price increase, but simply the deviation of the price
of oil from the highest price in recent memory. This behavioral
model can be captured by replacing the censored variable
![]() by the uncensored variable
by the uncensored variable
![]() where
where
![]() is the most recent maximum of the
real price of
is the most recent maximum of the
real price of
oil. The implied nonlinear forecasting model is:
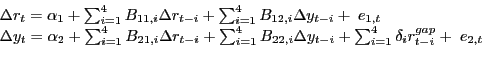
|
(6) |
The use of
![]() in this gap model allows
us to relax the assumption that the economy only responds to oil
prices exceeding recent peaks, while preserving the notion that
there is state dependence in the feedback from oil prices to the
economy.
in this gap model allows
us to relax the assumption that the economy only responds to oil
prices exceeding recent peaks, while preserving the notion that
there is state dependence in the feedback from oil prices to the
economy.
Another possible form of nonlinearity in the relationship between oil prices and the economy is discussed in Goldberg (1998), who observes that the feedback from oil price changes to the domestic economy may be limited to large oil price changes.4 The fact that small oil price changes might go unnoticed may be rationalized by the costs of monitoring energy prices and the costs of adjusting consumption patterns. The premise that only large oil price changes matter suggests a forecasting model of the form
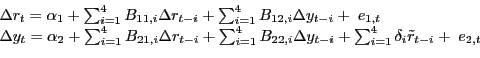
|
(7) |
where
![]()
![]() and
and ![]() refers to the sample standard deviation.
refers to the sample standard deviation.
An asymmetric version of this model in which only large oil price increases matter would be
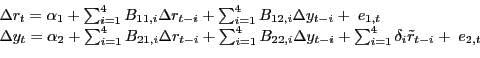
|
(8) |
where
![]()
![]()
All these models are a priori as reasonable as the models considered in Tables 2a and 2b. They can alternatively be specified in terms of the nominal price of oil and may be restricted further along the same lines of the models in Tables 2a and 2b, resulting in six distinct model specifications each. Yet another conjecture, we alluded to earlier, is that the disappointing accuracy of forecasts from linear VAR models arises because the regression fails to control for fluctuations in the share of crude oil expenditures in GDP. This problem may be addressed by specifying the forecasting model:
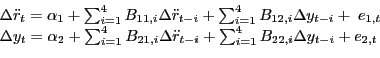
|
(9) |
where
![]() and
and ![]() is obtained by dividing the sum of U.S.
crude oil production and net crude oil imports, weighted by the
nominal U.S. refiners' acquisition cost for crude oil imports and
averaged by quarter, by quarterly U.S. nominal GDP. This approach
is similar to that taken by Edelstein and Kilian (2009) in modeling
the effects of shocks to retail energy prices on consumers'
purchasing power (also see Hamilton 2009). It can be shown that the
share of oil in output rises with the price of oil, so when the
price of oil is high, the same oil price increase receives a higher
weight in the construction of
is obtained by dividing the sum of U.S.
crude oil production and net crude oil imports, weighted by the
nominal U.S. refiners' acquisition cost for crude oil imports and
averaged by quarter, by quarterly U.S. nominal GDP. This approach
is similar to that taken by Edelstein and Kilian (2009) in modeling
the effects of shocks to retail energy prices on consumers'
purchasing power (also see Hamilton 2009). It can be shown that the
share of oil in output rises with the price of oil, so when the
price of oil is high, the same oil price increase receives a higher
weight in the construction of
![]() than when the price of oil is
low, making this weighted oil price model state-dependent
not unlike some of the earlier models. The upper panel of Figure 1
shows that the share of oil in U.S. GDP peaked in 1980/81, reached
a trough in the late 1980s and began to rebound systematically only
after 2003, although it never quite reached the level of
1980/81.5
than when the price of oil is
low, making this weighted oil price model state-dependent
not unlike some of the earlier models. The upper panel of Figure 1
shows that the share of oil in U.S. GDP peaked in 1980/81, reached
a trough in the late 1980s and began to rebound systematically only
after 2003, although it never quite reached the level of
1980/81.5
Tables 3a and 3b evaluate models (4) and (5). As in Tables
2a and 2b we focus on the U.S. refiners' acquisition cost for crude
oil. We find that nonlinear specifications based on the most recent
year of oil price data are systematically less accurate than
specifications based on the most recent three years of oil price
data. In the latter case, there is little difference between using
the nominal price of oil and the real price of oil. Imposing
![]() has only minor effects on
the MSPE, but imposing
has only minor effects on
the MSPE, but imposing
![]() helps especially at
short horizons.
helps especially at
short horizons.
A striking finding is that allowing for (weak) asymmetries increases the MSPE of the net change model. Overall, the most accurate forecasting model is the symmetric three-year net change model with all restrictions imposed, although alternative specifications that do not impose the exogeneity of the price of oil perform nearly as well. Whether one uses the nominal or the real price of oil makes little difference. The MSPE reductions of 8% at the one-quarter horizon, 28% at the four-quarter horizon, and 22% at the eight-quarter horizon when using the nominal price of oil compare favorably with the results for the best asymmetric model in Table 2b, which produced MSPE reductions of only -2%, 26%, and 17%, respectively. What is interesting about this finding is not how much we can improve on the net oil price increase model - indeed we are willing to simply postulate that these models are of comparable accuracy - but that much of the apparent forecasting success of the net oil price increase model in Table 2b had nothing to do with asymmetries, but with the other nonlinearities built in to the definition of the net oil price increase. This finding is reminiscent of the point we made earlier that models of pure asymmetries such as models based on Mork's oil price increase measure do not forecast very well. This result contrasts with common views in the literature. To date much of the empirical success of the net oil price increase specification has been attributed to the measure being asymmetric, with little attention to the fact that this definition embodies other nonlinearities. Our results suggest that these other nonlinearities may hold the key to improving our understanding of the transmission of oil price shocks to the economy.
The results in Tables 3a and 3b make it even more interesting to compare the performance of the three-year net change model to other nonlinear model specifications not involving asymmetries. Tables 4a and 4b focus on the models in equations (6) through (8). For the gap model we find that once again three-year oil price specifications are superior to one-year oil price specifications. At longer horizons, the three-year gap model specification can be more accurate than VAR models, but the results are sensitive to changes in the model specification. Even the most accurate three-year gap model in Table 4a is distinctly less accurate than the three-year net change model in Table 3b. Moreover, the large oil-price change model is not systematically more accurate than the linear VAR(4) model in Table 1, regardless of specification. Allowing for large oil price increases to matter more causes a substantial deterioration of forecast accuracy, reaffirming our conclusions about the role of asymmetries in forecasting.
Table 5 shows the results for the pseudo-linear VAR forecasting model in equation (9). In this model, the real price of oil has been weighted by the nominal share of oil in U.S. GDP. Table 5 shows that this pseudo-linear model does not work well, regardless of whether we impose exogeneity on the real price of oil, and is clearly less accurate than the linear VAR model.6 The lower panel of Figure 1 shows that until 2009, this model was slightly more accurate than the linear VAR model. Indeed, the model does a somewhat better job at predicting the recession of 2008. The forecast accuracy greatly deteriorates in 2009, however, when the oil share model predicts a much larger recovery than actually occurred on the basis of the preceding collapse of the real price of oil. We conclude that the overall forecast accuracy of the three-year net oil price change specification is not attained by any of these alternative specifications.
6. Sensitivity Analysis
An obvious question is how sensitive these results are to the choice of oil price series and evaluation period. Table 6 provides a systematic comparison of the performance of nonlinear forecasting models relative to the AR(4) benchmark model for real GDP growth for different oil price series and evaluation periods. In addition to reproducing the baseline results, we consider the composite U.S. refiner's acquisition cost, the U.S. refiners' acquisition cost for domestically produced crude oil, the price of West Texas Intermediate (WTI) crude oil and the U.S. producer price index for crude oil. To conserve space, we focus on the empirically most successful specification for the three-year net oil price increase and the corresponding net oil price change from Tables 2b and 3b, with all additional restrictions imposed.
6.1. Indications of Overfitting in the Forecasts of the Three-Year Net Increase Model
The first two columns in Table 6 show results for the evaluation period 1990.Q1-2011.Q4. While there is little evidence that three-year net oil price increase models outperform the benchmark at the one-quarter horizon, most specifications outperform the benchmark at the one-year horizon. Only two of ten alternative specifications reduce the one-quarter-ahead MSPE when evaluated on the full evaluation period of 1990.Q2-2011.Q4. In contrast, all but one model delivers four-quarter-ahead MSPE reductions.
There is no clear ranking between nominal and real oil price specifications at the one-quarter horizon, whereas at the four-quarter horizon forecasting models based on the nominal price tend to be somewhat more accurate. The largest MSPE reductions are obtained for the WTI price and for the U.S. refiners' acquisition cost for crude oil imports we used as a baseline for our analysis. The reduction in MSPE may be as high as 32% relative to the AR(4) benchmark model for real GDP growth. Models based on the PPI do not do well.7 The composite U.S. refiners' acquisition cost studied by Ravazzolo and Rothman (2012) appears to have lower predictive power than the U.S. refiners' acquisition cost for oil imports, whether nominal or real oil prices are used.
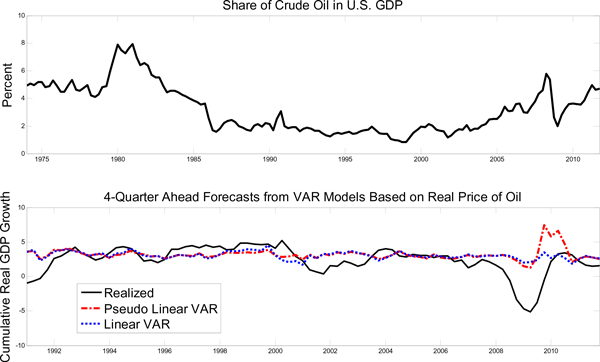
While the four-quarter-ahead MSPE reductions in Table 6 look impressive, there is reason to be cautious. It can be shown that much of the apparent gains in accuracy for the net oil price increase model are driven by data for the recession of 2008. An obvious concern is that these models may have forecast the 2008 recession for the wrong reasons. There is widespread agreement that the primary cause of this recession was the financial crisis of 2008. The financial crisis occurred immediately after a major surge in the price of oil, but itself was presumably not caused by that oil price surge. At best the oil price surge was a contributing factor to the subsequent economic decline. Plots of the recursive MSPE as shown in the lower panel of Figure 2 show that almost all of the apparent forecasting success of the net increase models at the four-quarter horizon arises during the 2008 recession. Hence, the seeming forecasting ability of these models may simply be an indication of overfitting. This concern is exacerbated by the fact that some net increase models in Table 6 imply that all of the 2008 recession was forecastable based on the preceding oil price increase, which does not seem credible.
It is usually thought that out-of-sample forecasts protect against such overfitting. This example illustrates why this perception need not be correct in the presence of historically unprecedented events when the evaluation sample is short. The problem is that, under quadratic loss, the ability of the nonlinear model to predict correctly one very large economic decline associated with the financial crisis, for example, could easily more than offset the sustained poor forecasting accuracy of the same nonlinear model during earlier episodes. This is a particular concern when dealing with a model that predicts a recession whenever there is a large net increase in the price of oil.
One way of gauging the importance of the 2008 episode in driving the MSPE ratio is to end the evaluation period in 2007.Q4, right before the financial crisis. The next two columns of Table 6 show that not one of the nonlinear models is able to forecast more accurately than the AR(4) benchmark model for real GDP growth during 1990.Q1-2007.Q4. This is true at the one-quarter and the four-quarter horizon, but especially at the four-quarter horizon. The four-quarter-ahead MSPE ratios are above 1 for all model specifications and exceed 2 for some specifications. In light of these results, it is fair to say that few forecasters by 2007.Q4 would have had the courage to stick with the forecasts implied by any of these nonlinear forecasting models given their sustained failure in the years leading up to the financial crisis. Especially noteworthy is the tendency of these models to forecast a major recession in 2005/06, which never occurred.
We conclude that the evidence that the net oil price increase transformation helps forecast cumulative U.S. real GDP growth is mixed at best. Not only are the results extremely sensitive to small extensions of the evaluation sample (with MSPE ratios in one case dropping from 2.05 to 0.92 with the addition of a few years of data), but the extent of the MSPE reductions vary greatly across models and can range from nonexistent or negligible to substantial in some cases.
6.2. Indications of Overfitting in the Forecasts of the Three-Year Net Change Model?
A similar concern applies to the results for the three-year net change model. We cannot take the results in Table 3b at face value without further scrutiny. It is instructive to subject this model to the same robustness checks as the 3-year net oil price increase model. For this purpose, the remaining columns of Table 6 have has been constructed analogously to the first four columns of results. We first focus on the evaluation period 1990.Q1-2011.QIV. Table 6 shows that the three-year net oil price change model has systematically lower MSPE than the AR(4) benchmark model for real GDP growth regardless of the forecast horizon. In addition, the results are much more robust across different oil price definitions than for the net oil price increase model, and the differences between specifications for the real price of oil and for the nominal price of oil are minor. Moreover, for seventeen of twenty specifications, the reductions in the MSPE are higher for the net change model than for the net increase model.
The last two columns show that the three-year net change model for the U.S. real refiners' acquisition cost for oil imports not only has a somewhat lower MSPE than the corresponding three-year net increase model over the 1990.Q1-2011.Q4 evaluation period, but also a lower MSPE when evaluated on the 1990.Q1-2007.Q4 period. This result again is largely robust across different oil price definitions. In short, unlike the net oil price increase model, the three-year net oil price change model is systematically more accurate than the AR(4) benchmark model for real GDP growth even prior to the financial crisis. While this evidence does not completely alleviate our concerns about overfitting in 1991 and 2008, it greatly improves our confidence in the forecast accuracy of this model during the financial crisis.
6.3. How Much Do Oil Prices Help Forecast the 2008 Recession?
A question of obvious interest is how much of the decline in U.S. real GDP growth during 2008/09 could have been forecast with the help of the three-year net oil price change measure. Figure 2 allows us to address this point. The upper panel shows a plot of the actual 4-step-ahead out-of-sample forecasts of each model against the realizations of cumulative real GDP growth, while the lower panel contains a time series plot of the recursive MSPE of each forecasting model relative to the AR(4) benchmark forecasting model for real GDP growth. Figure 2 shows a cumulative decline of -5% for 2008.Q1 through 2009.Q1 compared with an average annual growth rate near 2.5% prior to the crisis. The three-year net oil price change model forecast 0% growth for the same period, which roughly corresponds to one third of the decline that actually occurred.
Figure 2 also shows that the three-year net oil price change model provides more reasonable forecasts during 2005/06. Its predictions of an economic decline for 2005/06 are much more moderate than for the corresponding net increase model. In addition, the lower panel of Figure 2 illustrates that the three-year net oil price change model has on average been more accurate than the AR(4) benchmark model throughout most of evaluation period. In sharp contrast, the three-year net oil price increase model has been persistently less accurate than the AR(4) benchmark model except during the financial crisis. While this evidence alleviates concerns regarding overfitting to some extent, it does not eliminate them completely. In fact, Figure 2 shows that even the three-year net oil price change model shows some signs of overfitting. For example, it forecasts two spikes in economic activity in the 1990s that did not occur and - like the three-year net oil price increase model - it forecasts lower growth in 2005/06 than occurred. These forecast errors are a direct consequence of the estimation procedure choosing model estimates to fit the sharp recessions of 1991.
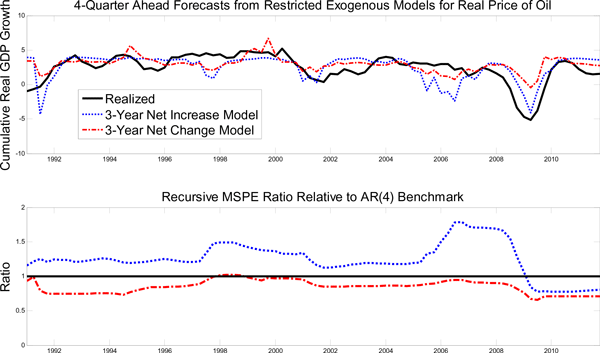
A simple way of exploring the consequences of this overfitting is to shrink the coefficient estimates on the lagged net oil price changes in the second equation of model (4) by a constant factor of one half, when constructing the forecasts. After shrinking these coefficients, we find that the model forecasts are much more reasonable during the remaining period of 1992.Q1-2007.Q4. At the same time, the modified three-year net oil price change model forecasts much smaller recessions in 1991 and 2008, as illustrated in Figure 3. For example, rather than forecasting one third of the actual decline in cumulative U.S. real GDP growth in 2008 one year in advance, as the original three-year net change model does, or forecasting virtually the entire recession, as the three-year net oil price increase model does, the model after scaling the oil price coefficients in the second equation forecasts about 15% of the observed decline in U.S. real GDP in 2008. This result seems much more economically reasonable and is still much larger than the decline implied by linear VAR forecasting models, consistent with the view that threshold nonlinearities matter for real GDP forecasts. It is also more in in line with forecasts from other nonlinear symmetric specifications such as the gap model, as shown in Figure 3, although the gap model overall does not appear as accurate as the scaled net change model.
7. Concluding Remarks
We first examined the ability of oil prices to improve simple univariate autoregressive forecasts of U.S. real GDP growth. We documented that there are at best small out-of-sample MSPE reductions when forecasting cumulative U.S. real GDP growth from bivariate VAR models that include the percent change in the price of oil in addition to real GDP growth. This finding was shown to be robust to whether the price of oil is specified in nominal or in real terms and whether the oil price is treated as exogenous or as endogenous with respect to U.S. real GDP. One possible explanation of this result is that the predictive relationship in question is nonlinear. Indeed this possibility has been discussed at length in the existing literature, but the out-of-sample forecasting performance of these nonlinear models has never been evaluated systematically.
We then evaluated and compared a wide range of forecasting models for U.S. real GDP based on nonlinear transformations of the price of oil that are asymmetric in oil price increases and decreases. Our work complements other recent studies such as Ravazzolo and Rothman (2012) in that it focuses on iterated forecasts from multivariate models rather than direct forecasts and that it greatly expands the set of nonlinear models under consideration. Of the asymmetric models only a multivariate generalization of the predictive model proposed by Hamilton (2003, 2011) produced systematic MSPE reductions at longer horizons. For example, based on the three-year net increase in the U.S. refiners' acquisition cost for crude oil imports, the MSPE reductions are between 19% and 26% at the one-year horizon and between 18% and 17% at the two-year horizon. At the one-quarter horizon, however, the results were less clear cut and depended on the precise definition of the oil price variable. We found no evidence in support of forecasting models based on the one-year net oil price increase of Hamilton (1996), models based on Mork's (1989) percent oil price increase measure, or models based on large percent increases in the price of oil (see, e.g., Goldberg 1998).
To date much of the empirical success of the three-year net oil price increase specification has been attributed to the fact that this oil price measure is asymmetric, with little attention to the fact that this definition also embodies other nonlinearities. In this regard, we demonstrated that reductions in the MSPE at least as large as for the three-year net oil price increase model can be obtained based on an alternative forecasting model that is symmetric in the three-year net oil price increases and decreases. The results for this net oil price change model specification suggest that the asymmetry embodied in the three-year net oil price increase measure is irrelevant for out-of-sample forecasting, if not harmful. This result is consistent with the fact that all other asymmetric specifications we considered appeared to be inferior to forecasting models that are symmetric in the price of oil. In short, if there are nonlinearities that matter for forecasting they are related to how far the current oil price deviates from its most recent extreme values, not to whether the price of oil increased or decreased relative to that threshold. This evidence directly addressed the common concern among many policy makers that the feedback from oil prices to the economy may become stronger once the price of oil passes certain possibly time-varying thresholds. We further demonstrated that a number of alternative and equally economically plausible symmetric nonlinear specifications (including models that focus on large oil price changes or models that control for time variation in the oil share) cannot replicate the forecasting success of the three-year net oil price change model.
The three-year net oil price change model not only tends to be at least as accurate as the corresponding three-year net oil price increase model, but it is more robust to the definition of the oil price variable, more robust across forecast horizons, and more robust to changes in the forecast evaluation period. A question of obvious interest is how much of the decline in U.S. real GDP growth during 2008/09 could have been forecast with the help of the three-year net oil price change model. Based on the four-quarter-ahead forecast, we showed that the three-year net oil price change model anticipated about one third of the observed decline in U.S. real GDP in 2008, while linear models essentially failed to predict any decline. These results appear much more plausible than the corresponding forecasts from the three-year net oil price increase model, which implies that virtually all of the 2008 recession could have been forecast one year in advance. We traced the latter economically implausible result to overfitting problems in small samples.
We then showed that a similar - if much less severe - overfitting problem also afflicts to the three-year net oil price change model. We illustrated how some simple ad hoc adjustments of the model coefficients can counter the effects of overfitting. With these corrections, we found that the three-year net change model would have forecast about 15% of the cumulative decline in U.S. real GDP in 2008 one year in advance, which is still much larger than the decline implied by linear VAR forecasts, but more similar to some other nonlinear symmetric forecasting models we studied. Our analysis added to a growing body of work that has questioned the role of asymmetries in the relationship between the price of oil and the U.S. economy, while drawing attention to a previously undocumented type of threshold nonlinearity in the predictive relationship between the price of oil and U.S. real GDP. The question of how important the threshold effects that we documented are deserves further study on extended samples and on other time series. Our findings in this regard have potentially important implications for applied forecasters, but also for economists interested in modeling the transmission of oil price shocks. For example, there is no theoretical model to date that would rationalize the type of the threshold effects embodied by three-year net oil price change models.
References
Alquist, R., Kilian, L., and R.J. Vigfusson (2012), "Forecasting the Price of Oil," prepared for: G. Elliott and A. Timmermann (eds.), Handbook of Economic Forecasting, 2, Amsterdam: North-Holland.
Bachmeier, L., Li, Q., and D. Liu (2008), "Should Oil Prices Receive So Much Attention? An Evaluation of the Predictive Power of Oil Prices for the U.S. Economy," EconomicInquiry, 46, 528-539.
Balke, N.S., Brown, S.P.A., and M.K. Yücel (2002), "Oil Price Shocks and the U.S. Economy: Where Does the Asymmetry Originate?" Energy Journal, 23, 27-52.
Baumeister, C., and L. Kilian (2011), "Real-Time Forecasts of the Real Price of Oil, forthcoming: Journal of Business and Economic Statistics.
Carlton, A.B. (2010), "Oil Prices and Real-Time Output Growth," mimeo, Department of Economics, University of Houston.
Clark, T.E., and M.W. McCracken (2009), "Nested Forecast Model Comparisons: A New Approach to Testing Equal Accuracy," mimeo, Federal Reserve Bank of St. Louis.
Clark, T.E., and M.W. McCracken (2012), "In-Sample Tests of Predictive Ability: A New Approach," forthcoming: Journal of Econometrics.
Davis, L.W., and L. Kilian (2011), "Estimating the Effect of a Gasoline Tax on Carbon Emissions," Journal of Applied Econometrics, 16, 1187-1214.
Edelstein, P., and L. Kilian (2009), "How Sensitive are Consumer Expenditures to Retail Energy Prices?" Journal of Monetary Economics, 56, 766-779.
Goldberg, P. (1998), "The Effects of the Corporate Average Fuel Economy Standards in the U.S.," Journal of Industrial Economics, 46, 1-33.
Hamilton, J.D. (1988) "A Neoclassical Model of Unemployment and the Business Cycle,"
Journal of Political Economy, 96, 593-617.
Hamilton, J. D. (1996), "This is What Happened to the Oil Price-Macroeconomy Relationship," Journal of Monetary Economics, 38, 215-220.
Hamilton, J. D. (2003), "What is an Oil Shock?" Journal of Econometrics, 113, 363-398.
Hamilton, J.D. (2009), "Causes and Consequences of the Oil Shock of 2007-08," Brookings Papers on Economic Activity, 1, Spring, 215-261.
Hamilton, J.D. (2011), "Nonlinearities and the Macroeconomic Effects of Oil Prices," Macroeconomic Dynamics, 15, 472-497.
Herrera, A.M., Lagalo, L.G., and T. Wada (2011), "Oil Price Shocks and Industrial Production: Is the Relationship Linear?" forthcoming: Macroeconomic Dynamics, 15(S3).
Inoue, A., and L. Kilian (2004), "In-Sample or Out-of-Sample Tests of Predictability: Which One Should We Use?" Econometric Reviews, 23, 371-402.
Kilian, L. (2009), "Not all Oil Price Shocks Are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market," American Economic Review, 99, 1053-1069.
Kilian, L., and R.J. Vigfusson (2011a), "Nonlinearities in the Oil Price-Output Relationship," Macroeconomic Dynamics, 15, 337-363.
Kilian, L., and R.J. Vigfusson (2011b), "Are the Responses of the U.S. Economy Asymmetric in Energy Price Increases and Decreases?" Quantitative Economics, 2(3), 419-453.
Koop, G., M.H. Pesaran, and S.M. Potter (1996), "Impulse Response Analysis in Nonlinear Multivariate Models," Journal of Econometrics, 74, 119-147.
Marcellino, M., J.H. Stock, and M.W. Watson (2006), "A Comparison of Direct and Iterated Multi-Step AR Methods for Forecasting Macroeconomic Time Series," Journal ofEconometrics, 135, 499-526.
Mork, K.A. (1989), "Oil and the Macroeconomy. When Prices Go Up and Down: An Extension of Hamilton's Results," Journal of Political Economy, 97, 740-744.
Ravazzolo, F., and P. Rothman (2012), "Oil and U.S. GDP: A Real Time Out-of-Sample Examination," forthccming: Journal of Money, Credit and Banking.
Ramey, V.A., and D.J. Vine (2010), "Oil, Automobiles, and the U.S. Economy: How Much Have Things Really Changed?" NBER Macroeconomics Annual 25, 333-368.
Figure 1: Pseudo-Linear VAR Models based on the Share of Crude Oil in U.S. GDP
NOTES: The linear VAR model refers to a bivariate VAR model for percent changes in the real price of oil and in U.S. real GDP. The pseudo-linear VAR model refers to a VAR model in which the real price of oil is weighted by the share of nominal oil use in nominal GDP. Oil use is defined as the sum of domestic crude oil production and net crude oil imports.
Data for Figure 1 (top)
| Date | Share of Crude Oil in U.S. GDP |
|---|---|
| 1974 | 4.94 |
| 1974.25 | 5.06 |
| 1974.5 | 4.98 |
| 1974.75 | 5.17 |
| 1975 | 5.19 |
| 1975.25 | 4.81 |
| 1975.5 | 4.88 |
| 1975.75 | 5.3 |
| 1976 | 4.9 |
| 1976.25 | 4.48 |
| 1976.5 | 4.48 |
| 1976.75 | 4.96 |
| 1977 | 5.33 |
| 1977.25 | 4.64 |
| 1977.5 | 4.56 |
| 1977.75 | 4.75 |
| 1978 | 4.95 |
| 1978.25 | 4.2 |
| 1978.5 | 4.09 |
| 1978.75 | 4.28 |
| 1979 | 4.81 |
| 1979.25 | 4.91 |
| 1979.5 | 5.93 |
| 1979.75 | 6.85 |
| 1980 | 7.91 |
| 1980.25 | 7.49 |
| 1980.5 | 7.28 |
| 1980.75 | 7.64 |
| 1981 | 7.93 |
| 1981.25 | 6.97 |
| 1981.5 | 6.42 |
| 1981.75 | 6.56 |
| 1982 | 6.38 |
| 1982.25 | 5.71 |
| 1982.5 | 5.5 |
| 1982.75 | 5.51 |
| 1983 | 4.89 |
| 1983.25 | 4.44 |
| 1983.5 | 4.57 |
| 1983.75 | 4.57 |
| 1984 | 4.46 |
| 1984.25 | 4.26 |
| 1984.5 | 4.14 |
| 1984.75 | 4.01 |
| 1985 | 3.83 |
| 1985.25 | 3.72 |
| 1985.5 | 3.54 |
| 1985.75 | 3.61 |
| 1986 | 2.57 |
| 1986.25 | 1.7 |
| 1986.5 | 1.57 |
| 1986.75 | 1.8 |
| 1987 | 2.22 |
| 1987.25 | 2.34 |
| 1987.5 | 2.44 |
| 1987.75 | 2.27 |
| 1988 | 1.97 |
| 1988.25 | 1.88 |
| 1988.5 | 1.74 |
| 1988.75 | 1.65 |
| 1989 | 2.03 |
| 1989.25 | 2.14 |
| 1989.5 | 1.96 |
| 1989.75 | 2.21 |
| 1990 | 2.16 |
| 1990.25 | 1.7 |
| 1990.5 | 2.52 |
| 1990.75 | 3.09 |
| 1991 | 1.99 |
| 1991.25 | 1.82 |
| 1991.5 | 1.91 |
| 1991.75 | 1.91 |
| 1992 | 1.61 |
| 1992.25 | 1.81 |
| 1992.5 | 1.88 |
| 1992.75 | 1.79 |
| 1993 | 1.65 |
| 1993.25 | 1.64 |
| 1993.5 | 1.48 |
| 1993.75 | 1.33 |
| 1994 | 1.23 |
| 1994.25 | 1.43 |
| 1994.5 | 1.51 |
| 1994.75 | 1.45 |
| 1995 | 1.5 |
| 1995.25 | 1.58 |
| 1995.5 | 1.44 |
| 1995.75 | 1.46 |
| 1996 | 1.62 |
| 1996.25 | 1.7 |
| 1996.5 | 1.74 |
| 1996.75 | 1.96 |
| 1997 | 1.72 |
| 1997.25 | 1.46 |
| 1997.5 | 1.45 |
| 1997.75 | 1.43 |
| 1998 | 1.04 |
| 1998.25 | 0.98 |
| 1998.5 | 0.94 |
| 1998.75 | 0.84 |
| 1999 | 0.83 |
| 1999.25 | 1.17 |
| 1999.5 | 1.52 |
| 1999.75 | 1.74 |
| 2000 | 1.94 |
| 2000.25 | 1.9 |
| 2000.5 | 2.13 |
| 2000.75 | 2.03 |
| 2001 | 1.72 |
| 2001.25 | 1.66 |
| 2001.5 | 1.61 |
| 2001.75 | 1.16 |
| 2002 | 1.3 |
| 2002.25 | 1.63 |
| 2002.5 | 1.76 |
| 2002.75 | 1.71 |
| 2003 | 2.06 |
| 2003.25 | 1.67 |
| 2003.5 | 1.79 |
| 2003.75 | 1.8 |
| 2004 | 2.01 |
| 2004.25 | 2.16 |
| 2004.5 | 2.46 |
| 2004.75 | 2.51 |
| 2005 | 2.52 |
| 2005.25 | 2.77 |
| 2005.5 | 3.4 |
| 2005.75 | 3.06 |
| 2006 | 3.11 |
| 2006.25 | 3.57 |
| 2006.5 | 3.63 |
| 2006.75 | 2.98 |
| 2007 | 2.94 |
| 2007.25 | 3.36 |
| 2007.5 | 3.77 |
| 2007.75 | 4.34 |
| 2008 | 4.6 |
| 2008.25 | 5.8 |
| 2008.5 | 5.38 |
| 2008.75 | 2.6 |
| 2009 | 2 |
| 2009.25 | 2.82 |
| 2009.5 | 3.26 |
| 2009.75 | 3.58 |
| 2010 | 3.63 |
| 2010.25 | 3.59 |
| 2010.5 | 3.57 |
| 2010.75 | 3.85 |
| 2011 | 4.41 |
| 2011.25 | 4.96 |
| 2011.5 | 4.62 |
| 2011.75 | 4.69 |
Data for Figure 1 (bottom)
| Date | Realized | Linear VAR | Pseudo Linear VAR |
|---|---|---|---|
| 1991 | -0.97 | 3.57 | 3.53 |
| 1991.25 | -0.69 | 3.87 | 3.7 |
| 1991.5 | -0.27 | 2.32 | 2.54 |
| 1991.75 | 1 | 2.92 | 2.99 |
| 1992 | 2.58 | 3.67 | 3.89 |
| 1992.25 | 2.96 | 3.77 | 3.82 |
| 1992.5 | 3.57 | 3.95 | 4.13 |
| 1992.75 | 4.22 | 3.67 | 3.74 |
| 1993 | 3.31 | 3.49 | 3.35 |
| 1993.25 | 2.89 | 2.99 | 3.08 |
| 1993.5 | 2.39 | 3.21 | 3.22 |
| 1993.75 | 2.66 | 3.34 | 3.22 |
| 1994 | 3.44 | 2.77 | 2.68 |
| 1994.25 | 4.16 | 3.31 | 3.15 |
| 1994.5 | 4.28 | 3.38 | 3.2 |
| 1994.75 | 4.07 | 4.09 | 3.7 |
| 1995 | 3.35 | 3.59 | 3.35 |
| 1995.25 | 2.21 | 3.01 | 3.19 |
| 1995.5 | 2.4 | 2.87 | 2.93 |
| 1995.75 | 1.99 | 2.94 | 3 |
| 1996 | 2.43 | 2.51 | 2.61 |
| 1996.25 | 3.93 | 2.86 | 2.84 |
| 1996.5 | 3.96 | 3.14 | 3.12 |
| 1996.75 | 4.35 | 3.05 | 3.08 |
| 1997 | 4.43 | 2.81 | 2.94 |
| 1997.25 | 4.19 | 3.32 | 3.37 |
| 1997.5 | 4.57 | 2.63 | 2.81 |
| 1997.75 | 4.25 | 2.78 | 2.87 |
| 1998 | 4.42 | 3.21 | 3.1 |
| 1998.25 | 3.85 | 3.73 | 3.5 |
| 1998.5 | 3.91 | 3.63 | 3.45 |
| 1998.75 | 4.86 | 3.68 | 3.4 |
| 1999 | 4.81 | 3.97 | 3.47 |
| 1999.25 | 4.69 | 3.84 | 3.4 |
| 1999.5 | 4.65 | 3.75 | 3.55 |
| 1999.75 | 4.71 | 4.55 | 3.89 |
| 2000 | 4.08 | 3.06 | 3.08 |
| 2000.25 | 5.24 | 2.4 | 2.83 |
| 2000.5 | 4.06 | 2.05 | 2.89 |
| 2000.75 | 2.87 | 2.23 | 3.13 |
| 2001 | 2.28 | 1.69 | 2.44 |
| 2001.25 | 1 | 3.06 | 3.22 |
| 2001.5 | 0.64 | 2.62 | 2.69 |
| 2001.75 | 0.4 | 3.27 | 3.26 |
| 2002 | 1.58 | 3.22 | 3.09 |
| 2002.25 | 1.45 | 3.6 | 3.48 |
| 2002.5 | 2.24 | 3.38 | 3.3 |
| 2002.75 | 1.92 | 3.73 | 3.56 |
| 2003 | 1.49 | 3.4 | 3.33 |
| 2003.25 | 1.8 | 3.18 | 3.28 |
| 2003.5 | 2.93 | 2.93 | 2.97 |
| 2003.75 | 3.79 | 2.3 | 2.53 |
| 2004 | 4.03 | 2.7 | 2.75 |
| 2004.25 | 3.83 | 3.11 | 3.16 |
| 2004.5 | 2.94 | 3.71 | 3.67 |
| 2004.75 | 2.85 | 3.21 | 3.15 |
| 2005 | 3.22 | 2.94 | 2.89 |
| 2005.25 | 3.03 | 2.87 | 2.84 |
| 2005.5 | 3.08 | 2.66 | 2.64 |
| 2005.75 | 2.77 | 3.13 | 3.19 |
| 2006 | 3 | 2.9 | 2.75 |
| 2006.25 | 2.96 | 2.67 | 2.61 |
| 2006.5 | 2.19 | 2.75 | 2.62 |
| 2006.75 | 2.35 | 2.81 | 2.82 |
| 2007 | 1.23 | 3.22 | 3.12 |
| 2007.25 | 1.72 | 2.86 | 2.73 |
| 2007.5 | 2.44 | 2.92 | 3.01 |
| 2007.75 | 2.18 | 3.08 | 3.05 |
| 2008 | 1.6 | 3 | 3 |
| 2008.25 | 1.03 | 3.15 | 3.13 |
| 2008.5 | -0.63 | 2.95 | 2.84 |
| 2008.75 | -3.38 | 2.59 | 2.32 |
| 2009 | -4.66 | 2.01 | 1.5 |
| 2009.25 | -5.16 | 2.09 | 1.26 |
| 2009.5 | -3.81 | 2.37 | 2.89 |
| 2009.75 | -0.55 | 3.49 | 7.41 |
| 2010 | 2.14 | 2.66 | 5.79 |
| 2010.25 | 3.25 | 3.19 | 6.63 |
| 2010.5 | 3.45 | 2.67 | 4.65 |
| 2010.75 | 3.09 | 1.88 | 2.11 |
| 2011 | 2.22 | 2.47 | 2.58 |
| 2011.25 | 1.62 | 2.96 | 2.9 |
| 2011.5 | 1.45 | 2.78 | 2.75 |
| 2011.75 | 1.6 | 2.58 | 2.54 |
Figure 2: Nonlinear Forecasts of Cumulative Real GDP Growth from the Fully Restricted Three-Year Net Oil Price Increase and Three-Year Net Oil Price Change Models
NOTES: The three-year net change model and the three-year net increase model are described in the text
Data for Figure 2 (top)
| Date | Realized | 3-year Net Increase Model | 3-year Net Change Model |
|---|---|---|---|
| 1991 | -0.97 | 3.91 | 3.42 |
| 1991.25 | -0.69 | 3.87 | 3.45 |
| 1991.5 | -0.27 | -4.34 | 1.17 |
| 1991.75 | 1 | -0.1 | 1.53 |
| 1992 | 2.58 | 1.19 | 2.44 |
| 1992.25 | 2.96 | 2.83 | 3.45 |
| 1992.5 | 3.57 | 3.96 | 3.35 |
| 1992.75 | 4.22 | 3.93 | 3.28 |
| 1993 | 3.31 | 3.94 | 3.53 |
| 1993.25 | 2.89 | 3.83 | 3.3 |
| 1993.5 | 2.39 | 3.81 | 3.27 |
| 1993.75 | 2.66 | 3.74 | 3.33 |
| 1994 | 3.44 | 3.59 | 3.08 |
| 1994.25 | 4.16 | 3.78 | 3.43 |
| 1994.5 | 4.28 | 3.74 | 3.9 |
| 1994.75 | 4.07 | 3.93 | 5.68 |
| 1995 | 3.35 | 3.71 | 4.61 |
| 1995.25 | 2.21 | 3.77 | 3.79 |
| 1995.5 | 2.4 | 3.55 | 3.67 |
| 1995.75 | 1.99 | 3.72 | 3.28 |
| 1996 | 2.43 | 3.47 | 2.86 |
| 1996.25 | 3.93 | 3.55 | 2.89 |
| 1996.5 | 3.96 | 3.68 | 3.14 |
| 1996.75 | 4.35 | 3.63 | 3.12 |
| 1997 | 4.43 | 3.01 | 2.85 |
| 1997.25 | 4.19 | 3.32 | 3.13 |
| 1997.5 | 4.57 | 1.31 | 2.25 |
| 1997.75 | 4.25 | 0.92 | 2.12 |
| 1998 | 4.42 | 2.46 | 2.57 |
| 1998.25 | 3.85 | 3.25 | 3.1 |
| 1998.5 | 3.91 | 3.49 | 3.15 |
| 1998.75 | 4.86 | 3.59 | 3.37 |
| 1999 | 4.81 | 3.68 | 4.76 |
| 1999.25 | 4.69 | 3.72 | 5.18 |
| 1999.5 | 4.65 | 3.84 | 4.72 |
| 1999.75 | 4.71 | 3.87 | 6.67 |
| 2000 | 4.08 | 3.64 | 4.32 |
| 2000.25 | 5.24 | 3.65 | 3.26 |
| 2000.5 | 4.06 | 3.33 | 3.29 |
| 2000.75 | 2.87 | 3.3 | 3.22 |
| 2001 | 2.28 | 0.56 | 1.96 |
| 2001.25 | 1 | 1.25 | 2.54 |
| 2001.5 | 0.64 | 0.28 | 1.83 |
| 2001.75 | 0.4 | 2.61 | 2.71 |
| 2002 | 1.58 | 3.11 | 2.68 |
| 2002.25 | 1.45 | 3.7 | 3.16 |
| 2002.5 | 2.24 | 3.65 | 2.96 |
| 2002.75 | 1.92 | 3.81 | 3.14 |
| 2003 | 1.49 | 3.83 | 3.23 |
| 2003.25 | 1.8 | 3.72 | 3.13 |
| 2003.5 | 2.93 | 3.25 | 2.9 |
| 2003.75 | 3.79 | 3.35 | 2.81 |
| 2004 | 4.03 | 3.16 | 2.86 |
| 2004.25 | 3.83 | 3.53 | 3.1 |
| 2004.5 | 2.94 | 3.79 | 3.33 |
| 2004.75 | 2.85 | 3.39 | 3.01 |
| 2005 | 3.22 | 2.07 | 2.43 |
| 2005.25 | 3.03 | 1.8 | 2.34 |
| 2005.5 | 3.08 | -0.86 | 1.47 |
| 2005.75 | 2.77 | 1.04 | 2.06 |
| 2006 | 3 | -1.29 | 1.3 |
| 2006.25 | 2.96 | -1.05 | 1.19 |
| 2006.5 | 2.19 | -2.41 | 0.71 |
| 2006.75 | 2.35 | 0.9 | 1.86 |
| 2007 | 1.23 | 1.28 | 2.24 |
| 2007.25 | 1.72 | 0.73 | 1.89 |
| 2007.5 | 2.44 | 2.16 | 2.35 |
| 2007.75 | 2.18 | 3.11 | 2.91 |
| 2008 | 1.6 | 3.08 | 2.83 |
| 2008.25 | 1.03 | 2.88 | 2.88 |
| 2008.5 | -0.63 | 1.9 | 2.45 |
| 2008.75 | -3.38 | 0.28 | 1.62 |
| 2009 | -4.66 | -1.61 | 0.59 |
| 2009.25 | -5.16 | -4.06 | -0.44 |
| 2009.5 | -3.81 | -0.94 | 0.54 |
| 2009.75 | -0.55 | 1.55 | 4 |
| 2010 | 2.14 | 2.07 | 3.64 |
| 2010.25 | 3.25 | 3.48 | 3.91 |
| 2010.5 | 3.45 | 3.62 | 3.76 |
| 2010.75 | 3.09 | 3.78 | 3.05 |
| 2011 | 2.22 | 3.77 | 3.03 |
| 2011.25 | 1.62 | 3.75 | 2.99 |
| 2011.5 | 1.45 | 3.63 | 2.82 |
| 2011.75 | 1.6 | 3.57 | 2.78 |
Data for Figure 2 (bottom)
| Date | 3-year Net Increase Model | 3-year Net Change Model |
|---|---|---|
| 1991 | 1.15 | 0.93 |
| 1991.25 | 1.22 | 0.99 |
| 1991.5 | 1.25 | 0.79 |
| 1991.75 | 1.21 | 0.75 |
| 1992 | 1.24 | 0.75 |
| 1992.25 | 1.24 | 0.75 |
| 1992.5 | 1.24 | 0.75 |
| 1992.75 | 1.21 | 0.75 |
| 1993 | 1.22 | 0.75 |
| 1993.25 | 1.23 | 0.75 |
| 1993.5 | 1.25 | 0.75 |
| 1993.75 | 1.26 | 0.76 |
| 1994 | 1.25 | 0.75 |
| 1994.25 | 1.23 | 0.75 |
| 1994.5 | 1.2 | 0.73 |
| 1994.75 | 1.2 | 0.77 |
| 1995 | 1.2 | 0.8 |
| 1995.25 | 1.21 | 0.82 |
| 1995.5 | 1.22 | 0.84 |
| 1995.75 | 1.24 | 0.85 |
| 1996 | 1.25 | 0.85 |
| 1996.25 | 1.24 | 0.85 |
| 1996.5 | 1.23 | 0.85 |
| 1996.75 | 1.21 | 0.86 |
| 1997 | 1.21 | 0.88 |
| 1997.25 | 1.21 | 0.89 |
| 1997.5 | 1.34 | 0.94 |
| 1997.75 | 1.48 | 0.99 |
| 1998 | 1.49 | 1.02 |
| 1998.25 | 1.49 | 1.02 |
| 1998.5 | 1.49 | 1.03 |
| 1998.75 | 1.45 | 1.02 |
| 1999 | 1.42 | 0.98 |
| 1999.25 | 1.4 | 0.96 |
| 1999.5 | 1.38 | 0.94 |
| 1999.75 | 1.37 | 0.98 |
| 2000 | 1.36 | 0.97 |
| 2000.25 | 1.33 | 0.97 |
| 2000.5 | 1.33 | 0.97 |
| 2000.75 | 1.32 | 0.96 |
| 2001 | 1.34 | 0.96 |
| 2001.25 | 1.23 | 0.91 |
| 2001.5 | 1.16 | 0.87 |
| 2001.75 | 1.12 | 0.85 |
| 2002 | 1.13 | 0.85 |
| 2002.25 | 1.14 | 0.85 |
| 2002.5 | 1.15 | 0.85 |
| 2002.75 | 1.17 | 0.86 |
| 2003 | 1.18 | 0.86 |
| 2003.25 | 1.19 | 0.86 |
| 2003.5 | 1.19 | 0.86 |
| 2003.75 | 1.19 | 0.86 |
| 2004 | 1.18 | 0.86 |
| 2004.25 | 1.18 | 0.86 |
| 2004.5 | 1.18 | 0.86 |
| 2004.75 | 1.18 | 0.86 |
| 2005 | 1.19 | 0.87 |
| 2005.25 | 1.2 | 0.87 |
| 2005.5 | 1.33 | 0.89 |
| 2005.75 | 1.35 | 0.89 |
| 2006 | 1.49 | 0.92 |
| 2006.25 | 1.62 | 0.94 |
| 2006.5 | 1.78 | 0.95 |
| 2006.75 | 1.79 | 0.95 |
| 2007 | 1.72 | 0.92 |
| 2007.25 | 1.71 | 0.91 |
| 2007.5 | 1.7 | 0.91 |
| 2007.75 | 1.7 | 0.91 |
| 2008 | 1.69 | 0.91 |
| 2008.25 | 1.66 | 0.9 |
| 2008.5 | 1.55 | 0.88 |
| 2008.75 | 1.29 | 0.82 |
| 2009 | 1.06 | 0.76 |
| 2009.25 | 0.84 | 0.67 |
| 2009.5 | 0.78 | 0.65 |
| 2009.75 | 0.78 | 0.71 |
| 2010 | 0.78 | 0.71 |
| 2010.25 | 0.78 | 0.71 |
| 2010.5 | 0.78 | 0.71 |
| 2010.75 | 0.78 | 0.71 |
| 2011 | 0.78 | 0.71 |
| 2011.25 | 0.79 | 0.71 |
| 2011.5 | 0.8 | 0.71 |
| 2011.75 | 0.81 | 0.71 |
Figure 3: Nonlinear Forecasts of Cumulative Real GDP Growth from Nonlinear Bivariate Forecasting Models Further Results
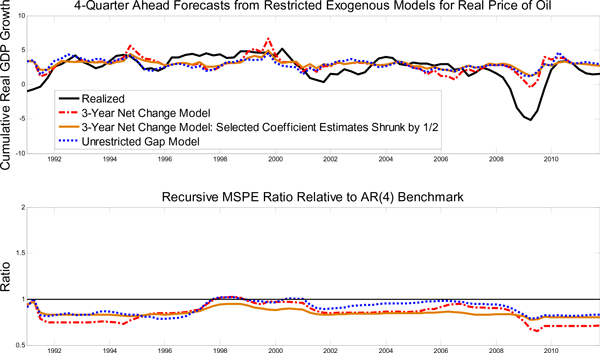
NOTES: The models are described in the text. The alternative 3-year net change model has been modified by shrinking the recursive estimates of the lagged net oil price change in the second model equation by 0.5, while retaining the remaining estimates. This ad hoc adjustment serves to prevent overfitting during the 1991 recession episode and as a result reduces subsequent forecast errors.
Data for Figure 3
| Date | Realized | 3-year Net Change Model | 3-year Net Change Model, Selected Coefficeint Estimated Shurnk by 1/2 | Unrestricted Gap Model |
|---|---|---|---|---|
| 1991 | -0.97 | 3.42 | 3.44 | 3.36 |
| 1991.25 | -0.69 | 3.45 | 3.33 | 3.59 |
| 1991.5 | -0.27 | 1.17 | 2.16 | 1.52 |
| 1991.75 | 1 | 1.53 | 2.19 | 2.31 |
| 1992 | 2.58 | 2.44 | 2.71 | 3.39 |
| 1992.25 | 2.96 | 3.45 | 3.44 | 3.81 |
| 1992.5 | 3.57 | 3.35 | 3.38 | 4.39 |
| 1992.75 | 4.22 | 3.28 | 3.24 | 4.05 |
| 1993 | 3.31 | 3.53 | 3.36 | 3.8 |
| 1993.25 | 2.89 | 3.3 | 3.26 | 3.41 |
| 1993.5 | 2.39 | 3.27 | 3.22 | 3.71 |
| 1993.75 | 2.66 | 3.33 | 3.24 | 3.71 |
| 1994 | 3.44 | 3.08 | 2.95 | 3.05 |
| 1994.25 | 4.16 | 3.43 | 3.24 | 3.64 |
| 1994.5 | 4.28 | 3.9 | 3.45 | 3.71 |
| 1994.75 | 4.07 | 5.68 | 4.49 | 4.25 |
| 1995 | 3.35 | 4.61 | 3.85 | 3.43 |
| 1995.25 | 2.21 | 3.79 | 3.49 | 2.32 |
| 1995.5 | 2.4 | 3.67 | 3.29 | 1.95 |
| 1995.75 | 1.99 | 3.28 | 3.17 | 2.36 |
| 1996 | 2.43 | 2.86 | 2.8 | 2.55 |
| 1996.25 | 3.93 | 2.89 | 2.93 | 2.88 |
| 1996.5 | 3.96 | 3.14 | 3.12 | 3.08 |
| 1996.75 | 4.35 | 3.12 | 3.11 | 2.85 |
| 1997 | 4.43 | 2.85 | 2.93 | 2.43 |
| 1997.25 | 4.19 | 3.13 | 3.24 | 2.68 |
| 1997.5 | 4.57 | 2.25 | 2.63 | 2.02 |
| 1997.75 | 4.25 | 2.12 | 2.58 | 2.18 |
| 1998 | 4.42 | 2.57 | 2.74 | 2.68 |
| 1998.25 | 3.85 | 3.1 | 3.2 | 3.29 |
| 1998.5 | 3.91 | 3.15 | 3.16 | 3.29 |
| 1998.75 | 4.86 | 3.37 | 3.22 | 3.54 |
| 1999 | 4.81 | 4.76 | 3.9 | 3.64 |
| 1999.25 | 4.69 | 5.18 | 4.16 | 3.55 |
| 1999.5 | 4.65 | 4.72 | 3.97 | 3.67 |
| 1999.75 | 4.71 | 6.67 | 5.01 | 4.54 |
| 2000 | 4.08 | 4.32 | 3.67 | 3.18 |
| 2000.25 | 5.24 | 3.26 | 3.11 | 2.76 |
| 2000.5 | 4.06 | 3.29 | 3.27 | 2.61 |
| 2000.75 | 2.87 | 3.22 | 3.33 | 2.56 |
| 2001 | 2.28 | 1.96 | 2.45 | 1.46 |
| 2001.25 | 1 | 2.54 | 2.98 | 2.38 |
| 2001.5 | 0.64 | 1.83 | 2.37 | 1.98 |
| 2001.75 | 0.4 | 2.71 | 2.95 | 2.89 |
| 2002 | 1.58 | 2.68 | 2.78 | 2.89 |
| 2002.25 | 1.45 | 3.16 | 3.24 | 3.38 |
| 2002.5 | 2.24 | 2.96 | 2.97 | 3.41 |
| 2002.75 | 1.92 | 3.14 | 3.12 | 3.71 |
| 2003 | 1.49 | 3.23 | 3.25 | 3.43 |
| 2003.25 | 1.8 | 3.13 | 3.16 | 3.43 |
| 2003.5 | 2.93 | 2.9 | 3 | 3.13 |
| 2003.75 | 3.79 | 2.81 | 2.84 | 2.56 |
| 2004 | 4.03 | 2.86 | 2.91 | 2.66 |
| 2004.25 | 3.83 | 3.1 | 3.14 | 2.98 |
| 2004.5 | 2.94 | 3.33 | 3.36 | 3.39 |
| 2004.75 | 2.85 | 3.01 | 3.09 | 2.91 |
| 2005 | 3.22 | 2.43 | 2.71 | 2.44 |
| 2005.25 | 3.03 | 2.34 | 2.66 | 2.25 |
| 2005.5 | 3.08 | 1.47 | 2.3 | 1.8 |
| 2005.75 | 2.77 | 2.06 | 2.59 | 2.45 |
| 2006 | 3 | 1.3 | 2.26 | 2.19 |
| 2006.25 | 2.96 | 1.19 | 2.11 | 2.13 |
| 2006.5 | 2.19 | 0.71 | 1.89 | 1.97 |
| 2006.75 | 2.35 | 1.86 | 2.46 | 2.3 |
| 2007 | 1.23 | 2.24 | 2.78 | 2.75 |
| 2007.25 | 1.72 | 1.89 | 2.48 | 2.46 |
| 2007.5 | 2.44 | 2.35 | 2.62 | 2.58 |
| 2007.75 | 2.18 | 2.91 | 3.01 | 2.8 |
| 2008 | 1.6 | 2.83 | 2.93 | 2.79 |
| 2008.25 | 1.03 | 2.88 | 3.07 | 2.86 |
| 2008.5 | -0.63 | 2.45 | 2.82 | 2.56 |
| 2008.75 | -3.38 | 1.62 | 2.32 | 2 |
| 2009 | -4.66 | 0.59 | 1.68 | 1.35 |
| 2009.25 | -5.16 | -0.44 | 1.28 | 1.22 |
| 2009.5 | -3.81 | 0.54 | 1.66 | 1.87 |
| 2009.75 | -0.55 | 4 | 3.01 | 2.97 |
| 2010 | 2.14 | 3.64 | 2.74 | 2.78 |
| 2010.25 | 3.25 | 3.91 | 3.23 | 4.67 |
| 2010.5 | 3.45 | 3.76 | 3.31 | 3.7 |
| 2010.75 | 3.09 | 3.05 | 3.05 | 3.01 |
| 2011 | 2.22 | 3.03 | 3.05 | 3.11 |
| 2011.25 | 1.62 | 2.99 | 3 | 3.29 |
| 2011.5 | 1.45 | 2.82 | 2.81 | 3.11 |
| 2011.75 | 1.6 | 2.78 | 2.76 | 2.99 |
Table 1: MSPE Ratios of Linear Autoregressive Models Relative to the AR (4) Benchmark Model Cumulative U.S. Real GDP Growth Rates
| Horizon | Real RAC Price of Imports Oil Price Endogenous | Real RAC Price of Imports Oil Price Exogenous | Nominal RAC Price of Imports Oil Price Endogenous | Nominal RAC Price of Imports Oil Price Exogenous |
|---|---|---|---|---|
| 1 | 1.10 | 1.10 | 1.11 | 1.11 |
| 2 | 1.04 | 1.04 | 1.05 | 1.05 |
| 3 | 0.98 | 0.98 | 0.99 | 0.99 |
| 4 | 0.96 | 0.96 | 0.97 | 0.96 |
| 5 | 0.95 | 0.94 | 0.96 | 0.95 |
| 6 | 0.94 | 0.93 | 0.94 | 0.93 |
| 7 | 0.95 | 0.94 | 0.95 | 0.94 |
| 8 | 0.96 | 0.94 | 0.96 | 0.95 |
NOTES: The benchmark model is an AR(4) for U.S. real GDP growth. The first alternative is a VAR(4) model for real GDP growth and the percent change in the price of oil that allows for unrestricted feedback from U.S. real GDP growth to the price of oil. The second alternative is a restricted VAR(4) model that treats the price of oil as exogenous. Boldface indicates gains in accuracy relative to the benchmark model. No tests of statistical significance have been conducted, given that these models are economically indistinguishable.
Table 2.a.1: MSPE Ratios of Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Real Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Unrestricted Model Mork Increase | Unrestricted Model Hamilton Net Increase: 1 Year | Unrestricted Model Hamilton Net Increase: 3 Year | Exogenous Model Mork Increase | Exogenous Model Hamilton Net Increase: 1 Year | Exogenous Model Hamilton Net Increase: 3 Year |
|---|---|---|---|---|---|---|
| 1 | 1.13 | 1.19 | 1.00 | 1.13 | 1.19 | 1.00 |
| 2 | 1.11 | 1.11 | 0.89 | 1.11 | 1.10 | 0.89 |
| 3 | 1.05 | 1.17 | 0.90 | 1.04 | 1.16 | 0.90 |
| 4 | 1.05 | 1.14 | 0.85 | 1.04 | 1.13 | 0.85 |
| 5 | 1.06 | 1.15 | 0.86 | 1.05 | 1.14 | 0.86 |
| 6 | 1.06 | 1.08 | 0.85 | 1.05 | 1.06 | 0.85 |
| 7 | 1.07 | 1.02 | 0.86 | 1.06 | 1.01 | 0.85 |
| 8 | 1.07 | 0.99 | 0.85 | 1.06 | 0.97 | 0.84 |
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The exogenous model suppresses feedback from lagged real GDP growth to the current price of oil.
Table 2.a.2: MSPE Ratios of Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Nominal Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Unrestricted Model Mork Increase | Unrestricted Model Hamilton Net Increase: 1 Year | Unrestricted Model Hamilton Net Increase: 3 Year | Exogenous Model Mork Increase | Exogenous Model Hamilton Net Increase: 1 Year | Exogenous Model Hamilton Net Increase: 3 Year |
|---|---|---|---|---|---|---|
| 1 | 1.13 | 1.19 | 1.00 | 1.13 | 1.19 | 1.00 |
| 2 | 1.11 | 1.11 | 0.89 | 1.11 | 1.10 | 0.89 |
| 3 | 1.05 | 1.17 | 0.90 | 1.04 | 1.16 | 0.90 |
| 4 | 1.05 | 1.14 | 0.85 | 1.04 | 1.13 | 0.85 |
| 5 | 1.06 | 1.15 | 0.86 | 1.05 | 1.14 | 0.86 |
| 6 | 1.06 | 1.08 | 0.85 | 1.05 | 1.06 | 0.85 |
| 7 | 1.07 | 1.02 | 0.86 | 1.06 | 1.01 | 0.85 |
| 8 | 1.07 | 0.99 | 0.85 | 1.06 | 0.97 | 0.84 |
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The exogenous model suppresses feedback from lagged real GDP growth to the current price of oil.
Table 2.b.1: MSPE Ratios of Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Real Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Restricted Model Mork Increase | Restricted Model Hamilton Net Increase: 1 Year | Restricted Model Hamilton Net Increase: 3 Year | Restricted Exogenous Model Mork Increase | Restricted Exogenous Model Hamilton Net Increase: 1 Year | Restricted Exogenous Model Hamilton Net Increase: 3 Year |
|---|---|---|---|---|---|---|
| 1 | 1.13 | 1.10 | 0.93 | 1.13 | 1.10 | 0.93 |
| 2 | 1.11 | 1.01 | 0.84 | 1.10 | 1.00 | 0.84 |
| 3 | 1.06 | 1.05 | 0.85 | 1.06 | 1.03 | 0.85 |
| 4 | 1.04 | 1.01 | 0.81 | 1.04 | 0.99 | 0.81 |
| 5 | 1.03 | 1.02 | 0.83 | 1.03 | 1.01 | 0.83 |
| 6 | 1.02 | 0.97 | 0.83 | 1.01 | 0.96 | 0.82 |
| 7 | 1.01 | 0.94 | 0.83 | 1.00 | 0.93 | 0.82 |
| 8 | 1.00 | 0.92 | 0.83 | 1.00 | 0.91 | 0.82 |
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The restricted model suppresses feedback from lagged percent changes in the price of oil to current real GDP growth, as proposed by Hamilton (2003, 2010). The restricted exogenous model combines this restriction with that of exogenous oil prices, further increasing the parsimony of the model.
Table 2.b.2: MSPE Ratios of Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Nominal Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Restricted Model Mork Increase | Restricted Model Hamilton Net Increase: 1 Year | Restricted Model Hamilton Net Increase: 3 Year | Restricted Exogenous Model Mork Increase | Restricted Exogenous Model Hamilton Net Increase: 1 Year | Restricted Exogenous Model Hamilton Net Increase: 3 Year |
|---|---|---|---|---|---|---|
| 1 | 1.12 | 1.10 | 1.02 | 1.12 | 1.10 | 1.02 |
| 2 | 1.09 | 0.96 | 0.79 | 1.08 | 0.96 | 0.79 |
| 3 | 1.04 | 0.99 | 0.79 | 1.04 | 0.98 | 0.79 |
| 4 | 1.02 | 0.95 | 0.74 | 1.01 | 0.94 | 0.74 |
| 5 | 1.01 | 0.99 | 0.82 | 1.00 | 0.98 | 0.81 |
| 6 | 0.99 | 0.95 | 0.84 | 0.98 | 0.94 | 0.83 |
| 7 | 0.98 | 0.93 | 0.85 | 0.97 | 0.91 | 0.84 |
| 8 | 0.97 | 0.91 | 0.85 | 0.97 | 0.90 | 0.83 |
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The restricted model suppresses feedback from lagged percent changes in the price of oil to current real GDP growth, as proposed by Hamilton (2003, 2010). The restricted exogenous model combines this restriction with that of exogenous oil prices, further increasing the parsimony of the model.
Table 3.a.1: MSPE Ratios of Alternative Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Real Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Unrestricted Model Net Change: 1 Year | Unrestricted Model Net Change: 3 Year | Unrestricted Model Asymmetric Net Change: 1 Year | Unrestricted Model Asymmetric Net Change: 3 Year | Exogenous Model Net Change: 1 Year | Exogenous Model Net Change: 3 Year | Exogenous Model Asymmetric Net Change: 1 Year | Exogenous Model Asymmetric Net Change: 3 Year | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.25 | 1.06 | 1.39 | 1.14 | 1.25 | 1.06 | 1.39 | 1.15 | |||
| 2 | 1.22 | 0.88 | 1.39 | 0.91 | 1.22 | 0.88 | 1.38 | 0.92 | |||
| 3 | 1.04 | 0.76 | 1.46 | 0.96 | 1.03 | 0.75 | 1.45 | 0.96 | |||
| 4 | 1.00 | 0.72 | 1.49 | 0.93 | 1.00 | 0.72 | 1.48 | 0.93 | |||
| 5 | 0.97 | 0.72 | 1.46 | 0.92 | 0.95 | 0.71 | 1.44 | 0.92 | |||
| 6 | 0.95 | 0.72 | 1.34 | 0.93 | 0.94 | 0.71 | 1.33 | 0.93 | |||
| 7 | 0.95 | 0.75 | 1.23 | 0.96 | 0.94 | 0.74 | 1.23 | 0.95 | |||
| 8 | 0.96 | 0.76 | 1.17 | 0.96 | 0.95 | 0.75 | 1.18 | 0.95 | |||
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The exogenous model suppresses feedback from lagged real GDP growth to the current price of oil.
Table 3.a.2: MSPE Ratios of Alternative Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Nominal Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Unrestricted Model Net Change: 1 Year | Unrestricted Model Net Change: 3 Year | Unrestricted Model Asymmetric Net Change: 1 Year | Unrestricted Model Asymmetric Net Change: 3 Year | Exogenous Model Net Change: 1 Year | Exogenous Model Net Change: 3 Year | Exogenous Model Asymmetric Net Change: 1 Year | Exogenous Model Asymmetric Net Change: 3 Year | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.37 | 1.09 | 1.66 | 1.26 | 1.37 | 1.09 | 1.66 | 1.26 | |||
| 2 | 1.36 | 0.91 | 1.69 | 0.90 | 1.36 | 0.91 | 1.69 | 0.90 | |||
| 3 | 1.15 | 0.75 | 1.95 | 0.95 | 1.14 | 0.74 | 1.93 | 0.94 | |||
| 4 | 1.12 | 0.71 | 1.99 | 0.86 | 1.11 | 0.70 | 1.96 | 0.85 | |||
| 5 | 1.13 | 0.71 | 2.08 | 0.96 | 1.11 | 0.70 | 2.04 | 0.95 | |||
| 6 | 1.10 | 0.73 | 1.82 | 0.98 | 1.08 | 0.72 | 1.80 | 0.97 | |||
| 7 | 1.07 | 0.76 | 1.59 | 1.00 | 1.05 | 0.75 | 1.60 | 0.99 | |||
| 8 | 1.05 | 0.77 | 1.47 | 0.99 | 1.04 | 0.76 | 1.49 | 0.98 | |||
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The exogenous model suppresses feedback from lagged real GDP growth to the current price of oil.
Table 3.b.1: MSPE Ratios of Alternative Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Real Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Restricted Model Net Change: 1 Year | Restricted Model Net Change: 3 Year | Restricted Model Asymmetric Net Change: 1 Year | Restricted Model Asymmetric Net Change: 3 Year | Restricted Exogenous Model Net Change: 1 Year | Restricted Exogenous Model Net Change: 3 Year | Restricted Exogenous Model Asymmetric Net Change: 1 Year | Restricted Exogenous Model Asymmetric Net Change: 3 Year | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.05 | 0.92 | 1.12 | 0.93 | 1.05 | 0.92 | 1.13 | 0.93 | |||
| 2 | 0.97 | 0.81 | 1.05 | 0.84 | 0.97 | 0.81 | 1.05 | 0.84 | |||
| 3 | 0.94 | 0.76 | 1.11 | 0.85 | 0.93 | 0.75 | 1.10 | 0.85 | |||
| 4 | 0.91 | 0.72 | 1.08 | 0.83 | 0.90 | 0.71 | 1.07 | 0.82 | |||
| 5 | 0.91 | 0.73 | 1.10 | 0.84 | 0.89 | 0.71 | 1.09 | 0.84 | |||
| 6 | 0.89 | 0.73 | 1.06 | 0.85 | 0.88 | 0.72 | 1.05 | 0.84 | |||
| 7 | 0.89 | 0.76 | 1.03 | 0.86 | 0.88 | 0.74 | 1.02 | 0.85 | |||
| 8 | 0.90 | 0.78 | 1.01 | 0.86 | 0.89 | 0.76 | 1.00 | 0.85 | |||
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The restricted model suppresses feedback from lagged percent changes in the price of oil to current real GDP growth, as proposed by Hamilton (2003, 2010). The restricted exogenous model combines this restriction with that of exogenous oil prices, further increasing the parsimony of the model.
Table 3.b.2: MSPE Ratios of Alternative Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Nominal Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Restricted Model Net Change: 1 Year | Restricted Model Net Change: 3 Year | Restricted Model Asymmetric Net Change: 1 Year | Restricted Model Asymmetric Net Change: 3 Year | Restricted Exogenous Model Net Change: 1 Year | Restricted Exogenous Model Net Change: 3 Year | Restricted Exogenous Model Asymmetric Net Change: 1 Year | Restricted Exogenous Model Asymmetric Net Change: 3 Year | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.05 | 0.92 | 1.12 | 0.93 | 1.05 | 0.92 | 1.13 | 0.93 | |||
| 2 | 0.97 | 0.81 | 1.05 | 0.84 | 0.97 | 0.81 | 1.05 | 0.84 | |||
| 3 | 0.94 | 0.76 | 1.11 | 0.85 | 0.93 | 0.75 | 1.10 | 0.85 | |||
| 4 | 0.91 | 0.72 | 1.08 | 0.83 | 0.90 | 0.71 | 1.07 | 0.82 | |||
| 5 | 0.91 | 0.73 | 1.10 | 0.84 | 0.89 | 0.71 | 1.09 | 0.84 | |||
| 6 | 0.89 | 0.73 | 1.06 | 0.85 | 0.88 | 0.72 | 1.05 | 0.84 | |||
| 7 | 0.89 | 0.76 | 1.03 | 0.86 | 0.88 | 0.74 | 1.02 | 0.85 | |||
| 8 | 0.90 | 0.78 | 1.01 | 0.86 | 0.89 | 0.76 | 1.00 | 0.85 | |||
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The restricted model suppresses feedback from lagged percent changes in the price of oil to current real GDP growth, as proposed by Hamilton (2003, 2010). The restricted exogenous model combines this restriction with that of exogenous oil prices, further increasing the parsimony of the model.
Table 4.a.1: MSPE Ratios of Alternative Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Real Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Unrestricted Model Gap Model: 1 Year | Unrestricted Model Gap Model: 3 Year | Unrestricted Model Large: Change | Unrestricted Model Large: Increase | Exogenous Model Gap Model: 1 Year | Exogenous Model Gap Model: 3 Year | Exogenous Model Large: Change | Exogenous Model Large: Increase | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.18 | 1.04 | 1.13 | 1.63 | 1.18 | 1.04 | 1.13 | 1.63 | |||
| 2 | 1.28 | 1.13 | 1.03 | 1.68 | 1.28 | 1.13 | 1.02 | 1.68 | |||
| 3 | 1.21 | 0.96 | 0.97 | 1.55 | 1.21 | 0.96 | 0.97 | 1.54 | |||
| 4 | 1.25 | 0.83 | 0.94 | 1.51 | 1.25 | 0.83 | 0.94 | 1.50 | |||
| 5 | 1.10 | 0.81 | 0.94 | 1.53 | 1.10 | 0.81 | 0.94 | 1.51 | |||
| 6 | 1.01 | 0.81 | 0.94 | 1.50 | 1.01 | 0.8 | 0.93 | 1.48 | |||
| 7 | 0.97 | 0.83 | 0.95 | 1.48 | 0.97 | 0.82 | 0.94 | 1.45 | |||
| 8 | 0.95 | 0.85 | 0.95 | 1.47 | 0.95 | 0.84 | 0.95 | 1.44 | |||
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The exogenous model suppresses feedback from lagged real GDP growth to the current price of oil.
Table 4.a.2: MSPE Ratios of Alternative Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Nominal Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Unrestricted Model Gap Model: 1 Year | Unrestricted Model Gap Model: 3 Year | Unrestricted Model Large: Change | Unrestricted Model Large: Increase | Exogenous Model Gap Model: 1 Year | Exogenous Model Gap Model: 3 Year | Exogenous Model Large: Change | Exogenous Model Large: Increase | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.16 | 1.03 | 1.01 | 1.51 | 1.16 | 1.03 | 1.01 | 1.51 | |||
| 2 | 1.29 | 1.19 | 1.00 | 1.53 | 1.29 | 1.19 | 1.00 | 1.52 | |||
| 3 | 1.17 | 0.95 | 0.97 | 1.32 | 1.17 | 0.95 | 0.97 | 1.31 | |||
| 4 | 1.24 | 0.89 | 0.94 | 1.27 | 1.24 | 0.88 | 0.94 | 1.25 | |||
| 5 | 1.05 | 0.81 | 0.94 | 1.28 | 1.05 | 0.81 | 0.93 | 1.26 | |||
| 6 | 0.98 | 0.81 | 0.94 | 1.23 | 0.97 | 0.80 | 0.93 | 1.21 | |||
| 7 | 0.93 | 0.82 | 0.95 | 1.21 | 0.93 | 0.81 | 0.94 | 1.19 | |||
| 8 | 0.91 | 0.84 | 0.96 | 1.21 | 0.91 | 0.83 | 0.95 | 1.19 | |||
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The exogenous model suppresses feedback from lagged real GDP growth to the current price of oil.
Table 4.b.1: MSPE Ratios of Alternative Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Real Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Unrestricted Model Gap Model: 1 Year | Unrestricted Model Gap Model: 3 Year | Unrestricted Model Large: Change | Unrestricted Model Large: Increase | Exogenous Model Gap Model: 1 Year | Exogenous Model Gap Model: 3 Year | Exogenous Model Large: Change | Exogenous Model Large: Increase | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.08 | 1.03 | 1.13 | 1.47 | 1.03 | 1.07 | 1.13 | 1.47 | |||
| 2 | 0.93 | 0.94 | 1.07 | 1.46 | 0.94 | 0.93 | 1.07 | 1.45 | |||
| 3 | 0.94 | 0.93 | 1.01 | 1.36 | 0.93 | 0.93 | 1.01 | 1.35 | |||
| 4 | 0.92 | 0.95 | 0.98 | 1.31 | 0.95 | 0.92 | 0.98 | 1.30 | |||
| 5 | 0.92 | 0.95 | 0.97 | 1.31 | 0.94 | 0.91 | 0.97 | 1.30 | |||
| 6 | 0.94 | 1.01 | 0.96 | 1.29 | 1.00 | 0.93 | 0.95 | 1.27 | |||
| 7 | 0.97 | 1.07 | 0.96 | 1.25 | 1.05 | 0.96 | 0.95 | 1.24 | |||
| 8 | 1.01 | 1.12 | 0.97 | 1.23 | 1.09 | 0.99 | 0.96 | 1.22 | |||
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The exogenous model suppresses feedback from lagged real GDP growth to the current price of oil.
Table 4.b.2: MSPE Ratios of Alternative Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates: Nominal Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Unrestricted Model Gap Model: 1 Year | Unrestricted Model Gap Model: 3 Year | Unrestricted Model Large: Change | Unrestricted Model Large: Increase | Exogenous Model Gap Model: 1 Year | Exogenous Model Gap Model: 3 Year | Exogenous Model Largel: Change | Exogenous Model Large: Increase |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.07 | 1.04 | 1.08 | 1.39 | 1.04 | 1.07 | 1.08 | 1.39 |
| 2 | 0.94 | 0.95 | 1.02 | 1.38 | 0.95 | 0.94 | 1.02 | 1.37 |
| 3 | 0.95 | 0.94 | 0.98 | 1.24 | 0.94 | 0.94 | 0.98 | 1.23 |
| 4 | 0.95 | 0.97 | 0.96 | 1.19 | 0.97 | 0.94 | 0.96 | 1.18 |
| 5 | 0.93 | 0.95 | 0.95 | 1.19 | 0.95 | 0.93 | 0.95 | 1.18 |
| 6 | 0.95 | 1.02 | 0.94 | 1.15 | 1.01 | 0.94 | 0.93 | 1.13 |
| 7 | 0.98 | 1.07 | 0.94 | 1.12 | 1.05 | 0.97 | 0.93 | 1.10 |
| 8 | 1.02 | 1.12 | 0.94 | 1.11 | 1.09 | 1.00 | 0.94 | 1.09 |
NOTES: The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The exogenous model suppresses feedback from lagged real GDP growth to the current price of oil.
Table 5: MSPE Ratios of Models with Oil Price Weighted by the Oil Share in U.S. GDP Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates
| Horizon | Real Refiners' Acquisition Cost for Imported Crude Oil Unrestricted Model | Real Refiners' Acquisition Cost for Imported Crude Oil Exogenous Model |
|---|---|---|
| 1 | 1.21 | 1.21 |
| 2 | 1.19 | 1.19 |
| 3 | 1.13 | 1.12 |
| 4 | 1.11 | 1.09 |
| 5 | 1.08 | 1.05 |
| 6 | 1.06 | 1.02 |
| 7 | 1.05 | 1.01 |
| 8 | 1.05 | 1.01 |
Table 6: MSPE Ratios for the Restricted and Exogenous Nonlinear Models Relative to AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates
| Oil Price | Three-Year Net Oil Price Increase Model 1990.Q1-2011.Q4: h=1 | Three-Year Net Oil Price Increase Model 1990.Q1-2011.Q4: h=4 | Three-Year Net Oil Price Increase Model 1990.Q1-2011.Q4: h=1 | Three-Year Net Oil Price Increase Model 1990.Q1-2011.Q4: h=4 | Three-Year Net Oil Price Change Model 1990.Q1-2011.Q4: h=1 | Three-Year Net Oil Price Change Model 1990.Q1-2011.Q4: h=4 | Three-Year Net Oil Price Change Model 1990.Q1-2007.Q4: h=1 | Three-Year Net Oil Price Change Model 1990.Q1-2007.Q4: h=4 |
|---|---|---|---|---|---|---|---|---|
| Real RAC Imports | 0.93 | 0.81 | 1.11 | 1.71 | 0.92 | 0.71 | 0.94 | 0.91 |
| Real RAC Composite | 1.16 | 0.92 | 1.49 | 2.05 | 0.93 | 0.74 | 0.95 | 0.98 |
| Real RAC Domestic | 1.22 | 0.86 | 1.55 | 1.73 | 0.95 | 0.76 | 0.96 | 0.95 |
| Real WTI | 1.04 | 0.70 | 1.23 | 1.22 | 0.95 | 0.74 | 0.96 | 0.85 |
| Real PPI | 1.21 | 1.00 | 1.63 | 2.28 | 0.94 | 0.74 | 0.99 | 0.97 |
| Nominal RAC Imports | 1.03 | 0.74 | 1.22 | 1.37 | 0.92 | 0.70 | 0.96 | 0.89 |
| Nominal RAC Composite | 1.25 | 0.81 | 1.58 | 1.54 | 0.93 | 0.72 | 0.98 | 0.90 |
| Nominal RAC Domestic | 1.23 | 0.80 | 1.50 | 1.40 | 0.95 | 0.74 | 0.97 | 0.89 |
| Nominal WTI | 0.94 | 0.68 | 1.02 | 1.08 | 0.95 | 0.72 | 0.95 | 0.83 |
| Nominal PPI | 1.22 | 0.84 | 1.59 | 1.78 | 0.95 | 0.70 | 1.00 | 0.90 |
NOTES: ![]() denotes the forecast horizon. The
forecasting models are described in the text. Boldface indicates
gains in accuracy relative to AR(4) benchmark model
for real GDP growth.
denotes the forecast horizon. The
forecasting models are described in the text. Boldface indicates
gains in accuracy relative to AR(4) benchmark model
for real GDP growth.
Footnotes
1. The work of Carlton (2010) is not comparable with ours or with Ravazzolo and Rothman's because of her use of pre-1973 data, which invalidates standard regression analysis and causes instabilities in the predictive relationships. The econometric implications of using pre-1973 oil price data are discussed in detail in Kilian and Vigfusson (2011) and Alquist, Kilian and Vigfusson (2012). Return to text
2. Our focus in this paper is on assessing whether the gains in forecast accuracy are economically significant. We do not conduct tests of statistical significance. Conventional tests of the null hypothesis of equal predictive accuracy are designed to test the null of no predictability in population rather than the null of equal MSPEs in finite samples (see Inoue and Kilian 2004). This fact makes them inappropriate for comparing out-of-sample forecasts and biased toward rejecting the null hypothesis. In other words, even a rejection of the null would not necessarily imply that the inclusion of oil prices significantly reduces the out-of-sample MSPE. This problem has recently been addressed by Clark and McCracken (2009, 2012), but their alternative tests of equal finite-sample MSPEs are not applicable in our setting. Return to text
3. In related work, Ramey and Vine (2010) propose an alternative adjustment to the price of gasoline that reflects the time cost of queuing in gasoline markets during the 1970s. That adjustment as well serves to remove a nonlinearity in the transmission process. Both the nonlinearity postulated in Edelstein and Kilian (2009) and that postulated in Ramey and Vine (2010) is incompatible with the specific nonlinearity embodied in the models of Mork (1989) and Hamilton (1996, 2003) in that these papers rely on linear regressions after adjusting the energy price data. Return to text
4. A similar idea has also been explored in Davis and Kilian (2011). Return to text
5. This pattern differs from the results reported in Edelstein and Kilian (2009) for the share of energy expenditures in consumer spending. One reason is that Edelstein and Kilian focus on retail energy prices and on expenditures on all forms of energy, whereas here we are more narrowly concerned with the share of crude oil in the economy. Return to text
6. The corresponding model for the nominal price of oil would be even less accurate. That model is not reported, because there is no obvious rationale for such a specification. Return to text
7. It can be shown that this result is qualitatively robust to using pre-1974 data in estimation. For further discussion of this point and a comparison with results reported in Hamilton (2011) see Alquist, Kilian, and Vigfusson (2012). Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text