Heterogeneous Workers, Optimal Job Seeking, and Aggregate Labor Market Dynamics

Brendan Epstein^**

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

In the United States, the aggregate vacancy-unemployment (V/U) ratio is strongly procyclical, and a large fraction of its adjustment associated with changes in productivity is sluggish. The latter is entirely unexplained by the benchmark homogeneous-agent model of equilibrium unemployment theory. I show that endogenous search and worker-side horizontal heterogeneity in production capacity can be important in accounting for this propagation puzzle. Driven by differences in unemployed and on-the-job seekers' search incentives, the probability that any given firm with a job opening matches with a worker endowed with a comparative advantage in that job exhibits a stage of procyclical slow-moving adjustment. Consequently, so do the expected gains from posting vacancies and, hence, the V/U ratio. The model has channels through which the majority of both the V/U ratio's sluggish-adjustment properties and its elasticity with respect to output per worker can be accounted for.

Keywords: Amplification, comparative advantage, endogenous search, heterogeneity, market tightness, mismatch, on-the-job search, propagation, search and matching, search intensity, unemployment, vacancies

JEL classification: E25, J24, J64

1 Introduction

The aggregate vacancy-unemployment (V/U) ratio broadly summarizes the state of the labor market, as it reflects the ease with which individuals can exit unemployment. Empirically, in the United States, the V/U ratio is strongly procyclical, and a large fraction of its adjustment given changes in productivity is sluggish. Hence, for instance, an increase in productivity is associated with an upward jump in the V/U ratio, followed by a protracted stage over which the V/U ratio continues to slowly rise (at a decreasing rate). The benchmark, homogeneous-agent model of equilibrium unemployment theory has no channels through which such slow-moving adjustment can be accounted for: given a change in productivity, the model predicts that full adjustment of the V/U ratio occurs instantly. This limitation is additional to the well-known fact that under standard calibrations, the benchmark model can account for less than half of the elasticity of the V/U ratio with respect to productivity.¹ Understanding the V/U ratio's stage of sluggish adjustment is important. Indeed, a slow-moving deterioration of the V/U ratio reflects the degree to which the labor market responds persistently, for example, in the wake of a recession. Moreover, as can be inferred from Fujita and Ramey (2007), around 60% of the total change in the V/U ratio that occurs given a change in productivity takes place during the V/U ratio's stage of sluggish adjustment.²

The objective of this paper is to develop an understanding of the extent to which endogenous search and horizontal worker-side heterogeneity in production capacity can have an impact on shaping the dynamic adjustment process of the V/U ratio relative to changes in productivity. I capture horizontal heterogeneity by considering a labor force composed of individuals who have a comparative advantage in a particular job, but are still able to work in jobs in which they have a comparative disadvantage. I assume no worker has an absolute advantage in production, and I endogenize the search behavior of all job seekers, both employed and unemployed, across all available job opportunities. The model I develop is not competing, but rather, complementary to the benchmark/standard model, which I show is nested within the present paper's framework.

Quantitative analysis reveals that the impact of horizontal worker-side heterogeneity and endogenous search can be substantial. Indeed, results imply that accounting for such factors can potentially help explain both the majority of the V/U ratio's slow-moving adjustment properties and the majority of its elasticity with respect to output per worker.

In the model, both workers and firms prefer comparative-advantage employment (matches between the same worker- and firm-type) over comparative-disadvantage employment (that is, matches between workers and firms whose type is different), since the former generates the highest surplus. Nonetheless, comparative disadvantage employment generates valuable surplus also; therefore, it represents an appealing alternative through which workers can exit unemployment, as well as an additional channel through which firms can fill positions and, accordingly, incur lower expected vacancy-posting costs. Given this environment, incentives are such that unemployed individuals search across all available job opportunities, and on-the-job (OTJ) search emerges naturally as the result of individuals who are employed in jobs in which they have a comparative disadvantage (alternatively, skill-mismatched employment), but search for comparative-advantage (alternatively, skill-matched) employment. The intensity of search that any given individual devotes to any given job opportunity is endogenous and contingent on: an individual's comparative advantage in production, the state of the economy, search costs, and an individual's employment state.

Given worker-side heterogeneity, vacancy-posting decisions are based on the expected value of a match, which depends on the slow-moving masses of unemployed and OTJ searchers. Consider, for example, an increase in productivity.³ This induces a sudden increase in the expected gains from posting vacancies, triggering a jump in the V/U ratio. Since unemployed individuals have a lower outside-search option compared to OTJ seekers, following the increase in productivity, as unemployment declines the ratio of OTJ searchers to unemployed individuals rises slowly. Consequently, the fraction of job seekers who direct search (exclusively) toward comparative-advantage employment opportunities increases. This leads to a slow-moving rise in the probability that any given firm with a job opening matches with a worker endowed with a comparative advantage in that job (that is, the probability that any given firm with a vacancy matches with a worker of its own type). Hence, the expected gains from posting vacancies exhibit a stage of sluggish increase, inducing the same in the V/U ratio. The opposite occurs in a contraction.

It follows that the process leading to slow-moving adjustment of the V/U ratio originates from endogenous changes in the composition of the pool of individuals searching for any particular type of job. Endogenous job-seeking magnifies this process and aids in accounting for the amplification of shocks by generating feedback between firm and worker-side decisions. In particular, this allows workers to respond optimally to relative changes in employment surpluses across job opportunities, which has a direct impact on cyclical changes in the composition of searchers, and hence, on firms' match-quality expectations.

As related to the role of worker-side heterogeneity, Albrecht and Vroman (2002), Gautier (2002), Chassamboulli (2009), and Dolado, Jansen, and Jimeno (2009) develop models that explore the impact of vertical worker-side skill differentiation on idiosyncratic differences in unemployment and wages, while Pries (2007) shows how vertical differentiation can help amplify aggregate productivity shocks. In turn, Bils, Chang, and Kim (2009) focus on understanding differences in unemployment and work hours across labor-force participants. In their analysis, worker-side heterogeneity operates in a context in which "comparative advantage" refers to individuals who have high market productivity relative to their home productivity. Furthermore, labor markets are segmented: although the labor force is heterogeneous, conditional on idiosyncratic characteristics individuals seek employment in only one production sector. In all of the previous, workers' search behavior is determined exogenously.

By accounting for horizontal worker-side differentiation and endogenous directed search, the analysis in the present paper complements the literature on three main fronts. First, it reveals the critical labor-market role of (directed) OTJ search. In the absence of this, workers' ability to refocus search given changes in productivity is limited to the extent that the model's channel for generating slow-moving adjustment of the V/U ratio is effectively shut down. Thus, comparative disadvantage employment emerges as necessary, but not sufficient for the V/U ratio to exhibit sluggish adjustment in response to changes in productivity. Second, analysis shows that the combination of worker-side heterogeneity and optimal search can generate amplification of changes in productivity broadly in line with the data even for relatively small values of net unemployment flow benefits. This stands in contrast to the fact that, as noted, for instance, in Hagedorn and Manovskii (2008), the standard model requires net unemployment flow benefits to be almost as large as output per worker in order to match the amplification of productivity shocks in the data. Finally, accounting for worker-side heterogeneity implies that output per worker (OPW) is endogenous. The theory reveals that, conditional on whether they stem from changes in productivity throughout or between job opportunities, otherwise identical changes in OPW can be associated with adjustment in aggregate labor-market variables of considerably different magnitude. Intuitively, changes in OPW that stem from changes in productivity between job opportunities are associated with greater changes in relative employment surpluses, and therefore with greater endogenous readjustment in the pool of individuals searching for any particular type of job.

This paper proceeds as follows. Section 2 develops the theory; although my ultimate interest lies in understanding the joint implications of worker-side heterogeneity and endogenous directed search, I develop the model sequentially, building it by initially focusing on the case in which search decisions are exogenous. Then, Section 3 details my methodology for numerical analysis, and Sections 4 and 5 present results. Finally, Section 6 concludes.

2 The Model

I consider an economy with two types of workers and two types of production sectors/firms, where worker-side differentiation is horizontal, and the environment is symmetric. This facilitates focus on developing an understanding of the extent to which arbitrarily small degrees of heterogeneity can have an impact on aggregate labor-market fluctuations relative to the standard, homogeneous-agent model of equilibrium unemployment theory.

I embed horizontal differentiation through assumptions on production. Let workers and production sectors/firms be indexed by $i,j\in\{1,2\}$ . In the notation subscripts refer to workers and superscripts to sectors/firms. Comparative advantage employment, which I alternatively refer to as skill-matched employment, occurs when the worker and firm type coincide. The output generated by a type- individual employed by a type- firm is $y_{i,t}^{i}=p_{t}$ , where $p_{t}$ is an economy-wide (exogenous) productivity parameter. For $j\neq i$ , the output generated by a type- individual employed by a type- firm (comparative disadvantage employment, or, alternatively, skill-mismatched employment) is $y_{j,t}^{i}=p_{t}(1-\phi_{t})$ , where $\phi_{t}\in(0,1)$ is an (exogenous) penalty parameter that captures the degree of comparative disadvantage of a type- individual employed by a type- firm. Unless noted otherwise, henceforth when and appear together in some expression, assume $i\neq j$ .

Symmetry implies that in all periods any type-specific worker/firm variable is equal to half of its aggregate counterpart, and that all model parameters are symmetric across worker and firm types. Given symmetry, whenever helpful I present the model from the point of view of type-1 economic agents. All statements carry over to type-2 agents by simple re-indexing. As in Hagedorn and Manovskii (2008) the model is cast in discrete time, but I assume that the time period is small enough to be a close approximation to continuous time. All economic agents discount the future at rate , and $\beta=1/\left( 1+r\right)$ is the discount factor. In addition, all variables are normalized by the aggregate labor force.

Job seekers are in employment state $\mathbb{S\in}\left\{ u,\chi\right\}$ , where means " unemployed" and $\chi$ means "skill-mismatch employed." Unemployed workers receive net unemployment flow benefits , which are equal to the difference between time-invariant gross unemployment flow benefits and time-invariant (for now) search costs $C_{u}$ . Unemployed individuals direct their search across all employment opportunities.⁴

The value of unemployment for a type-1 individual is given by $U_{1,t}$ . All job-finding probabilities are endogenous, and $F_{1,\mathbb{S},t}^{i}$ denotes the probability that a type-1 individual searching for a job in sector finds a job in that sector, given that he or she is in employment state $\mathbb{S}$ . Moreover, $W_{1,t}^{i}$ is the value of employment for a type-1 individual who is matched with a type firm. Letting $\mathbb{E}$ denote the expectation operator, it follows that

$\displaystyle U_{1,t}=z-C_{u}+\beta(F_{1,u,t}^{1}\cdot\mathbb{E}_{t}W_{1,t+1}^{1} +F_{1,u,t}^{2}\cdot\mathbb{E}_{t}W_{1,t+1}^{2}$
$\displaystyle +(1-F_{1,u,t}^{1}-F_{1,u,t}^{2})\cdot\mathbb{E}_{t}U_{1,t+1})$ .	(1)

Comparative advantage in production implies that in any period $W_{1,t} ^{1}>W_{1,t}^{2}$ . By assumption, it is always true that $W_{1,t}^{2}>U_{1,t}$ .

Let $w_{1,t}^{i}$ denote the wage of a type-1 individual who is matched with a type- firm. As noted in Shimer (2006), the standard Nash bargaining solution to wage determination in matching models is invalid given on-the-job search. Thus, in line with Pissarides (1994), Chassamboulli (2009), and Dolado, Jansen, and Jimeno (2009), I assume that wages are such that a constant fraction $\eta$ of the surplus of a match goes to the worker, where $\eta\in\left( 0,1\right)$ is the bargaining power of workers, $1-\eta$ goes to the firm, and also that wages can be continuously revised and that long-term contracts are not possible.⁵ Following the literature, there is an exogenous job-destruction probability $\delta>0$ with which any type of job, whether skill-matched or -mismatched, is destroyed. Since the value of skill-mismatch is less than that of skill-matched employment, it is optimal for an individual who is skill-mismatched to engage in on-the-job (OTJ) search directed toward the sector in which he or she has a comparative advantage (conditional on the type of match, the production functions of all firms within a sector are identical, so there are no gains in moving from one skill-mismatched employment relationship to another). It follows that the value of comparative disadvantage employment for a type-1 individual is

$\displaystyle W_{1,t}^{2}$	$\displaystyle =w_{1,t}^{2}-C_{\chi}+\beta((1-\delta-F_{1,\chi,t}^{1} )\cdot\mathbb{E}_{t}W_{1,t+1}^{2}$
	$\displaystyle +F_{1,\chi ,t}^{1}\cdot\mathbb{E}_{t}W_{1,t+1}^{1}+\delta\cdot\mathbb{E}_{t} U_{1,t+1})$ ,	(2)

where $C_{\chi}$ represents (for now, time invariant) OTJ search costs. Note that a job-to-job transition occurs with probability $F_{1,\chi,t}^{1}$ , meaning that there is an endogenous job-destruction component associated with skill-mismatched employment.

Using analogous reasoning, the relevant value of comparative advantage employment is

$\displaystyle W_{1,t}^{1}=w_{1,t}^{1}+\beta(\left( 1-\delta\right) \cdot\mathbb{E} _{t}W_{1,t+1}^{1}+\delta\cdot\mathbb{E}_{t}U_{1,t+1})$ .

(3)

In this case, there is no endogenous job-destruction component, since skill-matched individuals have already achieved their best possible match. Hence, they do not engage in OTJ search.

Let $u_{i,t}$ , $\chi_{i,t}$ and $n_{i,t}$ denote, respectively, the mass of type- individuals who are unemployed, skill-mismatch employed, and skill-match employed; each of these masses is determined endogenously. Then,

$\displaystyle \psi_{i}=u_{i,t}+\chi_{i,t}+n_{i,t}$ ,

(4)

where, by symmetry, $\psi_{i}=0.5$ is the economy's fraction of type- individuals.

Each period, the number of matches formed in sector is determined by the sectoral matching function $m_{t}^{i}=m(v_{t}^{i},s_{t}^{i})$ , which is increasing in sector- vacancies $v^{i}$ and searchers $s^{i}$ . Following related literature, such as Gautier (2002), I assume that has constant returns to scale. In particular, let $m_{t}=A(v_{t}^{i})^{\alpha}(s_{t} ^{i})^{1-\alpha}$ , where $\alpha\in\left( 0,1\right)$ is the elasticity of sectoral matches with respect to sectoral vacancies, and is the matching efficiency parameter.

The job-finding probability $F_{1,\mathbb{S},t}^{i}$ is given by $f_{t} ^{i}=m_{t}^{i}/s_{t}^{i}$ (sector- matches per sector- searchers), weighted by the worker-type/employment-state specific technological component $\ell_{1,\mathbb{S}}^{i}$ : effective search. For now, I assume that effective search is determined exogenously. Thus, in any period $F_{1,\mathbb{S},t}^{i}=\ell_{1,\mathbb{S}}^{i}f_{t}^{i}$ . The technological component of the search process summarizes the effectiveness with which all of an individual's job-seeking activities lead to a job offer given his or her employment state and the sector in which the individual is searching.⁶ Effective search includes different kinds of search activities and methods, the intensity with which search methods are used, etc. It follows that sectoral searchers are a weighted sum of all individuals searching in that sector, where the weights are effective search. Thus, for instance,

$\displaystyle s_{t}^{1}=\ell_{1,u}^{1}\cdot u_{1,t}+\ell_{2,u}^{1}\cdot u_{2,t}+\ell _{1,\chi}^{1}\cdot\chi_{1,t}$ .

(5)

Note that sector-1 searchers do not include the weighted mass of skill-mismatched type-2 individuals $\ell_{2,\chi}^{2}\cdot\chi_{2,t}$ , since type-2 individuals who are employed in sector 1 only search for sector-2 jobs.⁷ Given constant returns to scale $f_{t}^{i}=f(\theta_{t}^{i})$ , where $\theta_{t}^{i}=v_{t}^{i}/s_{t}^{i}$ denotes sectoral (market) tightness, and $f_{t}^{\prime}>0$ .

With the earlier development in mind, it is straightforward that the evolution of the mass of unemployed type- workers satisfies

$\displaystyle u_{1,t+1}-u_{1,t}=\delta\left( n_{1,t}+\chi_{1,t}\right) -(F_{1,u,t} ^{1}+F_{1,u,t}^{2}\mathcal{)}u_{1,t}$ ,

(6)

and the aggregate unemployment rate is $u_{t}=\sum_{i}u_{i,t}$ . Moreover, the evolution of the mass of type- workers who are skill mismatched is given by

$\displaystyle \chi_{1,t+1}-\chi_{1,t}=F_{1,u,t}^{2}u_{1,t}-(\delta+F_{1,\chi,t}^{1} )\chi_{1,t}$ ,

(7)

with the aggregate rate of skill-mismatch satisfying $\chi_{t}=\sum_{i} \chi_{i,t}$ . Finally, letting $e_{t}=\left( 1-u_{t}\right)$ denote the employment rate, $\chi_{t}/e_{t}$ is the aggregate rate of skill-mismatched employment.

Turning toward firms, let the value of a job for a sector-1 firm that is matched with a type- worker be denoted by $J_{i,t}^{1}$ , and the value of a vacancy by $V_{t}^{i}$ . The firm's value of skill-matched employment is

$\displaystyle J_{1,t}^{1}=y_{1,t}^{1}-w_{1,t}^{1}+\beta(\left( 1-\delta\right) \cdot\mathbb{E}_{t}J_{1,t+1}^{1}+\delta\cdot\mathbb{E}_{t}V_{t+1}^{1} )$ ,

(8)

and its value of skill-mismatched employment is

$\displaystyle J_{2,t}^{1}=y_{2,t}^{1}-w_{2,t}^{1}+\beta((1-\delta-F_{2,\chi,t}^{2} )\cdot\mathbb{E}_{t}J_{2,t+1}^{1}+(\delta+F_{2,\chi,t}^{2})\cdot\mathbb{E} _{t}V_{t+1}^{1})$ .

(9)

Comparative advantage in production implies that $J_{1,t}^{1}>J_{2,t}^{1}$ .

Following the literature, while a firm has a vacancy it incurs the time-invariant flow cost . The probability with which a sector- vacant job is filled is $q_{t}^{i}=m_{t}^{i}/v_{t}^{i}$ (sector- matches per sector- vacancies). Given constant returns to scale, this can be stated as $q_{t}^{i}=q(\theta_{t}^{i})$ , where $q_{t}^{\prime}<0$ . The probability that a sector- vacant job is filled with a worker who has a comparative advantage in that sector is $q_{t}^{1}(1-\pi_{2,t}^{1})$ , and $q_{t}^{1} \pi_{2,t}^{1}$ otherwise. If follows that

$\displaystyle V_{t}^{1}=-c+\beta(q_{t}^{1}(1-\pi_{2,t}^{1})\cdot\mathbb{E}_{t}J_{1,t+1} ^{1}+q_{t}^{1}\pi_{2,t}^{1}\cdot\mathbb{E}_{t}J_{2,t+1}^{1})+(1-q_{t} ^{1})\mathbb{E}_{t}V_{t+1}^{1})$ ,

(10)

and given the earlier development

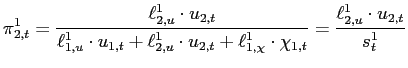$\displaystyle \pi_{2,t}^{1}=\frac{\ell_{2,u}^{1}\cdot u_{2,t}}{\ell_{1,u}^{1}\cdot u_{1,t}+\ell_{2,u}^{1}\cdot u_{2,t}+\ell_{1,\chi}^{1}\cdot\chi_{1,t}} =\frac{\ell_{2,u}^{1}\cdot u_{2,t}}{s_{t}^{1}}$ .

(11)

That is, $\pi_{2,t}^{1}$ is the effective fraction of type-2 individuals looking for jobs in sector 1. This probability is endogenous, and given its dependence on the slow-moving masses of unemployed and OTJ searchers, slow moving as well. For short, with some slight abuse of terminology, I henceforth refer to $\pi_{2,t}^{1}$ as the probability of skill-mismatch.

For $i\in\{1,2\}$ , $S_{1,t}^{i}=W_{1,t}^{i}-U_{1,t}+J_{1,t}^{i}$ is the surplus generated by an employment match between a type- worker and a sector- firm. The earlier noted assumptions on wage negotiations jointly imply that wages ultimately satisfy conditions identical to the standard Nash bargaining solution, implying the surplus-sharing rule

$\displaystyle (W_{1,t}^{i}-U_{1,t})/\eta=S_{1,t}^{i}=J_{1,t}^{i}/\left( 1-\eta\right)$ .

(12)

Since $S_{1,t}^{1}>S_{1,t}^{2}$ (and $S_{1,t}^{1}>S_{2,t}^{1}$ ), it follows that $w_{1,t}^{1}>w_{1,t}^{2}$ (and $w_{1,t}^{1}>w_{2,t}^{1}$ ). Therefore, the wage of an individual who is skill-mismatched is lower than his or her skill-matched wage, and the wage of an individual who is skill-mismatched in any given sector is lower than that of individuals who are skill-matched in that same sector.

Free entry into vacancy creation implies the zero-profit condition $V_{t} ^{i}=0$ . Implementing this condition in equation (10) along with the definition of surplus and rearranging yields the vacancy/job-creation condition:

$\displaystyle \beta\left( 1-\eta\right) ((1-\pi_{j,t}^{i})\cdot\mathbb{E}_{t}S_{i,t+1} ^{i}+\pi_{j,t}^{i}\cdot\mathbb{E}_{t}S_{j,t+1}^{i})=c/q(\theta_{t} ^{i})$ .

(13)

This is the model's fundamental equilibrium equation. Changes in economy-wide productivity induce changes in the expected gains from posting vacancies (the left-hand side (LHS)). These changes must be balanced out in terms of changes in expected costs (the right-hand side (RHS)). Such balancing occurs through changes in $q^{i}$ , which is a decreasing function of $\theta^{i}$ . It follows that $\theta^{1}$ and $\theta^{2}$ are the model's fundamental equilibrium variables.⁸

Henceforth, I refer to the model as developed so far, that is, with fixed effective search, as the multi-agent (MA) model.

2.1 The Role of Worker Heterogeneity

The MA model is not solvable analytically; however, the role of worker heterogeneity can be understood intuitively by initially focusing on the impact of the absence of heterogeneity. Assume all workers are identical and normalize all production to . Then, $\pi_{j}^{i}=0$ , $\chi_{i}=0$ , and symmetry implies that $s^{i}=Tu$ , where $T=\ell_{i,u} ^{i}+\ell_{j,u}^{i}$ , and additionally $v^{i}=v/2$ , where denotes aggregate vacancies. Thus, $\theta^{i}=\left( 0.5/T\right) \Theta$ , where $\Theta=v/u$ : the ratio of aggregate vacancies to aggregate unemployment (alternatively, the V/U ratio). Hence, $m^{i}=m\left( v,u\right)$ , and, more generally, super and subscripts become unnecessary since sectors and individuals are now entirely identical. Within this context, the job-creation condition reduces to

$\displaystyle \beta\left( 1-\eta\right) \mathbb{E}_{t}S_{t+1}=c/q(\Theta_{t} )$ ,

(14)

which is, in fact, the standard (homogeneous agent) model's job creation condition.⁹ Thus, the standard model is a special case of the MA model in which heterogeneity is done away with.

Consider a permanent increase in economy-wide productivity . This leads to a one time, permanent increase in the expected gains from posting vacancies (the LHS of equation $% latex2html id marker 4704 $ \left( \ref{JC Pissarides}\right) $$ ) that is balanced out by a one-time increase in the expected costs of posting vacancies (the equation's RHS). Since the job-filling probability is a decreasing function of the V/U ratio, this balancing occurs through a one-time increase in the V/U ratio, which is driven by an instantaneous increase in aggregate vacancies. Hence, given a change in , the V/U ratio does not exhibit post-shock slow-moving adjustment.

Now, return to the MA model, and once again consider a permanent increase in . At the moment of the shock, the expected gains from posting vacancies jump up (the LHS of equation (13), as do the expected costs (the equation's RHS). The latter is driven by an instantaneous increase in sectoral market tightness $\theta^{i}$ , which itself is driven by a jump in sectoral vacancies. However, unlike the standard model, all adjustments do not end there. This is because the probability of skill-mismatch $\pi_{j}^{i}$ is slow moving, and therefore, only after the change in productivity has occurred will this probability begin to adjust. By extension, the expected gains from posting vacancies will also continue to (slowly) adjust after the change in .

When economy-wide productivity rises, as the pool of unemployed individuals declines, type- workers take relatively longer to exit $s^{i}$ than type- searchers. This is because upon becoming skill-mismatched, type- individuals become OTJ searchers, and therefore continue to form part of $s^{i}$ ; however, type- workers exit $s^{i}$ whether they become skill-matched or -mismatched. Such relatively faster drainage of type- workers maps into a decrease in the probability of skill-mismatch $\pi_{j} ^{i}$ , which occurs slowly given its dependence on the slow-moving masses of unemployed and OTJ searchers. This leads to a slow-moving increase in the expected gains from posting vacancies, which is balanced out through a slow-moving increase in the expected costs, driven by a slow-moving increase in sectoral market tightness. By extension, the slow-moving increase in the availability of sectoral vacancies per searchers will lead to a slow-moving increase in the availability of aggregate vacancies per unemployed individual. Thus, in the MA model, an increase in economy-wide productivity results in a stage of slow-moving increase in the V/U ratio, with the reverse being true given a decline in .

More technically, note that given symmetry equation (11) can be stated as

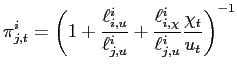$\displaystyle \pi_{j,t}^{i}=\left( 1+\frac{\ell_{i,u}^{i}}{\ell_{j,u}^{i}}+\frac {\ell_{i,\chi}^{i}}{\ell_{j,u}^{i}}\frac{\chi_{t}}{u_{t}}\right) ^{-1}$ .

(15)

As such, the expression for $\pi_{j}^{i}$ clearly shows that in an expansion it is a slow-moving increase in the ratio of skill-mismatched employment to unemployment that serves to foster a slow-moving decline in the probability of skill-mismatch. Note, in addition, that in the absence of OTJ search $\ell_{i,\chi}^{i}=0$ , and therefore $\pi_{j}^{i}$ reduces to being a constant, meaning that the model's channel for generating sluggish adjustment of the V/U ratio is effectively shut down.¹⁰

The employment surpluses associated with skill-matched and -mismatched employment can be expressed, in steady state, respectively as

$\displaystyle S_{1}^{1}=\left( y_{1}^{1}-z-\beta F_{1,u}^{2}\eta S_{1}^{2}\right) \cdot\left( 1-\beta\left( 1-\delta-F_{1,u}^{1}\eta\right) \right) ^{-1}$

(16)

and

$\displaystyle S_{1}^{2}=(y_{1}^{2}-z-\beta\left( F_{1,u}^{1}-F_{1,\chi}^{1}\right) \eta S_{1}^{1})\cdot(1-\beta(1-\delta-F_{1,u}^{2}\eta-F_{1,\chi}^{1}))^{-1}$ .

(17)

The term $\beta F_{1,u}^{2}\eta S_{1}^{2}$ in equation (16) and its analog in equation (17) capture, respectively, the opportunity costs of skill-matched and -mismatched employment.¹¹ As detailed in the appendix, a permanent increase in relative productivity $1-\phi$ induces an on impact decrease in the expected gains from posting vacancies. Intuitively, this reflects the relative importance of skill-matched surplus in firms' vacancy-posting decisions, and therefore, the extent to which a weighing down of the highest surplus-generating employment arrangement in the economy - due to higher opportunity costs - is particularly damaging for overall vacancy-posting incentives. It follows that in the MA model a decrease in $\phi$ will induce the economy to adjust opposite to an increase in economy-wide productivity , ultimately triggering a decline in the V/U ratio, part of which will be slow-moving. The reverse will occur given a decline in .

2.2 The Role of Optimal Effective Search

The costs of effective search directed toward a sector are simply the costs of generating job offers in that sector. As noted in Krueger and Mueller (2008), the time that unemployed individuals spend searching is small, which suggests that time constraints are not binding in optimal search decisions.¹² Given this, an intuitive reason for which unemployed individuals might limit the effective search that they devote to any given type of job opportunity is that search costs are sector specific. In turn, sector-specific search costs are a natural motivation for individuals to broaden their search to include jobs in which they do not have a comparative advantage. To capture this intuition, I assume that individuals bear the additively separable effective-search disutility function

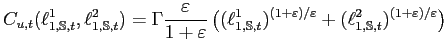$\displaystyle C_{u,t}(\ell_{1,\mathbb{S},t}^{1},\ell_{1,\mathbb{S},t}^{2})=\Gamma \frac{\varepsilon}{1+\varepsilon}\left( (\ell_{1,\mathbb{S},t}^{1} )^{(1+\varepsilon)/\varepsilon}+(\ell_{1,\mathbb{S},t}^{2})^{(1+\varepsilon )/\varepsilon}\right)$ ,

(18)

where $\Gamma,\varepsilon>0$ .

Of course, the only value functions that must be updated are a workers' value of skill-mismatched employment and unemployment. Quite simply, $W_{1,t}^{2}$ and $U_{1,t}$ are as before, except that now they are maximized, respectively, over $\ell_{1,\chi}^{1}$ , and $\mathcal{\ell}_{1u,t}^{1}\$ and $\mathcal{\ell }_{1,u,t}^{2}$ . Moreover, net unemployment flow benefits become endogenous, since $z_{t}$ is now equal to the difference between and $C_{u,t}$ . As before, I assume that in all states of the economy it is optimal for unemployed individuals to search for jobs across sectors. Given the surplus-sharing rule in equation (12) , the first-order conditions for optimal search can be stated as

$\displaystyle \Gamma(\ell_{1,\chi,t}^{1})^{1/\varepsilon}=f_{t}^{1}\beta\eta\mathbb{E} _{t}(S_{1,t+1}^{1}-S_{1,t+1}^{2})$

(19)

when skill-mismatched, and for $i\in\left\{ 1,2\right\}$

$\displaystyle \Gamma(\ell_{1,u,t}^{i})^{1/\varepsilon}=f_{t}^{i}\beta\eta\mathbb{E} _{t}S_{1,t+1}^{i}$

(20)

when unemployed.¹³ In each of these first-order conditions the RHS represents the expected gains from search. Note that effective search is a jump variable.

The intuitive nature of the cost function is reflected on several fronts. By symmetry $f^{1}=f^{2}=f$ . Therefore, since $S_{1}^{1}>S_{1}^{2}$ , given equation (20) unemployed individuals will always devote greater effective search toward skill-matched employment: $\ell _{1,u,t}^{1}>\ell_{1,u,t}^{2}$ $\forall t$ . This implies self selection. Furthermore, if non-symmetric environments were considered, the chosen cost function provides an additional and natural motivation for skill-mismatched employment to exist. Suppose $f^{1}=0$ . Then, it is optimal to set $\ell_{1,u,t}^{1}=0$ , but as long as the expected gains from skill-mismatched search are positive $\ell_{1,u,t}^{2}>0$ .

I henceforth refer to the MA model extended to account for endogenous effective search as the multi-agent optimal search (MA-OS) model. This is the paper's central model of interest.

The MA-OS model nests three models. These are the MA model (obtained by fixing effective search), the standard model (obtained by fixing effective search and setting $\phi=0$ ), and a version of the standard model in which effective search is endogenous (standard optimal search (standard-OS) model; set $\phi=0$ , but allow unemployed individuals to choose effective search). Given the absence of worker-side heterogeneity (and OTJ search), as is the case with the standard model, the standard-OS model has no channels through which sluggish adjustment of the V/U ratio can be generated.¹⁴

Related literature focuses on the response of models' endogenous variables relative to changes in output per worker (OPW). In the case of the standard and standard-OS models, OPW corresponds in straightforward fashion to the exogenous economy-wide productivity parameter . In contrast, in the MA and MA-OS models OPW is determined endogenously, and given by

$\displaystyle OPW=\left( p\left( 1-u-\chi\right) +p(1-\phi)\chi\right) \cdot\left( 1-u\right) ^{-1}$ .

(21)

Equation (21) calls explicit attention to the role of both economy-wide productivity and the skill-mismatch parameter $\phi$ in the determination of OPW. This highlights the fact that observed empirical changes in OPW need not stem from a unique source.

Although the MA-OS model is not solvable analytically, the impact of endogenous effective search can still be gauged. Since employment surpluses are procyclical in , then so are the expected gains from search, and therefore, effective search as well (recall equations (19) and (20)). Intuitively, in an expansion jobs are easier to find and employment surpluses are higher. This means that the opportunity cost of not having a job, and for that matter, of being skill-mismatched, increases. Hence, individuals react to above-average economic conditions by supplying above-average effective search. In a recession, the opposite occurs. For instance, think of discouraged workers as an extreme example of this; these are individuals who have set effective search equal to zero.¹⁵

Endogenous effective search enhances the amplification of economy-wide productivity shocks because it generates feedback between firm- and worker-side decisions. For instance, when the expected gains from search increase, effective search rises, which decreases expected vacancy-posting costs (all else equal, $\theta^{i}$ declines). This raises the expected gains from posting vacancies, therefore increasing vacancies, which raises the expected gains from search, and so on and so forth.

Endogenous effective search also enhances the magnitude of the model's sluggish adjustment properties. This is so because it induces greater adjustment in the ratio of skill-mismatched employment $\chi/u$ . Indeed, since employed job seekers have a more attractive outside option than unemployed ones, which is employment itself, it follows that unemployed effective search is more procyclical than OTJ search (mathematically, contrast equation (20) to equation (19)). Hence, in response to a rise in economy-wide productivity the probability of entering skill-mismatched employment will increase relatively more than the probability of exiting skill-mismatched employment. This will magnify the post shock increase in $\chi/u$ relative to the MA model, and, accordingly, the post shock decline in the probability of skill-mismatch $\pi_{j}^{i}$ . Note that regardless of any jump in $\pi_{j}^{i}$ , it is the slow-moving changes of this variable that matter for sluggish adjustment of the V/U ratio. Therefore, the magnified slow-moving decrease in $\pi_{j}^{i}$ that occurs under endogenous search will accordingly enhance the slow-moving adjustment of the V/U ratio. Of course, in terms of both amplification and sluggish adjustment, a decline in will induce opposite effects to those detailed above.

Now, consider instead the effects of a permanent increase in $1-\phi$ . Recall from analysis of the MA model that this will induce a reduction in the expected gains from posting vacancies. In the MA-OS model, this effect will be amplified because on impact of the the increase in $1-\phi$ there will be an accompanying strong instantaneous increase in the relative effective search that unemployed individuals devote to comparative disadvantage employment. This, of course, will lead to an instantaneous increase in the probability of skill-mismatch, further depressing the expected gains from posting vacancies.

However, the extent to which greater relative effective search devoted to skill-mismatched employment leads to (slow-moving) increases in the ratio of skill-mismatched employment to unemployment $\chi/u$ implies that following an increase in $1-\phi$ the probability of skill-mismatch will slowly decrease (recall, once more, equation (15)). In response to this, the V/U ratio will slowly rise. Hence, once effective search is endogenized, an increase in $1-\phi$ can in fact lead to an overall increase in the ratio of aggregate vacancies to unemployment, reversing the associated implications noted earlier for the MA model.

In addition, in the MA-OS model, because an increase in $1-\phi$ induces a relatively greater increase in effective search devoted toward skill-mismatched employment than an increase in (which has a direct and broad impact across all effective search), the ratio $\chi/u$ will (slowly) increase more following the former than following the latter. Given equation (15), this implies that changes in $1-\phi$ will tend to induce greater slow-moving adjustment of the V/U ratio than changes in . Moreover, it also follows that changes in $1-\phi$ will tend to have less of an impact on OPW than changes in . Indeed, note from equation (21) that while an increase in $1-\phi$ , all else equal, tends to increase OPW, a relative increase in $\chi$ , all else equal, tends to decrease OPW. In contrast, an increase in works broadly toward increasing OPW through increases in both skill-matched and -mismatched productivity. Of course, a decline in $1-\phi$ induces opposite effects to those stemming from an increase in relative productivity.

3 Basis for Numerical Analysis of Permanent Shocks

My analysis will focus on the impact of permanent changes in models' exogenous variables, as this substantially simplifies the explanation and interpretation of results while fully addressing the issues of central interest.¹⁶ In order to gain a full understanding of the MA-OS model, in analogous fashion to earlier in the paper, numerical analysis will contrast results to those stemming from nested models. There are no empirical time-series counterparts to the parameters and $\phi$ ; therefore, following related literature, results are put in context by highlighting changes in endogenous variables relative to changes in output per worker, when relevant. All henceforth cited tables and figures can be found in the appendix.

The choice of parameter values for each model is summarized in Table 1. I assume that the time period is equal to one week. Accordingly, I set the discount factor $\beta$ to 0.999, which is consistent with a quarterly interest rate of 0.012. I use the matching function efficiency parameter and the flow cost of vacancy posting to target the equilibrium aggregate unemployment rate and the equilibrium V/U ratio $\Theta=0.71$ ; this is in line with averages of US data spanning the last six decades. Using US unemployment data and the methodology described in Shimer (2005), I obtain the job-finding probability of an average unemployed individual. At monthly frequency, the mean of this is equal to 0.43. The associated job-finding probability at weekly frequency is given by $1-\left( 1-0.43\right) ^{1/4}$ , which is equal to 0.131; I take this as the relevant steady-state value. Using this and the target equilibrium unemployment rate, solving for the exogenous job-destruction probability implies $\delta=0.0081$ .¹⁷ In all cases, the matching function exponent $\alpha$ is chosen so that the partial elasticity of aggregate matches with respect to aggregate unemployment is in line with the corresponding evidence from Petrongolo and Pissarides (2001).¹⁸

The parameters $\Gamma$ and $\varepsilon$ are specific to the MA-OS and standard-OS models. Numerical analysis reveals that for each $\Gamma$ there is a value of that will hit the target equilibrium unemployment rate, but nothing else changes. Thus, I normalize $\Gamma$ by setting this parameter equal to one. In addition, I assume quadratic effective search disutility, meaning that $\varepsilon=1$ .

The skill-mismatch parameter $\phi$ is specific to the MA and MA-OS models. McLaughlin and Bils (2001) argue that average within-industry wage differentials between individuals who remain in an industry and those who switch can be interpreted as the result of equilibrium self-selection. They show that, empirically, the wages of industry switchers are, on average, 16 lower than those of industry non-switchers. I take this number as a reference point. Therefore, I use the skill-mismatch penalty parameter $\phi$ to set the equilibrium ratio of wages of skill-mismatched individuals to average wages in a sector equal to 0.84.

In the case of the MA model, effective search is assumed to be fixed at the equilibrium values implied endogenously by the MA-OS model. In order to further tighten the comparability of results, I purge the analysis from cross-model imbalances in bargaining power by setting the parameter $\eta$ equal to 0.5. In addition, I anchor all models around a common value for net unemployment flow benefits , which I set to 0.5. This is the average of the values advanced in Shimer (2005) and Hall and Milgrom (2008), assuming, in the latter, the lowest suggested replacement rate. Anchoring around is in line with the fact that it is the value of , not , which matters directly for the determination of the value of employment surpluses (recall equations (16) and (17)).

In all cases, the initial steady state of models is calculated at . Numerical analysis reveals that in the MA and MA-OS models the fraction of skill-mismatched employment is always small, making the equilibrium value of output per worker (OPW) arbitrarily close to one. Thus, across models, equilibrium net unemployment flow benefits are approximately 50% of OPW.¹⁹

4 Results I: Permanent Increases in Productivity

Figures 1 through 6 focus on the response of key endogenous variables to a 1 permanent (unanticipated) increase in economy-wide productivity . As shown in Figure 1, in the standard model on impact of the shock $\Theta$ instantaneously jumps to its new equilibrium value, while in the MA-OS model $\Theta$ initially jumps, and thereafter continues to slowly increase over 4 months. This slow-moving increase in the V/U ratio is driven by the slow-moving post-shock decline in the probability of skill-mismatch $\pi _{j}^{i}$ shown in Figure 2, which stems from the slow-moving post-shock increase in the ratio of skill-mismatched to unemployed individuals $\chi/u$ shown in Figure 3 (recall equation (15)).

In the MA-OS model $\pi_{j,t}^{i}=\ell_{j,u,t}^{i}u_{j,t}/s_{t}^{i}$ . The jump in $\pi_{j}^{i}$ noted in Figure 2 is driven by the greater procyclicality of effective search devoted to skill-mismatched jobs (U $\rightarrow$ skill-mismatch, $\ell_{j,u,t}^{i}$ , $i\neq j$ ) relative to unemployed and OTJ effective search devoted to skill-matched search (U $\rightarrow$ skill-match, $\ell_{i,u,t}^{i}$ , and OTJ search, $\ell_{i,\chi,t}^{i}$ , respectively); this is shown in Figure 4, and stems from the expected gains from search for skill-mismatched employment always being relatively lower.²⁰ The relatively greater procyclicality of $\ell_{j,u,t}^{i}$ also accounts for the relative adjustments in the slow-moving components of the probability of skill-mismatch, as shown in Figure 5 (given symmetry the percent changes in $u_{i}$ and $\chi_{i}$ are the same as those in their aggregate counterparts), and that of the fraction of skill-mismatched employment $\chi/e$ is shown in Figure 6.

Figures 7 and 8 show the individual responses of aggregate vacancies, , and unemployment, . In both models, on impact of the shock vacancies overshoot. In terms of the response of the V/U ratio, the key difference is that while in the standard model after the shock takes place vacancies decline at the same rate that unemployment does, in the MA-OS model the post-shock slow-moving decline in the probability of skill-mismatch maintains incentives for vacancy posting higher than otherwise. Hence, in the MA-OS model, after their initial jump vacancies decrease, but at a slower rate relative to unemployment than in the absence of a post-shock decline in the probability of skill-mismatch.

Of course, in the standard model the elasticity of OPW with respect to is one. In the MA-OS model, the 1% change in economy-wide productivity under consideration induces a 1.003% change in OPW. As shown in Figure 6, in the MA-OS model a permanent increase in ultimately induces a decline in the fraction of skill-mismatched employment $\chi/e$ . Hence, in terms of OPW, the change in is slightly amplified.

Figures 9 through 16 focus on the response of key endogenous variables to a 1% (unexpected) permanent increase in $1-\phi$ in the MA-OS model. As shown in Figure 9, while on impact of the shock the V/U ratio declines, thereafter it slowly increases across a period of roughly 15 months over which it fully reverses its initial decline, ultimately increasing relative to its starting value. Figures 10 and 11 show the corresponding changes in aggregate vacancies and unemployment. Of course, the on-impact decline in $\Theta$ is driven by an on-impact decline in vacancies, which now exhibit a stage of sluggish adjustment. Indeed, after their initial jump, vacancies slowly increase in the direction of change of the exogenous driving force.

Figure 12 shows adjustment in the probability of skill-mismatch $\pi_{j}^{i}$ . Its initial jump, along with its persistent post-shock direction of change, is driven by the initial response of endogenous effective search. As shown in Figure 13, on impact of the increase in $1-\phi$ the associated increase in skill-mismatched employment surplus triggers a substantial increase in effective search devoted to such jobs, partially at the expense of that devoted to skill-matched employment. Figure 14 details the ensuing changes in the rate of skill-mismatch $\chi$ and the ratio of skill-mismatched employment to unemployment $\chi/u$ . Overall, it follows that the lack of propagation slow-moving vacancies response given changes in economy-wide productivity , as shown earlier, is simply a reflection of accompanying changes in the probability of skill-mismatch not being sufficiently large.

As shown in Figure 15, unsurprisingly, the increase in $1-\phi$ induces a substantial increase in the fraction of skill-mismatched employment, $\chi/e$ . In terms of OPW, the relative increase in skill-mismatched employment acts opposite to the increase in relative productivity $1-\phi$ . This leads, in particular, to the elasticity of OPW with respect to $1-\phi$ to be a meager 0.002. Overall, the analysis reveals that once endogenous effective search is accounted for, changes in relative productivity have the potential to be a much more powerful driving force than economy-wide productivity in terms of both amplification and propagation of shocks in the model's key endogenous variables.

5 Results II: Permanent Increases in OPW

Following related literature, I now focus on changes in models' endogenous variables relative to changes in OPW.²¹ In addition, I extend the analysis to account for the impact of joint changes in and $\phi$ . In particular, I focus on joint shocks in which both economy-wide and relative productivity move in the same direction. This is intuitive given that in the MA-OS model the (unique) skill-mismatched employment opportunity is a stand-in for all jobs other than the one in which a worker is most productive. Therefore, to the extent that an increase in $1-\phi$ represents an increase in a worker's outside option relative to skill-matched employment, an increase in $1-\phi$ occurring jointly with an increase in is broadly analogous to it being the case that in an expansion individuals have relatively more viable work opportunities available than otherwise.

Row R1 of Table 2 summarizes information stemming from empirical US data. The elasticities of the V/U ratio $\Theta$ , aggregate vacancies , and aggregate unemployment with respect to OPW are, respectively, 7.79, 3.88, and -3.93 (columns C1, C4, C7). Moreover, the elasticity of vacancies with respect to unemployment, which implicitly captures the slope of the Beveridge curve, that is, the empirical negative relationship between aggregate vacancies and unemployment, is -0.86 (column C9).²² Turning toward the propagation of productivity shocks, some broadly applicable stylized facts can be inferred from the detailed analysis in Fujita and Ramey (2007). These are summarized in columns C2, C3, C5, C6, and C8. Empirically, in the United States, an impulse in OPW of around 0.7% is associated with: 1) an on-impact jump in the V/U ratio that is followed by a stage of slow-moving increase (that occurs at a decreasing rate) during which approximately 60% of the total rise in the V/U ratio takes place (the V/U ratio peaks around 12 months after the increase in OPW occurs), 2) a (decreasing rate) decline in the aggregate unemployment rate that lasts approximately 15 months before bottoming out, and 3) sluggishness in the adjustment of vacancies; on impact vacancies jump, and thereafter they continue to rise (at a decreasing rate) for about 12 months over which approximately 60% of their total increase occurs. It follows that, empirically, slow-moving adjustment of vacancies is an important contributing factor to the sluggish adjustment of the V/U ratio.

Rows R2 through R5 in Table 2 show model-specific responses to a -induced on-impact increase in OPW of 0.7%, broadly serving to summarize results already shown in Section 4, and also, for comparison, incorporating results pertaining to the standard-OS and MA models.²³ The standard model has limited explanatory power, accounting, in particular, for 27% of the empirical elasticity of the V/U ratio with respect to OPW, but none of its sluggish adjustment. The MA model accounts for a similar fraction of the empirical elasticity of the V/U ratio, but its dynamic adjustment is fundamentally different than in the standard model, as it is characterized by a stage of slow-moving response induced by vacancies adjusting at a slower rate than unemployment. Comparatively similar are the relative responses in the standard-OS and MA-OS models, with the former accounting for 55% of the empirical elasticity of $\Theta$ with respect to OPW, and the latter for 64%. The last column of Table 2 (C10) shows the elasticity of OPW with respect to the initial impulse of the relevant exogenous driving force(s).

It follows that limiting changes in OPW to being driven by changes in , relative to all other models MA-OS makes the most important gains in accounting for sluggish adjustment of $\Theta$ , with its post-shock stage of slow-moving adjustment lasting for 4 months over which 12% of its total increase occurs. Thus, in response to a -induced increase in OPW, the MA-OS model's slow-moving adjustment properties are approximately 25% of its empirical counterparts. Moreover, as noted above, the model accounts for around 2/3 of the empirical elasticity of the V/U ratio with respect to OPW. Overall, results highlight the extent to which endogenous effective search aids in accounting for the amplification of productivity shocks, worker-side heterogeneity aids with propagation, and the combination of both magnifies their individual effects.

Figures 16 through 20 show responses in the MA-OS model's key endogenous variables to joint increases in and $1-\phi$ that (in all cases) induce an on-impact increase in OPW of 0.7%, where the size of the shock to $1-\phi$ is, alternatively, half of the shock in , equal to the shock in , and two, three, four, and five times the shock in (the legend in Figure 16 applies to Figures 17 through 20). For reference, the noted set of figures also shows the case corresponding to row R5 of Table 2, which is the situation in which only a shock in occurs.

Figure 16 highlights that the greater the contribution of relative productivity to the shock, the greater the total response of the V/U ratio, as well as the magnitude of the extent to which it adjusts sluggishly. Moreover, when combined with an increase in economy-wide productivity, an increase in $1-\phi$ does not necessarily induce an on-impact decrease in the V/U ratio, as shown earlier to be the case given a stand-alone increase in $1-\phi$ . As shown in Figure 17, this carries over to vacancies; moreover, while vacancies do not exhibit sluggish adjustment for relatively small changes in $1-\phi$ , they do for higher ones. Figure 18 shows the corresponding changes in unemployment, and Figure 19 shows changes in $\chi/u$ ; greater and longer increases in $\chi/u$ are associated with greater and longer post-shock decreases in the the probability of skill-mismatch, which induces greater and longer post shock increases in the V/U ratio. Finally, Figure 20 shows the relevant adjustments in the fraction of skill-mismatched employment $\chi/e$ .

Rows R6 through R11 of Table 2 put in context the information shown in Figures 16 through 20. As the relative contribution of $1-\phi$ to the rise in OPW increases, the MA-OS model makes substantial progress in broadly accounting for the entirety of the US empirical data, both in terms of amplification and propagation of productivity shocks. This is particularly important on four fronts. First, the fact that the model is capable of generating sluggish adjustment of both the V/U ratio and vacancies implies substantial improvement relative to the standard model, which has no channels through which this can occur. Second, it is noteworthy that the MA-OS model can yield amplification broadly in line with the data, as captured by the elasticities noted in Table 2, even for relatively small values of net unemployment flow benefits. This stands in contrast to the fact that, as noted, for instance, in Hagedorn and Manovskii (2008), the standard model requires net unemployment flow benefits to be almost as large as OPW in order to match the amplification of productivity shocks in the data.²⁴ Third, results highlight that, given heterogeneity, not all productivity shocks induce equivalent dynamic adjustments. In particular, the model suggests that changes in relative productivity are a key factor driving observed changes in aggregate labor-market variables. Finally, it is particularly noteworthy that even in the absence of changes in relative productivity, the MA-OS model already makes substantial progress in accounting for both amplification and propagation of productivity shocks relative to the standard model, as noted earlier in row R5 of Table 2.

In terms of the relative response of vacancies to unemployment, as noted in column C9 of Table 2, compared to the data the standard model errs on the downside, whereas the MA-OS model errs on the upside. However, when joint shocks are considered, as the relative contribution of $1-\phi$ increases, results from the MA-OS model move increasingly in line toward the data. Overall, the results shown in Table 2 suggest that conditional on the response of vacancies relative to unemployment increasing, the MA-OS model can indeed potentially account for much, if not all, of the data. In that sense, it is important to keep in mind that once heterogeneity comes into play, the MA-OS model is in fact a vast simplification of reality, and there are a host of additional issues that could help readjust the response of vacancies relative to unemployment in the degree needed for the entirety of the data to be precisely matched. Intuitively, two reasons for which the effects of changes in the probability of skill-mismatch could be magnified in terms of the relative dynamic adjustment of vacancies are greater heterogeneity in both job types and/or the labor force, and job-training costs that are decreasing in the quality of an employment match. The former is sensible, given that heterogeneity is the basis for the model's propagation channel. The latter would imply that slow-moving increases in the firm-side probability of skill-matched employment would induce declines in expected training costs, therefore reinforcing increases in vacancy-posting incentives.

6 Conclusions

This paper explores the effects that worker-side heterogeneity and optimal job-seeking behavior have on aggregate labor-market fluctuations. The context of the analysis is one in which individuals have a comparative advantage in a particular job/sector, but are still able to work in jobs/sectors in which they are at a comparative disadvantage. Given this, firms with vacancies have expectations regarding match quality that are a function of the slow-moving masses of unemployed and on-the-job (OTJ) searchers: this provides a channel for slow-moving adjustment of the V/U ratio.

In an expansion, for instance, endogenous changes in the composition of the pool of individuals searching for any particular type of job lead to a stage of slow-moving increase in the firm-side probability of comparative advantage employment. This induces a slow-moving increase in the expected gains from posting vacancies, which keeps vacancy-posting incentives higher than otherwise. Coupled with declining unemployment, this leads to sluggish adjustment of the V/U ratio. Endogenous job-seeking magnifies this process and aids in accounting for the amplification of shocks by generating feedback between firm and worker-side decisions. Intuitively, allowing workers to respond optimally to relative changes in employment surpluses across job opportunities bears direct impact on cyclical changes in the composition of searchers, and hence, on firms' match-quality expectations. Sluggish adjustment of the aggregate vacancy-unemployment (V/U) ratio given changes in output per worker (OPW) is a key feature of the data that the standard, homogenous-agent model of equilibrium unemployment theory cannot account for. This limitation is additional to the well known fact that under standard calibrations, the benchmark model can account for less than half of the elasticity of the V/U ratio with respect to productivity.

Comparative-disadvantage employment emerges as necessary, but not sufficient for slow-moving adjustment of the V/U ratio to occur in response to changes in productivity. In the absence of this, workers' ability to refocus search given changes in productivity is limited to the extent that the model's channel for generating slow-moving adjustment of the V/U ratio is effectively shut down. In addition, the theory reveals that, conditional on whether they stem from changes in productivity throughout or between job opportunities, otherwise identical changes in OPW can be associated with adjustment in aggregate labor-market variables of considerably different magnitude. In particular, changes in OPW that stem from changes in productivity between job opportunities induce greater changes in relative employment surpluses. This induces greater readjustment in the pool of individuals searching for any particular job, and therefore, in firms' expectations regarding the probability of comparative advantage employment.

Overall, quantitative analysis shows that accounting for horizontal worker-side heterogeneity and optimal search can potentially help explain both the majority of the V/U ratio's slow-moving adjustment properties and the majority of its elasticity with respect to output per worker. Results hold for relatively small values of net unemployment flow benefits. This stands in contrast to the fact that, as noted, for instance, in Hagedorn and Manovskii (2008), the standard model requires net unemployment flow benefits to be almost as large as output per worker in order to match the amplification of productivity shocks in the data.

References

Albrecht, James, and Susan Vroman.2002. "A Matching Model with Endogenous Skill Requirements." International Economic Review, 43(1): 283-305.

Bils, Mark, Yongsung Chang, and Sun-Bin Kim. 2009. "Comparative Advantage and Unemployment." NBER Working Paper No. w15030.

Chassamboulli, Andri. 2009. "Cyclical Upgrading of Labor and Unemployment Differences Across Skill Groups."The B.E. Journal of Macroeconomics, 11(1), art. 14.

Christensen, Bent, Rasmus Lentz, Dale Mortensen, George Neumann, and Axel Werwatz. 2005. "On-the-Job Search and the Wage Distribution." Journal of Labor Economics, 23(1): 31-58.

Diamond, Peter. 1982. "Aggregate Demand Management in Search Equilibrium." The Journal of Political Economy, 90(5): 881-894.

Dolado, Juan, Marcel Jansen, and Juan Jimeno. 2008. "On-the-Job Search in a Matching Model with Heterogeneous Jobs and Workers." The Economic Journal, 119(534): 200-228.

Fujita, Shigeru, and Garey Ramey. 2007. "Job Matching and Propagation." Journal of Economic Dynamics and Control, 31(11): 3671-3698.

Gautier, Pieter. 2002. "Unemployment and Search Externalities in a Model with Heterogeneous Jobs and Workers." Economica, 69(273), 21-40.

Hagedorn, Marcus, and Iourii Manovskii. 2008. "The Cyclical Behavior of Equilibrium Unemployment and Vacancies Revisited." The American Economic Review, 98(2): 1692-1706.

Hall, Robert. 2005. "Employment Fluctuations with Equilibrium Wage Stickiness." American Economic Review, 95(1), 50-65.

Hall, Robert, and Paul Milgrom. 2008. "The Limited Influence of Unemployment on the Wage Bargain." The American Economic Review, 98(4): 1653-1674.

Krueger, Alan, and Andreas Mueller. 2008. "The Lot of the Unemployed." IZA discussion paper No. 3490.

McLaughlin, Kenneth, and Mark Bils. 2001. "Interindustry Mobility and the Cyclical Upgrading of Labor." Journal of Labor Economics, 19(1): 94-135.

Mortensen, Dale, and Eva Nagypal. 2007. "More on Unemployment and Vacancy Fluctuations." Review of Economic Dynamics, 10(3): 327-347.

Mortensen, Dale, and Christopher Pissarides. 1994. "Job Creation and Job Destruction in the Theory of Unemployment." The Review of Economic Studies, 61(3): 397-415.

Petrongolo, Barbara, and Christopher Pissarides. 2001. "Looking into the Black Box: A Survey of the Matching Function." Journal of Economic Literature, 39(2): 390-431.

Pissarides, Christopher. 1985. "Short-Run Equilibrium Dynamics of Vacancies, Unemployment, and Real Wages." The American Economic Review, 75(4): 676-690.

Pissarides, Christopher. 1994. "Search Unemployment with On-the-Job Search." The Review of Economic Studies, 61(3): 457-475.

Pissarides, Christopher. 2000. Equilibrium Unemployment Theory. Cambridge, MA: MIT Press.

Pissarides, Christopher. 2009. "The Unemployment Volatility Puzzle: Is Wage Stickiness the Answer?" Econometrica, 77(5): 1339-1369.

Pries, Michael. 2008. "Worker Heterogeneity and Labor Market Volatility in Matching Models." Review of Economic Dynamics, 11(3): 664-678.

Shimer, Robert. 2005. "The Cyclical Behavior of Equilibrium Unemployment and Vacancies." The American Economic Review, 95(1): 25-49.

Shimer, Robert. 2006. "On-the-Job Search and Strategic Bargaining," European Economic Review, 50(4): 811-830.

A Tables

Table 1: Model Calibrations (Weekly Frequency)

Model	Parameter = b	Parameter = α	Parameter = A	Parameter = Γ	Parameter = c	Parameter = φ	Parameter = ε	Parameter = $\ell_{1,u}^{1}$	Parameter = $\ell_{1,u}^{2}$	Parameter =
Standard	0.50	0.50	0.16	-	0.62	-	-	-	-	-
Standard-OS	0.72	0.50	0.19	1.00	0.62	-	1.00	-	-	-
MA	0.72	0.60	0.20	1.00	0.72	0.12	0.00	0.64	0.13	0.51
MA-OS	0.72	0.60	0.20	1.00	0.72	0.12	1.00	-	-	-

In all cases δ = 0.0081, η = 0.50, β = 0.999)

Notes (reasons for parameter choices): : - see text for details; $\alpha$ : Petrongolo and Pissarides (2001); : (data) target ; $\Gamma$ : normalization; $\delta$ : (data) implied by ; $\eta$ : symmetry - see text for details; : (data) $\Theta=0.71$ ; $\phi$ : McLaughlin and Bils (2001) - see text for details; $\varepsilon$ : quadratic search disutility when relevant; $\beta$ : quarterly interest rate at ; $\ell_{1,u}^{1}$ , $\ell_{1,u}^{2}$ , $\ell_{1,\chi}^{1}$ : MA-OS endogenously implied - see text for details.

Table 2: Properties and Model-Generated Elasticities of Key Variables

	V/U Ratio: C1	V/U Ratio: C2	V/U Ratio: C3	Vacancies: C4	Vacancies: C5	Vacancies: C6	Unemp.: C7	Unemp.: C8	∂v/∂u C9	OPW: C10
R1: US	7.79	12	60%	3.88	12	60%	-3.93	15	-0.86	-
R2: st.	2.12	0	0%	1.19	0	0%	-0.99	11	-1.13	1.00
R3: MA	2.19	3	5%	0.96	0	0%	-1.21	8	-0.79	1.00
R4: st.-OS	4.25	0	0%	1.23	0	0%	-2.91	14	-0.43	1.00
R5: MA-OS	4.58	4	12%	1.20	0	0%	-3.28	9	-0.37	1.00
R6: MA-OS	4.99	6	24%	1.40	0	0%	-3.47	11	-0.40	1.00
R7: MA-OS	5.44	10	35%	1.64	0	0%	-3.66	12	-0.45	0.99
R8: MA-OS	6.30	14	54%	2.09	0	0%	-4.03	13	-0.52	0.98
R9: MA-OS	7.15	15	68%	2.53	10	9%	-4.41	14	-0.57	0.97
R10: MA-OS	7.95	16	78%	2.94	12	42%	-4.75	15	-0.62	0.96
R11: MA-OS	8.49	17	85%	3.22	15	59%	-4.98	15	-0.65	0.96

Notes (columns and rows; see text for details on US data): : elasticity of V/U ratio with respect to output per worker (OPW); : months after shock over which V/U ratio continues to increase (propagation); : percent of total increase in V/U ratio occurring over period of slow-moving adjustment; : elasticity of aggregate vacancies with respect to OPW; : months after shock over which vacancies continue to increase (propagation); : percent of total increase in vacancies occurring over period of slow-moving adjustment; : elasticity of aggregate unemployment with respect to OPW; : month at which unemployment reaches a trough; : slope of Beveridge curve; : elasticity of output per worker with respect to on-impact size of exogenous shock (0.007). : US data; -: model-specific response given -induced on-impact increase in OPW of 0.7%; -: response in MA-OS model to joint increases in and $1-\phi$ that (in all cases) induce an on-impact increase in OPW of 0.7%, where size of shock to $1-\phi$ is half of shock in (), equal to shock in (), and two (), three (), four (), and five () times the shock in . Model-generated elasticities are based off permanent change in productivity.

B Figures

Figure 1: MA-OS and Standard Models

Figure 1: Figure 1 shows the impulse response of the V/U ratio given a 1 percent permanent unanticipated increase in economy-wide productivity in both the MA-OS and Standard models. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from 4.1 to 4.8. In the case of the MA-OS model, the figure shows that in month 0 the V/U ratio jumps to slightly less than 4.2 percent, and then increases slowly at a decreasing rate, reaching a maximum of approximately 4.75 percent by month 4. Then, the V/U ratio decreases slowly at a decreasing rate, and levels off by month 16 at approximately 4.6 percent. In the case of the Standard model, the figure shows that in month 0 the V/U ratio jumps to somewhat less than 4.4 percent, and remains constant at that level thereafter.

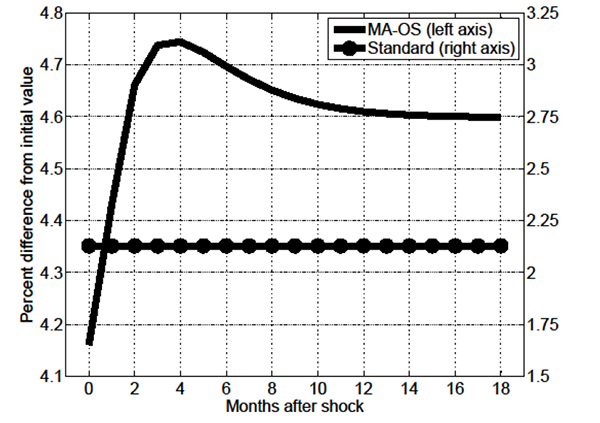
Figure 2: MA-OS Model

Figure 2: Figure 2 shows the impulse response function of the skill-mismatch probability in the MA-OS model given a 1 percent permanent unanticipated increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from 0.8 to 1.25. The figure shows that in month 0 the skill mismatch probability jumps by approximately 1.25 percent, then slowly decreases at a decreasing rate, reaching a low of slightly less than 0.85 percent by month 4, and thereafter slowly increases at a decreasing rate, finally leveling off at 0.95 percent by approximately month 16.

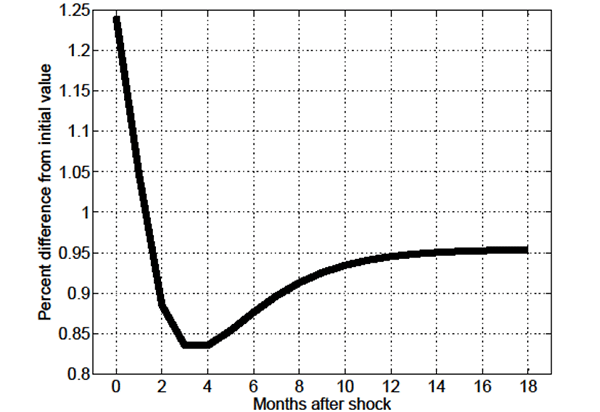
Figure 3: MA-OS Model

Figure 3: Figure 3 shows the impulse response function of the skill-mismatch to unemployment ratio in the MA-OS model given a 1 percent permanent unanticipated increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from -0.5 to 3. The figure shows that in month 0 the skill-mismatch to unemployment ratio is at 0 percent, and then starts to increase slowly at a decreasing rate, reaching a peak of slightly less than 3 percent by month 12, and thereafter decreases slowly at a decreasing rate, leveling off by approximately month 18 at 2 percent.

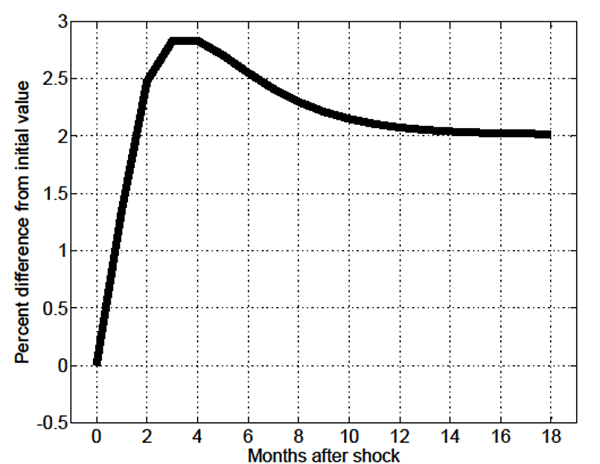
Figure 4: MA-OS Model

Figure 4: Figure 4 shows the impulse response function of effective search (devoted to skill-matched employment while individuals are unemployed, to skill-matched employment while individuals are searching on the job, and to skill-mismatched employment while unemployed) in the MA-OS model given a 1 percent permanent unanticipated increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from 1 to 4. The figure shows the following. In month 0 the effective search devoted to skill-matched employment by on-the-job searchers jumps to somewhat over 1.5 percent, thereafter increases slowly at a decreasing rate reaching approximately 1.75 percent by month 4, after which it remains constant at that level. In month 0 the effective search devoted to skill-matched employment by unemployed individuals jumps to approximately 2 percent, thereafter increases slowly at a decreasing rate reaching approximately 2.2 percent by month 4, after which it remains constant at that level. In month 0 the effective search devoted to skill-mismatched employment by unemployed individuals jumps to approximately 3.5 percent, thereafter increases slowly at a decreasing rate and peaks at 4 months a touch above 3.5 percent, after which it remains constant at that level.

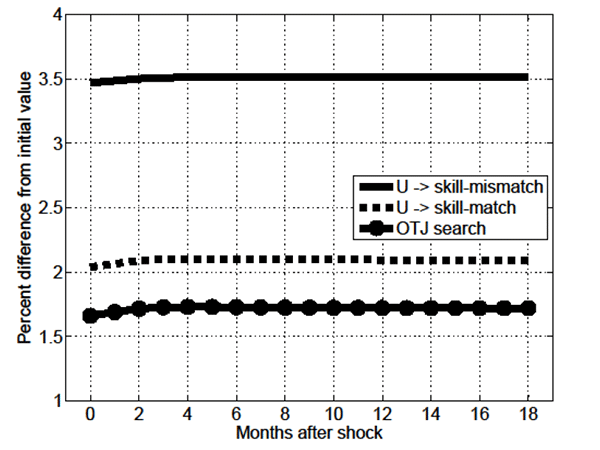
Figure 5: MA-OS Model

Figure 5: Figure 5 shows the impulse response function of the aggregate skill-mismatch rate and the aggregate unemployment rate in the MA-OS model given a 1 percent permanent unanticipated increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from -3.5 to 0.5. The figure shows that in month 0 the aggregate skill-mismatch rate is at 0 percent, then increases slowly at a decreasing rate, peaking at slightly less than 0.5 percent in month 2, and thereafter decreases slowly at a decreasing rate leveling off at about -1.3 percent by month 16. The figure also shows that in month 0 the aggregate rate of unemployment is at 0 percent, and then begins to slowly decline at a decreasing rate, almost leveling off by month 10 at approximately -3.25 percent.

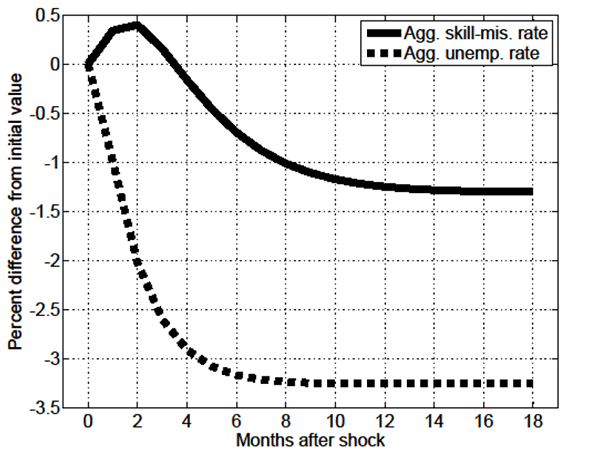
Figure 6: MA-OS Model

$Figure 6: Figure 6 shows the impulse response function of the aggregate fraction of skill-mismatch employment in the MA-OS model given a 1 percent permanent unanticipated increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from -2 to 0.5. The figure shows that in month 0 the aggregate fraction of skill-mismatch employment is at 0 percent, then increases slowly at a decreasing rate, peaking at about 0.4 percent in month 2, and thereafter decreases slowly at a decreasing rate leveling off at about -1.5 percent by month 16.$

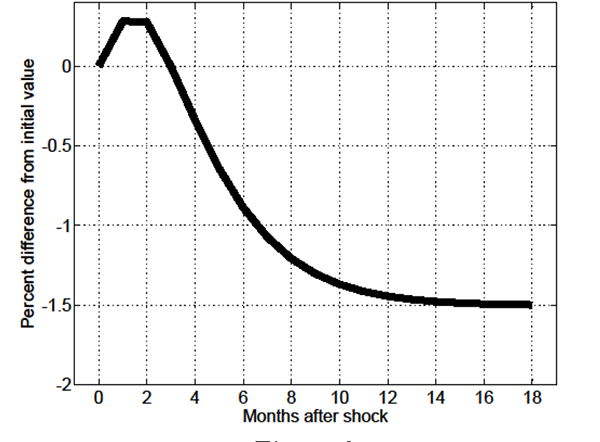
Figures 1-6: responses to 1% permanent (unanticipated) increase in economy-wide productivity of V/U ratio (Fig. 1: MA-OS and Standard models), skill-mismatch probability $\pi_{j}^{i}$ (Fig. 2: MA-OS model), skill-mismatch to unemployment ratio to $\chi/u$ (Fig. 3: MA-OS model), effective search $\ell_{i,u}^{i}$ : U - skill-match, $\ell_{j,u}^{i}$ : U - skill-mismatch, $\ell_{i,\chi}^{i}$ : OTJ search (Fig. 4: MA-OS model), rate of skill-mismatch $\chi$ and unemployment rate (Fig. 5: MA-OS model), and fraction of skill-mismatch employment $\chi/e$ (Fig. 6: MA-OS model).

Figure 7: MA-OS and Standard Models

Figure 7: Figure 7 shows the impulse response function of aggregate vacancies in the MA-OS and Standard models given a 1 percent permanent unanticipated increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from 0 to 4.5. In the case of the MA-OS model, the figure shows that in month 0 aggregate vacancies jump to slightly above 4 percent, and thereafter slowly decrease at a decreasing rate, leveling off at around 1.25 percent by month 14. In the case of the Standard model, the figure shows that in month 0 aggregate vacancies jump to slightly below 3.5 percent, and thereafter slowly decrease at a decreasing rate, leveling off at somewhat less than 0.5 percent by month 9.

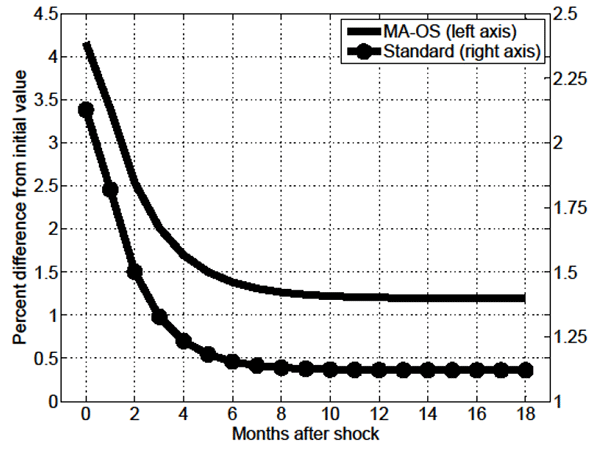
Figure 8: MA-OS and Standard Models

Figure 8: Figure 8 shows the impulse response function of aggregate unemployment rate in the MA-OS and Standard models given a 1 percent permanent unanticipated increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from a touch above 0 to -3.5. In the case of the Standard model, the figure shows the aggregate unemployment rate at 0 percent in month 0, and thereafter decreasing at a decreasing rate, leveling off at -1 percent by month 8. In the case of the MA-OS model, the figure shows the aggregate unemployment rate at 0 percent in month 0, and thereafter decreasing at a decreasing rate, leveling off at about -3.25 percent by month 10.

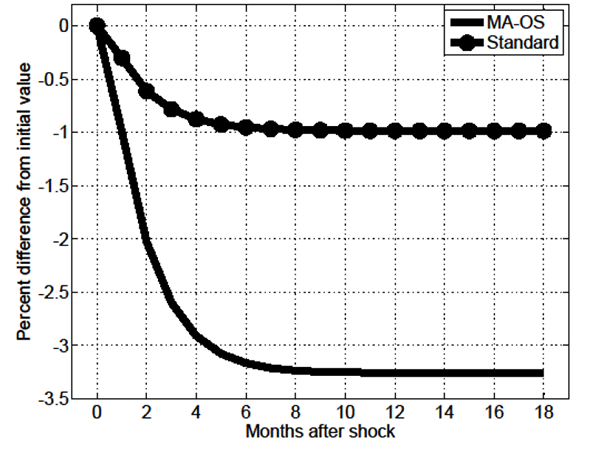
Figure 9: MA-OS and Standard Models

Figure 9: Figure 9 shows the impulse response function of the V/U ratio in the MA-OS model given a 1 percent permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter). The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from -0.8 to 1. The figure shows that in month 0 the V/U ratio jumps down to -0.6 percent, and then increases slowly at a decreasing rate, leveling off at slightly above 0.8 percent by month 16.

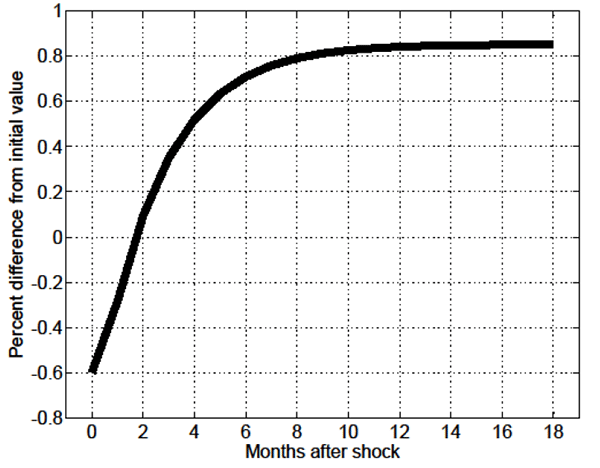
Figure 10: MA-OS and Standard models

Figure 10: Figure 10 shows the impulse response function of aggregate vacancies in the MA-OS model given a 1 percent permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter). The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from -0.8 to 0.6. The figure shows that in month 0 aggregate vacancies jump down to -0.6 percent, and then increase slowly at a decreasing rate, leveling off at somewhat above 0.6 percent by month 14.

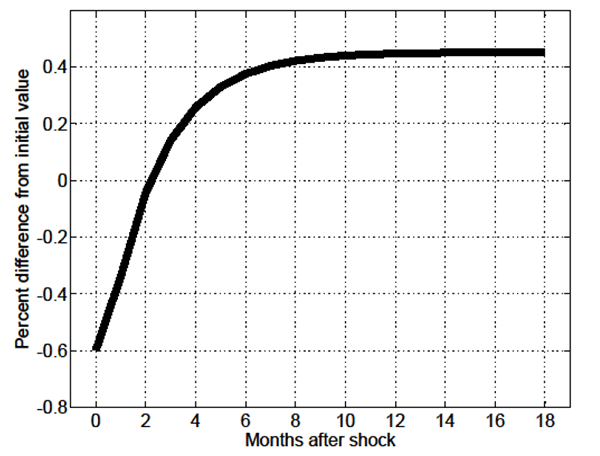
Figure 11: MA-OS and Standard Models

Figure 11: Figure 11 shows the impulse response function of aggregate unemployment in the MA-OS model given a 1 percent permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter). The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from -0.4 to somewhat above 0. The figure shows that in month 0 aggregate unemployment is at 0 percent, and then decreases slowly at a decreasing rate, leveling off at -0.4 percent by month 16.

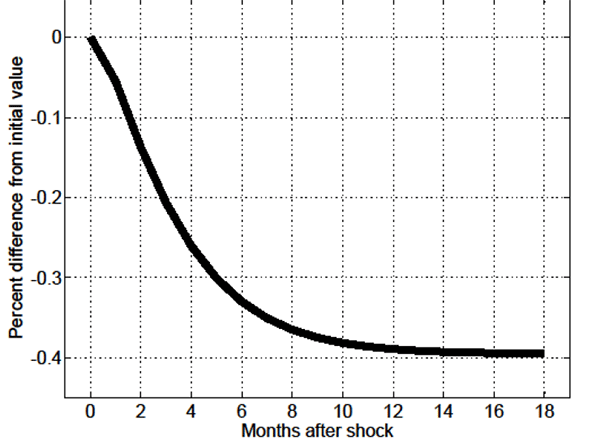
Figure 12: MA-OS and Standard Models

Figure 12: Figure 12 shows the impulse response function of the skill-mismatch probability in the MA-OS model given a 1 percent permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter). The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from 4.4 to 6. The figure shows that in month 0 the skill-mismatch probability jumps to slightly above 5.8 percent, and thereafter slowly declines at a decreasing rate, leveling off at a touch higher than 4.4 percent by month 14.

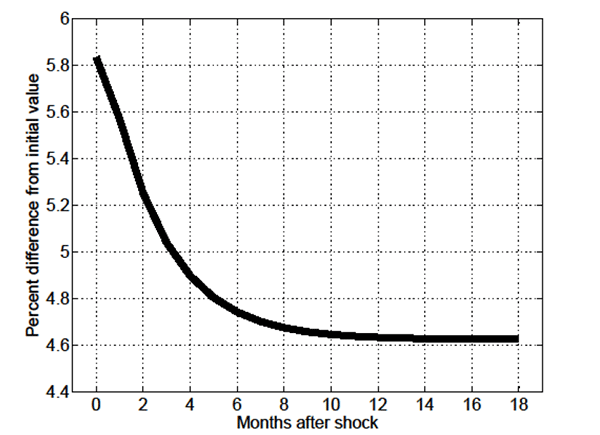
Figures 7-8: responses to 1% permanent (unanticipated) increase in economy-wide productivity of aggregate vacancies (Fig. 7: MA-OS and Standard models) and aggregate unemployment (MA-OS and Standard models).

Figures 9-12: responses in MA-OS model to 1% permanent (unanticipated) increase in relative productivity $1-\phi$ of V/U ratio (Fig. 9), aggregate vacancies (Fig. 10), aggregate unemployment (Fig. 11), and skill-mismatch probability $\pi_{j}^{i}$ (Fig. 12).

Figure 13: MA-OS and Standard models

Figure 13: Figure 13 shows the impulse response function of effective search (devoted to skill-matched employment while individuals are unemployed, to skill-matched employment while individuals are searching on the job, and to skill-mismatched employment while unemployed) in the MA-OS model given a 1 percent permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter). The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from -1 to 7. The figure shows the following. In month 0 the effective search devoted to skill-matched employment by on-the-job searchers jumps down to a touch below -2 percent, thereafter increases slowly at a decreasing rate reaching approximately -2 percent by month 4, after which it remains constant at that level. In month 0 the effective search devoted to skill-matched employment by unemployed individuals jumps down to somewhat less than 0 percent, thereafter increases slowly at a decreasing rate to a touch below 0 percent by month 4, after which it remains constant at that level. In month 0 the effective search devoted to skill-mismatched employment by unemployed individuals jumps to somewhat above 6 percent, thereafter increases slowly at a decreasing rate and peaks a touch above the level of its original jump by month 4, after which it remains constant.

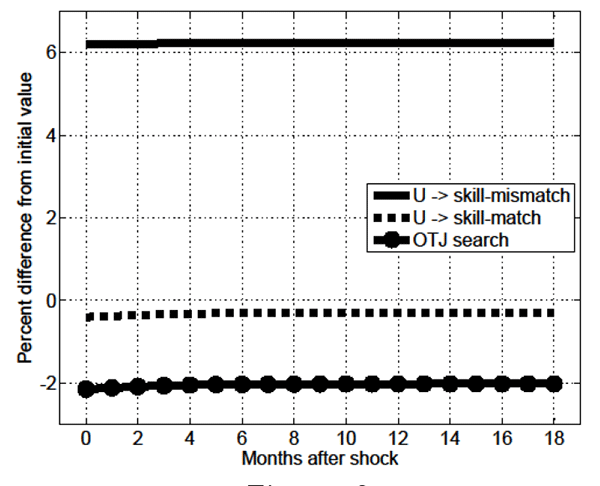
Figure 14: MA-OS and Standard models

Figure 14: Figure 14 shows the impulse response function of the aggregate skill-mismatch rate and the aggregate skill-mismatch to unemployment ratio in the MA-OS model given a 1 percent permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter). The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from 0 to 9. The figure shows that in month 0 both the aggregate skill-mismatch rate and the aggregate skill-mismatch to unemployment ratio are at 0 percent, then slowly increase at a decreasing rate, and level off at about 14 months: the aggregate skill-mismatch to unemployment ratio at a touch higher than 8 percent, and the aggregate skill-mismatch rate a bit below 8 percent.

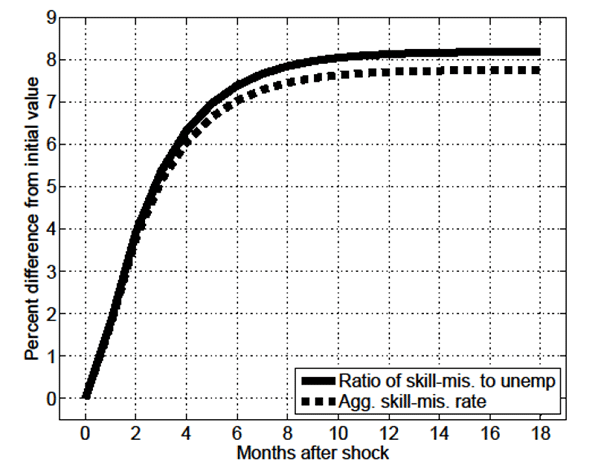
Figure 15: MA-OS and Standard Models

$Figure 15: Figure 15 shows the impulse response function of the aggregate fraction of skill-mismatched employment in the MA-OS model given a 1 percent permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter). The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from somewhat less than 0 to 9. The figure shows that in month 0 the aggregate fraction of skill-mismatched employment is at 0, and then slowly increases at a decreasing rate, leveling off at slightly less than 8 percent by month 14.$

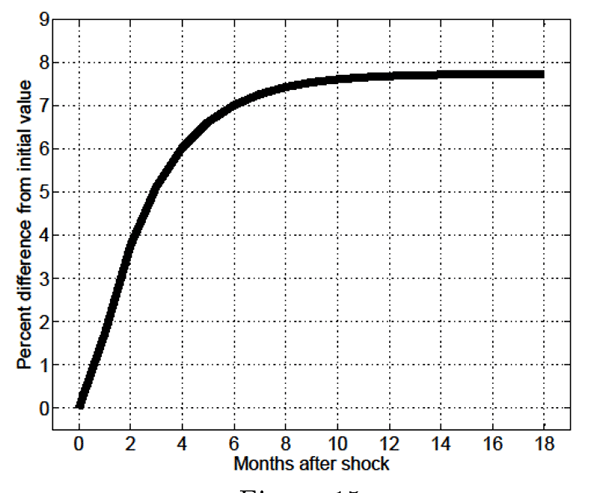
Figure 16: MA-OS and Standard Models

Figure 16: Figure 16 shows the impulse response function of the V/U ratio in the MA-OS model given an on impact increase in output per worker of 0.7 percent that is alternatively driven by: 1) a permanent unanticipated increase in economy-wide productivity only, 2) a joint permanent unanticipated increase in economy-wide productivity and permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter) such that the on impact increase in relative productivity is half as large as the on impact increase in economy-wide productivity, and 3) as large as the on impact increase in economy-wide productivity, 4) twice as large as the on impact increase in economy-wide productivity, 5) three times as large as the on impact increase in economy-wide productivity, 6) four times as large as the on impact increase in economy-wide productivity, and 7) five times as large as the on impact increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from somewhat below 1 to 6; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from somewhat less than 0 to 9. The figure shows the following. In case (1) the V/U ratio jumps in month 0 to about 3 percent, then increases slowly at a decreasing rate, peaks at a touch below 3.5 percent in month 4, and thereafter decreases slowly at a decreasing rate before leveling off at about 14 months at a level that is somewhat below its peak. In case (2) the V/U ratio jumps in month 0 to somewhat below 3 percent, then increases slowly at a decreasing rate and levels off at about 3.5 percent by month 6. In case (3) the V/U ratio jumps in month 0 to about 2.5 percent, then increases slowly at a decreasing rate and levels off at somewhat below 4 percent by month 10. In case (4) the V/U ratio jumps in month 0 to 2 percent, then increases slowly at a decreasing rate and levels off at somewhat below 4.5 percent by month 14. In case (5) the V/U ratio jumps in month 0 to a touch above 1.5 percent, then increases slowly at a decreasing rate and levels off at nearly 5 percent by month 15. In case (6) the V/U ratio jumps in month 0 to somewhat above 1 percent, then increases slowly at a decreasing rate and levels off at somewhat below 5.5 percent by month 16. In case (7) the V/U ratio jumps in month 0 to somewhat below 1 percent, then increases slowly at a decreasing rate and levels off at about 5.75 percent by month 17.

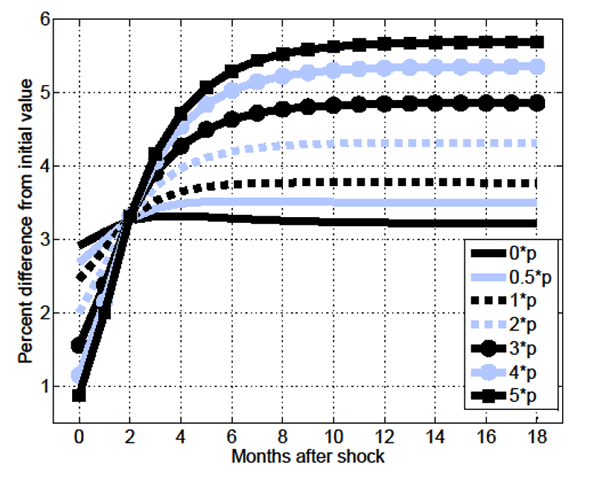
Figure 17: MA-OS and Standard Models

Figure 17: Figure 17 shows the impulse response function of aggregate vacancies in the MA-OS model given an on impact increase in output per worker of 0.7 percent that is alternatively driven by: 1) a permanent unanticipated increase in economy-wide productivity only, 2) a joint permanent unanticipated increase in economy-wide productivity and permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter) such that the on impact increase in relative productivity is half as large as the on impact increase in economy-wide productivity, and 3) as large as the on impact increase in economy-wide productivity, 4) twice as large as the on impact increase in economy-wide productivity, 5) three times as large as the on impact increase in economy-wide productivity, 6) four times as large as the on impact increase in economy-wide productivity, and 7) five times as large as the on impact increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from somewhat less than 0.5 to 3. The figure shows the following. In case (1) aggregate vacancies jump in month 0 to about 3 percent, then decrease slowly at a decreasing rate, leveling off at about 0.75 percent by month 13. In case (2) aggregate vacancies jump to somewhat below 3 percent, then decrease slowly at a decreasing rate, leveling off at about 1 percent by approximately month 13. In case (3) aggregate vacancies jump in month 0 to about 2.5 percent, then decrease slowly at a decreasing rate, leveling off at about 1.25 percent by month 12. In case (4) aggregate vacancies jump in month 0 to 2 percent, then decrease slowly at a decreasing rate, leveling off at a touch less than 1.5 percent at about month 10. In case (5) aggregate vacancies jump in month 0 to a touch above 1.5 percent, then increases slowly at a decreasing rate and level off at nearly 1.75 percent by month 10. In case (6) aggregate vacancies jump in month 0 to somewhat above 1 percent, then increases slowly at a decreasing rate and level off at 2 percent by month 12. In case (7) aggregate vacancies jump in month 0 to somewhat below 1 percent, then increase slowly at a decreasing rate and level at a touch below 2.25 percent by month 15.

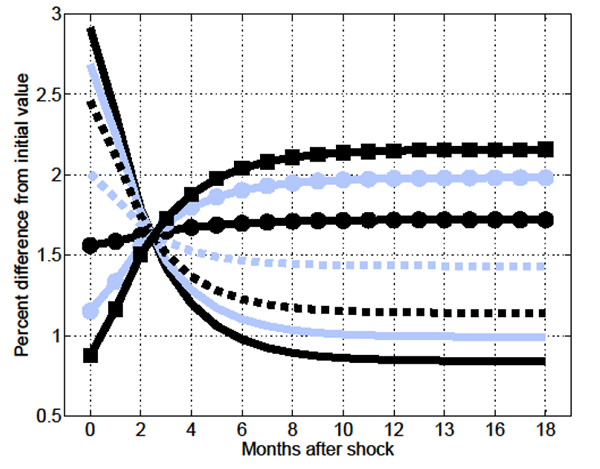
Figure 18: MA-OS and Standard Models

Figure 18: Figure 18 shows the impulse response function of aggregate unemployment in the MA-OS model given an on impact increase in output per worker of 0.7 percent that is alternatively driven by: 1) a permanent unanticipated increase in economy-wide productivity only, 2) a joint permanent unanticipated increase in economy-wide productivity and permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter) such that the on impact increase in relative productivity is half as large as the on impact increase in economy-wide productivity, and 3) as large as the on impact increase in economy-wide productivity, 4) twice as large as the on impact increase in economy-wide productivity, 5) three times as large as the on impact increase in economy-wide productivity, 6) four times as large as the on impact increase in economy-wide productivity, and 7) five times as large as the on impact increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from somewhat less than -3.5 to somewhat more than 0. The figure shows the following. In case (1) aggregate unemployment is at 0 percent in month 0, and thereafter decreases slowly at a decreasing rate, leveling off at about -2.25 percent by month 9. In case (2) aggregate unemployment is at 0 percent in month 0, and thereafter decreases slowly at a decreasing rate, leveling off at a touch above -2.5 percent by month 11. In case (3) aggregate unemployment is at 0 percent in month 0, and thereafter decreases slowly at a decreasing rate, leveling off at a touch below -2.5 percent by month 12. In case (4) aggregate unemployment is at 0 percent in month 0, and thereafter decreases slowly at a decreasing rate, leveling off at about -2.75 percent by month 13. In case (5) aggregate unemployment is at 0 percent in month 0, and thereafter decreases slowly at a decreasing rate, leveling off at about -3 percent by month 14. In case (6) aggregate unemployment is at 0 percent in month 0, and thereafter decreases slowly at a decreasing rate, leveling off at about -3.25 percent by month 15. In case (7) aggregate unemployment is at 0 percent in month 0, and thereafter decreases slowly at a decreasing rate, leveling off at somewhat below -3.25 percent by month 15.

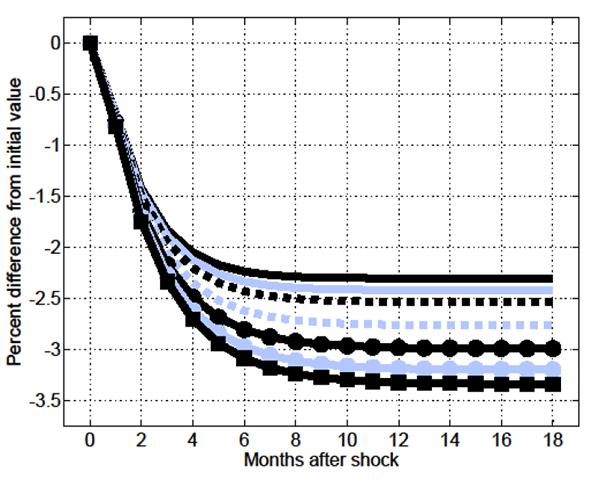
Figures 13-15: responses in MA-OS model to 1% permanent (unanticipated) increase in relative productivity $1-\phi$ of effective search (Fig. 13; legend as in Fig. 4), rate of skill-mismatch $\chi$ and unemployment rate (Fig. 14), and fraction of skill-mismatch employment $\chi/e$ (Fig. 15).

Figures 16-18 (legend in Fig. 16 applies to all): responses in MA-OS model to permanent (unanticipated) increase in economy-wide productivity , and joint shocks in and relative productivity $1-\phi$ ; 0*p indicates shock in , only. 0.5*p indicates that size of shock in $1-\phi$ is half as size as shock to , etc. In all cases, on impact of exogenous shocks OPW increases by 0.7%. Response of V/U ratio (Fig. 16), response of aggregate vacancies (Fig. 17), and response of aggregate unemployment (Fig. 18).

Figure 19: MA-OS and Standard Models

Figure 19: Figure 19 shows the impulse response function of the aggregate skill-mismatch to unemployment ratio in the MA-OS model given an on impact increase in output per worker of 0.7 percent that is alternatively driven by: 1) a permanent unanticipated increase in economy-wide productivity only, 2) a joint permanent unanticipated increase in economy-wide productivity and permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter) such that the on impact increase in relative productivity is half as large as the on impact increase in economy-wide productivity, and 3) as large as the on impact increase in economy-wide productivity, 4) twice as large as the on impact increase in economy-wide productivity, 5) three times as large as the on impact increase in economy-wide productivity, 6) four times as large as the on impact increase in economy-wide productivity, and 7) five times as large as the on impact increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from somewhat less than 0 to 30. The figure shows the following. In case (1) the aggregate skill-mismatch to unemployment ratio is at 0 percent in month 0, and then increases slowly at a decreasing rate, peaking at about 2.5 percent in month 3, then decreases at a decreasing rate before leveling off at somewhat below 2.5 percent by month 12. In case (2) the aggregate skill-mismatch to unemployment ratio is at 0 percent in month 0, then increases slowly at a decreasing rate before leveling off in month 6 at somewhat below 5 percent. In case (3) the aggregate skill-mismatch to unemployment ratio is at 0 percent in month 0, then increases slowly at a decreasing rate before leveling off in month 8 at about 7.5 percent. In case (4) the aggregate skill-mismatch to unemployment ratio is at 0 percent in month 0, then increases slowly at a decreasing rate and levels off at about month 10 at approximately 12.5 percent. In case (5) the aggregate skill-mismatch to unemployment ratio is at 0 percent in month 0, then increases slowly at a decreasing rate and levels off at somewhat below 20 percent by month 16. In case (6) the aggregate skill-mismatch to unemployment ratio is at 0 percent in month 0, then increases slowly at a decreasing rate and levels off at somewhat below 25 percent by month 16. In case (7) the aggregate skill-mismatch to unemployment ratio is at 0 percent in month 0, then increases slowly at a decreasing rate and levels off at about 27.5 percent by month 16.

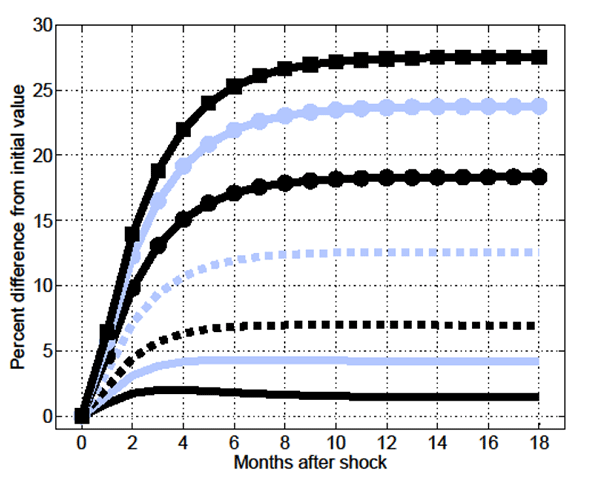
Figure 20: MA-OS and Standard Models

$Figure 20: Figure 20 shows the impulse response function of the fraction of skill-mismatched employment in the MA-OS model given an on impact increase in output per worker of 0.7 percent that is alternatively driven by: 1) a permanent unanticipated increase in economy-wide productivity only, 2) a joint permanent unanticipated increase in economy-wide productivity and permanent unanticipated increase in relative productivity (the difference between 1 and the skill-mismatch penalty parameter) such that the on impact increase in sectoral productivity is half as large as the on impact increase in economy-wide productivity, and 3) as large as the on impact increase in economy-wide productivity, 4) twice as large as the on impact increase in economy-wide productivity, 5) three times as large as the on impact increase in economy-wide productivity, 6) four times as large as the on impact increase in economy-wide productivity, and 7) five times as large as the on impact increase in economy-wide productivity. The figureâ€™s horizontal axis is labeled â€œMonths after shockâ€ and ranges from -1 to 19 months; the figureâ€™s vertical axis is labeled â€œPercent difference from initial valueâ€ and ranges from -5 to 25. The figure shows the following. In case (1) the fraction of skill-mismatched employment is at 0 percent in month 0, and then increases slowly at a decreasing rate, peaks a touch above 0 percent in month 2, and then decreases at a decreasing rate before leveling off at somewhat below 0 percent by month 15. In case (2) the fraction of skill-mismatched employment is at 0 percent in month 0, then increases slowly at a decreasing rate before more or less leveling off in month 4 at somewhat below 2.5 percent. In case (3) the fraction of skill-mismatched employment is at 0 percent in month 0, then increases slowly at a decreasing rate before leveling off in month 6 at somewhat below 5 percent. In case (4) the fraction of skill-mismatched employment is at 0 percent in month 0, then increases slowly at a decreasing rate and levels off at about month 10 at somewhat below 10 percent. In case (5) the fraction of skill-mismatched employment is at 0 percent in month 0, then increases slowly at a decreasing rate and levels off at a touch below 15 percent by month 12. In case (6) the fraction of skill-mismatched employment is at 0 percent in month 0, then increases slowly at a decreasing rate and levels off at a touch below 20 percent by month 12. In case (7) the fraction of skill-mismatched employment is at 0 percent in month 0, then increases slowly at a decreasing rate and levels off at about 22.5 percent by month 14.$

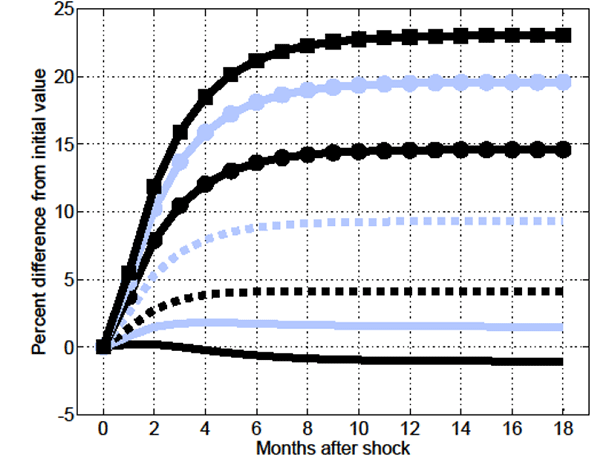
Figures 19-20 (legend in Fig. 16 applies to all): responses in MA-OS model to permanent (unanticipated) increase in economy-wide productivity , and joint shocks in and relative productivity $1-\phi$ ; 0*p indicates shock in , only. 0.5*p indicates that size of shock in $1-\phi$ is half as size as shock to , etc.Response of skill-mismatch to unemployment ratio $\chi/u$ (Fig. 19), and response of fraction of skill-mismatched employment $\chi/e$ (Fig. 20).

C Additional Details

As noted in Shimer (2005) and Mortensen and Nagypal (2007), the cyclical properties of models of the sort developed in this paper are well assessed by considering differences between steady states. Therefore, in what follows, relevant mathematical inferences are based on steady-state to steady-state changes.

C.1 The Role of Worker Heterogeneity

Proposition C.1.1. In the multi-agent model the probability of skill mismatched employment, $\pi_{j}^{i}$ , is countercyclical in economy-wide productivity .

Proof. Given symmetry, for $i\neq j$ $u_{i}=u_{j}=0.5u$ , and $\chi_{i}=\chi_{j}=0.5\chi$ . Then, using equation (11) and rearranging implies that $\pi_{j}^{i}=\left( 2+\chi/u\right) ^{-1}$ , where $i\neq j$ , and I have used the assumption that all effective search is fixed at unity. Therefore, if $\chi/u$ is procyclical, then $\pi_{j}^{i}$ is countercyclical. For $i\neq j$ symmetry implies that $f^{i}=f^{j}=f$ . Then,

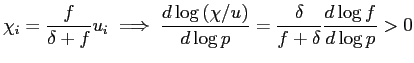$\displaystyle \chi_{i}=\frac{f}{\delta+f}u_{i}\implies\frac{d\log\left( \chi/u\right) }{d\log p}=\frac{\delta}{f+\delta}\frac{d\log f}{d\log p}>0$ ,

(22)

since is procyclical.

Proposition C.1.2. In the absence of OTJ search, in the multi-agent model $\pi_{j}^{i}$ is (always) constant.

Proof. Assuming OTJ search is not possible is equivalent to setting $\ell_{i,\chi}^{i}=0$ , in which case $\pi_{j}^{i}$ is equal to the constant $(1+\ell_{i,u}^{i}/\ell_{j,u}^{i})^{-1}$ .

Corollary C.1.1. In the multi-agent model skill-mismatched employment is necessary, but not sufficient, for propagation in the V/U ratio to occur in response to changes in economy-wide productivity .

Remark C.1.1. Within the context of the MA-OS model, Proposition 1 can be thought of carrying over as follows: on impact of an increase in economy-wide productivity the probability of skill-mismatch can jump, but relative to its position after this initial jump, the probability of skill-mismatch will thereafter decrease.

The Role of Optimal Effective Search

Proposition C.2.1. In the standard-OS model effective search is procyclical in economy-wide productivity .

Proof.²⁵Consistent with the functional forms assumed for the MA-OS model, for the standard-OS model let $C=\Gamma\ell^{\left( 1+\varepsilon\right) /\varepsilon}$ and $m=v^{\alpha}s^{1-\alpha}$ , where $s=\ell u$ . In this case, $q=A\theta^{\alpha-1}$ , where $\theta=v/\ell u$ . Moreover, denote the job-finding probability of unemployed individuals by $F=\ell f$ , where $f=A\theta^{\alpha}$ . The relevant first-order condition for optimal search implies that

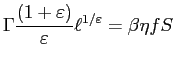$\displaystyle \Gamma\frac{\left( 1+\varepsilon\right) }{\varepsilon}\ell^{1/\varepsilon }=\beta\eta fS$ ,

(23)

where is the employment surplus (recall that individuals choose effective search taking market conditions as given). Moreover, the job-creation condition is now given by

$\displaystyle \beta\left( 1-\eta\right) S=c/q$ .

(24)

Substituting this into equation (23) implies, after total differentiation, that

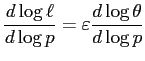$\displaystyle \frac{d\log\ell}{d\log p}=\varepsilon\frac{d\log\theta}{d\log p}$ .

(25)

Since $\theta$ is procyclical, the equation above implies that so is effective search $\ell$ . Showing formally that $\theta$ is procyclical, to which I now proceed, offers additional insight. Using the definition of surplus, , and substituting in for the relevant value functions implies that

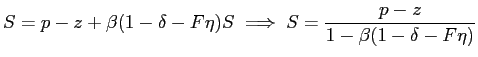$\displaystyle S=p-z+\beta(1-\delta-F\eta)S\implies S=\frac{p-z}{1-\beta(1-\delta-F\eta )}$ .

(26)

Combining with equation (24) yields

$\displaystyle \frac{p-z}{1-\beta(1-\delta-F\eta)}=\frac{c}{\beta\left( 1-\eta\right) q}$ .

(27)

Therefore,

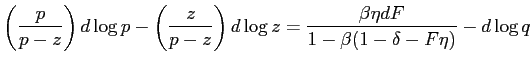$\displaystyle \left( \frac{p}{p-z}\right) d\log p-\left( \frac{z}{p-z}\right) d\log z=\frac{\beta\eta dF}{1-\beta(1-\delta-F\eta)}-d\log q$ .

(28)

Using the fact that $F=\ell f$ and $z=b-\Gamma\ell^{\left( 1+\varepsilon \right) /\varepsilon}$ , this can be stated as

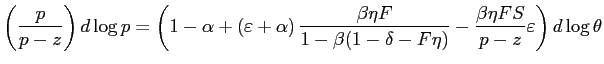$\displaystyle \left( \frac{p}{p-z}\right) d\log p=\left( 1-\alpha+\left( \varepsilon +\alpha\right) \frac{\beta\eta F}{1-\beta(1-\delta-F\eta)}-\frac{\beta\eta FS}{p-z}\varepsilon\right) d\log\theta$ .

(29)

Of course, $1-\alpha>0$ and , the latter by assumption: otherwise, it would not be optimal for individuals to seek employment. Moreover, $1>\beta(1-\delta-F\eta)$ ). Then, given equation (29), to show that $d\log\theta/d\log p>0$ it is enough to show that the second term in the coefficient on $d\log\theta$ is greater than the third term. Note that

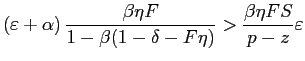
$\displaystyle \left( \varepsilon+\alpha\right) \frac{\beta\eta F}{1-\beta(1-\delta-F\eta )}>\frac{\beta\eta FS}{p-z}\varepsilon$
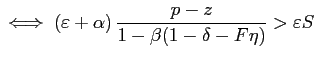
$\displaystyle \iff\left( \varepsilon+\alpha\right) \frac{p-z}{1-\beta(1-\delta-F\eta )}>\varepsilon S$
$\displaystyle \iff\left( \varepsilon+\alpha\right) S>\varepsilon S$ ,	(30)

which will always hold (in the second line above, I have made use of equation (26). Therefore, $d\log\theta/d\log p>0$ , $d\log z/d\log p<0$ , and $d\log\ell/d\log p>0$ .

Proposition C.2.2. If effective search is endogenized in the standard model, then the elasticity of the V/U ratio with respect to economy-wide productivity is greater than otherwise.

Proof.²⁶Consistent with the functional forms assumed for the MA-OS model, for the standard model let $m=v^{\alpha}u^{1-\alpha}$ . In this case, $q=A\Theta ^{\alpha-1}$ , where $\Theta=v/u$ . Moreover, denote the job-finding probability of unemployed individuals by , where $F=A\Theta^{\alpha}$ . Using the definition of surplus, , and substituting in for the relevant value functions implies that

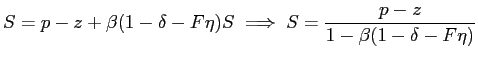$\displaystyle S=p-z+\beta(1-\delta-F\eta)S\implies S=\frac{p-z}{1-\beta(1-\delta-F\eta )}$ .

(31)

Combining with the job-creation condition $S=c/\beta\left( 1-\eta\right) q$ implies that

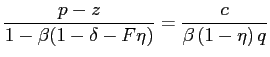$\displaystyle \frac{p-z}{1-\beta(1-\delta-F\eta)}=\frac{c}{\beta\left( 1-\eta\right) q}$ .

(32)

Hence,

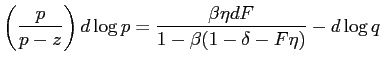$\displaystyle \left( \frac{p}{p-z}\right) d\log p=\frac{\beta\eta dF}{1-\beta (1-\delta-F\eta)}-d\log q$ ,

(33)

and

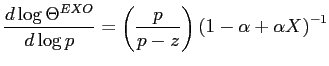$\displaystyle \frac{d\log\Theta^{EXO}}{d\log p}=\left( \frac{p}{p-z}\right) \left( 1-\alpha+\alpha X\right) ^{-1}$ ,

(34)

Above, $X=\beta\eta F/(1-\beta(1-\delta-F\eta))$ , and denotes that effective search is exogenous (and fixed at unity: $\ell=1$ ). Moreover, for reasonable values for $\beta$ , $\eta$ , $\delta$ , and , $X\in\left( 0,1\right)$ .

Note from the proof of Proposition 4 that equation (28) can be written as

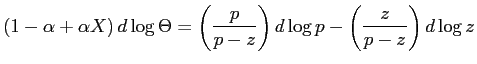
$\displaystyle \left( 1-\alpha+\alpha X\right) d\log\Theta=\left( \frac{p}{p-z}\right) d\log p-\left( \frac{z}{p-z}\right) d\log z$
$\displaystyle +\left( 1-\alpha \right) \left( 1-X\right) d\log\ell$
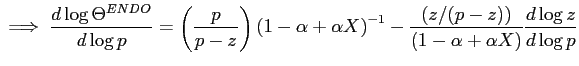
$\displaystyle \implies\frac{d\log\Theta^{ENDO}}{d\log p}=\left( \frac{p}{p-z}\right) \left( 1-\alpha+\alpha X\right) ^{-1}-\frac{\left( z/(p-z)\right) }{\left( 1-\alpha+\alpha X\right) }\frac{d\log z}{d\log p}$
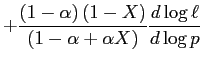$\displaystyle +\frac{\left( 1-\alpha\right) \left( 1-X\right) }{\left( 1-\alpha+\alpha X\right) }\frac{d\log\ell}{d\log p}$ ,	(35)

where denotes that effective search is endogenous. From earlier, $X\in\left( 0,1\right)$ ; therefore, $1-\alpha+\alpha X>0$ . Moreover, from the proof of Proposition 4 $d\log z/d\log p<0$ and $d\log\ell/d\log p>0$ . Of course, . Hence, using equation $% latex2html id marker 5517 $ \left( \ref{S}\right) $$ , equation $% latex2html id marker 5519 $ \left( \ref{U}\right) $$ can be stated as

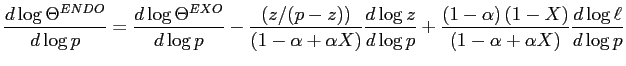
$\displaystyle \frac{d\log\Theta^{ENDO}}{d\log p}=\frac{d\log\Theta^{EXO}}{d\log p} -\frac{\left( z/(p-z)\right) }{\left( 1-\alpha+\alpha X\right) } \frac{d\log z}{d\log p}+\frac{\left( 1-\alpha\right) \left( 1-X\right) }{\left( 1-\alpha+\alpha X\right) }\frac{d\log\ell}{d\log p}$
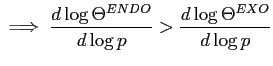$\displaystyle \implies\frac{d\log\Theta^{ENDO}}{d\log p}>\frac{d\log\Theta^{EXO}}{d\log p}$ .	(36)

C.3 Equilibrium in the MA and MA-OS Models

Once searchers $s^{i}$ are determined, sectoral vacancies can be backed out from $\theta^{i}$ . Given knowledge of the masses of unemployed and skill-mismatched individuals it is straightforward to derive $s^{i}$ , and therefore, $\pi_{j}^{i}$ , where $i\neq j$ . Hence, for $i,j\in\left\{ 1,2\right\}$ and $i\neq j$ knowledge of the key endogenous variables $\pi_{j}^{i}$ , $u_{i}$ , $\chi_{i}$ , and $\theta^{i}$ (eight variables total) is sufficient to derive all of the model's remaining endogenous variables. There are four employment values: $J_{1}^{1}$ , $J_{2}^{1}$ , $J_{2}^{2}$ , and $J_{1}^{2}$ . Using the surplus-sharing rule in equation (12) these can be stated in terms of employment surpluses, and solved for using the four job values implicit in equations (8) and (9). As noted before, $\theta^{1}$ and $\theta^{2}$ are defined by the two corresponding job creation conditions implied by equation (13). Finally, the remaining six key variables $\pi_{1}^{2}$ , $\pi_{2}^{1}$ , $u_{1}$ , $u_{2}$ , $\chi_{1}$ , and $\chi_{2}$ , are defined through the 6 expressions implicit in equations (11), (6), and (7); recall that the environment is symmetric. Thus, the model reduces to 8 equations in 8 unknowns.

C.4 MA Model: Changes in Relative Productivity

Consider the employment surpluses

$\displaystyle S_{1}^{1}=\left( y_{1}^{1}-z-\beta F_{1,u}^{2}\eta S_{1}^{2}\right) \cdot\left( 1-\beta\left( 1-\delta-F_{1,u}^{1}\eta\right) \right) ^{-1}$

and

$\displaystyle S_{1}^{2}=(y_{1}^{2}-z-\beta\left( F_{1,u}^{1}-F_{1,\chi}^{1}\right) \eta S_{1}^{1})\cdot(1-\beta(1-\delta-F_{1,u}^{2}\eta-F_{1,\chi}^{1}))^{-1}$ .

Given symmetry, for a type-1 firm the expected gains from posting vacancies satisfy

$\displaystyle \beta\left( 1-\eta\right) ((1-\pi_{2}^{1})S_{1}^{1}+\pi_{2}^{1}S_{2} ^{1})=\beta\left( 1-\eta\right) (\pi_{1}^{1}S_{1}^{1}+\pi_{2}^{1}S_{1} ^{2})$ .

Then, since the skill-mismatch probability is slow moving, what matters for the on-impact effect of a change in $\phi$ (or, for that matter, the on-impact effect of a change in ), is the expression

$\displaystyle \pi_{1}^{1}dS_{1}^{1}+\pi_{2}^{1}dS_{1}^{2}$ .

From the surplus definitions above, given a change in $\phi$ , that is, a change that only affects $y_{1}^{2}$ ,

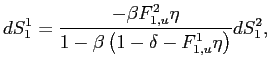
$\displaystyle dS_{1}^{1}=\frac{-\beta F_{1,u}^{2}\eta}{1-\beta\left( 1-\delta-F_{1,u} ^{1}\eta\right) }dS_{1}^{2}\text{,}$

and

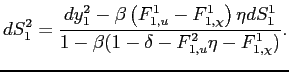
$\displaystyle dS_{1}^{2}=\frac{dy_{1}^{2}-\beta\left( F_{1,u}^{1}-F_{1,\chi}^{1}\right) \eta dS_{1}^{1}}{1-\beta(1-\delta-F_{1,u}^{2}\eta-F_{1,\chi}^{1})}\text{.}$

Let

$\displaystyle A=\beta F_{1,u}^{2}\eta$ , $\displaystyle B=1-\beta\left( 1-\delta-F_{1,u}^{1} \eta\right)$ ,

$\displaystyle C=\beta\left( F_{1,u}^{1}-F_{1,\chi}^{1}\right) \eta$ ,

and

$\displaystyle D=1-\beta(1-\delta-F_{1,u}^{2}\eta-F_{1,\chi}^{1})$

Then,

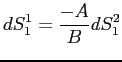$\displaystyle dS_{1}^{1}=\frac{-A}{B}dS_{1}^{2}$ ,

and

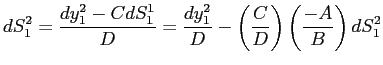
$\displaystyle dS_{1}^{2}=\frac{dy_{1}^{2}-CdS_{1}^{1}}{D}=\frac{dy_{1}^{2}}{D}-\left( \frac{C}{D}\right) \left( \frac{-A}{B}\right) dS_{1}^{2}$
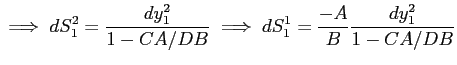$\displaystyle \implies dS_{1}^{2}=\frac{dy_{1}^{2}}{1-CA/DB}\implies dS_{1}^{1}=\frac{-A} {B}\frac{dy_{1}^{2}}{1-CA/DB}$ .

Note that if $F_{1,u}^{1}\leq F_{1,\chi}^{1}$ , then $C\leq0$ , meaning that (for reasonable parameter values, the same is true when $F_{1,u}^{1}>F_{1,\chi}^{1}$ ), in which case the sign of $dS_{1}^{2}$ is equal to the sign of $dy_{1}^{2}$ and the sign of $dS_{1}^{1}$ is opposite to that of $dy_{1}^{2}$ . In particular, an increase in $1-\phi$ induces an increase in $y_{1}^{2}$ , and therefore an increase in $S_{1}^{2}$ and a decrease in $S_{1}^{1}$ . Note, then, that

$\displaystyle \pi_{1}^{1}dS_{1}^{1}+\pi_{2}^{1}dS_{1}^{2}<0$

if and only if

$\displaystyle \frac{\pi_{1}^{1}}{\pi_{2}^{1}}\frac{-A}{B}\frac{dy_{1}^{2}}{1-CA/DB} <-\frac{dy_{1}^{2}}{1-CA/DB}$ .

If this is true if and only if

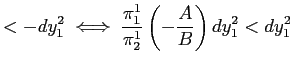
$\displaystyle \frac{\pi_{1}^{1}}{\pi_{2}^{1}}\frac{-A}{B}dy_{1}^{2}$	$\displaystyle <-dy_{1}^{2}\iff \frac{\pi_{1}^{1}}{\pi_{2}^{1}}\left( -\frac{A}{B}\right) dy_{1}^{2} <dy_{1}^{2}$
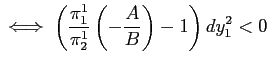	$\displaystyle \iff\left( \frac{\pi_{1}^{1}}{\pi_{2}^{1}}\left( -\frac{A}{B}\right) -1\right) dy_{1}^{2}<0$ ,

which holds for $dy_{1}^{2}>0$ since . Therefore, as long as , an increase in $y_{1}^{2}$ induces an on-impact decrease in the expected gains from posting vacancies.

C.5 Matching Function Elasticities

Petrongolo and Pissarides (2001) document that across a wide range of studies aggregate matching functions are found, empirically, to be approximately Cobb-Douglas in aggregate vacancies and unemployment. They note in their concluding section that the coefficient on unemployment is generally found to be in the range 0.5 to 0.7 when matches are formed with individuals exiting unemployment, only, and in the range 0.3-0.4 when total hires are used as the dependent variable (not only hires from unemployment). The nature of the standard and standard-OS models is such that the former applies, while the latter applies to the MA and MA-OS models.

In the standard and standard-OS models total matches are given by $M=A(v)^{\alpha}(\ell u)^{1-\alpha}$ , where $\ell$ denotes effective search; it clearly follows that in both cases the partial elasticities of with respect to and are, respectively, $\alpha$ and $1-\alpha$ . In the MA and MA-OS models, given sectoral matching functions and symmetry, it is straightforward to show that total matches in the economy are given by

$\displaystyle M=A(v^{\alpha}((\ell_{i,u}^{i}+\ell_{j,u}^{i})u+\ell_{i,\chi}^{i} \chi)^{1-\alpha}$ ,

where

$T=\ell_{i,u}^{i}+\ell_{j,u}^{i}$ . Then, $\partial\log M/\partial\log v=\alpha$ , and

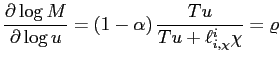$\displaystyle \frac{\partial\log M}{\partial\log u}=\left( 1-\alpha\right) \frac {Tu}{Tu+\ell_{i,\chi}^{i}\chi}=\varrho$ .

As the effective fraction of on-the-job searchers converges to zero, this elasticity converges to $\left( 1-\alpha\right)$ ,

as in the standard model. As long as $\alpha\geq0.6$ and $\ell_{i,\chi}^{i}\chi>0$ , then $\varrho \leq0.4$ . Furthermore, $\varrho\geq0.3$ if and only if

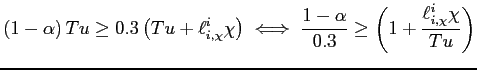$\displaystyle \left( 1-\alpha\right) Tu\geq0.3\left( Tu+\ell_{i,\chi}^{i}\chi\right) \iff\frac{1-\alpha}{0.3}\geq\left( 1+\frac{\ell_{i,\chi}^{i}\chi}{Tu}\right)$ .

Numerical analysis reveals that $\ell_{i,\chi}^{i}\chi<Tu$ . Hence, for $\alpha=0.6$ , the partial elasticities of aggregate matches with respect to and are broadly consistent with the findings in Petrongolo and Pissarides (2001).

C.6 Sensitivity to Changes in Key Parameters/Variables

Table C.6.1 Model calibrations (weekly frequency)

Difference in	Parameter: b	Parameter: ∝	Parameter: A	Parameter: T	Parameter: c	Parameter: Ø	Parameter: ε	Parameter: δ	Parameter: ß	Parameter: η
none	0.72	0.60	0.20	1.00	0.72	0.12	1.00	0.0081	0.999	0.50
ε	0.73	0.60	0.20	1.00	0.70	0.12	1.10	0.0081	0.999	0.50
Ø	0.72	0.60	0.20	1.00	0.71	0.13	1.00	0.0081	0.999	0.50
η	0.72	0.60	0.19	1.00	0.60	0.12	1.00	0.0081	0.999	0.55
z	0.75	0.60	0.20	1.00	0.63	0.13	1.00	0.0081	0.999	0.50

Notes for reference, first row shows benchmark calibration; second row refers to calibration in which $\varepsilon$ is 10 percent higher, but all targets remain as in benchmark; third row refers to calibration in which $\phi$ is 10% higher, but all targets remain as in benchmark except that implied ratio of skill-mismatched wage to average sectoral wage is now 0.83; fourth row refers to calibration in which $\eta$ is 10% higher, but all targets remain as in benchmark; fifth row refers to case in which net unemployment flow benefits are targeted to be 10% higher (0.55 instead of 0.5), but all other targets remain as in benchmark.

Table C.6.2: properties of key variables under ε = 1:1

	V/U Ratio: C1	V/U Ratio: C2	V/U Ratio: C3	Vacancies: C4	Vacancies: C5	Vacancies: C6	Unemp.: C7	Unemp.: C8	∂v/∂u C9	OPW: C10
R1: US	7.79	12	60%	3.88	12	60%	-3.93	15	-0.86	-
R2: MA-OS	4.81	4	11%	1.22	0	0%	-3.47	11	-0.35	1.00
R3: MA-OS	5.22	7	22%	1.43	0	0%	-3.65	12	-0.39	0.99
R4: MA-OS	5.66	8	32%	1.68	0	0%	-3.83	12	-0.44	0.99
R5: MA-OS	6.52	15	50%	2.15	0	0%	-4.19	12	-0.51	0.97
R6: MA-OS	7.40	15	63%	2.62	0	0%	-4.55	13	-0.58	0.96
R7: MA-OS	8.22	16	73%	3.10	12	26%	-4.89	13	-0.63	0.95
R8: MA-OS	8.79	16	78%	3.37	13	43%	-5.12	14	-0.66	0.94

Notes: Alternative calibration that applies to results in - implements value for $\varepsilon$ 10% higher than in benchmark calibration, but all targets remain the same. : elasticity of V/U ratio with respect to output per worker (OPW); : months after shock over which V/U ratio continues to increase (propagation); : percent of total increase in V/U ratio occurring over period of slow-moving adjustment; : elasticity of aggregate vacancies with respect to OPW; : months after shock over which vacancies continue to increase (propagation); : percent of total increase in vacancies occurring over period of slow-moving adjustment; : elasticity of aggregate unemployment with respect to OPW; : month at which unemployment reaches a trough; : slope of Beveridge curve; : elasticity of output per worker with respect to on-impact size of exogenous shock (0.007). : US data; : responses given -induced on-impact increase in OPW of 0.7% under benchmark calibration; -: response in MA-OS model to joint increases in and $1-\phi$ that (in all cases) induce an on-impact increase in OPW of 0.7%, where size of shock to $1-\phi$ is half of shock in (), equal to shock in (), and two (), three (), four (), and five () times the shock in .

Table C.6.3: properties of key variables under φ = 0:13

	V/U Ratio: C1	V/U Ratio: C2	V/U Ratio: C3	Vacancies: C4	Vacancies: C5	Vacancies: C6	Unemp.: C7	Unemp.: C8	∂v/∂u C9	OPW: C10
R 1: US	7.79	12	60%	3.88	12	60%	-3.93	15	-0.86	-
R2: MA-OS	4.62	4	12%	1.22	0	0%	-3.29	10	-0.37	1.00
R3: MA-OS	5.03	5	23%	1.43	0	0%	-3.47	10	-0.41	1.00
R4: MA-OS	5.45	9	34%	1.65	0	0%	-3.66	11	-0.45	0.99
R5: MA-OS	6.30	11	52%	2.10	0	0%	-4.03	11	-0.52	0.98
R6: MA-OS	7.15	14	65%	2.54	6	2%	-4.40	13	-0.58	0.96
R7: MA-OS	7.94	15	76%	2.95	11	34%	-4.75	14	-0.62	0.95
R8: MA-OS	8.49	15	81%	3.22	12	51%	-4.98	15	-0.65	0.95

Notes: Alternative calibration that applies to results in - implements skill-mismatch parameter 10% higher than in benchmark calibration, but all targets remain the same. Row and column references are as in Table C.5.2.

Table C.6.4: properties of key variables under η = 0:55

	V/U Ratio: C1	V/U Ratio: C2	V/U Ratio: C3	Vacancies: C4	Vacancies: C5	Vacancies: C6	Unemp.: C7	Unemp.: C8	∂v/∂u C9	OPW: C10
R 1: US	7.79	12	60%	3.88	12	60%	-3.93	15	-0.86	-
R2: MA-OS	4.61	4	14%	1.21	0	0%	-3.28	9	-0.37	1.00
R3: MA-OS	5.06	6	26%	1.45	0	0%	-3.48	12	-0.42	1.00
R4: MA-OS	5.52	9	37%	1.67	0	0%	-3.69	11	-0.46	0.99
R5: MA-OS	6.43	12	56%	2.16	0	0%	-4.09	12	-0.53	0.98
R6: MA-OS	7.35	14	70%	2.63	13	17%	-4.50	13	-0.59	0.96
R7: MA-OS	8.20	15	81%	3.07	13	49%	-4.87	13	-0.63	0.96
R8: MA-OS	8.79	18	87%	3.36	18	66%	-5.12	14	-0.66	0.95

Notes: Alternative calibration that applies to results in - implements bargaining power of workers 10% higher than in benchmark calibration, but all targets remain the same. Row and column references are as in Table C.5.2.

Table C.6.5: properties of key variables under z = 0:55

	V/U Ratio: C1	V/U Ratio: C2	V/U Ratio: C3	Vacancies: C4	Vacancies: C5	Vacancies: C6	Unemp.: C7	Unemp.: C8	∂v/∂u C9	OPW: C10
R 1: US	7.79	12	60%	3.88	12	60%	-3.93	15	-0.86	-
R2: MA-OS	5.19	4	13%	1.38	0	0%	-3.67	9	-0.38	1.00
R3: MA-OS	5.65	6	24%	1.62	0	0%	-3.88	10	-0.42	1.00
R4: MA-OS	6.12	8	34%	1.87	0	0%	-4.10	11	-0.46	0.99
R5: MA-OS	7.06	12	50%	2.36	0	0%	-4.48	14	-0.53	0.97
R6: MA-OS	8.00	13	63%	2.86	0	0%	-4.89	15	-0.59	0.96
R7: MA-OS	8.90	13	73%	3.32	10	27%	-5.27	15	-0.63	0.95
R8: MA-OS	9.51	15	78%	3.64	12	43%	-5.53	16	-0.66	0.94

Notes: Alternative calibration that applies to results in - targets net unemployment flow benefits 10% higher than in benchmark calibration, while all other targets remain the same. Row and column references are as in Table C.5.2.

Footnotes

**. International Finance Division, Board of Governors of the Federal Reserve System, Washington, D.C. 20551. E-mail: Brendan.Epstein@frb.gov. My greatest thanks to Mike Elsby, Etienne Gagnon, Miles Kimball, Toshihiko Mukoyama, Jeff Smith, and Brian Jacob for very helpful comments and discussions, and also to seminar participants at the Board of Governors of the Federal Reserve System, Brown University, McMaster University, the University of Michigan, the 2012 Midwest Macro Meetings hosted by the University of Notre Dame, and the 2012 Canadian Economics Association annual conference hosted by the University of Calgary. All errors are my own. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

1. See, for example, Shimer (2005), Hall (2005), Fujita and Ramey (2007), Mortensen and Nagypal (2007), and Hagedorn and Manovskii (2008) for additional discussion on the V/U ratio's emprical response to changes in productivity, and also with regards to the standard/benchmark model's limitations in fully accounting for the data. In broader reference to the standard model, see, for instance Diamond (1982), Pissarides (1985), Mortensen and Pissarides (1994), and Pissarides (2000). Return to text

2. In particular, given an increase in productivity of about 0.7% the V/U ratio jumps and thereafter continues to slowly rise over approximately 12 months. Return to text

3. As is standard in the literature, by this I mean an exogenous change in productivity. Return to text

4. I assume that it is always optimal for them to do so, as the central focus of this paper is tied to examining the implications of skill-mismatched employment. Return to text

5. I elaborate on the meaning of surplus further below, as well as on the overall determination of wages. Return to text

6. This is based on the theory developed in Pissarides (2000), chapter 5, in which the standard, homogeneous-agent model features an endogenous job-seeking technological component. Later in the paper I endogenize the choice of idiosyncratic search technologies within the present multi-agent framework. Return to text

7. Total matches in sector-1 are given by

$\displaystyle F_{1,u,t}^{1}u_{1,t}+F_{2,u,t}^{1}u_{2,t}+F_{1,\chi,t}^{1}\chi_{1,t} =\ell_{1,u,t}^{1}f_{t}^{1}u_{1,t}+\ell_{2,u,t}^{1}f_{t}^{1}u_{2,t} +\ell_{1,\chi,t}^{1}f_{t}^{1}\chi_{1,t}$
$\displaystyle =(\ell_{1,u,t}^{1}u_{1,t}+\ell_{2,u,t}^{1}u_{2,t}+\ell_{1,\chi,t}^{1} \chi_{1,t})f_{t}^{1}=s_{t}^{1}\cdot m_{t}^{1}/s_{t}^{1}=m_{t}^{1}$ .

Return to text

8. See the appendix for further details Return to text

9. See, for instance, Pissarides (2000). Return to text

10. See the appendix for further details. Return to text

11. Indeed, numerical analysis implies that $F_{1,u} ^{1}>F_{1,\chi}^{1}$ is endogenously optimal. Quite simply, this captures differences in outside options between unemployed and OTJ searchers. Return to text

12. In their cross-country investigation, Krueger and Mueller (2008) find that, conditional on searching, the average search time ranges from 40 minutes per week in Slovenia, to slightly less than 4 hours per week in Canada (which is a small amount more than in the U.S.). Return to text

13. Individuals choose effective search taking market conditions as given (in particular, $\theta^{i}$ ). Note that it is endogenously optimal to set $\ell_{1,\chi,t}^{2}=0$ . Return to text

14. See the appendix, as well as Pissarides (2000), chapter 5, for further details on what I refer to as the "standard-OS model." Return to text

15. With regards to procyclical effective search, see, for instance, Christensen et al. (2005). As noted earlier, the procyclicality of effective search is also a feature of the standard, homogenous-agent model enhanced to account for endogenous effective search (Pissarides (2000), chapter 5). Return to text

16. Numerical analysis reveals that differences in results stemming from temporary and permanent changes in the economy's driving forces are for all purposes negligible. In terms of impulse response functions, in particular, differences are broadly limited to the absence of mean reversion. This is broadly in line with the fact that, as noted in Shimer (2005) and Mortensen and Nagypal (2007), the cyclical properties of models of the sort developed in the present paper are well assessed by considering differences between steady states. Return to text

17. The unemployment rate is at monthly frequency, spans 1951:M1 through 2011:M10, and is taken from the Bureau of Labor Statistics (BLS). Vacancies are at monthly frequency and obtained by using the Job Openings and Labor Turnover Survey (JOLTS) data since 2000:M12 (when first available) combined with the Conference Board's Help-Wanted Index (HWI) from 1951:M1 through 2000:M11 (adjusted to the JOLTS units of measurement). Return to text

18. See the appendix for further details. Return to text

19. The appendix shows that implementing alternative values for , $\varepsilon$ , $\eta$ and $\phi$ does not substantially alter overall results. Return to text

20. To further understand this, consider an extreme example. Suppose the expected gains from skill-mismatched search were zero; then, the first-order conditions for optimal effective search imply that $\ell_{2,u}^{1}$ would be zero as well. Given a positive productivity shock, assume these expected gains increase by an arbitrarily small amount. Then, so will $\ell_{2,u}^{1}$ . However, because $\ell_{2,u}^{1}$ was originally zero, the percent change in $\ell_{2,u}^{1}$ would technically be infinity. However, recall from earlier that by comparative advantage $\ell_{1,u,t}^{1}>\ell_{2,u,t}^{1}$ in all states of the economy. Return to text

21. See, for instance, Pissarides (2009). Return to text

22. Empirical elasticities are based off the logarithm of quarterly data spanning 1951:Q1 through 2011:Q3 that, following Shimer (2005), is detrended using an HP-filter with smoothing parameter $10^{5}$ . Data on unemployment and output per worker is taken from Bureau of Labor Statistics. Vacancies are obtained by using the Job Openings and Labor Turnover Survey (JOLTS) data since 2000:M12 (when first available) combined with the Conference Board's Help-Wanted Index (HWI) from 1951:M1 through 2000:M11 (adjusted to the JOLTS units of measurement). Both unemployment and vacancy data are originally at monthly frequency (statistics are based off quarterly averages); the series of output per worker is only available at quarterly frequency. Return to text

23. In line with the overall preceding analysis, note that in all cases referred to henceforth, model-generated elasticities are based off permanent changes in productivity, and hence are implied by changes between steady states. Return to text

24. In particular, net unemployment flow benefits must be approximately 96% of OPW in order for the standard model to match the data's amplification properties. Recall that the present calibration is such that net unemployment flow benefits are approximately 50% of OPW. Intuitively, the fact that employment surpluses are a function of the difference between the productivity of a match and net unemployment flow benefits means that the smaller this difference is, the more percentage-wise sensitive it is to changes in productivity, and therefore, the greater the elasticity of $\Theta$ with respect to OPW. Return to text

25. For simplicity, this proof assumes functional forms consistent with the overall development of the model. Return to text

26. For simplicity, this proof assumes functional forms consistent with the overall development of the model. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text