
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1080, May 2013 --- Screen Reader
Version*
Do Central Banks' Forecasts Take Into Account Public Opinion and Views?
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
The Federal Reserve through the Federal Open Market Committee (FOMC) regularly releases macroeconomic forecasts to the general public and the US congress with the purpose of explaining the likely evolution of the economy and the appropriate stance of monetary policy. Immediately before doing so, the FOMC receives a forecast produced by the Federal Reserve staff which remains private for five years. The literature has pointed out that, despite the informational advantage of the FOMC, its forecast differs from and is not always more accurate than the staff forecast. This finding has raised concerns regarding the loss of relevant information and the usefulness of the FOMC forecasts. This paper brings evidence that the FOMC forecast also incorporates other publicly available forecasts and views, and that the weight attributed to public forecasts is larger than what is optimal given a mean squared error objective. These findings are consistent with i) the institutional role of the FOMC in being representative of a variety of public views, ii) the academic literature recommendation to use equal weights and not to overfit specific forecasts based on past performance. The statistical model can also account for several empirical regularities of the forecasts.
Keywords: Monetary policy design, central banks' forecasts
JEL classification: E52, E58, E31.
1. Introduction
Economic projections are often presented to the public and its political representatives by central banks as part of their mandates. The public disclosure of forecasts is a common practice of central banks which are designed to be transparent and accountable to the democratic societies that they represent. These forecasts help society understand the likely evolution of the economy and the trade-offs that the society faces as well as the policy choices that best represent its interests.
More specifically in the United States, the Federal Reserve regularly discloses to the public the forecasts produced by the Federal Open Market Committee (FOMC) - the body that sets the Federal Funds rate. The FOMC meetings devote substantial amount of time preparing these forecasts and they draw on considerable expertise and resources. The FOMC forecast is then heavily discussed and scrutinized in the U.S. Congress and the media. Given the importance of the FOMC forecast, both as part of appropriate monetary policy and as an accountable and transparent policy-making process of democratic societal choice, it is worthwhile to ascertain the factors that affect this forecast.
Romer and Romer (2008) and other subsequent papers show a puzzling result concerning the usefulness of the FOMC forecast. The staff of the Federal Reserve prepares the so-called Greenbook forecasts.1 The Greenbook forecast is prepared specifically for and one week prior to the FOMC meetings. This forecast constitutes a key input into the FOMC forecast, and the FOMC could simply adopt it without changes. The FOMC has an informational advantage as it releases its forecast later and also has insider knowledge of their own preferences regarding the interest rate setting. Romer and Romer (2008) find that despite these advantages, the FOMC forecast is not more accurate than the Greenbook forecast. Optimal predictions of inflation and unemployment place a zero, or a very low weight, on the FOMC forecast.
This paper examines the determinants of the FOMC forecast. In order to do so, it is critical to use the Greenbook forecast as a control because it is prepared just before and specifically for the FOMC. A key characteristic that I explore is the public exposure and the institutional role of the FOMC. The Greenbook forecast remains private for five years and is not mandated to fulfil any public role. Following this line of thought, I find that the FOMC forecast seems to reflect or incorporate other publicly available forecasts and information, namely I explore both the role of private sector and White House forecasts.
The statistical model I estimate can account for several empirical regularities of the forecasts. More precisely, the statistical results can explain the puzzle of Romer and Romer (2008). The model can also capture the cases in which the FOMC produces better forecasts than the Greenbook, as well as the cases in which it produces better forecasts than the SPF and the White House.
The White House forecast data are obtained from the Budget of the United States Government and the Mid-Session Review. Private sector forecast data are available through the Survey of Professional Forecasters. Because all the variables in our regressions are forecasts, the statistical framework is straightforward and interpretable.
There are a variety of reasons for which the FOMC forecast may reflect other publicly available information besides what is already contained in the Greenbook. This paper opens avenues for future research into the underlying motivations for doing so, as several possible explanations are observationally equivalent. The goal of this paper is not to distinguish between these but to establish whether the FOMC does or does not take into account publicly available forecasts of relevant economic agents and institutions. Having said that, the results are consistent with the role assigned in the Federal Reserve Act to the FOMC.2 The FOMC is a diverse committee institutionally designed to represent the public and a variety of views, and the Greenbook could potentially be one among several views. The finding in this paper that the FOMC does not depart randomly from the Greenbook, and instead takes it heavily into account but also incorporates other public information is a comforting result for the FOMC given its mandate. In addition, the FOMC explicitly and publicly compared its forecasts with the ones of the White House and the private sector both in public statements and official documents, being very transparent in doing so.
I also examine whether the weights attributed to public forecasts reflect an optimal pooling of information. I find that the weights on public forecasts are larger than the optimal weights computed from a mean squared error (MSE) perspective. According to this perspective, the public forecasts considered seem to be overweighted. However, the forecasting literature often recommends giving equal weights to relevant forecasts rather than following a strict MSE perspective (e.g. Zarnowitz (1992), Clements and Hendry (1998, 2002)). The rationale is that the methods of each forecaster as well as the structure of the economy change frequently and it may be difficult to identify good forecasters based on past performance. The literature shows here some tension between using MSE or equal weights, and the FOMC forecast seems to follow good forecasting practice and draw on both - the weights estimated in the statistical regressions are in between both approaches.
Several papers have compared different forecasts by examining their similarity and ranking their forecasting performance (Romer and Romer (2008), Reifschneider and Tulip (2007), and Faust and Wright (2009) and among many others). Studies focus often on the inflation forecast because it is the variable most related to the mission of central banks and for which they have specific expertise. Consistent with these arguments, there is a consensus that the Greenbook inflation forecast seems to be the most efficient. Other papers have examined the effects of the public opinion (Tootell (1999)) and regional factors (Meade and Sheets (2005)) on the FOMC members' policy votes, and the patterns of forecast disagreement among individual members of the FOMC (Banternghansa and McCracken (2009)). None of these papers, however, provides an explanation for the difference between the FOMC and Greenbook forecasts; to the best of my knowledge the present paper is the first to empirically address this issue.
It is beyond the scope of the present paper to examine welfare or normative questions. Such questions are as interesting as they are ill posed since they depend on the objective functions of society and the central bank. For instance, Ellison and Sargent (2012) provide a theoretical explanation where the FOMC behaves optimally. The authors argue that the FOMC is a robust policymaker, as in Hansen and Sargent (2008). Unlike the Greenbook, the FOMC forecasts follow the probabilities of robust policy rather than aim to be optimal in a pure forecasting sense. In fact, the results found here could also be justified by claiming that the FOMC did not follow a purely MSE forecasting perspective. The mechanisms pointed out here and in Ellison an dSargent (2012) are not contradictory but complementary. Most likely many factors play a role. A later section discusses the insights that can be gained from both papers.
The paper is organized as follows: Section 2 describes the forecasts and key statistics. Section 3 provides the main results and Section 4 addresses their implications. Section 5 presents robustness analysis, including the use of individual level forecasts of the FOMC participants. Section 6 concludes.
2. The Forecasts
The FOMC forecast: The course of monetary policy in the US is decided at the FOMC meetings. The Humphrey-Hawkins Full Employment and Balanced Growth Act requires the Federal Reserve to submit to Congress twice a year a document - the Monetary Policy Report (MPR) - discussing the conduct of monetary policy and the outlook on the economy. To this effect, preceding the MPR submission and in conjunction with FOMC meetings, each Federal Reserve Bank president plus seven members of the Federal Reserve Board submit their forecasts.
The range and central tendency of these forecasts are released to the public as part of the MPR and are discussed in a congressional hearing. I use the midpoint of the central tendency and, if not available, the midpoint of the range. A later section examines the individual responses of the FOMC members.
Starting in July 1979 the FOMC forecasts are prepared in February and July of each year. The forecasts in February are for the current year; the forecasts in July are for both the current year and next year. The forecasts for inflation and real growth are for fourth quarter over fourth quarter. The forecasts for unemployment are for the fourth quarter level. The definitions of the forecasted variables changed overtime, which poses an extra difficulty in matching definitions across sources.3
The Fed staff forecast (Greenbook): The staff of the Board of Governors of the Federal Reserve System produces these forecasts one week before each FOMC meeting. All FOMC participants have access to them. The Greenbook takes five years to become public and the data sample in this paper observes that condition. All variables forecasted by the FOMC are forecasted by the staff.
The White House forecast: The forecasts of the White House are included because the MPR frequently shows these forecasts and compares them directly with the FOMC forecast. These comparisons are present from the inception of the MPR until 2000.4 The forecasts of the White House and the Administration are interconnected with the Administration policies and goals. The Administration opinion on the evolution of the economy are disclosed to the public in a variety of formats: speeches, interviews, debates, articles, press releases, and so on. Even though all of these sources are important for this paper, one needs to rely on a systematic process to record the White House forecasts.
The data-set was constructed by manually collecting the forecasts from the Budget of the United States Government and the Mid-Session Review.5 Around January or February of each year, the budget for the subsequent fiscal year is presented. The forecasts for several years are contained in the chapter "Economic Assumptions". The table with forecasts also contains a note usually indicating that information only up to November of the previous year is used.
For the corresponding July forecasts of the FOMC, I use the Mid-Session Review of the Budget, which is available around June or July of each year. The "Economic Assumptions" table also contains a note usually indicating that information only up to May or June is used. The timing of the forecasts is addressed later in the analysis.
The number of variables being forecasted is less than those in the Greenbook but more than those in the FOMC. For inflation, one can match the forecasts of inflation until July 1999.6 A later section extends the sample for the inflation results. For real growth and unemployment, one can match the definitions in the entire sample.
The private sector forecast: Comparisons with private sector forecasts are never present in the MPR but occasionally appear during the testimony and hearings. For instance, testifying at the Senate Banking Committee on 14 February 2008 Chairman Bernanke referred that the forecasts to be released in the following weeks were "reasonably consistent" with private-sector forecasts.7
I use the Survey of Professional Forecasters (SPF) because of several reasons. First, it is the oldest survey of macroeconomic forecasts in the United States conducted at a quarterly frequency. Second, the respondents produce regular forecasts of economic variables as part of their routine tasks in the business world and Wall Street. Third, this survey contains forecasts for several variables at different horizons that allow us to match the FOMC definitions. A later analysis shows results with the Blue Chip forecasts.
For inflation, one can match the FOMC inflation forecast until July 1999.8 For real growth and unemployment the entire sample of FOMC forecasts is matched. The SPF forecasts from the fourth quarter of the preceding year and the second quarter of the corresponding year match the February and July FOMC forecasts, respectively. The professional forecasters need to submit their responses at late in the second or third week of the middle month of each quarter.9 The results of the survey are released to the public around the fourth week of the middle month of the quarter.
Outcomes: For actual outcomes, I try to match what the staff and the FOMC were trying to forecast. For NIPA variables I use the final estimates released after three months and for non-NIPA I use the data as originally released.
2.1 Preliminary Analysis
Mean Squared Errors: The results are particularly relevant for the inflation forecast. First, the Greenbook inflation forecast seems to be quite accurate. Second, the Fed has specific expertise in monitoring and forecasting inflation - unlike real growth and unemployment, which are affected to a greater extent by other policies and institutions. Third, as shown in Svensson (1997, 1999), the modern framework of inflation targeting can be implemented and depends crucially on the evolution and monitoring of the inflation forecast.
Table 1 shows the Mean Squared Errors (MSE) for the updated sample. The Greenbook performs quite well in this dimension. With respect to inflation, the Greenbook outperforms the others. This result is not surprising given that the main mandate of central banks is to stabilize and, therefore, forecast inflation. Also, inflation is mainly a monetary phenomenon and central banks should have a very good sense of future developments in that area.
With respect to unemployment and real growth, Table 1 does not dictate a clear winner. The forecasts are similar and none is found to perform much better. Unlike inflation, real growth and unemployment depend to a greater extent on policies and factors outside the Fed's control. Unsurprisingly, others can forecast those two variables equally well.
Table 1a: Mean Squared Errors: White House
| MSE: G | MSE: F | MSE: W | MSE: | rank {G,F, | rank {W,F, | |
|---|---|---|---|---|---|---|
| Inflation | 0.7570 | 0.9331 | 1.2649 | 0.8609 | ✔ | ✔ |
| Unemp. | 0.4539 | 0.4744 | 0.6109 | 0.4787 | ✔ | ✔ |
| Real growth | 1.7870 | 1.6884 | 2.4482 | 1.8374 | ✔ |
Table 1b: Mean Squared Errors: SPF
| MSE: G | MSE: F | MSE: S | MSE: | rank {G,F, | rank {S,F, | |
|---|---|---|---|---|---|---|
| Inflation | 0.6658 | 0.8157 | 1.3629 | 0.7748 | ✔ | ✔ |
| Unemp. | 0.4015 | 0.3895 | 0.5087 | 0.3943 | ✔ | ✔ |
| Real growth | 1.7901 | 1.6181 | 1.8501 | 1.6907 | ✔ | ✔ |
Notes: The table reports Mean Squared Errors for
Greenbook (G), FOMC (F), White House (W), SPF (S), and FOMC
predicted by the model in section 3 (![]() ). The sample is the same for all variables in each
panel. The upper and lower panel display different values even for
common series because the sample does not coincide as some values
for the SPF forecasts cannot be constructed in the earlier part of
the sample. The fourth column displays a checkmark if the MSE
ranking of F and G is replicated by
). The sample is the same for all variables in each
panel. The upper and lower panel display different values even for
common series because the sample does not coincide as some values
for the SPF forecasts cannot be constructed in the earlier part of
the sample. The fourth column displays a checkmark if the MSE
ranking of F and G is replicated by ![]() and G;
the fifth column is analogous to the fourth but considers the MSE
ranking relative to public forecasts rather than G.
and G;
the fifth column is analogous to the fourth but considers the MSE
ranking relative to public forecasts rather than G.
Average Forecast: The upper panel of Table 2 shows the
averages of the Greenbook (![]() ), FOMC (
), FOMC (![]() ), and White House forecasts (
), and White House forecasts (![]() ), and the
outcome of the variables being forecasted. The fourth column
displays a checkmark if the FOMC forecast is in between the
Greenbook and the White House. The FOMC average forecast is always
in between the other two. This pattern is present even when
disaggregating the forecasts by date and horizon. The lower panel
of Table 2 performs the
same analysis comparing the Greenbook, FOMC, and SPF forecasts
(
), and the
outcome of the variables being forecasted. The fourth column
displays a checkmark if the FOMC forecast is in between the
Greenbook and the White House. The FOMC average forecast is always
in between the other two. This pattern is present even when
disaggregating the forecasts by date and horizon. The lower panel
of Table 2 performs the
same analysis comparing the Greenbook, FOMC, and SPF forecasts
(![]() ). The same patterns are present.
). The same patterns are present.
Even though, the average forecast of F, S, and W are similar,
there is variability over time that can be explored. Table A.1 in the
appendix shows the standard deviations of the difference between
two forecasts. For instance, for real growth
![]() is equal to 0.8.
is equal to 0.8.
Sign Predictions: Table 3 examines
whether having access to the Greenbook and either the SPF or the
White House forecast would help predict whether the FOMC forecast
would be higher or lower than the Greenbook. If the FOMC bases its
forecast on the Greenbook but also incorporates some information
from the SPF, one would think that
![]() should imply
should imply
![]() , and
, and
![]() should imply
should imply
![]() . Even with such a direct
approach, Table 3 shows that the
success rate is above 75% when predicting the direction of the FOMC
forecast relative to the Greenbook.
. Even with such a direct
approach, Table 3 shows that the
success rate is above 75% when predicting the direction of the FOMC
forecast relative to the Greenbook.
Table 2a: Average Forecast Comparison: White House
| Average: G | Average: F | Average: W | In between? | Outcome | |
|---|---|---|---|---|---|
| Overall: Inflation | 4.1731 | 4.3054 | 4.3887 | ✔ | 3.9319 |
| Overall: Unemp. | 6.2318 | 6.1685 | 6.0965 | ✔ | 6.0694 |
| Overall: Real Growth | 2.6178 | 2.6882 | 2.8553 | ✔ | 2.7303 |
| Inflation: Jan. Cur. | 4.1295 | 4.2312 | 4.3550 | ✔ | 3.8712 |
| Inflation: Jul. Cur. | 4.2093 | 4.3512 | 4.4000 | ✔ | 4.1093 |
| Inflation: Jul. Nex | 4.1785 | 4.3304 | 4.4095 | ✔ | 3.8121 |
| Unemp: Jan. Cur. | 6.3000 | 6.2231 | 6.2222 | ✔ | 6.1222 |
| Unemp: Jul. Cur. | 6.2393 | 6.2228 | 6.1571 | ✔ | 6.1143 |
| Unemp: Jul. Nex | 6.2393 | 6.1451 | 5.9893 | ✔ | 6.0750 |
| Real Growth: Jan. Cur. | 2.5416 | 2.6389 | 2.6741 | ✔ | 2.7552 |
| Real Growth: Jul. Cur. | 2.5400 | 2.5804 | 2.6357 | ✔ | 2.6911 |
| Real Growth: Jul. Nex | 2.7202 | 2.7946 | 3.2250 | ✔ | 2.7410 |
Table 2b: Average Forecast Comparison: SPF
| Average: G | Average: F | Average: S | In between? | Outcome | |
|---|---|---|---|---|---|
| Overall: Inflation | 3.9657 | 4.0900 | 4.2877 | ✔ | 3.7416 |
| Overall: Unemp. | 6.1825 | 6.1291 | 6.1153 | ✔ | 6.0000 |
| Overall: Real Growth | 2.6431 | 2.7094 | 2.7414 | ✔ | 2.8354 |
| Inflation: Jan. Cur. | 4.1295 | 4.2312 | 4.4549 | ✔ | 3.8712 |
| Inflation: Jul. Cur. | 4.2093 | 4.3512 | 4.3983 | ✔ | 4.1093 |
| Inflation: Jul. Nex | 3.4996 | 3.6285 | 3.9728 | ✔ | 3.1686 |
| Unemp: Jan. Cur. | 6.3000 | 6.2231 | 6.2146 | ✔ | 6.1222 |
| Unemp: Jul. Cur. | 6.2393 | 6.2228 | 6.1641 | ✔ | 6.1143 |
| Unemp: Jul. Nex | 5.9920 | 5.9225 | 5.9534 | 5.7400 | |
| Real Growth: Jan. Cur. | 2.5416 | 2.6389 | 2.6774 | ✔ | 2.7552 |
| Real Growth: Jul. Cur. | 2.5400 | 2.5804 | 2.7183 | ✔ | 2.6911 |
| Real Growth: Jul. Nex | 2.8680 | 2.9300 | 2.8363 | 3.0835 |
Notes: The table reports the average forecast of the Greenbook (G), FOMC (F), White House (W), SPF (S), and the outcome. The fourth column displays a check if the FOMC forecast is in between the other two. The sample is the same for all variables in each panel. The upper and lower panel display different values even for common series because the sample does not coincide as some values for the SPF forecasts cannot be constructed in the earlier part of the sample.
The remaining columns in the table show that the results are
robust to only incorporating predictions in which ![]() are above or below a certain threshold. Taking
as an example the unemployment forecast, the last column shows that
when
are above or below a certain threshold. Taking
as an example the unemployment forecast, the last column shows that
when ![]() is below the 25th or above the
75th percentile, in 92% of all observations one can correctly
predict the direction of the FOMC forecast relative to the
Greenbook.
is below the 25th or above the
75th percentile, in 92% of all observations one can correctly
predict the direction of the FOMC forecast relative to the
Greenbook.
Table 3: Percentage of Correct Sign Predictions
| Predicting Sign: W | Predicting Sign: S | Predicting Sign percentiles (40-60): W | Predicting Sign percentiles (40-60): S | Predicting Sign percentiles (25-75): W | Predicting Sign percentiles (25-75): S | |
|---|---|---|---|---|---|---|
| Inflation | 75.9259 | 75.4717 | 73.4694 | 73.3333 | 76.6667 | 75.0000 |
| Unemp. | 81.0811 | 83.7838 | 85.0000 | 83.8710 | 92.3077 | 88.3721 |
| Real Growth | 76.7123 | 76.9231 | 78.9474 | 77.4194 | 78.5714 | 82.0513 |
Notes: The table reports the percentage
of correct predictions of the sign of ![]() .
The first column plots the percentage of correct predictions
.
The first column plots the percentage of correct predictions
![]() and
and
![]() implying
implying
![]() and
and ![]() ,
respectively. The third column computes the percentage of correct
predictions with
,
respectively. The third column computes the percentage of correct
predictions with
![]() and
and
![]() implying
implying
![]() and
and
![]() , respectively. The fifth
column does the analysis with the 25th and 75th percentile. The
second, fourth, and sixth column make the same analysis for the SPF
forecast.
, respectively. The fifth
column does the analysis with the 25th and 75th percentile. The
second, fourth, and sixth column make the same analysis for the SPF
forecast.
3. Main Results
The analysis in the previous section was indicative of the
channels being examined. This section performs a more formal
econometric evaluation. The main specification examines why the
FOMC deviates from the Greenbook forecast instead of just adopting
it. In other words, the question is whether movements in the
dependent variable ![]() reflect other
forecasts. To this effect, the two equations below are estimated
separately:
reflect other
forecasts. To this effect, the two equations below are estimated
separately:
![]()
Table 4 presents the results. The equations are estimated with ordinary and weighted least squares. The WLS regression captures the different timings of the forecasts. Newey-West standard errors with three lags are reported when using WLS. A constant is included in the regressions because the average forecast was already examined in Table 2. Here, a crucial and stricter point is being tested, whether time-variations in the FOMC forecast reflect time-variations in public forecasts.
Table 4: Regression Results
| constant | W | S | R2 of (F-G) | R2 of F | |
|---|---|---|---|---|---|
| Inflation: W, OLS |
0.0791 (0.0333) | 0.2466 (0.0527) | - | 0.2673 | 0.9878 |
| Inflation: W, WLS |
0.0783 (0.0484) | 0.2519 (0.0677) | - | 0.2608 | 0.9878 |
| Inflation: S, OLS |
0.0569 (0.0382) | - | 0.2093 (0.0574) | 0.1892 | 0.9856 |
| Inflation: S, WLS |
0.0443 (0.0722) | - | 0.2420 (0.1136) | 0.2526 | 0.9856 |
| Unemployment: W, OLS |
-0.0076 (0.018) | 0.4114 (0.0454) | - | 0.4971 | 0.9874 |
| Unemployment: W, WLS |
-0.0005 (0.0225) | 0.4026 (0.063) | - | 0.4748 | 0.9873 |
| Unemployment: S, OLS |
-0.0272 (0.0165) | - | 0.3897 (0.0397) | 0.5530 | 0.9888 |
| Unemployment: S, WLS |
-0.0256 (0.0191) |
- | 0.3882 (0.0656) | 0.5408 | 0.9888 |
| Real Growth: W, OLS |
0.0005 (0.031) | 0.2945 (0.0372) | - | 0.4307 | 0.9605 |
| Real Growth: W, WLS |
-0.0021 (0.0412) | 0.2942 (0.0333) | - | 0.4226 | 0.9605 |
| Real Growth: S, OLS |
0.0417 (0.0312) | - | 0.2505 (0.0423) | 0.3100 | 0.9602 |
| Real Growth: S, WLS |
0.0367 (0.0419) | - | 0.2409 (0.0715) | 0.2920 | 0.9602 |
Notes: The table reports the estimates of equations (1) - (2). W and S denote White House and SPF forecasts, respectively. The equations are estimated both with OLS and WLS. Newey-West standard errors with three lags are reported in the WLS regression.
The results show that indeed the difference between the FOMC and
the Greenbook can be explained by, or is correlated with, the White
House and the SPF. In the inflation forecast the weight put on the
non-Greenbook forecast is roughly 0.25. The weight goes up slightly
for real growth, and regarding unemployment the weight goes up to
roughly 0.40. In all specifications the coefficients are
statistically significant. Two ![]() measures are
reported, the first related to explaining
measures are
reported, the first related to explaining ![]() , the second in explaining
, the second in explaining ![]() . Obviously, explaining
. Obviously, explaining ![]() is
a daunting task as the two forecasts are formulated within a one
week interval. Despite these difficulties, the econometric model
presented here is statistically significant.
is
a daunting task as the two forecasts are formulated within a one
week interval. Despite these difficulties, the econometric model
presented here is statistically significant.
3.1 Discussion of Results
It is not the claim of this paper that the results in Table 4 are causal. Causality and correlation may lead to observationally equivalent FOMC forecasts. For instance, the FOMC mandate of representing the public may lead the FOMC to actively want to understand some public views regarding the evolution of the economy, and to incorporate the views that it agrees with. But it could also be that the FOMC already had shared views with other forecasters. Reverse causality seems less plausible given our results. Below I discuss the timings of the forecasts and I present additional evidence on this issue.
Discussion of timings:
It is always the case that the Greenbook is completed roughly
one week before the FOMC meetings. The SPF is a quarterly survey
forecasting several periods ahead. I chose the quarter in which the
forecast is completed such that the SPF forecast is finished and
publicly available before the Greenbook and the FOMC
forecasts.10 This
timing helps to establish that it is the variable ![]() reflecting information in
reflecting information in ![]() instead of the opposite.11 Also, this
choice of timing for the SPF puts this forecast at an informational
disadvantage, making it harder to obtain the result claimed here
because the FOMC should put even more weight on the Greenbook.
instead of the opposite.11 Also, this
choice of timing for the SPF puts this forecast at an informational
disadvantage, making it harder to obtain the result claimed here
because the FOMC should put even more weight on the Greenbook.
Regarding the White House forecast, the dates of the documents
indicate that it is completed before the Greenbook. Namely, the
Economic Assumptions tables in the budget documents have a footnote
indicating that only information up to a certain date is
incorporated. That date is before the Greenbook. This timing helps
to establish that it is the variable ![]() reflecting information in
reflecting information in ![]() instead
of the opposite.
instead
of the opposite.
The results also suggest that reverse causality is much less
likely. For instance, the FOMC mean forecast is in between the
White House and the Greenbook mean (Table 2). Such
evidence is at odds with the explanation that it is the White House
incorporating the other two forecasts. The same pattern can be
found in the results of Table 4. If one
postulates that the variable ![]() reacts to
reacts to
![]() then it does so with a coefficient
larger than one. Such reasoning is implausible because it would
imply that if, for instance, the Greenbook forecasts inflation to
be 3% and the FOMC forecasts 3.5%, then the White House would
extrapolate and forecast 4%. While extrapolative models of
inflation are not necessarily wrong, it is hard to argue that such
behavior is likely or optimal for the US inflation time series. The
timings and statistical evidence do not seem to suggest reverse
causality.
then it does so with a coefficient
larger than one. Such reasoning is implausible because it would
imply that if, for instance, the Greenbook forecasts inflation to
be 3% and the FOMC forecasts 3.5%, then the White House would
extrapolate and forecast 4%. While extrapolative models of
inflation are not necessarily wrong, it is hard to argue that such
behavior is likely or optimal for the US inflation time series. The
timings and statistical evidence do not seem to suggest reverse
causality.
Further evidence:
Even if the White House forecast is completed before the Greenbook, it may happen that it is only published after. For that reason one cannot claim that the FOMC had knowledge of the forecast in the Budget. Also, in some years the dates in the the Economic Assumptions tables are missing or are indicative only. This issue is in fact not problematic. The forecasts and views of the Administration are discussed widely in the media and in policymaking circles. A strong evidence of this claim is that the MPR makes reference to the White House forecasts even in times when they were not publicly available through the Budget, as they were available through the media and other sources.
For instance, the MPR dated 20th of July 1983 specifically shows the White House forecast even though the Mid-Session Review of the Budget was only released on the 25th of July 1983. Another example is contained in the MPR of July 1993, "The Administration has not yet released the midyear update to its economic and budgetary projections. However, statements by Administration officials suggest that the revised forecasts for real growth and inflation in 1993 and 1994 are not likely to differ significantly from those of the Federal Reserve."
In addition to this evidence, further analysis is presented to clarify the results. One may be concerned that the FOMC may not know exactly and in every period the White House forecast contained in the Budget. This issue translates in econometric terms into a problem of measurement error. Also one would like to observe perfectly the perception of the FOMC regarding the White House forecasts as well as the FOMC perception of other Administration signals. Instead, one observes only the White House forecasts contained in the US budget. As it is well known, measurement error creates a downward bias in the estimates. The fact that the estimates in Table 4 are significant is, therefore, supportive of the channels proposed in this paper.
Table 5 presents further evidence. I use a known correction for measurement error in regressions with one variable. The method of group averages was first advocated by Wald (1940) and is described, for instance, in Greene (2000). This method uses an instrumental variable based on groups of the original variable. For example, with three groups one creates the instrumental variable -1,0,1 if the variable is below the 33th percentile, in between, or above the 67th percentile, respectively. The table reports the results when two and three groups are used, in both cases the instruments are not weak.12 The main results still hold.
Table 5: Further Evidence
| constant | W | First st. F-stat. | |
|---|---|---|---|
| Inflation: IV, 2 groups |
0.0651 (0.0354) | 0.3119 (0.0776) | 50.7000 |
| Inflation: IV, 3 groups |
0.0748 (0.034) | 0.2669 (0.0664) | 94.1480 |
| Unemployment: IV, 2 groups |
-0.0044 (0.0186) | 0.4350 (0.0589) | 115.6200 |
| Unemployment: IV, 3 groups |
0.0004 (0.0183) | 0.4702 (0.0523) | 250.6580 |
| Real Growth: IV, 2 groups |
0.0038 (0.032) | 0.2806 (0.0533) | 74.9500 |
| Real Growth: IV, 3 groups |
0.0065 (0.0314) | 0.2695 (0.0463) | 143.1370 |
Notes: The table reports the estimates of equations (1) - (2). The first panel uses instrumental variables with the method of group averages
Summary of further evidence:
Making causal arguments in economics is extremely hard. Given that the data is not a pure time-series, it is impossible to use Granger causality and similar tests. Such tests are also subjective once forward looking variables are involved, as is the case here. Having said that, the results do not suggest that the causality runs in the opposite direction for three reasons. First, the timings of forecasts are such that the non-Fed forecasts are completed before the FOMC meetings. Second, the estimated coefficients also confirm the claims in the paper, otherwise one would need to appeal to extrapolative forecasting in the US. Third, the instrumental variable regressions provide further evidence.
With this evidence at hand one should also clarify that the
results do not dismiss the explanations of Ellison and Sargent (2012). One can argue that the forecasts are
independent and the regression coefficient ![]() is
capturing the similarity between the robustness degree of the
agents producing the forecasts.
is
capturing the similarity between the robustness degree of the
agents producing the forecasts.
If this is the explanation, then this paper is still surprising. First, the White House would also have to behave as a robust policymaker, instead of trying to be more optimistic in order to win the elections or push certain political agendas. Second, a crucial observation is that the private sector does not decide on monetary policy and has no incentive to publish policymaking robust forecasts. Third, one could claim that robust forecasting is the norm for all agents; if that is so it would be interesting to examine why the Fed staff is so different and what determines different degrees of robustness.
4 Additional Results
4.1 Replicating MSE
I now examine whether the statistical model can account for the
observed patterns of the MSEs. To examine this issue, one can first
compute the FOMC forecast implied by the model, denoted as
![]() . In other words,
. In other words, ![]() is the fitted values of
is the fitted values of ![]() based on the
OLS estimates of equations (1) and (2).
based on the
OLS estimates of equations (1) and (2).
The MSE of ![]() can gauge the improvement or
deterioration in the MSE caused by the channels modeled in this
paper. The model is successful along this dimension. For all cases
except one, Table 1 shows that the ranking of MSEs of
can gauge the improvement or
deterioration in the MSE caused by the channels modeled in this
paper. The model is successful along this dimension. For all cases
except one, Table 1 shows that the ranking of MSEs of ![]() relative to
relative to
![]() is replicated by the ranking of MSEs of
is replicated by the ranking of MSEs of
![]() relative to
relative to ![]() (described in second to last column in Table 1). For instance,
the MSE of the inflation forecast
(described in second to last column in Table 1). For instance,
the MSE of the inflation forecast ![]() is
always worse than the Greenbook. The model can also explain cases
in which the FOMC performs better than the Greenbook; also the last
column in Table 1 shows that the model can capture the better accuracy of the FOMC
relative to the other public forecasts.
is
always worse than the Greenbook. The model can also explain cases
in which the FOMC performs better than the Greenbook; also the last
column in Table 1 shows that the model can capture the better accuracy of the FOMC
relative to the other public forecasts.
4.2 Forecast Accuracy and Optimal Weights
A natural question arises: is it optimal for the FOMC to incorporate the White House and SPF forecasts? Part of the answer can be seen in Table 1. The FOMC inflation forecast is worse than the Greenbook and therefore, if MSE forecast accuracy were the objective, the FOMC would have been better off by just adopting the Greenbook inflation forecast. However, the pooling of forecasts usually leads to an improved forecast but determining the optimal weights may not be straightforward.
An important step is to compare the weights actually used
![]() with the optimal weights. This comparison
allows one to analyze more carefully whether the FOMC reflects too
much or too little the non-Greenbook forecasts. Optimality here is
defined from a forecasting perspective, the weights that would
minimize the MSE of the FOMC forecast.
with the optimal weights. This comparison
allows one to analyze more carefully whether the FOMC reflects too
much or too little the non-Greenbook forecasts. Optimality here is
defined from a forecasting perspective, the weights that would
minimize the MSE of the FOMC forecast.
Table 6 reports the
optimal weights, which are directly comparable with the weights
![]() in Table 4. For all
cases except one, the weights on the non-Fed forecasts are larger
than the optimal ones. This result shows that for all variables -
inflation, unemployment, and real growth - publicly available
forecasts are overweighed. For instance, for inflation the weight
on the White House forecast is 0.25 whereas the optimal weight is
0.
in Table 4. For all
cases except one, the weights on the non-Fed forecasts are larger
than the optimal ones. This result shows that for all variables -
inflation, unemployment, and real growth - publicly available
forecasts are overweighed. For instance, for inflation the weight
on the White House forecast is 0.25 whereas the optimal weight is
0.
One possible reason for the overweight of the non-Greenbook forecasts relates to the institutional design of the FOMC. The FOMC is a plural body that is designed to represent a variety of views, and in that sense it is comforting to know that the difference between the FOMC and Greenbook is not noise, and instead reflects other public views. There are also other potential reasons based on forecasting grounds that I investigate below.
First, I investigate if the Greenbook was a poor forecast at the beginning of the sample, in which case the FOMC could have taken substantial time to learn that the Greenbook is accurate. Such patterns can occur in a model of learning as in Marcet and Sargent (1989) and Marcet and Nicolini (2003). Figure 4.2 shows the evolution over time of the optimal MSE weight - the recursive estimates using data up to the date in the horizontal axis.13 The figures show that the optimal weights on public forecasts vis-à-vis the Greenbook were always low or converged quite fast to a low number. Therefore, a potentially "bad start" of the Greenbook forecast does not seem to be the reason for overweighing public forecasts.
Table 6: Optimal Weights
| constant | W | S | ||
|---|---|---|---|---|
| Inflation: W | -0.2399 (0.1148) | -0.0062 (0.1816) | - | 0.8499 |
| Inflation: S | -0.1723 (0.1179) | - | -0.1611 (0.177) |
0.8434 |
| Unemployment: W | -0.1833 (0.076) | -0.1550 (0.1914) | - | 0.8083 |
| Unemployment: S | -0.1742 (0.0694) | - | 0.1235 (0.1666) | 0.8115 |
| Real Growth: W | 0.1164 (0.1525) | -0.0162 (0.1831) | - | 0.4382 |
| Real Growth: S | 0.1513 (0.1472) | - | 0.4176 (0.1995) | 0.4222 |
Notes: The table reports the weights that would be optimal to use in the full sample.
Second, I investigate if the forecasting literature advocates other approaches rather than using optimal MSE weights.14 Indeed, there are several approaches advocated, and fitting MSE weights is sometimes not recommended because of several arguments (e.g. Zarnowitz (1992), Clements and Hendry (1998, 2002) among others).
One reason is that forecasters or forecasts change their methods and views often; also the structure of the economy changes, and a good method for a time-period may not necessarily be valid for another time-period. Hence, the success of a particular forecast may be occasional and fortuitous or intuitive. And a particular's forecast record may not be reliable as a basis for inferences on how it will perform in the future. When no model coincides with a non-constant data generation process (DGP), Clements and Hendry (2002) show that averaging may then dominate over estimated weights in the combination.15
In results not shown, the optimal MSE weights do show some variability. While excluding the Volker disinflation alone does not lead to significant changes, there is increased uncertainty in the optimal MSE weights after 1990. Indeed, after 1990 the White House inflation forecast is slightly under-weighted. This literature and results suggest that there may be periods in which the FOMC forecast is superior or inferior to the Greenbook. And that ranking may largely depend on how perfect or imperfect other public forecasts and views are, as well their optimal weight, which is not easy to determine ex-ante.
The forecasting literature shows that there is a tension between using optimal MSE weights based on past record versus using equal weights among several forecasts. Both approaches have advantages and disadvantages, and can be defended or criticized accordingly. Interestingly, it seems that the weights characterizing the FOMC forecast are in between these two approaches. For five cases out of six, the weights shown in Table 4 are in between the optimal MSE weights shown in Table 6 and the equal weights of 0.5.16
Figure 1: Optimal Weights
![]() .
.
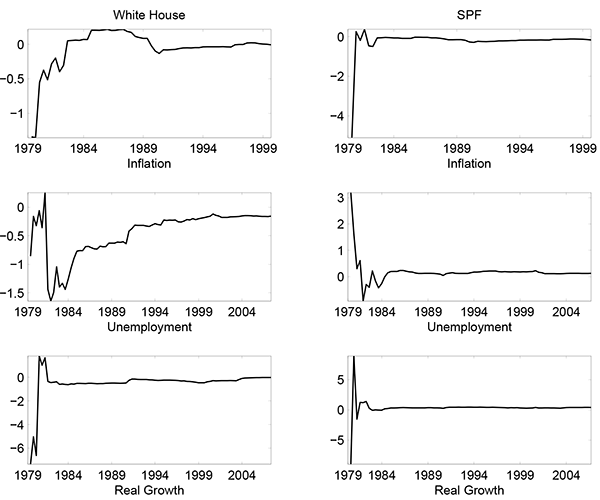
Notes: The figure plots the optimal weights in equations (1) - (2) using OLS. The graphs on the left and right refer to the White House and SPF forecasts, respectively.
4.3 Replication of Regressions Predicting Actual Values
This subsection examines whether the statistical model is able to capture some stylized facts in the literature. In order to determine the forecasting power of the FOMC relative to the Greenbook, the following regression is usually estimated:
| (3) |
where ![]() is the outcome. For inflation Romer and Romer (2008) find that the weight on
is the outcome. For inflation Romer and Romer (2008) find that the weight on ![]() is small or negative. For unemployment the same happens but to a
lesser extent, and for real growth the weights show that none of
the forecasts has a clear advantage.17
is small or negative. For unemployment the same happens but to a
lesser extent, and for real growth the weights show that none of
the forecasts has a clear advantage.17
Table 7 examines whether
the model can account for the findings of Romer and Romer (2008). The table displays their original
regression using the updated sample of this paper (first two rows
in the table). Then it substitutes the forecast ![]() by the forecast as predicted by the models (
by the forecast as predicted by the models (![]() ). The weights on
). The weights on ![]() and
and
![]() broadly replicate the patterns of the
weights on
broadly replicate the patterns of the
weights on ![]() and
and ![]() ; namely the
weight on
; namely the
weight on ![]() is small and lower than the
weight on
is small and lower than the
weight on ![]() .
.
Table 7: Role in Predicting Actual Values
| constant | G | Non-Staff | R2 | |
|---|---|---|---|---|
| Inflation: F OLS | -0.1822 (0.2501) | 1.0548 (0.4173) | -0.0668 (0.3986) | 0.8500 |
| Inflation: F WLS | -0.2216 (0.1635) | 1.3537 (0.3926) | -0.3322 (0.3791) | 0.8996 |
| Inflation: OLS | -0.1792 (0.2633) | 0.9969 (0.7496) | -0.0114 (0.744) | 0.8499 |
| Inflation: WLS | -0.2237 (0.1914) | 0.8828 (0.6355) | 0.1239 (0.6217) | 0.8956 |
| Inflation: OLS | 0.0011 (0.2964) | 1.8428 (0.8637) | -0.8723 (0.8754) | 0.8435 |
| Inflation: WLS | -0.0718 (0.222) | 1.7455 (0.5258) | -0.7516 (0.5386) | 0.8921 |
| Unemployment: F OLS | 0.1356 (0.335) | 0.9136 (0.3306) | 0.0390 (0.339) | 0.8048 |
| Unemployment: F WLS | 0.1236 (0.5701) | 0.7373 (0.478) | 0.2205 (0.4394) | 0.8324 |
| Unemployment: OLS | 0.3629 (0.3581) | 1.6987 (0.5048) | -0.7910 (0.5315) | 0.8099 |
| Unemployment: WLS | 0.3072 (0.5299) | 1.5402 (0.7774) | -0.6184 (0.7782) | 0.8312 |
| Unemployment: OLS | 0.3791 (0.3393) | 0.9312 (0.449) | -0.0222 (0.4706) | 0.8126 |
| Unemployment: WLS | 0.2801 (0.5358) | 0.8243 (0.5657) | 0.1039 (0.563) | 0.8277 |
| Real Growth: F OLS | 0.4970 (0.3235) | 0.2649 (0.4004) | 0.5728 (0.4316) | 0.4488 |
| Real Growth: F WLS | 0.5777 (0.4672) | 0.2432 (0.5349) | 0.5651 (0.5723) | 0.4829 |
| Real Growth: OLS | 0.9877 (0.3532) | 1.7340 (0.6494) | -1.0403 (0.7007) | 0.4517 |
| Real Growth: WLS | 0.9848 (0.5227) | 1.7001 (0.8988) | -1.0120 (0.9898) | 0.4833 |
| Real Growth: OLS | 0.7698 (0.4666) | 0.4539 (1.067) | 0.3196 (1.1695) | 0.4291 |
| Real Growth: WLS | 0.7576 (0.748) | 0.3857 (1.461) | 0.3867 (1.6435) | 0.4655 |
Notes: The table reports the estimates of equation
(3). All
the regressions include as dependent variable the actual outcome
and as independent variable the Greenbook forecast. The regressions
also include as independent variable either the FOMC forecast
(![]() ), the FOMC forecasts predicted by equations
(1) and
(2) (
), the FOMC forecasts predicted by equations
(1) and
(2) (
![]() and
and
![]() ).
).
5. Robustness
5.1 Extending the Inflation Regression and Sub-Sample Analysis
Because the Greenbook inflation forecast seems to be better than the other non-Fed forecasts, the results gain extra interest with respect to this variable. However, the change in definitions of the FOMC inflation forecast limited the analysis until July 1999, while for the other variables one can use all the data up to the five year lag of Greenbook confidentiality.
This section extends the inflation forecast in the following
way. Until 1999 one can use the definition of variables as before.
From February 2000 until February 2004, the variable ![]() refers to CPI and the variable
refers to CPI and the variable ![]() refers to PCE. From July 2004 onwards, the
variable
refers to PCE. From July 2004 onwards, the
variable ![]() refers to CPI and the variable
refers to CPI and the variable
![]() refers to PCE core. The spirit
of the regression is the same as before, but the definitions in the
independent and dependent variables do not match exactly. Table 8 shows that the
results largely hold in the extended sample, as well as from 2000
onwards only.
refers to PCE core. The spirit
of the regression is the same as before, but the definitions in the
independent and dependent variables do not match exactly. Table 8 shows that the
results largely hold in the extended sample, as well as from 2000
onwards only.
Table A.3 in the appendix examines sub-sample analysis and shows that the results still hold.
Table 8: Extending the Inflation Regression
| constant | W | S | R2 of (F-G) | R2 of F | |
|---|---|---|---|---|---|
| 1979-: W, OLS | 0.0636 (0.0275) | 0.2358 (0.0457) | - | 0.2428 | 0.9896 |
| 2000-: W, OLS | 0.0220 (0.0546) | 0.2190 (0.1077) | - | 0.1646 | 0.8752 |
| 1979-: S, OLS | 0.0460 (0.0313) | - | 0.2097 (0.049) | 0.1902 | 0.9874 |
| 2000-: S, OLS | 0.0041 (0.055) | - | 0.2370 (0.0986) | 0.2330 | 0.8554 |
Notes: The table reports the estimates with the inflation forecast for the extended sample. The first and third rows consider the sample from 1979 until the availability of the Greenbook. The second and fourth rows consider the sample after 2000 where the definitions of inflation do not coincide.
5.2. Results With Individual FOMC Responses
The statistical analysis presented so far employed the central tendency of the FOMC forecasts. The central tendency is less prone to extreme responses that may reflect some strategic behavior by some FOMC participants. I am not discarding strategic behavior at the individual level responses, what the results presented so far suggest is that the central tendency seems to be incorporate information from the White House and SPF forecasts.
This subsection uses the individual responses data described in Romer (2010). On the one hand, the individual responses are released only after a ten year lag and, therefore, are less interesting to analyze than the central tendency that is released immediately. On the other hand, the individual responses contain additional statistical information with sixteen to eighteen individual forecasts per MPR.
Table 9 reports the results of a panel data fixed effects regression where the individual elements are the Fed regional banks and the individual governors.18 The main results are still present. The coefficients attached with the non-Greenbook forecasts are statistically significant and are even larger than the values reported in Table 4. The larger coefficients in the panel data are largely explained by the sample period. Table A.4 in the appendix reports the central tendency regressions for the same sample period where one can observe that the coefficients become quite similar to the ones obtained in the panel data.
Table 9. Panel Data Regression Results
| W | S | R2 of (F-G) | |
|---|---|---|---|
| Inflation: W | 0.6651 (0.0481) | - | 0.3922 |
| Inflation: S | - | 0.4572 (0.0352) | 0.3796 |
| Unemployment: W | 0.4571 (0.0308) | - | 0.4557 |
| Unemployment: S | - | 0.4492 (0.0288) | 0.4888 |
| Real Growth: W | 0.3789 (0.0421) | - | 0.3210 |
| Real Growth: S | - | 0.3058 (0.0296) | 0.3721 |
Notes: The table reports the panel data estimates of equations (1) - (2). W and S denotes White House and SPF forecasts, respectively. The equations are estimated with fixed effects. Panel data Newey-West standard errors with three lags are reported.
6. Conclusion
This paper aimed at contributing to a better understanding of the forecasts that central banks produce and present to the public. The reliability of the forecasts that central banks present to the public and its representatives provides a strong pilar for transparent and accountable central banks as part of democratic societies.
This paper focuses on the United States given the amount of data that is available. The Greenbook forecast is produced just before the official forecast is released, but is kept private for five years; using the Greenbook forecast as a control is crucial for the analysis. Also, for the United States one can rely on a large amount of forecasts representing other views in the economy.
I find that the FOMC forecast does not discard the Greenbook forecast, in fact the weight given to the Greenbook is large. In addition, the difference between the FOMC and the Greenbook forecast is not random or white noise. I find that the FOMC also takes into account, or reflects, forecasts and views of the public and relevant institutions. The statistical model can capture several characteristics of the forecasts in terms of accuracy and their relative ranking. For instance, the model captures that the FOMC forecast does not always improve relative to the Greenbook, but remains the best forecast among the set of forecasts that are published immediately.
This paper opens avenues for future research questions regarding the underlying motivations of the FOMC because several possible explanations are observationally equivalent. This paper focused first in examining whether certain results are or are not present. Having said that, two key explanations are consistent with the results that I find in this paper.
First, the FOMC is institutionally designed to reflect or represent a variety of views in the economy. The finding that the FOMC incorporates views from the general public and its representatives is consistent with its mandate. Some may have preferred that officially published central bank forecasts resemble more heavily or rely on their internal forecasts and methods. Others may find comfort that public views, regardless of how perfect or imperfect they may be, play a role in institutions that are designed to represent and serve the public.
Second, the forecasting literature recommends pooling different forecasts and views. Practice and theory suggest that combining forecasts adds value, and can even dominate the best individual forecast. However, determining in real-time the weights to attribute to each forecast is not straightforward. The literature recommends using optimal weights from a MSE perspective or using equal weights for relevant forecasts. Both approaches can be defended or criticized. The weights obtained in this paper seem to be in between those two approaches.
References
Banternghansa, Chanont and Michael W. McCracken (2009). "Forecast disagreement among FOMC members." Working Papers 2009-059, Federal Reserve Bank of St. Louis.
Clements, Michael P. and David F. Hendry (1998). Forecasting Economic Time Series. Cambridge, Cambridge University Press.
Clements, Michael P. and David F. Hendry (2002). "Pooling of Forecasts." Econometrics Journal, 5, 1-26.
Ellison, Martin and Tom Sargent (2012). "A defence of the FOMC." International Economic Review, forthcoming.
Faust, Jon and Jonathan H. Wright (2009). "Comparing Greenbook and Reduced Form Forecasts Using a Large Realtime Dataset." Journal of Business & Economic Statistics, 27(4), 468-479.
Greene, William H. (2000). Econometric Analysis. Prentice Hall. Hansen, L.P. and T.J. Sargent (2008). Robustness. Princeton, New Jersey, Princeton University Press.
Marcet, Albert and J.P. Nicolini (2003). "Recurrent Hyperinflations and Learning." American Economic Review, 93 (5), 1476-1498.
Marcet, Albert and T.J. Sargent (1989). "Convergence of Least-Squares Learning mechanisms in Self-Referential Linear Stochastic Models." Journal of Economic Theory, 48, 337-368.
Meade, Ellen E and D Nathan Sheets (2005). "Regional Influences on FOMC Voting Patterns." Journal of Money, Credit and Banking, 37(4), 661-77.
Reddy, Sudeep (2008). "The Economy: Bernanke Open to a Sizable Rate Cut - Job and Housing Markets May Worsen, Posing Risks To Growth, Fed Chief Says." The Wall Street Journal, 15 February 2008.
Reifschneider, David and Peter Tulip (2007). "Gauging the uncertainty of the economic outlook from historical forecasting errors." Finance and economics discussion series, Board of Governors of the Federal Reserve System (U.S.).
Romer, Christina D. and David H. Romer (2000). "Federal Reserve Information and the Behavior of Interest Rates." American Economic Review, 90(3), 429-457.
Romer, Christina D. and David H. Romer (2008). "The FOMC versus the Staff: Where Can Monetary Policymakers Add Value?" American Economic Review, 98(2), 230-35.
Romer, David (2010). "A New Data Set on Monetary Policy: The Economic Forecasts of Individual Members of the FOMC." Journal of Money, Credit and Banking, 42(5), 951-957.
Svensson, Lars E. O. (1997). "Inflation forecast targeting: Implementing and monitoring inflation targets." European Economic Review, 41(6), 1111-1146.
Svensson, Lars E. O. (1999). "Inflation targeting as a monetary policy rule." Journal of Monetary Economics, 43(3), 607-654.
Tootell, Geoffrey M. B. (1999). "Whose monetary policy is it anyway?" Journal of Monetary Economics, 43(1), 217-235.
Wald, Abraham (1940). "The Fitting of Straight Lines if Both Variables are Subject to Error." The Annals of Mathematical Statistics, 11(3), pp. 284-300.
Zarnowitz, Victor (1992). "Has Macro-Forecasting Failed?" Cato Journal, 12, 129-164.
Appendix:
A.1 Standard Deviations
Table A.1. Standard Deviations of Forecast Differences
| | | | |
|---|---|---|---|
| Inflation | 0.2858 | 0.5878 | 0.5990 |
| Unemp. | 0.2192 | 0.4136 | 0.3757 |
| Real Growth | 0.3604 | 0.7357 | 0.8032 |
Notes: The table reports the standard
deviations of ![]() ,
, ![]() ,
,
![]() .
. ![]() ,
, ![]() ,
and
,
and ![]() denote the FOMC, White House, and SPF
forecasts, respectively.
denote the FOMC, White House, and SPF
forecasts, respectively.
A.2. Optimal Weights
Figure A.1. Optimal Weights
![]() .
.
Notes: The figure plots the optimal
weights in equations (1) - (2), but the
constant is eliminated from the regression and the coefficient
![]() is limited to be between zero and one. The
graphs on the left and right refer to the White House and SPF
forecasts, respectively.
is limited to be between zero and one. The
graphs on the left and right refer to the White House and SPF
forecasts, respectively.
A.3 Role in predicting actual values
Table A.2. Role in Predicting Actual Values
| constant | G | Non-Staff | R2 | |
|---|---|---|---|---|
Inflation: F, OLS | -0.1822 (0.2501) | 1.0548 (0.4173) | -0.0668 (0.3986) | 0.8500 |
| Inflation: F, WLS | -0.2216 (0.1635) | 1.3537 (0.3926) | -0.3322 (0.3791) | 0.8996 |
Inflation: W, OLS | -0.1801 (0.251) | 0.9883 (0.1948) | -0.0028 (0.1835) | 0.8499 |
| Inflation: W, WLS | -0.2140 (0.1729) | 0.9755 (0.1735) | 0.0312 (0.1566) | 0.8956 |
Inflation: S, OLS | -0.0485 (0.2723) | 1.1531 (0.1789) | -0.1826 (0.1832) | 0.8435 |
| Inflation: S, WLS | -0.1051 (0.2062) | 1.1757 (0.122) | -0.1819 (0.1303) | 0.8921 |
Unemployment: F, OLS | 0.1356 (0.335) | 0.9136 (0.3306) | 0.0390 (0.339) | 0.8048 |
| Unemployment: F, WLS | 0.1236 (0.5701) | 0.7373 (0.478) | 0.2205 (0.4394) | 0.8324 |
Unemployment: W, OLS | 0.3689 (0.3598) | 1.2331 (0.1962) | -0.3254 (0.2186) | 0.8099 |
| Unemployment: W, WLS | 0.3075 (0.5299) | 1.1708 (0.3205) | -0.2490 (0.3133) | 0.8312 |
Unemployment: S, OLS | 0.3797 (0.3442) | 0.9176 (0.1667) | -0.0087 (0.1834) | 0.8126 |
| Unemployment: S, WLS | 0.2774 (0.5366) | 0.8878 (0.2328) | 0.0403 (0.2185) | 0.8277 |
Real Growth: F, OLS | 0.4970 (0.3235) | 0.2649 (0.4004) | 0.5728 (0.4316) | 0.4488 |
| Real Growth: F, WLS | 0.5777 (0.4672) | 0.2432 (0.5349) | 0.5651 (0.5723) | 0.4829 |
Real Growth: W, OLS | 0.9872 (0.353) | 1.0000 (0.1766) | -0.3063 (0.2063) | 0.4517 |
| Real Growth: W, WLS | 0.9869 (0.524) | 0.9859 (0.2307) | -0.2978 (0.2912) | 0.4833 |
Real Growth: S, OLS | 0.7832 (0.4301) | 0.6934 (0.2101) | 0.0800 (0.2929) | 0.4291 |
| Real Growth: S, WLS | 0.7718 (0.6989) | 0.6792 (0.2438) | 0.0932(0.396) | 0.4655 |
Notes: The table reports the estimates of equation
(3). All
the regressions include as dependent variable the actual outcome
and as independent variable the Greenbook forecast. The regressions
also include as independent variable either the forecasts of the
FOMC (![]() ), the White House (
), the White House (![]() ), or the
SPF (
), or the
SPF (![]() ).
).
A.4. Sub-Sample Analysis
Table A.3a. Regression Results: Sub-Sample Analysis: After 1985
| constant | W | S | R2of (F-G) | R2of F | |
|---|---|---|---|---|---|
| Inflation: W, OLS | 0.0054 (0.0279) | 0.3341 (0.0771) | - | 0.3197 | 0.9470 |
| Inflation: W, WLS | 0.0070 (0.0356) | 0.3531 (0.0993) | - | 0.3242 | 0.9468 |
| Inflation: S, OLS | -0.0577 (0.0323) | - | 0.3729 (0.0837) | 0.3317 | 0.9513 |
| Inflation: S, WLS | -0.0632 (0.0315) | - | 0.3858 (0.0807) | 0.3410 | 0.9513 |
| Unemployment: W, OLS | -0.0155 (0.0193) | 0.4641 (0.0577) | - | 0.5065 | 0.9720 |
| Unemployment: W, WLS | -0.0110 (0.0259) | 0.4507 (0.0876) | - | 0.4865 | 0.9717 |
| Unemployment: S, OLS | -0.0317 (0.0178) | - | 0.4995 (0.0541) | 0.5827 | 0.9745 |
| Unemployment: S, WLS | -0.0294 (0.0227) | - | 0.4989 (0.0766) | 0.5780 | 0.9745 |
| Real Growth: W, OLS | 0.0062 (0.03) | 0.3099 (0.0481) | - | 0.3973 | 0.9055 |
| Real Growth: W, WLS | 0.0064 (0.0455) | 0.3074 (0.0514) | - | 0.3871 | 0.9056 |
| Real Growth: S, OLS | 0.0218 (0.0273) | - | 0.3977 (0.0486) | 0.5228 | 0.9240 |
| Real Growth: S, WLS | 0.0080 (0.0335) | - | 0.3893 (0.0504) | 0.5431 | 0.9242 |
Table A.3b. Regression Results: Sub-Sample Analysis: After 1990
| constant | W | S | R2of (F-G) | R2of F | |
|---|---|---|---|---|---|
| Inflation: W, OLS | -0.0248 (0.0328) | 0.4852 (0.1334) | - | 0.3461 | 0.9270 |
| Inflation: W, WLS | -0.0186 (0.0334) | 0.4856 (0.1307) | - | 0.3529 | 0.9270 |
| Inflation: S, OLS | -0.0628 (0.0378) | - | 0.2958 (0.0887) | 0.3081 | 0.9288 |
| Inflation: S, WLS | -0.0708 (0.0355) | - | 0.2965 (0.0883) | 0.3124 | 0.9288 |
| Unemployment: W, OLS | -0.0289 (0.0224) | 0.5147 (0.0702) | - | 0.5285 | 0.9730 |
| Unemployment: W, WLS | -0.0249 (0.0302) | 0.4971 (0.0942) | - | 0.5128 | 0.9725 |
| Unemployment: S, OLS | -0.0093 (0.0205) | - | 0.5293 (0.0592) | 0.6347 | 0.9813 |
| Unemployment: S, WLS | -0.0097 (0.0279) | - | 0.5229 (0.086) | 0.6229 | 0.9812 |
| Real Growth: W, OLS | 0.0690 (0.0355) | 0.4266 (0.0619) | - | 0.4972 | 0.9136 |
| Real Growth: W, WLS | 0.0763 (0.05) | 0.4297 (0.0587) | - | 0.5113 | 0.9135 |
| Real Growth: S, OLS | 0.0306 (0.0331) | - | 0.4187 (0.0541) | 0.5653 | 0.9264 |
| Real Growth: S, WLS | 0.0182 (0.0402) | - | 0.4043 (0.059) | 0.5731 | 0.9266 |
Notes: The table reports the estimates of equations (1) - (2). W and S denotes White House and SPF forecasts, respectively. The equations are estimated both with OLS and WLS. Newey-West standard errors with three lags are reported in the WLS regression. The upper panel only includes the sample after 1985, the lower panel includes the sample after 1990.
Table A.4. Regression Results: Sub-Sample Coinciding with Panel Data
| constant | W | S | R2of (F-G) | R2of F | |
|---|---|---|---|---|---|
| Inflation: W, OLS | -0.0045 (0.0264) | 0.6377 (0.1082) | - | 0.6124 | 0.9319 |
| Inflation: W, WLS | -0.0076 (0.031) | 0.6109 (0.0798) | - | 0.5901 | 0.9324 |
| Inflation: S, OLS | -0.0498 (0.0326) | - | 0.4093 (0.0865) | 0.5043 | 0.9147 |
| Inflation: S, WLS | -0.0705 (0.0286) | - | 0.4181 (0.0824) | 0.5257 | 0.9143 |
| Unemployment: W, OLS | -0.0673 (0.0267) | 0.4795 (0.0716) | - | 0.6158 | 0.9812 |
| Unemployment: W, WLS | -0.0663 (0.0343) | 0.4779 (0.0949) | - | 0.6209 | 0.9812 |
| Unemployment: S, OLS | -0.0390 (0.0243) | - | 0.4754 (0.0606) | 0.6875 | 0.9857 |
| Unemployment: S, WLS | -0.0420 (0.0301) | - | 0.4894 (0.087) | 0.7292 | 0.9859 |
| Real Growth: W, OLS | 0.1249 (0.0414) | 0.3711 (0.1066) | - | 0.3023 | 0.8782 |
| Real Growth: W, WLS | 0.1366 (0.0501) | 0.3972 (0.0725) | - | 0.3660 | 0.8759 |
| Real Growth: S, OLS | 0.0945 (0.0401) | - | 0.2752 (0.0701) | 0.3550 | 0.8841 |
| Real Growth: S, WLS | 0.0887 (0.0436) | - | 0.2733 (0.0574) | 0.3494 | 0.8843 |
Notes: The table reports the estimates of equations (1) - (2). W and S denotes White House and SPF forecasts, respectively. The equations are estimated both with OLS and WLS. Newey-West standard errors with three lags are reported in the WLS regression. The sample goes from 1992 to 2001.
Footnotes
† Acknowledgments: I am grateful to Isabel Correia, Martin Ellison, Neil Ericsson, Jon Faust, Jordi Gali, Luca Guerrieri, Chris Gust, Thomas Laubach, Jesper Linde, David Lopez-Salido, Albert Marcet, Caterina Mendicino, David Reifshneider, John Rogers, Pedro Teles, seminar participants at the University of Oxford, Federal Reserve Board, Universidade Catolica Portuguesa, Bank of Portugal, and several economists at the Federal Reserve Board for comments. John Weber, Walker Ray, and Erica Reisman provided superb research assistance. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with teh Federal Reserve System. Email: [email protected]. Return to text
1. The Greenbook has recently been merged with the Bluebook and relabeled "Tealbook". For convenience, I will continue to use the term Greenbook throughout this paper. Return to text
2. See the Federal Reserve Act, Section 4, Article 10, 11, 12 and Section 10, Article 1. Return to text
3. The initial inflation definition was GNP inflation, in February 1989 changed to CPI, in February 2000 changed to personal consumption expenditures (PCE), in July 2004 changed to core PCE, and after February 2008 changed to both PCE and core PCE. The initial real growth definition was GNP, in February 1992 changed to GDP. The unemployment definition did not change. Return to text
4. The MPRs are available at http://fraser.stlouisfed.org/historicaldocs/680/. After 2000 explicit comparisons are no longer present, as the definitions of variables being forecasted by the White House and FOMC no longer coincides exactly. A later section shows that the results still hold after 2000. Return to text
5. These forecasts gather inputs from the Council of Economic Advisors, Department of the Treasury, Office of Management and Budget, and also from the Department of Commerce (Bureau of Economic Analysis and Economics and Statistics Administration), and the Department of Labor (Bureau of Labor Statistics). Return to text
6. Unfortunately, the budget documents do not contain PCE inflation, the definition of the FOMC after 2000 as explained in footnote 3. Return to text
7. The corresponding MPR is dated 27 February 2008; the reader is referred to The Wall Street Journal article Reddy (2008). Return to text
8. In the SPF, PCE and core PCE inflation are only available after 2007, which does not allow to match the definitions of the FOMC immediately after 2000 as explained in footnote 3. Return to text
9. This timing always allows the participants to have access to the advance report of the Bureau of Economic Analysis. Return to text
10. The studies examining the accuracy of different forecasts try to use forecasts formed at roughly the same time period. That treatment of timings can be problematic for the current study. Taking as an example the February FOMC meetings, if I used the SPF forecasts formed in the first quarter of the year rather than the last quarter of the previous year, the SPF participants could already have access to the FOMC forecasts and blur the results. Return to text
11. This result is still consistent with the FOMC forecasts (and monetary policy actions) influencing the SPF forecasts at a later date. Return to text
12. The results are also robust to running the regression when the number of groups equals the number of observations, in which case the instrumental variable is the ranking of the observations. Return to text
13. The
appendix shows the figures where the constant is omitted from the
regressions and the weight ![]() is restricted to be
between 0 and 1. The results are similar. Return to text
is restricted to be
between 0 and 1. The results are similar. Return to text
14. Excluding the constant or minimizing the MSE in the 10% largest errors leads to the same conclusions. Return to text
15. Another reason relates to herding, where forecasters try not to differ too much among themselves. The Greenbook is the only forecast that cannot be made available in real-time. Accordingly, the FOMC forecast may attach less weight to the Greenbook than to public forecasts based on a herding motive. Return to text
16. A later section shows the results when combining more than two forecasts. Return to text
17. Table A.2 in the appendix
reproduces these results for the updated sample used here. The
table also shows the results of the same regressions with
![]() and
and ![]() or
or ![]() and
and ![]() , which confirms the limited usefulness of
, which confirms the limited usefulness of
![]() and
and ![]() . Return to text
. Return to text
18. This panel is unbalanced because there is turnover among governors. The results are very similar when the group of governors is treated as a cluster. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text