
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1091, November 2013 --- Screen Reader
Version*
Portfolio Diversification and the Cross-Sectional Distribution of Foreign Investment
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
In this paper I explore the role of portfolio diversification in explaining the distribution of foreign investment across countries. I capture the portfolio diversification motive by a measure of country-specific riskiness, "covariance risk", which I construct as how countries' growth rates covary with the stochastic discount factor of a representative international investor. My key new empirical finding is a strong and significant correlation between this new measure of country riskiness and foreign investment allocations. Less risky countries, i.e. countries whose growth rates are more highly correlated with the investor's stochastic discount factor, receive larger investment shares than more risky countries. I interpret this result as evidence that investors do take into account diversification opportunities, not only for portfolio investment decisions, but also for foreign direct investment decisions. My empirical results confirm the theoretical predictions of standard portfolio allocation models.
Keywords: Foreign direct investment, global risk, international portfolio choice, portfolio diversification
JEL classification: F21, F34, F41, G11
1 Introduction
This paper contributes to the literature on the determinants of foreign investment by considering the role of portfolio diversification. Unlike the literature on portfolio investment, the literature on foreign direct investment (FDI) does not explore the portfolio selection motive behind investors' decisions. The literature on FDI looks at the cross-sectional distribution of investment as the result of investors evaluating countries on their individual merits. Real-world evidence, however, suggests that multinational corporations (MNCs) take diversification opportunities into account when making investment decisions. For example, in the last year the Wall Street Journal documented the experience of several MNCs such as HSBC, Banco Santander and Tesco PLC that benefited from regional diversification, especially in the current economic downturn.
My objective is to explore the role of diversification in the cross-sectional distribution of total foreign investment, which includes FDI as well as portfolio investment. To do so I extend the existing analyses of the determinants of foreign investment by adopting a portfolio allocation approach to risk. I capture the portfolio diversification motive by a measure of country-specific riskiness, which I refer to as "covariance risk". I construct this measure as how countries' growth rates covary with the stochastic discount factor (SDF) of a representative international investor. The idea is to capture the extent to which investments in a foreign economy provide a hedge against the investor's overall risk.
I find evidence that investors do take into account diversification opportunities. My key new finding is that less risky countries, i.e. countries whose growth rates are more highly correlated with the investor's SDF, receive larger investment shares than more risky countries. This result has both statistical as well as strong economic significance. For example, if a country's riskiness declines from the 25th percentile to the 75th percentile, on average the total foreign investment per capita increases by more than 135%.
My approach allows me to study the role of portfolio diversification in the distribution of foreign investment in general and across a large sample of countries that includes low-income countries. First, I look at total foreign investment that includes both FDI and portfolio investment. The role of diversification has been studied for portfolio investment allocations, but not for FDI allocations. It is important to explore FDI allocations because the data shows that FDI is the main component of foreign investment for the majority of countries. Portfolio investment constitutes a significant share of total foreign investment only for high-income countries, while for the majority of low- and middle-income countries FDI is more than 90 percent of total foreign investment. Second, my measure of covariance risk that captures the investors' diversification motive is available for 104 countries. In contrast, the empirical literature on portfolio investment usually uses stock market return correlations, which limits the country coverage to countries with well developed stock markets and reliable stock market data.
I study the role of portfolio diversification in the distribution of foreign investment using both a theoretical and an empirical approach. In the theoretical motivation I show that the share of investment a foreign economy receives is a decreasing function of the covariance of its returns with the returns of the investor's domestic economy. This covariance of returns captures the idea of diversification in the model. I use a standard portfolio allocation model based on Merton (1969, 1971) and incorporate elements that have been used in the literature (see for example Kraay and Ventura (2000); Kraay et al. (2005); Asiedu et al. (2009); Coeurdacier and Guibaud (2010)), but have either been studied separately or have not been thoroughly explored. This allows for a general theoretical framework of allocation of foreign investment that includes both FDI and portfolio investment.
Next, I test whether this theoretical prediction finds support in the data. In my empirical investigation I capture the portfolio diversification motive by a new measure of country-specific riskiness: "covariance risk". This measure is constructed in Burnside and Tabova (2009) as the covariance between countries' growth rates and a measure of global risk that is a proxy for the stochastic discount factor (SDF) of a representative international investor. The approach is analogous to the two-pass regression method used in empirical finance to explain cross-sectional variation in expected returns across portfolios, with country growth rates replacing portfolio returns in the regressions. The first step is to obtain country-specific exposures to global risk factors. The risk factors are: the US real GDP growth, the US real interest rate, the change in the relative prices of oil, metals, and agricultural commodities, and the US stock market excess return. The second step is to obtain the cost of risk by regressing average growth rates on the estimated exposures to the risk factors. Using this approach Burnside and Tabova (2009) construct a measure of global risk that is a proxy for the global investor's SDF. All relevant information about a country's exposure to global risk factors can be summarized in the covariance between its growth rate and this proxy SDF. This single variable is my covariance risk measure. Countries with higher values of this measure are less risky because their growth rates are more highly correlated with the stochastic discount factor.
For the empirical analysis I use two measures of foreign investment: (i) the stock of FDI originating from the US; and (ii) the stock of total FDI and portfolio investment, adjusted for valuation effects (see Lane and Milesi-Ferretti, 2009).
My key empirical finding is a strong and significant correlation between my measure of country riskiness and the foreign investment allocations across countries. Riskier countries receive smaller shares of FDI originating from the US than less risky countries. Riskier countries also attract less total FDI and portfolio investment. The results show that the diversification motive, captured by countries' riskiness, has statistical as well as strong economic significance. In my analysis I control for factors that the existing literature has identified as important determinants of investment allocations, including expropriation risk (see Asiedu et al., 2009; and Blonigen, 2005 for an extensive overview of the empirical literature). The results are also robust when I use an estimation procedure that accounts for the fact that the measure of covariance risk is a generated regressor.
The results of the paper suggest that mitigation of covariance risk has the potential to make countries more attractive for foreign investment. This has important implications especially for developing countries where foreign investment finances development projects and is crucial in bridging the gap between domestic savings and investment needs.
The rest of the paper is organized as follows. Section 2 introduces the theoretical model that links foreign investment to covariance risk. Section 3 describes the data and variables used in the empirical analysis. It provides the details of how the new measure of covariance risk is constructed. Section 4 describes the empirical methodology and presents the main results and robustness checks. Section 5 outlines the policy implications and concludes.
2 A Model of Foreign Investment and Portfolio Diversification
I use a portfolio allocation approach to model the role of portfolio diversification in the distribution of foreign investment. The model is based on Merton (1969, 1971). It relates closely to Kraay and Ventura (2000) and Kraay et al. (2005) who use portfolio selection models to examine classical questions in international economics. In the model a representative investor chooses how to distribute his/her capital stock among the domestic economy, (N-1) foreign economies, and a riskless asset. The representative investor's lifetime utility is:
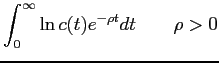
|
(1) |
where ![]() is consumption and
is consumption and ![]() is the
rate of time preference (
is the
rate of time preference (![]() ). Capital is the only
factor of production and there is a single good that can be used
for consumption and investment. To simplify the exposition, I
assume that capital does not depreciate over time. The production
function is linear in the capital stock in all economies. The
stochastic rate of return for the domestic and foreign economies
is:
). Capital is the only
factor of production and there is a single good that can be used
for consumption and investment. To simplify the exposition, I
assume that capital does not depreciate over time. The production
function is linear in the capital stock in all economies. The
stochastic rate of return for the domestic and foreign economies
is:
![$ \mathbf{R} = \left[ \begin{array}{c} R_P \ \mathbf{R_F} \end{array} \right] \qquad \textrm{ is the vector of mean returns in the domestic} (R_P) \textrm{and foreign economies} (R_F)$](img8.gif)
![$ \mathbf{\Sigma} = \left[ \begin{array}{cc} \sigma^2_{P} & \omega'\ \omega & \Sigma_{F} \end{array} \right] \qquad \textrm{is the covariance matrix of returns}$](img9.gif)
![]() is the variance of the domestic
economy's returns,
is the variance of the domestic
economy's returns,
![]() is the vector of covariances
of the foreign economies' returns with the domestic economy's
returns,
is the vector of covariances
of the foreign economies' returns with the domestic economy's
returns,
![]() is the covariance matrix of
the foreign economies' returns,
is the covariance matrix of
the foreign economies' returns,
![]() is the vector of Wiener
processes. Since contracts across borders cannot be enforced, the
international investor faces the risk that the host country may
either expropriate or unilaterally modify the contract governing
the investment. The probability of expropriation is captured by the
term
is the vector of Wiener
processes. Since contracts across borders cannot be enforced, the
international investor faces the risk that the host country may
either expropriate or unilaterally modify the contract governing
the investment. The probability of expropriation is captured by the
term ![]() , which is a Poisson process.1 In this
formulation the threat of expropriation is exogenous from the
investor's point of view. This is analogous to the set-up in the
theoretical literature on the role of expropriation where although
the decision of expropriation is endogenously determined by the
recipient country, it is taken as given by the international
investor (Eaton and Gersovitz, 1984).2 If expropriation occurs
the entire output accrues to the host country and the
representative investor does not invest in this country in the
future. This assumption is standard in the literature.
, which is a Poisson process.1 In this
formulation the threat of expropriation is exogenous from the
investor's point of view. This is analogous to the set-up in the
theoretical literature on the role of expropriation where although
the decision of expropriation is endogenously determined by the
recipient country, it is taken as given by the international
investor (Eaton and Gersovitz, 1984).2 If expropriation occurs
the entire output accrues to the host country and the
representative investor does not invest in this country in the
future. This assumption is standard in the literature.
Denote by ![]() the aggregate capital stock. Let
the aggregate capital stock. Let
![]() be the share invested in the domestic
economy,
be the share invested in the domestic
economy,
![]() : the vector of shares
invested in foreign economies. Then the fraction employed in the
riskless activity,
: the vector of shares
invested in foreign economies. Then the fraction employed in the
riskless activity, ![]() , is:
, is:
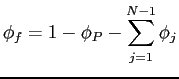
The investor's budget constraint can be expressed as follows:
![$\displaystyle dk\, =\, \Big[ \{ \phi'(R\,-\, r^f \iota) \,+\, r^f \} \,k \,-\, c \Big]\,dt \,+\, k \, \phi'\, \Sigma^{1/2}\,dz - k \, \phi'\, dq$](img20.gif)
|
(2) |
where
![]() . The budget
constraint illustrates the trade-off between risk and return that
underlies investment decisions. To determine the optimal
consumption and capital allocation rules the representative
investor maximizes his/her lifetime utility subject to the budget
constraint. The optimization problem is:
. The budget
constraint illustrates the trade-off between risk and return that
underlies investment decisions. To determine the optimal
consumption and capital allocation rules the representative
investor maximizes his/her lifetime utility subject to the budget
constraint. The optimization problem is:
![$\displaystyle max_{\{c,\mathbf{\phi}\}}\Big\{\, ln(c) \,+\, \frac{\partial J}{\partial k} \, \Big[ \{ \phi'(R\,-\,r^f \mathbf{\iota}) \,+\, r^f \} \,k \,-\, c \Big] + {}$](img24.gif)
|
|||
![$\displaystyle {} + \, \frac{1}{2} \frac{\partial^2 J}{\partial k^2} \, k^2 [\phi'\, \Sigma \, \phi] \,+\, \alpha'[J(k^d)\,- \,{J}(k) \iota] \Big\}$](img25.gif)
|
(3) |
where ![]() is the capital stock in the event of
expropriation,
is the capital stock in the event of
expropriation,
![]() is the vector of
probabilities of expropriation. Throughout I impose the usual
transversality condition and assume that the investor's holdings of
capital in all economies are nonnegative.3 In this framework closed
form solutions for the portfolio allocations are obtained.4 The
optimal consumption rule is:
is the vector of
probabilities of expropriation. Throughout I impose the usual
transversality condition and assume that the investor's holdings of
capital in all economies are nonnegative.3 In this framework closed
form solutions for the portfolio allocations are obtained.4 The
optimal consumption rule is:
| (4) |
The optimal investment shares are:
| (5) |
| (6) |
where ![]() is a diagonal matrix with the
capital shares
is a diagonal matrix with the
capital shares
![]() on the diagonal. Equations
(4),(5), and (6) show that both the consumption-capital ratio and
the fractions of capital employed in the foreign economies are
constant. Equation (4) states that consumption depends only on the
aggregate stock of capital. For the special case of logarithmic
utility that I use here, the consumption decision is independent of
the expected return or the variances and covariances of the
economies' returns. Equations (5) and (6) state that the
international investor behaves as a mean-variance investor. For
example, the share of capital invested in each foreign economy
equals its expected excess return relative to its variance and
covariance and corrected for the risk of expropriation. For
constant relative risk aversion utility the investment decision is
independent of the consumption decision (Samuelson, 1969 and
Merton, 1969).5 6
on the diagonal. Equations
(4),(5), and (6) show that both the consumption-capital ratio and
the fractions of capital employed in the foreign economies are
constant. Equation (4) states that consumption depends only on the
aggregate stock of capital. For the special case of logarithmic
utility that I use here, the consumption decision is independent of
the expected return or the variances and covariances of the
economies' returns. Equations (5) and (6) state that the
international investor behaves as a mean-variance investor. For
example, the share of capital invested in each foreign economy
equals its expected excess return relative to its variance and
covariance and corrected for the risk of expropriation. For
constant relative risk aversion utility the investment decision is
independent of the consumption decision (Samuelson, 1969 and
Merton, 1969).5 6
Denote by ![]() the covariance between foreign
economy
the covariance between foreign
economy ![]() and the domestic economy, and by
and the domestic economy, and by
![]() the share of investment in the foreign
country
the share of investment in the foreign
country ![]() . I interpret
. I interpret
![]() as the measure of country i's
covariance risk. Then the role of county i's covariance risk on the
share of foreign investment it receives can be expressed as:
as the measure of country i's
covariance risk. Then the role of county i's covariance risk on the
share of foreign investment it receives can be expressed as:
![$\displaystyle \frac{\partial \, \phi_i}{\partial \, \omega_i}\, = \, \frac{-\, \phi_P \, (\mathbf{\Sigma_F}^{-1})_{ii} \,-\, \frac{\partial \, \phi_P}{\partial \, \omega_i}\, [\mathbf{(\Sigma_F}^{-1})_{i~}\, \omega]}{\mathbf{\alpha_i \, (1-\phi_i)^{-2}\,(\Sigma_F}^{-1})_{ii} + \, 1}$](img38.gif)
|
(7) |
where
![]() is
the
is
the
![]() coefficient on the diagonal of
matrix
coefficient on the diagonal of
matrix
![]() ;
;
![]() is the
is the
![]() row of matrix
row of matrix
![]() . In the model this derivative
captures the role of portfolio diversification in the distribution
of foreign investment. The first term of the numerator, i.e.
. In the model this derivative
captures the role of portfolio diversification in the distribution
of foreign investment. The first term of the numerator, i.e.
![]() , and
the denominator are positive, so the sign of the derivative depends
on the sensitivity of the share of investment in the domestic
economy to its covariance with the foreign economies. To evaluate
the sign of the derivative I use two approaches. First, I follow
the literature on "home bias" that allows me to analytically sign
the derivative. Second, I use numerical evaluation. In both cases I
find that the derivative is strictly negative: the share of foreign
investment is decreasing in its covariance with the domestic
economy.
, and
the denominator are positive, so the sign of the derivative depends
on the sensitivity of the share of investment in the domestic
economy to its covariance with the foreign economies. To evaluate
the sign of the derivative I use two approaches. First, I follow
the literature on "home bias" that allows me to analytically sign
the derivative. Second, I use numerical evaluation. In both cases I
find that the derivative is strictly negative: the share of foreign
investment is decreasing in its covariance with the domestic
economy.
First, equation (7) shows that the share of foreign investment
is decreasing in the covariance,
![]() ,
if the share of investment in the domestic economy is not sensitive
to its covariance with the foreign economies, i.e. when
,
if the share of investment in the domestic economy is not sensitive
to its covariance with the foreign economies, i.e. when
![]() .
The literature on "home bias" provides a reason why this might be
the case. I follow this literature and introduce an investment
constraint that states that the share of capital invested in the
domestic economy must exceed a certain threshold; this restriction
is binding (see for example Coeurdacier and Guibaud, 2010):
.
The literature on "home bias" provides a reason why this might be
the case. I follow this literature and introduce an investment
constraint that states that the share of capital invested in the
domestic economy must exceed a certain threshold; this restriction
is binding (see for example Coeurdacier and Guibaud, 2010):
where ![]() is the optimal share for the
unconstrained problem and
is the optimal share for the
unconstrained problem and
![]() is fixed. This type of
restriction reflects both regulatory constraints faced by investors
as well as risk management practices of MNCs or institutional
investors. Since the constraint is binding, the investor is forced
to invest more in its economy than it is optimal under the
unconstrained problem. The portfolio constraint forces a "home
bias": a widely documented and studied phenomenon in the
literature on international portfolio allocations. The constraint
limits the investor's portfolio choice by fixing the share of
investment in the domestic economy. Therefore:
is fixed. This type of
restriction reflects both regulatory constraints faced by investors
as well as risk management practices of MNCs or institutional
investors. Since the constraint is binding, the investor is forced
to invest more in its economy than it is optimal under the
unconstrained problem. The portfolio constraint forces a "home
bias": a widely documented and studied phenomenon in the
literature on international portfolio allocations. The constraint
limits the investor's portfolio choice by fixing the share of
investment in the domestic economy. Therefore:
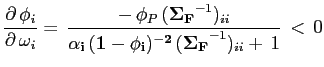
Second, using a numerical evaluation, I show that even if the
share invested in the domestic economy, ![]() , is
sensitive to changes in the covariance,
, is
sensitive to changes in the covariance, ![]() , the
share invested in the foreign economy i is strictly
decreasing in
, the
share invested in the foreign economy i is strictly
decreasing in ![]() . I evaluate the derivative
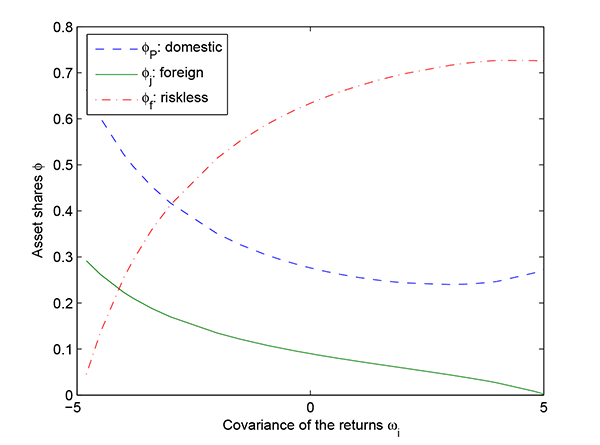
numerically for the case of a single foreign economy i.
Figures 1 and 2 show the simulated fractions of capital for a range
of plausible values for the covariance and for different magnitudes
of the risk of expropriation. I set the range of values for
. I evaluate the derivative
numerically for the case of a single foreign economy i.
Figures 1 and 2 show the simulated fractions of capital for a range
of plausible values for the covariance and for different magnitudes
of the risk of expropriation. I set the range of values for
![]() to correspond to the range of values
observed in the data for the covariance of the US per capita GDP
growth rate with the GDP growth rates of 106 countries. The time
period is 1971-2007. I set
to correspond to the range of values
observed in the data for the covariance of the US per capita GDP
growth rate with the GDP growth rates of 106 countries. The time
period is 1971-2007. I set
![]() equal to the variance of the US
per capita GDP growth, which is 0.036; and
equal to the variance of the US
per capita GDP growth, which is 0.036; and
![]() equal to the median
variance of per capita GDP growth for the sample of countries,
which is 0.15. The plot does not change much for a broader range of
values for
equal to the median
variance of per capita GDP growth for the sample of countries,
which is 0.15. The plot does not change much for a broader range of
values for
![]() and
and
![]() . Finally, I set
. Finally, I set ![]() and
and ![]() to correspond to the
average growth rates in the US,
to correspond to the
average growth rates in the US,
![]() , and the median of the average
growth rates of countries in the sample,
, and the median of the average
growth rates of countries in the sample, ![]() ,
such that
,
such that
![]() . The
plots show the negative relation between the fraction of investment
employed in the foreign economy,
. The
plots show the negative relation between the fraction of investment
employed in the foreign economy, ![]() , and its
covariance with the domestic economy
, and its
covariance with the domestic economy ![]() :
:
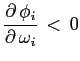
Figure 1: Investment Shares
for a Range of Values for ![]() ,
,
![]()

Although the focus of this paper is on the role of covariance risk, I also take into account the risk of expropriation. The role of expropriation risk on foreign country i's investment allocation, , can be expressed as follows:
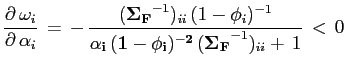
To summarize, the model shows that the covariance of returns does play a role in the decision making process of a representative international investor. The more negatively correlated the return of a foreign economy is with the investor's home economy, the larger the share of capital that the investor is willing to allocate to that economy. This relationship captures the role of diversification in the foreign investment allocations across countries. In what follows, I develop a general empirical specification to study whether this relationship holds in the data.
Figure 2: Investment Shares
for a Range of Values for
![]() ,
,
![]()
3 Measures of Covariance Risk and Foreign Investment
Before proceeding with the empirical analysis, in this Section I first describe the main variables for the analysis: foreign investment and my measure of covariance risk that captures the diversification motive behind investors' allocation decisions.
3.1 Covariance Risk
In my empirical investigation I capture the portfolio diversification motive by a new measure of country-specific riskiness, which I refer to as covariance risk. This new measure is constructed in Burnside and Tabova (2009) as the covariance between countries' growth rates and a measure of global risk that is a proxy for the stochastic discount factor (SDF) of a representative international investor. The approach is analogous to the two-pass regression method used in empirical finance to explain cross-sectional variation in expected returns across portfolios, with country growth rates replacing portfolio returns in the regressions. Ideally one would assess whether risk explains differences in rates of return across countries by gathering data on rates of return to investment, and estimating an explicit model of the international investor's stochastic discount factor. Unfortunately this approach is fraught with difficulty.7
The first step is to obtain country-specific exposures to global
risk factors. The risk factors are: the US real GDP growth, the US
real interest rate, the change in the relative prices of oil,
metals, and agricultural commodities, and the US stock market
excess return. This involves time series regression of each
country's real growth rate, ![]() , on a vector
of six risk factors,
, on a vector
of six risk factors,
![]() :
:
the time period is 1971-2007 for a total of 104 countries. The
choice of the factors is motivated by the notion that to some
extent they reflect global demand conditions, global financial
conditions, and terms of trade shocks that might be considered
important to the small economies in our sample. The betas,
![]() , measure countries' exposure to the
risk factors. There are two important findings from this
estimation. First, the results show a considerable spread among the
betas,
, measure countries' exposure to the
risk factors. There are two important findings from this
estimation. First, the results show a considerable spread among the
betas, ![]() , across countries. Second, between
roughly 15 and 30 percent of the estimated betas are individually
statistically significant at the 5 percent level (see Burnside and
Tabova, 2009 for more details).
, across countries. Second, between
roughly 15 and 30 percent of the estimated betas are individually
statistically significant at the 5 percent level (see Burnside and
Tabova, 2009 for more details).
The second step is to obtain the cost of risk by regressing
average growth rates on the estimated exposures to the risk factors
using a single cross-sectional regression of average growth rates
![]() on the estimated
on the estimated ![]() from the time series regression:
from the time series regression:
where
![]() is the OLS estimate
of
is the OLS estimate
of
![]() obtained in the time
series regression, and
obtained in the time
series regression, and ![]() is an error term. The
parameter
is an error term. The
parameter ![]() measures the cost in percentage
points of growth, of different exposures to risk. Using this
approach Burnside and Tabova (2009) construct a measure of global
risk that is a proxy for the global investor's SDF
measures the cost in percentage
points of growth, of different exposures to risk. Using this
approach Burnside and Tabova (2009) construct a measure of global
risk that is a proxy for the global investor's SDF
![]() :
:
All relevant information about a country's exposure to global
risk factors can be summarized in the covariance (or beta) between
its growth rate and this proxy SDF. This single variable is my
"covariance risk" measure,
![]() :
:
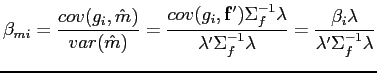
Countries with higher values of this measure are less
risky because their growth rates are more highly correlated with
the stochastic discount factor. The degree of a country's
riskiness,
![]() , depends on the sign and magnitude
of its exposure to the specific risk factors,
, depends on the sign and magnitude
of its exposure to the specific risk factors, ![]() . For example, countries with more negative exposures
to US interest rates and more positive exposures to changes in oil
and metals prices are riskier. Risk exposure is highly correlated
with initial income: the highest-income countries tend to have
roughly zero
. For example, countries with more negative exposures
to US interest rates and more positive exposures to changes in oil
and metals prices are riskier. Risk exposure is highly correlated
with initial income: the highest-income countries tend to have
roughly zero
![]() , while lower income countries tend
to have negative
, while lower income countries tend
to have negative
![]() .
.
It is useful to establish the explicit link between the
empirical measure of covariance risk and the measure ![]() that I used in the theoretical model. Recall that
the empirical measure of covariance risk is:
that I used in the theoretical model. Recall that
the empirical measure of covariance risk is:
![]() .
Since the global stochastic discount factor
.
Since the global stochastic discount factor ![]() is the same for all countries,
is the same for all countries,
![]() identifies the
country-specific riskiness. Replacing
identifies the
country-specific riskiness. Replacing ![]() with
with
![]() does not change the sign of the
covariance: the sign of
does not change the sign of the
covariance: the sign of
![]() will be the same
as the sign of
will be the same
as the sign of
![]() .8 The
direct link between the empirical and theoretical measure of
covariance risk can be expressed as:
.8 The
direct link between the empirical and theoretical measure of
covariance risk can be expressed as:
Therefore, for the data to confirm the theoretical predictions
of the role of portfolio diversification, in the empirical
investigation we would expect to find a positive correlation
between
![]() and the foreign investment
allocations across countries:
and the foreign investment
allocations across countries:
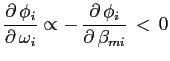
3.2 Foreign Investment
In the empirical analysis I use two measures of foreign investment: (i) the stock of FDI originating from the US; and (ii) the stock of total FDI and portfolio investment. I do not consider the debt-creating component of capital flows for two main reasons. First, the focus of the paper is on pure investment motives that are not reflected in debt flows. Second, official concessional lending, which is not determined by investment objectives, is the main component of the debt stock for the majority of low-income countries in the sample.
The source of data for FDI originating from the US is the International Economics Accounts reported by the Bureau of Economic Analysis. The data is available for 93 countries. For total FDI and portfolio investment I use a database constructed by Lane and Milesi-Ferretti (2006) where the stock measures are adjusted for valuation effects, such as exchange rate changes, variations in the price of capital goods and changes in the values of stock market indices. The stock data also takes into account unrecorded capital flight and debt reductions that are not captured in "crude" cumulative current account data. The data is available for 145 countries.
Given that most of the variation in the data is across countries, it is appropriate to consider average stock of foreign investment and estimate a single cross-sectional regression. Since capital liberalization plays an important role for the dynamics of foreign inflows, I use average stock for each recipient country for the period 1995-2007.9 Before the early 1990s capital movements were still restricted in many economies, and foreign investment was, therefore, less sensitive to the economic and institutional environment (see Lane and Milesi-Ferretti (2003, 2005, 2006), Harms and Lutz (2006)).
4 Empirical Analysis
The theoretical model in Section 2 shows that portfolio diversification does play a role in the decision making process of a representative international investor. The more negatively correlated the return of a foreign economy is with the investor's home economy, the larger the share of capital that the investor is willing to allocate to this foreign economy. Now I develop a general empirical specification to study whether this relationship holds in the data. I first use data on FDI originating from the US. Next, I capture the role of portfolio diversification on total foreign investment by using data on recipient countries' total stock of FDI and portfolio investment. In the empirical analysis I use my measure of covariance risk to capture the portfolio diversification motive behind investors' decisions.
4.1 Portfolio Diversification and FDI Originating From the US
Figure 3 shows that the covariance risk measure,
![]() , is positively related with the
US FDI allocations across countries. This positive relation can be
interpreted as initial evidence that the theoretical predictions
find support in the data. Note that by construction countries with higher values of
, is positively related with the
US FDI allocations across countries. This positive relation can be
interpreted as initial evidence that the theoretical predictions
find support in the data. Note that by construction countries with higher values of
![]() are less risky since their
growth rates are more positively correlated with the investor's
stochastic discount factor. In Figure 3 countries are sorted by
their stock of FDI scaled either by the total stock of US FDI
across all recipient countries or by population and are then
grouped into quartiles. The vertical axis shows the average
are less risky since their
growth rates are more positively correlated with the investor's
stochastic discount factor. In Figure 3 countries are sorted by
their stock of FDI scaled either by the total stock of US FDI
across all recipient countries or by population and are then
grouped into quartiles. The vertical axis shows the average
![]() .
.
Figure 3:
![]() Versus Covariance
Risk
Versus Covariance
Risk
![]()
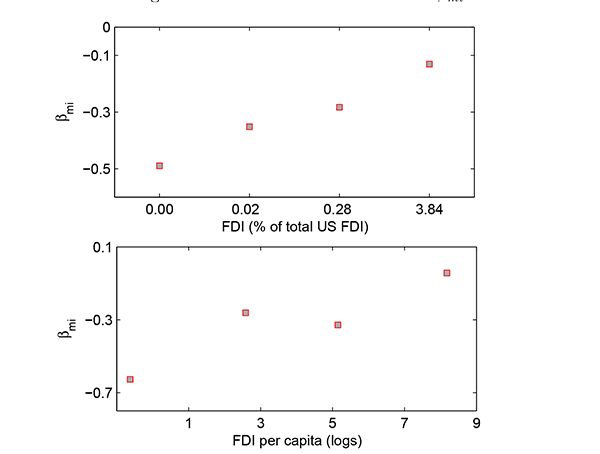
The horizontal axis of each graph shows the average stock of FDI expressed either as a share of the total US FDI across all countries or in per capita terms.
In addition, I use simple bivariate cross-sectional regressions
to show that the correlation between covariance risk and foreign
investment is strongly statistically significant (see Table 1). The
results hold for either measure of FDI. The full sample includes
all 92 countries for which I have constructed the new measure of
country-specific riskiness (covariance risk) and for which data is
available of FDI originating from the US. For a robustness check I
also exclude the largest recipients of ![]() .
These are Canada (CAN), the Netherlands (NLD), and Great Britain
(GBR) in the case of
.
These are Canada (CAN), the Netherlands (NLD), and Great Britain
(GBR) in the case of
![]() ; and the financial centers
Bahamas (BHS), Bermuda (BMU), Luxembourg (LUX), and Panama (PAN)
for the case of FDI per capita.
; and the financial centers
Bahamas (BHS), Bermuda (BMU), Luxembourg (LUX), and Panama (PAN)
for the case of FDI per capita.
Table 1: FDI Originating From the US and Covariance Risk (1995-2007)
| Dependent variable | Constant | Covariance risk | R2 |
|---|---|---|---|
| FDI per capita: Full Sample | 4.54*** (0.40) | 2.06*** (0.54) | 0.127 |
| Excluding LUX, BMU, BHS, PAN | 4.21*** (0.40) | 1.77*** (0.58) | 0.102 |
| FDI as a share of total: Full Sample | -2.55*** (0.41) | 1.71*** (0.62) | 0.085 |
| Excluding CAN, NLD, GBR | -2.77*** (0.41) | 1.60*** (0.61) |
Notes: Heteroscedasticity-consistent standard errors in parentheses.
4.1.1 Holding Companies and Redirection of FDI
US parent companies funnel a share of their direct investments
abroad through holding company affiliates.10 Data from BEA
shows that in 2007 30 percent of the US direct investment position
abroad is accounted for by holding companies, which may have
invested the funds in other countries. To take this into account, I
check if the positive relationship between the stock of FDI and
![]() is preserved for bilateral FDI
originating from the countries with the largest share in
is preserved for bilateral FDI
originating from the countries with the largest share in
![]() and the largest
share of holding companies recipients of
and the largest
share of holding companies recipients of
![]() : the Netherlands
(NL) and the United Kingdom (UK). In 2007 the Netherlands held 14
percent of total
: the Netherlands
(NL) and the United Kingdom (UK). In 2007 the Netherlands held 14
percent of total
![]() and 68 percent
was accounted for by holding companies; the UK held 13 percent of
total
and 68 percent
was accounted for by holding companies; the UK held 13 percent of
total
![]() and 22 percent
was accounted for by holding companies (source: BEA 2008, 2009).
The source of data on bilateral FDI stock originating from the
Netherlands and the UK is OECD International Direct Investment
Statistics, the sample period and methodology are identical to the
ones used above for the FDI originating from the US. When I regress
the FDI per capita (in logs) on
and 22 percent
was accounted for by holding companies (source: BEA 2008, 2009).
The source of data on bilateral FDI stock originating from the
Netherlands and the UK is OECD International Direct Investment
Statistics, the sample period and methodology are identical to the
ones used above for the FDI originating from the US. When I regress
the FDI per capita (in logs) on
![]() , I obtain the following
estimates:
, I obtain the following
estimates:
| (8) |
| (9) |
where heteroskedasticity-consistent standard errors are in
parentheses. The results show that for both the Netherlands and the
United Kingdom the positive relationship between
![]() and FDI allocations is preserved.
Therefore, even though the final destination of the funds channeled
through holding companies is unknown, there is evidence that the
countries with the largest share of holding companies in the FDI
portfolio of the US follow the logic of portfolio
diversification.
and FDI allocations is preserved.
Therefore, even though the final destination of the funds channeled
through holding companies is unknown, there is evidence that the
countries with the largest share of holding companies in the FDI
portfolio of the US follow the logic of portfolio
diversification.
4.1.2 Controlling for Traditional Determinants of FDI
Next, I show that my key empirical finding on the role of
portfolio diversification, captured by my covariance risk measure,
is preserved if I control for country-specific characteristics
drawn from the empirical literature on the determinants of
FDI.11 In the cross sectional regression I
include an expropriation risk rating to capture the risk that host
countries might either expropriate the foreign investment or
unilaterally modify the contract governing the investment. This is
a more traditional measure of risk that has been used in recent
empirical studies. The source of data is the International Country
Risk Guide database.12 A high score implies less
risk.13 The rating is available for 80 of
the 93 countries in my sample. I also include GDP growth rates to
capture growth opportunities in the host country; the level of GDP
as a measure of market size;
![]() as a measure
of trade openness; the number of phones per 1000 people as a
measure of infrastructure availability and the level of
development.14 The data source for these variables
is the World Development Indicators (2009). To be consistent with
the dependent variable, I average the control variables over the
same period. An additional control variable is the distance between
the capitals of the originating country and the host country as a
proxy for the relative magnitude of transaction costs. Transaction
costs of control and potential problems stemming from cultural
differences are expected to increase with distance.15 The
descriptive statistics are reported in Appendix A.
as a measure
of trade openness; the number of phones per 1000 people as a
measure of infrastructure availability and the level of
development.14 The data source for these variables
is the World Development Indicators (2009). To be consistent with
the dependent variable, I average the control variables over the
same period. An additional control variable is the distance between
the capitals of the originating country and the host country as a
proxy for the relative magnitude of transaction costs. Transaction
costs of control and potential problems stemming from cultural
differences are expected to increase with distance.15 The
descriptive statistics are reported in Appendix A.
Since most of the variation in the data is across countries, reflecting conditions that change slowly, I use cross-sectional regressions. All variables are averages for the period 1995-2007. The model I estimate is:
| (10) |
where
![]() is the measure of covariance
risk,
is the measure of covariance
risk,
![]() is the vector of control
variables described above, and
is the vector of control
variables described above, and
![]() is the coefficient vector
associated with the control variables. I first estimate the model
using the shares of countries' FDI,
is the coefficient vector
associated with the control variables. I first estimate the model
using the shares of countries' FDI,
![]() , as the dependent variable
, as the dependent variable
![]() . This estimation provides a direct link
to the predictions of the theoretical model where the
representative investor solves for optimal investment shares across
the foreign economies. I also estimate the model using per capita
FDI originating from the US, as the dependent variable.
. This estimation provides a direct link
to the predictions of the theoretical model where the
representative investor solves for optimal investment shares across
the foreign economies. I also estimate the model using per capita
FDI originating from the US, as the dependent variable.
First, I estimate the model by OLS. The sample includes 78
countries due to data availability of the expropriation risk
rating. Columns 1 and 3 in Table 2 presents the results of this
estimation. The coefficient on covariance risk,
![]() , is positive and significant at
the 3 percent level. This means that less risky countries from the
international investor's perspective, i.e. those with higher values
for
, is positive and significant at
the 3 percent level. This means that less risky countries from the
international investor's perspective, i.e. those with higher values
for
![]() , receive on average a larger
share of the total stock of FDI. Less risky countries have also a
higher level of FDI per capita.
, receive on average a larger
share of the total stock of FDI. Less risky countries have also a
higher level of FDI per capita.
The results show that the diversification motive, captured by my
covariance risk measure, has statistical as well as strong economic
significance. The 25th percentile value for the
![]() in the sample is -0.69, while the 75th is 0.02. The point estimates
for the coefficient associated with
in the sample is -0.69, while the 75th is 0.02. The point estimates
for the coefficient associated with
![]() suggest that the cross-sectional
regression predicts that if a country's riskiness declines from the
25th percentile to the 75th percentile, on average per capita FDI
from the US increases by more than 183 percent. The magnitude is
similar for the case when the share of FDI is the dependent
variable. This empirical result confirms the theoretical
prediction: the stock of FDI in a foreign economy, measured either
in per capita terms or as a share of total FDI across all
countries, is a decreasing function of the covariance of its return
with the return of the investor's home economy.
suggest that the cross-sectional
regression predicts that if a country's riskiness declines from the
25th percentile to the 75th percentile, on average per capita FDI
from the US increases by more than 183 percent. The magnitude is
similar for the case when the share of FDI is the dependent
variable. This empirical result confirms the theoretical
prediction: the stock of FDI in a foreign economy, measured either
in per capita terms or as a share of total FDI across all
countries, is a decreasing function of the covariance of its return
with the return of the investor's home economy.
I now turn my attention to the other explanatory variables. Table 2 shows that consistent with Asiedu et al. (2009) the coefficient on the expropriation risk variable is positive and significant for all specifications. Recall from the data description section that higher values of the expropriation risk rating imply less risk. I find that openness to trade, infrastructure availability, and the size of the domestic market, measured by either level of GDP or population, have a positive and significant effect on FDI. As expected, oil producers attract on average a larger share of FDI; while distance is negatively and significantly correlated with FDI.
Because
![]() is a generated regressor, it may
be the case that the estimate of
is a generated regressor, it may
be the case that the estimate of ![]() is biased
towards zero because of measurement error.16 This would only
reinforce my finding of a positive relationship between FDI
holdings and the measure of covariance risk
is biased
towards zero because of measurement error.16 This would only
reinforce my finding of a positive relationship between FDI
holdings and the measure of covariance risk
![]() . A related concern in the case of
generated regressors is that OLS standard errors understate the
true standard errors. To address this issue I use maximum
likelihood estimation (MLE). My approach follows Kim (1995) who
derives a maximum likelihood estimator that takes into account the
measurement error of the generated regressor. Kim (1995) develops
the correction for the two-pass estimation methodology of expected
returns, but the correction can easily be applied for more general
problems. Appendix B contains a detailed description of the MLE
methodology. The correction provides a robustness check for the
validity of the uncorrected OLS estimates and standard errors.
. A related concern in the case of
generated regressors is that OLS standard errors understate the
true standard errors. To address this issue I use maximum
likelihood estimation (MLE). My approach follows Kim (1995) who
derives a maximum likelihood estimator that takes into account the
measurement error of the generated regressor. Kim (1995) develops
the correction for the two-pass estimation methodology of expected
returns, but the correction can easily be applied for more general
problems. Appendix B contains a detailed description of the MLE
methodology. The correction provides a robustness check for the
validity of the uncorrected OLS estimates and standard errors.
Columns 2 and 4 in Table 2 present the MLE results along with
the OLS coefficients for comparison. Consistent with the theory,
the results show that the OLS estimation results in an
underestimation of the coefficient associated with
![]() (the variable measured with
error). The correction does not change the main findings and serves
as a robustness check for the link between FDI and covariance
risk.
(the variable measured with
error). The correction does not change the main findings and serves
as a robustness check for the link between FDI and covariance
risk.
Table 2: Impact of Covariance Risk on the Stock of FDI Originating From the US After Controlling for Country-Specific Factors
| Dependent var: FDIi/FDIUS(log): OLS | Dependent var: FDIi/FDIUS(log): MLE | Dependent var: FDI per capita (log): OLS | Dependent var: FDI per capita (log): MLE | |
|---|---|---|---|---|
| Covariance risk (βmi) | 0.978** (0.472) | 1.533** (0.722) | 0.836** (0.419) | 1.217** (0.583) |
| GDP growth | -0.279** (0.137) | -0.270** (0.123) | -0.287** (0.131) | -0.278** (0.110) |
| In(GDP) | 1.326*** (0.152) | 1.351*** (0.141) | 0.536*** (0.138) | 0.544*** (0.124) |
| Trade/GDP | 0.014** (0.003) | 0.015*** (0.004) | 0.015*** (0.003) | 0.016*** (0.003) |
| ln(1 + Phones) | 1.337*** (0.237) | 1.263*** (0.206) | 0.759** (0.306) | 0.702*** (0.245) |
| ln(Distance) | -0.915*** (0.317) | -0.904** (0.345) | -1.039*** (0.365) | -1.025*** (0.318) |
| Expropriation risk | 2.318* (1.231) | 2.349** (1.178) | 2.144* (1.193) | 2.130** (1.039) |
| Oil exporter dummy | 0.918 (0.729) | 1.149* (0.602) | 0.606 (0.688) | 0.755 (0.525) |
| Constant | -24.756*** (3.977) | -25.021*** (4.355) | -6.505 (4.071) | -6.564 (4.115) |
| obs | 78 | 78 | 78 | 78 |
| R2 | 0.776 | 0.767 | 0.800 | 0.795 |
Notes: Heteroscedasticity-consistent standard errors in parentheses. *(10%), **(5%), ***(1%).
Countries with higher values of ![]() are less risky. Similarly, higher values of the
expropriation risk variable imply lower expropriation risk.
are less risky. Similarly, higher values of the
expropriation risk variable imply lower expropriation risk.
4.2 Portfolio Diversification and Total Stock of Foreign Investment
In this section I explore the role of portfolio diversification using (i) the entire stock of FDI in the recipient countries, and (ii) the stock of total foreign investment that includes FDI as well as portfolio investment (PO). The data is adjusted for valuation effects (see Lane and Milesi-Ferretti, 2009).
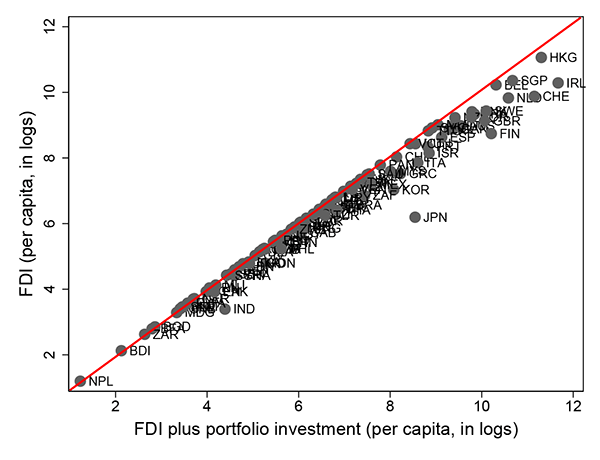
The scatter plot of FDI versus total foreign investment shows that FDI is the main component of total foreign investment for the majority of countries. Portfolio investment constitutes a significant share of total foreign investment only for the high-income countries (see Figure 4). The summary statistics in Table 3 confirm this fact. Therefore, in the cross-section the majority of variation in foreign investment is explained by the variation in FDI rather than portfolio investment.
Figure 4: FDI Versus FDI Plus Portfolio Investment (Average 1995-2007)
Using this new database I again find evidence that the
international investors take into account diversification
opportunities in their allocation decisions. Figure 5 shows that
foreign investment across countries is positively associated with
my covariance risk measure,
![]() . By construction countries with
higher values
. By construction countries with
higher values
![]() are less risky since their
growth rates are more positively correlated with the investor's
stochastic discount factor. In the Figure countries are sorted
either by the stock of FDI per capita or by the total stock of
foreign investment and are then grouped into quartiles. The
vertical axis shows the average
are less risky since their
growth rates are more positively correlated with the investor's
stochastic discount factor. In the Figure countries are sorted
either by the stock of FDI per capita or by the total stock of
foreign investment and are then grouped into quartiles. The
vertical axis shows the average
![]() , while the horizontal axis of
each graph shows either the average per capita FDI or the average
per capita total foreign investment.
, while the horizontal axis of
each graph shows either the average per capita FDI or the average
per capita total foreign investment.
In addition, in Table 4 I use simple bivariate cross-sectional
regressions to show that the correlation between covariance risk
and foreign investment is statistically significant. The relation
between
![]() and foreign investment is
preserved if the sample includes only low- and middle-income
countries. The results also confirm the evidence from Figure 5 that
for low- and middle-income countries the majority of foreign
investment is explained by FDI rather than portfolio
investment.
and foreign investment is
preserved if the sample includes only low- and middle-income
countries. The results also confirm the evidence from Figure 5 that
for low- and middle-income countries the majority of foreign
investment is explained by FDI rather than portfolio
investment.
Table 3: Share of FDI in Total Foreign Investment: FDI/(FDI+PO) (Mean 1995-2007)
| Obs. | Mean | Median | St.Dev. | |
|---|---|---|---|---|
| Low-income countries | 34 | 0.933 | 0.989 | 0.131 |
| Middle-income countries | 29 | 0.864 | 0.920 | 0.141 |
| High-income countries | 30 | 0.633 | 0.611 | 0.236 |
Figure 5: Foreign Investment
Versus Covariance Risk
![]()
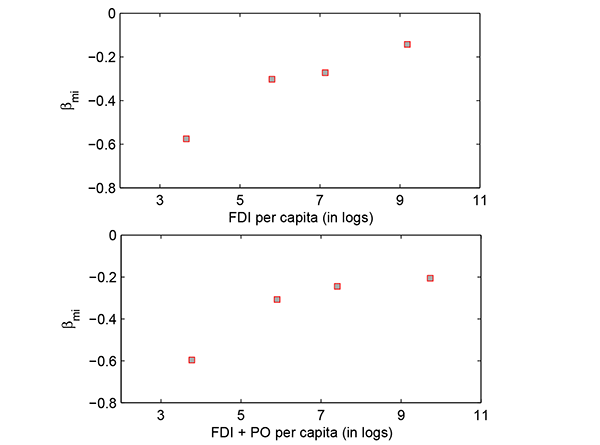
Table 4: Impact of Covariance Risk on the Total Stock of Foreign Investment
| Right-hand side variables: Constant | Right-hand side variables: Covariance risk | R2 | obs | |
|---|---|---|---|---|
| A. Full sample: Regressions with FDI | 6.96 (0.26) | 1.16 (0.30) | 0.104 | 90 |
| A. Full sample: Regressions with FDI + PO | 7.24 (0.28) | 1.24 (0.32) | 0.100 | 90 |
| B. Low and middle-income countries: Regressions with FDI | 5.67 (0.22) | 0.61 (0.23) | 0.069 | 61 |
| B. Low and middle-income countries: Regressions with FDI + PO | 5.81 (0.23) | 0.63 (0.23) | 0.071 | 61 |
Notes. Dependent variable: in log per capita.
Heteroscedasticity-consistent standard errors in parentheses.
4.2.1 Controlling for Traditional Determinants of Foreign Investment
Next, I show that my key empirical finding on the role of portfolio diversification, captured by my covariance risk measure, is preserved if I control for the country-specific characteristics described in the previous Section. For the regressions where the dependent variable is total foreign investment I include dummies for the high-income countries in the sample to account for the fact that portfolio investment constitutes a significant share of foreign investment only for these countries.
The results show a strong and significant relation between my measure of covariance risk and foreign investment, measured either by per capita FDI or per capita total foreign investment that includes portfolio investment. Countries that are perceived as more risky, i.e. countries with lower values of the covariance risk measure, receive lower levels of per capita foreign investment.
This relationship is not only statistically significant, but has
economic significance as well. The 25th percentile value for the
![]() in the sample is -0.69, while the 75th
percentile value is 0.02. The
point estimates for the coefficient associated with
in the sample is -0.69, while the 75th
percentile value is 0.02. The
point estimates for the coefficient associated with
![]() suggest that the cross-sectional
regression predicts that if a country's covariance risk declines
from the 25th percentile to the 75th percentile, on average total
foreign investment per capita increases by more than 165 percent.
The estimated increase for FDI per capita is 135 percent. Also, the
role of the control variables is preserved: the coefficient on the
expropriation risk variable is positive and significant for all
specifications, openness to trade, infrastructure availability, and
the size of the domestic market, have a positive and significant
effect on total foreign investment. The results do not change if
the size of the domestic market is measured by the countries'
population instead of the level of their GDP.
suggest that the cross-sectional
regression predicts that if a country's covariance risk declines
from the 25th percentile to the 75th percentile, on average total
foreign investment per capita increases by more than 165 percent.
The estimated increase for FDI per capita is 135 percent. Also, the
role of the control variables is preserved: the coefficient on the
expropriation risk variable is positive and significant for all
specifications, openness to trade, infrastructure availability, and
the size of the domestic market, have a positive and significant
effect on total foreign investment. The results do not change if
the size of the domestic market is measured by the countries'
population instead of the level of their GDP.
Table 5: Impact of Covariance Risk on the Total Stock of Foreign Investment After Controlling for Country-Specific Factors
| FDI: OLS | FDI: MLE | FDI + Portfolio investment: OLS | FDI + Portfolio investment: MLE | |
|---|---|---|---|---|
| Covariance risk (βmi) | 0.420** (0.203) | 0.461** (0.230) | 0.431** (0.204) | 0.489** (0.248) |
| GDP growth | -0.087 (0.047) | -0.067 (0.051) | -0.062 (0.047) | -0.062 (0.057) |
| ln(GDP) | -0.067 (0.067) | -0.079 (0.065) | 0.023 (0.068) | 0.023 (0.072) |
| Trade/GDP | 0.010*** (0.003) | 0.009*** (0.002) | 0.009*** (0.003) | 0.009*** (0.002) |
| ln(1 + Phones) | 1.211*** (0.157) | 1.234*** (0.122) | 0.947*** (0.184) | 0.938*** (0.160) |
| Expropriation risk | 1.726*** (0.599) | 1.540*** (0.577) | 1.469*** (0.577) | 1.460*** (0.651) |
| Oil exporter dummy | 0.985*** (0.307) | 0.972*** (0.277) | 0.826*** (0.275) | 0.851*** (0.307) |
| High-income country dummy | 1.242*** (0.297) | 1.248*** (0.338) | ||
| Constant | 1.254 (1.984) | 1.941 (1.888) | 0.140 (1.901) | 0.182 (2.106) |
| obs | 80 | 80 | 80 | 80 |
| R2 | 0.882 | 0.893 | 0.890 | 0.889 |
Notes. Dependent variable: in log per capita; *(10%), **(5%), ***(1%).
Heteroscedasticity-consistent standard errors in parentheses.
5 Concluding Remarks
In this paper I explore the role of diversification in the cross-sectional distribution of total foreign investment, which includes FDI as well as portfolio investment. To do so I extend the existing analyses of the determinants of foreign investment by adopting a portfolio allocation approach to risk. I capture the portfolio diversification motive by a measure of country-specific riskiness, which I refer to as "covariance risk". I construct this measure as how countries' growth rates covary with the stochastic discount factor of a representative international investor. I develop a general empirical specification that highlights the role of diversification but allows for host country specific characteristics to also influence portfolio allocations. My key new result is that the diversification motive, captured by my covariance risk measure, has statistical as well as strong economic significance. Therefore, I find empirical evidence that international investors take into account diversification opportunities in their investment allocation decisions, which confirms the predictions of standard portfolio allocation models.
References
Alfaro, L., 2003. Foreign Direct Investment and Growth: Does the Sector Matter? Unpublished. Harvard Business School.
Asiedu, E., 2002. On the Determinants of Foreign Direct Investment to Developing Countries: Is Africa Different? World Development, 30(1), 107-119.
Asiedu E., Jin, Y., and Nandwa, B., 2009. Does foreign aid mitigate the adverse effect of expropriation risk on foreign direct investment? Journal of International Economics.
Benigno, P. and Nisticò, S., 2009. International Portfolio Allocation under Model Uncertainty. NBER Working Paper No. 14734
Blonigen, B., 2005. A Review of the Empirical Literature on FDI Determinants. NBER Working Paper No. 11299.
Borga, M. and R. J. Mataloni, Jr., 2001. Direct Investment Positions for 2000: Country and Industry Detail. Technical Note. Survey of Current Business 81 (July 2001): 23–25.
Brainard, S.L., 1993. A simple theory of multinational corporations and trade within a trade-off between proximity and concentration. NBER Working Paper No. 4269.
Brainard, S.L., 1997. An empirical assessment of the proximity-concentration trade-off between multinational sales and trade. Am. Econ. Rev. 87, 520–544.
Burnside, C. and Tabova, A., 2009. Risk, Volatility, and the Global Cross-Section of Growth Rates. NBER Working Paper 15225.
Carroll, R., Ruppert, D., Stephanski, L. and Crainiceanu, C., 2006. Measurement error in nonlinear models: a modern perspective. Second Edition, Chapman & Hall/CRC.
Coeurdacier, N., 2009. Do trade costs in goods market lead to home bias in equities? Journal of International Economics 77 (2009) 86-100.
Coeurdacier, N. and Guibaud, S., 2008. A Dynamic Equilibrium Model of Imperfectly Integrated Financial Markets. Working Paper, London Business School.
Coeurdacier, N. and Guibaud, S., 2010. International Portfolio Diversification Is Better Than You Think. Journal of International Money and Finance, forthcoming
Coeurdacier, N., Kollmann, R. and Martin, P., 2010. International Portfolios, Capital Accumulation and Foreign Asset Dynamics. Journal Of International Economics 80 (2010) 100-112.
Eaton, J. and Gersovitz, M., 1984. A Theory of Expropriation and Deviations from Perfect Capital Mobility. The Economic Journal 94, 16-40.
Fama, E. and James D. MacBeth, J., 1973. Risk, Return, and Equilibrium: Empirical Tests. Journal of Political Economy 81(3, May-Jun.), 607-36.
Ferri, G., 2004. More analysts, better ratings: do rating agencies invest enough in less developed countries? Journal of Applied Economics 12, 77–98.
Fuller, W. (1987). Measurement error models. John Wiley
![]() Sons.
Sons.
Gourinchas, P. and O. Jeanne. Capital Flows to Developing Countries: The Allocation Puzzle. NBER Working Paper 2009.
Harms, P., Lutz, M., 2006. Aid, governance and private foreign investment: some puzzling findings for the 1990s. The Economic Journal 116, 773–790.
Hausmann, R. and Fernandez-Arias, E., 2001. Foreign Direct Investment: Good Cholesterol? In Foreign Direct Investment Versus Other Flows to Latin America. Development Center Seminars, OECD.
Hines, J., 1995. Forbidden payment: Foreign bribery and American business after 1977. NBER Working Paper no. 5266. Cambridge, Mass.: National Bureau of Economic Research, September.
Hnatkovska, V., 2010. Home Bias and High Turnover: Dynamic Portfolio Choice with Incomplete Markets. Journal of International Economics 80 (1), 2010.
Ibarra, M. and Koncz, J., 2008. Direct Investment Positions for 2008: Country and Industry Detail. Survey of Current Business (July 2008), 20-34.
Kaufmann, D., Kraay, A. and Mastruzzi, M., 2009. Governance matters VIII: Aggregate and Individual Governance Indicators, 1996–2008. Policy Research Working Paper 4978, World Bank.
Kim, D. (1995). The errors in the variables problem in the cross-section of expected stock returns. Journal of Finance, 50(5).
Klenow, P. and Andrés Rodríguez-Clare, 1997. The Neoclassical Revival in Growth Economics: Has it Gone too Far? NBER Macroeconomics Annual 1997. Cambridge, MA: MIT Press.
Kraay, A., Loayza, N., Serven, L., Ventura, J. (2005). Country Portfolios. Journal of the European Economic Association. 3 (4): 914-945.
Lane, P.R. and Milesi-Ferretti, G.M., 2000. External Capital Structure: Theory and Evidence. IMF Working Paper 152.
Lane, P.R. and G.M. Milesi-Ferretti (2006). The External Wealth of Nations Mark II: Revised and Extended Estimates of Foreign Assets and Liabilities, 1970-2004. IMF Working Paper, March 2006.
Lane, P.R. and G.M. Milesi-Ferretti (2008). International Investment Patterns. The Review of Economics and Statistics, August 2008, 90(3): 538-549.
Loree, D., Guisinger, S., 1995. Policy and non-Policy Determinants of U.S. Foreign Direct Investment. Journal of International Business Studies 26(2), 281-299.
Lucas, R., 1990. Why Doesn't Capital Flow from Rich to Poor Countries? American Economic Review 80(2), 92-96.
Merton, R. (1969). Lifetime Portfolio Selection under Uncertainty: The Continuous-Time Case. The Review of Economics and Statistics, Vol. 51, No. 3, 247-257.
Merton, R. (1971). Optimum Consumption and Portfolio Rules in a Continuous-Time Model. Journal of Economic Theory 3, 373-413
Merton, R. (1990). Continuous-Time Finance. Basil Blackwell, Cambridge.
Pinheiro-Alves, R., 2008. Behavioural Determinants of Foreign Direct Investment. MPRA Paper No. 10297.
Political Risk Services, 2009. International Country Risk Guide. NY.
Samuelson, P.A., 1969. Lifetime Portfolio Selection by Dynamic Stochastic Programming. Review of Economics and Statistics 51, August: 239-46.
Van Nieuwerburgh, S. and Veldkamp, L., 2007. Information Immobility and the Home Bias Puzzle. Working Paper, New York University.
Wei, S.J., 2000. How taxing is corruption on international investors? Review of Economics and Statistics 82 (1): 1–11.
Woodridge, J.M., 2002. Econometric Analysis of Cross Section and Panel Data. MIT Press, Cambridge, Massachusetts.
World Bank, 2009. World Development Indicators, Washington, D.C.
A Appendix: Control Variables and Country List
Table 6: Descriptive Statistics
| Variable | Mean | St.Dev. | Min | Max |
|---|---|---|---|---|
| ln(FDIUS per capita) | 4.08 | 3.05 | -3.44 | 9.25 |
| ln(FDI per capita) | 6.45 | 2.19 | -1.20 | 10.87 |
| ln((FDI + PO) per capita) | 6.72 | 2.36 | -1.20 | 11.36 |
| Covariance risk | -0.33 | 0.56 | -1.98 | 1.16 |
| GDP growth (%) | 2.27 | 1.56 | -1.68 | 8.05 |
| ln(GDP) | 24.49 | 1.97 | 19.90 | 28.02 |
| ln(Population) | 16.55 | 1.56 | 12.56 | 20.96 |
| Trade/GDP (%) | 40.85 | 31.00 | 10.50 | 218.7 |
| ln(Phones) | 21.95 | 22.12 | 0.03 | 69.27 |
| ln(Distance) | 8.90 | 0.57 | 6.31 | 9.69 |
| Expropriation risk | 8.09 | 1.66 | 4.08 | 10.64 |
Table 7: Correlation Matrix of the Independent Variables
| Inv. risk | >Growth | ln(GDP) | Trade/GDP | ln(Phones) | ln(Distance) | |
|---|---|---|---|---|---|---|
| Covariance risk | 1.000 | |||||
| GDP growth | 0.057 | 1.000 | ||||
| ln(GDP) | 0.149 | 0.344 | 1.000 | |||
| Trade/GDP | 0.135 | 0.116 | -0.007 | 1.000 | ||
| ln(Phones) | 0.312 | 0.189 | 0.563 | 0.320 | 1.000 | |
| ln(Distance) | -0.178 | 0.003 | -0.041 | 0.089 | -0.263 | 1.000< |
| Expropriation risk | 0.326 | 0.287 | 0.344 | 0.374 | 0.713 | -0.251 |
Institutional Variables
In the empirical analysis I use an expropriation risk variable that specifically measures the risk of expropriation or arbitrary contract modifications. The table below shows that the expropriation risk variable and three empirical indicators (Source: Kaufmann et al., 2009) that capture different dimensions of institutional quality (political stability, rule of law and control of corruption) are very highly correlated. Therefore, expropriation risk can be interpreted more broadly as a measure of public governance, which can include bureaucratic corruption, deviations from rule of law, arbitrary government regulations.
Table 8: Institutional Variables: Correlation Matrix
| Expropriation risk | Political stability | Rule of law | Control of corruption | |
|---|---|---|---|---|
| Expropriation risk | 1.00 | 0.81 | 0.84 | 0.85 |
| Political stability | 0.81 | 1.00 | 0.89 | 0.85 |
| Rule of law | 0.84 | 0.89 | 1.00 | 0.97 |
| Control of corruption | 0.85 | 0.85 | 0.97 | 1.00 |
Country List for Multivariate Regressions:
Algeria, Argentina, Australia, Austria, Belgium, Burkina Faso, Bangladesh, Bahamas*, Brazil, Botswana, Canada, Chile, China, Cote d'Ivoire, Cameroon, Rep. of Congo, Colombia, Costa Rica, Denmark, Dominican Republic, Ecuador, Egypt, Finland, France, Gabon, United Kingdom, Ghana, Gambia, Greece, Guatemala, Hong Kong, Honduras, Hungary, India, Indonesia, Ireland, Iran, Island, Israel, Italy, Jamaica, Kenya, Korea, Luxembourg*, Malaysia, Morocco, Madagascar, Mexico, Mali, Malta, Malawi, Niger, Nigeria, the Netherlands, Norway, New Zealand, Pakistan, Panama*, Peru, Philippines, Papua New Guinea, Portugal, Sudan, Senegal, Sierra Leone, Singapore, South Africa, Spain, Sri Lanka, Sweden, Switzerland, Syria, Togo, Thailand, Trinidad and Tobago, Tunisia, Turkey, Venezuela, Zambia, Zimbabwe.
B Appendix: MLE Estimation With a Generated Regressor
The model I estimate is:
where
![]() is the vector of control
variables measured without error, and
is the vector of control
variables measured without error, and
![]() is the coefficient vector
associated with the control variables. Let the measurement error of
the generated regressor be
is the coefficient vector
associated with the control variables. Let the measurement error of
the generated regressor be ![]() :
:
where the covariance risk variable
![]() is the true variable, while
is the true variable, while
![]() is the estimated or
observed variable. The idea behind the adjusted estimator is to
choose
is the estimated or
observed variable. The idea behind the adjusted estimator is to
choose
![]() to minimize the
quadratic form
to minimize the
quadratic form
![]() where:
where:
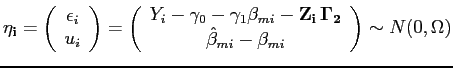
![$\displaystyle \mathbf{\Omega} = \left[ \begin{array}{cc} \Sigma_{\epsilon} & 0 \ 0 & \Sigma_{u} \end{array} \right] $](img184.gif)
where
![]() is the covariance matrix
of the residuals from the cross-sectional regression regression;
and
is the covariance matrix
of the residuals from the cross-sectional regression regression;
and
![]() is the covariance matrix of the
measurement error in
is the covariance matrix of the
measurement error in
![]() .
.
The MLE is a function of ![]() : the relative
magnitude of the error variances of Y and
: the relative
magnitude of the error variances of Y and
![]() . Without additional
information about the error terms,
. Without additional
information about the error terms, ![]() and
and
![]() , the MLE of the unknown parameter vector
that minimizes the likelihood function does not exist. Fuller
(1987) assumes the relative magnitude of the error variances is
known, while Kim (1995) derives it for the two-pass estimation of
expected returns. Since in my case the relative variance is neither
known nor can be easily derived from the model, I get
, the MLE of the unknown parameter vector
that minimizes the likelihood function does not exist. Fuller
(1987) assumes the relative magnitude of the error variances is
known, while Kim (1995) derives it for the two-pass estimation of
expected returns. Since in my case the relative variance is neither
known nor can be easily derived from the model, I get ![]() and
and
![]() using a bootstrap
procedure and set
using a bootstrap
procedure and set ![]() equal to the median of
the diagonal of
equal to the median of
the diagonal of
![]() . In what
follows I use the simulated relative variances and apply the
correction proposed Kim (1995). The MLE of
. In what
follows I use the simulated relative variances and apply the
correction proposed Kim (1995). The MLE of ![]() ,
,
![]() , and
, and ![]() are given by:
are given by:
![$\displaystyle \hat{\gamma}_1 = \frac{S + \Big[S^2 + 4\delta\Big(m_{Y \hat{\beta}_{mi}}-\mathbf{M}'_{\hat{\beta}_{mi}\mathbf{Z}} \mathbf{M}^{-1}_{\mathbf{Z}\mathbf{Z}}\mathbf{M}_{Y\mathbf{Z}}\Big)^2 \Big]^{1/2}}{2\Big(m_{Y \hat{\beta}_{mi}}-\mathbf{M}'_{\hat{\beta}_{mi}\mathbf{Z}} \mathbf{M}^{-1}_{\mathbf{Z}\mathbf{Z}}\mathbf{M}_{Y\mathbf{Z}}\Big)} $](img199.gif)
where:
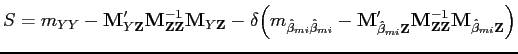
and ![]() and
and
![]() are the second co-moment
between variables
are the second co-moment
between variables ![]() and
and ![]() (the
boldface represents a vector or a matrix). Let
(the
boldface represents a vector or a matrix). Let
![]() ,
then Kim (1995) shows that the asymptotic distribution of
,
then Kim (1995) shows that the asymptotic distribution of
![]() is given by:
is given by:
![$\displaystyle \mathbf{\Sigma}_{\mathbf{\hat{\Gamma}}} = \left[ \begin{array}{ccc} (1+\mathbf{\mu}'_z \Sigma^{-1}_{zz}\mathbf{\mu}_z)\sigma^2_w + \phi^2 \sigma^2_{\hat{\gamma}_1} & -\phi \sigma^2_{\hat{\gamma}_1} & -\sigma^2_w \Sigma^{-1}_{zz}\mathbf{\mu}_z + \phi\Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z}\sigma^2_{\hat{\gamma}_1}\\ [10pt] -\phi \sigma^2_{\hat{\gamma}_1} & \sigma^2_{\hat{\gamma}_1} & - \Sigma'_{\beta_{mi}z} \Sigma^{-1}_{zz}\sigma^2_{\hat{\gamma}_1} \\ [10pt] -\sigma^2_w \Sigma^{-1}_{zz}\mathbf{\mu}_z + \phi\Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z}\sigma^2_{\hat{\gamma}_1} & -\Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z}\sigma^2_{\hat{\gamma}_1} & \sigma^2_w \Sigma^{-1}_{zz} + \Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z}\Sigma'_{\beta_{mi}z}\Sigma^{-1}_{zz} \sigma^2_{\hat{\gamma}_1} \end{array} \right], $](img210.gif)
![$\displaystyle \textrm{and} \qquad (\mu_{\beta_{mi}}, \mathbf{\mu}_z) \qquad \textrm{and} \qquad \left[ \begin{array}{cc} \sigma^2_{\beta_{mi}} & \Sigma'_{\beta_{mi}z} \ \Sigma_{\beta_{mi}z} & \Sigma_{zz} \end{array} \right] $](img213.gif)
are the mean vector and variance matrix of
![]() and explanatory variables
and explanatory variables
![]() . The variance matrix,
. The variance matrix,
![]() is estimated by
replacing the unknown parameters with their sample estimates:
is estimated by
replacing the unknown parameters with their sample estimates:
where:
Footnotes
** Staff economist in the Division of International Finance, Board of Governors of the Federal Reserve System, Washington, D.C. 20551 USA. E-mail: [email protected]. This paper is based on a chapter of my PhD dissertation. I thank Craig Burnside for guidance and valuable advice; Barbara Rossi, Pietro Peretto, Gian Maria Milesi-Ferretti, Daniele Terlizzese and participants at Duke University seminars, MOOD 10th Doctoral Workshop in Economic Theory and Econometrics, IMF Research Seminar, Board of Governors IF seminar, and 2011 SEA meetings for helpful comments. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. The Poisson process is a continuous-time process which allows discrete (i.e. discontinuous) changes in the variables. Return to text
2. In their seminal paper, Eaton and Gersovitz (1984) the decision of expropriation is determined by the binding expropriation constraint that states that the host country's discounted income if expropriation occurs equals the host country's discounted income if no expropriation occurs. Return to text
3. See Merton (1990) for proof and discussion of the role of the form of the value function for the solution of the problem. Return to text
4. For utility functions of the form yielding constant relative risk aversion the problem can be solved explicitly. Return to text
5. I consider only interior optimal solutions. If the problem is formulated in the more general Khun-Tucker form the equalities of (4),(5), and (6) will be replaced with inequalities. Return to text
6. Merton (1990) shows that the sample paths of consumption and capital are identical to those generated in the complete markets case. Return to text
7. One might, for example, assume a Cobb-Douglas production technology and measure the marginal product of capital in each country and at each point in time, using assumptions about model parameters and data on output and capital stocks. It is not trivial to measure capital stocks. See, for example, Klenow and Rodriguez-Clare's (1997) analysis of the neoclassical growth model, in which they measure capital stocks by accumulating investment data in the Penn World Tables. However, if rates of return are inclusive of adjustment costs, further assumptions about functional forms need to be made. Measuring returns to investment in human capital would be even more difficult. Return to text
8. The covariances are time-series
statistics. In standard stochastic growth models rates of return
and growth rates of GDP are highly correlated in the time series
dimension because changes in technology and labor inputs (as
opposed to the slow-moving changes in capital inputs) drive the
comovements. Improvements in technology and increases in labor
inputs due to other shocks increase growth and the marginal product
of capital, and, hence, the rate of return to investments in
capital. Hence, at a minimum, the sign of
![]() will be the same
as the sign of
will be the same
as the sign of
![]() . Return to text
. Return to text
9. It is customary in the empirical literature on FDI to smooth out cyclical fluctuations by averaging the dependent and independent variables. See Harms and Lutz (2006), Asiedu et al. (2009) among others. Return to text
10. A holding company is a company whose primary activity is holding the securities or financial assets of other companies. Return to text
11. Hausmann and Fernandez-Arias (2001); Asiedu et al. (2002, 2009) among others. Return to text
12. See International country risk guide (2007). Return to text
13. The consensus in the empirical literature is that expropriation risk has a negative effect on FDI (see Loree and Guisinger (1995), Asiedu et al. (2009) among others). Return to text
14. Some empirical studies use GDP per capita as a proxy for development. Since the number of phones is highly correlated with GDP per capita (correlation coefficient 0.91) and can be used as a proxy for availability of infrastructure in the host country (see Asiedu et al., 2009), it is an appropriate control variable for this study. Return to text
15. Distance is usually featured in gravity models that are widely used in empirical international economics, most commonly in trade studies. A number of studies, however, have shown that the gravity model also has explanatory power when applied to FDI. Brainard (1993, 1997) provides a theoretical model for gravity-like forces for FDI analyses. Return to text
16. This is in the case of classical attenuation bias (see Wooldridge 2001), assuming that measurement errors are orthogonal to the other variables of interest. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text