
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1093, November 2013 --- Screen Reader
Version*
Surprise and Uncertainty Indexes: Real-Time Aggregation of Real-Activity Macro Surprises
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
I construct two real-time, real activity indexes: (i) a surprise index that summarizes recent economic data surprises and measures optimism/pessimism about the state of the economy, and (ii) an uncertainty index that measures uncertainty related to the state of the economy. The indexes, on a given day, are weighted averages of the surprises or squared surprises from a set of macro releases, where the weights depend on the contribution of the associated real activity indicator to a business condition index à la Aruoba, Diebold, and Scotti (2009). I construct indexes for the United States, Euro Area, the United Kingdom, Canada, Japan. I show that the surprise index preserves the properties of the underlying series in affecting asset prices, with the advantage of being a parsimonious summary measure of real-activity surprises. For the United States, I present the real-activity uncertainty index in relation to other proxies commonly used to measure uncertainty and compare their macroeconomic impact. I find evidence that when uncertainty is strictly related to real activity it has a potentially milder impact on economic activity than when it also relates to the financial sector.
Keywords: Business cycle, dynamic factor model, state space model, forecasting weights
JEL classification: C38, E32
1 Introduction
This paper proposes a new methodology to construct two real-time, real activity indexes: (i) a surprise index that summarizes recent economic data surprises and measures deviation from consensus expectations and (ii) an uncertainty index that measures uncertainty related to the state of the economy. The indexes, on a given day, are weighted averages of the surprises or squared surprises from a set of releases, where the weights depend on the contribution of the associated real activity indicator to a business condition index à la Aruoba, Diebold, and Scotti (2009). The surprise index measures whether agents are more optimistic or pessimist about the real economy than indicated by actual data releases. A positive (negative) reading of the surprise index suggests that economic releases have on balance been higher (lower) than consensus, meaning that agents were more pessimistic (optimistic) about the economy. The uncertainty index measures how uncertain agents are about current real activity conditions. A greater (smaller) reading of the uncertainty index suggests that agents have on balance been more (less) uncertain about the state of the economy. I apply this methodology to construct indexes for the United States, Euro Area, the United Kingdom, Canada, Japan, and an aggregate of the five countries over the 2003-2012 period.
The Aruoba, Diebold, and Scotti (ADS) index maintained by the Federal Reserve Bank of Philadelphia has proven to be a successful economic indicator and as such it has been classified by the Wall Street Journal among the 50 economic indicators that really matter (Constable and Wright, 2011) and has been added by Bloomberg to the data that can be followed in real time through its platform (ADS BCI Index).2 The ADS index measures the state of the economy and serves as a summary statistics of the information market participants have received thus far about real activity. However, in efficient markets, asset prices react to new information. Thus it is important to measure the surprise component of the information that has just arrived and the uncertainty surrounding that information. To this end, the surprise index presented in this paper aggregates the information contained in the surprises to construct a summary measure of the deviation of the real economy from consensus expectations, and the uncertainty index quantifies economic uncertainty, which is otherwise challenging to measure. The indexes are not competitors but complements to the existing business condition indicators such as the ADS index and to existing uncertainty indexes.
This paper relates to several branches of the literature. First and foremost is the uncertainty literature, which has thrived in recent years. Because uncertainty is not observable, a number of proxies have been used to measure it, ranging from stock market realized and implied volatilities (Bloom, 2009), to the cross-sectional dispersion of survey-based forecasts (Bachmann, Elstner and Sims, 2013), the frequency of newspaper references to economic policy uncertainty (Baker, Bloom, and Davis, 2013), or the common variability in the purely unforecastable component of the future value of a big number of variables (Jurado, Ludvigson, and Ng, 2013). However, these measures tend to combine economic uncertainty with other notions. For example, stock return volatility combines information about stock market volatility with economic uncertainty, and forecast disagreement could measure divergence of opinions among forecasters rather than just the underlying uncertainty about the economy. My paper contributes to this literature by providing a daily macroeconomic information uncertainty measure which quantifies the part of uncertainty that specifically relates to the state of the real economy. It also contributes by helping to disentangle the impact of purely macro uncertainty versus more general uncertainty. Second, this paper relates to those papers that study the impact of news surprises on asset price such as Andersen, Bollerslev, Diebold and Vega (2003, 2007), and Gilbert, Scotti, Strasser and Vega (2012), and contributes to this literature by providing a parsimonious summary measure of real-activity macroeconomic surprises. The paper also relates to papers that use similar factors models to extract a business condition index or to nowcast GDP such as the seminal Stock and Watson paper (1989), Aruoba, Diebold, and Scotti (2009), and Banbura, Giannone, and Reichlin (2010) among others. It also employs the idea of forecasting weights developed in Koopman and Harvey (2003) and applied by Banbura and Rünstler (2010) and Camacho and Perez-Quiros (2010), among others, to study the impact of news releases on GDP forecast revisions.
In order to construct the surprise and uncertainty indexes, I first employ a dynamic factor model to estimate monthly business condition indexes for the aforementioned countries and compute the weights representing the contribution of the economic indicators to these business condition indexes. I then use those weights to average the surprises or squared surprises in order to construct the surprise and the uncertainty indexes, respectively. The weights depend on (i) the time elapsed since the release of the associated information and (ii) the unbalancedness pattern of the underlying releases. The former is a time decay feature that reduces the contribution of each surprise over time. The latter is a missing data characteristic that sets to zero the contributions of an indicator in months in which no data is available.
I find that, surprise indexes tend to be negative during the recession associated with the 2008 financial crisis, the so-called Great Recession, suggesting that agents were more optimistic about the real economy than it warranted.3 There appear to be other episodes when the indexes are negative. Of note are the most recent decline in the euro-area surprise index, the sharp drop in the Japanese surprise index after the March 2011 earthquake, and the prolonged low levels of the U.K. index in 2010 and 2011. On the other hand, there are also several instances where the surprise indexes are positive, especially coming out of the recession in the United States, the United Kingdom and Canada. I show that the surprise index preserves the properties of the underlying series in affecting asset prices, with the advantage of being a parsimonious summary measure of real-activity surprises. In light of this, Demiralp, King, and Scotti (2013) make use of it as a control variable when investigating the effects of political commentaries on policy rate decisions and policy expectations in the United States and the Euro Area, and find it to be significant determinant of policy expectations. Similarly, Brunetti, Buyuksahin, and Harris (2013) employ it as a control variable in studying the impact of speculation activity in the crude oil market.
The uncertainty indexes tend to be higher during recession periods. Interestingly, the euro-area uncertainty index reaches its highest values just before and after the 2008-2009 recession, suggesting that agents were more uncertain about the economy as the Euro Area was entering and exiting the recession. The daily U.S. uncertainty index is remarkably similar to the U.S. stock market implied volatility as measured by the VIX. Implied volatility, a forward-looking measure, is computed from option prices. The uncertainty index, a historical measure, is calculated from current and past macroeconomic news surprises. The former is a wider measure that combines information about risk aversion and future stock market volatility/uncertainty, and to the extent that these two move with news surprises, the VIX also contains information about current and future economic uncertainty. Although understanding the exact link between the two goes beyond the scope of this paper, it is nonetheless quite astonishing that macroeconomic uncertainty seems to be such an important component of the VIX during the period analyzed.4 The monthly version of the uncertainty index appears to be less correlated to other uncertainty proxies mentioned above.5
In a bivariate VAR exercise with employment and uncertainty proxies for the United States over the last decade, I find that, when uncertainty is strictly related to real activity as measured by real-activity uncertainty index, it has a potentially milder impact on economic activity. Just flipping the argument, when uncertainty is more generally related to economic and financial conditions as measured by the VIX, its impact on real-activity variables is stronger and more prolonged. This finding supports recent work by Caldara, Fuentes-Albero, Gilchrist and Zakrajsek (2013) which finds that the financial channel is key in the transmission of uncertainty shocks.
The surprise and uncertainty indexes tend to be negatively correlated, meaning that bad news increases volatility.6 This results is similar to the inverse relationship between first and second moments of asset returns found in the financial literature, phenomenon that Fostel and Geanakopoplos (2012) provide a theoretical explanation to, together with explaining a decrease in leverage.
The remainder of the paper is organized as follows: section 2 presents the data and the rationale behind using Bloomberg forecasts; section 3 presents the details of the dynamic factor model, the forecasting weights and the construction of the surprise and uncertainty indexes; section 4 covers the estimation details; section 5 presents the results; section 6 shows some applications; and section 7 concludes.
2 Data
Before getting into the model, this section presents information about the data used to construct the surprise and uncertainty indexes. I use two different types of data: the actual first release of the macroeconomic variable, say gross domestic product (GDP) or nonfarm payroll, and its forecast as measured by the Bloomberg median expectation. The actual releases of macroeconomic variables are used to estimate the underlying factor model from which I gather the weights. The difference between actual releases and Bloomberg expectations, also known as news surprise or forecast error, is then used together with the weights to construct the surprise and uncertainty indexes. In what follows, I describe the details of the data and study some of the properties of the news surprises.
The analysis covers five countries: the United States, the Euro Area, the United Kingdom, Canada, and Japan. I use five indicators for each country, except the United States for which I use six. Several considerations guide the choice of variables. First, I want to use those variables that are regarded as the main real activity indicators and as such followed by the business community, governments, and central banks as indication of the state of the economy. Second, I choose indicators for which analysts form expectations that are publicly available. Table 1 lists the indicators, together with their frequency, publication lags and transformations that I use to construct the real activity factor. The two rightmost columns list the source of the data series that I use to construct the factor, and the corresponding Bloomberg data series that I use to construct the surprise and uncertainty indexes.
The analysis for the surprise and uncertainty indexes covers the period from May 15, 2003 through September 30, 2012. However, a longer dataset is used to estimate the underlying business condition indexes: January 1980 to September 30, 2012, except for the Euro area where the sample starts in January 1985.
The first indicator is quarterly real GDP. For each country, the first GDP release for the corresponding quarter is used. The second indicator is industrial production (IP), which is a monthly indicator. The third indicator is employees on nonagricultural payrolls, when available, or the unemployment rate.7 The former tends to be more timely than the latter, but unfortunately it is not available for all countries.8 The fourth indicator is retail sales, which is another monthly variable. The fifth indicator is a survey measure of the manufacturing sector or the overall economy (composite) depending on the availability of the Bloomberg forecast. I use the ISM manufacturing index for the United States, the composite PMI for the Euro Area, the manufacturing PMI for the United Kingdom and Canada (Ivy survey), and the Tankan survey for Japan. The Tankan survey is a quarterly series, whereas the other surveys are all monthly.9 Although monthly series are generally preferred when available, the Tankan survey has the advantage of being very timely, as it is released on average four days before the end of the quarter it refers to.10 The average publication lag for the other series vary a lot as shown in table 1. Survey measures are the most timely of all: the euro-area Flash composite PMI is the first indicator to be released, followed by the Japanese Tankan survey, the U.S. ISM and the U.K. PMI. On the other hand, GDP and IP data tend to be the last information to be released.
The additional indicator for the United States is the Bureau of Economic Analysis (BEA) personal income. Household income or personal income are generally available for the other countries but because their expectation is not, I drop them from the dataset.
As already mentioned, while the announcement itself is used in
constructing the real activity factor, the news surprise, that is
the difference between announcement realizations
![]() and their corresponding Bloomberg
expectations
and their corresponding Bloomberg
expectations
![]() , is used
in constructing the surprise and uncertainty indexes. Because units
of measurement vary across macroeconomic variables, I standardize
the resulting surprises by dividing each of them by their sample
standard deviation
, is used
in constructing the surprise and uncertainty indexes. Because units
of measurement vary across macroeconomic variables, I standardize
the resulting surprises by dividing each of them by their sample
standard deviation
![]() . The standardized news surprise
associated with the macroeconomic indicator
. The standardized news surprise
associated with the macroeconomic indicator ![]() at
time
at
time ![]() is therefore computed as:
is therefore computed as:
![$\displaystyle s_{t}^{i}=\frac{y_{t}^{i}-E[y_{t}^{i}\vert\mathcal{F}_{t}]}{\sigma ^{i}}.$](img7.gif) |
(1) |
Table 1. Summary Information of the Real Activity Indicators Used in the Paper to Construct the Surprise and Uncertainty Indexes for the United States, Euro Area, United Kingdom, Canada, and Japan
| Country | Series Name | Description | Frequency | Publication Lag (days) | Transformation for Factor | Source | Bloomberg Mnemonic |
|---|---|---|---|---|---|---|---|
| United States | GDP | Real GDP, level | Q | 29 | log diff | BEA | GDP CQQQ |
| United States | IP | Index, level | M | 16 | log diff | FRB | IP CHNG |
| United States | Employment | Level | M | 5 | log diff | BLS | NFP TCH |
| United States | Retail Sales | Level | M | 13 | log diff | ISM | RSTAMOM |
| United States | ISM Manufacturing | Index | M | 2 | diff | ISM | NAPMPMI |
| United States | Personal Income | Level | M | 29 | log diff | BEA | PITLCHNG |
| Euro Area | GDP | Real GDP, level | Q | 48 | log diff | EUROSTAT | EUGNEMUQ |
| Euro Area | IP | Index, level | M | 46 | log diff | EUROSTAT | EUITEMUM |
| Euro Area | Unemployment rate | Level, percent | M | 32 | log diff | EUROSTAT | UMRTEMU |
| Euro Area | Retail Sales | Level | M | 41 | log diff | EUROSTAT | RSSAEMUM |
| Euro Area | PMI Composite (Flash) | Index | M | -9 | diff | Markit | ECPMICOU |
| United Kingdom | GDP | Real GDP, level | Q | 24 | log diff | UK ONS | UKGRABIQ |
| United Kingdom | IP | Index, level | M | 38 | log diff | UK ONS | UKIPMOM |
| United Kingdom | Unemployment rate | Level, percent | M | 15 | log diff | UK ONS | UKUER |
| United Kingdom | Retail Sales | Level | M | 20 | log diff | UK ONS | UKRVAMOM |
| United Kingdom | PMI Manufacturing | Index | M | 2 | diff | Markit | PMITMUK |
| Canada | GDP | Real GDP, level | Q | 61 | log diff | STCA | CGE9ANN |
| Canada | IP (monthly GDP) | Index, level | M | 60 | log diff | STCA | CAIPMOM |
| Canada | Employment | Level | M | 7 | log diff | STCA | CANLNETJ |
| Canada | Retail Sales | Level | M | 52 | log diff | STCA | CARSCHNG |
| Canada | Ivey PMI | Index | M | 6 | diff | PMAC | IVEY |
| Japan | GDP | Real GDP, level | Q | 46 | log diff | ESRI | JGDPAGDP |
| Japan | IP | Index, level | M | 28 | log diff | METI | JNIPMOM |
| Japan | Unemployment rate | Level, percent | M | 28 | log diff | MIC | JNUE |
| Japan | Retail Sales | Level | M | 27 | log diff | METI | JNRETMOM |
| Japan | Tankann Survey | Index | Q | -4 | diff | BoJ | JNTSMFG |
2.1 News Surprises
Market participants watch, and react to, scheduled macroeconomic
announcements because these announcements potentially contain new
information that was not previously incorporated into market
participants' expectations about the state of the economy. Several
studies have looked into the forecast efficiency, or rationality,
of market expectations. Under rationality, the surprise component,
measured as difference between the actual release and its forecast,
should truly represent "news," meaning that market agents
optimally use available information in forming their forecasts, and
therefore the forecast error should be orthogonal to information
available when the forecast is produced. This is equivalent to
testing whether the error term
![]() is orthogonal to the
forecast
is orthogonal to the
forecast
![]() in the
equation
in the
equation
| (2) |
In particular, testing for forecast efficiency boils down to
testing that
![]() in the regression
in the regression
| (3) |
where
![]() is the
forecast error, a.k.a news surprise. This is sometimes known as the
Mincer
is the
forecast error, a.k.a news surprise. This is sometimes known as the
Mincer![]() Zarnowitz test (Mincer and Zarnowitz 1969).
Several earlier papers have applied these tests mainly using data
revisions (among others, see Croushore and Stark (2001) and Faust,
Rogers and Wright (2005)). Table 2 reports evidence
from the baseline tests of forecast rationality
Zarnowitz test (Mincer and Zarnowitz 1969).
Several earlier papers have applied these tests mainly using data
revisions (among others, see Croushore and Stark (2001) and Faust,
Rogers and Wright (2005)). Table 2 reports evidence
from the baseline tests of forecast rationality ![]() tests of the hypothesis that
tests of the hypothesis that
![]() in equation
(3). As can be
seen in the middle columns,
in equation
(3). As can be
seen in the middle columns,
![]() and
and ![]() are
very often significantly different from zero and the F test fails
to reject the null hypothesis that
are
very often significantly different from zero and the F test fails
to reject the null hypothesis that
![]() only in
1/3 of the cases.
only in
1/3 of the cases.
But given that Bloomberg median forecasts are not efficient, why are they so important? Why do I use them rather than using efficient forecasts that I could construct within the factor model? The answer is simple: financial markets react neither to my own private forecast nor yours; financial markets react to Bloomberg forecasts, which are public and everyone can see.
A wide literature has documented the asset price response to macroeconomic news announcements. Andersen, Bollerslev, Diebold and Vega (2003, 2007) and Gilbert, Scotti, Strasser and Vega (2012) among others have looked into this question. Table 3 displays the results of univariate regressions of foreign exchange returns on the individual macro announcement surprises over the sample period 2003-2012. These results do not necessarily correspond to what reported in the existing literature because of the different samples used. However, they clearly state the point that Bloomberg forecasts (and surprises) are important because financial markets react to them.
Table 2. Forecast Efficiency Regression Results
| Country | Series Name | | | F | pvalue |
|---|---|---|---|---|---|
| United States | GDP | -0.02 | -0.04 | 0.71 | 0.50 |
| United States | IP | -0.12*** | 0.27*** | 6.62 | 0.00 |
| United States | Employment | -12.94** | -0.06* | 4.00 | 0.02 |
| United States | Retail Sales | -0.02 | 0.08 | 0.52 | 0.59 |
| United States | ISM | 1.40 | -0.02 | 1.25 | 0.29 |
| United States | Personal Income | 0.05 | -0.01 | 1.10 | 0.34 |
| Euro area | GDP | -0.01 | 0.11** | 2.76 | 0.08 |
| Euro area | IP | -0.06 | -0.16*** | 4.49 | 0.01 |
| Euro area | Unemployment | 0.04 | 0.00 | 0.21 | 0.81 |
| Euro area | Retail Sales | -0.12** | -0.26* | 4.65 | 0.01 |
| Euro area | PMI | 1.27 | -0.03 | 0.41 | 0.66 |
| United Kingdom | GDP | -0.15*** | 0.27*** | 6.13 | 0.01 |
| United Kingdom | IP | -0.23*** | -0.02 | 7.32 | 0.00 |
| United Kingdom | Unemployment | 0.04 | -0.01** | 3.12 | 0.05 |
| United Kingdom | Retail Sales | 0.20*** | -0.04 | 3.56 | 0.03 |
| United Kingdom | PMI | 2.89 | -0.05 | 1.16 | 0.32 |
| Canada | GDP | 0.05 | -0.01 | 0.11 | 0.90 |
| Canada | IP | -0.07*** | 0.06 | 6.56 | 0.00 |
| Canada | Employment | 5.70 | 0.12 | 2.52 | 0.09 |
| Canada | Retail Sales | -0.06 | 0.26** | 2.66 | 0.07 |
| Canada | Ivey Survey | 15.95*** | -0.27*** | 4.06 | 0.02 |
| Japan | GDP | 0.12 | -0.01 | 1.79 | 0.18 |
| Japan | IP | -0.44*** | 0.06 | 10.41 | 0.00 |
| Japan | Unemployment | 0.29** | -0.07** | 4.44 | 0.01 |
| Japan | Retail Sales | 0.13 | 0.25*** | 3.80 | 0.03 |
| Japan | Tankann | 0.17 | 0.01 | 0.22 | 0.80 |
* 10 percent significance, ** 5 percent significance, and *** 1 percent significance
Table 3. Results of Univariate Regressions in Which Exchange Rate Returns are Regressed on Each Individual Macroeconomic News Announcement Surpise (July 2003-Sept 2012), ![]()
| Euro/$: Beta | Euro/$: R2 | GBP/$: Beta | GBP/$: R2 | CAD/$: Beta | CAD/$: R2 | JPY/$: Beta | JPY/$: R2 | |
| US: IP | 0.058 | 0.007 | 0.022 | 0.001 | 0.046** | 0.005 | -0.053 | 0.005 |
| US: Employment | 0.258*** | 0.091 | 0.186*** | 0.094 | -0.058 | 0.008 | 0.377*** | 0.210 |
| US: Retail sales | 0.033 | 0.003 | 0.091* | 0.026 | -0.097** | 0.024 | 0.215*** | 0.117 |
| US: Personal income | 0.013 | 0.000 | -0.019 | 0.001 | 0.036 | 0.003 | -0.057 | 0.010 |
| US: PMI | 0.021 | 0.001 | 0.010 | 0.000 | -0.029 | 0.002 | 0.091** | 0.022 |
| US: GDP | 0.139* | 0.043 | -0.106* | 0.030 | 0.054* | 0.006 | 0.025 | 0.002 |
| Foreign: IP | -0.107*** | 0.033 | -0.131*** | 0.066 | -0.029 | 0.002 | 0.114 | 0.021 |
| Foreign: Employment/unemployment | 0.133*** | 0.035 | -0.037 | 0.002 | -0.260*** | -0.124 | 0.023 | 0.002 |
| Foreign: Retail sales | -0.190*** | 0.079 | -0.131*** | 0.044 | -0.215*** | 0.094 | -0.067** | 0.001 |
| Foreign: PMI/Ivey/Tankann | 0.014 | 0.000 | -0.250*** | 0.092 | -0.120*** | 0.025 | -0.099* | 0.029 |
| Foreign: GDP | -0.107 | 0.034 | -0.394*** | 0.295 | -0.108 | 0.035 | 0.049 | 0.013 |
* 10 percent, ** 5 percent, and *** 1 percent significance with Newey-West standard errors.
Employment is used for US and CA, unemployment for EA, UK, and JA. IP, empl, rtsales, and pers.income have around 104-110 observations depending on the country. GDP has 35-36 observations. PMI observations vary the most: 110 (US), 64 (EA), 78 (UK), 102 (CA), 37 (JA, quarterly).
3 The Model
I use a standard dynamic factor model at a monthly frequency which explicitly accounts for missing data and temporal aggregation.
3.1 The Dynamic Factor Model
I model the unobserved factor as a VAR process of order
![]() :
:
| (4) | |||
| (5) |
The model includes both monthly and quarterly variables. The
monthly variables ![]() follow a single
factor model representation of the type:
follow a single
factor model representation of the type:
| (6) | |||
| (7) |
where ![]() represents the underlying real activity
factor,
represents the underlying real activity
factor,
![]() is a vector of idiosyncratic
components, and
is a vector of idiosyncratic
components, and ![]() represent the factor loadings
for the monthly variables.
represent the factor loadings
for the monthly variables.
![]() follows an
follows an ![]() process, as shown in equation (7), and
process, as shown in equation (7), and
![]() .
.
The quarterly variables ![]() follow a
similar factor model representation:
follow a
similar factor model representation:
| (8) | |||
| (9) |
with
![]() . Quarterly
variables in the model are GDPs for all countries and the Japanese
Tankan survey. I follow Mariano and Murasawa (2003) in the way I
incorporate quarterly GDP into the monthly factor model. I define
. Quarterly
variables in the model are GDPs for all countries and the Japanese
Tankan survey. I follow Mariano and Murasawa (2003) in the way I
incorporate quarterly GDP into the monthly factor model. I define
![]() , then
, then
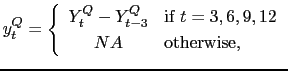 |
(10) |
and using the Mariano and Murasawa (2003) approximation I get that
for
![]()
| (11) |
Based on this I can link the quarterly variables to the monthly factor as
| (12) | |||
A similar treatment can be applied to any other quarterly series in the dataset.11
Stacking monthly and quarterly variables, this model can be easily cast in a state space representation:12
| (13) | |||
| (14) |
where
![]()
![]() and the
state vector includes both the common factor and the idiosyncratic
components:
and the
state vector includes both the common factor and the idiosyncratic
components:
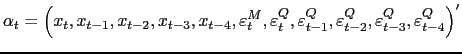 |
(15) |
We define the total number of indicators as ![]() . Of course, the model could be extended to a multiple
factor model.
. Of course, the model could be extended to a multiple
factor model.
3.2 Forecast Weights
With the dynamic factor model approach described above, each of
the real activity variables is used to extract information about
the common (unobserved) factor. The contribution of each series to
the determination of the factor represents the weight applied to
construct the surprise index. As shown in Koopman and Harvey
(2003), the weights
![]() are used to
calculate the estimator of the state vector based on information
available as of time
are used to
calculate the estimator of the state vector based on information
available as of time ![]() and can therefore be used
to compute the contribution of variable
and can therefore be used
to compute the contribution of variable ![]() in
forecasting the factor
in
forecasting the factor ![]() at time
at time ![]() :
:
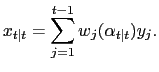 |
(16) |
As in the previous section, ![]() can contain
vectors of monthly or quarterly series
can contain
vectors of monthly or quarterly series
![]() Each series is
indicated by
Each series is
indicated by ![]()
I consider the real-time release schedule of each real activity
series ![]() . For example, if I want to calculate
the factor for the month of March 2012, information about that
month will be released gradually. In the United States, the ISM
index will be the first series to be released, most likely followed
by employment, retail sales, industrial production, and personal
income. The advance reading of GDP for the first quarter (i.e. the
one which includes January) will be released with an average delay
of 29 days from the end of the quarter. Based on this real-time
schedule, I can recursively compute the underlying unobserved
factor at time
. For example, if I want to calculate
the factor for the month of March 2012, information about that
month will be released gradually. In the United States, the ISM
index will be the first series to be released, most likely followed
by employment, retail sales, industrial production, and personal
income. The advance reading of GDP for the first quarter (i.e. the
one which includes January) will be released with an average delay
of 29 days from the end of the quarter. Based on this real-time
schedule, I can recursively compute the underlying unobserved
factor at time ![]() based on the data availability
until day
based on the data availability
until day ![]() , that is
, that is ![]() .
Equation (16)
displays the factor at time
.
Equation (16)
displays the factor at time ![]() as a weighted
average of the data
as a weighted
average of the data ![]() released between day
released between day
![]() and
and ![]() The weights
implicitly display a time decay feature with more recent data
exhibiting higher importance in determining the factor.
The weights
implicitly display a time decay feature with more recent data
exhibiting higher importance in determining the factor.
For each data series included in ![]() , say
, say
![]() , there exist a time series of weights
, there exist a time series of weights
![]() , so that cumulative forecast
weights can be computed as in Banbura and Rünstler (2010)
, so that cumulative forecast
weights can be computed as in Banbura and Rünstler (2010)
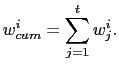 |
(17) |
Forecast weights do not depend on time ![]() , but depend
on the forecast horizon and the real-time release pattern of the
data. In this paper, I abstract from data revisions.
, but depend
on the forecast horizon and the real-time release pattern of the
data. In this paper, I abstract from data revisions.
An alternative to using the forecast weights as outlined above,
would be to use the weights as described in Banbura and Modugno
(2010). In this case, the weights would have a different
interpretation, as they would represent the contribution of the
news releases to the factor revision from period ![]() to
to ![]() . The Banbura and Modugno (2010) weights
are represented by the
. The Banbura and Modugno (2010) weights
are represented by the
![]() in:
in:
![$\displaystyle E[x_{t}^{i}\vert\Omega_{\nu+1}]-E[x_{t}^{i}\vert\Omega_{\nu}] = \sum_{j=1}^{J_{\nu+1}}b_{\nu+1,j} (y_t - E[y_{t}^{i}\vert\Omega_{\nu}])$](img145.gif) |
(18) |
where
![]() represents the revision to the factor implied by the new data
release,
represents the revision to the factor implied by the new data
release,
![]() is the
news surprise, and
is the
news surprise, and
![]() and
and
![]() are two consecutive data
vintages with
are two consecutive data
vintages with
![]() . In the
Banbura and Modugno (2010) framework,
. In the
Banbura and Modugno (2010) framework,
![]() is the model
implied expectation of the variable
is the model
implied expectation of the variable ![]() , while in my
framework
, while in my
framework
![]() would be the
Bloomberg expectation for the macro variable
would be the
Bloomberg expectation for the macro variable ![]() .
The advantage of their set-up is that the weights represents the
impact of the news release of a variable
.
The advantage of their set-up is that the weights represents the
impact of the news release of a variable ![]() on the
underlying factor forecast, rather than the importance of the
underlying series
on the
underlying factor forecast, rather than the importance of the
underlying series ![]() in determining the factor.
The drawback, however, is that the weight
in determining the factor.
The drawback, however, is that the weight ![]() is
practically the Kalman gain and as such, this set-up does not
provide me with a time series of the weights similar to what I have
in my framework. A way to overcome this issue could be to apply
some arbitrary time decay feature similar to what applied by
Citigroup to construct the so-called "Citigroup Economic Surprise
Indexes." These indexes are defined as weighted historical
standard deviations of data surprises where the weights of economic
indicators are derived from the announcement's impact that these
data surprises have on foreign exchange markets to which a
subjective decay function is applied.
is
practically the Kalman gain and as such, this set-up does not
provide me with a time series of the weights similar to what I have
in my framework. A way to overcome this issue could be to apply
some arbitrary time decay feature similar to what applied by
Citigroup to construct the so-called "Citigroup Economic Surprise
Indexes." These indexes are defined as weighted historical
standard deviations of data surprises where the weights of economic
indicators are derived from the announcement's impact that these
data surprises have on foreign exchange markets to which a
subjective decay function is applied.
3.3 The Surprise Index
I construct the surprise index starting from equation (16). With the idea
that forecast weights represent the importance of the series in
determining the underlying unobservable factor, I use those same
weights to combine the standardized surprises so that the surprise
index
![]() at time
at time ![]() is:
is:
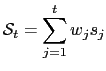 |
(19) |
where
![]() contains the vectors of the standardized surprise
contains the vectors of the standardized surprise ![]() corresponding to each data series
corresponding to each data series ![]() In the application, I construct the underlying series
that feed into the factor so that a higher (lower) number means
that the economy is doing better (worse). Likewise, I construct
each surprise such that a positive surprise means good (bad) news
for the economy. This implies that the weights should be positive.
In the application, I construct the underlying series
that feed into the factor so that a higher (lower) number means
that the economy is doing better (worse). Likewise, I construct
each surprise such that a positive surprise means good (bad) news
for the economy. This implies that the weights should be positive.
3.4 The Uncertainty Index
The uncertainty index is computed starting from equation (16) and averaging squared surprises
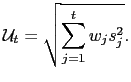 |
(20) |
The link with realized volatility is straightforward. Just like
realized volatility is computed as the square root of the average
of squared returns,
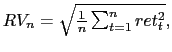 the
uncertainty index is computed as the square root of the weighted
average of the squared surprises.13 The weights are not
simply
the
uncertainty index is computed as the square root of the weighted
average of the squared surprises.13 The weights are not
simply ![]() but are time varying. Moreover, unlike
the volatility which is computed on one instrument at a time using
the history from
but are time varying. Moreover, unlike
the volatility which is computed on one instrument at a time using
the history from
![]() , the uncertainty index is
computed across different instruments/surprises as well as across
time.
, the uncertainty index is
computed across different instruments/surprises as well as across
time.
4 Estimation
The construction of the indexes requires three steps:
(i) estimation of the state space model of equations (13) and (14),
(ii) determination of the weights ![]() as defined in
equation (16) and
as defined in
equation (16) and
(iii) construction of the indexes as for equations (19) and (20).
For step (i), the estimation of the model in equations (13) and (14) requires
estimation of the parameters
![]() . The missing
data pattern complicates the estimation of the model. Missing data
occur both because the data are at different frequencies and
because indicators are released at different times after the end of
the reference period (ragged edge). A number of papers have dealt
with different frequencies and missing observations either within a
Kalman filter framework (see among others Aruoba, Diebold, and
Scotti (2009), Giannone, Reichlin and Small (2008), and Banbura and
Modugno (2010)) or within a mixed data sampling (MIDAS) regression
framework (Andreou, Kourtellos, and Ghysels (2011)). I estimate the
parameters by maximum likelihood implemented by the Expectation
Maximization (EM) algorithm as proposed by Doz, Giannone, and
Reichlin (2012) and extended by Banbura and Modugno (2010) to deal
with missing observations and idiosyncratic dynamics.14 The
EM algorithm iterates over two steps: in the expectation step, the
log-likelihood conditional on the data is calculated using the
estimated parameters from the previous iteration; in the
maximization step, the parameters are re-estimated by maximizing
the expected log-likelihood with respect to
. The missing
data pattern complicates the estimation of the model. Missing data
occur both because the data are at different frequencies and
because indicators are released at different times after the end of
the reference period (ragged edge). A number of papers have dealt
with different frequencies and missing observations either within a
Kalman filter framework (see among others Aruoba, Diebold, and
Scotti (2009), Giannone, Reichlin and Small (2008), and Banbura and
Modugno (2010)) or within a mixed data sampling (MIDAS) regression
framework (Andreou, Kourtellos, and Ghysels (2011)). I estimate the
parameters by maximum likelihood implemented by the Expectation
Maximization (EM) algorithm as proposed by Doz, Giannone, and
Reichlin (2012) and extended by Banbura and Modugno (2010) to deal
with missing observations and idiosyncratic dynamics.14 The
EM algorithm iterates over two steps: in the expectation step, the
log-likelihood conditional on the data is calculated using the
estimated parameters from the previous iteration; in the
maximization step, the parameters are re-estimated by maximizing
the expected log-likelihood with respect to ![]() Following Doz, Giannone, and Reichlin (2011, 2012),
the initial parameters
Following Doz, Giannone, and Reichlin (2011, 2012),
the initial parameters
![]() are obtained through principal
components and the iteration between the two steps is stopped when
the increase in likelihood between two steps is small.
are obtained through principal
components and the iteration between the two steps is stopped when
the increase in likelihood between two steps is small.
In step (ii), once the parameters ![]() are
estimated, the weights can be computed by running the algorithm
defined in Koopman and Harvey (2003) to get the smoothed weights.
The history of weights
are
estimated, the weights can be computed by running the algorithm
defined in Koopman and Harvey (2003) to get the smoothed weights.
The history of weights
![]() for
for ![]() is computed in real time for any
is computed in real time for any ![]() based on the information available up until that time.
based on the information available up until that time.
Finally, in step (iii), the surprise and uncertainty indexes are computed based on (19) and (20).
Each country is estimated separately. The estimation of the underlying business condition index is based on the longest common sample across countries (1980-2012), except for the euro area for which not enough indicators are available before 1985. The Kalman filter is then run based on the estimated parameters in a real time framework (i.e. based on data that are released sequentially), and steps (ii) and (iii) are repeated to get the smoothed weight matrix and the real-time surprise and uncertainty indexes for each day from May 15, 2003 to September 30, 2012.15 Step (i) is run over the entire sample, unlike steps (ii) and (iii), because for countries in which data series become available later in the sample estimates are not accurate at first.16 For the United States, where there are no issues of data availability, there are no significant differences in the surprise indexes constructed according to the two methodologies. 17
5 Results
Here I discuss the results following the steps described in the estimation section.
5.1 Real Activity Indexes
The real activity indexes that I estimate based on the indicators listed in table 1 are displayed in figure 1. As mentioned, I use a longer history for the estimation of these factors in order to have more reliable estimates. The figure shows the latest factors, which include information as of September 30, 2012, for the United States, the Euro Area, the United Kingdom, Canada, Japan, and an aggregate of the five countries.
The average value of each index is zero by construction. Therefore, a value of zero is interpreted as average economic activity for that country, whereas progressively bigger positive values indicate progressively better-than-average conditions and progressively more negative values indicate progressively worse-than-average conditions. Importantly, average conditions differ across countries. For example, a value of zero for Japan corresponds to a number akin to 0.7 percent annual real GDP growth while a value of zero in the United States corresponds to around 2.5 percent annual real GDP growth. The shaded areas in the panels represent official recessions as defined by the NBER, CEPR, and ECRI. The indexes fall sharply during recessions and tend to reach relatively high values during good times, for example the late 1990s. As expected, the U.S. business condition index is very similar to the Aruoba, Diebold, and Scotti (ADS) index maintained by the Federal Reserve Bank of Philadelphia, with the difference that the ADS index is daily and also includes weekly data such as initial jobless claims. Because the other countries do not have relevant weekly data, I opted here for a monthly frequency. The last panel shows the aggregate business condition index, which is created by aggregating the other indexes weighing them by each country's GDP.
Table 4. Average cumulative weights for each indicator used to construct the surprise index. For comparability across countries, weights are standardized so that the sum of all weights in each country is equal to 1. The average is computed over the last five years of the sample when all the indicators are available.
| United States | Euro area | United Kingdom | Canada | Japan | |
| GDP | 0.04 | 0.06 | 0.13 | 0.00 | 0.01 |
| IP | 0.35 | 0.31 | 0.39 | 0.02 | 0.57 |
| Employment/Unemployment | 0.30 | 0.40 | 0.30 | 0.92 | 0.17 |
| Retail Sales | 0.14 | 0.15 | 0.11 | 0.01 | 0.13 |
| PMI | 0.12 | 0.09 | 0.08 | 0.04 | 0.12 |
| Personal Income | 0.05 |
5.2 Weights
To gauge the importance of the various indicators in
constructing the surprise and uncertainty indexes, I consider two
different standpoints in analyzing the weights: (i) I construct the
cumulative weights as in equation (17) and (ii) I
analyze, at each time ![]() the vector of
the vector of ![]() weights,
weights, ![]() , that are
multiplied by the announcements to get the time
, that are
multiplied by the announcements to get the time ![]() surprise index based on equation (19).
surprise index based on equation (19).
To be clear, for
![]() , the variable
, the variable ![]() that represents the weights in equation (19) is a matrix of
dimension
that represents the weights in equation (19) is a matrix of
dimension
![]() which contains those
weights applied to all the announcements available up to time
which contains those
weights applied to all the announcements available up to time
![]() that are used in the
construction of the index. The sum of these weights over time
represents the cumulative weight for indicator
that are used in the
construction of the index. The sum of these weights over time
represents the cumulative weight for indicator ![]() at time
at time
![]() , that is
, that is
![]() .
.
The average cumulative weights are reported in table 4. 18 The
weights are averages because I calculate the mean of ![]() over the last five years of the sample. The choice of
the five years is arbitrary to some extent and is linked to the
availability of PMI data in the euro area and in the United
Kingdom.19 Based on this measure, employment
(or unemployment) and industrial production have the highest weight
in the United States, the Euro Area, and in the United Kingdom. In
Canada, most of the weight (92 percent) is concentrated on
employment. In Japan, industrial production is the most important
series followed by unemployment and retail sales.
over the last five years of the sample. The choice of
the five years is arbitrary to some extent and is linked to the
availability of PMI data in the euro area and in the United
Kingdom.19 Based on this measure, employment
(or unemployment) and industrial production have the highest weight
in the United States, the Euro Area, and in the United Kingdom. In
Canada, most of the weight (92 percent) is concentrated on
employment. In Japan, industrial production is the most important
series followed by unemployment and retail sales.
Cumulative weights, however, are not constant over time and
therefore looking at their mean is not enough. They are affected by
the pattern of missing observations due to the different release
schedule of the underlying indicators (ragged edge). Figure 2 shows
the evolution of the cumulative forecast weights
![]() for each indicator over the
first quarter of 2012. Each panel in the figure displays the
weights for a specific country. A clear pattern stands out: as soon
as new information about an indicator becomes available, the
contribution of that particular indicator increases. So, for
example, the weight of the U.S. nonfarm payroll series (NFP),
represented by the green line in the top leftmost panel, increases
on January 6, February 3, and March 9 (solid vertical lines) when
the December, January and February figures are announced. Until the
IP numbers are released (dotted vertical lines), nonfarm payroll
has the biggest weight. With the release of the IP figures, the
weight for IP (red line) increases and becomes the highest of all.
However, as additional information about real activity in the
United States is released, nonfarm payroll and IP weights start to
decline gradually. A similar pattern can be observed in the other
countries: as the more timely information becomes available, its
weight jumps up and it declines as other indicators are
subsequently released. In the euro area (the top rightmost panel),
unemployment tends to have the highest weight overall, but when IP
numbers are released, IP weights become slightly bigger than those
of the unemployment data. In the United Kingdom, IP weights are
always bigger than any other weight. In Canada unemployment is
consistently and by far the highest weight. Finally, in Japan, the
Tankan survey has the highest weight at the beginning of the
quarter when it represents the only available information for that
quarter, but its weight is immediately overtaken as other
information become available and, in particular, as IP numbers are
released.
for each indicator over the
first quarter of 2012. Each panel in the figure displays the
weights for a specific country. A clear pattern stands out: as soon
as new information about an indicator becomes available, the
contribution of that particular indicator increases. So, for
example, the weight of the U.S. nonfarm payroll series (NFP),
represented by the green line in the top leftmost panel, increases
on January 6, February 3, and March 9 (solid vertical lines) when
the December, January and February figures are announced. Until the
IP numbers are released (dotted vertical lines), nonfarm payroll
has the biggest weight. With the release of the IP figures, the
weight for IP (red line) increases and becomes the highest of all.
However, as additional information about real activity in the
United States is released, nonfarm payroll and IP weights start to
decline gradually. A similar pattern can be observed in the other
countries: as the more timely information becomes available, its
weight jumps up and it declines as other indicators are
subsequently released. In the euro area (the top rightmost panel),
unemployment tends to have the highest weight overall, but when IP
numbers are released, IP weights become slightly bigger than those
of the unemployment data. In the United Kingdom, IP weights are
always bigger than any other weight. In Canada unemployment is
consistently and by far the highest weight. Finally, in Japan, the
Tankan survey has the highest weight at the beginning of the
quarter when it represents the only available information for that
quarter, but its weight is immediately overtaken as other
information become available and, in particular, as IP numbers are
released.
Turning to (ii), figure 3 shows the weights ![]() when computed on March 31, 2012 for the six months prior to that
day.20 The weights in all the countries
display a time decay feature. For the United States, nonfarm
payroll and IP (the green and red bars) have the highest weight for
the month of February based on information as of March 31, 2012.
Interestingly, IP weights are more persistent than the others,
suggesting that past IP information continues to be important
whereas the nonfarm payroll information value is limited to the
latest available month. Because no data about March are released as
of March 31, all the weights are zero for the month of March.
Weights are close to zero for all indicators after about six
months. Of note, the time decay feature implies that an increase in
the index might be due to a smaller weight given to an old negative
surprise or to a new positive surprise.
when computed on March 31, 2012 for the six months prior to that
day.20 The weights in all the countries
display a time decay feature. For the United States, nonfarm
payroll and IP (the green and red bars) have the highest weight for
the month of February based on information as of March 31, 2012.
Interestingly, IP weights are more persistent than the others,
suggesting that past IP information continues to be important
whereas the nonfarm payroll information value is limited to the
latest available month. Because no data about March are released as
of March 31, all the weights are zero for the month of March.
Weights are close to zero for all indicators after about six
months. Of note, the time decay feature implies that an increase in
the index might be due to a smaller weight given to an old negative
surprise or to a new positive surprise.
The Euro Area represents an interesting case because as of March 31, 2012, flash euro-area PMI numbers for February and March are available, whereas any other real activity information refers to January. While past PMI numbers have a very small weight, the February and March PMI figures have a relatively high weight. Once more, the weights for IP are the slowest to decline and the last available unemployment data displays the highest weight.
The United Kingdom seems to have the slowest time decay in its weights compared to the other countries. In Canada, the employment weights dominate every other weight. Japan displays the quickest time decay with weights reaching practically zero already after only four months. Unlike the other countries, unemployment does not have the highest weight.
These weights are computed based on the available information as of March 31, 2012. Of course, the pattern would be different if the weights were to be computed on another day when different information was available.
5.3 Surprise Indexes
The news surprise indexes for the United States, the Euro area, the United Kingdom, Canada, Japan, and the aggregate of the five countries are displayed in figure 4 (solid lines).21 A positive (negative) reading of the surprise index suggests that economic releases have on balance been higher (lower) than consensus, meaning that agents were more pessimistic (optimistic) about the economy. A positive number does not mean the economy is doing well on any ordinary measure, but merely that economic forecasts were overly pessimistic. The surprise index reaches its lowest value during the global financial crisis of 2008-2009 in all the countries. This suggests that, as the crisis was unfolding, agents were less pessimistic about its possible outcome and its impact on the real economy, while the actual data turned out to depict a grimmer picture of the stance of economic activity around the globe.
The euro-area surprise index dropped sharply in March 2012. As agents became more optimistic on a resolution of the European debt crisis with the bond exchange taking place in Greece, real activity indicators for 2012 that were released in March were disappointing. The January unemployment rate, released on March 1, was 10.70 percent versus an expectation of 10.40 percent. The February and March euro-area PMIs released on February 22 and March 22 were 49.70 and 48.70 respectively, versus expected values of 50.50 and 49.60, respectively. Finally, based on data released on March 14, euro-area industrial production increased 0.2 percent from December 2011 to January 2012 versus an expectation of a 0.5 increase.
Interestingly, the U.K. index dropped sharply on January 25, 2011 when a very disappointing Q4 GDP for 2010 was released (-0.5 percent versus an expectation of +0.5 percent). Although subsequent data helped the index to move higher, it continued to be depressed until the second half of 2011. Agents reportedly attributed the slowdown to a series of temporary factors (such as bad weather, the Japanese earthquake, and the royal wedding) that were believed to be short-lived. The transitory nature of these events most probably made agents mark up their economic outlook, but as a series of temporary factors occurred, these expectation were always disappointed.
The Japanese surprise index dropped sharply on April 27, 2011 as the actual number for IP turned out to be a lot lower than expected following the March 2011 earthquake: IP decreased 15.30 percent between February and March versus the expectation of a 10.60 percent decrease.
On the other hand, there are also several instances where the surprise indexes are positive, especially coming out of the recession in the United States, the United Kingdom, and Canada.
For comparison, the dotted lines in figure 4 show the Citi Economic Surprise Indexes (CESI). Although CESIs also measure economic news, they are constructed based on a different methodology. CESIs are defined as weighted historical standard deviations of data surprises (actual releases versus Bloomberg median survey) and are calculated daily in a rolling three-month window. The weights of the economic indicators are derived from relative high-frequency spot foreign exchange impacts of 1 standard deviation data surprises adjusted to include a time decay feature so as to replicate the limited memory of markets. Because the index constructed in this paper does not rely on the impact that macroeconomic surprises have on asset prices, it represents a more objective measure of deviation from consensus expectations. Although the two indexes follow very similar patterns for all the countries, they also present some differences because both the set of indicators and the weights are different. For example, the euro-area surprise index tends to lag the CESI especially during the shaded area which represents the 2008-2009 recession.
5.4 Uncertainty Indexes
The uncertainty indexes for the United States, the Euro area,
the United Kingdom, Canada, Japan and the aggregate of the five
countries are displayed in figure 5 (solid lines). These indexes
measure how uncertain agents are about current real activity
conditions. A greater (smaller) reading of the uncertainty index
suggests that agents have on balance been more (less) uncertain
about the state of the economy. The indexes tend to be elevated
during recessions, although there are other episodes when the
indexes spike up. In the United States, economic uncertainty was
also relatively high in 2004 and a big jump was observed at the end
of 2005. The euro-area uncertainty index reaches its highest values
just before and after the 2008-2009 recession, suggesting that
agents were more uncertain about the economy as the euro-zone was
entering and exiting the recession. Increased macro uncertainty
characterized also the beginning of 2010 when the Greece "problem" started to be in prime time and the period between the
end of 2011 and the start of 2012. Uncertainty in the United
Kingdom has been particularly elevated since early 2009, when
compared to its value in the first part of the sample. Canada has
experienced several episodes of elevated economic uncertainty,
whereas in Japan, the period after the March 2011 earthquake was by
far the one with the highest uncertainty regarding the state of the
Japanese economy.
The dotted lines in the panels show stock market implied
volatilities in the United States, Euro Area, United Kingdom,
Canada, and Japan as represented by the VIX, VSTOXX, VTFSE, VIXC
and VXJ. The dashed lines display the stock market realized
volatilities for the respective countries. Notably, especially in
the latter part of the sample, the uncertainty index and the VIX
are very similar, whereas the uncertainty index of the euro area
differs somewhat from the VSTOXX. The two measures (implied
volatility and uncertainty index) are constructed in completely
independent ways. Implied volatility, a forward-looking measure, is
computed from option prices. The uncertainty index, a historical
measure, is calculated from current and past macroeconomic news
surprises. The former is a wider measure that combines information
about risk aversion and future stock market volatility, and to the
extent that these two move with news surprises, the VIX also
contains information about current and future economic uncertainty.
On the other hand, the uncertainty index presented here is a clean
measure of agents' uncertainty about the current state of the
economy.
6 Applications
In this section, I present a couple applications for the surprise and uncertainty indexes. In the first application, the surprise index is shown to preserve the properties of the underlying macro series in affecting asset prices in replicating the regressions shown in table 3. Combining several macro series into one, the surprise index has the advantage of being potentially easier to use and very parsimonious. In light of this, Demiralp, King, and Scotti (2013) make use of it as a control variable when investigating the effects of political commentaries on policy rate decisions and policy expectations in the United States and the Euro Area, and find it to be significant determinant of policy expectations. Similarly, Brunetti, Buyuksahin, and Harris (2013) employ it as a control variable in studying the impact of speculation activity in the crude oil market.
In the second application, the U.S. uncertainty index is compared to other uncertainty measures commonly used in the literature. The uncertainty index has a negative impact on real-activity series. Papers like Bloom (2009), Baker, Bloom, and Davis (2013), and Bachmann, Elstner, and Sims (2013) have documented a similar analysis with different measures of uncertainty. I find that, in the United States over the last decade, when uncertainty is strictly related to the state of the economy as measured by real activity, it has a potentially milder impact on macro activity than when the uncertainty is related to both the macro and the financial sectors as measured by the VIX.
Table 5. Results of univariate regressions in which exchange rate returns are regressed on the surprise index (July 2003 - Sept 2012): ![]()
Euro/$: |
Euro/$: R2 |
GBP/$: |
GBP/$: R2 |
CAD/$: |
CAD/$: R2 |
JPY/$: |
JPY/$: R2 |
|
| US surprise index | 0.362*** | 0.022 | 0.263*** | 0.014 | -0.096 | 0.002 | 0.418*** | 0.031 |
| Foreign surprise index | -0.332*** | 0.013 | -0.140 | 0.007 | -0.691*** | 0.042 | 0.128 | 0.002 |
* 10 percent, ** 5 percent, and *** 1 percent significance with Newey-West standard errors.
6.1 Surprise Indexes and News Impact on Foreign Exchanges
As shown in section 2, macroeconomic news announcement affect asset prices. The surprise index presented in this paper represents a nice summary measure that can be used to parsimoniously control for news announcement surprises in more general models.
Table 5 presents the results of a set of regression where the euro/$, GBP/$, CAD/$, and JPY/$ exchange rate returns are regressed on the U.S. surprise index and the respective foreign surprise index, i.e. the euro/$ return is regressed on the U.S surprise index and the euro-area surprise index, the GBP/$ return is regressed on the U.S surprise index and the U.K. surprise index, etc. I cover approximately the sample period for which the surprise indexes are available (July 2003 to Sept. 2012).22 As shown in the table, the surprise indexes tend to have the right sign and be significant: a positive change in the U.S. surprise index (i.e. the U.S. economy doing better than expected) appreciates the U.S. dollar versus the foreign currency, whereas a positive change in the foreign surprise index depreciated the U.S. dollar.
6.2 Uncertainty Measures and the Business Cycle
A "true" measure of economic uncertainty does not exist and stock market realized and implied volatilities have been commonly used as proxies for uncertainty. Bloom (2009), for example, uses the Chicago Board of Option Exchange VXO index as a proxy for uncertainty.23 More recently, a growing literature has focused on finding new measures of macroeconomic uncertainty. Bachmann, Elstner and Sims (2012) use survey expectation data to construct time-varying business-level uncertainty. For Germany and the United States, they construct a measure of uncertainty with forecast disagreement from the IFO Business Climate Survey and the Business Outlook Survey, respectively. Baker, Bloom, and Davis (2013) create an economic policy uncertainty (EPU) measure based on the frequency of newspaper references to economic policy uncertainty, the number and size of the federal tax code provisions set to expire in future years, and the disagreement among economic forecasters about policy relevant variables. Leduc and Liu (2012) use a measure of perceived uncertainty of consumers and businesses from the Thomson Reuters/University of Michigan Surveys of Consumers in the United States and the Confederation of British Industry (CBI) Industrial Trends Survey in the United Kingdom. Jurado, Ludvigson, and Ng (2013) define uncertainty as the variability in the purely unforecastable component of the future value of a variable and measure macro uncertainty as the uncertainty factors common to individual measures of uncertainty across a large number of series. Similarly to Jurado et al. (2013), my measure uses forecast errors, which however are not the objective and efficient forecast errors from a model. Instead they are market based forecast errors and as such my uncertainty index measures the perceived uncertainty about the state of the economy. Agents base decisions on their perceived uncertainty rather than an objective uncertainty that they do not observe.
Figure 6 compares the real-activity uncertainty index developed here against some of the available other measures of uncertainty for the United States. All measures are de-meaned and standardized for comparison; they are all countercyclical, rising during economic downturns. Their pairwise correlations range from about 20-25 percent between the uncertainty index and Baker, Bloom, and Davis or Bachmann, Elstner, and Sims to over 50 percent between the uncertainty index and the VIX.24 The uncertainty index exceeds 1.65 standard deviations above its mean only three times but the peaks do not always correspond with the peaks of the other series suggesting that these uncertainty measures might indeed carry slightly different information.
A growing literature has also focused on analyzing the relationship between real activity and uncertainty, and the latter has been generally found to have a significant role in firms' hiring decisions (employment) and output. To estimate such effects, I estimate a bivariate VAR with log employment and each one of the uncertainty proxies from figure 6, separately. Because of the short data set (monthly data from May 2003 to September 2012), the bivariate VAR represents a parsimonious way to model the joint dynamics between these variables. As shown in Bachmann, Elstner and Sims (2013), the results are robust to estimating a larger VAR similar to Bloom (2009).25 Each VAR is estimated selecting the lag length based on the Schwarz Information Criterion; employment enters in log levels, while uncertainty measures in levels.
Figure 7 shows the recursive impulse responses of employment to a one-standard-deviation uncertainty shock as measured by the different proxies, where uncertainty is ordered first. The shaded region is the +/- one standard error confidence interval for the real-activity uncertainty shock. Employment decreases after an uncertainty shock between 0.9 and 1.2 percent on average at its trough, with the exception of the Baker, Bloom and Davis EPU measure which shows a lower impact over this period. As shown in figure 8 by the confidence intervals for the real-activity uncertainty index and the VIX, when uncertainty is strictly related to real activity, it has potentially milder impact on economic activity. Just flipping the argument, when uncertainty is more generally related to economic as well as financial conditions as measured by the VIX, its impact on real-activity variables appears to be stronger and more prolonged. This finding supports recent work by Caldara, Fuentes-Albero, Gilchrist and Zakrajsek (2013) which finds that the financial channel is key in the transmission of uncertainty shocks. Although I do not explicitly introduce a financial channel, using the real-activity uncertainty index and the VIX allows me to distinguish between purely macro versus the more general macro and financial uncertainty.
For robustness, some alternative specifications are considered. The result just described holds true with other measures of real activity, such as industrial production or unemployment rate. Although a similar comparison is not shown for the other countries, the negative impact of an uncertainty shock on employment is generally significant across countries. A part of the uncertainty literature, considers uncertainty as a consequence of depressed economic activity, rather than a cause. In this case, the recursive identification scheme implemented above should be inverted. As a robustness check, I estimate generalized impulse responses from Pesaran and Shin (1998) which do not depend on the ordering of the variables and the results actually remain quite consistent across uncertainty proxies and variables.
7 Summary and Concluding Remarks
The goal of this paper is to construct measures of (i) real-time economic news and their deviation from consensus expectations and (ii) real-time uncertainty about the state of the economy. I view this paper as a "complement" to the Aruoba, Diebold and Scotti (2009) business condition index updated on a daily basis by the Federal Reserve Bank of Philadelphia. While the ADS index is a real time measurement of the state of the economy, the surprise index presented in this paper measures agents' optimism or pessimism about the economy by combining macroeconomic news surprises, and the uncertainty index measures agents' uncertainty about the current state of the economy. This paper is also a "complement" to other papers that develop uncertainty measures in that it only measures perceived uncertainty about the state of the economy and as such is mostly linked to Bachmann, Elstner, and Sims (2013).
I look forward to a variety of variations and extensions of this basic theme, including but not limited to:
- constructing indexes for nominal variables to gauge optimism/pessimism about inflation stance
- incorporating additional indicators and surprises for each country to construct a summary measure of real and nominal variables
- extending the framework to include U.S. macro surprises into foreign economies to exploit the correlation/causation across business cycles
- including vintages of data so that the indexes change not only when new information is released but also when past information is revised
- expanding the dataset to construct indexes with a longer history
- analyzing in more depth the impact of different types of uncertainty.
Bibliography
Andersen, T.G., Bollerslev, T., Diebold, F.X. and Vega, C. (2003). "Micro Effects of Macro Announcements: Real-Time Price Discovery in Foreign Exchange," American Economic Review, 93, 38-62.
Andersen, T.G., Bollerslev, T., Diebold, F.X. and Vega, C. (2007). "Real-Time Price Discovery in Stock, Bond and Foreign Exchange Markets," Journal of International Economics, 73, 251-277
Andreou, E., Kourtellos, A. and Ghysels, E. (2011) "Forecasting with Mixed-Frequency Data," Oxford Handbook of Economic Forecasting, Michael P. Clements and David F. Hendry (ed.) Chapter 8.
Aruoba, B.S., Diebold, F.X., and Scotti, C. (2009), "Real-Time Measurement of Business Conditions," Journal of Business and Economic Statistics, 27, 417-427
Bachmann, R., Elstner, S., and Sims, E. (2013), "Uncertainty and Economic Activity: Evidence from Business Survey Data," American Economic Journal: Macroeconomics, 5(2), 217-249
Banbura, M., Giannone, D., and Reichlin, L. (2010), "Nowcasting," in Handbook on Economic Forecasting, Michael P. Clements and David F. Hendry editors, Oxford
Banbura, M. and Modugno, M. (2010) "Maximum Likelihood Estimation of Large Factor Model on Dataset with Arbitrary Pattern of Missing Data," International Journal of Forecasting, forthcoming
Banbura, M. and Rünstler, G. (2010), "A Look into the Factor Model Black Box: Publication Lags and the Role of Hard and Soft Data in forecasting GDP," International Journal of Forecasting, 27, 333-346
Baum, C. and Wan, C.(2010) "Macroeconomic Uncertainty and Credit Default Swap Spreads," Applied Financial Economics, 20, 1163-1171
Baker, S.R., Bloom, N., and Davis S.J. (2013), "Measuring Economic Policy Uncertainty," mimeo
Bloom, N. (2009), "The impact of Uncertainty Shocks," Econometrica, 77, 623-685
Brunetti, C. Buyuksahin, B. and Harris, J. (2013), "Do Institutional Traders Predict Bull and Bear Markets?," mimeo
Caldara, D., Fuentes-Albero C., Gilchrist, S., and Zakrajsek, E. (20131) "On the Identification of Financial and Uncertainty Shocks," mimeo
Camacho, M. and Perez-Quiroz, G. (2009) "Introducing the euro-sting: Short-term indicator of euro area growth," Journal of Applied Econometrics, 25, 663-694
Constable, S. and Wright, R.E. (2011) "The WSJ Guide to the 50 Economic Indicators That Really Matter: From Big Macs to "Zombie Banks," the Indicators Smart Investors Watch to Beat the Market," HarperCollins, ISBN 0062001388
Croushore, D., and Stark, T. (2001) "A Real-time Dataset for Macroeconomists," Journal of Econometrics 105, 111-130
Demiralp, S., King, S., and Scotti, C. (2013) "Does Anyone Listen when Politicians Talk? The Impact of Political Commentaries on Policy Rate Decisions and Expectations," mimeo
Doz, C., Giannone, D. and Reichlin, L. (2011), "A Two-Step Estimator for Large Approximate Dynamic Factor Models Based on Kalman Filtering," Journal of Econometrics, 64(1), 188-205
Doz, C., Giannone, D. and Reichlin, L. (2012), "A Quasi Maximum Likelihood Approach for Large Approximate Dynamic Factor Models," Review of Economics and Statistics, forthcoming
Faust, J., Rogers, J.H. and Wright J. (2005), "News and Noise in G-7 GDP Announcements," Journal of Money, Credit and Banking 37-3, 403-419
Fostel, A. and Geanakoplos, J. (2012), "Why Does Bad News Increase Volatility and Decrease Leverage?," Journal of Economic Theory 147(2), 501-525
Giannone D., Reichlin L., and Small, D. (2008), "Nowcasting: The Real-Time Informational Content of Macroeconomic Data," Journal of Monetary Economics , 55(4), 665-676
Gilbert, T., Scotti, C., Strasser, G., and Vega, C. (2012) "Why do certain macroeconomic news announcements have a big impact on asset prices?" mimeo
Jagannathan, R. and Wang, Z. (1996), "The Conditional CAPM and the Cross-Section of Expected Returns," Journal of Finance 51-1, 3-53
Jurado, K., Ludvigson, S., and Ng, S. (2013), "Measuring Uncertainty," mimeo
Koopman, S.J. and Harvey, A. (2003), "Computing observation weights for signal extraction and filtering," Journal of Economic Dynamics & Control, 27, 1317-1333
Leduc, S. and Liu, Z. (2012), "Uncertainty shocks are aggregate demand shocks," FRBSF WP 2012-10, http://www.frbsf.org/publications/economics/papers/2012/wp12-10bk.pdf
Mariano, R.S. and Murasawa, Y. (2003), "A New Coincident Index of Business Cycles Based on Monthly and Quarterly Series," Journal of Applied Econometrics, 18, 427-443
Pesaran, H.H. and Shin, Y. (1998), "Generalized Impulse Response Analysis in Linear Multivariate Models," Economic Letters, 58, 17-29
Stock, J. H., and Watson, M.W. (1989), "New Indexes of Coincident and Leading Economic Indicators," in NBER Macro Annual, 4, Cambridge,MA: MIT Press
Appendix - The State Space Representation
We report below the details of the state space representation as specified by equations (13) and (14) when the only quarterly variable is GDP:
![$\displaystyle \underset{y_{t}}{\underbrace{\left[ \begin{array}{c} {\small y}_{t}^{M} \\ {\small y}_{t}^{Q} \end{array} \right] }}=\underset{Z}{\underbrace{\left[ \begin{array}{c} {\small\mu }^{M} \\ {\small\mu }^{Q} \end{array} \right] +\left[ \begin{array}{ccccccccccc} {\small Z}^{M} & {\small0} & {\small0} & {\small0} & {\small0} & {\small I}_{n^{M}} & {\small0} & {\small0} & {\small0} & {\small0} & {\small0} \\ {\small Z}^{Q} & {\small 2Z}^{Q} & {\small 3Z}^{Q} & {\small 2Z}^{Q} & {\small Z}^{Q} & {\small0} & {\small 1} & {\small 2} & {\small 3} & {\small 2} & {\small 1} \end{array} \right] }}\underset{\alpha _{t}}{\underbrace{\left[ \begin{array}{c} {\small x}_{t} \\ {\small x}_{t-1} \\ {\small x}_{t-2} \\ {\small x}_{t-3} \\ {\small x}_{t-4} \\ {\small\varepsilon }_{t}^{M} \\ {\small\varepsilon }_{t}^{Q} \\ {\small\varepsilon }_{t-1}^{Q} \\ {\small\varepsilon }_{t-2}^{Q} \\ {\small\varepsilon }_{t-3}^{Q} \\ {\small\varepsilon }_{t-4}^{Q} \end{array} \right] }}$](img209.gif) |
![$\displaystyle \left[ \begin{array}{c} {\small x}_{t} \\ {\small x}_{t-1} \\ {\s... ...^{Q} \\ {\small0} \\ {\small0} \\ {\small0} \\ {\small0} \end{array} \right] }}$](img210.gif) |
with ![]() and
and ![]() representing
the number of monthly and quarterly variables,
representing
the number of monthly and quarterly variables,
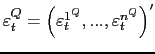 and
and
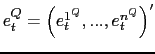 . Because we are considering the case of only one quarterly
variable,
. Because we are considering the case of only one quarterly
variable,
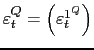 and
and
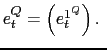 Also
Also
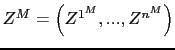 and
and
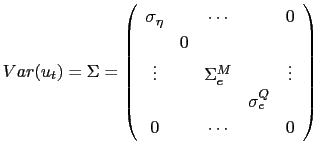 with with 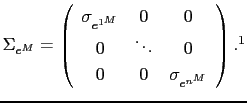 |
26 |
The parameters to be estimate are
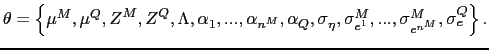
Figure 1: Real activity indexes (factors) for the United States, Euro Area, United Kingdom, Canada, Japan, and aggregate of the five countries.
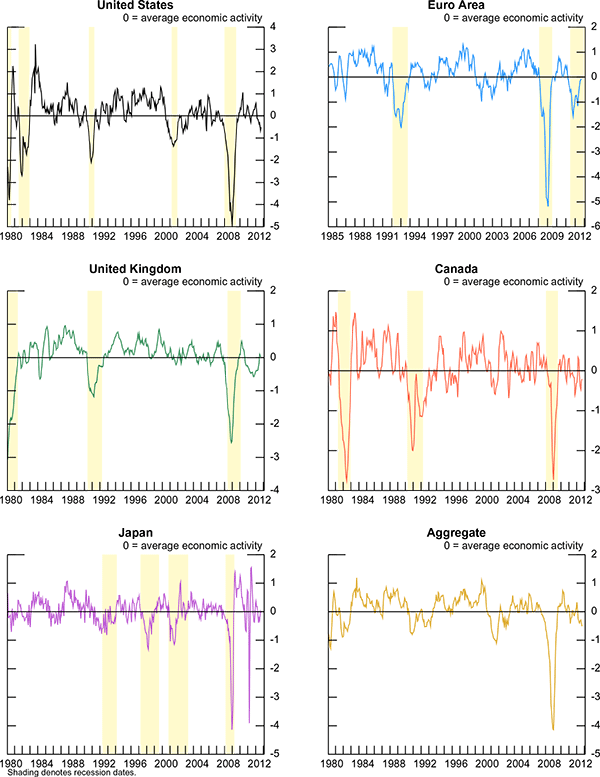
Data for Figure 1
|
Figure 2: Average cumulative weights for the United States, Euro Area, United Kingdom, Canada, and Japan over the first quarter of 2012.
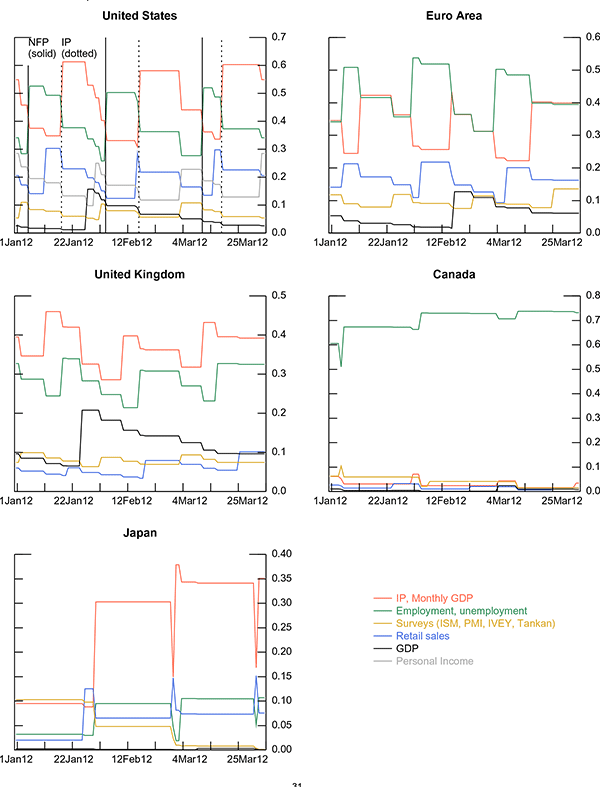
Data for Figure 2
| date | us_ip | us_nonfarm | us_rtsales | us_pincome | us_ism | us_gdp | eu_ip | eu_rtsales | eu_pmi | eu_unemp | eu_gdp | uk_ip | uk_rtsales | uk_pmi | uk_unemp | uk_gdp | ca_gdp_m | ca_employ | ca_rtsales | ca_pmi | ca_gdp | ja_ip | ja_rtsales | ja_unemp | ja_gdp | ja_tankan |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-Jan-12 | 0.549535 | 0.341012 | 0.20617 | 0.284823 | 0.053925 | 0.025681 | 0.345613 | 0.140711 | 0.11719 | 0.341589 | 0.053383 | 0.395334 | 0.060005 | 0.074717 | 0.327352 | 0.096968 | 0.061491 | 0.6065 | 0.027006 | 0.062705 | 0.010762 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 2-Jan-12 | 0.549535 | 0.341012 | 0.20617 | 0.284823 | 0.053925 | 0.025681 | 0.345613 | 0.140711 | 0.11719 | 0.341589 | 0.053383 | 0.395334 | 0.060005 | 0.074717 | 0.327352 | 0.096968 | 0.061491 | 0.6065 | 0.027006 | 0.062705 | 0.010762 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 3-Jan-12 | 0.458178 | 0.28432 | 0.171895 | 0.237473 | 0.109985 | 0.021411 | 0.345613 | 0.140711 | 0.11719 | 0.341589 | 0.053383 | 0.34669 | 0.052622 | 0.099143 | 0.287073 | 0.085036 | 0.061491 | 0.6065 | 0.027006 | 0.062705 | 0.010762 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 4-Jan-12 | 0.458178 | 0.28432 | 0.171895 | 0.237473 | 0.109985 | 0.021411 | 0.345613 | 0.140711 | 0.11719 | 0.341589 | 0.053383 | 0.34669 | 0.052622 | 0.099143 | 0.287073 | 0.085036 | 0.061491 | 0.6065 | 0.027006 | 0.062705 | 0.010762 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 5-Jan-12 | 0.458178 | 0.28432 | 0.171895 | 0.237473 | 0.109985 | 0.021411 | 0.345613 | 0.140711 | 0.11719 | 0.341589 | 0.053383 | 0.34669 | 0.052622 | 0.099143 | 0.287073 | 0.085036 | 0.05166 | 0.509534 | 0.022688 | 0.104864 | 0.009041 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 6-Jan-12 | 0.375685 | 0.526384 | 0.140946 | 0.194717 | 0.08396 | 0.017557 | 0.244563 | 0.212322 | 0.090569 | 0.508032 | 0.037775 | 0.34669 | 0.052622 | 0.099143 | 0.287073 | 0.085036 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 7-Jan-12 | 0.375685 | 0.526384 | 0.140946 | 0.194717 | 0.08396 | 0.017557 | 0.244563 | 0.212322 | 0.090569 | 0.508032 | 0.037775 | 0.34669 | 0.052622 | 0.099143 | 0.287073 | 0.085036 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 8-Jan-12 | 0.375685 | 0.526384 | 0.140946 | 0.194717 | 0.08396 | 0.017557 | 0.244563 | 0.212322 | 0.090569 | 0.508032 | 0.037775 | 0.34669 | 0.052622 | 0.099143 | 0.287073 | 0.085036 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 9-Jan-12 | 0.375685 | 0.526384 | 0.140946 | 0.194717 | 0.08396 | 0.017557 | 0.244563 | 0.212322 | 0.090569 | 0.508032 | 0.037775 | 0.34669 | 0.052622 | 0.099143 | 0.287073 | 0.085036 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 10-Jan-12 | 0.375685 | 0.526384 | 0.140946 | 0.194717 | 0.08396 | 0.017557 | 0.244563 | 0.212322 | 0.090569 | 0.508032 | 0.037775 | 0.34669 | 0.052622 | 0.099143 | 0.287073 | 0.085036 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 11-Jan-12 | 0.375685 | 0.526384 | 0.140946 | 0.194717 | 0.08396 | 0.017557 | 0.244563 | 0.212322 | 0.090569 | 0.508032 | 0.037775 | 0.34669 | 0.052622 | 0.099143 | 0.287073 | 0.085036 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 12-Jan-12 | 0.348532 | 0.493002 | 0.303287 | 0.180644 | 0.078554 | 0.016288 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.460422 | 0.044384 | 0.086261 | 0.244543 | 0.071724 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 13-Jan-12 | 0.348532 | 0.493002 | 0.303287 | 0.180644 | 0.078554 | 0.016288 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.460422 | 0.044384 | 0.086261 | 0.244543 | 0.071724 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 14-Jan-12 | 0.348532 | 0.493002 | 0.303287 | 0.180644 | 0.078554 | 0.016288 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.460422 | 0.044384 | 0.086261 | 0.244543 | 0.071724 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 15-Jan-12 | 0.348532 | 0.493002 | 0.303287 | 0.180644 | 0.078554 | 0.016288 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.460422 | 0.044384 | 0.086261 | 0.244543 | 0.071724 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 16-Jan-12 | 0.348532 | 0.493002 | 0.303287 | 0.180644 | 0.078554 | 0.016288 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.460422 | 0.044384 | 0.086261 | 0.244543 | 0.071724 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 17-Jan-12 | 0.348532 | 0.493002 | 0.303287 | 0.180644 | 0.078554 | 0.016288 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.460422 | 0.044384 | 0.086261 | 0.244543 | 0.071724 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 18-Jan-12 | 0.613305 | 0.377493 | 0.230312 | 0.133672 | 0.059931 | 0.012053 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.421163 | 0.040599 | 0.078209 | 0.340636 | 0.065608 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 19-Jan-12 | 0.613305 | 0.377493 | 0.230312 | 0.133672 | 0.059931 | 0.012053 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.421163 | 0.040599 | 0.078209 | 0.340636 | 0.065608 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 20-Jan-12 | 0.613305 | 0.377493 | 0.230312 | 0.133672 | 0.059931 | 0.012053 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.419892 | 0.06057 | 0.077961 | 0.339536 | 0.065418 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 21-Jan-12 | 0.613305 | 0.377493 | 0.230312 | 0.133672 | 0.059931 | 0.012053 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.419892 | 0.06057 | 0.077961 | 0.339536 | 0.065418 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 22-Jan-12 | 0.613305 | 0.377493 | 0.230312 | 0.133672 | 0.059931 | 0.012053 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.419892 | 0.06057 | 0.077961 | 0.339536 | 0.065418 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 23-Jan-12 | 0.613305 | 0.377493 | 0.230312 | 0.133672 | 0.059931 | 0.012053 | 0.422926 | 0.172617 | 0.079955 | 0.415641 | 0.03007 | 0.419892 | 0.06057 | 0.077961 | 0.339536 | 0.065418 | 0.031058 | 0.673609 | 0.01364 | 0.059924 | 0.005436 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 24-Jan-12 | 0.613305 | 0.377493 | 0.230312 | 0.133672 | 0.059931 | 0.012053 | 0.362793 | 0.148074 | 0.118483 | 0.356543 | 0.025794 | 0.419892 | 0.06057 | 0.077961 | 0.339536 | 0.065418 | 0.03094 | 0.671999 | 0.032277 | 0.059769 | 0.005415 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 25-Jan-12 | 0.613305 | 0.377493 | 0.230312 | 0.133672 | 0.059931 | 0.012053 | 0.362793 | 0.148074 | 0.118483 | 0.356543 | 0.025794 | 0.325611 | 0.048903 | 0.063784 | 0.283 | 0.207759 | 0.03094 | 0.671999 | 0.032277 | 0.059769 | 0.005415 | 0.095112 | 0.020337 | 0.032413 | 0.002433 | 0.102902 |
| 26-Jan-12 | 0.613305 | 0.377493 | 0.230312 | 0.133672 | 0.059931 | 0.012053 | 0.362793 | 0.148074 | 0.118483 | 0.356543 | 0.025794 | 0.325611 | 0.048903 | 0.063784 | 0.283 | 0.207759 | 0.03094 | 0.671999 | 0.032277 | 0.059769 | 0.005415 | 0.088033 | 0.125472 | 0.030081 | 0.002306 | 0.097695 |
| 27-Jan-12 | 0.529394 | 0.337594 | 0.197972 | 0.097976 | 0.052685 | 0.157495 | 0.362793 | 0.148074 | 0.118483 | 0.356543 | 0.025794 | 0.325611 | 0.048903 | 0.063784 | 0.283 | 0.207759 | 0.03094 | 0.671999 | 0.032277 | 0.059769 | 0.005415 | 0.088033 | 0.125472 | 0.030081 | 0.002306 | 0.097695 |
| 28-Jan-12 | 0.529394 | 0.337594 | 0.197972 | 0.097976 | 0.052685 | 0.157495 | 0.362793 | 0.148074 | 0.118483 | 0.356543 | 0.025794 | 0.325611 | 0.048903 | 0.063784 | 0.283 | 0.207759 | 0.03094 | 0.671999 | 0.032277 | 0.059769 | 0.005415 | 0.088033 | 0.125472 | 0.030081 | 0.002306 | 0.097695 |
| 29-Jan-12 | 0.529394 | 0.337594 | 0.197972 | 0.097976 | 0.052685 | 0.157495 | 0.362793 | 0.148074 | 0.118483 | 0.356543 | 0.025794 | 0.325611 | 0.048903 | 0.063784 | 0.283 | 0.207759 | 0.03094 | 0.671999 | 0.032277 | 0.059769 | 0.005415 | 0.088033 | 0.125472 | 0.030081 | 0.002306 | 0.097695 |
| 30-Jan-12 | 0.484021 | 0.309753 | 0.180928 | 0.25053 | 0.048259 | 0.143332 | 0.362793 | 0.148074 | 0.118483 | 0.356543 | 0.025794 | 0.325611 | 0.048903 | 0.063784 | 0.283 | 0.207759 | 0.03094 | 0.671999 | 0.032277 | 0.059769 | 0.005415 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 31-Jan-12 | 0.484021 | 0.309753 | 0.180928 | 0.25053 | 0.048259 | 0.143332 | 0.266981 | 0.108968 | 0.093454 | 0.537275 | 0.018982 | 0.325611 | 0.048903 | 0.063784 | 0.283 | 0.207759 | 0.071232 | 0.662695 | 0.031605 | 0.058832 | 0.0053 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 1-Feb-12 | 0.403605 | 0.25829 | 0.150868 | 0.208907 | 0.1046 | 0.119519 | 0.266981 | 0.108968 | 0.093454 | 0.537275 | 0.018982 | 0.28563 | 0.042898 | 0.087574 | 0.248251 | 0.182249 | 0.071232 | 0.662695 | 0.031605 | 0.058832 | 0.0053 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 2-Feb-12 | 0.403605 | 0.25829 | 0.150868 | 0.208907 | 0.1046 | 0.119519 | 0.266981 | 0.108968 | 0.093454 | 0.537275 | 0.018982 | 0.28563 | 0.042898 | 0.087574 | 0.248251 | 0.182249 | 0.071232 | 0.662695 | 0.031605 | 0.058832 | 0.0053 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 3-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.28563 | 0.042898 | 0.087574 | 0.248251 | 0.182249 | 0.024784 | 0.730769 | 0.010997 | 0.02047 | 0.001844 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 4-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.28563 | 0.042898 | 0.087574 | 0.248251 | 0.182249 | 0.024784 | 0.730769 | 0.010997 | 0.02047 | 0.001844 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 5-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.28563 | 0.042898 | 0.087574 | 0.248251 | 0.182249 | 0.024784 | 0.730769 | 0.010997 | 0.02047 | 0.001844 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 6-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.28563 | 0.042898 | 0.087574 | 0.248251 | 0.182249 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 7-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.28563 | 0.042898 | 0.087574 | 0.248251 | 0.182249 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 8-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.28563 | 0.042898 | 0.087574 | 0.248251 | 0.182249 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 9-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.397958 | 0.037025 | 0.077396 | 0.214736 | 0.156651 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 10-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.397958 | 0.037025 | 0.077396 | 0.214736 | 0.156651 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 11-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.397958 | 0.037025 | 0.077396 | 0.214736 | 0.156651 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 12-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.397958 | 0.037025 | 0.077396 | 0.214736 | 0.156651 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 13-Feb-12 | 0.331392 | 0.503499 | 0.123875 | 0.171529 | 0.079702 | 0.098135 | 0.256422 | 0.217871 | 0.091409 | 0.51902 | 0.018232 | 0.397958 | 0.037025 | 0.077396 | 0.214736 | 0.156651 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 14-Feb-12 | 0.307728 | 0.472151 | 0.285484 | 0.159281 | 0.074665 | 0.091127 | 0.432886 | 0.176913 | 0.080591 | 0.424108 | 0.014502 | 0.397958 | 0.037025 | 0.077396 | 0.214736 | 0.156651 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 15-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.363522 | 0.147401 | 0.075201 | 0.364365 | 0.127285 | 0.365121 | 0.03397 | 0.070336 | 0.310184 | 0.143725 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 16-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.363522 | 0.147401 | 0.075201 | 0.364365 | 0.127285 | 0.365121 | 0.03397 | 0.070336 | 0.310184 | 0.143725 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 17-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.363522 | 0.147401 | 0.075201 | 0.364365 | 0.127285 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 18-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.363522 | 0.147401 | 0.075201 | 0.364365 | 0.127285 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 19-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.363522 | 0.147401 | 0.075201 | 0.364365 | 0.127285 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 20-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.363522 | 0.147401 | 0.075201 | 0.364365 | 0.127285 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024718 | 0.729167 | 0.010967 | 0.041532 | 0.001839 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 21-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.363522 | 0.147401 | 0.075201 | 0.364365 | 0.127285 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024643 | 0.728209 | 0.021337 | 0.041461 | 0.001834 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 22-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.311863 | 0.126455 | 0.113979 | 0.312586 | 0.109197 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024643 | 0.728209 | 0.021337 | 0.041461 | 0.001834 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 23-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.311863 | 0.126455 | 0.113979 | 0.312586 | 0.109197 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024643 | 0.728209 | 0.021337 | 0.041461 | 0.001834 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 24-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.311863 | 0.126455 | 0.113979 | 0.312586 | 0.109197 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024643 | 0.728209 | 0.021337 | 0.041461 | 0.001834 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 25-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.311863 | 0.126455 | 0.113979 | 0.312586 | 0.109197 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024643 | 0.728209 | 0.021337 | 0.041461 | 0.001834 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 26-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.311863 | 0.126455 | 0.113979 | 0.312586 | 0.109197 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024643 | 0.728209 | 0.021337 | 0.041461 | 0.001834 | 0.303096 | 0.065096 | 0.094874 | 0.001104 | 0.048212 |
| 27-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.311863 | 0.126455 | 0.113979 | 0.312586 | 0.109197 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024643 | 0.728209 | 0.021337 | 0.041461 | 0.001834 | 0.149502 | 0.147542 | 0.046797 | 0.000544 | 0.02378 |
| 28-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.311863 | 0.126455 | 0.113979 | 0.312586 | 0.109197 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024643 | 0.728209 | 0.021337 | 0.041461 | 0.001834 | 0.379019 | 0.081517 | 0.019098 | 0.000222 | 0.009705 |
| 29-Feb-12 | 0.580792 | 0.362991 | 0.217714 | 0.118213 | 0.057201 | 0.067632 | 0.311863 | 0.126455 | 0.113979 | 0.312586 | 0.109197 | 0.36234 | 0.079447 | 0.069826 | 0.307977 | 0.14263 | 0.024643 | 0.728209 | 0.021337 | 0.041461 | 0.001834 | 0.379019 | 0.081517 | 0.019098 | 0.000222 | 0.009705 |
| 1-Mar-12 | 0.441383 | 0.276786 | 0.16539 | 0.228665 | 0.10847 | 0.050719 | 0.230702 | 0.093545 | 0.090487 | 0.502122 | 0.080779 | 0.31779 | 0.069679 | 0.094122 | 0.270111 | 0.125094 | 0.024643 | 0.728209 | 0.021337 | 0.041461 | 0.001834 | 0.343705 | 0.073914 | 0.105413 | 0.000195 | 0.008537 |
| 2-Mar-12 | 0.441383 | 0.276786 | 0.16539 | 0.228665 | 0.10847 | 0.050719 | 0.230702 | 0.093545 | 0.090487 | 0.502122 | 0.080779 | 0.31779 | 0.069679 | 0.094122 | 0.270111 | 0.125094 | 0.044101 | 0.706461 | 0.019835 | 0.039786 | 0.023866 | 0.343705 | 0.073914 | 0.105413 | 0.000195 | 0.008537 |
| 3-Mar-12 | 0.441383 | 0.276786 | 0.16539 | 0.228665 | 0.10847 | 0.050719 | 0.230702 | 0.093545 | 0.090487 | 0.502122 | 0.080779 | 0.31779 | 0.069679 | 0.094122 | 0.270111 | 0.125094 | 0.044101 | 0.706461 | 0.019835 | 0.039786 | 0.023866 | 0.343705 | 0.073914 | 0.105413 | 0.000195 | 0.008537 |
| 4-Mar-12 | 0.441383 | 0.276786 | 0.16539 | 0.228665 | 0.10847 | 0.050719 | 0.230702 | 0.093545 | 0.090487 | 0.502122 | 0.080779 | 0.31779 | 0.069679 | 0.094122 | 0.270111 | 0.125094 | 0.044101 | 0.706461 | 0.019835 | 0.039786 | 0.023866 | 0.343705 | 0.073914 | 0.105413 | 0.000195 | 0.008537 |
| 5-Mar-12 | 0.441383 | 0.276786 | 0.16539 | 0.228665 | 0.10847 | 0.050719 | 0.221774 | 0.200709 | 0.088601 | 0.485619 | 0.077653 | 0.31779 | 0.069679 | 0.094122 | 0.270111 | 0.125094 | 0.044101 | 0.706461 | 0.019835 | 0.039786 | 0.023866 | 0.343705 | 0.073914 | 0.105413 | 0.000195 | 0.008537 |
| 6-Mar-12 | 0.441383 | 0.276786 | 0.16539 | 0.228665 | 0.10847 | 0.050719 | 0.221774 | 0.200709 | 0.088601 | 0.485619 | 0.077653 | 0.31779 | 0.069679 | 0.094122 | 0.270111 | 0.125094 | 0.044101 | 0.706461 | 0.019835 | 0.039786 | 0.023866 | 0.343705 | 0.073914 | 0.105413 | 0.000195 | 0.008537 |
| 7-Mar-12 | 0.441383 | 0.276786 | 0.16539 | 0.228665 | 0.10847 | 0.050719 | 0.221774 | 0.200709 | 0.088601 | 0.485619 | 0.077653 | 0.31779 | 0.069679 | 0.094122 | 0.270111 | 0.125094 | 0.044101 | 0.706461 | 0.019835 | 0.039786 | 0.023866 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 8-Mar-12 | 0.441383 | 0.276786 | 0.16539 | 0.228665 | 0.10847 | 0.050719 | 0.221774 | 0.200709 | 0.088601 | 0.485619 | 0.077653 | 0.31779 | 0.069679 | 0.094122 | 0.270111 | 0.125094 | 0.044101 | 0.706461 | 0.019835 | 0.039786 | 0.023866 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 9-Mar-12 | 0.361989 | 0.519975 | 0.135641 | 0.187534 | 0.082743 | 0.041597 | 0.221774 | 0.200709 | 0.088601 | 0.485619 | 0.077653 | 0.432225 | 0.059697 | 0.082405 | 0.231485 | 0.106123 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 10-Mar-12 | 0.361989 | 0.519975 | 0.135641 | 0.187534 | 0.082743 | 0.041597 | 0.221774 | 0.200709 | 0.088601 | 0.485619 | 0.077653 | 0.432225 | 0.059697 | 0.082405 | 0.231485 | 0.106123 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 11-Mar-12 | 0.361989 | 0.519975 | 0.135641 | 0.187534 | 0.082743 | 0.041597 | 0.221774 | 0.200709 | 0.088601 | 0.485619 | 0.077653 | 0.432225 | 0.059697 | 0.082405 | 0.231485 | 0.106123 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 12-Mar-12 | 0.361989 | 0.519975 | 0.135641 | 0.187534 | 0.082743 | 0.041597 | 0.221774 | 0.200709 | 0.088601 | 0.485619 | 0.077653 | 0.432225 | 0.059697 | 0.082405 | 0.231485 | 0.106123 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 13-Mar-12 | 0.335874 | 0.487116 | 0.298068 | 0.174004 | 0.077435 | 0.038596 | 0.221774 | 0.200709 | 0.088601 | 0.485619 | 0.077653 | 0.432225 | 0.059697 | 0.082405 | 0.231485 | 0.106123 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 14-Mar-12 | 0.335874 | 0.487116 | 0.298068 | 0.174004 | 0.077435 | 0.038596 | 0.402465 | 0.163846 | 0.078518 | 0.398913 | 0.062015 | 0.395803 | 0.054666 | 0.074773 | 0.327551 | 0.097181 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 15-Mar-12 | 0.335874 | 0.487116 | 0.298068 | 0.174004 | 0.077435 | 0.038596 | 0.402465 | 0.163846 | 0.078518 | 0.398913 | 0.062015 | 0.395803 | 0.054666 | 0.074773 | 0.327551 | 0.097181 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 16-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.402465 | 0.163846 | 0.078518 | 0.398913 | 0.062015 | 0.395803 | 0.054666 | 0.074773 | 0.327551 | 0.097181 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 17-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.402465 | 0.163846 | 0.078518 | 0.398913 | 0.062015 | 0.395803 | 0.054666 | 0.074773 | 0.327551 | 0.097181 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 18-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.402465 | 0.163846 | 0.078518 | 0.398913 | 0.062015 | 0.395803 | 0.054666 | 0.074773 | 0.327551 | 0.097181 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 19-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.402465 | 0.163846 | 0.078518 | 0.398913 | 0.062015 | 0.395803 | 0.054666 | 0.074773 | 0.327551 | 0.097181 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 20-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.402465 | 0.163846 | 0.078518 | 0.398913 | 0.062015 | 0.395803 | 0.054666 | 0.074773 | 0.327551 | 0.097181 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 21-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.402465 | 0.163846 | 0.078518 | 0.398913 | 0.062015 | 0.395803 | 0.054666 | 0.074773 | 0.327551 | 0.097181 | 0.016569 | 0.737667 | 0.007452 | 0.014948 | 0.008967 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 22-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.39832 | 0.162159 | 0.135181 | 0.394805 | 0.061376 | 0.392689 | 0.101468 | 0.074211 | 0.325135 | 0.096416 | 0.016526 | 0.736899 | 0.015649 | 0.014915 | 0.008944 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 23-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.39832 | 0.162159 | 0.135181 | 0.394805 | 0.061376 | 0.392689 | 0.101468 | 0.074211 | 0.325135 | 0.096416 | 0.016526 | 0.736899 | 0.015649 | 0.014915 | 0.008944 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 24-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.39832 | 0.162159 | 0.135181 | 0.394805 | 0.061376 | 0.392689 | 0.101468 | 0.074211 | 0.325135 | 0.096416 | 0.016526 | 0.736899 | 0.015649 | 0.014915 | 0.008944 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 25-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.39832 | 0.162159 | 0.135181 | 0.394805 | 0.061376 | 0.392689 | 0.101468 | 0.074211 | 0.325135 | 0.096416 | 0.016526 | 0.736899 | 0.015649 | 0.014915 | 0.008944 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 26-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.39832 | 0.162159 | 0.135181 | 0.394805 | 0.061376 | 0.392689 | 0.101468 | 0.074211 | 0.325135 | 0.096416 | 0.016526 | 0.736899 | 0.015649 | 0.014915 | 0.008944 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 27-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.39832 | 0.162159 | 0.135181 | 0.394805 | 0.061376 | 0.392689 | 0.101468 | 0.074211 | 0.325135 | 0.096416 | 0.016526 | 0.736899 | 0.015649 | 0.014915 | 0.008944 | 0.341604 | 0.073457 | 0.10485 | 0.003702 | 0.00797 |
| 28-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.39832 | 0.162159 | 0.135181 | 0.394805 | 0.061376 | 0.392689 | 0.101468 | 0.074211 | 0.325135 | 0.096416 | 0.016526 | 0.736899 | 0.015649 | 0.014915 | 0.008944 | 0.168427 | 0.152305 | 0.051696 | 0.001825 | 0.003929 |
| 29-Mar-12 | 0.603596 | 0.373283 | 0.226542 | 0.128817 | 0.059126 | 0.028573 | 0.39832 | 0.162159 | 0.135181 | 0.394805 | 0.061376 | 0.392689 | 0.101468 | 0.074211 | 0.325135 | 0.096416 | 0.016526 | 0.736899 | 0.015649 | 0.014915 | 0.008944 | 0.350887 | 0.075478 | 0.107217 | 0.000653 | 0.001406 |
| 30-Mar-12 | 0.549535 | 0.341012 | 0.20617 | 0.284823 | 0.053925 | 0.025681 | 0.39832 | 0.162159 | 0.135181 | 0.394805 | 0.061376 | 0.392689 | 0.101468 | 0.074211 | 0.325135 | 0.096416 | 0.034598 | 0.732313 | 0.01546 | 0.014735 | 0.008829 | 0.350887 | 0.075478 | 0.107217 | 0.000653 | 0.001406 |
| 31-Mar-12 | 0.549535 | 0.341012 | 0.20617 | 0.284823 | 0.053925 | 0.025681 | 0.39832 | 0.162159 | 0.135181 | 0.394805 | 0.061376 | 0.392689 | 0.101468 | 0.074211 | 0.325135 | 0.096416 | 0.034598 | 0.732313 | 0.01546 | 0.014735 | 0.008829 | 0.350887 | 0.075478 | 0.107217 | 0.000653 | 0.001406 |
Figure 3: Time Series of weights for each indicator based on the information available as of March 31, 2012.
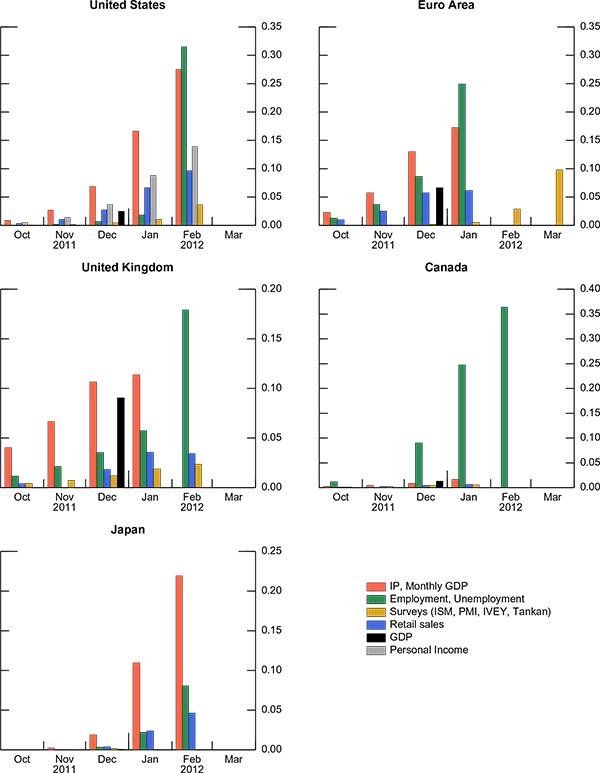
Data for Figure 3
| date | us_ip3 | us_nonfarm3 | us_rtsales3 | us_pincome3 | us_ism3 | us_gdp3 | eu_ip3 | eu_rtsales3 | eu_pmi3 | eu_unemp3 | eu_gdp3 | uk_ip3 | uk_rtsales3 | uk_pmi3 | uk_unemp3 | uk_gdp3 | ca_ip3 | ca_emp3 | ca_rtsales3 | ca_ivey3 | ca_gdp3 | ja_ip3 | ja_rtsales3 | ja_unemp3 | ja_gdp3 | ja_tankan3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011m8 | 0.0003 | -0.0006 | 0.0001 | 0.0002 | 0 | 0 | 0.0029 | 0.0013 | -0.0001 | 0.0014 | 0 | 0.015 | 0 | 0.0017 | 0.0045 | 0 | 0.0003 | 0.0041 | 0.0002 | 0.0002 | 0 | -0.0001 | 0 | 0 | 0 | 0 |
| 2011m9 | 0.0024 | -0.0008 | 0.001 | 0.0013 | 0.0001 | 0.0026 | 0.0081 | 0.0037 | -0.0002 | 0.0041 | -0.0062 | 0.0242 | 0.0042 | 0.0027 | 0.007 | 0.0002 | 0.0008 | 0.0104 | 0.0005 | 0.0005 | -0.0061 | -0.0004 | -0.0001 | -0.0001 | 0 | -0.001 |
| 2011m10 | 0.0093 | -0.0005 | 0.0037 | 0.0049 | 0.0005 | 0 | 0.023 | 0.0103 | -0.0002 | 0.0133 | 0 | 0.0403 | 0.004 | 0.0045 | 0.0118 | 0 | 0.0023 | 0.0119 | 0.0012 | 0.0012 | 0 | -0.0001 | 0 | -0.0001 | 0 | 0 |
| 2011m11 | 0.027 | 0.002 | 0.0108 | 0.0143 | 0.0017 | 0 | 0.0578 | 0.0257 | 0.0006 | 0.0373 | 0 | 0.0667 | 0 | 0.0076 | 0.0214 | 0 | 0.005 | 0 | 0.0025 | 0.0024 | 0 | 0.0028 | 0.0006 | 0.0005 | 0 | 0 |
| 2011m12 | 0.0688 | 0.0071 | 0.0275 | 0.0365 | 0.0044 | 0.025 | 0.1303 | 0.0578 | 0.0021 | 0.0864 | 0.0664 | 0.1067 | 0.0184 | 0.0121 | 0.0354 | 0.0906 | 0.0088 | 0.0904 | 0.0046 | 0.0046 | 0.0134 | 0.0191 | 0.0042 | 0.0038 | 0.0007 | 0.0021 |
| 2012m1 | 0.1664 | 0.0184 | 0.0664 | 0.0883 | 0.0107 | 0 | 0.1727 | 0.0617 | 0.0058 | 0.2498 | 0 | 0.1138 | 0.0357 | 0.0188 | 0.0576 | 0 | 0.017 | 0.2477 | 0.0064 | 0.0058 | 0 | 0.1098 | 0.0242 | 0.0222 | 0 | 0 |
| 2012m2 | 0.275 | 0.3153 | 0.0965 | 0.1391 | 0.0365 | 0 | 0 | 0 | 0.0292 | 0 | 0 | 0 | 0.0345 | 0.0238 | 0.1792 | 0 | 0 | 0.3642 | 0 | 0 | 0 | 0.2194 | 0.0465 | 0.0808 | 0 | 0 |
| 2012m3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.098 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Figure 4: The solid lines show the surprise indexes for the United States, Euro Area, United Kingdom, Canada, Japan, and the aggregate of the five countries. The dotted lines show the Citigroup Economic Surprise Indexes for the corresponding country (left axis).
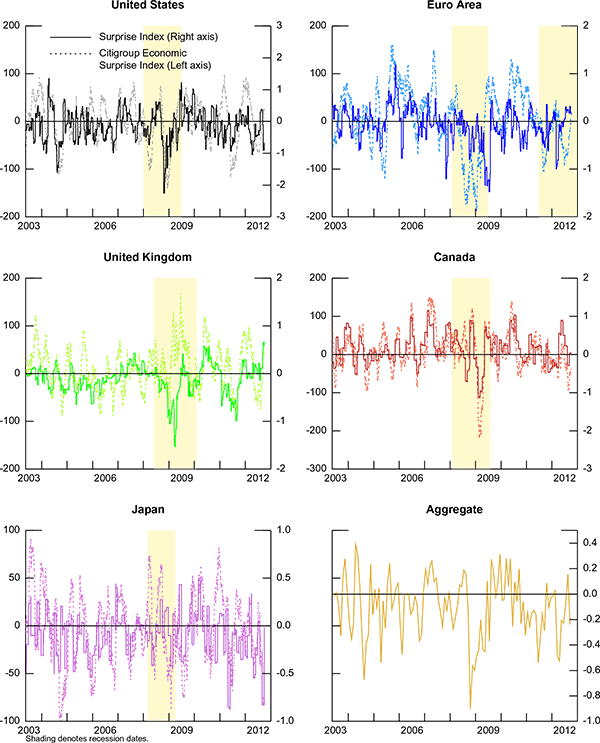
Figure 5: The solid lines show the uncertainty indexes for the United States, Euro Area, United Kingdom, Canada, Japan, and the aggregate of teh five countries. The dotted and dashed lines show stock market implied and realized volatilities respectively (left axis).
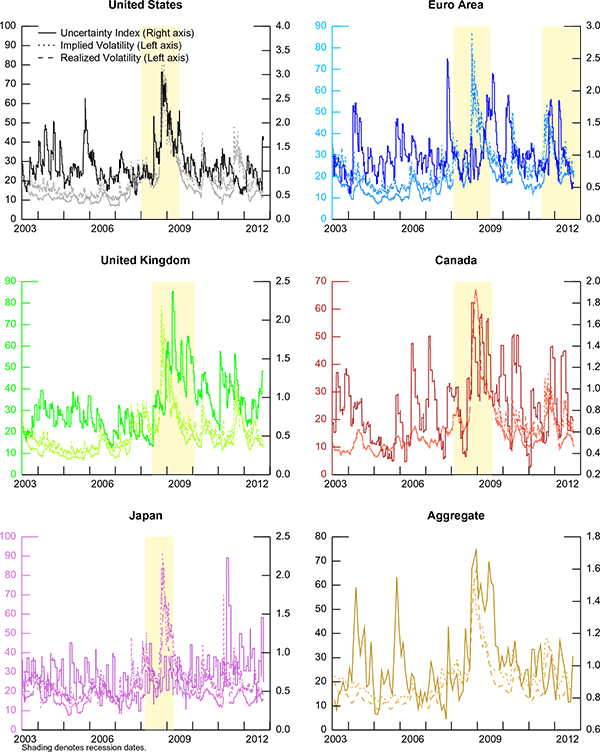
Figure 6: The solid line represent the uncertainty index withich is compared against other common proxies for uncertainty, namely the Baker, Bloom and Davis measure, the Bachmann, Elstner and Sims measure, and the VIX. All series are demeaned and standardized. The horizontal ine represents the 1.65 standard deviation limit.
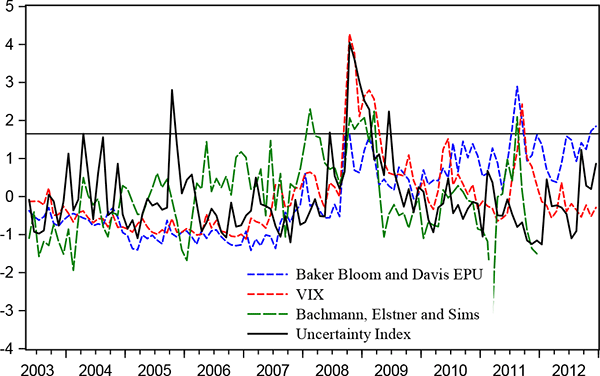
Figure 7: Employment response to a 1 standard deviation shock in the different uncertainty proxies. The shaded area represents the +/- one standard error confidence intreval for the uncertainty index.
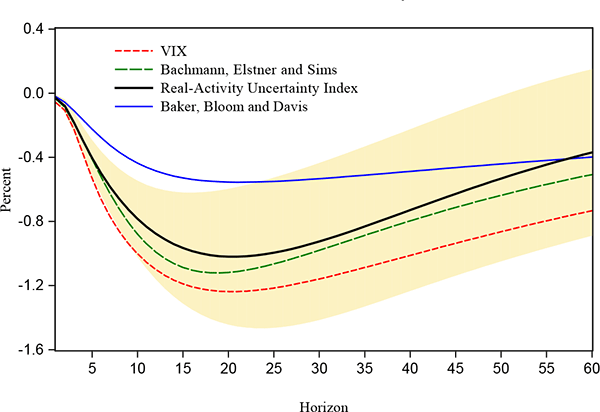
Figure 8: +/- one standard error confidence intreval for the real-activity uncertainty shock and the VIX.
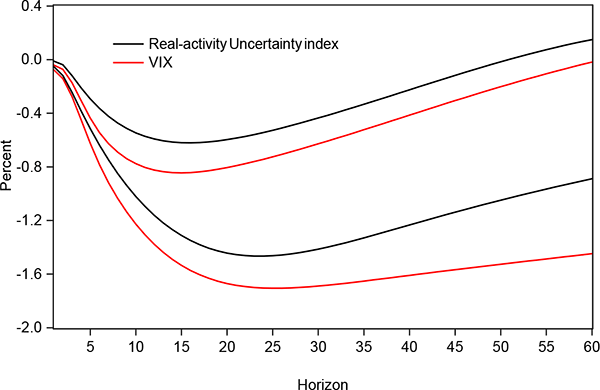
Footnotes
1. I would like to thank for their useful comments Boragan Aruoba, David Bowman, Celso Brunetti, Domenico Giannone, Raffaella Giacomini, Rob Martin, Andrew Patton, Barbara Rossi, Jonathan Wright, Clara Vega as well as various participants of conferences and seminars: 2012 Computing in Economics and Finance; 2012 European Meeting of the Econometric Society; 2012 Conference on Real-Time Data Analysis, Methods, and Applications at the Philadelphia Fed; 2012 NBER-NSF Time Series Conference; Third IFO conference on Macroeconomics and Survey Data; 2013 Econometric Society Australasian Meeting; Boston College; and Board of Governors of the Federal Reserve System. For outstanding research assistance I thank Rebecca DeSimone, Eric English, and Olivia Kim. The views expressed in this paper are solely the responsibility of the author and should not be interpreted as reflecting the view of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Correspondence to [email protected] Return to text
2. http://www.philadelphiafed.org/research-and-data/real-time-center/business-conditions-index/ Return to text
3. Unfortunately, we are not able to see whether this is a characteristic of all recessions because the surprise indexes only start in 2003 and hence only cover one recession episode. Expectation data are available from Bloomberg for all countries since 2003. Return to text
4. The correlation between the daily U.S. uncertainty index and the VIX is 53 percent over the sample period analyzed. Return to text
5. The correlation is 14 and 26 percent with the Baker, Bloom and Davis (2013) and the Bachmann, Elstner and Sims (2013) measures, respectively. Return to text
6. The correlation ranges between -0.26 to -0.45 for the United States, Euro Area, the United Kingdom and Japan, whereas it is positive in Canada over the sample period analyzed in the paper. Return to text
7. Employment data and expectations are available only for the United States and Canada. For the other countries we use the unemployment rate. Return to text
8. To avoid confusion, because for all the indicators a higher number means that the economy is doing good, I feed the negative of the unemployment rate into the model. Return to text
9. For Canada, Bloomberg used to provide expectations for the non-seasonally-adjusted IVY index, but as of March 2011, it started to provide expectations for the seasonally adjusted series. I splice the two series together being aware of the break point. Return to text
10. The Tankan survey has an average publication lag of -4 days, but only Q4 numbers are released before the end of the quarter (around mid-December). Other releases occur at the beginning of the following quarter. Return to text
11. The other quarterly series in the
dataset is the Japanese Tankan survey. Because it is an index, I do
not compute the ![]() difference (growth rate) as for
GDP. By defining
difference (growth rate) as for
GDP. By defining
![]()
![]() and
and
![]() the same argument goes through and equation (11) holds
exactly. Return to text
the same argument goes through and equation (11) holds
exactly. Return to text
12. Details about the state space representation can be found in the appendix. Return to text
13. Realized volatility is more
precisely defined as
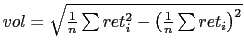 but because the second term, the average return, tends to be zero
it is frequently dropped. Similarly, we abstract from using the
second term,
but because the second term, the average return, tends to be zero
it is frequently dropped. Similarly, we abstract from using the
second term,
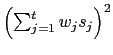 in the definition of the uncertainty index. In practice, this term
is very close to zero. Return to
text
in the definition of the uncertainty index. In practice, this term
is very close to zero. Return to
text
14. I thank Banbura, Giannone and Reichlin for sharing their EM codes. Return to text
15. The surprise index is computed on a shorter sample due to the limited availability of expectation data for all the countries. Return to text
16. The underlying real activity factor is estimated on the full sample to avoid parameter instability problems due to the fact that, for some of the countries, some macroeconomic releases become available later in the sample (namely retail sales and pmi series). Return to text
17. That means, running (i), (ii) and (iii) in real time versus running (i)over the entire sample, and (ii) and (iii) in real time does not give significant differences for the United States. Return to text
18. For comparability across countries, the table shows standardized weights so that the sum of all weights in each country is equal to 1. Return to text
19. Euro-area flash PMI becomes available in June 2007 and U.K. PMI becomes available in March 2006. Return to text
20. The idea is that ![]() represents the bars in figure 3, while
represents the bars in figure 3, while
![]() represent the lines in figure
2. Return to text
represent the lines in figure
2. Return to text
21. The indexes continue to be updated daily and are available from the author upon request. Return to text
22. For comparison with the exercise in table 3, I run the regression only on days in which there are news releases. This implies that I will have 556, 423, 443, 417, and 298 observations for the U.S., euro-area, U.K., Canadian and Japanese news, respectively. Return to text
23. The VXO is equivalent to the VIX series that I use. The VIX was launched in 1993. In 2003, its formula was modified substantially. Data from the new 2003 VIX formula, also used to reconstruct historical data going back to 1990, is known as the VIX. The data associated with the original and revised VIX formulae is known as VXO. In my sub-sample VIX and VXO coincide. Return to text
24. The smallest correlation is between Bachmann, Elstner, and Sims and Baker, Bloom, and Davis measures (about 10 percent). The highest correlation is between Baker, Bloom, and Davis EPU measure and the VIX (over 70 percent). Return to text
25. Given the short dataset, I only estimate the bivariate VAR. Return to text
26. We use the notation Σ to indicate a variance-covariance matrix and σ to indicate its elements. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text