
Board of Governors of the Federal Reserve System
International Finance Discussion Papers Number 1094, December 2013 --- Screen Reader Version*Local Currency Sovereign Risk1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Do governments default on debt denominated in their own currency? We introduce a new measure of sovereign credit risk, the local currency credit spread, defined as the spread of local currency bonds over the synthetic local currency risk-free rate constructed using cross currency swaps. We find that local currency credit spreads are positive and sizable. Compared with credit spreads on foreign currency denominated debt, local currency credit spreads have lower means, lower cross-country correlations, and are less sensitive to global risk factors. Global risk aversion and liquidity factors can explain more time variation in these credit spread differentials than macroeconomic fundamentals.
Keywords: Local currency, sovereign debt, currency swaps
JEL classification: F31, F34, G15
1 Introduction
If governments can potentially default on debt denominated in their own currency, then their borrowing costs should reflect both currency and credit risk. In order to study the credit risk on local currency sovereign debt, we introduce a simple model-free empirical measure of emerging market sovereign credit risk on LC denominated debt, the local currency credit spread, and contrast this new measure with the conventional measures of emerging market sovereign risk based on foreign currency (FC) denominated external debt. Despite the increasingly important role of local currency (LC) debt for emerging market sovereign issuers and its increasing share in the portfolio of domestic and foreign investors, emerging market LC debt markets are little understood and explicit LC sovereign risk measures are absent from the academic literature. When sovereigns borrow in their own currency, foreign lenders face the risk that the the sovereign will repay but in a depreciated currency and the risk that the country will outright default on the debt or impose capital controls for repatriation of capital. In this paper, we present a new metric to disentangle the risk of currency depreciation (currency risk) from outright default and capital controls (credit risk). In our 10 sample countries for the sample period 2005-2011, the mean spread of LC nominal yields over U.S. Treasuries is equal to 5 percentage points. Our decomposition attributes 3.72 percentage points to currency risk and the other 1.28 percentage points to the credit risk.
We define the LC credit spread as the difference between the nominal yield on an LC bond and the LC risk-free rate implied from the cross currency swap (CCS) market. While government bond yields are often used directly as the risk-free rate for developed country currencies, they cannot be used as the risk-free rate in emerging markets where the risk of sovereign default and capital controls are non-negligible. Instead, we use the dollar risk-free rate combined with the long-term forward rate implied from currency swap markets as the risk-free benchmark in each LC. From a dollar investor's perspective, the LC credit spread is equivalent to the synthetic dollar spread on an LC bond over the U.S. Treasury rate with the currency risk of promised cash flows fully hedged using cross currency swaps. By holding an LC bond and a currency swap with the same tenor and promised cash flows, the dollar investor can lock in the LC credit spread even if the value of the currency plummets as long as explicit default is avoided. From the sovereign issuer's perspective, the LC credit spread measures the synthetic dollar borrowing cost in the LC debt market.
Understanding the credit risk on local currency sovereign debt is important for several reasons. First, from total sovereign financing perspective, total LC debt outstanding in 2011 was on average 5-6 times greater than FC debt outstanding in our sample countries (BIS, 2013). Second, while there is an important literature examining why emerging markets cannot borrow in their own currency from foreigners (Eichengreen and Hausmann, 1999 and Eichengreen adn Hausmann, 2005), the situation has changed dramatically over the last decade. Foreigners are increasingly willing to purchase LC debt under domestic law. Du and Schreger (2013) construct a new dataset on foreign ownership of domestic government debt for 14 emerging markets. Figure 1 shows that foreign holdings of LC debt increased from around 5 percent of total LC debt outstanding in 2004 to over 20 percent in 2011. The growth of foreign holdings of LC debt far outpaced the growth of FC debt outstanding. The mean share of LC debt in total external debt held by foreigners increased from 20 percent to over 50 percent over the past decade. Furthermore, in terms of trading volume of foreign investors, according to volume surveys conducted by the Emerging Market Trading Association, the share of LC debt in total offshore emerging market debt trading volume has increased from 35 percent in 2000 to 71 percent in 2011, reaching 4.64 trillion U.S. dollars (Figure 2).
The growing importance of LC debt markets stands in stark contrast to the declining role of FC sovereign financing. This shift is rendering conventional measures of sovereign risk increasingly obsolete. In many emerging markets, government policy is to retire outstanding FC debt and end new FC issuance.3 The popular country-level JP Morgan Emerging Market Bond Index (EMBI), commonly used in academic research to measure sovereign risk, is today forced to track a dwindling number of outstanding FC eurobonds with declining liquidity and trading volume. In countries such as Egypt, Thailand, Malaysia, Morocco, South Korea and Qatar, FC debt has shrunk to the point that EMBI+ has been forced to discontinue these countries' indices. In addition to FC credit spreads, sovereign CDS spreads are used as an alternative measure of sovereign risk. However, defaults on local currency bonds governed under domestic law do not constitute credit events that trigger CDS contracts in emerging markets.4 As a result, sovereign CDS also offers an incomplete characterization of emerging market sovereign risk.
Using new data and a new measure, we document a new set of stylized facts about LC sovereign risk. To construct LC and FC sovereign credit spreads, we build a new dataset of zero-coupon LC and FC yield curves and swap rates for 10 major emerging markets at the daily frequency for a common sample period from 2005 to 2011. Using the 5-year zero-coupon benchmark, we find that LC credit spreads are significantly above zero, indicating an important credit component of LC debt, robust to taking into account transaction costs for entering into swaps. This result demonstrates the failure of long-term covered interest rate parity between government bond yields in emerging markets and the United States. Removing the currency risk highlights an important credit component in LC yields, as shown by the positive correlation between the LC credit spread and the conventional sovereign risk measure, the FC credit spread.
Despite a positive correlation, LC and FC credit spreads are different along three important dimensions. First, while LC credit spreads are large and economically significant, they are generally lower than FC credit spreads. The gap between LC and FC credit spreads significantly widened during the peak of the crisis following the Lehman bankruptcy. Second, FC credit spreads are much more correlated across countries than LC credit spreads. Over 80% of the variation in FC spreads is explained by the first principal component. In contrast, only 53 of the variation in LC credit spreads is explained by the first principal component, pointing to the relative importance of country-specific factors in driving LC spreads. Third, FC credit spreads are much more correlated with global risk factors than are LC credit spreads. These ex-ante results in the yield spread space are mirrored ex-post in the excess return space. Despite the common perception of emerging market LC debt as extremely risky, we find that swapped LC debt is actually safer than FC bonds for global investors measured in terms of global equity betas. The removal of currency risk is central to this finding, as the currency unhedged LC excess returns have larger betas with global equity returns than FC excess returns.
After documenting the differences between LC and FC credit spreads, we turn to examining the sources of these credit spread differentials. We discuss three broad hypotheses to explain the difference in LC and FC credit spreads: (1) differential cash flow risk, (2) differential liquidity risk and (3) differential pass-throughs of global risk aversion. Although differential cash flow risks are important for understanding persistent level differences between credit spreads, further regression analysis with country fixed effects shows that liquidity risks and shocks to global risk aversion matter more for time series variations in credit spread differentials.
FC and swapped LC bonds may have differential cash flow risks for several reasons. First, LC and FC credit spreads are defined with respect to risk-free rates in the respective currency, the unhedged covariance between LC credit and currency risk introduces a wedge between the LC and FC credit spreads. From a dollar investor's perspective, swapped LC debt can have lower cash flow risk if investors expect to gain profits from unwinding the swap position with unmatched LC bond cash flows in the event of an LC bond default. This is the case if the local currency is expected to depreciate upon default. Given the observed mean credit spreads, our simple calibration suggests that from a dollar investor's perspective a 34 percent expected LC depreciation upon default would lead to equal expected losses on LC and FC debt as a fraction of the face value on average. Second, the sovereign may choose to selectively default on LC or FC debt because of the currency composition of the debt, the holders of the debt or other considerations. It is unclear a priori whether we should expect higher default probabilities or recovery on LC or FC debt. Third, foreign holders of LC debt face several risks not present in FC bonds, including convertibility risk, as well as the risks of changing taxation and regulation, and differing legal risks arising from domestic jurisdiction, such as a more uncertain bankruptcy process.
In addition to differential cash flow risk, swapped LC and FC bonds may have different liquidity risk. We use data on the bid-ask spreads on LC bonds, FC bonds and currency swaps, as well as trading volume and turnover ratios of the bond market to assess differential liquidity risk of swapped LC and FC bonds. Since LC bonds generally have better liquidity than currency swaps and FC bonds, the synthetic swapped LC bond goes long in the more liquid security and short in the more illiquid security and thus has better liquidity overall.
Finally, in addition to differential cash flow and liquidity risks, we also examine why risk premia (in particular, the pass-through of global risk aversion) can be different across the two types of debt. We allow LC and FC credit spread differentials to also depend on the effectiveness of arbitrage between domestic and external debt markets. In a world with imperfect capital markets, collateral frictions and slow-moving capital can create limits to arbitrage (See, for example, Shleifer and Vishny, 1997, and Duffie, 2010). While an increasing fraction of LC debt is being purchased by foreign investors, the majority is still owned by domestic residents, commercial banks, and pension funds. We study a model where the arrival rate of credit events for FC and LC debt to respond differently to a local and global risk factor in the style of Duffie and Singleton (1999), diversified global investors are the primary clientele for FC debt, domestic investors are the primarily clientele for LC debt, and risk-averse arbitrageurs partially integrate the two markets (as in the preferred habitat model of Greenwood and Vayanos (2010) and Vila (2009). A key feature of the model is that shocks to global risk aversion have perfect pass-through into the FC credit spread, but incomplete pass-through into the LC credit spread due to imperfect market integration and risky arbitrage, driving credit spread differentials.
After laying out different hypotheses for the credit spread differentials, we perform an empirical decomposition to study the relative importance of each channel. We control for a host of global and local macroeconomic fundamentals to allow the cash flow risk to depend on fundamentals. We use VIX as a proxy for global risk aversion and bid-ask spreads on bonds and swaps to measure liquidity. While cash-flow risks are important for understanding the levels of the credit spreads, in a regression framework with country-fixed effects, we show that global risk aversion and liquidity risks are far more important in explaining the within country time series variations in the credit spread differential than macroeconomic fundamentals. We find that time-varying global risk aversion and liquidity alone can explain 46.7 percent of the variation in the difference between LC and FC credit spreads. This represents 83 percent of total explained variation conditional on economic fundamentals. In the excess return space, global risk aversion and liquidity factors significantly forecast excess returns of FC over the swapped LC bonds, whereas fundamentals do not forecast returns. Finally, consistent with the model featuring risky arbitrage, we find that LC credit spreads are more sensitive to global risk aversion in countries with more correlated swapped LC and FC bond returns.
The paper is structured as follows. We begin by explaining this paper's place in the existing literature. Section 2 explains the mechanics of cross currency swaps and formally introduces the LC credit spread measure. Section 3 presents new stylized facts on LC sovereign risk. Section 4 lays out different hypotheses to explain credit spread differentials and develops a no-arbitrage model of partially segmented markets with risky credit arbitrage. Section 5 performs empirical decomposition to assess the different hypotheses. Section 6 concludes.
1.1 Relation to the Literature
Our work is related to several distinct strands of literature: the enormous sovereign debt literature in international macroeconomics, the empirical sovereign and currency risk premia literature, the literature on currency-specific corporate credit spreads, and the segmented market asset pricing literature.
Recent work by Carmen Reinhart and Kenneth Rogoff demonstrates (Reinhart and Rogoff 2008, 2011) that LC sovereign borrowing and default are not new phenomena. While Reinhart and Rogoff document that default on domestic law bonds occur throughout history, a large fraction of the defaults they document concern real bonds (inflation or foreign currency linked) rather than explicit default on purely nominal bonds. The pricing of LC debt was also examined by Burger and Warnock (2007) and Burger et al. (2012), who studied ex-post returns on LC bonds using the J.P. Morgan Emerging Market Government Bond Index (EM-GBI) index.
Using our dataset of daily yield curves and currency swaps, we document a series of new stylized facts that we believe are important to integrate into the quantitative sovereign debt literature that builds on Aguiar and Gopinath (2006) and Arellano (2008). Given that an increasing fraction of sovereign borrowing is in LC, our findings on how LC credit spreads behave differently than FC credit spreads highlight the importance of moving away from the standard assumption in this literature that governments borrow solely from foreign lenders using real debt. In addition, a new theoretical literature has been trying to answer the question of when a country would choose to explicitly default on debt denominated in its own currency. Papers in this literature, including Aguiar et al. (2013), Araujo et al. (2013), Corsetti and Dedola (2013), Da-Rocha et al. (2012) and Jeanne (2012), present theoretical models where a sovereign might find it optimal to default on local currency debt. These papers, and the rest of the literature, are missing an empirical measure of the credit risk on these local currency bonds. We fill this gap by using cross currency swaps to disentangle the two theoretically distinct types of risk on local currency sovereign debt: currency and credit risk.
Our paper is also closely related to the literature on FC sovereign risk premia and currency risk premia. Borri and Verdelhan (2011) demonstrate that FC spreads can be explained by modeling a risk-averse investor who demands risk premia for holding sovereign debt because default generally occurs during bad times for global investors. Using data on credit default swaps (CDS) denominated in dollars, Longstaff et al. (2011) show that global risk factors explain more of the variation in CDS spreads than do local factors. Our analysis confirms these findings. In addition, we find support for the results of Lustig and Verdelhan (2007) and Lustig et al. (2012) that there is a common global factor in currency returns. This motivates our use of cross currency swaps to separate this currency risk from the credit risk on LC sovereign debt.
Cross currency swaps have previously been used to test long-term covered interest parity among government bond yields in developed countries. Popper (1993) and Fletcher and Taylor (1994, 1996) document some deviations from covered parity, but they are an order of magnitude smaller and much less persistent than those we document in our dataset of emerging markets. Currency-dependent credit spreads implied from cross currency swaps have also received attention in the empirical corporate finance literature. McBrady and Schill (2007) demonstrate that firms gauge credit spread differentials across different currencies when choosing the currency denomination of their debt. Jankowitsch and Stefan (2005) highlight the role of the correlation between FX and default risk in affecting currency-specific credit spreads. Using one year forwards and the JP Morgan EMBI, Didier and Garcia (2003) and Garcia and Lowenkron (2005) perform an exercise similar to ours, documenting that currency and credit risk, the so-called "cousin risks", are positively linked in some emerging markets but not in others.
Finally, our theoretical model builds on the asset pricing literature on investors' preferred habitats and the limits to arbitrage. Greenwood and Vayanos (2010), building on Vayanos and Vila (2009), examine the effect of increases in bond supply across the yield curve for U.S. Treasuries. The framework assumes that different maturities have different clienteles and each type of investor invests only in a certain range of maturities (their "preferred habitat"). We study an environment where preferred habitats correspond to currencies and markets rather than maturities, building on the cross-asset arbitrage theory presented by Gromb and Vayanos (2010), and solving analytically for the endogenous LC bond price.
2 Cross Currency Swaps and Sovereign Credit Spreads
2.1 Cross Currency Swaps
For short-term instruments, FX forward contracts allow investors to purchase foreign exchange at pre-determined forward rates. Beyond one year, liquidity is scarce in the forward markets and long-term currency hedging via forwards is very costly. CCS contracts, on the other hand, allow investors to conveniently hedge long-term currency risk. A CCS is an interest rate derivative contract that allows two parties to exchange interest payments and principal denominated in two currencies. A real-world example of hedging currency risk of an LC bond using CCS is given in Appendix A. For emerging markets, CCS counterparties are usually large offshore financial institutions. To mitigate the counterparty risk embedded in CCS contracts, the common market practice is to follow the Credit Support Annex of the International Swap and Derivative Association Master Agreement, which requires bilateral collateralization of CCS positions, and thus counterparty risk is fairly negligible. For countries with non-deliverable FX forwards, CCS contracts are cash settled in dollars based on LC notional amount and are free from currency convertibility risk.
For our cross-country study, it is cumbersome to deal with coupon bearing bonds and par swap rates due to the mismatch in coupon rates and payment dates between bonds and swaps. We can extract the long-term FX forward premium (the zero-coupon swap rate) implicit in the term structure of par swaps. Intuitively, a fixed for fixed LC/dollar CCS package can always be considered as the sum of two interest rate swaps. First, the investor swaps the fixed LC cash flow into a floating U.S. Libor cash flow5 and then swaps the floating U.S. Libor cash flow into a fixed dollar cash flow. We can exploit the fact that the receiver of U.S. Libor must be indifferent between offering a fixed LC or a fixed dollar cash flow. Thus, the difference in the two swap rates implies the long-term currency view of the financial market. After performing this transformation, a CCS is completely analogous to a standard forward contract. The specifics are given in the following proposition.
Proposition 1. Given implied log spot rates
![]() from the fixed LC for
U.S. Libor CCS and
from the fixed LC for
U.S. Libor CCS and
![]() from the fixed dollar
for Libor interest rate swap, the implicit long-term forward
premium is equal to
from the fixed dollar
for Libor interest rate swap, the implicit long-term forward
premium is equal to
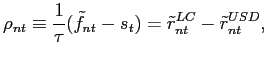
where
![]() is the pre-determined log
forward exchange rate at which a transaction between LC and dollars
takes place
is the pre-determined log
forward exchange rate at which a transaction between LC and dollars
takes place ![]() years ahead.
years ahead.
2.2 LC and FC Credit Spreads
The core of our dataset is daily zero-coupon yield curves and swap curves for LC and FC sovereign bonds issued by 10 different emerging market governments from January, 2005 to December, 2011. We use a benchmark tenor of 5 years. The choice of countries is mainly constrained by the lack of sufficient numbers of FC bonds outstanding. Furthermore, all 10 sample countries belong to the J.P. Morgan EM-GBI index, an investable index for emerging market LC bonds. The length of the sample period is constrained by the availability of long-term currency swap data. All data on cross currency swaps are collected from Bloomberg.6 Zero coupon yield curves are collected or estimated from various data sources. The details on the yield curve construction are given in Appendix B.
We work with log yields throughout the paper. To fix notations,
we let
![]() denote the
denote the ![]() -year
zero-coupon U.S. Treasury bond yield, the long-term risk-free rate
used throughout the paper. Nominal LC and FC yields are denoted by
-year
zero-coupon U.S. Treasury bond yield, the long-term risk-free rate
used throughout the paper. Nominal LC and FC yields are denoted by
![]() and
and
![]() , respectively. We let
, respectively. We let ![]() denote the zero-coupon swap rate, the implicit
forward premium as defined in Proposition 1. All yields and
swap rates are for the
denote the zero-coupon swap rate, the implicit
forward premium as defined in Proposition 1. All yields and
swap rates are for the ![]() -year zero-coupon benchmark
at date
-year zero-coupon benchmark
at date ![]() . The conventional measure of sovereign
risk, the FC credit spread, measures the difference between the
yield on FC debt and the U.S. Treasury yield:
. The conventional measure of sovereign
risk, the FC credit spread, measures the difference between the
yield on FC debt and the U.S. Treasury yield:
Our new measure for LC sovereign risk, the LC credit spread, is defined as the nominal LC spread over the the U.S. Treasury yield, minus the zero-coupon swap rate:
or the deviation from long-term covered interest rate parity between the government bond yields. There are two ways to interpret this measure. First, we can combine a U.S. Treasury bond with a fixed for fixed CCS to create an LC risk-free bond. The sum of the dollar risk-free and the CCS rate gives the LC risk free rate
and thus the LC credit spread measures the yield spread of the LC bond over the LC risk-free rate:
and is a pure credit spread measure for local currency. Second, the dollar investor can create a swapped LC bond by combining an LC bond with a CCS with the same promised cash flows. The synthetic dollar yield on the swapped LC bond is given by
The LC credit spread is therefore equal to the dollar spread on this synthetic asset:
Hence, by holding the swapped LC bond to maturity, the LC credit spread gives the promised dollar spread on the LC bond to dollar investors even if the LC depreciates, provided that explicit default is avoided. In the event of default, the dollar investor can choose to unwind the swap with an unmatched LC bond payment, which could result in additional FX profits or losses from the swap. We will discuss the effect of this hedging error in Section 4.1.1.
Finally, the LC over FC credit spread differential measures the spread between the yield on the synthetic dollar asset combining an LC bond and CCS over the FC bond yield:
From the issuer's perspective, it gives the the difference between the synthetic dollar borrowing cost in the local market and the actual dollar borrowing cost in the external market.
3 New Stylized Facts on LC Sovereign Risk
3.1 Deviations from Long-Term CIP
If the only risk on LC bonds was currency risk, then covered interest parity (CIP) would hold for government bond yields. If this were the case, LC credit spreads would equal zero in the absense of transaction costs. In Figure 3, we plot the 5-year swapped U.K. Treasury yield in dollars and the U.S. Treasury yield from 2000 to 2011, and show that this is roughly the case for the U.S. and the U.K.. The difference between the two curves, the U.K. LC credit spread, averages 10 basis points for the full sample and 6 basis points excluding 2008-2009. Long-term CIP holds quite well between the U.S. and the U.K. Treasury yields excluding 2008-2009. At the peak of the Global Financial Crisis around the Lehman bankruptcy, the U.K. credit spread temporarily increased to 100 basis points but converged back towards zero within a few months.
LC credit spreads in emerging markets offer a very different
picture. As can be seen in Figure 4, where the
5-year zero-coupon yield spreads are plotted for our sample
countries, large persistent deviations from long-term covered
interest parity are the norm rather than the exception. Column 1 in
Table 1 presents summary statistics for 5-year LC spreads for the sample
period 2005-2011 at the daily frequency. LC credit spreads,
![]() , have a cross-country mean of 128
basis points, calculated using the mid-rates on the swaps. Brazil
records the highest mean LC spreads equal to 313 basis points while
Mexico and Peru have the lowest means of about 60 basis points. All
mean LC credit spreads are positive and statistically significantly
different from zero using Newey-West standard errors allowing for
heteroskedasticity and serial correlation.7 Positive mean LC
spreads are robust to taking into account the transaction costs of
carrying out the swaps. Column 4 provides summary statistics for
liquidity of the cross currency swaps,
, have a cross-country mean of 128
basis points, calculated using the mid-rates on the swaps. Brazil
records the highest mean LC spreads equal to 313 basis points while
Mexico and Peru have the lowest means of about 60 basis points. All
mean LC credit spreads are positive and statistically significantly
different from zero using Newey-West standard errors allowing for
heteroskedasticity and serial correlation.7 Positive mean LC
spreads are robust to taking into account the transaction costs of
carrying out the swaps. Column 4 provides summary statistics for
liquidity of the cross currency swaps,
![]() , defined as half of the bid-ask
spread of cross currency swap rates, with the sample average equal
to 19 basis points. We perform statistical tests and find that LC
credit spread remains significantly positive for every country
after subtracting one half of the bid-ask spread on the CCS in
order to incorporate the transaction costs. Positive LC credit
spreads suggest that emerging market nominal LC sovereign bonds are
not free from credit risk from the investor's perspective.
, defined as half of the bid-ask
spread of cross currency swap rates, with the sample average equal
to 19 basis points. We perform statistical tests and find that LC
credit spread remains significantly positive for every country
after subtracting one half of the bid-ask spread on the CCS in
order to incorporate the transaction costs. Positive LC credit
spreads suggest that emerging market nominal LC sovereign bonds are
not free from credit risk from the investor's perspective.
3.2 Mean Levels of Credit Spreads
To compare the sovereign's dollar borrowing costs using FC debt
with the synthetic dollar borrowing costs using LC debt, we perform
an ex-ante credit spread comparison. FC credit spreads, ![]() , reported in Column 2 in Table 1 have a mean of
195 basis points, 67 basis points higher than LC credit spreads
based on the mid-rates for CCS. The difference increases to 86
basis points after taking into account the transaction cost of
carrying out the swaps. In Column 3, we compute the difference
between LC and FC credit spreads by country. The swapped LC over FC
spread,
, reported in Column 2 in Table 1 have a mean of
195 basis points, 67 basis points higher than LC credit spreads
based on the mid-rates for CCS. The difference increases to 86
basis points after taking into account the transaction cost of
carrying out the swaps. In Column 3, we compute the difference
between LC and FC credit spreads by country. The swapped LC over FC
spread,
![]() , is significantly negative for all
of our sample countries except Brazil. Although all our sample
countries have LC bond markets open to foreign investors,
foreigners may still need to incur transaction costs to buy into LC
markets. In addition to taxes on capital inflows, LC bonds are
often subject to local taxation, whereas FC international bonds are
exempt from interest withholding taxes. For 9 out of 10 countries
with negative LC swapped over FC spreads, the promised dollar
spread on LC bonds is unambiguously lower than that on FC bonds,
since swapped LC over FC spreads would become more negative after
taking into account positive taxes on LC bonds.
, is significantly negative for all
of our sample countries except Brazil. Although all our sample
countries have LC bond markets open to foreign investors,
foreigners may still need to incur transaction costs to buy into LC
markets. In addition to taxes on capital inflows, LC bonds are
often subject to local taxation, whereas FC international bonds are
exempt from interest withholding taxes. For 9 out of 10 countries
with negative LC swapped over FC spreads, the promised dollar
spread on LC bonds is unambiguously lower than that on FC bonds,
since swapped LC over FC spreads would become more negative after
taking into account positive taxes on LC bonds.
Brazil offers an important exception. As a country offering one of the highest nominal interest rates in the world, Brazil has implemented various measures to curb portfolio investment flows and cross-border derivative trading as macro-prudential and exchange rate policy. The Imposto sobre Operaçoes Financieras (IOF), or tax on financial transactions, was introduced in October 2009 and abandoned in the face of large capital outflows in June 2013, and varied between 2 and 6% on foreign investment in fixed income instruments during its time in effect. Figure 5 indicate four changes in the IOF tax rate. LC and FC credit spreads in Brazil diverged significantly after the IOF rate was changed to 6 percent in October 2010, reaching a record high of 400 basis points in November 2011. On June 5, 2013, Brazil removed the IOF tax amidst large FX depreciation pressure following the start of the Federal Reserve taper talk. The onshore LC and offshore FC credit spread differential dramatically converged to around 50 basis points after the removal of the IOF.
Even in the absence of transaction cost in the form of direct taxes on cross-boarder capital flows, currency convertibility and capital control risks are still non-negligible. Fortunately for our analysis, Brazil conducted four large issuances of eurobonds denominated in reais traded at the Luxembourg Stock Exchange and in the over-the-counter market. These bonds give offshore investors direct access to real-denominated sovereign rates without paying the onshore taxes. In addition, these bonds are payable in dollars and thus foreign investors are free from currency convertibility risk. Figure 5 shows that two long-term offshore real-denominated bonds are traded at significantly lower spreads than 10-year onshore bonds. Applying the CCS to the offshore LC yield generally gives a negative LC over FC spread. Besides Brazil, Colombia and the Philippines, more recently, have also issued several LC eurobonds cash settled in dollars. All the offshore LC bonds are currently traded significantly tighter than onshore bonds, which suggests that taxes and convertibility risk are important components of the LC credit spread from the offshore investors' perspective.
Despite the level difference in credit spreads, one might expect LC and FC credit risk to be correlated within countries, as in a downturn a country might find it more tempting to explicitly default on both types of debt. Column 5 confirms this conjecture. The within-country correlation between LC and FC credit spreads is positive for every country with a mean of 54 percent. However, there is significant cross-country heterogeneity. The correlation is highest for Hungary at 91% and lowest for Indonesia at 18%. This cross-country heterogeneity is a source of variation that suggests that incomplete market integration is potentially important in the relative pricing of the two types of debt, a hypothesis we will return to discuss in Section 4.3.
3.3 Widening Credit Spread Differentials During the Crisis
Despite the relatively short sample period, the years 2005-2011
cover dynamic world economic events: the end of the great
moderation, the Global Financial Crisis and the subsequent
recovery. Figure 6 plots the
difference in LC and FC credit spreads,
![]() , across 10 countries over the
sample period. While swapped LC over FC spreads largely remain in
negative territory (with the exception of Brazil), the spreads
significantly widened during the peak of the crisis following the
Lehman bankruptcy. The maximum difference between LC and FC credit
spreads for any country during the crisis was negative 10
percentage points for Indonesia.
, across 10 countries over the
sample period. While swapped LC over FC spreads largely remain in
negative territory (with the exception of Brazil), the spreads
significantly widened during the peak of the crisis following the
Lehman bankruptcy. The maximum difference between LC and FC credit
spreads for any country during the crisis was negative 10
percentage points for Indonesia.
Table 2 documents the behavior of the credit spreads during the crisis peak (defined approximately as the year following the Lehman bankruptcy from September 2008 to September 2009), measured as the increase in spreads relative to their pre-crisis means. FC credit spreads significantly increase in all countries and LC credit spreads increase significantly in 8 out of the 10 sample countries, with the exceptions of Indonesia and Peru. However, the increase in swapped LC spreads are generally less than the increase in FC spreads, as LC over FC credit spread differentials are reduced for all countries except Brazil. The divergent behavior of these credit spreads during the crisis peak highlights significant differences between LC and FC bonds, and offers a key stylized fact to be examined in Sections 4 and 5.
3.4 Cross-Country Correlations of Credit Spreads
In Table 3, we conduct a principal component (PC) analysis to determine the extent to which fluctuations in LC and FC credit spreads are driven by common components or by idiosyncratic country shocks. In the first column, we see that the first principal component explains less than 54% of the variation in LC credit spreads across countries. This is in sharp contrast to the FC spreads (Column 2) where over 81% of total variation is explained by the first PC. The first three principal components explain slightly less than 80% of the total variation for LC credit spreads whereas for FC credit spreads they explain about 97%. In addition, we find that the average pairwise correlation of LC credit spreads between countries is only 42%, in contrast to 78% for FC credit spreads. These findings point to country-specific idiosyncratic components as important drivers of LC credit spreads, in contrast to the FC market where global factors are by far the most important.8
To link these results to the literature using CDS spreads as a measure of sovereign risk, we perform the same principal component analysis for 5-year sovereign CDS spreads. The results, in Column 3, are very similar to the FC results in Column 2: the first principal component explains 80 percent of total variation of CDS spreads and the pairwise correlation averages 77 percent. Our result that an overwhelming amount of the variation in CDS spreads is explained by the first PC supports the findings of () who show that 64% of CDS spreads are explained by the first principal component of 26 developed and emerging markets. The sample period for their study is 2000-2010, but the authors find in the crisis subsample of 2007-2010 that the first principal component accounts for 75% of the variation.
3.5 Correlation of Sovereign Risk with Global Risk Factors
3.5.1 Credit Spreads
After identifying an important global component in both LC and FC credit spreads, we now try to understand what exactly this first principal component is capturing. In Table 4, we first examine the correlation of the first PC's of credit spreads with each other and with global risk factors. The global risk factors include the Merrill Lynch U.S. BBB corporate bond spread over the Treasuries, BBB/T, the implied volatility on S&P options, VIX, and the Chicago Fed National Activity Index, CFNAI, which is the first PC of 85 monthly real economic indicators. Panel (A) indicates that the first PC of FC credit spreads has remarkably high correlations with these three global risk factors, 93% with VIX, 88% with BBB/T and 76% with global macro fundamentals (or, more precisely, US fundamentals) proxied by the CFNAI index. The correlation between the first PC of LC credit spreads and global risk factors are lower, but still substantial, with a 76% correlation with VIX, 71% with BBB/T and 57% with CFNAI.
Furthermore, since the first PC explains much more variation in FC credit spreads than in LC credit spreads, the cross-country average correlation between raw credit spreads and global risk factors is much higher for FC than for LC debt (Panel B). Notably, VIX has a mean correlation of 70 percent with FC credit spreads, but only 41 percent with LC credit spreads. This leads us to conclude that the observed global factors are more important in driving spreads on FC debt than on swapped LC debt. Unsurprisingly, the correlations between the global factors and the CDS spread are very similar to the correlations between these factors and the FC spread.
3.5.2 Excess Returns
Having examined the ex-ante promised yields in Tables 3 and 4, we next turn to
ex-post realized returns. The natural measures to study are the
excess returns of LC and FC bonds over U.S. Treasury bonds. In
particular, we run a series of beta regressions to examine how LC
and FC excess returns vary with global and local equity markets.
Before turning to these results, we first define the different
types of returns. Since all yield spreads are for zero-coupon
benchmarks, we can quickly compute various excess returns for the
holding period ![]() .9 The FC over US excess
holding period return for an
.9 The FC over US excess
holding period return for an ![]() -year FC bond is
equal to
-year FC bond is
equal to
which represents the change in the log price of the FC bond over a U.S. Treasury bond of the same maturity. Similarly, the currency-specific return differential of an LC bond over a U.S. Treasury bond is given by
Depending on the specific FX hedging strategies, we can translate
![]() into three types of
dollar excess returns on LC bonds. First, the unhedged LC
over US excess return,
into three types of
dollar excess returns on LC bonds. First, the unhedged LC
over US excess return,
![]() , is equal to the
currency-specific return differential minus the ex-post LC
depreciation:
, is equal to the
currency-specific return differential minus the ex-post LC
depreciation:
where ![]() denotes the log spot exchange rate.
Second, the holding-period hedged LC over US excess return,
denotes the log spot exchange rate.
Second, the holding-period hedged LC over US excess return,
![]() , is equal to the
currency-specific return differential minus the ex-ante holding
period forward premium:
, is equal to the
currency-specific return differential minus the ex-ante holding
period forward premium:
where
![]() denotes the log forward rate
at
denotes the log forward rate
at ![]() for carrying out FX forward transaction
for carrying out FX forward transaction
![]() ahead. Third, swapped LC over US
excess returns,
ahead. Third, swapped LC over US
excess returns,
![]() , is equal to the
currency-specific return differential minus the return on the
currency swap:
, is equal to the
currency-specific return differential minus the return on the
currency swap:
All three LC excess returns share the same component measuring the LC and US currency-specific return differential. Depending on the specific FX hedging strategy, the ex-post LC depreciation, ex-ante holding period forward premium and ex-post return on the currency swap affect unhedged, hedged and swapped excess returns, respectively.10
Table 5 presents panel regression results for excess bond returns over local and global equity excess returns. Global equity excess returns are defined as the quarterly return on the S&P 500 index over 3 month U.S. Treasury bills. We define two measures of LC equity excess returns (holding-period hedged and long-term swapped) so that a foreign investor hedging her currency risk in the local equity market has the same degree of hedging on her bond position. We find that FC excess returns have significantly positive betas on both global and hedged LC equity returns, with the loading on S&P being greater. Hedged and swapped LC excess returns do not load on the S&P, but have a significantly positive beta on local equity returns. In contrast, FX unhedged LC excess returns have positive betas on both the S&P and local equity returns.
We therefore conclude that, for foreign investors, the main risk of LC bonds is that emerging market currencies depreciate when returns on global equities are low. This supports the results of () that common factors are important drivers of currency returns. Our new result, however, is that once currency risk is hedged using cross currency swaps, LC debt appears to be much less risky than FC debt in the sense that it has significantly lower loadings on global equity returns than FC debt.
3.6 Summary of Stylized Facts
We briefly summarize the results of Section 3. We first establish that emerging markets are paying positive spreads over the LC risk-free rate on their LC sovereign borrowing. This result indicates the failure of long-term covered interest parity for government bond yields between our ten emerging markets and the United States. With the mean LC credit spread equal to 128 basis points, the failure is so large as to make clear the importance of credit risk on LC debt, rather than only pointing to a temporary deviation from an arbitrage relationship as documented in developed markets. Positive within-country correlations between LC credit spreads and the conventional measure of sovereign risk, FC credit spreads, also highlight the role of sovereign risk on LC debt.
Despite the positive correlation, LC and FC credit spreads differ along three important dimensions. First, while LC credit spreads are large and economically significant, they are generally lower than FC credit spreads. The difference between LC and FC credit spreads significantly widened during the peak of the crisis following the Lehman bankruptcy. Second, FC credit spreads are much more correlated across countries than LC credit spreads. Over 80% of the variation in FC spreads is explained by the first principal component. In contrast, only 53% of the variation in LC credit spreads is explained by the first principal component, pointing to the relative importance of country-specific factors in driving LC spreads. Third, FC credit spreads are much more correlated with global risk factors than LC credit spreads. We find that FC spreads are very strongly correlated with global risk factors, including a remarkable 93% correlation between the first PC of FC credit spreads and VIX. These results are mirrored in the return space, as excess holding period returns on FC debt load heavily on global equity returns while excess returns on swapped LC debt do not load on global equity returns once local equity returns are controlled.
The differences between LC and FC credit spreads have important implications. Given the fact that the bulk of emerging market sovereign borrowing takes the form of LC debt, conventional measures of sovereign risk based on FC credit spreads and CDS spreads no longer fully characterize the costs of sovereign borrowing, the cross-country dependence of sovereign risk, and sensitivities of sovereign spreads to global risk factors. Understanding why LC and FC credit spreads differ is the main focus of the next two sections.
4 Hypotheses For Credit Spread Differentials
Having documented a series of new stylized facts on the differential behavior of LC and FC credit spreads, we now turn to explaining them. We first layout different sources of credit spread differentials in terms of differential cash flow risk, liquidity risk and differential sensitivity to global risk aversion. Finally, we perform further empirical analysis to the assess the importance of cash flow, liquidity and risk aversion factors in a regression framework in Section 5.
4.1 Differential Cash Flow Risks
4.1.1 Linking Credit Spreads to Cash Flow Risks
We start with the benchmark of perfect capital markets and
risk-neutral investors and examine the implications of LC and FC
credit spreads on cash flow risks of LC and FC debt. Let
![]() denote the risk-neutral expectation
of a dollar-based global investor. Suppose we have one-period LC
and FC bonds with default losses denoted by
denote the risk-neutral expectation
of a dollar-based global investor. Suppose we have one-period LC
and FC bonds with default losses denoted by
![]() and
and
![]() , with the loss measured as a
fraction of face value in the respective currency. The dollar price
of the FC bond is given by
, with the loss measured as a
fraction of face value in the respective currency. The dollar price
of the FC bond is given by
and the FC credit spread is then given by
The FC credit spread measures the expected default loss for the
dollar investor as a fraction of the face value of the dollar debt.
Analogous to the FC credit spread, we define the LC credit spread
as the pricing differential between a risk-free LC bond and a
defaultable LC bond. Let
![]() denote the risk-neutral
expectation of the local investor using the LC risk-free rate as
the numeraire, and then the LC credit spread is given by
denote the risk-neutral
expectation of the local investor using the LC risk-free rate as
the numeraire, and then the LC credit spread is given by
| (1) |
where
![]() is the
synthetic LC risk-free rate. The LC credit spread measures the
expected loss for the local investor as a fraction of the face
value of the LC debt. Therefore, the difference in LC and FC credit
spread measures the difference in risk-neutral expected default
losses perceived by local and dollar investors, respectively:
is the
synthetic LC risk-free rate. The LC credit spread measures the
expected loss for the local investor as a fraction of the face
value of the LC debt. Therefore, the difference in LC and FC credit
spread measures the difference in risk-neutral expected default
losses perceived by local and dollar investors, respectively:
One subtle but important issue with this comparison is that the
expected recovery rate measured as a fraction of the face value in
the LC is not equal to the expected recovery rate measured in the
dollar if the covariance between currency and default risk is
nonzero. To make the change of numeraire adjustment, we consider
the pricing of the LC credit spread under the dollar risk-neutral
expectation. The dollar price of the LC bond
![]() is given by
is given by
where
![]() is the price of the LC bond
expressed in LC, and
is the price of the LC bond
expressed in LC, and
![]() denotes the spot exchange
defined as local currency per dollar. Using the no-arbitrage
condition between LC and the dollar:
denotes the spot exchange
defined as local currency per dollar. Using the no-arbitrage
condition between LC and the dollar:
we can re-write the expression above as
![$\displaystyle \exp(-y_{t}^{*LC})E_{t}^{*}(1-L_{t+1}^{LC})\left[1+\frac{Cov_{t}^{*}(1-L_{t+1}^{LC},\mathcal{E}_{t}/\mathcal{E}_{t+1})}{E_{t}^{*}(1-L_{t+1}^{*})E_{t}^{*}(\mathcal{E}_{t}/\mathcal{E}_{t+1})}\right]$](img59.gif) |
So the LC credit spread under the dollar expectation is given by
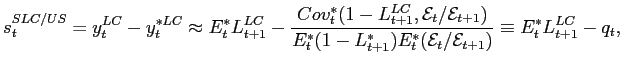 |
(2) |
where
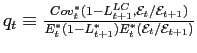 is referred the "quanto adjustment" for the covariance between
currency and default risk. If credit and currency risks are
positively correlated, the LC credit spread is lower than the
expected default loss under the dollar measure. If there is no
covariance between currency and credit,
is referred the "quanto adjustment" for the covariance between
currency and default risk. If credit and currency risks are
positively correlated, the LC credit spread is lower than the
expected default loss under the dollar measure. If there is no
covariance between currency and credit, ![]() and the
credit spreads are equal using the two risk-neutral measures.
Comparing the pricing equations (1) and (2), the covariance
between currency and default risk introduces a wedge between the
local and dollar valuations of the LC credit spread. The dollar
investor values the swapped LC bond more than the expected default
loss under the dollar measure if the LC depreciates upon default
(i.e.,
and the
credit spreads are equal using the two risk-neutral measures.
Comparing the pricing equations (1) and (2), the covariance
between currency and default risk introduces a wedge between the
local and dollar valuations of the LC credit spread. The dollar
investor values the swapped LC bond more than the expected default
loss under the dollar measure if the LC depreciates upon default
(i.e.,
![]() ). Intuitively, the covariance between credit and currency risks
essentially measures the hedging error of going long in the LC bond
hedged by shorting the currency swap. If the currency depreciates
upon default, the dollar investor is over-hedged and has additional
gain by unwinding the swap position from the unmatched LC bond cash
flow upon default. These profits would be passed into an ex-ante
negative credit spread adjustment. Therefore, from the dollar
investor's perspective, the credit spread differential is given by
). Intuitively, the covariance between credit and currency risks
essentially measures the hedging error of going long in the LC bond
hedged by shorting the currency swap. If the currency depreciates
upon default, the dollar investor is over-hedged and has additional
gain by unwinding the swap position from the unmatched LC bond cash
flow upon default. These profits would be passed into an ex-ante
negative credit spread adjustment. Therefore, from the dollar
investor's perspective, the credit spread differential is given by
4.1.2 A Simple Calibration for the Covariance Adjustment
To calibrate the size of the quanto-adjsutment, we assume a
one-period bond with zero-recovery rate upon default.11 We
also assume the spot exchange rate jumps upon default by a fraction
![]() relative to the non-default state.
Positive
relative to the non-default state.
Positive ![]() corresponds to depreciation upon
default. Following Khuong-Huu (1999), we assume that
corresponds to depreciation upon
default. Following Khuong-Huu (1999), we assume that
![]() is non-stochastic. Let
is non-stochastic. Let
![]() denote the
risk-neutral probability of an LC default. We define the
unconditional exchange rate as
denote the
risk-neutral probability of an LC default. We define the
unconditional exchange rate as
where
![]() and
and
![]() denote the spot
exchange rate in the non-default and default states, respectively.
Therefore, the spot rates conditional on non-default and default
are given as follows:12
denote the spot
exchange rate in the non-default and default states, respectively.
Therefore, the spot rates conditional on non-default and default
are given as follows:12
It follows that the quanto adjustment is equal to
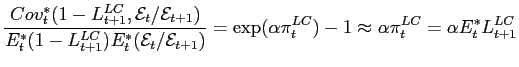 |
Therefore, the LC credit spread can be lower than the dollar expectation of expected default loss.
From an empirical perspective, although a country's exchange
rate typically depreciates during sovereign defaults, it is
difficult to estimate how much additional depreciation occurs upon
default relative to the relevant non-default counterfactual.
Instead of relying on historical experiences, we follow Mano (2013) use CDS traded in different currencies to back
out dollar investor's risk-neutral expectation upon a default on FC
sovereign debt. These CDS contracts denominated in the LC (quanto
CDS) are still linked to default on FC debt, and thus spreads
between dollar CDS and LC quanto CDS reflect the covariance between
currency and FC default risk. Liquidity of these quanto CDS
contracts is generally very thin with a few exceptions. Figure 7 shows CDS
spreads for Turkey denominated in dollars and in the Turkish lira.
LC CDS spreads are consistently below dollar CDS spreads. Despite
the level difference, the two CDS spreads have a correlation of 99
percent. Given the observed difference between LC and dollar CDS
spreads, under the assumption of full default13, we can compute
the expected depreciation upon default ![]() as
as

where
![]() denotes the spread on the dollar
CDS and
denotes the spread on the dollar
CDS and
![]() denotes the spread on the quanto
LC CDS. The implied depreciation upon default is fairly stable
throughout the entire sample with a mean equal to 38 percent and a
2.7 percent standard deviation.
denotes the spread on the quanto
LC CDS. The implied depreciation upon default is fairly stable
throughout the entire sample with a mean equal to 38 percent and a
2.7 percent standard deviation.
In order to better understand what LC and FC credit spreads imply about the differential default risk on the two types of debt, we perform a thought experiment to see how large expected depreciation upon default would need to be in order for the mean credit spreads we observe to correspond to equal credit risk between LC and FC debt. In our sample countries, the mean LC over FC credit spread differential is equal to -67 basis points and the mean FC credit spread is equal to 1.97 basis points. If the level difference between the two credit spreads were entirely driven by the quanto adjustment, meaning that the actual default probabilities and recovery rates were equal, then our data would imply 34 percent (0.67/1.97) expected depreciation upon default, similar to the estimate using Turkey's quanto CDS. If market participants expect higher depreciation upon default than this level and both types of debt are priced by dollar investors, then our empirical results would actually imply a larger default probability on LC debt than on FC debt. Therefore, even if the LC credit spreads are consistently lower than FC credit spreads, we cannot conclude that a lower default probability on LC debt than on FC debt from a dollar investor's perspective.
4.1.3 Can the Covariance Adjustment Explain All the Observed Variations?
Although the covariance between currency and credit risk can
explain large persistent level differences between LC and FC credit
spreads, it cannot be the only source to explain all variations in
the observed credit spread differentials. First, the expected
depreciation upon default ![]() would need to
be implausibly volatile if LC and FC credit spreads only differed
by the covariance adjustment. Appendix Table A3 summarizes the
implied depreciation upon default under our thought experiment of
equal default probabilities. As shown in Column 2, the mean
standard deviation for the expected depreciation upon default needs
to be as high as 56 percent, compared with the 2 percent standard
deviation observed in the Turkish CDS data.
would need to
be implausibly volatile if LC and FC credit spreads only differed
by the covariance adjustment. Appendix Table A3 summarizes the
implied depreciation upon default under our thought experiment of
equal default probabilities. As shown in Column 2, the mean
standard deviation for the expected depreciation upon default needs
to be as high as 56 percent, compared with the 2 percent standard
deviation observed in the Turkish CDS data.
Second, in the cross section, the estimated mean expected
depreciation upon default is at odds with the observed correlation
between currency and credit risk across countries. Although there
is no default in the model, we can use changes in credit spreads
and FX to infer the correlation between credit and currency risk.
When the dollar investor dynamically hedges the FX risk of the
synthetic LC spread,14 positive (negative) covariance
between currency and LC credit risk makes the dollar investor
over-hedge (under-hedge) when the credit spread widens (narrows)
and the local currency depreciates (appreciates) relative to the
forward rate. The hedging error gives rise to additional profits
(losses) for the dollar investor for holding the swapped LC bond
and should result in a negative (positive) credit spread
adjustment. Column 5 in Table A3 reports
correlation between changes in LC credit spreads and changes in the
spot exchange rate at the quarterly frequency. A positive number
indicates that credit risk and currency risk are positively
correlated. Brazil, Hungary and Poland have the highest correlation
between currency and credit, but on average have the lowest
![]() 's (in fact, expected
appreciation upon default), whereas Indonesia, Mexico and Peru have
low or even negative correlation between currency and credit, but
have the highest
's (in fact, expected
appreciation upon default), whereas Indonesia, Mexico and Peru have
low or even negative correlation between currency and credit, but
have the highest
![]() 's. The cross-country correlation
between the
's. The cross-country correlation
between the
![]() 's and correlation between
currency and credit is equal to negative 0.75 percent, instead of
being strongly positive. Therefore, the covariance adjustment alone
cannot explain the cross-country variations in the credit spread
differentials.
's and correlation between
currency and credit is equal to negative 0.75 percent, instead of
being strongly positive. Therefore, the covariance adjustment alone
cannot explain the cross-country variations in the credit spread
differentials.
4.1.4 Selective Default on LC and FC Debt
In addition to the positive covariance between currency and default risk, another more obvious cash-flow risk based explanation for why the mean credit spread on LC debt is lower than the mean credit spread on FC debt is that the risk of default on LC debt is lower. Although there are many reasons to expect differences in the default probabilities for the two types of debt, it is ambiguous a priori whether we should expect higher default probabilities or recovery on LC or FC debt. First, sovereigns have the ability to print the currency in which with the bond is denominated, so they always have the ability to make the contracted bond payments. However, inflation may be costly, and a government might find it preferable to explicitly default rather than tolerate the necessary money-printing to make the contracted bond payments. Second, the sovereign may have different incentives to repay the two types of debt. FC debt is mainly held by global investors whereas LC bonds are mainly held by local pension funds and commercial banks. On one hand, the government might favor the welfare of its citizens and be more inclined to default on FC obligations held predominantly by foreign investors. On the other hand, sovereigns may care about their reputation among international creditors and the access to global capital markets. These opposing forces make it unclear whether we should expect higher default probabilities on LC or FC debt.
4.1.5 Taxes, Convertibility and Legal Risks
Furthermore, taxes, convertibility and legal risks represent additional sources of risk for LC debt that are absent from FC debt. While tax and legal risks are theoretically distinct from the currency of the debt, in our sample nearly all LC debt is issued in domestic markets and governed under domestic law. Because of this, LC debt is subject to the risks of changing taxation, regulation, and custody, as well as a more uncertain bankruptcy procedure. Offshore investors also face convertibility risk whereby a government prevents the repatriation of funds by introducing capital controls while avoiding technical default. None of these risks can be hedged away by offshore currency swaps, often cash settled in dollars for non-deliverable currencies. FC bonds, on the other hand, are predominantly governed under international law and are therefore free from withholding taxes and from local government regulations. As discussed in Section 3.2, comparing yields on Brazilian LC bonds issued onshore and offshore, we see that differential taxes, convertibility and legal risks are positive and sizable. However, it is clear that these risks alone cannot explain the main empirical results as they would make the LC credit spreads higher than FC credit spreads across our sample countries.
4.2 Differential Liquidity Risk
In addition to differential credit risk, differential liquidity risk between the swapped LC and FC debt can create a wedge between the two credit spreads. Investors, especially short term investors, may need to be compensated for holding illiquid securities. We assess the liquidity of swapped LC debt and FC debt by comparing bid-ask spreads, market sizes and trading volume on both types of debt. A summary table of liquidity and trading volume at the country level can be found in Appendix Table A4. We obtain bid-ask spreads on LC and FC bonds by averaging bid-ask spreads across all sovereign bonds with pricing information in Bloomberg for each sample country. The sample mean bid-ask spread is equal to 28.6 basis point for the LC debt and 45.3 basis point for FC debt. The mean bid-ask spread on the currency swaps is equal to 39.4 basis points, greater than the bid-ask spread on the LC bonds.
In terms of market sizes and trading volume, we obtain data from the quarterly Debt Trading Volume Survey compiled by the Emerging Market Trading Association (EMTA). The survey participants consist of around 60 offshore large financial institutions, including most of the well-known investment banks and a few hedge funds. Since the survey participants are based offshore, these data do not include onshore trading volume by local investors. According to EMTA surveys, the mean reported quarterly trading volume is equal to $48 billion for LC bonds and $19 billion for FC bonds. Since the size of the LC bond market is about 5 times as large as the FC bond market, the turnover ratio (defined as trading volume decided by total debt outstanding) by offshore participants is lower for LC debt (30 percent for LC bonds and 61 percent for FC bonds). However, given that foreign holdings represent 15 percent of LC debt outstanding on average in the sample, a back-of-envelope calculation suggests that if local investors traded 18 percent as frequently as foreigners, the total turnover ratios for LC and FC debt would be same. Though we do not have detailed data on the trading volume of currency swaps, conversations with traders and anecdotal evidence suggest that the trading volume for long-dated currency hedging instruments is relatively low.
Therefore, investors of the synthetic swapped LC bonds have long positions in the more liquid cash market and short positions in the less liquid swap market, and hence have overall better liquidity compared to holding FC bonds. The potential liquidity premium would be translated into lower spreads for swapped LC bonds. We will return in Section 5 to analyze the effect the time-varying liquidity risk on the spread differential.
4.3 Differential Pass-Throughs of Global Risk Aversion
In addition to differential cash flow and liquidity risks, the overwhelmingly strong correlation between FC credit spreads and VIX and the lack of strong correlation between LC credit spreads and risk motivate us to consider differential risk premia embedded in the swapped LC and FC bonds. We view risk premia as excess returns that cannot be explained by cash flow and liquidity risk. We propose an explanation based on risky arbitrage in an imperfect capital market to shed light on why the risk premium (in particular, the pass-through of global risk aversion) can be different across the two types of the debt.
In a world with imperfect capital markets, margins, haircuts and other collateral frictions create limits to arbitrage, and slow-moving capital may permit the arbitrage opportunities to persist for extended periods of time (for example, Shleifer and Vishny, 1997 and Duffie, 2010). For emerging market debt, FC bonds are issued offshore, mainly targeting global investors. Although there has been increasing foreign ownership in LC debt markets, the bulk of the LC debt is still held by local investors, such as local pension funds, insurance companies, commercial banks and other government agencies. In emerging markets, these domestic entities are often required by law to hold a large fraction of their portfolios in LC treasury bonds, which gives rise to a distinct local clientele demand that is absent from the external debt market.15 The local clientele demand can have equilibrium impacts in the presence of frictions that create limits to arbitrage. These financial frictions are particularly severe during the peak of the global financial crisis, precisely when the dislocation between LC and FC credit spreads are the greatest. LC and FC credit spread differentials can also heavily depend on the effectiveness of arbitrage between domestic and external debt markets.
We formalize a parsimonious model allowing for different degrees of market integration via risky credit arbitrage in Appendix C. The model builds on the preferred habitat framework presented in Vayanos adn Vila (2009), Greenwood adn Vayanos (2010) and Hamilton and Wu (2012), and surveyed in Gromb and Vayanos (2010). Following Duffie and Singleton (1999), we take a reduced form approach to model arrival rates of credit events and allow them to depend on a local and a global factor. We introduce partial market segmentation through three main building blocks. First, we assume that FC bonds are priced by risk-averse diversified global investors with a complete-market stochastic discount factor (SDF) that only depends on the global factor. Global risk aversion shocks affect FC credit spreads directly through FC bonds' systematic exposure to the global shock. Second, we allow for the existence of local clientele demand, modeled as downward sloping outside demand with respect to the price of swapped LC bonds. Third, we assume that a risk-averse credit arbitrageur integrates LC and FC markets by equalizing the price of risk across the two markets adjusting for the onshore and offshore pricing wedge. As a result, the equilibrium LC credit spread is an endogenous outcome of the arbitrageurs' optimal portfolio demand and local clientele demand. The equilibrium impact of the risky arbitrage depends on the size of the position the arbitrageur is willing to take, which in turn depends on the arbitrageur's risk aversion, the asset return correlation, and the size and elasticity of local clientele demand. In particular, we show that shocks to global risk aversion have perfect pass-through into the FC credit spread, but incomplete pass-through into the LC credit spread due to imperfect market integration and risky arbitrage, driving credit spread differentials.
5 Decomposition of Credit Spread Differentials
5.1 Benchmark Regressions
After laying out different hypotheses to explain credit spread differentials, we now perform further empirical analysis to the assess the importance of cash flow, liquidity and risk aversion factors in a regression framework. The benchmark regression we perform is as follows:
where ![]() denotes country and
denotes country and ![]() denote
three different spreads, the LC credit spread (SLC), the FC credit
spread (FC), and the swapped LC over FC spread (SLC/FC). We include
country fixed effects in the regression to allow each country to
have a different intercept for credit spreads. The term
denote
three different spreads, the LC credit spread (SLC), the FC credit
spread (FC), and the swapped LC over FC spread (SLC/FC). We include
country fixed effects in the regression to allow each country to
have a different intercept for credit spreads. The term
![]() captures the effect on
global risk aversion on credit spreads. We first assume that
captures the effect on
global risk aversion on credit spreads. We first assume that
![]() , the pass-through coefficient of
global risk aversion, is the same across all countries, which will
be relaxed in Section 5.3. Sensitivity to
global and local risk factors is also assumed to be the same across
countries and to be time-invariant. We use VIX as a proxy for the
global risk aversion
, the pass-through coefficient of
global risk aversion, is the same across all countries, which will
be relaxed in Section 5.3. Sensitivity to
global and local risk factors is also assumed to be the same across
countries and to be time-invariant. We use VIX as a proxy for the
global risk aversion
![]() .16 The term
.16 The term
![]() captures the effect of liquidity
of LC, FC debt and currency swap markets, as proxied by the bid-ask
spreads on these instruments, and it enters the regression with the
coefficient
captures the effect of liquidity
of LC, FC debt and currency swap markets, as proxied by the bid-ask
spreads on these instruments, and it enters the regression with the
coefficient ![]() .
.
Finally, we control for a host of global and local macroeconomic
variables as proxies for ![]() and
and ![]() to capture the potentially differential cash flow
risks of LC and FC bonds conditional on economic fundamentals. As
our primary measure of global economic fundamentals, we use the
Chicago Fed National Activity Index (CFNAI), which is the first
principal component 85 monthly economic indicators of the U.S.
economy. For local controls, we first include,
to capture the potentially differential cash flow
risks of LC and FC bonds conditional on economic fundamentals. As
our primary measure of global economic fundamentals, we use the
Chicago Fed National Activity Index (CFNAI), which is the first
principal component 85 monthly economic indicators of the U.S.
economy. For local controls, we first include,
![]() , the realized standard
deviation of local equity returns, measured using the daily local
MSCI equity returns for 30-day rolling windows. We expect this
measure to reflect omitted local fundamentals and local risk
aversion. In addition, we include a set of country-specific
macroeconomic controls that previous literature (for example, Hilscher adn Nosbusch, 2010) has emphasized as potentially
important in explaining sovereign spreads. These include the FC
debt/GDP ratio, the LC debt/GDP ratio, the level and volatility of
monthly inflation and changes in the terms of trade, as well as
monthly changes in foreign exchange reserves.17
, the realized standard
deviation of local equity returns, measured using the daily local
MSCI equity returns for 30-day rolling windows. We expect this
measure to reflect omitted local fundamentals and local risk
aversion. In addition, we include a set of country-specific
macroeconomic controls that previous literature (for example, Hilscher adn Nosbusch, 2010) has emphasized as potentially
important in explaining sovereign spreads. These include the FC
debt/GDP ratio, the LC debt/GDP ratio, the level and volatility of
monthly inflation and changes in the terms of trade, as well as
monthly changes in foreign exchange reserves.17
Table 6 reports regression results for (1) the LC credit spread (2) the FC credit spread and (3) the swapped LC over FC spread, the difference between (1) and (2). By construction, the LC credit spread is equal to the difference between the nominal LC over US spread and the swap rate. We thus also report the regression results for the nominal LC over US spread in Column (4) and the swap rate in Column (5) to better understand the determinants of the LC credit spread. Following Driscoll and Kraay (1998), all regressions are run at monthly frequency with country fixed effects using the Newey-West type standard errors with 12-month lags to account for within-country serial correlation and clustering by month to correct for spatial correlation across countries for the same month.
VIX has a smaller impact on the LC credit spread than on the FC credit spread conditional on macroeconomic fundamentals.18 The coefficient on VIX for the FC credit spread is three times as large as the coefficient for the LC credit spread. The coefficient on VIX in the LC over FC credit spread differential regression (Column 3) is negative and statistically significant. The magnitude of the coefficient suggests that an expected one percentage point increase in the volatility of the S&P 500 over the next 30 days is associated with an 8 basis point increase in the LC credit spread, a 19 basis point increase in the FC credit spread, and therefore a 11 basis point reduction in the LC over FC credit spread differential. This risk aversion pass-through differential is economically significant. In our estimated sample, a one standard deviation increase in VIX over its mean decreases the credit spread differential by 33 basis points. The largest spike in VIX following the Lehman bankruptcy corresponds to a 3.5 standard deviation increase in VIX over the mean, which can generate around a negative115 basis point differential in LC and FC credit spreads, controlling for illiquidity in the bond and swap markets and the worsening local and global economic fundamentals during the crisis.
In addition, conditional on VIX and our host of macro controls, the liquidity of LC and FC bonds and currency swaps are significant explanatory variables for credit spreads. A wider bid-ask spread on LC bonds makes the LC credit spread higher and increases the credit spread differential. A wider bid-ask spread for FC bonds increases the FC credit spread and thus decreases the credit spread differential. Swap liquidity does not significantly affect the LC credit spread. On the other hand, the FC credit spread significantly increases with the swap bid-ask spread, despite the fact that no swaps are used in the construction of the measure. This suggests that the bid-ask on the currency swap as a general measure of offshore liquidity as well as a direct measure of swap liquidity.
The importance of VIX and liquidity risk in explaining credit spread differentials can also be seen from the R-squared of regressions. VIX and liquidity alone explain large fractions of the total variation in all the credit spread regressions, particularly for the FC credit spread. The within R-squared of a panel regression with VIX and liquidity as the only regressors is equal to 29.4 for the LC credit spread, 71 percent for the FC credit spread, and 46.7 percent for the credit spread differential. Conditional on macroeconomic fundamentals, VIX and liquidity increase the R-squared of the regression from 26.6 to 34.1 percent for the LC credit spread, from 53.7 to 78.6 percent for the FC credit spread and from 29.3 percent to 56.1 percent for the differential. Therefore, VIX and liquidity alone account for 86 percent of total explained variations in the credit spread differential.
In terms of the effect of macro fundamentals in explaining the credit spread differential, it is worth nothing that high debt to GDP ratios significantly reduce the credit spread differential, suggesting that FC bond cash flows are more at risk compared with LC bond cash flows with higher indebtedness. However, the additional explanatory power of macro fundamentals conditional on VIX and liquidity is very limited. This is not to say that macroeconomic fundamentals do not explain a significant portion of the level of the respective credit spreads. Rather, our results emphasizes their weaker ability to explain the within-country time-variation of credit spread measures.
5.2 Excess Returns Predictability
We now present evidence on whether risk aversion, liquidity and macro fundamentals can forecast bond excess returns.19 Since VIX has a contemporaneous positive impact on credit spreads through the risk premium channel, high levels of VIX are associated with high risk premia, and hence high excess returns over U.S. Treasury bonds. Since VIX has a differential contemporaneous pass-through into LC and FC credit spreads, we should also expect VIX to have differential predictive power for LC and FC excess returns. Consistent with the prediction, Table 7 shows that high VIX predicts higher FC excess returns (top panel) than swapped LC excess returns (middle panel), and thus positive FC over swapped LC excess returns (bottom panel). The result is robust to using a univariate predictive regression with VIX only and to using multivariate regressions with a host of other controls. The positive predictive power of VIX for FC over swapped LC excess returns naturally gives rise to an investment strategy. When global risk aversion is high, an arbitrageur can long FC bonds and short swapped LC bonds. Since FC spreads are much more sensitive to the global risk aversion shocks than swapped LC, high risk aversion predicts positive excess returns on this strategy, which compensates for the risk that the arbitrageur takes. On the other hand, global macroeconomic fundamentals (as proxied by CNFAI) do not forecast excess returns on swapped LC bonds nor LC bonds after VIX is controlled. After controlling for all the other macro fundamentals, CFNAI marginally forecasts persistence, rather than mean reversion in FC over swapped LC excess returns conditional on the VIX. Therefore, it is unlikely that the predictive power of VIX is due to its correlation with unobserved macroeconomic fundamentals. Conditional on fundamentals, a one standard deviation increase in VIX over its mean forecasts positive 3.7 percent annualized excess returns of FC over swapped LC bonds.
Liquidity factors also have strong predictive power for bond excess returns. The top panel of Table 7 shows that the bid-ask spreads on FC bonds and offshore currency swaps predict positive excess return on the FC bonds, while the bid-ask spread on the LC bonds does not predict FC bond excess returns. Although currency swaps are not used in constructed FC excess returns, liquidity of currency swaps is indicative of the overall offshore liquidity condition. In the middle panel for swapped LC bonds, illquidity of LC bonds positively forecasts excess returns and illiquidity of FC bonds and currency swaps negatively forecasts excess returns. This is consistent with the fact that investors holding swapped LC bonds go long in the liquidity risk in the cash market and go short offshore liquidity risk in the swap market. Liquidity factors contribute additional 7 percent of predictable R-squared for both FC and swapped LC excess returns. Finally, the same set of liquidity factors are the most powerful predictors of the FC over swapped LC excess returns. Therefore, compared with the 4 percent predictable R-squared due to VIX and CFNAI, adding the three liquidity factors bring the predictable R-squared to 20 percent. Further addition of all the other macro fundamentals only marginally increases the R-squared by 3 percent. The results suggest that the strategy of going long in FC bonds and shorting swapped LC bonds is most profitable when FC bonds and currency swaps are more illiquid and LC bonds are more liquid.
5.3 Cross-Country Variation
When VIX goes up, the LC over FC credit spread differential widens. The convergence trade of going long in FC bonds and short in swapped LC bonds should narrow the credit spread differential. However, this trading strategy is not risk-free as the asset returns are not perfectly correlated. The model based on risky credit arbitrage we discussed in Section 4.3 and detailed in the Appendix suggests the effectiveness of arbitrage crucially depends on the return correlation between the two assets.
To test this empirically, we relax the assumption that the
pass-through of global risk-aversion into FC debt,
![]() , is the same across all
countries. The theory predicts that the ratio of swapped LC to FC
pass-thorough
, is the same across all
countries. The theory predicts that the ratio of swapped LC to FC
pass-thorough
![]() increases
in
increases
in
![]() . We obtain estimates of
. We obtain estimates of
![]() and
and
![]() from the coefficients
on the interaction terms between country dummies and VIX in the
regression:
from the coefficients
on the interaction terms between country dummies and VIX in the
regression:
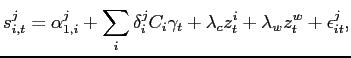 |
(3) |
where the country dummy ![]() for country
for country
![]() . Columns 1 and 2 of Table 8 report the
coefficient estimates for
. Columns 1 and 2 of Table 8 report the
coefficient estimates for
![]() and
and
![]() . For our model to find
empirical support, we would expect countries with a higher ratio
. For our model to find
empirical support, we would expect countries with a higher ratio
![]() to have a higher return correlation. As demonstrated by comparing
Column 3, where we compute this ratio country by country, and
Column 4, where we present the return correlations, this is
precisely what we find, with the correlation between the two
columns at a remarkable 84 percent. Differential sensitivities to
VIX explain the bulk of the cross-sectional variations in excess
return correlations. We present this result visually in Figure 8, showing
once again that the strong positive relationship between the
pass-through of risk aversion into the LC credit spread relative to
the FC credit spread and the return correlation between the two
assets. The result is robust to excluding the crisis period. The
differential sensitivities of LC and FC credit spreads to global
risk aversion shocks sheds light on the degree of market
integration between domestic and external debt markets.
to have a higher return correlation. As demonstrated by comparing
Column 3, where we compute this ratio country by country, and
Column 4, where we present the return correlations, this is
precisely what we find, with the correlation between the two
columns at a remarkable 84 percent. Differential sensitivities to
VIX explain the bulk of the cross-sectional variations in excess
return correlations. We present this result visually in Figure 8, showing
once again that the strong positive relationship between the
pass-through of risk aversion into the LC credit spread relative to
the FC credit spread and the return correlation between the two
assets. The result is robust to excluding the crisis period. The
differential sensitivities of LC and FC credit spreads to global
risk aversion shocks sheds light on the degree of market
integration between domestic and external debt markets.
6 Conclusion
The last decade has seen a remarkable change in emerging market government finance. While European countries find themselves borrowing in a currency they cannot print, major emerging markets sovereigns are increasingly borrowing in their own currency. These changes make it important to understand sovereign risk on local currency debt. In this paper, we studied this question by introducing a new measure of LC sovereign risk, the LC credit spread, defined as the difference between LC bond yield and the LC risk-free rate implied from the swap market. We then compared this measure of sovereign risk on local currency debt to credit spreads on foreign currency debt to understand how sovereign risk differs across the two types of sovereign debt.
Using this new measure, we document several key findings. First, emerging market LC bonds promise to pay a significant positive credit spread over the LC risk-free rate when they borrow in their own currency, measured as the size of the failure of long-term covered interest rate parity for government bond yields between emerging markets and the United States. This suggests that LC nominal bonds are not default free, despite of the sovereign's option to inflate away the debt. Second, LC bonds have lower credit spreads than FC bonds issued by the same sovereign at the same tenor. The LC over FC credit spread differential becomes even more negative during the peak of the global financial crisis. Third, FC credit spreads are very integrated across countries and more responsive to global risk factors, but LC credit spreads are much less so. From an offshore investor's perspective, the commonly perceived systematic risk on LC debt mainly comes from the currency risk. Once the currency risk is hedged to the first order, LC bonds are safer than FC bonds in terms of the correlations between asset returns and global risk factors.
A cash-flow risk based explanation suggests the difference between the two credit spreads reflects differences in expected default probabilities and the covariance between currency and credit risk. A discount factor and liquidity risk based explanation highlights the role of differential risk premia and liquidity premia embedded in the two types of the debt. While cash-flow risks are important for understanding the levels of the credit spreads, in a regression framework, we show that global risk aversion and liquidity risks are far more important in explaining the within country time series variations in the credit spread differential than macroeconomic fundamentals. The strong predictive power of risk aversion and liquidity factors in forecasting bond excess returns and the lack of forecasting power of macro fundamentals further support the role of risk and liquidity premia in driving time variations in credit spread differentials.
References
Mark Aguiar and Gita Gopinath. Defaultable debt, interest rates and the current account. Journal of International Economics, 69(1):64–83, 2006.
Mark Aguiar, Manuel Amador, Emmanuel Farhi, and Gita Gopinath. Crisis and commit- ment: Inflation credibility and the vulnerability to sovereign debt crises. Working Paper, July 2013.
Aloisio Araujo, Marcia Leon, and Rafael Santos. Welfare analysis of currency regimes with defaultable debts. Journal of International Economics, 89:143–153, 2013.
Cristina Arellano. Default risk and income fluctuations in emerging economies. American Economic Review, 98(3):690–712, 2008.
Cristina Arellano and Ananth Ramanarayanan. Default and the maturity structure in sovereign bonds. Journal of Political Economy, 120(2):187–232, April 2012.
Patrick Augustin and Romeo Tedongap. Real economic shocks and sovereign credit risk. Stockhold School of Economics Working Paper, April 2013.
BIS. Bank of international settlemement debt securities statistics. 2013.
Nicola Borri and Adrien Verdelhan. Sovereign risk premia. Working Paper, 2011.
John D. Burger and Francis E. Warnock. Foreign participation in local currency bond markets. Review of Financial Economics, 16(3):291–304, 2007.
John D. Burger, Francis E. Warnock, and Veronica Cacdac Warnock. Emerging local cur- rency bond markets. Financial Analysts Journal, 68(5), 2012.
John Campbell and Luis Viceira. Strategic Asset Allocation. Oxford University Press, 2002.
Giancarlo Corsetti and Luca Dedola. The mystery of the printing press: Self-fulfilling debt crises and monetary sovereignty. Working Paper, April 2013.
Jose-Maria Da-Rocha, Eduardo-Luis Gimenez, and Francisco-Xavier Lores. Self-fulfilling crises with default and devaluation. Economic Theory, March 2012.
Deepa Dhume Datta and Wenxin Du. Nonparametric hac estimation for time series data with missing observations. International Finance Discussion Paper No.1060, Federal Reserve Board, 2012.
Tatiana Didier and Marcio Garcia. Very high interest rates and the cousin risks: Brazil during the real plan. In Jose Gonzales and Anne O. Krueger, editors, Macroeconomic Reforms: The 2nd Generation. University of Chicago Press, 2003.
Francis Diebold and Canlin Li. Forecasting the term structure of government bond yields. Journal of Econometrics, 130(2):337–364, 2006.
John C. Driscoll and Aart Kraay. Consistent covariance matrix estimation with spatially dependent panel data. Review of Economics and Statistics, 80(4):549–560, 1998.
Wenxin Du and Jesse Schreger. The currency composotion of sovereign external portfolios. Working Paper, 2013.
Darell Duffe. Asset pricing dynamics with slow-moving capital. Journal of Finance, 65(4): 1237–1267, August 2010.
Darrell Duffe and Kenneth J. Singleton. Modeling term structures of defaultable bonds. The Review of Financial Studies, 12(4):687–720, 1999.
Barry Eichengreen and Ricardo Hausmann. "exchange rates and financial fragility". In New Challenges for Monetary Policy, pages 329–68. Federal Reserve Bank of Kansas City, 1999.
Barry Eichengreen and Ricardo Hausmann, editors. Other People’s Money: Debt Denomi- nation And Financial Instability In Emerging Market Economies. University of Chicago Press, 2005.
Donna J. Fletcher and Larry W. Taylor. A non-parametric analysis of covered interest parity in long-date capital markets. Journal of International Money and Finance, 13(4):459–475, August 1994.
Donna J. Fletcher and Larry W. Taylor. Swap covered interest parity in long-date capital markets. Review of Economics and Statistics, 78:530–538, 1996.
Marcio Garcia and Alexandre Lowenkron. Cousin risks: The extent and the causes of positive correlation between country and currency risks. Working Paper, PUC-Rio, 2005.
Robin Greenwood and Dimitri Vayanos. Bond supply and excess bond returns. Working Paper, August 2010.
Dennis Gromb and Dimitri Vayanos. Limits of arbitrage: The state of the theory. Annual Review of Finanical Economics, 2010.
James D. Hamilton and Jing Cynthia Wu. The effectiveness of alternative monetary policy tools in a zero lower bound environment. Journal of Money, Credit and Banking, 44(1): 3–46, February 2012.
Jens Hilscher and Yves Nosbusch. Determinants of sovereign risk: Macroeconomic funda- mentals and the pricing of sovereign debt. Review of Finance, 14(2):235–262, 2010.
ISDA. Credit derivative physical settlement matrix. International Swaps and Derivatives Association, May 2012.
Rainer Jankowitsch and PIchler Stefan. Currency dependence of corporate credit spreads. Journal of Risk, 8(1):1–24, 2005.
Olivier Jeanne. Fiscal challenges to monetary dominance in the euro area: A theoretical perspective. Working Paper, February, 2012.
Philippe Khuong-Huu. The price of credit. Risk, pages 68–71, December 1999.
Ajantha S. Kumara and Wade D. Pfau. Would emerging market pension funds benefit from international diversification. Annals of Finance, pages 1–17, 2011.
Michael Lee. Bloomberg fair value market curves. In International Bond Market Conference, Taipei, 2007.
Francis A. Longstaff, Jun Pan, Lasse H. Pedersen, and Kenneth J. Singleton. How sovereign is sovieregn credit risk? American Economic Journal: Macroeconomics, 3:75–103, April 2011.
Hanno Lustig and Adrien Verdelhan. The cross section of foreign currency risk premia and consumption growth risk. American Economic Review, 97(1):89–117, March 2007.
Hanno Lustig, Nikolai Roussanov, and Adrien Verdelhan. Common risk factors in currency markets. Working Paper, May 2011.
Hanno Lustig, Nikolai Roussanov, and Adrien Verdelhan. Countercyclical currency risk premia. Working Paper, January 2012.
Rui Mano. Exchange rates upon sovereign defaults. Working Paper, 2013.
Matthew R. McBrady and Michael J. Schill. Foreign currnecy-denominated borrowing in the absence of operating incentives. Journal of Financial Economics, 86:145–177, 2007.
Charles Nelson and Andrew Siegel. Parsimonious modeling of yield curves. Journal of Business, 60:473–489, 1987.
Helen Popper. Long-term covered interest parity: evidence from currency swaps. Journal of International Money and Finance, 12:439–448, 1993.
Carmen M. Reinhart and Kenneth S. Rogoff. This Time is Different: Eight Centuries of Financial Folly. Princeton University Press, 2008.
Carmen M. Reinhart and Kenneth S. Rogoff. The forgotten history of domestic debt. The Economic Journal, 121:319–350, May 2011.
SHCP. Criterios generales de política económica. Secretaría de Hacienda y Crédito Público de Mexico, 2008.
Andrei Shleifer and Robert Vishny. The limits of arbitrage. Journal of Finance, 52:35–55, 1997.
Dimitri Vayanos and Jean-Luc Vila. A preferred-habitat model of the term structure of interest rates. Working Paper, November 2009.
Figure 1: Evolution of Emerging Market Sovereign Debt Portfolios
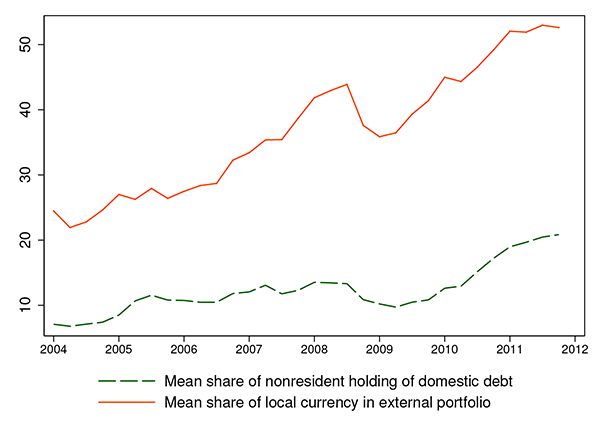
Notes: This figure displays the mean share of LC debt held by foreigners in total LC government debt (the dotted line) and the mean share of LC debt in total external debt held by foreigners (the solid line). The 14 sample countries are: Brazil, Colombia, Hungary, Indonesia, Israel, South Korea, Mexico, Malaysia, Peru, Poland, Russia, Thailand, Turkey and South Africa. See Du and Schreger (2013) for details on the dataset construction.
Figure 2: Offshore Trading Volume by Instrument Types (Trillions of USD)
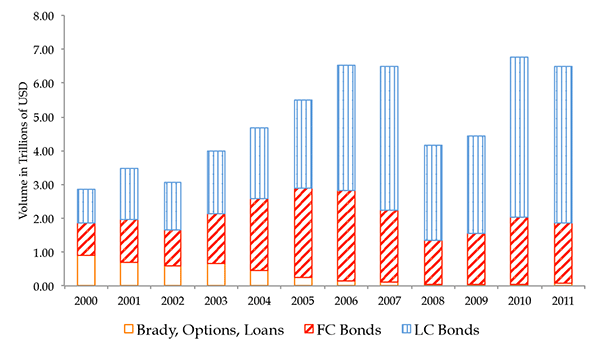
Source: Annual Debt Trading Volume Survey (2000-2011) by Emerging Market Trading Association
(EMTA)
Notes: This figure plots total trading volumes of
emerging market debt by instrument type in trillions of dollars. In
addition to FC bonds, the "Brady, Option, Loans" category also
refers to debt instruments denominated in foreign currencies. The
survey participants consist of large offshore financial
institutions.
Figure 3: 5-Year U.S. and Swapped UK Treasury Yields in Percentage Points
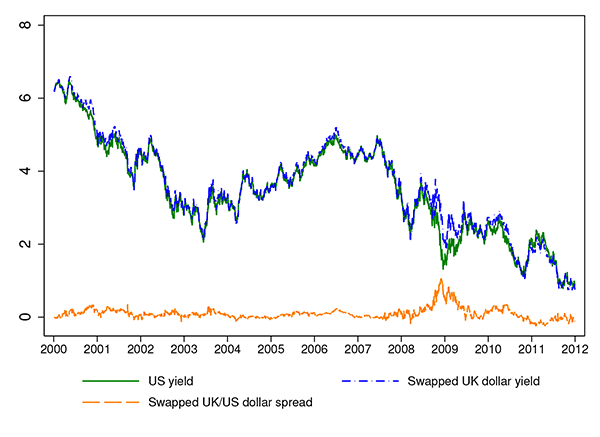
Notes: The green solid line plots the 5-Year zero-coupon U.S. Treasury yield. The blue dash-dotted line plots the 5-year zero-coupon swapped UK Treasury yield after applying a cross currency swap package consisting of two plain vanilla interest rate swaps (dollar and sterling) and the U.S. and UK Libor cross-currency basis swap. The orange dashed line plots the yield spread of the swapped UK Treasury yield over the U.S. Treasury. The mean of the yield spreads is 10 basis points with standard deviation equal to 16 basis points. The minimum spread is equal to negative 25 basis points and the maximum spread is equal to 106 basis points during the peak of the crisis. Excluding 2008-2009, the mean spread is 6 basis points with standard deviation equal to 10 basis points. The U.S. zero-coupon yield is from St. Louis Fed. The UK zero-coupon yield is from Bank of England. Swap rates are from Bloomberg.
Figure 4: 5-Year Swapped LC and FC Spreads in Percentage Points
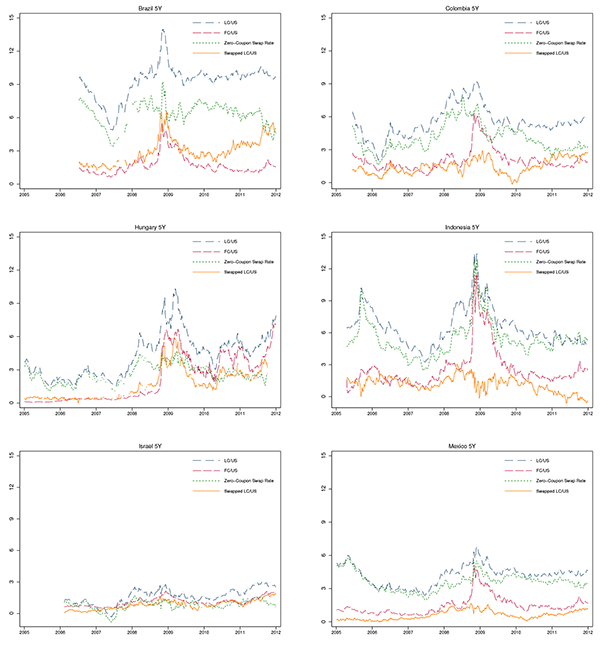
Notes: Each figure plots 10-day moving averages of zero-coupon LC and FC spreads over the U.S. Treasury at 5 years. LC/US denotes the LC yield over the U.S. Treasury yield. FC/US denotes the FC yield over the U.S. Treasury yield. Zero-coupon swap rate is the zero-coupon fixed for fixed CCS rate implied from par fixed for floating CCS and plain vanilla interest rate swap rates. Swapped LC/US denotes the swapped LC over U.S. Treasury yield spread. All yields and swap rates are for the 5-year tenor. Data sources and details on yield curve construction are given in Appendix Table A5.
Figure 4: 5-Year Swapped LC and FC Spreads in Percentage Points (Continued)
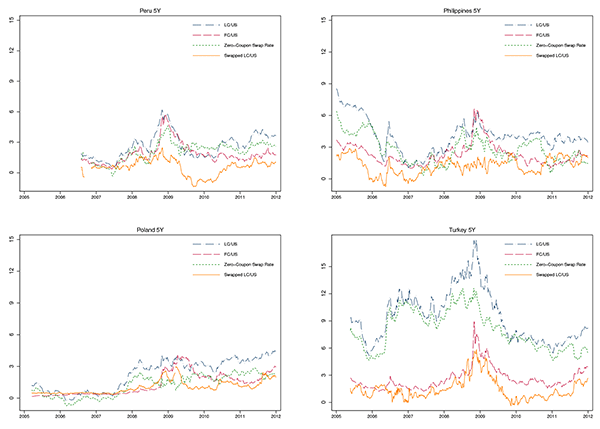
Notes: Each figure plots 10-day moving averages of zero-coupon LC and FC spreads over the U.S. Treasury at 5 years. LC/US denotes the LC yield over the U.S. Treasury yield. FC/US denotes the FC yield over the U.S. Treasury yield. Zero-coupon swap rate is the zero-coupon fixed for fixed CCS rate implied from par fixed for floating CCS and plain vanilla interest rate swap rates. Swapped LC/US denotes the swapped LC over U.S. Treasury yield spread. All yields and swap rates are for the 5-year tenor. Data sources and details on yield curve construction are given in Appendix Table A5.
Figure 5: Brazil Onshore and Offshore Yield Spread Comparison
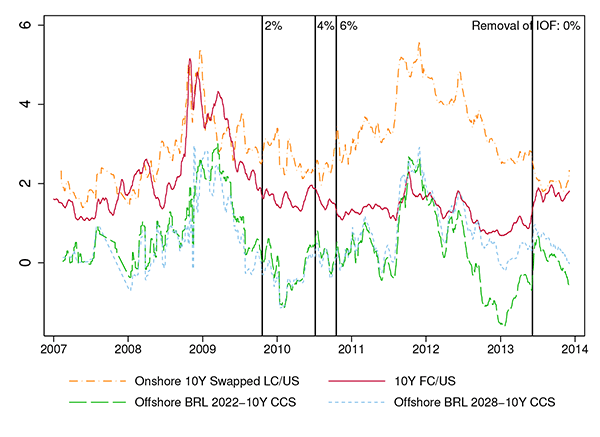
Notes: This figure plots nominal yields minus 10-year zero-coupon real/dollar swap rates on two Eurobonds denominated in Brazilian reals traded at the Luxembourg Stock Exchange with maturity years 2022 and 2028 (BRL 2022 by the green long-dashed line and BRL 2028 by the blue short-dashed line). Offshore swapped yields are compared with the 10-year zero-coupon onshore LC swapped yield plotted by the orange dash-dotted line and the offshore FC dollar yield plotted by the red solid line. The onshore LC zero-coupon yield is obtained from ANBIMA. The FC zero-coupon yield is estimated from Bloomberg BFV par yield curve. LC Eurobond yields are provided by the Luxembourg Stock Exchange and Bloomberg. The vertical lines indicate changes n the IOF tax rate on Oct 20, 2009 (from 0 to 2 percent), October 5, 2010 (from 2 to 4 percent), October 20, 2010 (from 4 to 6 percent) and June 5, 2013 (from 6 to 0 percent). Backward 2-week rolling averages of yield spreads are used in plotting the figure.
Figure 6: Swapped LC Over FC Spreads
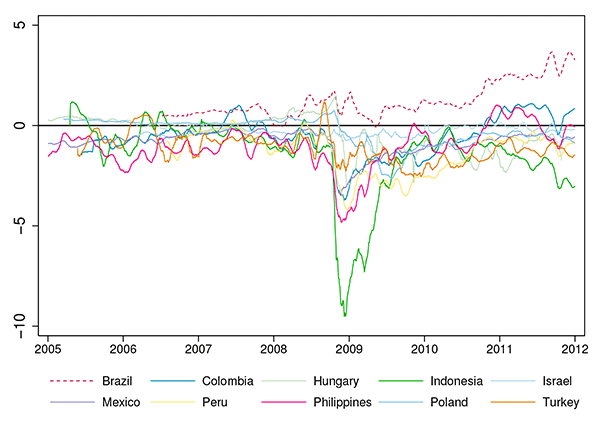
Notes: This figure plots 30-day moving averages of 5-year zero-coupon swapped LC over FC spreads (the difference between LC and FC credit spreads) using 5-year cross currency swaps for all 10 sample countries. Data sources and details on yield curve construction are given Appendix Table A5.
Figure 7: LC and Dollar Denominated CDS in Turkey
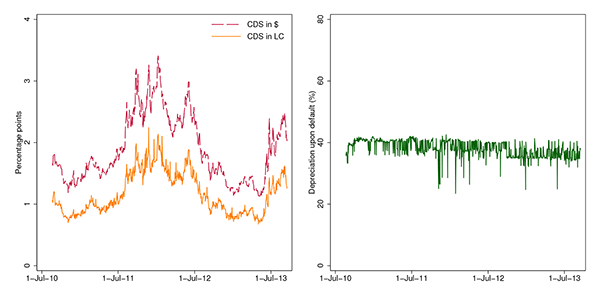
Notes: The left figure plots the CDS spreads in
percentage points for contracts denominated in dollars (dashed
cranberry line) and contracts denominated in Turkish liras (solid
orange line). The right figure plots risk-neutral expected
[percentage depreciation upon default calculated as
![]() .
The CDS data are from Markit.
.
The CDS data are from Markit.
Figure 8: Differential Risk Aversion Pass-Though and Return Correlation
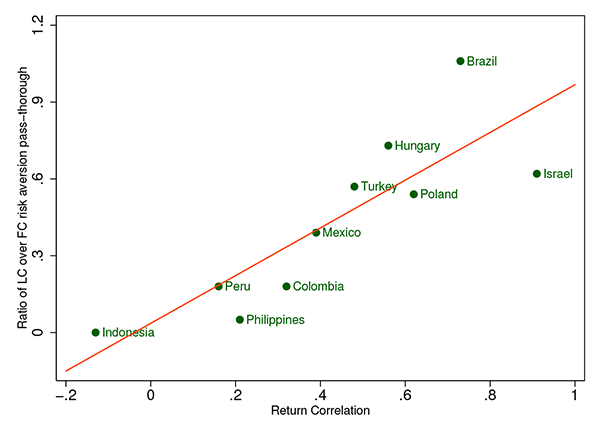
Notes: This figure plots the ratio of global risk aversion pass-through into LC credit spreads over the pass-through into FC credit spreads on the y-axis (Column 3 in Table 8) and correlation between swapped LC and FC quarterly holding period returns over U.S. Treasury bill rates on the x-axis (Column 4 in Table 8). The ratio of pass-through is computed based on Columns 1 and 2 in Table 8. The full regression specification is given by Equation 3.
Table 1: Mean LC and FC Credit Spread Comparison, 2005-2011
| Country | Sample Start | (1) SSLC/US | (2) SFC/US | (3) SSLC/FC | (4) baCCS/2 | (5) Corr(SLC,FC) |
|---|---|---|---|---|---|---|
| Brazil | Jul. 2006 | 3.13*** (1.13) | 1.78*** (0.91) | 1.35*** (0.94) | 0.32 (0.13) | 0.56 |
| Colombia | Jun. 2005 | 1.47*** (0.69) | 2.03*** (1.01) | -0.56*** (1.01) | 0.16 (0.10) | 0.34 |
| Hungary | Jan. 2005 | 1.69*** (1.23) | 2.15*** (2.01) | -0.47** (1.03) | 0.19 (0.14) | 0.91 |
| Indonesia | Apr. 2005 | 1.14*** (0.73) | 2.52*** (1.59) | -1.38*** (1.61) | 0.38 (0.23) | 0.18 |
| Israel | Feb. 2006 | 0.86*** (0.43) | 1.12*** (0.42) | -0.26*** (0.21) | 0.12 (0.03) | 0.84 |
| Mexico | Jan. 2005 | 0.60*** (0.40) | 1.44*** (0.79) | -0.83*** (0.60) | 0.09 (0.06) | 0.66 |
| Peru | Jul. 2006 | 0.55*** (0.80) | 1.97*** (1.05) | -1.42*** (1.09) | 0.16 (0.07) | 0.34 |
| Philippines | Mar. 2005 | 1.25*** (0.80) | 2.31*** (1.04) | -1.07*** (1.07) | 0.28 (0.14) | 0.34 |
| Poland | Mar. 2005 | 1.04*** (0.60) | 1.29*** (1.01) | -0.25** (0.62) | 0.12 (0.08) | 0.78 |
| Turkey | May 2005 | 1.46*** (1.19) | 2.57*** (1.20) | -1.12*** (0.81) | 0.11 (0.08) | 0.78 |
| Total | Jan. 2005 | 1.28*** (1.06) | 1.95*** (1.23) | -0.67*** (1.22) | 0.19 (0.15) | 0.54 |
| Observations | 13151 | 13151 | 13151 | 13151 |
Notes: This table reports sample starting date, mean and
standard deviation of 5-year log yield spreads at daily frequency.
The variables are (1)
![]() , swapped LC over U.S. Treasury
spread; (2)
, swapped LC over U.S. Treasury
spread; (2) ![]() , FC over U.S. Treasury spread;
(3)
, FC over U.S. Treasury spread;
(3)
![]() , swapped LC over FC spread, or
column (2) - column (1). (4)
, swapped LC over FC spread, or
column (2) - column (1). (4)
![]() , half of bid-ask spread of
cross-currency swaps. Standard deviations of the variables are
reported in the parentheses. We test significance of means using
Newey-West standard errors with 120-day lags. Standard errors are
omitted. Test results are reported for columns (1), (2) and (3),
*** p
, half of bid-ask spread of
cross-currency swaps. Standard deviations of the variables are
reported in the parentheses. We test significance of means using
Newey-West standard errors with 120-day lags. Standard errors are
omitted. Test results are reported for columns (1), (2) and (3),
*** p![]() 0.01, ** p
0.01, ** p![]() 0.05, *
p
0.05, *
p![]() 0.1. Since the bid-ask spread is always
nonnegative, significance tests are not performed for column 4. Two
additional tests are conducted for hypotheses (1)
0.1. Since the bid-ask spread is always
nonnegative, significance tests are not performed for column 4. Two
additional tests are conducted for hypotheses (1)
![]() and
and
![]() , both tests can be
rejected at 5 percent or lower confidence levels for all countries
using Newey-West standard errors with 120-day lags. Column (5)
reports within-country correlations between
, both tests can be
rejected at 5 percent or lower confidence levels for all countries
using Newey-West standard errors with 120-day lags. Column (5)
reports within-country correlations between
![]() and
and ![]() .
.
Table 2: Changes in Credit Spreads During Crisis Peak (09/01/08 - 09/01/09)
| Country | (1) ΔsSLC/US | (2) ΔsFC/US | (3) ΔsSLC/FC | (4) ΔbaCCS/2 |
|---|---|---|---|---|
| Brazil | 1.93*** (1.13) | 1.82*** (0.99) | 0.11 (0.66) | 0.26*** (0.13) |
| Colombia | 0.64*** (0.67) | 2.31*** (1.21) | -1.66*** (0.82) | 0.10*** (0.18) |
| Hungary | 2.70*** (1.12) | 3.80*** (2.17) | -1.10** (1.48) | 0.31*** (0.22) |
| Indonesia | 0.07 (0.65) | 3.67*** (2.17) | -3.61*** (2.41) | 0.45*** (0.39) |
| Israel | 0.54*** (0.26) | 0.68*** (0.26) | -0.15*** (0.21) | 0.05*** (0.04) |
| Mexico | 0.60*** (0.30) | 1.97*** (0.87) | -1.38*** (0.80) | -0.03*** (0.01) |
| Peru | -0.05 (0.95) | 2.21*** (1.12) | -2.26*** (0.81) | 0.07*** (0.08) |
| Philippines | 0.36*** (0.40) | 1.91*** (1.28) | -1.55*** (1.33) | 0.18*** (0.22) |
| Poland | 1.26*** (0.58) | 2.35*** (0.92) | -1.09*** (1.01) | 0.17*** (0.09) |
| Turkey | 1.89*** (1.44) | 2.70*** (1.47) | -0.81*** (0.86) | -0.06*** (0.07) |
| Total | 0.91*** (1.16) | 2.30*** (1.48) | -1.40*** (1.51) | 0.14*** (0.22) |
| Observations | 2058 | 2058 | 2058 | 2058 |
Notes: This table reports the mean and standard deviation
of changes in LC and FC credit spreads during the peak of the
Global Financial Crisis (09/01/2008-09/01/2009) relative to their
pre-crisis means. (1)
![]() is the increase in swapped
LC over U.S. Treasury spreads; (2)
is the increase in swapped
LC over U.S. Treasury spreads; (2)
![]() is the increase in the FC
over U.S. Treasury spreads; (3)
is the increase in the FC
over U.S. Treasury spreads; (3)
![]() is the increase in swapped
LC over FC spreads, or column (2)-column (1); and (4)
is the increase in swapped
LC over FC spreads, or column (2)-column (1); and (4)
![]() is the increase in one
half of bid-ask spreads. Standard deviations of variables are
reported in the parentheses. Statistical significance of the means
are tested using Newey-West standard errors with 120-day lags.
Significance levels are denoted by *** p
is the increase in one
half of bid-ask spreads. Standard deviations of variables are
reported in the parentheses. Statistical significance of the means
are tested using Newey-West standard errors with 120-day lags.
Significance levels are denoted by *** p![]() 0.01, **
p
0.01, **
p![]() 0.05, * p
0.05, * p![]() 0.1.
0.1.
Table 3: Cross-Country Correlation of Credit Spreads, 2005-2011
| Principal Components | (1) sSLC/US percentage | (1) sSLC/US total | (2) sFC/US percentage | (2) sFC/US total | (3) 5Y CDS percentage | (3) 5Y CDS total |
|---|---|---|---|---|---|---|
| First | 53.49 | 53.49 | 81.52 | 81.52 | 80.02 | 80.02 |
| Second | 16.30 | 69.78 | 11.70 | 93.22 | 15.34 | 95.36 |
| Third | 10.17 | 79.95 | 3.68 | 96.90 | 2.06 | 97.41 |
| Pairwise Corr. | 0.42 | 0.42 | 0.78 | 0.78 | 0.77 | .077 |
Notes: This table reports summary statistics of principal
component analysis and cross-country correlation matrices of
monthly 5-Year LC and FC credit spreads and sovereign credit
default swap spreads. The variables are (1)
![]() , swapped LC over U.S. Treasury
spreads; (2)
, swapped LC over U.S. Treasury
spreads; (2) ![]() , FC over U.S. Treasury
spreads; (3) 5Y CDS, five-year sovereign
CDS spreads. The rows "First", "Second", "Third" report
percentage and cumulative percentage of total variations explained
by the first, second and third principal components, respectively.
The row "Pairwise Corr." reports the mean of all bilateral
correlations for all country pairs. All variables are
end-of-the-month observations.
, FC over U.S. Treasury
spreads; (3) 5Y CDS, five-year sovereign
CDS spreads. The rows "First", "Second", "Third" report
percentage and cumulative percentage of total variations explained
by the first, second and third principal components, respectively.
The row "Pairwise Corr." reports the mean of all bilateral
correlations for all country pairs. All variables are
end-of-the-month observations.
Table 4: Correlation among Credit Spreads and Global Risk Factors. 2005-2011
| (A) First PC of Credit Spreads: sSLC/US | (A) First PC of Credit Spreads: sFC/US | (A) First PC of Credit Spreads: 5Y CDS | (B) Raw Credit Spreads: sSLC/US | (B) Raw Credit Spreads: sFC/US | (B) Raw Credit Spreads: 5Y CDS | (C) Global Risk Factors: BBB/T | (C) Global Risk Factors: -CFNAI | (C) Global Risk Factors: VIX | |
|---|---|---|---|---|---|---|---|---|---|
| sSLC/US | 1.00 | 1.00 | |||||||
| sFC/US | 0.81 | 1.00 | 0.49 | 1.00 | |||||
| 5Y CDS | 0.80 | 0.94 | 1.00 | 0.48 | 0.91 | 1.00 | |||
| BBB/T | 0.71 | 0.88 | 0.89 | 0.38 | 0.66 | 0.62 | 1.00 | ||
| -CFNAI | 0.57 | 0.76 | 0.75 | 0.33 | 0.58 | 0.52 | 0.87 | 1.00 | |
| VIX | 0.76 | 0.93 | 0.87 | 0.41 | 0.70 | 0.61 | 0.80 | 0.68 | 1.00 |
Notes: This table reports correlations among credit
spreads and global risk factors. Panel (A) reports correlations
between the first principal component of credit spreads and global
risk factors. Panel (B) reports average correlations between raw
credit spreads in 10 sample countries and global risk factors.
Panel (C) reports correlations between global risk factors only.
The three credit spreads are (1)
![]() , 5-year swapped LC over U.S.
Treasury spread; (2)
, 5-year swapped LC over U.S.
Treasury spread; (2) ![]() , 5-year FC over
U.S. Treasury spread; and (3) 5Y CDS, 5-year
sovereign credit default swap spread. The three global risk factors
are (1) BBB/T, Merrill Lynch BBB over 10-year Treasury
spread; (2) -CFNAI, negative of the real-time Chicago Fed National
Activity Index, or the first principal component of 85 monthly
economic indicators (positive CFNAI indicates improvement in
macroeconomic fundamentals), and (3) VIX, implied
volatility on the S&P index options. All variables use
end-of-the-month observations.
, 5-year FC over
U.S. Treasury spread; and (3) 5Y CDS, 5-year
sovereign credit default swap spread. The three global risk factors
are (1) BBB/T, Merrill Lynch BBB over 10-year Treasury
spread; (2) -CFNAI, negative of the real-time Chicago Fed National
Activity Index, or the first principal component of 85 monthly
economic indicators (positive CFNAI indicates improvement in
macroeconomic fundamentals), and (3) VIX, implied
volatility on the S&P index options. All variables use
end-of-the-month observations.
Table 5: Regressions of Bond Excess Returns on Equity Returns, 2005-2011
| (1) rxFC/US | (2) hrxLC/US | (3) uhrxLC/US | (4) rxFC/US | (5) srxLC/US | (6) uhrxLC/US | |
|---|---|---|---|---|---|---|
| S&P $ rx | 0.17*** (0.060) | -0.023 (0.057) | 0.26*** (0.081) | 0.22*** (0.055) | 0.0011 (0.025) | 0.42*** (0.086) |
| LC equity hedged $rx | 0.11*** (0.036) | 0.21*** (0.036) | 0.33*** (0.049) | |||
| LC equity swapped $rx | 0.066*** (0.022) | 0.099*** (0.021) | 0.19*** (0.047) | |||
| Observations | 12,122 | 12,122 | 12,122 | 12,122 | 12,122 | 12,122 |
| R-squared | 0.485 | 0.314 | 0.498 | 0.438 | 0.159 | 0.416 |
Notes: This table reports contemporaneous betas of bond
quarterly excess returns on global and local equity excess returns.
The dependent variables are (1) and (4)
![]() , FC over U.S. Treasury bond
excess returns; (2)
, FC over U.S. Treasury bond
excess returns; (2)
![]() , hedged LC over U.S. Treasury
bond excess return using 3-month forward contracts; (3) and (6)
, hedged LC over U.S. Treasury
bond excess return using 3-month forward contracts; (3) and (6)
![]() , unhedged LC over U.S. Treasury
bond excess returns; and (5)
, unhedged LC over U.S. Treasury
bond excess returns; and (5)
![]() , swapped LC over U.S. Treasury
bond excess returns All excess returns are computed based on the
quarterly holding period returns on 5-year zero-coupon benchmarks
(annualized). The independent variables are S&P $rx, quarterly return on the S&P 500 index over
3-month U.S. T-bills; LC
equity hedged $rx,
quarterly return on local MSCI index hedged using 3-month FX
forward over 3-month U.S. T-bills; and LC equity swapped $rx, quarterly return on local MSCI index combined with
a 5-year CCS over 3-month U.S. T-bills; All regressions are run at
daily frequency with country fixed effects using Newey-West
standard errors with 120-day lags and clustering by date following
Driscoll and Kraay (1998). Significance levels are denoted by ***
p
, swapped LC over U.S. Treasury
bond excess returns All excess returns are computed based on the
quarterly holding period returns on 5-year zero-coupon benchmarks
(annualized). The independent variables are S&P $rx, quarterly return on the S&P 500 index over
3-month U.S. T-bills; LC
equity hedged $rx,
quarterly return on local MSCI index hedged using 3-month FX
forward over 3-month U.S. T-bills; and LC equity swapped $rx, quarterly return on local MSCI index combined with
a 5-year CCS over 3-month U.S. T-bills; All regressions are run at
daily frequency with country fixed effects using Newey-West
standard errors with 120-day lags and clustering by date following
Driscoll and Kraay (1998). Significance levels are denoted by ***
p![]() 0.01, ** p
0.01, ** p![]() 0.05, *
p
0.05, *
p![]() 0.1.
0.1.
Table 6: Regression of 5-Year Credit Spreads on VIX, 2005m1-2011m12
| (1) sSLC/US | (2) sFC/US | (3) sSLC/FC | (4) sLC/US | (5) ccs | |
|---|---|---|---|---|---|
| VIX | 0.077*** (0.027) | 0.19*** (0.022) | -0.11*** (0.023) | 0.12** (0.048) | 0.040 (0.033) |
| baLC/2 | 0.021*** (0.0023) | 0.0045* (0.0027) | 0.017*** (0.0026) | 0.026*** (0.0057) | 0.0044 (0.0054) |
| baFC/2 | -0.0051 (0.0045) | 0.015*** (0.0034) | -0.020*** (0.0019) | 0.0041 (0.0036) | 0.0092*** (0.0036) |
| baCCS/2 | 0.0047 (0.0032) | 0.015*** (0.0027) | -0.010*** (0.0031) | 0.018 (0.011) | 0.013 (0.0090) |
| CFNAI | -0.054 (0.064) | -0.21*** (0.055) | 0.16 (0.098) | -0.14 (0.13) | -0.083 (0.14) |
| Other Controls: FC Debt/GDP | -0.024 | 0.092*** | -0.12*** | -0.011 | 0.013 |
| Other Controls: LC Debt/GDP | -0.017 | 0.011 | -0.028*** | -0.046*** | -0.029*** |
| ΔReserve | 0.0011 | -0.0022 | 0.0033 | -0.020 | -0.021 |
| ΔIP | -0.0062*** | -0.0038** | -0.0024 | -0.0078** | -0.0015 |
| ΔCPI | 0.085* | 0.081 | 0.0042 | 0.34*** | 0.26*** |
| Std(ΔCPI) | 0.083 | 0.15*** | -0.072 | 0.27*** | 0.19*** |
| ΔToT | -0.0071 | 0.0064 | -0.014** | 0.010 | 0.017*** |
| Std(ΔToT) | 0.032 | 0.039** | -0.0067 | 0.27*** | 0.24*** |
| Vol(ΔMSCI) | 0.14** | 0.25*** | -0.11* | 0.26 | 0.11 |
| Observations | 754 | 754 | 754 | 754 | 754 |
| Within R-Squared: Full model | 0.341 | 0.786 | 0.541 | 0.471 | 0.327 |
| Within R-Squared: Without VIX or Liquidity | 0.266 | 0.537 | 0.293 | 0.380 | 0.257 |
| Within R-Squared: With VIX and Liquidity Only | 0.294 | 0.710 | 0.467 | 0.323 | 0.172 |
Notes: This table reports fixed-effect panel regression
results of yield spreads and the swap rate on VIX and controls. The
dependent variables are as follows: (1)
![]() , swapped LC over U.S. Treasury
spread; (2)
, swapped LC over U.S. Treasury
spread; (2) ![]() , FC over U.S. Treasury spread;
(3)
, FC over U.S. Treasury spread;
(3)
![]() , swapped LC over FC spread; (4)
, swapped LC over FC spread; (4) ![]() , unhedged LC over US Treasury
spread; (5)CCS, 5-year
zero-coupon cross-currency swap rate. The independent variables
are: VIX, monthly standard deviation of implied
volatility on S&P index options (conventional quote/
, unhedged LC over US Treasury
spread; (5)CCS, 5-year
zero-coupon cross-currency swap rate. The independent variables
are: VIX, monthly standard deviation of implied
volatility on S&P index options (conventional quote/![]() );
); ![]() ,
, ![]() and
and ![]() , mean one half of bid-ask
spread on all LC and FC bonds in Bloomberg and on 5-year par CCS in
basis points; CFNAI,
Chicago Fed National Activity Index, or the first principal
component of 85 monthly economic indicators; FC Debt/GDP and LC
Debt/GDP, monthly LC and FC
debt to GDP ratios aggregating from the entire universe of
Bloomberg sovereign bonds outstanding;
, mean one half of bid-ask
spread on all LC and FC bonds in Bloomberg and on 5-year par CCS in
basis points; CFNAI,
Chicago Fed National Activity Index, or the first principal
component of 85 monthly economic indicators; FC Debt/GDP and LC
Debt/GDP, monthly LC and FC
debt to GDP ratios aggregating from the entire universe of
Bloomberg sovereign bonds outstanding;
![]() , monthly percentage change in
FX reserves;
, monthly percentage change in
FX reserves; ![]() , monthly percentage change in
country-specific industrial production index;
, monthly percentage change in
country-specific industrial production index;
![]() , monthly percentage change in
consumer price index;
, monthly percentage change in
consumer price index;
![]() , standard deviation of
, standard deviation of
![]() for the past 12 months;
for the past 12 months;
![]() , monthly percentage change in
terms of trade;
, monthly percentage change in
terms of trade;
![]() , standard deviation of
, standard deviation of
![]() for the past 12 months;
and
for the past 12 months;
and
![]() , realized standard deviation of daily local MSCI
equity returns computed using a moving window of 30 days. All
regressions are run at monthly frequency with country fixed effects
using Newey-West standard errors with 12-month lags clustered by
month following Driscoll and Kraay (1998) *** p
, realized standard deviation of daily local MSCI
equity returns computed using a moving window of 30 days. All
regressions are run at monthly frequency with country fixed effects
using Newey-West standard errors with 12-month lags clustered by
month following Driscoll and Kraay (1998) *** p![]() 0.01, ** p
0.01, ** p![]() 0.05, * p
0.05, * p![]() 0.1. Within R-squared is reported for the panel
regressions.
0.1. Within R-squared is reported for the panel
regressions.
Table 7: Forecasting Quarterly Holding-Period Excess Returns, 2005m1-2011m12
| VIX | CFNAI | baLC | baFC | baCCS | Other Controls | R2 | |
|---|---|---|---|---|---|---|---|
| 2.14*** (0.55) | No | 0.137 | |||||
| -4.09* (2.32) | No | 0.0430 | |||||
| 2.53*** (0.87) | 1.950 (3.41) | No | 0.142 | ||||
| 2.09** (0.88) | 2.700 (3.39) | -0.0320 (0.039) | 0.10*** (0.036) | 0.27*** (0.075) | No | 0.207 | |
| 2.77** (1.15) | 3.310 (3.00) | -0.0160 (0.044) | 0.092** (0.039) | 0.24*** (0.059) | Yes | 0.276 | |
| 0.89*** (0.29) | No | 0.0280 | |||||
| -2.18** (0.97) | No | 0.0150 | |||||
| 0.86* (0.51) | -0.120 (1.81) | No | 0.0280 | ||||
| 1.23** (0.56) | -0.580 (1.61) | 0.21*** (0.074) | -0.21*** (0.051) | -0.0640 (0.042) | No | 0.0990 | |
| 1.56** (0.73) | -0.440 (1.45) | 0.20*** (0.073) | -0.23*** (0.060) | -0.092** (0.039) | Yes | 0.141 | |
| 1.25*** (0.37) | No | 0.0350 | |||||
| -1.910 (1.88) | No | 0.00700 | |||||
| 1.68*** (0.43) | 2.090 (2.21) | No | 0.0390 | ||||
| 0.87** (0.42) | 3.300 (2.13) | -0.24*** (0.075) | 0.31*** (0.043) | 0.34*** (0.077) | No | 0.204 | |
| 1.22** (0.62) | 3.78** (1.87) | -0.22*** (0.075) | 0.32*** (0.042) | 0.34*** (0.062) | Yes | 0.234 |
Notes: This table reports annualized quarterly return
forecasting results for
![]() , FC over US excess returns,
, FC over US excess returns,
![]() , swapped LC over U.S.
excess returns, and
, swapped LC over U.S.
excess returns, and
![]() , FC over swapped LC excess
returns. See Table 6 for definition
of predictive variables. Other Controls refer to all other macroeconomic controls used in
Table 6.
All regressions are run at monthly frequency with country fixed
effects using Newey-West standard errors with 12-month lags
clustered by month following Driscoll and Kraay (1998) ***
p
, FC over swapped LC excess
returns. See Table 6 for definition
of predictive variables. Other Controls refer to all other macroeconomic controls used in
Table 6.
All regressions are run at monthly frequency with country fixed
effects using Newey-West standard errors with 12-month lags
clustered by month following Driscoll and Kraay (1998) ***
p![]() 0.01, ** p
0.01, ** p![]() 0.05, *
p
0.05, *
p![]() 0.1.
0.1.
Table 8: Impact of VIX on Credit Spreads by Country
(1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Brazil | 0.19*** (0.049) | 0.18*** (0.028) | 1.06 | 0.73 |
| Colombia | 0.049* (0.027) | 0.27*** (0.030) | 0.18 | 0.32 |
| Hungary | 0.31*** (0.065) | 0.43*** (0.064) | 0.73 | 0.56 |
| Indonesia | -0.00023 (0.044) | 0.45*** (0.079) | 0.00 | -0.13 |
| Israel | 0.034 (0.041) | 0.055 (0.039) | 0.62 | 0.91 |
| Mexico | 0.068* (0.037) | 0.18*** (0.021) | 0.39 | 0.39 |
| Peru | 0.046 (0.031) | 0.26*** (0.040) | 0.18 | 0.16 |
| Philippines | 0.013 (0.050) | 0.27*** (0.044) | 0.05 | 0.21 |
| Poland | 0.12*** (0.035) | 0.22*** (0.039) | 0.54 | 0.62 |
| Turkey | 0.21*** (0.052) | 0.36*** (0.035) | 0.57 | 0.48 |
| All Macro Controls | Yes | Yes | Correlation (3) and (4) | Correlation (3) and (4) |
| Observations | 757 | 757 | 0.84 | |
| R-squared | 0.407 | 0.746 |
Notes: The table reports results of cross-country
variations in the impact of VIX on credit spreads. Columns (1) and
(2) report coefficients on VIX interacting with country dummies in
credit spread regressions with macroeconomic controls, as specified
by Equation 3. Column (1)
reports the pass-through of VIX into LC credit spreads and Column
(2) reports the pass-through of VIX into FC credit spreads. All
controls are the same as in regression Table 6. All
regressions are run at monthly frequency with country fixed effects
using Newey-West standard errors with 12-month lags clustered by
month following Driscoll and Kraay (1998) *** p![]() 0.01, ** p
0.01, ** p![]() 0.05, * p
0.05, * p![]() 0.1. Column (3) computes the ratios of coefficients in
Column (1) over Column (2) and Column (4) reports the correlation
between swapped LC and FC quarterly excess returns over the U.S.
T-bill rates. A scatter plot of columns (3) against (4) is shown in
Figure 8.
0.1. Column (3) computes the ratios of coefficients in
Column (1) over Column (2) and Column (4) reports the correlation
between swapped LC and FC quarterly excess returns over the U.S.
T-bill rates. A scatter plot of columns (3) against (4) is shown in
Figure 8.
Appendix
A A Real-World Example
Figure A1 illustrates a concrete example of swapping an LC yield into a
dollar yield using CCS. Let ![]() denote the spot
peso/dollar exchange rate. Suppose a dollar-based investor lends to
the Mexican government by purchasing LC bonds traded at par with
notional amount equal to
denote the spot
peso/dollar exchange rate. Suppose a dollar-based investor lends to
the Mexican government by purchasing LC bonds traded at par with
notional amount equal to ![]() pesos. If the government
does not default, she will receive
pesos. If the government
does not default, she will receive ![]() percent
coupons at each coupon date and the principal of
percent
coupons at each coupon date and the principal of ![]() pesos at maturity. Without any currency hedging, even if the bond
does not default, the dollar payoff is uncertain since both the
coupons and the principal are subject to exchange rate risk. If the
dollar investor does not wish to bear the currency risk, she can
enter into a CCS package with a swapmaker (e.g., a bank) to lock in
a dollar yield. The details are as follows. At the inception of the
swap, the dollar investor gives 1 dollar to the bank. In exchange,
she receives
pesos at maturity. Without any currency hedging, even if the bond
does not default, the dollar payoff is uncertain since both the
coupons and the principal are subject to exchange rate risk. If the
dollar investor does not wish to bear the currency risk, she can
enter into a CCS package with a swapmaker (e.g., a bank) to lock in
a dollar yield. The details are as follows. At the inception of the
swap, the dollar investor gives 1 dollar to the bank. In exchange,
she receives ![]() pesos from the bank to lend to the
Mexican government. At each coupon date, the dollar investor passes
the
pesos from the bank to lend to the
Mexican government. At each coupon date, the dollar investor passes
the ![]() percent fixed coupons she receives in
pesos from the Mexican government to the bank and receives
percent fixed coupons she receives in
pesos from the Mexican government to the bank and receives
![]() percent fixed coupon in dollars,
where
percent fixed coupon in dollars,
where ![]() is the fixed peso for dollar swap rate.
At the maturity of the swap, the investor gives the
is the fixed peso for dollar swap rate.
At the maturity of the swap, the investor gives the ![]() pesos in principal repaid by the government to the bank and gets 1
dollar back. Therefore, the net cash flow of the investor is
entirely in dollars. The CCS swap package transforms the LC bond
into a synthetic dollar bond that promises to yield
pesos in principal repaid by the government to the bank and gets 1
dollar back. Therefore, the net cash flow of the investor is
entirely in dollars. The CCS swap package transforms the LC bond
into a synthetic dollar bond that promises to yield ![]() percent.
percent.
B Yield Curve Construction
Zero-coupon LC and FC yield curves for our sample countries are obtained or constructed from three main sources.20 First, our preference is to use zero-coupon LC curves constructed by the central bank of government agencies when they are available. Second, when national data are unavailable, we use the Bloomberg Fair Value (BFV) curve. The BFV curves are par yield curves estimated by Bloomberg on actively traded bonds using piecewise linear zero-coupon curves (Lee, 2007). These curves often serve as the benchmark reference rate in respective currencies. Traders using the Bloomberg trading platform can easily select these BFV curves for asset swap analysis. We use the standard Nelson-Siegel methodology to convert the par yield curves into zero curves with the scaling parameter for the curvature factor fixed using the value in Diebold and Li (2006).
Finally, for countries without national data or BFV curves, and to ensure reliability of the existing BFV curves, we estimate zero coupon yield curves using the individual bond data. We collected these data from Bloomberg by performing an exhaustive search for all available yields on active and matured bonds under <Govt TK> for our sample countries. We supplement Bloomberg FC bond yield data with additional data from Cbonds. We use nominal, fixed-coupon, bullet bonds without embedded options. LC curve estimation follows the Diebold and Li (2006) formulation of Nelson and Siegel (1987) and FC curve estimation follows Arellano and Ramanarayanan (2012) by fitting level, slope and curvature factors to the spread of zero-coupon FC curves over the corresponding dollar, Euro (Bundesbank), Yen and Sterling zero-coupon Treasury yields, depending on the currency denomination of the FC bonds. As in Arellano and Ramanarayanan (2012), we perform yield curve estimation when there are at least four bond yields observed on one day. We calculate yields using estimated parameters only up to the maximum tenor of the observed yields to avoid problems from extrapolation. When the Bloomberg BFV curves exists, our estimated yield curves track them very closely (details available upon request). However, since Bloomberg has partially removed historical yields for matured bonds from the system, the BFV curves offer more continuous series than our estimates. Therefore, we use BFV curves when they are available. For countries without BFV curves or earlier samples when BFV curves are not available, our estimated zero-coupon curves are used instead.
C A No-Arbitrage Model with Risky Arbitrage
We begin by specifying a reduced form default process for the
bonds. We define ![]() as the time when bonds of
type
as the time when bonds of
type ![]() issued by country
issued by country ![]() default, and the conditional survival intensity,
default, and the conditional survival intensity,
![]() as the probability that the
bond does not default in period
as the probability that the
bond does not default in period ![]() conditional on
the fact that it has not yet defaulted by period
conditional on
the fact that it has not yet defaulted by period ![]() We let the survival intensity for bond
We let the survival intensity for bond ![]() in country
in country
![]() depend on local
depend on local
![]() and global
and global
![]() factors:
factors:
For simplicity, we assume zero-recovery upon default. The local and global factors follow two AR(1) processes:
where
![]() and
and
![]() are independent standard
normal innovations,
are independent standard
normal innovations,
![]() and
and
![]() are AR(1) drifts, and
are AR(1) drifts, and
![]() and
and ![]() are
the autoregressive coefficients. We interpret an increase in the
factors as worsening macroeconomic fundamentals that make default
more likely. The global SDF is given by
are
the autoregressive coefficients. We interpret an increase in the
factors as worsening macroeconomic fundamentals that make default
more likely. The global SDF is given by
where ![]() indicates the risk aversion of global
investors. The one-period risk-free rate is therefore
indicates the risk aversion of global
investors. The one-period risk-free rate is therefore
C.0.1 Pricing FC and LC Bonds
In the case of one period bonds when defaulted bonds have zero
recovery rates, the survival process fully determines the bond
returns. We let
![]() denote the variance of one
period log returns. Given the global SDF and the one-period
survival rate, the one-period log FC spread over the risk-free rate
is given by
denote the variance of one
period log returns. Given the global SDF and the one-period
survival rate, the one-period log FC spread over the risk-free rate
is given by
The first set of terms
![]() is the expected default loss of the bond conditional on the
factors. The term
is the expected default loss of the bond conditional on the
factors. The term
![]() is the Jensen's
inequality correction from working with log yields. The third term
is the risk premium on the FC bond. When
is the Jensen's
inequality correction from working with log yields. The third term
is the risk premium on the FC bond. When
![]() , defaults are more
likely in the bad states of the world for the global investor,
leading the FC bond to carry a positive risk premium due to its
systematic exposure to global shocks. This is the empirically
relevant case as demonstrated in Borri and Verdelhan (2011) and Augustin and Tedongap (2013).
, defaults are more
likely in the bad states of the world for the global investor,
leading the FC bond to carry a positive risk premium due to its
systematic exposure to global shocks. This is the empirically
relevant case as demonstrated in Borri and Verdelhan (2011) and Augustin and Tedongap (2013).
Now suppose that the local bond market has an outside clientele
demand, i.e., local pension funds, and there are risk-averse
arbitrageurs who arbitrage between LC and FC markets. The
arbitrageurs take the FC spread priced by the global investor as
given. The LC credit spread is an equilibrium outcome of
arbitrageurs' portfolio demand and local clientele demand. Assume
that the arbitrageurs have power utility over next-period wealth
with constant relative risk aversion
![]() . As demonstrated in Campbell and Viceira (2002), the first-order condition of an
arbitrageur's optimal portfolio decision is given by
. As demonstrated in Campbell and Viceira (2002), the first-order condition of an
arbitrageur's optimal portfolio decision is given by
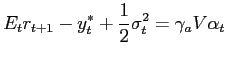
where ![]() is a column vector of one-period log
returns of the swapped LC and FC bonds,
is a column vector of one-period log
returns of the swapped LC and FC bonds,
![]() is the variance of log excess
returns,
is the variance of log excess
returns, ![]() is the variance-covariance matrix of log
excess returns, and
is the variance-covariance matrix of log
excess returns, and
![]() is a column vector with the
arbitrageur's portfolio weights in LC and FC debt.
is a column vector with the
arbitrageur's portfolio weights in LC and FC debt.
We conjecture that the LC credit spread
![]() is affine in the local and
global factors
is affine in the local and
global factors ![]() and
and ![]() and is given by
and is given by
where the spread parameters
![]() and
and ![]() will be solved for in the equilibrium. The expected dollar return
on swapped LC bonds is then equal to
will be solved for in the equilibrium. The expected dollar return
on swapped LC bonds is then equal to
where ![]() is the transaction cost (e.g.
capital inflow taxes or interest withholding taxes) for offshore
investors and
is the transaction cost (e.g.
capital inflow taxes or interest withholding taxes) for offshore
investors and
![]() gives the quanto adjustment as discussed in Section 4.1.1. By inverting
the variance-covariance matrix
gives the quanto adjustment as discussed in Section 4.1.1. By inverting
the variance-covariance matrix ![]() , we can calculate
the arbitrageur's optimal portfolio weights in local and foreign
currency bonds,
, we can calculate
the arbitrageur's optimal portfolio weights in local and foreign
currency bonds,
![]() and
and
![]() from the first-order condition:
from the first-order condition:
![$\displaystyle \left[\begin{array}{c} a_{t}^{SLC}\ a_{t}^{FC} \end{array}\right]=\frac{1}{\gamma_{a}(1-\rho_{r}^{2})(\sigma^{SLC})^{2}(\sigma^{FC})^{2}}\left[\begin{array}{cc} (\sigma^{FC})^{2} & -\rho_{r}\sigma^{SLC}\sigma^{FC}\ -\rho_{r}\sigma^{SLC}\sigma^{FC} & (\sigma^{SLC})^{2} \end{array}\right]\left[\begin{array}{c} (b_{0}+b_{c}z_{t}^{i}+b_{w}z_{t}^{w})-\tau_{0}+\alpha\tilde{s}_{t}^{LC}\ \gamma\sigma_{\lambda w}^{FC} \end{array}\right], $](img300.gif)
where ![]() is the correlation in log returns
between FC and the swapped LC bonds for the dollar investor. When
log returns are positively correlated,
is the correlation in log returns
between FC and the swapped LC bonds for the dollar investor. When
log returns are positively correlated,
![]() , the arbitrageur takes
offsetting positions in LC and FC bonds to hedge risk.
, the arbitrageur takes
offsetting positions in LC and FC bonds to hedge risk.
Following Greenwood and Vayanos (2010), we close the model
by positing a downward sloping excess clientele demand for LC bonds
![]() (normalizing the supply of LC
bonds to zero), which is decreasing in the price of the swapped LC
bond,
(normalizing the supply of LC
bonds to zero), which is decreasing in the price of the swapped LC
bond,
![]() ,
,
with ![]() . Local investors care about the
price of the swapped LC bond because it can be translated into how
much the LC bond yields relative to the LC risk-free rate.
Following (), we normalize the clientele
demand by the level of arbitrageur's wealth,
. Local investors care about the
price of the swapped LC bond because it can be translated into how
much the LC bond yields relative to the LC risk-free rate.
Following (), we normalize the clientele
demand by the level of arbitrageur's wealth, ![]() .
Furthermore, we assume that
.
Furthermore, we assume that ![]() is affine
in factors and takes the form:
is affine
in factors and takes the form:
In the absence of arbitrage, the market clearing condition requires
that excess demand is zero, and thus
![]() and the expected excess
return on swapped LC bonds is then equal to
and the expected excess
return on swapped LC bonds is then equal to
![]() . This
parametrization of
. This
parametrization of ![]() allows us to
conveniently summarize local demand as the deviation from zero
expected excess returns on swapped LC bonds for local investors
that would occur in the absence of arbitrage.21 Negative values
of
allows us to
conveniently summarize local demand as the deviation from zero
expected excess returns on swapped LC bonds for local investors
that would occur in the absence of arbitrage.21 Negative values
of
![]() and
and
![]() dampen the sensitivity of the LC
credit spread to local and global shocks.
dampen the sensitivity of the LC
credit spread to local and global shocks.
Equilibrium requires that asset markets clear, or the arbitrageur's optimal portfolio demand exactly offsets local clientele demand:
Using the above equilibrium condition, we can solve for the
equilibrium spread parameters ![]() ,
, ![]() and
and ![]() in closed forms as follows:
in closed forms as follows:
| (A4) |
where
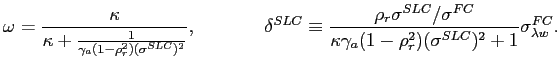
Therefore, the equilibrium LC credit spread depends on the local
demand shifters
![]() ,
,
![]() and
and
![]() , the offshore pricing wedge
, the offshore pricing wedge
![]() , the depreciation upon default
, the depreciation upon default
![]() , and the global investor's risk
aversion
, and the global investor's risk
aversion ![]() . The exact magnitude of these
equilibrium effects depend on the arbitrageur's risk aversion, the
return correlation and the elasticity of local demand. These will
be examined in the next subsection. The case of
. The exact magnitude of these
equilibrium effects depend on the arbitrageur's risk aversion, the
return correlation and the elasticity of local demand. These will
be examined in the next subsection. The case of ![]() corresponds complete segmentation between domestic
and external markets: the tax wedge and depreciation upon default
play no role in pricing the LC credit spread. The case of
corresponds complete segmentation between domestic
and external markets: the tax wedge and depreciation upon default
play no role in pricing the LC credit spread. The case of
![]() corresponds to perfect integration:
the mis-pricing induced by local clientele demand
corresponds to perfect integration:
the mis-pricing induced by local clientele demand ![]() does not affect the equilibrium pricing.
does not affect the equilibrium pricing.
C.0.2 Comparative Statics
To gain intuition, we perform several comparative statics.
First, we study the pass-through of global risk aversion into the
LC credit spread. The pass-through of global risk aversion into the
LC spread is the derivative of the spread
![]() with respect to risk
aversion
with respect to risk
aversion ![]() :
:
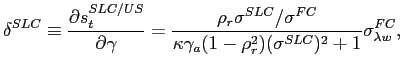 |
(A5) |
where we refer to
![]() as the pass-though parameter
for swapped LC debt. Similarly, for FC debt, we have that the
pass-through of risk aversion
as the pass-though parameter
for swapped LC debt. Similarly, for FC debt, we have that the
pass-through of risk aversion ![]() into FC
spreads
into FC
spreads
![]() is given by:
is given by:
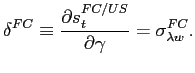
It is straightforward to establish the following proposition using Equation A5:
Proposition 2. (Pass-through of Global Risk Aversion) If the asset
return correlation times the standard deviation of swapped LC
returns is less than the standard deviation of FC returns
![]() , the
pass-through of global risk aversion shocks into the swapped LC
spread is less than into FC spreads,
, the
pass-through of global risk aversion shocks into the swapped LC
spread is less than into FC spreads,
![]() . Furthermore,
the pass-through into LC spreads is increasing in the return
correlation
. Furthermore,
the pass-through into LC spreads is increasing in the return
correlation
![]() ,
decreasing in the arbitrageur's risk aversion
,
decreasing in the arbitrageur's risk aversion
![]() ,
and decreasing in the elasticity of local demand
,
and decreasing in the elasticity of local demand
![]() .
.
Although the price of risk is equalized across the two markets by
the arbitrageur, the quantity of risk can still be different. Under
the condition that
![]() , swapped
LC bonds have a lower quantity of risk. We can re-express this
condition as
, swapped
LC bonds have a lower quantity of risk. We can re-express this
condition as
![]() in the beta regression of running swapped LC excess returns on FC
excess returns:
in the beta regression of running swapped LC excess returns on FC
excess returns:
Due to the lower quantity of risk, swapped LC bonds carry a lower
risk premium. In the one-period model, both ![]() and
and
![]() are given exogenously by
the default processes and do not depend on the local demands
are given exogenously by
the default processes and do not depend on the local demands
![]() and
and
![]() . We can relax this feature of the
model in a multi-period specification in which the price of the
bond next period is also uncertain even in the absence of default
and the price sensitivity depends on the local demand parameters
(available upon request). The mechanism of pass-through of global
risk aversion into the LC credit spread is as follows. An increase
in global risk aversion
. We can relax this feature of the
model in a multi-period specification in which the price of the
bond next period is also uncertain even in the absence of default
and the price sensitivity depends on the local demand parameters
(available upon request). The mechanism of pass-through of global
risk aversion into the LC credit spread is as follows. An increase
in global risk aversion ![]() increases the FC
spread and the expected excess returns on the FC bond. Holding the
arbitrageur's risk aversion constant, the arbitrageur takes
advantage of this opportunity by going long in FC bonds and hedges
her position by shorting swapped LC bonds, which drives up the
swapped LC spread. The pass-through of global risk aversion is
lower into the LC bond if the quantity of risk in LC bonds is
lower.
increases the FC
spread and the expected excess returns on the FC bond. Holding the
arbitrageur's risk aversion constant, the arbitrageur takes
advantage of this opportunity by going long in FC bonds and hedges
her position by shorting swapped LC bonds, which drives up the
swapped LC spread. The pass-through of global risk aversion is
lower into the LC bond if the quantity of risk in LC bonds is
lower.
The extent of the trade and its subsequent impact on the LC
credit spread depends on three key parameters. First, the
differential pass-through depends on the return correlation
![]() . Higher correlations increase LC
pass-through by allowing the arbitrageur to better hedge her risk
and hence take a larger position. When returns are uncorrelated (
. Higher correlations increase LC
pass-through by allowing the arbitrageur to better hedge her risk
and hence take a larger position. When returns are uncorrelated (
![]() ), the pass-through is zero, and
when returns are perfectly correlated (
), the pass-through is zero, and
when returns are perfectly correlated (
![]() ), pass-through achieves its
maximum at
), pass-through achieves its
maximum at
![]() .
Second, the differential pass-through depends on the arbitrageur's
risk aversion
.
Second, the differential pass-through depends on the arbitrageur's
risk aversion
![]() an increase in arbitrageur risk
aversion decreases pass-through. When
an increase in arbitrageur risk
aversion decreases pass-through. When
![]() is infinite, pass-through is zero
because the arbitrageur is too risk-averse to make any trades. When
is infinite, pass-through is zero
because the arbitrageur is too risk-averse to make any trades. When
![]() is zero, meaning that the
arbitrageur is risk-neutral, pass-through is maximized for a given
return correlation,
is zero, meaning that the
arbitrageur is risk-neutral, pass-through is maximized for a given
return correlation, ![]() . Third, the
differential pass-through depends on the elasticity of local
clientele demand
. Third, the
differential pass-through depends on the elasticity of local
clientele demand ![]() An increase in the
elasticity of local clientele demand decreases pass-though. A more
elastic local demand increases the ability of the LC credit spread
to absorb larger positions taken by arbitrageurs. When
An increase in the
elasticity of local clientele demand decreases pass-though. A more
elastic local demand increases the ability of the LC credit spread
to absorb larger positions taken by arbitrageurs. When ![]() is infinite, local clientele demand is perfectly
elastic and therefore the LC credit spread is completely determined
by local conditions, leaving no room for arbitrageurs to play a
role. On the other hand, when
is infinite, local clientele demand is perfectly
elastic and therefore the LC credit spread is completely determined
by local conditions, leaving no room for arbitrageurs to play a
role. On the other hand, when ![]() , local
clientele demand is zero and thus pass-through is maximized.
, local
clientele demand is zero and thus pass-through is maximized.
Figure A1: An Illustration of Swap Covered Local Currency Investment
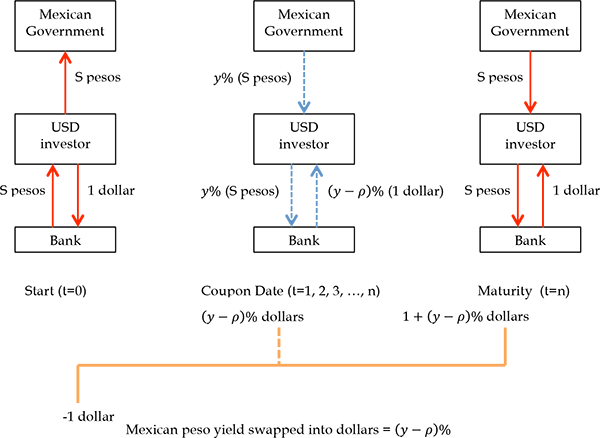
Notes: This figure illustrates how a dollar based
investor can use a fixed peso for fixed dollar cross-currency swap
package to fully hedge currency risk for all coupons and the
principal of a Mexican peso denominated LC bond and receive fixed
dollar cash flows. We let ![]() denote the spot
peso/dollar exchange rate at the inception of the swap,
denote the spot
peso/dollar exchange rate at the inception of the swap, ![]() denote the yield on the peso bond, and
denote the yield on the peso bond, and ![]() denote the fixed peso for fixed dollar swap rate. By
purchasing the peso bond while entering the asset swap, the LC bond
is transformed into a dollar bond with a dollar yield equal to
denote the fixed peso for fixed dollar swap rate. By
purchasing the peso bond while entering the asset swap, the LC bond
is transformed into a dollar bond with a dollar yield equal to ![]() .
.
Table A1: Cross-Currency Swaps and Currency Forward Comparison, 2005-2011
| Country | NDS | Floating Leg | Corr(CCS,FWD) | CCS | Fwd | CC-Fwd |
|---|---|---|---|---|---|---|
| Brazil | Yes | N/A | 97.16 | 7.19 (1.28) | 7.45 (1.28 | -0.27 (0.30) |
| Colombia | Yes | N/A | 99.19 | 3.52 (2.25) | 3.57 (2.24) | -0.05 (0.26) |
| Hungary | No | Bubor | 99.16 | 3.75 (1.35) | 3.80 (1.41) | -0.04 (0.27) |
| Indonesia | Yes | N/A | 97.79 | 5.67 (3.48) | 5.61 (3.82) | -0.06 (0.83) |
| Israel | Yes | Telbor | 98.10 | 0.52 (0.74) | 0.48 (0.74) | 0.05 (0.13) |
| Mexico | No | TIIE | 99.58 | 3.68 (1.24) | 4.05 (1.32) | -0.37 (0.14) |
| Peru | Yes | N/A | 98.76 | 0.98 (1.38) | 0.96 (1.42) | 0.02 (0.22) |
| Philippines | Yes | N/A | 97.25 | 1.96 (2.00) | 1.83 (2.02) | -0.13 (0.47) |
| Poland | No | Wibor | 98.96 | 1.69 (1.62) | 1.47 (1.51) | 0.23 (0.25) |
| Turkey | No | N/A | 98.69 | 9.36 (2.90) | 9.51 (2.93) | -0.15 (0.15) |
| Total | 98.68 | 3.95 (3.42) | 3.99 (3.54) | -0.04 (0.40) |
Notes: This table reports summary statistics for 1-year fixed for fixed cross currency swap (CCS) rates and 1-year offshore forward premium (Fwd) implied by outright forward contracts. Column 1 lists whether the currency swap is non-deliverable. Column 2 lists the name of the local floating leg against U.S. Libor if the currency swap consists of a plain-vanilla interest rate swap and a cross-currency basis swap. Corr(CCS,Fwd) reports correlation between swap rates and forward rates. The difference between the two variables are reported in the last column (CCS-Fwd). Forward rates are from Datastream and fixed for fixed CCS rates are computed by authors based on CCS and interest rate swap data from Bloomberg. Data are at daily frequency for the sample periods 2005-2011.
Table A2: Half of Bid-ask Spreads on FX Spots, Forwards and Swaps, 2005-2011
| Country | (1) 1M Fwd | (2) 3M Fwd | (3) 6M Fwd | (4) 1Y Fwd | (5) 5Y CCS |
|---|---|---|---|---|---|
| Brazil | 98.34 (17.1) | 53.80 (18.3) | 30.99 (15.0) | 22.41 (14.0) | 32.13 (13.5) |
| Colombia | 123.37 (14.7) | 68.71 (12.3) | 42.23 (9.43) | 30.19 (10.8) | 16.24 (10.7) |
| Hungary | 112.04 (10.8) | 52.88 (11.2) | 37.88 (14.5) | 28.08 (23.1) | 18.54 (14.2) |
| Indonesia | 315.96 (69.8) | 139.57 (51.3) | 90.30 (47.3) | 52.87 (37.9) | 37.49 (23.1) |
| Israel | 88.03 (12.9) | 36.52 (8.50) | 23.86 (6.78) | 16.62 (7.45) | 11.39 (4.31) |
| Mexico | 31.20 (7.76) | 12.88 (5.65) | 8.58 (4.94) | 6.12 (6.12) | 8.59 (6.17) |
| Peru | 100.25 (13.7) | 47.61 (10.0) | 29.39 (6.97) | 23.87 (6.92) | 16.00 (7.15) |
| Philippines | 126.57 (7.69) | 46.34 (4.53) | 37.24 (5.72) | 27.05 (5.79) | 28.00 (14.7) |
| Poland | 72.40 (8.56) | 27.38 (5.80) | 17.67 (6.86) | 11.98 (6.30) | 11.50 (8.33) |
| Turkey | 126.76 (25.8) | 59.79 (19.4) | 41.72 (18.9) | 25.85 (15.2) | 11.00 (8.14) |
| Total | 117.55 (33.3) | 53.75 (25.6) | 35.41 (23.5) | 23.96 (20.1) | 19.07 (15.7) |
Notes: This table reports mean and standard deviations of half of the bid-ask spreads of FX forward and CCS contracts in basis points for 10 sample countries at daily frequency from 2005 to 2011. Columns 1 to 4 report half of annualized bid-ask spreads for FX forward contracts at 1, 3, 6, and 12 months. Column 5 reports the half of the bid-ask for the spread for the 5-year swap contracts. Annualized standard deviations are reported in the parentheses. Spot and Forward data use closing quotes from WM/Reuter (access via Datastream) with the exceptions of Indonesia and Philippines for which the offshore forward rates use closing quotes of non-deliverable forwards from Tullet Prebon (access via Datastream). Swap rates are from Bloomberg.
Table A3: Summary Statistics for
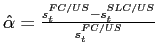
| Country | Full Sample (2005-11): (1) Mean | Full Sample (2005-11): (2) S.d. | Crisis Year (08/09-09/09): (3) Mean | Crisis Year (08/09-09/09): (4) S.d. | Full Sample: (5) |
|---|---|---|---|---|---|
| Brazil | -85.57 | (69.53) | -28.22 | (19.34) | 0.44 |
| Colombia | 19.15 | (48.38) | 55.98 | (13.75) | 0.28 |
| Hungary | -56.94 | (169.32) | 19.09 | (33.68) | 0.65 |
| Indonesia | 40.18 | (52.68) | 68.50 | (17.57) | -0.33 |
| Israel | 30.14 | (23.83) | 31.51 | (19.78) | -0.03 |
| Mexico | 59.91 | (20.78) | 66.42 | (9.83) | -0.05 |
| Peru | 66.61 | (46.31) | 91.23 | (39.23) | -0.06 |
| Philippines | 46.59 | (41.63) | 60.18 | (15.55) | -0.18 |
| Poland | -10.19 | (55.15) | 35.91 | (34.45) | 0.48 |
| Turkey | 45.02 | (35.36) | 43.72 | (22.80) | 0.36 |
| Mean | 16.68 | (56.30) | 44.53 | (39.76) | Corr (1) and (5) = -0.75 |
Notes: This table computes the hypothetical depreciation
upon default
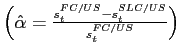 assuming the covariance between
currency and default risk is the only wedge between LC and FC
credit spreads. See Section 4.1.2 on details of
this estimator.
assuming the covariance between
currency and default risk is the only wedge between LC and FC
credit spreads. See Section 4.1.2 on details of
this estimator.
Table A4: Liquidity Measures of Bond and Swap Markets
| Country | (1) | (2) FC bidask | (3) FC badask | (4) LC Volume ($bln) | (5) FC Volume ($bln) | (6) LC Turnover (%) | (7) FC Turnover (%) |
|---|---|---|---|---|---|---|---|
| Brazil | 32.60 (13.50) | 13.43 (21.01) | 61.47 (28.66) | 149.00 (29.72) | 69.39 (32.53) | 20.11 (5.552) | 119.15 (40.31) |
| Colombia | 49.47 (20.84) | 11.34 (2.875) | 37.92 (21.84) | 16.03 (9.178) | 10.08 (3.164) | 34.59 (18.98) | 60.45 (22.43) |
| Hungary | 46.85 (47.40) | 20.56 (11.37) | 38.71 (31.98) | 21.43 (8.646) | 5.14 (2.911) | 39.52 (17.43) | 21.79 (12.38) |
| Indonesia | 92.39 (120.9) | 67.99 (28.86) | 73.87 (48.80) | 10.45 (4.604) | 10.81 (3.440) | 16.85 (6.459) | 79.34 (32.63) |
| Israel | 29.90 (17.60) | 13.62 (3.066) | 23.42 (8.197) | 14.01 (7.825) | 3.35 (2.535) | 15.61 (7.389) | 35.43 (25.27) |
| Mexico | 43.68 (21.47) | 37.21 (31.79) | 17.29 (11.60) | 134.47 (111.9) | 38.24 (10.97) | 75.01 (69.27) | 89.77 (26.18) |
| Peru | 40.56 (13.35) | 38.24 (15.35) | 39.34 (14.60) | 2.21 (1.920) | 6.08 (2.217) | 32.17 (30.19) | 61.15 (26.11) |
| Philippines | 37.26 (10.72) | 39.33 (19.95) | 55.37 (26.00) | 3.18 (2.327) | 15.66 (4.874) | 4.94 (2.677) | 63.46 (17.12) |
| Poland | 37.78 (19.55) | 23.92 (23.57) | 23.20 (17.33) | 51.71 (22.02) | 11.03 (6.778) | 18.32 (8.102) | 22.88 (14.82) |
| Turkey | 34.88 (9.065) | 9.94 (6.020) | 23.11 (16.16) | 74.19 (23.13) | 24.27 (12.00) | 32.87 (11.93) | 58.84 (31.68) |
| Total | 44.59 (46.90) | 27.82 (26.08) | 39.24 (31.30) | 47.66 (63.98) | 19.40 (22.69) | 29.33 (31.53) | 60.63 (38.08) |
Notes: This table reports mean and standard deviations of various liquidity measures of bond and swap markets. Columns 1-3 report the mean bid-ask spread on LC bonds, FC bonds and currency swaps in the monthly sample used in later regressions. The bid-ask spreads for LC and FC bonds are computed as the mean of all daily bid-ask spreads on all LC and FC bonds available in Bloomberg. Columns 4-5 summarize trading volume for LC and FC bonds provided in quarterly Debt Trading Volume Surveys conducted by Emerging Market Trading Association. The last two columns divide the trading volume by the amount debt outstanding from the BIS data to compute the turnover ratios.
Table A5a: Data Sources and Variable Construction: (A) Yield Curve Construction
| Country | Curve Currency | Zero-Soupon Curve Type | Data Source |
|---|---|---|---|
| Brazil | LC | Svensson | Brazilian Financial and Capital Market Associations (ANBIMA) |
| Brazil | FC | Nelson-Siegel | Bloomberg Fair Value par to zero |
| Colombia | LC | Nelson-Siegel | Bloomberg Fair Value par to zero |
| Colombia | FC | Nelson-Siegel | Bloomberg Fair Value par to zero |
| Hungary | LC | Svensson | Hungary Government Debt Management Office (AKK) |
| Hungary | FC | Nelson-Siegel | Authors' estimation based on individual bond prices Bloomberg and CBonds |
| Indonesia | LC | Nelson-Siegel | Bloomberg Fair Value par to zero |
| Indonesia | FC | Nelson-Siegel | Authors' estimation based on individual bond prices Bloomberg and CBonds |
| Israel | LC | Svensson | Bank of Israel |
| Israel | FC | Nelson-Siegel | Authors' estimation based on individual bond prices Bloomberg and CBonds |
| Mexico | LC | Nelson-Siegel | Bloomberg Fair Value par to zero |
| Mexico | FC | Nelson-Siegel | Bloomberg Fair Value par to zero |
| Peru | LC | Nelson-Siegel | Bloomberg Fair Value par to zero |
| Peru | FC | Nelson-Siegel | BFV and authors' estimation based on Bloomberg individual bond prices |
| Philippines | LC | Nelson-Siegel | Authors' estimation based on constant maturity yield curves provided by Philippines Dealing and Exchange Corp (PDEx) and average coupon rates from individual bonds from Bloomberg |
| Philippines | FC | Nelson-Siegel | Bloomberg Fair Value par to zero |
| Poland | LC | Nelson-Siegel | Bloomberg Fair Value par to zero |
| Poland | FC | Nelson-Siegel | Authors' estimation based on individual bond prices Bloomberg and CBonds |
| Turkey | LC | Svensson | Central Bank of Turkey |
| Turkey | FC | Nelson-Siegel | Bloomberg Fair Value par to zero |
Table A5b: Data Sources and Variable Construction: (B) Other Variables
| Variable | Data Source | Description |
|---|---|---|
| CDS | Bloomberg | Sovereign credit default swaps at various tenors denominated in dollars. |
| lc eq vol | Datastream | Local equity volatility: volatility of daily equity returns measured in local currency computed using backward-looking rolling windows equal to 30 days. |
| BBB/T | Datastream | Merrill-Lynch BBB U.S. corporate bond spread over the 10-year U.S. Treasury yield |
| CFNAI | Chicago Fed | Chicago Fed National Activity Index |
| VIX | WRDS | Implied volatility on S&P index options. |
| ΔIP | Haver | Monthly log change in the industrial production index |
| FC Debt/GDP | Authors' calculations | FC debt to GDP ratio, aggregated from face value of all FC bonds in Bloomberg. |
| LC Debt/GDP | Authors' calculations | LC debt to GDP ratio, aggregated from face value of all LC bonds in Bloomberg. |
| ΔCPI, Std(ΔCPI) | Haver | Monthly log change in the consumer priceand standard deviations of Δ CPI in last 12 months. |
| ΔToT, Std(ΔToT) | Bank of International Settlement | Monthly log change in terms of trade and standard deviations of Δ ToT in last 12 months. |
| ΔReserve | International Financial Statistics | Monthly log change in foreign exchange reserves. |
Footnotes
1. We are especially grateful to John Campbell, Gita Gopinath, Robin Greenwood, Kenneth Rogoff and Luis Viceira for their invaluable advice and guidance. We thank Javier Bianchi, Emmanuel Farhi, Donna Fletcher, Jeffrey Frankel, Jeffry Frieden, Jakub Jurek, Sebnem Kalemli-Ozcan, Rui Mano, Michael Rashes, Helene Rey, Jeremy Stein, Lawrence Summers, Vivian Yue, Adrien Verdelhan, and seminar participants at the AQR Capital Management, Federal Reserve Board, Harvard, IMF Institute, Maryland, NBER IFM, Stanford GSB, UCLA Anderson, Wharton, UCSD, UVA Darden, Western Finanace Association, and World Bank for comments and suggestions. Our discussants Matteo Maggiori and Michael Michaux provided excellent comments. We thank Cristina Arellano and Guido Lorenzoni for sharing their code and data. We are also indebted to numerous people at governments, central banks, investment banks, the Emerging Market Trading Association and Luxembourg Stock Exchange who helped us gather data on emerging market fixed income securities. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. All errors are our own. Return to text
2. Du: Federal Reserve Board, 20th and C Street NW, Washington, D.C. 20551. Email: [email protected]. Schreger: Department of Economics, Harvard University, Littauer Center, Cambridge, MA 02138. Email: [email protected]. Return to text
3. For example in Mexico, the 2008 guidelines for public debt management is to "Continue emphasis on the use of domestic debt to finance the entire federal government deficit and the stock of external debt" (SHCP, 2008) Return to text
4. This is different from the case of developed country sovereign CDS for which a default on local bonds would trigger CDS contracts (ISDA, 2012). Return to text
5. For Mexico, Hungary, Israel and Poland in our sample, this step itself combines two interest rate swaps: an onshore plain vanilla LC fixed for LC floating interest rate swap and a cross-currency LC floating for U.S. Libor basis swap. Return to text
6. Extremely illiquid trading days with bid-ask spreads over 400 basis points on CCS are excluded from the analysis (mainly for Indonesia during the 2008 crisis). All main results are not affected by including these extreme values. We compare the difference in 1-year forward premia implied by the swap and the forward markets in Table A1. The mean correlation is 99 percent. Using annualized bid-ask spreads as a proxy for liquidity, swap contracts are, on average, more liquid than short-term forward contracts (Table A2) . Return to text
7. Following Datta adn Du (2012), missing data are treated as non-serially correlated for Newey-West implementations throughout the paper. Return to text
8. To assess how measurement errors in LC credit spreads relative to FC affect these results, we start with the null hypothesis that LC and FC credit spreads are the same and then introduce i.i.d. Gaussian shocks to FC credit spreads using simulations. We show that the variance of shocks to FC credit spreads need to be at least 90 basis points to match the observed cross-country correlation in LC credit spreads, which corresponds to 6 times of the standard deviation of observed one-way transaction costs (half of the observed bid-ask spread on cross currency swaps). These simulation results are available upon request. Return to text
9. For quarterly returns, ![]() is a quarter and we approximate
is a quarter and we approximate
![]() with
with
![]() . Return to text
. Return to text
10. The hedged excess return is a first-order approximation of the mark-to-market (MTM) dollar return on money market hedging strategy by combining the LC bond with a long position in the domestic risk-free rate and a short position in the dollar risk-free rate over the U.S. Treasury bond. The swapped excess return is the first order approximation of the MTM dollar return on the bond and the CCS over the U.S. Treasury bond. The hedging notional is equal to the initial market value of the LC bond and is dynamically rebalanced. All the results are robust to using daily rebalancing under exact MTM accounting allowing for the second-order hedging errors. Return to text
11. A continuous time version with short rates following CIR processes is available upon request. Return to text
12. Under this assumption, we have
13. Again, this assumption can be relaxed but the exposition is clearer under full default. Return to text
14. Strictly speaking, dynamic hedging requires continuous rebalancing of the market value of the bond and the swap position. Return to text
15. Kumara and Pfau (2011) document stringent caps faced by emerging market pension funds in investing in local equities and overseas assets. Return to text
16. We divide the conventional quote of
VIX by ![]() to measure unannualized implied
volatility over the next 30 days. Return to text
to measure unannualized implied
volatility over the next 30 days. Return to text
17. Debt to GDP ratios are computed by aggregating the entire universe of individual sovereign bond issuance in Bloomberg. Using this index, rather than the aggregated data from the Bank for International Settlements (BIS), we obtain a higher frequency measure of the debt outstanding than the quarterly measure produced by the BIS. The correlation between our debt/GDP ratios with the BIS official statistics is 96 percent for FC debt and 80 percent for LC debt. More details on construction of macroeconomic controls are given in the Appendix Table A5. Return to text
18. This is consistent with Proposition 2 in the Appendix. Return to text
19. Exact mark-to-market accounting is used to calculate returns for swapped LC bonds to take into account second-order currency hedging errors due to covariance between currency and credit. The LC swap and bond positions are re-balanced at the daily frequency so that the two positions have the same market value. Return to text
20. Full details on LC and FC yield curve construction are given in the data appendix Table A5. Return to text
21. Covariance between currency and credit does not affect local investors' credit valuation for the LC bond. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text