
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1107, June 2014 --- Screen Reader
Version*
Understanding the Great Recession1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We argue that the vast bulk of movements in aggregate real economic activity during the Great Recession were due to financial frictions interacting with the zero lower bound. We reach this conclusion looking through the lens of a New Keynesian model in which firms face moderate degrees of price rigidities and no nominal rigidities in the wage setting process. Our model does a good job of accounting for the joint behavior of labor and goods markets, as well as inflation, during the Great Recession. According to the model the observed fall in total factor productivity and the rise in the cost of working capital played critical roles in accounting for the small size of the drop in inflation that occurred during the Great Recession.
Keywords: Inflation, unemployment, labor force, zero lower bound
JEL classification: E2, E24, E32
1. Introduction
The Great Recession has been marked by extraordinary contractions in output, investment and consumption. Mirroring these developments, per capita employment and the labor force participation rate have dropped substantially and show little sign of improving. The unemployment rate has declined from its Great Recession peak. But, this decline primarily reflects a sharp drop in the labor force participation rate, not an improvement in the labor market. Indeed, while vacancies have risen to their pre-recession levels, this rise has not translated into an improvement in employment. Despite all this economic weakness, the decline in inflation has been relatively modest.
We seek to understand the key forces driving the US economy in the Great Recession. To do so, we require a model that provides an empirically plausible account of key macroeconomic aggregates, including labor market outcomes like employment, vacancies, the labor force participation rate and the unemployment rate. To this end, we extend the medium-sized dynamic, stochastic general equilibrium (DSGE) model in Christiano, Eichenbaum and Trabandt (2013) (CET) to endogenize the labor force participation rate. To establish the empirical credibility of our model, we estimate its parameters using pre-2008 data. We argue that the model does a good job of accounting for the dynamics of twelve key macroeconomic variables over this period.
We show that four shocks can account for the key features of the Great Recession. Two of these shocks capture in a reduced form way frictions which are widely viewed as having played an important role in the Great Recession. The first of these is motivated by the literature stressing a reduction in consumption as a trigger for a zero lower bound (ZLB) episode (see Eggertsson and Woodford (2003), Eggertsson and Krugman (2012) and Guerrieri and Lorenzoni (2012)). For convenience, we capture this idea as in Smets and Wouters (2007) and Fisher (2014), by introducing a perturbation to agents' intertemporal Euler equation governing the accumulation of the risk-free asset. We refer to this perturbation as the consumption wedge. The second friction shock is motivated by the sharp increase in credit spreads observed in the post-2008 period. To capture this phenomenon, we introduce a wedge into households' first order condition for optimal capital accumulation. Simple financial friction models based on asymmetric information with costly monitoring imply that credit market frictions can be captured in a reduced form way as a wedge in the household's first order condition for capital (see Christiano and Davis 2006). We refer to this wedge as the financial wedge. Also, motivated by models like e.g. Bigio (2013), we allow the financial wedge to impact on the cost of working capital.
The third shock in our analysis is a neutral technology shock that captures the observed decline, relative to trend, in total factor productivity (TFP). The final shock in our analysis corresponds to the changes in government consumption that occurred during the Great Recession.
Our main findings can be summarized as follows. First, our model can account, quantitatively, for the key features of the Great Recession, including the ongoing decline in the labor force participation rate. Second, according to our model the vast bulk of the decline in economic activity is due to the financial wedge and, to a somewhat smaller extent, the consumption wedge.5 The rise in government consumption associated with the American Recovery and Reinvestment Act of 2009 did have a peak multiplier effect in excess of 2. But, the rise in government spending was too small to have a substantial effect. In addition, for reasons discussed in the text, we cannot attribute the long duration of the Great Recession to the substantial decline in government consumption that began around the start of 2011. Third, consistent with the basic findings in CET, we are able to account for the observed behavior of real wages during the Great Recession, even though we do not allow for sticky wages. Fourth, our model can account for the relatively small decline in inflation with only a moderate amount of price stickiness.
Our last finding is perhaps surprising in light of arguments by Hall (2011) and others that New Keynesian (NK) models imply inflation should have been much lower than it was during the Great Recession.6 Del Negro et al. (2014) argue that Hall's conclusions do not hold if the Phillips curve is sufficiently flat.7 In contrast, our model accounts for the behavior of inflation after 2008 by incorporating two key features of the data into our analysis: (i) the prolonged slowdown in TFP growth during the Great Recession and (ii) the rise in the cost of firms' working capital as measured by the spread between the corporate-borrowing rate and the risk-free interest rate. In our model, these forces drive up firms' marginal costs, exerting countervailing pressures on the deflationary forces operative during the post 2008 period.
Our paper may be of independent interest from a methodological perspective for three reasons. First, our analysis of the Great Recession requires that we do stochastic simulations of a model that is highly non-linear in several respects: (i) we work with the actual nonlinear equilibrium conditions; (ii) we confront the fact that the ZLB on the nominal interest rate is binding in parts of the sample and not in others; and (iii) our characterization of monetary policy allows for forward guidance, a policy rule that is characterized by regime switches in response to the values taken on by endogenous variables. The one approximation that we use in our solution method is certainty equivalence. Second, as we explain below, our analysis of the Great Recession requires that we adopt an unobserved components representation for the growth rate of neutral technology. This leads to a series of challenges in solving the model and deriving its implications for the data. Third, we note that traditional analyses of vacancies and unemployment based on the Beveridge curve would infer that there was a deterioration in the efficiency of labor markets during the Great Recession. We argue that this conclusion is based on a technical assumption which is highly misleading when applied to data from the Great Recession.
The remainder of this paper is organized as follows. The next section describes our model. The following two sections describe the data, methodology and results for estimating our model on pre-2008 data. In the next two sections, we use our model to study the Great Recession. We close with a brief conclusion. Many technical details of our analysis are relegated to a separate technical appendix that is available on request.
2. The Model
In this section, we describe a medium-sized DSGE model whose structure is, with one important exception, the same as the one in CET. The exception is that we modify the framework to endogenize labor force participation rates.
2.1 Households and Labor Force Dynamics
The economy is populated by a large number of identical
households. Each household has a unit measure of members. Members
of the household can be engaged in three types of activities: (i)
![]() members specialize in home production
in which case we say they are not in the labor force and that they
are in the non-participation state; (ii)
members specialize in home production
in which case we say they are not in the labor force and that they
are in the non-participation state; (ii) ![]() members of the household are in the labor force and are employed in
the production of a market good, and (iii)
members of the household are in the labor force and are employed in
the production of a market good, and (iii) ![]() members of the household are unemployed, i.e.
they are in the labor force but do not have a job.
members of the household are unemployed, i.e.
they are in the labor force but do not have a job.
We now describe aggregate flows in the labor market. We derive
an expression for the total number of people searching for a job at
the end of a period. This allows us to define the job finding rate,
![]() and the rate,
and the rate, ![]() at
which workers transit from non-participation into labor force
participation.
at
which workers transit from non-participation into labor force
participation.
At the end of each period a fraction ![]() of
randomly selected employed workers is separated from the firm with
which they had been matched. Thus, at the end of period
of
randomly selected employed workers is separated from the firm with
which they had been matched. Thus, at the end of period ![]() a total of
a total of
![]() workers separate
from firms and
workers separate
from firms and ![]() workers remain attached to
their firm. Let
workers remain attached to
their firm. Let ![]() denote the unemployment rate
at time
denote the unemployment rate
at time ![]() so that the number of unemployed workers
at time
so that the number of unemployed workers
at time ![]() is
is
![]() . The sum of separated and
unemployed workers is given by:
. The sum of separated and
unemployed workers is given by:
We assume that a separated worker and an unemployed worker have an
equal probability, ![]() of exiting the labor
force. It follows that
of exiting the labor
force. It follows that ![]() times the number of separated
and unemployed workers,
times the number of separated
and unemployed workers,
![]() remain
in the labor force and search for work. We refer to
remain
in the labor force and search for work. We refer to ![]() as
the 'staying rate'.
as
the 'staying rate'.
The household chooses ![]() the number of workers
that it transfers from non-participation into the labor force.
Thus, the labor force in period
the number of workers
that it transfers from non-participation into the labor force.
Thus, the labor force in period ![]() is:
is:
| (2.1) |
By its choice of ![]() the household in effect chooses
the household in effect chooses
![]() The total number of workers searching
for a job at the start of
The total number of workers searching
for a job at the start of ![]() is:
is:
| (2.2) |
Here we have used (2.1)
to substitute out for ![]() on the left hand side of
(2.2).
on the left hand side of
(2.2).
It is of interest to calculate the probability, ![]() that a non-participating worker is selected to be in
the labor force. We assume that the
that a non-participating worker is selected to be in
the labor force. We assume that the
![]() workers
who separate exogenously into the non-participation state do not
return home in time to be included in the pool of workers relevant
to the household's choice of
workers
who separate exogenously into the non-participation state do not
return home in time to be included in the pool of workers relevant
to the household's choice of ![]() As a result,
the universe of workers from which the household selects
As a result,
the universe of workers from which the household selects
![]() is
is ![]() It follows
that
It follows
that ![]() is given by:8
is given by:8
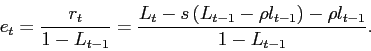 |
(2.3) |
The law of motion for employment is:
| (2.4) |
The job finding rate is the ratio of the number of new hires divided by the number of people searching for work, given by (2.2):
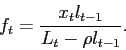 |
(2.5) |
2.2 Household Maximization
Members of the household derive utility from a market
consumption good and a good produced at home.9 The home good is
produced using the labor of individuals that are not in the labor
force, ![]() and the labor of the unemployed,
and the labor of the unemployed,
![]()
| (2.6) |
The term
![]() captures the idea that it is costly to change the number of people
who specialize in home production,
captures the idea that it is costly to change the number of people
who specialize in home production,
| (2.7) |
We assume
![]() so that in steady
state the unemployed contribute less to home production than do
people who are out of the labor force. Finally,
so that in steady
state the unemployed contribute less to home production than do
people who are out of the labor force. Finally, ![]() and
and ![]() are processes that
ensure balanced growth. We discuss these processes in detail below.
We included the adjustment costs in
are processes that
ensure balanced growth. We discuss these processes in detail below.
We included the adjustment costs in ![]() so that
the model can account for the gradual and hump-shaped response of
the labor force to a monetary policy shock (see subsection 4.3).
so that
the model can account for the gradual and hump-shaped response of
the labor force to a monetary policy shock (see subsection 4.3).
Workers experience no disutility from working and supply their labor inelastically. An employed worker brings home the wages that he earns. Unemployed workers receive government-provided unemployment compensation which they give to the household. Unemployment benefits are financed by lump-sum taxes paid by the household. The details of how workers find employment and receive wages are explained below. All household members have the same concave preferences over consumption, so each is allocated the same level of consumption.
The representative household maximizes the objective function:
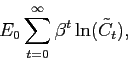 |
(2.8) |
where
Here, ![]() and
and ![]() denote
market consumption and consumption of the good produced at home.
The elasticity of substitution between
denote
market consumption and consumption of the good produced at home.
The elasticity of substitution between ![]() and
and
![]() is
is
![]() in steady
state
in steady
state![]() The parameter
The parameter ![]() controls the
degree of habit formation in household preferences. We assume
controls the
degree of habit formation in household preferences. We assume
![]() A bar over a variable indicates
its economy-wide average value.
A bar over a variable indicates
its economy-wide average value.
The flow budget constraint of the household is as follows:
| (2.9) |
The variable ![]() denotes lump-sum taxes net of
transfers and firm profits,
denotes lump-sum taxes net of
transfers and firm profits, ![]() denotes
beginning-of-period
denotes
beginning-of-period ![]() purchases of a nominal bond
which pays rate of return
purchases of a nominal bond
which pays rate of return ![]() at the start of
period
at the start of
period ![]() and
and ![]() denotes the
nominal rental rate of capital services. The variable
denotes the
nominal rental rate of capital services. The variable ![]() denotes the utilization rate of capital. As in
Christiano, Eichenbaum and Evans (2005) (CEE), we assume that the
household sells capital services in a perfectly competitive market,
so that
denotes the utilization rate of capital. As in
Christiano, Eichenbaum and Evans (2005) (CEE), we assume that the
household sells capital services in a perfectly competitive market,
so that
![]() represents the
household's earnings from supplying capital services.The increasing
convex function
represents the
household's earnings from supplying capital services.The increasing
convex function ![]() denotes the cost, in
units of investment goods, of setting the utilization rate
to
denotes the cost, in
units of investment goods, of setting the utilization rate
to![]() The variable
The variable ![]() denotes the nominal price of an investment good and
denotes the nominal price of an investment good and
![]() denotes household purchases of
investment goods. In addition, the nominal wage rate earned by an
employed worker is
denotes household purchases of
investment goods. In addition, the nominal wage rate earned by an
employed worker is ![]() and
and
![]() denotes exogenous
unemployment benefits received by unemployed workers from the
government. The term
denotes exogenous
unemployment benefits received by unemployed workers from the
government. The term ![]() is a process that
ensures balanced growth and will be discussed below.
is a process that
ensures balanced growth and will be discussed below.
When the household chooses ![]() it takes the
aggregate job finding rate,
it takes the
aggregate job finding rate, ![]() and the law of
motion linking
and the law of
motion linking ![]() and
and ![]() as
given:
as
given:
| (2.10) |
Relation (2.10) is
consistent with the actual law of motion of employment because of
the definition of ![]() (see (2.5)).
(see (2.5)).
The household owns the stock of capital which evolves according to,
| (2.11) |
The function ![]() is an increasing and convex
function capturing adjustment costs in investment. We assume that
is an increasing and convex
function capturing adjustment costs in investment. We assume that
![]() and its first derivative are both
zero along a steady state growth path.
and its first derivative are both
zero along a steady state growth path.
The household chooses state-contingent sequences,
![]() to maximize utility, (2.8),
subject to, (2.6), (2.7), (2.9), (2.10) and (2.11). The household
takes
to maximize utility, (2.8),
subject to, (2.6), (2.7), (2.9), (2.10) and (2.11). The household
takes ![]()
![]() ,
, ![]() and the state and date-contingent sequences,
and the state and date-contingent sequences,
![]() as given. As in CEE, we assume that the
as given. As in CEE, we assume that the ![]()
![]()
![]()
![]()
![]()
![]()
![]() decisions are made before the
realization of the current period monetary policy shock and after
the realization of the other shocks. This assumption captures the
notion that monetary policy shocks occur at a higher frequency of
time than the other shocks discussed below.
decisions are made before the
realization of the current period monetary policy shock and after
the realization of the other shocks. This assumption captures the
notion that monetary policy shocks occur at a higher frequency of
time than the other shocks discussed below.
2.3 Final Good Producers
A final homogeneous market good, ![]() is
produced by competitive and identical firms using the following
technology:
is
produced by competitive and identical firms using the following
technology:
![\begin{displaymath} Y_{t}=\left[ \int_{0}^{1}\left( Y_{j,t}\right) ^{\frac{1}{\lambda} }dj\right] ^{\lambda},\text{ } \end{displaymath}](img107.gif) |
(2.12) |
where ![]() The representative firm chooses
specialized inputs,
The representative firm chooses
specialized inputs, ![]() to maximize
profits:
to maximize
profits:
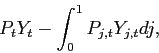
subject to the production function (2.12). The firm's
first order condition for the ![]() input is:
input is:
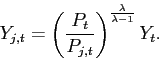 |
(2.13) |
2.4 Retailers
As in Ravenna and Walsh (2008), the ![]() input
good is produced by a monopolist retailer, with production
function:
input
good is produced by a monopolist retailer, with production
function:
| (2.14) |
The retailer is a monopolist in the product market and is
competitive in the factor markets. Here ![]() denotes
the total amount of capital services purchased by firm
denotes
the total amount of capital services purchased by firm ![]() . Also,
. Also,
![]() represents an exogenous
fixed cost of production, where
represents an exogenous
fixed cost of production, where ![]() is a positive
scalar and
is a positive
scalar and
![]() is a process, discussed
below, that ensures balanced growth. We calibrate the fixed cost so
that retailer profits are zero along the balanced growth path. In
(2.14),
is a process, discussed
below, that ensures balanced growth. We calibrate the fixed cost so
that retailer profits are zero along the balanced growth path. In
(2.14),
![]() is a technology shock whose properties
are discussed below. Finally,
is a technology shock whose properties
are discussed below. Finally, ![]() is the
quantity of an intermediate good purchased by the
is the
quantity of an intermediate good purchased by the ![]() retailer. This good is purchased in competitive markets
at the price
retailer. This good is purchased in competitive markets
at the price ![]() from a wholesaler.
Analogous to CEE, we assume that to produce in period
from a wholesaler.
Analogous to CEE, we assume that to produce in period ![]() the retailer must borrow a share
the retailer must borrow a share![]() of
of
![]() at the interest rate,
at the interest rate,
![]() that he expects to prevail in the
current period. In this way, the marginal cost of a
unit of
that he expects to prevail in the
current period. In this way, the marginal cost of a
unit of ![]() is
is
| (2.15) |
where![]() is the fraction of the intermediate
input that must be financed. The retailer repays the loan at the
end of period
is the fraction of the intermediate
input that must be financed. The retailer repays the loan at the
end of period ![]() after receiving sales revenues. The
after receiving sales revenues. The
![]() retailer sets its price,
retailer sets its price, ![]() subject to the demand curve, (2.13), and the Calvo
sticky price friction (2.16). In
particular,
subject to the demand curve, (2.13), and the Calvo
sticky price friction (2.16). In
particular,
![\begin{displaymath} P_{j,t}=\left\{ \begin{array}[c]{cl} P_{j,t-1} & \text{with probability }\xi\ \tilde{P}_{t} & \text{with probability }1-\xi \end{array}\right. . \end{displaymath}](img135.gif) |
(2.16) |
Here, ![]() denotes the price set by the
fraction
denotes the price set by the
fraction ![]() of producers who can re-optimize. We
assume these producers make their price decision before observing
the current period realization of the monetary policy shock, but
after the other time
of producers who can re-optimize. We
assume these producers make their price decision before observing
the current period realization of the monetary policy shock, but
after the other time ![]() shocks. Note that, unlike
CEE, we do not allow the non-optimizing firms to index their prices
to some measure of inflation. In this way, the model is consistent
with the observation that many prices remain unchanged for extended
periods of time (see Eichenbaum, Jaimovich and Rebelo, 2011, and
Klenow and Malin, 2011).
shocks. Note that, unlike
CEE, we do not allow the non-optimizing firms to index their prices
to some measure of inflation. In this way, the model is consistent
with the observation that many prices remain unchanged for extended
periods of time (see Eichenbaum, Jaimovich and Rebelo, 2011, and
Klenow and Malin, 2011).
2.5 Wholesalers and the Labor Market
A perfectly competitive representative wholesaler firm produces
the intermediate good using labor only. Let ![]() denote employment of the wholesaler at the end of period
denote employment of the wholesaler at the end of period
![]() Consistent with our discussion above, a
fraction
Consistent with our discussion above, a
fraction ![]() of workers separates exogenously from
the wholesaler at the end of period. A total of
of workers separates exogenously from
the wholesaler at the end of period. A total of ![]() workers are attached to the wholesaler at the
start of period
workers are attached to the wholesaler at the
start of period ![]() To meet a worker at the beginning
the period, the wholesaler must pay a fixed cost,
To meet a worker at the beginning
the period, the wholesaler must pay a fixed cost,
![]() , and post a suitable
number of vacancies. Here,
, and post a suitable
number of vacancies. Here, ![]() is a positive
scalar and
is a positive
scalar and
![]() is a process, discussed
below, that ensures balanced growth. To hire
is a process, discussed
below, that ensures balanced growth. To hire ![]() workers, the wholesaler must post
workers, the wholesaler must post
![]() vacancies where
vacancies where
![]() denotes the aggregate vacancy filling
rate which the representative firm takes as given. Posting
vacancies is costless. We assume that the representative firm is
large, so that if it posts
denotes the aggregate vacancy filling
rate which the representative firm takes as given. Posting
vacancies is costless. We assume that the representative firm is
large, so that if it posts
![]() vacancies, then it meets
exactly
vacancies, then it meets
exactly ![]() workers.
workers.
Because of the linearity of the firm's problem, in equilibrium
it must make zero profits. That is, the cost of a worker must equal
the value, ![]() of a worker:
of a worker:
| (2.17) |
where the objects in (2.17) are expressed in units of the final good.
At the beginning of the period, the representative
wholesaler is in contact with a total of ![]() workers (see equation (2.4)).
This pool of workers includes workers with whom the firm was
matched in the previous period, plus the new workers that the firm
has just met. Each worker in
workers (see equation (2.4)).
This pool of workers includes workers with whom the firm was
matched in the previous period, plus the new workers that the firm
has just met. Each worker in ![]() engages in
bilateral bargaining with a representative of the wholesaler,
taking the outcome of all other negotiations as given. The
equilibrium real wage rate,
engages in
bilateral bargaining with a representative of the wholesaler,
taking the outcome of all other negotiations as given. The
equilibrium real wage rate,
is the outcome of the bargaining process described below. In
equilibrium all bargaining sessions conclude successfully, so the
representative wholesaler employs ![]() workers
workers![]() Production begins immediately after wage
negotiations are concluded and the wholesaler sells the
intermediate good at the real price,
Production begins immediately after wage
negotiations are concluded and the wholesaler sells the
intermediate good at the real price,
![]() .
.
Consistent with Hall and Milgrom (2008) and CET, we assume that
wages are determined according to the alternating offer bargaining
protocol proposed in Rubinstein (1982) and Binmore, Rubinstein and
Wolinsky (1986). Let ![]() denote the expected
present discounted value of the wage payments by a firm to a worker
that it is matched with:
denote the expected
present discounted value of the wage payments by a firm to a worker
that it is matched with:
Here ![]() is the time
is the time ![]() household
discount factor which firms and workers view as an exogenous
stochastic process beyond their control.
household
discount factor which firms and workers view as an exogenous
stochastic process beyond their control.
The value of a worker to the firm, ![]() can be
expressed as follows:
can be
expressed as follows:
Here
![]() denotes the expected
present discounted value of the marginal revenue product associated
with a worker to the firm:
denotes the expected
present discounted value of the marginal revenue product associated
with a worker to the firm:
| (2.18) |
Let ![]() denote the value to a worker of being
matched with a firm that pays
denote the value to a worker of being
matched with a firm that pays ![]() in period
in period
![]()
| (2.19) |
Here, ![]() denotes the value of working
for another firm in period
denotes the value of working
for another firm in period ![]() . In equilibrium,
. In equilibrium,
![]() . Also,
. Also, ![]() in (2.19) is
the value of being an unemployed worker in period
in (2.19) is
the value of being an unemployed worker in period ![]() and
and ![]() is the value of being out-of-the
labor force in period
is the value of being out-of-the
labor force in period ![]() The objects,
The objects, ![]() ,
, ![]() and
and ![]() were
discussed in the previous section. Relation (2.19) reflects our
assumption that an employed worker remains in the same job with
probability
were
discussed in the previous section. Relation (2.19) reflects our
assumption that an employed worker remains in the same job with
probability ![]() transits to another job without
passing through unemployment with probability
transits to another job without
passing through unemployment with probability
![]() to
unemployment with probability
to
unemployment with probability
![]() and to
non-participation with probability
and to
non-participation with probability
![]()
It is convenient to rewrite (2.19) as follows:
| (2.20) |
where
| (2.21) |
According to (2.20),
![]() consists of two components. The first
is the expected present value of wages received by the worker from
the firm with which he is currently matched. The second corresponds
to the expected present value of the payments that a worker
receives in all dates and states when he is separated from that
firm.
consists of two components. The first
is the expected present value of wages received by the worker from
the firm with which he is currently matched. The second corresponds
to the expected present value of the payments that a worker
receives in all dates and states when he is separated from that
firm.
The value of unemployment, ![]() , is given
by,
, is given
by,
| (2.22) |
Recall that
![]() represents unemployment
compensation at time
represents unemployment
compensation at time ![]() The variable,
The variable,
![]() denotes the continuation value
of unemployment:
denotes the continuation value
of unemployment:
| (2.23) |
Expression (2.23) reflects
our assumption that an unemployed worker finds a job in the next
period with probability ![]() remains unemployed
with probability
remains unemployed
with probability
![]() and exits the labor
force with probability
and exits the labor
force with probability ![]()
The value of non-participation is:
| (2.24) |
Expression (2.24) reflects
our assumption that a non-participating worker is selected to join
the labor force with probability ![]() defined in (2.3).
defined in (2.3).
The structure of alternating offer bargaining is the same as it
is in CET. 10 Each matched worker-firm pair (both
those who just matched for the first time and those who were
matched in the past) bargain over the current wage rate,
![]() Each time period (a quarter) is
subdivided into
Each time period (a quarter) is
subdivided into ![]() periods of equal length, where
periods of equal length, where
![]() is even. The firm makes a wage offer at the
start of the first subperiod. It also makes an offer at the start
of every subsequent odd subperiod in the event that all previous
offers have been rejected. Similarly, workers make a wage offer at
the start of all even subperiods in case all previous offers have
been rejected. Because
is even. The firm makes a wage offer at the
start of the first subperiod. It also makes an offer at the start
of every subsequent odd subperiod in the event that all previous
offers have been rejected. Similarly, workers make a wage offer at
the start of all even subperiods in case all previous offers have
been rejected. Because ![]() is even, the last offer is
made, on a take-it-or-leave-it basis, by the worker. When the firm
rejects an offer it pays a cost,
is even, the last offer is
made, on a take-it-or-leave-it basis, by the worker. When the firm
rejects an offer it pays a cost,
![]() of making a
counteroffer. Here
of making a
counteroffer. Here ![]() is a positive scalar
and
is a positive scalar
and
![]() is a process that ensures
balanced growth.
is a process that ensures
balanced growth.
In subperiod
![]() the recipient of an offer can
either accept or reject it. If the offer is rejected the recipient
may declare an end to the negotiations or he may plan to make a
counteroffer at the start of the next subperiod. In the latter case
there is a probability,
the recipient of an offer can
either accept or reject it. If the offer is rejected the recipient
may declare an end to the negotiations or he may plan to make a
counteroffer at the start of the next subperiod. In the latter case
there is a probability, ![]() that bargaining breaks
down and the wholesaler and worker revert to their outside option.
For the firm, the value of the outside option is zero and for the
worker the outside option is unemployment.11 Given our
assumptions, workers and firms never choose to terminate bargaining
and go to their outside option.
that bargaining breaks
down and the wholesaler and worker revert to their outside option.
For the firm, the value of the outside option is zero and for the
worker the outside option is unemployment.11 Given our
assumptions, workers and firms never choose to terminate bargaining
and go to their outside option.
It is always optimal for the firm to offer the lowest wage rate subject to the condition that the worker does not reject it. To know what that wage rate is, the wholesaler must know what the worker would counteroffer in the event that the firm's offer was rejected. But, the worker's counteroffer depends on the firm's counteroffer in case the worker's counteroffer is rejected. We solve for the firm's initial offer beginning with the worker's final offer and working backwards. Since workers and firms know everything about each other, the firm's opening wage offer is always accepted.
Our environment is sufficiently simple that the solution to the bargaining problem has the following straightforward characterization:
| (2.25) |
where
![]() for
for
![]() and,
and,
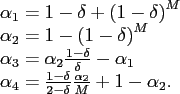
The technical appendix contains a detailed derivation of (2.25) and describes the procedure that we use for solving the bargaining problem.
To summarize, in period ![]() the problem of
wholesalers is to choose the hiring rate,
the problem of
wholesalers is to choose the hiring rate, ![]() and
to bargain with the workers that they meet. These activities occur
before the monetary policy shock is realized and after the other
shocks are realized.
and
to bargain with the workers that they meet. These activities occur
before the monetary policy shock is realized and after the other
shocks are realized.
2.6 Innovations to Technology
In this section we describe the laws of motion of
technology![]() Turning to the investment-specific
shock, we assume that
Turning to the investment-specific
shock, we assume that
![]() follows an AR(1) process
follows an AR(1) process
Here,
![]() is the innovation in
is the innovation in
![]() i.e., the error in the
one-step-ahead forecast of
i.e., the error in the
one-step-ahead forecast of
![]() based on the history of past
observations of
based on the history of past
observations of
![]()
For reasons explained later, it is convenient for our post-2008
analysis to adopt a components representation for neutral
technology.12 In particular, we assume that the
growth rate of neutral technology is the sum of a permanent
![]() and a transitory
and a transitory ![]() component:
component:
| (2.26) |
where
| (2.27) |
and
| (2.28) |
In (2.27) and (2.28),
![]() and
and
![]() are mean zero, unit
variance, iid shocks. To see why (2.28) is the
transitory component of
are mean zero, unit
variance, iid shocks. To see why (2.28) is the
transitory component of
![]() , suppose
, suppose
![]() so that
so that ![]() is the only component of technology and (ignoring
the constant term)
is the only component of technology and (ignoring
the constant term)
![]() or
or
Diving by ![]() where
where ![]() denotes the
lag operator, we have:
denotes the
lag operator, we have:
Thus, a shock to
![]() has only a transient effect
on the forecast of
has only a transient effect
on the forecast of
![]() . By contrast a shock,
say
. By contrast a shock,
say
![]() to
to
![]() shifts
shifts
![]() ,
,
![]() by the amount,
by the amount,
![]()
We assume that when there is a shock to
![]() agents do not know
whether it reflects the permanent or the temporary component. As a
result, they must solve a signal extraction problem when they
adjust their forecast of future values of
agents do not know
whether it reflects the permanent or the temporary component. As a
result, they must solve a signal extraction problem when they
adjust their forecast of future values of
![]() in response to an
unanticipated move in
in response to an
unanticipated move in
![]() Suppose, for
example, there is a shock to
Suppose, for
example, there is a shock to
![]() but that agents believe
most fluctuations in
but that agents believe
most fluctuations in
![]() reflect shocks to
reflect shocks to
![]() In this case they will
adjust their near term forecast of
In this case they will
adjust their near term forecast of
![]() leaving their
longer-term forecast of
leaving their
longer-term forecast of
![]() unaffected. As time
goes by and agents see that the change in
unaffected. As time
goes by and agents see that the change in
![]() is too persistent to
be due to the transitory component, the long-run component of their
forecast of
is too persistent to
be due to the transitory component, the long-run component of their
forecast of
![]() begins to adjust.
Thus, a disturbance in
begins to adjust.
Thus, a disturbance in
![]() triggers a sequence of
forecast errors for agents who cannot observe whether a shock to
triggers a sequence of
forecast errors for agents who cannot observe whether a shock to
![]() originates in the temporary or
permanent component of
originates in the temporary or
permanent component of ![]() (
(![]() .
.
Because agents do not observe the components of technology directly, they do not use the components representation to forecast technology growth. For forecasting, they use the univariate Wold representation that is implied by the components representation. The shocks to the permanent and transitory components of technology enter the system by perturbing the error in the Wold representation. To clarify these observations we first construct the Wold representation.
Multiply
![]() in (2.26) by
in (2.26) by
![]() where
where
![]() denotes the lag operator:
denotes the lag operator:
| (2.29) |
Let the stochastic process on the right of the equality be denoted
by
![]() . Evidently,
. Evidently,
![]() has a second order moving
average representation, which we express in the following form:
has a second order moving
average representation, which we express in the following form:
| (2.30) |
We obtain a mapping from
![]() to
to
![]() by first
computing the variance and two lagged covariances of the object to
the right of the first equality in (2.29). We then find
the values of
by first
computing the variance and two lagged covariances of the object to
the right of the first equality in (2.29). We then find
the values of ![]()
![]() and
and
![]() for which the variance and two
lagged covariances of
for which the variance and two
lagged covariances of
![]() and the object on the right
of the equality in (2.29)
are the same. In addition, we require that the eigenvalues in the
moving average representation of
and the object on the right
of the equality in (2.29)
are the same. In addition, we require that the eigenvalues in the
moving average representation of
![]() (2.30), lie inside the
unit circle. The latter condition is what guarantees that the shock
in the Wold representation is the innovation in technology. In sum,
the Wold representation for
(2.30), lie inside the
unit circle. The latter condition is what guarantees that the shock
in the Wold representation is the innovation in technology. In sum,
the Wold representation for
![]() is:
is:
| (2.31) |
The mapping from the structural shocks,
![]() and
and
![]() , to
, to ![]() is obtained by equating the objects on the right of
the equalities in (2.29)
and (2.30):
is obtained by equating the objects on the right of
the equalities in (2.29)
and (2.30):
| (2.32) |
According to this expression, if there is a positive disturbance to
![]() this triggers a sequence
of one-step-ahead forecast errors for agents, consistent with the
intuition described above.
this triggers a sequence
of one-step-ahead forecast errors for agents, consistent with the
intuition described above.
When we estimate our model, we treat the innovation in
technology, ![]() as a primitive and are not
concerned with the decomposition of
as a primitive and are not
concerned with the decomposition of ![]() into
the
into
the
![]() 's and
's and
![]() 's. In effect, we replace
the unobserved components representation of the technology shock
with its representation in (2.31). That
representation is an autoregressive, moving average representation
with two autoregressive parameters, two moving average parameters
and a standard deviation parameter. Thus, in principle it has five
free parameters. But, since the Wold representation is derived from
the unobserved components model, it has only four free parameters.
Specifically, we estimate the following parameters:
's. In effect, we replace
the unobserved components representation of the technology shock
with its representation in (2.31). That
representation is an autoregressive, moving average representation
with two autoregressive parameters, two moving average parameters
and a standard deviation parameter. Thus, in principle it has five
free parameters. But, since the Wold representation is derived from
the unobserved components model, it has only four free parameters.
Specifically, we estimate the following parameters:
![]() and the ratio
and the ratio
![]()
Although we do not make use of the decomposition of the
innovation, ![]() into the structural shocks
when we estimate our model, it turns out that the decomposition is
very useful for interpreting the post-2008 data.
into the structural shocks
when we estimate our model, it turns out that the decomposition is
very useful for interpreting the post-2008 data.
2.7 Market Clearing, Monetary Policy and Functional Forms
The total supply of the intermediate good is given by
![]() which equals the total quantity of
labor used by the wholesalers. So, clearing in the market for
intermediate goods requires
which equals the total quantity of
labor used by the wholesalers. So, clearing in the market for
intermediate goods requires
| (2.33) |
where
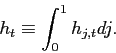
The capital services market clearing condition is:
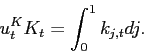
Market clearing for final goods requires:
| (2.34) |
The right hand side of the previous expression denotes the quantity
of final goods. The left hand side represents the various ways that
final goods are used. Homogeneous output, ![]() can
be converted one-for-one into either consumption goods, goods used
to hire workers, or government purchases,
can
be converted one-for-one into either consumption goods, goods used
to hire workers, or government purchases, ![]() . In
addition, some of
. In
addition, some of ![]() is absorbed by capital
utilization costs. Homogeneous output,
is absorbed by capital
utilization costs. Homogeneous output, ![]() can also
be used to produce investment goods using a linear technology in
which one unit of the final good is transformed into
can also
be used to produce investment goods using a linear technology in
which one unit of the final good is transformed into ![]() units of
units of ![]() Perfect competition in
the production of investment goods implies,
Perfect competition in
the production of investment goods implies,
Finally, clearing in the loan market requires that the demand for
loans by wholesalers,
![]() , equals the supply,
, equals the supply, ![]()
We adopt the following specification of monetary policy:
![\begin{align} \ln(R_{t}/R) & =\rho_{R}\ln(R_{t-1}/R) \ & +\left( 1-\rho_{R}\right) \left[ 0.25r_{\pi}\ln\left( \frac{\pi_{t}^{A} }{\pi^{A}}\right) +r_{y}\ln\left( \frac{\mathcal{Y}_{t}}{\mathcal{Y} _{t}^{\ast}}\right) +0.25r_{\Delta y}\ln\left( \frac{\mathcal{Y}_{t}}{ \mathcal{Y}_{t-4}\mu_{\mathcal{Y}}^{A}}\right) \right] +\sigma _{R}\varepsilon_{R,t},\nonumber \end{align}](img303.gif) |
(2.35) |
where
![]() and
and
![]() is the monetary authority's inflation
target
is the monetary authority's inflation
target![]() The object,
The object, ![]() is also
the value of
is also
the value of ![]() in nonstochastic steady
state. The shock,
in nonstochastic steady
state. The shock,
![]() is a unit variance, zero
mean and serially uncorrelated disturbance to monetary policy. The
variable,
is a unit variance, zero
mean and serially uncorrelated disturbance to monetary policy. The
variable,
![]() denotes Gross Domestic
Product (GDP):
denotes Gross Domestic
Product (GDP):
where ![]() denotes government consumption, which
is assumed to have the following representation:
denotes government consumption, which
is assumed to have the following representation:
| (2.36) |
Here, ![]() is a process that guarantees
balanced growth and
is a process that guarantees
balanced growth and ![]() is an exogenous
stochastic process. The variable,
is an exogenous
stochastic process. The variable,
![]() is defined as
follows:
is defined as
follows:
| (2.37) |
where ![]() is a process that guarantees
balanced growth and
is a process that guarantees
balanced growth and ![]() is a constant chosen to
guarantee that
is a constant chosen to
guarantee that
![]() converges to zero in nonstochastic steady state. The constant,
converges to zero in nonstochastic steady state. The constant,
![]() is the value of
is the value of
![]() in
nonstochastic steady state
in
nonstochastic steady state![]() Also,
Also, ![]() denotes the steady state value of
denotes the steady state value of ![]()
The sources of long-term growth in our model are the neutral and
investment-specific technological progress shocks discussed in the
previous subsection. The growth rate in steady state for the model
variables is a composite, ![]() of these
two technology shocks:
of these
two technology shocks:
The variables
![]() and
and
![]() converge to
constants in nonstochastic steady state.
converge to
constants in nonstochastic steady state.
If objects like the fixed cost of production, the cost of
hiring, etc., were constant, they would become irrelevant over
time. To avoid this implication, it is standard in the literature
to suppose that such objects are proportional to the underlying
source of growth, which is ![]() in our
setting. However, this assumption has the unfortunate implication
that technology shocks of both types have an immediate effect on
the vector of objects
in our
setting. However, this assumption has the unfortunate implication
that technology shocks of both types have an immediate effect on
the vector of objects
| (2.38) |
Such a specification seems implausible and so we instead proceed as
in Christiano, Trabandt and Walentin (2012) and
Schmitt-Grohé and Uribe (2012). In particular, we suppose
that the objects in ![]() are proportional to
a long moving average of composite technology,
are proportional to
a long moving average of composite technology, ![]()
| (2.39) |
where ![]() denotes the
denotes the ![]() element of
element of ![]() ,
, ![]() . Also,
. Also, ![]() is a
parameter to be estimated. Note that
is a
parameter to be estimated. Note that ![]() has the same growth rate in steady state as GDP. When
has the same growth rate in steady state as GDP. When ![]() is very close to zero,
is very close to zero, ![]() is
virtually unresponsive in the short-run to an innovation in either
of the two technology shocks, a feature that we find very
attractive on a priori grounds.
is
virtually unresponsive in the short-run to an innovation in either
of the two technology shocks, a feature that we find very
attractive on a priori grounds.
We adopt the investment adjustment cost specification proposed in CEE. In particular, we assume that the cost of adjusting investment takes the form:
![\begin{align*} S\left( I_{t}/I_{t-1}\right) & =0.5\exp\left[ \sqrt{S^{\prime\prime}} \left( I_{t}/I_{t-1}-\mu_{\Phi}\times\mu_{\Psi}\right) \right] \ & +0.5\exp\left[ -\sqrt{S^{\prime\prime}}\left( I_{t}/I_{t-1}-\mu_{\Phi }\times\mu_{\Psi}\right) \right] -1. \end{align*}](img343.gif)
Here, ![]() and
and ![]() denote the steady state growth rates of
denote the steady state growth rates of ![]() and
and
![]() . The value of
. The value of ![]() in nonstochastic steady state is
in nonstochastic steady state is
![]() In addition,
In addition,
![]() represents a model
parameter that coincides with the second derivative of
represents a model
parameter that coincides with the second derivative of
![]() , evaluated in steady
state
, evaluated in steady
state![]() It is straightforward to verify that
It is straightforward to verify that
![]() Our specification of the adjustment costs has the convenient
feature that the steady state of the model is independent of the
value of
Our specification of the adjustment costs has the convenient
feature that the steady state of the model is independent of the
value of
![]()
We assume that the cost associated with setting capacity utilization is given by,
where ![]() and
and ![]() are
positive scalars. We normalize the steady state value of
are
positive scalars. We normalize the steady state value of
![]() to unity, so that the adjustment
costs are zero in steady state, and
to unity, so that the adjustment
costs are zero in steady state, and ![]() is
equated to the steady state of the appropriately scaled rental rate
on capital. Our specification of the cost of capacity utilization
and our normalization of
is
equated to the steady state of the appropriately scaled rental rate
on capital. Our specification of the cost of capacity utilization
and our normalization of ![]() in steady state has
the convenient implication that the model steady state is
independent of
in steady state has
the convenient implication that the model steady state is
independent of ![]()
Finally, we discuss the determination of the equilibrium vacancy
filling rate, ![]() We posit a standard matching
function:
We posit a standard matching
function:
| (2.40) |
where ![]() denotes the economy-wide average
number of vacancies and
denotes the economy-wide average
number of vacancies and ![]() denotes the aggregate
vacancy rate. Then,
denotes the aggregate
vacancy rate. Then,
| (2.41) |
3. Data and Econometric Methodology for Pre-2008 Sample
We estimate our model using a Bayesian variant of the strategy in CEE that minimizes the distance between the dynamic response to three shocks in the model and the analog objects in the data. The latter are obtained using an identified VAR for post-war quarterly U.S. times series that include key labor market variables. The particular Bayesian strategy that we use is the one developed in Christiano, Trabandt and Walentin (2011), henceforth CTW.
CTW estimate a 14 variable VAR using quarterly data that are
seasonally adjusted and cover the period 1951Q1 to 2008Q4. To
facilitate comparisons, our analysis is based on the same VAR that
CTW use. As in CTW, we identify the dynamic responses to a monetary
policy shock by assuming that the monetary authority observes the
current and lagged values of all the variables in the VAR, and that
a monetary policy shock affects only the Federal Funds Rate
contemporaneously. As in Altig, Christiano, Eichenbaum and Linde
(2011), Fisher (2006) and CTW, we make two assumptions to identify
the dynamic responses to the technology shocks: (i) the only shocks
that affect labor productivity in the long-run are the innovations
to the neutral technology shock, ![]() and the
innovations to the investment-specific technology shock
and the
innovations to the investment-specific technology shock
![]() and (ii) the only
shocks that affects the price of investment relative to consumption
in the long-run are the innovations to the investment-specific
technology shock
and (ii) the only
shocks that affects the price of investment relative to consumption
in the long-run are the innovations to the investment-specific
technology shock
![]() . These assumptions are
satisfied in our model. Standard lag-length selection criteria lead
CTW to work with a VAR with 2 lags.13 The assumptions used
to identify the effects of monetary policy and technology shocks
are satisfied in our model.
. These assumptions are
satisfied in our model. Standard lag-length selection criteria lead
CTW to work with a VAR with 2 lags.13 The assumptions used
to identify the effects of monetary policy and technology shocks
are satisfied in our model.
We include the following variables in the VAR:
![\begin{displaymath} \left( \begin{array}[c]{c} \Delta\ln(\text{relative price of investment}_{t}\text{)}\ \Delta\ln(\operatorname{real}GDP_{t}/\text{hours}_{t})\ \Delta\ln(GDP\text{ deflator}_{t})\ \text{unemployment rate}_{t}\ \ln(\text{capacity utilization}_{t})\ \ln(\text{hours}_{t})\ \ln(\operatorname{real}GDP_{t}/\text{hours}_{t})-\ln(\text{real wage} _{t}\text{)}\ \ln(\text{nominal }C_{t}/\text{nominal }GDP_{t})\ \ln(\text{nominal }I_{t}/\text{nominal }GDP_{t})\ \ln(\text{job vacancies}_{t})\ \text{job separation rate}_{t}\ \text{job finding rate}_{t}\ \ln\left( \text{hours}_{t}/\text{labor force}_{t}\right) \ \text{federal funds rate}_{t} \end{array}\right) . \end{displaymath}](img370.gif) |
(3.1) |
See section A of the technical appendix in CTW for details about
the data. Here, we briefly discuss the job vacancy data. Our time
series on vacancies splices together a help-wanted index produced
by the Conference Board with a job openings measure produced by the
Bureau of Labor Statistics in their Job Openings and Labor Turnover
Survey (JOLTS). According to JOLTS, a 'job opening' is a position
that the firm would fill in the event that a suitable candidate
appears. A job vacancy in our model corresponds to this definition
of a 'job opening'. To see this, recall that in our model the
representative firm is large. We can think of our firm as
consisting of a large number of plants. Suppose that the firm wants
to hire ![]() people per plant when the vacancy filling
rate is
people per plant when the vacancy filling
rate is ![]() The firm instructs each plant to post
The firm instructs each plant to post
![]() vacancies with the understanding that
each vacancy which generates a job application will be turned into
a match.14 This is the sense in which vacancies
in our model meet the JOLTS definition of a job opening. Of course,
it is possible that the people responding to the JOLTS survey
report job opening numbers that correspond more closely to
vacancies with the understanding that
each vacancy which generates a job application will be turned into
a match.14 This is the sense in which vacancies
in our model meet the JOLTS definition of a job opening. Of course,
it is possible that the people responding to the JOLTS survey
report job opening numbers that correspond more closely to
![]() To the extent that this is true, the JOLTS
data should be thought of as a noisy indicator of vacancies in our
model. This measurement issue is not unique to our model. It arises
in the standard search and matching model (see, for example, Shimer
(2005)).
To the extent that this is true, the JOLTS
data should be thought of as a noisy indicator of vacancies in our
model. This measurement issue is not unique to our model. It arises
in the standard search and matching model (see, for example, Shimer
(2005)).
Given an estimate of the VAR we compute the implied impulse
response functions to the three structural shocks. We stack the
contemporaneous and 14 lagged values of each of these impulse
response functions for 13 of the variables listed above in a
vector, ![]() We do not include the job
separation rate because that variable is constant in our model. We
include the job separation rate in the VAR to ensure the VAR
results are not driven by an omitted variable bias.
We do not include the job
separation rate because that variable is constant in our model. We
include the job separation rate in the VAR to ensure the VAR
results are not driven by an omitted variable bias.
The logic underlying our model estimation procedure is as
follows. Suppose that our structural model is true. Denote the true
values of the model parameters by ![]() Let
Let
![]() denote the
model-implied mapping from a set of values for the model parameters
to the analog impulse responses in
denote the
model-implied mapping from a set of values for the model parameters
to the analog impulse responses in ![]() Thus,
Thus,
![]() denotes the
true value of the impulse responses whose estimates appear in
denotes the
true value of the impulse responses whose estimates appear in
![]() According to standard classical
asymptotic sampling theory, when the number of observations,
According to standard classical
asymptotic sampling theory, when the number of observations,
![]() is large, we have
is large, we have
Here, ![]() denotes the true values of the
parameters of the shocks in the model that we do not formally
include in the analysis. Because we solve the model using a
log-linearization procedure,
denotes the true values of the
parameters of the shocks in the model that we do not formally
include in the analysis. Because we solve the model using a
log-linearization procedure,
![]() is not a
function of
is not a
function of ![]() However, the sampling
distribution of
However, the sampling
distribution of ![]() is a function of
is a function of
![]() We find it convenient to express
the asymptotic distribution of
We find it convenient to express
the asymptotic distribution of ![]() in the
following form:
in the
following form:
| (3.2) |
where
For simplicity our notation does not make the dependence of
![]() on
on
![]() and
and ![]() explicit. We use a consistent estimator of
explicit. We use a consistent estimator of ![]() Motivated by small sample considerations, that estimator has only
diagonal elements (see CTW). The elements in
Motivated by small sample considerations, that estimator has only
diagonal elements (see CTW). The elements in ![]() are graphed in Figures 1-3 (see the
solid lines). The gray areas are centered, 95 percent
probability intervals computed using our estimate of
are graphed in Figures 1-3 (see the
solid lines). The gray areas are centered, 95 percent
probability intervals computed using our estimate of ![]() .
.
In our analysis, we treat ![]() as the
observed data. We specify priors for
as the
observed data. We specify priors for ![]() and then
compute the posterior distribution for
and then
compute the posterior distribution for ![]() given
given
![]() using Bayes' rule. This
computation requires the likelihood of
using Bayes' rule. This
computation requires the likelihood of ![]() given
given ![]() Our asymptotically valid
approximation of this likelihood is motivated by (3.2):
Our asymptotically valid
approximation of this likelihood is motivated by (3.2):
![\begin{displaymath} f\left( \hat{\psi}\vert\theta,V\right) =\left( \frac{1}{2\pi}\right) ^{\frac{N }{2}}\left\vert V\right\vert ^{-\frac{1}{2}}\exp\left[ -\frac{1}{2}\left( \hat{\psi}-\psi\left( \theta\right) \right) ^{\prime}V^{-1}\left( \hat{ \psi}-\psi\left( \theta\right) \right) \right] . \end{displaymath}](img406.gif) |
(3.3) |
The value of ![]() that maximizes the above function
represents an approximate maximum likelihood estimator of
that maximizes the above function
represents an approximate maximum likelihood estimator of
![]() It is approximate for three reasons:
(i) the central limit theorem underlying (3.2) only holds
exactly as
It is approximate for three reasons:
(i) the central limit theorem underlying (3.2) only holds
exactly as
![]() (ii) our proxy for
(ii) our proxy for
![]() is guaranteed to be correct only for
is guaranteed to be correct only for
![]() and (iii)
and (iii)
![]() is calculated using
a linear approximation.
is calculated using
a linear approximation.
Treating the function, ![]() as the likelihood
of
as the likelihood
of ![]() it follows that the Bayesian
posterior of
it follows that the Bayesian
posterior of ![]() conditional on
conditional on ![]() and
and ![]() is:
is:
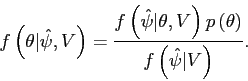 |
(3.4) |
Here,
![]() denotes the priors on
denotes the priors on
![]() and
and
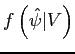 denotes the
marginal density of
denotes the
marginal density of ![]()
The mode of the posterior distribution of ![]() is
computed by maximizing the value of the numerator in (3.4), since the
denominator is not a function of
is
computed by maximizing the value of the numerator in (3.4), since the
denominator is not a function of ![]()
4. Empirical Results, Pre-2008 Sample
This section presents results for the estimated model. First, we discuss the priors and posteriors of structural parameters. Second, we discuss the ability of the model to account for the dynamic response of the economy to a monetary policy shock, a neutral technology shock and an investment-specific technology shock.
4.1 Calibration and Parameter Values Set a Priori
We set the values for a subset of the model parameters a priori.
These values are reported in Panel A of Table 1. We also set the
steady state values of five model variables, listed in Panel B of
Table 1. We specify ![]() so that the steady state
annual real rate of interest is three percent. The depreciation
rate on capital,
so that the steady state
annual real rate of interest is three percent. The depreciation
rate on capital, ![]() is set to imply an annual
depreciation rate of 10 percent. The growth rate of
composite technology,
is set to imply an annual
depreciation rate of 10 percent. The growth rate of
composite technology, ![]() is equated to the
sample average of real per capita GDP growth. The growth rate of
investment-specific technology,
is equated to the
sample average of real per capita GDP growth. The growth rate of
investment-specific technology, ![]() is set so
that
is set so
that
![]() is equal to the sample
average of real, per capita investment growth. We assume the
monetary authority's inflation target is 2 percent
per year and that the profits of intermediate good producers are
zero in steady state. We set the steady state value of the vacancy
filling rate,
is equal to the sample
average of real, per capita investment growth. We assume the
monetary authority's inflation target is 2 percent
per year and that the profits of intermediate good producers are
zero in steady state. We set the steady state value of the vacancy
filling rate, ![]() to 0.7, as in den Haan,
Ramey and Watson (2000) and Ravenna and Walsh (2008). The steady
state unemployment rate,
to 0.7, as in den Haan,
Ramey and Watson (2000) and Ravenna and Walsh (2008). The steady
state unemployment rate, ![]() is set to the average
unemployment rate in our sample, 0.05. We assume the parameter
is set to the average
unemployment rate in our sample, 0.05. We assume the parameter
![]() to be equal to 60 which
roughly corresponds to the number of business days in a quarter. We
set
to be equal to 60 which
roughly corresponds to the number of business days in a quarter. We
set ![]() which implies a match survival rate
that is consistent with both HM and Shimer (2012). Finally, we
assume that the steady state value of the ratio of government
consumption to gross output is 0.20.
which implies a match survival rate
that is consistent with both HM and Shimer (2012). Finally, we
assume that the steady state value of the ratio of government
consumption to gross output is 0.20.
Two additional parameters pertain to the household sector. We
set the elasticity of substitution in household utility between
home and market produced goods,
![]() to 3. This magnitude
is similar to what is reported in Aguiar, Hurst and Karabarbounis
(2013).15 We set the steady state labor force
to population ratio,
to 3. This magnitude
is similar to what is reported in Aguiar, Hurst and Karabarbounis
(2013).15 We set the steady state labor force
to population ratio, ![]() to 0.67.
to 0.67.
To make the model consistent with the 5 calibrated values for
![]()
![]()
![]()
![]() and profits, we select values for 5
parameters: the weight of market consumption in the utility
function,
and profits, we select values for 5
parameters: the weight of market consumption in the utility
function, ![]() the constant in front of the
matching function,
the constant in front of the
matching function, ![]() the fixed cost of
production,
the fixed cost of
production, ![]() the cost for the firm to make a
counteroffer,
the cost for the firm to make a
counteroffer, ![]() and the scale parameter,
and the scale parameter,
![]() in government consumption. The values for
these parameters, evaluated at the posterior mode of the set of
parameters that we estimate, are reported in Table 3.
in government consumption. The values for
these parameters, evaluated at the posterior mode of the set of
parameters that we estimate, are reported in Table 3.
4.2 Parameter Estimation
The priors and posteriors for the model parameters about which we do Bayesian inference are summarized in Table 2. A number of features of the posterior mode of the estimated parameters of our model are worth noting.
First, the posterior mode of ![]() implies a
moderate degree of price stickiness, with prices changing on
average once every 4 quarters. This value lies
within the range reported in the literature.
implies a
moderate degree of price stickiness, with prices changing on
average once every 4 quarters. This value lies
within the range reported in the literature.
Second, the posterior mode of ![]() implies that
there is a roughly 0.05 percent chance of an
exogenous break-up in negotiations when a wage offer is
rejected.
implies that
there is a roughly 0.05 percent chance of an
exogenous break-up in negotiations when a wage offer is
rejected.
Third, the posterior modes of our model parameters, along with the assumption that the steady state unemployment rate equals 5.5 percent, implies that it costs firms 0.81 days of marginal revenue to prepare a counteroffer during wage negotiations (see Table 3).
Fourth, the posterior mode of steady state hiring costs as a percent of gross output is equal to 0.5 percent. This result implies that steady state hiring costs as a percent of total wages of newly-hired workers is equal to 7 percent. Silva and Toledo (2009) report that, depending on the exact costs included, the value of this statistic is between 4 and 14 percent, a range that encompasses the corresponding statistic in our model.
Fifth, the posterior mode of the replacement ratio is 0.19. To put this number in perspective, consider the following narrow measure of the fraction of unemployment benefits to wages in the data. The numerator of the fraction is total payments of the government for unemployment insurance divided by the total number of unemployed people. The denominator of the fraction is total compensation of labor divided by the number or employees, i.e. the average wage per worker. The average of the numerator divided by denominator in our sample period is 0.14. This fraction represents the lower bound on the average replacement rate because it leaves out some other government contributions that unemployed people are eligible for. HM summarize the literature and report a range of estimates from 0.12 to 0.36 for the replacement ratio. It is well know that Diamond (1982), Mortensen (1982) and Pissarides (1985) (DMP) style models require a replacement ratio in excess of 0.9 to account for fluctuations in labor markets (see e.g. CET for an extended discussion). For the reasons stressed in CET, alternating offer bargaining between workers and firms mutes the sensitivity of real wages to aggregate shocks. This property underlies our model's ability to account for the estimated response of the economy to monetary policy shocks and shocks to neutral and investment-specific technology with a low replacement ratio.
Sixth, the posterior mode of ![]() implies that a
separated or unemployed worker leaves the labor force with
probability
implies that a
separated or unemployed worker leaves the labor force with
probability ![]()
Seventh, the posterior mode for ![]() is
0.02, implying that people out-of-the labor
force account for virtually all of home production.
is
0.02, implying that people out-of-the labor
force account for virtually all of home production.
Eighth, the posterior mode of ![]() which governs
the responsiveness of the elements of
which governs
the responsiveness of the elements of ![]() to
technology shocks, is small (0.16). So, variables
like government purchases and unemployment benefits are very
unresponsive in the short-run to technology shocks.
to
technology shocks, is small (0.16). So, variables
like government purchases and unemployment benefits are very
unresponsive in the short-run to technology shocks.
Ninth, the posterior modes of the parameters governing monetary policy are similar to those reported in the literature (see for example Justiniano, Primiceri, and Tambalotti, 2010).
Tenth, we turn to the parameters of the unobserved components representation of the neutral technology shock. According to the posterior mode, the standard deviation of the shock to the transient component is roughly 5 times the standard deviation of the permanent component. So, according to the posterior mode, most of the fluctuations (at least, at a short horizon) are due to the transitory component of neutral technology. This result is driven primarily by our prior, the rationale for which is discussed in section 5.2. The permanent component of neutral technology has an autocorrelation of roughly 0.8, so that a one percent shock to the permanent component eventually drives the level of technology up by about 5 percent. The temporary component is also fairly highly autocorrelated.
Many authors conclude that the growth rate of neutral technology
follows roughly a random walk (see, for example, Prescott, 1986).
Our model is consistent with this view. We find that the first
order autocorrelation of
![]() in our model
is 0.06, which is very close to zero. For
discussions of how a components representation, in which the
components are both highly autocorrelated, can nevertheless
generate a process that looks like a random walk, see Christiano
and Eichenbaum (1990) and Quah (1990).
in our model
is 0.06, which is very close to zero. For
discussions of how a components representation, in which the
components are both highly autocorrelated, can nevertheless
generate a process that looks like a random walk, see Christiano
and Eichenbaum (1990) and Quah (1990).
Table 4 reports the frequency with which workers transit between the three states that they can be in. The table reports the steady state frequencies implied by the model and the analog statistics calculated from data from the Current Population Survey. Note that we did not use these data statistics when we estimated or calibrated the model.16 Nevertheless, with two minor exceptions, the model does very well at accounting for those statistics of the data. The exceptions are that the model somewhat understates the frequency of transition from unemployment into unemployment and slightly overstates the frequency of transition from unemployment to out-of-the labor force. Finally, we note that in the data over half of newly employed people are hired from other jobs (see Diamond 2010, page 316). Our model is consistent with this fact: in the steady state of the model, 51 percent of newly employed workers in a given quarter come from other jobs.17 Overall, we view these findings as additional evidence in support of the notion that our model of the labor market is empirically plausible.
4.3 Impulse Response Functions
The solid black lines in Figures 1-3 present the impulse response functions to a monetary policy shock, a neutral technology shock and an investment-specific technology shock implied by the estimated VAR. The grey areas represent 95 percent probability intervals. The solid blue lines correspond to the impulse response functions of our model evaluated at the posterior mode of the structural parameters. Figure 1 shows that the model does very well at reproducing the estimated effects of an expansionary monetary policy shock, including the hump-shaped rises in real GDP and hours worked, the rise in the labor force participation rate and the muted response of inflation. Notice that real wages respond by much less than hours worked to a monetary policy shock. Even though the maximal rise in hours worked is roughly 0.14 percent, the maximal rise in real wages is only 0.06 percent. Significantly, the model accounts for the hump-shaped fall in the unemployment rate as well as the rise in the job finding rate and vacancies that occur after an expansionary monetary policy shock. The model does understate the rise in the capacity utilization rate. The sharp rise of capacity utilization in the estimated VAR may reflect that our data on the capacity utilization rate pertains to the manufacturing sector, which probably overstates the average response across all sectors in the economy.
From Figure 2 we see that the model does a good job of
accounting for the estimated effects of a negative innovation,
![]() to neutral technology (see
(2.31)). Note that the
model is able to account for the initial fall and subsequent
persistent rise in the unemployment rate. The model also accounts
for the initial rise and subsequent fall in vacancies and the job
finding rate after a negative shock to neutral technology. The
model is consistent with the relatively small response of the labor
force participation rate to a technology shock.
to neutral technology (see
(2.31)). Note that the
model is able to account for the initial fall and subsequent
persistent rise in the unemployment rate. The model also accounts
for the initial rise and subsequent fall in vacancies and the job
finding rate after a negative shock to neutral technology. The
model is consistent with the relatively small response of the labor
force participation rate to a technology shock.
Turning to the response of inflation after a negative neutral technology shock, note that our VAR implies that the maximal response occurs in the period of the shock.18 Our model has no problem reproducing this observation. See CTW for intuition.
Figure 3 reports the VAR-based estimates of the responses to an
investment-specific technology shock. The figure also displays the
responses to
![]() implied by our model
evaluated at the posterior mode of the parameters. Note that in all
cases the model impulses lie in the 95 percent probability interval
of the VAR-based impulse responses.
implied by our model
evaluated at the posterior mode of the parameters. Note that in all
cases the model impulses lie in the 95 percent probability interval
of the VAR-based impulse responses.
Viewed as a whole, the results of this section provide evidence that our model does well at accounting for the cyclical properties of key labor market and other macro variables in the pre-2008 period.
5. Modeling The Great Recession
In this section we provide a quantitative characterization of the Great Recession. We suppose that the economy was buffeted by a sequence of shocks that began in 2008Q3. Using simple projection methods, we estimate how the economy would have evolved in the absence of those shocks. The difference between how the economy would have evolved and how it did evolve is what we define as the Great Recession. We then extend our modeling framework to incorporate four candidate shocks that in principle could have caused the Great Recession. In addition, we provide an interpretation of monetary policy during the Great Recession, allowing for a binding ZLB and forward guidance. Finally, we discuss our strategy for stochastically simulating our model.
5.1 Characterizing the Great Recession
The solid line in Figure 4 displays the behavior of key macroeconomic variables since 2001. To assess how the economy would have evolved absent the large shocks associated with the Great Recession, we adopt a simple and transparent procedure. With five exceptions, we fit a linear trend from 2001Q1 to 2008Q2, represented by the dashed red line. To characterize what the data would have looked like absent the shocks that caused the financial crisis and Great Recession, we extrapolate the trend line (see the thin dashed line) for each variable. According to our model, all the nonstationary variables in the analysis are difference stationary. Our linear extrapolation procedure implicitly assumes that the shocks in the period 2001-2008 were small relative to the drift terms in the time series. Given this assumption, our extrapolation procedure approximately identifies how the data would have evolved, absent shocks after 2008Q2.
Four of the exceptions to our extrapolation method are inflation, the federal funds rate, the unemployment rate and the job finding rate. For these variables, we assume a no-change trajectory after 2008Q2. In the case of these four variables, our linear projection procedure led to implausible results. For example, the federal funds rate would be projected to be almost 6 percent in 2013Q2.
The fifth exception pertains to a measure of the spread between the corporate-borrowing rate and the risk-free interest rate. The measure that we use corresponds to the one provided in Gilchrist and Zakrajšek (2012) (GZ). These data are displayed in the (3,4) element of Figure 4. Our projection for the period after 2008Q2 is that the GZ spread falls linearly to 1 percent, its value during the relatively tranquil period, 1990-1997.
There are of course many alternative procedures for projecting the behavior of the economy. For example, we could use separate ARMA time series models for each of the variables or we could use multivariate methods including the VAR estimated with pre-2008Q2 data. A challenge for a multivariate approach is the nonlinearity associated with the ZLB. Still, it would be interesting to pursue alternative projection approaches in the future.
The projections for the labor force and employment after 2008Q2 are controversial because of ongoing demographic changes in the U.S. population. Our procedure attributes roughly 1.5 percentage points of the 2.5 percentage points decline in the labor force participation rate since 2008 to cyclical factors. Projections for the labor force to population ratio published by the Bureau of Labor Statistics in November 2007 suggest that the cyclical component in the decline in this ratio was roughly 2 percentage points.19 Reifschneider, Wascher and Wilcox (2013) and Sullivan (2013) estimate that the cyclical component of the decline in the labor force to population ratio is equal to 1 percentage point and 0.75 percentage points, respectively. So, we are roughly at the mid-point of these estimates.
According to Figure 4, the employment to population ratio fell by about 5 percentage points from 2008 to 2013. According to our procedure only a small part, about 0.5 percentage points, of this drop is accounted for by non-cyclical factors. Krugman (2014) argues that 1.6 percentage points of the 5 percentage points are due to demographic factors. So, like us, he ascribes a small portion of the decline in the employment to population ratio to non-cyclical factors. In contrast, Tracy and Kapon (2014) argue that the cyclical component of the decline was smaller. To the extent that this is true, it would be easier for our model to account for the data. In this sense we are adopting a conservative stance.
The distances between the solid lines and the thin-dashed lines in Figure 4 represents our estimates of the economic effects of the shocks that hit the economy in 2008Q3 and later. In effect, these distances are the Great Recession targets that we seek to explain.
Some features of the targets are worth emphasizing. First, there is large drop in log GDP. While some growth began in late 2009, per capita GDP has still not returned to its pre-crisis level as of the end of our sample. Second, there was a very substantial decline in consumption and investment. While the latter showed strong growth since late 2009 it has not yet surpassed its pre-crisis peak in per capita terms. Strikingly, although per capita consumption initially grew starting in late 2009, it stopped growing around the middle of 2012. The stop of consumption growth is mirrored by a slowdown in the growth rate of GDP and investment at around the same time.
An obvious candidate for a macro shock during this time period were the events surrounding the debt ceiling crisis and the sequester. It is obviously difficult to pick one particular date for when agents took seriously the possibility that the U.S. government was going to fall off the fiscal cliff. Still, it is interesting to note that in Spring 2012, Chairman Bernanke warned lawmakers of a 'massive fiscal cliff' involving year-end tax increases and spending cuts.20
Third, vacancies dropped sharply before 2009 and then rebounded almost to their pre-recession levels. At the same time, unemployment rose sharply, but then only fell modestly. Kocherlakota (2010) interprets these observations as implying that firms had positions to fill, but the unemployed workers were simply not suitable. This explanation is often referred to as the mismatch hypothesis. Davis, Faberman, and Haltiwanger (2012) provide a different interpretation of these observations. In their view, what matters for filling jobs is the intensity of firms' recruiting efforts, not vacancies per se. They argue that the intensity with which firms recruited workers after 2009 did not rebound in the same way that vacancies did. Perhaps surprisingly, our model can account for the joint behavior of unemployment and vacancies, even though the forces stressed by Kocherlakota and Davis, et al. are absent from our framework.
Finally, we note that despite the steep drop in GDP, inflation dropped by only about 1/2 - 1 percentage points. Authors like Hall (2011) argue that this joint observation is particularly challenging for NK models.
5.2 The Shocks Driving the Great Recession
We suppose that the Great Recession was triggered by four shocks. Two of these shocks are wedges which capture in a reduced form way frictions which are widely viewed as having been important during the Great Recession. The other sources of shocks that we allow for are government consumption and technology.
We begin by discussing the two financial shocks. The first is a
shock to households preferences for safe and/or liquid assets. We
capture this shock by introducing a perturbation,
![]() to agents' intertemporal
Euler equation associated with saving via risk-free bonds. The
object,
to agents' intertemporal
Euler equation associated with saving via risk-free bonds. The
object,
![]() is the consumption
wedge we discussed in the introduction. The Euler equation
associated with the nominally risk-free bond is given by:
is the consumption
wedge we discussed in the introduction. The Euler equation
associated with the nominally risk-free bond is given by:
See Fisher (2014) for a discussion of how a positive realization of
![]() can, to a first-order
approximation, be interpreted as reflecting an increase in the
demand for risk-free bonds.21
can, to a first-order
approximation, be interpreted as reflecting an increase in the
demand for risk-free bonds.21
We do not have data on
![]() We suppose that in 2008Q3,
agents think that
We suppose that in 2008Q3,
agents think that
![]() goes from zero to a constant
value, 0.33 percent per quarter, for 20 quarters,
i.e. until 2013Q2. They expected
goes from zero to a constant
value, 0.33 percent per quarter, for 20 quarters,
i.e. until 2013Q2. They expected
![]() to return to zero after that
date (see the dashed line in the (2,2) element in Figure 7). We
then assume that in 2012Q3, agents revised their expectations and
thought that
to return to zero after that
date (see the dashed line in the (2,2) element in Figure 7). We
then assume that in 2012Q3, agents revised their expectations and
thought that
![]() would remain at 0.33 percent until 2014Q3. We interpret this revision to
expectations as a response to the events associated with the fiscal
cliff and the sequester. We chose the particular value of
would remain at 0.33 percent until 2014Q3. We interpret this revision to
expectations as a response to the events associated with the fiscal
cliff and the sequester. We chose the particular value of
![]() to help the model achieve our
targets.
to help the model achieve our
targets.
To assess the magnitude of the shock to ![]() , it is useful to think of
, it is useful to think of ![]() as a shock to agents' discount rate. Recall from Table 1 that
as a shock to agents' discount rate. Recall from Table 1 that
![]() implying an annual discount
rate of about 1.3 percent.22 With
implying an annual discount
rate of about 1.3 percent.22 With ![]() the discount factor is in effect
the discount factor is in effect
![]() which
implies an annual discount rate of roughly zero percent.23 So,
our
which
implies an annual discount rate of roughly zero percent.23 So,
our ![]() shock implies that the annual
discount rate drops 1.3 percentage points. This
drop is substantially smaller than the 6 percentage point drop
assumed by Eggertsson and Woodford (2003).
shock implies that the annual
discount rate drops 1.3 percentage points. This
drop is substantially smaller than the 6 percentage point drop
assumed by Eggertsson and Woodford (2003).
The second financial shock represents a wedge to agents' intertemporal Euler equation for capital accumulation:
A simple financial friction model based on asymmetric information
with costly monitoring implies that credit market frictions can be
captured as a tax,
![]() on the gross return on
capital (see Christiano and Davis (2006)). The object,
on the gross return on
capital (see Christiano and Davis (2006)). The object,
![]() , is the financial wedge
that we discussed in the introduction.
, is the financial wedge
that we discussed in the introduction.
Recall that firms finance a fraction,
![]() , of the intermediate input in advance of revenues (see (2.15)). In contrast
to the existing DSGE literature, we allow for a risky working
capital channel in the sense that the financial wedge also
applies to working capital loans. Specifically, we replace
(2.15) with
, of the intermediate input in advance of revenues (see (2.15)). In contrast
to the existing DSGE literature, we allow for a risky working
capital channel in the sense that the financial wedge also
applies to working capital loans. Specifically, we replace
(2.15) with
| (5.1) |
where
![]() =1/2 as before. The risky working
capital channel captures in a reduced form way the frictions
modeled in e.g. Bigio (2013).
=1/2 as before. The risky working
capital channel captures in a reduced form way the frictions
modeled in e.g. Bigio (2013).
We measure the financial wedge using the GZ interest rate
spread. The latter is based on the average credit spread on senior
unsecured bonds issued by non-financial firms covered in Compustat
and by the Center for Research in Security Prices. The average and
median duration of the bonds in GZ's data is 6.47 and 6.00 years,
respectively. We interpret the GZ spread as an indicator of
![]() . We suppose that the
. We suppose that the
![]() 's are related to the GZ spread
as follows:
's are related to the GZ spread
as follows:
![\begin{displaymath} \Gamma_{t}=E\left[ \frac{\Delta_{t}^{k}+\Delta_{t+1}^{k}+...+\Delta _{t+23}^{k}}{6}\vert\Omega_{t}\right] , \end{displaymath}](img524.gif) |
(5.2) |
where ![]() denotes the GZ spread minus the
projection of that spread as of 2008Q2. Also,
denotes the GZ spread minus the
projection of that spread as of 2008Q2. Also, ![]() denotes the information available to agents at time
denotes the information available to agents at time
![]() In (5.2) we sum over
In (5.2) we sum over
![]() for
for ![]() because
because
![]() is a tax on the one quarter
return to capital while
is a tax on the one quarter
return to capital while ![]() applies to
applies to
![]()
![]() (i.e., 6
years). Also, we divide the sum in (5.2) by 6 to take
into account that
(i.e., 6
years). Also, we divide the sum in (5.2) by 6 to take
into account that
![]() is measured in quarterly
decimal terms while our empirical measure of
is measured in quarterly
decimal terms while our empirical measure of ![]() is measured in annual decimal terms.
is measured in annual decimal terms.
We feed the difference between the projected and actual
![]() 's, for
's, for ![]() 2008Q3, to the model. The projected and
actual
2008Q3, to the model. The projected and
actual ![]() 's are displayed in the (3,4)
element of Figure 4. The difference is displayed in the (1,1)
element of Figure 7. We assume that at each date agents must
forecast the future values of the
's are displayed in the (3,4)
element of Figure 4. The difference is displayed in the (1,1)
element of Figure 7. We assume that at each date agents must
forecast the future values of the ![]() 's.
They do so using a mean zero, first order autoregressive
representation (AR(1)), with autoregressive coefficient,
's.
They do so using a mean zero, first order autoregressive
representation (AR(1)), with autoregressive coefficient,
![]() This low value of
This low value of
![]() captures the idea that agents
thought the sharp increase in the financial wedge was transitory in
nature. This belief is consistent with the actual behavior of the
GZ spread. To solve their problem, agents actually work with the
captures the idea that agents
thought the sharp increase in the financial wedge was transitory in
nature. This belief is consistent with the actual behavior of the
GZ spread. To solve their problem, agents actually work with the
![]() 's. But, for any sequence,
's. But, for any sequence,
![]()
![]()
![]() , they can compute a sequence,
, they can compute a sequence,
![]()
![]()
![]() that satisfies (5.2). 24
that satisfies (5.2). 24
We now turn to a discussion of TFP. Various measures produced by the Bureau of Labor Statistics (BLS) are reported in the (1,1) panel of Figure 5. Each measure is the log of value-added minus the log of capital and labor services weighted by their shares in the income generated in producing the measure of value-added.25 In each case, we report a linear trend line fitted to the data from 2001Q1 through 2008Q2. We then project the numbers forward after 2008Q2. We do the same for three additional measures of TFP in the (1,2) panel of Figure 5. Two are taken from Fernald (2012) and the third is taken from the Penn World Tables. The bottom panel of Figure 5 displays the post-2008Q2 projection for log TFP minus the log of its actual value. Note that, with one exception, (i) TFP is below its pre-2008 trend during the Great Recession, and (ii) it remains well below its pre-2008 trend all the way up to the end of our data set. The exception is Fernald's (2012) utilization adjusted TFP measure, which briefly rises above trend in 2009. Features (i) and (ii) of TFP play an important role in our empirical results.
To assess the robustness of (i) and (ii), we redid our calculations using an alternative way of computing the trend lines. Figure 6 reproduces the basic calculations for three of our TFP measures using a linear trend that is constructed using data starting in 1982Q2. While there are some interesting differences across the figures, they have all share the two key features, (i) and (ii), discussed above. Specifically, it appears that TFP was persistently low during the Great Recession.
We now explain why we adopt an unobserved components time series
representation of
![]() If we assume that
agents knew in 2008Q3 that the fall in TFP would turn out to be so
persistent, then our model generates a counterfactual surge in
inflation. We infer that agents only gradually became aware of the
persistence in the decline of TFP. The notion that it took agents
time to realize that the drop in TFP was highly persistent is
consistent with other evidence. For example, Figure 4 in Swanson
and Williams (2013) shows that professional forecasts consistently
underestimated how long it would take the economy to emerge from
the ZLB.
If we assume that
agents knew in 2008Q3 that the fall in TFP would turn out to be so
persistent, then our model generates a counterfactual surge in
inflation. We infer that agents only gradually became aware of the
persistence in the decline of TFP. The notion that it took agents
time to realize that the drop in TFP was highly persistent is
consistent with other evidence. For example, Figure 4 in Swanson
and Williams (2013) shows that professional forecasts consistently
underestimated how long it would take the economy to emerge from
the ZLB.
The previous considerations are the reason that we work with the
unobserved components representation for
![]() in (2.26). In addition,
these considerations underlie our prior that the standard deviation
of the transitory shock is substantially larger than the standard
deviation of the permanent shock. We imposed this prior in
estimating the model on pre-2008 data.
in (2.26). In addition,
these considerations underlie our prior that the standard deviation
of the transitory shock is substantially larger than the standard
deviation of the permanent shock. We imposed this prior in
estimating the model on pre-2008 data.
At this point, it is worth to repeat the observation made in section 4.2 that we have not assumed anything particularly exotic about technology growth. As noted above, our model implies that the growth rate of technology is roughly a random walk, in accordance with a long tradition in business cycle theory. What our analysis in effect exploits is that a process that is as simple as a random walk can have components that are very different from a random walk.
Our analysis involves simulating the response of the model to
shocks. So, we must compute a sequence of realized values of
![]() Unlike government
spending and interest rate spreads, we do not directly observe
Unlike government
spending and interest rate spreads, we do not directly observe
![]() In our model log TFP
does not coincide with
In our model log TFP
does not coincide with
![]() . The principle reason
for this is the presence of the fixed cost in production in our
model. But, the behavior of model-implied TFP is sensitive to
. The principle reason
for this is the presence of the fixed cost in production in our
model. But, the behavior of model-implied TFP is sensitive to
![]()
To our initial surprise, the behavior is also very sensitive to
![]() So, from this
perspective both inflation and TFP contain substantial information
about
So, from this
perspective both inflation and TFP contain substantial information
about
![]() These observations
led us to choose a sequence of realized values for
These observations
led us to choose a sequence of realized values for
![]() that, conditional on
the other shocks, allows the model to account reasonably well for
inflation and log TFP.
that, conditional on
the other shocks, allows the model to account reasonably well for
inflation and log TFP.
The bottom panel of Figure 5 reports the measure of TFP for our model, computed using a close variant of the Bureau of Labor Statistics' procedure. 26 The black line with dots displays the model's simulated value of TFP relative to trend (how we detrend and solve the model is discussed below). Note that model TFP lies within the range of empirical measures reported in Figure 5. The bottom panel of Figure 6 shows that we obtain the same result when we detrend our three empirical measures of TFP when using a trend that begins in 1982.
Nonlinear versions of the standard Kalman smoothing methods
could be used to combine our model, the values for its parameters,
and our data to estimate the sequence of
![]() (and,
(and,
![]() ) in the post 2008Q2 data. In
practice, this approach is computationally challenging and we defer
it to future work.27 For convenience, we assume there was
a one-time shock to
) in the post 2008Q2 data. In
practice, this approach is computationally challenging and we defer
it to future work.27 For convenience, we assume there was
a one-time shock to
![]() in 2008Q3. For the
reasons given above, we assume that the shock was to the permanent
component of
in 2008Q3. For the
reasons given above, we assume that the shock was to the permanent
component of
![]() i.e.,
i.e.,
![]() We selected a value of
-0.25 percent for that shock so that, in
conjunction with our other assumptions, the model does a reasonable
job of accounting for post 2008Q2 inflation and log TFP. This
one-time shock leads to a persistent move in
We selected a value of
-0.25 percent for that shock so that, in
conjunction with our other assumptions, the model does a reasonable
job of accounting for post 2008Q2 inflation and log TFP. This
one-time shock leads to a persistent move in
![]() which eventually puts
which eventually puts
![]() roughly 1.2 percent below the level it
would have been in the absence of the shock. The shock to
roughly 1.2 percent below the level it
would have been in the absence of the shock. The shock to
![]() also leads to a sequence
of one-step-ahead forecast errors for agents, via (2.32). Our
specification of
also leads to a sequence
of one-step-ahead forecast errors for agents, via (2.32). Our
specification of
![]() captures features (i)
and (ii) of the TFP data that were discussed above.
captures features (i)
and (ii) of the TFP data that were discussed above.
Next we consider the shock to government consumption. The
variable ![]() defined in (2.36) is computed
using the simulated path of neutral technology,
defined in (2.36) is computed
using the simulated path of neutral technology,
![]() (see (2.38) and (2.39)).28
Then,
(see (2.38) and (2.39)).28
Then, ![]() is measured by dividing actual
government consumption in Figure 4, by
is measured by dividing actual
government consumption in Figure 4, by ![]() Agents forecast the period
Agents forecast the period ![]() value of
value of
![]() using current and past
realizations of the technology shocks. We assume that agents
forecast
using current and past
realizations of the technology shocks. We assume that agents
forecast ![]() by using the following AR(2)
process:
by using the following AR(2)
process:
where
![]() is a mean zero, unit
variance iid shock. We chose the roots for the AR(2) process such
that the first and second order autocorrelations of
is a mean zero, unit
variance iid shock. We chose the roots for the AR(2) process such
that the first and second order autocorrelations of
![]() in our estimated model are
close to the data for the sample 1951Q1 to 2008Q2.
in our estimated model are
close to the data for the sample 1951Q1 to 2008Q2.
5.3 Monetary Policy
We make two key assumptions about monetary policy during the post 2008Q3 period. We assume that the Fed initially followed a version of the Taylor rule that respects the ZLB on the nominal interest rate. We assume that there was an unanticipated regime change in 2011Q3, when the Fed switched to a policy of forward guidance.
5.3.1 Taylor Rule
We now define our version of the Taylor rule that takes the
non-negativity constraint on the nominal interest rate into
account. Let ![]() denote a gross 'shadow' nominal
rate of interest, which satisfies the following Taylor-style
monetary policy rule:
denote a gross 'shadow' nominal
rate of interest, which satisfies the following Taylor-style
monetary policy rule:
| (5.3) |
The actual policy rate, ![]() is determined as
follows:
is determined as
follows:
| (5.4) |
In 2008Q2, the federal funds rate was close to two percent (see
Figure 4). Consequently, because of the ZLB, the federal funds rate
could only fall by at most two percentage points. To capture this
in our model, we set the scalar ![]() to 1.004825.
to 1.004825.
Absent the ZLB constraint, the policy rule given by (5.3)-(5.4) coincides with (2.35), the policy rule that we estimated using pre-2008 data.
5.3.2 Forward Guidance
We interpret forward guidance as a monetary policy that commits to keeping the nominal interest rate zero until there is substantial improvement in the state of the economy. Initially, in 2011Q3 the Fed did not quantify what they meant by 'substantial improvement'. Instead, they reported how long they thought it would take until economic conditions would have improved substantially. In December 2012 the Fed became more explicit about what the state of the economy would have to be for them to consider leaving the ZLB. In particular, the Fed said that it would keep the interest rate at zero as long as inflation remains below 2.5 percent and unemployment remains above 6.5 percent. They did not commit to any particular action in case one or both the thresholds are breached.
In modeling forward guidance we begin with the period, 2011Q3-2012Q4. We do not know what the Fed's thresholds were during this period. But, we do know that in 2011Q3, the Fed announced that it expected the interest rate to remain at zero until mid-2013 (see Campbell, et al., 2012). According to Swanson and Williams (2013), when the Fed made its announcement the number of quarters that professional forecasters expected the interest rate to remain at zero jumped from 4 quarters to 7 or more quarters. We assume that forecasters believed the Fed's announcement and thought that the nominal interest rate would be zero for about 8 quarters. Interestingly, Swanson and Williams (2013) also report that forecasters continued to expect the interest rate to remain at zero for 7 or more quarters in each month through January 2013. Clearly, forecasters were repeatedly revising upwards their expectation of how long the ZLB episode would last. To capture this scenario in a parsimonious way we assume that in each quarter, beginning in 2011Q3 and ending in 2012Q4, agents believed the ZLB would remain in force for another 8 quarters. Thereafter, we suppose that they expected the Fed to revert back to the Taylor rule, (5.3) and (5.4).29
Beginning in 2013Q1, we suppose that agents believed the Fed switched to an explicit threshold rule. Specifically, we assume that agents thought the Fed would keep the Federal Funds rate close to zero until either the unemployment rate fell below 6.5 percent or inflation rose above 2.5 percent. We assume that as soon as these thresholds are met, the Fed switches back to our estimated Taylor rule, (5.3) and (5.4). The latter feature of our rule is an approximation because, as noted above, the Fed did not announce what it would do when the thresholds were met.
5.4 Solving the Model
Our specification of monetary policy includes a non-negativity
constraint on the nominal interest rate, as well as regime
switching. A subset of the latter depend on realizations of
endogenous variables. We search for a solution to our model in the
space of sequences.30 The solution satisfies the
equilibrium conditions which take the form of a set of stochastic
difference equations that are restricted by initial and end-point
conditions. Our solution strategy makes one approximation:
certainty equivalence. That is, wherever an expression like
![]() is encountered,
we replace it by
is encountered,
we replace it by
![]() for
for ![]()
Let ![]() denote the vector of shocks operating
in the post-2008Q2 period:
denote the vector of shocks operating
in the post-2008Q2 period:
The law of motion and agents' information sets about
Let ![]() denote the
denote the ![]() vector of period
vector of period ![]() endogenous
variables, appropriately scaled to account for steady growth. We
express the equilibrium conditions of the model as follows:
endogenous
variables, appropriately scaled to account for steady growth. We
express the equilibrium conditions of the model as follows:
| (5.5) |
Here, the information set is given by
Our solution strategy proceeds as follows. As discussed above,
we fix a sequence of values for ![]() for the periods
after 2008Q2. We suppose that at date
for the periods
after 2008Q2. We suppose that at date ![]() agents
observe
agents
observe ![]()
![]() for each
for each
![]() after 2008Q2. At each such date
after 2008Q2. At each such date ![]() they compute forecasts,
they compute forecasts, ![]()
![]()
![]() of the future values of
of the future values of
![]() . It is convenient to use the notation
. It is convenient to use the notation
![]()
We adopt an analogous notation for ![]() In
particular, denote the expected value of
In
particular, denote the expected value of ![]() formed at time
formed at time ![]() by
by
![]() , where
, where
![]() The
equilibrium value of
The
equilibrium value of ![]() is the first
element in the sequence,
is the first
element in the sequence,
![]()
![]() To
compute this sequence we require
To
compute this sequence we require ![]()
![]() and
and
![]() For
For ![]() greater
than 2008Q3 we set
greater
than 2008Q3 we set
![]() For
For
![]() corresponding to 2008Q3, we set
corresponding to 2008Q3, we set ![]() to its non-stochastic steady state value.
to its non-stochastic steady state value.
We now discuss how we computed
![]()
![]() We
do so by solving the equilibrium conditions and imposing certainty
equivalence. In particular,
We
do so by solving the equilibrium conditions and imposing certainty
equivalence. In particular,
![]() must satisfy:
must satisfy:
![]()
Evidently, to solve for
![]() requires
requires
![]() Relation (5.5) implies:
Relation (5.5) implies:
Proceeding in this way, we obtain a sequence of equilibrium
conditions involving
![]()
![]() Solving for this sequence requires a terminal condition. We obtain
this condition by imposing that
Solving for this sequence requires a terminal condition. We obtain
this condition by imposing that
![]() converges to the
non-stochastic steady state value of
converges to the
non-stochastic steady state value of ![]() With this procedure it is straightforward to implement our
assumptions about monetary policy.
With this procedure it is straightforward to implement our
assumptions about monetary policy.
6. The Great Recession: Empirical Results
In this section we analyze the behavior of the economy from 2008Q3 to the end of our sample, 2013Q2. First, we investigate how well our model accounts for the data. Second, we use our model to assess which shocks account for the Great Recession. In addition, we also investigate the role of the risky working capital channel and forward guidance.
6.1 The Model's Implications for the Great Recession
Figure 8 displays our empirical characterization of the Great Recession, i.e., the difference between how the economy would have evolved absent the post 2008Q2 shocks and how it did evolve. In addition, we display the relevant model analogs. For this, we assume that the economy would have been on its steady state growth path in the absence of the post-2008Q2 shocks. This is an approximation that simplifies the analysis and is arguably justified by the fact that the volatility of the economy is much greater after 2008 than it was before. The model analog to our empirical characterization of the Great Recession is the log difference between the variables on the steady state growth path and their response to the post-2008Q2 shocks.
Figure 8 indicates that the model does quite well at accounting for the behavior of our 11 endogenous variables during the Great Recession. Notice in particular that the model is able to account for the modest decline in real wages despite the absence of nominal rigidities in wage setting. Also, notice that the model accounts very well for the average level of inflation despite the fact that our model incorporates only a moderate degree of price stickiness: firms change prices on average once a year. In addition, the model also accounts well for the key labor market variables: labor force participation, employment, unemployment, vacancies and the job finding rate.
Figure 9 provides another way to assess the model's implications
for vacancies and unemployment. There, we report a scatter plot
with vacancies on the vertical axis and unemployment on the
horizontal. The variables in Figure 9 are taken from the 2,1 and
4,1 panels of Figure 8. Although the variables are expressed in
deviations from trend, the resulting Beveridge curve has the same
key features as those in the raw data (see, for example, Diamond
2010, Figure 4). In particular, notice how actual vacancies fall
and unemployment rises from late 2008 to late 2009. This downward
relationship is referred to as the Beveridge curve. After 2009,
vacancies rise but unemployment falls by less than one would have
predicted based on the Beveridge curve that existed before 2009.
That is, it appears that after 2009 there was a shift up in the
Beveridge curve. This shift is often interpreted as reflecting a
deterioration in match efficiency, captured in a simple environment
like ours by a fall in the parameter governing productivity in the
matching function (see ![]() in (2.40)). This
interpretation reflects a view that models like ours imply a stable
downward relationship between vacancies and unemployment, which can
only be perturbed by a change in match efficiency. However, this
downward relationship is in practice derived as a steady state
property of models, and is in fact not appropriate for interpreting
quarterly data. To explain this, we consider a simple
example.31
in (2.40)). This
interpretation reflects a view that models like ours imply a stable
downward relationship between vacancies and unemployment, which can
only be perturbed by a change in match efficiency. However, this
downward relationship is in practice derived as a steady state
property of models, and is in fact not appropriate for interpreting
quarterly data. To explain this, we consider a simple
example.31
Suppose that the matching function is given by:
where ![]()
![]() and
and ![]() denote hires, vacancies and unemployment, respectively.
Also,
denote hires, vacancies and unemployment, respectively.
Also, ![]() denotes a productivity parameter
that can potentially capture variations in match efficiency.
Dividing the matching function by the number of unemployed, we
obtain the job finding rate
denotes a productivity parameter
that can potentially capture variations in match efficiency.
Dividing the matching function by the number of unemployed, we
obtain the job finding rate
![]() so that:
so that:
The simplest search and matching model assumes that the labor force is constant so that:
where ![]() denotes employment and the labor force
is assumed to be of size unity. The change in the number of people
unemployed is given by:
denotes employment and the labor force
is assumed to be of size unity. The change in the number of people
unemployed is given by:
where
![]() denotes the
employed workers that separate into unemployment in period
denotes the
employed workers that separate into unemployment in period
![]() and
and ![]() is the
number of unemployed workers who find jobs. In steady state,
is the
number of unemployed workers who find jobs. In steady state,
![]() so that:
so that:
Combining this expression with the definition of the finding rate
and solving for ![]() we obtain:
we obtain:
![\begin{displaymath} V_{t}=\left[ \frac{\left( 1-\rho\right) \left( 1-U_{t}\right) } {\sigma_{m,t}U_{t}^{1-\alpha}}\right] ^{\frac{1}{\alpha}} \end{displaymath}](img655.gif) |
(6.1) |
This equation clearly implies (i) a negative relationship between ![]() and
and ![]() and (ii) the
only way that relationship can shift is with a change in the value
of
and (ii) the
only way that relationship can shift is with a change in the value
of ![]() or in the value of the other
matching function parameter,
or in the value of the other
matching function parameter, ![]() .32
Results (i) and (ii) are apparently very robust, as they do not
require taking a stand on many key relations in the overall
economy. In the technical appendix, we derive a similar result for
our model, which also does not depend on most of our model details,
such as the costs for arranging meetings between workers and firms,
the determination of the value of a job, etc.
.32
Results (i) and (ii) are apparently very robust, as they do not
require taking a stand on many key relations in the overall
economy. In the technical appendix, we derive a similar result for
our model, which also does not depend on most of our model details,
such as the costs for arranging meetings between workers and firms,
the determination of the value of a job, etc.
While the steady state Beveridge curve described in the previous
paragraph may be useful for many purposes, it is misleading for
interpreting data from the Great Recession, when the steady state
condition,
![]() is far from being satisfied.
To see this, note in Figure 9 that our model is able to account for
the so-called shift in the Beveridge curve, even though the
productivity parameter in our matching function is constant. The
only difference between the analysis in Figure 9 and our model's
steady state Beveridge curve is that we do not impose the
is far from being satisfied.
To see this, note in Figure 9 that our model is able to account for
the so-called shift in the Beveridge curve, even though the
productivity parameter in our matching function is constant. The
only difference between the analysis in Figure 9 and our model's
steady state Beveridge curve is that we do not impose the
![]() condition. Thus, according to
our analysis the data on vacancies and unemployment present no
reason to suppose that there has been a deterioration in match
efficiency. No doubt such a deterioration has occurred to some
extent, but it does not seem to be a first order feature of the
Great Recession.
condition. Thus, according to
our analysis the data on vacancies and unemployment present no
reason to suppose that there has been a deterioration in match
efficiency. No doubt such a deterioration has occurred to some
extent, but it does not seem to be a first order feature of the
Great Recession.
We conclude this section by noting that our model does not fully account for the Great Recession targets in the case of two variables. First, it does not capture the full magnitude of the collapse in investment in 2009. In the data, the maximal drop is a little less than 40 percent while in the model the drop is a little over 25 percent. After 2010 the model and data line up reasonably well with respect to investment. Second, the model does not account for the sharp drop in consumption relative to trend that began in 2012.
6.2 The Causes of the Great Recession
Figures 10 through 14 decompose the impact of the different shocks and the risky working capital channel on the economy in the post 2008Q3 period. We determine the role of a shock by setting that shock to its steady state value and redoing the simulations underlying Figure 8. The resulting decomposition is not additive because of the nonlinearities in the model.
Figure 10 displays the effect of the neutral technology shock on
post-2008 simulations. For convenience, the solid line reproduces
the corresponding solid line in Figure 8. The dashed line displays
the behavior of the economy when neutral technology shock is shut
down (i.e.,
![]() in 2008Q3). Comparing
the solid and dashed lines, we see that the neutral technology
slowdown had a significant impact on inflation. Had it not been for
the decline in neutral technology, there would have been
substantial deflation, as predicted by very simple NK models that
do not allow for a drop in technology during the ZLB period. The
negative technology shock also pushes up output, investment,
consumption, employment and the labor force. Abstracting from
wealth effects on labor force participation, a fall in neutral
technology raises marginal cost and, hence, inflation. In presence
of the ZLB, the latter effect lowers the real interest rate,
driving up aggregate spending and, hence, output and employment. In
fact, the wealth effect of a negative technology shock does lead to
an increase in the labor force participation rate. Other things the
same, this effect exerts downward pressure on the wage and, hence,
on marginal cost. Evidently, this effect is outweighed by the
direct effect of the negative technology shock, so that marginal
costs rise.33
in 2008Q3). Comparing
the solid and dashed lines, we see that the neutral technology
slowdown had a significant impact on inflation. Had it not been for
the decline in neutral technology, there would have been
substantial deflation, as predicted by very simple NK models that
do not allow for a drop in technology during the ZLB period. The
negative technology shock also pushes up output, investment,
consumption, employment and the labor force. Abstracting from
wealth effects on labor force participation, a fall in neutral
technology raises marginal cost and, hence, inflation. In presence
of the ZLB, the latter effect lowers the real interest rate,
driving up aggregate spending and, hence, output and employment. In
fact, the wealth effect of a negative technology shock does lead to
an increase in the labor force participation rate. Other things the
same, this effect exerts downward pressure on the wage and, hence,
on marginal cost. Evidently, this effect is outweighed by the
direct effect of the negative technology shock, so that marginal
costs rise.33
Medium-sized DSGE models typically abstract from the working capital channel. A natural question is: how important is that channel in allowing our model to account for the moderate degree of inflation during the Great Recession? To answer that question, we redo the simulation underlying Figure 8, replacing (5.1) with (2.15). The results are displayed in Figure 11. We find that the risky working capital channel plays a very important role in allowing the model to account for the moderate decline in inflation that occurred during the Great Recession. In the presence of a risky working capital requirement, a higher interest rate due to a positive financial wedge shock directly raises firms' marginal cost. Other things equal, this rise leads to inflation. Gilchrist, Schoenle, Sim and Zakrajšek (2013) provide firm-level evidence consistent with the importance of our risky working capital channel. They find that firms with bad balance sheets raise prices relative to firms with good balance sheets. From our perspective, firms with bad balance sheets face a very high cost of working capital and therefore, high marginal costs.
Taken together, the negative technology shocks and the risky working capital channel explain the relatively modest disinflation that occurred during the Great Recession. Essentially they exerted countervailing pressure on the disinflationary forces that were operative during the Great Recession. The output effects of the risky working capital channel are much weaker than those of the neutral technology shocks. In part this reflects the fact that the working capital risk channel works via the financial wedge shocks and these are much less persistent than the technology shocks.
Figures 12 and 13 report the effects of the financial and consumption wedges, respectively. The latter plays an important role in driving the economy into the ZLB and has substantial effects on real quantities and inflation. The fact that the nominal interest rate remains at zero after 2011 when there is no consumption wedge reflects our specification of monetary policy. The financial wedge has a relatively small impact on inflation and on the interest rate, but it has an enormous impact on real quantities. For example, the financial wedge is overwhelmingly the most important shock for investment. Notice that the model attributes the substantial drop in the labor force participation rate almost entirely to the consumption and financial wedges. This reflects that these wedges lead to a sharp deterioration in labor market conditions: drops in the job vacancy and finding rates and in the real wage. We do not think these wedge shocks were important in the pre-2008 period. In this way, the model is consistent with the fact that labor force participation rates are not very cyclical during normal recessions, while being very cyclical during the Great Recession.34
We now turn to Figure 14, which analyzes the role of government consumption in the Great Recession. Government consumption passes through two phases (see Figure 7). The first phase corresponds to the expansion associated with the American Recovery and Reinvestment Act of 2009. The second phase involves a contraction that began at the start of 2011. The first phase involves a maximum rise of 3 percent in government consumption (i.e., 0.6 percent relative to steady state GDP) and a maximum rise of 1.4 percent in GDP. This implies a maximum government consumption multiplier of 1.4/.6 or 2.17. In the second phase the decline in government spending is much more substantial, falling a maximum of nearly 10 percent, or 2 percent relative to steady state GDP. At the same time, the resulting drop in GDP is about 1.5 percent (see Figure 14). So, in the second phase, the government spending multiplier is only 1.5/2 or 0.75. In light of this result, it is difficult to attribute the long duration of the Great Recession to the recent decline in government consumption.
The second phase findings may at first seem inconsistent with existing analyses, which suggest that the government consumption multiplier may be very large in the ZLB. Indeed, Christiano, Eichenbaum and Rebelo (2011) show that a rise in government consumption that is expected to not extend beyond the ZLB has a large multiplier effect. But, they also show that a rise in government consumption that is expected to extend beyond the ZLB has a relatively small multiplier effect. The intuition for this is straightforward. An increase in spending after the ZLB ceases to bind has no direct impact on spending in the ZLB. But, it has a negative impact on household consumption in the ZLB because of the negative wealth effects associated with the (lump-sum) taxes required to finance the increase in government spending. A feature of our simulations is that the increase in government consumption in the first phase is never expected by agents to persist beyond the ZLB. In the second phase the decrease in government consumption is expected to persist beyond the end of the ZLB.
Figure 15 displays the impact of the switch to forward guidance in 2011. The dashed line represents the model simulation with all shocks, when the Taylor rule is in place throughout the period. The figure indicates that without forward guidance the Fed would have started raising the interest rate in 2012. By keeping the interest rate at zero, the monetary authority caused output to be 2 percent higher and the unemployment rate to be one percentage point lower. Interestingly, this relationship is consistent with Okun's law.
We also examined the role, in our simulations, of the unexpected
extension in the duration of the consumption wedge,
![]() in 2012Q3. To save space, we
simply report the key results. The extension has two important
effects. First, it helps the model account for the slowdown in
consumption that occurred around end-2011 (see panel 2,4 of Figure
4). Second, it helps the model account for fact that inflation
remains low for so long.
in 2012Q3. To save space, we
simply report the key results. The extension has two important
effects. First, it helps the model account for the slowdown in
consumption that occurred around end-2011 (see panel 2,4 of Figure
4). Second, it helps the model account for fact that inflation
remains low for so long.
7. Conclusion
This paper argues that the bulk of movements in aggregate real economic activity during the Great Recession were due to financial frictions interacting with the ZLB. We reach this conclusion looking at the data through the lens of a New Keynesian model in which firms face moderate degrees of price rigidities and no nominal rigidities in the wage setting process. Our model does a good job of accounting for the joint behavior of labor and goods markets, as well as inflation, during the Great Recession. According to the model the observed fall in TFP relative to trend and the rise in the cost of working capital played key roles in accounting for the small size of the drop in inflation that occurred during the Great Recession.
Bibliography
Aguiar, Mark, Erik Hurst and Loukas Karabarbounis, 2012, "Time Use During the Great Recession," American Economic Review, forthcoming.
Altig, David, Lawrence Christiano, Martin Eichenbaum and Jesper Linde, 2011, "Firm-Specific Capital, Nominal Rigidities and the Business Cycle," Review of Economic Dynamics , Elsevier for the Society for Economic Dynamics, vol. 14(2), pages 225-247, April.
Binmore, Ken, Ariel Rubinstein, and Asher Wolinsky, 1986, "The Nash Bargaining Solution in Economic Modelling," RAND Journal of Economics, 17(2), pp. 176-88.
Bigio, Saki, 2013, "Endogenous Liquidity and the Business Cycle," manuscript, Columbia Business School.
Boot, J. and W. Feibes and J. Lisman, 1967, "Further Methods of Derivation of Quarterly Figures from Annual Data," Applied Statistics 16, pp. 65 - 75.
Campbell, Jeffrey R., Charles L. Evans, Jonas D. M. Fisher, and Alejandro Justiniano, 2012, "Macroeconomic Effects of Federal Reserve Forward Guidance," Brookings Papers on Economic Activity, Economic Studies Program, The Brookings Institution, vol. 44, Spring, pages 1-80.
Christiano, Lawrence J. and Joshua M. Davis, 2006, "Two Flaws In Business Cycle Accounting," NBER Working Paper No. 12647, National Bureau of Economic Research, Inc.
Christiano, Lawrence J., Roberto Motto and Massimo Rostagno, 2003, "The Great Depression and the Friedman-Schwartz Hypothesis," Journal of Money, Credit and Banking , Vol. 35, No. 6, Part 2: Recent Developments in Monetary Economics, December, pp. 1119-1197.
Christiano, Lawrence J., and Martin S. Eichenbaum, 1990, "Unit Roots in GNP: Do We Know and Do We Care?", Carnegie-Rochester Conference Series on Public Policy 32, pp. 7-62.
Christiano, Lawrence J., Martin S. Eichenbaum and Charles L. Evans, 2005, "Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy," Journal of Political Economy, 113(1), pp. 1-45.
Christiano, Lawrence J., Martin S. Eichenbaum and Sergio Rebelo, 2011, "When Is the Government Spending Multiplier Large?," Journal of Political Economy, University of Chicago Press, vol. 119(1), pages 78 - 121.
Christiano, Lawrence J., Martin S. Eichenbaum and Mathias Trabandt, 2013, "Unemployment and Business Cycles," NBER Working Paper No. 19265, National Bureau of Economic Research, Inc.
Christiano, Lawrence J., Martin S. Eichenbaum and Robert Vigfusson, 2007. "Assessing Structural VARs," NBER Chapters, in: NBER Macroeconomics Annual 2006, Volume 21, pages 1-106 National Bureau of Economic Research, Inc.
Christiano, Lawrence J., Mathias Trabandt and Karl Walentin, 2011, "DSGE Models for Monetary Policy Analysis," in Benjamin M. Friedman, and Michael Woodford, editors: Handbook of Monetary Economics, Vol. 3A, The Netherlands: North-Holland.
Christiano, Lawrence J., Mathias Trabandt and Karl Walentin, 2012, "Involuntary Unemployment and the Business Cycle," manuscript, Northwestern University, 2012.
Davis, Steven, J., R. Jason Faberman, and John C. Haltiwanger, 2012, "Recruiting Intensity During and After the Great Recession: National and Industry Evidence," American Economic Review: Papers and Proceedings, vol. 102, no. 3, May.
den Haan, Wouter, Garey Ramey, and Joel Watson, 2000, "Job Destruction and Propagation of Shocks," American Economic Review, 90(3), pp. 482-98.
Del Negro, Marco, Marc P. Giannoni and Frank Schorfheide, 2014, "Inflation in the Great Recession and New Keynesian Models," Federal Reserve Bank of New York Staff Report no. 618, January.
Dupor, Bill and Rong Li, 2012, "The 2009 Recovery Act and the Expected Inflation Channel of Government Spending," Federal Reserve Bank of St. Louis Working Paper No. 2013-026A.
Diamond, Peter A., 1982, "Aggregate Demand Management in Search Equilibrium," Journal of Political Economy, 90(5), pp. 881-894.
Diamond, Peter A., 2010, "Unemployment, Vacancies and Wages," Nobel Prize lecture, December 8.
Edge, Rochelle M., Thomas Laubach, John C. Williams, 2007, "Imperfect credibility and inflation persistence," Journal of Monetary Economics 54, 2421-2438.
Eichenbaum, Martin, Nir Jaimovich and Sergio Rebelo, 2011, " Reference Prices and Nominal Rigidities,", American Economic Review, 101(1), pp. 242-272.
Eggertsson, Gauti B. and Paul Krugman, 2012, "Debt, Deleveraging, and the Liquidity Trap: A Fisher-Minsky-Koo Approach," The Quarterly Journal of Economics, Oxford University Press, vol. 127(3), pages 1469-1513.
Eggertsson, Gauti and Michael Woodford, 2003, "The zero interest-rate bound and optimal monetary policy," Brookings Papers on Economic Activity, Economic Studies Program, The Brookings Institution, vol. 34(1), pages 139-235.
Erceg, Christopher J., and Andrew T. Levin, 2003, "Imperfect credibility and inflation persistence," Journal of Monetary Economics, 50, 915-944.
Erceg, Christopher J., and Andrew T. Levin, 2013, "Labor Force Participation and Monetary Policy in the Wake of the Great Recession", CEPR Discussion Paper No. DP9668, September.
Fair, Ray C., and John Taylor, 1983, "Solution and Maximum Likelihood Estimation of Dynamic Nonlinear Rational Expectations Models," Econometrica, vol. 51, no. 4, July, pp. 1169-1185.
Fernald, John, 2012, "A Quarterly, Utilization-Adjusted Series on Total Factor Productivity," Federal Reserve Bank of San Francisco Working Paper 2012-19.
Fisher, Jonas, 2006, "The Dynamic Effects of Neutral and Investment-Specific Technology Shocks," Journal of Political Economy, 114(3), pp. 413-451.
Fisher, Jonas, 2014, "On the Structural Interpretation of the Smets-Wouters 'Risk Premium' Shock," manuscript, Federal Reserve Bank of Chicago.
Gilchrist, Simon and Egon Zakrajšek, 2012, Credit Spreads and Business Cycle Fluctuations, American Economic Review, 102(4): 1692-1720.
Gilchrist, Simon, Raphael, Schoenle, Jae Sim and Egon Zakrajš ek (2013), "Inflation Dynamics during the Financial Crisis," manuscript, December.
Gust, Christopher J., J. David Lopez-Salido, and Matthew E. Smith (2013), "The Empirical Implications of the Interest-Rate Lower Bound," Finance and Economics Discussion Series 2012-83. Board of Governors of the Federal Reserve System.
Hall, Robert E., 2005, "Employment Fluctuations with Equilibrium Wage Stickiness," American Economic Review, 95(1), pp. 50-65.
Hall, Robert E. and Paul R. Milgrom, 2008, "The Limited Influence of Unemployment on the Wage Bargain," The American Economic Review, 98(4), pp. 1653-1674.
Hall, Robert E., 2011, "The Long Slump," American Economic Review, 101, 431-469.
Justiniano, Alejandro, Giorgio E. Primiceri, and Andrea Tambalotti, 2010, "Investment Shocks and Business Cycles," Journal of Monetary Economics 57(2), pp. 132-145.
Kapon, Samuel and Joseph Tracy, 2014, "A Mis-Leading Labor Market Indicator," Federal Reserve Bank of New York, http://libertystreeteconomics.newyorkfed.org/2014/02/a-mis-leading-labor-market-indicator.html, February 3, 2014.
Klenow, Pete and Benjamin Malin, 2011, "Microeconomic Evidence on Price-Setting," in the Handbook of Monetary Economics 3A, editors: B. Friedman and M. Woodford, Elsevier, pp. 231-284.
Kocherlakota, Narayana, 2010, "Inside the FOMC," Federal Reserve Bank of Minneapolis, http://www.minneapolisfed.org/news_events/pres/speech_display.cfm?id=4525.
Krugman Paul, 2014, "Demography and Employment," http://krugman.blogs.nytimes.com/2014/02/03/demography-and-employment-wonkish. February 3, 2014.
Lorenzoni, Guido and Veronica Guerrieri, (2012), "Credit Crises, Precautionary Savings and the Liquidity Trap," Quarterly Journal of Economics.
Mortensen, Dale T., 1982, "Property Rights and Efficiency in Mating, Racing, and Related Games," American Economic Review, 72(5), pp. 968-79.
Paciello, Luigi, (2011), "Does Inflation Adjust Faster to Aggregate Technology Shocks than to Monetary Policy Shocks," Journal of Money, Credit and Banking, 43(8).
Pissarides, Christopher A., 1985, "Short-Run Equilibrium Dynamics of Unemployment, Vacancies, and Real Wages," American Economic Review, 75(4), pp. 676-90.
Prescott, Edward, C., 1986, "Theory Ahead of Business Cycle Measurement," Federal Reserve Bank of Minneapolis Quarterly Review, Fall, vol. 10, no. 4.
Quah, Danny, 1990, "Permanent and Transitory Movements in Labor Income: An Explanation for 'Excess Smoothness' in Consumption," Journal of Political Economy, Vol. 98, No. 3, June, pp. 449-475.
Ravenna, Federico and Carl Walsh, 2008, "Vacancies, Unemployment, and the Phillips Curve," European Economic Review, 52, pp. 1494-1521.
Reifschneider, David, William Wascher and David Wilcox, 2013, "Aggregate Supply in the United States: Recent Developments and Implications for the Conduct of Monetary Policy," Federal Reserve Board Finance and Economics Discussion Series No. 2013-77, December.
Rubinstein, Ariel, 1982, "Perfect Equilibrium in a Bargaining Model," Econometrica, 50(1), pp. 97-109.
Schmitt-Grohé, Stephanie, and Martin Uribe, 2012, "What's News in Business Cycles?," Econometrica, 80, pp. 2733-2764.
Silva, J. and M. Toledo, 2009, "Labor Turnover Costs and the Cyclical Behavior of Vacancies and Unemployment," Macroeconomic Dynamics, 13, Supplement 1.
Shimer, Robert, 2005, "The Cyclical Behavior of Equilibrium Unemployment and Vacancies," The American Economic Review, 95(1), pp. 25-49.
Shimer, Robert, 2012, "Reassessing the Ins and Outs of Unemployment," Review of Economic Dynamics , 15(2), pp. 127-48.
Smets, Frank and Rafael Wouters, 2007, "Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach," American Economic Review, 97(3), pp. 586-606.
Sullivan, Daniel, 2013, "Trends In Labor Force Participation, Presentation, Federal Reserve Bank of Chicago," https://www.chicagofed.org/digital_assets/others/people/research _resources/ sullivan_daniel/sullivan_cbo_labor_force.pdf.
Swanson, Eric T. and John C. Williams, 2013, 'Measuring the Effect of the Zero Lower Bound On Medium- and Longer-Term Interest Rates,' forthcoming, American Economic Review.
Yashiv, Eran, 2008, "The Beveridge Curve," The New Palgrave Dictionary of Economics , Second Edition, Edited by Steven N. Durlauf and Lawrence E. Blume.
Table 1a: Non-Estimated Model Parameters and Calibrated Variables - Panel A: Parameters
| Parameter | Value | Description |
|---|---|---|
| δK | 0.025 | Depreciation rate of physical capital |
| β | 0.9968 | Discount factor |
| ρ | 0.9 | Job survival probability |
| M | 60 | Maximum bargaining rounds per quarter |
| (1-χ)-1 | 3 | Elasticity of substitution market and home consumpion |
| 100(πA-1) | 2 | Annual net inflation rate target |
| 400ln(μφ) | 1.7 | Annual output per capita growth rate |
| 400ln(μφ x μψ) | 2.9 | Annual investment per capita growth rate |
Table 1b: Non-Estimated Model Parameters and Calibrated Variables - Panel B: Steady State Values
| Parameter | Value | Description |
|---|---|---|
| profits | 0 | Intermediate goods producers profits |
| Q | 0.7 | Vacancy filling rate |
| u | 0.055 | Unemployment rate |
| L | 0.67 | Labor force to population ratio |
| G/Y | 0.2 | Government consumption to gross output ratio |
Table 2: Priors and Posteriors of Model Parameters
| Parameter | Prior: Distribution | Prior: Mean, Std. | Posterior: Mode | Posterior: Std. | |
|---|---|---|---|---|---|
| Price Setting Parameters: Price Stickiness | ξ | Beta | 0.66,0.15 | 0.737 | 0.022 |
| Price Setting Parameters: Price Markup Parameter | λ | Gamma | 1.20,0.05 | 1.322 | 0.042 |
| Monetary Authority Parameters: Taylor Rule: Interest Rate Smoothing | ρR | Beta | 0.75,0.15 | 0.792 | 0.015 |
| Monetary Authority Parameters: Taylor Rule: Inflation Coefficient | rπ | Gamma | 1.70,0.10 | 1.672 | 0.093 |
| Monetary Authority Parameters: Taylor Rule: GDP Gap Coefficient | ry | Gamma | 0.01,0.01 | 0.012 | 0.007 |
| Monetary Authority Parameters: Taylor Rule: GDP Growth Coefficient | rΔy | Gamma | 0.20,0.05 | 0.184 | 0.048 |
| Preferences and Technology: Market and Home Consumption Habit | b | Beta | 0.50,0.15 | 0.889 | 0.013 |
| Preferences and Technology: Capacity Utilization Adjustment Cost | σa | Gamma | 0.50,0.30 | 0.036 | 0.028 |
| Preferences and Technology: Investment Adjustment Cost | S" | Gamma | 8.00,2.00 | 12.07 | 1.672 |
| Preferences and Technology: Capital Share | α | Beta | 0.33,0.03 | 0.247 | 0.018 |
| Preferences and Technology: Technology Diffusion | θ | Beta | 0.50,0.20 | 0.115 | 0.024 |
| Labor Market Parameters: Probability of Bargaining Breakup | 100δ | Gamma | 0.50,0.20 | 0.051 | 0.015 |
| Labor Market Parameters: Replacement Ratio | D/w | Beta | 0.40,0.10 | 0.194 | 0.058 |
| Labor Market Parameters: Hiring Cost to Output Ratio | sl | Gamma | 1.00,0.30 | 0.474 | 0.146 |
| Labor Market Parameters: Labor Force Adjustment Cost | φL | Gamma | 100,50.0 | 134.7 | 28.34 |
| Labor Market Parameters: Unemployed Share in Home Production | αcH | Beta | 0.03,0.01 | 0.015 | 0.005 |
| Labor Market Parameters: Probability of Staying in Labor Force | s | Beta | 0.85,0.05 | 0.816 | 0.060 |
| Labor Market Parameters: Matching Function Parameter | σ | Beta | 0.50,0.10 | 0.506 | 0.039 |
| Shocks: Standard Deviation Monetary Policy Shock | 400σR | Gamma | 0.65,0.05 | 0.650 | 0.035 |
| Shocks: AR(1) Persistent Component of Neutral Techn. | ρP | Gamma | 0.50,0.07 | 0.792 | 0.041 |
| Shocks: Stdev. Persistent Component of Neutral Techn. | 100σP | Gamma | 0.15,0.04 | 0.037 | 0.004 |
| Shocks: AR(1) Transitory Component of Neutral Techn. | ρT | Beta | 0.75,0.07 | 0.927 | 0.033 |
| Shocks: Stdev. Ratio Transitory and Perm. Neutral Techn. | σT/σP | Gamma | 6.00,0.45 | 4.916 | 0.403 |
| Shocks: AR(1) Investment Technology | ρψ | Beta | 0.75,0.10 | 0.714 | 0.056 |
| Shocks: Standard Deviation Investment Technology Shk. | 100σψ | Gamma | 0.10,0.05 | 0.114 | 0.017 |
Notes: Sl denotes the steady state hiring to gross output ratio (in percent).
Table 3: Model Steady States and Implied Parameters
| Variable | At Estimated Posterior Mode | Description |
|---|---|---|
| K/Y | 7.01 | Capital to gross output ratio (quarterly) |
| C/Y | 0.57 | Market consumption to gross output ratio |
| I/Y | 0.22 | Investment to gross output ratio |
| l | 0.63 | Employment to population ratio |
| R | 1.0125 | Gross nominal interest rate (quarterly) |
| Rreal | 1.0075 | Gross real interest rate (quarterly) |
| mc | 0.76 | Marginal cost (inverse markup) |
| σb | 0.036 | Capacity utilization cost parameter |
| Y | 0.83 | Gross output |
| φ/Y | 0.32 | Fixed cost to gross output ratio |
| σm | 0.66 | Level parameter in matching function |
| f | 0.63 | Job finding rate |
| ϑ | 0.98 | Marginal revenue of wholesaler |
| x | 0.1 | Hiring rate |
| J | 0.06 | Value of firm |
| V | 197.1 | Value of work |
| U | 193.3 | Value of unemployment |
| N | 185.1 | Value of not being in the labor force |
| v | 0.18 | Vacancy rate |
| e | 0.06 | Probability of leaving non-participation |
| ω | 0.47 | Home consumption weight in utility |
| CH | 0.31 | Home consumption |
| w | 0.97 | Real wage |
| γ(ϑ/M) | 0.81 | Counteroffer costs as share of daily revenue |
Table 4: Labor Market Status Transition Probabilities
| To: E (Data) | To: E (Model) | To: U (Data) | To: U (Model) | To: N (Data) | To: N (Model) | |
|---|---|---|---|---|---|---|
| From: E | 0.89 | 0.95 | 0.03 | 0.03 | 0.08 | 0.02 |
| From: U | 0.46 | 0.52 | 0.17 | 0.30 | 0.37 | 0.18 |
| From: N | 0.14 | 0.04 | 0.05 | 0.02 | 0.81 | 0.94 |
Notes: Transition probabilities between employment (E), unemployment (U) and non-participation (N). Model refers to transition probabilities in steady state at estimated parameter values. Data are based on Current Population Survey. We take the average of monthly transition probabilities from January 1990 to December 2013. To convert from monthly to quarterly frequency we take the average monthly transition probability matrix to the power of three.
Figure 1: Impulse Responses to an Expansionary Monetary Policy Shock
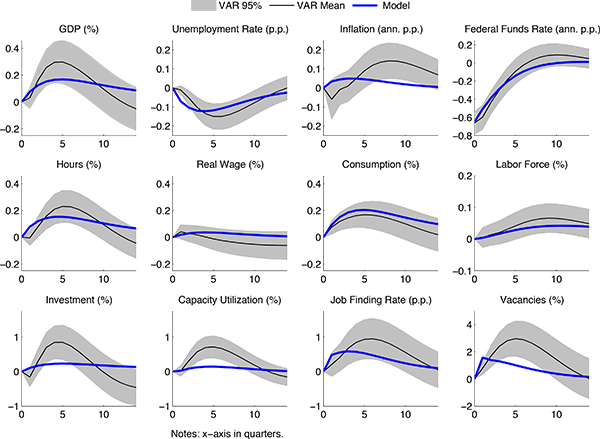
Figure 2: Impulse Responses to Negative Innovation in Neutral Technology
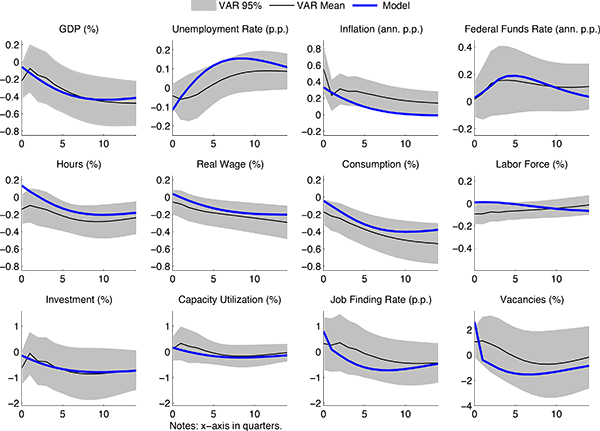
Figure 3: Impulse Responses to Negative Innovation in Investment-Specific Technology
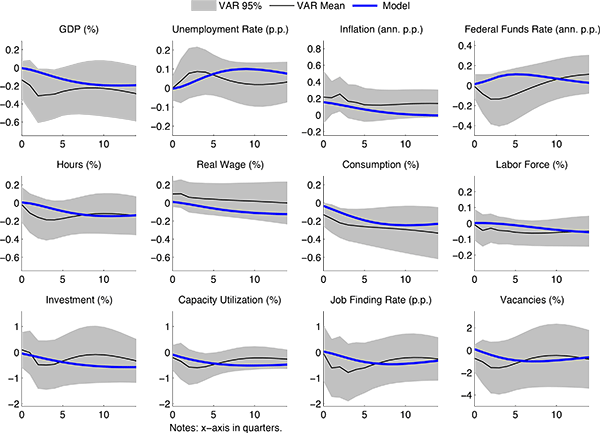
Figure 4: The Great Recession in the U.S.
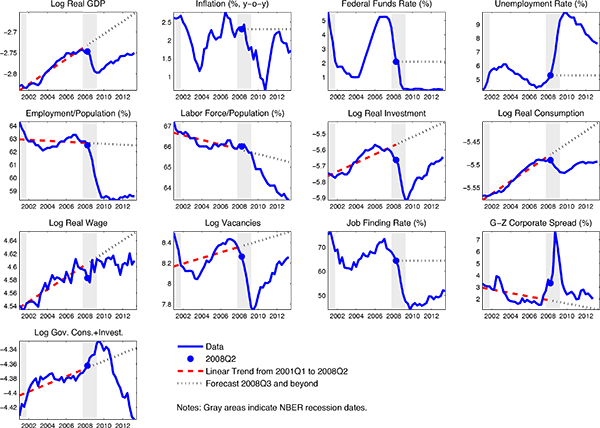
Figure 5: Measures of Total Factor Productivity (TFP): 2001 to 2013
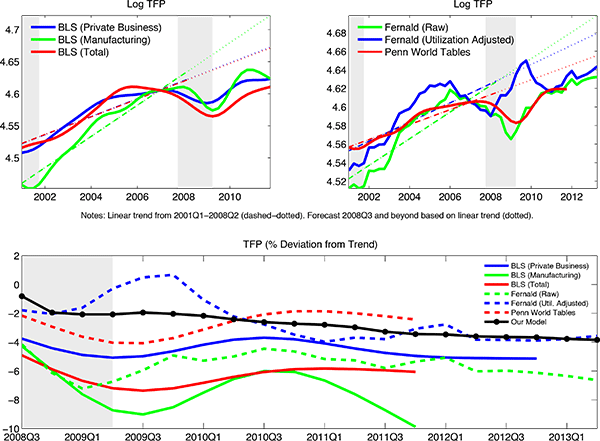
Figure 6: Measures of Total Factor Productivity: 1982-2013
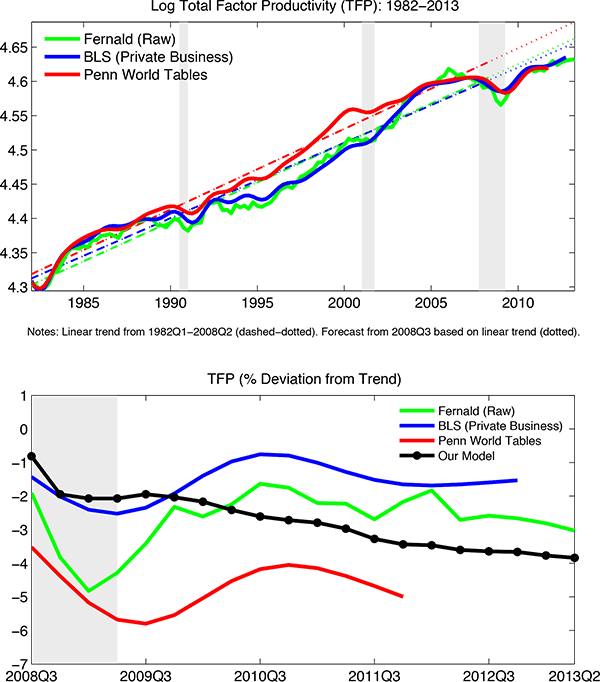
Figure 7: The U.S. Great Recession: Exogenous Variables
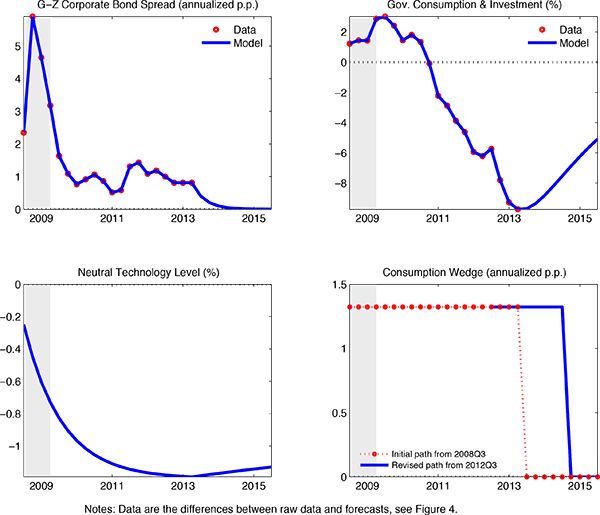
Figure 8: The U.S. Great Recession: Data vs. Model
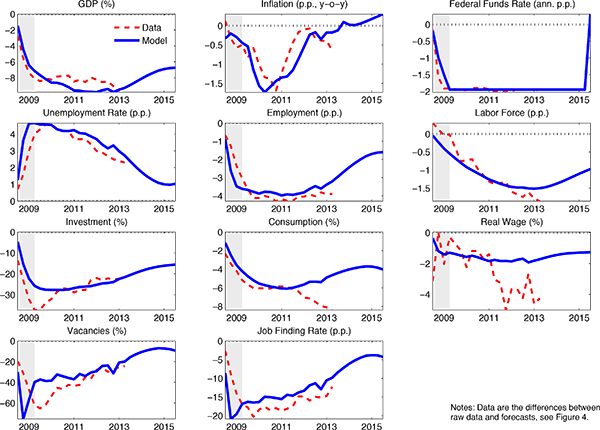
Figure 9: Beveridge Curve: Data vs. Model
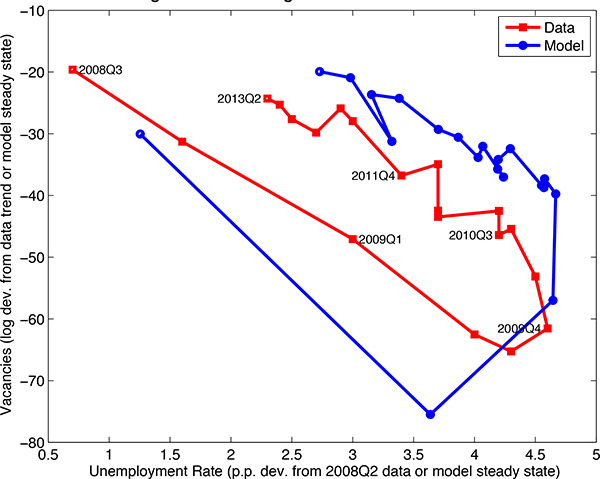
Figure 10: The U.S. Great Recession: Effects of Neutral Technology
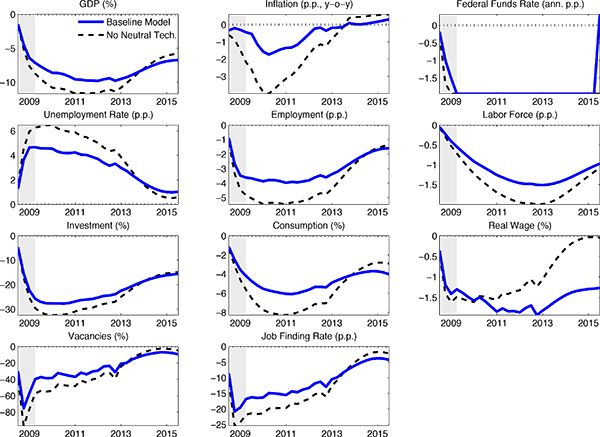
Figure 11: The U.S. Great Recession: Effects of Spread on Working Capital
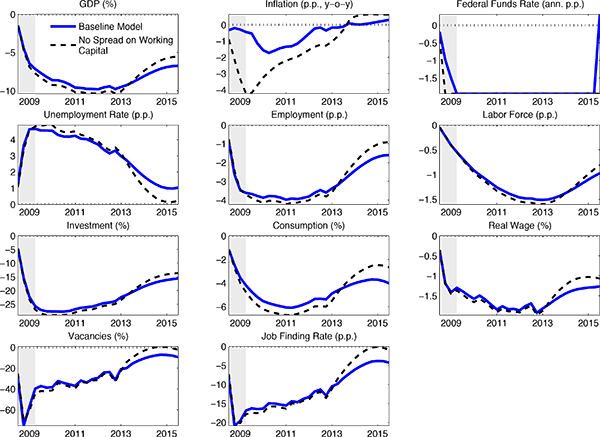
Figure 12: The U.S. Great Recession: Effects of Financial Wedge
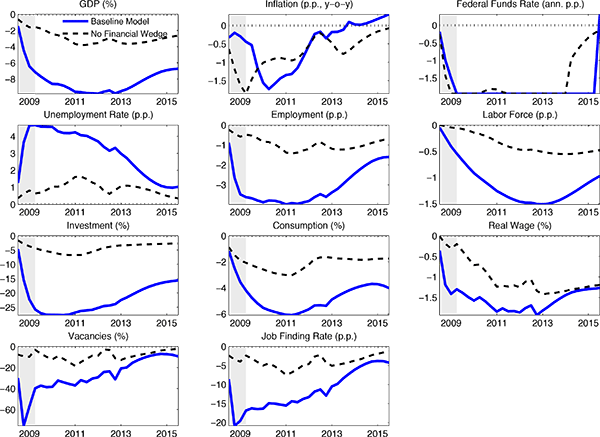
Figure 13: The U.S. Great Recession: Effects of Consumption Wedge
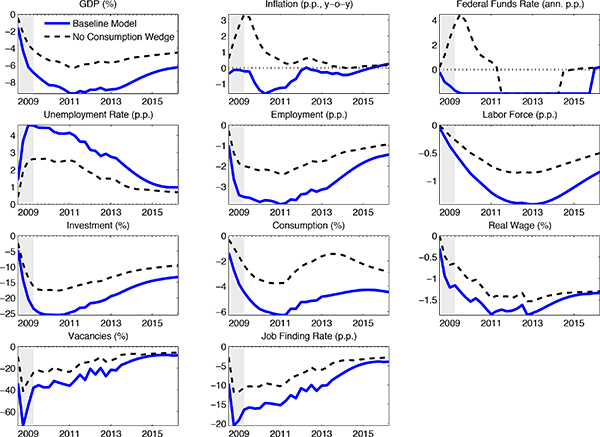
Figure 14: The U.S. Great Recession: Effects of Government Consumption and Investment
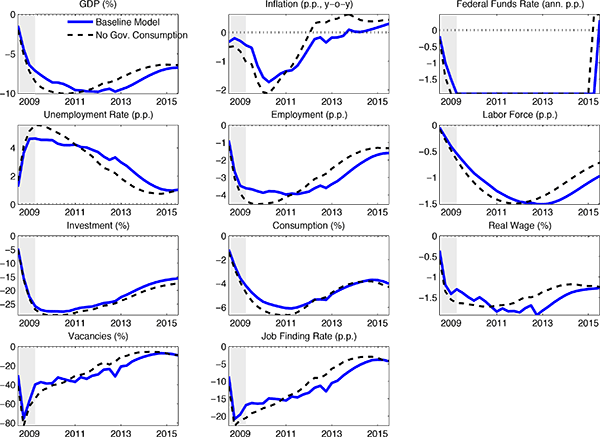
Figure 15: The U.S. Great Recession: Effects of Forward Guidance
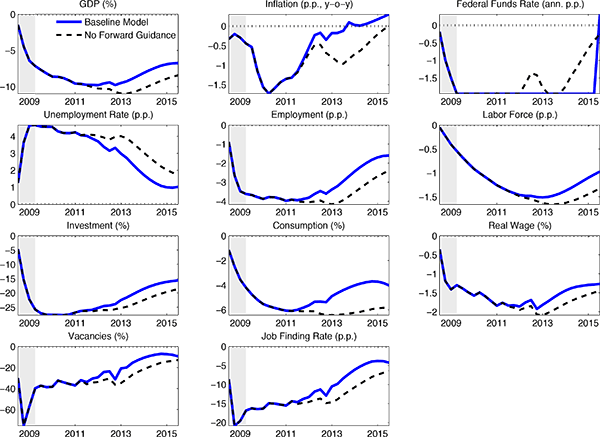
Footnotes
1. The views expressed in this paper are those of the authors and do not necessarily reflect those of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. We are grateful for discussions with Gadi Barlevy. Return to text
2. Northwestern University, Department of Economics, 2001 Sheridan Road, Evanston, Illinois 60208, USA. Phone: +1-847-491-8231. E-mail: [email protected]. Return to text
3. Northwestern University, Department of Economics, 2001 Sheridan Road, Evanston, Illinois 60208, USA. Phone: +1-847-491-8232. E-mail: [email protected]. Return to text
4. Board of Governors of the Federal Reserve System, Division of International Finance, Trade and Financial Studies Section, 20th Street and Constitution Avenue N.W., Washington, D.C. 20551, USA, E-mail: [email protected]. Return to text
5. The findings with respect to the financial wedge is consistent Del Negro, Giannoni and Schorfheide (2014), who reach their conclusion using a different methodology than ours. Return to text
6. In a related criticism Dupor and Li (2013) argue that the behavior of actual and expected inflation during the period of the American Recovery and Reinvestment Act is inconsistent with the predictions of NK style models. Return to text
7. Christiano, Eichenbaum and Rebelo (2011) reach a similar conclusion based on data up to the end of 2010. Return to text
8. We include the staying rate,
![]() in our analysis for a substantive as well
as a technical reason. The substantive reason is that, in the data,
workers move in both directions between unemployment,
non-participation and employment. The gross flows are much bigger
than the net flows. Setting
in our analysis for a substantive as well
as a technical reason. The substantive reason is that, in the data,
workers move in both directions between unemployment,
non-participation and employment. The gross flows are much bigger
than the net flows. Setting ![]() helps the model
account for these patterns. The technical reason for allowing
helps the model
account for these patterns. The technical reason for allowing
![]() can be seen by setting
can be seen by setting ![]() in (
in (![]() ). In that case,
if the household wishes to make
). In that case,
if the household wishes to make
![]() , it must set
, it must set ![]() That would require withdrawing from the labor
force some workers who were unemployed in
That would require withdrawing from the labor
force some workers who were unemployed in ![]() and
stayed in the labor force as well as some workers who were
separated from their firm and stayed in the labor force. But, if
some of these workers are withdrawn from the labor force then their
actual staying rate would be lower than the fixed number,
and
stayed in the labor force as well as some workers who were
separated from their firm and stayed in the labor force. But, if
some of these workers are withdrawn from the labor force then their
actual staying rate would be lower than the fixed number,
![]() So, the actual staying rate would be a
non-linear function of
So, the actual staying rate would be a
non-linear function of ![]() with the staying
rate below
with the staying
rate below ![]() for
for
![]() 0 and equal to
0 and equal to ![]() for
for
![]() This kink point is a
non-linearity that would be hard to avoid because it occurs
precisely at the model's steady state. Even with
This kink point is a
non-linearity that would be hard to avoid because it occurs
precisely at the model's steady state. Even with ![]() there is a kink point, but it is far from steady state
and so it can be ignored when we solve the model. Return to text
there is a kink point, but it is far from steady state
and so it can be ignored when we solve the model. Return to text
9. Erceg and Levin (2013) also exploit this type of tradeoff in their model of labor force participation. However, their households find themselves in a very different labor market than ours do. In our analysis the labor market is a version of the Diamond-Mortensen-Pissarides model, while in their analysis, the labor market is a competitive spot market. Return to text
10. When bargaining breaks down, we assume that workers are sent to unemployment, not out-of-the labor force. Return to text
11. We could allow for the possibility that when negotiations break down the worker has a chance of leaving the labor force. To keep our analysis relatively simple, we do not allow for that possibility here. Return to text
12. Unobserved components representations have played an important role in macroeconomic analysis. See, for example, Erceg and Levin (2003) and Edge, Laubach and Williams (2007). Return to text
13. See CTW for a sensitivity analysis with respect to the lag length of the VAR. Return to text
14. Some plants will hire more than
![]() people and others will hire fewer. By the
law of large numbers, there is no uncertainty at the firm level
about how many people will be hired. Return to text
people and others will hire fewer. By the
law of large numbers, there is no uncertainty at the firm level
about how many people will be hired. Return to text
15. We take our elasticity of
substitution parameter from the literature to maintain
comparability. However, there is a caveat. To understand this,
recall the definition of the elasticity of substitution. It is the
percent change in ![]() in response to a one
percent change in the corresponding relative price, say
in response to a one
percent change in the corresponding relative price, say ![]() . From an empirical standpoint, it is difficult to
obtain a direct measure of this elasticity because we do not have
data on
. From an empirical standpoint, it is difficult to
obtain a direct measure of this elasticity because we do not have
data on ![]() or
or ![]() As a result,
structural relations must be assumed, which map from observables to
As a result,
structural relations must be assumed, which map from observables to
![]() and
and ![]() Since
estimates of the elasticity are presumably dependent on the details
of the structural assumptions, it is not clear how to compare
values of this parameter across different studies, which make
different structural assumptions. Return
to text
Since
estimates of the elasticity are presumably dependent on the details
of the structural assumptions, it is not clear how to compare
values of this parameter across different studies, which make
different structural assumptions. Return
to text
16. Our data does include the job finding rate. However, our impulse response matching procedure only uses the dynamics of that variable and not its level. Return to text
17. We reached this conclusion as
follows. Workers starting a new job at the start of period
![]() come from three states: employment,
unemployment and not-in-the labor force. The quantities of these
people are
come from three states: employment,
unemployment and not-in-the labor force. The quantities of these
people are
![]()
![]() and
and
![]() respectively. We computed these three objects in steady state using
the information in Tables 1, 2 and 3. The fraction reported in the
text is the ratio of the first number to the sum of all
three. Return to text
respectively. We computed these three objects in steady state using
the information in Tables 1, 2 and 3. The fraction reported in the
text is the ratio of the first number to the sum of all
three. Return to text
18. This finding is consistent with results in e.g. Altig, Christiano, Eichenbaum and Linde (2011) and Paciello (2011). Return to text
19. See Erceg and Levin (2013), Figure 1. Return to text
20. According to the Huffington Post (http://www.huffingtonpost.com/2012/12/27/fiscal-cliff-2013_n _2372034.html) in Autumn of 2012, many economists warned that if left unaddressed, concerns about the 'fiscal cliff', could trigger a recession. Return to text
21. The shock is also similar to the 'flight-to-quality' shock found to play a substantial role in the start of the Great Depression in Christiano, Motto and Rostagno (2003). Return to text
22. In particular,
![]() , after
rounding. Return to text
, after
rounding. Return to text
23. In particular,
![]() after
rounding. Return to text
after
rounding. Return to text
24. In performing this computation, we
impose that
![]() as
as
![]() and
and
![]() , where the
subscript
, where the
subscript ![]() signifies the nonstochastic steady
state. Return to text
signifies the nonstochastic steady
state. Return to text
25. The BLS measure is only available at an annual frequency. We interpolate the annual data to a quarterly frequency using a standard interpolation routine described in Boot, Feibes, and Lisman (1967). Return to text
26. Our measure of TFP is the ratio of
GDP (i.e., ![]() to capital and labor services,
each raised to a power that corresponds to their steady state share
of total income. Return to text
to capital and labor services,
each raised to a power that corresponds to their steady state share
of total income. Return to text
27. See e.g. Gust, Lopez-Salido and Smith (2013) who estimate a nonlinear DSGE model subject to an occasionally binding ZLB constraint. Return to text
28. For simplicity, in our calculations we assume that the investment-specific technology shock remains on its steady state growth path after 2008. Return to text
29. Our model of monetary policy is clearly an approximation. For example, it is possible that in our stochastic simulations the Fed's actual thresholds are breached before 8 quarters. Since we do not know what those thresholds were, we do not see a way to substantially improve our approach. Later, in December 2013, the Fed did announce thresholds, but there is no reason to believe that those were their thresholds in the earlier period. Return to text
30. Our procedure is related to the one proposed in Fair and Taylor (1983). Return to text
31. We include this example for completeness. It can be found in other places, for example, Yashiv (2008). Return to text
32. In principle, a change in the
separation rate, ![]() could also have shifted the
Beveridge curve during the Great Recession. This explanation does
not work because the separation rate fell from an average level of
3.7 percent before the Great Recession to an average of 3.1 percent
after 2009. These numbers were calculated using JOLTS data
available at the BLS website. Return to
text
could also have shifted the
Beveridge curve during the Great Recession. This explanation does
not work because the separation rate fell from an average level of
3.7 percent before the Great Recession to an average of 3.1 percent
after 2009. These numbers were calculated using JOLTS data
available at the BLS website. Return to
text
33. There are other forces at work in the ZLB that can cause a persistent decrease in technology to generate more inflation than a transitory decrease. Return to text
34. See Erceg and Levin (2013), for an analysis which reaches a qualitatively similar conclusion using a small scale, calibrated model. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text