Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2011-22 Screen Reader version ^♣

Volatility, Money Market Rates, and the Transmission of Monetary Policy*

Seth B. Carpenter

Senior Associate Director
Division of Monetary Affairs
Board of Governors of the Federal Reserve System
20th and C Street, NW, Washington, DC 20551
[email protected]

Selva Demiralp

Associate Professor
Department of Economics Koc University
Rumeli Feneri Yolu
Sariyer, Istanbul 34450 Turkey
[email protected]

February 2011

Keywords: Monetary transmission mechanism, expectations hypothesis, term premium

Abstract:

Central banks typically control an overnight interest rate as their policy tool, and the transmission of monetary policy happens through the relationship of this overnight rate to the rest of the yield curve. The expectations hypothesis, that longer-term rates should equal expected future short-term rates plus a term premium, provides the typical framework for understanding this relationship. We explore the effect of volatility in the federal funds market on the expectations hypothesis in money markets. We present two major results. First, the expectations hypothesis is likely to be rejected in money markets if the realized federal funds rate is studied instead of an appropriate measure of the expected federal funds rate. Second, we find that lower volatility in the bank funding markets market, all else equal, leads to a lower term premium and thus longer-term rates for a given setting of the overnight rate. The results appear to hold for the US as well as the Euro Area and the UK. The results have implications for the design of operational frameworks for the implementation of monetary policy and for the interpretation of the changes in the Libor-OIS spread during the financial crisis. We also demonstrate that the expectations hypothesis is more likely to hold the more closely linked the short- and long-term interest rates are.

JEL codes: E43, E52, E58

Introduction

Central banks typically control an overnight interest rate as their policy tool, and most economists think that the transmission of monetary policy happens through the relationship of this overnight rate to the rest of the yield curve. The expectations hypothesis, that longer-term rates should equal expected future short-term rates plus a term premium, provides the typical framework for understanding this relationship. The degree of control that the Federal Reserve has exercised over the funds rate has not been constant through time, and the recent financial crisis led to dislocations in many money markets. We explore the effect that volatility in the federal funds market has on the expectations hypothesis in money markets. Specifically, we look for evidence that volatility in the overnight rate can affect the term premium embedded in longer-term money market rates.

The Federal Reserve has had a target for the federal funds rate for decades. Although from 1979 to 1982, the path of nonborrowed reserves was the official operating framework, both before and after, the Federal Open Market Committee had an intended level for the funds rate (see Bernanke and Blinder, 1992, Rudebusch, 1995, Meulendyke, 1998). The volatility in the funds market, however, has not been constant (see Bennett and Peristiani, 2002, Hilton, 2005, Demiralp and Farley, 2005, Nautz and Schmidt, 2009). Demiralp and Farley have documented the decline in volatility in the funds market during the 1990s, for example, and attribute the trend to higher frequency of open market operations on the part of the Federal Reserve, improved reserve management of banks, and consolidations in the banking system. Nautz and Schmidt (2009) note that the steps taken towards transparency since 1994 further stabilized the funds rate volatility. As monetary policy in the United States has become more transparent and predictable, the anticipation of changes to the target rate led to movements in the funds rate before many target rate changes. Carpenter and Demiralp (2006) investigate this phenomenon and document that there is some evidence that the anticipation effect is transmitted to the very near end of the yield curve. In this paper, we try to estimate what effect more generalized volatility in the federal funds rate has on longer-term money market rates.

The expectations hypothesis has been studied extensively in the economics literature. Among the more notable examples are Shiller, Campbell, and Schoenholtz, 1983, Campbell and Schiller, 1991, Mankiw and Miron, 1986, and Rudebusch, 1995. The literature provides mixed support for the expectations hypothesis in its most simple form, however, with the allowance for (potentially time-varying) term premiums, the record improves. For the short end of the yield curve, Lange, Sack, and Whitesell (2003), as an example, provide evidence that the link between expected future short rates and longer-term rates has become stronger with more transparent and predictable monetary policy.

Many researchers who have tested the expectations hypothesis, however, have found very weak evidence at the short end of the yield curve. Mankiw and Miron (1986) attributed the negligible predictive power of the spread between long rates and short rates to the Federal Reserve's interest smoothing policies. They argued that the Federal Reserve's interest stabilization policies induced a random walk behavior at the short end of the yield curve. Under these circumstances and assuming rational expectations, the short rate expected by the market would always equal the current short rate, and the term spread would always equal the term premium. Fluctuations in the spread would have no predictive power for the path of the short rate. Mankiw and Miron's argument is that the Fed's interest rate smoothing weakens the term structure relationship by preventing any information about the near-term expectations to be reflected in short term rates. In this paper, we note that the performance of the expectations hypothesis at the short end of the yield curve improves when an appropriate measure of the expected federal funds rate is used.

Using data from 1992 through 2010, we find that lower volatility in the funds market leads, all else equal, to a lower term premium and thus lower longer-term rates for a given setting of the overnight rate. The result is fairly intuitive. One reason for the expectations hypothesis to hold is through arbitrage. If the term rate was expected to be above the expected overnight rate, a bank could borrow at the overnight rate to fund a term loan and earn the spread. Volatility in the overnight rate, however, creates uncertainty in funding costs. If this uncertainty leads potential arbitrageurs to demand a risk premium for funding a term loan through overnight funds, the term premium should rise.

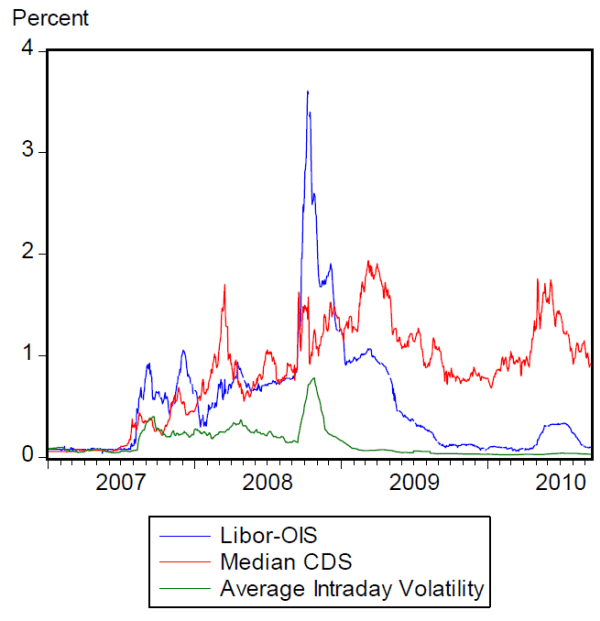
These results bear on the design of the framework for the implementation of monetary policy with regard to the desirable degree of control over the overnight rate. For example, while a simple framework may be desirable from an operational perspective, if a simple framework were to lead to an overnight rate that is volatile, term premiums, and therefore longer-term rates, would likely be higher. The results also suggest a different, or perhaps additional, interpretation of the changes in the Libor-OIS spread during the financial crisis. Researchers who studied the crisis have looked for a link between the Libor-OIS spread and counterparty risk, often measure by credit-default-swap (CDS) spreads (see for example, Taylor and Williams, 2009, McAndrews et al., 2009). Additionally, researches have attributed narrowing in the spread to the Federal Reserve's liquidity provision through various facilities (see McAndrews et al., 2009, Christensen et al., 2009). Our results suggest an alternative, but easily complementary, channel for the narrowing of the spread. Figure 1 plots the three-month Libor-OIS spread together with average intraday volatility over the previous 30 days, along with the median CDS spread for the banks in the Libor panel from January 2007 to September 2010.¹ Note that volatility in the federal funds rate fell following the autumn of 2008, and the Libor-OIS spread declined steadily over the first half of 2009. The decline in volatility could have led to at least some of the narrowing of the Libor-OIS spread in addition to any contribution from reduced credit risk or central bank interventions.

The rest of the paper is laid out as follows. The next section discusses estimation strategies for the expectations hypothesis, following the existing literature. We look at the effect of including different measures of expectations in the funds market into a standard empirical specification and show that the expectations measures that we use matters. The following section shifts the focus to term bank funding rates. We demonstrate that the expectations hypothesis appears to work well for bank funding rates and that volatility in the overnight rate can contribute significantly to explaining term premiums. This main result is established for the US as well as the Euro Area and the UK. This result is of particular interest in understanding the term premium during the financial crisis and in understanding the implications of different operating environments for the implementation of monetary policy. The final section concludes.

The Expectations Hypothesis

The expectations hypothesis of the term structure of interest rates states that current longer-term rates should equal to the average of the expected overnight rate plus some term premium that accounts for liquidity risk, credit risk, or other factors. In practice, we could think of the three-month Treasury bill rate (TB3) as the long-term rate and the overnight federal funds rate (FFR) to be the short-term rate. We could write the expectations hypothesis as follows:

$TB3_{t} =\frac{1}{90} \left[FFR_{t} +E_{t} (FFR_{t+1} )+E_{t} (FFR_{t+2} )+...+E_{t} (FFR_{t+90} )\right]+c$

(1)

Where $E_{t}$ denotes the expectations operator at time t and c is a term premium. In many empirical analysis of the term structure such as Campbell and Schiller, 1991, Mankiw and Miron, 1986, Roberds et al., 1996, and Lange et al., 2003, a common practice is to assume "perfect foresight" such that $E_{t} (FFR_{t+i} )=FFR_{t+i}$ and test whether today's 90-day Treasury rate is equal to the average realized (not expected) funds rates over the next 90 days.² Furthermore, the term premium is assumed to be constant and captured by the residual in the regression.

The perfect foresight assumption can be removed by replacing the realized funds rates with expectations derived from, for example, federal funds futures contracts on the right hand side. The appendix describes the calculation of daily expectations over the next ninety days based on federal funds futures contracts.

Expressing equation (1) in first differences gives us:

$\Delta TB3_{t} =\frac{1}{90} \left[\Delta FFR_{t} +\Delta E_{t} (FFR_{t+1} )+\Delta E_{t} (FFR_{t+2} )+...+\Delta E_{t} (FFR_{t+90} )\right]$

(2)

In equation (2), the term premium drops due to differencing, under the assumption that it changes only a negligible amount from one day to another, which is an even weaker assumption than a constant term premium throughout the maturity of the long-term contract. This specification is particularly convenient for our purposes because it allows us to investigate the importance of imposing the perfect foresight assumption and its implications in testing the expectations hypothesis without worrying about the term premium.

The first column in Table 1 shows the results from the regression where changes in the three-month rate are regressed onto changes in the realized funds rate over the next 90 days, as is typically assumed in the literature. The sample period extends from January 1, 1990 through September 15, 2010. The purpose of this exercise is to re-estimate a well-accepted specification from the term structure literature and use it for comparison in the later analysis. Note that the slope coefficient is significantly different from its theoretical value of one and the $R^{2}$ is very low. Instead, the second column shows the regression results where the change in the three-month rate is regressed onto the expected changes in the funds rate over the next 90 days. Expected changes in the funds rate over the next 90 and 180 days are derived from federal funds futures contracts. The appendix describes our methodology of deriving longer term policy expectations in this manner. This time, the coefficient estimate is insignificantly different from its theoretical value of one. Furthermore, the $R^{2}$ of the regression increases noticeably.

The third and fourth columns in Table 1 show the results from a similar exercise with changes in six-month Treasury yield regressed onto the change in the average funds rate in the next six months and the change in the average expected funds rate in the next six months. The results are similar to the results for the three-month bill rate. When the expected funds rate is used instead of the realized funds rate, the coefficient estimate equals its theoretical value of one and $R^{2}$ increases substantially.

Market expectations of the funds rate over the future months can also be derived from the overnight-indexed swap (OIS) rate. Overnight indexed swaps are over-the-counter traded derivatives in which one party agrees to pay a fixed rate in exchange for the average of a floating central-bank rate over the life of the swap. For dollar swaps, the floating rate is the daily effective federal funds rate. The OIS rate is a measure of market participants' expected average federal funds rate over the relevant term. One drawback, however, is that data on overnight-indexed swaps were not available prior to December 2001 because the market was still developing. In contrast, the measure of expectations that we used in Table 1 goes back to 1989 and allows for a longer sample. Table 2 illustrates how the results based on federal funds futures contracts compare to those based on OIS rates. The first column in Table 2 replicates the first column Table 1 for the sample after December 2001 where the three-month Treasury bill rate is regressed onto the average funds rate over the next 90 days. The coefficient estimate is comparable to the one obtained for the longer sample and is significantly smaller than one. The second and third columns replace the average funds rate with the expected funds rate based on federal funds futures contracts and three-month OIS rate respectively. In both cases, the coefficient estimate associated with the expected funds rate is insignificantly different from its theoretical value of one. The close resemblance between the results using either expectations measure is consistent with the discussion in the Appendix regarding the close match between the two expectations measures.

Term premiums and bank funding rates

The results presented in the previous section suggest that estimation of the expectations hypothesis at the near end of the yield curve is sensitive to the use of realized rates versus market-based expectations of future short rates. Using market-based measures of expected rates produces results where the expectations hypothesis appears to hold at the short end of the yield curve. This finding suggests that the previously established results regarding the weak evidence in favor of the expectations hypothesis arise from the inappropriate proxy used for market expectations. When proper measures of expectations are used instead, the evidence strongly supports the expectations hypothesis. We now turn to studying the term premium and analyze its behavior during the current crisis.

The estimation in the previous section was done in changes, following much of the literature, to avoid potential issues of nonstationarity with the interest rates and to avoid the term premium. The level of rates, or more precisely, the level of the term rate relative to the expected overnight rate, however, may also be of interest. Term spreads are typically thought to capture risk premiums, and estimating term-structure relationships from spreads are a way to avoid stationarity problems. That said, in the simplest form, using a term spread as the dependent variable and estimating the effect of other variables on that spread essentially imposes the expectations hypothesis on the data. Estimating the relationship in levels to be able to test the hypothesis is valid if residuals from the regression are stationary, implying that there is a cointegrating relationship in the nonstationary variables. Furthermore, estimating the regression in levels allows us to quantify the components of this term premium and better understand the reasons behind interest rate fluctuations during the recent financial turmoil.

While the results of the previous section appear to be supportive of the expectations hypothesis, the comparison of the federal funds rate--an unsecured, bank funding rate--to the Treasury bill rate--a riskless, government funding rate--may be a bit problematic especially when we consider the variables in levels. Spreads between these rates will likely reflect risk premiums that we would expect, but because the instruments are inherently different and the markets have different participants, the comparison is not direct. To make a more direct comparison, we use different bank funding rates, three-month Libor, three-month Eurodollar, and three-month federal funds to test the expectations hypothesis. We run the same estimation using the three-month Treasury bill rate as a comparison. In the level regressions, the dependent variable is one of the term rates. According to the expectations hypothesis, the term rate should equal expected short rate over the maturity of the term rate and a term premium. In order to capture the expectations component we use the OIS rate or the expected funds rate derived from federal funds futures contracts as an independent variable. In this simple specification, the residuals are non-stationary, suggesting that the cointegrating relationship, if it exists, has not been captured. Adding a measure of federal funds volatility to capture part of the term premium, we obtain a co-integrating relationship that gives stationary residuals. To compare the results to other research, we also include a measure of credit risk, although the latter alone is not sufficient to generate stationary errors in the absence of a measure for federal funds volatility.

Table 3 presents the results of benchmark regressions. Here, we start our sample period in January 2001 to be able to use CDS spreads for large banks as a measure of credit risk. Taylor and Williams (2009) use the median five-year CDS annual rate for the banks in the US dollar Libor survey starting in 2007. Importantly, this sample includes relatively calm periods in the bank funding market as well as some rather turbulent episodes. In the upper panel (panel A), we regress the level of the term rate on a constant, comparable maturity OIS rate, the realized volatility of the federal funds rate, and the median CDS spread for large banks. This is our benchmark specification. The last two terms are intended to capture the term premium. Volatility in the federal funds market can be measured in different ways. In these results, we show the results from using the average intraday volatility over the preceding 30 days as a proxy for expected volatility in the near future. However, the results are robust to using other measures of funds rate volatility, such as realized daily standard deviation of the federal funds rate or the mean absolute deviation of the funds rate from the target over the prior 30 days (not shown). If the expectations hypothesis were to hold perfectly, the constant term would equal a time-invariant term premium and the slope on the OIS rate would equal one.

Column 1 in the upper panel of Table 3 shows that for three-month Libor, the coefficient on the OIS rate is very close to one.³ The coefficient, however, is rather precisely measured and is statistically significantly different from one. The median CDS spread has a positive and statistically significant coefficient, confirming the results in other research that, conditional on a given level of the expected path for the funds rate, greater credit risk among banks is associated with a wider term premium. Volatility in the federal funds market is also statistically significant and associated with a wider term premium. Finally, the R-squared of the regression is very high. The high R-squared, however might lead one to suspect that the regression is subject to spurious correlation, given the fact that interest rates are typically found to be nonstationary. However, the stationarity of the residuals, and thus the presence of the cointegrating relationship, implies that the regression is valid and the coefficients are estimated consistently.

What does the first column of results tell us? Essentially, the slope coefficient suggests that the expectations hypothesis basically holds for bank funding markets from the overnight rate to the three-month rate. The term premium, however, is importantly linked to credit risk. This result should be unsurprising, as many studies of the Libor-OIS spread during the current financial crisis have found a robust correlation between the spread and CDS spreads, other measures of credit risk, and other measures of liquidity risk, see for example Schwarz, 2009, Taylor and Williams, 2009, and Christensen, Lopez, and Rudebusch, 2009. Other researchers have examined the role risk or central bank intervention has played in determining the Libor-OIS spread. What is novel here, is the fact that the volatility in the federal funds rate is also statistically and economically significant. During normal times, volatility in the federal funds rate is around 5 basis points. During the financial crisis, average monthly intraday volatility got as high as 90 basis points, implying that this volatility could be responsible for as much as 278 (=90 $\times$ 3.09) basis points of the Libor-OIS spread. Figure 2 plots the Libor-OIS spread, the fitted value from our regression, and the spread that our model suggests is attributable to federal funds volatility. Of note, following year end 2008, volatility in the federal funds rate declined notably and the Libor-OIS spread narrowed even more. To be sure, general market conditions improved, however, the ability of a bank that might be inclined to arbitrage term markets was clearly enhanced by greater certainty over the path of the funds rate.

Columns 2 and 3 provide robustness checks and present a similar picture for the three-month Eurodollar rate and the three-month federal funds rate. Qualitatively, the results are virtually identical. The slope coefficient is close to one, credit market risk is a significant explanatory variable, and volatility in the overnight market is statistically significant.

The picture is a bit different when the term rate is the three-month Treasury bill rate. The coefficients on CDS spreads and on federal funds rate volatility are both statistically significant, but negative. These results, however, are intuitive. The Treasury bill is a risk-free instrument and, more importantly, a safe-haven asset. When markets experience elevated risk or volatility, demand for the safest assets increases, driving down the yield on Treasury bills. The fact that the coefficients are of opposite signs, however, underscores the advantages of comparing like types of funding rates.

As an additional robustness check, we repeat the analysis by replacing the OIS rate with the measure of the expected funds rate that is derived from federal funds futures contracts. As shown in the lower panel of table 3 (panel B), the results are essentially identical, reflecting the fact that our two expectations measures are very similar. This result is reassuring because the federal funds futures data are available prior to 2001, allowing us to extend our sample period backwards and yet be confident that the results are not dependent on a single measure of expectations.

Taylor and Williams (2009) note that in addition to credit-default-swap spreads, the spread between the yen-denominated Libor and Tibor, or the spread between Libor and repo rates can be used as alternative measures of counterparty risk. These measures of risk not only provide a robustness check for our results, they also allow us to extend our sample period. In Table 4, we repeat the analysis in Table 3 but replace the CDS spread with the Libor-Tibor spread.⁴ The upper panel (panel A) uses the OIS rate as a measure of expectations. Overall, the results are comparable to Table 3 although the credit risk measure has the opposite sign in the Eurodollar equation and insignificant in the funds rate equation. In the lower panel (panel B), we replace the OIS rate with the federal funds futures based measure of expectations and expand the sample period backwards to November 1995.⁵ When we take advantage of a longer sample, all the coefficient estimates become significant and their values are comparable to those in Table 3. The coefficient estimates associated with the Libor-Tibor spread are significantly larger than those associated with the CDS spread and the difference is statistically significant.

Table 5 contemplates yet another measure of counterparty risk considered in Taylor and Williams (2009). Instead of using the median CDS spread as we have considered in Table 3, we use an index of the CDS spread constructed by the Board of Governors. The results are comparable to the benchmark specification in Table 3.

The main focus in Taylor and Williams (2009) is to analyze the effectiveness of the Term Auction Facility in driving down the spread on term lending rates. To that end, they test for the significance of dummy variables for the day of TAF auctions and each of the four days following the auction. In order to check how their results change after we control for federal funds volatility, we add dummy variables for TAF days into our specification and adjust our sample period to match with theirs. While the coefficient estimates for the TAF dummies are negative, none of them are significant (not shown). The literature has not reached an agreement on how to measure the effectiveness of TAF. As an alternative to Taylor and Williams (2009), Wu (2008) defined a TAF dummy that equals zero before the TAF was first introduced on December 12, 2007, and one afterwards.⁶ This specification assumes that the TAF facility would permanently reduce liquidity risk affecting interbank lending markets. Table 6 shows the results from the specification using this dummy variable. As shown, the TAF dummy is negative and highly significant for all term rates. While we do not take a stand on the interpretation of these types of analyses, our main results are robust to the inclusion of these measures. We conclude that, however effective the TAF was in narrowing spreads and lowering rates, the role of volatility in the funds market also needs to be considered.

Robustness Analysis

One question regarding the interpretation of our results is whether the impact of intraday volatility on the term premium is driven by the extraordinary fluctuations in this variable during the crisis period. In order to control for the crisis, we generate a dummy variable that captures the crisis period and interact this dummy variable with intraday volatility in our benchmark specification.⁷ Table 7 shows the results from this analysis. As shown, intraday volatility is significant both before and after the crisis. The difference between the two periods is statistically insignificant for most rates except for the Treasury rate. For the Treasury rate, the volatility enters with a negative sign only during the crisis period, suggesting that the volatility in the crisis affected that market differently.

One way to reconcile our results with the liquidity premium theory is to note that intraday volatility may at least partially capture the liquidity risk component of the term premium. This way of interpreting our results would go against Taylor and Williams (2009) argument that the Libor-OIS spread should not contain any liquidity risk. In order to test this argument more thoroughly we add additional measures of liquidity risk to our benchmark specification such as the spread between the six-month and three-month Treasury bill rates and the volume in the federal funds market. Furthermore, in order to control for potential spillovers between the major financial markets, we also add the interbank volatilities in the Euro area and UK.⁸ Table 8 shows the results from this exercise. Two observations are noticeable. First, the additional liquidity risk measures are highly significant in most of the regressions. From a theoretical perspective, Eisenschmidt and Tapking (2009) reached a similar conclusion for the Euro area, arguing that the rates in the interbank markets could not be explained with credit risk alone and the liquidity risk should play a role. Second, intraday volatility is still significant even in the presence of the additional liquidity measures. Finally, intraday volatilities in the Euro area and the UK are generally significant in affecting the money market rates in the US both in the period before and after the crisis

As a final robustness test, we check for GARCH effects. We show the results for the Libor equation in Table 9. Intraday volatility is significant for the mean equation before and after the crisis. Meanwhile, measures of credit and liquidity risk have a negative impact on the variance of Libor.⁹

An Extension for the Euro Area and the UK

So far we have established the role of volatility on short term interest rates in the US. In this section, we extend our analysis to the Euro Area and the UK. The first column in Table 10 shows the results for the Euro Area where the benchmark specification is estimated for this region. Here, Libor is replaced by Euribor and the thirty-day trailing standard deviation of the Eonia is used as a measure for volatility. The second column adds intraday volatility in the US and the UK to the Euribor equation before and after the crisis. Eonia volatility is significant in affecting Euribor similar to our results for the US. However, the impact of volatility after the crisis is significantly different from its impact before the crisis. Furthermore, intraday volatility in the federal funds marketvolatility in the US as well as the UK is are significant in affecting Eonia both before and after the crisis as well, although its their significance increases dramatically during the crisis. In the last column, Tthe spread between the six-month and three-month German bond rates, which is added as an additional measure of liquidity risk, is insignificant. Intraday volatility still maintains its significance. Table 11 checks for the presence of GARCH effects. Most of the regressors that are significant in the mean equation are also significant in the variance equation. US volatility has a larger impact on the mean equation for Euribor relative to Eonia volatility during the crisis period.

Tables 12 and 13 are the counterparts of Tables 10 and 11 for the UK. This time, the dependent variable is Sterling-denominated Libor and the measure of volatility is the 30-day standard deviation of the Sonia. As the additional measure of liquidity risk, we use the spread between the three month and overnight repo rates. The results are very similar to those obtained for the Euro Area. Own overnight volatility as well as foreign overnight volatilities are significant in determining the term premium which is more pronounced after the crisis.Intraday volatility in the US is significant in affecting the mean as well as the variance of the interbank rates in the Euro Area and the UK. Evidence of GARCH effects are detected in the variance equation.

Conclusions

The results presented above have a variety of implications. First, the results provide another set of evidence that the expectations hypothesis is generally a valid characterization of the term structure of interest rates, at least at the very near end of the yield curve. In terms of levels, a higher degree of volatility in the overnight rate is associated with a greater term premium. That is to say, greater volatility leads to a higher longer-term rate for a given level of the short rate. If one mechanism through which the expectations hypothesis holds is intertemporal arbitrage, lenders lending long while funding themselves short, volatility in the short rate increases the risk associated with this trade, making the lender demand a higher term premium.

The implications of these findings are varied. Failure to find empirical support for the expectations hypothesis could reflect mismeasurement of expectations, not simply a refutation of the hypothesis. Our results confirm that using measures of the expected federal funds rate instead of the realized federal funds rate yields results that tend to support the expectations hypothesis. Second, in the current financial crisis, a great deal of attention has been paid to the Libor-OIS spread. The popular view is that this spread reflects liquidity and term premiums in the bank funding market, and thus the spread can be used as a summary statistic for those strains. Those effects are surely present, however these results suggest also considering the volatility in the overnight rate when interpreting that spread. Essentially, the higher volatility adds to the liquidity risk that exists in the market. This result is true for the US as well as the Euro Area and the UK. Furthermore, interbank volatility in one market has spillovers in other markets. Finally, the Federal Reserve has changed its operating procedure for the daily implementation of monetary policy. The high level of reserve balances in the banking system has led to a discussion of various tools at the central bank's disposal for its "exit strategy" from its current accomodative stance. If those tools lead to an operating framework where the overnight rate is more volatile than it had been, even conditional on being able to hit a target rate on avearge, then the results presented above suggest that term premiums should be higher and, all else equal, longer-term interest rates will be higher conditional on a given setting of the overnight rate.

References

Bennett, P., and Peristiani, S., 2002, Are U.S. Reserve Requirements Still Binding?, Federal Reserve Bank of New York Economic Policy Review 8, no. 1, 53-68.

Bernanke, B., and Blinder, A., 1992, The Federal Funds Rate and the Channels of Monetary Transmission, American Economic Review 82(4), 901-921.

Campbell, J.Y., and Shiller, R.J., 1991, Yield Spreads and Interest Rate Movements: A Bird's Eye View, Review of Economic Studies 58, 495-514

Carpenter, S., and Demiralp, S., 2006, Anticipation of Monetary Policy and Open Market Operations, International Journal of Central Banking June, 25-63

Christensen, J. H. E., Lopez, J.A., and Rudebusch, G.D., 2009, Do Central Bank Liquidity Facilities Affect Interbank Lending Rates?, FRBSF Working Paper 2009-13 (June).

Cook, T., and Hahn, T., 1989, The Effect of Changes in the Federal Funds Rate on Market Interest Rates in the 1970s, Journal of Monetary Economics 24, 331-351.

Demiralp, S., 2008, Monetary Policy Surprises and the Expectations Hypothesis at the Short End of the Yield Curve, Economics Letters, 101: 1-3.

Demiralp, S., Farley, D., 2005, Declining required reserves, funds rate volatility, and open market operations, Journal of Banking and Finance 29, 1131-1152.

Eisenschmidt, J., Tapking, J., 2009, Liquidity risk premia in unsecured interbank money markets, European Central Bank Working Paper No: 1025.

Gurkaynak, R., Sack, B. and Swanson, E., 2007, Market-Based Measures of Monetary Policy Expectations, Journal of Business and Economic Statistics 25(2), April, 201-12.

Hilton, S., 2005, Trends in Federal Funds Rate Volatility, Current issues in Economics and Finance, Federal Reserve Bank of New York, July 2005 Volume 11, Number 7

Kuttner, K., 2001. Monetary Policy Surprises and Interest Rates: Evidence from the Fed Funds Futures Market, Journal of Monetary Economics,47, 447-76.

Lange, J., Sack, B., and Whitesell, W., 2003, Anticipations of Monetary Policy in Financial Markets, Journal of Money, Credit, and Banking 35, 889-909.

Mankiw, N.G., and Miron, J.A., 1986, The Changing Behavior of the Term Structure of Interest Rates, Quarterly Journal of Economics 101, 211-228

McAndrews, J., Sarkar, A., and Wang, Z., 2008, The Effect of the Term Auction Facility on the London Inter-Bank Offered Rate, FRB New York Staff Report 335(July).

Meulendyke, A. M., 1998, U.S. Monetary Policy and Financial Markets, New York, Federal Reserve Bank of New York.

Nautz, D., Schmidt, S., 2009. Monetary policy implementation and the federal funds rate. Journal of Banking and Finance 33, 1274-1284.

Rudebusch, G., 1995, Federal Reserve Interest Rate Targeting, Rational Expectations, and the Term Structure, Journal of Monetary Economics 35, 245-274.

Schwarz, K., 2009, Mind the Gap: Disentangling Credit and Liquidity in Risk Spreads, Columbia University, unpublished manuscript

Shiller, R.J., Campbell, J.Y., and Schoenholtz, K.L., 1983, Forward Rates and Future Policy: Interpreting the Term Structure of Interest Rates, Brookings Papers on Economic Activity no. 1, 173-224

Taylor, J., and Williams, J., 2009, A Black Swan in the Money Market, American Economic Journal: Macroeconomics 1(1), 58-83.

Wu, T., 2008, On the Effectiveness of the Federal Reserve's New Liquidity Facilities, Federal Reserve Bank of Dallas Working Paper 0808.

**Table 1: Testing the Expectations Hypothesis**
	$\Delta TB3_{t}$ 1/1/90-6/18/10: I	$\Delta TB3_{t}$ 1/1/90-6/18/10: II	$\Delta TB6_{t}$ 1/1/90-3/22/10: III	$\Delta TB6_{t}$ 1/1/90-3/22/10: IV
Constant	0.00**	0.00	0.00**	0.00
Constant (t-statistic)	-2.04	-0.70	-2.28	-0.80
$\Delta Avg(FFR_{90} )$	0.42**	-	0.51**	-
$\Delta Avg(FFR_{90} )$ (t-statistic)	2.85		4.51
$\Delta E_{t} \left[Avg(FFR_{90} )\right]$	-	1.00**	-	1.04**
$\Delta E_{t} \left[Avg(FFR_{90} )\right]$ (t-statistic)		15.00		29.41
Adjusted $R^{2}$	0.01	0.26	0.01	0.51
Number of Obs.	4897	4897	4835	4835

t-statistics (based on White heteroskedasticity consistent standard errors) are below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance.

Realized average funds rate for TB3 (TB6) equation is calculated over the next 90 (180) days.

Expected average funds rate ( $E_{t} \left[Avg(FFR_{} )\right]$ ) for the TB3 (TB6) equation is calculated from federal funds futures contracts over the next 90 (180) days as described in the appendix.

Table 2: Testing the Expectations Hypothesis with Alternative Measures of Expectations

Sample Period: 12/4/2001-6/18/2010

Dependent variable: $\Delta TB3_{t}$

	I	II	III
Constant	0.00	0.00	0.00
Constant (t-statistic)	-1.45	-0.97	-1.12
$\Delta Avg(FFR_{90} )$	0.39	-	-
$\Delta Avg(FFR_{90} )$ (t-statistic)	1.04
$\Delta E_{t} \left[Avg(FFR_{90} )\right]$	-	1.16**	-
$\Delta E_{t} \left[Avg(FFR_{90} )\right]$ (t-statistic)		6.35
$\Delta$ OIS (Three month)	-	-	0.95**
$\Delta$ OIS (Three month) (t-statistic)			6.46
Adjusted R ${}^{2}$	0.00	0.21	0.15
Number of Obs.	2046	2046	2046

t-statistics (based on White heteroskedasticity consistent standard errors) are below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance.

Table 3: Testing the Expectations Hypothesis for various Interest Rates

Panel A: Using OIS rate as a measure of expectations

Sample Period: 12/4/2001-9/15/2010

	I: Libor	II: ED	III: Term FFR	IV: T-Bill
1. Constant	-0.12**	-0.30**	-0.20**	0.12**
1. Constant (t-statistic)	-12.37	-18.91	-15.09	13.00
2. OIS (3-month)	0.99**	0.98**	0.97**	0.92**
2. OIS (3-month) (t-statistic)	376.51	238.98	288.06	282.88
3. Intraday Vol.	3.09**	4.21**	3.89**	-0.99**
3. Intraday Vol. (t-statistic)	30.57	25.79	30.73	-10.18
4. CDS (median)	0.33**	0.61**	0.42**	-0.10**
4. CDS (median) (t-statistic)	20.44	25.15	20.18	-7.83
5. Adjusted R ${}^{2}$	0.99	0.97	0.98	0.99
6. Number of Obs.	2197	2195	2201	2198

Panel B: Using federal funds futures based measure of expectations

Sample Period: 12/4/2001-9/15/2010

	I: Libor	II: ED	III: Term FFR	IV: T-Bill
1. Constant	-0.11**	-0.28**	-0.19**	0.13**
1. Constant (t-statistic)	-10.74	-17.61	-13.71	14.50
2. $E_{t} \left[Avg(FFR_{} )\right]$	0.99**	0.99**	0.98**	0.93**
2. $E_{t} \left[Avg(FFR_{} )\right]$ (t-statistic)	365.08	232.65	276.59	263.07
3. Intraday Vol.	3.14**	4.24**	3.91**	-0.97**
3. Intraday Vol. (t-statistic)	31.22	25.80	30.27	-9.04
4. CDS (median)	0.32**	0.60**	0.41**	-0.10**
4. CDS (median) (t-statistic)	19.75	24.40	19.41	-8.03
5. Adjusted R ${}^{2}$	0.99	0.97	0.98	0.99
6. Number of Obs.	2217	2197	2202	2199

t-statistics (based on White heteroskedasticity consistent standard errors) are below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance.

One day forward Libor rate is used in the regressions to adjust for the time difference between New York and London.

$E_{t} \left[Avg(FFR_{} )\right]$ is the expected funds rate calculated from federal fund futures contracts over the maturity of the security (which is 90-days for all the securities considered in this table).

The maturities for the Libor, Eurodollar, Term fed funds, and Treasury Bills are three months.

Table 4: Testing the Expectations Hypothesis using Libor-Tibor spread as a measure of risk

Panel A: Using OIS rate as a measure of expectations

Sample Period: 12/4/2001-9/15/2010

	I: Libor	II: ED	III: Term FFR	IV: T-Bill
1. Constant	0.19**	0.10**	0.09**	0.01
1. Constant (t-statistic)	13.32	3.93	5.02	0.47
2. OIS (3-month)	0.92**	0.89**	0.90**	0.95**
2. OIS (3-month) (t-statistic)	286.55	158.51	201.16	490.73
3. Intraday Vol.	3.27**	5.32**	4.54**	-0.95**
3. Intraday Vol. (t-statistic)	32.77	31.24	35.17	-7.43
4. Libor-Tibor	0.66**	-0.44**	-0.05	-0.37**
4. Libor-Tibor (t-statistic)	8.69	-3.30	-0.46	-3.30
5. Adjusted R ${}^{2}$	0.99	0.96	0.98	0.99
6. Number of Obs.	2073	2017	2020	2020

Panel B: Using federal funds futures based measure of expectations

Sample Period: 11/14/1995-9/15/2010

	I: Libor	II: ED	III: Term FFR	IV: T-Bill
1. Constant	0.28**	0.40**	0.29**	-0.01**
1. Constant (t-statistic)	31.89	27.39	25.62	-2.57
2. $E_{t} \left[Avg(FFR)\right]$	0.93**	0.87**	0.91**	0.96**
2. $E_{t} \left[Avg(FFR)\right]$ (t-statistic)	301.30	172.58	215.93	562.77
3. Intraday Vol.	2.18**	2.94**	2.77**	-0.56**
3. Intraday Vol. (t-statistic)	21.86	18.17	20.53	-10.10
4. Libor-Tibor	1.03**	1.44**	1.11**	-0.39**
4. Libor-Tibor (t-statistic)	16.71	15.11	14.07	-6.76
5. Adjusted R ${}^{2}$	0.99	0.97	0.98	0.99
6. Number of Obs.	3540	3437	3413	3419

t-statistics (based on White heteroskedasticity consistent standard errors) are below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance.

One day forward Libor rate is used in the regressions to adjust for the time difference between New York and London. Similarly, Tibor rate is forwarded one period relative to Libor in computing the Libor-Tibor spread to adjust for the time difference between London and Tokyo.

Tibor data is available after 1995, which determines the beginning of the sample size in panel B.

The maturities for the Libor, Eurodollar, Term fed funds, and Treasury Bills are three months.

Table 5: Testing the Expectations Hypothesis using CDS index as a measure of risk

Sample Period: 12/4/2001-9/15/2010

	I: Libor	II: ED	III: Term FFR	IV: T-Bill
1. Constant	-0.14**	-0.35**	-0.24**	0.11**
1. Constant (t-statistic)	-16.97	-28.67	-22.18	12.68
2. OIS (3-month)	0.99**	0.99**	0.98**	0.93**
2. OIS (3-month) (t-statistic)	456.73	299.32	350.07	298.58
3. Intraday Vol.	3.05**	4.09**	3.81**	-1.01**
3. Intraday Vol. (t-statistic)	30.95	25.61	30.41	-10.22
4. CDS index	0.32**	0.62**	0.43**	-0.08**
4. CDS index (t-statistic)	28.00	41.41	30.35	-6.59
5. Adjusted R ${}^{2}$	0.99	0.98	0.98	0.99
6. Number of Obs.	2198	2196	2202	2199

t-statistics (based on White heteroskedasticity consistent standard errors) are below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance

One day forward Libor rate is used in the regressions to adjust for the time difference between New York and London.

Table 6: Testing the effectiveness of TAF

Sample Period: 1/3/2007-6/4/2009

	I: Libor	II: ED	III: Term FFR	IV: T-Bill
1. Constant	-0.51**	-0.64**	-0.54**	0.08**
1. Constant (t-statistic)	-21.59	-15.24	-15.32	2.75
2. OIS (3-month)	1.03**	1.01**	1.01**	0.92**
2. OIS (3-month) (t-statistic)	217.93	127.08	150.08	129.45
3. Intraday Vol.	3.32**	4.48**	4.11**	-0.95**
3. Intraday Vol. (t-statistic)	33.34	27.53	32.72	-8.49
4. CDS index	0.64**	0.89**	0.67**	-0.05**
4. CDS index (t-statistic)	29.62	23.99	21.04	-2.08
5. TAF dummy	-0.16**	-0.16**	-0.10**	-0.01**
5. TAF dummy (t-statistic)	-9.61	-5.89	-4.30	-0.46
6. Adjusted R ${}^{2}$	0.99	0.97	0.98	0.99
7. Number of Obs.	915	925	931	929

t-statistics (based on White heteroskedasticity consistent standard errors) are below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance

One day forward Libor rate is used in the regressions to adjust for the time difference between New York and London.

The maturities for the Libor, Eurodollar, term fed funds, and Treasury Bills are three months.

Table 7: Robustness Analysis I

Sample Period: 12/4/2001-9/15/2010

	I: Libor	II: ED	III: Term FFR	IV: T-Bill
1. Constant	-0.10**	-0.25**	-0.18**	-0.06**
1. Constant (t-statistic)	-6.55	-11.18	-9.13	-5.57
2. OIS (3-month)	0.99**	0.99**	0.97**	0.91**
2. OIS (3-month) (t-statistic)	356.49	221.55	265.75	286.02
3. Intraday Vol. $\times (1-D^{Crisis} )$	2.64**	3.40**	3.42**	2.24**
3. Intraday Vol. $\times (1-D^{Crisis} )$ (t-statistic)	11.47	9.34	11.36	11.77
4. Intraday Vol. $\times D^{Crisis}$	3.07**	4.17**	3.87**	-0.84**
4. Intraday Vol. $\times D^{Crisis}$ (t-statistic)	29.35	24.63	29.63	-9.30
5. CDS median	0.31**	0.57**	0.40**	0.03**
5. CDS median (t-statistic)	16.63	20.72	16.37	2.67
6. Adjusted R ${}^{2}$	0.99	0.97	0.98	0.99
7. Number of Obs.	2197	2194	2200	2197

t-statistics (based on White heteroskedasticity consistent standard errors) are below the coefficient estimates.

$D^{Crisis}$ takes the value of 1 between August 9, 2007 through September 15, 2010.

Table 8: Robustness Analysis II

Sample Period: 12/4/2001-9/15/2010

	I: Libor	II: ED	III: Term FFR	IV: T-Bill
1. Constant	-1.34**	-0.72	-1.05**	1.80**
1. Constant (t-statistic)	-4.17	-1.36	-2.46	7.05
2. OIS (3-month)	1.00**	0.98**	0.98**	0.91**
2. OIS (3-month) (t-statistic)	338.57	194.00	223.02	261.68
3. Intraday Vol. $\times (1-D^{Crisis} )$	1.11**	2.40**	2.00**	2.84**
3. Intraday Vol. $\times (1-D^{Crisis} )$ (t-statistic)	5.85	7.73	7.89	12.83
4. Intraday Vol. $\times D^{Crisis}$	1.98**	2.71**	2.51**	-0.51**
4. Intraday Vol. $\times D^{Crisis}$ (t-statistic)	13.74	12.59	15.69	-5.07
5. CDS_median	0.30**	0.47**	0.34**	-0.09**
5. CDS_median (t-statistic)	16.49	13.37	11.31	-5.10
6. TB6-TB3	0.49**	0.70 **	0.62**	-0.54**
6. TB6-TB3 (t-statistic)	12.97	8.91	9.11	-12.32
7. FF Volume	0.10**	0.04	0.08**	-0.16**
7. FF Volume (t-statistic)	3.54	0.84	1.99	-6.94
8. Eonia Vol. $\times (1-D^{Crisis} )$	0.45**	0.62**	0.49**	-0.03
8. Eonia Vol. $\times (1-D^{Crisis} )$ (t-statistic)	10.50	8.99	9.11	-0.94
9. Eonia Vol. $\times D^{Crisis}$	0.25**	0.58**	0.09	0.48**
9. Eonia Vol. $\times D^{Crisis}$ (t-statistic)	2.12	3.15	0.60	9.24
10. Sonia Vol. $\times (1-D^{Crisis} )$	0.14**	-0.13**	-0.03	-0.12**
10. Sonia Vol. $\times (1-D^{Crisis} )$ (t-statistic)	7.39	-4.24	-1.22	-5.59
11. Sonia Vol. $\times D^{Crisis}$	1.00**	1.42**	1.45**	0.11**
11. Sonia Vol. $\times D^{Crisis}$ (t-statistic)	15.47	15.04	17.36	2.47
12. Adjusted R ${}^{2}$	0.99	0.98	0.99	0.99
13. Number of Obs.	2139	2192	2194	2198

t-statistics (based on White heteroskedasticity consistent standard errors) are below the coefficient estimates.

Table 9: GARCH Effects for the US

Sample Period: 12/4/2001-9/15/2010

Dependent Variable: Libor (3-month)

	I: Mean Equation	II: Variance Equation
1. Constant	-1.23**	0.01**
1. Constant (z-statistic)	-13.94	286.84
2. OIS (3-month)	0.99**	-0.00**
2. OIS (3-month) (z-statistic)	1230.20	-10.23
3. Intraday Vol. $\times (1-D^{Crisis} )$	0.60**	-0.01
3. Intraday Vol. $\times (1-D^{Crisis} )$ (z-statistic)	15.06	-1.18
4. Intraday Vol. $\times D^{Crisis}$	1.41**	0.01**
4. Intraday Vol. $\times D^{Crisis}$ (z-statistic)	58.87	3.51
5. CDS_median	0.08**	-0.00**
5. CDS_median (z-statistic)	23.94	-6.88
6. TB6-TB3	0.08**	-0.00**
6. TB6-TB3 (z-statistic)	13.54	-8.10
7. FF Volume	0.11**	-0.00**
7. FF Volume (z-statistic)	14.09	-1327.46
8. Eonia Vol. $\times (1-D^{Crisis} )$	0.07**	-0.00
8. Eonia Vol. $\times (1-D^{Crisis} )$ (z-statistic)	3.71	-1.01
9. Eonia Vol. $\times D^{Crisis}$	0.37**	-0.01**
9. Eonia Vol. $\times D^{Crisis}$ (z-statistic)	20.96	-8.83
10. Sonia Vol. $\times (1-D^{Crisis} )$	0.07**	-0.00**
10. Sonia Vol. $\times (1-D^{Crisis} )$ (z-statistic)	16.02	-10.23
11. Sonia Vol. $\times D^{Crisis}$	1.28**	0.01**
11. Sonia Vol. $\times D^{Crisis}$ (z-statistic)	74.34	2.46
12. $Residual_{-1}^{2}$		0.81**
12. $Residual_{-1}^{2}$ (z-statistic)		21.44
13. $GARCH_{-1}$		-0.18**
13. $GARCH_{-1}$ (z-statistic)		-4.44
14. Adjusted R ${}^{2}$	0.99
15. Number of Obs.	2156

z-statistics (based on Bollerslev-Wooldrige robust standard errors & covariance) are shown below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance

Table 10: Testing the Expectations Hypothesis for the Euro Area using median CDS as a measure of Expectations

Sample Period: 1/2/2001-9/15/2010

Dependent Variable: Euribor (3-month)

	I	II
1. Constant	-0.12**	0.04**
1. Constant (t-statistic)	-12.75	8.01
2. OIS (3-month)	1.06**	1.00**
2. OIS (3-month) (t-statistic)	327.08	452.65
3. Eonia Vol. $\times (1-D^{Crisis} )$	-0.39**	0.07**
3. Eonia Vol. $\times (1-D^{Crisis} )$ (t-statistic)	-12.96	7.07
4. Eonia Vol. $\times D^{Crisis}$	2.62**	0.83**
4. Eonia Vol. $\times D^{Crisis}$ (t-statistic)	23.37	16.28
5. CDS (median)	0.22**	0.15**
5. CDS (median) (t-statistic)	14.66	17.57
6. German Bond (6m)-German Bond (3m)	-	0.02
6. German Bond (6m)-German Bond (3m) (t-statistic)		1.13
7. Intraday Vol. $\times (1-D^{Crisis} )$	-	-0.06*
7. Intraday Vol. $\times (1-D^{Crisis} )$ (t-statistic)		-1.81
8. Intraday Vol. $\times D^{Crisis}$	-	1.26**
8. Intraday Vol. $\times D^{Crisis}$ (t-statistic)		28.68
9. Sonia Vol. $\times (1-D^{Crisis} )$	-	-0.08**
9. Sonia Vol. $\times (1-D^{Crisis} )$ (t-statistic)		-7.08
10.Sonia Vol. $\times D^{Crisis}$	-	0.86**
10.Sonia Vol. $\times D^{Crisis}$ (t-statistic)		24.16
11. Adjusted R ${}^{2}$	0.99	0.99
12. Number of Obs.	2485	2479

t-statistics (based on White heteroskedasticity consistent standard errors) are below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance

Table 11: GARCH Effects for the Euro Area

Sample Period: 1/2/2001-9/15/2010

Dependent Variable: Euribor (3-month)

	I: Mean Equation	II: Variance Equation
1. Constant	0.06**	0.00**
1. Constant (z-statistic)	22.27	12.30
2. OIS (3-month)	1.00**	-0.00**
2. OIS (3-month) (z-statistic)	1282.70	-6.76
3. STD_Eonia $\times (1-D^{Crisis} )$	0.05**	-0.00**
3. STD_Eonia $\times (1-D^{Crisis} )$ (z-statistic)	7.03	-2.80
4. STD_Eonia $\times D^{Crisis}$	0.05**	-0.01**
4. STD_Eonia $\times D^{Crisis}$ (z-statistic)	7.03	-5.29
5. CDS (median)	0.13**	-0.01**
5. CDS (median) (z-statistic)	48.93	-5.29
6. German Bond (6m)-German Bond (3m)	0.00	-0.00**
6. German Bond (6m)-German Bond (3m) (z-statistic)	0.17	-3.48
7. Intraday Vol. $\times (1-D^{Crisis} )$	-0.01	-0.01**
7. Intraday Vol. $\times (1-D^{Crisis} )$ (z-statistic)	-0.45	-6.48
8. Intraday Vol. $\times D^{Crisis}$	1.24**	-0.00*
8. Intraday Vol. $\times D^{Crisis}$ (z-statistic)	75.58	-1.62
9. Sonia Vol. $\times (1-D^{Crisis} )$	-0.07**	-0.00**
9. Sonia Vol. $\times (1-D^{Crisis} )$ (z-statistic)	-15.52	-2.74
10.Sonia Vol. $\times D^{Crisis}$	0.83**	0.01**
10.Sonia Vol. $\times D^{Crisis}$ (z-statistic)	48.25	4.80
11. $Residual_{-1}^{2}$		0.57**
11. $Residual_{-1}^{2}$ (z-statistic)		9.25
12. $GARCH_{-1}$		-0.05
12. $GARCH_{-1}$ (z-statistic)		-0.48
13. R ${}^{2}$	0.99
14. Number of Obs.	2478

z-statistics (based on Bollerslev-Wooldrige robust standard errors & covariance) are shown below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance

Table 12: Testing the Expectations Hypothesis for the UK

Sample Period:1/2/2001-9/15/2010

Dependent Variable: Sterling denominated Libor (3-month)

	I	II
1. Constant	-0.18**	-0.09**
1. Constant (t-statistic)	-10.33	-5.84
2. OIS (3-month)	1.06**	1.03**
2. OIS (3-month) (t-statistic)	286.60	291.10
3. Sonia Vol. $\times (1-D^{Crisis} )$	-0.25**	-0.04**
3. Sonia Vol. $\times (1-D^{Crisis} )$ (t-statistic)	-20.45	-2.95
4. Sonia Vol. $\times (D^{Crisis} )$	2.29**	1.44**
4. Sonia Vol. $\times (D^{Crisis} )$ (t-statistic)	24.77	21.33
5. CDS (median)	0.50**	0.27**
5. CDS (median) (t-statistic)	28.96	13.11
6. RP(3m)-RP(ON)	-	0.02**
6. RP(3m)-RP(ON) (t-statistic)		3.68
7. Intraday Vol. $\times (1-D^{Crisis} )$	-	0.12**
7. Intraday Vol. $\times (1-D^{Crisis} )$ (t-statistic)		2.42
8. Intraday Vol. $\times D^{Crisis}$	-	0.95**
8. Intraday Vol. $\times D^{Crisis}$ (t-statistic)		13.64
9. Eonia Vol. $\times (1-D^{Crisis} )$	-	0.14**
9. Eonia Vol. $\times (1-D^{Crisis} )$ (t-statistic)		8.63
10. Eonia Vol. $\times D^{Crisis}$	-	1.47**
10. Eonia Vol. $\times D^{Crisis}$ (t-statistic)		13.84
11. Adjusted R ${}^{2}$	0.99	0.99
12. Number of Obs.	2444	2442

t-statistics (based on White heteroskedasticity consistent standard errors) are below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance

Table 13: GARCH Effects for the UK

Sample Period: 1/2/2001-9/15/2010

Dependent Variable: Sterling Denominated Libor (3-month)

	I: Mean Equation	II: Variance Equation
1. Constant	-0.07**	0.01**
1. Constant (z-statistic)	-11.31	10.68
2. OIS (3-month)	1.03**	-0.00**
2. OIS (3-month) (z-statistic)	755.22	-4998.93
3. Sonia Vol. $\times (1-D^{Crisis} )$	-0.02**	-0.00**
3. Sonia Vol. $\times (1-D^{Crisis} )$ (z-statistic)	-3.46	-3.84
4. Sonia Vol. $\times (D^{Crisis} )$	1.52**	0.06**
4. Sonia Vol. $\times (D^{Crisis} )$ (z-statistic)	38.43	5.06
5. CDS (median)	0.14**	-0.00**
5. CDS (median) (z-statistic)	20.11	-4.21
6. RP(3m)-RP(ON)	0.01**	-0.00**
6. RP(3m)-RP(ON) (z-statistic)	2.45	-2.08
7. Intraday Vol. $\times (1-D^{Crisis} )$	0.04**	-0.02**
7. Intraday Vol. $\times (1-D^{Crisis} )$ (z-statistic)	2.29	-6.48
8. Intraday Vol. $\times D^{Crisis}$	1.27**	-0.01
8. Intraday Vol. $\times D^{Crisis}$ (z-statistic)	42.19	-1.58
9. Eonia Vol. $\times (1-D^{Crisis} )$	0.12**	-0.01**
9. Eonia Vol. $\times (1-D^{Crisis} )$ (z-statistic)	9.08	-5.00
10. Eonia Vol. $\times D^{Crisis}$	1.46**	-0.04**
10. Eonia Vol. $\times D^{Crisis}$ (z-statistic)	40.84	-6.36
11. $Residual_{-1}^{2}$		0.58**
11. $Residual_{-1}^{2}$ (z-statistic)		8.87
12. $GARCH_{-1}$		-0.04
12. $GARCH_{-1}$ (z-statistic)		-0.40
13. Adjusted R ${}^{2}$	0.99
14. Number of Obs.	2442

z-statistics (based on Bollerslev-Wooldrige robust standard errors & covariance) are shown below the coefficient estimates.

*/** indicates significance at 90%/95% level of significance

Figure 1: The Libor-OIS Spread over the Course of the Crisis

Accessible Version

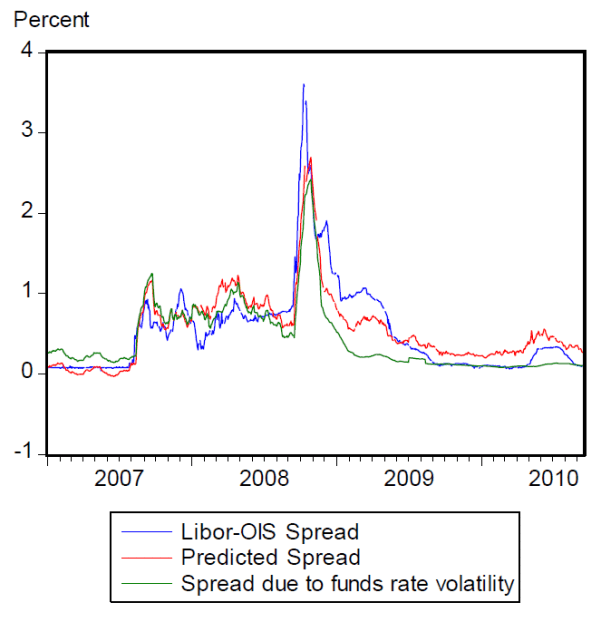
Figure 2: Predicted Libor-OIS spread

Accessible Version

Predicted Spread=(Predicted Libor from Table 3, column 1)-OIS

Spread due to FFR volatility= $\mathop{\beta _{Vol} }\limits^{\wedge } \times$ FFR Volatility

Appendix: Calculation of 90-day Expectations

The following diagram illustrates our logic in calculating 90-day expectations

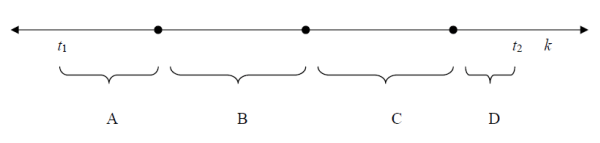
Diagram illustrates 90-day expectation calculation, as described in text below.

where

$t_{1}$ : the current day

$m_{i}$ : the number of days in month i

$t_{2}$ : the number of days included from the 4th month ( $t_{2}$ $=90-\left[m_{2} +m_{3} +(m_{1} -t_{1} )\right]$ )

: day of FOMC meeting in month 4.

A: Average expected funds rate in the remaining days of the current month

B: Average expected funds rate in month 2

C: Average expected funds rate in month 3

D: Average expected funds rate until $t_{2}$ in month 4

We now describe how we calculate each of these components A through D.

A: Average expected funds rate in the remaining days of the current month

On day t, spot month futures contract ( $FF1_{t}$ ) reflects the expected funds rate for the current month. That is:

$FF1_{t} =\frac{1}{m_{1} } E_{t} \sum _{i=1}^{m_{1} }FFR_{i} +\mu _{t}$

(A.1)

where $m_{1}$ is the total number of days in month 1 (current month), $E_{t}$ is the expectations operator based on information as of day t, is the effective funds rate, and $\mu _{t}$ is a term that may represent the risk premium or day of month effects in the futures market. In an efficient market with risk-neutral investors, this term would be zero.

Rearranging equation A.1:

$FF1_{t} =\frac{1}{m_{1} } \left(\sum _{i=1}^{t-1}FFR_{i} \right)+\frac{1}{m_{1} } \left(E_{t} \sum _{i=t}^{m_{1} }FFR_{i} \right)+\mu _{t}$

(A.2)

Equation (A.2) notes that the spot month futures contract on day t has two components. The first component is the funds rate that is realized up to that date, and the second component is the expected funds rate on the remaining days of the month. Solving for the second term gives us the average expected funds rate for the remaining days in the month, A:

$A=\frac{1}{m_{1} -t+1} \left(E_{t} \sum _{i=t}^{m_{1} }FFR_{i} \right)=\frac{m_{1} (FF1_{t} -\mu _{t} )-\sum _{i=1}^{t-1}FFR_{i} }{m_{1} -t+1}$

(A.3)

B and C: Average expected funds rates in months 2 and 3

Average expected funds rates in months 2 and 3 as of day t are equal to the futures rates for the two-month and three-month contracts less the term premium respectively.

D: Average expected funds rate until $t_{2}$ in month 4

Note that $t_{2}$ denotes the last day included in 90-day expectations from the fourth month. Calculating the average expected funds rate over that time period is a bit trickier than the previous months. If there is no FOMC meeting in that month, then, average expected funds rate until $t_{2}$ is simply equal to the futures rate for the four-month contract less the term premium. If there is an FOMC meeting at a date after $t_{2}$ (i.e. $t_{2}$ k) , then the average expected funds rate is equal to the expected target for the third month.¹⁰ If the FOMC meeting is scheduled prior to $t_{2}$ (i.e. $t_{2} >k$ ), then the average expected funds rate is equal to the expected target for the third month for the first days, and it is equal to the expected target for the fourth month from day through day $t_{2}$ .

Average expected funds rate over the next 90-days

Once these components are calculated, we can derive the average expected funds rate over the next 90 days (Exp_90) as:

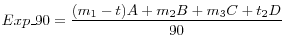
$\displaystyle Exp\_ 90=\frac{(m_{1} -t)A+m_{2} B+m_{3} C+t_{2} D}{90}$

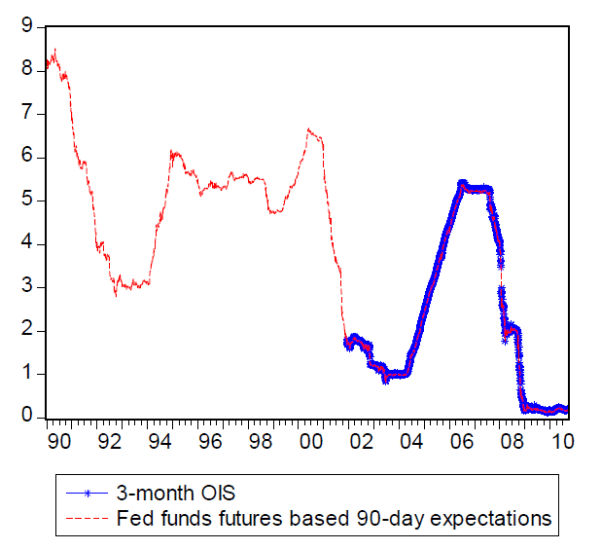
Expectations calculated in this manner are comparable to the three-month OIS rate. Figure A.1 illustrates the close resemblance between these two series.¹¹ Note that the OIS series is only available after 2001 while the expectations calculated from federal funds futures are available since May 1989. The correlation coefficient between these two measures of expectations is 0.99.

Figure A.1. Alternative measures for expected funds rate over the next 90 days

Accessible Version

Footnotes

* The views expressed are those of the authors and do not necessarily reflect those of the Federal Reserve, the Board of Governors, or other members of the staff. Demiralp's research was funded by the Turkish Academy of Sciences (TUBA). David Lucca,Ruslan Bikbov, Rehim Kilic, Benoit Mojon and the participants at the ECB's workshop on "Challenges to monetary policy implementation beyond the financial market turbulence" provided useful discussions. We thank Zenide Avellaneda and Peter Andersen for excellent research assistance. Return to Text

1. Intraday volatility is a volume-weighted measure of standard deviation based on total brokered funds rate transactions on a given day. Return to Text

2. More specifically, the tests check whether the spread between today's 90-day Treasury rate and the funds rate help explain the spread between the average funds rate over the next 90 days and today's funds rate. Return to Text

3. One day forward Libor rate is used in the regressions to adjust for the time difference between New York and London. Return to Text

4. Tibor rate is forwarded one period relative to Libor in computing the Libor-Tibor spread to adjust for the time difference between London and Tokyo. Return to Text

5. Tibor data is available after November 1995, which determines the beginning of the sample size in panel B. Return to Text

6. In our specification the TAF dummy takes the value of one between 12/17/2007 and 9/15/2010. Return to Text

7. The dummy variable takes the value fo 1 from August 9, 2007 through the end of our sample on September 15, 2010. Return to Text

8. Interbank volatility in the Euro area and the UK are measured by the standard deviations in the overnight lending rates in these regions (Eonia and Sonia respectively) over the last 30 days. Return to Text

9. For further robustness checks, we consider adding a dummy variable to control for volatility on quarter-ends (McAndrews et al. (2009) which turns out to be insignificant (not shown). Return to Text

10. Expected target for any month

, $E_{t} (T_{j} )$ , can be calculated in a recursive manner as $E_{t} (T_{j} )=\frac{m_{j} (FFJ_{t} -\mu _{t} )-kE_{t} (T_{j-1} )}{m_{j} -k}$ Where

is the

-month federal funds futures contract rate. If

corresponds to the last five days of a month, then, $E_{t} (T_{j} )=FF(J+1)_{t} -\mu _{t}$ . If there is no FOMC in month j, then $E_{t} (T_{j} )=E_{t} (T_{j-1} ).$ See Demiralp (2008) for more details. Return to Text

11. In our calculations we set $\mu _{t}$ to three basis points, consistent with the calculations in Gurkaynak, Sack and Swanson (2007). Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text