
Financial Capital and the Macroeconomy:
A Quantitative Framework*
Board of Governors of the Federal Reserve System
Keywords: Capital market friction, financial intermediary, capital constraint, liquidity based asset pricing, credit provision, uncertainty, aggregate fluctuation.
Abstract:
JEL Classifications: E32, E44.
1 Introduction
The global financial crisis has shown that the balance sheet/liquidity condition of financial institutions can have important real effects on the macroeconomy. Indeed, a root cause of financial instability appears to be the reliance on short-term funding of financial investment in potentially illiquid capital assets. To the extent that the essence of financial intermediation lies in the transformation of short-term liquid assets into long-term capital assets, the potential imbalance between the liquidity of intermediaries' funding and their investment assets is an inherent feature of modern finance.
Such an imbalance, however, could cause a significant disruption in the financial intermediation process, taking a large toll on real economic activity, especially when capital markets suffer from information problems. For instance, if outside capital is costly to raise because of information asymmetries between insiders and outsiders, financial institutions may take preemptive measures to reduce their exposure to an increase in uncertainty, thereby foregoing otherwise profitable investment opportunities. Likewise, if interbank transactions involving balance sheet assets is costly because of lack of transparency and growing counter-party risks, financial institutions may employ caution against taking large unhedged positions because undoing such positions may involve a substantial degree of distressed sales. Such preemptive measures, though individually rational, could collectively bring about a tightening in the availability of credit and decline in economic activity, which in the extreme could manifest itself in a financial crisis.
The discussion above suggests an important link between economic uncertainty and activity, mediated by capital market friction facing financial intermediaries. However, within the workhorse academic framework for macroeconomic analysis, the links between financial intermediation and macroeconomic outcomes are thin to non-existent (although the field is growing, e.g., Adrian and Shin (2010), Brunnermeier and Pedersen (2009), Gertler and Kiyotaki (2010) and He and Krishnamurthy (2008)). Meanwhile, banking, finance, and macroeconomics are typically not integrated in the models used at policy institutions (e.g., the discussion in Boivin et al. (2010)).
Our goal is to take a deeper look at how such a link operates in a modern economy, quantifying the significance of capital market frictions, and potentially identifying intervention points for future public policies. To that end, we take a dual approach. First, we develop a dynamic model in which the balance sheet/liquidity condition of financial intermediaries plays an important role in the determination of asset prices and economic activity under time-varying uncertainty. Second, we present new evidence on the importance of uncertainty facing financial intermediaries for credit terms and quantity and for aggregate economic activity, thus quantifying the significance of capital market frictions. We adopt a structural identification strategy in which the predictions of our theory, in the form of sign restrictions, play an important role.
In our model, we provide a general-equilibrium, business-cycle framework that generalizes the liquidity based asset pricing framework (LAPM, Holmström and Tirole (2001)) from the viewpoint of financial intermediaries operating under a capital (margin) constraint. The financial intermediaries in the model are required to make investment commitments before a complete resolution of idiosyncratic funding risk that can be addressed only by costly refinancing (of the type emphasized by, for example, Myers and Majluf (1984) and Bolton and Freixas (2000)); this environment forces intermediaries to behave in a risk-averse manner. The resulting caution against taking a large unhedged position given short-run funding uncertainty creates an intermediary specific pricing kernel that can deviate from the stochastic discount factor of a representative household even when the intermediary is fully owned by the household, pushing equilibrium asset returns away from their counterpart in the absence of such intermediation frictions, causing aggregate investment and output to respond to shocks to intermediaries.1
It is worthwhile to emphasize that the caution adopted by our otherwise risk-neutral intermediaries arises because of the frictions in financial markets we assume; other approaches have resorted to assuming risk-aversion on the part of intermediaries to generate similar behavior (e.g., He and Krishnamurthy (2008)). Using this model, we show that an increase in uncertainty, in the sense of mean preserving spread, can have a powerful impact on credit market conditions and economic activity even though such an uncertainty shock does not have any direct implication for real allocations in a frictionless economy.
We then use the theoretical predictions of our model regarding the impact of an uncertainty shock to financial intermediaries to quantify the macroeconomic importance of capital market frictions facing financial institutions. We start by constructing an uncertainty measure, an empirical counterpart of the time-varying idiosyncratic uncertainty in the theoretical model, using daily equity price movements at large bank-holding companies in the United States. To quantify the impact of structural shocks to the uncertainty measure, we frame our structural econometric analysis in a set of Bayesian sign restrictions informed by our model's predictions, which identify the dynamic effects of disturbances to the intermediation sector on macroeconomic variables.
Implementation of our identifying assumptions finds quantitatively important effects of shocks to the intermediation sector on economic activity, with increased uncertainty leading to a tightening in lending terms and declines in lending and economic activity. The use of theoretical restrictions to inform identification of intermediation shocks is a notable advance over previous macroeconomic efforts, which have used debatable assumptions, such as recursive timing assumptions, to identify such effects (e.g., Berrospide and Edge (2010), Lown and Morgan (2006) and Ciccarelli et al. (2010) ).2 In particular, our approach allows us to purge `" business cycle" correlations between lending and activity from our estimates of the effects of shocks to intermediaries on real activity, following a strategy similar to Uhlig (2005) and Mountford and Uhlig (2009) in their analyses of monetary policy and fiscal policy, respectively.
Indeed, our results reveal clearly that the financial shocks we identify are different from those in these other VAR approaches. This result is not very surprising because our focus on uncertainty shocks is a fairly narrow perspective, as our model framework implies that nearly any shock affecting the balance sheet/liquidity position of financial intermediaries will impact financial markets and real activity. In this sense, our new evidence helps highlight some of the possibly important economic mechanisms, but allows for the possibility of much richer investigations of financial shocks in the future. Finally, our focus on uncertainty shocks provides novel evidence on the role of this type of factor in macroeconomic fluctuations, evidence complementary to, for example, Bloom (2009).3
2 The Model
In our model, financial intermediation is central to the provision of credit and the management of household portfolios. The following three assumptions make intermediation important: (i) households need liquidity services from deposits at financial intermediaries, which implies that households accept returns on intermediary deposits below the risk free rate; (ii) households lack the skill necessary to invest and manage their financial resources and turn to financial intermediaries to manage investment decisions; and (iii) intermediaries themselves face capital market frictions, owing to the conflicts of interests and the information asymmetry between the financial intermediaries and their owners, the households, which creates a dilution cost for the intermediaries when raising equity capital.
The model economy consists of a representative household, a continuum of financial intermediaries, a continuum of competitive final-goods producers, and a continuum of competitive investment-goods producers. We start with the financial intermediaries.
2.1.1 Return Structure
Financial intermediaries use a mix of debt (deposits) and equity from households to invest in capital assets. A financial intermediary ![]() purchases capital asset
purchases capital asset
![]() at a market price
at a market price ![]() and rents out this capital to final-goods firms
for net rental income defined as
and rents out this capital to final-goods firms
for net rental income defined as
To model the balance sheet/liquidity risk that financial intermediaries face, we assume that the rate of return from investment is subject to a multiplicative idiosyncratic shock such that the total rate of return can be decomposed into two components, idiosyncratic and aggregate,
where
where the idiosyncratic return volatility evolves over time according to a Markov process,
Note that an increase in uncertainty is a mean preserving spread: while the second moment of the distribution (2) is time-varying, the first moment of the distribution is time-invariant, i.e.,
2.1.2 Capital Constraint
We assume that financial intermediaries are subject to a minimum capital ratio (or margin requirement) that may vary over time. Denoting this minimum capital ratio by ![]() , the capital constraint is given by
, the capital constraint is given by
The equation states that the ratio of debts to assets must be less than
In equilibrium, the capital constraint is always binding for two reasons: First, as discussed further below, the household is willing to pay a liquidity premium for its deposits since the intermediary deposits create non-pecuniary returns for the household. Second, even without the liquidity premium, financial intermediaries prefer to issue debt rather than to issue equity owing to the dilution cost associated with equity issuance, which will be explained shortly. As a consequence, the financial intermediaries follow a "pecking order" in their capital structure choice. We will prove that the capital constraint binds in the steady state.
2.1.3 Timing of Events
As highlighted in the introduction, a key aspect of our analysis involves the disconnect between intermediaries' lending commitments and their short-run funds. To model this disconnect in a tractable manner, we adopt the following timing convention: (1) At the beginning of each period, the
aggregate component of returns (![]() ) becomes known. (2) After observing the aggregate shocks, the intermediary makes investment (
) becomes known. (2) After observing the aggregate shocks, the intermediary makes investment (
![]() ) and borrowing (
) and borrowing (
![]() ) decisions. (3) After the investment/borrowing decisions, the level of the idiosyncratic shock (
) decisions. (3) After the investment/borrowing decisions, the level of the idiosyncratic shock (
![]() ) becomes known to the intermediary and dividend payout /equity issuance decisions (
) becomes known to the intermediary and dividend payout /equity issuance decisions (
![]() ) are made.
) are made.
The timing convention implies that the financial intermediaries have to make investment commitments before they know their (random) realization of internal funds. It also implies that the revenue shock becomes known only after the borrowing markets for intermediaries are closed. While this precise timing is somewhat arbitrary, it captures important features of reality. In particular, the timing convention represents parsimoniously the short-run funding risks that financial intermediaries face. For example, financial intermediaries always face uncertainty about the balance between their short-run loanable funds and/or the cost of such funds in retail/wholesale borrowing markets and the use of outstanding loan commitments; alternatively, realized income can fall short of the funding needs associated with their precommitments due to credit losses or fluctuations in asset values. Under such conditions and when outside equity is more expensive than borrowing, funding uncertainty can make the intermediaries adopt a precautionary stance in making investment/deposit decisions even when all intermediaries are risk-neutral.6
2.1.4 Evolution of Capital
To capture the role of financial market frictions for the intermediaries, we adopt a costly equity finance framework. Owing to the information asymmetry between the intermediaries and the potential owners, equity issuance involves a dilution effect, a phenomenon that a dollar amount of equity
issuance reduces the value of existing shares more than a dollar. We operationalize this effect by assuming that the actual cash flow related with equity is given by a function
![]() defined as,
defined as,
![\displaystyle =\left\{ \begin{array}[c]{cl} D_{t}(i) & \text{ if }D_{t}(i)\geq0\\ (1-\bar{\varphi})D_{t}(i) & \text{ if }D_{t}(i)<0 \end{array} \right.](img46.gif) |
||
In words, when the intermediary pays out a positive amount of dividends, the cash outflow associated with equity is simply given by the dividends payout, ![]() . However when the
intermediary issues new equities (
. However when the
intermediary issues new equities (
![]() ), the cash inflow associated with the notional value
), the cash inflow associated with the notional value ![]() is
reduced to
is
reduced to
![]() . Following Bolton and Freixas (2000), we call the foregone cash flow
. Following Bolton and Freixas (2000), we call the foregone cash flow
![]() a dilution cost.7
a dilution cost.7
In each period, financial intermediaries face the following flow of funds constraint,
| 0 | 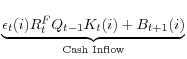 |
(6) |
![\displaystyle \underset{\text{Cash Outflow}}{\underbrace{[R_{t}^{B}B_{t} (i)+Q_{t}K_{t+1}(i)+\varphi(D_{t}(i))]}}.](img56.gif) |
The cash inflow is composed of revenue from last period's investment (lending)
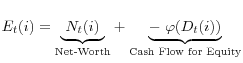
2.1.5 Value Maximization Problem
To define the optimization problem of an intermediary, it is useful to introduce an expectation operator that accounts for idiosyncratic uncertainty,
![]() . The conditioning set of the operator includes all information up to time
. The conditioning set of the operator includes all information up to time ![]() except the current realization of the idiosyncratic shock
except the current realization of the idiosyncratic shock
![]() . We can then formally state the value maximization problem of the intermediary as follows. The intermediary optimizes over
. We can then formally state the value maximization problem of the intermediary as follows. The intermediary optimizes over
![]() ,
,
![]() and
and ![]() to maximize
to maximize
where
Note that the intermediary is risk-neutral and discounts the future dividends by the marginal utility of representative household, the owner of the institution. Also note that the flow of funds constraint and its shadow value
![]() are within the expectation operator
are within the expectation operator
![]() -under our timing assumption, the intermediary has to decide how much to borrow and invest before it comes to know the value of idiosyncratic shock
-under our timing assumption, the intermediary has to decide how much to borrow and invest before it comes to know the value of idiosyncratic shock
![]() . This implies that the intermediary does not know its own shadow value of internal funds until the idiosyncratic cash flow shock becomes known and the intermediary needs to
form an expectation based on aggregate conditions. We can summarize the efficiency conditions of the problem as follows,
. This implies that the intermediary does not know its own shadow value of internal funds until the idiosyncratic cash flow shock becomes known and the intermediary needs to
form an expectation based on aggregate conditions. We can summarize the efficiency conditions of the problem as follows,
- FOC for
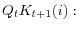
- FOC for
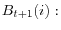
- FOC for
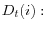
where
![]() . On the right side of the FOCs for investment and borrowing, all macroeconomic variables at
. On the right side of the FOCs for investment and borrowing, all macroeconomic variables at ![]() are taken out of the expectation operator
are taken out of the expectation operator
![]() , since the conditioning set of
, since the conditioning set of
![]() includes those variables at time
includes those variables at time ![]() . In contrast, the
FOC for dividends is not integrated over the idiosyncratic uncertainty. This is because the dividends/equity financing decisions are made after the realization of the shock.
. In contrast, the
FOC for dividends is not integrated over the idiosyncratic uncertainty. This is because the dividends/equity financing decisions are made after the realization of the shock.
To see that the capital constraint binds in the steady state, consider the version of (9) that arises in the absence of aggregate uncertainty, i.e., when
![]() ,
,
![]() , and
, and
![]() ,
,
This is the version of the efficiency condition that will be used extensively in our analysis that follows. To operationalize (11) for a sharper characterization of the equilibrium, we need to show how the intermediaries in the model form expectations regarding their liquidity condition, which is summarized by two measures,
2.1.6 Intermediary Asset Pricing
Our model has a symmetric equilibrium for three reasons: financial intermediaries are risk-neutral; the first moment of the idiosyncratic shock is time-invariant; and finally, the intermediaries decide how much to invest and to borrow before the realization of their idiosyncratic shocks. In this
symmetric equilibrium: all financial intermediaries choose the same level of investment and borrowing, i.e.,
![]() and
and
![]() for all
for all ![]() and
and
![]() . This greatly facilitates aggregation. However, dividends/equity issuance decisions are conditioned upon the realization of the idiosyncratic shock. The same thing can be
said about the shadow value of the flow of funds constraint, which is the summary measure of the liquidity condition of a particular intermediary.
. This greatly facilitates aggregation. However, dividends/equity issuance decisions are conditioned upon the realization of the idiosyncratic shock. The same thing can be
said about the shadow value of the flow of funds constraint, which is the summary measure of the liquidity condition of a particular intermediary.
After imposing the binding capital constraint and the symmetric equilibrium condition, we can express the flow of funds constraint as
At the time of dividend payout/equity issuance decision, all other quantities of the above expression are predetermined. Since the LHS is strictly increasing in
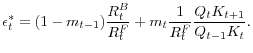
The discussion above regarding the equity finance threshold can be used to transform the efficiency condition (11) into a form that is more convenient for a quantitative analysis of the model, which requires us to evaluate two measures of liquidity condition:
![]() and
and
![]() . To that end, let
. To that end, let ![]() be a
standardization of
be a
standardization of
![]() defined as
defined as
Since
(14) implies that the intermediary's ex ante valuation of a sure dollar is always greater than a dollar as long as the probability of costly recapitalization is strictly positive. What is uncertain here is not the dollar, but its valuation. While the realized shadow value takes only two values: it is either 1 or
Using properties of the lognormal distribution and noting that
![]() for all bounded positive parameter
for all bounded positive parameter
![]() , one can easily see that
, one can easily see that
where
as long as
In summary, the caution created by the commitment structure imposed on the investment technology amid unresolved idiosyncratic funding risk manifests itself in the conservative ex ante valuation of random and non-random cash flow. This sets a higher bar for the required return on investment as will be shown below.
Using (14) and (15), we can eliminate all expressions involving the expectation operator
![]() in (11) and transform the efficiency condition for investment into an asset pricing formula. To that end, it is convenient to rewrite the FOC
as
in (11) and transform the efficiency condition for investment into an asset pricing formula. To that end, it is convenient to rewrite the FOC
as
![\displaystyle m_{t}=\beta\mathbb{E}_{t}\left\{ \frac{\Lambda_{t+1}}{\Lambda_{t}} \frac{\mathbb{E}_{t+1}^{i}[\lambda_{t+1}(i)]}{\mathbb{E}_{t}^{i}[\lambda _{t}(i)]}\left[ \dfrac{\mathbb{E}_{t+1}^{i}[\lambda_{t+1}(i)\epsilon _{t+1}(i)]}{\mathbb{E}_{t+1}^{i}[\lambda_{t+1}(i)]}\frac{R_{t+1}^{F}} {\Pi_{t+1}}-\left( 1-m_{t}\right) \frac{R_{t+1}^{B}}{\Pi_{t+1}}\right] \right\} .](img132.gif)
where the intermediary's pricing kernel is given by
![\displaystyle M_{t,t+1}^{B}=M_{t,t+1}^{H}\left[ \frac{1+\eta\Phi(s_{t+1}^{\ast})} {1+\eta\Phi(s_{t}^{\ast})}\right] =\beta\frac{\Lambda_{t+1}}{\Lambda_{t} }\left[ \frac{1+\eta\Phi(s_{t+1}^{\ast})}{1+\eta\Phi(s_{t}^{\ast})}\right]](img135.gif)
![\displaystyle \tilde{R}_{t+1}^{F}=R_{t+1}^{F}\left[ \frac{1+\eta\Phi(s_{t+1}^{\ast} -\sigma_{t+1})}{1+\eta\Phi(s_{t+1}^{\ast})}\right] <R_{t+1}^{F}.](img136.gif)
The above asset pricing formula looks different from a textbook version mainly for two reasons. First, the formula is a levered asset pricing formula. Unlike in the textbook version which assumes away leverage choice, the returns are levered up to the inverse of
capital ratio. To see this point, assume ![]() . One can then see the second term vanish and the formula looks closer to the conventional one, i.e.,
. One can then see the second term vanish and the formula looks closer to the conventional one, i.e.,
![]()
Second, the intermediary specific pricing kernel is a filtered version of the representative household's pricing kernel, where the filter is the ratio of the shadow value of internal funds today vs. tomorrow. The filter could potentially weaken the role of the representative household as a
marginal investor even though all financial intermediaries are owned by the households. Suppose that in the beginning of current period, a bad news about aggregate returns arrives. This, holding other things constant, increases the probability of costly recapitalization
![]() since even a normal range of idiosyncratic return may not be enough to meet the funding needs associated with today's investment. If the aggregate shock is strong enough,
the ratio of shadow values tomorrow vs. today substantially declines, making overall required return on capital (
since even a normal range of idiosyncratic return may not be enough to meet the funding needs associated with today's investment. If the aggregate shock is strong enough,
the ratio of shadow values tomorrow vs. today substantially declines, making overall required return on capital (
![]() ) rise, which suppresses today's investment.
) rise, which suppresses today's investment.
The intermediary asset pricing formula can be applied to price any asset with arbitrary random/non-random return structure. To fix the idea, suppose an asset ![]() whose price must be
determined in general equilibrium. For instance, one can think of an arbitrary lending opportunity with no default risk. If the representative household can directly purchase such an asset, the asset will be priced according to
whose price must be
determined in general equilibrium. For instance, one can think of an arbitrary lending opportunity with no default risk. If the representative household can directly purchase such an asset, the asset will be priced according to
Our discussion of the intermediary asset pricing can also shed light on the nature of the fluctuations in lending standards. A well known empirical fact is that the lending standards, measured by Senior Loan Officer Opinion Survey, which reports the proportion of senior loan officers who have
tightened their lending standards recently, is highly correlated with a popular measure of credit spreads such as the difference between BBB-rated bond and 10 year Treasury yields, with their correlation coefficient being close to 0.8. The survey on lending standards may be revealing that the
lending institutions tighten standards and increase spreads when the shadow value of their internal funds increases; in principle, such tighter lending standards can occur without any changes in borrowers' fundamentals if the balance sheet condition of lending institutions is impaired. In our
framework, such an attitude (or willingness to lend) toward new lending opportunity is summarized by
![]() . Of course, another natural interpretation of such survey results is that they reflect the time-varying quality of borrowers, e.g., the creditworthiness of potential bank
borrowers. While we do not object such conventional interpretation, our discussion of the intermediary asset pricing formula points to another possibility, and research has demonstrated that fluctuations in default risk and recovery rates of non-financial borrowers may be insufficient to understand
movements in borrowing spreads and lending standards (see Huang and Huang (2003) and Chen et al. (2009)).
. Of course, another natural interpretation of such survey results is that they reflect the time-varying quality of borrowers, e.g., the creditworthiness of potential bank
borrowers. While we do not object such conventional interpretation, our discussion of the intermediary asset pricing formula points to another possibility, and research has demonstrated that fluctuations in default risk and recovery rates of non-financial borrowers may be insufficient to understand
movements in borrowing spreads and lending standards (see Huang and Huang (2003) and Chen et al. (2009)).
The form of the intermediary asset pricing formula is superficially similar to Jermann and Quadrini (2009), who derive a similar pricing kernel from a reduced-form convex adjustment cost of dividend; however, our approach derives from a specific set of structural frictions. It is also superficially similar to the intermediary asset pricing formula of He and Krishnamurthy (2008); however, they derive their intermediary-specific pricing kernel from the assumption of risk averse intermediaries. The link to the LAPM (Liquidity-Based Asset Pricing Model) of Holmström and Tirole (2001) is more direct: In our case, the liquidity premium arises from costly recapitalization of financial intermediaries, while the premium exists for non-financial corporations with potential investment opportunity or working capital needs in Holmström and Tirole (2001).
Finally, we note that, when
![]() , the asset pricing formula collapses to
, the asset pricing formula collapses to
![\displaystyle 1=\mathbb{E}_{t}\left\{ M_{t,t+1}^{H}\left[ \frac{1}{m_{t}}\left( \frac{ R_{t+1}^{F}}{\Pi_{t+1}}-(1-m_{t})\frac{R_{t+1}^{B}}{\Pi_{t+1}}\right) \right] \right\}](img149.gif)
2.1.7 Illiquidity of Balance Sheet Assets and Adjustment Costs
In our timing convention, we assume that there exist factors that make the intraperiod adjustment of balance sheet assets difficult, requiring the commitment of participants. In reality, there are also reasons why interperiod as well as intraperiod adjustments of loan portfolio can be costly. As pointed out by many, for instance, Diamond and Rajan (2000), financial assets of intermediaries are inherently illiquid: First, a substantial knowledge about the characteristics of borrowers is an indispensable prerequisite for successful selections of new borrowers and churning out inefficient existing borrowers. Second, a substantial part of balance sheet assets is composed of items that are not easily marketable since the intermediaries cannot commit themselves to work for the second buyers after the sale of such financial assets. Such an illiquidity of balance sheet assets may be the fundamental force behind the slow dynamics often found in balance sheet data.
To capture this aspect in a parsimonious way, we assume that there exists a constant return-to-scale convex adjustment cost associated with changing the nominal stock of financial assets of the intermediaries:
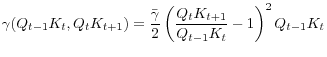 ,
, Though not explicit in (17), the flow of funds constraint and the equity finance threshold need to be modified accordingly as well.
These dynamic costs of adjusting the balance sheet of financial intermediaries are not important for the qualitative predictions of the model, but will help match the dynamics of adjustment apparent in the data.
2.1.8 Cost of Capital
From a theoretical perspective, the relevant cost facing intermediaries is a marginal cost of funds (or a weighted average of marginal costs), as can be seen directly by rewriting (11) as
![\displaystyle \overset{}{\underset{\text{MB of Investment}}{\underbrace{\mathbb{E} _{t}\{M_{t,t+1}^{H}\mathbb{E}_{t+1}^{i}[\lambda_{t+1}(i)\epsilon _{t+1}(i)]R_{t+1}^{F}\}}}}](img155.gif) |
||
![\displaystyle =\underset{\text{MC of Investment}}{\underbrace{m_{t}\mathbb{E}_{t} ^{i}[\lambda_{t}(i)]+(1-m_{t})\mathbb{E}_{t}\left\{ M_{t,t+1}^{H} \mathbb{E}_{t+1}^{i}[\lambda_{t+1}(i)]\frac{R_{t+1}^{B}}{\Pi_{t+1}}\right\} }}.](img156.gif) |
The above equates the marginal benefit (LHS) and the marginal cost (RHS) of investment. Evidently it is an weighted average of two components, the one associated with the marginal cost of raising capital and the one associated with marginal borrowing cost.
However, policy debates often center around a slightly different concept, so called weighted average cost of capital (WACC). Given the importance of the concept in policy discussion, we show how such a measure can be constructed in our environment. To that end, we
need show how the return on equity, i.e., the stock market return on financial shares
![]() evolves over time. Exploiting the recursive structure in (7), we can express the value of intermediary as
evolves over time. Exploiting the recursive structure in (7), we can express the value of intermediary as
where
The textbook version of weighted average cost of capital is defined as
where
![\displaystyle R_{t+1}^{S}\equiv\Pi_{t+1}\left[ \frac{v_{t+1}^{B}}{\mathbb{E}_{t} [M_{t,t+1}^{H}\cdot v_{t+1}^{B}]}\right]](img168.gif)
The return on equity has two components: the conventional stock market return and the average cost of new equity issuance per unit of total market value. At this point, the formula may looks arbitrary to some readers, but we show below that (20) is consistent with the household optimization condition.
3.1 Household
The representative household consumes the final-goods and earns market wages by supplying labor inputs for the production of final goods. We assume that the household lacks necessary skills to directly manage investment projects. For this reason, the household invests its saving through financial intermediaries. The household can either invest in the shares of the intermediaries or make deposits to the intermediaries.
3.1.1 Budget Constraint
Under the assumptions made above, the budget constraint of the representative household can be expressed as
| 0 | 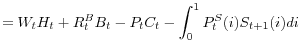 |
(21) |
![\displaystyle -B_{t+1}+\int_{0}^{1}[\max\{D_{t}(i),0\}+P_{t-1,t}^{S}(i)]S_{t} (i)di](img173.gif) |
where
where
Substituting (22) and (23) in the budget constraint of the representative household, one can see that the budget constraint is equivalent to
| 0 | 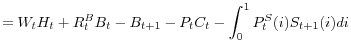 |
(24) |
![\displaystyle +\int_{0}^{1}[\max\{D_{t}(i),0\}+(1-\bar{\varphi})\min\{D_{t}(i),0\}+P_{t} ^{S}(i)]S_{t}(i)di.](img185.gif) |
3.1.2 Preferences
For the preferences of the representative household, we adopt the most standard specifications for quantitative analyses in the literature. One such specification can be found in Smets and Wouters (2007). More specifically, we adopt internal habit formation in consumption and a labor disutility separable from the utility of consumption. To model the value households place on their deposits, we adopt the deposit in the utility specification originating from Sidrauski (1967), which captures the non-pecuniary benefits provided by financial institutions.12 Formally, the preferences are given by
The household problem is straightforward: the household chooses
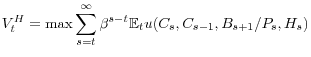
3.1.3 Pricing Financial Intermediaries
We now show how the representative household prices the debts and equities of the financial intermediaries. The FOCs for consumption, deposits and shares are given by
- FOC for
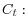
- FOC for
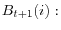
- FOC for
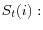
The FOC for consumption is standard. The FOC for intermediary debt is different from a standard asset pricing formula because of the non-pecuniary benefit of deposit. This creates a liquidity premium that the household is willing to fore-go in making deposits at a rate lower than risk-free rate. Formally, the liquidity premium can be defined as
![\displaystyle \beta\mathbb{E}_{t}\left[ \frac{\Lambda_{t+1}}{\Lambda_{t}}\left( \frac{R_{t+1}}{\Pi_{t+1}}-\frac{R_{t+1}^{B}}{\Pi_{t+1}}\right) \right] =\frac{\theta/\Lambda_{t}}{B_{t+1}(i)/P_{t}}\geq0](img201.gif)
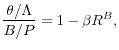
We now turn to the issue of how to price the shares of the financial intermediaries. In discussing the cost of capital for intermediaries, we made a claim that the asset pricing formula for the intermediary shares must have a correction term to the conventional one, reflecting the costly equity
financing friction. To show this, first note that since there is no persistence in the first moment of the idiosyncratic shock and the second moment shock is shared by all intermediaries, the ex-dividend price of all shares are the same regardless of realization of idiosyncratic shock today. Hence,
![]() for all
for all ![]() , and trivially,
, and trivially,
![]() . Next, noting that
. Next, noting that
![]() ,
,
![]() and
and
![]() , we can rewrite the asset pricing formula (28) as
, we can rewrite the asset pricing formula (28) as
![\displaystyle 1=\beta\mathbb{E}_{t}\left[ \frac{\Lambda_{t+1}}{\Lambda_{t}}\left( \frac{ D_{t+1}+P_{t+1}^{S}}{P_{t}^{S}}\right) \right] +\beta\mathbb{E}_{t}\left[ \frac{\Lambda_{t+1}}{\Lambda_{t}}\frac{\bar{\varphi}D_{t+1}^{-}}{P_{t}^{S}} \right]](img213.gif)
In equilibrium,
![]() for all
for all ![]() . We can then see that (24)
is equivalent to
. We can then see that (24)
is equivalent to
where
3.2 Technology
To save space, our description of the rest of the model economy will be brief. Our goal in this analysis is to investigate the role of funding-market frictions facing financial intermediaries. Given that these frictions arise independently of others such as nominal frictions, we take the model as close as possible to a real business cycle benchmark for the virtue of simplicity. While we keep distinctions between nominal and real variables in our notation (thereby allowing easy integration of monetary policy questions at a later stage), price adjustment is frictionless in this analysis.
3.2.1 Final Goods
A continuum of competitive firms produce final goods using capital and labor in a constant return-to-scale (CRS) Cobb-Douglas technology. They solve the following static profit maximization problem,
3.2.2 Investment
A continuum of competitive firms produce investment goods by combining an input of final goods and a CRS adjustment technology. Following Christiano et al. (2003) and Smets and Wouters (2007), we specify a convex investment adjustment cost and model the investment problem as follows,
![\displaystyle V_{t}^{I}=\max\mathbb{E}_{t}\sum_{s=t}^{\infty}\beta^{t-s}\frac{\Lambda_{s} }{P_{s}}\left\{ Q_{s}I_{s}(k)-P_{s}\left[ I_{s}(k)+\frac{\bar{\chi}}{2} \left( \frac{I_{s}(k)}{I_{s-1}(k)}-1\right) ^{2}I_{s-1}(k)\right] \right\} .](img222.gif)
3.3 Market Clearing Condition
Goods market clearing requires that aggregate production equal the sum of consumption, investment, and the various resource costs (adjustment costs) assumed in our quantitative framework
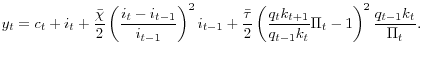
4 Predictions and Model-Based Identification
Insight into the quantitative predictions of our model for the effects of shocks to the intermediation sector for economic activity and credit spreads requires a calibration closely tied to the data. To develop such an anchoring, we examine the predictions of our model for a range of variables following an increase in idiosyncratic uncertainty, create a new data series on idiosyncratic uncertainty within the intermediation sector based on the cross-sectional variance of daily equity returns for large financial institutions, and then use the predictions of our model for the sign of the response of financial institutions' value of internal funds and lending following an increase in uncertainty to identify the impact of shocks to the intermediation sector on real activity while ensuring that such identified disturbances are purged of typical "business-cycle" fluctuations. After these discussions, we then return to our model and illustrate how a broader array of financial developments - indeed, any that affect the balance sheet of intermediaries - can have important macroeconomic consequences in our model.
4.1 Uncertainty Shock: Model's Prediction
As we highlighted earlier, developments within the intermediation sector, such as an increase in the idiosyncratic uncertainty regarding returns facing intermediaries, are important for macroeconomic fluctuations given the financial frictions in our model (and would be neutral with respect to macroeconomic outcomes in the absence of such frictions). While this qualitative point is clear from the (complex) system of equations governing the economy's equilibrium, the quantitative nature of these effects is less clear, and we illustrate the qualitative predictions of our model along this dimension via a simulation exercise.
To perform these simulations, we first assign parameter values. There are three parameters that govern key aspects of the model's predictions for the macroeconomic effects of intermediation shocks: the cost of equity issuance
![]() , the long run standard deviation of return on asset
, the long run standard deviation of return on asset
![]() , and the weight on the deposit in the utility
, and the weight on the deposit in the utility ![]() . We try to
adopt reasonable values for the first two parameters by tying these values to data from financial markets. The estimates/calibrations for the equity issuance cost varies a lot in the literature ranging from 0.08 in Gomes (2001) to 0.30 in Cooley and
Quadrini (2001). We chose
. We try to
adopt reasonable values for the first two parameters by tying these values to data from financial markets. The estimates/calibrations for the equity issuance cost varies a lot in the literature ranging from 0.08 in Gomes (2001) to 0.30 in Cooley and
Quadrini (2001). We chose
![]() , following Cooley and Quadrini (2001). While this choice is on the high side of the range, we made this choice to replicate the harsh
financing environment seen during the recent financial turmoil. Regarding the volatility, we set
, following Cooley and Quadrini (2001). While this choice is on the high side of the range, we made this choice to replicate the harsh
financing environment seen during the recent financial turmoil. Regarding the volatility, we set
![]() , implying an annual volatility level of 0.10, to match the standard deviation of return on asset (profits/total asset) of U.S. banking sector reported in Demirguc et al. (2003). With regard to the weight of deposits in the utility function (
, implying an annual volatility level of 0.10, to match the standard deviation of return on asset (profits/total asset) of U.S. banking sector reported in Demirguc et al. (2003). With regard to the weight of deposits in the utility function (![]() ), we choose its value to match (roughly) the net interest margin of
financial intermediaries,
), we choose its value to match (roughly) the net interest margin of
financial intermediaries,
![]() . Saunders and Schumacher (2000) and Demirguc et al. (2003) provide an international comparison of such
margins, which range from a low of 160 bps (Swiss) to a high of 500 bps (Spain and U.S.) on average during the period of 1988-1995. Conditioned upon
. Saunders and Schumacher (2000) and Demirguc et al. (2003) provide an international comparison of such
margins, which range from a low of 160 bps (Swiss) to a high of 500 bps (Spain and U.S.) on average during the period of 1988-1995. Conditioned upon
![]() and
and
![]() , setting
, setting
![]() roughly matches the interest rate margin in the data. Note that the interest rate margin is a sum of two components,
roughly matches the interest rate margin in the data. Note that the interest rate margin is a sum of two components,
![]() . With
. With
![]() , about half of the margin is explained by a return premium over risk free rate
, about half of the margin is explained by a return premium over risk free rate ![]() and the rest of the margin is explained by the liquidity premium
and the rest of the margin is explained by the liquidity premium ![]() in our framework.
in our framework.
With regard to other parameters, we choose the investment and balance sheet adjustment cost parameters and the parameter governing habit persistence so as to deliver hump-shaped impulses response function to typical shocks. To deliver the slow dynamics for intermediaries' balance sheet observed
in the data, we specify a small loan adjustment cost by setting
![]() equal to 1. This choice, together with the choice of investment adjustment cost parameter, helps us match the persistent response of lending. For the investment adjustment cost
parameter, we set
equal to 1. This choice, together with the choice of investment adjustment cost parameter, helps us match the persistent response of lending. For the investment adjustment cost
parameter, we set
![]() , a moderate value similar to those reported in macroeconomic analyses (of other issues). We calibrate the habit persistence parameter as
, a moderate value similar to those reported in macroeconomic analyses (of other issues). We calibrate the habit persistence parameter as ![]() , a value in the typical range.
, a value in the typical range.
For the parameters that can be considered traditional, we make standard choices whenever possible. The risk free rate in the steady state is set at
![]() in quarterly frequency. The depreciation rate
in quarterly frequency. The depreciation rate ![]() is set equal
to 0.025. We assume a relatively elastic labor supply by setting the inverse of Frisch elasticity parameter
is set equal
to 0.025. We assume a relatively elastic labor supply by setting the inverse of Frisch elasticity parameter ![]() equal to 0.1 and we choose the weight of the labor disutility as
equal to 0.1 and we choose the weight of the labor disutility as ![]() . We set
. We set
![]() , a fairly standard setting.
, a fairly standard setting.
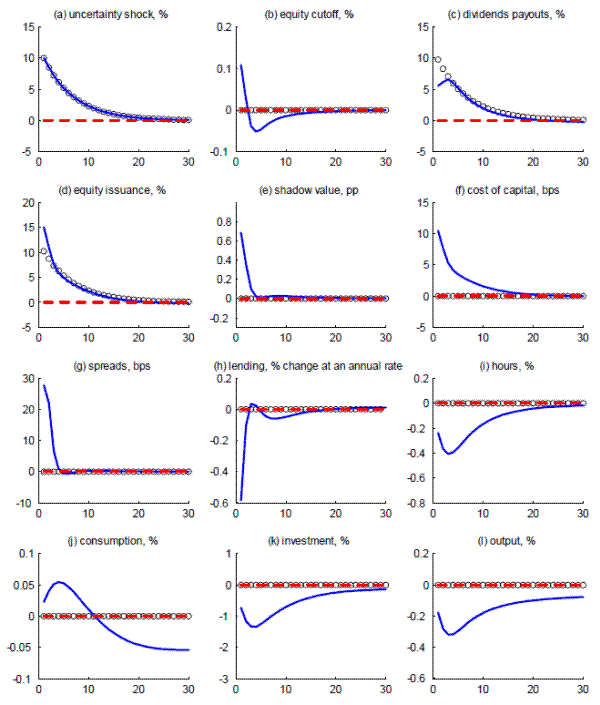
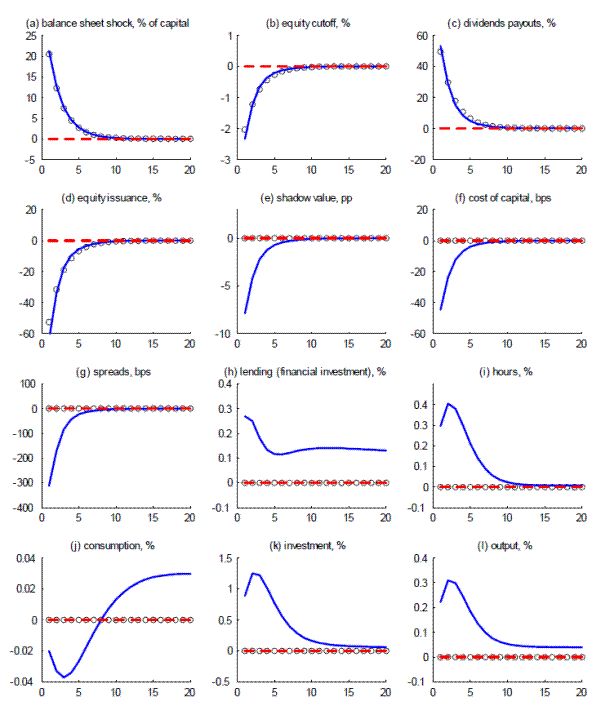
We can now illustrate the effects of an uncertainty shock. Figure 1 shows the impact of an increase in (idiosyncratic) uncertainty within the financial sector. In this experiment, we consider a fairly persistent shock process. We set
![]() , near the value in Bloom (2009) and a choice that will be broadly consistent with our empirical evidence below. We consider a shock that increases the
level of uncertainty 10 percent immediately. The frictionless economy (black circles) exhibits a complete dichotomy between financial flows and real variables: the changes in uncertainty create large adjustment in dividends and equity finance, with no first order consequences for real
allocations.
, near the value in Bloom (2009) and a choice that will be broadly consistent with our empirical evidence below. We consider a shock that increases the
level of uncertainty 10 percent immediately. The frictionless economy (black circles) exhibits a complete dichotomy between financial flows and real variables: the changes in uncertainty create large adjustment in dividends and equity finance, with no first order consequences for real
allocations.
To understand the economic impact of uncertainty shock under the financial friction, it is useful to remember that the uncertainty shock becomes known at the beginning of the period, before the realization of idiosyncratic returns. While such a second moment shock is a mean preserving spread as emphasized earlier, implying both greater upside and downside potential to investment, the increase in downside risk (the left tail) is especially important in our environment, a phenomenon known as "the bad news principle" (Bernanke (1983)). Because of the greater dispersion in idiosyncratic returns, some intermediaries find themselves with unusually large amount of cash inflow. However, at the time of investment/borrowing decisions, the increased probability of costly equity financing aggravates intermediaries' concern for liquidity and increases the internal valuation of internal funds, as displayed in panel (e). The cost of intermediary capital increases relative to the risk-free rate, which is transmitted to other credit markets as shown by the increase in the spreads in panel (g).
The funding pressure facing the financial intermediaries should be met by raising internal funds (e.g., cutting back in dividends), by outside equity, or by downsizing the balance sheet (e.g., cutting back in lending or sales of assets). Each of these options is costly to the intermediaries as
the outside capital requires dilution costs and deleveraging of the balance sheet implies the loss of the intermediation margin. As a consequence, the intermediaries in the model economy respond by trying to strike a balance between their options for balance sheet adjustment. In panel (c), we can
see that the dividends payouts, while increasing, are substantially lower relative to the frictionless case. Panel (d) shows that equity issuance in the presence of the financial friction responds to the shock more strongly than in the frictionless case. Panel (h) shows that the intermediaries
deleverage their balance sheet substantially by cutting back on lending. Panel (i)![]() (l) display the consequence of such deleveraging on real allocations: aggregate hours, investment and
output contract persistently.
(l) display the consequence of such deleveraging on real allocations: aggregate hours, investment and
output contract persistently.
With regard to model predictions, we note three aspects that we will emphasize in our empirical analysis below. In particular, figure 1 shows that an increase in uncertainty within the intermediation sector leads to an increase in the value of funds within the sector, a widening in the borrowing spread, and a decline in lending. We take these predictions to the data after discussing our empirical measure of uncertainty within the intermediation sector.
4.2 Some Data on Uncertainty
In order to examine the magnitude of the quantitative effects of developments within the intermediation sector, we need to bring some data on developments at intermediaries and examine their interaction with macroeconomic developments. Given the earlier discussion, we focus on the degree of idiosyncratic uncertainty within the intermediation sector.
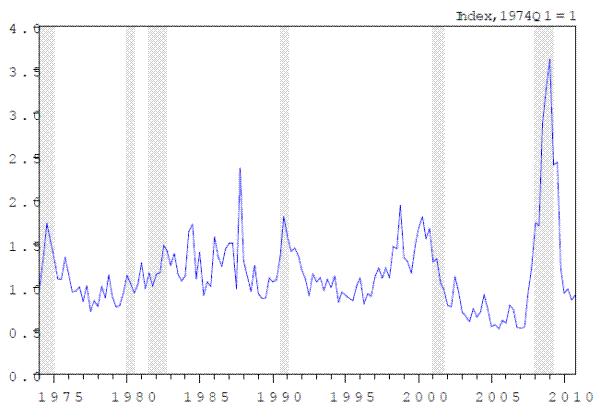
Several approaches to gauging such uncertainty within the intermediation sector are possible. For example, a possibly fruitful approach could examine the indicators of (firm-specific) uncertainty derived from financial market prices, e.g. options on intermediaries. However, we are interested in constructing a long time series on uncertainty that is representative of the majority of the intermediation sector within the United States, and construction of an options-implied volatility measure for a broad set of financial firms over the past forty years was not feasible for this study. Our measure of uncertainty with the intermediation sector is based in realized volatility. Specifically, we analyze the period from the first quarter of 1973 until the third quarter of 2010 and gather daily equity prices for the top-25 banking organizations (as measured by total assets) within the United States each quarter (e.g., the composition of the top-25 is allowed to change each quarter). We then construct the cross-sectional standard deviation of the daily percent change in equity prices across these financial intermediaries; our focus on cross-sectional variation is consistent with our emphasis on idiosyncratic uncertainty. We take the average of this cross-sectional standard deviation within a quarter as our measure of idiosyncratic uncertainty.
Figure 2 shows the variation in this measure (indexed to equal 1 in 1974Q1) over the 1974-2010 period. Several points are apparent. First, this measure of uncertainty, while varying significantly over time, is not especially strongly correlated with recessions as defined by the National Bureau of Economic Research (the shaded regions); this may help our empirical identification strategy below, as we want to illustrate the independent effect of financial-sector developments on macroeconomic outcomes, rather than developments "in the other direction" (i.e., the impact of macroeconomic developments on the financial sector). Second, this measure exploded to unprecedented levels during the financial crisis that (according to this data) began in the third quarter of 2008 and remained high through the third quarter of 2009. Other notable periods include the elevated level of uncertainty regarding financial intermediaries from late 1990 to early 1993 (which corresponded to a portion of the period covering the U.S. Savings and Loan crisis and the financial headwinds of the early 1990s) and the quite low level of uncertainty during the 2003-2006 period (a time at which excesses in leverage were building according to many analysts, ex post).
4.3 A Bayesian Approach to Identification
With the model predictions and data discussed in the previous two sections in hand, we now turn to an exploration of the data to see whether the role of uncertainty within the intermediation sector, and hence the role of balance-sheet considerations at financial intermediaries more generally, for macroeconomic fluctuations are borne out empirically.
As highlighted above, we view three predictions of our theoretical framework as informative with regard to developments at intermediaries following an increase in uncertainty within the intermediation sector. Specifically, in response to an increase in uncertainty, our model predicts
- An increase in the value of internal funds at intermediaries that reduces the willingness to lend;
- A widening in the borrowing spread; and
- A decline in lending.
It is straightforward to use these theoretical restrictions to identify the effects of shocks to the financial intermediation sector on macroeconomic outcomes. Specifically, we apply the Bayesian approach of Uhlig (2005), which considers the set of impulse responses in a vector autoregression (VAR) consistent with these identifying restrictions.13 This approach finds all responses consistent with the identifying restrictions and develops the set of responses for all variables embedded in the VAR. As a result, the findings regarding macroeconomic responses can be considered reasonably robust, especially as compared to relatively atheoretical identifying restrictions within a VAR approach (such as recursive orderings, which assume delayed responses for certain variables as in the analysis of banking shocks in Lown and Morgan (2006) and Berrospide and Edge (2010)).14
With that said, it is also important, especially within a large VAR, to include restrictions outside those of specific interest, as the Bayesian approach defines a set of responses satisfying the imposed restrictions using orthogonal rotations of the shocks to the system; inclusion of restrictions on responses to shocks outside those of interest help insure robustness, as such additional restrictions help to more sharply delineate the differences across orthogonal innovations within the system. This is potentially valuable in our analysis, as it is possible that a (negative, recessionary) general business cycle shock would result in a decline in lending and willingness to lend along with a decline in real GDP. We purge our system of these types of shocks, to focus especially on a causal effect associated with intermediation shocks. Therefore, our analysis identifies two orthogonal shocks - an (uncertainty) intermediation shock and a business cycle shock. The restrictions imposed on these shocks are
- A financial (uncertainty) intermediation shock increases our measure of idiosyncratic uncertainty and the borrowing spread, decreases willingness to lend and lending, and is orthogonal to the business-cycle shock;
- A Business cycle (recession) shock lowers real GDP and real investment, increases the unemployment rate, and is orthogonal to the other identified shocks.
For each shock, we impose these restrictions over the first four periods of the impulse. Note especially that by including a business cycle shock we attempt to purge the response to financial intermediation shocks of the endogenous fluctuations in lending associated with typical fluctuations in aggregate demand/supply. Other uses of sign restrictions (e.g., Mountford and Uhlig (2009)) adopt a similar business-cycle shock.
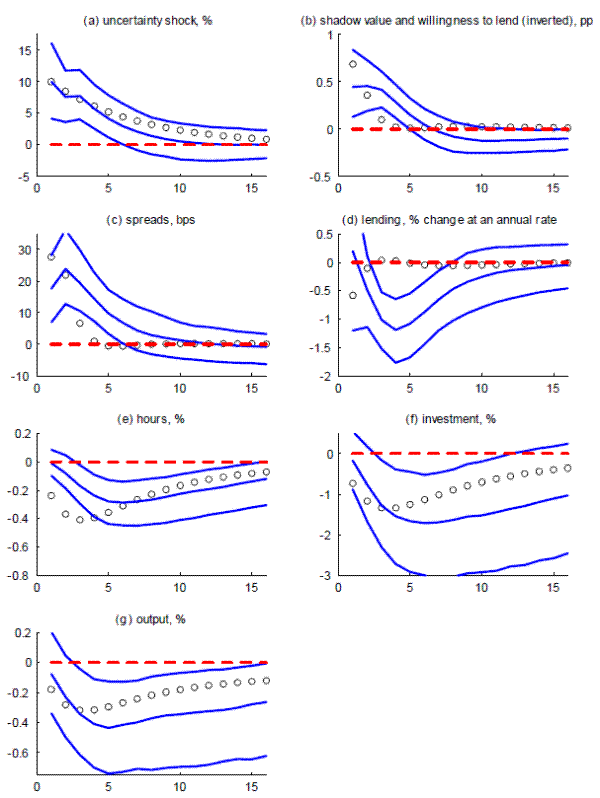
Our VAR includes eight variables: (the log of) real GDP; (the log of) real fixed investment; the unemployment rate; the real federal funds rate (defined as the nominal federal funds rate minus the change in the core Personal Consumption Expenditures (PCE) price index over the previous four quarters); the spread between the BBB corporate bond rate and the 10-yr Treasury rate; the share of banks more willing to lend to consumers from the Senior Loan Officer Opinion Survey; (the log of) bank lending; and (the log of) our measure of idiosyncratic uncertainty within the intermediation sector. The intermediation (uncertainty) shock restrictions are applied to the last four variables, with a decline in willingness to lend and lending accompanying an increase in uncertainty. The estimation sample is 1974:Q1 to 2010:Q3 and the VAR includes two lags; (By using willingness to lend to consumers, our sample period is considerably longer than that of other VAR analyses using other questions from the Senior Loan Officer's Opinion Survey(e.g., Lown and Morgan (2006) and Berrospide and Edge (2010); we discuss the robustness of our results later).
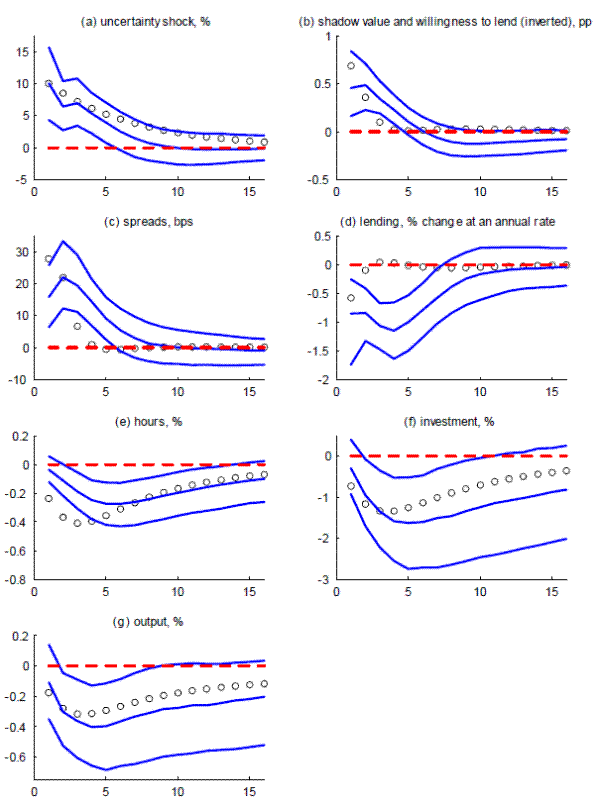
The impulse responses to an intermediation (uncertainty) shock identified via this procedure are reported in figure 3; the lines represent the 68-percent confidence intervals and the dots represent the model predictions that were presented in the previous section.15 Panel (a) shows that the structural shock immediately increases the uncertainty measure by 10 percent. As shown in panel (b), willingness to lend falls (as indicated by the jump in the lines, as willingness to lend is reported on an inverted scale); this jump is reminiscent of the jump in the internal value of funds (shown in the dots, but not comparable empirically; the presentation is meant to illustrate the correspondence).16 Lending (panel (d)) also jumps down. This shock has important macroeconomic effects: The BBB-bond spread rises notably (e.g., by about 20 basis points), indicating spillovers to financial conditions more generally (panel (c)); moreover, hours, real investment, and real GDP decline notably (by about 1/3 percent, 1 1/4 percent, and 1/3 percent, respectively).17 Overall, both lending and real investment decline substantially more sharply than real GDP, with peak responses just below a decline of 1 percent. The more pronounced effect on investment and lending is similar, qualitatively, to the predictions of our model.
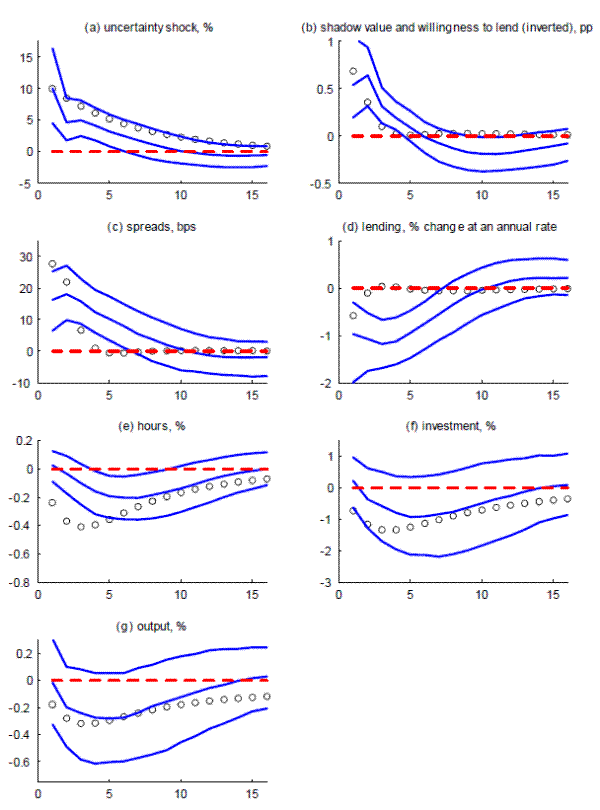
With regard to robustness, we considered two alternatives to the identification scheme we highlight as our main analysis. First, we relaxed the restriction that lending must fall following an uncertainty shock (on the view that some readers may view a restriction on lending as too close to a direct restriction on the real effects of uncertainty shocks). Relaxing this restriction, as shown in figure 4, had essentially no effect on the impact of uncertainty shocks for financial and real outcomes within our VAR. Second, we ended the estimation sample in 2007Q4, before the jump in our uncertainty measure recorded in 2008; this shift allows us to consider the robustness of the empirical links we identify to episodes prior to the recent financial crisis. As shown in figure 5, the shift in sample period increased the standard errors associated with the impact of uncertainty shocks on financial and real variables (and now only with 68-percent confidence set for the impact on the BBB spread continues to exclude zero, while other confidence intervals are wide). However, the nature of the impulse responses at the median are very similar to those for the entire sample period for lending, real GDP, the unemployment rate, and the BBB spread. These two exercises suggest that the broad implications of our framework capture important empirical regularities, although the importance of these regularities is more apparent using developments during the 2008 financial crisis.
4.4 Comparison to Other VAR approaches
Another dimension of robustness regards the correspondence between the intermediation (uncertainty) shocks estimated by our approach and those found using other approaches. As mentioned previously, one popular approach involves a recursive ordering scheme, as pursued in Lown and Morgan (2006), Berrospide and Edge (2010), and Ciccarelli et al. (2010). In this approach, researchers typically include a measure from surveys of financial institution of willingness to lend or net tightening in lending standards, and identify shocks to intermediation by assuming that such shocks immediately impact standards but only affect spending with a lag (e.g., a standard Cholesky ordering for identification in a VAR).
In a more recent approach, Bassett III et al. (2010) use micro-level information on banks responding to the Senior Loan Officer's Opinion Survey in the United States to identify changes in standards that are orthogonal to a long list of conditions at the bank level; these authors suggest this approach may better identify the change in loan supply than the macroeconomic VAR approach. Interestingly, these authors show that their identified loan supply shocks are very similar to those using the recursive ordering in a VAR.
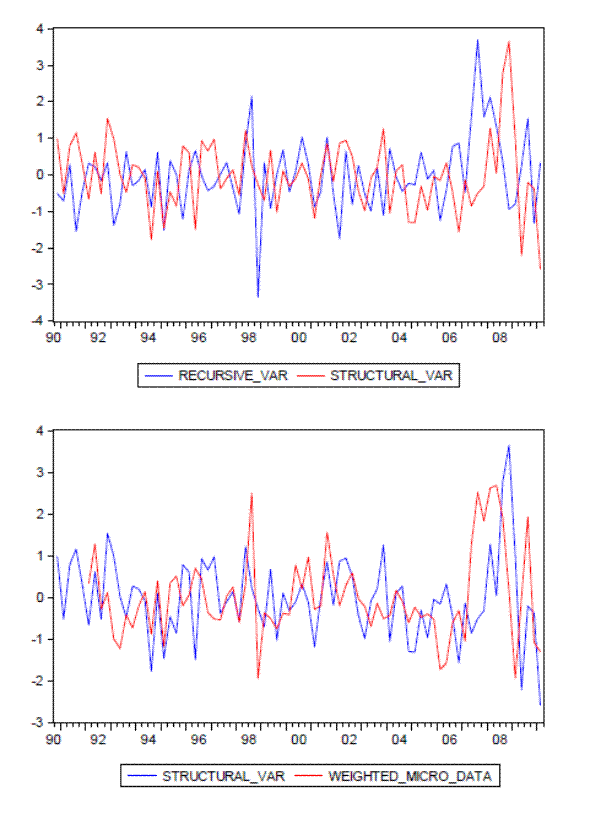
We compare our uncertainty shocks to the loan supply shocks from Bassett III et al. (2010) (both those from their micro-level and recursive VAR approaches) in figure 6. As shown in the upper panel, our uncertainty shocks are not
very correlated with either the VAR recursive shocks (upper panel) or the micro-based shocks (the lower panel), with simple correlations near 0 (as opposed to a correlation near ![]() for the
two alternatives). In this sense, our uncertainty shocks are capturing a different factor from those found using these measures of loan supply shocks. We view this result as unsurprising, as our model implies that loan supply should be affected by uncertainty and by a wide
range of other factors as well.
for the
two alternatives). In this sense, our uncertainty shocks are capturing a different factor from those found using these measures of loan supply shocks. We view this result as unsurprising, as our model implies that loan supply should be affected by uncertainty and by a wide
range of other factors as well.
4.5 Balance Sheet Shock
Indeed, we would like to emphasize that we have taken a very focused approach in our empirical exercise and examined the impact of a shift in idiosyncratic uncertainty within our model and empirically. Our model implies a much broader set of implications. Specifically, any disturbance that alters the balance-sheet (or liquidity) position of intermediaries has important macroeconomic effects in our model. In this sense, our empirical analysis confirms the important role of intermediation, but probably underplays the overall macroeconomic significance of shocks to the intermediation sector by not considering a comprehensive set of developments impacting intermediaries' balance sheet positions.
We illustrate this basic point in figure 7, in which we consider a hypothetical aggregate shock to the balance sheets of financial intermediaries. For this experiment, we modify the flow of funds constraint as
| 0 | ||
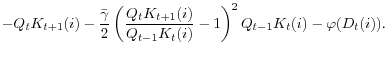 |
where
Note that the shock is additive to the profit: as such, the shock does not have direct implication for the marginal profitability of intermediary investment. As a result, the shock would not have substantial real effects on a frictionless economy (i.e., an economy with
![]() ). However, under the funding market friction that we consider, the shock is relevant information for the risk management of the intermediaries. The shock affects the
liquidity condition of the intermediaries, which influences the marginal valuation of investment opportunity. For a straightforward comparison, figure 7 also displays the case of the frictionless economy (denoted by black circles) together with the case of the model economy
(blue solid lines).
). However, under the funding market friction that we consider, the shock is relevant information for the risk management of the intermediaries. The shock affects the
liquidity condition of the intermediaries, which influences the marginal valuation of investment opportunity. For a straightforward comparison, figure 7 also displays the case of the frictionless economy (denoted by black circles) together with the case of the model economy
(blue solid lines).
Consider the frictionless case first. The windfall cash inflow improves the internal funds substantially, hence less need for outside equity, reflected in the large drop in the equity issuance cutoff shown in panel (b). Since the shock does not have implication for the marginal profitability of financial investment, a large number of intermediaries simply disburse the extra cash flow as dividends (panel (c)). Equity issuance, shown in panel (d) also substantially decreases as there is less need for outside funds. Such financial flows, however, do not have any consequences for real allocations. Since the financial markets are frictionless, the shadow value of extra cash is always equal to one, not responding to the liquidity condition as shown in panel (e). As a result, weighted average cost of capital of intermediaries (panel (f)) and spreads (panel (g)) show zero responses. With no changes in the costs of capital at various levels of the economy, the level of lending is also unresponsive to the shock (panel (h)), implying no changes in employment, real investment, and output (panel (i), (k) and (l)). Finally, it is notable that the consumption also exhibits zero response. While the balance sheet shock is a transfer from the households to the intermediaries, such transfer is exactly offset by the reverse transfer, increase in dividends and decrease in equity issuance, resulting in zero response in consumption.
We now turn to the case with the financial friction. As in the frictionless case, the liquidity condition of the financial intermediaries is dramatically improved by the shock and the probability of having to tap the equity market for additional funding declines substantially, indicated by the
plunge in the equity issuance threshold
![]() . The responses of dividends and equity issuance are more or less the same as in the frictionless case. What is different is the massive drop in the expected shadow value
of internal funds shown in panel (e). As a consequence, the cost of intermediary capital declines about 50 basis points in panel (f) and a strong positive spill over effect for general lending terms ensues as the credit spreads decline as much as 300 basis points in panel (g). While the shock does
not affect the fundamentals of investment, the much lower valuation of internal funds allow the intermediaries to substantially expand their balance sheet as seen in the expansion of lending in panel (h). This would not be the case if the intermediaries were not constrained by the financial
friction before the shock.
. The responses of dividends and equity issuance are more or less the same as in the frictionless case. What is different is the massive drop in the expected shadow value
of internal funds shown in panel (e). As a consequence, the cost of intermediary capital declines about 50 basis points in panel (f) and a strong positive spill over effect for general lending terms ensues as the credit spreads decline as much as 300 basis points in panel (g). While the shock does
not affect the fundamentals of investment, the much lower valuation of internal funds allow the intermediaries to substantially expand their balance sheet as seen in the expansion of lending in panel (h). This would not be the case if the intermediaries were not constrained by the financial
friction before the shock.
Panel (i)![]() (l) exhibit the responses of variables related with economic activity. In panel (i), one can see that hours increase substantially. While consumption initially declines to
allow a greater investment in intermediary debts, the response of consumption shown in panel (j) is very much muted relative to other endogenous variables. Aggregate investment and output all show strong positive response to the balance sheet shock. In particular, aggregate investment leads the
upside business cycle, responding to the large increase in the price of capital. One can easily see a meaningful interaction between the financial and the real sectors: the initial increase in the price of capital is caused by the decisions of the intermediaries to expand their financial
investment. Such investment leads to the higher asset prices of the economy, initiating strong real investment cycle. The resulting upturn in business cycle improves the return on intermediary financial investment, further strengthening the liquidity condition of the intermediaries, supporting an
even stronger gain in real economic activity.
(l) exhibit the responses of variables related with economic activity. In panel (i), one can see that hours increase substantially. While consumption initially declines to
allow a greater investment in intermediary debts, the response of consumption shown in panel (j) is very much muted relative to other endogenous variables. Aggregate investment and output all show strong positive response to the balance sheet shock. In particular, aggregate investment leads the
upside business cycle, responding to the large increase in the price of capital. One can easily see a meaningful interaction between the financial and the real sectors: the initial increase in the price of capital is caused by the decisions of the intermediaries to expand their financial
investment. Such investment leads to the higher asset prices of the economy, initiating strong real investment cycle. The resulting upturn in business cycle improves the return on intermediary financial investment, further strengthening the liquidity condition of the intermediaries, supporting an
even stronger gain in real economic activity.
Overall, these simulations emphasize how a broad range of shocks that impact the position of financial intermediaries have macroeconomic consequences in our model. In turn, this consideration implies that various policies vis-a-vis the financial sector can prove important for macroeconomic outcomes.
5 Conclusion
In our analysis, we consider a tractable macroeconomic model in which real investment is intermediated through institutions that commit financial resources in the face of idiosyncratic funding risk and a binding capital constraint. We show that the liquidity/balance sheet condition of intermediaries can be an important driver of asset prices and aggregate activity. This prediction is confirmed by empirical evidence from our structural econometric analysis framed in a set sign restrictions implied by our model. Indeed, we examine only a small portion of the potential empirical importance of intermediation for macroeconomic outcomes by focusing exclusively on a shift in uncertainty within the intermediation sector. To that end, we develop a new measure of such uncertainty and identify important effects on real GDP and unemployment from such disturbances. Our model implies a much broader range of shocks to financial intermediaries may be important, a subject for further research.
Our framework allows consideration of several short term credit policies designed to address a liquidity/balance sheet crisis as well as long-term policies such as capital requirements. Given the empirical validation of our model herein, we pursue analysis of policy implications in companion research (see Kiley and Sim (2011)).
Research Papers, 2065, Stanford University, Graduate School of Business.
Volume 3 of Handbook of Monetary Economics, pp. 601 - 650. Elsevier.
SSRN eLibrary.
Journal of Money, Credit and Banking 26(3), pp. 585-628.
The Quarterly Journal of Economics 98(1), pp. 85-106.
Volume 1, Part 3 of Handbook of Macroeconomics, pp. 1341 - 1393. Elsevier.
International Journal of Central Banking 6(34), 1-50.
Interim report of the macroeconomic assessment group, Basel Committee on Banking Supervision, Basel, Switzerland.
Econometrica 77(3), pp. 623-685.
Volume 3 of Handbook of Monetary Economics, pp. 369 - 422. Elsevier.
The Journal of Political Economy 108(2), pp. 324-351.
Review of Financial Studies 22(6), 2201-2238.
Journal of Monetary Economics 49(6), 1131-1159.
Review of Financial Studies 22(9), 3367-3409.
Journal of Money, Credit and Banking 35(6), 1119-1197.
Working Paper Series, 1228, European Central Bank.
The American Economic Review 91(5), pp. 1286-1310.
Policy Research Working Paper Series, 3030, The World Bank.
The Journal of Finance 55(6), pp. 2431-2465.
Carnegie-Rochester Conference Series on Public Policy 49, 207 - 244.
Volume 3 of Handbook of Monetary Economics, pp. 547 - 599. Elsevier.
The American Economic Review 91(5), pp. 1263-1285.
Journal of Housing Economics 3(1), 31 - 50.
Journal of Economic Perspectives 25(1), 3-28.
NBER Working Papers, 14517, National Bureau of Economic Research, Inc.
The Journal of Finance 56(5), pp. 1837-1867.
SSRN eLibrary.
NBER Working Papers, 15338, National Bureau of Economic Research, Inc.
Wiley.
Finance and Economics Discussion Series 2011-28, Board of Governors of the Federal Reserve System (U.S.).
Journal of Money, Credit and Banking 38(6), 1575-1597.
Journal of Applied Econometrics 24(6), 960-992.
Journal of Financial Economics 13(2), 187 - 221.
mimeo, Board of Governors of the Federal Reserve System.
The Bell Journal of Economics 8(1), pp. 23-40.
Review of Economic Studies 77(2), 665-696.
Journal of International Money and Finance 19(6), 813 - 832.
The Journal of Political Economy 75(6), 796-810.
The American Economic Review 97(3), 586-606.
Journal of Monetary Economics 52(2), 381 - 419.
Journal of Monetary Economics 55(2), 298 - 320.
Technical report.
Footnotes
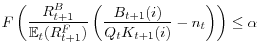
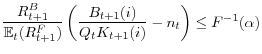
One could call the right hand side of the inequality a minimum capital ratio (or margin requirement) and denote it by
What can help the situation, if exists, is an efficient secondary market in which capital assets on intermediary balance sheets can be traded such that a cash strapped intermediary can sell some portion of its assets to a cash rich intermediary and use the proceeds to buy back a portion of its debt, thereby satisfying the capital constraint without issuing new shares, which is assumed to be costly in this research as will be explained below. However, it is natural to assume that the same information problem that makes the equity finance costly also makes interbank transfer of balance sheet assets difficult (as was apparent in the financial crisis of 2008, where secondary markets for bank loans became severely distressed). Given that such frictions in a hypothetical secondary market for bank assets have similar implications as costly equity financing, we simplify the analysis by assuming either the absence of such secondary market or at least that the marginal cost of interbank transfer of assets are greater than the marginal cost of equity issuance. Return to Text
![\displaystyle \int_{\epsilon\geq\epsilon_{t}^{\ast}}\epsilon f(\epsilon\vert\sigma_{t} )d\epsilon=[1-\Phi(s_{t}^{\ast}-\sigma_{t})]\int_{0}^{\infty}\epsilon f(\epsilon\vert\sigma_{t})d\epsilon,](img126.gif)
![\displaystyle =\epsilon_{t+1}(i)\left[ \frac{R_{t+1}^{K}+(1-\delta)Q_{t+1}}{Q_{t}}\right]](img15.gif)
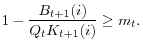
![\displaystyle =\max\sum_{s=t}^{\infty}\beta^{s-t}\mathbb{E}_{t}\left[ \frac{\Lambda_{s}}{P_{s}}\mathbb{E}_{t}^{i}[D_{s}(i)]\right]](img72.gif)
![\displaystyle +\sum_{s=t}^{\infty}\beta^{s-t}\mathbb{E}_{t}\left\{ \left. \left. \frac{ \Lambda_{s}}{P_{s}}\mu_{s}(i)\right[ (1-m_{s})Q_{s}K_{s+1} (i)-B_{s+1}(i) \right] \right\}](img73.gif)
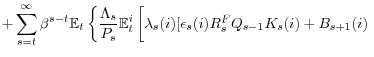
![\displaystyle \left. \left. -R_{s}^{B}B_{s}(i)-Q_{s}K_{s+1}(i)-\overset{\overset{}{}}{\varphi(D_{s}(i))} ]\right] \right\}](img75.gif)
![\displaystyle \beta\mathbb{E}_{t}\left[ \frac{\Lambda_{t+1}}{\Lambda_{t}} \mathbb{E}_{t+1}^{i}[\lambda_{t+1}(i)\epsilon_{t+1}(i)]\frac{R_{t+1}^{F}}{ \Pi_{t+1}}\right]](img84.gif)
![\displaystyle \mathbb{E}_{t}^{i}[\lambda_{t}(i)]=\mu_{t}(i)+\beta\mathbb{E}_{t}\left[ \frac{\Lambda_{t+1}}{\Lambda_{t}}\mathbb{E}_{t+1}^{i}[\lambda_{t+1}(i)] \frac{R_{t+1}^{B}}{\Pi_{t+1}}\right]](img86.gif)
![\displaystyle =\beta\mathbb{E}_{t}\left[ \frac{\Lambda_{t+1}}{\Lambda_{t}}\mathbb{E}_{t+1}^{i}[\lambda_{t+1} (i)\epsilon_{t+1}(i)]\frac{R_{t+1}^{F}}{\Pi_{t+1}}\right]](img99.gif)
![\displaystyle -\beta\mathbb{E}_{t}\left[ \frac{\Lambda_{t+1}}{\Lambda_{t}} (1-m_{t})\mathbb{E}_{t+1}^{i}[\lambda_{t+1}(i)]\frac{R_{t+1}^{B}}{\Pi_{t+1} }\right]](img100.gif)
![\displaystyle \lambda_{t}(i)=1/\varphi^{\prime}(D_{t}(i))=\left\{ \begin{array}[c]{c} 1\\ 1/(1-\bar{\varphi})>1 \end{array} \right. \begin{array}[c]{c} \text{if }\epsilon_{t}(i)\geq\epsilon_{t}^{\ast}\\ \text{if }\epsilon_{t}(i)<\epsilon_{t}^{\ast} \end{array} .](img114.gif)
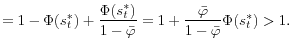
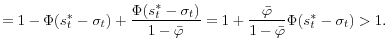
![\displaystyle 1=\mathbb{E}_{t}\left\{ M_{t,t+1}^{B}\left[ \frac{1}{m_{t}}\left( \frac{\tilde{R}_{t+1}^{F}}{\Pi_{t+1}}-\left( 1-m_{t}\right) \frac {R_{t+1}^{B}}{\Pi_{t+1}}\right) \right] \right\}](img134.gif)
![\displaystyle =\mathbb{E}_{t}\left\{ M_{t,t+1}^{B}\left[ \frac{1}{m_{t}}\left( \frac{\tilde{R}_{t+1}^{F}}{\Pi_{t+1}}-\left( 1-m_{t}\right) \frac {R_{t+1}^{B}}{\Pi_{t+1}}\right) \right] \right\}](img153.gif)
![\displaystyle -\frac{\bar{\gamma}}{m_{t}}\left( \frac{Q_{t}K_{t+1}}{Q_{t-1}K_{t} }-1\right) -\mathbb{E}_{t}\left\{ M_{t,t+1}^{B}\frac{\bar{\gamma}}{2m_{t} }\left[ \left( \frac{Q_{t+1}K_{t+2}}{Q_{t}K_{t+1}}\right) ^{2}-1\right] \right\} .](img154.gif)
![\displaystyle R_{t+1}^{S}\equiv\Pi_{t+1}\left[ \frac{v_{t+1}^{B}}{\mathbb{E}_{t} [M_{t,t+1}^{H}\cdot v_{t+1}^{B}]}+\frac{\bar{\varphi}d_{t+1}^{B-}} {\mathbb{E}_{t}[M_{t,t+1}^{H}\cdot v_{t+1}^{B}]}\right] .](img171.gif)
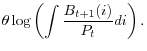
![\displaystyle \Lambda_{t}=\frac{1}{C_{t}-aC_{t-1}}-\beta\mathbb{E}_{t}\left[ \frac{a}{ C_{t+1}-aC_{t}}\right]](img195.gif)
![\displaystyle 1=\frac{\theta/\Lambda_{t}}{B_{t+1}(i)/P_{t}}+\beta\mathbb{E}_{t}\left[ \frac{\Lambda_{t+1}}{\Lambda_{t}}\frac{R_{t+1}^{B}}{\Pi_{t+1}}\right]](img196.gif)
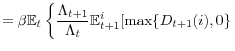
![\displaystyle \left. \underset{}{\overset{}{+(1-\bar{\varphi})\min\{D_{t+1} (i),0\}+P_{t+1}^{S}(i)]}}\right\}](img200.gif)
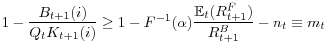 .
.