
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 795, April 2004 - Screen Reader Version*
Price-Level Determinacy, Lower Bounds on the Nominal Interest Rate, and Liquidity Traps
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We consider monetary-policy rules with inflation-rate targets and interest-rate or money-growth instruments using a flexible-price, perfect-foresight model. There is always a locally-unique target equilibrium. There may also be below-target equilibria (BTE) with inflation always below target and constant, asymptotically approaching or eventually reaching a below-target value, or oscillating. Liquidity traps are neither necessary nor sufficient for BTE which can arise if monetary policy keeps the interest rate above a lower bound. We construct monetary rules that preclude BTE when fiscal policy does not. Plausible fiscal policies preclude BTE for any monetary policy; those policies exclude surpluses and, possibly, balanced budgets.
Keywords: price-level indeterminacy, multiple equilibria, zero bound, monetary policy, monetary rule, fiscal policy, money demand.
JEL Classification: E31, E50, E62, E41
1 Introduction and summary
In this paper we discuss price-level determinacy when there is a lower bound on the (nominal) interest rate. The lower bound may arise either because of the behavior of (private) agents or because of monetary policy. For generality and relevance, our analysis is conducted in terms of the inflation rate instead of the price level.1 In our terminology, a model exhibits (inflation-rate) indeterminacy if it has multiple equilibria.
Determinacy in flexible-price models is of both theoretical and practical interest. As regards theory, inflation-rate determinacy is a standard topic. Furthermore, in models with synchronized price contracts, agents must be able to determine what expected inflation would be under price flexibility in order to set their contract prices. As regards practice, the current situation in Japan, with deflation and zero short-term interest rates, makes it more urgent to ascertain whether the possible existence of multiple equilibria is more than a theoretical curiosum.
Recently, the possibility of indeterminacy has received much
attention. Models with standard interest-rate rules or money-growth
rules and a locally unique steady-state target equilibrium
(![]() ) for the inflation
rate may have additional equilibria. To be more precise, there may
be multiple below-target equilibria (
) for the inflation
rate may have additional equilibria. To be more precise, there may
be multiple below-target equilibria (![]() ), paths along which the inflation rate is always
below target and is constant or either asymptotically approaches or
eventually reaches a below-target value.2 Fiscal policy may preclude
), paths along which the inflation rate is always
below target and is constant or either asymptotically approaches or
eventually reaches a below-target value.2 Fiscal policy may preclude ![]() ; in particular, a balanced-budget
fiscal policy precludes
; in particular, a balanced-budget
fiscal policy precludes ![]() in which the interest rate is always at a zero lower bound.3
in which the interest rate is always at a zero lower bound.3
We illustrate, modify, and extend recent analysis using a perfect-foresight, superneutral model with flexible prices which may have a liquidity trap. We adopt what we regard as the conventional definition of a liquidity trap: a liquidity trap is a region of the money-demand function in which bonds and money are perfect substitutes so that open-market operations in bonds cannot lower the interest rate any further.4 In our model, a liquidity trap may arise at a zero or at a strictly positive interest rate.
It is useful to summarize what we do. We present accessible
derivations of the central results regarding indeterminacy given
the existence of a lower bound on the interest rate.5 We distinguish clearly between a lower
bound that arises because of monetary policy and one that arises
because agents are in a liquidity trap. It turns out that a
liquidity trap is neither necessary nor sufficient for ![]() .
.
We also consider monetary-policy rules that preclude
![]() . The monetary policy
rules used in deriving indeterminacy results are monotonic in the
inflation rate. We present two kinds of monetary-policy rules that
may preclude
. The monetary policy
rules used in deriving indeterminacy results are monotonic in the
inflation rate. We present two kinds of monetary-policy rules that
may preclude ![]() . First,
elaborating on an observation in Benhabib, Schmitt-Grohe, and Uribe
(2001b), we demonstrate that monetary-policy rules that are not
monotonic in the inflation rate may preclude
. First,
elaborating on an observation in Benhabib, Schmitt-Grohe, and Uribe
(2001b), we demonstrate that monetary-policy rules that are not
monotonic in the inflation rate may preclude ![]() . Second, we present a rule under
which the interest rate responds to expected future inflation as
well as to current inflation. This rule is asymmetric: the interest
rate responds more strongly to expected future inflation if the
current inflation rate is below the target rate.
. Second, we present a rule under
which the interest rate responds to expected future inflation as
well as to current inflation. This rule is asymmetric: the interest
rate responds more strongly to expected future inflation if the
current inflation rate is below the target rate.
In addition, we show how conclusions about determinacy under
alternative monetary rules depend on fiscal policy. For simplicity,
we characterize fiscal policy by the growth rate of total nominal
government debt![]() 6 There is always a growth rate of debt
high enough to preclude
6 There is always a growth rate of debt
high enough to preclude ![]() no matter what the monetary policy because
no matter what the monetary policy because ![]() paths would violate the
transversality condition. A balanced-budget fiscal policy (a zero
growth rate of debt) is not expansionary enough if the interest
rate is positive at least part of the time either because of a
positive lower bound or, for example, because of foreseen variation
in productivity. Within a range, the combination of a small deficit
with a standard interest-rate or money-supply rule guarantees that
the
paths would violate the
transversality condition. A balanced-budget fiscal policy (a zero
growth rate of debt) is not expansionary enough if the interest
rate is positive at least part of the time either because of a
positive lower bound or, for example, because of foreseen variation
in productivity. Within a range, the combination of a small deficit
with a standard interest-rate or money-supply rule guarantees that
the ![]() is the unique
equilibrium because the deficit precludes
is the unique
equilibrium because the deficit precludes ![]() .
.
In the next section we lay our model and discuss two specific
money-demand functions. Section 3 is a presentation of some
results regarding the existence of ![]() with interest-rate rules. We discuss indeterminacy
under money-growth rules in section 4. In section 5, we
present monetary-policy rules that assure determinacy.
Section 6 is a discussion of some implications of fiscal
policy for determinacy. Concluding remarks are provided in
section 7.
with interest-rate rules. We discuss indeterminacy
under money-growth rules in section 4. In section 5, we
present monetary-policy rules that assure determinacy.
Section 6 is a discussion of some implications of fiscal
policy for determinacy. Concluding remarks are provided in
section 7.
2 The model
2.1 Agents
Our model economy is populated by a continuum of agents each of which acts simultaneously as a consumer and a producer. For simplicity, we assume that the product market is perfectly competitive, that prices are flexible, and that agents have perfect foresight. The problem of each agent is to find the
![$\displaystyle \underset{C_{t},B_{t},M_{t},Y_{t}}{Max}\sum_{t=0}^{\infty}\beta^{... ...U(C_{t})+V(m_{t})-\left[ 1/\left( 2\rho_{t}\right) \right] Y_{t}{} ^{2}\right\}$](img6.gif)
|
||
| (1) | ||
subject to the following period budget and positivity constraints:
| (2) | |
Period utility is increasing in consumption, weakly increasing in real (money) balances
| (3) |
where
To simplify exposition, in sections 2-6 we express the nominal interest rate, the real interest rate and inflation rate in gross terms and refer to them as `the interest rate', `the real interest rate', and `the inflation rate' respectively. In the introductory and concluding sections, we refer to the net nominal interest rate as `the interest rate' in order to facilitate comparison of our results to those of others.
Three necessary conditions for an optimum are
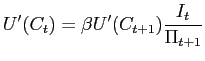 (bonds)
(bonds) |
(4) |
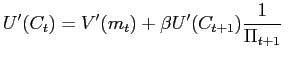 (money)
(money) |
(5) |
| (6) |
where
| (7) |
Informally, since the marginal utility of consumption is always positive, it cannot be optimal for the present value of agents' `end of horizon' net financial assets to be strictly positive. The first order conditions have been written as equilibrium conditions:
We assume that productivity is constant
![]() except in section 6.3.
Under this assumption, the four equilibrium conditions (4), (5),
(6), and (7) reduce to the Fisher equation, the money market
equilibrium condition, the output determination equation, and the
transversality condition:
except in section 6.3.
Under this assumption, the four equilibrium conditions (4), (5),
(6), and (7) reduce to the Fisher equation, the money market
equilibrium condition, the output determination equation, and the
transversality condition:
| (8) |
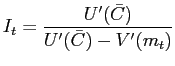
|
(9) |
| (10) |
| (11) |
where
2.2 Policy
We assume that fiscal policy determines the total amount of
nominal government bonds outstanding, ![]() , through control of the budget
deficit inclusive of interest payments. Monetary policy determines
whether these bonds are held by the monetary authority as a match
for the money supply,
, through control of the budget
deficit inclusive of interest payments. Monetary policy determines
whether these bonds are held by the monetary authority as a match
for the money supply, ![]() , or directly by the public,
, or directly by the public, ![]() , through control of open-market
operations. The consolidated government balance sheet implies that
, through control of open-market
operations. The consolidated government balance sheet implies that
![]() . Most
of this paper is devoted to the analysis of determinacy under
alternative monetary-policy rules which are specified below. Except
in section 6, we assume that fiscal policy is conducted so that
(11) holds for any path of the nominal interest rate.9Fiscal policy and equation (11),
therefore, may be disregarded until that section.
. Most
of this paper is devoted to the analysis of determinacy under
alternative monetary-policy rules which are specified below. Except
in section 6, we assume that fiscal policy is conducted so that
(11) holds for any path of the nominal interest rate.9Fiscal policy and equation (11),
therefore, may be disregarded until that section.
So that we can discuss indeterminacy in our stripped-down model,
we assume that there is a target equilibrium (![]() ) with a target value for inflation (
) with a target value for inflation (
![]() ) given by
) given by
![]() because of
considerations not included in the model. Since the target nominal
interest rate (
because of
considerations not included in the model. Since the target nominal
interest rate (![]() ) must satisfy
) must satisfy
![]() ,
it is given by
,
it is given by
![]() .
Absent such considerations, the optimal values for
.
Absent such considerations, the optimal values for ![]() and
and ![]() would be
would be
![]() and
and
![]() , respectively.
Our main focus is on the possible existence of below-target
equilibria
, respectively.
Our main focus is on the possible existence of below-target
equilibria ![]() We
define
We
define ![]() as weakly
increasing or decreasing paths for inflation and the interest rate
along which they are always below
as weakly
increasing or decreasing paths for inflation and the interest rate
along which they are always below
![]() and
and
![]() respectively,
and are either constant at, asymptotically approach, or eventually
reach values represented by
respectively,
and are either constant at, asymptotically approach, or eventually
reach values represented by ![]() and
and ![]() , respectively, where
, respectively, where
![]() .
.
2.3 Money demand and lower bounds on the interest rate
We consider two particular specifications of money demand. Under both specifications the gross nominal interest rate has a lower bound (possibly one). Equation (9) implies
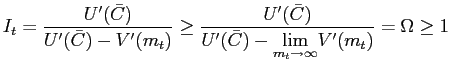
|
(12) |
Of course, a lower bound of one for
The lower bound ![]() may be unattainable or attainable. To model an attainable lower
bound (
may be unattainable or attainable. To model an attainable lower
bound (![]() ) for
) for
![]() , we assume that
the utility of real balances is given by
, we assume that
the utility of real balances is given by
![$\displaystyle V(m_{t})=\left\{ \begin{array}[c]{cc} \underline{V}^{\prime}m_{t}... ...m_{t} & \text{for }m_{t}>\overline{m} \end{array} \right. ,\qquad\overline{m}>0$](img67.gif)
|
(13) |
As before,
![$\displaystyle I_{t}=\left\{ \begin{array}[c]{cc} \frac{U^{\prime}(\bar{C})}{U^{... ...U^{\prime}(\bar{C})}{U^{\prime}(\bar{C})-\underline {V}^{\prime}}=\Omega^{ALB},$](img69.gif)
|
(14) |
To model an unattainable lower bound (![]() ), we assume that the utility of
real balances is given by
), we assume that the utility of
real balances is given by
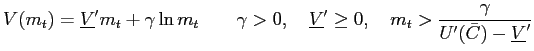
|
(15) |
where
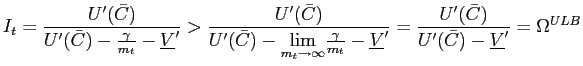
|
(16) |
Money-demand functions with an ![]() and an
and an ![]() are represented in figure 1.10 In
both cases,
are represented in figure 1.10 In
both cases, ![]() if
and only if
if
and only if
![]() . With an
. With an ![]() there is a liquidity trap, as
conventionally defined, at the lower bound. Purchases of bonds with
money can not lower the interest rate. With an
there is a liquidity trap, as
conventionally defined, at the lower bound. Purchases of bonds with
money can not lower the interest rate. With an ![]() there is never a liquidity trap.
Purchases of bonds with money can always lower the interest rate,
if only by an infinitessimal amount.
there is never a liquidity trap.
Purchases of bonds with money can always lower the interest rate,
if only by an infinitessimal amount.
From (16), (14), and ![]() (from (4)) we know that there exists a minimum
level for real money balances denoted by
(from (4)) we know that there exists a minimum
level for real money balances denoted by
![]() :
:
![]() with an
with an ![]() model, and
model, and
![]() with an
with an ![]() . In
order for
. In
order for
![]() in the
in the
![]() model, we need
model, we need
![]() .
.
3 Interest-rate rules and BTE
We begin by assuming that monetary policy takes the form of interest-rate rules and consider two examples. The general form of the interest-rate rules is
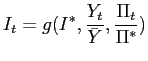
|
(17) |
where
3.1 A preference-determined lower bound
First, consider the case of an interest-rate rule under which
the interest rate may go all the way to the preference-determined lower bound,
![]() ,
associated with an
,
associated with an ![]() money-demand function:12
money-demand function:12
![$\displaystyle I_{t}=\max\left[ \Omega^{ALB},I^{\ast}\left( \frac{\Pi_{t}}{\Pi^{\ast} }\right) ^{\lambda}\right] ,\qquad\lambda>1$](img94.gif)
|
(18) |
The piecewise log-linear rule (18) is globally (weakly) increasing in the inflation rate, and the elasticity of the interest rate with respect to the inflation rate in the strictly increasing part is
The Fisher equation (8), the interest-rate rule (18), and
![]() imply a log-linear difference equation in
imply a log-linear difference equation in ![]() when
when
![]() :
:
![$\displaystyle \begin{tabular}[c]{l} $\Pi_{t+1}=\frac{I^{\ast}}{R}\left( \frac{\... ...\Pi}_{t+1}=(1-\lambda)\hat{\Pi}^{\ast}+\lambda\hat{\Pi}_{t}$ \end{tabular} \ \ $](img97.gif)
|
(19) |
where variables with hats over them represent logarithms. The solution is
| (20) |
One possible steady-state equilibrium is inflation equal to the
target rate. If one could disregard the lower bound on the interest
rate, this would be the only equilibrium. Deviations from the
inflation target would result in explosive or implosive paths of
inflation since ![]() .
.
However, equation (20) applies only when it calls for an
interest rate at or above
![]() . The
inflation rate cannot decline forever. If the inflation rate given
by (20) calls for an interest rate below
. The
inflation rate cannot decline forever. If the inflation rate given
by (20) calls for an interest rate below
![]() the
inflation rate is determined by the Fisher equation (8) together
with
the
inflation rate is determined by the Fisher equation (8) together
with
![]() instead of by (20). That is, the inflation rate will stop declining
when it is equal to its lower bound:
instead of by (20). That is, the inflation rate will stop declining
when it is equal to its lower bound:
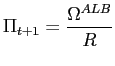 |
(21) |
The difference equation reflecting the lower bound has the form shown in figure 2:14
![$\displaystyle \Pi_{t+1}=\max\left[ \frac{\Omega^{ALB}}{R},(\Pi^{\ast})^{1-\lambda}(\Pi _{t})^{\lambda}\right]$](img106.gif)
|
(22) |
The list of equilibria as indexed by ![]() is
is
- 1.
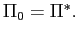 Steady-state
Steady-state  .
.
2.
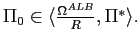
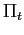 decreases to
decreases to
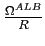 in finite time
in finite time
3.
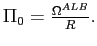 Steady-state
Steady-state
 equilibrium.
equilibrium.4.
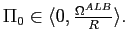 Equilibria with
Equilibria with
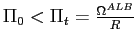 ,
,
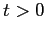 .15
.15
Along any ![]() path, the
inflation rate eventually reaches
path, the
inflation rate eventually reaches
![]() so that
so that ![]() reaches
its liquidity-trap value
reaches
its liquidity-trap value
![]() at which
the levels of the nominal and real money supplies are
indeterminate.16 Hence,
the number of equilibria is even larger than indicated above. Let
the liquidity trap be reached in period
at which
the levels of the nominal and real money supplies are
indeterminate.16 Hence,
the number of equilibria is even larger than indicated above. Let
the liquidity trap be reached in period ![]() at price level
at price level ![]() , given a particular initial
, given a particular initial
![]() There is an
infinity of equilibria associated with each initial
There is an
infinity of equilibria associated with each initial
![]() Once the
liquidity trap is reached, the set of possible paths for
Once the
liquidity trap is reached, the set of possible paths for
![]()
![]() includes all paths for which
includes all paths for which
![]()
![]() since agents
are indifferent between money and bonds.
since agents
are indifferent between money and bonds.
There may be more equilibria than those listed above. Beginning
on any initial inflation rate above
![]() the
inflation rate follows follows a divergent path. Such divergent
paths have been referred to as speculative hyperinflations, for
example, by Obstfeld and Rogoff, who have discussed ways of
precluding them.17
Throughout this paper we assume that paths with ever increasing
inflation are precluded.
the
inflation rate follows follows a divergent path. Such divergent
paths have been referred to as speculative hyperinflations, for
example, by Obstfeld and Rogoff, who have discussed ways of
precluding them.17
Throughout this paper we assume that paths with ever increasing
inflation are precluded.
For the sake of comparison, we briefly consider the case of an
interest-rate peg in which ![]() and the difference equation in figure 2 is a
horizontal line. Suppose it is announced that
and the difference equation in figure 2 is a
horizontal line. Suppose it is announced that ![]() will equal
will equal ![]() in period
in period ![]() and all future periods. The Fisher
equation (8), implies that
and all future periods. The Fisher
equation (8), implies that ![]() would be associated with
would be associated with
![]() from period
from period
![]() on. However, this
interest-rate rule would not pin down the initial inflation rate.
There would be a continuum of equilibria, indexed by the initial
inflation rate
on. However, this
interest-rate rule would not pin down the initial inflation rate.
There would be a continuum of equilibria, indexed by the initial
inflation rate
![]() . However, if the
monetary authorities specify the initial level of the money supply
in addition to the interest-rate peg, the initial inflation rate is
determinate, since there is a unique level of real balances
associated with
. However, if the
monetary authorities specify the initial level of the money supply
in addition to the interest-rate peg, the initial inflation rate is
determinate, since there is a unique level of real balances
associated with
![]()
3.2 A policy-determined lower bound
Now consider interest-rate rules designed to keep the gross
nominal interest rate from falling below a policy-determined lower bound, ![]() , that may be above
, that may be above
![]() . The
policy-determined lower bound may be attainable,
. The
policy-determined lower bound may be attainable,
![]() , or
unattainable,
, or
unattainable,
![]() . For
example, with the interest-rate rule
. For
example, with the interest-rate rule
![$\displaystyle I_{t}=\max\left[ \Lambda^{ALB},I^{\ast}\left( \frac{\Pi_{t}}{\Pi^{\ast} }\right) ^{\lambda}\right] ,\qquad\Lambda^{ALB}\geq\Omega,\qquad\lambda>1$](img131.gif)
|
(23) |
the policy-determined lower bound is attainable. This rule and the difference equation in inflation that it implies are identical to the ones considered in the last subsection except that the lower bounds on the interest rate and inflation are determined by policy, not by preferences. The rule is implementable with both
It is useful to consider a rule that is very similar to the
continuously differentiable rules used in the seminal papers on the
existence of ![]() :
:
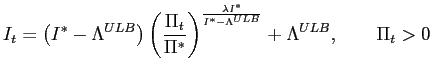
|
(24) |
With the rule (24), there must be two steady-state equilibrium
inflation rates: one is
![]() and the
other is
and the
other is ![]() which is below
which is below
![]() and
above
and
above
![]() but
which may or may not involve deflation.
Combining the rule (24) with the Fisher equation (8) yields a
difference equation in inflation of the form plotted in figure
3:21
but
which may or may not involve deflation.
Combining the rule (24) with the Fisher equation (8) yields a
difference equation in inflation of the form plotted in figure
3:21
![$\displaystyle \Pi_{t+1}=\frac{1}{R}\left[ \left( I^{\ast}-\Lambda^{ULB}\right) ... ...\ast}}\right) ^{\frac{\lambda R}{I^{\ast}-\Lambda^{ULB}} }+\Lambda^{ULB}\right]$](img148.gif)
|
(25) |
This equation is a convex function that has a lower bound of
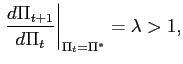
|
(26) |
that is,
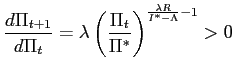
|
(27) |
Therefore, it must intersect the
There is a continuum of equilibria, indexed by ![]() . Each
. Each ![]() is associated with one of the
two possible steady-state inflation rates.
is associated with one of the
two possible steady-state inflation rates.
- 1.
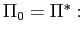 Steady-state
Steady-state 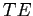 .
.
2.
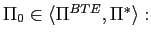 Non-steady-state
Non-steady-state 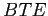 ;
;
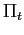
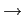
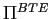 from
above
from
above3.
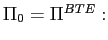 Steady-state
Steady-state 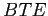 .
.4.
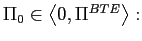 Non-steady-state
Non-steady-state 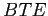 ;
;
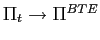 from below.23
from below.23
4 Indeterminacy under money-growth rules
4.1 Indeterminacy with 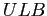 money demand
money demand
When the money-demand function has an ![]() , money-growth rules are consistent
with the existence of both a
, money-growth rules are consistent
with the existence of both a ![]() and
and ![]() in
which real money balances are forever increasing and the interest
rate is approaching its lower bound.24
in
which real money balances are forever increasing and the interest
rate is approaching its lower bound.24
Consider the money-growth rule:
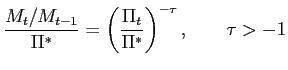
|
(28) |
If
The Fisher equation (8) and the money market equilibrium
condition (9) with the functional form for ![]() in equation (15) imply an
expression for the inflation rate in terms of real balances:
in equation (15) imply an
expression for the inflation rate in terms of real balances:
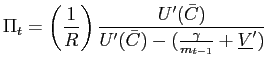
|
(29) |
Furthermore, the money-growth rule can be rewritten as
| (30) |
Combining (30) and (29), yields a difference equation in real balances,
![$\displaystyle m_{t}=m_{t-1}(\Pi^{\ast})^{1+\tau}\left[ \left( \frac{1}{R}\right... ...e}(\bar{C})-\frac{\gamma}{m_{t-1} }-\underline{V}^{\prime}}\right] ^{-(1+\tau)}$](img176.gif)
|
(31) |
with the form plotted in figure 4.26 Given the definition of
The unique steady-state solution for equation (31) is
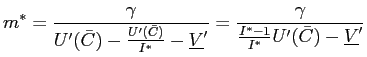
|
(32) |
If the steady-state level of real balances is to be positive, it must be that
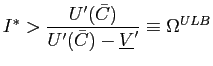
|
(33) |
The money-growth rule may be associated not only with the
![]() , but also with a
range of
, but also with a
range of ![]() in which
inflation declines forever and approaches the limit
in which
inflation declines forever and approaches the limit
![]() . The
equilibria may be indexed by
. The
equilibria may be indexed by ![]() :
:
- 1.
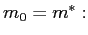 Steady state
Steady state  with
with
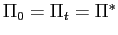 .
.
2.
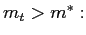
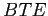 with positive growth
in
with positive growth
in 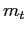 ,
,
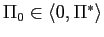 and
and
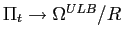 from
above
from
above
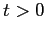 .
.
The money-growth rule has a representation as an interest-rate rule that is related to but somewhat different from the one discussed in section 3.2.28
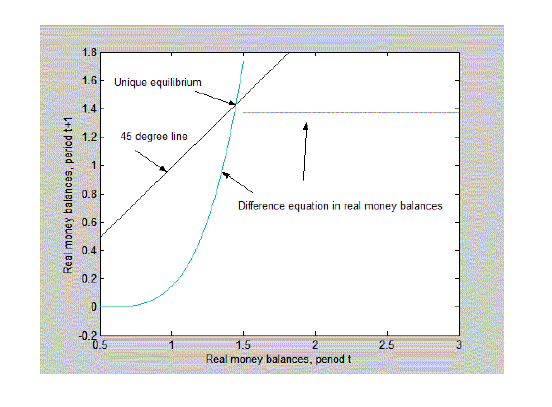
4.2 Indeterminacy with 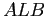 money demand
money demand
With ![]() money
demand money-growth rules are also consistent with the existence of
both a
money
demand money-growth rules are also consistent with the existence of
both a ![]() and
and
![]() . In the
. In the ![]() real money balances are forever
increasing money demand, as with
real money balances are forever
increasing money demand, as with ![]() money demand, but the interest rate reaches its
lower bound. The Fisher equation (8) and the
money demand, but the interest rate reaches its
lower bound. The Fisher equation (8) and the
![]() -part of the money-demand
function (14) imply an expression for inflation in terms of real
balances:
-part of the money-demand
function (14) imply an expression for inflation in terms of real
balances:
![$\displaystyle \Pi_{t}=\left( \frac{1}{R}\right) \left[ \frac{U^{\prime}(\bar{C} )}{U^{\prime}(\bar{C})-\overline{m}+m_{t-1}-\underline{V}^{\prime}}\right]$](img204.gif)
|
(34) |
Combining the money-growth rule (30) with (34) we obtain a difference equation in real balances:
![$\displaystyle m_{t}=m_{t-1}\left[ \left( \frac{1}{R}\right) \frac{U^{\prime}(\b... ...^{\prime}}\right] ^{-(1+\tau)}\Pi^{\ast(1+\tau)},\qquad m_{t-1}\leq\overline{m}$](img205.gif)
|
(35) |
Given the definition of
There exists a steady-state equilibrium with positive real balances equal to
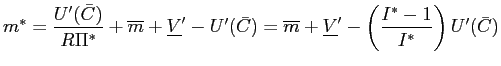
|
(36) |
under weak conditions that we assume are met.29 This equilibrium is a
Figure 5 is a diagram for the case where
![]() because
because
![]() .31
.31
The list of equilibria indexed by ![]() is now
is now![]()
- 1.
 steady state with
steady state with
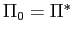
2.
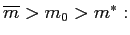
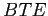 with
with
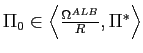 ,
, 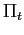 reaches
reaches
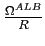 from above,
from above, 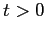 .
.
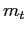 reaches
reaches
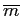 from
below,
from
below,3.
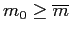
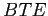 with
with
![$ \Pi_{0}\in\left\langle 0,\frac{\Omega^{ALB}}{R}\right] $](img232.gif) and
and
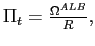
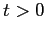 . The
. The 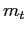 growth rate is constant at
growth rate is constant at
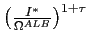 .
.
There is a second steady-state equilibrium with zero real
balances when
![]() so that
so that
![]() .32 This
case is not of particular interest to us because we want to focus
on equilibria in which inflation is below target (real balances are
above target). However, it is quite important for those considering
the existence of hyperinflation equilibria.
.32 This
case is not of particular interest to us because we want to focus
on equilibria in which inflation is below target (real balances are
above target). However, it is quite important for those considering
the existence of hyperinflation equilibria.
The money-growth rule in the ![]() model also has a representation as an
interest-rate rule as long as
model also has a representation as an
interest-rate rule as long as
![]() .33 However,
.33 However,
![]() for all
for all
![]() .
Hence, the interest-rate rule representation requires an additional
specification of policy when
.
Hence, the interest-rate rule representation requires an additional
specification of policy when
![]() in
order to uniquely pin down the path of real money balances for each
initial
in
order to uniquely pin down the path of real money balances for each
initial ![]() . For
example, Eggertson and Woodford (2003) add a rule for money growth
that applies whenever the interest rate reaches its lower
bound.
. For
example, Eggertson and Woodford (2003) add a rule for money growth
that applies whenever the interest rate reaches its lower
bound.
5 Monetary-policy rules that imply uniqueness
5.1 A nonmonotonic interest-rate rule
First, we show that making the interest-rate rule a nonmonotonic function of the inflation rate may insure a unique equilibrium, following up on an observation by Benhabib, Schmitt-Grohe, and Uribe (2001b). Consider the piecewise log-linear interest-rate rule
![$\displaystyle I_{t}=\left\{ \begin{array}[c]{cc} \begin{array}[c]{c} I_{t}^{\as... ...i_{t}}{\Pi^{\ast}}\right) ^{\lambda} \leq\Omega \end{array} \end{array} \right.$](img241.gif)
|
(37) |
This rule is similar to the one described in section 3.2, but the interest rate is pegged at
The difference equation in the inflation rate that follows from
(37) and the Fisher equation (8) is illustrated in figure
6.34 Consider
a situation where the inflation rate is so low that if ![]() were given by
were given by
![]() it would be less than or equal to the lower bound,
it would be less than or equal to the lower bound, ![]() . In such a situation,
. In such a situation,
![]() jumps up to
jumps up to
![]() . In the
next period, the inflation rate must be higher than the target
inflation rate given the Fisher equation and the fact that
. In the
next period, the inflation rate must be higher than the target
inflation rate given the Fisher equation and the fact that
![]() . But such a path is not
a possible solution, because it implies that the inflation rate
increases without limit. Hence, the economy cannot start out on a
path of declining inflation.
. But such a path is not
a possible solution, because it implies that the inflation rate
increases without limit. Hence, the economy cannot start out on a
path of declining inflation.
5.2 A monotonic but asymmetric interest-rate rule
Next, we demonstrate that there is an asymmetric interest-rate rule that is associated with a unique steady-state inflation rate and a determinate price level. Consider the following rule35,
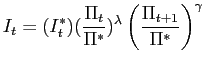
|
(38) |
Combining equation (38) with the Fisher equation (8) and using
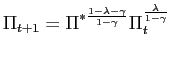
|
(39) |
Taking logs, we have
| (40) |
where
The rule (38) implies asymmetric responses under the following assumptions:
![]() If
If
![]() ,
,
![]() , and
, and
![]() , so that
, so that
![]() and
and
![]() .
.
![]() If
If
![]() ,
,
![]() and
and
![]() , so that
, so that
![]() and
and
![]() .
.
Under these assumptions, the rule calls for a stronger response to expected future inflation when current inflation is below target.
With the asymmetric rule the difference equation for inflation
(39) has the form shown in figure 7.36 In contrast with the symmetric rule
(19), the asymmetric rule (39) implies a difference equation for
inflation for which
![]() no matter how low the value of
no matter how low the value of ![]() .
.
![]() is a unique
steady-state equilibrium, and
is a unique
steady-state equilibrium, and
![]() is
the only equilibrium.37 If the
initial inflation rate is in the interval
is
the only equilibrium.37 If the
initial inflation rate is in the interval
![]() , the economy
embarks on a path with ever-increasing inflation. The part of the
difference equation that applies when
, the economy
embarks on a path with ever-increasing inflation. The part of the
difference equation that applies when
![]() implies
implies
![]() ,
and the inflation rate continues to increase because the part that
applies when
,
and the inflation rate continues to increase because the part that
applies when
![]() is
now relevant.
is
now relevant.
5.3 A nonmonotonic money-growth rule
Finally, we demonstrate that a nonmonotonic money-growth rule can work analogously to the nonmonotonic interest-rate rule in section 5.1. We assume a money-growth rule of the form
![$\displaystyle M_{t}=\left\{ \begin{array}[c]{ccc} \begin{array}[c]{c} \left( \f... ...rline{m}\\ \\ \text{if }m_{t-1}\geq\overline{m} \end{array} \end{array} \right.$](img279.gif)
|
(41) |
and an
The top relationship in equation (41) is a rewrite of the
money-growth rule (28) and ![]() is the steady-state level of real money
balances when following that relationship:
is the steady-state level of real money
balances when following that relationship:
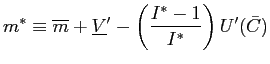
|
(42) |
The second part of (41) tells us that the level of real balances in period
6 Fiscal policy and BTE
6.1 Fiscal policy can always preclude BTE
There is always a fiscal policy that precludes ![]() no matter what the monetary policy
rule. Fiscal policy determines the path of total nominal government
debt measured as total nominal government bonds,
no matter what the monetary policy
rule. Fiscal policy determines the path of total nominal government
debt measured as total nominal government bonds, ![]() . The consolidated government
balance sheet implies that
. The consolidated government
balance sheet implies that ![]() must equal the money supply (which equals the
government bonds held by the monetary authority) plus government
bonds held by the public:
must equal the money supply (which equals the
government bonds held by the monetary authority) plus government
bonds held by the public:
| (43) |
For simplicity, we devote most of our attention to fiscal policies under which there is a constant gross growth rate (
| (44) |
where
Fiscal policy and the transversality condition (11) taken
together have implications for the possibility of ![]() . First, consider a candidate
steady-state
. First, consider a candidate
steady-state ![]() in which
the interest rate is constant at
in which
the interest rate is constant at ![]() . The path
. The path
![]()
![]()
![]() can be a steady-state equilibrium
only if
can be a steady-state equilibrium
only if
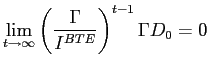
|
(45) |
Therefore if
One important implication of the previous paragraph, is that if
![]() , the
Friedman rule (
, the
Friedman rule (![]()
![]()
![]() ) cannot be implemented exactly under
any type of monetary policy. This result for the case of
) cannot be implemented exactly under
any type of monetary policy. This result for the case of
![]() is obtained
by Schmitt-Grohe and Uribe (2000) in cases in which the
monetary-policy rule is either an interest-rate rule or a
money-growth rule. Another important implication is that if
is obtained
by Schmitt-Grohe and Uribe (2000) in cases in which the
monetary-policy rule is either an interest-rate rule or a
money-growth rule. Another important implication is that if
![]() , there
may be
, there
may be ![]() with small
deficits (
with small
deficits (
![]() ).
).
Next, consider a candidate ![]() path on which the interest-rate path is some
weakly decreasing sequence
path on which the interest-rate path is some
weakly decreasing sequence ![]() with
with
![]() . Let
. Let
![]()
![]() where
where
![]() is a
weakly decreasing sequence with
is a
weakly decreasing sequence with
![]() . Let the value
of
. Let the value
of
![]() at some
time
at some
time ![]() given by
given by
![]() be arbitrarily close to one. This sequence of interest rates can be
an equilibrium only if
be arbitrarily close to one. This sequence of interest rates can be
an equilibrium only if
| (46) |
The condition (46) cannot hold if
The class of fiscal policies for which
![]() is especially
interesting. As just shown, this class precludes
is especially
interesting. As just shown, this class precludes ![]() for any monetary policy. It follows
that a combination of a member of this class with a standard
interest-rate rule like equation (18) or money-supply rule like
equation (28) is sufficient to insure that
for any monetary policy. It follows
that a combination of a member of this class with a standard
interest-rate rule like equation (18) or money-supply rule like
equation (28) is sufficient to insure that
![]() is the
unique equilibrium value for the inflation rate. These observations
suggest that
is the
unique equilibrium value for the inflation rate. These observations
suggest that ![]() may not be
a matter for concern in OECD countries. Most, if not all, of these
countries run positive but relatively small government deficits on
average so their fiscal policies may preclude
may not be
a matter for concern in OECD countries. Most, if not all, of these
countries run positive but relatively small government deficits on
average so their fiscal policies may preclude ![]() . This possibility is yet another
reminder of the importance of analyzing monetary and fiscal policy
jointly.40
. This possibility is yet another
reminder of the importance of analyzing monetary and fiscal policy
jointly.40
6.2 Uniqueness with money growth through transfers
In subsection 4.2 we show that with an ALB money-demand
function, the money-growth rule (28) is associated with multiple
equilibria. There, as well as in all of the paper before section 6,
we assume that ![]() can take on any value implied by the open-market purchases used to
increase the money supply. In particular,
can take on any value implied by the open-market purchases used to
increase the money supply. In particular, ![]() can be as negative as necessary,
or, in other words, government interest-bearing claims on the
public can increase without limit.
can be as negative as necessary,
or, in other words, government interest-bearing claims on the
public can increase without limit.
In this subsection, we assume that there is a finite lower bound
on ![]() designated by
designated by
![]() where
where
![]() ; that is, government claims
on the public cannot exceed the finite amount
; that is, government claims
on the public cannot exceed the finite amount
![]() Once
this limit is reached, the money supply can be increased only by
money-financed transfers (`money rain'). The required policy is
best viewed as a combination of fiscal policy and monetary policy:
the fiscal authority makes a bond-financed transfer to the private
sector, and the monetary authority buys the bonds.
Once
this limit is reached, the money supply can be increased only by
money-financed transfers (`money rain'). The required policy is
best viewed as a combination of fiscal policy and monetary policy:
the fiscal authority makes a bond-financed transfer to the private
sector, and the monetary authority buys the bonds.
If ![]() are to be precluded,
the transversality condition (11) implies that
are to be precluded,
the transversality condition (11) implies that
![]() (the target
rate of inflation and money growth) must be chosen so that
(the target
rate of inflation and money growth) must be chosen so that
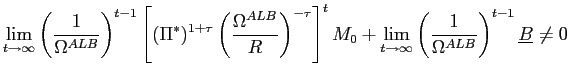
|
(47) |
where
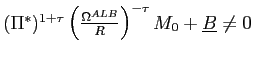 . Since
. Since 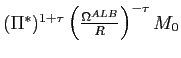 if
if
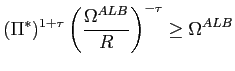
|
(48) |
or, equivalently, so that
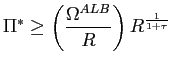
|
(49) |
The second term is either zero or bounded at
6.3 An illustration of the insufficiency
of balanced-budget fiscal policy for precluding 
In section 6.1, we show that a balanced-budget policy precludes
![]() when the interest
rate is always at a lower bound of one. Here we show that a
balanced-budget policy may not preclude
when the interest
rate is always at a lower bound of one. Here we show that a
balanced-budget policy may not preclude ![]() even if the interest rate is at a
lower bound of one infinitely often. We assume that there is
regular and perfectly foreseen variation in productivity, e.g.
seasonal variation. In our example, there is a
even if the interest rate is at a
lower bound of one infinitely often. We assume that there is
regular and perfectly foreseen variation in productivity, e.g.
seasonal variation. In our example, there is a ![]() in which the interest rate
fluctuates between one and a value greater than one.
in which the interest rate
fluctuates between one and a value greater than one.
Consider the following period utility function with time-varying
productivity, ![]() :
:
| (50) |
Solutions for the model with this utility function can be obtained using the procedure for the constant-productivity case. We report only the results needed to make our point.
Equations (50), (4) and (6) imply that the nominal and real interest rates are given by
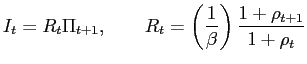
|
(51) |
Today's real interest rate,
| (52) |
We consider a simple example in which (a) the attainable lower
bound on the nominal interest rate is unity,
![]() , (b)
, (b)
![]() alternates
between a high value (
alternates
between a high value (
![]() ) in even
periods and a low value (
) in even
periods and a low value (
![]() ) in odd
periods,
) in odd
periods,
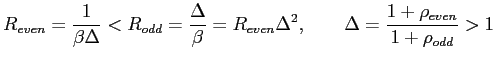
|
(53) |
and (c)
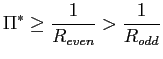
|
(54) |
If ![]() is at the lower
bound of one, equations (51) and (54) imply that
is at the lower
bound of one, equations (51) and (54) imply that
![]() . From the
interest-rate rule (18) with a time varying
. From the
interest-rate rule (18) with a time varying
![]() and
equation (52), it follows that
and
equation (52), it follows that ![]() is above the lower bound if
is above the lower bound if
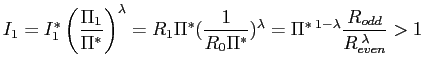
|
(55) |
From equation (53) it follows that the condition (55) is satisfied if
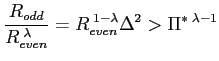
|
(56) |
Given
![]() is at the lower
bound again. Given
is at the lower
bound again. Given ![]() and
and
![]() ,
,
![]() is given by
the difference equation (19) that applies when
is given by
the difference equation (19) that applies when ![]() :
:
| (57) |
Given the interest-rate rule (18) and inequality (54),
![$\displaystyle I_{2}=\max\left[ 1,\left( R_{even}\Pi^{\ast}\right) \left( \frac{... ...ght] =\max\left[ 1,\left( R_{even}\Pi^{\ast}\right) ^{1-\lambda^{2} }\right] =1$](img372.gif)
|
(58) |
By induction, interest rates, real interest rates, and inflation rates are
![$\displaystyle \begin{tabular}[c]{lll} $I_{even}=1$\ & & $I_{odd}=\left( R_{even... ..._{even}=(R_{even}\Pi^{\ast})^{1-\lambda }(1/R_{even})<1/R_{even}$ \end{tabular}$](img373.gif)
|
(59) |
since we are assuming that
It follows that ![]() are
possible in our example with variable productivity and a balanced
budget. The transversality condition is met because the interest
rate alternates between one and a value greater than one. As
pointed out by Benhabib, Schmitt-Grohe, and Uribe (2001a), a
balanced-budget policy precludes only equilibria in which the
central bank commits to keep the interest rate equal to one no
matter what happens to inflation.
are
possible in our example with variable productivity and a balanced
budget. The transversality condition is met because the interest
rate alternates between one and a value greater than one. As
pointed out by Benhabib, Schmitt-Grohe, and Uribe (2001a), a
balanced-budget policy precludes only equilibria in which the
central bank commits to keep the interest rate equal to one no
matter what happens to inflation.
7 Concluding remarks
Under many specifications of monetary policy, standard models
may exhibit price-level indeterminacy. That is, they may have
multiple equilibria that include both a locally-unique steady-state
target (inflation-rate) equilibrium (![]() ) and multiple below-target equilibria (
) and multiple below-target equilibria (![]() ), equilibria in which the inflation
rate is always below target and is constant or eventually reaches
or asymptotically approaches a below-target value.
), equilibria in which the inflation
rate is always below target and is constant or eventually reaches
or asymptotically approaches a below-target value.
Rules with either the (nominal) interest rate or money growth as instruments are consistent with price-level indeterminacy in the presence of a conventionally-defined liquidity trap, a situation in which bonds and money are perfect substitutes at either a positive or zero nominal interest rate. Interest-rate and money-growth rules may also be consistent with indeterminacy even if there is no liquidity trap for one of two reasons. First, an interest-rate rule may keep the interest rate above a policy-determined lower bound. Second, with either an interest-rate rule or a money-growth rule, money demand may imply a lower bound on the interest rate so that the interest rate cannot be lowered `enough' even though it can always be lowered somewhat.
We have found that implementing monetary policy by setting money
growth instead of the interest rate makes a difference only if the
economy is in a liquidity trap and money is injected without
open-market operations, e.g. by lump sum transfers. Under these
conditions, a money-growth rule, more accurately viewed as a
combination of a money-growth and fiscal-policy rules, may preclude
![]() when an
interest-rate rule does not.
when an
interest-rate rule does not.
The above results all apply when the interest rate and money growth respond monotonically to eliminate deviations in the current inflation rate from its target value. We have expanded on the observation made in Benhabib, Schmitt-Grohe, and Uribe (2001b) that a unique steady-state inflation rate may be implied by interest-rate rules that are non-monotonic in the current inflation rate and have shown that an analogous result holds for non-monotonic money-growth rules. We also show that a unique steady state inflation rate is implied by an asymmetric interest-rate rule that calls for a response not only to current inflation but also to expected future inflation, with the response to expected future inflation being stronger when the current inflation rate is below target.
Conclusions about determinacy under alternative monetary rules
depend on fiscal policy as measured by the growth rate of total
nominal government debt. There is always a class of fiscal policies
that can preclude ![]() no
matter what the monetary policy because with those policies
no
matter what the monetary policy because with those policies
![]() paths violate the
transversality condition. Balanced budget fiscal policy can
preclude
paths violate the
transversality condition. Balanced budget fiscal policy can
preclude ![]() if the
interest rate is always at a zero lower bound. However, it cannot
do so if the lower bound on the interest rate is positive or if
productivity is variable even though the interest rate is at a
lower bound of zero infinitely often.
if the
interest rate is always at a zero lower bound. However, it cannot
do so if the lower bound on the interest rate is positive or if
productivity is variable even though the interest rate is at a
lower bound of zero infinitely often.
As stated in the introduction, it is not yet clear whether the
existence of ![]() is an
important problem or a curiosum. Some have argued that
is an
important problem or a curiosum. Some have argued that ![]() are of little interest for
theoretical reasons. McCallum (2001, 2003) uses his `minimum state
variable' criterion as one way of determining which equilibria are
of interest. In terms of our model, he shows that the
locally-unique
are of little interest for
theoretical reasons. McCallum (2001, 2003) uses his `minimum state
variable' criterion as one way of determining which equilibria are
of interest. In terms of our model, he shows that the
locally-unique ![]() meets
this criterion while the multiplicity of
meets
this criterion while the multiplicity of ![]() equilibria associated with the
below-target steady state, often referred to as `sun-spot'
equilibria, do not. Both McCallum (2001, 2003) and Evans and
Honkapohja (2002) use stability under a particular type of learning
as an alternative criterion. In terms of our model, they show that
the
equilibria associated with the
below-target steady state, often referred to as `sun-spot'
equilibria, do not. Both McCallum (2001, 2003) and Evans and
Honkapohja (2002) use stability under a particular type of learning
as an alternative criterion. In terms of our model, they show that
the ![]() is stable under
learning while the
is stable under
learning while the ![]() are
not. Although these theoretical arguments are attractive, not all
analysts are completely convinced by them.
are
not. Although these theoretical arguments are attractive, not all
analysts are completely convinced by them.
Our analysis suggests another more practical reason for focusing
on the ![]() The
combination of any of a range of small deficits with a standard
interest-rate or money-supply rule guarantees that the
The
combination of any of a range of small deficits with a standard
interest-rate or money-supply rule guarantees that the ![]() is the unique equilibrium because
the deficit precludes
is the unique equilibrium because
the deficit precludes ![]() .
This observation suggests that
.
This observation suggests that ![]() may not be a matter for concern in most OECD
countries. Most of these countries run positive but relatively
small government deficits on average so their fiscal policies may
preclude
may not be a matter for concern in most OECD
countries. Most of these countries run positive but relatively
small government deficits on average so their fiscal policies may
preclude ![]() . This
possibility provides another illustration of the importance of
analyzing monetary and fiscal policy jointly.
. This
possibility provides another illustration of the importance of
analyzing monetary and fiscal policy jointly.
It might be argued that Japan has been in a ![]() for the last several years.
Although this argument cannot be rejected out of hand, there is a
good reason to question it. Japan has had near-zero interest rates
and deflation despite the fact that the growth rate of nominal
government debt has exceeded nominal interest rates on government
debt. That is, according to our analysis, fiscal policy was too
expansionary to be consistent with a
for the last several years.
Although this argument cannot be rejected out of hand, there is a
good reason to question it. Japan has had near-zero interest rates
and deflation despite the fact that the growth rate of nominal
government debt has exceeded nominal interest rates on government
debt. That is, according to our analysis, fiscal policy was too
expansionary to be consistent with a ![]() .
.
Many analysts have concluded that the Japanese situation is
better described as a standard `liquidity-trap equilibrium'
(![]() ). A
). A ![]() could arise, for example, if
there were a large negative demand shock in the presence of wage
and price inertia. In order for output to be equal to potential it
would be necessary for the real interest rate to fall below zero.
However, the nominal interest rate could not be driven below zero
because of a liquidity trap as conventionally defined. Furthermore,
expected inflation might not move in the right direction or by the
right amount to reduce the real interest rate as much as is
required.
could arise, for example, if
there were a large negative demand shock in the presence of wage
and price inertia. In order for output to be equal to potential it
would be necessary for the real interest rate to fall below zero.
However, the nominal interest rate could not be driven below zero
because of a liquidity trap as conventionally defined. Furthermore,
expected inflation might not move in the right direction or by the
right amount to reduce the real interest rate as much as is
required.
For some policies, appropriateness depends crucially on whether
one is concerned about ![]() or
or ![]() , but,
for others, it does not. For example, it is often suggested that
Japan should announce a higher target inflation rate. Raising the
target inflation rate (or increasing the money supply even though
the interest rate is at the lower bound) can help an economy escape
from an
, but,
for others, it does not. For example, it is often suggested that
Japan should announce a higher target inflation rate. Raising the
target inflation rate (or increasing the money supply even though
the interest rate is at the lower bound) can help an economy escape
from an ![]() by
raising expected future inflation thereby lowering the real
interest rate.47 However,
we have shown that this policy cannot help escape from a
by
raising expected future inflation thereby lowering the real
interest rate.47 However,
we have shown that this policy cannot help escape from a
![]() because the target
inflation rate is irrelevant for this type of equilibrium. In
contrast, no matter which type of unintended equilibrium one is
trying to avoid, there is a strong case for a more aggressive
response to inflation when it is below target. It has been stressed
that more aggressive easing reduces the chances of falling into
because the target
inflation rate is irrelevant for this type of equilibrium. In
contrast, no matter which type of unintended equilibrium one is
trying to avoid, there is a strong case for a more aggressive
response to inflation when it is below target. It has been stressed
that more aggressive easing reduces the chances of falling into
![]() in which
policymakers must rely on less familiar instruments with more
uncertain effects.48 We have
shown that responding more aggressively to expected inflation when
current inflation is below target makes it possible to avoid
in which
policymakers must rely on less familiar instruments with more
uncertain effects.48 We have
shown that responding more aggressively to expected inflation when
current inflation is below target makes it possible to avoid
![]() .
.
References
Benhabib, J., S. Schmitt-Grohe, and M. Uribe (1998) ``Monetary Policy and Multiple Equilibria'', Finance and Economics Discussion Series 1998-29, Federal Reserve Board.
Benhabib, J., S. Schmitt-Grohe, and M. Uribe (2001a) ``Avoiding Liquidity Traps'', Journal of Political Economy, 110, 535--563.
Benhabib, J., S. Schmitt-Grohe, and M. Uribe (2001c) ``Monetary Policy and Multiple Equilibria'', American Economic Review, 91, 167--185.
Benhabib, J., S. Schmitt-Grohe, and M. Uribe (2001b) ``The Perils of Taylor Rules'', Journal of Economic Theory, 96, 40--69.
Bernanke, B. S., and V. Reinhart (2004) ``Monetary Policy at Very Low Nominal Interest Rates'', American Economic Review, 94, forthcoming.
Canzoneri, M. B., R. E. Cumby, and B. T. Diba (2001) ``Is the Price Level Determined by the Needs of Fiscal Solvency?'', American Economic Review, 91, 1221--1238.
Christiano, L. J., and M. Rostagno (2001) ``Money Growth Monitoring and the Taylor Rule'', NBER Working Paper 8539, National Bureau of Economic Research.
Eggertson, G., and M. Woodford (2003) ``The Zero Bound on Interest Rates and Optimal Monetary Policy'', Processed, IMF and Princeton University.
Evans, G. W., and S. Honkapohja (2002) ``Policy Interaction, Learning and the Fiscal Theory of Prices'', Processed, University of Helsinki, http://ideas.repec.org/e/pho12.html).
Evans, G. W., and S. Honkapohja (2003) ``Policy Interaction, Expectations and the Liquidity Trap'', Processed, University of Helsinki, (http://ideas.repec.org/e/pho12.html).
Krugman, P. (1998) ``It's Baack: Japan's Slump and Return of the Liquidity Trap'', Brookings Papers on Economic Activity, 2, 137--187.
Leeper, E. (1991) ``Equilibria under `Active' and `Passive'Monetary Policies'', Journal of Monetary Economics, 27, 129--147.
McCallum, B. T. (2001) ``Inflation Targeting and the Liquidity Trap'', in N. Loayza and R. Soto (eds.) Inflation Targeting: Design, Performance, Challenges, Central Bank of Chile, Santiago, 395-497 (NBER Working Paper 8225).
Loayza and R. Soto (eds.) Inflation Targeting: Design, Performance, Challenges, Central Bank of Chile, Santiago, 395--497 (NBER Working Paper 8225).
Obstfeld, M., and K. Rogoff (1983) ``Speculative hyperinflations in maximizing models: Can we rule them out?'', Journal of Political Economy, 91, 675--687.
Obstfeld, M., and K. Rogoff (1986) ``Ruling Out Divergent Speculative Bubbles'', Journal of Monetary Economics, 17, 349--362. 24
Obstfeld, M., and K. Rogoff (1996) Foundations of International Macroeconomics, MIT Press, Cambridge.
Orphanides, A., and V. Wieland (2000) ``Efficient Monetary Policy Design Near Price Stability'', Journal of the Japanese and International Economies, 14, 327--365.
Sargent, T. J. (1987) Macroeconomic Theory, Academic Press, New York, Second Edition.
Schmitt-Grohe, S., and M. Uribe (2000) ``Price Level Determinacy and Monetary Policy under a Balanced-Budget Requirement'', Journal of Monetary Economics, 45, 211--246.
Svensson, L. E. O. (2000) ``The Zero Bound in an Open Economy: A Foolproof Way of Escaping from a Liquidity Trap'', NBER Working Paper 7957, National Bureau of Econonmic Research.
Woodford, M. (1994) ``Monetary Policy and Price Level Determinacy in a Cash-in-Advance Economy'', Economic Theory, 4, 345--380.
Woodford, M. (2001a) ``Fiscal Requirements for Price Stability'', Journal of Money, Credit and Banking, 33, 669--728.
Woodford, M. (2001b) ``The Taylor Rule and Optimal Monetary Policy'', processed, Princeton University.
Woodford, M. (2003) Interest and Prices: Foundations of a Theory of Monetary Policy, Princeton University Press, Princeton.
Figure 1: ULB and ALB money demands
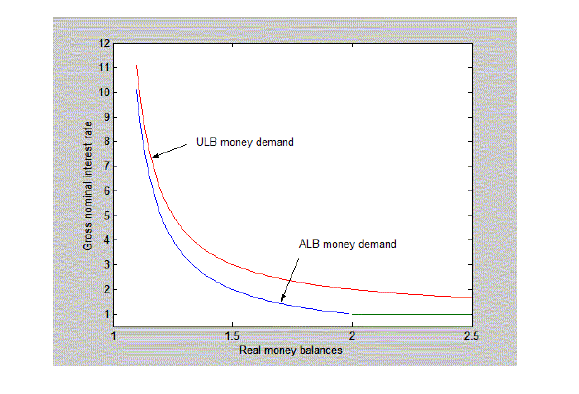
Figure 2: Interest-rate rule and preference-determined lower bound.
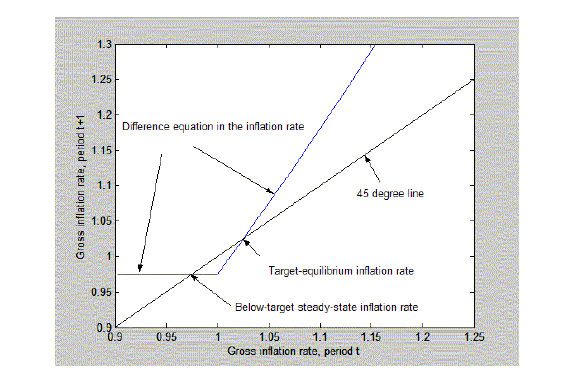
Figure 3: Interest-rate rule and policy-determined lower bound.
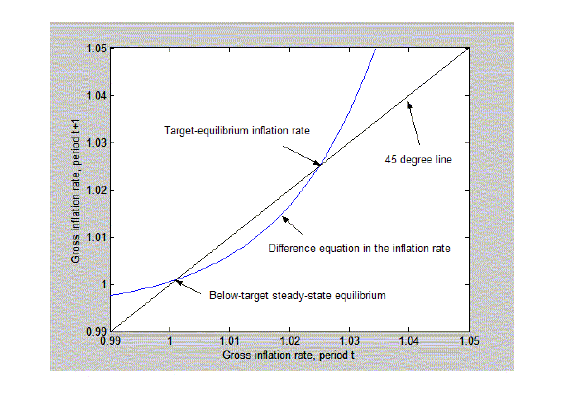
Figure 4: Money-growth rule with unattainable lower bound.
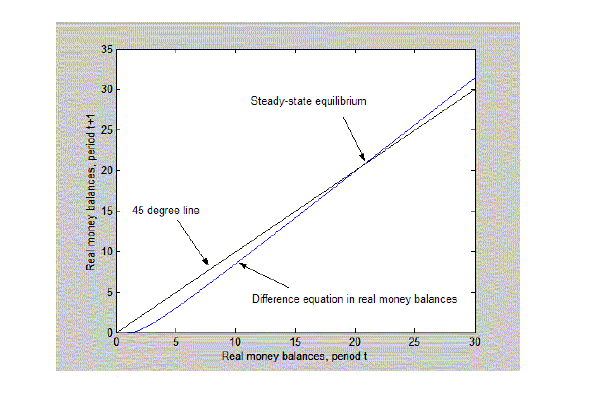
Figure 5: Money-growth rule with attainable lower bound.
Figure 6: Non-monotonic interest-rate rule.
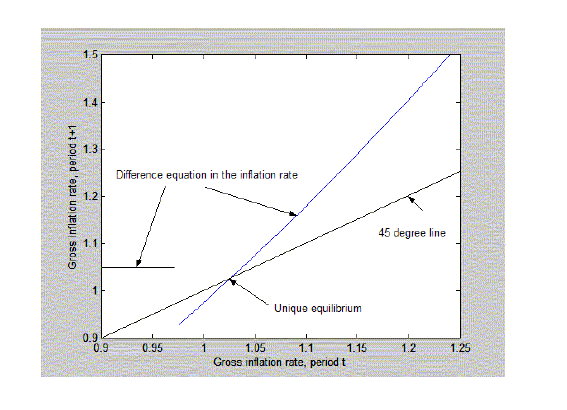
Figure 7: Asymmetric intrest-rate rule
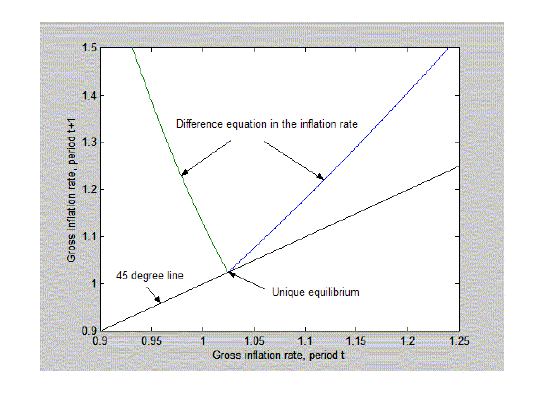
Figure 8: Non-monotonic money-growth rule
Footnotes
* Alstadheim is an Assistant Professor at Howard University, and Henderson is a Special Adviser in the Division of International Finance at the Federal Reserve Board. For helpful comments, we thank David Bowman, Matthew Canzoneri, Behzad Diba, Refet Gurkaynak, Berthold Herrendorf, Lars Svensson, and participants in a session at the 2001 meetings of the Southern Economics Association; in seminars at Georgetown University, the Federal Reserve Board, and the European Central Bank; and in the Konstanz Seminar on Monetary Theory and Monetary Policy. Remaining errors are our own. Alstadheim thanks the Center for Monetary and Financial Research in Norway and the Federal Reserve Board for financial support and hospitality. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting those of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. The email addresses of the authors are, respectively, [email protected] and [email protected] . Return to text
1. Of course, inflation-rate determinacy and price-level determinacy are linked. If the inflation rate (defined as the percentage change in the price level between today and yesterday) is determined and yesterday's price level is known, then today's price level is determined. Return to text
2. A 1999 version of Woodford (2003) cited by Benhabib, Schmitt-Grohe, and Uribe (2001b) contains an explanation of the possible existence of BTE with both interest-rate rules and money-supply rules. In Woodford (2003) and Benhabib, Schmitt-Grohe, and Uribe (2001a) the inflation rate may asymptotically approach a below-target steady state; in Schmitt-Grohe and Uribe (2000), Benhabib, Schmitt-Grohe, and Uribe (2001b) and Eggertsson and Woodford (2003) it may eventually reach a below-target steady state. Return to text
3. Woodford (2001a) and Benhabib, Schmitt-Grohe, and Uribe (2001b) consider fiscal policy. Schmitt-Grohe and Uribe (2000) analyze balanced-budget fiscal policy. Return to text
4. McCallum (2001) refers to a `liquidity trap situation' as a situation in which `the (usual) interest rate instrument is immobilized'. Svensson (2000) refers to a liquidity trap as a situation with a binding zero lower bound on the nominal interest rate. Krugman (1998) refers to a liquidity trap as a situation where `monetary policy loses its grip because the nominal interest rate is essentially zero [and] the quantity of money becomes irrelevant because money and bonds are essentially perfect substitutes'. Our definition is the same as Krugman's except that, like Sargent (1987) among others, we explicitly allow for a liquidity trap at a positive interest rate. Return to text
5. Since our model has flexible prices and exhibits superneutrality, a lower bound can give rise to only nominal indeterminacy. However, using a model with sticky prices, Benhabib, Schmitt-Grohe, and Uribe (2001a) show that a lower bound can give rise not only to nominal indeterminacy but also to real indeterminacy. Return to text
6. The characterization of fiscal policy in Eggertsson and Woodford (2003) is more general and includes ours as a special case. Return to text
7. We consider specific functional
forms for ![]() in
section 2.3 and for
in
section 2.3 and for
![]() in section 6.3. Return to text
in section 6.3. Return to text
8. Increases in ![]() can be interpreted either as
increases in productivity or decreases in the disutility of labor
if agents supply their desired amounts of labor either because they
are consumer-producers or because they participate in a labor
market that clears. Following Obstfeld and Rogoff (1996), let
can be interpreted either as
increases in productivity or decreases in the disutility of labor
if agents supply their desired amounts of labor either because they
are consumer-producers or because they participate in a labor
market that clears. Following Obstfeld and Rogoff (1996), let
![]() be the
disutility associated with labor (
be the
disutility associated with labor (![]() ) and let
) and let
![]() be the production function.
Inverting the production function yields
be the production function.
Inverting the production function yields ![]()
9. This means that (except in section 6) fiscal policy is assumed to be Ricardian according to the definition of Benhabib, Schmitt-Grohe, and Uribe (1998). A sufficient condition for (11) to hold is that the gross growth rate of total government debt is low enough. Since the nominal interest rate enters equation (11), the maximum permissible growth rate depends on monetary policy and the rest of the model. Return to text
10. For figure 1,
![]() ,
, ![]() ,
,
![]() , and
, and
![]() . Return to text
. Return to text
11. For these funds to survive, there must be some spread between the market rates they earn and the deposit rates they pay as noted by Bernanke and Reinhart (2004). Return to text
12. In this sense, the rule (18) is similar to the one used in Schmitt-Grohe and Uribe (2000) and in the appendix of Benhabib, Schmitt-Grohe, and Uribe (2001b). Return to text
13. We use an interest-rate rule of the form (18) so that the inflation-rate term in the strictly increasing range is directly comparable to the inflation-rate term in the money-supply rule (28). Return to text
14. For figure 2,
![]() ,
,
![]()
![]() and
and
![]() . Return to text
. Return to text
15. The
initial inflation rate is not constrained by the lower bound
![]() . The
reason is that the constraint on the inflation rate is implied by
the Fisher equation in combination with the interest rate given by
the interest-rate rule. The Fisher equation has no implications for
the initial price level or the inflation rate
. The
reason is that the constraint on the inflation rate is implied by
the Fisher equation in combination with the interest rate given by
the interest-rate rule. The Fisher equation has no implications for
the initial price level or the inflation rate
![]() , but it has implications
for the inflation rate
, but it has implications
for the inflation rate
![]() .
Hence,
.
Hence,
![]() Return to text
Return to text
16. Otherwise, the nominal money supply is determined by the nominal interest rate and the money-demand function, given the unique inflation rate associated with the TE. Return to text
17. See Obstfeld and Rogoff (1983) and Obstfeld and Rogoff (1986). Return to text
18. Consider the family of interest-rate rules given by
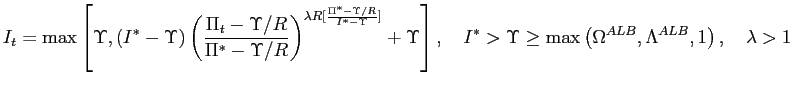
19. The continuous-time policy rule used in Benhabib, Schmitt-Grohe, and Uribe (2001a) and the main text of Benhabib, Schmitt-Grohe, and Uribe (2001b) has a policy-determined unattainable lower bound. The discrete-time analogue of this rule is
![$\displaystyle I_{t}=\left( I^{\ast}-\Lambda^{ULB}\right) \exp\left[ \frac{RA}{I^{\ast }-\Lambda^{ULB}}(\Pi_{t}-\Pi^{\ast})\right] +\Lambda^{ULB},\qquad A>1 $](img142.gif)
We employ the rule (24) because it is
directly comparable to the other interest-rate rules and the
money-supply rules (28)
used in this paper. Rule (24) is also used by
Evans and Honkapohja (2003), who assume that
![]() . Return to
text
. Return to
text
20. That is
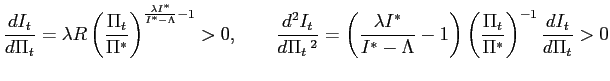
21. For figure 3,
![]() ,
,
![]()
![]() and
and
![]() Return to
text
Return to
text
22. If ![]() there would be a unique
steady state at
there would be a unique
steady state at
![]() , but
there would be multiple initial equilibrium inflation rates because
all paths that start below the target rate would approach
it. Return to text
, but
there would be multiple initial equilibrium inflation rates because
all paths that start below the target rate would approach
it. Return to text
23. ![]() can be lower than
can be lower than
![]() , see footnote 15. Return to text
, see footnote 15. Return to text
24. This possibility is pointed out,
for example, in Woodford (1994), Woodford (2003),
Christiano (2001), and Benhabib, Schmitt-Grohe, and Uribe (2001b)). We
begin with the case of ![]() money demand because it is somewhat simpler. Return to text
money demand because it is somewhat simpler. Return to text
25. With
![]() nominal balances increase when the inflation rate is above target.
For further discussion of this case, see footnote 27. Return to text
nominal balances increase when the inflation rate is above target.
For further discussion of this case, see footnote 27. Return to text
26. For figure 4, ![]()
![]()
![]()
![]()
![]() and
and ![]() , so
, so
![]() Return to text
Return to text
27. ![]() is
an unstable steady state since equation (31) and the
expression for
is
an unstable steady state since equation (31) and the
expression for
![]() given by
(29) imply that for
all
given by
(29) imply that for
all ![]()
![$\displaystyle \begin{tabular}[c]{l} $\left. \frac{dm_{t}}{dm_{t-1}}\right\vert ... ...R(1+\tau)\gamma\Pi^{\ast}}{m^{\ast}U^{\prime}(\bar{C})}>1$ \end{tabular}\ \ $](img191.gif)
28. Equation (16) can be used to
obtain an expression for ![]() in terms of
in terms of ![]() . Using this expression and assuming
. Using this expression and assuming
![]() , it follows from equations
(30) and (8) that
, it follows from equations
(30) and (8) that
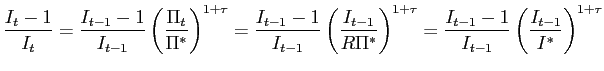
29. The positive steady state exists
only if
![]() or equivalently
or equivalently
![]() That is, the target interest rate must be smaller than the
maximum possible interest rate. For parameter values for which
That is, the target interest rate must be smaller than the
maximum possible interest rate. For parameter values for which
![]() ,
,
![]() , so the condition is definitely met. In order to exist,
the strictly positive steady state equilibrium must also satisfy
, so the condition is definitely met. In order to exist,
the strictly positive steady state equilibrium must also satisfy
![]() which
means that
which
means that
![]() . This condition is always satisfied as long as
. This condition is always satisfied as long as
![]() is not too large. Return to text
is not too large. Return to text
30. ![]() is an unstable steady state since (36) and the
definition of
is an unstable steady state since (36) and the
definition of ![]() imply
imply
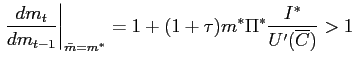
31. For figure 5,
![]()
![]()
![]() 1/
1/![]() ,
,
![]() , so
, so
![]() Return
to text
Return
to text
32. See section 2.3. In this case
(not shown), the line representing the difference equation would
start at the origin and have a slope that is below one at the
origin, increases until it exceeds one, and is constant for
![]() Return to text
Return to text
33. Using (30),(8) and (14), we get
![$\displaystyle \frac{I_{t}-1}{I_{t}}U^{\prime}(\bar{C})=\left[ \frac{I_{t-1}-1}{... ...rac{I^{\ast}}{I_{t-1}}\right] ^{1+\tau}+(\underline{V}^{\prime} +\overline{m}) $](img238.gif)
34. For figure 6,
![]() ,
,
![]()
![]() and
and
![]() . Return to text
. Return to text
35. Benhabib, Schmitt-Grohe, and Uribe (2001c) also consider interest-rate rules where the interest rate responds to both current and future inflation, but in a different context. Return to text
36. For figure 7,
![]()
![]() and
and
![]() .
.
![]() when
when
![]() ,
and
,
and ![]() otherwise. Return to text
otherwise. Return to text
37. All it takes for equation
(39) to be
associated with a unique steady-state ![]() is that
is that
![]() when
when
![]() and
and
![]() when
when
![]() .
One could, for example, let
.
One could, for example, let ![]() so that there was zero response to future
inflation, and vary
so that there was zero response to future
inflation, and vary ![]() to meet these requirements. Return to
text
to meet these requirements. Return to
text
38. For figure 8,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() , and
, and
![]() so
that
so
that
![]() . Return
to text
. Return
to text
39. Of course, there are many other
parameterizations of fiscal policy which are consistent with the
existence of ![]() . Return to text
. Return to text
40. An early joint analysis of monetary and fiscal policy is Leeper (1991); more recent analyses include Canzoneri, Cumby, and Diba (2001) and Evans and Honkapohja (2002). Return to text
41. Woodford (2003) and Woodford (1994) restrict attention to the case of ![]() (and
(and
![]() ) and
argue that the restriction on the range of the target inflation
rate,
) and
argue that the restriction on the range of the target inflation
rate,
![]() necessary to preclude
necessary to preclude ![]() is a limitation of money-supply rules relative to interest-rate
rules. However, the condition in equation (48) implies that if
is a limitation of money-supply rules relative to interest-rate
rules. However, the condition in equation (48) implies that if
![]() , the
authorities can follow a money-supply rule that implies uniqueness
and still target a gross inflation rate below
, the
authorities can follow a money-supply rule that implies uniqueness
and still target a gross inflation rate below
![]() . In
particular, with
. In
particular, with
![]() one can
get arbitrarily close to the Friedman rule by choosing
one can
get arbitrarily close to the Friedman rule by choosing ![]() large enough. Return to text
large enough. Return to text
42. In a model in which the lower
bound on the gross interest rate is one, Woodford (1994) shows
that a money-growth rule in combination with the condition that
![]()
![]()
![]() is associated with uniqueness as
long as gross money growth is equal to or larger than one (
is associated with uniqueness as
long as gross money growth is equal to or larger than one (
![]() in our
notation). When the public holds no government bonds, money must be
increased by money-transfers. A money-growth rule with
in our
notation). When the public holds no government bonds, money must be
increased by money-transfers. A money-growth rule with
![]() then corresponds to the
class of fiscal policies discussed in is subsection with
then corresponds to the
class of fiscal policies discussed in is subsection with
![]() , since the nominal growth rate of money is equal to the nominal
growth rate of government bonds.
Benhabib, Schmitt-Grohe, and Uribe (2001b) show that multiple equilibria
are precluded under money-growth rules when
, since the nominal growth rate of money is equal to the nominal
growth rate of government bonds.
Benhabib, Schmitt-Grohe, and Uribe (2001b) show that multiple equilibria
are precluded under money-growth rules when
![]() As we have
shown the lower bound on
As we have
shown the lower bound on ![]() can be negative. What is needed is that money be
supplied with lump-sum transfers instead of open-market operations
after some point Return to text
can be negative. What is needed is that money be
supplied with lump-sum transfers instead of open-market operations
after some point Return to text
43. Woodford (1994) (2003) restricts
attention to the case of ![]() (and
(and
![]() ) and
argues that the restriction on the range of the target inflation
rate,
) and
argues that the restriction on the range of the target inflation
rate,
![]() necessary to preclude
necessary to preclude ![]() is a limitation of money-supply rules relative to interest-rate
rules. Return to text
is a limitation of money-supply rules relative to interest-rate
rules. Return to text
44. A similar relation is discussed in Woodford (2001b). Return to text
45. A
![]()
![]() cannot be
attained because
cannot be
attained because ![]() would be below a lower bound of one. As noted by Krugman (1998)
being in a liquidity trap in which
would be below a lower bound of one. As noted by Krugman (1998)
being in a liquidity trap in which ![]() is at its lower bound has only nominal
consequences in a flexible-price model but has real consequences in
a sticky-price model because output has to adjust. For example,
Svensson (2000) considers what happens when
is at its lower bound has only nominal
consequences in a flexible-price model but has real consequences in
a sticky-price model because output has to adjust. For example,
Svensson (2000) considers what happens when
![]() is too low
and how it can credibly be raised. Return to text
is too low
and how it can credibly be raised. Return to text
46. For example, the combination
![]() ,
,
![]() ,
,
![]() , and
, and
![]() satisfy
both (54) and
(56), since
satisfy
both (54) and
(56), since
![]() .
.
![]() and (
and (
![]()
47. See, for example, Krugman (1998). Return to text
48. See, for example, Orphanides and Wieland (2000). Return to text
This version is optimized for use by screen readers. A printable pdf version is available.