
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 799, April 2004, Revised Version: late 2004--Screen Reader Version*.
This HTML version of this discussion paper is a revised and updated version of the same paper available as a PDF file at http://www.federalreserve.gov/pubs/ifdp/2004/799/ifdp799.pdf.
The Great Inflation of the 1970s1
International Finance Discussion Papers numbers 797-807 were presented on November 14-15, 2003 at the second conference sponsored by the International Research Forum on Monetary Policy sponsored by the European Central Bank, the Federal Reserve Board, the Center for German and European Studies at Georgetown University, and the Center for Financial Studies at the Goethe University in Frankfurt.
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
The two leading explanations for the poor inflation performance during the 1970s are policy opportunism (Barro and Gordon, 1982) and '' inadvertently'' bad monetary policy (Clarida, Gali and Gertler, 2000, Orphanides, 2003). In this paper we show that models of the latter category not only can account for high and persistent inflation but also have satisfactory overall performance. Moreover, both the Orphanides thesis (that loose monetary policy was the outcome of mis-perceptions about potential output rather than of inflation tolerance) and the Clarida, Gali and Gertler one (that weak policy reaction to expected inflation led to indeterminacies) are consistent with the data as long as there was a very large decrease in productivity at the time. Our result suggest that the assumption of policy opportunism does not seem essential for understanding the inflation experience of the 70s. JEL class: E32 E52
Keywords: Inflation, imperfect information, learning, monetary policy rule, indeterminacy
JEL Classification: E32, E52
Introduction
During the 1970s, the inflation rate in the US reached its 20-th century peak, with levels exceeding 10%. The causes of this ''great'' inflation remain the subject of considerable academic debate. Broadly speaking, the proposed explanations fall into two categories. Those that claim that the high inflation was due to the lack of proper incentives on the part of policymakers who chose to accept (or even induce) high inflation in order to prevent a recession (the inflation bias suggested by Barro and Gordon, 1982; see also Ireland, 1999). And those that claim that it may have been the result of the honest mistakes of a well-meaning central bank. The latter category can be further subdivided into a group of explanations that emphasize either bad lack under significant imperfect information or bad luck together with technical, inadvertent errors in policy design.
According to the latter view, the FED inadvertently committed a ''technical'' error by implementing an interest policy rule in which nominal interest rates were moved less than expected inflation (Clarida, Gali and Gertler, 2000). The resulting decrease in real interest rates fuelled inflation inducing instability (indeterminacy) in the economy and exaggerating inflation movements. The implication of this view is that adoption of the standard Henderson-McKibbin-Taylor (HMT)rule would have prevented the persistent surge in inflation.
The bad luck under imperfect information view claims that loose monetary policy and inflation reflected an unavoidable mistake on the part of a monetary authority whose tolerance of inflation did not differ significantly from that commonly attributed to the authorities in the 80s and 90s. Orphanides (2003) has argued that the large decrease in actual output following the persistent downward shift in potential output was interpreted as a decrease in the output gap4. It led to expansionary monetary policy that exaggerated the inflationary impact of the decrease in potential output. Eventually and after a long delay, the FED realized that potential output growth was lower and adjusted policy to bring inflation down. Imperfect information about the substantial productivity slowdown rather than tolerance of inflation played the critical role in the inflation process.
All these theories seem plausible. Identifying the most empirically relevant one has not been an easy task. A subset of the literature has tackled the issue of the contribution of policy to inflation directly, by examining whether monetary actions can be captured by a policy rule, and if yes, what the properties of such rule are. Relying on single equation estimation, Clarida, Gali and Gertler, 2000, claim that the FED indeed followed an interest rule during the 1970s but that rule contained a weak reaction to inflation that led to indeterminacies. Orphanides, 2001, disputes this claim. Using real time data, he documents the existence of a rule too, but he also finds no significant difference between pre and post Volcker tolerance regarding inflation. Lubic and Schforheide, 2003, estimate a small new Keynesian model (without learning, though, on the part of monetary authorities) and arrive at results similar to those of Clarida, Gertler and Gali's. According to their estimated model, post 1982 U.S. monetary policy is consistent with determinacy, whereas the pre-Volcker policy is not. Nelson and Nicolov, 2002, estimate a similar small scale model for the UK and find that both output gap mis-measurement and a weak policy response to inflation played an important role. And that the weak reaction to inflation does not seem to have encouraged multiple equilibria.
A second subset of the literature again uses a small scale model but imposes --rather than estimates-- a policy rule. Lansing, 2001, finds that a specification with sufficiently large reaction to inflation is consistent with the patterns of inflation and output observed during the 1970s.
Finally, a third subset of the empirical literature has investigated the events of the 70s within the context of calibrated, stochastic general equilibrium models. Christiano and Gust, 1999, argue that the new Keynesian model cannot replicate that experience, while a limited participation model with indeterminacy can (they do not address the role of imperfect information, though). Cukierman and Lippi, 2002, demonstrate how, within a backward looking version of the Keynesian model, imperfect information leads to serially correlated forecast errors and loose monetary policy. Bullard and Eusepi, 2003, argue that a persistent increase in inflation can obtain in the new Keynesian model even when policy responds strongly to inflation when the policymakers learn gradually about changes in trend productivity. Finally, in related work which however, looks at the disinflation of the 80s, Erceg and Levin, 2003, argue that the disinflation experience can be accounted for by a shift in the inflation target of the FED with the public only gradually learning about the policy regime switch.
Our objective in this paper is twofold. First, to examine whether explanations based on rules -as opposed to discretion- are consistent with the macroeconomic performance of the 70s. We emphasize overall macroeconomic performance because we find attempts to validate particular theories based solely on the behavior of inflation too narrow. And second, to undertake a direct comparison of the two leading explanations from this group (Orphanides vs Clarida, Gali and Gertler). This is an important task, as the two explanations carry dramatically different implications for inflation scenaria in the future. If the Orphanides view is correct, then strong reaction to expected inflation is not sufficient to prevent bad inflation outcomes. The experience of the 70s can be repeated. If the Clarida, Gali and Gertler view is correct, then inflation is likely to remain tamed as long as the central bank reacts sufficiently strongly to expected inflation.
We address these questions within the New Keynesian (NK) model. We ask whether and under what conditions the NK model with policy commitment can replicate the evolution of inflation following a severe, persistent slowdown in the rate of productivity growth. And if yes, whether the model also meets additional fitness criteria.
We first examine whether the model can generate a ''great inflation'' under the assumption that the HMT policy rule pursued at the time did not differ from that commonly attributed to the ''Volcker-Greenspan'' FED (see Clarida, Gali and Gertler, 2000, Orphanides, 2001). We find that this is the case if the productivity slowdown is very large and there exists a high degree of imperfect information5. Imperfect information introduces stickiness in inflation forecasts, making the expected inflation ''gap''(the deviation of expected from target inflation) small. The underestimation of the inflation gap leads to weak policy reaction even when the inflation reaction coefficient is large. We also find that the overall macroeconomic performance of this model is good with two exceptions: The predicted recession is too severe. And the required shock is very large.
We then examine the performance of the model under HMT rules that allow for indeterminacy (following Clarida, Gali and Gertler, CGG hereafter) due to a small reaction coefficient to inflation. Some of these rules have good properties: They generate inflation persistence and realistic overall macroeconomic volatility. Their main weakness, though, is that they also generate too severe of a recession.
Our conclusion from these exercises is that the data support the view that the FED did not react to inflation developments in the 70s strongly enough, in the sense that it did not raise nominal interest rates sufficiently. Thus policy contributed to higher inflation. Nevertheless, this behavior may not have arisen from policy opportunism, an inappropriate policy rule would have sufficed. It is difficult, though, to identify the source of the weak reaction. Interestingly, our analysis also suggests that output stabilization motives may not have played as important a role in the great inflation as commonly assumed.
The remaining of the paper is organized as follows. Section 1 presents the model. Section 2 discusses the calibration. Section 3 presents the main results. An appendix describes the mechanics of the solution to the model under imperfect information and learning based on the Kalman filter.
1 The model
The set up is the standard New Keynesian model. The economy is populated by a large number of identical infinitely-lived households and consists of two sectors: one producing intermediate goods and the other a final good. The intermediate good is produced with capital and labor and the final good with intermediate goods. The final good is homogeneous and can be used for consumption (private and public) and investment purposes.
1.1 The household
Household preferences are characterized by the lifetime utility function:6
where
The household is subject to the following time constraint
where
In each and every period, the representative household faces a budget constraint of the form
where
Capital accumulates according to the law of motion
where
The household determines her consumption/savings, money holdings and leisure plans by maximizing her utility (1) subject to the time constraint (2), the budget constraint (3) and taking the evolution of physical capital (4) into account.
1.2 Final goods sector
The final good is produced by combining intermediate goods. This process is described by the following CES function
where
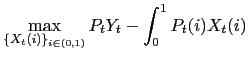 d
d |
(6) |
subject to (5), where
and the following general price index
The final good may be used for consumption -- private or public -- and investment purposes.
1.3 Intermediate goods producers
Each firm ![]() ,
,
![]() , produces an
intermediate good by means of capital and labor according to a
constant returns-to-scale technology, represented by the
Cobb-Douglas production function
, produces an
intermediate good by means of capital and labor according to a
constant returns-to-scale technology, represented by the
Cobb-Douglas production function
where
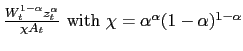
Intermediate goods producers are monopolistically competitive,
and therefore set prices for the good they produce. We follow
Calvo, 1983, in assuming that firms set their prices for a
stochastic number of periods. In each and every period, a firm
either gets the chance to adjust its price (an event occurring with
probability ![]() ) or it
does not. In order to maintain long term money neutrality (in the
absence of monetary frictions) we also assume that the price set by
the firm grows at the steady state rate of inflation. Hence, if a
firm
) or it
does not. In order to maintain long term money neutrality (in the
absence of monetary frictions) we also assume that the price set by
the firm grows at the steady state rate of inflation. Hence, if a
firm ![]() does not reset its
price, the latter is given by
does not reset its
price, the latter is given by
![]() . A firm
. A firm
![]() sets its price,
sets its price,
![]() ,
in period
,
in period ![]() in order to
maximize its discounted profit flow:
in order to
maximize its discounted profit flow:
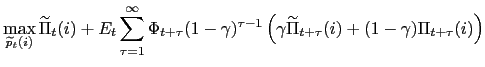
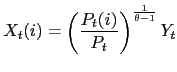
![]()
Since the price setting scheme is independent of any firm specific characteristic, all firms that reset their prices will choose the same price.
In each period, a fraction ![]() of contracts ends, so there are
of contracts ends, so there are
![]() contracts surviving from period
contracts surviving from period ![]() , and therefore
, and therefore
![]() from period
from period ![]() . Hence,
from (8), the aggregate intermediate price
index is given by
. Hence,
from (8), the aggregate intermediate price
index is given by
1.4 The monetary authorities
We assume that monetary policy is conducted according to a standard HMT rule. Namely,
whereThere exists disagreement in the literature regarding the
empirically relevant values of ![]() and
and ![]() for the 1970s. Clarida, Gali and Gertler, 2000,
claim that the pre-Volcker, HMT monetary rule involved a policy
response to inflation that was too weak. Namely, that
for the 1970s. Clarida, Gali and Gertler, 2000,
claim that the pre-Volcker, HMT monetary rule involved a policy
response to inflation that was too weak. Namely, that ![]() which led to real
indeterminacies and excessive inflation. They estimate the triplet
which led to real
indeterminacies and excessive inflation. They estimate the triplet
![]() . Orphanides,
2001, disputes this claim. He argues that the reaction to --
expected -- inflation was broadly similar in the pre and
post-Volcker period, but the reaction to output was stronger in the
earlier period. In particular, using real time date, he estimates
. Orphanides,
2001, disputes this claim. He argues that the reaction to --
expected -- inflation was broadly similar in the pre and
post-Volcker period, but the reaction to output was stronger in the
earlier period. In particular, using real time date, he estimates
![]()
We investigate the consequences of using alternative values for
![]() and
and
![]() in order to shed
some light on the role of policy preferences relative to that of
the degree of imperfect information for the behavior of
inflation.
in order to shed
some light on the role of policy preferences relative to that of
the degree of imperfect information for the behavior of
inflation.
1.5 The government
The government finances government expenditure on the domestic final good using lump sum taxes. The stationary component of government expenditures is assumed to follow an exogenous stochastic process, whose properties will be defined later.
1.6 The equilibrium
We now turn to the description of the equilibrium of the economy.
such that:
- (i)
- given a sequence of prices
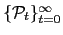 and a sequence of
shocks,
and a sequence of
shocks,
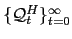 is a solution
to the representative household's problem;
is a solution
to the representative household's problem; - (ii)
- given a sequence of prices
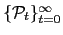 and a sequence of
shocks,
and a sequence of
shocks,
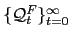 is a solution
to the representative firms' problem;
is a solution
to the representative firms' problem; - (iii)
- given a sequence of quantities
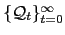 and a sequence of
shocks,
and a sequence of
shocks,
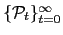 clears the markets
clears the markets
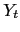
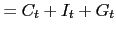
(12) 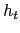
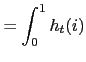 d
d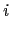
(13) 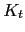
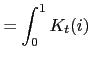 d
d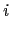
(14) 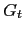
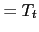
(15)
and the money market. - (iv)
- Prices satisfy (1.3) and (11).
2 Parametrization
The model is parameterized on US quarterly data for the period 1960:1-1999:4. The data are taken from the Federal Reserve Database.8 The parameters are reported in table 1.
![]() , the discount
factor is set such that households discount the future at a 4%
annual rate, implying
, the discount
factor is set such that households discount the future at a 4%
annual rate, implying ![]() equals 0.988. The instantaneous utility function
takes the form
equals 0.988. The instantaneous utility function
takes the form
![$\displaystyle U\left( C_{t},\frac{M_{t}}{P_{t}},\ell_{t}\right) =\frac{1}{1-\si... ...^{\eta}\right) ^{\frac{\nu}{\eta}}\ell_{t}^{1-\nu}\right) ^{1-\sigma}-1\right] $](img92.gif)
![]() , the probability
of price resetting is set in the benchmark case at 0.25, implying
that the average length of price contracts is about 4 quarters. The
nominal growth of the economy,
, the probability
of price resetting is set in the benchmark case at 0.25, implying
that the average length of price contracts is about 4 quarters. The
nominal growth of the economy, ![]() , is set such that the average quarterly rate of
inflation over the period is
, is set such that the average quarterly rate of
inflation over the period is
![]() per quarter. The quarterly depreciation rate,
per quarter. The quarterly depreciation rate, ![]() , was set equal to 0.025.
, was set equal to 0.025. ![]() in the benchmark case is set
such that the level of markup in the steady state is 15%.
in the benchmark case is set
such that the level of markup in the steady state is 15%.
![]() , the elasticity
of the production function to physical capital, is set such that
the model reproduces the US labor share -- defined as the ratio of
labor compensation over GDP -- over the sample period (0.575).
, the elasticity
of the production function to physical capital, is set such that
the model reproduces the US labor share -- defined as the ratio of
labor compensation over GDP -- over the sample period (0.575).
The evolution of technology is assumed to contain two
components. One capturing deterministic growth and the other
stochastic growth. The stochastic one,
![]() is
assumed to follow a stationary AR(1) process of the form
is
assumed to follow a stationary AR(1) process of the form
Alternative descriptions of the productivity process may be
equally plausible. For instance, productivity growth may have
followed a deterministic trend that permanently
Table 1: Calibration, benchmark case
| Preferences | Preferences | Preferences |
|---|---|---|
| Discount Factor | 0.988 | |
| Relative risk aversion | 1.500 | |
| Parameter of CES in utility function | -1.560 | |
| Weight of money in the utility function | 0.065 | |
| CES weight in utility function | 0.344 | |
| Technology | Technology | Technology |
| Capital elasticity of intermediate output | 0.281 | |
| Capital adjustment costs parameter | 1.000 | |
| Depreciation rate | 0.025 | |
| Parameter of markup | 0.850 | |
| Probability of price resetting | 0.250 | |
| Shocks and policy parameters | Shocks and policy parameters | Shocks and policy parameters |
| Persistence of technology shock | 0.950 | |
| Standard deviation of technology shock |
|
0.008 |
| Persistence of government spending shock | 0.970 | |
| Volatility of government spending shock |
|
0.020 |
| Government share | 0.200 | |
| Nominal growth | 1.012 |
The government spending shock11 is assumed to follow an AR(1) process
An important feature of our analysis is that the policymakers have imperfect knowledge about the true state of the economy. In particular, we assume that both actual12 and potential output are observed with noise13. Potential output can be written as
- i)
-
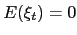 for all
for all
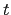 ;
; - ii)
-
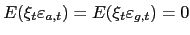 ;
; - iii)
- and
![\begin{displaymath} E(\xi_{t}\xi_{k})=\left\{ \begin{array}[c]{ll} \sigma_{\xi}^{2} & \mbox{ if } t=k\ 0 & \mbox{Otherwise} \end{array}\right. \end{displaymath}](img118.gif)
In order to facilitate the interpretation of
![]() we set
its value in relation to the volatility of the technology shock.
More precisely, we define
we set
its value in relation to the volatility of the technology shock.
More precisely, we define ![]() as
as
![]() . Different values
were assigned to
. Different values
were assigned to ![]() in order to gauge the effects of imperfect
information in the model.
in order to gauge the effects of imperfect
information in the model.
3 The results
The model is first log-linearized around the deterministic steady state and then solved according to the method outlined in the appendix.
We start by assuming the standard specification for the HMT
rule, namely, ![]() ,
,
![]() and
and
![]() (Hereafter
we denote
(Hereafter
we denote
![]() ) and vary the
degree of uncertainty -- the quality of the signal -- about
potential output.14 The
objective of this exercise is to determine i) whether a policy reaction function of the type
commonly attributed to the FED during the 80s and 90s is consistent
with high and persistent inflation of the type observed in the 70s;
and ii) the role played by imperfect
information. This exercise may then prove useful for determining
whether the great inflation can be attributed mostly to bad luck
and incomplete information (as Orphanides, 2001, 2003 has argued).
Or to insufficiently aggressive reaction to inflation developments
-- a low
) and vary the
degree of uncertainty -- the quality of the signal -- about
potential output.14 The
objective of this exercise is to determine i) whether a policy reaction function of the type
commonly attributed to the FED during the 80s and 90s is consistent
with high and persistent inflation of the type observed in the 70s;
and ii) the role played by imperfect
information. This exercise may then prove useful for determining
whether the great inflation can be attributed mostly to bad luck
and incomplete information (as Orphanides, 2001, 2003 has argued).
Or to insufficiently aggressive reaction to inflation developments
-- a low ![]() , as
emphasized by Clarida, Gertler and Gali, 2000. Or to an inherent
inflation bias, as emphasized by Ireland, 1999.
, as
emphasized by Clarida, Gertler and Gali, 2000. Or to an inherent
inflation bias, as emphasized by Ireland, 1999.
We report two sets of statistics. The volatility of H-P filtered
actual output, annualized inflation and investment. And the impulse
response functions (IRF) of actual output and inflation following a
negative technology shock for the perfect information model (Perf.
Info.), the imperfect information model with
![]() (Imp.
Info. (I)) and
(Imp.
Info. (I)) and
![]() (Imp.
Info. (II)). The IRF for the inflation rate is annualized and
expressed in percentage points. The actual rate of inflation
following a shock is simply found by adding the response reported
in the IRF to the steady state value (
(Imp.
Info. (II)). The IRF for the inflation rate is annualized and
expressed in percentage points. The actual rate of inflation
following a shock is simply found by adding the response reported
in the IRF to the steady state value (
![]() =4.8%).
=4.8%).
There exists considerable uncertainty about the (type and) size of the shock that triggered the productivity slowdown of the 70s. We do not take a position on this. We proceed by selecting a value for the supply shock that can generate a large and persistent increase in the inflation rate under at least one of the informational assumptions considered. By large, we mean an increase in the inflation rate of the order of 5-7 percentage points, implying that the maximum rate of inflation obtained during that period is about 10%-12%. We then feed a series of shocks that include this value for the first quarter of 1973 into our model and generate the other statistics described above.
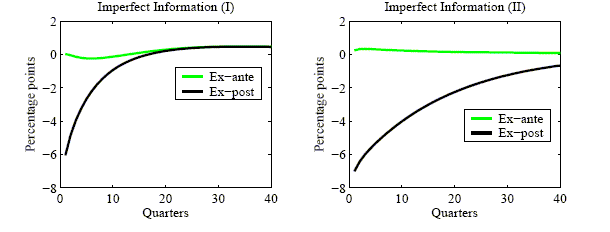
Figure 1 reports the IRFs in the case of a
standard HMT rule. The model can produce a large and persistent
increase in the inflation rate if two conditions are met: The shock
is very large (of the order of 33%) and the degree of imperfect
information is very high (say,
![]() ).
Moreover, table 3 indicates that the model
can generate a realistic degree of macroeconomic volatility in the
case of a high degree of imperfect information. For instance, the
volatility of output, investment and inflation in the case
).
Moreover, table 3 indicates that the model
can generate a realistic degree of macroeconomic volatility in the
case of a high degree of imperfect information. For instance, the
volatility of output, investment and inflation in the case
![]() (4
quarters contracts) and
(4
quarters contracts) and
![]() (Imp. Info
(II)) are 1.820%, 6.736% and 0.619% respectively, to be compared to
1.639%, 7.271% and 0.778% in the data. The model fails, though, in
its prediction of the maximal effect on output following such a
shock. In particular, the maximal predicted effect is -19.812%
which seems implausibly high (table 2). On
the other hand, the performance of the model under perfect
information is bad. The increase in inflation is quite small,
output and investment volatility is too large and inflation
volatility too low and the maximal effects are even higher.
(Imp. Info
(II)) are 1.820%, 6.736% and 0.619% respectively, to be compared to
1.639%, 7.271% and 0.778% in the data. The model fails, though, in
its prediction of the maximal effect on output following such a
shock. In particular, the maximal predicted effect is -19.812%
which seems implausibly high (table 2). On
the other hand, the performance of the model under perfect
information is bad. The increase in inflation is quite small,
output and investment volatility is too large and inflation
volatility too low and the maximal effects are even higher.
Imperfect information is critical for the ability of the model
to generate a persistent increase in inflation as well as
sufficient volatility following a persistent supply shock. When the
variance of the noise is large, much of the change in actual
inflation is attributed to cyclical rather than ''core''
developments. This means that estimated future inflation --and
hence the inflation ''gap''-- is sticky, i.e., it does not move much with the current shocks
and actual inflation (see Figure 2).
Imperfect information introduces a serially correlated error term
in the Phillips curve, whose size and persistence depends on the
size of
![]() and the
speed of learning. As a result, the policy reaction to a perceived
small inflation gap proves too weak even if
and the
speed of learning. As a result, the policy reaction to a perceived
small inflation gap proves too weak even if
![]() is large,
resulting in countercyclical policy. The real interest rate is
decreased significantly, see Figure
3, fuelling inflation while smoothing output
out. As long as the inflation forecast error is persistent (as this
will be the case for a persistent shock and slow learning) the
increase in actual inflation will be persistent too. This
requirement does not seem to pose a problem for the model as the
magnitude of the predicted gap between actual and expected
inflation seems to be in line with that observed in the 70s.
is large,
resulting in countercyclical policy. The real interest rate is
decreased significantly, see Figure
3, fuelling inflation while smoothing output
out. As long as the inflation forecast error is persistent (as this
will be the case for a persistent shock and slow learning) the
increase in actual inflation will be persistent too. This
requirement does not seem to pose a problem for the model as the
magnitude of the predicted gap between actual and expected
inflation seems to be in line with that observed in the 70s.
The choice of the inflation variable that enters the policy rule plays an important role. The argument above has suggested that the source of the persistence in inflation is the stickiness of expected inflation. Were the FED to react to current or past actual inflation relative to target then inflation would be contained more quickly. In this case, however, the model would behave less satisfactorily. Inflation volatility would be further away from that in the data, output volatility would be exaggerated and the maximal effect on output would be even higher. Thus, excessive policymaker optimism about the future inflation path plays an important role.
The strength of the stabilization motive (the coefficient
![]() ) does not play an
important role in the analysis. We have repeated the analysis under
) does not play an
important role in the analysis. We have repeated the analysis under
![]() =1.2 and
=1.2 and
![]() =1.7 with almost
identical results (Figure 4 and Table
4). This is a comforting finding because it
is difficult to justify differences in stabilization motives
between the pre and post 1980 policymakers. Differences in luck and
information are much less controversial.
=1.7 with almost
identical results (Figure 4 and Table
4). This is a comforting finding because it
is difficult to justify differences in stabilization motives
between the pre and post 1980 policymakers. Differences in luck and
information are much less controversial.
The model does not perform as well with a lower ![]() (lower panels of Figure
4 and Table 4). In
this case it is difficult to both match volatility and generate the
appropriate inflation dynamics. If the model matches volatility
well then it exaggerates the increase in inflation.
(lower panels of Figure
4 and Table 4). In
this case it is difficult to both match volatility and generate the
appropriate inflation dynamics. If the model matches volatility
well then it exaggerates the increase in inflation.
Increasing the degree of degree of price flexibility (say, from
![]() to
to
![]() does not
alter the basic picture but improves things somewhat. A smaller
shock is now required, inflation volatility moves closer to that in
the data and the maximal effect on output is reduced. At the same
time, inflation persistence is somewhat reduced.
does not
alter the basic picture but improves things somewhat. A smaller
shock is now required, inflation volatility moves closer to that in
the data and the maximal effect on output is reduced. At the same
time, inflation persistence is somewhat reduced.
We have run a larger number of experiments involving this HMT rule and alternative values of the other parameters of the model without changing overall model performance. To summarize our main results: The NK model under the standard HMT policy rule and imperfect information can generate plausible inflation dynamics and good overall fit in the face of a very substantial productivity slowdown and expected inflation gap targeting. Nonetheless, this specification has some weaknesses, found in the requirement of a very large shock, and of a very severe predicted recession.
We now turn to specifications in which policy is conducted in a
way that destabilizes rather than constrains inflation (as
suggested by Clarida, Gertler and Gali, 2000). We have investigated
the properties of the model under the policy rule parametrization
suggested by CGG, namely,
![]() . Such
a rule leads to real indeterminacy. This specification can generate
a large, persistent increase in inflation (see Figure 5), but the associated response of output is
implausible and macroeconomic volatility is too low (Tables
5 and 6). An
important feature of this specification is that real indeterminacy
introduces an additional source of uncertainty related to a sunspot
shock that affects beliefs. We assume that the sunspot shock is
purely extrinsic and is therefore not correlated with any
fundamental shock. Since we have no information that would allow us
to calibrate this shock we have explored several cases. In the
first one, the volatility of the sunspot shock is set to 0. In this
case, the model overestimates output volatility, but significantly
underestimates that of both investment, consumption and inflation.
This is also the case when the volatility is set at the same level
as that of the technology shock. When the sunspot shock is
calibrated in order for the model to match inflation volatility,
the implied standard deviation of output is widely overestimated
(by almost 40%). The same obtains when the sunspot is calibrated to
match investment volatility, and this is highly magnified when the
sunspot is used to mimic the volatility of the nominal interest
rate.15
Nonetheless, we have encountered more successful policy
specifications within the range of indeterminate equilibria. Figure
6 and Tables 7 and
8 correspond to such a case with
. Such
a rule leads to real indeterminacy. This specification can generate
a large, persistent increase in inflation (see Figure 5), but the associated response of output is
implausible and macroeconomic volatility is too low (Tables
5 and 6). An
important feature of this specification is that real indeterminacy
introduces an additional source of uncertainty related to a sunspot
shock that affects beliefs. We assume that the sunspot shock is
purely extrinsic and is therefore not correlated with any
fundamental shock. Since we have no information that would allow us
to calibrate this shock we have explored several cases. In the
first one, the volatility of the sunspot shock is set to 0. In this
case, the model overestimates output volatility, but significantly
underestimates that of both investment, consumption and inflation.
This is also the case when the volatility is set at the same level
as that of the technology shock. When the sunspot shock is
calibrated in order for the model to match inflation volatility,
the implied standard deviation of output is widely overestimated
(by almost 40%). The same obtains when the sunspot is calibrated to
match investment volatility, and this is highly magnified when the
sunspot is used to mimic the volatility of the nominal interest
rate.15
Nonetheless, we have encountered more successful policy
specifications within the range of indeterminate equilibria. Figure
6 and Tables 7 and
8 correspond to such a case with
![]() As can
be seen, this specification performs fairly well. The model has
little difficulty producing high and persistent inflation and can
account for volatility fairly well (but it underestimates
investment volatility). If it has an Achilles heel, it is to be
found in its excessive reaction of output (Figure 6), a weakness that it shares with the imperfect
information version under the standard HMT rule. Hence, the main
advantage of this specification may be that it works even with a
much smaller shock.
As can
be seen, this specification performs fairly well. The model has
little difficulty producing high and persistent inflation and can
account for volatility fairly well (but it underestimates
investment volatility). If it has an Achilles heel, it is to be
found in its excessive reaction of output (Figure 6), a weakness that it shares with the imperfect
information version under the standard HMT rule. Hence, the main
advantage of this specification may be that it works even with a
much smaller shock.
How can we explain the similarity in the results under the two specifications of the policy rule? The reaction of the nominal interest rates to inflation is the product of the inflation reaction coefficient and the estimated inflation ''gap''. High and persistent inflation can occur following a productivity slowdown either because the reaction coefficient is low (the Clarida-Gali-Gertler scenario of bad policy ) or because the estimated inflation gap to which policy is reacting is low (the Orphanides scenario of imperfect information). information. This reasoning indicates that there may be a serious difficulty in identifying the policy rule. The difference in the results of CGG and Orphanides who rely on different information assumptions (actual vs real time data) can be explained using this argument.
Before concluding, let us point out that there is a widespread belief that the great inflation did not actually start in the early 70s but rather in the mid-60s. In our model a series of unperceived negative supply shocks, culminating with an oil shock in 1973 --that was misperceived as temporary-- can reproduce the upward trend as well as the spike in the inflation series16.
4 Conclusions
Inflation in the US reached high levels during the 1970s, to a large extent due to what proved to be excessively loose monetary policy. There exist two conflicting views concerning the conduct of policy at that time. One sees it as reflecting opportunistic (discretionary) behavior on the part of the FED (Barro and Gordon, 1982). According to this view, the problem of inflation arises from poorly designed institutions, and the only way to prevent inflationary episodes in the future is by creating institutions that provide the ''right'' incentives to the policymakers.
The other view attributes looseness to inadvertent policy mistakes committed by a central bank that follows a rule. Such mistakes can arise even when the central bank is sufficiently averse to inflation, due to imperfect information about the true state of the economy (Orphanides, 2003). Or when the bank does not fully understand the properties of the rule it uses (Clarida, Gali and Gertler, 2000). The recommended solution in these cases is to improve the technical aspects of policymaking, that is, to adopt better rules, allow for imperfect information and so on.
Our analysis has established that policy opportunism is not necessary for obtaining persistently bad inflation outcomes. And that, conditional on accepting the occurrence of a very large supply shock, these two rule-based explanations represent empirically compelling scenarios. Nevertheless, the information contained in the data does not suffice to conclusively discriminate between. Additional races are needed. Although Lubic and Schforheide, 2003, argue that the data support a policy specification with indeterminacy over one with determinacy (for the 70s) their model does not include the key elements emphasized by Orphanides. We are currently investigating this issue using the Lubic and Schforheide methodology but also incorporating learning on the part of the policymakers. Whether this approach will break the observational equivalence between the competing theories remains an open issue.
References
Barro, Robert and David Gordon, 1983,''Rules, Discretion and Reputation in a Model of Monetary Policy'', Journal of Monetary Economics, 12 (1), 101-21.
Bils, Mark and Peter Klenow, 2002, ''Some Evidence on the Importance of Sticky Prices,'' NBER wp #9069.
Bullard, James and Stefano Eusepi, 2003, ''Did the Great Inflation Occur Despite Policymaker Commitment to a Taylor Rule,'' Federal Reserve Bank of Atlanta, October, WP 2003-20.
Clarida, Richard, Jordi Gali, and Mark Gertler, 2000, ''Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory'', Quarterly Journal of Economics, 147-180.
Christiano, Larry and Christopher Gust, 1999, ''The Great Inflation of the 1970s'', mimeo.
Cukierman, Alex and Francesco Lippi, 2002, '' Endogenous Monetary Policy with Unobserved Potential Output,'' manuscript.
DeLong, Bradford, 1997, ''America's Peacetime Inflation: The 1970s'', In Reducing Inflation: Motivation and Strategy, eds. C. Romer and D. Romer, 247-276. Chicago: Univ. of Chicago Press.
Erceg, Christopher and Andrew Levin. (2003). ''Imperfect Credibility and Inflation Persistence.''Journal of Monetary Economics, 50(4), 915-944.
Ehrmann, Michael and Frank Smets, 2003, ''Uncertain Potential Output: Implications for Monetary Policy, ''Journal of Economic Dynamics and Control, 27, 1611--1638.
Ireland, Peter, 1999, ''Does the Time-Consistency Problem Explain the Behavior of Inflation in the United States?'' Journal of Monetary Economics, 44(2) 279-91.
Lansing, Kevin J, 2001, ''Learning about a Shift in Trend Output: Implications for Monetary Policy and Inflation.'' Unpublished manuscript. FRB San Francisco.
Nelson, Edward and Kalin Nicolov, 2002, ''Monetary Policy and Stagflation in the UK,''CEPR Discussion Paper No. 3458, July.
Orphanides, Athanasios, 2001, ''Monetary Policy Rules, Macroeconomic Stability and Inflation: A View from the Trenches,'' BGFRS.
Orphanides, Athanasios and John C. Williams, 2002, ''Imperfect Knowledge, Inflation Expectations, and Monetary Policy,'' BGFRS.
Orphanides, Athanasios, 2003, ''The Quest for Prosperity without Inflation.'' Journal of Monetary Economics, 50(3) 633-63.
Sargent, Thomas J, 1999, ''The Conquest of American Inflation''. Princeton: Princeton Univ. Press.
Svensson, Lars and Michael Woodford, 2003, ''Indicator Variables for Optimal Policy,'' Journal of Monetary Economics, 50(3), 691-720.
5 Appendix
The solution of the model under imperfect information with a Kalman filter
Let's consider the following system
Note that, from (16), we have
where
with
5.1 Solving the system
Step 1:
We first solve equation 17 without the error term:
Plugging (20) into (21), we have
where
| (23) | ||
| (24) |
Step 2:
We now use these results in the original system of equations. Equation (17) is
Taking expectations, we have
Subtracting, we get
![$\displaystyle M_{ss0} \left( \begin{array}[c]{c} X^{b}_{t+1}-X^{b}_{t+1\vert t}... ...ray} \right) + \left( \begin{array}[c]{c} M_{e} u_{t+1}\\ 0 \end{array} \right)$](img171.gif)
|
(25) |
or,
where,
Now considering the first block we have
We also have
Finally, we have
5.2 Filtering
Since our solution involves terms in
![]() , we
need to compute this quantity. However, the only information we can
exploit is a signal
, we
need to compute this quantity. However, the only information we can
exploit is a signal ![]() that we described previously. We therefore use a Kalman filter
approach to compute the optimal prediction of
that we described previously. We therefore use a Kalman filter
approach to compute the optimal prediction of
![]() .
.
In order to recover the Kalman filter, it is a good idea to think in terms of expectational errors. Therefore, let us define
The first thing we have to do is to rewrite the system in terms of
state-space representation. Since
![]() , we
have
, we
have
where
Now, consider the law of motion of backward state variables, we get
where
We therefore end-up with the following state-space representation
| (27) | ||
| (28) |
For which the Kalman filter is given by
where
Note however that the above solution is obtained for a given
![]() matrix that remains
to be computed. We can do that by using the basic equation of the
Kalman filter:
matrix that remains
to be computed. We can do that by using the basic equation of the
Kalman filter:
Solving for
where we made use of the identity
![$\displaystyle = P S^{0^{\prime}}(I+S^{1} K)^{\prime}\left[ (I+S^{1} K)(S^{0} P S^{0^{\prime}} +\Sigma_{vv})(I+S^{1} K)^{\prime}\right] ^{-1}$](img236.gif)
|
||
Hence, we obtain
Now, recall that
Plugging the definition of
5.3 Summary
We finally end-up with the system of equations:
| (32) | ||
| (33) | ||
| (34) | ||
| (35) | ||
| (36) | ||
| (37) |
which describe the dynamics of our economy.
6 Determinate Equilibrium: The Volcker-Greenspan rule
Figure 1: IRF to a negative technology shock
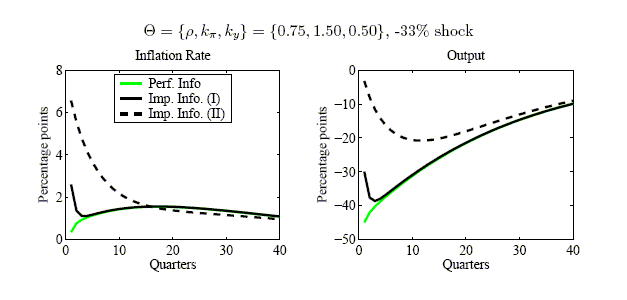
Table 2: Impact and extreme effect of a technology shock
Perf. Info Impact
|
Perf. Info Max
|
Imp. Info (I) Impact
|
Imp. Info (I) Max
|
Imp. Info (II) Impact
|
Imp. Info (II) Max
|
|
| Output | -45.074 | -45.074 | -29.977 | -38.695 | -3.163 | -20.803 |
| Inflation | 0.335 | 1.543 | 2.597 | 2.597 | 6.569 | 6.569 |
Note: Perfect information, Imperfect information (I) and Imperfect information
(II) correspond to ![]() =0,1,8 respectively, where
=0,1,8 respectively, where ![]() is the amount of noise.
is the amount of noise.
Table 3: Standard Deviations:
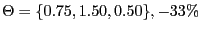 Shock
Shock
|
|
|
|
|
|---|---|---|---|
| Data | 1.639 | 7.271 | 0.778 |
| Perf. Info. | 4.349 | 15.625 | 0.097 |
| Imp. Info (I) | 3.891 | 14.324 | 0.212 |
| Imp. Info (II) | 1.820 | 6.736 | 0.619 |
and ![]() are output,
investment and inflation respectively. Perfect informa-
are output,
investment and inflation respectively. Perfect informa-
tion, Imperfect information I and Imperfect information II correspond to
![]() =0,1,8 respectively
where
=0,1,8 respectively
where ![]() is the amount of
noise.
is the amount of
noise. ![]() =
=
![]()
Figure 2: Expected versus realized inflation rate =  =
=
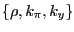 =
{0.75, 1.50, 0.50}
=
{0.75, 1.50, 0.50}
Figure 3: Figure 3: Ex-ante versus Ex-post real interest rate 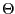 = {0.75, 1.50, 0.50}
= {0.75, 1.50, 0.50}
7 Determinacy: Reactions to inflation and output
Table 4: Standard Deviations
|
|
|
|
|
|---|---|---|---|
| Data |
1.639 |
7.271 |
0.778 |
| Perf. Info. | 3.509 | 12.774 | 0.108 |
| Imp. Info. (I) | 3.146 | 11.549 | 0.154 |
| Imp. Info. (II) | 1.598 | 5.865 | 0.483 |
|
|
|
|
|
| Perf. Info. | 3.255 | 11.612 | 0.093 |
| Imp. Info. (I) | 2.957 | 10.821 | 0.188 |
| Imp. Info. (II) | 1.509 | 5.521 | 0.478 |
|
|
|
|
|
| Perf. Info. | 3.103 | 10.810 | 0.278 |
| Imp. Info. (I) | 2.856 | 10.251 | 0.313 |
| Imp. Info. (II) | 1.468 | 5.269 | 0.492 |
Note: The standard deviations are computed for HP-filtered series. y, i
and ![]() are output,
investment and inflation respectively.
are output,
investment and inflation respectively. ![]() =
=
![]()
Figure 4: IRF to a negative -33% technology shock
Panel A: ![]() = {0.75, 1.50, 0.20}
= {0.75, 1.50, 0.20}
8 Real Indeterminancy: The Clarida-Gali-Gertler rule
Figure 5: IRF to a -12% technology shock 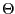 = {0.75,0.80,0.40}
= {0.75,0.80,0.40}
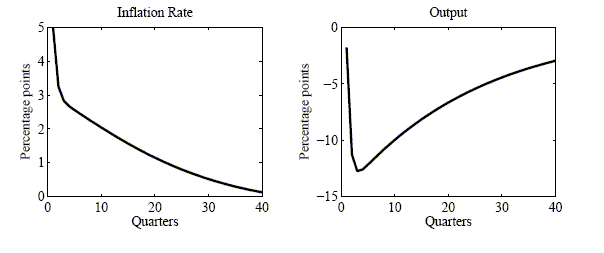
Table 5: Effects of a -12% technology shock  = {0.75,0.80,0.40}
= {0.75,0.80,0.40}
| Impact | Max. | |
|---|---|---|
| Output | -1.773 | -12.755 |
| Inflation | 5.000 | 5.000 |
Table 6: Standard Deviations  = {0.75,0.80,0.40}
= {0.75,0.80,0.40}
|
|
|
|
|
|---|---|---|---|
| Data | 1.639 | 7.271 | 0.778 |
| q=0.25, -12% shock | q=0.25, -12% shock | q=0.25, -12% shock | |
| 0 | 1.702 | 5.545 | 0.529 |
|
|
1.727 | 5.689 | 0.542 |
| 0.0400 |
2.272 | 8.463 | 0.777 |
| 0.0294 |
2.030 | 7.278 | 0.676 |
| 0.1294 |
5.065 | 21.029 | 1.861 |
Note: The standard deviations are computed for HP-filtered series. y, i
and ![]() are output,
investment and inflation respectively. (a), (b) and (c)
are output,
investment and inflation respectively. (a), (b) and (c)
match
![]() ,
,
![]() and
and
![]() .
. ![]() =
=
![]()
9 Indeterminacy: Other cases
Figure 6: IRF to a -8% technology shock,  = {0.75,1.20,0.80}
= {0.75,1.20,0.80}
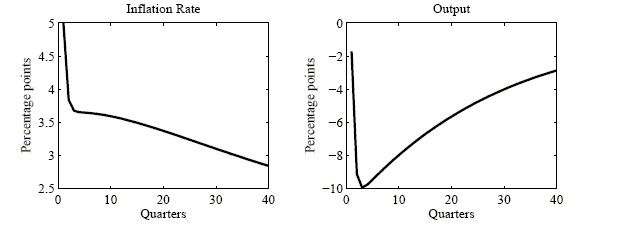
Table 7: Effects of a -8% technology shock,  = {0.75,1.20,0.80}
= {0.75,1.20,0.80}
| Impact | Max. | |
|---|---|---|
| Output | -1.718 | -9.972 |
| Inflation | 5.020 | 5.020 |
Table 8: Standard Deviations,  = {0.75,1.20,0.80}
= {0.75,1.20,0.80}
|
|
|
|
|
|---|---|---|---|
| Data | 1.639 | 7.271 | 0.778 |
| 0 | 1.625 | 5.274 | 0.689 |
|
|
1.650 | 5.394 | 0.714 |
| 0.006 |
1.639 | 5.340 | 0.704 |
| 0.035 |
2.072 | 7.271 | 1.042 |
| 0.016 |
1.724 | 5.736 | 0.778 |
| 0.058 |
2.681 | 9.827 | 1.461 |
Note: The standard deviations are computed for HP-filtered series. y, i
and ![]() are output,
investment and inflation respectively. (a), (b), (c) and
are output,
investment and inflation respectively. (a), (b), (c) and
(d) match
![]() ,
,
![]() , and
, and
![]() .
. ![]() =
=
![]()
Footnotes
1. We would like to thank Andy Levin, Mike Spagat and the participants at the International Research Forum on Monetary Policy in DC and at the European Monetary Forum in Bonn for valuable comments. Return to text
2. CNRS-GREMAQ, Manufacture des Tabacs, bât. F, 21 allée de Brienne, 31000 Toulouse, France. Tel: (33-5) 61-12-85-60, Fax: (33- 5) 61-22-55-63, email: [email protected], Homepage: http://fabcol.free.fr Return to text
3. Department of Economics, University of Bern, CEPR, IMOP. Address: VWI, Gesellschaftsstrasse 49, CH 3012 Bern, Switzerland. Tel: (41) 31-6313989, Fax: (41) 31-631-3992, email: [email protected], Homepage: http://www-vwi.unibe.ch/amakro/dellas.htm Return to text
4. Related explanations are that the FED was the ''victim'' of conventional macroeconomic wisdom of the time that claimed the existence of a stable, permanent tradeoff between inflation and unemployment (De Long, 1997). Or, that the FED was the ''victim'' of econometrics. Sargent, 1999, for instance, has argued that the data periodically give the impression of the existence of a Phillips curve with a favorable trade-off between inflation and unemployment. High inflation then results as the central bank attempts to exploit this Return to text
5. We follow Svensson and Woodford, 2003, in modelling imperfect information using the Kalman filter. Return to text
6. ![]() denotes mathematical conditional
expectations. Expectations are conditional on information available
at the beginning of period
denotes mathematical conditional
expectations. Expectations are conditional on information available
at the beginning of period ![]() . Return to text
. Return to text
7. See Ehrmann and Smets, 2003, for a discussion of optimal monetary policy in a related model. Return to text
8. URL: http://research.stlouisfed.org/fred/ Return to text
9. There is a non-negligible change in the volatility of the Solow residual between the pre and the post Volcker period. That up to 1979:4 is 0.0084 while that after 1980:1 is 0.0062. For the evaluation of the model it is the former period that is relevant. Note that for the government spending shock the difference between the two periods is negligible. Return to text
10. For instance, this is the assumption made by Bullard and Eusepi, 2003. Nonetheless, there is very little agreement regarding the type of change in the productivity process that took place around 1970. Other differences between our model and that of Bullard and Eusepi are to be found the learning mechanism and the interest policy rule employed. Return to text
11. The -logarithm of the- government expenditure series is first detrended using a linear trend. Return to text
12. Making some variable other than actual output noisy -for instance, inflation- does not materially affect the results. Return to text
13. The public too has imperfect information about actual and potential output. Return to text
14. To be more precise, we vary the
size of ![]() . Return to
text
. Return to
text
15. We could not set the sunspot volatility so as to match consumption volatility as it is already overestimated when the standard deviation of the sunspot is set to 0. Return to text
16. There is considerable evidence, based, for instance, on the behavior of the current account, that the increase in the oil price in 1973 was perceived as temporary. Return to text
This version is optimized for use by screen readers. A printable pdf version is available.
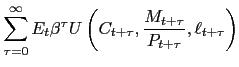
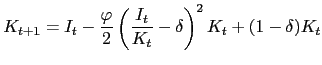
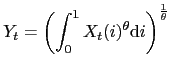
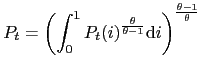
![$\tilde{p}_{t}(i)=\frac{1}{\theta}\frac{E_{t}
{\displaystyle\sum\limits_{\tau=0}^{\infty}}
\left[ (1-\gamma)\overline{\pi}^{\frac{1}{\theta-1}}\right] ^{\tau}
\Phi_{t+\tau}P_{t+\tau}^{\frac{2-\theta}{1-\theta}}S_{t+\tau}Y_{t+\tau}}{E_{t}
{\displaystyle\sum\limits_{\tau=0}^{\infty}}
\left[ (1-\gamma)\overline{\pi}^{\frac{\theta}{\theta-1}}\right] ^{\tau}
\Phi_{t+\tau}P_{t+\tau}^{\frac{1}{\theta-1}}Y_{t+\tau}}$](img3_10.gif)
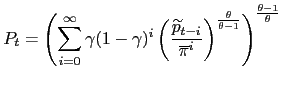
![$\displaystyle M_{cc} Y_{t}= M_{cs} \left( \begin{array}[c]{c} X^{b}_{t}\\ X^{f}... ...ft( \begin{array}[c]{c} X^{b}_{t\vert t}\\ X^{f}_{t\vert t} \end{array} \right)$](img134.gif)
![$\displaystyle M_{ss0} \left( \begin{array}[c]{c} X^{b}_{t+1}\\ X^{f}_{t+1\vert ... ..._{sc1} Y_{t} + \left( \begin{array}[c]{c} M_{e} u_{t+1}\\ 0 \end{array} \right)$](img135.gif)
![$\displaystyle S_{t}= C^{0} \left( \begin{array}[c]{c} X^{b}_{t}\\ X^{f}_{t} \en... ...gin{array}[c]{c} X^{b}_{t\vert t}\\ X^{f}_{t\vert t} \end{array} \right) +v_{t}$](img136.gif)
![$\displaystyle Y_{t}=B^{0} \left( \begin{array}[c]{c} X^{b}_{t}\\ X^{f}_{t} \end... ...ft( \begin{array}[c]{c} X^{b}_{t\vert t}\\ X^{f}_{t\vert t} \end{array} \right)$](img152.gif)
![$\displaystyle Y_{t\vert t}=B\left( \begin{array}[c]{c} X^{b}_{t\vert t}\\ X^{f}_{t\vert t} \end{array} \right)$](img155.gif)
![$\displaystyle M_{ss0} \left( \begin{array}[c]{c} X^{b}_{t+1\vert t}\\ X^{f}_{t+... ..._{t\vert t} \end{array} \right) = M_{sc0} Y_{t+1\vert t} + M_{sc1} Y_{t\vert t}$](img157.gif)
![$\displaystyle \left( \begin{array}[c]{c} X^{b}_{t+1\vert t}\\ X^{f}_{t+1\vert t... ...ft( \begin{array}[c]{c} X^{b}_{t\vert t}\\ X^{f}_{t\vert t} \end{array} \right)$](img158.gif)
![$\displaystyle M_{ss0} \left( \begin{array}[c]{c} X^{b}_{t+1}\\ X^{f}_{t+1\vert ... ...ft( \begin{array}[c]{c} X^{b}_{t\vert t}\\ X^{f}_{t\vert t} \end{array} \right)$](img165.gif)
![$\displaystyle = M_{sc0} B \left( \begin{array}[c]{c} X^{b}_{t+1\vert t}\\ X^{f}... ...sc1} B^{0} \left( \begin{array}[c]{c} X^{b}_{t}\\ X^{f}_{t} \end{array} \right)$](img166.gif)
![$\displaystyle + M_{sc1} B^{1} \left( \begin{array}[c]{c} X^{b}_{t\vert t}\\ X^{... ...ray} \right) + \left( \begin{array}[c]{c} M_{e} u_{t+1}\\ 0 \end{array} \right)$](img167.gif)
![$\displaystyle M_{ss0} \left( \begin{array}[c]{c} X^{b}_{t+1\vert t}\\ X^{f}_{t+... ...ft( \begin{array}[c]{c} X^{b}_{t\vert t}\\ X^{f}_{t\vert t} \end{array} \right)$](img168.gif)
![$\displaystyle = M_{sc0} B \left( \begin{array}[c]{c} X^{b}_{t+1\vert t}\\ X^{f}... ...ft( \begin{array}[c]{c} X^{b}_{t\vert t}\\ X^{f}_{t\vert t} \end{array} \right)$](img169.gif)
![$\displaystyle + M_{sc1} B^{1} \left( \begin{array}[c]{c} X^{b}_{t\vert t}\\ X^{f}_{t\vert t} \end{array} \right)$](img170.gif)
![$\displaystyle \left( \begin{array}[c]{c} X^{b}_{t+1}-X^{b}_{t+1\vert t}\\ 0 \en... ... + M_{ss0}^{-1}\left( \begin{array}[c]{c} M_{e} u_{t+1}\\ 0 \end{array} \right)$](img172.gif)