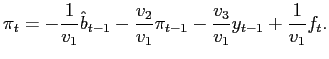Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 806, April 2004--Screen Reader Version*
Optimal Monetary and Fiscal Policy: A Linear-Quadratic Approach
International Finance Discussion Papers numbers 797-807 were presented on November 14-15, 2003 at the second conference sponsored by the International Research Forum on Monetary Policy sponsored by the European Central Bank, the Federal Reserve Board, the Center for German and European Studies at Georgetown University, and the Center for Financial Studies at the Goethe University in Frankfurt.
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We propose an integrated treatment of the problems of optimal monetary and fiscal policy, for an economy in which prices are sticky (so that the supply-side effects of tax changes are more complex than in standard fiscal analyses) and the only available sources of government revenue are distorting taxes (so that the fiscal consequences of monetary policy must be considered alongside the usual stabilization objectives). Our linear-quadratic approach allows us to nest both conventional analyses of optimal monetary stabilization policy and analyses of optimal tax-smoothing as special cases of our more general framework. We show how a linear-quadratic policy problem can be derived which yields a correct linear approximation to the optimal policy rules from the point of view of the maximization of expected discounted utility in a dynamic stochastic general-equilibrium model. Finally, in addition to characterizing the optimal dynamic responses to shocks under an optimal policy, we derive policy rules through which the monetary and fiscal authorities may implement the optimal equilibrium. These take the form of optimal targeting rules, specifying an appropriate target criterion for each authority.
Keywords: Loss function, output gap, tax smoothing, targeting rules
JEL Classifications: E52, E61, E63
Non-technical summary
We propose an integrated treatment of the problems of optimal monetary and fiscal policy, for an economy in which prices are sticky and the only available sources of government revenue are distorting taxes. The integrated treatment allows us to consider how familiar characterizations of optimal monetary policy must be generalized to take account of the consequences of alternative monetary policies for the government budget, and to consider fiscal shocks as one of the types of disturbances to which monetary policy may need to respond. It also allows us to show how conventional characterizations of optimal tax policy can be generalized to the case in which economic activity depends not solely upon supply-side incentives, but on aggregate (nominal) demand as well.
We show how a linear-quadratic policy problem can be derived that yields a correct linear approximation to the optimal policy rules from the point of view of the maximization of expected discounted utility. This requires that we take account of the effects of stabilization policy (i.e., of the variances of endogenous variables) on the average levels of consumption and hours worked; but we show that such effects can be incorporated into the quadratic objective, so that we need not consider nonlinearities in the constraints on our policy problem.
We show that a quadratic loss function can be derived that consists of a weighted average of two terms each period: squared deviations of the inflation rate from an optimal rate of zero, and squared deviations of log output from a target output level that varies over time as a function of exogenous disturbances to preferences, technology, and the government�s exogenous fiscal constraints. Thus consideration of the effects of tax distortions does not introduce any additional stabilization objectives beyond the ones (inflation stabilization and output-gap stabilization) considered in conventional treatments of monetary stabilization policy; both monetary and fiscal instruments should be used to stabilize inflation and the (appropriately defined) output gap. However, allowing for the distortions associated with raising government revenue can affect the weights on these objectives, and the proper definition of the target rate of output.
We consider how the optimal responses to shocks vary depending on the degree of price stickiness, and show, in a calibrated example, that the optimal responses that would be derived under the assumption of complete price flexibility are quite different than those that are optimal if prices are even slightly sticky; this indicates that allowing for price stickiness is quite important in exercises of this kind. In particular, optimal policy involves much greater stability of the inflation rate if prices are sticky, while shocks should instead have permanent effects on the level of government debt and on tax rates, even in the presence of nominal government debt.
Finally, we derive targeting rules through which the monetary and fiscal authorities may implement the optimal equilibrium. An optimal targeting rule for monetary policy in the case of distorting taxes still has the form of a flexible inflation targeting rule, as in the literature that ignores the fiscal consequences of monetary policy, but the output gap should modify the inflation target in a different way. We also obtain a targeting rule for the fiscal authority, and this too requires the fiscal authority to base policy on the projected consequences of alternative government budgets for future inflation.
Introduction
While there are by now substantial literatures seeking to characterize optimal monetary and fiscal policy respectively, the two literatures have largely developed in isolation, and upon apparently contradictory foundations. The modern literature on dynamically optimal fiscal policy often abstracts from monetary aspects of the economy altogether, and so implicitly allows for no useful role for monetary policy. When monetary policy is considered within the theory of optimal fiscal policy, it is most often in the context of models with flexible prices; in these models, monetary policy matters only (i) because the level of nominal interest rates (and hence the opportunity cost of holding money) determines the size of certain distortions that result from the attempt to economize on money balances, and (ii) because the way in the price level varies in response to real disturbances determines the state-contingent real payoffs on (riskless) nominally-denominated government debt, which may facilitate tax-smoothing in the case that explicitly state-contingent debt is not available. The literature on optimal monetary policy has instead been mainly concerned with quite distinct objectives for monetary stabilization policy, namely the minimization of the distortions that result from prices or wages that do not adjust quickly enough to clear markets. At the same time, this literature typically ignores the fiscal consequences of alternative monetary policies; the characterizations of optimal monetary policy that are obtained are thus strictly correct only for a world in which lump-sum taxes are available.
Here we wish to consider the way in which the conclusions reached in each of these two familiar literatures must be modified if one takes simultaneous account of the basic elements of the policy problems addressed in each literature. On the one hand, we wish to consider how conventional conclusions with regard to the nature of an optimal monetary policy rule must be modified if one recognizes that the government's only sources of revenue are distorting taxes, so that the fiscal consequences of monetary policy matter for welfare. And on the other hand, we wish to consider how conventional conclusions with regard to optimal tax policy must be modified if one recognizes that prices do not instantaneously clear markets, so that output determination depends on aggregate demand, in addition to the supply-side factors stressed in the conventional theory of optimal taxation.
A number of recent papers have also sought to jointly consider optimal monetary and fiscal policy, in the context of models with sticky prices; important examples include Correia et al., (2001), Schmitt-Grohé and Uribe (2001), and Siu (2001). Our approach differs from those taken in these papers, however, in several respects. First, we model price stickiness in a different way than in any of these papers, namely, by assuming staggered pricing of the kind introduced by Calvo (1983). This particular form of price stickiness has been widely used both in analyses of optimal monetary policy in models with explicit microfoundations (e.g., Goodfriend and King, 1997; Clarida et al., 1999; Woodford, 2003) and in the empirical literature on optimizing models of the monetary transmission mechanism (e.g., Rotemberg and Woodford, 1997; Gali and Gertler, 1999; Sbordone, 2002).
Perhaps more importantly, we obtain analytical results rather than purely numerical ones. To obtain these results, we propose a linear-quadratic approach to the characterization of optimal monetary and fiscal policy, that allows us to nest both conventional analyses of optimal monetary policy, such as that of Clarida et al. (1999), and analyses of optimal tax-smoothing in the spirit of Barro (1979), Lucas and Stokey (1983), and Aiyagari et al. (2002) as special cases of our more general framework. We show how a linear-quadratic policy problem can be derived which yields a correct linear approximation to the optimal policy rules from the point of view of the maximization of expected discounted utility in a dynamic stochastic general-equilibrium model, building on the work of Benigno and Woodford (2003) for the case of optimal monetary policy when lump-sum taxes are available.
Finally, we do not content ourselves with merely characterizing the optimal dynamic responses of our policy instruments (and other state variables) to shocks under an optimal policy, given one assumption or another about the nature and statistical properties of the exogenous disturbances to our model economy. Instead, we also wish to derive policy rules that the monetary and fiscal authorities may reasonably commit themselves to follow, as a way of implementing the optimal equilibrium. In particular, we seek to characterize optimal policy in terms of optimal targeting rules for monetary and fiscal policy, of the kind proposed in the case of monetary policy by Svensson (1999), Svensson and Woodford (2003), and Giannoni and Woodford (2002, 2003). The rules are specified in terms of a target criterion for each authority; each authority commits itself to use its policy instrument each period in whatever way is necessary in order to allow it to project an evolution of the economy consistent with its target criterion. As discussed in Giannoni and Woodford (2002), we can derive rules of this form that are not merely consistent with the desired equilibrium responses to disturbances, but that in addition (i) imply a determinate rational-expectations equilibrium, so that there are not other equally possible (but less desirable) equilibria consistent with the same policy; and (ii) bring about optimal responses to shocks regardless of the character of and statistical properties of the exogenous disturbances in the model.
1 The Policy Problem
Here we describe our assumptions about the economic environment and pose the optimization problem that jointly optimal monetary and fiscal policies are intended to solve. The approximation method that we use to characterize the solution to this problem is then presented in the following section. Further details of the derivation of the structural equations of our model of nominal price rigidity can be found in Woodford (2003, chapter 3).
The goal of policy is assumed to be the maximization of the level of expected utility of a representative household. In our model, each household seeks to maximize
where
with an elasticity of substitution equal to
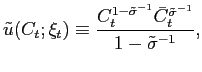
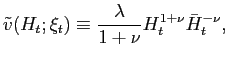
We assume a common technology for the production of all goods, in which (industry-specific) labor is the only variable input,
We can furthermore express the relative quantities demanded of
the differentiated goods each period as a function of their
relative prices. This allows us to write the utility flow to the
representative household in the form
![]() where
where
is a measure of price dispersion at date
and the vector
The producers in each industry fix the prices of their goods in
monetary units for a random interval of time, as in the model of
staggered pricing introduced by Calvo (1983). We let
![]() be the
fraction of prices that remain unchanged in any period. A supplier
that changes its price in period
be the
fraction of prices that remain unchanged in any period. A supplier
that changes its price in period ![]() chooses its new price
chooses its new price ![]() to maximize
to maximize
where
The function
![]() , defined in the appendix,
indicates the after-tax nominal profits of a supplier with price
, defined in the appendix,
indicates the after-tax nominal profits of a supplier with price
![]() in an industry with
common price
in an industry with
common price ![]() when
the aggregate price index is equal to
when
the aggregate price index is equal to ![]() , aggregate demand is equal to
, aggregate demand is equal to
![]() , and sales revenues
are taxed at rate
, and sales revenues
are taxed at rate ![]() Profits are equal to after-tax sales revenues net of the wage bill,
and the real wage demanded for labor of type
Profits are equal to after-tax sales revenues net of the wage bill,
and the real wage demanded for labor of type ![]() is assumed to be given by
is assumed to be given by
where
Each of the suppliers that revise their prices in period
![]() choose the same new
price
choose the same new
price
![]() Under our
assumed functional forms, the optimal choice has a closed-form
solution
Under our
assumed functional forms, the optimal choice has a closed-form
solution
where
The price index then evolves according to a law of motion
as a consequence of (4). Substitution of (9) into (10) implies that equilibrium inflation in any period is given by
where
for the dispersion measure defined in (3). This is the source in our model of welfare losses from inflation or deflation.
We abstract here from any monetary frictions that would account
for a demand for central-bank liabilities that earn a substandard
rate of return; we nonetheless assume that the central bank can
control the riskless short-term nominal interest rate ![]() 6 which is in turn related to other
financial asset prices through the arbitrage relation
6 which is in turn related to other
financial asset prices through the arbitrage relation
Our abstraction from monetary frictions, and hence from the
existence of seignorage revenues, does not mean that monetary
policy has no fiscal consequences, for interest-rate policy and the
equilibrium inflation that results from it have implications for
the real burden of government debt. For simplicity, we shall assume
that all public debt consists of riskless nominal one-period bonds.
The nominal value ![]() of
end-of-period public debt then evolves according to a law of
motion
of
end-of-period public debt then evolves according to a law of
motion
where the real primary budget surplus is given by
Here
Rational-expectations equilibrium requires that the expected path of government surpluses must satisfy an intertemporal solvency condition
in each state of the world that may be realized at date
Under the standard (Ramsey) approach to the characterization of
an optimal policy commitment, one chooses among state-contingent
paths
![]() from some
initial date
from some
initial date ![]() onward
that satisfy (11), (12), and (15) for each
onward
that satisfy (11), (12), and (15) for each
![]() given
initial government debt
given
initial government debt
![]() and price
dispersion
and price
dispersion
![]() so as
to maximize (5). Such a
so as
to maximize (5). Such a ![]() optimal plan requires
commitment, insofar as the corresponding
optimal plan requires
commitment, insofar as the corresponding ![]() optimal plan for some later date
optimal plan for some later date
![]() , given the conditions
, given the conditions
![]() obtaining at that date, will not involve a continuation of the
obtaining at that date, will not involve a continuation of the
![]() optimal plan.
This failure of time consistency occurs because the constraints on
what can be achieved at date
optimal plan.
This failure of time consistency occurs because the constraints on
what can be achieved at date ![]() consistent with the existence of a
rational-expectations equilibrium, depend on the expected paths of
inflation, output and taxes at later dates; but in the absence of a
prior commitment, a planner would have no motive at those later
dates to choose a policy consistent with the anticipations that it
was desirable to create at date
consistent with the existence of a
rational-expectations equilibrium, depend on the expected paths of
inflation, output and taxes at later dates; but in the absence of a
prior commitment, a planner would have no motive at those later
dates to choose a policy consistent with the anticipations that it
was desirable to create at date ![]()
However, the degree of advance commitment that is necessary to bring about an optimal equilibrium is of only a limited sort. Let
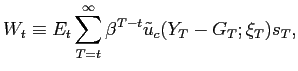
In the first stage, values of the endogenous variables
![]() , where
, where
![]() ,
and state-contingent commitments
,
and state-contingent commitments
![]() for the following period,
are chosen, subject to a set of constraints stated in the appendix,
including the requirement that the choices
for the following period,
are chosen, subject to a set of constraints stated in the appendix,
including the requirement that the choices
![]() for each possible state of the world
for each possible state of the world
![]() . These
variables are chosen so as to maximize the objective
. These
variables are chosen so as to maximize the objective
![]() where we define the functional
where we define the functional
In the second stage, the equilibrium evolution from period
The optimization problem in stage two of this reformulation of
the Ramsey problem is of the same form as the Ramsey problem
itself, except that there are additional constraints associated
with the precommitted values for the elements of
![]() Let us consider a problem
like the Ramsey problem just defined, looking forward from some
period
Let us consider a problem
like the Ramsey problem just defined, looking forward from some
period ![]() except
under the constraints that the quantities
except
under the constraints that the quantities ![]() must take certain given
values, where
must take certain given
values, where
![]() This constrained problem can similarly be expressed as a two-stage
problem of the same form as above, with an identical stage two
problem to the one described above. Stage two of this constrained
problem is thus of exactly the same form as the problem itself.
Hence the constrained problem has a recursive form. It can be
decomposed into an infinite sequence of problems, in which in each
period
This constrained problem can similarly be expressed as a two-stage
problem of the same form as above, with an identical stage two
problem to the one described above. Stage two of this constrained
problem is thus of exactly the same form as the problem itself.
Hence the constrained problem has a recursive form. It can be
decomposed into an infinite sequence of problems, in which in each
period ![]() ,
,
![]() are chosen to maximize
are chosen to maximize
![]() , subject to the
constraints of the stage one problem, given the predetermined state
variables
, subject to the
constraints of the stage one problem, given the predetermined state
variables
![]() and the precommitted values
and the precommitted values ![]()
Our aim here is to characterize policy that solves this
constrained optimization problem (stage two of the original Ramsey
problem), i.e., policy that is optimal
from some date ![]() onward
given precommitted values for
onward
given precommitted values for ![]() . Because of the recursive form of this problem,
it is possible for a commitment to a time-invariant policy rule
from date
. Because of the recursive form of this problem,
it is possible for a commitment to a time-invariant policy rule
from date ![]() onward to
implement an equilibrium that solves the problem, for some
specification of the initial commitments
onward to
implement an equilibrium that solves the problem, for some
specification of the initial commitments ![]() A time-invariant policy rule
with this property is said by Woodford (2003, chapter 7) to be
``optimal from a timeless perspective.''10 Such a rule is one that a policymaker
that solves a traditional Ramsey problem would be willing to commit
to eventually follow, though the
solution to the Ramsey problem involves different behavior
initially, as there is no need to internalize the effects of prior
anticipation of the policy adopted for period
A time-invariant policy rule
with this property is said by Woodford (2003, chapter 7) to be
``optimal from a timeless perspective.''10 Such a rule is one that a policymaker
that solves a traditional Ramsey problem would be willing to commit
to eventually follow, though the
solution to the Ramsey problem involves different behavior
initially, as there is no need to internalize the effects of prior
anticipation of the policy adopted for period ![]() 11 One might also argue that it is
desirable to commit to follow such a rule immediately, even though
such a policy would not solve the (unconstrained) Ramsey problem,
as a way of demonstrating one's willingness to accept constraints
that one wishes the public to believe that one will accept in the
future.
11 One might also argue that it is
desirable to commit to follow such a rule immediately, even though
such a policy would not solve the (unconstrained) Ramsey problem,
as a way of demonstrating one's willingness to accept constraints
that one wishes the public to believe that one will accept in the
future.
2 A Linear-Quadratic Approximate Problem
In fact, we shall here characterize the solution to this problem (and similarly, derive optimal time-invariant policy rules) only for initial conditions near certain steady-state values, allowing us to use local approximations in characterizing optimal policy.12 We establish that these steady-state values have the property that if one starts from initial conditions close enough to the steady state, and exogenous disturbances thereafter are small enough, the optimal policy subject to the initial commitments remains forever near the steady state. Hence our local characterization would describe the long run character of Ramsey policy, in the event that disturbances are small enough, and that deterministic Ramsey policy would converge to the steady state.13 Of greater interest here, it describes policy that is optimal from a timeless perspective in the event of small disturbances.
We first must show the existence of a steady state, i.e., of an optimal policy (under appropriate
initial conditions) that involves constant values of all variables.
To this end we consider the purely deterministic case, in which the
exogenous disturbances
![]()
![]()
![]()
![]()
![]()
![]() each take
constant values
each take
constant values
![]() and
and
![]() for
all
for
all
![]() and assume
an initial real public debt
and assume
an initial real public debt
![]() . We wish to find an initial
degree of price dispersion
. We wish to find an initial
degree of price dispersion
![]() and
initial commitments
and
initial commitments
![]() such
that the solution to the ``stage two'' problem defined above
involves a constant policy
such
that the solution to the ``stage two'' problem defined above
involves a constant policy
![]() each period, in which
each period, in which
![]() is equal to
the initial real debt and
is equal to
the initial real debt and
![]() is equal
to the initial price dispersion. We show in the appendix that the
first-order conditions for this problem admit a steady-state
solution of this form, and we verify below that the second-order
conditions for a local optimum are also satisfied.
is equal
to the initial price dispersion. We show in the appendix that the
first-order conditions for this problem admit a steady-state
solution of this form, and we verify below that the second-order
conditions for a local optimum are also satisfied.
Regardless of the initial public debt ![]() we show that
we show that
![]() (zero
inflation), and correspondingly that
(zero
inflation), and correspondingly that
![]() (zero
price dispersion). Note that our conclusion that the optimal
steady-state inflation rate is zero generalizes the result of
Benigno and Woodford (2003) for the case in which taxes are
lump-sum at the margin. We may furthermore assume without loss of
generality that the constant values of
(zero
price dispersion). Note that our conclusion that the optimal
steady-state inflation rate is zero generalizes the result of
Benigno and Woodford (2003) for the case in which taxes are
lump-sum at the margin. We may furthermore assume without loss of
generality that the constant values of ![]() and
and ![]() are chosen (given the initial
government debt
are chosen (given the initial
government debt ![]() ) so that in the optimal steady state,
) so that in the optimal steady state,
![]() and
and
![]() each
period.14 The
associated steady-state tax rate is given by
each
period.14 The
associated steady-state tax rate is given by
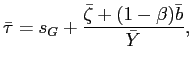
We next wish to characterize the optimal responses to small perturbations of the initial conditions and small fluctuations in the disturbance processes around the above values. To do this, we compute a linear-quadratic approximate problem, the solution to which represents a linear approximation to the solution to the ``stage two'' policy problem, using the method introduced in Benigno and Woodford (2003). An important advantage of this approach is that it allows direct comparison of our results with those obtained in other analyses of optimal monetary stabilization policy. Other advantages are that it makes it straightforward to verify whether the second-order conditions hold that are required in order for a solution to our first-order conditions to be at least a local optimum,15 and that it provides us with a welfare measure with which to rank alternative sub-optimal policies, in addition to allowing computation of the optimal policy.
We begin by computing a Taylor-series approximation to our
welfare measure (5), expanding around the
steady-state allocation defined above, in which
![]() for
each good at all times and
for
each good at all times and ![]() at all times.16 As a second-order (logarithmic)
approximation to this measure, we obtain17
at all times.16 As a second-order (logarithmic)
approximation to this measure, we obtain17
where
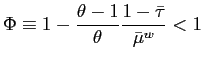
Under the Calvo assumption about the distribution of intervals between price changes, we can relate the dispersion of prices to the overall rate of inflation, allowing us to rewrite (17) as
for a certain coefficient
We note that when ![]() there is a non-zero linear term in
(18), which means that we cannot expect to
evaluate this expression to second order using only an approximate
solution for the path of aggregate output that is accurate only to
first order. Thus we cannot determine optimal policy, even up to
first order, using this approximate objective together with
approximations to the structural equations that are accurate only
to first order. Rotemberg and Woodford (1997) avoid this problem by
assuming an output subsidy (i.e., a
value
there is a non-zero linear term in
(18), which means that we cannot expect to
evaluate this expression to second order using only an approximate
solution for the path of aggregate output that is accurate only to
first order. Thus we cannot determine optimal policy, even up to
first order, using this approximate objective together with
approximations to the structural equations that are accurate only
to first order. Rotemberg and Woodford (1997) avoid this problem by
assuming an output subsidy (i.e., a
value
![]() ) of
the size needed to ensure that
) of
the size needed to ensure that ![]() Here we do not wish to make this assumption,
because we assume that lump-sum taxes are unavailable, in which
case
Here we do not wish to make this assumption,
because we assume that lump-sum taxes are unavailable, in which
case ![]() would be
possible only in the case of a particular initial level of
government assets
would be
possible only in the case of a particular initial level of
government assets
![]() Furthermore, we are more interested in the case in which government
revenue needs are more acute than that would imply.
Furthermore, we are more interested in the case in which government
revenue needs are more acute than that would imply.
Benigno and Woodford (2003) propose an alternative way of
dealing with this problem, which is to use a second-order
approximation to the aggregate-supply relation to eliminate the
linear terms in the quadratic welfare measure. In the model that
they consider, where taxes are lump-sum (and so do not affect the
aggregate supply relation), a forward-integrated second-order
approximation to this relation allows one to express the expected
discounted value of output terms
![]() as a
function of purely quadratic terms (except for certain transitory
terms that do not affect the ``stage two'' policy problem). In the
present case, the level of distorting taxes has a first-order
effect on the aggregate-supply relation (see equation (22) below), so that the forward-integrated
relation involves the expected discounted value of the tax rate as
well as the expected discounted value of output. However, as shown
in the appendix, a second-order approximation to the intertemporal
solvency condition (15 )19 provides another relation between the
expected discounted values of output and the tax rate and a set of
purely quadratic terms. These two second-order approximations to
the structural equations that appear as constraints in our policy
problem can then be used to express the expected discounted value
of output terms in (18) in terms of purely
quadratic terms.
as a
function of purely quadratic terms (except for certain transitory
terms that do not affect the ``stage two'' policy problem). In the
present case, the level of distorting taxes has a first-order
effect on the aggregate-supply relation (see equation (22) below), so that the forward-integrated
relation involves the expected discounted value of the tax rate as
well as the expected discounted value of output. However, as shown
in the appendix, a second-order approximation to the intertemporal
solvency condition (15 )19 provides another relation between the
expected discounted values of output and the tax rate and a set of
purely quadratic terms. These two second-order approximations to
the structural equations that appear as constraints in our policy
problem can then be used to express the expected discounted value
of output terms in (18) in terms of purely
quadratic terms.
In this manner, we can rewrite (18) as
where again the coefficients are defined in the appendix. The expression
where a lower value of (20) implies a higher value of (19). Because this loss function is purely quadratic (i.e., lacking linear terms), it is possible to evaluate it to second order using only a first-order approximation to the equilibrium evolution of inflation and output under a given policy. Hence log-linear approximations to the structural relations of our model suffice, yielding a standard linear-quadratic policy problem.
In order for this linear-quadratic problem to have a bounded
solution (which then approximates the solution to the exact
problem), we must verify that the quadratic objective (20) is convex. We show in the appendix that
![]() so
that the objective is convex, as long as the steady-state tax rate
so
that the objective is convex, as long as the steady-state tax rate
![]() and share
of government purchases
and share
of government purchases ![]() in the national product are below certain
positive bounds. We shall here assume that these conditions are
satisfied, i.e., that the government's
fiscal needs are not too severe. Note that in this case, our
quadratic objective turns out to be of a form commonly assumed in
the literature on monetary policy evaluation; that is, policy
should seek to minimize the discounted value of a weighted sum of
squared deviations of inflation from an optimal level (here zero)
and squared fluctuations in an ``output gap''
in the national product are below certain
positive bounds. We shall here assume that these conditions are
satisfied, i.e., that the government's
fiscal needs are not too severe. Note that in this case, our
quadratic objective turns out to be of a form commonly assumed in
the literature on monetary policy evaluation; that is, policy
should seek to minimize the discounted value of a weighted sum of
squared deviations of inflation from an optimal level (here zero)
and squared fluctuations in an ``output gap''
![]() where the
target output level
where the
target output level
![]() depends on the various exogenous disturbances in a way discussed in
the appendix. It is also perhaps of interest to note that a ``tax
smoothing'' objective of the kind postulated by Barro (1979) and
Bohn (1990) does not appear in our welfare measure as a separate
objective. Instead, tax distortions are relevant only insofar as they result in ``output gaps'' of
the same sort that monetary stabilization policy aims to
minimize.
depends on the various exogenous disturbances in a way discussed in
the appendix. It is also perhaps of interest to note that a ``tax
smoothing'' objective of the kind postulated by Barro (1979) and
Bohn (1990) does not appear in our welfare measure as a separate
objective. Instead, tax distortions are relevant only insofar as they result in ``output gaps'' of
the same sort that monetary stabilization policy aims to
minimize.
We turn next to the form of the log-linear constraints in the approximate policy problem. A first-order Taylor series expansion of (11) around the zero-inflation steady state yields the log-linear aggregate-supply relation
for certain coefficients
It is useful to write this approximate aggregate-supply relation
in terms of the welfare-relevant output gap ![]() . Equation (21) can be equivalently be written as
. Equation (21) can be equivalently be written as
where
where
The effects of the various exogenous disturbances in
![]() on the
``cost-push'' term
on the
``cost-push'' term ![]() are explained in the appendix. It is worth noting that under
certain conditions
are explained in the appendix. It is worth noting that under
certain conditions ![]() is unaffected by some disturbances. In the case that
is unaffected by some disturbances. In the case that ![]() the cost-push term is given
by
the cost-push term is given
by
where in this case,
Even when ![]() if
there are no government purchases (so that
if
there are no government purchases (so that ![]() ) and no fiscal shocks
(meaning that
) and no fiscal shocks
(meaning that
![]() and
and
![]() ),
then the
),
then the ![]() term is
again of the form (24), but with
term is
again of the form (24), but with
![]() as discussed in Benigno
and Woodford (2003). Hence in this case neither taste or technology
shocks have ``cost-push'' effects. The reason is that in this
``isoelastic'' case, if neither taxes nor the wage markup ever
vary, the flexible-price equilibrium value of output and the
efficient level vary in exactly the same proportion in response to
each of the other types of shocks; hence inflation stabilization
also stabilizes the gap between actual output and the efficient
level. Another special case is the limiting case of linear utility
of consumption (
as discussed in Benigno
and Woodford (2003). Hence in this case neither taste or technology
shocks have ``cost-push'' effects. The reason is that in this
``isoelastic'' case, if neither taxes nor the wage markup ever
vary, the flexible-price equilibrium value of output and the
efficient level vary in exactly the same proportion in response to
each of the other types of shocks; hence inflation stabilization
also stabilizes the gap between actual output and the efficient
level. Another special case is the limiting case of linear utility
of consumption (
![]() ); in
this case,
); in
this case, ![]() is
again of the form (24 ), for a different
value of
is
again of the form (24 ), for a different
value of ![]() In
general, however, when
In
general, however, when ![]() and
and ![]() all of the disturbances shift the
flexible-price equilibrium level of output (under a constant tax
rate) and the efficient level of output to differing extents,
resulting in ``cost-push'' contributions from all of these
shocks.
all of the disturbances shift the
flexible-price equilibrium level of output (under a constant tax
rate) and the efficient level of output to differing extents,
resulting in ``cost-push'' contributions from all of these
shocks.
The other constraint on possible equilibrium paths is the intertemporal government solvency condition. A log-linear approximation to (15) can be written in the form
where
together with a transversality condition.21
We note that the only reason why it should not be possible to completely stabilize both
inflation and the output gap from some date ![]() onward is if the sum
onward is if the sum
![]() is
non-zero. The composite disturbance
is
non-zero. The composite disturbance ![]() therefore completely summarizes the information
at date
therefore completely summarizes the information
at date ![]() about the
exogenous disturbances that determines the degree to which
stabilization of inflation and output is not possible; and under an
optimal policy, the state-contingent evolution of the inflation
rate, the output gap, and the real public debt depend solely on the
evolution of the single composite disturbance process
about the
exogenous disturbances that determines the degree to which
stabilization of inflation and output is not possible; and under an
optimal policy, the state-contingent evolution of the inflation
rate, the output gap, and the real public debt depend solely on the
evolution of the single composite disturbance process
![]()
This result contrasts with the standard literature on optimal
monetary stabilization policy, in which (in the absence of a motive
for interest-rate stabilization, as here) it is instead the
cost-push term ![]() that summarizes the extent to which exogenous disturbances require
that fluctuations in inflation and in the output gap should occur.
Note that in the case that there are no government purchases and no
fiscal shocks,
that summarizes the extent to which exogenous disturbances require
that fluctuations in inflation and in the output gap should occur.
Note that in the case that there are no government purchases and no
fiscal shocks, ![]() corresponds simply to (24). Thus, for
example, it is concluded (in a model with lump-sum taxes) that
there should be no variation in inflation in response to a
technology shock (Khan et al., 2002;
Benigno and Woodford, 2003). But even in this simple case, the
fiscal stress is given by an expression of the form
corresponds simply to (24). Thus, for
example, it is concluded (in a model with lump-sum taxes) that
there should be no variation in inflation in response to a
technology shock (Khan et al., 2002;
Benigno and Woodford, 2003). But even in this simple case, the
fiscal stress is given by an expression of the form
where the expressions
Finally, we wish to consider optimal policy subject to the
constraints that
![]() and
and ![]() take given
(precommitted) values. Again, only log-linear approximations to
these constraints matter for a log-linear approximate
characterization of optimal policy. As discussed in the appendix,
the corresponding constraints in our approximate model are
precommitments regarding the state-contingent values of
take given
(precommitted) values. Again, only log-linear approximations to
these constraints matter for a log-linear approximate
characterization of optimal policy. As discussed in the appendix,
the corresponding constraints in our approximate model are
precommitments regarding the state-contingent values of
![]() and
and
![]()
To summarize, our approximate policy problem involves the choice
of state-contingent paths for the endogenous variables
![]() from
some date
from
some date ![]() onward
so as to minimize the quadratic loss function (20), subject to the constraint that conditions
(23) and (25) be
satisfied each period, given an initial value
onward
so as to minimize the quadratic loss function (20), subject to the constraint that conditions
(23) and (25) be
satisfied each period, given an initial value
![]() and
subject also to the constraints that
and
subject also to the constraints that
![]() and
and
![]() equal
certain precommitted values (that may depend on the state of the
world in period
equal
certain precommitted values (that may depend on the state of the
world in period ![]() ).
We shall first characterize the state-contingent evolution of the
endogenous variables in response to exogenous shocks, in the
rational-expectations equilibrium that solves this problem. We then
turn to the derivation of optimal policy rules, commitment to which
should implement an equilibrium of this kind.
).
We shall first characterize the state-contingent evolution of the
endogenous variables in response to exogenous shocks, in the
rational-expectations equilibrium that solves this problem. We then
turn to the derivation of optimal policy rules, commitment to which
should implement an equilibrium of this kind.
3 Optimal Responses to Shocks: The Case of Flexible Prices
In considering the solution to the problem of stabilization
policy just posed, it may be useful to first consider the simple
case in which prices are fully flexible. This is the limiting case
of our model in which ![]() with the consequence that
with the consequence that ![]() in (20), and that
in (20), and that
![]() in
(23). Hence our optimization problem reduces
to the minimization of
in
(23). Hence our optimization problem reduces
to the minimization of
subject to the constraints
and (25). It is easily seen that in this case, the optimal policy is one that achieves
This last equation implies that unexpected inflation must equal the innovation in the fiscal stress,
We thus obtain simple conclusions about the determinants of fluctuations in inflation, output and the tax rate under optimal policy. Unexpected inflation variations occur as needed in order to prevent taxes from ever having to be varied in order to respond to variations in fiscal stress, as in the analyses of Bohn (1990) and Chari and Kehoe (1999). This allows a model with only riskless nominal government debt to achieve the same state-contingent allocation of resources as the government would choose to bring about if it were able to issue state-contingent debt, as in the model of Lucas and Stokey (1983).
Because taxes do not have to adjust in response to variations in
fiscal stress, as in the tax-smoothing model of Barro (1979), it is
possible to ``smooth'' them across states as well as over time.
However, the sense in which it is desirable to ``smooth'' tax rates
is that of minimizing variation in the gap
![]() , rather than
variation in the tax rate itself.24 In other words, it is really the ``tax
gap''
, rather than
variation in the tax rate itself.24 In other words, it is really the ``tax
gap''
![]() that should be
smoothed. Under certain special circumstances, it will not be
optimal for tax rates to vary in response to shocks; these are the
conditions, discussed above, under which shocks have no cost-push
effects, so that there is no change in
that should be
smoothed. Under certain special circumstances, it will not be
optimal for tax rates to vary in response to shocks; these are the
conditions, discussed above, under which shocks have no cost-push
effects, so that there is no change in
![]() .
For example, if there are no government purchases and there is no
variation in the wage markup, this will be the case. But more
generally, all disturbances will have some cost-push effect, and
result in variations in
.
For example, if there are no government purchases and there is no
variation in the wage markup, this will be the case. But more
generally, all disturbances will have some cost-push effect, and
result in variations in
![]() There will then be variations in the tax rate in response to these
shocks under an optimal policy. However, there will be no unit root
in the tax rate, as in the Barro (1979) model of optimal tax
policy. Instead, as in the analysis of Lucas and Stokey (1983), the
optimal fluctuations in the tax rate will be stationary, and will
have the same persistence properties as the real disturbances
(specifically, the persistence properties of the composite
cost-push shock).
There will then be variations in the tax rate in response to these
shocks under an optimal policy. However, there will be no unit root
in the tax rate, as in the Barro (1979) model of optimal tax
policy. Instead, as in the analysis of Lucas and Stokey (1983), the
optimal fluctuations in the tax rate will be stationary, and will
have the same persistence properties as the real disturbances
(specifically, the persistence properties of the composite
cost-push shock).
Variations in fiscal stress will instead require changes in the
tax rate, as in the analysis of Barro (1979), if we suppose that
the government issues only riskless indexed debt, rather than the
riskless nominal debt assumed in our baseline model. (Again, for
simplicity we assume that only one-period riskless debt is issued.)
In this case the objective function (20) and
the constraints (25) and (29) remain the same, but b
![]() the real value of
private claims on the government at the beginning of period
the real value of
private claims on the government at the beginning of period
![]() , is now a
predetermined variable. This means that unexpected inflation
variations are no longer able to relax the intertemporal government
solvency condition. In fact, rewriting the constraint (25) in terms of
, is now a
predetermined variable. This means that unexpected inflation
variations are no longer able to relax the intertemporal government
solvency condition. In fact, rewriting the constraint (25) in terms of
![]() we see
that the path of inflation is now completely irrelevant to
welfare.
we see
that the path of inflation is now completely irrelevant to
welfare.
The solution to this optimization problem is now less trivial, as complete stabilization of the output gap is not generally possible. The optimal state-contingent evolution of output and taxes can be determined using a Lagrangian method, as in Woodford (2003, chapter 7). The Lagrangian for the present problem can be written as
where
The resulting first-order condition with respect to ![]() is
is
that with respect to
and that with respect to b
Each of these conditions must be satisfied for each
An analytical solution to these equations is easily given. Using
equation (29) to substitute for
![]() in the
forward-integrated version of (25), then
equations (31) and (32) to
substitute for
in the
forward-integrated version of (25), then
equations (31) and (32) to
substitute for ![]() as a function of the path of
as a function of the path of
![]() and
finally using (33) to replace all terms of the
form
and
finally using (33) to replace all terms of the
form
![]() (for
(for ![]() ) by
) by
![]() we
obtain an equation that can be solved for
we
obtain an equation that can be solved for
![]() The
solution is of the form
The
solution is of the form
![$\displaystyle \varphi_{2t}={\frac{m_{b}}{m_{b}+n_{b}}}\varphi_{2,t-1}-{\frac{1}{m_{b}+n_{b} }}[f_{t}+{\text{\b{b}}}_{t-1}], $](img258.gif)
In this case, unlike that of nominal debt, inflation is
not affected by a pure fiscal shock (or
indeed any other shock) under the optimal policy, but instead the
output gap and the tax rate are. Note also that in the above
solution, the multiplier
![]() the
output gap, and the tax rate all follow unit root processes: a temporary disturbance to the fiscal stress
permanently changes the level of each of these variables, as in the
analysis of the optimal dynamics of the tax rate in Barro (1979)
and Bohn (1990). However, the optimal evolution of the tax rate is
not in general a pure random walk as in the analysis of Barro and
Bohn. Instead, the tax gap is an IMA(1,1) process, as in the local
analysis of Aiyagari et al. (2002); the
optimal tax rate
the
output gap, and the tax rate all follow unit root processes: a temporary disturbance to the fiscal stress
permanently changes the level of each of these variables, as in the
analysis of the optimal dynamics of the tax rate in Barro (1979)
and Bohn (1990). However, the optimal evolution of the tax rate is
not in general a pure random walk as in the analysis of Barro and
Bohn. Instead, the tax gap is an IMA(1,1) process, as in the local
analysis of Aiyagari et al. (2002); the
optimal tax rate
![]() may
have more complex dynamics, in the case that
may
have more complex dynamics, in the case that
![]() exhibits stationary fluctuations. In the special case of linear
utility (
exhibits stationary fluctuations. In the special case of linear
utility (
![]() ),
),
![]() and
both the output gap and the tax gap follow random walks (as both
co-move with
and
both the output gap and the tax gap follow random walks (as both
co-move with
![]() ). If the
only disturbances are fiscal disturbances (
). If the
only disturbances are fiscal disturbances (
![]() and
and
![]() ), then
there are also no fluctuations in
), then
there are also no fluctuations in
![]() in
this case, so that the optimal tax rate follows a random walk.
in
this case, so that the optimal tax rate follows a random walk.
More generally, we observe that optimal policy ``smooths''
![]() the
value (in units of marginal utility) of additional government
revenue in period
the
value (in units of marginal utility) of additional government
revenue in period ![]() , so
that it follows a random walk. This is the proper generalization of
the Barro tax-smoothing result, though it only implies smoothing of
tax rates in fairly special cases. We find a similar result in the
case that prices are sticky, even when government debt is not
indexed, as we now show.
, so
that it follows a random walk. This is the proper generalization of
the Barro tax-smoothing result, though it only implies smoothing of
tax rates in fairly special cases. We find a similar result in the
case that prices are sticky, even when government debt is not
indexed, as we now show.
4 Optimal Responses to Shocks: The Case of Sticky Prices
We turn now to the characterization of the optimal responses to
shocks in the case that prices are sticky (![]() ). The optimization
problem that provides a first-order characterization of optimal
responses in this case is that of choosing processes
). The optimization
problem that provides a first-order characterization of optimal
responses in this case is that of choosing processes
![]() from
date
from
date ![]() onward to
minimize (20), subject to the constraints
(23) and (25) for
each
onward to
minimize (20), subject to the constraints
(23) and (25) for
each
![]() , together
with initial constraints of the form
, together
with initial constraints of the form
![$\displaystyle =E_{t_{0}}\sum_{t=t_{0}}^{\infty}\beta^{t-t_{0} }\{\frac{1}{2}q_{... ..._{1t}[-\kappa^{-1}\pi_{t}+y_{t}+\psi\hat{\tau}_{t}+\kappa^{-1}\beta\pi _{t+1}]+$](img273.gif)
|
||
by analogy with (30).
The first-order condition with respect to ![]() is given by
is given by
that with respect to
that with respect to
and finally that with respect to
These together with the two structural equations and the initial conditions are to be solved for the state-contingent paths of
In the unique bounded solution to these equations, the dynamics
of government debt and of the shadow value of government revenue
![]() are again
of the form
are again
of the form
![$\displaystyle \varphi_{2t}={\frac{\tilde{m}_{b}}{\tilde{m}_{b}+n_{b}}}\varphi_{2,t-1} -{\frac{1}{\tilde{m}_{b}+n_{b}}}[f_{t}+{\hat{b}}_{t-1}], $](img281.gif)
where
We now discuss the optimal response of the variables to a
disturbance to the level of fiscal stress. The laws of motion just
derived for government debt and the Lagrange multiplier imply that
temporary disturbances to the level of fiscal stress cause a
permanent change in the level of both the Lagrange multiplier and
the public debt. This then implies a permanent change in the level
of output as well, which in turn requires (since inflation is
stationary) a permanent change in the level of the tax rate. Since
inflation is proportional to the change in the Lagrange multiplier,
the price level moves in proportion to the multiplier, which means
a temporary disturbance to the fiscal stress results in a permanent
change in the price level, as in the flexible-price case analyzed
in the previous section. Thus in this case, the price level, output
gap, government debt, and tax rate all
have unit roots, combining features of the two special cases
considered in the previous section.29 Both price level and
![]() are
random walks. They jump immediately to new permanent level in
response to change in fiscal stress. In the case of purely
transitory (white noise) disturbances, government debt also jumps
immediately to a new permanent level. Given the dynamics of the
price level and government debt, the dynamics of output and tax
rate then jointly determined by the aggregate-supply relation and
the government budget constraint.
are
random walks. They jump immediately to new permanent level in
response to change in fiscal stress. In the case of purely
transitory (white noise) disturbances, government debt also jumps
immediately to a new permanent level. Given the dynamics of the
price level and government debt, the dynamics of output and tax
rate then jointly determined by the aggregate-supply relation and
the government budget constraint.
Figure 1: Impulse response of the public debt to a pure fiscal shock, for alternative degrees of price stickiness
![Figure 1 shows the optimal impulse response of the government debt to a pure fiscal shock, for each of 7 different values for $\kappa$: 0.0236 (baseline), 0.05, 0.1, 0.25, 1, 25, and infinity. Quarter zero is the quarter of the shock, $\kappa$ is the slope of the short-run aggregate-supply relation, and the other parameters of the model are maintained at the values stated in the text. The x-axis has a range of [-2,8] quarters; the y-axis has a range of [0,0.4]. The response for each value of $\kappa$ is zero for negative quarters, jumps to a positive value in quarter zero, and remains at that value for all positive quarters. In quarter zero, the baseline response jumps to about 0.36, the response with $\kappa=25$ jumps to about 0.16, and the responses for the other values of $\kappa$ all jump to between 0.35 and 0.4.](Figure1.gif)
Figure 2: Impulse response of the tax rate to a pure fiscal shock
![Figure 2 shows the optimal responses of the tax rate to the disturbance in Figure 1, for each of the 7 values of $\kappa$. The x-axis has a range of [-2,8] quarters; the y-axis has a range of [-0.4,0.3]. The response for each value of $\kappa$ is zero for negative quarters, jumps to a positive or negative value in quarter zero, jumps to a non-negative value for quarter 1, and remains at that value for the remaining positive quarters. In quarter zero, the baseline response jumps to about 0.2, whereas the impulses for all other values of $\kappa$ jump to negative values, ranging from -0.05 to -0.35. In quarter one, the response with $\kappa=\infty$ is about zero, that for \kappa=25$ is about 0.03, and those for all other values of $\kappa$ (including the baseline response) are about 0.07.](Figure2.gif)
Figure 3: Impulse response of the inflation rate to a pure fiscal shock
![Figure 3 shows the optimal responses of the inflation rate to the disturbance for Figure 1, for each of the 7 values of $\kappa$. The x-axis has a range of [-2,8] quarters; the y-axis has a range of [0,1.8]. The response for each value of $\kappa$ is zero for negative quarters, jumps to a positive value in quarter zero, and returns to zero for positive quarters. In quarter zero, the baseline response jumps to about 0.08, that for $\kappa=0.1$ to about unity, that for $\kappa=0.05$ to about 1.6, and those for all other values of $\kappa$ to a very small value (around 0.05 or less).](Figure3.gif)
Table 1: Immediate responses for alternative degrees of price stickiness.
|
|
|
|
|---|---|---|---|
| .024 | 29 | .072 | .021 |
| .05 | 20 | .076 | .024 |
| .10 | 14 | .077 | .030 |
| .25 | 9 | .078 | .044 |
| 1.0 | 5.4 | .075 | .113 |
| 25 | 2.4 | .032 | .998 |
|
0 | 0 | 1.651 |
We further find that the degree to which fiscal stress is
relieved by a price-level jump (as in the flexible-price,
nominal-debt case) as opposed to an increase in government debt and
hence a permanently higher tax rate (as in the flexible-price,
indexed-debt case) depends on the degree of price stickiness. We
illustrate this with a numerical example. We calibrate a quarterly
model by assuming that
![]() and
and
![]() in
accordance with the estimates of Rotemberg and Woodford (1997). We
furthermore assume an elasticity of substitution among alternative
goods of
in
accordance with the estimates of Rotemberg and Woodford (1997). We
furthermore assume an elasticity of substitution among alternative
goods of ![]() , an
overall level of steady-state distortions
, an
overall level of steady-state distortions ![]() a steady-state tax rate of
a steady-state tax rate of
![]() and a
steady-state debt level
and a
steady-state debt level
![]() (debt equal to 60 percent of a year's GDP). Given the assumed
degree of market power of producers (a steady-state gross price
markup of 1.11) and the assumed size of the tax wedge, the value
(debt equal to 60 percent of a year's GDP). Given the assumed
degree of market power of producers (a steady-state gross price
markup of 1.11) and the assumed size of the tax wedge, the value
![]() corresponds
to a steady-state wage markup of
corresponds
to a steady-state wage markup of
![]() If
we assume that there are no government transfers in the steady
state, then the assumed level of tax revenues net of debt service
would finance steady-state government purchases equal to a share
If
we assume that there are no government transfers in the steady
state, then the assumed level of tax revenues net of debt service
would finance steady-state government purchases equal to a share
![]() of
output.
of
output.
Let us suppose that the economy is disturbed by an exogenous
increase in transfer programs
![]() , equal
to one percent of aggregate output, and expected to last only for
the current quarter. Figure 1 shows the optimal impulse response of
the government debt
, equal
to one percent of aggregate output, and expected to last only for
the current quarter. Figure 1 shows the optimal impulse response of
the government debt
![]() to this
shock (where quarter zero is the quarter of the shock), for each of
7 different values for
to this
shock (where quarter zero is the quarter of the shock), for each of
7 different values for ![]() the slope of the short-run aggregate-supply
relation, maintaining the values just stated for the other
parameters of the model. The solid line indicates the optimal
response in the case of our baseline value for
the slope of the short-run aggregate-supply
relation, maintaining the values just stated for the other
parameters of the model. The solid line indicates the optimal
response in the case of our baseline value for ![]() , based on the estimates of
Rotemberg and Woodford; the other cases represent progressively
greater degrees of price flexibility, up to the limiting case of
fully flexible prices (the case
, based on the estimates of
Rotemberg and Woodford; the other cases represent progressively
greater degrees of price flexibility, up to the limiting case of
fully flexible prices (the case
![]() ).
Figures 2 and 3 similarly show the optimal responses of the tax
rate and the inflation rate to the same disturbance, for each of
the same 7 cases.30
).
Figures 2 and 3 similarly show the optimal responses of the tax
rate and the inflation rate to the same disturbance, for each of
the same 7 cases.30
We see that the volatility of both inflation and tax rates under
optimal policy depends greatly on the degree of stickiness of
prices. Table 1 reports the initial quarter's response of the
inflation rate, and the long-run response of the tax rate, for each
of the 7 cases. The table also indicates for each case the implied
average time (in weeks) between price changes,
![]() where
where
![]() is
the fraction of prices unchanged for an entire quarter implied by
the assumed value of
is
the fraction of prices unchanged for an entire quarter implied by
the assumed value of ![]() .31 We first
note that our baseline calibration implies that price changes occur
only slightly less frequently than twice per year, which is
consistent with survey evidence.32 Next, we observe that even were we to
assume an aggregate-supply relation several times as steep as the
one estimated using U.S. data, our conclusions with regard to the
size of the optimal responses of the (long-run) tax rate and the
inflation rate would be fairly similar. At the same time, the
optimal responses with fully flexible prices are quite different:
the response of inflation is 80 times as large as under the
baseline sticky-price calibration (implying a variance of inflation
6400 times as large), while the long-run tax rate does not respond
at all in the flexible-price case.33 But even a small degree of stickiness
of prices makes a dramatic difference in the optimal responses; for
example, if prices are revised only every five weeks on average,
the variance of inflation is reduced by a factor of more than 200,
while the optimal response of the long-run tax rate to the
increased revenue need is nearly the same size as under the
baseline degree of price stickiness. Thus we find, as do
Schmitt-Grohé and Uribe (2001) in the context of a
calibrated model with convex costs of price adjustment, that the
conclusions of the flexible-price analysis are quite misleading if
prices are even slightly sticky. Under a realistic calibration of
the degree of price stickiness, inflation should be quite stable,
even in response to disturbances with substantial consequences for
the government's budget constraint, while tax rates should instead
respond substantially (and with a unit root) to variations in
fiscal stress.
.31 We first
note that our baseline calibration implies that price changes occur
only slightly less frequently than twice per year, which is
consistent with survey evidence.32 Next, we observe that even were we to
assume an aggregate-supply relation several times as steep as the
one estimated using U.S. data, our conclusions with regard to the
size of the optimal responses of the (long-run) tax rate and the
inflation rate would be fairly similar. At the same time, the
optimal responses with fully flexible prices are quite different:
the response of inflation is 80 times as large as under the
baseline sticky-price calibration (implying a variance of inflation
6400 times as large), while the long-run tax rate does not respond
at all in the flexible-price case.33 But even a small degree of stickiness
of prices makes a dramatic difference in the optimal responses; for
example, if prices are revised only every five weeks on average,
the variance of inflation is reduced by a factor of more than 200,
while the optimal response of the long-run tax rate to the
increased revenue need is nearly the same size as under the
baseline degree of price stickiness. Thus we find, as do
Schmitt-Grohé and Uribe (2001) in the context of a
calibrated model with convex costs of price adjustment, that the
conclusions of the flexible-price analysis are quite misleading if
prices are even slightly sticky. Under a realistic calibration of
the degree of price stickiness, inflation should be quite stable,
even in response to disturbances with substantial consequences for
the government's budget constraint, while tax rates should instead
respond substantially (and with a unit root) to variations in
fiscal stress.
We can also compare our results with those that arise when taxes
are lump-sum. In this case, ![]() and the first-order condition (36) requires that
and the first-order condition (36) requires that
![]() The
remaining first-order conditions reduce to
The
remaining first-order conditions reduce to
Note that the familiar case from the literature on monetary
stabilization policy does not result simply from assuming that
sources of revenue that do not shift the aggregate-supply relation
are available ; it is also important
that the sort of tax that does shift
the AS relation (like the sales tax here) is not available. We could nest both the standard
model and our present baseline case within a single, more general
framework by assuming that revenue can be raised using either the
sales tax or a lump-sum tax, but that there is an additional convex
cost (perhaps representing ``collection costs'', assumed to reduce
the utility of the representative household but not using real
resources) of increases in either tax rate. The standard case would
then appear as the limiting case of this model in which the
collection costs associated with the sales tax are infinite, while
those associated with the lump-sum tax are zero; the baseline model
here would correspond to an alternative limiting case in which the
collection costs associated with the lump-sum tax are infinite,
while those associated with the sales tax are zero. In intermediate
cases, we would continue to find that fiscal stress affects the
optimal evolution of both inflation and the output gap, as long as
there is a positive collection cost for the lump-sum tax. At the
same time, the result that the shadow value of additional
government revenue follows a random walk under optimal policy
(which would still be true) will not in general imply, as it does
here, that the price level should also be a random walk; for the
perfect co-movement of
![]() and
and
![]() that
characterizes optimal policy in our baseline case will not be
implied by the first-order conditions except in the case that there
are no collection costs associated with the sales tax. Nonetheless,
the price level will generally contain a unit root under optimal
policy, even if it will not generally follow a random walk.
that
characterizes optimal policy in our baseline case will not be
implied by the first-order conditions except in the case that there
are no collection costs associated with the sales tax. Nonetheless,
the price level will generally contain a unit root under optimal
policy, even if it will not generally follow a random walk.
We also obtain results more similar to those in the standard
literature on monetary stabilization policy if we assume
(realistically) that it is not possible to adjust tax rates on such
short notice in response to shocks as is possible with monetary
policy. As a simple way of introducing delays in the adjustment of
tax policy, suppose that the tax rate ![]() has to be fixed in period
has to be fixed in period
![]() . In this case, the
first-order conditions characterizing optimal responses to shocks
are the same as above, except that (36) is
replaced by
. In this case, the
first-order conditions characterizing optimal responses to shocks
are the same as above, except that (36) is
replaced by
for each
5 Optimal Targeting Rules for Monetary and Fiscal Policy
We now wish to characterize the policy rules that the monetary and fiscal authorities can follow in order to bring about the state-contingent responses to shocks described in the previous section. One might think that it suffices to solve for the optimal state-contingent paths for the policy instruments. But in general this is not a desirable approach to the specification of a policy rule, as discussed in Svensson (2003) and Woodford (2003, chapter 7). A description of optimal policy in these terms would require enumeration of all of the types of shocks that might be encountered later, indefinitely far in the future, which is not feasible in practice. A commitment to a state-contingent instrument path, even when possible, also may not determine the optimal equilibrium as the locally unique rational-expectations equilibrium consistent with this policy; many other (much less desirable) equilibria may also be consistent with the same state-contingent instrument path.
Instead, we here specify targeting rules in the sense of Svensson (1999, 2003) and Giannoni and Woodford (2003). These targeting rules are commitments on the part of the policy authorities to adjust their respective instruments so as to ensure that the projected paths of the endogenous variables satisfy certain target criteria. We show that under an appropriate choice of these target criteria, a commitment to ensure that they hold at all times will determine a unique non-explosive rational-expectations equilibrium, in which the state-contingent evolution of inflation, output and the tax rate solves the optimization problem discussed in the previous section. Moreover, we show that it is possible to obtain a specification of the policy rules that is robust to alternative specifications of the exogenous shock processes.
We apply the general approach of Giannoni and Woodford (2002), which allows the derivation of optimal target criteria with the properties just stated. In addition, Giannoni and Woodford show that such target criteria can be formulated that refer only to the projected paths of the target variables (the ones in terms of which the stabilization objectives of policy are defined -- here, inflation and the output gap). Briefly, the method involves constructing the target criteria by eliminating the Lagrange multipliers from the system of the system of first-order conditions that characterize the optimal state-contingent evolution, regardless of character of the (additive) disturbances. We are left with linear relations among the target variables, that do not involve the disturbances and with coefficients independent of the specification of the disturbances, that represent the desired target criteria.
Recall that the first-order conditions that characterize the
optimal state-contingent paths in the problem considered in the
previous section are given by (34) -
(37). As explained in the previous section,
the first three of these conditions imply that the evolution of
inflation and of the output gap must satisfy (38) - (39) each period. We
can solve (38) - (39) for the values of
![]() implied by the values of
implied by the values of
![]() that are
observed in an optimal equilibrium. We can then replace
that are
observed in an optimal equilibrium. We can then replace
![]() in
these two relations by the multiplier implied in this way by observed values of
in
these two relations by the multiplier implied in this way by observed values of
![]() Finally, we can eliminate
Finally, we can eliminate
![]() from
these two relations, to obtain a necessary relation between
from
these two relations, to obtain a necessary relation between
![]() and
and
![]() , given
, given
![]() and
and
![]() given by
given by
This target criterion has the form of a ``flexible inflation target,'' similar to the optimal target criterion for monetary policy in model with lump-sum taxation (Woodford, 2003, chapter 7). It is interesting to note that, as in all of the examples of optimal target criteria for monetary policy derived under varying assumptions in Giannoni and Woodford (2003), it is only the projected rate of change of the output gap that matters for determining the appropriate adjustment of the near-term inflation target; the absolute level of the output gap is irrelevant.
The remaining first-order condition from the previous section,
not used in the derivation of (41), is
(37). By similarly using the solutions for
![]() implied by observations
of
implied by observations
of
![]() to
substitute for the multipliers in this condition, one obtains a
further target criterion
to
substitute for the multipliers in this condition, one obtains a
further target criterion
(Note that the fact that this always holds in the optimal equilibrium -- i.e., that the price level must follow a random walk -- has already been noted in the previous section.) We show in the appendix that policies that ensure that (41) - (42) hold for all
Moreover, this equilibrium solves the above first-order
conditions for a particular specification of the initial lagged
multipliers
![]() , which are
inferred from the initial values
, which are
inferred from the initial values
![]() in the way just explained.
Hence this equilibrium minimizes expected discounted losses
(20) given
in the way just explained.
Hence this equilibrium minimizes expected discounted losses
(20) given
![]() and
subject to constraints on initial outcomes of the form
and
subject to constraints on initial outcomes of the form
Furthermore, these constraints are self-consistent in the sense that the equilibrium that solves this problem is one in which
We have established a pair of target criteria with the property that if they are expected to be jointly satisfied each period, the resulting equilibrium involves the optimal responses to shocks. This result in itself, however, does not establish which policy instrument should be used to ensure satisfaction of which criterion. Since the variables referred to in both criteria can be affected by both monetary and fiscal policy, there is not a uniquely appropriate answer to that question. However, the following represents a relatively simple example of a way in which such a regime could be institutionalized through separate targeting procedures on the part of monetary and fiscal authorities.
Let the central bank be assigned the task of maximizing social
welfare through its adjustment of the level of short-term interest
rates, taking as given the
state-contingent evolution of the public debt
![]() , which
depends on the decisions of the fiscal authority. Thus the central
bank treats the evolution of the public debt as being outside its
control, just like the exogenous disturbances
, which
depends on the decisions of the fiscal authority. Thus the central
bank treats the evolution of the public debt as being outside its
control, just like the exogenous disturbances
![]() and
simply seeks to forecast its evolution in order to correctly model
the constraints on its own policy. Here we do not propose a regime
under which it is actually true that
the evolution of the public debt would be unaffected by a change in
monetary policy. But there is no inconsistency in the central
bank's assumption (since a given bounded process
and
simply seeks to forecast its evolution in order to correctly model
the constraints on its own policy. Here we do not propose a regime
under which it is actually true that
the evolution of the public debt would be unaffected by a change in
monetary policy. But there is no inconsistency in the central
bank's assumption (since a given bounded process
![]() will
continue to represent a feasible fiscal
policy regardless of the policy adopted by the central bank), and
we shall show that the conduct of policy under this assumption does
not lead to a suboptimal outcome, as long as the state-contingent
evolution of the public debt is correctly forecasted by the central
bank.
will
continue to represent a feasible fiscal
policy regardless of the policy adopted by the central bank), and
we shall show that the conduct of policy under this assumption does
not lead to a suboptimal outcome, as long as the state-contingent
evolution of the public debt is correctly forecasted by the central
bank.
The central bank then seeks to bring about paths for
![]() from date
from date
![]() onward that
minimize (20), subject to the constraints
(23) and (25) for
each
onward that
minimize (20), subject to the constraints
(23) and (25) for
each
![]() , together
with initial constraints of the form (43) - (44), given the
evolution of the processes
, together
with initial constraints of the form (43) - (44), given the
evolution of the processes
![]() . The
first-order conditions for this optimization problem are given by
(34), (35) and
(37) each period, which in turn imply that
(41) must hold each period, as shown above.
One can further show that a commitment by the central bank to
ensure that (41) holds each period determines
the equilibrium evolution that solves this problem, in the case of
an appropriate (self-consistent) choice of the initial constraints
(43) - (44).
Thus (41) is an optimal target criterion for a
policy authority seeking to solve the kind of problem just posed;
and since the problem takes as given the evolution of the public
debt, it is obviously a more suitable assignment for the central
bank than for the fiscal authority. The kind of interest-rate
reaction function that can be used to implement a ``flexible
inflation target'' of this kind is discussed in Svensson and
Woodford (2003) and Woodford (2003, chapter 7).
. The
first-order conditions for this optimization problem are given by
(34), (35) and
(37) each period, which in turn imply that
(41) must hold each period, as shown above.
One can further show that a commitment by the central bank to
ensure that (41) holds each period determines
the equilibrium evolution that solves this problem, in the case of
an appropriate (self-consistent) choice of the initial constraints
(43) - (44).
Thus (41) is an optimal target criterion for a
policy authority seeking to solve the kind of problem just posed;
and since the problem takes as given the evolution of the public
debt, it is obviously a more suitable assignment for the central
bank than for the fiscal authority. The kind of interest-rate
reaction function that can be used to implement a ``flexible
inflation target'' of this kind is discussed in Svensson and
Woodford (2003) and Woodford (2003, chapter 7).
Correspondingly, let the fiscal authority be assigned the task
of choosing the level of government revenue each period that will
maximize social welfare, taking as given the state-contingent
evolution of output ![]() , which it regards as being determined by
monetary policy. (Again, it need not really be the case that the
central bank ensures a particular state-contingent path of output,
regardless of what the fiscal authority does. But again, this
assumption is not inconsistent with our model of the economy, since
it is possible for the central bank to bring about any bounded
process
, which it regards as being determined by
monetary policy. (Again, it need not really be the case that the
central bank ensures a particular state-contingent path of output,
regardless of what the fiscal authority does. But again, this
assumption is not inconsistent with our model of the economy, since
it is possible for the central bank to bring about any bounded
process ![]() that it wishes, regardless of fiscal policy, in the case that
prices are sticky.) If the fiscal authority regards the evolution
of output as outside its control, its objective reduces to the
minimization of
that it wishes, regardless of fiscal policy, in the case that
prices are sticky.) If the fiscal authority regards the evolution
of output as outside its control, its objective reduces to the
minimization of
But this is a possible objective for fiscal policy, given the effects of tax policy on inflation dynamics (when taxes are not lump-sum) indicated by (23).
Forward integration of (23) implies that
Thus what matters about fiscal policy for current inflation determination is the present value of expected tax rates; but this in turn is constrained by the intertemporal solvency condition (25). Using (25) to substitute for the present value of taxes in (46), we obtain a relation of the form
for certain coefficients
The first-order condition for the optimal choice of
![]() is then
simply (42), which we find is indeed a
suitable target criterion for the fiscal authority. The decision
rule implied by this target criterion is seen to be
is then
simply (42), which we find is indeed a
suitable target criterion for the fiscal authority. The decision
rule implied by this target criterion is seen to be
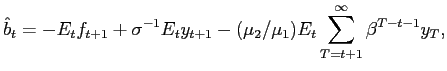
6 Conclusion
We have shown that it is possible to jointly analyze optimal monetary and fiscal policy within a single framework. The two problems, often considered in isolation, turn out to be more closely related than might have been expected. In particular, we find that variations in the level of distorting taxes should be chosen to serve the same objectives as those emphasized in the literature on monetary stabilization policy: stabilization of inflation and of a (properly defined) output gap. A single output gap can be defined that measures the total distortion of the level of economic activity, resulting both from the stickiness of prices (and the consequent variation in markups) and from the supply-side effects of tax distortions. It is this cumulative gap that one wishes to stabilize, rather than the individual components resulting from the two sources; and both monetary policy and tax policy can be used to affect it. Both monetary policy and tax policy also matter for inflation determination in our model, because of the effects of the tax rate on real marginal cost and hence on the aggregate-supply relation. Indeed, we have exhibited a pair of robustly optimal targeting rules for the monetary and fiscal authorities respectively, under which both authorities consider the consequences of their actions for near-term inflation projections in determining how to adjust their instruments.
And not only should the fiscal authority use tax policy to serve the traditional goals of monetary stabilization policy; we also find that the monetary authority should take account of the consequences of its actions for the government budget. In the present model, that abstracts entirely from transactions frictions, these consequences have solely to do with the implications of alternative price-level and interest-rate paths for the real burden of interest payments on the public debt, and not any contribution of seignorage to government revenues. Nonetheless, under a calibration of our model that assumes a debt burden and a level of distorting taxes that would not be unusual for an advanced industrial economy, taking account of the existence of a positive shadow value of additional government revenue (owing to the non-existence of lump-sum taxes) makes a material difference for the quantitative characterization of optimal monetary policy. In fact, we have found that the crucial summary statistic that indicates the degree to which various types of real disturbances should be allowed to affect short-run projections for either inflation or the output gap is not the degree to which these disturbances shift the aggregate-supply curve for a given tax rate (i.e., the extent to which they represent ``cost-push'' shocks), but rather the degree to which they create fiscal stress (shift the intertemporal government solvency condition).
Our conclusion that monetary policy should take account of the requirements for government solvency does not imply anything as strong as the result of Chari and Kehoe (1999) for a flexible-price economy with nominal government debt, according to which surprise variations in the inflation rate should be used to completely offset variations in fiscal stress, so that tax rates need not vary (other than as necessary to stabilize the output gap). We find that in the case of even a modest degree of price stickiness -- much less than what seems to be consistent with empirical evidence for the U.S. -- it is not optimal for inflation to respond to variations in fiscal stress by more than a tiny fraction of the amount that would be required to eliminate the fiscal stress (and that would be optimal with fully flexible prices); instead, a substantial part of the adjustment should come through a change in the tax rate. But the way in which the acceptable short-run inflation projection should be affected by variations in the projected output gap is substantially different in an economy with only distorting taxes than would be the case in the presence of lump-sum taxation. For with distorting taxes, the available tradeoff between variations in inflation and in the output gap depends not only on the way these variables are related to one another through the aggregate-supply relation, but also on the way that each of them affects the government budget.
A Appendix
A.1 Derivation of the aggregate-supply relation (equation (11))
In this section, we derive equation (11)
in the main text and we define the variables ![]() and
and ![]() In the Calvo model, a supplier
that changes its price in period
In the Calvo model, a supplier
that changes its price in period ![]() chooses a new price
chooses a new price ![]() to maximize
to maximize
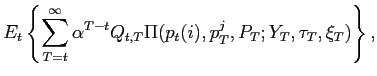
Here Dixit-Stiglitz monopolistic competition implies that the individual supplier faces a demand curve each period of the form
We note that supplier ![]() 's profits are a concave function of the quantity
sold
's profits are a concave function of the quantity
sold ![]() since
revenues are proportional to
since
revenues are proportional to
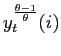 and hence concave
in
and hence concave
in ![]() , while costs
are convex in
, while costs
are convex in ![]() .
Moreover, since
.
Moreover, since ![]() is proportional to
is proportional to
![]() the profit function is also concave in
the profit function is also concave in
![]() .
The first-order condition for the optimal choice of the price
.
The first-order condition for the optimal choice of the price
![]() is the same as
the one with respect to
is the same as
the one with respect to
![]() hence the first-order condition with respect to
hence the first-order condition with respect to ![]() is both necessary and
sufficient for an optimum.
is both necessary and
sufficient for an optimum.
For this first-order condition, we obtain
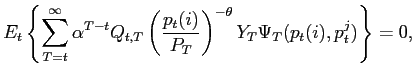
![$\displaystyle \Psi_{T}(p,p^{j})\equiv\left[ (1-\tau_{T})-\frac{\theta}{\theta-1... ...{T}f^{\prime}(f^{-1} (Y_{T}(p/P_{T})^{-\theta}/A_{T}))}}\frac{P_{T}}{p}\right] $](img362.gif)
![$\displaystyle E_{t}\left\{ \sum_{T=t}^{\infty}(\alpha\beta)^{T-t}Q_{t,T}\left( ... ...xi _{T})}{u_{c}(Y_{T};\xi_{T})}}\frac{P_{T}}{p_{t}^{\ast}}\right] \right\} =0. $](img366.gif)
Using the isoelastic functional forms given in the text, we obtain a closed-form solution to (49), given by
where
in which expressions
and where in the function
yields a short-run aggregate-supply relation between inflation and output of the form (11) in the text.
A.2 Recursive formulation of the policy problem
Under the standard (Ramsey) approach to the characterization of
an optimal policy commitment, one chooses among state-contingent
paths
![]() from some
initial date
from some
initial date ![]() onward
that satisfy
onward
that satisfy
where
for each
Here we note that the definition (3) of the index of price dispersion implies the law of motion
which can be written in the form (57); this is the origin of that constraint.
We now show that the ![]() optimal plan (Ramsey problem) can be obtained as
the solution to a two-stage optimization problem. To this purpose,
let
optimal plan (Ramsey problem) can be obtained as
the solution to a two-stage optimization problem. To this purpose,
let
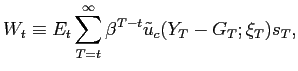
in order for (58) to be satisfied. Thus a specified value for
The two-stage optimization problem is the following. In the
first stage, values of the endogenous variables ![]() , where
, where
![]() ,
and state-contingent commitments
,
and state-contingent commitments
![]() for the following period,
are chosen so as to maximize an objective defined below. In the
second stage, the equilibrium evolution from period
for the following period,
are chosen so as to maximize an objective defined below. In the
second stage, the equilibrium evolution from period ![]() onward is chosen to solve the
maximization problem that defines the value function
onward is chosen to solve the
maximization problem that defines the value function
![]() ,
given the state of the world
,
given the state of the world
![]() and the
precommitted values for
and the
precommitted values for
![]() associated
with that state.
associated
with that state.
In defining the objective for the first stage of this equivalent
formulation of the Ramsey problem, it is useful to let ![]() denote the value of
denote the value of
![]() that solves
(56) for given values of
that solves
(56) for given values of ![]() and
and ![]() , and to let
, and to let ![]() denote the real primary
surplus
denote the real primary
surplus ![]() defined
by (59) in the case of given values of
defined
by (59) in the case of given values of
![]() and
and ![]() . We also define the functional
relationships
. We also define the functional
relationships
Then in the first stage, ![]() and
and
![]() are
chosen so as to maximize
are
chosen so as to maximize
over values of
(i)
![]() and
and
![]() satisfy
(57);
satisfy
(57);
(ii) the values
satisfy
(iii) the value
satisfies (62) for
(iv) the choices
![]() for each possible state of the world
for each possible state of the world
![]() .
.
These constraints imply that the objective
![]() is
well-defined, and that values
is
well-defined, and that values
![]() are chosen for which
the stage two problem will be well-defined, whichever state of the
world is realized in period
are chosen for which
the stage two problem will be well-defined, whichever state of the
world is realized in period ![]() Furthermore, in the case of any stage-one
choices consistent with the above constraints, and any subsequent
evolution consistent with the constraints of the stage-two problem,
(66) implies that (56)
is satisfied in period
Furthermore, in the case of any stage-one
choices consistent with the above constraints, and any subsequent
evolution consistent with the constraints of the stage-two problem,
(66) implies that (56)
is satisfied in period ![]() while (62) implies that
(58) is satisfied in period
while (62) implies that
(58) is satisfied in period ![]() Constraint (i) above implies
that (57) is also satisfied in period
Constraint (i) above implies
that (57) is also satisfied in period
![]() Finally, the
constraints of the stage-two problem imply that both (56), (57) and (58)
are satisfied in each period
Finally, the
constraints of the stage-two problem imply that both (56), (57) and (58)
are satisfied in each period
![]() thus
the state-contingent evolution that solves the two-stage problem is
a rational-expectations equilibrium. Conversely, one can show that
any possible rational-expectations equilibrium satisfies all of
these constraints.
thus
the state-contingent evolution that solves the two-stage problem is
a rational-expectations equilibrium. Conversely, one can show that
any possible rational-expectations equilibrium satisfies all of
these constraints.
One can then reformulate the Ramsey problem, replacing the set
of requirements for rational-expectations equilibrium by the
stage-one constraints plus the stage-two constraints. Since no
aspect of the evolution from period ![]() onward, other than the specification of
onward, other than the specification of
![]() ,
affects the stage-one constraints, the optimization problem
decomposes into the two stages defined above, where the objective
(63) corresponds to the maximization of
,
affects the stage-one constraints, the optimization problem
decomposes into the two stages defined above, where the objective
(63) corresponds to the maximization of
![]() in the first
stage.
in the first
stage.
The optimization problem in stage two of this reformulation of
the Ramsey problem is of the same form as the Ramsey problem
itself, except that there are additional constraints associated
with the precommitted values for the elements of
![]() Let us consider a problem
like the Ramsey problem just defined, looking forward from some
period
Let us consider a problem
like the Ramsey problem just defined, looking forward from some
period ![]() except
under the constraints that the quantities
except
under the constraints that the quantities ![]() must take certain given
values, where
must take certain given
values, where
![]() This constrained problem can similarly be expressed as a two-stage
problem of the same form as above, with an identical stage two
problem to the one described above. The stage one problem is also
identical to stage one of the Ramsey problem, except that now the
plan chosen in stage one must be consistent with the given values
This constrained problem can similarly be expressed as a two-stage
problem of the same form as above, with an identical stage two
problem to the one described above. The stage one problem is also
identical to stage one of the Ramsey problem, except that now the
plan chosen in stage one must be consistent with the given values
![]() so that
conditions (64), (65) and
(67) are now added to the constraints on the
possible choices of
so that
conditions (64), (65) and
(67) are now added to the constraints on the
possible choices of
![]() in stage one. (The
stipulation that
in stage one. (The
stipulation that
![]() implies that the constraint set remains non-empty despite these
additional restrictions.)
implies that the constraint set remains non-empty despite these
additional restrictions.)
Stage two of this constrained problem is thus of exactly the
same form as the problem itself. Hence the constrained problem has
a recursive form. It can be decomposed into an infinite sequence of
problems, in which in each period ![]() ,
,
![]() are chosen to maximize
are chosen to maximize
![]() , given the
predetermined state variables
, given the
predetermined state variables
![]() and the precommitted values
and the precommitted values ![]() subject to the constraints that
subject to the constraints that
(i) ![]() is
given by (66),
is
given by (66), ![]() is then given by (62), and
is then given by (62), and
![]() is given by
(57);
is given by
(57);
(ii) the precommitted values ![]() are fulfilled, i.e.,
are fulfilled, i.e.,
and
(iii) the choices
![]() for each
possible state of the world
for each
possible state of the world ![]() .
.
Our aim in the paper is to provide a local characterization of
policy that solves this recursive optimization, in the event of
small enough disturbances, and initial conditions
![]() that are close enough to consistency with the steady state
characterized in the next section of this appendix.
that are close enough to consistency with the steady state
characterized in the next section of this appendix.
A.3 The deterministic steady state
Here we show the existence of a steady state, i.e., of an optimal policy (under appropriate
initial conditions) of the `recursive policy problem just defined
that involves constant values of all variables. We now consider a
deterministic problem in which the exogenous disturbances
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() each take
constant values
each take
constant values ![]() ,
, ![]() ,
, ![]() ,
,
![]() and
and
![]() for all
for all
![]() , and we
start from initial conditions
, and we
start from initial conditions
![]() . (The value of
. (The value of ![]() is arbitrary, subject to an
upper bound discussed below.) We wish to find an initial degree of
price dispersion
is arbitrary, subject to an
upper bound discussed below.) We wish to find an initial degree of
price dispersion
![]() and
initial commitments
and
initial commitments
![]() such
that the recursive (or ``stage two'') problem involves a constant
policy
such
that the recursive (or ``stage two'') problem involves a constant
policy
![]() ,
,
![]() each
period, in which
each
period, in which ![]() is equal to the initial real debt and
is equal to the initial real debt and
![]() is equal
to the initial price dispersion.
is equal
to the initial price dispersion.
We thus consider the problem of maximizing
subject to the constraints
and given the specified initial conditions
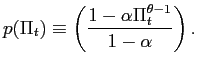
We introduce Lagrange multipliers ![]() through
through ![]() corresponding to constraints (72) through (77) respectively. We
also introduce multipliers dated
corresponding to constraints (72) through (77) respectively. We
also introduce multipliers dated ![]() corresponding to the constraints implied by the
initial conditions
corresponding to the constraints implied by the
initial conditions
![]() ; the
latter multipliers are normalized in such a way that the
first-order conditions take the same form at date
; the
latter multipliers are normalized in such a way that the
first-order conditions take the same form at date ![]() as at all later dates. The
first-order conditions of the maximization problem are then the
following. The one with respect to
as at all later dates. The
first-order conditions of the maximization problem are then the
following. The one with respect to ![]() is
is
that with respect to
that with respect to
that with respect to
that with respect to
that with respect to
that with respect to
and finally, that with respect to
We search for a solution to these first-order conditions in
which
![]()
![]()
![]() ,
,
![]() and
and
![]() at all
times. A steady-state solution of this kind also requires that the
Lagrange multipliers take constant values. We furthermore
conjecture the existence of a solution in which
at all
times. A steady-state solution of this kind also requires that the
Lagrange multipliers take constant values. We furthermore
conjecture the existence of a solution in which
![]() as stated
in the text. Note that such a solution implies that
as stated
in the text. Note that such a solution implies that
![]()
![]()
![]() and
and
![]() . Using
these substitutions, we find that (the steady-state version of)
each of the first-order conditions (78) -
(85) is satisfied if the steady-state values
satisfy
. Using
these substitutions, we find that (the steady-state version of)
each of the first-order conditions (78) -
(85) is satisfied if the steady-state values
satisfy
Similarly, (the steady-state versions of) the constraints (72) - (77) are satisfied if
We have thus verified that a constant solution to the
first-order conditions exists. With a method to be explained below,
we check that this solution is indeed at least a local optimum.
Note that as asserted in the text, this deterministic steady state
involves zero inflation, and a steady-state tax rate
![]()
A.4 A second-order approximation to utility (equations (17) and (18))
We derive here equations (17) and (18) in the main text, taking a second-order approximation to (equation (60)) following the treatment in Woodford (2003, chapter 6). We start by approximating the expected discounted value of the utility of the representative household
First we note that
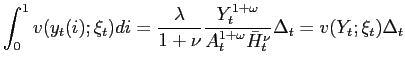
The first term in (89) can be approximated using a second-order Taylor expansion around the steady state defined in the previous section as
where a bar denotes the steady-state value for each variable, a tilde denotes the deviation of the variable from its steady-state value (e.g.,
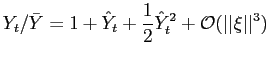
We may similarly approximate
![]() by
by
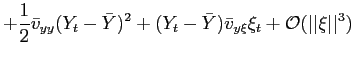
|
||
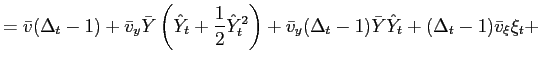
|
||
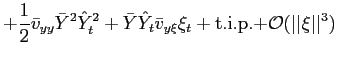
|
||
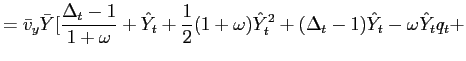
|
||
![$\displaystyle -\frac{\Delta_{t}-1}{1+\omega}\omega q_{t}]+{\mathrm{t.i.p.+}}{{\mathcal{O} }}(\vert\vert\xi\vert\vert^{3}).$](img536.gif)
|
We take a second-order expansion of (61), obtaining
This in turn allows us to approximate
where we have used the steady state relation
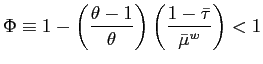
Combining (90) and (92), we finally obtain equation (17) in the text,
where
 |
We finally observe that (91) can be integrated to obtain
By substituting (94) into (93), we obtain
![$\displaystyle =\overline{Y}\bar{u}_{c}\cdot E_{t_{0}}\sum_{t=t_{0}}^{\infty }\b... ...{2}u_{yy}\widehat{Y}_{t} ^{2}+\widehat{Y}_{t}u_{\xi}\xi_{t}-u_{\pi}\pi_{t}^{2}]$](img159.gif)
|
||
This coincides with equation (18) in the text, where we have further defined
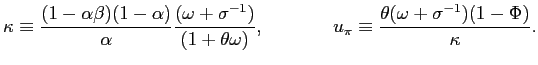
A.5 A second-order approximation to the AS equation (equation (11))
We now compute a second-order approximation to the aggregate supply equation (56), or equation (11) in the main text. We start from (50) that can be written as
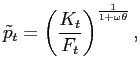
where we define
![$\displaystyle Z_{t}\equiv E_{t}\left\{ \sum_{T=t}^{+\infty}(\alpha\beta)^{T-t} [X_{T}+(1-2\theta-\omega\theta)\hat{P}_{t,T}]\right\} , $](img561.gif)
We next take a second-order expansion of the law of motion (55) for the price index, obtaining
where we have used the fact that
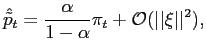
We note further that a second-order approximation to the
identity
![]() yields
yields
and that
where
This can be expressed compactly in the form
where we have defined
![\begin{displaymath} x_{t}\equiv\left[ \begin{array}[c]{c} \hat{\tau}_{t}\ \hat{Y}_{t} \end{array}\right] , \end{displaymath}](img579.gif)
![\begin{displaymath} C_{x}=\left[ \begin{array}[c]{cc} \psi & (1-\sigma^{-1})\psi... ...}(1-s_{C}^{-1} )(\omega+\sigma^{-1})^{-1} \end{array}\right] , \end{displaymath}](img582.gif)
![\begin{displaymath} C_{\xi}=\left[ \begin{array}[c]{ccccc} 0 & 0 & \psi\sigma^{-... ...& \frac{(1+\omega)}{(\omega+\sigma^{-1})} \end{array}\right] , \end{displaymath}](img583.gif)
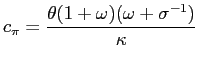
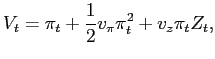
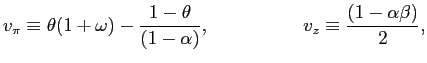
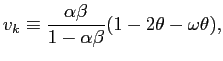
Note that in a first-order approximation, (100) can be written as simply
where
where the term
A.6 A second-order approximation to the intertemporal government solvency condition (equation (15))
We now derive a second-order approximation to the intertemporal government solvency condition. We use the definition
where
and
First, we take a second-order approximation of the term
where we have followed previous definitions and use the isoelastic functional forms assumed and note that we can write
by using previous definitions.
We recall now that the primary surplus is defined as
where we have defined
Substituting (109) into (103), we obtain
where
![\begin{displaymath} B_{x}=\left[ \begin{array}[c]{cc} (1+\omega_{g}) & (1-\sigma... ...1}+\sigma^{-2}-2\sigma^{-1}(1+\omega_{g}) \end{array}\right] , \end{displaymath}](img634.gif)
![\begin{displaymath} B_{\xi}=\left[ \begin{array}[c]{ccccc} 0 & 0 & \sigma^{-1}(1... ...ma^{-1}(\sigma^{-1}-1-\omega_{g}) & 0 & 0 \end{array}\right] , \end{displaymath}](img635.gif)
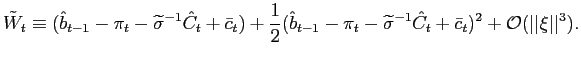
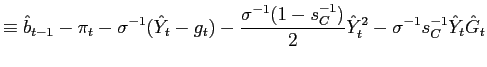
|
||
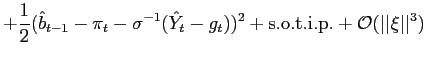
|
which can be written as
![$\displaystyle =\hat{b}_{t-1}-\pi_{t}+w_{x}^{\prime}x_{t}+w_{\xi}^{\prime} \xi_{... ...c{1}{2}[\hat{b}_{t-1}-\pi_{t}+w_{x}^{\prime}x_{t}+w_{\xi}^{\prime}\xi _{t}]^{2}$](img639.gif)
|
||
![\begin{displaymath} W_{x}=\left[ \begin{array}[c]{cc} 0 & 0\ 0 & (s_{C}^{-1}-1)\sigma^{-1} \end{array}\right] , \end{displaymath}](img642.gif)
![\begin{displaymath} W_{\xi}=\left[ \begin{array}[c]{ccccc} 0 & 0 & 0 & 0 & 0\ 0 & -s_{C}^{-1}\sigma^{-1} & 0 & 0 & 0 \end{array}\right] . \end{displaymath}](img643.gif)
Note that in the first-order approximation we can simply write (110) as
Moreover integrating forward (110), we obtain that
where we have moved
A.7 A quadratic policy objective (equations (19) and (20))
We now derive a quadratic approximation to the policy objective
function. To this end, we combine equation (102) and (112) in a way to
eliminate the linear term in (93). Indeed, we
find
![]() such that
such that
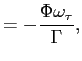 |
||
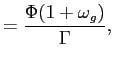 |
where
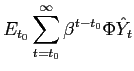
|
![$\displaystyle =E_{t_{0} }\sum_{t=t_{0}}^{\infty}\beta^{t-t_{0}}[\vartheta_{1}b_{x}^{\prime} +\vartheta_{2}c_{x}^{\prime}]x_{t}$](img657.gif)
|
|
![$\displaystyle =-E_{t_{0}}\sum_{t=t_{0}}^{\infty}\beta^{t-t_{0}}[\frac{1}{2}x_{t}^{\prime }D_{x}x_{t}+x_{t}^{\prime}D_{\xi}\xi_{t}+\frac{1}{2}d_{\pi}\pi_{t}^{2}]$](img658.gif)
|
||
where
Hence
In particular, we obtain that
![]() and that
and that
![\begin{displaymath} Q_{x}=\left[ \begin{array}[c]{cc} 0 & 0\ 0 & q_{y} \end{array}\right] , \end{displaymath}](img666.gif)
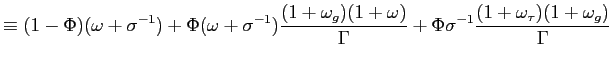
|
||
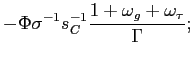
|
moreover we have defined
![\begin{displaymath} Q_{\xi}=\left[ \begin{array}[c]{ccccc} 0 & 0 & 0 & 0 & 0\ ... ...q_{\xi2} & q_{\xi3} & q_{\xi4} & q_{\xi5} \end{array}\right] , \end{displaymath}](img670.gif)
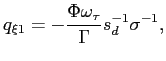
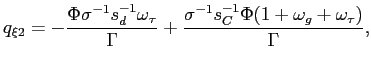
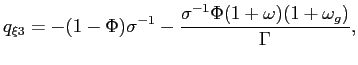
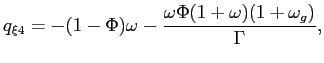
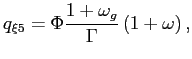
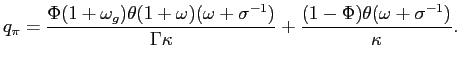
We have further defined
![]() ,
the desired level of output, as
,
the desired level of output, as
It follows that we may rank policies in terms of the implied value of the discounted quadratic loss function (114) which corresponds to equation (20) in the main text. Because this loss function is purely quadratic (i.e., lacking linear terms), it is possible to evaluate it to second order using only a first-order approximation to the equilibrium evolution of inflation and output under a given policy. Hence the log-linear approximate structural relations (101) and (111) are sufficiently accurate for our purposes. Similarly, it suffices that we use log-linear approximations to the variables
Then an optimal policy from a timeless perspective is a policy
from date ![]() onward
that minimizes the quadratic loss function (114) subject to the constraints implied by the linear
structural relations (101) and (111) holding in each period
onward
that minimizes the quadratic loss function (114) subject to the constraints implied by the linear
structural relations (101) and (111) holding in each period
![]() given the
initial values
given the
initial values
![]()
![]() and subject also to the
constraints that certain predetermined values for
and subject also to the
constraints that certain predetermined values for
![]() and
and
![]() (or
alternatively, for
(or
alternatively, for
![]() and for
and for
![]() ) be
achieved.40 We note
that under the assumption that
) be
achieved.40 We note
that under the assumption that
![]() ,
, ![]() ,
which implies that
,
which implies that ![]() . Moreover, if
. Moreover, if
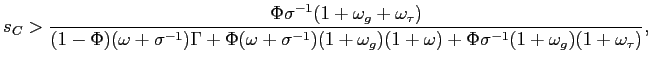
A.8 The log-linear aggregate-supply relation and the cost-push disturbance term
The AS equation (101) can be written as
where
where we have further defined
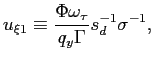
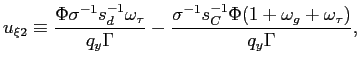
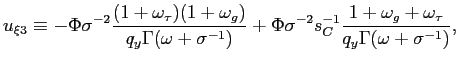
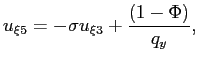
which is equation (23) in the text.
A.9 The log-linear intertemporal solvency condition and the ``fiscal stress'' disturbance term
The flow budget constraint (111) can be solved forward to yield the intertemporal solvency condition
where
![$\displaystyle \equiv\sigma^{-1}(g_{t}-\hat{Y}_{t}^{\ast})-(1-\beta)E_{t}\sum _{... ...b_{y}\hat{Y}_{T}^{\ast}+b_{\tau}\hat{\tau} _{T}^{\ast}+b_{\xi}^{\prime}\xi_{T}]$](img714.gif)
|
||
![$\displaystyle =\sigma^{-1}(g_{t}-\hat{Y}_{t}^{\ast})+(1-\beta)E_{t}\sum_{T=t}^{... ...at{Y}_{T}^{\ast}-(b_{\xi}^{\prime }-b_{\tau}\psi^{-1}c_{\xi}^{\prime})\xi_{T}].$](img715.gif)
|
This can be rewritten in a more compact way as
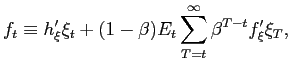
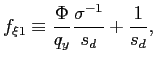
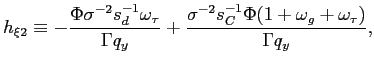
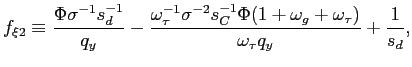
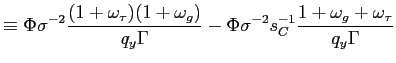
|
||
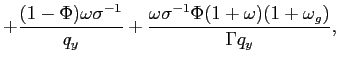
|
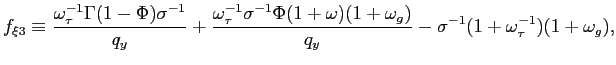
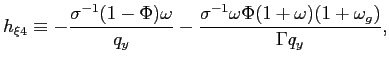
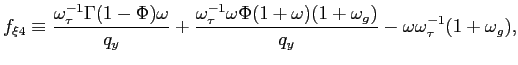
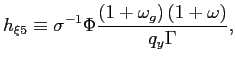
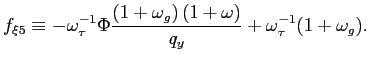
A.10 Definition of the coefficients in sections 3, 4 and 5
The coefficients
![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
,
![]() are
defined as
are
defined as
The coefficients ![]() and
and ![]() of section 5
are defined as
of section 5
are defined as
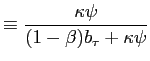
|
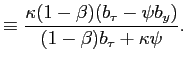
|
A.11 Proof of determinacy of equilibrium under the optimal targeting rules
We now show that there is a determinate equilibrium if policy is conducted so as to ensure that the two target criteria
and
are satisfied in each period
where
Use (119), combined with
and
Then further use (120) to eliminate
![\begin{displaymath} z_{t}\equiv\left[ \begin{array}[c]{l} \pi_{t}\ \pi_{t-1}\\... ...egin{array}[c]{l} 0\ 0\ 0\ n_{41} \end{array}\right] . \end{displaymath}](img767.gif)
Because ![]() is lower
triangular, its eigenvalues are the four diagonal elements: 0, 0,
1, and
is lower
triangular, its eigenvalues are the four diagonal elements: 0, 0,
1, and
![]() Hence
there is exactly one eigenvalue outside the unit circle, and
equilibrium is determinate (but possesses a unit root). Because of
the triangular form of the matrix, one can also easily solve
explicitly for the elements of the left eigenvector
Hence
there is exactly one eigenvalue outside the unit circle, and
equilibrium is determinate (but possesses a unit root). Because of
the triangular form of the matrix, one can also easily solve
explicitly for the elements of the left eigenvector
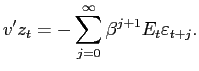
The solution for
References
[1] Aiyagari, S. Rao, Albert Marcet, Thomas Sargent, and Juha Seppala (2002), `` Optimal Taxation without State-Contingent Debt, '' Journal of Political Economy.
[2] Barro, Robert J. (1979), `` On the Determination of Public Debt,'' Journal of Political Economy 87: 940-971.
[3] Benigno, Pierpaolo, and Michael Woodford (2003), `` Inflation Stabilization and Welfare: The Case of Large Distortions,'' in preparation.
[4] Bohn, Henning (1990), `` Tax Smoothing with Financial Instruments,'' American Economic Review 80: 1217-1230.
[5] Chari, V.V., Lawrence Christiano J., and Patrick Kehoe (1991), `` Optimal Fiscal and Monetary Policy: Some Recent Results,'' Journal of Money, Credit, and Banking 23: 519-539.
[6] Chari, V.V., Lawrence Christiano J., and Patrick Kehoe, (1994) `` Optimal Fiscal Policy in a Business Cycle Model, '' Journal of Political Economy 102: 617-652.
[7] Chari, V.V., and Patrick J. Kehoe (1999), `` Optimal Fiscal and Monetary Policy,'' in J.B. Taylor and M. Woodford, eds., Handbook of Macroeconomics, vol. 1C, North-Holland.
[8] Clarida, Richard, Jordi Gali, and Mark Gertler (1999), `` The Science of Monetary Policy: a New Keynesian Perspective,'' Journal of Economic Literature, 37 (4), pp. 1661-1707
[9] Correia, Isabel, Juan Pablo Nicolini and Pedro Teles (2001), `` Optimal Fiscal and Monetary Policy: Equivalence Results,'' unpublished manuscript, Bank of Portugal.
[10] Friedman, Milton (1969),`` The Optimum Quantity of Money,'' in The Optimum Quantity of Money and Other Essays, Chicago: Aldine.
[11] Giannoni, Marc, and Michael Woodford (2002), `` Optimal Interest-Rate Rules: I. General Theory,'' NBER working paper no. 9419, December.
[12] Giannoni, Marc, and Michael Woodford (2003), `` Optimal Inflation Targeting Rules,'' in B.S. Bernanke and M. Woodford, eds., Inflation Targeting, Chicago: University of Chicago Press, forthcoming.
[13] Hall, George, and Stefan Krieger (2000), `` The Tax Smoothing Implications of the Federal Debt Paydown,'' Brookings Papers on Economic Activity 2: 253-301.
[14] Khan, Aubhik, Robert G. King, and Alexander L. Wolman (2002), `` Optimal Monetary Policy,'' NBER working paper no. 9402, December.
[15] Lucas, Robert E., Jr., and Nancy L. Stokey (1983), `` Optimal Fiscal and Monetary Policy in an Economy without Capital,'' Journal of Monetary Economics 12: 55-93.
[16] Rotemberg, Julio J., and Michael Woodford (1997), `` An Optimization-Based Econometric Framework for the Evaluation of Monetary Policy'', in B.S. Bernanke and Rotemberg (eds.), NBER Macroeconomic Annual 1997, Cambridge, MA: MIT Press. 297-346.
[17] Sbordone, Argia M. (2002), `` Prices and Unit Labor Costs: A New Test of Price Stickiness,'' Journal of Monetary Economics 49: 265-292.
[18] Schmitt-Grohé, Stephanie, and Martin Uribe (2001), `` Optimal Fiscal and Monetary Policy under Sticky prices,'' Rutgers University working paper no. 2001-06, June.
[19] Siu, Henry E. (2001), `` Optimal Fiscal and Monetary Policy with Sticky Prices,'' unpublished manuscript, Northwestern University, November.
[20] Svensson, Lars E.O. (1999), `` Inflation Targeting as a Monetary Policy Rule,'' Journal of Monetary Economics 43: 607-654.
[21] Svensson, Lars E.O. (2003), `` What Is Wrong with Taylor Rules? Using Judgment in Monetary Policy through Targeting Rules,'' Journal of Economic Literature, forthcoming.
[22] Svensson, Lars E.O., and Michael Woodford (2003), `` Implementing Optimal Policy through Inflation-Forecast Targeting,'' in B.S. Bernanke and M. Woodford, eds., Inflation Targeting, Chicago: University of Chicago Press, forthcoming.
[23] Woodford, Michael (1999), `` Commentary: How Should Monetary Policy Be Conducted in an Era of Price Stability?'' in Federal Reserve Bank of Kansas City, New Challenges for Monetary Policy.
[24] Woodford, Michael (2001), `` Fiscal Requirements for Price Stability,'' Journal of Money, Credit and Banking 33: 669-728.
[25] Woodford, Michael (2003), Interest and Prices: Foundations of a Theory of Monetary Policy, Princeton: Princeton University Press.
Footnotes
1. Published in Mark Gertler and Kenneth Rogoff, eds., NBER Macroeconomics Annual 2003, Cambridge: MIT Press, http://mitpress.mit.edu. Reprinted with permission of The MIT Press. We would like to thank Stefania Albanesi, Marios Angeletos, Albert Marcet, Ramon Marimon, seminar participants at New York University, Rutgers University, Universitat Pompeu Fabra, the NBER Macroeconomics Annual conference, and the editors for helpful comments, Brad Strum and Vasco Curdia for research assistance, and the National Science Foundation for research support through a grant to the NBER. Return to text
2. We might alternatively assume specialization across households in the type of labor supplied; in the presence of perfect sharing of labor income risk across households, household decisions regarding consumption and labor supply would all be as assumed here. Return to text
3. The government is assumed to need
to obtain an exogenously given quantity of the Dixit-Stiglitz
aggregate each period, and to obtain this in a cost-minimizing
fashion. Hence the government allocates its purchases across the
suppliers of differentiated goods in the same proportion as do
households, and the index of aggregate demand ![]() is the same function of the
individual quantities
is the same function of the
individual quantities
![]() as
as
![]() is of the
individual quantities consumed
is of the
individual quantities consumed
![]() , defined
in (2). Return to
text
, defined
in (2). Return to
text
4. In the case that we assume that
![]() at all
times, our model is one in which both households and firms are
wage-takers, or there is efficient contracting between
them. Return to text
at all
times, our model is one in which both households and firms are
wage-takers, or there is efficient contracting between
them. Return to text
5. The disturbance vector
![]() is now
understood to include the current value of the wage markup
is now
understood to include the current value of the wage markup
![]() Return to
text
Return to
text
6. For discussion of how this is possible even in a ``cashless'' economy of the kind assumed here, see Woodford (2003, chapter 2). Return to text
7. This can be shown to be true in
the case of small enough disturbances, given that the nominal
interest rate is equal to
![]() under the optimal policy in
the absence of disturbances. Return to
text
under the optimal policy in
the absence of disturbances. Return to
text
8. See Woodford (2003, chapter 2) for derivation of this condition from household optimization together with market clearing. The condition should not be interpreted as an a priori constraint on possible government policy rules, as discussed in Woodford (2001). However, when we consider the problem of choosing an optimal plan from the among the possible rational-expectations equilibria, this condition must be imposed among the constraints on the set of equilibria that one may hope to bring about. Return to text
9. In our notation for the value
function ![]()
![]() denotes not
simply the vector of disturbances in period
denotes not
simply the vector of disturbances in period ![]() , but all information in period
, but all information in period
![]() about current and
future disturbances. This corresponds to the disturbance vector
about current and
future disturbances. This corresponds to the disturbance vector
![]() referred to
earlier in the case that the disturbance vector follows a Markov
process. Return to text
referred to
earlier in the case that the disturbance vector follows a Markov
process. Return to text
10. See also Woodford (1999) and Giannoni and Woodford (2002). Return to text
11. For example, in the case of
positive initial nominal government debt, the ![]() optimal policy would involve a
large inflation in period
optimal policy would involve a
large inflation in period ![]() in order to reduce the pre-existing debt
burden, but a commitment not to respond similarly to the existence
of nominal government debt in later periods. Return to text
in order to reduce the pre-existing debt
burden, but a commitment not to respond similarly to the existence
of nominal government debt in later periods. Return to text
12. Local approximations of the same
sort are often used in the literature in numerical
characterizations of Ramsey policy. Strictly speaking, however,
such approximations are valid only in the case of initial
commitments ![]() near enough to the steady-state values of these variables, and the
near enough to the steady-state values of these variables, and the
![]() optimal (Ramsey)
policy need not involve values of
optimal (Ramsey)
policy need not involve values of ![]() near the steady-state values, even in the
absence of random disturbances. Return
to text
near the steady-state values, even in the
absence of random disturbances. Return
to text
13. Benigno and Woodford (2003)
gives an example of an application in which Ramsey policy does
converge asymptotically to the steady state, so that the solution
to the approximate problem approximates the response to small
shocks under the Ramsey policy, at dates long enough after
![]() . We cannot make a
similar claim in the present application, however, because of the
unit root in the dynamics associated with optimal
policy. Return to text
. We cannot make a
similar claim in the present application, however, because of the
unit root in the dynamics associated with optimal
policy. Return to text
14. Note that we may assign
arbitrary positive values to
![]() without changing the nature of the implied preferences, as long as
the value of
without changing the nature of the implied preferences, as long as
the value of ![]() is
appropriately adjusted. Return to
text
is
appropriately adjusted. Return to
text
15. Benigno and Woodford (2003) show that these conditions can fail to hold, so that a small amount of arbitrary randomization of policy is welfare-improving, but argue that the conditions under which this occurs in their model are not empirically plausible. Return to text
16. Here the elements of
![]() are assumed to
be
are assumed to
be
![]() and
and
![]() so that a value of zero for this vector corresponds to the
steady-state values of all disturbances. The perturbations
so that a value of zero for this vector corresponds to the
steady-state values of all disturbances. The perturbations
![]() and
and
![]() are not
defined to be logarithmic so that we do not have to assume positive
steady-state values for these variables. Return to text
are not
defined to be logarithmic so that we do not have to assume positive
steady-state values for these variables. Return to text
17. See the appendix for details. Our calculations here follow closely those of Woodford (2003, chapter 6) and Benigno and Woodford (2003). Return to text
18. Specifically, we use the
notation
![]() as shorthand
for
as shorthand
for
![]() where in each case hats refer to log deviations from the
steady-state values of the various parameters of the policy
problem. We treat
where in each case hats refer to log deviations from the
steady-state values of the various parameters of the policy
problem. We treat
![]() as an expansion parameter,
rather than
as an expansion parameter,
rather than
![]() because (12) implies that deviations of the
inflation rate from zero of order
because (12) implies that deviations of the
inflation rate from zero of order ![]() only result in deviations in the dispersion
measure
only result in deviations in the dispersion
measure
![]() from one of
order
from one of
order
![]() We are
thus entitled to treat the fluctuations in
We are
thus entitled to treat the fluctuations in
![]() as being
only of second order in our bound on the amplitude of disturbances,
since if this is true at some initial date it will remain true
thereafter. Return to text
as being
only of second order in our bound on the amplitude of disturbances,
since if this is true at some initial date it will remain true
thereafter. Return to text
19. Since we are interested in
providing an approximate characterization of the ``stage two''
policy problem, in which a precommitted value of ![]() appears as a constraint, it is
actually a second-order approximation to that constraint that we
need. However, this latter constraint has the same form as
(15); the difference is only in which
quantities in the relation are taken to have predetermined
values. Return to text
appears as a constraint, it is
actually a second-order approximation to that constraint that we
need. However, this latter constraint has the same form as
(15); the difference is only in which
quantities in the relation are taken to have predetermined
values. Return to text
20. See, e.g., Clarida et al. (1999) or Woodford (2003, chapter 3). Return to text
21. If we restrict attention to
bounded paths for the endogenous variables, then a path satisfies
(25) in each period
![]() if and
only if it satisfies the flow budget constraint (26) in each period. Return to text
if and
only if it satisfies the flow budget constraint (26) in each period. Return to text
22. Note that this preference can be
justified in terms of our model, in the case that ![]() is positive though extremely
small. For there will then be a very small positive value for
is positive though extremely
small. For there will then be a very small positive value for
![]() , implying that
reduction of the expected discounted value of inflation is
preferred to the extent that this does not require any increase in
the expected discounted value of squared output gaps. Return to text
, implying that
reduction of the expected discounted value of inflation is
preferred to the extent that this does not require any increase in
the expected discounted value of squared output gaps. Return to text
23. The result relies upon the fact that the distortions created by the monetary frictions are minimized in the case of a zero opportunity cost of holding money each period, as argued by Friedman (1969). Neither the existence of effects of nominal interest rates on supply costs (so that an interest-rate term should appear in the aggregate-supply relation (29)) nor the contribution of seignorage revenues to the government budget constraint make any difference to the result, since unexpected changes in revenue needs can always be costlessly obtained through unexpected inflation, while any desired shifts in the aggregate-supply relation to offset cost-push shocks can be achieved by varying the tax rate. Return to text
24. A number of authors (e.g., Chari et al., 1991, 1994; Hall and Krieger, 2000; Aiyagari et al., 2002) have found that in calibrated flexible-price models with state-contingent government debt, the optimal variation in labor tax rates is quite small. Our results indicate this as well, in the case that real disturbances have only small cost-push effects, and we have listed earlier various conditions under which this will be the case. But under some circumstances, optimal policy may involve substantial volatility of the tax rate, and indeed, more volatility of the tax rate than of inflation. This would be the case if shocks occur that have large cost-push effects while having relatively little effect on fiscal stress. Return to text
25. Alternatively,
![]() is the
multiplier associated with constraint (25). Return to
text
is the
multiplier associated with constraint (25). Return to
text
26. It should be recalled that in
order for policy to be optimal from a timeless perspective, the
state-contingent initial commitment
![]() must
be chosen in a way that conforms to the state-contingent commitment
regarding
must
be chosen in a way that conforms to the state-contingent commitment
regarding ![]() that
will be chosen in all later periods, so that the optimal policy can
be implemented by a time-invariant rule. Hence it is convenient to
present the first-order conditions in a time-invariant
form. Return to text
that
will be chosen in all later periods, so that the optimal policy can
be implemented by a time-invariant rule. Hence it is convenient to
present the first-order conditions in a time-invariant
form. Return to text
27. In the only such solution, the
variables
![]() ,
,
![]() and
and
![]() are all
permanently affected by shocks, even when the disturbances are all
assumed to be stationary (and bounded) processes. Hence a bounded
solution exists only under the assumption that random disturbances
occur only in a finite number of
periods. However, our characterization of optimal policy
does not depend on a particular bound on the number of periods in
which there are disturbances, or which periods these are; in order
to allow disturbances in a larger number of periods, we must assume
a tighter bound on the amplitude of disturbances, in order for the
optimal paths of the endogenous variables to remain within a given
neighborhood of the steady-state values. Aiyagari et al. (2002) discuss the asymptotic behavior of
the optimal plan in the exact nonlinear version of a problem
similar to this one, in the case that disturbances occur
indefinitely. Return to text
are all
permanently affected by shocks, even when the disturbances are all
assumed to be stationary (and bounded) processes. Hence a bounded
solution exists only under the assumption that random disturbances
occur only in a finite number of
periods. However, our characterization of optimal policy
does not depend on a particular bound on the number of periods in
which there are disturbances, or which periods these are; in order
to allow disturbances in a larger number of periods, we must assume
a tighter bound on the amplitude of disturbances, in order for the
optimal paths of the endogenous variables to remain within a given
neighborhood of the steady-state values. Aiyagari et al. (2002) discuss the asymptotic behavior of
the optimal plan in the exact nonlinear version of a problem
similar to this one, in the case that disturbances occur
indefinitely. Return to text
28. The initial condition for
![]() is
in turn chosen so that the solution obtained is consistent with the
initial constraint
is
in turn chosen so that the solution obtained is consistent with the
initial constraint
![]() Under policy that is
optimal from a timeless perspective, this initial commitment is in
turn chosen in a self-consistent fashion, as discussed further in
section 5. Note that the specification of
Under policy that is
optimal from a timeless perspective, this initial commitment is in
turn chosen in a self-consistent fashion, as discussed further in
section 5. Note that the specification of
![]() does not affect our conclusions about the optimal responses to
shocks, emphasized in this section. Return to text
does not affect our conclusions about the optimal responses to
shocks, emphasized in this section. Return to text
29. Schmitt-Grohé and Uribe (2001) similarly observe that in a model with sticky prices, the optimal response of the tax rate is similar to what would be optimal in a flexible-price model with riskless indexed government debt. Return to text
30. In figure 1, a response of 1
means a one percent increase in the value of ![]() from 60 percent to 60.6
percent of a year's GDP. In figure 2, a response of 1 means a one
percent decrease in
from 60 percent to 60.6
percent of a year's GDP. In figure 2, a response of 1 means a one
percent decrease in ![]() , from 20 percent to 20.2 percent. In figure
3, a response of 1 means a one percent per annum increase in the
inflation rate, or an increase of the price level from 1 to 1.0025
over the course of a quarter (given that our model is quarterly).
The responses reported in Table 1 are measured in the same
way. Return to text
, from 20 percent to 20.2 percent. In figure
3, a response of 1 means a one percent per annum increase in the
inflation rate, or an increase of the price level from 1 to 1.0025
over the course of a quarter (given that our model is quarterly).
The responses reported in Table 1 are measured in the same
way. Return to text
31. We have used the relation
between ![]() and
and
![]() for a continuous-time
version of the Calvo model in order to express the degree of price
stickiness in terms of an average time between price
changes. Return to text
for a continuous-time
version of the Calvo model in order to express the degree of price
stickiness in terms of an average time between price
changes. Return to text
32. The indicated average time
between price changes for the baseline case is shorter than that
reported in Rotemberg and Woodford (1997), both because we here
assume a slightly larger value of ![]() implying a smaller value of
implying a smaller value of ![]() and because of the
continuous-time method used here to convert
and because of the
continuous-time method used here to convert ![]() into an implied average time
interval. Return to text
into an implied average time
interval. Return to text
33. The tax rate does respond in the
quarter of the shock in the case of flexible prices, but with the
opposite sign to that associated with optimal policy under our
baseline calibration. Under flexible prices, as discussed above,
the tax rate does not respond to variations in fiscal stress at
all. Because the increase in government transfers raises the
optimal level of output
![]() for
reasons explained in the appendix, the optimal tax rate
for
reasons explained in the appendix, the optimal tax rate
![]() actually falls, in order to induce equilibrium output to increase;
and under flexible prices, this is the optimal response of
actually falls, in order to induce equilibrium output to increase;
and under flexible prices, this is the optimal response of
![]() Return to
text
Return to
text
34. See Benigno and Woodford (2003)
for detailed analysis of the determinants of ![]() and
and
![]() in
this case. Return to text
in
this case. Return to text
35. See Woodford (2003, chapters 7, 8) for further discussion of the self-consistency condition that the initial constraints are required to satisfy. Return to text
36. As stated in the text, in our
notation for the value function ![]()
![]() denotes not simply the vector of disturbances in period
denotes not simply the vector of disturbances in period
![]() , but all information
in period
, but all information
in period ![]() about
current and future disturbances. Return
to text
about
current and future disturbances. Return
to text
37. There is plainly no possibility
of positive supply of output by producers in the case that
![]() in any
period; hence the steady state must involve
in any
period; hence the steady state must involve
![]() Return to
text
Return to
text
38. This is true for any tax rate at
which
![]() exceeds
exceeds
![]() Fixing any value
Fixing any value ![]() our Inada conditions imply that this
inequality holds for all small enough values of
our Inada conditions imply that this
inequality holds for all small enough values of ![]() . And if the inequality holds
for some
. And if the inequality holds
for some ![]() then by continuity it must hold for an
open interval of values of
then by continuity it must hold for an
open interval of values of ![]() Return to
text
Return to
text
39. In fact, there must exist at
least two such solutions, since the Inada conditions also imply
that
![]() for all
for all ![]() close enough to 1. These
multiple solutions correspond to a ``Laffer curve'' result, under
which two distinct tax rates result in the same equilibrium level
of government revenues. We select the lower-tax, higher-output
solution as the one around which we compute our Taylor-series
expansions; this is clearly the higher-utility
solution. Return to text
close enough to 1. These
multiple solutions correspond to a ``Laffer curve'' result, under
which two distinct tax rates result in the same equilibrium level
of government revenues. We select the lower-tax, higher-output
solution as the one around which we compute our Taylor-series
expansions; this is clearly the higher-utility
solution. Return to text
40. The constraint associated with a
predetermined value for ![]() can be neglected, in a first-order
characterization of optimal policy, because the variable
can be neglected, in a first-order
characterization of optimal policy, because the variable
![]() does not appear
in the first-order approximation to the aggregate-supply
relation. Return to text
does not appear
in the first-order approximation to the aggregate-supply
relation. Return to text
This version is optimized for use by screen readers. A printable pdf version is available.
![$\displaystyle U_{t_{0}}\equiv E_{t_{0}}\sum_{t=t_{0}}^{\infty}\beta^{t-t_{0}}\left[ \tilde{u}(C_{t};\xi_{t})-\int_{0}^{1}\tilde{v}(H_{t}(j);\xi_{t})dj\right] ,$](img1.gif)
![$\displaystyle C_{t}\equiv\left[ \int_{0}^{1}c_{t}(i)^{\frac{\theta}{\theta-1}}di\right] ^{\frac{\theta-1}{\theta}},$](img3.gif)
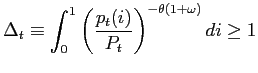
![$\displaystyle P_{t}\equiv\left[ \int_{0}^{1}p_{t}(i)^{1-\theta}di\right] ^{\frac{1} {1-\theta}},$](img26.gif)
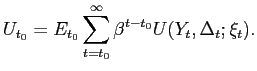
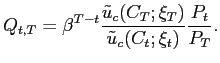
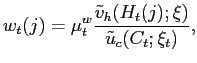
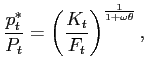
![$\displaystyle P_{t}=\left[ (1-\alpha)p_{t}^{*1-\theta}+\alpha P_{t-1}^{1-\theta}\right] ^{\frac{1}{1-\theta}},$](img53.gif)
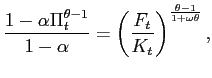
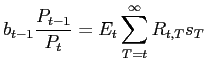
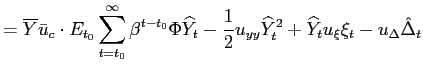
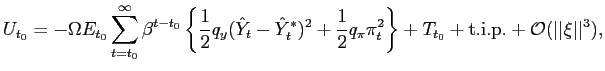
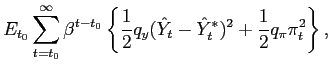
![$\displaystyle \hat{b}_{t-1}-\pi_{t}-\sigma^{-1}y_{t}=-f_{t}\;+(1-\beta)E_{t}\su... ...\infty}\beta^{T-t}[b_{y}y_{T}+b_{\tau}(\hat{\tau}_{T}-\hat{\tau} _{T}^{\ast})],$](img198.gif)
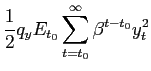
![$\displaystyle =E_{t_{0}}\sum_{t=t_{0}}^{\infty}\beta^{t-t_{0} }\{\frac{1}{2}q_{... ...y_{t}+\psi\hat{\tau}_{t} ]+\varphi_{2t}[({\text{\b{b}}}_{t-1}-\sigma^{-1}y_{t})$](img239.gif)
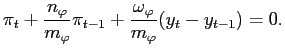
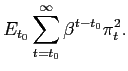
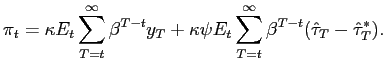
![$\displaystyle \pi_{t}=\mu_{1}[\hat{b}_{t-1}-\sigma^{-1}y_{t}+f_{t}]+\mu_{2}E_{t}\sum _{T=t}^{\infty}\beta^{T-t}y_{T},$](img344.gif)
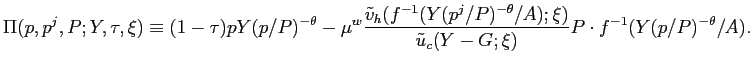
![$\displaystyle E_{t}\left\{ \sum_{T=t}^{\infty}\alpha^{T-t}u_{c}(Y_{T};\xi_{T})\... ...t}^{\ast}/P_{T})^{-\theta};\xi_{T})}{u_{c}(Y_{T};\xi_{T})}}\right] \right\} =0.$](img367.gif)
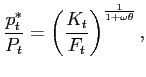
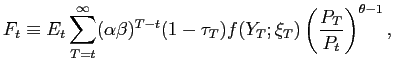
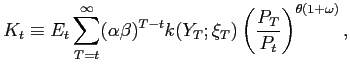
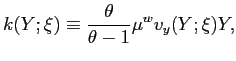
![$\displaystyle P_{t}=\left[ (1-\alpha)p_{t}^{\ast1-\theta}+\alpha P_{t-1}^{1-\theta}\right] ^{\frac{1}{1-\theta}}$](img375.gif)
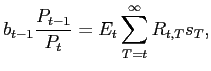
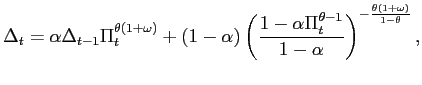
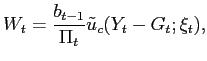
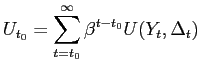
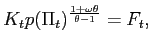
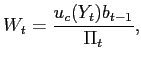
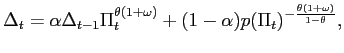
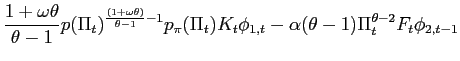
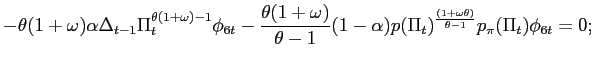
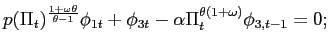
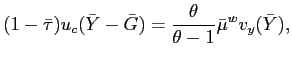
![$\displaystyle U_{t_{0}}=E_{t_{0}}\sum_{t=t_{0}}^{\infty}\beta^{t-t_{0}}\left[ u(Y_{t} ;\xi_{t})-\int_{0}^{1}v(y_{t}(i);\xi_{t})di\right] .$](img502.gif)
![$\displaystyle U_{t_{0}}=E_{t_{0}}\sum_{t=t_{0}}^{\infty}\beta^{t-t_{0}}\left[ u(Y_{t} ;\xi_{t})-v(Y_{t};\xi_{t})\Delta_{t}\right] .$](img504.gif)
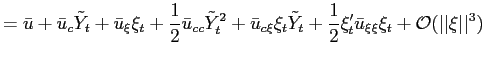
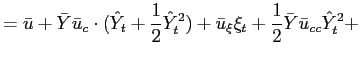
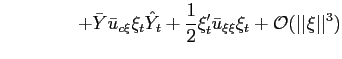
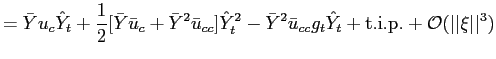
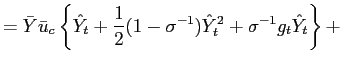
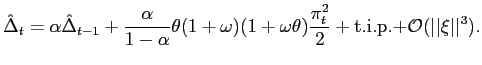
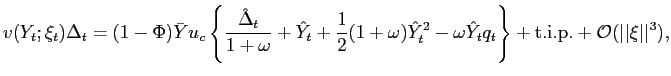
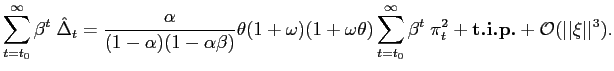
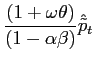
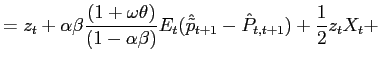
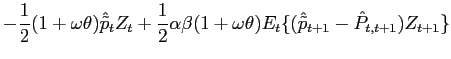
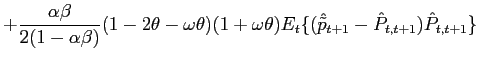
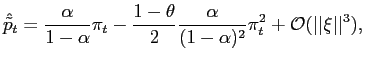
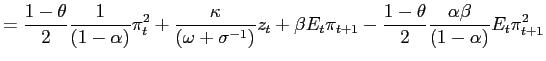
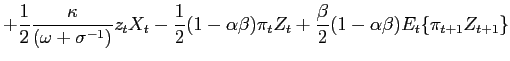
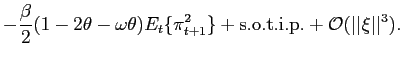
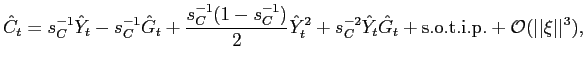
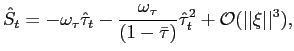
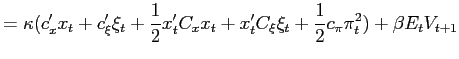
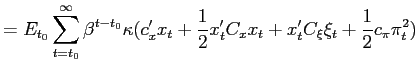
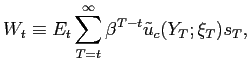
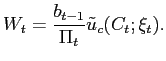
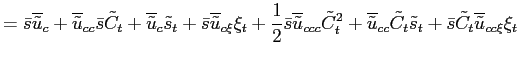
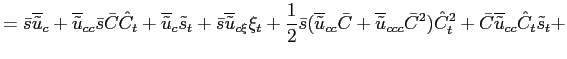
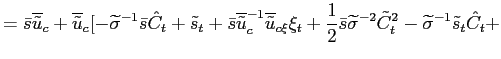
![$\displaystyle =\bar{s}\overline{\tilde{u}}_{c}+\overline{\tilde{u}}_{c}[-\tilde... ...t}(\hat {C}_{t}-\bar{c}_{t})-\tilde{\sigma}^{-2}\bar{s}\bar{c}_{t}\hat{C} _{t}]$](img609.gif)
![$\displaystyle =\bar{s}\overline{\tilde{u}} _{c}[1-\sigma^{-1}\hat{Y}_{t}+\sigma... ...ilde{s}_{t} +\frac{1}{2}[\sigma^{-1}(s_{C}^{-1}-1)+\sigma^{-2}]\hat{Y}_{t}^{2}+$](img613.gif)
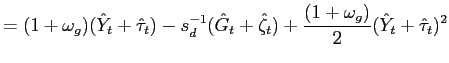
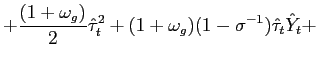
![$\displaystyle +\frac{1}{2}\left[ 1+\omega_{g}+\sigma^{-1}(s_{C}^{-1}-1)+\sigma ^{-2}-2\sigma^{-1}(1+\omega_{g})\right] \hat{Y}_{t}^{2}+$](img625.gif)
![$\displaystyle =(1-\beta)[b_{x}^{\prime}x_{t}+b_{\xi}^{\prime}\xi_{t} +\frac{1}{... ...{t}^{\prime}B_{x}x_{t}+x_{t}^{\prime}B_{\xi}\xi_{t}]+\beta E_{t}\tilde{W}_{t+1}$](img629.gif)
![$\displaystyle \tilde{W}_{t_{0}}=(1-\beta)E_{t_{0}}\sum_{t=t_{0}}^{\infty}\beta^... ...xi_{t}]+{\text{\textbf{t.i.p.}}}+{{\mathcal{O}}}(\vert\vert\xi\vert\vert^{3} ),$](img647.gif)
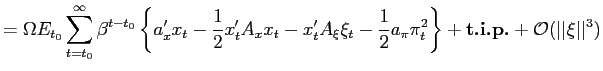
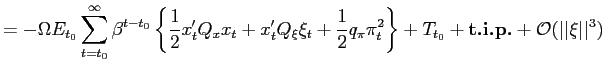
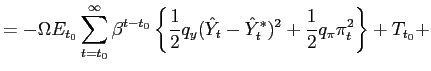
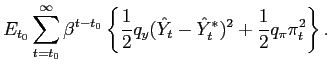
![$\displaystyle \hat{b}_{t-1}-\pi_{t}-\sigma^{-1}y_{t}=-f_{t}\;+(1-\beta)E_{t}\su... ...{\infty}\beta^{T-t}[b_{y}y_{T}+b_{\tau}(\hat{\tau}_{T}-\hat{\tau} _{T}^{\ast})]$](img711.gif)