
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 860, May 2006-Screen Reader Version*
Can the U.S. Monetary Policy Fall (Again) in an Expectation Trap?1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We provide a tractable model to study monetary policy under discretion. We focus on Markov equilibria. For all parametrizations with an equilibrium inflation rate around 2%, there is a second equilibrium with an inflation rate just above 10%. Thus the model can simultaneously account for the low and high inflation episodes in the U.S. We carefully characterize the set of Markov equilibria along the parameter space and find our results to be robust.
Keywords: Time inconsistency, inflation, expectation traps
JEL classification: E31, E52, E58
1 Introduction
After more than 20 years of low inflation in the U.S., the study of past high inflation episodes may not seem a pressing issue. We think otherwise. The high inflation of the 70s was preceded by a decade of low inflation. Can the current record of low inflation also be suddenly reversed? No doubt, monetary policy has gone a long way since the 70s, yet the institutional framework is largely unchanged. Could the possibility of high inflation episodes be an inherent feature of discretionary monetary policy?
The 70s in the U.S. is the classic case study for high inflation episodes in developed economies. The hypothesis that oil shocks were responsible for the high and persistent inflation has long been rejected--see De Long (1997), Bernanke, Gertler and Watson (1997) and references therein. Among other evidence, it has been argued that the take-off of inflation preceded the oil price shocks.
The expectation trap hypothesis conjectures that high inflation during the 70s was the outcome of a shift in private sector beliefs which were then validated by monetary policy. For example, Clarida, Gali and Gertler (2000) argues that monetary policy in the pre-Volcker period was highly accommodative to expected inflation. The authors show that the estimated policy rule for the pre-Volcker period gives rise to sunspot equilibria, as it `` leaves open the possibility of bursts of inflation and output that result from self-fulfilling changes in expectations.''3 Christiano and Gust (2000) also develops a model of `expectation traps,' defined as `` a situation in which an increase in private agents' expectations of inflation pressures the central bank into increasing actual inflation.'' 4 Both papers build on the assumption that monetary policy is given by an exogenous policy rule.
This paper argues instead that monetary policy discretion was responsible for the high U.S. inflation in the 70s. Monetary policy is modelled as the outcome of a benevolent policymaker who is unable to commit. Thus monetary policy is subject to the time inconsistency problem as in Kydland and Prescott (1977) and Barro and Gordon (1983). Without commitment, the optimal monetary policy may be incompatible with rational expectations.
Yet monetary policy discretion can also induce multiple equilibria. We pursue the idea that expectation traps arise from the lack of commitment rather than from the properties of a specific policy rule. This theoretical possibility was first explored by Albanesi, Chari and Christiano (2003) in the context of Markov equilibria, i.e., without resorting to trigger strategies.5
We argue that expectation traps should be considered more than just a theoretical possibility. For this purpose, we introduce a tractable monetary economy for the study of Markov equilibria under full policy discretion.
The main result is our model's quantitative match of the U.S. inflation experience. We calibrate the model to match the average U.S. inflation rate over the period 1983-2004. For all parametrizations with an equilibrium inflation rate between 2% and 2.5%, there is an additional Markov equilibrium with inflation just above 10%. This property of the model is robust and it does not rely upon large nominal frictions.
Our model is tractable enough to provide an insight into the economics of expectation traps. We assume there are some firms that are financially constrained and have to borrow the wage bill in nominal terms. There is also a subset of monopolistic firms which set the nominal price in advance. Monetary policy has a different impact on each type of firm. For financially constrained firms, inflation drives the cost of money up and hinders their productivity. On the other hand, unexpected inflation eases the monopoly distortion by eroding nominal prices.
There is a low inflation equilibrium where the monopoly and financial distortions are balanced. The monetary authority has little to gain from further inflation: any sticky price firms' output expansion is nearly offset by the output loss in the financially constrained sector. In order to have a positive inflation rate in equilibrium, the share of sticky price firms must be larger than the share of financially constrained firms. When the private sector expects high inflation, the situation is vastly different. Since sticky prices are set according to expectations, low actual inflation would imply very high real prices. On the other hand, if high inflation expectations are validated, then the financially constrained firm's decisions will be severely distorted. The monetary authority chooses to validate the high inflation expectations when the sticky price firms predominate over financially constrained firms. Hence, any economy with a 2% equilibrium inflation rate has a high inflation equilibrium as well.
Our model provides a tractable framework to discuss key issues on credibility and monetary policy. For example, Goodfriend (1993) and Goodfriend and King (2005) discuss how, under Paul Volcker's tenure, the Federal Reserve had to respond to `` inflation scares,'' i.e., abrupt changes in the long term inflation expectations. Such a shift in the private sector beliefs is not at odds with rational expectations in our model. Without doubt, the possibility of high and persistent inflation is a first order concern for policymakers.
There is a growing literature on expectation traps due to policy discretion. Yet this paper is the first to put a tractable model to quantitative evaluation. Albanesi et al. (2003), for example, presents a model of limited tractability which does not match the actual U.S. inflation figures. The authors provide three examples with low and high inflation pairs of 38% and 107%, 10% and 217% and 8% and 227%.6
Khan, King and Wolman (2001) also presents an economy with multiple Markov equilibria. However, this model has to be solved by backward induction which complicates the analysis. In a more recent paper, King and Wolman (2004) provides a stylized version of Khan et. al. (2001) but does not pursue a quantitative evaluation of the model. Sui (2004) also explores multiple policy equilibria in an economy where firms can insulate themselves against monetary phenomena. We view our model as performing strongly along the quantitative dimension while being at least as tractable as any other in the field.
The remainder of this paper is as follows. In Section 2 we characterize the private sector equilibrium and in Section 3 we define the concept of Markov equilibrium. Section 4 offers a brief preview of the model's match of the U.S. inflation experience. The monetary authority decision is carefully studied in Section 5. Finally Section 6 explores the set of Markov equilibria, in depth. Section 7 concludes.
2 Private Sector Equilibrium
The infinite-horizon economy is populated by a representative household, a representative final good firm, a continuum of intermediate good firms and a monetary authority.
Figure 1 illustrates the timing of the model. Several of the decisions
relevant for period ![]() are
made one period in advance. First, a fraction of the intermediate
good firms--the sticky price firms indexed by
are
made one period in advance. First, a fraction of the intermediate
good firms--the sticky price firms indexed by ![]() --set their nominal price for
period
--set their nominal price for
period ![]() ,
,
![]() , at the
start of period
, at the
start of period ![]() .
Second, the monetary authority chooses the policy instrument to
maximize the representative household's welfare taking
.
Second, the monetary authority chooses the policy instrument to
maximize the representative household's welfare taking
![]() as given.
Then households choose nominal deposits
as given.
Then households choose nominal deposits ![]() along with consumption
along with consumption![]() and labor
and labor
![]() . On the demand
side of the market for nominal deposits, a subset of financially
constrained firms borrow their wage bill for date
. On the demand
side of the market for nominal deposits, a subset of financially
constrained firms borrow their wage bill for date ![]() . As indicated in Figure 1, date
. As indicated in Figure 1, date
![]() consumption and labor
decisions are made at the end of period
consumption and labor
decisions are made at the end of period ![]() .
.
We assume that the monetary policy instrument is the nominal
interest rate, ![]() ,
that is paid at date
,
that is paid at date ![]() on
nominal deposits carried from period
on
nominal deposits carried from period ![]() . The nominal interest rate is implemented by
intervening in the market for nominal deposits. As shown below,
there is a one-to-one relationship between the nominal interest
rate and the inflation rate at date
. The nominal interest rate is implemented by
intervening in the market for nominal deposits. As shown below,
there is a one-to-one relationship between the nominal interest
rate and the inflation rate at date ![]() ,
,
![]() Hence, we can
think of the inflation rate as the policy instrument.
Hence, we can
think of the inflation rate as the policy instrument.
Before the monetary policy decision, the sticky price firms must
form a belief about inflation in period ![]() , denoted
, denoted
![]() , in order
to set their nominal price
, in order
to set their nominal price
![]() . Following
the literature, we commonly refer to
. Following
the literature, we commonly refer to
![]() as private
sector inflation expectations, although `` beliefs'' would be more
accurate.
as private
sector inflation expectations, although `` beliefs'' would be more
accurate.
We show that real prices and allocations in a private sector
equilibrium at date ![]() are
fully determined by the state of the economy
are
fully determined by the state of the economy
![]() . Neither past
nor future policy decisions are relevant and there is no physical
state variable in the economy. By focusing on Markov perfect
equilibria, we can study the monetary authority's decision as a
sequence of static problems.
. Neither past
nor future policy decisions are relevant and there is no physical
state variable in the economy. By focusing on Markov perfect
equilibria, we can study the monetary authority's decision as a
sequence of static problems.
We do not model money directly. Implicitly, nominal deposits are as good as cash balances. This feature of the model allows us to abstract from money demand considerations and to focus on nominal frictions on the supply side of the economy.7
Figure 1. Timing of Relevant Decisions for Period t

2.1 Households
Household preferences at date ![]() are given by
are given by
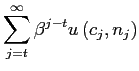
The household's problem at date ![]() is
is
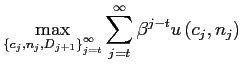 |
(1) |
subject to
| 0 |
and
| (2) |
for all ![]() , where
, where
![]() are nominal
deposits, which pay a nominal interest rate
are nominal
deposits, which pay a nominal interest rate ![]() , and
, and ![]() are profits. Nominal
deposits,
are profits. Nominal
deposits, ![]() , are the
unique asset holdings of the household.
, are the
unique asset holdings of the household.
The intertemporal Euler equation associated with the household's
problem (1) at date
![]() is
is
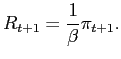
Labor supply is characterized by the first order condition
Neither the level of deposits ![]() nor the price level
nor the price level ![]() appear in the intertemporal
Euler equation and the labor supply condition. Therefore we write
both equilibrium conditions in terms of the economy wide state
appear in the intertemporal
Euler equation and the labor supply condition. Therefore we write
both equilibrium conditions in terms of the economy wide state
![]() .8 First the labor supply condition
.8 First the labor supply condition
| (3) |
As the policy choice for period ![]() is made at period
is made at period ![]() , the relevant pricing equation for the date
, the relevant pricing equation for the date
![]() private sector
equilibrium is given by the household problem at date
private sector
equilibrium is given by the household problem at date ![]() ,
,
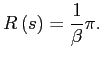 |
(4) |
We will drop the time subscripts for the remaining of the paper
and normalize the last period's aggregate price index to
![]() in order to resolve
the nominal indeterminacy.
in order to resolve
the nominal indeterminacy.
2.2 Firms
There is a representative final good firm which combines a
continuum
![]() of
intermediate inputs,
of
intermediate inputs, ![]() ,
to produce the final good,
,
to produce the final good, ![]() , according to
, according to
![$\displaystyle y\left( s\right) =\left[ \int y_{i}\left( s\right) ^{\eta}di\right] ^{\frac{1}{\eta}}$](img48.gif) |
(5) |
where ![]() . Its
profit-maximization problem is
. Its
profit-maximization problem is
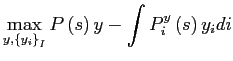
subject to (5).
Hence, the demand for good ![]() is given by
is given by
| (6) |
where
 .
.
There is monopolistic competition in the intermediate good
sector. Each intermediate good is produced by a single firm
![]() according to a simple
linear technology
according to a simple
linear technology
There are three types of intermediate good firms. Let
![]() denote the
measure of firms of type
denote the
measure of firms of type ![]() .
The aggregate measure of intermediate good firms is normalized to
one. We assume that the firms' decisions are symmetric within each
type.
.
The aggregate measure of intermediate good firms is normalized to
one. We assume that the firms' decisions are symmetric within each
type.
Firms of type ![]() --the
sticky price firms--set their nominal prices before the monetary
authority's policy choice. As a consequence, they set the nominal
price,
--the
sticky price firms--set their nominal prices before the monetary
authority's policy choice. As a consequence, they set the nominal
price,
![]() , according to the
private sector inflation expectations
, according to the
private sector inflation expectations ![]() . Given our specification for
the demand for each good
. Given our specification for
the demand for each good ![]() in (6), profit
maximization implies that the nominal price equals a constant
markup over the expected marginal cost
in (6), profit
maximization implies that the nominal price equals a constant
markup over the expected marginal cost
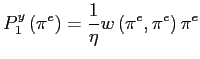 |
(7) |
where
![]() is the nominal
wage consistent with the inflation belief
is the nominal
wage consistent with the inflation belief ![]() .
.
Firms of type ![]() are
flexible price setters, i.e., they set the nominal price,
are
flexible price setters, i.e., they set the nominal price,
![]() , after the monetary
authority's decision. The price is a function of both
, after the monetary
authority's decision. The price is a function of both ![]() and
and ![]() . Firms of type
. Firms of type ![]() are financially constrained and they must borrow the
nominal wage bill
are financially constrained and they must borrow the
nominal wage bill ![]() one
period in advance at the nominal interest rate
one
period in advance at the nominal interest rate
![]() .
Their optimal pricing rule is
.
Their optimal pricing rule is
 |
(8) |
The fact that their marginal cost is augmented by
![]() is
reflected in the real price.
is
reflected in the real price.
Finally, firms of type ![]() are flexible price setters and financially
unconstrained. Therefore we have
are flexible price setters and financially
unconstrained. Therefore we have
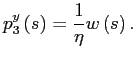 |
(9) |
Note that if the expectation and the actual inflation rate are
the same,
![]() , (7) and (9) imply that
prices and output are the same across sticky and non-financially
constrained flexible price firms, i.e.,
, (7) and (9) imply that
prices and output are the same across sticky and non-financially
constrained flexible price firms, i.e.,
![]() and
and
![]() . Moreover,
if
. Moreover,
if
![]() , all firms' prices and
production are identical. Since the production function for the
final good (5) is
convex, symmetry across firm types is a necessary condition for
production efficiency. In other words,
, all firms' prices and
production are identical. Since the production function for the
final good (5) is
convex, symmetry across firm types is a necessary condition for
production efficiency. In other words,
![]() and
and
![]() introduce costly price distortions.
introduce costly price distortions.
2.3 Market Clearing Conditions and Private Sector Equilibrium Definition
The aggregate resource constraint is
![$\displaystyle c\left( s\right) =\left[ \int n_{i}\left( s\right) ^{\eta}di\right] ^{1/\eta}$](img74.gif) |
(10) |
where (5) has been combined with each intermediate good production technology. The market clearing condition for the labor market is
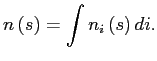 |
(11) |
Equations (3)-(11) are sufficient
to solve for all real prices and allocations as functions of
![]() . We proceed to define a
Private Sector Equilibrium (PSE) given
. We proceed to define a
Private Sector Equilibrium (PSE) given ![]() as a collection of allocation
and price functions and a sticky nominal price
as a collection of allocation
and price functions and a sticky nominal price
![]() .
.
- The household optimality conditions, (3) and (4), are satisfied.
- Firms maximize profits, (7)-(9) are satisfied.
- Markets clear, (6) and (10)-(11) hold.
A Private Sector Equilibrium
outcome in state
![]() is the collection of
allocations and prices which occur at a PSE given
is the collection of
allocations and prices which occur at a PSE given ![]() evaluated at
evaluated at ![]() .
.
Our definition of the PSE is sufficient to characterize the monetary authority's problem. Note that nominal prices, deposits and monetary transfers are not included in the PSE. Now we show how to characterize these variables and why they are not relevant for the monetary authority's problem.
It is straightforward to recover all nominal prices under our
normalization
![]() .
The nominal deposit market clearing condition is
.
The nominal deposit market clearing condition is
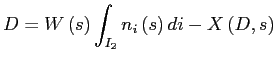 |
(12) |
where
![]() are
monetary transfers by the monetary authority. Note that for any
level of nominal deposits
are
monetary transfers by the monetary authority. Note that for any
level of nominal deposits ![]() and state
and state ![]() ,
there is
,
there is
![]() that clears the nominal deposits market. Hence, for any
that clears the nominal deposits market. Hence, for any
![]() and
and ![]() , the monetary authority can
implement its policy decision in terms of an inflation rate by
setting
, the monetary authority can
implement its policy decision in terms of an inflation rate by
setting
![]() accordingly.
accordingly.
Finally, the household budget constraint (2) gives a law of
motion for nominal deposits,
![]() . Since
. Since
![]() ,
the path for nominal deposits is strictly positive given
,
the path for nominal deposits is strictly positive given
![]() .
.
2.4 Solving for the Private Sector Equilibrium
In our model, the PSE can be solved for analytically. We start
by taking ![]() , a
number, as given. Then we solve for the PSE functions that map the
actual inflation rate
, a
number, as given. Then we solve for the PSE functions that map the
actual inflation rate ![]() into allocations and prices. Using these PSE functions, we can
characterize the sticky price firms decision as function of the
expected inflation rate,
into allocations and prices. Using these PSE functions, we can
characterize the sticky price firms decision as function of the
expected inflation rate,
![]() .
.
From the Fischer equation (4), the nominal interest rate and inflation are simply linked by
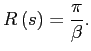
![$\displaystyle \frac{y_{i}\left( s\right) }{y_{j}\left( s\right) }=\left[ \frac ... ...}^{y}\left( s\right) }{p_{i}^{y}\left( s\right) }\right] ^{\frac {1}{1-\eta}}, $](img93.gif)
|
![$\displaystyle =\left[ \frac {1}{\eta}\frac{w\left( s\right) }{p_{1}^{y}\left( s\right) }\right] ^{\frac{1}{1-\eta}},$](img96.gif)
|
|

|
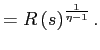 |
These wedges between sectorial production are the result of relative price distortions.
From (5) and the relative quantity relations obtained above, we obtain that
![$\displaystyle y\left( s\right) =y_{3}\left( s\right) \left[ \mu_{3}+\mu_{2}R\le... ...1}^{y}\left( s\right) }\right] ^{\frac{\eta}{1-\eta} }\right] ^{\frac{1}{\eta}}$](img99.gif) |
(13) |
and from (11)
![$\displaystyle n\left( s\right) =y_{3}\left( s\right) \left( \mu_{3}+\mu_{2}R\le... ...left( s\right) }{p_{1}^{y}\left( s\right) }\right] ^{\frac{1}{1-\eta}}\right) .$](img100.gif) |
(14) |
In order to characterize the real wage rate, use the previous expression and combine it with the demand function (6) and pricing equation (9) for goods of type 3
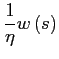 ![$\displaystyle =\left( \mu_{3}+\mu_{2}R\left( s\right) ^{\frac{\eta}{\eta-1}}+\m... ...}\left( s\right) }\right] ^{\frac{\eta}{1-\eta}}\right) ^{\frac{1-\eta}{\eta}},$](img102.gif)
|
||
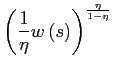 ![$\displaystyle =\mu_{3}+\mu_{2}R\left( s\right) ^{\frac{\eta}{\eta-1}}+\mu_{1}\l... ...ac{w\left( s\right) }{p_{1}^{y}\left( s\right) }\right] ^{\frac{\eta}{1-\eta}},$](img104.gif)
|
||
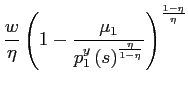 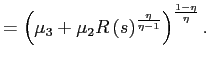
|
Hence, the real wage rate can be solved for
![$\displaystyle w\left( s\right) =\eta\left[ \frac{\mu_{3}+\mu_{2}R\left( s\right... ..._{1}^{y}\left( s\right) ^{\frac{\eta} {\eta-1}}}\right] ^{\frac{1-\eta}{\eta}}.$](img107.gif) |
(15) |
This expression is the key to solve for the PSE. With knowledge
of
![]() , the
rest of equilibrium allocations and prices follow easily. Labor,
, the
rest of equilibrium allocations and prices follow easily. Labor,
![]() , is
given by (3).
Then, combining (13)
with (14),
, is
given by (3).
Then, combining (13)
with (14),
![$\displaystyle \varphi\left( s\right) =\frac{\left[ \mu_{3}+\mu_{2}R\left( s\rig... ...rac{w\left( s\right) }{p_{1}^{y}\left( s\right) }\right] ^{\frac{1}{1-\eta}}}. $](img109.gif)
To close the PSE, we still need to solve for
![]() .
Given an expectation
.
Given an expectation ![]() ,
(7) implies that
,
(7) implies that
![]() will satisfy
will satisfy
![]() .
This allows us to write the real wage as
.
This allows us to write the real wage as
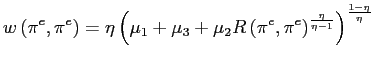
and, using (7) again,
![]() as
as
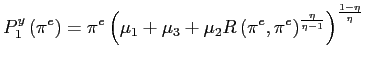 |
(16) |
Note that
![]() is increasing in
is increasing in
![]() .
.
3 Policy Equilibrium
In this section we introduce our policy equilibrium concepts. First, we state the monetary authority's problem and the definition of a Markov equilibrium. We also show that the optimal monetary policy with commitment is the Friedman rule. We provide a simple condition such that the Friedman rule is time inconsistent, i.e., it does not constitute a Markov equilibrium.
3.1 The Monetary Authority Problem and Markov Equilibrium
The monetary authority's problem is to choose the inflation rate
which maximizes household welfare taking nominal prices
![]() as given. Hence the
monetary authority has no ability to manipulate the private sector
inflation expectations.
as given. Hence the
monetary authority has no ability to manipulate the private sector
inflation expectations.
The choice of the inflation rate is constrained as follows.
First, the nominal interest rate is bounded below by one, i.e.,
![]() .
This bound is implied by the arbitrage condition between nominal
bonds and cash balances. The latter are not explicitly modelled
here, yet we can use (4) to establish
that the lower bound for inflation equals the intertemporal
discount rate,
.
This bound is implied by the arbitrage condition between nominal
bonds and cash balances. The latter are not explicitly modelled
here, yet we can use (4) to establish
that the lower bound for inflation equals the intertemporal
discount rate,
![]() .
.
Second, the existence of a PSE outcome also imposes an upper
bound,
![]() , on the inflation
rate. This upper bound is an increasing function of the private
sector inflation expectations. As
, on the inflation
rate. This upper bound is an increasing function of the private
sector inflation expectations. As ![]() approaches the upper bound
approaches the upper bound ![]() , the sticky price firms
have unbounded losses.9
, the sticky price firms
have unbounded losses.9
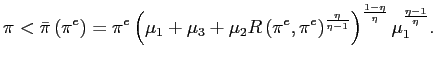
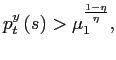
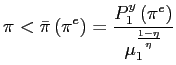
![]()
In the Appendix we show that the policy choice set can be defined without any loss of generality as
Because a PSE outcome fully determines the household period welfare, we can state the monetary authority's problem as an intratemporal optimization problem
| (17) |
where
![]() and
and
![]() belong to a PSE given
belong to a PSE given ![]() . Let
. Let
![]() be the best policy
response function which solves (17) given any
be the best policy
response function which solves (17) given any
![]() .10
.10
All is set for the definition of a Markov equilibrium. The nomenclature emphasizes that equilibria based on trigger strategies are ruled out.
We will say that a policy ![]() is time consistent if there exists a Markov
equilibrium with
is time consistent if there exists a Markov
equilibrium with
![]() . The
definition is for an one-period economy. We will spare the reader
from the corresponding definition for the infinite horizon
economy.
. The
definition is for an one-period economy. We will spare the reader
from the corresponding definition for the infinite horizon
economy.
3.2 Friedman Rule
Optimal monetary policy with commitment can be thought as a
policy equilibrium under an alternative timing. Let the monetary
authority decide once and for all on the inflation rate at the
beginning of period ![]() .
Sticky nominal prices and remaining private sector variables are
then set with the knowledge of the policy decision. Thus the
monetary authority's decision pins down uniquely private sector
inflation expectations.
.
Sticky nominal prices and remaining private sector variables are
then set with the knowledge of the policy decision. Thus the
monetary authority's decision pins down uniquely private sector
inflation expectations.
Not surprisingly, the optimal monetary policy with commitment
turns out to be the Friedman rule. All distortions associated with
price dispersion are zeroed by setting the nominal interest rate to
zero,
![]() .
The distortion that arises from monopoly pricing remains. However,
there is nothing monetary policy can do to curtail the market power
of the intermediate good firms.11 Hence, labor remains
undersupplied.
.
The distortion that arises from monopoly pricing remains. However,
there is nothing monetary policy can do to curtail the market power
of the intermediate good firms.11 Hence, labor remains
undersupplied.
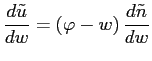
Does the Friedman Rule constitute a Markov Equilibrium? Assume
the private sector believes that the Friedman Rule will be in
place,
![]() , and
sets nominal prices accordingly. Ex-post, the monetary authority
considers to set inflation above expectations
, and
sets nominal prices accordingly. Ex-post, the monetary authority
considers to set inflation above expectations
![]() in
order to cut the markup of the sticky price firms. Such a move
increases price dispersion. The price difference between the sticky
and flexible price firms is welcome as it reflects the improved
efficiency in the sticky price firms sector. However, financially
constrained firms have their marginal cost augmented by
in
order to cut the markup of the sticky price firms. Such a move
increases price dispersion. The price difference between the sticky
and flexible price firms is welcome as it reflects the improved
efficiency in the sticky price firms sector. However, financially
constrained firms have their marginal cost augmented by
![]() .
On the margin, the welfare benefits and losses of inflation are
weighted by the size of the sticky price firm and financially
constrained firm sector respectively.
.
On the margin, the welfare benefits and losses of inflation are
weighted by the size of the sticky price firm and financially
constrained firm sector respectively.
The next Proposition follows from this discussion. It formally shows that the Friedman Rule is not a Markov equilibrium as long as the sticky price firm sector is strictly larger than the sector of financially constrained firms.
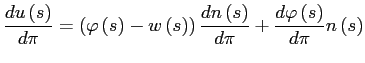
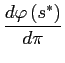 |
where the first two equations result from simple algebra. For the last one, note that
![$ \left[ \int x^{\eta}di\right] ^{\frac{1}{\eta}} \leq\int xdi$](img162.gif) .
From the fact that
.
From the fact that Finally, differentiating (15) and evaluating
at ![]()
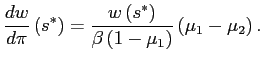
We find that
![]() is
not a sufficient condition to establish the time consistency of the
optimal monetary policy.
is
not a sufficient condition to establish the time consistency of the
optimal monetary policy.
4 A Preview of the Main Result
In this section we briefly preview the model's match of the U.S. inflation experience. Previous studies have focused on the existence of multiple equilibria. Here we take a step forward and ask whether the quantitative results of our model lend support to the expectation trap hypothesis.
To evaluate the model, we first fix all parameters that are not directly related to the monetary policy transmission mechanism. These are the Frisch labor elasticity, the intertemporal discount rate and the elasticity of substitution between intermediate goods. Values for these parameters are readily available in the literature and they are discussed in Section 6. In short, we assume a unit Frisch labor elasticity, an intertemporal discount rate consistent with an annual real interest rate of 3% and an elasticity of substitution implying a 10% markup in the price of intermediate goods.
It remains to pick the share of sticky price firms, ![]() , and financially constrained
firms,
, and financially constrained
firms, ![]() .
These two parameters govern all the nominal frictions in our model.
Unexpected inflation provides a real stimulus by eroding the markup
charged by sticky price firms. On the other side, the cost of
inflation arises from the financial constraints that firms of type
2 face. We calibrate
the composition of the intermediate good sector in order to match
the average U.S. inflation in the period 1984-2004.12
.
These two parameters govern all the nominal frictions in our model.
Unexpected inflation provides a real stimulus by eroding the markup
charged by sticky price firms. On the other side, the cost of
inflation arises from the financial constraints that firms of type
2 face. We calibrate
the composition of the intermediate good sector in order to match
the average U.S. inflation in the period 1984-2004.12
We find that all parametrizations with a Markov equilibrium in
the range of 2 - 2.5% inflation also feature a high inflation equilibrium between 10 % and 11%. This is quite surprising since
there are many pairs
![]() which imply a 2 - 2.5% Markov
equilibrium.
which imply a 2 - 2.5% Markov
equilibrium.
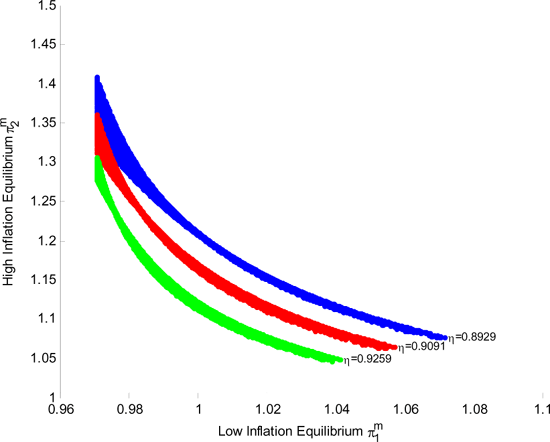
Figure 2. Markov Equilibria: Several Economies
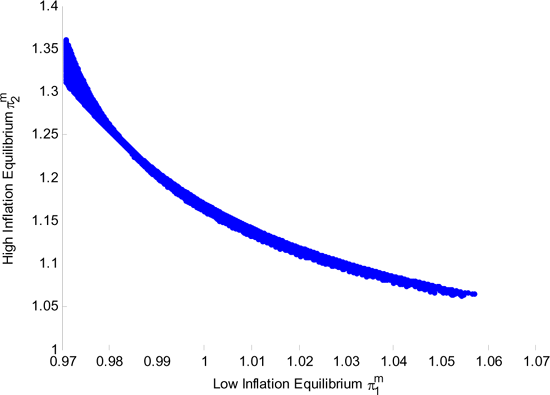
Figure 2
illustrates this noteworthy property of the model. We compute the
Markov equilibria for all feasible pairs
![]() , holding the remaining
parameters constant. For the vast majority of parametrizations
there are two Markov equilibria. In Figure 2 we plot for each
pair
, holding the remaining
parameters constant. For the vast majority of parametrizations
there are two Markov equilibria. In Figure 2 we plot for each
pair
![]() the set of Markov
equilibria as a point in
the set of Markov
equilibria as a point in ![]() . The abscissa is the low inflation equilibrium
and the ordinate is the high inflation equilibrium. The only pairs
. The abscissa is the low inflation equilibrium
and the ordinate is the high inflation equilibrium. The only pairs
![]() not displayed here are
those for which there is no equilibrium or the Friedman rule is
time consistent. Figure 2 makes clear that
the set of Markov equilibria spanned by all pairs is tightly
clustered around a downward sloping locus. We have two degrees of
freedom in
not displayed here are
those for which there is no equilibrium or the Friedman rule is
time consistent. Figure 2 makes clear that
the set of Markov equilibria spanned by all pairs is tightly
clustered around a downward sloping locus. We have two degrees of
freedom in ![]() and
and
![]() , yet the level
of the low inflation equilibrium pins down the high inflation
equilibrium in a very small interval.
, yet the level
of the low inflation equilibrium pins down the high inflation
equilibrium in a very small interval.
In short, when the model is calibrated to match the average inflation in the US over the last 20 years, an additional Markov equilibrium arises around a 10.5% inflation rate--a level consistent with the U.S. high inflation experience in the 70s.
Figure 3. Markov Equilibria for Preferred Calibration
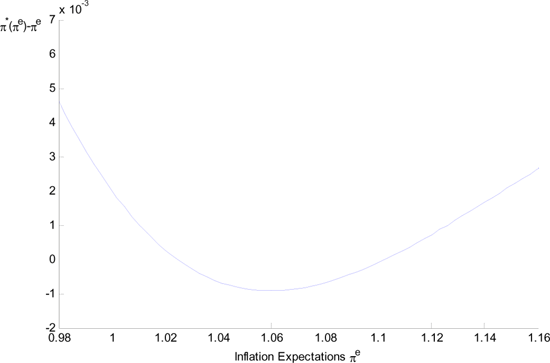
Figure 3
displays the Markov equilibria for our preferred calibration with
![]() and
and
![]() . Private
sector inflation expectations,
. Private
sector inflation expectations, ![]() , are displayed on the horizontal axis. The
solid line plots the difference between the best policy response
and private sector expectations,
, are displayed on the horizontal axis. The
solid line plots the difference between the best policy response
and private sector expectations,
![]() . A Markov
equilibrium is given by
. A Markov
equilibrium is given by
![]() .
.
Our preferred calibration has a low inflation equilibrium at 2.45% and a high inflation equilibrium of 10.25% . We emphasize that there is no need to assume large nominal frictions as in our case less than 20% of the firms are subject to any friction.
Below we want to understand the monetary policy decision and the economics behind the multiplicity of equilibria. Finally Section 6 gets back to the quantitative exercise, details our preferred calibration and explores the robustness of the results.
5 Monetary Policy Decision
This section provides an insight into the monetary policy decision. The economy is simple enough to keep track of the incentives that shape the monetary authority's decision. However the monetary authority's problem is considerably complex. We emphasize the role of high inflation expectations.
We start by discussing the relationship between employment and inflation in the model. Under low inflation expectations, the Phillips curve has the conventional shape: inflation leads to employment gains. However, the Phillips curve can be non-monotone for high inflation expectations. As a result, the nature of the monetary authority's problem changes with the level of inflation expectations.
5.1 The Phillips Curve
We start by studying how allocations depend on the policy choice
![]() . In particular, we
want to characterize the relationship between inflation and labor
demand which forms the basis of the monetary policy transmission
mechanism.
. In particular, we
want to characterize the relationship between inflation and labor
demand which forms the basis of the monetary policy transmission
mechanism.
It is necessary to impose a cap on inflation expectations to prove that labor demand is monotonically increasing with inflation. For inflation expectations below this cap, employment expands as result of additional inflation. This is a classic upward sloping Phillips curve. For high inflation expectations--defined as expectations that exceed the cap--the Phillips curve can be non-monotone.
![$\displaystyle P_{1}^{y}\left( \pi^{e}\right) \leq\bar{P}_{1}^{y}=\beta\left[ \l... ...2}\right) \left( \frac{\mu_{1}}{\mu_{2}}\right) \right] ^{\frac{1-\eta}{\eta}} $](img191.gif)
Recall that
![]() is a strictly
increasing function of the private sector inflation expectations
is a strictly
increasing function of the private sector inflation expectations
![]() . Hence the
condition
. Hence the
condition
![]() is
equivalent to a cap on inflation expectations.
is
equivalent to a cap on inflation expectations.
Figure 4. Inflation and Employment
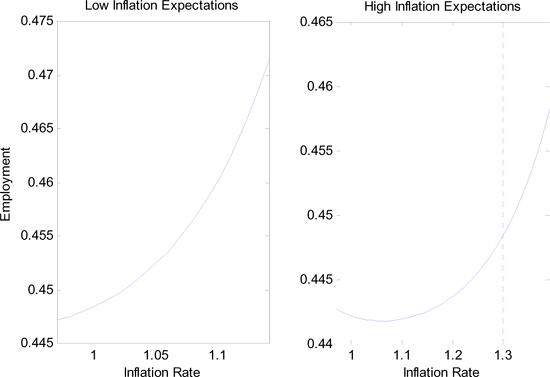
We illustrate the possibility of a non-monotonic Phillips curve
with a numerical example. Figure 4 displays
employment as a function of the inflation rate ![]() for two different inflation
expectations
for two different inflation
expectations ![]() .13 The left
graph corresponds to an expected inflation of 2%, as indicated by the dashed
vertical line. Employment is strictly increasing with
inflation.
.13 The left
graph corresponds to an expected inflation of 2%, as indicated by the dashed
vertical line. Employment is strictly increasing with
inflation.
The right graph in Figure 4 corresponds to high inflation expectations, around 30%. The relationship between employment and inflation is not monotone. For any inflation rate below 8%, more inflation actually reduces employment. The Phillips curve has the ``wrong'' shape only when inflation is clearly below inflation expectations but it looks standard elsewhere.
Figure 5. Inflation and Firm i = 1, 2 Output
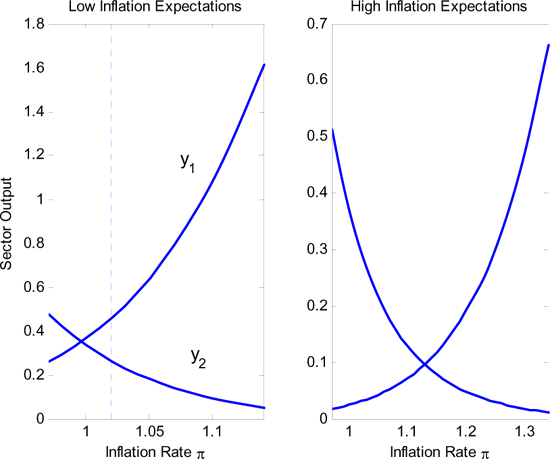
Figure 5 shows
the output for sticky price firms, ![]() , and financially constrained firms,
, and financially constrained firms, ![]() , as function of the inflation
rate for inflation expectations of 2% and 30%.
The output of the sticky price firms is strictly increasing in the
inflation rate as their relative price decreases with inflation.
The output of the financially constrained firms decreases as
inflation augments their marginal cost through a higher nominal
interest rate. It is easy to see why the welfare benefits and costs
of inflation arise from the output response of sticky price and
financially constrained firm respectively.
, as function of the inflation
rate for inflation expectations of 2% and 30%.
The output of the sticky price firms is strictly increasing in the
inflation rate as their relative price decreases with inflation.
The output of the financially constrained firms decreases as
inflation augments their marginal cost through a higher nominal
interest rate. It is easy to see why the welfare benefits and costs
of inflation arise from the output response of sticky price and
financially constrained firm respectively.
The left panel in Figure 5 depicts the case of low inflation expectations. Around the expected inflation rate, inflation displaces production from financially constrained firms to sticky price firms. The monetary authority may still do some fine tuning, shifting the distortion--and hence employment--from one sector to the other to achieve greater efficiency.
The right graph in Figure 5 makes clear that
high inflation expectations deliver a different scenario.
Validating the inflation expectations hurts the financially
constrained sector: the output of financially constrained firms
![]() is close to
0 at
is close to
0 at
![]() . Low
inflation can restore the financially constrained firm sector close
to efficient levels but this comes at the cost of depressing the
sticky price firm sector. Rather than fine tuning, the monetary
authority problem resembles a `` pick-your-poison'' decision.
. Low
inflation can restore the financially constrained firm sector close
to efficient levels but this comes at the cost of depressing the
sticky price firm sector. Rather than fine tuning, the monetary
authority problem resembles a `` pick-your-poison'' decision.
The non-montone Phillips curve arises because, in a severely distorted sector, output reacts very little to additional inflation. For example, increasing inflation from 2% to 4% has a large negative impact on the output of financially constrained firms. However, output of sticky price firms barely improves and there is an aggregate employment loss.
5.2 Under Low Inflation Expectations: Fine Tuning
We further discuss the monetary authority's problem when
inflation expectations are low, i.e.,
![]() as
given by Proposition 6. We have
previously argued that in this case the monetary policy decision is
one of fine tuning. In line with this argument, we only need a mild
technical assumption to show that the first order condition of the
monetary authority problem (17) is sufficient
to characterize the best policy response function
as
given by Proposition 6. We have
previously argued that in this case the monetary policy decision is
one of fine tuning. In line with this argument, we only need a mild
technical assumption to show that the first order condition of the
monetary authority problem (17) is sufficient
to characterize the best policy response function
![]() .
.
Proposition 7 Consider a PSE with
![]() .
Let
.
Let
![]() be the final good
production associated with
be the final good
production associated with ![]() such that
such that
![]() .
Then
.
Then
![]() is a differentiable
function. Moreover, if
is a differentiable
function. Moreover, if
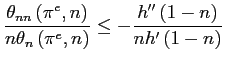 |
(18) |
for all ![]() , then the
first order condition of the monetary authority problem is
sufficient to characterize
, then the
first order condition of the monetary authority problem is
sufficient to characterize
![]() . Moreover,
. Moreover,
![]() is
continuous.
is
continuous.
While the set of first best allocations is convex given standard
assumptions on technology, similar conditions for the convexity of
the set of second best allocations are restrictive and often
without of interpretation. The condition (18) is weaker than
the convexity of the aggregate resource set spanned by monetary
policy. If the aggregate resource set is indeed convex,
![]() , the
first order condition is sufficient because
, the
first order condition is sufficient because ![]() is a concave function. Quite
interestingly, (3)
implies that the RHS of (18) is the inverse
of the Frisch labor supply elasticity. The labor literature has
reported very low estimates for the Frisch labor supply elasticity,
between 0 and 0.25. Hence (18) does not seem
to be a strong restriction. In our preferred calibration the Frisch
labor supply elasticity is one, yet condition (18) is
satisfied.
is a concave function. Quite
interestingly, (3)
implies that the RHS of (18) is the inverse
of the Frisch labor supply elasticity. The labor literature has
reported very low estimates for the Frisch labor supply elasticity,
between 0 and 0.25. Hence (18) does not seem
to be a strong restriction. In our preferred calibration the Frisch
labor supply elasticity is one, yet condition (18) is
satisfied.
As long as inflation expectations are low, Proposition 7 asserts it is safe to explore the monetary policy decision on the margin. In the Appendix, we include a discussion of the first order condition associated with (17). We show that it can be rewritten as
 |
(19) |
where

The sufficiency of the first order condition (19) also implies that the monetary authority's problem can be studied with a quadratic approximation. We emphasize that a quadratic approximation is safe only as long as inflation expectations are low.
Figure 6. Allocations and Welfare Under Inflation Expectation ![]()
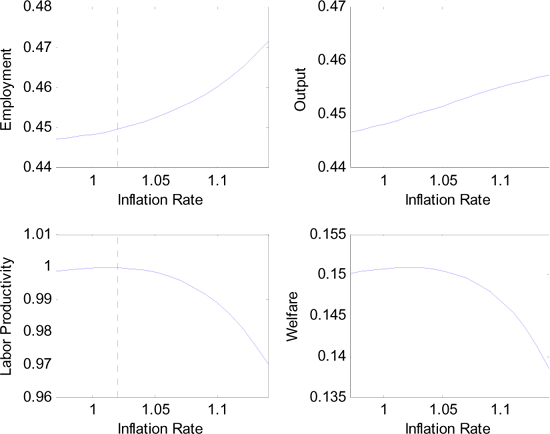
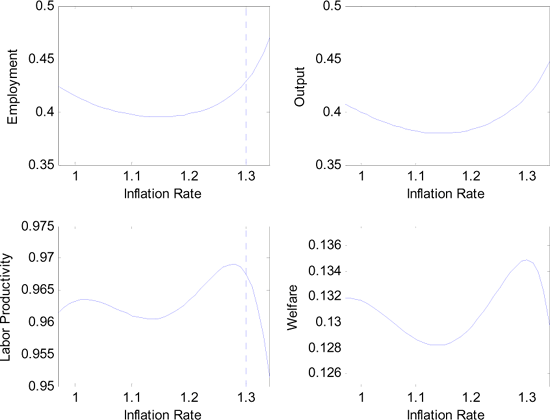
For a low expected inflation of 2%, Figure 6 displays several allocations and welfare in response to changes in the inflation rate. The top left graph is the Phillips curve. Output also increases with inflation, but labor productivity does not once actual inflation exceeds expected inflation ( marked with a vertical dashed line ). Hence while the monetary authority can further increase output, it does so at the cost of reduced production efficiency. Both price distortions and the impact of financial constraints contribute to the latter.
Welfare is displayed in the bottom right graph of Figure 6. Welfare peaks somewhere above the inflation expectation. The resulting monetary policy decision reflects the trade-off between stimulating the labor demand and maintaining high labor productivity.
5.3 Under High Inflation Expectations: Pick Your Poison
Confronted with high inflation expectations, the monetary authority faces a pick-your-poison problem. There is no way out of severe distortions. Fulfilling the high inflation expectations implies a large wedge between the price and the marginal cost for financially constrained firms. However, low inflation also delivers large distortions--only in this case on the sector of sticky price firms.
Figure 7 graphs allocations and welfare as a function of the monetary authority's inflation choice under an expectation of a 30% inflation rate. As discussed earlier, the relationship between employment and inflation is not monotone. Output also displays the same U-shape, as shown in the two top graphs.
Figure 7. Allocations and Welfare Under Inflation Expectation ![]()
The bottom right graph depicts welfare. The monetary authority faces a double-peaked indirect utility function. Note that labor productivity also displays two peaks. Low inflation brings the financially constrained firms close to the optimal production level; high inflation improves production efficiency in the sticky price firms. In each case, the more efficient sector is also larger.
From Figure 7 it is obvious that the monetary authority's problem cannot be characterized by first order welfare changes. Instead, the monetary authority compares two local maxima: one close to inflation expectations and the other close to the Friedman rule. This is what we understand by pick-your-poison.
5.4 The Best Policy Response
Next we characterize the best policy response function
![]() , i.e., the inflation
rate which solves the monetary authority's problem given inflation
expectation
, i.e., the inflation
rate which solves the monetary authority's problem given inflation
expectation ![]() .
Nonlinear methods are used: given our discussion above, linear
approximation methods are not reliable for high inflation
expectations.
.
Nonlinear methods are used: given our discussion above, linear
approximation methods are not reliable for high inflation
expectations.
Figure 8 plots
the best policy response function
![]() for our preferred
calibration and two additional parametrizations. Inflation
expectations
for our preferred
calibration and two additional parametrizations. Inflation
expectations ![]() are on
the horizontal axis and the best policy response in the vertical
axis. The thick line is the best policy response function. The thin
line indicates additional local maxima. A crossing of the best
policy response function and the 45-degree (dashed) line indicates
a Markov equilibrium
are on
the horizontal axis and the best policy response in the vertical
axis. The thick line is the best policy response function. The thin
line indicates additional local maxima. A crossing of the best
policy response function and the 45-degree (dashed) line indicates
a Markov equilibrium
![]() .
.
Figure 8. Best Policy Response Different Parametrizations
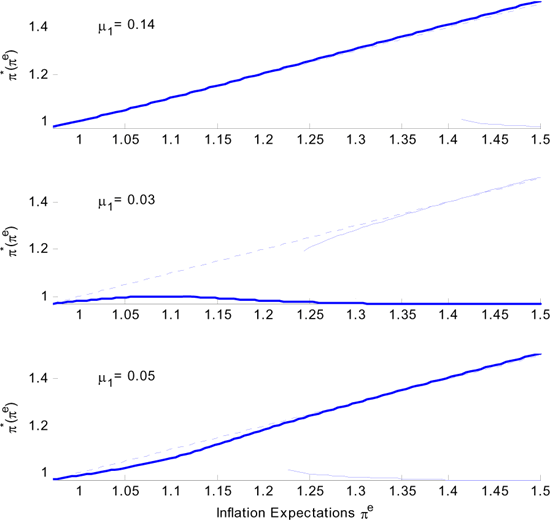
The top graph displays the best policy response function for our
preferred calibration
![]() and
and
![]() . The best
policy response tracks inflation expectations closely--indeed, so
close that the reader is referred to Figure 3 to actually spot
Markov equilibria. Note the best policy response would be well
approximated by a linear function yet a linear approximation would
necessarily miss the second equilibrium. The indirect welfare
function is double peaked only for very high inflation
expectations, well past the second Markov equilibrium.
. The best
policy response tracks inflation expectations closely--indeed, so
close that the reader is referred to Figure 3 to actually spot
Markov equilibria. Note the best policy response would be well
approximated by a linear function yet a linear approximation would
necessarily miss the second equilibrium. The indirect welfare
function is double peaked only for very high inflation
expectations, well past the second Markov equilibrium.
The middle graph corresponds to a parametrization with a very
small share of sticky price firms,
![]() . For
inflation expectations of 25% and above, there are two local maxima. The local
maximum in the low inflation region always dominates. This rules
out the possibility of a high inflation equilibrium.
. For
inflation expectations of 25% and above, there are two local maxima. The local
maximum in the low inflation region always dominates. This rules
out the possibility of a high inflation equilibrium.
The bottom graph in Figure 8 shows the best
policy response function for a very similar parameter choice,
![]() . Again
there are two local maxima, but this time high inflation is the
best policy response by the monetary authority. Now there are two
Markov equilibria: a low inflation equilibrium close to the
Friedman rule and a high inflation equilibrium above 30%.
. Again
there are two local maxima, but this time high inflation is the
best policy response by the monetary authority. Now there are two
Markov equilibria: a low inflation equilibrium close to the
Friedman rule and a high inflation equilibrium above 30%.
In all three cases the best policy response function is continuous. This does not need to be the case. The best policy response may alternate between local maxima. The discontinuity in the best policy response function must be in the region of high inflation expectations where the indirect welfare function can be double peaked. By continuity of the indirect welfare function, the monetary authority is actually indifferent between a certain pair of low and high inflation at the discontinuity of the best policy response.
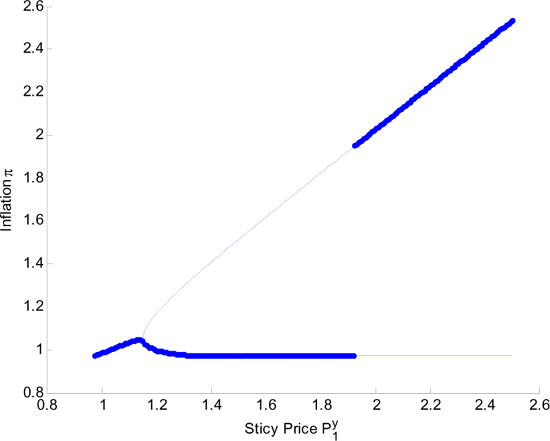
Figure 9 illustrates such a case. The thick line now indicates the best
policy response given the sticky price ![]() .15 The thin lines indicate local maxima.
Note that the location of the global maximum changes so the
resulting best policy response function is not continuous. This
discontinuity leads us to consider the possibility that the
monetary authority has a mixed strategy in equilibrium, i.e., it
randomizes between two inflation choices. We will carefully explore
the role of mixed strategies in Section 6.3 and the
Appendix.
.15 The thin lines indicate local maxima.
Note that the location of the global maximum changes so the
resulting best policy response function is not continuous. This
discontinuity leads us to consider the possibility that the
monetary authority has a mixed strategy in equilibrium, i.e., it
randomizes between two inflation choices. We will carefully explore
the role of mixed strategies in Section 6.3 and the
Appendix.
Figure 9. Best Policy Response as Function of Sticky Prive ![]() Parameters
Parameters ![]() ,
, ![]()
6 Expectation Traps
The main feature of the economy is the multiplicity of Markov equilibria. In this section we argue that the model quantitatively matches the U.S. inflation in the last 40 years, including low and high inflation episodes. We first document our preferred calibration and then go on to explore other parametrizations. We also discuss the possibility of Markov equilibria with mixed strategies.
Clarida et al. (2000) and Christiano and Gust (2000) also provide an account of the high inflation in the U.S. based on policymaking. However, they take monetary policy as given by an exogenous Taylor rule. Under our assumption of full discretion, policy decisions are determined by the economy's primitives. We do not have a separate set of parameters to calibrate policy.
6.1 The Economics of Expectations Traps
Expectation traps are the rule in our economy--exceptions involve either non-existence of equilibrium or the Friedman rule being time consistent.16 The simplicity of the model allows us to discuss the economics behind this property.
Expectation traps arise from the heterogeneous impact that inflation expectations have on firms' output levels. The efficiency gains from unexpected inflation stem from the sticky price firms while the welfare costs of inflation are linked to the financially constrained firms.
Consider first the low inflation equilibrium. The output of sticky price and financially constrained firms is slightly distorted by monopolistic pricing. The small but positive nominal interest rate further distorts the financially constrained firm's output. The monetary authority's problem is then to fine tune the economy. There are little net welfare gains from shifting the distortion from sticky price to financially constrained firms as both are at a similar distance from efficiency. Hence an equilibrium is achieved at a low inflation rate where the cost of price distortion is small.
The situation under high inflation is quite different. Financially constrained firms are severely distorted because of high cost of money. As a result, financially constrained firms operate at reduced scale. Because in equilibrium sticky price firms anticipate high inflation and set nominal prices accordingly, the distortion on the sticky price firm's output is unchanged.
Hence the sticky price firm's output is larger than that of the financially constrained firms'. This leads the monetary authority to validate the high inflation expectations. Efficiency gains in the sticky price firm sector greatly outweigh the losses in the smaller financially constrained sector. Hence the monetary authority's incentives are also balanced at a high inflation rate despite the larger costs of price distortion.
How common are expectations traps? Several papers find multiple equilibria in a variety of monetary economies.17 Albanesi et al. (2003) explores a cash/credit good model and show that monetary policy discretion may lead to expectation traps. King and Wolman (2004) also finds multiple equilibria in a simple new Keynesian model with two-period staggered pricing. Siu (2004) allows firms to set their degree of price stickiness and shows that, once again, equilibrium multiplicity arises. Finally, Armenter (2004) argues that the necessary conditions for the existence of expectation traps are very general.
6.2 Calibration
We start with the utility function which we assume to be of the form
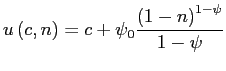
We define one period to be one year. The inverse of ![]() is the real interest rate in
our economy. We take the annual real interest rate to be 3%, implying a value
is the real interest rate in
our economy. We take the annual real interest rate to be 3%, implying a value
![]() . The last
of the pre-set parameters is the constant elasticity of
substitution
. The last
of the pre-set parameters is the constant elasticity of
substitution ![]() . We
choose to replicate a 10% markup in the price of intermediate goods.
. We
choose to replicate a 10% markup in the price of intermediate goods.
We choose the share of the sticky price and financially
constrained firms, ![]() and
and ![]() respectively,
to match an inflation rate in the range 2 - 2.5% . This corresponds to the
average US inflation over the period 1983-2004. The annual PPI
inflation rate is 1.8%
for the period, the CPI around 3% and the core inflation only a little above
3% .19
respectively,
to match an inflation rate in the range 2 - 2.5% . This corresponds to the
average US inflation over the period 1983-2004. The annual PPI
inflation rate is 1.8%
for the period, the CPI around 3% and the core inflation only a little above
3% .19
We find that all parametrizations with a low inflation equilibrium between 2 and 2.5% also have a high inflation equilibrium in the interval 10 - 11 . Hence the model naturally provides an excellent account of U.S. inflation in the 70s as well. During the period 1973-1983, inflation rates peaked at 10.5% for the GDP deflator, 13.4% for the CPI and 10.8% for the PCE. Averages over the period are all above 7%.
Our preferred calibration is summarized in Table 1. It features a small amount of nominal frictions. Over 80% of the firms are not subject to any friction and there are more sticky price firms than financially constrained firms, 14% over 4%.
Table 1. Preferred Calibration
| Parameter | Value |
|---|---|
| .9709 | |
| .5 | |
| 1 | |
| .91 | |
| .14 | |
| .04 |
The quantitative performance of the model is robust. Figure 10 reproduces
Figure 2 for
different values of parameter ![]() . Values
. Values ![]() to
to ![]() cover the most widely accepted values for the
markup, from 8% to
12%. In each case, a
calibrated Markov equilibrium in the range of 2 - 2.5% implies an additional
equilibrium with higher inflation. The range for the high inflation
equilibrium changes with
cover the most widely accepted values for the
markup, from 8% to
12%. In each case, a
calibrated Markov equilibrium in the range of 2 - 2.5% implies an additional
equilibrium with higher inflation. The range for the high inflation
equilibrium changes with ![]() but it stays within reasonable bounds, from
8% to 16%. We have also explored
variations in the parameters in the labor supply and the results
remain unchanged. The robustness of our main result does not imply
that Markov equilibria are not sensitive to parameters
but it stays within reasonable bounds, from
8% to 16%. We have also explored
variations in the parameters in the labor supply and the results
remain unchanged. The robustness of our main result does not imply
that Markov equilibria are not sensitive to parameters ![]() and
and ![]() .
.
Figure 10. Markov Equilibria: Robustness Analysis
6.3 The Set of Markov Equilibria
Our economy usually has two Markov equilibria. In order to deliver a complete analysis of the model, we now carefully explore the set of Markov equilibria across the parameter space to detect less typical cases.
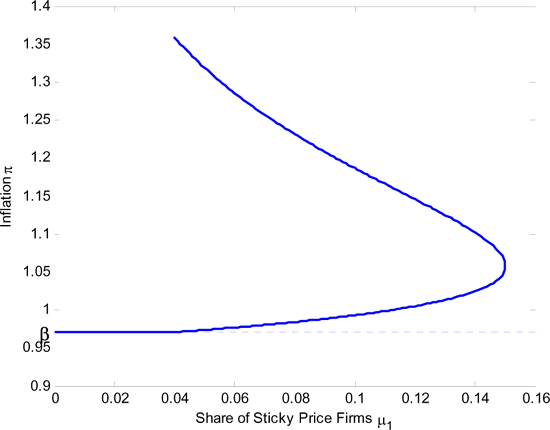
Figure 11 shows the
set of Markov equilibria for different parametrizations of the
share of sticky price firms ![]() , displayed along the horizontal axis.
Remaining parameters are set to the corresponding values in our
preferred calibration. In particular, the share of financially
constrained firms is fixed at
, displayed along the horizontal axis.
Remaining parameters are set to the corresponding values in our
preferred calibration. In particular, the share of financially
constrained firms is fixed at
![]() . The zero
nominal interest bound is indicated with the dashed line.
. The zero
nominal interest bound is indicated with the dashed line.
We first abstract from the possibility of mixed strategies in
equilibrium. We distinguish three parameter subspaces. For
![]() , the
Friedman rule is time consistent and it constitutes the unique
equilibrium of the economy. For the interval between .04 and .15 there are two Markov equilibria.
Finally, for
, the
Friedman rule is time consistent and it constitutes the unique
equilibrium of the economy. For the interval between .04 and .15 there are two Markov equilibria.
Finally, for
![]() there
is no equilibrium. Figure 11 shows how the
low and high inflation equilibrium become closer as
there
is no equilibrium. Figure 11 shows how the
low and high inflation equilibrium become closer as ![]() grows. Indeed, there exists
grows. Indeed, there exists
![]() such that
there is a unique equilibrium around 5% inflation rate. The unique interior Markov
equilibrium is not generic, however, as any perturbation of
such that
there is a unique equilibrium around 5% inflation rate. The unique interior Markov
equilibrium is not generic, however, as any perturbation of
![]() produces
either none or two Markov equilibria.
produces
either none or two Markov equilibria.
Figure 11. Markov Equilibrium Set
Once we allow for mixed strategies, a fourth possibility arises. In Section 5 we mentioned that the monetary authority may be indifferent between two policy decisions given an inflation expectation. It is then possible that there exists a Markov equilibrium where the monetary authority plays a mixed strategy. For brevity, we relegate the definition of a Markov equilibrium with mixed strategies to the Appendix.
Mixed strategies are present in equilibrium for a small but
generic region of the parameter space. Sticky price firms set their
nominal price, ![]() , taking into account that inflation is a
random variable. In equilibrium,
, taking into account that inflation is a
random variable. In equilibrium, ![]() leaves the monetary authority indifferent
between several inflation rates.
leaves the monetary authority indifferent
between several inflation rates.
In Figure 12 we
focus on the parameter region
![]() where there are
Markov equilibria with mixed strategies. For each value
where there are
Markov equilibria with mixed strategies. For each value
![]() the monetary
authority finds it optimal to randomize between two inflation rates
displayed on the left panel of Figure 12. One inflation
rate is always at the lower bound
the monetary
authority finds it optimal to randomize between two inflation rates
displayed on the left panel of Figure 12. One inflation
rate is always at the lower bound ![]() . The other inflation rate is very high and it
decreases with
. The other inflation rate is very high and it
decreases with ![]() .
.
Figure 12. Markov Equilibria With Mixed Strategies
![Figure 12 focuses on the parameter region $ \mu_{1}\in\left[ .0397,.04\right] $ where there are Markov equilibria with mixed strategies. For each value $ \mu_{1}$ the monetary authority finds it optimal to randomize between two inflation rates displayed on the left panel. One inflation rate is always at the lower bound $ \beta$. The other inflation rate is very high and it decreases with $ \mu_{1}$.
The figure shows the probability of the high inflation outcome in the right panel. We find that the equilibrium mixed strategy is such that expected inflation is close to the high inflation. As $ \mu_{1}$ approaches .04, the probability of the high inflation outcome converges to 1 and the mixed strategy degenerates into a pure strategy equilibrium. Hence for $ \mu_{1} \geq.04$ there are two Markov equilibria with pure strategies.](figure12.gif)
Figure 12 shows
the probability of the high inflation outcome in the right panel.
We find that the equilibrium mixed strategy is such that expected
inflation is close to the high inflation. As ![]() approaches .04, the probability of the high
inflation outcome converges to 1 and the mixed strategy degenerates into a pure
strategy equilibrium. Hence for
approaches .04, the probability of the high
inflation outcome converges to 1 and the mixed strategy degenerates into a pure
strategy equilibrium. Hence for
![]() there
are two Markov equilibria with pure strategies.
there
are two Markov equilibria with pure strategies.
7 Conclusions
This paper makes an important step forward in exploring the hypothesis that the high inflation experienced by the U.S. in the 70s was driven by expectations. We present an economy where policy discretion gives rise to multiple Markov equilibria. The model's match of the U.S. inflation experience is noteworthy. For any parametrization featuring an equilibrium inflation rate around 2%, there is an additional high inflation equilibrium just above 10%. We find this property of the model to be robust.
The model is tractable enough to provide an insight into the economics behind expectation traps. The forces at work are quite general and the equilibrium multiplicity does not rely on large nominal frictions. These results strongly suggest that expectation traps are more than just a theoretical curiosity.
We acknowledge that the indeterminacy of inflation expectations is unsatisfactory. One possibility is to explore learning in the spirit of Marcet and Sargent (1989) and, more recently, Marcet and Nicolini (2003). Another possibility is to relax the common knowledge assumption. Recent literature has successfully applied global games to several policy problems as in Morris and Shin (1998), Morris and Shin (2004), Rochet and Vives (2004) and many others.
Expectation traps are specially relevant for applied monetary policy. For example Armenter adn Bodenstein (2005) discusses exchange rate regimes in the presence of expectation traps: the equilibrium multiplicity makes a stronger case for a fixed exchange rate.
The possibility of a high inflation equilibrium is a first order concern for the policymaker. Credibility is not about getting the inflation rate right up to a tenth of a percent. It is about avoiding a 70s encore.
References
Albanesi, S., Chari, V. and Christiano, L. J.: 2003, Expectation traps and monetary policy, The Review of Economic Studies 70(4), 715—742.
Altonji, J.: 1986, Intertemporal labor supply: Evidence from micro data, Journal of Political Economy 94(3), 176—215.
Armenter, R.: 2004, A general theory (and some evidence) of expectation traps in monetary policy. Working Paper, Federal Reserve Bank of New York.
Armenter, R. and Bodenstein, M.: 2005, Does the time inconsistency problemmake flexible exchange rates look worse than you think? Working Paper, Federal Reserve Bank of New York.
Barro, R. J. and Gordon, D.: 1983, A positive theory of monetary policy in a natural rate model, Journal of Political Economy 91(4), 589—610.
Bernanke, B., Gertler, M. andWatson, M.: 1997, Systematic monetary policy and the effects of oil price shocks, Brookings Papers on Economic Activity (Issue 1), 91—157.
Chari, V., Christiano, L. J. and Eichenbaum, M.: 1998, Expectation traps and discretion, Journal of Economic Theory 81(2), 462—492.
Christiano, L. J. and Gust, C.: 2000, The expectations trap hypothesis, Federal Reserve Bank of Chicago Economic Perspectives 24(Issue 2), 21—39.
Clarida, R., Gali, J. and Gertler, M.: 2000, Monetary policy rules and macroeconomic stability: Evidence and some theory, Quarterly Journal of Economics 115(1), 147—180.
De Long, J. B.: 1997, America’s peacetime inflation: The 1970s, in C. Romer and D. Romer eds), Reducing Inflation: Motivation and Strategy, Chicago University Press, Chicago.
Domeij, D. and Floden, M.: 2004, The labor-supply elasticity and borrowing constraints: Why estimates are biased. Stockholm School of Economics, Working Paper.
Dupor, B.: 2003, Optimal random monetary policy with nominal rigidity, Journal of Economic Theory 112(1), 66—78.
Goodfriend, M.: 1993, Interest rate policy and the inflation scare problem: 1979-1992, Economic Quarterly 79(1).
Goodfriend, M. and King, R.: 2005, The incredible Volcker disinflation. NBER Working Paper 11562.
Judd, J. P. and Rudebusch, G. D.: 1998, Taylor’s rule and the Fed: 1970-1997, Economic Review (Issue 3), 3—14.
Khan, A., King, R. G. andWolman, A. L.: 2001, The pitfalls of monetary discretion. Federal Reserve Bank of Richmond Working Paper 01-08.
King, R. G. and Wolman, A. L.: 2004, Monetary discretion, pricing complementarity and dynamic multiple equilibria, Quarterly Journal of Economics 119(4), 1513—1553.
Kydland, F. and Prescott, E. C.: 1977, Rules rather than discretion: The inconsistency of optimal plans, Journal of Political Economy 85(3), 473—491.
Marcet, A. and Nicolini, J. P.: 2003, Recurrent hyperinflations and learning, American Economic Review 93(5), 1476—1498.
Marcet, A. and Sargent, T. J.: 1989, Least-squares learning and the dynamics of hyperinflation, in W. Barnett, J. Geweke and K. Shell (eds), International Symposia in Economic
Theory and Econometrics, Cambridge University Press, Cambridge, pp. 119—37. Morris, S. and Shin, H. S.: 1998, Unique equilibrium in a model of self-fulfilling currency attacks, The American Economic Review 88(3), 587—597.
Morris, S. and Shin, H. S.: 2004, Coordination risk and the price of debt, European Economic Review 48(1), 133—153.
Rochet, J.-C. and Vives, X.: 2004, Coordination failures and the lender of last resort: Was Bagehot right after all?, Journal of the European Economic Association 2(6), 1116—47.
Siu, H. E.: 2004, Time consistent monetary policy with endogenous price rigidity. Working Paper, University of British Columbia.
Woodford, M.: 2003, Interest and Prices, Princeton University Press, Princeton.A.1 Appendix
A.1 Closure of the Policy Choice Set
To show that the set is not empty, note that
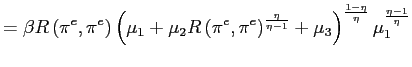 |
||
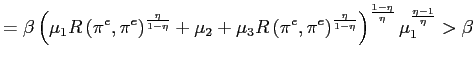 |
using
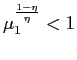
A.2 First Order Welfare Changes
We drop the dependence on ![]() for convenience. Solving the monetary authority
problem's in (17) we
have the following first order condition:
for convenience. Solving the monetary authority
problem's in (17) we
have the following first order condition:

With some algebra, the previous expression can be rewritten in terms of wedges and elasticities. Using (10) and (11), we have that
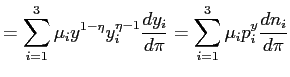
|
||
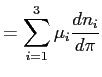 |
so we can rewrite the necessary first order condition, using

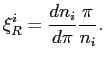
Expression (19)
relates to the classic second best theory. Because of monopolistic
competition, there is a wedge between the price and marginal cost
in every sector. Each wedge is weighted by the `size' of the
sector, i.e.,
![]() , and then
the production elasticity with respect to inflation. Each sector
has a different elasticity. We show that for
, and then
the production elasticity with respect to inflation. Each sector
has a different elasticity. We show that for
![]() ,
,
![]() .
.
We solve first for
![]() .
Using (9) and (6),
.
Using (9) and (6),
![$\displaystyle n_{3}=y\left[ \frac{1}{\eta}w\right] ^{\frac{1}{\eta-1}} $](img285.gif)
![$\displaystyle \frac{dn_{3}}{d\pi}=\frac{dy}{d\pi}\left[ \frac{1}{\eta}w\right] ... ...}y\left[ \frac{1}{\eta}w\right] ^{\frac{1} {\eta-1}}\frac{1}{w}\frac{dw}{d\pi} $](img286.gif)
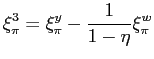
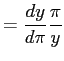 |
||
 |
Similarly for ![]() , we
have
, we
have
![$\displaystyle n_{2}=y\left[ \frac{1}{\eta}Rw\right] ^{\frac{1}{\eta-1}} $](img293.gif)
![$\displaystyle \frac{dn_{2}}{d\pi}=\frac{dy}{d\pi}\left[ \frac{1}{\eta}\pi w\rig... ... \frac{1}{\eta}\pi w\right] ^{\frac{1}{\eta-1}}\frac{w+\pi\frac{dw}{d\pi}}{Rw} $](img294.gif)
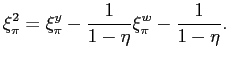
![$\displaystyle n_{1}=y\left[ \frac{P^{y}}{\pi}\right] ^{\frac{1}{\eta-1}} $](img296.gif)
![$\displaystyle \frac{dn_{1}}{d\pi}=\frac{dy}{d\pi}\left[ \frac{P^{y}}{\pi}\right... ...ac{1}{1-\eta}y\left[ \frac{P^{y}}{\pi}\right] ^{\frac{1}{\eta-1}}\frac{1}{\pi} $](img297.gif)
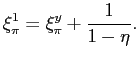
A.3 Monetary Authority Problem
A PSE outcome solves a system of non-linear equations
First we prove Proposition 6.
![$\displaystyle w=\eta\left[ \frac{\mu_{2}x^{-1}+\mu_{3}}{1-\tilde{\mu}_{1}x}\right] ^{\frac{1-\eta}{\eta}} $](img304.gif)
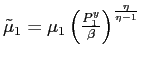 . Note it is sufficient to establish that
. Note it is sufficient to establish that
![$\displaystyle \frac{d}{dx}\left[ \frac{\mu_{2}+\mu_{3}x}{x-\tilde{\mu}_{1}x^{2}}\right]$](img309.gif) |
||
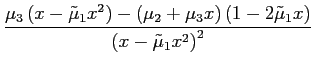 |
||
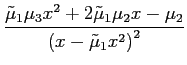 |
||
Note
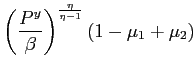 |
or
![$\displaystyle P^{y}\leq\beta\left[ \frac{\mu_{1}}{\mu_{2}}\left( 1-\mu_{1}+\mu_{2}\right) \right] ^{\frac{1-\eta}{\eta}} $](img318.gif)
![]()
Proposition 6 has an important implication. Because labor is a monotone function
of ![]() , we can think of
labor being the policy instrument. This is only possible under the
restriction
, we can think of
labor being the policy instrument. This is only possible under the
restriction
![]() .
.
Let
where
![]() . Under the condition
. Under the condition
![$ P^{y}\left( \pi^{e}\right) \leq\beta\left[ \frac{\mu_{1}}{\mu_{2}}\left( 1-\mu_{1}+\mu_{2}\right) \right] ^{\frac{1-\eta}{\eta}}$](img321.gif) ,
,
![]() is a differentiable
function of
is a differentiable
function of ![]() for
for
![]() as implied by
Proposition 6
.20 Hence
the monetary authority's problem becomes
as implied by
Proposition 6
.20 Hence
the monetary authority's problem becomes
| (20) |
and the optimal policy decision
![]() can be obtained using (3), (4) and (15).
can be obtained using (3), (4) and (15).
All is set for the proof of Proposition 7.
A.4 Markov Equilibria with Mixed Strategies
We adapt the definition of the Markov equilibrium to allow the
monetary authority to play mixed strategies. Now the policy
decision is given by probability distribution
![]() defined over
defined over
![]() . We start by changing
the definition of the state of the private sector economy to
. We start by changing
the definition of the state of the private sector economy to
![]() . This reflects
that now firms have a belief with respect to
. This reflects
that now firms have a belief with respect to
![]() .
It is easy to check that all private sector allocations can be
solved given
.
It is easy to check that all private sector allocations can be
solved given ![]() .
.
Our preferences' assumptions imply that firms weigh all states equally. Hence the sticky price firm's problem is to maximize expected profits
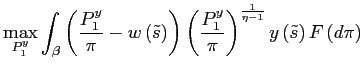
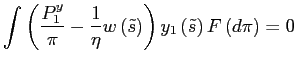
and hence
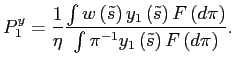 |
(21) |
We confirm that ![]() is function of monetary policy distribution
is function of monetary policy distribution
![]() .
.
A Markov equilibrium with mixed strategies is defined as follows.
Footnotes
1. The authors are grateful to Lawrence Christiano and Etienne Gagnon for comments and suggestions. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System, or the Federal Reserve Bank of New York. Return to text
2. Armenter: Federal Reserve Bank of New York, e-mail: [email protected]; Bodenstein: Board of Governors of the Federal Reserve System, e-mail: [email protected]. Return to text
3. Clarida et al. (2000), page 149. See also Judd and Rudebusch (1998). Return to text
4. Christiano and Gust (2000), page 22. Return to text
5. Chari, Christiano and Eichenbaum (1998) shows that there exist Nash equilibria with expectation traps in an infinite horizon economy. Albeit the term `expectation trap' was introduced in that paper, attention is often restricted to Markov equilibria, thereby ruling out trigger strategies. Return to text
6. In private correspondence, Etienne Gagnon confirmed that several versions of the model in Albanesi et al. (2003) fail to produce equilibria with reasonable levels of low and high inflation. Return to text
7. This in the spirit of the cashless economies discussed in Woodford (2003). Return to text
8. We can do this because we restrict our analysis to Markov equilibrium. Return to text
9. It is possible to allow firms to
shut down or re-set nominal prices if profits fall below some
arbitrary level. A PSE would then exist for all
![]() . Whether
we allow for negative profits or not does not affect our
results. Return to text
. Whether
we allow for negative profits or not does not affect our
results. Return to text
10. Existence of
![]() follows from
follows from
![]() being bounded above and the closure of the policy choice set
previously discussed. However, the solution of (17) can be a
correspondence. We will get back to this possibility in Section 6.3. For simplicity
we proceed here with
being bounded above and the closure of the policy choice set
previously discussed. However, the solution of (17) can be a
correspondence. We will get back to this possibility in Section 6.3. For simplicity
we proceed here with
![]() as a
function. Return to text
as a
function. Return to text
11. Dupor (2003) shows that optimal monetary policy with commitment may have a random component which can alleviate the monopoly distortion. We do not allow for such randomizations in our model. Return to text
12. The growth rate of the GDP deflator was 2.45% over 1984-2004. See Section 6 for a more detailed account of inflation in the U.S. Return to text
13. All figures in this section are based on our preferred calibration that is detailed in Section 6. Return to text
14. We prove the proposition under a weaker requirement, namely that condition (18) only needs to be satisfied in a neighborhood of any critical point associated with (17). Return to text
15. In Section 6.3 we make clear
why it is necessary to use ![]() rather than
rather than ![]() when dealing with the (rare) possibility of a
best policy response correspondence. Return to text
when dealing with the (rare) possibility of a
best policy response correspondence. Return to text
16. There is also the rare case of Markov equilibria with mixed strategies, which we discuss later in more detail. Of course, there are also non-generic cases of a unique interior Markov equilibrium. Return to text
17. All of them focus on Markov perfect equilibria and so none of the equilibrium multiplicity results hinge on trigger strategies. Return to text
18. Most estimates in the labor literature are well below 1--for example, see Altonji (1986). However, recent work as pointed out that estimates may be biased downwards. See Domeij and Floden (2004) and references herein. Return to text
19. We used data from the Federal Reserve Bank of St. Louis' FRED database. Return to text
20. Again, this set can be closed without loss of generality following the same steps as in Claim 8. Return to text
This version is optimized for use by screen readers. A printable pdf version is available.