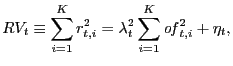Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 862, May 2006-Screen Reader Version*
FRB: What Drives Volatility Persistence in the Foreign Exchange Market?1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We analyze the factors driving the widely-noted persistence in asset return volatility using a unique dataset on global euro-dollar exchange rate trading. We propose a new simple empirical specification of volatility, based on the Kyle-model, which links volatility to the information flow, measured as the order flow in the market, and the price sensitivity to that information. Through the use of high-frequency data, we are able to estimate the time-varying market sensitivity to information, and movements in volatility can therefore be directly related to movements in two observable variables, the order flow and the market sensitivity. The empirical results are very strong and show that the model is able to explain almost all of the long-run variation in volatility. Our results also show that the variation over time of the market's sensitivity to information plays at least as important a role in explaining the persistence of volatility as does the rate of information arrival itself. The econometric analysis is conducted using novel estimation techniques which explicitly take into account the persistent nature of the variables and allow us to properly test for long-run relationships in the data.
Keywords: Volatility persistence, news sensitivity, exchange rates, long memory, fractional cointegration, narrow band spectral regression
JEL classification: F31, G1, G15.
1 Introduction
The past two decades have seen the estimation of many variations of ARCH/GARCH and stochastic volatility models, and, more recently, direct inference on realized volatility. The results all point towards the conclusion that the volatility of asset prices changes over time in the manner of a fairly persistent process. However, there is still no clear agreement on why this is the case. The most common hypothesis is that the rate of information arrival affecting the price of an asset is itself persistent, perhaps because economic data relevant to the price are released in a clustered fashion or because analysis relevant to the price is produced in a clustered fashion. A less common explanation, which does not exclude the first one, is that variation over time in the sensitivity of market participants to information may also help explain the pattern of volatility persistence. We present in this paper a simple, direct empirical test of the roles of both information arrival and market sensitivity in driving volatility persistence, using a unique high-frequency dataset covering several years of global interdealer foreign exchange trading.
Much of the research on this topic derives from studies of `mixture of distributions' models proposed by Clark (1973), Tauchen and Pitts (1983), and Andersen (1996), among others, where volatility and trading volume are jointly directed by the process of information arrival. Thus, in these models, persistence in the information arrival process generates persistence in asset price volatility and trading volume. In practice, however, the estimated persistence of volatility in such bivariate volatility-volume models has typically been found to be much lower than in univariate time-series models of volatility, which points to the conclusion that volatility and volume cannot both be well explained by a single factor. Motivated by these findings, Liesenfeld (2001) extends previous mixture models to allow for volume and volatility to be driven not only by a latent information arrival process, but also by an additional latent process that governs the impact of information on prices. He shows that such a model, where the dynamics of volatility are associated with both the rate of information arrival and the time-varying sensitivity to information, is able to capture much more of the persistence in volatility. In the same spirit, McQueen and Vorkink (2004) present a model in which the sensitivity of investors to news temporarily rises after a shock to their wealth, and show that such a model can help explain GARCH effects.3
Our paper is inspired by the results of Liesenfeld (2001), but it takes a very different approach from previous work on the study of volatility persistence. We propose a simple alternative empirical specification of volatility derived from the well-known equilibrium result in the trading model of Kyle (1985), which states that returns in each time period are determined by the interaction of the order imbalance in that period (the order flow) and a price sensitivity parameter (`` Kyle's lambda''). This simple relationship linking order flow to returns has been studied extensively in the foreign exchange market in the past few years (e.g., Evans and Lyons, 2002, 2004), and has been found to account for a substantial share of the observed variation in exchange rates. Here we show that there are large variations across time in this relationship, and that this variation is linked to the time-variation in volatility. Evans and Lyons and other authors have also argued that the contemporaneous explanatory power of order flow for exchange rate movements derives in great part from the fact that information relevant to the price is transmitted to the market through order flow, a point previously demonstrated by Hasbrouck (1991) for the stock market. To the extent that order flow represents information, our empirical specification therefore allows us to decompose the factors affecting volatility into two time-varying components: the flow of information itself and the sensitivity of the market to that information. We stress, however, that none of the results in the paper depend upon the interpretation of order flow as information, although we focus on that interpretation.
We test this specification using a unique high-frequency dataset which represents a majority of global interdealer trading in the spot euro-dollar exchange rate over a period of several years. Besides the price and the trading volume, the data also include high frequency signed order flow, which allows us to estimate the time-varying market sensitivity parameter by regressing high-frequency returns onto high-frequency order flow. We can thus treat the market sensitivity as an observed variable, along with the order flow and the realized volatility. The empirical specification used in this paper therefore differs substantially from those used in previous work on the topic, where latent variable specifications have been the norm.
The aim of this paper is then to relate the persistent component in volatility to other observable variables, in order to gain understanding of what drives the long-run time-series variations in volatility. In particular, as mentioned above, we analyze how the time-series behaviour in volatility relates to both the order flow in the market and the market's sensitivity to that order flow. Since the slow-moving persistent component in volatility dominates its time-series behaviour, we focus in the paper on capturing this part of the variance in volatility.
There are two primary challenges in testing this relationship. First, there is no a priori reason to believe that the variables on the right-hand side are exogenous and that the relationship is causal. Rather, the main purpose of the empirical analysis is to determine whether there is a long-run equilibrium relationship, or co-movement, between volatility and the measures of market sensitivity and information flow. Second, the persistence in both volatility and the explanatory variables makes spurious regression results a possibility. Standard OLS inference is therefore likely to be biased, and possibly completely spurious.4
Since the object of interest is the persistent, or long-run, components in the variables and how they relate to each other, it is useful to think of the empirical analysis as a test of cointegration. Typically, cointegration refers to a stationary combination of non-stationary unit-root processes, and is usually interpreted as a long-run equilibrium relationship. However, it is also possible for stationary processes to cointegrate, in the sense that they share a long-run component, even though that component is stationary (e.g. Robinson, 1994); this is usually referred to as fractional cointegration to distinguish it from the traditional usage of the word.
Importantly, by focusing on the long-run components in the data, it is possible to consistently estimate the cointegrating relationship in the stationary case with endogenous regressors, a case where OLS estimation would clearly deliver biased estimates. Intuitively, consistent estimation in the presence of endogeneity is possible because the long-run behaviour in the processes is dominated by the persistent component, and the endogeneity of the regressors will be of a second-order importance. A more economic interpretation is that, since the variables contain a long-run slow-moving component, it makes sense to think of the cointegrating relationship as a long-run equilibrium, similar to the non-stationary case, and causality is thus not a concern. In practice, focusing on the long-run movements is done by transforming the data to the frequency domain and using only the frequencies close to zero, which correspond to the long-run movements in the data. Least squares estimation of the cointegration vector can then be performed in the frequency domain, using only frequencies close to zero. Since most of the information in a persistent process is contained in these lower frequencies, there is in fact little loss of efficiency by excluding the higher ones.
Formally, we assume that the data follow long-memory, or fractionally integrated processes, and we test for fractional cointegration through the use of narrow band least squares methods and estimation of the long-memory parameters in the original data as well as the cointegration residuals. It is well documented that long-memory models provide a good description of the time-series behaviour of volatility (e.g. Andersen, Bollerslev, Diebold, and Labys, 2003). However, there have been few attempts at extending the univariate time-series analysis to tests of fractional cointegration.5 The long-memory framework is convenient since it provides a concise summary statistic of the degree of persistence in a process and thus easily enables comparison between the persistence in the original data and the cointegration residuals.
Using these methods, we estimate the Kyle-based empirical specification for volatility. Overall, the results are striking. We show that most, if not all, of the persistence in volatility can be explained by variations in the market's sensitivity to order flow (Kyle's lambda) and the variations in the order flow itself. Thus, if one interprets order flow as information, the results show that persistent behaviour in volatility can be attributed to both persistence in the market's sensitivity to new information, as well as the persistence in the information flow itself.
The empirical analysis clearly shows that the time variation in the sensitivity parameter plays a central role in explaining the time series properties of volatility. Indeed, all the results indicate that variations in market sensitivity may well be more important in explaining volatility persistence than the time variation in the flow of information itself. From an econometric point of view, this result is fairly easy to explain. The persistence in the information flow is simply not large enough to capture the persistence in volatility, whereas the persistence of the sensitivity parameter is very similar to that of volatility, and thus potentially capable of explaining its behavior. These results are also consistent with the conclusions of Liesenfeld (2001), namely that the information flow accounts for the somewhat shorter-, or medium-term, behaviour in volatility, whereas the sensitivity to information accounts for the longer-run behaviour.
The paper proceeds as follows. Section 2 introduces the high-frequency exchange rate data used in our analysis. Section 3 first derives our empirical specification, addressing its motivation, its empirical validity, and the constructed variables that we use in our estimations. It then presents some preliminary OLS analysis of the contemporaneous relationships between our constructed variables. Section 4 presents the fractional integration and cointegration methodology used in the remainder of the paper. Section 5 presents our main estimation results, based on the empirical specification presented in section 3. Section 6 discusses the relationship between trading volume and volatility in our data. Section 7 concludes.
2 The Data
We analyze high-frequency spot euro-dollar exchange rate data spanning January 1999 through December 2004. We have access not only to data on the exchange rate itself, but also to the volume of trade and the order flow. Our price data are available at the one-second frequency, from which we construct time series sampled at either the one-minute or the five-minute frequencies, and the transaction variables are available at the one-minute and five-minute frequencies. The transactions data are proprietary and confidential. The data were provided by EBS (Electronic Broking System), which operates an electronic limit order book used by all large foreign exchange dealers across the globe to trade in a number of major currency pairs. Since the late 1990's, interdealer trading in the spot euro-dollar exchange rate, the most-traded currency pair, has, on a global basis, become heavily concentrated on EBS. As a result, over our sample period, EBS processed a clear majority of the world's interdealer transactions in spot euro-dollar, and the price on the EBS system was the reference price used by all dealers to generate derivatives prices and spot prices for their customers.6 Further details on the EBS trading system and the data can be found in Chaboud et al. (2004) and Berger et al. (2005).
The exchange rate data we use are the midpoint of the highest bid and lowest ask quotes in the EBS limit-order book at the top of each time interval (one-minute or five-minute). These quotes are executable, not just indicative, and therefore represent a true price series. The trading volume data are the amount traded per time interval, expressed in millions of the base currency (the euro). Order flow is measured as the net of buyer-initiated trading volume minus seller-initiated trading volume per time interval. The direction of trade is based on actual trading records: A trade is recorded as, for instance, buyer-initiated, if it is the result of a `` hit'' on a posted ask quote. Order flow is also expressed in millions of base currency, with a positive number representing net buying pressure on the base currency.
We exclude all data collected from Friday 17:00 New York time to Sunday 17:00 New York time from our sample, as trading activity during these hours is minimal and not encouraged by the foreign exchange trading community.7 We also drop several holidays and days of unusually light volume near these holidays: December 24-26, December 31-January 2, Good Friday, Easter Monday, Memorial Day, Labor Day, Thanksgiving and the following day, and July 4 or the day on which it is observed. Similar conventions have been used in other research on foreign exchange markets, such as Andersen, Bollerslev, Diebold, and Vega (2003). In addition, we also exclude September 22, 2000, the day of the coordinated intervention operation in support of the euro by the G7, which was accompanied by record volatility, and September 11, 2001 and the three following days, days with very low market activity on EBS.8
For the analysis in this paper, we construct a sample at the five-minute frequency over the entire 24-hour trading day and a sample at the one-minute frequency that uses only observations from the busiest trading hours of the day, obtained between 03:00 and 11:00 New York time, when the global foreign exchange market is most active. Figure 1 presents a graph of average minute-by-minute trading volume throughout the day in euro-dollar on the EBS system, indexed to the average one-minute trading volume in our entire sample.
3 Empirical Specification and Preliminary Results
3.1 Motivation
The starting point for our analysis is the behaviour of intra-daily foreign exchange returns. Motivated by one of the key equilibrium relationships in Kyle (1985), we consider the following contemporaneous relationship between returns and order flow,
where
In the original Kyle model, the
![]() parameter
represents the depth of the market, with a smaller
parameter
represents the depth of the market, with a smaller
![]() corresponding to a deeper market. Alternatively (the difference is,
in large part, semantic) these
corresponding to a deeper market. Alternatively (the difference is,
in large part, semantic) these
![]() coefficients can, and have been, interpreted as the sensitivity of
the price to the information that traders receive through the
trading process. A number of researchers, including Hasbrouck
(1991), Payne (2003) and Evans and Lyons (2002, 2004) have argued
that the well-documented impact of order flow on prices in the
foreign exchange market and other asset markets reflects the fact
that order flow reveals to traders information that is either
private or just widely dispersed among economic agents, such as
risk parameters or even early indications of changes in the pace of
economic activity. Even if one does not fully accept that
interpretation, the
coefficients can, and have been, interpreted as the sensitivity of
the price to the information that traders receive through the
trading process. A number of researchers, including Hasbrouck
(1991), Payne (2003) and Evans and Lyons (2002, 2004) have argued
that the well-documented impact of order flow on prices in the
foreign exchange market and other asset markets reflects the fact
that order flow reveals to traders information that is either
private or just widely dispersed among economic agents, such as
risk parameters or even early indications of changes in the pace of
economic activity. Even if one does not fully accept that
interpretation, the
![]() coefficients unquestionably reflect how traders adjust the price in
reaction to order flow. Without directly appealing to the link
between order flow and information, changes over time in the
behavior of traders in reaction to order flow may also reflect
factors such as changes in the traders' willingness or ability to
hold inventory or changes in their appetite for risk.
coefficients unquestionably reflect how traders adjust the price in
reaction to order flow. Without directly appealing to the link
between order flow and information, changes over time in the
behavior of traders in reaction to order flow may also reflect
factors such as changes in the traders' willingness or ability to
hold inventory or changes in their appetite for risk.
By squaring and summing up each side in equation (1) over all daily intervals, the following equation
for daily realized volatility, ![]() , is obtained,
, is obtained,
where
That is, daily volatility is a function of the aggregate daily squared order flow and of the squared sensitivity of the price to order flow.
The usefulness of this derivation, of course, hinges on the
validity of the original equation (1). Table 1 shows the results from estimating equation
(1) with a fixed slope coefficient
![]() for the entire
sample, allowing for a non-zero intercept. The results are
promising with an
for the entire
sample, allowing for a non-zero intercept. The results are
promising with an ![]() of
46% in the full-day
five-minute sample and an
of
46% in the full-day
five-minute sample and an ![]() of 41% in the 3-11am one-minute sample, which must be
considered highly successful for any asset-return.9, 10
of 41% in the 3-11am one-minute sample, which must be
considered highly successful for any asset-return.9, 10
Of course, the parameter
![]() is not
assumed to be fixed over time, and it is thus likely that an even
better fit of equation (1) can be obtained by
estimating
is not
assumed to be fixed over time, and it is thus likely that an even
better fit of equation (1) can be obtained by
estimating
![]() separately
for each day. A summary of the results from such daily regressions
are shown in Table 2, and the logged daily
separately
for each day. A summary of the results from such daily regressions
are shown in Table 2, and the logged daily
![]() are
plotted in Figure 2. The mean of the daily
estimates are a bit larger than the overall estimates reported in
Table 1, whereas the median daily estimates
are in fact very close to those in Table 1.
The
are
plotted in Figure 2. The mean of the daily
estimates are a bit larger than the overall estimates reported in
Table 1, whereas the median daily estimates
are in fact very close to those in Table 1.
The ![]() are also
somewhat larger with a median of 52.5% for the full-day sample estimates at the
five-minute frequency. The percentiles of the daily
are also
somewhat larger with a median of 52.5% for the full-day sample estimates at the
five-minute frequency. The percentiles of the daily ![]() shown in Table 2 provide additional support for a strong
relationship between returns and order flow at high-frequencies;
the lower 5% quantile
for the daily regressions run on the full-day sample at a
five-minute frequency is above 34% .11
shown in Table 2 provide additional support for a strong
relationship between returns and order flow at high-frequencies;
the lower 5% quantile
for the daily regressions run on the full-day sample at a
five-minute frequency is above 34% .11
In summary, the results reported in Tables 1 and 2 show that, at high
frequencies, returns and order flow tend to move in a consistent
direction to a large degree, thus giving support to equation
(1). The estimation of the
![]() in
equation (1) at a daily frequency allows us to
replace the unobserved
in
equation (1) at a daily frequency allows us to
replace the unobserved
![]() in
equation (3) with these `realized' daily
in
equation (3) with these `realized' daily
![]() , in the
same manner as we use realized volatility instead of the true
unobserved integrated volatility.12
, in the
same manner as we use realized volatility instead of the true
unobserved integrated volatility.12
3.2 Empirical Specification
The empirical specification that we are interested in testing is the following log-version of equation (3),
This specification is, of course, not a precise generalization of equation (3) since it does not properly take into account the additive error term in (3). However, it provides for a convenient empirical specification since it allows for tests of whether variations in both the
The daily data used in estimating equation (4) are constructed in a manner identical to that
described in the derivations above. That is, from the five-minute
exchange rate data, we construct continuously-compounded returns
(log differences), where ![]() is the return on day
is the return on day ![]() in interval
in interval ![]() . There are 288 five-minute intervals
each day; interval 1 is the time period from 17:00 to 17:05 (New
York time), since, by convention, each trading day in the global
foreign exchange market begins and ends at 17:00. We then calculate
realized volatility on day
. There are 288 five-minute intervals
each day; interval 1 is the time period from 17:00 to 17:05 (New
York time), since, by convention, each trading day in the global
foreign exchange market begins and ends at 17:00. We then calculate
realized volatility on day ![]() as
as
![]() . Similarly, squared
integrated order flow is created as
. Similarly, squared
integrated order flow is created as
![]() where
where
![]() is
the five-minute order flow in interval
is
the five-minute order flow in interval ![]() on day
on day ![]() . Daily variables based on the
one-minute frequency intra-daily data for the busiest trading hours
between 3-11am are constructed in an analogous manner. The
. Daily variables based on the
one-minute frequency intra-daily data for the busiest trading hours
between 3-11am are constructed in an analogous manner. The
![]() variables
are obtained from the daily OLS estimates of equation (1), as described above. There are
variables
are obtained from the daily OLS estimates of equation (1), as described above. There are ![]() daily observations in the
data.13
daily observations in the
data.13
Tables 3 and 4 show
summary statistics of the data, including the volume of trade which
is used briefly in the latter analysis, as well as the correlations
between the variables. The first moment of trading volume is
proprietary and cannot be displayed. The log-data is graphed in
Figure 2. Figure 3 shows
40-day moving averages of the demeaned log-transformed variables.
The graphs certainly suggest the possibility that movements in
![]() and the
integrated squared order flow could explain some of the movements
in volatility, but it seems unlikely that either of the two
explanatory variables by themselves could account for much of the
movements in volatility. The formal econometric analysis confirm
these speculations.
and the
integrated squared order flow could explain some of the movements
in volatility, but it seems unlikely that either of the two
explanatory variables by themselves could account for much of the
movements in volatility. The formal econometric analysis confirm
these speculations.
3.3 Preliminary OLS Analysis
It is well known that realized volatility exhibits a persistent behaviour, often modelled as long-memory or fractional integration, which may invalidate standard OLS inference in equation (4). In addition, it is likely that the right-hand side variables are endogenous in some manner, which would also imply that OLS estimates are biased. However, it is still instructive to consider the OLS estimates of equation (4) and compare them to the results obtained from regression analyses that explicitly take into account the persistence in the data.
Table 5 shows the results from the OLS
estimation of equation (4). Based on these
results, it would seem that equation (4)
provides a reasonably good fit of the data, with a large
![]() around
around
![]() and highly
significant
and highly
significant ![]() statistics
for all parameters. The parameters
statistics
for all parameters. The parameters
![]() and
and
![]() are
statistically significantly different from their theoretical values
of unity, however, and also deviate rather substantially from one
in absolute terms, with most estimates in the range of 0.8 to 0.9. The OLS analysis thus seems to imply that
equation (4) provides a good description of the
data, given the high
are
statistically significantly different from their theoretical values
of unity, however, and also deviate rather substantially from one
in absolute terms, with most estimates in the range of 0.8 to 0.9. The OLS analysis thus seems to imply that
equation (4) provides a good description of the
data, given the high ![]() ,
but there is less support of the more specific model given by
equation (3) which (approximately) implies
that
,
but there is less support of the more specific model given by
equation (3) which (approximately) implies
that
![]() . Table 5 also reports the results from estimating equation
(4) when either
. Table 5 also reports the results from estimating equation
(4) when either
![]() or
or
![]() are
restricted to equal zero; that is, the results from regressing
realized volatility onto either the
are
restricted to equal zero; that is, the results from regressing
realized volatility onto either the
![]() or the
squared order flow by themselves. Judging by the
or the
squared order flow by themselves. Judging by the ![]() , it is apparent from these
results that both of the regressors in equation (4) help explain the movements of volatility over time.
By themselves, the
, it is apparent from these
results that both of the regressors in equation (4) help explain the movements of volatility over time.
By themselves, the
![]() appear to
explain more of the variation in volatility than the squared order
flow, but neither of the variables does a very good job alone.
appear to
explain more of the variation in volatility than the squared order
flow, but neither of the variables does a very good job alone.
Given the fairly strong support that was found for equation
(1), the results shown in Table 5 might not seem totally surprising. Indeed, it seems
justified to ask whether the analysis of equation (4) adds much insight to that already gained from
equation (1). However, it is quite possible
that equation (1) is well specified, while
equation (4) is spurious in an econometric
sense. As shown below, realized volatility is fairly persistent and
well characterized as a long-memory or fractionally integrated
process. Thus, in order for equation (4) to
provide a meaningful econometric relationship, some of the
persistence in realized volatility must be explained by the
![]() and the
integrated squared order flow. Otherwise, the error term will have
the same persistence as the original data and equation (4) will make little sense from an econometric point of
view. The analysis of equation (1), however,
does not reveal whether this is the case or not, since it is
focused on the first moment of the data, whereas the long-memory is
in the second moment. A somewhat simplified, but perhaps more
intuitive way of understanding the differences between equations
(1) and (4) is to consider
the extreme case when the instantaneous volatility of returns is
constant within each day, but changes from day to day. Clearly, the
daily estimates of equation (1) could not then
tell us how the changes in volatility are related to changes in
and the
integrated squared order flow. Otherwise, the error term will have
the same persistence as the original data and equation (4) will make little sense from an econometric point of
view. The analysis of equation (1), however,
does not reveal whether this is the case or not, since it is
focused on the first moment of the data, whereas the long-memory is
in the second moment. A somewhat simplified, but perhaps more
intuitive way of understanding the differences between equations
(1) and (4) is to consider
the extreme case when the instantaneous volatility of returns is
constant within each day, but changes from day to day. Clearly, the
daily estimates of equation (1) could not then
tell us how the changes in volatility are related to changes in
![]() and the
integrated squared order flow, since in each estimation of equation
(1), volatility would be fixed.
and the
integrated squared order flow, since in each estimation of equation
(1), volatility would be fixed.
In the next section we outline econometric methods that take into account the persistent nature of the data, and provide explicit tests of the validity of equation (4).
4 Econometric Methodology
As we explained, the analysis performed in the previous section ignores two potential issues in the data that may render standard OLS inference invalid, long-memory and endogeneity. In this section we outline methods which explicitly take these issues into account.
4.1 Fractional Integration and Cointegration
The high degree of serial correlation, even at long lags, in
volatility is a well established empirical regularity. One of the
most common models for capturing this `long-memory' property is the
so-called fractionally integrated model, which is also often
referred to simply as a long-memory model. A process ![]() is said to be fractionally
integrated with memory parameter
is said to be fractionally
integrated with memory parameter ![]() , if
, if
where
Equation (5) has been used successfully to
capture much of the variance in realized volatility series (e.g.
Andersen, Bollerslev, Diebold, and Labys, 2003). The key parameter
of the model is the memory parameter ![]() , which determines the degree of persistence in the
process. For
, which determines the degree of persistence in the
process. For
![]() , the process
, the process
![]() is stationary,
although it will only slowly return to its long-run unconditional
mean, and for
is stationary,
although it will only slowly return to its long-run unconditional
mean, and for
![]() ,
, ![]() is a non-stationary process.
is a non-stationary process.
In a manner analogous to fractional integration generalizing
standard integrated processes, the concept of cointegration can
also be expanded to fractional cointegration. If ![]() is a vector process of
fractionally integrated variables, each with memory parameter
is a vector process of
fractionally integrated variables, each with memory parameter
![]() , and there exists a
non-zero linear combination of the elements in
, and there exists a
non-zero linear combination of the elements in ![]() with memory
with memory ![]() then
then ![]() is said to be fractionally
cointegrated. This concept was noted in the seminal paper by Engle
and Granger (1987), although it is only recently that it has
received much attention. Fractional cointegration generalizes
standard cointegration both in that the original component
processes in
is said to be fractionally
cointegrated. This concept was noted in the seminal paper by Engle
and Granger (1987), although it is only recently that it has
received much attention. Fractional cointegration generalizes
standard cointegration both in that the original component
processes in ![]() can be
fractionally integrated and in that the residuals in the
cointegrating relationship may possess long-memory, as long as
can be
fractionally integrated and in that the residuals in the
cointegrating relationship may possess long-memory, as long as
![]() .
.
The subsequent econometric analysis in this paper is based
around these concepts of fractional integration and cointegration.
We show that the variables in equation (4)
appear to possess long-memory and then test if equation (4) is a fractional cointegrating relationship. This
approach allows us to directly assess how much of the persistence
in volatility that can be attributed to the persistence in the
explanatory variables, by estimating the parameter ![]() from the fractional cointegrating
residuals.
from the fractional cointegrating
residuals.
To fix ideas, let
![]() ,
,
![]() and
and
![]() . We assume
the following data generating process,
. We assume
the following data generating process,
where
The parameters of interest are thus given by
![]() , although
we will estimate a separate
, although
we will estimate a separate ![]() parameter for each variable. The cointegration
vector
parameter for each variable. The cointegration
vector ![]() is
estimated using narrow band frequency domain methods that are
consistent also when the regressors are endogenous. Finally, the
long-memory parameter for the residuals,
is
estimated using narrow band frequency domain methods that are
consistent also when the regressors are endogenous. Finally, the
long-memory parameter for the residuals, ![]() , is estimated from the
cointegration residuals. This is crucial, since only if
, is estimated from the
cointegration residuals. This is crucial, since only if
![]() is less than
is less than
![]() , and hence there is
fractional cointegration, is the rest of the analysis valid.
, and hence there is
fractional cointegration, is the rest of the analysis valid.
4.2 Estimation of 
Univariate estimation of the long-memory parameter ![]() for each variable has been well
analyzed and a number of different procedures have been proposed in
the literature. Since the short-run dynamics of the data,
determined by the properties of
for each variable has been well
analyzed and a number of different procedures have been proposed in
the literature. Since the short-run dynamics of the data,
determined by the properties of ![]() , are not of primary interest, we focus on
methods that are semi-parametric in nature and make no specific
parametric assumptions regarding the dynamics of
, are not of primary interest, we focus on
methods that are semi-parametric in nature and make no specific
parametric assumptions regarding the dynamics of ![]() . In particular, we use a recent
estimator developed by Shimotsu and Phillips (2004) and Shimotsu
(2004), which they refer to as the exact local
Whittle (ELW) estimator. The ELW estimator is more efficient
than the commonly used log-periodogram regression estimator (Geweke
and Porter-Hudak, 1983, and Robinson, 1995a) and unlike the
standard local Whittle estimator (Künsch, 1987, and Robinson,
1995b), it is consistent and asymptotically normally distributed
for any value of
. In particular, we use a recent
estimator developed by Shimotsu and Phillips (2004) and Shimotsu
(2004), which they refer to as the exact local
Whittle (ELW) estimator. The ELW estimator is more efficient
than the commonly used log-periodogram regression estimator (Geweke
and Porter-Hudak, 1983, and Robinson, 1995a) and unlike the
standard local Whittle estimator (Künsch, 1987, and Robinson,
1995b), it is consistent and asymptotically normally distributed
for any value of ![]() . No prior assumptions on
. No prior assumptions on ![]() are therefore required and standard
errors and confidence intervals can easily be calculated based on
the asymptotic distribution that applies for all
are therefore required and standard
errors and confidence intervals can easily be calculated based on
the asymptotic distribution that applies for all ![]() . The analysis in the paper was also
performed using the standard local Whittle estimator and the
results were almost identical. For brevity, we only show the
results from the ELW estimator.14
. The analysis in the paper was also
performed using the standard local Whittle estimator and the
results were almost identical. For brevity, we only show the
results from the ELW estimator.14
The ELW estimator relies on a frequency domain representation of
the data and uses only the first ![]() frequencies closest to the origin, where
frequencies closest to the origin, where
![]() and
and
![]() , as
, as
![]() .15 By using only the frequencies around
zero, the short-run dynamics of the data do not affect the
estimator. Shimotsu and Phillips (2004) show that the limiting
distribution of the estimator is asymptotically normal with
variance
.15 By using only the frequencies around
zero, the short-run dynamics of the data do not affect the
estimator. Shimotsu and Phillips (2004) show that the limiting
distribution of the estimator is asymptotically normal with
variance
![]() for all values of
for all values of ![]() . Since
we are not aware of any studies on the optimal choice of bandwidth
for this estimator, we follow the usual convention in the
literature and report the results for a range of alternatives.
. Since
we are not aware of any studies on the optimal choice of bandwidth
for this estimator, we follow the usual convention in the
literature and report the results for a range of alternatives.
4.3 Cointegration Estimation and Testing
It is well known that in a standard cointegration framework with
unit-root regressors and stationary errors, the standard OLS
estimates of the cointegration vector are still consistent when the
regressors are endogenous. Briefly speaking, this holds because the
strength of the signal in the non-stationary regressors is of an
order of magnitude stronger than the biasing effect resulting from
the endogeneity; hence, the endogeneity will only cause the OLS
estimator to be inefficient, rather than inconsistent. On a more
intuitive level, cointegration represents a long-run equilibrium,
or co-movement, between variables; it is thus not a causal
relationship and endogeneity is not a first order concern. A
similar argument can be made in the non-stationary fractionally
cointegrated case, with ![]() . However, in the stationary case with
. However, in the stationary case with
![]() , which seems
to be the relevant case for the present study, standard OLS will no
longer deliver consistent estimates.
, which seems
to be the relevant case for the present study, standard OLS will no
longer deliver consistent estimates.
In order to understand the advantages and need for the more
complicated methods described below, it is useful to quickly
consider the properties of OLS for stationary and non-stationary
variables. For simplicity, suppose
![]() , where the error term
, where the error term
![]() is
is ![]() and correlated with
and correlated with ![]() . For OLS to be a consistent
estimator of
. For OLS to be a consistent
estimator of ![]() , it must
hold that
, it must
hold that
![]() as
as
![]() .
This condition is satisfied in the unit-root case, as well as in
the case where
.
This condition is satisfied in the unit-root case, as well as in
the case where ![]() , since the variation in the non-stationary
process
, since the variation in the non-stationary
process ![]() will be
of an order of magnitude larger than that of the stationary noise
will be
of an order of magnitude larger than that of the stationary noise
![]() ; that is, the
denominator will grow faster than the numerator and the ratio will
converge to zero. However, in the stationary case with
; that is, the
denominator will grow faster than the numerator and the ratio will
converge to zero. However, in the stationary case with ![]() ,
,
![]() , since
, since ![]() is
endogenous. Thus, despite the long-memory, the variance in the
regressor
is
endogenous. Thus, despite the long-memory, the variance in the
regressor ![]() no
longer dominates that of the error term
no
longer dominates that of the error term ![]() and the OLS estimator is
inconsistent. However, although the overall variance in
and the OLS estimator is
inconsistent. However, although the overall variance in
![]() does not dominate
that of
does not dominate
that of ![]() , it is
still the case that the long-memory in
, it is
still the case that the long-memory in ![]() causes the variance coming from
the long-run movements in
causes the variance coming from
the long-run movements in ![]() to dominate the long-run variance in
to dominate the long-run variance in
![]() . Therefore, by
focusing exclusively on the long run movements in the data, it is
possible to consistently estimate
. Therefore, by
focusing exclusively on the long run movements in the data, it is
possible to consistently estimate ![]() also in the case with
also in the case with ![]() . Indeed, since (fractional)
cointegration represents a long-run relationship, it is intuitively
appealing to use only the long-run data movements in the estimation
procedure.
. Indeed, since (fractional)
cointegration represents a long-run relationship, it is intuitively
appealing to use only the long-run data movements in the estimation
procedure.
The most convenient way of extracting the long-run movements in
the data is by transforming the data into the frequency domain,
where the frequencies close to zero represent the long-run.16 Thus, for observations around the zero
frequency the strength of the cointegrating relationship dominates
the endogeneity effect and deliver consistent estimates. A least
squares estimator that relies only on observations in a narrow band
of frequencies is referred to as a narrow band least squares (NBLS)
estimator. Robinson (1994) shows that in the presence of fractional
cointegration, with ![]() , the NBLS estimator around the zero frequency
does yield consistent estimates of the cointegrating vector. It
should be stressed that this result holds also when the
cointegration residuals possess long-memory, as long as the memory
in the residuals is less than in the original data; i.e., when
there is fractional cointegration. The NBLS estimator is also
consistent in the non-stationary case of
, the NBLS estimator around the zero frequency
does yield consistent estimates of the cointegrating vector. It
should be stressed that this result holds also when the
cointegration residuals possess long-memory, as long as the memory
in the residuals is less than in the original data; i.e., when
there is fractional cointegration. The NBLS estimator is also
consistent in the non-stationary case of ![]() , as long as there is
fractional cointegration.
, as long as there is
fractional cointegration.
Although the NBLS estimator ensures consistent estimation of
fractional cointegrating relationships, we can improve upon this
estimator when the regressors are endogenous. Nielsen and
Frederiksen (2005) show how to modify the NBLS estimator and
achieve estimates that are more closely centered around the true
parameter values; they label the resulting estimator fully modified
NBLS (FMNBLS). Apart from providing better point estimates, the
FMNBLS estimator also has the desirable property that it is
asymptotically normally distributed for ![]() ; this is not generally true
for the standard NBLS estimator.
; this is not generally true
for the standard NBLS estimator.
In addition, Nielsen and Frederiksen (2005) show that estimates
of ![]() , the long-memory
parameter for the cointegration residuals, can be consistently
estimated from the fitted regression residuals, and that the
asymptotic distribution of the estimator for
, the long-memory
parameter for the cointegration residuals, can be consistently
estimated from the fitted regression residuals, and that the
asymptotic distribution of the estimator for ![]() will be the same as if the true
cointegration errors were used. This result holds for estimated
regression residuals based either on the NBLS or FMNBLS
estimates.
will be the same as if the true
cointegration errors were used. This result holds for estimated
regression residuals based either on the NBLS or FMNBLS
estimates.
The NBLS estimator is a function of the number of frequencies
close to zero used in the estimation; we call that number the
bandwidth parameter ![]() .
Similarly, we label as
.
Similarly, we label as ![]() the bandwith parameter used in the ELW
estimation of
the bandwith parameter used in the ELW
estimation of ![]() for the
NBLS residuals. The FMNBLS estimator relies on a preliminary NBLS
estimation, using bandwidth
for the
NBLS residuals. The FMNBLS estimator relies on a preliminary NBLS
estimation, using bandwidth ![]() , as well as estimates of
, as well as estimates of ![]() and
and ![]() , based on the NBLS residuals, using bandwidth
, based on the NBLS residuals, using bandwidth
![]() . The correction
term used in the FMNBLS estimator is calculated using a bandwidth
. The correction
term used in the FMNBLS estimator is calculated using a bandwidth
![]() and the actual
FMNBLS estimates are obtained using a bandwidth
and the actual
FMNBLS estimates are obtained using a bandwidth ![]() , which is set equal to
, which is set equal to
![]() . The estimate of
. The estimate of
![]() in the FMNBLS
residuals is calculated using the bandwidth
in the FMNBLS
residuals is calculated using the bandwidth ![]() . The NBLS and FMNBLS
estimators, along with relevant bandwidth conditions, are discussed
further in the Appendix.
. The NBLS and FMNBLS
estimators, along with relevant bandwidth conditions, are discussed
further in the Appendix.
5 Empirical Results
At the end of Section 3, we presented some
preliminary support for equation (4) based on
OLS analysis. In this section we use the econometric tools
described above to show that the initial conclusions from the OLS
estimation can in fact be substantially strengthened. We estimate
equations (6)-(8), which
formalize the time-series properties of the variables in equation
(4), and find strong evidence of a fractional
cointegrating relationship between realized volatility, the
integrated squared order flow and the realized
![]() . Indeed,
in many cases, we cannot reject the null hypothesis that all of the
long-memory in volatility is explained by these two co-variates.
This is especially true for the sample based only on data for the
busiest hours between 3-11am, sampled at the one-minute frequency.
In this case, the null hypothesis cannot be rejected for any of the
bandwidths that are used.
. Indeed,
in many cases, we cannot reject the null hypothesis that all of the
long-memory in volatility is explained by these two co-variates.
This is especially true for the sample based only on data for the
busiest hours between 3-11am, sampled at the one-minute frequency.
In this case, the null hypothesis cannot be rejected for any of the
bandwidths that are used.
The empirical results from the estimation of equation (4), of formally equations (6)-(8), are shown in Table 6. Panel A shows the results for the samples based on
intra-daily data sampled at the five-minute frequency, using all
hours of the day. Panels B show the corresponding results when only
intra-daily data between the hours of 03:00 and 11:00, sampled at
the one minute frequency, are used. In both panels, the ELW
estimates of ![]() for each of
the daily log-transformed variables, including volume, are shown,
along with the estimates of the cointegrating vector, using either
the NBLS or FMNBLS estimators, and the corresponding estimates of
the long-memory parameter,
for each of
the daily log-transformed variables, including volume, are shown,
along with the estimates of the cointegrating vector, using either
the NBLS or FMNBLS estimators, and the corresponding estimates of
the long-memory parameter, ![]() , in the residuals. All estimates are calculated
for a number of different bandwidths.
, in the residuals. All estimates are calculated
for a number of different bandwidths.
5.1 Estimates of 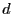
The top of both panels in Table 6 shows the
estimated long-memory parameters for each data series. The
estimates are all based on the ELW estimator, allowing for a
non-zero mean as described by Shimotsu (2004). Three different
bandwidths are considered,
![]() ,
,
![]() , and
, and
![]() , where
, where
![]() indicates the integer part of a real number.17 For the larger bandwidths,
indicates the integer part of a real number.17 For the larger bandwidths,
![]() and
and
![]() , the estimates of
, the estimates of
![]() for realized
volatility are all between
for realized
volatility are all between ![]() and
and ![]() ,
similar to those found in other studies (e.g. Andersen, Bollerslev,
Diebold, and Labys, 2003, and Bollerslev and Wright, 2000). The
estimates for the
,
similar to those found in other studies (e.g. Andersen, Bollerslev,
Diebold, and Labys, 2003, and Bollerslev and Wright, 2000). The
estimates for the
![]() are
similar to those for realized volatility, but generally somewhat
larger. The estimates for the integrated squared order flow are
smaller and are all in the region
are
similar to those for realized volatility, but generally somewhat
larger. The estimates for the integrated squared order flow are
smaller and are all in the region
![]() . It is interesting to note,
however, that for the smallest bandwidth
. It is interesting to note,
however, that for the smallest bandwidth
![]() , the point estimates of
, the point estimates of
![]() for both realized
volatility and the realized
for both realized
volatility and the realized
![]() are
greater than
are
greater than ![]() , and
thus in the non-stationary region; the estimates of
, and
thus in the non-stationary region; the estimates of ![]() for the
for the
![]() is, in
fact, greater than
is, in
fact, greater than ![]() also for
also for
![]() when the one minute data from
03:00 to 11:00 are used. This is in contrast to the commonly held
belief that realized volatility is a stationary process with
when the one minute data from
03:00 to 11:00 are used. This is in contrast to the commonly held
belief that realized volatility is a stationary process with
![]() , although
Bandi and Perron (2004) also find similar results for stock-return
volatility. Of course, for all bandwidths considered here, a
, although
Bandi and Perron (2004) also find similar results for stock-return
volatility. Of course, for all bandwidths considered here, a
![]() confidence
interval for
confidence
interval for ![]() , for realized
volatility, would always include values greater than
, for realized
volatility, would always include values greater than ![]() . The estimates for volume are
generally larger than those for the squared order flow but smaller
than the ones for realized volatility and the
. The estimates for volume are
generally larger than those for the squared order flow but smaller
than the ones for realized volatility and the
![]() .
.
There is thus strong evidence of significant long-memory in all
variables, and the estimates indicate that the memory in realized
volatility and the
![]() are quite
similar whereas the squared order flow appear to have somewhat less
memory. We should stress again, however, that the subsequent
fractional cointegration analysis does not require identical memory
in the variables. It can also not be ruled out statiscally that
some of the variables are non-stationary, although most point
estimates of
are quite
similar whereas the squared order flow appear to have somewhat less
memory. We should stress again, however, that the subsequent
fractional cointegration analysis does not require identical memory
in the variables. It can also not be ruled out statiscally that
some of the variables are non-stationary, although most point
estimates of ![]() are in the
stationary region. The NBLS and FMNBLS estimators described above
will remain consistent for non-stationary data, although they will
no longer be asymptotically normally distributed. Since most
estimates point towards stationarity, however, inference based on
the assumption of a stationary fractional cointegration
relationship still seems the most suitable. One would also expect
that small deviations from stationarity, i.e. for
are in the
stationary region. The NBLS and FMNBLS estimators described above
will remain consistent for non-stationary data, although they will
no longer be asymptotically normally distributed. Since most
estimates point towards stationarity, however, inference based on
the assumption of a stationary fractional cointegration
relationship still seems the most suitable. One would also expect
that small deviations from stationarity, i.e. for ![]() greater than, but close to
greater than, but close to
![]() , the estimators
are close to normally distributed asymptotically. Perhaps most
importantly, the ELW estimator of
, the estimators
are close to normally distributed asymptotically. Perhaps most
importantly, the ELW estimator of ![]() for the regression residuals, will have the same
asymptotic distribution regardless of whether the data are
stationary or not.
for the regression residuals, will have the same
asymptotic distribution regardless of whether the data are
stationary or not.
5.2 Cointegration Estimates
The bottom parts of the panels in Table 6 show the results from the fractional cointegration analysis, using
either the NBLS or FMNBLS estimator with a set of different
bandwidths. The FMNBLS estimator is asymptotically normally
distributed provided the regressors are stationary, which seems
likely to hold.18 Thus,
the standard errors given below the FMNBLS estimates can be used
for standard inference; standard errors are given for the intercept
but the asymptotic properties for the intercept estimator are
unknown.19 As a
comparison to the narrow band estimates, the last row in each panel
gives the results from a full bandwidth or, equivalently, OLS
estimation; these results are thus identical to those shown in
Table 5, except for the additional estimates of
![]() , based on the OLS
residuals, which is now also shown.
, based on the OLS
residuals, which is now also shown.
The results for the sample based on intra-daily five-minute
returns from all hours of the day, are shown in Panel A of Table 6. It is immediately obvious that there is a
fairly large difference between the standard OLS estimates and the
narrow band estimates. The NBLS and FMNBLS estimates of
![]() and
and
![]() are
much closer to unity, as the model would predict, and based on the
standard errors, we can typically not reject the null hypothesis
that
are
much closer to unity, as the model would predict, and based on the
standard errors, we can typically not reject the null hypothesis
that
![]() . The FMNBLS
estimates are typically somewhat closer to unity than the plain
NBLS estimates, although the difference here is smaller than that
between the OLS and the NBLS estimates. The differences across
bandwidths are fairly small, and do not change the overall outcome
of the estimates. This is somewhat striking, given that the
smallest bandwidth used for the regression estimates,
. The FMNBLS
estimates are typically somewhat closer to unity than the plain
NBLS estimates, although the difference here is smaller than that
between the OLS and the NBLS estimates. The differences across
bandwidths are fairly small, and do not change the overall outcome
of the estimates. This is somewhat striking, given that the
smallest bandwidth used for the regression estimates,
![]() , in fact only
contain the first eight frequencies; a reflection of how much of
the signal in a persistent process that is concentrated to the
first few frequencies. The OLS estimates show, however, that the
introduction of higher frequencies will eventually bias the results
downward.
, in fact only
contain the first eight frequencies; a reflection of how much of
the signal in a persistent process that is concentrated to the
first few frequencies. The OLS estimates show, however, that the
introduction of higher frequencies will eventually bias the results
downward.
Given these results, it seems that equation (4) is best interpreted as a long-run relationship and
the primary question therefore becomes whether the realized
![]() and the
squared order flow can indeed explain the long-run characteristics
of realized volatility. The answer to this question, of course,
lies in the estimates of
and the
squared order flow can indeed explain the long-run characteristics
of realized volatility. The answer to this question, of course,
lies in the estimates of ![]() , the long-memory parameter for the residuals in
equation (4). These estimates are shown in both
panels of Table 6, and focusing again on Panel
A, it is evident that the memory in the residuals
, the long-memory parameter for the residuals in
equation (4). These estimates are shown in both
panels of Table 6, and focusing again on Panel
A, it is evident that the memory in the residuals ![]() , is substantially less than the
memory in the original realized volatility. Although for most
bandwidths it is possible to reject the null hypothesis that
, is substantially less than the
memory in the original realized volatility. Although for most
bandwidths it is possible to reject the null hypothesis that
![]() the evidence
of fractional cointegration is very strong, with estimates of
the evidence
of fractional cointegration is very strong, with estimates of
![]() typically much
smaller than the estimates of
typically much
smaller than the estimates of ![]() . Only for the smallest bandwidth is the estimate of
. Only for the smallest bandwidth is the estimate of
![]() , equal to about
0.17, substantially
larger than zero in absolute terms. However, for that bandwidth the
estimate of
, equal to about
0.17, substantially
larger than zero in absolute terms. However, for that bandwidth the
estimate of ![]() for realized
volatility is equal to 0.559 and the results thus suggest a memory reduction
of almost 0.4. When
using the OLS residuals, the estimate of
for realized
volatility is equal to 0.559 and the results thus suggest a memory reduction
of almost 0.4. When
using the OLS residuals, the estimate of ![]() , 0.237, is much larger than the corresponding estimates
from the narrow band residuals, which are equal to about
0.08, with the same
bandwidth used for the estimation of
, 0.237, is much larger than the corresponding estimates
from the narrow band residuals, which are equal to about
0.08, with the same
bandwidth used for the estimation of ![]() . The results based on the NBLS and FMNBLS
residuals are very similar, reflecting the closeness of these
regression estimates.
. The results based on the NBLS and FMNBLS
residuals are very similar, reflecting the closeness of these
regression estimates.
There is thus very strong evidence that equation (4) should be seen as a fractional cointegrating relationship. It cannot be ruled out that there is still a small long-memory component in the residuals, but it is evident that the amount of persistence in the residuals is much less than in the realized volatility.
The results for the one-minute sample shown in Panels B of Table 6, are generally in line with those just
discussed for the full-day five-minute sample. For the one-minute
sample, the cointegration results are even stronger, and we cannot
reject the hypothesis of ![]() for any bandwidths; the point estimates of
for any bandwidths; the point estimates of
![]() are are also
typically very close to zero. The estimates of
are are also
typically very close to zero. The estimates of
![]() are
somewhat smaller than those for the full-day five-minute data shown
in Panel A, and on the borderline of being significantly different
from one.
are
somewhat smaller than those for the full-day five-minute data shown
in Panel A, and on the borderline of being significantly different
from one.
Some additional graphical evidence of fractional cointegration are shown in Figures 4 and 5. Figure 4 shows plots of realized volatility and the corresponding FMNBLS regression residuals. The difference between the original data and the residuals is striking, and the graphs clearly show the large reduction in persistent behaviour in the residuals.20 A similar case is made in Figure 5, which plots the auto-corellograms for realized volatility and the FMNBLS residuals. Again, there is an obvious and remarkable difference in the autocorrelation of realized volatility and the regression residuals. In summary, the results presented in this section show strong evidence that most, if not all, of the long-run time-series behaviour in exchange rate volatility can be explained by movements in the associated order flow and market sensitivity.
5.3 Order Flow or Market Sensitivity: Which Influence Dominates?
The results in the previous section give strong support for the
joint ability of market sensitivity and integrated squared order
flow to explain the persistence in volatility. Although the
estimated slope coefficients for both of these variables are highly
significant and close to their theoretical values, it cannot be
ruled out that the fractional cointegration result is primarily
driven by one of these variables. We test this possibility here by
using the same fractional cointegration tests as above on each of
the two explanatory variables separately. The results are shown in
Table 8; for brevity we only show the FMNBLS
results. Starting with the results for
![]() , it is
clear that the estimated slope coefficient
, it is
clear that the estimated slope coefficient
![]() is
smaller than in the specification with two regressors, but still of
a somewhat similar magnitude. The estimates of
is
smaller than in the specification with two regressors, but still of
a somewhat similar magnitude. The estimates of
![]() , the
memory parameter for the residuals, is now substantially larger,
however, with values around 0.3. This is still smaller than the estimates of
, the
memory parameter for the residuals, is now substantially larger,
however, with values around 0.3. This is still smaller than the estimates of
![]() for the original
realized volatility data, which are typically around 0.45, but it is evident that the
for the original
realized volatility data, which are typically around 0.45, but it is evident that the
![]() explain
less of the persistence in volatility by themselves than they do
jointly with the squared order flow.
explain
less of the persistence in volatility by themselves than they do
jointly with the squared order flow.
The results for the integrated squared order flow, however, show
no evidence that this variable can explain any of the persistence
in volatility by itself; the estimates of ![]() are very similar to the
estimates of
are very similar to the
estimates of ![]() in realized
volatility. Given the apparent lack of fractional cointegration in
this regression, the estimates are likely to be spurious. This may
explain why the slope coefficient now is negative for the FMNBLS
estimates and also the large variation across bandwidths. The OLS
estimates are in fact the only ones that appear somewhat similar to
the results found for the model with both explanatory variables
included. However, the lack of any evidence of cointegration also
in this case, and the subsequent spurious nature of the regression,
makes it difficult to interpret the coefficient estimates. Still,
all the evidence we have uncovered strongly suggests that the role
of market sensitivity in explaining volatility persistence is at
least as large as that of the rate of information arrival.
in realized
volatility. Given the apparent lack of fractional cointegration in
this regression, the estimates are likely to be spurious. This may
explain why the slope coefficient now is negative for the FMNBLS
estimates and also the large variation across bandwidths. The OLS
estimates are in fact the only ones that appear somewhat similar to
the results found for the model with both explanatory variables
included. However, the lack of any evidence of cointegration also
in this case, and the subsequent spurious nature of the regression,
makes it difficult to interpret the coefficient estimates. Still,
all the evidence we have uncovered strongly suggests that the role
of market sensitivity in explaining volatility persistence is at
least as large as that of the rate of information arrival.
The failure of the integrated squared order flow to capture any
of the persistence in volatility by itself is not very surprising,
given the estimates of the long-memory parameters shown in Table 6. The point estimates clearly indicates that
the persistence in volatility is likely to be greater than that in
the squared order flow. Hence, there is simply not enough
persistence in the squared order flow to explain the long-run
movements in volatility. The
![]() , on the
other hand, seem to have a very similar degree of persistence to
that in volatility.
, on the
other hand, seem to have a very similar degree of persistence to
that in volatility.
Taken together, the results in Tables 6 and 8 suggest the possibility that the
![]() primarily
explain the most persistent behaviour in volatility, captured by
the reduction in memory from 0.45 to 0.3,
whereas the integrated squared order flow captures the somewhat
less persistent behaviour represented by the remaining memory, of
about 0.3, that is not
explained by the
primarily
explain the most persistent behaviour in volatility, captured by
the reduction in memory from 0.45 to 0.3,
whereas the integrated squared order flow captures the somewhat
less persistent behaviour represented by the remaining memory, of
about 0.3, that is not
explained by the
![]() . The
graphs in Figure 3 also gives some support to
this notion, where it appears that the
. The
graphs in Figure 3 also gives some support to
this notion, where it appears that the
![]() co-move
with the big swings in volatility whereas the squared order flow
picks up the less persistent shocks. Liesenfeld (2001) advances a
similar conclusion.
co-move
with the big swings in volatility whereas the squared order flow
picks up the less persistent shocks. Liesenfeld (2001) advances a
similar conclusion.
5.4 The Unconditional Distribution
So far we have shown that the regression equation (4) does a good job of capturing the time series
properties of realized volatility, in the sense that almost all of
its persistence can be explained by the
![]() and the
integrated squared order flow. It is, however, also interesting to
briefly consider whether equation (4) can
adequately capture the unconditional distribution of realized
volatility. As highlighted in Andersen, Bollerslev, Diebold, and
Ebens (2001) and Andersen, Bollerslev, Diebold, and Labys (2001,
2003), the unconditional distribution of log-realized-volatilty
appears close to normal. Table 3 gives some
support to this conjecture, although the kurtosis is on the large
side, especially in the five-minute full day sample.
and the
integrated squared order flow. It is, however, also interesting to
briefly consider whether equation (4) can
adequately capture the unconditional distribution of realized
volatility. As highlighted in Andersen, Bollerslev, Diebold, and
Ebens (2001) and Andersen, Bollerslev, Diebold, and Labys (2001,
2003), the unconditional distribution of log-realized-volatilty
appears close to normal. Table 3 gives some
support to this conjecture, although the kurtosis is on the large
side, especially in the five-minute full day sample.
Table 7 shows the corresponding summary
statistics for the fitted values of realized volatility, obtained
from the estimate of equation (4). The skewness
and kurtosis in the fitted data is similar to those of the actual
data in the 3-11am one minute sample, but less so in the full day
five minute sample. The most noticeable difference is the large
kurtosis in the fitted five minute data, which is likely a result
of the large kurtosis in the five-minute
![]() , as seen
in Table 3. Figure 6
shows kernel density estimates of the unconditional distributions
for the fitted values as well as for the actual realized volatility
data. The densities are standardized to have zero mean and unit
variance, and as a comparison the standard normal density is also
plotted. It is quite evident that the original log-data is close to
normally distributed, whereas the fitted values deviate somewhat
from normality, although less so for the one-minute data. Overall,
the evidence in Table 7 and Figure 6 show that the fitted equation (4) captures the salient features of the unconditional
distribution of the log-realized-volatility.
, as seen
in Table 3. Figure 6
shows kernel density estimates of the unconditional distributions
for the fitted values as well as for the actual realized volatility
data. The densities are standardized to have zero mean and unit
variance, and as a comparison the standard normal density is also
plotted. It is quite evident that the original log-data is close to
normally distributed, whereas the fitted values deviate somewhat
from normality, although less so for the one-minute data. Overall,
the evidence in Table 7 and Figure 6 show that the fitted equation (4) captures the salient features of the unconditional
distribution of the log-realized-volatility.
6 The Role of Trading Volume
As stated in the introduction, the most common hypothesis used for explaining volatility persistence in stock returns is that the rate of arrival of information affecting the asset price is itself persistent. The arrival of information generates price changes and, in most models, trading activity; the theoretical models of Clark (1973) and Tauchen and Pitts (1983) are based around these ideas. This line of reasoning implies that the volume of trade is also likely to be persistent and co-move with volatility. Ideally, of course, one would want to test this theory by directly relating volatility to the flow of information. Unfortunately, the actual arrival of information is hard to measure and quantify.21
Given the problems of directly measuring information arrival, most empirical research in this field has attempted to link volatility and volume (e.g., Lamoureux and Lastrapes, 1990, 1994, Andersen, 1996, and Bollerslev and Jubinski, 1999). To account for the simultaneity of volatility and volume, it is popular to use a model with a latent unobserved information arrival process that affects both volatility and volume. The estimated volatility persistence from such bivariate volatility-volume models is typically much smaller than that found in univariate ARCH/GARCH or stochastic volatility estimates, however.
Given this empirical tradition of relating volatility and volume in stock markets, we investigate this relationship in our foreign exchange data. This relationship has not been analyzed previously in the foreign exchange market, as trading volume data representing a substantial share of the market have not been previously available. At the highest of frequencies (tick by tick), absolute (squared) order flow and (squared) trading volume are, by definition, equal. As the sampling frequency decreases, the two series diverge quickly, and intervals with high trading volume could have an order flow of, for instance, zero. At the relatively-high frequencies that we consider in this paper, squared order flow integrated over a day and daily trading volume (not squared) are still fairly highly correlated, as seen in Table 4. Figure 7 shows a 40-day moving average plot of the logged value of volume, next to the log of realized volatility; it is evident that the time-series for volume share many of characteristics of the integrated squared order flow, shown in Figure 3.22
We regress daily volatility onto either just daily volume or
onto both volume and the
![]() , to
evaluate if volume does as well as order flow in explaining
volatility persistence. In addition, we also test if one can do
even better at explaining volatility persistence by including both
volume and order flow, as well as the
, to
evaluate if volume does as well as order flow in explaining
volatility persistence. In addition, we also test if one can do
even better at explaining volatility persistence by including both
volume and order flow, as well as the
![]() , in the
regression. This specification can be motivated by the possibility
that, ceteris paribus, a greater order
flow is needed to move returns when the overall volume is
relatively high. By including volume in the regression, such
effects are controlled for. As discussed previously, in the
presence of fractional cointegration, narrow band least squares
around the zero frequency will deliver consistent estimates of the
regression coefficients also in the presence of endogeneity. Again,
we show only the results from the FMNBLS estimation. Standard OLS
estimates are given as a comparison, however.
, in the
regression. This specification can be motivated by the possibility
that, ceteris paribus, a greater order
flow is needed to move returns when the overall volume is
relatively high. By including volume in the regression, such
effects are controlled for. As discussed previously, in the
presence of fractional cointegration, narrow band least squares
around the zero frequency will deliver consistent estimates of the
regression coefficients also in the presence of endogeneity. Again,
we show only the results from the FMNBLS estimation. Standard OLS
estimates are given as a comparison, however.
Table 9 shows the results from using volume
instead of integrated squared order flow in equation (4). As expected, given the results in Table 8, volume by itself cannot explain any of the
persistence in volatility. Note, however, that if one performed
just a plain OLS regression and based the inference on the standard
errors of the slope coefficient, one would conclude that volume is
highly significant. When including both volume and the
![]() in the
regression, the results change substantially. The estimates of
in the
regression, the results change substantially. The estimates of
![]() are still
somewhat larger than those found when using the integrated squared
order flow together with the
are still
somewhat larger than those found when using the integrated squared
order flow together with the
![]() shown in
Table 6, but they are much smaller than when
only the
shown in
Table 6, but they are much smaller than when
only the
![]() are
included as shown in Table 8. There is thus
clear evidence that volume enters into the fractional cointegration
relationship, together with the
are
included as shown in Table 8. There is thus
clear evidence that volume enters into the fractional cointegration
relationship, together with the
![]() , and
helps explain the persistence in volatility. In general, however,
the null hypothesis of
, and
helps explain the persistence in volatility. In general, however,
the null hypothesis of
![]() is
rejected. The coefficients in front of the
is
rejected. The coefficients in front of the
![]() and
volume are quite close to one; there is no strong reason that they
should equal one, however, since volume played no part in the
derivation of the regression equation.
and
volume are quite close to one; there is no strong reason that they
should equal one, however, since volume played no part in the
derivation of the regression equation.
In Table 10, the results from regressing
volatility onto volume, integrated squared order flow, and the
![]() are
shown. For the 3-11am one-minute data, the estimates of
are
shown. For the 3-11am one-minute data, the estimates of
![]() are
similar to those found for the case with just the integrated
squared order flow, except for the smallest bandwidth where the
estimate in Table 10 is substantially larger.
For the other bandwidths, the null hypothesis of
are
similar to those found for the case with just the integrated
squared order flow, except for the smallest bandwidth where the
estimate in Table 10 is substantially larger.
For the other bandwidths, the null hypothesis of ![]() cannot be rejected. The
estimates of the coefficients for the squared order flow and the
volume are estimated very imprecisely, reflecting the high
correlation between order flow and volume at the one-minute
frequency. At the five-minute frequency, however, the estimates of
cannot be rejected. The
estimates of the coefficients for the squared order flow and the
volume are estimated very imprecisely, reflecting the high
correlation between order flow and volume at the one-minute
frequency. At the five-minute frequency, however, the estimates of
![]() are in
fact considerably smaller than those in Table 6. The coefficients for squared order flow and volume
are now also more precisely estimated, although less so than in the
case with just squared order flow. This regression also highlights
the bias in the plain OLS regression; the OLS estimates deviate
substantially from the FMNBLS estimates, which is also reflected in
the much larger value for
are in
fact considerably smaller than those in Table 6. The coefficients for squared order flow and volume
are now also more precisely estimated, although less so than in the
case with just squared order flow. This regression also highlights
the bias in the plain OLS regression; the OLS estimates deviate
substantially from the FMNBLS estimates, which is also reflected in
the much larger value for
![]() . Overall,
there is some evidence that when sampling data at the five-minute
frequency, the additional information contained in volume can help
explain the long-run behaviour in volatility. It is also clear,
however, that squared order flow is more important in explaining
volatility persistence than is trading volume.
. Overall,
there is some evidence that when sampling data at the five-minute
frequency, the additional information contained in volume can help
explain the long-run behaviour in volatility. It is also clear,
however, that squared order flow is more important in explaining
volatility persistence than is trading volume.
7 Conclusion
We have shown that movements in the market's sensitivity to information, jointly with movements in the rate of information arrival, can, to a very large degree, explain the long-run dynamics of realized exchange rate volatility. Our results are based on a new simple empirical specification of volatility derived from the trading model of Kyle (1985). In contrast with previous research on the determinants of volatility, which have primarily relied on latent variable models, our specification allows us to directly study how the order flow and its time-varying impact on the price relates to movements in volatility. To the extent that order flow brings new information to the market, our results therefore provide strong direct empirical support for the explanation of volatility persistence advanced in a model by Liesenfeld (2001), which highlighted the role of the time-varying market sensitivity to information.
The empirical analysis is focused on detecting co-movements between the long-run slow-moving components that dominate the time-series behaviour in realized volatility as well as in the explanatory variables. The results indicate that the very long-run movements in volatility are primarily associated with changes in the market sensitivity, whereas the somewhat less persistent variation is captured by changes in the information flow itself. Importantly, we rely on recent econometric methods which allow us to avoid the potential simultaneity bias that may affect regressions involving asset price volatility and variables such as order flow and trading volume, and also address the potential spuriousness that may arise in the study of the joint behavior of these fairly persistent variables. Our robust methods, for instance, show little or no evidence that trading volume explains volatility persistence, whereas standard OLS inference on the same data indicates strongly that trading volume co-moves with volatility.
This work is made possible by the availability for the first time of a unique set of euro-dollar spot exchange rate trading data, which covers a majority of global interdealer activity in that currency pair at very high frequency over several years. This owes to a change in the structure of the foreign exchange market in recent years: On a global scale, interdealer trading in this exchange rate, while still fully over-the-counter, has been heavily concentrated on a single electronic trading platform. The immense size of the euro-dollar spot market and the availability of these data make it an ideal candidate to estimate our measure of market sensitivity and to study the impact of its variation over time.
It would, of course, be of interest to repeat the same exercise using data from other asset markets. One interesting question is whether the strength of our findings regarding the link between variations in market sensitivity and the long-run time series behavior of volatility is peculiar to the foreign exchange market or would also be present in equity and bond markets. It is widely believed that there is less of a consensus among market participants about an equilibrium model for prices in the foreign exchange market than in other financial markets. It is therefore possible that the role of order flow in driving prices and conveying information is greater in the foreign exchange market than in other markets, which would make order flow and our market sensitivity parameter more relevant to the study of volatility in the foreign exchange market than in other markets. However, papers such as Hasbrouck (1991), for instance, have demonstrated the important role of order flow in conveying information in equity markets, and recent work by Brandt and Kavajecz (2004) has found the same phenomenon in the Treasury market. This suggests that our results would likely extend to other asset prices, although perhaps not with the same strength.
Given the importance of the time-varying market sensitivity in explaining volatility movements, an obvious question for further research is what actually drives the observed changes in market sensitivity. In the original model of Kyle (1985), from which our specification for volatility is derived, the response of the price to order flow depends upon the amount of informed trading in the market. The more informed traders in the market, the more private information is conveyed through the order flow. It is possible that some variant of this idea could be at play here, although the role of purely private information in exchange rate markets is widely thought to be small. But if one expands the definition of `` private'' to include information that is not necessarily confidential or held only by a few traders at the time of the trade, but perhaps just widely dispersed among market participants, Kyle's original concept could still apply. It is also possible that the observed variation over time in market sensitivity may be due to factors affecting market liquidity over time in a more mechanical way, that is without reference to the information present in the market. Changes in the ability or willingness of traders to hold inventory, for instance, could come from variations in the amount of capital assigned to trading or even, simply, to seasonal closings in various countries active in this market, although we see little obvious evidence of seasonal factors at the relevant frequencies. It is also possible that, for instance, times of heightened uncertainty about economic conditions, such as inflexion points in economic activity or in monetary policy could be associated with higher market sensitivity to the actions of other market participants. Finally, a more drastic explanation would be that the variation over time in market sensitivity could also reflect changes in deeper, more fundamental parameters among market participants, including changes in risk aversion over time. Extending this work to other asset markets and studying whether the pattern of variation in market sensitivity is specific to certain markets or assets, or if there is a common component, would help narrow the list of possible factors driving the variation in market sensitivity. Research into these topics is currently being undertaken by the authors and will be reported in future work.
A Narrow Band Least Squares
Define the discrete Fourier transform of a generic time-series
![]() , evaluated at the
fundamental frequencies, as
, evaluated at the
fundamental frequencies, as
|
(9) |
for
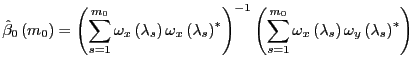
|
(10) |
where
Nielsen and Frederiksen (2005) show that estimates of
![]() , the long-memory
parameter for the cointegration residuals, can be consistently
estimated from the fitted regression residuals, and that the
asymptotic distribution of the estimator for
, the long-memory
parameter for the cointegration residuals, can be consistently
estimated from the fitted regression residuals, and that the
asymptotic distribution of the estimator for ![]() will be the same as if the true
cointegration errors were used. However, some additional bandwidth
restrictions are required. In particular, if
will be the same as if the true
cointegration errors were used. However, some additional bandwidth
restrictions are required. In particular, if ![]() is the bandwidth used in the
NBLS estimation, and
is the bandwidth used in the
NBLS estimation, and ![]() is the bandwidth used in the estimation of
is the bandwidth used in the estimation of ![]() , then
, then ![]() and
and ![]() must satisfy
must satisfy
![]() as
as
![]() ,
in addition to the usual restrictions. That is, the bandwidth for
the estimation of
,
in addition to the usual restrictions. That is, the bandwidth for
the estimation of ![]() must be of a magnitude larger than the one used in the estimation
of the cointegration vector.
must be of a magnitude larger than the one used in the estimation
of the cointegration vector.
The FMNBLS estimator relies on a first stage NBLS estimate of
![]() and ELW estimates
of
and ELW estimates
of ![]() and
and ![]() .23 These can be estimated using
bandwidths
.23 These can be estimated using
bandwidths ![]() and
and
![]() , respectively,
satisfying the above restrictions. The correction term that is used
in the FMNBLS estimator is estimated using a bandwidth
, respectively,
satisfying the above restrictions. The correction term that is used
in the FMNBLS estimator is estimated using a bandwidth ![]() , where
, where
![]() as
as
![]() .
The final FMNBLS estimates are obtained using a bandwidth
.
The final FMNBLS estimates are obtained using a bandwidth
![]() , where
, where
![]() is most
conveniently set equal to
is most
conveniently set equal to ![]() . The bandwidth
. The bandwidth ![]() is also used to estimate the long-memory
parameter
is also used to estimate the long-memory
parameter ![]() from the
residuals in the final FMNBLS regression.
from the
residuals in the final FMNBLS regression.
Under these bandwidth restrictions, Nielsen and Frederiksen
(2005) show that the FMNBLS estimates are asymptotically normally
distributed when
![]() and
and
![]() ; i.e. when
there is fractional cointegration in the stationary domain.
Finally, the FMNBLS estimates reported in this paper also
incorporate the finite sample bias correction suggested by Nielsen
and Frederiksen (2005).
; i.e. when
there is fractional cointegration in the stationary domain.
Finally, the FMNBLS estimates reported in this paper also
incorporate the finite sample bias correction suggested by Nielsen
and Frederiksen (2005).
References
Andersen, T.G., 1996. Return Volatility and Trading Volume: An Information Flow Interpretation of Stochastic Volatility, Journal of Finance 51, 169-204.
Andersen, T.G., T. Bollerslev, F.X. Diebold, and H. Ebens, 2001. The distribution of realized stock return volatility, Journal of Financial Economics 61, 43-76.
Andersen, T.G., T. Bollerslev, F.X. Diebold, and P. Labys, 2001. The Distribution of Realized Exchange Rate Volatility, Journal of the American Statistical Association 96, 42-55.
Andersen, T.G., T. Bollerslev, F.X. Diebold, and P. Labys, 2003. Modeling and Forecasting Realized Volatility, Econometrica 71, 579-625.
Andersen, T.G., T. Bollerslev, F.X. Diebold, and C. Vega, 2003. Micro Effects of Macro Announcements: Real-Time Price Discovery in Foreign Exchange, American Economic Review 93, 38-62.
Andersen, T.G., T. Bollerslev, F.X. Diebold, and J. Wu, 2004. Realized Beta: Persistence and Predictability, Working paper, University of Pennsylvania.
Baillie, R.T, and T. Bollerslev, 1994. Cointegration, Fractional Cointegration, and Exchange Rate Dynamics, Journal of Finance 49, 737-745.
Bandi, F., and B. Perron, 2004. Long Memory and the relation between implied and realized volatility, Working Paper, Graduate School of Business, University of Chicago.
Berger D.W., A.P. Chaboud, S.V. Chernenko, E. Howorka, R.S. Krishnasami Iyer, D. Liu, and J.H. Wright, 2005. Order Flow and Exchange Rate Dynamics in Electronic Brokerage System Data, International Finance Discussion Paper 830, Federal Reserve Board.
Berry, T.D. and K.M. Howe, 1994. Public Information Arrival, Journal of Finance 49, 1331-1346.
Bollerslev, T., and D. Jubinski, 1999. Equity Trading Volume and Volatility: Latent Information Arrivals and Common Long-Run Dependencies, Journal of Business and Economics Statistics 17, 9-21.
Brandt, M. and K. Kavajecz, 2004, Price Discovery in the U.S. Treasury Market: The Impact of Orderflow and Liquidity on the Yield Curve, Journal of Finance 54, 2623-2654.
Chaboud, A., S. Chernenko, E. Howorka, R. K. Iyer, D. Liu, J. Wright, 2004. The High-Frequency Effect of U.S. Macroeconomic Data Releases on Prices and Trading Activity in the Global Interdealer Foreign Exchange Market, International Finance Discussion Paper 823, Federal Reserve Board.
Christensen, B.J., and M.Ø Nielsen, 2004. Asymptotic normality of narrow-band least squares in the stationary fractional cointegration model and volatility forecasting, Journal of Econometrics, forthcoming.
Clark, P., 1973. A Subordinated Stochastic Process Model with Finite Variance for Speculative Prices, Econometrica 41, 135-155.
Engle, R.F., 1974. Band Spectrum Regression, International Economic Review 15, 1-11.
Engle, R.F., and C.W.J. Granger, 1987. Co-Integration and Error Correction: Representation, Estimation, and Testing, Econometrica 55, 251-276.
Evans, M., and R. Lyons, 2002. Order Flow and Exchange Rate Dynamics, Journal of Political Economy 110, 170-180.
Evans, M. and R. Lyons, 2004. Exchange Rate Fundamentals and Order Flow, Working Paper, University of California Berkeley Haas School of Busines.
Geweke, J., and S. Porter-Hudak, 1983. The estimation and application of long-memory time series models, Journal of Time Series Analysis 4, 221-238.
Granger, C.W.J., and P. Newbold, 1974. Spurious regression in econometrics, Journal of Econometrics 2, 111-120.
Hannan, E.J., 1970. Multiple Time Series, Wiley, New York.
Hasbrouck, J., 1991. Measuring the Information Content of Stock Trades, Journal of Finance 46, 179-207.
Künsch, H., 1987. Statistical aspects of self-similar processes. In Proceedings of the first World Congress of the Bernoulli Society (Yu. Prokhorov and V.V. Sazanov, eds.) 1, 67-74. VNU Science Press, Utrecht.
Kyle, A.S., 1985. Continuous Auctions and Insider Trading. Econometrica 53, 1315-1336.
Lamoureux C.G., and W.D. Lastrapes, 1990. Heteroskedasticity in Stock Return Data: Volume versus GARCH Effects, Journal of Finance 45, 221-229.
Lamoureux C.G., and W.D. Lastrapes, 1994. Endogenous Trading Volume and Momentum in Stock-Return Volatility, Journal of Business and Economic Statistics 12, 253-260.
Liesenfeld, R., 2001. A generalized bivariate mixture model for stock price volatility and trading volume, Journal of Econometrics 104, 141-178.
Liesenfeld, R., 2002. Identifying Common Long-Range Dependence in Volume and Volatility Using High-Frequency Data, manuscript.
McQueen, G., and K. Vorhink, 2004. Whence GARCH? A Preference-Based Explanation for Conditional Volatility, Review of Financial Studies 17, 915-949.
Mitchell, M.L. and J.H. Mulherin, 1994. The Impact of Public Information on the Stock Market, Journal of Finance 49, 923-950.
Phillips, P.C.B., 1986. Understanding spurious regressions in econometrics. Journal of Econometrics 33, 311-340.
Robinson, P.M., 1994. Semiparametric Analysis of Long-Memory Time Series, Annals of Statistics 22, 515-539.
Robinson, P.M., 1995a. Log-periodogram regression of time series with long range dependence. Annals of Statistics 23, 1048-1072.
Robinson, P.M., 1995b. Gaussian semiparametric estimation of long range dependence. Annals of Statistics 23, 1630-1661.
Shimotsu, K., 2004. Exact Local Whittle Estimation of Fractional Integration with Unknown Mean and Time Trend, Working Paper, Queen's University.
Shimotsu, K., and P.C.B. Phillips, 2004. Exact Local Whittle Estimation of Fractional Integration, Cowles Foundation Discussion Paper 1367.
Tauchen, G. and M. Pitts, 1983. The Price Variability - Volume Relationship on Speculative Markets, Econometrica 51, 485-505.
Tsay, W.J., and C.F. Chung, 2000. The spurious regression of fractionally integrated processes, Journal of Econometrics 96, 155-182.
Table 1. Results From Regressing Returns Onto Contemporaneous Orderflow
| Intercept | | |||
|---|---|---|---|---|
Panel A: Full Day, Five Minute |
429,984 |
-0.114 (0.005) |
52.518 (0.223) |
0.46 |
Panel B: 3-11am, One Minute |
715,147 |
-0.038 (0.002) |
48.720 (0.163) |
0.41 |
Results from regressing returns
onto contemporaneous orderflow. This table shows the OLS estimates
of equation (1), allowing for a non-zero
intercept and treating ![]() as identical for all
as identical for all ![]() while using the entire sample of
intra-daily observations. The
while using the entire sample of
intra-daily observations. The ![]()
![]() should
be interpreted as the estimated exchange rate movement, in basis
points, per billion euros of orderflow. The first column state the
number of observations
should
be interpreted as the estimated exchange rate movement, in basis
points, per billion euros of orderflow. The first column state the
number of observations ![]() used in each regression, and the following two columns give the
estimates of the intercepts in the regressions and of the
coefficient
used in each regression, and the following two columns give the
estimates of the intercepts in the regressions and of the
coefficient ![]() ,
respectively; robust standard errors are given in parentheses below
the estimates. The last column shows the
,
respectively; robust standard errors are given in parentheses below
the estimates. The last column shows the ![]() of the regressions.
of the regressions.
Table 2. Summary of Daily Results From Regressing Returns Onto Contemporaneous Orderflow
| Mean | Std.dev. | 1% | 5% | 10% | 25% | 50% | 75% | 90% | 95% | 99% | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Full Day, Five Minute - | 55.147 | 15.901 | 26.779 | 34.643 | 38.199 | 44.333 | 53.306 | 63.300 | 73.906 | 83.870 | 108.238 |
| Panel A: Full Day, Five Minute - | 0.511 | 0.096 | 0.155 | 0.339 | 0.403 | 0.467 | 0.525 | 0.573 | 0.614 | 0.633 | 0.674 |
| Panel B: 3-11am, One Minute - | 50.573 | 14.219 | 26.949 | 32.329 | 35.232 | 40.536 | 48.291 | 58.054 | 68.237 | 76.719 | 95.447 |
| Panel B: 3-11am, One Minute - | 0.463 | 0.076 | 0.185 | 0.340 | 0.379 | 0.430 | 0.471 | 0.509 | 0.542 | 0.562 | 0.588 |
This table
reports a summary of the daily estimates of ![]() from estimating equation
(1) day-by-day using intra-daily data. That
is, for each day in the sample, a separate
from estimating equation
(1) day-by-day using intra-daily data. That
is, for each day in the sample, a separate ![]() is estimated, based only on
intra-daily observations for that day and allowing for a non-zero
intercept. Summary statistics for the resulting estimates of
is estimated, based only on
intra-daily observations for that day and allowing for a non-zero
intercept. Summary statistics for the resulting estimates of
![]() and the
and the
![]() for the regressions
are reported. The
for the regressions
are reported. The ![]()
![]() should
be interpreted as the estimated exchange rate movement, in basis
points, per billion euros of orderflow. The first two columns
report the mean and standard deviations of the daily estimates and
should
be interpreted as the estimated exchange rate movement, in basis
points, per billion euros of orderflow. The first two columns
report the mean and standard deviations of the daily estimates and
![]() . The remaining
columns give the percentiles of the empirical distributions of the
daily estimates and
. The remaining
columns give the percentiles of the empirical distributions of the
daily estimates and ![]()
Table 3. Summary Statistics of the Daily Data
| Variable | Mean | Std.dev | Skewness | Kurtosis | Min | Max |
|---|---|---|---|---|---|---|
Panel A: Full day, Five Minute | -0.917 | 0.523 | 0.185 | 3.871 | -2.697 | 1.873 |
Panel A: Full day, Five Minute | 3.974 | 0.279 | -0.367 | 7.912 | 1.416 | 5.008 |
Panel A: Full day, Five Minute | 13.502 | 0.471 | -0.911 | 5.393 | 10.957 | 14.761 |
Panel A: Full day, Five Minute | 0.333 | -1.207 | 6.687 | 8.706 | 11.551 | |
Panel B: 3-11am, One Minute
| -1.634 | 0.565 | 0.167 | 3.549 | -3.447 | 1.086 |
Panel B: 3-11am, One Minute
| 3.890 | 0.265 | 0.174 | 3.338 | 2.678 | 4.837 |
Panel B: 3-11am, One Minute
| 12.823 | 0.459 | -1.046 | 5.801 | 10.332 | 14.203 |
Panel B: 3-11am, One Minute
| 0.352 | -1.215 | 6.515 | 8.054 | 11.196 |
The mean, standard deviation, skewness and kurtosis, as well
as the minimum and maximum values are shown for each variable. The
summary statistics are given for both samples used in the analysis
and ![]() is the number of daily
observations available in each of these samples. The variables are
defined in the main text and log
is the number of daily
observations available in each of these samples. The variables are
defined in the main text and log![]() , log
, log
![]() , log
, log
![]() , and
log
, and
log![]() represent the
daily series for realized volatility, the realized
represent the
daily series for realized volatility, the realized ![]()
![]() , the integrated squared orderflow,
and the volume of trade, respectively. The first moment of the
volume of trade is proprietary and cannot be displayed.
, the integrated squared orderflow,
and the volume of trade, respectively. The first moment of the
volume of trade is proprietary and cannot be displayed.
Table 4. Correlation Matrices for the Data
| Variable |
|
|
|
|
|---|---|---|---|---|
Panel A: Full Day, Five Minute - | 1.000 |
|||
Panel A: Full Day, Five Minute - | 0.564 |
1.000 |
||
Panel A: Full Day, Five Minute - | 0.433 |
-0.398 |
1.000 |
|
Panel A: Full Day, Five Minute - | 0.528 |
-0.232 |
0.882 |
1.000 |
Panel B: 3-11am, One Minute - | 1.000 |
|||
Panel B: 3-11am, One Minute - | 0.602 |
1.000 |
||
Panel B: 3-11am, One Minute - | 0.467 |
-0.321 |
1.000 |
|
Panel B: 3-11am, One Minute - | 0.595 |
-0.136 |
0.933 |
1.000 |
Each panel shows the correlation structure between the
variables in each sample. The variables are defined in the main
text and log![]() , log
, log
![]() , log
, log
![]() , and
log
, and
log![]() represent the
daily series for realized volatility, the realized
represent the
daily series for realized volatility, the realized ![]()
![]() , the integrated squared orderflow,
and the volume of trade, respectively.
, the integrated squared orderflow,
and the volume of trade, respectively.
Table 5. Results From OLS Estimation
| | | | |||
|---|---|---|---|---|---|
Panel A: Full Day, Five Minute | 1487 | -19.154 (0.223) | 0.822 (0.011) | 0.867 (0.013) | 0.831 |
Panel A: Full Day, Five Minute | 1487 | -5.127 (0.160) | 0.530 (0.020) | 0.318 | |
Panel A: Full Day, Five Minute | 1487 | -7.410 (0.351) | 0.481 (0.026) | 0.187 | |
Panel B: 3-11am, One Minute | 1487 | -20.206 (0.214) | 0.894 (0.011) | 0.905 (0.013) | 0.849 |
Panel B: 3-11am, One Minute | 1487 | -6.636 (0.172) | 0.642 (0.022) | 0.363 | |
Panel B: 3-11am, One Minute | 1487 | -9.003 (0.362) | 0.574 (0.028) | 0.218 |
This table reports the results from estimating equation (4) by ordinary least squares; the standard errors are
given in parantheses below the estimates. The first column gives
the number of daily observations in the samples and the last column
shows the ![]() . The first
row in each panel shows the results from the unrestricted
estimation of equation (4), whereas rows two and
three in each panel shows the results from the restricted
estimation of equation (4), with
. The first
row in each panel shows the results from the unrestricted
estimation of equation (4), whereas rows two and
three in each panel shows the results from the restricted
estimation of equation (4), with
![]() and
and
![]() ,
respectively.
,
respectively.
Table 6a. Results From Narrow Band Estimation - Panel A: Full Day, Five Minute: Long Memory Estimates ![]()
| Bandwidth | ELW Estimates of |
ELW Estimates of |
ELW Estimates of |
ELW Estimates of |
|---|---|---|---|---|
![\begin{displaymath} \begin{array}[c]{c} m=\left[ T^{0.5}\right] \ \text{ } \end{array}\end{displaymath}](img307.gif) |
0.559 (0.081) | 0.604 (0.081) | 0.329 (0.081) | 0.379 (0.081) |
![\begin{displaymath} \begin{array}[c]{c} m=\left[ T^{0.6}\right] \ \text{ } \end{array}\end{displaymath}](img312.gif) |
0.445 (0.056) | 0.476 (0.056) | 0.363 (0.056) | 0.414 (0.056) |
![\begin{displaymath} \begin{array}[c]{c} m=\left[ T^{0.7}\right] \ \text{ } \end{array}\end{displaymath}](img317.gif) |
0.456 (0.039) | 0.488 (0.039) | 0.309 (0.039) | 0.388 (0.039) |
Table 6b. Results From Narrow Band Estimation - Panel A: Full Day, Five Minute: Cointegration Analysis
| Bandwidths |
NBLS - |
NBLS - |
NBLS - |
NBLS - |
FMNBLS - |
FMNBLS - |
FMNBLS - |
FMNBLS - |
|---|---|---|---|---|---|---|---|---|
![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.5}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img322.gif) |
-21.390 (0.234) | 0.949 (0.039) | 0.958 (0.088) | 0.173 (0.081) | -21.816 (0.235) | 0.945 (0.040) | 0.992 (0.091) | 0.175 (0.081) |
![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img331.gif) |
-21.390 (0.234) | 0.949 (0.039) | 0.958 (0.088) | 0.085 (0.056) | -21.954 (0.237) | 0.956 (0.040) | 0.996 (0.089) | 0.083 (0.056) |
![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img337.gif) |
-21.559 (0.235) | 0.955 (0.032) | 0.967 (0.058) | 0.082 (0.056) | -22.382 (0.240) | 0.970 (0.032) | 1.019 (0.059) | 0.075 (0.056) |
![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img346.gif) |
-21.559 (0.235) | 0.955 (0.032) | 0.967 (0.058) | 0.084 (0.039) | -22.851 (0.244) | 0.983 (0.033) | 1.046 (0.061) | 0.081 (0.039) |
![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.5}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img352.gif) |
-21.125 (0.234) | 0.953 (0.026) | 0.936 (0.045) | 0.088 (0.039) | -22.071 (0.240) | 0.984 (0.027) | 0.988 (0.046) | 0.081 (0.039) |
![\begin{displaymath} \begin{array}[c]{l} m_{0}=T\text{ (OLS),}\ m_{1}=\left[ T^{0.6}\right] \end{array}\end{displaymath}](img360.gif) |
-19.154 (0.223) | 0.822 (0.011) | 0.867 (0.013) | 0.237 (0.056) |
Table 6c. Results From Narrow Band Estimation - Panel B: 3-11am, One Minute: Long Memory Estimates,
![]()
| Bandwidth |
ELW Estimates of |
ELW Estimates of |
ELW Estimates of |
ELW Estimates of |
|---|---|---|---|---|
![\begin{displaymath} \begin{array}[c]{c} m=\left[ T^{0.5}\right] \ \text{ } \end{array}\end{displaymath}](img307.gif) |
0.548 (0.081) | 0.586 (0.081) | 0.303 (0.081) | 0.364 (0.081) |
![\begin{displaymath} \begin{array}[c]{c} m=\left[ T^{0.6}\right] \ \text{ } \end{array}\end{displaymath}](img312.gif) |
0.429 (0.056) | 0.552 (0.056) | 0.328 (0.056) | 0.379 (0.056) |
![\begin{displaymath} \begin{array}[c]{c} m=\left[ T^{0.7}\right] \ \text{ } \end{array}\end{displaymath}](img317.gif) |
0.441 (0.039) | 0.487 (0.039) | 0.317 (0.039) | 0.366 (0.039) |
Table 6d. Results From Narrow Band Estimation - Panel B: 3-11am, One Minute: Cointegration Analysis
| Bandwidths | NBLS - | NBLS - | NBLS - | NBLS - | FMNBLS - | FMNBLS - | FMNBLS - | FMNBLS - |
|---|---|---|---|---|---|---|---|---|
![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.5}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img322.gif) | -20.433 (0.217) | 0.957 (0.028) | 0.885 (0.060) | 0.116 (0.081) | -20.345 (0.216) | 0.947 (0.028) | 0.884 (0.061) | 0.116 (0.081) |
![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img331.gif) | -20.433 (0.217) | 0.957 (0.028) | 0.885 (0.060) | -0.010 (0.056) | -21.415 (0.217) | 0.957 (0.028) | 0.884 (0.060) | -0.010 (0.056) |
![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img337.gif) | -20.674 (0.217) | 0.965 (0.027) | 0.899 (0.049) | -0.011 (0.056) | -20.889 (0.217) | 0.970 (0.027) | 0.913 (0.049) | -0.010 (0.056) |
![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img346.gif) | -20.674 (0.217) | 0.965 (0.027) | 0.899 (0.049) | 0.021 (0.039) | -21.294 (0.218) | 0.982 (0.028) | 0.937 (0.050) | 0.022 (0.039) |
![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.5}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img352.gif) | -20.521 (0.217) | 0.967 (0.023) | 0.886 (0.037) | 0.023 (0.039) | -21.091 (0.219)) | 0.991 (0.023) | 0.915 (0.038) | 0.027 (0.039) |
![\begin{displaymath} \begin{array}[c]{l} m_{0}=T\text{ (OLS),}\ m_{1}=\left[ T^{0.6}\right] \end{array}\end{displaymath}](img360.gif) | -20.206 (0.214) | 0.894 (0.011) | 0.905 (0.013) | 0.093 (0.056) |
Tables 6a - 6d reports the estimates of the long-memory
parameters in the data as well as the narrow band least squares
(NBLS) regression estimates of equation (4); the
standard errors are given in parentheses below the estimates. The
first part of each panel shows the exact local Whittle (ELW)
estimates of ![]() for the log
of realized volatility
for the log
of realized volatility ![]() , the log of the
, the log of the
![]() , and the
log of the squared integrated orderflow
, and the
log of the squared integrated orderflow
![]() , as
well as for the log of the daily volume
, as
well as for the log of the daily volume ![]() which is used later in the
analysis. The estimates for three different bandwidths,
which is used later in the
analysis. The estimates for three different bandwidths,
![]() , are reported. The
second part of each panel report the NBLS and fully modified NBLS
(FMNBLS) estimates of equation (4), for
different bandwidth choices; the last row in each panel corresponds
to OLS estimation. The columns labeled
, are reported. The
second part of each panel report the NBLS and fully modified NBLS
(FMNBLS) estimates of equation (4), for
different bandwidth choices; the last row in each panel corresponds
to OLS estimation. The columns labeled ![]() give the ELW estimates of
the long-memory parameter for the residuals of the respective
regression. The bandwidths that are used are all integer parts of
fractional powers of the sample size. Observe that
give the ELW estimates of
the long-memory parameter for the residuals of the respective
regression. The bandwidths that are used are all integer parts of
fractional powers of the sample size. Observe that
![]() and
and ![]() .
.
Table 7. The Unconditional Distribution of the Fitted Volatility
| Variable | Mean | Std.dev | Skewness | Kurtosis |
|---|---|---|---|---|
Panel A: Full Day, Five Minute - | -0.917 |
0.523 |
0.185 |
3.872 |
Panel A: Full Day, Five Minute - | -0.917 |
0.562 |
-0.562 |
6.308 |
Panel B: 3-11am, One Minute - | -1.639 |
0.565 |
0.167 |
3.549 |
Panel B: 3-11am, One Minute - | -1.639 |
0.549 |
-0.233 |
3.327 |
This table reports summary statistics for
the fitted values of the log realized volatility based on the
narrow band estimates of equation equation (4).
In particular, the fitted values are calculated from the FMNBLS
estimates of equation (4), using bandwidths
![]() and
and
![]() . The
first row in each panel shows the summary statistics for the actual
data and the second row shows the statistics for the fitted
values.
. The
first row in each panel shows the summary statistics for the actual
data and the second row shows the statistics for the fitted
values.
Table 8. Results From Restricted Narrow Band Estimation
| Bandwidths | | | | | | |
|---|---|---|---|---|---|---|
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.5}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img322.gif) | -6.972 (0.167) | 0.762 (0.133) | 0.337 (0.081) | 16.364 (0.710) | -1.280 (0.768) | 0.629 (0.081) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img331.gif) | -6.947 (0.167) | 0.759 (0.133) | 0.335 (0.056) | 17.104 (0.726) | -1.335 (0.778) |
0.371 (0.056) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img337.gif) | -6.959 (0.167) | 0.760 (0.115) | 0.335 (0.056) | 0.269 (0.403) | -0.088 (0.387) | 0.438 (0.056) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img346.gif) | -7.175 (0.169) | 0.788 (0.116) | 0.305 (0.039) | 3.857 (0.457) | -0.354 (0.403) | 0.412 (0.039) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.5}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img352.gif) | -6.870 (0.167) | 0.749 (0.084) | 0.309 (0.039) | 0.974 (0.413) | -0.140 (0.248) | 0.438 (0.039) |
| Panel A: Full Day, Five Minute - | -5.127 (0.160) | 0.530 (0.020) | 0.370 (0.056) | -7.410 (0.351) | 0.481 (0.026) | 0.481 (0.056) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.5}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img322.gif) | -7.754 (0.174) | 0.786 (0.130) | 0.294 (0.081) | 12.343 (0.662) | -1.090 (0.737) | 0.661 (0.081) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img331.gif) | -7.707 (0.174) | 0.780 (0.130) | 0.271 (0.056) | 14.085 (0.700) | -1.226 (0.761) | 0.336 (0.056) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img337.gif) | -7.721 (0.174) | 0.782 (0.110) | 0.271 (0.056) | 0.738 (0.442) | -0.185 (0.390) | 0.409 (0.056) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img346.gif) | -7.802 (0.175) | 0.792 (0.110) | 0.300 (0.039) | 4.081 (0.496) | -0.446 (0.408) | 0.393 (0.039) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.5}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img352.gif) | -7.529 (0.174) | 0.757 (0.083) | 0.302 (0.039) | 0.638 (0.440) | -0.178 (0.248) | 0.420 (0.039) |
Panel B: 3-11am, One Minute - | -6.636 (0.172) | 0.642 (0.022) | 0.289 (0.056) | -9.003 (0.362) | 0.574 (0.028) | 0.486 (0.056) |
This table reports the FMNBLS regression estimates
of equation (4) with either
![]() or
or
![]() restricted to be equal to zero; the standard errors are given in
parentheses below the estimates. The first column shows the
bandwidths used in the estimation, where the last row in each panel
correspond to OLS estimation. The left-hand side of each panel
shows the results for
restricted to be equal to zero; the standard errors are given in
parentheses below the estimates. The first column shows the
bandwidths used in the estimation, where the last row in each panel
correspond to OLS estimation. The left-hand side of each panel
shows the results for
![]() and
the right-hand side shows the results for
and
the right-hand side shows the results for
![]() .
The columns labeled
.
The columns labeled ![]() give the ELW estimates of the long-memory
parameter for the residuals of the respective regression. The
bandwidths that are used are all integer parts of fractional powers
of the sample size. Observe that
give the ELW estimates of the long-memory
parameter for the residuals of the respective regression. The
bandwidths that are used are all integer parts of fractional powers
of the sample size. Observe that
![]() and
and ![]() .
.
Table 9. Results From Narrow Band Regressions With Volume
Bandwidths | | | | | | | |
|---|---|---|---|---|---|---|---|
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.5}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img322.gif) | -17.051 (0.298) | 0.892 (0.053) | 0.845 (0.131) | 0.209 (0.081) | 7.991 (0.592) | -0.832 (0.809) | 0.539 (0.081) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img331.gif) | -17.263 (0.301) | 0.906 (0.054) | 0.855 (0.134) | 0.148 (0.056) | 8.701 (0.606) | -0.899 (0.819) | 0.421 (0.056) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img337.gif) | -18.560 (0.291) | 0.914 (0.043) | 0.970 (0.089) | 0.137 (0.056) | -3.575 (0.404) | 0.248 (0.423) | 0.455 (0.056) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img346.gif) | -18.482 (0.297) | 0.928 (0.044) | 0.952 (0.092) | 0.148 (0.039) | -1.446 (0.429) | 0.050 (0.433) | 0.459 (0.039) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.5}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img352.gif) | -18.249 (0.293) | 0.911 (0.033) | 0.943 (0.065) | 0.142 (0.039) | -3.049 (0.410) | 0.199 (0.275) | 0.468 (0.039) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=T\text{ (OLS),}\ m_{1}=\left[ T^{0.6}\right] \end{array}\end{displaymath}](img360.gif) | -18.041 (0.251) | 0.682 (0.012) | 1.094 (0.020) | 0.302 (0.056) | -9.790 (0.371) | 0.829 (0.035) | 0.478 (0.056) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.5}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img322.gif) | -16.089 (0.246) | 0.843 (0.039) | 0.765 (0.093) | 0.153 (0.081) | -0.852 (0.442) | -0.076 (0.732) | 0.550 (0.081) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img331.gif) | -16.298 (0.245) | 0.850 (0.038) | 0.780 (0.092) | 0.047 (0.056) | 1.206 (0.477) | -0.276 (0.754) | 0.416 (0.056) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img337.gif) | -17.263 (0.235) | 0.858 (0.036) | 0.867 (0.073) | 0.029 (0.056) | -5.985 (0.374) | 0.421 (0.410) | 0.453 (0.056) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img346.gif) | -17.252 (0.237) | 0.868 (0.036) | 0.859 (0.075) | 0.108 (0.039) | -4.458 (0.391) | 0.273 (0.417) | 0.456 (0.039) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.5}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img352.gif) | -17.603 (0.233) | 0.866 (0.027) | 0.894 (0.053) | 0.103 (0.039) | -5.543 (0.378) | 0.378 (0.265) | 0.463 (0.039) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=T\text{ (OLS),}\ m_{1}=\left[ T^{0.6}\right] \end{array}\end{displaymath}](img360.gif) | -18.741 (0.213) | 0.738 (0.012) | 1.100 (0.018) | 0.211 (0.056) | -11.488 (0.345) | 0.954 (0.033) | 0.481 (0.056) |
This table reports the FMNBLS regression
estimates of equation (4) with the integrated
squared orderflow replaced by volume ![]() ; the standard errors are given in parentheses
below the estimates. The first column shows the bandwidths used in
the estimation, where the last row in each panel corresponds to OLS
estimation. The left-hand side of each panel shows the results for
the unrestricted regression, where
; the standard errors are given in parentheses
below the estimates. The first column shows the bandwidths used in
the estimation, where the last row in each panel corresponds to OLS
estimation. The left-hand side of each panel shows the results for
the unrestricted regression, where ![]() is the coefficient in front of volume in
the regression. The left-hand side of each panel shows the results
with
is the coefficient in front of volume in
the regression. The left-hand side of each panel shows the results
with
![]() imposed as a restriction. The columns labeled
imposed as a restriction. The columns labeled ![]() give the ELW estimates of
the long-memory parameter for the residuals of the respective
regression The bandwidths that are used are all integer parts of
fractional powers of the sample size. Observe that
give the ELW estimates of
the long-memory parameter for the residuals of the respective
regression The bandwidths that are used are all integer parts of
fractional powers of the sample size. Observe that
![]() and
and ![]() .
.
Table 10. Results From Narrow Band Regressions With Both Volume and Squared Orderflow
| Bandwidths | | | | | |
|---|---|---|---|---|---|
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.5}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img322.gif) | -21.987 (0.237) | 0.952 (0.035) | 0.727 (0.218) | 0.344 (0.219) | -0.055 (0.081) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img331.gif) | -21.736 (0.239) | 0.955 (0.033) | 0.662 (0.203) | 0.401 (0.204) | -0.089 (0.056) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img337.gif) | -21.617 (0.243) | 0.954 (0.029) | 0.569 (0.148) | 0.509 (0.156) | -0.063 (0.056) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img346.gif) | -21.566 (0.245) | 0.961 (0.029) | 0.565 (0.150) | 0.504 (0.158) | 0.013 (0.039) |
Panel A: Full Day, Five Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.5}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img352.gif) | -20.422 (0.247) | 0.945 (0.026) | 0.494 (0.113) | 0.498 (0.122) | 0.014 (0.039) |
Panel A: Full Day, Five Minute -
| -19.504 (0.221) | 0.795 (0.011) | 0.654 (0.027) | 0.322 (0.036) | 0.221 (0.056) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.5}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img322.gif) | -21.042 (0.219) | 0.919 (0.063) | 0.498 (0.408) | 0.568 (0.409) | 0.228 (0.081) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.3}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img331.gif) | -20.566 (0.222) | 0.919 (0.060) | 0.422 (0.388) | 0.617 (0.389) | 0.018 (0.056) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.6}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img337.gif) | -20.484 (0.219) | 0.934 (0.038) | 0.570 (0.211) | 0.414 (0.222) | -0.069 (0.056) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.4}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img346.gif) | -20.778 (0.219) | 0.947 (0.038) | 0.616 (0.213) | 0.376 (0.224) | 0.003 (0.039) |
Panel B: 3-11am, One Minute - ![\begin{displaymath} \begin{array}[c]{l} m_{0}=\left[ T^{0.5}\right] ,m_{1}=\left... ...right] \ m_{2}=\left[ T^{0.7}\right] ,m_{3}=m_{0} \end{array}\end{displaymath}](img352.gif) | -20.156 (0.223) | 0.938 (0.030) | 0.483 (0.147) | 0.487 (0.159) | 0.013 (0.039) |
Panel B: 3-11am, One Minute -
| -20.081 (0.212) | 0.856 (0.013) | 0.675 (0.041) | 0.303 (0.051) | 0.098 (0.056) |
This table
reports the FMNBLS regressions estimates of
![]() , with the standard errors given in parentheses below the
estimates. The first column shows the bandwidths used in the
estimation, where the last row in each panel corresponds to OLS
estimation. The columns labeled
, with the standard errors given in parentheses below the
estimates. The first column shows the bandwidths used in the
estimation, where the last row in each panel corresponds to OLS
estimation. The columns labeled ![]() give the ELW estimates of the long-memory
parameter for the residuals of the respective regression. The
bandwidths that are used are all integer parts of fractional powers
of the sample size. Observe that
give the ELW estimates of the long-memory
parameter for the residuals of the respective regression. The
bandwidths that are used are all integer parts of fractional powers
of the sample size. Observe that
![]() and
and ![]() .
.
Figure 1. The Average One-Minute Volume of Trade Over the Day
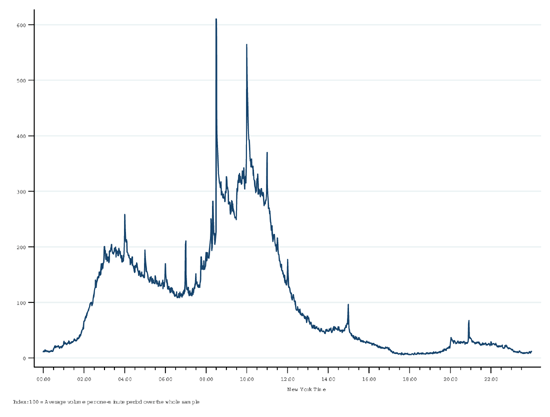
Figure 2. Plots of the Logged Daily Data
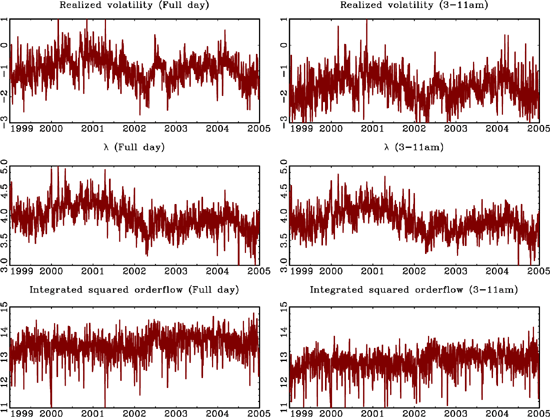
Figure 3. Plots of the
40-day moving average of the demeaned log-transformed realized
volatility
![]() , the estimated
, the estimated
![]() , and the
integrated squared orderflow
, and the
integrated squared orderflow
![]()
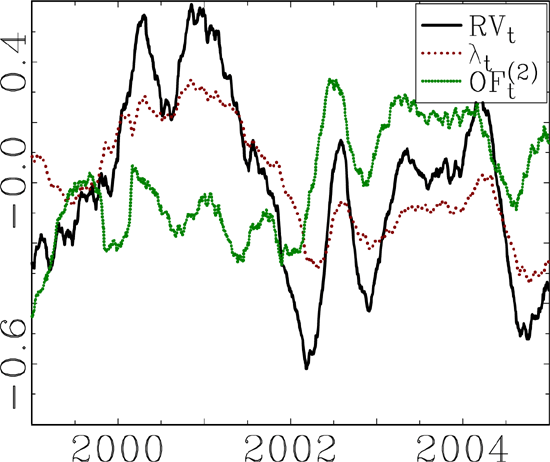
Figure 4. Plots of Realized Volatility and the Corresponding Regression Residuals
![Figure 4 shows plots of realized volatility and the corresponding regression residuals. The top two panels show plots of the realized volatility, constructed from the full-day five-minute and 3-11am one-minute intra-daily data, respectively. The lower panels show the corresponding regression residuals from the FMNBLS estimation of equation (4), using bandwidths $ m_{0}=m_{3}=\left [ T^{0.4}\right ] $ and $ m_{1}=m_{2}=\left [ T^{0.6} \right ] .$](figure4.gif)
Figure 5. Auto-Correlograms of Realized Volatility and the Corresponding Regression Residuals
![Figure 5 shows auto-correlograms of realized volatility and the corresponding regression residuals. The top two panels show the auto-correlograms of realized volatility, constructed from the full-day five-minute
and 3-11am one-minute intra-daily data, respectively. The lower panels show the auto-correlograms for the corresponding regression
residuals from the FMNBLS estimation of equation 4), using bandwidths $ m_{0}=m_{3}=\left [ T^{0.4}\right ] $ and $ m_{1}=m_{2}=\left [ T^{0.6} \right ] .$](figure5.gif)
Figure 6. The Standardized Unconditional Distribution of the Actual and Fitted Values of the Log of Realized Volatility
![The standardized unconditional distribution of the actual and fitted values of the log of realized volatility. The graphs show kernel density estimates for the standardized values of the actual logtransformed realized volatility as well as for the fitted values of log-realized volatility obtained from FMNBLS estimates of equation $ m_{0}=m_{3}=\left [ T^{0.4}\right ] $ and $ m_{1}=m_{2}=\left [ T^{0.6} \right ] .$ The dotted line shows the standard normal density.](figure6.gif)
Figure 7. Plots of the
40-day moving average of the demeaned log-transformed realized
volatility
![]() , and volume of trade
, and volume of trade
![]()
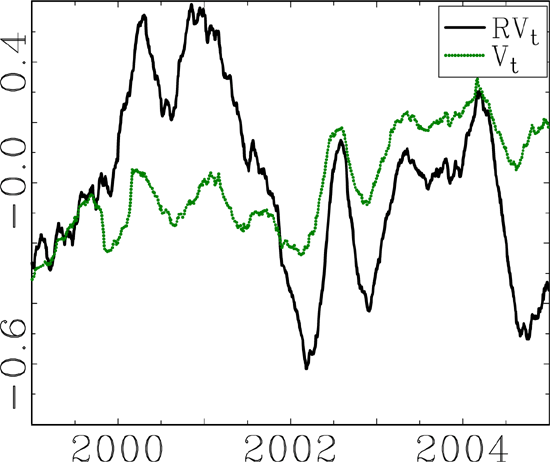
Footnotes
1. We have benefitted from comments by David Bowman, Mark Carey, Frank Diebold, Jon Faust, Joe Gagnon, Dale Henderson, Lennart Hjalmarsson, Mico Loretan, Mark Seasholes, Clara Vega, Jon Wongswan, Jonathan Wright, Pär Österholm, and seminar participants at the Federal Reserve Board. The views presented in this paper are solely those of the authors and do not represent those of the Federal Reserve Board or its staff. Return to text
2. Berger, Chaboud, and Hjalmarsson are with the Division of International Finance, Federal Reserve Board, Mail Stop 20, Washington, DC 20551, USA. Howorka is with EBS, 535 Madison Avenue, New York, NY 10022. Corresponding author: Erik Hjalmarrson. Tel.: +1-202-452-2436; fax: +1-202-263-4850; email: [email protected]. Return to text
3. Another line of research has attempted to use the number of news stories released by financial wire services as measures of the rate of information arrival in the stock market, such as Mitchell and Mulherin (1994) and Berry and Howe (1994). This has met with very limited success, as the number of news stories explains only a small fraction of stock return volatility. Return to text
4. In models relating volatility and volume there are indications that failure to account for the endogeneity of volume leads to biased inference. Lamoureux and Lastrapes (1990), for instance, find apparently strong evidence that volume can explain the GARCH effects in return volatility. However, in later work, Lamoureux and Lastrapes (1994) use a mixture model with a latent factor to relax the exogeneity assumption and find that this model cannot explain the persistence in volatility. The latter model is, however, fairly restrictive in nature, which makes it difficult to draw any strong conclusions regarding the causes of its failure. Return to text
5. Bollerslev and Jubinski (1999) and Liesenfeld (2002) consider the long-memory in volatility and trading volume, although only Liesenfeld (2002) performs any formal tests of fractional cointegration; both articles find little or no support that volatility and trading volume share a common long-run component. Bandi and Perron (2004) use fractional cointegration to analyze the relationship between implied and realized volatility. Return to text
6. EBS does not publish trading volume data per currency pair. To give a sense of an order of magnitude, average daily trading volume (the dollar amount traded) on EBS in euro-dollar in 2003, for instance, was well above that of the NYSE as a whole. Average daily trading volume on the NYSE in 2003 was about $40 billion. Traders on EBS can transact in amounts ranging from 1 to 999 million of the base currency. In practice, however, as large deals are routinely broken down, most transactions are for amounts of 1 to 5 million, and the average trade size varies little over time. As a result, there is a very high correlation between the trading volume in a given time period and and the number of transactions in that same period. Return to text
7. In this market, by global convention, the value date changes at 17:00 New York time (whether or not it is Eastern Standard time or Eastern Daylight time), which therefore represents the official cutoff between two trading days. Return to text
8. One of EBS's computer centers, located near the World Trade Center in New York, was temporarily disabled after the September 11 attack. Return to text
9. These results are close to what Evans and Lyons (2002) report in their study of the impact of daily order flow on daily exchange rate returns. Return to text
10. Empirical work conducted on the
same dataset supports the conclusion that the
![]() coefficients can be interpreted as the market sensitivity to new
information. Berger et al. (2005, table 9) estimate a
Hasbrouck-style (1991) VAR at the one-minute frequency. They report
that order flow shocks account for about 40 percent of permanent
exchange rate variation. Breaking the day into several intervals,
they also show that order flow explains the largest share of
exchange rate variation during the periods of highest global
trading volume, including the times when most macroeconomic data
are released. These results suggest that order flow is conveying
information to the traders through the trading process and thus
that the
coefficients can be interpreted as the market sensitivity to new
information. Berger et al. (2005, table 9) estimate a
Hasbrouck-style (1991) VAR at the one-minute frequency. They report
that order flow shocks account for about 40 percent of permanent
exchange rate variation. Breaking the day into several intervals,
they also show that order flow explains the largest share of
exchange rate variation during the periods of highest global
trading volume, including the times when most macroeconomic data
are released. These results suggest that order flow is conveying
information to the traders through the trading process and thus
that the
![]() 's can
reasonably be interpreted as capturing the market sensitivity to
new information. Return to text
's can
reasonably be interpreted as capturing the market sensitivity to
new information. Return to text
11. In Kyle's (1985) analysis,
![]() represents
unexpected orderflow, rather than total
observed orderflow, which all the empirical results reported in
this paper are based on. As a robustness check, we also constructed
a proxy for unexpected orderflow by AR-filtering the observed
orderflow. The results from the filtered data were very similar to
those reported here for the total orderflow and are not shown in
the paper. Return to text
represents
unexpected orderflow, rather than total
observed orderflow, which all the empirical results reported in
this paper are based on. As a robustness check, we also constructed
a proxy for unexpected orderflow by AR-filtering the observed
orderflow. The results from the filtered data were very similar to
those reported here for the total orderflow and are not shown in
the paper. Return to text
12. In the same vein, Andersen et al. (2004) study the time series properties of realized CAPM betas. Return to text
13. In both of the two daily samples
thus obtained, there are two days for which the estimated
![]() is
negative, although not statistically significantly different from
zero. Interestingly, these are days when U.S. monthly payroll data
were released, with large jumps in the exchange rate
instantaneously associated with the data releases. Since negative
values of
is
negative, although not statistically significantly different from
zero. Interestingly, these are days when U.S. monthly payroll data
were released, with large jumps in the exchange rate
instantaneously associated with the data releases. Since negative
values of
![]() make little
economic sense and prevent a log-transformation, we drop these rare
days from our sample. The actual number of days used in each sample
is thus
make little
economic sense and prevent a log-transformation, we drop these rare
days from our sample. The actual number of days used in each sample
is thus ![]() . Return to
text
. Return to
text
14. We use the estimator developed
by Shimotsu (2004) that allows for an unknown mean in the data. In
particular, following the results of Shimotsu (2004), if
![]() ,
, ![]() represent the data, the ELW
estimator is applied to
represent the data, the ELW
estimator is applied to
![]() where
where
![]() , with
, with
![]() for
for ![]() ,
,
![]() for
for ![]() ,
,
![]() for
for ![]() , and
, and ![]() is the sample mean. Return to text
is the sample mean. Return to text
15. The bandwidth restrictions given here, and below, are typically simplified versions of the exact restrictions given in the orginal papers. The rate restrictions provided here are meant to convey the primary intuition behind the choice of bandwidth and not a formal result. Return to text
16. Hannan (1970) provides a textbook treatment on frequency domain methods and Engle (1974) gives an early economic application. Return to text
17. The bandwidths used here for the
estimation of ![]() , and below in
the NBLS and FMNBLS estimation, are all of the form
, and below in
the NBLS and FMNBLS estimation, are all of the form
![]() , for
, for
![]() and
and ![]() . The highest
frequencies included in the spectral analysis for these bandwidths
correspond approximately to time-domain horizons of 185, 80, 40,
20, and 10 days, respectively. Return to
text
. The highest
frequencies included in the spectral analysis for these bandwidths
correspond approximately to time-domain horizons of 185, 80, 40,
20, and 10 days, respectively. Return to
text
18. The NBLS estimates are
asymptotically normal under the stronger assumptions that
![]() , and
that the long-run correlation between the regressors and the error
terms is zero; that is the regressors can be endogenous in the
short run (the higher frequencies in the spectral domain) but not
in the long run (the frequencies close to zero); Christensen and
Nielsen (2004). Whereas the former condition is likely to hold,
there is no a priori reason to assume
that the latter one holds. Return to
text
, and
that the long-run correlation between the regressors and the error
terms is zero; that is the regressors can be endogenous in the
short run (the higher frequencies in the spectral domain) but not
in the long run (the frequencies close to zero); Christensen and
Nielsen (2004). Whereas the former condition is likely to hold,
there is no a priori reason to assume
that the latter one holds. Return to
text
19. Since the
![]() are
generated regressors, this may affect the econometric analysis.
However, we conjecture that the strength of the fractional
cointegrating relationship dominates the potential effects arising
from the use of a generated regressor, and that, at least
asymptotically, there should be no difference between using the
true values and the generated values of the
are
generated regressors, this may affect the econometric analysis.
However, we conjecture that the strength of the fractional
cointegrating relationship dominates the potential effects arising
from the use of a generated regressor, and that, at least
asymptotically, there should be no difference between using the
true values and the generated values of the
![]() . Monte
Carlo simulations, not reported in the paper, show that there is
little or no difference between the estimates resulting from the
use of the true
. Monte
Carlo simulations, not reported in the paper, show that there is
little or no difference between the estimates resulting from the
use of the true
![]() or the
generated ones. Return to text
or the
generated ones. Return to text
20. There are 23 days where either
the one minute residuals or the five minute residuals are greater
than ![]() (which is
approximately equal to two standard deviations). On 16 of these
days there are US macroannouncements and on an additional five more
of these days there are ECB or German macro announcements. In
summary, 21 of the 23 of the outlier days are thus days with macro
announcements. Return to text
(which is
approximately equal to two standard deviations). On 16 of these
days there are US macroannouncements and on an additional five more
of these days there are ECB or German macro announcements. In
summary, 21 of the 23 of the outlier days are thus days with macro
announcements. Return to text
21. We made one attempt at directly
measuring the arrival of information, using the number of
international Dow Jones news stories per day. The data collected
was the total number of daily Dow Jones international news wire
stories (collected from Factiva) excluding repeated stories, fixed
market updates and sports stories (a fixed market update says, for
instance, that the euro-dollar exchange rate was 1.21 at 1:00 GMT).
We choose this flexible categorization because other than sports,
all the other subcategories under Dow Jones international seemed as
if they could be relevant. Also, the EBS terminal provides users
with a real time Dow Jones news feed so this series was the natural
choice to try. We regressed realized volatility onto the Dow Jones
news stories variable by itself, as well as jointly with the
![]() . The
lattter multiple regression was motivated by the finding that there
was little evidence that squared orderflow in itself could explain
volatility persistence, and to the extent that both squared
orderflow and the Dow Jones stories proxy for some information
arrival we might expect similar results here. The regression
results, which are omitted here, showed no evidence that the Dow
Jones variable could explain any of the persistence in volatility,
either by itself or jointly with the
. The
lattter multiple regression was motivated by the finding that there
was little evidence that squared orderflow in itself could explain
volatility persistence, and to the extent that both squared
orderflow and the Dow Jones stories proxy for some information
arrival we might expect similar results here. The regression
results, which are omitted here, showed no evidence that the Dow
Jones variable could explain any of the persistence in volatility,
either by itself or jointly with the
![]() . Return to
text
. Return to
text
22. In the stock-market literature, it is common to use the number of transactions, rather than the volume of trade, as a measure of market activity. We therefore performed the same analysis as just described, but with volume replaced by the number of transactions. Overall, the results were similar, but perhaps a bit weaker, when using the number of transactions and the results are not reported here for brevity. As stated previously, in the electronic interdealer foreign exchange data that we study, the majority of trades is for amounts between 1 and 5 million euros, as large orders are routinely broken up before execution. As a result, the average trade size shows little time variation, and the number of transactions and the trading volume show a high degree of correlation. Return to text
23. As pointed out above, separate
![]() parameters are
estimated for each variable and these distinct estimates are used
in forming the FMNBLS estimator. Return
to text
parameters are
estimated for each variable and these distinct estimates are used
in forming the FMNBLS estimator. Return
to text
This version is optimized for use by screen readers. A printable pdf version is available.