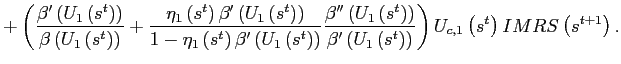Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 867, August 2006-Screen Reader Version*
Closing Open Economy Models*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Several methods have been proposed to obtain stationarity in open economy models. I find substantial qualitative and quantitative differences between these methods in a two-country framework, in contrast to the results of Schmitt-Grohé and Uribe (2003). In models with a debt elastic interest rate premium or a convex portfolio cost, both the steady state and the equilibrium dynamics are unique if the elasticity of substitution between the domestic and the foreign traded good is high. However, there are three steady states if the elasticity of substitution is sufficiently low. With endogenous discounting, there is always a unique and stable steady state irrespective of the magnitude of the elasticity of substitution. Similar to the model with convex portfolio costs or a debt elastic interest rate premium, though, there can be multiple convergence paths for low values of the elasticity in response to shocks.
Keywords: multiple equilibria, stationarity, incomplete markets
JEL Classification: D51, F41
1 Introduction
In open economy models with incomplete asset markets the deterministic steady state depends on the initial conditions of the economy and the steady state is compatible with any level of net foreign assets. In a stochastic environment the model generates non-stationary variables as net foreign assets follow a unit root process.1
Several modifications of the standard model have been proposed in order to induce stationarity among which are an endogenous discount factor (Uzawa-type preferences), a debt elastic interest rate premium or convex portfolio costs. Schmitt-Grohé and Uribe (2003) present quantitative comparisons of these alternative approaches and find that all of them deliver virtually identical dynamics. However, their analysis is restricted to the case of a small open economy, and therefore further scrutiny is justified. Nevertheless, their work has been cited extensively by others to claim irrelevance of the chosen approach that induces stationarity in a specific model even in multi-country setups.2
In this paper, I investigate the theoretical differences between several stationarity inducing approaches in a standard two-country model with limited substitutability between traded goods. If goods are highly substitutable across countries, the stationarity inducing approaches that I investigate have very similar properties. However, for low values of the elasticity of substitution between traded goods there are important nonlinearities which give rise to substantial differences across methods.
Each of the two countries produces one good. These imperfectly substitutable goods are traded in a frictionless goods market. International financial markets are incomplete as the only asset that is traded between countries is one non-state-contingent bond. I consider three approaches to obtain stationarity: an endogenous discount factor, a debt elastic interest rate premium and convex portfolio costs. While I focus on these three most popular approaches, there are other approaches. Ghironi (2003) solves the stationarity problem by introducing an overlapping generations structure.3 Huggett (1993) solves the stationarity problem by introducing explicit limits on the level of asset holdings.4
In the standard model with incomplete markets the steady state is undetermined since the growth rate of marginal utility does not depend on the allocation of net foreign assets. Absent arbitrage opportunities, the price of the non-state-contingent bond is equalized across countries implying that expected marginal utility growth is equalized across countries. In the deterministic steady state, this condition contains no information about the steady state values of the system and the system of equilibrium conditions becomes underdetermined. Any level of net foreign asset holdings is a steady state.
If stationarity is induced by convex portfolio costs, there is a
unique stable steady state only if the elasticity of substitution
between the domestic and foreign traded goods
![]() is
sufficiently large, i.e.,
is
sufficiently large, i.e.,
![]() is above
some threshold level
is above
some threshold level
![]() . For
lower values of the elasticity of substitution, however, I find
three steady states two of which are locally stable, but the third
one is not. It is important to note that this multiplicity of
steady states is unrelated to the aforementioned indeterminacy in
the non-stationary model. I also analyze the dynamic implications
of shocks under different values of the elasticity of substitution
. For
lower values of the elasticity of substitution, however, I find
three steady states two of which are locally stable, but the third
one is not. It is important to note that this multiplicity of
steady states is unrelated to the aforementioned indeterminacy in
the non-stationary model. I also analyze the dynamic implications
of shocks under different values of the elasticity of substitution
![]() . For a high
value of the elasticity of substitution, there is a unique impulse
response function for a small technology shock. If
. For a high
value of the elasticity of substitution, there is a unique impulse
response function for a small technology shock. If
![]() this finding no
longer holds true. Assume that the economy is in one of the two
stable steady states. For a small technology shock there are two
paths that lead the economy back into the original steady state.
However, for the same shock, the economy can also converge to the
other stable steady state. For example, if the shock improves
country
this finding no
longer holds true. Assume that the economy is in one of the two
stable steady states. For a small technology shock there are two
paths that lead the economy back into the original steady state.
However, for the same shock, the economy can also converge to the
other stable steady state. For example, if the shock improves
country ![]() 's technology,
the real exchange rate may either depreciate on impact by a small,
an intermediate or a large amount relative to the original steady
state. The model with a debt elastic interest rate shares these
features with the model of convex portfolio costs.
's technology,
the real exchange rate may either depreciate on impact by a small,
an intermediate or a large amount relative to the original steady
state. The model with a debt elastic interest rate shares these
features with the model of convex portfolio costs.
If, following Uzawa (1968), the discount factor is assumed to be
endogenous, an agent's rate of time preference is strictly
decreasing in the agent's utility level.5 In this setup there is always a unique
and stable steady state irrespective of the value of the elasticity
of substitution between foreign and domestic goods
![]() .
Ironically, the unique and stable steady state in the model with
endogenous discounting features the same allocations as the
unstable steady state in the model with portfolio costs for
.
Ironically, the unique and stable steady state in the model with
endogenous discounting features the same allocations as the
unstable steady state in the model with portfolio costs for
![]() . In response to a
technology shock a high elasticity of substitution
. In response to a
technology shock a high elasticity of substitution
![]() implies a
unique adjustment path of the economy. However, if
implies a
unique adjustment path of the economy. However, if
![]() is below
the critical value
is below
the critical value
![]() I
find three different impulse response functions for a given small
technology shock. If the shock raises country
I
find three different impulse response functions for a given small
technology shock. If the shock raises country ![]() 's technology the real exchange rate
may either appreciate on impact by a small or a large amount
relative to the magnitude of the shock or it may depreciate by a
large amount on impact.
's technology the real exchange rate
may either appreciate on impact by a small or a large amount
relative to the magnitude of the shock or it may depreciate by a
large amount on impact.
The reason for the striking differences between the models lies
in the nonlinearities that arise for low values of the elasticity
of substitution. Absent international financial markets, there are
multiple equilibria if
![]() is below
is below
![]() .
Consider an endowment economy with two countries and two traded
goods that are imperfect substitutes.6Assume that the countries are just
mirroring each other with respect to preferences and
endowments.7 Then,
there is always one equilibrium with the relative price of the
traded goods equal to unity. However, there can be two more
equilibria. If the price of the domestic good is very high relative
to the price of the foreign good, domestic agents are very wealthy
compared to the foreign agents. If the elasticity of substitution
is low, foreigners are willing to give up most of their good in
order to consume at least some of the domestic good, and domestic
agents end up consuming most of the domestic and the foreign good.
The reverse is true as well. Foreign agents consume most of the
goods, if the foreign good is very expensive in relative terms. Of
course, these last two scenarios cannot be an equilibrium for high
values of the elasticity of substitution. In the limiting case of
perfect substitutability the unique equilibrium features each
country consuming its own endowment.
.
Consider an endowment economy with two countries and two traded
goods that are imperfect substitutes.6Assume that the countries are just
mirroring each other with respect to preferences and
endowments.7 Then,
there is always one equilibrium with the relative price of the
traded goods equal to unity. However, there can be two more
equilibria. If the price of the domestic good is very high relative
to the price of the foreign good, domestic agents are very wealthy
compared to the foreign agents. If the elasticity of substitution
is low, foreigners are willing to give up most of their good in
order to consume at least some of the domestic good, and domestic
agents end up consuming most of the domestic and the foreign good.
The reverse is true as well. Foreign agents consume most of the
goods, if the foreign good is very expensive in relative terms. Of
course, these last two scenarios cannot be an equilibrium for high
values of the elasticity of substitution. In the limiting case of
perfect substitutability the unique equilibrium features each
country consuming its own endowment.
In the dynamic economy with incomplete asset markets, the
equilibria of the economy without international financial markets
are the candidate steady states. Consider the case of a low
elasticity of substitution, i.e.,
![]() . Under the assumption
that portfolio costs are zero if and only if net foreign assets are
zero, all three candidate steady states are in fact steady states
of the bond economy with convex portfolio costs. Similarly, if the
debt elastic interest rate premium is zero if and only if net
foreign assets are zero, there are three steady states. However, if
the discount factor is endogenous, absence of arbitrage requires
that the discount factors are equalized across countries in any
steady state. As the discount factor is assumed to be strictly
decreasing in the agent's utility level, this condition uniquely
determines the steady state allocations (provided a strictly
concave utility function and a convex technology).
. Under the assumption
that portfolio costs are zero if and only if net foreign assets are
zero, all three candidate steady states are in fact steady states
of the bond economy with convex portfolio costs. Similarly, if the
debt elastic interest rate premium is zero if and only if net
foreign assets are zero, there are three steady states. However, if
the discount factor is endogenous, absence of arbitrage requires
that the discount factors are equalized across countries in any
steady state. As the discount factor is assumed to be strictly
decreasing in the agent's utility level, this condition uniquely
determines the steady state allocations (provided a strictly
concave utility function and a convex technology).
In the simple model presented in this paper, the critical value
of the elasticity of substitution
![]() lies
in the range of
lies
in the range of ![]() for reasonable choices of the remaining parameters. However, the
value of
for reasonable choices of the remaining parameters. However, the
value of
![]() is
sensitive to changes in the model. For example, if the model is
extended along the lines of Corsetti and Dedola (2005) to allow for
non-traded goods and a strong complementarity between traded and
non-traded goods,
is
sensitive to changes in the model. For example, if the model is
extended along the lines of Corsetti and Dedola (2005) to allow for
non-traded goods and a strong complementarity between traded and
non-traded goods,
![]() can
easily assume values larger than
can
easily assume values larger than ![]() for reasonable parameterizations of the model.
for reasonable parameterizations of the model.
The empirical literature reports a wide range of trade
elasticities at the aggregate level from 0 to ![]() .8 Whalley
(1985) reports an elasticity of
.8 Whalley
(1985) reports an elasticity of ![]() . In a recent study, Hooper, Johnson and Marquez
(2000) estimate trade elasticities for the G7 countries. They
report a short-run trade elasticity of
. In a recent study, Hooper, Johnson and Marquez
(2000) estimate trade elasticities for the G7 countries. They
report a short-run trade elasticity of ![]() for the U.S., and values ranging
between 0 and
for the U.S., and values ranging
between 0 and ![]() for the remaining G7 countries.
Earlier studies by Houthakker and Magee (1969) and Marquez (1990)
also suggest trade elasticities between 0
and
for the remaining G7 countries.
Earlier studies by Houthakker and Magee (1969) and Marquez (1990)
also suggest trade elasticities between 0
and ![]() . In his study, Taylor
(1993) estimates an import demand equation for the US and finds a
short-run trade elasticity of
. In his study, Taylor
(1993) estimates an import demand equation for the US and finds a
short-run trade elasticity of ![]() and a long-run trade elasticity of
and a long-run trade elasticity of ![]() .9
.9
The remainder of the paper is organized as follows. Section 2 presents the model and analyses it under the assumption that there are no international financial markets. In section 3, agents have access to one non-state-contingent bond. I analyze the characteristics of the steady states under the different stationarity inducing approaches. The impulse response functions for the model with endogenous discounting and convex portfolio costs are investigated in section 4. Finally, section 5 offers concluding remarks.
2 The model
In the remainder of this section, I analyze the simple two-country model under the assumption of balanced trade, i.e., there are no international financial markets. Absent capital accumulation this assumption allows me to present the issues of multiple equilibria without the additional complications that occur in a dynamic model. Furthermore, under financial autarchy the model is stationary.10
In Section ![]() the simple
model is augmented by the assumption that agents have access to
international financial markets. I first present the standard model
with incomplete markets in order to illustrate the stationarity
problem. Three different approaches to induce stationarity are
studied: convex portfolio costs, debt elastic interest rate, and
endogenous discount factor. The analysis is guided by two
questions. How does the number of steady states in the closed model
relate to the number of equilibria in the model with financial
autarchy? How are the dynamic properties of a steady state related
to the slope of the excess demand function for the different
stationarity inducing approaches?
the simple
model is augmented by the assumption that agents have access to
international financial markets. I first present the standard model
with incomplete markets in order to illustrate the stationarity
problem. Three different approaches to induce stationarity are
studied: convex portfolio costs, debt elastic interest rate, and
endogenous discount factor. The analysis is guided by two
questions. How does the number of steady states in the closed model
relate to the number of equilibria in the model with financial
autarchy? How are the dynamic properties of a steady state related
to the slope of the excess demand function for the different
stationarity inducing approaches?
2.1 Financial autarchy
There are two countries, each populated by an infinite number of households with a total measure of one. Each country produces only one good that can be traded without frictions in the international goods market. The two goods are assumed to be imperfect substitutes in the household's utility function. Labor, which is supplied endogenously, is the sole input into the production process.
Time is discrete and each period the economy experiences one of
finitely many events ![]() .
.
![]() denotes the
history of events up through and including period
denotes the
history of events up through and including period ![]() . The probability, as of period
0, of any particular history
. The probability, as of period
0, of any particular history ![]() is
is
![]() . The initial realization
. The initial realization
![]() is given.
is given.
Households maximize their expected lifetime utility subject to the budget constraint
where
![$ c_{i}\left( s^{t}\right) =\left[ \alpha_{i1}^{1-\rho}c_{i1}^{\rho}\left( s^{t}\right) +\alpha _{i2}^{1-\rho}c_{i2}^{\rho}\left( s^{t}\right) \right] ^{\frac{1}{\rho}}$](img41.gif) with
with
The strictly concave period utility function
![]() is
assumed to satisfy the following sign conditions:
is
assumed to satisfy the following sign conditions:
Agent ![]() chooses
consumption of the two traded goods such that
chooses
consumption of the two traded goods such that
where
![$\displaystyle \equiv\frac{\bar {P}_{1}\left( s^{t}\right) }{P_{1}\left( s^{t}\right) }=\left[ \alpha_{11}\left( \frac{1}{\bar{q}\left( s^{t}\right) }\right) ^{\frac{\rho}{\rho-1}}+\alpha_{12}\right] ^{\frac{1-\rho}{\rho}}\frac{1} {\bar{q}\left( s^{t}\right) }$](img65.gif) with
with |
||
![$\displaystyle \equiv\frac{\bar {P}_{2}\left( s^{t}\right) }{P_{2}\left( s^{t}\right) }=\left[ \alpha_{21}\left( \frac{1}{\bar{q}\left( s^{t}\right) }\right) ^{\frac{\rho}{\rho-1}}+\alpha_{22}\right] ^{\frac{1-\rho}{\rho}}$](img68.gif) with
with |
I normalize the price of the consumption basket in country
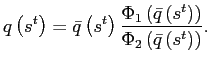
Similar expressions can be derived for the demand of good
The optimal allocation of labor relative to consumption is determined from
Firms in country ![]() produce the traded good
produce the traded good ![]() using a linear production technology,
using a linear production technology,
![]() . Appendix
. Appendix ![]() shows that equations (6) - (8) can be used to express
shows that equations (6) - (8) can be used to express ![]() and
and ![]() as functions of the prices
as functions of the prices ![]() ,
, ![]() and
and ![]() (and
(and ![]() ) only.
) only.
Perfect competition and the linear technology imply that the
equilibrium wage equals the productivity parameter, i.e.
![]() .
As shown in appendix
.
As shown in appendix ![]() the
equilibrium conditions for this model can be fully summarized by
the excess demand function for good
the
equilibrium conditions for this model can be fully summarized by
the excess demand function for good ![]() :
:
An equilibrium is a relative price
Figure 1 plots
the excess demand for good ![]() as a function of
as a function of
![]() for different values of the
elasticity of substitution
for different values of the
elasticity of substitution
![]() . In
plotting
. In
plotting ![]() , I
assume the following utility function
, I
assume the following utility function
The parameter values are
| parameter | value | explanation of the parameter |
|---|---|---|
| -2.75 |
|
|
| 7.00 | ||
| 3.00 | coefficient of relative risk aversion | |
|
|
0.90 | weight on domestic good in CES aggregator |
|
|
0.10 | weight on foreign good in CES aggregator |
|
|
1.00 | technology level |
Figure 1: Excess demand
for good 2 for different values of
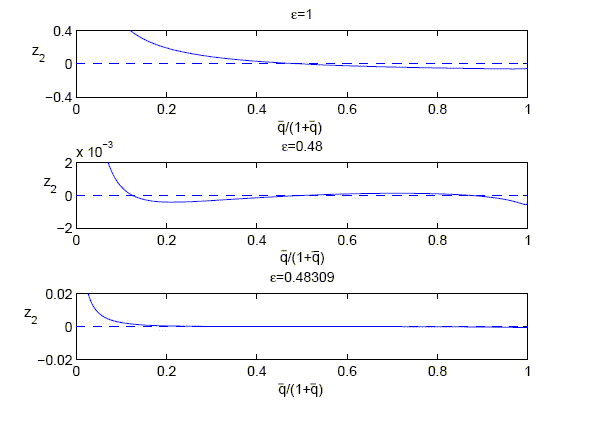
Figure 1 description:
Figure 1 consists of three graphs presented in a 3-by-1 matrix. The caption for figure 1 reads �excess demand for good 2 for different values of epsilon�. The x-axis of each graph is labeled q-bar over 1 plus q-bar, and ranges in values from 0 to 1 in increments of 0.2. The top graph is titled epsilon equals 1. The y-axis is labeled Z sub 2, and ranges in values from -0.4 to 4 in increments of 0.4. A dashed horizontal line exists in the graph where Z sub 2 equals 0. The curve begins at (0.11,0.4), it steadily decreases to (0.5,0), and continues to decrease, albeit more slowly, until (1,-0.05). The middle graph is titled epsilon equals 0.48. The y-axis is labeled Z sub 2, and ranges in values from -0.002 to 0.002 in increments of 0.002. A dashed horizontal line exists in the graph where Z sub 2 equals 0. The curve begins at (0.08,0.002). It decreases quickly to (0.2,-0.0005). It then very slowly increases, crosses the dashed horizontal line at (0.5,0) and continues to (0.7,0.0005). Afterwards, it slowly decreases until (1,-0.0005). The bottom graph is titled epsilon equals 0.48309. The y-axis is labeled Z sub 2, and ranges in values from -0.02 to 0.02 in increments of 0.02. A dashed horizontal line exists in the graph where Z sub 2 equals 0. The curve begins at (0.05,0.02). It quickly decreases until converging to (0.2, 0). It remains at this value for the rest of q-bar over 1 plus q-bar.
For a given parameterization of the remainder of the model I
distinguish three cases for the elasticity of substitution,
![]() :
:
- If
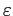 is
sufficiently high, as in the first panel, the excess demand
function has exactly one zero. Hence, the equilibrium is unique and
it features
is
sufficiently high, as in the first panel, the excess demand
function has exactly one zero. Hence, the equilibrium is unique and
it features
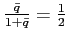 . Furthermore,
the slope of the excess demand function at
. Furthermore,
the slope of the excess demand function at
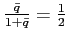 is
negative.
is
negative. - If
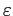 is
sufficiently low, as in the second panel, the excess demand
function has three zeros. While the excess demand function is
downward sloping at the first and third equilibrium, it is upward
sloping in the second one (counted from left to right).
is
sufficiently low, as in the second panel, the excess demand
function has three zeros. While the excess demand function is
downward sloping at the first and third equilibrium, it is upward
sloping in the second one (counted from left to right). - There is a critical value
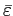 (here
(here
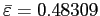 ) of the elasticity of
substitution such that there is a continuum of equilibria because
the slope of the excess demand function is zero around
) of the elasticity of
substitution such that there is a continuum of equilibria because
the slope of the excess demand function is zero around
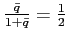 .
.
Multiple equilibria arise at low values of the elasticity of
substitution for the following reason. Consider the first
equilibrium in the second panel. If the price of good ![]() is high relative to the price of good
is high relative to the price of good
![]() ,
,
![]() , agents
of country
, agents
of country ![]() produce more
of their good than agents of country
produce more
of their good than agents of country ![]() . As the elasticity of substitution between the goods
is very low, country
. As the elasticity of substitution between the goods
is very low, country ![]() agents
are willing to pay the high price for good
agents
are willing to pay the high price for good ![]() and country
and country ![]() ends up consuming most of the two
goods. The same logic applied in the third equilibrium,
ends up consuming most of the two
goods. The same logic applied in the third equilibrium,
![]() , with
the roles of country
, with
the roles of country ![]() and
and
![]() being reversed. The
second equilibrium is the symmetric equilibrium featuring
being reversed. The
second equilibrium is the symmetric equilibrium featuring
![]() . If the
elasticity of substitution is high, equilibria
. If the
elasticity of substitution is high, equilibria ![]() and
and ![]() cannot exist. In fact, if the elasticity of
substitution is infinite, agents in both countries only consume
their own goods and the relative price in the unique equilibrium
has to be equal to
cannot exist. In fact, if the elasticity of
substitution is infinite, agents in both countries only consume
their own goods and the relative price in the unique equilibrium
has to be equal to ![]() .
.
2.2 More about multiple equilibria
The above findings are not surprising. The analogous endowment economy with a CES aggregator has been used extensively in general equilibrium theory to study equilibrium multiplicity. For instance see Mas-Colell (1991), Kehoe (1991), Gjerstad (1996) and Bela (1997). In appendix A.3, I summarize some of the findings of general equilibrium theory in the context of the model presented here in this paper. In general, the number of equilibria is odd. If the excess demand function is upward sloping in an equilibrium, there have to be at least two more. Unfortunately, nothing can be said with certainty about the number of equilibria unless one can prove that the equilibrium is unique.
To gain an idea about the relationship between the critical
value
![]() and
the remaining model parameters, consider the case of
and
the remaining model parameters, consider the case of
![]() ,
,
![]() and identical preferences over
consumption and leisure in the two countries. Irrespective of the
value of the elasticity of substitution,
and identical preferences over
consumption and leisure in the two countries. Irrespective of the
value of the elasticity of substitution, ![]() is an equilibrium. As shown
more generally in appendix
is an equilibrium. As shown
more generally in appendix ![]() , the critical value
, the critical value
![]() is
given by
is
given by
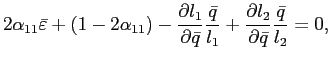
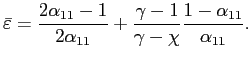
- Even without home bias in consumption, i.e.,
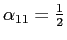 ,
,
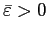 if agents are sufficiently risk averse (
if agents are sufficiently risk averse (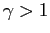 ).
). -
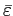 is
strictly increasing in
is
strictly increasing in 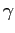 .
. - If
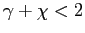 ,
,
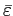 is
increasing in the home bias. Otherwise,
is
increasing in the home bias. Otherwise,
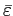 is
decreasing in
is
decreasing in
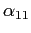 .
. - If
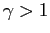 ,
,
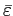 is
increasing in the Frish labor supply elasticity
is
increasing in the Frish labor supply elasticity
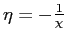 .
Otherwise,
.
Otherwise,
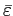 is
decreasing in
is
decreasing in
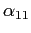 .
. - If
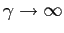 and
and
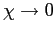 ,
,
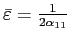 .
.
If the household's preferences over consumption and leisure are
Cobb-Douglas the appendix shows that
![]() ,
, ![]() and
and
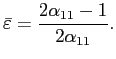
As these examples show, the critical value of
![]() (and
therefore the presence of multiple equilibria) is greatly affected
by certain model choices. In the technical appendix to this paper,
which is available upon request, I also show the following:
(and
therefore the presence of multiple equilibria) is greatly affected
by certain model choices. In the technical appendix to this paper,
which is available upon request, I also show the following:
- In a model with endogenous capital formation,
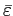 also
depends on the elasticity of substitution between labor and
capital. Relative to the model without capital,
also
depends on the elasticity of substitution between labor and
capital. Relative to the model without capital,
 can
be lower or higher for otherwise identical parameters.
can
be lower or higher for otherwise identical parameters. - In a model with non-traded goods,
 can
be very high (much larger than unity) for reasonable parameter
choices if there is some complementarity between traded and
non-traded goods as in Corsetti, Dedola and Leduc (2005).
can
be very high (much larger than unity) for reasonable parameter
choices if there is some complementarity between traded and
non-traded goods as in Corsetti, Dedola and Leduc (2005).
The value of
![]() also has an
important impact on the comparative static properties of the model.
Consider a small increase in the productivity level of country
also has an
important impact on the comparative static properties of the model.
Consider a small increase in the productivity level of country
![]() . Such a change deforms
the excess demand function and shifts it upwards. Figure 2 shows the
excess demand function for
. Such a change deforms
the excess demand function and shifts it upwards. Figure 2 shows the
excess demand function for
![]() (upper panel) and
(upper panel) and
![]() (lower panel)
for two technology shocks of different magnitude. The solid line
depicts the original excess demand function with
(lower panel)
for two technology shocks of different magnitude. The solid line
depicts the original excess demand function with
![]() . The
dashed line shows the case of
. The
dashed line shows the case of
![]() and
the dashed-dotted line is the case of
and
the dashed-dotted line is the case of
![]() . If
the elasticity of substitution is large (
. If
the elasticity of substitution is large (
![]() ) the increase in
) the increase in
![]() leads to a small
increase in the equilibrium value of the relative price of traded
goods irrespective of the magnitude of the shock.
leads to a small
increase in the equilibrium value of the relative price of traded
goods irrespective of the magnitude of the shock.
The situation is quite different if the elasticity is low (
![]() ). For a small
relative increase in
). For a small
relative increase in ![]() all three equilibria are preserved. While the price of traded goods
rises in the first and third equilibrium relative to the original
equilibrium,
all three equilibria are preserved. While the price of traded goods
rises in the first and third equilibrium relative to the original
equilibrium,
![]() ,
,
![]() drops in the
second equilibrium. However, if the technology shock is
sufficiently large, the first two equilibria disappear. Only the
third equilibrium survives. The dashed-dotted line in panel 2 has
only one zero, which occurs around
drops in the
second equilibrium. However, if the technology shock is
sufficiently large, the first two equilibria disappear. Only the
third equilibrium survives. The dashed-dotted line in panel 2 has
only one zero, which occurs around
![]() .
.
Figure 2: Equilibria for
small changes in
 .
.
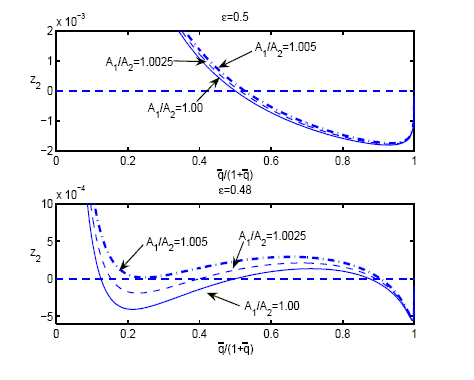
Figure 2 description:
Figure 2 consists of two graphs presented in a 2-by-1 matrix. The caption reads �Equilibria for small changes in A sub 1 over A sub 2.� The x-axis of each graph is labeled q-bar over 1 plus q-bar, and ranges in values from 0 to 1 in increments of 0.2. The top graph is titled epsilon equals 0.5. The y-axis is labeled Z sub 2, and ranges in values from -0.002 to 0.002 in increments of 0.001. A dashed horizontal line exists in the graph where Z sub 2 equals 0. The first curve is labeled A sub 1 over A sub 2 equals 1. The second curve is labeled A sub 1 over A sub 2 equals 1.0025. The third curve is labeled A sub 1 over A sub 2 equals 1.005. The curves all take the same shape. The first and third curves lie on both sides of the second curve. The second curve begins at the point (0.35, 0.002). It decreases to (0.95,-0.0015) before increasing to (1,0). The difference between the second curve and the first curve (below it) and the difference between the second curve and the third curve (above it) varies. Initially, it is 0.0001 on each side of curve 2. This difference decreases, and by the end, all three curves end at the same point (1,0). The bottom graph is titled epsilon equals 0.48. The y-axis is labeled Z sub 2, and ranges in values from -0.0005 to 0.001 in increments of 0.0005. A dashed horizontal line exists in the graph where Z sub 2 equals 0. The first curve is labeled A sub 1 over A sub 2 equals 1. The second curve is labeled A sub 1 over A sub 2 equals 1.0025. The third curve is labeled A sub 1 over A sub 2 equals 1.005. The curves all take the same shape. The first and third curves lie on both sides of the second curve. The second curve begins at (0.1,0.001). It quickly decreases to (0.2,-0.0005), then increases slowly to (0.8,0.0001) before falling back down again to (1,-0.0005). The difference between the second curve and the first curve (below it) and the difference between the second curve and the third curve (above it) varies. Initially, it appears to be 0.0001 on each side of curve 2. By the time, q-bar over 1 plus q-bar equals 0.2, this difference has increased to 0.0003. Afterwards, this difference decreases, and by the end, all three curves end at the same point (1,-0.0005).
3 Bond economies
In contrast to the last section agents are now assumed to have
access to international financial markets. Following the standard
assumption in international macroeconomics, financial markets are
exogenously incomplete in the sense that the only asset that is
traded internationally is one non-state-contingent bond. This bond
is in zero net supply, i.e.,
![]() .
.
In order to illustrate the stationarity problem, I begin with the standard incomplete markets setup without stationarity-inducing features.
3.1 The non-stationary model
In the standard two-country model a household faces the following maximization problem
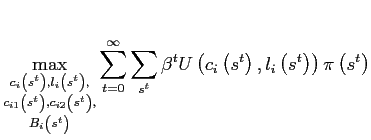
|
||
Given the assumptions on technology, preferences, and trade stated in the previous section the equilibrium dynamics are fully summarized by
- the excess demand function for good
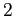
whereand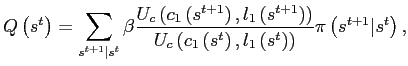
 in equilibrium,
in equilibrium, - the familiar risk sharing equation, states that expected
marginal utility growth is equalized across countries:
where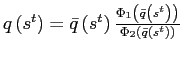 .
.
I have used the assumption that bonds are in zero net supply. As
shown in appendix ![]() ,
consumption and labor choices can be expressed as functions of the
relative price
,
consumption and labor choices can be expressed as functions of the
relative price ![]() .
Moreover, this system of difference equations has to satisfy the
appropriate initial and transversality conditions.
.
Moreover, this system of difference equations has to satisfy the
appropriate initial and transversality conditions.
Unfortunately, the deterministic steady state of this model is
not unique. With
![]() and
and
![]() as shown in
Appendix
as shown in
Appendix ![]() , equations (11) and (12)
have to solve for the steady state values of
, equations (11) and (12)
have to solve for the steady state values of ![]() and
and ![]() . However, in a steady state,
equation (12) collapses to an identity and contains no information about
the endogenous variables. Hence, there is one equations but two
unknowns.
. However, in a steady state,
equation (12) collapses to an identity and contains no information about
the endogenous variables. Hence, there is one equations but two
unknowns.
Admittedly, it is possible to choose a particular steady state
amongst the set of feasible solutions to (11). It is common practice see, e.g., Baxter and Crucini (1995)
to assume
![]() .
Although this choice pins down the original steady state, the
dynamic system that describes the behavior of the economy in the
neighborhood of the steady state is not stationary. Even a
completely temporary shock has long lasting effects on the economy:
whatever the level of bond holdings materializes in the period
immediately following a shock becomes the new long-run position
until a new shock occurs.
.
Although this choice pins down the original steady state, the
dynamic system that describes the behavior of the economy in the
neighborhood of the steady state is not stationary. Even a
completely temporary shock has long lasting effects on the economy:
whatever the level of bond holdings materializes in the period
immediately following a shock becomes the new long-run position
until a new shock occurs.
This problem is easily seen by looking at the linear
approximation of the dynamic system around a candidate steady state
with
![]() . For
simplicity assume that preferences are additive-separable in
consumption and leisure, i.e.,
. For
simplicity assume that preferences are additive-separable in
consumption and leisure, i.e.,
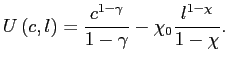
![$\displaystyle c_{1}\left( s^{t}\right) =\chi_{0}^{\frac{1}{\chi}}\left[ \Phi_{1}\left( \bar{q}\left( s^{t}\right) \right) A_{1}\left( s^{t}\right) \right] ^{\frac{\chi-1}{\chi}}\left[ c_{1}\left( s^{t}\right) \right] ^{\frac{\gamma}{\chi}}+B_{1}\left( s^{t-1}\right) -Q\left( s^{t}\right) B_{1}\left( s^{t}\right)$](img185.gif) .
.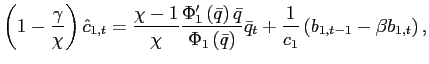
![$\displaystyle \frac{\partial z_{2}}{\partial\bar{q}}\bar{q}\bar{q}_{t}+\frac{\partial z_{2} }{\partial dW_{1}}\left[ b_{1,t-1}-\beta b_{1,t}\right] =0\text{.} $](img190.gif)
Finally, the log-linear approximation of equation (12) is given by
![$\displaystyle -\gamma\left( \left( \hat{c}_{1,t+1}-\hat{c}_{2,t+1}\right) -\left( \hat{c}_{1,t}-\hat{c}_{2,t}\right) \right) =\left[ 1+\frac{\Phi_{1} ^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{1}\left( \bar{q}\right) }-\frac{\Phi_{2}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{2}\left( \bar{q}\right) }\right] \left( \hat{q}_{t}-\hat{q}_{t+1}\right) . $](img193.gif)
![\begin{displaymath} \left( \begin{array}[c]{c} \bar{q}_{t+1}\ b_{t} \end{array}\right) =\left( \begin{array}[c]{cc} 1 & 0\ \frac{1}{\beta}\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}} {\frac{\partial z_{2}}{\partial dW_{1}}} & \frac{1}{\beta} \end{array}\right) \left( \begin{array}[c]{c} \bar{q}_{t}\ b_{t-1} \end{array}\right) \end{displaymath}](img197.gif)
3.2 Bond economy with convex portfolio costs
Similar to Heathcote and Perri (2002), and Schmitt-Grohé
and Uribe (2003) let agents face a convex cost for holding/issuing
bonds. The collected fees are reimbursed to the agents by a
lump-sum transfer.
![]() denotes the
portfolio costs in terms of country
denotes the
portfolio costs in terms of country ![]() 's traded good, where
's traded good, where
![]() and
and
![]() otherwise. The representative household in country
otherwise. The representative household in country ![]() solves
solves
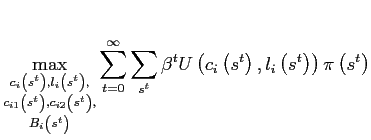
|
||
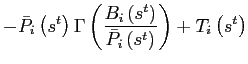 ,
, |
where
The equilibrium dynamics are fully summarized by
![]() with
with ![]() given
by equation (11),
given
by equation (11),
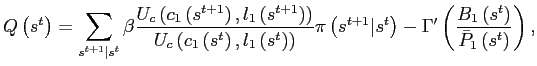
As
![]() for
for
![]() and larger
than zero otherwise, equation (13) implies that in a steady state
and larger
than zero otherwise, equation (13) implies that in a steady state
![]() .
Although the steady state value of bond holdings is uniquely
determined, there can still be multiple steady states if
.
Although the steady state value of bond holdings is uniquely
determined, there can still be multiple steady states if
![]() has multiple solutions
in
has multiple solutions
in ![]() . Hence, any
steady state of the financial autarchy model is also a steady state
of the model with convex portfolio costs. Consequently, for
. Hence, any
steady state of the financial autarchy model is also a steady state
of the model with convex portfolio costs. Consequently, for
![]() the portfolio cost
model has multiple steady states.
the portfolio cost
model has multiple steady states.
The global equilibrium dynamics in an economy with perfect
foresight are depicted in figures 3 and 4 in a phase diagram. The
dashed lines are the
![]() locus and the
locus and the
![]() locus of the dynamic
system, respectively. Each intersection of the two loci corresponds
to a steady state. The manifold which has been computed by a
reverse shooting algorithm is depicted by the solid line.11 If the elasticity of substitution is
high
locus of the dynamic
system, respectively. Each intersection of the two loci corresponds
to a steady state. The manifold which has been computed by a
reverse shooting algorithm is depicted by the solid line.11 If the elasticity of substitution is
high
![]() , there
is a unique and stable steady state, see figure 4.
, there
is a unique and stable steady state, see figure 4.
However, there are three steady states if the elasticity of
substitution is low
![]() as
depicted in figure 5. As indicated by the arrows the first and the
third steady state are locally stable, but the second one
as
depicted in figure 5. As indicated by the arrows the first and the
third steady state are locally stable, but the second one
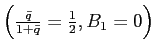 is not. For intermediate values of initial bond holdings the
economy converges either to the first or to the third steady state.
Convergence to a steady state is unique only if the initial bond
holdings are sufficiently high in absolute value.
is not. For intermediate values of initial bond holdings the
economy converges either to the first or to the third steady state.
Convergence to a steady state is unique only if the initial bond
holdings are sufficiently high in absolute value.
The (local) dynamic properties of the model with convex portfolio costs are summarized in the following theorem.
Appendix ![]() provides
an exact definition of
provides
an exact definition of
![]() and a proof
of the above theorem.
and a proof
of the above theorem.
![]() measures how
sensitive the portfolio costs are in the steady state with respect
to changes in the bond distribution. To keep the model with convex
portfolio costs close to the original model, the portfolio costs
need to be small and quite insensitive to changes in the allocation
of assets. In fact, if
measures how
sensitive the portfolio costs are in the steady state with respect
to changes in the bond distribution. To keep the model with convex
portfolio costs close to the original model, the portfolio costs
need to be small and quite insensitive to changes in the allocation
of assets. In fact, if ![]() is quadratic as in Heathcote and Perri (2002),
is quadratic as in Heathcote and Perri (2002),
![]() is sufficiently
small for portfolio costs that are of realistic magnitude.
is sufficiently
small for portfolio costs that are of realistic magnitude.
If portfolio costs are chosen to be very large, the model becomes similar to the model with financial autarchy. Under financial autarchy, any steady state is locally stable in this set-up.
Figure 3: Stability of the
steady state for
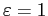 with
convex portfolio costs.
with
convex portfolio costs.
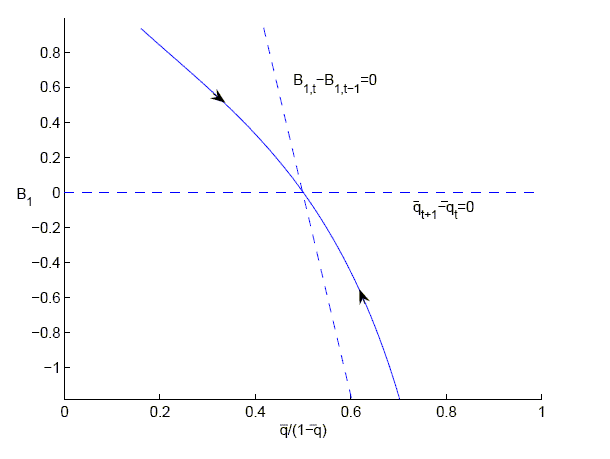
Figure 3 description:
Figure 3 consists of one graph. The caption reads �stability of the steady state for epsilon equals one with convex portfolio costs.� The x-axis is labeled q-bar over 1 minus q-bar, and ranges in values from 0 to 1 in increments of 0.2. The y-axis is labeled B sub 1, and ranges in values from -1.2 to 1 in increments of 0.2. A dashed horizontal line exists where B sub 1 equals 0. The line is labeled q-bar sub (t plus 1) minus q-bar sub t equals 0. A dashed diagonal line exists starting at about (0.5, 1) and running to (0.6,-1.2). The line is labeled B sub 1 comma t minus B sub 1 comma (t minus 1) equals 0. Note that the dashed lines create four quadrants. The dashed lines intersect at (0.5,0). A single parabolic-shaped curve exists starting at about (0.2, 1) running through (0.5, 0) and then to (0.7, -1.2). Recall that the two dashed lines intersect to create four quadrants. The portion of the curve in the upper left quadrant contains an arrow pointing southeast. The portion of the curve in the lower right quadrant contains an arrow pointing northwest.
Figure 4: Stability of the
steady state for
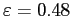 with
convex portfolio costs.
with
convex portfolio costs.
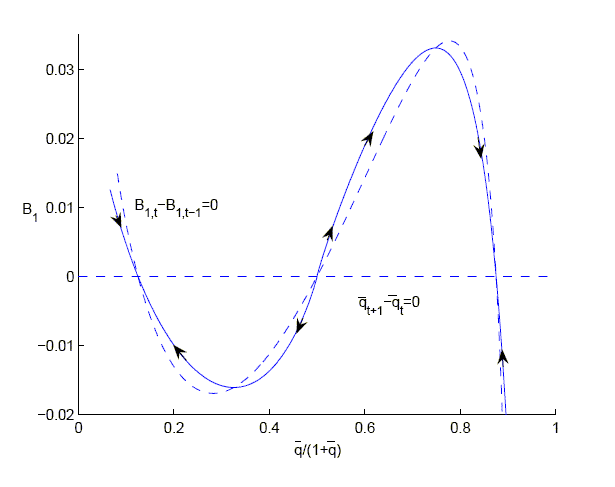
Figure 4 description:
Figure 4 consists of one graph. The caption reads �stability of the steady state for epsilon equals 0.48 with convex portfolio costs.� The x-axis is labeled q-bar over 1 plus q-bar, and ranges in values from 0 to 1 in increments of 0.2. The y-axis is labeled B sub 1, and ranges in values from -0.02 to 0.035 in increments of 0.01. A dashed horizontal line exists where B sub 1 equals 0. The line is labeled q-bar sub (t plus 1) minus q-bar sub t equals 0. A dashed curve and a solid curve exist with similar polynomial shapes. Each curve crosses the dashed horizontal line at (0.1,0), (0.5,0) and (0.85,0). The dashed line is labeled B sub 1 comma t minus B sub 1 comma (t minus 1) equals 0. It begins at (0.08,0.015). The solid curve begins at (0.08,0.01) and decreases, crosses the dashed line at (0.1,0) and decreases until (0.35,-0.015). It then increases, crosses the dashed horizontal line at (0.5,0) and reaches a high point of (0.7, 0.035). It then decreases, crosses the dashed horizontal line at (0.85,0), and reaches the value (0.9,-0.02). In the part of the curve where q-bar over 1 plus q-bar is less than 0.1, there exists an arrow pointing southeast. In the part of the curve where q-bar over 1 plus q-bar is between 0.1 and 0.3, there exists an arrow pointing northwest. In the part of the curve where q-bar over 1 plus q-bar is between 0.3 and 0.5, there exists an arrow pointing southwest. In the part of the curve where q-bar over 1 plus q-bar is between 0.5 and 0.7, there exists an arrow pointing northeast. In the part of the curve where q-bar over 1 plus q-bar is between 0.7 and 0.85, there exists an arrow point southeast. In the part of the curve where q-bar over 1 plus q-bar is between 0.85 and 0.9, there exists an arrow pointing north.
3.3 Bond economy with debt elastic interest rate
In the setup of this paper the portfolio cost approach is very
similar to a model with a debt elastic interest rate. The latter
approach assumes that the consumers in countries ![]() and
and ![]() face different prices for the bond, and that the
spread between the prices is a function of the net foreign asset
position. This approach appears among others in Boileau and
Normandin (2005), Devereux and Smith (2003), and
Schmitt-Grohé and Uribe (2003). The households budget
constraint is given by
face different prices for the bond, and that the
spread between the prices is a function of the net foreign asset
position. This approach appears among others in Boileau and
Normandin (2005), Devereux and Smith (2003), and
Schmitt-Grohé and Uribe (2003). The households budget
constraint is given by
where the function
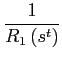 |
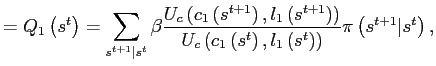
|
|
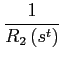 |
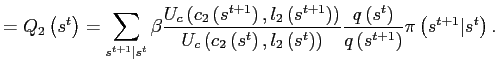
|
Furthermore, equation (14) implies
As
In a steady state equation (15) implies
![]() given
the assumption
given
the assumption
![]() . Hence, in the model with a
debt elastic interest rate all the steady states of the financial
autarchy model are preserved.
. Hence, in the model with a
debt elastic interest rate all the steady states of the financial
autarchy model are preserved.
As in the model with convex portfolio costs the stability of a steady state can be linked to the slope of the excess demand function.
Appendix ![]() provides
an exact definition of
provides
an exact definition of
![]() . Similar to
the model with convex portfolio costs, the condition
. Similar to
the model with convex portfolio costs, the condition
![]() implies
that the interest rate does not react too strongly to changes in
the bond holdings. Hence, to the extent that the model with a debt
elastic interest rate is supposed to behave close to the original
model, any steady state with an upward-sloping excess demand
function is unstable.12
implies
that the interest rate does not react too strongly to changes in
the bond holdings. Hence, to the extent that the model with a debt
elastic interest rate is supposed to behave close to the original
model, any steady state with an upward-sloping excess demand
function is unstable.12
3.4 Bond economy with endogenous discounting
In this section agents' discount factors are assumed to be endogenous as in Mendoza (1991), Corsetti, Dedola and Leduc (2005), and Schmitt-Grohé and Uribe (2003).13 This concept of preferences with intertemporal dependences was introduced by Uzawa (1968) and it has been extended and clarified by Epstein (1983, 1987). Uzawa-Epstein preferences fall into the broader class of recursive preferences. The subjective discount factor is assumed to be a decreasing function of the period utility level, i.e., agents become more impatient as current utility rises. For most of the analysis, I assume that agents do not internalize the effect that their current consumption and labor choices have on their discount factor. As the model is solved by a backward shooting algorithm, this assumption simplifies the analysis drastically because it reduces the number of state variables from three to just one.
The problem of the representative household is given by
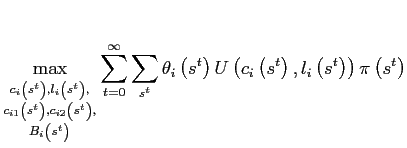
|
||
The equilibrium dynamics are fully summarized by
![$\displaystyle Q\left( s^{t}\right) =\sum_{s^{t+1}\vert s^{t}}\beta_{1}\left[ U\left( c_{1}\left( s^{t}\right) ,l_{1}\left( s^{t}\right) \right) \right] \frac{U_{c,1}\left( c_{1}\left( s^{t+1}\right) ,l_{1}\left( s^{t+1} \right) \right) }{U_{c,1}\left( c_{1}\left( s^{t}\right) ,l_{1}\left( s^{t}\right) \right) }\pi\left( s^{t+1}\vert s^{t}\right) $](img251.gif)
where
Equation (16) implies that in a steady state the discount factors are equalized across countries
As
The following theorem about the stability of the steady state is proven in the appendix
If the discount factor is assumed to be strictly increasing in the utility level, the model dynamics are always explosive irrespective of the slope of the excess demand function.
Using a phase diagram, figures 5 and 6 illustrate the global dynamics for the model with
endogenous discounting.14 The
dashed lines are the
![]() and
and
![]() locus, respectively.
locus, respectively.
The unique steady state is always saddle-path stable for both
high and low values of the elasticity of substitution. However, if
![]() is low the
path to the steady state given an initial wealth distribution is
not unique. For initial bond holdings close enough to 0 the initial value of
is low the
path to the steady state given an initial wealth distribution is
not unique. For initial bond holdings close enough to 0 the initial value of ![]() determines the starting point on the stable
manifold.
determines the starting point on the stable
manifold.
Figure 5: Stability of the
steady state for
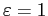 with an
endogenous discount factor.
with an
endogenous discount factor.
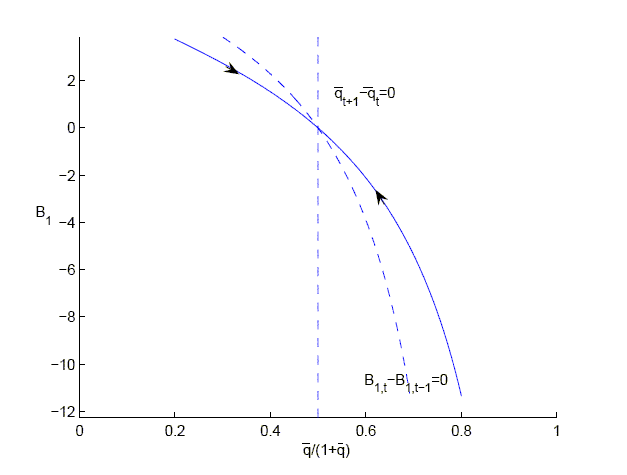
Figure 5 description:
Figure 5 consists of one graph. The caption reads �stability of the steady state for epsilon equals 1 with an endogenous discount factor.� The x-axis is labeled q-bar over 1 plus q-bar, and ranges in values from 0 to 1 in increments of 0.2. The y-axis is labeled B sub 1, and ranges from -12 to 4 in increments of 2. A dashed vertical line exists where q-bar over 1 plus q-bar equals 0.5. This line is labeled q-bar sub t plus 1 minus q-bar sub t equals 0. A dashed curved line with a parabolic shape exists. It begins at (0.3,4) through (0.5,0) to (0.7,-12). This line is labeled B sub 1 comma t minus B sub 1 comma (t minus 1) equals 0. A solid parabolic line runs from (0.2,4) through (0.5, 0) and to (0.8, -12). The part of the curve to the left of the vertical line contains an arrow pointing southeast. The part of the curve to the right of the vertical line contains an arrow pointing northwest.
Figure 6: Stability of the
steady state for
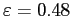 with
an endogenous discount factor.
with
an endogenous discount factor.
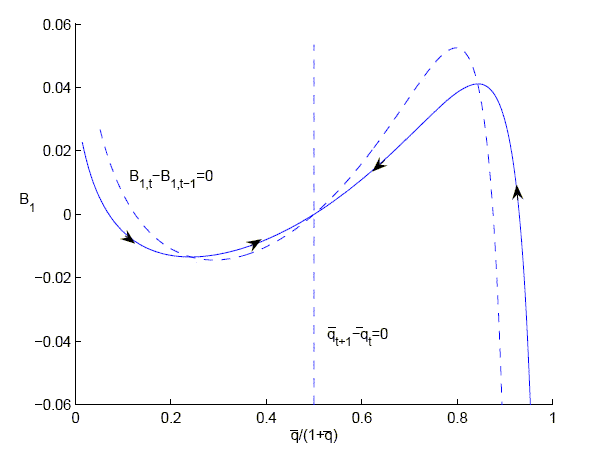
Figure 6 description:
Figure 6 consists of one graph. The caption reads �stability of the steady state for epsilon equals 0.48 with an endogenous discount factor.� The x-axis is labeled q-bar over 1 plus q-bar, and ranges in values from 0 to 1 in increments of 0.2. The y-axis is labeled B sub 1, and ranges from -0.06 to 0.06 in increments of 0.02. A dashed vertical line exists where q-bar over 1 plus q-bar equals 0.5. The line is labeled q-bar sub t plus 1 minus q-bar sub t equals 0. A dashed curve and a solid curved line with a polynomial shape exist. Both lines cross the dashed vertical line at (0.5,0). The dashed curve is labeled B sub 1 comma t minus B sub t minus B sub 1 comma (t minus 1) equals 0. The solid curve begins at (0,0.02). It decreases to (0.2,-0.015). It then increases, crosses the dashed vertical line at (0.5,0) and continues to increase until a high point at (0.9,0.04). It then decreases to (0.95,-0.06). In the part of the curve where q-bar over 1 plus q-bar is less than 0.2, there exists an arrow pointing southeast. In the part of the curve where q-bar over 1 plus q-bar is between 0.2 and 0.5, there exists an arrow pointing northeast. In the part of the curve where q-bar over 1 plus q-bar is between 0.5 and 0.8, there exists an arrow pointing southwest. In the part of the curve where q-bar over 1 plus q-bar is between 0.8 and 0.9, there exists an arrow pointing northwest.
If agents internalize the effects of their consumption and labor decisions on the discount factor, the risk sharing condition is given by
Again, a steady state requires that the discount factors are equalized across countries, i.e.,
A weaker version of theorem 3 applies if agents internalize the effects of their choices on the discount factor.
To the extent that the model with endogenous discounting is supposed to be close to the original model, the discount factor should not change excessively as the utility level deviates from its steady state level. Note, that the (in-)stability of the steady state is not at all related to the slope of the excess demand function, but merely to the parameterization of the endogenous discount factor itself.
3.5 Discussion and intuition
Table 2 summarizes the above results:
| Model | portfolio cost | debt elastic interest rate | endog. dcf. (no internalization) |
endog. dcf. (internalization) |
|---|---|---|---|---|
|
# steady states |
1 | 1 | 1 | 1 |
|
dynamics |
(saddle) stable | (saddle) stable | (saddle) stable | (saddle) stable |
|
# steady states
|
3 | 3 | 1 | 1 |
|
dynamics
|
#1, 3 (saddle) stable, #2 unstable |
#1, 3 (saddle) stable, #2 unstable |
(saddle) stable
|
(saddle) stable
|
Multiplicity of steady states
If there are no international financial markets in the model as
in section ![]() ,
international bond holdings are zero by definition. In the model
with convex portfolio costs, the risk sharing equation imposes the
restriction that bond holdings are zero in the steady state. Hence,
any equilibrium of the financial autarchy model is a steady state
in the bond economy with convex portfolio costs. The same result
occurs if the interest rate is assumed to be debt elastic.
,
international bond holdings are zero by definition. In the model
with convex portfolio costs, the risk sharing equation imposes the
restriction that bond holdings are zero in the steady state. Hence,
any equilibrium of the financial autarchy model is a steady state
in the bond economy with convex portfolio costs. The same result
occurs if the interest rate is assumed to be debt elastic.
With an endogenous discount factor (both with and without
internalization), however, the risk sharing condition implies a
unique value of the relative price ![]() in the steady state. Bond holdings are
determined as the residual from the excess demand function. This
difference manifests itself in the
in the steady state. Bond holdings are
determined as the residual from the excess demand function. This
difference manifests itself in the
![]() locus being a horizontal
line in the first two cases and a vertical line in the remaining
two cases.
locus being a horizontal
line in the first two cases and a vertical line in the remaining
two cases.
To illustrate the intuition behind these differences consider
the simplified model with fixed labor supply. Furthermore, focus on
the case
![]() . There are three
equilibria in the model without international financial markets.
These three equilibria are the candidate equilibria for the bond
economies, with case
. There are three
equilibria in the model without international financial markets.
These three equilibria are the candidate equilibria for the bond
economies, with case ![]() featuring
featuring
![]() , case
, case
![]()
![]() , and case
, and case
![]()
![]() . In
situation
. In
situation ![]() , country
, country
![]() 's consumption is much
higher than country
's consumption is much
higher than country ![]() 's, and
vice versa in case
's, and
vice versa in case ![]() .
.
Consider the candidate steady state ![]() for the economy with endogenous
discounting. Agents in country
for the economy with endogenous
discounting. Agents in country ![]() consume more and they are substantially less
patient, i.e.,
consume more and they are substantially less
patient, i.e., ![]() is smaller than
is smaller than ![]() . Country
. Country ![]() agents are willing to borrow
resources at an interest rate of
agents are willing to borrow
resources at an interest rate of
![]() while country
while country ![]() agents only
demand
agents only
demand
![]() .
Hence, country
.
Hence, country ![]() finds
it optimal to borrow from country
finds
it optimal to borrow from country ![]() . With
. With ![]() , case
, case ![]() cannot be an equilibrium. For the same reason case
cannot be an equilibrium. For the same reason case
![]() is not an
equilibrium with the roles of the two countries reversed.
is not an
equilibrium with the roles of the two countries reversed.
In the portfolio cost model the steady state interest rate is
independent of the allocations and always equals
![]() .
Hence, there are no incentives to borrow and lend in any of the
three candidate steady states. All candidate steady states with
.
Hence, there are no incentives to borrow and lend in any of the
three candidate steady states. All candidate steady states with
![]() are steady
states of the model with convex portfolio costs. Again, the same
applies under a debt elastic interest rate.
are steady
states of the model with convex portfolio costs. Again, the same
applies under a debt elastic interest rate.
Stability of steady states
Theorems 1 and 2 show that under reasonable parameterizations of the convex portfolio cost and the debt elastic interest rate the stability of the dynamic system in the neighborhood of a steady state depends on the sign of the slope of the excess demand function in this steady state. Whenever the excess demand function is upward-sloping in a steady state, the steady state is locally unstable.
Under endogenous discounting (theorems 3 and 4) the stability of the system in the neighborhood of a steady state does not depend on the slope of the excess demand function in the steady state. The stability depends solely on the parameterization of the endogenous discount factor.
The logic behind the stability of the steady state in the model
with endogenous discounting is closely related to the argument
about its uniqueness. Assume that ![]() is below its steady state value. This implies
that consumption in country
is below its steady state value. This implies
that consumption in country ![]() (2) is
above (below) its steady state value. Suppose, that the relative
price is even lower in the next period, suggesting that the economy
moves away from the steady state. This implies an increasing
(decreasing) consumption profile in country
(2) is
above (below) its steady state value. Suppose, that the relative
price is even lower in the next period, suggesting that the economy
moves away from the steady state. This implies an increasing
(decreasing) consumption profile in country ![]() (2). In
addition, the discount factor in country
(2). In
addition, the discount factor in country ![]() (2) falls
(rises). Hence, the price of the non-state-contingent bond falls in
country
(2) falls
(rises). Hence, the price of the non-state-contingent bond falls in
country ![]() but rises in
country
but rises in
country ![]() . Obviously,
the opposite movement of bond prices is inconsistent with the
absence of arbitrage dictated by the risk sharing condition,
equation (16). Hence, if
. Obviously,
the opposite movement of bond prices is inconsistent with the
absence of arbitrage dictated by the risk sharing condition,
equation (16). Hence, if ![]() is below its steady state value at time
is below its steady state value at time ![]() ,
, ![]() must rise in
must rise in ![]() and the economy converges to its unique steady
state.
and the economy converges to its unique steady
state.
Consider the case of a low elasticity of substitution in the
bond economy with convex portfolio costs. All equilibria of the
financial autarchy model are also steady states in this setup.
However, only cases ![]() and
and
![]() are stable. The
intuition behind the instability of case
are stable. The
intuition behind the instability of case ![]() is as follows. The price of bonds
consists of two pieces: the intertemporal marginal rate of
substitution and the derivative of the portfolio costs. Consider
the neighborhood of any of the three steady states. If
is as follows. The price of bonds
consists of two pieces: the intertemporal marginal rate of
substitution and the derivative of the portfolio costs. Consider
the neighborhood of any of the three steady states. If ![]() is slightly below its steady
state value, consumption in country
is slightly below its steady
state value, consumption in country ![]() (2) is
above (below) its corresponding steady state value. Stability of a
certain steady state requires
(2) is
above (below) its corresponding steady state value. Stability of a
certain steady state requires ![]() to rise and
to rise and ![]() to fall over time. As a result, the
intertemporal marginal rate of substitution in country
to fall over time. As a result, the
intertemporal marginal rate of substitution in country ![]() (2) rises
(falls), which leads to a divergence of bond prices. However, when
(2) rises
(falls), which leads to a divergence of bond prices. However, when
![]() rises, bond
holdings and, due to the convexity of the portfolio costs, the
derivative of the portfolio costs fall. The effect on bond prices
is negative in both countries. However, it is stronger in country
rises, bond
holdings and, due to the convexity of the portfolio costs, the
derivative of the portfolio costs fall. The effect on bond prices
is negative in both countries. However, it is stronger in country
![]() since portfolio costs
are measured in terms of each country's good. This second effect
operates towards a rise of the bond price in country
since portfolio costs
are measured in terms of each country's good. This second effect
operates towards a rise of the bond price in country ![]() relative to country
relative to country ![]() . If this effect is strong enough,
bond prices can be prevented from drifting apart. In cases
. If this effect is strong enough,
bond prices can be prevented from drifting apart. In cases
![]() and
and ![]() , small changes in
, small changes in ![]() imply relatively large changes
in bond holdings and therefore relatively large changes in the
derivative of the portfolio costs. In case
imply relatively large changes
in bond holdings and therefore relatively large changes in the
derivative of the portfolio costs. In case ![]() , however, the change in bond
holdings is small owing to the fact that the excess demand function
is fairly flat around this steady state. Hence, bond prices drift
apart and case
, however, the change in bond
holdings is small owing to the fact that the excess demand function
is fairly flat around this steady state. Hence, bond prices drift
apart and case ![]() is
unstable.
is
unstable.
Although conceptually different, these results are related to
the concept of tâtonnement stability by Samuelson (1947). In
the model without international financial markets and
![]() , the second
equilibrium is locally totally unstable as relative prices diverge.
The first and third equilibrium are locally stable since for an
initial price vector that is sufficiently close to the equilibrium
the dynamic trajectory causes relative prices to converge. As in
the case of convex portfolio costs or a debt elastic interest rate,
stability of a steady state is related to the slope of the excess
demand function. However, it is not really clear what is the
concept of "time" used in the tâtonnement analysis. In sharp
contrast to the models presented in this paper, it cannot be real
time as the economy is not in equilibrium along the
tâtonnement path and thereby violates feasibility.
, the second
equilibrium is locally totally unstable as relative prices diverge.
The first and third equilibrium are locally stable since for an
initial price vector that is sufficiently close to the equilibrium
the dynamic trajectory causes relative prices to converge. As in
the case of convex portfolio costs or a debt elastic interest rate,
stability of a steady state is related to the slope of the excess
demand function. However, it is not really clear what is the
concept of "time" used in the tâtonnement analysis. In sharp
contrast to the models presented in this paper, it cannot be real
time as the economy is not in equilibrium along the
tâtonnement path and thereby violates feasibility.
4 Technology shocks
4.1 Impulse response functions
This section studies the dynamic response to a technology shock in the model with an endogenous discount factor (without internalization) and with convex portfolio costs, respectively. To keep the discussion simple I do not discuss the cases of a debt elastic interest rate or the endogenous discount factor with internalization. Not surprisingly, though, the results in this section for the debt elastic interest rate are similar to the ones for convex portfolio costs. The case of endogenous discounting with internalization behaves close to the case without internalization.
At time ![]() country
country
![]() experiences an
unexpected
experiences an
unexpected ![]() rise in its
technology. The shock follows an
rise in its
technology. The shock follows an ![]() process with a persistence parameter of
process with a persistence parameter of
![]() . Once the shock is
realized, agents perfectly foresee the future path of the economy.
The economy is assumed to be in a steady state prior to the
shock.
. Once the shock is
realized, agents perfectly foresee the future path of the economy.
The economy is assumed to be in a steady state prior to the
shock.
High elasticity of substitution
Consider first the case of a large value of the elasticity of
substitution, i.e.,
![]() . The steady state is
unique and stable for both approaches. Figure 7 plots the impulse response
functions in the two economies for different variables of interest.
The impulse responses for the endogenous discount factor model are
given by the solid lines, and are given by the dashed lines for the
portfolio cost model. All variables are shown in levels rather than
deviations from the steady state. In the example shown, the steady
state values are
. The steady state is
unique and stable for both approaches. Figure 7 plots the impulse response
functions in the two economies for different variables of interest.
The impulse responses for the endogenous discount factor model are
given by the solid lines, and are given by the dashed lines for the
portfolio cost model. All variables are shown in levels rather than
deviations from the steady state. In the example shown, the steady
state values are
![]() ,
,
![]() and
and
![]() . The impulse
responses are strikingly similar for the two approaches. Only the
dynamics of bond holdings differ, but apparently this has almost no
impact on the remaining variables given that bond holdings are
small.
. The impulse
responses are strikingly similar for the two approaches. Only the
dynamics of bond holdings differ, but apparently this has almost no
impact on the remaining variables given that bond holdings are
small.
The increase in country ![]() 's productivity reduces the costs of production in
country
's productivity reduces the costs of production in
country ![]() . Therefore,
output in country
. Therefore,
output in country ![]() rises
relative to country
rises
relative to country ![]() . So
does consumption, however, its rise is smaller since country
. So
does consumption, however, its rise is smaller since country
![]() borrows from country
borrows from country
![]() . The price of good
. The price of good
![]() relative to good
relative to good
![]() increases, reflecting
the relative abundance of good
increases, reflecting
the relative abundance of good ![]() in the world market. Despite the modelling
differences, the impulse response functions look very much alike
for the two models. Given the remaining parameters of the models,
changes in
in the world market. Despite the modelling
differences, the impulse response functions look very much alike
for the two models. Given the remaining parameters of the models,
changes in
![]() do not
substantially change the picture as long as
do not
substantially change the picture as long as
![]() .
.
Figure 7: Impulse response
functions for a 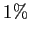 technology innovation in country
technology innovation in country 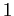 and
and
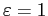 . All
variables are plotted in levels. Solid line shows the response for
endogenous discounting, dashed line for convex portfolio
costs.
. All
variables are plotted in levels. Solid line shows the response for
endogenous discounting, dashed line for convex portfolio
costs.
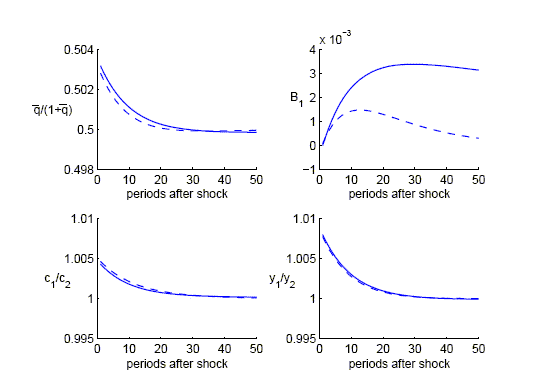
Figure 7 description:
Figure 7 consists of four graphs presented in a two-by-two matrix. The caption reads �impulse response functions for a one percent technology in country 1 and epsilon equals 1. All variables are plotted in levels. Sold line shows the response for endogenous discounting, dashed line for convex portfolio costs.� The x-axis for each graph is labeled periods after shock, and ranges in values from 0 to 50 in increments of 10. Each graph contains two curves. In the top left graph, the y-axis is labeled q-bar over one plus q-bar, and ranges in values form 0.498 to 0.504 to 0.002. The first curve begins at (0,0.5035) and decreases to 0.5 by period 30. It remains at this value for the remaining periods. The second curve is represented as a dashed line. It begins at 0.503 and decrease to 0.5 by period 25. It remains at this value for the remaining periods. In the top right graph, the y-axis is labeled B, and ranges in values from -0.001 to 0.004, in increments of 0.001. The first curve begins at 0 and increases to 0.003 by period 20. It remains at roughly that value for the remaining periods. The second curve is represented as a dashed line. It begins at 0 and increases to 0.0015 by period 15. It then slowly decreases to 0 by period 50. In the bottom left graph, the y-axis is labeled c sub 1 over c sub 2, and ranges in values from 0.995 to 1.01 in increments of 0.005. The curves are both very close. They begin at 1.005 and decrease to 1 by period 20. It remains at this value for the remaining periods. In the bottom right graph, the y-axis is labeled y sub 1 over y sub 2, and ranges in values from 0.995 to 0.01 in increments of 0.005. The curves are both very close. They begin at 1.007 and decrease to 1 by period 20. It remains at this value for the remaining periods.
Low elasticity of substitution
However, once
![]() drops below
drops below
![]() , the
two models differ drastically owing to the potential multiplicity
of steady states. Figures 8 and 9 show the impulse response
functions in the two models for
, the
two models differ drastically owing to the potential multiplicity
of steady states. Figures 8 and 9 show the impulse response
functions in the two models for
![]() .
.
In the model with endogenous discounting (figure 8) there are three possible impulse
response functions for a ![]() technology shock (
technology shock (![]() dashed,
dashed, ![]() solid and
solid and
![]() dashed-dotted
line). As the steady state is unique and globally stable, the
economy converges back in each case to the old steady state with
dashed-dotted
line). As the steady state is unique and globally stable, the
economy converges back in each case to the old steady state with
![]() ,
,
![]() and
and
![]() .
.
In the first case (dashed line) the technology shock leads to a
fall in the relative price, ![]() . As the elasticity of substitution between
traded goods is low, production in country
. As the elasticity of substitution between
traded goods is low, production in country ![]() rises relative to country
rises relative to country
![]() to generate more
income in order to prevent a too strong fall in income. With
country
to generate more
income in order to prevent a too strong fall in income. With
country ![]() increasing
its consumption relative to country
increasing
its consumption relative to country ![]() , but lowering its relative use of labor,
, but lowering its relative use of labor,
![]() falls
relative to
falls
relative to ![]() .
The resulting borrowing by country
.
The resulting borrowing by country ![]() shifts additional resources to country
shifts additional resources to country ![]() and reinforces the effects. The
second case (solid line) behaves qualitatively like the first case.
However, the effects are considerably smaller.
and reinforces the effects. The
second case (solid line) behaves qualitatively like the first case.
However, the effects are considerably smaller.
However, in the third case (dashed-dotted line) the shock leads
to a rise of the relative price of good ![]() , but to an increase of
, but to an increase of ![]() relative to
relative to ![]() . As the price effect is not
compensated by the increased production of good
. As the price effect is not
compensated by the increased production of good ![]() , consumption in country
, consumption in country ![]() declines relative to country
declines relative to country
![]() . Furthermore, agents
in country
. Furthermore, agents
in country ![]() become less
patient which leads to increased borrowing by country
become less
patient which leads to increased borrowing by country ![]() and this reinforces the effects.
and this reinforces the effects.
Figure 8: Impulse response
functions for a 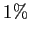 technology innovation in country
technology innovation in country 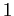 . All variables are plotted in levels. Agents'
discount factors are endogenous and
. All variables are plotted in levels. Agents'
discount factors are endogenous and
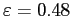 .
.
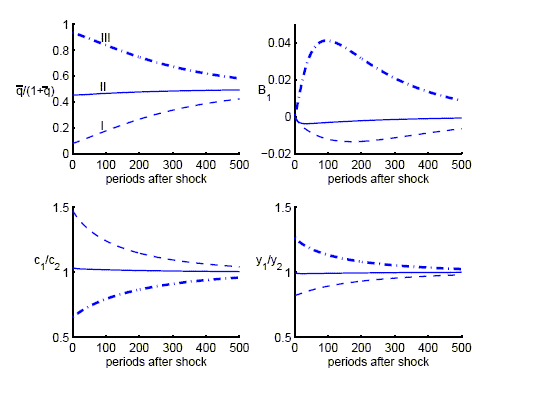
Figure 8 description:
Figure 8 consists of four graphs presented in a two-by-two matrix. The caption reads �impulse response functions for a one percent technology innovation in country 1. All variables are plotted in levels. Agents� discount factors are endogenous and epsilon equals 0.48.� The x-axis for each graph is labeled periods after shock, and ranges in values from 0 to 500 in increments of 100. Each graph contains three curves. In the top left graph, the y-axis is labeled q-bar over 1 plus q-bar, and ranges in values from 0 to 1 in increments of 0.2. The first curve begins at 0.1 and steadily increases (almost linearly) until reaching 0.4 at period 500. The second curve is roughly horizontal at 0.5. The third curve begins at about 0.9 and steadily decreases (almost linearly) until reaching 0.6 at period 500. In the top right graph, the y-axis is labeled B, and ranges in values from -0.02 to 0.04 in increments of 0.02. The first curve begins at 0 and decreases to -0.01 by period 150. It then steadily increases to -0.05 by period 500. The second curve is roughly horizontal at 0. The third curve begins at 0 and increases to 0.04 by period 100. It then steadily decreases to 0.01 y period 500. In the bottom left graph, the y-axis is labeled c sub 1 over c sub 2, and ranges in values from 0.5 to 1.5 in increments of 0.5. The first curve begins at 1.5, steadily decreases, and eventually converges to 1 by period 500. The second curve is roughly horizontal at 1. The third curve begins at 0.75, steadily increases, and converges to 1 by period 500. In the bottom right graph, the y-axis is labeled y sub 1 over y sub 2, and ranges in values from 0.5 to 1.5 in increments of 0.5. The first curve begins at 0.8, steadily increases, and converges to 1 by period 500. The second curve is roughly horizontal at 1. The third curve begins at 1.25, steadily decreases, and eventually converges to 1 by period 500.
Figure 9: Impulse response
functions for a 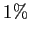 technology innovation in country
technology innovation in country 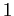 . All variables are plotted in levels. Agents face
convex portfolio costs and
. All variables are plotted in levels. Agents face
convex portfolio costs and
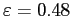 .
.
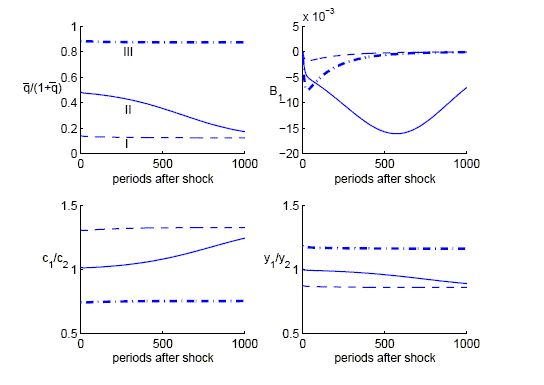
Figure 9 description:
Figure 9 consists of four graphs presented in a two-by-two matrix. The caption reads �impulse response functions for a one percent technology innovation in country 1. All variables are plotted in levels. Agents face convex portfolio costs and epsilon equals 0.48.� The x-axis for each graph is labeled periods after shock, and ranges in values from 0 to 1000 in increments of 500. Each graph contains three curves. In the top left graph, the y-axis is labeled q-bar over 1 plus q-bar, and ranges in values from 0 to 1 in increments of 0.2. The first curve is roughly horizontal at 0.18. The second curve begins at 0.5 and steadily decreases until 0.2 at period 1000. The third curve begins is roughly horizontal at 0.9. In the top right graph, the y-axis is labeled B, and ranges in values from -0.02 to 0.005 in increments of 0.005. The first curve begins at -0.001, steadily increases, and converges to 0 by period 500. It remains there for the remaining periods. The second curve begins at 0 and decreases to -0.015 by period 600. It then steadily increases to -0.007 by period 1000. The third curve begins at -0.007, steadily increases, and converges to 0 by period 500. It remains there for the remaining periods. In the bottom left graph, the y-axis is labeled c sub 1 over c sub 2, and ranges in values from 0.5 to 1.5 in increments of 0.5. The first curve is roughly horizontal at 1.25. The second curve begins at 1 and increase to 1.4 by period 1000. The third curve is roughly horizontal at 0.75. In the bottom right graph, the y-axis is labeled y sub 1 over y sub 2, and ranges in values from 0.5 to 1.5 in increments of 0.5. The first curve is roughly horizontal at 0.9. The second curve begins at 1, slowly decreases, and reaches a value just over 0.9 by period 1000. The third curve is roughly horizontal at 1.25.
If the model is closed by introducing convex portfolio costs,
there are two locally stable steady states with
![]() and
and ![]() . The third one, featuring
. The third one, featuring
![]() , is unstable. In
figure 9, I assume that the
economy is originally in the steady state with
, is unstable. In
figure 9, I assume that the
economy is originally in the steady state with
![]() . In the first two cases
(solid and dashed lines) the economy reverts to its original steady
state. However, in the third one, the economy moves into a
different regime: after an initial massive depreciation of
. In the first two cases
(solid and dashed lines) the economy reverts to its original steady
state. However, in the third one, the economy moves into a
different regime: after an initial massive depreciation of
![]() the economy
converges to the other stable steady state with
the economy
converges to the other stable steady state with
![]() . All
three cases have in common that higher productivity in country
. All
three cases have in common that higher productivity in country
![]() leads to an increase
in the production of good
leads to an increase
in the production of good ![]() and a relative decline of its price. Consumption
drops below its (new) steady state value. Given the low
substitutability between traded goods, the decline in the price of
good
and a relative decline of its price. Consumption
drops below its (new) steady state value. Given the low
substitutability between traded goods, the decline in the price of
good ![]() is too large to be
compensated by the additional income that is due to the rise in
production of good
is too large to be
compensated by the additional income that is due to the rise in
production of good ![]() . Even
as agents in country
. Even
as agents in country ![]() borrow
from country
borrow
from country ![]() , they cannot
prevent their consumption from falling relative to consumption in
country
, they cannot
prevent their consumption from falling relative to consumption in
country ![]() starting
from the original steady state.
starting
from the original steady state.
The multiplicity of the impulse response functions is closely
related to the multiplicity of steady states in the model of
financial autarchy. Consider the model with endogenous discounting
and
![]() . Although, there is a
unique steady state in this model, the corresponding model without
financial markets has three steady states. For simplicity, consider
a permanent shock to technology. This situation is depicted in
figure 10. Before the shock, the
stable manifold is given by the solid line and the unique steady
state features
. Although, there is a
unique steady state in this model, the corresponding model without
financial markets has three steady states. For simplicity, consider
a permanent shock to technology. This situation is depicted in
figure 10. Before the shock, the
stable manifold is given by the solid line and the unique steady
state features
![]() and
and ![]() . In response to the shock,
the manifold shifts upwards as indicated by the dashed line. In the
new steady state - labeled by the small circle -
. In response to the shock,
the manifold shifts upwards as indicated by the dashed line. In the
new steady state - labeled by the small circle -
![]() and
and
![]() . How does
the transition occur? As bond holdings are predetermined, the
economy has to start in a point on the new manifold with
. How does
the transition occur? As bond holdings are predetermined, the
economy has to start in a point on the new manifold with
![]() . There are
three points that satisfy this condition, each marked by a little
square and an arrow. The arrows indicate the movements of
. There are
three points that satisfy this condition, each marked by a little
square and an arrow. The arrows indicate the movements of
![]() and
and
![]() along the new
manifold. Absent other restrictions on the adjustment path, each of
the points
along the new
manifold. Absent other restrictions on the adjustment path, each of
the points ![]() -
-![]() can
be the starting point of the transition dynamics.
can
be the starting point of the transition dynamics.
Figure 10: Shift of the stable manifold for a permanent technology shock.
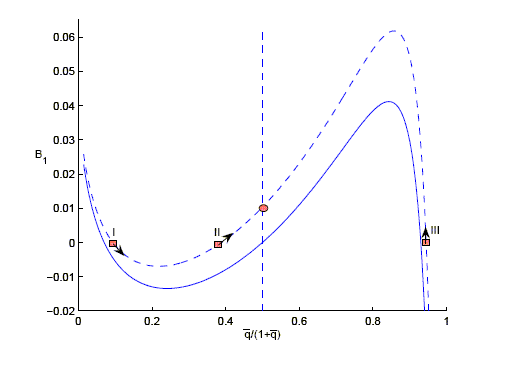
Figure 10 description:
Figure 10 consists of one graph. The caption reads �shift of the stable manifold for a permanent technology shock.� The x-axis is labeled q-bar over 1 plus q-bar, and ranges in value from 0 to 1 in increments of 0.2. The y-axis is labeled B, and ranges in values from -0.02 to 0.06 in increments of 0.01. A dash vertical line exists where q-bar over 1 plus q-bar equals 0.5. A dashed line with a parabolic shape exists. It begins at (0,0.02) and decreases to (0.2,-0.01). It then increases, crosses the dashed vertical line at (0,0.01), and reaches a high point at (0.8,0.06). It then decreases to (0.95,-0.02). The curve beings at (0, 0.02). It decreases to (0.2,-0.015). It then increases, crosses the dashed vertical line at (0.5, 0) and reaches a high point at (0.8,0.04). It then decreases to (0.9,-0.02).
Note, that if the technology shock is too large, there is only
one impulse response function. In figure 10 a large enough shock to technology
can shift the manifold (and the new steady state) sufficiently up
such that points ![]() and
and
![]() disappear. The
unique starting point of the transition dynamics is then point
disappear. The
unique starting point of the transition dynamics is then point
![]() .
.
In the case of figures 8 and 9 technology shocks larger than
![]() , would imply
unique impulse response functions for this very reason. The unique
response resembles case
, would imply
unique impulse response functions for this very reason. The unique
response resembles case ![]() , the dashed-dotted line. The economy with
portfolio costs converges to a new steady state after the effects
of the shock are foregone. While a
, the dashed-dotted line. The economy with
portfolio costs converges to a new steady state after the effects
of the shock are foregone. While a ![]() rise in technology seems large, this threshold
number can be very close to 0 for more
persistent shocks or for
rise in technology seems large, this threshold
number can be very close to 0 for more
persistent shocks or for
![]() closer to
closer to
![]() .
.
In the above discussion I have presented examples for which the
endogenous variables do not oscillate along the equilibrium path.
However, if the eigenvalues that go along with the linear
approximation of the dynamic system around a steady state are
complex there can be other interesting equilibria. For example, it
is straightforward to show that in the case of convex portfolio
costs there can be parameterizations of the cost function such that
for
![]() the middle steady
state is an unstable focus. In this case, there are most likely
more than three impulse response functions. However, to the extent
that these additional impulse responses exist, they would not be
directly related to the fact that there are multiple steady states
under financial autarchy. For this reason, I omit the analysis of
such cases.15
the middle steady
state is an unstable focus. In this case, there are most likely
more than three impulse response functions. However, to the extent
that these additional impulse responses exist, they would not be
directly related to the fact that there are multiple steady states
under financial autarchy. For this reason, I omit the analysis of
such cases.15
4.2 Implications for applied modelling
One lesson from applied general equilibrium modelling is that it is practically impossible to find all the equilibria of a given model unless it can be proven that the equilibrium is unique. As illustrated in this paper, failing to detect equilibrium multiplicity and its associated nonlinearities renders an incomplete description of the model's dynamics.
In particular, equilibrium multiplicity implies that the model
dynamics cannot be reliably captured by a log-linear approximation
around a given steady state. In the endogenous discount factor
model, for example, only the second impulse response function in
figure 8 is detected if the
model is solved by linearization. For larger shocks, the predicted
impulse response function is merely an amplified version of the
response under small shocks (case ![]() ). Obviously, for larger shocks such a prediction is
far off the true impulse responses which resemble case
). Obviously, for larger shocks such a prediction is
far off the true impulse responses which resemble case ![]() . This failure to recover the
correct dynamics of the model is very different from the typical
approximation error for large shocks.
. This failure to recover the
correct dynamics of the model is very different from the typical
approximation error for large shocks.
In practice, researchers often calibrate their models to a specific steady state and log-linearize around it, thereby assuming away the issues addressed in this paper. Since different methods of closing open economy models can have diverse dynamic implications - in particular with respect to the stability of certain steady states - applied general equilibrium researchers may find it instructive to solve their models for various stationarity-inducing methods.
However, for the purpose of inducing stationarity into the model with incomplete international financial markets, the endogenous discount factor approach can be misleading. This approach forces the model to have a unique and stable steady state irrespective of the number of steady states that occur under other approaches that can be used to close open economy models. Important nonlinearities may remain undetected. As shown in this paper, convex portfolio costs or a debt elastic interest rate allow for multiple steady states whenever there are multiple solutions to the excess demand function under financial autarchy. These approaches at least do not rule out by construction the ability to detect steady state multiplicity. If the excess demand function is upward-sloping in a steady state - which proves the existence of multiple steady states - these two models turn out to be unstable in the neighborhood of this steady state
5 Conclusions
This paper analyzes different approaches that resolve the stationarity problem in models with incomplete asset markets. If stationarity is induced by an endogenous discount factor, there is always a unique saddle stable steady state. However, despite the uniqueness of the steady state, the equilibrium may not be unique away from the steady state. If the analogous model without international financial markets has multiple equilibria, there are multiple paths that lead the economy back to its steady state in response to a technology shock.
If stationarity is induced by a convex portfolio cost or a debt elastic interest rate, the number of steady states coincides with the number of equilibria in the analogous model without international financial markets. If the excess demand function in the financial autarchy model has multiple zeros not all steady states are saddle stable: a steady state in which the excess demand function is upward sloping is typically unstable. Similar to the model with endogenous discounting, there can be multiple impulse responses to a technology shock. However, in the case of convex portfolio costs or a debt elastic interest rate the economy may or may not converge back to its former steady state but to one of the other steady states of the model.
In the present paper, the differences across stationarity
inducing methods hinge on the value of the elasticity of
substitution between traded goods,
![]() , as the
elasticity governs the multiplicity of equilibria in the financial
autarchy model. Although the critical value
, as the
elasticity governs the multiplicity of equilibria in the financial
autarchy model. Although the critical value
![]() for
which these differences become an issue depends on the specific
model, the relevance of the findings in this paper goes
further.
for
which these differences become an issue depends on the specific
model, the relevance of the findings in this paper goes
further.
In applied macroeconomic studies it is common to chose values
between ![]() and
and
![]() (see e.g. Backus
and Smith (1995), Chari, Kehoe and McGrattan (2003), and Heathcote
and Perri (2002)). Recently, however, various authors have argued
in favor of low values of the trade elasticity. In straightforward
extensions of the model presented in this paper Heathcote and Perri
(2002) and Collard and Dellas (2004) argue that they improve their
models' performance in accounting for features of the international
business cycle like the volatility of the terms of trade when
moving to elasticities in the range of
(see e.g. Backus
and Smith (1995), Chari, Kehoe and McGrattan (2003), and Heathcote
and Perri (2002)). Recently, however, various authors have argued
in favor of low values of the trade elasticity. In straightforward
extensions of the model presented in this paper Heathcote and Perri
(2002) and Collard and Dellas (2004) argue that they improve their
models' performance in accounting for features of the international
business cycle like the volatility of the terms of trade when
moving to elasticities in the range of ![]() . In Benigno and Thoenissen (2006)
the model with an elasticity of
. In Benigno and Thoenissen (2006)
the model with an elasticity of ![]() outperforms their baseline calibration with a
value of
outperforms their baseline calibration with a
value of ![]() .
.
Other researchers have refrained from assuming such low
elasticities directly. Instead, they augment the standard model by
distribution costs in nontraded goods to obtain a low implied
elasticity of substitution. Representative work is by Burstein,
Neves and Rebelo (2003), Burstein, Eichenbaum and Rebelo (2003),
Corsetti and Dedola (2005), and Corsetti, Dedola and Leduc (2005).
Corsetti, Dedola and Leduc build a two country general equilibrium
model with distribution costs in nontraded goods. Only for a low
implied value of the elasticity of substitution does their
linearized model successfully address two important puzzles in
international economics: the high volatility of the real exchange
rate relative to fundamentals and the observed negative correlation
between the real exchange rate and relative consumption (Backus and
Smith (1993)). Corsetti and Dedola (2005) show that this framework
admits multiple equilibria in the absence of international
borrowing and lending even if the direct elasticity of substitution
between traded goods is larger than ![]() .
.
As Kollmann (2005) shows, a low elasticity of substitution may
also be responsible for the apparent home bias in equity holdings.
Rabanal and Tuesta (2005) estimate a DSGE model with sticky prices
using a Bayesian approach. Their median estimates for the
elasticity of substitution range from ![]() to
to ![]() for different specifications of
their model. Lubik and Schorfheide (2005) estimate the elasticity
of substitution to be around
for different specifications of
their model. Lubik and Schorfheide (2005) estimate the elasticity
of substitution to be around ![]() .
.
This list of papers indicates that low values of trade elasticities at the aggregate level may be behind many of the puzzles in international macroeconomics. However, to the extent that the assumption of low (implied) trade elasticities gives rise to multiple equilibria and important nonlinearities, the choice of how to induce stationarity in a model with incomplete international asset markets is no longer innocuous.
References
[1] Backus, D. and G. Smith (1993). Consumption and real exchange rates in dynamic economies with non-traded goods. Journal of International Economics 35, 297-316.
[2] Bayoumi, T. (1999). Estimating trade equations from aggregate bilateral data. IMF Working Paper 99/74.
[3] Baxter, M. and M Crucini (1995). Business cycles and the asset structure of foreign trade. International Economic Review 36, 133-157.
[4] Bela, V. (1997). A pitchfork bifurcation in the t�tonnement process. Economic Theory 10, 521-530.
[5] Benigno, G. and C. Thoenissen (2006). Consumption and real exchange rates with incomplete markets and non-traded goods. CEPR Discussion Papers 5580.
[6] Boileau, M., and M. Normandin (2005). Closing international real business cycle models with restricted financial markets. Center for Economic Analysis, University of Colorado at Boulder.
[7] Broda, C. and D. Weinstein (2006). Globalization and the gains from variety. Quarterly Journal of Economics 121, 541-585.
[8] Burstein, A., J. Neves and S. Rebelo (2003). Distribution costs and real exchange rate dynamics during exchange-rate-based stabilizations. Journal of Monetary Economics 50, 1189-1214. 36
[9] Burstein, A., M. Eichenbaum and S. Rebelo (2005). Large devaluations and the real exchange rate. Journal of Political Economy 113, 742-784.
[10] Chari, V.V., P. Kehoe and E. McGrattan (2002). Can sticky prices generate volatile and persistent real exchange rates? Review of Economic Studies 69, 633-63.
[11] Collard, F., and H. Dellas (2002). Technology Shocks and Employment. CEPR Discussion Papers 3680.
[12] Corsetti, G. and L. Dedola (2005). A macroeconomic model of international price discrimination. Journal of International Economics 67, 129-155.
[13] Corsetti, G., L. Dedola and S. Leduc (2005). International risk-sharing and the transmission of productivity shocks. International Finance Discussion Papers 826, Board of Governors of the Federal Reserve System.
[14] Devereux, M. and G. Smith (2002). Transfer Problem Dynamics: Macroeconomics of the Franco-Prussian War Indemnity. University of British Comlumbia.
[15] Dotsey, M. and R. King (2005). Implications of state-dependent pricing for dynamic macroeconomic models. Journal of Monetary Economics 52, 213-242.
[16] Epstein, L. (1983). Stationary cardinal utility and optimal growth under uncertainty. Journal of Economic Theory 31, 133-152.
[17] Epstein, L. (1987). A simple dynamic general equilibrium model. Journal of Economic Theory 41, 68-95.
[18] Ghironi, F. (2003). Macroeconomic interdependence under incomplete markets. Forthcoming Journal of International Economics
[19] Gjerstad, S. (1996). Multiple equilibria in exchange economies with homothetic, nearly identical preferences. Discussion Paper 228, Federal Reserve Bank of Minneapolis.
[20] Heathcote, J. and F. Perri (2002). Financial autarchy and international business cycles. Journal of Monetary Economics 49, 601-627.
[21] Hooper, P., K. Johnson and J. Marquez (2000). Trade elasticities for the G-7 countries. Princeton Studies in International Economics 87.
[22] Houthakker, H. and S.Magee (1969). Income and price elasticities in world trade. Review of Economics and Statistics 51, 111-25. 37
[23] Huggett, M. (1993). The risk free rate in heterogeneous-agents, incomplete insurance economies. Journal of Economic Dynamics and Control 17, 953-969.
[24] Judd, K. (1998). Numerical methods in economics. MIT Press, Cambridge, MA.
[25] Kehoe, T. (1980). An index theorem for general equilibrium models with production. Econometrica 48, 1211-1232.
[26] Kehoe, T. (1985). Multiplicity of equilibria and comparative statics. Quarterly Journal of Economics 100, 119-147.
[27] Kehoe, T. (1991). Computation and multiplicity of equilibria. Chap. 38 in Handbook of Mathematical Economics, vol. IV, edited by W. Hildenbrand, and H. Sonnenschein. North-Holland Press, Amsterdam.
[28] Kim, S. and M. Kose (2003). Dynamics of open-economy business-cycle models: role of the discount factor. Macroeconomic Dynamics 7, 263-290.
[29] Kollmann, R. (2005). International portfolio equilibrium and the current account: a dynamic general equilibrium perspective. University of Paris XII.
[30] Lubik, T. (2003). Non-stationarity and instability in small open economy models when they are �closed�. Johns Hopkins University.
[31] Lubik, T. and Schorfheide F. (2005). A Bayesian look at new open economy macroeconomics. NBER Macroeconomics Annual 2005.
[32] Marquez, J. (1990). Income and price elasticities of foreign trade flows: econometric estimation and analysis of the U.S. trade deficit. Economics in theory and practice: An eclectic approach Essays in honor of F. G. Adams, 1989, 129-76, Advanced Studies in Theoretical and Applied Econometrics, vol. 17 Dordrecht, Boston and London, Kluwer Academic.
[33] Mas-Colell, A. (1991). On the uniqueness of the equilibrium once again. In equilibrium theory and applications, edited by W. Barnett, C. Cornet, C. Daspremont, J. Gabszwewicz and Mas-Colell. Cambridge University Press, Cambridge, MA.
[34] Mas-Colell, A., M. Whinston and J. Green (1995). Microeconomic Analysis. Oxford University Press, Oxford, UK.
[35] Mendoza, E. (1991). Real business cycles in a small-open economy. American Economic Review 81, 797-818. 38
[36] Rabanal, P. and V. Tuesta (2005). Euro-Dollar real exchange rate dynamics in an estimated two-country model: what is important and what is not. International Monetary Fund.
[37] Samuelson, P. (1947). Foundations of economic analysis. Harvard University Press, Cambridge, MA.
[38] Schmitt-Groh�, S. and M. Uribe (2003). Closing small open economy models. Journal of International Economics 61, 163-185.
[39] Taylor, J. (1993). Macroeconomic policy in a world economy: from economic design to practical operation. Norton, New York, NY.
[40] Uzawa, H. (1968). Time preference, the consumption function and optimum asset holdings. In Wolfe J.N. (Ed.), Value, capital and growth: papers in honor of Sir John Hicks. The University of Edinburgh Press, Edinburgh, 485-504.
[41] Whalley, J. (1985). Trade liberalization among major world trading areas. MIT Press, Cambridge, MA.
A. A formal analysis of existence and multiplicity
This appendix shows the existence of the equilibrium in the model with financial autarchy. In addition, I discuss conditions under which multiple equilibria arise. The appendix ends by discussing different parameterizations for which multiple equilibria occur.
A.1 A more general setup
I assume that ![]() is
given by the linear homogenous aggregator
is
given by the linear homogenous aggregator
![]() .16
.16![]() is assumed to satisfy
is assumed to satisfy
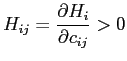 ,
, 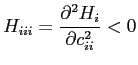 ,
, 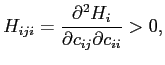
The strictly concave period utility function
Linear homogeneity of
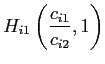 |
||
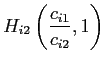 |
Given the properties of
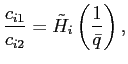
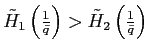 for all
for all ![$\displaystyle \equiv\frac{\bar{P}_{1}}{P_{1}}=\frac {\bar{q}H_{1}\left( \tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) ,1\right) }{\bar{q}\left[ \tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) +\bar {q}\right] }$](img330.gif) with
with |
||
![$\displaystyle \equiv\frac{\bar{P}_{2}}{P_{2}}=\frac {\bar{q}H_{2}\left( \tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) ,1\right) }{\left[ \tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right] }$](img333.gif) with
with |
I normalize the price of the consumption basket in country
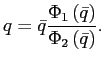
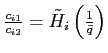 , the demand functions for good
, the demand functions for good ![$\displaystyle =\frac{1}{\left( \tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right) }\left[ w_{1}l_{1}+\frac{1}{\Phi_{1}\left( \bar{q}\right) }dW_{1}\right] ,$](img338.gif)
|
||
![$\displaystyle =\frac{1}{\left( \tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) \frac{1}{\bar{q}}+1\right) }\left[ w_{2}l_{2}+\frac{1}{\bar{q}\Phi _{1}\left( \bar{q}\right) }dW_{2}\right] ,$](img340.gif)
|
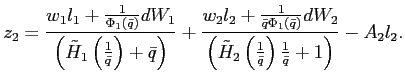
Combining
allows to express
![$\displaystyle \frac{dc}{dl}=-\frac{\left[ \Phi_{i}\left( \bar{q}\right) A_{i} U_{lc}+U_{ll}\right] }{\left[ U_{lc}+\Phi_{i}\left( \bar{q}\right) A_{i}U_{cc}\right] }<0 $](img349.gif)
A.2 Existence of the equilibrium
In the following I closely follow Kehoe (1980, 1985 and 1991).
Let ![]() be the time
endowment of agents in country
be the time
endowment of agents in country ![]() . Kehoe defines the excess demand for a good as the
difference between the demand for a specific good and the aggregate
endowment with this good. The economy's endowment with goods
. Kehoe defines the excess demand for a good as the
difference between the demand for a specific good and the aggregate
endowment with this good. The economy's endowment with goods
![]() and
and ![]() is zero, while the leisure
endowments are
is zero, while the leisure
endowments are ![]() and
and ![]() . I denote the
excess demand for goods
. I denote the
excess demand for goods ![]() and
and ![]() by
by
![]() ,
,
![]() . The excess
demand for leisure is given by
. The excess
demand for leisure is given by
![]() .
Furthermore, let
.
Furthermore, let
![]() .
.
The production side of the economy is given by a ![]() activity analysis matrix
activity analysis matrix
![]() . Each column of
. Each column of
![]() represents an
activity, which transforms inputs taken from the vector of
aggregate initial endowments or from the outputs of other
activities into outputs, which are either consumed or further used
as inputs. Positive entries in an activity denote quantities of
outputs produced by the activity; negative entries denote
quantities of inputs consumed. Aggregate production is denoted by
represents an
activity, which transforms inputs taken from the vector of
aggregate initial endowments or from the outputs of other
activities into outputs, which are either consumed or further used
as inputs. Positive entries in an activity denote quantities of
outputs produced by the activity; negative entries denote
quantities of inputs consumed. Aggregate production is denoted by
![]() , where
, where
![]() is a
is a ![]() vector of nonnegative
activity levels:
vector of nonnegative
activity levels:
![\begin{displaymath} A=\left[ \begin{array}[c]{rrrrrr} -1 & 0 & 0 & 0 & A_{1} & 0\ 0 & -1 & 0 & 0 & 0 & A_{2}\ 0 & 0 & -1 & 0 & -1 & 0\ 0 & 0 & 0 & -1 & 0 & -1 \end{array}\right] , \end{displaymath}](img362.gif)
An equilibrium of this economy is a price vector
![]() that satisfies the following three properties: first
that satisfies the following three properties: first
![]() ; second there exists a
nonnegative vector of activity levels
; second there exists a
nonnegative vector of activity levels ![]() such that
such that
![]() ; and third
; and third
![]() . The
first condition requires that there be no excess profits available.
The second one requires that supply equals demand. The third one is
simply a price normalization.
. The
first condition requires that there be no excess profits available.
The second one requires that supply equals demand. The third one is
simply a price normalization.
Existence of an equilibrium follows directly from Theorem
![]() in Kehoe (1985).
Notice, how Kehoe's presentation of the problem can be reduced to
the presentation in the main text. Let the activity vector be
in Kehoe (1985).
Notice, how Kehoe's presentation of the problem can be reduced to
the presentation in the main text. Let the activity vector be
![]() . Then
. Then
![\begin{displaymath} d\left( p\right) -Ay^{\prime}=\left( \begin{array}[c]{c} c_{11}+c_{21}\ c_{12}+c_{22}\ -l_{1}\ -l_{2} \end{array}\right) -\left( \begin{array}[c]{c} A_{1}l_{1}\ A_{2}l_{2}\ -l_{1}\ -l_{2} \end{array}\right) \text{.} \end{displaymath}](img369.gif)
A.3 Multiplicity of equilibria
If all the equilibria of an economy are locally unique, the
economy is referred to as regular. Kehoe (1980) provides general
conditions that ensure regularity. In addition, he shows that the
number of equilibria in a production economy is odd. Let the index
of an equilibrium ![]() be defined as
be defined as
![\begin{displaymath} index\left( \hat{p}\right) =sgn\left( \det\left[ \begin{array}[c]{cc} -\bar{J} & \bar{B}\ -\bar{B}^{\prime} & 0 \end{array}\right] \right) . \end{displaymath}](img374.gif)
Theorem ![]() in Kehoe
(1985) states that the sum of the indices across all equilibria
equals
in Kehoe
(1985) states that the sum of the indices across all equilibria
equals ![]() , i.e.,
, i.e.,
![]() . Hence the
number of equilibria in a regular economy is finite and odd. If it
cannot be proven that there is a unique equilibrium, this is
usually all that can be said about the number of equilibria.
Although there has been substantial progress in the development of
fixed point algorithms, it is in general impossible to find all the
equilibria of an economy if there is no guarantee that there is
only one.
. Hence the
number of equilibria in a regular economy is finite and odd. If it
cannot be proven that there is a unique equilibrium, this is
usually all that can be said about the number of equilibria.
Although there has been substantial progress in the development of
fixed point algorithms, it is in general impossible to find all the
equilibria of an economy if there is no guarantee that there is
only one.
What can be said about the equilibria in the model presented in this paper? Using Kehoe's approach,
![\begin{displaymath} \bar{J}=\left[ \begin{array}[c]{ccc} \partial d_{c,2}/\partial\bar{q} & 0 & 0\ \partial d_{l,1}/\partial\bar{q} & 0 & 0\ \partial d_{l,2}/\partial\bar{q} & 0 & 0 \end{array}\right] ,\bar{B}=\left[ \begin{array}[c]{rr} 0 & A_{2}\ -1 & 0\ 0 & -1 \end{array}\right] , \end{displaymath}](img381.gif)
![\begin{displaymath} \det\left[ \begin{array}[c]{cc} -\bar{J} & \bar{B}\ -\bar{B}^{\prime} & 0 \end{array}\right] =-\frac{\partial d_{c,2}}{\partial\bar{q}}+A_{2}\frac{\partial d_{l,1}}{\partial\bar{q}}=-\frac{\partial z_{2}}{\partial\bar{q}}\text{.} \end{displaymath}](img382.gif)
In order to find calibrated economies with multiple equilibria for the model presented in this paper, I search for parameters such that the slope of the excess demand function is zero in equilibrium. Totally differentiating equation (9) delivers
![$\displaystyle =\frac{A_{1}l_{1}}{\bar{q}\left[ \tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right] }\left[ \frac{\tilde{H}_{1}^{\prime}\left( \frac{1}{\bar{q}}\right) \frac{1}{\bar {q}}-\bar{q}}{\tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) +\bar{q}} +\frac{\partial l_{1}}{\partial\bar{q}}\frac{\bar{q}}{l_{1}}\right]$](img386.gif)
|
||
![$\displaystyle +\frac{\tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) A_{2}l_{2}}{\bar {q}\left[ \tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right] }\left[ \frac{\frac{\tilde{H}_{2}^{\prime}\left( \frac{1}{\bar{q}}\right) }{\tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) }+\bar{q}}{\left[ \tilde {H}_{2}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right] }-\frac{\partial l_{2}}{\partial\bar{q}}\frac{\bar{q}}{l_{2}}\right] .$](img387.gif)
|
Let the (possibly variable) elasticity of substitution between traded goods in country
The slope of
![$\displaystyle \frac{\partial z_{2}}{\partial\bar{q}}\vert _{\bar{q}=\bar{q}^{\ast}}=-\frac {A_{1}l_{1}}{\bar{q}\left[ \tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right] }\left[ \frac{\varepsilon_{1}\left( \bar{q}\right) \tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) \frac{1}{\bar{q}}+1}{\tilde {H}_{1}\left( \frac{1}{\bar{q}}\right) \frac{1}{\bar{q}}+1}+\frac {\varepsilon_{2}\left( \bar{q}\right) -1}{\tilde{H}_{2}\left( \frac{1} {\bar{q}}\right) \frac{1}{\bar{q}}+1}-\frac{\partial l_{1}}{\partial\bar{q} }\frac{\bar{q}}{l_{1}}+\frac{\partial l_{2}}{\partial\bar{q}}\frac{\bar{q} }{l_{2}}\right] . $](img393.gif)
To find an expression for
![]() notice that equations (4) and (5) together with (3) and the consumption aggregators,
notice that equations (4) and (5) together with (3) and the consumption aggregators,
![]() , imply
, imply
![]() . Total
differentiation of
. Total
differentiation of
![]() and (8) yields
and (8) yields
![$\displaystyle \frac{\partial l_{i}}{\partial\bar{q}}\frac{\bar{q}}{l_{i}}=-\left[ \frac{-\eta_{i}\left[ \frac{U_{lc,i}^{2}}{U_{cc,i}}\frac{U_{c,i}}{U_{l,i} }-U_{ll,i}\frac{U_{c,i}}{U_{l,i}}\right] +\left[ U_{lc,i}-\frac{U_{l,i} }{U_{c,i}}U_{cc,i}\right] }{\left[ U_{lc,i}-U_{ll,i}\frac{U_{c,i}}{U_{l,i} }\right] +\left[ U_{lc,i}-\frac{U_{l,i}}{U_{c,i}}U_{cc,i}\right] }\right] \frac{\Phi_{i}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{i}\left( \bar{q}\right) }, $](img400.gif)
To gain additional insights, I define the share of imports in GDP of country
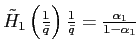 . Analogously, it is
. Analogously, it is
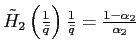 . Let the relative country size,
. Let the relative country size,
![$\displaystyle \frac{\partial z_{2}}{\partial\bar{q}}\vert _{\bar{q}=\bar{q}^{\ast}}=-\frac {A_{1}l_{1}}{\bar{q}\left[ \tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right] }\left[ \varepsilon_{1}\left( \bar{q}\right) \alpha _{1}+\varepsilon_{2}\left( \bar{q}\right) \alpha_{2}+\left( 1-\alpha _{1}-\alpha_{2}\right) -\frac{\partial l_{1}}{\partial\bar{q}}\frac{\bar{q} }{l_{1}}+\frac{\partial l_{2}}{\partial\bar{q}}\frac{\bar{q}}{l_{2}}\right] , $](img416.gif)
I consider the following three classes of utility functions:
- Additive separable in consumption and leisure (labor)
and
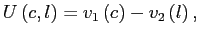 Since
Since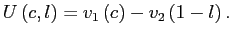
 ,
where
,
where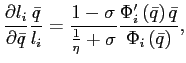
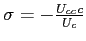 , the relative risk
aversion, and
, the relative risk
aversion, and 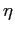 is the
Frisch labor supply elasticity.
is the
Frisch labor supply elasticity. - Preferences without wealth effects
and
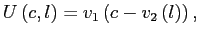
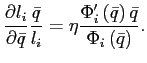
- Cobb-Douglas aggregator
where
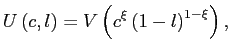
 is strictly monotone in its argument. In this case
is strictly monotone in its argument. In this case
To obtain an idea, how likely it is to observe multiple
equilibria in a calibrated economy, I proceed as follows. For the
case of additive-separable preferences, assume that the two
countries share the same constant values for the elasticity of
substitution, the Frisch labor supply elasticity and the relative
risk aversion. The critical value
![]() that
separates the case of a unique equilibrium from the case of
multiple equilibria is then determined by setting
that
separates the case of a unique equilibrium from the case of
multiple equilibria is then determined by setting
![]() ,
,
![$\displaystyle \bar{\varepsilon}=\frac{\alpha_{1}+\alpha_{2}-1}{\alpha_{1}+\alpha_{2}} +\frac{\frac{1-\sigma}{\frac{1}{\eta}+\sigma}}{\alpha_{1}+\alpha_{2}}\left[ \alpha_{1}+\alpha_{2}-2\right]$](img430.gif) .
.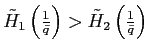 for all
for all Figure 11 plots
![]() as a
function of
as a
function of ![]() and
and
![]() for
for
![]() . For the most appropriate
choices of
. For the most appropriate
choices of ![]() and
and
![]() ,
,
![]() lies
around
lies
around ![]() . For
example,
. For
example,
![]() for
for ![]() and
and
![]() .
.
Figure 11:
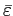 as a
function of risk aversion,
as a
function of risk aversion, 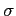 , and the Frisch labor supply elasticity,
, and the Frisch labor supply elasticity,
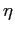 , for given
, for given
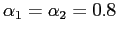 .
.
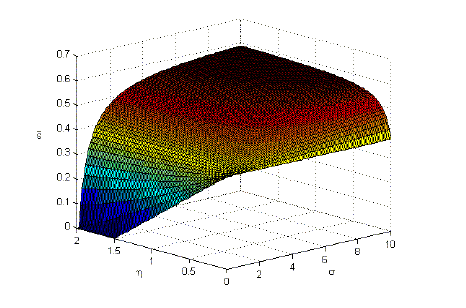
Figure 11 description:
Figure 11 consists of a single three-dimensional graph. The caption reads �epsilon-bar as a function of risk aversion, sigma, and the Frisch labor supply elasticity, eta, for given alpha sub 1 equals alpha sub 2 equals 0.8.� The x-axis is labeled sigma and runs from 0 to 10 in increments of 2. The y-axis is labeled eta and runs from 0 to 2 in increments of 0.5. The z-axis is labeled epsilon-bar and runs from 0 to 0.7 in increments of 0.1. At eta equal to 2, sigma 0, epsilon-bar is 0 and at eta equal to 2 and sigma equal to 10, epsilon-bar is 0.6. As eta is held constant and sigma rises, epsilon-bar rises in a concave manner. Similarly, for other values of eta. If eta equals 1, and sigma equals 0, epsilon-bar equals 0.1 and at eta equal 1 and sigma equal to 10, epsilon-bar is again 0.6. In between epsilon-bar rises in a concave manner.
Figure 12 shows
![]() as a
function
as a
function
![]() and
and
![]() for
for
![]() and
and
![]() .
Since
.
Since ![]() ,
,
![]() is
increasing in
is
increasing in
![]() and
and
![]() (or
decreasing in the import share in GDP).
(or
decreasing in the import share in GDP).
Figure 12:
 as a
function of
as a
function of
 and
and
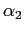 for
for
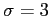 and
and
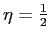 .
.
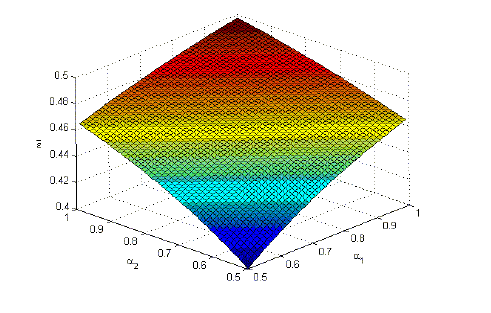
Figure 12 description:
Figure 12 consists of a single three-dimensional graph. The caption reads �epsilon-bar as a function of alpha sub 1 and alpha sub 2 for sigma equals 3 and eta = 0.5.� The x-axis is labeled alpha sub 1 and runs from 0.5 to 1 in increments of 0.1. The y-axis is labeled alpha sub 2 and runs from 0.5 to 1 in increments of 0.1. The z-axis is labeled epsilon-bar and runs from 0.4 to 0.5 in increments of 0.02. At alpha sub 1 and alpha sub 2 equal to 0.5, epsilon-bar is 0.4. If alpha sub 1 is constant but alpha sub 2 rises, epsilon-bar rises to 0.46 at alpha sub 2 equal to 1. In between epsilon-bar rises in a concave manner. If alpha sub 2 is constant but alpha sub 1 rises, epsilon-bar rises to 0.46 at alpha sub 1 equal to 1. In between epsilon-bar rises in a concave manner. If alpha sub 1 and alpha sub 2 rise to 1, epsilon-bar rises in a concave manner and reaches 0.5 when alpha sub 1 and alpha sub 2 are 1.
B. Stability and the slope of the excess demand function
This appendix proves theorems 1-4 in the main text. Section
![]() provides the
algebraic derivations needed for these proofs. Section
provides the
algebraic derivations needed for these proofs. Section ![]() provides the proofs themselves.
All derivations and proofs are based on the more general model
described in appendix
provides the proofs themselves.
All derivations and proofs are based on the more general model
described in appendix ![]() .
.
B.1 Preliminaries
In this section I derive a log-linear approximation of the
model's dynamics solely in terms of the relative price ![]() and bond holdings
and bond holdings ![]() . I assume that the model is
parameterized such that in any steady state bond holdings are
zero.
. I assume that the model is
parameterized such that in any steady state bond holdings are
zero.
Consumption and labor
With constant technology, equations imply
where
![$\displaystyle =\frac{\left[ U_{lc,i}-\frac{U_{l,i}}{U_{c,i}}U_{cc,i} \right] }{\left[ U_{lc,i}-\frac{U_{l,i}}{U_{c,i}}U_{cc,i}\right] +\left[ U_{cl,i}-\frac{U_{c,i}}{U_{l,i}}U_{ll,i}\right] },$](img458.gif)
|
||
![$\displaystyle =\frac{-U_{c,i}\frac{1}{l_{i}}}{\left[ U_{lc,i}-\frac{U_{l,i} }{U_{c,i}}U_{cc,i}\right] +\left[ U_{cl,i}-\frac{U_{c,i}}{U_{l,i}} U_{ll,i}\right] },$](img460.gif)
|
||
With the assumptions on the utility function
Excess demand function
Using equations (26) - (29) the log-linear approximation of the excess demand function
in equilibrium,
![]() , can be written
as
, can be written
as
with
![$\displaystyle =\frac{A_{1}l_{1}}{\left[ \tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right] }\left[ \frac{\tilde{H}_{1}^{\prime}\left( \frac{1}{\bar{q}}\right) \frac{1}{\bar {q}}-\bar{q}}{\tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) +\bar{q}} +\frac{\partial l_{1}}{\partial\bar{q}}\frac{\bar{q}}{l_{1}}\right] +\frac{\tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) A_{2}l_{2}}{\bar {q}\left[ \tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right] }\left[ \frac{\frac{\tilde{H}_{2}^{\prime}\left( \frac{1}{\bar{q}}\right) }{\tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) }+\bar{q}}{\tilde{H} _{2}\left( \frac{1}{\bar{q}}\right) +\bar{q}}-\frac{\partial l_{2}} {\partial\bar{q}}\frac{\bar{q}}{l_{2}}\right]$](img469.gif)
|
||
![$\displaystyle =c_{12}\left\{ \left[ \varepsilon_{1}\left( \bar{q}\right) \tilde{H} _{1}\left( \frac{1}{\bar{q}}\right) \frac{1}{\bar{q}}+1+\omega_{q,1}\right] \frac{\Phi_{1}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{1}\left( \bar{q}\right) }+\left[ \frac{1-\varepsilon_{2}\left( \bar{q}\right) }{\tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) \frac{1}{\bar{q}}} -\omega_{q,2}\right] \frac{\Phi_{2}^{\prime}\left( \bar{q}\right) \bar{q} }{\Phi_{2}\left( \bar{q}\right) }\right\} ,$](img470.gif)
|
||
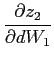 |
![$\displaystyle =\frac{A_{1}l_{1}}{\left[ \tilde {H}_{1}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right] }\frac{\partial l_{1}}{\partial dW_{1}}\frac{1}{l_{1}}+\frac{\tilde{H}_{2}\left( \frac {1}{\bar{q}}\right) \frac{1}{\bar{q}}A_{2}l_{2}}{\tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) \frac{1}{\bar{q}}+1}\frac{\partial l_{2}}{\partial dW_{2}}\frac{1}{l_{2}}+\frac{\frac{1}{\Phi_{1}\left( \bar{q}\right) } }{\left[ \tilde{H}_{1}\left( \frac{1}{\bar{q}}\right) +\bar{q}\right] }-\frac{\frac{1}{q\Phi_{2}\left( \bar{q}\right) }}{\tilde{H}_{2}\left( \frac{1}{\bar{q}}\right) \frac{1}{\bar{q}}+1}$](img472.gif)
|
|
![$\displaystyle =-\frac{1}{\bar{q}\Phi_{1}\left( \bar{q}\right) }\left\{ 1+\left[ 1-\omega_{b,1}\right] \frac{\Phi_{1}^{\prime}\left( \bar{q}\right) \bar{q} }{\Phi_{1}\left( \bar{q}\right) }-\left[ 1-\omega_{b,2}\right] \frac {\Phi_{2}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{2}\left( \bar {q}\right) }\right\} .$](img473.gif) |
In simplifying the expressions for
B.2 Linearized models
Convex portfolio costs
Using equations (26) - (29) and the log-linearized risk sharing condition, that is derived from equation (13), delivers the following system of linear difference equations
![\begin{displaymath} \left( \begin{array}[c]{c} \bar{q}_{t+1}\ b_{t} \end{array}\right) =\left( \begin{array}[c]{cc} 1+\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}}{\frac{\partial z_{2} }{\partial dW_{1}}d_{q}-\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}d_{b} }\check{\Gamma} & \frac{\frac{\partial z_{2}}{\partial dW_{1}}}{\frac{\partial z_{2}}{\partial dW_{1}}d_{q}-\frac{\partial z_{2}}{\partial\bar{q}}\bar {q}d_{b}}\check{\Gamma}\ \frac{1}{\beta}\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}} {\frac{\partial z_{2}}{\partial dW_{1}}} & \frac{1}{\beta} \end{array}\right) \left( \begin{array}[c]{c} \bar{q}_{t}\ b_{t-1} \end{array}\right) , \end{displaymath}](img483.gif)
![$\displaystyle =\frac{\Gamma^{\prime\prime}\left( 0\right) }{\beta ^{2}\Phi_{1}\left( \bar{q}\right) }\left[ 1+\frac{1}{\bar{q}}\right] ,$](img485.gif)
|
||
![$\displaystyle =-\left[ \frac{U_{cc,1}c_{1}}{U_{c,1}}-\left( \frac{U_{cc,1}c_{1} }{U_{c,1}}+\frac{U_{cl,1}l_{1}}{U_{c,1}}\right) \omega_{b,1}\right] \frac{\Phi_{1}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{1}\left( \bar{q}\right) }\frac{1}{\bar{q}\Phi_{1}\left( \bar{q}\right) c_{12}}$](img487.gif)
|
||
![$\displaystyle +\left[ \frac{U_{cc,2}c_{2}}{U_{c,2}}-\left( \frac{U_{cc,2}c_{2}}{U_{c,2} }+\frac{U_{cl,2}l_{2}}{U_{c,2}}\right) \omega_{b,2}\right] \frac{\Phi _{2}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{2}\left( \bar{q}\right) }\frac{1}{\bar{q}\Phi_{1}\left( \bar{q}\right) c_{12}},$](img488.gif)
|
||
![$\displaystyle =-\bar{q}\Phi_{1}\left( \bar{q}\right) c_{12}d_{b}+1+\left[ 1-\omega_{b,1}\right] \frac{\Phi_{1}^{\prime}\left( \bar{q}\right) \bar{q} }{\Phi_{1}\left( \bar{q}\right) }-\left[ 1-\omega_{b,2}\right] \frac {\Phi_{2}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{2}\left( \bar {q}\right) }.$](img490.gif)
|
Note that
![$ -\frac{U_{cc,i}c_{i}}{U_{c,i}}+\left( \frac {U_{cc,i}c_{i}}{U_{c,i}}+\frac{U_{cl,i}l_{i}}{U_{c,i}}\right) \omega _{b,i}=-\frac{U_{ll,i}U_{cc,i}-U_{lc,i}^{2}}{\left[ U_{lc,i}-\frac{U_{l,i} }{U_{c,i}}U_{cc,i}\right] +\left[ U_{cl,i}-\frac{U_{c,i}}{U_{l,i}} U_{ll,i}\right] }\frac{l_{i}}{U_{c,i}}>0$](img492.gif) .
.
The original (non-stationary) model is obtained for ![]()
![]() .
.
Debt elastic interest rate
The model with a debt elastic interest rate is very similar to the model with portfolio costs. Following the standard assumption that agents do not internalize the effects of their decisions on the interest rate, it is
![\begin{displaymath} \left( \begin{array}[c]{c} \bar{q}_{t+1}\ b_{t} \end{array}\right) =\left( \begin{array}[c]{cc} 1-\frac{\Psi^{\prime}\left( 0\right) }{\beta}\frac{\frac{\partial z_{2} }{\partial\bar{q}}\bar{q}}{\frac{\partial z_{2}}{\partial dW_{1}}d_{q} -\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}d_{b}} & -\frac{\Psi^{\prime }\left( 0\right) }{\beta}\frac{\frac{\partial z_{2}}{\partial dW_{1}}} {\frac{\partial z_{2}}{\partial dW_{1}}d_{q}-\frac{\partial z_{2}} {\partial\bar{q}}\bar{q}d_{b}}\ \frac{1}{\beta}\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}} {\frac{\partial z_{2}}{\partial dW_{1}}} & \frac{1}{\beta} \end{array}\right) \left( \begin{array}[c]{c} \bar{q}_{t}\ b_{t-1} \end{array}\right) . \end{displaymath}](img495.gif)
Endogenous discounting without internalization
If agents do not internalize the effects of their consumption and leisure choices on the discount factor, the risk sharing condition, equation (16), implies the following system of difference equations
![\begin{displaymath} \left( \begin{array}[c]{c} \bar{q}_{t+1}\ b_{t} \end{array}\right) =\left( \begin{array}[c]{cc} 1+\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}}{\frac{\partial z_{2} }{\partial dW_{1}}d_{q}-\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}d_{b} }\check{\Gamma} & \frac{\frac{\partial z_{2}}{\partial dW_{1}}}{\frac{\partial z_{2}}{\partial dW_{1}}d_{q}-\frac{\partial z_{2}}{\partial\bar{q}}\bar {q}d_{b}}\check{\Gamma}\ \frac{1}{\beta}\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}} {\frac{\partial z_{2}}{\partial dW_{1}}} & \frac{1}{\beta} \end{array}\right) \left( \begin{array}[c]{c} \bar{q}_{t}\ b_{t-1} \end{array}\right) , \end{displaymath}](img483.gif)
![$\displaystyle =\left[ U_{c,1}c_{1}\frac{\beta_{1}^{\prime}}{\beta_{1}}\frac {\Phi_{1}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{1}\left( \bar {q}\right) }-U_{c,2}c_{2}\frac{\beta_{2}^{\prime}}{\beta_{2}}\frac{\Phi _{2}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{2}\left( \bar{q}\right) }\right] \frac{1}{\bar{q}\Phi_{1}\left( \bar{q}\right) c_{12}},$](img498.gif)
|
||
Endogenous discounting with internalization
In this last model, agents take into account the effects of
their consumption and leisure choices on the discount factor. As
equations (18) and (19) reveal this implies two additional state variables. In
addition to ![]() ,
,
![]() and
and
![]() are
also state variables of the linearized system:
are
also state variables of the linearized system:
![\begin{displaymath} \left( \begin{array}[c]{c} \bar{q}_{t+1}\ \hat{\eta}_{1,t+1}\ \hat{\eta}_{2,t+1}\ b_{t} \end{array}\right) =\left( \begin{array}[c]{cccc} 1 & -zm_{1} & zm_{2} & 0\ \frac{a\phi_{1}}{m_{1}} & \left[ \frac{1}{\beta_{1}}-za\phi_{1}\right] & za\phi_{1}\frac{m_{2}}{m_{1}} & 0\ \frac{a\phi_{2}}{m_{2}} & -za\phi_{2}\frac{m_{1}}{m_{2}} & \left[ \frac {1}{\beta_{2}}+za\phi_{2}\right] & 0\ \frac{1}{\beta}\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}} {\frac{\partial z_{2}}{\partial dW_{1}}} & 0 & 0 & \frac{1}{\beta} \end{array}\right) \left( \begin{array}[c]{c} \bar{q}_{t}\ \hat{\eta}_{1,t}\ \hat{\eta}_{2,t}\ b_{t-1} \end{array}\right) , \end{displaymath}](img510.gif)
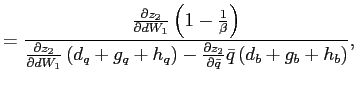
|
||
![$\displaystyle =\left[ 1+\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}} {\frac{\partial z_{2}}{\partial dW_{1}}}\frac{1}{\bar{q}\Phi_{1}\left( \bar{q}\right) c_{12}}\right] ,$](img514.gif)
|
||
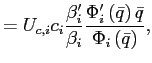
|
||
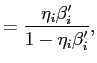
|
for
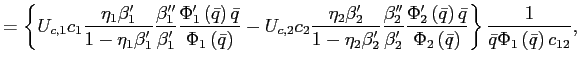
|
||
Important sign restrictions
Before I study the local stability in the next section, it is useful to find the signs of the following expressions:
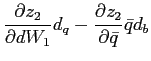
|
![$\displaystyle =-\frac{1}{\bar{q}\Phi_{1}\left( \bar{q}\right) }\left( 1+\left[ 1-\omega_{b,1}\right] \frac{\Phi_{1}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{1}\left( \bar{q}\right) }-\left[ 1-\omega_{b,2}\right] \frac{\Phi_{2}^{\prime}\left( \bar{q}\right) \bar{q} }{\Phi_{2}\left( \bar{q}\right) }\right) ^{2}+\Upsilon c_{12}d_{b}<0,$](img524.gif)
|
|
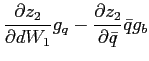
|
where
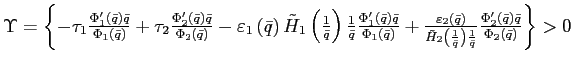 .
.
The sign of
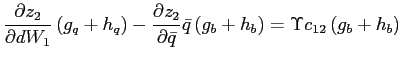
B.3 Stability of the steady states
As most of the dynamic systems that are studied in this section are systems with two variables, consider
- i.
- if
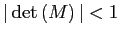 and
and  tr
tr
 , the
modulus of all eigenvalue is smaller than
, the
modulus of all eigenvalue is smaller than 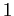 ,
, - ii.
- if
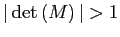 and
and 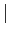 tr
tr
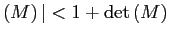 , the
modulus of all eigenvalues is larger than
, the
modulus of all eigenvalues is larger than 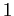 ,
, - iii.
- if
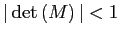 and
and  tr
tr
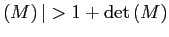 or
or
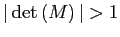 and
and  tr
tr
 , the
modulus of one eigenvalue is larger than
, the
modulus of one eigenvalue is larger than  , while the other one is smaller than
, while the other one is smaller than
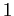 .
.
With these results in mind I proof theorems 1-4 in the main text:
![\begin{displaymath} M_{P}=\left( \begin{array}[c]{cc} 1+\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}}{\frac{\partial z_{2} }{\partial dW_{1}}d_{q}-\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}d_{b} }\check{\Gamma} & \frac{\frac{\partial z_{2}}{\partial dW_{1}}}{\frac{\partial z_{2}}{\partial dW_{1}}d_{q}-\frac{\partial z_{2}}{\partial\bar{q}}\bar {q}d_{b}}\check{\Gamma}\ \frac{1}{\beta}\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}} {\frac{\partial z_{2}}{\partial dW_{1}}} & \frac{1}{\beta} \end{array}\right) \text{.} \end{displaymath}](img544.gif)
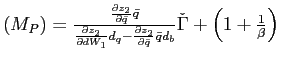 , respectively. Since
, respectively. Since If
![]() , tr
, tr
![]() and the
modulus of one eigenvalue is larger than
and the
modulus of one eigenvalue is larger than ![]() , while the other one is smaller than
, while the other one is smaller than
![]() . Given that bond
holdings are the only state variable, the system is saddle-path
stable.
. Given that bond
holdings are the only state variable, the system is saddle-path
stable.
If
![]() , the
modulus of each eigenvalue is larger than
, the
modulus of each eigenvalue is larger than ![]() for
for
![$\displaystyle \equiv-2\beta\frac{\left( 1+\beta\right) \Phi_{1}\left( \bar{q}\right) }{\bar{q}\left[ 1+\frac{1}{\bar{q}}\right] }\frac {\frac{\partial z_{2}}{\partial dW_{1}}d_{q}-\frac{\partial z_{2}} {\partial\bar{q}}\bar{q}d_{b}}{\frac{\partial z_{2}}{\partial\bar{q}}} >\Gamma^{\prime\prime}\left( 0\right) >0.$](img556.gif)
|
Otherwise, the modulus of exactly one of the eigenvalues is larger than
![]() measures the
sensitivity of the portfolio costs in the neighborhood of the
steady state. In most applications, this sensitivity is low. If
measures the
sensitivity of the portfolio costs in the neighborhood of the
steady state. In most applications, this sensitivity is low. If
![]() is assumed to be
very large, the economy is very similar to the economy in financial
autarchy. In the latter, any steady state is saddle-path stable.
Hence, any steady state can be turned into a saddle point in the
model with portfolio costs if the marginal costs of portfolio
holdings increase strongly enough as the economy deviates from the
steady state.
is assumed to be
very large, the economy is very similar to the economy in financial
autarchy. In the latter, any steady state is saddle-path stable.
Hence, any steady state can be turned into a saddle point in the
model with portfolio costs if the marginal costs of portfolio
holdings increase strongly enough as the economy deviates from the
steady state.
However, given that the model with convex portfolio costs is supposed to behave closely to the original (non-stationary) model, it is common practice to specify portfolio costs that are small and that do not change dramatically in the neighborhood of the steady state. Such specifications are also in line with actual portfolio costs.
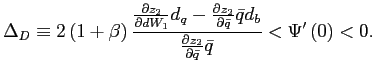
![]()
![\begin{displaymath} M_{E}=\left( \begin{array}[c]{cc} 1+\frac{\frac{\partial z_{2}}{\partial dW_{1}}g_{q}-\frac{\partial z_{2} }{\partial\bar{q}}\bar{q}g_{b}}{\frac{\partial z_{2}}{\partial dW_{1}} d_{q}-\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}d_{b}} & 0\ \frac{1}{\beta}\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}} {\frac{\partial z_{2}}{\partial dW_{1}}} & \frac{1}{\beta} \end{array}\right) \text{.} \end{displaymath}](img563.gif)
![$ \det\left( M_{E}\right) =\frac{1}{\beta }\left[ 1+\frac{\frac{\partial z_{2}}{\partial dW_{1}}g_{q}-\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}g_{b}}{\frac{\partial z_{2}}{\partial dW_{1} }d_{q}-\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}d_{b}}\right] $](img564.gif) and tr
and tr
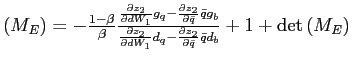 , respectively. Since
, respectively. Since
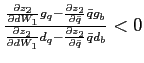 irrespective of the sign of the slope of the excess demand
function, the modulus of exactly one eigenvalue is smaller than
irrespective of the sign of the slope of the excess demand
function, the modulus of exactly one eigenvalue is smaller than
Notice that it is crucial to assume that the endogenous discount
factor is decreasing in the utility level. Otherwise
![]() and
and ![]() tr
tr
![]() irrespective of the slope of the excess demand function. In this
case, both eigenvalues would be larger than
irrespective of the slope of the excess demand function. In this
case, both eigenvalues would be larger than ![]() .
.
If agents internalize the effects of their choices on the
endogenous discount factor, only a weaker theorem can be proven
since the sign of
![]() cannot be determined. In preparation for this theorem, consider an
increase in the wealth of agents in country
cannot be determined. In preparation for this theorem, consider an
increase in the wealth of agents in country ![]() . I am interested in the change of the
intertemporal marginal rate of substitution under the assumption
that current and future prices as well as future allocations remain
unchanged. The only variables that are allowed to change are
current consumption and leisure and therefore also utility in the
current period. I refer to this experiment as the direct impact of
a wealth increase.
. I am interested in the change of the
intertemporal marginal rate of substitution under the assumption
that current and future prices as well as future allocations remain
unchanged. The only variables that are allowed to change are
current consumption and leisure and therefore also utility in the
current period. I refer to this experiment as the direct impact of
a wealth increase.
The intertemporal marginal rate of substitution in country
![]() is given by
is given by
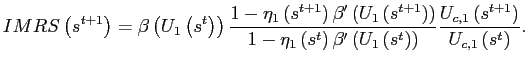
|
||
The first equation states the familiar equilibrium condition that the marginal rate of substitution between labor and consumption equals the real wage. As shown earlier, the second equation can be derived straight from the intertemporal budget constraint of the agents.
The direct impact of a wealth increase on the intertemporal marginal rate of substitution is given by
The first term in equation (31) measures the direct impact of the wealth transfer on the marginal utility of consumption under the assumption that the marginal rate of substitution between leisure and consumption is held constant. Under the assumptions on the utility function the first term is positive. In the experiment the increase in the wealth of the agents of country
The second term measures the effect of the wealth increase on
![]() through the
endogeneity of the discount factor. There are two effects. First,
as consumption and leisure rise in the current period, so does
utility
through the
endogeneity of the discount factor. There are two effects. First,
as consumption and leisure rise in the current period, so does
utility
![]() . As the discount factor is
decreasing in the utility level this effect operates towards a
decline of the
. As the discount factor is
decreasing in the utility level this effect operates towards a
decline of the ![]() . Furthermore, the change in the discount
factor effects the
. Furthermore, the change in the discount
factor effects the ![]() also through its impact on the discounted
future utility summarized in
also through its impact on the discounted
future utility summarized in
![]() . Absent assumptions on
. Absent assumptions on
![]() this expression cannot be signed.
this expression cannot be signed.
If the discount factor is constant,
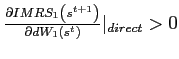 . Hence, if the discount factor
. Hence, if the discount factor ![]() does not react too strongly
to changes in
does not react too strongly
to changes in ![]() , the
effect will still be positive.
, the
effect will still be positive.
Given the original questions this restriction is not too
restrictive and
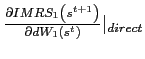 is most likely to be positive. Endogenous discounting is
introduced to obtain stationarity in the model with incomplete
asset markets. To the extent that the stationary model is supposed
to behave closely to the original non-stationary model it is
desirable that the discount factor does not move around too
much.
is most likely to be positive. Endogenous discounting is
introduced to obtain stationarity in the model with incomplete
asset markets. To the extent that the stationary model is supposed
to behave closely to the original non-stationary model it is
desirable that the discount factor does not move around too
much.
Under the assumption that
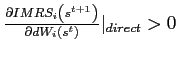 ,
, ![]() , theorem
, theorem
![]() can be proven.
can be proven.
![\begin{displaymath} M_{I}=\left( \begin{array}[c]{cccc} 1 & -zm_{1} & zm_{2} & 0\ \frac{a\phi_{1}}{m_{1}} & \left[ \frac{1}{\beta_{1}}-za\phi_{1}\right] & za\phi_{1}\frac{m_{2}}{m_{1}} & 0\ \frac{a\phi_{2}}{m_{2}} & -za\phi_{2}\frac{m_{1}}{m_{2}} & \left[ \frac {1}{\beta_{2}}+za\phi_{2}\right] & 0\ \frac{1}{\beta}\frac{\frac{\partial z_{2}}{\partial\bar{q}}\bar{q}} {\frac{\partial z_{2}}{\partial dW_{1}}} & 0 & 0 & \frac{1}{\beta} \end{array}\right) \text{.} \end{displaymath}](img594.gif)
![$\displaystyle -\left( \lambda-\frac{1}{\beta}\right) ^{2}\left( \lambda^{2}-\left[ \frac{1}{\beta}+1+za\left[ \phi_{2}-\phi_{1}\right] \right] \lambda +\frac{1}{\beta}\right) =0$](img595.gif) ,
,![$\displaystyle za\left[ \phi_{2}-\phi_{1}\right] =\frac{\frac{1}{\beta}\left( 1-\beta\right) \Upsilon\bar{q}\Phi_{1}\left( \bar{q}\right) c_{12}g_{b} }{\left( 1+\left[ 1-\omega_{b,1}\right] \frac{\Phi_{1}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{1}\left( \bar{q}\right) }-\left[ 1-\omega_{b,2}\right] \frac{\Phi_{2}^{\prime}\left( \bar{q}\right) \bar{q} }{\Phi_{2}\left( \bar{q}\right) }\right) ^{2}-\Upsilon\bar{q}\Phi _{1}\left( \bar{q}\right) c_{12}\left( d_{b}+h_{b}+g_{b}\right) }\text{,} $](img596.gif)
![$\displaystyle za\left[ \phi_{2}-\phi_{1}\right] <-2\left( 1+\frac{1}{\beta}\right)$](img600.gif) .
.![$\displaystyle =\left[ -\frac{U_{cc,1}c_{1}}{U_{c,1}}+\left( \frac{U_{cc,1}c_{1}} {U_{c,1}}+\frac{U_{cl,1}l_{1}}{U_{c,1}}\right) \omega_{b,1}+\left( \frac{\beta_{1}^{\prime}}{\beta_{1}}+\frac{\eta_{1}\beta_{1}^{\prime}} {1-\eta_{1}\beta_{1}^{\prime}}\frac{\beta_{1}^{\prime\prime}}{\beta _{1}^{\prime}}\right) U_{c,1}c_{1}\right] \frac{\Phi_{1}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{1}\left( \bar{q}\right) }$](img604.gif)
|
||
![$\displaystyle -\left[ -\frac{U_{cc,2}c_{2}}{U_{c,2}}+\left( \frac{U_{cc,2}c_{2}} {U_{c,2}}+\frac{U_{cl,2}l_{2}}{U_{c,2}}\right) \omega_{b,2}+\left( \frac{\beta_{2}^{\prime}}{\beta_{2}}+\frac{\eta_{2}\beta_{2}^{\prime}} {1-\eta_{2}\beta_{2}^{\prime}}\frac{\beta_{2}^{\prime\prime}}{\beta _{2}^{\prime}}\right) U_{c,2}c_{2}\right] \frac{\Phi_{2}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{2}\left( \bar{q}\right) }$](img605.gif)
|
Under the assumption that
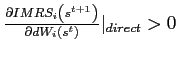 ,
, Obviously the assumption that
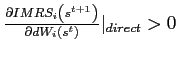 for each
for each ![]() is
unnecessarily strong. However, this expression is somewhat more
intuitive than other possible restrictions.
is
unnecessarily strong. However, this expression is somewhat more
intuitive than other possible restrictions.
Most notably theorems 3 and 4 show that under endogenous discounting the stability of the system in the neighborhood of a steady state does not depend on the slope of the excess demand function in the steady state. The stability depends solely on the parameterization of the endogenous discount factor. This is very different from the economies studied in theorems 1 and 2. With convex portfolio costs or a debt-elastic interest rate the stability of the system around a steady state depends very much on the slope of the excess demand function in this steady state.18
Footnotes
* I am grateful to Roc Armenter, David Bowman, Paul Bergin, Chris Erceg, Fabio Ghironi, Luca Guerrieri, Chris Gust, Sylvain Leduc, Paolo Pesenti and Cedric Tille for insightful comments. I have also benefited from seminar participants at the Federal Reserve Board and the Federal Reserve Bank of New York. All remaining errors are mine. The views expressed in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. Return to text
† Board of Governors of the Federal Reserve System, Washington D.C. E-mail: [email protected]. Return to text
1. Obviously, this problem is not unique to international economics. The same issues occur in models with heterogeneous agents and incomplete asset markets. Return to text
2. See also Kim and Kose (2003) for a related study in a small open economy framework. Lubik (2003) analyses some additional approaches that induce stationarity and finds substantial qualitative differences. Hence, the implicit generalization of the results in Schmitt-Grohé and Uribe (2003) by many researchers is not even appropriate for the case of a small open economy. Boileau and Normandin (2005) extend the analysis to a two-country model with one homogeneous good. Interesting quantitative differences can occur in their setup depending on the persistence of technology shocks. Return to text
3. In the technical appendix to this paper, which is available upon request, I study the overlapping generations structure of Ghironi (2003). The mathematical properties of his approach turn out to be closely related to the models with convex portfolio costs or a debt elastic interest rate premium. Return to text
4. Models with occasionally binding constraints, however, cannot be solved reliably using local approximation techniques. This complicates the analysis and explains why Huggett's approach is typically avoided in international macroeconomics. Return to text
5. If the discount factor is increasing in the agent's utility level, the dynamics around any steady state are explosive. Return to text
6. This static example has been subject to numerous studies in general equilibrium theory, see Kehoe (1991) and Mas-Colell et al (1995). Return to text
7. By mirroring I mean, that good
![]()
![]() enters
the utility function of country
enters
the utility function of country ![]() agents the same way that good
agents the same way that good
![]() enters the utility function of country
enters the utility function of country ![]() agents. The same holds for the
agents' endowments with goods
agents. The same holds for the
agents' endowments with goods ![]() and
and ![]() . Return to text
. Return to text
8. Obviously, these marco estimates
are in sharp contrast to the micro evidence where mean estimates
vary between ![]() and
and
![]() . See, e.g., Broda and
Weinstein (2005). Return to text
. See, e.g., Broda and
Weinstein (2005). Return to text
9. One of the most comprehensive empirical study on trade elasticities is Bayoumi (1999), who uses data on 420 bilateral trade flows between 21 industrialized countries. Under the restriction (not rejected statistically) that elasticities are identical for all country pairs, the estimated long-run price elasticity ranges between 0.38 and 0.89 depending on the model specification. Return to text
10. Introducing capital into the model is unlikely to change the results presented in this paper. It is straightforward to show, that in financial autarchy multiple equilibria also occur in a model with capital if the elasticity of substitution is sufficiently low. The nonlinearities underlying this finding are very likely to cause the same differences between the approaches that induce stationarity as in the model without capital. Return to text
11. See Judd (1998). In plotting the
stable manifold I have assumed that the portfolio costs are
quadratic, i.e.,
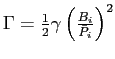 with
with
![]() . Return to
text
. Return to
text
12. Before I move to the case of a bond economy with endogenous discounting, a short comment about Ghironi's (2003) overlapping generations structure seems to be appropriate. Like the model with a debt elastic interest rate, Ghironi's framework preserves all the candidate steady states that occur in the model without international financial markets. Therefore, it is not surprising, that in his framework a steady state is dynamically unstable (saddle-path stable) if the excess demand function is upward (downward) sloping in the steady state. Return to text
13. Mendoza (1991) uses the endogenous discount factor approach in a small open economy model. Corsetti, Dedola and Leduc (2005) employ this technique in a two country model of the international business cycle. Return to text
14. The stable manifold is
calculated using a reverse shooting algorithm. The endogenous
discount factor is assumed to be of the form
![]() , where the constant
, where the constant ![]() is chosen such that
is chosen such that
![]() in the
steady state.
in the
steady state. ![]() is
a constant that ensures that
is
a constant that ensures that ![]() . Return to
text
. Return to
text
15. Only in the model with
endogenous discounting without internalization can it be shown that
the steady state cannot be a focus. In all other models
oscillations can occur for appropriate parameterizations if
![]() . Return to text
. Return to text
16. An aggregator that satisfies the
restrictions imposed on ![]() is given by the straightforward extension of the
is given by the straightforward extension of the
![]() aggregator which
has been suggested by Dotsey and King (2005):
aggregator which
has been suggested by Dotsey and King (2005):
![$\displaystyle \frac{\alpha_{i1}}{\left( 1+\eta\right) \rho}\left[ \frac{\left( 1+\eta\right) }{\alpha_{i1}}\left( \frac{c_{i1}}{c_{i}}\right) -\eta\right] ^{\rho}+\frac{\alpha_{i2}}{\left( 1+\eta\right) \rho}\left[ \frac{\left( 1+\eta\right) }{\alpha_{i2}}\left( \frac{c_{i2}}{c_{i} }\right) -\eta\right] ^{\rho}=\frac{1}{\left( 1+\eta\right) \rho}. $](img309.gif)
17. The Frisch (or constant marginal utility of wealth) labor supply elasticity is defined as
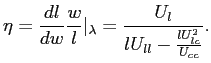
18. One notable exception to this statement are the cases of very sensitive portfolio costs or debt elastic interest rate. In these cases the model behaves like the economy under financial autarchy and every steady state is stable in the simple model without capital. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available.
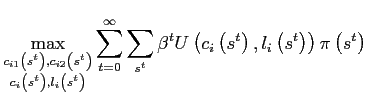
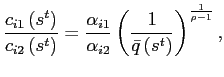
![$\displaystyle =\frac{1}{\left( \frac{\alpha_{11}} {\alpha_{12}}\left( \frac{1}{\bar{q}\left( s^{t}\right) }\right) ^{\frac{1}{\rho-1}}+\bar{q}\left( s^{t}\right) \right) }\left[ w_{1}\left( s^{t}\right) l_{1}\left( s^{t}\right) +\frac{1}{\Phi _{1}\left( \bar{q}\left( s^{t}\right) \right) }dW_{1}\left( s^{t}\right) \right] ,$](img77.gif)
![$\displaystyle =\frac{1}{\left( \frac{\alpha_{21}} {\alpha_{22}}\left( \frac{1}{\bar{q}\left( s^{t}\right) }\right) ^{\frac{\rho}{\rho-1}}+1\right) }\left[ w_{2}\left( s^{t}\right) l_{2}\left( s^{t}\right) +\frac{1}{\bar{q}\left( s^{t}\right) \Phi _{1}\left( \bar{q}\left( s^{t}\right) \right) }dW_{2}\left( s^{t}\right) \right] .$](img79.gif)
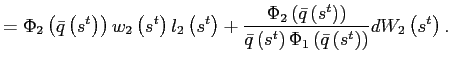
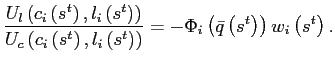
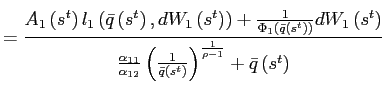
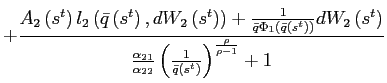
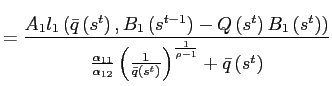
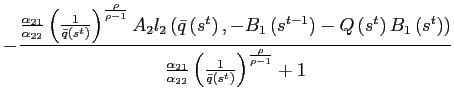
![$\displaystyle +\left[ \frac{1}{\frac{\alpha_{11}}{\alpha_{12}}\left( \frac{1}{\bar {q}\left( s^{t}\right) }\right) ^{\frac{1}{\rho-1}}+\bar{q}\left( s^{t}\right) }-\frac{1}{\frac{\alpha_{21}}{\alpha_{22}}\left( \frac{1} {\bar{q}\left( s^{t}\right) }\right) ^{\frac{\rho}{\rho-1}}+1}\right] \frac{1}{\Phi_{1}\left( \bar{q}\left( s^{t}\right) \right) }\left[ B_{1}\left( s^{t-1}\right) -Q\left( s^{t}\right) B_{1}\left( s^{t}\right) \right] ,$](img170.gif)
![$\displaystyle \sum_{s^{t+1}\vert s^{t}}\beta\left[ \frac{U_{c}\left( c_{1}\left( s^{t+1}\right) ,l_{1}\left( s^{t+1}\right) \right) }{U_{c}\left( c_{1}\left( s^{t}\right) ,l_{1}\left( s^{t}\right) \right) }-\frac {U_{c}\left( c_{2}\left( s^{t+1}\right) ,l_{2}\left( s^{t+1}\right) \right) }{U_{c}\left( c_{2}\left( s^{t}\right) ,l_{2}\left( s^{t}\right) \right) }\frac{q\left( s^{t}\right) }{q\left( s^{t+1}\right) }\right] \pi\left( s^{t+1}\vert s^{t}\right) =0,$](img173.gif)
![$\displaystyle \sum_{s^{t+1}\vert s^{t}}\beta\left[ \frac{U_{c}\left( c_{1}\left( s^{t+1}\right) ,l_{1}\left( s^{t+1}\right) \right) }{U_{c}\left( c_{1}\left( s^{t}\right) ,l_{1}\left( s^{t}\right) \right) }-\frac {U_{c}\left( c_{2}\left( s^{t+1}\right) ,l_{2}\left( s^{t+1}\right) \right) }{U_{c}\left( c_{2}\left( s^{t}\right) ,l_{2}\left( s^{t}\right) \right) }\frac{q\left( s^{t}\right) }{q\left( s^{t+1}\right) }\right] \pi\left( s^{t+1}\vert s^{t}\right)$](img207.gif)
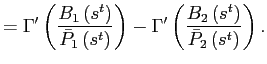
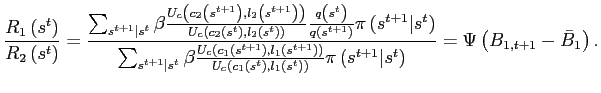
![$\displaystyle \sum_{s^{t+1}\vert s^{t}}\left[ \beta_{1}\left[ U\left( s^{t}\right) \right] \frac{U_{c}\left( c_{1}\left( s^{t+1}\right) ,l_{1}\left( s^{t+1}\right) \right) }{U_{c}\left( c_{1}\left( s^{t}\right) ,l_{1}\left( s^{t}\right) \right) }-\beta_{2}\left[ U\left( s^{t}\right) \right] \frac{U_{c}\left( c_{2}\left( s^{t+1}\right) ,l_{2}\left( s^{t+1}\right) \right) } {U_{c}\left( c_{2}\left( s^{t}\right) ,l_{2}\left( s^{t}\right) \right) }\frac{q\left( s^{t}\right) }{q\left( s^{t+1}\right) }\right] \pi\left( s^{t+1}\vert s^{t}\right) =0,$](img252.gif)
![$\displaystyle \sum_{s^{t+1}\vert s^{t}}\left[ \beta_{1}\left( s^{t}\right) \frac {U_{c,1}\left( s^{t+1}\right) -\eta_{1}\left( s^{t+1}\right) \beta _{c,1}\left( s^{t+1}\right) }{U_{c,1}\left( s^{t}\right) -\eta_{1}\left( s^{t}\right) \beta_{c,1}\left( s^{t}\right) }\right] \pi\left( s^{t+1}\vert s^{t}\right)$](img269.gif)
![$\displaystyle =\sum_{s^{t+1}\vert s^{t}}\left[ \beta_{2}\left( s^{t}\right) \frac {U_{c,2}\left( s^{t+1}\right) -\eta_{2}\left( s^{t+1}\right) \beta _{c,2}\left( s^{t+1}\right) }{U_{c,2}\left( s^{t}\right) -\eta_{2}\left( s^{t}\right) \beta_{c,2}\left( s^{t}\right) }\frac{\bar{q}\left( s^{t}\right) }{\bar{q}\left( s^{t+1}\right) }\frac{\Phi_{1}\left( \bar {q}\left( s^{t}\right) \right) }{\Phi_{1}\left( \bar{q}\left( s^{t+1}\right) \right) }\frac{\Phi_{2}\left( \bar{q}\left( s^{t+1}\right) \right) }{\Phi_{2}\left( \bar{q}\left( s^{t}\right) \right) }\right] \pi\left( s^{t+1}\vert s^{t}\right) .$](img270.gif)
![$\displaystyle \eta_{i}\left( s^{t}\right) =\sum_{s^{t+1}\vert s^{t}}\left[ -U_{i}\left( s^{t+1}\right) +\beta_{i}\left( s^{t+1}\right) \eta\left( s^{t+1}\right) \right] \pi\left( s^{t+1}\vert s^{t}\right) .$](img272.gif)
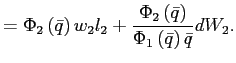
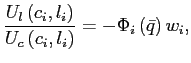
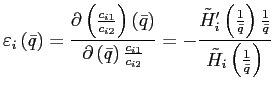 .
.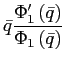
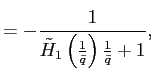
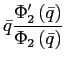
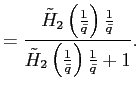
![$\displaystyle =\omega_{q,1}\frac{\Phi_{1}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{1}\left( \bar{q}\right) }\bar{q}_{t}-\omega_{b,1}\frac {1}{c_{1}}\left[ b_{1,t-1}-\beta b_{1,t}\right] ,$](img447.gif)
![$\displaystyle =\omega_{q,2}\frac{\Phi_{2}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{2}\left( \bar{q}\right) }\bar{q}_{t}+\omega_{b,2}\frac {\Phi_{2}\left( \bar{q}\right) }{\bar{q}\Phi_{1}\left( \bar{q}\right) }\frac{1}{c_{2}}\left[ b_{1,t-1}-\beta b_{1,t}\right] ,$](img449.gif)
![$\displaystyle =\left[ 1+\omega_{q,1}\right] \frac{\Phi_{1}^{\prime }\left( \bar{q}\right) \bar{q}}{\Phi_{1}\left( \bar{q}\right) }\bar{q} _{t}+\left[ 1-\omega_{b,1}\right] \frac{1}{c_{1}}\left[ b_{1,t-1}-\beta b_{1,t}\right] ,$](img451.gif)
![$\displaystyle =\left[ 1+\omega_{q,2}\right] \frac{\Phi_{2}^{\prime }\left( \bar{q}\right) \bar{q}}{\Phi_{2}\left( \bar{q}\right) }\bar{q} _{t}-\left[ 1-\omega_{b,2}\right] \frac{\Phi_{2}\left( \bar{q}\right) }{\bar{q}\Phi_{1}\left( \bar{q}\right) }\frac{1}{c_{2}}\left[ b_{1,t-1}-\beta b_{1,t}\right] ,$](img453.gif)
![$\displaystyle \frac{\partial z_{2}}{\partial\bar{q}}\bar{q}\bar{q}_{t}+\frac{\partial z_{2} }{\partial dW_{1}}\left[ b_{1,t-1}-\beta b_{1,t}\right] =0$](img467.gif)
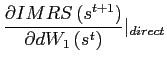
![$\displaystyle =\left[ -\frac{U_{cc,1}\left( s^{t}\right) c_{1}\left( s^{t}\right) }{U_{c,1}\left( s^{t}\right) }+\left( \frac{U_{cc,1}\left( s^{t}\right) c_{1}\left( s^{t}\right) }{U_{c,1}\left( s^{t}\right) }+\frac {U_{cl,1}\left( s^{t}\right) l_{1}\left( s^{t}\right) }{U_{c,1}\left( s^{t}\right) }\right) \omega_{1b}\left( s^{t}\right) \right] \frac {1}{c_{1}\left( s^{t}\right) }IMRS\left( s^{t+1}\right)$](img580.gif)