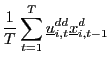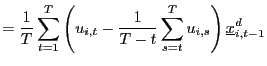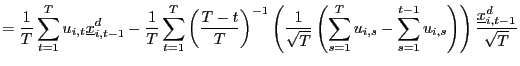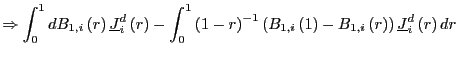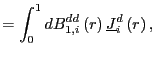Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 869, August 2006 --- Screen Reader Version*
Predictive Regressions with Panel Data
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper analyzes panel data inference in predictive regressions with endogenous and nearly persistent regressors. The standard fixed effects estimator is shown to suffer from a second order bias; analytical results, as well as Monte Carlo evidence, show that the bias and resulting size distortions can be severe. New estimators, based on recursive demeaning as well as direct bias correction, are proposed and methods for dealing with cross sectional dependence in the form of common factors are also developed. Overall, the results show that the econometric issues associated with predictive regressions when using time-series data to a large extent also carry over to the panel case. However, practical solutions are more readily available when using panel data. The results are illustrated with an application to predictability in international stock indices.
Keywords: Cross-sectional dependence; Panel data; Pooled regression; Predictive regression; Stock return predictability.
JEL classification: C22, C23, G1.
1 Introduction
Predictive regressions are important tools for evaluating and testing economic models. Although tests of stock return predictability, and the related market efficiency hypothesis, are probably the most common application, many rational expectations models can be tested in a similar manner (Mankiw and Shapiro, 1986). Traditionally, forecasting regressions have been evaluated in time-series frameworks. However, with the increased availability of data, in particular international financial and macroeconomic data, it becomes natural to extend the single time-series framework to a panel data setting.
It has gradually been discovered that the apparently simple
linear regression model most often used for evaluating
predictability in fact raises some very tough econometric issues.
The high degree of persistence found in many predictor variables,
such as the earnings- or dividend-price ratios in the prototypical
stock return forecasting regression, is at the root of most
econometric problems associated with predictive regressions. The
near persistence of the regressors, coupled with a strong
contemporaneous correlation between the innovations in the
regressor and the regressand, causes standard OLS estimates to be
inefficient and normal ![]() tests to have the wrong size. If the regressor is a
unit-root process, the predictive regression becomes a
cointegrating relationship and well established methods for dealing
with endogenous regressors can be used. However, if the regressor
is not a pure unit-root process, but rather a so called
near-unit-root process, standard cointegration methods can yield
misleading results (c.f. Cavanagh et al., 1995 and Elliot,
1998).2
tests to have the wrong size. If the regressor is a
unit-root process, the predictive regression becomes a
cointegrating relationship and well established methods for dealing
with endogenous regressors can be used. However, if the regressor
is not a pure unit-root process, but rather a so called
near-unit-root process, standard cointegration methods can yield
misleading results (c.f. Cavanagh et al., 1995 and Elliot,
1998).2
In this paper, I analyze econometric inference in predictive regressions in a panel data setting, when the regressors are nearly persistent and endogenous. The main contributions are the derivations of the asymptotic properties of pooled estimators in forecasting equations and the proposal of new procedures to deal with the bias effects arising from the persistence and endogeneity of the regressors. New results for controlling for the effects of common factors in panels are also derived. The methods developed in the paper are used to test for stock-return predictability in a panel of international stock returns.
By pooling the data, the econometric issues encountered in the time-series case can, to some extent, be dealt with more easily. Intuitively, persistent regressors cause no problems when they are exogenous. When pooling the data, independent cross-sectional information dilutes the endogeneity effects, and thus potentially alleviates the bias effects seen in the time-series case. This intuition holds when no individual intercepts, or fixed effects, are allowed in the specification. In this case, the standard pooled estimator has an asymptotically normal distribution; the summing up over the cross-section in the pooled estimator eliminates the usual near unit-root asymptotic distributions found in the time-series case. It follows immediately that test statistics have standard distributions and normal inference can be performed.
However, when fixed effects are allowed for, the asymptotic
properties of the pooled estimator change. The time-series
demeaning of the data, which is implicit in a fixed effects
estimation, causes the fixed effects estimator to suffer from a
second order bias that invalidates inference from standard
test-statistics. To correct for this bias, I develop an estimator
based on the idea of recursive demeaning (e.g. Moon and Phillips,
2000, and Sul et al., 2005). When demeaning each time-series in the
panel, information after time ![]() is used to form the time
is used to form the time ![]() regressor; this induces a correlation
between the lagged value of the demeaned regressor, used in the
estimation of the predictive regression, and the error term in the
forecasting equation, which gives rise to the second order bias in
the fixed effects estimator. By using information only up till time
regressor; this induces a correlation
between the lagged value of the demeaned regressor, used in the
estimation of the predictive regression, and the error term in the
forecasting equation, which gives rise to the second order bias in
the fixed effects estimator. By using information only up till time
![]() in the demeaning of
the regressor and only information after time
in the demeaning of
the regressor and only information after time ![]() in the demeaning of the dependent
variable, the distortive effects arising from standard demeaning
are eliminated. The estimator based on recursively demeaned data is
shown to have an asymptotically normal distribution and standard
inference can again be performed.
in the demeaning of the dependent
variable, the distortive effects arising from standard demeaning
are eliminated. The estimator based on recursively demeaned data is
shown to have an asymptotically normal distribution and standard
inference can again be performed.
Although the estimator based on recursive demeaning is asymptotically normally distributed, it gives up some efficiency by disregarding parts of the data in the demeaning process. An alternative approach to control for the bias in the standard fixed effects estimator is to directly estimate the bias term and subtract it from the original estimator. Monte Carlo simulations show that such a correction works very well in practice, and produces unbiased estimators as well as correctly sized tests with good power. This bias corrected fixed effects estimator thus provides a simple and relatively efficient way of dealing with the bias and size distortions induced by the near persistence and endogeneity of the forecasting variables.
The overall conclusion from the theoretical results and the supporting Monte Carlo simulations is that, in the typical panel data case, persistent and endogenous regressors will cause standard inference to be biased. In the time-series case, this result is well established and the results in this paper show that equal caution is required when working with panel data. However, unlike the time-series case, bias correction methods can be implemented in a relatively straightforward manner and normally distributed test-statistics can be achieved. Unbiased point estimates are also easily calculated, in contrast to the time-series case where the popular Bonferroni bound methods lead to correctly sized tests but not unique unbiased point estimates (Cavanagh et al., 1995, and Campbell and Yogo, 2005).
Another econometric issue that arises in the analysis of panels of financial or macroeconomic data is the potential presence of common factors. The standard panel data assumption of cross-sectional independence is often too restrictive, and I show how the framework in this paper can be extended to a setting where common factors are present in the data. These methods follow the work of Pesaran (2006) and extend his methods to a setting with nearly integrated regressors.
As an illustration of the methods derived in this paper, I consider the classical issue of stock return predictability. I use an international panel of returns from 18 different stock indices and the corresponding dividend- and earnings-price ratios, as well as the book-to-market values. The empirical results from the forecasting regressions with stock returns illustrate well the theoretical results derived in the paper. Based on the results from the standard fixed effects estimator, the evidence in favour of return predictability is very strong, using either of the three predictor variables. However, when using the robust methods developed here, the evidence disappears almost completely.
The rest of the paper is organized as follows. Section 2 describes the model, while Sections 3 and 4 derive the main asymptotic properties of the pooled estimators. The finite sample properties of the procedures developed in this paper are analyzed through Monte Carlo experiments in Section 5. Some generalizations of the econometric model are considered in Section 6, and Section 7 contains the empirical application to stock return predictability. Section 8 concludes and technical proofs are found in the appendix.
Following the work of Phillips and Moon (1999), results for the
panel estimators are derived using sequential limits, which usually
implies first keeping the cross-sectional dimension, ![]() , fixed and letting the time-series
dimension,
, fixed and letting the time-series
dimension, ![]() , go to
infinity, and then letting
, go to
infinity, and then letting ![]() go to infinity. Such sequential convergence is
denoted
go to infinity. Such sequential convergence is
denoted
![]() .
Subject to potential rate restrictions, such as
.
Subject to potential rate restrictions, such as
![]() , these
results can generally be shown to hold as
, these
results can generally be shown to hold as ![]() and
and ![]() go to infinity jointly, denoted
go to infinity jointly, denoted
![]() , by showing that
the sufficient conditions in Phillips and Moon (1999) are
satisfied; proofs of such joint convergence are not pursued here,
however. Otherwise, standard notation is used.
, by showing that
the sufficient conditions in Phillips and Moon (1999) are
satisfied; proofs of such joint convergence are not pursued here,
however. Otherwise, standard notation is used.
![]() denotes a Brownian motion with covariance matrix
denotes a Brownian motion with covariance matrix ![]() ,
,
![]() signifies
weak convergence, and
signifies
weak convergence, and
![]() denotes
convergence in probability.
denotes
convergence in probability.
2 Model and assumptions
2.1 The data generating process
Consider a panel model with dependent variables ![]() ,
, ![]() ,
, ![]() , and the corresponding
vector of regressors,
, and the corresponding
vector of regressors, ![]() , where
, where ![]() is an
is an ![]() vector. The behavior of
vector. The behavior of ![]() and
and ![]() are modelled as follows,
are modelled as follows,
where
This model is a panel analogue of the time-series models studied by Mankiw and Shapiro (1986), Cavanagh et al. (1995), Stambaugh (1999), Jansson and Moreira (2004), Lewellen (2004), and Campbell and Yogo (2005).
1.
![]()
2.
![]() where
where
![]() and
and
![]() .
.
3.
![]() ,
,
![]() and
and
![]()
4.
![]() for all
for all ![]() and
and
![]() .
.
Assumption1 specifies that the innovation processes follow a martingale
difference sequence (mds) with finite fourth moments. The regressor
can be endogenous in the sense that ![]() and
and ![]() may be contemporaneously correlated. The
common factors,
may be contemporaneously correlated. The
common factors, ![]() ,
are assumed independent of the specific error components, and
Assumption 2 specifies
that the factor loadings are distributed independently of other
random variables in the model. At the expense of some extra
notation, the model could allow for a more general time-series
structure in the innovation process
,
are assumed independent of the specific error components, and
Assumption 2 specifies
that the factor loadings are distributed independently of other
random variables in the model. At the expense of some extra
notation, the model could allow for a more general time-series
structure in the innovation process ![]() ; the results in the paper would carry through
with virtually no changes. The mds assumption for the errors in the
dependent variables,
; the results in the paper would carry through
with virtually no changes. The mds assumption for the errors in the
dependent variables, ![]() ,
is standard in predictive regressions, and is often based on some
orthogonality condition from an underlying rational expectations
model. For instance, in financial forecasting regressions the mds
assumption is motivated by the efficient markets hypothesis. The
rank condition in Assumption 3 is used for
identification in the estimation procedures that control for the
common factors. It essentially states that all information
regarding the common factors in the data can potentially be
recovered from the innovation processes of the regressors. This
condition turns out to be less restrictive than it seems, since it
is the factors in the regressor errors that play the key role in
the asymptotic properties of the pooled estimators. That is, a
common factor that is only present in the dependent variable will
not affect the analysis in any fundamental way. This is analyzed in
more detail later in the paper.
,
is standard in predictive regressions, and is often based on some
orthogonality condition from an underlying rational expectations
model. For instance, in financial forecasting regressions the mds
assumption is motivated by the efficient markets hypothesis. The
rank condition in Assumption 3 is used for
identification in the estimation procedures that control for the
common factors. It essentially states that all information
regarding the common factors in the data can potentially be
recovered from the innovation processes of the regressors. This
condition turns out to be less restrictive than it seems, since it
is the factors in the regressor errors that play the key role in
the asymptotic properties of the pooled estimators. That is, a
common factor that is only present in the dependent variable will
not affect the analysis in any fundamental way. This is analyzed in
more detail later in the paper.
It is also assumed that all the time-series in the panel share
the same auto-regressive root, ![]() . This assumption is imposed due to the
presence of the common factors in the regressors, which would make
it difficult to allow for heterogenous persistence. The effects of
relaxing this assumption are briefly discussed later in the paper.
Given a common auto-regressive root, the
. This assumption is imposed due to the
presence of the common factors in the regressors, which would make
it difficult to allow for heterogenous persistence. The effects of
relaxing this assumption are briefly discussed later in the paper.
Given a common auto-regressive root, the ![]() process can be expressed in a
convenient component form,
process can be expressed in a
convenient component form,
| (3) |
Under Assumption 1,
by standard arguments (Phillips and Solo, 1992),
![]() , where
, where
![]() denote a
denote a ![]() dimensional Brownian motion. Further, by the
results in Phillips (1987,1988), it follows that as
dimensional Brownian motion. Further, by the
results in Phillips (1987,1988), it follows that as
![]() ,
,
![]() , where
, where
![]() and
and
![]() . Analogous results hold for the time-series demeaned data,
. Analogous results hold for the time-series demeaned data,
![]() ,
with
,
with ![]() replaced by
replaced by
![]() ; when there
is no risk of confusion, the dependence of
; when there
is no risk of confusion, the dependence of
![]() and
and
![]() on
on ![]() will be suppressed. The following
lemma summarizes the key asymptotic results used in the paper.
will be suppressed. The following
lemma summarizes the key asymptotic results used in the paper.
(a)
![]() where
where
![$ \Phi_{ux}\equiv E\left[ \left( \int_{0}^{1}dB_{1,i}J_{i}\right) \left( \int_{0}^{1}dB_{1,i} J_{i}\right) ^{\prime}\right] $](img69.gif) ,
,
![$ \Phi_{uz}\equiv\Gamma^{\prime}E\left[ \left. \left( \int_{0}^{1}dB_{1,i}J_{f}\right) \left( \int_{0}^{1} dB_{1,i}J_{f}\right) ^{\prime}\right\vert \mathcal{C}\right] \Gamma$](img70.gif) , and
, and
![]() is the
is the
![]() field generated
by
field generated
by
![]() .
.
(b)
![]()
(c)
![]() where
where
![]() and
and
![]()
(d)
![]()
(e)
![]()
(f)
![]() where
where
![]() and
and
![]()
3 Cross-sectional independence
3.1 The standard pooled estimator
To understand the basic properties of the pooled estimator of
![]() , it is
instructive to start with analyzing the case when there are no
common factors in the data. That is, let
, it is
instructive to start with analyzing the case when there are no
common factors in the data. That is, let
![]() and
and
![]() , for
all
, for
all ![]() . To estimate the
parameter
. To estimate the
parameter ![]() consider
first the traditional pooled estimator when there are no individual
effects, i.e. when
consider
first the traditional pooled estimator when there are no individual
effects, i.e. when
![]() for
all
for
all ![]() .3 The pooled estimator is given by
.3 The pooled estimator is given by
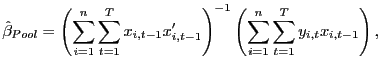
|
(4) |
and the following theorem gives its asymptotic properties.
The pooled estimator of ![]() is thus asymptotically normally distributed and
the limiting distribution depends on
is thus asymptotically normally distributed and
the limiting distribution depends on
![]() and
and
![]() . To perform
inference, estimates of these parameters are required. Let
. To perform
inference, estimates of these parameters are required. Let
![]() ,
,
![]() , and
, and
![]() . The estimator
. The estimator
![]() is thus
the panel equivalent of HAC estimators for long-run variances.
is thus
the panel equivalent of HAC estimators for long-run variances.
Standard tests can now be performed. For instance, the null
hypothesis
![]() ,
for some
,
for some ![]() , can be
tested using a
, can be
tested using a ![]() test.
Let
test.
Let
![]() . Using the results derived above, it follows easily that
under the null-hypothesis,
. Using the results derived above, it follows easily that
under the null-hypothesis,
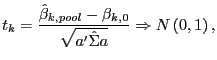
|
(6) |
in sequential limits, as
Thus, when there are no fixed effects in the pooled regression, inference in the panel case becomes trivial since the pooled estimator is asymptotically normally distributed. This is in contrast with the time-series case where the OLS estimator has a non-normal asymptotic distribution which depends on unknown nuisance parameters.
3.2 Fixed effects
In the above analysis, the individual intercepts
![]() were all
assumed to be equal to zero. This section considers the effects on
the pooled estimator when the
were all
assumed to be equal to zero. This section considers the effects on
the pooled estimator when the
![]() are no
longer zero and are allowed to vary across the panel.
are no
longer zero and are allowed to vary across the panel.
Let
![]() and
and
![]() denote the time-series demeaned data. That is,
denote the time-series demeaned data. That is,
![]() and
and
![]() .
The fixed effects pooled estimator, which allows for individual
intercepts, is then given by
.
The fixed effects pooled estimator, which allows for individual
intercepts, is then given by
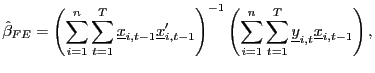
|
(7) |
and
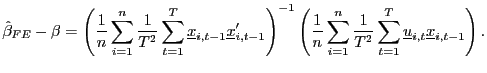
|
(8) |
Clearly, the estimator is still consistent. Its asymptotic distribution, however, will be affected by the demeaning. For fixed
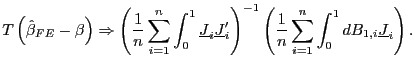
|
(9) |
Let
![$\displaystyle E\left[ \int_{0}^{1}dB_{1,i}\underline{J}_{i}\right]$](img111.gif)
|
![$\displaystyle =E\left[ \int _{0}^{1}dB_{1,i}\left( r\right) J_{i}\left( r\right) -\int_{0}^{1} dB_{1,i}\left( s\right) \int_{0}^{1}J_{i}\left( r\right) dr\right]$](img112.gif)
|
(10) |
![$\displaystyle =-\int_{0}^{1}\int_{0}^{1}\int_{0}^{r}e^{\left( r-q\right) C}E\left[ dB_{1,i}\left( s\right) dB_{2,i}\left( q\right) \right] dsdr$](img113.gif)
|
||
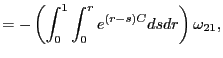
|
(11) |
which is different from zero whenever
and the estimator suffers from a second order bias from the demeaning process.
3.3 Recursive demeaning
The second order bias arises because the demeaning process
induces a correlation between the innovation processes ![]() and the demeaned regressors
and the demeaned regressors
![]() .4 Intuitively,
.4 Intuitively, ![]() and
and
![]() are correlated because, in the demeaning of
are correlated because, in the demeaning of ![]() , information available
after time
, information available
after time ![]() is used.
At the expense of some efficiency, one solution is therefore to use
recursive demeaning of
is used.
At the expense of some efficiency, one solution is therefore to use
recursive demeaning of ![]() and
and ![]() (e.g. Moon and Phillips, 2000, and Sul et al.,
2005). That is, define
(e.g. Moon and Phillips, 2000, and Sul et al.,
2005). That is, define
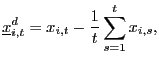
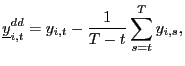 and
and 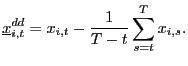
|
(13) |
The process
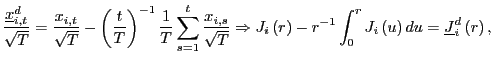
|
(14) |
and
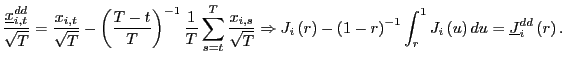
|
(15) |
Consider the following pooled estimator, using the recursively demeaned data,
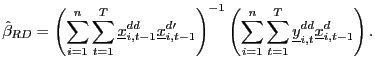
|
(16) |
To perform inference, let
![]() ,
,
![]() , and
, and
![]() . The
. The ![]() test and
Wald-test based on
test and
Wald-test based on
![]() and
and
![]() will satisfy the
usual properties and the results follow in the same manner as
above.
will satisfy the
usual properties and the results follow in the same manner as
above.
3.4 Direct bias correction
The estimator
![]() gives
up some efficiency through the recursive demeaning process. A more
efficient approach would be to directly estimate the bias term in
(12) and subtract it
from the standard pooled estimator. A simple biased corrected
estimator is given by
gives
up some efficiency through the recursive demeaning process. A more
efficient approach would be to directly estimate the bias term in
(12) and subtract it
from the standard pooled estimator. A simple biased corrected
estimator is given by
Provided that
where
An estimate of
![]() is easy to
obtain by averaging the estimates of
is easy to
obtain by averaging the estimates of
![]() obtained
from time-series regressions. As discussed below, it is possible to
consistently estimate
obtained
from time-series regressions. As discussed below, it is possible to
consistently estimate ![]() using panel data, unlike in the time-series case.
using panel data, unlike in the time-series case.
3.5 Estimation of 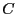
The estimator proposed above relies on an estimate of
![]() . Moon and Phillips
(2000) show how
. Moon and Phillips
(2000) show how ![]() can
be consistently estimated in equation (2) when
can
be consistently estimated in equation (2) when
![]() is a scalar. The
diagonal of
is a scalar. The
diagonal of ![]() can, of
course, be estimated by the individual univariate estimates; thus,
if one restricts
can, of
course, be estimated by the individual univariate estimates; thus,
if one restricts ![]() to be
diagonal, then an estimate of a matrix
to be
diagonal, then an estimate of a matrix ![]() can be obtained using the methods
of Moon and Phillips (2000).
can be obtained using the methods
of Moon and Phillips (2000).
Consider the case of a scalar ![]() , and assume that
, and assume that ![]() is generated according to equation (2). Noting that
is generated according to equation (2). Noting that
![]() it is
natural to consider estimators of the form
it is
natural to consider estimators of the form
![]() . The pooled
estimator of
. The pooled
estimator of ![]() is given
by,
is given
by,
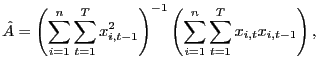
It is beyond the scope of this paper to formally consider the
effects of common factors in the data on the estimator ![]() . However, Monte Carlo
simulations not reported in the paper indicate that it also remains
unbiased in the presence of common factors.
. However, Monte Carlo
simulations not reported in the paper indicate that it also remains
unbiased in the presence of common factors.
4 Cross-sectional dependence
4.1 The effects of common factors
I now return to the general setup with common factors in the data. The following theorem summarizes the asymptotic properties of the standard pooled estimator, as well as the fixed effects estimator, when there are common factors.
Thus, in the presence of the general factor structure outlined in Assumptions 1 and 2, the standard pooled estimator exhibits a non-standard limiting distribution, although it is still consistent; standard tests can therefore not be used. Similarly, the limiting behavior of the fixed effects estimator is determined by the bias term arising from the time-series demeaning of the data, as well as an additional term that stems from the common factors in the data.
4.2 Robust estimators
Based on the methods of Pesaran (2006), I propose an estimator that is more robust to cross-sectional dependence in the data. Write the model in matrix form,
| (22) | ||
| (23) |
where
The idea of Pesaran (2006) is to project the data onto the space
orthogonal to the common factors, thereby removing the cross
sectional dependence from the data used in the estimation. However,
since the factors in ![]() are not observed in practice, an indirect approach is required.
are not observed in practice, an indirect approach is required.
Consider the following estimator of ![]() ,
,
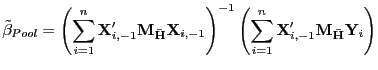
|
(24) |
where
Here,
The estimator
To form a better understanding behind the functioning of the
above estimator, let
![\begin{displaymath}\mathbf{Q}=\left( \begin{array}[c]{cc} \mathbf{f}\Gamma & \mathbf{Z}_{-1}\Gamma \end{array}\right) \end{displaymath}](img177.gif) , and
, and
![]() . Also, let
. Also, let
![\begin{displaymath}\mathbf{G=}\left( \begin{array}[c]{cc} \mathbf{f} & \mathbf{Z}_{-1} \end{array}\right) \end{displaymath}](img179.gif) and
and
![]() Observe that,
Observe that,
![$\displaystyle \sqrt{n}T\left( \tilde{\beta}_{Pool}-\beta\right) =\left( \frac{1}{n} \sum_{i=1}^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{\bar{H}} }\mathbf{X}_{i,-1}}{T^{2}}\right) ^{-1}\left[ \left( \frac{1}{\sqrt{n}} \sum_{i=1}^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{\bar{H}} }\mathbf{f}\gamma_{i}}{T}\right) +\left( \frac{1}{\sqrt{n}}\sum_{i=1} ^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{\bar{H}}} \mathbf{u}_{i}}{T}\right) \right] .$](img181.gif)
|
(27) |
Since
![$\displaystyle \sqrt{n}T\left( \tilde{\beta}_{Pool}-\beta\right) \Rightarrow MN\left( 0,\Omega_{xx}^{-1}E\left[ \left. \left( \int_{0}^{1}J_{i\cdot f\Gamma }dB_{1,i}\right) \left( \int_{0}^{1}J_{i\cdot f\Gamma}dB_{1,i}\right) ^{\prime}\right\vert \mathcal{C}\right] \Omega_{xx}^{-1}\right) ,$](img189.gif)
|
(28) |
where
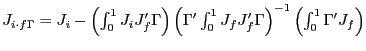 is the residual from the orthogonal projection of
is the residual from the orthogonal projection of
The estimator
![]() thus achieves a
thus achieves a
![]() convergence
rate and an asymptotic mixed normal distribution. The mixed
normality in this case arises from the common factors, which leads
to a mixed normal rather than a normal distribution as in the case
above with no common factors; a similar result is also noted in Jin
(2004). Andrews (2005) provides an extensive discussion on
convergence with common shocks. This theorem also extends the
results for stationary data in Pesaran (2006) to the nearly
integrated case, although using a somewhat different definition of
the
convergence
rate and an asymptotic mixed normal distribution. The mixed
normality in this case arises from the common factors, which leads
to a mixed normal rather than a normal distribution as in the case
above with no common factors; a similar result is also noted in Jin
(2004). Andrews (2005) provides an extensive discussion on
convergence with common shocks. This theorem also extends the
results for stationary data in Pesaran (2006) to the nearly
integrated case, although using a somewhat different definition of
the
![]() matrix.
Allowing for fixed effects in the arguments, it is easy to show the
following result.
matrix.
Allowing for fixed effects in the arguments, it is easy to show the
following result.
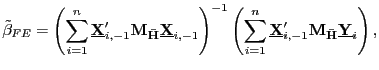
|
(29) |
and
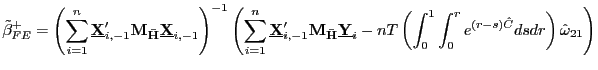
|
(30) |
where
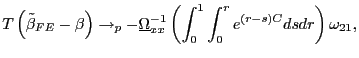
|
(31) |
and
![$\displaystyle \sqrt{n}T\left( \tilde{\beta}_{FE}^{+}-\beta\right) \Rightarrow MN\left( 0,\underline{\Omega}_{xx}^{-1}E\left[ \left. \left( \int_{0}^{1} \underline{J}_{i\cdot f\Gamma}dB_{1,i}\right) \left( \int_{0}^{1} \underline{J}_{i\cdot f\Gamma}dB_{1,i}\right) ^{\prime}\right\vert \mathcal{C}\right] \underline{\Omega}_{xx}^{-1}\right) .$](img198.gif)
|
(32) |
The fixed effects transformation thus has an identical bias
effect on the estimator that controls for common factors, and can
also be corrected in an identical manner. Similarly, it could also
be shown that using recursive demeaning on the data projected onto
the cross-sectional means would be asymptotically mixed normally
distributed, although these results are omitted here.
![]() and
and
![]() thus provide pooled estimators for predictive regressions that are
asymptotically mixed normally distributed in the presence of common
factors and with the allowance for fixed effects. Standard
thus provide pooled estimators for predictive regressions that are
asymptotically mixed normally distributed in the presence of common
factors and with the allowance for fixed effects. Standard
![]() tests and Wald-tests
can therefore be used; the variance-covariance matrix of
tests and Wald-tests
can therefore be used; the variance-covariance matrix of
![]() or
or
![]() can be estimated in an analogous manner as described above for the
case with no common factors, by simply using the defactored data.
The practical implementation of
can be estimated in an analogous manner as described above for the
case with no common factors, by simply using the defactored data.
The practical implementation of
![]() , or
, or
![]() ,
is thus very simple: Premultiply the data by
,
is thus very simple: Premultiply the data by
![]() , and use the resulting
variables in the original procedures for
, and use the resulting
variables in the original procedures for
![]() and
and
![]() .
Note that this also automatically facilitates the correct
estimation of
.
Note that this also automatically facilitates the correct
estimation of
![]() , which now
represents the correlation between the cross-sectionally
independent errors,
, which now
represents the correlation between the cross-sectionally
independent errors, ![]() and
and ![]() , rather than
the correlation between the total innovation processes in the
regressors and regressand.
, rather than
the correlation between the total innovation processes in the
regressors and regressand.
4.3 More general factor structures
The key assumption in deriving the results in Theorem 4 was the rank condition in Assumption 3. It essentially allows for the whole factor structure to be revealed through the innovations in the regressor variables alone. While this is a convenient assumption, since it does not require first stage estimates of the innovations in the regressand, it is also potentially limiting since it effectively restricts the factors in the dependent variable to be a subset of the factors in the regressors. However, it is easy to show that additional factors in the regressand do not fundamentally alter the above results.
Consider the following model, which is a generalization of the original model in equations (1) and (2),
where
![$\displaystyle \sqrt{n}T\left( \tilde{\beta}_{Pool}-\beta\right) \Rightarrow MN\left( 0,\Omega_{xx}^{-1}E\left[ \left. \left( \int_{0}^{1}J_{i\cdot f\Gamma }\left( dB_{1,i}+\eta^{\prime}dB_{g}\right) \right) \left( \int_{0} ^{1}J_{i\cdot f\Gamma}\left( dB_{1,i}+\eta^{\prime}dB_{g}\right) \right) ^{\prime}\right\vert \mathcal{C}\right] \Omega_{xx}^{-1}\right) ,$](img207.gif)
|
(35) |
where
The limiting distribution changes but remains mixed normal and inference can be performed in an identical manner using standard test-statistics. The procedures derived in the previous subsection are thus robust to additional factors in the dependent variable.
5 Finite sample evidence
5.1 No cross-sectional dependence
To evaluate the small sample properties of the panel data
estimators proposed in this paper, a Monte Carlo study is
performed. In the first experiment, the properties of the point
estimates are considered. Equations (1) and (2) are simulated
for the case with a single regressor. The innovations
![]() are drawn from normal
distributions with mean zero, unit variance, and correlations
are drawn from normal
distributions with mean zero, unit variance, and correlations
![]() and
and ![]() ; there is no
cross-sectional dependence. The slope parameter
; there is no
cross-sectional dependence. The slope parameter ![]() is set equal to
is set equal to ![]() and the local-to-unity parameter
and the local-to-unity parameter
![]() is set to
is set to
![]() . The sample size
is given by
. The sample size
is given by ![]()
![]() . The small value
of
. The small value
of ![]() is chosen in
order to reflect the fact that most forecasting regressions are
used to test a null of
is chosen in
order to reflect the fact that most forecasting regressions are
used to test a null of ![]() , and any plausible alternative is often close
to zero. The intercepts
, and any plausible alternative is often close
to zero. The intercepts
![]() are set
equal to zero but individual effects are still fitted for all the
estimators, except the standard pooled one, in order to evaluate
the second-order bias effects arising from demeaning. All results
are based on 10,000 repetitions.
are set
equal to zero but individual effects are still fitted for all the
estimators, except the standard pooled one, in order to evaluate
the second-order bias effects arising from demeaning. All results
are based on 10,000 repetitions.
Four different estimators are considered: the pooled estimator
with no fixed effects,
![]() ,
the fixed effects estimator using standard demeaning,
,
the fixed effects estimator using standard demeaning,
![]() , the
recursively demeaned pooled estimator,
, the
recursively demeaned pooled estimator,
![]() ,
and the bias corrected estimator
,
and the bias corrected estimator
![]() .
The bias correction in the estimator
.
The bias correction in the estimator
![]() is estimated by
is estimated by
![]() , where
, where ![]() is the panel estimate of the local-to-unity parameter and
is the panel estimate of the local-to-unity parameter and
![]() is
estimated as
is
estimated as
![]() with
with
![]() the
covariance between the residuals from a time-series estimation of
equation (1) and the
quasi-differenced regressors,
the
covariance between the residuals from a time-series estimation of
equation (1) and the
quasi-differenced regressors,
![]() . In general, the standard
pooled estimator does not work well when the
. In general, the standard
pooled estimator does not work well when the
![]() differ
across
differ
across ![]() , but is used
as a comparison here.
, but is used
as a comparison here.
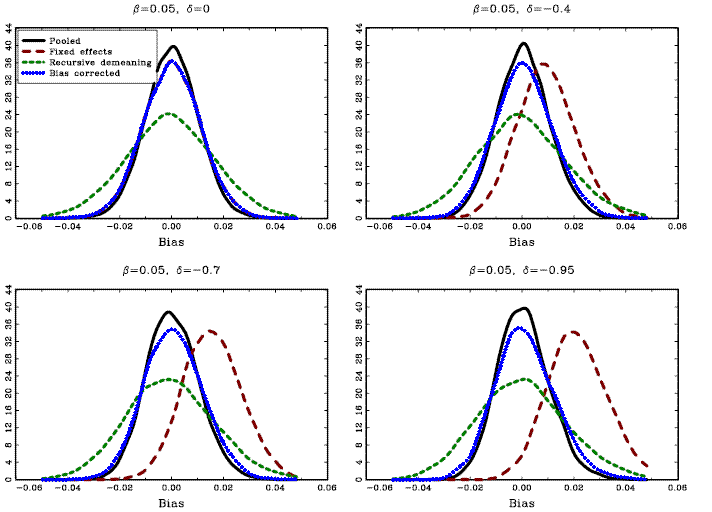
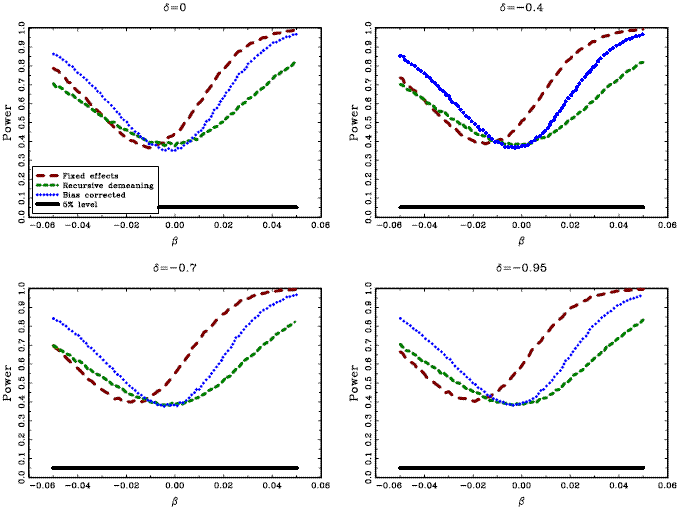
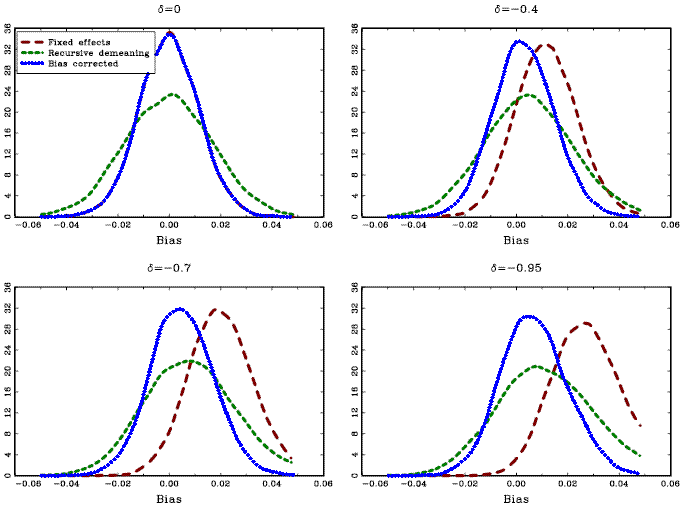
The results are shown in Figure 1. All estimators,
except
![]() , are
virtually unbiased. The estimator
, are
virtually unbiased. The estimator
![]() ,
which uses standard demeaning to account for individual effects,
exhibits a rather substantial bias when the absolute value of the
correlation
,
which uses standard demeaning to account for individual effects,
exhibits a rather substantial bias when the absolute value of the
correlation ![]() is
large. The recursively demeaned estimator,
is
large. The recursively demeaned estimator,
![]() ,
suffers from a lack of efficiency, but it is well centered around
the true value.
,
suffers from a lack of efficiency, but it is well centered around
the true value.
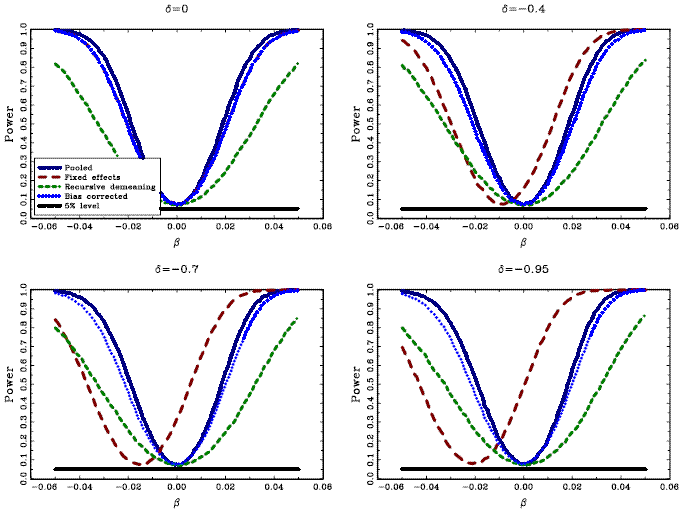
The second part of the Monte Carlo study concerns the size and
power of the pooled ![]() tests.
The same setup as above is used but, in order to calculate the
power of the tests, the slope coefficient
tests.
The same setup as above is used but, in order to calculate the
power of the tests, the slope coefficient ![]() now varies between
now varies between ![]() and
and ![]() . Figure 2 shows the
average rejection rates of the
. Figure 2 shows the
average rejection rates of the ![]() percent two-sided
percent two-sided ![]() tests, evaluating a null of
tests, evaluating a null of ![]() ; that is, the power curves of
the tests. Panel A in Table 1 shows the
average sizes of the nominal
; that is, the power curves of
the tests. Panel A in Table 1 shows the
average sizes of the nominal ![]() percent tests under the null hypothesis of
percent tests under the null hypothesis of
![]() for the two
sided
for the two
sided ![]() tests corresponding to
the four different estimators considered above. Again, the results
are based on 10,000 repetitions.
tests corresponding to
the four different estimators considered above. Again, the results
are based on 10,000 repetitions.
Apart from the test based on the standard fixed effects
estimator, all tests perform well in terms of size, although they
all tend to over reject the null hypothesis somewhat. Table
1 and the power
curves in Figure 2
clearly show the effects of the second order bias in the fixed
effects estimator. The three other tests all exhibit decent power
properties although the test based on
![]() has
lower power than the bias corrected estimator.
has
lower power than the bias corrected estimator.
In summary, the simulation evidence shows the importance of controlling for the second order bias arising from fitting individual intercepts in the pooled regression; the estimator based on recursive demeaning appears to do well and results in test-statistics with correct size and decent power properties. The bias correction of the fixed effects estimator also appears to work well, producing nearly unbiased results and correctly sized tests with good power. Overall, the simulations confirm the analytical results previously derived.
5.2 Common factors
In this section, I repeat the Monte Carlo experiments above,
with the exception that there is now a common factor in the
innovations. In particular, equations (1) and (2) are now
simulated with a single regressor and a single common factor
![]() , drawn from a
standard normal distribution. The factor loadings,
, drawn from a
standard normal distribution. The factor loadings,
![]() and
and
![]() , are also
normally distributed with means of minus one and plus one,
respectively, and standard deviations equal to
, are also
normally distributed with means of minus one and plus one,
respectively, and standard deviations equal to ![]() i
i![]() n both cases. The
innovations in the returns and regressor processes are formed as
and
n both cases. The
innovations in the returns and regressor processes are formed as
and
![]() ,
respectively, where
,
respectively, where
![]() are drawn from standard
normal distributions; the scaling by
are drawn from standard
normal distributions; the scaling by ![]() is performed in order to achieve an
approximate unit variance in the innovations which enables easier
comparison with the cross-sectionally independent case. As before,
the correlation between
is performed in order to achieve an
approximate unit variance in the innovations which enables easier
comparison with the cross-sectionally independent case. As before,
the correlation between ![]() and
and ![]() is set to
is set to
![]() and
and ![]() . Note that
. Note that
![]() no longer
represents the overall correlation between the innovations, but
rather that between the cross-sectionally independent parts of the
innovations. In addition, I allow
no longer
represents the overall correlation between the innovations, but
rather that between the cross-sectionally independent parts of the
innovations. In addition, I allow
![]() to vary
across
to vary
across ![]() according to
a normal distribution with mean and standard deviation equal to
according to
a normal distribution with mean and standard deviation equal to
![]() . Otherwise, the
setup is identical to that used in the case with no common factors.
Again, all results are based on
. Otherwise, the
setup is identical to that used in the case with no common factors.
Again, all results are based on ![]() repetitions.
repetitions.
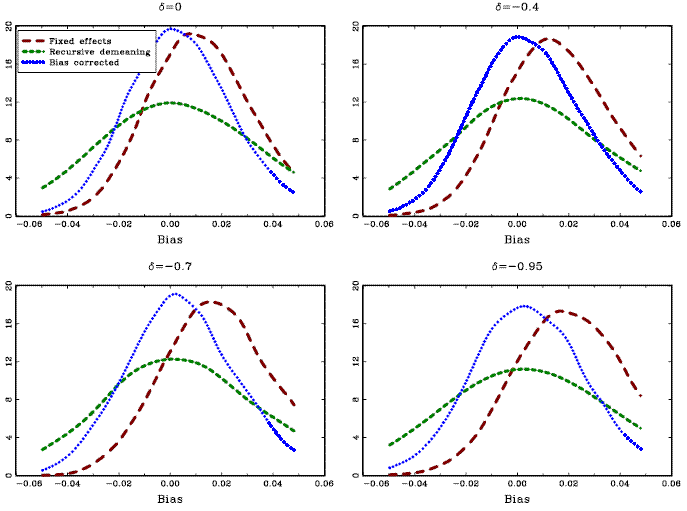
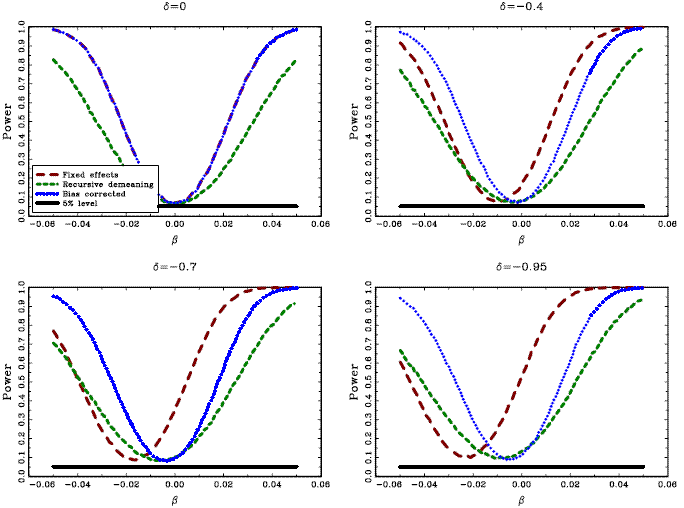
The results are shown in Panels B and C of Table 1 and in Figures
3-6. Panel B in
Table 1 and Figures
3 and 4 show the
outcomes of the Monte Carlo experiments when the model generated
with common factors is estimated using the standard estimators
![]() , and
, and
![]() ,
that do not control for cross-sectional dependence; since
,
that do not control for cross-sectional dependence; since
![]() now varies
across the panel, the standard pooled estimator without fixed
effects is not considered. Figure 3 shows that
now varies
across the panel, the standard pooled estimator without fixed
effects is not considered. Figure 3 shows that
![]() and
and
![]() are still fairly unbiased, in accordance with the asymptotic result
in Theorem 3, but
they are much more variable than in the case with no common factors
and exhibit a non-normal distribution. The real downside from not
controlling for the cross-sectional dependence is seen in the size
of the
are still fairly unbiased, in accordance with the asymptotic result
in Theorem 3, but
they are much more variable than in the case with no common factors
and exhibit a non-normal distribution. The real downside from not
controlling for the cross-sectional dependence is seen in the size
of the ![]() tests
displayed in Panel B of Table 1 and in the power
curves in Figure 3.
It is clear that when the common factors are ignored in the
estimation process, the actual size of the corresponding
tests
displayed in Panel B of Table 1 and in the power
curves in Figure 3.
It is clear that when the common factors are ignored in the
estimation process, the actual size of the corresponding
![]() tests is very far from
the nominal size of
tests is very far from
the nominal size of ![]() percent, with rejection rates between
percent, with rejection rates between ![]() and
and ![]() percent under the null.
percent under the null.
Panel C in Table 1
and Figures 5 and
6 show the same
results for the estimators
![]() , and
, and
![]() , which control for the common
factors;
, which control for the common
factors;
![]() represents the estimator with recursive demeaning using defactored
data. The distributions of the point estimates, as seen in Figure
5, are now much
better behaved and normal looking, as well as much more peaked than
in Figure 3. The
represents the estimator with recursive demeaning using defactored
data. The distributions of the point estimates, as seen in Figure
5, are now much
better behaved and normal looking, as well as much more peaked than
in Figure 3. The
![]() tests also possess
better size and power properties, although there is a slight
tendency to over-reject when
tests also possess
better size and power properties, although there is a slight
tendency to over-reject when ![]() is large in absolute numbers. As before, the
standard fixed effects estimator exhibits a finite sample bias and
extremely poor size properties.
is large in absolute numbers. As before, the
standard fixed effects estimator exhibits a finite sample bias and
extremely poor size properties.
In summary, the estimator
![]() ,
and
,
and
![]() , which were designed to control
for cross-sectional dependence, appear to work reasonably well in
small samples, although there is a small bias and over-rejection
when
, which were designed to control
for cross-sectional dependence, appear to work reasonably well in
small samples, although there is a small bias and over-rejection
when ![]() is large.
Compared to the estimators that do not take the common factors into
account, there is a huge improvement, however.
is large.
Compared to the estimators that do not take the common factors into
account, there is a huge improvement, however.
6 Heterogenous auto-regressive roots
One dimension along which the model in this paper can be
generalized is to allow the auto-regressive root ![]() to vary across
to vary across ![]() , such that each time-series
, such that each time-series
![]() possesses a root
possesses a root
![]() , where
, where
![]() may be modelled
as a random variable. Most of the analysis will carry through in
this setting, with the limiting expressions being expectations also
over the
may be modelled
as a random variable. Most of the analysis will carry through in
this setting, with the limiting expressions being expectations also
over the ![]() .
Problems arise in the bias correcting exercises, however. For
instance, the bias-corrected fixed effects estimator,
.
Problems arise in the bias correcting exercises, however. For
instance, the bias-corrected fixed effects estimator,
![]() ,
relies on an estimate of
,
relies on an estimate of ![]() ,
but when the
,
but when the ![]() are no
longer identical, panel methods cannot be used to form estimates of
the individual
are no
longer identical, panel methods cannot be used to form estimates of
the individual ![]() .
In particular, an estimate of
.
In particular, an estimate of
![]() is needed.
An approximate estimate of
is needed.
An approximate estimate of
![]() is given
by
is given
by
![]() .
Hjalmarsson (2005) shows that, in general, the pooled estimator of
Moon and Phillips (2000) will be an upward biased estimator of
.
Hjalmarsson (2005) shows that, in general, the pooled estimator of
Moon and Phillips (2000) will be an upward biased estimator of
![]() when the
when the ![]() are
non-identical. By Jensen's inequality,
are
non-identical. By Jensen's inequality,
![]() , so the bias term will be underestimated by this
approximation. The upward bias in the estimate of
, so the bias term will be underestimated by this
approximation. The upward bias in the estimate of
![]() ,
based on the Moon and Phillips (2000) estimator, will thus to some
extent counteract the downward bias induced by Jensen's inequality.
Alternatively, the estimator
,
based on the Moon and Phillips (2000) estimator, will thus to some
extent counteract the downward bias induced by Jensen's inequality.
Alternatively, the estimator
![]() ,
which is based on recursive demeaning, could be used instead since
it requires no knowledge of the
,
which is based on recursive demeaning, could be used instead since
it requires no knowledge of the ![]() .
.
The heterogenous ![]() also cause some difficulties when dealing with the common factors.
When the
also cause some difficulties when dealing with the common factors.
When the ![]() are
not identical, it is no longer possible to write
are
not identical, it is no longer possible to write
![]() and the
subsequent analysis becomes more involved and is outside the scope
of this paper.
and the
subsequent analysis becomes more involved and is outside the scope
of this paper.
7 Empirical application
To illustrate the methods developed in this paper, I consider
the question of stock-return predictability in an international
data set. The data are obtained from the MSCI database and consist
of a panel of total returns for stock markets in 18 different
countries and three corresponding forecasting variables: the
dividend- and earnings-price ratios as well as the book-to-market
values. With varying success, all three of these variables have
been used extensively in tests of stock-return predictability for
U.S. data (e.g. Campbell and Shiller, 1988, Fama and French 1988,
Lewellen, 2004, and Campbell and Yogo, 2005), and to a lesser
degree in international data (e.g. Ang and Bekaert, 2003, and
Campbell, 2003). All three of these forecasting variables are
highly persistent, and since they are all valuation ratios, their
innovations are likely to be highly correlated with the innovations
to the returns process. The data are on a monthly basis and the
returns data span the period 1970.1 to 2002.12, whereas not all
forecasting variables are available for this whole time-period, or
for all countries. In particular, I have data for stock indices in
the following countries: Australia, Austria, Belgium, Canada,
Denmark, France, Germany, Hong Kong, Italy, Japan, the Netherlands,
Norway, Singapore, Spain, Sweden, Switzerland, the UK, and the
USA.5 The
dividend price ratio
![]() is
available for all countries except Hong Kong and for the entire
sample period from 1970.1 onwards. The earnings price ratio
is
available for all countries except Hong Kong and for the entire
sample period from 1970.1 onwards. The earnings price ratio
![]() is
available for all countries except Italy and Switzerland, from
1974.12 onwards. The book-to-market value
is
available for all countries except Italy and Switzerland, from
1974.12 onwards. The book-to-market value
![]() is
available for all countries from 1974.12 onwards. The forecasting
variables are the valuation ratios provided by MSCI, with earnings
representing cash earnings.
is
available for all countries from 1974.12 onwards. The forecasting
variables are the valuation ratios provided by MSCI, with earnings
representing cash earnings.
All returns and forecasting variables are expressed in U.S. dollars, and excess returns over the 1-month U.S. T-bill rate are calculated. The dependent variable in all regressions is thus excess returns over the U.S. short rate. Finally, all data are log-transformed.
The results from the pooled forecasting regressions are shown in Table 2. Panel A displays the results when there is no control for common factors, whereas the results in Panel B are based on the methods developed for dealing with cross-sectional dependence.
The estimates of ![]() and
the estimates of the correlation between the innovations in the
returns and predictor processes show that the forecasting variables
are clearly near-unit processes and highly endogenous. Starting
with the results in Panel A, the standard pooled fixed effects
estimator,
and
the estimates of the correlation between the innovations in the
returns and predictor processes show that the forecasting variables
are clearly near-unit processes and highly endogenous. Starting
with the results in Panel A, the standard pooled fixed effects
estimator,
![]() ,
delivers highly significant estimates and clearly rejects the
null-hypothesis of no predictability. Given the high persistence
and endogeneity found in the data, however, these results are
likely to be upward biased and as seen from the estimates based on
the estimator using recursive demeaning,
,
delivers highly significant estimates and clearly rejects the
null-hypothesis of no predictability. Given the high persistence
and endogeneity found in the data, however, these results are
likely to be upward biased and as seen from the estimates based on
the estimator using recursive demeaning,
![]() and
the bias corrected fixed effects estimator,
and
the bias corrected fixed effects estimator,
![]() ,
the significance disappears when controlling for the bias induced
by the time-series demeaning in the fixed effects estimator.
,
the significance disappears when controlling for the bias induced
by the time-series demeaning in the fixed effects estimator.
In Panel B, the regression estimates are based on the methods
controlling for common factors across the different markets. For
the dividend price ratio, the standard fixed effects estimate is
now even more significant, but the ![]() statistics for the two other estimates,
statistics for the two other estimates,
![]() and
and
![]() , are in fact both negative and
insignificant. For the earnings-price ratio and the book-to-market
ratio, the results from the fixed effects estimator become less
strong when controlling for common factors and the two other
estimators are both negative for both variables. Overall, the case
for stock-return predictability in this international data set,
using either of the three predictor variables, must be considered
very weak.
, are in fact both negative and
insignificant. For the earnings-price ratio and the book-to-market
ratio, the results from the fixed effects estimator become less
strong when controlling for common factors and the two other
estimators are both negative for both variables. Overall, the case
for stock-return predictability in this international data set,
using either of the three predictor variables, must be considered
very weak.
The empirical results shown here again illustrate the difficulties of performing inference in regressions with persistent and endogenous variables, and that these difficulties also prevail when a panel of data, rather than a single time-series, is available. Indeed, judging by the vast difference between the estimates and test statistics resulting from the standard fixed effects estimator and those from the robust estimators, it is clear that the bias effects can be as large in panel estimations as in time-series regressions.
8 Conclusion
A panel data extension of the traditional linear forecasting model is considered. I analyze a setup where the regressors are nearly persistent processes and potentially endogenous, which captures the essential characteristics of many empirical situations. It is shown that when no fixed effects are present, the standard pooled estimator is asymptotically normal and standard inference can be performed; the cross-sectional information effectively dilutes the endogeneity effects that are present in the standard time-series case and as the cross-sectional dimension grows large, these effects disappear altogether. However, when individual intercepts, or fixed effects, are estimated, the endogeneity of the regressors cause the pooled estimator to have a second order bias. To control for these effects, an alternative pooled estimator based on the concept of recursive demeaning is proposed. Alternatively, a bias corrected version of the standard fixed effects estimator is also proposed. Following the work of Peseran (2006), I also extend the results to a setting that allows for cross-sectional dependence in the form of common factors in the panel.
Monte Carlo evidence suggests that the proposed estimators have good finite sample properties and also shows that, in a typical setup, the distortions to the standard fixed effects estimator can be quite severe when the regressors are endogenous. An application to predictability in international stock-returns also illustrates that failure to account for the endogeneity and persistence in the regressors can lead to highly biased inference.
The results in this paper provide an important extension to the existing literature on time-series methods for predictive regressions and show that a careful analysis of the impact of nearly persistent and endogenous regressors is required also in the panel data case.
A Preliminary results
1.
![]()
![]() and
and
![]() are of order
are of order
![]()
2.
![]()
![]()
![]()
![]() and
and
![]() are of order
are of order
![]()
3.
![]() and
and
![]() are of order
are of order
![]()
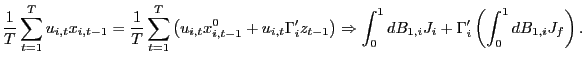
![$\displaystyle \frac{1}{\sqrt{n}}\sum_{i=1}^{n}\int_{0}^{1}dB_{1,i}J_{i}\Rightarrow N\left( 0,E\left[ \left( \int_{0}^{1}dB_{1,i}J_{i}\right) \left( \int_{0} ^{1}dB_{1,i}J_{i}\right) ^{\prime}\right] \right) . $](img268.gif)
![$\displaystyle \frac{1}{\sqrt{n}}\sum_{i=1}^{n}\Gamma_{i}^{\prime}\left( \int_{0} ^{1}dB_{1,i}J_{f}\right) \Rightarrow MN\left( 0,E\left[ \left. \Gamma _{i}^{\prime}\left( \int_{0}^{1}dB_{1,i}J_{f}\right) \left( \int_{0} ^{1}dB_{1,i}J_{f}\right) ^{\prime}\Gamma_{i}\right\vert \mathcal{C}\right] \right) . $](img271.gif)
(b) Similarly, as
![]()
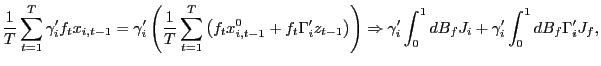
![$\displaystyle \frac{1}{n}\sum_{i=1}^{n}\gamma_{i}^{\prime}\int_{0}^{1}dB_{f}J_{i} \rightarrow_{p}\gamma^{\prime}E\left[ \left. \int_{0}^{1}dB_{f} J_{i}\right\vert \mathcal{C}\right] =0,$](img274.gif) and
and 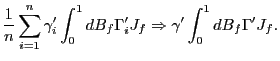
(c) Observe that
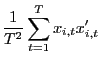
|
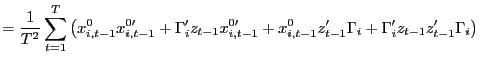
|
|
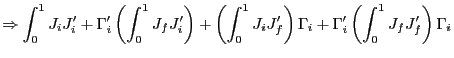
|
as
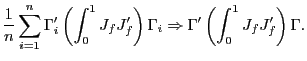
(d) As before, as
![]()
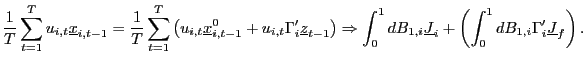
![$\displaystyle \frac{1}{n}\sum_{i=1}^{n}\frac{1}{T}\sum_{t=1}^{T}u_{i,t}\underline{x} _{i,t-1}\rightarrow_{p}-\left( \int_{0}^{1}\int_{0}^{r}E\left[ e^{\left( r-s\right) C}\right] dsdr\right) \omega_{21}. $](img285.gif)
(e) As
![]() ,
,
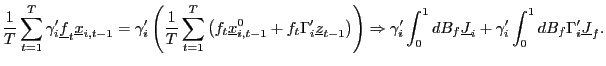
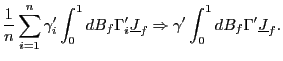
(f) The result follows in an
identical manner to that in (c). ![]()
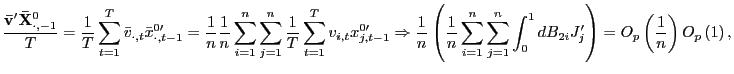
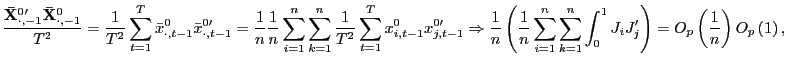
2. Similar to above, as
![]() ,
,
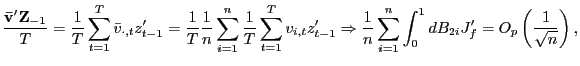
3.
![]() follows directly from Lemma 2 in Pesaran (2006). Further,
as
follows directly from Lemma 2 in Pesaran (2006). Further,
as
![]()
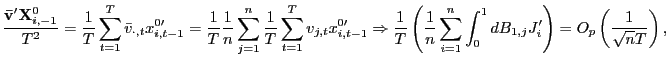
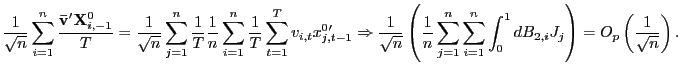
![]()
B Proofs of main results
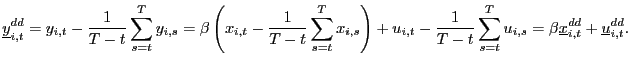
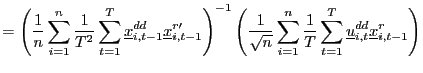
|
||
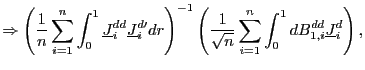
|
since
by standard arguments. By the independent increments property of the Brownian motion, it follows that the expectation of (36) is equal to zero and the result follows from similar arguments as before.
![\begin{displaymath} \mathbf{\bar{H}}D_{T}^{-1}=\left( \begin{array}[c]{cc} \mathbf{\Delta}_{C}\mathbf{\bar{X}} & \mathbf{\bar{X}}_{\cdot,-1} \end{array}\right) \left( \begin{array}[c]{cc} I_{m}\sqrt{T} & 0\ 0 & I_{m}T \end{array}\right) =\left( \begin{array}[c]{cc} \frac{\mathbf{\Delta}_{C}\mathbf{\bar{X}}}{\sqrt{T}} & \frac{\mathbf{\bar{X} }_{\cdot,-1}}{T} \end{array}\right) . \end{displaymath}](img314.gif)
![$\displaystyle \sqrt{n}T\left( \tilde{\beta}_{Pool}-\beta\right) =\left( \frac{1}{n} \sum_{i=1}^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{\bar{H}} }\mathbf{X}_{i,-1}}{T^{2}}\right) ^{-1}\left[ \left( \frac{1}{\sqrt{n}} \sum_{i=1}^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{\bar{H}} }\mathbf{f}\gamma_{i}}{T}\right) +\left( \frac{1}{\sqrt{n}}\sum_{i=1} ^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{\bar{H}}} \mathbf{u}_{i}}{T}\right) \right] , $](img315.gif)
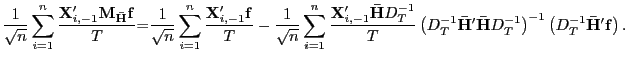
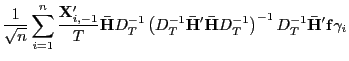
|
||
![$\displaystyle =\frac{1}{\sqrt{n}}\sum_{i=1}^{n}\frac{\mathbf{X}_{i,-1}^{\prime}}{T}\left( \par \begin{array}[c]{cc} \frac{\mathbf{f}\bar{\Gamma}+\mathbf{\bar{v}}}{\sqrt{T}} & \frac {\mathbf{\bar{X}}_{\cdot,-1}^{0}+\mathbf{Z}_{-1}\bar{\Gamma}}{T} \end{array} \right)$](img319.gif)
|
||
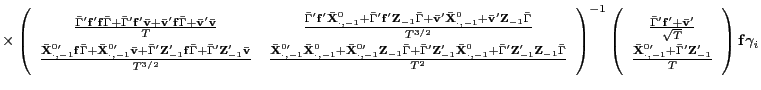
|
||
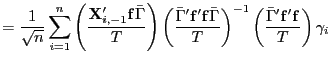
|
||
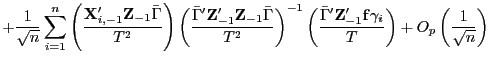
|
||
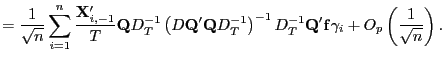
|
Thus,
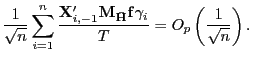
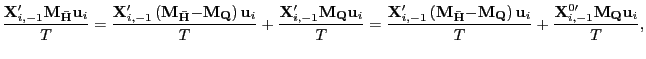
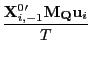
|
||
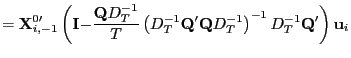
|
||
![$\displaystyle =\mathbf{X}_{i,-1}^{0\prime}\left( \mathbf{I-}\left( \begin{array}[c]{cc} \frac{\mathbf{f}\bar{\Gamma}}{\sqrt{T}} & \frac{\mathbf{Z}_{-1}\bar{\Gamma} }{T} \end{array} \right) \left( \begin{array}[c]{cc} \frac{\bar{\Gamma}^{\prime}\mathbf{f}^{\prime}\mathbf{f}\bar{\Gamma}}{T} & \frac{\bar{\Gamma}^{\prime}\mathbf{f}^{\prime}\mathbf{Z}_{-1}\bar{\Gamma} }{T^{3/2}}\\ \frac{\bar{\Gamma}^{\prime}\mathbf{Z}_{-1}^{\prime}\mathbf{f}\bar{\Gamma} }{T^{3/2}} & \frac{\bar{\Gamma}^{\prime}\mathbf{Z}_{-1}^{\prime} \mathbf{Z}_{-1}\bar{\Gamma}}{T^{2}} \end{array} \right) ^{-1}\left( \begin{array}[c]{c} \frac{\bar{\Gamma}^{\prime}\mathbf{f}^{\prime}}{\sqrt{T}}\\ \frac{\bar{\Gamma}^{\prime}\mathbf{Z}_{-1}^{\prime}}{T} \end{array} \right) \right) \mathbf{u}_{i}$](img328.gif)
|
||
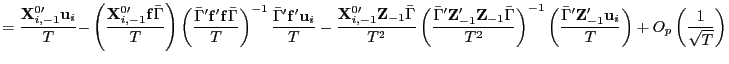
|
||
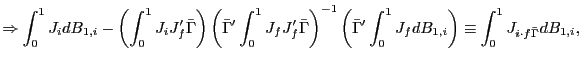
|
where
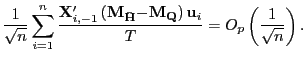
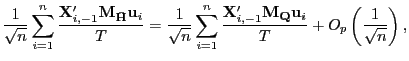
![$\displaystyle \frac{1}{\sqrt{n}}\sum_{i=1}^{n}\frac{\mathbf{X}_{i,-1}^{\prime} \mathbf{M}_{\mathbf{Q}}\mathbf{u}_{i}}{T}\Rightarrow MN\left( 0,E\left[ \left. \left( \int_{0}^{1}J_{i\cdot f\Gamma}dB_{1,i}\right) \left( \int_{0}^{1}J_{i\cdot f\Gamma}dB_{1,i}\right) ^{\prime}\right\vert \mathcal{C}\right] \right) , $](img337.gif)
![$\displaystyle \frac{1}{n}\sum_{i=1}^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M} _{\mathbf{\bar{H}}}\mathbf{X}_{i,-1}}{T^{2}}=\frac{1}{n}\sum_{i=1}^{n} \frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{Q}}\mathbf{X}_{i,-1} }{T^{2}}+O_{p}\left( \frac{1}{\sqrt{n}}\right) =\frac{1}{n}\sum_{i=1} ^{n}\frac{\mathbf{X}_{i,-1}^{0\prime}\mathbf{X}_{i,-1}^{0}}{T^{2}} +O_{p}\left( \frac{1}{\sqrt{n}}\right) \rightarrow_{p}E\left[ \int_{0} ^{1}J_{i}J_{i}^{\prime}\right] , $](img339.gif)
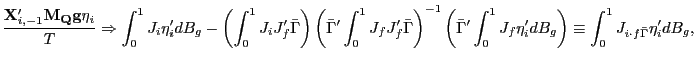
Bibliography
- 1
- Andrews, D.W.K., 2005. Cross-section Regression with Common Shocks, Econometrica 73, 1551-1585.
- 2
- Ang, A., and G. Bekaert, 2003. Stock Return Predictability: Is it There? Working paper, Columbia University.
- 3
- Campbell, J.Y., 2003. Consumption-Based Asset Pricing, in: Constantinides, G.M., Harris M., and Stulz R. eds., Handbook of the Economics of Finance, Vol. 1B (North-Holland, Amsterdam) 803-888.
- 4
- Campbell, J.Y., and M. Yogo, 2005. Efficient Tests of Stock Return Predictability, forthcoming Journal of Financial Economics.
- 5
- Cavanagh, C., G. Elliot, and J. Stock, 1995. Inference in models with nearly integrated regressors, Econometric Theory 11, 1131-1147.
- 6
- Elliot, G., 1998. On the Robustness of Cointegration Methods When Regressors Almost Have Unit Roots, Econometrica 66, 149-158;
- 7
- Goetzman W.N., and P. Jorion, 1993. Testing the Predictive Power of Dividend Yields, Journal of Finance 48, 663-679.
- 8
- Hjalmarsson, E., 2005. Estimation of average local-to-unity roots in heterogenous panels, International Finance Discussion Paper 852, Federal Reserve Board.
- 9
- Jansson, M., and M.J. Moreira, 2004. Optimal Inference in Regression Models with Nearly Integrated Regressors, Working Paper, Harvard University.
- 10
- Jin, S., 2004. Discrete Choice Modeling with Nonstationary Panels Applied to Exchange Rate Regime Choice, Mimeo, Yale University.
- 11
- Lewellen, J., 2004. Predicting returns with financial ratios, Journal of Financial Economics, 74, 209-235.
- 12
- Mankiw, N.G., and M.D. Shapiro, 1986. Do we reject too often? Small sample properties of tests of rational expectations models, Economics Letters 20, 139-145.
- 13
- Moon, H.R., and P.C.B. Phillips, 2000. Estimation of Autoregressive Roots near Unity using Panel Data, Econometric Theory 16, 927-998.
- 14
- Nelson, C.R., and M.J. Kim, 1993. Predictable Stock Returns: The Role of Small Sample Bias, Journal of Finance 48, 641-661.
- 15
- Pagan, A., and A. Ullah, 1999. Nonparametric Econometrics, Cambridge University Press.
- 16
- Pesaran, M.H., 2006. Estimation and Inference in Large Heterogeneous Panels with a Multifactor Error Structure, Econometrica, forthcoming.
- 17
- Phillips, P.C.B, and B. Hansen, 1990. Statistical Inference in Instrumental Variables Regression with I(1) Processes, Review of Economic Studies 57, 99-125.
- 18
- Phillips, P.C.B., and H.R. Moon, 1999. Linear Regression Limit Theory for Nonstationary Panel Data, Econometrica 67, 1057-1111.
- 19
- Phillips, P.C.B., and V. Solo, 1992. Asymptotics for Linear Processes, Annals of Statistics, 20, 971-1001.
- 20
- Phillips, P.C.B., and D. Sul, 2004. Bias in Dynamic Panel Estimation with Fixed Effects, Incidental Trends and Cross Section Dependence, Cowles Foundation Discussion Paper 1438.
- 21
- Polk, C., S. Thompson, and T. Vuolteenaho, 2004. Cross-sectional Forecasts of the Equity Premium, Working Paper, Department of Economics, Harvard University.
- 22
- Stambaugh, R., 1999. Predictive regressions, Journal of Financial Economics 54, 375-421.
- 23
- Sul, D., P.C.B. Phillips, and C.Y. Choi, 2005. Prewhitening bias in HAC estimation, Oxford Bulletin of Economics and Statistics 67, 517-546.
The table shows the average rejection rates under the null of
Panel A: No common factors
| Estimator |
|
|
|
|
|---|---|---|---|---|
|
|
||||
|
|
||||
|
|
||||
|
|
Panel B: Common factors with no correction
| Estimator |
|
|
|
|
|---|---|---|---|---|
|
|
||||
|
|
||||
|
|
Panel C: Common factors using correction
| Estimator |
|
|
|
|
|---|---|---|---|---|
|
|
||||
|
|
||||
|
|
The table shows the point estimates and corresponding
Panel A: No correction for common factors
| Variable |
|
|
|
|
|
||
|---|---|---|---|---|---|---|---|
|
|
|
|
|
![\begin{displaymath} \begin{array}[c]{c} -0.045\ \left( -2.740\right) \end{array}\end{displaymath}](img388.gif) |
![\begin{displaymath} \begin{array}[c]{c} -0.002\ \left( -0.800\right) \end{array}\end{displaymath}](img389.gif) |
|
|
|
|
|
|
|
![\begin{displaymath} \begin{array}[c]{c} -0.183\ \left( -0.591\right) \end{array}\end{displaymath}](img396.gif) |
![\begin{displaymath} \begin{array}[c]{c} 0.000\ \left( -0.051\right) \end{array}\end{displaymath}](img397.gif) |
|
|
|
|
|
|
|
![\begin{displaymath} \begin{array}[c]{c} -0.141\ \left( -0.895\right) \end{array}\end{displaymath}](img403.gif) |
|
|
|
Panel B: Correction for common factors
| Variable | | | | | ||
|---|---|---|---|---|---|---|
| |
|
|
|
![\begin{displaymath} \begin{array}[c]{c} -0.008\ \left( -1.588\right) \end{array}\end{displaymath}](img408.gif) |
![\begin{displaymath} \begin{array}[c]{c} -0.003\ \left( -0.770\right) \end{array}\end{displaymath}](img409.gif) |
|
| |
|
|
|
![\begin{displaymath} \begin{array}[c]{c} -0.009\ \left( -1.137\right) \end{array}\end{displaymath}](img413.gif) |
![\begin{displaymath} \begin{array}[c]{c} -0.005\ \left( -1.170\right) \end{array}\end{displaymath}](img414.gif) |
|
| |
|
|
|
![\begin{displaymath} \begin{array}[c]{c} -0.010\ \left( -1.710\right) \end{array}\end{displaymath}](img417.gif) |
![\begin{displaymath} \begin{array}[c]{c} -0.001\ \left( -0.194\right) \end{array}\end{displaymath}](img418.gif) |
|
The graphs show the kernel density estimates of the estimated slope coefficients, for samples with
The graphs show the average rejection rates for a two-sided
The graphs show the kernel density estimates of the estimated slope coefficients, for samples with
The graphs show the average rejection rates for a two-sided
The graphs show the kernel density estimates of the estimated slope coefficients, for samples with
The graphs show the average rejection rates for a two-sided
Footnotes
1. I am very grateful to Peter Phillips for providing much useful advice. Other helpful comments have been provided by Don Andrews, Lennart Hjalmarsson, Randi Hjalmarsson, Yuichi Kitamura, Vadim Marmer, Alex Maynard, Taisuke Otsu, Robert Shiller, Kevin Song, Pär Österholm, as well as participants in the summer workshop and econometrics seminar at Yale University, the finance seminar at Göteborg University, and the European Summer Meeting of the Econometric Society in Vienna. Tel.: +1-202-452-2426; fax: +1-202-263-4850; email: [email protected]. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
2. The literature on time-series forecasting regressions is very large. Some examples are Mankiw and Shapiro (1986), Nelson and Kim (1993), Goetzman and Jorion (1993), Cavanagh et al. (1995), Stambaugh (1999), Janson and Moreira (2004), Lewellen (2004), Polk et al. (2004), and Campbell and Yogo (2005). Many of these studies are primarily concerned with tests of stock-return predictability, although the results are generally applicable to more general forecasting regressions. Return to text
3. The results developed below also
hold in the case with a common non-zero
intercept ![]() . Return to
text
. Return to
text
4. The phenomenon is analogous to that found by Moon and Phillips (2000), in their estimation of local-to-unity roots in panels with incidental trends. Return to text
5. Hong Kong is, of course, not a country. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text
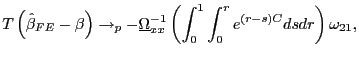
![$ \underline{\Phi}_{ux}^{RD}=E\left[ \left( \int_{0}^{1}dB_{1,i} ^{dd}\underline{J}_{i}^{d}\right) \left( \int_{0}^{1}dB_{1,i}^{dd} \underline{J}_{i}^{d}\right) ^{\prime}\right] $](img130.gif)
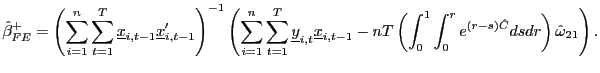
![$\displaystyle T\left( \hat{\beta}_{Pool}-\beta\right) \Rightarrow\left( \Omega _{xx}+\Omega_{zz}\right) ^{-1}\left[ \int_{0}^{1}\left( \gamma^{\prime }dB_{f}\right) \left( \Gamma^{\prime}J_{f}\right) \right] .$](img151.gif)
![$\displaystyle T\left( \hat{\beta}_{FE}-\beta\right) \Rightarrow\left( \underline{\Omega }_{xx}+\underline{\Omega}_{zz}\right) ^{-1}\left[ \int_{0}^{1}\left( \gamma^{\prime}dB_{f}\right) \left( \Gamma^{\prime}\underline{J}_{f}\right) -\left( \int_{0}^{1}\int_{0}^{r}e^{\left( r-s\right) C}dsdr\right) \omega_{21}\right] .$](img152.gif)
![$\displaystyle \bar{H}_{t}=\frac{1}{n}\sum_{i=1}^{n}H_{i,t}=\frac{1}{n}\sum_{i=1}^{n}\left( \begin{array}[c]{c} \Delta_{C}x_{i,t}\\ x_{i,t-1} \end{array} \right) =\left( \begin{array}[c]{c} \Delta_{C}\bar{x}_{\cdot,t}\\ \bar{x}_{\cdot,t-1} \end{array} \right) .$](img169.gif)
![$\displaystyle \mathbf{\bar{H}}\mathbf{=}\left( \begin{array}[c]{cc} \mathbf{\Delta}_{C}\mathbf{\bar{X}} & \mathbf{\bar{X}}_{\cdot,-1} \end{array} \right) =\left( \begin{array}[c]{cc} \mathbf{f}\bar{\Gamma}+\mathbf{\bar{v}} & \mathbf{\bar{X}}_{\cdot,-1} ^{0}+\mathbf{Z}_{-1}\bar{\Gamma} \end{array} \right) .$](img173.gif)