
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 870, September 2006-Screen Reader Version*

Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 870, September 2006-Screen Reader Version*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Heterogeneity between unemployed and employed individuals matters for optimal fiscal policy. This paper considers the consequences of welfare heterogeneity between these two groups for the determination of optimal capital and labor income taxes in a model with matching frictions in the labor market. In line with a recent finding in the literature, we find that the optimal capital tax is typically non-zero because it is used to indirectly mitigate an externality along the extensive labor margin that arises from search and matching frictions. However, the consideration of heterogeneity makes our result differ in an important way: even for a wellknown parameter configuration (the Hosios condition) that typically eliminates this externality, we show that the optimal capital income tax is still non-zero. We also show that labor adjustment along the intensive margin has an important effect on efficiency at the extensive margin, and hence on the optimal capital tax, independent of welfare heterogeneity. Taken together, our results show that these two empirically-relevant features of the labor market can have a quantitatively-important effect on the optimal capital tax.
Keywords: Optimal fiscal policy, labor search, Hosios condition
JEL Classification: E24, E62, H21, J64
Heterogeneity between unemployed and employed individuals matters for optimal fiscal policy. This paper considers the consequences of welfare heterogeneity between unemployed and employed individuals for the determination of optimal capital and labor income taxes in a model with matching frictions in the labor market. In line with a recent finding in the literature, we find that the optimal capital tax is typically non-zero because it is used to indirectly mitigate an externality that arises from search and matching frictions, one that cannot be corrected by the labor tax. However, the consideration of heterogeneity makes our result differ in an important way: even for a well-known parameter configuration that typically eliminates this externality, we continue to find a non-zero optimal capital tax. This difference stems from the heterogeneity in welfare between the employed and the unemployed. We also show that labor adjustment along the hours margin has an important effect on efficiency at the extensive margin, and hence on the optimal capital tax, independent of welfare heterogeneity.
Models featuring labor search and matching have two central features. First, because matches are costly to form, existing matches generate a surplus to be split between the worker and the firm. Second, matching models exhibit an externality due to the relative number of agents on each side of the labor market. This ``market-tightness" externality arises from the fact that one additional job-seeker in the market increases the probability that a firm will match with a worker but decreases the probability that job-seekers already in the market will match with a firm.1 Hosios (1990) shows these externalities are balanced when a worker's share of the match surplus equals his contribution to the formation of the match, yielding the socially-optimal market tightness. In a model with no taxes, the Hosios sharing rule typically boils down to a simple parameter restriction, specifically that the bargaining power of workers equals the elasticity of workers' input into the matching technology.
Much less is known about efficiency in this class of models in the presence of proportional taxes. As interest grows in using such models to answer policy questions, it seems important to understand the implications of policy for the nature of efficiency in frictional labor markets, and vice-versa.2 We show that proportional labor income taxes disrupt the usual Hosios efficiency rule for two distinct reasons: if unemployed and employed individuals do not experience the same level of welfare and if labor adjustment occurs not only at the extensive margin (number of people working) but also at the intensive margin (hours worked per person). With the Hosios condition disrupted for either (or both) of these reasons, a non-zero optimal capital tax can be used as an indirect instrument to steer the labor market towards efficiency along the extensive margin. This result is an instance of using the capital income tax to substitute for a missing tax instrument.3 Our results show that each of these channels -- welfare heterogeneity and intensive labor adjustment -- has a quantitatively important effect on the optimal capital income tax rate.
In each case, the link between the Hosios condition and a zero capital tax is severed through the Nash wage bargaining process, which is the typical assumption about how wages are set in this class of models, an assumption we maintain. The wage is the critical endogenous variable that affects efficiency along the extensive labor margin. In stylized form, the wage that emerges from Nash bargaining can be expressed as
A study closely related to ours is Domeij (2005). In an
important contribution to the literature, he also studies optimal
labor and capital income taxation in a model with labor matching
frictions. Building on the model of Shi and Wen (1999), Domeij
(2005) finds that when the Hosios parameter restriction is
satisfied, the optimal capital tax is always zero. An attractive
feature of their model is that it allows for an analytical
solution. Part of the analytic tractability of Domeij's (2005)
setup comes from the lack of an intensive margin and the assumption
that individuals are indifferent to whether or not they work. In
terms of the above stylized wage equation, Domeij's (2005) setup
can be interpreted as featuring ![]() and a
and a ![]() independent of
independent of ![]() .
However, for applied analysis, it may be important to allow for
ex-post heterogeneity and an intensive margin, two realistic
features a model of the labor market should capture. Our
quantitative results show that each of these features makes the
coincidence between the Hosios parameterization and a zero optimal
capital tax disappear.
.
However, for applied analysis, it may be important to allow for
ex-post heterogeneity and an intensive margin, two realistic
features a model of the labor market should capture. Our
quantitative results show that each of these features makes the
coincidence between the Hosios parameterization and a zero optimal
capital tax disappear.
In terms of our specific findings, three are noteworthy of mention at the outset. First, with neither welfare heterogeneity nor endogenous choice of hours, Ramsey allocations are socially-optimal when the Hosios condition is satisfied. That is, even though the Ramsey planner levies a proportional labor income tax in order to finance government spending, this tax turns out to be non-distortionary. The optimal labor tax here is thus somewhat akin to a levy on initial capital. To our knowledge, this is the first instance in the optimal taxation literature in which Ramsey allocations achieve social efficiency. Second, both of the channels we study -- welfare heterogeneity and intensive labor adjustment -- imply that optimal capital tax rates should be positive, which stands in contrast to the findings of, among others, Judd (2002), Schmitt-Grohe and Uribe (2005), and Chugh (2006) that negative optimal capital tax rates should be used to indirectly affect some types of market frictions.4 Third, in terms of welfare, following the standard prescription of a zero capital income tax rate instead of the positive tax rates we find entails a welfare loss of about 0.7 percent of steady-state consumption, which seems large enough to be worthy of attention.
The rest of the paper is organized as follows. In Section 2, we lay out our basic model without an intensive margin. Section 3 presents the Ramsey problem, and Section 4 describes how we parameterize our model. Quantitative results are presented in Section 5, along with a detailed analysis of how welfare heterogeneity between employed and unemployed individuals affects the extensive labor margin and the optimal capital income tax. In Section 6, we extend the basic model to include an intensive labor margin and show how it exerts a distorting effect on the extensive margin, one that can be corrected by a capital tax, independent of welfare heterogeneity. Section 7 computes the welfare losses that stem from implementing a zero capital income tax instead of the optimal non-zero capital taxes in our models. Section 8 concludes.
The model embeds the Pissarides (2000) textbook search model with capital into a general equilibrium framework. The crucial feature of the model in this section is that individuals who are employed may experience total utility different from individuals who are unemployed, and these utility differences stem from individuals' labor-status subutility functions. Bargaining occurs between an individual worker and a firm. The structure we employ ensures perfect consumption insurance between employed and unemployed individuals. While this simplification shuts down what may be an important source of heterogeneity between the unemployed and the employed, it allows us to focus on the implications for fiscal policy stemming from welfare heterogeneity due solely to the utility of work versus non-work.
There is a representative household in the economy. Each
household consists of a continuum of measure one of family members.
Each member of the household either works during a given time
period or is unemployed and searching for a job. There is a measure
![]() of employed
individuals in the household and a measure
of employed
individuals in the household and a measure ![]() of unemployed individuals. We
assume that total household income is divided evenly amongst all
individuals, so each individual has the same consumption.5
of unemployed individuals. We
assume that total household income is divided evenly amongst all
individuals, so each individual has the same consumption.5
The household's discounted lifetime utility is given by
![$\displaystyle \sum_{t=0}^{\infty} \beta^{t} \left[ u(c_{t}) + \int_{0}^{n_{t}} v^{i} di + \int_{n_{t}}^{1} A^{i} di \right] ,$](img16.gif)
|
(2) |
The household does not choose how many family members work. As
described below, the number of people who work is determined by a
random matching process. We also assume that each employed
individual works a fixed number of hours
![]() . This
assumption facilitates comparison of our baseline model without
intensive labor adjustment to our full model in
Section 6 with intensive
adjustment. The household chooses sequences of consumption, real
government bond holdings, and capital
. This
assumption facilitates comparison of our baseline model without
intensive labor adjustment to our full model in
Section 6 with intensive
adjustment. The household chooses sequences of consumption, real
government bond holdings, and capital
![]() , to maximize lifetime utility
subject to the flow budget constraint
, to maximize lifetime utility
subject to the flow budget constraint
Denote by ![]() the
time-
the
time-![]() Lagrange multiplier
on the flow budget constraint. The first order conditions with
respect to
Lagrange multiplier
on the flow budget constraint. The first order conditions with
respect to ![]()
![]() and
and ![]() are
are
We again point out that although all individuals are perfectly
insured against consumption risk, there is welfare heterogeneity,
measured by ![]() , between
unemployed and employed because of differences in their work
status.
, between
unemployed and employed because of differences in their work
status.
There is a representative firm that produces and sells a
homogenous final good in a perfectly competitive product market.
The firm must engage in costly search for a worker to fill each of
its job openings. In each job ![]() that will produce output, the worker and firm
bargain simultaneously over the pre-tax real wage
that will produce output, the worker and firm
bargain simultaneously over the pre-tax real wage ![]() paid in that position. Output
of job
paid in that position. Output
of job ![]() is given by
is given by
![]() , where
, where
![]() exhibits
diminishing returns in capital. Note again that we allow here for a
fixed
exhibits
diminishing returns in capital. Note again that we allow here for a
fixed
![]() number
of hours worked in each job. The capital
number
of hours worked in each job. The capital ![]() used in production is specific
to a particular job and is rented by the firm in a spot capital
market. Any two jobs
used in production is specific
to a particular job and is rented by the firm in a spot capital
market. Any two jobs ![]() and
and
![]() at the firm are
identical, so from here on we suppress the first subscript and
denote by
at the firm are
identical, so from here on we suppress the first subscript and
denote by ![]() the
capital used in any job, by
the
capital used in any job, by ![]() the wage in any job, and so on. Total output
thus depends on the production technology and the measure of
matches
the wage in any job, and so on. Total output
thus depends on the production technology and the measure of
matches ![]() that
produce,
that
produce,
| (10) |
The firm begins period ![]() with employment stock
with employment stock ![]() . Its future employment stock depends on its
current choices as well as the random matching process. With
probability
. Its future employment stock depends on its
current choices as well as the random matching process. With
probability ![]() ,
taken as given by the firm, a vacancy will be filled by a worker.
Labor-market tightness is
,
taken as given by the firm, a vacancy will be filled by a worker.
Labor-market tightness is
![]() , and
matching probabilities depends only on tightness given the
Cobb-Douglas matching function we will assume. The firm rents
capital
, and
matching probabilities depends only on tightness given the
Cobb-Douglas matching function we will assume. The firm rents
capital ![]() for use
in each job and chooses vacancies to post
for use
in each job and chooses vacancies to post ![]() and future employment
and future employment
![]() to maximize
to maximize
Associate the multiplier ![]() with the employment constraint. The
first-order conditions with respect to
with the employment constraint. The
first-order conditions with respect to ![]() ,
, ![]() , and
, and ![]() are, respectively,
are, respectively,
The government has a stream of purchases ![]() to finance using labor and
capital income taxes and real debt. The flow budget constraint of
the government is
to finance using labor and
capital income taxes and real debt. The flow budget constraint of
the government is
As is standard in the literature, we assume that the wage paid in any given job is determined in a Nash bargain between the matched worker and firm. Details of the solution are given in Appendix A. Here we present only the outcome of the Nash bargain. Bargaining over the wage payment yields
Here, we limit our attention to steady-states. In steady-state, the bargained wage payment reduces to
Matches between unemployed individuals searching for jobs and
firms searching to fill vacancies are formed according to a
matching technology,
![]() , where
, where
![]() is the number of
searching individuals and
is the number of
searching individuals and ![]() is the number of posted vacancies. A match
formed in period
is the number of posted vacancies. A match
formed in period ![]() will
produce in period
will
produce in period ![]() provided it survives exogenous separation at the beginning of
period
provided it survives exogenous separation at the beginning of
period ![]() . The
evolution of total employment is thus given by
. The
evolution of total employment is thus given by
The household optimality conditions are summarized by (4 ), (8), and (9). We condense (4) and (8) along with the firm's optimality condition with respect to capital, (15), into the single present-value expression,
The problem of the Ramsey planner is to raise revenue for the
government through labor and capital income taxes in such a way
that maximizes the welfare of the representative household, subject
to the equilibrium conditions of the economy. In period zero, the
Ramsey planner commits to a policy rule. Unlike the household, the
Ramsey planner does choose ![]() (subject to the matching frictions and
bargaining outcomes in the decentralized economy), and the
planner's explicit consideration of the aggregate welfare of
employed individuals versus unemployed individuals when making
these choices is important for our results.
(subject to the matching frictions and
bargaining outcomes in the decentralized economy), and the
planner's explicit consideration of the aggregate welfare of
employed individuals versus unemployed individuals when making
these choices is important for our results.
The Ramsey problem is thus to choose
![]() to maximize (3)
subject to (15), (16 ), (18), (20 ), (21), (22), and (23 ) and taking as given
to maximize (3)
subject to (15), (16 ), (18), (20 ), (21), (22), and (23 ) and taking as given ![]() . We leave the labor tax rate
as a choice of the Ramsey planner, rather than eliminating it in
order to cast the problem in terms of only allocations. Thus, we do
not adopt the strict primal approach and instead solve a hybrid
Ramsey problem that mixes allocation and policy variables as Ramsey
choices.6We could
eliminate
. We leave the labor tax rate
as a choice of the Ramsey planner, rather than eliminating it in
order to cast the problem in terms of only allocations. Thus, we do
not adopt the strict primal approach and instead solve a hybrid
Ramsey problem that mixes allocation and policy variables as Ramsey
choices.6We could
eliminate ![]() using
the wage equation, but to make the structure of the Ramsey problem
comparable to that of our full model in Section 6 we choose not to make this
substitution.
using
the wage equation, but to make the structure of the Ramsey problem
comparable to that of our full model in Section 6 we choose not to make this
substitution.
Because we are concerned only with steady-states, we consider
only the Ramsey first-order conditions for ![]() . We assume that the time-zero
Ramsey allocation is the same as the asymptotic steady-state Ramsey
allocation, thus endogenizing the initial condition of the
economy.7 This
assumption does not affect whether or not a zero capital income tax
rate is optimal in the asymptotic steady-state. Throughout, we
assume that the first-order conditions of the Ramsey problem are
necessary and sufficient and that all allocations are interior.
Once we have the Ramsey allocation, we back out the capital tax
rate that supports the allocation using (9).
. We assume that the time-zero
Ramsey allocation is the same as the asymptotic steady-state Ramsey
allocation, thus endogenizing the initial condition of the
economy.7 This
assumption does not affect whether or not a zero capital income tax
rate is optimal in the asymptotic steady-state. Throughout, we
assume that the first-order conditions of the Ramsey problem are
necessary and sufficient and that all allocations are interior.
Once we have the Ramsey allocation, we back out the capital tax
rate that supports the allocation using (9).
We characterize the Ramsey steady-state of our model numerically. Before turning to our results, we describe how we parameterize the model. We assume that the instantaneous utility function over consumption is
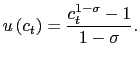
|
(24) |
Our timing assumptions are such that production in a period
occurs after the realization of separations. Following the
convention in the literature, we suppose that the unemployment rate
is computed before the realization of
separations. We set the quarterly probability of separation at
![]() ,
consistent with Shimer (2005). Thus, letting
,
consistent with Shimer (2005). Thus, letting ![]() denote the steady-state level of
employment,
denote the steady-state level of
employment,
![]() is
the employment rate, and
is
the employment rate, and
![]() is the steady-state unemployment rate.
is the steady-state unemployment rate.
The production function displays diminishing returns in capital,
| (25) |
As in much of the literature, the matching technology is Cobb-Douglas,
| (26) |
We normalize the disutility of working to ![]() . With this normalization, there
are two natural cases to consider regarding the calibration of
. With this normalization, there
are two natural cases to consider regarding the calibration of
![]() , the utility value of
not working. The first case is
, the utility value of
not working. The first case is ![]() , so that there is no difference at all in the
realized welfare of employed versus unemployed individuals. We
label this case model I. Although model I may not be an accurate
description of the relative welfare between unemployed and employed
individuals, it serves as a very useful benchmark for our main
results.
, so that there is no difference at all in the
realized welfare of employed versus unemployed individuals. We
label this case model I. Although model I may not be an accurate
description of the relative welfare between unemployed and employed
individuals, it serves as a very useful benchmark for our main
results.
In the second case, we introduce ex-post heterogeneity between
employed and unemployed individuals by allowing ![]() to differ from
to differ from ![]() . Here, our choice of a specific
value of
. Here, our choice of a specific
value of ![]() is guided by
Shimer (2005), who calibrates his model so that unemployed
individuals receive, in the form of unemployment benefits, about 40
percent of the wages of employed individuals. With his linear
utility assumption, unemployed individuals are therefore 40 percent
as well off as employed persons. Our model differs from Shimer's
(2005) primarily in that we assume full consumption insurance, but
also in that we have capital formation and curvature in both
utility and production. Thus, when we allow for welfare
heterogeneity, we interpret Shimer's (2005) calibration to mean
that unemployed individuals must receive 2.5 times more consumption
(in steady-state) than employed individuals in order for the total
utility of the two types of individuals to be equalized. That is,
we set
is guided by
Shimer (2005), who calibrates his model so that unemployed
individuals receive, in the form of unemployment benefits, about 40
percent of the wages of employed individuals. With his linear
utility assumption, unemployed individuals are therefore 40 percent
as well off as employed persons. Our model differs from Shimer's
(2005) primarily in that we assume full consumption insurance, but
also in that we have capital formation and curvature in both
utility and production. Thus, when we allow for welfare
heterogeneity, we interpret Shimer's (2005) calibration to mean
that unemployed individuals must receive 2.5 times more consumption
(in steady-state) than employed individuals in order for the total
utility of the two types of individuals to be equalized. That is,
we set ![]() such that in
steady-state
such that in
steady-state
| (27) |
With ![]() selected in
these two different ways, we calibrate
selected in
these two different ways, we calibrate ![]() and
and ![]() in model I to hit the firm and
worker matching rates
in model I to hit the firm and
worker matching rates
![]() and
and
![]() . The resulting values are
. The resulting values are
![]() and
and
![]() , which we
then hold fixed when we move to model II, as well as when we move
to the models in Section 6. We
thus view model I as the reference point for all of our
analysis.
, which we
then hold fixed when we move to model II, as well as when we move
to the models in Section 6. We
thus view model I as the reference point for all of our
analysis.
In each model, we focus on the case where the Nash bargaining
power of workers is set to
![]() ,
so that the usual Hosios condition for search efficiency is
satisfied. The implications of welfare heterogeneity (and, in
Section 6, the intensive margin)
for the optimal capital income tax when the
Hosios condition is satisfied is the focus of our study. We
choose steady-state government purchases
,
so that the usual Hosios condition for search efficiency is
satisfied. The implications of welfare heterogeneity (and, in
Section 6, the intensive margin)
for the optimal capital income tax when the
Hosios condition is satisfied is the focus of our study. We
choose steady-state government purchases ![]() so that they constitute 18
percent of total output. The same value of
so that they constitute 18
percent of total output. The same value of ![]() (
(
![]() )
delivers a government share of output very close to 18 percent in
both models (as well as the models in Section 6 ). Finally, the steady-state value of
government debt is assumed to be
)
delivers a government share of output very close to 18 percent in
both models (as well as the models in Section 6 ). Finally, the steady-state value of
government debt is assumed to be ![]() . While clearly not realistic, the assumption of
zero debt facilitates the welfare comparisons between the Ramsey
policy and alternative sub-optimal policies we conduct in
Section 7. Our quantitative results
are not very sensitive to
. While clearly not realistic, the assumption of
zero debt facilitates the welfare comparisons between the Ramsey
policy and alternative sub-optimal policies we conduct in
Section 7. Our quantitative results
are not very sensitive to ![]() . Table 1 summarizes the parameter values
that are common across all versions of our models.
. Table 1 summarizes the parameter values
that are common across all versions of our models.
| 0.99 | 1 | 0.70 | 0.02 | 0.40 | 0.10 | 0.40 |
After obtaining the dynamic first-order conditions of the Ramsey
problem described in Section 3, we impose steady-state and
numerically solve the resulting non-linear system. The capital
income tax rate ![]() is then determined from (9). With the exception of
Section 5.3, the usual
Hosios condition holds throughout this section, so that
is then determined from (9). With the exception of
Section 5.3, the usual
Hosios condition holds throughout this section, so that
![]() . The
Hosios condition typically achieves efficiency along the extensive
labor margin; we show that with proportional labor income taxation
and welfare heterogeneity between employed and unemployed
individuals, this is no longer true.
. The
Hosios condition typically achieves efficiency along the extensive
labor margin; we show that with proportional labor income taxation
and welfare heterogeneity between employed and unemployed
individuals, this is no longer true.
|
|
|
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.844 | 0.857 | 1.495 | 0.700 | 0.600 | 0.532 | 7.885 | 0.791 | 9.966 | 0.672 | 0.129 | 0 |
| 0.142 | 0 | 0.323 | 0.844 | 0.857 | 1.495 | 0.700 | 0.600 | 0.389 | 7.885 | 0.791 | 9.966 | 0.492 | 0.129 | 0.180 |
|
|
|
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -- | -- | 0.844 | 0.857 | 1.495 | 0.700 | 0.600 | 0.532 | 7.885 | 0.791 | 9.966 | 0.672 | 0.129 | 0 |
| 0.142 | -- | -- | 0.844 | 0.857 | 1.495 | 0.700 | 0.600 | 0.389 | 7.885 | 0.791 | 9.966 | 0.492 | 0.129 | 0.180 |
We begin by presenting results from model I, in which employed
and unemployed individuals are identical in welfare terms. The
upper panel of Table 2 presents the key steady-state allocation and policy variables under
the Ramsey plan for our calibrated value of ![]() as well as
as well as
![]() . The lower
panel of Table 2 presents
the social planner's allocations for these two cases. By social
efficiency here, we mean those allocations that are subject to the
technological constraints imposed by production and search and
matching but which are not necessarily implementable as a
decentralized equilibrium with proportional taxes, a requirement
which of course is imposed on the Ramsey planner.8 Thus, socially-optimal allocations are
the solution of a planning problem that maximizes (3) subject to (20), (22), and (23), taking as given
. The lower
panel of Table 2 presents
the social planner's allocations for these two cases. By social
efficiency here, we mean those allocations that are subject to the
technological constraints imposed by production and search and
matching but which are not necessarily implementable as a
decentralized equilibrium with proportional taxes, a requirement
which of course is imposed on the Ramsey planner.8 Thus, socially-optimal allocations are
the solution of a planning problem that maximizes (3) subject to (20), (22), and (23), taking as given ![]() .
.
Immediately striking in Table 2 is that, with the exception of
consumption, the allocation is invariant both to government
spending and to whether or not it is required to be implementable
as a decentralized equilibrium. With no government spending to
finance, the Ramsey planner has no need to impose any taxes as long
as the Hosios condition holds, as the first row of
Table 2 shows; in
section 5.3, we show that
away from the Hosios condition, the Ramsey planner does levy taxes
to try to mimic the efficient sharing delivered by the Hosios rule.
Once
![]() , the
Ramsey planner of course cannot set all taxes to zero. As shown in
the second row, the optimal capital income tax rate is zero, and
all government spending is financed through the labor income tax.
This echoes the hallmark Chamley (1986) zero-capital-taxation
result that arises in a model with homogenous (representative)
consumers. It is also consistent with the results of Domeij (2005)
for a model with no welfare heterogeneity between unemployed and
employed individuals. The only effect of government spending is to
crowd out private consumption one-for-one; despite a positive zero
labor tax, the Ramsey allocation remains identical to the
socially-efficient allocation.
, the
Ramsey planner of course cannot set all taxes to zero. As shown in
the second row, the optimal capital income tax rate is zero, and
all government spending is financed through the labor income tax.
This echoes the hallmark Chamley (1986) zero-capital-taxation
result that arises in a model with homogenous (representative)
consumers. It is also consistent with the results of Domeij (2005)
for a model with no welfare heterogeneity between unemployed and
employed individuals. The only effect of government spending is to
crowd out private consumption one-for-one; despite a positive zero
labor tax, the Ramsey allocation remains identical to the
socially-efficient allocation.
At first, it seems quite surprising that the Ramsey planner is
able to implement the first-best allocation because
![]() requires levying a proportional wage tax. The mechanism by which a
Ramsey policy typically transmits into a Ramsey allocation is that
it affects prices -- post-tax prices are different from pre-tax
prices and hence agents' decisions are affected. In the canonical
Ramsey fiscal policy problem with Walrasian labor markets -- as in,
say, Lucas and Stokey (1983) -- the two prices to be manipulated
are the real return on capital and the real wage. With a zero
optimal capital tax, the return on capital is clearly not altered.
The issue then is the reaction of the wage to the proportional
labor income tax in our model. In the simple environment of model
I, the labor tax does not affect the pre-tax wage (compare the
first two rows of Table 2.
The only decision in model I made according to wages is by firms
when choosing how many vacancies to post -- future wages appear in
the job-creation condition (16). Neither the household nor
individuals make any decisions regarding their labor market status.
Hence allocations turn out to be unaffected despite
requires levying a proportional wage tax. The mechanism by which a
Ramsey policy typically transmits into a Ramsey allocation is that
it affects prices -- post-tax prices are different from pre-tax
prices and hence agents' decisions are affected. In the canonical
Ramsey fiscal policy problem with Walrasian labor markets -- as in,
say, Lucas and Stokey (1983) -- the two prices to be manipulated
are the real return on capital and the real wage. With a zero
optimal capital tax, the return on capital is clearly not altered.
The issue then is the reaction of the wage to the proportional
labor income tax in our model. In the simple environment of model
I, the labor tax does not affect the pre-tax wage (compare the
first two rows of Table 2.
The only decision in model I made according to wages is by firms
when choosing how many vacancies to post -- future wages appear in
the job-creation condition (16). Neither the household nor
individuals make any decisions regarding their labor market status.
Hence allocations turn out to be unaffected despite
![]() ; in
other words, the proportional labor income tax is not
distortionary.
; in
other words, the proportional labor income tax is not
distortionary.
It is apparent from the Nash wage equation (19 ), reproduced here for convenience,
We think this result is quite interesting on its own, as we know
of no Ramsey model in which the socially-efficient allocation is
attained. The key to our result, of course, is that with wages
unaffected by taxes, the proportional labor tax acts as a lump-sum
``labor levy." It is also clear from the Nash wage equation that
this labor-levy feature of the Ramsey policy will not hold in the
empirically-relevant case ![]() because then labor taxes will affect wages.
This is the case to which we turn in the next section. Also, to
preview the richer model we develop in Section 6, this lump-sum nature of labor taxes will
not hold when there are both extensive and intensive labor margins.
With both extensive and intensive labor adjustment, the effect of
taxes on hours worked will exert independent influence on the wage.
Nonetheless, with the majority of empirically-observed labor
adjustment occurring at the extensive margin, it is interesting to
understand the benchmark results we have developed in this
section.
because then labor taxes will affect wages.
This is the case to which we turn in the next section. Also, to
preview the richer model we develop in Section 6, this lump-sum nature of labor taxes will
not hold when there are both extensive and intensive labor margins.
With both extensive and intensive labor adjustment, the effect of
taxes on hours worked will exert independent influence on the wage.
Nonetheless, with the majority of empirically-observed labor
adjustment occurring at the extensive margin, it is interesting to
understand the benchmark results we have developed in this
section.
To summarize these results so far: when the Hosios condition is
satisfied and labor adjustment occurs at only the extensive margin,
welfare homogeneity implies the optimal capital tax is zero,
confirming the results of Domeij (2005). In this environment, a
proportional labor tax ends up acting as a lump-sum tax instrument,
allowing Ramsey allocations to be first-best instead of only
second-best. The rest of our paper demonstrates that this result
depends critically on three key assumptions -- welfare homogeneity
(![]() ), the Hosios
condition (
), the Hosios
condition (
![]() ), and
the lack of an intensive margin (
), and
the lack of an intensive margin (![]() ). Relaxing any of these assumptions has an
important effect on the Ramsey policy prescription -- in
particular, on the optimal capital income tax rate -- and hence the
coincidence of the Ramsey solution and the social planning
solution.
). Relaxing any of these assumptions has an
important effect on the Ramsey policy prescription -- in
particular, on the optimal capital income tax rate -- and hence the
coincidence of the Ramsey solution and the social planning
solution.
We now turn to the case in which individuals differ in their
realized levels of utility according to their labor market status.
As described in Section 4, we model this ex-post
heterogeneity between unemployed and employed individuals by
choosing a value of ![]() different from
different from ![]() in a
way consistent with Shimer (2005). The value of
in a
way consistent with Shimer (2005). The value of ![]() needed to achieve this calibration
is
needed to achieve this calibration
is
![]() ; recalling
that the labor-status subutility of employed individuals is
normalized to
; recalling
that the labor-status subutility of employed individuals is
normalized to ![]() , this
means unemployed individuals are worse off than employed
individuals. The upper panel of Table 3 presents the key steady-state
allocation and policy variables under the Ramsey plan both with and
without government spending for model II. The lower panel of the
table presents the corresponding socially-efficient
allocations.
, this
means unemployed individuals are worse off than employed
individuals. The upper panel of Table 3 presents the key steady-state
allocation and policy variables under the Ramsey plan both with and
without government spending for model II. The lower panel of the
table presents the corresponding socially-efficient
allocations.
|
|
|
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.890 | 1.676 | 1.379 | 0.535 | 0.897 | 0.528 | 8.315 | 0.834 | 9.966 | 0.632 | 0.168 | 0 |
| 0.142 | 0.044 | 0.327 | 0.892 | 1.733 | 1.360 | 0.528 | 0.915 | 0.383 | 8.152 | 0.831 | 9.814 | 0.461 | 0.172 | 0.171 |
|
|
|
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -- | -- | 0.890 | 1.676 | 1.379 | 0.535 | 0.897 | 0.528 | 8.315 | 0.834 | 9.966 | 0.632 | 0.168 | 0 |
| 0.142 | -- | -- | 0.881 | 1.455 | 1.406 | 0.567 | 0.824 | 0.388 | 8.234 | 0.826 | 9.966 | 0.469 | 0.159 | 0.172 |
In order to understand how the introduction of welfare
heterogeneity alters the results in Section 5.1, it is useful to begin by comparing
the steady states of model I when ![]() (the first row of Table 2) and model II when
(the first row of Table 2) and model II when ![]() (the first row of
Table 3). Welfare
heterogeneity dampens the Nash wage because with
(the first row of
Table 3). Welfare
heterogeneity dampens the Nash wage because with ![]() lower than
lower than ![]() , individuals have a preference for
being employed over being unemployed, rather than being indifferent
as was the case in Section 5.1. In the interest of preserving jobs,
individuals are willing to accept lower wages. Lower wages in turn
raises the number of people working in the economy. The wage
equation (28) shows how the
first part of this transmission mechanism works:
, individuals have a preference for
being employed over being unemployed, rather than being indifferent
as was the case in Section 5.1. In the interest of preserving jobs,
individuals are willing to accept lower wages. Lower wages in turn
raises the number of people working in the economy. The wage
equation (28) shows how the
first part of this transmission mechanism works: ![]() erodes the bargaining
position of individuals, lowering the Nash wage (
erodes the bargaining
position of individuals, lowering the Nash wage (
![]() ). The firm's
vacancy-creation condition (16) shows how the second part of
this transmission mechanism works: a lower wage encourages firms to
post more vacancies because each job is now more profitable. The
ensuing tighter labor market (a higher
). The firm's
vacancy-creation condition (16) shows how the second part of
this transmission mechanism works: a lower wage encourages firms to
post more vacancies because each job is now more profitable. The
ensuing tighter labor market (a higher
![]() ) in
equilibrium leads to more individuals working because it is easier
for a given unemployed individual to make contact with a firm.
Thus, unemployment falls and output rises relative to the model I
economy in which individuals are indifferent to whether or not they
work. On the other hand, because vacancy posting is costly, it also
crowds out private consumption through the resource constraint.
Thus, heterogeneity by itself, without any government financing
considerations, lowers wages, raises employment, and crowds out
consumption.
) in
equilibrium leads to more individuals working because it is easier
for a given unemployed individual to make contact with a firm.
Thus, unemployment falls and output rises relative to the model I
economy in which individuals are indifferent to whether or not they
work. On the other hand, because vacancy posting is costly, it also
crowds out private consumption through the resource constraint.
Thus, heterogeneity by itself, without any government financing
considerations, lowers wages, raises employment, and crowds out
consumption.
Next, turn to the the solution of the Ramsey problem with
![]() ,
presented in the second row of Table 3. The optimal capital income tax rate
is no longer zero as in model I; this is due to an inefficiently
high level of vacancy creation by firms. Once again, understanding
the mechanism requires inspecting the wage equation (28) and the
vacancy-creation condition (16). The wage equation shows that
with
,
presented in the second row of Table 3. The optimal capital income tax rate
is no longer zero as in model I; this is due to an inefficiently
high level of vacancy creation by firms. Once again, understanding
the mechanism requires inspecting the wage equation (28) and the
vacancy-creation condition (16). The wage equation shows that
with ![]() , a positive
labor tax erodes workers' bargaining position and therefore reduces
the Nash wage.9 That is,
, a positive
labor tax erodes workers' bargaining position and therefore reduces
the Nash wage.9 That is,
![]() when
when ![]() . This dependence of the wage
on the labor tax rate is in contrast to model I, in which, because
individuals were indifferent between working and not working
(
. This dependence of the wage
on the labor tax rate is in contrast to model I, in which, because
individuals were indifferent between working and not working
(![]() ), the bargained
wage was invariant to the labor tax rate.
), the bargained
wage was invariant to the labor tax rate.
With the wages firms pay dampened by the positive labor income
tax, firms' incentives to post vacancies would rise above the
efficient level. That is, the extensive labor margin becomes
inefficient even though the Hosios condition holds. The Ramsey
planner, interested in balancing efficiency with the need to
finance government spending, tries to influence this outcome with
the policy instruments at his disposal. Thus far, we have limited
the Ramsey planner to using only labor and capital income taxes.
The positive capital income tax here balances two efficiency
considerations: the desire to not disrupt the capital accumulation
margin against indirectly promoting efficiency along the extensive
labor margin. A positive capital income tax, by dampening capital
accumulation, lowers the output
![]() of a
match, making vacancy-posting less profitable for firms. Thus,
lacking an instrument that directly affects the extensive labor
margin, the Ramsey planner uses the capital tax as a substitute
instrument.10
of a
match, making vacancy-posting less profitable for firms. Thus,
lacking an instrument that directly affects the extensive labor
margin, the Ramsey planner uses the capital tax as a substitute
instrument.10
This effect of the capital tax on firms' vacancy-posting incentives was first described by Domeij (2005). In Domeij's (2005) model, however, the capital tax needs to be used as an indirect instrument only when the Hosios condition is not satisfied -- in his model, when the Hosios parameterization is in place, there is never a need to influence the extensive margin via any (direct or indirect) instruments. As we mentioned in the introduction, Domeij's (2005) setup can be interpreted as one in which all individuals, whether employed or not, experience the same level of welfare. Our results show that when unemployed individuals are worse off than employed individuals, a positive capital tax acts to promote efficient job-creation even though the Hosios condition is satisfied. It is this consideration of heterogeneity that most sets our work and results apart from Domeij's (2005).
The indirect use of the capital tax to correct a labor market distortion suggests that other fiscal instruments might be able to more directly steer the economy towards efficiency along the extensive margin. We investigate this further in Section 5.4 by allowing for a vacancy tax. Before considering a vacancy tax, we briefly consider the behavior of the optimal capital tax away from the Hosios condition.
All of our analysis so far has been conducted at the Hosios
rule,
![]() , which
is known to deliver efficient sharing of the match surplus between
firms and workers in the absence of proportional taxes. Here we
consider how tax policy can be used to steer the economy towards
the efficient allocation when the Hosios rule is not satisfied. We
concentrate on the use of the capital tax as the indirect means of
affecting the labor market; the general lessons developed in this
section readily apply to the use of a vacancy tax in
Section 5.4. To focus
on the inefficiency stemming from non-Hosios sharing, we assume
, which
is known to deliver efficient sharing of the match surplus between
firms and workers in the absence of proportional taxes. Here we
consider how tax policy can be used to steer the economy towards
the efficient allocation when the Hosios rule is not satisfied. We
concentrate on the use of the capital tax as the indirect means of
affecting the labor market; the general lessons developed in this
section readily apply to the use of a vacancy tax in
Section 5.4. To focus
on the inefficiency stemming from non-Hosios sharing, we assume
![]() . Doing so
removes the issue of optimal financing of government spending from
the analysis.
. Doing so
removes the issue of optimal financing of government spending from
the analysis.
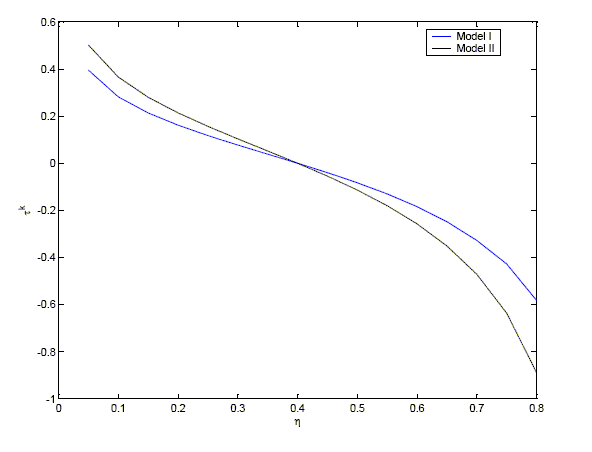
In Figure 1, we plot the optimal
steady-state capital tax rates as a function of the worker
bargaining share ![]() for
models I and II. Regardless of the assumed degree of heterogeneity
between unemployed and employed individuals,
for
models I and II. Regardless of the assumed degree of heterogeneity
between unemployed and employed individuals, ![]() is strictly decreasing in
is strictly decreasing in
![]() . The intuition is
as we discussed in Section 5.2 : the capital tax indirectly affects
firms' incentives to post vacancies by lowering the output of a
match. Here, when workers' Nash bargaining power is low (
. The intuition is
as we discussed in Section 5.2 : the capital tax indirectly affects
firms' incentives to post vacancies by lowering the output of a
match. Here, when workers' Nash bargaining power is low (
![]() ),
firms' incentives to create vacancies are inefficiently high
because they expect to receive a share of the match surplus
disproportionately large relative to their contribution to match
formation. This incentive is inefficiently high because Nash wages
are inefficiently low -- that is,
),
firms' incentives to create vacancies are inefficiently high
because they expect to receive a share of the match surplus
disproportionately large relative to their contribution to match
formation. This incentive is inefficiently high because Nash wages
are inefficiently low -- that is,
![]() . Thus, efficiency
requires that firms post fewer vacancies, which the Ramsey planner
attempts to replicate by levying a positive capital tax that lowers
the output of a match, dampening firms' incentives to post
vacancies. The opposite occurs when workers' bargaining power is
high (
. Thus, efficiency
requires that firms post fewer vacancies, which the Ramsey planner
attempts to replicate by levying a positive capital tax that lowers
the output of a match, dampening firms' incentives to post
vacancies. The opposite occurs when workers' bargaining power is
high (
![]() ):
firms receive a disproportionately small share of the match surplus
because wages are high, so the incentive to post vacancies is
inefficiently low. In this case, a capital subsidy boosts match
output, partially restoring the incentive to post vacancies.
):
firms receive a disproportionately small share of the match surplus
because wages are high, so the incentive to post vacancies is
inefficiently low. In this case, a capital subsidy boosts match
output, partially restoring the incentive to post vacancies.
We truncate Figure 1 at
![]() because for
larger values of
because for
larger values of ![]() the
optimal capital tax rates (subsidies) become implausibly large.
Note again that the results in Figure 1 are for
the
optimal capital tax rates (subsidies) become implausibly large.
Note again that the results in Figure 1 are for
![]() . The
results for our benchmark
. The
results for our benchmark
![]() are
very similar.
are
very similar.
We see at least two interesting issues our findings here raise.
We know from our results thus far that efficiency in the labor
market is associated with a zero optimal capital income
tax.11 A Nash
share ![]() that varied
appropriately with
that varied
appropriately with ![]() would achieve this. That is, one could imagine generalizing the
notion of the efficient sharing rule to depend on taxes, so that
efficient sharing would be described not by
would achieve this. That is, one could imagine generalizing the
notion of the efficient sharing rule to depend on taxes, so that
efficient sharing would be described not by
![]() but
instead by a function
but
instead by a function
![]() . For efficiency in the labor
market to come about solely through efficient bargaining when
. For efficiency in the labor
market to come about solely through efficient bargaining when
![]() ,
workers' share of the match surplus would need to be raised so long
as unemployed workers are worse off than employed workers -- that
is, efficiency would require
,
workers' share of the match surplus would need to be raised so long
as unemployed workers are worse off than employed workers -- that
is, efficiency would require
![]() so
long as
so
long as ![]() . An
efficient mix of fiscal policy then would need to consider the
response of
. An
efficient mix of fiscal policy then would need to consider the
response of ![]() to
to
![]() , perhaps
allowing the Ramsey planner to achieve efficiency in the long
run.
, perhaps
allowing the Ramsey planner to achieve efficiency in the long
run.
A second issue our findings raise is one of the effects of
time-varying taxes and wage-bargaining protocols. The bargaining
share ![]() , which is
descriptive of an institutional feature of the economy, may not be
something we think could move around at business cycle frequencies.
If this is the case, then it seems that it is impossible for
governments to deliver efficient, or even Ramsey, allocations over
the business cycle without having access to variable vacancy taxes
or using the capital tax to correct labor market inefficiencies at
business cycle frequencies. We leave consideration of these
interesting issues for future work.
, which is
descriptive of an institutional feature of the economy, may not be
something we think could move around at business cycle frequencies.
If this is the case, then it seems that it is impossible for
governments to deliver efficient, or even Ramsey, allocations over
the business cycle without having access to variable vacancy taxes
or using the capital tax to correct labor market inefficiencies at
business cycle frequencies. We leave consideration of these
interesting issues for future work.
The nonzero capital tax in our model is used to indirectly mitigate an inefficiency that the government does not have an instrument to address directly. By itself, this is not a very surprising result in the Ramsey literature. For example, Judd (2002), Schmitt-Grohe and Uribe (2005), and Chugh (2006) show that a capital subsidy can be used as part of the Ramsey policy to offset monopoly power by producers when there is no direct way of doing so. Here, we demonstrate that the capital income tax in our model is substituting for a more direct labor market instrument.
The two natural candidates for a direct labor market instrument
are a vacancy tax and an unemployment benefit. As Domeij (2005)
shows, the two instruments are perfect substitutes for each other,
as might be expected because all that matters for matching
efficiency is market tightness ![]() , so that affecting either
, so that affecting either ![]() or
or ![]() can do the job. Thus, we will only consider a
vacancy tax, which we introduce into our model in a straightforward
way. We replace
can do the job. Thus, we will only consider a
vacancy tax, which we introduce into our model in a straightforward
way. We replace ![]() with
with
![]() in the firm's profit function and the resulting job-creation
condition, and we introduce
in the firm's profit function and the resulting job-creation
condition, and we introduce
![]() as a revenue item in the
government budget constraint, where
as a revenue item in the
government budget constraint, where
![]() is the
vacancy tax rate. If
is the
vacancy tax rate. If
![]() ,
the firm must pay a tax for each vacancy it creates, while if
,
the firm must pay a tax for each vacancy it creates, while if
![]() ,
the firm receives a subsidy for each vacancy. Note that the total
vacancy tax adds to government revenues and is now part of the
optimal financing problem.
,
the firm receives a subsidy for each vacancy. Note that the total
vacancy tax adds to government revenues and is now part of the
optimal financing problem.
With this vacancy tax available, we again compute the Ramsey
allocations and policies. To isolate the effect of having a vacancy
tax available, we keep ![]() at its calibrated value above. Results are
presented in Table 4. The optimal capital
tax is now always zero as the vacancy tax, being the more direct
instrument to target the inefficiency in vacancy-creation stemming
from welfare heterogeneity, assumes the role previously played by
the capital tax. Domeij (2005) shows that using such a direct labor
market instrument is more efficient than using the capital tax, as
would be expected. Such a welfare gain of using a vacancy tax
arises in our model, as well. The steady-state welfare gain, in
terms of percentage of consumption, of using the vacancy tax is
documented in the last column on Table 4. In model I, there is
no welfare gain because the Ramsey allocation without the vacancy
tax already achieves socially efficiency. In model II, the welfare
gain of having access to the vacancy tax is about 0.4 percent of
steady-state consumption. Note that having access to the vacancy
tax allows the Ramsey planner to achieve the socially-optimal
allocation in model II (compare the second row of
Table 4 to
the last row of Table 3),
so this is another instance of the Ramsey allocation achieving
Pareto optimality -- that is, the proportional labor income tax is
not distortionary in the presence of welfare heterogeneity even
though the Hosios condition does not hold. In effect, the vacancy
tax acts to restore the Hosios sharing rule.
at its calibrated value above. Results are
presented in Table 4. The optimal capital
tax is now always zero as the vacancy tax, being the more direct
instrument to target the inefficiency in vacancy-creation stemming
from welfare heterogeneity, assumes the role previously played by
the capital tax. Domeij (2005) shows that using such a direct labor
market instrument is more efficient than using the capital tax, as
would be expected. Such a welfare gain of using a vacancy tax
arises in our model, as well. The steady-state welfare gain, in
terms of percentage of consumption, of using the vacancy tax is
documented in the last column on Table 4. In model I, there is
no welfare gain because the Ramsey allocation without the vacancy
tax already achieves socially efficiency. In model II, the welfare
gain of having access to the vacancy tax is about 0.4 percent of
steady-state consumption. Note that having access to the vacancy
tax allows the Ramsey planner to achieve the socially-optimal
allocation in model II (compare the second row of
Table 4 to
the last row of Table 3),
so this is another instance of the Ramsey allocation achieving
Pareto optimality -- that is, the proportional labor income tax is
not distortionary in the presence of welfare heterogeneity even
though the Hosios condition does not hold. In effect, the vacancy
tax acts to restore the Hosios sharing rule.
|
|
|
|
Welfare Gain | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.323 | 0.844 | 0.857 | 1.495 | 0.700 | 0.600 | 0.389 | 7.884 | 0.791 | 9.966 | 0.492 | 0.129 | 0.180 | 0 |
|
|
|
|
Welfare Gain | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.149 | 0 | 0.298 | 0.881 | 1.455 | 1.336 | 0.567 | 0.824 | 0.388 | 8.234 | 0.826 | 9.966 | 0.469 | 0.159 | 0.172 | 0.374 |
Having demonstrated that a capital tax is an imperfect proxy for a vacancy tax in our model, we continue our analysis by omitting the vacancy tax. Some justification for this might be that, given how much attention is usually paid to promoting job-creation, an explicit vacancy tax may be a politically infeasible issue.
For applied quantitative work, it may be of interest to model variations in the intensive labor margin as well as the extensive margin. In this section, we show that, even if the elasticity of hours supply is small as most micro evidence suggests, the presence of adjustment at the intensive margin has important consequences for the optimal capital tax. Specifically, the intensive margin introduces another channel through which the link between the Hosios condition and a zero optimal capital tax is broken. This channel is a standard-looking condition linking the marginal rate of substitution between consumption and hours and the marginal product of labor, one that is distorted by a proportional labor income tax. Thus, in this full version of our model, the proportional labor income tax is distortionary, in contrast to the model with only extensive adjustment in Section 2. We proceed by highlighting how the basic model we have been using up to now is modified to incorporate the intensive margin and then present quantitative results.
We enrich the household structure in the following way. Each
individual ![]() that works
in a time period spends
that works
in a time period spends ![]() hours working and suffers disutility
hours working and suffers disutility
![]() from working,
with
from working,
with
![]() . With
symmetry across working individuals, the household lifetime utility
is given by
. With
symmetry across working individuals, the household lifetime utility
is given by
Hours are no longer fixed as in Section 2. Rather, the number of hours worked by an individual is determined in Nash bargaining between the worker and the firm to which it is attached -- neither the worker nor the household unit directly chooses hours. The Nash solution for hours is presented below. The budget constraint of the household is modified in the obvious way to account for the fact that household labor earnings now depend on the total variable hours worked by family members,
Output of job ![]() is now
produced according to
is now
produced according to
![]() , where
, where ![]() has constant returns to scale.
Once again, jobs are symmetric, thus
has constant returns to scale.
Once again, jobs are symmetric, thus ![]() and
and ![]() are
common across matches. Total output is thus
are
common across matches. Total output is thus
| (31) |
| (32) |
The firm's dynamic profit function is
In the flow budget constraint of the government, total labor tax revenue now depends on hours worked by each individual,
We assume that hours worked and the wage paid in any given job are simultaneously determined in Nash bargaining between the matched worker and firm. More detail is provided in Appendix A. A useful way to think about the outcome of this simultaneous bargaining is that the choice of hours maximizes the joint surplus of the match, while the bargained wage payment divides the surplus between the worker and the firm.
The choice of hours that maximizes the joint surplus from the match satisfies a labor optimality condition that looks standard in a neoclassical labor market,
Bargaining over the wage payment yields a total wage payment
![]() ,
,
Note from (36) that
bargained hours depend on ![]() . To emphasize this dependence, we somtimes
write
. To emphasize this dependence, we somtimes
write
![]() . It is
clear then that the bargained wage payment depends on
. It is
clear then that the bargained wage payment depends on ![]() not only through the worker
threat point but also through
not only through the worker
threat point but also through ![]() . That is, in (38), even if
. That is, in (38), even if ![]() , meaning there is no welfare
heterogeneity between employed and unemployed persons,
, meaning there is no welfare
heterogeneity between employed and unemployed persons, ![]() is still a function of
is still a function of ![]() because hours depend on
because hours depend on
![]() , and the
production function
, and the
production function ![]() now
depends on a variable
now
depends on a variable ![]() .
This is how labor adjustment along the intensive margin opens up a
second channel through which a nonzero labor tax affects wages and
thus firms' incentives to create vacancies.
.
This is how labor adjustment along the intensive margin opens up a
second channel through which a nonzero labor tax affects wages and
thus firms' incentives to create vacancies.
The equilibrium conditions remain those in Section 2.6 appropriately modified to
include ![]() and now
also include (36). We
use (36) to eliminate
and now
also include (36). We
use (36) to eliminate
![]() from the
implementability constraint facing the Ramsey planner; the
implementability constraint in this version of our model is
thus
from the
implementability constraint facing the Ramsey planner; the
implementability constraint in this version of our model is
thus
The Ramsey problem is a straightforward extension of that
described in Section 3. To
the list of Ramsey choice variables, add ![]() and remove
and remove
![]() (because of our substitution using (36)). Thus, the unknown processes here
are
(because of our substitution using (36)). Thus, the unknown processes here
are
![]() .
The constraints facing the Ramsey planner are the same as those in
Section 3 with appropriate
inclusion of
.
The constraints facing the Ramsey planner are the same as those in
Section 3 with appropriate
inclusion of ![]() inside
the production function and factor prices. We continue to assume
commitment to a policy at time-zero and concern ourselves with only
the
inside
the production function and factor prices. We continue to assume
commitment to a policy at time-zero and concern ourselves with only
the ![]() Ramsey
first-order conditions. With the Ramsey allocation we compute the
steady-state capital and labor income tax rates from (9) and (36), respectively.
Ramsey
first-order conditions. With the Ramsey allocation we compute the
steady-state capital and labor income tax rates from (9) and (36), respectively.
We describe here the new elements of the parameterization. For those parameters we do not discuss here, our choices remain those in Section 4.
For the labor subutility function, we assume the functional form
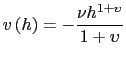
|
(40) |
Regarding ![]() , we define
analogs of our models I and II from Section 4. In model III, meant to parallel
model I, we calibrate
, we define
analogs of our models I and II from Section 4. In model III, meant to parallel
model I, we calibrate ![]() so that
so that
![]() , so there is no realized
welfare heterogeneity between employed and unemployed persons. In
model IV, we calibrate
, so there is no realized
welfare heterogeneity between employed and unemployed persons. In
model IV, we calibrate ![]() so that under the Ramsey plan
so that under the Ramsey plan
| (41) |
As before, after obtaining the dynamic first-order conditions of
the Ramsey problem, we impose steady-state, numerically solve the
resulting non-linear system, and then determine ![]() and
and ![]() residually from the
equilibrium conditions. Table 5 presents the Ramsey and
socially-optimal steady-states in models III and IV for
residually from the
equilibrium conditions. Table 5 presents the Ramsey and
socially-optimal steady-states in models III and IV for
![]() and our
benchmark calibration for
and our
benchmark calibration for
![]() from
models I and II.
from
models I and II.
|
|
|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.350 | 0.844 | 0.857 | 1.495 | 0.700 | 0.600 | 0.532 | 7.884 | 0.791 | 9.966 | 0.672 | 0.129 | 0 |
| 0.142 | 0.028 | 0.324 | 0.346 | 0.843 | 0.853 | 1.484 | 0.701 | 0.598 | 0.380 | 7.681 | 0.778 | 9.872 | 0.489 | 0.131 | 0.183 |
|
|
|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -- | -- | 0.350 | 0.844 | 0.857 | 1.495 | 0.700 | 0.600 | 0.532 | 7.884 | 0.791 | 9.966 | 0.672 | 0.129 | 0 |
| 0.142 | -- | -- | 0.367 | 0.844 | 0.863 | 1.512 | 0.698 | 0.602 | 0.420 | 8.270 | 0.830 | 9.966 | 0.506 | 0.123 | 0.172 |
|
|
|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.351 | 0.890 | 1.678 | 1.379 | 0.535 | 0.898 | 0.528 | 8.326 | 0.835 | 9.966 | 0.632 | 0.168 | 0 |
| 0.142 | 0.073 | 0.327 | 0.346 | 0.891 | 1.711 | 1.348 | 0.531 | 0.908 | 0.374 | 7.933 | 0.817 | 9.711 | 0.458 | 0.174 | 0.174 |
|
|
|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -- | -- | 0.350 | 0.844 | 0.857 | 1.495 | 0.700 | 0.600 | 0.532 | 7.884 | 0.791 | 9.966 | 0.672 | 0.129 | 0 |
| 0.142 | -- | -- | 0.367 | 0.884 | 1.512 | 1.421 | 0.558 | 0.843 | 0.419 | 8.658 | 0.869 | 9.966 | 0.483 | 0.154 | 0.164 |
The Ramsey allocation in model III when
![]() (the first
row of Table 5) is
identical to the (Ramsey and socially-efficient) allocation in
model I (Table 2). This is
by construction -- we calibrate
(the first
row of Table 5) is
identical to the (Ramsey and socially-efficient) allocation in
model I (Table 2). This is
by construction -- we calibrate ![]() in model III so that these results are the same,
making any new findings here due only to adjustment at the
intensive labor margin. The Ramsey allocation with
in model III so that these results are the same,
making any new findings here due only to adjustment at the
intensive labor margin. The Ramsey allocation with
![]() here is
again of course identical to the socially-efficient allocation (the
third row of Table 5).
here is
again of course identical to the socially-efficient allocation (the
third row of Table 5).
To understand the effect of the presence of adjustment at the
hours margin, compare the first two rows of Table 5. In the second row, with
![]() , the
Ramsey planner requires a positive labor income tax. The tax
reduces hours worked through the hours bargaining
solution (36), from 0.350 to
0.346. Fewer hours worked per job, ceteris
paribus, causes output per job,
, the
Ramsey planner requires a positive labor income tax. The tax
reduces hours worked through the hours bargaining
solution (36), from 0.350 to
0.346. Fewer hours worked per job, ceteris
paribus, causes output per job,
![]() , to
fall. The bargained wage thus also falls, as (38) shows. This effect on the wage arises
solely through
, to
fall. The bargained wage thus also falls, as (38) shows. This effect on the wage arises
solely through
![]() because
the second term on the right-hand-side of (38) is zero in model III since we
calibrate
because
the second term on the right-hand-side of (38) is zero in model III since we
calibrate ![]() . A
lower wage in turn raises the incentive for firms to post more
vacancies despite the Hosios rule being in effect. The Ramsey
planner would like to prevent this outcome because job-postings
would then be too high from the point of view of social efficiency.
As in Section 5, a
positive capital income tax indirectly dampens the job-posting
incentive and steers the economy closer towards efficiency along
the extensive margin. The second row of Table 5 show that a capital income tax
rate of
. A
lower wage in turn raises the incentive for firms to post more
vacancies despite the Hosios rule being in effect. The Ramsey
planner would like to prevent this outcome because job-postings
would then be too high from the point of view of social efficiency.
As in Section 5, a
positive capital income tax indirectly dampens the job-posting
incentive and steers the economy closer towards efficiency along
the extensive margin. The second row of Table 5 show that a capital income tax
rate of
![]() is
optimal when there is no heterogeneity between employed and
unemployed individuals but labor adjustment occurs at the intensive
margin.
is
optimal when there is no heterogeneity between employed and
unemployed individuals but labor adjustment occurs at the intensive
margin.
The upper half of Table 5 shows that when
![]() , the
Ramsey allocation no longer coincides with the socially-efficient
allocation as it did in model I. Model III, like model I, displays
no welfare heterogeneity between employed and unemployed
individuals. The divergence of the Ramsey allocation from the
socially-efficient allocation thus comes through the hours channel.
The nonzero labor income tax rate distorts the hours margin, just
like in a standard neoclassical model of the labor market. The
hours distortion then affects wage bargaining as described above.
Thus, the proportional labor income tax is distortionary in model
III (and model IV), unlike in model I, preventing the Ramsey
allocation from achieving full efficiency. In other words, the
labor-levy feature of the Ramsey policy described in
Section 5.1 vanishes with the
neoclassical intensive margin.
, the
Ramsey allocation no longer coincides with the socially-efficient
allocation as it did in model I. Model III, like model I, displays
no welfare heterogeneity between employed and unemployed
individuals. The divergence of the Ramsey allocation from the
socially-efficient allocation thus comes through the hours channel.
The nonzero labor income tax rate distorts the hours margin, just
like in a standard neoclassical model of the labor market. The
hours distortion then affects wage bargaining as described above.
Thus, the proportional labor income tax is distortionary in model
III (and model IV), unlike in model I, preventing the Ramsey
allocation from achieving full efficiency. In other words, the
labor-levy feature of the Ramsey policy described in
Section 5.1 vanishes with the
neoclassical intensive margin.
The lower half of Table 5 considers the joint effects of
welfare heterogeneity and intensive adjustment. In model IV, a
labor income tax distorts wage bargaining and hence the extensive
employment margin through two distinct channels: through
![]() in the
first term on the right-hand-side of (38) and through
in the
first term on the right-hand-side of (38) and through
![]() in the
second term of (38). The
optimal capital income tax rate here is
in the
second term of (38). The
optimal capital income tax rate here is
![]() ,
which is essentially just the sum of the optimal capital tax rates
that arise due to just the hours distortion (
,
which is essentially just the sum of the optimal capital tax rates
that arise due to just the hours distortion (
![]() in
the second row of Table 5) and just welfare heterogeneity (
in
the second row of Table 5) and just welfare heterogeneity (
![]() in the
second row of Table 3).
Thus, it seems heterogeneity and the hours distortion have somewhat
additive implications for the optimal capital income tax. To the
extent that labor is elastic at the intensive margin, it is
important to know that these intensive variations -- however small,
which we capture by calibrating the elasticity of intensive labor
supply to be very low -- can have what seem to be an important
quantitative effect on the optimal capital tax. Because our optimal
capital taxation results are driven by inefficiencies in the
extensive labor margin, our findings more fundamentally demonstrate
that the presence of an intensive margin when taxes are
proportional can have important consequences for efficiency along
the extensive labor margin, adding to our understanding of the
nature of efficiency of this class of models.
in the
second row of Table 3).
Thus, it seems heterogeneity and the hours distortion have somewhat
additive implications for the optimal capital income tax. To the
extent that labor is elastic at the intensive margin, it is
important to know that these intensive variations -- however small,
which we capture by calibrating the elasticity of intensive labor
supply to be very low -- can have what seem to be an important
quantitative effect on the optimal capital tax. Because our optimal
capital taxation results are driven by inefficiencies in the
extensive labor margin, our findings more fundamentally demonstrate
that the presence of an intensive margin when taxes are
proportional can have important consequences for efficiency along
the extensive labor margin, adding to our understanding of the
nature of efficiency of this class of models.
The largest of our optimal capital income tax rates is around
seven percent, in our model IV. One may think that it does not make
much difference whether the capital tax rate is set to the
seemingly small positive values we find in our models or simply set
exactly to
![]() , the
standard prescription in the optimal capital taxation literature.
We show here that in fact the welfare consequences, while small,
are not negligible. We quantify the welfare loss of following a
zero capital tax versus following the optimal policy in our
models.
, the
standard prescription in the optimal capital taxation literature.
We show here that in fact the welfare consequences, while small,
are not negligible. We quantify the welfare loss of following a
zero capital tax versus following the optimal policy in our
models.
We address this issue in the following way. Holding the level of
government spending fixed at our benchmark
![]() and
keeping intact the Hosios condition
and
keeping intact the Hosios condition ![]() , we compute steady-state welfare under the
Ramsey policy in each of our models according to
, we compute steady-state welfare under the
Ramsey policy in each of our models according to
| (42) |
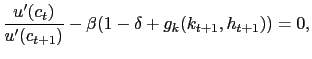
|
(43) |
Denote the allocation resulting from this restricted Ramsey
problem with a hat over variables. We follow the convention of
computing welfare by assuming it is only consumption compensation
that is required, so we compute the welfare loss from the
restricted Ramsey policy as the percentage increase ![]() in consumption that the
household requires in order to be just as well off as in the
unrestricted Ramsey allocation -- that is, we find the
in consumption that the
household requires in order to be just as well off as in the
unrestricted Ramsey allocation -- that is, we find the ![]() such that
such that
| (44) |
Table 6 compiles the welfare losses of following a zero capital income tax versus the optimal capital income tax in our four models. In model I, the optimal capital income tax rate is zero, thus welfare is identical under the unrestricted and restricted Ramsey solutions. In model IV, with both welfare heterogeneity and the distortion due to endogenous hours, the welfare loss is about 0.7 percent of steady-state consumption. This loss decomposes roughly additively into welfare losses due to each channel -- losses of about 0.5 percent of consumption due to welfare heterogeneity by itself (model II) and about 0.25 percent of consumption due to the hours distortion by itself (model III). This welfare decomposition seems consistent with our finding in Section 6.7 that the effects on the optimal capital tax themselves are roughly additive. While seemingly not huge, steady-state welfare losses of this magnitude are not negligible. For example, given that consumption constitutes around 70 percent of output, a welfare loss of 0.7 percent of consumption translates into roughly $50 billion for the U.S. economy.
| Model | Welfare Heterogeneity | Intensive Margin | Optimal |
Welfare Loss of
|
|---|---|---|---|---|
| I | no | no | 0 | 0 |
| II | yes | no | 0.044 | 0.479 |
| III | no | yes | 0.028 | 0.250 |
| IV | yes | yes | 0.073 | 0.679 |
This paper shows that heterogeneity between unemployed and employed individuals matters for optimal fiscal policy. Our main result is that when unemployed individuals are worse off than employed individuals, making them willing to accept lower wages in order to secure employment, a positive capital tax can be used as an indirect way of preventing firms from creating an inefficiently high number of jobs in response to lower wages. In contrast to Domeij (2005), we find that this result holds even at the well-known Hosios parameter configuration that typically sets the wage at its socially-optimal level. In addition, labor adjustment at the hours margin also implies a non-zero optimal capital tax even though the Hosios parameterization is satisfied. We find that the welfare loss of not taking into account welfare heterogeneity and intensive labor adjustment when setting capital income taxes, and instead just following the usual prescription of a zero tax rate, can be as high as 0.7 percent of steady-state consumption.
There are at least two directions in which this model could be extended in future research. First, heterogeneity enters our model through differences in the utility of employed versus unemployed individuals. While our results show that even this simple source of heterogeneity matters for optimal policy, it no doubt also is important to consider alternative sources of differences between employed and unemployed individuals. For example, we could move away from the consumption insurance assumed in this model, allowing individual consumption and capital holdings to differ across labor states. Moving in this direction, however, adds to the complexity of the problem by increasing the state space of the model.
Second, our results consider optimal steady state taxation and thus ignore dynamics. However, the solution to the wage bargaining problem shows that the dynamic effects of the labor tax on wage bargaining may be an important consideration for the dynamically optimal Ramsey policy. In particular, equation (18) shows that a time-varying tax rate drives an extra wedge into the division of the surplus created by a match. The way in which this wedge influences the optimal choice of fiscal policy may be interesting to study in future work.
Here we derive the Nash-bargaining solution between an individual worker and the firm for both the total wage payment and the number of hours worked. At the end of the derivations, we show how the bargaining outcome simplifies when there is no intensive labor margin.
The value of working for an individual is
The value of a filled job is
![$\displaystyle \frac{\gamma}{q(\theta_{t})} = \beta\left[ \left( \frac{u^{\prime}(c_{t+1} )}{u^{\prime}(c_{t})}\right) (1-\rho^{x}) \mathbf{J_{t+1}} \right] .$](img218.gif)
|
(48) |
| (49) |
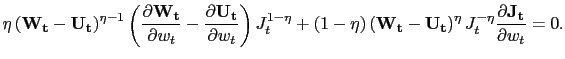
|
(50) |
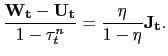
|
(51) |
Using the definitions of
![]() and
and
![]() ,
,
![$\displaystyle \mathbf{W_{t}} - \mathbf{U_{t}} = (1-\tau^{n}_{t})w_{t} h_{t} + \frac {v(h_{t})}{u^{\prime}(c_{t})} - \frac{A}{u^{\prime}(c_{t})} + \beta\left[ \left( \frac{u^{\prime}(c_{t+1})}{u^{\prime}(c_{t})}\right) \left( (1-\rho^{x})(1-\theta_{t} q(\theta_{t})) \mathbf{W_{t+1}} - (1-\rho ^{x})(1-\theta_{t} q(\theta_{t})) \mathbf{U_{t+1}} \right) \right] .$](img227.gif)
|
(52) |
![$\displaystyle \mathbf{W_{t}} - \mathbf{U_{t}} = (1-\tau^{n}_{t})w_{t} h_{t} + \frac {v(h_{t})}{u^{\prime}(c_{t})} - \frac{A}{u^{\prime}(c_{t})} + \beta\left[ \left( \frac{u^{\prime}(c_{t+1})}{u^{\prime}(c_{t})}\right) (1-\rho ^{x})(1-\theta_{t} q(\theta_{t})) (\mathbf{W_{t+1}} - \mathbf{U_{t+1}} ) \right] .$](img228.gif)
|
(53) |
![$\displaystyle \mathbf{W_{t}} - \mathbf{U_{t}} = (1-\tau^{n}_{t})w_{t} h_{t} + \frac {v(h_{t})}{u^{\prime}(c_{t})} - \frac{A}{u^{\prime}(c_{t})} + (1-\theta_{t} q(\theta_{t})) \left( \frac{\eta}{1-\eta}\right) \beta\left[ \left( \frac{u^{\prime}(c_{t+1})}{u^{\prime}(c_{t})}\right) (1-\rho^{x}) (1-\tau ^{n}_{t+1})\mathbf{J_{t+1}} \right] ,$](img230.gif)
|
(54) |
![$\displaystyle \frac{\mathbf{W_{t}} - \mathbf{U_{t}}}{1-\tau^{n}_{t}} = w_{t} h_{t} + \frac{1}{1-\tau^{n}_{t}} \left[ \frac{v(h_{t})}{u^{\prime}(c_{t})} - \frac {A}{u^{\prime}(c_{t})} \right] + \left( \frac{ (1-\theta_{t} q(\theta_{t})) }{1-\tau^{n}_{t}} \right) \left( \frac{\eta}{1-\eta}\right) \beta E_{t} \left[ \left( \frac{u^{\prime}(c_{t+1})}{u^{\prime}(c_{t})}\right) (1-\rho^{x}) (1-\tau^{n}_{t+1})\mathbf{J_{t+1}} \right] .$](img231.gif)
|
(55) |
![$\displaystyle w_{t} h_{t} + \frac{1}{1-\tau^{n}_{t}} \left[ \frac{v(h_{t})}{u^{\prime }(c_{t})} - \frac{A}{u^{\prime}(c_{t})} \right] + \left( \frac{ (1-\theta_{t} q(\theta_{t})) }{1-\tau^{n}_{t}} \right) \left( \frac{\eta }{1-\eta}\right) \beta\left[ \left( \frac{u^{\prime}(c_{t+1})}{u^{\prime }(c_{t})}\right) (1-\rho^{x}) (1-\tau^{n}_{t+1})\mathbf{J_{t+1}} \right] = \frac{\eta}{1-\eta} \mathbf{J_{t}}.$](img232.gif)
|
(56) |
![$\displaystyle {\tiny w_{t} h_{t} + \frac{1}{1-\tau^{n}_{t}} \left[ \frac{v(h_{t} )}{u^{\prime}(c_{t})} - \frac{A}{u^{\prime}(c_{t})} \right] + \left( \frac{ (1-\theta_{t} q(\theta_{t})) }{1-\tau^{n}_{t}} \right) \left( \frac{\eta }{1-\eta}\right) \beta\left[ \left( \frac{u^{\prime}(c_{t+1})}{u^{\prime }(c_{t})}\right) (1-\rho^{x}) (1-\tau^{n}_{t+1})\mathbf{J_{t+1}} \right] = \frac{\eta}{1-\eta} \left( g(k_{t},h_{t}) - w_{t} h_{t} - r_{t} k_{t} + \frac{\gamma}{q(\theta_{t})} \right) .}$](img234.gif)
|
(57) |
![$\displaystyle {\small w_{t} h_{t} = \eta\left[ g(k_{t},h_{t}) - r_{t} k_{t} + \frac{\gamma }{q(\theta_{t})}\right] +\frac{1-\eta}{1-\tau^{n}_{t}}\left[ \frac {A}{u^{\prime}(c_{t})} - \frac{v(h_{t})}{u^{\prime}(c_{t})} \right] - \eta\left( \frac{1-\theta_{t} q(\theta_{t})}{1-\tau^{n}_{t}}\right) \beta\left[ \frac{u^{\prime}(c_{t+1})}{u^{\prime}(c_{t})} (1-\rho^{x}) (1-\tau^{n}_{t+1}) \mathbf{J_{t+1}} \right] .}$](img235.gif)
|
(58) |
Make the substitution
![]() to write
to write
![$\displaystyle {\tiny w_{t} h_{t} = \eta\left[ g(k_{t},h_{t}) - r_{t} k_{t} + \frac{\gamma }{q(\theta_{t})}\right] + \frac{1-\eta}{1-\tau^{n}_{t}}\left[ \frac {A}{u^{\prime}(c_{t})} - \frac{v(h_{t})}{u^{\prime}(c_{t})} \right] - \eta\left( \frac{1-\theta_{t} q(\theta_{t})}{1-\tau^{n}_{t}}\right) \beta\left[ \frac{u^{\prime}(c_{t+1})}{u^{\prime}(c_{t})} (1-\rho^{x}) (1-\tau^{n}_{t+1}) \left( g(k_{t+1},h_{t+1}) - w_{t+1}h_{t+1} - r_{t+1}k_{t+1} + \frac{\gamma}{q(\theta_{t+1})} \right) \right] .}$](img237.gif)
|
(59) |
![$\displaystyle w_{t} h_{t} = \eta\left[ g(k_{t},h_{t}) - r_{t} k_{t}\right] + \frac{1-\eta}{1-\tau^{n}_{t}}\left[ \frac{A-v(h_{t} )}{u^{\prime}(c_{t})}\right] + \frac{\eta\gamma}{q(\theta_{t})} \left[ \frac{\tau^{n}_{t+1} - \tau^{n}_{t} + \theta_{t} q(\theta_{t}) (1-\tau ^{n}_{t+1})}{1-\tau^{n}_{t}} \right] ,$](img181.gif)
|
(60) |
Turning to the determination of hours worked in a match, the
first-order-condition of the Nash product with respect to
![]() is
is
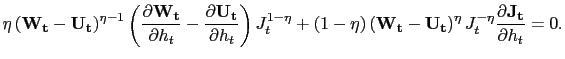
|
(61) |
![$\displaystyle \frac{\eta}{1-\eta} \mathbf{J_{t}} \left[ (1-\tau^{n}_{t})w_{t} + \frac{v^{\prime}(h_{t})}{u^{\prime}(c_{t})} \right] = \left( \mathbf{W_{t}} - \mathbf{U_{t}}\right) \left[ w_{t} - g_{h}(k_{t},h_{t})\right] .$](img243.gif)
|
(62) |
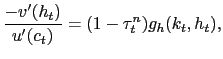
|
(63) |
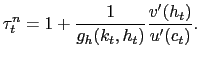
|
(64) |
In our simpler model without the intensive margin, the worker
and firm asset values
![]() and
and
![]() simplify
to
simplify
to
![$\displaystyle \mathbf{W_{t}} = (1-\tau^{n}_{t})w_{t} \bar{h} + \frac{v}{u^{\prime}(c_{t})} + \beta\left[ \left( \frac{u^{\prime}(c_{t+1})}{u^{\prime}(c_{t})}\right) \left( (1-\rho^{x}) \mathbf{W_{t+1}} + \rho^{x} \mathbf{U_{t+1}} \right) \right]$](img248.gif)
|
(65) |
![$\displaystyle \mathbf{J_{t}} = g(k_{t}, \bar{h}) - w_{t} \bar{h} - r_{t} k_{t} + \beta\left[ \left( \frac{u^{\prime}(c_{t+1})}{u^{\prime}(c_{t})}\right) (1-\rho^{x}) \mathbf{J_{t+1}} \right] .$](img249.gif)
|
(66) |
![$\displaystyle w_{t} \bar{h} = \eta\left[ g(k_{t}, \bar{h}) - r_{t} k_{t}\right] + \frac{1-\eta}{1-\tau^{n}_{t}} \left[ \frac{A-v}{u^{\prime}(c_{t})}\right] + \frac{\eta\gamma}{q(\theta_{t})} \left[ \frac{\tau^{n}_{t+1} - \tau^{n}_{t} + (1-\tau^{n}_{t+1}) \theta_{t} q(\theta_{t})}{1-\tau^{n}_{t}}\right] ,$](img251.gif)
|
(67) |
The derivation of the implementability constraint follows that laid out in Lucas and Stokey (1983) and Chari and Kehoe (1999). We present the derivation first for the full model with intensive adjustment and then show how the implementability constraint is modified in the model without intensive adjustment.
Start with the household flow budget constraint in equilibrium
| (68) |
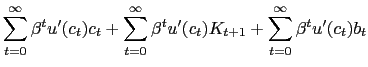
|
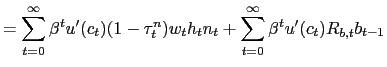
|
|
![$\displaystyle +\sum_{t=0}^{\infty}\beta^{t}u^{\prime}(c_{t})\left[ 1+\left( r_{t}-\delta\right) \left( 1-\tau_{t}^{k}\right) \right] K_{t}+\sum _{t=0}^{\infty}\beta^{t}u^{\prime}(c_{t})d_{t}.$](img256.gif)
|
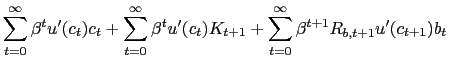
|
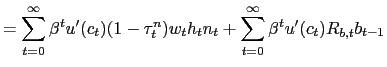
|
|
![$\displaystyle +\sum_{t=0}^{\infty}\beta^{t}u^{\prime}(c_{t})\left[ 1+\left( r_{t}-\delta\right) \left( 1-\tau_{t}^{k}\right) \right] K_{t}+\sum _{t=0}^{\infty}\beta^{t}u^{\prime}(c_{t})d_{t}.$](img256.gif)
|
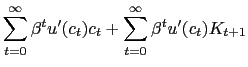
|
![$\displaystyle =\sum_{t=0}^{\infty}\beta^{t}u^{\prime }(c_{t})(1-\tau_{t}^{n})w_{t}h_{t}n_{t}+\sum_{t=0}^{\infty}\beta^{t}u^{\prime }(c_{t})\left[ 1+\left( r_{t}-\delta\right) \left( 1-\tau_{t}^{k}\right) \right] K_{t}$](img261.gif)
|
|
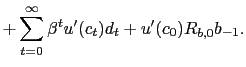
|
![$\displaystyle \sum_{t=0}^{\infty}\beta^{t}u^{\prime}(c_{t})c_{t}=\sum_{t=0}^{\infty} \beta^{t}u^{\prime}(c_{t})(1-\tau_{t}^{n})w_{t}h_{t}n_{t}+\sum_{t=0}^{\infty }\beta^{t}u^{\prime}(c_{t})d_{t}+u^{\prime}(c_{0})\left[ R_{b,0} b_{-1}+\left( 1+\left( r_{0}-\delta\right) \left( 1-\tau_{0}^{k}\right) \right) K_{0}\right] .$](img264.gif)
|
(69) |
Now insert equilibrium profits, given by
![]() on the right hand side to yield
on the right hand side to yield
![$\displaystyle \sum_{t=0}^{\infty}\beta^{t}u^{\prime}(c_{t})\left[ c_{t}-n_{t}g \left( k_{t},h_{t}\right) +\tau_{t}^{n}w_{t}h_{t}n_{t}+r_{t}k_{t}n_{t}+\gamma v_{t}\left( 1-\tau_{t}^{s}\right) \right] =u^{\prime}(c_{0})\left[ R_{b,0}b_{-1}+\left( 1+\left( r_{0}-\delta\right) \left( 1-\tau_{0} ^{k}\right) \right) K_{0}, \right]$](img266.gif)
|
(70) |
![$\displaystyle \sum_{t=0}^{\infty}\beta^{t}u^{\prime}(c_{t})\left[ c_{t}-\left( g_{h}\left( k_{t},h_{t}\right) -\tau_{t}^{n}w_{t}\right) n_{t}h_{t}+\gamma v_{t}\left( 1-\tau_{t}^{s}\right) \right] =u^{\prime}(c_{0})\left[ R_{b,0}b_{-1}+\left( 1+\left( g_{k}(k_{0},h_{0})-\delta\right) \left( 1-\tau_{0}^{k}\right) \right) K_{0}\right] .$](img269.gif)
|
(72) |
Using the Nash solution for hours
![]() we can write
we can write
![]() Inserting this into the previous expression, we arrive at
our form of the present value implementability constraint,
Inserting this into the previous expression, we arrive at
our form of the present value implementability constraint,
![$\displaystyle \sum_{t=0}^{\infty}\beta^{t}u^{\prime}(c_{t})\left[ c_{t}-n_{t}h_{t}\left( g_{h}\left( k_{t},h_{t}\right) -w_{t}-\frac{w_{t}}{g_{h}(k_{t},h_{t})} \frac{v^{\prime}(h_{t})}{u^{\prime}(c_{t})}\right) +\gamma v_{t}\left( 1-\tau_{t}^{s}\right) \right] =$](img272.gif)
|
|
![$\displaystyle \sum_{t=0}^{\infty}\beta^{t}\left[ u^{\prime}(c_{t})c_{t}+v^{\prime} (h_{t})h_{t}\right] =u^{\prime}(c_{0})\left[ R_{b,0}b_{-1}+\left( 1+\left( g_{k}(k_{0},h_{0})-\delta\right) \left( 1-\tau_{0}^{k}\right) \right) K_{0}\right] ,$](img277.gif)
|
(73) |
In the model without intensive adjustment, the manipulations
following expression (71) are unavailable because the
production function ![]() is
not constant returns to scale. We also cannot eliminate the labor
tax rate
is
not constant returns to scale. We also cannot eliminate the labor
tax rate ![]() as we
did above because there is no intensive margin with which to
eliminate it. Thus, in deriving the implementability constraint in
the model without intensive adjustment, we must stop at the analog
of expression (71),
as we
did above because there is no intensive margin with which to
eliminate it. Thus, in deriving the implementability constraint in
the model without intensive adjustment, we must stop at the analog
of expression (71),
![$\displaystyle \lefteqn{\sum_{t=0}^{\infty} \beta^{t} u'(c_{t}) \left[ c_{t} - \left( g(k_{t}, \bar{h}) - \tau^{n}_{t} w_{t} \bar{h} - g_{k}(k_{t}, \bar{h}) k_{t} \right) n_{t} + \gamma v_{t} (1-\tau^{s}_{t}) \right] = }$](img85.gif)
|
(74) | |
Andolfatto, David, 1996, Business Cycles and Labor-Market Search, American Economic Review, 86, 112-132.
Blanchard, Olivier and Peter Diamond, 1989, The Beveridge Curve, Brookings Papers on Economic Activity, 1, 1-76.
Chamley, Christophe, 1986, The Welfare Cost of Capital Income Taxation in a Growing Economy, Econometrica, 54, 607-622.
Chari V. V., and Patrick J. Kehoe, 1999, Optimal Fiscal and Monetary Policy, Handbook of Macroeconomics, John B. Taylor and Michael Woodford, Vol. 1C, Elsevier.
Chugh, Sanjay K, 2006, Optimal Fiscal and Monetary Policy with Sticky Wages and Sticky Prices, Review of Economic Dynamics.
Domeij, David, 2005, Optimal Capital Taxation and Labor Market Search, Review of Economic Dynamics, 8, 623-650.
Hagedorn, Marcus and Iourii Manovskii, 2006, The Cyclical Behavior of Equilibrium Unemployment and Vacancies Revisited, University of Pennsylvania.
Hosios, Arthur J, 1990, On the Efficiency of Matching and Related Models of Search and Unemployment, Review of Economic Studies, 57, 279-298.
Judd, Kenneth L, 2002, Capital Income Taxation with Imperfect Competition, American Economic Review, 92, 417-421.
Krause, Michael U. and Thomas A. Lubik, 2004, The (Ir)relevance of Real Wage Rigidity in the New Keynesian Model with Search Frictions, Johns Hopkins University.
Ljungqvist, Lars and Thomas J. Sargent, 2004, Recursive Macroeconomic Theory, MIT Press.
Lucas, Robert E. Jr. and Nancy L. Stokey, 1983, Optimal Fiscal and Monetary Policy in an Economy Without Capital, Journal of Monetary Economics, 12, 55-93.
Merz, Monika, 1995, Search in the Labor Market and the Real Business Cycle, Journal of Monetary Economics, 36, 269-300.
Pissarides, Christopher A, 2000, Equilibrium Unemployment Theory, MIT Press.
Rogerson, Richard, Robert Shimer, and Randall Wright, 2005, Search-Theoretic Models of the Labor Market: A Survey, Journal of Economic Literature, 43, 959-988.
Schmitt-Grohe, Stephanie and Martin Uribe, 2005, Optimal Fiscal and Monetary Policy in a Medium-Scale Macroeconomic Model, 2005.
Shi, Shouyong and Quan Wen, 1999, Labor Market Search and the Dynamic Effects of Taxes and Subsidies, Journal of Monetary Economics, 43, 457-495.
Trigari, Antonella, 2003, Equilibrium Unemployment, Job Flows and Inflation Dynamics, Bocconi University.
Walsh, Carl E, 2005, Labor Market Search, Sticky Prices, and Interest Rate Policies, Review of Economic Dynamics, 8, 829-849.
*Email address: [email protected]. Return to text
†Email address: [email protected]. We thank Shigeru Fujita, Sylvain Leduc, Robert Martin, and Thomas Tallarini for helpful discussions, and participants at the Board�s International Finance Workshop, the Spring 2006 Federal Reserve System Macroeconomics Meetings, the 2006 Midwest Macroeconomics Meetings, the 2006 Econometric Society Summer Meetings, and the 2006 Society of Computational Economics Meetings. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. Equivalently, the externality can be thought of as arising from the fact that one additional firm with a vacancy increases the probability that a job-seeker will match with a firm but decreases the probability that firms already in the market will match with a job-seeker. Return to text
2. Trigari (2003), Krause and Lubik (2004), and Walsh (2005) are just a few recent examples of the emerging use of labor search models to address policy questions. Return to text
3. In this case, the missing instrument is one that directly affects market tightness. See Ljungqvist and Sargent (2004, p. 478) for more discussion on using the capital tax as part of an incomplete tax system. Return to text
4. In these papers, a capital subsidy boosts output, which is inefficiently low due to the presence of a monopolistic distortion, closer to its efficient level by encouraging capital accumulation. Return to text
5. Thus, we follow Merz (1995), Andolfatto (1996), and much of the subsequent literature in this regard by assuming full consumption insurance between employed and unemployed individuals. Return to text
6. See Ljungqvist and Sargent (2004, Chapter 15) for more discussion about alternative setups of Ramsey problems. Return to text
7. This adoption of the ``timeless" perspective is innocuous here since we focus on only the steady-state rather than on transitional dynamics. We should also point out that, as is well-known in this literature, nothing guarantees a solution to the Ramsey problem, nor, if a solution exists, convergence to a steady-state. We do, however, numerically find a steady-state. Return to text
8. By the Second Welfare Theorem, the socially-efficient allocation can be implemented as an equilibrium with an appropriate set of lump-sum tax instruments. Return to text
9. On the other hand, if
![]() , the labor tax
raises workers' bargaining power and thus raises the bargained
wage. The intuition for this case is that individuals prefer to be
unemployed in an economy where
, the labor tax
raises workers' bargaining power and thus raises the bargained
wage. The intuition for this case is that individuals prefer to be
unemployed in an economy where ![]() . A rise in
. A rise in ![]() in this case increases the opportunity cost
of foregoing leisure and working instead. The bargained wage must
then compensate workers with a higher wage in order to entice them
to join a match. Return to text
in this case increases the opportunity cost
of foregoing leisure and working instead. The bargained wage must
then compensate workers with a higher wage in order to entice them
to join a match. Return to text
10. The ability of the capital tax to act as a substitute instrument in an incomplete tax system is well-known -- see Ljungqvist and Sargent (2004, p. 478). Return to text
11. Again, assuming no vacancy tax exists. Return to text
12. See Chari and Kehoe (1999, p. 1679-1680) for more discussion on this type of restriction in a Ramsey problem. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text