Skip to: [Printable Version (PDF)]

Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 872, September 2006 --- Screen Reader Version*

The Monetary Origins of Asymmetric Information in International Equity Markets

Gregory H. Bauer and Clara Vega^*

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

Existing studies using low-frequency data have found that macroeconomic shocks contribute little to international stock market covariation. However, these papers have not accounted for the presence of asymmetric information where sophisticated investors generate private information about the fundamentals that drive returns in many countries. In this paper, we use a new microstructure data set to better identify the effects of private and public information shocks about U.S. interest rates and equity returns. High-frequency private and public information shocks help forecast domestic money and equity returns over daily and weekly intervals. In addition, these shocks are components of factors that are priced in a model of the cross section of international returns. Linking private information to U.S. macroeconomic factors is useful for many domestic and international asset pricing tests.

Keywords: Private information, international equity returns, monetary policy, foreign exchange rates, exchange traded funds.

JEL classification: F3, G12, G14, G15

1 Introduction

The causes of international stock market covariation remain a puzzling issue in finance. Asset-pricing models dictate that expected stock returns vary in response to changes in risk-free interest rates, changes in expected future cash flows, and/or changes in the equity risk premium. In a rational asset-pricing framework, with international market integration, comovements in international stock returns would be driven by news about macroeconomic factors that affect cash flows, risk-free rates, or risk premiums in many countries.

Existing studies using low-frequency data, however, show that macroeconomic factors have a limited impact on international equity returns. For example, King, Sentana and Wadhwani (1994) construct a factor model of 16 national stock market monthly returns and examine the influence of 10 key macroeconomic variables. They conclude that the surprise components of these observable variables contribute little to world stock market variation. Rather, there is a dominant unobservable (i.e., non-public) factor driving international returns.¹ Karolyi and Stulz (1996) show that neither macroeconomic news announcements nor interest rate shocks significantly affect comovements between U.S. and Japanese stock returns. Connolly and Wang (2003) examine the open-to-close equity market returns of the U.S., the U.K., and Japan and find that foreign returns cause movements in domestic markets even after accounting for macroeconomic news announcements.

If public news about macroeconomic variables is not responsible for the comovements, could some `` market friction'' be responsible? One potential friction is trading based on asymmetric information. In the literature that examines the limits to international risk-sharing, asymmetric information is used as a theoretical explanation of the `` home bias'' and `` familiarity'' puzzles in international portfolio selection.<sup>2</sup> In contrast, the literature has been largely silent on the effects of trading based on private information on international asset-return covariability. When sophisticated agents trade, their private information is (partially) revealed to the market, causing revisions in asset prices. Trading based on private information could thus be a potential cause of the comovements in international stock returns if agents had superior knowledge about the common factors that price equities from many countries. However, the economic origins of such private information remain unexplored. Indeed, Goodhart and O'Hara (1997) wonder: `` in the international context, how could private information be expected to have a global impact?''

In this paper, we provide an answer to this question. We start by providing empirical estimates of trading based on private information in the U.S. money and equity markets. Using an analysis of microstructure data, we show that some agents have superior knowledge about both future U.S. interest rates and aggregate U.S. equity market returns. Trades based on private information have a significant impact on money and equity market returns over holding periods that range from one day to one week.

Our interpretation of these results is that sophisticated investors have good information about future macroeconomic factors that will affect both U.S. equity prices and interest rates. If international equity markets are integrated, then information about U.S. factors will give informed agents superior knowledge about the global factors that price stocks in many countries (Albuquerque, Bauer and Schneider 2003a). It is then likely that the private information of the sophisticated investors trading in these (liquid) U.S. markets will help explain the cross section of international equity returns.

We use a latent-factor model of international equity returns to evaluate the effects of private information originating in U.S. markets on foreign markets. The latent factor is composed of public and private information shocks from the U.S. money and equity markets. We examine how the factor is related to daily and weekly returns on foreign equity markets. We show that private and public information shocks arising in U.S. markets are components of the priced factor in a model of the cross section of international equity returns. Sophisticated investors have an impact on global markets when their superior information is incorporated into international equity returns. To the best of our knowledge, this is the first paper to show that private information is part of a priced factor in an international setting.

This paper extends the existing literature in three ways. The first extension is to adapt techniques from the microstructure literature (primarily Hasbrouck 1991) to identify information shocks in aggregate U.S. stock and money markets from quote revisions and order flows sampled at high frequencies. These shocks can be orthogonalized into those due to private and public information. Using order flow sampled at high frequencies provides a powerful method of obtaining private information shocks (e.g., Hasbrouck 1991, Brennan and Subrahmanyam 1996, Madhavan, Richardson and Roomans 1997, and Yu 2003). Similarly, the effect of public news on asset prices can be measured more accurately using high-frequency data (Andersen et al. 2003). We can use the high-frequency shocks obtained from our time-series regressions as elements of the latent factor in a conditional asset-pricing model of the cross section of international returns. The model reveals that the shocks are both statistically and economically important.

The second extension is to focus on shocks related to a specific macroeconomic fundamental: U.S. interest rates. Cochrane and Piazzesi (2002) and others have shown that unanticipated daily movements in short-term U.S. interest rates are good proxies for monetary policy innovations. Cochrane and Piazzesi (2002) also show that these public information shocks have a large impact on short and long-term U.S. bond yields. We extend their work in two ways. First, using time-series regressions on our microstructure data, we obtain both public and private information shocks about U.S. interest rates. We then show that these shocks affect prices in the U.S. equity market. Second, we show that the shocks have an affect on the cross section of international equity returns.

Our third extension is that, instead of focusing on the returns of foreign stocks traded in national markets, we use foreign stock indexes that trade in New York as exchange traded funds (ETFs). ETFs are bundles of foreign stocks that trade on the American Stock Exchange (AMEX) and are priced in U.S. dollars. They are designed to be a low-cost instrument that tracks a foreign stock index. Because the supply of an ETF can be altered at any time, arbitrage ensures that its price closely tracks the index. By using these contracts, we observe returns and order flows on foreign equities that trade contemporaneously with their U.S. counterparts. We can thus obtain high-frequency measures of public and private information shocks that affect the foreign indexes during U.S. trading times.

One potential problem in previous low-frequency studies of international equity market comovements is non-synchronous trading. Those studies examined the impact of information events that occurred during U.S. trading times on foreign (overnight) returns. The different time zones of the markets complicate the inference.³ In this paper, we avoid this problem by using foreign assets that trade contemporaneously with American stocks, and by focusing on public and private information shocks released during U.S. trading times only. The foreign assets, however, will respond to news released in the home markets as well. Thus, our approach does not measure the effects of all trading based on private information on the assets, but only a subset of the trades.⁴

A potential problem with our approach is that the foreign indexes (ETFs) trade less in the U.S. market than they do in their home market. The potential for stale prices will complicate any short-run analysis of the returns. In contrast, the focus in this paper is on changes in the foreign equity prices over holding periods ranging from one day to one week.⁵ At these intervals, stale prices will have much less of an influence. An additional benefit of examining daily and weekly intervals is that we obtain the aggregate U.S. and foreign market response to information released during U.S. trading times. This is important, because foreign market trading could negate the effects of information released during U.S. trading times, leaving no long-run impact on the price of the security. We find, however, that our high-frequency information shocks that occur during U.S. trading times continue to have an impact on foreign equity returns up to a week later.

Our focus on trading related to U.S. variables helps to fill in the gaps from previous studies. Albuquerque, Bauer and Schneider (2003a) identify a common global factor that accounts for approximately half of the variation in monthly trades by U.S. investors due to private information. Although they speculate on the origins of the private information, they do not test any particular factor. Other papers have hinted that private information in one market may spill over into a foreign equity market. For example, Werner and Kleidon (1996) examine the intra-day patterns in trading volume, return volatility, and bid-ask spreads of cross-listed stocks in the U.K. and U.S. equity markets. After testing several hypotheses that could cause the patterns, they conclude that the main cause is the private information revealed by U.S. order flow. Werner and Kleidon do not, however, indicate what the private information could be.

Our paper also contributes to areas other than international asset pricing. One contribution is to the growing literature that attempts to link microstructure concepts, such as private information and liquidity, to asset pricing.⁶ Easley, Hvidkjaer and O'Hara (2002) find that a measure of a stock's probability of private information based trading is priced in the cross section of U.S. stocks. In this paper, we provide additional support for their analysis by showing that part of the private information in the U.S. equity market is related to a specific macroeconomic fundamental.

We proceed as follows. In section 2, we describe the data and show how our Eurodollar interest rate series is related to U.S. monetary policy. In section 3, we describe our general microstructure model for extracting private and public information shocks from the U.S. money and equity markets. In section 4, we present our latent-factor model and show that private information is a priced factor in the cross section of international equity returns. We conclude in section 5.

2 Data Description and U.S. Monetary Policy Proxies

This section starts by explaining the sources of our data series. It also explains how to obtain signed trades (order flow) from the Eurodollar, U.S. equity, and foreign equity markets. We then show how shocks in the Eurodollar futures market are related to changes in U.S. monetary policy.

2.1 Data description

To capture public and private information shocks in the U.S. and foreign equity markets, we use high-frequency data on ETFs. ETFs are shares of a portfolio of stocks that trade continuously on an exchange and are designed to track closely the performance of a specific index.⁷ Managers of the ETFs may buy either all the stocks in the index or a sample of stocks, to track the index. It is important to emphasize that ETFs are not closed-end funds. Closed-end funds offer a fixed supply of shares, and as demand changes they frequently trade at appreciable discounts from (and sometimes premiums to) their net asset values (NAVs). In contrast, market participants are able to create and redeem shares in an ETF when its market price differs from the value of its underlying index. This ability to open the funds at any time ensures that ETFs trade near their NAVs.⁸

The U.S. ETF is the Standard and Poor's (S&P) 500 fund (SPDR, or `` Spider'') that began trading on the AMEX in 1993.⁹ Elton et al. (2002) discuss the investment and tracking performance of this fund. They conclude that the SPDR closely tracks the S&P 500 index, because the difference between the two is less than 1.8 basis points per annum. The SPDR is a very liquid security; in mid-2003, the fund had over U.S. $37 billion in assets under management, with average daily trading volume totalling U.S. $4 billion.

The foreign ETFs are shares of portfolios designed to track the performance of foreign market indexes compiled by Morgan Stanley Capital International (MSCI). They were launched under the World Equity Benchmark Shares (WEBS) brand and were renamed in 1998 as `` iShares,'' or index shares. They are managed by Barclays Global Fund Advisors and trade on the AMEX. We use bid quotes, ask quotes, and transactions prices for the ETFs of the U.S. and 10 foreign countries (Germany, Japan, the U.K., Switzerland, Canada, France, the Netherlands, Sweden, Australia, and Italy). We select these countries because they have developed equity markets and ETF data that are available over our sample period.

The U.S. and foreign ETF data are obtained from the Trades and Quotes (TAQ) database. The sample period consists of continuously recorded tick-by-tick data from April 1, 1996 to November 30, 2001 (1,206 days). To calculate ETF buyer-initiated orders and seller-initiated orders, we use the algorithm developed by Lee and Ready (1991).¹⁰ Order flow is the net amount of buyer-initiated less seller-initiated trades.

To estimate public and private information shocks in U.S. interest rates, we use high-frequency data on the Eurodollar futures contract that trades on the Chicago Mercantile Exchange (CME).¹¹ The Eurodollar contract is considered to be the most liquid exchange-traded money market instrument in the world. The contract is valued at 100 less the London Inter-Bank Offered Rate (LIBOR) on Eurodollars at maturity. We examine five different maturities: the 3-month, 6-month, 9-month, 1-year, and 5-year ( $k=3,6,9,12,$ and $60$) contracts. The contracts maturing in less than one year are the most liquid.

The CME records `` time and sales data,'' which contain the time and price of a transaction only if the price is different from the previously recorded price. Bid (ask) quotes appear in this file only if the bid quote is above (the ask quote is below) the previously recorded transaction price. Because quotes are generally not recorded, we use the `` tick test'' to estimate buyer-initiated and seller-initiated orders.¹² The order-flow series that we use is the net purchases (buyer-initiated less seller-initiated trades).

Using time and sales data produces two opposite effects on our measure of private information. The first effect is that we underestimate the number of `` liquidity trades'' as opposed to `` informed trades.'' Since we have time and sales data, we can measure trades only when the price of the asset changes, which is more likely to occur due to an informed trade rather than a liquidity-based trade. Thus, we systematically underestimate liquidity-based trades. This implies that our order-flow series is dominated by information-based trading.

The second effect results from not being able to observe quotes, which forces us to classify trades using the tick test. Our estimated order flows for the Eurodollar data using the tick test will be noisier than the order-flow measure for the other assets, which we obtain by using the Lee and Ready algorithm. However, Ellis, Michaely and O'Hara (2000) show that the tick test does not induce a systematic bias into the resulting order-flow data.

The foreign ETFs trade in U.S. dollars. As a robustness check to our results below, we wish to evaluate the effect of our public and private information shocks on foreign equity returns measured in foreign currencies. Unfortunately, we are unable to obtain high-frequency quote and transaction data on the spot market foreign exchange rates associated with our 12 foreign countries. We therefore use currency future contracts traded on the CME. We obtain time-and-sales data for the Euro, Japanese Yen, U.K. Pound, Swiss Franc, and Canadian Dollar futures contracts.¹³ The contracts are priced in U.S. dollars per unit of foreign currency. Again, we use the tick test to categorize the transactions data as purchases or sales. We use the 3-month futures contracts, because they are the most liquid.

One difficulty with combining our various data series is that the markets that we analyze have slightly different trading times. The Eurodollar and foreign currency futures contracts trade on the CME, where the trading hours are from 8:20 a.m. to 3.00 p.m. EST. The ETFs trade on the AMEX, where the trading hours are from 9:30 a.m. to 4.00 p.m. EST. In our analysis, we constrain the aggregate data set to a common period. We also divide the trading day into subperiods, to determine the influence of one market on the other. We therefore divide the day into eleven 30-minute intervals, with the first interval starting at 9:30 a.m. EST and the last interval ending at 3.00 p.m. EST. This results in a total of 15,598 half-hour observations for the entire data set. We use the last mid-quote recorded during each half-hour interval as our price.¹⁴Quote revisions are the log differences of these prices. Signed order flow is the total number of purchases less the total amount of sales during the interval.

Another difficulty with the data set is that the trades and quote revisions display an intra-day seasonality. We therefore perform an initial deseasonalization by projecting the order flows and quote revisions data on time-of-day dummy variables, and use the mean-centred residuals as our basic data series.

Table 1a shows sample statistics for the quote revisions on the Eurodollar futures contracts, the U.S. and foreign ETFs, and the foreign currency futures contracts. The Eurodollar futures contracts have a very small average mean return and a low standard deviation relative to the other series. The contracts with maturities of less than one year are very liquid, with almost all intervals recording a quote (transaction price). The ETFs are much more volatile, with standard deviations above $0.2$ per cent per half-hour of trading for all countries. The U.S. ETF (Spider) is very liquid, with observations recorded in $99.7$ per cent of all intervals. The foreign ETFs are naturally less liquid, with some contracts having a quote observation in only $40$ per cent of the intervals. This may complicate the short-horizon analysis of returns; however, our daily and weekly holding periods make this issue much less important. The foreign currency contracts are all liquid.

Table 1b shows the sample statistics of the order-flow data for the assets. These data are displayed in numbers of net purchases per half-hour period. For example, the 3-month Eurodollar futures contract has an average of $0.029$ contracts purchased net each half-hour during the sample period. As can be seen, the net number of contracts traded each interval ranges widely for the Eurodollar contracts, the U.S. ETF, and the foreign currency futures contracts, indicating a fair degree of trading activity.¹⁵ Some of the foreign ETFs trade much less frequently, with trades recorded in approximately $20$ per cent of all the intervals. We obtain the global private information shocks from trading in the Eurodollar and U.S. ETF markets, both of which are quite liquid.

Table 1c shows the correlation coefficients between the log price changes of the ETF and their underlying MSCI indexes for daily and weekly holding periods. The correlations range from $0.603$ to $0.802$ at the daily interval, whereas they rise to above $0.85$ at the weekly interval. There are two reasons for the less-than-perfect correlations. First, the ETF may not be able to hold stocks in the same composition as that of the MSCI index. For example, if a particular foreign stock is a large portion of the foreign index, then the ETF fund manager may have trouble tracking the index while keeping the ETF diversified enough for U.S. tax and regulatory purposes. Second, investors are not able to arbitrage all differences between the price of the ETF and the underlying stocks, due to transactions costs and differences in trading times.¹⁶ The effect of timing differences will be particularly large at daily intervals. Nevertheless, the correlations are high enough at the weekly interval that we are confident that the ETFs represent the U.S. prices of the foreign equities.

Table 2a shows the contemporaneous correlations between the quote revisions on the assets. The top part of the table shows the correlations between the Eurodollar futures, the U.S. ETF, and the foreign currency futures contracts. There is a high degree of correlation between price movements on the short-dated Eurodollar futures contracts. The negative correlation between the U.S. ETF quote revision and those on the Eurodollar contracts implies that price gains in the U.S. ETF are associated with rising Eurodollar interest rates. In our sample, the U.S. Federal Reserve raised interest rates as the equity market was gaining, and then lowered rates as the market declined. The correlations with the foreign currency contracts indicate that an increase in the U.S. equity market is associated with a strengthening U.S. dollar against all of the foreign currencies except the Canadian dollar. The correlations among the U.S. and foreign equity quotes at the bottom part of Table 2a indicate that common factors are affecting the returns on these assets during U.S. trading times.

The net purchases data also display common variation, though the correlations are not as high (Table 2b). Again, the short-dated Eurodollar contracts display common variation. Investors purchase Eurodollar contracts when they are selling the U.S. equity market, as shown in the middle of the table. The bottom part of the table indicates some common variation to net purchases across the ETF markets.

In our analysis below, we study the effects of information shocks that arise in the U.S. money and equity markets on foreign equities. This implies a causal (time-series) relation that we should establish first. We thus undertake a number of Granger causality tests. In the first set of tests, we examine whether foreign equity market order flows and quote revisions cause either quote revisions or order flow in the Eurodollar market. In these tests, we regress the quote revision or order flow in the U.S. money market on 12 lagged values of order flow and quote revisions in the market.¹⁷ We also include 12 lagged values of the U.S. or foreign ETF order flows and quote revisions, to determine whether the coefficients on the latter variables are jointly significant, yielding a test statistic that is distributed as $\chi^{2}(12)$.

Table 3a shows the asymptotic marginal significance levels ($P$-values) of the tests. A small value would indicate predictability of the U.S. or foreign equity market variable for the U.S. money market. None of the 44 statistics is significant at a $5$ per cent level, indicating that neither the order flows nor the quote revisions from the U.S. or foreign ETF markets Granger-cause the Eurodollar market.

We repeat the same test for the U.S. equity markets quote-revision and order-flow regressions. We also test (Table 3b) whether the Eurodollar variables help predict movements in the U.S. equity market. There is clear evidence that Eurodollar order flows and quote revisions cause movements in U.S. equity order flows and quote revisions. In contrast, only a few of the foreign ETF variables Granger-cause order flows or quote revisions in the U.S. ETF.

We also test (Table 3c) whether the U.S. money and equity markets Granger-cause the foreign equity markets. Lagged order flow in the Eurodollar and U.S. ETF markets is a significant predictor of future quotes and order flows in a number of countries. Lagged quote revisions in the Eurodollar and U.S. ETF markets yield a large amount of predictability in the foreign ETF order-flow processes. Investors who transact in U.S. trading times appear to base their foreign buying decisions on recent price movements in the U.S. markets. There is also a strong relationship in the foreign quote-revision regressions. ETF market makers respond to lagged order flows and quote revisions in the two U.S. markets when they set their quotes.

The tests indicate that price discovery occurs first in the U.S. money and then in the U.S. equity market. This information is subsequently impounded into foreign equity prices. This sequence is related to the relative liquidity of the markets. When investors receive private news about `` global'' factors (i.e., factors that affect many asset markets), they undertake transactions in those markets that are the most liquid. Thus, the initial price response in the Eurodollar and U.S. ETF markets may simply result from the relative liquidity of the markets. The market makers in the less-liquid market observe these prices and then adjust their quotes.

2.2 The Eurodollar futures contract and U.S. monetary policy

This paper uses the rate on Eurodollar futures contracts to estimate monetary policy shocks. Previous research has provided evidence on several components in the Eurodollar futures interest rate. Cochrane and Piazzesi (2002) show that the (spot) Eurodollar interest rate can successfully forecast moves in the Federal funds target rate, the rate which anchors moves in the spot Federal funds rate. Lee (2003) examines the close connection that exists between the overnight Federal funds market and its Eurodollar counterpart (the `` on-shore - off-shore interest differential''). He finds a small potential arbitrage between the two rates, but notes a number of frictions that may prevent arbitrage trades from happening. Stigum (1990, p. 911) also notes the close connection between the Eurodollar and domestic interest rate markets and quotes a Eurobanker as saying that `` Rarely does the tail wag the dog. The U.S. money market is the dog, the Euromarket the tail.'' She goes on to say that: `` The truth of this statement has created a foreign contingent of Fed watchers - in London, Paris, Singapore and other Eurocenters. ... Eurobankers must understand the workings of the U.S. money market and follow closely developments there.'' Piazzesi and Swanson (2004) show that Eurodollar futures rates predict future Federal funds rates. In addition, they find a significant time-varying risk premium in the futures rates, which can complicate the extraction of monetary policy forecasts from the futures' rates.

Thus, we can break the price of the Eurodollar futures contract into three components. The first is the forecast of the Federal funds rate (the `` monetary policy'' component). The second is the forecast of the difference between the Eurodollar interest rate (LIBOR) and the Federal funds rate (the `` on-shore - off-shore interest rate differential'' component). The third is the risk-premium component from holding the contract. Our assumption in this paper is that trades in the Eurodollar market reflect private information about the three components.

We use this framework to extract monetary policy innovations. Piazzesi and Swanson (2004) note that daily changes in the price of a Eurodollar futures contract can be used as a measure of a monetary policy shock, since the risk-premium component is relatively stable over their 2-day window. We use the change in the price of a short-term Eurodollar futures contract at the time of the target rate announcement as our measure of a monetary policy shock. Our assumption is that neither the risk-premium component nor the on-shore - off-shore interest differential component will change significantly during this half-hour period. Below, in our analysis of the microstructure data, we will show how to get a good measure of the unanticipated move in the rate at high frequencies. For now, we provide some simple forecasts using daily data. In Figure 1, we show how the price of the 6-month Eurodollar futures contract is related to future Federal funds target moves. From June 1999 to June 2000, the Eurodollar futures lead the Federal funds target rate increases. Likewise, from November 2000 to November 2001, the Eurodollar futures lead the target rate decreases. In the earlier part of the sample, from April 1996 to June 1999, there are two `` false'' predictions, but, for the most part, the Eurodollar futures correctly predicts no changes in the target and leads the increase and decrease in the target rate.

To formalize how well the Eurodollar futures contract can forecast target rate changes, we estimate the forecasting model of Cochrane and Piazzesi (2002). We estimate the model in price form; i.e., we calculate a `` price'' for the Federal funds target rate as $P_{\tau} ^{TR}=\log(100-TR_{\tau})$, where $TR_{\tau}$ is the target rate at time $\tau$. We make this estimation to be consistent with our public and private information system of equations used in section 3, which are in quote revision form. The forecast regression is then

$$\Delta P_{\tau}^{TR}=a+bP_{\tau-1}^{TR}+cSP_{j\tau-1}+\varepsilon_{j\tau },$$ (1)

where $\Delta P_{\tau}^{TR}=P_{\tau}^{TR}-P_{\tau-1}^{TR}$ is the `` return'' on the target rate at time $\tau$, when a change to the target rate is announced; $P_{\tau-1}^{TR}$ is the target rate 30 minutes before the announced change to the target rate; and $SP_{j\tau-1}=P_{\tau-1}^{TR}-\log(P_{\tau-1}^{ED})$ is the spread between the log target rate price and the log Eurodollar futures price on the $j$-month contract, also recorded 30 minutes before the change to the target rate. Note that the time index, $\tau,$ is an event time index. In our sample period, there are 19 changes to the target rate, so $\tau=1,...,19.$¹⁸

We run the Cochrane-Piazzesi regression separately using each of the Eurodollar futures contracts. Table 4 shows the results. The 6-month contract has the highest predictive power, with an $R^{2}$ of $0.918.$ The negative coefficient on the spread is to be expected; if the `` price'' of the target rate is above that on the Eurodollar contract, the negative coefficient indicates that a decrease in the Federal funds price is forecast, so that it moves closer to that of the Eurodollar contract. Overall, the regressions indicate that the spread between the Eurodollar futures contracts and the current level of the target contains significant information about future changes to the Federal funds target.

3 Private Information in U.S. Asset Markets

In this section, we use microstructure theory and a modification of a standard empirical model to obtain measures of private and public information shocks in the U.S. money and equity markets.¹⁹We start by outlining our general modelling approach and then apply it to the U.S. money and equity markets. The model yields public and private information shocks from the two markets that are used in the cross sectional analysis of international stock returns in section 4. However, they are also of interest in their own right for revealing the impact of trades based on private information in aggregate U.S. markets.

3.1 General modelling approach

Theoretical papers designed to explain price changes in a microstructure setting have emphasized two factors: the optimal inventory level of the specialist and the response of the quote to information revelation. Our approach is to focus on the information-revelation component while controlling for inventory and liquidity effects. Figure 2 shows the stylized timing convention that is present in the models. An investor observes the original quotes ( $q_{t-1}^{b}$ is the bid, $q_{t-1}^{a}$ is the ask) set by the market maker at time $t-1$. The investor then decides on their trade (i.e., net order flow), $x_{t},$ which is driven partially by private information and by liquidity needs. Public information news arrives after the trade is completed and the market maker sets new quotes at time $t$, prior to any new trades being completed.

To estimate the public and private information shocks in a particular asset market, we adopt the linear vector autoregression of Hasbrouck (1991). As he points out, many microstructure imperfections (e.g., inventory control effects, price discreteness, exchange mandated price smoothing) can cause lagged effects in order-flow and quote-revision dynamics. We therefore model investor order flow as a linear function of past flows and quote revisions:

$$x_{t}=c+\theta(L)r_{t}+\kappa(L)x_{t}+v(x)_{t},$$ (2)

where $x_{t}$ is the (net) order flow in the market; $r_{t}$ is the quote revision on the asset; and $\theta(L)$ and $\kappa(L)$ are polynomials in the lag operator. The residual in this equation ($v(x)_{t}$) includes two components. The first is unanticipated trades due to liquidity shocks: investors will undertake trades in an asset market in response to random shocks to their wealth. The second component is unanticipated trades due to new private information: investors will undertake trades when their private assessment of the asset's value differs from the prevailing market quote.²⁰

Quote revisions can be modelled using a similar autoregressive structure:

$$r_{t+1}=c+\gamma(L)r_{t}+\delta(L)x_{t}+\lambda v(x)_{t}+v(r)_{t} .$$ (3)

The lagged quote revision and order-flow variables are also present to capture transient microstructure effects. Note that contemporaneous unanticipated trades ($v(x)_{t}$) are included in this equation, given the above assumption about information revelation in microstructure time. Because the explanatory variables account for microstructure effects and private information, the disturbance $v(r)_{t}$ reflects public information news. The combined system of (2) and (3) thus provides two (orthogonal) shocks that represent private and public news in an asset market, respectively.

In this system, a private information shock will cause a sequence of quote revisions as the information becomes absorbed into the market price. The key difficulty is in identifying the private information component of the (unanticipated) trade ($v(x)_{t}$). The identifying assumption is that, in a market with informed and uninformed traders, order flow conveys information and therefore causes a persistent impact on the security's price.²¹ Trades based on liquidity or inventory have no information value and thus have only a transitory impact on prices. Therefore, with the passage of time, all rational agents expect quotes to revert (on average) to the fair value of the security,

$$s\rightarrow T,E\left[ (q_{s}^{b}+q_{s}^{a})/2-p_{T}\vert\Phi _{t}\right] \rightarrow0,$$ (4)

where $s$ is some future time; $T$ is the terminal time when the true value of the security, $p_{T}$, is revealed; and $\Phi_{t}$ is the current (time $t$) information set. Private information about an asset's value will cause a change in the fair value of the security as the information is revealed through trading and becomes incorporated in the market's expectation of the price. To calculate the effect of a private information shock on an asset's price, we calculate the long-run impact that unanticipated trade orders have on the security's quotes.

To measure the permanent effects of an unanticipated trade, we construct the change in the (log) price of the asset over the holding period, $H$:

$$r_{t,t+H}\equiv\log(P_{t+H})-\log(P_{t}).$$ (5)

We can then model the $H$-period return using the same structure as above:

$$r_{t,t+H}=c+\gamma(L)r_{t}+\delta(L)x_{t}+\lambda v(x_{t})+v(r)_{t} .$$ (6)

In this equation, the holding-period return is driven in part by private information `` news'' that has been revealed to the market in the form of unanticipated trades ($v(x_{t})$). These unanticipated trades are noisy measures of private information, because they include liquidity or inventory effects. The key economic identification that we obtain from the microstructure literature is that liquidity effects are transient, whereas information effects are permanent. The trades will represent private information if the $\lambda$ coefficient is statistically significant for longer holding periods.

Our econometric specification is similar to that by Hasbrouck (1991), in that a reduced-form specification for trades is used to obtain a residual that is a noisy measure of the private information news. He uses impulse-response functions to obtain the impact of an unanticipated net purchase on quote revisions. Our method has direct tests of the private information effects on returns via an examination of the significance of the $\lambda$ coefficient. Our approach provides robust standard errors on the impact of unanticipated trades on returns, something that is not easily available in a reduced-form VAR with simultaneous variables on the right-hand side.²²

3.2 Private and public information in U.S. money and equity markets

In this section, we describe our model of net purchases and quote revisions in the Eurodollar futures and U.S. ETF markets. While we base our model on the general approach of section 3.1, there are two additional issues that we must face. The first is that we are estimating the dynamics of quote revisions and order flows in the U.S. money and equity markets simultaneously. An assumption is therefore required about the information sets of the market makers in the two markets. We assume that the market makers in both markets can observe past order flows and prices from both markets.²³ In this way, private information shocks in one market may be transmitted to the other market.

The second issue is the assumed variance-covariance stationarity of the data needed to estimate the VAR, which is clearly not the case with the Eurodollar futures contract.²⁴ Figure 1 shows that the mean of the Eurodollar rate changes over time as it fluctuates around the Federal funds target rate. We therefore model the conditional mean of the Eurodollar rate as a function of the Federal funds target rate.

Following our general approach in section 3.1, the first equation in the system models the time-series process of the order flow in the Eurodollar futures market ( $x_{t}^{ED}$),

$$x_{t}^{ED} =c+a(L)r_{t}^{ED}+b(L)x_{t}^{ED}+c(L)r_{t}^{US} +$$ (7)

$$d(L)x_{t}^{US}+gP_{t-1}^{TR}+hSP_{t-1}+v(x)_{t}^{ED}.$$

In this equation, net purchases in the Eurodollar futures market are linear functions of past net purchases and quote revisions in both the Eurodollar and U.S. ETF markets. Current trades are a function of these public information variables, due to various microstructure effects, which, in our setting, may have an influence across several markets. We also include the two `` monetary policy'' variables that were used in the Cochrane-Piazzesi target rate regressions: the price of the lagged Federal funds target rate ( $P_{t-1}^{TR}$) and the spread between the log target-rate price and the log Eurodollar futures price ( $SP_{t-1}=P_{t-1} ^{TR}-\log(P_{t-1}^{ED})$). Recall that both variables were shown to have good explanatory power for forecasting future U.S. Federal Reserve policy moves in Table 4. If agents trade in the Eurodollar market in anticipation of future Fed moves, these variables should help capture those effects.

The order-flow process for the U.S. ETF can be modelled similarly:

$$x_{t}^{US} =c+a(L)r_{t}^{ED}+b(l)x_{t}^{ED}+c(L)r_{t}^{US}+d\left( L\right) x_{t}^{US}$$ (8)

$$+gP_{t-1}^{TR}+hSP_{t-1}+kv(x)_{t}^{ED}+v(x)_{t}^{US}.$$

Equity market order flow is also a function of past order flow and quote revisions in the two markets.²⁵ If sophisticated investors trade in the equity market in anticipation of interest rate changes by the Federal Reserve, then the monetary policy variables from the Cochrane-Piazessi regressions should help capture this flow. Following our Granger causality test results, we assume that the equity market maker sees the unanticipated order flow from the Eurodollar money market. The first two equations then provide (orthogonalized) residuals that contain the private information of sophisticated investors in the money and equity markets.

The third equation in the system models the quote revision process in the U.S. money market:

$$r_{t,t+H}^{ED} =c+\theta(L)r_{t}^{ED}+\varphi(L)x_{t}^{ED}+\omega (L)r_{t}^{US}+\eta(L)x_{t}^{US}$$ (9)

$$+\phi P_{t-1}^{TR}+\psi SP_{t-1}+\lambda_{ED}v(x)_{t}^{ED}+\lambda _{US}v(x)_{t}^{US}+v(r)_{t}^{ED}.$$

In this equation, the holding-period return on a Eurodollar futures contract is a function of past quote revisions and order flows in the two markets. These may have an influence over short holding periods, because microstructure effects are important. As the holding period lengthens, these variables are less likely to have an influence. We also include the monetary policy variables in this regression, for the reasons given above. The close relationship between the Eurodollar and target rates implies that the spread variable may help to capture the movement of the rates towards each other.

Quote revisions are also driven in part by private information `` news'' that has been revealed to the market in the form of unanticipated trades in both the money and equity markets ( $v(x)_{t}^{ED}$ and $v(x)_{t}^{US}$, respectively). These unanticipated trades are noisy measures of private information, because they include liquidity or inventory shocks. As stated above, the key economic identification that we obtain from the microstructure literature is that liquidity shocks are transient, whereas information shocks have a permanent effect on the price of the asset. To measure the permanent effects of information shocks, we look at quote revisions in the Eurodollar futures over the holding period, $H$:

$$r_{t,t+H}^{ED}\equiv\log(P_{t+H}^{ED})-\log(P_{t}^{ED}),$$

where $P_{t}^{ED}$ is the price of the Eurodollar futures contract.²⁶ Thus, the trades will represent private information if the $\lambda_{ED}$ or $\lambda_{US}$ coefficients are significant for longer holding periods.

We can gauge the effect of public and private information on U.S. equity returns similarly via:

$$r_{t,t+H}^{US}=c+\theta(L)r_{t}^{ED}+\varphi(L)x_{t}^{ED}+\omega(L)r_{t} ^{US}+\eta(L)x_{t}^{US}$$ (10)

$$+\phi P_{t-1}^{TR}+\psi SP_{t-1}+\lambda_{ED}v(x)_{t}^{ED}+\lambda _{US}v(x)_{t}^{US}$$

$$+\varsigma v(r)_{t}^{ED}\cdot1{\small (\Delta TR\neq0)}+v(r)_{t} ^{US}.$$

In this regression, accumulated U.S. equity returns over the holding period, $H$ ( $r_{t,t+H}^{US}\equiv\log(P_{t+H}^{US})-\log(P_{t}^{US})$) are a function of past public information originating in the U.S. money and equity markets. Unanticipated money and equity market order flows will forecast future equity returns if they contain private information that is relevant to the equity market maker. As in our money market analysis, the key test is that the unanticipated money and equity market trades have an effect on returns over longer holding periods ($H=1$ day or $5$ days).

The half-hour ($H=1$) version of the money market quote-revision regression (9) provides an estimate of the expected change in the price of the Eurodollar contract. The residual from this regression ( $v(r)_{t}^{ED}$) will be the unexpected change in interest rates due to public news innovations. We can further decompose this residual using dummy variables into those shocks that occur when there is a change to the Federal funds target rate ( $1{\small (\Delta TR\neq0)}$) and when there is not ( $1{\small (\Delta TR=0)}$). During the half-hour period when the Federal Reserve changes interest rates, there is a clear causal chain from the money market to the equity market. Thus, the change in the price of the Eurodollar contract during these particular half-hour periods ( $1{\small (\Delta TR\neq0)}$) provides a high-frequency counterpart to the monetary policy shocks constructed by Cochrane and Piazzesi (2002). We therefore include these residuals in the equity market order-flow regression.

3.3 Results

Table $5$a shows results of the first two equations from the model. The estimate of the Eurodollar order-flow regression is at the top. Overall, the instruments do a poor job in capturing expected Eurodollar order flow: the $R^{2}$ statistic is only $0.006$.²⁷ The monetary variables are not significant, which suggests that traders do not position themselves around monetary policy changes. This result may be misleading, however, because these trades could occur at any time, and thus trying to capture them with one lagged value may not be sufficient. The second regression is for U.S. equity market order flow. This regression has an adjusted $R^{2}$ statistic of $0.083$, which indicates that the instruments have some ability to forecast the next period's order flow. The sums of the U.S. ETF lagged order-flow and quote-revision coefficients are significant, as are the lagged Eurodollar quote revisions. The spread variable is also significant, with a positive coefficient.

The poor ability of the selected instruments to capture order-flow variation raises concern about the use of the residuals from these regressions in the holding-period return regressions (9) and (10 ). The low degree of explanatory power indicates that the instruments are not able to capture much of the short-run inventory dynamics that are present in the markets. The residuals will therefore contain more of these short-run influences, making them noisier signals of the long-run information component. This, in turn, makes our subsequent findings of significant information effects more conservative.

Table $5$b shows the results of estimating the holding-period returns (9) on the Eurodollar futures contract over periods ranging from one half-hour to five trading days. The ability of the selected instruments to model short-run movements in Eurodollar quote revisions is very high, with the half-hour regression having an $R^{2}$ statistic of $0.752.$ As the holding period lengthens, the statistics decrease rapidly, in line with similar estimates of daily and weekly returns throughout the asset-pricing literature. The spread variable is significant at conventional levels for all of the holding periods. When the spread is higher, the regressions in Table $4$ show that the price of the target asset was expected to fall (an increase in the target rate was likely). The spread shows that a decrease in the Eurodollar price (an increase in the Eurodollar rate) is also likely.

The regressions also include the unanticipated order flows from the money and equity markets (i.e., the residuals from the order-flow regressions in Table $5$a). The Eurodollar order-flow variable is significant at all holding periods, which indicates that trades based on private information are present in the Eurodollar futures market. Sophisticated agents appear to have superior information about the direction of future U.S. interest rates. When they trade, the information becomes incorporated into market rates. The market makers do not appear to use equity market order flow for longer-run pricing decisions, providing further evidence that the direction of causality is from the money market to the equity market.

Table $5$c shows the estimates of the holding-period returns on the U.S. ETF. As with the quote-revision regressions, the half-hour holding period returns display a large amount of predictability, with an $R^{2}$ statistic of
$20.3$ per cent. As the holding period lengthens, the degree of linear predictability again naturally falls. Neither of the two monetary policy variables from the Cochrane-Piazzesi regressions is significant. Rather, the influence of the money market is captured by the information shocks from the Eurodollar market. Unanticipated money market order flow is significant for the half-hour to $5$ day holding periods. Thus, private information revealed in the U.S. money market helps predict subsequent U.S. equity market movements. We note that the negative coefficients are in line with the unconditional negative correlation coefficients between the price of the ETF and U.S. equity market shown in Table $2$; traders are adjusting their positions in line with the movements between interest rates and equity returns during this period.

The effect of an unexpected change in the price of the Eurodollar contract when there is a Federal Reserve policy change ( $v(r)_{t}^{ED}1{\small (\Delta TR\neq0)}$) is shown in the next column of Table 5c. The positive coefficients are in line with other estimates in the literature: a policy-driven increase in interest rates causes a decline in equity market prices. However, the coefficients are significant at conventional levels for the half-hour and $1$ day holding periods only. At the $5$ day horizon, the coefficient has a P-value of $0.124$.

There are two ways to interpret this finding. The first is that, although public news about U.S. monetary policy changes is quickly incorporated into U.S. equity market returns, the news has no long-run effect on prices. However, this interpretation would be at odds with a large and growing literature that finds that unexpected changes to the Federal funds target have an effect on longer-run asset market returns.²⁸

The second interpretation of our results is that there are too few ($19$) changes to the target rate during our sample period. Longer-run returns are noisier and the power of the regressions to detect the effect of the changes declines. In addition, other macroeconomic announcements occur during the weekly holding periods. For example, there are U.S. payroll announcements during the week following six of the target rate changes in our sample. Five of these announcements are negative and would have the effect of decreasing U.S. equity returns, as Andersen et al. (2004) show. Thus, the effects of monetary policy shocks are being negated by the effects of the U.S. employment shocks. Under either interpretation of these public news shocks, it is important to note that the private information shocks have a long-run impact.

The last column in the table shows the effect of unanticipated equity market purchases over a half-hour period on future equity returns. The coefficients are positive and significant for all of the holding periods examined. While this variable may reflect both liquidity and information shocks at short horizons, only the information-based component will have an effect over longer holding periods. It is clear, then, that sophisticated investors have private information about the aggregate U.S. equity market. When they trade, this information is gradually incorporated into prices.

3.4 Interpretation

Our view of asymmetric information is different from the standard one, in which traders have good information about a specific firm. One way to view the equity market results in this section is that traders have correlated private information about many firms. Although the theoretical works of Subrahmanyam (1991) and Chan (1993) examine correlated private information, they are silent on the economic origins of the information.

Our contribution is to relate aggregate private information to factors that influence the returns on many assets; in particular, monetary policy. We have shown that unanticipated changes in the Eurodollar rate when there is a Federal Reserve policy change, a public news shock, affect U.S. stocks over a $1$ day interval.²⁹ However, private information originating in the U.S. money markets forecasts stock returns over $1$ to $5$ days.³⁰ This suggests that it may take longer for investors to interpret the trades based on private information about interest rates than the moves in the interest rate itself.

Saar (2001) notes that the price impact of trades may not be the result of superior knowledge about the cash flows on the assets being released to the market. It may, instead, be the result of the market maker assessing the distribution of demand in a heterogeneous investor environment. The market maker uses trades to obtain more information about investor preferences and endowments. We note that this private information is not `` insider'' information; rather, it is the superior interpretation of public signals. The expense devoted to `` Fed watching'' by many financial institutions suggests that the forecasting of Federal Reserve actions is a profitable activity. Fed watchers (or the agents who use their analyses) can thus be viewed as informed traders whose orders convey information.

Given these findings, we are indifferent as to whether the private information we find is about either the cash flows on the assets or how these cash flows will be demanded by market participants. Sophisticated investors could obtain superior knowledge of factors that affect the cash flows that U.S. equities are claims to, or superior knowledge about future interest rate levels, from macroeconomic analysis. Alternatively, they could obtain knowledge of future investor order flow in the U.S. markets. In either case, the information asymmetry would likely impact foreign equity markets, as we show below.

One question about our results is the long-lived nature of the private information shock. Our daily and weekly results are bracketed by results in other studies that examine the effects of trading based on private information. For example, Hasbrouck (1991) examines the impact of private information on quote revisions that occur up to 20 transactions later. In contrast, Easley, Hvidkjaer and O'Hara (2002) find that a measure of a stock's probability of information-based trading is priced in the cross section of U.S. stocks using monthly data.

Our results have implications for studies that attempt to link private information and other market frictions to domestic asset prices. For example, other work has explored systematic factors in liquidity and their link to the cross section of U.S. stock returns (Chordia, Roll and Subrahmanyam 2000, Hasbrouck and Seppi 2001, and Pastor and Stambaugh 2003). We note that liquidity and trading based on private information are linked in many microstructure models. Our finding of a role of common private information may therefore provide some guidance for the economic origins of systematic liquidity.

4 The Cross Section of International Equity Returns

The previous sections have shown that trading based on private information predicts both U.S. money and equity market returns over daily and weekly holding periods. In addition, public information shocks in the Eurodollar market associated with policy changes affect U.S. equity prices. If international equity markets are integrated, then the factors that affect U.S. equity markets will also affect international markets. In this section, we explore whether these shocks are priced by estimating a latent-factor model of the cross section of international equity returns.

4.1 Latent-factor model

To test whether the U.S. information shocks are priced factors in international markets, we use the latent-factor model of Hansen and Hodrick (1983) and Gibbons and Ferson (1985). In this model, the excess return on a foreign asset, $i,$ is a function of the realizations of $K$ factors:

$$r_{i,t+1}=E_{t}[r_{i,t+1}]+\beta_{i}f_{t+1}+\varepsilon_{i,t+1} ,$$ (11)

where $f$ is a $K\times1$ vector of factor realizations with $E_{t} [f_{t+1}]=0$; $\beta_{i}=cov(r_{i,t+1},f_{t+1})$ is a $1\times K$ vector of constants; and $\varepsilon_{i}$ is an idiosyncratic error, uncorrelated with $f.$ Equilibrium requires that the expected return on the asset be a function of the $K$ sources of risk:

$$E_{t}[r_{i,t+1}]=\beta_{i}\theta_{t},$$ (12)

where $\theta_{t}$ is a $K\times1$ vector that contains the market price of risk of the factors.

In the latent-factor approach, the factors are not specified directly. Rather, there are a number of instruments that forecast returns in the markets and are likely related to the true, but unknown, factors. The price of risk of the $k$-th factor, $\theta_{k,t}$, is written as a linear combination of the set of $N$ instruments, $I_{t}$:

$$\theta_{k,t}=\alpha_{k}I_{t},$$ (13)

where the $\alpha_{k}$ are coefficients.

Combining the assumption about the process driving returns (11), the equilibrium condition (12), and the assumption on the market price of risk (13) yields a non-linear pricing equation for asset $i$:

$$r_{i,t+1}=\beta_{i}\alpha I_{t}+\widetilde{\varepsilon}_{i,t+1},$$

where the $K\times N$ $\alpha$ matrix contains the $\alpha_{k}$ coefficients on the instruments for the $K$ factors and $\widetilde{\varepsilon} _{i,t+1}=\beta_{i}f_{t+1}+\varepsilon_{i,t+1}$ . This model is used to examine the cross section of $M$ assets via:

$$R_{t+1}=\beta\alpha I_{t}+\widetilde{\varepsilon}_{t+1}.$$

$R_{t+1}$ is the $M$ vector that contains the quote revisions on the foreign countries. The $M$ by $K$ matrix, $\beta,$ is the loading of the returns on the time-varying factor returns. The $K$ by $N$ matrix, $\alpha,$ are the coefficients on the instruments; the linear combination, $\alpha I_{t},$ represents the time-varying return on the latent factors.

Because the factors are latent in this model, its ability to price the cross section of international equity returns will depend on the selection of the instruments. Campbell (1996) asserts that the factors that price the cross section of asset returns should be the innovations on those variables that can forecast the moments of the investment-opportunity set. In our model, with the assumption of international market integration, the innovations on those variables that forecast U.S. asset returns will be able to forecast the international investment-opportunity set.³¹ Thus, we use the public and private information variables from our time-series regressions for our instruments:

$$I_{t} =( P_{t-1}^{TR},SP_{t-1},v(x)_{t}^{ED},v(r)_{t} ^{ED}\cdot1{\small (\Delta TR=0)},$$

$$v(r)_{t}^{ED}\cdot1{\small (\Delta TR\neq0)}, v(x)_{t}^{US}, v(r)_{t}^{US}).$$

Our information set, $I_{t},$ includes the monetary policy variables that were shown to have some predictability for the Eurodollar and U.S. ETF markets. We include the unanticipated order flow and quote revision from the Eurodollar money market regressions, (7) and (9), respectively. Note that we segregate the public information shocks into those that have occurred as a function of changes to the target rate ( $\Delta TR\neq0$) and those that have not ( $\Delta TR=0$). We also include the unanticipated order flow and quote revision from the U.S. equity market regressions, (8) and (10), respectively.

Our interest centres on the public and private information content of the shocks from the Eurodollar and U.S. equity markets. The unanticipated quote revisions represent public information news in the two markets. As stated earlier, the unanticipated order flows will contain elements related both to microstructure (e.g., liquidity or inventory) effects and to shocks to the private information sets of sophisticated investors. Over longer holding periods, the microstructure effects will disappear and the information effects of the trades may be obtained by estimating:

$$R_{t+H}=\beta_{H}\alpha_{H}I_{t}+\widetilde{\varepsilon}_{H,t+1} ,$$ (14)

where $R_{t+H}$ is the vector of $H$-period returns on the foreign equity markets. If private information is part of a priced factor, the $\alpha_{H}$ coefficients associated with the unanticipated order flows will be significant for longer holding periods (e.g., $H=1$ day or $1$ week).

The model is estimated by generalized method of moments (GMM). We estimate the system (14) separately for each holding period, $H$. The Newey-West (1987) form of the optimal weighting matrix is used to capture any autocorrelation of heteroskedasticity in the residuals. In its current form, the model is unidentified due to the $\beta_{H}\alpha_{H}$ combination. We thus impose the standard identification that the first $K$ rows of the matrix $\beta_{H}$ are equal to an identity matrix. The cross-equation restrictions of the model can be tested using the standard $\chi^{2}$ test statistic from a GMM system.

Using the latent-factor model to capture the cross section of returns has a number of advantages.³² In this study, as with other empirical studies of market frictions on asset prices (e.g., Pastor and Stambaugh 2002, Hou and Moskowitz 2003), we do not specify a model that directly ties asymmetric information to the cross section of expected international returns.³³ Rather, the cross section of returns should be explained by those variables that can predict time variation in the investment-opportunity set. Given the time-series results above, the variables we have chosen should have some power to explain the cross section. The advantage of the latent-factor model is that it can capture the pricing ability of all of the variables in a parsimonious setting.

Another advantage of the latent-factor model is that it allows the data to reveal the structure of the cross section of expected returns. This can answer a number of questions. For example, are private and public information shocks separate factors, or part of the same factor? Do all of the countries examined load on the same shocks? Alternatively, as noted by Campbell and Hamao (1992), the latent-factor model can be evaluated simply by its ability to describe the cross section of returns.

4.2 Results

Table 6 shows the summary statistics of a one-latent-factor model. The $\chi^{2}$ test statistics of the cross-equation restrictions on the parameters are shown at the top of the table, along with their asymptotic marginal significance levels ($P$-values). The statistics show that the one-factor model is rejected for the one-half-hour ($H=1$) returns, whereas it is not rejected for the daily and weekly returns ($H=1$ and $5$ days). To judge whether the model does a good job in capturing expected equity returns, we examine some variance ratios. The numerator of the ratio is the variance of the expected return on the foreign country ETF from the latent-factor model. The denominator is the variance of the expected return from a regression of the ETF return on the same instruments. If the model does a good job in capturing expected return variation, then the ratio should be near 1.00. As can be seen, the ratios are lower for the half-hour holding period, whereas they rise for most countries for the daily and weekly intervals.

The results of these tests contain a mixed message for the model. Formally, our choice of instruments and the over-identifying restrictions are rejected for the half-hour holding period, likely due to short-run microstructure effects such as inventory rebalancing or liquidity shocks. The microstructure effects will be captured (in part) by our instruments and will affect half-hour holding-period returns as the market maker adjusts their quotes to the shocks. The quote adjustment process, however, appears to be more complicated over half-hour intervals than the factor model indicates. The large number of data points ($15$,$598$) allows us to detect these small differences even though the model captures a large portion of the predictable returns based on these instruments.

At longer holding periods of a day to a week, the microstructure effects disappear and pricing decisions are driven by the assessment of information in the market. The combination of our instruments and the over-identifying restrictions of the model are not rejected, which indicates that the information effects driving longer horizon returns are less complicated than the shorter-run microstructure effects. In addition, the variance ratios indicate that the model captures a significant portion of expected return variation. Thus, given the formal model tests and the variance ratio results, we use the latent variable model as our starting point for analyzing the cross section of international returns.

Table $7$ shows the estimates of the $\beta_{H}$ coefficients for the $10$ foreign countries and the three holding periods. The coefficients on the German returns are normalized to $1.00$ for identification. For each holding period, all of the countries load on the factor with a significant coefficient. This shows that the instruments are doing a good job in capturing the common information effects that are driving the cross section of international returns.

An examination of the $\alpha_{H}$ coefficients reveals which of the individual variables are priced in the cross section. Table $8$ shows these estimates over the three holding periods. Each cell contains three numbers; the first two are the estimated coefficient from the model and its $t$-statistic. The third number [$\sigma$-shock] is designed to show the economic significance of the indicated variable. It is calculated as the absolute value of the estimated $\alpha_{H}$ coefficient times a one-standard-deviation shock to the variable, divided by the standard deviation of the latent factor. It is thus similar to a (normalized) one-standard-deviation shock analysis of an impulse response function.

The coefficients on the monetary policy variables are shown in the first two columns of Table 8. As with the U.S. equity return regressions, these instruments show little ability to price the cross section of international returns. The next three columns measure the effects of the Eurodollar market on the foreign equity markets. At the longer holding periods, the unanticipated Eurodollar purchases ( $v(x)_{t}^{ED}$) are noisy measures of private information released during U.S. trading times. The coefficients on this variable are significant and negative, again in line with the U.S. ETF results. Thus, private information released in the U.S. money market is part of the priced factor in the international cross section. The effects of the private information shocks are also economically important. A one-standard-deviation shock to the variable accounts for approximately $30$ per cent ($20$ per cent) of the volatility of the factor at a half-hour (weekly) horizon.

Unanticipated Eurodollar quote revisions ( $v(r)_{t}^{ED}$) represent public news shocks. Shocks that are not associated with monetary policy moves ( $\Delta TR=0$) have a negative coefficient and are statistically significant at all horizons. Shocks that are associated with monetary policy innovations ( $\Delta TR\neq0$) have a positive coefficient and are significant for the half-hour and 1-day horizons. The shocks account for approximately $19$ per cent of the factor's variability at the same intervals. The shocks are not significant for the weekly holding-period returns. The sign and significance of the coefficients attached to monetary policy innovations over the three horizons match those obtained for U.S. ETF returns.

Thus, during this period, the effect of interest rate changes on equity market returns depends on whether the change was driven by a policy move. However, both of the public information interest rate shocks (policy and non-policy driven) have smaller measures of economic significance than do the private information shocks.

The final two columns of Table 8 show the coefficients associated with private and public information shocks that arise in the U.S. equity market. Public information shocks in the U.S. equity market ( $v(r)_{t}^{US}$) are a part of the priced factor in foreign equity returns, in line with previous low-frequency studies that use excess U.S. equity market returns (e.g., Campbell and Hamao 1992, Bekaert and Hodrick 1992). The new result is that private information shocks are also a priced factor for the half-hour and daily intervals. The coefficients on unanticipated net purchases are positive and significant for these intervals. In addition, the private information shocks are large economically, with a one-standard-deviation shock being equivalent to $48.2$ per cent of the variation in daily expected returns. The $\sigma$-shock measures are large for the public information shocks even out to a weekly horizon, which suggests that public information shocks take a long time to be absorbed by the market. This may be misleading, however, since there will be factors other than the money market shocks, which will be analyzed by sophisticated investors. We conclude that sophisticated U.S. investors obtain information that is related to the common factors that influence asset prices around the world. When they trade in the U.S. equity index market, market makers in the ETFs can use this information to set foreign equity prices.

4.3 Interpretation

In the international literature, private information is used as an explanation of the home bias phenomenon (French and Poterba 1991, Gehrig 1993, Brennan and Cao 1997, and Coval 1999). In this literature, sophisticated agents have superior information about returns on stocks in their own countries; e.g., German investors have superior knowledge about German firms, which U.S. investors could not obtain. This generates an additional source of risk to investing in international stocks, which leads agents to invest in domestic equities.

This view of the structure of private information has been challenged by Albuquerque, Bauer, and Schneider (2003a), who show that sophisticated U.S. investors have private information about global factors that affect returns in many countries. They use a factor analysis of monthly international transactions by U.S. residents to generate the global factor. We improve on their findings in two ways. First, we use high-frequency data to identify public and private information shocks based on well-established approaches from the microstructure literature. Second, we show that international trading based on private information is related (in part) to U.S. interest rates. As with our domestic market analysis above, we acknowledge that there may be other important economic sources of private information that we are not modelling.

The origins of the private information can be motivated in two ways. Sophisticated agents, such as hedge funds, can conduct `` top-down'' analyses in which they generate private information about macroeconomic fundamentals from a superior interpretation of public information. The fundamentals could be related to either the U.S. or foreign economies. In either case, with integrated international markets, such information would be useful for capturing return variation in many countries. The large number of PhDs employed by such funds to generate private trading opportunities is consistent with this story. We note that, as with our domestic results, this private information about monetary policy does not come from information leakages from the Fed.

Alternatively, order flow in the U.S. markets could be acting as a `` bottom-up'' aggregator of diffuse private information. Evans and Lyons (2004) construct a model of the foreign exchange market where order flow aggregates the dispersed private information about productivity shocks in the two countries. They note that, whereas productivity shocks would occur at the level of the firm, aggregate trades by agents in the country would give a more precise estimate of the country's productivity shock for that period. Evans and Lyons also note that agents' trades could be aggregating information about other variables that are realized at the micro level, such as money demand. Our U.S. shocks can therefore be interpreted as money-demand shocks and real shocks that arise from firm-level information. Financial firms in the U.S. that observe a large cross section of customer order flow could then extract such information and use it for proprietary trading. Again, with integrated markets, such U.S. information shocks would have an international effect.

We acknowledge that our results could be consistent with investors having country-specific private information. Kodres and Pritsker (2002) present a model of rational contagion across countries. In their model, asset prices contain both a country-specific private-information component and a global public-information component. As informed agents trade securities of a specific country due to new private information, their portfolios will require rebalancing to maintain the desired exposure to the global risk factors. This will, in turn, cause trading in assets from other countries. Thus, private information revelation in one market causes trading in many other markets due to portfolio rebalancing.

While our story may be consistent with country-specific private information, we believe that global private information factors offer a better interpretation. We are obtaining the private information signals from aggregate U.S. money and equity markets. These signals are more likely to have value for equities in many markets than the country-specific signals originating in developing markets as in Kodres and Pritsker. For example, short-term U.S. interest rates have been found to have forecasting ability for international equity returns by Campbell and Hamao (1992), Dumas and Solnik (1995), Harvey (1991) and Ferson and Harvey (1994). One of the contributions of this paper is to show that private information about U.S. interest rates is also a useful variable in these tests. However, even if our private information shocks are specific to the U.S., our two main points remain valid: (i) trading based on private information is at least partially responsible for the correlated moves in international equity markets; and, (ii) this private information is, in part, related to U.S. interest rates.

One question that we cannot answer from our data set is the identity of the agents who are generating the private information. We are able to identify all private information generated during U.S. trading hours in U.S. markets. The information could come from sophisticated investors from many countries who are trading in U.S. markets. For example, foreign sophisticated investors (e.g., hedge funds) could obtain superior information about U.S. based factors if they devote significant resources to that purpose and are able to profit from trading on the information. In this sense, what matters more for international markets is the degree of investor sophistication, not the country in which they reside (Albuquerque, Bauer and Schneider 2003b).

4.4 Home currency returns

A number of studies have shown that asymmetric information is a significant driver of exchange rates (Lyons 1995, 2001; Evans and Lyons 2002; Covrig and Melvin 2002). If sophisticated investors generate private information about foreign exchange rates, they will be able to trade assets denominated in the foreign currencies and make a profit. This may be driving our results, since the return on the foreign ETF that is traded in U.S. markets is composed of a home currency return on the index plus a change in the value of the foreign exchange rate. It follows that the results of our previous analysis could be due to sophisticated investors generating private information about the foreign exchange component, rather than the foreign equity component.

To show that the results for the equity markets were not solely due to exchange rate effects, we construct home currency equity returns by dividing the U.S. dollar price of the foreign country ETF by the foreign exchange rate from the futures market:

$$r_{t,t+H}^{HC}\equiv\log(P_{t+H}^{ETF}/P_{t+H}^{FC})-\log(P_{t}^{ED} /P_{t}^{FC}),$$

where $P_{t}^{FC}$ is the price of the foreign currency futures contract at time $t$. We note that this return only approximates the home currency return, because the spot exchange rate price should have been used, but it is unavailable to us in microstructure time. The approximation, however, should be good because the variability of the futures price will be dominated by movements in the spot exchange rate. We can project these home currency equity returns on the estimated latent factor from our model:

$$r_{t,t+H}^{HC}=\varphi_{H}(\widehat{\alpha}_{H}I_{t})+\varepsilon _{H,t+1}^{\ast},$$ (15)

where $\widehat{\alpha}_{H}$ are the estimated coefficients from the GMM estimation of (14). If the exchange rate effects do not matter, then the $\varphi_{H}$ coefficients in this regression should be close to the $\beta_{H}$ coefficients from the original GMM estimation. The null hypothesis is then

$$H_{0}:\varphi_{H}=\beta_{H}$$ (16)

Table $9$ shows the ordinary least squares (OLS) estimates of (15) and the asymptotic $t$-test statistics associated with (16). The P-values of the test statistics associated with the test of (16) are also included. The parameter estimates of the loadings of the home currency returns are large for the half-hour holding period and then decline with the forecast horizon. None of the coefficients is statistically significant at the weekly horizon. The small P-values on the half-hour test results for all of the countries except Canada show that there is enough power to reject the joint equivalence of both estimates. As before, this is likely related to the poor ability of the model to capture the microstructure effects. The two estimates, however, are not statistically different in either the daily or weekly returns for all of the countries, which suggests that the information components of the returns are similar. We conclude that the changes in the foreign exchange rates are somewhat related to the linear combination of the selected instruments obtained from the equity pricing model. The earlier results, however, were not driven solely by this phenomenon.

5 Conclusions

Our goal in this study was to deepen our understanding of the links between foreign asset movements and news (public and private) originating in U.S. money and equity markets. Recent studies using high-frequency data show that public news about U.S. money and equity markets affects equity markets abroad (Andersen et al. 2003). Our main contribution has been to show that some agents have superior knowledge about future U.S. interest rates and aggregate equity market returns. This superior knowledge is partially revealed through trades that affect daily and weekly returns on international stocks. This finding gets to the core of Goodhart and O'Hara's (1997) question as to how private information can have a global impact. Not only have we shown that public and private information about U.S. interest rates and aggregate equity markets predicts future foreign equity market movements, but we have also shown that these are components of the factor that is priced in the international cross section.

These findings suggest that further research should be conducted into the behavior of domestic and foreign markets. In recent work, Pastor and Stambaugh (2002) and others show that market-wide liquidity is a state variable that is important for domestic asset pricing. Liquidity is defined as temporary price fluctuations induced by order flow. In contrast, private information is defined as permanent price fluctuations induced by order flow. The literature has largely treated these as distinct concepts. As Kyle (1985) notes, however, the two quantities are correlated, since informed traders prefer to strategically place trades in liquid markets to hide their behavior and maximize their profits. Future research on asset returns should attempt to distinguish between the two effects and determine their economic origins.

Bibliography

1

Albuquerque, Rui, Gregory H. Bauer, and Martin Schneider (2003a), `` Characterizing Asymmetric Information in International Equity Markets,'' mimeo, University of Rochester.

2

Albuquerque, Rui, Gregory H. Bauer, and Martin Schneider (2003b), `` International Equity Flows and Returns: A Quantitative Equilibrium Approach,'' mimeo, University of Rochester.

3

Andersen, T., T. Bollerslev, F.X. Diebold, and C. Vega (2003), `` Micro Effects of Macro Announcements: Real-Time Price Discovery in Foreign Exchange, '' American Economic Review, 93, 38-62.

4

Andersen, T., T. Bollerslev, F.X. Diebold, and C. Vega (2004), `` Real-Time Price Discovery in Stock, Bond and Foreign Exchange Markets, '' mimeo, Northwestern University.

5

Bekaert, Geert and Robert J. Hodrick (1992), `` Characterizing Predictable Components in Excess Returns on Equity and Foreign Exchange Markets'' Journal of Finance, 47(2) 467-509.

6

Bernanke, Ben and Kenneth N. Kuttner (2005), `` What Explains the Stock Market's Reaction to Federal Reserve Policy,'' Journal of Finance, forthcoming.

7

Brennan, Michael J., and H. Henry Cao (1997), `` International Portfolio Investment Flows,'' The Journal of Finance, 52, 1851-1880.

8

Brennan, Michael J. and Subrahmanyam A. (1996), `` Market Microstructure and Asset Pricing: On the Compensation for Illiquidity in Stock Returns,'' Journal of Financial Economics, 41, 441-464.

9

Brennan, Michael J., Narasimhan Jegadeesh, and Bhaskaran Swaminathan (1993), `` Investment Analysis and the Adjustment of Stock Prices to Common Information,'' The Review of Financial Studies, 6, 799-824.

10

Campbell, John Y. (1996), `` Understanding Risk and Return,'' Journal of Political Economy, 104, 298-345.

11

Campbell, John Y. and Yasushi Hamao (1992), `` Predictable Stock Returns in the United States and Japan: A Study of Long-Term Capital Market Integration'', The Journal of Finance, 47, 43-69.

12

Carlson, John B., Jean M. McIntire and James B. Thomson (1995), `` Federal Funds Futures as an Indicator of Future Monetary Policy: A Primer,'' Economic Review, 20-30.

13

Chan, Kalok (1993), `` Imperfect Information and Cross-Autocorrelation among Stock Prices,'' Journal of Finance 48:1211-1230.

14

Chordia, Tarun, Richard Roll and Avavidhar Subrahmanyam (2000), `` Commonality in Liquidity,'' Journal of Financial Economics, 56, 3-28.

15

Cochrane, John H. and Monika Piazzesi (2002), `` The Fed and Interest Rates: A High-Frequency Identification,'' American Economic Review Papers and Proceedings, 92, 90-95.

16

Connolly, R. and A. F. Wang (2003), `` International Equity Market Comovements: Economic Fundamentals or Contagion?'' Pacific-Basin Finance Journal 11: 23-43.

17

Coval, Joshua (1999), ``International Capital Flows when Investors have Local Information,'' University of Michigan, mimeo.

18

Covrig, Vincentiu and Michael Melvin (2002), `` Asymmetric Information and Price Discovery in the FX Market: Does Tokyo Know More About the Yen?,'' Journal of Empirical Finance, .

19

Craig, Alastair, Ajay Dravid and Matthew Richardson (1995), `` Market Efficiency Around the Clock Some Supporting Evidence in Using Foreign-Based Derivatives,'' Journal of Financial Economics, 39, 161-180.

20

Dumas, Bernard and Bruno Solnik (1995), `` The World Price of Foreign Exchange Risk,'' Journal of Finance 50: 445-479.

21

Easley, David, and Maureen O'Hara (1987), `` Prices, trade size and information in security markets,'' Journal of Financial Economics, 19, 69-90.

22

Easley, David, and Maureen O'Hara (2002), `` Microstructure and Asset Pricing, '' in G.M. Constantinides, M. Harris and R. Stulz (eds.), Handbook of Economics of Finance. Elsevier-North Holland, forthcoming.

23

Easley, David, Soeren Hvidkjaer and Maureen O'Hara (2002), `` Is Information Risk a Determinant of Asset Returns?'', The Journal of Finance, 57, 2185-2221.

24

Ellis, Katrina, Roni Michaely and Maureen O'Hara (2000), `` The Accuracy of Trade Classification Rules: Evidence from Nasdaq,'' Journal of Financial and Quantitative Analysis, 35, 529-551.

25

Elton, E. J., J. M. Gruber, G. Comer and K. Li (2002), `` Spiders: Where Are the Bugs?,'' Journal of Business, forthcoming.

26

Engle, Robert F., Ito Takatoshi and Wen-Ling Lin (1990), `` Meteor Showers or Heat waves? Heteroskedastci Intra-Day Volatility in the Foreign Exchange Market,'' Econometrica, 58, 525-542.

27

Evans, Martin D.D. and Richard K. Lyons (2002), `` Order Flow and Exchange Rates'', Journal of Political Economy, 110, 170-180.

28

Evans, Martin D.D. and Richard K. Lyons (2004), `` A New Micro Model of Exchange Rate Dynamics'', mimeo, University of California Berkeley.

29

Fair, C. Ray (2003), `` Shock Effects on Stocks, Bonds, and Exchange Rates,'' Journal of International Money and Finance, 22, 307-341.

30

Ferson, Wayne E. (1995), `` Theory and Empirical Testing of Asset Pricing Models,'' in R.Jarrow et al. (eds.), Handbooks in OR & MS, vol. 9, 145-200.

31

Ferson, Wayne E. and Campbell R. Harvey (1994), `` An Exploratory Investigation of the Fundamental Determinants of National Equity Market Returns,'' in The Internationalization of Equity Markets, Jeffrey A. Frankel (ed.). Chicago: The University of Chicago Press.

32

French, Kenneth, and James Poterba (1991), `` Investor Diversification and International Equity Markets,'' American Economic Review Papers and Proceedings, 81,222-226.

33

Gehrig, Thomas (1993), `` An Information Based Explanation of the Domestic Bias in International Equity Investment,'' Scandinavian Journal of Economics, 95, 97-109.

34

Gibbons, Michael R. and Wayne Ferson (1985), `` Testing Asset Pricing Models with Changing Expectations and an Unobservable Market Portfolio'', Journal of Financial Economics, 14, 217-236.

35

Glosten, Lawrence R., and Paul R. Milgrom (1985), `` Bid, Ask and Transaction Prices in a Specialist Market with Heterogeneously Informed Traders,'' Journal of Financial Economics, 14, 71-100.

36

Goodhart, A.E. Charles and Maureen O'Hara (1997), `` High Frequency Data in Financial Markets: Issues and Applications,'' Journal of Empirical Finance, 4, 73-114.

37

Hamao, Y., R.W. Masulis and V.K. Ng (1990), `` Correlations in Price Changes and Volatility across International Stock Markets,'' Review of Financial Studies, 3, 281-307.

38

Hansen, Lars P. and Robert J. Hodrick (1983), `` Risk Averse Speculation in the Forward Foreign Exchange Market: An Econometric Analysis of Linear Models'', in Jacob A. Frenkel (ed.), Exchange Rates and International Macroeconomics. Chicago: The University of Chicago Press.

39

Hardouvelis, Gikas A. (1987), `` Macroeconomic Information and Stock Prices,'' Journal of Economics and Business, 39, 131-140.

40

Harvey, Campbell R. (1991), `` The World Price of Covariance Risk'', The Journal of Finance 46: 111-157.

41

Hasbrouck, Joel (1991), `` Measuring The Information Content of Stock Trades,'' The Journal of Finance, 46, 179-207.

42

Hasbrouck, Joel (1996), `` Modeling Market Microstructure Time Series,'' Handbook of Statistics, 14, 647-692.

43

Hasbrouck, Joel and Duane J. Seppi (2001), `` Common Factors in Prices, Order Flows and Liquidity,'' Journal of Financial Economics, 59, 383-411.

44

Hou, Kewei and Tobias J. Moskowitz (2003), `` Market Frictions, Price Delay and the Cross-Section of Expected Returns,'' working paper.

45

Jensen, G. R., J.M. Mercer and R.R. Johnson (1996), `` Business Conditions, Monetary Policy, and Expected Security Returns,'' Journal of Financial Economics, 40, 213-237.

46

Karolyi, G. Andrew, and Rene M. Stulz (1996), `` Why Do Markets Move Together? An Investigation of U.S.-Japan Stock Return Comovements,'' The Journal of Finance, 51, 951-985.

47

Kim, Soyoung (2001), `` International Transmission of US Monetary Policy Shocks: Evidence from VAR's,'' Journal of Monetary Economics, 48, 339-372.

48

King, Mervyn and Sushil Wadhwani (1990), `` Transmission of Volatility Between Stock Markets'', The Review of Financial Studies, 3, 5-33.

49

King, Mervyn, Enrique Sentana and Sushil Wadhwani (1994), `` Volatility and the Link Between National Stock Markets'', Econometrica, 62, 901-33.

50

Kodres, Laura E. and Matthew Pritsker (2002), `` A Rational Expectations Model of Financial Contagion'', Journal of Finance, 57, 769-799.

51

Kuttner, Kenneth N. (2001), `` Monetary Policy Surprises and Interest Rates: Evidence from the Fed Funds Futures Market,'' Journal of Monetary Economics, 47, 523-544.

52

Kyle, Albert S. (1985), `` Continuous Auctions and Insider Trading,'' Econometrica, 53, 1315-1335.

53

Lee, Charles M. and Mark Ready (1991), `` Inferring Trade Direction from Intraday Data,'' The Journal of Finance, 46, 733-746.

54

Lee, Young-Sook (2003), `` The Federal funds market and the overnight Eurodollar market'', Journal of Banking and Finance, 27, 749-771.

55

Lin, W., Engle, R., and T. Ito (1994), `` Do Bulls and Bears Move accross Borders? International Transmission of Stock Returns and Volatility,'' Review of Financial Studies, 7, 507-538.

56

Lyons, Richard K. (1995), `` Tests of Microstructural Hypothese in the Foreign Exchange Market'', Journal of Financial Economics, 321-351.

57

Lyons, Richard K. (2001), The Microstructure Approach to Exchange Rates, MIT Press.

58

Madhavan, A., M. Richardson and M. Roomans, (1997), `` Why Do Security Prices Change? A Transaction-Level Analysis of NYSE Stocks,'' Review of Financial Studies 10(4), 1035-1064.

59

Melvin, Michael (2002), `` Exchange Rates and FOMC Days'', mimeo, Arizona State University.

60

Newey, W. and K. West (1987), `` A Simple Positive-Definite Heteroskedasticity and Autocorrelation Consistent Covariance Matrix,'' Econometrica 55, 703-708.

61

O'Hara, Maureen (1997), Market Microstructure Theory, Blackwell Publishers.

62

Pastor, Lubos and Robert F. Stambaugh (2003), `` Asset Prices and Exchange Rates'', mimeo, MIT.

63

Patelis, A. (1997), `` Stock Return Predictability and the Role of Monetary Policy,'' The Journal of Finance, 52, 1951-1972.

64

Pearce, Douglas K. and V. Vance Roley (1985), `` Stock Prices and Economic News,'' Journal of Business, 58, 49-67.

65

Piazzesi, Monika and Eric Swanson (2004), `` Futures Prices as Risk-Adjusted Forecasts of Monetary Policy'', NBER Working paper 10547.

66

Rudebusch, Glenn D. (1998), `` Do Measures of Monetary Policy in a VAR Make Sense'', International Economic Review 39(4), 907-31.

67

Saar, Gideon (2001), `` Investor Uncertainty and Order Flow Information'', working paper, New York University.

68

Saar, Gideon and Lei Yu (2002), `` Information Asymmetry about the Firm and the Permanent Price Impact of Trades: Is there a Connection?'', working paper, New York University.

69

Schwert G. William (1981), `` The Adjustment of Stock Prices to Information about Inflation,'' The Journal of Finance, 36, 15-29.

70

Subrahmanyam, Avanidhar (1991), `` A Theory of Trading in Stock Index Futures,'' Review of Financial Studies 4:17-51.

71

Stigum, Marcia (1990), The Money Market. Chicago: Richard D. Irwin, Inc.

72

Susmel, R. and R. F. Engle (1994), `` Hourly Volatility Spillovers Between International Equity Markets,'' Journal of International Money and Finance, 13, 3-25.

73

Thorbecke, W. (1997), `` On Stock Market Returns and Monetary Policy,'' The Journal of Finance, 52, 635-654.

74

Werner, Ingrid M. and Allan W. Kleidon (1996), `` U.K. and U.S. Trading of British Cross-Listed Stocks: An Intraday Analysis of Market Integration'', The Review of Financial Studies, 9, 619-664.

75

Yu, Lei (2003), `` Basket Securities, Price Formation and Informational Efficiency'', working paper, New York University.

Footnotes

*We thank Rui Albuquerque, Mike Barclay, Michael Fleming, Richard Lyons, Michael Melvin, Matthew Pritsker, Bill Schwert, JerryWarner as well as seminar participants at the Northern Finance Association meeting, Southern Finance Association meeting, Western Economics Association International meeting, Western Finance Association meeting, the Bank of Canada-Sauder School of Business Workshop on International Financial Markets, and the University of Rochester for their comments. Bauer is affiliated with the Financial Markets Department of the Bank of Canada. Address: 234 Wellington St., Ottawa, Ontario, Canada K1A 0G9. Vega is affiliated with the Board of Governors of the Federal Reserve System and William E. Simon Graduate School of Business Administration. Address: Carol Simon Hall, University of Rochester, Rochester, NY 14627. E-mail: [email protected] and [email protected]. The views in this paper are solely the responsibility of the authors and should not be interpreted as re.ecting the views of the Bank of Canada, the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

1.      King, Sentana and Wadhwani interpret the common factor that is unrelated to fundamentals as an index of `` investor sentiment.'' See also King and Wadhwani (1990) and Lin, Engle and Ito (1994). Return to text

2.      Sophisticated agents are believed to have superior (`` private'') information about the returns on assets in their own country. A broader definition of private information is given below. Return to text

3.      Low-frequency studies find conflicting results about causality. For example, Hammao, Masulis and Ng (1990), and King and Wadhwani (1990), find that correlations in volatility and prices appear to be causal from the United States to other countries. On the other hand, Lin, Engle and Ito (1994) find a bidirectional relationship between New York and Tokyo, and Susmel and Engle (1994) find a bidirectional relationship, albeit weak, between New York and London. Engle, Ito and Lin (1990) find a bidirectional relationship in the intraday yen/dollar exchange rate. Return to text

4.      Craig, Dravid and Richardson (1995) find that trading in Nikkei futures in the United States provides information about next-day Japanese equity returns. However, they do not identify the sources of the information. Return to text

5.      We construct the daily and weekly returns using overlapping samples of high-frequency data. This allows us to maintain the identification advantages of a microstructure analysis while focusing on the information content of longer holding-period returns. Return to text

6.      This literature is surveyed in Easley and O'Hara (2002). Return to text

7.      All the ETFs we use are listed on the AMEX; some of them are listed on other exchanges, including foreign exchanges. Nevertheless, the largest trading volume for these assets takes place on the AMEX during our sample period, and we confine ourselves to data from that exchange. Return to text

8.      Another advantage of ETFs is their tax efficieny. See Elton et al. (2002). Return to text

9.      The SPDR also traded on the NYSE and NASDAQ (as well as other exchanges) during our sample period. Howevere, trading on the AMEX remained quite liquid during this time. Return to text

10.       This algorithm compares transaction prices with the mid-quote five seconds before the transaction took place. If the transaction price is above the mid-quote, then we classify the trade as a buy; if the transaction price is below the mid-quote, we classify the trade as a sell. If the transaction price is equal to the mid-quote, then we use the tick test. Ellis, Michaely and O�Hara (2000) evaluate how well the Lee and Ready algorithm performs, and find that it is 81.05 per cent accurate.  Return to text

11.      We could also have used federal funds futures contract data (e.g., Rudebusch 1998, Kuttner 2001, and Carlson, McIntire and Thomson 1995). We use the Eurodollar futures contract because it is more liquid than the Federal funds futures contract, implying that it may better reflect information about the state of the economy. We use futures market data because no high-frequency transactions data are available in the spot market. Return to text

12.       The tick test is as follows: if the transaction price is higher than the previous price, we classify the trade as a buy, and if it is below the previous transaction price, we classify it as a sell. Ellis, Michaely and O�Hara (2000) find that the tick test correctly classifies 77.6 per cent of the trades. Return to text

13.      As in Fair (2003), the euro futures contract series is the German Deutsche Mark futures contract prior to 1 June 1999, and the euro futures contract after that. Both contracts traded somewhat before and after this date, but this date is a reasonable splicing date, because at that time liquidity started to switch from the German Deutsche Mark market to the euro market. Return to text

14.      For the Eurodollar and foreign currency futures contracts, we use the last transaction price recorded during the interval. Return to text

15.      The frequency of observations recorded for the Eurodollar and foreign currency contract data are the same for both the quotes and order flows for the series, due to the use of time-and-sales data. Return to text

16.      The prices of the ETFs are recorded at close of trade during U.S. trading hours, whereas the MSCI indexes are calculated at close of trade in the national markets. Return to text

17.       We use 12 lagged values to capture the effects of a full day of trading. Our results are robust to this choice. Return to text

18.       Following the literature, we exclude the change to the target rate following the terrorist attacks of September 11, 2001. Return to text

19.      See O'Hara (1997) for a discussion and derivation of domestic microstructure models. For a discussion and derivation of international microstructure models, see Lyons (2001). For a survey of empirical time-series microstructure models, see Hasbrouck (1996). Return to text

20.      We can improve our measures of private information by having as much of the effects of lagged public information removed from them as possible. This means that, instead of using a statistical criterion (such as AIC or SIC) to choose the optimal lag length, $L$, we choose large lag lengths that are likely to be longer than those mandated by a statistical test or casual economic reasoning. We thus choose a lag length equal to just over one day of trading ($12$ half-hour intervals) for our base-case analysis. Return to text

21.      Standard microstructure theory models with this set-up include: Kyle (1985), as an example of an auction or batch strategic trading model; and Glosten and Milgrom (1985) and Easley and O'Hara (1987), as examples of sequential trade models. Return to text

22.       Conventional measures of standard errors from this system are likely to be understated, due to two problems. The first is that extending the holding period of the asset out to $H$ periods will result in a moving-average error process in (9) and (10). The second problem is that the residuals in our intraday data are likely to be heteroscedastic, in line with other microstructure studies. We therefore report all results using Newey-West (1987) standard errors with a lag length equal to the minimum of $H-1,$ or $12$ half-hour trading intervals. Return to text

23.      We are assuming that sophisticated investors will trade on their superior knowledge of macroeconomic factors in several liquid markets simultaneously. Market makers would realize this and use as many sources of information as possible to reduce the information asymmetry. They can see aggregate trading activity in other asset markets and infer the signs of the recent trades from the cross-section of contemporaneous volume and price data. Return to text

24.      In the steady state of this system, information shocks would be absent and inventories would be at desired levels. Expected returns are constant and prices are thus a martingale. Return to text

25.      The coefficients in (8) are different from those in (7). The symbols are the same, because we do not wish to increase the notational burden. Return to text

26.      Under our assumption (4), this is equivalent, as time progresses, to the return on a buy-and-hold strategy over $H$ periods in a Eurodollar futures contract. Note that a one-period return, $r_{t,t+1}^{ED},$ represents the change in the price of the contract over a half-hour interval. Return to text

27.      Throughout this paper, the $R^{2}$ statistics are adjusted for degress of freedom. The low degree of explanatory power is similar to estimates of order flow in other asset markets. For example, Hasbrouck (1991) obtains an $R^{2}$ of 0.086 when he estimates the order flow of an individual stock. Return to text

28.      Researchers who find a significant influence of monetary policy on U.S. stocks include Schwert (1981), Pearce and Roley (1985), Hardouvelis (1987), Jensen, Mercer and Johnson (1996), Patelis (1997), Thorbecke (1997), and Bernanke and Kuttner (2005). Changes in U.S. monetary policy also affect foreign equity markets (Kim 2001). Return to text

29.      While monetary policy is one of the factors influencing prices, there are likely to be many others. See Andersen et al. (2004) for an analysis. Return to text

30.       Melvin (2002) finds that the exchange rate market switches to a more informed state on Federal Open Market Committee days, which suggests greater private information revelation. Return to text

31.      In previous asset-pricing tests, the instruments $I_{t}$ were the `` usual suspects'' that were found to forecast returns at monthly horizons. Examples include dividend yields, term structure slopes, short-term interest rates, and credit spreads. We focus on variables that have predictive ability over shorter horizons. Return to text

32.      Latent-factor models have been used in a number of domestic and international asset-pricing tests. See Ferson (1995) for a survey. Return to text

33.      See, however, Easley, Hvidkjaer and O'Hara (2002) for such a model on domestic stock returns. Albuquerque et al. (2003b) provide a model that relates returns and flows to private information in an international setting. However, they do not test the effects of private information on the cross section of asset prices. Return to text

Figure 1
Six-month Eurodollar Futures and Fed Funds Target Rate

The two solid lines are the daily 6-month Eurodollar futures rate and the actual target-rate. The sample period is from April 1, 1996 to November 30, 2001. There were 20 target-rate changes in this period. The Eurodollar futures data are from the Chicago Mercantile Exchange (CME). The target rate is from the Federal Reserve Bank of New York.

Figure 2
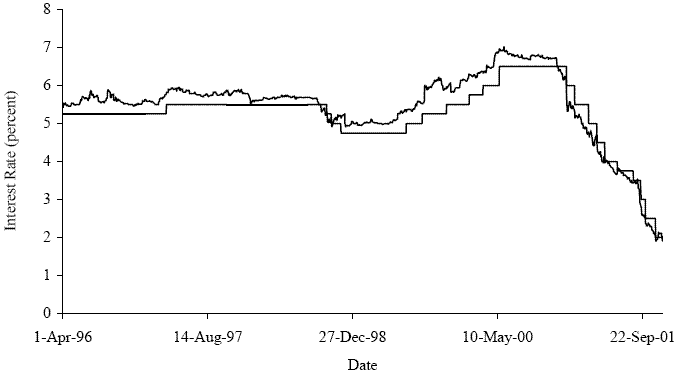
Timing of Quotes, Private Information, Trade Orders and Public Information

Private information is the persistent impact unanticipated trade orders have on the security price. To measure private information we estimate a system of equations similar to Hasbrouck (1991). The two main identification assumptions are the following: trade orders are in no part driven by public information and trade orders are driven partially by private information and liquidity needs. These two assumptions can be summarized as a timing convention. The timing is shown bellow, where $q^b_{t-1}$ is the bid quote, $q^a_{t-1}$ is the ask quote at time $t-1$ and $x^s_t$ are the seller-initiated orders and $x^b_t$ are the buyer-initiated orders.

Table 1a
Summary Statistics of Quote Revisions on Eurodollar Futures Contracts, Exchange Traded Funds and Foreign Currency Futures Contracts

The table shows summary statistics of quote revisions on Eurodollar futures contracts, Exchange Traded Funds (ETFs), and foreign currency futures contracts. The Eurodollar futures contracts are from the Chicago Mercantile Exchange (CME) and have a maturity of $k$ months. The US ETF is the Standard and Poor's 500 Depository Receipt (``Spider'') managed by State Street Global Advisors. The foreign country exchange traded funds are the ``ishares'' ETFs managed by Barclay's Global Advisors. The source of the ETF data is the TAQ database. The foreign currency futures data are also from the CME and are denominated in US dollars per unit of foreign exchange. All of the series are aggregated to 11 one-half hour intervals during the common trading times of the CME and the NYSE/AMEX exchanges. The sample period is April 1, 1996 to November 30, 2001 resulting in a total of 15,598 half-hour observations. The quote revisions are the (log) change in the last quote recorded during each one-half hour interval, multiplied by 100. The table shows the: mean; standard deviation; first and 99$^{th}$ fractiles; the per cent of all intervals which have an observation (``freq''); and asymptotic marginal significance levels ($P$-values) of the Ljung-Box test statistics for autocorrelation out to the indicated lags. The intra-day seasonality has been removed from all of the quote revisions; the final column shows the $P$-value of a test of the null hypothesis of no intra-day seasonality on the raw data.

Panel A: Eurodollar futures

	mean (%)	std. dev. (%)	fractiles: 1$^{st}$ (%)	fractiles: 99$^{th}$ (%)	freq. (%)	L.-B. Q-test: 1 lag (P - value)	L.-B. Q-test: 11 lags (P - value)	Intra-day seasonal (P - value)
$k$ = 3	0.0002	0.010	-0.021	0.021	91.197	$<0.001$	$<0.001$	0.007
$k$ = 6	0.0003	0.013	-0.031	0.031	94.961	$<0.001$	$<0.001$	0.001
$k$ = 9	0.0002	0.014	-0.037	0.036	95.313	0.059	$<0.001$	0.063
$k$ = 12	0.0001	0.015	-0.038	0.038	94.031	0.617	0.001	0.070
$k$ = 60	-0.0003	0.016	-0.053	0.044	42.797	0.028	$<0.001$	0.018

 

Panel B: Exchange Traded Funds

	mean (%)	std. dev. (%)	fractiles: 1$^{st}$ (%)	fractiles: 99$^{th}$ (%)	freq. (%)	L.-B. Q-test: 1 lag (P - value)	L.-B. Q-test: 11 lags (P - value)	Intra-day seasonal (P - value)
US	-0.002	0.275	-0.714	0.702	99.711	0.207	0.359	0.245
Germany	-0.002	0.251	-0.735	0.710	71.777	0.796	0.089	0.286
Japan	-0.009	0.273	-0.777	0.712	93.210	$<0.001$	$<0.001$	$<0.001$
UK	0.002	0.245	-0.747	0.714	61.384	0.028	$<0.001$	0.060
Switzerland	-0.002	0.226	-0.776	0.714	49.580	0.004	0.027	0.054
Canada	-0.004	0.273	-0.977	0.856	41.444	0.234	0.049	0.214
France	-0.002	0.217	-0.672	0.643	57.947	0.889	0.030	0.017
Netherlands	0.001	0.213	-0.598	0.632	46.624	0.048	0.301	0.052
Sweden	0.001	0.277	-0.825	0.823	46.759	0.012	0.016	0.003
Australia	-0.004	0.241	-0.727	0.654	46.458	$<0.001$	$<0.001$	0.090
Italy	-0.004	0.236	-0.714	0.687	54.754	0.538	0.036	0.011

 

Panel C: Foreign Currency Futures

	mean (%)	std. dev. (%)	fractiles: 1$^{st}$ (%)	fractiles: 99$^{th}$ (%)	freq. (%)	L.-B. Q-test: 1 lag (P - value)	L.-B. Q-test: 11 lags (P - value)	Intra-day seasonal (P - value)
Euro	0.001	0.120	-0.321	0.314	93.384	0.244	0.124	0.003
Yen	-0.002	0.122	-0.326	0.340	98.442	$<0.001$	$<0.001$	0.047
UK Pound	0.002	0.093	-0.249	0.259	98.211	$<0.001$	$<0.001$	0.001
Swiss Franc	-0.0001	0.137	-0.351	0.362	98.352	0.001	0.047	$<0.001$
Canadian $	-0.002	0.071	-0.198	0.201	98.282	$<0.001$	$<0.001$	$<0.001$

Table 1b
Summary Statistics of Signed Order Flows of Eurodollar Futures Contracts, Exchange Traded Funds and Foreign Currency Futures Contracts

The table shows summary statistics of signed order flows of Eurodollar futures contracts, Exchange Traded Funds (ETFs), and foreign currency futures contracts. The sources of the data are given in Table 1a. Using all observations, the signs of the trades in the Eurodollar and foreign currency futures contracts have been estimated using the ``tick rule'' as detailed in the text. The ETF trades from the TAQ database have been labeled as purchases or sales according to the Lee and Ready (1991) algorithm. All of the order flow series are aggregated to 11 one-half hour intervals during the common trading times of the CME and the NYSE/AMEX exchanges. The sample period is April 1, 1996 to November 30, 2001 resulting in a total of 15,598 half-hour observations. The table shows the: mean; standard deviation; the 1$^{st}$ and 99$^{th}$ fractiles; the per cent of all intervals which have an observation (``freq''); and asymptotic marginal significance levels ($P$-values) of the Ljung-Box test statistics for autocorrelation out to the indicated lags. The intra-day seasonality has been removed from all of the order flows; the final column shows the $P$-value of a test of the null hypothesis of no intra-day seasonality on the raw data.

Panel A: Eurodollar futures

	mean (#)	std. dev. (#)	fractiles: 1$^{st}$ (#)	fractiles: 99$^{th}$ (#)	freq. (%)	L.-B. Q-test: 1 lag (P - value)	L.-B. Q-test: 11 lags (P - value)	Intra-day seasonal (P - value)
$k$ = 3	0.029	1.521	-4.052	4.041	91.197	$<0.001$	$<0.001$	0.003
$k$ = 6	0.028	1.990	-5.907	5.093	94.961	$<0.001$	$<0.001$	0.001
$k$ = 9	0.029	2.257	-6.109	6.000	95.313	0.013	$<0.001$	0.015
$k$ = 12	0.011	2.359	-6.915	6.085	94.031	0.164	$<0.001$	0.195
$k$ = 60	-0.013	0.802	-2.024	2.020	42.797	0.131	$<0.001$	0.049

 

Panel B: Exchange Traded Funds

	mean (#)	std. dev. (#)	fractiles: 1$^{st}$ (#)	fractiles: 99$^{th}$ (#)	freq. (%)	L.-B. Q-test: 1 lag (P - value)	L.-B. Q-test: 11 lags (P - value)	Intra-day seasonal (P - value)
US	0.886	14.471	-41.506	40.329	99.679	$<0.001$	$<0.001$	$<0.001$
Germany	0.126	1.519	-3.959	4.080	56.101	$<0.001$	$<0.001$	$<0.001$
Japan	0.298	3.022	-7.156	9.183	88.145	$<0.001$	$<0.001$	$<0.001$
UK	0.067	1.103	-3.021	2.998	43.848	$<0.001$	$<0.001$	$<0.001$
Switzerland	0.038	0.691	-1.991	2.036	28.300	$<0.001$	$<0.001$	$<0.001$
Canada	0.039	0.661	-1.989	2.016	21.568	$<0.001$	$<0.001$	$<0.001$
France	0.049	0.884	-2.072	2.972	40.174	$<0.001$	$<0.001$	$<0.001$
Netherlands	0.032	0.580	-1.961	1.987	22.684	$<0.001$	$<0.001$	$<0.001$
Sweden	0.028	0.540	-1.030	1.990	19.818	$<0.001$	$<0.001$	$<0.001$
Australia	0.032	0.731	-2.025	2.020	30.916	$<0.001$	$<0.001$	$<0.001$
Italy	0.018	0.905	-2.042	2.968	36.404	$<0.001$	$<0.001$	$<0.001$

 

Panel C: Foreign Currency Futures

	mean (#)	std. dev. (#)	fractiles: 1$^{st}$ (#)	fractiles: 99$^{th}$ (#)	freq. (%)	L.-B. Q-test: 1 lag (P - value)	L.-B. Q-test: 11 lags (P - value)	Intra-day seasonal (P - value)
Euro	0.016	6.968	-18.139	18.108	98.384	$<0.001$	0.027	0.143
Yen	-0.020	7.255	-18.938	18.569	98.442	$<0.001$	$<0.001$	0.391
UK Pound	0.119	5.615	-14.298	14.189	98.211	$<0.001$	$<0.001$	$<0.001$
Swiss Franc	0.094	6.881	-17.845	17.964	98.352	$<0.001$	$<0.001$	0.171
Canadian $	-0.159	4.289	-11.116	11.198	98.282	$<0.001$	$<0.001$	$<0.001$

Table 1c
Correlation Coefficients of Foreign Exchange Traded Funds and M.S.C. I. Indexes

The tables shows correlation coefficients of the log price change in the foreign Exchange Traded Funds (ETFs) and the log change in the Morgan Stanley Capital Incorporated (MSCI) foreign stock index over the indicated holding period $H$. The sources of the data are given in Table 1a.

	$H$ = 1 day	$H$ = 5 days
Germany	0.767	0.934
Japan	0.674	0.909
UK	0.675	0.876
Switzerland	0.674	0.883
Canada	0.655	0.902
France	0.802	0.943
Netherlands	0.761	0.932
Sweden	0.725	0.896
Australia	0.603	0.856
Italy	0.801	0.932

Table 2a
Contemporaneous Correlations of Quote Revisions on Eurodollar Futures Contracts, Exchange Traded Funds and Foreign Currency Futures Contracts

The top part of the table shows contemporaneous correlation coefficients of quote revisions on the Eurodollar futures contracts, the US Exchange Traded Fund, and the foreign currency futures contracts. The bottom part of the table shows the contemporaneous correlation coefficients of quote revisions on the US and foreign Exchange Traded Funds. The sources of the data are given in Table 1a.

Panel A: Eurodollar futures

	Eurodollar futures: $k$ = 3	Eurodollar futures: $k$ = 6	Eurodollar futures: $k$ = 9	Eurodollar futures: $k$ = 12	Eurodollar futures: $k$ = 60	US ETF	Foreign Currency Futures: Euro	Foreign Currency Futures: Yen	Foreign Currency Futures: UK Pd	Foreign Currency Futures: Sw. Fr.
$k$ = 3	1
$k$ = 6	0.773	1
$k$ = 9	0.733	0.873	1
$k$ = 12	0.696	0.835	0.901	1
$k$ = 60	0.245	0.283	0.317	0.333	1
US ETF	-0.157	-0.168	-0.157	-0.154	-0.010	1

 

Panel B: Foreign Currency Futures

	Eurodollar futures: $k$ = 3	Eurodollar futures: $k$ = 6	Eurodollar futures: $k$ = 9	Eurodollar futures: $k$ = 12	Eurodollar futures: $k$ = 60	US ETF	Foreign Currency Futures: Euro	Foreign Currency Futures: Yen	Foreign Currency Futures: UK Pd	Foreign Currency Futures: Sw. Fr.
Euro	0.177	0.167	0.161	0.152	0.044	-0.309	1
Yen	0.102	0.086	0.068	0.054	0.008	-0.186	0.379	1
UK Pd	0.087	0.082	0.081	0.076	0.023	-0.174	0.540	0.229	1
Sw. Fr.	0.221	0.204	0.184	0.172	0.058	-0.325	0.883	0.396	0.496	1
Cdn $	0.022	0.017	0.025	0.026	0.033	0.100	-0.014	-0.005	-0.005	-0.024

 

Panel C: Exchange Traded Funds

	US	Ger.	Jap.	UK	Swiss	Can.	Fra.	Neth	Swe.	Aus.
US	1
Germany	0.196	1
Japan	0.144	0.148	1
UK	0.176	0.209	0.110	1
Switzerland	0.168	0.173	0.082	0.195	1
Canada	0.163	0.188	0.112	0.143	0.141	1
France	0.215	0.404	0.156	0.226	0.200	0.233	1
Netherlands	0.228	0.224	0.099	0.244	0.300	0.138	0.241	1
Sweden	0.251	0.197	0.101	0.225	0.256	0.143	0.219	0.352	1
Australia	0.113	0.168	0.101	0.145	0.108	0.147	0.171	0.144	0.073	1
Italy	0.166	0.331	0.142	0.193	0.192	0.209	0.402	0.226	0.167	0.183

Table 2b
Contemporaneous Correlations of Signed Order Flows of Eurodollar Futures Contracts, Exchange Traded Funds and Foreign Currency Futures Contracts

The top part of the table shows contemporaneous correlation coefficients of signed order flows of the Eurodollar futures contracts, the US Exchange Traded Fund, and the foreign currency futures contracts. The bottom part of the table shows the contemporaneous correlation coefficients of order flows of the US and foreign Exchange Traded Funds. The sources of the data are given in Table 1b.

Panel A: Eurodollar futures

	Eurodollar futures: $k$ = 3	Eurodollar futures: $k$ = 6	Eurodollar futures: $k$ = 9	Eurodollar futures: $k$ = 12	Eurodollar futures: $k$ = 60	US ETF	Foreign Currency Futures: Euro	Foreign Currency Futures: Yen	Foreign Currency Futures: UK Pd	Foreign Currency Futures: Sw. Fr.
$k$ = 3	1
$k$ = 6	0.672	1
$k$ = 9	0.647	0.814	1
$k$ = 12	0.619	0.774	0.836	1
$k$ = 60	0.185	0.239	0.267	0.285	1
US ETF	-0.121	-0.122	-0.114	-0.113	0.006	1

 

Panel B: Foreign Currency Futures

	Eurodollar futures: $k$ = 3	Eurodollar futures: $k$ = 6	Eurodollar futures: $k$ = 9	Eurodollar futures: $k$ = 12	Eurodollar futures: $k$ = 60	US ETF	Foreign Currency Futures: Euro	Foreign Currency Futures: Yen	Foreign Currency Futures: UK Pd	Foreign Currency Futures: Sw. Fr.
Euro	0.056	0.060	0.067	0.055	0.001	-0.092	1
Yen	0.008	0.015	0.006	0.004	-0.016	-0.027	0.158	1
UK Pd	0.027	0.031	0.029	0.033	0.001	-0.046	0.216	0.061	1
Sw. Fr.	0.035	0.031	0.035	0.030	-0.012	-0.062	0.292	0.110	0.152	1
Cdn $	0.014	0.008	0.007	0.010	0.020	0.024	-0.014	0.003	-0.018	-0.020

 

Panel C: Exchange Traded Funds

	US	Ger.	Jap.	UK	Swiss	Can.	Fra.	Neth	Swe.	Aus.
US	1
Germany	0.058	1
Japan	0.044	0.094	1
UK	0.050	0.172	0.091	1
Switzerland	0.037	0.155	0.058	0.161	1
Canada	0.033	0.066	0.054	0.040	0.051	1
France	0.055	0.256	0.093	0.188	0.158	0.053	1
Netherlands	0.024	0.126	0.047	0.131	0.209	0.040	0.196	1
Sweden	0.010	0.098	0.043	0.085	0.125	0.042	0.135	0.148	1
Australia	0.017	0.079	0.070	0.100	0.094	0.080	0.084	0.096	0.060	1
Italy	0.040	0.155	0.053	0.106	0.141	0.034	0.213	0.172	0.097	0.086

Table 3a
Granger Causality Tests of the Predictability of US and Foreign-Country ETF Variables in the Six-Month Eurodollar Order Flow and Quote Revision Regressions

The table presents asymptotic marginal significance levels ($P$-values) of the test statistics associated with Granger causality tests of the predictive ability of the indicated US and foreign country variables in the six-month Eurodollar futures quote revision and order flow regressions. The panel on the left shows the Granger causality tests for the Eurodollar order flow regression while the panel on the right shows the corresponding tests for the quote revision regression. The tests are for the joint significance of 12 lagged values of the indicated US or foreign country ETF variable in a regression that includes lagged Eurodollar quote revisions and order flows. The test statistics, which are robust to general forms of heteroskedasticity and autocorrelation (Newey and West (1987)), are $\chi$$^{2}$ distributed with 12 degree of freedom.

country $j$ =	Eurodollar Order Flow Regression: lagged order flow	Eurodollar Order Flow Regression: lagged quote revisions	Eurodollar Quote Revision Regression: lagged order flows	Eurodollar Quote Revision Regression: lagged quote revisions
US	0.686	0.139	0.869	0.309
Germany	0.564	0.431	0.539	0.679
Japan	0.544	0.084	0.747	0.054
UK	0.787	0.771	0.703	0.726
Switzerland	0.745	0.864	0.920	0.927
Canada	0.051	0.188	0.128	0.314
France	0.817	0.418	0.474	0.277
Netherlands	0.098	0.922	0.174	0.857
Sweden	0.855	0.785	0.952	0.816
Australia	0.581	0.100	0.657	0.159
Italy	0.877	0.957	0.601	0.931

Table 3b
Granger Causality Tests of the Predictability of Eurodollar and Foreign-Country ETF Variables in the US ETF Order Flow and Quote Revision Regressions

The table presents asymptotic marginal significance levels ($P$-values) of the test statistics associated with Granger causality tests of the predictive ability of the indicated Eurodollar and foreign-country ETF variables in the US ETF order flow and quote revision regressions. The panel on the left shows the Granger causality tests for the US ETF order flow regression while the panel on the right shows the corresponding tests for the quote revision regression. The tests are for the joint significance of 12 lagged values of the indicated Eurodollar (with maturity of $k$ months) or foreign-country ETF variable in a regression that includes lagged US ETF quote revisions and order flows. The test statistics, which are robust to general forms of heteroskedasticity and autocorrelation (Newey and West (1987)), are $\chi$$^{2}$ distributed with 12 degree of freedom.

Panel A: Eurodollar futures

	US ETF Order Flow Regression: lagged order flows	US ETF Order Flow Regression: lagged quote revisions	US ETF Quote Revision Regression: lagged order flows	US ETF Quote Revision Regression: lagged quote revisions
$k$ = 3	0.013	0.021	0.042	0.036
$k$ = 6	$<0.001$	$<0.001$	$<0.001$	$<0.001$
$k$ = 9	0.021	$<0.001$	0.212	0.010
$k$ = 12	0.217	0.101	0.142	0.154
$k$ = 60	0.117	0.207	0.425	0.856

 

Panel B: Exchange Traded Funds

	US ETF Order Flow Regression: lagged order flows	US ETF Order Flow Regression: lagged quote revisions	US ETF Quote Revision Regression: lagged order flows	US ETF Quote Revision Regression: lagged quote revisions
Germany	0.146	0.898	0.038	0.979
Japan	0.696	0.675	0.655	0.287
UK	0.882	0.177	0.939	0.769
Switzerland	0.007	0.567	0.681	0.509
Canada	0.269	0.092	0.101	0.219
France	0.221	0.400	0.933	0.911
Netherlands	0.672	0.010	0.862	0.023
Sweden	0.081	0.315	0.311	0.350
Australia	0.703	0.001	0.337	0.325
Italy	0.081	0.629	0.082	0.277

Table 3c
Granger Causality Tests of the Predictability of the Six-Month Eurodollar and US ETF Variables in the Foreign-Country ETF Order Flow and Quote Revision Regressions

The table presents asymptotic marginal significance levels ($P$-values) of the test statistics associated with Granger causality tests of the predictive ability of the indicated six-month Eurodollar and US ETF variables in the foreign country ETF order flow and quote revision regressions. The panel on the left shows the Granger causality tests for the foreign-country order flow regressions while the panel on the right shows the corresponding tests for the quote revision regressions. The tests are for the joint significance of 12 lagged values of the indicated six-month Eurodollar or US ETF variable in a regression that includes lagged Eurodollar, US ETF and foreign-country ETF quote revisions and order flows. The test statistics, which are robust to general forms of heteroskedasticity and autocorrelation (Newey and West (1987)), are $\chi$$^{2}$ distributed with 12 degree of freedom.

country$j$=	Country-$j$ ETF Order Flow Regressions: Eurodollar lagged order flows	Country-$j$ ETF Order Flow Regressions: Eurodollar lagged quote revisions	Country-$j$ ETF Order Flow Regressions: US ETF lagged order flows	Country-$j$ ETF Order Flow Regressions: US ETF lagged quote revisions	Country-$j$ ETF Quote Revision Regressions: Eurodollar lagged order flows	Country-$j$ ETF Quote Revision Regressions: Eurodollar lagged quote revisions	Country-$j$ ETF Quote Revision Regressions: US ETF lagged order flows	Country-$j$ ETF Quote Revision Regressions: US ETF lagged quote revisions
Germany	0.078	0.007	0.046	$<0.001$	$<0.001$	$<0.001$	0.263	$<0.001$
Japan	$<0.001$	$<0.001$	0.690	$<0.001$	$<0.001$	$<0.001$	0.078	$<0.001$
UK	0.113	0.001	0.274	$<0.001$	$<0.001$	$<0.001$	0.954	$<0.001$
Switzerland	0.081	0.066	0.060	0.297	0.085	$<0.001$	0.041	$<0.001$
Canada	0.350	0.096	0.435	$<0.001$	$<0.001$	$<0.001$	0.542	$<0.001$
France	0.504	0.332	0.188	$<0.001$	0.291	0.158	0.826	$<0.001$
Netherlands	0.004	$<0.001$	0.011	0.070	0.105	0.544	0.629	$<0.001$
Sweden	0.004	$<0.001$	0.355	0.472	0.369	0.089	0.017	$<0.001$
Australia	0.023	$<0.001$	0.741	$<0.001$	0.002	0.005	0.112	$<0.001$
Italy	0.114	0.135	0.811	$<0.001$	0.157	0.156	0.372	$<0.001$

Table 4
Cochrane-Piazzesi (2002) Regressions using Eurodollar Futures Contracts

The table provides estimates of the Cochrane and Piazzesi (2002) regressions to model the relationship between the Eurodollar futures contract and future monetary policy changes. The dependent variable in all of the regressions is the change in the ``price'' of the Federal funds target ( $\Delta P^{TR}_{ \tau })$, when a target change occurs$.$ Note that an increase in this variable implies a decrease in the target rate. The independent variables are the lagged level of the Federal funds target rate price ( $P^{TR}_{ \tau -1})$ and the spread between the log target-rate shadow price and the $j$-month log Eurodollar futures price (SP $_{\tau -1}=P^{TR}_{\tau -1 }-- P^{ED}_{\tau -1})$. These latter two variables are recorded 30-minutes before the target-rate change. The sample period is from April 1, 1996 to November 30, 2001. The time index is in event time: $\tau$ = 1,...19, as there were 19 target-rate changes in this period. (We exclude the target rate change following September 11, 2001). The White $t$ statistics (in parentheses) are asymptotically robust to general forms of heteroskedasticity. The $R^{2 }$statistics are adjusted for degrees of freedom.

futures contract maturity	$P^{TR}_{ \tau -1}$ ($t$-stat.)	SP$_{\tau -1}$ ($t$-stat.)	$R^{2 }$
$k$ = 3	0.043 (2.918)	-0.517 (-16.894)	0.907
$k$ = 6	0.079 (7.324)	-0.383 (-17.255)	0.918
$k$ = 9	0.105 (8.112)	-0.347 (-14.091)	0.874
$k$ = 12	0.137 (8.338)	-0.336 (-11.159)	0.851
$k$ = 60	0.384 (8.568)	-0.383 (-5.503)	0.583

Table 5a
Estimates of the Modified Hasbrouck (1991) Model for the Eurodollar Futures and US Exchange Traded Fund Order Flow Regressions

The table presents the results from OLS regressions of the six-month Eurodollar futures signed order flow (7) and the US ETF signed order flow (8) on the selected public information variables. The signed order flows on the two assets are accumulated over a one-half-hour interval. They are projected on 12 lagged values each of the Eurodollar and the US ETF order flows and quote revisions. For these variables the sum of the 12 coefficients is given along with a $t$ statistic of the significance of the sum. The regressions also include: the lagged Federal Funds target price ( $P^{TR}_{ t-1})$; and the lagged difference between the Fed Funds target price and the price of the Eurodollar contract (SP $_{t-1 }= P^{TR}_{t-1 }-- P^{ED}_{t-1})$. The US ETF order flow regression also includes the unanticipated net purchases from the Eurodollar order flow regressions ( $\nu (x)_{t}^{ED})$. The Newey-West $t$ statistics (in parentheses) are asymptotically robust to general forms of heteroskedasticity and autocorrelation. The $R^{2 }$ statistics are adjusted for degrees of freedom.

Panel A: Eurodollar Order Flow Regression

Eurodollar: lagged order flows ($t$-stat.)	Eurodollar: lagged quote revisions ($t$-stat.)	US ETF: lagged order flows ($t$-stat.)	US ETF: lagged quote revisions ($t$-stat.)	monetary policy:$P^{TR}_{ t-1}$ ($t$-stat.)	monetary policy: SP$_{t-1}$ ($t$-stat.)	$\nu$(x)$_{t}^{ED}$ ($t$-stat.)	$R^{2 }$
0.029 (0.480)	2.148 (0.224)	0.001 (0.320)	0.134 (0.561)	-0.016 (-0.640)	-0.022 (-0.501)		0.006

 

Panel B: US ETF Order Flow Regression

Eurodollar: lagged order flows ($t$-stat.)	Eurodollar: lagged quote revisions ($t$-stat.)	US ETF: lagged order flows ($t$-stat.)	US ETF: lagged quote revisions ($t$-stat.)	monetary policy:$P^{TR}_{ t-1}$ ($t$-stat.)	monetary policy: SP$_{t-1}$ ($t$-stat.)	$\nu$(x)$_{t}^{ED}$ ($t$-stat.)	$R^{2 }$
-0.041 (-0.094)	216.576 (3.227)	0.371 (12.282)	-6.749 (-3.673)	-0.953 (-5.387)	1.080 (3.844)	-0.894 (-9.687)	0.083

Table 5b
Estimates of the Modified Hasbrouck (1991) Model for the Six-Month Eurodollar Futures Contract Holding Period Returns

The table presents the results from OLS regressions of the six-month Eurodollar futures contract's holding period return on the selected private and public information variables (9). The holding period returns are the (log) difference in price of the contract over the holding period $H$. The returns are projected on 12 lagged values each of the six-month Eurodollar and US ETF order flows and quote revisions. For these variables the sum of the 12 coefficients is given along with a $t$ statistic of the significance of the sum. The regressions also include: the lagged Federal Funds target price ( $P^{TR}_{ t-1})$; the lagged difference between the Fed Funds target price and the price of the Eurodollar contract (SP $_{t-1 }= P^{TR}_{t-1 }-- P^{ED}_{t-1})$; the unanticipated net purchases from the Eurodollar and US ETF order flow regressions in Table 5a ( $\nu (x)_{t}^{ED}$ and $\nu (r)_{t}^{ED}$, respectively). The Newey-West $t$ statistics (in parentheses) are asymptotically robust to general forms of heteroskedasticity and autocorrelation. The $R^{2 }$statistics are adjusted for degrees of freedom.

$H$=	Eurodollar: lagged order flows ($t$-stat.)	Eurodollar: lagged quote revisions ($t$-stat.)	US ETF: lagged order flows ($t$-stat.)	US ETF: lagged quote revisions ($t$-stat.)	monetary policy: $P^{TR}_{ t-1}$ ($t$-stat.)	monetary policy: SP$_{t-1}$ ($t$-stat.)	Eurodollar: $\nu$(x)$_{t}^{ED}$ ($t$-stat.)	US ETF: $\nu$(x)$_{t}^{US}$ ($t$-stat.)	$R^{2 }$
$\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ hour	-0.000 (-0.695)	0.043 (2.329)	-0.000 (-0.842)	0.002 (1.091)	-0.000 (-0.719)	-0.000 (-2.821)	0.0006 (77.794)	0.00002 (1.886)	0.752
1 day	-0.009 (-2.587)	1.595 (3.012)	-0.000 (-1.241)	-0.015 (-0.685)	-0.001 (-0.558)	-0.010 (-2.728)	0.006 (18.597)	-0.00003 (-0.593)	0.038
5 days	-0.024 (-2.222)	2.287 (1.400)	-0.000 (-0.068)	-0.020 (-0.437)	-0.006 (-0.523)	-0.048 (-3.136)	0.005 (6.919)	0.00003 (0.311)	0.030

Table 5c
Estimates of the Modified Hasbrouck (1991) Model for the US ETF Holding Period Returns

The table presents the results from OLS regressions of the US ETF holding period return on the selected private and public information variables (10). The holding period returns are the (log) difference in price of the ETF over the holding period $H$. The returns are projected on 12 lagged values each of the six-month Eurodollar and US ETF order flows and quote revisions. For these variables the sum of the 12 coefficients is given along with a $t$ statistic of the significance of the sum. The regression also includes: the lagged Federal Funds target price ( $P^{TR}_{ t-1})$; the lagged difference between the Fed Funds target price and the price of the Eurodollar contract (SP $_{t-1 }= P^{TR}_{t-1 }-- P^{ED}_{t-1})$; the unanticipated net purchases from the Eurodollar and US ETF order flow regressions in Table 5a ( $\nu (x)_{t}^{ED}$ and $\nu$(x)$_{t}^{US}$, respectively); and the unanticipated quote revision on the Eurodollar contract from the $H$= $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ hour regression in Table 5b ( $\nu (r)_{t}^{ED})$ when there was a change in the Fed Funds target rate during the half-hour period (1($\Delta$TR$\ne$0)). The Newey-West $t$ statistics (in parentheses) are asymptotically robust to general forms of heteroskedasticity and autocorrelation. The $R^{2 }$ statistics are adjusted for degrees of freedom.

$H$=	Eurodollar: lagged order flows ($t$-stat.)	Eurodollar: lagged quote revisions ($t$-stat.)	US ETF: lagged order flows ($t$-stat.)	US ETF: lagged quote revisions ($t$-stat.)	monetary policy: $P^{TR}_{ t-1}$ ($t$-stat.)	monetary policy: SP$_{t-1}$ ($t$-stat.)	Eurodollar: $\nu$(x)$_{t}^{ED}$ ($t$-stat.)	Eurodollar: $\nu$(r)$_{t}^{ED}$ 1($\Delta$TR$\ne$0) ($t$-stat.)	US ETF: $\nu$(x)$_{t}^{US}$ ($t$-stat.)	$R^{2 }$
$\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ hour	0.006 (1.022)	0.574 (0.782)	0.001 (1.552)	-0.019 (-0.528)	0.002 (0.623)	0.004 (0.863)	-0.027 (-9.275)	16.858 (4.950)	0.008 (33.275)	0.203
1 day	0.047 (0.675)	-1.852 (-0.214)	-0.005 (-0.890)	0.767 (1.861)	0.010 (0.260)	0.035 (0.482)	-0.025 (-3.750)	18.423 (3.432)	0.010 (10.365)	0.015
5 days	0.070 (0.268)	-19.035 (-0.470)	-0.036 (-2.320)	-0.494 (-0.515)	0.037 (0.227)	0.170 (0.553)	-0.027 (-2.123)	17.203 (1.538)	0.005 (3.171)	0.007

Table 6
Summary Statistics from and Tests of the Latent Factor Model of International Stock Returns

The top part of the table presents the value of the $J$-statistics associated with the Wald tests of the over-identifying restrictions of the latent factor model of international stock returns. The statistics are distributed as $\chi$$^{2}$(63) and are presented along with their asymptotic marginal significance levels ($P$-value). The model is estimated separately for each holding period $H$ by Generalized Method of Moments. The bottom part of the table presents variance ratio measures of the statistical fit of the model. The ratio shows how the latent factor model captures the expected return variation in the data. The numerator is the variance of the expected return on the foreign ETF from the latent factor model while the denominator is the variance of the expected return from an OLS regression of the foreign ETF return on the global instruments.

Panel A: $J$-statistic model test

	$H=\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ hour	$H$ = 1 day	$H$ = 5 days
$\chi ^{2}$ (63) statistic	129.52	73.07	73.74
$P$-value	$<0.001$	0.181	0.167

 

Panel B: Variance ratios

	$H=\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ hour	$H$ = 1 day	$H$ = 5 days
Germany	0.256	0.917	1.189
Japan	0.546	0.857	1.032
UK	0.503	0.927	1.575
Switzerland	0.690	0.928	1.388
Canada	0.375	0.883	0.572
France	0.291	0.927	1.386
Netherlands	0.440	0.925	1.329
Sweden	0.879	0.814	0.237
Australia	0.023	0.742	0.417
Italy	0.150	0.810	1.450

Table 7
Beta Coefficients on the Implied Global Risk Premiums in the Latent Factor Model of International Stock Returns

The table shows the $\beta$ coefficients on the implied global risk premium from the latent factor model of international stock returns. The implied global risk premium is the linear combination of the global instruments given in Table 8. The beta coefficient for Germany is normalized for identification. The model is estimated separately for each holding period $H$ by Generalized Method of Moments. The Newey-West $t$ statistics (in parentheses) are asymptotically robust to general forms of heteroskedasticity and autocorrelation.

	$H=\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ hour: $\beta$ ($t$-stat.)	$H$ = 1 day: $\beta$ ($t$-stat.)	$H$ = 5 days: $\beta$ ($t$-stat.)
Germany	1.000	1.000	1.000
Japan	0.984 (11.675)	0.529 (10.207)	0.615 (5.439)
UK	1.164 (14.845)	0.753 (22.049)	0.681 (11.467)
Switzerland	0.988 (12.024)	0.580 (17.342)	0.698 (11.440)
Canada	1.103 (12.121)	1.149 (19.381)	1.130 (10.504)
France	1.012 (18.587)	0.951 (32.196)	0.881 (16.181)
Netherlands	1.176 (13.764)	0.8.14 (25.221)	0.766 (13.957)
Sweden	2.045 (14.690)	1.301 (21.092)	1.005 (11.438)
Australia	0.367 (6.805)	0.637 (11.550)	0.637 (7.954)
Italy	0.683 (12.215)	0.857 (23.544)	0.922 (11.838)

Table 8
Coefficients on the Global Instruments in the Latent Factor Model of International Stock Returns

The table shows the $\alpha$$_{H}$ coefficients on the global instruments in the latent factor model of international stock returns. The global instruments are: a constant; the lagged Federal funds target price ($P^{TR}_{ t-1})$; the lagged difference between the Fed Funds target price and the price of the Eurodollar contract (SP $_{t-1 }= P^{TR}_{t-1 }-- P^{ED}_{t-1})$; the unanticipated net purchases on the six-month Eurodollar contract from Table 5a ( $\nu (x)_{t}^{ED})$; the unanticipated quote revision on the Eurodollar contract from the $H=\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ hour regression in Table 5b ( $\nu (r)_{t}^{ED})$, which are separated into whether there was a change in the Fed Funds target rate during the half-hour period (1($\Delta$TR$\ne$0)) or not; and the unanticipated net purchases and quote revisions on the US ETF from Tables 5a and 5c ( $\nu (x)_{t}^{US}$ and $\nu (r)_{t}^{US })$. The model is estimated separately by Generalized Method of Moments for each holding period $H$. The Newey-West $t$ statistics (in parentheses) are asymptotically robust to general forms of heteroskedasticity and autocorrelation. The $\sigma$-shocks [in brackets] represent the effect of a one standard deviation shock to the indicated variable, normalized by the standard deviation of the latent factor.

Panel A: $H=\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ hour

constant ($t$-stat.)	monetary policy: $P^{TR}_{ t-1}$ ($t$-stat.) [$\sigma$-shock]	monetary policy: SP$_{t-1}$ ($t$-stat.) [$\sigma$-shock]	Eurodollar: $\nu$(x)$_{t}^{ED}$ ($t$-stat.) [$\sigma$-shock]	Eurodollar: $\nu$(r)$_{t}^{ED}$ 1($\Delta$TR=0) ($t$-stat.) [$\sigma$-shock]	Eurodollar: $\nu$(r)$_{t}^{ED}$ 1($\Delta$TR$\ne$0) ($t$-stat.) [$\sigma$-shock]	US ETF: $\nu$(x)$_{t}^{US}$ ($t$-stat.) [$\sigma$-shock]	US ETF: $\nu$(r)$_{t}^{US}$ ($t$-stat.) [$\sigma$-shock]
-0.641 (-1.246)	0.001 (1.245) [0.036]	0.0003 (0.169) [0.005]	-0.005 (-8.327) [0.311]	-0.797 (-6.462) [0.143]	3.001 (13.383) [0.192]	0.001 (10.664) [0.385]	0.112 (14.427) [0.827]

 

Panel B: $H$ = 1 day

constant ($t$-stat.)	monetary policy: $P^{TR}_{ t-1}$ ($t$-stat.) [$\sigma$-shock]	monetary policy: SP$_{t-1}$ ($t$-stat.) [$\sigma$-shock]	Eurodollar: $\nu$(x)$_{t}^{ED}$ ($t$-stat.) [$\sigma$-shock]	Eurodollar: $\nu$(r)$_{t}^{ED}$ 1($\Delta$TR=0) ($t$-stat.) [$\sigma$-shock]	Eurodollar: $\nu$(r)$_{t}^{ED}$ 1($\Delta$TR$\ne$0) ($t$-stat.) [$\sigma$-shock]	US ETF: $\nu$(x)$_{t}^{US}$ ($t$-stat.) [$\sigma$-shock]	US ETF: $\nu$(r)$_{t}^{US}$ ($t$-stat.) [$\sigma$-shock]
2.204 (0.148)	-0.005 (-0.146) [0.019]	0.029 (0.507) [0.067]	-0.027 (-5.096) [0.242]	-2.330 (-2.797) [0.064]	20.096 (13.353) [0.196]	0.008 (8.971) [0.482]	0.722 (13.089) [0.811]

 

Panel C: $H$ = 5 days

constant ($t$-stat.)	monetary policy: $P^{TR}_{ t-1}$ ($t$-stat.) [$\sigma$-shock]	monetary policy: SP$_{t-1}$ ($t$-stat.) [$\sigma$-shock]	Eurodollar: $\nu$(x)$_{t}^{ED}$ ($t$-stat.) [$\sigma$-shock]	Eurodollar: $\nu$(r)$_{t}^{ED}$ 1($\Delta$TR=0) ($t$-stat.) [$\sigma$-shock]	Eurodollar: $\nu$(r)$_{t}^{ED}$ 1($\Delta$TR$\ne$0) ($t$-stat.) [$\sigma$-shock]	US ETF: $\nu$(x)$_{t}^{US}$ ($t$-stat.) [$\sigma$-shock]	US ETF: $\nu$(r)$_{t}^{US}$ ($t$-stat.) [$\sigma$-shock]
118.18 (2.201)	-0.259 (-2.199) [0.730]	-0.123 (-0.579) [0.212]	-0.031 (-2.981) [0.208]	-7.940 (-4.984) [0.159]	1.442 (0.770) [0.010]	0.002 (1.377) [0.093]	0.745 (7.737) [0.614]

Table 9
OLS Regressions of Home-Currency Returns on Foreign Exchange Traded Funds on the Latent Factor

The table shows the OLS regression coefficients ($\hat {\varphi })$ of the (log) change in the home-currency price of the foreign-country ETF over holding period $H$ on the latent factor from the international equity pricing model. The home currency price of the ETF is calculated using the foreign currency futures prices. The latent factor is the linear combinations of the global instruments given in Table 8. The Newey-West $t$ statistics (in parentheses) are asymptotically robust to general forms of heteroskedasticity and autocorrelation. The $R^{2 }$ statistics are adjusted for degrees of freedom. The table also shows the values of the asymptotic marginal significance levels ($P$-values) associated with the $\chi$$^{2}$ statistics which test whether the indicated coefficient is equal to the value of the beta coefficient from the cross-sectional model that is shown in Table 7.

	$H$ = 1/2 hour: $\hat {\varphi }$ ($t$-stat.)	$H$ = 1/2 hour: $R^{2 }$ $P$-value ($\phi =\beta )$	$H$ = 1 day: $\hat {\varphi }$ ($t$-stat.)	$H$ = 1 day: $R^{2 }$ $P$-value ($\phi =\beta )$	$H$ = 5 days: $\hat {\varphi }$ ($t$-stat.)	$H$ = 5 days: $R^{2 }$ $P$-value ($\phi =\beta )$
Germany	2.803 (5.761)	0.111 $<0.001$	1.177 (13.676)	0.024 0.040	0.290 (0.607)	-0.001 0.137
Japan	2.001 (6.835)	0.049 0.001	0.602 (7.977)	0.007 0.331	-0.229 (-0.648)	-0.002 0.017
UK	1.923 (6.831)	0.059 0.007	0.847 (12.821)	0.019 0.156	0.378 (1.262)	0.001 0.312
Switzerland	2.604 (7.725)	0.107 $<0.001$	0.801 (10.248)	0.016 0.005	0.513 (1.401)	0.001 0.614
Canada	1.310 (4.353)	0.025 0.491	1.061 (13.507)	0.022 0.265	-0.059 (-0.115)	-0.000 0.020

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: December 20, 2006