
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 874, September 2006 --- Screen Reader
Version*

Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 874, September 2006 --- Screen Reader
Version*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We study the role played by private and public information in the process of price formation in the U.S. Treasury bond market. To guide our analysis, we develop a parsimonious model of speculative trading in the presence of two realistic market frictions -- information heterogeneity and imperfect competition among informed traders -- and a public signal. We test its equilibrium implications by analyzing the response of two-year, five-year, and ten-year U.S. bond yields to order flow and real-time U.S. macroeconomic news. We find strong evidence of informational effects in the U.S. Treasury bond market: unanticipated order flow has a significant and permanent impact on daily bond yield changes during both announcement and non-announcement days. Our analysis further shows that, consistent with our stylized model, the contemporaneous correlation between order flow and yield changes is higher when the dispersion of beliefs among market participants is high and public announcements are noisy.
Keywords: Treasury Bond Markets; Macroeconomic News Announcements; Strategic Trading; Market Microstructure; Order Flow; Real-Time Data; Expectations; Dispersion of Beliefs
JEL Classification: E44, G14
*Pasquariello is affiliated with the department of Finance at the Ross School of Business at University of Michigan and Vega is affiliated with the Board of Governors of the Federal Reserve System and the University of Rochester Simon School of Business. Please address comments to the authors via email at [email protected] and [email protected]. We benefitted from the comments of Sreedhar Bharath, Michael Brandt, Michael Fleming, Clifton Green, Nejat Seyhun, Guojun Wu, Kathy Yuan, and other participants in seminars at the 2005 European Finance Association meetings in Moscow, the 2006 Bank of Canada Fixed Income Markets conference in Ottawa, Federal Reserve Board of Governors, George Washington University, the University of Maryland, the University of Michigan, the University of Rochester, and the University of Utah. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System.� Return to text
Identifying the causes of daily asset price movements remains a puzzling issue in finance. In a frictionless market, asset prices should immediately adjust to public news surprises. Hence, we should observe price jumps only during announcement times. However, asset prices fluctuate significantly during non-announcement days as well. This fact has motivated the introduction of various market frictions to better explain the behavior of asset prices. One possible friction is asymmetric information.1 When sophisticated agents trade, their private information is (partially) revealed to the market, via order flow, causing revisions in asset prices even in the absence of public announcements.
The goal of this paper is to theoretically identify and empirically measure the effect of these two complementary mechanisms responsible for daily price changes: aggregation of public news and aggregation of order flow. In particular, we assess the relevance of each mechanism conditional on the dispersion of beliefs among traders and the public signals' noise.
To guide our analysis, we develop a parsimonious model of speculative trading in the spirit of Kyle (1985). The model builds upon two realistic market frictions: information heterogeneity and imperfect competition among informed traders (henceforth, speculators). In this setting, more diverse information among speculators leads to lower equilibrium market liquidity, since their trading activity is more cautious than if they were homogeneously informed, thus making the market-makers more vulnerable to adverse selection. We then introduce a public signal and derive equilibrium prices and trading strategies on announcement and non-announcement days. The contribution of the model is twofold. To our knowledge, it provides a novel theoretical analysis of the relationship between the trading activity of heterogeneously informed, imperfectly competitive speculators, the availability and quality of public information, and market liquidity. Furthermore, its analytically tractable closed-form solution, in terms of elementary functions, generates several explicit and empirically testable implications on the nature of that relationship.2In particular, we show that the availability of a public signal improves market liquidity (the more so the lower that signal's volatility) since its presence reduces the adverse selection risk for the market-makers and mitigates the quasi-monopolistic behavior of the speculators.
This model is not asset-specific, i.e., it applies to stock, bond, and foreign exchange markets. In this study, we test its implications for the U.S. government bond market for three reasons. First, Treasury market data contains signed trades; thus, we do not need to rely on algorithms (e.g., Lee and Ready, 1991) that add measurement error to our estimates of order flow. Second, government bond markets represent the simplest trading environment to analyze price changes while avoiding omitted variable biases. For example, most theories predict an unambiguous link between macroeconomic fundamentals and bond yield changes, with unexpected increases in real activity and inflation raising bond yields (e.g., Fleming and Remolona, 1997; Balduzzi, Elton, and Green, 2001, among others). In contrast, the link between macroeconomic fundamentals and the stock market is less clear (e.g., Andersen, Bollerslev, Diebold, and Vega, 2004; Boyd, Hu, and Jagannathan, 2005). Third, the market for Treasury securities is interesting in itself since it is among the largest, most liquid U.S. financial markets.
Our empirical results strongly support the main implications of
our model. During non-announcement days, adverse selection costs of
unanticipated order flow are higher when the dispersion of beliefs
-- measured by the standard deviation of professional forecasts of
macroeconomic news releases -- is high. For instance, we estimate
that a one standard deviation shock to abnormal order flow
decreases two-year, five-year, and ten-year bond yields by
![]() ,
, ![]() , and
, and ![]() basis points, respectively, on
high dispersion days compared to
basis points, respectively, on
high dispersion days compared to ![]() ,
, ![]() , and
, and
![]() basis points on low
dispersion days. These differences are economically and
statistically significant. Consistently, these higher adverse
selection costs translate into higher contemporaneous correlation
between order flow changes and bond yield changes. For example, the
adjusted
basis points on low
dispersion days. These differences are economically and
statistically significant. Consistently, these higher adverse
selection costs translate into higher contemporaneous correlation
between order flow changes and bond yield changes. For example, the
adjusted ![]() of
regressing daily five-year Treasury bond yield changes on
unanticipated order flow is
of
regressing daily five-year Treasury bond yield changes on
unanticipated order flow is ![]() on high dispersion days compared to
on high dispersion days compared to
![]() on low dispersion
days. Intuitively, when information heterogeneity is high, the
speculators' quasi-monopolistic trading behavior leads to a ``
cautious'' equilibrium where changes in unanticipated order flow
have a greater impact on bond yields.
on low dispersion
days. Intuitively, when information heterogeneity is high, the
speculators' quasi-monopolistic trading behavior leads to a ``
cautious'' equilibrium where changes in unanticipated order flow
have a greater impact on bond yields.
The release of a public signal, a trade-free source of
information about fundamentals, induces the speculators to trade
more aggressively on their private information. Accordingly, we
find that the correlation between unanticipated order flow and
day-to-day bond yield changes is lower during announcement days.
For example, comparing non-announcement days with Nonfarm Payroll
Employment release dates, the explanatory power of order flow
decreases from ![]() to
to ![]() ,
, ![]() to
to ![]() , and
, and ![]() to
to ![]() for the two-year, five-year,
and ten-year bonds, respectively. Yet, when both the dispersion of
beliefs and the noise of the public signal -- measured as the
absolute difference between the actual announcement and its last
revision -- are high, the importance of order flow in setting bond
prices increases. All of the above results are robust to
alternative measures of the dispersion of beliefs among market
participants, as well as to different regression specifications and
the inclusion of different control variables. Lastly, our evidence
cannot be attributed to transient inventory or portfolio
rebalancing considerations, since the unanticipated government bond
order flow has a permanent impact on yield changes during both
announcement and non-announcement days in the sample.
for the two-year, five-year,
and ten-year bonds, respectively. Yet, when both the dispersion of
beliefs and the noise of the public signal -- measured as the
absolute difference between the actual announcement and its last
revision -- are high, the importance of order flow in setting bond
prices increases. All of the above results are robust to
alternative measures of the dispersion of beliefs among market
participants, as well as to different regression specifications and
the inclusion of different control variables. Lastly, our evidence
cannot be attributed to transient inventory or portfolio
rebalancing considerations, since the unanticipated government bond
order flow has a permanent impact on yield changes during both
announcement and non-announcement days in the sample.
Our paper is most closely related to two recent studies of order
flow in the U.S. Treasury market. Brandt and Kavajecz (2004) find
that order flow accounts for up to ![]() of the variation in yields on days without major
macroeconomic announcements. Green (2004) examines the effect of
order flow on intraday bond price changes surrounding U.S.
macroeconomic news announcements. We extend both studies by
identifying a theoretical and empirical link between the price
discovery role of order flow and the degree of information
heterogeneity among investors and the quality of macroeconomic data
releases. In particular, we document important effects of both
dispersion of beliefs and public signal noise on the correlation
between daily bond yield changes and order flow during announcement
and non-announcement days. This evidence complements the weak
effects reported by Green (2004) over thirty-minute intervals
around news releases. Since the econometrician does not observe the
precise arrival time of private information signals, narrowing the
estimation window may lead to underestimating the effect of
dispersion of beliefs on market liquidity.3
of the variation in yields on days without major
macroeconomic announcements. Green (2004) examines the effect of
order flow on intraday bond price changes surrounding U.S.
macroeconomic news announcements. We extend both studies by
identifying a theoretical and empirical link between the price
discovery role of order flow and the degree of information
heterogeneity among investors and the quality of macroeconomic data
releases. In particular, we document important effects of both
dispersion of beliefs and public signal noise on the correlation
between daily bond yield changes and order flow during announcement
and non-announcement days. This evidence complements the weak
effects reported by Green (2004) over thirty-minute intervals
around news releases. Since the econometrician does not observe the
precise arrival time of private information signals, narrowing the
estimation window may lead to underestimating the effect of
dispersion of beliefs on market liquidity.3
Our work also belongs to the literature bridging the gap between asset pricing and market microstructure. Evans and Lyons (2003) find that signed order flow is a good predictor of subsequent exchange rate movements; Brandt and Kavajecz (2004) show that this is true for bond market movements; Easley, Hvidkjaer, and O'Hara (2002) argue that the probability of informed trading (PIN), a function of order flow, is a priced firm characteristic in stock returns. These studies enhance our understanding of the determinants of asset price movements, but do not provide any evidence on the determinants of order flow. Evans and Lyons (2004) address this issue by showing that foreign exchange order flow predicts future macroeconomic surprises, i.e., it conveys information about fundamentals. We go a step further in linking the impact of order flow on bond prices to macroeconomic uncertainty (public signal noise) and the heterogeneity of beliefs about real shocks.
We proceed as follows. In Section 2, we construct a stylized model of trading to guide our empirical analysis. In Section 3, we describe the data. In Section 4, we present the empirical results. We conclude in Section 5.
In this section we motivate our investigation of the impact of the dispersion of beliefs among sophisticated market participants and the release of macroeconomic news on the informational role of trading. We first describe a one-shot version of the multi-period model of trading of Foster and Viswanathan (1996) and derive closed-form solutions for the equilibrium market depth and trading volume. Then, we enrich the model by introducing a public signal and consider its implications for the equilibrium price and trading strategies. All proofs are in the Appendix unless otherwise noted.
The basic model is a two-date, one-period economy in which a
single risky asset is exchanged. Trading occurs only at the end of
the period (![]() ), after
which the asset payoff, a normally distributed random variable
), after
which the asset payoff, a normally distributed random variable
![]() with mean zero and
variance
with mean zero and
variance
![]() , is
realized. The economy is populated by three types of risk-neutral
traders: a discrete number (
, is
realized. The economy is populated by three types of risk-neutral
traders: a discrete number (![]() ) of informed traders (that we label speculators),
liquidity traders, and perfectly competitive market-makers (MMs).
All traders know the structure of the economy and the decision
process leading to order flow and prices.
) of informed traders (that we label speculators),
liquidity traders, and perfectly competitive market-makers (MMs).
All traders know the structure of the economy and the decision
process leading to order flow and prices.
At time ![]() there is
neither information asymmetry about
there is
neither information asymmetry about ![]() nor trading. Sometime between
nor trading. Sometime between ![]() and
and ![]() , each speculator
, each speculator ![]() receives a private and noisy signal of
receives a private and noisy signal of ![]() ,
, ![]() . We assume that the resulting signal vector
. We assume that the resulting signal vector
![]() is drawn from a
multivariate normal distribution (MND) with mean zero and
covariance matrix
is drawn from a
multivariate normal distribution (MND) with mean zero and
covariance matrix
![]() such that
such that
![]() and
and
![]() . We also
impose that the speculators together know the liquidation value of
the risky asset:
. We also
impose that the speculators together know the liquidation value of
the risky asset:
![]() ; therefore,
; therefore,
![]() .
This specification makes the total amount of information available
to the speculators independent from the correlation of their
private signals, albeit still implying the most general information
structure up to rescaling by a constant (see Foster and
Viswanathan, 1996).
.
This specification makes the total amount of information available
to the speculators independent from the correlation of their
private signals, albeit still implying the most general information
structure up to rescaling by a constant (see Foster and
Viswanathan, 1996).
These assumptions imply that
![]() and
and
![]() ,
where
,
where
![]() is the
correlation between any two private information endowments
is the
correlation between any two private information endowments
![]() and
and
![]() . As in
Foster and Viswanathan (1996), we parametrize the degree of
diversity among speculators' signals by requiring that
. As in
Foster and Viswanathan (1996), we parametrize the degree of
diversity among speculators' signals by requiring that
![]() . This restriction
ensures that
. This restriction
ensures that
![]() is positive
definite. If
is positive
definite. If ![]() , then
speculators' private information is homogeneous: All speculators receive the same
signal
, then
speculators' private information is homogeneous: All speculators receive the same
signal
![]() such
that
such
that
![]() and
and ![]() . If
. If
![]() , then speculators'
information is heterogeneous:
, then speculators'
information is heterogeneous:
![]() ,
,
![]() , and
, and
![]() . Otherwise,
speculators' signals are only partially correlated: Indeed,
. Otherwise,
speculators' signals are only partially correlated: Indeed,
![]() if
if
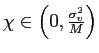 and
and
![]() if
if
![]() .4
.4
At time ![]() , both
speculators and liquidity traders submit their orders to the MMs,
before the equilibrium price
, both
speculators and liquidity traders submit their orders to the MMs,
before the equilibrium price ![]() has been set. We define the market order of the
has been set. We define the market order of the
![]() speculator to be
speculator to be ![]() .
Thus, her profit is given by
.
Thus, her profit is given by
![]() .
Liquidity traders generate a random, normally distributed demand
.
Liquidity traders generate a random, normally distributed demand
![]() , with mean zero and
variance
, with mean zero and
variance
![]() . For
simplicity, we assume that
. For
simplicity, we assume that ![]() is independent from all other random variables. MMs
do not receive any information, but observe the aggregate order
flow
is independent from all other random variables. MMs
do not receive any information, but observe the aggregate order
flow
![]() from all market
participants and set the market-clearing price
from all market
participants and set the market-clearing price
![]() .
.
Consistently with Kyle (1985), we define a Bayesian Nash
equilibrium as a set of ![]() functions
functions
![]() ,
and
,
and
![]() such that the following two
conditions hold:
such that the following two
conditions hold:
We restrict our attention to linear equilibria. We first conjecture general linear functions for the pricing rule and speculators' demands. We then solve for their parameters satisfying conditions 1 and 2. Finally, we show that these parameters and those functions represent a rational expectations equilibrium. The following proposition accomplishes this task.
The optimal trading strategy of each speculator depends on the
information she receives about the asset payoff (![]() ) and on the depth of the market (
) and on the depth of the market (
![]() ). If
). If
![]() , Eqs. (1) and (2) reduce to the well-known
equilibrium of Kyle (1985). The speculators, albeit risk-neutral,
exploit their private information cautiously (
, Eqs. (1) and (2) reduce to the well-known
equilibrium of Kyle (1985). The speculators, albeit risk-neutral,
exploit their private information cautiously (
![]() ), to avoid
dissipating their informational advantage with their trades. Thus,
the equilibrium market liquidity in
), to avoid
dissipating their informational advantage with their trades. Thus,
the equilibrium market liquidity in ![]() reflects MMs' attempt to be compensated for the
losses they anticipate from trading with speculators, as it affects
their profits from liquidity trading.
reflects MMs' attempt to be compensated for the
losses they anticipate from trading with speculators, as it affects
their profits from liquidity trading.
The intuition behind the parsimonious equilibrium of Eqs.
(1) and (2) is similar to
that in the multi-period models of Foster and Viswanathan (1996)
and Back et al. (2000). Yet, its closed-form solution (in
Proposition 1) translates that intuition into unambiguous
predictions on the impact of information heterogeneity on market
depth.5 The
optimal market orders ![]() depend on the number of speculators
(
depend on the number of speculators
(![]() ) and the correlation
among their information endowments (
) and the correlation
among their information endowments (![]() ). The intensity of competition among
speculators affects their ability to maintain the informativeness
of the order flow as low as possible. A greater number of
speculators trade more aggressively -- i.e., their aggregate amount
of trading is higher -- since (imperfect) competition among them
precludes any collusive trading strategy. For instance, when
). The intensity of competition among
speculators affects their ability to maintain the informativeness
of the order flow as low as possible. A greater number of
speculators trade more aggressively -- i.e., their aggregate amount
of trading is higher -- since (imperfect) competition among them
precludes any collusive trading strategy. For instance, when
![]() speculators are
homogeneously informed (
speculators are
homogeneously informed (![]() ), then
), then
![]() , which
implies that the finite difference
, which
implies that the finite difference
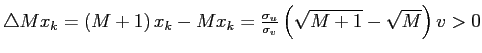 . This behavior reduces the adverse selection problem for
the MMs, thus leading to greater market liquidity (lower
. This behavior reduces the adverse selection problem for
the MMs, thus leading to greater market liquidity (lower
![]() ).
).
The heterogeneity of speculators' signals attenuates their
trading aggressiveness. When information is less correlated
(![]() closer to zero),
each speculator has some monopoly power on her signal, because at
least part of it is known exclusively to her. Hence, as a group,
they trade more cautiously -- i.e., their aggregate amount of
trading is lower -- to reveal less of their own information
endowments
closer to zero),
each speculator has some monopoly power on her signal, because at
least part of it is known exclusively to her. Hence, as a group,
they trade more cautiously -- i.e., their aggregate amount of
trading is lower -- to reveal less of their own information
endowments
![]() . For
example, when
. For
example, when ![]() speculators are heterogeneously informed (
speculators are heterogeneously informed (![]() ), then
), then
![]() , which
implies that
, which
implies that
![]() , i.e., lower than the aggregate amount of trading by
, i.e., lower than the aggregate amount of trading by
![]() homogeneously
informed speculators (
homogeneously
informed speculators (![]() ) but identical to the trade of a monopolistic
speculator (
) but identical to the trade of a monopolistic
speculator (![]() ). This
``quasi-monopolistic'' behavior makes the MMs more vulnerable to
adverse selection, thus the market less liquid (higher
). This
``quasi-monopolistic'' behavior makes the MMs more vulnerable to
adverse selection, thus the market less liquid (higher ![]() ). The following corollary
summarizes the first set of empirical implications of our
model.
). The following corollary
summarizes the first set of empirical implications of our
model.
To gain further insight on this result, we construct a simple
numerical example by setting
![]() . We then vary the parameter
. We then vary the parameter
![]() to study the
liquidity of this market with respect to a broad range of signal
correlations
to study the
liquidity of this market with respect to a broad range of signal
correlations ![]() (from
very highly negative to very highly positive) when
(from
very highly negative to very highly positive) when ![]() ,
, ![]() , and
, and ![]() . By
construction, both the private signals' variance (
. By
construction, both the private signals' variance (
![]() ) and
covariance (
) and
covariance (
![]() ) change
with
) change
with ![]() and
and ![]() , yet the total amount of information
available to the speculators is unchanged. We plot the resulting
, yet the total amount of information
available to the speculators is unchanged. We plot the resulting
![]() in Figure 1A.
Multiple, perfectly heterogeneously informed speculators
(
in Figure 1A.
Multiple, perfectly heterogeneously informed speculators
(![]() ) collectively
trade as cautiously as a monopolist speculator. Under these
circumstances, adverse selection is at its highest, and market
liquidity at its lowest (
) collectively
trade as cautiously as a monopolist speculator. Under these
circumstances, adverse selection is at its highest, and market
liquidity at its lowest (
![]() ). A greater
number of competing speculators improves market depth, but
significantly so only if accompanied by more correlated private
signals. However, ceteris paribus, the improvement in market
liquidity is more pronounced (and informed trading less cautious)
when speculators' private signals are negatively correlated. When
). A greater
number of competing speculators improves market depth, but
significantly so only if accompanied by more correlated private
signals. However, ceteris paribus, the improvement in market
liquidity is more pronounced (and informed trading less cautious)
when speculators' private signals are negatively correlated. When
![]() , each
speculator expects her competitors' trades to be negatively
correlated to her own (pushing
, each
speculator expects her competitors' trades to be negatively
correlated to her own (pushing ![]() against her signal), hence trading on it to be
more profitable.
against her signal), hence trading on it to be
more profitable.
We now extend the basic model of Section 2.1 by providing each
player with an additional, common source of information about the
risky asset before trading takes place. According to Kim and
Verrecchia (1994, p. 43), ``public disclosure has received little
explicit attention in theoretical models whose major focus is
understanding market liquidity.''6 More specifically, we assume that,
sometime between ![]() and
and
![]() , both the
speculators and the MMs also observe a public and noisy signal
, both the
speculators and the MMs also observe a public and noisy signal
![]() of the asset
payoff
of the asset
payoff ![]() . This signal
is normally distributed with mean zero and variance
. This signal
is normally distributed with mean zero and variance
![]() . We can think of
. We can think of
![]() as any surprise
public announcement (e.g., macroeconomic news) released
simultaneously to all market participants. We further impose that
as any surprise
public announcement (e.g., macroeconomic news) released
simultaneously to all market participants. We further impose that
![]() , so that the
parameter
, so that the
parameter
![]() controls
for the quality of the public signal and
controls
for the quality of the public signal and
![]() .
The private information endowment of each speculator is then given
by
.
The private information endowment of each speculator is then given
by
![]() , where
, where
![$ \alpha=\frac{M\sigma_{v}^{2}\left( \sigma_{p}^{2}-\sigma_{v} ^{2}\right) }{\sigma_{p}^{2}\left[ \sigma_{v}^{2}+M\left( M-1\right) \chi\right] -\sigma_{v}^{4}}>0$](img92.gif) and
and
![$ \beta=-\frac{\sigma_{v}^{4}\left( \sigma_{p}^{2}-\sigma_{v}^{2}\right) }{\sigma_{p}^{2}\left\{ \left[ \sigma_{v}^{2}+M\left( M-1\right) \chi\right] -\sigma_{v}^{4}\right\} } <0$](img93.gif) . Thus,
. Thus,
![]() , where
, where
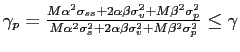 .
.
Again we search for linear equilibria. The following proposition summarizes our results.
![$ \lambda_{p}=\frac{\alpha^{\frac{1}{2}}\sigma_{v}\left( \sigma_{p} ^{2}-\sigma_{v}^{2}\right) ^{\frac{1}{2}}}{\sigma_{u}\sigma_{p}\left[ 2+\left( M-1\right) \gamma_{p}\right] }>0$](img98.gif) and
and
The optimal trading strategy of each speculator in Eq. (4) mirrors that of Proposition 1 (Eq. (2)), yet it now depends only on
![]() , the
truly private -- hence less correlated (
, the
truly private -- hence less correlated (
![]() )
-- component of speculator
)
-- component of speculator ![]() 's original private signal (
's original private signal (![]() ) in the presence of a public
signal of
) in the presence of a public
signal of ![]() . Hence, the
MMs' belief update about
. Hence, the
MMs' belief update about ![]() stemming from
stemming from ![]() makes
speculators' private information less valuable. The resulting
equilibrium price
makes
speculators' private information less valuable. The resulting
equilibrium price ![]() in
Eq. (3) can be rewritten as
in
Eq. (3) can be rewritten as
Foster and Viswanathan (1993) generalize the trading model of Kyle (1985) to distributions of the elliptically contoured class (ECC) and show that, in the presence of a discrete number of identically informed traders, the unexpected realization of a public signal has no impact on market liquidity regardless of the ECC used. This is the case for the equilibrium of Proposition 2 as well.7Nonetheless, Proposition 2 allows us to study the impact of the availability of noisy public information on equilibrium market depth in the presence of imperfectly competitive and heterogeneously informed speculators. To our knowledge, this analysis is novel to the financial literature. We start with the following result.
The availability of the public signal ![]() reduces the adverse selection
risk for the MMs, thus increasing the depth of this stylized
market, for two reasons. First, the public signal represents an
additional, trade-free source of information about
reduces the adverse selection
risk for the MMs, thus increasing the depth of this stylized
market, for two reasons. First, the public signal represents an
additional, trade-free source of information about ![]() . Second, speculators have to trade
more aggressively to extract rents from their private information.
In Figure 1B we plot the ensuing gain in liquidity,
. Second, speculators have to trade
more aggressively to extract rents from their private information.
In Figure 1B we plot the ensuing gain in liquidity,
![]() ,
as a function of private signal correlations
,
as a function of private signal correlations ![]() when the public signal's noise
when the public signal's noise
![]() ,
i.e., by varying
,
i.e., by varying ![]() and
and
![]() (so
(so
![]() and
and
![]() as well,
but not the total amount of information available to the
speculators) as in Figure 1A. The increase in market depth is
greater when
as well,
but not the total amount of information available to the
speculators) as in Figure 1A. The increase in market depth is
greater when ![]() is
negative and the number of speculators (
is
negative and the number of speculators (![]() ) is high. In those circumstances,
the availability of a public signal reinforces speculators'
existing incentives to place market orders on their private signals
) is high. In those circumstances,
the availability of a public signal reinforces speculators'
existing incentives to place market orders on their private signals
![]() more
aggressively. However, greater
more
aggressively. However, greater
![]() , ceteris
paribus, increases
, ceteris
paribus, increases
![]() , since the
poorer quality of
, since the
poorer quality of ![]() (lower information-to-noise ratio
(lower information-to-noise ratio
![]() ) induces the MMs
to rely more heavily on
) induces the MMs
to rely more heavily on
![]() to set
market-clearing prices, hence the speculators to trade less
aggressively.
to set
market-clearing prices, hence the speculators to trade less
aggressively.
In the presence of a public signal, information heterogeneity
among speculators plays a more ambiguous role on market liquidity.
If the volatility of the public signal is low, heterogeneously
informed (thus more cautious) speculators put less weight on their
private signals ![]() (lower
(lower ![]() in
in
![]() ) and
more weight on the public signal
) and
more weight on the public signal ![]() (higher
(higher ![]() in
in
![]() )
when updating their beliefs than homogeneously informed (thus more
aggressive) speculators. Hence, the ensuing trading behavior leads
to less adverse selection risk for the
MMs (lower
)
when updating their beliefs than homogeneously informed (thus more
aggressive) speculators. Hence, the ensuing trading behavior leads
to less adverse selection risk for the
MMs (lower
![]() ). Vice
versa, when
). Vice
versa, when
![]() is high,
speculators rely more heavily on their private signals, but more
cautiously so if gamma is low, leading to lower equilibrium market
depth (higher
is high,
speculators rely more heavily on their private signals, but more
cautiously so if gamma is low, leading to lower equilibrium market
depth (higher
![]() ), as in
Corollary 1.
), as in
Corollary 1.
The volatility of the public signal ![]() also affects its direct impact (
also affects its direct impact (
![]() ) on the
equilibrium price of Eq. (3). Everything else
equal, the poorer is the quality of the public signal (higher
) on the
equilibrium price of Eq. (3). Everything else
equal, the poorer is the quality of the public signal (higher
![]() ), the more
the speculators rely on their private signals
), the more
the speculators rely on their private signals ![]() (see Remark 1) and the MMs rely
on the aggregate order flow
(see Remark 1) and the MMs rely
on the aggregate order flow
![]() to infer
the asset payoff
to infer
the asset payoff ![]() .
Consequently, the MMs put less weight on
.
Consequently, the MMs put less weight on ![]() and more weight on
and more weight on
![]() in setting
the market-clearing price
in setting
the market-clearing price ![]() , toward the benchmark of Eq. (1):
, toward the benchmark of Eq. (1):
![]() and
and
![]() .
.
We test the implications of the model presented in the previous section using U.S. Treasury bond market data and U.S. macroeconomic announcements. As mentioned in Section 1, this choice is motivated not only by the quality and availability of data on U.S. government bond transactions, but also by the clear theoretical link between macroeconomic fundamentals and bond yield changes.
We use intraday U.S. Treasury bond yields, quotes, transactions, and signed trades for the most recently issued, ``on-the-run,'' two-year, five-year, and ten-year Treasury notes. We use these ``on-the-run'' notes because, according to Fleming (1997), Brandt and Kavajecz (2004), and Goldreich, Hanke, and Nath (2005), those are the securities with the greatest liquidity and where the majority of informed trading takes place. We are interested in studying the informational role of bond trading related to macroeconomic fundamentals. Therefore, we focus on the intermediate to long maturities, since these are the most responsive to macroeconomic aggregates (e.g., Balduzzi et al., 2001). Consistently, when we perform the analysis that follows on the remaining ``on-the-run'' and ``off-the-run'' Treasury securities in our database, we find that (i) the resulting inference for the former is weaker than the one described in the paper, and (ii) order flow has no impact on yield changes for the latter. These results are available upon request from the authors.
We obtain the data from GovPX, a firm that collects quote and
trade information from six of the seven main interdealer brokers
(with the notable exception of Cantor Fitzgerald).8 Fleming (1997) argues that these six
brokers account for approximately two-thirds of the
interdealer-broker market, which in turn translates into
approximately ![]() of the
trading volume in the secondary market for Treasury securities. Our
sample includes every transaction taking place during ``regular
trading hours,'' from 7:30 a.m. to 5:00 p.m. Eastern Standard Time
(EST), between January 2, 1992 and December 29, 2000. GovPX stopped
recording intraday volume afterward. Strictly speaking, the U.S.
Treasury market is open
of the
trading volume in the secondary market for Treasury securities. Our
sample includes every transaction taking place during ``regular
trading hours,'' from 7:30 a.m. to 5:00 p.m. Eastern Standard Time
(EST), between January 2, 1992 and December 29, 2000. GovPX stopped
recording intraday volume afterward. Strictly speaking, the U.S.
Treasury market is open ![]() hours a day; yet,
hours a day; yet, ![]() of
the trading volume occurs during those hours. Thus, to remove
fluctuations in bond yields due to illiquidity, we ignore trades
outside that narrower interval. Finally, the data contains some
interdealer brokers' posting errors not previously filtered out by
GovPX. We eliminate these errors following the procedure described
in Fleming's (2003) appendix.
of
the trading volume occurs during those hours. Thus, to remove
fluctuations in bond yields due to illiquidity, we ignore trades
outside that narrower interval. Finally, the data contains some
interdealer brokers' posting errors not previously filtered out by
GovPX. We eliminate these errors following the procedure described
in Fleming's (2003) appendix.
We report summary statistics for the daily raw yield and
transaction data in Table 1. Bond yields are in percentage, i.e.,
were multiplied by ![]() ;
bond yield changes are in basis points, i.e., were multiplied by
;
bond yield changes are in basis points, i.e., were multiplied by
![]() . Not
surprisingly, mean Treasury bond yields are increasing with
maturity and display large positive first-order autocorrelation (
. Not
surprisingly, mean Treasury bond yields are increasing with
maturity and display large positive first-order autocorrelation (
![]() ). Mean daily yield changes
are small or zero; yet, their sample variability suggests that
economically important fluctuations of the yield curve took place
over the sample period. Five-year Treasury notes are characterized
by the largest mean daily number of transactions (roughly
). Mean daily yield changes
are small or zero; yet, their sample variability suggests that
economically important fluctuations of the yield curve took place
over the sample period. Five-year Treasury notes are characterized
by the largest mean daily number of transactions (roughly
![]() ), hence by the
highest liquidity, consistent with the findings of Fleming (2003),
among others.
), hence by the
highest liquidity, consistent with the findings of Fleming (2003),
among others.
We also compare (but do not report here for economy of space) daily bond yield changes during days when one of the most closely observed U.S. macroeconomic announcement, the Nonfarm Payroll Employment report, is released to daily bond yield changes during non-announcement days.9 Bond yield changes are clearly more volatile on days when the Payroll numbers are announced, but yield changes during non-announcement days are economically significant as well. These dynamics, together with the poor performance of public macroeconomic surprises in explaining fluctuations in bond yields on non-announcement days, further motivate our study of the price discovery role of order flow when no public news arrive to the bond market.
We use the International Money Market Services (MMS) Inc.
real-time data on the expectations and realizations of ![]() of the most relevant U.S.
macroeconomic fundamentals to estimate announcement surprises.
Table 2 provides a brief description of the most salient
characteristics of U.S. economic news announcements in our sample:
the total number of observations, the agency reporting each
announcement, the time of the announcement release, and whether the
standard deviation across professional forecasts is available.
Fleming and Remolona (1997) and Andersen, Bollerslev, Diebold, and
Vega (2003) discuss the main properties of MMS forecasts; Balduzzi
et al. (2001) show that these forecasts are not stale and
unbiased.
of the most relevant U.S.
macroeconomic fundamentals to estimate announcement surprises.
Table 2 provides a brief description of the most salient
characteristics of U.S. economic news announcements in our sample:
the total number of observations, the agency reporting each
announcement, the time of the announcement release, and whether the
standard deviation across professional forecasts is available.
Fleming and Remolona (1997) and Andersen, Bollerslev, Diebold, and
Vega (2003) discuss the main properties of MMS forecasts; Balduzzi
et al. (2001) show that these forecasts are not stale and
unbiased.
We define announcement surprises as the difference between
announcement realizations and their corresponding expectations.
More specifically, since units of measurement vary across
macroeconomic variables, we standardize the resulting surprises by
dividing each of them by their sample standard deviation. The
standardized news associated with the macroeconomic indicator
![]() at time
at time ![]() is therefore computed as
is therefore computed as
We use the MMS standard deviation across professional forecasts
as a measure of dispersion of beliefs across sophisticated
investors. This measure of information heterogeneity is widely
adopted in the literature on investors' reaction to information
releases in the stock market (e.g., Diether, Malloy, and Scherbina,
2002; Kallberg and Pasquariello, 2004); Green (2004) recently uses
it in a bond market context. As indicated in Table 2, this variable
is only available for ![]() of the
of the ![]() macroeconomic news in our sample.
macroeconomic news in our sample.
Overall, the dispersion of beliefs is large (e.g., roughly
![]() on average of the
mean absolute monthly Nonfarm Payroll report), time-varying, and
positively correlated across macroeconomic announcements. To
conserve space, we do not show the correlation matrix of all the
announcements, but only report (in Table 2) the pairwise
correlation between each announcement and arguably the most
important of them, the Nonfarm Payroll report (e.g., Andersen and
Bollerslev, 1998; Andersen et al., 2004; Brenner et al., 2005).
This correlation is positive, albeit not statistically significant
for most of the announcements. Thus, dispersion of beliefs in
Nonfarm Payroll forecasts is not necessarily a good measure of
information heterogeneity about the state of the economy, which is
ultimately what we are interested in. This motivates us to
construct three alternative measures of dispersion of beliefs
during announcement and non-announcement days: one based
exclusively on the Payroll announcement, another based on
on average of the
mean absolute monthly Nonfarm Payroll report), time-varying, and
positively correlated across macroeconomic announcements. To
conserve space, we do not show the correlation matrix of all the
announcements, but only report (in Table 2) the pairwise
correlation between each announcement and arguably the most
important of them, the Nonfarm Payroll report (e.g., Andersen and
Bollerslev, 1998; Andersen et al., 2004; Brenner et al., 2005).
This correlation is positive, albeit not statistically significant
for most of the announcements. Thus, dispersion of beliefs in
Nonfarm Payroll forecasts is not necessarily a good measure of
information heterogeneity about the state of the economy, which is
ultimately what we are interested in. This motivates us to
construct three alternative measures of dispersion of beliefs
during announcement and non-announcement days: one based
exclusively on the Payroll announcement, another based on
![]() ``influential''
announcements (defined below), and the last one based on the
``influential''
announcements (defined below), and the last one based on the
![]() announcements for
which the standard deviation of professional forecasts is available
(i.e., those italicized in Table 2).
announcements for
which the standard deviation of professional forecasts is available
(i.e., those italicized in Table 2).
The use of the MMS database to calculate monthly measures of
dispersion of beliefs raises two issues: (i) the announcements in
Table 2 are released at different frequencies and (ii) the standard
deviation of professional forecasts only measures heterogenous
beliefs at the time of the announcement. We address these issues by
assuming that the dispersion of beliefs remains constant between
announcements. This assumption is empirically justified since the
first order autocorrelation in the standard deviation of
professional forecasts (
![]() in Table 2) is positive and mostly statistically significant.
Hence, if the dispersion of beliefs across investors is high in one
month (week or quarter), it is likely to remain high in the next
month (week or quarter).
in Table 2) is positive and mostly statistically significant.
Hence, if the dispersion of beliefs across investors is high in one
month (week or quarter), it is likely to remain high in the next
month (week or quarter).
To convert weekly and quarterly dispersions to a monthly frequency we use the following procedure. For the single weekly announcement in the sample, Initial Unemployment Claims, we average the dispersion of beliefs across four weeks. For the three quarterly announcements in the sample, GDP Advance, Preliminary, and Final, we assume that the dispersion of beliefs in the first month of the quarter is constant throughout the quarter. The dispersion of beliefs of monthly announcements is instead left unchanged and assumed to be constant between announcements.
We then define our monthly proxy for the aggregate degree of information heterogeneity about macroeconomic fundamentals as a weighted sum of monthly dispersions across announcements,
We use the monthly dispersion estimates from these three
methodologies to classify days in which the corresponding monthly
variable ![]() is
above (below) the top (bottom)
is
above (below) the top (bottom)
![]() (
(
![]() )
percentile of its empirical distribution as days with high (low)
information heterogeneity. The resulting time series of high
(
)
percentile of its empirical distribution as days with high (low)
information heterogeneity. The resulting time series of high
(![]() ) and low
(
) and low
(![]() ) dispersion days
are positively correlated: Their correlations (not reported here)
range from
) dispersion days
are positively correlated: Their correlations (not reported here)
range from ![]() (between
the Payroll-based series,
(between
the Payroll-based series, ![]() , and the series constructed with the influential
announcements,
, and the series constructed with the influential
announcements, ![]() ) to
) to
![]() (between the
series using all announcements,
(between the
series using all announcements, ![]() , and the one based only on the influential news
releases,
, and the one based only on the influential news
releases, ![]() ).
).
Finally, we report in Table 3 the differences in the mean daily
number of transactions (![]() ) in the two, five, and ten-year Treasury bond
markets across days with high (
) in the two, five, and ten-year Treasury bond
markets across days with high (![]() ) and low (
) and low (![]() ) dispersion of beliefs measured with the three
alternative methods described above. The corresponding
) dispersion of beliefs measured with the three
alternative methods described above. The corresponding ![]() statistics are computed using
Newey-West standard errors, because Table 1 shows that the number
of daily transactions is positively autocorrelated. Consistent with
Griffith, Smith, Turnbull, and White (2000) and Ranaldo (2004),
among others (but also with the spirit of the model of Section 2),
we interpret a big (small) number of daily transactions as a proxy
for a high (low) degree of trading aggressiveness. The ensuing
differences are economically and statistically significant: fewer
transactions take place in high dispersion days than in low
dispersion days (i.e.,
statistics are computed using
Newey-West standard errors, because Table 1 shows that the number
of daily transactions is positively autocorrelated. Consistent with
Griffith, Smith, Turnbull, and White (2000) and Ranaldo (2004),
among others (but also with the spirit of the model of Section 2),
we interpret a big (small) number of daily transactions as a proxy
for a high (low) degree of trading aggressiveness. The ensuing
differences are economically and statistically significant: fewer
transactions take place in high dispersion days than in low
dispersion days (i.e.,
![]() ).
Consistently, Spearman correlations between
).
Consistently, Spearman correlations between ![]() and either
and either ![]() ,
, ![]() , or
, or ![]() (not reported here) are
always negative for all maturities and mostly statistically
significant. This evidence provides support for the basic intuition
of our model and gives us further confidence in the heterogeneity
proxies of Eq. (7), since it suggests that, in
the government bond market, periods of greater dispersion of
beliefs among market participants are accompanied by more cautious
speculative trading activity, as argued in Section 2.1.1.
(not reported here) are
always negative for all maturities and mostly statistically
significant. This evidence provides support for the basic intuition
of our model and gives us further confidence in the heterogeneity
proxies of Eq. (7), since it suggests that, in
the government bond market, periods of greater dispersion of
beliefs among market participants are accompanied by more cautious
speculative trading activity, as argued in Section 2.1.1.
The U.S. government often revises previously released
macroeconomic information. Aruoba (2004) identifies these data
revisions as either ``informative,'' i.e., due to newly available
information, or ``uninformative,'' i.e., due to definitional
changes (such as changes in the base-year or changes in seasonal
weights). In this paper, we use the former revisions to measure
public signal noise. Specifically, we use the Federal Reserve Bank
of Philadelphia ``Real Time Data Set'' (RTDS), which records not
only real-time macroeconomic announcements but also their
subsequent revisions.11 Of the
![]() announcements in
Table 2 for which MMS forecasts are available, the RDTS contains
monthly data on Capacity Utilization, Industrial Production, and
Nonfarm Payroll Employment report. The only variable undergoing
``uninformative'' changes over the sample period is Industrial
Production, whose base-year was revised in February 1998. According
to extant literature (e.g., Mork, 1987; Faust, Rogers, and Wright,
2003; Aruoba, 2004), (i) the final published revision of each
actual announcement represents the most accurate measure for the
corresponding macroeconomic variable, and (ii) those revisions
should be interpreted as noise, for they are predictable (based on
past information).12 Hence,
we measure public news noise as the difference between each initial
announcement and its last revision. Since what matters in our model
is the magnitude of the noise (
announcements in
Table 2 for which MMS forecasts are available, the RDTS contains
monthly data on Capacity Utilization, Industrial Production, and
Nonfarm Payroll Employment report. The only variable undergoing
``uninformative'' changes over the sample period is Industrial
Production, whose base-year was revised in February 1998. According
to extant literature (e.g., Mork, 1987; Faust, Rogers, and Wright,
2003; Aruoba, 2004), (i) the final published revision of each
actual announcement represents the most accurate measure for the
corresponding macroeconomic variable, and (ii) those revisions
should be interpreted as noise, for they are predictable (based on
past information).12 Hence,
we measure public news noise as the difference between each initial
announcement and its last revision. Since what matters in our model
is the magnitude of the noise (
![]() of
Section 2.2), not its direction, we use the absolute value of this
difference in our empirical analysis.
of
Section 2.2), not its direction, we use the absolute value of this
difference in our empirical analysis.
Consistent with Aruoba (2004), the resulting time series of
simple and absolute macroeconomic data revisions -- i.e., the
simple and absolute differences between the real-time announcement
and the final revision for Capacity Utilization, Industrial
Production, and Nonfarm Payroll Employment -- display a few spikes
and are often negative, revealing a tendency for the government to
be overly conservative in its initial announcements. Interestingly,
the absolute value of the measurement error tends to be positively
correlated with the volatility of the underlying announcement, with
correlations (not reported here) varying between a low of
![]() (Industrial
Production) and a high of
(Industrial
Production) and a high of ![]() (Nonfarm Payroll). This suggests that the
measurement error is related to macroeconomic uncertainty. In our
theoretical model,
(Nonfarm Payroll). This suggests that the
measurement error is related to macroeconomic uncertainty. In our
theoretical model,
![]() arises
from either uncertainty about the macroeconomy or the quality of
the public signal. In the ensuing empirical analysis, we consider
both possibilities.
arises
from either uncertainty about the macroeconomy or the quality of
the public signal. In the ensuing empirical analysis, we consider
both possibilities.
The model of Section 2 generates several implications that we
now test in this section. In the database described in Section 3,
we are able to directly observe price changes,
![]() , as a
proxy for
, as a
proxy for ![]() , public
news surprises
, public
news surprises ![]() ,
as a proxy for
,
as a proxy for ![]() ,
and aggregate order flow
,
and aggregate order flow
![]() , as a proxy
for
, as a proxy
for
![]() . Yet, in
our setting, it is only the unexpected portion of aggregate order
flow that affects the equilibrium prices of Eqs. (1) and (3).13 Furthermore,
. Yet, in
our setting, it is only the unexpected portion of aggregate order
flow that affects the equilibrium prices of Eqs. (1) and (3).13 Furthermore,
![]() is assumed
to depend only on informed and liquidity trading. Yet, in reality,
many additional microstructure imperfections can cause lagged
effects in the observed order flow (see Hasbrouck, 2004).
Therefore, to implement our model, we estimate
is assumed
to depend only on informed and liquidity trading. Yet, in reality,
many additional microstructure imperfections can cause lagged
effects in the observed order flow (see Hasbrouck, 2004).
Therefore, to implement our model, we estimate
![]() , the
unanticipated portion of aggregate order flow.
, the
unanticipated portion of aggregate order flow.
For that purpose, we use the linear autoregressive model of Hasbrouck (1991),
GovPX calculates bond yields using transaction prices, so there
is a mechanical inverse relation between the two quantities. To be
consistent with the term-structure literature, we estimate the
impact of unanticipated order flow and public information arrivals
on daily yield changes (
![]() ) rather
than on price changes. Nonetheless, our results are robust to
either specification. We translate the equilibrium prices of
Propositions 1 and 2 into the following estimable equations:
) rather
than on price changes. Nonetheless, our results are robust to
either specification. We translate the equilibrium prices of
Propositions 1 and 2 into the following estimable equations:
Even in the absence of the information effects of our model,
inventory considerations (first formalized by Garman, 1976) may
explain, either in full or in part, any significant correlation
between price changes and order flow. Yield changes may in fact
react to net order flow imbalances, to compensate market
participants for providing liquidity, even when the order flow has
no information content. To assess the relevance of this alternative
hypothesis, we follow Hasbrouck (1991) and include lagged values of
unanticipated order flow and yield changes in both Eqs. (9) and (10). As in Hasbrouck
(1991), we assume the permanent impact of trades is due to
information shocks and the transitory impact is due to
noninformation (e.g., liquidity) shocks. Hence, negative and
significant estimates for ![]() and
and
![]() are driven
by transitory inventory control effects when accompanied by a
positive and significant impact of lagged unanticipated net order
flow on yield changes. In other words, significant contemporaneous
order flow effects are transient if
they are later reversed. On the other hand, negative and
significant estimates for
are driven
by transitory inventory control effects when accompanied by a
positive and significant impact of lagged unanticipated net order
flow on yield changes. In other words, significant contemporaneous
order flow effects are transient if
they are later reversed. On the other hand, negative and
significant estimates for ![]() and
and
![]() are driven
by permanent information effects (consistent with our model) when
accompanied by negative and significant, or statistically
insignificant, impact of lagged unanticipated net order flow on
yield changes.
are driven
by permanent information effects (consistent with our model) when
accompanied by negative and significant, or statistically
insignificant, impact of lagged unanticipated net order flow on
yield changes.
We start by estimating Eq. (9) across
non-announcement days and then testing the main implication of
Proposition 1, namely that market liquidity (
![]() ) is
decreasing in the heterogeneity of speculators' information
endowments. First, we define non-announcement days consistently
with our procedures to measure such heterogeneity (in Section
3.2.2). When
) is
decreasing in the heterogeneity of speculators' information
endowments. First, we define non-announcement days consistently
with our procedures to measure such heterogeneity (in Section
3.2.2). When ![]() , we
define non-announcement days as all trading Fridays in the sample
in which no Nonfarm Payroll Employment report is released, to
control for potential day-of-the-week effects. When
, we
define non-announcement days as all trading Fridays in the sample
in which no Nonfarm Payroll Employment report is released, to
control for potential day-of-the-week effects. When ![]() or
or ![]() , we define non-announcement days as all trading
days when none of the corresponding announcements (either the
influential ones or those italicized in Table 2) take place. We
then test Corollary 1 by amending Eq. (9) as
follows:
, we define non-announcement days as all trading
days when none of the corresponding announcements (either the
influential ones or those italicized in Table 2) take place. We
then test Corollary 1 by amending Eq. (9) as
follows:
The results in Table 4 provide strong evidence for information
effects of order flow on bond yield changes and no evidence for
inventory control effects. For all maturities and nearly all
measures of dispersion of beliefs, the estimated contemporaneous
correlation between unanticipated order flow and yield changes (
![]() ) is
negative and significant. The coefficients for one-period lagged
unanticipated order flow (
) is
negative and significant. The coefficients for one-period lagged
unanticipated order flow (
![]() ), not
reported here, are instead often negative, always statistically
insignificant at the
), not
reported here, are instead often negative, always statistically
insignificant at the ![]() level, and about ten times smaller in magnitude than the
contemporaneous coefficients
level, and about ten times smaller in magnitude than the
contemporaneous coefficients
![]() . Lastly,
the resulting cumulated impact of unanticipated order flow on yield
changes (
. Lastly,
the resulting cumulated impact of unanticipated order flow on yield
changes (
![]() in Table 4) is
mostly statistically significant, albeit more weakly so on
non-announcement days with low heterogeneity of beliefs. In other
words, we find no evidence that the impact of unanticipated U.S.
Treasury bond order flow on yield changes is reversed in the next
five trading days, except in correspondence with low dispersion of
beliefs about Nonfarm Payroll announcements (
in Table 4) is
mostly statistically significant, albeit more weakly so on
non-announcement days with low heterogeneity of beliefs. In other
words, we find no evidence that the impact of unanticipated U.S.
Treasury bond order flow on yield changes is reversed in the next
five trading days, except in correspondence with low dispersion of
beliefs about Nonfarm Payroll announcements (![]() ).
).
The results in Table 4 also provide strong evidence in favor of
Corollary 1, especially for the five-year bond, the most liquid
U.S. Treasury note. Regardless of whether we use only the Nonfarm
Payroll announcement to measure dispersion of beliefs or whether we
aggregate dispersion of beliefs across macroeconomic announcements,
we cannot reject the null hypothesis that
![]() . This evidence is
consistent with the basic intuition of the benchmark model of
Section 2.1: In the absence of a public signal, greater information
heterogeneity among investors translates into greater adverse
selection risk for the market-makers, hence into lower market
liquidity (
. This evidence is
consistent with the basic intuition of the benchmark model of
Section 2.1: In the absence of a public signal, greater information
heterogeneity among investors translates into greater adverse
selection risk for the market-makers, hence into lower market
liquidity (
![]() ).
).
The increase in adverse selection costs in correspondence with
high dispersion of beliefs among market participants is not only
statistically but also economically significant. For example, when
classifying trading days according to ![]() (i.e., only with respect to
the volatility of Nonfarm Payroll forecasts), we find that a one
standard deviation shock to unanticipated order flow in five-year
bonds decreases their yields by
(i.e., only with respect to
the volatility of Nonfarm Payroll forecasts), we find that a one
standard deviation shock to unanticipated order flow in five-year
bonds decreases their yields by ![]() basis points on high dispersion days
(
basis points on high dispersion days
(![]() ) and just
) and just
![]() basis points on
low dispersion days (
basis points on
low dispersion days (![]() ), as compared to a daily yield change one
standard deviation from its mean of roughly
), as compared to a daily yield change one
standard deviation from its mean of roughly ![]() basis points (in Table 1) over
the entire sample. Consistently, the correlation between daily
five-year bond yield changes and unanticipated daily net order flow
(the adjusted
basis points (in Table 1) over
the entire sample. Consistently, the correlation between daily
five-year bond yield changes and unanticipated daily net order flow
(the adjusted ![]() of the
above regression) is much greater during high dispersion days (
of the
above regression) is much greater during high dispersion days (
![]() )
than during low dispersion days (
)
than during low dispersion days (
![]() ).
).
We also find evidence in favor of Corollary 1 in the two-year
bond market, although only when we use the dispersion of analysts'
forecasts about Nonfarm Payroll Employment (![]() ) and Influential announcements
(
) and Influential announcements
(![]() ) as proxies for
information heterogeneity, and in the ten-year bond market when we
use the Nonfarm Payroll announcement alone. This may be due to the
fact that not all macroeconomic announcements are equally important
ex ante, thus making the aggregate dispersion of beliefs across
announcements a noisy measure of such heterogeneity. We explore
this issue in greater depth in Section 4.2.
) as proxies for
information heterogeneity, and in the ten-year bond market when we
use the Nonfarm Payroll announcement alone. This may be due to the
fact that not all macroeconomic announcements are equally important
ex ante, thus making the aggregate dispersion of beliefs across
announcements a noisy measure of such heterogeneity. We explore
this issue in greater depth in Section 4.2.
In the model of Section 2, equilibrium market liquidity (
![]() and
and
![]() ) is a
function of several parameters beyond the one determining the
intensity of information heterogeneity among speculators
(
) is a
function of several parameters beyond the one determining the
intensity of information heterogeneity among speculators
(![]() ). For example, in
the benchmark equilibrium with no public signal (Proposition 1),
). For example, in
the benchmark equilibrium with no public signal (Proposition 1),
![]() also depends on
the intensity of noise trading (
also depends on
the intensity of noise trading (
![]() ), the
number of informed traders (
), the
number of informed traders (![]() ), and the volatility of the intrinsic value of the
asset (
), and the volatility of the intrinsic value of the
asset (
![]() ). The
regression model of Eq. (11), whose estimates
are reported in Table 4, does not explicitly control for any of
these parameters. These omissions have the potential to bias our
inference.
). The
regression model of Eq. (11), whose estimates
are reported in Table 4, does not explicitly control for any of
these parameters. These omissions have the potential to bias our
inference.
To begin with, in our model the parameters
![]() ,
,
![]() , and
, and
![]() are unrelated to the
dispersion of beliefs. If this were true, the estimation of Eq.
(11) would in principle be unbiased.
Nevertheless, omitted variable biases may arise from relaxing some
of the model's most stringent assumptions. For example, if we
allowed for endogenous entry of informed traders, the equilibrium
number of market participants might be correlated with their
dispersion of beliefs, since the latter would affect investors'
potential profits from trading. In addition, misspecification
biases may arise from the intertemporal dynamics of either
speculators' participation, intensity of noise trading, or
fundamental uncertainty. It is difficult to control for these
variables. In this section, we do our best to gauge the robustness
of the results presented above to their inclusion. The analysis
that follows indicates that these results are indeed robust.
are unrelated to the
dispersion of beliefs. If this were true, the estimation of Eq.
(11) would in principle be unbiased.
Nevertheless, omitted variable biases may arise from relaxing some
of the model's most stringent assumptions. For example, if we
allowed for endogenous entry of informed traders, the equilibrium
number of market participants might be correlated with their
dispersion of beliefs, since the latter would affect investors'
potential profits from trading. In addition, misspecification
biases may arise from the intertemporal dynamics of either
speculators' participation, intensity of noise trading, or
fundamental uncertainty. It is difficult to control for these
variables. In this section, we do our best to gauge the robustness
of the results presented above to their inclusion. The analysis
that follows indicates that these results are indeed robust.
Specifically, we conduct several robustness checks. First, the
inclusion of lagged unanticipated order flow in Eq. (11) allows us to assess the relevance of any
transient, noninformation effect (hence not just inventory control
effects but also those due to noise trading,
![]() ) on the
relationship between trades and price changes (see Hasbrouck,
1991). As previously mentioned, the estimation of Eq. (11) in Table 4 indicates that the impact of
unanticipated government bond order flow on yield changes is
permanent, i.e., cannot be explained by transitory noise effects.
Alternatively, we determine the importance of noise trading by
computing order flow and yield changes over disjoint intervals of
each day in our sample, as in Brandt and Kavajecz (2004), rather
than concurrently. In particular, we aggregate unanticipated order
flow in the morning (from 7:30 a.m. to 12:00 p.m.), labeled as time
) on the
relationship between trades and price changes (see Hasbrouck,
1991). As previously mentioned, the estimation of Eq. (11) in Table 4 indicates that the impact of
unanticipated government bond order flow on yield changes is
permanent, i.e., cannot be explained by transitory noise effects.
Alternatively, we determine the importance of noise trading by
computing order flow and yield changes over disjoint intervals of
each day in our sample, as in Brandt and Kavajecz (2004), rather
than concurrently. In particular, we aggregate unanticipated order
flow in the morning (from 7:30 a.m. to 12:00 p.m.), labeled as time
![]() , and average yields
from 12:00 p.m. until the end of each trading day (5:00 p.m.),
labeled as time
, and average yields
from 12:00 p.m. until the end of each trading day (5:00 p.m.),
labeled as time ![]() . We
then regress bond yield changes at time
. We
then regress bond yield changes at time ![]() on unanticipated order flow at
time
on unanticipated order flow at
time ![]() . This procedure not
only prevents non-synchronous measurement errors (as argued by
Brandt and Kavajecz, 2004) but also allows us to identify the long
run or permanent effect of order flow on prices. The resulting
estimates of market liquidity, not reported here, are qualitatively
similar to those from Eq. (11) presented in
Table 4.
. This procedure not
only prevents non-synchronous measurement errors (as argued by
Brandt and Kavajecz, 2004) but also allows us to identify the long
run or permanent effect of order flow on prices. The resulting
estimates of market liquidity, not reported here, are qualitatively
similar to those from Eq. (11) presented in
Table 4.
We also control for the number of informed traders (![]() ) and the volatility of the intrinsic
value of the asset (
) and the volatility of the intrinsic
value of the asset (
![]() ). We do
so by including in Eq. (11) additional
variables capturing the interaction between (i.e., the product of):
(i) order flow and daily realized volatility,16(ii) order flow and the number of
transactions, and (iii) order flow and a weight linearly increasing
as the announcement date approaches.17 In our model, the degree of
information heterogeneity affects both equilibrium price volatility
and the aggressiveness of informed trading (proxied by the number
of transactions, as in Section 3.2.2). Depending on the strength of
these effects, the inclusion of those cross terms in Eq. (11) may reduce the statistical significance of the
relation between market liquidity and dispersion of beliefs.
Instead, we find no evidence that order flow interacts with either
the number of transactions or the proximity to the announcement
date. The product of order flow and daily realized volatility is
statistically significant only in the five-year Treasury bond
market.18 This is
not surprising, since we expect informed investors to be more
active in the most liquid trading venues (e.g., Chowdhry and Nanda,
1991), as so the five-year bond market is generally deemed (e.g.,
Fleming, 2003). It is therefore possible that our proxy for
realized volatility is successfully capturing the time-varying
participation of informed traders only in the market where such
participation is probably most important. Nonetheless, neither the
economic nor the statistical significance of the dispersion of
beliefs dummies in Table 4 are affected by the inclusion of these
interaction terms in Eq. (11).
). We do
so by including in Eq. (11) additional
variables capturing the interaction between (i.e., the product of):
(i) order flow and daily realized volatility,16(ii) order flow and the number of
transactions, and (iii) order flow and a weight linearly increasing
as the announcement date approaches.17 In our model, the degree of
information heterogeneity affects both equilibrium price volatility
and the aggressiveness of informed trading (proxied by the number
of transactions, as in Section 3.2.2). Depending on the strength of
these effects, the inclusion of those cross terms in Eq. (11) may reduce the statistical significance of the
relation between market liquidity and dispersion of beliefs.
Instead, we find no evidence that order flow interacts with either
the number of transactions or the proximity to the announcement
date. The product of order flow and daily realized volatility is
statistically significant only in the five-year Treasury bond
market.18 This is
not surprising, since we expect informed investors to be more
active in the most liquid trading venues (e.g., Chowdhry and Nanda,
1991), as so the five-year bond market is generally deemed (e.g.,
Fleming, 2003). It is therefore possible that our proxy for
realized volatility is successfully capturing the time-varying
participation of informed traders only in the market where such
participation is probably most important. Nonetheless, neither the
economic nor the statistical significance of the dispersion of
beliefs dummies in Table 4 are affected by the inclusion of these
interaction terms in Eq. (11).
Lastly, we control for variables outside our model that might spuriously affect our results. For example, Treasury auction dates might have a liquidity effect on the secondary bond market. Thus, if our proxies for dispersion of beliefs were spuriously correlated with auction dates, an additional omitted variable bias might arise. We account for this eventuality by including the interaction between order flow and dummies for these dates in Eq. (11).19 The liquidity of U.S. Treasury bonds may also be affected by their repurchase agreement (repo) rates, i.e., by their specialness. According to Moulton (2004), the relative repo specialness of on-the-run Treasury securities (such as those in our database) generally increases in proximity of auction dates. Hence, the inclusion of auction dummies in Eq. (11) may control for spurious liquidity shocks induced by time-varying specialness as well. Similarly, we include day-of-the-week and annual effects to control for weekly seasonality and temporal trends in the order flow and/or the dispersion of beliefs. None of these effects are statistically significant.
When we introduce a public signal in the model (Proposition 2),
market liquidity increases (Corollary 2), because the presence of a
trade-free source of information and more aggressive trading by the
speculators mitigates the adverse selection risk for the
market-makers. In our empirical analysis, this translates into
observing a negative difference (since we work with yields) between
![]() (of Eq.
(1)) and
(of Eq.
(1)) and
![]() (of Eq.
(3)) in the following regression:
(of Eq.
(3)) in the following regression:
Consistent with Table 4, the evidence in Table 5 indicates that,
even during announcement days, both the contemporaneous and
cumulative impact of unanticipated order flow on yield changes (
![]() and
and
![]() , respectively)
are negative and statistically significant (often at the
, respectively)
are negative and statistically significant (often at the
![]() level). Hence, the
correlation between unanticipated order flow and yield changes
during announcement days does not appear to be driven by inventory
control effects. Table 5 also shows that, in most cases, the
difference between
level). Hence, the
correlation between unanticipated order flow and yield changes
during announcement days does not appear to be driven by inventory
control effects. Table 5 also shows that, in most cases, the
difference between
![]() and
and
![]() is not
statistically significant (except for the five-year Treasury notes
when
is not
statistically significant (except for the five-year Treasury notes
when ![]() or
or ![]() ). Our model suggests that this
would be the case if the public news surprises in our sample
(
). Our model suggests that this
would be the case if the public news surprises in our sample
(![]() in Eq. (3)) were noisy, since
in Eq. (3)) were noisy, since
![]() .
Yet, our model (Corollary 3) also implies that noisy public signals
should have little or no impact on price changes (i.e.,
.
Yet, our model (Corollary 3) also implies that noisy public signals
should have little or no impact on price changes (i.e.,
![]() as
well). This interpretation, although intriguing, is not exhaustive
since in unreported analysis we find that seven of the
macroeconomic news releases in our sample (the ``influential''
ones) do have a statistically significant impact on day-to-day bond
yield changes between 1992 and 2000 (i.e., at least some
as
well). This interpretation, although intriguing, is not exhaustive
since in unreported analysis we find that seven of the
macroeconomic news releases in our sample (the ``influential''
ones) do have a statistically significant impact on day-to-day bond
yield changes between 1992 and 2000 (i.e., at least some
![]() are
statistically significant).
are
statistically significant).
An alternative interpretation of the statistically
indistinguishable estimates for ![]() and
and
![]() in Table 5
is that the release of public macroeconomic signals may increase
investors' information heterogeneity (as argued in Kim and
Verrecchia, 1994, 1997), hence compensating the reduction in
adverse selection costs due to the availability of trade-free
sources of information (as in our model). This interpretation is
consistent with the evidence reported by Green (2004), who finds
that the estimated half-hour price impact of order flow in the
Treasury bond market is actually higher during the thirty-minute
interval immediately after an announcement than during the
thirty-minute interval immediately before the announcement or on
non-announcement days.
in Table 5
is that the release of public macroeconomic signals may increase
investors' information heterogeneity (as argued in Kim and
Verrecchia, 1994, 1997), hence compensating the reduction in
adverse selection costs due to the availability of trade-free
sources of information (as in our model). This interpretation is
consistent with the evidence reported by Green (2004), who finds
that the estimated half-hour price impact of order flow in the
Treasury bond market is actually higher during the thirty-minute
interval immediately after an announcement than during the
thirty-minute interval immediately before the announcement or on
non-announcement days.
However, the analysis of both the estimated correlation between
bond yield changes and unanticipated net order flow and the average
cumulative impact of the latter on the former provides stronger
support for Corollary 2. Indeed, the adjusted ![]() of Eq. (12)
is always higher for non-announcement days than for announcement
days (i.e.,
of Eq. (12)
is always higher for non-announcement days than for announcement
days (i.e.,
![]() in Table 5), with the sole
exception of five-year notes when
in Table 5), with the sole
exception of five-year notes when ![]() . Furthermore, the impact of unanticipated order
flow in either the two-year or the ten-year Treasury notes on the
corresponding yield changes is permanent during non-announcement
days (statistically significant
. Furthermore, the impact of unanticipated order
flow in either the two-year or the ten-year Treasury notes on the
corresponding yield changes is permanent during non-announcement
days (statistically significant
![]() in Table 5), but
only transitory during Nonfarm Payroll announcement days
(statistically insignificant
in Table 5), but
only transitory during Nonfarm Payroll announcement days
(statistically insignificant
![]() in Table 5). This
suggests that dealers rely more heavily on unanticipated order flow
to set bond prices during non-announcement days than on
announcement days, consistent with our model and the findings in
Brandt and Kavajecz (2004).
in Table 5). This
suggests that dealers rely more heavily on unanticipated order flow
to set bond prices during non-announcement days than on
announcement days, consistent with our model and the findings in
Brandt and Kavajecz (2004).
Overall, the evidence reported in Table 5 indicates (albeit not
as strongly as in Section 4.1) that the release of public signals
does not increase (and occasionally reduces) adverse selection
costs and does not impair (and occasionally improves) market
liquidity. Nonetheless, both the above discussion and the
comparative statics of Figure 1B also indicate that any such
liquidity gain may crucially depend on the quality of the public
signal (
![]() ) and on
the degree of information heterogeneity among market participants
(
) and on
the degree of information heterogeneity among market participants
(![]() ). We explore
these issues next, starting with the latter.
). We explore
these issues next, starting with the latter.
In this section, we analyze the effect of information heterogeneity on market liquidity during announcement days. For that purpose, we estimate the following representation of Eq. (10):
According to our model (Remark 2), greater dispersion of beliefs
among speculators reduces market liquidity during announcement days
(i.e.,
![]() in Eq. (13)) only when the public signal is noisy, since the
latter induces those heterogeneously informed speculators to use
cautiously their private signals, thus increasing adverse selection
risks for the market-makers. Vice versa, if the quality of the
public signal is high (
in Eq. (13)) only when the public signal is noisy, since the
latter induces those heterogeneously informed speculators to use
cautiously their private signals, thus increasing adverse selection
risks for the market-makers. Vice versa, if the quality of the
public signal is high (
![]() is low),
more heterogeneously informed speculators display their caution by
relying less on their private signals (and more on the public
signal) in their trading activity, thus lowering the perceived
adverse selections risk for the market-makers and improving market
liquidity (i.e.,
is low),
more heterogeneously informed speculators display their caution by
relying less on their private signals (and more on the public
signal) in their trading activity, thus lowering the perceived
adverse selections risk for the market-makers and improving market
liquidity (i.e.,
![]() in Eq. (13)).
in Eq. (13)).
Table 6 reveals that the difference between
![]() and
and
![]() is
always negative and, in most cases, both economically and
statistically significant. For instance, when we measure dispersion
of beliefs using the Nonfarm Payroll announcement, a one standard
deviation shock to unanticipated order flow decreases ten-year bond
yields by
is
always negative and, in most cases, both economically and
statistically significant. For instance, when we measure dispersion
of beliefs using the Nonfarm Payroll announcement, a one standard
deviation shock to unanticipated order flow decreases ten-year bond
yields by ![]() basis
points during high dispersion days, while it increases bond yields by
basis
points during high dispersion days, while it increases bond yields by ![]() basis points during low
dispersion days. This evidence suggests that the dispersion of
beliefs among market participants has an important impact on
Treasury bond market liquidity, in the direction predicted by our
model, even in the presence of public signals of macroeconomic
fundamentals. This evidence is also (indirectly) consistent with
the conjecture made in Section 4.2 that public signal noise is
``sufficiently'' high in our sample. In Section 4.2.3 below, we
gauge more explicitly the potential role of public signal noise on
market liquidity.
basis points during low
dispersion days. This evidence suggests that the dispersion of
beliefs among market participants has an important impact on
Treasury bond market liquidity, in the direction predicted by our
model, even in the presence of public signals of macroeconomic
fundamentals. This evidence is also (indirectly) consistent with
the conjecture made in Section 4.2 that public signal noise is
``sufficiently'' high in our sample. In Section 4.2.3 below, we
gauge more explicitly the potential role of public signal noise on
market liquidity.
We now turn to the impact of public signals on yield changes.
According to the extended model of Section 2.2, a public signal can
induce price (and yield) changes through two channels that, in the
spirit of Evans and Lyons (2003), we call direct (through
market-makers' belief updating process) and indirect (through
speculators' trades in the order flow). Yet, in the model, the
direct channel is always more important than the indirect one. The
evidence presented in Table 6 confirms this latter result: The
adjusted ![]() of the
fully specified regressions of Eq. (13), i.e.,
including both the unanticipated order flow and the public
signal(s),
of the
fully specified regressions of Eq. (13), i.e.,
including both the unanticipated order flow and the public
signal(s), ![]() , is
between
, is
between ![]() and
and
![]() times bigger than
the adjusted
times bigger than
the adjusted ![]() of the
regressions estimated using only unanticipated order flow,
of the
regressions estimated using only unanticipated order flow,
![]() .
.
Many of the results in Section 4.2.1 above are generally weaker
in correspondence with the aggregate proxies for information
heterogeneity described in Eq. (7). In
particular, the relevance of public signals for bond yield changes
(i.e., the difference between ![]() and
and
![]() in Table
6) is declining in
in Table
6) is declining in ![]() , the
number of announcements used in the analysis. This may be explained
by a potentially mistaken classification of certain macroeconomic
releases as important public announcements. Indeed, both Eq.
(7) and the corresponding classification of
announcement days implicitly assume that all U.S. macroeconomic
news releases listed in Table 2 are equally important. However, the
literature (e.g., Fleming and Remolona, 1997) suggests that not all
public information may be equally relevant ex ante to participants
in the U.S. Treasury bond markets.
, the
number of announcements used in the analysis. This may be explained
by a potentially mistaken classification of certain macroeconomic
releases as important public announcements. Indeed, both Eq.
(7) and the corresponding classification of
announcement days implicitly assume that all U.S. macroeconomic
news releases listed in Table 2 are equally important. However, the
literature (e.g., Fleming and Remolona, 1997) suggests that not all
public information may be equally relevant ex ante to participants
in the U.S. Treasury bond markets.
This can be due to several factors: The dispersion of beliefs might be higher for certain announcements than for others, some announcements may not reveal any useful information to price bonds (i.e., the days in which they occur are effectively non-announcement days), or some announcements might be noisier than others. According to our model, the availability of a public signal of higher (lower) quality implies a higher (lower) impact of order flow on equilibrium price changes during announcement days. In this section, we examine the effect of public signal noise directly.
Specifically, Remark 1 and Corollary 3 state that adverse selection costs are higher and the price reaction to public announcement surprises is lower when the public signal noise is high. Intuitively, when the public signal is noisy, the market-makers rely more heavily on the order flow than on the public signal, thus requiring greater compensation for providing liquidity. The evidence in Table 7 supports this claim. There we report estimates of the following equation:
Table 7 shows that the impact of these public signals on bond
yield changes is generally more significant when their noise is
lower (columns
![]() and
and
![]() ).
Accordingly, we also find that (i) the coefficients measuring the
contemporaneous and permanent impact of unanticipated order flow on
bond yield changes are generally insignificant on announcement days
when the public signal noise is low (columns
).
Accordingly, we also find that (i) the coefficients measuring the
contemporaneous and permanent impact of unanticipated order flow on
bond yield changes are generally insignificant on announcement days
when the public signal noise is low (columns
![]() and
and
![]() in Table 7), and
(ii) the adjusted
in Table 7), and
(ii) the adjusted ![]() of
order flow alone is generally higher on days with high public
signal noise (
of
order flow alone is generally higher on days with high public
signal noise (![]() )
than on days with low public signal noise (
)
than on days with low public signal noise (![]() ), i.e.,
), i.e.,
![]() ; yet, these differences
are not large. These results suggest that the impact of the release
of macroeconomic data on the process of price formation in the U.S.
Treasury market is decreasing in the quality of the public signals,
as argued in the model of Section 2.2, albeit not importantly
so.
; yet, these differences
are not large. These results suggest that the impact of the release
of macroeconomic data on the process of price formation in the U.S.
Treasury market is decreasing in the quality of the public signals,
as argued in the model of Section 2.2, albeit not importantly
so.
Finally, we amend all the regression models specified above to
account for the potential omitted variable biases described in
Section 4.1.1. Many of these biases are in fact more likely to
arise when analyzing the impact of both information heterogeneity
and public signal noise on market liquidity during announcement
days. For example, the number of informed market participants is
likely to be endogenously higher during announcement days
regardless of their dispersion of beliefs, if they expect the
Treasury bond market to be more liquid then (e.g., Chowdhry and
Nanda, 1991). In addition, as observed in Section 3.2.3, public
signal noise may stem not only from the signal's intrinsic quality
but also from fundamental uncertainty (
![]() in our
model), which affects market liquidity directly as well
(Proposition 2). Yet, we find that all our conclusions are robust
to the inclusion of the same control variables employed for our
analysis of non-announcement days.
in our
model), which affects market liquidity directly as well
(Proposition 2). Yet, we find that all our conclusions are robust
to the inclusion of the same control variables employed for our
analysis of non-announcement days.
The main goal of this paper is to deepen our understanding of the links between daily bond yield movements, news about fundamentals, and order flow conditional on the investors' dispersion of beliefs and the public signals' noise. To that end, we theoretically identify and empirically document important news and order flow effects in the U.S. Treasury bond market. To guide our analysis, we develop a parsimonious model of speculative trading in the presence of asymmetric sharing of information among imperfectly competitive traders and a public signal of the terminal value of the traded asset. We then test its equilibrium implications by studying the relation between daily two-year, five-year, and ten-year U.S. Treasury bond yield changes and unanticipated order flow and real-time U.S. macroeconomic news releases.
Our evidence suggests that announcement and order flow surprises produce conditional, persistent mean jumps, i.e., that the process of price formation in the bond market is linked to information about fundamentals and agents' beliefs. The nature of this linkage is sensitive to the intensity of investors' dispersion of beliefs and the noise of the public announcement (albeit more weakly so). In particular, and consistent with our model, unanticipated order flow is more highly correlated with bond yield changes when the dispersion of beliefs across informed traders is high and the public announcement is noisy.
These findings allow us to draw several implications for future research. Existing term structure models are notorious for their poor out-of-sample forecast performance (e.g., Duffee, 2002). Recently, Diebold and Li (2003) use a variation of the Nelson and Siegel (1987) exponential components framework to forecast yield curve movements at short and long horizons, finding encouraging results at short horizons. We show here that U.S. Treasury bond order flow is contemporaneously correlated with daily yield changes and that the significance of this relation depends on the degree of information heterogeneity about macroeconomic fundamentals among market participants. In future work, we intend to include order flow information to forecast the term structure.
Our results also indicate that day-to-day bond yield changes and
order flow are most sensitive to Nonfarm Payroll Employment
announcements. Nominal bond yields depend on future inflation and
future capital productivity, hence naturally react to employment
announcement surprises. Previous studies observe that Nonfarm
Payroll Employment is the first news release for a given month
(e.g., Fleming and Remolona, 1997; Andersen et al., 2003). However,
our analysis implicitly accounts for the timing of the
announcements, by focusing exclusively on their surprise content.
Hence, the importance of this announcement should depend on its
predictive power. Yet, to the best of our knowledge, no study has
shown that the Nonfarm Payroll Employment is the best predictor for
future activity and inflation out of the ![]() macroeconomic announcements in our
sample.20 Thus, we
suspect that its importance goes beyond its predictive power for
real activity. Morris and Shin (2002) provide an interesting
theoretical explanation for this overreaction to Nonfarm Payroll news. They argue
that bond yields will be most reactive to the types of news
emphasized by the press. In their model, this overreaction to news
is rational and reflects the coordination role of public
information. We look forward to future research that further
investigates this possibility.
macroeconomic announcements in our
sample.20 Thus, we
suspect that its importance goes beyond its predictive power for
real activity. Morris and Shin (2002) provide an interesting
theoretical explanation for this overreaction to Nonfarm Payroll news. They argue
that bond yields will be most reactive to the types of news
emphasized by the press. In their model, this overreaction to news
is rational and reflects the coordination role of public
information. We look forward to future research that further
investigates this possibility.
| (A-1) |
| (A-2) |
| (A-3) | ||
| (A-4) |
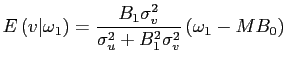 .
. |
(A-5) |
| (A-6) | ||
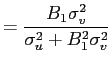 .
. |
(A-7) |
![$\displaystyle A_{1}=\frac{\psi}{B_{1}\left[ 2+\left( M-1\right) \gamma\right] }$](img267.gif) .
. |
(A-8) |
![$ A_{1}=\frac{\sigma_{v}\psi^{\frac{1}{2}}}{\sigma_{u}\left[ 2+\left( M-1\right) \gamma\right] }$](img269.gif) , where
, where
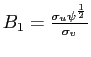 .
Both
.
Both ![$ \Delta\lambda=\lambda\left( \text{at }M+1\right) -\lambda\left( \text{at }M\right) =\frac{\sigma_{v}^{2}\sqrt{M+1}\left[ \sigma_{v} ^{2}+\left( M+1\right) M\chi\right] ^{\frac{1}{2}}}{\sigma_{u}\left[ \sigma_{v}^{2}\left( M+2\right) +\left( M+1\right) M\chi\right] } -\frac{\sigma_{v}^{2}\sqrt{M}\left[ \sigma_{v}^{2}+M\left( M-1\right) \chi\right] ^{\frac{1}{2}}}{\sigma_{u}\left[ \sigma_{v}^{2}\left( M+1\right) +M\left( M-1\right) \chi\right] }=0$](img276.gif) only when speculators' information is heterogeneous (
only when speculators' information is heterogeneous (
![$ \lambda=\frac{\sigma_{v} ^{2}\sqrt{M}\left[ \sigma_{v}^{2}+M\left( M-1\right) \chi\right] ^{\frac{1}{2}}}{\sigma_{u}\left[ \sigma_{v}^{2}\left( M+1\right) +M\left( M-1\right) \chi\right] }$](img280.gif) is a concave function of
is a concave function of ![$ \frac{\partial\lambda}{\partial\chi}=-\frac{M^{\frac{3}{2}}\left( M-1\right) ^{2}\sigma_{v}^{2}\left( M\chi-\sigma_{v}^{2}\right) } {2\sigma_{u}\left[ \sigma_{v}^{2}+M\left( M-1\right) \chi\right] ^{\frac{1}{2}}\left[ \sigma_{v}^{2}\left( M+1\right) +M\left( M-1\right) \chi\right] ^{2}}$](img281.gif) , implying that
, implying that
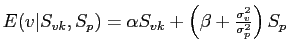 and
and
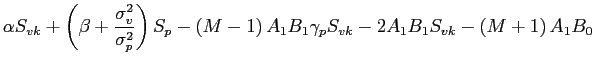
|
(A-9) | |
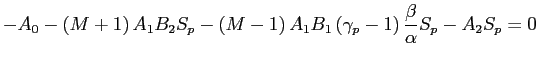 .
. |
| (A-10) | ||
| (A-11) | ||
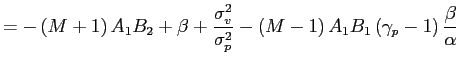
|
(A-12) |
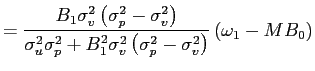
|
(A-13) | |
![$\displaystyle +\frac{\sigma_{v}^{2}\left[ \sigma_{u}^{2}-MB_{1}B_{2}\left( \sigma _{p}^{2}-\sigma_{v}^{2}\right) \right] }{\sigma_{u}^{2}\sigma_{p}^{2} +B_{1}^{2}\sigma_{v}^{2}\left( \sigma_{p}^{2}-\sigma_{v}^{2}\right) } S_{p}$](img300.gif) .
. |
| (A-14) | ||
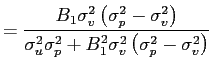
|
(A-15) | |
![$\displaystyle =\frac{\sigma_{v}^{2}\left[ \sigma_{u}^{2}-MB_{1}B_{2}\left( \sigma_{p}^{2}-\sigma_{v}^{2}\right) \right] }{\sigma_{u}^{2}\sigma_{p} ^{2}+B_{1}^{2}\sigma_{v}^{2}\left( \sigma_{p}^{2}-\sigma_{v}^{2}\right) }$](img302.gif) .
. |
(A-16) |
![$ A_{1}^{2}=\frac{\alpha\sigma_{v}^{2}\left( \sigma_{p} ^{2}-\sigma_{v}^{2}\right) }{\sigma_{u}^{2}\sigma_{p}^{2}\left[ 2+\left( M-1\right) \gamma_{p}\right] ^{2}}$](img305.gif) , since
, since
![$ A_{1}=\frac{\alpha^{\frac{1}{2}}\sigma _{v}\left( \sigma_{p}^{2}-\sigma_{v}^{2}\right) ^{\frac{1}{2}}}{\sigma _{u}\sigma_{p}\left[ 2+\left( M-1\right) \gamma_{p}\right] }>0$](img307.gif) , where
, where
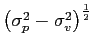 are the unique square roots of
are the unique square roots of ![$ B_{1}=\alpha\sigma_{u}\sigma_{p}\left[ \alpha\sigma_{v} ^{2}\left( \sigma_{p}^{2}-\sigma_{v}^{2}\right) \right] ^{-\frac{1}{2}}$](img312.gif) . Substituting the solution for
. Substituting the solution for 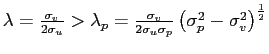 since
since
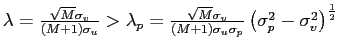 . When
. When 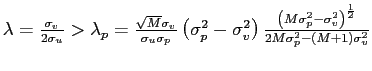 since
since
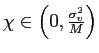 (
(
![$ \lambda=\frac{\sigma_{v} ^{2}\sqrt{M}\left[ \sigma_{v}^{2}+M\left( M-1\right) \chi\right] ^{\frac{1}{2}}}{\sigma_{u}\left[ \sigma_{v}^{2}\left( M+1\right) +M\left( M-1\right) \chi\right] }>\lambda_{p}=\frac{\alpha^{\frac{1}{2}}\sigma _{v}\left( \sigma_{p}^{2}-\sigma_{v}^{2}\right) ^{\frac{1}{2}}}{\sigma _{u}\sigma_{p}\left[ 2+\left( M-1\right) \gamma_{p}\right] }$](img320.gif) where
where
![$ \gamma_{p}=\frac{\sigma_{p}^{2}\left( \sigma_{v}^{2}-M\chi\right) -\sigma_{v}^{4}}{\sigma_{p}^{2}\left[ \sigma_{v}^{2}+M\left( M-1\right) \chi\right] -\sigma_{v}^{4}}$](img321.gif) and
and
![$ \alpha=\frac{M\sigma_{v}^{2}\left( \sigma_{p}^{2}-\sigma_{v}^{2}\right) }{\sigma_{p}^{2}\left[ \sigma_{v} ^{2}+M\left( M-1\right) \chi\right] -\sigma_{v}^{4}}$](img322.gif) . In addition,
. In addition,
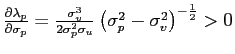 since
since
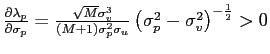 . When
. When ![$ \frac{\partial\lambda_{p}}{\partial\sigma_{p}} =\frac{\sqrt{M}\sigma_{v}^{3}\left[ \sigma_{v}^{4}\left( M+1\right) +\sigma_{p}^{2}\left( \sigma_{v}^{2}+2M^{2}\sigma_{p}^{2}-5M\sigma_{v} ^{2}\right) \right] }{\sigma_{p}^{2}\sigma_{u}\left[ 2\sigma_{p} ^{2}-\left( M+1\right) \sigma_{v}^{2}\right] ^{2}}\left( M\sigma_{p} ^{2}-\sigma_{v}^{2}\right) ^{-\frac{1}{2}}$](img326.gif) since
since
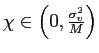 (
(
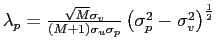 ; if speculators' private signals are uncorrelated, then
; if speculators' private signals are uncorrelated, then
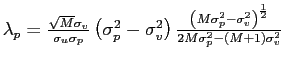 . It then follows that it exists a unique
. It then follows that it exists a unique
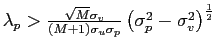 if
if
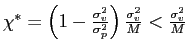 (i.e.,
(i.e.,
[1] Admati, A., and Pfleiderer, P., 1988, A Theory of Intraday Trading Patterns: Volume and Price Variability, Review of Financial Studies, 1, 3-40.
[2] Andersen, T., and Bollerslev, T., 1998, Deutsche Mark-Dollar Volatility: Intraday Activity Patterns, Macroeconomic Announcements, and Longer Run Dependencies, Journal of Finance, 53, 219-265.
[3] Andersen, T., Bollerslev, T., Diebold, F., and Labys, P., 2003, Modeling and Forecasting Realized Volatility, Econometrica, 71, 579-626.
[4] Andersen, T., Bollerslev, T., Diebold, F., and Vega, C., 2003, Micro Effects of Macro Announcements: Real-Time Price Discovery in Foreign Exchange, American Economic Review, 93, 38-62.
[5] Andersen, T., Bollerslev, T., Diebold, F., and Vega, C., 2004, Real-Time Price Discovery in Stock, Bond, and Foreign Exchange Markets, Working Paper, Northwestern University.
[6] Aruoba, B., 2004, Empirical Properties of Macroeconomic Revisions, Working Paper, University of Pennsylvania.
[7] Back, K., Cao, H., and Willard, G., 2000, Imperfect Competition Among Informed Traders, Journal of Finance, 55, 2117-2155.
[8] Balduzzi, P., Elton, E., and Green, C., 2001, Economic News and Bond Prices: Evidence From the U.S. Treasury Market, Journal of Financial and Quantitative Analysis, 36, 523-543.
[9] Bandi, F., and Russell, J., 2005, Separating Microstructure Noise from Volatility, Journal of Financial Economics, forthcoming.
[10] Berry, T., Howe, K., 1994, Public Information Arrival, Journal of Finance, 49, 1331-1346.
[11] Boyd, J., Hu, J., and Jagannathan, R., 2005, The Stock Market's Reaction to Unemployment News: Why Bad News Is Usually Good For Stocks, Journal of Finance, 60, 649-672.
[12] Brandt, M., and Kavajecz, K., 2004, Price Discovery in the U.S. Treasury Market: The Impact of Order Flow and Liquidity on the Yield Curve, Journal of Finance, 59, 2623-2654.
[13] Brenner, M., Pasquariello, P., and Subrahmanyam, M., 2005, Financial Markets and the Macro Economy, Working Paper, Ross School of Business, University of Michigan.
[14] Chowdhry, B., and Nanda, V., 1991, Multimarket Trading and Market Liquidity, Review of Financial Studies, 4, 483-511.
[15] Croushore, D., and Stark, T., 1999, A Real-Time Data Set of Macroeconomists: Does the Data Vintage Matter? Federal Reserve Bank of Philadelphia Working Paper No. 99-21.
[16] Croushore, D., and Stark, T., 2001, A Real-Time Data Set of Macroeconomists, Journal of Econometrics, 105, 111-130.
[17] Diamond, D., and Verrecchia, R., 1991, Disclosure, Liquidity, and the Cost of Capital, Journal of Finance, 46, 1325-1359.
[18] Diebold, F., and Li, C., 2003, Forecasting the Term Structure of Government Bond Yields, Journal of Econometrics, forthcoming.
[19] Diether, K., Malloy, C., and Scherbina, A., 2002, Differences of Opinion and the Cross Section of Stock Returns, Journal of Finance, 57, 2113-2141.
[20] Duffee, G., 2002, Term Premia and Interest Rate Forecasts in Affine Models, Journal of Finance, 57, 405-443.
[21] Easley, D., Hvidkjaer, S., and O'Hara, M., 2002, Is Information Risk a Determinant of Asset Returns? Journal of Finance, 57, 2185-2221.
[22] Estrella, A., and Mishkin, F., 1998, Predicting U.S. Recessions: Financial Variables as Leading Indicators, Review of Economics and Statistics, 80, 45-61.
[23] Evans, M., and Lyons, R., 2002, Order Flow and Exchange Rate Dynamics, Journal of Political Economy, 110, 170-180.
[24] Evans, M., and Lyons, R., 2003, How is Macro News Transmitted to Exchange Rates, NBER Working Paper No. 9433.
[25] Evans, M., and Lyons, R., 2004, Exchange Rate Fundamentals and Order Flow, Working Paper, Haas School of Business, University of California at Berkeley.
[26] Faust, J., Rogers, J., and Wright, J., 2003, News and Noise in G-7 GDP Announcements, Journal of Money, Credit and Banking, forthcoming.
[27] Fleming, M., 1997, The Round-the-Clock Market of U.S. Treasury Securities, Economic Policy Review, Federal Reserve Bank of New York, 3, 9-32.
[28] Fleming, M., 2003, Measuring Treasury Market Liquidity, Economic Policy Review, Federal Reserve Bank of New York, 83-108.
[29] Fleming, M., and Remolona, E., 1997, What Moves the Bond Market? Economic Policy Review, Federal Reserve Bank of New York, 31-50.
[30] Fleming, M., and Remolona, E., 1999, Price Formation and Liquidity in the U.S. Treasury Market: The Response to Public Information, Journal of Finance, 54, 1901-1915.
[31] Foster, F., and Viswanathan, S., 1990, A Theory of the Interday Variations in Volume, Variance, and Trading Costs in Securities Markets, Review of Financial Studies, 3, 593-624.
[32] Foster, F., and Viswanathan, S., 1993, The Effect of Public Information and Competition on Trading Volume and Price Volatility, Review of Financial Studies, 6, 23-56.
[33] Foster, F., and Viswanathan, S., 1996, Strategic Trading When Agents Forecast the Forecasts of Others, Journal of Finance, 51, 1437-1478.
[34] Garman, Mark B., 1976, Market Microstructure, Journal of Financial Economics, 3, 257-275.
[35] Goldreich, D., Hanke, B., and Nath, P., 2005, The Price of Future Liquidity: Time-Varying Liquidity in the U.S. Treasury Market, Review of Finance, forthcoming.
[36] Goodhart, C., and O'Hara, M., 1997, High Frequency Data in Financial Markets: Issues and Applications, Journal of Empirical Finance, 4, 73-114.
[37] Green, C., 2004, Economic News and the Impact of Trading on Bond Prices, Journal of Finance, 59, 1201-1233.
[38] Griffiths, M., Smith, B., Turnbull, D., and White, R., 2000, The Costs and the Determinants of Order Aggressiveness, Journal of Financial Economics, 56, 65-88.
[39] Hasbrouck, J., 1991, Measuring The Information Content of Stock Trades, Journal of Finance, 46, 179-207.
[40] Hasbrouck, J., 2003, Intraday Price Formation in U.S. Equity Index Markets, Journal of Finance, 58, 2375-2399.
[41] Hasbrouck, J., 2004, Economic and Statistical Perspectives on the Dynamics of Trade in Securities Markets, Teaching Notes, Stern School of Business, New York University.
[42] Kallberg, J., and Pasquariello, P., 2004, Time-Series and Cross-Sectional Excess Comovement in Stock Indexes, Working Paper, Ross School of Business at University of Michigan.
[43] Kavajecz, K., and Collins, S., 1995, Rationality of Preliminary Money Stock Estimates, Review of Economics and Statistics, 77, 32-41.
[44] Kim., O., and Verrecchia, R., 1994, Market Liquidity and Volume around Earnings Announcements, Journal of Accounting and Economics, 17, 41-67.
[45] Kim., O., and Verrecchia, R., 1997, Pre-Announcement and Event-Period Private Information, Journal of Accounting and Economics, 24, 395-419.
[46] Koski, J., and Michaely, R., 2000, Prices, Liquidity, and the Information Content of Trades, Review of Financial Studies, 13, 659-696.
[47] Kuttner, K., 2001, Monetary Policy Surprises and Interest Rates: Evidence from the Fed Funds Futures Market, Journal of Monetary Economics, 47, 523-544.
[48] Kyle, A., 1985, Continuous Auctions and Insider Trading, Econometrica, 53, 1315-1335.
[49] Lee, C., and Ready, M., 1991, Inferring Trade Direction from Intraday Data, Journal of Finance, 46, 733-746.
[50] Lucas, R., 1982, Interest Rates and Currency Prices in a Two-Country World, Journal of Monetary Economics, 10, 335-359.
[51] Mankiw, N., Runkle, D., and Shapiro, M., 1984, Are Preliminary Announcements of the Money Stock Rational Forecasts?, Journal of Monetary Economics, 14, 15-27.
[52] McKelvey, R., Page, T., 1990, Public and Private Information: An Experimental Study of Information Pooling, Econometrica, 58, 1321-1339.
[53] Moulton, P., 2004, Relative Repo Specialness in U.S. Treasuries, Journal of Fixed Income, 14, 40-47.
[54] Mork, K., 1987, Ain't Behavin': Forecast Errors and Measurement Errors in Early GNP Estimates, Journal of Business and Economic Statistics, 5, 165-175.
[55] Mork, K., 1990, Forecastable Money-Growth Revisions: A Closer Look at the Data, Canadian Journal of Economics, 23, 593-616.
[56] Morris, S., and Shin, H., 2002, Social Value of Public Information, American Economic Review, 92, 1521-1534.
[57] Novshek, W., 1984, Finding All n-Firm Cournot Equilibria, International Economic Review, 25, 61-70.
[58] Ranaldo, A., 2004, Order Aggressiveness in Limit Order Book Markets, Journal of Financial Markets, 7, 53-74.
[59] Zarnowitz, V., and Lambros, L., 1987, Consensus and Uncertainty in Economic Prediction, Journal of Political Economy, 95, 591-621.
In this table we report the mean,
standard deviation, maximum, minimum, and first-order
autocorrelation coefficient (![]() ) for the
following variables: Two-year, five-year and ten-year on-the-run
daily yields (in percentage, i.e., multiplied by 100), daily yield
changes (in basis points, i.e., multiplied by 10,000), number of
buys, number of sells, daily net order flow
) for the
following variables: Two-year, five-year and ten-year on-the-run
daily yields (in percentage, i.e., multiplied by 100), daily yield
changes (in basis points, i.e., multiplied by 10,000), number of
buys, number of sells, daily net order flow
![]() (number of buys minus number of sells),
daily abnormal order flow, and the daily number of transactions.
The daily abnormal, or unanticipated order flow (defined in Section
4 as
(number of buys minus number of sells),
daily abnormal order flow, and the daily number of transactions.
The daily abnormal, or unanticipated order flow (defined in Section
4 as
![]() ) is
computed by aggregating over each day
) is
computed by aggregating over each day ![]() all
half-hour intraday residuals from the estimation of the linear
autoregressive model of Hasbrouck (1991) in Eq. (8). The data source is GovPX. Our sample period starts
in January 2, 1992 and ends in December 29, 2000, for a total of
2,246 daily observations.
all
half-hour intraday residuals from the estimation of the linear
autoregressive model of Hasbrouck (1991) in Eq. (8). The data source is GovPX. Our sample period starts
in January 2, 1992 and ends in December 29, 2000, for a total of
2,246 daily observations.
| Mean: Two-Year | Stdev.: Two-Year | Max.: Two-Year | Min.: Two-Year | Two-Year
|
|||
|---|---|---|---|---|---|---|---|
| Daily Yield |
5.49 | 0.89 | 7.73 | 3.70 | 0.998 | ||
| Daily Yield
Change |
0.05 | 6.10 | 35.10 | -31.10 | 0.041 | ||
| Number of Buys | 202.07 | 80.00 | 604 | 25 | 0.559 | ||
| Number of Sells | 170.77 | 69.89 | 640 | 17 | 0.533 | ||
| Order Flow | 31.30 | 37.38 | 204 | -89 | 0.088 | ||
| Abnormal Order Flow | 0.00 | 33.74 | 187.58 | -102.49 | 0.032 | ||
| Number of Transactions | 372.84 | 145.50 | 1244 | 44 | 0.578 |
| Mean: Five-Year | Stdev.: Five-Year | Max.: Five-Year | Min.: Five-Year | Five-Year
|
|||
|---|---|---|---|---|---|---|---|
| Daily Yield |
5.97 | 0.74 | 7.90 | 3.98 | 0.996 | ||
| Daily Yield
Change |
-0.01 | 6.39 | 35.10 | -29.30 | 0.044 | ||
| Number of Buys | 324.70 | 127.36 | 816 | 34 | 0.633 | ||
| Number of Sells | 289.41 | 114.47 | 737 | 33 | 0.631 | ||
| Order Flow | 35.29 | 49.53 | 278 | -127 | 0.128 | ||
| Abnormal Order Flow | 0.00 | 47.85 | 262.72 | -129.44 | -0.007 | ||
| Number of Transactions | 614.11 | 237.05 | 1423 | 88 | 0.654 |
| Mean: Ten-Year | Stdev.: Ten-Year | Max.: Ten-Year | Min.: Ten-Year | Ten-Year
|
|||
|---|---|---|---|---|---|---|---|
| Daily Yield |
6.26 | 0.74 | 8.03 | 4.16 | 0.997 | ||
| Daily Yield
Change |
-0.04 | 5.99 | 33.60 | -23.00 | 0.044 | ||
| Number of Buys | 281.70 | 109.03 | 693 | 34 | 0.710 | ||
| Number of Sells | 260.55 | 102.44 | 553 | 22 | 0.692 | ||
| Order Flow | 21.14 | 36.45 | 153 | -105 | 0.160 | ||
| Abnormal Order Flow | 0.00 | 40.29 | 142.98 | -105.38 | 0.038 | ||
| Number of Transactions | 542.25 | 208.41 | 1246 | 73 | 0.718 |
In this table we report the number
of observations, source, and release time for the 25 U.S.
macroeconomic announcements in our sample. We also report summary
statistics for the corresponding standard deviation across
professional forecasts, our proxy for dispersion of beliefs among
market participants, whenever available. Specifically, we report
the mean, standard deviation, Spearman rank correlation with the
Nonfarm Payroll standard deviation (![]() Payroll
Payroll![]() ), and the first-order
autocorrelation coefficient (
), and the first-order
autocorrelation coefficient (![]() ) for each
series
) for each
series ![]() . A "*", "**", or "***" indicate the latter two measures'
significance at 10%, 5%, or 1% level, respectively. The release
time in the table, in Eastern Standard Time (EST, with Daylight
savings time starting on the first Sunday of April and ending on
the last Sunday of October), is constant throughout the sample
except in the following circumstances: In 01/94, the personal
income announcement time moved from 10:00 a.m. to 8:30 a.m.;
beginning in 01/96, consumer credit was released regularly at 3:00
p.m. while prior to this date, its release times varied; in 12/93,
the personal consumption expenditures announcement time moved from
10:00 a.m. to 8:30 a.m.; whenever GDP is released on the same day
as durable goods orders, the durable goods orders announcement is
moved to 10:00 a.m.; on 07/96 the durable goods orders announcement
was released at 9:00 a.m.; in 01/97, the business inventory
announcement was moved from 10:00 a.m. to 8:30 a.m.; beginning in
3/28/94, the fed funds rate was released regularly at 2:15 p.m.,
while prior to this date, the release times varied. The sources for
the MMS data are: Bureau of Labor Statistics (BLS), Bureau of the
Census (BC), Bureau of Economic Analysis (BEA), Federal Reserve
Board (FRB), National Association of Purchasing Managers (NAPM),
Conference Board (CB), Financial Management Office (FMO), and
Employment and Training Administration (ETA). The standard
deviation across professional forecasts of Capacity Utilization,
Personal Income, Consumer Credit, Personal Consumption
Expenditures, Business Inventories, Government Budget, and Target
Federal Funds Rate (announcements 7, 8, 9, 11, 15, 16, and 24) is
not available.
. A "*", "**", or "***" indicate the latter two measures'
significance at 10%, 5%, or 1% level, respectively. The release
time in the table, in Eastern Standard Time (EST, with Daylight
savings time starting on the first Sunday of April and ending on
the last Sunday of October), is constant throughout the sample
except in the following circumstances: In 01/94, the personal
income announcement time moved from 10:00 a.m. to 8:30 a.m.;
beginning in 01/96, consumer credit was released regularly at 3:00
p.m. while prior to this date, its release times varied; in 12/93,
the personal consumption expenditures announcement time moved from
10:00 a.m. to 8:30 a.m.; whenever GDP is released on the same day
as durable goods orders, the durable goods orders announcement is
moved to 10:00 a.m.; on 07/96 the durable goods orders announcement
was released at 9:00 a.m.; in 01/97, the business inventory
announcement was moved from 10:00 a.m. to 8:30 a.m.; beginning in
3/28/94, the fed funds rate was released regularly at 2:15 p.m.,
while prior to this date, the release times varied. The sources for
the MMS data are: Bureau of Labor Statistics (BLS), Bureau of the
Census (BC), Bureau of Economic Analysis (BEA), Federal Reserve
Board (FRB), National Association of Purchasing Managers (NAPM),
Conference Board (CB), Financial Management Office (FMO), and
Employment and Training Administration (ETA). The standard
deviation across professional forecasts of Capacity Utilization,
Personal Income, Consumer Credit, Personal Consumption
Expenditures, Business Inventories, Government Budget, and Target
Federal Funds Rate (announcements 7, 8, 9, 11, 15, 16, and 24) is
not available.
| Quarterly Announcements: Obs. | Quarterly Announcements: Source | Quarterly Announcements: Time | Quarterly Announcements: Mean | Quarterly Announcements: Stdev. | Quarterly Announcements: |
|
|
|---|---|---|---|---|---|---|---|
| 1- GDP Advance | 36 | BEA | 8:30 | 0.480 | 0.170 | 0.162* | -0.181 |
| 2- GDP Preliminary | 34 | BEA | 8:30 | 0.313 | 0.178 | 0.014 | 0.192 |
| 3- GDP Final | 35 | BEA | 8:30 | 0.128 | 0.051 | 0.083 | 0.250 |
| Monthly Announcements: Obs. | Monthly Announcements: Source | Monthly Announcements: Time | Monthly Announcements: Mean | Monthly Announcements: Stdev. | Monthly Announcements: |
|
|
|---|---|---|---|---|---|---|---|
| Real Activity: 4- Nonfarm Payroll | 108 | BLS | 8:30 | 41.814 | 14.212 | 1.000 | 0.424*** |
| Real Activity: 5- Retail Sales | 108 | BC | 8:30 | 0.302 | 0.158 | 0.109 | 0.047 |
| Real Activity: 6- Industrial Production | 107 | FRB | 9:15 | 0.183 | 0.135 | 0.236** | 0.358*** |
| Real Activity: 7- Capacity Utilization | 107 | FRB | 9:15 | n.a. | n.a. | n.a. | n.a. |
| Real Activity: 8- Personal Income | 105 | BEA | 10:00/8:30 | n.a. | n.a. | n.a. | n.a. |
| Real Activity: 9- Consumer Credit | 108 | FRB | 15:00 | n.a. | n.a. | n.a. | n.a. |
| Consumption: 10- New Home Sales | 106 | BC | 10:00 | 19.270 | 10.235 | 0.151 | 0.099 |
| Consumption: 11- Pers. Cons. Exp. | 107 | BEA | 10:00/8:30 | n.a. | n.a. | n.a. | n.a. |
| Investment: 12- Durable Goods Orders | 106 | BC | 8:30/9:00/10:00 | 1.034 | 0.333 | 0.077 | 0.412*** |
| Investment: 13- Factory Orders | 105 | BC | 10:00 | 0.587 | 0.577 | 0.219** | 0.015 |
| Investment: 14- Construction Spending | 105 | BC | 10:00 | 0.499 | 0.253 | 0.176* | 0.192*** |
| Investment: 15- Business Inventories | 106 | BC | 10:00/8:30 | n.a. | n.a. | n.a. | n.a. |
| Government Purchases: 16- Government Budget | 107 | FMO | 14:00 | n.a. | n.a. | n.a. | n.a. |
| Net Exports: 17- Trade Balance | 107 | BEA | 8:30 | 0.790 | 0.851 | 0.122 | 0.018 |
| Prices: 18- Producer Price Index | 108 | BLS | 8:30 | 0.130 | 0.049 | 0.186* | 0.287*** |
| Prices: 19- Consumer Price Index | 107 | BLS | 8:30 | 0.086 | 0.051 | 0.146 | 0.221** |
| Forward-Looking: 20- Consumer Conf. Index | 106 | CB | 10:00 | 1.646 | 0.609 | 0.079 | 0.230** |
| Forward-Looking: 21- NAPM Index | 107 | NAPM | 10:00 | 0.961 | 0.303 | 0.242** | 0.382*** |
| Forward-Looking: 22- Housing Starts | 106 | BC | 8:30 | 0.045 | 0.038 | 0.160 | 0.246*** |
| Forward-Looking: 23- Index of Leading Ind. | 108 | CB | 8:30 | 0.202 | 0.137 | 0.134 | 0.480*** |
| Six-Week Announcements: Obs. | Six-Week Announcements: Source | Six-Week Announcements: Time | Six-Week Announcements: Mean | Six-Week Announcements: Stdev. | Six-Week Announcements: |
|
|
|---|---|---|---|---|---|---|---|
| 24- Target Fed Funds Rate | 71 | FRB | 14:15 | n.a. | n.a. | n.a. | n.a. |
In this table we report estimates of the following equation:
| Announcement | Two-Year: b_{h} | Two-Year: b_{m} | Two-Year: b_{l} | Two-Year: b_ {h}-b_{l} | Two-Year: |
|---|---|---|---|---|---|
| Nonfarm Payroll Employment | 366.687 | 362.978 | 374.983 | -8.296 | 86.05% |
| Nonfarm Payroll Employment: s.e. | 5.729 | 4.811 | 5.773 | 8.133 | |
| Influential Announcements | 317.836 | 372.472 | 409.360 | -91.524*** | 86.80% |
| Influential Announcements: s.e. | 5.596 | 4.684 | 5.665 | 7.963 | |
| All Announcements | 321.120 | 362.468 | 421.500 | -100.38*** | 86.95% |
| All Announcements: s.e. | 5.543 | 4.655 | 5.659 | 7.921 |
| Announcement | Five-Year: b_{h} | Five-Year: b_{m} | Five-Year: b_{l} | Five-Year: b_ {h}-b_{l} | Five-Year: |
|---|---|---|---|---|---|
| Nonfarm Payroll Employment | 603.503 | 570.535 | 648.080 | -44.576*** | 85.73% |
| Nonfarm Payroll Employment: s.e. | 9.475 | 7.958 | 9.541 | 13.447 | |
| Influential Announcements | 562.774 | 626.650 | 599.127 | -36.353*** | 85.54% |
| Influential Announcements: s.e. | 9.617 | 8.044 | 9.721 | 13.675 | |
| All Announcements | 534.212 | 607.237 | 657.696 | -123.484*** | 85.91% |
| All Announcements: s.e. | 9.459 | 7.937 | 9.642 | 13.507 |
| Announcement | Ten-Year: b_{h} | Ten-Year: b_{m} | Ten-Year: b_{l} | Ten-Year: b_ {h}-b_{l} | Ten-Year: |
|---|---|---|---|---|---|
| Nonfarm Payroll Employment | 530.563 | 505.908 | 570.922 | -40.359*** | 85.56% |
| Nonfarm Payroll Employment: s.e. | 8.353 | 7.015 | 8.411 | 11.854 | |
| Influential Announcements | 496.024 | 554.288 | 527.157 | -31.132*** | 85.55% |
| Influential Announcements: s.e. | 8.490 | 7.096 | 8.576 | 12.068 | |
| All Announcements | 452.617 | 546.248 | 584.260 | -131.643*** | 86.20% |
| All Announcements: s.e. | 8.266 | 6.931 | 8.420 | 11.799 |
In this table we report estimates of the following regression model (Eq. (11)):
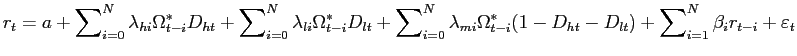 ,
,| Announcement |
|
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Nonfarm Payroll | -0.213*** | -0.182*** | -0.121*** | -0.092*** | -0.161** | -0.182*** | -0.072 | 28.54% | 6.66% | 21.69% |
| Nonfarm Payroll: s.e. | 0.033 | 0.025 | 0.034 | 0.048 | 0.067 | 0.050 | 0.056 | |||
| Influential | -0.140*** | -0.108*** | -0.080*** | -0.060*** | -0.106*** | -0.096*** | -0.049** | 14.61% | 10.65% | 15.52% |
| Influential: s.e. | 0.016 | 0.010 | 0.010 | 0.019 | 0.031 | 0.022 | 0.022 | |||
| All | -0.122*** | -0.093*** | -0.098*** | -0.024 | -0.152*** | -0.086*** | -0.086*** | 15.46% | 16.92% | 15.83% |
| All: s.e. | 0.017 | 0.012 | 0.014 | 0.022 | 0.032 | 0.024 | 0.027 |
| Announcement |
|
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Nonfarm Payroll | -0.210*** | -0.153*** | -0.085*** | -0.125*** | -0.285*** | -0.136*** | 0.019 | 41.38% | 9.65% | 23.30% |
| Nonfarm Payroll: s.e. | 0.029 | 0.022 | 0.027 | 0.040 | 0.078 | 0.049 | 0.062 | |||
| Influential | -0.151*** | -0.122*** | -0.087*** | -0.064*** | -0.142*** | -0.106*** | -0.050** | 19.14% | 11.97% | 20.31% |
| Influential: s.e. | 0.014 | 0.010 | 0.010 | 0.018 | 0.036 | 0.022 | 0.025 | |||
| All | -0.155*** | -0.097*** | -0.102*** | -0.053*** | -0.167*** | -0.079*** | -0.083*** | 21.37% | 18.76% | 19.40% |
| All: s.e. | 0.017 | 0.012 | 0.013 | 0.022 | 0.041 | 0.027 | 0.029 |
| Announcement |
|
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Nonfarm Payroll | -0.170*** | -0.129*** | -0.071 | -0.099 | -0.192** | -0.269*** | -0.017 | 15.10% | 1.02% | 10.29% |
| Nonfarm Payroll: s.e. | 0.043 | 0.032 | 0.043 | 0.061 | 0.093 | 0.058 | 0.079 | |||
| Influential | -0.081*** | -0.093*** | -0.079*** | -0.002 | -0.075** | -0.109*** | -0.053 | 2.83% | 4.72% | 6.05% |
| Influential: s.e. | 0.018 | 0.013 | 0.013 | 0.025 | 0.035 | 0.027 | 0.042 | |||
| All | -0.075*** | -0.086*** | -0.071*** | -0.004 | -0.109** | -0.119*** | -0.097** | 3.82% | 4.43% | 6.16% |
| All: s.e. | 0.023 | 0.017 | 0.019 | 0.029 | 0.053 | 0.033 | 0.038 |
In this table we report estimates of the following regression model (Eq. (12)):
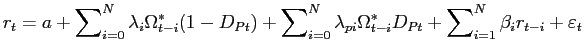 ,
,| Announcement |
|
|
||||||
|---|---|---|---|---|---|---|---|---|
| Nonfarm Payroll | -0.108*** | -0.087*** | -0.021 | -0.131*** | -0.013 | 15.31% | 6.47% | 14.72% |
| Nonfarm Payroll: s.e. | 0.021 | 0.027 | 0.034 | 0.041 | 0.064 | |||
| Influential | -0.103*** | -0.112*** | 0.009 | -0.075*** | -0.059*** | 15.34% | 12.29% | 13.98% |
| Influential: s.e. | 0.008 | 0.008 | 0.011 | 0.016 | 0.019 | |||
| All | -0.102*** | -0.109*** | 0.007 | -0.096*** | -0.059*** | 16.00% | 13.24% | 13.99% |
| All: s.e. | 0.011 | 0.006 | 0.013 | 0.023 | 0.015 |
| Announcement |
|
|
||||||
|---|---|---|---|---|---|---|---|---|
| Nonfarm Payroll | -0.124*** | -0.168*** | 0.044** | -0.121*** | -0.242*** | 21.03% | 19.61% | 21.37% |
| Nonfarm Payroll: s.e. | 0.017 | 0.025 | 0.019 | 0.043 | 0.062 | |||
| Influential | -0.117*** | -0.137*** | 0.020* | -0.095*** | -0.137*** | 19.88% | 20.88% | 20.76% |
| Influential: s.e. | 0.007 | 0.008 | 0.011 | 0.017 | 0.020 | |||
| All | -0.115*** | -0.131*** | 0.016 | -0.107*** | -0.115*** | 20.29% | 20.48% | 20.70% |
| All: s.e. | 0.011 | 0.006 | 0.012 | 0.024 | 0.016 |
| Announcement |
|
|
||||||
|---|---|---|---|---|---|---|---|---|
| Nonfarm Payroll | -0.087*** | -0.053* | -0.034 | -0.181*** | -0.020 | 6.74% | 3.59% | 7.07% |
| s.e. | 0.025 | 0.030 | 0.048 | 0.049 | 0.088 | |||
| Influential | -0.086*** | -0.086*** | 0.000 | -0.083*** | -0.086*** | 6.73% | 5.73% | 6.52% |
| Influential: s.e. | 0.010 | 0.011 | 0.015 | 0.021 | 0.026 | |||
| All | -0.077*** | -0.090*** | 0.013 | -0.103*** | -0.076*** | 7.08% | 5.99% | 6.49% |
| All: s.e. | 0.014 | 0.009 | 0.017 | 0.030 | 0.019 |
In this table we report estimates of the following regression model (Eq. (14)):
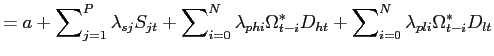
|
||
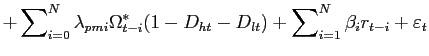 ,
, |
| Announcement |
|
|
|
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonfarm Pay. | 6.279*** | -0.141** | -0.117** | -0.116 | -0.025* | 0.087 | -0.301*** | -0.055 | 7.81% | -8.04% | 8.51% | 40.87% |
| Nonfarm Pay: s.e. | 0.883 | 0.060 | 0.047 | 0.092 | 0.014 | 0.151 | 0.113 | 0.176 | ||||
| Influential | 2.805*** | -0.179*** | -0.08*** | -0.106*** | -0.073*** | -0.152*** | -0.063** | -0.040 | 15.86% | 9.57% | 13.54% | 30.27% |
| Influential: s.e. | 0.322 | 0.019 | 0.012 | 0.016 | 0.024 | 0.047 | 0.031 | 0.036 | ||||
| All | 1.490*** | -0.165*** | -0.092*** | -0.093*** | -0.072*** | -0.130*** | -0.030 | -0.055** | 16.65% | 14.50% | 13.79% | 26.70% |
| All: s.e. | 0.196 | 0.015 | 0.010 | 0.012 | 0.020 | 0.034 | 0.026 | 0.027 |
| Announcement |
|
|
|
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonfarm Pay. | 6.028*** | -0.220*** | -0.179*** | -0.117** | -0.103*** | -0.209 | -0.253*** | -0.087 | 11.45% | -4.37% | 14.46% | 46.68% |
| Nonfarm Pay: s.e. | 0.855 | 0.065 | 0.042 | 0.049 | 0.034 | 0.161 | 0.097 | 0.138 | ||||
| Influential | 2.670*** | -0.184*** | -0.111*** | -0.124*** | -0.060*** | -0.202*** | -0.129*** | -0.083** | 24.16% | 15.27% | 21.45% | 34.00% |
| Influential: s.e. | 0.318 | 0.017 | 0.012 | 0.015 | 0.023 | 0.048 | 0.030 | 0.038 | ||||
| All | 1.259*** | -0.183*** | -0.111*** | -0.124*** | -0.059*** | -0.192*** | -0.100*** | -0.083*** | 23.94% | 24.78% | 21.83% | 31.27% |
| All: s.e. | 0.194 | 0.014 | 0.010 | 0.012 | 0.019 | 0.039 | 0.025 | 0.027 |
| Announcement |
|
|
|
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonfarm Pay. | 4.195*** | -0.239** | -0.017 | 0.076 | -0.315** | -0.157 | 0.040 | 0.109 | -10.27% | -3.53% | 0.26% | 22.81% |
| Nonfarm Pay: s.e. | 0.815 | 0.097 | 0.081 | 0.105 | 0.143 | 0.206 | 0.178 | 0.224 | ||||
| Influential | 2.445*** | -0.103*** | -0.068*** | -0.072*** | -0.031 | -0.130** | -0.064* | -0.038 | 3.55% | 5.33% | 5.58% | 16.95% |
| Influential: s.e. | 0.329 | 0.024 | 0.018 | 0.023 | 0.033 | 0.062 | 0.039 | 0.057 | ||||
| All | 1.329*** | -0.117*** | -0.079*** | -0.068*** | -0.049** | -0.120** | -0.070** | -0.014 | 4.26% | 6.71% | 6.31% | 15.04% |
| All: s.e. | 0.199 | 0.021 | 0.014 | 0.018 | 0.021 | 0.051 | 0.032 | 0.037 |
In this table we report estimates of the following regression model (Eq. (14)):
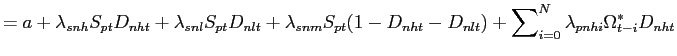
|
||
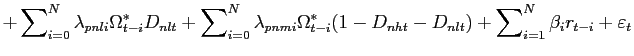 ,
, |
| Ann. |
|
|
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Non. P. | 6.861*** | 7.569*** | 5.205*** | -0.132* | -0.164*** | -0.108* | -0.105 | -0.378*** | 0.041 | 32.67% | 39.24% | 39.00% | 46.88% |
| Non. P: s.e. | 1.678 | 1.288 | 1.609 | 0.067 | 0.050 | 0.062 | 0.191 | 0.140 | 0.152 | ||||
| In. P. | 1.672* | 1.468 | 0.820 | -0.075* | -0.106*** | -0.130** | 0.037 | 0.154* | -0.008 | 2.38% | 10.93% | 9.50% | 23.40% |
| In. P: s.e. | 0.916 | 1.035 | 1.337 | 0.043 | 0.034 | 0.058 | 0.092 | 0.090 | 0.116 | ||||
| Cap. U. | 1.643 | 1.399 | 2.123 | -0.072 | -0.092*** | -0.097 | 0.113 | 0.075 | 0.052 | 9.01% | 18.20% | 18.80% | 25.73% |
| Cap. U: s.e. | 1.011 | 0.866 | 1.521 | 0.045 | 0.030 | 0.069 | 0.105 | 0.070 | 0.114 |
| Ann. |
|
|
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Non. P. | 5.959*** | 5.513*** | 4.267*** | -0.196*** | -0.212*** | -0.210*** | -0.411** | -0.343*** | -0.290*** | 26.77% | 39.16% | 38.21% | 51.06% |
| Non. P: s.e. | 1.580 | 1.202 | 1.546 | 0.052 | 0.053 | 0.052 | 0.158 | 0.131 | 0.111 | ||||
| Ind P. | 1.251 | 0.233 | 0.916 | -0.099** | -0.157*** | -0.122* | -0.035 | 0.048 | -0.096 | 2.44% | 22.80% | 20.82% | 23.05% |
| In. P: s.e. | 0.963 | 1.125 | 1.597 | 0.043 | 0.034 | 0.067 | 0.113 | 0.094 | 0.138 | ||||
| Cap. U. | 1.466 | 0.152 | 1.956 | -0.128** | -0.152*** | -0.085 | -0.053 | 0.065 | -0.135 | 7.66% | 27.80% | 24.85% | 28.06% |
| Cap. U: s.e. | 0.904 | 0.962 | 1.588 | 0.053 | 0.031 | 0.063 | 0.106 | 0.085 | 0.163 |
| Ann. |
|
|
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Non. P. | 3.702** | 3.165** | 4.225** | -0.139 | -0.078 | 0.036 | -0.566** | 0.267 | 0.116 | 20.88% | 21.29% | 19.84% | 27.62% |
| Non. P: s.e. | 1.648 | 1.209 | 1.615 | 0.101 | 0.087 | 0.085 | 0.220 | 0.182 | 0.183 | ||||
| Ind. P. | 0.281 | 2.025* | 1.940 | 0.059 | -0.117 | -0.131* | 0.020 | -0.071 | 0.036 | 3.70% | 5.47% | 7.69% | -0.96% |
| In. P: s.e. | 0.991 | 1.084 | 1.538 | 0.077 | 0.073 | 0.078 | 0.142 | 0.11 | 0.143 | ||||
| Cap. U. | 1.365 | 1.174 | 2.456* | -0.013 | -0.057 | -0.148** | 0.013 | -0.022 | -0.09 | 8.15% | 7.44% | 10.64% | 6.03% |
| Cap. U: s.e. | 0.994 | 1.008 | 1.443 | 0.089 | 0.058 | 0.074 | 0.137 | 0.103 | 0.135 |
In this figure we plot the market
liquidity parameter defined in Proposition 1,
![]() in Figure 1A, and the difference between the sensitivity of the equilibrium price to the order flow in the absence and in the presence of a public signal
in Figure 1A, and the difference between the sensitivity of the equilibrium price to the order flow in the absence and in the presence of a public signal
![]() in Figure 1B, as a function of the degree of
correlation of the speculators' signals,
in Figure 1B, as a function of the degree of
correlation of the speculators' signals, ![]() , in
the presence of M = 1, 2, or 4 speculators, when
, in
the presence of M = 1, 2, or 4 speculators, when
![]() . According to Proposition 1,
. According to Proposition 1,
![]() , while
, while
![$ \lambda_{p}=\frac{\alpha^{\frac{1}{2}}\sigma_{v}\left( \sigma_{p}^{2} -\sigma_{v}^{2}\right) ^{\frac{1}{2}}}{\sigma_{u}\sigma_{p}[2+(M-1)\gamma _{p}]}$](img2fig1eq.giforig874.gif) in Proposition 2, where
in Proposition 2, where
![$ \gamma_{p}=\frac{\sigma_{p}^{2}\left( \sigma_{v}^{2}-M\chi\right) -\sigma_{v}^{4} } {\sigma_{p}^{2}\left[ \sigma_{v}^{2}+M\left( M-1\right) \chi\right] -\sigma_{v}^{4}}$](img331.giforig874.gif) and
and
![]() . Since
. Since
![]() ,
,
![]() , and
, and
![]() , the range of correlations
compatible with a positive definite
, the range of correlations
compatible with a positive definite ![]() is obtained by varying the
parameter
is obtained by varying the
parameter
![]() within the interval [0, 10] when M = 2, and the interval [0, 5] when M = 4.
within the interval [0, 10] when M = 2, and the interval [0, 5] when M = 4.
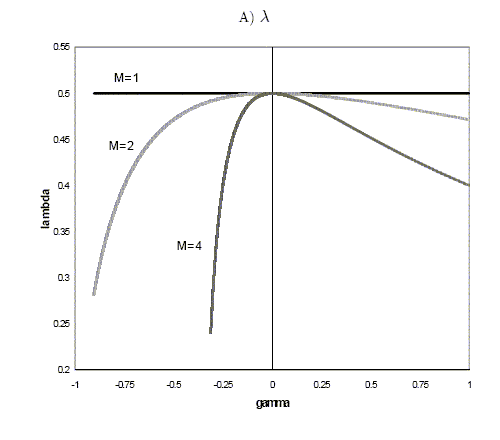
In this figure we plot the market liquidity parameter defined in
Proposition 1,
![]() . We construct a simple numerical example by setting
. We construct a simple numerical example by setting
![]() .
We then vary the range of signal correlations
.
We then vary the range of signal correlations ![]() (from very highly negative to
very highly positive) when the number of informed traders,
(from very highly negative to
very highly positive) when the number of informed traders,
![]() ,
, ![]() , and
, and ![]() . Multiple, perfectly heterogeneously informed
speculators (
. Multiple, perfectly heterogeneously informed
speculators (![]() )
collectively trade as cautiously as a monopolist speculator. Under
these circumstances, adverse selection is at its highest, and
market liquidity at its lowest (
)
collectively trade as cautiously as a monopolist speculator. Under
these circumstances, adverse selection is at its highest, and
market liquidity at its lowest (
![]() ). A greater
number of competing speculators improves market depth, but
significantly so only if accompanied by more correlated private
signals. However, ceteris paribus, the improvement in market
liquidity is more pronounced (and informed trading less cautious)
when speculators' private signals are negatively correlated. When
). A greater
number of competing speculators improves market depth, but
significantly so only if accompanied by more correlated private
signals. However, ceteris paribus, the improvement in market
liquidity is more pronounced (and informed trading less cautious)
when speculators' private signals are negatively correlated. When
![]() , each
speculator expects her competitors' trades to be negatively
correlated to her own (pushing
, each
speculator expects her competitors' trades to be negatively
correlated to her own (pushing ![]() against her signal), hence trading on it to be
more profitable.
against her signal), hence trading on it to be
more profitable.
More detail. Figure 1A plots lambda on the vertical axis with range [0.2, 0.55] and gamma on the horizontal axis with range [-1,+1]. For M=1, lambda is constant at 0.5 for all values of gamma. For M=2, lambda starts at about 0.28 for gamma=-0.9, with lambda increasing rapidly to 0.5 at gamma=0, then dropping off slowly to about 0.48 at gamma=1. For M=4, lambda starts at about 0.23 for gamma=-0.3, with lambda increasing rapidly to 0.5 at gamma=0, then dropping off to about 0.4 at gamma=1.
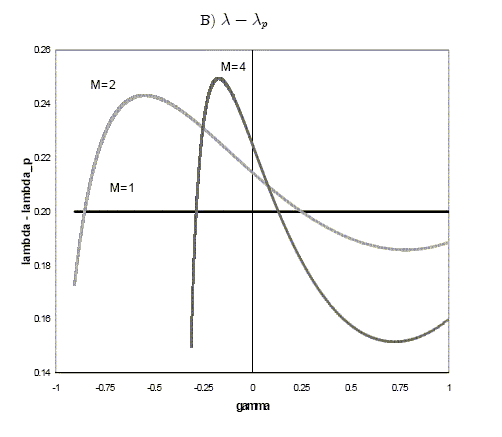
In Figure 1B we plot the difference between the sensitivity of
the equilibrium price to the order flow in the absence and in the
presence of a public signal ![]() ,
,
![]() , as
a function of the degree of correlation of the speculators'
signals,
, as
a function of the degree of correlation of the speculators'
signals, ![]() , in the
presence of
, in the
presence of ![]() ,
,
![]() , or
, or ![]() speculators, when
speculators, when
![]() and the public
signal's noise
and the public
signal's noise
![]() . The
increase in market depth is greater when
. The
increase in market depth is greater when ![]() is negative and the number of
speculators (
is negative and the number of
speculators (![]() ) is high. In
those circumstances, the availability of a public signal reinforces
speculators' existing incentives to place market orders on their
private signals
) is high. In
those circumstances, the availability of a public signal reinforces
speculators' existing incentives to place market orders on their
private signals ![]() more aggressively. However, greater
more aggressively. However, greater
![]() ,
ceteris paribus, increases
,
ceteris paribus, increases
![]() , since the
poorer quality of
, since the
poorer quality of ![]() (lower information-to-noise ratio
(lower information-to-noise ratio
![]() ) induces the
market makers to rely more heavily on
) induces the
market makers to rely more heavily on
![]() to set
market-clearing prices, hence the speculators to trade less
aggressively.
to set
market-clearing prices, hence the speculators to trade less
aggressively.
More detail. Figure 1B plots lambda-lambda_p on the vertical axis with range [0.14, 0.26] and gamma on the horizontal axis with range [-1,+1]. For M=1, lambda-lambda_p is constant at 0.2 for all values of gamma. For M=2, lambda-lambda_p starts at about 0.17 for gamma=-0.9, with lambda-lambda_p increasing rapidly to about 0.24 at gamma about -0.6, then dropping off slowly to about 0.19 at gamma=0.75, and increasing slightly to gamma=1. For M=4, lambda-lambda_p starts at about 0.15 for gamma=-0.3, with lambda-lambda_p increasing rapidly to about 0.25 at gamma about -0.2, then dropping off to about 0.15 at gamma=0.75, and increasing slightly to gamma=1.
1. According to Goodhart and O'Hara (1997, p. 102), ``one puzzle in the study of asset markets, either nationally or internationally, is that so little of the movements in such markets can be ascribed to identified public `news'. In domestic (equity) markets this finding is often attributed to private information being revealed.'' This friction has been recently studied by Brandt and Kavajecz (2004) and Green (2004) in the U.S. Treasury bond market, by Andersen and Bollerslev (1998) and Evans and Lyons (2002, 2003, 2004) in the foreign exchange market, by Berry and Howe (1994) in the U.S. stock market, and by Brenner, Pasquariello, and Subrahmanyam (2005) in the U.S. corporate bond market, among others. Return to text
2. Foster and Viswanathan (1996) and Back, Cao, and Willard (2000) extend Kyle (1985) to analyze the impact of competition among heterogeneously informed traders on market liquidity and price volatility in discrete-time and continuous-time models of intraday trading, respectively. Foster and Viswanathan (1993) show that, when the beliefs of perfectly informed traders are represented by elliptically contoured distributions, price volatility and trading volume depend on the surprise component of public information. Yet, neither model's equilibrium is in closed-form, except the (analytically intractable) inverse incomplete gamma function in Back et al. (2000). Hence, their implications are sensitive to the chosen calibration parameters. Further, neither model, by its dynamic nature, generates unambiguous comparative statics for the impact of information heterogeneity or the availability of public information on market liquidity. Finally, neither model can be easily generalized to allow for both a public signal of the traded asset's payoff and less than perfectly correlated private information. Return to text
3. For instance, heterogeneously informed investors may not trade immediately after public news are released but instead wait to preserve (and exploit) their informational advantage as long (and as much) as possible, as in Foster and Viswanathan (1996). Return to text
4. The assumption that the total
amount of information available to speculators is fixed (
![]() ) implies that
) implies that
![]() and
and
![]() , hence
, hence
![]() . Further, the absolute bound to the largest negative
private signal correlation
. Further, the absolute bound to the largest negative
private signal correlation ![]() compatible with a positive definite
compatible with a positive definite
![]() ,
,
![]() , is a decreasing
function of
, is a decreasing
function of ![]() . Return to text
. Return to text
5. This contrasts with the numerical examples of the dynamics of market depth reported in Foster and Viswanathan (1996, Figure 1C) and Back et al. (2000, Figure 3A). Return to text
6. Admati and Pfleiderer (1988) and Foster and Viswanathan (1990) consider dynamic models of intraday trading in which the private information of either perfectly competitive insiders or a monopolistic insider is either fully or partially revealed by the end of the trading period. McKelvey and Page (1990) provide experimental evidence that individuals make inferences from publicly available information using Bayesian updating. Diamond and Verrecchia (1991) argue that the disclosure of public information may reduce the volatility of the order flow, leading some market makers to exit. Kim and Verrecchia (1994) show that, in the absence of better informed agents but in the presence of better information processors with homogeneous priors, the arrival of a public signal leads to greater information asymmetry and lower market liquidity. Return to text
7. Specifically, it can be shown
that the one-shot equilibrium in Foster and Viswanathan (1993,
Proposition 1) is a special case of our Proposition 2 when private
signal correlations ![]() for any ECC. Return to text
for any ECC. Return to text
8. In our sample period (1992 to
2000), the major interdealer brokers in the U.S. Treasury market
are Cantor Fitzgerald Inc., Garban Ltd., Hilliard Farber & Co.
Inc., Liberty Brokerage Inc., RMJ Securities Corp., and Tullet and
Tokyo Securities Inc. Cantor Fitzgerald's share of the interdealer
Treasury market is about ![]() over our sample period (Goldreich et al., 2005).
Nevertheless, Cantor Fitzgerald is a dominant player only in the
``long end'' of the Treasury yield curve, which we do not study in
depth in this paper. Return to
text
over our sample period (Goldreich et al., 2005).
Nevertheless, Cantor Fitzgerald is a dominant player only in the
``long end'' of the Treasury yield curve, which we do not study in
depth in this paper. Return to
text
9. Andersen and Bollerslev (1998), among others, refer to the Nonfarm Payroll report as the ``king'' of announcements because of the significant sensitivity of most asset markets to its release. Return to text
10. In unreported analysis, we show that these announcements represent the most important information events in the U.S. Treasury Market, i.e., the only ones having a statistically significant impact on day-to-day bond yield changes, consistent with Fleming and Remolona (1997), among others. Return to text
11. See Croushore and Stark (1999, 2001) for details of this database and examples of empirical applications. The database is publicly available on the internet at http://www.phil.frb.org/econ/forecast/reaindex.html. Return to text
12. Much of this evidence stems from the analysis of either GDP or the RTDS variables listed above. The evidence is more controversial for money stock announcements. For instance, Mankiw, Runkle, and Shapiro (1984) and Mork (1990) find that the preliminary growth rates of several Federal Reserve's money aggregates are not efficient predictors of the growth rates of finally-revised data. Yet, according to Kavajecz and Collins (1995), the bias in preliminary monetary data may be attributed either to the specific seasonal adjustment procedure used by the Federal Reserve or to a different temporal aggregation than for finally-revised, not-seasonally adjusted data. Monetary aggregates are not included in our database. Return to text
13. Indeed, the distributional
assumptions in Section 2.1 imply that
![]() in both Propositions 1
and 2. Return to text
in both Propositions 1
and 2. Return to text
14. Our results are also robust to
different specifications of Eq. (8). For
example, we sample bond yields each time there is a transaction,
rather than at thirty-minute intervals. We also sample bond yields
at an `` optimal'' frequency determined according to the procedure
of Bandi and Russell (2005). The evidence presented below is
qualitatively and quantitatively similar to that obtained using
these alternative sampling procedures, as well as using the
aggregate raw (rather than unanticipated) order flow,
![]() . The
robustness of our results reflects the fact that aggregate
unanticipated order flow,
. The
robustness of our results reflects the fact that aggregate
unanticipated order flow,
![]() , is
very closely related to
, is
very closely related to
![]() . Indeed,
regardless of the selected specification, the resulting
. Indeed,
regardless of the selected specification, the resulting
![]() from Eq. (8) are lower than
from Eq. (8) are lower than ![]() . Return to text
. Return to text
15. Nonetheless, the inference that
follows is robust to smaller or bigger values for ![]() . Return
to text
. Return
to text
16. We estimate realized volatility applying the procedure of Andersen, Bollerslev, Diebold, and Labys (2003) to yield mid-quotes sampled at an ``optimal'' frequency determined according to Bandi and Russel (2005). Return to text
17. Presumably, the number of
informed traders might increase as the public announcement date
approaches. We do not include this product term when measuring
dispersion of beliefs only with forecasts of Nonfarm Payroll
announcements (i.e., ![]() ), since then we only use the Fridays before
the announcement dates to control for potential day-of-the-week
effects. Return to text
), since then we only use the Fridays before
the announcement dates to control for potential day-of-the-week
effects. Return to text
18. The resulting adjusted
![]() from the
introduction of this cross term in Eq. (8) for
five-year bond yield differentials increases from
from the
introduction of this cross term in Eq. (8) for
five-year bond yield differentials increases from ![]() ,
, ![]() , and
, and ![]() (i.e.,
(i.e., ![]() of Table 4) to
of Table 4) to ![]() ,
, ![]() , and
, and ![]() when measuring the dispersion
of beliefs with the standard deviation of professional forecasts of
Nonfarm Payroll (
when measuring the dispersion
of beliefs with the standard deviation of professional forecasts of
Nonfarm Payroll (![]() ),
``influential'' (
),
``influential'' (![]() ),
and all available macroeconomic news announcements (
),
and all available macroeconomic news announcements (![]() ), respectively. Return to text
), respectively. Return to text
19. The history of auction dates we use in the analysis is available on the U.S. Treasury website, at http://www.publicdebt.treas.gov/of/ofaicqry.htm. Return to text
20. The NBER's Business Cycle Dating Committee mentions that no single macroeconomic variable is the most important predictor of recessions and expansions (e.g., see http://www.nber.org/cycles/recessions.html). The committee takes into account real GDP, real income, employment, industrial production, and wholesale and retail sales to determine whether the U.S. is in a recession or in an expansion. When running a horse race between macroeconomic variables and financial variables to predict the business cycle, Estrella and Mishkin (1998) do not even consider Nonfarm Payroll announcements. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text