
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 876, September 2006 --- Screen Reader Version*
An Empirical Analysis of Specialist Trading Behavior at the New York Stock Exchange
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
I establish stylized empirical facts about the trading behavior of New York Stock Exchange specialists. Specifically, I look at the effect of future price movements, the specialist's explicit role, and the specialist's inventory levels on specialist trading behavior. The motivation for this empirical study is to infer whether the specialist behaves like an active investor who has an information advantage which he obtains while acting as a broker for other traders. If this were the case, one would expect that the specialist would engage in a profit maximizing strategy, buying low and selling high, which is opposite to the prediction of the traditional inventory model.
I find that specialists behave like active investors who seek to buy stocks when prices are low and to sell when prices are high. I also find that when specialists are not performing their trading obligations of being on the opposite side of the market they are in almost 85 percent of their trades, buying low and selling high. The findings of this paper indicate that the NYSE specialist is best represented in theoretical models as a constrained profit maximizing, informed investor rather than as a zero profit trader.
Keywords: Market microstructure; Specialist; NYSE; Market maker
JEL classification: G10; G14
1. Introduction
This paper examines empirically the trading behavior of specialists on the New York Stock Exchange. A specialist at the NYSE enjoys an exclusive right to make the market in securities assigned to him. With this comes the affirmative obligation of maintaining a `` fair and orderly market'' in the assigned security. This entails providing liquidity when liquidity is low, keeping prices somewhat continuous and acting as an agent for other traders. In return the specialist earns income through the bid-ask spread. In addition, the specialist uses the bid ask spread to insure himself against asymmetric information. Furthermore the NYSE specialist enjoys a `` last move'' advantage which may give rise to additional trading profits.
I find that when inventory levels and the specialist's explicit role is taken into account, the specialist behaves like active investors who seek to buy stocks when prices are low and to sell when prices are high. Another important result of the paper is that when it comes to generating income, the specialist loses money on market making trades while he makes a profit on self-initiated trades, this even despite that fact that liquidity trades by definition include the spread profit. Last I find that a specialist's trades are informative about future short term price movement.
In the past, the theoretical literature has emphasized inventory-based models when modeling the trading and price setting behavior of specialists. If a specialist faces inventory carrying costs or is risk averse, he will actively control his inventory position by setting prices to induce movements towards desired inventory levels. In a seminal contribution Garman (1976) modeled market makers as zero profit individuals who adjust prices in order to avoid failure under order uncertainty. His main conclusion was that the optimal bid-ask prices were monotone decreasing functions of the dealer's inventory position, while the spread remained fixed. Stoll (1978) and O'Hara and Oldfield (1986), to name a few, extended this model but eventually came to the same main conclusion, that is that the bid-ask prices depended on the specialist's inventory position. However, empirical studies connected to these inventory models have found only weak evidence of short-run inventory effects (Madhavan and Smidt 1991, and Hasbrouck and Sofianos 1993). Madhavan and Smidt (1993) examined inventory behavior over long horizons and also found only weak evidence for inventory effects. Overall, empirical research suggests that specialists' inventories have only a weak effect on changes in ask and bid prices. Madhavan and Panchapagesan (2000) even found that the only significant inventory effects were in the opposite direction to what the theory predicts. In an effort to explain these contradictions, Madhavan and Sofianos (1998) found that specialists control their inventories through the timing and direction of their trades rather than by adjusting their quotes. This implies that the current inventory control model of specialists excludes some important features which also affect specialists behavior.
By assuming that the specialist is an informed profit maximizer I do find evidence that specialists control their inventories through the timing and direction of their trades. The assumption that the specialist is an informed profit maximizer is motivated by two theoretical papers. First, Spiegel and Subrahmanyam (1996) modeled the specialist as a competitive trader who attempts to profit from minute-by-minute price fluctuations, as opposed to other traders who find continuous monitoring of market movements prohibitively costly. Second, Benveniste, Marcus and Wilhelm (1992) explicitly modeled the relationship between the specialist and the floor brokers as being informative for the specialist. In both of these models, the specialist will buy when prices are low and sell when prices are high. This is the exact opposite of the behavior predicted by inventory control models. A recent empirical paper by Harris and Panchapagesan (2003) finds that specialists use information from the limit order book to guide trading. Trade is not only influenced by order imbalance, but also by individual order properties, such as duration and price of limit orders relative to the market.
The empirical model below tests the connection between specialist trading behavior, specialists' inventories, and security prices. There is no attempt here to infer how the specialist gets his information, whether from continuously monitoring the market or from other floor brokers. Rather, the purpose is to infer from the specialist's behavior if he is informed and if he profits from that information. The analysis of 143 stocks on the NYSE provides evidence that, when comparing prevailing midpoints of quotes, specialist do sell at the high and buy at the low. They therefore behave as competitive traders attempting to profit from minute-by-minute price fluctuations. This contradicts the general view of the mainstream literature, which is that specialists are suppliers of immediacy to ordinary traders, and that the bid-ask spread is both the price they impose for the provision of this service and an insurance against asymmetric information (for example Glosten and Milgrom 1985). A main result of my paper is that specialists receive compensation from profitable self-initiated trading rather than just from the bid-ask spread. The results are statistically more significant for more liquid stocks, for which the specialists role of market making may be less important. Inventory positions also play a role in specialists' actions. If there is an inventory imbalance, specialists will adjust the direction of their trades to correct for it. This is in accordance with Madhavan and Sofianos (1998). One of the strongest characteristics of specialist behavior is being on the opposite side of the market when there is an order imbalance. Doing this so - which is unprofitable in the time period investigated here, lets specialists fulfill their obligation to the NYSE of maintaining a orderly market in the assigned security. Specialist's trades turn out to be informative about future short term price movement. That is, if a specialist initiates a trade at a price above the prevailing midquote, the price of the stock is more likely to move up in the near term, indicating that these specialists' trades are informative about future price movements. This leads to the last question explored in this paper. When it comes to generating income, what is more profitable for the specialist: trades that he initiates or trades in which he is a liquidity provider? Despite the fact that liquidity trades by definition include spread profit, the overall profit from specialist-initiated trades is higher for the stocks I examine. In the sample, the specialists lose money on market making trades while making a profit on self-initiated trades.
In the United States there has been a movement towards so-called automated trading systems (ATSs) which operate without any explicitly designated market makers. International exchanges have also widely adopted ATSs.2 In response to these market trends, the NYSE recently merged with ArcaEx, one of the leading Electronic Communication Networks (ECNs). The NYSE has stated that it will adopt a hybrid model of trading, where floor trading and electronic trading will coexist. This change will reduce the monopoly power of the specialist due to decreased order flow, and it may also be a move towards phasing out the increasingly debated specialist system entirely.3 Before that happens, it is important to understand the role of the specialist in the current trading environment. This paper contributes to that effect.
This paper is organized as follows. Section two discusses the empirical model. Section three describes the data. Section four presents the empirical results. Section five discusses how different strategies contribute to the specialist ´ s profit. Finally, section six concludes.
2. The Empirical Model
The question of interest is whether future price movements affect specialists' trades. Specialists' trading decisions potentially reveal more about their private information than their quotes, since other traders have trading priority at the quoted price. The dependent variable in the model is therefore whether specialists are buying or selling, with one of the independent variables being future prices. The maintained hypothesis is that specialists have some information about future prices.
Previous theoretical research identifies other factors likely to affect the direction of specialist trading activity at the transaction level for an individual stock. As mentioned in the introduction, empirical tests of inventory control theory have found only very weak or no relations between inventory levels and prices. On the other hand, Madhavan and Sofianos (1998) found that specialists control their inventories through the timing and direction of their trades. Inventory is therefore included in this model where it is expected that higher inventory will cause the market maker to take the seller side in a trade more frequently.
The bid-ask spread can also affect specialist trading activity. Seppi (1997) presents a model of a strategic specialist who faces competition from the limit order book. He shows that specialists are more likely to participate when the bid-ask spread is wide by improving the bid or ask price. Such actions can be profitable and also satisfy the specialist's affirmative exchange obligation to provide liquidity and maintain price continuity.
Accordingly, the specialist buying or selling at time
![]() is modeled as
follows,
is modeled as
follows,
where the indicator variable y
![]() is the
specialist's pre-trade signed inventory position (positive when
long and negative when short). In accordance with Madhavan and
Sofianos (1998), the hypothesis is that
is the
specialist's pre-trade signed inventory position (positive when
long and negative when short). In accordance with Madhavan and
Sofianos (1998), the hypothesis is that ![]() is negative, that is, when
the specialist has a high inventory position he uses the direction
of the trade to get rid of some of his risk.
is negative, that is, when
the specialist has a high inventory position he uses the direction
of the trade to get rid of some of his risk.
![]() is the
pre-trade posted dollar spread multiplied by the sign of the trade
(positive for trades classified as buyer-initiated and negative for
seller-initiated). The hypothesis is that
is the
pre-trade posted dollar spread multiplied by the sign of the trade
(positive for trades classified as buyer-initiated and negative for
seller-initiated). The hypothesis is that ![]() is negative, indicating that
specialists are more active on the opposite side of a trade when
the spread is wider, since that takes into account specialists
affirmative exchange obligation to provide liquidity and maintain
price continuity.
is negative, indicating that
specialists are more active on the opposite side of a trade when
the spread is wider, since that takes into account specialists
affirmative exchange obligation to provide liquidity and maintain
price continuity.
![]() is the
signed percentage change calculated at the midpoint of the
prevailing bid and ask quotes eight trades into the future. The
hypothesis is that
is the
signed percentage change calculated at the midpoint of the
prevailing bid and ask quotes eight trades into the future. The
hypothesis is that ![]() is positive, i.e., that specialists are buying low and selling
high.
is positive, i.e., that specialists are buying low and selling
high.
3. The Data
The time series data used in this paper consists of trade-by-trade information from the Trade, Order, Record, and Quote database (TORQ database). The TORQ database contains transactions and quotes for a sample of 144 stocks from November 1990 through January 1991. The age of this data is an issue but due to the NYSE data sharing policy, more recent data are not available. The TORQ data set consists of four different files, one of which includes detailed information on the identity of traders. This information is only partially complete. Certain traders' identities, including those of the specialists, are intentionally not revealed. In such cases, the relevant fields are not concealed, but merely left blank. Specialist trades are identified using an algorithm that was developed by Edward (1999) and later refined by Panchapagesan (1999). Omission of a trader's identity code is used to flag transactions as possibly involving a specialist. Using filters based on prior knowledge of the data files and the NYSE's policies and procedures, the algorithm was refined by Panchapagesan (1999) to identify specialist trades. This algorithm was verified by replicating studies that used validated specialist trade data and it was found to be highly accurate (Panchapagesan 1999). For a further discussion of the algorithm for identifying specialist trades, see Appendix A.
A procedure suggested by Lee and Ready (1991) is used to classify trades as buyer- or seller-initiated. Specifically, the trade price is compared with the midpoint of the prevailing bid and ask quotes. A 15-second lag on quotes is used to correct for differences in the clock speed with which trades and quotes are reported. Trades whose prices are above (below) the midpoint are classified as buyer-initiated (seller-initiated). Trades at the quote midpoint generally cannot be classified in this manner. However, following Madhavan and Sofianos (1998), mid-quote trades where specialists participate are classified as seller-initiated (buyer-initiated) if the specialist is buying (selling). That is, the specialist is specified as the liquidity provider.
An opening share inventory for each day and each stock is constructed as the sum of all signed specialist trades. Since the inventory level at the start of the sample is not observed, the inventory level is only correct up to an unknown constant.
Out of the 144 stocks in the TORQ database, 143 are used in this paper.4 All major results are given in trade frequency groups, with the stocks that trade with the highest frequency in this period in frequency 1 and those that trade with the lowest frequency in frequency 5.
Table 1 presents summary statistics on these frequency groups of stocks for November 1990 through January 1991. The sample stocks vary widely in important dimensions. Specialists for the most frequently traded stocks trade those shares on average almost once every minute, while for the least frequently traded stocks the specialist trades the shares on average less than once an hour. The specialist participation rate is inversely related to trading frequency, as would be expected because market making responsibilities are more essential for thinly traded stocks.
The data that is going to be of most interest is inventory data, spread data and the change in the mid-quote eight trades into the future. These are the data which are used in the model presented in the previous section. Table 1 gives the summary of these data for the five frequency groups mentioned above.
It is obvious that the units of these numbers vary greatly in magnitude, and this will have to be kept in mind when the results in the next section are interpreted. Inventories, for example, are in thousands, while price changes are in eighths of a dollar. The standard deviation of the inventory is lower for stocks with lower trading frequency. This is presumably because the increased risk of holding a position in a stock that is not very liquid leads to more inventory targeting. Also the standard deviation of prices goes up as the trading frequency declines, since stocks that are more thinly traded tend to have more volatile prices, and also since eight trades into the future is a longer time period for thinly traded stocks. As expected, the average spread is highest for the least liquid stocks.
As mentioned above, the age of this dataset is an issue, and it is important to keep in mind that there have been many changes made to the rules and regulations of the NYSE since these data were collected. One of the more important changes for the specialist may have been the opening of the limit order book in January 2002. Boehmer, Saar, and Yu (2005) find that specialists participation rate decreased after the limit order books were opened to other traders. This is consistent with an increased trading risk due to a decrease in information advantage. Other important changes occurred in June 1997, when NYSE began trading stocks in "sixteenths" of a dollar, and in January 2001, when decimal pricing was fully implemented. `` Last trade'' advantage becomes even more important in the new environment because the opportunity cost of increasing the buy price or of lowering the sell price has decreased. As a result the specialist participation rate appears to have increased considerably, indicating an increase in the use of information advantage.5Without more recent specialist specific trade data, the exact effects of these regulatory changes are unknown. However, the non-availability of more up-to-date data of this type does not change the basic hypothesis of this paper, which is that specialists trade on the information they have. This paper cannot say whether specialists still enjoy the same information advantage or to what extent they can trade on their information.
4. Empirical results
4.1. Binary Estimation
The model that will be estimated is the above mentioned binary model that estimates whether the specialist is buying or selling,
| (2) | ||
![$\displaystyle \begin{tabular}[c]{l} y$_{i}$=\textbf{1} when the specialist buys\\ y$_{i}$=\textbf{0} when the specialist sells. \end{tabular}$](img12.gif)
|
Equation 2 is estimated with both probit and logit MLE estimation methods, where each observation is treated as a single draw from a Bernoulli distribution.
Table 2 present the results from the
individual probit estimations. As mentioned before, the prior
hypothesis is that the coefficient for ![]() is negative,
is negative, ![]() is negative and
is negative and ![]() is positive, which means that
these are tested against a one sided alternative. The constant is
on the other hand tested against a two sided alternative since no
prior exists about the outcome of that estimator. For goodness of
fit a pseudo-R
is positive, which means that
these are tested against a one sided alternative. The constant is
on the other hand tested against a two sided alternative since no
prior exists about the outcome of that estimator. For goodness of
fit a pseudo-R
![]() is reported
as well as the likelihood ratio test statistic. The results for the
probit and logit estimations are similar, consistent with a
moderate balance between 0s and 1s for the dependent variable. Thus
only the results of the probit estimation are reported here and in
the rest of the paper.
is reported
as well as the likelihood ratio test statistic. The results for the
probit and logit estimations are similar, consistent with a
moderate balance between 0s and 1s for the dependent variable. Thus
only the results of the probit estimation are reported here and in
the rest of the paper.
The main result of the probit estimation is that in seventy-five percent of the stocks (107 out of 143) the price coefficient is positive, and that it is significantly so in twenty-eight percent of the cases. This supports the main hypothesis that specialists buy stocks when prices are about to go up and sell them when prices are about to down. This indicates that market makers obtain profits from exploiting future price fluctuations; presumably, they are able to earn these profits from the comparative advantage gained by continuously monitoring markets. These results are robust to changes in the number of future trades used for the price change estimation, that is, with price changes estimated either four or sixteen trades into the future. This means that the initial assumption that market makers are informed utility maximizers may be appropriate when theoretical models of specialist behavior are developed.
It is interesting to see that future price changes affect the specialist differently depending on the frequency group of the stock. There seems to be a inverted U-shape relationship between the liquidity of the stock and the opportunity the specialist has to time the market, since the lowest future price change coefficients are in the highest-trading and in the lowest-trading frequency. In the highest trading frequency this result is economically intuitive since these markets are more efficient and the specialist is therefore not in as good a position to predict and take advantage of future prices and take advantage of them. As for the most thinly traded stocks, it is likely that the specialist's role of providing liquidity is more important proportionally than profit maximization, which would explain why the future price change coefficient becomes smaller as stocks become more thinly traded.
The inventory coefficient is negative and significantly so in thirty percent of the cases. This supports the empirical results in Madhavan and Sofianos (1998), who find that specialists control their inventories through the timing and direction of their trades rather than through the adjustment of their quotes. The magnitude of the inventory effects is strongest in the most thinly traded stocks. This is economically intuitive because the time between trades, and hence inventory carrying costs, tend to be greater in less liquid stocks. This will cause the specialist in a thinly traded stock to want to promptly reverse his position to a optimal inventory level.
The coefficient of the variable signed spread is negative and significantly so in ninety eight percent of the regressions. This strongly supports the hypothesis that specialists are more active on the opposite side of a trade when the spread is wider, affirming their exchange obligation to provide liquidity and maintain price continuity. These obligations also appear to increase as the stocks become less liquid, with the coefficient being highest for the least liquid group.
The marginal effects can be seen in table 3 where the slope is estimated at the mean of each of the regressors.6 If prices go up by an eighth of a dollar in the future, the decision to buy (1) goes up by 0.2325. If inventories go up by 10,000, the decision to buy goes down by -0.06 for all stocks. It is interesting to see if any one of the exogenous parameters is driving the endogenous variable in any one direction. The effect of each coefficient is determined in table 4 for the mean of the regressor multiplied by the slope coefficients. To clarify even further that none of the variables drive the resulting endogenous variables, the absolute value of the standard deviation of the regressor times the slope is also given. The magnitude results indicate that no single variable dominates the specialist's choice whether to sell or buy. The spread size has the greatest effect in all groups of stocks though, indicating that the role of specialists in providing liquidity is an important factor in their decision to buy or sell.
4.2. Predictions
With the estimators for the model in hand it is of interest to
investigate how well the model does in predicting whether a
specialist will buy or sell at specific points in time. Table
5 gives the outcome of sample prediction
probabilities for the five groups of stocks. November and December
data was used to estimate probit and logit models and the models
were then used to predict specialist activities in January. The
naive prediction is both out of sample and in sample, which gives
the best possible naive alternative to the models' prediction. A
stock has a naive prediction of y![]() if P(buy) is
if P(buy) is ![]() For out of sample data, the naive prediction
number of sells and buys are counted in November and December, for
the in sample naive prediction the number of sells and buys in
January are counted. As before, only the probit results are
displayed. The results for the logit estimation were similar.
For out of sample data, the naive prediction
number of sells and buys are counted in November and December, for
the in sample naive prediction the number of sells and buys in
January are counted. As before, only the probit results are
displayed. The results for the logit estimation were similar.
The results indicate that the model presented and estimated above improves predictions considerably. The probit model correctly predicts the direction of the specialist's trade in 66% of all trades while an in sample naive predictor only predicts it correctly in less than 57% of all trades. For some trade frequency groups the difference is even greater. The probit model does increasingly well in predicting the direction of trade for trading frequencies one through four, with 61% prediction accuracy for the most frequently traded stocks and tops it with almost 70% accuracy for trading frequency group four. The model does not do as well for the least liquid stocks, but still does better than the naive predictors. The results suggest that the independent variables in the model do have a real effect on the specialists decision whether to buy or sell.
To refine the predictions a rolling update was made of the model to assess its performance when information is updated. November and December data was used to predict two trading days in January, then the data from those two trading days was added and the model estimated again and those results used to predict other two days into the future. This rolling prediction was done for group one, two, and three. It was not done for the other two groups since those stocks were too thinly traded to yield significant results. Updating the model with new data does not make a huge difference in the predictability, as can be seen in table 5 panel B. It does improve the probit predictions in all the groups but only marginally, the greatest improvement is in group three which is only half a percent improvement from 66.74% to 67.21%. This indicates that the model is robust when used for predictions up to a month into the future.
5. Trades Initiated by the Specialist
A specialists has two separate roles, he has to be a liquidity provider in the stock he is assigned to, and as shown above, he is an active trader trying to profit from short term price fluctuations. It is therefore interesting to try to split the trades into two categories, those done to fulfill market making obligations and those done to maximize profits. In this section the trades are decomposed into trades initiated by the specialist and trades initiated by other traders. It is assumed that the trades that are initiated by the specialist are profit maximizing trades.
As before, the procedure by Lee and Ready (1991) is used to classify trades as buyer- or seller-initiated and mid-quote trades are specified as market making trades. Table 6 gives the summary of the data.
In most of the trades, seventy one percent on average, the specialist is at the opposite side of the market; he is providing liquidity. When he is a liquidity provider, he collects the spread as a payment for his services and also as an insurance against information trading. As expected, the specialist's role as a liquidity provider increases as the stocks become more thinly traded, with seventy seven percent of trades being liquidity providing trades for the most thinly traded stocks.
Table 7 gives an overview of what the specialist does when he initiates trades. In eighty five percent of cases, the specialist buys (sells) the stock when the price is at a low (high). This is a profit maximizing strategy. For the more liquid stocks this is even a higher proportion, going up to 89% of trades for the most liquid stocks, while only about two thirds of initiated trades are a buy at low and sell at high for the least liquid stocks. In the remainder of this section, I will look at the profits specialists make from initiated trades as opposed to market making trades. Trading profits are defined similarly to Hasbrouck and Sofianos (1993). They can be measured either on a cash flow basis or a market-to-market basis, and are respectively defined as follows:
| (3) | ||
Since there is a limit to the current data set it is assumed that inventories at the beginning of the time period are zero. It is also assumed that inventories at the end of the period are zero, that is the inventory position accumulated during the period will be liquidated at market prices at the end of the period. One can also think of this as meaning that the inventories on hand are evaluated at current market prices. This means that both methods of evaluating profits are equivalent, since:
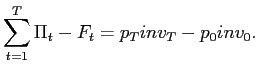
|
(4) |
The short sample period may cause a problem here with the end of period selling/buying of the whole inventory. If the horizon is short, and therefore the total profits not as high, inventory selling/buying may be driving the results. To test for the robustness of the results the end of period inventories were sold/bought for a number of different prices, end of period mid-quote, average price of the period, maximum price of the period, and the minimum price of the period. These different exercises did not lead to a different conclusion than what is presented below, which are the results for end of period mid-quote.
All trades that the specialist initiates are buys above mid-quote and sells below mid-quote, so there is no bid/ask spread bounce incorporated into the profits from those buys and sells. On the other hand the bid/ask spread bounce does decrease the potential loss that is incurred from market making. Taking this to the extreme, it is worth noting that if the mid-quote were the same throughout the sample then the profit from market making would be no less than zero. Loss from initiating a trade would, however, be no less than one eighth times the amount bought or sold. This can be seen quite simply by looking at trading profits.
Assume that the mid-quote is fixed throughout the sample. All
market making buys are executed at the mid-quote or below
![]() , all
market making sells are executed at the mid-quote or above
, all
market making sells are executed at the mid-quote or above
![]()
| (5) | ||
where M stands for market making, then,
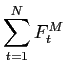 |
(6) | |
By same reasoning, trading profits for initiated trades would be:
| (7) | ||
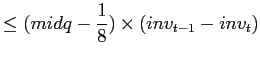 for sell
for sell |
||
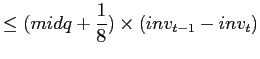 for buy
for buy |
where I stands for initiated trade, then,
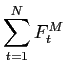 |
![$\displaystyle \leq0-\frac{1}{8}\sum_{t=1}^{N}abs\left[ inv_{t-1}-inv_{t}\right]$](img37.gif)
|
(8) |
So trading profits for market making are in part due to the spread, while there is no such thing in the initiated trade profits. In table 8 there is a summary of how much profit comes from each trading strategy. That is total revenues from that strategy summed over stocks divided by total trading turnover. The results for the least liquid stocks are omitted due to very infrequent trading in them. As shown in table 6, there are only on average twenty seven specialist initiated trades over the whole period for the least liquid stocks which does not give a good estimate of profitability.
Most noteworthy is that fact that the specialist is always doing better in the initiated trades than in the market making trades. This is so even though there is a bid ask spread bounce incorporated into the market making profits. For all the stocks, liquidity trades have a loss of 0.2 cents per dollar while initiated trades have a profit of 0.112 cents per dollar. The difference is most in the lowest frequency where the specialist was making 0.36 cents per dollar on initiated trades while he was loosing 0.59 cents a dollar on market making trades. On average specialists were losing money in this period, prices were going down, and their market making obligations appear to have been dominating.
It is worth noting, however, that the results are very different between stocks. For individual stocks, 63 out of the 115 reported in table 8 had a higher profit for liquidity trades, that is around fifty five percent. The main results did not change when some of the assumptions changed, for example, if the end of period inventory was sold of at average prices in the period instead of end of period mid-quote, 62/115 stocks still had a higher initiated trade profit. Profit for all the reported stocks changed from -0.096 cents per dollar to -1.06 cents per dollar, while liquidity trades had a loss of -0.125 cents per dollar and initiated trades had a profit of 0.044 cents per dollar (results not shown).
This further strengthens the main results of this paper, that specialists do profit from trades that they initiate, which strongly supports the hypothesis that they have some information about short term price fluctuations.
5.1. Future Price Movement
Since it appears that the specialist is mostly buying low and selling high it may be the case that specialist initiated trade is a good estimate of the future short run price change in a stock. The estimated model for the future price change is
There were too few observations in the lowest frequency stocks
to estimate the model. For many of the stocks, the Durbin Watson
test indicated the presence of first order autocorrelation, so the
Newey West procedure was used to estimate the disturbances.
![]() was tested
against a one sided alternative, since the prior is that it should
be positive. As we have no priors for
was tested
against a one sided alternative, since the prior is that it should
be positive. As we have no priors for
![]() it was
tested against a two sided alternative. The results for the more
frequently traded stocks are presented in table
9.
it was
tested against a two sided alternative. The results for the more
frequently traded stocks are presented in table
9.
The goodness of a fit of the model is not very high. Adjusted
R![]() goes from being 1%
in the highest frequency to being 4% in the lowest frequency. Still
eighty five percent of the trade coefficients are positive as
predicted and almost sixty percent of them are significant at the
10% level. This does indicate that specialist initiated trading
does contain some information about future price movements. This
information can, however, not be backed out of NYSE daily trading
data since traders identies are not revealed. Across the trade
frequencies, trade is most often significant in frequencies two and
three. This indicates that trade is more efficient in trading
frequency group one. The reason that the trade coefficient is less
significant in the lowest frequency is probably due to the number
of observations.
goes from being 1%
in the highest frequency to being 4% in the lowest frequency. Still
eighty five percent of the trade coefficients are positive as
predicted and almost sixty percent of them are significant at the
10% level. This does indicate that specialist initiated trading
does contain some information about future price movements. This
information can, however, not be backed out of NYSE daily trading
data since traders identies are not revealed. Across the trade
frequencies, trade is most often significant in frequencies two and
three. This indicates that trade is more efficient in trading
frequency group one. The reason that the trade coefficient is less
significant in the lowest frequency is probably due to the number
of observations.
6. Discussion
The main implications of the above empirical analysis is that specialists do behave like active investors with information advantages. Up until now most theories about specialists' trading behavior have focused on inventory control models which predict that specialists change their prices to affect their inventory position. This means that prices would move down after a specialist purchase and move up after a specialist sale. Empirical research has failed to bear out the main hypothesis of inventory control models, motivating this paper. Theories that assume that the specialist has an informational advantage from continuously monitoring the market or from continuous trading relationships predict, oposite to inventory control models, that specialists would buy stocks when prices are low and sell stocks when prices are high. The above analysis substantiates that specialists do behave like active investors while also managing their inventories. By controling for specialists' market making obligations I do find that specialists' trading direction is affected by future prices. They are indeed buying low and selling high.
It is quite noteworthy to see that when specialists are not performing their trading obligations by being on the opposite side of a market they are in almost eighty five percent of the trades buying low and selling high. This is the most convincing evidence supporting the theory that specialists are informed about future price movements. Specialists trading direction is effective in explaining future price movements when market making trades are excluded from the dataset, indicating that monitoring the specialist actions may be profitable. For the general trading public it is, however, impossible to monitor specialist trades since information on traders' identity is not public.
Trading profits were mostly negative in this period, but despite that, the trading profits for specialist initiated trades were positive in three out of four frequency groups. Furthermore there were always higher losses incurred on the market making trades than on the specialist initiated trades, even though the former trades incorporate spread profit.
It seems clear from the above results that the market maker is best represented as a profit maximizing informed investor rather than a zero profit trader. This gives rise to several interesting avenues for future research. It may be interesting to incorporate the above results into a theoretical model which could yield a testable hypothesis on available trade data. Another interesting aspect is to formalize a model with reputation to see how the floor brokers and specialists interact when the specialists are profit maximizing traders. Empirically it is also interesting to investigate if the same results hold in other markets where specialists have similar privileges and obligations.
References
- Admati, A.R. and Pfleiderer, P. 1989. `` Divide and Conquer: A theory of intraday and day-of-the week mean effects'' Review of Financial Studies 2, 189-223.
- Amihud, Y., Mendelson, H., 1980. `` Dealership market: market making with inventory'' Journal of Financial Economics 8,31-53
- Boehmer, E., Gideon, S. and Yu, L., 2005. `` Lifting the Veil: An Analysisi of Pre-Trade Transparency at the NYSE'' Journal of Finance 60, 783-815
- Garman, M.B., 1976. `` Market Microstructure'' Journal of Financial Economics, 3 257-275.
- Edwards, A. K., 1999, `` NYSE Specialists Competing with Limit Orders: A Source of Price Improvement'' working paper, Securities and Exchange Commission.
- Easley, D., and O'Hara, M., 1987. `` Price, Trade Size, and Information in Securities Markets'', Journal of Financial Economics 19, 69-90.
- French and Roll, 1986, `` Stock return variances: The arrival of information and the reaction of traders'' Journal of Financial Economics 17, 5-26.
- Glosten, L. R., and Milgrom, P.R., 1985. `` Bid, Ask and Transaction Prices in a Specialist Market with Heterogeneously Informed Traders'', Journal of Financial Economics, 14, 71-100.
- Greene, William H. ``Econometric Analysis'' (Prentice Hall, Upper Saddle River, New Jersey, 1993).
- Hamilton, James D. ``Time Series Analysis'' (Princeton University Press, Princeton, New Jersey, 1994).
- Harris, Lawrence E. and _Panchapagesan, Vankatesh, 2003. `` The Information-Content of the Limit Order Book: Evidence from NYSE Specialist Trading Decisions'' work in progress, version Febuary 27, 2003.
- Hasbrouck, J, 1992. Using the TORQ Database.
- Hasbrouck, J., Sofianos, G., 1993. `` The trades of market-makers: an analysis of NYSE specialists'' Journal of Finance 48, 1565-1594.
- Ho, T., and Stoll H., 1981. `` Optimal Dealer Pricing Under Transactions and Return Uncertainty'' Journal of Finance 38, 1053-1074.
- Ho, T., and Stoll H., 1983. `` The dynamics of dealer markets under competition'' Journal of Financial Economics 9, 47-73.
- Huang, Roger D. and Stoll, Hans R. 1997. `` The Components of the Bid-Ask Spread: A General Approach'' The Review of Financial Studies, Vol. 10, No. 4, 995-1034.
- Judge, Hill, Griffiths, Lutkepohl and Lee. `` Introduction to the Theory and Practice of Econometrics'' (John Wiley & Sons, New York: 1988)
- Kavajecz, A. Kenneth, 1999. `` A Specialist's Quoted Depth and the Limit Order Book'' Journal of Finance Vol. LIV, No 2, 747-771.
- Lee, C. and Ready, M., 1991. `` Inferring trade direction from intra day data'' Journal of Finance 46, 733-746.
- Madhava, A., and Smidt S., 1991. `` A Bayesian model of intraday specialist pricing'' Journal of Financial Economics 30, 99-134.
- Madhavan, A., and Panchapagesan, V., 2000. `` Price Discovery in Auction Markets: A Look Inside the Black Box'' The Review of Financial Studies, Vol. 13, No. 3. 627-658.
- Madhavan, A., and Smidt S., 1993. `` An analysis of Changes in Specialist Inventories and Quotations'' Journal of Finance 48, 1595-1628.
- Madhavan, A., and Sofianos, 1998. `` An empirical analysis of NYSE specialist trading'' Journal of Financial Economics 48, 159-188.
- New York Stock Exchange, 2003 web page.
- O'Hara and Oldfield, 1986, `` The Microeconomics of Market Making'' Journal of Financial and Quantitative Analysis, Vol 21, No. 4, 361-376.
- O'Hara, Maureen. `` Market Microstructure Theory'' (Blackwell Publishers Ltd.Malden 1995).
- Panchapagesan, Vankatesh, 1999. `` Identifying Specialist Trades in the TORQ Data - A Simple Algorithm'' working paper, Washington University in St. Louis..
- Seppi, Duane J., 1997, `` Liquidity Provision with Limit Orders and a Strategic Specialist'' Review of Financial Studies 10, 103-150.
- Spiegel, M., and Subrahmanyam, A., 1996. `` On Intraday Risk Premia'' Journal of Finance 50, 319-339.
- Stoll, H. 1978, `` The supply of Dealer Service in Securities Markets'' Journal of Finance 33, 1133-1151.
7. Appendix A.
The four files that form the TORQ data are: the Consolidated Transaction file (CT), the Consolidated Quotes file (CQ), the system Order Database file (SOD) and the Consolidated Audit Trail file (CD)7. The time series data in this paper uses all but the Consolidated Transaction (CT) file. The following is based on identifying specialist buys, identifying specialist sells is symmetric.
Specialist buys are represented by audit records (CD) where the:
- Account type (''BUYACCT'') is missing. NYSE rule 132 mandates the provision of account information for audit trail purposes by all traders. Therefore, account types cannot be missing in the audit data unless they were systematically excluded. Since specialist's account type (S) is missing in the TORQ data, the necessary condition for a specialist buy is that the buyer account type should be blank. Additional refinements are needed because account types can be missing for nonspecialist trades as well.
- Source (''BTYPe'') is D2, L2 or blank, i.e. the source of the buyer must be from the crowd side, and must not be ''uncompared''.
- For ITS trades (NYSE executing market or committing market), they must not have a matching record in the System Order Database (SOD). This is because ITS buys with missing account type that are not in SOD are likely to represent specialist buys.
This makes up a transaction file for specialists8. To match quotes with trades the transaction file for specialists is run together with the Consolidated Quotes file, connecting these two files through date and time. A 15-second lag is used to correct for difference in the clock speed with which trades and quotes are reported (Madhavan and Sofianos, 1998).
An example of a specialist buy from a TORQ CD data file can be seen in table 10:
The sample contains 65 trading days for 143 stocks in the TORQ database. Each frequency group average represents the simple mean of the daily averages of stocks within that frequency.
| Freq. 1 (high) | Freq. 2 | Freq. 3 | Freq. 4 | Freq. 5 (low) | |
|---|---|---|---|---|---|
| Av. trades per day | 354 |
64 |
28 |
13 |
5 |
| Av. participation rate | 20.3% |
22.2% |
26.5% |
30.8% |
36.4% |
| Inventory (std) | 13,749 (103,871) |
5,852 (25,922) |
-3,517 (16,074) |
-5,826 (11,541) |
-7,908 (10,049) |
| Price Change (std) | -0.0018 (0.0485) |
-0.0026 (0.0562) |
-0.0049 (0.0752) |
-0.0056 (0.1227) |
-0.0140 (0.2107) |
| Spread (std) | 0.4407 (0.6446) |
0.4742 (0.3860) |
0.4829 (0.2193) |
0.4815 (0.1842) |
0.5394 (0.3304) |
Table 2: Probit Analysis of Specialist Trading
This table reports the results of 143 probit maximum likelihood estimations, divided into5 frequency groups, for Nov. 1990 -Jan.1991. Each cell contains the mean of the estimated parameters for that frequency group and the percent of stocks for which the estimate issignificant at the 5% level.
|
Table 3: Probit Slope Parameters
This table reports the
estimated slope coefficients for 143 probit maximum likelihood
estimations divided into 5 frequency
groups, for Nov. 1990 -Jan.1991, the slope coefficients are
estimated at the mean of the regressors
using
![]() , where
, where
![]() is a vector of the
estimated parameters and
is a vector of the
estimated parameters and ![]() is the standard normal density. Each cell contains the mean
of the estimated parameters for that frequency.
is the standard normal density. Each cell contains the mean
of the estimated parameters for that frequency.
|
Table 4: Magnitude Effects of the Exogenous Parameters
This table reports the result of a multiplication of the slope and the mean value of the regressors. It also reports the absolute value of the standard deviation of the regressor times the slope of the estimator.
|
Table 5: Prediction Probabilities
This table shows the
prediction capabilities of the model when compared to a naive
prediction, a stockhas a naive prediction of
y
![]() if P(buy)
is
if P(buy)
is
![]() In panel B rolling updates on the model and
the naive predictors is
done.
In panel B rolling updates on the model and
the naive predictors is
done.
|
| Panel B Rolling Updates | All | 1 (high) | 2 | 3 | 4 | 5 (low) |
|---|---|---|---|---|---|---|
| Probit | 61.51% | 65.35% | 67.21% | |||
| Naive: Out of sample | 55.39% | 54.59% | 54.57% | |||
| Naive: In sample | 55.61% | 56.65% | 58.42% |
Table 6: Trades of the Specialist
This table presents the average number of trades in each category and below the percentage in each category. Trades are specified as liquidity providing trades if the specialist is a buyer to a seller-initiated trade and vice versa. A trade is buyer (seller) initiated if the trade price is above (below) the prevailing midpoint of the quotes. Trades at the midpoint are specified as liquidity trades.
|
|
Table 8: Profits for Trading Strategy Cents/Dollar
This table presents the average profits from trading strategies for each trading frequency. Each number represents a simple mean of the variables for each trading frequency. If the liquidity trades profits are corrected for the bid/ask bounce the difference becomes even more pronounced.
|
Table 9: Regression Analysis of Price Changes
The table reports the results of 115 regression estimations, divided into 4 frequency groups, for Nov. 1990 -Jan.1991. Each cell contains the mean of the estimated parameters for that frequency and the percent of stocks for which the estimate is significant at the 10% level.
|
|
||||||||||||||||||
| I represents nonprogram trading, nonmember, individual investor | ||||||||||||||||||
| P represents nonprogram trading, member proprietary |
Footnotes
1. Economist in the Division of International Finance of the Board of Governors of the Federal Reserve System. I thank George Hall, Matthiew Spiegel, Robert Shiller and Tony Smith for helpful comments and suggestions. For questions or comments, please contact Sigridur Benediktsdottir, email: [email protected]. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. All errors are sole responsibility of the authors. Return to text
2. The Electronic Communication Networks's ECN in the United States use fully automated trading systems. There are also electronic markets in for example the United Kingdom, Canada and Germany. Return to text
3. Specialists have been accused of trading ahead of the market for their own profit, harming other investors. Seven specialist firms settled such charges by paying a fine of 247 million dollars. In the spring of 2005 fifteen specialists were charged in a criminal indictment for making illegitimate trades at customers' expense. Return to text
4. One stock was too thinly traded in this period to yield any results. Return to text
5. See the NYSE website, http://www.nysedata.com/factbook/viewer_interactive.asp?hidCategory=3. Return to text
6. Even though `` current practice favors averaging the individual marginal effects'' (Greene 1997) this is done since same answers can be expected in large samples. Return to text
7. For further discussion about the TORQ data base see Hasbrouck (1992) Return to text
8. For further discussion about this algorithm see Panchapagesan (1999) and Madhavan and Panchapagesan (2000) Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text