
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 882, October 2006 --- Screen Reader
Version*
Changes in Job Quality and Trends in Labor Hours
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Many economic models featuring labor supply decisions, especially in macroeconomic analysis, assume away heterogeneity in the nature of work, or assume that the nature of work is irrelevant to the labor/leisure choice. This paper studies the macroeconomic implications of relaxing this assumption. Estimation from micro data using labor hours, wages, consumption, and nonpecuniary job characteristics suggests that labor supply responds to differences and to changes in the nature of work. Ceteris paribus, some job characteristics induce more labor hours than others do. Labeling the jobs that embed the labor-inducing characteristics as better quality jobs, the study estimates a Job Quality index for the aggregate U.S. economy from 1850 to 2000. The results suggest that over the same period, improvements in Job Quality accounted for at least 20.4 percent of growth in labor hours.
Keywords: Job Quality, Labor Supply, Trends in Labor Hours
JEL classification:E24; J22; O47
I. Introduction
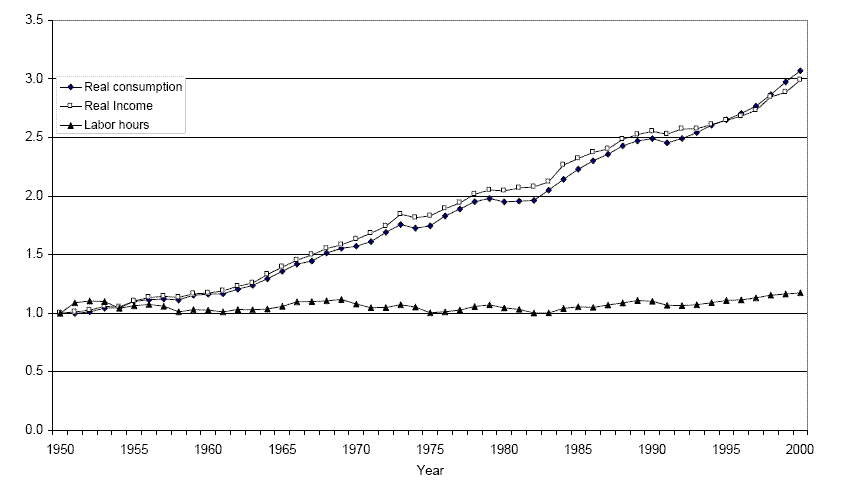
A well documented regularity of time series variables of the aggregate United States economy is the lack of trend in per capita labor hours. For example, between 1950 and 2000 economic variables such as consumption per capita and GDP per capita nearly tripled. Per capita labor hours, on the other hand, remained relatively stable with no sign of a strong trend. (See Figure I) While this observation is widely accepted among economists nowadays, it was not always expected. In his 1930 essay on the `` Economic Possibilities for Our Grandchildren'', Keynes predicted an increase in leisure as income rises.1 In other words, with the rise in income, we should have observed a strong downward trend in work hours. This decrease was quite conceivable, but didn't happen.
There are two leading explanations for the lack of trends in labor hours.2 One explanation is that the income and substitution effects offset each other. As the real wage grows, two opposing effects determine a worker's labor supply decision. The substitution effect tends to motivate a worker to increase labor hours to take advantage of the higher real wage rate, whereas the income effect induces a reduction in hours since the worker is wealthier for a given amount of labor input. Since the two effects have opposite signs and are equal in magnitudes, labor hours do not change.
A second explanation - provided by the home production literature - is based on the notion that the quantity and productivity of hours allocated to home production (home sector) is important in understanding labor supplied in the market sector (Benhabib, Rogerson, and Wright [1991], and Greenwood and Hercowitz [1991]).3 Technological progress in both the market sector and in the home sector affect labor supply. In a scenario where technological progress in both sectors occur at roughly the same pace, there would be no substitution away from one sector in favor of the other, hence labor hours remain relatively constant. Reservations about this theory include its reliance on specific technological progress in the two sectors, and on the size of the elasticity of substitution between the home and the market sector. There is, however, little independent empirical evidence on the estimation of home technological progress, or on the elasticity of substitution between the two sectors.
This study offers an alternative explanation. Specifically, it argues that the nature of work is relevant for the worker's labor supply decision. Some job characteristics induce more disutility for work than others do, and the quality of these jobs is lower. The lower the quality, the more likely a worker will reduce hours following an increase in the real wage, and as the economy grows, the aggregate Job Quality improves, thereby, causing a decline in disutility for work. The decline in disutility induces more labor. In other words, the income and substitution effects do not necessarily cancel. The observed cancellation is due to the Job Quality effect, which complements the substitution effect to counterbalance the income effect. An implication of this hypothesis is that holding the Job Quality constant, we should observe a domination of the income effect, consistent with predictions in Keynes [1930].
Using a unique dataset on labor hours, wages, and nonpecuniary job characteristics from the Health and Retirement Study (HRS)4, this study provides empirical evidence suggesting that some job characteristics induce more labor hours than others do. In the aggregate economy, the share of jobs with these characteristics has increased over time, resulting in an improvement in the economy wide Job Quality index. Between 1850 and 2000, the increase in Job Quality contributed to at least 20.4 percent of growth in labor hours in the U.S.
The remainder of the paper is organized as follows: Section II defines Job Quality and introduces the theory. Section III provides some empirical evidence supporting the theory. Section IV is devoted to the analysis of Job Quality in the aggregate economy. Section V suggests some implications of the results. Section VI discusses some caveats, and Section VII concludes.
II. The Job Quality Theory
The theory of job quality draws inspiration from observed changes in the nature of work over time and from the heterogeneity in hours by occupation. Table I displays the share of total employment by industry in the United States in 1850, 1920, and in 2000. In 1850, Agriculture made up approximately 58.0 percent of total employment. The percentage decreased to 26.2 percent in 1920, and to 2.9 percent in 2000. The shares of employment in the Manufacturing sector were 12.3 percent, 24.6 percent, and 14.9 percent in the corresponding years. For the retail sector, the corresponding percentages were 8.1 percent, 9.9 percent, and 17.9 percent. Table II, presents the share of employment by occupation in 1850, 1920, and in 2000. In 1850 3.3 percent of total employees were Professionals, the percentage increased to 5.5 percent in 1920 and to 21.1 percent in 2000. Farmers and Farm laborers made up 57.5 percent, 25.8 percent, and 1.7 percent of employment in 1850, 1920, and 2000, respectively.5
Furthermore, for some occupations, the nature the work has evolved over time. For example, some sales professions evolved from door-to-door to telemarketing.
In the cross-section, there is heterogeneity in average work hours by occupation. Rones, Gardner, and IIg [1997] analyzed trends in hours of work in the United States between 1976 and 1993. The most noteworthy observation is the increase in the share of persons who are working very long hours, exceeding the average workweek by a full eight-hour day. They further find that the long workweek itself is associated with certain types of occupations.6
In light of these significant changes in the nature of employment in the US in the last century and half, it is surprising that little research has been devoted to understanding how changes in nature of work have affected workers' labor supply decisions. This study investigates the issue.
II.1 Defining Job Quality
The fact that workers require some compensation in order to supply labor indicates that there is some distaste for working. The distaste for work results not only from the opportunity cost of going to work, but it also depends on the nature of the tasks involved. In this study, Job Quality is defined as the degree of satisfaction, or the pleasantness associated with the process of working. Job Quality does not refer to any benefits such as wages, employer-provided health care, fame, or status associated with or resulting from the job, nor does it refer to the quality of the output.7 Some illustrative examples are in order.
A few decades ago, an economics professor would have had to draw charts and graphs manually on the board to illustrate an economic theory. Nowadays, he/she can perform the same task with less pain by means of an overhead projector. Similarly, the construction of a tunnel or highway would have required several manually intensive labor hours. The same task is performed more efficiently and with far less discomfort by today's heavy machinery.8
A comparison of jobs in the cross-section illustrates the Job Quality theory as well. For example, ceteris paribus, a garbage worker will most likely display a higher disutility for work compared to an office worker for a given amount of labor hours. Collecting garbage is not as pleasant as sorting mail in a clean office environment. Likewise, Job Quality can differ for two workers in the same occupation. A computer programmer with a high-resolution computer screen will find work more pleasant compared to an identical worker whose computer screen resolution is poor.9
II.2 Modeling
To understand the Job Quality hypothesis, recall the following intratemporal equilibrium for a lifetime utility maximizing worker over consumption and leisure.
| (1) | 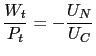 |
Intuitively, equation (1)
states that the real wage is equal to the marginal rate of
substitution between consumption and labor. A worker cannot
increase utility by giving up one unit of leisure, and spending the
proceeds
![]() on
units of consumption valued at
on
units of consumption valued at ![]() per unit. Neither can he/she improve utility by
giving up one unit of consumption, and spending the proceeds on
leisure valued at
per unit. Neither can he/she improve utility by
giving up one unit of consumption, and spending the proceeds on
leisure valued at ![]() per
unit.
per
unit.
Consider the same worker, and assume an improvement in the
quality of his/her work, or assume he/she switches to a higher
quality job with an equal wage while maintaining the same
consumption profile so that ![]() improves. Holding real wages and consumption
constant, the marginal utility for work improves, causing the rate
of substitution between labor and consumption to exceed the real
wage. The worker exploits the improvement in Job Quality to
increase utility by providing more labor until the marginal rate of
substitution between labor and consumption matches the real
wage.
improves. Holding real wages and consumption
constant, the marginal utility for work improves, causing the rate
of substitution between labor and consumption to exceed the real
wage. The worker exploits the improvement in Job Quality to
increase utility by providing more labor until the marginal rate of
substitution between labor and consumption matches the real
wage.
Another aspect of the Job Quality hypothesis is through the response of a worker to a permanent increase in the real wage rate. The Job Quality hypothesis suggests that following the increase in the real wage rate, a worker in a high-quality job will decrease labor hours by less, compared to a worker in a low quality job. In other words, the income effect tends to be higher in lower-quality jobs. Over time, as income grows, the share of employment in lower-quality jobs decreases causing an overall decline in the income effect.
Job Quality and the Consumer Problem
In most macroeconomic models, the utility function contains two
choice variables, labor or leisure, and consumption. Any utility
function with only consumption and labor (or leisure) implicitly
assumes homogeneity in the nature of work, that is, the nature of
work is irrelevant to the worker's labor supply decision. Allowing
for heterogeneity in jobs, consists of including a third variable
in the utility function that captures differences in Job Quality.
Suppose a job consists of several nonpecuniary characteristics that
are relevant to the worker's labor supply decision. The worker
chooses leisure ![]() and
consumption
and
consumption ![]() given a
bundle of nonpecuniary job characteristics
given a
bundle of nonpecuniary job characteristics
![]() and a
vector of demographic variables,
and a
vector of demographic variables, ![]() . The model assumes the wage rate and the
characteristics are exogenous for simplification.10
. The model assumes the wage rate and the
characteristics are exogenous for simplification.10
| (2) |
The utility function is maximized subject to the following budget
constraint: ![]() The
variable
The
variable ![]() represents
non-labor income,
represents
non-labor income, ![]() is
total labor annual hours and
is
total labor annual hours and ![]() , where
, where ![]() is the total time endowment.
is the total time endowment. ![]() represents the set of demographics
such as age, gender etc.
represents the set of demographics
such as age, gender etc. ![]() is
a composite of market consumption goods purchased with the labor
income
is
a composite of market consumption goods purchased with the labor
income ![]() .
.
![]() is the prevailing
wage rate. To simplify the model, let's omit
is the prevailing
wage rate. To simplify the model, let's omit ![]() , and let
, and let ![]() represent a composite of job
characteristics. We can rewrite the maximization problem as
follows:
represent a composite of job
characteristics. We can rewrite the maximization problem as
follows:
where
![]() is a composite
index of the nonpecuniary job characteristics. In addition to the
standard assumptions
is a composite
index of the nonpecuniary job characteristics. In addition to the
standard assumptions
![]() ,
,
![]() , let's assume that
agents prefer higher-quality jobs,
, let's assume that
agents prefer higher-quality jobs,
![]() , and that
, and that
![]() . The
last assumption states that job quality and labor hours are
interdependent. The higher
. The
last assumption states that job quality and labor hours are
interdependent. The higher ![]() is, the higher the marginal utility for work holding
labor hours constant. Let's further assume that consumption and
quality are independent
is, the higher the marginal utility for work holding
labor hours constant. Let's further assume that consumption and
quality are independent
![]() . With this modification
of the utility function, the first order conditions of utility
maximization can be re-written as follows:
. With this modification
of the utility function, the first order conditions of utility
maximization can be re-written as follows:
| (3) |
| (4) |
Equation (4)
captures labor supply for given levels of ![]() and
and ![]() . Combining equations (3) and (4)
results in equation (5) below:
. Combining equations (3) and (4)
results in equation (5) below:
| (5) | 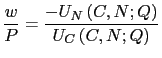 |
II.3 Econometric Model
Assume the utility function takes the following functional form:

where, ![]() denotes
the risk aversion parameter,
denotes
the risk aversion parameter, ![]() the real wage labor supply elasticity, and
the real wage labor supply elasticity, and
![]() the Job
Quality-labor hours elasticity.
the Job
Quality-labor hours elasticity. ![]() is the Job quality variable,
is the Job quality variable, ![]() consumption, and
consumption, and ![]() the observed labor hours. Normalize
the price for goods to unity and re-write equation (5)
as:
the observed labor hours. Normalize
the price for goods to unity and re-write equation (5)
as:
| (6) | 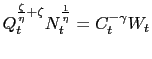 |
Taking logarithms of (6) and re-arranging terms results in the following testable cross-section and difference equations:
| (7) |
| (8) |
where ![]() denotes the
difference operator.
denotes the
difference operator.
![]() . Equations (7)
and (8) provide testable relationships between labor hours, real
wages, consumption, and Job Quality in the cross-section and
between two periods. Labor hours and real wages are available in
the data. The Job Quality variable is not. It is derived in the
following section.
. Equations (7)
and (8) provide testable relationships between labor hours, real
wages, consumption, and Job Quality in the cross-section and
between two periods. Labor hours and real wages are available in
the data. The Job Quality variable is not. It is derived in the
following section.
III. Measuring Job Quality and its Effect on Labor Supply
Measuring the effect of Job Quality on labor supply is a difficult exercise for several reasons. Job Quality appears to be an abstract concept, and as such, difficult to measure. Even with a good measure of Job Quality, how to assess its effect on labor supply is not obvious. After all, the set of job characteristics that generates disutility for one worker may be attractive to another worker. Workers may display different levels of disutility with respect to a given quality job. For example, a worker physically fit to lift twenty-five-pound boxes would have a lower disutility performing this task compared to another worker not well suited for the same task. Just as consumers have different tastes and preferences for products, workers have different tastes and preferences (for jobs), reflecting a combination of their individual interests and abilities. Just as consumers purchase goods and services that maximize their welfare, workers may sort into jobs that minimize their respective disutility for work. In an ideal scenario, where workers match perfectly to the jobs they desire, the effect of Job Quality on labor supply will be less significant in a cross-section analysis.
Despite these difficulties, the paper attempts the exercise using a unique data set from the Health and Retirement Study. The measurement of the effect of Job Quality on labor hours begins with an analysis of labor supply and job characteristics. I then build on the results from the analysis to obtain a measure of Job Quality in the cross-section. The cross-sectional measure provides the basis for the aggregate Job Quality index for the US economy.
III.1 Measurement of Job Quality in Micro Data
The Health and Retirement Study collects data on labor hours, compensations, and nonpecuniary job characteristics. The responses to the job characteristics questions provide the basis for the quality measure.
III.1.1 Job Characteristics Data
The Health and Retirement Study asks the following seventeen questions about job characteristics.
``...Thinking of your job, please tell how often these statements are true''
(1=All or almost all of the time, 2=Most of the time, 3=Some of the time, 4=None or almost none of the time)
- My job requires lots of physical effort (PHYSICAL)
- My job requires lifting heavy loads (LIFTING)
- My job requires stooping, kneeling, or crouching (BENDING)
- My job requires good eyesight (EYESIGHT)
- My job requires intense concentration or attention (ATTENTION)
- My job requires skill in dealing with other people (PEOPLE)
- My job requires me to work with computers (COMPUTERS)
- My job requires me to analyze data or information (DATA)
- My job requires me to keep up with the pace set by others (PACE)
- My job requires me to do the same things over and over (REPETITION)
- My job requires that I learn new things (LEARN)
- I have a lot of freedom to decide how I do my own work (FREEDOM)
- People I work with are helpful and friendly (COWORKERS)
In addition to these questions, the study asks respondents the following:
``...thinking of your job, this time please indicate how much you agree or disagree with each statement'' . (1=Strongly agree, 2=Agree, 3=Disagree, 4=Strongly disagree)
- I could do my job a lot better if I received training to update my job skills (TRAINING)
- My job requires me to do more difficult things than it used to (DIFFICULT)
- My job requires a very good memory (MEMORY)
- My job involves a lot of stress (STRESS)
Each of the above statements captures a specific job characteristic best described by the word in parentheses.11 One can argue that these questions do not cover every aspect of all jobs, but they do capture the main characteristics of most jobs. The following section constructs the Job Quality index by applying the common factor analysis technique to the answers to these questions.12
Results
Before performing the factor analysis, it is worth looking at the correlation matrix of the job characteristics in Table III. It provides insights in the correlation structure of the data. Some job characteristics correlate with others and some do not. For example, PHYSICAL, LIFTING, BENDING are strongly correlated with each other, and COMPUTERS is highly correlated with DATA. This indicates that the variables capture jobs with similar characteristics. On the other hand, there is little correlation between EYESIGHT and LIFTING or between ATTENTION and LIFTING. These attributes most likely reflect jobs that are not similar.
The results from the common factor analysis presented in Table IV suggest seven common factors for the jobs in our data. The first factor correlates positively with the following variables (in order of significance): DATA, COMPUTERS, LEARN, MEMORY, ATTENTION, DIFFICULT, STRESS, PEOPLE, PACE, and correlates negatively with PHYSICAL, LIFTING, BENDING, and REPETITION. The second factor correlates positively with such variables as PHYSICAL, LIFTING, BENDING, and correlates negatively with COMPUTERS. The last five factors appear to reflect some variation of the first two. For example, the third factor is not correlated with PHYSICAL, LIFTING, nor BENDING, but correlates positively with FREEDOM and COWORKERS, and negatively with TRAINING and DIFFICULT. Based on the significance of the contribution of the factors to the variability of the data, the first two factors are retained as our measure of job characteristics. The last five factors are not as desirable as the first two. They do not correlate highly with the observed variables as evidenced by their low factor loadings and small eigenvalues. Together the first two factors explain approximately 76 percent of the variation in the observed data. The remainder of the study focuses on these two factors.
Overall, the first factor reflects jobs that are non-physical in nature, whereas the second factor reflects physical jobs. To understand the factors, Tables V and VI present their means by industry and occupation. The results are in line with expectations. For example, we would expect jobs in the construction and mining industries to be physically intensive. The mean of the PHYSICAL factor is positive for this industry whereas the mean of the MENTAL factor is negative. Similarly, the mean for the MENTAL factor is positive for the Finance and Management industries. The means for the PHYSICAL factor are negative for the same industries. For the transportation industry, both means are positive, indicating that jobs in the transportation industry contain both mental and physical components. For occupations such as Managerial, Specialty Operation, Technical Support, or Sales, the mean of the MENTAL factor is positive. For the same occupations, the mean of the PHYSICAL factor is negative. Other occupations such as Household Services and Protection have negative means for both factors.
To further understand the differences in the two categories of jobs, Table VII displays the correlation between the factors and various job characteristics such as benefits, compensation, and job flexibility. The results show that the MENTAL factor correlates positively with Salary, and Net Wealth. The correlation coefficient for the PHYSICAL factor is negative for these variables. Workers in MENTAL jobs also tend to have a higher education. They tend to be white, male, and with the flexibility to increase hours, but they cannot decrease them. Furthermore, they tend to have better benefit packages such as higher number of paid vacation weeks per year, higher number of paid sick days, and an employer-provided retirement plan. They tend to make Pay and Promotion decisions for other employees, and they are healthier. Workers in PHYSICAL jobs, on the other hand, do not have such generous benefit packages. They tend to be members of an employee union, and do not work as much overtime as their counterparts in MENTAL jobs. Job insecurity and injury rates tend to be higher for workers in the PHYSICAL jobs.
III.2 Job Quality and Labor Supply
This section examines the relationship between job characteristics and labor supply by estimating the labor supply equations derived in section II.3 while controlling for other factors that could influence estimation. The first model estimates the cross-sectional equation (7). The second model estimates the corresponding difference equation (8). The benchmark cross-section and difference models are estimated for employed respondents only.
Furthermore, the models focus on the hours margin. Labor economists have recognized the importance of participation margin in labor supply. Focusing on the hour's margin allows extrapolation of the results to workers of all ages, for whom the hours choice is relevant but for whom the participation decision faced by respondents in this sample, namely retirement, is not relevant.
III.2.1 Regression Analysis: Cross-Section
To understand how the factors influence labor supply after controlling for all other covariates, the first model regresses logarithmic labor hours on the vector of factors scores, real wage, some demographics, and pecuniary work variables.13 All the data are from the first wave (1992) of the HRS.
| (9) |
The results from the O.L.S. estimation are presented in Table VIII. The coefficient of PHYSICAL factor variable is negative and insignificant, whereas the MENTAL factor has a positive, significant coefficient. Workers in jobs that are mentally intensive tend to work more hours compared to workers in physical jobs. The results imply that a unit improvement in the MENTAL factor accounts for approximately 3.4 percent of growth in annual labor hours.
III.2.2 Regression Analysis: Difference
The regression in this section uses data available in the first and second waves of the HRS. The data in both waves are identical except the second wave's data were collected two years after those of the first. The second wave contains questions on job characteristics for respondents who switched jobs between the two waves. The factor scores for these respondents are constructed as described above. No job characteristics data were collected for respondents who remained in the same job. For these respondents, the factor scores estimated in the first wave are used. In this estimation as in the cross-section, consumption is omitted. In the end, we have data on labor hours, factor scores, time-varying demographics, and pecuniary job characteristics for two waves of data collected approximately two years apart for the same respondents. These data allows us to test how changes in hours between 1992 and 1994 responded to changes in the factor scores, by estimating the following econometric model.
| (10) |
where ![]() denotes the
difference between the value of variable in 1994 and its value in
1992,
denotes the
difference between the value of variable in 1994 and its value in
1992,
![]() . From the
regression results in Table IX, we note
again that the coefficient on the change in the MENTAL factor is
positive and statistically significant, whereas for the PHYSICAL
factor, the coefficient is negative and insignificant. The results
from this model imply that a one-unit increase in the MENTAL factor
accounts for approximately 5.5 percent of growth in annual labor
hours.
. From the
regression results in Table IX, we note
again that the coefficient on the change in the MENTAL factor is
positive and statistically significant, whereas for the PHYSICAL
factor, the coefficient is negative and insignificant. The results
from this model imply that a one-unit increase in the MENTAL factor
accounts for approximately 5.5 percent of growth in annual labor
hours.
The results from the two regression models indicate that, of the two main job characteristics, only the MENTAL factor influences labor hours positively. The coefficient for the PHYSICAL factor is not statistically different from zero. In the remainder of the analysis, I retain the MENTAL factor as the Job Quality measure.
III.2.3 Robustness and Sensitivity Analysis
This section conducts several sensitivity and robustness tests. The results are reported for the Job Quality coefficient in Tables X and XI. The first sensitivity tests exclude the insignificant PHYSICAL factor from both models. The benchmark results are preserved. To better compare the results obtained from both models, the next sensitivities estimate both models using an identical sample. Reconciling the samples does not significantly alter the results.
Next, the sample in the Difference model is restricted to the set of respondents who switched jobs between 1992 and 1994. Excluding respondents who didn't change jobs allows more variation in the Job Quality variable and provides a firmer test of whether changes in Job Quality and changes in labor hours co-vary. The estimated coefficient for the Job Quality variable is 0.047. In the next set of sensitivity tests, the sample is split between males and females for both models. The split of the sample allows a test of whether the relationship between Job Quality and labor hours differs by gender. The estimates are identical for men and women.
The results obtained from the cross-section regression model can be biased if the sample is incidentally truncated along the Job Quality variable. For example, if poor Job Quality lowers the labor force participation rate, the sample would consist of workers with Job Quality over a certain threshold. The truncation introduces an omitted-variable bias that could drive the observed results if the omitted variable is correlated with the Job Quality measure. The estimation of a two-stage Heckman model where participation is modeled as a function of age, education, health, marital status, net wealth, gender, and occupation in previous jobs (proxy for Job Quality in previous job) addresses the issue. The estimated coefficient for Job Quality is identical to the estimate from the benchmark regression. The occupation dummy variables in the participation model are significant. So is the Job Quality variable in the hours equation. These results indicate that Job Quality matters for labor force participation as well as for labor supply. Controlling for the participation effect does not significantly change the results.
Marital status may also influence a respondent's labor supply, especially if there are strong interactions between the respondent's and the spouse's labor supply. To the extent that the unobserved factors due to marital status are correlated with the Job Quality measure, our results will be biased. When the analysis is conducted separately for married and single respondents, the results are preserved.
The next sensitivity analysis is motivated by potential biases introduced by the choice of the HRS data. This issue is of concern because in the HRS most respondents were born between 1931 and 1941.14 For these reasons, the average age in the sample (55 year of age) exceeds the national average worker's age. To the extent that the Job Quality effect is different for older and younger workers, the coefficient in our sample will not reflect the coefficient obtained using the entire population data. The regression analysis for various age brackets reveals a higher coefficient for younger respondents. For respondents below 55 years of age, the average coefficient is 0.043 and 0.027 for respondents over 55. One possible explanation for these results is that older workers are more experienced and accustomed to their jobs, and hence, tolerate more than younger works. The differences in coefficients for age groups are mostly insignificant. To the extent that differences in coefficients across age groups matter, they indicate a higher coefficient for younger workers, which indicates that our estimate of the quality effect would be higher if the age distribution of workers in the HRS sample were identical to the age distribution at the national level.
Another possible and related bias comes from sample selection. For example, if older workers tend to join specific types of occupations and industries, these occupations will be over represented in our sample. Given the close link between occupation and Job Quality, our estimate would be biased. To address this issue, we construct weights such that the distribution of employment in the HRS by industry and occupation cells matches the national distribution. The estimated coefficient increases slightly from 0.034 to 0.037.
A common problem in estimation of labor supply models using micro data is the `` division bias''. Division bias is present if there are measurement errors in labor hours, and the wage rate is computed as salary divided by the hours. For example, an over-estimation of the hours increases the dependent variable and decreases the independent variable, resulting in an upward bias in the wage coefficient. If the correlation between the wage rate and the Job Quality measure is high, the estimate quality coefficient will be biased. To test whether our results are affected by the division bias, the sample is restricted to employees paid hourly. In other words, the wage rate for respondents in this sample is no longer computed as the ratio of salary to total hours. These respondents make up approximately 56 percent of the sample. The regression coefficient (0.020) remains positive and statistically significant. Furthermore, the correlation between the Job Quality measure and the wage rate is weak so that even in the presence of a division bias, the main results are not likely to be affected.
In sum, the sensitivity analysis reveals that the Job Quality estimate obtained in the benchmark model remains positive and statistically significant, and that it is robust to various controls and cuts of the data.
IV. Aggregate Job Quality Index and Quality Controlled Hours
To construct the aggregate Job Quality index over time, the HRS data is limited since it is only available from 1992. I use IPMUS decennial data on employment by occupation and industry from 1850 to 2000.15 IPUMS reclassifies occupations and industries based on the census 1950 classification scheme. The reclassification makes the data comparable across years. I match these industry and occupation groups with those of the HRS. In the end, we obtain thirteen industries and eight occupations groups that are comparable between the IPMUS data and the HRS data (see Appendix A for the industry and occupation classification in both datasets).
Using the average Job Quality measure constructed from the HRS job characteristics by industry and occupation cells, we can infer the overall quality of jobs in the aggregate economy from the composition of the workforce. For example, if the fraction of workers in the higher-quality industries and occupations increases proportionally more than the fraction of workers in lower-quality industries, the aggregate Job Quality in the economy improves.16 The aggregate Job Quality index would decline if the opposite were true.
Let
![]() denote the
number of workers in occupation
denote the
number of workers in occupation ![]() and industry
and industry ![]() at time
at time ![]() ,
and
,
and ![]() the total
number of workers at time
the total
number of workers at time ![]() . Let
. Let ![]() be the improvement in aggregate Job Quality
between a base-year
be the improvement in aggregate Job Quality
between a base-year ![]() and
time
and
time ![]() .
.
| (11) | 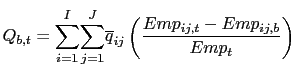 |
where ![]() is the total number
of industries in the economy, and
is the total number
of industries in the economy, and ![]() the total number of occupations.
the total number of occupations.
![]() is
the average quality for industry
is
the average quality for industry ![]() and occupation
and occupation ![]() calculated in section III.1. The Job Quality
variable is multiplied by 0.034, the quality coefficient estimated
in Table 2.6a, so that one hundredth of a unit change in the
quality measure implies a 1 percent corresponding change in labor
hours. For equation (11)
reduces to
calculated in section III.1. The Job Quality
variable is multiplied by 0.034, the quality coefficient estimated
in Table 2.6a, so that one hundredth of a unit change in the
quality measure implies a 1 percent corresponding change in labor
hours. For equation (11)
reduces to ![]() .
.
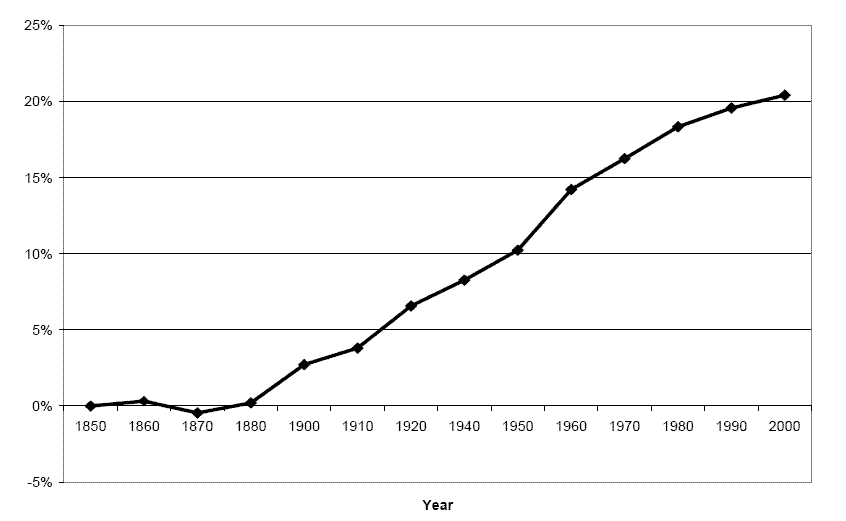
Figure II plots the aggregate Job Quality index for the U.S. from 1850 and 2000. The index increased by approximately 0.204. The results imply that the improvement in Job Quality was responsible for at least 20.4 percent growth in average annual labor hours between 1850 and 2000, which corresponds to approximately 0.14 percent of labor hours growth (less than three hours) per year.
Three features of the index are worth noting. From 1850 to 1880, the index did not change. Between 1880 and 1950, it improved almost exponentially, and after 1950, it continued to improve at a slower rate. The increase between 1880 and 1900 reflects the shift from Agriculture toward Manufacturing, Transportation, and Retail trade industries. For occupations, the significant shift occurred from Farmers to Machine operatives. Post 1950, the share in employment in Agriculture and Manufacturing declined drastically, and the share of Professional services industry rose. From 1950 on, employment in the Clerical and Professional occupations surged, while employment shares of Farmers and Operative laborers declined. These three phases seem to mark the movement from Agriculture to Manufacturing between 1880 and 1900, and from Manufacturing to Services after 1950.
Tables XII and XIII break down the growth in the Job Quality index by industry and occupation. Table XII shows the growth in quality attributed to industry only. This is the growth due to shifts in industry employment ignoring shifts in occupation employment. Similarly, Table XIII displays the growth in quality due to shifts in occupation employment, ignoring shifts in industry employment. The growth attributed to shifts in industry is 16.1 percent while the growth due to occupation changes is 19.5 percent.
The derivation of quality-controlled labor hours follows from the growth in the Job Quality index derived in the previous section. Let 1850 be the base year, quality-controlled labor hours can be derived using the following formula:
| (12) | 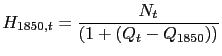 |
where ![]() denotes the
quality-controlled labor hours,
denotes the
quality-controlled labor hours, ![]() is actual annual per person observed labor
hours,
is actual annual per person observed labor
hours, ![]() is the
aggregate quality derived in the previous section. Given the
improvement in
is the
aggregate quality derived in the previous section. Given the
improvement in ![]() between 1850 and 2000, formula
(12)
implies that quality-controlled labor hours declined by
approximately 20.4 percent. These results support the Job Quality
hypothesis that the average hours would have been working
approximately 20.4 percent lower in 2000 had the nature of work
remained constant since 1850.
between 1850 and 2000, formula
(12)
implies that quality-controlled labor hours declined by
approximately 20.4 percent. These results support the Job Quality
hypothesis that the average hours would have been working
approximately 20.4 percent lower in 2000 had the nature of work
remained constant since 1850.
V. Some Caveats
From the observed changes in the nature of work, the study characterizes jobs in the United States and assesses the implications of changes in Job Quality on changes in labor supply. The measures provided are not without limitations.
First, the aggregate Job Quality measure assumes a constant ranking of industry and occupation cells across time. Sector-biased technological changes could cause quality in an occupation to exceed the Job Quality in occupations previously ranked higher. The assumption appears, however, reasonable. A correlation of the rankings of industry and occupation cells by education (a good proxy for Job Quality) is 0.90. Second, the derived relationship between Job Quality and work hours assumes that a worker in 1850 is identical to a worker in 2000. If the characteristics of workers change over time, this could influence our measured quality effect. Further, and perhaps more importantly, the current Job Quality index fails to account for within-jobs quality improvements. The derived index is entirely based on the reallocation of employment across industries and occupations over time.
From the micro-data standpoint, there are reservations about the HRS data. One unique feature of this data set is the over representation of older workers. The mean and median age of the respondents in the data are approximately 56. This average is much higher than the age of the national average worker. To the extent that the relationship between Job Quality and labor hours is sensitive to the age of the respondent, our estimates would be biased. The sensitivity analyses performed in section III.2 indicate some differences in the estimated Job Quality effect for various age brackets. The estimate is higher for respondents below 55 years of age. Any potential bias introduced by the over-representation of older workers would suggest that the actual estimate is higher than the one reported. This limitation and the inability to capture within-jobs quality improvements make our estimates of the growth in hours attributed to Job Quality, a lower bound of the true estimate.
VI. Conclusion
This study presents evidence of the heterogeneity in jobs, and analyzes the implications of this heterogeneity for labor supply. The results indicate that, ceteris paribus, some jobs tend to induce more labor hours. These jobs are prevalent in the services sector and in public administration, and in occupations such as management, professional specialty, sales, administrative, and technical support. Workers in these occupations tend to enjoy higher wages and more generous employer provided benefits packages. The share of employment in these industries and occupations has increased over time, inducing an overall increase in aggregate Job Quality. The increase in labor resulting from the improvement in Job Quality explains, in part, the lack of a strong downward trend in the average work hours in the United States. More precisely, the improvement in Job Quality between 1850 and 2000 accounts for at least 20.4 percent of growth in per capita labor hours. Once we control for changes in quality, we observe a decline in labor hours consistent with a domination of the income effect over the substitution effect.
One important limitation of the study is the inability to account for within-jobs quality improvements. As such, the measure only provides a lower bound of the true measure. To fully appreciate the extent to which changes in Job Quality impact trends in labor hours, more research along this line is warranted.
A. Appendix: IPUMS and HRS Industry and Occupation Classification
Panel 1. IPUMS and HRS Industry Classification
| IPUMS 1950 Industry Classification | HRS Industry Classification |
|---|---|
| Agriculture, forestry, fishing | Agriculture, forestry, fishing |
| Mining and construction | Mining and construction |
| Manufacturing: non-durable | Manufacturing: non-durable |
| Manufacturing: durable | Manufacturing: durable |
| Transportation | Transportation |
| Wholesale | Wholesale |
| Retail | Retail |
| Finance, insurance, and real estate | Finance, insurance, and real estate |
| Business and repair services | Business and repair services |
| Personal services | Personal services |
| Entertainment and recreation | Entertainment and recreation |
| Professional and related services | Professional and related services |
| Public administration | Public administration |
Note: IPUMS industry classification categories are idential to those in the Health and Retirement Survey.
Panel 2. IPUMS and HRS Occupation Classification
| IPUMS 1950 Occupation Classification | HRS Occupation Classification |
|---|---|
| Professional, Technical | Prof. Specialty oper. & tech support |
| Managers, Officials, and Proprietors | Managerial specialty operation |
| Sales workers | Sales |
| Clerical and Kindred | Clerical, administrative support |
| Service Workers (private household) | Service: priv. hshld, clean, building serv. |
| Service Workers (not private household) | Service: protection Service: food preparation Health services Personal services |
| Farmers, Farm Laborers | Farming, forestry, fishing |
| Operatives, Laborers | Operators: machine Operators: transport, etc. Operators: handlers, etc. |
| Craftsmen | Mechanics and repair Construction trade and extractors Precision production Member of armed forces |
References
1. Barsky, Robert, Miles Kimball, Thomas Juster and Matthew Shapiro, `` Preference Parameters and Behavioral. Heterogeneity: An Experimental Approach in the Health and Retirement Study,'' Quarterly Journal of Economics, CXII (1997), 537-579.
2. Basu, Susanto and Kimball, Miles, `` Long-Run Labor Supply and the Elasticity of Intertemporal Substitution for Consumption,'' Working Paper, (2002), University of Michigan.
3. Benhabib, Jess, Richard Rogerson and Randall Wright, `` Homework in Macroeconomics: Household Production and Aggregate Fluctuations,'' Journal of Political Economy, XCIX (1991), 1166-1187.
4. Campbell, John Y., and Sydney Ludvigson, `` Elasticities of Substitution in Real Business Cycle Models with Home Production,'' electronic file available at www.ny.frb.org-/rmaghome/economist/ludvigson/ludvigson.html, (2000).
5. Costa, Dora L., `` The Wage and the Length of the Work Day: From the 1890s to 1991,'' NBER Working Paper 6504 (1998).
6. Gardner, Jennifer M., Philip L.Rones, and Randy E. IIg, `` Trends in hours of work since the mid-1970s,'' BLS Monthly Labor Review, CXX (1997).
7. Greenwood, Jeremy and Zvi Hercowitz, `` The Allocation of Capital and Time over the Business Cycle,'' Journal of Political Economy, XCIX (1991), 1188-1214.
8. Greenwood, Jeremy, Richard Rogerson and Randall Wright, `` Household Production in Real Business Cycle Theory," in Thomas F. Cooley, eds., Frontiers of Real Business Cycle Theory, (Princeton, NY: Princeton University Press, 1995).
9. Hall, Robert E., `` Intertemporal Substitution in Consumption,'' Journal of Political Economy, XCVI (1988), 339-357.
10. -----, `` Stochastic Implications of the Life Cycle-Permanent Income Hypothesis: Theory and Evidence,'' Journal of Political Economy, LXXXVI (1978), 971-987.
11. Hamermesh, D., , `` Consumption During Retirement: The Missing Link in the Life Cycle,'' Review of Economics and Statistics, LXVI (1984), 1-7.
12. Hansen, G.D., and R. Wright, `` The Labor Market in Real Business Cycle Theory,'' Federal Reserve Bank of Minneapolis Quarterly Review, Spring (1992), 1-12.
13. Heckman, James and Mark R. Killingsworth, `` Female Labor Supply: A Survey,'' In Orley C. Ashenfelter, and Richard Layard, eds., Handbook of Labor Economics, Volume 1 (Amsterdam: North Holland, 1986).
14. Hurd, Michael and Kathleen McGarry, `` The relationship between job characteristics and Retirement,'' NBER Working paper 4558 (1993).
15. Juhn, Chinhui and Kevin M. Murphy, `` Wage Inequality and Family Labor Supply,'' NBER Working paper MMMMMCDLIX (1996).
16. King, Robert G., Charles I. Plosser, and Sergio T. Rebelo, `` Production, Growth and Business Cycles: I. The Basic Neoclassical Model,'' Journal of Monetary economics, XXI (1988),195-232.
17. ---, "Production, Growth and Business Cycles: II. New Directions,'' Journal of Monetary economics, XXI (1988), 309-341.
18. Keynes, John Maynard, `` Economic Possibilities for our Grandchildren,'' Nation and Athenaeum, October 11 and 18, 1930. (Reprinted in The Collected Writings of John Maynard Keynes, Volume IX, Essays in Persuasion, London, 1972).
19. Mariger, R., `` A Life-Cycle Consumption Model with Liquidity Constraints: Theory and Empirical Results'', Econometrica, LV ( 1987), 533-557.
20. McDonald, Roderick P., `` Factor Analysis and Related Methods,'' (Hillsdale, NJ: Lawrence Erlbaum Associates, 1985).
21. Nakamura, Alice and Susan, Houseman, `` Working Time in Comparative Perspective,'' (Kalamazoo, Michigan: W.E. Upjohn Institute for Employment Research Volume II, 2001).
22. Pencavel, John, `` Labor Supply of Men: A Survey,'' In Orley C. Ashenfelter, and Richard Layard, eds., Handbook of Labor Economics, Volume 1 (Amsterdam: North Holland,1986).
23. Rebelo, Sergio and Danyang Xie, `` Beyond Balanced Growth,'' NBER Working Paper 6159, (1997).
24. Rummel, R. J., `` Applied Factor Analysis,'' (Evanston, IL: Northwestern University Press, 1970).
25. Smith, James P. and Michael P. Ward, `` Trends in Women's work, Education, and Family Building,'' Journal of Labor Economics, III (1985), S59-S90.
26. Stock, James H., Mark W. Watson, `` Business Cycle Fluctuations in U.S. Macroeconomic Time Series,'' NBER working paper 6528 (1998).
27. Vissing-Jorgenson, `` Limited Asset Market Participation and the Elasticity of Intertemporal Substitution,'' NBER Working paper 8896, (2002).
28. Viscusi W, Kip, `` The Value of Risks to Life and Health,'' Journal of Economic Literature, Volume XXXI (1993 ), 1912-1946.
Table I. Share of Employment by Industry in 1850, 1920, and 2000 (percent)
Industry |
1850 | 1920 | 2000 |
|---|---|---|---|
Agriculture, forestry, fishing |
58.0 | 26.2 | 2.9 |
Mining and construction |
8.1 | 7.8 | 7.4 |
Manufacturing: non-durable |
5.6 | 12.9 | 8.6 |
Manufacturing: durable |
6.7 | 11.7 | 6.3 |
Transportation |
2.9 | 9.2 | 4.9 |
Wholesale |
0.1 | 2.1 | 3.3 |
Retail |
8.1 | 9.9 | 17.9 |
Finance, insurance, and real estate |
0.3 | 2.1 | 5.8 |
Business and repair services |
2.3 | 2.8 | 6.4 |
Personal services |
4.2 | 7.5 | 3.2 |
Entertainment and recreation |
0.1 | 0.6 | 2.6 |
Professional and related services |
3.0 | 4.8 | 24.8 |
Public administration |
0.6 | 2.5 | 5.9 |
Source: Author's calculations from 1 percent Sample of the Census Bureau collected in the Integrated Public Use Microdata Series by the Minnesota Population Center. (http://www.ipums.org). Industry in all years is redefined by IPUMS to be consistent with the 1950 classification.
Table II. Share of Employment by Occupation in 1850, 1920, and 2000 (percent)
| Industry | 1850 | 1920 | 2000 |
|---|---|---|---|
Professional |
3.3 | 5.5 | 21.1 |
Managers, officials, Proprietors |
5.1 | 6.5 | 10.3 |
Farmers / Farm laborers |
57.5 | 25.8 | 1.7 |
Service |
1.5 | 8.1 | 14.9 |
Clerical |
0.2 | 8.1 | 18.8 |
Sales |
2.5 | 4.9 | 6.5 |
Craftsmen |
18.7 | 14.4 | 11.0 |
Operative /Non farm Laborers |
11.2 | 26.7 | 15.9 |
Source: Author's calculations from 1 percent Sample of the Census Bureau collected in the Integrated Public Use Microdata Series by the Minnesota Population Center. (http://www.ipums.org). Occupation in all years is redefined by IPUMS to be consistent with the 1950 classification.
Table III. Correlation Matrix of Nonpecuniary Job Characteristics Variables
|
|
Phys. | Lifting | Bend. | Eye. | Attent. | People | Comp. | Data | Pace | Repet. | Learn | Freed. | Cowrk. | Train. | Diffic. | Mem. | Stress |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Physical |
1.00 | ||||||||||||||||
Lifting |
0.65 | 1.00 | |||||||||||||||
Bending |
0.60 | 0.64 | 1.00 | ||||||||||||||
Eyesight |
0.06 | 0.02 | 0.05 | 1.00 | |||||||||||||
Attention |
0.04 | 0.00 | -0.00 | 0.40 | 1.00 | ||||||||||||
People |
-0.04 | -0.06 | -0.03 | 0.18 | 0.31 | 1.00 | |||||||||||
Computers |
-0.35 | -0.28 | -0.25 | 0.16 | 0.18 | 0.15 | 1.00 | ||||||||||
Data |
-0.30 | -0.23 | -0.22 | 0.14 | 0.27 | 0.24 | 0.55 | 1.00 | |||||||||
Pace |
0.02 | 0.01 | -0.02 | 0.14 | 0.26 | 0.21 | 0.22 | 0.27 | 1.00 | ||||||||
Repetition |
0.22 | 0.16 | 0.18 | 0.11 | 0.10 | 0.01 | -0.08 | -0.14 | 0.17 | 1.00 | |||||||
Learn |
-0.04 | -0.05 | -0.03 | 0.18 | 0.30 | 0.32 | 0.26 | 0.39 | 0.28 | -0.06 | 1.00 | ||||||
Freedom |
-0.11 | -0.10 | -0.06 | 0.01 | 0.04 | 0.11 | 0.04 | 0.17 | -0.12 | -0.13 | 0.15 | 1.00 | |||||
Coworkers |
-0.02 | -0.04 | -0.01 | 0.08 | 0.05 | 0.11 | -0.01 | -0.01 | -0.01 | 0.04 | 0.08 | 0.23 | 1.00 | ||||
Training |
0.01 | 0.01 | 0.02 | 0.03 | 0.07 | 0.06 | 0.09 | 0.09 | 0.10 | -0.06 | 0.21 | -0.07 | -0.05 | 1.00 | |||
Difficult |
-0.01 | 0.01 | 0.01 | 0.09 | 0.18 | 0.12 | 0.22 | 0.26 | 0.17 | -0.06 | 0.31 | -0.01 | -0.09 | 0.36 | 1.00 | ||
Memory |
-0.06 | -0.05 | -0.05 | 0.22 | 0.32 | 0.30 | 0.20 | 0.30 | 0.20 | -0.01 | 0.33 | 0.11 | 0.04 | 0.14 | 0.26 | 1.00 | |
Stress |
0.02 | 0.01 | -0.02 | 0.10 | 0.29 | 0.23 | 0.17 | 0.25 | 0.24 | 0.04 | 0.26 | -0.03 | -0.16 | 0.15 | 0.36 | 0.29 | 1.00 |
Source: Author's calculations from wave I of the Health and Retirement Study
Table IV. Common Factor Analysis Results Using Nonpecuniary Job Characteristics Data
| Variable | Factor 1 | Factor 2 | Factor 3 | Factor 4 | Factor 5 | Factor 6 | Factor 7 | Factor Unique. | Description |
|---|---|---|---|---|---|---|---|---|---|
Physical |
-0.41 | 0.66 | 0.02 | 0.03 | 0.02 | -0.00 | -0.02 | 0.39 | My job requires lots of physical effort. |
Lifting |
-0.40 | 0.65 | -0.02 | 0.12 | 0.15 | -0.04 | -0.00 | 0.38 | My job requires lifting heavy loads. |
Bending |
-0.37 | 0.62 | 0.03 | 0.14 | 0.13 | -0.00 | 0.03 | 0.44 | My job requires stooping, kneeling, or crouching. |
Eyesight |
0.28 | 0.26 | 0.24 | -0.18 | -0.01 | -0.00 | 0.21 | 0.72 | My job requires good eyesight. |
Attention |
0.45 | 0.33 | 0.21 | -0.18 | -0.08 | -0.07 | 0.10 | 0.59 | My job requires intense concentration or attention |
People |
0.41 | 0.20 | 0.21 | 0.01 | -0.12 | -0.04 | -0.11 | 0.72 | My job requires skill in dealing with other people |
Computers |
0.58 | -0.12 | -0.06 | -0.04 | 0.30 | 0.03 | 0.07 | 0.55 | My job requires me to work with computers. |
Data |
0.68 | -0.03 | -0.00 | 0.10 | 0.28 | -0.04 | -0.02 | 0.45 | My job requires me to analyze data or information. |
Pace |
0.37 | 0.26 | -0.04 | -0.24 | 0.08 | 0.12 | -0.16 | 0.70 | My job requires me to keep up with the pace set by others |
Repetition |
-0.11 | 0.27 | 0.08 | -0.30 | -0.01 | 0.11 | -0.05 | 0.80 | My job requires me to do the same things over and over. |
Learn |
0.55 | 0.25 | 0.05 | 0.18 | -0.02 | 0.09 | -0.07 | 0.59 | My job requires that I learn new things. |
Freedom |
0.15 | -0.10 | 0.31 | 0.33 | -0.02 | -0.04 | -0.02 | 0.76 | I have a lot of freedom to decide how I do my own work |
Coworkers |
0.03 | -0.03 | 0.39 | 0.13 | -0.04 | 0.17 | -0.01 | 0.80 | The people I work with are helpful and friendly. |
Training |
0.22 | 0.17 | -0.30 | 0.13 | -0.14 | 0.17 | 0.08 | 0.76 | Could do job a lot better if I received training to update my job skills |
Difficult |
0.41 | 0.25 | -0.34 | 0.16 | -0.09 | 0.05 | 0.07 | 0.61 | My job requires me to do more difficult things than it used to. |
Memory |
0.48 | 0.23 | 0.08 | 0.06 | -0.13 | -0.07 | -0.01 | 0.69 | My job requires a very good memory. |
Stress |
0.41 | 0.29 | -0.22 | -0.06 | -0.11 | -0.16 | -0.08 | 0.66 | My job involves a lot of stress. |
Pct variance explained by factor |
57 | 39 | 14 | 10 | 6 | 3 | 3 |
Note: The first table displays each factor and its corresponding eigen-value. The second table displays the factor analysis results. First column contains the variables used in the regression. Columns 2-8 display the factors retained out of the possible set of 17. Only factors with positive eigen-values are retained. Column 9 captures the uniqueness of the variable, that is, the variability in the variable that no common factor can explain Column 10 gives detail description of the variables in column 1. Factor loadings greater than of equal to 0.3 in bold.<br>
Source: Author's calculations from Wave I of the Health and Retirement Study
Table V. Mean of "PHYSICAL" and "MENTAL" Factors by Industry
| Industry | MENTAL | PHYSICAL | Nobs |
|---|---|---|---|
Agriculture, forestry, fishing | -0.71 | 0.37 | 278 |
Mining and construction | -0.51 | 0.45 | 515 |
Manufacturing: non-durable | -0.16 | 0.04 | 614 |
Manufacturing: durable | -0.07 | 0.03 | 906 |
Transportation | 0.01 | 0.09 | 574 |
Wholesale | 0.06 | -0.02 | 324 |
Retail | -0.26 | 0.16 | 935 |
Finance, insurance, and real estate | 0.56 | -0.35 | 533 |
Business and repair services | -0.04 | -0.07 | 495 |
Personal services | -0.72 | -0.05 | 412 |
Entertainment and recreation | -0.35 | 0.05 | 125 |
Professional and related services | 0.20 | 0.05 | 2,255 |
Public administration | 0.60 | -0.21 | 409 |
Source: Author's calculations from wave I of the Health and Retirement Study.
Note: A positive high average for the MENTAL factor indicates a mentally intensive industry. A negative high average indicates a low mentally intensive industry. The same is true for the PHYSICAL factor.
Table VI. Mean of "PHYSICAL" and "MENTAL" Factors by Occupation
| Occupation | MENTAL | PHYSICAL | Nobs |
|---|---|---|---|
Managerial specialty operation |
0.55 | -0.25 | 1,247 |
Prof. Specialty oper. & tech support |
0.51 | -0.06 | 1,316 |
Sales |
0.10 | -0.08 | 855 |
Clerical, administrative support |
0.42 | -0.23 | 1,344 |
Service: priv. hshld, clean, building serv. |
-1.38 | -0.33 | 130 |
Service: protection |
-0.10 | -0.20 | 142 |
Service: food preparation |
-0.71 | 0.50 | 253 |
Health services |
-0.43 | 0.64 | 197 |
Personal services |
-0.82 | 0.15 | 570 |
Farming, forestry, fishing |
-0.84 | 0.42 | 265 |
Mechanics and repair |
-0.30 | 0.43 | 306 |
Construction trade and extractors |
-0.63 | 0.72 | 289 |
Precision production |
-0.22 | 0.16 | 285 |
Operators: machine |
-0.54 | 0.25 | 566 |
Operators: transport, etc. |
-0.50 | 0.31 | 424 |
Operators: handlers, etc. |
-0.93 | 0.49 | 212 |
Member of armed forces |
0.97 | -0.42 | 7 |
Source: Author's calculations from wave I of the Health and Retirement Study.
Note: A positive high average for the MENTAL factor indicates a mentally intensive industry. A negativehigh average indicates a low mentally intensive industry. The same is true for the PHYSICAL factor.
Table VII. Correlation of Mental and Physical Factors with Job Characteristics and other demographics (OBS = 2,822)
| Occupation | Mental Factor | Physical Factor |
|---|---|---|
Salary |
0.19 | -0.07 |
Education |
0.44 | -0.19 |
Marital Status |
0.03 | -0.03 |
Net Wealth |
0.13 | -0.12 |
Male |
0.13 | -0.02 |
White |
0.10 | -0.10 |
Num. Paid Vacation Weeks |
0.18 | -0.06 |
Num. Paid Sick Days |
0.21 | -0.07 |
Long-term Disability |
0.13 | -0.02 |
Can Decrease Hours |
-0.00 | -0.03 |
Can Increase Hours |
0.14 | -0.02 |
Employer Retirement Plan |
0.23 | -0.02 |
Job Security |
0.04 | -0.03 |
Union Membership |
-0.10 | 0.14 |
Make Pay/Promotion Decision |
0.28 | -0.12 |
Better Health |
0.18 | -0.07 |
Overtime Weeks |
0.03 | -0.04 |
Number of injuries |
-0.03 | 0.11 |
Source: Author's calculations from wave I of the Health and Retirement Study.
Table VIII. O.L.S. Regression of Log Annual Labor Hours on Log Wage rate, Job Characteristic, and demographic variables
| Variable | Coefficient | St. Error | P-Value |
|---|---|---|---|
Mental |
0.034 | 0.004 | 0.000 |
Physical |
-0.004 | 0.003 | 0.260 |
Log wage rate |
-0.017 | 0.008 | 0.031 |
Non labor income |
3.32e-09 | 3.08e-08 | 0.914 |
Net Wealth |
3.77e-09 | 9.15e-09 | 0.680 |
Male |
0.122 | 0.007 | 0.000 |
White |
0.011 | 0.007 | 0.096 |
Years on Job |
0.001 | 0.000 | 0.006 |
Marital Status |
-0.020 | 0.007 | 0.006 |
Age |
-0.002 | 0.001 | 0.000 |
Education |
-0.004 | 0.001 | 0.001 |
Household size |
-0.002 | 0.003 | 0.370 |
Health Status |
0.003 | 0.003 | 0.352 |
Survival probability to 85 |
0.002 | 0.001 | 0.018 |
Union Membership |
-0.058 | 0.006 | 0.000 |
Employer Retirement Plan |
0.011 | 0.008 | 0.138 |
Can Increase Hours |
0.024 | 0.006 | 0.000 |
Can Decrease Hours |
0.010 | 0.007 | 0.158 |
Num. Paid Vacation Weeks |
0.018 | 0.002 | 0.000 |
Long-term Disability |
0.030 | 0.006 | 0.000 |
Job Safety (num. Injuries) |
0.028 | 0.009 | 0.001 |
Constant |
7.714 | 0.040 | 0.000 |
Number of Observation: 5,037
R-squared: 0.17
Note: The dependent variable in is the natural log of annual labor hours worked reported by respondents in wave I of the Health and Retirement Study. `` wage rate'' is the employee's hourly wage rate. For salaried respondents, it is the total salary divided by the labor income. `` non labor income'' is the income from sources other than job. Age is the respondent's age, `` Education is the number of years of education. Health is the self-reported health status on a 1-5 scale.5=Excellent, 1=Poor. Net worth is households' net worth in U.S. dollars. `` White'' captures whether the respondent is White. `` Years on Job'' is the number of years at the current job. `` Marital Status'' is ``1'' if respondent is married and ``0'' if not. `` Employer Retirement Plan'' is ``1'' if employer provides some type of retirement plan such 401k, pension, tax-deferred plans etc. `` Can Decrease/Increase'' is an indicator for ability of employee to decrease/increase hours on the job. ``1'' if respondent can decrease/increase hours and `` 0'' otherwise. `` Long-term Disability'' is ``1'' if employer provides a long-term disability plan and `` 0'' if he does not. `` Job Safety'' is the number of injuries to respondent on the job in the year preceding the interview. Union Membership is `` 1'' if respondent belongs to a union and `` 0'' if not. Household size is the number of household members besides respondent. Survival probability to 85 is `` 0'' if respondent does not believe he/she'll live to 85 of age, and ``10'' if absolutely certain.
Source: Author's calculations from the Health and Retirement Study
Table IX. O.L.S. Regression of Log Change in Annual Labor Hours between 1992 and 1994 on Log Change in Wage rate, Change in Job Characteristic, and Change in other demographic variables
| Variable | Coefficient | St. Error | P-Value |
|---|---|---|---|
Change in Mental |
0.055 | 0.030 | 0.071 |
Change in Physical |
-0.027 | 0.020 | 0.179 |
Log change wage rate |
-0.107 | 0.040 | 0.008 |
Change in net Wealth |
0.000 | 0.003 | 0.984 |
Change in non labor income |
0.000 | 0.000 | 0.182 |
Change in safety (number of injuries) |
-0.029 | 0.017 | 0.081 |
Change in household size |
-0.002 | 0.002 | 0.266 |
Change in paid vacation weeks |
0.003 | 0.001 | 0.007 |
Change in marital status |
0.004 | 0.023 | 0.869 |
Health Improvement |
0.001 | 0.005 | 0.789 |
Change in ability to decrease hours |
0.016 | 0.009 | 0.095 |
Change in ability to increase hours |
0.007 | 0.006 | 0.200 |
Change in union membership |
-0.026 | 0.009 | 0.007 |
Change in long-term disability membership |
-0.005 | 0.009 | 0.626 |
Change in pension plan membership |
0.001 | 0.007 | 0.897 |
Constant |
-0.009 | 0.010 | 0.332 |
Number of Observation: 3,019
R-squared: 0.04
Note: The dependent variable is the change in log of annual labor hours worked between 1992 and 1994. Changes in all variables denote the values of the variable in 1994 minus the values in 1992.
Source: Author's calculations from the Health and Retirement Study
Table X. Sensitivity Analysis of Effect of Job Quality on Log Labor Hours
| Model/Sensitivity | Sample size | Job Quality Coefficient |
|---|---|---|
Cross-section/Benchmark |
5,037 | 0.034** (0.004) |
Difference/Benchmark |
3,019 | 0.055* (0.030) |
Cross-section/Exclude insignificant PHYSICAL factor from the model |
5,037 | 0.034** (0.004) |
Difference/Exclude insignificant PHYSICAL factor from the model |
3,019 | 0.0601* (0.030) |
Cross-section/Reconcile samples to use same respondents in both models |
2,880 | 0.030** (0.004) |
Difference/Reconcile samples to use same respondents in both models |
2,880 | 0.059* (0.031) |
Difference/Restrict sample to resp. who switched job between wave 1 & 2 |
574 | 0.047* (0.031) |
Cross-section/Female |
2,630 | 0.034** (0.005) |
Cross-section/Male |
2,407 | 0.034** (0.005) |
Cross-section/Control for Labor force participation in a two-stage Heckman model. Participation is modeled as a function of previous occupation (proxy for quality) and other demographics such as age, education, health, Marital status, net wealth, and Gender. |
All:8,402 cens:3,371 unc.:5,031 | 0.034** (0.004) |
Cross-section/For married workers |
4,008 | 0.036** (0.004) |
Cross-section/For single workers |
1,029 | 0.028** (0.008) |
Cross-section/Hourly wage workers only |
2,784 | 0.020** (0.004) |
Source: Author's calculations from wave I and II of the Health and Retirement Study.
Note: *Indicates significance at 5 percent level
**Indicates significance at the 1% level
Table XI: Sensitivity Analysis of Effect of Job Quality on Log Labor Hours
| Model/Sensitivity | Sample size | Job Quality Coefficient |
|---|---|---|
Cross-section/Respondents with non-labor income to labor income ratio below 0.10 |
3,334 | 0.037** (0.005) |
Cross-section/brackets: |
1,230 | 0.047** (0.007) |
Cross-section/Restrict sample to respondents with age below 52 years |
1,313 | 0.038** (0.008) |
Cross-section/Restrict sample to workers with age between 53 and 55 |
1,100 | 0.021** (0.007) |
Cross-section/Restrict sample to workers with age between 56 and 58 |
921 | 0.030** (0.008) |
Cross-section/Restrict sample to workers with age between 59 and 61 |
473 | 0.028** (0.012) |
Cross-section/Restrict sample to workers with age between 62 and over |
15,128 | 0.037** (0.002) |
Cross-section/Inclusion of frequency weigths in the benchmark model. Weights are assigned to match the distribution of industry and occupation frequencies in HRS to frequencies in the U.S. 1990 Census. |
2,063 | 0.020** (0.006) |
Cross-section/Occupations with non Mental Jobs |
2,974 | 0.050** (0.005) |
Cross-section/Occupation with Mental Jobs |
2,130 | 0.030** (0.005) |
Cross-section/Industries with non Mental Jobs |
2,907 | 0.050** (0.005) |
Cross-section/Industries with Mental Jobs |
2,907 | 0.050** (0.005) |
Source: Author's calculations from wave I and II of the Health and Retirement Study.
* Indicates significance at 5 percent level
** Indicates significance at the 1% level
Table XII. Growth in Labor Hours by Industry due to Improvements in Job Quality between 1850 and 2000 (Percent)
| Industry | 1850 | 1860 | 1870 | 1880 | 1900 | 1910 | 1920 | 1940 | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Agg../Forest/Fishing |
0.0 | -0.1 | 0.0 | -0.2 | -0.1 | 0.0 | 0.1 | -0.1 | 0.1 | 0.1 | 0.5 | 0.8 | 0.7 | 0.1 |
Mining/Construction |
0.0 | -0.7 | -0.4 | 0.1 | 0.3 | 0.6 | 0.8 | 0.1 | 2.2 | 3.8 | 4.4 | 5.6 | 6.2 | 4.5 |
Durable Manufacturing |
0.0 | -0.5 | -0.9 | -1.4 | -0.2 | 0.1 | 1.7 | 2.7 | 2.9 | 5.6 | 5.9 | 6.6 | 8.4 | 8.6 |
Nondurable Manufacturing |
0.0 | -0.7 | -1.8 | -2.0 | -2.0 | -1.6 | -1.1 | -0.3 | 0.3 | 1.3 | 1.9 | 2.9 | 4.6 | 5.1 |
Transportation |
0.0 | -1.2 | -1.0 | 2.8 | 3.3 | 4.4 | 6.1 | 6.8 | 6.9 | 9.2 | 9.6 | 10.4 | 10.8 | 10.4 |
Wholesale |
0.0 | 7.3 | 5.1 | 6.2 | -0.1 | -2.0 | -3.7 | -7.6 | -10.0 | -8.6 | -10.1 | -9.2 | -8.0 | -8.6 |
Retail |
0.0 | -2.0 | -2.1 | -4.2 | -2.0 | -1.8 | -2.4 | -1.6 | -1.6 | -1.1 | -1.4 | 0.4 | 0.8 | 2.2 |
Fin/Insurance/Real estate |
0.0 | -1.3 | -0.9 | 0.7 | -5.2 | -7.9 | -3.6 | -9.9 | -8.0 | -5.1 | -4.9 | -3.8 | -3.1 | -2.5 |
Business Repair |
0.0 | 1.5 | 0.2 | 6.0 | 7.3 | 5.5 | 8.4 | 4.3 | 5.9 | 9.6 | 11.5 | 13.3 | 14.1 | 14.8 |
Personal Services |
0.0 | -13.0 | -13.1 | -12.9 | -12.3 | -12.0 | -11.5 | -10.9 | -9.4 | -9.5 | -8.6 | -7.4 | -5.3 | -5.2 |
Ent. Recreation |
0.0 | 0.8 | 1.3 | 0.1 | -0.2 | -0.8 | -2.2 | -3.4 | -2.5 | -1.6 | -2.0 | -1.3 | -0.6 | -1.6 |
Prof. Related Services |
0.0 | -0.5 | -1.0 | -0.5 | -1.3 | -5.4 | -4.3 | -7.5 | -9.2 | -10.2 | -10.4 | -10.5 | -9.9 | -9.2 |
Pub. Administration |
0.0 | -0.2 | -0.8 | 3.3 | -1.4 | 0.7 | -1.3 | 2.4 | -0.2 | -1.0 | -0.6 | 1.7 | 2.2 | 3.8 |
Industry Total |
0.0 | 1.7 | 1.2 | 1.0 | 3.5 | 4.8 | 7.2 | 8.6 | 10.4 | 13.2 | 14.8 | 15.8 | 15.8 | 16.1 |
Total |
0.0 | 0.3 | -0.5 | 0.2 | 2.7 | 3.8 | 6.6 | 8.3 | 10.2 | 14.2 | 16.2 | 18.3 | 19.6 | 20.4 |
Source: The Job Quality data by occupation and industry cells are calculated from the Health and Retirement Study data.
Note: Aggregate improvement in Quality is calculated from Industry and Occupation employment data in IPUMS. The `` Industry Total'' row is the improvement in quality when occupation is held fixed so that the observed improvements are entirely caused by shifts in industries. The `` Total'' row is the overall improvement in quality occupation shifts and industry shifts combined.
Table XIII. Growth in Labor Hours by Occupation due to Improvements in Job Quality between 1850 and 2000 (Percent)
| Occupation | 1850 | 1860 | 1870 | 1880 | 1900 | 1910 | 1920 | 1940 | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Professional |
0.0 | 0.0 | -0.3 | -1.0 | -1.1 | -0.9 | -0.5 | -0.5 | -0.1 | 0.4 | 0.5 | 0.6 | 0.4 | 0.4 |
Man./Officials/Proprietor |
0.0 | 1.2 | 1.4 | 4.0 | 2.6 | 1.5 | 2.9 | 2.8 | 2.6 | 3.8 | 4.6 | 4.4 | 4.6 | 4.8 |
Farmers |
0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
Service |
0.0 | -9.3 | -9.0 | -8.3 | -7.6 | -6.1 | -4.2 | -1.9 | 1.9 | 2.2 | 3.2 | 5.5 | 6.3 | 7.0 |
Clerical |
0.0 | -1.5 | 0.0 | -1.4 | -1.6 | -0.7 | -0.5 | 0.7 | 1.0 | 1.0 | 1.0 | 1.0 | 0.4 | 0.6 |
Sales |
0.0 | 0.6 | 2.7 | 2.0 | 4.6 | 7.2 | 6.6 | 7.2 | 6.4 | 6.4 | 7.3 | 10.2 | 11.5 | 10.8 |
Craftsmen |
0.0 | 0.5 | 0.0 | 0.1 | 0.6 | 1.0 | 2.3 | 1.2 | 1.6 | 2.2 | 2.1 | 1.6 | 1.1 | -0.5 |
Operative/ Laborers |
0.0 | 0.1 | 0.8 | -0.7 | 0.1 | 0.2 | 0.5 | -0.9 | 0.1 | 0.0 | -0.2 | -0.3 | -1.2 | -1.0 |
Occupation Total |
0.0 | 0.3 | -0.2 | 0.7 | 3.3 | 4.3 | 6.7 | 8.8 | 10.2 | 13.9 | 15.6 | 17.3 | 18.7 | 19.5 |
Total |
0.0 | 0.9 | -0.5 | 0.2 | 2.7 | 3.8 | 6.6 | 8.3 | 10.2 | 14.2 | 16.2 | 18.3 | 19.6 | 20.4 |
Source: The Job Quality data by occupation and industry cells are calculated from the Health and Retirement Study data.
Note: Aggregate improvement in Quality is calculated from Industry and Occupation employment data in IPUMS. The `` Occupation Total'' row is the improvement in quality when industry is held fixed so that the observed improvements are entirely caused by shifts in occupations. The `` Total'' row is the overall improvement in quality occupation shifts and industry shifts combined.
Figure I. Per Capita Real Consumption, Income, Labor Hours Growth from 1950-2000
Data For Figure 1: Per Capita Real Consumption, Income, Labor Hours Growth from 1950-2000
| Year | Real Consumption | Income | Labor Hours Growth |
|---|---|---|---|
| 1950 | 1.00 | 1.00 | 1.00 |
| 1951 | 1.00 | 1.01 | 1.09 |
| 1952 | 1.01 | 1.03 | 1.10 |
| 1953 | 1.04 | 1.06 | 1.10 |
| 1954 | 1.05 | 1.05 | 1.04 |
| 1955 | 1.10 | 1.10 | 1.06 |
| 1956 | 1.11 | 1.14 | 1.07 |
| 1957 | 1.12 | 1.14 | 1.06 |
| 1958 | 1.11 | 1.13 | 1.01 |
| 1959 | 1.15 | 1.17 | 1.03 |
| 1960 | 1.16 | 1.17 | 1.03 |
| 1961 | 1.17 | 1.19 | 1.01 |
| 1962 | 1.21 | 1.23 | 1.03 |
| 1963 | 1.24 | 1.26 | 1.03 |
| 1964 | 1.29 | 1.33 | 1.04 |
| 1965 | 1.36 | 1.39 | 1.06 |
| 1966 | 1.42 | 1.45 | 1.10 |
| 1967 | 1.45 | 1.50 | 1.10 |
| 1968 | 1.51 | 1.55 | 1.11 |
| 1969 | 1.55 | 1.58 | 1.12 |
| 1970 | 1.57 | 1.63 | 1.08 |
| 1971 | 1.61 | 1.68 | 1.05 |
| 1972 | 1.69 | 1.74 | 1.05 |
| 1973 | 1.76 | 1.84 | 1.07 |
| 1974 | 1.73 | 1.81 | 1.05 |
| 1975 | 1.75 | 1.83 | 1.00 |
| 1976 | 1.83 | 1.89 | 1.01 |
| 1977 | 1.89 | 1.94 | 1.03 |
| 1978 | 1.95 | 2.02 | 1.06 |
| 1979 | 1.98 | 2.05 | 1.07 |
| 1980 | 1.95 | 2.04 | 1.04 |
| 1981 | 1.96 | 2.07 | 1.03 |
| 1982 | 1.96 | 2.08 | 1.00 |
| 1983 | 2.05 | 2.12 | 1.00 |
| 1984 | 2.14 | 2.26 | 1.04 |
| 1985 | 2.23 | 2.32 | 1.05 |
| 1986 | 2.30 | 2.37 | 1.05 |
| 1987 | 2.36 | 2.40 | 1.07 |
| 1988 | 2.43 | 2.48 | 1.09 |
| 1989 | 2.47 | 2.52 | 1.11 |
| 1990 | 2.49 | 2.55 | 1.10 |
| 1991 | 2.45 | 2.53 | 1.07 |
| 1992 | 2.49 | 2.57 | 1.07 |
| 1993 | 2.54 | 2.57 | 1.07 |
| 1994 | 2.60 | 2.61 | 1.09 |
| 1995 | 2.65 | 2.65 | 1.11 |
| 1996 | 2.70 | 2.68 | 1.11 |
| 1997 | 2.77 | 2.73 | 1.13 |
| 1998 | 2.86 | 2.84 | 1.15 |
| 1999 | 2.97 | 2.88 | 1.16 |
| 2000 | 3.07 | 2.99 | 1.17 |
Figure II. Growth in Labor Hours Due to Improvements in Job Quality
Data for Figure 2: Growth in Labor Hours Due to Improvements in Job Quality
| Year | Growth in Labor Hours due to Job Quality |
|---|---|
| 1850 | 0.0% |
| 1860 | 0.3% |
| 1870 | -0.5% |
| 1880 | 0.2% |
| 1900 | 2.7 |
| 1910 | 3.8% |
| 1920 | 6.6% |
| 1940 | 8.3% |
| 1950 | 10.2% |
| 1960 | 14.2% |
| 1970 | 16.2% |
| 1980 | 18.3% |
| 1990 | 19.6% |
| 2000 | 20.4% |
Footnotes
*Mailing address: Division of International Finance, Board of Governors, Federal Reserve System, Mail Stop 24, Washington DC 20551,USA; email: [email protected]. Tel.: (202)-452-2609; fax: (202)-736-5638. The author thanks Matthew Shapiro, Miles Kimball, Robert Barsky, and Charles Brown for encouraging work on this topic and for constructive feedback. Helpful comments by Gary Solon, John Laitner, Linda Tesar, Kerwin Charles, and Herman Kamil are gratefully acknowledged. My gratitude extends to seminar participants at the University of Michigan, the University of Notre Dame, Clemson University, Drexel University, the Federal Reserve Banks of Boston and Philadelphia, and at the Board of Governors of the Federal Reserve System. I am responsible for any remaining errors and omissions. Work on this project started while I was a graduate student in the Department of Economics and a Research Associate at the Institute for Social Research at the University of Michigan. The views expressed in the paper are those of the author and do not necessarily reflect those of the Board of Governors or the Federal Reserve System. Return to text
1. In fact, Keynes predicted that the allocation of the extra leisure time will be man's real and permanent problem. Noting that man needs to do some work if he needs to be contented, Keynes envisioned a widely shared shorter workweek resulting in three-hours shifts or a fifteen-hour workweek. Return to text
2. Another explanation for the lack of trends in labor hours is implicit the King-Plosser-Rebelo (KPR) utility function. Labor and consumption are complements, so that an increase in consumption makes work more pleasant and discourages workers from reducing hours. For some parameter restrictions on the utility function, the increase in consumption increases the marginal utility for work enough to justify a lack of trends in hours. Return to text
3. See Greenwood, Rogerson and Wright [1995] for a survey. Return to text
4. The Health and Retirement Study samples individuals born between the years 1931 and 1941 living in the United States. Respondents also include spouses of age eligible respondents even if these spouses are not age eligible themselves. It is a nationally representative sample. The exceptions are blacks and Florida residents that are over sampled. Return to text
5. The changes in the sectoral composition of employment and the nature of occupations in the US are consistent with a well-known international stylized fact, namely, that income levels tend to be correlated with the share of services in total employment. In low-income countries, agriculture tends to be the predominant employment sector. For middle-income countries, employment in manufacturing dominates, and for high-income countries, services makeup the biggest share of employment. The composition of employment by sector tends to change systematically with the income level. Most economies start with agriculture as the predominant employment sector, as the income level expands, employments shifts to manufacturing, and to the services sector. Return to text
6. See Costa [1998] for more evidence on heterogeneity of hours between occupations and over time. Return to text
7. Note that this definition is different from the definitions in some studies on jobs by the Center for National Policy, the Bureau of Labor Statistics, and International Labor Organization. According the their definitions, wages, fringe benefits, and health benefits define Job Quality. The definition does not deal with the nature of work. For example, the Average Job Quality index constructed by Harvard economist Medoff and used by the Bureau of Labor Statistics is entirely constructed based on compensation differences across jobs. The International Labor Organization in Geneva defines Job Quality based on Remuneration levels, Job Security, Social Protection, Safety and Health concerns, Human resource development, Management and Organization, Freely chosen employment. The definition of Job Quality in this paper focuses on the nature of the work itself and factors that influence the comfort or pleasantness of the working process. Return to text
8. The changes in nature of work was well predicted by Keynes when he said ``...in quite a few years-in our own lifetimes I mean- we may be able to perform all the operations of agriculture, mining, and manufacturing with a quarter of the human effort to which we have been accustomed'' Keynes [1930]. Return to text
9. Based on the examples provided, it appears that Job Quality and technology capture the same notion. Although, there could be a link between technological progress and improvements in Job Quality, the two concepts are not identical. Technological progress need not lead to improvements in work quality. An improvement in the miles-per-gallon of trucks due to technological progress does not improve the job quality for truck drivers. Return to text
10. The compensating differential literature recognizes the dependence of the wage rate on the job characteristics. In the macroeconomic context, the average job quality change is considered independent of the wage. In subsequent microanalysis, both wages and job quality will be included in the regression analysis. Given a weak correlation between the quality measure and the wage rate, the quality effect through the wage rate appears negligible. Return to text
11. Words in parentheses are not part of the survey. They are borrowed from Hurd and McGarry [1993] to capture the main job characteristic. Return to text
12. Common factor analysis is one method among others to perform factor analysis. Other techniques include Principal Components, Iterated Principal Factor, and Maximum likelihood. All these methods yield similar results. Return to text
13. Ideally, the list of regressors would include consumption. The inclusion of consumption is however, problematic because it is endogeneous. Furthermore, the data set does not contain good measures of household consumption. The omission of consumption, could potentially introduces a bias in the estimation. Given the assumption of independence between Job quality and consumption by construction, I expect bias on the coefficient of interest, namely the Job Quality coefficient, to be small. Return to text
14. The possible exception is the spouses of the respondents. Spouses were included in the study so long as their mates where age eligible (born between 1931 and 1941). Return to text
15. IPUMS (Integrated Public Use Microdata Series) consists of twenty-five high-precision samples of the American population drawn from thirteen federal censuses. This study uses the 1 random sample drawn from the census data. Return to text
16. The measure of aggregate quality does not take into account the within job improvement. The quality improvement is obtained from shifts in the industry and occupation mix. The resulting measure is therefore a lower bound of the true improvement in Job Quality. Furthermore, the methodology assumes a constant ranking of industry-occupation cells for Job Quality across time. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text