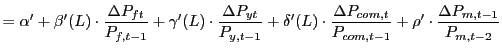Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 883, December 2006 --- Screen Reader
Version*
Measurement Matters for Modeling U.S. Import Prices
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We focus on capturing the increasingly important role that emerging economies play in determining U.S. import prices. Emerging market producers differ from others in two respects: (1) their cost structure is well below that of developed-market producers, and (2) their wide profit margins induce pricing policies that seek to exhaust production capacity. We argue that these features have dampened the short-run responses of import prices to changes in the value of the dollar but that they have not altered the associated long-run response. To capture these considerations, we develop a new method to measure foreign prices and adopt a formulation that differentiates between short- and long-run responses.
Our econometric work asks two questions: First, can one replicate the literature's dispersion of pass-through estimates? Second, is there any evidence of a change in the dynamic response of import prices to changes in the exchange value of the dollar? To address the first question, we estimate the parameters of our models using several alternative measures of U.S. and foreign prices, dynamic specifications, and sample periods. We find that these alternative inputs translate into a large range of parameter estimates, a finding that helps to rationalizing the existing dispersion of estimates. To address the second question, we compute the implied dynamic adjustment of import prices to a change in the value of the dollar using parameters estimated from two samples: 1974-2000 and 1974-2005. The long-run response of import prices is similar regardless of which sample is used---roughly one-half of the change in the exchange rate is passed through to import prices. However, the short-run response is quite sensitive to the sample period. Specifically, the short-run response based on data through 2005 is smaller than the short-run response based on data through 2000. We argue that one force behind the change in dynamics of the import-price process is the greater presence of producers from emerging economies and that their effect on import prices can be captured with their measure of foreign prices.
Keywords: aggregation methods, automated specification, exchange rates, pass-through, Penn World Tables.
JEL classification: F17, F41, C51, C53
1 Introduction
Just how much the dollar should depreciate to restore external balance is the subject of an on-going debate in which little agreement exists. The disagreements stem from several sources but an important one is the responsiveness of U.S. import prices to changes in the value of the dollar. Specifically, Goldberg and Knetter (1997), and Campa and Goldberg (2005) report that half of the movements of the dollar are passed through to import prices whereas Olivei (2002) and Marazzi et al. (2005) find that this pass-through, while significant in the past, has virtually disappeared. Using a new measure of foreign prices, we find that pass-through in the long-run - at the ten-year horizon - has been stable at one-half whereas pass-through in the short-run -at the two-year horizon - has declined markedly over the past decade. We believe these findings contribute to resolving the dispersion of recent estimates.
The general framework to model import prices used by previous studies is given in equation (1):
| (1) |
where ![]() is the price of U.S. imports;
is the price of U.S. imports;
![]() is the price of U.S. products;
is the price of U.S. products;
![]() is the foreign price expressed in
dollars; and
is the foreign price expressed in
dollars; and ![]() is the price of internationally
traded commodities. Equation (1) allows for the
possibility that foreign exporters seek to retain some parity with
general U.S. prices by adjusting their export prices to changes in
the prices prevailing in the U.S. market. Such a strategy, known as
pricing to market, implies that
is the price of internationally
traded commodities. Equation (1) allows for the
possibility that foreign exporters seek to retain some parity with
general U.S. prices by adjusting their export prices to changes in
the prices prevailing in the U.S. market. Such a strategy, known as
pricing to market, implies that
![]() .
Equation (1) also allows for the possibility that
an increase in the value of the dollar, which raises
.
Equation (1) also allows for the possibility that
an increase in the value of the dollar, which raises ![]() is then passed through to
is then passed through to ![]() Such a
response is known as the exchange-rate pass-through and it implies
that
Such a
response is known as the exchange-rate pass-through and it implies
that
![]() .2
.2
Equation (1) offers one way to rationalize the
dispersion of estimates of ![]() reported in the
literature: empirical studies differ in their choice of price
measures, econometric formulations, sample periods, and estimation
techniques. Another explanation is that this dispersion is
reflecting a structural change in the behavior of exporters to the
United States that is not adequately captured by recent studies.
Indeed, one recent development that qualifies as a structural
change is the increased importance of emerging economies as a
source of U.S. imports.3 To grasp how this possibility shapes
our strategy involves a brief expositional detour to which we now
turn.
reported in the
literature: empirical studies differ in their choice of price
measures, econometric formulations, sample periods, and estimation
techniques. Another explanation is that this dispersion is
reflecting a structural change in the behavior of exporters to the
United States that is not adequately captured by recent studies.
Indeed, one recent development that qualifies as a structural
change is the increased importance of emerging economies as a
source of U.S. imports.3 To grasp how this possibility shapes
our strategy involves a brief expositional detour to which we now
turn.
There are two salient features of emerging economies that may affect the behavior of U.S. import prices. First, emerging economies have low production costs relative to developed economies. Second, emerging economies have been increasing their capacity to produce exportable goods at a rapid rate. To the extent that emerging-market producers are pricing their exports to achieve a market share that exhausts their growing production capacity, we would expect two distinct effects on import prices. The first effect is straight-forward: we would expect some downward pressure on import prices as emerging-market exporters price somewhat below prevailing prices in order to gain market share. We would expect this expansion in supply to both increase the total volume of imports and to displace some imports from higher cost producers who are now no longer able to price above their variable costs. The second effect is more subtle and involves the responsiveness of import prices to changes in exchange rates. If the emerging market producers face short-run capacity constraints, then as their share in U.S. imports increases, we would expect import prices to become less responsive to exchange rate movements and more responsive to U.S. price developments.
To understand this change in price responsiveness, it is helpful to focus on the import-supply schedule. To the extent that capacity constraints are binding, the short-run supply schedule becomes more nearly vertical. Thus movements in exchange rates or foreign costs, which induce vertical shifts in the supply schedule, will have a relatively small impact on prices while a shift in the demand schedule will have a relatively large impact on prices. This situation does not imply that foreign prices, or exchange rates, are becoming less important in the determination of U.S. import prices but, rather, that the dynamics of the process are changing. In particular, the long-run (secular) movements are still determined in large part by foreign capacity and costs (with some rightward drift in the supply schedule), but the short-run movements are more closely tied to U.S. demand and U.S. domestic price developments (through the steepening of the supply schedule).
To model this phenomenon econometrically requires a measure of foreign prices that explicitly captures both the growing capacity of emerging-market producers and the fact that the cost structure of these producers is well below that of developed-market producers. Section 2 develops such a measure of foreign prices and contrasts it to existing measures of aggregate foreign prices. Section 2 also looks at the domestic price measures and notes that different measures of U.S. prices carry different implications for modeling import prices. If one chooses the U.S. GDP deflator, then foreign products are assumed to compete with U.S. goods and services whereas if one uses the GDP deflator for goods, then foreign products are assumed to compete with U.S. goods.4
Section 3 describes several different econometric specifications that have been used to estimate the parameters of equation (1) and notes how these specifications differ in their characterization of long-run behavior. Section 4, using annual observations from 1974 to 2005, estimates several versions of equation (1) and reports on the sensitivity of the estimation results to changes in measures of U.S. and foreign prices, dynamic specifications, and sample periods. The section also estimates the parameters using sample-selection techniques to exclude observations when emerging economies were not important in world trade. Accordingly, Section 4 divides the discussion in two parts: Full-sample Estimation and Sample-selection Estimation. We find that changes in estimation design give rise to a dispersion of estimates, as found in the literature. We also find, using our new measure of foreign prices and recent observations, that the short-run exchange rate pass-through is close to zero but that the long-run pass-through is about one-half. We interpret this result as suggesting that the growing importance of emerging economies does not imply that foreign prices, or exchange rates, are becoming less important in the determination of U.S. import prices but, rather, that the dynamics of the process are changing.
2 Measurement Matters
We measure the price of U.S. imports, ![]() as
the multilateral price deflator of U.S. merchandise imports
excluding oil, computers, and semiconductors. For work using
disaggregate import prices see Yang (1997), Olivei (2002), Campa
and Goldberg (2005). For the price of raw materials,
as
the multilateral price deflator of U.S. merchandise imports
excluding oil, computers, and semiconductors. For work using
disaggregate import prices see Yang (1997), Olivei (2002), Campa
and Goldberg (2005). For the price of raw materials, ![]() , we use the IMF's non-fuel commodity price index. For
foreign and U.S. domestic prices, however, we consider several
alternatives which are discussed below.
, we use the IMF's non-fuel commodity price index. For
foreign and U.S. domestic prices, however, we consider several
alternatives which are discussed below.
2.1 Foreign Prices (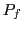 )
)
Measuring foreign prices is of interest because they serve as
proxies for foreign costs for which data are not readily available.
The general practice for measuring foreign prices aggregates
foreign CPIs, expressed in U.S. dollars, using bilateral trade
weights. We depart from this practice in several ways. First, we
argue that GDP deflators are a better proxy for domestic costs than
CPIs. Second, rather than aggregating foreign GDP deflators
expressed in U.S. dollars, we construct our measure of ![]() so as to ensure consistency with the evolution of U.S.
international relative prices. We attain this consistency in two
steps. The first step involves measuring U.S. international
relative prices,
so as to ensure consistency with the evolution of U.S.
international relative prices. We attain this consistency in two
steps. The first step involves measuring U.S. international
relative prices, ![]() :
:
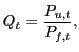 |
(2) |
where ![]() is the price level of U.S. products.
This first step is needed because data for absolute price levels
across countries are not easily available whereas the levels of the
associated bilateral relative prices are available. The second step
uses equation (2) to solve for
is the price level of U.S. products.
This first step is needed because data for absolute price levels
across countries are not easily available whereas the levels of the
associated bilateral relative prices are available. The second step
uses equation (2) to solve for ![]() taking as given data for
taking as given data for ![]() and
and
![]()
Implementing these two steps would be straightforward if there
were agreement on how to construct ![]() As Chinn
(2005) notes, however, such an agreement is not currently in place.
Indeed, the existing measures of
As Chinn
(2005) notes, however, such an agreement is not currently in place.
Indeed, the existing measures of ![]() constructed by the
Federal Reserve, the IMF, and the OECD differ in their mix of
countries, in their measure of prices, in their weighting schemes,
and in their aggregation methods. The one feature these measures of
constructed by the
Federal Reserve, the IMF, and the OECD differ in their mix of
countries, in their measure of prices, in their weighting schemes,
and in their aggregation methods. The one feature these measures of
![]() have in common is their reliance on
relative price indexes. As discussed further below, such measures
cannot fully capture the growing importance of the low-cost
producers because indexes indicate, by construction, the percent
change of the variable relative to a base year. Our measure focuses
on the level of international relative prices and not of its
change.
have in common is their reliance on
relative price indexes. As discussed further below, such measures
cannot fully capture the growing importance of the low-cost
producers because indexes indicate, by construction, the percent
change of the variable relative to a base year. Our measure focuses
on the level of international relative prices and not of its
change.
2.1.1 Measuring International Relative Prices
Central to our construct of ![]() is the measurement
of the level of the price of U.S. products relative to the level of
the price of the
is the measurement
of the level of the price of U.S. products relative to the level of
the price of the ![]() country,
country, ![]() We
measure this bilateral relative price as
We
measure this bilateral relative price as
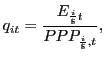
where
![]() is the spot dollar exchange
rate relative to the
is the spot dollar exchange
rate relative to the ![]() currency (a rise in
currency (a rise in
![]() constitutes an appreciation
of the dollar); and
constitutes an appreciation
of the dollar); and
![]() is the PPP exchange rate
reported by the Penn World Tables.5 This PPP rate is a
weighted average of the prices of the
is the PPP exchange rate
reported by the Penn World Tables.5 This PPP rate is a
weighted average of the prices of the ![]() country
relative to U.S. prices using as weights the production levels of
the
country
relative to U.S. prices using as weights the production levels of
the ![]() country. The prices used by the Penn data
are based on highly comparable products across countries and the
associated weights account for the full value of GDP. The Penn data
are constructed to allow cross-country comparisons and thus well
suited to our purposes.
country. The prices used by the Penn data
are based on highly comparable products across countries and the
associated weights account for the full value of GDP. The Penn data
are constructed to allow cross-country comparisons and thus well
suited to our purposes.
Note that ![]() differs importantly from the price
indexes used in macroeconomics. Typically, these price indexes are
constructed to equal 100 in a given year, so it would make no sense
to compare the level of price indexes in two countries. In
contrast,
differs importantly from the price
indexes used in macroeconomics. Typically, these price indexes are
constructed to equal 100 in a given year, so it would make no sense
to compare the level of price indexes in two countries. In
contrast, ![]() is unitless and easy to interpret:
A value of 2 means that the basket of the
is unitless and easy to interpret:
A value of 2 means that the basket of the ![]() country is twice as expensive in the United States as it is in the
country is twice as expensive in the United States as it is in the
![]() country.
country.
We aggregate these bilateral relative prices into our construct
![]() using two formulas: a geometric
aggregate, denoted as
using two formulas: a geometric
aggregate, denoted as
![]() and a Divisia aggregate, denoted
as
and a Divisia aggregate, denoted
as
![]() 6 The geometric aggregate is
6 The geometric aggregate is
where ![]() is the share of the
is the share of the ![]() country in the aggregate. Several factors affect the aggregate
country in the aggregate. Several factors affect the aggregate
![]() : an increase in U.S. prices raises
it, while an increase in foreign prices lowers it; a nominal
appreciation of the dollar (an increase in
: an increase in U.S. prices raises
it, while an increase in foreign prices lowers it; a nominal
appreciation of the dollar (an increase in
![]() ) raises
) raises ![]() . These three factors work through their effect on
the bilateral relative prices-the
. These three factors work through their effect on
the bilateral relative prices-the
![]() s. In addition, changing the
weights alone will affect
s. In addition, changing the
weights alone will affect ![]() even if
none of the underlying prices or exchange rates change.
Specifically, emerging-market economies have relatively low
production costs and their share in world trade has been
increasing. The resulting increase in their share in world markets
is captured by the increase in their weights. Loosely speaking,
raising the weight on these low-price countries lowers the
`average' price abroad and raises U.S. prices relative to the
average foreign price, even if no underlying prices change.
even if
none of the underlying prices or exchange rates change.
Specifically, emerging-market economies have relatively low
production costs and their share in world trade has been
increasing. The resulting increase in their share in world markets
is captured by the increase in their weights. Loosely speaking,
raising the weight on these low-price countries lowers the
`average' price abroad and raises U.S. prices relative to the
average foreign price, even if no underlying prices change.
In contrast, the Divisia aggregate of U.S. international relative prices is a weighted average of growth rates of bilateral relative prices:
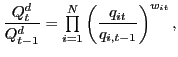 |
(3) |
where by convention,
![]() is set equal to 100 to a given
period and the index level for all other periods is defined
recursively. The chief drawback of this measure for our purposes is
that it cannot fully recognize the importance of low-price
countries such as China and Mexico. To be sure, the weights for
these two countries have increased but their relative prices have
been fairly stable which means that the large weights are being
multiplied by negligible growth rates. The geometric aggregate does
not suffer from this limitation because changes in weights affect
the aggregate even if all the relative prices are fixed.
is set equal to 100 to a given
period and the index level for all other periods is defined
recursively. The chief drawback of this measure for our purposes is
that it cannot fully recognize the importance of low-price
countries such as China and Mexico. To be sure, the weights for
these two countries have increased but their relative prices have
been fairly stable which means that the large weights are being
multiplied by negligible growth rates. The geometric aggregate does
not suffer from this limitation because changes in weights affect
the aggregate even if all the relative prices are fixed.
In constructing these aggregates, we consider two types of weights: U.S. bilateral non-oil imports and a broad measure of U.S. trade competitiveness.7 As shown in the top panel of figure 1, unlike the choice of weights, the choice of aggregation method matters for measuring the international relative price of U.S. products. Specifically, the geometric aggregate has an upward trend meaning that the price of U.S. products relative to foreign products has been increasing over time. Such a trend owes primarily to shifts in country weights away from the relatively high-price industrial countries toward the lower-price developing economies. In contrast, the Divisia aggregate of relative prices embodies a downward trend in U.S. international relative prices. Accounting for the difference in trends involves recognizing that the Divisia aggregate focuses on the movements in the bilateral real exchange rates alone while ignoring the general shift towards the relatively low-price producers. Capturing this general shift requires aggregation of the levels of bilateral relative prices, which is what geometric aggregation allows.8
2.1.2 Estimating Foreign Prices in Dollars
Given data for U.S. domestic prices-the GDP deflator-and for the
aggregate of U.S. international relative prices, we use equation
(2) to construct data for foreign prices.
Specifically, the measure of foreign prices in dollars implied by
![]() is
is
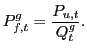
The measure of foreign prices in dollars implied by ![]() is
is
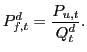
The bottom panel of figure (1) shows that,
given the data for ![]() differences in the
evolution of aggregate relative prices translate into differences
for the two measures of foreign prices. Specifically, after moving
in lock step from 1972 to 1986, the series diverge with
differences in the
evolution of aggregate relative prices translate into differences
for the two measures of foreign prices. Specifically, after moving
in lock step from 1972 to 1986, the series diverge with ![]() growing faster than
growing faster than
![]() The growing gap between these two
series reflects the growing gap associated with the choice of
aggregation method.
The growing gap between these two
series reflects the growing gap associated with the choice of
aggregation method.
2.2 U.S. Prices (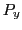 )
)
To measure the prices of U.S. products that compete with imports we consider three measures: the Producer Price Index, the overall GDP deflator, and the GDP deflator for goods alone. The distinction between goods and services might matter if one argues that imports of goods compete with U.S. goods, and not with U.S. goods and services. That such a distinction is potentially relevant is clear from figure 2. Indeed, since 1970, the price deflator for U.S. goods and services has grown faster than the PPI and the GDP deflator for goods. Furthermore, since 1995, the growth rate of price deflator for goods has a narrow range of fluctuations around zero whereas the growth rate for the overall GDP deflator is positive throughout the sample. For the PPI, the growth rate also fluctuates around zero but the range of the fluctuations exceed that of the deflator for GDP goods.
2.3 Measuring and Modeling
The left panels of figure 3 reveal a
close relation between ![]() and the price of
imports. The right panels reveal, in contrast, a growing distancing
between
and the price of
imports. The right panels reveal, in contrast, a growing distancing
between ![]() and the price of imports after
1985. Such a gap can be construed as suggesting a decline in the
responsiveness of U.S. import prices to the exchange rate. The data
also reveal a growing gap between the price deflator for imports
and the price deflator for U.S. goods and services. That distancing
is not present if one uses the U.S. deflator for goods alone.
and the price of imports after
1985. Such a gap can be construed as suggesting a decline in the
responsiveness of U.S. import prices to the exchange rate. The data
also reveal a growing gap between the price deflator for imports
and the price deflator for U.S. goods and services. That distancing
is not present if one uses the U.S. deflator for goods alone.
To evaluate the time-series properties of these variables, Table 1 shows the results from the Augmented Dickey-Fuller tests of stationarity. With one exception, the ADF tests cannot reject a unit-root for these series; the exception is the commodity price index for which the ADF test statistic exceeds by a good margin the 1% critical value. For the price of imports, the ADF test shows a marginal rejection of the unit-root hypothesis at certain lags.
3 Econometric Specifications
For parameter estimation we specify equation (1) as an autoregressive distributed lag:
| (4) |
where ![]() is the lag operator and
is the lag operator and
![]() 9 The appeal of
equation (4) is its flexibility in
differentiating between short-run effects and long run effects. The
exchange-rate pass-through is
9 The appeal of
equation (4) is its flexibility in
differentiating between short-run effects and long run effects. The
exchange-rate pass-through is ![]() in the
short-run and
in the
short-run and
![]() in the long-run. The
remaining long-run coefficients are
in the long-run. The
remaining long-run coefficients are
![]() for the pricing to
market and
for the pricing to
market and
![]() for the price of
commodities. The difference between short- and long-run effects is
determined by the parameter
for the price of
commodities. The difference between short- and long-run effects is
determined by the parameter ![]() which measures
the persistence of import prices.
which measures
the persistence of import prices.
A popular alternative to equation (4) explains the growth rate of import prices in terms of growth rates of its determinants:
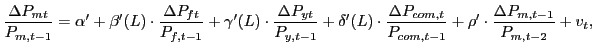 |
(5) |
where
![]() and we
attach an `
and we
attach an `![]() ' to the coefficients to
emphasize that they differ from those in equation (4). Again, the exchange-rate pass-through is
' to the coefficients to
emphasize that they differ from those in equation (4). Again, the exchange-rate pass-through is
![]() in the short run and
in the short run and
![]() in
the long-run. The remaining long-run coefficients are
in
the long-run. The remaining long-run coefficients are
![]() for the pricing to market and
for the pricing to market and
![]() for the price of commodities.
for the price of commodities.
Equations (4) and (5) differ in their characterization of long-run behavior. Specifically, the long-run import price implied by equation (5) is arbitrary because it depends on the value of the initial condition; the long-run import price implied by equation (4) is, however, uniquely determined. Specifically, equation (4) implies that, regardless of the initial condition, the long-run level of import prices is determined as
| (6) |
where
![]()
![]() and
and
![]() For these
coefficients to be consistent with the predictions of theory, they
need to meet the sign restrictions (
For these
coefficients to be consistent with the predictions of theory, they
need to meet the sign restrictions (![]()
![]() ,
, ![]() and the homogeneity condition (
and the homogeneity condition (
![]() ); the long-run
coefficients for equation (5) need to meet
comparable conditions.10
); the long-run
coefficients for equation (5) need to meet
comparable conditions.10
4 Econometric Results
4.1 Full-sample Estimation
Parameter estimation rests on the General-to-Specific strategy. The general formulations correspond to equations (4) and (5) where we include current values and 1 lag for each predetermined variable; the specific formulations are obtained by implementing the automated-specification algorithm developed by Hendry and Krolzig (2001). Their algorithm combines least squares with a selection criteria that excludes formulations lacking parameter constancy, white-noise residuals, and insignificant variables. Further, the critical values used in model selection are not fixed in advance but, rather, are calculated sequentially to recognize the joint nature of model specification and parameter estimation.
Table 2 reports the long-run coefficient estimates for the specific formulation associated with equation (4) along with the evaluation of the properties of the residuals; Table 3 reports the associated results for equation (5). To facilitate the discussion, figures 4-6 show the sensitivity of these estimates to changes in
- the econometric specification: equation (4) versus equation (5);
- the measure of U.S. prices,
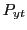 : GDP deflator
for goods and services (G&S), GDP deflator for goods (Goods),
Producer Price Index (PPI);
: GDP deflator
for goods and services (G&S), GDP deflator for goods (Goods),
Producer Price Index (PPI); - the measure of foreign price,
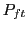 :
geometric aggregate and Divisia aggregate;
:
geometric aggregate and Divisia aggregate; - the weighting scheme,
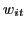 : U.S.
bilateral non-oil imports (non-oil) to using U.S. trade
competitiveness (broad);
: U.S.
bilateral non-oil imports (non-oil) to using U.S. trade
competitiveness (broad); - the estimation period: 1974-2000 and 1974-2005.
Based on the full sample, figure 4 reports the long-run estimates of the
pricing to market coefficient,
![]() and of exchange-rate
pass-through coefficient,
and of exchange-rate
pass-through coefficient,
![]() . Inspection of the results
reveals several findings. First, as shown in the top panel,
. Inspection of the results
reveals several findings. First, as shown in the top panel,
![]() is positive and significant
except when the estimation uses the formulation in levels with the
Divisia measure of foreign prices along with either the U.S. PPI or
the U.S. overall GDP deflator. Second, as shown in the bottom
panel,
is positive and significant
except when the estimation uses the formulation in levels with the
Divisia measure of foreign prices along with either the U.S. PPI or
the U.S. overall GDP deflator. Second, as shown in the bottom
panel,
![]() is positive, significantly
greater than zero, and exceeds 1/3. Third, values of
is positive, significantly
greater than zero, and exceeds 1/3. Third, values of
![]() based on the equation in
levels, equation (4), with the geometric foreign
price are close to 0.5 and are, in general, larger than estimates
based on the Divisia foreign price.
based on the equation in
levels, equation (4), with the geometric foreign
price are close to 0.5 and are, in general, larger than estimates
based on the Divisia foreign price.
The role of commodity prices depends on the specification. For
the equation in levels (Table 2) commodity prices are not relevant
whereas for the equation in growth rates (Table 3), they are. Such
a difference is not surprising because, as Table 1 shows, the level
of the price of commodities is stationary. In terms of the estimate
of persistence,
![]() , the results for the equation
in levels (Table 2) indicate that
, the results for the equation
in levels (Table 2) indicate that
![]() is significant and well below
one; for the equation in growth rates (Table 3),
is significant and well below
one; for the equation in growth rates (Table 3),
![]() is not statistically
different from zero. In terms of the properties of the residuals,
the evidence cannot reject the hypotheses of serial independence
and homoskedasticity for either specification.
is not statistically
different from zero. In terms of the properties of the residuals,
the evidence cannot reject the hypotheses of serial independence
and homoskedasticity for either specification.
Finding that the smallest value of
![]() exceeds 1/3 is at odds with
studies that focus on recent observations alone and report values
of
exceeds 1/3 is at odds with
studies that focus on recent observations alone and report values
of
![]() close to zero. One
possibility is that recent observations are responsible for a
decline in
close to zero. One
possibility is that recent observations are responsible for a
decline in
![]() In such a case, one should
expect that excluding them from our sample would raise the value of
In such a case, one should
expect that excluding them from our sample would raise the value of
![]() To explore this
possibility, we re-estimate the coefficients with a sample that
ends in 2000 and compare the resulting estimates to those based on
the full sample.
To explore this
possibility, we re-estimate the coefficients with a sample that
ends in 2000 and compare the resulting estimates to those based on
the full sample.
Figure 5 shows how the value of
![]() changes in response to
alternative sample periods while controlling for price measures and
functional forms.11We find no evidence of a higher
long-run exchange-rate pass-through for the sample ending in 2000.
Instead, for the level specifications and some U.S. price measures,
we find that extending the sample increases noticeably the
value of
changes in response to
alternative sample periods while controlling for price measures and
functional forms.11We find no evidence of a higher
long-run exchange-rate pass-through for the sample ending in 2000.
Instead, for the level specifications and some U.S. price measures,
we find that extending the sample increases noticeably the
value of
![]() . As shown in figure 6, the estimated pricing-to-market coefficient,
. As shown in figure 6, the estimated pricing-to-market coefficient,
![]() is somewhat more sensitive
to sample period, especially for the level specifications based on
the Divisia measure of foreign prices.
is somewhat more sensitive
to sample period, especially for the level specifications based on
the Divisia measure of foreign prices.
Several conclusions emerge from these estimation results. First,
the long-run effect of exchange rates on import prices is at least
one-third across all regressions. Second, the mere inclusion of
recent observations does not significantly lower the value of
![]() Third, the measurement of
foreign prices matters for estimating the exchange-rate
pass-through. Specifically, values of
Third, the measurement of
foreign prices matters for estimating the exchange-rate
pass-through. Specifically, values of
![]() based on the geometric
foreign price are larger (close to 0.5) and less sensitive to
changes in specification than estimates based on the Divisia
foreign price. Finally, changes in estimation design give rise to a
dispersion of estimates, as found in the literature. Such a
dispersion is problematic for policy applications: seemingly minor
changes in estimation design carry radically different implications
regarding the strength of the expenditure-switching effect of a
change in the exchange value of the dollar.
based on the geometric
foreign price are larger (close to 0.5) and less sensitive to
changes in specification than estimates based on the Divisia
foreign price. Finally, changes in estimation design give rise to a
dispersion of estimates, as found in the literature. Such a
dispersion is problematic for policy applications: seemingly minor
changes in estimation design carry radically different implications
regarding the strength of the expenditure-switching effect of a
change in the exchange value of the dollar.
To discriminate among these specifications, we argue that policy
applications benefit from formulations that exhibit three
properties: constancy of long-run parameters, white-noise
residuals, and consistency with price homogeneity. Applying this
criteria yields two specifications, reproduced in Table 4. One
specification uses the formulation in levels along with the
geometric foreign price and the U.S. deflator for GDP goods; this
specification is labeled as ![]() . The second
specification uses the formulation in growth rates along with the
Broad weighted Divisia measure of foreign price and the U.S. PPI;
this specification is labeled as
. The second
specification uses the formulation in growth rates along with the
Broad weighted Divisia measure of foreign price and the U.S. PPI;
this specification is labeled as ![]() .12
.12
These two specifications have similar values for
![]() : 0.5 for
: 0.5 for ![]() and 0.4 for
and 0.4 for ![]() However, these
specifications differ in their implications for the long-run: the
coefficient for
However, these
specifications differ in their implications for the long-run: the
coefficient for ![]() refers to a long-run response
of the level of import prices whereas the coefficient for
refers to a long-run response
of the level of import prices whereas the coefficient for
![]() refers to the short run (one year)
response of the growth rate of import prices. This
distinction would not be relevant if the estimated adjustment delay
in
refers to the short run (one year)
response of the growth rate of import prices. This
distinction would not be relevant if the estimated adjustment delay
in ![]() were brief, but it is not. Figure 7 shows how import prices respond to a
hypothetical one-percent sustained depreciation of the
dollar.13 The results reveal several features
of interest. First, the models differ greatly in their short-run
responses. Specifically, after one year,
were brief, but it is not. Figure 7 shows how import prices respond to a
hypothetical one-percent sustained depreciation of the
dollar.13 The results reveal several features
of interest. First, the models differ greatly in their short-run
responses. Specifically, after one year, ![]() predicts that import prices will increase by 0.4 percent (blue
line) whereas
predicts that import prices will increase by 0.4 percent (blue
line) whereas ![]() shows a negligible response (black
line).14 After four years, however, the two
specifications predict roughly the same effect on import prices.
Second, to emphasize how changes in the estimation sample have
changed the character of dynamic adjustment, the figure also
includes the response from
shows a negligible response (black
line).14 After four years, however, the two
specifications predict roughly the same effect on import prices.
Second, to emphasize how changes in the estimation sample have
changed the character of dynamic adjustment, the figure also
includes the response from ![]() using
parameter estimates based on data through 2000 (red line). The
responses from these two sample periods converge to virtually
identical values in the long run. Their short-run responses are,
however, quite different: the specification based on data through
2000 has a higher short-run response and a quicker adjustment to
the long-run than the estimate based on data through 2005. We
interpret this finding as being consistent with the idea that the
increased importance of emerging economies has changed the dynamics
of the process of import-price determination.
using
parameter estimates based on data through 2000 (red line). The
responses from these two sample periods converge to virtually
identical values in the long run. Their short-run responses are,
however, quite different: the specification based on data through
2000 has a higher short-run response and a quicker adjustment to
the long-run than the estimate based on data through 2005. We
interpret this finding as being consistent with the idea that the
increased importance of emerging economies has changed the dynamics
of the process of import-price determination.
Beyond stating the obvious-namely, that there is an important
difference between short and long run effects, these results are
not powerful enough to discriminate between ![]() and
and
![]() To that end, we examine the
out-of-sample accuracy of these two formulations. Specifically, we
apply the General-to-Specific algorithm with data through 2000 and
then use dynamic simulations to generate ex-post forecasts for
2001-2005.15 Figure 8 shows the 95 percent confidence bands of these ex-post
forecasts.16 The results indicate that, over the
first two years, both equations have statistically insignificant
prediction errors but that
To that end, we examine the
out-of-sample accuracy of these two formulations. Specifically, we
apply the General-to-Specific algorithm with data through 2000 and
then use dynamic simulations to generate ex-post forecasts for
2001-2005.15 Figure 8 shows the 95 percent confidence bands of these ex-post
forecasts.16 The results indicate that, over the
first two years, both equations have statistically insignificant
prediction errors but that ![]() is much more
accurate than
is much more
accurate than ![]() . Thus, if the sole purpose of
estimation is short-term forecasting, then
. Thus, if the sole purpose of
estimation is short-term forecasting, then ![]() is
the preferred specification. The evidence for horizons beyond two
years is, however, less supportive of
is
the preferred specification. The evidence for horizons beyond two
years is, however, less supportive of ![]() Even
though both equations show statistically significant prediction
errors, the root-mean squared error over the five-year horizon is
six percent for
Even
though both equations show statistically significant prediction
errors, the root-mean squared error over the five-year horizon is
six percent for ![]() but eight percent for
but eight percent for
![]() Thus, if the policy application
extends beyond two years then
Thus, if the policy application
extends beyond two years then ![]() carries
greater precision.
carries
greater precision.
At this point we would conclude that, of the two formulations that exhibit white-noise residuals and consistency with the homogeneity postulate, the one with the lowest average forecast error in the medium term uses our geometric measure of foreign prices. It has a long-run pass-through of one-half. This formulation captures the changing nature of the import-price process by using a measure of foreign prices that reflects the growing importance of emerging economies. There is, however, an alternative strategy that retains the conventional measures of foreign price and uses sample-selection methods so as to exclude observations when emerging economies were not important in world trade. In the next subsection we weigh the choice of retaining current (Divisia based) measures of foreign prices and shortening the sample period against replacing the Divisia measures of foreign prices with the geometric alternative and retaining the full sample period.
4.2 Sample-selection Estimation
The result of the recent decline in the pass-through is based on
quarterly data whereas our data are annual. Thus we begin by
confirming that this same feature is also present in the annual
analogue to these models. To this end, we apply rolling regressions
to the growth equation (5) using the Divisia
measure of ![]() and the producer price index for
and the producer price index for
![]() and a window of 15 years starting in
1974.17 Figure 9 shows the 95 percent confidence interval for
the estimated pass-through coefficient of equation (5),
and a window of 15 years starting in
1974.17 Figure 9 shows the 95 percent confidence interval for
the estimated pass-through coefficient of equation (5),
![]() The results reveal
a sustained decline in
The results reveal
a sustained decline in
![]() from 0.45 in 1995
to 0.17 in 2005, a pattern in line with the findings of Olivei
(2002) Marazzi and Sheets (2006).18
from 0.45 in 1995
to 0.17 in 2005, a pattern in line with the findings of Olivei
(2002) Marazzi and Sheets (2006).18
We now ask whether this decline in
![]() is robust to model
specification. In choosing an alternative formulation, we follow
Ericsson (2006, Table 6.2) who shows that equation (4) can be expressed as an error-correction
formulation:
is robust to model
specification. In choosing an alternative formulation, we follow
Ericsson (2006, Table 6.2) who shows that equation (4) can be expressed as an error-correction
formulation:
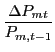 |
|
(7) |
Equation (7) is appealing because it
differentiates between short- and long-run responses. The
coefficients associated with the growth rates of the right-hand
side variables represent short-run responses; the coefficients
associated with the variables in levels capture the adjustment of
the price of imports to its long-run value. Indeed, the resulting
expression for the long-run level of import prices is equation
(6) above where
![]()
![]()
![]()
![]() and
and ![]() is the coefficient of the lagged import price in for the
equation in levels, equation (4).
is the coefficient of the lagged import price in for the
equation in levels, equation (4).
For estimation, we implement first a General-to-Specific
strategy using the full sample and then apply rolling regressions
to the selected specification![]() The top left panel
of figure 10 shows that
The top left panel
of figure 10 shows that
![]() declines from 0.5
in 1990 to 0.2 in 2005, just as in the rolling-regression results
reported in figure 9. This finding
suggests that the short-run pass-through has declined regardless of
functional form, a finding consistent with the results reported by
Olivei (2002) and Marazzi and Sheets (2006). The top right and
bottom panels of figure 10 show that both
declines from 0.5
in 1990 to 0.2 in 2005, just as in the rolling-regression results
reported in figure 9. This finding
suggests that the short-run pass-through has declined regardless of
functional form, a finding consistent with the results reported by
Olivei (2002) and Marazzi and Sheets (2006). The top right and
bottom panels of figure 10 show that both
![]() and
and
![]() start at zero
but increase (in absolute value) and remain constant since 1995. In
particular, figure 11 shows that the
implied estimate of the long-run pass-through,
start at zero
but increase (in absolute value) and remain constant since 1995. In
particular, figure 11 shows that the
implied estimate of the long-run pass-through,
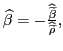 has fluctuated between 0.4 and 0.5 with a sample mean of 0.48,
which is close the value of
has fluctuated between 0.4 and 0.5 with a sample mean of 0.48,
which is close the value of
![]() of
of ![]() These findings support our view that the growing importance of
emerging economies does not imply that foreign prices, or exchange
rates, are becoming less important in the determination of U.S.
import prices but, rather, that the dynamics of the process are
changing. Indeed, the short-run exchange rate pass-through is now
close to zero but the long-run pass-through is about one-half.
These findings support our view that the growing importance of
emerging economies does not imply that foreign prices, or exchange
rates, are becoming less important in the determination of U.S.
import prices but, rather, that the dynamics of the process are
changing. Indeed, the short-run exchange rate pass-through is now
close to zero but the long-run pass-through is about one-half.
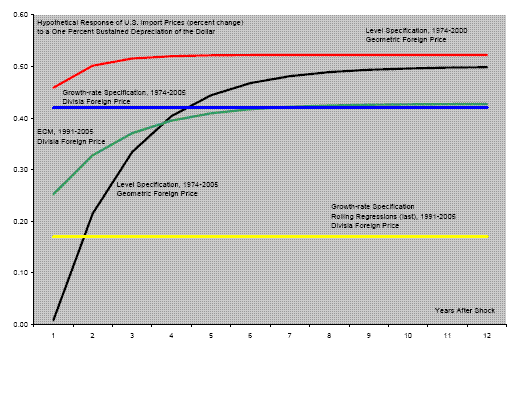
Again, this difference between short- and long-run responses would not be relevant if the adjustment process were swift. To estimate the delay in adjusting to the long-run, we examine the response of import prices to a sustained, one-percent increase in the value of the dollar.19 Figure 12 shows a similarity of short-run responses: 0.17 for the formulation in growth rates (yellow line) and 0.25 for the error-correction model (green line). This similarity is, however, short-lived with the response from the error-correction model being more that twice as large as that from the growth rate equation after three years. Further, figure 12 suggests that the dispersion in estimates found in the literature might be due to a failure to differentiate between short-run and long-run responses in the level of import prices.
Figure 12 also suggests that one can capture the increased role of emerging economies in two ways: by either modifying methods to measure foreign prices (black line) or by using conventional measures of prices combined with rolling regressions (green line). However, lacking a test to discriminate between the two approaches, we offer two reasons why modeling import prices benefits from a strategy that emphasizes measurement as opposed to sample selection. First, rolling regressions embody a tension relevant to policy work: whereas the parameter estimates are assumed to be constant during the forecast period, they are assumed to change during the estimation period. Second, as Marazzi and Sheets (2006) note, estimates from rolling regressions may be sensitive to the choice of the window used for estimation. Without objective criteria for choosing the estimation window, this introduces another subjective, but important, element to the modeling process.
5 Conclusions
This paper offers an empirical analysis of the behavior of U.S. import prices with a focus on assessing the dispersion of estimated pass-through of exchange rates. We find that, whereas the pass-through in the short-run has declined, the long-run pass-through has remained stable. We believe that these findings argue for employing formulations that differentiate between short- and long-run responses. We also argue that the one force behind the change in dynamics of the import-price process is the greater presence of producers from emerging economies. And we show that their effect on import prices can be captured with our measure of foreign prices.
Bibliography
1. Bodnar, G., B. Dumas, and R. Marston, 2002,"Pass-through and Exposure," Journal of Finance, 57, 199-231.
2. Bowman, D., 2000, "Notes on IF Exchange Rate Indexes," mimeo.
3. Bussiere, M., 2004, "Non-linear Exchange Rate Pass-through?", mimeo, Federal Reserve Board.
4. Campa, J. and L. Goldberg, 2005, "Exchange Rate Pass-Through into Import Prices," Review of Economics and Statistics, 87, 679-690.
5. Chinn, M., 2005, "A Primer on Real Effective Exchange Rates: Determinants, Overvaluation, Trade Flows and Competitive Devaluation," NBER Working Paper No. 11521.
6. Ericsson, N., 2006, Empirical Modelling of Economic Time Series, Oxford: Oxford University Press (forthcoming).
7. Goldberg, P. and M. Knetter, 1997, "Goods Prices and Exchange Rates: What Have We Learned?," Journal of Economic Literature, 35, 1243-1272.
8. Gron, A. and D. Swenson, 2000, "Cost Pass-through in the U.S. Automobile Market," Review of Economics and Statistics, 82, 316-324.
9. Gross, D. and N. Schmitt, 2000, "Exchange Rate Pass-Through and Dynamic Oligopoly: An Empirical Investigation," Journal of International Economics, 52, 89-112.
10. Gust, C., S. Leduc, and R. Vigfusson, 2006, "Trade Integration, Competition, and the Decline in Exchange Rate Pass-trhough," this compendium.
11. Hellerstein, R., 2004, "Who Bears the Cost of a Change in the Exchange Rate? The Case of Imported Beer," Federal Reserve Bank of New York, Staff Report no. 179.
12. Hendry, D. F. and H. Krolzig, 2001, Automatic Econometric Model Selection Using PcGets, London: Timberlake.
13. Loretan, M., 2005, "Indexes of the Foreign Exchange Value of the Dollar," Federal Reserve Bulletin, 91, No.1 (Winter), 1-8.
14. Marazzi, M., N. Sheets, R. J. Vigfusson, and others, 2005, "Exchange Rate Pass-through to U.S. Import Prices: Some New Evidence," International Finance Discussion Paper, No. 833.
15. Marazzi, M. and N. Sheets, 2006, "Declining Exchange Rate Pass-through to U.S. Import Prices: The Potential Role of Global Factors," this compendium.
16. Olivei, G., 2002, "Exchange Rates and the Prices of Manufacturing Products Imported into the United States," New England Economic Review, First Quarter, 3-18.
17. Pollard, P. and C. Coughlin, 2004, "Size Matters: Asymmetric Exchange Rate Pass-through at the Industry Level," Leverhulme Centre Research Paper 2004/13.
18. Summers, R. and A. Heston, 1991, "The Penn World Table (Mark 5): An expanded Set of International Comparisons, 1950-1988," Quarterly Journal of Economics, 106, 327-368.
19. Yang, J., 1997, "Exchange Rate Pass-Through in U.S. Manufacturing Industries," Review of Economics and Statistics, 89, 95-104.
Table 1: Augmented Dickey-Fuller Tests-1974-2005
Variable: Lags |
t-adf |
beta Y_1 |
SER |
AIC |
|---|---|---|---|---|
Import Price: 3 |
-2.896 | 0.899 | 0.030 | -6.891 |
Import Price: 2 |
-3.206* | 0.907 | 0.029 | -6.950 |
Import Price: 1 |
-2.173 | 0.938 | 0.032 | -6.808 |
Import Price: 0 |
-3.646* | 0.906 | 0.034 | -6.713 |
GDP Deflator: Goods & Services: 3 |
-2.014 | 0.976 | 0.009 | -9.321 |
GDP Deflator: Goods & Services: 2 |
-2.574 | 0.971 | 0.009 | -9.338 |
GDP Deflator: Goods & Services: 1 |
-1.721 | 0.981 | 0.009 | -9.234 |
GDP Deflator: Goods & Services: 0 |
-8.198** | 0.940 | 0.012 | -8.752 |
Foreign Price: Geometric Non-oil Weights: 3 |
-2.410 | 0.901 | 0.047 | -5.954 |
Foreign Price: Geometric Non-oil Weights: 2 |
-2.281 | 0.912 | 0.047 | -5.994 |
Foreign Price: Geometric Non-oil Weights: 1 |
-2.214 | 0.917 | 0.046 | -6.044 |
Foreign Price: Geometric Non-oil Weights: 0 |
-2.971* | 0.882 | 0.052 | -5.838 |
Foreign Price: Divisia Non-oil Weights: 3 |
-1.790 | 0.947 | 0.049 | -5.866 |
Foreign Price: Divisia Non-oil Weights: 2 |
-1.723 | 0.953 | 0.049 | -5.920 |
Foreign Price: Divisia Non-oil Weights: 1 |
-1.572 | 0.958 | 0.049 | -5.955 |
Foreign Price: Divisia Non-oil Weights: 0 |
-2.137 | 0.937 | 0.055 | -5.741 |
Producer Price Index: 3 |
-2.238 | 0.942 | 0.027 | -7.051 |
Producer Price Index: 2 |
-3.118* | 0.931 | 0.027 | -7.089 |
Producer Price Index: 1 |
-2.036 | 0.949 | 0.032 | -6.823 |
Producer Price Index: 0 |
-4.723** | 0.902 | 0.035 | -6.637 |
Commodity Price: 3 |
-4.712** | 0.292 | 0.085 | -4.783 |
Commodity Price: 2 |
-4.830** | 0.243 | 0.090 | -4.699 |
Commodity Price: 1 |
-4.936** | 0.266 | 0.088 | -4.755 |
Commodity Price: 0 |
-3.952** | 0.428 | 0.096 | -4.620 |
GDP Deflator: Goods: 3 |
-2.276 | 0.946 | 0.012 | -8.756 |
GDP Deflator: Goods: 2 |
-2.613 | 0.941 | 0.011 | -8.810 |
GDP Deflator: Goods: 1 |
-2.434 | 0.950 | 0.011 | -8.841 |
GDP Deflator: Goods: 0 |
-8.198** | 0.891 | 0.013 | -8.556 |
Foreign Price: Geometric Trade Weights: 3 |
-2.302 | 0.904 | 0.050 | -5.857 |
Foreign Price: Geometric Trade Weights: 2 |
-2.152 | 0.915 | 0.049 | -5.894 |
Foreign Price: Geometric Trade Weights: 1 |
-2.080 | 0.920 | 0.049 | -5.942 |
Foreign Price: Geometric Trade Weights: 0 |
-2.760 | 0.887 | 0.055 | -5.747 |
Foreign Price: Divisia Trade Weights: 3 |
-1.860 | 0.944 | 0.050 | -5.845 |
Foreign Price: Divisia Trade Weights: 2 |
-1.711 | 0.951 | 0.050 | -5.888 |
Foreign Price: Divisia Trade Weights: 1 |
-1.547 | 0.957 | 0.050 | -5.917 |
Foreign Price: Divisia Trade Weights: 0 |
-2.108 | 0.935 | 0.056 | -5.692 |
Legend
t-ADF: augmented Dickey-Fuller Test; an'*' means that the test rejects the hypothesis of a unit root
beta Y-1: Coefficient of the level of the lagged dependent variable
AIC: Akaike information criterion
Rejection values 5%=-2.96; 1%=-3.67. Constant included.
Table 2: Long-run Coefficients: Level Specification-Sensitivity to Foreign Prices, U.S. Prices, Weighting Schemes, and Sample Periods
Panel A. Foreign Price Measured by Geometric Aggregate; U.S. Price Measured by GDP Deflator for Goods and Services
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.72 | 0.04 | 0.26 | 0.03 | 0.10 | 0.03 | 0e | - | -0.31 | 0.12 | 1.09 | 0.06 | 0.014 | 0.35 | 0.54 |
| Nonoil Weights and Sample 1974-2005 | 0.49 | 0.05 | 0.46 | 0.04 | 0e | - | 0.29 | 0.06 | 0.36 | 0.13 | 0.95 | 0.06 | 0.018 | 0.02 | 0.76 |
| Broad Weights and Sample 1974-2000 | 0.71 | 0.04 | 0.27 | 0.03 | 0.10 | 0.02 | 0e | - | -0.27 | 0.11 | 1.08 | 0.05 | 0.013 | 0.36 | 0.36 |
| Broad Weights and Sample 1974-2005 | 0.47 | 0.05 | 0.47 | 0.04 | 0e | - | 0.29 | 0.06 | 0.41 | 0.13 | 0.94 | 0.06 | 0.017 | 0.02 | 0.66 |
Panel B. Foreign Price Measured by Geometric Aggregate; U.S. Price Measured by GDP Deflator for Goods
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.51 | 0.07 | 0.52 | 0.08 | 0e | - | 0e | - | 0e | - | 1.03 | 0.11 | 0.028 | 0.07 | 0.57 |
| Nonoil Weights and Sample 1974-2005 | 0.56 | 0.12 | 0.47 | 0.12 | 0e | - | 0.64 | 0.09 | 0e | - | 1.03 | 0.17 | 0.026 | 0.39 | 0.69 |
| Broad Weights and Sample 1974-2000 | 0.50 | 0.06 | 0.52 | 0.06 | 0e | - | 0.33 | 0.06 | 0e | - | 1.03 | 0.08 | 0.025 | 0.08 | 0.78 |
| Broad Weights and Sample 1974-2005 | 0.53 | 0.09 | 0.49 | 0.10 | 0e | - | 0.58 | 0.09 | 0e | - | 1.03 | 0.13 | 0.026 | 0.18 | 0.62 |
Panel C. Foreign Price Measured by Geometric Aggregate; U.S. Price Measured by Producer Price Index
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.52 | 0.08 | 0.48 | 0.09 | 0e | - | 0.56 | 0.16 | 0e | - | 1.00 | 0.12 | 0.020 | 0.16 | 0.76 |
| Nonoil Weights and Sample 1974-2005 | 0.35 | 0.16 | 0.57 | 0.12 | 0e | - | 0.66 | 0.15 | 0.45 | 0.35 | 0.91 | 0.20 | 0.020 | 0.49 | 0.51 |
| Broad Weights and Sample 1974-2000 | 0.54 | 0.05 | 0.46 | 0.06 | 0e | - | 0.41 | 0.16 | 0e | - | 1.00 | 0.08 | 0.018 | 0.12 | 0.76 |
| Broad Weights and Sample 1974-2005 | 0.46 | 0.05 | 0.50 | 0.05 | 0e | - | 0.27 | 0.08 | 0.23 | 0.13 | 0.95 | 0.07 | 0.020 | 0.05 | 0.52 |
Panel D. Foreign Price Measured by Divisia Aggregate; U.S. Price Measured by GDP Deflator for Goods and Services
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.77 | 0.07 | 0.18 | 0.05 | 0.13 | 0.04 | 0.33 | 0.08 | -0.42 | 0.20 | 1.08 | 0.09 | 0.014 | 0.44 | 0.68 |
| Nonoil Weights and Sample 1974-2005 | 0.26 | 0.21 | 0.48 | 0.18 | 0e | - | 0.69 | 0.08 | 0.98 | 0.40 | 0.75 | 0.28 | 0.021 | 0.02 | 0.09 |
| Broad Weights and Sample 1974-2000 | 0.78 | 0.07 | 0.17 | 0.05 | 0.13 | 0.04 | 0.32 | 0.08 | -0.39 | 0.19 | 1.08 | 0.09 | 0.014 | 0.40 | 0.50 |
| Broad Weights and Sample 1974-2005 | 0.27 | 0.20 | 0.47 | 0.14 | 0e | - | 0.68 | 0.08 | 1.02 | 0.38 | 0.74 | 0.24 | 0.022 | 0.16 | 0.05 |
Panel E. Foreign Price Measured by Divisia Aggregate; U.S. Price Measured by GDP Deflator for Goods
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.55 | 0.04 | 0.42 | 0.04 | 0e | - | 0.30 | 0.08 | 0e | - | 0.97 | 0.06 | 0.022 | 0.03 | 0.53 |
| Nonoil Weights and Sample 1974-2005 | 0.73 | 0.08 | 0.35 | 0.04 | 0.06 | 0.03 | 0.18 | 0.09 | -0.73 | 0.25 | 1.14 | 0.09 | 0.018 | 0.01 | 0.96 |
| Broad Weights and Sample 1974-2000 | 0.79 | 0.07 | 0.34 | 0.03 | 0e | - | 0e | - | -0.70 | 0.19 | 1.13 | 0.08 | 0.020 | 0.04 | 0.88 |
| Broad Weights and Sample 1974-2005 | 0.78 | 0.06 | 0.34 | 0.03 | 0e | - | 0e | - | -0.70 | 0.17 | 1.13 | 0.07 | 0.019 | 0.02 | 0.79 |
Panel F. Foreign Price Measured by Divisia Aggregate; U.S. Price Measured by Producer Price Index
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.63 | 0.03 | 0.32 | 0.03 | 0e | - | 0.33 | 0.13 | 0e | - | 0.95 | 0.04 | 0.015 | 0.22 | 0.29 |
| Nonoil Weights and Sample 1974-2005 | 0.15 | 0.28 | 0.47 | 0.16 | 0e | - | 0.78 | 0.12 | 1.51 | 0.74 | 0.63 | 0.32 | 0.020 | 0.46 | 0.37 |
| Broad Weights and Sample 1974-2000 | 0.63 | 0.03 | 0.32 | 0.03 | 0e | - | 0.29 | 0.12 | 0e | - | 0.95 | 0.04 | 0.014 | 0.23 | 0.39 |
| Broad Weights and Sample 1974-2005 | 0.19 | 0.25 | 0.46 | 0.14 | 0e | - | 0.76 | 0.12 | 1.41 | 0.64 | 0.65 | 0.29 | 0.020 | 0.38 | 0.48 |
Legend
0e: Algorithm excludes explanatory variable from specification.
(a): Entries for "Independent" and "Homoskedastic" are significance levels for rejecting the hypothesis of serial independence and homoskedasticity.
Table 3: Long-run Coefficients; Growth Specification-Sensitivity to Foreign Prices, U.S. Prices, Weighting Schemes, and Sample Periods
Panel A. Foreign Price Measured by Geometric Aggregate; U.S. Price Measured by GDP Deflator for Goods and Services
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.73 | 0.11 | 0.37 | 0.09 | 0.09 | 0.03 | 0e | - | 0e | - | 1.18 | 0.15 | 0.022 | 0.91 | 0.82 |
| Nonoil Weights and Sample 1974-2005 | 0.71 | 0.11 | 0.36 | 0.09 | 0.07 | 0.03 | 0e | - | 0e | - | 1.14 | 0.14 | 0.022 | 0.96 | 0.44 |
| Broad Weights and Sample 1974-2000 | 0.75 | 0.11 | 0.35 | 0.08 | 0.09 | 0.03 | 0e | - | 0e | - | 1.19 | 0.14 | 0.022 | 0.23 | 0.91 |
| Broad Weights and Sample 1974-2005 | 0.72 | 0.11 | 0.35 | 0.08 | 0.08 | 0.03 | 0e | - | 0e | - | 1.15 | 0.14 | 0.022 | 0.89 | 0.69 |
Panel B. Foreign Price Measured by Geometric Aggregate; U.S. Price Measured by GDP Deflator for Goods
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.83 | 0.16 | 0.42 | 0.10 | 0.10 | 0.04 | 0e | - | 0e | - | 1.36 | 0.19 | 0.026 | 0.70 | 0.98 |
| Nonoil Weights and Sample 1974-2005 | 0.85 | 0.15 | 0.41 | 0.09 | 0.09 | 0.04 | 0e | - | 0e | - | 1.36 | 0.18 | 0.024 | 0.76 | 0.97 |
| Broad Weights and Sample 1974-2000 | 0.86 | 0.16 | 0.40 | 0.10 | 0.11 | 0.04 | 0e | - | 0e | - | 1.37 | 0.19 | 0.026 | 0.60 | 0.97 |
| Broad Weights and Sample 1974-2005 | 0.88 | 0.14 | 0.39 | 0.08 | 0.10 | 0.04 | 0e | - | 0e | - | 1.37 | 0.17 | 0.024 | 0.62 | 0.88 |
Panel C. Foreign Price Measured by Geometric Aggregate; U.S. Price Measured by Producer Price Index
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.58 | 0.10 | 0.47 | 0.08 | 0.06 | 0.03 | 0e | - | 0e | - | 1.11 | 0.13 | 0.022 | 0.57 | 0.05 |
| Nonoil Weights and Sample 1974-2005 | 0.52 | 0.11 | 0.44 | 0.09 | 0.08 | 0.05 | 0e | - | 0e | - | 1.04 | 0.15 | 0.024 | 0.57 | 0.23 |
| Broad Weights and Sample 1974-2000 | 0.60 | 0.09 | 0.45 | 0.07 | 0.06 | 0.03 | 0e | - | 0e | - | 1.11 | 0.12 | 0.022 | 0.35 | 0.04 |
| Broad Weights and Sample 1974-2005 | 0.49 | 0.12 | 0.46 | 0.10 | 0.11 | 0.06 | 0.10 | 0.11 | 0e | - | 1.05 | 0.17 | 0.024 | 0.53 | 0.67 |
Panel D. Foreign Price Measured by Divisia Aggregate; U.S. Price Measured by GDP Deflator for Goods and Services
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.72 | 0.12 | 0.33 | 0.09 | 0.09 | 0.04 | 0e | - | 0e | - | 1.14 | 0.15 | 0.023 | 0.96 | 0.55 |
| Nonoil Weights and Sample 1974-2005 | 1.01 | 0.16 | 0.36 | 0.08 | 0.08 | 0.03 | 0e | - | -0.02 | 0.01 | 1.44 | 0.18 | 0.021 | 0.99 | 0.71 |
| Broad Weights and Sample 1974-2000 | 0.72 | 0.12 | 0.33 | 0.08 | 0.10 | 0.04 | 0e | - | 0e | - | 1.14 | 0.15 | 0.023 | 0.94 | 0.79 |
| Broad Weights and Sample 1974-2005 | 1.00 | 0.16 | 0.34 | 0.08 | 0.08 | 0.03 | 0e | - | -0.02 | 0.01 | 1.43 | 0.18 | 0.022 | 0.96 | 0.70 |
Panel E. Foreign Price Measured by Divisia Aggregate; U.S. Price Measured by GDP Deflator for Goods
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.83 | 0.16 | 0.39 | 0.09 | 0.10 | 0.04 | 0e | - | 0e | - | 1.33 | 0.19 | 0.026 | 0.68 | 0.89 |
| Nonoil Weights and Sample 1974-2005 | 0.77 | 0.15 | 0.36 | 0.08 | 0.15 | 0.05 | 0e | - | 0e | - | 1.28 | 0.17 | 0.023 | 0.49 | 0.95 |
| Broad Weights and Sample 1974-2000 | 0.83 | 0.16 | 0.39 | 0.09 | 0.11 | 0.04 | 0e | - | 0e | - | 1.32 | 0.19 | 0.026 | 0.64 | 0.93 |
| Broad Weights and Sample 1974-2005 | 0.77 | 0.15 | 0.35 | 0.08 | 0.16 | 0.05 | 0e | - | 0e | - | 1.28 | 0.17 | 0.023 | 0.40 | 0.93 |
Panel F. Foreign Price Measured by Divisia Aggregate; U.S. Price Measured by Producer Price Index
| Pricing to Market: coeff. | Pricing to Market: se | Pass-through: coeff | Pass-through: se | Commodity: coeff | Commodity: se | Lagged Dep. Variable: coeff | Lagged Dep. Variable: se | Intercept: coeff | Intercept: se | Homogeneity: coeff | Homogeneity: se | Residuals: SER | Residuals: Independent | Residuals: Homoskedastic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonoil Weights and Sample 1974-2000 | 0.55 | 0.10 | 0.41 | 0.07 | 0.12 | 0.05 | 0e | - | 0e | - | 1.08 | 0.13 | 0.022 | 0.24 | 0.87 |
| Nonoil Weights and Sample 1974-2005 | 0.59 | 0.12 | 0.44 | 0.09 | 0.08 | 0.06 | 0e | - | -0.01 | 0.01 | 1.11 | 0.16 | 0.024 | 0.68 | 0.82 |
| Broad Weights and Sample 1974-2000 | 0.54 | 0.10 | 0.40 | 0.07 | 0.13 | 0.05 | 0e | - | 0e | - | 1.07 | 0.13 | 0.022 | 0.20 | 0.72 |
| Broad Weights and Sample 1974-2005 | 0.58 | 0.12 | 0.42 | 0.09 | 0.09 | 0.06 | 0e | - | -0.01 | 0.01 | 1.09 | 0.16 | 0.025 | 0.60 | 0.78 |
Legend
0e: Algorithm excludes explanatory variable from specification.
(a): Entries for "Independent" and "Homoskedastic" are significance levels for rejecting the hypothesis of serial independence and homoskedasticity.
Table 4: Long-run Coefficient Estimates - OLS, 1974-2005
Selected Specifications
(standard errors in parentheses)
| Formulation |
Formulation |
Formulation |
Formulation |
|
|---|---|---|---|---|
| Pricing to Market | 0.50 (0.06) |
0.53 (0.09) |
0.54 (0.10) |
0.58 (0.12) |
| Pass-through | 0.52 (0.06) |
0.49 (0.10) |
0.40 (0.07) |
0.42 (0.09) |
| Persistence | 0.33 (0.06) |
0.58 (0.09) |
- | - |
| Homogeneity |
1.03 (0.08) |
1.03 (0.14) |
1.07 (0.13) |
1.09 (0.15) |
Legend
![]() Equation (4) with
geometric measure of foreign prices and GDP-goods deflator for U.S.
prices.
Equation (4) with
geometric measure of foreign prices and GDP-goods deflator for U.S.
prices.
![]() Equation (5)
with Divisia measure of foreign prices and PPI for U.S.
prices.
Equation (5)
with Divisia measure of foreign prices and PPI for U.S.
prices.
![]() Sum of pricing to market and
pass-through coefficients; standard error computed without taking
into account the covariance of the estimates.
Sum of pricing to market and
pass-through coefficients; standard error computed without taking
into account the covariance of the estimates.
Figure 1: U.S. International Relative Prices and Aggregate Foreign-GDP Deflators
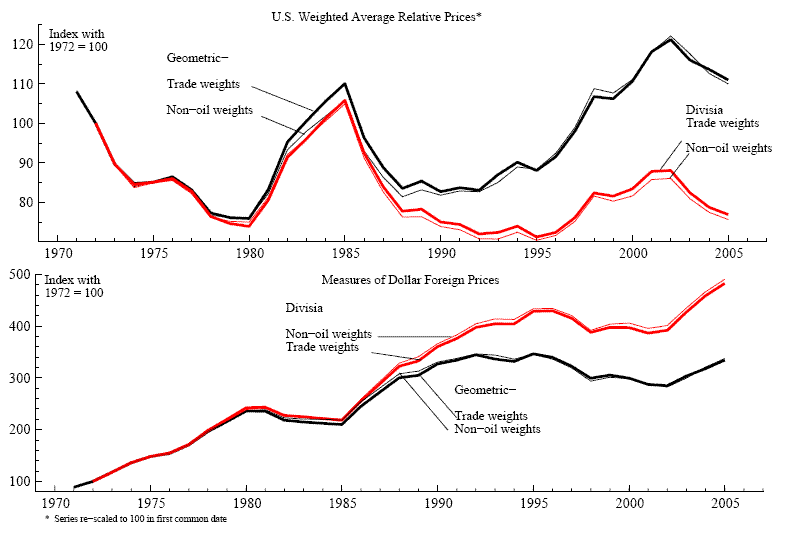
Figure 2: Alternative Measures of U.S. Prices
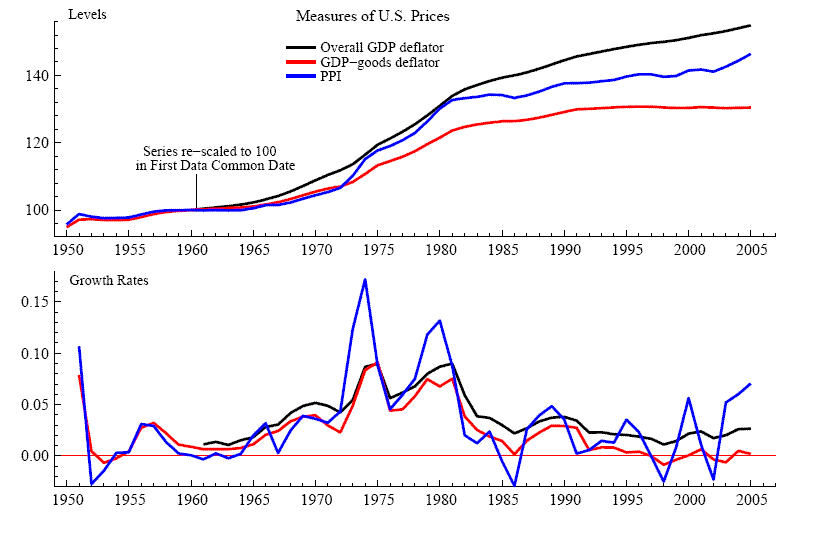
Figure 3: Import Prices, Domestic and Foreign Price Levels
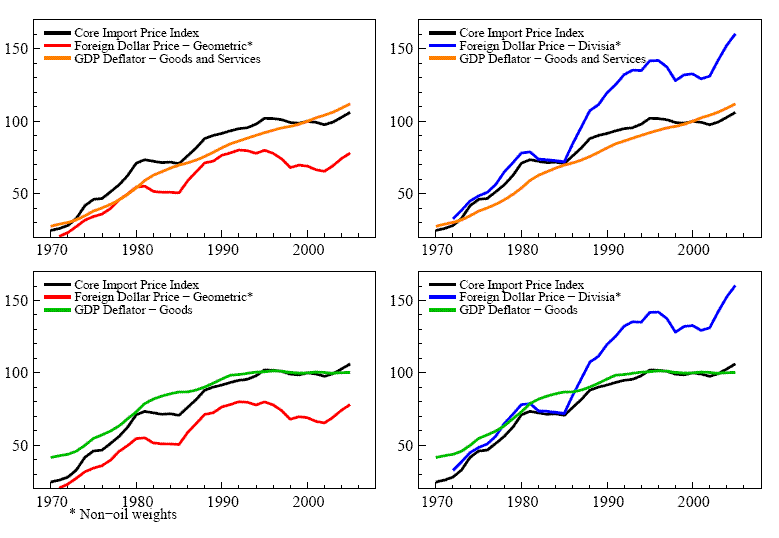
Figure 4: Long-run Coefficient Estimates - Sensitivity to Estimation Design
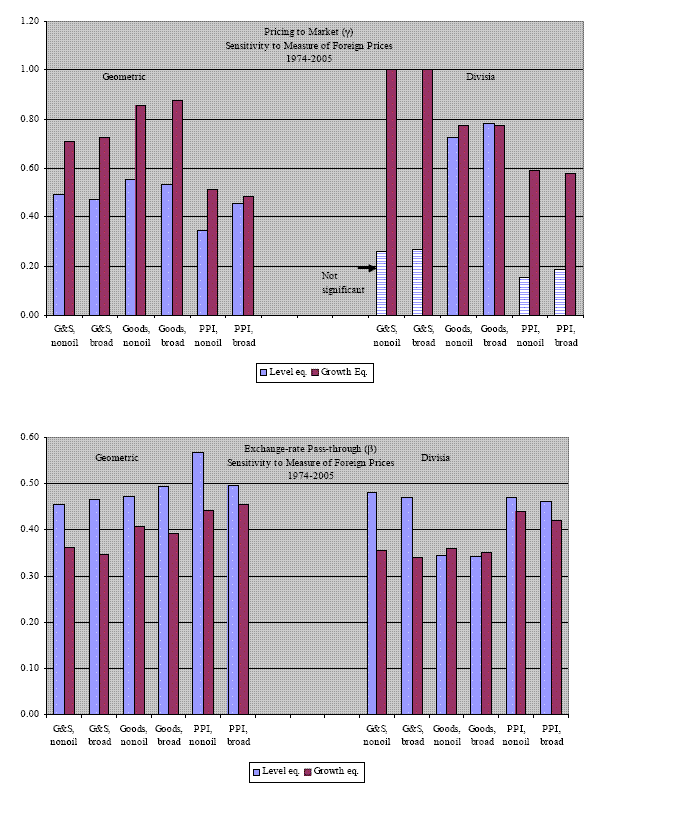
Figure 5: Long-run Estimates
of Exchange-rate Pass-through (
![]() ): Alternative Sample
Periods
): Alternative Sample
Periods
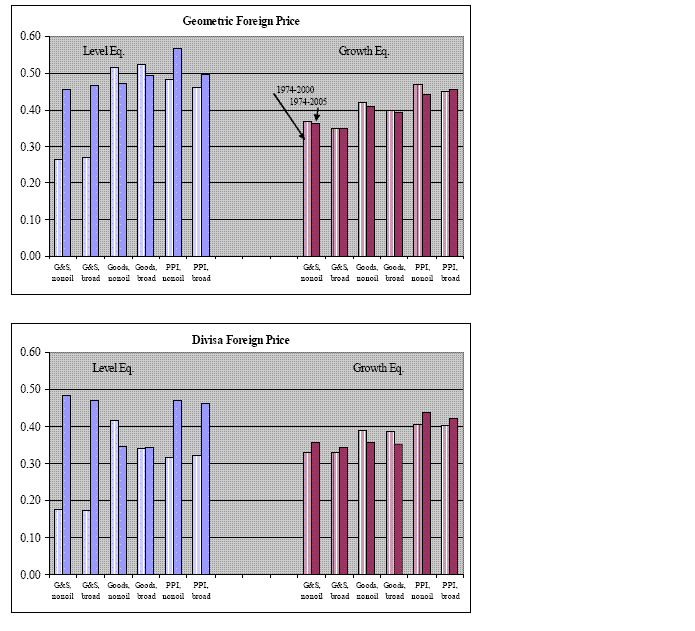
Figure 6: Long-run Estimates
of Pricing-to-Market (
![]() ): Alternative Sample
Periods (n denotes not statistically significant).
): Alternative Sample
Periods (n denotes not statistically significant).
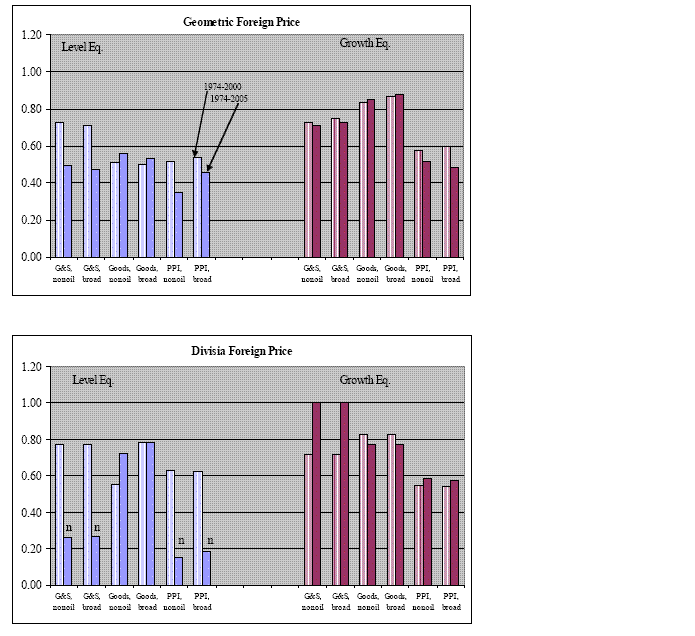
Figure 7: Short- and Long-run Exchange-rate Pass-through: Alternative Formulations
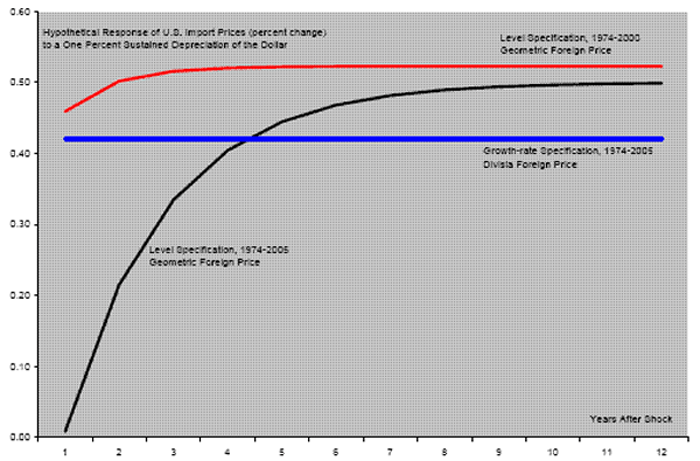
Figure 8: 95% Confidence Bands for Ex-post Dynamic Extrapolations of Import Prices
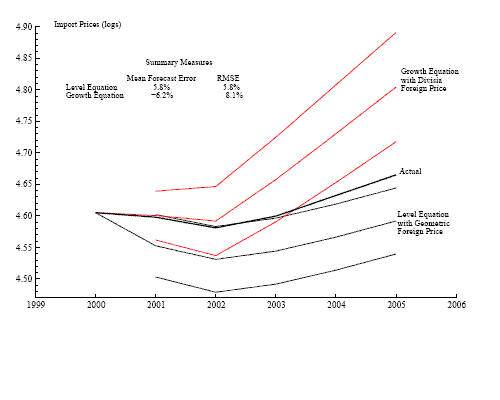
Figure 9: Estimated Short-run Exchange-Rate Pass-through: Growth-Rate Model with Rolling Regressions
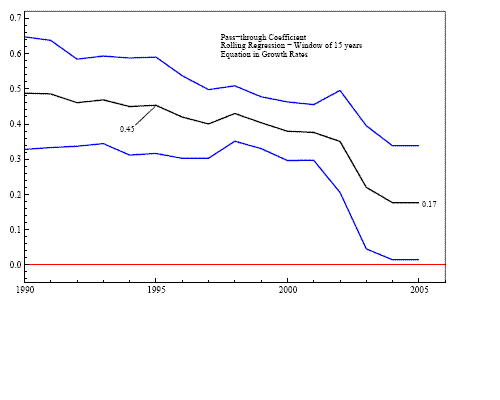
Figure 10: Rolling Regression Estimates of Error-Correction Model
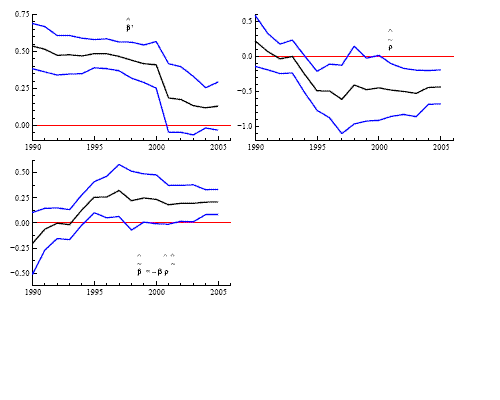
Figure 11: Long-run Estimate
of Exchange-Rate Pass-through of Error-Correction
Model: -
![]()
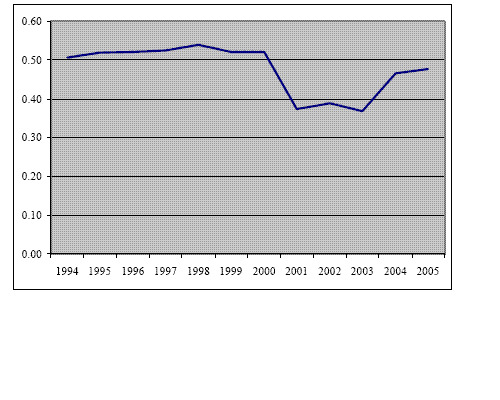
Figure 12: Short- and Long-run Exchange-rate Pass-through: Alternative Formulations and Sample-selection Methods
Footnotes
1. E-mail addresses are [email protected] and [email protected]. We are grateful to Neil Ericsson, Joe Gagnon, Mario Marazzi, Trevor Reeve, Nathan Sheets, and Robert Vigfusson for their detailed comments. A previous version of this paper was presented in the workshop series of the Federal Reserve Board and the meetings of the Fall 2005 meetings of the Midwest International Economics Group. The calculations use PcGets; see Hendry and Krolzig (2001). The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/ . Return to text
2. Not all studies are willing to extend
the benefit of the doubt to equation (1). Indeed,
recent studies recognize that strategic interactions among
producers means that ![]() and
and ![]() are not parameters to be estimated but rather
endogenous outcomes resulting from demand-supply interactions at
the micro level. See Gron and Swenson (2000), Gross and Schmitt
(2000), Hellerstein (2004); Bodnar et al. (2002); Gust et al.
(2006). Return to text
are not parameters to be estimated but rather
endogenous outcomes resulting from demand-supply interactions at
the micro level. See Gron and Swenson (2000), Gross and Schmitt
(2000), Hellerstein (2004); Bodnar et al. (2002); Gust et al.
(2006). Return to text
3. Recent data show that China displaced Canada as the largest provider of non-fuel goods to the United States. Return to text
4. As long as U.S. services and U.S. goods are not perfect substitute for each other, the measure of U.S. prices matters for estimation. Return to text
5. For an introduction to the Penn World Tables, see Summers and Heston (1991). Return to text
6. The countries we include are the ones included in the Federal Reserve's Broad index of the real effective value of the dollar. Other aggregation rules are available but we use geometric aggregation because of its widespread use in economics. See Bowman (2000). Return to text
7. These competitive weights are those used in the Broad index of the foreign exchange value of the dollar. See Loretan (2005) for the measurement of these weights. Return to text
8. Note, however, that just applying geometric aggregation to the levels of price indexes will not capture the shift towards low-price producers: one would be aggregating growth rates relative to a base period instead of the levels of the relative prices. Return to text
9. For papers examining the role of non-linearities, see Bussiere (2004); and Pollard and C. Coughlin (2004). Return to text
10. Note that the inclusion of an
intercept in equation (5) implies that the
implied level of the price of imports will include a trend. Thus
![]() changes at a rate of
changes at a rate of
![]() even
if all other prices are constant. Return
to text
even
if all other prices are constant. Return
to text
11. The General to Specific strategy is applied to each sample period separately. As a result, the specific formulation for the shorter sample is not influenced by observations outside the sample period. Return to text
12. Table 4 also offers an informal assessment of the degree to which there is cointegration among prices. For the geometric measure of foreign price, the best equation (parameter constancy, white-noise residuals, homogeneity) explains the level of the import prices. The cointegration test for this equation involves comparing the t-statistic of one minus the coefficient for the lagged dependent variable against the Ericsson-Mackinnon critical value. This coefficient is 0.42 (=1-0.58) and its standard error is 0.09; the associated t-statistic is 4.67. The Ericsson-Mackinnon critical value (5%) is 3.33 (Ericsson, 2006, p.302, table 6.7). Thus the evidence cannot reject cointegration if one uses the geometric measure of foreign prices. For the Divisia measure of foreign price, the best equation explains the growth rate of import prices. As a result, the evidence does not support cointegration in this case. Return to text
13. The response is computed as
![]() Return to text
Return to text
14. The estimates for ![]() show a negligible response in short-run pass-through
coefficients because
show a negligible response in short-run pass-through
coefficients because ![]() and
and ![]() have opposite signs with
have opposite signs with
![]() Return to text
Return to text
15. The re-application of the General to Specific algorithm avoids the specifications being influenced by observations beyond 2000. Return to text
16. For the equation in growth rates, we
generate the prediction for the level by augmenting the model with
the definition of the logarithm of the price level: ln![]() = ln
= ln
![]() ln
ln![]() Return to text
Return to text
17. Rolling regressions use a fixed sample the dates of which (the window) change systematically by excluding the earliest date and including the next date. Return to text
18. To attain greater comparability with previous results, we also treat the specification as known and invariant from one sample to another: only the estimated parameters change as the sample changes. Operationally, we implement first a General-to-Specific strategy using the full sample and then apply rolling regressions to the selected specification. The alternative would be to find a specific formulation for each estimation window. Studies reporting rolling-regression estimates do not search window by window and so we retain their practice. Return to text
19. We use parameter estimates based on the last window of the rolling regression (1991-2005). Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text