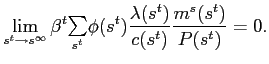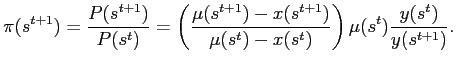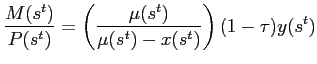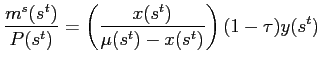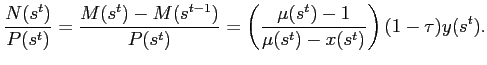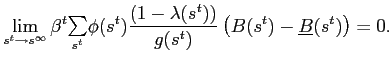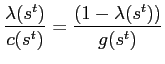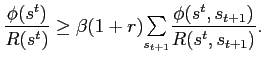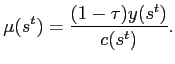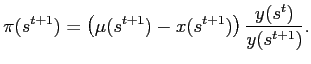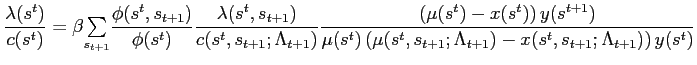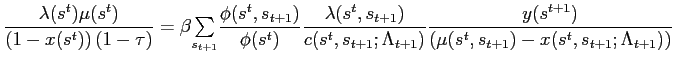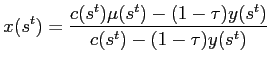Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 890, February 2007 --- Screen Reader
Version*
Dollarization and Financial Integration
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
How does a country's choice of exchange rate regime impact its ability to borrow from abroad? We build a small open economy model in which the government can potentially respond to shocks via domestic monetary policy and by international borrowing. We assume that debt repayment must be incentive compatible when the default punishment is equivalent to permanent exclusion from debt markets. We compare a floating regime to full dollarization. We find that dollarization is potentially beneficial, even though it means the loss of the monetary instrument, precisely because this loss can strengthen incentives to maintain access to debt markets. Given stronger repayment incentives, more borrowing can be supported, and thus dollarization can increase international financial integration. This prediction of theory is consistent with the experiences of El Salvador and Ecuador, which recently dollarized, as well as with that of highly-indebted countries like Italy which adopted the Euro as part of Economic and Monetary Union. In each case, spreads on foreign currency government debt declined substantially around the time of regime change.
Keywords: dollarization, sovereign debt
JEL classification: F33, F34, F36
1 Introduction
The recurrence of currency and financial crises in emerging markets has generated an intense debate on the appropriate exchange rate regime. Dollarization has attracted special attention, in part because of the recent official dollarization of Ecuador and El Salvador.1
The key difference between dollarizing and simply pegging the exchange rate is that dollarizing represents more permanent restrictions on domestic monetary policy. Thus thinking about dollarization leads one to thinking about what a government might have to gain by tying its hands more tightly with regards to monetary policy, which in turn leads to the issue of credibility. In discussing papers in a conference volume on the topic of dollarization, Sargent (2001) writes
`` In their papers and verbal discussions, proponents of dollarization often appealed to commitment and information problems that somehow render dollarization more credible and more likely to produce good outcomes. Those proponents presented no models of how dollarization was connected with credibility. We need some models."
In this paper we explore one avenue via which dollarization may increase credibility. In particular, we develop a model in which dollarization enhances a sovereign borrower's credibility in international financial markets, and thereby increases international financial integration.
Retaining the ability to print one's own currency gives governments a flexible way to raise revenue. Emerging markets economies are typically subject to big shocks, and large fractions of government revenue are linked to volatile commodity prices. Moreover, increasing traditional tax rates is difficult, and does not guarantee additional revenue when evasion is widespread and the informal sector is large. In this context seigniorage is a valuable fiscal instrument, since extra money can rapidly be printed as required. Click (1998) documents that seigniorage accounted for a large share of government spending in many Latin American countries in the 1970s and 1980s and that countries with more volatile spending relied more heavily on seigniorage as a fiscal instrument. Calvo and Guidotti (1993) find that inflation taxes tend to be much more volatile than regular taxes in practice. They rationalize this finding by developing a model in which it is optimal to let changes in the inflation tax do all the work in adjusting to unanticipated fluctuations in spending.2
At the same time, emerging markets economies issue debt on international markets to smooth fluctuations and to ease temporary liquidity problems. In the model developed in this paper, dollarization may help strengthen fragile sovereign debt markets. The logic is that because dollarizing rules out the use of monetary policy to respond to shocks, it may increase the value to the sovereign of maintaining access to the debt instrument. Thus if default is punished by exclusion from debt markets, dollarization effectively reduces the sovereign's incentive to default, and thereby increases the amount of borrowing that can be supported in equilibrium.
Our theoretical model is a small open exchange economy designed to highlight the trade-off that arises in the decision to dollarize between the loss of seigniorage as a flexible fiscal instrument on the one hand, and the potential gain from increased financial integration on the other. Consumers value private and public consumption goods. To ensure a role for two policy instruments, the growth rate of money and international debt, we assume the economy is subject to two sources of risk. First, output is stochastic, which introduces a motive for inter-temporal smoothing. Second, consumers' relative taste for private versus public consumption fluctuates, which introduces a motive for intra-temporal reallocation between the private and public sector.
In the tradition of the literature on optimal policy, we assume that the government is benevolent and rational, and seeks to maximize the utility of a representative consumer.3 Changes in the money growth rate affect the division of output between consumers and the government because of a cash-in-advance friction. In addition to revenue from seigniorage, the government also trades one period bonds in international financial markets at a constant real interest rate. However, the government cannot commit to repay international debts: contracts must be self-enforcing as in Zhang (1997). Thus foreign creditors set borrowing limits such that the government always has the incentive to honor its obligations, where the penalty in case of default is permanent financial autarky.
We compare a floating exchange rate regime to a dollarized regime. Under floating, the government sets the money growth rate and thus the inflation and devaluation rates at every date. Under dollarization, the inflation rate is constant, and the government's only policy instrument is its international debt position.
After defining the Ramsey problem for the government, we explore what determines how much international borrowing can be supported in equilibrium, and how this varies across exchange rate regimes. In an extensive sensitivity analysis we find that dollarizing can either increase or reduce the amount of borrowing that can be supported in equilibrium. Relative to a float, borrowing constraints tend to be looser under a dollarized regime (i) the larger are shocks to the relative taste for public versus private consumption, (ii) the less synchronized are periods of high output (and tax revenue) and high demand for government consumption, (iii) the lower is the interest rate, and (iv) the higher is the rate of time preference. In the floating economy, the process for demand shocks has no impact on the position of the borrowing constraint, since these shocks can always be perfectly smoothed with monetary policy. Comparing welfare across regimes, we find that dollarizing is welfare-improving in regions of the parameter space where dollarizing supports sufficient additional borrowing to offset the welfare loss associated with losing control of the rates of money growth, inflation and devaluation.
Finally, to get a sense of the quantitative relevance of the trade-off we explore, we consider a calibration to El Salvador (which dollarized in 2001) and to Mexico (which has been discussed as a potential candidate for dollarization). We find that in both cases large taste shocks are required to account for the high volatility of government spending relative to GDP. The model successfully replicates some key features of the data, such as the co-movement at business cycle frequencies between government consumption on the one hand, and output, private consumption, the inflation rate, and the change in the government's net foreign asset position on the other.
Comparing across the two regimes, we find that in the calibration to El Salvador the dollarized economy exhibits looser borrowing constraints and less frequent debt crises, identified as periods in which the borrowing constraint is binding. At the maximum value for debt that can be sustained in the floating regime, lifetime utility can be higher when dollarized, reflecting the benefit of a looser borrowing constraint. The results for the Mexico calibration are quite different: in this case, less borrowing can be supported in the dollarized economy. We interpret the different results for these two countries in terms of differences in the covariance matrix for the underlying shocks.
In Section 2 of the paper we describe a range of empirical evidence consistent with our thesis that reducing devaluation risk might also reduce default risk. We focus in particular on Ecuador, El Salvador, and countries that adopted the euro, and argue that for these countries abandoning an independent monetary policy has led to a reduction in financial markets' perceptions of default risk.
There is a large literature on the pros and cons of dollarization, and an even larger related literature on the relative merits of fixed versus floating exchange rates. Perhaps the two most discussed arguments in favor of dollarization are that it can reduce inflation by importing monetary policy credibility, and can increase trade by eliminating currency risk and foreign exchange transaction costs (Alesina and Barro 2002). The model we develop in this paper is deliberately designed to abstract from these potential benefits in order to clarify the trade-off in the dollarization decision between the loss of seigniorage as a flexible fiscal instrument on the one hand, and the potential increase in international financial integration on the other. However, because additional mechanisms would come into play in a richer model, we now briefly review the existing debate, and explain how it connects to the theory developed in this paper.
The evidence on the boost to trade from eliminating currency risk is mixed. Frankel and Rose (2002) find that currency unions boost bilateral trade significantly with other currency union countries in a sample of 186 countries. However, Lane (2006) notes that to date the Economic and Monetary Union (EMU) in Europe has not increased the importance of intra-euro-zone trade relative to trade outside the euro area. In contrast, there is strong evidence that the EMU has increased financial integration across the euro area along many dimensions, in particular by reducing bond spreads across member countries.
Dollarization does bring lower and less volatile inflation to countries adopting a stronger currency (Edwards 2001). A common interpretation of the high and volatile inflation rates in some emerging markets economies is that these countries face more severe time-consistency problems in setting monetary policy than countries whose currencies are being adopted (see, for example, Cooper and Kempf 2001). A competing explanation for why monetary independence leads to higher inflation is that countries perceive control of the printing press as an opportunity for beggar-thy-neighbor policy. Cooper and Kempf (2003) build a model in which inflation acts as a tax on foreigners wishing to purchase domestic goods, prompting competitive governments to choose inefficiently high inflation rates in equilibrium. Similarly, Cooley and Quadrini (2001) argue that Mexico may prefer a higher inflation rate than the US because higher nominal interest rates can have favorable effects on the terms of trade. In the model of this paper, there is no time consistency problem in monetary policy, and international prices are taken as given. Thus the key difference between the floating and dollarized economies is the volatility of the inflation rate, rather than the average level of inflation.
If dollarization is permanent, it eliminates the possibility of currency crises. Mendoza (2001) argues that eliminating distortionary uncertainty over the duration of stabilization policies can deliver substantial welfare gains (see also Calvo 1999 and Berg and Borensztein 2000). Dollarization also solves the `` fear of floating'' problem (Calvo 2001) which arises when international liabilities are denominated in dollars and currency devaluations therefore precipitate debt crises. In our endowment economy, devaluations are non-distortionary. Furthermore, the law of one price holds, so periods of inflation and devaluation do not make it more difficult to repay dollar debts.
Finally, Sims (2001) argues that dollarization is costly because it prevents the economy from issuing (state-contingent) nominal debt, without affecting dollar interest rates. However, governments in emerging markets are largely unable to issue external debt in their own currency, no matter what exchange rate regime they have, so it is not clear that this constitutes a strong argument against dollarization in practice.
2 Historical Experience
In the context of our theory, a country's choice for its exchange rate regime has implications for the volatility of its inflation rate, and for its ability to sell bonds in international sovereign debt markets. In practice, easier access to international credit should translate into some combination of additional borrowing or lower sovereign risk spreads. In this section we provide some empirical evidence that is consistent with the hypothesis that by surrendering monetary independence a government can effectively improve its credit rating as a sovereign borrower.
We first look at the experiences of four countries that recently delegated monetary policy offshore: Italy and Portugal, which adopted the European single currency in 1999, and Ecuador and El Salvador, which dollarized in 2000 and 2001 respectively. Figure 1 plots time series for sovereign spreads for loans issued by these four countries.4 Spreads are defined as the difference in yields between domestic and foreign government issued bonds, where paired bonds share similar maturities, coupon rates and currency. In each case, we are able to isolate default risk from devaluation risk by pairing bonds denominated in the same currency. For example, we compare the yield to maturity on a deutsche mark (DM) denominated bond issued by Italy to a DM denominated bond issued by Germany.
Italy and Portugal are interesting case studies among the set of European countries participating in the Economic and Monetary Union (EMU) because in addition to having issued foreign currency bonds that are traded in secondary markets, they have lived with very high levels of government debt relative to GDP: 116% and 95% respectively in 1996. The European single currency was officially introduced on January 1st 1999, but more relevant for markets' perceptions of default risk is the date when it became clear that these countries would be allowed to adopt the euro at the new currency's inception. For Italy, Bassetto (2006) argues that 1996 was the key year. The first panel of Figure 1 shows that spreads on Italian deutsche mark denominated bonds decreased substantially in that year, by about 100 basis points in total. The second panel plots spreads for Portuguese bonds. As in the Italian case, spreads on these bonds also decreased significantly in 1996 and 1997.5
Ecuador dollarized in 2000 in the midst of a severe economic crisis with a collapsing banking system, a sliding local currency, and after defaulting on its Brady bonds in late 1999. The regime was implemented in an attempt to reduce inflation, bring stability to the economy, and gain credibility with international investors. Since dollarization, Ecuador's inflation has been significantly reduced to single digits. Figure 1 shows that default risk increased significantly in 1998 prior to the 1999 crisis and default. In July 2000 spreads came down again after Ecuador dollarized and renegotiated its debts. Since the dollarization plan was implemented, spreads on Ecuadorian government bonds have decreased cumulatively by about 800 basis points.
El Salvador implemented its dollarization plan in 2001. Figure 1 shows that the spread on dollar loans has decreased by over 400 basis points since 2001. In fact the very day after the new currency was adopted, the interest rate on consumer mortgages fell from 17 to 11 percent. Consumer credit has been growing, and the government and the corporate sector have benefited from cheaper international borrowing.
Figure 1: Spreads and Dollarization
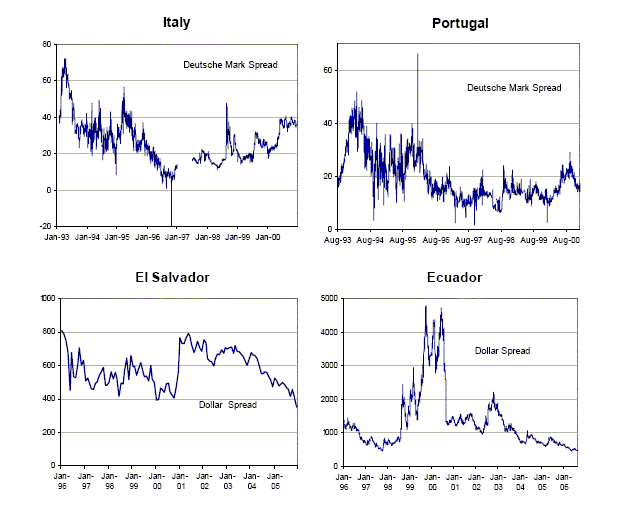
Description of Figure 1: Spreads and Dollarization
Figure 1 shows line plots for time series for sovereign spreads for loans issued by Italy, Portugal, El Salvador and Ecuador. Spreads are defined as the difference in yields between domestic and foreign government issued bonds, where paired bonds share similar maturities, coupon rates and currency. In each case, we isolate default risk from devaluation risk by pairing bonds denominated in the same currency. For example, we compare the yield to maturity on a deutsche mark (DM) denominated bond issued by Italy to a DM denominated bond issued by Germany.
The first panel of Figure 1 shows that the difference between the yield on Italian Deutschemark-denominated bonds and German Deutschemark-denominated bonds decreases in 1996, approximately from 25 to 10 basis points over the course of the year.
The second panel of Figure 1 shows that the difference between the yield on Italian Deutschemark-denominated bonds and German Deutschemark-denominated bonds decreases from around 30 basis points at the start of 1996, to around 10 basis points by the end of 1997.
The third panel in Figure 1 shows that the difference between the domestic dollar prime interest rate on loans of maturity greater than one year in El Salvador and the yield on a U.S. government bill with one year maturity decreases from 770 basis points to 350 basis points between January 2001 and the end of 2005.
The fourth panel in Figure 1 shows that the JP Morgan Emerging Market Bond Index Spread for Ecuador increases significantly in 1998 prior to the 1999 crisis and default. After dollarization, the spread declines to around 1400 basis points in August 2000, and then gradually declines further to around 500 basis points by August 2006.
Table 1. Correlations with International Investor Ratings
| Inflation | St.Dev Inflation | Fixed Exch. Rate | Debt / GDP | log(GDP/capita) |
|---|---|---|---|---|
| -0.46 | -0.43 | 0.29 | -0.31 | 0.89 |
Thus, in time series data for countries that have surrendered monetary policy, there is evidence that this reform has reduced the cost of international credit. We now turn to cross-sectional data, and consider a much larger set of countries. Here we find complementary evidence that countries with less flexibility in setting monetary policy - as evidenced by having a fixed exchange rate or less volatile inflation - are viewed as safer borrowers.
We study the relationship between inflation, the exchange rate regime, and default risk for the 76 countries that are rated by Moody's for its International Investor Ratings. These credit ratings are intended to convey default risk for foreign currency sovereign bonds. We use credit ratings as opposed to direct measures of spreads as our proxy for ease of access to international credit because ratings are available for a broader set of countries (in practice, ratings and spreads correlate very strongly). For each country in our sample, the statistics we record are (1) Moody's ratings for 2000 converted to a linear scale (higher numbers equate to better ratings), (2) CPI inflation in 2000, (3) the standard deviation of CPI inflation over the period 1985-2000, (4) GDP per capita in dollars in 2000, (5) a dummy variable corresponding to a fixed exchange rate regime in 2000, and (6) the ratio of foreign debt to GDP in 2001.6
Table 1 shows the correlations of credit ratings for government debt with these other variables. Ratings tend to be better for countries with low and stable inflation, low levels of foreign debt to GDP, fixed exchange rate regimes, and higher GDP per capita. These correlations are consistent with the notion that too much flexibility in monetary policy can crowd out flexibility in debt policy. Still, one should not over-interpret this evidence, for at least two reasons. First, nominally fixed exchange rate regimes vary enormously in how frequently and easily exchange rate parities can be adjusted, while our theory will strictly apply only to very hard pegs. Second, the exchange rate regime is a policy choice that likely correlates with institutional factors that also impact credibility in financial markets. Thus, to properly understand the relationship between dollarization and financial integration, we need an explicit model.
3 Model
We consider a small open economy populated by a large number of identical consumers, a representative firm, and a government. Consumers work for firms, and each period produce a stochastic quantity of goods that can be used for private or public consumption. Firms sell these goods in exchange for cash. Once the goods market has closed, firms pay their workers. Thus the cash that consumers spend on goods in the current period must be carried over from the previous period.
The government is benevolent and chooses policies to maximize consumer welfare. We compare two alternative exchange rate regimes. The first is a simple float. Under a float, trade in the cash goods market is conducted using the currency issued by the domestic government, which we label the peso. We allow the government to print new money after observing the firm's output and to spend it immediately to purchase goods that will be provided publicly. The second regime we consider is dollarization. Only foreign currency circulates in a dollarized economy. Thus the domestic government has no control over monetary policy and enjoys no seigniorage.
We assume that under both regimes, the government is the only actor in the economy with access to a competitive international bond market.7 In the bond market the domestic government can sell bonds that take the form of one-period dollar-denominated loans. International lenders decide whether to lend, how much to lend, and at what price to lend. However they cannot make the price of loans contingent on the borrowing government's net foreign asset position, or on the shocks that will hit the economy in the next period. Thus asset markets are far from complete. However, the assumed market structure is appropriate for most emerging markets economies, whose bonds typically specify repayment in foreign currency and on non-contingent terms.8
International debt contracts are notoriously difficult to enforce directly. We assume that lenders can commit to honor their contractual obligations, but that the domestic government cannot commit to repay any debt obligations. In the event of default, creditors are assumed to credibly punish the government by permanently excluding it from the bond market: a government that has defaulted in the past can neither buy nor sell bonds. When it is impossible to impose direct sanctions on defaulting sovereigns, this is the harshest feasible punishment.9
We assume that international lenders can earn a safe real return
![]() on the world market. Competition among
lenders combined with the assumption that lending rates must be
non-contingent drives all lenders to sell bonds at the same price
on the world market. Competition among
lenders combined with the assumption that lending rates must be
non-contingent drives all lenders to sell bonds at the same price
![]() and to ensure repayment by rationing
credit.10 Thus lenders impose endogenous
borrowing limits on the sovereign such that no borrowing occurs
beyond the point at which the probability of subsequent default
becomes positive. A key point of the paper is that because default
incentives depend on the menu of policy instruments available to
the government, the position of these endogenous borrowing
constraints will generally differ across the floating and
dollarized regimes.
and to ensure repayment by rationing
credit.10 Thus lenders impose endogenous
borrowing limits on the sovereign such that no borrowing occurs
beyond the point at which the probability of subsequent default
becomes positive. A key point of the paper is that because default
incentives depend on the menu of policy instruments available to
the government, the position of these endogenous borrowing
constraints will generally differ across the floating and
dollarized regimes.
We now lay out the model formally and describe in detail the problems solved by each agent in our economy.
In each period ![]() the economy
experiences one of finitely-many events
the economy
experiences one of finitely-many events
![]() An event is a stochastic
realization for output,
An event is a stochastic
realization for output, ![]() and a stochastic
realization for a preference parameter
and a stochastic
realization for a preference parameter
![]() We assume that the pair of
shocks
We assume that the pair of
shocks
![]() evolves according
to a first-order Markov process. We denote by
evolves according
to a first-order Markov process. We denote by
![]() the history
of events up to and including period
the history
of events up to and including period ![]() The
probability, as of date
The
probability, as of date ![]() of a particular history
of a particular history
![]() is
is
![]()
Output ![]() is produced by the
representative firm and can be converted into a private consumption
good
is produced by the
representative firm and can be converted into a private consumption
good ![]() or a public consumption good,
or a public consumption good,
![]() Output is produced at the start of
the period, and then allocated between consumers and the government
in a cash market in the middle of the period. At the end of the
period, firms pay their workers (consumers) nominal wages
Output is produced at the start of
the period, and then allocated between consumers and the government
in a cash market in the middle of the period. At the end of the
period, firms pay their workers (consumers) nominal wages
![]()
Consumers are infinitely-lived, discount at rate ![]() and derive utility from both privately and publicly
provided consumption goods. Expected lifetime utility is given
by
and derive utility from both privately and publicly
provided consumption goods. Expected lifetime utility is given
by
where period utility is
Variation in the taste parameter
![]() can be interpreted as
capturing changes through time in household preferences for public
versus private goods, or changes in the taste for the allocation
mechanism (government provision versus market provision). One
possible manifestation of these changes in taste would be electoral
cycles in which populist free-spending governments and more
fiscally conservative market-oriented governments take turns in
power. In the context of the model, these shocks play two roles.
First, a second source of uncertainty introduces a clear role for a
second policy instrument, and suggests a downside to renouncing the
monetary instrument by dollarizing. Second, when we later calibrate
the model to El Salvador and Mexico, we find that demand-side
shocks of some sort are required to account for the high volatility
of private and public consumption in the data.
can be interpreted as
capturing changes through time in household preferences for public
versus private goods, or changes in the taste for the allocation
mechanism (government provision versus market provision). One
possible manifestation of these changes in taste would be electoral
cycles in which populist free-spending governments and more
fiscally conservative market-oriented governments take turns in
power. In the context of the model, these shocks play two roles.
First, a second source of uncertainty introduces a clear role for a
second policy instrument, and suggests a downside to renouncing the
monetary instrument by dollarizing. Second, when we later calibrate
the model to El Salvador and Mexico, we find that demand-side
shocks of some sort are required to account for the high volatility
of private and public consumption in the data.
We assume that cash is the only savings vehicle available to
consumers. The representative consumer enters the period with money
savings from the previous period
![]() and wages from the previous
period
and wages from the previous
period
![]() He observes the endowment shock
He observes the endowment shock
![]() the taste shock
the taste shock
![]() and the price level
and the price level
![]() . He then decides how much of his
money to spend, subject to the cash-in-advance constraint and the
budget constraint:
. He then decides how much of his
money to spend, subject to the cash-in-advance constraint and the
budget constraint:
where
![]() denotes total nominal balances
carried into period
denotes total nominal balances
carried into period ![]() In the floating economy
consumers can only save and purchase goods using pesos.11 Note
that we do not assume at the outset that shocks are small
enough to rule out money saving because the variance of shocks is
an important determinant of the position of borrowing constraints.
In fact, for realistic amounts of volatility, we will find that
money saving typically does occur in equilibrium.
In the floating economy
consumers can only save and purchase goods using pesos.11 Note
that we do not assume at the outset that shocks are small
enough to rule out money saving because the variance of shocks is
an important determinant of the position of borrowing constraints.
In fact, for realistic amounts of volatility, we will find that
money saving typically does occur in equilibrium.
The household problem is to choose sequences for money savings
![]() and consumption
and consumption ![]() to maximize expected lifetime utility (eq. 1) subject to the cash-in-advance constraint (eq.
2), the budget constraint (eq. 3) and a non-negativity constraint on consumption,
to maximize expected lifetime utility (eq. 1) subject to the cash-in-advance constraint (eq.
2), the budget constraint (eq. 3) and a non-negativity constraint on consumption,
![]() taking as a given a complete
set of date and state contingent endowments
taking as a given a complete
set of date and state contingent endowments ![]() taste shocks
taste shocks
![]() wages
wages ![]() prices
prices ![]() probabilities
probabilities
![]() and initial money holdings
and initial money holdings
![]()
The inter-temporal first order condition for the household's problem is
 |
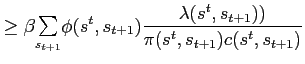
|
(4) |
where
![]() denotes the gross inflation rate when next period's state is
denotes the gross inflation rate when next period's state is
![]() .
.
The transversality condition is
3.1 Government Problem When Floating
At time zero, the government in the floating regime decides on a
policy
![]() which
defines government consumption
which
defines government consumption ![]() ,
dollar-denominated assets
,
dollar-denominated assets ![]() and the
quantity of pesos in circulation
and the
quantity of pesos in circulation ![]() for all
for all
![]() and for all
and for all ![]() given some initial assets
given some initial assets ![]() and nominal
balances
and nominal
balances ![]()
The government is not subject to a cash-in-advance constraint
since it can print new money after observing ![]() and
and
![]() and use this money immediately
to help finance public consumption,
and use this money immediately
to help finance public consumption, ![]() Let
Let
![]() denote the
aggregate stock of money in circulation at the end of period
denote the
aggregate stock of money in circulation at the end of period
![]() Thus the money growth rate
Thus the money growth rate
![]() is equal to
is equal to
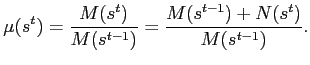
In addition to seigniorage and revenue from international
borrowing, the government also seizes a constant fraction
![]() of the endowment directly, with no money
changing hands. This can be interpreted as a constant tax rate on
private-sector output or, alternatively, as the government
producing fraction
of the endowment directly, with no money
changing hands. This can be interpreted as a constant tax rate on
private-sector output or, alternatively, as the government
producing fraction ![]() of output. We assume the
law of one price holds, so that the nominal exchange rate measured
in units of pesos per dollar is equal to the domestic price level:
of output. We assume the
law of one price holds, so that the nominal exchange rate measured
in units of pesos per dollar is equal to the domestic price level:
![]() Thus the government
nominal budget constraint, prior to default, is given by
Thus the government
nominal budget constraint, prior to default, is given by
where ![]() are dollar-denominated riskless
foreign assets purchased at
are dollar-denominated riskless
foreign assets purchased at ![]() .
.
In addition, assets purchased must exceed some state-contingent limit:
The government is allowed to default at any date. If the government chooses to default, then for all future histories the government budget constraint becomes
However, as noted above, lenders will not lend beyond the point
at which the default probability becomes positive. We assume that
the constraints
![]() are tight enough to
deter the government from ever defaulting in equilibrium, but ``
not too tight'' in the sense of Alvarez and Jermann (2000). In
particular, constraints would be too tight if it were possible to
loosen the constraint marginally for at least one
are tight enough to
deter the government from ever defaulting in equilibrium, but ``
not too tight'' in the sense of Alvarez and Jermann (2000). In
particular, constraints would be too tight if it were possible to
loosen the constraint marginally for at least one ![]() without this change ever inducing a
borrowing-constrained agent to default.
without this change ever inducing a
borrowing-constrained agent to default.
3.2 Government Problem When Dollarized
The problem for the government in a dollarized economy differs from the one described above in two respects.
First, the money growth rate is not a domestic policy instrument
but is chosen by the foreign government to maintain a constant
price level which we normalize to one. We assume that the domestic
dollar cash market for goods is open to foreigners as well as
domestic consumers. Thus arbitrage equates the domestic price level
to the foreign one:
![]() Given that the
domestic government cannot print new money, the term
Given that the
domestic government cannot print new money, the term ![]() drops out of the government budget constraints pre
and post default (eqs. 6 and 8) and the pre default constraint becomes
drops out of the government budget constraints pre
and post default (eqs. 6 and 8) and the pre default constraint becomes
Second, as we have already emphasized, the maximum amount of
borrowing allowed at a point in time,
![]() will differ across
regimes. In particular, suppose debt is used more actively under
dollarization to compensate for the lack of a monetary instrument.
Then the prospect of losing the debt instrument in the event of
default should be of greater concern in the dollarized regime, and
it may therefore be possible to support more sovereign debt in
equilibrium.
will differ across
regimes. In particular, suppose debt is used more actively under
dollarization to compensate for the lack of a monetary instrument.
Then the prospect of losing the debt instrument in the event of
default should be of greater concern in the dollarized regime, and
it may therefore be possible to support more sovereign debt in
equilibrium.
3.3 Equilibrium Relationships
The following relationships apply to both economies.
At the end of the period, firms pay as wages all the cash they hold. Thus
Since all the money circulating in the economy at the end of the period is held by households
In the floating regime, ![]() denotes the domestic
government's newly printed money, while in the dollarized economy,
denotes the domestic
government's newly printed money, while in the dollarized economy,
![]() denotes dollar net purchases of
domestically-produced goods by foreigners.12
denotes dollar net purchases of
domestically-produced goods by foreigners.12
The market clearing condition for the cash goods market is
Note that if households do no money saving
![]() we get the standard quantity
equation with velocity equal to one. Initial money holdings equal
the initial money supply
we get the standard quantity
equation with velocity equal to one. Initial money holdings equal
the initial money supply
![]()
The aggregate resource constraint under flexibility is:
while the corresponding constraint under dollarization is
These conditions can be interpreted as follows. Under a float, all
international borrowing and lending is conducted by the government,
and thus the change in the government's bond position is the only
item on the capital account. In the dollarized economy, there is an
additional private source of capital flows associated with changes
in the quantity of dollars circulating domestically, ![]() . For domestic households, dollar bills can be viewed
as international bonds that can be used to smooth shocks to wages
and preferences. However, their value as a self-insurance device is
limited by two factors: (i) they pay zero real interest, and (ii)
dollar holdings are bounded below by the cash-in-advance
constraint: the household must always carry at least
. For domestic households, dollar bills can be viewed
as international bonds that can be used to smooth shocks to wages
and preferences. However, their value as a self-insurance device is
limited by two factors: (i) they pay zero real interest, and (ii)
dollar holdings are bounded below by the cash-in-advance
constraint: the household must always carry at least
![]() dollars from
period
dollars from
period ![]() into period
into period ![]()
For each regime, combining the government budget constraint and the aggregate resource constraint (eqs. 6 and 13, or eqs. 9 and 14) gives an alternative expression for private consumption:
Let ![]() denote the fraction of aggregate
cash on hand that agents save at
denote the fraction of aggregate
cash on hand that agents save at ![]()
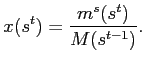
For solving the equilibrium allocations in the floating economy it
is convenient to express private consumption and the real money
variables in terms of the sequences ![]()
![]() and
and ![]() with
no reference to nominal variables
with
no reference to nominal variables ![]()
![]() or
or ![]()
First, from the goods market clearing condition, eq. 12, the price level is given by
Substituting ![]() into the consumer's budget
constraint (eq. 15) gives
into the consumer's budget
constraint (eq. 15) gives
Note that if the household is not doing any money saving
![]() ), then
), then
![]() However in general, the money growth rate has a direct effect on
consumption and an indirect effect via
However in general, the money growth rate has a direct effect on
consumption and an indirect effect via
![]()
The real return to money saving (the inflation rate) is given by
In the dollarized regime
![]() for all
for all ![]() and
thus the money growth rate
and
thus the money growth rate
![]() is endogenous and depends in
equilibrium on households' choices regarding money savings
is endogenous and depends in
equilibrium on households' choices regarding money savings
![]() In the floating economy the money
growth rate
In the floating economy the money
growth rate
![]() is the domestic government's
policy choice and the inflation rate
is the domestic government's
policy choice and the inflation rate
![]() is endogenous and depends on
money savings
is endogenous and depends on
money savings ![]() .
.
Making repeated use of the expression for the price level, eq. 16, real balances, real money savings, and the real value of seigniorage (corresponding to net purchases by foreigners in the dollarized regime) can be expressed, respectively as:
Note that
![]() Setting
Setting
![]() implies zero seigniorage. As
implies zero seigniorage. As
![]()
![]() and
thus
and
thus
![]() Note that for
Note that for
![]() seigniorage is (weakly)
positive. For
seigniorage is (weakly)
positive. For
![]() seigniorage is negative.
seigniorage is negative.
4 Definition of Equilibrium
We first define equilibria for two economies that are not of
direct interest, but that are useful for constructing borrowing
constraints that are not too tight. The first economy is one in
which: (i) the borrowing constraints
![]() are
exogenous, and (ii) the government must respect the constraints and
is not allowed to default. The second economy is one in which the
government has defaulted in the past and has no access to the
international debt market. The third economy, which is the economy
of interest, features endogenous borrowing constraints that are not
too tight. In this economy default is permitted but never occurs in
equilibrium.
are
exogenous, and (ii) the government must respect the constraints and
is not allowed to default. The second economy is one in which the
government has defaulted in the past and has no access to the
international debt market. The third economy, which is the economy
of interest, features endogenous borrowing constraints that are not
too tight. In this economy default is permitted but never occurs in
equilibrium.
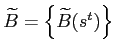
We will look for borrowing constraints that are tight enough, but not too tight. They are tight enough in that if the sovereign is at the borrowing constraint, then the probability that he will strictly prefer to default in the next period is zero. They are not too tight in that there is at least one combination of shocks under which he will be indifferent between repaying or defaulting. To formalize the difference between the values of repaying debts and defaulting, we introduce some new notation.
Let
![]()
![]()
![]() be a function defining the
value associated with a date
be a function defining the
value associated with a date ![]() Ramsey problem
given history
Ramsey problem
given history
![]() arbitrary bonds
arbitrary bonds ![]() (and in the dollarized economy money
(and in the dollarized economy money ![]() )
)![]() and a set of borrowing constraints
and a set of borrowing constraints
![]() Let
Let
![]()
![]()
![]() be a function defining the
difference between the value of the Ramsey equilibrium and the
value of default
be a function defining the
difference between the value of the Ramsey equilibrium and the
value of default
![]() :
:
We now note some useful properties of these functions:
- The function
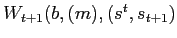
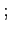
 is strictly increasing in
is strictly increasing in
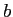 for any
for any
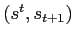 while the value of default
is independent of the quantity of debt defaulted on. It follows
immediately that if for some history
while the value of default
is independent of the quantity of debt defaulted on. It follows
immediately that if for some history 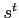 the
government weakly prefers not to default in every possible
the
government weakly prefers not to default in every possible
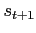 given bonds
given bonds 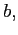 then
the government will strictly prefer to repay for any
then
the government will strictly prefer to repay for any
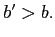 Conversely, if the
government is indifferent about default for some
Conversely, if the
government is indifferent about default for some 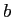 given
given 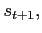 then if
then if
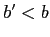 and
and 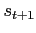 is realized, the government will strictly prefer to default.
is realized, the government will strictly prefer to default. - The function
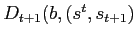
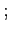
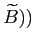 does not depend on the stock
of money balances consumers carry into the start of the period. In
the floating economy the nominal quantity of pesos is irrelevant,
since it has no impact on real allocations (we return to this point
in Proposition 1). In the dollarized economy, the Ramsey planner is
powerless to impact the time series for private consumption, and we
have assumed separability in utility between private and public
consumption. Thus the difference between the values of
repaying and defaulting does not depend on cash balances.
does not depend on the stock
of money balances consumers carry into the start of the period. In
the floating economy the nominal quantity of pesos is irrelevant,
since it has no impact on real allocations (we return to this point
in Proposition 1). In the dollarized economy, the Ramsey planner is
powerless to impact the time series for private consumption, and we
have assumed separability in utility between private and public
consumption. Thus the difference between the values of
repaying and defaulting does not depend on cash balances. - Under the solution to the date 0 Ramsey problem, the
continuation value at
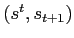 given equilibrium bonds
given equilibrium bonds
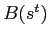 is equal to
is equal to
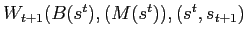
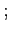
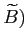 . This reflects the fact that
there is no time consistency problem in these economies, a point we
will return to later.
. This reflects the fact that
there is no time consistency problem in these economies, a point we
will return to later.
If the not-too-tight condition is satisfied then by virtue of properties (1) and (2)
Note that if all lenders but one were in aggregate willing to
lend an amount strictly less than
![]() given
given ![]() then the last lender could make a positive profit on a
marginal additional loan by charging a real interest rate greater
than
then the last lender could make a positive profit on a
marginal additional loan by charging a real interest rate greater
than ![]() and bearing no default risk. Thus the only
equilibrium in the lending market in which no excess profits remain
is one in which lenders are willing in aggregate to lend up to
and bearing no default risk. Thus the only
equilibrium in the lending market in which no excess profits remain
is one in which lenders are willing in aggregate to lend up to
![]() at the safe world
interest rate
at the safe world
interest rate ![]()
In the appendix we show that for a given feasible policy there is a unique monetary equilibrium in this economy.
4.1 Ramsey Equilibria
We now describe how we solve for the Ramsey equilibrium in our economies. Solving the Ramsey problem in the dollarized economy is simpler, because monetary policy in this case is exogenous, and the planner only needs to decide on the optimal debt policy.
4.1.1 Dollarized Economy
The Ramsey equilibrium in the dollarized monetary economy with riskless lending can be characterized by solving the following planner's problem. Consider a planner who maximizes expected lifetime utility (eq. 1) subject to budget constraints
and a set of borrowing constraints of the form eq. 7.
Sufficient conditions for a solution to this problem are the optimality conditions for bonds:
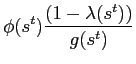 |
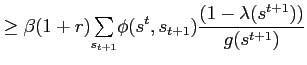
|
(24) |
Note that in the dollarized economy, separability between private and public consumption in preferences implies that consumers and the government end up solving completely separate problems. Consumers use dollar money savings to smooth the marginal utility of private consumption through time, taking as given inflation rates. The government uses debt to smooth the marginal utility of public consumption through time, taking as given the world interest rate and state-contingent borrowing constraints.
4.1.2 Floating Economy
Proposition 1. The Ramsey equilibrium in the floating monetary economy with riskless lending can be characterized by solving the problem of a planner who maximizes expected lifetime utility eq. (1) subject to an aggregate resource constraint (13) and a set of borrowing constraints of the form eq. (7) where these constraints are "not too tight."
Proof: See the appendix.
This result greatly simplifies the Ramsey problem because it effectively eliminates the constraint that the allocations chosen by the Ramsey planner must constitute a competitive equilibrium. At the simplest level, the intuition for the result is that control of the money growth rate is equivalent to access to lump-sum taxation in this economy: by choosing money growth rates appropriately, the government can achieve any possible division of total resources between private and public consumption. Since the government's problem reduces to a standard consumption-savings problem, there is no time-consistency problem in our economies, in the sense that the government never has an incentive to deviate from its pre-announced policy.13
Sufficient conditions for a solution to this planner's problem are the optimality conditions for bonds (eqs. 24 and 25) described above and an intra-temporal first order condition
which says that the planner wants to equate the marginal utilities of privately and publicly provided goods at each date and state.
Note that because the marginal utilities of private and public
consumption are equated state by state, the inter-temporal first
order condition 24 can be expressed in
terms of total resources available for domestic consumption
![]()
Thus in this case, the planner simply wants to smooth fluctuations
in the endowment through time, irrespective of the process for
taste shocks: a floating, credit-worthy government will typically
issue debt when the endowment is relatively low, and repay when the
endowment is high. Monetary policy will be used primarily to adjust
the mix between private and public consumption in response to taste
shocks. When
![]() is high, indicating a
preference for private consumption, the money growth rate
is high, indicating a
preference for private consumption, the money growth rate
![]() and thus seigniorage will be
relatively low.
and thus seigniorage will be
relatively low.
4.2 Questions
- Could the government do better by internalizing the
relationship between policy choices and not-too-tight borrowing
constraints in the floating regime?
In defining the Ramsey problem, we assumed that the government took borrowing constraints as given. Taking as given borrowing constraints that are not-too-tight, the Ramsey solution maximizes value. To increase value, an alternative policy would have to imply looser borrowing constraints. However, we can argue that not-too-tight constraints can only be tighter under alternative policies. First, note that changing policy prior to default will not change default values
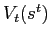 under a float. Second, since
values inside the contract,
under a float. Second, since
values inside the contract,
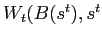
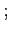
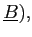 could only be lower under
alternative policies, not-too-tight borrowing constraints could
only be tighter. A similar argument applies to the dollarized
economy.
could only be lower under
alternative policies, not-too-tight borrowing constraints could
only be tighter. A similar argument applies to the dollarized
economy. - Would domestic consumers like to be able to buy dollars in
the floating regime?
Suppose households in the floating economy were able to exchange pesos for dollars, and buy or sell goods on an international market. We can argue that prior to default, dollars will not be used as a private savings vehicle. The first order condition for dollar savings will be
However, combining 27 and 30 gives![$\displaystyle \frac{\lambda(s^{t})\phi(s^{t})}{c(s^{t})}\geq\beta {\textstyle\sum\limits_{s_{t+1}}} \left[ \frac{\lambda(s^{t},s_{t+1})\phi(s^{t},s_{t+1})}{c(s^{t},s_{t+1} )}\right] . $](img234.gif)
![$\displaystyle \frac{\lambda(s^{t})\phi(s^{t})}{c(s^{t})}\geq\beta(1+r) {\textstyle\sum\limits_{s_{t+1}}} \left[ \frac{\lambda(s^{t},s_{t+1})\phi(s^{t},s_{t+1})}{c(s^{t},s_{t+1} )}\right] $](img235.gif)
Comparing these two inequalities, it is clear that as long as
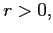 households will never want to save
in the form of dollars. The intuition is that the government can
save dollars at a positive interest rate, while households can only
hold dollar cash. Since they value consumption in different states
equally, it is efficient for the government to conduct all
international borrowing and lending.14 In the event of
default, households might want to save in the form of dollars. Thus
if allowed to do so, the value of default under a float would be
increased, and consequently borrowing constraints would be
tighter.
households will never want to save
in the form of dollars. The intuition is that the government can
save dollars at a positive interest rate, while households can only
hold dollar cash. Since they value consumption in different states
equally, it is efficient for the government to conduct all
international borrowing and lending.14 In the event of
default, households might want to save in the form of dollars. Thus
if allowed to do so, the value of default under a float would be
increased, and consequently borrowing constraints would be
tighter. - Is there a role for domestic debt in these economies?
In the floating economy, control over the money-growth rate by itself effectively amounts to having access to a state-contingent lump-sum tax. Thus domestic debt instruments, whether peso or dollar denominated, would be superfluous. In the dollarized model economy, endowing the government with the ability to buy and sell dollar-denominated bonds with domestic consumers would effectively introduce a valuable new instrument for reallocating resources between the private and public sector. In many emerging markets, domestic debt's usefulness as a re-allocative policy instrument is limited by poorly developed financial markets. By contrast, virtually the entire population is active in the cash goods market, and thus subject to the inflation tax associated with growth in the money supply.
5 Quantitative Analysis
5.1 Comparing debt constraints and welfare across regimes
Conditional on a particular exchange rate regime, the borrowing constraint is looser the more valuable is access to the debt instrument prior to default, or, equivalently, the more painful is the loss of the instrument post default. Comparing across regimes, the constraint tends to be looser in the regime in which debt is used more actively, which in turn depends on the nature of shocks hitting the economy.
It is instructive to consider two simple examples, in which only one type of shock is operative.
First, suppose there are only shocks to ![]() the relative taste for public versus private consumption. In this
case the only goal for policy is to allocate constant output
efficiently between public and private consumption. Control of the
money growth rate and thus the inflation rate can achieve this
perfectly. Thus, under a float there is no incentive for the
government to repay any debts, and the borrowing constraint is at
zero. Under dollarization, debt is a valuable though imperfect
instrument since it is the only way for the government to smooth
through taste shocks. Thus borrowing can be supported in this
case.
the relative taste for public versus private consumption. In this
case the only goal for policy is to allocate constant output
efficiently between public and private consumption. Control of the
money growth rate and thus the inflation rate can achieve this
perfectly. Thus, under a float there is no incentive for the
government to repay any debts, and the borrowing constraint is at
zero. Under dollarization, debt is a valuable though imperfect
instrument since it is the only way for the government to smooth
through taste shocks. Thus borrowing can be supported in this
case.
Second, consider the case with only shocks to output ![]() . Under a float, in response to a transitory increase in
output it is optimal to increase the money growth rate in order to
tax away some of the increase in private income via inflation. Debt
is used aggressively, since debt repayments must both offset the
increase in direct tax revenue and the increase in seigniorage
revenue. Activist debt policy translates into strong repayment
incentives and a loose borrowing constraint. Under dollarization,
by contrast, debt is used less prior to default, and consequently
the borrowing constraint is tighter.
. Under a float, in response to a transitory increase in
output it is optimal to increase the money growth rate in order to
tax away some of the increase in private income via inflation. Debt
is used aggressively, since debt repayments must both offset the
increase in direct tax revenue and the increase in seigniorage
revenue. Activist debt policy translates into strong repayment
incentives and a loose borrowing constraint. Under dollarization,
by contrast, debt is used less prior to default, and consequently
the borrowing constraint is tighter.
When both types of shocks are operational, the relative volatility and correlation of shocks are key to understanding the relative position of borrowing constraints under the two regimes.
Ranking welfare across the two regimes is more complicated than ranking borrowing constraints. Even if dollarizing means looser constraints, the associated benefits must be weighted against the costs of losing monetary policy as an instrument. If the economy is subject to only one source of risk, it is easy to see that a float necessarily welfare dominates. With only taste shocks, a float achieves the efficient allocation of resources across sectors and through time, even though no borrowing is supported in equilibrium. With only endowment shocks, a float welfare dominates because more borrowing can be supported in equilibrium. We conclude that a necessary condition for dollarization to be welfare-improving in our environment is that the variance of both types of shocks is positive.
5.2 Sensitivity
To understand how the choice of exchange rate regime impacts
debt constraints and welfare, we consider a simple baseline
parameterization, and conduct an extensive sensitivity analysis
with respect to alternative parameter values. We assume that both
shocks are drawn independently from the same two-point
distribution, with a mean of 0.85 and a standard
deviation of 5 percent. Thus
![]() We set the constant tax rate
We set the constant tax rate ![]() so that absent
any shocks, efficient allocations could be achieved with constant
debt and a constant money supply. Thus
so that absent
any shocks, efficient allocations could be achieved with constant
debt and a constant money supply. Thus
![]() Finally
we set the discount factor
Finally
we set the discount factor ![]() to 0.96 and the interest rate
to 0.96 and the interest rate ![]() to 2
percent. By exploring variations on this particular parameter
configuration we will learn a lot about the differences between the
two exchange rate regimes. Later we will introduce more discipline
in the choice of parameter values by calibrating the model to some
specific countries.
to 2
percent. By exploring variations on this particular parameter
configuration we will learn a lot about the differences between the
two exchange rate regimes. Later we will introduce more discipline
in the choice of parameter values by calibrating the model to some
specific countries.
In this section we explore how borrowing constraints and welfare
change as we vary (i) the variance of the taste shock ![]() (ii) the correlation between
(ii) the correlation between ![]() and
and ![]() (iii) the discount factor
(iii) the discount factor ![]() and (iv) the interest rate
and (iv) the interest rate ![]() Comparing
borrowing constraints across regimes is easy, because in our
example the position of the constraint is independent of the
current state.15 Comparing welfare is more difficult
because expected lifetime utility is conditional on all the state
variables in the economy. Moreover, in addition to the values for
shocks and for sovereign debt, there is one additional endogenous
state variable in the dollarized economy, namely domestic
consumers' holdings of dollars. We compare welfare by (i) setting
sovereign debt in both regimes equal to the value of the borrowing
constraint in the floating economy (which almost always exceeds the
constraint under dollarization), (ii) setting the real value of
dollars in the dollarized economy equal to the real value of pesos
in the floating economy, and (iii) taking an unconditional average
across lifetime utility under each possible configuration of
shocks. The welfare difference is reported as percentage difference
in lifetime aggregate consumption across regimes.
Comparing
borrowing constraints across regimes is easy, because in our
example the position of the constraint is independent of the
current state.15 Comparing welfare is more difficult
because expected lifetime utility is conditional on all the state
variables in the economy. Moreover, in addition to the values for
shocks and for sovereign debt, there is one additional endogenous
state variable in the dollarized economy, namely domestic
consumers' holdings of dollars. We compare welfare by (i) setting
sovereign debt in both regimes equal to the value of the borrowing
constraint in the floating economy (which almost always exceeds the
constraint under dollarization), (ii) setting the real value of
dollars in the dollarized economy equal to the real value of pesos
in the floating economy, and (iii) taking an unconditional average
across lifetime utility under each possible configuration of
shocks. The welfare difference is reported as percentage difference
in lifetime aggregate consumption across regimes.
At the parameter configuration described above, the borrowing constraint is extremely tight under a float, while the government can borrow almost twenty percent of GDP in the dollarized economy. Welfare is very similar. The intuition for these findings will become clear in the context of our sensitivity analysis.
Figure 2: Borrowing Constraints and Welfare
Description of Figure 2: Borrowing Constraints and Welfare
Figure 2 shows line plots documenting how debt limits and the welfare gain from dollarizing vary with some key model parameter values.
The first panel shows the effect of changing the variance of the taste shock, lamda, holding all other parameters constant. The variance of lamda does not impact the position of the borrowing constraint in the floating economy. In the dollarized economy, the borrowing constraint is looser the larger are the taste shocks. When taste shocks are very small, so that more borrowing is possible in the floating regime, then a float welfare dominates. For more volatile taste shocks, the figure shows that dollarizing is welfare-improving.
The second panel shows the effect of changing the correlation between the two shocks, from minus one to plus one. This correlation has no impact on the position of the borrowing constraint in the floating economy. In the dollarized economy, the higher is the shock's correlation, the looser is the borrowing constraint. Increasing the correlation of shocks makes dollarization relatively more attractive in welfare terms, and the welfare gain becomes positive once the correlation exceeds approximately 0.25.
The third panel shows the effect of varying the discount factor, beta. Borrowing constraints become tighter as beta is reduced. For sufficiently low beta, no borrowing can be supported in equilibrium. This threshold is much higher in the floating regime. As beta increases towards the reciprocal of the gross interest rate, the borrowing limit loosens substantially in the dollarized economy, such that when beta=0.98 it is at 27.5% of GDP, compared to 18.1% when beta=0.96. For values for beta such that no borrowing can be supported in either regime, floating welfare-dominates. The welfare gap between the two regimes narrows as beta is increased over the range where the borrowing constraint is becoming looser in the dollarized economy, but is still zero in the floating economy. There is a range of intermediate values for beta for which dollarization welfare-dominates. For large enough values for beta, the welfare ranking across regimes flips once more.
The fourth panel shows the effect of varying the interest rate, r. The position of the borrowing constraint is minimally sensitive to the interest rate in the floating regime, while the constraint becomes extremely loose for low interest rates in the dollarized economy. When r=0.1%, the government can borrow up to three times GDP at a risk-free interest rate. As the interest rates tends towards zero, the welfare gains from dollarizing become quite substantial, reaching 5.7 percent of consumption when r=0.1%.
5.2.1 Variance of 
We first vary the variance of ![]() holding all
other parameters constant. The first panel in Figure 2 shows
the impact on the position of the borrowing constraints as a
fraction of mean output, and relative welfare in the two
economies.
holding all
other parameters constant. The first panel in Figure 2 shows
the impact on the position of the borrowing constraints as a
fraction of mean output, and relative welfare in the two
economies.
First, note that the variance of ![]() plays
no role in determining the position of the constraint or debt
dynamics in the floating economy. As discussed above, this is
because shocks to
plays
no role in determining the position of the constraint or debt
dynamics in the floating economy. As discussed above, this is
because shocks to ![]() can be perfectly
insured with the money growth instrument. In the dollarized
economy, the borrowing constraint is looser the larger are the
taste shocks, since bigger shocks increase the role for
international borrowing and lending. When taste shocks are small
enough, the ranking of constraints across regimes switches. This is
consistent with the previous result for the economy with only
endowment shocks.
can be perfectly
insured with the money growth instrument. In the dollarized
economy, the borrowing constraint is looser the larger are the
taste shocks, since bigger shocks increase the role for
international borrowing and lending. When taste shocks are small
enough, the ranking of constraints across regimes switches. This is
consistent with the previous result for the economy with only
endowment shocks.
How the welfare ranking across regimes changes with the variance of taste shocks is also intuitive. Obviously, when taste shocks are very small, so that more borrowing is possible in the floating regime, then a float welfare dominates: dollarizing would mean losing an instrument, with no credibility gain in financial markets. For more volatile taste shocks, there is an interesting trade-off. Figure 2 shows that when taste shocks are large enough, the welfare gain from looser borrowing constraints in the dollarized economy more than offsets the loss of seigniorage as a policy instrument, and thus dollarizing is welfare-improving.
5.2.2 Correlation between  and
and 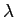
The second panel in Figure 2 shows the effect of varying the correlation between endowment and taste shocks. This correlation has no impact on the position of the borrowing constraint in the floating economy for the reason discussed above: taste shocks are perfectly insured via monetary policy.
In the dollarized economy, a positive correlation between the two shocks means that when output (and tax revenue) is high, government consumption is not especially valued (and vice versa). Thus the government would like to use debt aggressively, and the threat of losing the debt instrument in the event of default is potent. Thus the higher is the shock's correlation, the looser is the endogenous borrowing constraint.
The fact that increasing the correlation of shocks loosens the
borrowing constraint is one reason why higher correlation makes
dollarization relatively more attractive in welfare terms. A second
reason is that for higher correlations, the loss of the monetary
policy instrument under dollarization is less painful. The logic is
that if ![]() and
and ![]() co-move
positively, then private income tends to rise automatically in
times when private consumption is highly valued. Thus increasing
co-move
positively, then private income tends to rise automatically in
times when private consumption is highly valued. Thus increasing
![]() reduces the role for
monetary policy.
reduces the role for
monetary policy.
5.2.3 The discount factor 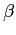
The third panel in Figure 2 shows
the effect of varying ![]() As in standard
repeated games, the more impatient are consumers, the less
effective is the threatened default punishment of exclusion from
international borrowing. Thus borrowing constraints become tighter
as
As in standard
repeated games, the more impatient are consumers, the less
effective is the threatened default punishment of exclusion from
international borrowing. Thus borrowing constraints become tighter
as ![]() is reduced. For sufficiently low
is reduced. For sufficiently low
![]() no borrowing can be supported in
equilibrium. This threshold
no borrowing can be supported in
equilibrium. This threshold ![]() is much higher
in the floating regime, reflecting the fact that in this case
monetary policy perfectly insures taste shocks, and endowment
shocks are small. Borrowing can be supported for a wider range of
values for
is much higher
in the floating regime, reflecting the fact that in this case
monetary policy perfectly insures taste shocks, and endowment
shocks are small. Borrowing can be supported for a wider range of
values for ![]() in the dollarized economy, because
in this regime debt has an additional valuable role smoothing
preference shocks. As
in the dollarized economy, because
in this regime debt has an additional valuable role smoothing
preference shocks. As ![]() increases towards the
discount rate,
increases towards the
discount rate, ![]() the borrowing limit loosens
substantially in the dollarized economy, such that when
the borrowing limit loosens
substantially in the dollarized economy, such that when
![]() it is at 27.5% of
GDP, compared to 18.1% when
it is at 27.5% of
GDP, compared to 18.1% when
![]()
When no borrowing can be supported in either regime, floating
clearly welfare-dominates, since dollarizing means losing an
instrument with no credibility gain in financial markets. The
welfare gap between the two regimes narrows as ![]() is increased over the range where the borrowing
constraint is becoming looser in the dollarized economy, but is
still zero in the floating economy. As the consumer's rate of time
preference approaches the interest rate, the position of the
borrowing constraint becomes increasingly irrelevant. The reason is
that as the opportunity time cost of holding bonds shrinks, the
government is willing to hold an increasingly large buffer stock of
precautionary bonds, and consequently the borrowing constraint
binds ever less frequently. This is why for large enough values for
is increased over the range where the borrowing
constraint is becoming looser in the dollarized economy, but is
still zero in the floating economy. As the consumer's rate of time
preference approaches the interest rate, the position of the
borrowing constraint becomes increasingly irrelevant. The reason is
that as the opportunity time cost of holding bonds shrinks, the
government is willing to hold an increasingly large buffer stock of
precautionary bonds, and consequently the borrowing constraint
binds ever less frequently. This is why for large enough values for
![]() the welfare ranking across regimes
flips once more.
the welfare ranking across regimes
flips once more.
5.2.4 The interest rate 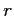
In the last panel of Figure 2 we
consider the effect of varying the interest rate, ![]() The results are rather striking. The position of the borrowing
constraint is minimally sensitive to the interest rate in the
floating regime, while the constraint becomes extremely loose for
low interest rates in the dollarized economy. When
The results are rather striking. The position of the borrowing
constraint is minimally sensitive to the interest rate in the
floating regime, while the constraint becomes extremely loose for
low interest rates in the dollarized economy. When ![]() the government can borrow up to three times GDP at a
risk-free interest rate.
the government can borrow up to three times GDP at a
risk-free interest rate.
To build some intuition for these results, first suppose there were no shocks in these economies. With a small but positive interest rate and no enforcement frictions, the government would like to borrow heavily initially, and enjoy a downward-sloping profile for consumption looking forward. This simply reflects the standard relationship between the desired growth rate for consumption and the differential between the rate of interest and the rate of time preference. If this differential is large, moving from a flat consumption profile to the optimal one can generate large welfare gains. But in a risk-free version of a model in which debt repayment cannot be enforced directly, these gains can never be realized. The reason is simply that the position of the borrowing constraint depends only on the borrower's incentives to maintain a good credit rating ex post: the ex ante potential gains from reallocating consumption inter-temporally are irrelevant. We conclude that when the interest rate is far below the rate of time preference, there are large welfare costs associated with the lack of an enforcement mechanism.
Now consider introducing shocks. As we reduce the interest rate, default incentives change in two ways. First, it becomes cheaper to pay interest on loans, and the incentive to default is reduced. Second, the cost of engaging in precautionary savings is larger because having bond holdings in excess of the borrowing constraint is expensive. In the limit, if the interest rate is sufficiently low relative to the rate of time preference, it is never optimal to move off the constraint, and since there is no use for debt, there is no cost to defaulting.
In the floating regime, as we have argued previously, the only
shocks relevant to debt repayment incentives are endowment shocks.
These shocks are quite small, so for sufficiently low ![]() (holding constant
(holding constant ![]() it will
rarely be worth doing any precautionary saving. Thus, even though
maintaining a good credit report is cheap (because
it will
rarely be worth doing any precautionary saving. Thus, even though
maintaining a good credit report is cheap (because ![]() is low), there is not much incentive to do so. This is why the
borrowing constraint remains very tight in the floating
economy.
is low), there is not much incentive to do so. This is why the
borrowing constraint remains very tight in the floating
economy.
Under dollarization, by contrast, the government also wants to
use debt to smooth preference shocks. In this case debt is used
more aggressively, and the punishment for default remains
significant even for ![]() Thus in this economy the
effect that debt repayment becomes cheaper when
Thus in this economy the
effect that debt repayment becomes cheaper when ![]() is reduced dominates, and the borrowing constraint becomes
extremely loose as
is reduced dominates, and the borrowing constraint becomes
extremely loose as
![]()
As
![]() the welfare gains from
dollarizing become quite substantial, reaching 5.7 percent of consumption when
the welfare gains from
dollarizing become quite substantial, reaching 5.7 percent of consumption when ![]() These
welfare gains are too large to be attributed solely to improved
smoothing of endowment shocks, since the endowment shocks are
relatively small, and Lucas' (1987) expressions for the welfare
costs of business cycles would suggest small welfare gains to
eliminating them. Rather, the bulk of the welfare gains in this
example comes from inter-temporal reallocation. Starting at the
tight floating constraint, dollarizing allows the government to
raise government spending in the short run and to then gradually
reduce spending over time.
These
welfare gains are too large to be attributed solely to improved
smoothing of endowment shocks, since the endowment shocks are
relatively small, and Lucas' (1987) expressions for the welfare
costs of business cycles would suggest small welfare gains to
eliminating them. Rather, the bulk of the welfare gains in this
example comes from inter-temporal reallocation. Starting at the
tight floating constraint, dollarizing allows the government to
raise government spending in the short run and to then gradually
reduce spending over time.
5.2.5 Relation to literature
There is now quite a large literature that explores this class of models with endogenous debt constraints. While these models are intuitively appealing and can shed light on some features of sovereign debt markets, several important features of the data remain hard to explain. One is that observed debt levels drastically exceed the amount of borrowing that can typically be supported in calibrated versions of these models. The usual fix to this problem has been to assume that default comes with additional negative consequences, in addition to exclusion from future credit markets. For example, many papers assume that post default, the mean endowment is permanently reduced by several percentage points.
The analysis above suggests an alternative resolution. In
particular, as long as the variance of shocks is positive, then as
![]() and
and
![]() the borrowing
constraint becomes arbitrarily loose. The intuition is simple: as
the borrowing
constraint becomes arbitrarily loose. The intuition is simple: as
![]() so does the cost of repaying
debts. As
so does the cost of repaying
debts. As
![]() the cost of holding
precautionary savings approaches zero, so that as long as the
borrower faces some risk, the borrower will want to self-insure
with debt, and will wish to avoid the punishment associated with
default. Thus it is tempting to conclude that if the model is
calibrated to a sufficiently short period length, one can support
realistic debt levels in equilibrium. However, validating this
hypothesis requires a careful evaluation of the nature of high
frequency risk that is beyond the scope of this paper.
the cost of holding
precautionary savings approaches zero, so that as long as the
borrower faces some risk, the borrower will want to self-insure
with debt, and will wish to avoid the punishment associated with
default. Thus it is tempting to conclude that if the model is
calibrated to a sufficiently short period length, one can support
realistic debt levels in equilibrium. However, validating this
hypothesis requires a careful evaluation of the nature of high
frequency risk that is beyond the scope of this paper.
5.3 Calibration
We now apply our model to the study of actual countries in which dollarization has been discussed or implemented. Given that the relative performance of the floating and dollarized regimes in terms of financial integration and welfare is very sensitive to various parameter values, it is important to consider parameterizations that are appropriate for specific countries. We calibrate to two countries: El Salvador, which dollarized in 2001, and Mexico, which retains the peso, but where dollarization has been discussed in the past (see, for example, Cooley and Quadrini, 2001). The strategy is to calibrate the model assuming a floating regime, and to then compare across exchange rate regimes holding all parameter values constant.
We solve the model at a quarterly frequency and compare annualized output from the model to the annual data that is available for these countries. The variables we focus on are real output, government consumption, household consumption, the change in government net foreign assets, and the inflation rate. The series for output, public and private consumption and inflation are from the World Development Indicators for 1960-2002.16 Inflation is the annual percentage change in consumer prices. To study the dynamics of foreign public debt in our model we use the series for Government Foreign Financing as a percentage of GDP from the IMF's International Financial Statistics for 1980-2002. We log the series for output and consumption, and filter all the data with a 15 year Band-Pass Filter.17
The stochastic structure for the shocks is country-specific. We
assume that ![]() and
and ![]() are drawn
from a time-invariant bivariate lognormal distribution, with
potentially correlated innovations:
are drawn
from a time-invariant bivariate lognormal distribution, with
potentially correlated innovations:
![\begin{displaymath} E[\varepsilon^{y\prime}\varepsilon^{\lambda}]=\Sigma=\left[ \begin{array}[c]{cc} \sigma_{y}^{2} & \sigma_{y\lambda}\ \sigma_{y\lambda} & \sigma_{\lambda}^{2} \end{array}\right] \end{displaymath}](img306.gif)
The three parameters in the variance-covariance matrix
![]() are chosen so that the floating
economy replicates the annualized volatilities of output and
government consumption, and the correlation between government
consumption and output. Shocks are discretized into a 9-state
Markov process following the Hussey and Tauchen (1991)
procedure.
are chosen so that the floating
economy replicates the annualized volatilities of output and
government consumption, and the correlation between government
consumption and output. Shocks are discretized into a 9-state
Markov process following the Hussey and Tauchen (1991)
procedure.
The quarterly interest rate ![]() is set to
1% which is the average quarterly yield on
a one-year U.S. Treasury Bill for the period 1996 to 2006. The time
preference parameter
is set to
1% which is the average quarterly yield on
a one-year U.S. Treasury Bill for the period 1996 to 2006. The time
preference parameter ![]() is set to 0.98 which is consistent with the 2% average quarterly interest rate in El Salvador on domestic
dollar-denominated loans.18 For the sake of simplicity, we
assume the same value for
is set to 0.98 which is consistent with the 2% average quarterly interest rate in El Salvador on domestic
dollar-denominated loans.18 For the sake of simplicity, we
assume the same value for ![]() in both
countries.
in both
countries.
The mean value for ![]() is set to 0.85 so that the mean government consumption to GDP ratio is
15%. This is approximately equal to the
government consumption to output ratio in both countries. As in the
sensitivity section we assume a constant labor tax rate
is set to 0.85 so that the mean government consumption to GDP ratio is
15%. This is approximately equal to the
government consumption to output ratio in both countries. As in the
sensitivity section we assume a constant labor tax rate
![]() Table 2 summarizes
the parameter values used.
Table 2 summarizes
the parameter values used.
Table 2: Calibration: Country-Specific Parameters
Parameter |
Symbol |
Mexico |
El Salvador |
|---|---|---|---|
std. dev. output |
0.0787 |
0.105 |
|
std. dev. pref. shock |
0.013 |
0.035 |
|
shock correlation |
-0.524 |
0.372 |
Table 2: Calibration: Common Parameters
Parameter |
Symbol |
Value |
|---|---|---|
| mean pref. shock | 0.85 | |
| interest rate | 0.01 | |
| labor tax rate | 0.15 | |
| discount factor | 0.98 |
5.4 El Salvador
Table 3 presents business cycle statistics for the El Salvadorean data, and for the corresponding model economy under the floating and dollarized regimes. Business cycle statistics from the model are based on annualized output from a long simulation designed to approximate the limiting distribution of asset holdings. Model output is filtered in the same way as the data.
In the data, government consumption is almost twice as volatile as output and private consumption is substantially more volatile than output. In the context of our calibration procedure, this generates an important role for taste shocks. Inflation and government consumption co-move positively, and are both counter-cyclical. To replicate the counter-cyclicality of government consumption, the calibration calls for positively correlated shocks (see Table 2). The change in net foreign public assets is acyclical and negatively correlated with government consumption in the data. Thus periods of high government expenditure are associated with both higher inflation and greater foreign borrowing.
Table 3: Business Cycle Statistics, El Salvador
|
Data: |
Data: |
Data: |
Floating
Economy: |
Floating
Economy: |
Floating
Economy: |
Dollarized Economy: |
Dollarized Economy: |
Dollarized Economy: |
|
|---|---|---|---|---|---|---|---|---|---|
| Output | 5.27 | - | -0.05 | 5.27 | - | -0.05 | 5.27 | - | -0.05 |
| Government cons. | 9.73 | -0.05 | - | 9.74 | -0.05 | - | 8.30 | -0.05 | - |
| Private cons. | 7.58 | 0.90 | -0.38 | 4.68 | 0.81 | -0.25 | 4.37 | 0.79 | 0.11 |
| Inflation | 4.46 | -0.29 | 0.19 | 8.92 | -0.22 | 0.68 | - | - | - |
| 0.48 | 0.03 | -0.19 | 3.11 | 0.67 | -0.25 | 3.27 | 0.54 | -0.84 |
Table 3: Business Cycle Statistics, El Salvador, continued
| Floating Economy | Dollarized Economy | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Borrowing constraint / GDP (%) | 7.01 | 8.31 | |||||||
| Mean money savings / GDP (%) | 0.80 | 1.20 | |||||||
| Mean debt / GDP (%) | 3.96 | 6.40 | |||||||
| Frequency constraint binds (%) | 10.0 | 6.0 | |||||||
The floating regime model calibrated to El Salvador fits the data well. The model replicates the negative empirical correlation between private and public consumption, the positive correlation between inflation and government consumption, and the countercyclicality of inflation. Given the shock process, periods of low output - when inter-temporal smoothing dictates additional foreign borrowing - also tend to be periods when the demand for government consumption is high - and intra-temporal smoothing dictates high inflation. Thus the model is able to replicate the fact that inflation is counter-cyclical, and the fact that the accumulation of net foreign assets is negatively correlated with government consumption.
Table 3 also presents the statistics for the dollarized regime. Dollarization increases financial integration for El Salvador. The dollarized economy is able to borrow a larger proportion of annual output (8.3 versus 7.0 percent in the floating regime) and debt is used more aggressively. Dollarization also reduces the frequency of financial crises, defined as periods in which the borrowing constraint is binding: the probability mass at the constraint is 10% under a float compared to 6% when dollarized. More active use of debt in the dollarized regime appears to be a good substitute for the loss of the inflation instrument, as evidenced by the similar volatility of government consumption across regimes. In the dollarized economy, the sovereign wants to borrow when output is low or when the taste for government consumption is high. Since these events tend to coincide in the El Salvador calibration, a single instrument can go a long way towards accommodating both sources of risk. We find that expected welfare under the dollarized regime is very similar to the floating regime. In light of the sensitivity analysis, the reason why dollarization looks quite attractive is twofold: (i) taste shocks are large, and (ii) taste and productivity shocks are positively correlated.
Average money savings - in excess of those dictated by the
cash-in-advance constraint - are quite small in these economies, on
the order of one percent of annual GDP. Nonetheless, adjustment of
money savings is quite a powerful instrument for smoothing the
marginal utility of private consumption inter-temporally. One
indication of the role played by money comes from comparing the
volatilities of output and private consumption in the dollarized
economy. In the absence of money saving, the consumer's budget
constraint would reduce to
![]() in which case
private consumption and output would be equally volatile. In
contrast, in the monetary equilibrium the percentage standard
deviation of output is 5.27, while the corresponding
figure for private consumption is 4.37. Note
also that on average there is more demand for money when dollarized
than under a float. This does not reflect a difference in the
average inflation rate across regimes. Rather private consumers
compensate for the absence of monetary policy as a device for
buffering shocks by engaging in additional precautionary saving and
self-insurance.
in which case
private consumption and output would be equally volatile. In
contrast, in the monetary equilibrium the percentage standard
deviation of output is 5.27, while the corresponding
figure for private consumption is 4.37. Note
also that on average there is more demand for money when dollarized
than under a float. This does not reflect a difference in the
average inflation rate across regimes. Rather private consumers
compensate for the absence of monetary policy as a device for
buffering shocks by engaging in additional precautionary saving and
self-insurance.
5.5 Mexico
Table 4 presents business cycle statistics for the data in Mexico and for the corresponding models. Consumption and output are roughly equally volatile in Mexican data, while government consumption is much more volatile than output. Inflation has been extremely volatile. In terms of correlations, the Mexican economy differs dramatically from El Salvador's. In Mexico, the correlations between private consumption, public consumption and output are all strongly positive. In further contrast to El Salvador, the change in net foreign assets is positively correlated with output and weakly positively correlated with government consumption. Thus the Mexican government borrows in recessions, while booms in government spending are typically financed by inflation or growth in the tax base rather than by international borrowing.
Our calibration suggests that in Mexico taste shocks are smaller than in El Salvador. Replicating the large positive correlation between government spending and output requires taste shocks that are negatively correlated with output.
Table 4: Business Cycle Statistics, Mexico
|
Data: |
Data: |
Data: |
Floating
Economy: |
Floating
Economy: |
Floating
Economy: |
Dollarized Economy: |
Dollarized Economy: |
Dollarized Economy: |
|
|---|---|---|---|---|---|---|---|---|---|
| Output | 3.95 | - | 0.78 | 3.95 | - | 0.79 | 3.95 | - | 0.79 |
| Government cons. | 5.67 | 0.78 | - | 5.66 | 0.79 | - | 3.76 | 0.79 | - |
| Private cons. | 3.84 | 0.94 | 0.67 | 2.83 | 0.80 | 0.69 | 3.37 | 0.76 | 0.77 |
| Inflation | 19.10 | -0.09 | 0.24 | 5.84 | 0.24 | 0.40 | - | - | - |
| 1.31 | 0.41 | 0.14 | 2.10 | 0.64 | 0.28 | 0.30 | 0.35 | -0.17 |
Table 4: Business Cycle Statistics, Mexico, continued
| Parameter | Floating Economy | Dollarized Economy | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Borrowing constraint / GDP (%) | 3.47 | 0.66 | |||||||
| Mean money savings / GDP (%) | 0.38 | 0.66 | |||||||
| Mean debt / GDP (%) | 1.66 | 0.19 | |||||||
| Frequency constraint binds (%) | 12.1 | 14.8 | |||||||
As was the case with El Salvador, the floating economy
calibrated to Mexico successfully matches many features of the
data. Output and private and public consumption are strongly
positively correlated with each other. In our formulation of taste
shocks, an increase in ![]() makes households
simultaneously value private consumption more and public
consumption less, which tends to make the correlation between the
two negative. Productivity shocks, by contrast, induce a positive
correlation. Because productivity shocks are the most important
source of risk for Mexico, the model reproduces the strong positive
correlation between public and private consumption observed
empirically.
makes households
simultaneously value private consumption more and public
consumption less, which tends to make the correlation between the
two negative. Productivity shocks, by contrast, induce a positive
correlation. Because productivity shocks are the most important
source of risk for Mexico, the model reproduces the strong positive
correlation between public and private consumption observed
empirically.
The floating model economy also predicts a positive correlation
between inflation and government spending, in line with Mexican
data. A positive correlation emerges because the government
finances taste-shock driven fluctuations in government consumption
by adjusting the inflation tax rate. However, because periods of
high output tend to be periods of high demand for government
consumption
![]() the
inflation rate does not have to fluctuate too much to deliver the
efficient level of government consumption. This is why the model
fails to account for the high volatility of inflation observed in
Mexico. The model does match the procyclicality of changes in
foreign assets because debt is used to smooth output fluctuations:
the government runs down its assets in periods of low output, and
engages in precautionary savings in periods of relatively high
output.
the
inflation rate does not have to fluctuate too much to deliver the
efficient level of government consumption. This is why the model
fails to account for the high volatility of inflation observed in
Mexico. The model does match the procyclicality of changes in
foreign assets because debt is used to smooth output fluctuations:
the government runs down its assets in periods of low output, and
engages in precautionary savings in periods of relatively high
output.
Table 4 also presents statistics for the dollarized economy. Dollarization reduces international financial integration for Mexico by several metrics: the borrowing constraint is much tighter, the change in net foreign assets is much less volatile, and the frequency of periods in which the constraint binds is greater. Because dollarization means both the loss of an instrument and the loss of credibility in international financial markets, it comes as no surprise that welfare is higher under a float, on average by 0.2% of lifetime consumption.
6 Conclusion
This paper presents a simple model designed to study the interaction between the choice of exchange rate regime and integration in international financial markets. The advantage of a floating regime is that control of the money growth rate and thus of seigniorage constitutes a flexible policy instrument for cushioning shocks. At the same time, dollarization may be attractive precisely because eliminating the monetary instrument can strengthen incentives to repay debts, and thereby increase access to international credit. This is a new way to think about how relinquishing monetary independence may strengthen credibility. It is a complement to the existing literature, which has largely focused on dollarization as a source of external credibility in environments in which monetary independence would lead to excessive inflation.
We find that the historical experience of countries that have delegated control of monetary policy is consistent with the idea that dollarizing can make it easier for a country to borrow. In particular, countries that have dollarized saw the cost of sovereign borrowing fall around the time they abandoned the domestic currency.
An important message from our model is that the effect of dollarization on financial integration and on welfare depends critically on the type of shocks economies face, and on the level of international interest rates. Low interest rates make dollarization especially attractive, because debt becomes a very cheap instrument for smoothing fluctuations. We also find that economies in which the demand for government revenue is counter-cyclical will likely experience the greatest gains from relinquishing control of monetary policy. In part this is because debt is used very actively to respond to shocks in this case. Thus the loss of the debt instrument in the event of default is costly, which means that a lot of borrowing can be supported in equilibrium.
When calibrating our model to actual countries, El Salvador, which dollarized in 2001, appears a better candidate for dollarization than Mexico. The model indicates that dollarization in El Salvador should improve the country's degree of integration with financial markets, which is consistent with empirical evidence, and can even increase consumer welfare. By contrast, the model suggests that for Mexico dollarization would reduce access to foreign credit, since demand side shocks appear small and government spending is pro-cyclical.
We conclude by noting that while the decision of whether to conduct an independent monetary policy or to adopt another country's currency is a very important one, the basic economic mechanisms we emphasize in this paper have much broader potential application. In related work, Krueger and Perri (2005) study the connection between the extent of government insurance against idiosyncratic risk at the household level, and the depth of private domestic credit markets. They find that progressive taxation can increase incentives to default on private debts, and thus crowd out private insurance. In the international arena, there are various examples of international policy choices that shrink a country's choice set for domestic policy, and which may thereby increase a country's access to international credit. One example is the decision to joint a customs union, such as the North American Free Trade Area, which requires candidate member countries to give up control of taxes on trade. A second example is the Economic and Monetary Union in Europe, which requires eliminating restrictions on cross-border flows of capital and labor and thus limits countries' ability to respond to shocks by adjusting domestic tax rates. In these and many other examples the theory outlined in this paper suggests a connection between the extent of domestic economic sovereignty and the treatment a country can expect in sovereign debt markets.
References
[1] Aguiar, M., and G. Gopinath. Emerging Market Business Cycles: The Cycle Is the Trend. Journal of Political Economy, forthcoming.
[2] Alesina, A., and R. Barro. 2002. Currency Unions. Quarterly Journal of Economics, 117(2), 409-436.
[3] Alvarez, F., and U. J. Jermann. 2000. Efficiency, Equilibrium, and Asset Pricing with Risk of Default. Econometrica, 68(4), 775-798.
[4] Arellano, C. 2005. Default Risk and Income Fluctuations in Emerging Economies. University of Minnesota Working Paper.
[5] Bassetto, M. 2006. Fiscal Policy and Price Stability: The Case of Italy, 1992-98. Chicago Fed Letter 233.
[6] Berg, A., and E. Borensztein. 2000. Full Dollarization: The Pros and Cons. IMF Policy Discussion Paper, Washington DC.
[7] Bernoth, K., J. von Hagen, and L. Schuknecht. 2006. Sovereign Risk Premiums in the European Government Bond Market. University of Bonn Working Paper.
[8] Calvo, G. 1999. On Dollarization. University of Maryland Working Paper.
[9] Calvo, G. 2001. Capital Markets and the Exchange Rate: with Special Reference to the Dollarization Debate in Latin America. Journal of Money, Credit, and Banking, 33(2), 312-334.
[10] Calvo, G. and P. Guidotti. 1993. On the Flexibility of Monetary Policy: The Case of the Optimal Inflation Tax. Review of Economic Studies, 60(3), 667-687.
[11] Canzoneri M., and C. Rogers. 1990. Is the European Community an Optimal Currency Area? Optimal Taxation Versus the Cost of Multiple Currencies. American Economic Review, 80(3), 419-433.
[12] Chari, V.V., and Kehoe, P. 1999. Optimal Fiscal and Monetary Policy. In Handbook of Macroeconomics, ed. J. B. Taylor and M. Woodford, vol. 1, chap. 26, 1671-1745, Elsevier.
[13] Click, R. 1998. Seigniorage in a Cross-Section of Countries. Journal of Money, Credit and Banking, 30(2), 154-171.
[14] Cooley, T., and V. Quadrini. 2001. The Costs of Losing Monetary Independence: The Case of Mexico. Journal of Money, Credit and Banking, 33(2), 370-397.
[15] Cooper, R., and H. Kempf. 2001. Dollarization and the Conquest of Hyperinflation in Divided Societies. Federal Reserve Bank of Minneapolis Quarterly Review, 25(3), 3-12.
[16] Cooper, R., and H. Kempf. 2003. Commitment and the Adoption of a Common Currency. International Economic Review, 44(1), 119-142.
[17] Cooper, R., and H. Kempf. 2004. Overturning Mundell: Fiscal Policy in a Monetary Union. Review of Economic Studies, 71, 371-97.
[18] Edwards, S., 2001. Dollarization and Economic Performance: An Empirical Investigation. NBER Working Paper 8274.
[19] Eichengreen B., and R. Hausmann. 2005. Other People's Money: Debt Denomination and Financial Instability in Emerging Market Economies. Chicago: University of Chicago Press.
[20] Frankel, J., and A. Rose. 2002. An Estimate of the Effect of Common Currencies Unions on Trade and Income. Quarterly Journal of Economics, 117(2), 437-466.
[21] Hussey, R., and G. Tauchen. 1991. Quadrature-Based Methods for Obtaining Approximate Solutions to Nonlinear Asset Pricing Models. Econometrica, 59(2), 371-396.
[22] Kletzer, K. M., and B. D. Wright. 2000. Sovereign Debt as Intertemporal Barter. American Economic Review, 90(3), 621-639.
[23] Krueger, D., and F. Perri. 2005. Public versus Private Risk Sharing. University of Minnesota Working Paper.
[24] Lane, P. 2006. The Real Effects of European Monetary Union. Journal of Economic Perspectives, 20(4), 47-66.
[25] Levy-Yeyati, E., and F. Sturzenegger. 2003. To Float or to Fix: Evidence on the Impact of Exchange Rate Regimes on Growth. American Economic Review, 94(4), 1173-1193.
[26] Lucas, R., and N. Stokey. 1983. Optimal Fiscal and Monetary Policy in an Economy without Capital. Journal of Monetary Economics, 12(1), 55-93.
[27] Mendoza, E. 2001. The Benefits of Dollarization When Stabilization Policy Lacks Credibility and Financial Markets Are Imperfect. Journal of Money, Credit and Banking, 33(2), 440-474.
[28] Sargent, T. 2001. Comment on Fiscal Consequences for Mexico of Adopting the Dollar. Journal of Money, Credit and Banking, 33(2), 619-625.
[29] Sims, C. 2001. Fiscal Consequences for Mexico of Adopting the Dollar. Journal of Money, Credit and Banking, 33(2), 597-616.
[30] Zhang, H. 1997. Endogenous Borrowing Constraints with Incomplete Markets. Journal of Finance, 52(5), 2187-2209.
Appendix
Proof for decentralization proposition in the floating economy
We want to show that the government in the monetary economy, in
which control of the money growth rate is the only way to
reallocate resources between the public and private sectors, can
achieve the same allocations as a planner who can effectively use
lump-sum taxes and transfers to redistribute freely period by
period. In particular, we need to show that there exist sequences
for the money growth rates
![]() , associated savings rates
, associated savings rates
![]() and inflation rates
and inflation rates
![]() that satisfy (i) the consumer's
budget constraint (eq. 17) given the
planner's target values for private consumption (eq. 27) (ii) the government's budget constraint (eq.
6) given the planner's target values for
government consumption (eq. 28), (iii)
the conditions for household optimization (eqs. 4 and 5).
that satisfy (i) the consumer's
budget constraint (eq. 17) given the
planner's target values for private consumption (eq. 27) (ii) the government's budget constraint (eq.
6) given the planner's target values for
government consumption (eq. 28), (iii)
the conditions for household optimization (eqs. 4 and 5).
Consider an arbitrary future date and state, ![]() and
and ![]() and an arbitrary feasible monetary
policy from
and an arbitrary feasible monetary
policy from ![]() onwards. For our desired
decentralization result it is sufficient to show that for all
onwards. For our desired
decentralization result it is sufficient to show that for all
![]() and for all
and for all ![]() the planner in the monetary economy can implement any value for
the planner in the monetary economy can implement any value for
![]() where
total resources
where
total resources ![]() are given by eq. 29, given an appropriate choice for
are given by eq. 29, given an appropriate choice for
![]()
To show this we begin by making a few useful observations.
- Because this is an endowment economy, neither money growth nor inflation have any distortionary effects on factor supplies.
- Past monetary policy does not restrict the set of feasible allocations that can be achieved looking forward, because current and future policy determine the real value of the pesos consumers carry into the period, which is what matters for real allocations.19
Given ![]() and
and ![]() we first show
that the government can implement any value for
we first show
that the government can implement any value for
![]() and in
particular can implement the target value from eq. 27. We then work backwards to compute the value
for
and in
particular can implement the target value from eq. 27. We then work backwards to compute the value
for
![]() that delivers the target
that delivers the target
![]() exploiting the fact that changes
in
exploiting the fact that changes
in
![]() do not impact
do not impact
![]() In this fashion we can
work backwards all the way to period 0, along the way deriving
sequences for
In this fashion we can
work backwards all the way to period 0, along the way deriving
sequences for
![]()
![]() and
and ![]() that
decentralize the planner's solution.
that
decentralize the planner's solution.
We guess, and will verify, that given a particular monetary
policy from tomorrow onwards, there will be a critical money growth
rate
![]() such that for any
such that for any
![]() the
money savings rate
the
money savings rate ![]() is constant and
equal to zero, while for
is constant and
equal to zero, while for
![]() the
savings rate
the
savings rate ![]() is continuous and decreasing in
is continuous and decreasing in
![]() with the property that
with the property that
![]() as
as
![]()
If the target value for ![]() is less
than or equal to
is less
than or equal to
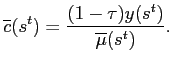
then from the consumer's budget constraint 17 it can be implemented with a money growth
rate
![]() defined by
defined by
where
![]() and
and
![]() In this case, the lower is the
target value for
In this case, the lower is the
target value for ![]() the higher is the required
the higher is the required
![]() . As
. As
![]()
![]() From eq. 18 the inflation rate
From eq. 18 the inflation rate
![]() in this case is given by
in this case is given by
If the target value for ![]() is greater
than
is greater
than
![]() then it will not be
possible to implement in a monetary economy without money savings.
In this case, the required money growth rate will be low or
negative, savings
then it will not be
possible to implement in a monetary economy without money savings.
In this case, the required money growth rate will be low or
negative, savings ![]() will be positive,
and the inter-temporal first order condition for money saving will
be an equality. From the consumer's budget constraint, eq. 17,
will be positive,
and the inter-temporal first order condition for money saving will
be an equality. From the consumer's budget constraint, eq. 17,
![]() implies
implies
![]() for
all
for
all ![]() Given the expressions 17 and 18 for current
consumption and the inflation rate between
Given the expressions 17 and 18 for current
consumption and the inflation rate between ![]() and
and
![]() the inter-temporal first order condition
equation implicitly defines
the inter-temporal first order condition
equation implicitly defines ![]() as a
continuous function of
as a
continuous function of
![]() . In particular, the
inter-temporal first order condition may be written
. In particular, the
inter-temporal first order condition may be written
Using eq. 17 to express consumption as a
function of ![]() and
and
![]() gives
gives
It is immediate from this expression that the savings rate
![]() is everywhere decreasing in
is everywhere decreasing in
![]() 20 For
20 For
![]() given
(i) a continuation policy
given
(i) a continuation policy
![]() (ii) future money growth
rates
(ii) future money growth
rates
![]() , (iii) future savings
rates
, (iii) future savings
rates
![]() and (iv)
future consumption
and (iv)
future consumption
![]() , the current
money growth rate
, the current
money growth rate
![]() is defined by the solution to eq.
34 when the money savings rate
is defined by the solution to eq.
34 when the money savings rate ![]() is given by re-arranging eq. 17, i.e.
is given by re-arranging eq. 17, i.e.
The critical money growth rate
![]() is the value of
is the value of
![]() that solves 34 when
that solves 34 when
![]() For
For
![]() the
inter-temporal first order condition will be a strict inequality
with
the
inter-temporal first order condition will be a strict inequality
with
![]() confirming the guess that for
money growth rates exceeding
confirming the guess that for
money growth rates exceeding
![]() household
maximization will imply no money saving.
household
maximization will imply no money saving.
The important point relating to our decentralization result is
that with log utility the savings rate ![]() is
uniformly decreasing in the money growth rate
is
uniformly decreasing in the money growth rate
![]() The implication is that if the
government had infinite resources, it could make seigniorage
arbitrarily small and consumption arbitrarily large by reducing
The implication is that if the
government had infinite resources, it could make seigniorage
arbitrarily small and consumption arbitrarily large by reducing
![]() towards the point at which
towards the point at which
![]() (see eq. 17)
(see eq. 17)![]() In practice, the government
always has at least
In practice, the government
always has at least
![]() resources from
direct taxation and international borrowing. So it can reduce the
money growth rate to the point at which seigniorage is equal to the
negative of this number, in which case
resources from
direct taxation and international borrowing. So it can reduce the
money growth rate to the point at which seigniorage is equal to the
negative of this number, in which case
![]() Thus we have shown that
the monetary authority can implement any value for
Thus we have shown that
the monetary authority can implement any value for
![]() with an appropriate
choice for
with an appropriate
choice for
![]() .
.
Corollary: Equilibrium uniqueness
There is a unique monetary equilibrium in our economy. This
follows immediately from the fact that the savings rate ![]() is everywhere decreasing in
is everywhere decreasing in
![]() In particular, for any policy
In particular, for any policy
![]() defining policy from period
defining policy from period
![]() and onwards, each possible money growth
rate
and onwards, each possible money growth
rate
![]() at
at ![]() implies
a unique value for
implies
a unique value for ![]() and thus for
and thus for
![]() and
and
![]() A similar argument can
be applied, recursively, at each date
A similar argument can
be applied, recursively, at each date ![]()
Footnotes
* Arellano: [email protected]; Heathcote: [email protected]. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. Dollarization is meant in the broad sense of unilaterally adopting a stronger foreign currency such as the U.S. dollar, euro, or yen. Return to text
2. Canzoneri and Rogers (1990) explore the importance of seigniorage in the European Union. They find that the optimal inflation rate is country-specific and depends on the efficiency of the domestic tax collection system. Return to text
3. See, for example, Lucas and Stokey (1983) and Chari and Kehoe (1999). Most of the literature on Ramsey optimal taxation has been developed for closed economies. Return to text
4. Data for Italy and Portugal are from Bloomberg. Italian bonds are matured in 12-31-97 and 12-31-06 respectively. The Portuguese bond matured 7-02-03. We do not report spreads when the time to maturity drops below one year. Ecuador's spread is the JP Morgan Emerging Market Bond Index (EMBI) Spread for Ecuador. Data for El Salvador are the difference between the domestic dollar prime interest rate on loans of maturity greater than one year and the yield on a U.S. government bill with one year maturity. We use this spread measure for El Salvador because El Salvador issued its first Global Bonds in international markets only in 2001. Return to text
5. Bernoth, von Hagen and Schuknecht (2006) document that spreads on newly issued DM-denominated bonds decreased prior to the start of EMU for all member countries. Return to text
6. The series for GDP per capita and inflation (2, 3 and 4) are from the World Bank's World Development Indicators. The exchange rate dummy (5) is from a classification by Levy-Yeyati and Sturzenegger (2003). The dummy variable takes the value of 1 for countries with fixed exchange rates. It takes the value of 0 if the regime is `` Flexible" or ``Interim" in their classification. The ratio of foreign debt to GDP (6) is from the World Bank Statistics on External Debt and the Central Government Debt Statistical Yearbook. We use debt data for 2001 due to limited data availability for 2000. For the developed countries that are not present in the World Bank Statistics on External Debt, we use central government foreign debt, estimated as the percentage of marketable debt held by non-residents times total central government debt. Return to text
7. In reality, non-government international trade in financial assets is growing, but it is still the case that most external debt in countries where dollarization is considered a possibility represents government borrowing. For example, as of March 2003, Argentinean government debt accounted for 67% of the total stock of foreign debt; in Mexico and Ecuador the corresponding figures were 56% and 73%. Return to text
8. The difficulty emerging-markets face in borrowing abroad in their own currencies is referred to as `` original sin." See Chapter 1 of Eichengreen and Hausmann (2005) for empirical evidence on the currency denomination of sovereign debt. Return to text
9. Permanent exclusion from trade might sound counter-factually harsh. However, since default is not an equilibrium outcome, what matters for observed allocations is the value of the threatened punishment, and not precisely how it is implemented. Kletzer and Wright (2000) develop a model of sovereign debt in which the effective punishment for default is equivalent to permanent autarky, but where the punishment is delivered in a way that permits trade to continue, but on worse terms from the borrower's perspective. Return to text
10. One could imagine an alternative market structure in which lenders offer a menu of contracts, each of which specifies a loan amount and an interest rate. Contracts for greater loan amounts would then be associated with higher interest rates to compensate for greater risk of default. In equilibrium the unconditional expected return to the lender would be equalized across contracts. This market structure is adopted in Arellano (2005). Return to text
11. Later we will argue that in equilibrium consumers in the flexible economy would not want to save in the form of dollars, even if they were allowed to do so. Return to text
12. Negative ![]() can be
interpreted as follows. Under a float the domestic government is
borrowing goods abroad, selling them on the domestic market, and
taking the domestic money it receives in exchange out of
circulation. Under dollarization, domestic consumers are buying
goods from abroad. Return to
text
can be
interpreted as follows. Under a float the domestic government is
borrowing goods abroad, selling them on the domestic market, and
taking the domestic money it receives in exchange out of
circulation. Under dollarization, domestic consumers are buying
goods from abroad. Return to
text
13. Potential deviations from the
pre-announced policy would be to default on outstanding debts, or
to deviate from pre-announced debt or monetary policy. Default will
reduce welfare, given borrowing constraints that are not too tight.
Deviating from pre-announced debt policy will reduce welfare, since
the pre-announced policy smooths the marginal utility of government
consumption as effectively as possible. Deviating from
pre-announced monetary policy will be welfare-reducing, because
such a change can only alter the mix between private and public
consumption (in a welfare-reducing fashion) without changing the
total resources ![]() (eq. 29) in the economy. Return to text
(eq. 29) in the economy. Return to text
14. The government enjoys an additional advantage relative to private households: it can borrow, while private households cannot hold negative quantities of dollar currency. Return to text
15. This reflects the fact that the date
![]() probability of each possible event
probability of each possible event
![]() is always strictly positive,
irrespective of
is always strictly positive,
irrespective of ![]() Return to text
Return to text
16. The specific series we used from WDI are: General government final consumption expenditure, Household final consumption expenditure, GDP and Inflation. All these series (except inflation) are in per capita terms, and in real units of local currency. Return to text
17. We use a longer filter to keep some of the lower frequency movements that have been documented by Aguiar and Gopinath (forthcoming) to be important for emerging-markets economies. Return to text
18. The series used is the prime lending rate in dollars for loans of more than one year, as reported by the El Salvador Central Bank, for the post-dollarization period. Return to text
19. The real purchasing power of
consumers' money balances entering the goods market at
![]() is given by
is given by
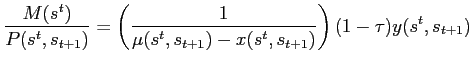
20. Here is some intuition for the
response of ![]() to
to
![]() . Absent a change in the savings
rate, a reduction in the money growth rate
. Absent a change in the savings
rate, a reduction in the money growth rate
![]() reduces the current price level
reduces the current price level
![]() and increases expected inflation
and increases expected inflation
![]() which tends to reduce savings.
It also increases current consumption, and reduces the marginal
utility of consumption, making consumers want to save more. With no
change in the savings rate the second effect would dominate,
leaving the marginal utility of consumption at
which tends to reduce savings.
It also increases current consumption, and reduces the marginal
utility of consumption, making consumers want to save more. With no
change in the savings rate the second effect would dominate,
leaving the marginal utility of consumption at ![]() too low (see 34). Of course, in
equilibrium prices and decisions adjust so that the household's
inter-temporal first order condition is satisfied. The equilibrium
adjustment mechanism is that the expected inflation rate rises by
more than under the no-savings-adjustment hypothsis, and the
savings rate rises. This increase in the savings rate is consistent
with the inflation dynamic, and the reduced return to saving
reduces the right hand side of the intertemporal first order
condition. At the same time, a higher savings rate actually
increases equilibrium consumption (see eq. 17), reducing the left hand side of the first
order condition, but for log utility the first effect
dominates. Return to text
too low (see 34). Of course, in
equilibrium prices and decisions adjust so that the household's
inter-temporal first order condition is satisfied. The equilibrium
adjustment mechanism is that the expected inflation rate rises by
more than under the no-savings-adjustment hypothsis, and the
savings rate rises. This increase in the savings rate is consistent
with the inflation dynamic, and the reduced return to saving
reduces the right hand side of the intertemporal first order
condition. At the same time, a higher savings rate actually
increases equilibrium consumption (see eq. 17), reducing the left hand side of the first
order condition, but for log utility the first effect
dominates. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text