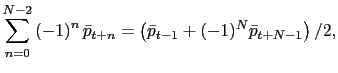Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 896, May 2007--- Screen Reader
Version*
Price Setting during Low and High Inflation:
Evidence from Mexico
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper provides new insight into the relationship between inflation and consumer price setting by examining a large data set of Mexican consumer prices covering episodes of both low and high inflation, as well as the transition between the two. Overall, the economy shares several characteristics with time-dependent models when the annual inflation rate is low (below 10-15%), while displaying strong state dependence when inflation is high (above 10-15%). At low inflation levels, the aggregate frequency of price changes responds little to movements in inflation because movements in the frequency of price decreases partly offset movements in the frequency of price increases. When the annual inflation rate rises beyond 10-15 percent, however, there are no longer enough price decreases to counterbalance the rising occurrence of price increases, making the frequency of price changes more responsive to inflation. It is shown that a simple menu-cost model with idiosyncratic technology shocks predicts remarkably well the level of the average frequency and magnitude of price changes over a wide range of inflation.
Keywords: Price setting, consumer prices, frequency of price changes, time-dependent pricing, state-dependent pricing.
JEL classification: E31, D40, C23.
1. Introduction
This paper presents new evidence on the setting of consumer prices during low and high inflation that sheds light on the empirical plausibility of competing models of price rigidities. It uses a new store-level data set containing more than six million individual price quotes that is representative of more than two-thirds of Mexican consumers' expenditures. The data starts in January 1994 and ends in December 2004. Over that 11-year period, CPI inflation rose from 6.8% in 1994 to a high of 41.8% in 1995 before falling to a low of 3.9% in 2001. Given these considerable fluctuations, this data set can potentially be used to discriminate among competing models of nominal price rigidities, as these models' predictions diverge most in the presence of large shocks.
Many macroeconomic models assume that price rigidities exist. There is, however, no consensus on how to model these rigidities. In time-dependent models, the set of firms optimizing their prices is fixed exogenously within the period.2 In state-dependent models, on the other hand, the timing of price changes is an endogenous decision. In these models, price stickiness results from frictions like menu costs, imperfect or costly information and shifts in demand that accompany price changes.3 Recently, several authors have argued that variants of time-dependent models can deliver empirically plausible predictions despite their simplicity.4 Even advocates of time-dependent models would agree, however, that the performance of these models should decline as inflation becomes high or volatile. The inflation level at which time-dependent models break down remains an open question, as does the more general question of what price-setting models are empirically plausible at both low and high inflation levels.
My data set captures considerably more variation in inflation than do other studies of consumer prices with comparable product coverage.5 As Figure 1 indicates, inflation is low and stable in the United States and Euro area relative to Mexico over the periods covered by these studies. In the case of high-inflation economies, the evidence is limited mainly to food products in Israel (Lach and Tsiddon (1992); Baharad and Eden (2004)) and Poland (Konieczny and Skrzypacz (2005)) and supermarket products in Argentina (Burstein, Eichenbaum, and Rebelo (2005)). This paper differs from these studies because my data set is representative of most goods and services in the CPI with the exception of housing rents, and I provide evidence for both high and low levels of inflation.
Figure 1. Inflation and time coverage of U.S., Euro-area and Mexican CPI studies
I find sharp differences in the price-setting behaviors of low- and high-inflation economies: Whereas low-inflation economies exhibit several features of time-dependent pricing models, high-inflation economies show strong state dependence. More specifically, when inflation is low (below 10-15%), the frequency of price changes is only mildly correlated with inflation, especially when I restrict the sample to nonregulated goods, in which case I find no correlation. On the other hand, the average magnitude of price changes in such low-inflation environments displays a tight and linear relationship with inflation. As a result, movements in the frequency of price changes account for little of the inflation variance: at most 17% for all nonregulated products and 5% for nonregulated goods, figures that fall in line with Klenow and Kryvtsov (2005) for the United States (5%).
In contrast, when inflation is high (above 10-15%), both the frequency and average magnitude of price changes are strongly correlated with inflation. In this case, a 1-percent increase in the annual inflation rate is associated with a rise of about 0.4 percentage-point in the monthly frequency of price changes for nonregulated consumer products. Movements in the frequency of price changes therefore comprise an important component of inflation variance. This central role of the frequency of price changes in inflation dynamics is best revealed by a rise of the value added tax from 10 to 15% in April 1995: The adjustment of prices occurs almost entirely through an increased frequency of price changes -- not an increased magnitude -- and is completed within a month of the tax change.
Price decreases are key to the dramatically different behaviors of low- and high-inflation economies. When I decompose the frequency of price changes into the sum of the frequencies of price increases and decreases, I find that the frequency of price decreases diminishes rapidly as inflation rises from 0 to 10-15%. This decline partly offsets a simultaneous rise in the frequency of price increases, thereby dampening movements in the overall frequency of price changes. Moreover, the decline in the occurrence of price decreases relative to price increases leads to a rise in the average magnitude of price changes. This change in the composition of price changes largely explains the strong correlation between inflation and the average magnitude of price changes in my data when inflation is low. Once inflation moves beyond 10-15%, however, there are no longer enough price decreases to offset price increases, so the frequency of price changes becomes highly correlated with inflation.
The important role of price decreases for inflation dynamics in Mexico is likely to be found in the United States and euro area. At similar levels of inflation, price decreases account for 42% of price changes in Mexico, a level comparable to the euro area (42%, Dhyne et al. (2005)) and the United States (45%, Klenow and Kryvtsov (2005)). For most groups of products, however, price changes are more frequent in the United States. I conjecture that the greater number of price decreases in the United States relative to Mexico likely will have similar dampening effects on the frequency of price changes at low levels of inflation.
The above empirical findings shed light on what types of pricing models deliver realistic predictions at various levels of inflation. Overall, my results suggest that pricing models should endogenize the timing of price changes if they wish to make realistic predictions at both low and high inflation levels. Above a 10-15% inflation rate, the predictions of time-dependent models are clearly inconsistent with the strong state-dependence found in my data with respect to inflation. When inflation falls below 10-15%, the muted response of the frequency of price changes in the nonregulated good sector is more consistent, at least on the surface, with time-dependent models like Calvo's. These facts suggest that macroeconomists may need to resort to different price-setting models when focusing on either low or high inflation economies. They also present the challenge of finding a model offering empirically plausible predictions at all levels of inflation.
I calibrate a discrete-time version of the Golosov and Lucas (2003) menu-cost model. The model embeds idiosyncratic technology shocks giving rise to a distribution of both positive and negative nominal price changes. I show that the model performs remarkably well in terms of predicting the average frequency and magnitude of price changes over a wide range of inflation. In particular, the model generates a slow increase in the frequency of price changes as inflation takes off from a low level. The success of the model comes in part from the presence of offsetting movements in the frequency of price increases and decreases, and highlights the importance of idiosyncratic shocks in this class of models for delivering empirically plausible predictions.
The paper is organized as follows. In Section 2, I provide a brief overview of the Mexican macroeconomic context over the sample period. In Section 3, I describe the assemblage of my data set and discuss features of the data that are important for interpreting my results. Then, Section 4 defines the statistics computed in this paper. In Section 5, I explain how the average frequency and magnitude of individual price changes differ across low- and high-inflation episodes, and I investigate the inflation pass-through resulting from an April 1995 hike in the value added tax. Section 6 offers a comparison of consumer price stickiness between the Mexican economy and that of the United States and Euro area. In Section 7, I calibrate a discrete-time version of the Golosov-Lucas model and investigate its ability to match the main empirical features of consumer price setting when subject to levels of inflation similar to the ones experienced by Mexico over my sample period. The last section provides concluding remarks.
2. Macroeconomic Context
The sample period was marked by a severe economic downturn in the wake of the December 1994 peso devaluation. To most observers of the Mexican economy, however, 1994 opened rather positively.6 Inflation had been stabilized successfully below 10 percent, a major achievement in light of the three-digit rates of the late 1980s.7 The real interest rate also had decreased. The excess return on the three-month, dollar-denominated Tesobonos was only two percentage points above the American T-Bill. The budget deficit, seen by many as the culprit of previous economic crises, had been eliminated in 1992. Moreover, the North American Free Trade Agreement had taken effect on January 1, 1994. This treaty was part of a broad set of Mexican government initiatives to deregulate the country's economy and open it to foreign trade and capital. Foreign capital entered abundantly with a net inflow over 8% of GDP in 1993. However, growth in real GDP per capita remained modest, averaging 2.5% from 1991 to 1993. Many observers saw this situation as part of a restructuring process that soon would bring strong growth to the country.
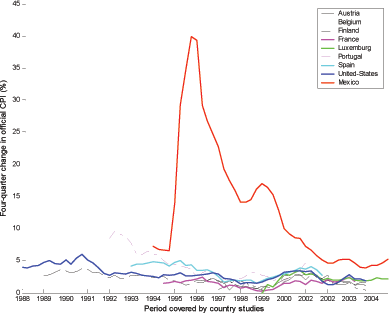
Figure 2. Main macroeconomic indicators
The devaluation brought a radical change of mood. On December 22, 1994, the exchange rate collapsed and lost more than 40% of its value vis-à-vis the U.S. dollar in the week that followed.8 As depicted in Figure 2, interest rates were pushed upward substantially as Banxico tightened the supply of money to prevent further erosion of the peso and a capital flight. The devaluation left a major stagflation in its wake. Inflation took off almost immediately, increasing from 6.5% in November 1994, to 44.3% in January 1995 before peaking at 92.0% in April 1995. Real output per capita contracted by 9.5% in 1995, while private consumption per capita fell by a solid 13.2%. Mexicans would have to wait until 1998 for real GDP per capita to surpass its 1994 level and until 1999 for inflation to settle below 10%.
The decline in aggregate income, coupled with a rise in fiscal evasion, brought a sharp decline in government revenues.9 To prevent further revenue erosion, the government raised the general rate of the value added tax rate (VAT) from 10 to 15 percent on April 1, 1995. This change affected all Mexican regions, with the notable exceptions of Baja California and a corridor along the country's southern and northern borders where the rate remained at 10%.
3. Mexican Micro Data on Consumer Prices
3.1 Description of Sources
The data comprise price quotes collected by Banco de México (Banxico) for computing the Mexican CPI. Most price quotes correspond to narrowly defined items sold in specific outlets (e.g., corn flour, brand Maseca, bag of 1 kg, sold in outlet 1100 in Mexico City). A limited number of quotes are city-wide indexes, or the average price of a small sample of narrowly defined items belonging to the same category and outlet. Since January 1994, the official gazette of the Mexican government, the Diario Oficial de la Federación, has published price quotes. This publication releases each quote with a key linking the item to a specific outlet, city and good category; these keys allow me to track individual prices over time.10 In this paper, I refer to an item's complete price history as its price trajectory. A price trajectory comprises one or several successive price spells, episodes when the price remained constant.
The data set contains 6.5 million price quotes from January 1994 to December 2004. Banxico makes individual prices available up to six months after their publication, but it does not keep a historical data set of individual prices. The data set was assembled by merging the information released in the Diario. The data for the months of January 1994 to February 1995 could not be extracted electronically, so they were typed from original hard paper copies of the Diario using double-entry keying, a process ensuring a character-wise accuracy in excess of 99.998%.11 About 430,000 price quotes were added to the database in this way.
Precise item descriptions were published in March 1995 and August 2002. The Diario also includes lists of items that are periodically added, dropped or substituted from the CPI basket. Unlike additions, substitutions are not planned events. They occur when the characteristics of an item (weight, size, model, presentation, etc.) change, when an outlet stops carrying an item or, in rarer cases, when an outlet goes out of business.
The weights used in the CPI are derived from the Survey of Households' Income and Expenditures (ENIGH) . The CPI categories are representative of all ENIGH categories accounting for at least 0.02 percent of households' expenditures. This ensures a coverage well above 95% of Mexican households' expenditures.
3.2 Sample coverage
In January 1994, the CPI contained 30,692 price quotes spread over 302 categories. By December 2004, it had expanded to more than 60,000 price quotes distributed over 315 categories. Two major revisions of the basket occurred over that period. The first occurred in March 1995, when the number of cities covered in the CPI grew from 35 to 46. At the same time, 29 new good categories were introduced into the basket, and 18 were abandoned. This revision had been planned long before the peso's devaluation. Secondly, in July 2002, Banxico updated the basket again to reflect the structure of Mexican households' consumption in 2000. In the process, 60 product categories merged into 27, another 36 were introduced into the basket and one was dropped. I cannot link items before and after the 2002 basket revision because of a change to the item keys.
To ensure the greatest comparability across time, I compute my core results for a sample covering January 1994 - June 2002 using the expenditure weights implemented in March 1995.12 Unless otherwise indicated, the sample is restricted to the 266 product categories comprising nonregulated individual prices that were unaffected by the 1995 basket revision.13 This restricted sample covers 63.4% of CPI expenditures. The largest three excluded product categories are homeowners' imputed rents, gasoline and rents, whose weight in the CPI are respectively 11.6%, 3.2% and 2.4%. This more homogenous sample contains 3.8 million price quotes from over 51,000 price trajectories. Summary statistics of the data used in this paper are provided in Table 1.
Table 1. Summary statistics
| Period | January 1994 - June 2002 | July 2002 - December 2004 |
|---|---|---|
| Price Quotes: Total | 3,804,885 | 1,580,618 |
| Price Quotes: Average per month | 37,303 | 52,687 |
| Trajectories | 51,299 | 99,435 |
| Substitutions | 11,291 | 38,981 |
| Unweighted frequency (%)a: Price changes | 29.8 | 27.8 |
| Unweighted frequency (%)a: Price increases | 20.9 | 16.0 |
| Unweighted frequency (%)a: Price decreases | 8.9 | 11.7 |
| Product categories: Dataset | 266 | 289 |
| Product categories: Full CPIbb | 313 | 315 |
| CPI weight (%) | 63.4 | 65.9 |
Notes: (a) The unweighted frequencies are computed by dividing the number of positive or negative price changes by the total number of price quotes for which a price change can be computed. (b) The total number of product categories was expanded from 302 to 313 in March 1995.
3.3 Other Aspects of the Data
I now address features of the data that are important to consider when interpreting of the results. The most significant issue is price averaging. Banxico collects prices twice monthly for all items but food; food price collection occurs four times per month.14 The collected prices are then averaged to produce the monthly figures reported in the Diario. Observing the monthly average rather than the actual price of an item complicates the inference about price changes. For example, an average price of $2 for an item is consistent with an actual price of $2 throughout the month. It also is consistent with an actual price of $1.50 in the first half of the month and $2.50 in the second, or any combination of positive prices with $2 as their average. Moreover, changes to an average price series are typically more frequent and of smaller magnitude than changes to an actual price series. For example, a price hike from $1.50 to $2.50 in the middle of the month results in an average price of $2, which is $0.50 short of the new actual price. Thus, if the actual price remains constant over the next month, another change to the average price series will be recorded.
To make my results as comparable as possible to other studies, which do not use averaged price quotes, I have constructed alternative price trajectories that filter the effect of averaging observations whenever possible. These new series correspond to the end-of-month series of actual prices, which are both consistent with the published averages and minimizes the number of price changes. In addition to being closer to the unobserved series of actual prices, the filtered series provide a lower bound on how frequently prices change. Appendix A discusses details of the filtering procedure.
Another issue in the data is that price collectors do not always directly observe prices. Indeed, sometimes an item is out of stock, out of season or, in rarer cases, the outlet is closed when the CPI agent visits. In such situations, the price from the previous period is carried forward. Although I cannot identify prices that were imputed in my sample, I do find clear indications that the number of imputations was larger at the beginning of the sample. Item substitutions represented less than 0.1% of all published price quotes in 1994, a proportion that rose to 1.2% in 2001 and 3.0% in 2004; this trend likely will create a downward bias in the estimated frequency of price changes at the beginning of the sample.15
Furthermore, prices are inclusive of sales as long as they are conditional on the purchase of a single item. For example, in a 3-for-2 promotion, the regular price would be reported. In such cases, the unobserved effective price is lower than the observed reported price. There is no variable in the data set signaling that an item is on sale or that a promotion is ongoing. To assess the prevalence of sales in the sample, I define sales as a price spell that lasts three months or less, begins with a price decline and is ended by a price increase of the same magnitude. When goods are weighted by expenditure shares, sales amount to 4% of price changes over the sample period and 9% over the year prior before the 2002 basket revision. These figures are lower than the 20% reported by Klenow and Kryvtsov for the United States (cited by Bils and Klenow (2004)). This difference likely reflects a greater prevalence of sales and promotions in the United States than Mexico as well as methodological differences.16 All the results in my paper are inclusive of unconditional sales.
In interpreting the data, one must also consider that most price quotes for the product categories of textiles, clothing, shoes and their related accessories are an average of a small sample of item prices; all items within a sample pertain to the same outlet whenever possible. Using the descriptions published in the Diario, I identified the exact number of items and brands within each store sample. A store sample typically contains two to four items (e.g., two cotton-based pants for men, brands Lee and Cimarron), with a mode of three for the number of both items and brands. Price changes generally are more frequent and of smaller magnitude for a sample than for its individual components, but the severity of this divergence depends on the price synchronization within the sample. For example, if an outlet runs a 30 sale on all jeans, then the average price of a sample of three pairs of jeans also decreases by 30%. I discard all store samples whenever a product category contains a large proportion of individual observations. For 34 categories encompassing all clothing and shoes categories except school uniforms, I retain only samples comprising three items and discard all other observations. I then treat those observations like other individual observations. Appendix B explores the extent of the bias this procedure introduces.
A final issue is that item substitutions often accompany changes in product characteristics, thereby raising the question of whether substitutions should be treated as price changes. The Inflation Persistence Network's approach is to assume that all substitutions not previously planned by the CPI agency involve a price change. In this paper, I instead exclude all substitutions from the computation of price changes because their treatment varies over the sample period. The main conclusions are not affected by this decision.
3.4 Example of Individual Price Trajectory
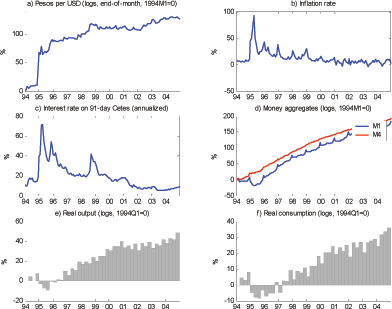
The next figure shows an actual price trajectory and illustrates how the effect of averaging several price observations over the month is filtered out. It displays two years of monthly average prices for a copy of the book "The Universal History of Literature" sold in a Mexico City outlet. This series was computed by Banxico by averaging the two prices its CPI agent collected each month. From January 1994 to December 1995, there were six changes to the series. The first happened in August 1994 when the average price increased from $23 to $25. Because the average price remained at $25 in September, I conclude that the two prices collected in August also equaled $25. The next two changes occurred in January and February 1995. The published price for January, $28.5, is the exact average of the published prices for December and February ($25 and $32, respectively). This figure is consistent with the occurrence of a single change in the actual price from $25 to $32 during the second half of January. The last three price changes occurred in May, June and July of 1995; the published price increased from $32 to $36.5, then to $47 and finally to $53. This series is consistent with a change in the actual price from $32 to $41 after the first price collection in May and then $41 to $53 after the first price collection in June. The filtered series, which contains only the last observation of each month, is displayed at the bottom of Figure 3. It contains only four price changes, and their magnitude is greater on average than those in the published average price series.
Figure 3. Illustration of a price trajectory correction
Note: The dashed line represents the actual monthly average price published in the Diario of a single copy of the book "The Universal History of Literature" sold in a Mexico City outlet. The solid represents the filtered point-in-time series.
Data for Figure 3
| Month | Price: Unfiltered | Price: Filtered |
|---|---|---|
| Jan-94 | 23.00 | 23.00 |
| Feb-94 | 23.00 | 23.00 |
| Mar-94 | 23.00 | 23.00 |
| Apr-94 | 23.00 | 23.00 |
| May-94 | 23.00 | 23.00 |
| Jun-94 | 23.00 | 23.00 |
| Jul-94 | 23.00 | 23.00 |
| Aug-94 | 25.00 | 25.00 |
| Sep-94 | 25.00 | 25.00 |
| Oct-94 | 25.00 | 25.00 |
| Nov-94 | 25.00 | 25.00 |
| Dec-94 | 25.00 | 25.00 |
| Jan-95 | 28.50 | 32.00 |
| Feb-95 | 32.00 | 32.00 |
| Mar-95 | 32.00 | 32.00 |
| Apr-95 | 36.50 | 41.00 |
| May-95 | 47.00 | 53.00 |
| Jun-95 | 53.00 | 53.00 |
| Jul-95 | 53.00 | 53.00 |
| Aug-95 | 53.00 | 53.00 |
| Sep-95 | 53.00 | 53.00 |
| Oct-95 | 53.00 | 53.00 |
| Nov-95 | 53.00 | 53.00 |
| Dec-95 | 53.00 | 53.00 |
4. Inflation Accounting Principles
Whenever a price is reported for two consecutive months, an indicator that a price change has occurred is created:
![\begin{displaymath} I_{it}=\left\{ \begin{array}[c]{cc} 1 & \text{if }p_{it}\neq p_{it-1}\ 0 & \text{if }p_{it}=p_{it-1} \end{array}\right. \end{displaymath}](img21.gif)
where ![]() is the price of item
is the price of item ![]() (in logs) during month
(in logs) during month ![]() . Inflation is defined as
. Inflation is defined as
where
![]() ,
,
![]() is the weight of item
is the weight of item ![]() , and
, and
![]() is the set of all items for
which
is the set of all items for
which ![]() is defined. For
is defined. For
![]() , I use the weight of the CPI
category to which item
, I use the weight of the CPI
category to which item ![]() belongs, divided by the
number of items in that category for which I can compute a price
change at
belongs, divided by the
number of items in that category for which I can compute a price
change at ![]() . Inflation also can be expressed as
. Inflation also can be expressed as
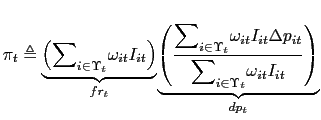
The term ![]() , henceforth referred to as the
frequency of price changes, is the total CPI weight of items whose
price changes at
, henceforth referred to as the
frequency of price changes, is the total CPI weight of items whose
price changes at ![]() . The term
. The term ![]() is
the average magnitude of those price changes. In the popular Calvo
and Taylor models with uniform staggering of price changes,
is
the average magnitude of those price changes. In the popular Calvo
and Taylor models with uniform staggering of price changes,
![]() is the only possible source of
variation in
is the only possible source of
variation in ![]() .
.
It is convenient to decompose inflation further into a weighted sum of price increases and decreases:
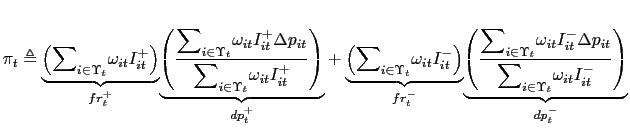
This decomposition carries information about the relationship
between the distribution of price changes and inflation. In the
next section, the frequency of price increases and decreases,
![]() and
and
![]() , will play a central role in the
dynamics of inflation.
, will play a central role in the
dynamics of inflation.
The statistic ![]() yields information about the
economy's degree of price stickiness; all else equal, the greater
yields information about the
economy's degree of price stickiness; all else equal, the greater
![]() is, the more flexible prices are. A
closely related measure of price stickiness is the duration of
price spells. Although price spells' length can be measured
directly in the data, the literature generally has preferred
duration measures derived from the frequency of price changes.
Assuming price changes occur at a constant rate over the month, the
average duration is given by
is, the more flexible prices are. A
closely related measure of price stickiness is the duration of
price spells. Although price spells' length can be measured
directly in the data, the literature generally has preferred
duration measures derived from the frequency of price changes.
Assuming price changes occur at a constant rate over the month, the
average duration is given by
![]() .
Aggregate measures of average or median durations are obtained by
computing
.
Aggregate measures of average or median durations are obtained by
computing ![]() and
and ![]() at the
category level and then aggregating them using the CPI product
category weights.17
at the
category level and then aggregating them using the CPI product
category weights.17
5. Main Results
This section presents the main results regarding the frequency and magnitude of price changes and emphasizes their relationships to inflation. I leave aside all items whose price is regulated to focus on prices that are free to adjust. In addition, I treat separately non-regulated goods and non-regulated services as their behavior differ markedly.
5.1 Frequency
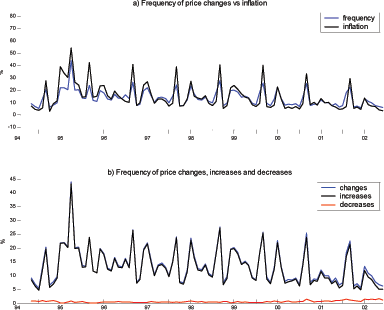
I first present the results for nonregulated goods which represents 73.1% of all expenditures in the main basket. For those items, movements in the frequency of price changes and inflation were very large over the sample period. In April 1995, the rate of inflation for nonregulated goods peaked at 82.9% (6.9% in monthly terms). This rate is much greater than the 7.2 percent average in 1994 and the 1.5 percent average in the last year of the sample. The frequency of price changes also peaked in April 1995, when the price of 64.3% of nonregulated goods, measured in CPI weight, changed over that month. This number is more than twice the average level of 24.2% in 1994 and 30.3% in the last year of the sample. In the case of services, inflation peaked at 54.3% in annual terms in April 1995 (4.5% in monthly terms).
Figure 4
presents the main time series statistics for non-regulated goods.
Positive comovement between ![]() and
and
![]() is clearly visible in the figure. The
correlation coefficient between the two linearly detrended series
equals 0.93 for the whole period. This correlation
is largely driven by the high inflation episode, however; it falls
to -0.02 if I consider only the last three years
of the sample. After mid-1996, it is difficult to spot any downward
trend in the frequency of price changes even though inflation
trends down. The reason behind this loose relationship is apparent
in the lower part of Figure 4, where I break
down
is clearly visible in the figure. The
correlation coefficient between the two linearly detrended series
equals 0.93 for the whole period. This correlation
is largely driven by the high inflation episode, however; it falls
to -0.02 if I consider only the last three years
of the sample. After mid-1996, it is difficult to spot any downward
trend in the frequency of price changes even though inflation
trends down. The reason behind this loose relationship is apparent
in the lower part of Figure 4, where I break
down ![]() into
into
![]() and
and
![]() . As inflation declined, so did the
frequency of price increases. At the same time, however, price
decreases became more frequent, thereby dampening movements in the
frequency of price changes. A look at the correlation between
. As inflation declined, so did the
frequency of price increases. At the same time, however, price
decreases became more frequent, thereby dampening movements in the
frequency of price changes. A look at the correlation between
![]()
![]() and
and ![]() provides further evidence of this dampening effect. In the last
three years of the sample, the correlation is 0.55 between
provides further evidence of this dampening effect. In the last
three years of the sample, the correlation is 0.55 between
![]() and
and ![]() and
-0.72 between
and
-0.72 between
![]() and
and ![]() . (All
series are linearly detrended.) The net result is an absence of
correlation between
. (All
series are linearly detrended.) The net result is an absence of
correlation between ![]() and
and ![]() over that period.
over that period.
Figure 4. Frequency of price changes (nonregulated goods)
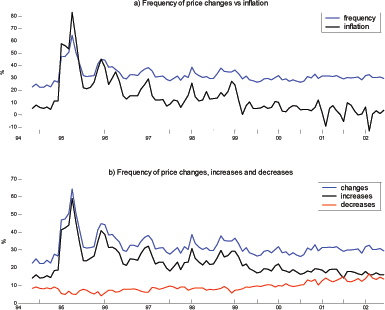
The offsetting effect of price decreases operates mainly at low
levels of inflation. Indeed, when inflation reaches above 10 to 15% in my sample,
there are few price decreases left to offset movements in the
frequency of price increases. At the peak of inflation, for
example, only 8% of price changes were price
decreases. In contrast, 45% of price changes were
negative in the last year of the sample (42% if I
include nonregulated services), a figure echoing those on the
United States and the Euro area. This disappearance of price
decreases creates the observed nonlinearity in the relationship of
![]() to
to ![]() .
.
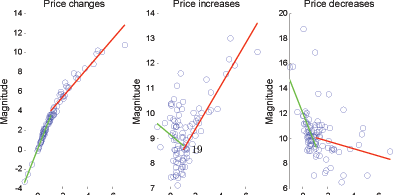
Figure 5 shows evidence
of the offsetting effect from a different angle by presenting
scatterplots of ![]() ,
,
![]() and
and
![]() against the inflation rate. The
sample is divided into low- and high-inflation subsamples. The
low-inflation subsample features a rapid fall in the frequency of
price decreases as inflation takes off, thereby generating the
offsetting effect. In comparison, in the high-inflation subsample,
the frequency of price decreases is closer to its lower bound and
responds less directly to movements in inflation. This change in
behavior, seen as a "kink" in the relation, occurs for an
inflation rate of 10 - 15%.18 The plots also
show the predicted values from simple linear regressions on each
subsample, using 12.5% as the cutoff inflation. The
regression results are presented in Table 2.
against the inflation rate. The
sample is divided into low- and high-inflation subsamples. The
low-inflation subsample features a rapid fall in the frequency of
price decreases as inflation takes off, thereby generating the
offsetting effect. In comparison, in the high-inflation subsample,
the frequency of price decreases is closer to its lower bound and
responds less directly to movements in inflation. This change in
behavior, seen as a "kink" in the relation, occurs for an
inflation rate of 10 - 15%.18 The plots also
show the predicted values from simple linear regressions on each
subsample, using 12.5% as the cutoff inflation. The
regression results are presented in Table 2.
Figure 5. Scatterplot of the frequency of price changes and inflation (nonregulated goods)
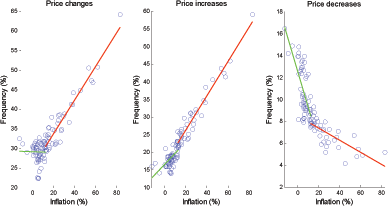
Note: Each graph displays linear regression lines using all observations below and above 12.5% annual inflation respectively. The regression statistics are presented in Table 2.
Table 2. Linear regression results for nonregulated goods (Panel 1: Frequency of Price Changes)
| Observations | fr: Constant |
fr: π |
fr: R2 |
fr+: Constant |
fr+: π |
fr+: R2 |
fr-: Constant |
fr-: π |
fr-: R2 |
|---|---|---|---|---|---|---|---|---|---|
| All | 26.92, (0.42) |
0.37, (0.02) |
0.78 |
15.86, (0.31) |
0.50, (0.01) |
0.92 |
11.06, (0.25) |
-0.13, (0.01) |
0.56 |
| π<=12.5% | 29.16, (0.52) |
-0.01, (0.07) |
0.00 |
16.66, (0.42) |
0.31, (0.05) |
0.36 |
12.51, (0.32) |
-0.32, (0.04) |
0.51 |
| π>12.5% | 25.14, (0.79) |
0.43, (0.02) |
0.90 |
16.66, (0.67) |
0.49, (0.02) |
0.94 |
8.47, (0.27) |
-0.05, (0.01) |
0.55 |
Note: numbers in parentheses are standard errors
Table 2: Linear regression results for nonregulated goods (Panel 2: Magnitude of Price Changes)
| Observations | dp: Constant |
dp: π |
dp: R2 |
dp+: Constant |
dp+: π |
dp+: R2 |
dp-: Constant |
dp-: π |
dp-: R2 |
|---|---|---|---|---|---|---|---|---|---|
| All | 0.91, (0.11) |
2.02, (0.06) |
0.92 |
8.58, (0.14) |
0.54, (0.08) |
0.34 |
11.06, (0.24) |
-0.58, (0.14) |
0.16 |
| π<=12.5% | 0.10, (0.04) |
3.27, (0.06) |
0.98 |
9.15, (0.21) |
-0.42, (0.32) |
0.03 | 11.99, (0.32) |
-2.53, (0.50) |
0.31 |
| π>12.5% | 2.44, (0.20) |
1.50, (0.08) |
0.91 |
7.67, (0.18) |
0.86, (0.07) |
0.82 |
10.41, (0.52) |
-0.30, (0.20) |
0.06 |
Note: numbers in parentheses are standard errors
When inflation is high, there is a clear positive relation
between ![]() and
and ![]() : each
percentage-point increase in the annual inflation rate is
associated with a 0.37 (0.02)
percentage-point increase
in the frequency of price changes of nonregulated goods.19 In
stark contrast, in the low-inflation subsample, the frequency of
price changes shows no statistical relation to inflation in the low
inflation subsample; the best point estimate for the slope of the
regression line is actually negative at -0.01 (0.07)
. The reason behind this
very different behavior of
: each
percentage-point increase in the annual inflation rate is
associated with a 0.37 (0.02)
percentage-point increase
in the frequency of price changes of nonregulated goods.19 In
stark contrast, in the low-inflation subsample, the frequency of
price changes shows no statistical relation to inflation in the low
inflation subsample; the best point estimate for the slope of the
regression line is actually negative at -0.01 (0.07)
. The reason behind this
very different behavior of ![]() over the low-
and high-inflation subsamples can be understood by taking a second
look at
over the low-
and high-inflation subsamples can be understood by taking a second
look at
![]() and
and
![]() . When inflation is low, a one
percentage-point change in the inflation rate has a similar effect
in magnitude on
. When inflation is low, a one
percentage-point change in the inflation rate has a similar effect
in magnitude on
![]() and
and
![]() , 0.31 (0.05)
versus -0.32 (0.04),
but this effect takes opposite
signs. The net effect renders unresponsive
, 0.31 (0.05)
versus -0.32 (0.04),
but this effect takes opposite
signs. The net effect renders unresponsive ![]() to
movements in inflation. As inflation moves toward high values,
however, the rate at which
to
movements in inflation. As inflation moves toward high values,
however, the rate at which
![]() falls decreases as it approaches
its lower bound of 0. The frequency of price increases still has
room to respond, though, resulting in the significant, positive
statistical relationship that surfaces between
falls decreases as it approaches
its lower bound of 0. The frequency of price increases still has
room to respond, though, resulting in the significant, positive
statistical relationship that surfaces between ![]() and
and ![]() . The offsetting effect of
price decreases when inflation is low is robust to choosing any
cutoff for the low- and high-inflation subsamples within the
10-15% range. Furthermore, the results are
similar if I include nonregulated services, if I drop observations
before the 1995 sample revision or around the inflation peak, and
if I exclude all small-store samples.
. The offsetting effect of
price decreases when inflation is low is robust to choosing any
cutoff for the low- and high-inflation subsamples within the
10-15% range. Furthermore, the results are
similar if I include nonregulated services, if I drop observations
before the 1995 sample revision or around the inflation peak, and
if I exclude all small-store samples.
Nonregulated services represent a much smaller share of
expenditures than nonregulated goods in the basket at 26.9%. The upper part of Figure 6 displays the
frequency of price changes and the inflation rate of nonregulated
services over the sample period. There are several notable
differences in price setting behaviors with respect to nonregulated
goods. First, price changes are less frequent for nonregulated
services than goods, a fact noted by several author (e.g.
Bils and Klenow (2004) and Dhyne et al. (2005)). Second, the frequency of price changes is a
much more important margin of adjustment for services inflation
than for goods. Even at low levels of aggregate inflation, I
observe large increases in the price index for nonregulated
services associated with important movements in ![]() . These movements have a strong seasonal component,
with the large adjustments of each year occurring almost inevitably
in January and September. Second, the sample peak in inflation
around April 1995 is associated with a smaller rise in the
frequency of price changes. The frequency averaged 10.4% in the
second half of 1994 and 24.7% in the first half of 1995 compared to
24.3% and 50.2% for nonregulated goods. Finally, most nonregulated
services price changes are price increases. In the last year of the
sample, less than 1 out of every 8 price changes was a price
decrease. The strong movements in the frequency of price changes at
low levels of inflation may be associated with this relative
absence of price decreases. Movements in the frequency of price
decreases are negligible for the dynamics of the frequency of price
changes, in sharp contrast with nonregulated goods.
. These movements have a strong seasonal component,
with the large adjustments of each year occurring almost inevitably
in January and September. Second, the sample peak in inflation
around April 1995 is associated with a smaller rise in the
frequency of price changes. The frequency averaged 10.4% in the
second half of 1994 and 24.7% in the first half of 1995 compared to
24.3% and 50.2% for nonregulated goods. Finally, most nonregulated
services price changes are price increases. In the last year of the
sample, less than 1 out of every 8 price changes was a price
decrease. The strong movements in the frequency of price changes at
low levels of inflation may be associated with this relative
absence of price decreases. Movements in the frequency of price
decreases are negligible for the dynamics of the frequency of price
changes, in sharp contrast with nonregulated goods.
Figure 6. Frequency of price changes (nonregulated services)
Data for Figure 6
Month |
Inflation |
Frequency changes |
Frequency increases |
Frequency decreases |
|---|---|---|---|---|
May-94 |
7.1 |
9.1 |
8.4 |
0.7 |
Jun-94 |
4.6 |
6.9 |
6.2 |
0.7 |
Jul-94 |
3.7 |
5.3 |
4.6 |
0.7 |
Aug-94 |
5.6 |
13.4 |
12.4 |
1.0 |
Sep-94 |
27.7 |
20.3 |
19.6 |
0.7 |
Oct-94 |
2.9 |
6.5 |
5.7 |
0.8 |
Nov-94 |
8.9 |
7.8 |
6.9 |
0.9 |
Dec-94 |
11.2 |
9.6 |
9.0 |
0.6 |
Jan-95 |
38.8 |
21.8 |
21.7 |
0.1 |
Feb-95 |
33.6 |
21.9 |
21.8 |
0.1 |
Mar-95 |
30.3 |
20.5 |
20.1 |
0.4 |
Apr-95 |
54.3 |
43.9 |
43.2 |
0.7 |
May-95 |
26.5 |
20.1 |
19.8 |
0.2 |
Jun-95 |
24.1 |
20.3 |
20.0 |
0.4 |
Jul-95 |
14.2 |
13.7 |
13.1 |
0.7 |
Aug-95 |
14.6 |
13.4 |
13.2 |
0.3 |
Sep-95 |
42.5 |
23.9 |
23.8 |
0.1 |
Oct-95 |
14.4 |
11.6 |
11.6 |
0.1 |
Nov-95 |
15.1 |
10.9 |
10.9 |
0.0 |
Dec-95 |
23.5 |
19.8 |
19.6 |
0.2 |
Jan-96 |
24.0 |
17.9 |
17.5 |
0.4 |
Feb-96 |
15.6 |
12.7 |
12.3 |
0.3 |
Mar-96 |
13.0 |
12.0 |
11.6 |
0.5 |
Apr-96 |
19.4 |
16.6 |
16.2 |
0.4 |
May-96 |
15.7 |
13.5 |
12.9 |
0.5 |
Jun-96 |
12.9 |
13.2 |
12.8 |
0.5 |
Jul-96 |
11.0 |
16.2 |
15.9 |
0.4 |
Aug-96 |
10.0 |
13.2 |
12.7 |
0.5 |
Sep-96 |
40.8 |
26.6 |
26.4 |
0.2 |
Oct-96 |
7.6 |
7.6 |
7.3 |
0.3 |
Nov-96 |
9.7 |
8.9 |
8.6 |
0.3 |
Dec-96 |
24.1 |
19.5 |
19.2 |
0.3 |
Jan-97 |
26.9 |
21.8 |
21.5 |
0.3 |
Feb-97 |
16.5 |
15.5 |
14.9 |
0.6 |
Mar-97 |
9.4 |
10.3 |
9.9 |
0.4 |
Apr-97 |
12.8 |
13.8 |
13.5 |
0.3 |
May-97 |
12.9 |
14.5 |
14.1 |
0.4 |
Jun-97 |
11.0 |
13.0 |
12.7 |
0.4 |
Jul-97 |
7.3 |
9.9 |
9.5 |
0.4 |
Aug-97 |
9.3 |
15.1 |
14.8 |
0.3 |
Sep-97 |
39.1 |
24.1 |
23.7 |
0.4 |
Oct-97 |
7.2 |
7.7 |
7.4 |
0.2 |
Nov-97 |
7.4 |
7.4 |
6.9 |
0.5 |
Dec-97 |
13.0 |
12.0 |
11.4 |
0.6 |
Jan-98 |
27.3 |
23.5 |
22.8 |
0.7 |
Feb-98 |
14.9 |
17.0 |
16.4 |
0.6 |
Mar-98 |
13.7 |
12.4 |
11.9 |
0.5 |
Apr-98 |
13.0 |
12.2 |
11.6 |
0.6 |
May-98 |
15.6 |
14.2 |
13.9 |
0.3 |
Jun-98 |
9.6 |
10.8 |
10.3 |
0.5 |
Jul-98 |
7.7 |
9.8 |
9.4 |
0.3 |
Aug-98 |
10.8 |
18.5 |
18.2 |
0.4 |
Sep-98 |
40.4 |
27.5 |
27.2 |
0.3 |
Oct-98 |
5.3 |
7.4 |
6.7 |
0.7 |
Nov-98 |
7.5 |
9.6 |
9.0 |
0.6 |
Dec-98 |
22.0 |
19.5 |
19.4 |
0.1 |
Jan-99 |
24.0 |
20.1 |
19.8 |
0.2 |
Feb-99 |
20.9 |
18.4 |
17.9 |
0.5 |
Mar-99 |
17.1 |
14.2 |
14.0 |
0.2 |
Apr-99 |
14.5 |
15.2 |
14.9 |
0.3 |
May-99 |
13.8 |
13.8 |
13.6 |
0.2 |
Jun-99 |
8.1 |
9.4 |
9.1 |
0.3 |
Jul-99 |
6.9 |
8.5 |
8.3 |
0.2 |
Aug-99 |
9.4 |
18.5 |
18.2 |
0.3 |
Sep-99 |
40.1 |
25.7 |
25.4 |
0.3 |
Oct-99 |
6.8 |
9.3 |
8.8 |
0.6 |
Nov-99 |
6.0 |
7.5 |
7.0 |
0.5 |
Dec-99 |
7.8 |
12.9 |
12.2 |
0.7 |
Jan-00 |
22.5 |
22.6 |
22.0 |
0.6 |
Feb-00 |
12.8 |
13.1 |
12.8 |
0.3 |
Mar-00 |
5.4 |
7.9 |
7.2 |
0.7 |
Apr-00 |
6.5 |
8.5 |
7.8 |
0.7 |
May-00 |
5.2 |
8.4 |
8.1 |
0.4 |
Jun-00 |
6.8 |
9.1 |
8.7 |
0.5 |
Jul-00 |
4.7 |
6.7 |
6.2 |
0.5 |
Aug-00 |
9.0 |
14.2 |
13.6 |
0.6 |
Sep-00 |
33.2 |
25.3 |
23.8 |
1.5 |
Oct-00 |
8.4 |
7.6 |
6.7 |
0.9 |
Nov-00 |
10.3 |
8.7 |
8.2 |
0.5 |
Dec-00 |
8.0 |
8.5 |
7.9 |
0.6 |
Jan-01 |
13.3 |
12.0 |
11.4 |
0.6 |
Feb-01 |
9.9 |
9.9 |
9.1 |
0.8 |
Mar-01 |
10.4 |
9.9 |
9.1 |
0.8 |
Apr-01 |
7.6 |
7.6 |
7.0 |
0.6 |
May-01 |
6.3 |
9.1 |
8.1 |
1.0 |
Jun-01 |
4.5 |
6.6 |
5.6 |
1.0 |
Jul-01 |
4.9 |
7.4 |
6.3 |
1.0 |
Aug-01 |
7.0 |
18.2 |
16.8 |
1.4 |
Sep-01 |
29.6 |
22.5 |
21.4 |
1.1 |
Oct-01 |
5.3 |
6.2 |
5.2 |
1.0 |
Nov-01 |
6.4 |
7.0 |
6.2 |
0.8 |
Dec-01 |
4.4 |
5.5 |
4.9 |
0.6 |
Jan-02 |
13.6 |
13.2 |
11.8 |
1.4 |
Feb-02 |
8.4 |
10.8 |
9.5 |
1.3 |
Mar-02 |
7.3 |
10.0 |
8.6 |
1.4 |
Apr-02 |
6.9 |
7.7 |
6.5 |
1.2 |
May-02 |
3.9 |
6.8 |
5.1 |
1.7 |
Jun-02 |
3.3 |
6.2 |
5.0 |
1.2 |
5.2 Magnitude of Price Changes
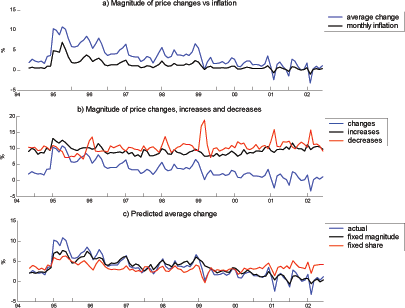
In the case of nonregulated goods, the average magnitude of
price changes moves strongly with inflation, regardless of whether
inflation is low or high. The series ![]() and
and
![]() , displayed in Figure 7, follow similar
patterns over the sample period.20 They register sharp
increases during the Tequila crisis, followed by a protracted
decline and ultimately a stabilization. The correlation between the
two linearly detrended series is 0.94 over the full
sample period. The high inflation episode does not drive this
strong correlation, as was the case with the frequency of price
changes; indeed, the correlation actually rises to a solid
0.998 over the last three years of the
sample. As the scatterplot of
, displayed in Figure 7, follow similar
patterns over the sample period.20 They register sharp
increases during the Tequila crisis, followed by a protracted
decline and ultimately a stabilization. The correlation between the
two linearly detrended series is 0.94 over the full
sample period. The high inflation episode does not drive this
strong correlation, as was the case with the frequency of price
changes; indeed, the correlation actually rises to a solid
0.998 over the last three years of the
sample. As the scatterplot of ![]() against
against
![]() (Figure 8, with
regression coefficients presented in Table 2) indicates,
(Figure 8, with
regression coefficients presented in Table 2) indicates,
![]() and
and ![]() have a
tight, almost linear relation when inflation is below 1% per month, or roughly 10-15 percent per year. When
inflation is greater than 1% per month, the
relation is still strongly positive, albeit noisier and slightly
concave.
have a
tight, almost linear relation when inflation is below 1% per month, or roughly 10-15 percent per year. When
inflation is greater than 1% per month, the
relation is still strongly positive, albeit noisier and slightly
concave.
Figure 7. Average magnitude of price changes (nonregulated goods)
Data for Figure 7
Month |
Inflation |
Magnitude changes |
Magnitude increases |
Magnitude decreases |
Predicted average change (fixed magnitude) |
Predicted average change (fixed share) |
|---|---|---|---|---|---|---|
May-94 | 0.4 | 1.9 | 9.0 | 10.3 | 2.0 | 3.2 |
Jun-94 | 0.7 | 2.7 | 9.9 | 10.2 | 2.1 | 3.9 |
Jul-94 | 0.5 | 2.2 | 9.5 | 10.2 | 2.0 | 3.6 |
Aug-94 | 0.4 | 1.9 | 8.1 | 9.2 | 2.3 | 2.9 |
Sep-94 | 0.5 | 2.2 | 8.6 | 9.5 | 2.2 | 3.2 |
Oct-94 | 0.4 | 1.6 | 8.6 | 10.8 | 2.2 | 2.8 |
Nov-94 | 0.9 | 3.4 | 10.2 | 10.3 | 2.7 | 4.1 |
Dec-94 | 1.0 | 3.6 | 9.2 | 9.4 | 3.3 | 3.7 |
Jan-95 | 4.8 | 10.2 | 13.0 | 10.9 | 6.9 | 5.9 |
Feb-95 | 4.7 | 9.9 | 12.2 | 10.4 | 7.2 | 5.4 |
Mar-95 | 4.5 | 8.8 | 11.6 | 9.5 | 6.6 | 5.3 |
Apr-95 | 6.9 | 10.7 | 12.5 | 9.0 | 7.7 | 6.0 |
May-95 | 5.1 | 10.1 | 11.9 | 7.1 | 7.3 | 6.2 |
Jun-95 | 3.2 | 7.8 | 10.9 | 7.1 | 5.8 | 5.5 |
Jul-95 | 1.8 | 5.8 | 10.0 | 7.5 | 4.5 | 4.8 |
Aug-95 | 1.8 | 5.7 | 9.6 | 7.3 | 4.6 | 4.5 |
Sep-95 | 1.9 | 6.0 | 9.3 | 8.4 | 5.5 | 4.0 |
Oct-95 | 2.2 | 6.9 | 9.8 | 7.7 | 6.0 | 4.6 |
Nov-95 | 3.1 | 7.4 | 10.1 | 6.6 | 6.1 | 5.1 |
Dec-95 | 3.8 | 8.4 | 10.2 | 9.2 | 7.4 | 4.4 |
Jan-96 | 3.2 | 7.3 | 10.2 | 12.3 | 6.7 | 3.4 |
Feb-96 | 2.0 | 5.3 | 9.7 | 13.6 | 5.5 | 2.7 |
Mar-96 | 2.5 | 6.4 | 10.1 | 9.2 | 5.5 | 4.3 |
Apr-96 | 2.9 | 7.9 | 11.4 | 9.0 | 5.9 | 5.3 |
May-96 | 2.3 | 6.6 | 10.2 | 9.1 | 5.5 | 4.4 |
Jun-96 | 1.3 | 4.3 | 9.0 | 9.1 | 4.2 | 3.6 |
Jul-96 | 1.1 | 3.6 | 8.2 | 8.7 | 3.9 | 3.1 |
Aug-96 | 1.3 | 4.0 | 8.6 | 10.7 | 4.5 | 2.8 |
Sep-96 | 1.3 | 4.0 | 8.6 | 10.1 | 4.4 | 3.0 |
Oct-96 | 1.3 | 4.0 | 8.6 | 10.6 | 4.5 | 2.9 |
Nov-96 | 1.7 | 5.0 | 8.8 | 11.0 | 5.4 | 2.9 |
Dec-96 | 2.0 | 5.5 | 8.5 | 9.8 | 6.0 | 3.0 |
Jan-97 | 2.4 | 6.4 | 9.3 | 9.2 | 6.1 | 3.8 |
Feb-97 | 1.3 | 3.7 | 8.3 | 10.2 | 4.3 | 2.7 |
Mar-97 | 1.0 | 3.3 | 8.7 | 10.2 | 3.7 | 3.0 |
Apr-97 | 1.0 | 3.2 | 7.6 | 9.6 | 4.3 | 2.4 |
May-97 | 1.0 | 3.3 | 7.9 | 9.6 | 4.1 | 2.7 |
Jun-97 | 0.6 | 2.0 | 7.1 | 9.1 | 3.1 | 2.3 |
Jul-97 | 0.7 | 2.6 | 9.5 | 10.7 | 2.5 | 3.5 |
Aug-97 | 1.0 | 3.4 | 9.1 | 9.2 | 3.2 | 3.6 |
Sep-97 | 0.9 | 3.0 | 7.6 | 10.1 | 4.1 | 2.3 |
Oct-97 | 0.5 | 1.8 | 7.7 | 10.5 | 2.8 | 2.3 |
Nov-97 | 0.9 | 2.9 | 7.9 | 9.6 | 3.6 | 2.6 |
Dec-97 | 1.3 | 4.4 | 8.4 | 8.6 | 4.6 | 3.3 |
Jan-98 | 2.2 | 5.6 | 9.8 | 10.9 | 5.2 | 3.6 |
Feb-98 | 1.2 | 3.6 | 9.5 | 13.6 | 4.3 | 2.6 |
Mar-98 | 0.9 | 3.0 | 8.2 | 11.1 | 4.0 | 2.4 |
Apr-98 | 1.0 | 3.3 | 8.1 | 8.6 | 3.6 | 3.1 |
May-98 | 1.6 | 5.0 | 9.5 | 9.5 | 4.6 | 3.8 |
Jun-98 | 1.1 | 3.7 | 8.7 | 10.3 | 4.0 | 3.0 |
Jul-98 | 1.1 | 3.7 | 8.6 | 10.5 | 4.2 | 2.8 |
Aug-98 | 1.1 | 3.4 | 7.9 | 11.4 | 4.7 | 2.1 |
Sep-98 | 1.5 | 3.9 | 8.1 | 11.1 | 5.0 | 2.4 |
Oct-98 | 1.3 | 3.6 | 8.8 | 11.1 | 4.0 | 2.9 |
Nov-98 | 1.6 | 4.5 | 9.1 | 10.7 | 4.7 | 3.1 |
Dec-98 | 2.3 | 6.5 | 9.6 | 9.3 | 6.0 | 4.0 |
Jan-99 | 2.0 | 5.5 | 9.1 | 9.3 | 5.4 | 3.6 |
Feb-99 | 1.0 | 3.0 | 8.7 | 16.9 | 4.8 | 1.0 |
Mar-99 | 0.0 | 0.1 | 7.5 | 18.8 | 3.8 | -0.4 |
Apr-99 | 0.6 | 2.0 | 7.5 | 11.0 | 3.5 | 1.9 |
May-99 | 0.9 | 3.1 | 7.8 | 7.1 | 3.0 | 3.3 |
Jun-99 | 0.4 | 1.6 | 7.6 | 9.9 | 2.6 | 2.3 |
Jul-99 | 0.4 | 1.6 | 8.3 | 10.1 | 2.1 | 2.8 |
Aug-99 | 0.5 | 1.7 | 7.6 | 9.1 | 2.3 | 2.6 |
Sep-99 | 0.6 | 2.0 | 8.0 | 9.6 | 2.6 | 2.8 |
Oct-99 | 0.4 | 1.5 | 7.9 | 10.2 | 2.3 | 2.5 |
Nov-99 | 0.5 | 1.8 | 8.4 | 9.9 | 2.1 | 3.0 |
Dec-99 | 0.9 | 3.0 | 9.1 | 10.9 | 3.3 | 3.1 |
Jan-00 | 0.9 | 2.7 | 8.4 | 10.1 | 3.2 | 2.9 |
Feb-00 | 0.2 | 0.9 | 7.5 | 12.0 | 2.6 | 1.7 |
Mar-00 | 0.2 | 0.8 | 8.1 | 11.4 | 1.8 | 2.3 |
Apr-00 | 0.5 | 1.7 | 9.5 | 11.5 | 2.0 | 3.2 |
May-00 | 0.6 | 2.2 | 8.2 | 9.8 | 2.7 | 2.8 |
Jun-00 | 0.6 | 2.2 | 8.7 | 9.5 | 2.3 | 3.3 |
Jul-00 | 0.3 | 1.3 | 8.6 | 10.1 | 1.6 | 3.0 |
Aug-00 | 0.4 | 1.3 | 9.2 | 11.2 | 1.7 | 3.1 |
Sep-00 | 0.4 | 1.2 | 9.1 | 9.7 | 1.1 | 3.4 |
Oct-00 | 0.3 | 0.9 | 9.0 | 10.5 | 1.2 | 3.1 |
Nov-00 | 0.5 | 1.5 | 10.2 | 10.9 | 1.2 | 3.8 |
Dec-00 | 1.0 | 3.4 | 10.5 | 9.8 | 2.4 | 4.4 |
Jan-01 | 0.2 | 0.6 | 9.2 | 12.2 | 1.3 | 2.8 |
Feb-01 | -0.8 | -2.5 | 8.7 | 15.8 | 0.3 | 1.3 |
Mar-01 | 0.4 | 1.4 | 9.5 | 10.6 | 1.4 | 3.5 |
Apr-01 | 0.6 | 2.0 | 9.7 | 10.5 | 1.7 | 3.7 |
May-01 | 0.3 | 0.8 | 9.5 | 12.1 | 1.4 | 3.0 |
Jun-01 | 0.0 | 0.1 | 10.4 | 11.8 | 0.2 | 3.7 |
Jul-01 | -0.4 | -1.5 | 9.6 | 12.1 | -0.8 | 3.1 |
Aug-01 | 0.8 | 2.7 | 11.6 | 10.2 | 1.2 | 5.1 |
Sep-01 | 0.7 | 2.2 | 10.3 | 9.8 | 1.3 | 4.3 |
Oct-01 | 0.2 | 0.8 | 9.8 | 11.2 | 0.9 | 3.5 |
Nov-01 | 0.0 | -0.1 | 9.9 | 11.9 | 0.3 | 3.3 |
Dec-01 | 0.1 | 0.2 | 9.1 | 11.2 | 0.7 | 3.0 |
Jan-02 | 0.5 | 1.7 | 11.1 | 10.3 | 0.6 | 4.7 |
Feb-02 | -1.1 | -3.3 | 9.5 | 15.7 | -0.7 | 1.9 |
Mar-02 | 0.1 | 0.2 | 10.3 | 11.2 | 0.0 | 3.9 |
Apr-02 | 0.3 | 0.9 | 10.6 | 11.2 | 0.6 | 4.0 |
May-02 | 0.1 | 0.3 | 10.4 | 10.6 | -0.2 | 4.1 |
Jun-02 | 0.3 | 1.1 | 9.7 | 9.1 | 0.2 | 4.1 |
Figure 8. Scatterplot of the average magnitude of price changes and inflation (nonregulated goods)
These results should come as no surprise given the findings
described earlier regarding the frequency of price changes and
inflation. By definition,
![]() . When inflation
is low,
. When inflation
is low, ![]() moves little with inflation, implying
that
moves little with inflation, implying
that ![]() moves strongly and almost linearly
with
moves strongly and almost linearly
with ![]() . In contrast, when inflation is
greater than 10-15% per year,
. In contrast, when inflation is
greater than 10-15% per year, ![]() moves strongly and positively with
moves strongly and positively with ![]() . This second source of variation in
. This second source of variation in ![]() introduces some curvature as well as some noise in
the relationship between
introduces some curvature as well as some noise in
the relationship between ![]() and
and ![]() .
.
To better understand what drives ![]() , it is
convenient to express it as
, it is
convenient to express it as
where
![]() is the
fraction of price increases among price changes. Thus, variations
in the absolute magnitude of price increases and decreases, as well
as their relative occurrence (the composition effect), affects the
average magnitude of price changes. It is clear from Figure
7 that
is the
fraction of price increases among price changes. Thus, variations
in the absolute magnitude of price increases and decreases, as well
as their relative occurrence (the composition effect), affects the
average magnitude of price changes. It is clear from Figure
7 that
![]() and
and
![]() are less
correlated with inflation than
are less
correlated with inflation than ![]() . The point
estimates for the correlation over the full sample are 0.65 and -0.23, respectively. Moreover,
. The point
estimates for the correlation over the full sample are 0.65 and -0.23, respectively. Moreover,
![]() and
and
![]() display
much less variation over the sample period than their weighted
sum.21 Except for a short period around the
peak of inflation, the two series show relatively small
oscillations around their sample mean: 9.2% for
price increases and 10.4% for price decreases.
This pattern leaves a potentially large role for movements in
display
much less variation over the sample period than their weighted
sum.21 Except for a short period around the
peak of inflation, the two series show relatively small
oscillations around their sample mean: 9.2% for
price increases and 10.4% for price decreases.
This pattern leaves a potentially large role for movements in
![]() to affect average price change. The
relation between inflation and
to affect average price change. The
relation between inflation and
![]() or
or
![]() also is
much noisier than the relation between inflation and
also is
much noisier than the relation between inflation and ![]() . The bottom of Table 2 presents results
from linear regressions of the magnitude of price changes on
inflation. There is no significant statistical relationship between
. The bottom of Table 2 presents results
from linear regressions of the magnitude of price changes on
inflation. There is no significant statistical relationship between
![]() and
and
![]() in the low-inflation sample nor
between
in the low-inflation sample nor
between
![]() and
and
![]() in the high- inflation subsample.
in the high- inflation subsample.
To assess the importance of this composition effect, I compute
two counterfactual series in Figure 7. I obtain the
first by holding ![]() at its sample mean to show how
movements in
at its sample mean to show how
movements in
![]() and
and
![]() alone
affect
alone
affect ![]() . In the second series,
. In the second series,
![]() and
and
![]() are held
at their sample mean so the relative occurrence of price increases
and decreases is the only source of variation in
are held
at their sample mean so the relative occurrence of price increases
and decreases is the only source of variation in ![]() . The main finding indicates that the composition
effect drives
. The main finding indicates that the composition
effect drives ![]() when inflation is below 10-15%,
whereas movements in both the composition and absolute magnitude of
price changes are important when inflation is high. Had
when inflation is below 10-15%,
whereas movements in both the composition and absolute magnitude of
price changes are important when inflation is high. Had ![]() been constant,
been constant, ![]() would have
sloped up counterfactually in the last three years of the sample
because of a mild upward trend in
would have
sloped up counterfactually in the last three years of the sample
because of a mild upward trend in
![]() after 1999. In contrast, the
series allowing only for the composition effect predicts remarkably
well the level of
after 1999. In contrast, the
series allowing only for the composition effect predicts remarkably
well the level of ![]() over that period. When
inflation nears its peak, the composition effect alone is
insufficient to match the level of
over that period. When
inflation nears its peak, the composition effect alone is
insufficient to match the level of ![]() , but it
is a better predictor than merely allowing for changes in the
absolute magnitude.
, but it
is a better predictor than merely allowing for changes in the
absolute magnitude.
5.3 Distribution of Price Changes
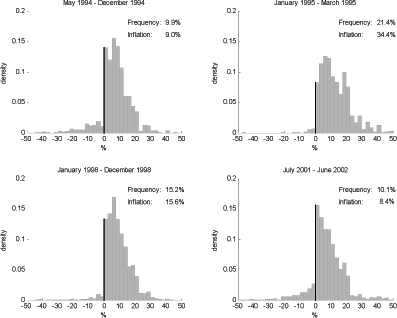
There is much heterogeneity in the size of price changes at all levels of inflation. In the case of nonregulated goods, the distribution of price changes is very spread out; both small and large price changes arise (see Figure 9).22 When inflation is low, many large and small price decreases occur. Furthermore, the entire distribution shifts to the right as inflation increases. On the other hand, price decreases, which are almost as frequent as price increases at low inflation, become less prevalent as inflation rises. This behavior leads to the weak response of the frequency and the strong response of the magnitude of price changes discussed earlier.
Figure 9. Distribution of nonzero price changes (nonregulated goods)
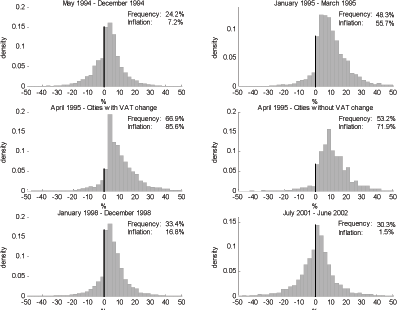
When inflation is high, price increases between 0 and
20% compose the bulk of price changes. The
increased density of this region comes from two sources. First,
prices that change often ![]() food products in particular
food products in particular
![]() see their distribution moving up. Second,
several prices that would have remained fixed otherwise are updated
by positive amounts. Recall that the price of 59.1% of all nonregulated items changed in April 1995
compared with only 25.6% in the last year of
the sample.
see their distribution moving up. Second,
several prices that would have remained fixed otherwise are updated
by positive amounts. Recall that the price of 59.1% of all nonregulated items changed in April 1995
compared with only 25.6% in the last year of
the sample.
The distributions are not symmetric, even when inflation is at its lowest. Indeed, small decreases are less frequent than small increases. Furthermore, price increases are more spread out than price decreases when inflation is high, but the opposite is true when inflation hovers around 1.7% in the last year of the sample. Price changes for food items primarily drive this pattern: the variance of these changes is large, and food items represent a sizable share of price changes. Other product categories have less frequent, mainly positive price adjustments. This finding support the idea that at least two product categories are required in macroeconomics models to be consistent with the empirical distribution of price changes. To produce the long tails, I need a category of items whose magnitude of price changes has a large variance. When mixed with a category displaying less variable and mainly positive changes, an asymmetry around zero could arise.
I find a clear effect of changes in the VAT on the distribution of price changes. The two middle graphs show the distribution when the 5% VAT hike occurred in April 1995. The density of the interval comprising the mode of the distribution stands out as unusually high and falls within the band corresponding to the change in the VAT. I provide a more detailed analysis of the VAT tax change in a later subsection.
Figure 10 displays the corresponding distributions of price changes for nonregulated services. The graphs corresponding to the VAT tax change are omitted given the small number of services impacted by the change. As noted earlier, there are few price decreases for nonregulated services, even at low levels of inflation. This striking difference between the distributions of price changes for nonregulated goods versus nonregulated services offers support to the idea that an empirically successful microfounded model should embed at least two sectors. There is a slight increase in the frequency of price changes conditional on inflation toward the end of the sample period. Interestingly, the figure indicates that some of these additional price changes are price decreases.
Figure 10. Distribution of nonzero price changes (nonregulated services)
5.4 Sector statistics
Similar to the findings for the United States and Euro area, a substantial heterogeneity in consumer price stickiness exists across major product groups in Mexico (see Figure 11).23 In particular, Foods and nonalcoholic beverages stands out for its high frequency of price changes and the prevalence of price decreases. Its frequency averages 40.0% over the last three years of the sample when inflation was low, a percentage almost identical to its 40.2% average over the full sample period; in contrast, the average frequency of other groups is generally half of those numbers or less. The share of price decreases for Food and nonalcoholic beverages is 35.8% over the full sample and 45.3% in the last three years. Other groups experience few or no price decreases over most of the sample period. Only when inflation settled comfortably below 10% did price decreases rise mildly. Given these observations, food products clearly are key to the importance of price decreases at the aggregate level.
Figure 11. Sector frequencies of price changes
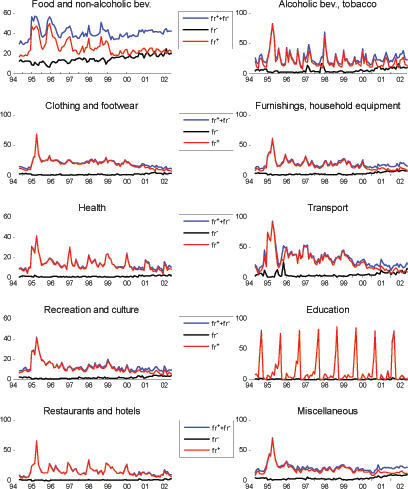
Figure 11 also shows that almost every sector rapidly felt the inflationary pressure accompanying the devaluation. In January 1995, all groups but Education experienced a sharp rise in the frequency of price changes. A second wave of rapid increases in the frequency of price changes also surfaced in most groups in April 1995. The clear spikes in the series relate to a change in the value added tax, which I will discuss in greater detail at the end of the section.
I also find evidence of seasonality in the timing of price changes for groups containing a large proportion of services. In particular, Health, Restaurants and Hotels as well as Transportation display some seasonality in January. Education is a striking case, with more than 90% its prices changing in either August or September and few if any prices changing at other times of the year. These seasonal patterns can be considered as a form of time dependence in which prices are adjusted at fixed time intervals. The strong seasonality particular to Education stems largely from the nature of the items it encompasses; tuition, registration fees and room and board in academic institutions constitute the bulk of observations in that category. These items are distinctive because both the price and quantity consumed are fixed for a certain time period (say, a semester or an academic year). In that sense, they differ from the staggered pricing model where the price is fixed but the quantity can fluctuate freely.
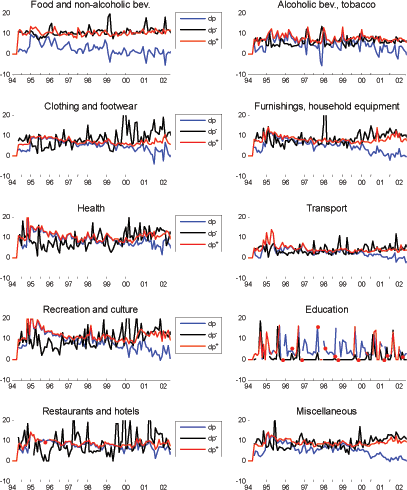
There are less striking differences across sectors with respect to the magnitude of price changes (see Figure 12). Overall, the average magnitude of price changes is similar in magnitude across sector. The sector of Transport has the overall smallest price changes. The sector of Education also has unusually small price changes for several months of the year. Price increases are typically larger than average in September, however, when the frequency of price changes is the highest in September. Finally, I notice that the devaluation brought larger price increases mainly in the service sectors while Food and non-alcoholic beverages displayed little change.
Figure 12. Sector average magnitude of price changes
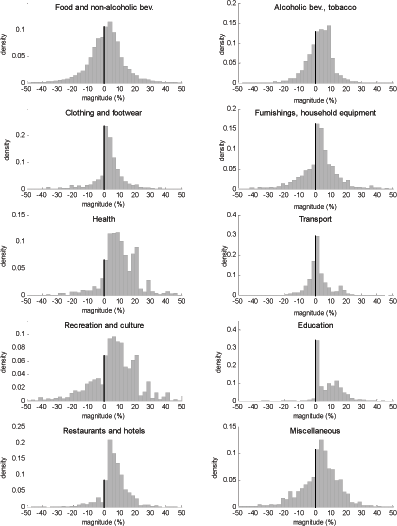
Finally, I present the distributions of price changes for two-digit COICOP groups over the last two years of the sample. The purpose of this figure is to illustrate that a large amount of price change dispersion is found at lower levels of aggregations. Very small price changes are found in all COICOP group considered. A particularly large number of them is found in the Transport industry, which includes items such as airfares, and in Education, for which prices were found to be changed at regular intervals. An unusually large number of small price changes are also found in the Clothing and footwear sector. Recall, however, that most observations in that sector are an average the price of three similar items belonging to the same store. The large number of small price changes thus likely reflects the fact that changes to the average price are typically smaller than individual price changes themselves.
Figure 13. Distribution of nonzero price changes (2-digit COICOP groups, July 2000 to June 2002)
5.5 Inflation Variance Decomposition
In this section, I quantify the importance of fluctuations in
the frequency and magnitude of price changes for the variance of
inflation. The starting point is a first-order Taylor-series
expansion of
![]() around
around
![]() and
and ![]() ,
as implemented by Klenow and Kryvtsov (2005):
,
as implemented by Klenow and Kryvtsov (2005):
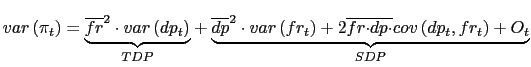
This expression provides a decomposition into a time dependent
(TDP) and a state dependent (SDP) part. TDP is the only term
depending solely on ![]() , whereas all terms in
SDP, including the higher-order terms
, whereas all terms in
SDP, including the higher-order terms ![]() , are
functions of
, are
functions of ![]() . In the Calvo model, as well as
in the Taylor pricing model with uniform staggering, the TDP term
accounts for all of the inflation variance. Finding non-zero terms
in SDP therefore can serve as evidence against these time dependent
models. Using U.S. CPI data for 1988-2003, Klenow and Kryvtsov find
only a minor role for the terms in SDP, and around 95% of the
variance in the monthly inflation series stem from fluctuations in
. In the Calvo model, as well as
in the Taylor pricing model with uniform staggering, the TDP term
accounts for all of the inflation variance. Finding non-zero terms
in SDP therefore can serve as evidence against these time dependent
models. Using U.S. CPI data for 1988-2003, Klenow and Kryvtsov find
only a minor role for the terms in SDP, and around 95% of the
variance in the monthly inflation series stem from fluctuations in
![]() . This aspect of the United States'
recent inflation experience therefore conforms to time dependent
models.
. This aspect of the United States'
recent inflation experience therefore conforms to time dependent
models.
The figures for Mexico differ markedly from those for the United
States. As shown in Table 3, the TDP term
represents only 41.9% of the inflation variance
over the full sample period, leaving a much greater role for
fluctuations in ![]() . This comes as no surprise
given the high correlation between
. This comes as no surprise
given the high correlation between ![]() and
and
![]() over the sample period. The smaller
share of variance that the TDP terms account for also appears in
both the goods and services sectors. This share is particularly
small for services at 14.3%, but this figure stems
primarily from the strong seasonal pattern in the pricing of
Education services.24 In the case of goods, movements in
over the sample period. The smaller
share of variance that the TDP terms account for also appears in
both the goods and services sectors. This share is particularly
small for services at 14.3%, but this figure stems
primarily from the strong seasonal pattern in the pricing of
Education services.24 In the case of goods, movements in
![]() also are important, with the notable
exception of unprocessed food, which I will discuss
shortly.
also are important, with the notable
exception of unprocessed food, which I will discuss
shortly.
Table 3: Inflation variance decomposition - Panel 1: Full Sample Period (January 1994 - June 2002)
Inflation: Average |
Inflation: Average |
Share of Inflation Variance (%): TDP |
Share of Inflation Variance (%): SDP1 |
Share of Inflation Variance (%): SDP2 |
Share of Inflation Variance (%): Other |
|
|---|---|---|---|---|---|---|
| Full CPI | 14.4 |
13.2 |
41.9 |
4.6 |
21.6 |
31.9 |
| Full CPI: Nonregulated goods | 14.4 |
15.3 |
46.0 |
2.8 |
17.1 |
34.2 |
| Full CPI: Nonregulated goods: Unprocessed food | 12.8 |
18.2 |
86.6 |
0.5 |
3.8 |
9.1 |
| Full CPI: Nonregulated Goods: Processed food | 15.3 |
18.4 |
32.2 |
4.9 |
18.8 |
44.1 |
| Full CPI: Nonregulated goods: Nonenergy ind. goods | 14.9 |
15.4 |
27.0 |
8.3 |
24.0 |
40.7 |
| Full CPI: Nonregulated services | 14.6 |
10.6 |
14.3 |
35.9 |
26.7 |
23.1 |
Table 3: Inflation variance decomposition - Panel 2: Precrisis (January 1994 - December 1994)
Inflation: Average |
Inflation: Average |
Share of Inflation Variance (%): TDP |
Share of Inflation Variance (%): SDP1 |
Share of Inflation Variance (%): SDP2 |
Share of Inflation Variance (%): Other |
|
|---|---|---|---|---|---|---|
| Full CPI | 7.7 |
3.2 |
58.3 |
5.3 |
32.1 |
4.4 |
| Full CPI: Nonregulated goods | 7.2 |
2.8 |
57.2 |
4.6 |
30.5 |
7.7 |
| Full CPI: Nonregulated goods: Unprocessed food | 8.7 |
5.2 |
88.9 |
0.6 |
12.3 |
-1.7 |
| Full CPI: Nonregulated goods: Processed food | 6.2 |
3.6 |
61.1 |
6.9 |
32.8 |
-0.9 |
| Full CPI: Nonregulated goods: Nonenergy ind. goods | 6.7 |
3.4 |
40.0 |
8.0 |
29.6 |
22.5 |
| Full CPI: Nonregulated services | 9.0 |
8.1 |
18.2 |
25.8 |
21.0 |
35.0 |
Table 3: Inflation variance decomposition - Panel 3: Crisis (January 1995 - June 1999)
Inflation: Average |
Inflation: Average |
Share of Inflation Variance (%): TDP |
Share of Inflation Variance (%): SDP1 |
Share of Inflation Variance (%): SDP2 |
Share of Inflation Variance (%): Other |
|
|---|---|---|---|---|---|---|
| Full CPI | 21.4 |
13.8 |
34.6 |
9.6 |
30.3 |
25.5 |
| Full CPI: Nonregulated goods | 22.5 |
16.1 |
38.8 |
6.7 |
27.4 |
27.1 |
| Full CPI: Nonregulated goods: Unprocessed food | 20.1 |
18.3 |
88.0 |
1.2 |
10.3 |
0.5 |
| Full CPI: Nonregulated goods: Processed food | 24.0 |
20.8 |
26.4 |
12.4 |
30.4 |
30.9 |
| Full CPI: Nonregulated goods: Nonenergy ind. goods | 23.2 |
16.3 |
17.7 |
16.5 |
26.6 |
39.2 |
| Full CPI: Nonregulated services | 18.4 |
10.9 |
15.4 |
41.5 |
27.8 |
15.3 |
Table 3: Inflation variance decomposition - Panel 4: Postcrisis (July 1999 - June 2002)
Inflation: Average |
Inflation: Average |
Share of Inflation Variance (%): TDP |
Share of Inflation Variance (%): SDP1 |
Share of Inflation Variance (%): SDP2 |
Share of Inflation Variance (%): Other |
|
|---|---|---|---|---|---|---|
| Full CPI | 5.5 |
4.7 |
82.7 |
0.9 |
5.7 |
10.6 |
| Full CPI: Nonregulated goods | 3.9 |
5.0 |
94.9 |
0.2 |
-2.3 |
7.2 |
| Full CPI: Nonregulated goods: Unprocessed food | 2.8 |
14.8 |
92.3 |
0.0 |
0.0 |
7.7 |
| Full CPI: Nonregulated goods: Processed food | 4.3 |
4.4 |
92.8 |
1.5 |
2.7 |
3.1 |
| Full CPI: Nonregulated goods: Nonenergy ind. goods | 4.3 |
3.8 |
86.4 |
1.1 |
10.1 |
2.5 |
| Full CPI: Nonregulated services | 10.1 |
8.3 |
11.3 |
32.6 |
17.3 |
38.8 |
Notes: The full CPI includes all nonregulated goods and services less housing rents and product categories containing an insufficient number of individual observations.
As I have shown, the high inflation episode drives the
correlation between ![]() and
and ![]() , which becomes essentially zero as inflation levels
off. This elusive relationship has a direct consequence for the
variance breakdown. When restricted to the low-inflation period
after mid-1999, the share of inflation variance represented by the
TDP climbs to 82.7%. This proportion reaches
94.9% when services are excluded, a figure
comparable to Klenow and Kryvtsov's finding for the United States.
In contrast, the proportion is lowest when inflation is most
variable. The short subperiod before 1995 represents an
intermediate case. Taken together, these findings help indicate
when time-dependent models have realistic implications for the
inflation variance. As Figure 8 showed,
there is a tight, almost linear relation between
, which becomes essentially zero as inflation levels
off. This elusive relationship has a direct consequence for the
variance breakdown. When restricted to the low-inflation period
after mid-1999, the share of inflation variance represented by the
TDP climbs to 82.7%. This proportion reaches
94.9% when services are excluded, a figure
comparable to Klenow and Kryvtsov's finding for the United States.
In contrast, the proportion is lowest when inflation is most
variable. The short subperiod before 1995 represents an
intermediate case. Taken together, these findings help indicate
when time-dependent models have realistic implications for the
inflation variance. As Figure 8 showed,
there is a tight, almost linear relation between ![]() and
and ![]() when the latter is below
10-15%. This strong comovement drives the
variance decomposition during the low-inflation period. Then, as
inflation takes off,
when the latter is below
10-15%. This strong comovement drives the
variance decomposition during the low-inflation period. Then, as
inflation takes off, ![]() becomes more
positively correlated with
becomes more
positively correlated with ![]() and
and
![]() . This relationship induces a
substantial role for terms involving
. This relationship induces a
substantial role for terms involving ![]() ,
especially for the covariance and higher-order terms.
,
especially for the covariance and higher-order terms.
As noted earlier, the time-dependent part accounts for most of the variance of unprocessed food inflation, presumably because the frequency is high even when inflation is low. This finding means there is little room for the frequency to adjust when inflation takes off. I uncover support for this conjecture at the product category level: The TDP term accounts for a larger share of the variance in product categories with especially frequent price adjustments.25
5.6 Effects of the VAT Change
Changes to value added taxes are observable events that can reveal precious information about how an economy adjusts in response to such shocks. On April 1, 1995, the generate rate of the VAT rose from 10 to 15% everywhere in Mexico, with the exception of cities located in a corridor along the northern and southern borders, as well as the whole Baja California. Mexican retailers are required to include the VAT in their sales prices. All else equal, an increase in the VAT squeezed retailer's profit margins, thereby creating an incentive for adjusting prices upward. In TDP models, this adjustment occurs only through larger price changes. In this section, I investigate whether this prediction was actually realized.
Two features make the April 1995 VAT increase particularly interesting. First, retailers were given a very short notice of the VAT change. The decree was adopted March 18 and published in the Diario on March 27. A large number of price quotes for March 1995 were collected before the public learned of the change and the tax was in full force when collection started in April. Second, the change did not affect all items and cities. Prices from excluded groups of products and geographic areas can serve as controls to disentangle the effect of the VAT from other factors.
The results are presented in Figure 14. The sample was divided into four groups according to whether items are taxed rate or tax-exempt (respectively labelled "general rate" and "excluded items") and whether they are located in cities affected or unaffected by the change (labelled "Center" and "Border", respectively). Inflation rates, expressed in the graph as monthly rates, differed markedly across regions and goods in April 1995. The inflation rate of center cities exceeded the rate for border cities by 3.5 percentage points in the case of goods affected by the general rate. That same month, the difference was -0.6 percentage points for goods exempted from the VAT. These differences clearly indicate that most of the price adjustment occurred within a month. Notably, the adjustment occurred mainly through more frequent rather than larger price changes. For the items taxed under the general rate, the fraction of price changes in April is 76.2% for the cities affected by the change, and 39.2% for the cities where the rate remained at 10%. For items that are taxed-exempt, the frequency of price changes are very similar across regions where the tax rate increased (47.1%) and where it did not (47.9%). The average magnitude of price change is similar across regions, which might be surprising given that I previously noticed a spike in the price change distribution of items in cities affected by the change. The effect of the tax change on the average price increase was minute.
Figure 14. Effect of April 1, 1995 VAT change
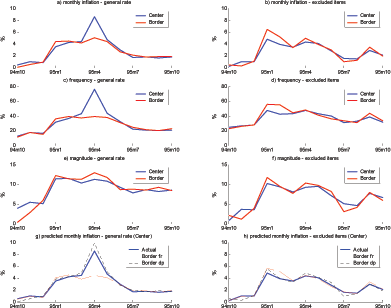
The sharp increase in the frequency of price changes was the
main source of inflation pass-through. Direct proof of this
conclusion appears at the bottom of Figure 14, where three
inflation rates are reported. The first is the actual inflation
rate for the cities affected by the tax; this rate is the product
of the frequency and magnitude of price changes,
![]() . The
other two series are obtained by replacing
. The
other two series are obtained by replacing
![]() and
and
![]() by their respective values
for cities along the borders. The three series are computed first
for items under the general rate and then repeated for tax-exempt
items. The predicted inflation rate is almost identical to the
actual rate when I replace the magnitude of price changes. However,
when I use the lower frequency of border cities, there is no
increase in inflation.
by their respective values
for cities along the borders. The three series are computed first
for items under the general rate and then repeated for tax-exempt
items. The predicted inflation rate is almost identical to the
actual rate when I replace the magnitude of price changes. However,
when I use the lower frequency of border cities, there is no
increase in inflation.
Note that inflation rose more rapidly in border cities. This behavior is consistent with the greater exchange rate pass-through along the border. I found the difference in inflation to be particularly large for Food and nonalcoholic beverages and Restaurants and hotels. Although items in the latter category usually are classified as nontradables, the importance of tourism in border cities might have contributed to the greater pass-through.
Several authors have noted the effect of VAT changes on the
frequency of price changes.26 The Mexican tax change is
especially interesting, however, because of its unusually large
size and the regional differences in its application. The change in
the frequency, over 35 percentage points, is larger than any other
documented frequency change. Furthermore, because price decreases
were nearly absent in April 1995, one could conjecture that their
buffering effect did little to prevent the aggregate frequency from
rising. However, VAT hikes do not seem to be associated with
unusually large falls in ![]() in Europe.
in Europe.
6. International Comparisons
A priori, it is difficult to know how the findings for Mexico might generalize to other countries because there are no comparable studies with similar product and inflation coverage. In this section, I construct baskets of goods similar to the ones used for the low-inflation studies in the United States and Euro area studies. I also break down the Mexican sample into low- and high-inflation subperiods to provide more direct comparisons. In show that Mexico is an intermediate case between the United States and the Euro area in terms of price stickiness. I then compare my results with the sectorial studies done at high inflation.
6.1 Low-Inflation Studies
6.1.1 Time and Product Coverage
Three time periods of 24 months were selected. The first starts in March 1995, immediately after the CPI basket revision, and captures a period when inflation averaged nearly 30%. The second period covers the last two years of data before the second revision of the CPI basket in 2002. The third period runs from January 2003 to December 2004. The inflation rate over the last two samples is only a few percentage-points higher than the United States and Euro area studies. The third period is the most directly comparable to the U.S. and Euro-area studies in terms of methodology and product coverage.
Statistics for the frequency of price changes are computed for two different baskets. The first, the BK basket, has a product coverage similar to the one Bils and Klenow (2004) used for the United States. Its construction was detailed in Section 2.2.27 This sample covers 63.4% of Mexican consumption expenditures before the 2002 revision of the CPI basket. In the third time period, I use all categories with individual observations, resulting in a CPI coverage of 65.9%. In comparison, Bils and Klenow's sample covers 68.9% of U.S. consumption expenditures. To produce comparable statistics, I classified the Mexican product categories according to the BLS classification system used from 1989 to 1997.
The second basket matches the one used by the Inflation Persistence Network and is consequently labeled the IPN basket. This smaller basket is restricted to 50 product categories to facilitate comparisons across countries. Categories are representative of 2-digit groups in the Classification Of Individual COnsumption by Purpose (COICOP) and of the following five main components: unprocessed food, processed food, energy, nonenergy industrial goods (NEIG) and services. Details of the basket construction are relegated to Appendix C.
6.1.2 Results
The results are presented in Table 4. Because they are very similar for the BK and IPN baskets, I will focus on the broad findings. The CPI inflation rate averages 27.9% in Mexico over the first time period, a rate well above the 2.3% and 1.6% averages in the U.S. and Euro-area samples, respectively. Not surprisingly, the aggregate frequency of price changes is much higher in Mexico, averaging 32.5% in the BK sample, more than twice the Euro area average, and 6 percentage points higher than the United States. The higher frequency is reflected in terms of shorter durations. The median duration in Mexico is about three months compared with 4.6 months in the United States and 10.6 months in the Euro area. I also report the average duration and the inverse of the aggregate frequency. Although both are sensitive to the underlying heterogeneity, they nevertheless confirm the previous ranking. Notably, the difference between the mean and the median declines considerably during the high-inflation period.
Table 4: Comparison of price stickiness in Mexico, the United States and the Euro area
| Period | Mexico: Mar 1995 - Feb 1997 |
Mexico: Jul 2000 - Jun 2002 |
Mexico: Jan 2003 - Dec 2004 |
United States: Jan 1995 - Dec 1997 |
Euro area: Jan 1996 - Dec 2000 |
|---|---|---|---|---|---|
| Average inflation | 27.9 |
4.4 |
3.8 |
2.3 |
1.6 |
| Aggregate frequency: BK sample | 32.5 |
24.9 |
22.6 |
26.1 |
15.3 |
| Aggregate frequency: IPN sample | 32.9 |
24.0 |
19.9 |
24.8 |
15.1 |
| Duration: Mean Duration: BK sample | 3.1 |
6.6 |
7.0 |
6.7 |
n.a |
| Duration: Mean Duration: IPN sample | 3.7 |
6.6 |
7.9 |
n.a |
13.0 |
| Duration: Inverse of aggregate frequency: BK sample | 3.1 |
4.0 |
4.4 |
3.8 |
6.5 |
| Duration: Inverse of aggregate frequency: IPN sample | 3.0 |
4.2 |
5.0 |
4.0 |
6.6 |
| Duration: Median duration: BK sample | 3.0 |
5.6 |
5.7 |
4.6 |
n.a. |
| Duration: Median duration: IPN sample | 2.6 |
5.7 |
5.2 |
n.a. |
10.6 |
Note: Figures for the United States and Euro area come from Dhyne et al (2005).
In the second and third time periods, Mexican inflation rates are much closer to their American and European counterparts than in the first time period. The frequency of price changes falls a few percentage points below that of the United States despite a slightly higher inflation rate, and it stops about five to 10 percentage points higher than that of the Euro area depending on the basket considered. Overall, the Mexican economy appears less flexible than the U.S. economy and more flexible than the Euro-area economy for comparable inflation rates.
A higher aggregate frequency does not necessarily imply increased flexibility for prices at the product-category level, however. Indeed, differences in CPI composition may also play role because of the considerable heterogeneity at the sector level documented earlier. Table 5 reports the expenditure weights for major groups of products under the BLS and COICOP classifications. The weights represent the shares of the BK and IPN baskets each special group accounts for. The most striking difference is the relatively large share of Food in the Mexican consumption basket. In contrast, both Durable goods and Services account for smaller shares in Mexico than in the United States.
Table 5: Expenditures weights of special aggregates - Panel 1: BK Sample
| Base year | Mexico: 1993 |
Mexico: 2000 |
United States: 1995 |
|---|---|---|---|
| Share of total consumption expenditures | 63.4 |
65.9 |
68.9 |
| Nondurable goods | 72.4 |
65.1 |
44.1 |
| Durable goods | 11.7 |
11.6 |
14.7 |
| Services | 15.9 |
23.3 |
41.2 |
| Food | 49.4 |
41.2 |
22.6 |
| Home furnishing | 12.0 |
15.6 |
24.9 |
| Apparel | 10.7 |
8.6 |
8.5 |
| Transportation | 6.8 |
6.7 |
23.1 |
| Medical care | 4.9 |
6.1 |
7.5 |
| Entertainment | 3.8 |
5.1 |
6.2 |
| Other | 12.4 |
16.8 |
7.2 |
Table 5: Expenditures weights of special aggregates - Panel 2: IPN Sample
| Base year | Mexico: 1993 |
Mexico: 2000 |
Euro Area: 1995 |
|---|---|---|---|
| Unprocessed food | 19.2 |
13.5 |
9.3 |
| Processed food | 20.3 |
18.5 |
14.3 |
| Energy | 6.5 |
8.0 |
5.8 |
| Nonenergy industrial goods | 24.7 |
25.8 |
34.4 |
| Services | 29.2 |
34.2 |
36.2 |
Note: Weights with base year 1993 and 2000 were introduced by Banxico during the March 1995 and July 2002 revisions of the CPI basket.
Table 6 provides frequency statistics for the main BLS special groups, and 2-digit COICOP groups. For the high-inflation period, the frequency of price changes for the Food, Home Furnishing, Medical Care and Others categories was higher in Mexico than the United States.28 As inflation leveled, the frequency remained higher for Food and Other in Mexico, but was comparable to the United States or lower for all other special groups. With respect to the Euro area, prices appear more flexible in Mexico for all observed inflation levels, and for all 2-digit COICOP groups except Energy. The table also indicates how differences in composition affect the aggregate frequency of price changes. Holding the frequency of special groups constant, I computed the aggregate frequency that would have resulted if Mexico had had the same category weights as the United States and Euro area. For the BK sample, using the U.S. weights for Mexico lowers its frequency from 32.5% to 31.7% for the high-inflation period and from 22.6% to 20.0% for the lowest inflation period. In the case of the IPN basket, the frequency would have dropped from 32.9% to 28.9% for the high-inflation period. In short, the relatively large share of CPI expenditures for food, particularly unprocessed food, contributes to the overall flexibility of consumer prices in Mexico.
Table 6: Comparison of the frequency of price changes between Mexico, the United States and the Euro area for some special groups - Panel 1: BK Sample
| Period | Mexico: Mar 1995 - Feb 1997 |
Mexico: Jul 2000 - Jun 2002 |
Mexico: Jan 2003 - Dec 2004 |
United States: Jan 1995 - Dec 1997 |
|---|---|---|---|---|
| Average inflation | 27.9 |
4.4 |
3.8 |
2.3 |
| Nondurable goods | 35.7 |
29.4 |
28.2 |
29.9 |
| Durable goods | 35.8 |
16.9 |
17.8 |
30.3 |
| Services | 15.1 |
10.5 |
9.1 |
20.6 |
| Major groups: Food | 39.5 |
35.2 |
33.8 |
25.3 |
| Major groups: Home furnishing | 27.1 |
17.5 |
17.2 |
26.4 |
| Major groups: Apparel | 27.0 |
14.4 |
9.1 |
29.2 |
| Major groups: Transportation | 44.6 |
19.6 |
19.9 |
39.5 |
| Major groups: Medical care | 17.1 |
10.2 |
11.4 |
9.3 |
| Major groups: Entertainment | 11.1 |
7.3 |
11.8 |
11.3 |
| Major groups: Other | 20.1 |
14.6 |
15.2 |
11.0 |
| Aggregate frequency: United States weights | 31.7 |
20.3 |
20.0 |
26.1 |
| Aggregate frequency: Mexico weights | 32.5 |
24.9 |
22.6 |
- |
Table 6: Comparison of the frequency of price changes between Mexico, the United States and the Euro area for some special groups - Panel 2: IPN Sample
| Period | Mexico: Mar 1995 - Feb 1997 | Mexico: Jul 2000 - Jun 2002 | Mexico: Jan 2003 - Dec 2004 | Euro area: Jan 1996 - Dec 2000 |
|---|---|---|---|---|
| Average inflation | 27.9 | 4.4 | 3.8 | 1.6 |
| Unprocessed food | 54.7 | 55.0 | 26.4 | 28.3 |
| Processed food | 34.5 | 20.0 | 12.5 | 13.7 |
| Nonenergy industrial goods | 55.5 | 39.3 | 18.7 | 9.2 |
| Energy | 28.8 | 16.8 | 54.9 | 78.0 |
| Services | 15.8 | 8.9 | 6.1 | 5.6 |
| Aggregate frequency: Euro area weights | 28.9 | 19.3 | 26.4 | 15.1 |
| Aggregate frequency: Mexico weights | 32.9 | 24.0 | 19.9 | - |
Notes: The U.S. statistics are computed using the figures in Bils and Klenow (2004) and are inclusive of sales. The figures for the Euro area are from Dhyne et al. (2005).
6.2 High-Inflation Studies
The amount of empirical evidence on the setting of consumer prices during high inflation is very limited. Lach and Tsiddon (1992) consider a sample of 26 food products in Israel (mainly meat and alcohol products). For the period 1978-79, 39.5% of prices changed in their sample every month while the annual inflation rate averaged 60%. This figure is the same as the average frequency of price changes for food products in my high-inflation sample, even though the average inflation rate in Mexico (27.9%) was only half that of Israel. A related study featuring Konieczny and Skrzypacz (2005), who study the transition from a planned to a market economy in Poland. They use monthly data on 52 products, of which 37 are food products, from January 1990 to December 1996. They report a monthly frequency of price change of 59 as inflation peaked at 249% in 1990. In contrast, the frequency of price changes was 30% in 1996 when inflation averaged 19%. Interestingly, the frequency was only from 35% in 1993 although inflation was double its 1996 rate (38%). This finding supports the idea that movements in the frequency of price changes are dampened in the food sector due to the presence of price decreases. Burstein, Eichenbaum, and Rebelo (2005) conduct a weekly survey of supermarket prices for a broader basket covering 58 good categories in Argentina from March to December 2002, when the annual inflation rate averaged 33%. They find a 66.5% median frequency of price changes. This percentage is much larger than what I find for Mexico. Part of the difference is likely explained by differences in the type of outlets surveyed.29
7. Empirical Performance of Menu-Cost Models
In this last section, I calibrate a discrete-time version of the menu-cost model developed by Golosov and Lucas (2003) . The objective is to investigate whether this state-dependent model can correctly predict the average magnitude and frequency of price changes at levels of inflation similar to the ones observed in Mexico over my sample period. This particular model was chosen because it embeds three desirable features. First, the presence of menu costs gives rise to infrequent, lumpy nominal price adjustments. Second, it leaves the frequency of price changes free to vary with inflation, a feature not found in most time-dependent models and in state-dependent models in which nominal prices adjust every period. Third, the model contains idiosyncratic technology shocks generating a distribution of both positive and negative price changes. The first two features means that, a priori, both the frequency and magnitude of price changes can respond to a change in inflation, while the simultaneous presence of price increases and decreases might help to generate an initially slow rise in the frequency of price changes as inflation takes off from a low level. Throughout the discussion, I focus on a stationary equilibrium with constant aggregate inflation. A discussion of the model's calibration is relegated to Appendix D.
7.1 Economic Environment
The economy consists of three types of agents. An
infinitely-lived representative household supplies labor and
consumes a basket of differentiated consumption goods. These goods
are produced by a continuum of monopolistically competitive firms
subject to idiosyncratic technology shocks, the only source of
uncertainty in the economy. Finally, there is a monetary authority
whose only role is to expand the money supply at a constant rate
![]() .
.
7.1.1 Households
The problem of the household is to choose a sequence for
consumption,
![]() , and an hours worked,
, and an hours worked,
![]() , in order to maximize
its present discounted utility,
, in order to maximize
its present discounted utility,
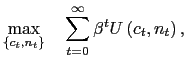
subject to a budget constraint
and a simple cash-in-advance constraint
The variable ![]() is the price index at time
is the price index at time
![]() ,
, ![]() is the wage
rate and
is the wage
rate and ![]() are the household's cash balances that
correspond to the money stock. Real profits,
are the household's cash balances that
correspond to the money stock. Real profits, ![]() , are remitted every period by intermediate firms. The
budget constraint states that consumption spending equals the sum
of a household's labor income and profits received from firms.
Following Golosov and Lucas, I further assume that utility is
separable, logarithmic in consumption and linear in labor:
, are remitted every period by intermediate firms. The
budget constraint states that consumption spending equals the sum
of a household's labor income and profits received from firms.
Following Golosov and Lucas, I further assume that utility is
separable, logarithmic in consumption and linear in labor:
The household's problem is fully static. In the stationary equilibrium, all aggregate real quantities are constant while aggregate nominal quantities grow at the same rate as the money stock. Under the above assumptions, the intratemporal Euler equation implies that the wage rate is proportional to the stock of money.
Consumption is a composite of intermediate consumption goods aggregated using a Dixit-Stiglitz specification
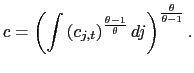
The demand for individual consumption goods must satisfy
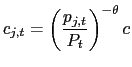
where the price index is given by
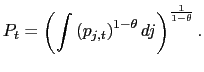
7.1.2 Intermediate Firms
There is a continuum of measure one of monopolistically
competitive firms. At the beginning of the each period, firms draw
idiosyncratic productivity shocks. They then decide whether to keep
selling their goods at the same nominal price as in the previous
period, or to incur a menu cost (expressed in units of labor),
![]() , in order to optimize their price. Once
prices are set for the period, firms must satisfy the demand at
those prices.
, in order to optimize their price. Once
prices are set for the period, firms must satisfy the demand at
those prices.
The production function of the ![]() firm is
linear in labor
firm is
linear in labor
I assume that labor productivity,
![]() , evolves according to
, evolves according to
where technological innovations,
![]() , are drawn from a normal
distribution .
, are drawn from a normal
distribution .
![]()
Firms maximize the present discounted value of their profits. It
is convenient to express their problem recursively in order to
solve it using dynamic programming techniques. Let
![]() be the Bellman
equation of an optimally behaving firm just before it decides
whether to change its nominal price or not. The state of the firm
comprises its nominal price relative to the price index,
be the Bellman
equation of an optimally behaving firm just before it decides
whether to change its nominal price or not. The state of the firm
comprises its nominal price relative to the price index,
![]() , and its technological level,
, and its technological level, ![]() . The value function is given by
. The value function is given by
where
![]() is the value
function associated with the firm's decision to keep its nominal
price constant in the current period and behave optimally
thereafter, and
is the value
function associated with the firm's decision to keep its nominal
price constant in the current period and behave optimally
thereafter, and
![]() is the
corresponding value function of a firm choosing to optimize its
nominal price in the current period. These functions are expressed
as
is the
corresponding value function of a firm choosing to optimize its
nominal price in the current period. These functions are expressed
as
and
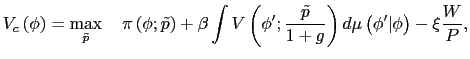
respectively. The first right hand-side term,
![]() , is the period
gross profit function. Taking into account the production function
and the demand curve, it is expressed as
, is the period
gross profit function. Taking into account the production function
and the demand curve, it is expressed as
![]() . The integral gives the expected value function in the next
period, taking into account price erosion due to inflation and the
distribution of technology shocks.
. The integral gives the expected value function in the next
period, taking into account price erosion due to inflation and the
distribution of technology shocks.
7.2 Main Results
As described in Appendix D, the model is calibrated to match the average frequency and magnitude of price changes over the last two years of the sample, a period when annual inflation averaged 4.5 percent. The model's predictions are then recorded for steady state inflation rates ranging from 0 to 50 percent. Overall, the model matches remarkably well the behavior of the average frequency and magnitude of price changes. The fit of the frequency of price changes is reported in Figure 15. The diamonds, squares and triangles represent the average monthly frequency of price changes, increases and decreases, respectively, for each calendar year in the sample. The lines indicate the corresponding predictions of the model. As inflation is increased from a low to a high level, the model produces a slow rise in the average monthly frequency of price changes similar to the one observed in the data. The main outlier is the year 1994 for which the model predicts a frequency of price changes around 26% compared to 21.2% in the data. This poor fit may be related to data collection and sample composition issues (see Section 3 for a discussion). The model fares rather well at reproducing the underlying opposite movements in the average frequency of price increases and decreases. The model's simple calibration slightly underpredicts the size of the initial fall in the frequency of price changes and simultaneous rise in the occurrence of price increases, although any strong judgement on this aspect is also potentially subject to data issues.
Figure 15. Average frequency of price changes predicted by the model compared to the sample annual averages
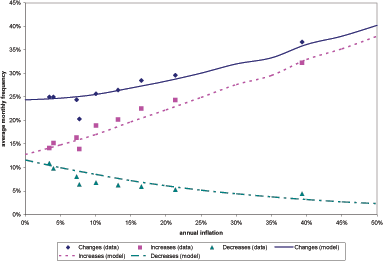
As shown in Figure 16, the model fits equally well the average magnitude of price changes. When inflation is low, the average magnitude of price changes responds almost linearly to a change in steady state inflation, a counterpart to the weak response of the frequency of price changes. Interestingly, the goodness of fit arises despite much poorer fits of the average magnitudes of price increases and decreases. Figure 16 thus hints that in the model, as it is the case in the data, movements in the average magnitude of price changes are driven mainly by changes to the relative occurrence of price increases and decreases, not by movements in the average absolute magnitude.
Figure 16. Average magnitude of price changes, increases and decreases predicted by the model compared to the sample's annual averages
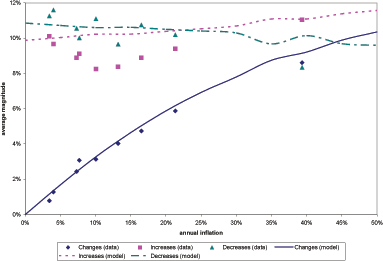
It has been argued by Rotemberg (2004) that menu-cost models often
imply movements in the size of price changes that are too
large compared to the data. Rotemberg illustrates this point
using a version of the Sheshinski and Weiss (1977) menu-cost model in which
idiosyncratic shocks are absent. Under a wide range of parameter
values, he finds that this model overpredicts movements in the size
of price changes as average inflation varies. This conclusion
clearly does not apply to the menu-cost model considered above: The
average absolute magnitude of price changes moves little with
inflation. This is despite a clear prediction of menu-cost models
that the width of the ![]() band widens when steady
state inflation increases30. In the steady state of the
Sheshinski and Weiss model, the average and absolute magnitude of
price changes are identical because all price changes are positive
whenever inflation is positive and predictable. In the
Golosov-Lucas model, the two statistics are disconnected due to the
presence of price decreases.
band widens when steady
state inflation increases30. In the steady state of the
Sheshinski and Weiss model, the average and absolute magnitude of
price changes are identical because all price changes are positive
whenever inflation is positive and predictable. In the
Golosov-Lucas model, the two statistics are disconnected due to the
presence of price decreases.
As I have shown, the Golosov-Lucas model is consistent with key features of individual consumer price setting at both relatively low and high levels of inflation. Despite this success, the model suffers from several known inconsistencies with the data. As discussed by Golosov and Lucas (2003) and Midrigan (2006), the model generates too few small price changes and has an implausibly small amount of intrinsic persistence. Nevertheless, my findings offer hope that a state-dependent model addressing these short-comings, such as a model in which the hypotheses of constant and time-invariant menu costs are relaxed, might provide a good fit the average magnitude and frequency of price changes if it embeds a distribution of positive and negative price changes.
8. Conclusion
This paper provides new evidence about the relationship between inflation and the adjustment of individual consumer prices. It uses a large dataset of Mexican consumer prices covering episodes of both low and high inflation, as well as the transition between the two. The overall portrait is of an economy sharing several characteristics of time dependent models when inflation is low (below 10-15%), while displaying strong state dependence when inflation is high (above 10-15%).
At low inflation levels, the frequency of price changes varies little and its relationship to inflation is elusive. In contrast, the average magnitude of price change covaries strongly with inflation. As a result, movements in the frequency account for little of the inflation variance of inflation. Thus, at low inflation levels, the economy resembles time-dependent models with a constant frequency of price changes. When annual inflation runs above 10-15%, however, inflation becomes positively correlated with the frequency of price changes: A one percentage-point increase in the annual inflation rate is associated with a roughly 0.4-percentage-point increase in the frequency of price changes of nonregulated goods. Variations in both the frequency and magnitude of price changes are key in determining the variance of inflation. In this sense, my analysis provides a natural distinction between low- and high-inflation environments: In a low-inflation environment, price decreases matter.
Behind the radically different behaviors of the low- and high-inflation economies lies the central role of price decreases. As inflation varies, opposite movements in the frequency of price decreases offset movements in the frequency of price increases. When inflation is low, this mechanism is strong enough to render the frequency of price changes of nonregulated goods unresponsive to movements in inflation. When inflation is high, however, too few price decreases are left to counterbalance movements in the frequency of price increases. In this situation, the economy displays strong state dependence with respect to inflation.
Several authors (e.g., Dhyne et al. (2005)) have argued that macroeconomics models should incorporate at least two sectors. The first sector, which corresponds to food products in Mexico, features very flexible prices that respond to frequent idiosyncratic shocks. The other sectors encompass a greater degree of price stickiness to capture items with infrequent and lumpy price adjustments. My analysis reinforces this view by showing the central role of price decreases in the dynamic of inflation in the sectors displaying the largest price flexibility.
One important challenge is to find a price-setting model offering empirically plausible predictions at both low and high levels of inflation. I have shown that the Golosov-Lucas menu-cost model offers some important success. The key to the model's good fit of the average frequency and magnitude of price changes is the joint presence of nominal rigidities and idiosyncratic shocks generating a distribution of both negative and positive nonzero price changes that is free to move with the level of inflation. Note that time-dependent models such as Calvo are not inconsistent with the presence of a distribution of both positive and negative price changes, however. In fact, it is possible to augment the baseline Calvo model with idiosyncratic technology shocks and obtain, after linearization, the same reduced-form equation for inflation. While this alternative model generates movements in the relative share of price decreases and increases, it fails to produce a rise in the frequency of price changes as inflation takes off.
Finally, my analysis suggests the "right" price-setting model might depend importantly on the characteristics of the shock at hand. I documented that a hike in the value added tax led to an almost complete pass-through after one month, most of which occurred through a high frequency of price changes. The speed of transmission was much higher than the speed commonly assumed for monetary and technology shocks. Price-setting models generating highly persistent responses to all types of shocks would mispredict the price adjustment entirely.
References
Aucremanne, L. and E. Dhyne (2004). How frequently do prices change? Evidence based on the micro data underlying the Belgian CPI. European Central Bank, Working Paper Series: 331.
Aucremanne, L. and E. Dhyne (2005). Time-dependent versus state-dependent pricing - a panel data approach to the determinants of Belgian consumer price changes. European Central Bank, Working Paper Series: 462.
Baharad, E. and B. Eden (2004). Price rigidity and price dispersion: Evidence from micro data. Review of Economic Dynamics 7(3), 613-41.
Baudry, L., H. L. Bihan, P. Sevestre, and S. Tarrieu (2004). Price rigidity. Evidence from the French CPI micro-data. European Central Bank, Working Paper Series: 384.
Bils, M. and P. J. Klenow (2004). Some evidence on the importance of sticky prices. Journal of Political Economy 112(5), 947-985.
Burstein, A., M. Eichenbaum, and S. Rebelo (2005). Large devaluations and the real exchange rate. Journal of Political Economy 113(4), 742-84.
Burstein, A. T. (2006). Inflation and output dynamics with state-dependent pricing decisions. Journal of Monetary Economics 53(7) 1235-1257.
Calvo, G. A. (1983). Staggered prices in a utility-maximizing framework. Journal of Monetary Economics 12(3), 383-98.
Chari, V. V., P. J. Kehoe, and E. R. McGrattan (2002). Can sticky price models generate volatile and persistent real exchange rates? Review of Economic Studies 69(3), 533-63.
Christiano, L. J., M. Eichenbaum, and C. L. Evans (2005). Nominal rigidities and the dynamic effects of a shock to monetary policy. Journal of Political Economy 113(1), 1-45.
Danziger, L. (1999). A dynamic economy with costly price adjustments. American Economic Review 89(4), 878-901.
Dhyne, E., L. J. Alvarez, H. L. Bihan, G. Veronese, D. Dias, J. Hoffmann, N. Jonker, P. Lunnemann, F. Rumler, and J. Vilmunen (2005). Price setting in the euro area: some stylized facts from individual consumer price data. European Central Bank Working Paper Series: 524.
Dias, M., D. Dias, and P. Neves (2004). Stylised features of price setting behaviour in Portugal: 1992 - 2001. European Central Bank Working Paper Series: 332.
Dotsey, M., R. G. King, and A. L. Wolman (1999). State-dependent pricing and the general equilibrium dynamics of money and output. Quarterly Journal of Economics 114(2), 655-90.
Eden, B. (1994). The adjustment of prices to monetary shocks when trade is uncertain and sequential. Journal of Political Economy 102(3), 493-509.
Edwards, S. (1997). The Mexican Peso Crisis? How Much Did We Know? When Did We Know It? National Bureau of Economic Research, Working Papers: 6334.
Eichenbaum, M. and J. D. M. Fisher (2004). Evaluating the Calvo Model of Sticky Prices. National Bureau of Economic Research, Working Papers: 10617.
Gali, J. and M. Gertler (1999). Inflation dynamics: A structural econometric analysis. Journal of Monetary Economics 44(2), 195-222.
Gertler, M. and J. Leahy (2006). A Phillips Curve with an Ss Foundation. National Bureau of Economic Research, Working Papers: 11971.
Golosov, M. and R. E. Lucas (2003). Menu Costs and Phillips Curves. National Bureau of Economic Research, Working Papers: 10187.
Hoffmann, J. and J.-R. Kurz-Kim (2006). Consumer price adjustment under the microscope - Germany in a period of low inflation. European Central Bank Working Paper Series: 652.
Instituto Nacional de Estad�stica Geograf�a e Inform�tica (various editions). S�ntesis metodol�gica de la encuesta nacional de ingresos y gastos de los hogares. Instituto Nacional de Estad�stica Geograf�a e Inform�tica.
Jonker N., C. Folkertsma, and H. Blijenberg (2004). An empirical analysis of price setting behaviour in the Netherlands in the period 1998-2003 using micro data. European Central Bank Working Paper Series: 413.
Klenow, P. J. and O. Kryvtsov (2005). State-Dependent or Time-Dependent Pricing: Does it Matter for Recent U.S. Inflation? National Bureau of Economic Research, Working Papers: 11043.
Konieczny, J. D. and A. Skrzypacz (2005). Inflation and price setting in a natural experiment. Journal of Monetary Economics 52(3), 621-32.
Lach, S. and D. Tsiddon (1992). The behavior of prices and inflation: An empirical analysis of disaggregated price data. Journal of Political Economy 100(2), 349-89.
Lucas, R. E. and M. Woodford (1993). Real Effects of Monetary Shocks in an Economy with Sequential Purchases. National Bureau of Economic Research, Working Papers: 4250.
�lvarez, L. J. and I. Hernando (2006). Price setting behaviour in Spain: Evidence from consumer price micro-data. Economic Modelling 23(4), 699-716.
Mackowiak, B. and M. Wiederholt (2004). Optimal Sticky Prices under Rational Inattention. Collaborative Research Center Discussion Papers: 649.
Mankiw, N. G. and R. Reis (2002). Sticky information versus sticky prices: A proposal to replace the new keynesian phillips curve. Quarterly Journal of Economics 117(4), 1295-1328.
Midrigan, V. (2006). Menu Costs, Multi-Product Firms, and Aggregate Fluctuations. Mimeo, Ohio State University.
Organisation for Economic Co-operation and Development (2000). OECD economic surveys, 1999-2000: Mexico.
Rotemberg, J. J. (2002). Customer Anger at Price Increases, Time Variation in the Frequency of Price Changes and Monetary Policy. National Bureau of Economic Research, Working Papers: 9320.
Rotemberg, J. J. (2004). Fair Pricing. National Bureau of Economic Research, Working Papers: 10915.
Sheshinski, E. and Y. Weiss (1977). Inflation and costs of price adjustment. Review of Economic Studies 44, 287-303.
Sims, C. A. (2003). Implications of rational inattention. Journal of Monetary Economics 50(3), 665-90.
Smets, F. and R. Wouters (2004). Comparing Shocks and Frictions in US and Euro Area Business Cycles: A Bayesian DSGE Approach. C.E.P.R. Discussion Papers: 4750.
Taylor, J. B. (1980). Aggregate dynamics and staggered contracts. Journal of Political Economy 88(1), 1-23.
A. Price Averaging
In Mexico, price collectors visit outlets four times every month to collect prices of food items, and they visit twice per month to collect prices for all other items. The prices published in the Diario are an average of the prices collected over the month. In this appendix, I first discuss how observing a price's average rather than its actual value complicates inferences about the timing and magnitude of price changes. I then describe how I filtered the data to make the results in this paper more directly comparable to results from studies using prices collected once per month.
A.1 Effects of Averaging on Frequency and Magnitude
Suppose a price collector observes the price of an item twice every month and then computes two time series. The first is a simple average of the prices collected over the month (the average-price series). The other contains the second price collected each month (the point-in-time series). The average-price series corresponds Banxico's current method, whereas point-in-time series are used in the United States and Euro area.
Changes to the average-price series typically are more frequent
and of a smaller magnitude than changes to the point-in-time
series. To illustrate this point, consider a price that is constant
over the months ![]() ,
, ![]() and
and
![]() , with the exception of a single
adjustment at month
, with the exception of a single
adjustment at month ![]() . If the price changes
before the first price is collected at
. If the price changes
before the first price is collected at ![]() , then both
prices collected over that month equal the new price. Thus, the
average- and point-in-time series are identical and correctly
reflect the timing and magnitude of the actual price change. If the
price change occurs between the two price collections, the
point-in-time series still accurately represents the actual price.
The average-price series, on the other hand, now displays
two price changes: one at month
, then both
prices collected over that month equal the new price. Thus, the
average- and point-in-time series are identical and correctly
reflect the timing and magnitude of the actual price change. If the
price change occurs between the two price collections, the
point-in-time series still accurately represents the actual price.
The average-price series, on the other hand, now displays
two price changes: one at month ![]() and one at
and one at
![]() . The average-price series records a
second price change because the average price at
. The average-price series records a
second price change because the average price at ![]() has increased by only half of the change in the actual price.
Finally, if the price adjustment occurs after the second
collection, both the average price and point-in-time series display
a change of the correct magnitude but with a one-month lag.31
has increased by only half of the change in the actual price.
Finally, if the price adjustment occurs after the second
collection, both the average price and point-in-time series display
a change of the correct magnitude but with a one-month lag.31
A.2 Filtration of Average Price Trajectories
In the above example, a price change detected at the second price collection created two consecutive price changes of equal magnitude in the average-price series. My strategy entails finding such patterns and constructing a trajectory for the last price collected over the month that matches the average price and minimizes the number of price changes.
A.2.1 Two consecutive price changes
Let ![]() be the unobserved
be the unobserved ![]() price of an item for which collection happens twice a
month, and let
price of an item for which collection happens twice a
month, and let
![]() be its
observed monthly average. Consider the case of two consecutive
price changes starting at month
be its
observed monthly average. Consider the case of two consecutive
price changes starting at month ![]() . (Additional price
changes might precede or follow them.) If
. (Additional price
changes might precede or follow them.) If
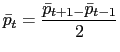
then I can construct a bimonthly sequence
![]() consistent with the observed average price sequence
consistent with the observed average price sequence
![]() that
features no price change at
that
features no price change at ![]() . I simply set
. I simply set
![]() and
and
![]() , and assume the
price change occurred between the two price collections at
, and assume the
price change occurred between the two price collections at
![]() so that
so that
![]() and
and
![]() . The point-in-time
sequence using the last price collected each month,
. The point-in-time
sequence using the last price collected each month,
![]() , features
no price changes at
, features
no price changes at ![]() .
.
Similarly, consider an item whose price is collected four times per month. If
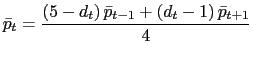
for some
![]() , I can
construct a sequence
, I can
construct a sequence
![]() consistent with the observed average price sequence that contains
no price change at
consistent with the observed average price sequence that contains
no price change at ![]() . As before, I set
. As before, I set
![]() and
and
![]() . I then assume a
unique price change was detected at the
. I then assume a
unique price change was detected at the ![]() visit
of the price collector at
visit
of the price collector at ![]() so that
so that
![]() and
and
![]() . The
point-in-time sequence
. The
point-in-time sequence
![]() contains no
change at
contains no
change at ![]() , and all its elements are strictly
positive. Moreover, aside from possible rounding issues, there is
at most one sequence
, and all its elements are strictly
positive. Moreover, aside from possible rounding issues, there is
at most one sequence
![]() consistent with
consistent with
![]() that
features no price change within periods
that
features no price change within periods ![]() and
and
![]() and contains a single change at
and contains a single change at
![]() .32
.32
A.2.2 Multiple price changes
Suppose now there are ![]() consecutive changes to
the average-price series starting at
consecutive changes to
the average-price series starting at ![]() . If the
price of the item is collected twice per month and the following
condition holds
. If the
price of the item is collected twice per month and the following
condition holds
then I can construct a unique bimonthly series
![]() that is (a) consistent with the observed monthly averages
that is (a) consistent with the observed monthly averages
![]() , (b)
features no price change within periods
, (b)
features no price change within periods ![]() and
and
![]() , (c) has at most one price change per
period detected at price collector's second visit and such that (d)
the point-in-time sequence
, (c) has at most one price change per
period detected at price collector's second visit and such that (d)
the point-in-time sequence
![]() features no
price change at
features no
price change at ![]() . This series is constructed by
setting
. This series is constructed by
setting
![]() ,
,
![]() , and then
constructing recursively
, and then
constructing recursively
for
![]() .
.
Similarly, consider the case of an item whose price is collected
four times per month. If there exists
![]() , with
, with
![]() , such that
the following relation holds:
, such that
the following relation holds:
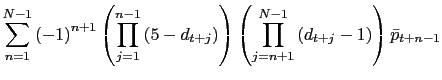
|
(2) | |
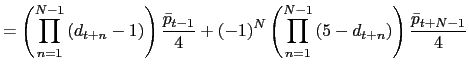
|
then I can construct a sequence of prices collected
![]() that is (a) consistent with the observed monthly averages
that is (a) consistent with the observed monthly averages
![]() , (b) features
no price change within periods
, (b) features
no price change within periods ![]() and
and ![]() , (c) contains a unique price change detected at
, (c) contains a unique price change detected at
![]() and such that (d) there is no change at
and such that (d) there is no change at ![]() in the
monthly point-in-time series
in the
monthly point-in-time series
![]() . I proceed
by setting
. I proceed
by setting
![]() ,
,
![]() and then
recursively computing
and then
recursively computing
![\begin{displaymath} p_{t+n}^{i}=\left\{ \begin{array}[c]{cc} p_{t+n-1}^{4} & \text{if }i<d_{t+n}\ \left( 4\bar{p}_{t+n}-\left( d_{t+n}-1\right) p_{t+n-1}^{4}\right) /\left( 5-d_{t+n}\right) & \text{otherwise} \end{array}\right. . \end{displaymath}](img349.gif)
Notice that if
(1)
or
(2)
is satisfied for some ![]() , there is no need
to adjust the average price at
, there is no need
to adjust the average price at ![]() . Unlike the case
of two consecutive price changes, there is no guarantee that
. Unlike the case
of two consecutive price changes, there is no guarantee that
![]() and
and
![]() have strictly positive entries. In the case of food items, there
also might be more than one sequence of detection times
have strictly positive entries. In the case of food items, there
also might be more than one sequence of detection times
![]() such that
condition
(2)
is satisfied. Thus, in the implementation of the filter, one
should make a correction only if it is plausible.
such that
condition
(2)
is satisfied. Thus, in the implementation of the filter, one
should make a correction only if it is plausible.
A.2.3 Implementation of the filter
The filter is applied on an average-price series to extract a
point-in-time series of the last price collected over the month.
The identifying assumptions are stringent enough to recover the
full set of prices collected,
![]() . Those
assumptions are:
. Those
assumptions are:
- a)
- The actual price changes at most once per month;
- b)
- If
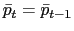 , then
, then
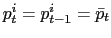 ;
; - c)
- For the first month
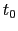 of a price trajectory,
of a price trajectory,
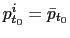 ;
; - d)
- Starting with
 , I identify all sequences
of
, I identify all sequences
of 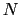 consecutive changes to the average-price
series. Starting with the oldest sequence of such consecutive price
changes,
consecutive changes to the average-price
series. Starting with the oldest sequence of such consecutive price
changes,
Bimonthly observations
if (1) holds and no elements in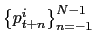 previously have been set to a particular value, then I construct a
candidate sequence of collected prices
previously have been set to a particular value, then I construct a
candidate sequence of collected prices
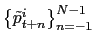 as
described above. If all elements of
as
described above. If all elements of
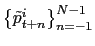 are
strictly positive, and the absolute price changes are smaller than
are
strictly positive, and the absolute price changes are smaller than
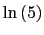 , I set
, I set
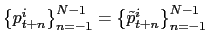 . I then repeat the procedure with the next sequence of
. I then repeat the procedure with the next sequence of 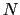 consecutive price changes.
consecutive price changes.
Food items
for all possible detection times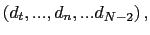
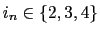 such that
(2)
holds, I construct a candidate sequence of collected prices
such that
(2)
holds, I construct a candidate sequence of collected prices
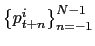 as
described above. I discard all sequences containing negative prices
or price changes greater than
as
described above. I discard all sequences containing negative prices
or price changes greater than
 . If some candidate
corrections remain, I randomly select one of them and use it to set
. If some candidate
corrections remain, I randomly select one of them and use it to set
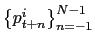 .
I repeat the procedure with the next sequence of
.
I repeat the procedure with the next sequence of 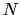 consecutive price changes.
consecutive price changes.
Once all cases with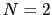 have been considered, I
repeat the entire procedure again with
have been considered, I
repeat the entire procedure again with
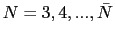 .
. - e)
- For all other cases, I set
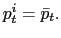
Once I have identified
![]() , I easily can
recover the price trajectories for the last price of the month,
, I easily can
recover the price trajectories for the last price of the month,
![]() or
or
![]() .
.
A.3 Discussion of the Filter
In practice, I allow the left- and right-hand sides of
(1)
and
(2)
to differ by up to 0.005 to account for the
rounding of prices. In the case of food items, I find a
multiplicity of candidate solutions in 3% of the
cases for which
(2)
is satisfied when ![]() . This proportion grows to
10% when
. This proportion grows to
10% when ![]() . As a robustness
check, I apply the filter for food items on the price trajectories
of bimonthly items. Any correction made with
. As a robustness
check, I apply the filter for food items on the price trajectories
of bimonthly items. Any correction made with ![]() or
or ![]() for some
for some
![]() indicates the filter spuriously eliminates
a price change not induced by averaging. The filter's performance
for various
indicates the filter spuriously eliminates
a price change not induced by averaging. The filter's performance
for various ![]() is presented in Table 7.
is presented in Table 7.
Table 7: Performance of the filter
| N | Cases | Exact | Mixed | Spurious |
|---|---|---|---|---|
| 2 | 142,730 | 94.5% | 1.0% | 4.5% |
| 3 | 7,138 | 75.8% | 2.1% | 22.1% |
| 4 | 1,415 | 32.9% | 2.9% | 64.2% |
| 5 | 596 | 12.2% | 4.0% | 83.7% |
In the case of two consecutive price changes, the filter
corrects 142,730 sequences. Of those sequences,
94.5% have a corresponding unique solution
with ![]() . For an additional 1.0% of cases, a solution with
. For an additional 1.0% of cases, a solution with ![]() is
mixed with a spurious solution. In less than one sequence out of
twenty, the criterion is satisfied but all candidate solutions have
either
is
mixed with a spurious solution. In less than one sequence out of
twenty, the criterion is satisfied but all candidate solutions have
either ![]() or
or ![]() . As
. As
![]() increases, the proportion of spurious
corrections grows quickly. The number of cases detected falls even
more rapidly, however, which suggests that leaving long sequences
of price changes uncorrected should not effect the overall results.
For those reasons, I set
increases, the proportion of spurious
corrections grows quickly. The number of cases detected falls even
more rapidly, however, which suggests that leaving long sequences
of price changes uncorrected should not effect the overall results.
For those reasons, I set ![]() for food items and
for food items and
![]() for bimonthly observations, which
are not subject to multiplicity issues. Before computing the
statistics in this paper, I drop the first four observations of
each price trajectory because they cannot be filtered for all
values of
for bimonthly observations, which
are not subject to multiplicity issues. Before computing the
statistics in this paper, I drop the first four observations of
each price trajectory because they cannot be filtered for all
values of ![]() considered.
considered.
Finally, all the results in this paper regarding the
relationship between inflation and price setting stand if I use the
published averaged data directly. The main effect of filtering is
to reduce the occurrence of price changes, lowering ![]()
![]() and
and ![]() while
increasing the average absolute magnitude of price changes
while
increasing the average absolute magnitude of price changes
![]() ,
, ![]() and
and
![]() .
.
B. Store Samples
Store samples are used to deal with the high turnover rate of individual items in the clothing categories. When the price of one item in the sample is no longer available, it is substituted by a similar item whose price has been tracked simultaneously. The average price of the sample is then rescaled to avoid creating a price change. The Diario does not report such substitutions. If no substitute is available in the store, the CPI agent might use the price of an item with similar characteristics from a different outlet. For 34 product categories, Banxico mainly reports prices pertaining to store samples rather than to individual items. Using the descriptions published in the Diario, I counted the number of items in each sample and discarded those that did not comprise exactly three elements, the most common sample size.
In this paper, I treat those observations are treated like individual items, which might create an upward bias in the frequency of price changes: Only one item price needs to change to induce a change in the average price in the sample. Moreover, the absolute magnitude of changes typically will be smaller than the underlying changes to individual prices. A lower bound on the aggregate frequency of price changes in the CPI was derived by assuming independent price changes within store samples.33 Under this assumption, the average biases are 1.3 percentage points for nonregulated products and 1.7 percentage points for nonregulated goods in the sample. All the main patterns found in the data are preserved.
C. IPN Basket
This appendix details the construction of products baskets similar to that of the Inflation Persistence Network. The original product categories in the IPN basket are listed in Tables 8 and 9 along with corresponding matches for Mexico. I use the same method as the IPN to construct product category weights. I first assign a 2-digit COICOP group and one of the five main components (unprocessed food, processed food, nonenergy industrial goods, energy and services) to each product category in the Mexican CPI, and exclude product categories under Health Care, Education, Cars and Electricity. I then compute the total weight of each stratum -- a combination of a COICOP group and main component -- for the remaining categories. Finally, the item weights in each stratum are set such that relative weights are the same as in the CPI and add up to the stratum share of all consumer expenses considered.34 The flip side of this procedure is that some product categories are attributed a disproportionate share of the basket weight because other categories selected within their stratum have relatively small expenditure shares. Milk is the clearest example, receiving more than 13% of the IPN basket weight while accounting for less than 2% of total CPI expenditures.
There are a few product categories in the IPN basket that lack direct matches in the Mexican CPI. Following the IPN procedure, substitutes are randomly chosen within the same stratum. Substitutes are sought before the 2002 basket revision for Mineral water, Dog Food, Fax Machine, Hotel Room and Videotape Hiring because no category with individual observations was available at this time35. Furthermore, Gasoline, Car Maintenance and Household Maintenance in the Mexican CPI are matched with several products in the IPN basket when no finer breakdown is available. In the case of Gasoline, I use city indexes because there is no alternative category with individual prices in the same stratum. Gas stations are required to post prices set by the Mexican government, and changes follow pre-established rules that are updated periodically. The Household Maintenance and Photographic items product categories from the Mexican CPI mixes both goods and services before 2002 and for the entire time period, respectively. Separate indexes for goods and services are computed by classifying each items within those product categories accordingly. The weights in the IPN sample are then set proportionally to each stratum's share of observations in the product category.
Finally, four product categories in the Mexican basket, Household Maintenance, Other electric devices, Other entertainment and Phone Line, were introduced in March 1995. The frequency statistics for March to June 1995 must be imputed for those categories because the filter eliminates the first few observations of every trajectory. In the case of Household Maintenance and Other electric devices, the frequency of price changes for March to June 1995 is imputed using a linear projection on the frequency of price changes of nonregulated goods subject to the value added tax and a linear trend. For Phone Line and Other entertainment, the procedure is repeated using nonregulated services subject to the value added tax and a linear trend.
Table 8: Correspondence table with IPN sample (March 1995 - June 2002)
2-digit COICOP | Main component | IPN description | Mexican description | Key | Weight | Frequency: Mar 1995 - Feb 1997 | Frequency: Jul 2000 - Jun 2002 |
|---|---|---|---|---|---|---|---|
| 1 | UF | Steak | Special beef cuts | 21 | 7.50 | 38.7 | 23.8 |
| 1 | UF | Fresh fish | Mojarra fish | 42 | 3.44 | 66.2 | 57.7 |
| 1 | UF | Lettuce | Lettuce | 99 | 1.89 | 76.3 | 87.2 |
| 1 | UF | Banana | Banana (tabasco) | 71 | 6.41 | 65.8 | 83.6 |
| 1 | PF | Milk | Pasteurized milk | 49 | 11.66 | 62.9 | 14.3 |
| 1 | PF | Sugar | Sugar | 109 | 3.79 | 46.4 | 13.2 |
| 1 | PF | Frozen spinach | Canned vegetables | 107 | 0.41 | 55.3 | 27.9 |
| 1 | PF | Mineral water | Bottled juices and nectars | 133 | 0.54 | 56.6 | 23.8 |
| 1 | PF | Coffee | Instant coffee | 113 | 1.08 | 76.3 | 28.5 |
| 2 | PF | Whisky | Rum | 135 | 0.62 | 50.4 | 29.9 |
| 2 | PF | Beer in a shop | Beer | 134 | 2.22 | 63.0 | 9.3 |
| 3 | NEIG | Socks | Socks | 216 | 0.67 | 45.3 | 18.9 |
| 3 | NEIG | Jeans | Cotton-based pants (men) | 210 | 1.73 | 37.0 | 22.5 |
| 3 | NEIG | Sport (shoes) | Tennis shoes | 248 | 3.15 | 32.7 | 21.0 |
| 3 | NEIG | Shirt (men) | Shirts (men) | 213 | 2.68 | 38.7 | 25.8 |
| 3 | S | Dry (cleaning) | Laundry and dry cleaning | 182 | 0.77 | 20.7 | 8.6 |
| 4 | NEIG | Acrylic (painting) | Housing maintenance (goods) | 364 | 1.85 | 47.5 | 15.2 |
| 4 | NEIG | Cement | Housing maintenance (goods) | 364 | - | - | - |
| 4 | S | Hourly rate of an electrician | Housing maintenance (services) | 364 | 0.40 | 28.1 | 10.5 |
| 4 | S | Hourly rate of a plumber | Housing maintenance (services) | 364 | - | - | - |
| 4 | E | Heating oil | Heating oil | 367 | 1.77 | 59.6 | 7.7 |
| 5 | NEIG | Toaster | Other electric devices | 336 | 0.32 | 28.8 | 13.4 |
| 5 | NEIG | Electric bulb | Electric bulbs | 180 | 0.63 | 48.6 | 15.5 |
| 5 | NEIG | 1 type of furniture | Bedroom sets | 270 | 4.46 | 26.2 | 14.8 |
| 5 | NEIG | Towel | Towels | 279 | 1.00 | 28.3 | 11.2 |
| 5 | S | Domestic services | Domestic services | 181 | 1.68 | 20.7 | 2.2 |
| 7 | E | Fuel type 1 | Gasoline | 351 | 4.70 | 100.0 | 35.4 |
| 7 | E | Fuel type 2 | Gasoline | 351 | - | - | - |
| 7 | NEIG | Car tyre | Car tire | 356 | 0.57 | 49.6 | 15.4 |
| 7 | S | Hourly rate in a garage | Car maintenance | 354 | 5.74 | 29.4 | 9.9 |
| 7 | S | Car wash | Car maintenance | 354 | - | - | - |
| 7 | S | Balancing of wheels | Car maintenance | 354 | - | - | - |
| 7 | S | Taxi | Taxi | 342 | 6.10 | 32.1 | 1.0 |
| 8 | S | Fax machine | Phone line | 381 | 2.62 | 8.6 | 0.0 |
| 9 | NEIG | Television set | Televisions and VCRs | 319 | 2.25 | 39.2 | 11.5 |
| 9 | NEIG | Dog food | Magazines | 334 | 1.04 | 19.3 | 0.0 |
| 9 | NEIG | Tennis ball | Sport equipment | 325 | 0.25 | 29.6 | 10.6 |
| 9 | NEIG | Construction game (Lego) | Toys | 324 | 0.23 | 21.7 | 5.9 |
| 9 | S | Movie | Movie | 327 | 1.62 | 16.4 | 14.1 |
| 9 | S | Videotape hiring | Other entertainment | 371 | 0.39 | 15.8 | 0.7 |
| 9 | S | Photo development | Photographic items (services) | 323 | 0.18 | 41.5 | 11.3 |
| 11 | S | Hotel room | Night club | 328 | 0.38 | 33.6 | 5.0 |
| 11 | S | Glass of beer in a café | Bars | 160 | 2.04 | 35.5 | 4.2 |
| 11 | S | 1 meal in a restaurant | Restaurants, pubs and similar | 163 | 3.80 | 25.4 | 9.7 |
| 11 | S | Hot-dog | Snackbars | 161 | 1.58 | 23.3 | 7.9 |
| 11 | S | Cola based lemonade in a café | Coffeeshops | 162 | 0.42 | 38.1 | 6.8 |
| 12 | NEIG | Toothpaste | Toothpaste | 193 | 3.23 | 70.1 | 15.9 |
| 12 | NEIG | Suitcase | Purses, suitcases and belts | 250 | 0.67 | 33.3 | 8.0 |
| 12 | S | Haircut (men) | Haircut | 200 | 1.10 | 8.9 | 1.8 |
| 12 | S | Hairdressing (ladies) | Beauty salon | 201 | 0.41 | 11.9 | 9.6 |
Notes: 2-digit COICOP: (1) Food and non-alcoholic beverages, (2) Alcoholic beverages, tobacco and narcotics, (3) Clothing and footwear, (4) Housing, water, electricity and other fuels, (5) Furnishing, household equipment and routine, (7)Transport, (8) Communication, (9) Recreation and culture, (11) Restaurants and hotels, (12) Miscellaneous goods and services. Main component: (UF) Unprocessed food, (PF) Processed Food, (NEIG) Nonenergy industrial goods, (E) Energy, (S) Services.
Table 9. Correspondence table with IPN sample (July 2002 - December 2004)
2-digit COICOP | Main component | IPN description | Mexican description | Key | Weight | Frequency: Jan 2003 - Dec 2004 |
|---|---|---|---|---|---|---|
| 1 | UF | Steak | Special beef cuts | 25 | 2.33 | 28.2 |
| 1 | UF | Fresh fish | Mojarra fish | 37 | 3.06 | 56.4 |
| 1 | UF | Lettuce | Lettuce | 83 | 1.87 | 86.1 |
| 1 | UF | Banana | Banana | 58 | 6.26 | 73.5 |
| 1 | PF | Milk | Pasteurized milk | 43 | 10.43 | 18.0 |
| 1 | PF | Sugar | Sugar | 98 | 1.16 | 26.1 |
| 1 | PF | Frozen spinach | Canned vegetables | 94 | 0.25 | 24.8 |
| 1 | PF | Mineral water | Bottled water | 102 | 1.98 | 23.3 |
| 1 | PF | Coffee | Instant coffee | 99 | 0.66 | 34.8 |
| 2 | PF | Whisky | Rum | 119 | 0.31 | 37.9 |
| 2 | PF | Beer in a shop | Beer | 116 | 3.65 | 21.3 |
| 3 | NEIG | Socks | Socks | 136 | 0.25 | 17.6 |
| 3 | NEIG | Jeans | Cotton-based pants (men) | 137 | 1.79 | 12.5 |
| 3 | NEIG | Sport (shoes) | Tennis shoes | 163 | 2.94 | 13.0 |
| 3 | NEIG | Shirt (men) | Shirts (men) | 134 | 2.09 | 14.9 |
| 3 | S | Dry (cleaning) | Laundry and dry cleaning | 169 | 0.65 | 14.2 |
| 4 | NEIG | Acrylic (painting) | Housing maintenance (goods) | 184 | 1.20 | 13.5 |
| 4 | NEIG | Cement | Housing maintenance (goods) | 184 | - | - |
| 4 | S | Hourly rate of an electrician | Housing maintenance (services) | 186 | 2.76 | 10.2 |
| 4 | S | Hourly rate of a plumber | Housing maintenance (services) | 186 | - | - |
| 4 | E | Heating oil | Domestic gas | 189 | 2.61 | 88.5 |
| 5 | NEIG | Toaster | Other electric devices | 216 | 2.48 | 17.6 |
| 5 | NEIG | Electric bulb | Electric bulbs | 226 | 0.79 | 8.1 |
| 5 | NEIG | 1 type of furniture | Bedroom sets | 213 | 1.87 | 10.5 |
| 5 | NEIG | Towel | Towels | 239 | 0.56 | 11.6 |
| 5 | S | Domestic services | Domestic services | 194 | 2.11 | 10.0 |
| 7 | E | Fuel type 1 | Gasoline | 313 | 5.37 | 14.0 |
| 7 | E | Fuel type 2 | Gasoline | 314 | - | - |
| 7 | NEIG | Car tyre | Car tire | 316 | 0.34 | 27.9 |
| 7 | S | Hourly rate in a garage | Car maintenance | 321 | 1.86 | 10.0 |
| 7 | S | Car wash | Car maintenance | 322 | - | - |
| 7 | S | Balancing of wheels | Car maintenance | 323 | - | - |
| 7 | S | Taxi | Taxi | 307 | 6.18 | 5.4 |
| 8 | S | Fax machine | Phone line | 193 | 5.11 | 3.4 |
| 9 | NEIG | Television set | Televisions and VCRs | 221 | 2.11 | 12.0 |
| 9 | NEIG | Dog food | Pet food | 360 | 0.79 | 20.8 |
| 9 | NEIG | Tennis ball | Sport equipment | 364 | 0.17 | 9.5 |
| 9 | NEIG | Construction game (Lego) | Toys | 358 | 2.57 | 18.1 |
| 9 | S | Movie | Movie | 349 | 2.81 | 47.7 |
| 9 | S | Videotape hiring | Videotape hiring | 362 | 0.43 | 8.2 |
| 9 | S | Photo development | Photographic items (services) | 361 | 0.28 | 17.3 |
| 11 | S | Hotel room | Hotel room | 348 | 0.15 | 38.4 |
| 11 | S | Glass of beer in a café | Bars | 380 | 0.65 | 10.7 |
| 11 | S | 1 meal in a restaurant | Restaurants, pubs and similar | 379 | 3.60 | 11.2 |
| 11 | S | Hot-dog | Snackbars | 378 | 5.52 | 12.4 |
| 11 | S | Cola based lemonade in a café | Coffeeshops | 381 | 0.27 | 13.2 |
| 12 | NEIG | Toothpaste | Toothpaste | 284 | 4.71 | 33.7 |
| 12 | NEIG | Suitcase | Purses, suitcases and belts | 171 | 1.16 | 6.1 |
| 12 | S | Haircut (men) | Haircut | 279 | 1.43 | 11.5 |
| 12 | S | Hairdressing (ladies) | Beauty salon | 280 | 0.41 | 5.8 |
Notes: 2-digit COICOP: (1) Food and non-alcoholic beverages, (2) Alcoholic beverages, tobacco and narcotics, (3) Clothing and footwear, (4) Housing, water, electricity and other fuels, (5) Furnishing, household equipment and routine, (7)Transport, (8) Communication, (9) Recreation and culture, (11) Restaurants and hotels, (12) Miscellaneous goods and services. Main component: (UF) Unprocessed food, (PF) Processed Food, (NEIG) Nonenergy industrial goods, (E) Energy, (S) Services.
D. Calibration of the Golosov-Lucas Model
Some parameters of the model are taken directly from the
literature while others are chosen to match particular moments of
the distribution of price changes. For the elasticity of
substitution across items, I pick a value of 7,
the same number as Golosov and Lucas. The discount factor is set to (1.05)-1/12, while the log
of inflation is calibrated to 0.045/12, its sample
average over the July 2000 to June 2002 period. The persistence of
technology shocks is set to 0.75, a value
similar to that implied by Golosov and Lucas' quarterly calibration
(
![]() per month) but higher
than Midrigan's (0.5 per month). The remaining free
parameters are the marginal disutility of labor,
per month) but higher
than Midrigan's (0.5 per month). The remaining free
parameters are the marginal disutility of labor, ![]() , the variance of technological innovations,
, the variance of technological innovations,
![]() , and the size of
menu costs,
, and the size of
menu costs, ![]() . The parameter
. The parameter ![]() is chosen so that households would work exactly 25% of
their time if menu costs were zero. The other two parameters are
calibrated so that the model matches exactly the average frequency
of price changes and the average absolute magnitude of nonzero
price changes in the data. The calibrated values are 0.0029 and 0.00511 for
is chosen so that households would work exactly 25% of
their time if menu costs were zero. The other two parameters are
calibrated so that the model matches exactly the average frequency
of price changes and the average absolute magnitude of nonzero
price changes in the data. The calibrated values are 0.0029 and 0.00511 for
![]() and
and ![]() , respectively.
, respectively.
The model is solved using dynamic programming techniques. As a first step, I guess a value for the price index from which I derive aggregate consumption and the real wage. The value functions are then approximated using Chebyshev polynomials. Conditional on the aggregate variables, a fixed point is found by value function iteration and the policy functions are recovered. A long Markov chain is then generated by sampling from the distribution of shocks and assuming that firms behave according to the policy functions. A price index is computed from the Markov chain and the associated aggregate quantities are derived. Finally, the initial guess for the price index is updated. The procedure is repeated until convergence.
Footnotes
1. E-mail: [email protected]. I would like to thank the members of my dissertation committee, Lawrence J. Christiano, Alexander Monge-Naranjo, Sergio Rebelo, and especially my chair Martin Eichenbaum, for their continuous guidance and support. I also am grateful to Martin Bodenstein, Jeff Campbell, Reinout DeBock, Rodrigo García Verdú, Jon Huntley, Eugene Orlov and Nicolas Vincent for their insightful comments and suggestions. Chris Ahlin, Allan Collard-Wexler, Martha Carillo and José Antonio Murillo Garza provided valuable help with the data. Financial support for this research was provided in part by the Center for International Economics and Development (CIED), Northwestern University Graduate Research Grant and the Fonds québécois pour les chercheurs et l'aide à la recherche (FCAR). All errors and omissions are mine. The views expressed in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. Return to text
2. Time-dependent models include Taylor's
(1980) staggered pricing model, in which firms optimize every
![]() periods, and the Calvo (1983) model, in which
firms face a constant probability
periods, and the Calvo (1983) model, in which
firms face a constant probability ![]() of
optimizing their prices. Recent implementations of time-dependent
rules can be found, for example, in Chari, Kehoe, and McGrattan (2002); Christiano, Eichenbaum and Evans (2005); Gali and Gertler (1999); and Smets and Wouters (2004). Return to
text
of
optimizing their prices. Recent implementations of time-dependent
rules can be found, for example, in Chari, Kehoe, and McGrattan (2002); Christiano, Eichenbaum and Evans (2005); Gali and Gertler (1999); and Smets and Wouters (2004). Return to
text
3. For a modern treatment of menu-cost models, see, for example, Dotsey, King and Wolman (1999); Danziger (1999); Golosov and Lucas (2003); Burstein (2006); and Gertler and Leahy (2006). Recent developments in models of information frictions includes Mankiw and Reis (2002); Sims (2003); and Mackowiak and Wiederholt (2004). Other state-dependent approaches include fair-pricing models (Rotemberg (2002); Rotemberg (2004)) and uncertain and sequential trading (e.g., Eden (1994); Lucas and Woodford (1993)). Return to text
4. See Klenow and Kryvtsov (2005), Burstein (2006) and Eichenbaum and Fisher (2004). Return to text
5. For studies on the United States, see Bils and Klenow (2004) and Klenow and Kryvtsov (2005). Dhyne et al. (2005) review the main findings for the Euro area. Return to text
6. See Edwards (1997) for a review of observers' opinions in 1994. Return to text
7. Unless otherwise indicated, all percentage figures are in logartihmic differences. The inflation rate is the annualized change in the CPI over the previous month. Return to text
8. Mexico pegged its exchange rate to the dollar in May 1992. In February 1994, the country switched to pre-announced crawling bands around the U.S. dollar. Return to text
9. See OECD economic surveys, 1999-2000: Mexico for a detailed description of the taxation system. Return to text
10. Items from the same outlet are attributed store keys independently to ensure confidentiality. Return to text
11. I thank Chris Ahlin for lending me original copies of the Diario. Return to text
12. These weights are derived from the 1989 ENIGH survey. They were updated using relative prices to reflect consumer expenditures in 1993. Return to text
13. Seven product categories common to both periods were dropped from the analysis because they contained indexes rather than individual observations. Return to text
14. In the United States, the BLS collects prices monthly for food consumed at home, energy, and a few additional items with volatile prices. Other prices are collected monthly for the three largest metropolitain areas (New York, Los Angeles, and Chicago) and every other month for the remaining areas. Return to text
15. A more systematic treatment of substitutions was implemented in 2001. Prices can now be carried forward for at most a month and a half before a substitution is sought. If the scarcity is generalized, this allowance can be extended up to three months. Systematic rotation of items was introduced in July 2002 to keep the CPI basket up to date. Return to text
16. The BLS reports prices net of sales and promotions whenever possible. For example, a 3-for-2 promotion would result in a temporary 33% price decrease. Return to text
17. The above average duration measure is biased downward because of Jensen's inequality. See Baharad and Eden (2004) and Dhyne et al. (2005) for a discussion of this bias. Return to text
18. A more formal way of choosing this cutoff is to regress the frequency of price decreases on inflation, allowing for a break in the relation. The hypothesis that the coefficients are equal for the two subsamples is rejected at the 1% for all points over that interval. Formal tests for choosing the break's location are sensitive to dropping all observations before April 1995. Return to text
19. The number in parentheses is the standard error. Return to text
20. The inflation series is the nonannualized monthly inflation rate to facilitate visual comparisons. Return to text
21. The few large spikes in
![]() , all occuring at the beginning of
the year, stem from seasonal variations in the price of a few fresh
food items. Return to text
, all occuring at the beginning of
the year, stem from seasonal variations in the price of a few fresh
food items. Return to text
22. The distribution is conditional on observing a price change such that its density integrates to one. Prices from all nonregulated product categories are used to construct the graphs. Return to text
23. To facilitate comparisions, I classify each product category according to the Euro area Classification Of Individual COnsumption by Purpose (COICOP). I report the results for 2-digit COICOP groups using all product categories unaffected by the 1995 basket revision, regardless of whether they are regulated or not. For Housing, water, electricity, gas and other fuels and Communications, I could not compute the frequency because of a lack of data. Return to text
24. Although seasonality sometimes is interpreted as evidence of time dependency, it does not feed into the TDP term here because the benchmark assumes uniform staggering. Return to text
25. A simple unweighted linear regression
of the share of variance the TDP term accounts for over the average
product category frequency has a slope of 0.85 for
the full sample and 1.13 for the high-inflation
period. Both slopes are significant at the 95% confidence level,
and the respective ![]() are 0.45 and 0.78. Return to text
are 0.45 and 0.78. Return to text
26. Particularly for Spain Álvarez and Hernando (2006)), Belgium (Aucremanne and Dhyne (2004 and 2005)), France (Baudry et al. (2004)), Portugal (Dias, Dias, and Neves (2004)), Germany (Hoffmann and Kurz-Kim (2006)) and the Netherlands (Jonker et al. (2004)). Return to text
27. It excludes all product categories introduced in March 1995; their price changes are not observed until July 1995 because the first four months of all price trajectories are cut during the filtering procedure. Excluding those categories has a negligible effect on the results after July 1995. Return to text
28. The special group Others includes tobacco and smoking products, personal care goods and services, personal services and educational expenses. Return to text
29. Baudry et al. (2004) report that the outlet size is positively correlated with the frequency of price changes in French CPI data. Return to text
30. The gentle fall in the average magnitude of price decreases in Figure 16 seems inconsistent with this prediction. It occurs in the model because the proportion of very large price decreases falls with inflation. As inflation takes off, technology shocks must be increasingly large to generate price decreases of a given magnitude due to greater relative price erosion. Depending on the idiosyncratic shock distributional assumptions, the average magnitude of price decreases might therefore fall over some inflation range, despite a rise the threshold. Return to text
31. If several price changes occur within a month, then the magnitude of price changes can be either under- or overestimated. Return to text
32. Rounding occurs because the price of items sold for a specific volume or weight generally are converted into a standard unit before appearing in the Diario. For example, the price of a 300 ml bottle of juice would be multiplied by 10/3 to be expressed in pesos per liter. Return to text
33. If the frequency of price change is
![]() for a sample of three items, and
individual price changes are independent within the sample, then
the frequency of price changes of an individual item is
for a sample of three items, and
individual price changes are independent within the sample, then
the frequency of price changes of an individual item is
![]() . Return to text
. Return to text
34. The IPN classifies Frozen spinash under process food even though it is part of unprocessed food according to the COICOP classification. To ensure the greatest comparability between our baskets, I exceptionally treat the corresponding Mexican product category as processed food in the derivation of the statistics related to the IPN basket. Return to text
35. A Fax Machine is categorized as a communication service under the COICOP, even though it refers to the price of acquiring the good, if no break down between telephone and telefax equipment and services is available. A substitution was sought in the Mexican sample because fax machines fall into a product category associated with a different stratum. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text