Exchange Rates and Fundamentals: A Generalization^*

James M. Nason and John H. Rogers^†

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

Exchange rates have raised the ire of economists for more than 20 years. The problem is that few, if any, exchange rate models are known to systematically beat a naive random walk in out of sample forecasts. Engel and West (2005) show that these failures can be explained by the standard-present value model (PVM) because it predicts random walk exchange rate dynamics if the discount factor approaches one and fundamentals have a unit root. This paper generalizes the Engel and West (EW) hypothesis to the larger class of open economy dynamic stochastic general equilibrium (DSGE) models. The EW hypothesis is shown to hold for a canonical open economy DSGE model. We show that all the predictions of the standard-PVM carry over to the DSGE-PVM. The DSGE-PVM also yields an unobserved components (UC) models that we estimate using Bayesian methods and a quarterly Canadian-U.S. sample. Bayesian model evaluation reveals that the data support a UC model that calibrates the discount factor to one implying the Canadian dollar-U.S. dollar exchange rate is a random walk dominated by permanent cross-country monetary and productivity shocks.

Keywords: Exchange rates, present-value model and fundamentals, random walk, DSGE model, unobserved components model, Bayesian model comparison

JEL classification: E31, E37, F41

1 Introduction

The search for satisfactory exchange rate models continues to be elusive. This paper studies a workhorse theory of currency market equilibrium determination, the present-value model (PVM) of exchange rates, in the spirit of Engel and West (2005). Starting with the PVM and using uncontroversial assumptions about fundamentals and the discount factor, Engel and West (EW) hypothesize that the PVM generates an approximate random walk in exchange rates if the PVM discount factor approaches one and fundamentals are I(1). An important implication of the EW hypothesis is that fundamentals have no power to forecast future exchange rates, even with the PVM dictating equilibrium in the currency market. EW support their hypothesis with a key theorem and empirical and simulation evidence.

This paper complements Engel and West (2005) by generalizing their main hypothesis in two ways. First, the EW hypothesis is generalized using a canonical two-country monetary dynamic stochastic general equilibrium (DSGE) model. Its linearized uncovered interest parity (UIP) and money demand equations yield the DSGE-PVM that coincides with the standard PVM of the exchange rate. Second, we show the standard- and DSGE-PVMs make equivalent predictions for exchange rates. The predictions are summarized in five propositions: (1) the exchange rate and fundamental cointegrate [Campbell and Shiller (1987)], (2) the PVM yields an error correction model (ECM) for currency returns in which the lagged cointegrating relation is the only regressor, (3) the PVM predicts a limiting economy (i.e., the PVM discount factor approaches one from below) in which the exchange rate is a martingale, (4) given fundamental growth depends only on the lagged cointegrating relation, the exchange rate and fundamental have a common trend-common cycle decomposition [Vahid and Engle (1993)], and (5) the EW hypothesis is also satisfied when the exchange rate and fundamental share a common feature and the PVM discount factor approaches one. A corollary to (5) is that the exchange rate is unpredictable when the PVM discount factor goes to one.

We report evidence from vector autoregression (VARs) about the propositions using quarterly floating rate Canadian-, Japanese-, and U.K.-U.S. samples. The VAR evidence rejects cointegration and reveals substantial serial correlation for the exchange rate and the fundamental. There is also evidence that a common feature exists between the Canadian dollar-, Yen-, and Pound-U.S. dollar exchange rates and the relevant fundamentals. Nonetheless, the VAR approach is unable to address the EW hypothesis question of whether the PVM discount factor approaches one.¹

The DSGE-PVM possesses a deep structure tied to the primitives of the underlying open economy unlike the standard-PVM. Rather than rely on the entire set of DSGE optimality and equilibrium condition, we give empirical content to the DSGE-PVM by placing restrictions on its fundamentals (cross-country money and consumption). We restrict these fundamentals with permanent-transitory decompositions. This decomposition allows us to cast the DSGE-PVM as a tri-variate unobserved components (UC) model in the exchange rate and observed fundamentals. The UC model also incorporates DSGE-PVM cross-equation restrictions conditional on whether the discount factor is calibrated or estimated. Three UC models calibrate the discount factor to one, which disconnects the exchange rate from the transitory component(s) of fundamentals. Transitory fundamentals restrict the exchange rate in three other UC models in which the DSGE-PVM discount factor is estimated.

We estimate six UC models on a Canadian-U.S. sample running from 1976Q1 to 2004Q4. The UC models yield state space systems for the DSGE-PVM, which allows us to recruit the Kalman filter to evaluate likelihoods. We compute likelihoods of the UC models using the Metropolis-Hastings (MH) simulator described by Rabanal and Rubio-Ramírez (2005) to draw Markov chain Monte Carlo (MCMC) replications from posteriors. We conduct model comparisons using marginal posterior likelihoods of the six UC models to find which is favored by the data. We find that the data favors the UC model that calibrates the discount factor to one and in which cyclical fluctuations are driven only with the transitory shock to cross-country consumption. Favored next is the UC model with the same transitory shock and in which the estimated posterior mean of the DSGE-PVM discount factor is 0.9962. The posterior of this UC model reveals that permanent shocks to fundamentals dominate exchange rate fluctuations. Thus, the data prefer UC models that are consistent with the EW hypothesis. Moreover, we find that the data fail to support UC models that tie the exchange rate to the transitory monetary shock. Rogoff (2007) also notes that exchange rates appear disconnected from 'mean reverting monetary fundamentals'. These results stand in contrast to those of open economy DSGE models which assign key roles to nominal rigidities, UIP shock persistence, and monetary disturbances.²

The next section constructs the standard- and DSGE-PVMs of the exchange rate. Section 3 presents five propositions that generalize the EW hypothesis. Our Bayesian econometric strategy is discussed in section 4. Section 5 reports estimates of six UC models. We conclude in section 6.

2 Two Present-Value Models of Exchange Rates

This section fleshes out the standard PVM, in which the equilibrium exchange rate is determined by melding a liquidity-money demand function, UIP condition, purchasing power parity (PPP), and flexible prices. This is a workhorse exchange rate model used by, among others, Dornbusch (1976), Bilson (1978), Frankel (1979), Meese (1986), Mark (1995), and Engel and West (2005). This section also develops a PVM of the exchange rate derived from a canonical optimizing two-country monetary DSGE model. We show that the EW hypothesis generalizes to this wider class of models.

2.A The Standard Present-Value Model of Exchange Rates

The standard-PVM of the exchange rate starts with the liquidity-money demand function

$\displaystyle m_{h,t} \; - \; p_{h,t} \; \; = \; \; \psi\hspace{0.01in} y_{h,t} \; - \; \phi\hspace{0.01in} r_{h,t}, \quad0 \; < \; \psi, \, \phi,$

(1)

where $m_{h,t}$ $\,p_{h,t}$ , $\,y_{h,t}$ , and $r_{h,t}$ denote the home country's natural logarithm of money stock, price level, output, and the level of the nominal interest rate. The parameter $\psi$ measures the income elasticity of money demand. Since the nominal interest rate is in its level, $\phi$ is the interest rate semi-elasticity of money demand. Define cross-country differentials $m_{t}$ $m_{h,t}$ $m_{f,t}$ , $\,p_{t}$ $p_{h,t}$ $p_{f,t}$ , $\,y_{t}$ $y_{h,t}$ $y_{f,t}$ , and $\,r_{t}$ $r_{h,t}$ $\,-\,$ $r_{f,t}$ , where denotes the foreign country. Assuming PPP holds, $e_{t}$ $p_{t}$ , where $e_{t}$ is the log of the (nominal) exchange rate in which the U.S dollar is the home country's currency.

Under UIP, the law of motion of the exchange rate is approximately

$\displaystyle \mathbf{E}_{t} e_{t+1} \, - \, e_{t} \; \; = \; \; r_{t}.$

(2)

Substitute for $r_{t}$ in the law of motion of the exchange rate (2) with the money demand function (1) and impose PPP to produce the Euler equation $e_{t} - \omega\mathbf{E}_{t} e_{t+1} = (1 - \omega) \bigl ( m_{t} - \psi y_{t} \bigr )$ , where the standard-PVM discount factor is $\omega\equiv\frac{\displaystyle \phi}{ \displaystyle 1+\phi}$ and $m_{t} - \psi y_{t}$ is the standard-PVM fundamental, which nets cross-country money with its income demand. Iterate on the Euler equation through date T and recognize that the transversality condition $\lim_{T \, \rightarrow\infty }\omega^{T+1} \mathbf{E}_{t} e_{t+T} = 0$ to obtain the standard PVM relation

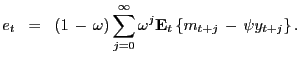
$\displaystyle e_{t} \; \; = \; \; (1 \, - \, \omega) \sum_{j=0}^{\infty} \omega^{j} \mathbf{E}_{t} \left\{ m_{t+j} \, - \, \psi y_{t+j} \right\} .$

(3)

The standard PVM (3) sets the log exchange rate equal to the annuity value of the fundamental $m_{t} - \psi y_{t}$ at the standard-PVM discount factor $\omega$ .³

2.B The DSGE Model

The optimizing monetary DSGE model consists of the preferences of domestic and foreign economies and their resource constraints. For the home (h) and foreign (f) countries, the former objects take the form

$\displaystyle \mathcal{U}\left( C_{i,t}, \, \, \frac{M_{i,t}}{P_{i,t}} \right) \; \; = \; \; \frac{\left[ C_{i,t}^{ \displaystyle \nu}\left( \frac {\displaystyle M_{i,t} }{\displaystyle P_{i,t}} \right) ^{\displaystyle (1 - \nu)}\right] ^{ \displaystyle (1 - \varphi)}}{1 - \varphi}, \; \; \; \; 0 \, < \, \nu\, < 1, \; \; \; 0 \, < \, \varphi,$

(4)

where $C_{i,t}$ and $M_{i,t}$ represent the th country's consumption and the th country's holdings of its money stock. The resource constraint of the home country is

$\displaystyle \qquad B^{h}_{h,t} \, + \, s_{t} B^{f}_{h,t} \, + \, P_{h,t} C_{h,t} \, + \, M_{h,t} \; = \; (1 + r_{h,t-1}) B^{h}_{h,t-1} \, + \, s_{t} (1 + r_{f,t-1}) B^{f}_{h,t-1} \, + \, M_{h,t-1} \, + \, P_{h,t} Y_{h,t},$

(5)

where $B^{i}_{i,t}$ , $B^{\ell}_{i,t}$ , $r_{i,t-1}$ , $r_{\ell ,t-1}$ , $Y_{i,t}$ , and $s_{t}$ denote the ith country's nominal holding of its own bonds at the end of date t, the ith country's nominal holding of the $\ell$ th country's bonds at the end of date t, the return on the ith country's bond, the return on the $\ell$ th country's bond, the output level of the ith country, and the level of the exchange rate. The two-country DSGE model is closed with $B^{h}_{h,t}$ $\, + \,$ $B^{f}_{h,t}$ $\, + \,$ $B^{h}_{f,t}$ $\, + \,$ $B^{f}_{f,t}$ . This condition forces the world stock of nominal debt to be in zero net supply, period-by-period, along the equilibrium path.

In section 2, analysis of the standard-PVM relies on I(1) fundamentals. Likewise, we assume that the processes for labor-augmenting total factor productivity (TFP), $A_{i,t}$ , and $M_{i,t}$ satisfy

ASSUMPTION 1: $\, ln[A_{i,t}]$ and $ln[M_{i,t}]$ $\sim I(1), \; i \; = \; h, \, f$ .

ASSUMPTION 2: Cross-country TFP and money stock differentials are I(1) and do not cointegrate.

Assumptions 1 and 2 impose stochastic trends on the two-country DSGE model.

2.C Optimizing UIP and Money Demand

The home country maximizes its expected discounted lifetime utility over uncertain streams of consumption and real balances,

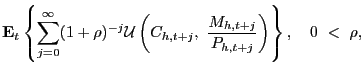
$\displaystyle \mathbf{E}_{t} \left\{ \sum^{\infty}_{j=0} (1 + \rho)^{-j} \mathcal{U}\left( C_{h,t+j}, \, \, \frac{M_{h,t+j}}{P_{h,t+j}} \right) \right\} , \quad0 \, \, < \, \, \rho,$

subject to (5). The first-order necessary conditions of economy i yield optimality conditions that describe UIP and money demand. The utility-based UIP condition of the home country is

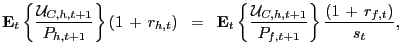
$\displaystyle \mathbf{E}_{t} \left\{ \frac{\mathcal{U}_{C,h,t+1}}{P_{h,t+1}} \right\} (1 \, + \, r_{h,t}) \; \; = \; \; \mathbf{E}_{t} \left\{ \frac{\mathcal{U} _{C,h,t+1}}{P_{f,t+1}} \right\} \frac{(1 \, + \, r_{f,t})}{s_{t} },$

(6)

where $\mathcal{U}_{C,h,t}$ is the marginal utility of consumption of the home country at date t. Given the utility specification (4), the exact money demand function of country i is

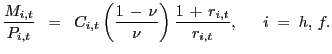
$\displaystyle \frac{M_{i,t}}{P_{i,t}} \; \; = \; \; C_{i,t} \left( \frac{1 \, - \, \nu} {\nu} \right) \frac{1 \, + \, r_{i,t}}{r_{i,t}}, \; \quad\; i \; = \; h, \, f.$

(7)

The consumption elasticity of money demand is unity, while the interest elasticity of money demand is a nonlinear function of the steady state bond return.

The UIP condition (6) and money demand equation (7) can be stochastically detrended and then linearized to produce an equilibrium DSGE-law of motion for the exchange rate. Begin by combining the utility function (4) and the UIP condition (6) to obtain

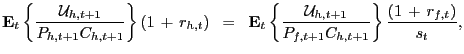
$\displaystyle \mathbf{E}_{t} \left\{ \frac{\mathcal{U}_{h,t+1}}{P_{h,t+1} C_{h,t+1}} \right\} (1 \, + \, r_{h,t}) \; \; = \; \; \mathbf{E}_{t} \left\{ \frac{ \mathcal{U}_{h,t+1}} {P_{f,t+1}C_{h,t+1}} \right\} \frac{(1 \, + \, r_{f,t}) }{s_{t}},$

where $\mathcal{U}_{i,t}$ is the utility level of country i at date t. Prior to stochastically detrending the previous expression, define $\widehat{\mathcal{U}}_{i,t} = \mathcal{U}_{i,t}/A_{i,t}$ , $\, \widehat {P}_{i,t} = P_{i,t} A_{i,t}/M_{i,t}$ , $\, \widehat{C}_{i,t} = C_{i,t}/A_{i,t}$ , $\gamma_{A,i,t} = A_{i,t}/A_{i,t-1}$ , $\gamma_{M,i,t} = M_{i,t}/M_{i,t-1}$ , $\, \widehat{s}_{t} = s_{t} A_{t} /M_{t}$ , $\, A_{t} = A_{h,t}/A_{f,t}$ , and $M_{t} = M_{h,t}/M_{f,t}$ . Note that $\widehat{C} _{i,t}$ is the transitory component of consumption of the th economy, $\gamma_{A,i,t} (\gamma _{M,i,t})$ is the TFP (money) growth rate of country , and the cross-country TFP (money stock) differential $A_{t} \, (M_{t})$ are I(1). Applying the definitions, the stochastically detrended UIP condition becomes

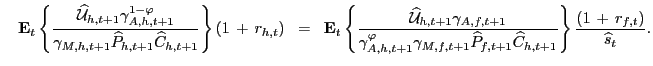
$\displaystyle \quad\mathbf{E}_{t} \left\{ \frac{\widehat{\mathcal{U}}_{h,t+1} \gamma^{1 - \varphi}_{A,h,t+1}}{\gamma_{M,h,t+1}\widehat{P}_{h,t+1} \widehat{C}_{h,t+1} } \right\} (1 \, + \, r_{h,t}) \; \; = \; \; \mathbf{E}_{t} \left\{ \frac{ \widehat{\mathcal{U}}_{h,t+1} \gamma_{A,f,t+1}} {\gamma^{\varphi}_{A,h,t+1} \gamma_{M,f,t+1} \widehat{P}_{f,t+1} \widehat{C}_{h,t+1}} \right\} \frac{(1 \, + \, r_{f,t})}{\widehat{s}_{t}}.$

A log linear approximation of the stochastically detrended UIP condition yields

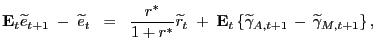
$\displaystyle \mathbf{E}_{t} \widetilde{e}_{t+1} \; - \; \widetilde{e}_{t} \; \; = \; \; \frac{r^{\ast}}{1 + r^{\ast}} \widetilde{r}_{t} \; + \; \mathbf{E}_{t} \left\{ \widetilde{\gamma}_{A,t+1} \, - \, \widetilde{\gamma}_{M,t+1} \right\} ,$

(8)

where, for example, $\widetilde{e}_{t} = \ln[\widehat{s}_{t}] - \ln[s^{\ast}]$ and $r^{\ast} (= r_{h}^{\ast} = r_{f}^{\ast})$ denotes the steady state world real rate.

2.D A DSGE-PVM of the Exchange Rate

We use the linear approximate law of motion of the exchange rate (8), and a stochastically detrended version of the money demand equation (7) to produce the DSGE-PVM. When linearized, the unit consumption elasticity-money demand equation (7) produces $\, -\widetilde{p}_{t}$ $\widetilde{c}_{t} - \frac{\displaystyle 1 \; \;} {\displaystyle 1 + r^{\ast}} \widetilde{r}_{t}$ . Impose PPP on the stochastically detrended version of the money demand equation and combine it with the law of motion (8) of the transitory component of the exchange rate to find

$\displaystyle \left[ 1 \; - \; \frac{1 \; \;}{1 + r^{\ast}} \mathbf{E}_{t} \mathbf{L}^{-1} \right] \widetilde{e}_{t} \; \; = \; \; \frac{1 \; \;}{1 + r^{\ast}} \mathbf{\ E}_{t} \left\{ \widetilde{\gamma}_{M,t+1} \, - \, \widetilde {\gamma}_{A,t+1} \right\} \; \; - \; \; \frac{r^{\ast}}{1 + r^{\ast}} \widetilde{c}_{t}.$

Solving this stochastic difference equation forward gives a present value relation for the transitory component of the exchange rate

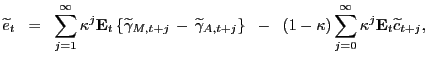
$\displaystyle \widetilde{e}_{t} \; \; = \; \; \sum_{j=1}^{\infty} \kappa^{j}\mathbf{E}_{t} \left\{ \widetilde{\gamma}_{M,t+j} \, - \, \widetilde{\gamma}_{A,t+j} \right\} \; \; - \; \; (1 - \kappa) \sum_{j=0}^{\infty} \kappa^{j} \mathbf{E}_{t} \widetilde{c}_{t+j},$

(9)

where the relevant tranversality conditions are invoked and the DSGE-PVM discount factor $\kappa$ $\equiv$ $\frac{\displaystyle 1 \; \;}{\displaystyle 1+r^{\ast}}$ . Note that the DSGE-PVM and permanent income hypothesis discount factors are equivalent.

The DSGE-PVM relation (9) is the equilibrium law of motion of the cyclical component of the exchange rate. Transitory movements in the exchange rate are equated with the future discounted expected path of cross-country money and TFP growth and the (negative of the) annuity-value of the transitory component of cross-country consumption. The DSGE model identifies the exchange rate's unobserved time-varying risk premium with the expected path of cross-country TFP growth and transitory consumption, which suggest additional sources of exchange rate fluctuations.

The DSGE model produces a present value relation that resembles the standard-PVM (3). The DSGE-PVM follows from unwinding the stochastic detrending of the present value (9)

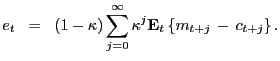
$\displaystyle e_{t} \; \; = \; \; (1 - \kappa) \sum_{j=0}^{\infty} \kappa^{j} \mathbf{E}_{t} \left\{ m_{t+j} \, - \, c_{t+j} \right\} .$

(10)

Thus, the standard-PVM (3) and DSGE-PVM (10) are identical up to differences in their discount factors and real fundamentals. The standard-PVM discount factor $\omega$ is tied to the interest rate semi-elasticity of money demand, $\phi$ , while the DSGE-PVM sets $\kappa$ to the inverse of the gross steady state real world interest rate, $1 + r^{\ast}$ . For the standard-PVM (DSGE-PVM), the real fundamental is cross-country output $y_{t}$ (consumption $c_{t}$ ). Table 1 summarizes the notable elements of the standard- and DSGE-PVMs.

3 Generalizing the Engel-West Hypothesis

This section presents five propositions that generalize the EW hypothesis. This allows a broader empirical analysis of the EW hypothesis, and does so using standard time series tools. The propositions apply to the standard-PVM and the DSGE-PVM because their present value relations coincide. Thus, we generalize the EW hypothesis to the large class of two-country monetary DSGE models.

We collapse the differences in the discount factor and real fundamental of the standard-PVM (3) and DSGE-PVM (10) to stress their mutual predictions in this section. These differences are put aside by defining a PVM discount factor $\mathcal{B}$ equal to either $\omega$ or $\kappa$ , while the fundamental $z_{t}$ is equivalent to either $m_{t}$ $\psi y_{t}$ or $m_{t}$ $c_{t}$ . With these assumptions, the focus is on the PVM

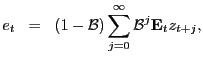
$\displaystyle e_{t} \; \; = \; \; (1 - \mathcal{B}) \sum_{j=0}^{\infty} \mathcal{B}^{j} \mathbf{E}_{t} z_{t+j},$

(11)

which subsumes the standard- and DSGE-PVMs. The PVM (11) provides several predictions given

ASSUMPTION 3: $\, z_{t} \sim I(1)$ .

ASSUMPTION 4: $\, (1 - \mathbf{L}) z_{t}$ has a Wold representation, $(1 - \mathbf{L}) z_{t} \; = \; \Delta z^{\ast} \, + \, \zeta(\mathbf{L}) \, \upsilon_{t}$ , where $\mathbf{L}\,z_{t} = z_{t-1}$ .⁴

Engel and West (2005) employ Assumption 3, but they do not require restrictions as strong as Assumption 4. However, Assumption 4 is standard for linear rational expectation models; see Hansen, Roberds, and Sargent (1991). Assumption 4 is also an implication of a linear approximate solution of the open economy DSGE model, while Assumption 3 is consistent with Assumptions 1 and 2.

3.A Cointegration Restrictions

The first prediction is that $e_{t}$ and $z_{t}$ share a common trend. This follows from subtracting the latter from both sides of the equality of the present-value relation (11) and combining terms to produce the exchange rate-fundamental cointegrating relation

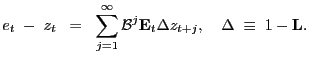
$\displaystyle e_{t} \; - \; z_{t} \; \; = \; \; \sum^{\infty}_{j=1} \mathcal{B}^{j} \mathbf{E}_{t} \Delta z_{t+j}, \quad\Delta\; \equiv\; 1 - \mathbf{L} .$

(12)

Equation (12) reflects the forces - expected discounted value of fundamental growth - that push the exchange rate toward long-run PPP. The explanation is

PROPOSITION 1: If $z_{t}$ satisfies Assumptions 3 and 4, $\mathcal{X}_{t} = \beta^{\prime} q_{t}$ forms a cointegrating relation with cointegrating vector $\beta^{\prime} = [1 \; \; -1]$ , where $q_{t} \equiv[e_{t} \; \; \; z_{t}]^{\prime}$ .

The proposition is a variation of results found in Campbell and Shiller (1987). We interpret the cointegration relation $\mathcal{X}_{t}$ as the 'adjusted' exchange rate because movements in fundamentals are eliminated from it. According to the cointegration present value relation (12), the 'adjusted' exchange rate is stationary and forward-looking in fundamental growth. Moreover, the cointegration relation $\mathcal{X}_{t}$ is an infinite-order moving average, MA $(\infty)$ equal to $\mathcal{B} \left( \mathbf{L} \right) \zeta _{\mathcal{B}} \left( \mathbf{L} \right)$ $\hspace{-1mm} \upsilon_{t}$ , where $\mathcal{B} \left( \mathbf{L} \right)$ $\sum^{\infty}_{j=0} \mathcal{B}^{j} \mathbf{L}^{j}$ and $\zeta_{\mathcal{B}} \left( \mathbf{L} \right)$ $\sum^{\infty}_{j=0} (\mathcal{B} \zeta)^{j} \mathbf{L}^{j-1}$ under Assumptions 3 and 4 (i.e., $z_{t}$ is and its growth rate has a Wold representation). Thus, the 'adjusted' exchange rate is a "cycle generator" - as defined by Engle and Issler (1995) - because shocks to serially correlated fundamental growth create persistent PPP deviations.

The standard- and DSGE-PVM require Assumptions 3 and 4 to satisfy Proposition 1. Rather than these assumptions, we can construct a cointegration relation from the DSGE model using Assumptions 1 and 2 because $\mathcal{X}_{t}$ is implied by the balanced growth restriction, $e_{t} \equiv\ln[s_{t}] = \widetilde{e}_{t} + m_{t} - a_{t}$ , where $m_{t} = \ln[M_{t}]$ and $a_{t} = \ln[A_{t}]$ . In this case, PPP deviations arise from the DSGE-PVM because of restrictions the present-value relation (9) places on the transitory component of the exchange rate, $\widetilde{e}_{t}$ .

3.B Equilibrium Currency Return Dynamics

The second PVM prediction is that currency returns depend only on the lagged 'adjusted' exchange rate and fundamental forecast innovation. We show this by first rewriting the PVM of (11) as $e_{t}$ $(1 - \mathcal{B}) z_{t}$ $= (1 - \mathcal{B}) \sum^{\infty}_{j=1} \mathcal{B}^{j} \mathbf{E}_{t} z_{t+j}$ . Differencing this equation produces, $\Delta e_{t} - (1 - \mathcal{B}) \Delta z_{t} = (1 - \mathcal{B}) \displaystyle \sum^{\infty}_{j=1} \mathcal{B}^{j} \left[ \mathbf{E}_{t} z_{t+j} - \mathbf{E}_{t-1} z_{t+j-1} \right]$ . Next, add and subtract $\mathbf{E}_{t-1} z_{t+j}$ inside the brackets, and substitute with the cointegration-present-value relation (12) to obtain

$\displaystyle \Delta e_{t} \; - \; \frac{1 - \mathcal{B}}{\mathcal{B}} \mathcal{X}_{t-1} \; \; = \; \; (1 - \mathcal{B}) \sum^{\infty}_{j=0} \mathcal{B}^{j} \bigl[ \mathbf{E}_{t} \, - \, \mathbf{E}_{t-1} \bigr] z_{t+j} .$

(13)

In equilibrium, currency return are generated by the lagged cointegration relation, $\mathcal{X}_{t-1}$ , and the expected annuity value of the forecast innovations of the fundamental. The lagged cointegration relation is the error correction mechanism of (13) that reflects the only force that restores currency returns to equilibrium and PPP in response to the shock innovation $u_{\Delta e, t}$ . These ideas are summarized by

PROPOSITION 2: Under Proposition 1, the PVM predicts that the equilibrium currency return is an error correction mechanism in which the lagged 'adjusted' exchange rate (or cointegration relation) is the only factor that drives the exchange rate to PPP in response to fundamental shock innovations.

Equation (13) is an ECM that regresses currency returns only on the lagged `adjusted' exchange rate. The regression is $\Delta e_{t}$ $\, \vartheta\mathcal{X}_{t-1}$ $u_{\Delta e, t}$ with factor loading $\vartheta$ $\frac{\displaystyle 1 - \mathcal{B} }{ \displaystyle \mathcal{B}}$ and currency return forecast error $u_{\Delta e,t}$ $(1 - \mathcal{B}) \sum^{\infty}_{j=0} \mathcal{B}^{j} \bigl[ \mathbf{E}_{t} \, - \, \mathbf{E}_{t-1} \bigr] z_{t+j}$ .⁵

3.C A Limiting Model of Exchange Rate Determination

Proposition 2 relies on $\mathcal{B}$ < 1 to define short- to medium-run currency return dynamics. This raises the question of the impact of relaxing this bound.

PROPOSITION 3: The exchange rate approaches a martingale (in the strict sense) as $\mathcal{B} \, \longrightarrow\, 1$ , according to the present-value relation (13) assuming Proposition 1.

Proposition 3 relies on $\mathcal{B} \longrightarrow1$ to produce the martingale $\mathbf{E}_{t} e_{t+1}$ $e_{t}$ and random walk behavior in the exchange rate.⁶ This behavior suggests an equilibrium path for $e_{t+1}$ in which its best forecast is $e_{t}$ , given relevant information, because the source of serial correlation, $\mathcal{X}_{t}$ disappears as $\mathcal{B} \longrightarrow1$ .⁷

3.D PVM Exchange Rate Dynamics Redux

Engel and West (2005) show that the PVM of the exchange rate yields an approximate random walk as $\mathcal{B}$ approaches one. This section affirms the EW hypothesis, but unlike Proposition 3 does not rely on Proposition 2. Rather than follow the EW proof exactly, we invoke Assumptions 3 and 4, the present-value relation (3), the Weiner-Kolmogorov prediction formula, and the conjecture $e_{t} \, =$ a $z_{t}$ to find that currency returns are unpredictable.

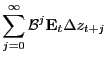The EW hypothesis is $plim_{\displaystyle \mathcal{B} \longrightarrow\displaystyle 1} [\Delta e_{t} - \mbox{\texttt{a}} \zeta(\mathbf{1}) \upsilon_{t}] = 0$ . Its hypothesis test begins by noting $e_{t}$ $\, = \,$ $z_{t-1}$ $\, + \,$ $\displaystyle \sum_{j=0}^{\infty}\mathcal{B}^{j}\mathbf{E}_{t} \Delta z_{t+j}$ , which is obtained from the present-value relation (3). Use this equation to construct $\Delta e_{t} - \mathbf{E}_{t-1} \Delta e_{t}$ $\zeta\left( \mathcal{B} \right) \upsilon_{t}$ , given Assumptions 3 and 4 and the Weiner-Kolmogorov prediction formula. 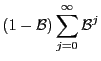The PVM of (11) also sets currency returns equal to the annuity value of fundamental growth, $\Delta e_{t}$ $(1 - \mathcal{B}) \displaystyle \sum_{j=0}^{\infty} \mathcal{B} ^{j}$ $\mathbf{E}_{t} \Delta z_{t+j}$ . The last two equations yield

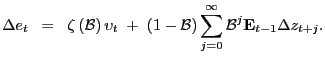
$\displaystyle \Delta e_{t} \; \; = \; \; \zeta\left( \mathcal{B} \right) \upsilon_{t} \; + \; (1 - \mathcal{B}) \sum_{j=0}^{\infty} \mathcal{B}^{j}\mathbf{E}_{t-1} \Delta z_{t+j}.$

(14)

By letting $\mathcal{B} \longrightarrow1$ , the random walk hypothesis of EW is verified independent of the ECM of Proposition 2 (and cointegration prediction of Proposition 1).⁸

The ECM (13) and Proposition 2 maps into the EW currency return generating equation (14). First, apply the change of index to the present value of (14) to obtain the present-value cointegration relation (12) lagged once. For the ECM (13), its present value $(1 - \mathcal{B}) \sum^{\infty}_{j=0} \mathcal{B}^{j} \bigl[ \mathbf{E}_{t} - \mathbf{E}_{t-1} \bigr] z_{t+j}$ equals $\zeta\left( \mathcal{B} \right)$ $\hspace{-0.75mm} \upsilon_{t}$ subsequent to evoking Assumptions 3 and 4 and the Weiner-Kolmogorov prediction formula. Thus, when the PVM discount factor $\mathcal{B}$ is arbitrarily close to one, the EW hypothesis predicts $\Delta e_{t}$ $\zeta\left( \mathbf{1} \right)$ $\hspace{-0.75mm} \upsilon_{t}$ which is consistent with currency returns following an ECM with no own lags or lags of fundamental growth. Since the standard- and DSGE-PVMs produce the ECM, the EW hypothesis is generalized to the larger class of two-country monetary DSGE models.

3.E A Common Trend-Common Cycle Model of Exchange Rates and Fundamentals

Proposition 2 predicts an ECM for currency returns that is consistent with the EW currency return generating equation (14). These results rely, at most, on assumptions 3 and 4 under which fundamentals are I(1) and have a Wold representation in growth rates. However, empirical work on exchange rates often employ multivariate time series models (i.e., VARs) instead of the deeper notion of a Wold representation.

This section studies the impact on the bivariate exchange rate-fundamental process, $q_{t} = \bigl[e_{t} \; \; z_{t} \bigr]^{\prime}$ of endowing an ECM on fundamental growth. In this case, $\Delta q_{t}$ forms a VECM(0)

$\displaystyle \Delta q_{t} \; \; = \; \; \left[ \begin{array}[c]{c} \vartheta\\ \eta \end{array} \right] \mathcal{X}_{t-1} \; + \; \left[ \begin{array}[c]{c} u_{\Delta e,t}\\ u_{\Delta z,t} \end{array} \right] ,$

(15)

where $\eta$ is the factor loading on $\mathcal{X}_{t-1}$ for $\Delta z_{t}$ and $u_{\Delta z,t}$ is its forecast innovation. Pre-multiplying the VECM(0) by $\overline{\beta}^{\, \prime} = \Bigl [1 \; \; -\hspace{-0.65mm}\frac{\displaystyle \vartheta}{\displaystyle \eta} \Bigr]$ creates the common feature

$\displaystyle \overline{\beta}^{\, \prime} \Delta q_{t} \; \; = \; \; \overline{\beta}^{\, \prime} \left[ u_{\Delta e, t} \; \; \; \; u_{\Delta z,t} \right] ^{\prime }.$

(16)

The vector $\overline{\beta}^{\, \prime}$ satisfies the Engle and Kozicki (1993) notion of a common feature because it creates a linear combination of $\Delta e_{t}$ and $\Delta z_{t}$ that is unpredictable conditional on their history. Given this common feature restriction and the cointegration relation of Proposition 1, Vahid and Engle (1993) provide a method to construct a Stock and Watson (1988) multivariate Beveridge and Nelson (1981) common trend-common cycle decomposition. We summarize these results with

PROPOSITION 4: Assume fundamental growth is the ECM process $\, \Delta z_{t}$ $\eta\mathcal{X}_{t-1}$ $u_{\Delta z,t}$ , where the forecast innovation $u_{\Delta z,t}$ is Gaussian. When Proposition 2 holds, $\, q_{t}$ has a common feature, $\overline{\beta }^{\, \prime} \Delta q_{t}$ , in the sense of Engle and Kozicki (1993), where $\overline{\beta}^{\, \prime} = \Bigl [1 \; \; -\hspace{-0.65mm}\frac{\displaystyle \vartheta}{\displaystyle \eta} \Bigr]$ . The cointegrating and common feature vectors $\beta$ and $\overline{ \beta}$ restrict the trend-cycle decomposition of $q_{t}$ , as described by Vahid and Engle (1993).

The common feature of Proposition 4 endows $q_{t} = [e_{t} \; \; z_{t}]^{\prime}$ with a common trend and a common cycle Beveridge-Nelson-Stock-Watson (BNSW) decomposition. Vahid and Engle (1993) provide an example in which the cointegration and common feature vectors restrict the trend of $q_{t}$ to $\mathbf{I}_{2}$ $\overline{\beta} (\beta^{\prime} \, \overline{\beta})^{-1} \beta^{\prime}$ , which gives trend and cycle components $\frac{\displaystyle -\mathcal{B} \eta }{\displaystyle 1 - \mathcal{B}(1 + \eta)} \overline{\beta}^{\, \prime} q_{t}$ and $\frac{\displaystyle 1 - \mathcal{B}}{\displaystyle 1 - \mathcal{B} (1 + \eta)} \beta^{\prime} q_{t}$ , respectively.⁹ The BNSW decomposition imposes a common cycle on $e_{t}$ and $z_{t}$ in the short-, medium-, and long-run, which restricts the exchange rate to be unpredictable at all forecast horizons. This prediction is at odds with the empirical evidence of Mark (1995).

The common feature relation (16) also provides another approach to verify the EW hypothesis, $plim_{\displaystyle \mathcal{B} \longrightarrow\displaystyle 1} [\Delta e_{t} - \mbox{\texttt{a}} \zeta(\mathbf{1}) \upsilon_{t}] = 0$ .

PROPOSITION 5: Let the exchange rate and fundamental have the VECM(0) (15). Then, the EW hypothesis requires currency returns and fundamental growth to share a common feature defined by $\overline{\beta}^{\, \prime} = [1 \; \; -\hspace{-0.65mm} \frac{\displaystyle \vartheta}{\displaystyle \eta}]$ and that $\vartheta$ $\longrightarrow$ 0 or $\mathcal{B} \longrightarrow1$ .

Proposition 5 differs from other approaches to the EW hypothesis. First, the common feature relation (16) imposes cross-equation restrictions on $\Delta q_{t}$ because its cycle generator, the lagged cointegrating relation $\mathcal{X}_{t-1}$ , is annihilated by $\overline {\beta}^{\, \prime}$ . Having eliminated $\mathcal{X}_{t-1}$ , the EW hypothesis decouples the exchange rate from fundamental growth and its forecast innovation $u_{\Delta z, t}$ ( $\zeta(\mathbf{1})\upsilon_{t}$ ). Finally, observe that when $\vartheta$ $\longrightarrow$ 0 (or $\mathcal{B} \longrightarrow1)$ , $\overline{\beta}^{\, \prime}$ $\longrightarrow$ $[1 \; \; 0]$ . This leaves only the forecast innovation $u_{\Delta e, t}$ to generate movements in $\Delta e_{t}$ . Thus, the EW hypothesis is affirmed by Proposition 5.¹⁰

A corollary of Proposition 5 is that changes in fundamentals do not Granger cause currency returns as $\mathcal{B} \longrightarrow1$ . Only if $\mathcal{B} \in(0, \, 1)$ , do movements in fundamentals have predictive power for currency returns according to the PVM. However, currency returns Granger cause growth in the fundamental as long as it is predicted by its own lagged forecast innovations. The equilibrium currency return generating equation (13) and Proposition 2 shows that this holds even if $\mathcal{B} \longrightarrow1$ .

3.F Reduced Form Evidence

The propositions suggest testable restrictions on exchange rates and fundamentals. Table 3 describes details of the tests and summarizes results. Fisrt, if the lag length of the levels VAR of the exchange rate and fundamental exceeds one, the VECM (15) is rejected. Second, cointegration tests are sufficient to examine Proposition 1. Finally, common feature tests are used, following Vahid and Engel (1993) and Engel and Issler (1995), that yield information about Proposition 4.

We estimate VARs of foreign currency-U.S. dollar exchange rates and fundamentals using Canadian, Japanese, U.K., and U.S. data on a 1976Q1 - 2004Q4 sample.¹¹ VAR lag lengths are chosen using likelihood ratio (LR) statistics, given a VAR(8), $\, \ldots$ , VAR(1).¹² As described in Table 3, the Canadian-, Japanese-, and U.K.-U.S. samples yield a VAR(8), VAR(5), and VAR(4), respectively.¹³ Thus, the Canadian, Japanese, U.K., and U.S. data reject the VECM (15) because $\Delta q_{t}$ has more serial correlation than explained by the lagged cointegration relation $\mathcal{X} _{t-1}$ .

Table 3 also presents Johansen (1991, 1994) trace and $\lambda-$ max test statistics that fail to confirm the cointegration prediction of Proposition 1 for the Canadian-, Japanese-, and U.K.-U.S. samples. This finding is consistent with Engel and West (2005), who argue there is little evidence that exchange rates and fundamentals cointegrate.

Finally, the common feature test is described in Table 3. This uses squared canonical correlations of currency returns and fundamental growth. The common feature null is that the smallest correlation equals zero. We use a $\chi^{2}$ statistic of Vahid and Engle (1993) and a F-statistic developed by Rao (1973) to test this null. The tests reject the null for the largest canonical correlation, but not for the smaller one in the three samples. This is evidence that currency returns and fundamental share a common feature in the Canadian-, Japanese-, and U.K.-U.S. samples. Given a common feature, the exchange rate approximates a random walk when $\mathcal{B} \longrightarrow1$ . The next section explores the empirical content of this hypothesis in the Canadian-U.S. data.

4 Econometric Models and Methods

Propositions 1-5 broaden our understanding of the EW hypothesis, which is also generalized to hold for the DSGE-PVM. Although the previous section discusses VAR methods that yield evidence about the joint behavior of the exchange rate and standard-PVM fundamentals, this approach is not informative about estimates of the PVM discount factor.

This section presents methods to estimate a PVM discount factor and test the EW hypothesis. Instead of relying on VARs, we employ unobserved components (UC) models to estimate the DSGE-PVM and test the EW hypothesis using Bayesian methods. A brief example motivates our approach. Consider the PVM (11) where the fundamental $z_{t}$ has the permanent-transitory decomposition $z_{t}$ $\tau_{t}$ $\widetilde {z}_{t}$ , $\tau_{t+1}$ $\tau_{t}$ $\varepsilon_{\tau,t+1}$ , $(1 - \sum_{i=1}^{p_{z}} \mathcal{A}_{\widetilde{z},i} \mathbf{L}^{i})$ $\widetilde{z}_{t}$ $\varepsilon_{\widetilde{z},t}$ , $\mathbf{E}_{t} \varepsilon_{\tau,t+1}$ $\mathbf{E}_{t} \varepsilon_{\widetilde{z},t+1}$ 0, $\mathbf{E}_{t} \varepsilon_{\tau,t+1}^{2}$ $\sigma_{\tau}^{2}$ , $\mathbf{E}_{t} \varepsilon_{\widetilde{z},t+1}^{2}$ $\sigma _{\widetilde{z}}^{2}$ , and $\mathbf{E}_{t} \varepsilon_{\tau,t+i} \, \varepsilon_{\widetilde{z},t+j}$ 0 for all and .¹⁴ Combining the PVM (11) and the permanent-transitory decomposition of $z_{t}$ gives an equilibrium permanent-transitory decomposition of the exchange rate, $e_{t} = \tau_{t} + (1 - \mathcal{B}) \iota_{\widetilde{z}} \left[ \mathbf{I} \, - \, \mathcal{B} \mathcal{A} _{\widetilde{z}} \right] ^{-1} \widetilde{z}_{t}$ , where $\iota _{\widetilde{z}}$ is a 1 $\times$ $p_{z}$ row vector with a first element of one and zeros elsewhere and $\mathcal{A}_{\widetilde{z}}$ is the companion matrix of the AR of $\widetilde{z}_{t}$ . The exchange rate trend is identified with the random walk of $z_{t}$ under its permanent-transitory decomposition. Transitory exchange rate fluctuations are driven by the fundamental cyclical component, $\widetilde{z}_{t}$ , which is the common dynamic factor of the exchange rate and observed fundamental. The permanent-transitory decomposition of the exchange rate is useful for the EW hypothesis because it becomes possible to estimate $\mathcal{B}$ , along with the coefficients of the permanent-transitory decomposition of $z_{t}$ . Note also that as $\mathcal{B}$ approaches one, the permanent component $\tau_{t}$ comes to dominate exchange rate fluctuations as predicted by the EW hypothesis.

We use Bayesian methods to estimate multivariate UC models of the DSGE-PVM. The models represent different combinations of restrictions imposed by the DSGE-PVM on the exchange rate, cross-country money, and cross-country consumption. For example, $\kappa$ is estimated for three UC models, which ties the exchange rate to the transitory component(s) of fundamentals. The exchange rate is disconnected from transitory shocks in remaining three UC models because $\kappa$ is calibrated to one. We cast the UC models in state space form to evaluate numerically the likelihoods. We use a sample of the Canadian dollar-U.S. dollar (CDN$/US$) exchange rate and the Canadian-U.S. money and consumption differentials from 1976Q1-2004Q4. The random walk MH simulator is used to generate MCMC draws from the UC model posterior distributions conditional on this sample. We compute model moments, such as parameter means, unconditional variance ratios, permanent-transitory decompositions, and forecast error variance decompositions (FEVDs), from the posterior distributions. Model comparisons are based on marginal likelihoods, which we construct by integrating the likelihood function of each model across its parameter space where the weighting function is the model prior.

4.A State Space Systems of the UC Models

The state space systems of the six UC models begin with the balanced growth restriction the DSGE model imposes on the exchange rate. This restriction is equivalent to the permanent-transitory decomposition $e_{t} = m_{t} - a_{t} + \widetilde{e}_{t}$ . The DSGE-PVM (9) places cross-equation restrictions on the stationary component of the exchange rate, $\widetilde{e}_{t}$ .

Cross-equation restrictions are conditioned on the permanent and transitory components of cross-country money and cross-country consumption. The permanent components of money and consumption are $\mu_{t+1} = \mu^{\ast} + \mu_{t} + \varepsilon_{\mu,t+1}$ , $\, \varepsilon_{\mu,t+1} \sim\mathcal{N}(0, \sigma^{2}_{\varepsilon_{\mu}})$ , and $a_{t+1} = a^{\ast} + a_{t} + \varepsilon_{a,t+1}$ , $\varepsilon_{a,t+1} \sim\mathcal{N}(0, \sigma^{2}_{\varepsilon_{a}})$ , respectively. Note that $\mu^{\ast}$ and $a^{\ast}$ are the deterministic trend growth rates of cross-country money and TFP. We assume $\widetilde{m}_{t}$ is a MA $(k_{\widetilde{m}})$ , $\widetilde{m}_{t} = \sum^{k_{\widetilde{m}}}_{j=0} \alpha_{j} \varepsilon _{\widetilde{m},t-j}$ , where $\alpha_{0} \equiv1$ and $\varepsilon _{\widetilde{m},t} \sim\mathcal{N}(0, \sigma^{2}_{\varepsilon_{\widetilde{m}} })$ . For $\widetilde{c}_{t}$ , we employ a AR $(k_{\widetilde{c}})$ , $\widetilde{c}_{t} = \sum^{k_{\widetilde{c}}}_{j=1} \theta_{j} \widetilde {c}_{t-j} + \varepsilon_{\widetilde{c},t}$ , where $\varepsilon_{\widetilde {c},t} \sim\mathcal{N}(0, \sigma^{2}_{\varepsilon_{\widetilde{c}}})$ . Put these elements together to form the balanced growth version of the DSGE-PVM

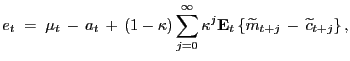
$\displaystyle e_{t} \; = \; \mu_{t} \, - \, a_{t} \, + \, (1 - \kappa) \sum_{j=0}^{\infty} \kappa^{j} \mathbf{E}_{t} \left\{ \widetilde{m}_{t+j} \, - \, \widetilde {c}_{t+j} \right\} ,$

(17)

which satisfies the DSGE balanced growth path restrictions. The balanced growth DSGE-PVM (17) implies the cointegrating relation of Proposition 1. Thus, the exchange rate responds only to trends in cross-country money, $\mu_{t}$ , and TFP, $a_{t}$ , in the long-run. Serial correlation in the exchange rate is produced by the transitory components of cross-country money and consumption, $\widetilde{m}_{t}$ and $\widetilde {c}_{t}$ . Also, if a common cycle generates these transitory components, the exchange also shares the restriction. Thus, the permanent and transitory components of cross-country money and consumption drive exchange rate fluctuations, which give rise to cross-equation restrictions in the UC models.

The UC models are classified according to whether there are two cycles or a common cycle and whether $\kappa$ is calibrated to one or estimated. Three UC models follow from solving the DSGE-PVM (17) given $\widetilde{m}_{t} \sim$ MA $(k_{\widetilde{m}})$ and $\widetilde{c}_{t} \sim$ AR $(k_{\widetilde{c}})$ or a common cycle is imposed using either the MA $(k_{\widetilde{m}})$ or AR $(k_{\widetilde{c}})$ . The three UC models are estimated when $\kappa$ is calibrated to one. We also use the UC models to estimate $\kappa$ . The six UC models have in common the cross-country money trend, $\mu_{t}$ , and TFP trend, $a_{t}$ .

A rich set of cross-equation restrictions arises in the 2-trend, 2-cycle UC model with $\kappa\in(0, \, 1)$ . In part, its state space system consists of the observation equations

$\displaystyle \qquad\left[ \begin{array}[c]{c} e_{t}\\ m_{t}\\ c_{t} \end{array} \right] \; \; = \; \; \left[ \begin{array}[c]{cccccccccc} 1 & -1 & \delta_{\widetilde{m},0} & \delta_{\widetilde{m},1} & \ldots & \delta_{\widetilde{m},k_{\widetilde{m}}} & \delta_{\widetilde{c},0} & \delta_{\widetilde{c},1} & \ldots & \delta_{\widetilde{c},k_{\widetilde{c}} -1}\\ 1 & 0 & 1 & \alpha_{1} & \ldots & \alpha_{k_{\widetilde{m}}} & 0 & 0 & \ldots & 0\\ 0 & 1 & 0 & 0 & \ldots & 0 & 1 & 0 & \ldots & 0\\ & & & & & & & & & \end{array} \right] \mathcal{S}_{\widetilde{m},c,t},$

(18)

where $\mathcal{S}_{\widetilde{m},c,t} = \left[ \mu_{t} \; a_{t} \; \varepsilon_{\widetilde{m},t} \; \varepsilon_{\widetilde{m},t-1} \, \ldots\, \varepsilon_{\widetilde{m},t-k_{\widetilde{m}}} \; \; \widetilde {c}_{t} \; \, \widetilde{c}_{t-1} \, \ldots\, \widetilde{c}_{t-k_{\widetilde {c}}+1} \right] ^{\prime}$ , factor loadings on $\varepsilon_{\widetilde{m} ,t}$ and its lags are

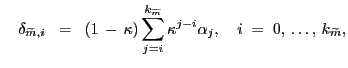
$\displaystyle \quad\delta_{\widetilde{m},i} \; \; = \; \; (1 \, - \, \kappa) \displaystyle \sum^{k_{\widetilde{m}}}_{j=i} \kappa^{j-i} \alpha_{j}, \quad i \; = \; 0, \, \ldots, \, k_{\widetilde{m}},$

(19)

factor loadings on $\widetilde{c}_{t}$ , $\ldots$ , $\widetilde {c}_{t-k_{\widetilde{c}}}$ are elements of the row vector

$\displaystyle \delta_{\widetilde{c}} \; \; = \; \; -s_{\widetilde{c}} (1 \, - \, \kappa) \biggl [\mathbf{I}_{k_{\widetilde{c}}} \, \, - \, \, \kappa\Theta\biggr]^{-1}, \quad s_{\widetilde{c}} \; = \; [1 \; \; \, \mathbf{0}_{1 \times k_{\widetilde{c}}-1}],$

(20)

and $\Theta$ is the companion matrix of the AR $(k_{\widetilde{c} })$ of $\widetilde{c}_{t}$ . The system of first-order state equations is

$\displaystyle \mathcal{S}_{\widetilde{m},c,t+1} \; \; = \; \; \left[ \begin{array}[c]{c} \mu^{\ast}\\ a^{\ast}\\ 0\\ \vdots\\ 0\\ \vdots \end{array} \right] \; \; + \; \; \left[ \begin{array}[c]{ccccccc} 1 & 0 & \ldots & 0 & 0 & \ldots & 0\\ 0 & 1 & \ldots & 0 & 0 & \ldots & 0\\ 0 & 0 & \ldots & 0 & 0 & \ldots & 0\\ \vdots & \vdots & \mathbf{I}_{k_{\widetilde{m}}} & \vdots & \vdots & & \vdots\\ 0 & 0 & \ldots & 0 & \theta_{1} & \ldots & \theta_{k_{\widetilde{c}}}\\ \vdots & \vdots & & \vdots & & \mathbf{I}_{k_{\widetilde{c}}-1} & \mathbf{0}_{(k_{\widetilde{c}}-1) \times1}\\ & & & & & & \end{array} \right] \, \mathcal{S}_{\widetilde{m},c,t} \; \; + \; \; \left[ \begin{array}[c]{c} \varepsilon_{\mu,t+1}\\ \varepsilon_{a,t+1}\\ \varepsilon_{\widetilde{m},t+1}\\ \mathbf{0}_{k_{\widetilde{m}} \times1}\\ \varepsilon_{\widetilde{c},t+1}\\ \mathbf{0}_{(k_{\widetilde{c}}-1) \times1}\\ \end{array} \right] ,$

(21)

with covariance matrix $\Omega_{m,\widetilde{c}} = \varepsilon _{\widetilde{m},c,t} \varepsilon_{\widetilde{m},c,t}^{\prime}$ , where $\varepsilon_{\widetilde{m},c,t} = [\varepsilon_{\mu,t+1} \, \, \varepsilon _{a,t+1} \, \, \varepsilon_{\widetilde{m},t+1} \, \, \mathbf{0}_{k_{\widetilde {m}} \times1} \, \, \varepsilon_{\widetilde{c},t+1} \, \, \mathbf{0} _{(k_{\widetilde{c}}-1) \times1}]^{\prime}$ .

We also study UC models that impose one common transitory factor on $m_{t}$ and $c_{t}$ . When the common component is $\widetilde{m}_{t}$ , the response of $c_{t}$ to $\widetilde{m}_{t}$ is denoted $\pi_{m,\widetilde{c}}$ . This implies $\widetilde{c}_{t}$ $\pi _{m,\widetilde{c}} \widetilde{m}_{t}$ and gives rise to the 2-trend, money cycle UC model. Identifying the common transitory component with $\widetilde{c}_{t}$ defines $\widetilde{m}_{t}$ $\pi_{m,\widetilde{c}} \widetilde{c}_{t}$ which restricts the 2-trend, consumption cycle UC model. The appendix describes the state space systems of the 2-trend, money cycle and 2-trend, consumption cycle UC models.

The three remaining UC models set $\kappa= 1$ . The restriction on the state space of the 2-trend, 2-cycle UC model is that the exchange rate is decoupled from transitory cross-country money and consumption shocks. Similar restrictions arise in the observer equation of the 2-trend, money cycle and 2-trend, consumption cycle UC models. Thus, we are able to compare DSGE-PVMs in which $\kappa$ is estimated to those in which $\kappa$ is calibrated to one. This provides an empirical appraisal of the EW hypothesis.

4.B The UC Model and Its Likelihood Function

We label the 2-trend, 2-cycle UC model with $\kappa\in(0, \, 1)$ $UC_{2,2,\kappa}$ . Likewise, $UC_{2,\widetilde{m},\kappa }$ and $UC_{2,\widetilde{c},\kappa}$ denote the 2-trend, money cycle and 2-trend, consumption cycle, $\kappa\in(0, \, 1)$ UC models. The state space system of $UC_{2,2,\kappa}$ is (18) and (21), while the appendix presents these systems for $\, UC_{2,\widetilde{m},\kappa}$ and $UC_{2,\widetilde{c},\kappa}$ . These state space systems represent the dynamics of $\mathcal{Y}_{t} = \bigl [e_{t} \; \; m_{t} \; \; c_{t} \bigr ]^{\prime}$ restricted by the DSGE-PVM and permanent-transitory specifications of $m_{t}$ and $c_{t}$ . We calibrate $\kappa= 1$ in $UC_{2,2,\kappa=1}$ , $\, UC_{2,\widetilde{m},\kappa=1}$ , and $UC_{2,\widetilde{c},\kappa=1}$ . The state space systems are mapped into the Kalman filter to evaluate likelihood functions as proposed by Harvey (1989) and Hamilton (1994).¹⁵ Denote the likelihood $\mathcal{L} \bigl(\mathcal{Y}_{t} \vert\, \, \Gamma_{2,i,\kappa}, \, \, UC_{2,i,\kappa} \bigr)$ , where 2, $\, \widetilde{m}, \, \widetilde{c}$ , $\kappa$ is either calibrated to one or estimated, and $\Gamma_{2,i,\kappa }$ is the parameter vector of $UC_{2,i,\kappa}$ .

The largest parameter vector is $\Gamma _{2,2,\kappa}$ . It contains $11 + k_{\widetilde{m}} \, + \, k_{\widetilde{c}}$ elements, $\, \Gamma_{2,2,\kappa} = \bigl [\kappa$ $\, \, \alpha_{1}$ $\, \, \ldots\, \, \alpha_{k_{\widetilde{m}}}$ $\, \, \theta_{1} \, \, \ldots\, \, \theta_{k_{\widetilde{c}}}$ $\, \, \mu^{\ast}$ $\, \, a^{\ast}$ $\, \, \sigma_{\mu} \; \, \, \sigma_{a}$ $\, \, \sigma_{\widetilde{m}} \; \, \, \sigma_{\widetilde{c}} \, \, \; \varrho_{a,\widetilde{c}} \; \, \, \pi_{e,0} \; \, \, \pi_{e,t} \; \, \, \pi_{e,a} \bigr]^{\prime}$ . We add the parameters $\varrho_{a,\widetilde{c}}$ , $\, \pi_{e,0}$ , $\, \pi_{e,t}$ , and $\pi_{e,a}$ to $\Gamma_{2,2,\kappa}$ to better fit $UC_{2,2,\kappa}$ to the data. For example, the Canadian-U.S. TFP differential exhibits more variation than $c_{t}$ if the correlation coefficient of innovations to $a_{t}$ and $\widetilde{c}_{t}$ , $\mathbf{E} \{ \varepsilon_{a,t} \, \varepsilon _{\widetilde{c},t} \} = \varrho_{a,\widetilde{c}}$ , is negative.¹⁶ The remaining three parameters allow for an unrestricted exchange rate intercept, $\pi_{e,0}$ , a linear exchange rate trend, $\pi_{e,t}$ , and a factor loading on the Canadian-U.S. TFP differential, $\pi_{e,a}$ , rather than set the (1, 2) element in the matrix of the observation system (18) to negative one.¹⁷ We estimate $\pi_{e,a}$ to ask if the data supports the cointegration-balanced growth path restriction imposed on the DSGE-PVM (17).

The parameter vectors of the other five UC models are smaller. The $UC_{2,\widetilde{m},\kappa}$ model drops two plus $k_{\widetilde{c}}$ parameters from $\Gamma_{2,\widetilde{m},\kappa}$ $\bigl [\kappa$ $\, \, \alpha_{1}$ $\, \, \ldots\, \, \alpha_{k_{\widetilde {m}}}$ $\; \, \, \mu^{\ast}$ $\, \, a^{\ast}$ $\, \, \sigma_{\mu} \; \, \, \sigma_{a}$ $\, \, \sigma_{\widetilde{m}} \; \, \, \pi_{e,0} \; \, \, \pi_{e,t} \; \, \, \pi_{e,a} \; \, \, \pi_{c,\widetilde{m}} \bigr]^{\prime}$ , while adding the factor loading on $\widetilde{m}_{t}$ for $c_{t}$ , $\pi_{c,\widetilde{m}}$ . The factor loading $\pi_{m,\widetilde{c}}$ enters the parameter vector of $UC_{2,\widetilde{m},\kappa}$ , while $\alpha_{1}$ $\, \, \ldots\, \, \alpha_{k_{\widetilde{m}}}$ and $\sigma_{\widetilde{m}}$ are dropped from $\, \Gamma_{2,\widetilde{c},\kappa} = \bigl [\kappa$ $\, \, \theta_{1} \, \, \ldots\, \, \theta_{k_{\widetilde{c}}}$ $\, \, \mu^{\ast}$ $\, \, a^{\ast}$ $\, \, \sigma_{\mu} \; \, \, \sigma_{a}$ $\; \, \, \sigma_{\widetilde{c}} \, \, \; \varrho_{a,\widetilde{c}} \; \, \, \pi_{e,0} \; \, \, \pi_{e,t} \; \, \, \pi_{e,a} \; \, \, \pi_{m,\widetilde{c}} \bigr]^{\prime}$ . The parameter vectors of the UC models $UC_{2,2,\kappa=1}$ , $\, UC_{2,\widetilde{m},\kappa=1}$ , and $UC_{2,\widetilde{c},\kappa=1}$ are identical to $\, \Gamma_{2,2,\kappa}$ , $\, \Gamma_{2,\widetilde{m},\kappa}$ , and $\Gamma_{2,\widetilde{c},\kappa}$ except that $\kappa= 1$ .

4.C The Data

The sample runs from 1976Q1 to 2004Q4, T = 116. We have observations on the Canadian dollar-U.S. dollar exchange rate (average of period). The Canadian monetary aggregate is M1 in current Canadian dollars, while for the U.S. it is the Board of Governors monetary base (adjusted for changes in reserve requirements) in current U.S. dollars. Consumption is the sum of non-durable and services expenditures in constant local currency units.¹⁸ The aggregate quantity data is converted to per capita units. The data is logged and multiplied by 100, but is neither demeaned nor detrended.

4.D Estimation Methods

The likelihood functions of the UC models do not have analytic solutions. We approximate the likelihoods $\mathcal{L} (\mathcal{Y}_{t} \vert\, \, \Gamma_{2,i,\kappa=1}, \, \, UC_{2,i,\kappa=1})$ and $\mathcal{L}(\mathcal{Y}_{t} \vert\, \, \Gamma_{2,i,\kappa}, \, \, UC_{2,i,\kappa})$ with posterior distributions of $\, \Gamma_{2,i,\kappa=1}$ and $\, \Gamma_{2,i,\kappa}$ , generated by the MCMC replications of the random walk MH simulator. Our estimates of $\, \Gamma_{2,i,\kappa=1}$ and $\, \Gamma_{2,i,\kappa}$ and marginal likelihoods build on the Bayesian estimation tools of Fernández-Villaverde and Rubio-Ramírez (2004), Rabanal and Rubio-Ramírez (2005), Geweke (1999, 2005), An and Schorfheide (2007), and Gelman, Carlin, Stern, and Rubin (2004). The MH simulator creates 1.5 million MCMC draws from the posterior. The initial 750,000 draws are treated as a burn-in sample and therefore discarded. We base our estimates on the remaining 750,000 draws from the posteriors of the $\, UC_{2,2,\kappa=1}$ , $\, UC_{2,\widetilde{m} ,\kappa=1}$ , $\, UC_{2,\widetilde{c},\kappa=1}$ , $\, UC_{2,2,\kappa}$ , $\, UC_{2,\widetilde{m},\kappa}$ , and $UC_{2,\widetilde{c},\kappa}$ models.¹⁹

4.E Priors

The second column of table 4 (5) list the priors of $\, \Gamma_{2,i,\kappa=1}$ $\, (\Gamma_{2,i,\kappa})$ , 2, $\, \widetilde{m}$ , $\, \widetilde{c}$ . Under a normal prior, the first element is the degenerate mean and second its standard deviation. The inverse-gamma priors are parameterized by its degrees of freedom, the first element, and its mean, the second element. The left and right end points of a uniform prior is denoted by its first and second elements.

We choose degenerate priors for the lag lengths of the MA $(k_{\widetilde{m}})$ of $\widetilde{m}_{t}$ and AR $(k_{\widetilde{c}})$ of $\widetilde{c}_{t}$ that set $k_{\widetilde{m}} = k_{\widetilde{c}} = 2$ . Normal priors for the MA ( $\alpha_{1}$ and $\alpha_{2}$ ) and AR ( $\theta_{1}$ and $\theta_{2}$ ) coefficients allow for disparate transitory behavior in $\widetilde{m}_{t}$ and $\widetilde{c}_{t}$ . The prior means of $\alpha_{1}$ , $\alpha_{2}$ , $\, \theta_{1}$ , and $\theta_{2}$ guarantee that the relevant eigenvalues are strictly less than one. The eigenvalues of the MA(2) (AR(2)) of $\widetilde{m}_{t}$ ( $\widetilde{c}_{t}$ ) are 0.60 ± 0.20i (0.95 and -0.10). The standard deviation of the normal priors of the MA and AR coefficients provide for a wide set of realizations for $\alpha_{1}$ , $\alpha_{2}$ , $\, \theta_{1}$ , and $\theta_{2}$ . However, when a draw generates an eigenvalue greater than one (in absolute value) for either the MA or AR coefficients, the draw is discarded. Nonetheless, the MA and AR priors admit transitory cycles in cross-country money and consumption that allow for power at the business cycle frequencies, if the data wants.

We opt for priors of $\mu^{\ast}$ and $a^{\ast}$ that rely on the Canadian-U.S. money stock and consumption differentials samples. Since $\mu^{\ast}$ and $a^{\ast}$ represent deterministic trend growth, we ground the priors on normal distributions. The prior standard deviations of $\mu^{\ast}$ and $a^{\ast}$ match sample moments.

Priors on the standard deviations of the shock innovations reflect standard practice for estimating DSGE models with Bayesian methods. For example, Adolfson, Laséen, Lindé, and Villani (2007) employ inverse-gamma priors for the standard deviations of the shock innovations of their sticky price open economy DSGE model. However, there is a lack of good information about $\sigma_{\mu}$ , $\, \sigma_{a}$ , $\sigma_{\widetilde{m}}$ , and $\sigma_{\widetilde{c}}$ . This explains why we impose a prior with two degrees of freedom, which forces these standard deviations to be positive. On the other hand, we attach a normally distributed prior to the correlation of innovations to $a_{t}$ and $\widetilde{c}_{t}$ , $\varrho_{a,\widetilde{c}}$ . Its mean is negative to capture our prior that the TFP differential, $a_{t}$ , is smoother than cross-country consumption, $c_{t}$ . Since we have no information about the extent of the smoothness, the mean is -0.5 with a standard deviation of 0.2 that places draws close to negative one or zero in the 95 percent coverage interval of the prior. Draws greater than one or less than negative one are ignored. The correlation of innovations to $\mu_{t}$ and $\widetilde{m}_{t}$ is fixed at zero, reflecting our assumption that the sources and causes of permanent and transitory monetary shocks are orthogonal.

The exchange rate intercept and linear time trend priors are set according to a linear regression of the exchange rate on these objects. This motivates our choice of normally distributed priors for $\, \pi_{e,0}$ and $\pi_{e,t}$ and of their degenerate means and standard deviations.

The remaining factor loadings have priors that reflect a dearth of information on our part. The uniform priors of $\, \pi_{e,a}$ , $\, \pi_{c,\widetilde{m}}$ , and $\pi_{c,\widetilde{m}}$ are wide and include zero. If, for example, $\pi_{e,a}$ is small it indicates the inadequacy of the balanced growth restriction and the impact of permanent fluctuations in Canadian-U.S. TFP differentials on the exchange rate. The same holds for the response of $c_{t} \, (m_{t})$ to transitory movements in the Canadian-U.S. money stock (consumption) differential.

The $UC_{2,i,\kappa}$ models have only one 'economic' parameter, the DSGE-PVM discount factor $\kappa\equiv \frac{\displaystyle 1 \; \;} {\displaystyle 1 + r^{\ast}}$ , in common. We adopt the Engel and West (2005) prior for $\kappa$ . They argue that it is necessary for $\kappa\in[0.9, \; 0.999]$ to generate an approximate random walk exchange rate from the standard-PVM. Hence, our prior on $\kappa$ is constructed to provide information about the EW hypothesis from the posteriors of the $UC_{2,i,\kappa}$ models. We impose an inverse-gamma prior on the DSGE-PVM discount factor $\kappa$ , which follows Del Negro and Schorfheide (2006). The degenerate prior means of $\kappa= 0.988$ and exp([a* = 0.158]/400) imply an annual average real world interest rate of about five percent. Although a five percent real world interest rate is large for the floating rate period, the standard deviation of 0.038 guarantees draws for $\kappa$ that cover a wide interval. However, MCMC draws from the random walk MH simulator of the $UC_{2,i,\kappa}$ models obey the EW prior because we ignore draws for which $\kappa\, \notin\, [0.9, \; 0.999]$ .

5 Results

This section presents the results of implementing our empirical strategy. Tables 4 and 5 provide the posterior means and standard deviations of $\, \Gamma_{2,i,\kappa=1}$ and $\, \Gamma_{2,i,\kappa}$ vectors, i 2, $\, \widetilde{m}$ , $\, \widetilde{c}$ , for the six UC models. We include marginal likelihoods of the six UC models, using methods described by Fernández-Villaverde and Rubio-Ramírez (2004), Rabanal and Rubio-Ramírez (2005), and Geweke (1999), to conduct inference across these models. We present densities of the prior and posteriors of $\kappa$ for $\, UC_{2,2,\kappa}$ , $\, UC_{2,\widetilde{m},\kappa}$ , and $UC_{2,\widetilde{c},\kappa}$ in figure 1. Tables 6, 7, 8, and 9 report factor loadings on the exchange rate of the transitory components of money and consumption differentials, unconditional variance ratios of the present discounted value of the shock innovations to the exchange rate, FEVDs of the trend-cycle decomposition of the exchange rate with respect to these shocks, and summary statistics of trend-cycle decompositions, respectively. Figures 2, 3, and 4 plot the trend-cycle decomposition of the CDN$/US$ exchange rate.

5.A Parameter Estimates

Tables 4 and 5 list the posterior means and standard deviations of the parameters of the six UC models. Estimates of $\, UC_{2,2,\kappa=1}$ , $\, UC_{2,\widetilde{m},\kappa=1}$ , $\, UC_{2,\widetilde {c},\kappa=1}$ appear in table 4. These three models exhibit persistence in the transitory components of the money and consumption differentials, $\widetilde{m}_{t}$ and $\widetilde{c}_{t}$ . For example, the $\, UC_{2,\widetilde{m},\kappa=1}$ $\, ( UC_{2,\widetilde{c},\kappa=1})$ model yields AR (MA) estimates that imply the half life of a shock to $\widetilde {c}_{t} \, ( \widetilde{m}_{t})$ is 17 (7) years.²⁰ However, only $\widetilde{c}_{t}$ is persistent in the $\, UC_{2,2,\kappa=1}$ model. The half life of a shock to $\widetilde{m}_{t}$ is less than two quarters, while for $\widetilde{c}_{t}$ it is between nine and ten years. Note also that the priors and posterior means of the MA coefficients, $\alpha_{1}$ and $\alpha_{2}$ , only differ for the $\, UC_{2,\widetilde{m},\kappa=1}$ model. Although the posterior means of the AR coefficients have moved away from the prior means, a one standard deviation of the posterior of $\theta_{2}$ covers zero for the $\, UC_{2,2,\kappa=1}$ and $\, UC_{2,\widetilde{c},\kappa=1}$ models.

The posterior means of $\mu^{\ast}$ and $a^{\ast}$ show that Canada experiences slower (faster) trend money (TFP) growth than the U.S. over the sample. Trend U.S. money growth is on average about 0.05 percent higher annually according to the posteriors of the $UC_{2,2,\kappa=1}$ , $\, UC_{2,\widetilde{m},\kappa=1}$ , and $UC_{2,\widetilde{c},\kappa=1}$ models. Across these models, $a^{\ast} \approx0.16$ indicates Canadian deterministic trend TFP growth dominates its U.S. counterpart by about 0.06 percent at an annual rate.

The $UC_{2,2,\kappa=1}$ , $\, UC_{2,\widetilde {m},\kappa=1}$ , and $UC_{2,\widetilde{c},\kappa=1}$ models show differences across estimates of the posterior means of the shock innovation standard deviations. Only the estimated impulse structure of the $UC_{2,\widetilde {m},\kappa=1}$ model is dominated by movements in the permanent innovations of the money shock, $\sigma_{\mu}$ . The converse is that this model yields the smallest posterior means of the standard deviation of the TFP differential shock and $\widetilde{m}_{t}$ shock innovations, $\sigma_{a}$ and $\sigma_{\widetilde{m}}$ . The $UC_{2,\widetilde{c},\kappa=1}$ model yields the largest estimates of $\sigma_{a}$ and $\sigma_{\widetilde{c}}$ , but these posterior means are about the same magnitude. Note also that the correlation of the innovations to the TFP shock and $\widetilde{c}_{t}$ shock is estimated to be $\varrho_{a,\widetilde{c}} = -0.88$ and by the $UC_{2,2,\kappa =1}$ and $UC_{2,\widetilde{c},\kappa=1}$ models, respectively. Thus, these models are consistent with the TFP trend being more volatile than observed Canadian-U.S. consumption.

Estimates of the exchange rate intercept and linear time trend indicate that the $UC_{2,\widetilde{m},\kappa=1}$ model provides the largest value for the US$ in steady state and the largest deterministic growth rate for the CDN$/US$ exchange rate. The posterior means of $\pi_{e,0}$ and $\pi_{e,t}$ imply that the steady state CDN$/US$ exchange rate is 1.23 with a deterministic annual growth rate of about 0.8 percent. For the $UC_{2,2,\kappa=1} \, (UC_{2,\widetilde{c},\kappa=1})$ model, the analogous values are 1.10 (1.03) and 0.3 (0.2) percent per annum. Thus, the $UC_{2,\widetilde{m},\kappa=1}$ model places more emphasis on deterministic elements to fit the data compared to the other two UC models that calibrate $\kappa$ to one.

The remaining coefficients are the factor loadings $\pi_{e,a}$ , $\, \pi_{e,\widetilde{m}}$ , and $\pi_{e,\widetilde{c}}$ . Posterior mean estimates of $\pi_{e,a}$ and -9.02 reveal that there are statistically and economically large deviations from the balanced growth path by the $UC_{2,2,\kappa=1}$ and $UC_{2,\widetilde{m},\kappa=1}$ models. The $UC_{2,\widetilde{c},\kappa=1}$ model is closer to satisfying the balanced growth hypothesis that $\pi_{e,a} = -1$ . This UC model has a posterior mean of -0.72 for $\pi_{e,\widetilde{c}}$ whose two standard deviation interval contains the balanced growth restriction. The response of the Canadian-U.S. money stock differential to $\widetilde{c}_{t}$ is also close to negative one for the $UC_{2,\widetilde{c},\kappa=1}$ model because the posterior mean of $\pi_{m,\widetilde{c}} = -0.90$ with a standard deviation of 0.21. The $UC_{2,\widetilde{m},\kappa=1}$ model reveals that a one percent rise in $\widetilde{c}_{t}$ results in a 4.4 percent rise in the Canadian-U.S. consumption differential.

The key economic parameter of the DSGE-PVM is its discount factor $\kappa$ . Table 5 lists the posterior means and standard deviations of the $\Gamma_{2,2,\kappa}$ and $\, \Gamma_{2,\widetilde{m} ,\kappa}$ , and $\, \Gamma_{2,\widetilde{c},\kappa}$ vectors that include estimates of $\kappa$ . Aside from the inclusion of the prior, posterior mean, and standard deviation $\kappa$ at the top of table 5, the posterior means and standard deviations of the remaining coefficients resemble those reported in table 4. The only notable exceptions are that the posterior means of $\sigma_{a}$ , $\, \sigma_{\widetilde{c}}$ , $\, \pi_{e,a}$ , and $\pi _{e,\widetilde{c}}$ are smaller for the $UC_{2,\widetilde{c},\kappa}$ model compared to its cousin with the calibration $\kappa= 1$ . The result is that $\sigma_{\mu}$ is the largest innovation shock standard deviation of the $UC_{2,\widetilde{c},\kappa}$ model. Also, this UC model and the data produce an estimate of $\pi_{e,a}$ whose one standard deviation coverage interval contains negative one. Thus, the $UC_{2,\widetilde{c},\kappa}$ model is closer to the balanced growth hypothesis and relies to a greater extent on permanent shocks to the Canadian-U.S. money stock differential.

The posterior means of $\kappa$ range from 0.966 for the $UC_{2,2,\kappa}$ model, to 0.974 for the $UC_{2,\widetilde{m},\kappa }$ model, to the largest estimate of 0.9962 for the $UC_{2,\widetilde {c},\kappa}$ model. These estimates are consistent with annual world real interest rates of 15.1, 11.4, and 1.7 percent given the posteriors of the $UC_{2,2,\kappa}$ , $\, UC_{2,\widetilde{m},\kappa}$ and $UC_{2,\widetilde {c},\kappa}$ models, respectively. Although the $UC_{2,2,\kappa}$ , $\, UC_{2,\widetilde{m},\kappa}$ models have posteriors that suggest unreasonably large world real interest rates, these UC models yield 95 percent coverage intervals whose upper end is 0.999. The $UC_{2,\widetilde{c},\kappa}$ model produces a posterior of $\kappa$ with a 95 percent coverage interval whose lower end equals 0.987. This value of $\kappa$ is greater than the posterior means of $\kappa$ for the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde{m},\kappa}$ models. Thus, the $UC_{2,\widetilde{c},\kappa}$ model generates a posterior distribution of $\kappa$ that is to the right of those produced by the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde{m},\kappa}$ models.

Figure 1 reinforces the view that the $UC_{2,\widetilde{c},\kappa}$ model posteriors yield estimates of $\kappa$ that are to the right of those of the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde {m},\kappa}$ models. Posterior densities of $\kappa$ appear in figure 1 for these UC models, along with the density of the inverse-gamma prior restricted to the EW prior of $\kappa\in[0.9, \, 0.999]$ . The solid (black) line is the $\kappa$ prior density. It is close to the posterior density of $\kappa$ derived from the $UC_{2,2,\kappa}$ model, which is the dashed (blue) line. The $UC_{2,\widetilde{m},\kappa}$ model generates a posterior density of $\kappa$ , the dot-dash (green) plot, that moves off the prior by placing less weight on $\kappa$ s less than 0.97 and more weight above it. The dot-dot (red) plot is the density of $\kappa$ from the $UC_{2,\widetilde{c},\kappa}$ model posterior. This density is deflated by ten percent to ease comparison to the other densities. A striking feature of figure 1 is that the $UC_{2,\widetilde {c},\kappa}$ model posterior pushes $\kappa$ off of its prior because its mass lays between 0.98 and 0.999.

Table 6 contains the posterior means of the exchange rate factor loadings with respect to $\widetilde{m}_{t}$ and $\widetilde{c}_{t}$ , the $\delta_{\widetilde{m},i}$ s and $\delta _{\widetilde{c},i}$ s.²¹ A striking aspect of the estimates of $\delta _{\widetilde{m},0}$ , $\, \delta_{\widetilde{m},1}$ , and $\delta_{\widetilde {m},2}$ is that the response of the CDN$/US$ exchange rate to innovations in $\widetilde{m}_{t}$ is economically small for either the $UC_{2,2,\kappa}$ or $UC_{2,\widetilde{m},\kappa}$ models. The large posterior standard errors on these factor loading also indicate the imprecision the Canadian-U.S. data give to these estimates. The data yield a more precise estimate of $\delta_{\widetilde{c},0}$ for the $UC_{2,2,\kappa}$ model. The posterior mean of this factor loading shows that the exchange rate falls by 0.6 percent given a one percent increase in $\widetilde{c}_{t}$ . These estimates drop to -0.33 for the $UC_{2,\widetilde{c},\kappa}$ model. Also, the associated 95 percent coverage interval contains zero. In summary, the $UC_{2,2,\kappa}$ , $\, UC_{2,\widetilde{m},\kappa}$ , and $UC_{2,\widetilde {c},\kappa}$ models have posteriors in which there is either a negligible exchange rate response to $\widetilde{m}_{t}$ shocks or an economically large negative reaction by the CDN$/US$ exchange rate to $\widetilde{c}_{t}$ fluctuations. However, the latter exchange rate response is sometimes estimated imprecisely.

5.B Unconditional Variance Ratios and FEVDs of the Exchange Rate

Tables 7 and 8 present unconditional variance ratios and FEVDs computed using the posteriors of the $UC_{2,2,\kappa}$ , $UC_{2,\widetilde{m},\kappa}$ , and $UC_{2,\widetilde{c},\kappa}$ models. We calculate the variances of the present discounted values (PDVs) of the money, TFP, and consumption shock innovations using the DSGE-PVM version of the equilibrium currency return generating equation (14) and UC model restrictions when $\kappa$ is estimated. The variance ratios are these values divided by the sample variance of the CDN$/US$ exchange rate ( 2.04). According to the unconditional variance ratios, only permanent shocks to the Canadian-US money differential, $\varepsilon_{\mu,t}$ , and the TFP differential, $\varepsilon_{a,t}$ , explain variation in the CDN$/US$ exchange rate. The variances of the PDVs of shock innovations to $\widetilde{m}_{t}$ and $\widetilde{c}_{t}$ are small and lack precision. Note that except for the $UC_{2,\widetilde{m},\kappa}$ model, the variance of the PDV of $\varepsilon_{a,t}$ is larger than that of $\varepsilon_{\mu,t}$ .

We report FEVDs in table 8 with implications similar to the unconditional variance ratios.²² The top panel of figure 8 shows that the posterior of the $UC_{2,2,\kappa}$ model yields a FEVD in which the TFP shock $\varepsilon_{a,t}$ makes a large and increasing contribution to exchange rate fluctuations at longer horizons. The money shock $\varepsilon_{\mu,t}$ remains economically important for exchange rate movements out to a three to five year horizon, but shocks to $\widetilde {m}_{t}$ and $\widetilde{c}_{t}$ are unimportant at any horizon. Much the same is true for the FEVDs found using the $UC_{2,\widetilde{m},\kappa}$ model posterior. However, the relative shares of the $\varepsilon_{\mu,t}$ and $\varepsilon_{a,t}$ shocks are unchanged at a two-thirds/one-third split from the one quarter to ten year horizons.

The posterior of the $UC_{2,\widetilde{c},\kappa}$ model imbues a sluggish dynamic to the exchange rate FEVDs found in the bottom panel of table 8. The $\varepsilon_{\mu,t}$ and $\varepsilon_{a,t}$ shocks are responsible for about 60 and 40 percent, respectively, of fluctuations in the exchange rate at short horizons. At a 10 year horizon, the contribution of $\varepsilon_{\mu,t}$ ( $\varepsilon_{a,t}$ ) only falls (rises) to 55 (45) percent. Thus, only the posterior of the $UC_{2,\widetilde {c},\kappa}$ model predicts that permanent shocks to money dominate exchange rate movements at longer horizons.

5.C Trend-Cycle Decompositions

Trend-cycle decompositions of the CDN$/US$ exchange rate and Canadian-U.S. money and consumption differentials are plotted in figures 2 and 3 with summary statistics given in table 9. We run $UC_{2,2,\kappa}$ , $UC_{2,\widetilde{m},\kappa}$ , and $UC_{2,\widetilde {c},\kappa}$ model posteriors through the Kalman smoother to create trend-cycle decompositions and summary statistics. Figures 2 and 3 and table 9 contain moments that are averages over 750,000 draws from UC model posteriors. Trend exchange rate growth is labeled $\Delta e^{\tau}$ in table 9.

The top window of figure 2 contains plots of the exchange rate and smoothed trends taken from the posteriors of the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde{c},\kappa}$ models.²³ The solid (black) line is $e_{t}$ , the log of the actual exchange rate. The smoothed trends of the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde{c},\kappa}$ models are the dashed (blue) and dotted (red) plots, respectively. Note that these UC models generate smoothed exchange rate trends that are more volatile than the actual exchange rate. The top row of table 9 indicate that the posteriors of the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde{c},\kappa}$ models generate standard deviations of $\Delta e^{\tau}$ equal to 2.66 and 2.44, respectively. The standard deviation of $\Delta e^{\tau}$ equals 2.04.

The smoothed exchange rate cycles appear in the bottom window of figure 2. The dotted (blue) line is the smoothed exchange rate cycle, $\widetilde{e}_{t}$ , based on the posterior of the $UC_{2,2,\kappa }$ model, while the dotted (red) line is associated with the $UC_{2,\widetilde {c},\kappa}$ model. Although the former $\widetilde{e}_{t}$ exhibits more variability than the latter (the standard deviations are 3.68 and 2.44), these $\widetilde{e}_{t}$ s are persistent with AR1 correlation statistics of 0.97 and 0.98. Note that only the posterior of the $UC_{2,\widetilde{m},\kappa}$ model yields a (close to) non-zero correlation for $\Delta e^{\tau}$ and $\widetilde{e}$ , according to table 9.

Figure 3 depicts smoothed permanent-transitory decompositions of the Canadian-U.S. money and consumption differentials. The actual differentials and smoothed trends appear in the top row of windows, while smoothed cycles are found in the bottom row of windows. The money (consumption) differentials are the right (left) side windows. The posterior of the $UC_{2,2,\kappa}$ model produces a money trend, $\mu_{t}$ that almost perfectly mimics the actual Canadian-U.S. money differentials, as shown in the top left window of figure 3. The result is that smoothed $\widetilde{m}_{t}$ is much less volatile, with a standard deviation of 0.68 compared to a standard deviation of 1.62 for $\mu_{t}$ . The bottom left window of figure 3 shows a saw-toothed pattern in $\widetilde{m}_{t}$ , conditional on the posterior of the $UC_{2,2,\kappa}$ model. This explains the AR1 correlation statistic of -0.68 for $\widetilde{m}_{t}$ (middle of the second column of table 9).

Table 9 reveals that the posterior of $UC_{2,\widetilde{c},\kappa}$ model produces a smoothed money trend, $\mu_{t}$ , that is about as volatile as in the $UC_{2,2,\kappa}$ model. The relevant standard deviations are 1.62 and 1.71 (second and fourth columns of table 9). However, the smoothed $\Delta\mu$ and $\Delta e^{\tau}$ have a positive correlation of 0.62 only in the posterior of the $UC_{2,\widetilde{c},\kappa}$ model (bottom half of the fourth column of table 9).

The posteriors of the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde{c},\kappa}$ models yield qualitatively similar plots for the smoothed TFP trend differential, $a_{t}$ . These plots appear in the top right window of figure 3 as dashed (blue) and dotted (red) lines for the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde{c},\kappa}$ models, respectively, where observed cross country consumption is the solid (black) line. The smoothed TFP growth differential, $\Delta a$ , is 50 percent more volatile for the $UC_{2,\widetilde{c},\kappa}$ model than it is for the $UC_{2,2,\kappa}$ model. The posteriors of these two UC models also produce correlations of -0.71 and -0.85 between $\Delta e^{\tau}$ and $\Delta a$ . Thus, a rising U.S. TFP is associated with an appreciation of the U.S. dollar. The late 1970s is one such period because Canada experienced a greater relative productivity slowdown. By the 1980s, Canadian TFP is growing more rapidly than in the U.S., which continues into the early 1990s. Subsequently, U.S. TFP recovers relative to Canadian TFP. At the end of the sample, the Canadian-U.S. TFP differential is expanding once more.

The bottom right window of figure 3 presents the smoothed $\widetilde{c}_{t}$ of the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde {c},\kappa}$ models. The former cycle is the dashed (blue) line and the latter is the dotted (red) plot. These cycles are persistent, with AR1 correlation statistics of 0.97 and 0.98, but the $UC_{2,2,\kappa}$ model generates a third less volatility in smoothed $\widetilde{c}_{t}$ than found for the $UC_{2,\widetilde{c},\kappa}$ model.

The smoothed $\widetilde{c}_{t}$ has peaks and troughs that coincide with several U.S.-Canadian business cycle dates. For example, troughs in the posterior mean of $\widetilde{c}_{t}$ appear in 1981 and 1990, which also represent recessions dates in the U.S. and Canada. Since the end of the 1990-1991 recession, the rise in $\widetilde{c}_{t}$ points to a persistent, but transitory, rise in U.S. consumption relative to Canada. Nonetheless, $\widetilde{c}_{t}$ has been falling rapidly since a peak in late 2001, which corresponds to the end of the last U.S. recession.

The bottom row of table 9 shows that $\widetilde{c}_{t}$ and $\widetilde{e}_{t}$ are perfectly negatively correlated in the posteriors of the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde {c},\kappa}$ models. The negative correlation of the transitory component of the exchange rate with $\widetilde{c}_{t}$ helps to interpret exchange rate fluctuations. Peaks in the transitory component of the exchange rate occur either at or shortly after the end of recessions. For example, the smoothed exchange rate cycles have a tendency to peak and trough around dates usually associated with U.S. and Canadian business cycle dates (i.e., the late 1970s, early 1990s, and 2001). A specific case is the peak in $\widetilde{e}_{t}$ during the 1990-1991 recession in the U.S., which is a moment at which the Canadian dollar approached par against the U.S. dollar. An exception is the end of the 2001 recession when the Canadian dollar reached a low of nearly 0.62 to the U.S. dollar.

5.D Comparing the UC models

The bottom row of table 4 reports the log marginal likelihoods, $\ln\widehat{\mathcal{L}}$ , of the $UC_{2,2,\kappa=1}$ , $\, UC_{2,\widetilde{m},\kappa=1}$ , and $UC_{2,\widetilde{c},\kappa=1}$ models. These marginal likelihoods show that our Canadian-U.S. sample gives most support to the $UC_{2,\widetilde{c},\kappa=1}$ model. The difference between this model and the $UC_{2,2,\kappa=1}$ model is about 29, so that the Bayes factor prefers the UC model with only transitory consumption. For the data to give more credence to the latter model, its prior probability must be raised by the prior probability of the $UC_{2,\widetilde{c},\kappa=1}$ model multiplied by 4.7 × 10¹²[=exp(29.18)]. Since the magnitude of this factor is large, it seems unreasonable to include the transitory money shock in the UC model when $\kappa$ is calibrated to one.

The last row of table 5 contains the log marginal likelihoods of the $UC_{2,2,\kappa}$ , $\, UC_{2,\widetilde{m},\kappa}$ , and $UC_{2,\widetilde{c},\kappa}$ models. The ranking of these models matches that of the UC models with the $\kappa= 1$ calibration. The $UC_{2,\widetilde {m},\kappa}$ model dominates the $UC_{2,2,\kappa}$ and $\, UC_{2,\widetilde {m},\kappa}$ models. A key reason is that the posteriors of these models yield economically implausible estimates of the DGSE-PVM discount factor $\kappa$ .

This raises the question of whether it is difficult to choose between the $UC_{2,\widetilde{c},\kappa=1}$ and $UC_{2,\widetilde{c},\kappa}$ models. Our sample favors the $UC_{2,\widetilde {c},\kappa=1}$ and $UC_{2,\widetilde{c},\kappa}$ models compared to the other four. The $UC_{2,\widetilde{c},\kappa=1}$ model has the largest marginal likelihood, which suggests that the data support it over the $UC_{2,\widetilde {c},\kappa}$ model. This choice relies on the belief that scaling up the prior probability of the $UC_{2,\widetilde{c},\kappa}$ model by 167.3 = exp(5.12) is too large to be justified. If, on the other hand, this factor is regarded as inconclusive in rejecting the $UC_{2,\widetilde{c},\kappa}$ model, it could be argued that our Canadian-U.S. sample cannot pick between the $UC_{2,\widetilde{c},\kappa=1}$ and $UC_{2,\widetilde{c},\kappa}$ models.²⁴ Nonetheless, these UC models support for the EW hypothesis.

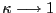
5.E Exchange Rate Dynamics as $\kappa \longrightarrow1$

Engel and West (2005) argue that the exchange rate will approximate a random walk when the discount factor is close to one and fundamentals have a unit root. Propositions 3 and 5 also predict that $\widetilde{e}_{t}$ will collapse to random walk as $\kappa \longrightarrow1$ .

We extract evidence about the EW hypothesis from the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde{c},\kappa}$ model posteriors. The focus is on these UC models rather than the $UC_{2,\widetilde{c},\kappa=1}$ model because it attributes all exchange rate movements to permanent shocks. We conduct this comparison with $\kappa$ s at the 16th and 84th percentiles, along with the largest $\kappa$ s, from the $\Gamma_{2,2,\kappa}$ and $\Gamma_{2,\widetilde{c},\kappa}$ vectors. For the $UC_{2,2,\kappa}$ ( $UC_{2,\widetilde{c},\kappa}$ ) model, the 16th percentile, 84th percentile, and largest $\kappa$ s are 0.9425, 0.9883, and 0.9990 (0.9943, 0.9987, and 0.9990), respectively. Fixing $\kappa$ at these values, we simulate the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde{c},\kappa}$ models extracting 2000 draws from the posteriors, discard the first 1000, run the Kalman smoother on the remaining 1000, and average the ensemble to generate exchange rate cycles that respect the rational expectations hypothesis.

Figure 4 plots the smoothed exchange rate cycles. The top (bottom) window contains the $\widetilde{e}_{t}$ created from the posterior of the $UC_{2,2,\kappa}$ ( $UC_{2,\widetilde{c},\kappa}$ ) model. The dot-dash (blue), dotted (green), and dotted (red) lines are conditional on the 16th percentile, 84th percentile, and largest $\kappa$ s, respectively. Across the top and bottom windows, the volatility of $\widetilde{e}_{t}$ is compressed as $\kappa$ approaches 0.999. This is reflected in the standard deviations of $\widetilde{e}_{t}$ that equal 4.44, 2.84, and 0.57 moving from the smallest to largest $\kappa$ for the $UC_{2,2,\kappa}$ model. The equivalent standard deviations are 3.74, 1.64, and 1.30 for the $UC_{2,\widetilde{c},\kappa}$ model. Although the $UC_{2,2,\kappa}$ model generates exchange rate cycles that are smoother than at its posterior mean only for the largest $\kappa$ s, this UC model is able to produce smoother exchange rate cycles at the 84th percentile and largest $\kappa$ s. Thus, pushing $\kappa$ increases the smoothness of the exchange rate cycle. This is evidence that lends credence to the EW hypothesis.

6 Conclusion

Economists have little to say about the impact of policy on currency markets without an equilibrium theory of exchange rate determination that is empirically relevant. According to Engel and West (2005), the near random walk behavior of exchange rates explains the failure of equilibrium models to fit the data or to find any model that systematically beats it at out-of-sample forecasting. They conjecture that the standard-present value model (PVM) of exchange rates yields the random walk prediction when fundamentals are persistent and the discount factor is close to one.

This paper generalizes the Engel and West (EW) hypothesis by constructing a PVM from a two-country monetary dynamic stochastic general equilibrium (DSGE) model. The standard- and DSGE-PVMs yield identical predictions for the exchange rate. These predictions are summarized by five propositions. Thus, we generalize the EW hypothesis to the larger class of open economy DSGE models.

Our empirical results support the view that the Canadian-U.S. data prefer a random walk exchange rate and a DSGE-PVM with a discount factor calibrated to one. At the same time we obtain evidence on the nature of the shocks driving exchange rates. Bayesian estimates of the DSGE-PVM indicate that the Canadian dollar-U.S. dollar exchange rate is dominated by permanent shocks, whether the discount factor is estimated or calibrated to one, which supports the EW hypothesis. Our evidence is also consistent with the recent VAR literature suggesting that monetary policy shocks have only a minor impact on exchange rate fluctuations. Monetary policy shocks are also found to be unimportant for exchange rate movements by Lubik and Schorfheide (2006) within the context of an estimated open economy DSGE model. Whether this result holds across a wider set of open economy DSGE models is a worthy goal of future research.

References

Adolfson, M., S. Laséen, J. Lindé, and M. Villani. 2007. Bayesian Estimation of an Open Economy DSGE Model with Incomplete Pass-Through. Journal of International Economics 72, 481-511.

An, S., F. Schorfheide. 2007. Bayesian analysis of DSGE models. Econometric Reviews 26, 113-172.

Beveridge, S., C.R. Nelson. 1981. A New Approach to Decomposition of Economic Time Series into Perman- ent and Transitory Components with Particular Attention to Measurement of the Business Cycle. Journal of Monetary Economics 7, 151-174.

Bilson, J.F.O. 1978. Rational Expectations and the Exchange Rate. in Frenkel, J.A., H.G. Johnson, THE ECONOMICS OF EXCHANGE RATES: SELECTED STUDIES, Addison-Wesley, Reading, MA.

Campbell, J.Y., R. Shiller. 1987. Cointegration and Tests of Present Value Models. Journal of Political Economy 93, 1062-1088.

Del Negro, M., F. Schorfheide. 2006. Forming Priors for DSGE Models (and How it Affects the Assessment of Nominal Rigidites). Working Paper 2006-16, Federal Reserve Bank of Atlanta.

Dornbusch, R. 1976. Expectations and Exchange Rate Dynamics. Journal of Political Economy 84, 1161-1176.

Eichenbaum, M., C. Evans, 1995. Some Empirical Evidence on the Effects of Monetary Policy Shocks on Exchange Rates. Quarterly Journal of Economics 110, 975-1010.

Engel, C., K.D. West, 2005. Exchange Rates and Fundamentals. Journal of Political Economy 113, 485-517.

Engle, R.F., J.V. Issler, 1995. Estimating Common Sectoral Cycles. Journal of Monetary Economics 35, 83-113.

Engle, R.F., S. Kozicki, 1993. Testing for Common Features. Journal of Business and Economics Statistics 11, 369-395.

Faust, J., J. Rogers, 2003. Monetary Policy's Role in Exchange Rate Behavior. $\,$ Journal of Monetary Economics 50, 1403-1424.

Fernández-Villaverde, J., J.F. Rubio-Ramírez. 2004. Comparing Dynamic Equilibrium Models to Data: A Bayesian Approach. Journal of Econometrics 123, 153-187.

Frankel, J.A., 1979. On the Mark: A Theory of Floating Exchange Rates Basedon Real Interest Rate Differentials. American Economics Review 69, 610-622.

Gelman, A., J.B. Carlin, H.S. Stern, D.B. Rubin, 2004, BAYESIAN DATA ANALYSIS, SECOND EDITION, Chapman and Hall, New York, NY.

Geweke, J., 1999. Using Simulation Methods for Bayesian Econometric Models: Inference, Development and Communication. Econometric Reviews 18, 1-126.

Geweke, J., 2005. CONTEMPORARY BAYESIAN ECONOMETRICS AND STATISTICS, J. Wiley and Sons, Inc., Hoboken, NJ.

Hamilton, J.D., 1994, TIME SERIES ANALYSIS, Princeton University Press, Princeton, NJ.

Hansen, L.P., W. Roberds, T.J. Sargent. 1991. Time Series Implications of Present Value Budget Balance and of Martingale Models and Consumption and Taxes. in Hansen, L.P., T.J. Sargent (eds.), RATIONAL EXPECTATIONS ECONOMETRICS, Westview Press, Boulder, CO.

Harvey, A.C., FORECASTING, STRUCTURAL TIME SERIES MODELS AND THE KALMAN FILTER, Cambridge University Press, Cambridge, England.

Harvey, A.C., T.M. Trimbur, H.K. van Dijk. 2007. Trends and Cycles in Economic Time Series: A Bayesian Approach. Journal of Econometrics 140, 618-649.

Hecq, A., F.C. Palm, J-P. Urbain. 2000. Permanent-Transitory Decomposition in VAR Models with Cointegration and Common Cycles. Oxford Bulletin of Economics and Statistics 62, 511-532.

Jeffreys, H., 1998. THEORY OF PROBABILITY, Oxford University Press, Oxford, UK.

Johansen, S. 1991. Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Auto- regressive Models. Econometrica 59, 1551-1580.

Johansen, S. 1994. The Role of the Constant and Linear Terms in Cointegration Analysis and Nonstationary Variables. Econometric Reviews 13, 205-229.

Kim, S., N. Roubini. 2000. Exchange Rate Anomalies in the Industrial Countries: A Solution with a Structural VAR Approach. Journal of Monetary Economics 45, 561-586.

Lubik, T., F. Schorfheide. 2006. A Bayesian Look at New Open Economy Macroeconomics. in Gertler, M., K. Rogoff (eds.), NBER MACROECONOMICS ANNUAL 2005. MIT Press, Cambrigde, MA.

MacKinnon, J.G., A.A. Haug, L. Michelis. 1999. Numerical Distributions of Likelihood Ratio Tests of Cointegration. Journal of Applied Econometrics 14, 563-577.

Maheswaran, S., C.A. Sims. 1993. Empirical Implications of Arbitrage-Free Asset Markets. in Phillips, P.C.B. (ed.), MODELS, METHODS AND APPLICATIONS OF ECONOMETRICS, Blackwell Publishing, Oxford, UK.

Mark, N. 1995. Exchange Rates and Fundamentals: Evidence on Long-Horizon Predictability. American Economics Review 85, 201-218.

Mark, N., D. Sul, 2003. Cointegration Vector Estimation by Panel DOLS and Long-Run Money Demand. Oxford Bulletin of Economics and Statistics 65, 665-680.

Meese, R.A., 1986. Testing for Bubbles in Exchange Markets: A Case of Sparkling Rates. Journal of Political Economy 94, 345-373.

Morley, J.C., C.R. Nelson, E. Zivot. 2003. Why Are Beveridge-Nelson and Unobserved Component Decompositions of GDP So Different? Review of Economics and Statistics 85, 235-234.

Osterwald-Lenum, M. 1992. Quantiles of the Asymptotic Distribution of the Maximum Likelihood Cointegration Rank Test Statistics, Oxford Bulletin of Economics and Statistics 54, 461-472.

Rabanal, P., J.F. Rubio-Ramírez. 2005. Comparing New Keynesian Models of the Business Cycle: A Bayesian Approach. Journal of Monetary Economics 52, 1151-1166.

Rao, C.S. 1973. LINEAR STATISTICAL INFERENCE, Wiley, Ltd., New York, NY.

Rogers, J.H., 2000. Monetary Shocks and Real Exchange Rates. Journal of International Economics 49, 269-288.

Rogoff, K. 2007. Comments on: Engel, Mark, and West's Exchange Rate Models Are Not as Bad as You Think. in Acemoglu, D., K. Rogoff, M. Woodford (eds.), NBER MACROECONOMICS ANNUAL 2007, VOL. 22, MIT Press, Cambridge, MA.

Rossi, B. 2007. Comments on: Engel, Mark, and West's Exchange Rate Models Are Not as Bad as You Think. in Acemoglu, D., K. Rogoff, M. Woodford (eds.), NBER MACROECONOMICS ANNUAL 2007, VOL. 22, MIT Press, Cambridge, MA.

Scholl, A., Uhlig, H., 2005. New Evidence on the Puzzles. Results from Agnostic Identification on Monetary Policy and Exchange Rates. SFB 649 Discussion Paper No. 2005-037.

Sims, C.A. 1980. Macroeconomics and Reality. Econometrica 48, 1-48.

Sims, C.A., Stock, J.H., M.W. Watson. 1990. Inference in Linear Time Series Models with Some Unit Roots. Econometrica 58, 113-144.

Stock, J.H., M.W. Watson. 1988. Testing for Common Trends. Journal of the American Statistical Association 83, 1097-1107.

Vahid, F., R.F. Engle. 1993. Common Trends and Common Cycles. Journal of Applied Econometrics 8, 341-360.

Table 1: Summary of Standard PVM and DSGE-PVM: Panel A: Standard-PVM

ECM(0):	(13) $\Delta e_{t} - \frac{\displaystyle 1 - \omega} {\displaystyle \omega} \mathcal{X}_{t-1} = (1 - \omega) \sum ^{\infty}_{j=0} \omega^{j} \bigl[\mathbf{E}_{t} - \mathbf{E}_{t-1} \bigr] z_{t+j}$ .
EW Equation:	(14) $\Delta e_{t} \; = \; \zeta\left( \omega\right) \upsilon_{t} \, + \, (1 - \omega) \sum_{j=0}^{\infty} \omega^{j}\mathbf{E}_{t-1} \Delta z_{t+j}$ .
Parameters:	$\omega\equiv\frac{\displaystyle \phi}{ \displaystyle 1+\phi} =$ Discount Factor, $\phi=$ Money Demand Interest Rate Semi-Elasticity, $\psi=$ Money Demand Income Elasticity.
Fundamentals:	$\mathcal{X}_{t} \; = \; e_{t} - z_{t}$ , $z_{t} \; = \; m_{t} - \psi y_{t}$ , $m_{t} =$ Cross Country Money, $y_{t} =$ Cross-Country Output.

Table 1: Summary of Standard PVM and DSGE-PVM: Panel B: DSGE-PVM

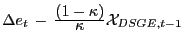ECM(0):	(13) $\Delta e_{t} \, - \, \frac {\displaystyle (1 - \kappa)}{\displaystyle \kappa} \mathcal{X}_{DSGE,t-1}$ $= \; \; (1 - \kappa) \sum_{j=0}^{\infty} \kappa^{j} \left[ \mathbf{E}_{t} - \mathbf{E}_{t-1} \right] \left\{ m_{t+j} \, - \, c_{t+j} \right\}$ .
EW Equation:	(14) $\Delta e_{t} \, = \, \sum _{j=0}^{\infty} \kappa^{j} \left[ \mathbf{E}_{t} - \mathbf{E}_{t-1} \right] \left\{ \Delta m_{t+j} \, - \, \Delta c_{t+j} \right\}$ $+ \; (1 - \kappa) \sum_{j=0}^{\infty} \kappa^{j} \mathbf{E}_{t} \left\{ \Delta m_{t+j} \, - \, \Delta c_{t+j} \right\}$ .
Parameters:	$\kappa\equiv\frac{\displaystyle 1 \; \;}{ \displaystyle 1 + r^{\ast}} =$ Discount Factor, $r^{\ast} =$ Steady State Real World Interest Rate.
Fundamentals:	$\mathcal{X}_{DSGE, t} \; = \; e_{t} - m_{t} + c_{t}$ , $m_{t} =$ Cross Country Money, $c_{t} =$ Cross-Country Output.

Table 2: Summary of Propositions for Standard- and DSGE-PVMs

Proposition 1:	PVM Predicts Exchange Rate and Fundamentals Cointegrate; Campbell and Shiller (1987).
Proposition 2:	Currency Returns Are an ECM(0).
Proposition 3:	Exchange Rate Approximates a Martingale as $\mathcal{B} \longrightarrow1$ .
Proposition 4:	VECM(0) Imply Common Trend and Common Cycle for Exchange Rate and Fundamental.
Proposition 5:	EW's (2005) Hypothesis Needs Currency Returns and Fundamental Growth Share a Co-Feature and $\mathcal{B} \longrightarrow1$ .

Table 3: Tests of Propositions 1, 3, and 5: Sample 1976Q1 - 2004Q4: Panel A: Proposition 3: VECM(0)

Statistic	Canada & U.S.	Japan & U.S.	U.K. & U.S.
Levels VAR Lag Length	8	5	4
LR statistic p-value	(0.02)	(0.01)	(0.09)

Table 3: Tests of Propositions 1, 3, and 5: Sample 1976Q1 - 2004Q4: Panel B: Proposition 1: Common Trend Cointegration Tests

Model	Canada & U.S. Case 2*	Japan & U.S. Case 1	U.K. & U.S. Case 1
λ-Max statistic: Two Unit Root	$\; \,$ 4.86	0.20	2.27
λ-Max statistic: One Unit Root	17.28	4.64	12.32
Trace statistic: Two Unit Root	$\;$ 4.86	0.20	2.27
Trace statistic: One Unit Root	12.42	4.43	10.04

Table 3: Tests of Propositions 1, 3, and 5: Sample 1976Q1 - 2004Q4: Panel C: Proposition 5: Common Cycle

Statistic	Canada & U.S.	Japan & U.S.	U.K. & U.S.
Sq. Canonical Correlations	0.30, 0.09	0.44, 0.08	0.19, 0.07
χ²-statistic p-value	(0.01), (0.69)	(0.00), (0.21)	(0.00), (0.12)
F-statistic p-value	(0.00), (0.61)	(0.00), (0.19)	(0.00), (0.11)

The level of fundamentals equals cross-country money netted with cross-country output calibrated to a unitary income elasticity of money demand. The money stocks (outputs) are measured in current (constant) local currency units and per capita terms. A constant and linear time trend are included in the level VARs. The LR statistics employ the Sims (1980) correction and have standard asymptotic distribution according to results in Sims, Stock, and Watson (1990). The case 2* and case 1 model definitions are based on Osterwald-Lenum (1992). MacKinnon, Haug, and Michelis (1999) provide five percent critical values of 8.19 (8.19) and 18.11 (15.02) for the case 2* model λ-max (trace) tests and 3.84 (3.84) and 15.49 (14.26) for the case 1 model. The common feature tests compute the canonical correlations of Δe_t and Δm_t - Δy_t. The common feature null is all or a subset of the canonical correlations are zero. See Engle and Issler (1995) and Vahid and Engle (1993) for details.

Table 4: UC Model Posterior Means, κ = 1

Parameter	Priors	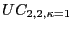$\, UC_{2,2,\kappa=1}$	$\, UC_{2,\widetilde{m},\kappa=1}$	$\, UC_{2,\widetilde{c},\kappa=1}$
$\alpha_{1}$	Normal	-1.1906	-0.8691	-
$\alpha_{1}$ : [parameters] (std. devs)	[-1.2, 0.10]	(0.0613)	(0.0470)	-
$\alpha_{2}$	Normal	0.4133	0.9501	-
$\alpha_{2}$ : [parameters] (std. devs)	[0.40, 0.17]	(0.1092)	(0.0528)	-
$\theta_{1}$	Normal	0.9407	-	0.9830
$\theta_{1}$ : [parameters] (std. devs)	[0.85, 0.10]	(0.0491)	-	(0.0296)
$\theta_{2}$	Normal	0.0403	-	0.0069
$\theta_{2}$ : [parameters] (std. devs)	[0.10, 0.15]	(0.0488)	-	(0.0291)
$\mu^{\ast}$	Normal	-0.1260	-0.1258	-0.1258
$\mu^{\ast}$ : [parameters] (std. devs)	[-0.126, 0.015]	(0.0150)	(0.0150)	(0.0120)
$a^{\ast}$	Normal	0.1615	0.1645	0.1571
$a^{\ast}$ : [parameters] (std. devs)	[0.158, 0.025]	(0.0229)	(0.0213)	(0.0199)
$\sigma_{\mu}$	Inv-Gamma	1.8838	2.4629	1.6784
$\sigma_{\mu}$ : [parameters] (std. devs)	[2.0, 1.5]	(0.1436)	(0.1507)	(0.1264)
$\sigma_{a}$	Inv-Gamma	1.0471	0.3971	1.9461
$\sigma_{a}$ : [parameters] (std. devs)	[2.0, 0.4]	(0.2206)	(0.0345)	(0.3831)
$\sigma_{\widetilde{m}}$	Inv-Gamma	0.6002	0.4728	-
$\sigma_{\widetilde{m}}$ : [parameters] (std. devs)	[2.0, 0.6]	(0.0899)	(0.1168)	-
$\sigma_{\widetilde{c}}$	Inv-Gamma	1.2874	-	2.0135
$\sigma_{\widetilde{c}}$ : [parameters] (std. devs)	[2.0, 0.7]	(0.2354)	-	(0.3823)
$\varrho_{a,\widetilde{c}}$	Normal	-0.8758	-	-0.9475
$\varrho_{a,\widetilde{c}}$ : [parameters] (std. devs)	[-0.5, 0.2]	(0.0462)	-	(0.0234)
$\pi_{e,0}$	Normal	80.1528	138.8984	62.9442
$\pi_{e,0}$ : [parameters] (std. devs)	[100.0, 15.0]	(6.8283)	(5.7281)	(2.9991)
$\pi_{e,t}$	Normal	0.7038	1.9366	0.3831
$\pi_{e,t}$ : [parameters] (std. devs)	[1.0, 0.5]	(0.1710)	(0.1106)	(0.1306)
$\pi_{e,a}$	Uniform	-2.6822	-9.0223	-0.7208
$\pi_{e,a}$ : [parameters] (std. devs)	[-10.0, 0.0]	(0.6316)	(0.5377)	(0.1886)
$\pi_{c,\widetilde{m}}$	Uniform	-	4.3973	-
$\pi_{c,\widetilde{m}}$ : [parameters] (std. devs)	[-2.0, 7.5]	-	(1.1057)	-
$\pi_{m,\widetilde{c}}$	Uniform	-	-	-0.8985
$\pi_{m,\widetilde{c}}$ : [parameters] (std. devs)	[-7.5, 2.0]	-	-	(0.2099)
$\ln\widehat{\mathcal{L}}$	-	-53.95	-226.76	-24.76

Table 5: UC Model Posterior Means, κ ∈ [0.9, 0.999]

Parameter	Priors	$UC_{2,2,\kappa}$	$\, UC_{2,\widetilde {m},\kappa}$	$\, UC_{2,\widetilde{c},\kappa}$
$\kappa$	Inv-Gamma	0.9658	0.9738	0.9962
$\kappa$ : [parameters] (std. devs)	[0.988, 0.038]	(0.0219)	(0.0196)	(0.0046)
$\alpha_{1}$	Normal	-1.1892	-0.8828	-
$\alpha_{1}$ : [parameters] (std. devs)	[-1.20, 0.10]	(0.0673)	(0.0369)	-
$\alpha_{2}$	Normal	0.4131	0.8465	-
$\alpha_{2}$ : [parameters] (std. devs)	[0.40, 0.17]	(0.1179)	(0.0223)	-
$\theta_{1}$	Normal	0.9396	-	0.9799
$\theta_{1}$ : [parameters] (std. devs)	[0.85, 0.10]	(0.0431)	-	(0.0315)
$\theta_{2}$	Normal	0.0421	-	0.0018
$\theta_{2}$ : [parameters] (std. devs)	[0.10, 0.15]	(0.0422)	-	(0.0314)
$\mu^{\ast}$	Normal	-0.1256	-0.1260	-0.1260
$\mu^{\ast}$ : [parameters] (std. devs)	[-0.126, 0.015]	(0.0148)	(0.0149)	(0.0147)
$a^{\ast}$	Normal	0.1621	0.1630	0.1578
$a^{\ast}$ : [parameters] (std. devs)	[0.158, 0.025]	(0.0227)	(0.0205)	(0.0243)
$\sigma_{\mu}$	Inv-Gamma	1.8914	2.4241	1.7188
$\sigma_{\mu}$ : [parameters] (std. devs)	[2.0, 1.5]	(0.1484)	(0.1663)	(0.1112)
$\sigma_{a}$	Inv-Gamma	1.0842	0.4043	1.5738
$\sigma_{a}$ : [parameters] (std. devs)	[2.0, 0.4]	(0.2477)	(0.0378)	(0.2727)
$\sigma_{\widetilde{m}}$	Inv-Gamma	0.6068	0.5752	-
$\sigma_{\widetilde{m}}$ : [parameters] (std. devs)	[2.0, 0.6]	(0.0865)	(0.0975)	-
$\sigma_{\widetilde{c}}$	Inv-Gamma	1.3828	-	1.6742
$\sigma_{\widetilde{c}}$ : [parameters] (std. devs)	[2.0, 0.7]	(0.2346)	-	(0.2772)
$\varrho_{a,\widetilde{c}}$	Normal	-0.8990	-	-0.9256
$\varrho_{a,\widetilde{c}}$ : [parameters] (std. devs)	[-0.5, 0.2]	(0.0409)	-	(0.0291)
$\pi_{e,0}$	Normal	85.2271	135.7241	67.8714
$\pi_{e,0}$ : [parameters] (std. devs)	[100.0, 15.0]	(6.7620)	(6.3363)	(3.7506)
$\pi_{e,t}$	Normal	0.7955	1.9076	0.4526
$\pi_{e,t}$ : [parameters] (std. devs)	[1.0, 0.5]	(0.1774)	(0.1211)	(0.1112)
$\pi_{e,a}$	Uniform	-3.2825	-8.8023	-1.2605
$\pi_{e,a}$ : [parameters] (std. devs)	[-10.0, 0.0]	(0.6426)	(0.5900)	(0.3087)
$\pi_{c,\widetilde{m}}$	Uniform	-	4.4186	-
$\pi_{c,\widetilde{m}}$ : [parameters] (std. devs)	[-2.0, 7.5]	-	(0.7952)	-
$\pi_{m,\widetilde{c}}$	Uniform	-	-	-1.0380
$\pi_{m,\widetilde{c}}$ : [parameters] (std. devs)	[-7.5, 2.0]	-	-	(0.2179)
$\ln\widehat{\mathcal{L}}$	-	-53.94	-253.03	-29.88

Table 6: UC Model Posterior Means, κ ∈ [0.9, 0.999], Factor Loadings on Money and Consumption Cycles

Parameter	$UC_{2,2,\kappa}$	$\, UC_{2,\widetilde{m},\kappa}$	$\, UC_{2,\widetilde{c},\kappa}$
$(1 - \pi_{c,\widetilde{m}})\delta_{\widetilde{m},0}$	0.0086	-0.0841	-
$(1 - \pi_{c,\widetilde{m}})\delta_{\widetilde{m},0}$ std. dev.	(0.0096)	(0.0676)	-
$(1 - \pi_{c,\widetilde{m}})\delta_{\widetilde{m},1}$	-0.0269	0.0064	-
$(1 - \pi_{c,\widetilde{m}})\delta_{\widetilde{m},1}$ std. dev.	(0.0188)	(0.0082)	-
$(1 - \pi_{c,\widetilde{m}})\delta_{\widetilde{m},2}$	0.0143	-0.0762	-
$(1 - \pi_{c,\widetilde{m}})\delta_{\widetilde{m},2}$ std. dev.	(0.0108)	(0.0624)	-
$(1 - \pi_{c,\widetilde{m}})\Sigma_{i} \delta_{\widetilde{m},i}$	-0.0040	-0.1542	-
$(1 - \pi_{c,\widetilde{m}})\Sigma_{i} \delta_{\widetilde{m},i}$ std. dev.	(0.0202)	(0.1237)	-
$(1 - \pi_{m,\widetilde{c}})\delta_{\widetilde{c},0}$	-0.6044	-	-0.3252
$(1 - \pi_{m,\widetilde{c}})\delta_{\widetilde{c},0}$ std. dev.	(0.2042)	-	(0.2052)
$(1 - \pi_{m,\widetilde{c}})\delta_{\widetilde{c},1}$	-0.0238	-	-0.0004
$(1 - \pi_{m,\widetilde{c}})\delta_{\widetilde{c},1}$ std. dev.	(0.0261)	-	(0.0111)
$(1 - \pi_{m,\widetilde{c}})\Sigma_{i} \delta_{\widetilde{c},i}$	-0.6283	-	-0.3256
$(1 - \pi_{m,\widetilde{c}})\Sigma_{i} \delta_{\widetilde{c},i}$ std. dev.	(0.2117)	-	(0.2053)

^† The factor loadings $\pi_{c,\widetilde{m}}$ and $\pi_{m,\widetilde{c}}$ equal zero for the $UC_{2,2,\kappa}$ model.

Table 7: US Model Posterior Means, κ ∈ [0.9, 0.999], Variance(PDV-ε) / Variance(Δe)

Parameter	$UC_{2,2,\kappa}$	$\, UC_{2,\widetilde{m},\kappa}$	$\, UC_{2,\widetilde{c},\kappa}$
$Var(PDV-\varepsilon_{\mu}) / Var(\Delta e)$	0.92	1.48	0.71
$Var(PDV-\varepsilon_{\mu}) / Var(\Delta e)$ std. dev.	(0.15)	(0.22)	(0.09)
$Var(PDV-\varepsilon_{a}) / Var(\Delta e)$	3.04	0.36	0.96
$Var(PDV-\varepsilon_{a}) / Var(\Delta e)$ std. dev.	(0.73)	(0.06)	(0.53)
$Var(PDV-\varepsilon_{\widetilde{m}}) / Var(\Delta e)$	0.00	0.00	-
$Var(PDV-\varepsilon_{\widetilde{m}}) / Var(\Delta e)$ std. dev.	(0.00)	(0.00)	-
$Var(PDV-\varepsilon_{\widetilde{c}}) / Var(\Delta e)$	0.22	-	0.12
$Var(PDV-\varepsilon_{\widetilde{c}}) / Var(\Delta e)$ std. dev.	(0.16)	-	(0.22)

Table 8: UC-Models, κ ∈ [0.9, 0.999], Exchange Rate FEVDs^†: Panel A: $UC_{2,2,\kappa}$ Model

Forecast Horizon	$\varepsilon_{\mu}$	$\varepsilon_{A}$	$\varepsilon_{\widetilde{c}}$
1	0.23	0.77	0.00
4	0.23	0.77	0.00
12	0.21	0.79	0.00
20	0.19	0.80	0.01
40	0.15	0.82	0.03

Table 8: UC-Models, κ ∈ [0.9, 0.999], Exchange Rate FEVDs^†: Panel B: $UC_{2,\widetilde{m},\kappa}$ Model

Forecast Horizon	$\varepsilon_{\mu}$	$\varepsilon_{A}$	$\varepsilon_{\widetilde{c}}$
1	0.32	0.68	-
4	0.32	0.68	-
12	0.32	0.68	-
20	0.32	0.68	-
40	0.32	0.68	-

Table 8: UC-Models, κ ∈ [0.9, 0.999], Exchange Rate FEVDs^†: Panel C: $UC_{2,\widetilde{c},\kappa}$ Model

Forecast Horizon	$\varepsilon_{\mu}$	$\varepsilon_{A}$	$\varepsilon_{\widetilde{c}}$
1	0.59	0.40	0.01
4	0.58	0.41	0.01
12	0.57	0.42	0.01
20	0.57	0.43	0.01
40	0.55	0.45	0.01

^† The summary statistics are the means of the ensemble of FEVDs with respect to permanent and transitory Canadian-U.S. money differential and Canadian-U.S. consumption differential shocks generated from the $UC_{2,2,\kappa}$ , $UC_{2,\widetilde{m},\kappa}$ , and $UC_{2,\widetilde {c},\kappa}$ model posterior distributions.

Table 9: UC-Models, κ ∈ [0.9, 0.999], Summary of the Trend-Cycle Decomposition^†

Parameter	$UC_{2,2,\kappa}$	$\, UC_{2,\widetilde{m},\kappa}$	$\, UC_{2,\widetilde{c},\kappa}$
$STD( \Delta e^{\tau} )$	2.66	104.28	2.44
$STD( \widetilde{e} )$	3.68	106.84	2.55
$AR1( \widetilde{e} )$	0.97	0.55	0.98
$Corr(\Delta e^{\tau}, \; \widetilde{e})$	-0.06	-0.37	-0.02
$STD(\Delta\mu)$	1.62	4.54	1.71
$STD(\widetilde{m})$	0.68	3.03	-
$AR1(\widetilde{m})$	-0.68	0.13	-
$Corr(\Delta\mu, \; \widetilde{m})$	0.26	-0.24	-
$STD(\Delta a)$	0.99	12.18	1.56
$STD(\widetilde{c})$	5.73	-	7.73
$AR1(\widetilde{c})$	0.97	-	0.98
$Corr(\Delta a, \; \widetilde{c})$	-0.16	-	-0.14
$Corr(\Delta e^{\tau}, \; \Delta\mu)$	0.01	-0.40	0.62
$Corr(\Delta e^{\tau}, \; \Delta a)$	-0.85	-0.93	-0.71
$Corr(\Delta\mu, \; \Delta a)$	0.52	0.55	0.10
$Corr(\widetilde{e}, \; \widetilde{m})$	0.04	-0.73	-
$Corr(\widetilde{e}, \; \widetilde{c})$	-1.00	-	-1.00

^† The summary statistics are the means of the ensemble of CDN$/US$ exchange rate, Canadian-U.S. money differential, and Canadian-U.S. consumption differential trends and cycles generated from the $UC_{2,2,\kappa}$ , $UC_{2,\widetilde{m},\kappa}$ , and $UC_{2,\widetilde {c},\kappa}$ model posterior distributions.

Figure 1: Prior and Posterior PDFs of DSGE-PVM Discount Factor

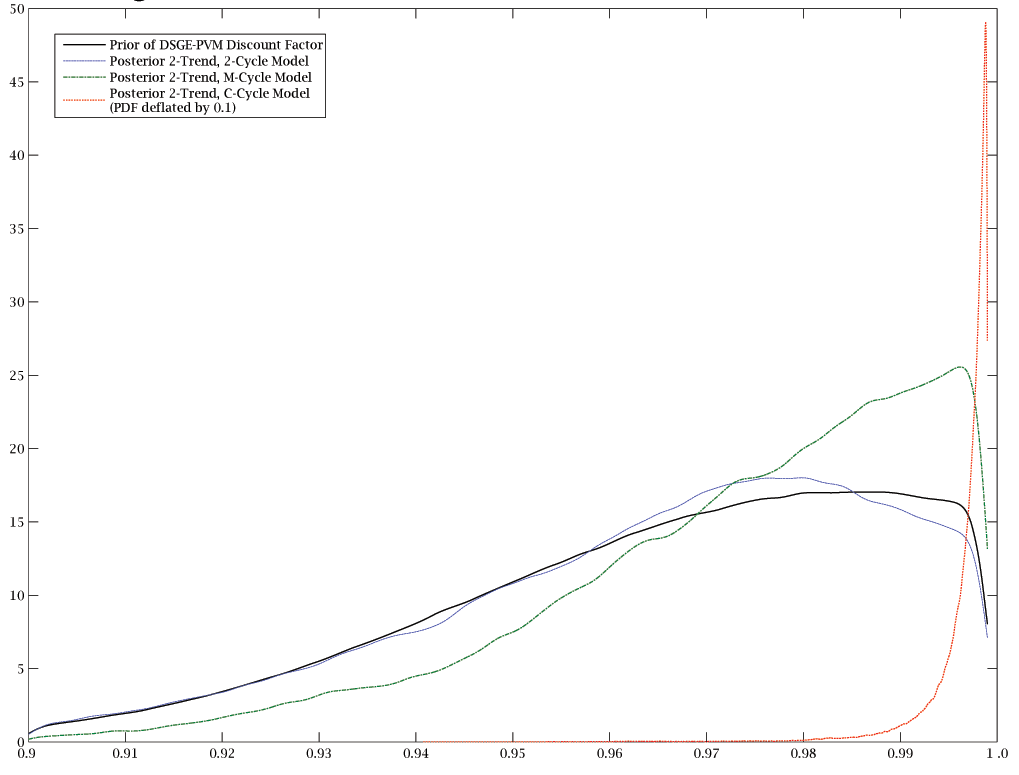
$Figure 1 presents densities of the prior and posteriors of kappa for UC_{2,2,kappa}, UC_{2,m,kappa}, and UC_{2,c,kappa}. The UC_{2,c,kappa} model posteriors yield estimates of kappa that are to the right of those of the UC_{2,2,kappa} and UC_{2,m,kappa} models. The kappa prior density is close to the posterior density of kappa derived from the UC_{2,2,kappa} model. The UC_{2,m,kappa} model generates a posterior density of kappa that moves off the prior by placing less weight on kappa_s less than 0.97 and more weight above it. The density of kappa from the UC_{2,c,kappa} model posterior is deflated by ten percent to ease comparison to the other densities. A striking feature of figure 1 is that the UC_{2,c,kappa} model posterior pushes kappa off of its prior because its mass lays between 0.98 and 0.999.$

Figure 2: CDN$/US$ Exchange Rate Trend and Cycle, 1976Q1 - 2004Q4

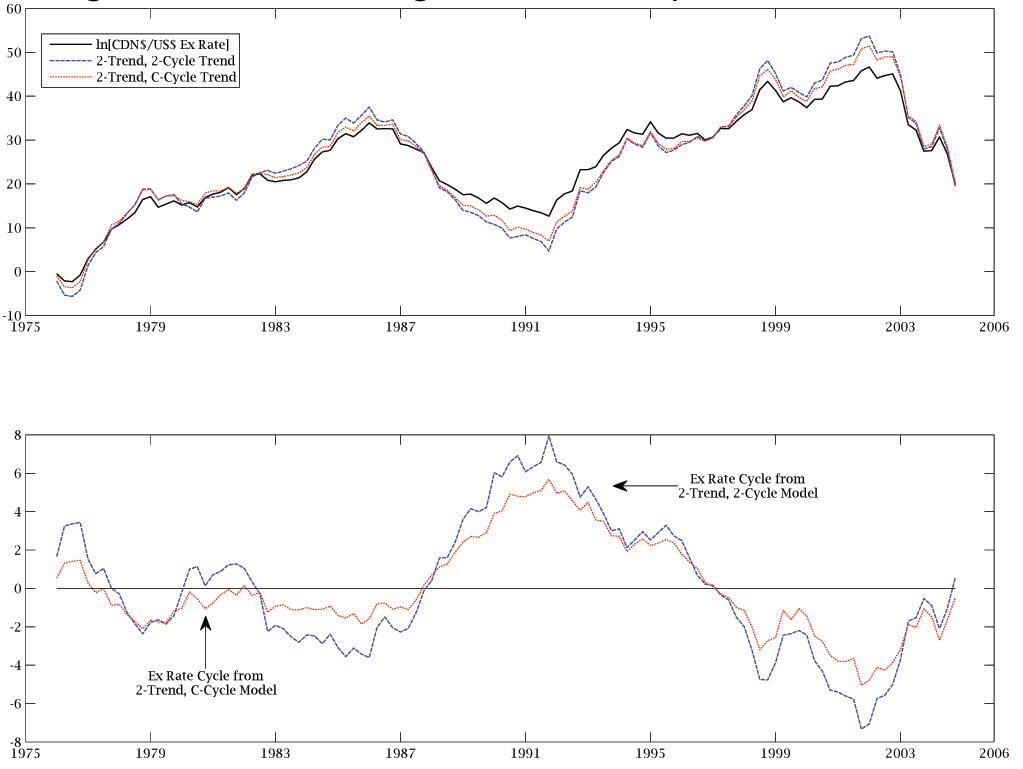
$In Figure 2, the top window contains plots of the exchange rate and smoothed trends taken from the posteriors of the UC_{2,2,kappa} and UC_{2,c,kappa} models. These UC models generate smoothed exchange rate trends that are more volatile than the actual exchange rate. The smoothed exchange rate cycles appear in the bottom window of figure 2. Although the smoothed exchange rate cycle, e_{t}, based on the posterior of the UC_{2,2,kappa} model exhibits more variability than the one associated with the UC_{2,c,kappa} model (the standard deviations are 3.68 and 2.44), these e_{t}s are persistent with AR1 correlation statistics of 0.97 and 0.98.$

Figure 3: CDN-US Money, Consumption Trends and Cycles, 1976Q1 - 2004Q4

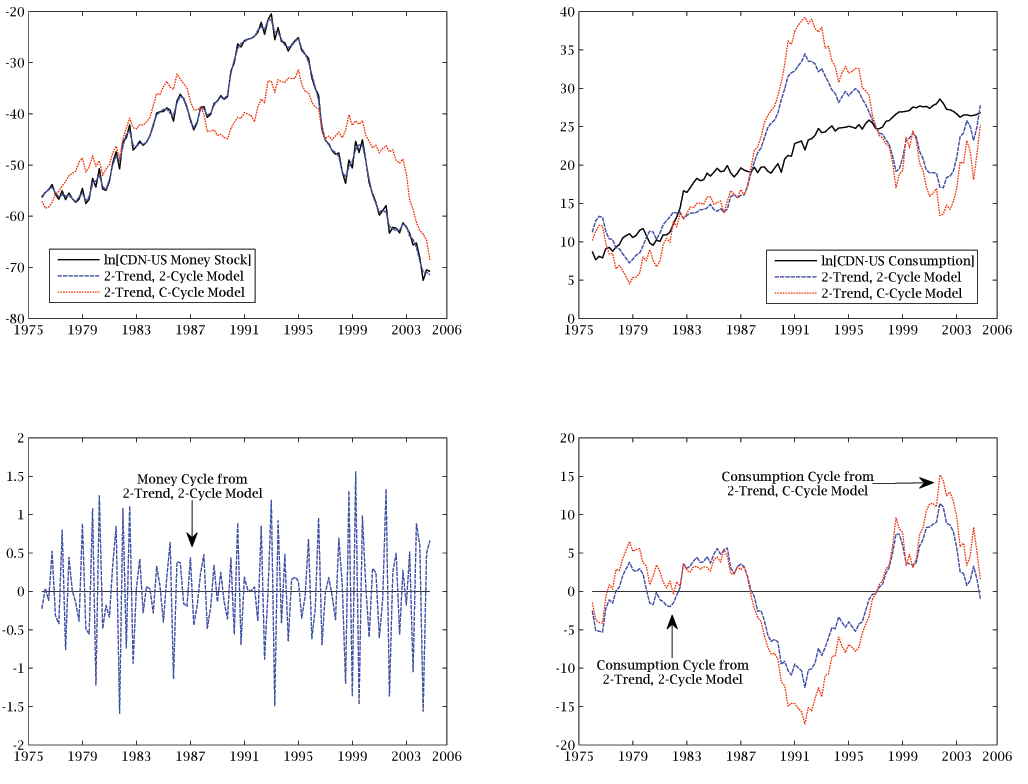
$Figure 3 presents smoothed permanent-transitory decompositions of the Canadian-U.S. money and consumption differentials. The actual differentials and smoothed trends appear in the top row of windows, while smoothed cycles are found in the bottom row of windows. The money (consumption) differentials are the right (left) side windows. The posterior of the UC_{2,2,kappa} model produces a money trend, mu_{t} that almost perfectly mimics the actual Canadian-U.S. money differentials, as shown in the top left window. The result is that smoothed m_{t} is much less volatile, with a standard deviation of 0.68 compared to a standard deviation of 1.62 for mu_{t}. The bottom left window shows a saw-toothed pattern in m_{t}, conditional on the posterior of the UC_{2,2,kappa} model. The posteriors of the UC_{2,2,kappa} and UC_{2,c,kappa} models yield qualitatively similar plots for the smoothed TFP trend differential, a_{t}. These plots appear in the top right window. The smoothed TFP growth differential, delta a, is 50 percent more volatile for the UC_{2,c,kappa} model than it is for the UC_{2,2,kappa} model. The posteriors of these two UC models also produce correlations of -0.71 and -0.85 between delta e to the power of tau and delta a. The bottom right window of figure 3 presents the smoothed c_{t} of the UC_{2,2,kappa} and UC_{2,c,kappa} models. These cycles are persistent, with AR1 correlation statistics of 0.97 and 0.98, but the UC_{2,2,kappa} model generates a third less volatility in smoothed c_{t} than found for the UC_{2,c,kappa} model. The smoothed c_{t} has peaks and troughs that coincide with several U.S.-Canadian business cycle dates. For example, troughs in the posterior mean of c_{t} appear in 1981 and 1990, which also represent recessions dates in the U.S. and Canada. Since the end of the 1990--1991 recession, the rise in c_{t} points to a persistent, but transitory, rise in U.S. consumption relative to Canada. Nonetheless, c_{t} has been falling rapidly since a peak in late 2001, which corresponds to the end of the last U.S. recession.$

Figure 4: CDN$/US$ Ex Rate Cycles at Different DSGE-PVM Discount Factors

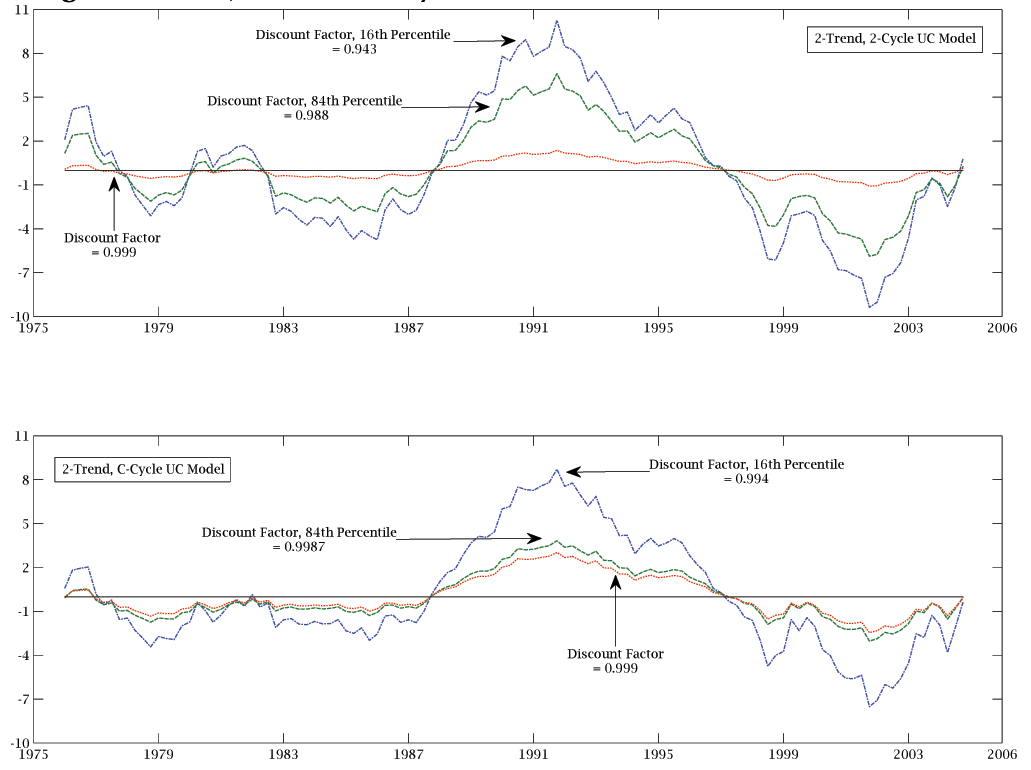
$Figure 4 plots the smoothed exchange rate cycles. The top (bottom) window contains the e_{t} created from the posterior of the UC_{2,2,kappa} (UC_{2,c,kappa}) model, conditional on the 16th percentile, 84th percentile, and largest kappa_s. Across the top and bottom windows, the volatility of e_{t} is compressed as kappa approaches 0.999. This is reflected in the standard deviations of e_{t} that equal 4.44, 2.84, and 0.57 moving from the smallest to largest kappa for the UC_{2,2,kappa} model. The equivalent standard deviations are 3.74, 1.64, and 1.30 for the UC_{2,c,kappa} model. Although the UC_{2,2,kappa} model generates exchange rate cycles that are smoother than at its posterior mean only for the largest kappa_s, this UC model is able to produce smoother exchange rate cycles at the 84th percentile and largest kappa_s. Thus, pushing kappa increases the smoothness of the exchange rate cycle. This is evidence that lends credence to the EW hypothesis.$

Footnotes

* We wish to thank Toni Braun, Fabio Canova, Menzie Chinn, Frank Diebold, John Geweke, Fumio Hayashi, Sharon Kozicki, Adrian Pagan, Juan F. Rubio-Ramírez, Tom Sargent, Pedro Silos, Ellis Tallman, Noah Williams, Farshid Vahid, Kenji Wada, Ken West, Tao Zha, the Federal Reserve Bank of Atlanta macro lunch study group, and seminar participants at the 2006 NBER Summer Institute Working Group on Forecasting and Empirical Methods in Macroeconomics and Finance, the 2007 Norges Bank Workshop on, "Prediction and Monetary Policy in the Presence of Model Uncertainty", the 2007 Bank of Canada-European Central Bank Exchange Rate Modeling Workshop, the 2007 Reserve Bank of Australia Research Workshop, "Monetary Policy in Open Economies", Ohio State, Houston, Tokyo, and Washington University for useful comments. The views in this paper represent those of the authors and are not those of either the Federal Reserve Bank of Atlanta, the Board of Governors of the Federal Reserve System, or any of its staff. Errors in this paper are the responsibility of the authors. Return to text

^† Authors' contact details: James M. Nason, Research Department, Federal Reserve Bank of Atlanta, 1000 Peachtree St., N.E., Atlanta, GA 30309, email: jim.nason@atl.frb.org. John H. Rogers, International Finance Division, Board of Governors of the Federal Reserve System, Washington, D.C. 20551, email: john.h.rogers@frb.gov. Return to text

1. Actual data most often rejects the standard-PVM. Typical are tests Meese (1986) reported that employed the first ten years of the floating rate regime. He finds that exchange rates are infected with persistent deviations from fundamentals, which reject the standard-PVM and its cross-equation restrictions. However, Meese is unable to uncover the source of the rejections. Instead of a condemnation of the standard-PVM, we view results such as Meese's as a challenge to update and deepen its analysis. Return to text

2. The open economy VAR literature offers mixed evidence on the importance of various shocks for the exchange rate. Early papers including Eichenbaum and Evans (1995), Rogers (2000) and Kim and Roubini (2000) found some significance for identified monetary shocks. Recent contributions, however, suggest that monetary policy shocks have only a minor impact on exchange rate fluctuations, consistent with Rogoff's view, for example, see Faust and Rogers, (2003) and Scholl and Uhlig (2005). Return to text

3. The present-value relation (3) yields the weak prediction that Granger-causes . Engel and West (2005) and Rossi (2007) report that this prediction is often not rejected in G -7 data. Return to text

4. The restrictions on the moving average are $\Delta z^{\ast}$ is linearly deterministic, $\zeta_{0} = 1$ , $\zeta(\mathbf{L})$ is an infinite order lag polynominal with roots outside the unit circle, the $\zeta_{i}$ s are square summable, and $\upsilon_{t}$ is mean zero, homoskedastic, linearly independent given history and is serially uncorrelated with itself and the past of $\Delta z_{t}$ . Return to text

5. The error $u_{\Delta e, t}$ is also justified if the econometrician's information set is strictly within that of currency traders. Return to text

6. Maheswaran and Sims (1993) show that the martingale restriction has little empirical content for tests of asset pricing models when data is sampled at discrete moments in time. Return to text

7. Hansen, Roberds, and Sargent (1991) study linear rational expectations models that anticipate Proposition 3. Return to text

8. This analysis matches equations A.3 - A.11 and the surrounding discussion of Engel and West (2005). Return to text

9. Vahid and Engle show a n-dimension VAR(1) with d cointegrating relations has n - d common feature relations. Return to text

10. Proposition 5 can also be cast as an implication of the BNSW representation of $\Delta q_{t}$ . In this case, $\overline{\beta}^{\, \prime}$ removes the vector MA $(\infty)$ in $u_{\Delta e,t}$ and $u_{\Delta x,t}$ from the BNSW representation of $\Delta q_{t}$ . Only a linear combination of pure forecast innovations, $u_{\Delta e,t}$ and $u_{\Delta x,t}$ , are left to drive $\Delta q_{t}$ . Let $\vartheta$ $\longrightarrow$ 0 to obtain the random walk exchange rate with innovation $u_{\Delta e,t}$ $\zeta(\mathbf{1})\upsilon_{t}$ . Return to text

11. Fundamentals equal cross-country money minus cross-country output, which implies an income elasticity of money demand, $\psi$ , calibrated to one. This calibration is consistent with estimates reported by Mark and Sul (2003). The money stocks (outputs) are measured in current (constant) local currency units and per capita terms. Return to text

12. The VARs include a constant and linear time trend. The LR statistics employ the Sims (1980) correction and have standard asymptotic distribution according to results in Sims, Stock, and Watson (1990). Return to text

13. The Canadian-U.S. and Japanese-U.S. VARs are selected when the p-value of the LR test is five percent or less. Since the U.K.-U.S. VAR offers ambiguous results, we settle on a VAR(4). Return to text

14. We thank Farshid Vahid for suggesting this example. Return to text

15. A related example is Harvey, Trimbur, and van Dijk (2007) who use Bayesian methods to estimate permanent-transitory decompositions of aggregate time series, but without rational expectations cross-equation restrictions. Return to text

16. Morley, Nelson, and Zivot (2003) show that this restriction applied to an univariate UC model resolves its differences with the Beverage and Nelson (1981) decomposition. Return to text

17. The factor loading on the permanent component of $m_{t}$ remains (normalized to) one. Return to text

18. The appendix discusses the data and explains, for example, that Canadian consumption includes semi-durable expenditures. Return to text

19. The posterior distributions are based on acceptance rates of between 25 and 36 percent. Besides the 750,000 MCMC draws used to compute the moments reported below, four more sequences of 750,000 MCMCs are generated from disparate starting values to assess across chain and within chain convergence. We compute the $\widehat{R}$ statistic of Gelman, Carlin, Stern, and Rubin (2004) to evaluate across chain across and the separated partial means test of Geweke (2005) convergence, which is distributed asymptotically $\chi^{2}$ . Across the 77 parameters of the six UC models, the two largest $\widehat{R}$ s are 1.20 and 1.04, while Gelman, et al suggest a $\widehat{R}$ of about 1.10. On five subsamples, the Geweke separated partial means test has no p-value smaller than 0.21 across the six UC models and five MCMC simulation sequences. Return to text

20. The half life equals log[0.5]/log[q], where q is the largest modulus of the companion matrix of the AR or MA coefficients. Return to text

21. For the $UC_{2,\widetilde {m},\kappa}$ and $UC_{2,\widetilde{c},\kappa}$ models, the relevant factor loadings are multiplied by $1 - \pi_{e,\widetilde{m}}$ or $1 - \pi _{e,\widetilde{c}}$ . Return to text

22. The FEVDs are computed using the VECM implied by equation (13). The VECM is placed in state space form as outlined by Heqc, Palm, and Urbain (2000) and iterated to create the FEVDs of table 8. Return to text

23. We do not present the trend-cycle decompositions based on the posterior of the $UC_{2,\widetilde{m},\kappa}$ model because its log marginal likelihood is far below those of the other UC models. Table 9 includes standard deviations of $\Delta e^{\tau}$ and $\widetilde{e}$ from the posterior of the $UC_{2,\widetilde{m},\kappa}$ model that are larger by a factor of 30 or compared to these statistics from the $UC_{2,2,\kappa}$ and $UC_{2,\widetilde{c},\kappa}$ models. This signals the lack of acceptance of the $UC_{2,\widetilde{m},\kappa}$ model by our Canadian-U.S. sample. Return to text

24. Jeffreys (1998, p. 432) contends that Bayes factors differing by 3.16 is evidence about the two models just between 'not worth more than a bare mention' and substantially in favor of the model with the larger marginal likelihood. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Exchange Rates and Fundamentals: A Generalization*