Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

FRB: Central Banking Before, During and After the Crisis Conference: Screen Reader Version - Monetary Aggregates and the Central Bank's Financial Stability Mandate - An Integrated Framework for Multiple Financial Regulations Screen Reader Version^♣

An Integrated Framework for Multiple Financial Regulations*

Charles A. E. Goodhart

Financial Markets Group, London School of Economics

Anil K Kashyap

University of Chicago Booth School of Business, Federal Reserve Bank of Chicago, and National Bureau of Economic Research

Dimitrios P. Tsomocos

Said Business School and St Edmund Hall, University of Oxford

Alexandros P. Vardoulakis

Banque de France

First draft: March 2012

Abstract:

In this companion paper to Goodhart, Kashyap, Tsomocos and Vardoulakis (2012), we explore the interactions of various types of financial regulation. We find that regulations that control fire sale risk are critical for delivering financial stability and improving the welfare of savers and borrowers. We describe the combinations of capital regulations, margin requirements, liquidity regulation and dynamic provisioning that are most effective in this respect. A policy featuring margin requirements together with counter-cyclical capital requirements delivers equal or better outcomes for the economy than does an unregulated financial system. But it is easy to produce combinations " />

To understand the model it is helpful to realize that the only uncertainty in the model stems from whether the quantity of potatoes in period two is high or low relative to the amount of houses. When potatoes are abundant then the borrowers from the first period can repay their loans and potentially even acquire more housing. So in this case there is no default and instead the financial institutions (and agents R and P who are also housing owners) experience capital gains on those assets. The only actor that suffers in this case are the new homebuyers, F, who face high home prices and have to compete to rent it with others in the economy who are rebalancing their portfolios to reflect the capital gains.

The outcomes are much more subtle and complicated when the endowment of potatoes is low because in this case house prices will collapse. This collapse is unavoidable and default on mortgages is optimal from an individual's point of view. However, there are several channels through which the financial system may amplify the initial impulse that will lead to other inefficiencies. Regulations may be useful if they can limit this amplification.

The trigger for any amplification starts with the choice of the non-bank over whether to repay the repo loan or return the MBS which serve as collateral on the loan. Arbitrage guarantees that the effective return from buying MBS backed by defaulted mortgages must be same as buying the underlying houses. So mortgage default must depress MBS prices. When the fall in housing prices is big enough, it becomes rational for the N to suffer the reputational penalty associated with defaulting and return the collateral rather than repay the loan. In this case, the bank not only sees its asset values drop because of its losses on the mortgages that it retained, but also because the MBS it finds returned are worth less than the loan it was carrying on its books.

Given the asset impairment, B faces a decision over whether to default on its deposit obligations. In deciding whether to honor its deposit contracts the bank trades off a reputational penalty associated with default, against the profits that can be had from deploying the resources for other investments.

One alternative to defaulting is for the bank to sell assets to pay off the deposits. However, the only assets which can potentially be sold at the time when the deposits are due are the MBS that have been returned by the shadow banks. Depending on the availability of buyers to purchase MBS, selling assets may contribute to a fire-sale.

We assume that MBS prices are subject to cash-in-the-market pricing (Allen and Gale (1994)) whereby that the value of the MBS is determined by the wealth of the potential buyers of the assets rather than the future cash flows generated by the assets. The shadow bank, which is the natural buyer of mortgage backed securities, finds its capital depleted in the state of the world where housing prices collapse. Thus, given the limited resources of the shadow banks, the more MBS that the commercial bank returns to the market, the lower is the price of MBS. This simple formulation is intended to capture the Shleifer and Vishny (2011) characterization of a fire sale whereby prices for assets are depressed because the natural buyers of the assets are impaired at the time of sale. Obviously, any regulation that limits the size of the initial repo default can potentially influence the size of the fire sale.

But the presence of the fire sale also creates three follow-on effects. The first comes because banks must make an active portfolio choice between holding onto its mortgage backed securities and extending new loans. The bank is assumed to be unable to issue equity (in the immediate aftermath of the bad shock), so its balance sheet capacity is limited. Thus, the bank must trade off using its capital to hold a mortgage backed security or to initiate new loans. So the losses on the MBS sales from the cash-in-the-market pricing tighten this capital constraint and potentially create a "credit crunch" for new borrowers (in that the bank's capital problem reduces the supply of loans that are available).

The second potential inefficiency comes because the repo default also raises the incentive for the bank to default on its deposit contracts. The losses to the depositor (R) reduce his wealth, causing him to sell additional housing to finance his purchases of goods. The additional housing sales will lead to lower housing prices.

Finally, there is a third channel that arises from the interaction of the cash-in-the-market fire sale and the other two follow-on effects. B always considers the arbitrage relation between MBS prices and the price of houses. When the bank receives the MBS that are issued against defaulted mortgages (from the shadow bank), either it can hold the MBS to maturity or it can sell the MBS right away, which depresses further not only MBS but also house prices. Therefore, the model also embodies the kind of downward spiral described in Brunnermeier and Pedersen (2009).

One prominent feature of the model is the asymmetry between the rich households and the other agents in the model. The combination of the risky deposit, money which can be used as a store of value, and the durable asset means that household R can invest in ways that protect itself from financial problems. But the way in which R responds to different risks or regulations will matter for the other agents. To take one particularly important example, depending on the extent of fire sale risk, R will decide whether to retain some housing that can be sold in the second period (rather than saving through the banking system or with money). If R is selling more housing in the second period and the good state materializes, then the extent of the house appreciation in that scenario is limited (relative to the case where R is selling less). The relative price of housing is a key factor in determining whether P and F's welfare rises or falls. So even though R may be relatively immune to interventions that alter the financial system, R's response to these developments can be critical. This is why a full general equilibrium model is needed to study regulation and why partial equilibrium reasoning can be potentially misleading.

4 The Baseline Equilibrium and the Role of Financial Regulation

The remainder of our analysis proceeds using particular choices for the model parameters. The assumed values for endowments, wealth, financial institution's capital, central bank lending rates, default penalties, risk aversion, probabilities of good and bad states, discount rates and housing depreciation rates are given in Table A-2 in appendix I.

In reviewing the calibration keep in mind that a period is presumed to be 5 years, so with the probability of the bad state being 10 percent, a crisis would be expected roughly every 50 years. We see the key choices in Table A-2 as relating to those that directly govern the size of the fire sale in the bad state. As we just explained, when the fire sale risk is large then financial sector amplification of the initial house price decline is strong (and vice versa).

The two most important factors directly affecting the fire sale are the wealth of N (because that influences the degree of cash-in-the-market pricing) and the endowments of P and F who are the house price buyers. The baseline version of the model (see Table A-3) is calibrated so that MBS prices fall by 26% in the crisis (and rise by 44% in the boom), so that the real estate collapse is very much in line with the recent U.S. experience; the fire sale involves the bank selling only six percent of the MBS that it receives back as collateral.

In a crisis households default on mortgages by only repaying 45 cents on each 1 dollar borrowed. The down payment that they make is assumed to 37% of the mortgage. The bank's willingness to permit the household to have more leverage is tempered by the bank's own risk aversion. One direction for future work is to explore the effects of presuming more willingness to take risks by the banks and non-banks. The banks in the current version repay 60 cents on every dollar of deposits.⁴

Before exploring the effects of regulation on the equilibrium it is helpful to note the channels through which regulation can improve the welfare of the households and financial institutions. Cataloging the various channels makes it easier to see the distributional effects of different policies.

R's welfare is almost immune to regulatory interventions as he can undo almost all adverse effects by re-optimizing his mix of deposits and housing sales. However, as demonstrated above his actions create pecuniary externalities through relative prices on P and F because they do not face complete markets. As a rule he will save more through the banking system when defaults are less severe. But, the attractiveness of retaining housing and selling the extra housing also depends on the size of the fire-sale and the house price collapse in the bad state. In order for a policy to make R definitely worse off, it must effectively reduce his wealth by making his endowment less valuable by changing the relative price of potatoes and houses, otherwise he can adjust his savings strategy to evade the effects - we will see that there are regulations that can operate this way.

P can gain if he can get more housing in period 1 or 2, (or if in a crisis he defaults less). He can increase his first period housing if more short-term lending in period 1 becomes available or more mortgage lending in period 1 is available. He can acquire more housing in the good state in period 2 if its relative price is lower because R is selling more, or if short-term lending terms are better.

F's gains depend solely on the relative price of potatoes to houses. In the good state, he can get more housing if potatoes prices are high, either because R is selling more housing or if short term lending terms are better so that the same amount of potatoes can support a higher housing purchase. In the bad state, if the relative price of housing is lower, then he can buy more of it.

B gains in the good state when it makes more capital gains on the mortgages that it holds on the balance sheet. So, ceteris paribus, this can happen if it retains more mortgages or if it sees a bigger price appreciation on houses. Its welfare in the bad state depends on the size of its default. It also gains whenever the spread between its lending rate and its cost of funding is higher (in either period 1 or 2).

Finally the shadow bank gains in the good state when it makes more capital gains on its MBS holdings. These gains come from being able to hold more MBS or from larger house price appreciation. In the bad state, the non-bank gains if its default is smaller.

With these mechanisms in mind we explore the potential effects five regulatory tools: limits on loan to value ratios, capital requirements for banks, liquidity coverage ratios for banks, dynamic loan loss provisioning for banks, and margin requirement on repurchase agreements used by shadow banks. The point of each of the regulations is to limit the consequences of the housing price collapse. Each of these interventions will limit fire sales in the bad state by reducing either the size of the non-bank's default on its repo loan or the size of the bank deposit default.

But because they differ in ways of inducing this stability the effects can differ across agents. In particular, margin requirements, liquidity requirements, loan to value and initial capital requirements all directly reduce mortgage lending in period 1. They differ in whether their incidence limits bank or non-bank lending more. The capital requirements in period 2 guarantee that banks are healthier after a default occurs to reduce directly the costs of the default; the equilibrium adjustments though involve large lending changes in period 1. Dynamic provisioning damps the credit boom in the good state and thus only indirectly influences the fallout from a house price drop. The precise mathematical formulas for the regulations are given in appendix III. In the text we focus on the key prices and quantities that govern welfare for the households and financial institutions.

Loan to value (LTV) requirements force households to use more of their own wealth to obtain a mortgage loan. The effects on the key endogenous variables in the model are shown in Table 1. This regulation is unique among those we consider because it directly acts on P to limit his ability to obtain credit, rather than creating incentives for the bank or non-bank to extend less credit. Because the bank is risk-averse it will prefer smoother profit streams to more variable ones, so given that P will be able to obtain less total credit B will spread this reduction over both the first and second period. Since the households endowed with potatoes are the primary borrowers in the economy, this credit contraction forces them to sell more potatoes which lowers the price of potatoes relative to houses in both periods.

Table 1: Impact of Alternative Regulations on Key Endogenous Variables

(Change relative to baseline equilibrium)

	LTV	MR	${CR}_{1}$	${CR}_{2b}$	${LCR}_{1}$	DP
Securitization	-	-	+	+	+	+
Relative price of potatoes to housing-good state	-	$\approx$ 0	$\approx$ 0	+	+	+
Profits of the Bank period 1	+	+	+	-	-	-
Profits of Bank good state	+	+	-	-	-	-

+ indicates increase, - indicates decrease, ˜0 indicates no change

Table 2: Impact of Alternative Regulations on Household Utilities and Financial Institutions' Welfare (Change relative to baseline equilibrium)

	LTV	MR	${CR}_{1}$	${CR}_{2b}$	${LCR}_{1}$	DP
P's Utility	-	$\approx$ 0	+	+	+	+
F's Utility	-	$\approx$ 0	$\approx$ 0	+	+	+
R's Utility	$\approx$ 0	$\approx$ 0	$\approx$ 0	$\approx$ 0	-	-
B's Payoff	+	+	+	-	-	-
N's Payoff	+	+	$\approx$ 0	-	$\approx$ 0	-

+ indicates increase, - indicates decrease, $\approx$ 0 indicates no change

The impact on the different agents is shown in Table 2. Given the reduction in relative price of potatoes, both P and F suffer from increasing the down-payment requirements on houses. The higher relative prices of houses deliver slightly higher capital gains on mortgages and MBS for the financial institutions in the good state. But more importantly, the lower loan to value ratio makes the homeowner absorb more of the losses from a home price collapse, so that the financial institutions' defaults are much lower than without the loan to value regulation.

Margin requirements force non-banks to pledge more equity to secure their repo loans. This reduces the attractiveness of securitization and so that relatively more of the housing financing that occurs comes via mortgages that remain on the balance sheets of the banks. These changes in the structure of financing benefit the banks in two ways. First, by virtue of a higher market share in housing financing the banks capture more of the gains from the house price appreciation in boom scenario. Second, the non-banks' higher equity contribution reduces the size of their repo default. This latter effect also benefits the bank. Households are essentially unaffected by the imposition of margin requirements: the relative price of houses is not much affected, and while P has a smaller default that is because he was able to acquire less housing in period 1.

Capital ratios for banks in the baseline equilibrium are higher in period 1 than in the bad state.⁵ The starting capital positions, therefore, are counter-cyclical. So, care must be taken in thinking about which comparative static exercise to consider: a local perturbation to either the first period ratio or ratio in the bad state will mean that the counter-cyclical rule would still be in place. Alternatively, one can examine a large enough change in the capital requirement in the bad state so that it becomes equal to the level observed in the good state. We first describe the local experiments and explore combined changes in the last section of the paper.

Raising the capital requirement in period 1 induces the bank to hold fewer mortgages on its balance sheet. It substitutes by securitizing more of the mortgages it originates and by making more short-term loans in period 1. This portfolio shift generates slightly more profits in period 1 and fewer profits in the good state. But the bank's default is much lower in the bad state, which makes B better off. Because P is able to obtain less mortgage credit his default is less severe, so he also is better off. As usual R is essentially unaffected. The relative price of houses and potatoes are not altered enough to change the outcomes for F. The non-bank becomes riskier by virtue of the additional MBS that it is holding: this generates additional profits in the good state and default in the bad state larger. On net N's welfare is about the same.

Raising capital requirements in the bad state triggers several general equilibrium responses. First, the bank does less mortgage lending in period 1 to avoid losses in period 2. The bank's reduction in mortgage financing means that the bank also needs fewer deposits, so that R saves more using his housing endowment. This leads R to sell more houses in period 2, raising the relative price of potatoes in both states, making both P and F better off. The lower relative price of houses in the good state, and the lower overall reduction in first period mortgages means N is worse off. B suffers for these reasons (and also because its profits are lower in period 1), but does default by less when house prices crash. The net effect is still negative for the bank.

Liquidity requirements can also be applied in the first period or during the second period. Imposing liquidity requirements in the bad state leads to a massive fire sale because the only way for the bank to obtain liquidity is to sell its MBS. So this regulation makes no sense to consider.⁶ Imposing liquidity requirements during the good state runs into the same problem as imposing capital requirements during booms. When asset prices are high many assets can be easily sold. So to make this ratio bind, the regulation would have to be extremely aggressive, changing substantially as a boom developed. Since we do not view this as plausible we also do not consider this regulation.

These choices leave a first period liquidity requirement for consideration. Banks meet this kind of liquidity requirement by making more short term loans in period 1 and by securitizing the mortgages it does make - notice the similarity to the period 1 choices that are made by the bank when it is faced with an ex-post capital requirement. The bank sees profits fall in period 1 and the good state, and it is not better protected against default in the bad state. So the bank sees its payoffs reduced. The non-bank (just as with the initial capital requirement) sees its risk rise due to the additional securitization, but on net its overall payoff is not much affected. Because it has reduced mortgage issuance the bank also reduces its deposit taking, which pushes R to do more saving using its housing endowment. The additional housing sales in the second period make F and P better off; P also benefits from defaulting less due to having less housing credit. R's utility drops very slightly because the housing sales in the good state are so large that they create a big decline the relative price of houses, reducing his purchasing power.

Finally, it is possible to use dynamic provisioning, which we formalize as a direct tax on increasing real estate related lending in the good state. This makes it very different than the other tools in two respects. First, it is the only one of the regulatory options that it is targeted directly at leaning against the credit boom. Second, it is the only regulation that by construction must impair R. Normally R has portfolio substitution possibilities involving shifting savings between deposits and housing that allow him side-step regulation. But by making real estate lending more expensive in the good state, dynamic provision acts as a tax on R's endowment and forces him to sell more houses at a lower price. This leaves R worse off and P and F better off. Because the bank and non-bank both make much lower capital gains in the good state their profits suffer as well.

5 Combined Regulations

The foregoing results suggest combinations of regulation that should work well together and those that would not be expected to interact well. We proceed under the assumption that the goal of financial regulation to increase stability and credit availability so that both the financial institutions and the households are better off relative to the unregulated equilibrium. As a practical matter we have seen that R's utility is very insensitive to regulation, so we concentrate on the other agents.

From Table 2 we can see that certain tools are likely to be more effective than others. In particular, both margin requirements and loan to value regulations increase financial stability by making defaults less traumatic, and in doing so make the payoffs to the financial institutions higher than in the absence of regulation. But loan to value regulation depresses credit supply making borrowers worse off, while margin requirements are much less restrictive. So it appears easier to find a bundle that makes everyone better off when margin requirements are used instead of requiring larger down payments.

Likewise, raising capital requirements in the bad state and dynamic provisioning each reduce the relative price of houses in the good state. This benefits P and F at the expense of the financial institutions. But dynamic provisioning operates as a tax on R, while the capital requirements do not. So using ex-post capital requirements should be more attractive than using our depiction of provisioning.

Capital requirements and liquidity requirements in the initial period are similar in that both reduce mortgage extensions and prevent P from defaulting as much in the bust. Capital requirements reduce the bank's default as well, while a liquidity requirement does not. In contrast, a higher liquidity ratio raises the relative price of potatoes in the good state which benefits F.

Taken together these observations suggest that combinations of regulation involving margins, capital ratios and the initial liquidity ratio are the most promising to explore. The same reasoning suggests that substituting LTV requirements for margin requirements should deliver worse outcomes. Table 3 shows the change in welfare relative to the baseline from different regulatory packages of this sort - the three-way combinations dominate the two way versions, so to limit the possibilities we concentrate on these.

Table 3: Impact of Combining Regulations on Household Utilities and Financial Institutions' Welfare (Change relative to baseline equilibrium)
	${CR}_{1}$ & ${CR}_{2b}$ &MR	${CR}_{1}$ & L ${CR}_{1}$ &MR	${CR}_{1}$ & ${CR}_{2b}$ &LTV
P's Utility	+	+	$\approx$ 0
F's Utility	+	-	-
R's Utility	$\approx$ 0	$\approx$ 0	$\approx$ 0
B's Payoff	+	+	+
N's Payoff	+	+	+

+ indicates increase, - indicates decrease, $\approx$ 0 indicates no change

The column one combination includes margins and the two capital ratios. When all three are in place, R's utility is equivalent to that of the baseline and the other agents are better off. The regulations interact in interesting ways. In particular, raising capital requirements in period 1 leads to a carryover of capital into the second period, so that the incremental increase of capital needed in the bad state is reduced (relative to the case when capital requirements in the first period are not altered). This endogenous response weakens the adverse effects of ex-post capital requirements on financial institutions payoffs. Therefore, putting these two requirements together a small margin requirement makes everyone at least as well off as in the baseline case.

We also considered a combination that involves margins, along with period 1 liquidity requirements and capital requirements in the bad state. Any time a liquidity requirement is imposed, it triggers the same portfolio adjustments by the bank in period 1 as if the bank had its capital requirement in the bad state increased. This effect proves so powerful that the capital ratio in the bad state becomes so much higher that the regulation is not binding. Hence, these bundles amount to studying liquidity requirements, with margin requirements, and a less counter-cyclical set of capital standards; the capital ratio in period 1 is little affected, but remains above the capital ratio in period 2. So it is not really possible to do an isolated experiment that moves only margins, ex-ante liquidity and ex-post capital regulations.

The second column of table 3 shows a regulatory bundle featuring higher margins, along with increased ex-ante capital and liquidity regulations. This combination leaves F worse off. Based purely on the individual effects from table 2 this might at first seem surprising. The reason why this combination delivers a strange interaction is because it stifles the bank's ability to expand credit. On the one hand, the liquidity requirements forces it to expand short term lending (which is naturally limited by the first period wealth of the R and P), while on the other, the margin requirements limit the shadow bank's ability to absorb securitization. Faced with these roadblocks the bank cuts total credit, and because of its preference for smooth profits it spreads the credit reduction over both period 1 and period 2. P benefits partly because the lower loan limits reduce the size of this default in the bad state, but F only sees the reduction in credit and winds up worse off.

The last combination considered in table 3 shows the effects of packaging capital requirements in both periods with tighter loan to value regulation. This amounts to substituting a loan to value restriction for a margin requirement. From our analysis of the one-at-a-time regulatory interventions we would expect this to be a less good permutation. This intuition is confirmed as the welfare of both P and F drop when the LTV rules are imposed.⁷ The losses are attributable to the reduction in total credit that is induced by the increased down-payment requirements - just as when it was imposed as a single regulation. Credit availability falls in both periods, so P sees a sharp drop in mortgage credit and F is able to borrow less in the boom state. Thus, both borrowers are made worse off by raising down payment requirements instead of margin requirements.

We draw three conclusions from the results from analyzing the results in Table 3. First, while this model has multiple ways in which the financial system can amplify shocks, it is not the case that regulatory interventions with multiple tools is necessarily welfare enhancing. One of the more obvious policy packaging that at first glance might be appealing actually is welfare-reducing. Indeed, it is easy to put together many other combinations of policies that have unintended effects.

Second, the reason why some of the policy bundles in Table 3 did not work accords with the intuition we have emphasized about paying attention to the channels through which regulations operate. For example, combining two ex-ante regulations that control bank risk-taking is unnatural when considering their expected economic effects, even though blindly using the results in Table 2 might suggest trying this combination. The more successful package combines regulations that operate via fairly different channels.

Finally, and most importantly, the only way to conduct this type of exercise is to use a full general equilibrium model. There would simply be no way to guess confidently based on partial equilibrium hunches which policies would be complements and substitutes and which ones would have unfortunate interactions when they are implemented simultaneously.

6 Conclusions

Our approach to studying financial regulation highlights the substantial payoff to having a formal general equilibrium model that takes a clear stand on the purpose and risks associated with having a financial system that includes both banks and shadow banks that deliver funding to the economy. Given many complex interactions between the various agents in the model, no single regulatory tool is going to be sufficient to offset the many distortions arising from a default. But it does appear that a bundle of tools can improve outcomes relative to the unregulated equilibrium that the economy would reach.

We highlight groups of regulations that work in harmony towards alleviating the knock-on effects from asset fire sales. Margin requirements are a valuable complement to other regulations because they contribute to the stability of shadow banking system. Similarly, capital requirements that force banks to be better capitalized after an asset price collapse also work well with other regulatory tools. The ex-post requirement on bank health reduces bank risk-taking and thereby contributes to the stability of the banking system. It also creates incentives for savers to diversify their portfolio choices which bring other benefits.

The best regulatory combination that we identify also includes raising capital requirements ahead of an asset price boom or bust. This restriction reduces bank risk-taking without too severely limiting overall credit supply and also lowers the burden of requiring higher capital during bad times.

Importantly, we find that indiscriminate combinations of regulations can easily be welfare reducing. Simply piling on multiple regulations because there are multiple channels of financial contagion is not necessarily good. Instead, wise regulation requires that considerable care is taken to anticipate the ways in which policies will interact and to guard against creating perverse incentives and reactions.

As Kohn (2010, 2011) emphasized, we are in the early days of macroprudential analysis. There are still many unanswered questions. But the prospects of addressing these questions using this style of general equilibrium model are bright.

7 References

Adrian, Tobias and Hyun Song Shin. 2009, "The Shadow Banking System: Implications for Financial Regulation", Federal Reserve Bank of New York Staff Reports, no. 382.

Allen, Franklin and Douglas Gale. 1994, "Liquidity Preference, Market Participation and Asset Price Volatility," American Economic Review, 84, 933-955.

Bernanke, Ben S. 2007, "The Financial Accelerator and the Credit Channel" speech at the Credit Channel of Monetary Policy in the Twenty-first Century Conference, Federal Reserve Bank of Atlanta, Atlanta, Georgia, June 15, 2007

Bernanke, Ben S., Mark Gertler, and Simon Gilchrist. 1999. "The financial accelerator in a quantitative business cycle framework," in: John. B. Taylor & Michael Woodford (ed.), Handbook of Macroeconomics, edition 1, volume 1, chapter 21, pp. 1341-1393, Elsevier

Brunnermeier, Markus and Lasse H. Pedersen, 2009, "Market Liquidity and Funding Liquidity", Review of Financial Studies 22 (6), pp. 2201-2238.

Curdia, Vasco and Michael Woodford, 2010, "Credit Spreads and Monetary Policy", Journal of Money, Credit and Banking, 42(1), 3-35

Dubey, Pradeep, Geanakoplos, John, and Martin Shubik (2005), Default and Punishment in General Equilibrium, Econometrica 73(1), pp. 1-37.

Goodhart, Charles A.E., Anil K Kashyap, Dimitrios P. Tsomocos, and Alexandros P. Vardoulakis, 2012, "Financial Regulation in General Equilibrium",National Bureau of Economic ResearchWorking Paper Number 17909.

Kashyap, Anil K, Berner, Richard, and Charles A.E. Goodhart, 2011, "The macroprudential toolkit", IMF Economic Review,59(2), 145-161. doi:10.1057/imfer.2011.4.

Kohn, Donald, L., 2011, "The Financial Policy Committee at the Bank of England" speech at the U.S. Department of the Treasury Conference, 2 December 2011

http://www.bankofengland.co.uk/publications/Documents/speeches/2011/speech536.pdf

Kohn, Donald, L., 2010, "Monetary Policy in the Crisis: Past, Present, and Future" speech at the Brimmer Policy Forum, American Economic Association Annual Meeting, Atlanta, Georgia, January 3, 2010

http://www.federalreserve.gov/newsevents/speech/kohn20100103a.htm

Kohn, Donald, L., 2007, "Financial stability and policy issues" speech at the Federal Reserve Bank of Atlanta's 2007 Financial Markets Conference, Sea Island, Georgia, May 16, 2007

Kroszner, Randall S., 2007, "Analyzing and Assessing Banking Crises" speech at the Federal Reserve Bank of San Francisco, Conference on the Asian Financial Crisis Revisited, San Francisco, California (via videoconference), September 6, 2007

Mishkin, Frederic S., 2007, "Will Monetary Policy Become More of a Science?" Finance and Economics Discussion Series: 2007-44, Board of Governors of the Federal Reserve System

Shleifer, Andrei and Robert Vishny, 2011, " Fire Sales in Finance and Macroeconomics", Journal of Economic Perspectives, 25(1), pp. 29-48.

Tucker, Paul 2010. "Shadow Banking: Financing Markets and Financial Stability", speech at the BCG Partners Seminar, London, January 21, 2010

Woodford, Michael. 2003, Interest and Prices: Foundations of a Theory of Monetary Policy. Princeton: Princeton University Press.

8 Appendix I: Notation and Parameterization

The labeling convention indentifies agents with superscripts ( , and goods (, and periods/states ( with subscripts. The following table presents the notation used for the exogenous and endogenous variables in the model. Superscripts and subscripts are not shown to save space.

**Table A-1: List of variables**
e	Endowments of potatoes or houses
Money	Monetary endowments of households
E	Capital of financial institutions
P	Prices of potatoes, housing or MBS
r	Interest rates on short-term loans, on discount window borrowing, on deposits, on mortgages or on repo loans
$\tau$	Marginal non-pecuniary penalty for default on mortgages, deposits or repo loans
$\gamma$	Risk aversion coefficients
$\omega$	Probability of good or bad state
$\xi$	Time discount factor
$\delta$	Depreciation rate
U	Utility of households
Prof	Profit function
$\pi$	Profits of financial institutions
c	Consumption of potatoes or housing
q	Quantity of potatoes or housing sold
LST	Quantity of short-term loans
MORT	Quantity of mortgages
REPO	Quantity of repo loans
D	Quantity of deposits
DISC	Quantity of discount window loans made by the central bank to the commercial bank
MBS	Quantity of mortgage backed securities sold
$\sigma$	Percentage of retained mortgages sold
$\theta$	Percentage of returned MBS that are re-sold (Rate of fire-sales)
V	Repayment rate on mortgages or deposits
CC	Cash committed for mortgage extension by the commercial bank
cash	Cash assets held by the commercial bank

**Table A-2: Exogenous variables**
Endowments of goods	Households' wealth	F.I. capital	CB rates	Default penalties	Risk aversion	Other parameters
$e^P_{1,p}=10$	${Money}^P_1=4.1$		$r^{CB}_1=0.12$	${\tau }^P_{2b}=4$	${\gamma }^P=2.1$	${\omega }_{2b}=0.1$
$e^P_{2g,p}=32$	${Money}^P_{2g}=4.1$	$E^B_{2g}=0.5$	$r^{CB}_{2g}=0.12$	${\tau }^B_{2g}=1.2$	${\gamma }^F=2.1$	$\xi =0.85$
$e^P_{2b,p}=5.8$	${Money}^P_{2b}=0.1$	$E^B_{2b}=0$	$r^{CB}_{2b}=0.20$	${\tau }^{\beta }_{2b}=1.2$	${\gamma }^R=2.4$	$\delta =0.15$
$e^F_{2g,p}=11$	${Money}^F_{2g}=4.1$			${\tau }^N_{2b}=0.2$	${\gamma }^B=1.4$
$e^F_{2b,p}=11$	${Money}^F_{2b}=2.1$	$E^N_{2g}=2$			${\gamma }^N=$ 0.7
$e^R_{1,h}=1$	${Money}^R_1=6.5$	$E^N_{2b}=1$
$e^R_{2g,h}=0$	${Money}^R_{2g}=0$
$e^R_{2b,h}=0$	${Money}^R_{2b}=0$

**Table A-3: Initial Equilibrium variables**
Prices	Interest rates	Aggregate Consumption	Aggregate Consumption	Loans	Loans	Securitization	Delivery rates	F.I. profits
$P_{1,p}=1.48$	$r^{ST}_1=0.12$	$c^P_{1,p}=0.827$	$c^R_{1,p}=9.173$	${LST}^P_1=12.10$	${LST}^B_1=50.70$	${MBS}^B_1=21.95$	$V^{MORT}_{2g}=1$	${\pi }^B_1=0.68$
$P_{2g,p}=1.33$	$r^{ST}_{2g}=0.12$	$c^P_{2g,p}=1.289$	$c^R_{2g,p}=41.320$	${LST}^P_{2g}=38.48$	${LST}^B_{2g}=64.11$	${ \sigma }^B_{2g}=0.281$	$V^{MORT}_{2b}=0.55$	${\pi }^B_{2g}=1.01$
$P_{2b,p}=1.60$	$r^{ST}_{2b}=0.20$	$c^P_{2b,p}=0.295$	$c^R_{2b,p}=15.874$	${LST}^P_{2b}=7.33$	${LST}^B_{2b}=21.13$	${ \sigma }^B_{2b}=0$	$V^D_{2g}=1$	${\pi }^B_{2b}=1.00$
$P_{1,h}=676.02$		$c^P_{1,h}=0.064$	$c^R_{1,h}=0.936$	${MORT}^P=27.02$	${DISC}^B_1=44.68$	$?^B_{2b}=0.063$	$V^D_{2b}=0.60$	${CC}^B=5.60$
$P_{2g,h}=1,111.18$	$r^{MORT}=0.58$	$c^P_{2g,h}=0.052$	$c^R_{2g,h}=0.783$	${LST}^F_{2g}=12.63$	${DISC}^B_{2g}=96.94$	${MBS}^N_{2g}=1.42$		${cash}^B_1=6.74$
$P_{2b,h}=362.83$	$r^{REPO}=0.57$	$c^P_{2b,h}=0.020$	$c^R_{2b,h}=0.796$	${LST}^F_{2b}=13.80$	${DISC}^B_{2b}=38.74$	${MBS}^N_{2b}=1.39$		${\pi }^N_{2g}=4.82$
$P_{1,MBS}=0.98$	$M^{CB}_1=44.68$	$c^F_{2g,p}=0.391$		${LST}^R_1=38.59$	${REPO}^B=20.41$			${\pi }^N_{2b}=1.20$
$P_{2g,MBS}=1.41$	$M^{CB}_{2g}=96.94$	$c^F_{2b,p}=0.631$		${LST}^R_{2g}=13.00$
$P_{2b,MBS}=0.72$	$M^{CB}_{2b}=38.74$	$c^F_{2g,h}=0.015$		${LST}^R_{2b}=0.005$
		$c^F_{2b,h}=0.044$

9 Appendix II: Optimization and Equilibrium

This section presents the objective functions and budget constraints for the main actors in the model. For full details see GKTV (2012).

Household P's optimization problem

Household P maximizes its intertemporal expected utility from the consumption of potatoes and housing. The last term in the utility function represents the reputational penalty from default, which is proportional to the loss given default on mortgages.

$\displaystyle {\max {\overline{U}}^P }=U^P\left(c^P_{1,p}, c^P_{1,h}\right)+\xi \cdot{\omega}_{2g}\left[U^P\left(c^P_{2g,p },\left(1-\delta \right)c^P_{1,h}+c^P_{2g,h}\right)\right]+$

$\displaystyle \xi \cdot{\omega }_{2b}\left[U^P\left(c^P_{2b,p}, c^P_{2b,h}\right)-{\tau }^P_{2b}\left[{MORT}^P\left(1+r^{MORT}\right)-P_{2b,h}c^P_{1,h}\right]\right]$

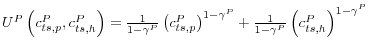
where $U^{P} \left(c_{ts,p}^{P} ,c_{ts,h}^{P} \right)=\frac{1}{1-\gamma ^{P} } \left(c_{ts,p}^{P} \right)^{1-\gamma ^{P} } +\frac{1}{1-\gamma ^{P} } \left(c_{ts,h}^{P} \right)^{1-\gamma ^{P} }$

subject to the following budget constraints

$\displaystyle P_{1,h}c^P_{1,h}={Money}^P_1+{MORT}^P+{LST}^P_1$

i.e. the purchase of housing in the initial period is funded by own monetary endowments, a mortgage and short-term borrowing

$\displaystyle {LST}^P_1(1+r^{ST}_1)= P_{1,p}q^P_{1,p}$

i.e. the revenues from potatoes sales are used to repay the short-term loans at the end of the initial period

$\displaystyle {MORT}^P\left(1+r^{MORT}\right)+P_{2g,h}c^P_{2g,h}={Money}^P_{2g}+{LST}^P_{2g}$

i.e. the repayment of the mortgage in the good state and the new housing purchases are funded by own monetary endowments and short-term borrowing

$\displaystyle {LST}^P_{2g}(1+r^{ST}_{2g})= P_{2g,p}q^P_{2g,p}$

i.e. the revenues from potatoes sales in the good state are used to repay the short-term loans at the end of the second period

$\displaystyle P_{2b,h}c^P_{2b,h}={Money}^P_{2b}+{LST}^P_{2b}$

i.e. own monetary endowments and short-term borrowing are the only funds used for the new housing purchases in the bad state, since households default on their mortgages

$\displaystyle {LST}^P_{2b}(1+r^{ST}_{2b})= P_{2b,p}q^P_{2b,p}$

i.e. the revenues from potatoes sales in the bad state are used to repay the short-term loans at the end of the second period

Household F's optimization problem

Household F enters the economy only in the second period. Thus, it lives either in the good or in the bad state and it aims at maximizing utility in either state from the consumption of potatoes and housing.

$\displaystyle {\max { U}^F\left(c^F_{2s,p},c^F_{2s,h}\right) }$

where $U^{F} \left(c_{2p}^{F} ,c_{2h}^{F} \right)=\frac{1}{1-\gamma ^{F} } \left(c_{2p}^{F} \right)^{1-\gamma ^{F} } +\frac{1}{1-\gamma ^{F} } \left(c_{2h}^{F} \right)^{1-\gamma ^{F} }$

subject to the following budget constraints

$\displaystyle P_{2s,h}c^F_{2s,h}={Money}^F_{2s}+{LST}^F_{2s}$

i.e. housing purchases are funded by own monetary endowments and short-term borrowing

$\displaystyle {LST}^F_{2s}(1+r^{ST}_{2s})= P_{2s,p}q^F_{2s,p}$

i.e. the revenues from potatoes sales are used to repay the short-term loans

Household R's optimization problem

Household R maximizes its intertemporal expected utility from the consumption of potatoes and houses.

$\displaystyle {\max {\overline{U}}^R }=U^R\left(c^R_{1,p}, c^R_{1,h}\right)+ \xi \cdot{\omega }_{2g}\left[U^R\left(c^R_{2g,p},\left(1-\delta \right)c^R_{1,h}+c^R_{2g,h}\right)\right]+\xi \cdot{\omega }_{2b}\left[U^R\left(c^R_{2b,p},\left(1-\delta \right)c^R_{1,h}+c^R_{2b,h}\right)\right]$

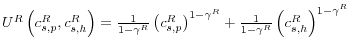
where $U^{R} \left(c_{s,p}^{R} ,c_{s,h}^{R} \right)=\frac{1}{1-\gamma ^{R} } \left(c_{s,p}^{R} \right)^{1-\gamma ^{R} } +\frac{1}{1-\gamma ^{R} } \left(c_{s,h}^{R} \right)^{1-\gamma ^{R} } {\rm }$

subject to the following budget constraints

$\displaystyle P_{1,p}c^R_{1,p}+D^R={Money}^R_1+{LST}^R_1$

i.e. potatoes purchases and deposits at the commercial bank are funded by own monetary endowments and short-term borrowing

$\displaystyle {LST}^R_1(1+r^{ST}_1)= P_{1,h}q^R_{1,h}$

i.e. the revenues from housing sales are used to repay the short-term loans at the end of the initial period

$\displaystyle P_{2s,p}c^R_{2s,p}={Money}^R_{2s}+{LST}^R_{2s}+{V^D_{2s}D}^R\left(1+r^D\right)$

i.e. potatoes purchases in state s in the second period are funded by own monetary endowments, short-term borrowing and the received repayment on deposits

$\displaystyle {LST}^R_{2s}(1+r^{ST}_{2s})= P_{2s,h}q^R_{2s,h}$

i.e. the revenues from housing sales in state s are used to repay the short-term loans at the end of the second period

Commercial bank B's optimization problem

The commercial bank aims at maximizing a concave function of profits made in both periods. The last term in the payoff function represents the reputational loss from default, which is proportional to the loss given default on deposits.

$\displaystyle {\max {\overline{Prof}}^B }={Prof}^B\left({\pi }^B_1\right)+\xi \sum_s{{\omega }_{2s}\left[{Prof}^B\left({\pi }^B_{2s}\right)-{\tau }^B_{2s}\left[1-v^B_{2s}\right]D^B(1+r^D)\right]}$

where $Prof\left(\pi _{ts}^{B} \right)=\frac{1}{1-\gamma ^{B} } \left(\pi _{ts}^{B} \right)^{1-\gamma ^{B} } {\rm }$

subject to the following budget constraints

$\displaystyle {LST}^B_1+{REPO}^B+{CC}^B= E^B_1+{DISC}^B_1+D^B$

i.e. the commercial bank uses its own capital together with funds borrowed from the discount window and deposits to supply short-term and repo loans and to hold a cash amount committed to the extension of mortgages

$\displaystyle {MORT}^B={CC}^B+P_{1,MBS}{MBS}^B_1$

i.e. the commercial bank funds the extension of mortgages with its own committed cash and with the proceeds from the securitization of mortgages

$\displaystyle {DISC}^B_1\left(1+r^{CB}_1\right)+{cash}^B_1={LST}^B_1(1+r^{ST}_1)$

i.e. a part of the proceeds from the repayment of short-term loans are used to repay the loans from the discount window and the rest is held as cash reserves

$\displaystyle {LST}^B_{2g}+v^B_{2g}D^B\left(1+r^D\right)= {cash}^B_1+E^B_{2g}+{DISC}^B_{2g}+P_{2g,MBS}{ \sigma }^B_{2g}\left({MORT}^B-{MBS}^B_1\right)$

i.e. the commercial bank uses its cash reserves and new capital together with borrowed funds from the discount window and revenues from further securitization of retained mortgages to repay depositors and extend new short-term lending in the good state in the second period

$\displaystyle {\pi }^B_{2g}={LST}^B_{2g}\left(1+r^{ST}_{2g}\right)+{REPO}^B(1+r^{REPO})+(1-{ \sigma }^B_{2g})\left({MORT}^B-{MBS}^B_1\right)(1+r^{MORT})-{DISC}^B_{2g}(1+r^{CB}_{2g})$

i.e. the profits in the good state are equal to the profit on short-term lending plus the repayment on repo loans and the mortgages remaing in the balance sheet less the loans that must be repaid to the central bank

$\displaystyle {LST}^B_{2b}+v^B_{2b}D^B\left(1+r^D\right)={cash}^B_1+E^B_{2b}+{DISC}^B_{2b}+P_{2b,MBS}\left[?^B_{2b} {MBS}^B_1+ { \sigma }^B_{2b}\left({MORT}^B-{MBS}^B_1\right)\right]$

i.e. the commercial bank uses its cash reserves and new capital together with borrowed funds from the discount window and revenues from further securitization of retained mortgages and from returned MBS that are resold to repay depositors and extend new short-term lending in the bad state in the second period

$\displaystyle {\pi }^B_{2b}={LST}^B_{2b}\left(1+r^{ST}_{2b}\right)+V^{MORT}_{2b}\left({MORT}^B-?^B_{2b}{MBS}^B_1-{ \sigma }^B_{2b}\left({MORT}^B-{MBS}^B_1\right)\right)\left(1+r^{MORT}\right)-{DISC}^B_{2b}(1+r^{CB}_{2b})$

i.e. the profits in the bad state are equal to the profits on short-term lending plus the repayment on the mortgages remaing in the balance sheet less loans that must be repaid to the central bank

Shadow bank N's optimization problem

The non-bank aims at maxizing a concave function of profits made in the second period, since it does not make any profits in the initial one. The last term in the payoff function represents the reputational loss from default, which is proportional to the loss given default on repo loans.

$\displaystyle {\max {\overline{Prof}}^N }=\xi \cdot{\omega }_{2g}{Prof}^N\left({\pi }^N_{2g}\right)+\xi \cdot{\omega }_{2b}\left[{Prof}^N\left({\pi }^N_{2b}\right)-{\tau }^N_{2b}\left[{REPO}^N(1+r^{REPO})-V^{MORT}_{2b}{MBS}^N_1\left(1+r^{MORT}\right)\right]\right]$

where $Prof\left(\pi _{2s}^{N} \right)=\frac{1}{1-\gamma ^{N} } \left(\pi _{2s}^{N} \right)^{1-\gamma ^{N} } {\rm }$

subject to the following budget constraints

$\displaystyle P_{1,MBS}{MBS}^N_1=E^N_1+{REPO}^N$

i.e. the initial purchase of mortgage backed securities is funded by own capital and a repo loan

$\displaystyle P_{2s,MBS}{MBS}^N_{2s}=E^N_{2s}$

i.e. the purchase of mortgage backed securities in the second period is funded out of new capital which implies cash-in-market pricing

$\displaystyle {\pi }^N_{2g}=\left({MBS}^N_1+{MBS}^N_{2g}\right)\left(1+r^{MORT}\right)-{REPO}^N\left(1+r^{REPO}\right)$

i.e. the profits in the good state are equal to the repayment on the mortgage backed securities purchased in both the initial period and the good state minus the repayment of the repo loan

$\displaystyle {\pi }^N_{2b}={V^{MORT}_{2b}MBS}^N_{2b}\left(1+r^{MORT}\right)$

i.e. the profits in the bad state are equal to the repayment of returned mortgages backed securities repurchased

Markets and Equilibrium

Equilibrium is reached when all agents maximize their payoff functions subject to their budget constraints, all markets clear and their expectations are rational. Potatoes prices in equilibrium are determined by the clearing of the potatoes market. Supply equals demand in every period and state in equilibrium, i.e. $q^P_{1,p}=c^R_{1,p}$ and $q^P_{2s,p}+q^F_{2s,p}=c^R_{2s,p}$ . Similarly, $q^R_{1,h}=c^P_{1,h}$ , $q^R_{2g,h}=c^P_{2g,h}+c^F_{2g,h}$ and $q^R_{2b,h}+c^P_{1,h}=c^P_{2b,h}+c^F_{2b,h}$ for the housing market in equilibrium. Moreover, the loan/deposit markets clear when ${MORT}^P={MORT}^B$ , ${REPO}^B={REPO}^N$ , , ${LST}^B_1={LST}^P_1+{LST}^R_1$ and ${LST}^B_{2s}={LST}^P_{2s}+{LST}^R_{2s}+{LST}^F_{2s}$ . The market clearing for mortgage backed securities requires ${MBS}^B_1={MBS}^N_1$ , ${ \sigma }^B_{2g}\left({MORT}^B-{MBS}^B_1\right)={MBS}^N_{2g}$ and $?^B_{2b} {MBS}^B_1+ { \sigma }^B_{2b}\left({MORT}^B-{MBS}^B_1\right)={MBS}^N_{2b}$ . Finally, the demand from the commercial bank determines the equilibrium level of borrowing from the discount window, since there is a perfectly elastic supply from the central bank at predetermined interest rates.

10 Appendix III: Definition of Regulatory Ratios

Loan-to-value regulation on mortgages

Loan-to-value regulation sets the maximum level of mortgage borrowing for a given value of collateral pledged. Given that mortgage extension takes place only in the initial period, this is an ex-ante tool.

$\displaystyle \frac{{MORT}^P}{P_{1,h}c^P_{1,h}}\le {\rm Maximum permissible l}oan to value ratio$

Haircut regulation on repo loans

Haircut regulation sets the minimum down-payment for a repo loan used to purchase mortgage backed securities. As such, it can be implemented before the resolution of uncertainty and it is an ex-ante tool as well.

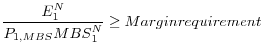
$\displaystyle \frac{E^N_1}{P_{1,MBS}{MBS}^N_1}\ge Margin requirement$

Bank capital regulation

Contrary to the aforementioned regulatory interventions, capital regulation does not attempt to regulate specific markets (mortgage or repo loan markets), but rather attempts to affect the incentives of the commercial bank to extend credit. Capital requirements are risk weighted in the spirit of the Basel accord. Short-term loans are safe and thus should have a zero risk weight, i.e. they are not included in the calculation of risk weighted assets. Capital regulation will differ depending on the point in time that is implemented. For example, regulating capital requirements in the initial period affects the extension of repo loans is different than imposing them once the default state has realized. In the former case, repo loans multiplied by their ex-ante risk weight counts as part of risk-weighted assets. While, in the latter case, after default they are written off and thus generate losses that reduce equity that is in the numerator of the ratio. Thus, capital requirements can be both an ex-ante and an ex-post regulatory tool.

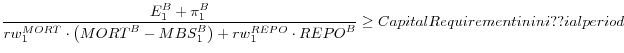
$\displaystyle \frac{E^B_1+{\pi }^B_1}{{rw}^{MORT}_1\cdot \left({MORT}^B-{MBS}^B_1\right)+{rw}^{REPO}_1\cdot {REPO}^B}\ge Capital Requirement in ini??ial period$

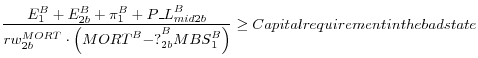
$\displaystyle \frac{E^B_1+E^B_{2b}+{\pi }^B_1+{P\_L}^B_{mid2b}}{{rw}^{MORT}_{2b}\cdot \left({{MORT}^B-?}^B_{2b}{MBS}^B_1\right)}\ge Capital requirement in the bad state$

Bank liquidity regulation

Like capital regulation, liquidity requirements alter the commercial bank's incentives offer different types of credit But these regulations skew choices based on an asset's liquidity rather than the asset's credit risk. Short-term loans are considered liquid, while mortgages and repo loans, being long-term and partially collateralized, are illiquid. As explained in the text, if liquidity requirements are imposed in the bad state they exacerbate fire sales. So we consider liquidity regulation only in the initial period.

$\displaystyle \frac{{LST}^B_1}{{LST}^B_1+{REPO}^B+{MORT}^B-{MBS}^B_1}\ge Liquidity requirement in initial period$

Dynamic provisioning

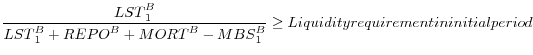
Dynamic provisioning is formalized as a requirement for the bank to keep cash on its balance sheet throughout the good state of the world when the growth of real estate related credit, g%, exceeds a certain threshold x%. Letting the per unit requirement be denoted by $\kappa$ , such regulation would imply that the gross dynamic provisioning is $\left(g\%-x\%\right)\kappa$ .

The budget constraints of the bank is the good state would then become

$\displaystyle {LST}^B_{2g,p}+{LST}^B_{2g,h}+v^B_{2g}D^B\left(1+r^D\right)+\left(g\%-x\%\right)\kappa \le {cash}^B_1+E^B_{2g}+{DISC}^B_{2g}+P_{2g,MBS}{ \sigma }^B_{2g}\left({MORT}^B-{MBS}^B_1\right)$

and

$\displaystyle {\pi }^B_{2g}\le {\left(g\%-x\%\right)\kappa +LST}^B_{2g,p}\left(1+r^{ST}_{2g,p}\right)+{LST}^B_{2g,h}\left(1+r^{ST}_{2g,h}\right)+{REPO}^B\left(1+r^{REPO}\right)$

$\displaystyle + (1-{ \sigma }^B_{2g})\left({MORT}^B-{MBS}^B_1\right)\left(1+r^{MORT}\right)-{DISC}^B_{2g}(1+r^{CB}_{2g}).$

Where the growth rate in real estate related credit is

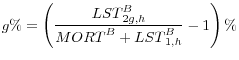
$\displaystyle g\%=\left(\frac{{LST}^B_{2g,h}}{{MORT}^B+{LST}^B_{1,h}}-1\right)\%$

Note that the short-term real estate related credit in the first period, ${LST}^B_{1,h}$ , is equal to the short-term loan demand of household P, ${LST}^P_1$ , while in the good state it is equal to the loan demands of both P and F, i.e. ${LST}^B_{2g,h}={LST}^P_{2g}+{LST}^F_{2g}$ .

Footnotes

* Prepared for the Board of Governors of the Federal Reserve System and International Journal of Central Banking conference on "Central Banking: Before, During, and After the Crisis", March 23/24, 2012. The views in this paper are those of the authors only and not necessarily of the institutions with which they are affiliated. Kashyap thanks the Initiative on Global Markets and the Center for Research on Securities Prices at Chicago Booth for research support. For information on his outside compensated activities, see http://faculty.chicagobooth.edu/anil.kashyap/. All errors are our own. Return to Text

1. See for example Bernanke (2007), Kohn (2007), Kroszner (2007) and Mishkin (2007) and in fact most of them gave more than one speech on this topic. Return to Text

2. If the first time home buyers were absent, then in the event of default all the goods would wind up being by the same agents, in which case default is much less important than in real situations where defaulting agents do not merely get to reacquire any assets against which they had borrowed. Return to Text

3. This is not the only reason why shadow banks exist. Even with identical capital charges for mortgages and MBS, their assumed differences in risk aversion create an incentive to securitize and even with no differences in risk aversion, there would still be pure diversification benefits to sharing the housing risk. Return to Text

4. The repayment rate can also be thought of as the expected probability of default when the decision to default is endogenous and there is no repayment on deposits in the event of default. Return to Text

5. In the good state all assets are essentially risk-less so capital ratios are technically infinite. Return to Text

6. We conjecture that this intuition that it is dangerous to impose a common liquidity requirement all the way through a credit cycle will carry over to other versions of the model. Return to Text

7. To make sure the comparison between columns 1 and 3 is reasonable, we calibrate the increase in LTV in column 3 to match the endogenous change in the LTV that occurs naturally in column 1. If the LTV and margins were identical tools then the equilibrium should not change, but as seen in the table things change considerably.

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Last update: February 1, 2013