
Complexity and Monetary Policy
Keywords:
Abstract:
Keywords: Financial crisis, complexity, monetary policy, model uncertainty, robust simple rules, ECB. JEL Classification: E50, E52, E58.
1 Introduction
In the aftermath of every major crisis, collective introspection among central bankers and economists invariably leads to the acknowledgement that the complexity of the economy is far greater than fathomed before. The ability to measure and diagnose incipient problems and avert trouble may seem diminished. The understanding of the workings of the economy may seem worse than appreciated earlier. The effectiveness of policy tools to tackle an initial shock and maintain stability may seem less certain.
The intensity of the resulting sense of misapprehension, however, varies with the confidence one had in our ability to measure, understand and control the economy. To those who fundamentally believe that the macroeconomy is too complex to measure and control very effectively to begin with, a crisis merely confirms our imperfect understanding of its functioning. In this sense, the present crisis, like every major crisis in the past, has served to reaffirm the limits of our knowledge and temper optimism that central banks can stabilize the economy with great precision. In this light, the crisis has reaffirmed that our efforts should be focused on improving robustness in policy design, acknowledging that our measurement may be imperfect and our models misspecified.1
In this paper we explore the design of robust policy guides aiming to maintain stability in the economy while recognizing the potential misspecification in modelling and mismeasurement of the state of the economy.We focus our analysis on the euro area and explore how a simple interest rate rule can help interpret ECB policy over the past dozen years. We then compare the performance of 11 models of the euro area under alternative policy rules, exploring implications and limits of robustness analysis.
The paper is organized in 10 sections. Section 2 reviews some of the sources of complexity in the economy and in policy design. Section 3 looks at the stability-oriented approach of the ECB in this light. Section 4 examines the evolution of macroeconomic models of the euro area and resulting changes in perceptions of macroeconomic dynamics over the past decade. Section 5 introduces a generalized policy rule for evaluation in the euro area models. Differences between the models are illustrated by means of impulse response and autocorrelation functions in section 6. Section 7 presents optimized model-specific rules. Sections 8 and 9 set up and perform the robustness analysis. Section 10 concludes.
2 Complexity: Intertwined Uncertainties
For this study, we consider that the objective of monetary policy is to maintain price stability and economic stability.2That is, the central bank is given the task of maintaining a low and stable rate of inflation, consistent with the central bank's definition of price stability and of avoiding major macroeconomic fluctuations.
A broad consensus has evolved over the past decades on a number of areas regarding monetary policy strategy. First, the central bank should have a clear numerical definition of price stability, for example a rate of inflation equal to a fixed low number, ![]() . This can serve as the central bank's primary objective or target. Second, and in contrast to the above, in light of the unknown and evolving potential of the economy, no similarly fixed target for real economic activity
should be adopted. Thus, although we can define conceptually
. This can serve as the central bank's primary objective or target. Second, and in contrast to the above, in light of the unknown and evolving potential of the economy, no similarly fixed target for real economic activity
should be adopted. Thus, although we can define conceptually ![]() to be the economy's potential output, consistent with price stability, no precise numerical value would be sensible to adopt
over time as a target. Third policy must be clearly communicated and be systematic in nature, based on a well understood contingency plan that avoids unnecessary discretion and unpredictability. Fourth, policy design must be forward-looking, in the sense that it needs to account for changes in the
economy resulting from market participants behavior and expectations formation, or for anticipated shocks and other developments that could be foreseen. Fifth, policy must ensure that inflation expectations over the medium and longer term remain well anchored in line with the central bank's
definition of price stability.
to be the economy's potential output, consistent with price stability, no precise numerical value would be sensible to adopt
over time as a target. Third policy must be clearly communicated and be systematic in nature, based on a well understood contingency plan that avoids unnecessary discretion and unpredictability. Fourth, policy design must be forward-looking, in the sense that it needs to account for changes in the
economy resulting from market participants behavior and expectations formation, or for anticipated shocks and other developments that could be foreseen. Fifth, policy must ensure that inflation expectations over the medium and longer term remain well anchored in line with the central bank's
definition of price stability.
Intertwined uncertainties in a number of areas create difficulties in arriving at a more precise description of policy strategy. Consider, for example, the question of how we judge "ideal" performance for the macroeconomy. Since aggregating over individual preferences in any economy is
impossible except under very unrealistic modeling assumptions, irreducible uncertainty prevails over the precise aggregate performance criterion. We can consider that good performance should keep inflation close to its target--that is the inflation gap, ![]() , close to zero, and similarly keep the output gap,
, close to zero, and similarly keep the output gap,
![]() , close to zero. But in light of the measurement difficulties associated with providing a precise numerical definition of full employment and potential output in real time,
defining "ideal" performance is necessarily elusive.
, close to zero. But in light of the measurement difficulties associated with providing a precise numerical definition of full employment and potential output in real time,
defining "ideal" performance is necessarily elusive.
Consider next the uncertainties regarding the structure of the economy. What are the key frictions at any point in time and what are their dynamic interactions over time? The need for simplicity in building models and the need for parsimony in estimating their empirical properties with our limited data, forces modellers to focus on only a few key frictions at a time. Some frictions will be missing from each model. To accommodate labor frictions with greater realism, for example, one may need to abstract from credit frictions, financial market frictions, or financial intermediation altogether. And conversely, to model effectively the intricacies of financial intermediation with a rich financial sector, one may abstract from numerous frictions in the real economy sector of a model.
Similarly, uncertainty regarding the determinants of inflation in the short run (the Phillips curve), the formation and evolution over time of inflation expectations are all areas where our knowledge is necessarily limited. Any simple macroeconomic model, however "sophisticated" or "modern" will be, at best, incomplete. Alternative competing models will have relative strengths and weaknesses but a suite of models may be best suited to address a range of potential questions in greater detail.
A crisis, like the present one, may also highlight specific blind spots that could not be effectively dealt with because of lack of similar experiences and data configurations in the recent past that are needed for estimation and calibration. Consider, for example, the uncertainty regarding the monetary policy transmission mechanism. Even under normal conditions this uncertainty is recognized to be considerable. The crisis brought us to an even more complex situation as the policy transmission had to be evaluated in an environment of policy rates approaching the zero lower bound. In most advanced economies, a similar data configuration had not been observed in decades, at least, except for the Japanese economy in the late 1990s. For an early exposition of the role of longer-term interest rates, exchange rates and quantitative easing at the zero bound in Japan, we refer the reader to (Orphanides & Wieland, 2000). Even so, quantitative evaluation of the channels of transmission and relative effectiveness of alternative unconventional policies were hard to come by when some decisions about these policies had to be taken.
As a result of the complexity resulting from these intertwined uncertainties, the exact form of the systematic policy rule that a central bank should pursue, or the degree to which its orientation should be forward-looking or the intensity with which it should aim to stabilize inflation over the near term, and so on, cannot be determined with precision.
This is one way to interpret the quest for robustness, searching for fairly simple rules that can be evaluated over a great number of competing models, aiming to identify policy guides that can achieve reasonably good performance overall.
3 Monetary Policy in the Euro Area
The considerations regarding the pursuit of robustness highlighted in the preceding section are helpful for understanding some of the drivers of monetary policy in the euro area.
First, the monetary policy of the ECB emphasizes the importance of maintaining well-anchored inflation expectations, in line with its numerical definition of price stability. Figure 1 compares the evolution of inflation in the euro area to survey results on inflation expectations five-years ahead from the ECB's Survey of Professional Forecasters (SPF). As can be seen, despite the volatility of actual inflation, the mean forecast is extremely stable and the majority of respondents in each quarter expect that the ECB will achieve inflation in line with its objective of close to but below 2 percent over the medium term.
Second, the ECB's stability oriented approach does not put great emphasis on output gap estimates when policy decisions are made. One reason for this is the extreme unreliability of real-time estimates of the output gap for the euro area.3Figure 2 provides an example of how misleading the information embedded in real-time estimates of the output gap can be in real time. The figure traces the evolution of the output gap estimates produced by the European Commission (EC) for the two years prior to the present crisis. With the benefit of hindsight, one can consider whether use of the estimate for the gap for 2006 would have helped guide monetary policy in the right direction. As can be seen, the opposite is the case, reliance on the gap would have hindered policy. Looked at from the latest perspective (the Autumn 2011 estimate), the output gap was significantly positive in 2006, suggesting the euro area economy was, if anything, overheated before the crisis. But according to the European Commission in 2006 the economy was operating below its potential. Had policymakers relied on this information, they would have loosened policy, a serious mistake in light of the information now available. The same story applies to the estimates for the year 2007, when the turbulence in financial markets started.
By contrast, euro area monetary aggregates had already indicated a sustained upward shift in trend money growth - a potential indication of overheating - for some years. Such signals are regularly analyzed as part of the monetary pillar in the ECB's strategy. ECB President Trichet has credited the monetary pillar in particular for the ECB's decision to start raising policy rates in December 2005 (see (Trichet, 2008)).
The unreliability of measuring the output gap is not confined to these years but is more general in nature. One illustration is provided in Figure 3 that compares the EC real-time estimates of the output gap for each year available with the most recent estimates. As can be seen, the errors are substantial and very persistent. In this small sample, a significant bias is also evident, resulting from the fact that, over the past decade, experts have generally become more pessimistic about growth prospects in the euro area, marking down estimates of potential output growth. The revisions in the growth rates of potential have been small--just a few tenths of a percentage point--but they accumulate into noticeable differences on the level of the output gap.
A simple policy rule that determines the change in the policy rate in response to inflation and the difference of the output gap reduces the impact of such measurement problems:
| (1) |
Interestingly, such a rule can also be used to illustrate the systematic and forward-looking nature of ECB policy over the past dozen years. It may be noted that the difference of growth from potential output growth,
Figures 6 and 7 show the policy prescriptions derived from using the one-year ahead forecasts as inputs to the simple rule. The shaded area is the envelope of the two rules corresponding to the two alternative guides for ![]() . As can be seen, despite its simplicity, the illustration based on inputs from the EC and private forecasters indicates that the contours of the resulting simple rule prescriptions are similar to the evolution of actual ECB policy over this period.5The most significant deviations can be observed during 2009 and 2010, a period when changes in unconventional measures complemented conventional policy in a manner
not reflected in the basic policy rate (the MRO) that is shown in the figures. Figure 8 shows the effects of these unconventional measures on money market rates.
. As can be seen, despite its simplicity, the illustration based on inputs from the EC and private forecasters indicates that the contours of the resulting simple rule prescriptions are similar to the evolution of actual ECB policy over this period.5The most significant deviations can be observed during 2009 and 2010, a period when changes in unconventional measures complemented conventional policy in a manner
not reflected in the basic policy rate (the MRO) that is shown in the figures. Figure 8 shows the effects of these unconventional measures on money market rates.
As noted earlier, the ECB's strategy also involves a special role for monetary aggregates in making interest rate decisions. A formal approach for including ECB-style cross-checking of near-term inflation and output forecasts with longer-term monetary trends in simple interest rules such as equation (1) has been proposed in (Beck & Wieland, 2007) and (Beck & Wieland, 2008) but is not exploited here.
4 Complexity: Changing perceptions/models of euro area macroeconomic dynamics
Researchers at central banks and other institutions use structural macroeconomic models to understand the interaction of monetary policy and macroeconomic fluctuations. The uncertainty about the transmission of monetary policy to aggregate output and inflation is reflected in the uncertainty about the appropriate model of the economy. Changing perceptions regarding the impact of policy decisions on the economy in turn are reflected in changing modeling structures and parameter estimates. We capture this development in policy modeling by considering 11 models of euro area macroeconomic dynamics that were built and estimated over the years by researchers at the ECB and other central banks as well as at universities, the International Monetary Fund and the European Commission.6The 11 models are listed in Table 1. They have been made available in the context of a large-scale model comparison project. An exposition of this new approach to comparative modeling is available in (Wieland et al., 2012) (see also (Taylor & Wieland, 2012) and (Wieland, 2012)).
Each of these models exhibits long-run monetary neutrality as well as short-run nominal inertia. As a result, monetary policy has short-run real effects and the central bank has the ability to stabilize output and inflation fluctuations. The models differ in many other dimensions, for example in the degree of forward-looking expectation formation, the extent of optimizing behavior by economic agents, and in terms of magnitude, scope and parameter estimates. Some of the models are fairly small and focus primarily on the interactions of output, inflation and interest rates. Several models are of medium-size and some are rather large and comprise between two to seven economies. Some models provide more detailed information on the structure of certain sectors of the economy such as the government, labor markets or the financial sector. Some of the models are estimated using harmonized data from the years prior to the start of European Monetary Union while others which were built and estimated at a later date also cover part of the EMU period.
| # | Type | Name | Description |
| 1. | Traditional Keynesian-style models | EA_AWM05 | ECB's (old) area-wide model of Dieppe et al (2005) |
| 2. | New Keynesian models with nominal rigidities and rational expectations (NK1) | G7_TAY93 | G7 model of Taylor (1993a) |
| 3. | New Keynesian models with nominal rigidities and rational expectations (NK1) | EA_CW05fm | Coenen and Wieland (2005), (Fuhrer-Moore-staggered contracts) |
| 4. | New Keynesian models with nominal rigidities and rational expectations (NK1) | EA_CW05ta | Coenen and Wieland (2005), (Taylor-staggered contracts) |
| 5. | New Keynesian models with nominal rigidities and rational expectations (NK1) | G3_CW03 | G3 model of Coenen and Wieland (2003) |
| 6. | Pre-Crisis New Keynesian DSGE models (NK-DSGE) | EA_SW03 | Smets and Wouters (2003) |
| 7. | Pre-Crisis New Keynesian DSGE models (NK-DSGE) | EACZ_GEM03 | Laxton and Pesenti (2003), euro area and Czech republic |
| 8. | Pre-Crisis New Keynesian DSGE models (NK-DSGE) | EA_SR07 | Sveriges Riksbank euro area model of Adolfson et al (2007) |
| 9. | Pre-Crisis New Keynesian DSGE models (NK-DSGE) | EA_QUEST09 | EU Commission's QUEST III model of Ratto et al (2009) |
| 10. | New Keynesian DSGE models built during the crisis | EA_CKL09 | Christoffel et al (2009), model with labor market frictions |
| 11. | New Keynesian DSGE models built during the crisis | EA_GNSS10 | Gerali et al (2010) model with financial frictions and banking |
The 11 models are not ordered by the date of publication but rather by the "age" of the underlying theoretical structure.
First, given that some recent commentators have questioned the usefulness of macroeconomic modeling in the last three decades in general7 and state-of-the-art Dynamic Stochastic General Equilibrium (DSGE) modeling in particular, it seems helpful to start with a traditional Keynesian-style model. This criteria is fulfilled by the European Central Bank's "old" Area-Wide model linearized as in (Dieppe et al., 2005), (EA_AWM05). Expectation formation in this model is largely backward-looking. It has been used for many years in the context of the ECB's forecasting process.8
The other models can be classified as New Keynesian models because they assume rational expectations, imperfect competition and wage or price rigidities. Many of these New-Keynesian models fully incorporate recent advances in terms of microeconomic foundations. Such models are often referred to as monetary business cycle models or monetary dynamic stochastic general equilibrium (DSGE) models.
Models 2 to 5 in Table 1 can be grouped into the first wave of New Keynesian modeling. In the following we use NK1 to label this group. The G7 model of (Taylor, 1993b) is a fairly large-scale example of this type of model. It includes staggered wage contracts, partial adjustment of prices and a detailed decomposition of the demand side in durable, non-durable and services consumption, fixed-, equipment- and inventory investment, government purchases, exports and imports. The model equations exhibit many similarities to current-generation New-Keynesian DSGE models, but they are not derived as stringently from the optimization problems of representative households and firms. We fix the exchange rates between Germany, France and Italy and simulate them as a euro zone bloc. Output is assumed to return to a long-run potential that is exogenous to monetary policy and government spending. The two models of (Coenen & Wieland, 2005) are much less disaggregated and focus on aggregate demand, inflation and interest rates. The EA_CW05ta variant uses Taylor-style staggered wage contracting ((Taylor, 1980)) and exhibits less nominal rigidity than the EA_CW05fm variant with Fuhrer-Moore style contracts ((Fuhrer & Moore, 1995)). The model of (Coenen & Wieland, 2003), (G3_CW03), is a three-country version covering the United States, the euro area and Japan and was previously used to evaluate monetary policy making at the zero lower bound on nominal interest rates in Japan.
Models 6 to 9 in Table 1 are modern New Keynesian DSGE models that were built and available for use in policy analysis at central banks and international institutions prior to the global financial crisis. In the following, we use the term NK-DSGE as a label referring to this group. The (Smets & Wouters, 2003) model that was developed at the European Central bank, (EA_SW03), is representative of current thinking in macroeconomics. It is very similar to, and 'largely based on' according to Smets and Wouters, the well-known empirically-estimated New-Keynesian DSGE model developed by (Christiano et al., 2005). The Smets and Wouters study received much attention in the literature because it showed that the current generation of DSGE models with sticky prices and wages was able to capture the time series properties of the data as long as a sufficient number of structural frictions and shocks was considered.
We include, model 7 from (Laxton & Pesenti, 2003) in the analysis, because it is a two-economy model that accounts for an endogenous response of exports and imports. The Laxton and Pesenti (2003) model,(EACZ_GEM03), was created at the International Monetary Fund at about the same time as the Smets-Wouters model. Model parameters were not estimated with macroeconomic data but calibrated to values considered reasonable in light of other studies. Certain parameters and shock variances were matched to euro area and Czech macroeconomic volatility.
In addition, we have included two fairly large-scale estimated DSGE models of the euro area developed at the Sveriges Riksbank ((Adolfson et al., 2007), EA_SR07) and the European Commission ((Ratto et al., 2009), EA_QUEST09). The open-economy model of the euro area by Ratto et al. (2009) is estimated with quarterly euro area data from 1981Q1 to 2006Q1 thereby including a significant part of EMU history. They named their model 'QUEST III'. It was built specifically for the joint analysis of fiscal and monetary policy and provides a thorough treatment of the government sector. Another important departure from the assumptions made by Smets and Wouters (2003) and Laxton and Pesenti (2003) concerns the inclusion of a share of rule-of-thumb households.
Finally, we also consider two models that have been built since the start of the financial crisis. The model of (Christoffel et al., 2009), EA_CKL09, incorporates unemployment and search frictions in labor market dynamics. Though the model was revised in 2008, the data used in estimation only extends to the end of 2006. In this respect, it is still a pre-crisis model. More importantly, the model of (Gerali et al., 2010), (EA_GNSS10) covers recent advances in the modeling of the financial sector in response to criticism regarding the lack of such detail in pre-crisis DSGE models. With regard to credit supply, they add a stylized banking sector to a model with credit frictions and borrowing constraints as in (Iacoviello, 2005). Banks have market power in loan and deposit markets and set different rates for households and firms. Furthermore, banks face costs in adjusting retail rates and changes in central bank rates are only passed through to loan and deposit rates over time. Banks accumulate capital out of retained earnings and aim to keep the ratio to assets close to a target. Their capital position affects lending and introduces feedback between the real and financial sector.
In sum, these 11 models capture the progression in scientific advances and the practice of macroeconomic modeling at central banks over the last twenty years very well. In this manner, they capture changing perceptions of the macroeconomic structure and monetary policy transmission in the euro
area.
5 A class of policy rules
Next, we consider a general monetary policy rule that we want to include in all eleven models for the purpose of a comparative analysis.
| (2) |
![]() refers to the short-term nominal interest rate. The rule incorporates interest rate smoothing with a smoothing parameter
refers to the short-term nominal interest rate. The rule incorporates interest rate smoothing with a smoothing parameter ![]() .
. ![]() denotes the (log of) the price level. Thus, the rule implies a response to the inflation rate over four quarters,
denotes the (log of) the price level. Thus, the rule implies a response to the inflation rate over four quarters,
![]() , with the response coefficient
, with the response coefficient ![]() . The inflation
target
. The inflation
target ![]() shown previously in equation (1) is normalized at a value of zero for our model simulations.
shown previously in equation (1) is normalized at a value of zero for our model simulations. ![]() is the deviation of output from the level that would be realized with flexible prices.
is the deviation of output from the level that would be realized with flexible prices. ![]() measures the magnitude of the response to the level of the gap
and
measures the magnitude of the response to the level of the gap
and
![]() to the growth rate over four quarters.
to the growth rate over four quarters. ![]() denotes the relevant
horizon. We consider rules based on current outcomes, two-quarter-ahead forecasts and four-quarter-head forecasts, i.e.
denotes the relevant
horizon. We consider rules based on current outcomes, two-quarter-ahead forecasts and four-quarter-head forecasts, i.e.
![]() .
.
In comparing the choice of forecast horizon in model simulations of this rule to the forecast horizon of the rule used in the empirical analysis in section 3, it is important to keep in mind that the most recent GDP data available in policy practice dates from one or two quarters prior to the policy decisions. To a large extent, the tremendous efforts undertaken at central banks in analyzing recent data and producing forecasts concern the "now-casting" for the current and following quarter. For this reason, the four-quarter-ahead forecast in the empirical analysis of section 3 is actually closer to a rule with a two-quarter-ahead forecast in the model simulations.
We will explore how simpler rules perform relative to this generalized five parameter rule,
![]() . For example, the well-known Taylor rule only contains a response to current inflation and the output gap with the following parameter values:
. For example, the well-known Taylor rule only contains a response to current inflation and the output gap with the following parameter values:
![]() . Outcome- and forecast-based Taylor-style rules with interest-rate smoothing instead imply the following parameter restrictions:
. Outcome- and forecast-based Taylor-style rules with interest-rate smoothing instead imply the following parameter restrictions:
![]() .
.
Another simplification that we evaluate is a response to output growth instead of the output gap, i.e.
![]() .9If the
coefficient on the lagged interest rate is restricted to unity,
.9If the
coefficient on the lagged interest rate is restricted to unity, ![]() , these rules are often referred to as first-difference rules. The policy rule in equation (1) that was used to review
euro area policy decisions in section 3 is such a difference rule with
, these rules are often referred to as first-difference rules. The policy rule in equation (1) that was used to review
euro area policy decisions in section 3 is such a difference rule with
![]() . It can be used with current values of output and inflation and with forecasts. In the subsequent simulation we will use the label DIF0 to
refer to the outcome-based version of this difference rule.
. It can be used with current values of output and inflation and with forecasts. In the subsequent simulation we will use the label DIF0 to
refer to the outcome-based version of this difference rule.
6 Differences in model dynamics
The sources of euro area macroeconomic fluctuations and the transmission of central bank policy to euro area aggregates can only be understood through the lens of a macroeconomic model. Each model provides a different perspective and emphasizes different elements of the macroeconomic structure.
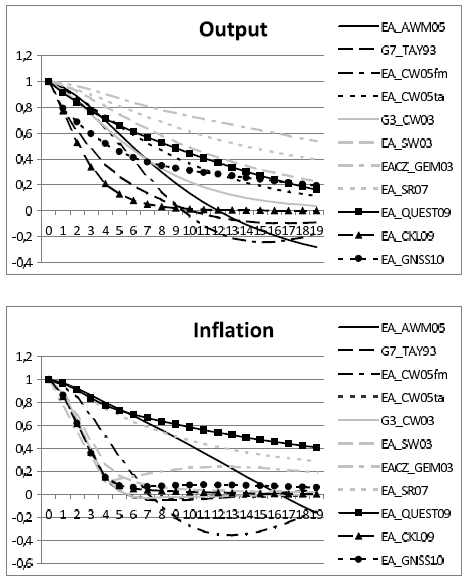
To illustrate differences and similarities between models we compute two types of objects: (i) the impulse response functions of output and inflation to a monetary policy shock and (ii) the autocorrelation functions of output and inflation given the stochastic properties of all other shocks, excluding the monetary policy shock.
We introduce the identical monetary policy rule in all models. Thus, any differences that are revealed by our comparison are due to differences in the non-policy part of the macroeconomic structure. For this purpose we use a Taylor-style rule with interest-rate smoothing that was estimated
empirically by (Gerdesmeier & Roffia, 2004) and also employed as a benchmark in (Kuester & Wieland, 2010). The GR rule is a restricted version of the generalized rule in equation (1) with only the lagged interest rate,
current inflation and the output gap. The response coefficients are
![]() .10
.10
Figure 9 reports the impact of a 100 basis points increase in the nominal interest rate on euro area real GDP and inflation in the 11 models when interest rates in subsequent periods are set according to the GR rule. Thus, differences in the transmission of monetary policy to output and inflation are solely due to differences in the structural assumptions and parameter estimates of these models. All models have Keynesian features. Due to nominal rigidities the increase in the nominal interest rate raises real interest rates and lowers real output. Inflation typically reacts more slowly and declines in response to slowing output consistent with a Phillips curve. There are substantial differences in terms of magnitude and persistence of the effect of such a monetary policy shock. They arise because of different structural assumptions and different data used in estimation. Some models use more data series than others and the sample periods vary.
Figure 10 reports the autocorrelation functions of output and inflation in the 11 models given the variance-covariance matrix of the respective model's structural disturbances but excluding monetary policy surprises. Both output and inflation exhibit persistence in all models. The degree of persistence, however, varies substantially.
These findings confirm that the 11 models considered have fairly different implications for euro area macroeconomic dynamics and monetary policy transmission. Given many of these models have been built and used at policy institutions they represent a policy-relevant range of model uncertainty.
7 Model-specific rules
How well would the generalized rule defined by equation (2) perform in stabilizing output and inflation dynamics in the different models of the euro area? To answer this question we search for the values of the parameters of the rule that are most effective in a given model. To evaluate policy performance we use the weighted sum of unconditional variances of inflation deviations from target (normalized at zero), the output gap, and the quarterly change in the interest rate.
| (3) |
This loss function is of practical relevance as it captures the two objectives outlined in section 2, that is maintaining a low and stable rate of inflation and avoiding major macroeconomic fluctuations. In addition, it includes moderating the volatility of policy rates as a third objective. This term captures central banks' tendency to smooth interest rates and avoid frequent policy reversals of great magnitude.
We then choose the response coefficients
![]() and the horizon
and the horizon ![]() to minimize the above loss
function. In doing so we consider three different horizons,
to minimize the above loss
function. In doing so we consider three different horizons,
![]() .
. ![]() is restricted to lie between 0 and 1.5 and the other
coefficients between -3 and 3. These boundaries only matter in one model. The coefficient values and horizons that deliver the minimum loss in each model are reported in Table 2 together with the resulting absolute loss.
is restricted to lie between 0 and 1.5 and the other
coefficients between -3 and 3. These boundaries only matter in one model. The coefficient values and horizons that deliver the minimum loss in each model are reported in Table 2 together with the resulting absolute loss.
| # | Name |
|
Min(L) | L(Tay) | L(GR) | L(Dif,h=0) | ||||
| 1. | EA_AWM05 | 0.83 | 0.49 | 1.19 | 0.21 | 4 | 3.05 | 5.8 | 7.9 | |
| 2. | G7_TAY93 | 1.16 | 0.51 | 1.85 | -0.09 | 2 | 11.69 | 19.5 | 19.4 | 17.5 |
| 3. | EA_CW05fm | 0.85 | 0.52 | 0.58 | 0.07 | 0 | 5.71 | 10.3 | 9.5 | 8.8 |
| 4. | EA_CW05ta | 0.86 | 0.14 | 0.90 | -0.24 | 2 | 2.63 | 4.7 | 4.8 | 3.8 |
| 5. | G3_CW03 | 0.87 | 0.13 | 0.55 | 0.00 | 0 | 1.95 | 3.5 | 3.3 | 2.6 |
| 6. | EA_SW03 | 0.98 | 0.10 | 1.09 | -0.28 | 0 | 1.46 | 4.9 | 5.1 | 2.6 |
| 7. | EACZ_GEM03 | 0.98 | 2.02 | 0.25 | 1.50 | 4 | 1.26 | 1.6 | 3.3 | 1.6 |
| 8. | EA_SR07 | 1.03 | 0.11 | -0.03 | 0.79 | 0 | 5.77 | 19.4 | 16.0 | 8.3 |
| 9. | EA_QUEST09 | 1.05 | 0.75 | 0.15 | 0.42 | 0 | 3.03 | 18.0 | 8.0 | 3.2 |
| 10. | EA_CKL09 | 1.50 | 3.00 | -0.39 | -0.51 | 4 | 4.36 | 8.8 | 5.8 | 6.2 |
| 11. | EA_GNSS10 | 1.21 | 0.76 | 0.55 | -0.18 | 0 | 13.7 | 23.1 | 21.0 |
Optimized model-specific rules almost always involve the lagged interest rate, inflation, the output gap and output growth. One model has a coefficient of zero on output growth, (G3_CW03), and another one a near-zero coefficient on the output gap, (EA_SR07). The EA_CKL09 model exhibits very extreme coefficients which represent a corner solution at the pre-set boundaries of 1.5 for the coefficient on the lagged interest rate and 3 for the coefficient on inflation.
Six of the models prefer a policy response to current outcomes of inflation, the output gap and output growth over forecasts of these variables. In 3 models, the optimal forecast horizon is four quarters and in two models the best performance is achieved with two-quarter ahead forecasts.
The response coefficients on inflation, the output gap and output growth vary substantially across models. The minimum losses achieved under the model-specific rules are quite a bit lower than under Taylor's rule, the GR rule or the outcome-based version of the first-difference rule from
equation (1), DIF0. DIF0 implies explosive dynamics in the ECB's Area-Wide model as indicated by the ![]() sign in Table 1. As noted in Kuester and Wieland (2010) this model does not
tolerate a unit root in the nominal policy rate because it exhibits largely backward-looking dynamics and assigns almost no role to forward-looking, rational expectations. Taylor's rule typically implies greater losses than the GR or DIF0 rules because it restricts the coefficient on the lagged
interest rate to zero. Models with rational expectations typically attribute substantial improvements in stabilization performance to interest rate smoothing ((Levin et al., 1999)). Somewhat surprisingly, however, the Taylor rule implies equilibrium
indeterminacy in the
sign in Table 1. As noted in Kuester and Wieland (2010) this model does not
tolerate a unit root in the nominal policy rate because it exhibits largely backward-looking dynamics and assigns almost no role to forward-looking, rational expectations. Taylor's rule typically implies greater losses than the GR or DIF0 rules because it restricts the coefficient on the lagged
interest rate to zero. Models with rational expectations typically attribute substantial improvements in stabilization performance to interest rate smoothing ((Levin et al., 1999)). Somewhat surprisingly, however, the Taylor rule implies equilibrium
indeterminacy in the
![]() model with financial frictions and banking. This outcome is also signaled by an
model with financial frictions and banking. This outcome is also signaled by an ![]() sign in the table.
sign in the table.
8 Robustness
Unfortunately, model-specific rules that are optimized for one model are typically not robust to model uncertainty. They often deliver much worse or even disastrous performance in other models. To the extent another model provides a better match for the unknown structure of the euro area economy
than the policy maker's preferred framework, the policy recommendations resulting from the model-specific rule favored by this policy maker would induce much greater macroeconomic fluctuations than anticipated. Table 3 illustrates this model risk by reporting outcomes for each of the 11
model-specific rules from Table 1 in the other 10 models. The values shown are percentage increases in the loss function under each rule relative to the rule optimal in the specific model. Thus, values on the diagonal are equal to zero by definition. Off diagonal we observe many cases with
explosive dynamics or equilibrium indeterminacy as indicated by ![]() . Furthermore, there are many cases where losses more than double or triple relative to the model-specific rule. Thus, it
would be of great benefit to know exactly which model constitutes the best possible representation of the macroeconomic structure of the euro area economy. In the absence of this knowledge, policymakers are best advised not to use purely model-specific policy recommendations as guidance in making
policy decisions.
. Furthermore, there are many cases where losses more than double or triple relative to the model-specific rule. Thus, it
would be of great benefit to know exactly which model constitutes the best possible representation of the macroeconomic structure of the euro area economy. In the absence of this knowledge, policymakers are best advised not to use purely model-specific policy recommendations as guidance in making
policy decisions.
| # | Rule | 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | 11. |
| 1. | EA_AWM05 | 0 | 30 | 48 | 61 | 58 | 16 | 113 | 228 | 113 | 74 | 126 |
| 2. | G7_TAY93 | 232 | 0 | 31 | 32 | 26 | 5 | 216 | 285 | 229 | 35 | 107 |
| 3. | EA_CW05fm | 107 | 11 | 0 | 11 | 10 | 24 | 81 | 171 | 93 | 28 | 47 |
| 4. | EA_CW05ta | 38 | 10 | 235 | 0 | 1 | 21 | 5032 | 54 | |||
| 5. | G3_CW03 | 92 | 5 | 105 | 0 | 18 | 2624 | 29 | ||||
| 6. | EA_SW03 | 775 | 8 | 153 | 35 | 26 | 0 | 1539 | 1624 | 29 | ||
| 7. | EACZ_GEM03 | 183 | 159 | 25 | 49 | 54 | 321 | 0 | 76 | 57 | 880 | 5643 |
| 8. | EA_SR07 | 85 | 27 | 80 | 17 | 15 | 29 | 32 | 0 | 83 | 210 | 101 |
| 9. | EA_QUEST09 | 63 | 58 | 67 | 54 | 68 | 43 | 61 | 0 | 28 | 35 | |
| 10. | EA_CKL09 | 869 | 482 | 221 | 162 | 3227 | 25 | 1115 | 20 | 0 | 35 | |
| 11. | EA_GNSS10 | 151 | 832 | 1333 | 326 | 115 | 93 | 115 | 17 | 11 | 0 |
An alternative approach that promises more robust performance across models is Bayesian model averaging ( (Levin et al., 2003), (Brock et al., 2007) and Kuester and Wieland (2010)). We start by considering a
Bayesian policy with flat priors that assigns equal probabilities or weights to each model. Thus, we pick the response coefficients
![]() and the horizon
and the horizon ![]() to minimize average model
loss:
to minimize average model
loss:
![\displaystyle \sum_{m=1}^M \frac{1}{M}\L _m = \sum_{m=1}^M \frac{1}{M} \left[Var (\pi_m) + Var (y_m) + Var (\Delta i_m)\right]](img32.gif) |
(4) |
where
| (5) |
The coefficient on the lagged interest rate is near unity. The coefficients on inflation, output gap and growth are all positive. Output gap and growth are calculated relative to the flexible-price benchmark.
This model averaging rule delivers fairly robust performance across all eleven models. To illustrate its robustness we compute the increase in loss in percentage terms that results from the model averaging rule in each of the 11 models relative to the best model-specific rule in that model (i.e. the rules from Table 1). It is shown in the first row of Table 4.
The increase in losses is much more moderate than in the case of the model-specific rules. There is no case of indeterminacy or explosiveness. Except for two cases the percentage increase does not exceed 50 percent of the minimum loss. It is 62 percent in the EA_SR07 model and 122 percent in the ECB's old Area-Wide model EA_AWM05. Thus, robustness comes at a significant cost in terms of performance deterioration relative to a scenario where the correct model is known. However, the model averaging rule achieves great improvements under model uncertainty, i.e. relative to a scenario where the policy maker follows a rule that is optimized for one model but one of the other models turns out be a better match to the structure of the euro area economy.
The robustness exhibited by the model-averaging rule is in a sense, in sample. It performs robustly across the sample of 11 models that is included in the average loss that the rule minimizes. An open question, however, is how well such a procedure for deriving robust policies performs out of sample. For example, what if only a subset of models is used in averaging? How robust is such a rule in models not considered in the average loss?
As discussed earlier, the models are ordered in a certain chronological order, not in terms publication date but in terms of the "age" of the theory underlying the models. EA_AWM05 stands out as a traditional Keynesian-style model with largely backward-looking expectations formation. Some economists might have considered this feature a reason for dropping the model from consideration. Then, there are the models numbered 2 to 5, that is the T_93_EU, EA_CW05fm, EA_CW05ta and G3_CW03 models. These models are best described as first-generation New Keynesian models. They include rational expectations and nominal rigidities such as staggered contracts. However, they do not fully enforce all the cross-equation restrictions that result from utility maximization of households and profit-maximization of imperfectly competitive firms as in more New Keynesian DSGE models. Given the earlier-mentioned criticism of DSGE modeling prior to the crisis, this property need not necessarily be a drawback. We refer to these four models as the NK1 group.
The models numbered 6 to 9, that is the EA_SW0, EACZ_GEM03, EA_SR07 and EA_QUEST09 models are monetary business cycle models that are derived consistently from the optimizing behavior of households and firms under rational expectations. New Keynesian features include imperfect competition and staggered nominal contracts. These four models were built and used at policy institutions for policy analysis prior to the global financial crisis. We term these four models the NK-DSGE group.
We then derive model-averaging rules for the NK1 and NK-DSGE group and evaluate how robust they are out of sample. The out of sample models include the old ECB's Area-Wide model as well as the new DSGE models built and estimated during the financial crisis, that is EA_CKL09, which includes search frictions in labor markets, and EA_GNSS10, which includes financial frictions, credit and banking.
Model averaging with the NK1 group implies minimizing the loss
![]() , while model averaging with the NK-DSGE group implies minimizing the loss
, while model averaging with the NK-DSGE group implies minimizing the loss
![]() . The resulting model-averaging rules are given by:
. The resulting model-averaging rules are given by:
| NK1: |
(6) | ||
| NK-DSGE: |
(7) |
Both rules exhibit near unity values on the lagged interest rate. The NK1 rule responds to inflation, output and output growth forecasts four-quarters into the future. The NK-DSGE rule is essentially a first difference rule for interest rates responding to current inflation and output growth relative to four quarters earlier. The current output gap has a near-zero coefficient.
The in-sample and out-of-sample robustness of these two rules is indicated in Table 5 by the increase in loss in percentage terms in each of the 11 models relative to the respective model-specific rule.
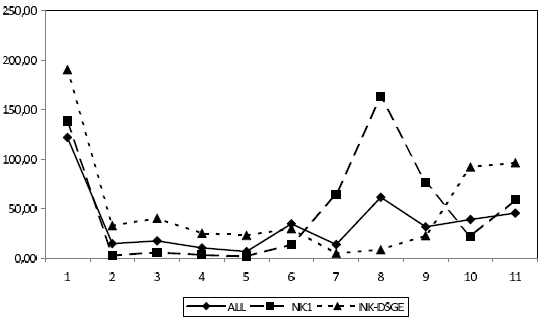
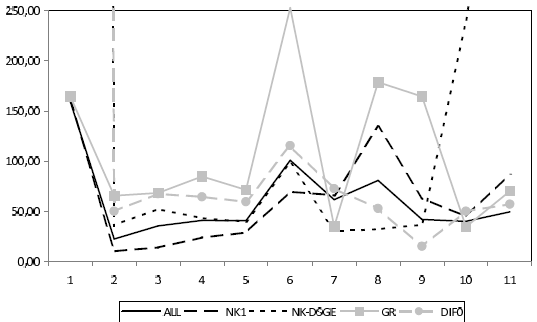
The NK1 and NK-DSGE rules also perform fairly robustly across models. There are no cases of indeterminacy or explosiveness. In some models the performance relative to the model-specific rule is better than for the rule that averages over all models (ALL), but in others it is worse. The performance of the three model averaging rules is most easily compared by the graphic representation in Figure 11. The horizontal axis indicates models 1 to 11. The blue line refers to the increase in loss relative to model-specific rules under the ALL rule. The red line indicates the robustness of the NK1 rule and the green line the NK-DSGE rule.
Not surprisingly, the NK1 rule performs best for the models of the NK1 group and the NK-DSGE rule for the models of the NK-DSGE group. Performance deteriorates out of sample. Somewhat surprisingly the NK1 rule is better in models 1, 10 and 11, (EA_AWM05, EA_CKL09, EA_GNSS10), than the NK-DSGE rule.
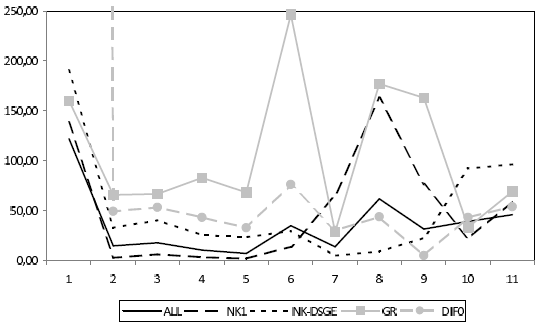
Figure 12 also includes the performance of the GR and DIF0 rules from Table 1 across models. The GR rule performs worse than the other rules in 7 out of 11 models. The difference to the ALL rule is greater than 50% of the minimum loss in 7 of the models. As noted earlier, the outcome-based DIF0 rule implies explosive behavior in model 1, the ECB's old Area-Wide model (EA_AWM05). However, if one removes this model from consideration this difference rule is surprisingly robust. The difference to the minimum loss is close to or less than 50 percent of the minimum loss in 9 of the models. Importantly, however, robustness of the difference rule is weakened substantially once it is based on forecasts. For example, the version with four-quarter-ahead forecasts suffers from drastic increases in losses in models 2,6, 9, 10 and 11 of magnitudes much greater than 200 % of the minimum loss.
9 Output Gap Mismeasurement and Robustness
As discussed in section 3 an important source of model uncertainty is the concept of potential output, that is the level of output consistent with long-run price stability. This variable is unobservable. It can only be computed using a particular model of potential output. As a result, estimates
of potential output are frequently revised and revisions are made even many years after the date to which the estimates apply. The difference between real-time and fall 2011 estimates of the euro area output gap by the European Commission was previously reviewed in section 3. The persistence of the
degree of mismeasurement of the output gap is due to the revision of potential output estimates and not of actual output. The high degree of persistence of output gap mismeasurement can be illustrated by modeling it with a simple autoregressive process and estimating its parameters. We denote the
difference between the real-time gap estimate and the 2011 gap estimate by ![]() . OLS estimates of this process with the data shown previously in Figure 3 imply:
. OLS estimates of this process with the data shown previously in Figure 3 imply:
The estimate of the autoregressive parameter is highly significant with a 95% confidence interval of [0.79,1.03]. The
To investigate the implications of output mismeasurement for monetary stabilization policy we add the estimated process for
![]() to the output gap(s) that appear in the interest rate rule as in (Orphanides, 2003b) and (Orphanides, 2003a). The
policy maker does not observe the correct output gap and sets interest rates persistently too high or too low. Then we evaluate the performance of the different policy rules and optimize their coefficients in the 11 models. Typically, the response coefficient(s) on the output gap(s) decline
relative to the case without output gap mismeasurement while the coefficient on inflation increases (results not shown here).
to the output gap(s) that appear in the interest rate rule as in (Orphanides, 2003b) and (Orphanides, 2003a). The
policy maker does not observe the correct output gap and sets interest rates persistently too high or too low. Then we evaluate the performance of the different policy rules and optimize their coefficients in the 11 models. Typically, the response coefficient(s) on the output gap(s) decline
relative to the case without output gap mismeasurement while the coefficient on inflation increases (results not shown here).
Market participants in the models we consider are assumed to form rational expectations knowing the correct output gaps as well as the error process entering the central bank's policy rule. Thus, there is asymmetric information between the central bank and market participants. As pointed out by Beck and Wieland (2008) the potential impact of output gap misperceptions is much greater in the more realistic case of symmetric misperceptions regarding the aggregate output gap. In this regard, our approach tends to understate the possible consequences of noisy output gaps.
We also re-optimize the model-averaging rules in the presence of output gap mismeasurement and re-compute the losses under the Taylor, GR and DIF0 rules from Table 2. Table 6 indicates the coefficients of the model-averaging rules with noisy output measurement relative to the earlier values
obtained when the output gap is observed without error.
For the ALL rule that was derived by averaging over all 11 models and for the NK1 rule that averaged over four early New Keynesian models the optimal horizon ![]() stays the same. The ALL rule
uses current values and the NK1 rule 4-quarter ahead forecasts. Thus, for the ALL and NK1 rules the response coefficients with and without noisy output gaps are directly comparable. Typically the coefficient on inflation increases and the coefficients on the output gap and the output growth rate
stay the same or decline in absolute value with output gap mismeasurement. The coefficient on the lagged interest rate also declines a bit.In the case of the four New-Keynesian DSGE models built before the financial crisis the rule using two-quarter-ahead forecasts now slightly dominates the rule
responding to current outcomes. For the NK-DSGE rules the coefficients are not directly comparable because of the change in horizon.
stays the same. The ALL rule
uses current values and the NK1 rule 4-quarter ahead forecasts. Thus, for the ALL and NK1 rules the response coefficients with and without noisy output gaps are directly comparable. Typically the coefficient on inflation increases and the coefficients on the output gap and the output growth rate
stay the same or decline in absolute value with output gap mismeasurement. The coefficient on the lagged interest rate also declines a bit.In the case of the four New-Keynesian DSGE models built before the financial crisis the rule using two-quarter-ahead forecasts now slightly dominates the rule
responding to current outcomes. For the NK-DSGE rules the coefficients are not directly comparable because of the change in horizon.
Figure 13 displays percent increases in loss under the ALL, NK1, NK-DSGE, GR and DIF0 rules relative to the model-specific rules when the output gap is mis-measured. Due to the additional noise, losses and percent loss increases relative to minimum loss are greater than in Figure 12. The NK-DSGE
rule turns out to be less robust and delivers substantially worse performance in model 11, (EA_GNSS10). The DIF0 rule remains fairly close to the ALL and NK1 model averaging rules. Its robustness properties, however, deteriorate again if forecasts are used in place of recent outcomes (not
shown).
10 Conclusions
The complexity resulting from intertwined uncertainties regarding potential model misspecification and mismeasurement of the state of the economy defines the monetary policy landscape. Policymakers, including at the ECB, are sensitive to the complexity of the environment in which policy is set. Using the euro area as laboratory in this paper we explore the design of robust policy guides aiming to maintain stability in the economy while recognizing the complexity facing policymakers.
As we show, the main ECB policy rate is characterized rather well by a simple first difference rule that explains the quarterly change in the policy rate in terms of the near term forecast of inflation deviation from the ECB's definition of price stability and the near term output growth deviation from its trend. An advantage of this simple rule is that its implementation does not require real-time estimates for the output gap that have been subject to severe mismeasurement before the crisis.
To capture the complex environment facing policymakers we conduct an evaluation of alternative policy rules across 11 quarterly models of the euro area. We use these models to examine implications and limits of robustness analysis. To capture as wide a range of alternative modeling strategies as possible, we consider the development of models of the euro area from the beginning of the EMU to just prior the financial crisis. We also incorporate models that include more detailed characterization of financial intermediation and banking risks informed by the first years of the crisis.
The analysis confirms the fragility of policy analysis optimized for any specific model and shows the merits of model averaging in policy design. Rules derived by averaging over all 11 euro area models are found to perform better when they use current outcomes rather than forecasts of output and inflation. Model averaging rules serve as useful benchmarks against which the robustness of other policy prescriptions may be evaluated. Interestingly, a simple difference rule with coefficients of 1/2 on inflation and output growth deviations, just like the rule shown to be useful for interpreting ECB interest rate policy, is quite robust as long as it responds to current outcomes rather than forecasts.
Bibliography
Journal of International Economics 72:481-511.
Journal of the European Economic Association 5(2-3).
Journal of Monetary Economics 55(1).
Journal of Econometrics 136(2):629-664.
Washington, D.C.: The Brookings Institution.
Journal of Political Economy 113(1):1-45.
ECB Working Paper Series 944.
European Economic Review 53:908-936.
Journal of Monetary Economics 50:1071-1101.
European Economic Review 49:1081-1104.
Journal of Common Market Studies 43(3):507-5372.
The Quarterly Journal of Economics 110(1):127-159.
Journal of Money, Credit and Banking 42:107-141.
Swiss Journal of Economics and Statistics 140(1):37-66.
The American Economic Review 95(3):739-764.
Journal of the European Economic Association 8(4):872-912.
Journal of Monetary Economics 50:1109-1146.
In J. B. Taylor (ed.), Monetary Policy Rules. Chicago: University of Chicago Press.
The American Economic Review 93(3):622-645.
Carnegie-Rochester Conference Series on Public Policy 29:173-204.
Journal of Monetary Economics 50:605-631.
Journal of Monetary Economics 50:633-663.
Journal of the Japanese and International Economies 14:327-365.
Economic Modelling 26(1):222-233.
Manuscript.
Journal of the European Economic Association. 1 (5):1123-1175.
Journal of Political Economy 88(1):1-24.
Carnegie-Rochester Conference Series on Public Policy 39:195-214.
W.W. Norton, New York.
Online Edition available on: http://www.stanford.edu/ johntayl/MacroPolicyWorld.htm.
Review of Economics and Statistics forthcoming.
In B. Friedman & M. Woodford (eds.), Handbook for Monetary Economics. Elsevier Science.
FEDS Working Paper 2010-15.
Frankfurter Allgemeine Zeitung.
In R. Solow & J.-P. Touffut (eds.), What's right with Macroeconomics? Edward Elgar Publishers.
Journal of Economic Behavior and Organisation forthcoming.
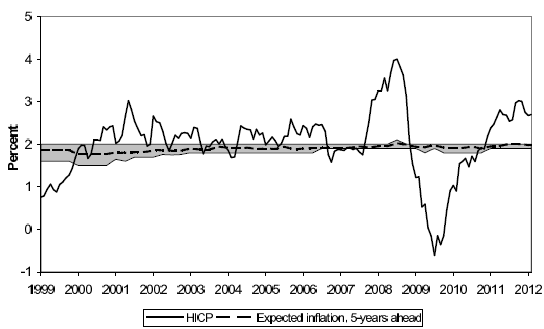
Notes: HICP shows the rate of increase of the index over 12 months. Expected inflation is the average five-year ahead forecast reported in the ECB SPF. The thin lines denote the 25% and 75% percentiles and the shaded area reflects the interquartile range of the cross-sectional distribution of the individual responses.
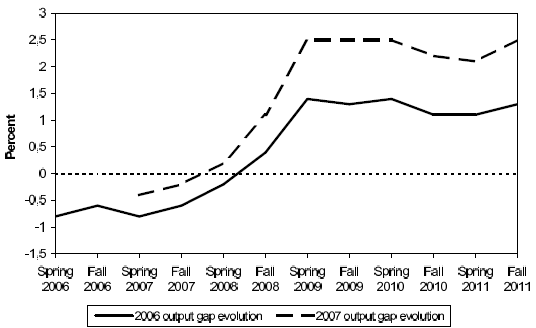
Notes: The two series trace the evolution of output gap estimates for the year 2006 and 2007, as reported by the European Commission in the Spring and Autumn forecasts.
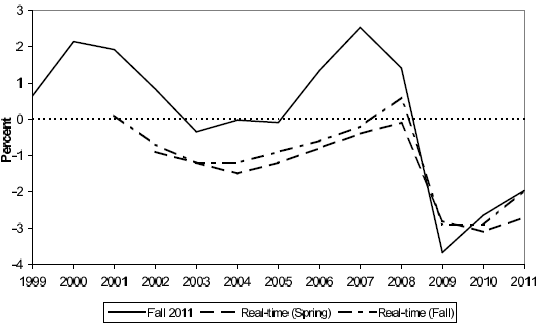
Notes: The Fall 2011 series shows the historical output gap estimates from the latest European Commission forecast (Fall 2011). The real-time series shows, in each year, the output gap estimate of the year from the European Commission Spring and Fall forecasts.
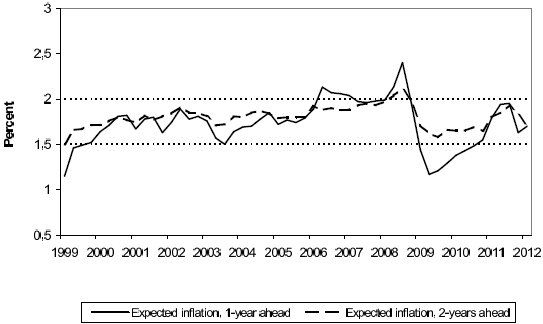
Notes: Expected inflation, one-year and two-years ahead, represent the average responses in the ECB SPF.
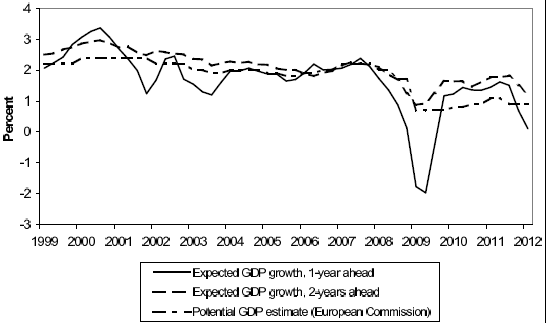
Notes: Expected growth one-year and two-years ahead represent the average responses in the ECB SPF. Potential output growth reflects the real-time estimate for the year as reported in the European Commision's Spring and Autumn forecasts.
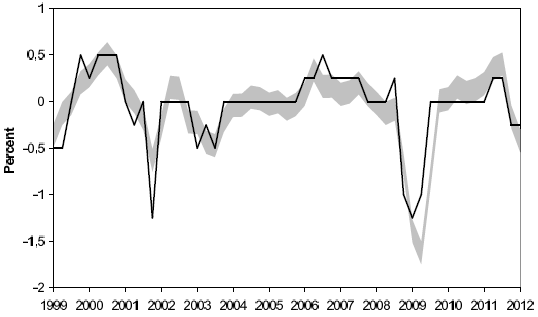
Notes: The shaded area represents the envelope of prescriptions from the simple policy rule:
![]() .
.
![]() reflects the deviations in the SPF one-year ahead inflation forecasts from either of two bounds as shown in Figure 4.
reflects the deviations in the SPF one-year ahead inflation forecasts from either of two bounds as shown in Figure 4.
![]() reflects the deviations in the SPF one-year ahead GDP growth forecasts from the potential output growth shown in Figure 5. The solid line shows the quarterly change in
the ECB policy rate (MRO) following the policy meeting of the 2nd month in each quarter.
reflects the deviations in the SPF one-year ahead GDP growth forecasts from the potential output growth shown in Figure 5. The solid line shows the quarterly change in
the ECB policy rate (MRO) following the policy meeting of the 2nd month in each quarter.
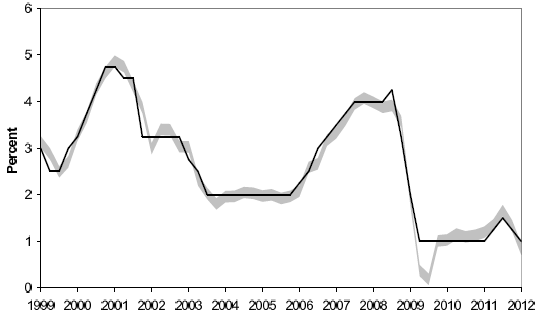
Notes: The shaded area represents the envelope of prescriptions from the simple policy rule:
![]() , that emerge from applying the prescribed change to the level of the policy rate a quarter earlier.
, that emerge from applying the prescribed change to the level of the policy rate a quarter earlier.
![]() reflects the deviations in the SPF one-year ahead inflation forecasts from either of two bounds as shown in Figure 4.
reflects the deviations in the SPF one-year ahead inflation forecasts from either of two bounds as shown in Figure 4.
![]() reflects the deviations in the SPF one-year ahead GDP growth forecasts from the potential output growth shown in Figure 5. The solid line shows the ECB policy rate (MRO)
following the policy meeting of the 2nd month in each quarter.
reflects the deviations in the SPF one-year ahead GDP growth forecasts from the potential output growth shown in Figure 5. The solid line shows the ECB policy rate (MRO)
following the policy meeting of the 2nd month in each quarter.
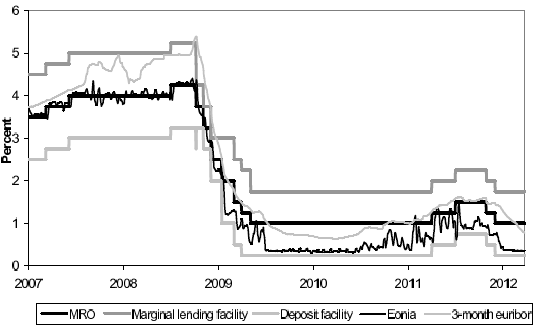
Notes: Eonia is the 5-day trailing moving average.
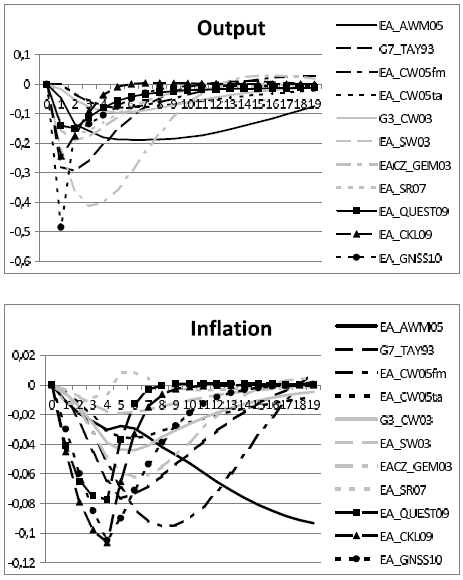
Notes: Impact of a one percentage point shock to monetary policy.
Footnotes
Last update: February 1, 2013