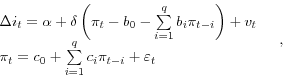ANCHORING BIAS IN CONSENSUS FORECASTS AND ITS EFFECT ON MARKET PRICES*
Keywords: forecasts, anchoring bias, bond yields
Abstract:
Previous empirical studies that test for the "rationality" of economic and financial forecasts generally test for generic properties such as bias or autocorrelated errors, and provide limited insight into the behavior behind inefficient forecasts. In this paper we test for a specific behavioral bias -- the anchoring bias described by Tversky and Kahneman (1974). In particular, we examine whether expert consensus forecasts of monthly economic releases from Money Market Services surveys from 1990-2006 have a tendency to be systematically biased toward the value of previous months' data releases. We find broad-based and significant evidence for the anchoring hypothesis; consensus forecasts are biased towards the values of previous months' data releases, which in some cases results in sizable predictable forecast errors. Then, to investigate whether the market participants anticipate the bias, we examine the response of interest rates to economic news. We find that bond yields react only to the residual, or unpredictable, component of the surprise and not to the expected piece of the forecast error apparently induced by anchoring. This suggests market participants anticipate the anchoring bias embedded in expert forecasts.
I Introduction
Professional forecasts of macroeconomic releases play an important role in markets, informing the decisions of both policymakers and private economic decision-makers. In light of this, and the substantial effects that data surprises have on asset prices, we might expect professional forecasters to avoid making systematic prediction errors. Previous research has approached this topic by testing time series of forecasts for "rationality", an approach with a fairly long and not entirely satisfying history. Generally, such studies focus on testing for a few generic properties such as bias or autocorrelation in errors, tests that have yielded mixed results which provide limited insight into the behavior driving any apparent biases. Such studies provoke - but do not answer - the question: What are the implications of non-rational forecasts for market prices? In particular, where persistent biases in forecasts exist, do the users of these forecasts take the predictions at face value when making investment decisions or dispensing advice? Or do they see through the biases, which would make such anomalies irrelevant for market prices?
As noted by Tversky and Kahneman (1974), psychological studies of forecast behavior find that predictions by individuals are prone to systematic biases that induce large and predictable forecast errors. One widely-documented form of systematic bias that influences predictions by non-professionals is "anchoring," defined as choosing forecasts that are too close to some easily observable prior or arbitrary point of departure. Such behavior results in forecasts that underweight new information and can thus give rise to predictable forecast errors.
We investigate whether anchoring influences expert consensus forecasts collected in surveys by Money Market Services (MMS) between 1991 and 2006. MMS is a widely-used source of forecasts in financial markets, which have also been subjected to tests of forecast efficiency (Aggarwal, et al., 1995; and Schirm, 2003). Our study focuses on monthly macroeconomic data releases that were previously found to have substantial effects on market interest rates (Balduzzi, et. al., 2001, Gurkaynak, et al, 2005; Goldman Sachs, 2006). We test a hunch - born of years spent monitoring data releases and market reactions - that recent past values of the data release act as an anchor on expert forecasts. For instance, in the case of retail sales, we investigate whether the forecast of January sales growth tends to be too close to the previously-released estimate of December sales growth.
We find broad-based and significant evidence that professional consensus forecasts are anchored towards the recent past values of the series being forecasted. The degree and pattern of anchoring we measure is remarkably consistent across the various data releases. Moreover, the influence of the anchor in some cases is quite substantial. We find that the typical forecast is weighted too heavily towards its recent past, on the order of 30 percent. These results thus indicate that anchoring on the recent past is a pervasive feature of expert consensus forecasts of economic data releases known to move market interest rates.
These findings imply that the forecast errors or "surprises" are at least partly predictable. Given that data surprises measured in this way have significant financial market effects, one must wonder whether these effects represent efficient responses to economic news. If market participants simply take consensus forecasts at face value and treat the entire surprise as news, then interest rate reactions to data releases would display greater volatility, relative to a world with rational forecasts.
Our second major contribution thus involves assessing whether anchoring bias in economic forecasts affects market interest rates. Specifically, do interest rates respond to the predictable, as well as the unpredictable, component of the surprise? To answer this question, we decompose the surprise in each data release into a predictable component induced by anchoring, plus the residual - the latter being the true surprise to the econometrician. We then test whether market participants anticipate the bias by regressing the change in the two-year (or ten-year) U.S. Treasury yield in the minutes surrounding the release onto these two components of the forecast error.
We find that the bond market reacts strongly and in the expected direction to the residual, or unpredictable, component of the surprises. On the other hand, interest rates do not appear to respond to the predicted piece of the surprise induced by anchoring. The results are similar for almost every release we consider. We thus conclude that, by and large, the market looks through the anchoring bias embedded in expert forecasts, so this behavioral bias does not induce interest rate predictability or excess volatility.
The remainder of this paper is organized as follows. Section II lays out the conceptual and empirical framework for the analysis. Section III describes basic properties of the data releases and MMS consensus forecasts. Section IV estimates the proposed model of anchoring bias. Section V tests whether the anchoring bias affects the response of market interest rates to data releases. Section VI concludes.
II. Forecast Bias, Anchoring, and Research Design
A. Rationality tests and anchoring
Many psychological and behavioral studies find that, in a variety of situations, predictions by individuals systematically deviate too little from seemingly arbitrary reference points, or anchors, which serve as starting points for these predictions. As a result, those predictions give too little weight to the forecasters' own information. 1 Tversky and Kahneman (1974) define anchoring to be when "people make estimates by starting from an initial value that is adjusted to yield the final answer ... adjustments are typically insufficient ... [and] different starting points yield different estimates, which are biased towards the initial values." In this section, we characterize the relation between traditional tests of forecast rationality and our proposed model of anchoring.
Testing whether macroeconomic forecasts have the properties of rational expectations has a fairly long tradition. A variety of earlier studies (e.g., Mullineaux, 1978; Zarnowitz, 1985) investigate whether consensus macroeconomic forecasts are consistent with conditional expectations. More recently, Aggarwal, Mohanty and Song (1995) and then Schirm (2003) applied this line of investigation to surveys of forecasts compiled by MMS.
While the more recent studies brought some new methodological considerations to the table, they have largely followed the basic formulation of this line of research. In particular, the typical analysis involves running regressions with the actual (realized) values of the data
release,![]() , as the dependent variable on the forecast available prior to the data release,
, as the dependent variable on the forecast available prior to the data release,![]() , or
, or
If forecasts could be improved by systematically magnifying them, the implication would be that forecasters are too slow or cautious when incorporating new information. Indeed, in a different setting, Nordhaus (1987) provides direct evidence of forecast inertia - that forecasters "hold on to their prior view too long." That inference is drawn from an analysis of fixed-event forecasts of GDP growth, which shows that forecast revisions tend to be highly serially correlated. 3 That setting differs from the more conventional time series with rolling-event forecasts, including the MMS forecasts that we analyze.
If forecasters in the standard rolling-event setting put too little weight on new information, this raises the question: What is the prior, or anchor, on which forecasters place too much weight? One plausible scenario is that forecasters treat the value of the previous month's data as the most salient single piece of information that has come to the fore in the time between their previous-month and current-month forecasts. If so, then the previous month's realization might be treated as a starting point, or anchor, for the current forecast. 4 More generally, forecasters might place some weight on a few lags of the release, particularly when the forecasted series tends to bounce around from month to month (i.e., exhibits negative autocorrelation). At the extreme, forecasters might conceivably anchor their forecast on a long-run average value for the series.
To develop this set of ideas more formally, consider the following transformation of equation (1), whereby the forecast is subtracted from both sides. This yields an alternative version of the basic rationality test, where the forecast error or "surprise" (![]() is regressed on the forecast:
is regressed on the forecast:
where
![]() represents the forecaster's unbiased prediction of next month's release and
represents the forecaster's unbiased prediction of next month's release and ![]() represents the average value of the forecasted series over the previous
represents the average value of the forecasted series over the previous![]() months. If
months. If ![]() , then we would conclude that consensus forecasts are anchored to the recent past. Using the implication from equation (2) that
, then we would conclude that consensus forecasts are anchored to the recent past. Using the implication from equation (2) that
![]() and plugging this relation into (3) and rearranging, implies that
and plugging this relation into (3) and rearranging, implies that
Equation (4) implies that the surprise, or forecast error, is partly predictable; in particular, it is positively related to the gap between the forecast and the average release value over the previous![]() months. This is a straightforward modification of the rationality regression (2). Here, a positive coefficient estimate would imply that consensus forecasts are systematically biased toward lagged values of the release (and
months. This is a straightforward modification of the rationality regression (2). Here, a positive coefficient estimate would imply that consensus forecasts are systematically biased toward lagged values of the release (and ![]() in equation (3)). Such a finding could be interpreted as evidence in favor of the Tversky and Kahneman (1974) "adjustment and anchoring" heuristic.
in equation (3)). Such a finding could be interpreted as evidence in favor of the Tversky and Kahneman (1974) "adjustment and anchoring" heuristic.
B. Market relevance of economic data and consensus forecasts
Along a separate line of research, several studies have analyzed the news content of data releases by measuring the surprise component of a release as the discrepancy between its actual value and the consensus forecast from MMS Services. Balduzzi, Elton and Green (2001) as well as Gurkaynak, Sack and Swanson (2005) study the impact of macroeconomic news on interest rates using MMS consensus forecasts to gauge surprises. Aggarwal and Schirm (1992) use the deviation between macroeconomic releases and consensus MMS forecasts to investigate the reaction of exchange rates to innovations in the U.S. trade balance. Andersen, Bollerslev, Diebold and Vega (2003) examine the effects of this and other macroeconomic news on exchange rates. In each study, these surprises are shown to have large and significant effects on financial market prices.
In light of the strength of financial market reactions to surprises measured in this way, it would be of both academic and practitioner interest to understand how systematic biases in economic forecasts might influence financial market reactions to news. Do financial market prices react to the predictable component of the surprise, or forecast error, arising from anchoring bias in the same way that they react to the residual component of the surprise? Or do market participants anticipate the bias, and thus respond only to the residual component of the surprise?
We study this question by estimating second-stage event-study regressions in which the change in the 2-year or 10-year Treasury yield around the time of the release is regressed on the two components of equation (4):
III Data and Sample Characteristics
A. Macroeconomic Releases, Forecasts and Surprises
Our analysis covers eight macroeconomic data releases: Consumer Confidence, Consumer Price Index (CPI), Durable Goods Orders, Industrial Production, ISM Manufacturing Index, New Homes Sales, and Retail Sales. 5 In two cases, we also examine the consensus forecasts of a key subcomponent of the top-line figure in the release - CPI ex-Food and Energy (Core CPI) and Retail Sales ex-Auto. In both cases, these data are released simultaneously with the top line release and are considered by market participants to contain more value-relevant news than the top line.
Table I lists each release, the beginning of our sample period, the timing of the release and the reporting convention, that is, whether the release is reported as a level, a change, or a percent change. While our last observation is March 2006 in each case, the starting date varies between
September 1992 and June 1996, determined by the availability of the forecast data. For each release, we define the consensus forecast, ![]() , as the mean forecast from the Money Market Services
(MMS ) survey. 6 The surprise is measured as the difference between the release and the associated MMS mean forecast.
, as the mean forecast from the Money Market Services
(MMS ) survey. 6 The surprise is measured as the difference between the release and the associated MMS mean forecast.
We focus on these eight key releases because of their previously identified and important influence on interest rate markets. Specifically, Balduzzi, Elton and Green (2001) show that each of these releases has statistically significant and economically important effects on bond yields at both the two-year and ten-year maturity; specifically, surprises explain 20 to 60 percent of the variability in the movements of the two-year and ten-year Treasury yields in the moments surrounding each release.
In Table II we present some summary statistics for each release (![]() , its associated MMS forecast, (
, its associated MMS forecast, (![]() , and forecast surprise (
, and forecast surprise (![]() . For each variable we report the sample mean,
. For each variable we report the sample mean,![]() , standard deviation,
, standard deviation, ![]() , and the sum of the autoregressive coefficients from a fifth order auto-regression,
, and the sum of the autoregressive coefficients from a fifth order auto-regression,
![]() , a measure of persistence. 7 Releases expressed in levels appear at the top of Table II, followed by the remaining releases. The mean surprise, reported
in Table II, is typically close to zero, suggesting that the forecasts are unconditionally unbiased. Also, the standard deviations of the forecasts are in every case smaller than that of the releases. As one would hope, the standard deviation of the surprises is typically smaller than that for the
underlying release, with Core CPI being the only exception. Not surprisingly, for data releases that are expressed in levels, which have a high degree of persistence, surprises are a lot less variable than the underlying release.
, a measure of persistence. 7 Releases expressed in levels appear at the top of Table II, followed by the remaining releases. The mean surprise, reported
in Table II, is typically close to zero, suggesting that the forecasts are unconditionally unbiased. Also, the standard deviations of the forecasts are in every case smaller than that of the releases. As one would hope, the standard deviation of the surprises is typically smaller than that for the
underlying release, with Core CPI being the only exception. Not surprisingly, for data releases that are expressed in levels, which have a high degree of persistence, surprises are a lot less variable than the underlying release.
The persistence properties of the variables listed in Table II are informative about the conditional properties of the MMS forecasts. In the case of the level variables, both the release and the forecast are highly persistent. The remaining releases and forecasts show small to moderate degrees
of persistence, with the exception of Durable Goods Orders and Retail Sales. These releases exhibit a substantial and statistically significant degree of negative serial correlation; for Durable Goods Orders
![]() , while for Retail Sales
, while for Retail Sales
![]() . 8
. 8![]() 9
However, neither of the associated forecasts exhibits a significant amount of negative serial correlation, and thus the negative serial correlation of the data shows up in the surprises. Interestingly, these are not the only releases where the surprise exhibits significant negative serial
correlation. The surprise is negatively serially correlated in every case except for the ISM release. It is also statistically significant in the case of the CPI, New Home Sales, Retail Sales and Retail Sales ex-Auto, suggesting that the MMS forecasts are conditionally biased.
9
However, neither of the associated forecasts exhibits a significant amount of negative serial correlation, and thus the negative serial correlation of the data shows up in the surprises. Interestingly, these are not the only releases where the surprise exhibits significant negative serial
correlation. The surprise is negatively serially correlated in every case except for the ISM release. It is also statistically significant in the case of the CPI, New Home Sales, Retail Sales and Retail Sales ex-Auto, suggesting that the MMS forecasts are conditionally biased.
The finding that the serial correlation in surprises tends to be negative rather than positive suggests that serial correlation in surprises could be due to the anchoring of forecasts on the most recent lagged value of the release. This can be illustrated by a simple example in which the release
is serially uncorrelated. Suppose forecasts were strongly anchored toward the recent past - in particular, that the current forecast is set equal to the lagged actual value,![]() . In
this simplified setting it is easy to see that,
. In
this simplified setting it is easy to see that,
Finally, before moving on to the main results, we note the unusual empirical properties of the Core CPI and its associated forecasts. As shown in Table II, the Core CPI is by far the least variable of all releases; that is, both the release and the associated surprise are significantly less volatile than any other release or surprise. Over our sample period, the MMS forecast of Core CPI is nearly constant, equal to 0.2% (monthly inflation rate) in 117 out of 176 months. Thus, in the case of the Core CPI, this sample period seems poorly suited to conducting our tests. Still, we include the Core CPI release in our analysis because Core CPI surprises have substantial interest rate effects, which might otherwise be spuriously attributed to top line CPI surprises.
B. Interest Rate Reactions to Macroeconomic News Releases
We measure the reaction of the two-year and ten-year U.S. Treasury yield in the moments surrounding each macroeconomic release using quote data from Bloomberg. For each release and maturity we extract the quoted yield from a trade occurring both five minutes prior and ten minutes after the release. The interest rate reaction is defined as the difference between the post- and pre-release quote. If no quote exists five minutes before (ten minutes after) the release, we use the last quote available between five and thirty minutes before the release (the first quote available between ten and thirty minutes after the release). 10
In Table III we display the mean, standard deviation and the sum of autoregressive coefficients of the interest rate reactions. The average interest rate response is always close to zero, which is consistent with the near-zero mean of the associated surprises. The standard deviations of the interest rate reactions provide some information about how much releases affect interest rates. Consistent with the findings of Gurkaynak, et. al., (2005) the standard deviations of the two-year and ten-year yield change are roughly similar. Also, consistent with the findings of Balduzzi, Elton and Green (2001) the Non-farm Payroll Employment release produces the largest interest rate reactions.
Looking at the persistence properties of the interest rate reactions indicates that the degree of serial correlation in the interest rate responses is typically small, ranging from -0.3 to 0.3 in most cases. In the case of Consumer Confidence, ISM, Durable Goods Orders and Industrial Production, however, the serial correlation is statistically significant, which suggests that interest rate reactions might be partly predictable. In what follows we examine whether any of the apparent predictability in these reactions can be traced to predictability of the associated surprises.
As laid out in equation (4) of section II, we test for anchoring bias in MMS consensus forecasts by running regressions with the forecast error as the dependent variable and the difference between the forecast and the anchor as the independent variable,
![]() . 11 In order to estimate equation (4) we need to specify the number of periods (
. 11 In order to estimate equation (4) we need to specify the number of periods (![]() used in constructing the anchor,
used in constructing the anchor, ![]() . We focus on two cases; in the first
. We focus on two cases; in the first![]() is simply the lagged value of the release (
is simply the lagged value of the release (![]() , while in the second it equals the
average release value over the prior three months (
, while in the second it equals the
average release value over the prior three months (![]() . 12 A positive value of
. 12 A positive value of![]() would constitute evidence that forecast errors are biased in a predictable way and that the form of the bias is consistent with anchoring.
would constitute evidence that forecast errors are biased in a predictable way and that the form of the bias is consistent with anchoring.
In Table IV we present the two alternative estimates of equation (4) for each of the macroeconomic releases listed in Table I. The first two columns show the coefficient on the forecast-anchor gap, the![]() , and the
, and the![]() for the case where the anchor is simply the prior month's release,
for the case where the anchor is simply the prior month's release,![]() . The third and fourth columns show the results when the anchor is the average value of the release over the prior three months,
. The third and fourth columns show the results when the anchor is the average value of the release over the prior three months,![]() . For each macroeconomic release, the
results from the model with the highest
. For each macroeconomic release, the
results from the model with the highest ![]() are shown in bold. Finally, the results for the three releases that are reported as levels appear at the top of Table IV. The results for the
remaining releases follow.
are shown in bold. Finally, the results for the three releases that are reported as levels appear at the top of Table IV. The results for the
remaining releases follow.
Broadly speaking, the results indicate a fairly consistent pattern of bias in macroeconomic forecasts. The estimated coefficient on the gap between the consensus forecast and the previous month's release (1-month anchoring), is positive for every release; and, in six of ten cases it is
significant at the 1% level. Together with the results from the 3-month anchoring model, we find that the dominant model (in bold) has a significantly positive coefficient for 8 of 10 releases. Aside from the Core CPI, which earlier was shown to be a poor candidate for this analysis, the
coefficient in the dominant (bold) model is not significant only in the case of the ISM Manufacturing Index. The![]() of the dominant models (again excluding the Core CPI) ranges from 1.3 to 25
percent, with an average value of around 11 percent.
of the dominant models (again excluding the Core CPI) ranges from 1.3 to 25
percent, with an average value of around 11 percent.
The pattern of results is also sensible in light of the time series properties of the releases. The top three data releases, each of which is expressed in levels, were shown in Table III to display a high degree of persistence. In all three of these cases, we find that the model with the one-month lag as the anchor clearly dominates the model based on the three-month anchor. Although anchoring itself may or may not be rational, the forecasters seem sophisticated enough to treat further lags of these three releases as largely redundant.
In the case of Consumer Confidence and New Home Sales, looking at the point estimates of ![]() suggests the anchoring bias is not only statistically significant but that its influence
also can be sizable. In the case of Consumer Confidence, the point estimate of 0.71 suggests that, to minimize the mean squared error, the average forecast would have to be shifted by 71 percent further from the lagged release value (in the direction indicated by the sign of the gap). In
terms of the framework laid out it equations (3) and (4), forecasters are placing roughly 40 percent of the weight on the previous month's release and only 60 percent on the expected value.
suggests the anchoring bias is not only statistically significant but that its influence
also can be sizable. In the case of Consumer Confidence, the point estimate of 0.71 suggests that, to minimize the mean squared error, the average forecast would have to be shifted by 71 percent further from the lagged release value (in the direction indicated by the sign of the gap). In
terms of the framework laid out it equations (3) and (4), forecasters are placing roughly 40 percent of the weight on the previous month's release and only 60 percent on the expected value.
![]() . The
. The![]() statistics of 11.5 percent for Consumer confidence and 4.9 percent for New How Sales are also notable. Given the importance of these releases for bond markets and the relatively large variance of surprises, an
statistics of 11.5 percent for Consumer confidence and 4.9 percent for New How Sales are also notable. Given the importance of these releases for bond markets and the relatively large variance of surprises, an![]() of even 5 percent represents a substantial amount of predictability with potentially noticeable implications for interest rate responses to these releases.
of even 5 percent represents a substantial amount of predictability with potentially noticeable implications for interest rate responses to these releases.
The remaining releases in the table are expressed in terms of changes or percent changes. Among these, the evidence in favor of one-month versus three-month anchoring is mixed. In three of the six cases (again leaving aside the Core CPI), the one-month anchoring model yields the best fit. Even so, we find robust evidence of anchoring behavior for Durable Goods Orders, Industrial Production, Retail Sales and Retail Sales ex-Auto. In each of these cases the null hypothesis of no anchoring is rejected at all conventional significance levels regardless of whether a one or three month anchor is employed. For the CPI and Non-farm Payroll Employment, anchoring is significant in the case of the three month anchor but not the one month anchor.
The magnitude of anchoring in the MMS forecasts of the change variables is generally somewhat less than that of the level variables, though it appears to be economically meaningful in most cases. The magnitude for Retail Sales falls close to middle of the pack; the coefficient of 0.25 in the
one-lag model for Retail Sales implies forecasters place roughly 20 percent (
![]() ) of the weight on that anchor. In addition, the forecast errors for Retail Sales appear to be unusually predictable: the
) of the weight on that anchor. In addition, the forecast errors for Retail Sales appear to be unusually predictable: the![]() suggests that the forecast-anchor gap explains 25 percent of the variance in surprises. Among the other change variables, the
suggests that the forecast-anchor gap explains 25 percent of the variance in surprises. Among the other change variables, the ![]() covers a range comparable to that of the level variables.
covers a range comparable to that of the level variables.
The results in Table IV indicate that the gap between the current forecast and the anchor predicts future surprises in almost every release we consider. In those tests, the alternative hypothesis is that forecast errors are unpredictable, that is, orthogonal to all known information. A more demanding test of our model would involve testing it against a more general model, for instance, a model where the forecast error might be related to the current forecast for some unspecified reason. To implement this, we test whether the coefficient on the hypothesized anchor is opposite in sign and equal in magnitude to the coefficient on the current forecast.
In Table V we show estimates of the following unrestricted anchoring model,
A quick perusal of the point estimates reveals a pattern of coefficients on forecasts and anchors that is remarkably consistent with our model of anchoring bias. In particular, in every case aside from the Core CPI, the estimate for![]() is positive while that for
is positive while that for ![]() is negative. In most cases, both the current forecast and the anchor are statistically important
for predicting future surprises. What is more, the difference in the coefficients' magnitudes is often remarkably small. For instance, for Consumer Confidence,
is negative. In most cases, both the current forecast and the anchor are statistically important
for predicting future surprises. What is more, the difference in the coefficients' magnitudes is often remarkably small. For instance, for Consumer Confidence,
![]() and
and
![]() .
.
The Wald tests reported in the fourth column of Table V show that only in the aberrant case of Core CPI is the null hypothesis that
![]() rejected at all conventional significance levels. Elsewhere, the Wald statistic provides scant evidence against the null hypothesis. The possible exceptions are
Industrial Production and Non-farm Payroll Employment, where the null hypothesis can be rejected at the 10%, but not the 5%, level. Even there, the discrepancies between
rejected at all conventional significance levels. Elsewhere, the Wald statistic provides scant evidence against the null hypothesis. The possible exceptions are
Industrial Production and Non-farm Payroll Employment, where the null hypothesis can be rejected at the 10%, but not the 5%, level. Even there, the discrepancies between ![]() and
and
![]() are relatively small. Finally, comparing the fit of the unrestricted and restricted (Table IV, bold) models reveals only a small deterioration in fit when we impose the
are relatively small. Finally, comparing the fit of the unrestricted and restricted (Table IV, bold) models reveals only a small deterioration in fit when we impose the
![]() restriction (in the original specification); the decline in
restriction (in the original specification); the decline in![]() is typically on the order of a percentage point.
is typically on the order of a percentage point.
Our model of anchoring bias assumes that forecasters always tilt their forecast toward the value of the previous month's (or few months') release by a similar proportion. On the other hand, it is plausible that the extent to which forecasters treat a lagged release as reasonable starting point for current-month forecasts could depend on whether that lagged release is viewed as representative or normal. For instance, when lagged realizations are far out of line with recent trends or broader historical experience, they may have less influence on current forecasts. Of course, the opposite might be true; that is, it might be that most of the anchoring occurs on the heels of outliers or trend-breaking observations, while very little anchoring occurs in normal times.
In principle such considerations would suggest that a more complex specification than our simple anchoring model might be informative, but there is no clear a priori case for any particular alternative. Thus, rather than postulate a more complicated anchoring model, we simply re-estimate
equation (4) on a sub-sample of observations that excludes outliers. Specifically, we exclude observations in which the change in the release from month ![]() to
to ![]() is larger than 1.5 standard deviations of the historical monthly change in the release. The results are contained in Table VI.
is larger than 1.5 standard deviations of the historical monthly change in the release. The results are contained in Table VI.
As with the model restriction tests in Table V, we report results only for the best-fitting model (1-month or 3-month anchoring) based on the Table IV regressions. The second and third columns report the estimates of![]() and the
and the![]() statistics from the full sample, while the final two columns report the same for the sample that excludes the outliers. Broadly speaking, the
outlier exclusion does not substantially alter the picture. The estimates of
statistics from the full sample, while the final two columns report the same for the sample that excludes the outliers. Broadly speaking, the
outlier exclusion does not substantially alter the picture. The estimates of ![]() are all still positive; in most cases, the estimated degree of anchoring appears to increase somewhat. The
most notable change is in the case of the ISM Manufacturing Index release, where the coefficient doubles to 0.44 and becomes statistically significant, while the
are all still positive; in most cases, the estimated degree of anchoring appears to increase somewhat. The
most notable change is in the case of the ISM Manufacturing Index release, where the coefficient doubles to 0.44 and becomes statistically significant, while the ![]() rises to 5%. The Nonfarm
Payrolls release is the only case showing a notable decline in the coefficient estimate when outliers are excluded, from 0.25 to 0.17, reducing its significance.
rises to 5%. The Nonfarm
Payrolls release is the only case showing a notable decline in the coefficient estimate when outliers are excluded, from 0.25 to 0.17, reducing its significance.
The broad picture that emerges from Tables IV, V and VI is one in which anchoring plays a statistically and economically meaningful role in determining MMS forecasts of key macroeconomic releases. In some cases the estimates imply that the anchor receives as much as a 40 percent weighting (Consumer Confidence) in the current forecast and the anchoring variable can account for up to 25 percent (Retail Sales) of the variance in future surprises. The pattern in the results is remarkably uniform. Accordingly, anchoring appears to be an important and robust feature of the MMS forecast data. These findings thus raise the question that we examine in the second part of our analysis: How does anchoring bias in these forecasts affect market reactions to the measured surprises?
V. Testing Market Reactions
A. The Framework
This section examines the implications of anchoring bias in macroeconomic forecasts for bond market reactions to the data releases. A large literature uses MMS forecasts to measure surprises in macroeconomic releases, which are then used to gauge the effect of macroeconomic news on asset prices
(Aggarwal and Schirm, 1992; Balduzzi, et al., 2001; Andersen, et al., 2003, Gurkaynak, et al, 2005 ). These studies examine the reaction of equity prices, exchange rates, and interest rates to differences between macroeconomic releases and the associated forecasts in the minutes surrounding the
releases. The typical specification in these studies takes on the following form:
The results above imply that these surprises- or forecast errors, to be precise - are partly predictable due to anchoring bias in the MMS forecasts. If markets are informationally efficient and market participants understand the nature of this bias, then market prices should anticipate this
component of the forecast error. In particular, market interest rates should not respond to the predictable component of the forecast error. We investigate this hypothesis using the model laid out in equation (5) of Section II,
![]() . Again,
. Again,![]() represents the change in either the two-year or ten-year U.S. Treasury bond yield in the moments surrounding the release and
represents the change in either the two-year or ten-year U.S. Treasury bond yield in the moments surrounding the release and
![]() represents the predicted component of the surprise induced by anchoring. We thus refer to the second regressor as the residual component of the
surprise - the true surprise from the econometrician's point of view.
represents the predicted component of the surprise induced by anchoring. We thus refer to the second regressor as the residual component of the
surprise - the true surprise from the econometrician's point of view.
We focus on two hypotheses concerning how market participants react to the predicted and residual components of the surprise. If market participants take the forecasts at face value and are unaware of the predictability in surprises then we would expect to find no difference in the response to
the predicted and residual components of the surprise, or
![]() . Finding
. Finding
![]() would indicate that the bond markets are not informationally efficient in the sense that data known at the time of the forecast can help predict movements in bond prices.
Alternatively, if market forecasts are informationally efficient - market participants are aware of the predictability induced by anchoring in the MMS forecasts - then we would expect to find no response of interest rates to variation in the predictable component of the surprise, or
would indicate that the bond markets are not informationally efficient in the sense that data known at the time of the forecast can help predict movements in bond prices.
Alternatively, if market forecasts are informationally efficient - market participants are aware of the predictability induced by anchoring in the MMS forecasts - then we would expect to find no response of interest rates to variation in the predictable component of the surprise, or![]() .
.
Our investigation of the response of interest rates to the predicted and residual components of surprises in macroeconomic releases is related to the previous work of Mishkin (1981). Mishkin examines whether the surprise implied by the reaction of interest rates to inflation news is consistent
with the unpredictable component of inflation identified from an autoregressive specification. Specifically, Mishkin estimates the following system,
B. Empirical Results
Before reviewing the empirical results, we first introduce two variations on the basic specification of equation (5) that apply to some of the releases. First, we control for revisions to previously released data that are announced along with the current month's data. This is done by including
the value of the revision as an additional regressor. Revisions are announced with the release of Industrial Production, Non-farm Payrolls and Retail Sales (both the top-line and ex-Auto release). For Non-farm Payrolls and Retail Sales, revisions to two previous months of data are released and
included as regressors; but to conserve space, we only report the parameter estimate for the most recent month's revision. In the Non-farm Payrolls regression, we also include a control for the surprise to the unemployment rate (based on the MMS survey), which is released simultaneously but
generally with less market impact than the payroll numbers. Thus, our general event-study regression can be written as:
Here,
The model is estimated via GMM. In particular, note that the terms
![]() that appear in equation (10) and (11) are not directly observed and must be estimated from the first stage anchoring model in equation (4). These generated regressors influence
the sampling distribution of the interest rate response coefficients
that appear in equation (10) and (11) are not directly observed and must be estimated from the first stage anchoring model in equation (4). These generated regressors influence
the sampling distribution of the interest rate response coefficients
![]() . In particular, the sampling variability induced by using generated regressors tends to increase the amount of sampling variability in the
second stage coefficients. We follow the approach of Newey (1984) by including the first stage anchoring model, equation (4), along with the second stage event-study regressions, equations (10) and (11), in the GMM system. 14 The resulting variance-covariance matrix fully
accounts for the use of generated regressors in equations (10) and (11).
. In particular, the sampling variability induced by using generated regressors tends to increase the amount of sampling variability in the
second stage coefficients. We follow the approach of Newey (1984) by including the first stage anchoring model, equation (4), along with the second stage event-study regressions, equations (10) and (11), in the GMM system. 14 The resulting variance-covariance matrix fully
accounts for the use of generated regressors in equations (10) and (11).
The results from GMM estimation of equations (10) and (11) are contained in Table VII. The parameter estimates have been scaled so that they reflect the effect on yields, in basis points, of a change in the independent variable equal to one standard deviation of the (total) surprise,
![]() . The first three columns report the parameter estimates. The fourth column reports the model
. The first three columns report the parameter estimates. The fourth column reports the model![]() . The fifth column reports the Wald test of the null hypothesis that bond yields react symmetrically to the predictable and unpredictable component of the MMS surprise,
. The fifth column reports the Wald test of the null hypothesis that bond yields react symmetrically to the predictable and unpredictable component of the MMS surprise,
![]() . 15
. 15
Looking down the columns of Table VII reveals three broad findings. First, consistent with previous research, we find that the releases account for a significant fraction of bond yield movements, ranging from roughly 20 to 50 percent. Second, the effect of the unexpected component of the
surprise on bond yields,![]() , is significant at the 1% level for every release except the CPI. Third,
, is significant at the 1% level for every release except the CPI. Third,![]() , the effect of the expected component of the surprise on bond yields, is small for almost every release, typically an order of magnitude smaller than that of
, the effect of the expected component of the surprise on bond yields, is small for almost every release, typically an order of magnitude smaller than that of![]() ; and it is insignificant in every case. The Wald test of the null hypothesis that bond yields react symmetrically to the unexpected and expected components of the surprise is rejected at the 10% level or lower in 5 out of 8 cases. 16 This is notable
since the Wald test fully accounts for the extra variability in the measurement of
; and it is insignificant in every case. The Wald test of the null hypothesis that bond yields react symmetrically to the unexpected and expected components of the surprise is rejected at the 10% level or lower in 5 out of 8 cases. 16 This is notable
since the Wald test fully accounts for the extra variability in the measurement of ![]() resulting from
resulting from![]() being a generated regressor. Finally, the results are quite similar across the short and long end of the yield curve.
being a generated regressor. Finally, the results are quite similar across the short and long end of the yield curve.
Focusing on the results for individual releases indicates that the exceptions to the broad pattern of results can largely be rationalized as special situations. First, for the (top line) CPI, both the expected and unexpected components of the surprise are not significant; and so we obviously
would be unable to reject the hypothesis that the components have the same effect. But this owes to the finding that, conditional on Core CPI, shocks to the total CPI (including Food and Energy) have little incremental effect on bond yields. 17 The market perceives the Core CPI as a better indicator of future inflation and Federal Reserve policy. The other obvious exception is in the Core CPI results. Here, we find that the estimated magnitude of
![]() is large and not significantly different from
is large and not significantly different from![]() . But this result
presumably owes to the poor performance of the anchoring model for the Core CPI, which explains less than 1 percent of the variation in the surprise. As argued already, this could be attributable to the granularity of Core CPI and its resultant lack of time-series variation in our sample
period.
. But this result
presumably owes to the poor performance of the anchoring model for the Core CPI, which explains less than 1 percent of the variation in the surprise. As argued already, this could be attributable to the granularity of Core CPI and its resultant lack of time-series variation in our sample
period.
A few other aspects to our findings in Table VII are notable, even if not central to our main hypotheses. First, we are comforted by the finding - consistent with previous research findings and views on Wall Street - that the employment release shows the largest interest rate effects and has the
most explanatory power of all the releases (in the event study window). It is also interesting to note that in every case where it is available, the revision to the previous month's data (![]() also has a significant positive effect on interest rates. Surprisingly, in most of these cases, the coefficient on the revision is almost as large as the coefficient on the current month (residual) surprise.
also has a significant positive effect on interest rates. Surprisingly, in most of these cases, the coefficient on the revision is almost as large as the coefficient on the current month (residual) surprise.
Summing up, the results in Table VII suggest that market participants do react to the unpredictable component but not to the predictable component of the MMS surprises. Accordingly, these results suggest that the informational inefficiency of MMS forecasts identified in Tables 4, 5 and 6 does not lead to any important source of inefficiency in interest rate markets. Market participants apparently anticipate the anchoring behavior of professional forecasters.
VI. Conclusions
We find that professional economic forecasts are biased in a manner consistent with a specific behavioral model of forecasting behavior: the anchoring and adjustment hypothesis of Kahneman and Tversky (1974). Specifically, we find that forecasts of any given release are anchored toward recent months' realized values of that release, thereby giving rise to predictable surprises. In some cases, such as Retail Sales, we find that up to 25% of the surprise in the macroeconomic release is predictable, due to a substantial weight being placed on the anchor by professional forecasters. Moreover, the evidence in favor of anchoring is remarkably consistent across each of the key releases that we study and is robust to the exclusion of outliers.
In light of the significant evidence of systematic bias in professional forecasts, we examine the implications for market prices of U.S. Treasury bonds. Specifically, we examine whether yields on 2-year and 10-year Treasury yields react to the predictable component of forecast surprises induced by anchoring behavior. Across the board, we find that interest rates only respond to the unpredictable component of the surprise. Estimates of the market reaction to the predictable component of data surprise in every case are small and insignificant, whereas the estimated reaction to the unpredictable component is large and significant.
We thereby conclude that, market participants do not take professional forecasts at face value when responding to macroeconomic news. To the contrary, at least some influential market participants are apparently able to parse the stale component of these forecasts, due to anchoring, from the component of the forecasts containing useful information about the expected future path of these macroeconomic variables. As a result, the behavioral bias displayed by the forecasts does not translate into a similar behavioral bias in market reactions to macroeconomic news.
These findings suggest a variety of directions for future research. We have identified a source of forecast bias consistent with a single behavioral hypothesis. Given the evidence presented here, it is of interest to know whether professional forecasts are subject to other behavioral biases that have been documented in experimental settings. It is also of interest to know whether other markets such as foreign exchange and equity markets are as adept as the U.S. Treasury market at processing the information in professional forecasts. In particular, it is worth considering whether the behavioral bias in professional forecasts is a source of inefficiency in markets that are commonly perceived to be less efficient than the U.S. Treasury market, such as markets for individual stocks.
Finally, because our analysis examines the behavior of consensus, or average, forecasts, the findings really only provide a characterization of the bias of a "representative forecaster". But there are likely to be significant cross-sectional differences in ability, in which case our results only capture average behavior, which we are presuming to be the average degree of anchoring. What is more, as argued for instance by Ehrbeck and Waldmann (1996) and Ottaviani and Sorensen (2006), forecasts are likely to be influenced by strategic considerations, which would add further complexity to any micro-level empirical analysis and its interpretation.
Appendix
Following Newey (1984), we account for the generated regressors in equations (10) and (11) by including the specification of the anchoring model, equation (4), in the GMM system. Specifically, we estimate the following exactly identified GMM system for each data release (row) contained in Table VII.
![g_T \left( \theta \right)=\frac{1}{T}h_t \left( \theta \right)=\frac{1}{T}\sum... ...t -S_t^e } \right)-\phi R_t } \right)R_t } \hfill \ \end{array} }} \right]}](img69.gif) (A.1)
(A.1)
in the case of Consumer Confidence, ISM index, New Homes Sales, Durable Goods, Industrial Production and Non-farm Payroll employment. In the case of Retail Sales and CPI we estimate the system,
![g_T \left( \theta \right)=\frac{1}{T}\sum\limits_{t=1}^T {h_t \left( \theta \r... ...SX_t^e } \right)-\phi R_t } \right)R_t } \hfill \ \end{array} }} \right]} }](img70.gif) (A.2)
(A.2)
in the case of Retail Sales and the CPI. In each case the GMM system is estimated by minimizing,
![]() , over
, over ![]() and note the
omission of a weighting matrix due to the just identified nature of the system. Finally, the variance-covariance matrix is estimated by:
and note the
omission of a weighting matrix due to the just identified nature of the system. Finally, the variance-covariance matrix is estimated by:
![]() (A.3)
(A.3)
where,
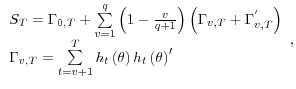 (A.4)
(A.4)
and,
![]() (A.5)
(A.5)
Finally, we note that a separate system is estimated for each release and each bond maturity (2 and 10 year).
Aggarwal R., Mohanty S., and F. Song, 1995, Are Survey Forecasts of Macroeconomic
Variables Rational?, Journal of Business, 68,1,99-119.
Aggarwal R., and D. Schirm, 1992, Balance of Trade Announcements and Asset Prices:
Influence on Equity Prices, Exchange Rates and Interest Rates, Journal of
International Money and Finance, 11, 80-95.
Andersen T., Bollerslev T., Diebold F., and Clara Vega, 2003, Micro Effects of
Macro Announcements: Real Time Price Discovery in Foreign Exchange,
American Economic Review, 93, 38-62.
Balduzzi P., Elton E., and T.C. Green, 2001, Economic News and Bond Prices: Evidence
from the U.S. Treasury Market, Journal of Financial and Quantitative Analysis,
36, 4, 523-543.
Frankel J. and K. Froot, 1987, Using Survey Data to Test Standard Propositions
Regarding Exchange Rate Expectations, American Economic Review, 77, 1, 133-153.
Gurkaynak R., Sack B. and E. Swanson, 2005, The Sensitivity of Long-Term Interest
Rates to Economic News: Evidence and Implications for Macroeconomic Models,
American Economic Review, 95, 1, 425-436.
Mishkin F., 1981, Are Market Forecasts Rational?, American Economic Review, 71, 3,
295-306.
Mullineaux, D., 1978, On Testing for Rationality: Another Look at the Livingston Price
Expectations, Journal of Political Economy, 86, 2, 329-336.
Northcraft G., and M. Neale, 1987, Experts, Amateurs, and Real Estate: An Anchoring
and Adjustment Perspective on Property Pricing Decisions, Organizational
Behavior and Human Decision Processes, 39, 84-97.
Newey W., 1984, A Method of Moments Interpretation of Sequential Estimators,
Economics Letters, 14, 201-206.
Nordhaus W., Forecasting Efficiency: Concepts and Applications, Review of Economics
and Statistics, 69, 4, 667-674.
Ottavani M., and P. Sorensen, 2006, The Strategy of Professional Forecasting, Journal of
Financial Economics, 81, 441-466.
Schirm D ., 2003, A Comparative Analysis of the Rationality of Consensus Forecasts of
U.S. Economic Indicators, Journal of Business, 76, 4, 547-561.
Tillman E., and R. Waldmann, 1996, Why Are Professional Forecasters Biased? Agency
Versus Behavioral Explanations, Quarterly Journal of Economics, 111, 1, 21-40.
Tversky A. and D. Kahneman, 1974, Judgment Under Uncertainty: Heuristics and
Biases, Science, 185, 1124-1131.
Zarnowitz V., 1985, Rational Expectations and Macroeconomic Forecasts, Journal of
Business and Economic Statistics, 3, 4, 293-311.
| Release | Beginning of Sample | Release Day (Next Month) | Release Time (AM) | Reporting Convention |
|---|---|---|---|---|
| Consumer Confidence | 09/1992 | Final Tuesday* | 10:00 | Level |
| Consumer Price Index (CPI) | 01/1993 | 3rd Wednesday | 08:30 | % Change |
| Core CPI | 01/1993 | 3rd Wednesday | 08:30 | % Change |
| Durable Goods Orders | 12/1992 | 4th Thursday | 08:30 | % Change |
| Industrial Production | 12/1992 | 3rd Week | 09:15 | % Change |
| ISM Index | 10/1992 | 1st Business Day | 08:30 | Level |
| Non-Farm Payroll Employment | 10/1992 | 1st Friday | 08:30 | Change |
| New Home Sales (in thousands) | 06/1996 | 4th Wednesday | 10:00 | Level |
| Retail Sales | 01/1993 | 2nd Week | 08:30 | % Change |
| Retail Sales ex-Auto | 01/1993 | 2nd Week | 08:30 | % Change |
* Released in current month
Notes: We report each data release, the month and year in which our sample period begins, the period in the following month when it is released, the time of the release and whether the release is reported as a level, change or percent change.
| Release |
Release |
Release
|
Forecast |
Forecast |
Forecast
|
Surprise |
Surprise |
Surprise
|
|
|---|---|---|---|---|---|---|---|---|---|
| Consumer Confidence | 104.73 | 22.40 | 0.96*** | 104.24 | 21.87 | 0.96*** | 0.50 | 4.97 | -0.14 |
| ISM Index | 52.92 | 5.07 | 0.88*** | 53.02 | 4.64 | 0.89*** | -0.10 | 2.06 | 0.18 |
| New Home Sales | 986.70 | 167.33 | 0.94*** | 970.47 | 160.68 | 0.98*** | 16.23 | 68.35 | -0.94*** |
| Consumer Price Index (CPI) | 0.20 | 0.22 | -0.05 | 0.23 | 0.13 | 0.34* | -0.02 | 0.13 | -0.60** |
| Core CPI | 0.20 | 0.10 | 0.28 | 0.21 | 0.05 | 0.81*** | 0.00 | 0.10 | -0.25 |
| Durable Goods Orders | 0.42 | 3.36 | -2.08*** | 0.28 | 1.25 | 0.01 | 0.14 | 2.73 | -1.34*** |
| Industrial Production | 0.22 | 0.48 | 0.42** | 0.20 | 0.34 | 0.59*** | 0.02 | 0.27 | -0.10 |
| Non-Farm Payroll
Employment |
130.64 | 164.84 | 0.70*** | 145.43 | 106.76 | 0.87*** | -14.78 | 111.00 | -0.13 |
| Retail Sales | 0.33 | 0.95 | -1.41*** | 0.35 | 0.54 | -0.13 | -0.02 | 0.60 | -0.58*** |
| Retail Sales ex-Auto | 0.35 | 0.49 | -0.25 | 0.37 | 0.20 | 0.36 | -0.01 | 0.40 | -0.45* |
Notes: We report the sample mean (![]() , standard deviation (
, standard deviation (![]() and the sum
of the autoregressive coefficients from an AR(5) (
and the sum
of the autoregressive coefficients from an AR(5) (
![]() for the underlying release (
for the underlying release (![]() , its forecast (
, its forecast (![]() and the surprise (
and the surprise (![]() . In the case of the sum of the autoregressive coefficients (
. In the case of the sum of the autoregressive coefficients (
![]() , * denotes significance at the 10% level, ** denotes significance at the 5% level and *** denotes significance at the 1% level.
, * denotes significance at the 10% level, ** denotes significance at the 5% level and *** denotes significance at the 1% level.
| 2 Year Response ( |
2 Year Response ( |
2 Year Response (
|
10 Year Response (
|
10 Year Response (
|
10 Year Response (
|
|
|---|---|---|---|---|---|---|
| Consumer Confidence | 0.00 | 0.02 | 0.27** | 0.00 | 0.03 | 0.37*** |
| ISM Index | 0.00 | 0.03 | 0.37*** | 0.00 | 0.03 | 0.28** |
| New Home Sales | 0.00 | 0.02 | 0.38 | 0.00 | 0.02 | -0.27 |
| Consumer Price Index (CPI) | 0.00 | 0.03 | -0.05 | 0.00 | 0.03 | -0.05 |
| Core CPI | 0.00 | 0.03 | -0.05 | 0.00 | 0.03 | -0.05 |
| Durable Goods Orders | 0.00 | 0.03 | -0.69*** | 0.00 | 0.02 | -0.33** |
| Industrial Production | 0.00 | 0.02 | 0.27** | 0.00 | 0.02 | 0.29** |
| Retail Sales | -0.01 | 0.04 | 0.17 | -0.01 | 0.03 | 0.12 |
| Retail Sales ex-Auto | -0.01 | 0.04 | 0.17 | -0.01 | 0.03 | 0.12 |
| Non-Farm Payroll
Employment |
0.00 | 0.09 | -0.18 | 0.00 | 0.07 | -0.28 |
| 1 Month Anchoring |
1 Month Anchoring |
3 Month Anchoring |
3 Month Anchoring |
|
|---|---|---|---|---|
| Consumer Confidence | 0.71
(6.10) |
11.52 | 0.11
(1.60) |
1.38 |
| ISM Index | 0.22
(1.26) |
1.34 | 0.09
(0.88) |
0.75 |
| New Home Sales | 0.53
(2.75) |
4.85 | -0.11
(0.57) |
0.36 |
| Durable Goods Orders | 0.16
(4.51) |
6.61 | 0.49
(5.74) |
13.28 |
| Industrial Production | 0.14
(3.24) |
7.30 | 0.19
(2.92) |
6.81 |
| Non-farm Payroll
Employment |
0.06
(0.75) |
0.48 | 0.25
(1.91) |
3.36 |
| Retail Sales | 0.25
(4.74) |
25.09 | 0.34
(2.82) |
17.79 |
| Retail Sales ex-Auto | 0.29
(4.04) |
15.36 | 0.37
(3.12) |
7.50 |
| Consumer Price Index (CPI) | 0.06
(1.52) |
1.49 | 0.26
(4.89) |
15.36 |
| Core CPI | 0.04
(0.67) |
0.18 | -0.06
(0.41) |
0.10 |
| Wald | |||||
|---|---|---|---|---|---|
| Consumer Confidence | 1 | 0.76
(5.92) |
-0.74
(6.03) |
0.27 | 12.00 |
| ISM Index | 1 | 0.25
(1.29) |
-0.24
(1.31) |
0.72 | 1.43 |
| New Home Sales | 1 | 0.46
(2.14) |
-0.50
(2.50) |
0.38 | 5.40 |
| Durable Goods Orders | 3 | 0.55
(3.35) |
-0.42
(2.00) |
0.68 | 13.38 |
| Industrial Production | 1 | 0.23
(3.11) |
-0.11
(2.47) |
0.06 | 9.42 |
| Non-farm Payroll
Employment |
3 | 0.36
(2.18) |
-0.23
(1.77) |
0.08 | 4.92 |
| Retail Sales | 1 | 0.31
(2.59) |
-0.23
(5.80) |
0.43 | 25.43 |
| Retail Sales ex-Auto | 1 | 0.36
(2.11) |
-0.27
(3.48) |
0.61 | 15.53 |
| Consumer Price Index (CPI) | 3 | 0.35
(6.81) |
-0.15
(1.58) |
0.07 | 17.22 |
| Core CPI | 1 | -0.34
(2.54) |
-0.09
(1.47) |
0.00 | 5.05 |
| Lags |
All Observations |
All Observations |
Outliers Excluded |
Outliers Excluded |
|
|---|---|---|---|---|---|
| Consumer Confidence | 1 | 0.71
(6.10) |
11.52 | 0.79
(5.48) |
13.16 |
| ISM Index | 1 | 0.22
(1.26) |
1.34 | 0.44
(2.17) |
4.89 |
| New Home Sales | 1 | 0.53
(2.75) |
4.85 | 0.54
(2.01) |
3.41 |
| Consumer Price Index (CPI) | 3 | 0.26
(4.89) |
15.36 | 0.21
(1.41) |
10.54 |
| Core CPI | 1 | 0.04
(0.67) |
0.18 | 0.03
(2.24) |
0.03 |
| Durable Goods Orders | 3 | 0.49
(5.74) |
13.28 | 0.61
(3.67) |
17.98 |
| Industrial Production | 1 | 0.14
(3.24) |
7.30 | 0.17
(2.19) |
4.89 |
| Non-farm Payroll
Employment |
3 | 0.25
(1.91) |
3.36 | 0.17
(1.83) |
1.68 |
| Retail Sales | 1 | 0.25
(4.74) |
25.09 | 0.23
(3.78) |
15.59 |
| Retail Sales ex-Auto | 1 | 0.29
(4.04) |
15.36 | 0.41
(3.33) |
15.86 |
| Consumer Price Index (CPI) | 3 | 0.26
(4.89) |
15.36 | 0.21
(1.41) |
10.54 |
| Core CPI | 1 | 0.04
(0.67) |
0.18 | 0.03
(2.24) |
0.03 |
Notes: We report estimates from the model,
![]() , using the full sample and a sub-sample that excludes observations in which the change in the previous month's release over the prior
month is large (see text for details). The first column reports the number of months (
, using the full sample and a sub-sample that excludes observations in which the change in the previous month's release over the prior
month is large (see text for details). The first column reports the number of months (![]() used in constructing the anchor (
used in constructing the anchor (![]() . The second and third column report the parameter estimate,
. The second and third column report the parameter estimate,![]() , and
, and ![]() from the full sample. The fourth and fifth column report the parameter estimate,
from the full sample. The fourth and fifth column report the parameter estimate,![]() , and
, and ![]() from the sub-sample. Newey-West (1987) t-statistics appear in parentheses.
from the sub-sample. Newey-West (1987) t-statistics appear in parentheses.
|
|
|||||
|---|---|---|---|---|---|
| Consumer Confidence 2 Year | 0.19 | 1.69*** | - | 46.9 | 0.00 |
| Consumer Confidence 10 Year | 0.07 | 1.60*** | - | 44.0 | 0.00 |
| ISM Index 2 Year | -2.33 | 2.31*** | - | 52.4 | 0.23 |
| ISM Index 10 Year | -3.45 | 2.09*** | - | 51.9 | 0.21 |
| New Home Sales 2 Year | 0.09 | 0.85*** | - | 17.3 | 0.21 |
| New Home Sales 10 Year | 0.10 | 0.82*** | - | 17.6 | 0.23 |
| Durable Goods Orders 2 Year | -0.25 | 1.39*** | - | 22.6 | 0.00 |
| Durable Goods Orders 10 Year | -0.45 | 1.16*** | - | 19.4 | 0.00 |
| Industrial Production 2 Year | -0.12 | 0.76*** | 0.55*** | 20.7 | 0.07 |
| Industrial Production 10 Year | 0.00 | 0.74*** | 0.49*** | 19.2 | 0.09 |
| Non-farm Payroll Employment 2 Year | 1.06 | 6.27*** | 1.65*** | 57.3 | 0.08 |
| Non-farm Payroll Employment 10 Year | 0.97 | 4.96*** | 1.08*** | 50.8 | 0.07 |
| Retail Sales: Auto 2 Year | 0.03 | 1.44*** | 1.62*** | 30.4 | 0.17 |
| Retail Sales: Auto 10 Year | 0.09 | 1.31*** | 1.02** | 29.2 | 0.12 |
| Retail Sales: ex-Auto 2 Year | -0.20 | 3.28*** | 1.23** | 30.4 | 0.02 |
| Retail Sales: ex-Auto 10 Year | -0.32 | 2.80*** | 1.08*** | 29.2 | 0.01 |
| CPI: Food and Energy 2 Year | -0.32 | -0.38 | - | 28.8 | 0.96 |
| CPI: Food and Energy 10 Year | -0.74 | -0.36 | - | 28.6 | 0.71 |
| Core CPI 2 Year | 7.43 | 2.29*** | - | 28.8 | 0.68 |
| Core CPI 10 Year | 6.50 | 2.14*** | - | 28.6 | 0.69 |
We report GMM estimates of the model,
![]() . *** denotes statistical significance at the 1% level and ** denotes significance at the 5% level. We also
report the model's
. *** denotes statistical significance at the 1% level and ** denotes significance at the 5% level. We also
report the model's![]() and the p-value of the Wald test that
and the p-value of the Wald test that
![]() in the final two columns.
in the final two columns.
Footnotes
 in the columns labeled
in the columns labeled