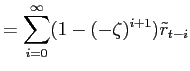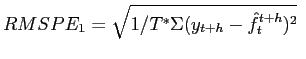Forecasting Professional Forecasters1
This version: March 23, 2006
Keywords: Survey forecasts, Mixed frequency data sampling, Forecast evaluation, Rational expectations, Kalman filter, Kalman smoother, News Announcements.
Surveys of forecasters, containing respondents' predictions of future values of growth, inflation and other key macroeconomic variables, receive a lot of attention in the financial press, from investors, and from policy makers. They are apparently widely perceived to provide useful information about agents' expectations. Nonetheless, these survey forecasts suffer from the crucial disadvantage that they are often quite stale, as they are released only infrequently, such as on a quarterly basis. In this paper, we propose methods for using asset price data to construct daily forecasts of upcoming survey releases, which we can then evaluate. Our methods allow us to estimate what professional forecasters would predict if they were asked to make a forecast each day, making it possible to measure the effects of events and news announcements on expectations. We apply these methods to forecasts for several macroeconomic variables from both the Survey of Professional Forecasters and Consensus Forecasts.
JEL Classifications: C22, C53.
1 Introduction
Surveys of professional forecasters are released, typically on a quarterly or monthly basis, containing respondents' predictions of key macroeconomic variables. These releases get wide coverage in the financial press and many of the forecasters being surveyed have a large clientele base paying considerable sums of money for their services. The sources and methods that these forecasters use are somewhat opaque, but a large quantity of their information is economic news that is in the public domain. Through the market process of price discovery, this economic news is also impounded in financial asset prices. In this paper, we propose methods for using financial market data that are readily available at a daily frequency to construct forecasts of upcoming survey releases, which we can then evaluate. Our methods allow us to estimate what professional forecasters would predict if they were asked to make a forecast each day. The challenge of formulating models to accomplish these tasks is that financial data are abundant, and arrive at much higher frequency than the releases of macroeconomic forecasts. It quickly becomes obvious that, unless a parsimonious model can be formulated, there is no practical solution for linking the quarterly forecasts to daily financial data.
There are various reasons why we are interested in measuring professional forecasters' expectations at a daily frequency:
(i) First, agents' expectations are of critical importance to policy makers, and policy makers apparently perceive surveys of forecasters to be providing useful information about those expectations. Monetary policy communications such as the minutes of the Federal Open Market Committee, and the semiannual Monetary Policy Report to the Congress of the Federal Reserve Board frequently point to survey expectations of inflation. These surveys are however released only at low frequency and are generally somewhat stale while perceptions of the outlook for the economy can move very fast. Policy makers, monitoring the economy in real time, would presumably like to be able to measure these expectations at a higher frequency. The methods that we propose allow us to measure expectations immediately before and after a specific event (e.g. macroeconomic news announcements, Federal Reserve policy shifts or major financial crises) and so measure the impact of such events on agents' expectations.4
(ii) Second, expectations in a multi-agent economy involve "forecasting the forecasts of others" (to paraphrase Townsend (1983)) and therefore private sector agents would likewise also wish to obtain higher frequency measures of others' expectations.
(iii) A third reason (closely related to the first two) is that surveys may be (approximately) rational or efficient forecasts of future economic data and may thus contain information for policy makers not just about agents' expectations, but also about likely future outcomes. In this paper we do not, however, make an assumption that surveys represent rational conditional expectations-for one thing their timing is too murky for this to be literally true. Nevertheless, the hypothesis of rationality of survey expectations has been examined and tested. The evidence is mixed. Froot (1989), Lamont (1995), Zarnowitz (1995), Ehrbeck and Waldmann (1996) and Romer and Romer (2000) report evidence against the efficiency of survey forecasts, but Keane and Runkle (1998), Thomas (1999), Mehra (2002) and Ang, Bekaert and Wei (2005) report more favorable evidence.5 Much of the discrepancy appears to relate to the sample period considered. In the 1970s, the surveys appear to have had poor success in forecasting some variables, especially inflation, but have been more successful subsequently.6 Our empirical work is going to focus on recent periods where the evidence on survey forecasts is relatively favorable. Ang, Bekaert and Wei run a horse-race for predicting inflation using macro variables, financial variables and survey forecasts. They argue quite persuasively that, in recent years, surveys appear to be the best predictors. They also investigate several optimal methods of combining forecasts and show that surveys outperform the other forecasting methods based on combining surveys with forecasts of macro variables and asset markets. Hence, Ang, Bekaert and Wei argue that surveys give very useful information regarding future inflation, that beats forecasts constructed from macro variables and asset prices. However, even if surveys provide useful information about future economic outcomes, they nevertheless have the drawback of being infrequent and generally somewhat stale, while the outlook for the economy can move very fast. The methods presented in this paper can overcome this drawback. Indeed, one might wonder how our forecasts of upcoming survey releases fare when interpreted as predictions of actual outcomes. We show that in some cases they can outperform a simple random walk benchmark.
While there are many reasons for measuring professional forecasters' expectations at high frequency, the task itself is, as noted before, not so trivial. One may first of all wonder which data would be most suitable to use. The task is very much related to the construction of leading indicators, or the extraction of a common factor as in, for example, Stock and Watson (1989, 2002). We could use low-frequency macroeconomic data, or high-frequency asset price data.7 But the latter will allow us to make predictions at any point in time, which is our goal in this paper. Thus, in this paper we use daily asset price data. Indeed, while we focus on the daily frequency, the methods that we propose apply to intradaily frequencies as well.
A priori, it is not clear how to use daily financial market data to formulate a parsimonious model. We first consider using a regression model to predict the next survey release. But, if surveys of forecasters are released quarterly and we are, say, two months from the last release, how would we use these two months of data to predict the next release? A simple linear regression will not work well as it would entail estimating a large number of parameters. For example if we use two months of data it would require estimation of 44 parameters, assuming 22 trading days a month. The estimation uncertainty would nullify any underlying predictable patterns that might exist. Matters are further complicated by the fact that there is some fuzziness in the timing of the surveys: although we have a notional date for each survey (the deadline for submission of responses), we have no way of knowing whether the forecasters actually formed their predictions on the survey deadline date or several days earlier. To allow for this we might want to use more than two months of data. We resolve the challenge by using Mixed Data Sampling, or MIDAS regression models, proposed in recent work of Ghysels, Santa-Clara and Valkanov (2002, 2003, 2005). MIDAS regressions are designed to handle large high-frequency data sets with judiciously chosen parameterizations, tightly parameterized yet versatile enough to yield predictions of low frequency forecast releases with daily financial data. The virtue of our approach is that we have for any day prior to a release a prediction model that conveniently adapts to the time remaining until the next forecast release. In our empirical work we use the median forecasts of output growth, inflation, unemployment and certain interest rates, from the Survey of Professional Forecasters (Croushore (1993)) and Consensus Forecasts (Zarnowitz (1995)). The financial market data that we use to predict these forecasts are daily changes in interest rates and interest rate futures prices, and also daily stock returns. We find that these asset price changes give us considerable predictive power for upcoming Survey of Professional Forecasters releases, and, to a lesser extent, Consensus Forecasts releases.
In addition to using these regression models to predict upcoming survey releases, we consider a more structural approach in which we use the Kalman filter to estimate what forecasters would predict if they were asked to make a forecast each day, treating their forecasts as "missing data" to be interpolated (see e.g. Harvey and Pierse (1984), Harvey (1989), Bernanke, Gertler and Watson (1997)). As a by-product, this also gives forecasts of upcoming releases. But again, we have to contend with the fact that although we have a notional date for each survey, agents likely formed their expectations sometime earlier. Again, we resolve this problem by using mixed data sampling methods. The theory of the Kalman Filter applies only to linear homoskedastic Gaussian systems and this assumption is clearly inadequate for daily financial market data. However, the Kalman filter nonetheless provides optimal linear prediction even when the errors are in fact fat-tailed and heteroksedastic. The Kalman filter models have the useful feature of allowing us to estimate forecasters' expectations on a day-to-day basis. We cannot precisely accomplish this task with a reduced form regression model that allows only predictions of future observed forecasts.
Having obtained estimates of agents' daily forecasts, we can then relate these to macroeconomic news announcements. For example, we can measure the average effect of a nonfarm payrolls announcement that is 100,000 better-than-expected on agents' forecasts.
Our work is conceptually related to several recent papers that use high-frequency financial data to form a daily indicator of the state of the economy (see e.g. Evans (2005) and Giannone, Reichlin and Small (2005)). However, our aim is not to construct a high-frequency coincident economic indicator, nor even a high-frequency leading economic indicator-an indicator designed to have maximal predictive power for future economic realizations (though we may be doing this indirectly). Our direct aim is to obtain high-frequency measures of forecasters' expectations.
There is of course an enormous literature on using asset price data to forecast future inflation, growth and other macroeconomic variables (see e.g. Stock and Watson (2003)), though not generally at the daily frequency. It is well known that it is hard to beat naive time series models in predicting future macroeconomic variables. This paper is, however, concerned with forecasting survey predictions of macroeconomic variables, rather than with forecasting the future macroeconomic variables. Forecasting survey predictions might be a somewhat easier task because if surveys were to approximate rational forecasts of future macroeconomic data, then a regression relating the forecast of the survey prediction to asset price returns should have a higher R-squared than a corresponding regression relating the future macroeconomic outcomes to asset price returns, because rational forecasts and actual realizations differ by a pure noise component that reduces the empirical fit of the latter regression.
The remainder of this paper is organized as follows. In section 2 we present a theoretical framework that succinctly represents the salient features of predicting forecasters with financial data. Reduced form MIDAS regression methods appear in section 3. A more structural approach that uses the Kalman filter to interpolate at the daily frequency is described in section 4. Empirical results appear in section 5. Section 6 concludes the paper.
2 Forecasting and financial market signals
In this section we present a stylized model of forecasting and financial market signals. The objective is to show, in a very stylized setting, how if asset prices and forecasts both respond to news about the state of the economy, we can use asset returns to glean high-frequency information about agents' forecasts. At the outset it is important to emphasize that we want to keep the model in this section simple. Therefore, we make some compromises with regards to generality and do not aim at matching all salient data features that will appear in our empirical analysis. The empirical specifications considered in the next sections will be richer and more general.
Assume that we observe forecasts of some future macroeconomic variable (e.g. inflation four quarters hence) once a quarter and suppose, for simplicity in this model, that these are observed on the last day of each quarter. Assume that the underlying macroeconomic variable 
is autoregressive of order one:
Let
denote the forecast of 
made on the last day of quarter 
If the forecaster knows the DGP, knows 
at the end of quarter t (when the forecast is being made), and is constructing a rational forecast then this h-quarter-ahead forecast will be:
and, after a little algebra, this is related to the previous h-quarter-ahead forecast and the shock
as follows:
We are interested in predicting
at some time between the end of quarter t-1
and the end of quarter t. During the quarter all sorts of news is released pertaining to the macroeconomic variable 
and this news is impounded into financial asset returns. Although the errors
occur quarterly, we construct a fictitious set of daily shocks
where 
denotes the last day of quarter t. While there are many financial assets traded, we focus on a single asset and assume that its price on day 
relates to the fictitious shocks as follows:
where
is the price at the beginning of the quarter t. Equation (4) tells us that daily prices provide a noisy signal of the underlying economic shocks. Assume that the fictitious shocks 
are Gaussian with mean zero and variance
and that the noise is also Gaussian with mean zero and variance
and is orthogonal to the 
process. We make these assumptions for convenience, but will comment on them later. The two related problems we then consider are: (1) predicting
during quarter t with concurrent and past daily financial market data via a regression model, or (2) treating agents' h-quarter-ahead expectations during the quarter as "missing" values of a process only observed at the end of the quarter. There is a fundamental difference between predicting
during the quarter, and "guessing"
, the unobserved h-quarter-ahead expectation on day 
The former is a prediction problem that can be formulated via a regression, whereas the latter is a filtering problem. We describe both of these in turn in the next two subsections.2.1 The regression approach
From equation (4) we note that the partial sums process 
behaves like a random walk and therefore asset price
behaves like a random walk plus noise (in practice stock prices are not a random walk, but this is one of our simplifying assumptions). To predict
, we would like to know
and the best predictor on day 
would be 
which is not observed but can be extracted from asset returns. In particular, in appendix A we show that conditional linear prediction given daily returns, denoted
can be approximated as:
![LaTex Encoded Math: \displaystyle \mathcal{P}[f_{t}^{t+h}\vert r_{d},d=l_{t-1} + 1,\ldots,\tau]](img38.gif){kind=small}
where
is a function of the signal-to-noise ratio 
=
(see below equation (A.2)) and 
is the asset return on day 
for days 
, 
, 
during quarter 
Equation (5) indicates that daily asset returns, which contain the daily accumulation of "news" allow us to predict forecasts.
The stylized model presented so far is based on a number of simplifying assumptions. It is worth discussing some of the critical assumptions and how they can be relaxed.
Firstly, the above analysis assumes that forecasters have rational expectations and know the DGP. The analysis in the remainder of the paper will not exclude the possibility of rational forecasting, and that would clearly strengthen the motivation for real-time forecasting of the forecasters. Nevertheless, our empirical model does not rely on such an assumption and, throughout this paper, we remain strictly agnostic about the rationality of forecasters' expectations.
Secondly, to derive equation (5) we assumed Gaussian errors. The resulting prediction formula only depended on the signal to noise ratio 
and the linear prediction is optimal in a MSE sense. With the Gaussian distributional assumptions, we are in fact in the context of the Kalman filter, the topic of the next subsection. Here we consider equation (5) as a linear projection or regression equation. Obviously, this regression equation is tightly parameterized because the analysis has been kept simple for the purpose of exposition. In particular, the process 
was assumed to be AR(1) and this yielded convenient formulas in this example. In practice, we prefer to have reduced form regressions that do not explicitly hinge on the specifics of the DGP. The empirical specification of the regression models is a topic that will be discussed further in the next section.
2.2 The filtering approach
We now turn to the second problem, namely how to extract
For this, it is very natural to specify and estimate a state space model using the Kalman filter to interpolate respondents' expectations, viewing these as "missing data" (see e.g. Harvey and Pierse (1984), Harvey (1989), Bernanke, Gertler and Watson (1997)). It is worth noting that the regression approach of the previous subsection can be viewed as less "structural" in the sense that we do not need to specify an explicit state space model. The Kalman filter applies to homoskedastic Gaussian systems, assumptions we make here for analytic convenience. To be specific, let us reconsider equation (3) and apply it to a daily setting:
The shocks
are not directly observable, only the returns are.8 The above equation, combined with equation (4), therefore holds the ingredients for a state space model to determine
namely daily returns are a noisy signal of daily changes in
where at the end of each quarter we observe
=
. This gives us an explicit state space model.3 Regression model specifications
In this section, we deal with regression models for predicting
. Let 
denote the survey deadline date for quarter 
: survey respondents submit their forecasts on or before this day: the survey results are released a few days later. We suppose that the researcher wishes to forecast
using asset return data on days up to and including day 
Our forecasting model is:
where
denotes the return on day 
for asset 
, 
denotes the number of assets and 
is a lag polynomial of order 
so that
is a distributed lag of daily returns on asset 
over the 
days up to and including day 
= 
where
In empirical work we will consider 
and 
corresponding to forecasts for
made on the survey deadline date, about one month earlier, and about two months earlier, respectively. Equation (8) uses mixed frequency data:
and
are observed at the quarterly frequency, 
, while the returns are at the daily frequency, but there is only one observation of the distributed lag of daily returns,
, in each quarter.9 Hence, as suggested by equation (5 ), asset returns up to a fraction 
of the time from the quarter 
survey deadline date to the quarter 
survey deadline date are used to predicting the quarter 
survey. We run a different regression for each 
and so should strictly put a 
-subscript on 
,
, 
, and 
in equation (8), but do not do so, in order to avoid excessively cumbersome notation. In order to identify 
in this equation, we constrain the polynomial 
to have weights that add up to one. The discussion in the previous section yielded a polynomial 
governed by one single parameter 
While this is certainly attractive, it is very limited as a parameterization and besides the very specific context of our particular theoretical model, may not be empirically plausible. In other words, we want a more flexible approach that keeps the number of parameters small. A solution to this problem can be found with MIDAS regression models. Following Ghysels, Sinko and Valkanov (2003) we use a flexible specification for 
with only two parameters,
and
In particular, the lag 
coefficient is written as:
where:
=
with 
=
Specification (9) has weights that add up to one and is based on the Beta function and we refer to it as the "Beta Lag." Ghysels, Sinko and Valkanov (2003) discuss its features in detail.
We consider three MIDAS regression models for the prediction of
. The first, which we refer to as model M1, is simply given by equations (8) and (9) with unknown parameters 
,
, 
,
and
. The second, which we refer to as model M2, imposes that
, implying that the weights in 
are equal. In this case,
is simply the average return over the 
days up until day 
and 
=
. Lastly, we consider an equal-weighted MIDAS regression in which the average returns from day 
to day 
are used to predict the upcoming release, i.e. 
=
and 
=
We refer to this as model M3. The difference between models M2 and M3 is that model M2 has a fixed lag length parameter, 
, while model M3 will always use returns from exactly day 
to day 
.
We estimate MIDAS models M2 and M3 by linear regression of
on
with 
fixed and 
=
respectively. We estimate MIDAS model M1 by nonlinear least squares, i.e. the parameters are chosen so as to minimize
where
is given by equation (9).4 Kalman filter specifications
We now turn to the extraction of
for horizon 
on day 
The methods outlined in the previous section allow for prediction of upcoming survey releases in a simple regression framework with minimal assumptions. In this section we deal with filtering a process that remains latent during the quarter. As noted before, it is very natural to specify and estimate a state space model using the Kalman filter to interpolate respondents' expectations, viewing these as "missing data". The Kalman filter applies to homoskedastic Gaussian systems and this assumption is clearly inadequate for financial data. However, the Kalman filter provides optimal linear prediction even with non-Gaussian errors.
We consider two thought-experiments that go beyond the simple stylized example of section 2. The first is that forecasters form expectations each day, but only send these expectations into the compilers of the survey once a quarter, on survey deadline dates. Thus, we observe respondents' expectations on survey deadline dates, but these expectations are missing data that must be interpolated on all other days. We let
denote the respondents' 
-quarter-ahead expectations on day 
and write the following model
where
is i.i.d. normal with mean zero and diagonal variance-covariance matrix. This model is clearly a linear Gaussian model in state-space form with
as the unobserved state, equation (12) as the transition equation, and (11) and (13) as the elements of the measurement equation.10
However, this model assumes that surveys correctly measure respondents' expectations on survey deadline dates. As discussed earlier, there is some fuzziness about the exact timing of respondents' expectations that it seems we should allow for. We can do so by amending equation (13) to specify instead that
where
is a MIDAS polynomial given by equation (9). The thought-experiment here is that individual respondents form their expectations each day, but that some of these get transmitted to the compilers of the survey faster than others, with the compilers of the survey using the latest numbers from each respondent to construct the survey releases once a quarter, on survey deadline dates. Our objective is to back out our estimates of respondents' underlying expectations given by
Of course, the model in which surveys correspond exactly to respondents' expectations on survey deadline dates is nested within this specification, as we can specify that
and
, implying that
.
We refer to the simple Kalman filter model (equations (11), (13) and (12)) as model K1. We refer to the MIDAS Kalman filter model (equations (11), (14) and (12)) as model K2. In either case, we can use the Kalman filter to find maximum-likelihood estimates of the parameters, giving filtered estimates of
and forecasts of
(made a fraction 
of the way through the prior inter-survey period) as by-products. We can also use the Kalman smoother to obtain estimates of
conditional on the entire dataset.
5 Empirical results
There are two surveys that we consider in the empirical work in this paper:
(i) The Survey of Professional Forecasters (SPF), conducted at a quarterly frequency. The respondents include Wall Street financial firms, banks, economic consulting groups, and economic forecasters at large corporations. Prior to 1990, it was a joint project of the American Statistical Association and the National Bureau of Economic Research; now it is run by the Federal Reserve Bank of Philadelphia. We use median SPF forecasts of real GDP growth, CPI inflation, three-month T-Bill yields and the unemployment rate at horizons one- through four- quarters ahead. Real GDP growth and CPI inflation are constructed as the annualized growth rates from quarter 
to quarter 
, where 
is the quarter in which the survey is taken and 
is the horizon of the forecast (
). Three-month T-Bill yields and the unemployment rate are simply expressed in levels. In the notation of the previous section,
refers to the forecast made in the quarter 
SPF forecast for any one of these variables in quarter 
and our forecasting models are the MIDAS models exactly as defined earlier. We start with the forecasts made in 1990Q3 and end with forecasts made in 2005Q4 for a total of 62 forecasts. For each of these forecasts we have the survey deadline dates that are about in the middle of each quarter. The survey deadline date is not the date that the survey results are released, but is the last day that respondents can send in their forecasts. We do not use SPF forecasts made before 1990Q3 because we do not have the associated survey deadline dates. Besides, the use of a relatively recent sample minimizes issues of structural change that seem to be very important using data that spans earlier time periods (Ang, Bekaert and Wei (2005) and Stock and Watson (2005)).
(ii) Consensus Forecasts, a survey that is conducted at a monthly frequency by Consensus Economics. We use median predictions from Consensus Forecasts for year-over-year real GDP growth, year-over-year CPI inflation, the level of three-month T-Bill yields, the level of the unemployment rate and the level of ten-year yields for the current and subsequent years, from October 1989 to June 2003, inclusive, for a total of 165 forecasts. As with the SPF, we have the survey deadline dates.11
We can use daily asset prices to predict the upcoming releases of either of these surveys, using MIDAS regression models M1, M2 and M3, or our Kalman filter models K1 and K2. We consider models with the following daily asset returns: (a) excess stock market returns, (b) the daily change in the rate on the fourth three-month eurodollar futures contract (a futures contract on a three-month interest rate about one year hence), (c) the daily changes in the rates on the first and twelfth eurodollar futures contracts (futures contract on three-month interest rates about three months and three years hence), (d) the daily changes in three-month and ten-year Treasury yields, and, finally, (e) the daily change in two-year Treasury yields.12 The number of assets, 
, is thus either 1 or 2. Our predictors are thus stock returns and changes in measures of the level and/or slope of the yield curve. In MIDAS models M1 and M2, the lag length 
is a fixed parameter that we set to 90 for the SPF and 40 for Consensus Forecasts. As our data are at the business day frequency, this corresponds to substantially more than one quarter or one month of data, respectively. We do this because we have no way of knowing whether the forecasters actually formed their predictions on the survey deadline date or several days earlier, and because preliminary investigation revealed that this choice of 
generally gave the best empirical fit.
We evaluate the forecasts by comparing the in-sample and pseudo-out-of-sample root mean-square prediction error (RMSPE) of each of the models M1, M2, M3, K1 and K2, used to predict the upcoming survey release, relative to the RMSPE from using the prior survey release as a predictor (a "random walk" forecast). This seems like a natural benchmark; it tells us what fraction of the revision to survey forecasts we are failing to predict. The empirical results for predictors (a)-(e) are reported in Tables 1-5, respectively. Each Table gives results for the Survey of Professional Forecasters in the top panel and for Consensus Forecasts in the lower panel. In each Table we report the in-sample and pseudo-out-of-sample relative RMSPE of models M1, M2, M3, K1 and K2, used to predict the upcoming survey release, relative to the random walk benchmark, for
. The first observation for out-of-sample prediction is the first observation in 1998, with parameters estimated using data from 1997 and earlier, and prediction then continues from this point on in the usual recursive manner, forecasting in each period using data that were actually available at that time. Note that because we are working with asset price data and survey forecasts (rather than actual macroeconomic realizations), we have no issues of data revisions to contend with; the out-of-sample forecasting exercise is a fully real-time forecasting exercise.
5.1 Discussion of the Forecasting Results for the SPF
We first discuss the simple regression results (models M1, M2 and M3) for the SPF. The in-sample relative RMSPEs from MIDAS models M1, M2 and M3 are generally well below one. Not surprisingly, relative RMSPEs are higher in the pseudo-out-of-sample forecasting exercise. Survey forecasts of the unemployment rate and T-Bill yields appear to be generally the most predictable out-of-sample, but relative RMSPEs are in many cases below one out-of-sample for GDP growth and CPI inflation as well. Overall, the best out-of-sample results appear to obtain for predictors (d), the daily changes in the three-month and ten-year Treasury yields, but the other yield curve variables (predictors (b), (c) and (e)) had similar performance. On average, across all four variables and all four horizons, the pseudo-out-of-sample relative RMSPE from MIDAS model M1 with 
and predictors (d) is 0.78. MIDAS model M1 also beats the benchmark out-of-sample (averaging across all variables and horizons), but the performance is notably weaker with predictors (a) (stock returns). It is perhaps not surprising that the best forecasting performance is given by daily changes in the slope and/or level of the yield curve rather than stock return data13, as the former exhibit a stronger relationship with the state of the economy. In particular, it is consistent with much work finding that the level and slope of the yield curve alone has the best predictive power for several key macroeconomic variables.
Even though MIDAS model M1 involves estimation of two additional parameters, it generally gives smaller out-of-sample RMSPEs than models M2 or M3. Thus, perhaps in part because the surveys represent agents' beliefs at a substantial lag relative to the survey deadline date (a lag that furthermore varies by respondent), allowing for non-equal weights in 
appears to result in some improvement in forecasting performance.
Not surprisingly, the relative RMSPE is generally somewhat smaller for forecasts made using asset price data up through the survey deadline date (
) than for forecasts made earlier in the inter-survey period (
).
We next discuss the results using the Kalman filter (models K1 and K2) for the SPF. Models K1 and K2 give quite similar RMSPEs to the MIDAS regression models. Again, the best results obtain when predicting the forecasts for three-month T-Bill yields and the unemployment rate, and when using predictors (d). Model K2, which allows for surveys to represent some respondents' beliefs at a substantial lag relative to the survey deadline date, generally gives smaller out-of-sample RMSPEs than model K1, even though the former involves estimation of two additional parameters. This reinforces the evidence that surveys represent agents' beliefs a considerable lag to the survey deadline date..
Models K1 and K2 seem to generally give less good forecasts of what the upcoming survey release is going to be than the reduced form MIDAS regression models M1, M2 and M3. Nonetheless, they have the useful feature of allowing us to estimate forecasters' expectations on a day-to-day basis, (
in the notation of equation (11)) and these estimates can be either conditional on past data (filtered estimates) or the whole sample (smoothed estimates). We cannot precisely accomplish these tasks with the reduced form MIDAS regression models.
As an illustration, in Figures 1 - 4, we show the time series of Kalman filtered and smoothed estimates of two-quarter-ahead real GDP growth expectations from models K1 and K2, using predictors (d), over the period since January 1998. SPF releases of actual two-quarter real GDP growth expectations are also shown on the figure (dated as of the survey deadline date). The Kalman filtered estimates jump on each survey deadline date as the information from the survey becomes incorporated in the model, but the jumps are quite a bit smaller in magnitude than the revisions to the survey forecasts, consistent with the results in Tables 1-5 on the RMSPE of the Kalman filter forecasts relative to that of the random walk benchmark. The Kalman smoothed estimates adjust more smoothly, as is of course to be expected.
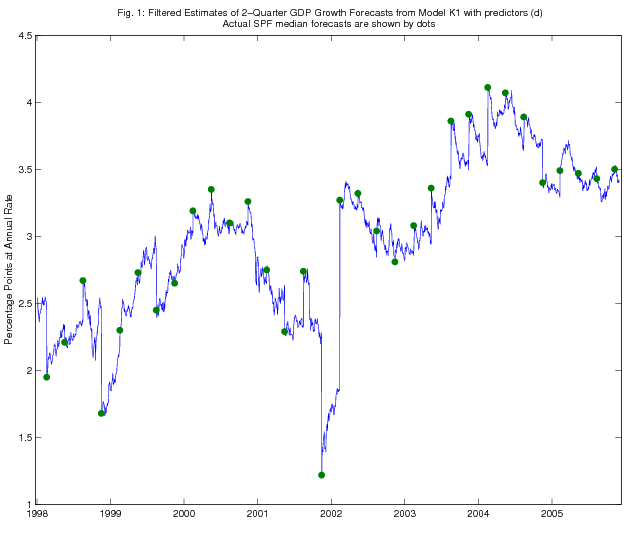
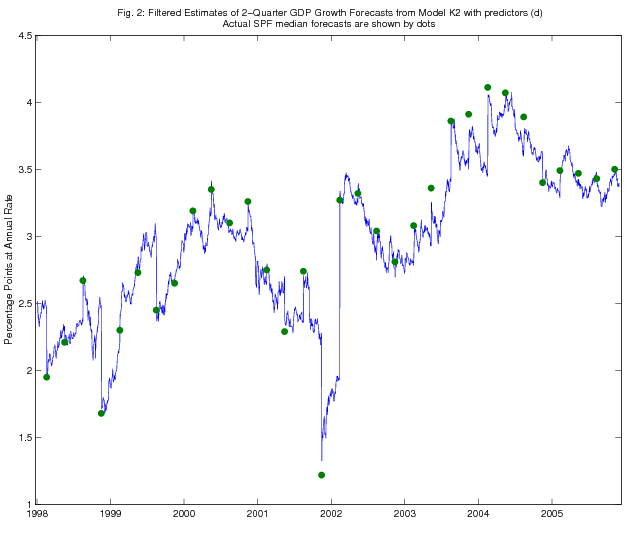
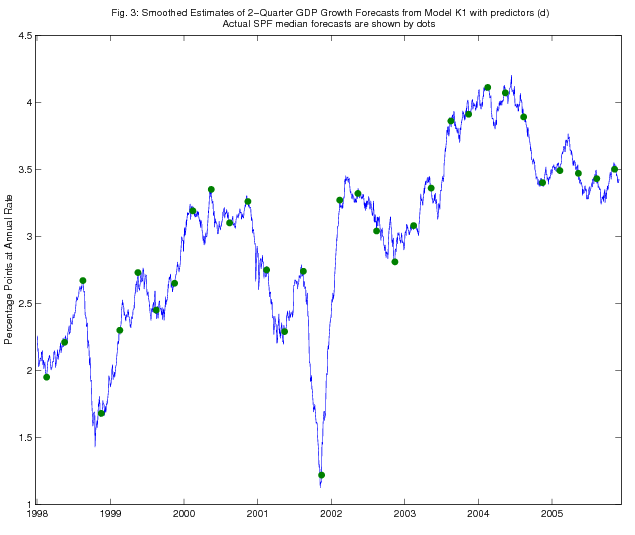
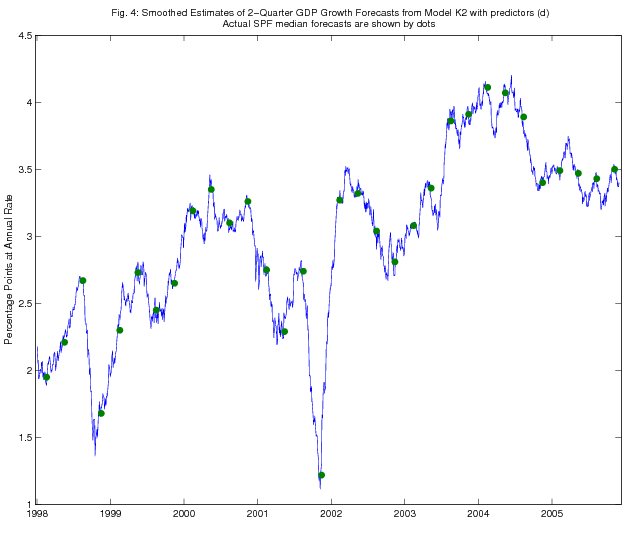
5.2 Discussion of the Forecasting Results for Consensus Forecast
We next briefly summarize the corresponding results for median Consensus Forecasts, reported in the lower panels of Tables 1-5. The results are fairly consistent with what we found for the SPF, but the improvements in RMSPE relative to the random walk benchmark are more modest than for the SPF. The most favorable results in predicting median Consensus Forecasts are for the three-month T-Bill yield and the ten-year yield. Averaging across all variables and all horizons, the pseudo-out-of-sample relative RMSPE for median Consensus Forecasts with 
is below one for all five models with any of the predictors, with the sole exception of predictor (a) (excess stock returns). Overall, the best results for forecasting median Consensus forecasts again obtain with predictors (d).
5.3 Measuring the Effect of News Announcements on Agents' Expectations
Applying the Kalman smoother to models, K1 and K2, we can estimate what forecasters' expectations were on a day-to-day basis conditional on the whole sample. Hence, we can, in principle, measure agents' expectations immediately before and after a specific event (e.g. macroeconomic news announcements, Federal Reserve policy shifts or major financial crises) and so measure the impact of such events on their expectations. The impacts of some events can even be seen in Figures 2 and 4, for models K1 and K2, respectively.
As an illustration, we show how our method can be used to estimate the average effect of a nonfarm payrolls data release (one of the most important macroeconomic news announcements) coming in 100,000 stronger than expected on the expectations of respondents to the SPF. Nonfarm payrolls data are released by the Bureau of Labor Statistics once a month, at 8:30 AM sharp. We measure ex-ante expectations for nonfarm payrolls releases from the median forecast from Money Market Services (MMS) taken the previous Friday. The surprise component of the nonfarm payrolls release is then the released value less the MMS survey expectation.14 Since the Kalman smoother gives us measures of the expectations of SPF respondents each day, we can regress the change in these expectations from the day before the nonfarm payrolls release to the day of the nonfarm payroll release on the surprise component of that release.15 Concretely, the regression that is estimated is
where
denotes the Kalman smoothed estimates of the h-quarter-ahead forecast for any variable being predicted in the SPF, 
denotes the surprise component of the nonfarm payrolls release,
is an error term, and the regression is run only over days on which there is a nonfarm payrolls release. This gives us a sample size of 182 - one observation for each monthly nonfarm payroll release from 1990Q3 to 2005Q4. The regression gives an estimate of the average effect of a one unit (100,000) positive nonfarm payrolls surprise on
. OLS coefficient estimates from equation (15) are given in Table 6, along with t-statistics constructed using heteroskedasticity-robust standard errors. Most entries are highly statistically significant with any of predictors (b)-(e). The estimated coefficients seem to be of a reasonable magnitude. For example, using predictors (d) and model K2, a 100,000 positive nonfarm payrolls surprise (which is approximately a one standard deviation announcement surprise) is estimated to raise one-quarter-ahead growth forecasts by 
ths of a percentage point and to raise four-quarter-ahead growth forecasts by 
th of a percentage point. And the same positive labor market news is estimated to raise four-quarter inflation forecasts by 
th of a percentage points, and to raise four-quarter T-Bill yield forecasts by 3 basis points. These estimated effects are all small, but it seems reasonable that forecasts are not adjusted much in response to a one-standard deviation surprise in employment growth for one month. And, though small, these effects are all highly significant.5.4 Using our Forecasts of Survey Forecasts as Forecasts of Future data
So far in this paper, we have focused on forecasting upcoming releases of surveys of forecasters. Part of our motivation for doing so is that these surveys, though released infrequently, might contain useful information about future outcomes. If our forecasts are conditional expectations of the upcoming survey forecasts, and those survey forecasts are in turn conditional expectations of actual future outcomes then, by the law of iterated expectations, our forecasts must also be conditional expectations of those actual future outcomes.
Accordingly, it is natural to ask how our daily forecasts for upcoming survey releases fare when they are interpreted as forecasts of actual future outcomes. We can compare this with a benchmark of a random walk forecast. Though this may seem like a very naive benchmark, it is well-known that it is quite hard to beat (see, for example, Atkeson and Ohanian (2001)), particularly for such a short sample period.
We therefore computed the RMSPE of our pseudo-out-of-sample forecasts for upcoming SPF releases, interpreted as forecasts of the actual outcomes. That is to say, we computed
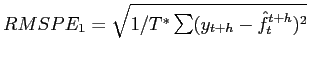
where 
denotes the realization in quarter 
,
denotes our pseudo-out-of-sample prediction of
, the 
-period-ahead survey forecast taken in quarter 
, and 
denotes the number of out-of-sample predictions. And we also computed the RMSPE of a random walk forecast. That is, we computed
Table 7 reports the relative RMSPE from these two methods for forecasting 
,
, for models M1, M2, M3, K1 and K2 with predictor (d), for
.16Entries in the Table less than one indicate that the forecasts of
give better predictors of 
than the random walk forecasts. Note that for
the random walk forecast might have an unfair artificial advantage in this comparison, because these might correspond to forecasts made before 
was known.17 It turns out that our predictions of survey forecasts beat the random walk forecast in forecasting future real GDP growth and CPI inflation. The latter is perhaps not surprising in the light of the results of Ang, Bekaert and Wei (2005). On the other hand our predictions of survey forecasts do less well than the random walk forecast in predicting future yields. Results for unemployment are mixed, but our predictions of survey forecasts generally underperform here as well. Taken together, these results indicate that daily forecasts for upcoming survey releases, in addition to being of interest in their own right, may also be useful as forecasts of actual future outcomes.
6 Conclusions
Survey forecasts provide useful information about agents' expectations, and perhaps also about the likely future evolution of the economy. Or at least, policy makers and financial markets appear to perceive this to be the case, judging by the amount of attention that is paid to these survey forecasts. However, since they are released infrequently, these surveys are often stale, and it would seem useful to be able to measure respondents' expectations, and to predict upcoming survey releases, at a higher frequency. We have proposed methods for doing so using daily financial market data, and found that the resulting predictions allow researchers to anticipate a substantial portion of the revisions to survey forecasts. We have also shown how daily estimates of respondents' expectations can allow us to measure the effects of events and news announcements on these expectations. MIDAS methods can also be used for forecasting outcomes (as opposed to survey expectations) using daily asset price data. We leave this for future research.
A Derivation of projection equation
In this appendix we derive equation (5). We noted that according to equation (4) the partial sums process 
behaves like a random walk and therefore the price
behaves like a random walk plus noise. Note that this is a 'local behavior' during the quarter from 
to 
Here we will assume a standard random walk plus noise process (as if it applied throughout, not just locally) to derive an approximate prediction formula. To distinguish the model from that in section 2 we use, at first different notation, and subsequently map the results into the setting of section 2. More specifically, we start from the standard random walk plus noise model (see e.g. Whittle (1983) and Harvey and De Rossi (2004)):
where
and 
are mutually uncorrelated Gaussian white noise disturbances with variances
and
respectively. Define the signal-to-noise ratio 
=
0 then the one-sided signal extraction filter for 
given
denoted
has weights
(see Whittle (1983) and Harvey and De Rossi (2004)):
where
=
![[(\sqrt{q^{2} + 4q} - 2 - q]/2.](img242.gif){kind=small}
This formula is approximate, in the sense that it applies to observations "near" 
whereas observations in the remote past have weights of the two-sided filter, namely
18 From equation (A.2) we can derive the first-difference version
=
namely:
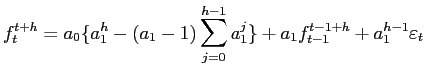
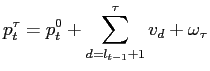
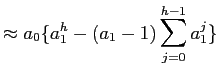
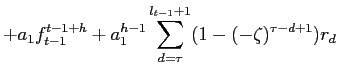
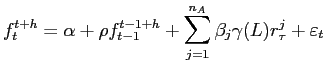
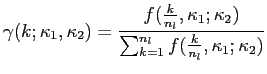
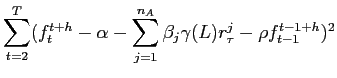
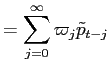
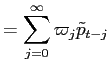
![LaTex Encoded Math: \displaystyle = (1+\zeta)[\tilde{r}_{t} + \sum_{i=1}^{\infty}\sum_{j=0}^{i}(-\zeta)^{j} \tilde{r}_{{t-i}} ]](img251.gif)
![LaTex Encoded Math: \displaystyle = (1+\zeta)[\tilde{r}_{t} + \sum_{i=1}^{\infty}\frac{1-(-\zeta)^{i+1}% }{1+\zeta}\tilde{r}_{{t-i}} ]](img252.gif)
As noted, the partial sum process
implied by equation (4) behaves locally like a random walk plus noise. Hence, we can use the above formula as an approximation, treating returns as if they are zero prior to the beginning of the quarter (
0 in section 2) and substituting into (3) yields equation (5). The formula is only an approximation and a more rigorous formula can be derived, using the finite sample exact filters weights. Deriving such filters is rather involved, see e.g. Whittle (1983) and Schleicher (2003), and we don't really need the exact filter weights for motivational purpose.
