A Fully-Rational Liquidity-Based Theory of
IPO Underpricing and Underperformance
Keywords: Liquidity, IPO, Asset Pricing, Market Microstructure
Abstract:
1 Introduction
Two of the important functions of a financial system are to facilitate risk sharing among investors and capital formation by firms. The initial public offering (IPO) process performs both functions by allowing the initial owners of a firm to raise capital by transferring and sharing some of the firm's risk with the wider investing public. If the IPO process was fully efficient, an IPO should maximize the issuer's proceeds, the investors who most value the shares should receive them, and in the absence of news or private information, there should be little trade after the shares are allocated. Additionally, the fact that a stock is a new issue should not influence its risk-adjusted expected returns in aftermarket trading.
Relative to this benchmark, U.S. IPOs appear to be highly inefficient: post-IPO share trading is initially very heavy2, and the allocation price of U.S. IPOs is on average nearly 19 percent below the closing price on the first day of trade [Ritter and Welch (2002)]. This underpricing is an apparent loss to issuers who would prefer to have sold at the higher price in the IPO aftermarket. The IPO process has other inefficiencies: allocations tends to favor institutional investors3 and, after the first trading day, the returns of new issues underperform on a market and characteristic adjusted basis for a period of time as long as three years [Loughran and Ritter (1991), Ritter and Welch (2002)].4
This paper presents a fully rational, symmetric information, theoretical model of IPO share allocation and price-setting, and of trading in the IPO aftermarket. The paper is built around the idea that trading conditions in the aftermarket may simultaneously explain underpricing, underperformance, and why allocations favor institutional investors. The model of the aftermarket is imperfectly competitive in the sense that there are some "large" investors who have market power, that is their trades move prices and they account for this when trading. The IPO is modeled as a bargaining game between the underwriter and the aftermarket investors: The underwriter must sell a fixed number of shares at the IPO or shortly afterwards in aftermarket trading. To do so, he sets a uniform IPO offer price and offers take it or leave it share allocations to the investors. Any shares that go unallocated are sold by the underwriter in aftermarket trading that follows the IPO. Large investors' market power in the aftermarket gives them bargaining power at the IPO because they can turn down their share allocation and force the underwriter to sell into the aftermarket, where large investors can influence (and lower) the price. To avoid this outcome, the underwriter distorts IPO asset allocations towards investors with market power, and gives them a favorable IPO offer price.5
From the initial asset allocations at the IPO, investors trade towards efficient asset allocations along an equilibrium transition path. Because large investors' trades move prices, the market is not perfectly liquid from their perspective, and this illiquidity influences returns and asset prices. In particular, when initial asset allocations favor large investors, along the equilibrium transition path large investors sell slowly through time to minimize the price impact of their trades. This restricts the supply of shares that is available to price-taking small investors. As a result small investors bid up the new issue's price, and because they don't expect to acquire many assets in the short-term, they bid down its expected returns, causing return underperformance. The magnitude and duration of the underperformance depends on the severity of illiquidity in the aftermarket, and on how the assets are allocated at the IPO.
There is a voluminous related literature on IPO underpricing, underperformance, and share allocations at the IPO.6 Most of the theoretical models in this literature explain only one or two of these phenomena. Only behavioral models can explain all three.7 Relative to this literature, this paper makes three contributions. First, to the best of my knowledge, it presents the only fully-rational theoretical model to date that can explain all three phenonomena. Second, the model shows that these phenomena are related to the competitiveness of the aftermarket, which in turn can be related to the distribution of the size of the investors that participate in the IPO or trade in the aftermarket (as measured by their wealth, or assets under management). Therefore, summary statistics of the distribution of investor size constitute a new set of state variables that can be used to test theories of IPOs, and to distinguish the predictions of this model from the related literature. Finally, this paper helps to fill a gap in the small literature on IPOs and liquidity. Within that literature, Ellul and Pagano (2003) present a theoretical model in which markets are illiquid, but competitive. Within their framework, they show that underpricing is required to compensate IPO participants for aftermarket illiquidity; they also find empirical support for the theory because aftermarket illiquidity has a large and positive correlation with more underpricing.8 Extending Ellul and Pagano's logic suggests IPOs should also earn a positive liquidity premium in aftermarket trading, but this is belied by the fact that IPO's underperform, and suggests that the Ellul and Pagano model cannot on its own explain both underpricing and underperformance. By contrast, this paper shows that a liquidity-based model can explain underpricing and underperformance provided one drops the perfect competition assumption in Ellul and Pagano and replaces it with the imperfect competition assumption that is used here.9
The rest of the paper proceeds in six parts. Section 2 provides a model overview; section 3 provides details on aftermarket trading; section 4 describes the process for share allocation and price setting at the IPO. Section 5 studies underpricing and underperformance using simulations; section 6 discusses the empirical implications of the model and provides a brief review of the most closely related empirical literature; a final section concludes.
2 Model Overview
The basic model is a stylized IPO in which a firm that wishes to
raise capital by selling ![]() shares of stock enlists a single underwriting
firm to market the issue. To abstract from agency issues, the
underwriter is assumed to act on behalf of the issuer. The
underwriter sells the issue to an investor base that consists of
shares of stock enlists a single underwriting
firm to market the issue. To abstract from agency issues, the
underwriter is assumed to act on behalf of the issuer. The
underwriter sells the issue to an investor base that consists of
![]() risk-averse investors
who participate in the IPO and trade in the aftermarket. Investor 1
represents a continuum of small investors who each take prices as
given. Investors
risk-averse investors
who participate in the IPO and trade in the aftermarket. Investor 1
represents a continuum of small investors who each take prices as
given. Investors ![]() through
through
![]() are large investors
whose desired aftermarket trades are large enough to move asset
prices. Because of differences in their size, the small investors
can be viewed as representing the demands of retail investors,
while the large investors represent the demands of institutional
investors. The process for setting the IPO offer price and share
allocations is modeled as a two-stage game. In the first stage, the
underwriter assesses the demand for the new issue by learning about
the characteristics of the investor base, and about aftermarket
trading conditions. Based on his information, the underwriter sets
a uniform IPO offer price and offers take-it or leave-it share
allocations to the investors.10 In the second stage, investors decide
whether to accept their allocations. Any shares that are turned
down by investors at the IPO are sold by the underwriter in the
aftermarket.
are large investors
whose desired aftermarket trades are large enough to move asset
prices. Because of differences in their size, the small investors
can be viewed as representing the demands of retail investors,
while the large investors represent the demands of institutional
investors. The process for setting the IPO offer price and share
allocations is modeled as a two-stage game. In the first stage, the
underwriter assesses the demand for the new issue by learning about
the characteristics of the investor base, and about aftermarket
trading conditions. Based on his information, the underwriter sets
a uniform IPO offer price and offers take-it or leave-it share
allocations to the investors.10 In the second stage, investors decide
whether to accept their allocations. Any shares that are turned
down by investors at the IPO are sold by the underwriter in the
aftermarket.
In much of the theoretical IPO literature, the primary explanation for underpricing is that it represents equilibrium compensation for various types of information asymmetries in the IPO process.11 To establish that the channels for underpricing and underperformance in the present model do not rely on informational differences, asymmetric information is ruled out by assumption. More specifically, I assume that information on investors' risk preferences, asset holdings, all knowledge of asset values, and the entire model of aftermarket trading is publicly available at all points of time and is common knowledge. The next section formally models the IPO aftermarket; and the following section models the share allocation and price-setting process at the IPO.
3 The IPO aftermarket
The framework for aftermarket trading is a partial equilibrium
extension of Pritsker's (2004) model of imperfect competition in
asset markets.12 Investors in the economy hold
diversified portfolios, but also specialize in trading the assets
that belong to a particular market-segment or industry-group.
Although there are many market segments, most of the analysis
focuses on the assets within a particular segment. For
informational or other reasons, the ![]() investors in the model are the only investors in the
economy that trade and hold the assets within this segment.13 Hereafter, these assets are referred
to as segment-assets. All investors in the economy trade a riskless
asset with gross return
investors in the model are the only investors in the
economy that trade and hold the assets within this segment.13 Hereafter, these assets are referred
to as segment-assets. All investors in the economy trade a riskless
asset with gross return ![]() per period that is in perfectly elastic supply, and a broadly-held
index that is in zero net supply.14 The index proxies for systematic risk
and can be thought of as a futures market. Because the index is
broadly held, the
per period that is in perfectly elastic supply, and a broadly-held
index that is in zero net supply.14 The index proxies for systematic risk
and can be thought of as a futures market. Because the index is
broadly held, the ![]() investors collective trades do not affect the price of the
index.
investors collective trades do not affect the price of the
index.
Risky Assets
The prices of the segment and index assets are ![]() and
and ![]() ; and have stacked price vector
; and have stacked price vector
![]() . The segment-assets
are in fixed supply
. The segment-assets
are in fixed supply ![]() .
The assets pay i.i.d. dividends
.
The assets pay i.i.d. dividends ![]() ,
, ![]() , represented by stacked vector
, represented by stacked vector ![]() , that has distribution:
, that has distribution:
Because prices can be negative, the assets' excess returns are best expressed on a per share basis, and are denoted:
For simplicity
where
Investors
Each investor ![]() chooses risky asset holdings
chooses risky asset holdings ![]() and consumption
and consumption ![]() to maximize his discounted
expected Constant Absolute Risk Aversion (CARA) utility of
consumption:
to maximize his discounted
expected Constant Absolute Risk Aversion (CARA) utility of
consumption:
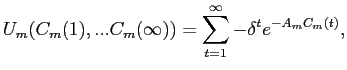
|
(B4) |
with discount factor
| (B5) |
An investor's liquid wealth, ![]() , is that part of her wealth that can be
liquidated at current prices. Because large investors' trades have
price impact, their wealth and liquid wealth differ; and it is
their liquid wealth that appears as an argument in their value
functions. Therefore it is useful to express their budget
constraints in terms of their beginning of period liquid
wealth:
, is that part of her wealth that can be
liquidated at current prices. Because large investors' trades have
price impact, their wealth and liquid wealth differ; and it is
their liquid wealth that appears as an argument in their value
functions. Therefore it is useful to express their budget
constraints in terms of their beginning of period liquid
wealth:
![\begin{displaymath}\begin{split}W_{ml}(t) = Q_{m}^{1} & (t)'D^{1}(t) + Q_{m}^{2}(t)'Z^{2}(t) \\ & + r \left [ W_{ml}(t-1) - \Delta Q^{1}_{m}(t-1)'P^{1}(t-1) - C_{m}(t-1) \right ] \quad t=1,\hdots T. \end{split}\end{displaymath}](img33.gif)
|
(B6) |
Below, I show that investors who differ in their risk-aversion
have different trading styles; this affects other investors ability
to acquire illiquid assets. As a result, which investors hold the
segment assets is a critical argument of investors value functions.
It is summarized by ![]() (
(
![]() vech
vech![]() ), the vector of
all investors segment-asset holdings.
), the vector of
all investors segment-asset holdings.
Trading Dynamics
Segment assets are traded over a total of ![]() time periods. The sequence of
actions is as follows: At the beginning of each period
time periods. The sequence of
actions is as follows: At the beginning of each period ![]() , investors enter the period
with risky-asset holdings
, investors enter the period
with risky-asset holdings
![]() ;
they then receive dividends and choose their risky asset trades
;
they then receive dividends and choose their risky asset trades
![]() . These
trades determine risky asset prices
. These
trades determine risky asset prices ![]() . Investors then choose consumption
. Investors then choose consumption ![]() ; the period ends; and the
same sequence is repeated through time
; the period ends; and the
same sequence is repeated through time ![]() . After period
. After period ![]() , investors continue to consume and
trade other assets, but trading of segment assets ends. The final
period of trade in the segment-assets facilitates solution of the
model via backwards induction.
, investors continue to consume and
trade other assets, but trading of segment assets ends. The final
period of trade in the segment-assets facilitates solution of the
model via backwards induction.
The process of trade for the segment-assets is modeled as a
dynamic Cournot-Stackelberg game of full information. In each
period ![]() , each
small investor optimally computes his demand for the segment assets
conditional on the state-variable
, each
small investor optimally computes his demand for the segment assets
conditional on the state-variable
![]() . Inverting
the aggregated demands of the small investors defines a linear
schedule of prices at which they are willing to absorb all possible
quantities of the large investors trades for the segment
assets:
. Inverting
the aggregated demands of the small investors defines a linear
schedule of prices at which they are willing to absorb all possible
quantities of the large investors trades for the segment
assets:
The matrix
![]() measures
the impact of large investor
measures
the impact of large investor ![]() 's segment asset trades on the price of the segment
assets.15 Large investors account for this price
impact when choosing their trades. Given the price schedule in
equation (7), large investors choose
their time
's segment asset trades on the price of the segment
assets.15 Large investors account for this price
impact when choosing their trades. Given the price schedule in
equation (7), large investors choose
their time ![]() risky asset
trades and consumption choices to solve the maximization
problem:
risky asset
trades and consumption choices to solve the maximization
problem:
subject to the budget constraint:
Large investors' equilibrium trades are found by solving for
trades that are best-responses to each other under the
Cournot-Stackelberg assumption that each large investor chooses his
own trades while taking the price schedule and the trades of the
other large investors as given. The resulting trades within a
period are a Cournot-Nash equilibrium. The model of trade is solved
by backwards induction from period ![]() , and the resulting equilibrium is subgame perfect.
Additional details on model solution and investors' value functions
are contained in the appendix.
, and the resulting equilibrium is subgame perfect.
Additional details on model solution and investors' value functions
are contained in the appendix.
Intuition for the main results on asset prices and trades comes
from examining the first order condition for large investor
![]() 's optimal trade
vector for the segment assets:
's optimal trade
vector for the segment assets:
where
The first term in braces on the right hand side measures the expected net benefit from borrowing money to buy a bit more of a segment asset when trades have no price impact. This is the only term of the first order condition that should be present in a competitive setting. Therefore, in a competitive setting all investors would immediately trade to a point where the first term is equal to 0. When there is imperfect competition, it will never be optimal for a large investor to trade immediately to such a point because the second term in his first order condition would be non-zero, implying his trades had too much price impact. Instead, to reduce their price impact, large investors trade in a way that allows their positions to converge towards a point at which further trade is no longer optimal. Therefore, if a large investor believes an asset is overvalued, or provides too low a return, he will not liquidate its holdings immediately, but will instead sell the asset slowly over time. Because he sells slowly, prices will also adjust slowly, making it possible for low returns to persist in equilibrium, as will be discussed further below.
3.1 Asset
Pricing
The intuition in the previous section and the results below both
show that when markets are illiquid, asset returns will satisfy one
equilibrium relationship when asset holdings are at their long-run
equilibrium, and satisfy a different relationship during the
transition to the long run. To illustrate the exact pricing
relationship, additional notation is required. More specifically,
let
![]() represent
investor
represent
investor ![]() 's long-run
holdings of the segment-assets; these holdings are also the same as
if all investors were price-takers, and are also associated with
the efficient sharing of risks. When risk sharing is efficient,
each investor holds assets in proportion to his risk-tolerance as a
fraction of the sum total of all investors' risk tolerances:
's long-run
holdings of the segment-assets; these holdings are also the same as
if all investors were price-takers, and are also associated with
the efficient sharing of risks. When risk sharing is efficient,
each investor holds assets in proportion to his risk-tolerance as a
fraction of the sum total of all investors' risk tolerances:
The following proposition shows that when markets are illiquid, the deviation from investors' efficient asset holdings behaves like a priced factor when computing one-period returns:
where
Proof: See section D of the appendix.
The proposition is intuitive. Because investors can perfectly
hedge the segment risk that is correlated with the index, the
reward for bearing that risk is exactly the same as is provided by
trading the index. Investors are left to share the segment assets
portfolio of residual risk,
![]() Segment-assets covariance with that residual risk is
Segment-assets covariance with that residual risk is
![]() . I
refer to this covariance as segment risk; segment risk is rewarded
because the investors in the segment cannot diversify it
away.16 In section D.1
of the appendix I show that in a competitive setting, index-risk
and segment-risk are the only priced risks in the model.
. I
refer to this covariance as segment risk; segment risk is rewarded
because the investors in the segment cannot diversify it
away.16 In section D.1
of the appendix I show that in a competitive setting, index-risk
and segment-risk are the only priced risks in the model.
When some investors trades move prices, imperfect risk sharing
among investors introduces additional transient priced factors that
vanish only when investors asset holdings converge to those
associated with perfect risk sharing. Because of illiquidity, the
convergence process takes time; therefore, imperfect risk sharing
at period ![]() affects one
period risk-premia at period
affects one
period risk-premia at period ![]() , as shown in the following corollary:
, as shown in the following corollary:
Proof: See section D of the appendix.
In both the corollary and the proposition, the prices of risk of
the transient factors (the
![]() 's) are
negative because when large investors hold more than their
efficient share of risky assets, the marginal investors, in this
case the small investors, hold less and hence require a smaller
premium for holding the residual risk.
's) are
negative because when large investors hold more than their
efficient share of risky assets, the marginal investors, in this
case the small investors, hold less and hence require a smaller
premium for holding the residual risk.
Potential Explanations for Underperformance
There are two notions of return underperformance after an IPO. The first is that an asset's expected returns in the short-run are lower than its expected returns in the long-run. The second are that its expected returns underperform after adjusting for some benchmark measure of risk. This section deals with the first type of underperformance; the second type of underperformance is discussed in section 5.3.
Corollary 1 illustrates how
underperformance of the first type can occur. More specifically,
because investors trade to efficient asset holdings, the third term
in equation (14) is transient, while the
first two terms are not. Therefore, short-run underperformance will
occur whenever the third-term is negative. Because the market
prices of risk
![]() are
negative, the third term generates return underperformance when
each large investor's IPO share allocation is greater than is
consistent with optimal risk sharing; this is consistent with
allocations being tilted towards institutional investors and away
from retail investors at the IPO.
are
negative, the third term generates return underperformance when
each large investor's IPO share allocation is greater than is
consistent with optimal risk sharing; this is consistent with
allocations being tilted towards institutional investors and away
from retail investors at the IPO.
The magnitude of underperformance depends on whether allocations
are distorted towards large investors, and it depends on the risk
preferences of the large investors that receive the allocations. In
a model with illiquidity, differences in investors' risk tolerances
correspond to differences in investors' willingness to sell assets
quickly and pay a high liquidity cost in order to share risk. The
more risk tolerant large investors are less willing to pay a high a
liquidity cost to share risk; therefore, risk sharing progresses
more slowly when asset allocations are initially tilted towards
them. This reduces the amount of risk that must be borne by the
marginal (small) investors and reduces the assets required rate of
return. Consistent with this reasoning, in simulations the
![]() functions (which measure the impact of allocation distortions
towards investor
functions (which measure the impact of allocation distortions
towards investor ![]() at
time
at
time ![]() on excess returns at
time
on excess returns at
time ![]() ) show that when
allocations are distorted towards large investors with more risk
tolerance, the effect on excess returns is longer-lived and larger
in magnitude.
) show that when
allocations are distorted towards large investors with more risk
tolerance, the effect on excess returns is longer-lived and larger
in magnitude.
The amount and persistence of underperformance also depends on
the competitiveness of the aftermarket. When the aftermarket is
highly competitive, the
![]() functions rapidly asymptote toward 0 as
functions rapidly asymptote toward 0 as ![]() increases, generating little
underperformance. When the aftermarket is less competitive, the
functions asymptote slowly, generating longer-lived
underperformance.
increases, generating little
underperformance. When the aftermarket is less competitive, the
functions asymptote slowly, generating longer-lived
underperformance.
Because IPO allocations affect post-IPO excess returns, they should also affect the initial trading price of the segment assets in the aftermarket. This is established in the appendix17, where I show that segment-asset prices at the beginning of each time period have the form:
where the scalars
5 Simulation Analysis
The model's properties are studied for a single case in which an underwriter sells 40 shares to a continuum of small investors (investor 1) and five large investors (investors 2-6) under a variety of liquidity conditions. For simplicity, the only segment asset is the new issue, and investors risk tolerances are normalized so that they sum to 1.
Aftermarket liquidity depends on the concentration of risk bearing capacity among investors, and on the number of periods of aftermarket trade. An investors share of a segment's risk bearing capacity is his risk tolerance as a percentage of the sum total of all investors risk tolerances. Concentration of risk bearing capacity provides investors with market power in the aftermarket; and this makes the market more illiquid. Results on concentration of risk bearing capacity are reported using the Herfindahl index, which ranges from 10,000 when risk bearing capacity is concentrated with one investor, to 0 when all investors are small and there is no concentration.25
The number of post-IPO trading periods consider ranges from 200 trading days (a bit less than a year) up to 2000 trading days (8 years).26 To explain the relationship between the number of post-IPO trading periods and liquidity, note that the more shares an investor trades within a period, the more he moves the price. Therefore, he would prefer to break up his trades through time to minimize their price impact. When fewer periods of trade remain, opportunities to break up trades are limited; therefore risk sharing becomes more costly. Consequently, shares acquire a greater liquidity premium when fewer periods of trade remain. Conversely, as the number of tradings periods grow, the liquidity premium vanishes and the market becomes perfectly competitive.27 Because my focus is on imperfect competition, I assume the number of trading periods is finite.
To illustrate the role of imperfect competition, the main results focus on two benchmark cases that differ only in whether the investors behave competitively. In both cases, investor 2 has more than a fifty percent share of the segment's risk bearing capacity (Table 1, Panel A); and the other investors differ in their risk tolerances.
When investors behave competitively, and the underwriter must sell all 40 shares, the IPO is no different than if the underwriter sold the shares directly in the aftermarket. Therefore, he raises $420 at the competitive price of $10.50 per share; additionally investors share allocations are proportional to their share of risk bearing capacity, which implies investor 2 should receive 21.82 shares.
When the aftermarket is imperfectly competitive, investor 2's
large share of risk bearing capacity gives him enormous bargaining
power at the IPO, because if he turns down his share allocation
then the underwriter will have to sell shares into an aftermarket
where investor 2 has substantial influence over price.
Alternatively, if the underwriter instead chooses to allocate
shares to other more risk averse investors, then they will be
exploited by investor 2 in the aftermarket--and this will depress
the price that other investors are willing to pay for shares. To
illustrate these points, I studied a sequence of IPOs in which
investor 2 can trade in the aftermarket but is restricted in the
amounts that he can acquire at the IPO. More specifically investor
2's aquistion was progressively restricted to be no larger than
![]() shares.28If the aftermarket is perfectly
competitive, the allocation restrictions are of little consequence
because other investors can aquire the shares at the IPO and then
quickly sell them to investor 2 in the aftermarket at the
competitive price; therefore the IPO offer price is barely
discounted from the competitive price. By contrast, if the
aftermarket is imperfectly competitive, then the IPO offer price is
severely discounted relative to the competitive price; moreover,
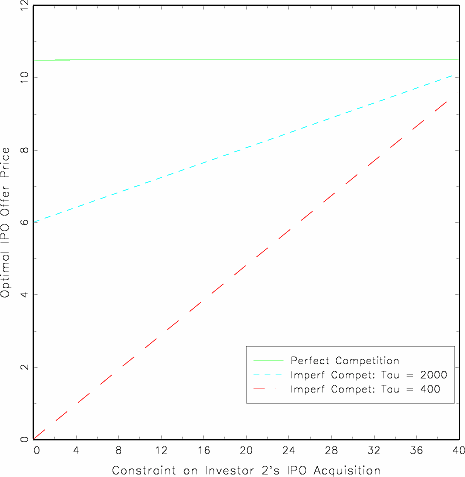
the feasible offer price (Figure 1) and
proceeds (not shown) are monotone increasing in the amount that can
be offered to investor 2 up to the total outstanding supply of the
issue. Investor 2's enormous bargaining power has implications for
allocations and trading volume, as well as for underpricing, and
return underperformance.
shares.28If the aftermarket is perfectly
competitive, the allocation restrictions are of little consequence
because other investors can aquire the shares at the IPO and then
quickly sell them to investor 2 in the aftermarket at the
competitive price; therefore the IPO offer price is barely
discounted from the competitive price. By contrast, if the
aftermarket is imperfectly competitive, then the IPO offer price is
severely discounted relative to the competitive price; moreover,
the feasible offer price (Figure 1) and
proceeds (not shown) are monotone increasing in the amount that can
be offered to investor 2 up to the total outstanding supply of the
issue. Investor 2's enormous bargaining power has implications for
allocations and trading volume, as well as for underpricing, and
return underperformance.
5.1 Allocation Distortions and Trading Volume
Because prices and proceeds are increasing in the amount that investor 2 can purchase, all of the shares are allocated to him at the IPO. This shows that allocations are distorted towards investors who have market power and away from retail investors (who each have none) (Table 1,Panel C). Additionally, among investors with market power, in the example the allocations are distorted towards the large investor with the most power. This illustrates that differences in investors market power provide a noninformation based explanation for why some large investors receive share allocations while others do not.
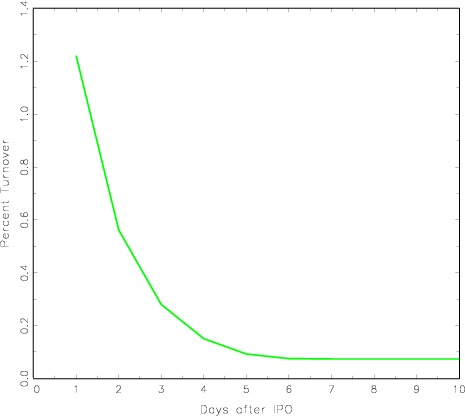
Because allocations at the IPO are not pareto optimal, the distortions create a basis for trade in the aftermarket. The resulting trading volume is heaviest on the first day of trading, constituting 1.2 percent of shares issued; daily volume drops off to about 0.1 percent of shares issued after the first week of trading (Figure 2). The example's pattern of heavy trading volume that rapidly drops off is qualitatively consistent with the empirical literature on post-IPO trading (Ellis et al. 2000), but the model fails to match the empirical magnitude of the first day's trading, which averaged 33.3 percent of shares issued in the 1980's, and 148.7 percent of shares issued in 1999-2000 (Ritter, 2005).
5.2 IPO Underpricing
The example shows the model is capable of generating substantial IPO underpricing. Underpricing ranges from a low of 40 percent when many trading periods remain to a high of 159 percent when relatively few periods remain (Table 1, Panel B). The underpricing has three pronounced features. First, the offer price is low relative to the asset's competitive price. Second, the aftermarket price is inflated relative to the asset's competitive price. If the competitive price is interpreted as the asset's "fundamental value" then it appears as if the IPO is associated with irrational price-overshooting even though the model is fully rational. The third feature is that the first two features are most pronounced when there are fewer periods of trade following the IPO.
Intuition for the first feature is related to investor 2's bargaining power; additional intuition for the underpricing comes from interpreting illiquidity as a tax on risk sharing. Because the tax makes risk sharing more costly, it pushes down the IPO offer price; in addition because of the tax less risk sharing takes place, which means investor 2 sells less in the aftermarket--and this constraint on supply pushes up the aftermarket price. When fewer trading periods remain, illiquidity is more severe, making the first two features more pronounced.
5.3
Underperformance
Recall that there are two types of return
underperformance--underperformance relative to an assets long-run
return--and underperformance relative to a risk adjusted benchmark.
Section 3.1 shows that the former is
associated with IPOs; to address the latter, post-IPO expected
excess returns were computed for up to 2000 business days and then
adjusted for market-risk by subtracting the asset's beta times the
expected excess return on the market portfolio. To compute the
excess return on the market portfolio, I aggregated up the excess
returns across all market segments. Recall from equation (12) (reproduced below) that in each segment
![]() , assets excess
expected returns can be decomposed into a component that is
correlated with the index, a second that is associated with market
segmentation (due to imperfect sharing of idiosyncratic risk), and
a third that is associated with allocation distortions and
illiquidity:
, assets excess
expected returns can be decomposed into a component that is
correlated with the index, a second that is associated with market
segmentation (due to imperfect sharing of idiosyncratic risk), and
a third that is associated with allocation distortions and
illiquidity:
![LaTex Encoded Math: \displaystyle \bar{Z}^{j}(t) = \beta_{j2} \bar{Z}^{2}(t) + \lambda_{[X^{j}]} \Omega_{e_{j}} X^{j} + \sum_{m=2}^{M_{j}} \lambda(m,t) \Omega_{e_{j}} (Q^{j}_{m}(t) - Q^{jW}_{m}).](img90.gif)
Under these circumstances, if investors trade the liquid index and specialize in trading the assets within different market-segments, then in the context of a one-period example (appendix F), the assets in each segment and the market portfolio earn a segmentation premium. Therefore, after adjustment for market-risk, the assets average segmentation premia are 0, and do not depend on whether the assets are new issues. Using similar reasoning, because relatively few firms are new issues, these firms will only have a minor effect on the market return. Therefore, after market adjustment, IPO firms will retain a large negative liquidity premium; that is they will underperform on a risk-adjusted basis.
Under simplifying circumstances (see appendix F), if ![]() is the fraction of firms that are new issues,
then the average market adjusted underperformance at time
is the fraction of firms that are new issues,
then the average market adjusted underperformance at time
![]() for segments with
IPO's should be approximately
for segments with
IPO's should be approximately ![]() times the allocation distortion / liquidity
component of excess returns:
times the allocation distortion / liquidity
component of excess returns:
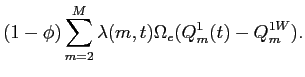
5.3.1 Adjusting for Characteristics
A stylized fact of measured underformance is that it is strongest when returns are market-adjusted, and weaken after adjustment for additional characteristics such as market-to-book (Ritter and Welch, 2002). Under some interpretations, these stylized facts are consistent with the liquidity-based explanation in the model; in particular, if assets' long-run competitive prices are interpreted as book-value, then the model predicts that because of illiquidity and allocation distortions at the IPO, then just after the IPO, market to book is high and consistent with the market-to-book effect, IPO returns underperform. It is important to bear in mind that in the empirical asset pricing literatature, market-to-book's ability to explain asset returns is an empirical regularity, not a theory of asset pricing. The contribution of the present model is that it provides a theoretical reason why market-to-book appears to "explain" post IPO return underperformance. This result has empirical implications; in particular, it shows that controlling for market-to-book can be problematic when testing the present model because a finding of no underperformance after adjustment for market-to-book is consistent with the model, and not evidence against it. This topic is discussed further in footnote 33 of section 6.1.
5.4 Money Left on the Table
IPO underpricing makes it appears as if the IPO should have raised more revenue. The loss in revenue is referred to as "money left on the table", hereafter MLOTT, and is usually measured as the differential between the IPO-offer price and closing price on the first day of trade times the number of shares issued. MLOTT often has the interpretation of a measure of the issuer's losses due to imperfections in the IPO process.29 For the present model, the imperfection is illiquidity; and it should be clear that the usual MLOTT calculation overstates issuer losses because it incorrectly assumes that all of the shares could be sold at the artificially high price that prevails in an illiquid aftermarket. An alternative measure of MLOTT instead compares the revenues that were raised at the IPO against the revenues that could have been raised if the aftermarket was perfectly competitive, which in this model means perfectly liquid. Computing losses by this alternative metric shows that the usual calculation can very significantly overstate issuer losses; in the case of the example it overstates them by a factor of 5 to 10 (Table 1, Panel B).
5.5 Alternative market configurations
To study how differences in investors risk tolerances affect the
results, I solved the model under two alternative market
configurations. In the first, some of investor 2's risk tolerance
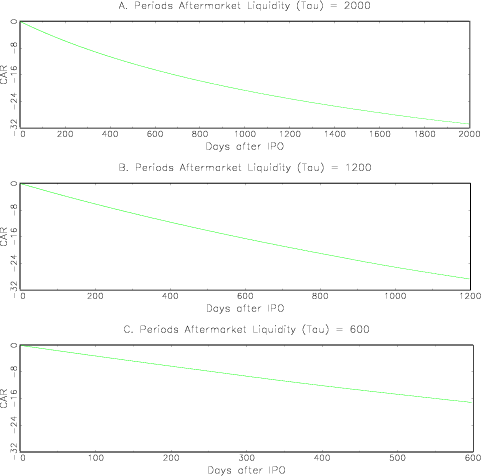
is spread evenly among the other large investors (Table 2). This change makes the aftermarket more competitive,
and has three further effects on the aftermarket. First, when the
number of aftermarket trading periods is ![]() , or
, or ![]() , the market is sufficiently
competitive that differences in who receives shares at the IPO have
a very small effect on prices (no more than 6 cents per share). In
this circumstance, the optimal allocation problem is ill-posed. I
simply assume that the competitive allocation results in these
cases. Second, the magnitude and persistence of underperformance
diminish somewhat, with the liquidity component of the CAR reduced
to -16 percent over 5 years. Third, the prices charged by the
underwriter at the IPO are actually above the competitive price.
This occurs because when the aftermarket is a little bit more
competitive, investor 2 has less market power in the aftermarket,
and hence has less bargaining power at the IPO. In this
circumstance, the underwriter can extract some of investor 2's
surplus from acquiring the new issue. Because the aftermarket is
still not perfectly liquid, the aftermarket price is inflated above
the IPO offer price, but now the underwriter is actually generating
more revenue for the issuer than if the aftermarket were
competitive. Compared with the earlier results, this shows that the
underwriter and issuer actually benefit if the aftermarket is a bit
less than perfectly competitive, but is hurt if the aftermarket
becomes too imperfectly competitive. Because a little bit of
imperfect competition can sometimes help the underwriter, this
result may help to explain underwriter practices that restrain
trade in the aftermarket, such as restrictions on investors ability
to flip shares.
, the market is sufficiently
competitive that differences in who receives shares at the IPO have
a very small effect on prices (no more than 6 cents per share). In
this circumstance, the optimal allocation problem is ill-posed. I
simply assume that the competitive allocation results in these
cases. Second, the magnitude and persistence of underperformance
diminish somewhat, with the liquidity component of the CAR reduced
to -16 percent over 5 years. Third, the prices charged by the
underwriter at the IPO are actually above the competitive price.
This occurs because when the aftermarket is a little bit more
competitive, investor 2 has less market power in the aftermarket,
and hence has less bargaining power at the IPO. In this
circumstance, the underwriter can extract some of investor 2's
surplus from acquiring the new issue. Because the aftermarket is
still not perfectly liquid, the aftermarket price is inflated above
the IPO offer price, but now the underwriter is actually generating
more revenue for the issuer than if the aftermarket were
competitive. Compared with the earlier results, this shows that the
underwriter and issuer actually benefit if the aftermarket is a bit
less than perfectly competitive, but is hurt if the aftermarket
becomes too imperfectly competitive. Because a little bit of
imperfect competition can sometimes help the underwriter, this
result may help to explain underwriter practices that restrain
trade in the aftermarket, such as restrictions on investors ability
to flip shares.
The second alternative market configuration contained two dominant large investors that each have 30% of the risk bearing capacity.30 Because this configuration was highly competitive, unless a small number of trading periods followed the IPO, results are only discussed for when there are 200 post-IPO trading periods. Unlike the previous examples in which the optimum involved allocating all of the shares to one investor, in this example the optimal share allocations involved splitting the shares evenly between investors 2 and 3 while distorting the share allocations away from all other investors. As in the previous example, the resulting IPO offer price was above the price that would prevail if the aftermarket was perfectly competitive. Nevertheless, the aftermarket price following the IPO was even higher, resulting in IPO underpricing of about 12%. Additionally, cumulative abnormal returns indicate short-lived underperformance; the liquidity component of the underperformance was 4.5% over 200 trading days.
6 Empirical Implications
The purpose of this section is to outline a rough strategy for testing the theory in this paper. The main implication of the theory is that IPO illiquidity and imperfect competition in the aftermarket following an IPO lead to allocation distortions towards large investors and IPO underpricing and underperformance. These implications lead to the following testable predictions:
- Allocation distortions are associated with underperformance in the aftermarket.
- Allocation distortions are associated with IPO underpricing.
- The above two effects are associated with illiquidity and imperfect competition in aftermarket trading.
Prediction 1 imposes restrictions on the coefficients of empirical versions of equation (14):
The empirical version provided above differs from equation
(14) because it is parameterized with
additional ![]() coefficients, and because expected excess returns have been
replaced by their realization on the left hand-side, which
introduces an expectational error
coefficients, and because expected excess returns have been
replaced by their realization on the left hand-side, which
introduces an expectational error
![]() on
the right-hand side. The main coefficient of interest is
on
the right-hand side. The main coefficient of interest is
![]() . Under the
null hypothesis that allocation distortions at the IPO are
unrelated to underperformance,
. Under the
null hypothesis that allocation distortions at the IPO are
unrelated to underperformance, ![]() should be equal to 0; while under the
alternative
should be equal to 0; while under the
alternative ![]() should be positive and the coefficients
should be positive and the coefficients
![]() should
be negative. Estimation of
should
be negative. Estimation of ![]() in cross-section requires information on
in cross-section requires information on
![]() and
investors holdings of all assets within each segment. However, if
and
investors holdings of all assets within each segment. However, if
![]() is nearly
diagonal, or if allocation distortions are only significantly
different from zero for new issues, then it is sufficient to create
an allocation distortion measure for each new issue that only
depends on its own idiosyncratic risk and own asset holdings. This
simplified approach is outlined below.
is nearly
diagonal, or if allocation distortions are only significantly
different from zero for new issues, then it is sufficient to create
an allocation distortion measure for each new issue that only
depends on its own idiosyncratic risk and own asset holdings. This
simplified approach is outlined below.
The allocation distortion measure that I propose for firm
![]() has the form:
has the form:
distort![LaTex Encoded Math: \displaystyle _{i} = \Omega_{ii} \sum_{m=2}^{M} g(RBC_{m}) \left [ \frac{x_{m}}{\sum_{m=1}^{M} x_{m}} - RBC_{m} \right ],](img102.gif)
|
(B23) |
where
Proxies for ![]() are needed to operationalize the distortion measure. Because the
model assumes that investors have CARA utility primarily for
tractability, a sensible way to proceed is to use a more realistic
assumption about investors utility. For example, if all investors
have power utility with coefficient of relative risk aversion
are needed to operationalize the distortion measure. Because the
model assumes that investors have CARA utility primarily for
tractability, a sensible way to proceed is to use a more realistic
assumption about investors utility. For example, if all investors
have power utility with coefficient of relative risk aversion
![]() , then investors
absolute risk tolerance is
, then investors
absolute risk tolerance is
![]() , and each
investors risk bearing capacity is equal to their own wealth as a
fraction of the sum total of the wealth of other investors in the
segment (
, and each
investors risk bearing capacity is equal to their own wealth as a
fraction of the sum total of the wealth of other investors in the
segment (
![]() ).31 Since wealth is a measure of
investors's size, the allocation distortion measure them becomes a
measure of how assets are allocated relative to the size of the
investors involved. Armed with this measure of allocation
distortions it should be possible to test prediction 1 by
estimating variants of equation (22) in
cross-section and then test whether
).31 Since wealth is a measure of
investors's size, the allocation distortion measure them becomes a
measure of how assets are allocated relative to the size of the
investors involved. Armed with this measure of allocation
distortions it should be possible to test prediction 1 by
estimating variants of equation (22) in
cross-section and then test whether ![]() is positive.32. A full analysis of how to estimate
the equation is well beyond the scope of the present paper. To test
prediction 2, the same measures of allocation distortions that are
used to estimate equation (22) can be used
to attempt to explain the cross-section of IPO underpricing.
is positive.32. A full analysis of how to estimate
the equation is well beyond the scope of the present paper. To test
prediction 2, the same measures of allocation distortions that are
used to estimate equation (22) can be used
to attempt to explain the cross-section of IPO underpricing.
To test the third prediction, measures of aftermarket illiquidity should be interacted with the allocation distortion variable. The theory predicts that the allocation distortions should only have an effect when there is illiquidity in the aftermarket. Hence, the interaction with the illiquidity variables should provide a sharper test of theory. The coefficients on the interaction terms are expected to have the same sign as the coefficients on the allocation distortions, and including these terms should cause the coefficients on the allocation distortions to weaken.
Allocation distortions are predicted by other theories, such as for example bookbuilding and adverse selection, in which the allocations are based on investors information. However, neither of those theories predicts a relationship between allocation distortions and IPO return underperformance. Therefore, if allocation distortions explain both underpricing and underperformance, it should be interpreted as evidence that an explanation based on illiquidity and imperfect competition in the aftermarket helps contribute to our understanding of IPOs.
To close this section, I briefly review the most closely related empirical literature on underpricing and underperformance.
6.1 Related
literature
The empirical literature that is most closely related to this paper studies the relationship between after-market liquidity and underpricing or underperformance. The relationship between IPO underpricing and illiquidity has been empirically studied by Booth and Chua (1996), Hahn and Ligon (2004), and Ellul and Pagano (2003). In closely related work, Butler et. al. (2005) study the relationship between a stock's liquidity, and the underwriting fees that are paid during a seasoned equity offering.
Although the Booth and Chua model makes predictions about the relationship between underpricing and aftermarket liquidity, they don't test this implication of their model; instead their tests focus on underpricing as compensation for costs of information gathering. Because such costs could generate underpricing irrespective of illiquidity, the implications of their tests for the relationship between underpricing and aftermarket liquidity are unclear. Hahn and Ligon attempt to directly test the Booth and Chua hypothesis that underpricing is used to increase liquidity by running OLS regressions of market microstructure measures of aftermarket liquidity on IPO underpricing. In regressions that account for other determinants of illiquidity, their results are mixed; with coefficients on underpricing sometimes statistically significant and positive, sometimes statistically significant and negative, and sometimes not statistically significant at all. A potential difficulty with the Hahn and Ligon methodology is that causality may run from underpricing to illiquidity (as in Booth and Chua) as well as from illiquidity to underpricing (as in Ellul and Pagano). The possibility that causality runs in both directions suggests that an instrumental variable approach is needed. In Ellul and Pagano, they regress underpricing on a set of determinants for underpricing, including measures of aftermarket liquidity. Additionally, they recognize the potential for simultaneity bias and instrument for it in some of their regressions.33 In all of Ellul and Pagano's regressions they find that more aftermarket illiquidity increases the amount of IPO underpricing. Butler et. al. find qualitatively similar relationship between illiquidity and underwriter fees in SEO's, but quantitatively the effects of illiquidity are much smaller than in Ellul and Pagano. This suggests the Ellul and Pagano results, while favorable for liquidity based theories, should be interpreted with caution. An additional reason for caution is if underpricing is a risk premium for aftermarket illiquidity, then the logical extension of Ellul and Pagano's theory would suggest that in the aftermarket, IPO's should earn a positive and significant risk premium for aftermarket illiquidity. If we believe the empirical evidence that IPO returns underperform in the aftermarket, this suggests that the mechanism driving aftermarket returns is more complicated than the theory of illiquidity considered by Ellul and Pagano. Eckbo and Norli (2002) take this argument one step further; they claim that newly issued stocks are more liquid than other stocks with similar risk characteristics; and thus their returns should underperform. To establish this point empirically, Eckbo and Norli compare the returns of a rolling portfolio of newly issued stocks that are held for up to five years against the returns a portfolio of more seasoned issues that are matched on size and book to market. They find that after adjusting for these factors, and controlling for differences in liquidity, new issues do not underperform.
The Eckbo and Norli and Ellul and Pagano findings, taken
together are puzzling because the latter suggests that IPOs are
very illiquid, while the former suggests the opposite. Both papers
can only be correct if liquidity conditions change rapidly after
the IPO, and if participants in IPOs are very concerned about a
short-term need to liquidate. This paper points towards a different
resolution in which illiquidity, when combined with imperfect
competition, generates both underpricing and underperformance. To
make a strong case that this is the correct resolution requires
careful future research on how to measure underperformance and
which measures of liquidity are relevant for large
investors.34![]() 35
35
7 Conclusions
In this paper I have presented a fully-rational, symmetric-information model to simultaneously explain IPO underpricing, underperformance, and a tilt in IPO share allocations towards institutional investors, and away from retail investors. The key model features that generate these results are illiquidity and imperfect competition in aftermarket trading. The model also generates a new set of testable predictions that tie the market structure of aftermarket trading and allocation distortions at the IPO, to the cross-sectional pattern of return underperformance following an IPO. Hopefully the results in this paper will stimulate new empirical research that studies the relationship between the structure of the IPO aftermarket trading environment and IPO underpricing and underperformace.
8 Notation
There are ![]() investors and
investors and
![]() risky assets. The first
risky assets. The first ![]() assets are illiquid. The next
assets are illiquid. The next ![]() assets are perfectly liquid.
The risky asset holdings of investor
assets are perfectly liquid.
The risky asset holdings of investor ![]() at time
at time ![]() are denoted by
are denoted by
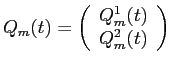
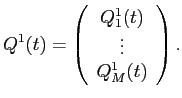
![]() represents the net asset holdings of a continuum of infinitesimal
small investors indexed by
represents the net asset holdings of a continuum of infinitesimal
small investors indexed by ![]() :
:
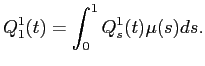
The algebra which follows requires many matrix summations and
the use of selection matrices. Rather than write summations
explicitly, I use the matrix
![]() to perform summations
where
to perform summations
where ![]() is an
is an
![]() by
by ![]() vector of ones, and
vector of ones, and ![]() is the
is the
![]() identity
matrix.36 In some cases, the matrix
identity
matrix.36 In some cases, the matrix ![]() may have different dimensions to
conform to the vector whose elements are being added. In all such
cases,
may have different dimensions to
conform to the vector whose elements are being added. In all such
cases, ![]() will always
have
will always
have ![]() , or
, or ![]() rows. The matrix
rows. The matrix ![]() is used for selecting
submatrices of a larger matrix.
is used for selecting
submatrices of a larger matrix. ![]() has form
has form
In the rest of the exposition, I will occasionally suppress time subscripts to save space.
9 Proof of Proposition 2
Large investor
and the price function for illiquid assets has the functional form:
Proof: The proof is by induction. Part I of the proof
establishes that if the value function has this form at time
![]() , then it has the same
form at time
, then it has the same
form at time ![]() . Part II of
the proof establishes the result for time
. Part II of
the proof establishes the result for time ![]() , the first period in which trade
cannot occur.
, the first period in which trade
cannot occur.
9.1 Part I:
Suppose the form of the value function is correct for time
![]() . Then, to establish
the form of the value function at time
. Then, to establish
the form of the value function at time ![]() , I first solve for the competitive
fringe's demand curve for absorbing the net order flow of the large
investors. I then solve the large investors and competitive
fringe's equilibrium portfolio and consumption choices, and then
solve for the value function at time
, I first solve for the competitive
fringe's demand curve for absorbing the net order flow of the large
investors. I then solve the large investors and competitive
fringe's equilibrium portfolio and consumption choices, and then
solve for the value function at time ![]() .
.
9.1.1 The competitive fringe's demand curve
The competitive fringe represents a continuum of infinitesimal
investors that are distributed uniformly on the unit interval with
total measure 1, i.e.
![]() for
for
![]() . At time
. At time
![]() , each participant
, each participant
![]() of the competitive
fringe solves:
of the competitive
fringe solves:
where, ![]() is the
stacked vector of small investor
is the
stacked vector of small investor ![]() 's holdings of illiquid (
's holdings of illiquid (![]() ) and perfectly liquid
(
) and perfectly liquid
(![]() ) risky
assets:
) risky
assets:
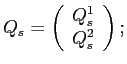
![]() is the stacked
vector of excess returns for the illiquid and liquid assets:
is the stacked
vector of excess returns for the illiquid and liquid assets:
and small investors liquid wealth is given by
In equation (B5),
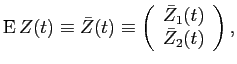
and
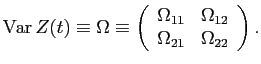
Substituting the expression for ![]() in (B4) and taking
expectations shows that small investors maximization becomes:
in (B4) and taking
expectations shows that small investors maximization becomes:
In solving the model, it is useful to break small investors
maximization into pieces by first solving for optimal ![]() as a function of
as a function of
![]() , and then
solving for optimal
, and then
solving for optimal ![]() . For given
. For given ![]() , the first order condition for optimal
, the first order condition for optimal
![]() shows that
optimal
shows that
optimal ![]() is
given by
is
given by
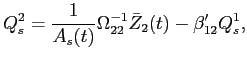
|
(B7) |
where
Plugging the solution for ![]() into the small investors value function and
simplifying then shows that the small investors maximization
problem reduces to:
into the small investors value function and
simplifying then shows that the small investors maximization
problem reduces to:
where
To gain intuition for the above expression, note that the excess return on each illiquid asset can be decomposed into a component that is correlated with the liquid assets and into a second idiosyncratic component.
![]() is the vector
of expected returns on the idiosyncratic components at time
is the vector
of expected returns on the idiosyncratic components at time
![]() and
and
![]() is the
variance covariance matrix of the idiosyncratic returns. The
expression shows that small investors portfolio maximization
problem can equivalently be written in terms of choosing an
exposure to the returns of the liquid assets, and to the
idiosyncratic component of returns of the illiquid assets.
is the
variance covariance matrix of the idiosyncratic returns. The
expression shows that small investors portfolio maximization
problem can equivalently be written in terms of choosing an
exposure to the returns of the liquid assets, and to the
idiosyncratic component of returns of the illiquid assets.
Solving for optimal
![]() then
shows
then
shows
The aggregate demand for ![]() at time
at time ![]() by all small investors can be found by integrating
both sides of equation (B9) with respect to
by all small investors can be found by integrating
both sides of equation (B9) with respect to
![]() , the density
of small investors, yielding:
, the density
of small investors, yielding:
9.1.2 The Price Schedule Faced by Large Investors
The price schedule faced by large investors at time ![]() maps large investors desired
orderflow of the illiquid assets into the time
maps large investors desired
orderflow of the illiquid assets into the time ![]() prices at which the competitive
fringe is willing to absorb the net orderflow. To solve for the
price schedule, I solve for prices
prices at which the competitive
fringe is willing to absorb the net orderflow. To solve for the
price schedule, I solve for prices ![]() in equation (B10)
such that when the large investors choose trade
in equation (B10)
such that when the large investors choose trade
![]() at time t-1, then the competitive fringe chooses trade
at time t-1, then the competitive fringe chooses trade
![]() .
.
Rearranging, equation (B10) while
making the substitutions
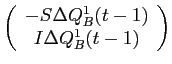
|
and
![LaTex Encoded Math: \displaystyle \frac{1}{r} \left ( \alpha(t) - \Gamma(t) [Q^{1}(t-1) + \Delta Q^{1}(t-1)] \right )](img185.gif)
|
then produces the price schedule faced by large investors at time
where,
Given the price schedule in equation (B11), large investors at time ![]() solve the maximization problem:
solve the maximization problem:
9.1.3 Large Investors Maximization Problem
where, substituting in the budget constraint, liquid wealth at
the beginning of time ![]() is given by
is given by
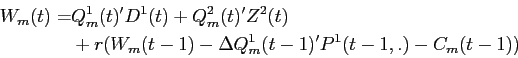
|
(B16) |
Note: Because dividends are paid in cash, the dividend payments received for holdings of illiquid asset are counted as part of liquid wealth even though the illiquid assets themselves are not counted.
Note that in equation (B15),
![]() and
and
![]() are
deterministic functions of time that are parameters of the value
function. Keeping this in mind, large investors holdings of the
liquid assets are solved in the same way as for small investors.
Taking expectations in equation (B15), solving
for optimal
are
deterministic functions of time that are parameters of the value
function. Keeping this in mind, large investors holdings of the
liquid assets are solved in the same way as for small investors.
Taking expectations in equation (B15), solving
for optimal ![]() given
given ![]() , and
substituting the optimal choice back into the large investor's
value function, transforms the large investors maximization problem
so that it has the following form:
, and
substituting the optimal choice back into the large investor's
value function, transforms the large investors maximization problem
so that it has the following form:
where,
The large investors play a Cournot game in which each choose his
time ![]() trade
trade
![]() in
the illiquid assets to solve the maximization problem in (B17) while taking the trades of the other large
investors as given, but while taking into account the effect that
his own trades have on the prices of the illiquid assets. Recall
the price impact function for the illiquid assets at time
in
the illiquid assets to solve the maximization problem in (B17) while taking the trades of the other large
investors as given, but while taking into account the effect that
his own trades have on the prices of the illiquid assets. Recall
the price impact function for the illiquid assets at time
![]() is given by equation
(B11).
is given by equation
(B11).
The first order condition for large investors illiquid asset choices is given by:
After substituting for
![]() from
equation (B11), writing
from
equation (B11), writing
![]() as
as
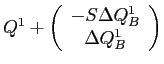 and simplifying, this produces the following reaction
function for large investor
and simplifying, this produces the following reaction
function for large investor ![]() :
:
where,
![\begin{displaymath}\begin{split}\pi_{m}(t-1) = & A_{m}(t) (-S_{1} + S_{m})[(\theta_{m}(t) + \theta_{m}(t)')/2]\left( \begin{array}{c} -S \\ I \end{array} \right ) \\ & - \beta_{Q^{1}_{B}}(t-1) - S_{m} \beta_{Q^{1}_{B}}(t-1)' S_{m} \\ \end{split}\end{displaymath}](img209.gif)
|
(B22) |
Stacking the (M-1) reaction functions produces a system of
![]() linear
equations in
linear
equations in ![]() unknowns:
unknowns:
Assume that ![]() is invertible. Then the solution for
is invertible. Then the solution for
![]() is unique, and given by
is unique, and given by
9.1.4 Equilibrium Asset Holdings
The solution for
![]() is
is
![]() . Therefore, the solution for
. Therefore, the solution for
![]() can be written as:
can be written as:
where,
With the above notation, the equilibrium purchases by large
participant ![]() in period
in period
![]() are given by
are given by
Additionally, the equilibrium transition dynamics for beginning of period illiquid risky asset holdings are given by:
where
9.1.5 Equilibrium Price Function
Recall that the equilibrium price function in each time period
maps investors beginning of period holdings of risky assets to an
equilibrium price after trade. The equilibrium price function for
period ![]() is found by
plugging the solution for large investors equilibrium trades from
equation (B26) into the price schedule faced
by large investors (equation (B11)). The
resulting price function for illiquid asset in period
is found by
plugging the solution for large investors equilibrium trades from
equation (B26) into the price schedule faced
by large investors (equation (B11)). The
resulting price function for illiquid asset in period ![]() has form:
has form:
where,
9.1.6 Large Investors Consumption
Large investors optimal time ![]() consumption depends on optimal time
consumption depends on optimal time ![]() trades. After plugging the
expressions for equilibrium prices, and equilibrium trades
[equations (B30), (B31),
and (B27)] into equation (B17), large investors consumption choice problem has
form:
trades. After plugging the
expressions for equilibrium prices, and equilibrium trades
[equations (B30), (B31),
and (B27)] into equation (B17), large investors consumption choice problem has
form:
where
![\begin{displaymath}\begin{split}\psi_{m}(Q^{1}, W_{m}(t-1),t-1) = & e^{-.5 \bar{Z}^{2}'\Omega_{22}^{-1} \bar{Z}^{2} -A_{m}(t) r W_{m}(t-1)} \\ & \times e^{+A_{m}(t) r [S_{m}(H_{0}(t-1) + H_{1}(t-1)Q^{1}(t-1)]'(\alpha(t-1) - \Gamma(t-1) Q^{1}(t-1))/r } \\ & \times e^{-A_{m}(t) (G_{0}(t-1) + G_{1}(t-1) Q^{1}(t-1))'\bar{v}_{m}(t)} \\ & \times e^{ .5 A_{m}(t)^{2} [G_{0}(t-1) + G_{1}(t-1) Q^{1}(t-1)]'\theta_{m}(t) [G_{0}(t-1) + G_{1}(t-1) Q^{1}(t-1)]} \end{split}\end{displaymath}](img233.gif)
|
(B35) |
The first order condition for choice of consumption implies that optimal consumption is given by:
9.1.7 Large investors value function at time
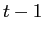
Define
![]() as the value function to
large investor
as the value function to
large investor ![]() from
entering period
from
entering period ![]() when
the vector of illiquid risky asset holdings is
when
the vector of illiquid risky asset holdings is ![]() , and his liquid asset holdings
are
, and his liquid asset holdings
are
![]() . After
substituting the optimal consumption choice in (B36) into equation (B34),
this value function is given by:
. After
substituting the optimal consumption choice in (B36) into equation (B34),
this value function is given by:
where,
Tedious algebra then shows that large investor ![]() 's value function at time
's value function at time
![]() has form:
has form:
where the parameters of the value function at time ![]() are given by the following Riccati
difference equations.
are given by the following Riccati
difference equations.
9.1.8 Small investors optimal consumption
The solution for each small investors consumption depends on
small investors optimal trades. To solve for optimal consumptions,
I first use equation (B9) to substitute out
for ![]() in equation
(B8). I then substitute out for
in equation
(B8). I then substitute out for
![]() with the
expression:
with the
expression:
| (B44) |
where,
Finally I substitute out
where,
![\begin{displaymath}\begin{split}\psi_{s}(Q^{1}(t-1),W_{s}(t-1),& t-1) = e^{-A_{s}(t) r W_{s}(t-1) -.5 \bar{Z}_{2}'\Omega_{22}^{-1} \bar{Z}_{2}} \\ \times & e^{-.5 [a_{0}(t-1) + a_{1}(t-1) Q^{1}(t-1)]'\Omega_{e}^{-1}[a_{0}(t-1) + a_{1}(t-1) Q^{1}(t-1)]} \\ \times & e^{-[G_{0}(t-1) + G_{1}(t-1) Q^{1}(t-1)]'\bar{v}_{s}(t)}\\ \times & e^{ - [G_{0}(t-1) + G_{1}(t-1) Q^{1}(t-1)]' \theta_{s}(t) [G_{0}(t-1) + G_{1}(t-1) Q^{1}(t-1)]} \end{split}\end{displaymath}](img253.gif)
|
(B48) |
The first order condition for choice of optimal consumption implies that optimal consumption is given by:
9.1.9 Small investors value function at time
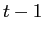
Define
![]() as the value function
to small investor
as the value function
to small investor ![]() from
entering period
from
entering period ![]() when
the vector of illiquid risky asset holdings is
when
the vector of illiquid risky asset holdings is
![]() , and his
liquid wealth is
, and his
liquid wealth is
![]() . After
substituting the optimal consumption choice in (B49) into equation (B47), this value function is given by:
. After
substituting the optimal consumption choice in (B49) into equation (B47), this value function is given by:
where,
| (B51) |
Simplification then shows that the value function has form:
The parameters in the small investors value functions at time
![]() are a function of
time
are a function of
time ![]() parameters as
expressed in the following Riccati equations:
parameters as
expressed in the following Riccati equations:
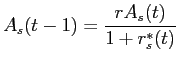
|
(B53) |
![\begin{displaymath}\begin{split}k_{s}(t-1) = & \left [ \frac{r^{*}_{s}(t) + 1}{r^{*}_{s}(t)} \right ] \left [\delta k_{s}(t-1) r^{*}_{s}(t) e^{-.5 \bar{Z}^{2}'\Omega_{22}^{-1} \bar{Z}^{2}} \right ]^{\frac{1}{1+r^{*}_{s}(t)}} \\ & \times \operatorname{Exp}\left \{\frac{ - a_{0}(t-1)'\Omega_{e}^{-1} a_{0}(t-1) - G_{0}(t-1)'\bar{v}_{s}(t) - G_{0}(t-1)'\theta_{s}(t) G_{0}(t-1)}{1+r^{*}_{s}(t)} \right \}, \end{split}\end{displaymath}](img263.gif)
|
(B54) |
This completes part I of the proof because equations (B39) and (B52) verify
that the value functions at time ![]() have the same form as at time
have the same form as at time ![]() .
.
9.2 Part II
To establish part II of the proof, I need to show that investors
value functions for entering entering period ![]() , the last period of trade, has the
same functional form as given in the proposition. To establish this
result, I first need to solve for investors value function at time
, the last period of trade, has the
same functional form as given in the proposition. To establish this
result, I first need to solve for investors value function at time
![]() , the first period
when investors cannot trade the illiquid assets (recall they can
continue to trade the riskless asset and the liquid assets
indefinitely). Then, given this value function, I use backwards
induction to solve for investors value function at time
, the first period
when investors cannot trade the illiquid assets (recall they can
continue to trade the riskless asset and the liquid assets
indefinitely). Then, given this value function, I use backwards
induction to solve for investors value function at time
![]() .
.
9.2.1 Investors Value
Functions at Time T+1
Recall that investors are infinitely lived but that from time
![]() onwards they cannot
alter their holdings of illiquid assets, but they can continue to
alter their consumption, and their holdings of liquid and riskless
assets. Because investors cannot trade in period
onwards they cannot
alter their holdings of illiquid assets, but they can continue to
alter their consumption, and their holdings of liquid and riskless
assets. Because investors cannot trade in period ![]() and after, the distinction
between small and large investors after this period is irrelevant.
Hence, the index
and after, the distinction
between small and large investors after this period is irrelevant.
Hence, the index ![]() used
below could be for either a large or small investor. Using the
Bellman principle, the value function
used
below could be for either a large or small investor. Using the
Bellman principle, the value function ![]() of entering period
of entering period
![]() (
(![]() ) with illiquid asset holdings
) with illiquid asset holdings
![]() and liquid
wealth
and liquid
wealth ![]() satisfies the functional equation:
satisfies the functional equation:
where,
and,
Inspection shows that the function
with
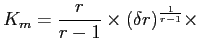 exp
exp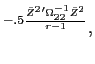
Given the value function at time ![]() , to solve for investors value functions at time
, to solve for investors value functions at time
![]() , I follow the same
steps as in equations (B4) through equation
(B56). Therefore, substituting in from
equation (B59), small investors
maximization problem at time
, I follow the same
steps as in equations (B4) through equation
(B56). Therefore, substituting in from
equation (B59), small investors
maximization problem at time ![]() has form:
has form:
such that,
| (B61) |
where,
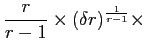 exp
exp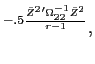
|
(B62) | ||
| (B63) | |||
![LaTex Encoded Math: \displaystyle \frac{(1/r)[\bar{D}^{1} - \beta_{12} \bar{Z}^{2}]}{1-(1/r)},](img285.gif)
|
(B64) | ||
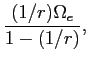
|
(B65) | ||
| (B66) | |||
| (B67) |
Substituting the expression for
![]() into the
value function, taking expectations, and then solving for optimal
into the
value function, taking expectations, and then solving for optimal
![]() given
given
![]() , and
substituting that into the value function shows that small
investors optimal choice of
, and
substituting that into the value function shows that small
investors optimal choice of ![]() and
and ![]() problem has form:
problem has form:
where
Integrating the solution for optimal ![]() over the set of small
investors then reveals that the net demand for the illiquid assets
by the competitive fringe is:
over the set of small
investors then reveals that the net demand for the illiquid assets
by the competitive fringe is:
![LaTex Encoded Math: \displaystyle Q^{1}_{1}(T+1) = \frac{1}{A_{1}(T+1)}[\Omega_{e}(t+1)]^{-1} [\bar{v}_{s}(T+1) - rP(t)]](img300.gif)
|
(B71) |
Following the approach that was used earlier to solve for the price schedule faced by large investors in equation (B11), inverting the small investors demand schedule for the illiquid assets reveals that the price schedule faced by large investors has the form:
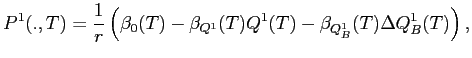
|
(B72) |
Given the price schedule at time ![]() , and the value function in equation (B59), large investors maximization problem at time
, and the value function in equation (B59), large investors maximization problem at time
![]() can be written in the
form:
can be written in the
form:
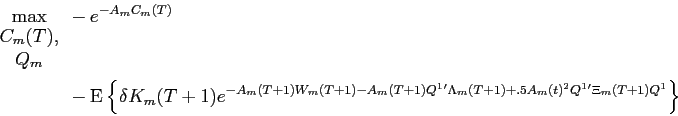
|
(B76) |
where,
Substituting in the budget constraint, liquid wealth at the
beginning of time ![]() is
given by
is
given by
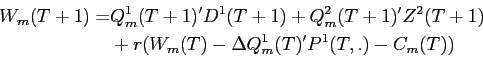
|
(B81) |
Large investors maximization problem at time ![]() has exactly the same form as given
in equation (B15). Therefore, the optimal
trades and consumption of large investors follow precisely the same
equations as given in Part I of the proof. Large investors value
function at time
has exactly the same form as given
in equation (B15). Therefore, the optimal
trades and consumption of large investors follow precisely the same
equations as given in Part I of the proof. Large investors value
function at time ![]() also
has the same functional form as in part I. The equilibrium price
function at time
also
has the same functional form as in part I. The equilibrium price
function at time ![]() also
has the same functional form as in part I. Therefore, to complete
the proof, it suffices to solve for small investors consumption and
then value function and verify that the value function has the
appropriate functional form.
also
has the same functional form as in part I. Therefore, to complete
the proof, it suffices to solve for small investors consumption and
then value function and verify that the value function has the
appropriate functional form.
To do so, note that from equation (B68), it is straightforward to show that the
optimal choice of
![]() is
is
![LaTex Encoded Math: \displaystyle Q^{1}_{s}(T+1) = \frac{1}{A_{s}(T+1)} [\Omega_{e}(T+1)]^{-1} \times [\bar{v}_{s}(T+1) - r P^{1}(T)],](img318.gif)
| (B82) |
where,
![\begin{displaymath}\begin{split}\Psi_{s}(T,Q^{1}) = & \operatorname{Exp}\left \{ -.5 \bar{Z}_{2}'\Omega_{22}^{-1} \bar{Z}_{2} - A_{s}(T) r W_{s}(T) \right \} \\ & \times \operatorname{Exp}\left \{ -.5 [\bar{v}_{s}(T+1) - \alpha(T)]' [\Omega_{e}(T+1)]^{-1} [\bar{v}_{s}(T+1) - \alpha(T)] \right \} \\ & \times \operatorname{Exp}\left \{ -Q^{1}(T)'\Gamma(T)'[\Omega_{e}(T+1)]^{-1} [\bar{v}_{s}(T+1) - \alpha(T)] \right \} \\ & \times \operatorname{Exp}\left \{ -.5 Q^{1}(T)' \Gamma(T)'[\Omega_{e}(T+1)]^{-1} \Gamma(T) Q^{1}(T) \right \} \end{split}\end{displaymath}](img321.gif)
|
(B83) |
Using the same approach that was used to solve for large
investors optimal consumption and then value function in part I of
the proof, tedious algebra shows that small investors value
function at time ![]() has
form
has
form
| (B84) | |||
| (B85) |
![\begin{displaymath}\begin{split}K_{s}(T) = & \left [ \frac{r^{*}_{s}(T+1) + 1}{r^{*}_{s}(T+1)} \right ] \left [\delta K_{s}(T+1) r^{*}_{s}(T+1) \right ]^{\frac{1}{1+r^{*}_{s}(T+1)}} \\ & \times \operatorname{Exp}\left ( \frac{-.5 \bar{Z}^{2} ' \Omega_{22}^{-1} \bar{Z}^{2} -.5 [\bar{v}_{s}(T+1) - \alpha(T)]' [\Omega_{e}(T+1)]^{-1} [\bar{v}_{s}(T+1) - \alpha(T)]}{1+r^{*}_{s}(T+1)} \right ), \end{split}\end{displaymath}](img328.gif)
|
(B86) |
![LaTex Encoded Math: \displaystyle \theta_{s}(T) = \frac{\Gamma(T)'[\Omega_{e}(T+1)]^{-1} \Gamma(T)}{1+r^{*}_{s}(T+1)}.](img330.gif)
|
(B88) |
This completes the proof by establishing that large and small
investors value functions take the hypothesized form in all periods
that involve trade. ![]()
10 Solutions for Value Function Parameters
Proof:
For
![]() and
and
![]() :
:
The proof is by induction. First, suppose that the results for
![]() and
and
![]() are true at
time
are true at
time ![]() . Then, from equation
(B12),
. Then, from equation
(B12),
![]() . This implies that from
equation (B23) that
. This implies that from
equation (B23) that
![]() .
As a result
.
As a result
![]() , which
implies from equation (B32) that
, which
implies from equation (B32) that
![]() and from equations
(B28) and (B30) that
and from equations
(B28) and (B30) that
![]() Substituting for
Substituting for
![]() and
and
![]() in equation
(B42) and simplifying then shows:
in equation
(B42) and simplifying then shows:
| (C6) |
Finally, substituting this result in equation (B18) proves the result for
For ![]() and
and
![]() :
:
The proof is by backwards induction. We know
![]() from equation (B77). Using this expression, and iterating on
equations (B40) and (B38)
proves the result for all times
from equation (B77). Using this expression, and iterating on
equations (B40) and (B38)
proves the result for all times
![]()
For ![]() :
:
The proof is by backwards induction. Equation (B80) establishes that it is true at time ![]() . Plugging the solution for
. Plugging the solution for
![]() into
equation (B41) while using the solutions for
into
equation (B41) while using the solutions for
![]() and the
result
and the
result
![]() confirms the result for
periods
confirms the result for
periods
![]() .
.
![]()
The next proposition provides information on the value functions of the small investors:
Proof:
For ![]() and
and
![]() :
Plugging the solutions for
:
Plugging the solutions for ![]() and
and
![]() from
proposition 3 into equation (B45) shows that
from
proposition 3 into equation (B45) shows that
![]() for all
times
for all
times ![]() . Since
. Since
![]() for all
times
for all
times ![]() , it then follows from
equation (B55) that if
, it then follows from
equation (B55) that if
![]() ,
then so does
,
then so does
![]() . To
complete the induction, note that substituting the solutions for
. To
complete the induction, note that substituting the solutions for
![]() (equation (B69)) and
(equation (B69)) and ![]() (proposition 3) into equation (B87)
confirms the result.
(proposition 3) into equation (B87)
confirms the result.
For ![]() ,
,
![]() , and
, and
![]() :
:
The form of the proof is identical to that given in proposition
3.![]()
| (C12) |
where,
| (C13) |
where,
Proof: The proof is by induction. First, assume that the
theorem is true at time ![]() .
Then, from equations (B14) and (B13)
.
Then, from equations (B14) and (B13)
![]() ,
and
,
and
![]() , where
, where
![]() is
is
![]() and
and
![]() is
is
![]() . Applying
these substitutions in large investors reaction functions and then
stacking the results reveals that in equation (B25),
. Applying
these substitutions in large investors reaction functions and then
stacking the results reveals that in equation (B25),
![]() and
and
![]() . The assumption
that the Nash Equilibrium trades in each period are unique implies
that
. The assumption
that the Nash Equilibrium trades in each period are unique implies
that
![]() is
invertible. Solving for
is
invertible. Solving for
![]() and
and
![]() then shows
that
then shows
that
![]() and
and
![LaTex Encoded Math: \displaystyle \left ( \begin{array}{c}-S[P(t-1)^{-1} Z(t-1)] \otimes I_{N_{1}}\\ (P(t-1)^{-1} Z(t-1)) \otimes I_{N_{1}} \end{array} \right )](img404.gif)
|
(C14) | ||
![LaTex Encoded Math: \displaystyle \left ( \begin{array}{c} [-\iota_{M}' {\cal P}(t-1)^{-1}Z(t-1)] \otimes I_{N_{1}} \\ ({\cal P}(t-1)^{-1} Z(t-1)) \otimes I_{N_{1}} \end{array} \right )](img405.gif)
|
(C15) | ||
| (C16) |
where
Proof: Straightforward induction involving application of the results from proposition 5.
11 Proofs of Asset Pricing
Propositions
Proof: When investors risky asset holdings are
![]() , then investors
asset holdings are identical to those associated with a competitive
equilibrium and complete markets in which trading is restricted to
the set of market participants that has been modeled. Hence, when
trade in the first set of assets is restricted to be among the
market participants, asset holdings are pareto optimal in all time
periods; and investors asset holdings will remain at
, then investors
asset holdings are identical to those associated with a competitive
equilibrium and complete markets in which trading is restricted to
the set of market participants that has been modeled. Hence, when
trade in the first set of assets is restricted to be among the
market participants, asset holdings are pareto optimal in all time
periods; and investors asset holdings will remain at ![]() because investors have no
basis to trade away from asset holdings that are associated with
perfect risk sharing. Because
because investors have no
basis to trade away from asset holdings that are associated with
perfect risk sharing. Because ![]() is the vector of asset holdings from a
competitive equilibrium, the resulting prices and expected returns
which support
is the vector of asset holdings from a
competitive equilibrium, the resulting prices and expected returns
which support ![]() are the
same as in the competitive equilibrium.
are the
same as in the competitive equilibrium. ![]()
Proof: Algebra shows that when asset holdings of asset 1
at time ![]() are
are
![]() , then excess
returns of asset 1 are equal to:
, then excess
returns of asset 1 are equal to:
![LaTex Encoded Math: \displaystyle P^{1}(t+1) + \bar{D}^{1} - rP^{1}(t) = \beta_{12} \bar{Z}^{2} + [\Gamma(t) - \frac{1}{r}\Gamma(t+1)G_{1}(t) ]Q^{1W}.](img423.gif)
Proposition 1: When investors
asset holdings of the first asset are not ![]() , then equilibrium expected
asset returns satisfy a linear factor model in which one factor is
the returns on asset 2, another factor corresponds to perfect
risk-sharing, but imperfect diversification of the idiosyncratic
risk of asset 1, and the remaining factors correspond to the
deviation of large investors asset holdings from those associated
with the large investors perfectly sharing the idiosyncratic risk
of asset 1.
, then equilibrium expected
asset returns satisfy a linear factor model in which one factor is
the returns on asset 2, another factor corresponds to perfect
risk-sharing, but imperfect diversification of the idiosyncratic
risk of asset 1, and the remaining factors correspond to the
deviation of large investors asset holdings from those associated
with the large investors perfectly sharing the idiosyncratic risk
of asset 1.
Proof: Let ![]() denote the vector of asset holdings of asset 1 that is associated
with perfect risk sharing among the investors that trade in asset
1. Manipulation of the equation for equilibrium prices given in
proposition 2, and substitution of
denote the vector of asset holdings of asset 1 that is associated
with perfect risk sharing among the investors that trade in asset
1. Manipulation of the equation for equilibrium prices given in
proposition 2, and substitution of
![]() for
for ![]() shows:
shows:
![LaTex Encoded Math: \displaystyle P^{1}(t+1) + \bar{D}^{1} - rP^{1}(t) = [\frac{1}{r} \alpha(t+1) + \bar{D^{1}} - \alpha(t)] -[\frac{1}{r}\Gamma(t+1)G_{0}(t)] + [\Gamma(t) - \frac{1}{r}\Gamma(t+1)G_{1}(t) ]Q^{1}(t)](img428.gif)
Plugging in the solution for
![]() shows the first term in braces on the right hand side of
the equation is equal to
shows the first term in braces on the right hand side of
the equation is equal to
![]() . The second term in braces is
zero since proposition 3 shows that
. The second term in braces is
zero since proposition 3 shows that
![]() Adding
and subtracting
Adding
and subtracting ![]() to
to ![]() , the above
equation can be rewritten as:
, the above
equation can be rewritten as:
Using the fact that
![LaTex Encoded Math: \displaystyle \left[ \begin{array}{c}(X^{1} - SQ^{1}_{B}) - (X^{1}-SQ^{1W}_{B}) \\ Q^{1}_{B} - Q^{1W}_{B} \end{array} \right ]](img436.gif)
|
|||
![LaTex Encoded Math: \displaystyle \left [\begin{array}{c} -S \\ I \end{array} \right ] (Q^{1}_{B} - Q^{1W}_{B})](img437.gif)
|
Applying the substitution for
![]() , and
the result of corollary 3 in equation
(D1) shows
, and
the result of corollary 3 in equation
(D1) shows
![LaTex Encoded Math: \displaystyle P^{1}(t+1) + \bar{D}^{1} - rP^{1}(t) = \beta_{12} \bar{Z}^{2} + \lambda_{[X^{1}]} \Omega_{e} X^{1} + [\Gamma(t) - \frac{1}{r}\Gamma(t+1)G_{1}(t) ]\left ( \begin{array}{c} -S \\ I \end{array} \right ) (Q^{1}_{B}(t) - Q^{1W}_{B})](img438.gif)
Finally, applying the algebra used in the derivation of proposition 5 shows
![LaTex Encoded Math: \displaystyle [\Gamma(t) - \frac{1}{r}\Gamma(t+1)G_{1}(t) ]\left ( \begin{array}{c} -S \\ I \end{array} \right ) = \lambda(t) \otimes \Omega_{e}](img439.gif)
|
(D2) |
where
![\begin{displaymath}\begin{array}{rcl} P^{1}(t+1) + \bar{D}^{1} - rP^{1}(t) & = & \beta_{12} \bar{Z}^{2} + \lambda_{[X^{1}]} \Omega_{e} X^{1} + [\lambda(t) \otimes \Omega_{e}] (Q^{1}_{B}(t) - Q^{1W}_{B}) \\ & = & \beta_{12} \bar{Z}^{2} + \lambda_{[X^{1}]} \Omega_{e} X^{1} + \sum_{m=2}^{M} \lambda(m,t) \Omega_{e} (Q^{1}_{m}(t) - Q^{1W}_{m}) \end{array}\end{displaymath}](img441.gif)
|
(D3) |
where
Corollary 1: When asset
holdings at time ![]() are
not efficient, then asset returns at time
are
not efficient, then asset returns at time ![]() follow a factor model in which
the market portfolio, the portfolio of segment residual risk, and
the deviation of large investors time
follow a factor model in which
the market portfolio, the portfolio of segment residual risk, and
the deviation of large investors time ![]() asset holdings from efficient asset
holdings are factors.
asset holdings from efficient asset
holdings are factors.
Proof: Iterating equation (D1),
by ![]() periods shows:
periods shows:
Iterating the equation for equilibrium trades in each period shows
![LaTex Encoded Math: \displaystyle Q^{1}(t+\tau) = [\prod_{j=0}^{\tau-1} G_{1}(t+j)] Q^{1}(t).](img444.gif)
![LaTex Encoded Math: \displaystyle [\prod_{j=0}^{\tau-1} G_{1}(t+j)] Q^{1W} = Q^{1W}.](img445.gif)
![LaTex Encoded Math: \displaystyle \beta_{12} \bar{Z}^{2} + \lambda_{[X^{1}]} \Omega_{e} X^{1} + \sum_{m=2}^{M} \lambda_{m}(t,\tau) \Omega_{e} (Q^{1}_{m}(t) - Q_{m}^{1W})](img448.gif)
|
where,
![LaTex Encoded Math: \displaystyle \lambda(t,\tau) \otimes \Omega_{e} = [\Gamma(t+\tau) - \frac{1}{r}\Gamma(t+1+\tau)G_{1}(t+\tau) ] \prod_{j=0}^{\tau-1} G_{1}(t+j),](img449.gif)
11.1
Competitive Benchmark Model
It is useful to contrast the behavior in the multi-market model with large investors with the behavior of asset prices and trades in the same model when all investors are price takers and can trade forever.
In this infinite period set-up with competitive markets, the
equilibrium risk-premium should be time invariant. Denote this risk
premium by ![]() ,
where,
,
where,
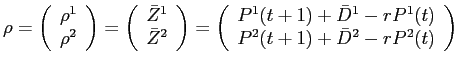
|
(D5) |
Note that
![]() is taken
as exogenous. The goal is to solve for
is taken
as exogenous. The goal is to solve for
![]() and
and
![]() that makes the
prices of the first group of assets (the ones that are illiquid in
the imperfect competition model) consistent with equilibrium in all
time periods.
that makes the
prices of the first group of assets (the ones that are illiquid in
the imperfect competition model) consistent with equilibrium in all
time periods.
Solving the equation for ![]() forward while imposing the transversality
condition
forward while imposing the transversality
condition
![]() shows that
shows that
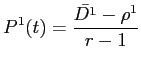
Given the hypothesized behavior of prices, it remains to solve
for ![]() and then to
show that the hypothesized behavior of prices is consistent with
equilibrium.
and then to
show that the hypothesized behavior of prices is consistent with
equilibrium.
The function,
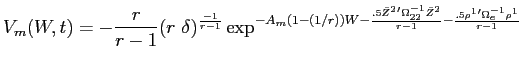
and the risk premium solution
where,
![LaTex Encoded Math: \displaystyle \lambda_{[X^{1}]} = \frac{(1-(1/r))}{\sum_{m=1}^{M}(1/A_{m})}](img461.gif)
|
(D7) |
satisfies the Bellman equation,
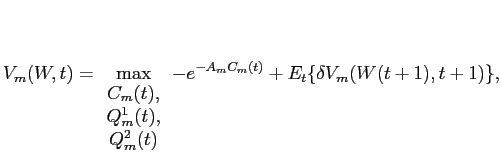
In addition, in the competitive equilibrium, investors optimal
choices of ![]() are
constant through time, and are market clearing for the hypothesized
are
constant through time, and are market clearing for the hypothesized
![]() . Investor
. Investor
![]() competitive
equilibrium holdings of
competitive
equilibrium holdings of ![]() is denoted by
is denoted by
![]() and is
equal to
and is
equal to
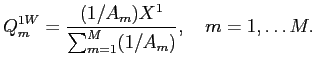
|
(D8) |
Substituting the hypothesized ![]() into the expression for equilibrium
into the expression for equilibrium
![]() , it follows that
in a competitive equilibrium, the equilibrium price is given by
, it follows that
in a competitive equilibrium, the equilibrium price is given by
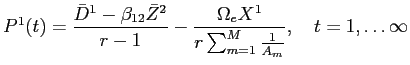
|
(D9) |
12 Solving the IPO Allocation and
Price-Setting Problem
The underwriter's problem in equations (16) - (18) problem requires
that he maximize a nonlinear objective function subject to the
equality constraint that the total issue is allocated at the IPO or
sold in the aftermarket, and subject to a set of nonlinear
participation constraints. To solve the maximation, the
participation constraints were expressed in terms of investors
certainty equivalent wealth. The transformed participation
constraints are quadratic in the state variables. Additionally, the
equality constraint was used to express ![]() in terms of the size of the
issue, and the allocations to other investors:
in terms of the size of the
issue, and the allocations to other investors:
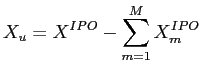
To economize on notation, I will drop the "IPO" superscript below in what follows. The Lagrangian for the transformed maximization problem is:
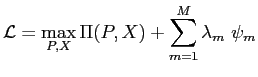
|
(E1) |
The necessary conditions for an optimum are given by the Kuhn-Tucker conditions:
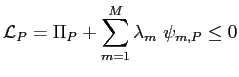 with c.s.
with c.s. |
(E2) |
and for
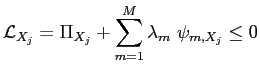 with c.s.
with c.s. |
(E3) |
If an investor purchases any shares at the IPO, then his utility is decreasing in the IPO offer price. Therefore, if shares are issued at the IPO, then the incentive constraints must be binding for some investors, because if they were not the underwriter could profit by raising the offer price until the incentive constraints do bind.
Although it is clear the incentive constraints must bind for at
least one investor, it is not clear for how many other investors
the constraints will bind. I solved the model in the special case
when there are 6 investors (![]() ) and the only asset in the segment is the new
issue. To solve the model, I assumed that the underwriters short
position is limited, i.e.
) and the only asset in the segment is the new
issue. To solve the model, I assumed that the underwriters short
position is limited, i.e.
![]() With
this added constraint, the feasible choices of
With
this added constraint, the feasible choices of ![]() lie on a simplex. I discretized
the simplex so that each investor's post IPO asset holdings could
take one of 21 values. Given a vector of asset holdings, I then
solved for the highest IPO offer price that satisfies all investors
incentive compatibility constraints,38, and then evaluated the objective
function. The point on the discretized simplex for which the
objective function was highest was treated as being in a
neighborhood of the global optimum, and was used as a starting
point for a second stage optimization. Additionally, the investor
or investors for whom the incentive compatibility constraints were
binding, were deemed as the investors for whom the constraints will
be binding at the optimum.
lie on a simplex. I discretized
the simplex so that each investor's post IPO asset holdings could
take one of 21 values. Given a vector of asset holdings, I then
solved for the highest IPO offer price that satisfies all investors
incentive compatibility constraints,38, and then evaluated the objective
function. The point on the discretized simplex for which the
objective function was highest was treated as being in a
neighborhood of the global optimum, and was used as a starting
point for a second stage optimization. Additionally, the investor
or investors for whom the incentive compatibility constraints were
binding, were deemed as the investors for whom the constraints will
be binding at the optimum.
The second stage optimization minimized the squared norm of the
Kuhn-Tucker conditions while checking for changes in the set of
investors for whom the constraints are binding. A quadratic
hillclimbing algorithm with safeguards was used in the second stage
optimization. When the investors all differ in their risk aversion,
as they do in some of the examples in the paper, then the incentive
compatability constraints tended to bind for a single investor.
Under this circumstance, the Kuhn Tucker condition for price
produce an analytical expression for
![]() , which
simplifies the second-stage optimization. A complicating factor in
the second stage is that the Hessians of the first and second stage
objective functions are singular. I believe (but cannot show), that
Gauss' nonlinear constrained optimization crashed because of this
property. To compensate for this problem in the second stage, at
each iteration I projected the direction vector onto the range and
null spaces of the hessian matrix, and then solved for the
projection coefficients that guarantee an increasing step in the
objective function. Finally, I found the book Practical Optimization, by Gill, Murray, and
Wright (1981) to be a very useful reference for solving nonlinear
optimization problems.
, which
simplifies the second-stage optimization. A complicating factor in
the second stage is that the Hessians of the first and second stage
objective functions are singular. I believe (but cannot show), that
Gauss' nonlinear constrained optimization crashed because of this
property. To compensate for this problem in the second stage, at
each iteration I projected the direction vector onto the range and
null spaces of the hessian matrix, and then solved for the
projection coefficients that guarantee an increasing step in the
objective function. Finally, I found the book Practical Optimization, by Gill, Murray, and
Wright (1981) to be a very useful reference for solving nonlinear
optimization problems.
13 Market Segmentation and Market
Adjusted Abnormal Returns
The purpose of this section is to study the properties of market
adjusted abnormal returns when there is market segmentation. The
analysis and results are closely related to Merton (1987). The
model contains two time-periods and ![]() blocks of risky assets, and a riskfree asset that is
in perfectly elastic supply and has return
blocks of risky assets, and a riskfree asset that is
in perfectly elastic supply and has return ![]() . The supply of shares outstanding in
block
. The supply of shares outstanding in
block ![]() is denoted by the
vector
is denoted by the
vector ![]() . Note
that the number of assets can vary from block to block. Investors
trade the assets in period 1 and consume in period 2. The period 2
payoff vector per share in block
. Note
that the number of assets can vary from block to block. Investors
trade the assets in period 1 and consume in period 2. The period 2
payoff vector per share in block ![]() is equal to
is equal to ![]() . The payoff of
. The payoff of ![]() is further decomposed into its mean
is further decomposed into its mean ![]() , a component that is
sensitive to systematic risk factor
, a component that is
sensitive to systematic risk factor ![]() , and an idiosyncratic component
, and an idiosyncratic component
![]() :
:
| (F1) |
I assume that
In addition to the ![]() blocks of assets, there is a single asset in zero net supply whose
payoff vector is:
blocks of assets, there is a single asset in zero net supply whose
payoff vector is:
| (F2) |
The N'th market can be viewed as a market for sharing systematic risk.
At time period 1, the price vector of the risky assets is
denoted by ![]() ,
,
![]() .
.
I assume that for some reason that is not specified here, asset
markets are segmented. This means that each block of assets has its
own set of investors that only take positions in the segment assets
and in asset ![]() . For
simplicity, the investors in each block are modelled as a single
representative price-taking investor with CARA utility of period 2
wealth and risk tolerance
. For
simplicity, the investors in each block are modelled as a single
representative price-taking investor with CARA utility of period 2
wealth and risk tolerance ![]() .
.
The market portfolio has payoff
![]() , and price
, and price
![]() . Its excess return over the
risk free rate is denoted by
. Its excess return over the
risk free rate is denoted by
![]() ; and the excess return of the
assets in block
; and the excess return of the
assets in block ![]() over
the risk free rate is denoted by
over
the risk free rate is denoted by
![]() .
.
Armed with this notation,
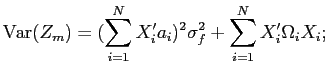
|
(F3) |
and,
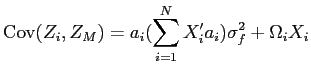
|
(F4) |
If I use the primitive assets to construct ![]() assets with payoffs
assets with payoffs
![]() , and a single asset with payoff
, and a single asset with payoff
![]() , then the new assets
will span the same space as the old, but they are easier to work
with. In particular, working from the new assets, it is
straightforward to show that for each block
, then the new assets
will span the same space as the old, but they are easier to work
with. In particular, working from the new assets, it is
straightforward to show that for each block ![]() , under the assumption of market
segmentation,
, under the assumption of market
segmentation,
| (F5) | |||
| (F6) |
where
Using the above expression to solve for the market's excess expected return then shows:
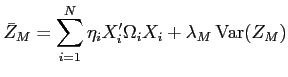
|
(F7) |
The expression for
![]() contains
two components. The second component is the standard risk premium
for an assets covariance with market risk when investors fully
diversify their asset holdings. The first component is an
additional premium for imperfect diversification. Examination will
show that each term of the imperfect diversification premium is
positive, which implies that imperfect diversification increases
the return on the market portfolio.
contains
two components. The second component is the standard risk premium
for an assets covariance with market risk when investors fully
diversify their asset holdings. The first component is an
additional premium for imperfect diversification. Examination will
show that each term of the imperfect diversification premium is
positive, which implies that imperfect diversification increases
the return on the market portfolio.
Below, I seek to examine how imperfect diversification affects
market adjusted abnormal returns. Letting
![]() ,
algebra then shows:
,
algebra then shows:
The term on the right hand of equation (F8) is the vector of Jensen's alphas for block
![]() that is due to
market segmentation. These alphas capture the risk premium for
inefficiently sharing risk across market segments (or blocks). My
goal here is to characterize the average behavior of the
that is due to
market segmentation. These alphas capture the risk premium for
inefficiently sharing risk across market segments (or blocks). My
goal here is to characterize the average behavior of the
![]() . Simple
algebra shows
. Simple
algebra shows
![]() . Because
. Because
![]() , it
follows that some of the market corrected
, it
follows that some of the market corrected ![]() must be positive and some
must be negative. Additionally, if the number of shares outstanding
of each asset is the same, then the average value of
must be positive and some
must be negative. Additionally, if the number of shares outstanding
of each asset is the same, then the average value of
![]() is equal to
0. This suggests that to a first approximation when the market is
perfectly competitive, and there is segmentation, then the average
market adjusted
is equal to
0. This suggests that to a first approximation when the market is
perfectly competitive, and there is segmentation, then the average
market adjusted ![]() is 0.
is 0.
When there is imperfect competition, I showed that asset returns
have two components.39 The first component is compensation
for imperfect risk sharing across blocks (or segments), and is
identical to the component above for the competitive case. The
second component is for inefficient risk sharing among the
investors who trade within a segment. Because investors within each
segment eventually share risks optimally, this second component is
transitory. For simplicity here, I will write it as ![]() .
. ![]() should be close to 0 for
segments that have not experienced an IPO recently, but may be
nonzero if they did. Note: if the first asset in a segment is an
IPO, and the risks of the other assets are shared efficiently
within the segment, then the allocation distortions at the IPO will
cause
should be close to 0 for
segments that have not experienced an IPO recently, but may be
nonzero if they did. Note: if the first asset in a segment is an
IPO, and the risks of the other assets are shared efficiently
within the segment, then the allocation distortions at the IPO will
cause ![]() to depart from
0 for all assets within the segment, but the size of the departure
for each asset is proportional to the first column of
to depart from
0 for all assets within the segment, but the size of the departure
for each asset is proportional to the first column of
![]() . If
. If
![]() is
diagonal, then the other assets in the segment are not affected by
the IPO; but they will be otherwise. To examine the role that this
term plays in market adjusted excess returns, note that
is
diagonal, then the other assets in the segment are not affected by
the IPO; but they will be otherwise. To examine the role that this
term plays in market adjusted excess returns, note that
![]() should be
added to each segments excess returns, and
should be
added to each segments excess returns, and
![]() should be added to the excess return on the market. Arithmetic then
shows that:
should be added to the excess return on the market. Arithmetic then
shows that:
The second term on the right hand side of the above equation
reflects how an IPO affects the returns within a particular market
segment. To get a feel for the magnitude of this term, with great
loss of generality suppose for a moment that an IPO occurs only in
segment 1, that there is only 1 risky asset per segment, and that
the characteristics of the assets in each segment are identical
(same number of shares, etc). Then ![]() is nonzero in segment
is nonzero in segment ![]() , and 0 in the other
, and 0 in the other ![]() segments. Algebra shows that
segments. Algebra shows that
![]() ;
solving for
;
solving for ![]() and
substituting in the right hand side of (F10)
then shows that if segment 1 has an IPO then
and
substituting in the right hand side of (F10)
then shows that if segment 1 has an IPO then
![LaTex Encoded Math: \displaystyle \alpha_{1} + \left [\pi_{1} - \frac{1}{N X_{1}} \sum X_{i}'\pi_{i} \right ]](img520.gif)
|
|||
where the last line follows because by assumption in this specialized case,
- Aggarwal, R., 2003, "Allocation of initial public offerings and flipping activity," Journal of Financial Economics, 68, 111-135.
- Benveniste, L.M., and P.A. Spindt, 1989, "How Investment Bankers Determine the Offer Price and Allocation of New Issues," Journal of Financial Economics 24, 343-61.
- Biais, B., Bossaerts, P., and J.C. Rochet, 2002, "An Optimal IPO Mechanism," Review of Economic Studies 69, 117-46.
- Boehmer, E., and R.P.H. Fishe, 2000, "Do Underwriters Encourage Stock Flipping? A New Explanation for the Underpricing of IPOs," Mimeo.
- Booth, J.R., and L. Chua, 1996, "Ownership dispersion, costly information, and IPO underpricing," Journal of Financial Economics 41, 291-310.
- Brav, A., Geczy, C., and P.A. Gompers, 2000, "Is the abnormal return following equity issuance anomalous?", Journal of Financial Economics 56, 209-249.
- Butler, A., Grullon, G., and J. Weston, 2005 "Stock Market Liquidity and the Cost of Issuing Equity," Journal of Financial and Quantitative Analysis, 40, 331-348.
- Cornelli, F., and D. Goldreich, (2003): "Bookbuilding: How Informative is the Order Book?," Journal of Finance, 58, 1415-44.
- Corwin, S.A., Harris, J.H., and M.L. Lipson, 2004, "The Development of Secondary Market Liquidity for NYSE-Listed IPOs," Journal of Finance, 59, no. 5, 2339-2373.
- DeMarzo, P.M., and B. Urosevic, 2000 "Optimal Trading by a Large Shareholder," Working Paper, Haas School of Business, University of California at Berkeley.
- de Jong, F. and M. Dahlquist, 2003, "Pseudo-Market Timing, Fact or Fiction," Mimeo, the University of Amsterdam.
- Derrien, F., and K.L. Womack, 2003, "Auctions vs. Bookbuilding and the Control of Underpricing in Hot IPO Markets," Review of Financial Studies 16, no. 1, 31-61.
- Eckbo, B.E., and Ø. Norli, 2002, "Liquidity risk, leverage, and long-run IPO returns," Mimeo, Dartmouth Tuck School of Business.
- Ellis, K., Michaely, R., and M. O'Hara, 2000, "When the Underwriter is the Market Maker: An Examination of Trading in the IPO Aftermarket," Journal of Finance, 55, no. 3, 1039-1074.
- Ellis, K., Michaely, R., and M. O'Hara, 2002, "The Making of a Dealer Market: From Entry to Equilibrium in the Trading of NASDAQ Stocks," Journal of Finance 57, no. 5, 2289 - 2316.
- Ellul, A., and M. Pagano, 2003, "IPO Underpricing and After-Market Liquidity," CSEF Working Paper no. 99, University of Salerno Centre for Studies in Economics and Finance.
- Gill, P.E., Murray, W., and M.H. Wright, 1981, Practical Optimization, Academic Press, London.
- Hahn, T., and J.A. Ligon, 2004, "Liquidity and Initial Public Offering Underpricing," Mimeo, College of Business and Economics, The University of Idaho.
- Hoberg, G., 2004, "Strategic Underwriting in Initial Public Offers," Yale ICF Working Paper No. 04-07.
- Jenkinson, T., and H. Jones, 2004, "Bids and Allocations in European IPO Bookbuilding," Journal of Finance , 59, no. 5, 2309-2338.
- Ljungqvist, A.P., Nanda, V., and R. Singh, 2003, "Hot Markets, Investor Sentiment, and IPO Pricing," Mimeo, Stern School of Business, New York University.
- Ljungvist, A., 2004, "IPO Underpricing," Handbooks in Finance: Empirical Corporate Finance, Chapter III.4, edited by B. E. Eckbo, forthcoming.
- Kihlstrom, R., 2001, "Monopoly Power in Dynamic Securities Markets,"Working Paper, The Wharton School, University of Pennsylvania.
- Loughran, T., and J.R. Ritter, 2000, "Uniformly Least Powerful Tests of Market Efficiency," Journal of Financial Economics 55, 361-389.
- Loughran, T., and J.R. Ritter, 2004, "Why has IPO Underpricing Changed over time?", Financial Management, 33, no. 3, 5-37.
- Merton, R.C., 1987, "A Simple Model of Capital Market Equilibrium with Incomplete Information", The Journal of Finance, 42 no. 3, 483-510.
- Pritsker, M., 2004, "Large Investors: Implications for Equilibrium Asset Returns, Shock Absorption and Liquidity," Mimeo, The Federal Reserve Board.
- Reuter, J., 2005, "Are IPO Allocations for Sale? Evidence from Mutual Funds," The Journal of Finance, Forthcoming.
- Ritter, J.R., 2005, "Some Factoids About the 2004 IPO Market," mimeo, the University of Florida, http://bear.cba.ufl.edu/ritter.
- Ritter, J.R., and I. Welch, 2002, "A Review of IPO Activity, Pricing, and Allocations," Journal of Finance 57, no. 4, 1795 - 1828.
- Rock, K., 1986, "Why New Issues Are Underpriced," Journal of Financial Economics 15, 187-212.
- Schultz, P., 2003, "Pseudo Market Timing and the Long-Run Underperformance of IPOs," Journal of Finance 58, no. 2, 483-517.
- Stapleton, R.C., and M.G. Subrahmanyam, 1978, "A Multi-period Equilibrium Asset Pricing Model," Econometrica, 46, 1077-1096.
- Urosevic, B., 2002a, "Moral Hazard and Dynamics of Insider Ownership Stakes," Working Paper, Universitat Pompeu Fabra.
- Urosevic, B., 2002b, "Essays in Optimal Dynamic Risk Sharing in Equity and Debt Markets," Ph.D. Dissertation, University of California at Berkeley, May.
- Vayanos, D., 2001, "Strategic Trading in a Dynamic Noisy Market," Journal of Finance, 56, 131-171.
- Viswanathan, S, and B. Wei, 2004, "Endogenous Events and Long Run Returns," Mimeo, Duke University.
- Westerfield, M.M., 2003, "Market Composition and the Participation Externality in Equity Market Formation," Mimeo, MIT Sloan School of Business.
| Investor Number | Type | Risk Bearing Capacity |
|---|---|---|
| 1 | Retail | 10.00 |
| 2 | Institutional | 54.56 |
| 3 | Institutional | 21.82 |
| 4 | Institutional | 8.73 |
| 5 | Institutional | 3.49 |
| 6 | Institutional | 1.40 |
| Risk Bearing Concentration (Herfindahl Index) | 3543.26 | |
Table 1: IPO Under-Pricing and Money Left on the Table: I.
B. IPO Under-Pricing and
Money Left on the Table (MLOTT)
| Periods Liq | Prices P_Offer | Prices P_Open | Prices P_Comp | Prices % Und_Price | MLOTT Raw | MLOTT Liq. Adj. |
|---|---|---|---|---|---|---|
| 2000 | 10.13 | 14.25 | 10.50 | 40.66 | 164.75 | 14.90 |
| 1800 | 10.06 | 14.83 | 10.50 | 47.38 | 190.73 | 17.38 |
| 1600 | 10.00 | 15.43 | 10.50 | 54.26 | 217.12 | 19.79 |
| 1400 | 9.94 | 16.04 | 10.50 | 61.33 | 243.93 | 22.23 |
| 1200 | 9.88 | 16.66 | 10.50 | 68.61 | 271.18 | 24.72 |
| 1000 | 9.82 | 17.29 | 10.50 | 76.10 | 298.87 | 27.24 |
| 800 | 9.75 | 17.93 | 10.50 | 83.82 | 327.01 | 29.81 |
| 600 | 9.69 | 18.58 | 10.50 | 91.76 | 355.60 | 32.41 |
| 400 | 9.62 | 19.24 | 10.50 | 99.94 | 384.65 | 35.06 |
| 200 | 7.95 | 20.62 | 10.50 | 159.36 | 506.89 | 101.74 |
Table 1: IPO Under-Pricing and Money Left on the Table: I.
C. IPO Allocation
Distortions (Percent)
| Investor Number | ||||||
| Post-IPO Trading Periods | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 2000 | -100.00 | 83.29 | -100.00 | -100.00 | -100.00 | -100.00 |
| 1800 | -100.00 | 83.29 | -100.00 | -100.00 | -100.00 | -100.00 |
| 1600 | -100.00 | 83.29 | -100.00 | -100.00 | -100.00 | -100.00 |
| 1400 | -100.00 | 83.29 | -100.00 | -100.00 | -100.00 | -100.00 |
| 1200 | -100.00 | 83.29 | -100.00 | -100.00 | -100.00 | -100.00 |
| 1000 | -100.00 | 83.29 | -100.00 | -100.00 | -100.00 | -100.00 |
| 800 | -100.00 | 83.29 | -100.00 | -100.00 | -100.00 | -100.00 |
| 600 | -100.00 | 83.29 | -100.00 | -100.00 | -100.00 | -100.00 |
| 400 | -100.00 | 83.29 | -100.00 | -100.00 | -100.00 | -100.00 |
| 200 | -100.00 | 83.29 | -100.00 | -100.00 | -100.00 | -100.00 |
Notes: When there is a continuum of small retail investors (investor 1), and 5 large investors (investors 2-6), the table reports expected IPO underpricing and money left on the table for 10 IPOs that vary by the number of days of trading that take place in the IPO aftermarket (Periods Liq). Fewer trading days correspond to less aftermarket liquidity. Each investors risk bearing capacity (panel A) is his own risk tolerance as a percent of the sum total of all investors risk tolerances. Percentage underpricing (panel B) is equal to the net expected one-day return associated with purchasing at the offer price (P_Offer) and then selling at the first days closing price (P_Open). Raw money left on the table is the difference in P_Offer and P_Open times the number of shares issued. Liquidity adjusted money left on the table is equal to the shares issued times the one day return associated with purchasing at P_Offer and then selling into a competitive (and perfectly liquid) aftermarket at price P_Comp. In a competive market, each investors allocation at the IPO should be equal to risk capacity times the number of shares issued. Allocation distortions (panel C) measure are the percentage difference in investors allocations at the IPO relative to the allocation he would have received in an efficient market.
| Investor Number | Type | Risk Bearing Capacity |
|---|---|---|
| 1 | Retail | 10.00 |
| 2 | Institutional | 40.00 |
| 3 | Institutional | 12.50 |
| 4 | Institutional | 12.50 |
| 5 | Institutional | 12.50 |
| 6 | Institutional | 12.50 |
| Risk Bearing Concentration (Herfindahl Index) | 2225 | |
Table 2: IPO Under-Pricing and Money Left on the Table: II.A.
B. IPO Under-Pricing and Money Left on the Table (MLOTT)
| Periods Liq | Prices P_Offer | Prices P_Open | Prices P_Comp | Prices % Und_Price | MLOTT Raw | MLOTT Liq. Adj. |
|---|---|---|---|---|---|---|
| 10.50 | 10.50 | 10.50 | 0.00 | 0.00 | 0.00 | |
| 10.50 | 10.50 | 10.50 | 0.00 | 0.00 | 0.00 | |
| 1600 | 10.53 | 10.71 | 10.50 | 1.70 | 7.14 | -1.38 |
| 1400 | 10.69 | 11.65 | 10.50 | 8.97 | 38.33 | -7.62 |
| 1200 | 10.85 | 12.61 | 10.50 | 16.27 | 70.59 | -14.07 |
| 1000 | 11.01 | 13.60 | 10.50 | 23.49 | 103.48 | -20.65 |
| 800 | 11.18 | 14.61 | 10.50 | 30.62 | 136.94 | -27.34 |
| 600 | 11.35 | 15.63 | 10.50 | 37.65 | 170.96 | -34.14 |
| 400 | 11.52 | 16.66 | 10.50 | 44.59 | 205.55 | -41.06 |
| 200 | 11.70 | 17.72 | 10.50 | 51.43 | 240.70 | -48.09 |
Table 2: IPO Under-Pricing and Money Left on the Table: II.A.
C. IPO Allocation Distortions (Percent)
| Investor Number | ||||||
| Post-IPO Trading Periods | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 1600 | -100.00 | 147.50 | -100.00 | -100.00 | -100.00 | -100.00 |
| 1400 | -100.00 | 149.57 | -100.00 | -100.00 | -100.00 | -100.00 |
| 1200 | -100.00 | 149.77 | -100.00 | -100.00 | -100.00 | -100.00 |
| 1000 | -100.00 | 149.84 | -100.00 | -100.00 | -100.00 | -100.00 |
| 800 | -100.00 | 149.88 | -100.00 | -100.00 | -100.00 | -100.00 |
| 600 | -100.00 | 149.90 | -100.00 | -100.00 | -100.00 | -100.00 |
| 400 | -100.00 | 149.92 | -100.00 | -100.00 | -100.00 | -100.00 |
| 200 | -100.00 | 149.93 | -100.00 | -100.00 | -100.00 | -100.00 |
Notes: This table is similar to Table 1 except that investors risk bearing capacity is less concentrated. When there are 2000, and 1800 post-IPO trading perids (marked with an asterisk), the aftermarket is sufficiently competitive that investors and the underwriter are nearly indifferent over how shares are allocated. I have assigned efficient share holdings in this case at competitive prices. When the aftermarket is slightly more competitive than in Table 1, but not perfectly competitive, the underwriter can allocate shares at a price that is higher than the competitive price (which is also the price with perfect liquidity). In such circumstances, liquidity adjusted money left on the table is negative.
Notes: For the market structure in panel A of Table 1, the figure presents optimal IPO offer prices as a function of constraints on the amount of shares that investor 2 can acquire at the IPO. Results are presented for when the aftermarket is perfectly competitive (nearly flat solid line), and when it is imperfectly competitive and there are 2000 (short dashes) or 400 (long dashes) periods of aftermarket trading following the IPO. The figure shows that when there is imperfect competition, the underwriter should distort share holdings towards investor 2 in order to increase the revenue raised at the IPO.
Notes: For the market structure in panel A of Table 1, when there are 2000 periods of trade remaining following the IPO, the figure presents share turnover [(buy volume + sell volume)/2] as a percent of shares outstanding.
Notes: For the market structure in panel A of Table
1, the figure presents expected cumulative
abnormal returns (CARs) relative to the market portfolio for
differing numbers of periods of liquid trading in the aftermarket
following the IPO. The figure is constructed under the assumption
that IPO's are an infinitesimal fraction of the market portfolio.
If instead, new issues represent ![]() percent of the market, then the CAR should be
adjusted downward in magnitude by approximately
percent of the market, then the CAR should be
adjusted downward in magnitude by approximately ![]() percent. See appendix F for details.
percent. See appendix F for details.
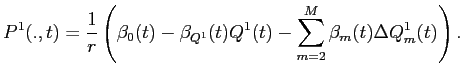
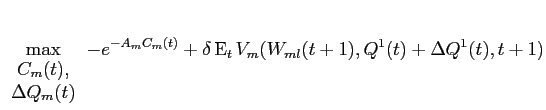
![LaTex Encoded Math: \displaystyle \frac{\partial \operatorname{E}V_{m}}{\partial \Delta Q^{1}_{m}} = \left [ \operatorname{E}V_{m,W}(.) ( D_{1}(t) - r P^{1}) + \operatorname{E}V_{m,Q^{1}_{m}}(.) \right ] - \left [\operatorname{E}V_{m,W}(.)r \Delta Q^{1}_{m}' P_{m}^1(.) \right ] = 0,](img47.gif)
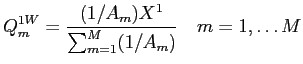
![LaTex Encoded Math: \displaystyle \bar{Z}^{1}(t) = \beta_{12} \bar{Z}^{2}(t) + \lambda_{[X^{1}]} \Omega_{e} X^{1} + \sum_{m=2}^{M} \lambda(m,t) \Omega_{e} (Q^{1}_{m}(t) - Q^{1W}_{m})](img51.gif)
![LaTex Encoded Math: \displaystyle \lambda_{[X^{1}]} = \frac{1-(1/r)}{\sum_{m=1}^{M} 1/A_{m}}](img52.gif)
![LaTex Encoded Math: \displaystyle \operatorname{E}_{t} [Z^{1}(t+\tau + 1)] = \beta_{12} \bar{Z}^{2} + \lambda_{[X^{1}]} \Omega_{e} X^{1} + \sum_{m=2}^{M} \lambda_{m}(t,\tau) \Omega_{e} (Q^{1}_{m}(t) - Q_{m}^{1W})](img57.gif)
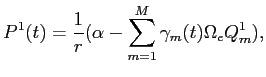
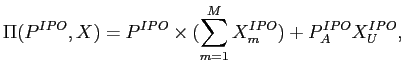
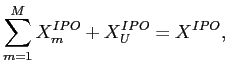
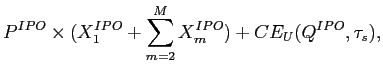
![LaTex Encoded Math: \displaystyle Z_{i}(t+\tau + 1) = \beta_{i,2} \pi_{IND} + [\lambda_{[X^{1}]} \Omega_{e} X^{1}] \pi_{SEG} + [\sum_{m=2}^{M} \lambda_{m}(t,\tau) \Omega_{e} (Q^{1}_{m}(t) - Q_{m}^{1W})] \pi_{LIQ} + \epsilon_{i}(t+\tau)](img96.gif)
![\begin{displaymath}\begin{array}{rcl} V_{s}(W_{s},Q^{1},t) & = & -K_{1}(t) \ F(Q^{1},t) \ e^{-A_{s}(t)W_{s}}, \\ [0.06in] \mbox{where} \ F(Q^{1},t) & = & e^{-Q^{1}(t)'\bar{v}_{s}(t) - Q^{1}(t)'\theta_{s}(t) Q^{1}(t).} \end{array}\end{displaymath}](img146.gif)
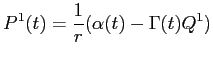
![LaTex Encoded Math: \displaystyle \max_{\begin{array}{c}C_{s}(t-1),\\ Q_{s},\\ q_{s} \end{array}} -e^{-A_{s} C_{s}(t-1)} - \delta \operatorname{E}[ K_{s}(t) F(Q^{1},t) e^{-A_{s}(t) W_{s}(t)} ]](img152.gif)
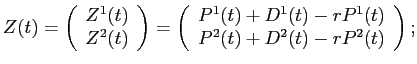
![LaTex Encoded Math: \displaystyle \max_{\begin{array}{c} C_{s}(t-1),\\ Q_{s} \end{array}} -e^{-A_{s} C_{s}(t-1)} - \delta F(Q^{1},t) e^{-A_{s}(t) r [W_{s}(t-1) - C_{s}(t-1)] -A_{s}(t) Q_{s}'\bar{Z}(t) + .5 A_{s}(t)^{2} Q_{s}' \Omega Q_{s} }](img161.gif)
![\begin{displaymath}\begin{split}\max_{\begin{array}{c} C_{s}(t-1),\\ Q^{1}_{s} \end{array}} -e^{-A_{s} C_{s}(t-1)} - & \delta F(Q^{1},t) K_{s}(t) \operatorname{Exp}\left \{ -.5 \bar{Z}_{2}'\Omega_{22}^{-1} \bar{Z}_{2} - A_{s}(t) r [W_{s}(t-1) - C_{s}(t-1)] \right \} \\ & \times \operatorname{Exp}\left \{ -A_{s}(t) Q^{1}_{s}'[\bar{Z}_{1}(t) - \beta_{12} \bar{Z}_{2}(t)] + .5 A_{s}(t)^{2} Q^{1}_{s}' \Omega_{e} Q^{1}_{s} \right \} \end{split}\end{displaymath}](img164.gif)
![LaTex Encoded Math: \displaystyle Q^{1}_{s}(t) = \frac{1}{A_{s}(t)} \Omega_{e}^{-1} [\bar{Z}_{1}(t) - \beta_{12} \bar{Z}_{2}(t)]](img169.gif)
![\begin{displaymath}\begin{array}{rcl} Q^{1}_{1}(t) & = & \int_{0}^{1} Q^{1}_{s}(t) \mu_{s} ds \\ [0.08in] & = & \left [\int_{0}^{1} \frac{1}{A_{s}(t)} \mu_{s} ds \right ] \Omega_{e}^{-1} [\bar{Z}_{1}(t) - \beta_{12} \bar{Z}_{2}(t)] \\ [0.08in] & = & \frac{1}{A_{1}(t)} \Omega_{e}^{-1} [\bar{Z}_{1}(t) - \beta_{12} \bar{Z}_{2}(t)] \end{array}\end{displaymath}](img171.gif)
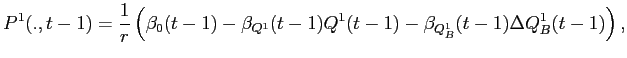
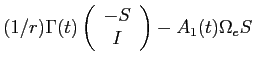
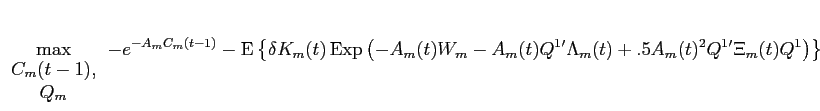
![\begin{displaymath}\begin{split}\max_{\begin{array}{c}C_{m}(t-1),\\ Q^{1}_{m} \end{array}} & -e^{-A_{m} C_{m}(t-1)} \\ & - \delta K_{m}(t) \left \{ \operatorname{Exp}( -.5 \bar{Z}^{2}'\Omega_{22}^{-1} \bar{Z}_{2} -A_{m}(t) r [W_{m}(t-1) - \Delta Q_{m}(t-1)'P^{1}(t-1,.) - C_{m}(t-1) ] \right. \\ & \left. \times \operatorname{Exp}(-A_{m}(t) Q^{1}'\bar{v}_{m}(t) + .5 A_{m}(t)^{2} Q^{1}'\theta_{m}(t) Q^{1} ) \right \} \end{split}\end{displaymath}](img198.gif)
![\begin{displaymath}\begin{split}0 = -A_{m}(t) [(-S_{1} + & S_{m})\bar{v}_{m}(t)] + A_{m}(t)^2 (-S_{1} + S_{m})[(\theta_{m}(t) + \theta_{m}(t)')/2](Q^{1} + \Delta Q^{1}) \\ & + A_{m}(t) \left [r P^{1}(.,t-1) - S_{m} \beta_{Q^{1}_{B}}(t-1)' S_{m} \Delta Q^{1}_{B} \right ], \end{split}\end{displaymath}](img204.gif)
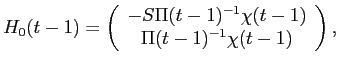 and
and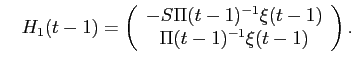
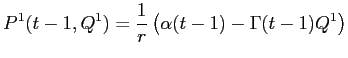
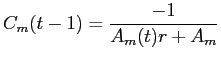 ln
ln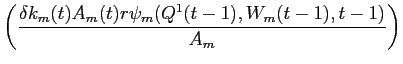
![LaTex Encoded Math: \displaystyle V_{m}(W_{m}(t-1),Q^{1},t-1) = -\left [\frac{1+r^{*}_{m}(t)}{r^{*}_{m}(t)} \right ] \left [\delta k_{m}(t) r^{*}_{m}(t) \psi_{m}(Q^{1}, W_{m}(t-1), t-1) \right ]^{\frac{1}{1+r^{*}_{m}(t)}}](img238.gif)
![\begin{displaymath}\begin{split}k_{m}(t-1) = & \left [ \frac{r^{*}_{m}(t) + 1}{r^{*}_{m}(t)} \right ] \left [\delta k_{m}(t) r^{*}_{m}(t) \right ]^{\frac{1}{1+r^{*}_{m}(t)}} \\ & \times e^{\frac{-.5 \bar{Z}^{2} ' \Omega_{22}^{-1} \bar{Z}^{2}}{1+r^{*}_{m}(t)}} \\ & \times e^{A_{m}(t-1) H_{0}(t-1)'S_{m}' \alpha(t-1)/r - A_{m}(t-1)G_{0}(t-1)'\bar{v}_{m}(t)/r + .5 A_{m}(t-1)^{2} ((1+r^{*}_{m}(t))/r^{2})(G_{0}(t-1)'\theta_{m}(t) G_{0}(t-1))} \end{split}\end{displaymath}](img242.gif)
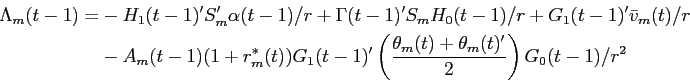
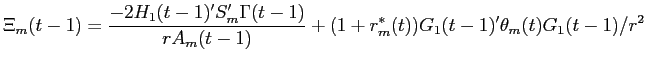
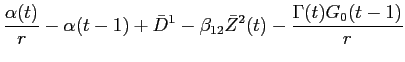
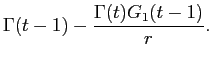
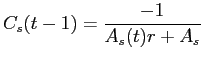 ln
ln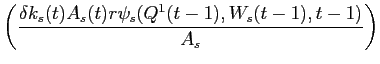
![\begin{displaymath}\begin{split}V_{s}(W_{s}(t-1),Q^{1}(t-1),t-1) = \\ & -\left [\frac{1+r^{*}_{s}(t)}{r^{*}_{s}(t)} \right ] \left [\delta k_{s}(t) r^{*}_{s}(t)\psi_{s}(Q^{1}(t-1),W_{s}(t-1), t-1)\right ]^{\frac{1}{1+r^{*}_{s}(t)}} \end{split}\end{displaymath}](img259.gif)
![\begin{displaymath}\begin{array}{ccl} V_{s}(W_{s}(t-1),Q^{1}(t-1),t-1) & = & -K_{s}(t-1) \ F(Q^{1},t-1) \ e^{-A_{s}(t-1)W_{s}(t-1)} , \\ [0.06in] \mbox{where} \ F(Q^{1}(t-1),t-1) & = & e^{- Q^{1}(t-1)'\bar{v}_{s}(t-1) - Q^{1}(t-1)'\theta_{s}(t-1) Q^{1}(t-1)} \end{array}\end{displaymath}](img261.gif)
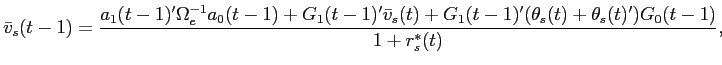
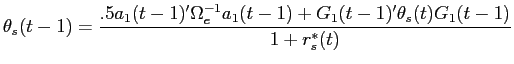
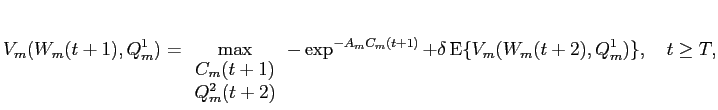
![LaTex Encoded Math: \displaystyle ^{-A_{m}[1-(1/r)] W_{m} - A_{m}[1-(1/r)] Q^{1}_{m}'\frac{(1/r)[\bar{D}^{1} - \beta_{12} \bar{Z}^{2}]}{1-(1/r)} + \frac{1}{2} A_{m}^{2}[1-(1/r)]^{2} Q_{m}^{1}'\frac{(1/r)\Omega_{e}}{1-(1/r)} Q_{m}^{1} }](img274.gif)
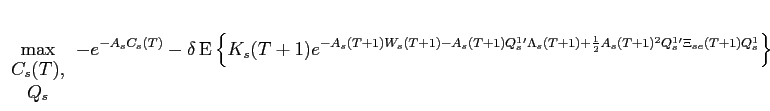
![\begin{displaymath}\begin{split}\max_{\begin{array}{c} C_{s}(T),\\ Q^{1}_{s} \end{array}} -e^{-A_{s} C_{s}(T)} - & \delta K_{s}(T+1) \operatorname{Exp}\left \{ -.5 \bar{Z}_{2}'\Omega_{22}^{-1} \bar{Z}_{2} - A_{s}(T) r [W_{s}(T) - C_{s}(T)] \right \} \\ & \times \operatorname{Exp}\left \{ -A_{s}(T+1) Q^{1}_{s}' [\bar{v}_{s}(T+1) - r P^{1}(T)] + .5 A_{s}(T+1)^{2} Q^{1}_{s}' \Omega_{e}(T+1) Q^{1}_{s} \right \} \end{split}\end{displaymath}](img294.gif)
![LaTex Encoded Math: \displaystyle \left [\frac{\bar{D}^{1}(T+1) - \beta_{12} \bar{Z}_{2}(T+1)}{1-(1/r)}\right ]](img296.gif)
![LaTex Encoded Math: \displaystyle \left [\frac{\Omega_{e}}{1-(1/r)} \right ]](img298.gif)
![LaTex Encoded Math: \displaystyle S_{m}' \left [ \frac{(1/r)[\bar{D}^{1} - \beta_{12} \bar{Z}^{2}]}{1-(1/r)} \right ],](img311.gif)
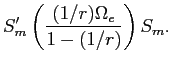
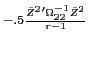
![LaTex Encoded Math: \displaystyle \bar{v}_{s}(T) = \frac{\Gamma(T)'[\Omega_{e}(T+1)]^{-1} [\bar{v}_{s}(T+1) - \alpha(T)]}{1+r^{*}_{s}(T+1)},](img329.gif)
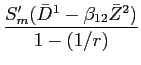
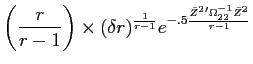
![LaTex Encoded Math: \displaystyle [\Gamma(t) - \frac{1}{r}\Gamma(t+1)G_{1}(t) ] Q^{1W} = \lambda_{[X^{1}]} \Omega_{e} X^{1}.](img422.gif)
 - Q^{W}) + [\Gamma(t) - \frac{1}{r}\Gamma(t+1)G_{1}(t) ]Q^{1W}](img432.gif)
 - Q^{1W}) \\ &+ [\Gamma(t+\tau) - \frac{1}{r}\Gamma(t+\tau + 1)G_{1}(t+\tau) ]Q^{1W}. \end{split}\end{displaymath}](img443.gif)
![LaTex Encoded Math: \displaystyle \bar{Z}_{i} - \beta_{i} \bar{Z}_{M} = \alpha_{i} + \left[ \pi_{i} - \beta_{i} \sum X_{i}'\pi_{i} \right ]](img515.gif)