Do Macro Variables, Asset Markets, or Surveys Forecast Inflation Better?
Keywords:
Abstract:
JEL Classification: E31, E37, E43, E44
1 Introduction
Obtaining reliable and accurate forecasts of future inflation is crucial for policymakers conducting monetary and fiscal policy; for investors hedging the risk of nominal assets; for firms making investment decisions and setting prices; and for labor and management negotiating wage contracts. Consequently, it is no surprise that a considerable academic literature evaluates different inflation forecasts and forecasting methods. In particular, economists use four main methods to forecast inflation. The first method is atheoretical, using time series models of the ARIMA variety. The second method builds on the economic model of the Phillips curve, leading to forecasting regressions that use real activity measures. Third, we can forecast inflation using information embedded in asset prices, in particular the term structure of interest rates. Finally, survey-based measures use information from agents (consumers or professionals) directly to forecast inflation.
In this article, we comprehensively compare and contrast the ability of these four methods to forecast inflation out of sample. Our approach makes four main contributions to the literature. First, our analysis is the first to comprehensively compare the four methods: time-series forecasts, forecasts based on the Phillips curve, forecasts from the yield curve, and all three available surveys (the Livingston, Michigan, and SPF surveys). The previous literature has concentrated on only one or two of these different forecasting methodologies. For example, Stockton and Glassman (1987) show that pure time-series models out-perform more sophisticated macro models, but do not consider term structure models or surveys. Fama and Gibbons (1984) compare term structure forecasts with the Livingston survey, but they do not consider forecasts from macro factors. Whereas Grant and Thomas (1999), Thomas (1999) and Mehra (2002) show that surveys out-perform simple time-series benchmarks for forecasting inflation, none of these studies compares the performance of survey measures with forecasts from Phillips curve or term structure models.
The lack of a study comparing these four methods of inflation forecasting implies that there is no well-accepted set of findings regarding the superiority of a particular forecasting method. The most comprehensive study to date, Stock and Watson (1999), finds that Phillips curve-based forecasts produce the most accurate out-of-sample forecasts of U.S. inflation compared with other macro series and asset prices, using data up to 1996. However, Stock and Watson only briefly compare the Phillips-curve forecasts to the Michigan survey and to simple regressions using term structure information. Stock and Watson do not consider no-arbitrage term structure models, non-linear forecasting models, or combined forecasts from all four forecasting methods. Recent work also casts doubts on the robustness of the Stock-Watson findings. In particular, Atkeson and Ohanian (2001), Fisher, Liu and Zhou (2002), Sims (2002), and Cecchetti, Chu and Steindel (2000), among others, show that the accuracy of Phillips curve-based forecasts depends crucially on the sample period. Clark and McCracken (2006) address the issue of how instability in the output gap coefficients of the Phillips curve affects forecasting power. To assess the stability of the inflation forecasts across different samples, we consider out-of-sample forecasts over both the post-1985 and post-1995 periods.
Our second contribution is to evaluate inflation forecasts implied by arbitrage-free asset pricing models. Previous studies employing term structure data mostly use only the term spread in simple OLS regressions and usually do not use all available term structure data (see, for example, Mishkin, 1990, 1991; Jorion and Mishkin, 1991; Stock and Watson, 2003). Frankel and Lown (1994) use a simple weighted average of different term spreads, but they do not impose no-arbitrage restrictions. In contrast to these approaches, we develop forecasting models that use all available data and impose no-arbitrage restrictions. Our no-arbitrage term structure models incorporate inflation as a state variable because inflation is an integral component of nominal yields. The no-arbitrage framework allows us to extract forecasts of inflation from data on inflation and asset prices taking into account potential time-varying risk premia.
No-arbitrage constraints are reasonable in a world where hedge funds and investment banks routinely eliminate arbitrage opportunities in fixed income securities. Imposing theoretical no-arbitrage restrictions may also lead to more efficient estimation. Just as Ang, Piazzesi and Wei (2004) show that no-arbitrage models produce superior forecasts of GDP growth, no-arbitrage restrictions may also produce more accurate forecasts of inflation. In addition, this is the first article to investigate non-linear, no-arbitrage models of inflation. We investigate both an empirical regime-switching model incorporating term structure information and a no-arbitrage, non-linear term structure model following Ang, Bekaert and Wei (2006) with inflation as a state variable.
Our third contribution is that we thoroughly investigate combined forecasts. Stock and Watson (2002a, 2003), among others, show that the use of aggregate indices of many macro series measuring real activity produces better forecasts of inflation than individual macro series. To investigate this further, we also include the (Phillips curve-based) index of real activity constructed by Bernanke, Boivin and Eliasz (2005) from 65 macroeconomic series. In addition, several authors (see, e.g., Stock and Watson, 1999; Brave and Fisher, 2004; Wright, 2004) advocate combining several alternative models to forecast inflation. We investigate five different methods of combining forecasts: simple means or medians, OLS based combinations, and Bayesian estimators with equal or unit weight priors.
Finally, our main focus is forecasting inflation rates. Because of the long-standing debate in macroeconomics on the stationarity of inflation rates, we also explicitly contrast the predictive power of some non-stationary models to stationary models and consider whether forecasting inflation changes alters the relative forecasting ability of different models.
Our major empirical results can be summarized as follows. The first major result is that survey forecasts outperform the other three methods in forecasting inflation. That the median Livingston and SPF survey forecasts do well is perhaps not surprising, because presumably many of the best analysts use time-series and Phillips Curve models. However, even participants in the Michigan survey who are consumers, not professionals, produce accurate out-of-sample forecasts, which are only slightly worse than those of the professionals in the Livingston and SPF surveys. We also find that the best survey forecasts are the survey median forecasts themselves; adjustments to take into account both linear and non-linear bias yield worse out-of-sample forecasting performance.
Second, term structure information does not generally lead to better forecasts and often leads to inferior forecasts than models using only aggregate activity measures. Whereas this confirms the results in Stock and Watson (1999), our investigation of term structure models is much more comprehensive. The relatively poor forecasting performance of term structure models extends to simple regression specifications, iterated long-horizon VAR forecasts, no-arbitrage affine models, and non-linear no-arbitrage models. These results suggest that while inflation is very important for explaining the dynamics of the term structure (see, e.g., Ang, Bekaert and Wei, 2006), yield curve information is less important for forecasting future inflation.
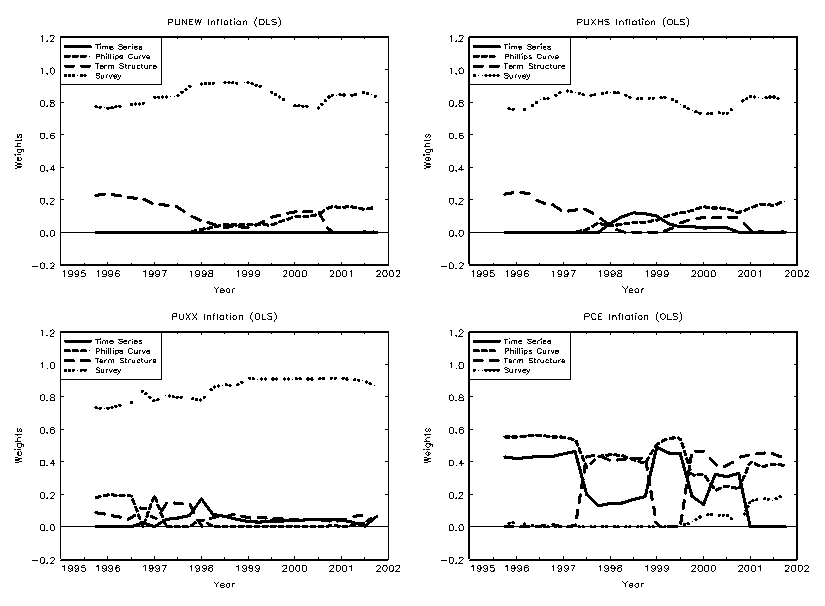
Our third major finding is that combining forecasts does not generally lead to better out-of-sample forecasting performance than single forecasting models. In particular, simple averaging, like using the mean or median of a number of forecasts, does not necessarily improve the forecast performance, whereas linear combinations of forecasts with weights computed based on past performance and prior information generate the biggest gains. Even the Phillips curve models using the Bernanke, Boivin and Eliasz (2005) forward-looking aggregate measure of real activity mostly does not perform well relative to simpler Phillips curve models and never outperforms the survey forecasts. The strong success of the surveys in forecasting inflation out-of-sample extends to surveys dominating other models in forecast combinination methods. The data consistently place the highest weights on the survey forecasts and little weight on other forecasting methods.
The remainder of this paper is organized as follows. Section 2 describes the data set. In Section 3, we describe the time-series models, predictive macro regressions, term structure models, and forecasts from survey data, and detail the forecasting methodology. Section 4 contains the empirical out-of-sample results. We examine the robustness of our results to a non-stationary inflation specification in Section 5. Finally, Section 6 concludes.
2.1 Inflation
We consider four different measures of inflation. The first three are consumer price index (CPI) measures, including CPI-U for All Urban Consumers, All Items (PUNEW), CPI for All Urban Consumers, All Items Less Shelter (PUXHS) and CPI for All Urban Consumers, All Items Less Food and Energy (PUXX), which is also called core CPI. The latter two measures strip out highly volatile components in order to better reflect underlying price trends (see the discussion in Quah and Vahey, 1995). The fourth measure is the Personal Consumption Expenditure deflator (PCE). While all three surveys forecast a CPI-based inflation measure, PCE inflation features prominently in policy work at the Federal Reserve. All measures are seasonally adjusted and obtained from the Bureau of Labor Statistics website. The sample period is 1952:Q2 to 2002:Q4 for PUNEW and PUXHS, 1958:Q2 to 2002:Q4 for PUXX, and 1960:Q2 to 2002:Q4 for PCE.
We define the quarterly inflation rate, ![]() , from
, from ![]() to
to ![]() as:
as:
where
where
Empirical work on inflation has failed to come to a consensus regarding its stationarity properties. For example, Bryan and Cecchetti (1993) assume a stationary inflation process, while Nelson and Schwert (1977) and Stock and Watson (1999) assume that the inflation process has a unit root. Most of our analysis assumes that inflation is stationary for two reasons. First, it is difficult to generate non-stationary inflation in standard economic models, whether they are monetary in nature, or of the New Keynesian variety (see Fuhrer and Moore, 1995; Holden and Driscoll, 2003). Second, the working paper version of Bai and Ng (2004) recently rejects the null of non-stationarity for inflation. That being said, Cogley and Sargent (2005) and Stock and Watson (2005) find evidence of changes in inflation persistence over time, with a random walk or integrated MA-process providing an accurate description of inflation dynamics during certain times. Furthermore, the use of a parsimonious non-stationary model may be attractive for forecasting. In particular, Atkeson and Ohanian (2001) have made the random walk a natural benchmark to beat in forecasting exercises. Therefore, we consider whether our results are robust to assuming non-stationary inflation in Section 5.
Table 1 reports summary statistics for all four measures of inflation for the full sample in Panel A, and the post-1985 sample and the post-1995 sample in Panels B and C, respectively. Our statistics pertain to annual inflation,
![]() , but we sample the data quarterly. Therefore, we report the fourth autocorrelation for quarterly inflation, which corresponds to the first autocorrelation for annual inflation.
Table 1 shows that all four inflation measures are lower and more stable during the last two decades, in common with many other macroeconomic series, including output (see Kim and Nelson, 1999; McConnell and Perez-Quiros, 2000; Stock and Watson, 2002b). Core CPI (PUXX)
has the lowest volatility of all the inflation measures. PUXX volatility ranges from 2.56% per annum over the full sample to only 0.24% per annum post-1996. The higher variability of the other measures in the latter part of the sample must be due to food and energy price changes. In the later
sample periods, PCE inflation is, on average, lower than CPI inflation, which may be partly due to its use of a chain weighting in contrast to the other CPI measures which use a fixed basket (see Clark, 1999).
, but we sample the data quarterly. Therefore, we report the fourth autocorrelation for quarterly inflation, which corresponds to the first autocorrelation for annual inflation.
Table 1 shows that all four inflation measures are lower and more stable during the last two decades, in common with many other macroeconomic series, including output (see Kim and Nelson, 1999; McConnell and Perez-Quiros, 2000; Stock and Watson, 2002b). Core CPI (PUXX)
has the lowest volatility of all the inflation measures. PUXX volatility ranges from 2.56% per annum over the full sample to only 0.24% per annum post-1996. The higher variability of the other measures in the latter part of the sample must be due to food and energy price changes. In the later
sample periods, PCE inflation is, on average, lower than CPI inflation, which may be partly due to its use of a chain weighting in contrast to the other CPI measures which use a fixed basket (see Clark, 1999).
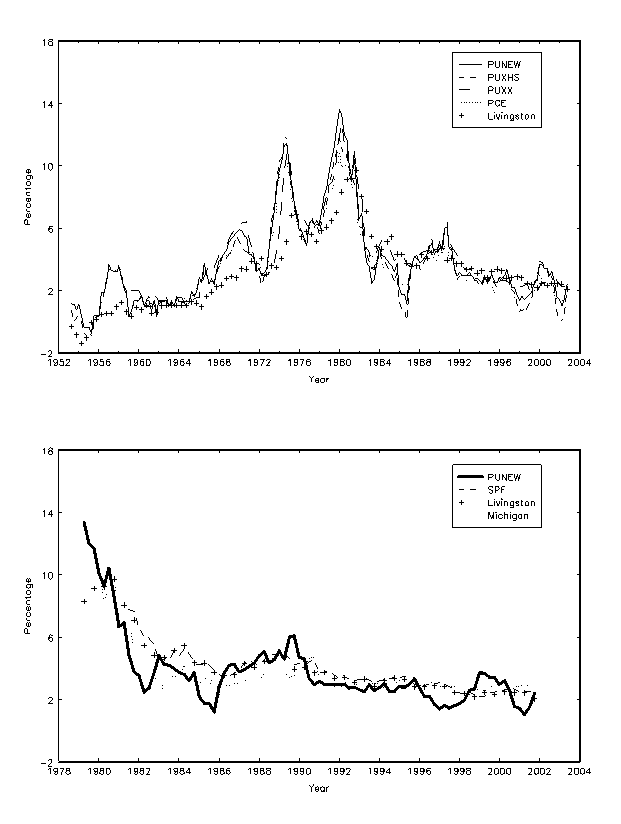
Inflation is somewhat persistent (0.79% for PUNEW over the full sample), but its persistence decreases over time, as can be seen from the lower autocorrelation coefficients for the PUNEW and the PUXHS measures after 1986, and for all measures after 1995. The correlations of the four measures of inflation with each other are all over 75% over the full sample. The comovement can be clearly seen in the top panel of Figure 1. Inflation is lower prior to 1969 and after 1983, but reaches a high of around 14% during the oil crisis of 1973-1983. PUXX tracks both PUNEW and PUXHS closely, except during the 1973-1975 period, where it is about 2% lower than the other two measures, and after 1985, where it appears to be more stable than the other two measures. During the periods when inflation is decelerating, such as in 1955-1956, 1987-1988, 1998-2000 and most recently 2002-2003, PUNEW declines more gradually than PUXHS, suggesting that housing prices are less volatile than the prices of other consumption goods during these periods.
2.2 Real Activity Measures
We consider six individual series for real activity along with one composite real activity factor. We compute GDP growth (GDPG) using the seasonally adjusted data on real GDP in billions of chained 2000 dollars. The unemployment rate (UNEMP) is also seasonally adjusted and computed for the civilian labor force aged 16 years and over. Both real GDP and the unemployment rate are from the Federal Reserve Economic Data (FRED) database. We compute the output gap either as the detrended log real GDP by removing a
quadratic trend as in Gali and Gertler (1999), which we term GAP1, or by using the Hodrick-Prescott (1997) filter (with the standard smoothness parameter of 1,600), which we term GAP2. At time ![]() , both measures are constructed using only current and past GDP values, so the filters are run recursively. We also use the labor income share (LSHR), defined as the ratio of nominal compensation to total
nominal output in the U.S. nonfarm business sector. We use two forward-looking indicators: the Stock-Watson (1989) Experimental Leading Index (XLI) and their Alternative Nonfinancial Experimental Leading Index-2 (XLI-2).
, both measures are constructed using only current and past GDP values, so the filters are run recursively. We also use the labor income share (LSHR), defined as the ratio of nominal compensation to total
nominal output in the U.S. nonfarm business sector. We use two forward-looking indicators: the Stock-Watson (1989) Experimental Leading Index (XLI) and their Alternative Nonfinancial Experimental Leading Index-2 (XLI-2).
Because Stock and Watson (2002a), among others, show that aggregating the information from many factors has good forecasting power, we also use a single factor aggregating the information from 65 individual series constructed by Bernanke, Boivin and Eliasz (2005). This single real activity series, which we term FAC, aggregates real output and income, employment and hours, consumption, housing starts and sales, real inventories, and average hourly earnings. The sample period for all the real activity measures is 1952:Q2 to 2001:Q4, except the Bernanke-Boivin-Eliasz real activity factor, which spans 1959:Q1 to 2001:Q3. We use the composite real activity factor at the end of each quarter for forecasting inflation over the next year.1
The real activity measures have the disadvantage that they may use information that is not actually available at the time of the forecast, either through data revisions, or because of full sample estimation in the case of the Bernanke-Boivin-Eliasz measure. This biases the forecasts from Phillips curve models to be better than what could be actually forecasted using a real-time data set. The use of real time economic activity measures produces much worse forecasts of future inflation compared to the use of revised economic series in Orphanides and van Norden (2001) but only slightly worse forecasts for both inflation and real activity in Bernanke and Boivin (2003). Nevertheless, our forecast errors using real activity measures are likely biased downwards.
2.3 Term Structure Data
The term structure variables are zero-coupon yields for the maturities of 1, 4, 8, 12, 16, and 20 quarters from CRSP spanning 1952:Q2 to 2001:Q4. The one-quarter rate is from the CRSP Fama risk-free rate file, while all other bond yields are from the CRSP Fama-Bliss discount bond file. All yields are continuously compounded and expressed at a quarterly frequency. We define the short rate (RATE) to be the one-quarter yield and define the term spread (SPD) to be the difference between the 20-quarter yield and the short rate. Some of our term structure models also use four-quarter and 12-quarter yields for estimation.
2.4 Surveys
We examine three inflation expectation surveys: the Livingston survey, the Survey of Professional Forecasters (SPF), and the Michigan survey.2 The Livingston survey is conducted twice a year, in June and in December, and polls economists from industry, government, and academia. The Livingston survey records participants' forecasts of non-seasonally-adjusted CPI levels six and twelve months in the future and is usually conducted in the middle of the month. Unlike the Livingston survey, participants in the SPF and the Michigan survey forecast inflation rates. Participants in the SPF are drawn primarily from business, and forecast changes in the quarterly average of seasonally-adjusted CPI-U levels. The SPF is conducted in the middle of every quarter and the sample period for the SPF median forecasts is from 1981:Q3 to 2002:Q4. In contrast to the Livingston survey and SPF, the Michigan survey is conducted monthly and asks households, rather than professionals, to estimate expected price changes over the next twelve months. We use the median Michigan survey forecast of inflation over the next year at the end of each quarter from 1978:Q1 to 2002:Q4.
There are some reporting lags between the time the surveys are taken and the public dissemination of their results. For the Livingston and the SPF surveys, there is a lag of about one week between the due date of the survey and their publication. However, these reporting lags are largely inconsequential for our purposes. What matters is the information set used by the forecasters in predicting future inflation. Clearly, survey forecasts must use less up to date information than either macro-economic or term structure forecasts. For example, the Livingston survey forecasters presumably use information up to at most the beginning of June and December, and mostly do not even have the May and November official CPI numbers available when making a forecast. The SPF forecasts can only use information up to at most the middle of the quarter and while we take the final month of the quarter for the Michigan survey, consumers do not have up-to-date economic data available at the end of the quarter. But, for the economist forecasting annual inflation with the surveys, all survey data is publicly available at the end of each quarter for the SPF and Michigan surveys, and at the end of each semi-annual period for the Livingston survey. Together with the slight data advantages present in revised, fitted macro data, we are in fact biasing the results against survey forecasts.
The Livingston survey is the only survey available for our full sample. In the top panel of Figure 1, which graphs the full sample of inflation data, we also include the unadjusted median Livingston forecasts. We plot the survey forecast lagged one year, so that in December 1990, we plot inflation from December 1989 to December 1990 together with the survey forecasts of December 1989. The Livingston forecasts broadly track the movements of inflation, but there are several large movements that the Livingston survey fails to track, for example the pickup in inflation in 1956-1959, 1967-1971, 1972-1975, and 1978-1981. In the bottom panel of Figure 1, we graph all three survey forecasts of future one-year inflation together with the annual PUNEW inflation, where the survey forecasts are lagged one year for direct comparison. After 1981, all survey forecasts move reasonably closely together and track inflation movements relatively well. Nevertheless, there are still some notable failures, like the slowdowns in inflation in the early 1980s and in 1996.
3 Forecasting Models and Methodology
In this section, we describe the forecasting models and describe our statistical tests. In all our out-of-sample forecasting exercises, we forecast future annual inflation. Hence, for all our models, we compute annual inflation forecasts of:
where
In Sections 3.1 to 3.4, we describe our 39 forecasting models. Table 2 contains a full nomenclature. Section 3.1 focuses on time-series models of inflation, which serve as our benchmark forecasts; Section 3.2 summarizes our OLS regression models using real activity macro variables; Section 3.3 describes the term structure models incorporating inflation data; and finally, Section 3.4 describes our survey forecasts. In Section 3.5, we define the out-of-sample periods and list the criteria that we use to assess the performance of out-of-sample forecasts. Finally, Section 3.6 describes our methodology to combine model forecasts.
For all models except OLS regressions, we compute implied long-horizon forecasts from single-period (quarterly) models. While Schorfheide (2005) shows that in theory, iterated forecasts need not be superior to direct forecasts from horizon-specific models, Marcellino, Stock and Watson (2006) document the empirical superiority of iterated forecasts in predicting U.S. macroeconomic series. For the OLS models, we compute the forecasts directly from the long-horizon regression estimates.
3.1 Time-Series Models
ARIMA Models
If inflation is stationary, the Wold theorem suggests that a parsimonious ARMA(![]() ) model may perform well in forecasting. We consider two ARMA(
) model may perform well in forecasting. We consider two ARMA(![]() ) models: an ARMA(1,1) model and a pure autoregressive model with
) models: an ARMA(1,1) model and a pure autoregressive model with ![]() lags, AR(
lags, AR(![]() ). The optimal lag length for the AR model is recursively selected using the Schwartz criterion (BIC) on the in-sample data. The motivation for the ARMA(1,1) model derives from a long tradition in rational expectations
macroeconomics (see Hamilton, 1985) and finance (see Fama, 1975) that models inflation as the sum of expected inflation and noise. If expected inflation follows an AR(1) process, then the reduced-form model for inflation is given by an ARMA(1,1) model. The ARMA(1,1) model also nicely fits the
slowly decaying autocorrelogram of inflation.
). The optimal lag length for the AR model is recursively selected using the Schwartz criterion (BIC) on the in-sample data. The motivation for the ARMA(1,1) model derives from a long tradition in rational expectations
macroeconomics (see Hamilton, 1985) and finance (see Fama, 1975) that models inflation as the sum of expected inflation and noise. If expected inflation follows an AR(1) process, then the reduced-form model for inflation is given by an ARMA(1,1) model. The ARMA(1,1) model also nicely fits the
slowly decaying autocorrelogram of inflation.
The specifications of the ARMA(1,1) model,
and the AR(
are entirely standard. The ARMA(1,1) model is estimated by maximum likelihood, conditional on a zero initial residual. We compute the implied inflation level forecast over the next year expressed at a quarterly frequency. For the ARMA(1,1) model, the forecast is:
![$\displaystyle \mathrm{E} _{t}(\pi_{t+4,4}) =\frac{1}{1-\phi}\left[ 4-\frac{\phi\left( 1-\phi^{4}\right) }{\left( 1-\phi\right) }\right] \mu+ \frac{\phi\left( 1-\phi^{4}\right) }{\left( 1-\phi\right) }\pi_{t} + \frac{\left( 1-\phi^{4}\right) \psi}{\left( 1-\phi\right) }\varepsilon_{t}. $](img21.gif)
![\begin{displaymath} X_{t}=\left[ \begin{array}[c]{c}% \pi_{t}\ \pi_{t-1}\ \vdots\ \pi_{t-p+1}% \end{array}\right] ,\text{ }A=\left[ \begin{array}[c]{c}% \mu\ 0\ \vdots\ 0 \end{array}\right] ,\text{ }\Phi=\left[ \begin{array}[c]{cccc}% \phi_{1} & \phi_{2} & ... & \phi_{p}\ 1 & 0 & ... & 0\ \vdots & \vdots & \ddots & \vdots\ 0 & 0 & ... & 0 \end{array}\right] \text{ and }U_{t}=\left[ \begin{array}[c]{c}% \varepsilon_{t}\ 0\ \vdots\ 0 \end{array}\right] . \end{displaymath}](img23.gif)
Our third ARIMA benchmark is a random walk (RW) forecast where
![]() , and
, and
![]() . Inspired by Atkeson and Ohanian (2001), we also forecast inflation using a random walk model on annual inflation, where the forecast is given by
. Inspired by Atkeson and Ohanian (2001), we also forecast inflation using a random walk model on annual inflation, where the forecast is given by
![]() . We denote this forecast as AORW.
. We denote this forecast as AORW.
Regime-Switching Models
Evans and Wachtel (1993), Evans and Lewis (1995), and Ang and Bekaert (2004), among others, document regime-switching behavior in inflation. A regime-switching model may potentially account for non-linearities and structural changes, such as a sudden shift in inflation expectations after a supply shock, or a change in inflation persistence.
We estimate the following univariate regime-switching model for inflation, which we term RGM:
The regime variable
3.2 Regression Forecasts Based on the Phillips Curve
In standard Phillips curve models of inflation, expected inflation is linked to some measure of the output gap. There are both forward- and backward-looking Phillips curve models, but ultimately even forward-looking models link expected inflation to the current information set. According to the Phillips curve, measures of real activity should be an important part of this information set. We avoid the debate regarding the actual measure of the output gap (see, for instance, Gali and Gertler, 1999) by taking an empirical approach and using a large number of real activity measures. We choose not to estimate structural models because the BIC criterion is likely to choose the empirical model best suitable for forecasting. Previous work often finds that models with the clearest theoretical justification often have poor predictive content (see the literature summary by Stock and Watson, 2003).
The empirical specification we estimate is:
where
In our next section, we extend the information set to include term structure information. Regression models where term structure information is included in ![]() along with inflation and
real activity are potentially consistent with a forward-looking Phillips curve that includes inflation and real activity measures in the information set. Such models can approximate the reduced form of a more sophisticated, forward-looking rational expectations Phillips curve model of inflation
(see, for instance, Bekaert, Cho and Moreno, 2005).
along with inflation and
real activity are potentially consistent with a forward-looking Phillips curve that includes inflation and real activity measures in the information set. Such models can approximate the reduced form of a more sophisticated, forward-looking rational expectations Phillips curve model of inflation
(see, for instance, Bekaert, Cho and Moreno, 2005).
3.3 Models Using Term Structure Data
We consider a variety of term structure forecasts, including augmenting the simple Phillips Curve OLS regressions with short rate and term spread variables; long-horizon VAR forecasts; a regime-switching specification; affine term structure models; and term structure models incorporating regime switches. We outline each of these specifications in turn.
Linear Non-Structural Models
We begin by augmenting the OLS Phillips Curve models in equation (7) with the short rate, RATE, and the term spread, SPD, as regressors in ![]() . Specifications
TS1-TS8 add RATE to the Phillips Curve Curve specifications PC1-PC8. TS9 and
. Specifications
TS1-TS8 add RATE to the Phillips Curve Curve specifications PC1-PC8. TS9 and
![]() only use inflation and term structure variables as predictors. TS9 uses inflation and the lagged term spread, producing a forecasting model similar to
the specification in Mishkin (1990, 1991). TS10 adds the short rate to this specification. Finally, TS11 adds GDP growth to the TS10 specification.
only use inflation and term structure variables as predictors. TS9 uses inflation and the lagged term spread, producing a forecasting model similar to
the specification in Mishkin (1990, 1991). TS10 adds the short rate to this specification. Finally, TS11 adds GDP growth to the TS10 specification.
We also consider forecasts with a VAR(1) in ![]() , where
, where ![]() contains RATE,
SPD, GDPG, and
contains RATE,
SPD, GDPG, and ![]() :
:
Although the VAR is specified at a quarterly frequency, we compute the annual horizon forecast of inflation implied by the VAR. We denote this forecasting specification as VAR. As Ang, Piazzesi and Wei (2004) and Cochrane and Piazzesi (2005) note, a VAR specification can be economically motivated from the fact that a reduced-form VAR is equivalent to a Gaussian term structure model where the term structure factors are observable yields and certain assumptions on risk premia apply. Under these restrictions, a VAR coincides with a no-arbitrage term structure model only for those yields included in the VAR. However, the VAR does not impose over-identifying restrictions generated by the term structure model for yields not included as factors in the VAR.
An Empirical Non-Linear Regime-Switching Model
A large empirical literature has documented the presence of regime switches in interest rates (see, among others, Hamilton, 1988; Gray, 1996; Bekaert, Hodrick and Marshall, 2001). In particular, Ang and Bekaert (2002) show that regime-switching models forecast interest rates better than linear models. As interest rates reflect information in expected inflation, capturing the regime-switching behavior in interest rates may help in forecasting potentially regime-switching dynamics of inflation.
We estimate a regime-switching VAR, denoted as RGMVAR:
where
No-Arbitrage Term Structure Models
We estimate two no-arbitrage term structure models. Because such models have implications for the complete yield curve, it is straightforward to incorporate additional information from the yield curve into the estimation. Such additional information is absent in the empirical VAR specified in
equation (8). Concretely, both no-arbitrage models have two latent variables and quarterly inflation as state variables, denoted by ![]() . We estimate the models by
maximum likelihood, and following Chen and Scott (1993), assume that the one- and 20-quarter yields are measured without error, and the other four- and 12-quarter yields are measured with error. The estimated models build on Ang, Bekaert and Wei (2006), who formulate a real pricing kernel as:
. We estimate the models by
maximum likelihood, and following Chen and Scott (1993), assume that the one- and 20-quarter yields are measured without error, and the other four- and 12-quarter yields are measured with error. The estimated models build on Ang, Bekaert and Wei (2006), who formulate a real pricing kernel as:
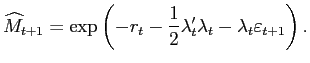 |
Here,
The first no-arbitrage model (MDL1) is an affine model in the class of Duffie and Kan (1996) with affine, time-varying risk premia (see Dai and Singleton, 2002; Duffee, 2002) modelled as:
where
The second model (MDL2) incorporates regime switches and is developed by Ang, Bekaert and Wei (2006). Ang, Bekaert and Wei show that this model fits the moments of yields and inflation very well and almost exactly matches the autocorrelogram of inflation. MDL2 replaces equation (12) with the regime-switching VAR:
and also incorporates regime switches in the prices of risk, replacing equation (11) with
There are four regime variables
In estimating MDL1 and MDL2, we impose the same parameter restrictions necessary for identification as Ang, Bekaert and Wei (2006) do. For both MDL1 and MDL2, we compute out-of-sample forecasts of annual inflation, but the models are estimated using quarterly data.
3.4 Survey Forecasts
We produce estimates of
![]() from the Livingston, SPF, and the Michigan surveys. We denote the actual forecasts from the SPF, Livingston and Michigan surveys as SPF1, LIV1, and MCH1, respectively.
from the Livingston, SPF, and the Michigan surveys. We denote the actual forecasts from the SPF, Livingston and Michigan surveys as SPF1, LIV1, and MCH1, respectively.
Producing Forecasts from Survey Data
Participants in the Livingston survey are asked to forecast a CPI level (not an inflation rate). Given the timing of the survey, Carlson (1977) carefully studies the forecasts of individual participants in the Livingston survey and finds that the participants generally forecast inflation over the next 14 months. We follow Thomas (1999) and Mehra (2002) and adjust the raw Livingston forecasts by a factor of 12/14 to obtain an annual inflation forecast.
Participants in both the SPF and the Michigan surveys do not forecast log year-on-year CPI levels according to the definition of inflation in equation (1). Instead, the surveys record simple expected inflation changes,
![]() . This differs from
. This differs from
![]() by a Jensen's inequality term. In addition, the SPF participants are asked to forecast changes in the quarterly average of seasonally-adjusted PUNEW
(CPI-U), as opposed to end-of-quarter changes in CPI levels. In both the SPF and the Michigan survey, we cannot directly recover forecasts of expected log changes in CPI levels. Instead, we directly use the SPF and Michigan survey forecasts to represent forecasts of future annual inflation as
defined in equation (3). We expect that the effects of these measurement problems are small.3 In any case, the Jensen's term biases our survey
forecasts upwards, imparting a conservative upward bias to our Root Mean Squared Error (RMSE) statistics.
by a Jensen's inequality term. In addition, the SPF participants are asked to forecast changes in the quarterly average of seasonally-adjusted PUNEW
(CPI-U), as opposed to end-of-quarter changes in CPI levels. In both the SPF and the Michigan survey, we cannot directly recover forecasts of expected log changes in CPI levels. Instead, we directly use the SPF and Michigan survey forecasts to represent forecasts of future annual inflation as
defined in equation (3). We expect that the effects of these measurement problems are small.3 In any case, the Jensen's term biases our survey
forecasts upwards, imparting a conservative upward bias to our Root Mean Squared Error (RMSE) statistics.
Adjusting Surveys for Bias
Several authors, including Thomas (1999), Mehra (2002), and Souleles (2004), document that survey forecasts are biased. We take into account the survey bias by estimating
![]() and
and ![]() in the regressions:
in the regressions:
where
Table 3 provides empirical evidence regarding these biases using the full sample. For each inflation measure, the first three rows report the results from regression (15). The SPF survey forecasts produce ![]() s that are smaller than one for all inflation measures, which are, with the exception of PUXX, significant at the 95% level. However, the point estimates of
s that are smaller than one for all inflation measures, which are, with the exception of PUXX, significant at the 95% level. However, the point estimates of
![]() are also positive, although mostly not significant, which implies that at low levels of inflation, the surveys under-predict future inflation and at high levels of inflation the
surveys over-predict future inflation. The turning point is
are also positive, although mostly not significant, which implies that at low levels of inflation, the surveys under-predict future inflation and at high levels of inflation the
surveys over-predict future inflation. The turning point is
![]() , so that the SPF survey mostly over-predicts inflation. The Livingston and Michigan surveys produce largely unbiased forecasts because the slope coefficients are
insignificantly different from one and the constants are insignificantly different from zero. Nevertheless, because the intercepts are positive (negative) for the Livingston (Michigan) survey, and the slope coefficients largely smaller (larger) than one, the Livingston (Michigan) survey tends to
produce mostly forecasts that are too low (high).
, so that the SPF survey mostly over-predicts inflation. The Livingston and Michigan surveys produce largely unbiased forecasts because the slope coefficients are
insignificantly different from one and the constants are insignificantly different from zero. Nevertheless, because the intercepts are positive (negative) for the Livingston (Michigan) survey, and the slope coefficients largely smaller (larger) than one, the Livingston (Michigan) survey tends to
produce mostly forecasts that are too low (high).
Thomas (1999) and Mehra (2002) suggest that the bias in the survey forecasts may vary across accelerating versus decelerating inflation environments, or across the business cycle. To take account of this possible asymmetry in the bias, we augment equation (15) with a
dummy variable, ![]() , which equals one if inflation at time
, which equals one if inflation at time ![]() exceeds its past
two-year moving average,
exceeds its past
two-year moving average,

We denote the survey forecasts that are non-linearly bias-adjusted using equation (16) as SPF3, LIV3, and MCH3 for the SPF, Livingston, and Michigan surveys, respectively.4
The bottom three rows of each panel in Table 3 report results from regression (16). Non-linear biases are reflected in significant ![]() or
or ![]() coefficients. For the SPF survey, there is no statistical evidence of non-linear biases. For all inflation measures, the SPF's negative
coefficients. For the SPF survey, there is no statistical evidence of non-linear biases. For all inflation measures, the SPF's negative ![]() and positive
and positive ![]() coefficients indicates that accelerating inflation implies a
smaller intercept and a higher slope coefficient, bringing the SPF forecasts closer to unbiasedness. For the Michigan survey, the biases are larger in magnitude (except for the PUXX measure) but there is only one significant coefficient: accelerating inflation yields a significantly higher slope
coefficient for the PUXHS measure. Economically, the Michigan survey is very close to unbiasedness in decelerating inflation environments, but over- (under-) predicts future inflation at low (high) inflation levels in accelerating inflation environments.
coefficients indicates that accelerating inflation implies a
smaller intercept and a higher slope coefficient, bringing the SPF forecasts closer to unbiasedness. For the Michigan survey, the biases are larger in magnitude (except for the PUXX measure) but there is only one significant coefficient: accelerating inflation yields a significantly higher slope
coefficient for the PUXHS measure. Economically, the Michigan survey is very close to unbiasedness in decelerating inflation environments, but over- (under-) predicts future inflation at low (high) inflation levels in accelerating inflation environments.
The Livingston survey has the strongest evidence of non-linear bias, for which we also have the longest data sample. The coefficients have the same sign as for the other surveys, but now the ![]() slope coefficients significantly increase in accelerating inflation environments for all inflation measures except PUXX. As in the case of the SPF survey, the Livingston survey is closer to being unbiased in accelerating inflation environments. Without accounting for
non-linearity, the Livingston survey produces largely unbiased forecasts in Table 3. However, the results of regression (16) for the Livingston survey show it produces mostly biased forecasts in decelerating inflation environments,
under-predicting future inflation when inflation is relatively low, and over-predicting future inflation when inflation is relatively high.
slope coefficients significantly increase in accelerating inflation environments for all inflation measures except PUXX. As in the case of the SPF survey, the Livingston survey is closer to being unbiased in accelerating inflation environments. Without accounting for
non-linearity, the Livingston survey produces largely unbiased forecasts in Table 3. However, the results of regression (16) for the Livingston survey show it produces mostly biased forecasts in decelerating inflation environments,
under-predicting future inflation when inflation is relatively low, and over-predicting future inflation when inflation is relatively high.
3.5 Assessing Forecasting Models
Out-of-Sample Periods
We select two starting dates for our out-of-sample forecasts, 1985:Q4 and 1995:Q4. Our main analysis focuses on recursive out-of-sample forecasts, which use all the data available at time ![]() to forecast annual future inflation from
to forecast annual future inflation from ![]() to
to ![]() . Hence, the windows used for
estimation lengthen through time. We also consider out-of-sample forecasts with a fixed rolling window. All of our annual forecasts are computed at a quarterly frequency, with the exception of forecasts from the Livingston survey, where forecasts are only available for the second and fourth quarter
each year.5 The out-of-sample periods end in 2002:Q4, except for forecasts with the composite real activity factor, which end in 2001:Q3.
. Hence, the windows used for
estimation lengthen through time. We also consider out-of-sample forecasts with a fixed rolling window. All of our annual forecasts are computed at a quarterly frequency, with the exception of forecasts from the Livingston survey, where forecasts are only available for the second and fourth quarter
each year.5 The out-of-sample periods end in 2002:Q4, except for forecasts with the composite real activity factor, which end in 2001:Q3.
Measuring Forecast Accuracy
We assess forecast accuracy with the Root Mean Squared Error (RMSE) of the forecasts produced by each model and also report the ratio of RMSEs relative to a time-series ARMA(1,1) benchmark that uses only information in the past series of inflation. We show below that the ARMA(1,1) model nearly always produces the lowest RMSE among all of the ARIMA time-series models that we examine.
To compare the out-of-sample forecasting performance of the various models, we perform a forecast comparison regression, following Stock and Watson (1999):
where
Stock and Watson (1999) note that inference about ![]() is complicated by the fact that the forecasts errors,
is complicated by the fact that the forecasts errors,
![]() , follow a MA(3) process because the overlapping annual observations are sampled at a quarterly frequency. We compute standard errors that account for the overlap by using
Hansen and Hodrick (1980) standard errors. To also take into account the estimated parameter uncertainty in one or both sets of the forecasts,
, follow a MA(3) process because the overlapping annual observations are sampled at a quarterly frequency. We compute standard errors that account for the overlap by using
Hansen and Hodrick (1980) standard errors. To also take into account the estimated parameter uncertainty in one or both sets of the forecasts,
![]() and
and ![]() , we also compute West (1996) standard errors. The
Appendix provides a detailed description of the computations involved.
, we also compute West (1996) standard errors. The
Appendix provides a detailed description of the computations involved.
3.6 Combining Models
A long statistics literature documents that forecast combinations typically provide better forecasts than individual forecasting models.6 For inflation forecasts, Stock and
Watson (1999) and Wright (2004), among others, show that combined forecasts using real activity and financial indicators are usually more accurate than individual forecasts. To examine if combining the information in different forecasts leads to gains in out-of-sample forecasting accuracy, we
examine five different methods of combining forecasts. All these methods involve placing different weights on ![]() individual forecasting models. The five model combination methods can be
summarized as follows:
individual forecasting models. The five model combination methods can be
summarized as follows:
Combination Methods
1. Mean
2. Median
3. OLS
4. Equal-Weight Prior
5. Unit-Weight Prior
All our model combinations are ex-ante. That is, we compute the weights on the models using the history of out-of-sample forecasts up to time ![]() . Hence, the ex-ante method assesses actual
out-of-sample forecasting power of combination methods. For example, the weights used to construct the ex-ante combined forecast at 2000:Q4 is based on a regression of realized annual inflation over 1985:Q4 to 2000:Q4 on the constructed out-of-sample forecasts over the same period.
. Hence, the ex-ante method assesses actual
out-of-sample forecasting power of combination methods. For example, the weights used to construct the ex-ante combined forecast at 2000:Q4 is based on a regression of realized annual inflation over 1985:Q4 to 2000:Q4 on the constructed out-of-sample forecasts over the same period.
In the first two model combination methods, we simply look at the overall mean and median, respectively, over ![]() different forecasting models. Equal weighting of many forecasts has been
used as early as Bates and Granger (1969) and, in practice, simple equal-weighting forecasting schemes are hard to beat. In particular, Stock and Watson (2003) show that this method produces superior out-of-sample forecasts of inflation.
different forecasting models. Equal weighting of many forecasts has been
used as early as Bates and Granger (1969) and, in practice, simple equal-weighting forecasting schemes are hard to beat. In particular, Stock and Watson (2003) show that this method produces superior out-of-sample forecasts of inflation.
In the last three combination methods, we compute different individual model weights that vary over time. These weights are estimated as slope coefficients in a regression of realized inflation on model forecasts:
where
To describe the last two combination methods, we set up some notation. Suppose we have ![]() forecast observations with
forecast observations with ![]() individual models. Let
individual models. Let ![]() be the
be the ![]() matrix of forecasts and
matrix of forecasts and ![]() the
the ![]() vector of actual future inflation levels
that are being forecast. Consequently, the
vector of actual future inflation levels
that are being forecast. Consequently, the ![]() -th row of
-th row of ![]() is given by
is given by
![]() . The mixed regression estimator can be viewed as a Bayesian estimator with the prior
. The mixed regression estimator can be viewed as a Bayesian estimator with the prior
![]() , where
, where
![]() is a scalar and
is a scalar and ![]() the
the ![]() identity matrix. The estimator can be derived as:
identity matrix. The estimator can be derived as:
where the parameter
We use empirical Bayes methods and estimate the shrinkage parameter as:
where
![$\displaystyle \widehat{\sigma}^{2}=\frac{1}{T}\pi^{\prime}\left[ I-F\left( F^{\prime }F\right) ^{-1}F^{\prime}\right] \pi $](img114.gif)
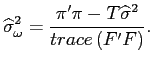
We examine the effect of two priors. In Model Combination 4, we use an equal-weight prior where each element of ![]() ,
,
![]() , which leads to the Ridge regressor used by Stock and Watson (1999). In the second prior (Model Combination 5), we assign unit weight to one type of forecast, for
example,
, which leads to the Ridge regressor used by Stock and Watson (1999). In the second prior (Model Combination 5), we assign unit weight to one type of forecast, for
example,
![]() . One natural choice for a unit weight prior would be to choose the best performing univariate forecast model.
. One natural choice for a unit weight prior would be to choose the best performing univariate forecast model.
When we compute the model weights, we impose the constraint that the weight on each model is positive and the weights sum to one. This ensures that the weights represent the best combination of models that produce good forecasts in their own right, rather than place negative weights on models that give consistently wrong forecasts. This is also very similar to shrinkage methods of forecasting (see Stock and Watson, 2005). For example, Bayesian Model Averaging uses posterior probabilities as weights, which are, by construction, positive and sum to one.7
The positivity constraint is imposed by minimizing the usual loss function, ![]() , associated with OLS for combination method 3:
, associated with OLS for combination method 3:
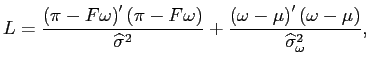
4 Empirical Results
Section 4.1 lays out our main empirical results for the forecasts of time-series models, OLS Phillips curve regressions, term structure models, and survey forecasts. We summarize these results in Section 4.2. Section 4.3 investigates how consistently the best models perform through time and Section 4.4 considers the effect of rolling windows. Section 4.5 reports the results of combining model forecasts.
4.1 Forecast Accuracy
Time-Series Models
In Table 4, we report RMSE statistics, in annual percentage terms, for the ARIMA model out-of-sample forecasts over the the post-1985 and post-1995 periods. The ARIMA RMSEs generally range from around 0.4-0.7% for PUXX to around 1.4-2.2% for PUXHS. For the post-1985 sample, the ARMA (1,1) model generates the lowest RMSE among all ARIMA models in forecasting PUNEW and PUXHS, but the annual Atkeson-Ohanian (2001) random walk is superior in forecasting core inflation (PUXX) and PCE. As the best quarterly ARIMA model, we select the ARMA(1,1) model for the remainder of the paper.8 In the post-1995 period, it beats both the quarterly RW and AR models in forecasting the PUXHS and PCE measure, but the AR model has a lower RMSE in forecasting PUNEW and PUXX, whereas the quarterly RW generates a lower RMSE in forecasting PUXX . Yet, the improvements are minor and the ARMA(1,1) model remains overall best among the three quarterly ARIMA models. However, the annual random walk is the best forecasting model for PUXX and PCE. It beats the ARMA(1,1) model for three of the four inflation measures and generates a much lower RMSE for forecasting core inflation (PUXX).
Table 4 also reports the RMSEs of the non-linear regime-switching model, RGM. Over the post-1985 period, RGM generally performs in line with, and slightly worse than, a standard ARMA model. There is some evidence that non-linearities are important for forecasting in the post-1995 sample, where the regime-switching model outperforms all the ARIMA models in forecasting PUNEW and PUXHS. Both these inflation series become much less persistent post-1995, and the RGM model captures this by transitioning to a regime of less persistent inflation. However, the Hamilton (1989) RGM model performs worse than a linear ARMA model for forecasting PUXX and PCE.
OLS Phillips Curve Forecasts
Table 5 reports the out-of-sample RMSEs and the model comparison regression estimates (equation (17)) for the Phillips curve models described in Section 3.2, relative to the benchmark of the ARMA(1,1) model. The overall
picture in Table 5 is that the ARMA(1,1) model typically outperform the Phillips curve forecasts. Of the 80 comparisons (10 models, 2 out-samples, and 4 inflation measures), the model comparison regression coefficient
![]() is not significantly positive at the 95% level in any of 80 cases using West (1996) standard errors! It must be said that the coefficients are sometimes positive and far away
from zero, but the standard errors are generally rather large. When we compute Hansen-Hodrick (1980) standard errors, we still only obtain 14 cases of significant
is not significantly positive at the 95% level in any of 80 cases using West (1996) standard errors! It must be said that the coefficients are sometimes positive and far away
from zero, but the standard errors are generally rather large. When we compute Hansen-Hodrick (1980) standard errors, we still only obtain 14 cases of significant
![]() coefficients with p-values less than 5%, and of these 14 cases, only nine are positive.
coefficients with p-values less than 5%, and of these 14 cases, only nine are positive.
The OLS Phillips curve regressions are most successful in forecasting core inflation, PUXX. Of the nine cases where the Phillips curve produces lower RMSEs than the ARMA(1,1) model, five occur for PUXX. The best model forecasting PUXX inflation uses the composite Bernanke-Boivin-Eliasz aggregate
real activity factor (PC8). While the
![]() coefficients are large for PC8, their West (1996) standard errors are also large, so they are insignificant for both samples. Another relatively successful Phillips curve
specification is the PC7 model that uses the Stock-Watson nonfinancial Experimental Leading Index-2. This index does not embed asset pricing information. PC7 for PUXHS post-1985 is the only case, out of 80 cases, that generates a positive
coefficients are large for PC8, their West (1996) standard errors are also large, so they are insignificant for both samples. Another relatively successful Phillips curve
specification is the PC7 model that uses the Stock-Watson nonfinancial Experimental Leading Index-2. This index does not embed asset pricing information. PC7 for PUXHS post-1985 is the only case, out of 80 cases, that generates a positive
![]() coefficient which is significant at a level higher than the 90% level using West standard errors, but its performance deteriorates for the post-1995 sample. All of the RMSEs of
PC7 are also higher than the RMSE of an ARMA(1,1) model. In contrast, the PC1 model, which simply uses past inflation and past GDP growth, delivers five of the nine relative RMSEs below one and beats PC7 in all but one case.
coefficient which is significant at a level higher than the 90% level using West standard errors, but its performance deteriorates for the post-1995 sample. All of the RMSEs of
PC7 are also higher than the RMSE of an ARMA(1,1) model. In contrast, the PC1 model, which simply uses past inflation and past GDP growth, delivers five of the nine relative RMSEs below one and beats PC7 in all but one case.
Among the various Phillips curve models, it is also striking that the PC4 model consistently beats the PC2 and PC3 models, sometimes by a wide margin in terms of RMSE. The PC2 and PC3 models use detrended measures of output that are often used to proxy for the output gap. PC4 uses the labor share as a real activity measure, which is sometimes used as a proxy for the marginal cost concept in New Keynesian models. This is interesting because the recent Phillips curve literature (see Gali and Gertler, 1999) stresses that marginal cost measures provide a better characterization of (in-sample) inflation dynamics than detrended output measures. Our results suggest that the use of marginal cost measures also leads to better out-of-sample predictive power. However, the use of GDP growth leads to significantly better forecasts than the labor share measure, but GDP growth remains, so far, conspicuously absent in the recent Phillips curve literature.
Finally, using Table 4 together with Table 5, it is easy to verify whether the Atkeson-Ohanian (2001) results hold up for our models and data. Essentially, they do: the annual random walk beats the Phillips curve models in 72 out of 80 cases. All the cases where a Phillips curve model beats the annual random walk occur in forecasting the PUNEW or PUXHS measures.
Term Structure Forecasts
In Table 6, we report the out-of-sample forecasting results for the various term structure models (see Section 3.3). Generally, the term structure based forecasts perform worse than the Phillips-curve based forecasts. Over a total of 120 statistics
(15 models, 4 inflation measures, 2 sample periods), term structure based-models beat the ARMA(1,1) model in only eight cases in terms of producing smaller RMSE statistics. The
![]() coefficients are usually positive for forecasting PUXX in the post-1985 period, but half are negative in the post-1995 sample. Unfortunately, the use of West (1996) standard
errors turns 10 cases of significantly positive
coefficients are usually positive for forecasting PUXX in the post-1985 period, but half are negative in the post-1995 sample. Unfortunately, the use of West (1996) standard
errors turns 10 cases of significantly positive
![]() coefficients using Hansen-Hodrick (1980) standard errors into insignificant coefficients. The performance of the term structure forecasts is so poor that using West (1996)
standard errors, in none of the 120 cases is the
coefficients using Hansen-Hodrick (1980) standard errors into insignificant coefficients. The performance of the term structure forecasts is so poor that using West (1996)
standard errors, in none of the 120 cases is the
![]() parameters significant at the 95% level. This may be caused by many of the term structure models, especially the no-arbitrage models, having relatively large numbers of
parameters.
parameters significant at the 95% level. This may be caused by many of the term structure models, especially the no-arbitrage models, having relatively large numbers of
parameters.
The term structure models most successfully forecast core inflation, PUXX, which delivers six of the eight cases with smaller RMSEs than an ARMA(1,1) model. In particular, the TS1 model that includes inflation, GDP growth, and the short rate beats an ARMA(1,1) model and has a positive
![]() , but insignificant, coefficient in both the post-1985 and post-1995 samples. The other models with term structure information that are successful at forecasting PUXX are TS6 and
TS8, both of which also include short rate information.
, but insignificant, coefficient in both the post-1985 and post-1995 samples. The other models with term structure information that are successful at forecasting PUXX are TS6 and
TS8, both of which also include short rate information.
The finance literature has typically used term spreads, not short rates, to predict future inflation changes (see, for example, Mishkin, 1990, 1991). In contrast to the relative success of the models with short rate information, models TS9-TS11, which incorporate information from the term spread, perform badly. They produce higher RMSE statistics than the benchmark ARMA(1,1) model for all four inflation measures. This is consistent with Estrella and Mishkin (1997) and Kozicki (1997), who find that the forecasting ability of the term spread is diminished after controlling for lagged inflation. However, we show that the short rate still contains modest predictive power even after controlling for lagged inflation. Thus, the short rate, not the term spread, contains the most predictive power in simple forecasting regressions.
Table 6 shows that the performance of iterated VAR forecasts is mixed. VARs produce lower RMSEs than ARMA(1,1) models. The relatively poor performance of long-horizon VAR forecasts for inflation contrasts with the good performance for VARs in forecasting GDP (see Ang, Piazzesi and Wei, 2004) and for forecasting other macroeconomic time series (see Marcellino, Stock and Watson, 2006). The non-linear empirical regime-switching VAR (RGMVAR) generally fares worse than the VAR. This result stands in contrast to the relatively strong performance of the univariate regime-switching model using only inflation data (RGM in Table 4) for forecasting PUNEW and PUXX. This implies that the non-linearities in term structure data have no marginal value for forecasting inflation above the non-linearities already present in inflation itself.
The last two lines of each panel in Table 6 shows that there is some evidence that no-arbitrage forecasts (MDL1-2) are useful for forecasting PUXX in the post-1985 sample. While the
![]() coefficients are significant using Hansen-Hodrick (1980) standard errors, they are not significant with West (1996) standard errors. Moreover, both no-arbitrage term structure
models always fail to beat the ARMA(1,1) forecasts in terms of RMSE. While the finance literature shows that inflation is a very important determinant of yield curve movements, our results show that the no-arbitrage cross-section of yields appears to provide little marginal forecasting ability for
the dynamics of future inflation over simple time-series models.
coefficients are significant using Hansen-Hodrick (1980) standard errors, they are not significant with West (1996) standard errors. Moreover, both no-arbitrage term structure
models always fail to beat the ARMA(1,1) forecasts in terms of RMSE. While the finance literature shows that inflation is a very important determinant of yield curve movements, our results show that the no-arbitrage cross-section of yields appears to provide little marginal forecasting ability for
the dynamics of future inflation over simple time-series models.
Surveys
Table 7 reports the results for the survey forecasts and reveals several notable results. First, surveys perform very well in forecasting PUNEW, PUXHS, and PUXX. With only one exception, the raw survey forecasts SPF1, LIV1 and MICH1 have lower RMSEs than ARMA(1,1)
forecasts over both the post-1985 and the post-1995 samples (the exception is MICH1 for PUXX over the post-1985 sample). For example, for the post-1985 (post-1995) sample, the RMSE ratio of the raw SPF forecasts relative to an ARMA(1,1) is 0.779 (0.861) when predicting PUNEW. The horse races always
assign large, positive
![]() weights to the pure survey forecasts (the lowest one is 0.383) in both out-of-sample periods. Ignoring parameter uncertainty, the coefficients are significantly different from
zero in every case, but taking into account parameter uncertainty, statistical significance disappears for the post-1995 samples, and in the case of the PUXX measure, even for the post-1985 sample. This is true for all three surveys.
weights to the pure survey forecasts (the lowest one is 0.383) in both out-of-sample periods. Ignoring parameter uncertainty, the coefficients are significantly different from
zero in every case, but taking into account parameter uncertainty, statistical significance disappears for the post-1995 samples, and in the case of the PUXX measure, even for the post-1985 sample. This is true for all three surveys.
Second, while the SPF and Livingston surveys do a good job at forecasting all three measures of CPI inflation (PUNEW, PUXHS, and PUXX) out-of-sample, the Michigan survey is relatively unsuccessful at forecasting core inflation, PUXX. It is not surprising that consumers in the Michigan survey fail to forecast PUXX, since PUXX excludes food and energy which are integral components of the consumer's basket of goods. Note that while the annual PUNEW and PUXHS measures have the highest correlations with each other (99% in both out-samples), core inflation is less correlated with the other CPI measures. In particular, post-1995, the correlation of annual PUXX with annual PUNEW (PUXHS) is only 33% (21%). Surveys do less well at forecasting PCE inflation, always producing worse forecasts in terms of RMSE than an ARMA(1,1). This result is expected because the survey participants are asked to forecast CPI inflation, rather than the consumption deflator PCE.
Third, the raw survey forecasts outperform the linear or non-linear bias adjusted forecasts (with the only notable exception being the bias-adjusted forecasts for PCE). As a specific example, for PUNEW, the relative RMSE ratios are always higher for the models with suffix 2 (linear bias adjustment) or the models with suffix 3 (non-linear bias adjustment) compared to the raw survey forecasts across all three surveys. This result is perhaps not surprising given the mixed evidence regarding biases in the survey data (see Table 3). While there are some significant biases, these biases must be small, relative to the total amount of forecast error in predicting inflation.
Finally, we might expect that the Livingston and SPF surveys produce good forecasts because they are conducted among professionals. In contrast, participants in the Michigan survey are consumers, not professionals. It is indeed the case that the professionals uniformly beat the consumers in forecasting inflation. Nevertheless, in most cases, the Michigan forecasts are of the same order of magnitude as the Livingston and SPF surveys. For example, for PUNEW over the post-1995 sample, the Michigan RMSE ratio is 0.862, just slightly above the RMSE ratio of 0.861 for the SPF survey. It is striking that information aggregated over non-professionals also produces accurate forecasts that beat ARIMA time-series models.
It is conceivable that consumers simply extrapolate past information to the future and that the Michigan survey forecasts are simply random walk forecasts, similar to the Atkeson and Ohanian (2001) (AORW) random walk forecasts. Indeed, Table 3 demonstrated the relatively good forecasting performance of the annual random walk model, which beats the ARMA(1,1) model in a number of cases. Nevertheless, comparing the performance of the survey forecasts relative to the AORW model, we find that the random walk model produces smaller RMSEs than the Michigan survey only for PUXX and PCE inflation, which consumers are not directly asked to forecast. The AORW also outperforms the SPF survey for PUXX inflation over the post-1995 period, but the AORW model always performs worse than the Livingston survey for the CPI inflation measures. Looking at PUNEW, the inflation measure which the survey participants are actually asked to forecast, the AORW model performs worse than all the surveys, including the Michigan surveys. Thus, survey forecasts clearly are not simply random walk forecasts!
4.2 Summary
Let us summarize the results so far. First, among ARIMA time-series models, the ARMA (1,1) model is the best overall quarterly model, but the annual random walk also performs very well. Nevertheless, some models that incorporate real activity information, term structure information, or, especially, survey information, beat the ARMA(1,1) model, even when ARMA(1,1) forecasts are used as the benchmark in a forecast comparison regression. Second, the simplest Phillips curve model using only past inflation and GDP growth is a good predictor. Third, adding term structure information occasionally leads to an improvement in inflation forecasts, but generally only for core inflation. No-arbitrage restrictions do not improve forecasting performance. Fourth, the survey forecasts perform very well in forecasting all inflation measures except PCE inflation.
To get an overall picture of the relative forecasting power of the various models, Table 8 reports the relative RMSE ratios of the best models from each of the first three categories (pure time-series, Phillips-curve, and term structure models) and of each raw survey forecast. The most remarkable result in Table 8 is that for CPI inflation (PUNEW, PUXHS, and PUXX), the survey forecasts completely dominate the Phillips curve or term structure models in both out-of-sample periods. For the post-1985 sample, the RMSEs are around 20% smaller for the survey forecasts compared to forecasts from Phillips-curve or term structure models. The natural exception is PCE inflation, where the best model in both samples is just the annual random walk model!
For the post-1985 sample, a survey forecast delivers the overall lowest RMSE for all CPI inflation measures. The performance of the survey forecasts remains impressive in the post-1995 sample, but the Hamilton (1989) regime-switching model (RGM) has a slightly lower RMSE for PUNEW and PUXHS. Impressively, the Livingston survey continues to deliver the most accurate forecast of PUXX post-1995.
For the Phillips curve forecasts, the simple PC1 regression using only past inflation and GDP growth frequently outperforms more complicated models for both PUNEW and PUXHS. Other measures of economic growth are more successful at forecasting PUXX and PCE. For PUXX inflation, PC8 produces forecasts that beat an ARMA(1,1) model for both the post-1985 and post-1995 sample. The PC8 forecasting model uses the Bernanke et al. (2005) composite indicator. For the PCE measure, models combining multiple time series (PC6 through 8) continue to do well, and the PC6 measure, which uses the Stock and Watson experimental leading index (XLI), produces the lowest RMSE for the post-1995 sample. For the post-1985 sample, PC4, which uses the labor share performs best. However, all the Phillips curve models are always beaten by time-series models or surveys.
Among the term structure models, models incorporating past inflation, the short rate, and one of the combination real activity measures (TS6 through TS8) perform relatively well. TS7 (using XLI-2) is best for the PUNEW and PCE measure for the post-1985 sample, whereas TS8 (using the Bernanke et al., 2005, composite indicator) is best for all measures except PUXX in the post-1995 sample. For PUXX, the TS6 model (which uses XLI as the real activity measure) produces the lowest RMSE. Like the Phillips curve models, all the term structure forecasts are also soundly beaten by time-series models or survey forecasts.
4.3 Stability of the Best Forecasting Models
One requirement for a good forecasting model is that it must consistently perform well. In Table 9, we report the ex-ante best models within each category (time-series, Phillips curve, term structure, and surveys) and across all models over the post-1995 sample. Since we record the best models at the end of each quarter, we include only the SPF and Michigan survey forecasts because the Livingston survey is only available semi-annually. This understates the performance of the surveys as the Livingston survey sometimes outperforms the other two survey measures, especially for PUXX (see Table 8). The best models are evaluated recursively, so at each point in time, we select the model within each group that yields the lowest forecast RMSEs over the sample from 1985:Q4 to the present. Naturally, as we roll through the sample, the best ex-ante models up to the end of each quarter converge to the best models reported for the post-1985 period in Table 8. If the best ex-ante models for 2002:Q4 were reported, these would be identical to the best models in the post-1985 sample in Table 8, with the exception that the Livingston survey is excluded.
Table 9 shows that for PUNEW and PUXHS, the ARMA(1,1) model is consistently the best time-series model, whereas for PUXX and PCE, the Atkeson-Ohanian (2001) model is always best. Given the good forecasting performance of these time-series models, this implies that the time-series models represent extremely good benchmarks. In contrast, there is little stability for the best ex-ante Phillips curve model, which is also stressed by Brave and Fisher (2004). For PUNEW, the best Phillips curve models alternate between PC1 (using GDP growth) and PC5 (using unemployment). For PUXHS, the best Phillips curve is PC7 (using XLI-2) at the beginning of the period, but transitions to PC1 at the end of the sample. For core inflation, PUXX, PC8 (using the composite Bernanke, Boivin and Eliasz, 2005, factor) alternates with PC1. This instability further reduces the usefulness of the Phillips curve forecasts and hence, the knowledge that sometimes these Phillips curve forecasts may beat an ARMA(1,1) model is hard to translate into consistent, accurate forecasts.
The best term structure models are also generally unstable over time for PUNEW and PUXX. While the VAR model is consistently the best performer for PUXHS and TS7 (using XLI-2 with the short rate) is always the best term structure model for PCE, this consistent performance is less useful because both of these models cannot beat an ARMA(1,1). A sharp contrast to the unstable Phillips curve and term structure models are the survey results. For all three CPI measures (PUNEW, PUXHS, and PUXX), professionals always forecast better than consumers, with the SPF beating the Michigan survey. A remarkable result is that the raw SPF survey always dominates all other models throughout the period for the CPI measures. Surveys consistently deliver superior inflation forecasts!
4.4 Rolling Window Forecasts
McConnell and Perez-Quiros (2000) and Stock and Watson (2002b), among others, document that there has been a structural break since the mid-1980s. This has been called the "Great Moderation" because it is characterized by lower volatility of many macro variables. It is conceivable that professional forecasters fast adapt to structural changes. In contrast, the models use relatively long windows (necessary to retain some estimation efficiency and power) to estimate parameters. These model parameters would respond only slowly to a structural break as new data points are added. If changes in the time series properties of inflation play a role in the relative forecasting prowess of models versus the surveys, allowing the model parameters to change more quickly through rolling windows should generate superior model performance.
In Table 10, we use a constant 10-year rolling window to estimate all the linear time-series, Phillips curve, and term structure models. We do not consider the regime-switching models (RGM, RGMVAR) and the no-arbitrage term structure models, (MDL1, which is an affine model, and MDL2, which is a regime-switching model). The regime-switching data generating processes in the RGM, RGMVAR, and MDL2 models produce forecasts that may already potentially account for structural breaks. We report the relative RMSEs of the ex-post best models in each category together with the raw survey forecasts results, using the same recursively estimated ARMA(1,1) model as the benchmark.
Table 10 shows that over both the post-1985 and post-1995 samples, surveys still provide the best forecasts for all CPI inflation measures. Note that with a 10-year rolling window, the post-1995 sample results involve models estimated only on the post-Great Moderation sample. Thus, surveys still out-perform even when the models are estimated only with data from the Great Moderation regime. But, estimating the models with only post-1985 data does improve their performance, as a comparison between the RMSE ratios between Tables 8 and 10 reveals, especially for the PUXX and PCE measures. This implies that the model parameters may indeed only have adjusted to the new situation by 1995 and raises the possibility that the out-performance of the surveys may not last. In fact, it is striking that an older literature, summarized by Croushore (1998), stressed that the surveys performed relatively poorly in forecasting compared to models.
To investigate this, we use the Livingston survey, which is the only survey available over our full sample, from 1952-2002. We compute the RMSE ratio of the out-of-sample forecasts for the Livingston survey relative to an ARMA(1,1) model for 1960-1985 and 1986-2002, where the first eight years are used as an in-sample estimation period for the ARMA(1,1) model. Over the pre-1985 sample, the Livingston RMSE ratio is 1.046 (with a RMSE level of 2.324), while over the post-1985 sample, the RMSE ratio is 0.789 (with a RMSE level of 0.896). Consequently, professionals are more adept at forecasting inflation in the post-1985 period.9
4.5 Combining Model Forecasts
Surveys may be averaging information from many different sources, whereas our models implicitly always constrain the information set to a limited number of variables. If this is the source of the out-performance of the surveys, the model combination techniques should perform better than any individual model by itself.
Table 11 investigates whether we can improve the forecasting performance by combining different models. We first combine models within each of the four categories (time-series, Phillips curve, term structure, and survey models), then combine the four ex-ante best models from each category in the column labelled "Best Models," and finally combine across all the models in the last column labelled "All Models." The models in the survey category comprise only the SPF and Michigan surveys because the Livingston survey is conducted at a semiannual frequency. Table 7 shows that the Livingston forecasts are very similar to the SPF and Michigan surveys for PUNEW and PUXHS, and that the Livingston survey is the best single forecaster for PUXX. Thus, excluding the Livingston survey places a conservative higher bound on the RMSEs for the forecast combinations involving surveys.
We use five methods of model combination: means or medians over all the models, linear combinations using weights recursively computed by OLS, and linear combinations using weights recursively computed by mixed combination regressions either with an equal-weight prior or a prior that places a unit weight on the ex-ante best model. We start the model combination regressions at 1995:Q4 using realized inflation and the out-of-sample forecasts over 1985:Q4 to 1995:Q4. At each subsequent period, we advance the data sample by one quarter and re-run the model combination regression to obtain the slope coefficient estimates. For comparison, the last row in each panel reports the RMSE ratio, relative to an ARMA(1,1) forecast, of the recursively-updated ex-ante best performing individual model, as reported in Table 9.10
There are three main findings in Table 11. First, using mean or median forecasts mostly does not improve the forecast performance relative to the best individual ex-ante model. There are 24 cases to consider: four inflation measures and six different sets of model combinations. Combining forecasts by taking their means only improves out-of-sample forecasts in six out of 24 cases. Taking medians produces the same results, improving forecasts for exactly the same cases as taking means. The mean or median combination methods work best for PUNEW and PUXHS using time-series models. However, when these forecasting improvements occur for model combinations, the improvements are small. Thus, simple methods of combining forecasts provide little additional predictive power relative to the best model.
Second, updating the model weights based on previous model performance does not always lead to superior performance. For the Phillips Curve models, OLS model combinations outperform means and medians for all inflation measures. However, when OLS model combinations are taken across all models, using an OLS combination is never better than the best individual model.
Finally, the performance of the equal-weight prior and the unit prior that places weight only the best ex-ante model are generally close to the OLS forecast combination method. Across all models, the unit weight prior produces lower RMSE ratios than the OLS or equal-weight priors. However, it is only for PUXX that the various regression-based model combination methods produce better forecasts than the best individual forecasts. For PUNEW, PUXHS, and PCE, the best individual models beat the model combinations, and for PUNEW and PUXHS, the best individual ex-ante forecasts are surveys.
To help interpret the results, we investigate the ex-ante OLS weights on some selected models. In Figure 2, we plot the OLS slope estimates of regression (18) for various inflation measures over the period of 1995:Q4 to 2002:Q4. For clarity, we restrict the regression to combinations of the ex-ante best model within each category (time-series, Phillips Curve, term structure) together with the SPF survey. Note that by choosing the best model in each category, we handicap the survey forecasts. We compute the weights in the regression recursively like the forecasts in Table 11; that is, we start in 1995:Q4, and recursively compute forecasts from 1985:Q4 to 1995:Q4.
Figure 2 shows that when forecasting all the CPI inflation measures (PUNEW, PUXHS, and PUXX), the data consistently place the largest ex-ante weights on survey forecasts and very little weight on the other models. The weights on the SPF survey forecast are generally constant and lie around 0.8 for PUNEW, PUXX, and PUXHS. There is no consistent, best model that dominates for the remaining 0.1-0.2 weights. The weights on the time-series models are always zero for PUNEW, but temporarily spike upward in the middle of the sample to around 0.15 for PUXHS and 0.20 for PUXX. For PUNEW and PUXHS, the Phillips curves fare best at the beginning of the sample, but the regressions place very little weight on Phillips curve forecasts at the end of the sample. For PCE inflation, surveys contain little information. The weight on the best survey stays close to zero until late 1999, then rises to 0.2. For forecasting PCE among the other categories of models, the Phillips Curve forecast stands out, with weights ranging from 0.2 to 0.6. Term structure models receive the highest weight at the end of the sample. We conclude that combining model forecasts, at least using the techniques here, is not a very useful forecasting tool, especially compared to using just survey data for forecasting CPI inflation.
5.1 Definition and Models
In this section we investigate the robustness of our results to the alternative assumption that quarterly inflation is difference stationary. Our exercise is now to forecast four-quarter ahead inflation changes:
where
We now replace quarterly inflation, ![]() , by quarterly inflation changes,
, by quarterly inflation changes,
![]() in all the models considered in Sections 3.1 to 3.3. For example, we estimate an ARMA(1,1) on first
differences of inflation:
in all the models considered in Sections 3.1 to 3.3. For example, we estimate an ARMA(1,1) on first
differences of inflation:
There are three models for which we do not estimate a counterpart using quarterly inflation differences. We do not consider a random walk model for inflation changes and do not specify the no-arbitrage term structure models (MLD1 and MLD2) to have non-stationary inflation dynamics, although we still consider the forecasts of annual inflation changes implied by the original stationary models. In all other cases, we examine the forecasts of both the original stationary models and the new non-stationary models that use first differences of inflation.
The original models estimated on inflation levels generate RMSEs for forecasting annual inflation changes that are identical to the RMSEs for forecasting annual inflation levels. Hence, the question is whether models estimated on differences provide superior forecasts to models estimated on levels. By including a new set of models estimated on inflation changes, we also enrich the set of forecasts which we can combine. We maintain the ARMA(1,1) model estimated on inflation rate levels as a benchmark.
5.2 Performance of Individual Models
Table 12 reports the RMSE ratios of the best performing models estimated on levels or differences within each model category. Time-series models estimated on levels always provide lower RMSEs than time-series models estimated on differences. For both Phillips curve and term structure models, using inflation differences or levels produces similar forecasting performance for both the PUNEW and PUXHS measures. For these inflation measures, the Phillips curve models are slightly better estimated on levels, but for term structure models, there is no clear overall winner. However, for the PUXX and PCE measures, Phillips curve and term structure regressions using past inflation changes are more accurate than regressions with past inflation levels.
Our major finding that surveys generally outperform other model forecasts is robust to specifying the models in inflation differences. For the CPI inflation measures (PUNEW, PUXHS, PUXX) over the post-1985 sample, surveys deliver lower RMSEs than the best time-series, Phillips curve, and term structure forecasts. First difference models are most helpful for lowering RMSEs for core inflation (PUXX) over the post-1995 sample, where the best time-series model estimated on differences (ARMA) produces a relative RMSE ratio of 0.649. This is still beaten by the raw Livingston survey, with a RMSE ratio of 0.557.11
5.3 Performance of Combining Models
In this section, we run forecast combination regressions to determine the best combination of models to forecast inflation changes (similar to Section 3.6 for inflation levels). The model weights are computed from the regression:
We repeat the exercise of Table 11 and compute ex-ante recursive weights over 1995:Q4-2002:Q4 using the best ex-ante forecasting models in each category and across all models. In unreported results available upon request, we find that our original results for forecasting inflation levels also extends to forecasting inflation changes. Specifically, there is generally no improvement in combining model forecasts, or when model combinations result in out-performance, the improvement is small. Specifically, for PUNEW and PUXHS, using means, medians, OLS, or an equal-weight prior produces higher RMSEs than the best individual model. For these inflation measures, all model combinations produce RMSEs that are higher than the survey forecasts. This result is robust to both combining models in levels and also combining models in differences. There are some improvements for forecasting PCE inflation using models in differences, but the forecasting gains are very small.
In Figures 3 and 4, we plot the OLS coefficient estimates of equation (22) for the models specified in differences and the models specified in levels, respectively, together with the best survey forecast. We consider only the SPF and the Michigan surveys at the end of each quarter, and the SPF survey always dominates the Michigan survey. Similar to Figure 2, we choose the best ex-ante performing time-series, Phillips Curve, and term structure models at each time, and compute the OLS ex-ante weights recursively over 1995:Q4 to 2004:Q4. Both Figures 3 and 4 confirm that the surveys produce superior forecasts of inflation changes.
In Figure 3, the weight on the SPF survey for PUNEW and PUXHS changes is above or around 0.8. The surveys clearly dominate the I(1) time-series, Phillips Curve, and term structure models. For PUXX changes, the regressions still place the largest weight on the survey, but the weight is around 0.5. In contrast, for forecasting PUXX inflation levels, the weights on the survey range from 0.6 to above 0.9. Thus, there is now additional information in the other models for forecasting PUXX changes, most particularly the Phillips Curve PC1 model, which has a weight around 0.4. Nevertheless, surveys still receive the highest weight. Consistent with the results for forecasting inflation levels, surveys provide little information to forecast PCE changes. For PCE changes, the largest ex-ante weight in the forecast combination regression is for the ARMA(1,1) estimated on inflation differences.
Figure 4 combines the surveys with stationary models. While Table 12 reveals that the RGM model estimated on inflation levels yields the lowest RMSE over the post-1995 sample in forecasting PUNEW and PUXHS differences, there appears to be little additional value in the RGM forecast once surveys are included. Figure 4 shows that the forecast combination regression places almost zero ex-ante weight on the RGM model. The weights on the other I(0) models are also low, whereas the survey weights are around 0.8 or higher. Compared to the other stationary model categories, surveys also have an edge at forecasting PUXX inflation. Again, surveys do not perform well relative to I(0) models for forecasting PCE changes.
6 Conclusions
We conduct a comprehensive analysis of different inflation forecasting methods using four inflation measures and two different out-of-sample periods (post-1985 and post-1995). We investigate forecasts based on time-series models; Phillips curve inspired forecasts; and forecasts embedding information from the term structure. Our analysis of term structure models includes linear regressions, non-linear regime switching models, and arbitrage-free term structure models. We compare these model forecasts with the forecasting performance of three different survey measures (the SPF, Livingston, and Michigan surveys), examining both raw and bias-adjusted survey measures.
Our results can be summarized as follows. First, the best time series model is mostly a simple ARMA(1,1) model, which can be motivated by thinking of inflation comprising stochastic expected inflation following an AR(1) process, and shocks to inflation. Post-1995, the annual random walk used by Atkeson and Ohanian (2001) is a serious competitor. Second, while the ARMA(1,1) model is hard to beat in terms of RMSE forecast accuracy, it is never the best model. For CPI measures, the survey measures consistently deliver better forecasts than ARMA(1,1) models, and in fact, much better forecasts than Phillips curve-based regressions, term structure models based on OLS regressions, non-linear models, iterated VAR forecasts, and even no-arbitrage term structure models that use information from the entire cross-section of yields. Naturally, surveys do a relatively poor job at forecasting PCE inflation, which they are not designed to forecast.
Some of our results shed light on the validity of some simple explanations of the superior performance of survey forecasts. One possibility is that the surveys simply aggregate information from many different sources, not captured by a single model. The superior information in median survey forecasts may be due to an effect similar to Bayesian Model Averaging, or averaging across potentially hundreds of different individual forecasts and extracting common components (see Stock and Watson, 2002a; Timmermann, 2004). For example, it is striking that the Michigan survey, which is conducted among relatively unsophisticated consumers, beats time-series, Phillips curve, and term structure forecasts. The Livingston and SPF surveys, conducted among professionals, do even better.
If there is information in surveys not included in a single model, combining model forecasts may lead to superior forecasts. However, when we examine forecasts that combine information across models or from various data sources (like the Bernanke et al., 2005, index of real activity that uses 65 macro factors measuring real activity), we find that the surveys still outperform. Across all models, combination methods of simple means or medians, or forecast combination regressions which use prior information never outperform survey forecasts. In ex-ante model combination exercises for forecasting CPI inflation, almost all the weight is placed on survey forecasts. One avenue for future research is to investigate whether alternative techniques for combining forecasts perform better (see Inoue and Killian, 2005, for a survey and study of one promising technique).
Another potential reason why surveys outperform is because survey information is not captured in any of the variables or models that we use. If this is the case, our results strongly suggest that there would be additional information to include survey forecasts in the large datasets used to construct a small number of composite factors, which are designed to summarize aggregate macroeconomic dynamics (see, among others, Bernanke et al., 2005; Stock and Watson, 2005).
Our results also have important implications for term structure modelling. Extant sophisticated no-arbitrage term structure models, while performing well in sample, seem to provide relatively poor forecasts relative to simpler term structure or Phillips curve models out-of-sample. A potential solution is to introduce the information present in the surveys as additional state variables in the term structure models. Pennacchi (1991) was an early attempt in that direction and Kim (2004) is a recent attempt to build survey expectations into a no-arbitrage quadratic term structure model. Brennan, Wang and Xia (2004) also recently use the Livingston survey to estimate an affine asset pricing model.
Finally, surveys may forecast well because they quickly react to changes in the data generating process for inflation in the post-1985 sample. In particular, since the mid-1980s, the volatility of many macroeconomic series, including inflation, has declined. This "Great Moderation" may also explain why a univariate regime-switching model for inflation provides relatively good forecasts over this sample period. Nevertheless, when we re-do our forecasting exercises using a 10-year rolling window, the surveys forecasts remain superior.
We conjecture that the surveys likely perform well for all of these reasons: the pooling of large amounts of information; the efficient aggregation of that information; and the ability to quickly adapt to major changes in the economic environment such as the Great Moderation. While our analysis shows that surveys provide superior forecasts of CPI inflation, the PCE deflator is often the Federal Reserve's preferred inflation indicator for the conduct of monetary policy. Since existing surveys target only the CPI index, professional surveys designed to forecast the PCE deflator may also deliver superior forecasts of PCE inflation.
Appendix: Computation of West (1996) Standard Errors
By subtracting
![]() from both sides of equation (17) and letting
from both sides of equation (17) and letting
![]() denote the forecast residuals of the ARMA(1,1) model and
denote the forecast residuals of the ARMA(1,1) model and
![]() denote the forecast residuals of candidate model
denote the forecast residuals of candidate model ![]() , we can write:
, we can write:
The estimated slope coefficient
 |
where
We use the notation based on West (2006). The forecast horizon is four quarters ahead. For each model ![]() there are
there are ![]() out-of-sample forecasts in all, which rely on estimates of a
out-of-sample forecasts in all, which rely on estimates of a
![]() unknown parameter vector
unknown parameter vector
![]() . The first forecast uses data from a sample of length
. The first forecast uses data from a sample of length ![]() to predict a
time
to predict a
time ![]() variable, while the last forecast uses data from time
variable, while the last forecast uses data from time
![]() to forecast a time
to forecast a time ![]() variable. The total sample size is
variable. The total sample size is
![]()
For the ![]() th candidate model,
th candidate model,
![]() , the small-sample estimate of the parameters
, the small-sample estimate of the parameters ![]() satisfies:
satisfies:
where
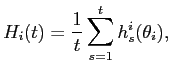 |
for the recursive forecast case which we investigate, where
We stack the parameters of the ARMA(1,1) benchmark model and the parameters of the ![]() th candidate model in the vector
th candidate model in the vector
![]() . Then, we can write
. Then, we can write
![]() , where
, where
![]() , where:
, where:
![\begin{displaymath}\left[ \begin{array}[c]{cc} B_{ARMA}(t) & 0\ 0 & B_i(t) \end{array}\right],\end{displaymath}](img176.gif) |
|||
![\begin{displaymath}\left[ \begin{array}[c]{c} h_{t}^{ARMA}(\theta_{ARMA}) \ h_{t}^{i}(\theta_{i}) \end{array}\right],\end{displaymath}](img178.gif) |
and
![$\displaystyle B =\left[ \begin{array}[c]{cc} B_{ARMA} & 0\\ 0 & B_i \end{array} \right].$](img180.gif) |
We define the derivative ![]() of the moment conditions with respect to
of the moment conditions with respect to ![]() as:
as:
![$\displaystyle F= \ensuremath{{\rm E}}\left[ \frac{\partial f_{t,t+4}(\theta)} {\partial \theta} \right] = \left[ \begin{array}[c]{c} F_{1} \\ F_{2} \end{array} \right],$](img182.gif) |
where
![$\displaystyle \ensuremath{{\rm E}}\left[ \frac{\partial f_{t,t+4}\left( \theta\right) } {\partial\theta_{ARMA}}\right] = \ensuremath{{\rm E}}\left[ \left( 2e_{t,t+4}^{ARMA} -e_{t,t+4}^{x}\right) \frac{\partial e_{t,t+4}^{ARMA}}{\partial\theta_{ARMA} }\right]$](img186.gif) |
|||
![$\displaystyle \ensuremath{{\rm E}}\left[ \frac{\partial f_{t,t+4}\left( \theta\right) } {\partial\theta_{i}}\right] =-\ensuremath{{\rm E}}\left[ e_{t,t+4}^{ARMA}\frac{\partial e_{t,t+4}^{x}}{\partial\theta_{i}}\right].$](img188.gif) |
Finally, for the asymptotic results, we need
![]() and
and
![]() with
with
 |
Following West (2006), we define the constants
Under these assumptions, West (1996) derives that the asymptotic variance
![]() is given by:
is given by:
where
Note that the estimate without parameter uncertainty is simply
A consistent estimator can be constructed using the small-sample counterparts. In particular, we compute
![]() and
and
![]() setting
setting
![]() ,
,
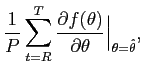 |
|||
and construct
![$\displaystyle \hat{g}_{t}=\left[ \begin{array}[c]{cc} \hat{f}_{t,t+4} & \hat{F}\hat{B}\hat{h}_{t} \end{array} \right].$](img222.gif) |
To construct a non-singular estimate for the covariance of
![$\displaystyle \hat{\Omega} = \left[ \begin{array}[c]{cc} \hat{\Omega}_{11} & \hat{\Omega}_{12} \\ \hat{\Omega}_{21} & \hat{\Omega}_{22} \end{array} \right].$](img226.gif) |
Then, a consistent estimate of
Bibliography
| PUNEW | PUXHS | PUXX | PCE | |
|---|---|---|---|---|
| Mean | 3.84 | 3.60 | 4.24 | 3.84 |
| Standard Error: Mean | (0.20) | (0.20) | (0.19) | (0.19) |
| Standard Deviation | 2.86 | 2.78 | 2.56 | 2.45 |
| Standard Error: Standard Deviation | (0.14) | (0.14) | (0.14) | (0.13) |
| Autocorrelation | 0.78 | 0.74 | 0.77 | 0.79 |
| Standard Error: Autocorrelation | (0.08) | (0.09) | (0.11) | 0.09) |
| Correlations: PUXHS | 0.99 | |||
| Correlations: PUXX | 0.94 | 0.91 | ||
| Correlations: PCE | 0.98 | 0.98 | 0.93 |
| PUNEW | PUXHS | PUXX | PCE | |
|---|---|---|---|---|
| Mean | 3.09 | 2.87 | 3.21 | 2.58 |
| Standard Error: Mean | (0.14) | (0.17) | 0.12) | (0.14) |
| Standard Deviation | 1.12 | 1.37 | 0.97 | 1.08 |
| Standard Error: Standard Deviation | (0.10) | (0.12) | (0.09) | (0.10) |
| Autocorrelation | 0.47 | 0.37 | 0.77 | 0.69 |
| Standard Error: Autocorrelation | (0.07) | (0.10) | (0.08) | (0.07) |
| Correlations PUXHS | 0.99 | |||
| Correlations PUXX | 0.85 | 0.79 | ||
| Correlations PCE | 0.95 | 0.93 | 0.90 |
| PUNEW | PUXHS | PUXX | PCE | |
|---|---|---|---|---|
| Mean | 2.27 | 1.84 | 2.32 | 1.70 |
| Standard Error: | (0.17) | (0.25) | (0.05) | (0.13) |
| Standard Deviation | 0.81 | 1.19 | 0.24 | 0.62 |
| Standard Error: Standard Deviation | (0.12) | (0.17) | (0.03) | (0.09) |
| Autocorrelation | -0.13 | -0.19 | -0.38 | 0.05 |
| Standard Error: Autocorrelation | (0.23) | (0.23) | (0.14) | (0.18) |
| Correlations PUXHS | 0.99 | |||
| Correlations PUXX | 0.33 | 0.21 | ||
| Correlations PCE | 0.89 | 0.88 | 0.19 |
** For PUXX, the start date is 1958:Q2 and for PCE, the start date is 1960:Q2.
| Abbreviation | Specification | Type of Model |
|---|---|---|
| ARMA | ARMA(1,1) | Time-Series Model |
| AR | Autoregressive model | Time-Series Model |
| RW | Random walk on quarterly inflation | Time-Series Model |
| AORW | Random walk on annual inflation | Time-Series Model |
| RGM | Univariate regime-switching model | Time-Series Model |
| PC1 | INFL + GDPG | Phillips Curve (OLS) |
| PC2 | INFL + GAP1 | Phillips Curve (OLS) |
| PC3 | INFL + GAP2 | Phillips Curve (OLS) |
| PC4 | INFL + LSHR | Phillips Curve (OLS) |
| PC5 | INFL + UNEMP | Phillips Curve (OLS) |
| PC6 | INFL + XLI | Phillips Curve (OLS) |
| PC7 | INFL + XLI-2 | Phillips Curve (OLS) |
| PC8 | INFL + FAC | Phillips Curve (OLS) |
| PC9 | INFL + GAP1 + LSHR | Phillips Curve (OLS) |
| PC10 | INFL + GAP2 + LSHR | Phillips Curve (OLS) |
| TS1 | INFL + GDPG + RATE | OLS Term Structure Model |
| TS2 | INFL + GAP1 + RATE | OLS Term Structure Model |
| TS3 | INFL + GAP2 + RATE | OLS Term Structure Model |
| TS4 | INFL + LSHR + RATE | OLS Term Structure Model |
| TS5 | INFL + UNEMP + RATE | OLS Term Structure Model |
| TS6 | INFL + XLI + RATE | OLS Term Structure Model |
| TS7 | INFL + XLI-2 + RATE | OLS Term Structure Model |
| TS8 | INFL + FAC + RATE | OLS Term Structure Model |
| TS9 | INFL + SPD | OLS Term Structure Model |
| TS10 | INFL + RATE + SPD | OLS Term Structure Model |
| TS11 | INFL + GDPG + RATE + SPD | OLS Term Structure Models |
| VAR | VAR(1) on RATE, SPD, INFL, GDPG | Empirical Term Structure Model |
| RGMVAR | Regime-switching model on RATE, SPD, INFL | Empirical Term Structure Model |
| MDL1 | Three-factor affine model | No-Arbitrage Term Structure Model |
| MDL2 | General three-factor regime-switching model | No-Arbitrage Term Structure Model |
| SPF1 | Survey of Professional Forecasters | Inflation Surveys |
| SPF2 | Linear bias-corrected SPF | Inflation Surveys |
| SPF3 | Non-linear bias-corrected SPF | Inflation Surveys |
| LIV1 | Livingston Survey | Inflation Surveys |
| LIV2 | Linear bias-corrected Livingston | Inflation Surveys |
| LIV3 | Non-linear bias-corrected Livingston | Inflation Surveys | MICH1 | Michigan Survey | Inflation Surveys |
| MICH2 | Linear bias-corrected Michigan | Inflation Surveys |
| MICH3 | Non-linear bias-corrected Michigan | Inflation Surveys |
|
|
| |||
|---|---|---|---|---|
| SPF | 1.321 | 0.482 | ||
| Standard Error: SPF | (0.694) | (0.190) | ||
| Livingston | 0.637 | 0.993 | ||
| Standard Error: Livingston | (0.375) | (0.161) | ||
| Michigan | -0.823 | 1.276 | ||
| Standard Error: Michigan | (0.658) | (0.205) | ||
| SPF | 1.437* | -0.188 | 0.414** | 0.128 |
| Standard Error: SPF | (0.671) | (0.585) | (0.180) | (0.140) |
| Livingston | 0.589** | -0.295 | 0.806** | 0.461** |
| Standard Error: Livingston | (0.184) | (0.506) | (0.068) | (0.160) |
| Michigan | 0.039 | -1.261 | 0.959 | 0.482 |
| Standard Error: Michigan | (0.429) | (0.822) | (0.099) | (0.249) |
|
|
| |||
|---|---|---|---|---|
| SPF | 0.638 | 0.601* | ||
| Standard Error: SPF | (0.803) | (0.199) | ||
| Livingston | 0.561 | 0.942 | ||
| Standard Error: Livingston | (0.337) | (0.130) | ||
| Michigan | -0.741 | 1.167 | ||
| Standard Error: Michigan | (0.621) | (0.166) | ||
| SPF | 0.612 | -0.269 | 0.580* | 0.147 |
| Standard Error: SPF | (0.717) | (1.085) | (0.164) | (0.279) |
| Livingston | 0.568** | -0.191 | 0.765** | 0.389** |
| Standard Error: Livingston | (0.202) | (0.576) | (0.070) | (0.129) |
| Michigan | -0.267 | -0.723 | 1.002 | 0.262* |
| Standard Error: Michigan | (0.613) | (0.571) | (0.143) | (0.132) |
|
|
| |||
|---|---|---|---|---|
| SPF | 0.852 | 0.694 | ||
| Standard Error: SPF | (0.612) | (0.179) | ||
| Livingston | 0.381 | 1.055 | ||
| Standard Error: Livingston | (0.429) | (0.133) | ||
| Michigan | -0.279 | 1.194 | ||
| Standard Error: Michigan | (0.466) | (0.124) | ||
| SPF | 0.966 | -0.201 | 0.643 | 0.100 |
| Standard Error: SPF | (0.662) | (0.495) | (0.192) | (0.123) |
| Livingston | 0.433 | 0.124 | 0.931 | 0.165 |
| Standard Error: | (0.303) | (0.558) | (0.104) | (0.136) |
| Michigan | -0.160 | -0.042 | 1.137 | 0.059 |
| Standard Error: Michigan | (0.579) | (0.842) | (0.146) | (0.245) |
|
|
| |||
|---|---|---|---|---|
| SPF | 0.041 | 0.728* | ||
| Standard Error: SPF | (0.500) | (0.125) | ||
| Livingston | 0.234 | 0.949 | ||
| Standard Error: Livingston | (0.479) | (0.136) | ||
| Michigan | -0.547 | 1.058 | ||
| Standard Error: Michigan | (0.521) | (0.139) | ||
| SPF | 0.122 | -0.571 | 0.689** | 0.213 |
| Standard Error: SPF | (0.482) | (0.751) | (0.108) | (0.187) |
| Livingston | 0.278 | -0.094 | 0.785* | 0.399** |
| Standard Error: Livingston | (0.453) | (0.480) | (0.087) | (0.085) |
| Michigan | -0.061 | -0.688 | 0.900 | 0.228 |
| Standard Error: Michigan | (0.581) | (0.559) | (0.145) | (0.117) |
| Post-1985 Sample RMSE |
Post-1985 Sample ARMA=1 |
Post-1995 Sample RMSE |
Post-1995 Sample ARMA=1 |
|
|---|---|---|---|---|
| ARMA | 1.136 | 1.000 | 1.144 | 1.000 |
| AR | 1.140 | 1.003 | 1.130 | 0.988 |
| RGM | 1.420 | 1.250 | 0.873 | 0.764 |
| AORW | 1.177 | 1.036 | 1.128 | 0.986 |
| RW | 1.626 | 1.431 | 1.529 | 1.337 |
| Post-1985 Sample RMSE |
Post-1985 Sample ARMA=1 |
Post-1995 Sample RMSE |
Post-1995 Sample ARMA=1 |
|
|---|---|---|---|---|
| ARMA | 1.490 | 1.000 | 1.626 | 1.000 |
| AR | 1.515 | 1.017 | 1.634 | 1.005 |
| RGM | 1.591 | 1.068 | 1.355 | 0.833 |
| AORW | 1.580 | 1.061 | 1.670 | 1.027 |
| RW | 2.172 | 1.458 | 2.146 | 1.320 |
| Post-1985 Sample RMSE |
Post-1985 Sample ARMA=1 |
Post-1995 Sample RMSE |
Post-1995 Sample ARMA=1 |
|
|---|---|---|---|---|
| ARMA | 0.630 | 1.000 | 0.600 | 1.000 |
| AR | 0.644 | 1.023 | 0.593 | 0.988 |
| RGM | 0.677 | 1.075 | 0.727 | 1.211 |
| AORW | 0.516 | 0.819 | 0.372 | 0.620 |
| RW | 0.675 | 1.072 | 0.549 | 0.915 |
| Post-1985 Sample RMSE |
Post-1985 Sample ARMA=1 |
Post-1995 Sample RMSE |
Post-1995 Sample ARMA=1 |
|
|---|---|---|---|---|
| ARMA | 0.878 | 1.000 | 0.944 | 1.000 |
| AR | 0.942 | 1.073 | 1.014 | 1.074 |
| RGM | 0.945 | 1.077 | 1.081 | 1.145 |
| AORW | 0.829 | 0.945 | 0.869 | 0.921 |
| RW | 1.140 | 1.298 | 1.215 | 1.288 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| PC1 | 0.979 | 0.639 | 0.392 | 0.596 | 0.977 | 0.673 | 0.624 | 0.984 |
| PC2 | 1.472 | 0.066 | 0.145 | 0.155 | 1.956 | -0.117 | 0.199 | 0.169 |
| PC3 | 1.166 | 0.269 | 0.233 | 0.258 | 1.295 | 0.171 | 0.349 | 0.344 |
| PC4 | 1.078 | -1.043 | 0.632 | 1.266 | 1.025 | 0.046 | 0.890 | 1.389 |
| PC5 | 1.032 | 0.354 | 0.288 | 0.372 | 1.115 | -0.174 | 0.222 | 0.458 |
| PC6 | 1.103 | -0.303 | 0.575 | 0.634 | 1.086 | -0.633 | 0.488 | 1.054 |
| PC7 | 1.022 | 0.460 | 0.161** | 0.283 | 1.040 | 0.367 | 0.406 | 0.531 |
| PC8 | 1.039 | 0.319 | 0.477 | 0.515 | 0.993 | 0.468 | 0.793 | 0.901 |
| PC9 | 1.576 | 0.006 | 0.119 | 0.144 | 1.994 | -0.121 | 0.174 | 0.159 |
| PC10 | 1.264 | 0.146 | 0.205 | 0.235 | 1.426 | 0.119 | 0.246 | 0.287 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| PC1 | 1.000 | 0.498 | 0.458 | 0.758 | 0.992 | 0.618 | 0.814 | 1.182 |
| PC2 | 1.328 | -0.022 | 0.218 | 0.239 | 1.586 | -0.192 | 0.317 | 0.266 |
| PC3 | 1.113 | 0.200 | 0.310 | 0.329 | 1.105 | 0.239 | 0.522 | 0.519 |
| PC4 | 1.096 | -0.988 | 0.497* | 1.064 | 1.029 | 0.008 | 0.745 | 1.229 |
| PC5 | 1.083 | -0.080 | 0.299 | 0.491 | 1.076 | -0.411 | 0.358 | 0.708 |
| PC6 | 1.131 | -1.074 | 0.519* | 0.822 | 1.061 | -1.316 | 0.512** | 1.463 |
| PC7 | 1.001 | 0.498 | 0.186** | 0.301 | 1.070 | 0.085 | 0.529 | 0.590 |
| PC8 | 1.094 | -0.325 | 0.466 | 0.713 | 1.007 | 0.101 | 1.259 | 1.337 |
| PC9 | 1.394 | -0.055 | 0.186 | 0.224 | 1.624 | -0.204 | 0.290 | 0.254 |
| PC10 | 1.165 | 0.125 | 0.273 | 0.308 | 1.202 | 0.150 | 0.340 | 0.392 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| PC1 | 0.866 | 1.432 | 0.340** | 1.632 | 0.825 | 1.182 | 0.120** | 1.384 |
| PC2 | 2.463 | -0.120 | 0.072 | 0.100 | 3.257 | -0.227 | 0.093* | 0.119 |
| PC3 | 1.664 | 0.054 | 0.213 | 0.190 | 2.076 | -0.063 | 0.275 | 0.226 |
| PC4 | 1.234 | 0.126 | 0.143 | 0.261 | 1.330 | 0.187 | 0.214 | 0.230 |
| PC5 | 1.024 | 0.460 | 0.207* | 0.370 | 1.185 | 0.134 | 0.445 | 0.551 |
| PC6 | 1.005 | 0.479 | 0.477 | 1.053 | 0.916 | 1.009 | 0.277** | 1.935 |
| PC7 | 1.074 | 0.381 | 0.277 | 0.426 | 1.089 | 0.293 | 0.500 | 0.731 |
| PC8 | 0.862 | 0.809 | 0.297** | 0.751 | 0.767 | 1.127 | 0.275** | 1.340 |
| PC9 | 2.485 | -0.076 | 0.069 | 0.100 | 3.262 | -0.168 | 0.069* | 0.120 |
| PC10 | 1.873 | 0.079 | 0.136 | 0.153 | 2.562 | 0.038 | 0.150 | 0.151 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| PC1 | 1.053 | 0.029 | 0.469 | 0.972 | 1.088 | -0.240 | 0.434 | 1.119 |
| PC2 | 1.698 | -0.136 | 0.141 | 0.178 | 1.997 | -0.240 | 0.223 | 0.218 |
| PC3 | 1.274 | -0.031 | 0.280 | 0.252 | 1.407 | -0.239 | 0.354 | 0.340 |
| PC4 | 1.027 | 0.343 | 0.392 | 1.004 | 1.031 | 0.339 | 0.535 | 1.138 |
| PC5 | 1.125 | -0.080 | 0.327 | 0.434 | 1.214 | -0.635 | 0.389 | 0.629 |
| PC6 | 1.053 | 0.036 | 0.484 | 1.233 | 1.020 | 0.273 | 0.509 | 1.795 |
| PC7 | 1.033 | 0.436 | 0.175* | 0.359 | 1.116 | 0.034 | 0.334 | 0.651 |
| PC8 | 1.040 | 0.269 | 0.476 | 0.807 | 1.044 | 0.044 | 1.101 | 2.018 |
| PC9 | 1.518 | -0.100 | 0.166 | 0.193 | 1.786 | -0.282 | 0.258 | 0.258 |
| PC10 | 1.247 | 0.120 | 0.201 | 0.297 | 1.432 | -0.068 | 0.235 | 0.322 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| TS1 | 1.096 | 0.137 | 0.332 | 0.393 | 1.030 | 0.362 | 0.410 | 0.653 |
| TS2 | 1.444 | 0.019 | 0.145 | 0.148 | 1.826 | -0.147 | 0.229 | 0.182 |
| TS3 | 1.176 | 0.193 | 0.229 | 0.259 | 1.226 | 0.156 | 0.335 | 0.358 |
| TS4 | 1.166 | -0.108 | 0.249 | 0.321 | 1.018 | 0.370 | 0.474 | 0.959 |
| TS5 | 1.134 | 0.088 | 0.186 | 0.278 | 1.122 | 0.006 | 0.187 | 0.429 |
| TS6 | 1.194 | -0.241 | 0.326 | 0.371 | 1.112 | -0.162 | 0.406 | 0.578 |
| TS7 | 1.091 | 0.309 | 0.252 | 0.290 | 1.039 | 0.373 | 0.434 | 0.523 |
| TS8 | 1.119 | 0.116 | 0.332 | 0.365 | 1.010 | 0.380 | 0.816 | 0.864 |
| TS9 | 1.363 | 0.086 | 0.085 | 0.129 | 1.229 | -0.008 | 0.083 | 0.305 |
| TS10 | 1.196 | -0.024 | 0.143 | 0.220 | 1.043 | 0.132 | 0.639 | 0.685 |
| TS11 | 1.198 | -0.124 | 0.431 | 0.414 | 1.052 | 0.286 | 0.318 | 0.611 |
| VAR | 1.106 | 0.307 | 0.187 | 0.225 | 1.328 | -0.101 | 0.259 | 0.270 |
| RGMVAR | 1.647 | 0.050 | 0.050 | 0.090 | 1.518 | -0.170 | 0.198 | 0.226 |
| MDL1 | 1.323 | 0.161 | 0.064* | 0.356 | 1.345 | -0.088 | 0.192 | 0.247 |
| MDL2 | 1.192 | 0.225 | 0.117 | 0.392 | 1.329 | -0.118 | 0.251 | 0.278 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| TS1 | 1.080 | -0.025 | 0.413 | 0.508 | 1.014 | 0.373 | 0.553 | 0.824 |
| TS2 | 1.345 | -0.017 | 0.205 | 0.216 | 1.584 | -0.197 | 0.329 | 0.265 |
| TS3 | 1.116 | 0.186 | 0.278 | 0.309 | 1.118 | 0.195 | 0.435 | 0.463 |
| TS4 | 1.085 | -0.275 | 0.499 | 0.670 | 0.996 | 0.542 | 0.592 | 1.077 |
| TS5 | 1.113 | -0.082 | 0.214 | 0.358 | 1.094 | -0.191 | 0.265 | 0.557 |
| TS6 | 1.140 | -0.566 | 0.342 | 0.534 | 1.069 | -0.360 | 0.419 | 0.776 |
| TS7 | 1.081 | 0.161 | 0.298 | 0.342 | 1.070 | 0.089 | 0.410 | 0.564 |
| TS8 | 1.083 | -0.054 | 0.411 | 0.497 | 0.975 | 0.559 | 1.057 | 1.055 |
| TS9 | 1.173 | 0.114 | 0.105 | 0.201 | 1.130 | -0.123 | 0.211 | 0.478 |
| TS10 | 1.140 | -0.594 | 0.468 | 0.658 | 1.032 | -0.034 | 0.090 | 0.855 |
| TS11 | 1.102 | -0.121 | 0.423 | 0.482 | 1.049 | 0.093 | 0.164 | 0.667 |
| VAR | 1.001 | 0.496 | 0.264 | 0.354 | 1.137 | 0.041 | 0.426 | 0.433 |
| RGMVAR | 1.363 | 0.070 | 0.085 | 0.159 | 1.285 | -0.149 | 0.366 | 0.383 |
| MDL1 | 1.225 | 0.127 | 0.081 | 0.263 | 1.186 | -0.048 | 0.266 | 0.320 |
| MDL2 | 1.047 | 0.395 | 0.203 | 0.702 | 1.156 | 0.000 | 0.406 | 0.386 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| TS1 | 0.945 | 0.667 | 0.322* | 0.655 | 0.945 | 0.665 | 0.317* | 0.924 |
| TS2 | 2.262 | -0.092 | 0.084 | 0.100 | 2.982 | -0.225 | 0.099* | 0.117 |
| TS3 | 1.399 | 0.121 | 0.260 | 0.249 | 1.698 | -0.057 | 0.344 | 0.288 |
| TS4 | 1.232 | 0.260 | 0.156 | 0.229 | 1.268 | 0.319 | 0.225 | 0.248 |
| TS5 | 1.081 | 0.392 | 0.203 | 0.299 | 1.258 | 0.085 | 0.407 | 0.454 |
| TS6 | 0.969 | 0.567 | 0.294 | 0.601 | 0.866 | 0.788 | 0.078** | 0.882 |
| TS7 | 1.068 | 0.419 | 0.203* | 0.354 | 1.118 | 0.342 | 0.289 | 0.505 |
| TS8 | 0.948 | 0.568 | 0.197** | 0.459 | 0.958 | 0.520 | 0.253* | 0.832 |
| TS9 | 1.372 | 0.050 | 0.239 | 0.247 | 1.282 | -0.101 | 0.457 | 0.504 |
| TS10 | 1.034 | 0.433 | 0.284 | 0.467 | 1.208 | -0.048 | 0.548 | 0.737 |
| TS11 | 1.017 | 0.474 | 0.246 | 0.439 | 1.192 | 0.099 | 0.502 | 0.686 |
| VAR | 1.651 | 0.041 | 0.178 | 0.154 | 2.238 | -0.276 | 0.151 | 0.183 |
| RGMVAR | 1.572 | 0.120 | 0.138 | 0.147 | 1.622 | -0.211 | 0.340 | 0.278 |
| MDL1 | 1.506 | 0.253 | 0.091** | 0.381 | 1.593 | -0.004 | 0.280 | 0.303 |
| MDL2 | 1.834 | 0.262 | 0.039** | 0.443 | 1.329 | 0.355 | 0.069** | 0.298 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| TS1 | 1.075 | -0.073 | 0.453 | 0.847 | 1.078 | -0.207 | 0.433 | 1.192 |
| TS2 | 1.670 | -0.149 | 0.145 | 0.181 | 1.966 | -0.247 | 0.226 | 0.221 |
| TS3 | 1.279 | -0.053 | 0.288 | 0.259 | 1.373 | -0.245 | 0.376 | 0.360 |
| TS4 | 1.075 | 0.018 | 0.372 | 0.864 | 1.059 | 0.234 | 0.442 | 0.816 |
| TS5 | 1.126 | -0.115 | 0.331 | 0.456 | 1.202 | -0.645 | 0.383 | 0.663 |
| TS6 | 1.094 | -0.149 | 0.428 | 0.896 | 1.100 | -0.358 | 0.397 | 1.322 |
| TS7 | 1.018 | 0.443 | 0.271 | 0.481 | 1.106 | 0.033 | 0.303 | 0.673 |
| TS8 | 1.027 | 0.374 | 0.414 | 0.720 | 1.025 | 0.346 | 1.058 | 1.855 |
| TS9 | 1.141 | -0.024 | 0.192 | 0.304 | 1.121 | -0.825 | 0.584 | 0.939 |
| TS10 | 1.087 | -0.569 | 0.549 | 0.992 | 1.110 | -0.850 | 0.638 | 1.177 |
| TS11 | 1.086 | 0.006 | 0.418 | 0.665 | 1.132 | -0.396 | 0.288 | 0.878 |
| VAR | 1.286 | -0.179 | 0.274 | 0.298 | 1.511 | -0.337 | 0.392 | 0.327 |
| RGMVAR | 1.507 | -0.242 | 0.131 | 0.237 | 1.461 | -0.356 | 0.233 | 0.424 |
| MDL1 | 1.169 | 0.144 | 0.235 | 0.432 | 1.271 | -0.374 | 0.284 | 0.481 |
| MDL2 | 1.314 | -0.205 | 0.159 | 1.220 | 1.339 | -0.331 | 0.120** | 0.589 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| SPF1 | 0.779 | 1.051 | 0.177** | 0.439* | 0.861 | 0.869 | 0.407* | 0.554 |
| SPF2 | 0.964 | 0.564 | 0.216** | 0.308 | 0.902 | 0.745 | 0.377* | 0.484 |
| SPF3 | 0.976 | 0.541 | 0.207** | 0.302 | 0.915 | 0.728 | 0.414 | 0.479 |
| LIV1 | 0.789 | 1.164 | 0.102** | 0.585 | 0.792 | 1.140 | 0.203** | 0.913 |
| LIV2 | 1.180 | 0.335 | 0.177 | 0.281 | 1.092 | 0.403 | 0.437 | 0.550 |
| LIV3 | 1.299 | 0.251 | 0.163 | 0.226 | 1.152 | 0.275 | 0.517 | 0.549 |
| MICH1 | 0.902 | 0.771 | 0.324* | 0.379* | 0.862 | 1.113 | 0.520* | 0.684 |
| MICH2 | 0.961 | 0.675 | 0.327* | 0.370 | 0.930 | 0.861 | 0.644 | 0.609 |
| MICH3 | 0.968 | 0.655 | 0.347 | 0.375 | 0.947 | 0.776 | 0.653 | 0.567 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| SPF1 | 0.819 | 0.939 | 0.171** | 0.430* | 0.914 | 0.773 | 0.394* | 0.546 |
| SPF2 | 0.924 | 0.666 | 0.227** | 0.312* | 0.888 | 0.825 | 0.357* | 0.504 |
| SPF3 | 1.348 | 0.103 | 0.183 | 0.193 | 0.958 | 0.582 | 0.323 | 0.362 |
| LIV1 | 0.844 | 1.098 | 0.099** | 0.573 | 0.856 | 1.072 | 0.214** | 0.878 |
| LIV2 | 1.054 | 0.554 | 0.176** | 0.386 | 1.031 | 0.550 | 0.366 | 0.615 |
| LIV3 | 1.199 | 0.327 | 0.156* | 0.299 | 1.053 | 0.502 | 0.443 | 0.605 |
| MICH1 | 0.881 | 0.876 | 0.273** | 0.398* | 0.937 | 0.750 | 0.434 | 0.476 |
| MICH2 | 0.918 | 0.815 | 0.290** | 0.395* | 0.932 | 0.814 | 0.515 | 0.528 |
| MICH3 | 0.970 | 0.608 | 0.251* | 0.347 | 0.953 | 0.684 | 0.492 | 0.474 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| SPF1 | 0.691 | 0.968 | 0.140** | 0.654 | 0.699 | 1.260 | 0.225** | 1.437 |
| SPF2 | 1.145 | 0.125 | 0.362 | 0.555 | 1.104 | 0.091 | 0.852 | 1.177 |
| SPF3 | 1.179 | 0.035 | 0.373 | 0.555 | 1.180 | -0.358 | 0.956 | 1.390 |
| LIV1 | 0.655 | 0.803 | 0.192** | 0.730 | 0.557 | 1.227 | 0.134** | 1.453 |
| LIV2 | 1.355 | -0.185 | 0.177 | 0.185 | 1.387 | -0.423 | 0.415 | 0.557 |
| LIV3 | 1.289 | -0.095 | 0.259 | 0.262 | 1.278 | -0.496 | 0.735 | 0.850 |
| MICH1 | 1.185 | 0.383 | 0.159* | 0.301 | 0.822 | 1.041 | 0.208** | 2.124 |
| MICH2 | 1.343 | -0.153 | 0.248 | 0.272 | 1.566 | -0.385 | 0.286 | 0.356 |
| MICH3 | 1.360 | -0.242 | 0.253 | 0.285 | 1.617 | -0.493 | 0.273 | 0.363 |
| Post-1985 Sample Relative RMSE |
Post-1985 Sample |
Post-1985 Sample HH SE |
Post-1985 Sample West SE |
Post-1995 Sample Relative RMSE |
Post-1995 Sample |
Post-1995 Sample HH SE |
Post-1995 Sample West SE |
|
|---|---|---|---|---|---|---|---|---|
| SPF1 | 1.199 | 0.147 | 0.267 | 0.241 | 1.250 | 0.090 | 0.395 | 0.349 |
| SPF2 | 0.980 | 0.537 | 0.206** | 0.375 | 0.924 | 0.655 | 0.325* | 0.570 |
| SPF3 | 1.034 | 0.454 | 0.180* | 0.306 | 1.040 | 0.453 | 0.234 | 0.362 |
| LIV1 | 1.082 | 0.175 | 0.325 | 0.300 | 1.101 | 0.132 | 0.412 | 0.400 |
| LIV2 | 1.397 | -0.050 | 0.189 | 0.234 | 1.303 | -0.026 | 0.265 | 0.358 |
| LIV3 | 1.380 | -0.123 | 0.149 | 0.212 | 1.341 | -0.191 | 0.272 | 0.375 |
| MICH1 | 1.217 | 0.108 | 0.216 | 0.192 | 1.338 | -0.030 | 0.327 | 0.283 |
| MICH2 | 1.194 | 0.039 | 0.253 | 0.216 | 1.205 | 0.056 | 0.415 | 0.350 |
| MICH3 | 1.248 | -0.022 | 0.239 | 0.200 | 1.255 | -0.003 | 0.399 | 0.334 |
| PUNEW | PUNEW | PUXHS | PUXHS | PUXX | PUXX | PCE | PCE | |
|---|---|---|---|---|---|---|---|---|
| Best Time-Series Model | ARMA | 1.000 | ARMA | 1.000 | AORW | 0.819 | AORW | 0.945* |
| Best Phillips-Curve Model | PC1 | 0.979 | PC1 | 1.000 | PC8 | 0.862 | PC4 | 1.027 |
| Best Term-Structure Model | TS7 | 1.091 | VAR | 1.001 | TS1 | 0.945 | TS7 | 1.018 |
| Raw Survey Forecasts | SPF1 | 0.779* | SPF1 | 0.819* | SPF1 | 0.691 | SPF1 | 1.199 |
| Raw Survey Forecasts | LIV1 | 0.789 | LIV1 | 0.844 | LIV1 | 0.655* | LIV1 | 1.082 |
| Raw Survey Forecasts | MICH1 | 0.902 | MICH1 | 0.881 | MICH1 | 1.185 | MICH1 | 1.217 |
| PUNEW | PUNEW | PUXHS | PUXHS | PUXX | PUXX | PCE | PCE | |
|---|---|---|---|---|---|---|---|---|
| Best Time-Series Model | RGM | 0.764* | RGM | 0.833* | AORW | 0.620 | AORW | 0.921* |
| Best Phillips-Curve Model | PC1 | 0.977 | PC1 | 0.992 | PC8 | 0.767 | PC6 | 1.020 |
| Best Term-Structure Model | TS8 | 1.010 | TS8 | 0.975 | TS6 | 0.866 | TS8 | 1.025 |
| Raw Survey Forecasts | SPF1 | 0.861 | SPF1 | 0.914 | SPF1 | 0.699 | SPF1 | 1.250 |
| Raw Survey Forecasts | LIV1 | 0.792 | LIV1 | 0.856 | LIV1 | 0.557* | LIV1 | 1.101 |
| Raw Survey Forecasts | MICH1 | 0.862 | MICH1 | 0.937 | MICH1 | 0.822 | MICH1 | 1.338 |
| Date | PUNEW Time Series | PUNEW Phillips Curve | PUNEW Term Structure | PUNEW Surveys | PUNEW All Models | PUXHS Time Series | PUXHS Phillips Curve | PUXHS Term Structure | PUXHSSurveys | PUXHS All Models |
|---|---|---|---|---|---|---|---|---|---|---|
| 1995Q4 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1996Q1 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1996Q2 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1996Q3 | ARMA | PC1 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1996Q4 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1997Q1 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1997Q2 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1997Q3 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1997Q4 | ARMA | PC1 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1998Q1 | ARMA | PC1 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1998Q2 | ARMA | PC1 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1998Q3 | ARMA | PC1 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1998Q4 | ARMA | PC1 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1999Q1 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1999Q2 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1999Q3 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 1999Q4 | ARMA | PC5 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 2000Q1 | ARMA | PC1 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 2000Q2 | ARMA | PC1 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 2000Q3 | ARMA | PC1 | VAR | SPF1 | SPF1 | ARMA | PC7 | VAR | SPF1 | SPF1 |
| 2000Q4 | ARMA | PC1 | TS1 | SPF1 | SPF1 | ARMA | PC1 | VAR | SPF1 | SPF1 |
| 2001Q1 | ARMA | PC1 | TS1 | SPF1 | SPF1 | ARMA | PC1 | VAR | SPF1 | SPF1 |
| 2001Q2 | ARMA | PC1 | TS1 | SPF1 | SPF1 | ARMA | PC1 | VAR | SPF1 | SPF1 |
| 2001Q3 | ARMA | PC1 | TS1 | SPF1 | SPF1 | ARMA | PC1 | VAR | SPF1 | SPF1 |
| 2001Q4 | ARMA | PC1 | TS7 | SPF1 | SPF1 | ARMA | PC1 | VAR | SPF1 | SPF1 |
| Date | PUXX Time Series | PUXX Phillips Curve | PUXX Term Structure | PUXX Surveys | PUXX All Models | PCE Time Series | PCE Phillips Curve | PCE Term Structure | PCESurveys | PCE All Models |
|---|---|---|---|---|---|---|---|---|---|---|
| 1995Q4 | AORW | PC1 | TS11 | SPF1 | SPF1 | AORW | PC7 | TS7 | MICH1 | TS7 |
| 1996Q1 | AORW | PC1 | TS11 | SPF1 | SPF1 | AORW | PC7 | TS7 | MICH1 | TS7 |
| 1996Q2 | AORW | PC1 | TS11 | SPF1 | SPF1 | AORW | PC7 | TS7 | MICH1 | TS7 |
| 1996Q3 | AORW | PC1 | TS11 | SPF1 | SPF1 | AORW | PC7 | TS7 | MICH1 | TS7 |
| 1996Q4 | AORW | PC8 | TS11 | SPF1 | SPF1 | AORW | PC7 | TS7 | MICH1 | AORW |
| 1997Q1 | AORW | PC1 | TS11 | SPF1 | SPF1 | AORW | PC7 | TS7 | MICH1 | AORW |
| 1997Q2 | AORW | PC8 | TS11 | SPF1 | SPF1 | AORW | PC7 | TS7 | MICH1 | AORW |
| 1997Q3 | AORW | PC8 | TS11 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | AORW |
| 1997Q4 | AORW | PC8 | TS11 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | AORW |
| 1998Q1 | AORW | PC8 | TS1 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | AORW |
| 1998Q2 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | AORW |
| 1998Q3 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | AORW |
| 1998Q4 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | AORW |
| 1999Q1 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC7 | TS7 | MICH1 | TS7 |
| 1999Q2 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC7 | TS7 | MICH1 | TS7 |
| 1999Q3 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC7 | TS7 | MICH1 | TS7 |
| 1999Q4 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | TS7 |
| 2000Q1 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | AORW |
| 2000Q2 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | AORW |
| 2000Q3 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | AORW |
| 2000Q4 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | MICH1 | AORW |
| 2001Q1 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | SPF1 | AORW |
| 2001Q2 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | SPF1 | AORW |
| 2001Q3 | AORW | PC8 | TS8 | SPF1 | SPF1 | AORW | PC4 | TS7 | SPF1 | AORW |
| 2001Q4 | AORW | PC8 | TS1 | SPF1 | SPF1 | AORW | PC4 | TS7 | SPF1 | AORW |
| PUNEW | PUNEW | PUXHS | PUXHS | PUXX | PUXX | PCE | PCE | |
|---|---|---|---|---|---|---|---|---|
| Best Time-Series Model | AR | 0.967 | AR | 1.002 | AORW | 0.819 | AORW | 0.945* |
| Best Phillips-Curve Model | PC7 | 1.070 | PC1 | 1.068 | PC8 | 1.179 | PC8 | 1.082 |
| Best Term-Structure Model | TS1 | 1.199 | TS9 | 1.073 | TS6 | 1.350 | TS6 | 1.182 |
| Raw Survey Forecasts | SPF1 | 0.779* | SPF1 | 0.819* | SPF1 | 0.691 | SPF1 | 1.199 |
| Raw Survey Forecasts | LIV1 | 0.789 | LIV1 | 0.844 | LIV1 | 0.655* | LIV1 | 1.082 |
| Raw Survey Forecasts | MICH1 | 0.902 | MICH1 | 0.881 | MICH1 | 1.185 | MICH1 | 1.217 |
| PUNEW | PUNEW | PUXHS | PUXHS | PUXX | PUXX | PCE | PCE | |
|---|---|---|---|---|---|---|---|---|
| Best Time-Series Model | AR | 0.879 | AR | 0.914 | ARMA | 0.635 | ARMA | 0.730* |
| Best Phillips-Curve Model | PC6 | 0.951 | PC6 | 0.955 | PC7 | 0.560 | PC6 | 0.799 |
| Best Term-Structure Model | VAR | 0.987 | VAR | 0.998 | TS5 | 0.881 | TS3 | 0.990 |
| Raw Survey Forecasts | SPF1 | 0.861* | SPF1 | 0.914 | SPF1 | 0.699 | SPF1 | 1.250 |
| Raw Survey Forecasts | LIV1 | 0.792 | LIV1 | 0.856* | LIV1 | 0.557* | LIV1 | 1.101 |
| Raw Survey Forecasts | MICH1 | 0.862 | MICH1 | 0.937 | MICH1 | 0.822 | MICH1 | 1.338 |
| Model Combination Method | Time-Series | Phillips Curve | Term Structure | Surveys | Best Models | All Models |
|---|---|---|---|---|---|---|
| Mean | 0.898 | 1.123 | 1.057 | 0.851 | 0.992 | 0.998 |
| Median | 0.934 | 1.093 | 1.079 | 0.851 | 1.016 | 1.045 |
| OLS | 0.970 | 1.007 | 1.116 | 0.858 | 0.867 | 0.876 |
| Equal Weight Prior | 0.955 | 1.007 | 1.102 | 0.858 | 0.861 | 0.879 |
| Unit Weight Prior | 0.977 | 0.951 | 1.115 | 0.859 | 0.862 | 0.873 |
| Best Individual Model | 1.000 | 0.960 | 1.207 | 0.861 | 0.861 | 0.861 |
| Model Combination Method | Time-Series | Phillips Curve | Term Structure | Surveys | Best Models | All Models |
|---|---|---|---|---|---|---|
| Mean | 0.954 | 1.065 | 1.012 | 0.921 | 0.975 | 0.992 |
| Median | 0.953 | 1.082 | 1.053 | 0.921 | 1.009 | 1.039 |
| OLS | 0.963 | 1.001 | 1.069 | 0.917 | 0.919 | 0.924 |
| Equal Weight Prior | 0.950 | 1.008 | 1.058 | 0.918 | 0.920 | 0.935 |
| Unit Weight Prior | 0.977 | 0.992 | 1.085 | 0.916 | 0.914 | 0.914 |
| Best Individual Model | 1.000 | 1.029 | 1.137 | 0.914 | 0.914 | 0.914 |
| Model Combination Method | Time-Series | Phillips Curve | Term Structure | Surveys | Best Models | All Models |
|---|---|---|---|---|---|---|
| Mean | 0.835 | 1.547 | 1.322 | 0.719 | 0.727 | 1.235 |
| Median | 0.940 | 1.167 | 1.211 | 0.719 | 0.735 | 1.052 |
| OLS | 0.631 | 0.885 | 0.964 | 0.699 | 0.665 | 0.706 |
| Equal Weight Prior | 0.687 | 0.878 | 0.956 | 0.699 | 0.652 | 0.661 |
| Unit Weight Prior | 0.650 | 0.836 | 0.947 | 0.699 | 0.658 | 0.658 |
| Best Individual Model | 0.620 | 0.779 | 0.977 | 0.699 | 0.699 | 0.699 |
| Model Combination Method | Time-Series | Phillips Curve | Term Structure | Surveys | Best Models | All Models |
|---|---|---|---|---|---|---|
| Mean | 0.968 | 1.160 | 1.127 | 1.285 | 0.999 | 1.105 |
| Median | 0.979 | 1.136 | 1.130 | 1.285 | 0.999 | 1.118 |
| OLS | 0.935 | 0.974 | 1.019 | 1.288 | 0.921 | 0.964 |
| Equal Weight Prior | 0.938 | 0.984 | 1.017 | 1.287 | 0.922 | 0.968 |
| Unit Weight Prior | 0.917 | 0.967 | 1.010 | 1.287 | 0.911 | 0.948 |
| Best Individual Model | 0.921 | 1.057 | 1.106 | 1.289 | 0.887 | 0.887 |
| Post-1985 Sample Estimated on Levels Model |
Post-1985 Sample Estimated on Levels RMSE |
Post-1985 Estimated on Differences Sample Model |
Post-1985 Estimated on Differences Sample RMSE |
Post-1995 Sample Estimated on Levels Model |
Post-1995 Sample Estimated on Levels RMSE |
Post-1995 Estimated on Differences Sample Model |
Post-1995 Estimated on Differences Sample RMSE |
|
|---|---|---|---|---|---|---|---|---|
| Best Time-Series Model | ARMA | 1.000 | ARMA | 1.071 | RGM | 0.764* | ARMA | 1.025 |
| Best Phillips-Curve Model | PC1 | 0.979 | PC7 | 1.005 | PC1 | 0.977 | PC7 | 0.976 |
| Best Term-Structure Model | TS7 | 1.091 | TS7 | 1.023 | TS8 | 1.010 | TS1 | 0.968 |
| Raw Survey Forecasts | SPF1 | 0.779* | SPF1 | 0.861 | ||||
| Raw Survey Forecasts | LIV1 | 0.789 | LIV1 | 0.792 | ||||
| Raw Survey Forecasts | MICH1 | 0.902 | MICH1 | 0.862 |
| Post-1985 Sample Estimated on Levels Model |
Post-1985 Sample Estimated on Levels RMSE |
Post-1985 Estimated on Differences Sample Model |
Post-1985 Estimated on Differences Sample RMSE |
Post-1995 Sample Estimated on Levels Model |
Post-1995 Sample Estimated on Levels RMSE |
Post-1995 Estimated on Differences Sample Model |
Post-1995 Estimated on Differences Sample RMSE |
|
|---|---|---|---|---|---|---|---|---|
| Best Time-Series Model | ARMA | 1.000 | ARMA | 1.098 | RGM | 0.833* | ARMA | 1.046 |
| Best Phillips-Curve Model | PC1 | 1.000 | PC7 | 1.027 | PC1 | 0.992 | PC1 | 1.023 |
| Best Term-Structure Model | VAR | 1.001 | TS7 | 1.004 | TS8 | 0.975 | TS7 | 0.987 |
| Raw Survey Forecasts | SPF1 | 0.819* | SPF1 | 0.914 | ||||
| Raw Survey Forecasts | LIV1 | 0.844 | LIV1 | 0.856 | ||||
| Raw Survey Forecasts | MICH1 | 0.881 | MICH1 | 0.937 |
| Post-1985 Sample Estimated on Levels Model |
Post-1985 Sample Estimated on Levels RMSE |
Post-1985 Estimated on Differences Sample Model |
Post-1985 Estimated on Differences Sample RMSE |
Post-1995 Sample Estimated on Levels Model |
Post-1995 Sample Estimated on Levels RMSE |
Post-1995 Estimated on Differences Sample Model |
Post-1995 Estimated on Differences Sample RMSE |
|
|---|---|---|---|---|---|---|---|---|
| Best Time-Series Model | AORW | 0.819 | ARMA | 0.837 | AORW | 0.620 | ARMA | 0.649 |
| Best Phillips-Curve Model | PC8 | 0.862 | PC1 | 0.722 | PC8 | 0.767 | PC1 | 0.652 |
| Best Term-Structure Model | TS1 | 0.945 | TS8 | 0.861 | TS6 | 0.866 | TS6 | 0.655 |
| Raw Survey Forecasts | SPF1 | 0.691 | SPF1 | 0.699 | ||||
| Raw Survey Forecasts | LIV1 | 0.655* | LIV1 | 0.557* | ||||
| Raw Survey Forecasts | MICH1 | 1.185 | MICH1 | 0.822 |
| Post-1985 Sample Estimated on Levels Model |
Post-1985 Sample Estimated on Levels RMSE |
Post-1985 Estimated on Differences Sample Model |
Post-1985 Estimated on Differences Sample RMSE |
Post-1995 Sample Estimated on Levels Model |
Post-1995 Sample Estimated on Levels RMSE |
Post-1995 Estimated on Differences Sample Model |
Post-1995 Estimated on Differences Sample RMSE |
|
|---|---|---|---|---|---|---|---|---|
| Best Time-Series Model | AORW | 0.945 | ARMA | 1.029 | AORW | 0.921 | ARMA | 1.004 |
| Best Phillips-Curve Model | PC4 | 1.027 | PC8 | 0.978 | PC6 | 1.020 | PC6 | 1.018 |
| Best Term-Structure Model | TS7 | 1.018 | TS8 | 0.945* | TS8 | 1.025 | TS4 | 0.951* |
| Raw Survey Forecasts | SPF1 | 1.199 | SPF1 | 1.250 | ||||
| Raw Survey Forecasts | LIV1 | 1.082 | LIV1 | 1.101 | ||||
| Raw Survey Forecasts | MICH1 | 1.217 | MICH1 | 1.338 |
Figure 3: Ex-Ante Weights on Best I(1) Models for Forecasting Annual Inflation Changes
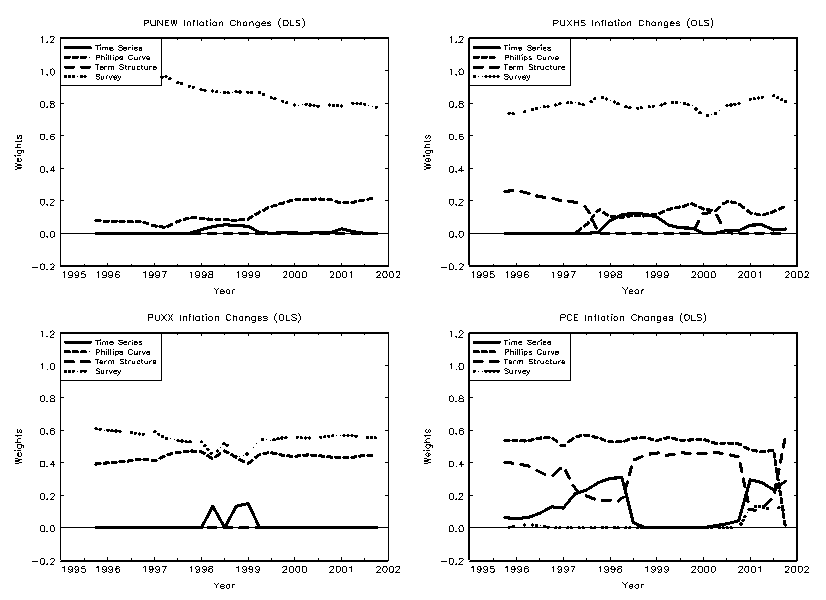
Figure 4: Ex-Ante Weights on Best I(0) Models for Forecasting Annual Inflation Changes
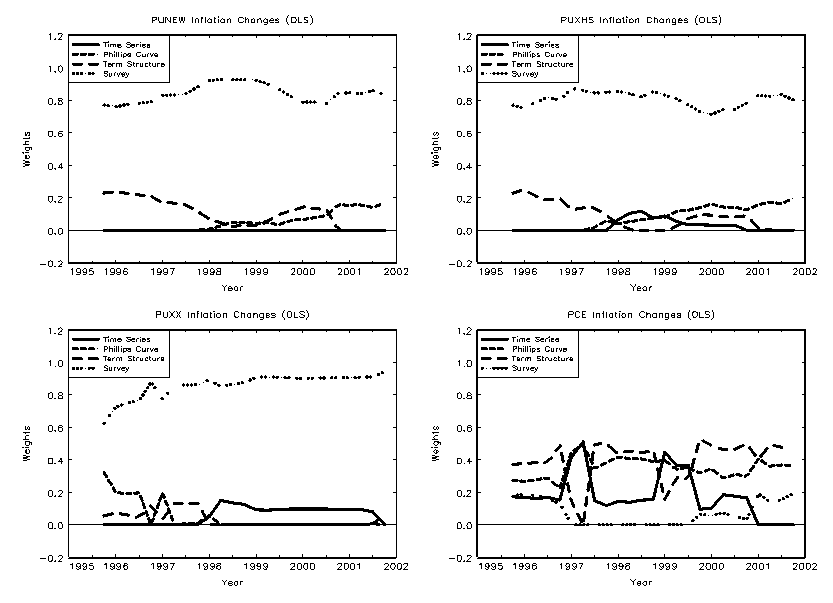
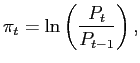
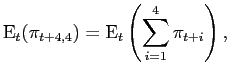
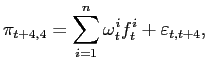
![$\displaystyle =\mathrm{E}_{t}\left[ \sum_{i=-3}^{3} (4-\vert i\vert)\Delta\pi_{t+1+i}\right]$](img127.gif)
![$\displaystyle = \mathrm{E}_{t} \left[ \sum_{i=0}^{3} (4-i) \Delta\pi_{t+1+i} \right] + 4 \pi_{t} - \pi_{t,4},$](img128.gif)
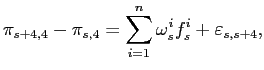
![$\displaystyle \sum_{j=-\infty}^{\infty} \ensuremath{{\rm E}}\left[ ( f_{t,t+4}-\ensuremath{{\rm E}} f_{t,t+4})(f_{t-j,t-j+4}-\ensuremath{{\rm E}}f_{t,t+4})^{\prime} \right],$](img200.gif)
![$\displaystyle \sum_{j=-\infty}^{\infty}\ensuremath{{\rm E}}\left[( f_{t,t+4}-\ensuremath{{\rm E}} f_{t,t+4}) h_{t-j}^{\prime} \right],$](img202.gif)
![$\displaystyle \sum_{j=-\infty}^{\infty}\ensuremath{{\rm E}} \left[h_{t}h_{t-j}^{\prime} \right].$](img204.gif)