
Monetary Policy Implementation
Without Averaging or Rate Corridors
Keywords: Policy implementation, overnight interest rate
Abstract:
JEL classifications: E4, E5
Introduction
In recent years, most central banks in industrialized countries have implemented monetary policy by trying to hit a target overnight interest rate, employing a system of reserve averaging, a corridor for interest rates between the central bank's lending and deposit rates, or a combination of a corridor and averaging. Averaging systems and rate corridors each have features that can assist a central bank in hitting its target for the overnight interest rate. However, each also has some potential weaknesses, and the balance among the costs and benefits for the two types of regimes tends to differ across central banks and financial systems. The disadvantages of both averaging and rate corridor regimes may become more salient in environments of relatively high short-term interest rates. Because short-term interest rates are now rising in many economies, it may be an apt time to consider an alternative framework for the implementation of monetary policy that does not suffer from the drawbacks of either averaging systems or rate corridors.
This paper develops and analyzes a new type of framework for policy implementation that provides a mechanism for generating a flat demand curve for central bank balances each day at the target overnight interest rate. With a highly elastic daily demand curve, the overnight interest rate would tend to stay close to the central bank's target, even if the central bank made errors in estimating either the position of the demand curve or the autonomous factors affecting the supply of reserves. The paper shows that a highly elastic daily demand curve can be achieved if a central bank provides a facility to pay daily interest on balances up to some maximum amount, with no penalty on shortfalls of balances from their maximum. Depository institutions would choose their own ceiling on interest-earning balances, subject to a small facility fee proportional to the ceiling. The paper describes how a daily interest facility of this nature could potentially allow for effective policy implementation.
The plan of the paper is as follows: After a review of monetary policy implementation regimes currently in place or soon to be implemented, a theoretical model is developed to depict an alternative possible framework using a daily interest facility. The elasticity of demand for central bank balances with such a facility is then compared with estimates of the elasticity of demand under an averaging regime, taking the Federal Reserve's case as an example. The paper then investigates the implications for the ability of a central bank to hit its target interest rate and the associated volatility of overnight interest rates. Caveats regarding the model's predictions, and complications associated with possible heterogeneity of behavior among depository institutions, are then discussed. A brief summary concludes.
Rate Corridors
Because funds held as account balances at the central bank may be traded for immediate settlement, overnight financing markets tend to be dominated by interbank trading of such balances. The central bank can in principle control the aggregate supply of such balances with open market operations. However, the central bank must also make forecasts of the effect on the aggregate supply of its balances of movements of other elements of its balance sheet that it does not directly control, such as the Treasury's account balance, currency outstanding, and check float.
Aside from these autonomous reserve supply factors, a central bank must know something about the demand curve for its balances in order to determine the right quantity of balances to supply through open market operations to hit its target overnight interest rate. Both averaging frameworks and interest rate corridors offer some advantages to a central bank regarding the type of demand curve it faces. While interest rate corridors are a more recent development, they are simpler than averaging systems, and so are discussed first.
In a rate corridor regime, the central bank's lending rate provides a ceiling for overnight interest rates while its deposit rate provides a floor (Woodford, 2001). The interest rate corridor is carefully positioned so that the central bank's target interest rate is at the midpoint of the corridor. Then, in the absence of reserve requirements or other types of contractual balance requirements, the opportunity costs of holding positive and negative balances at the central bank are equal at the target interest rate, and therefore the demand for such balances should equal zero at that rate. Aggregating the demand for balances across diverse depository institutions (DIs) would affect the slope of the demand curve, but would not in principle change the result that the demand for balances equals zero at the target interest rate. Thus, to hit its target, a central bank merely has to provide zero aggregate balances to the banking sector.
Central banks in Canada, Australia, and New Zealand implemented rate corridor regimes in the late 1990s and found they could hit their target interest rates fairly closely on a daily basis, with little associated volatility, even without the traditional policy implementation tools of reserve requirements or other types of averaging systems. Observing these results, Woodford (2001) argued that rate corridors were an improvement over traditional regimes in positioning central banks for future developments in the information economy.
However, interest rate corridors have not always worked out as theory predicts, as indicated by the experience of the Bank of England since it implemented such a regime in mid-2001 (described below). In practice, it is difficult to ensure symmetry of opportunity costs around the target interest rate, because transactions with private market participants are not perfect substitutes for similar transactions with the central bank. Loans to DIs, unlike deposits at the central bank, involve credit risk, while borrowing from a central bank requires collateral, unlike overnight borrowing from other DIs. For both of these reasons, the demand curve for central bank balances lies above the curve that would obtain with perfect substitution. Therefore, the key feature of a rate corridor regime (zero demand at the target interest rate) tends to be undermined and the central bank has to predict the possibly time-varying positive demands for balances at the target rate. The divergences from perfect substitution may be larger when interest rates are high because risk spreads and the opportunity cost of collateral may also tend to widen at such times. In addition, a central bank may err in predicting the supply of reserves coming from autonomous factors on its balance sheet. The resulting errors in the aggregate supply of balances will cause movements along the demand curve, and the demand curve in rate corridor systems tends to be steepest at the target interest rate. For these reasons, substantial volatility in interest rates can occur between the ceiling and floor of a rate corridor (Whitesell, 2006). A central bank may be concerned about such volatility partly because of its potential transmission out the yield curve or, even in the absence of substantial transmission to longer-term yields, because of possible adverse reputation effects of sizable and frequent errors in hitting its target interest rate. The central bank may be reluctant to respond to frequent target misses and associated rate volatility by substantially narrowing the interest rate corridor because of possible unpredictable effects of drying up trading in the private money market.
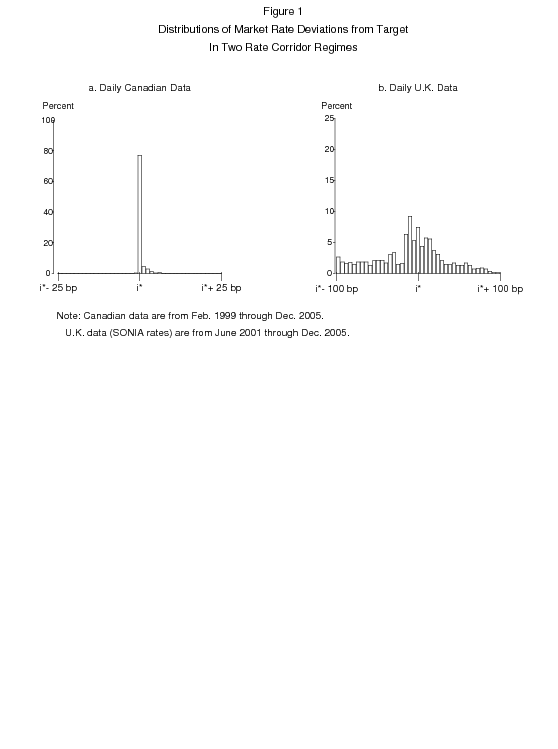
The volatility that arises in rate corridor regimes, owing either to imperfect substitution between private and central bank transactions or to errors in forecasting central bank balance sheet items, are likely to be larger when financial systems are complex and heterogeneous. Some empirical evidence supporting this contention is provided in Figure 1. It compares the experience of Canada and the United Kingdom under rate corridor regimes, showing the distribution of deviations of average daily interest rates from the central bank's target. The Bank of Canada sample begins in February 1999, when the averaging requirement on settlement balances was dropped. Despite a relatively narrow spread of 50 basis points between the Bank of Canada's lending and deposit rates, Canadian overnight interest rates have rarely moved close to the ceiling or floor. The root mean square deviation from the target interest rate has been a mere 3.5 basis points over this period. By contrast, the Bank of England (BOE) has employed a wide rate corridor of 200 basis points since June 2001, but has nevertheless seen the sterling overnight interbank average lending rate (SONIA) range across the full width of the corridor.1 The root mean square deviation of the SONIA from the BOE's target interest rate has been 45 basis points over this period. Although this volatility in the SONIA apparently has not resulted in greater volatility in three-month interest rates in the U.K. than in Canada, the BOE's dissatisfaction with the frequent misses in its interest rate target induced it to drop the rate corridor framework in favor of an innovative system of averaging with voluntary reserves, which is discussed below.
Averaging Systems
Reserve averaging systems include traditional reserve requirements that must be maintained on average over a multi-day maintenance period, and voluntary arrangements, such as the Federal Reserve's contractual clearing balance facility or the regime soon to be implemented by the BOE (Clews, 2005). An averaging system can aid the implementation of monetary policy in two ways: First, in most cases, the central bank knows the average aggregate level of balances that DIs need to hold over the maintenance period before the period begins.2 Second, with averaging, DIs have an incentive to vary their daily holdings of central bank balances, relative to their average requirement, in a way that helps to keep the overnight interest rate on target. For instance, when the overnight interest rate is low relative to its expected level later in the maintenance period, DIs will bulk up on their reserve holding relative to period-average requirements. As DIs bid for central bank balances, they will tend to push up the overnight interest rate. Conversely, when the overnight rate is high, DIs will go short on reserve holding, relative to their requirement, and this will put downward pressure on rates. This intertemporal arbitrage makes the reserve demand curve relatively more elastic on days of the maintenance period prior to the final ("settlement") day. In the extreme, the overnight interest rate earlier in the period would equal the expected rate on settlement day (as noted by Hamilton, 1996, and others). This is a key advantage if the expected overnight interest rate on settlement day is about equal to the target rate.
However, the downside to such arbitrage is that when market participants expect the central bank to change its interest rate target before the end of a reserve maintenance period, the central bank may find it difficult to keep the rate on target early in the period before the expected policy change is made. This adverse "anticipation effect" has become empirically important in the United States of late, as noted by Carpenter and Demiralp (2006b).
Another key weakness of an averaging regime is that some other type of mechanism is needed to limit volatility of the overnight interest rate on the last day of the maintenance period. In the United States, for example, this is accomplished in part through regulatory provisions that allow a certain percentage of reserve deficiencies or excess reserves to be carried over to the next period.3 In practice, carryover systems can be administratively cumbersome and sometimes fail to check an increase in interest rate volatility on settlement day. Volatility on that day is likely to be especially elevated if the opportunity cost of holding excess reserve balances is high; that is, if the general level of market interest rates is high and little or no interest is paid on excess reserves.
When compulsory reserve requirements are not accompanied by the payment of interest on required reserve balances, they also impose a distortionary reserve tax on DIs. The efforts of DIs to avoid the reserve tax involve a socially unnecessary expenditure of real resources and in consequence result in an impairment of financial efficiency.4 Reserve avoidance activities are likely to become more extensive the greater is the reserve tax; that is, the higher the general level of interest rates and the lower the interest, if any, paid on required reserve balances. In addition, the administrative and reporting burdens associated with collection of the reserve tax, including detailed, high-frequency reporting of deposit data on which reserve requirements are calculated, also represent an avoidable use of social resources.
The BOE is now planning to adopt an innovative policy implementation regime that uses averaging while striving to avoid many of the problems mentioned above (for details about the new regime, see Bank of England, 2005, and Clews, 2005). In brief, the system will be free from reserve avoidance and deposit reporting burdens because DI participation will be voluntary and a participant will be allowed to choose its own average requirement up to a maximum of £1 billion or 2 percent of its sterling deposits (net of interbank deposits), whichever is larger. Average balances will earn interest at the BOE's target rate. Adverse effects from anticipated policy changes will be avoided because the maintenance period will vary in length between four and five weeks so that it corresponds to the interval between meetings of the Monetary Policy Committee. In addition to the averaging of voluntary reserve holdings, the system will also employ an interest rate corridor.
However, the BOE's new regime will still be subject to potential rate volatility on the last day of the maintenance period. The central bank will employ two procedures to cope with this problem¯a penalty free band and a narrower rate corridor on settlement day. Similar to the system used for the Federal Reserve's contractual clearing balance program, a participating bank will incur a penalty only if its month-average balance drops more than 1 percent below the agreed target, and will earn a reduced rate of interest only to the extent that average balances are more than 1 percent above the agreed target balance. In addition, the interest rate corridor, normally 2 percentage points in width, will be reduced to a 50-basis-point width on settlement day.
In sum, the new BOE policy implementation regime will avoid many of the problems associated with previous averaging systems. However, it remains to be seen whether its administrative complexity or the resulting settlement-day interest rate volatility become problematic.
An Alternative Implementation Regime
Consider how policy could be implemented if a central bank established a voluntary, daily, interest-earning facility with features as discussed below. A DI would establish a daily interest facility, or DIF, choosing its own ceiling on the amount of daily balances held at the central bank that could earn interest. Any funds in the account in excess of that ceiling would earn nothing (or significantly less than the DIF rate). While banks could select any ceiling they wished on their daily interest facility, they would have to pay a facility fee of, say, 5 to 15 basis points, on the ceiling amount they choose. The DIF would pay interest at the target overnight rate, less an estimate of the average credit risk premium embedded in overnight market loans, reflecting the fact that a deposit at the central bank is risk-free.5 Any overdraft on the DI's account at the end of the day would result in a borrowing from the central bank at a penalty interest rate, which would automatically bring the account balance back to zero. However, any positive balances up to the DIF ceiling would earn interest at the DIF rate, with no penalties on shortfalls from the ceiling.
DIs would have an incentive to establish a DIF if, in its absence, they would hold excess reserves for clearing purposes and earn no interest (or interest at a much reduced rate). With a daily interest facility in place, a DI would have an incentive to lend at any risk-adjusted rate above the DIF rate, as long as its balance at the central bank remained in the black, and to withhold funds from the market at risk-adjusted rates below the DIF rate. This arbitrage activity would imply a relatively flat demand curve near the central bank's target interest rate. No averaging over a multi-day reserve period would be needed to generate this incentive to arbitrage. In principle, policy implementation under such a system would not require a precise estimate of the position of the aggregate reserve demand curve on each day, as a broad range of aggregate reserve supplies would be consistent with a market interest rate close to the central bank's target.
To formalize these ideas, consider a theoretical model of daily account management for a representative, risk-neutral DI in the style of Woodford (2001) and Whitesell (2006). Suppose, initially, that there were no DIF. Penalty rates on discount window loans or overnight overdrafts, along with
account posting uncertainties, would lead the DI to shoot for a positive end-of-day balance in its account at the central bank. Denoting the DI's target end-of-day balance as ![]() , the actual
end-of-day account balance would be T+
, the actual
end-of-day account balance would be T+![]() , reflecting a zero-mean account shock,
, reflecting a zero-mean account shock, ![]() , that represents possible late-in-the-day wire transfers of customers or other account postings after the DI's key interbank counterparties have exited the market for the day. Borrowing to cover account overdrafts is at a
penalty rate of
, that represents possible late-in-the-day wire transfers of customers or other account postings after the DI's key interbank counterparties have exited the market for the day. Borrowing to cover account overdrafts is at a
penalty rate of ![]() above the central bank's target interest rate of
above the central bank's target interest rate of ![]() . The marginal
cost of using collateral to borrow from the central bank, and any non-pecuniary or stigma effects, are assumed to be included in the penalty
. The marginal
cost of using collateral to borrow from the central bank, and any non-pecuniary or stigma effects, are assumed to be included in the penalty ![]() . The model abstracts from intraday movements of
interest rates and assumes that the DI observes the market interest rate for the day before choosing its target account balance for that day. The market interest rate,
. The model abstracts from intraday movements of
interest rates and assumes that the DI observes the market interest rate for the day before choosing its target account balance for that day. The market interest rate, ![]() , includes a spread for
expected credit losses of
, includes a spread for
expected credit losses of ![]() . The DI finds its optimal target account balance,
. The DI finds its optimal target account balance, ![]() , by
minimizing the expected opportunity costs of either holding zero-interest excess reserves or incurring an overdraft, given by the following expression:
, by
minimizing the expected opportunity costs of either holding zero-interest excess reserves or incurring an overdraft, given by the following expression:
The first-order condition, assuming
where
When the market rate is at the central bank's target (![]() *), equation (3) can be rewritten as:
*), equation (3) can be rewritten as:
From (3), the demand for balances responds positively, but less than one-for-one to the DIF ceiling:
The semi-elasticity is more useful here than the slope because, when aggregating over numerous representative DIs, the slope decreases while the semi-elasticity doesn't change, as explained below. A semi-elasticity is also preferable to a full elasticity when investigating volatility issues, because volatility is generally expressed in basis points rather than as a proportion of the level of interest rates.
In the above analysis, a DI's choice of an optimal target balance on a particular day is conditional, based on knowledge of the market interest rate for that day. However, the choice of an optimal DIF ceiling, ![]() , would not be conditional on a specific overnight interest rate, but rather based on the expected opportunity costs across the distribution of overnight interest rates. To complete the model, it is assumed that DIs know the distribution of the overnight market
interest rate (based on the historical interaction, day-to-day, of the aggregate demand curve with the aggregate supply of balances by the central bank), but this distribution abstracts from any expected changes in the target interest rate,
, would not be conditional on a specific overnight interest rate, but rather based on the expected opportunity costs across the distribution of overnight interest rates. To complete the model, it is assumed that DIs know the distribution of the overnight market
interest rate (based on the historical interaction, day-to-day, of the aggregate demand curve with the aggregate supply of balances by the central bank), but this distribution abstracts from any expected changes in the target interest rate, ![]() *.8 The DI therefore chooses the optimal
*.8 The DI therefore chooses the optimal ![]() by taking the unconditional expectation of (2) across the distribution of overnight market interest rates and then setting the derivative of that expression with respect to
by taking the unconditional expectation of (2) across the distribution of overnight market interest rates and then setting the derivative of that expression with respect to ![]() equal to zero, giving:
equal to zero, giving:
Now, it is evident from the first order conditions (3) and (7) that
As an aside, it may be worth noting that, while the semi-elasticity is preferable to the slope for purposes of aggregating over representative DIs, in some circumstances the slope of the aggregate demand curve may be a more relevant metric for a central bank than the semi-elasticity. For instance, either the slope or an arc elasticity would need to be used around the target overnight interest rate if the aggregate demand for balances equaled zero at or near that point. Also, the slope of the aggregate demand curve would serve well if the size of the central bank's errors in forecasting autonomous supply factors did not depend on the level of central bank balances outstanding.
While elasticity issues will be discussed further below, it is evident that the demand curve will be highly elastic when the two probability densities in the denominator of (6) are close to zero, which occurs when the ratios, ![]() /
/![]() and (
and (![]() /
/![]() , are fairly large. And as suggested by (7), the size of these ratios varies inversely with the ratio of
, are fairly large. And as suggested by (7), the size of these ratios varies inversely with the ratio of ![]() to
to ![]() .
.
Numerical methods were used to find the optimal ![]() from the first order conditions (3) and (7), given a distribution for
from the first order conditions (3) and (7), given a distribution for ![]() and parameter values for
and parameter values for ![]() ,
, ![]() , and
, and ![]() . This was fairly straightforward, as (3) and (7) are monotonic in
. This was fairly straightforward, as (3) and (7) are monotonic in ![]() and
and ![]() , respectively. First, a trial value of M was chosen. Then, 10,000 draws were taken from the distribution of interest
rates. For each interest rate draw, given the trial value of
, respectively. First, a trial value of M was chosen. Then, 10,000 draws were taken from the distribution of interest
rates. For each interest rate draw, given the trial value of ![]() , the optimal choice of
, the optimal choice of ![]() was found using a search based on equation (3). The cumulative normal probability on the left hand side of equation (7) was then computed and the average of those probability values, over the 10,000 draws of
was found using a search based on equation (3). The cumulative normal probability on the left hand side of equation (7) was then computed and the average of those probability values, over the 10,000 draws of ![]() , was used to evaluate, from (7), the trial value of
, was used to evaluate, from (7), the trial value of ![]() . The value of
. The value of ![]() was then incremented and the entire procedure was iterated until the value of
was then incremented and the entire procedure was iterated until the value of ![]() had been determined to an acceptable tolerance
level.
had been determined to an acceptable tolerance
level.
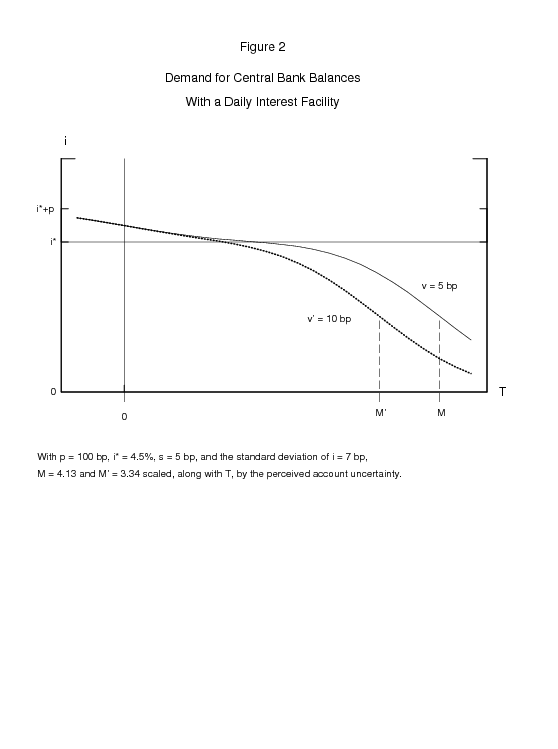
Figure 2 plots demand curves derived from such simulations, assuming a target interest rate, ![]() *, of 4
*, of 4
![]() percent, a penalty on central bank lending,
percent, a penalty on central bank lending, ![]() , of 1 percentage point, a private credit risk spread,
, of 1 percentage point, a private credit risk spread, ![]() , of 5 basis points, and a normal distribution for deviations of the market
interest rate from target, with a standard deviation of 7 basis points (equal to the root-mean-squared-error of the intraday brokered funds rate relative to the FOMC's target since 2002). The reserve demand curves were not sensitive to small adjustments of these assumptions.
, of 5 basis points, and a normal distribution for deviations of the market
interest rate from target, with a standard deviation of 7 basis points (equal to the root-mean-squared-error of the intraday brokered funds rate relative to the FOMC's target since 2002). The reserve demand curves were not sensitive to small adjustments of these assumptions.
However, the demand curves were quite responsive to the assumed facility fee, ![]() . Figure 2 shows a representative DI's demand curves for facility fees of 5 and 10 basis points. The demand
price for each curve rises above
. Figure 2 shows a representative DI's demand curves for facility fees of 5 and 10 basis points. The demand
price for each curve rises above ![]() * as a DI's balance drops close to zero because the DI is then willing to pay up to obtain funds from the market to offset the risk of a negative account shock
that puts it into an overdraft position. The demand price drops below
* as a DI's balance drops close to zero because the DI is then willing to pay up to obtain funds from the market to offset the risk of a negative account shock
that puts it into an overdraft position. The demand price drops below ![]() * as a DI's balance approaches
* as a DI's balance approaches ![]() because the DI will then buy funds from the market only at rates below the risk-adjusted DIF rate because of the risk of a positive account shock that leaves it with some zero-interest excess balances at the end of the day.
because the DI will then buy funds from the market only at rates below the risk-adjusted DIF rate because of the risk of a positive account shock that leaves it with some zero-interest excess balances at the end of the day.
The optimal choice of the DIF ceiling was ![]() = 4.1
= 4.1![]() for
for ![]() = 5 and
= 5 and ![]() = 3.3
= 3.3![]() for
for
![]() = 10, respectively. When
= 10, respectively. When ![]() *, a DI's target balance,
*, a DI's target balance, ![]() , from (4), equaled 0.43
, from (4), equaled 0.43![]() and 0.39
and 0.39![]() , respectively. These were both less than half the ceiling, as expected, because the penalty on overdrafts is smaller than the opportunity cost of excess balances. At
, respectively. These were both less than half the ceiling, as expected, because the penalty on overdrafts is smaller than the opportunity cost of excess balances. At ![]() *, the interest rate semi-elasticities of demand were -.030 and -.019, respectively.
*, the interest rate semi-elasticities of demand were -.030 and -.019, respectively.
A similar, but more symmetric policy implementation regime could be envisioned that combines a DIF with a penalty-free-overdraft facility. In this framework, a DI could also choose a maximum amount, say ![]() , of penalty-free borrowings from the central bank for an additional facility fee of vm. Borrowings up to the level
, of penalty-free borrowings from the central bank for an additional facility fee of vm. Borrowings up to the level ![]() would be at the target rate,
would be at the target rate,
![]() *, while borrowings in excess of
*, while borrowings in excess of ![]() would be booked at the rate of
would be booked at the rate of ![]() *+
*+![]() . In this formulation, the first-order condition for
. In this formulation, the first-order condition for ![]() , equation (3), would become:
, equation (3), would become:
The first order condition for the maximum level of penalty-free borrowing,
and the dependence of
The addition of a penalty-free borrowing facility to the DIF model would allow a DI to arbitrage the market interest rate to the central bank's target using either deposits or borrowings at the central bank. It would lower a DI's target account balance, in effect shifting the demand curve to the left. However, the symmetry of the roles and fees for the DIF and the penalty-free borrowing facility suggests that, in principle, DIs would choose the same width of arbitrage region whether using a DIF, penalty-free borrowing, or both, and DIs would be indifferent regarding the distinctions. In effect, the first-order conditions (7), (9), and (11) would determine only the sum of
Comparison with Reserve Demand Elasticities in an Averaging Regime
It is interesting to compare the semi-elasticities of demand found for the basic DIF model with those for a central bank using an averaging regime for policy implementation, such as the Federal Reserve. Identification problems have often plagued attempts to estimate the daily demand for reserves in the United States, as shifts in the demand curve cause interest rate movements that tend to trace out the supply curve. Perhaps largely for this reason, many researchers have found it difficult to identify a response of the federal funds rate to changes in the supply of reserves (a "liquidity effect"). The absence of a response would imply a perfectly elastic demand for reserves, if indeed there were no shifts in the demand curve to worry about. However, Hamilton (1997) and Carpenter and Demiralp (2006a) were able to find daily liquidity effects using a variable that causes shifts in the supply curve but not in the demand curve. Hamilton used forecast errors from a model of the Treasury's balance at the Federal Reserve over the April 1989 to November 1991 sample period, while Carpenter and Demiralp employed the Federal Reserve's actual errors in projecting the overall daily supply of reserves, other than through open market operations, over the mid-1989 to mid-2003 period. Each also tried to control for predictable, calendar-related shifts in the reserve demand curve.
Hamilton found a large liquidity effect of 22.7 basis points per billion dollars of balances on the last day of the two-week maintenance period and a very small effect of 0.84 basis points on other days. Given the average level of Fed balances of $32 billion over his sample period, this would
correspond to semi-elasticities of reserve demand of -.001 on settlement Wednesdays and -.037 on other days. With their improved specification and longer sample period, Carpenter and Demiralp found an average liquidity effect of 1 basis point per billion dollars of balances, and 3
![]() basis points on settlement Wednesday. Given average balances of $24 billion over their sample
period, the implied semi-elasticities of reserve demand are -.042 on average and -.012 on settlement day. These estimates for the
basis points on settlement Wednesday. Given average balances of $24 billion over their sample
period, the implied semi-elasticities of reserve demand are -.042 on average and -.012 on settlement day. These estimates for the
Fed's current averaging regime bracket the semi-elasticities of -.030 and -.019 derived for the DIF regime with facility fees of 5 and 10 basis points respectively.
Implications for Interest Rate Volatility
Aside from attempts to estimate and compare demand elasticities, the DIF model can also be used to derive interest rate volatilities that would arise from typical errors in forecasting autonomous reserve supply factors. Those results can then be contrasted to actual interest volatilities under existing regimes. For that purpose, the first column of Table 1 shows the Open Market Desk's report of average absolute errors in recent years in daily forecasts of reserve supply factors (Federal Reserve Bank of New York, 2005). Column 3 expresses the mean absolute forecast error as a percent of average balances that DIs held at the Federal Reserve during the year. Then, using the model semi-elasticities indicated above for facility fees of 5 and 10 basis points, the fourth column indicates the typical deviations of the overnight interest rate from target that the DIF model would predict, given those factor forecast errors.9 These numbers are smaller than the actual volatility in the federal funds rate over the last four years, given in the last column, which has nevertheless been quite low by historical standards. The results reflect the fact that the volatility of the overnight rate depends not only on the interaction of the reserve demand elasticity with reserve supply forecast errors, but also on the ability of a central bank to predict and offset shifts in the position of the reserve demand curve. Of course, the steeper the demand curve,
the greater will be the effect on rates of shifts in its position.
| Absolute
Factors Forecast Miss ($ millions) |
Average
Level of Fed Balances ($ millions) |
Absolute
Factors Miss (percent) |
Implied
Model Funds Rate Error (bp),
|
Actual Average Ab-solute Deviation of Effective Funds Rate
From Target (bp) |
|
|---|---|---|---|---|---|
| 2002 | 721 | 19,154 | 3.8 | 1.3 - 2.0 | 4 |
| 2003 | 803 | 22,816 | 3.5 | 1.2 - 1.8 | 4 |
| 2004 | 654 | 23,137 | 2.8 | 0.9 - 1.5 | 3 |
| 2005 | 876 | 20,417 | 4.3 | 1.4 - 2.3 | 5 |
| Using data from Federal Reserve Bank of New York (2005). | |||||
Practical Considerations Regarding Responses to a DIF
The above model may underestimate the response of DIs to a DIF regime for a number of reasons. First, DIs may choose to establish a higher ceiling on the DIF than predicted by the model in order to facilitate intraday clearing activities. In the U.S., for instance, DIs currently incur an intraday overdraft fee of 36 basis points at an annual rate. Balances held in a DIF would protect against such costs.
In addition, some larger DIs may choose a higher ceiling in order to arbitrage, not the daily average interest rate, as indicated in the model, but intraday movements of interest rates. Some money center banks in the U.S. at present are often both buyers and sellers of fed funds on a given day because of such arbitrage activities.
If DIs tended to establish higher ceilings than predicted by the model because of intraday market considerations, the elasticity of the aggregate demand curve could be substantially higher than indicated above. For instance, the model predicts that, with a facility fee of 5 basis points, a DI with end-of-day account uncertainty of $50 million would create a DIF with a maximum balance of only around $200 million, and its target end-of-day balance would be only a little over $80 million at the central bank's target interest rate. If the DI instead selected a ceiling of $300 million because of intraday market considerations or other reasons exogenous to the daily average analysis used in the model, its predicted demand for balances would be $125 million at the central bank's target interest rate, and the semi-elasticity of its demand function at that rate would rise substantially in absolute value, from -.03 to -.20. A demand elasticity that high would greatly facilitate monetary policy implementation.
DIs may also choose a higher DIF ceiling if they are risk-averse in their dealings with the central bank or attach significant non-pecuniary costs or stigma effects to borrowing from the central bank, which would in effect increase the penalty, ![]() . However, the effects of risk-aversion or a higher penalty on the elasticity of the demand curve at the target interest rate are uncertain. On one hand, DIs would choose a higher ceiling, which would tend to increase the elasticity. On
the other hand, DIs would be less willing to run down their balances in order to arbitrage market interest rates because of the increased concerns about overdraft risk.
. However, the effects of risk-aversion or a higher penalty on the elasticity of the demand curve at the target interest rate are uncertain. On one hand, DIs would choose a higher ceiling, which would tend to increase the elasticity. On
the other hand, DIs would be less willing to run down their balances in order to arbitrage market interest rates because of the increased concerns about overdraft risk.
The behavior of participants in the Federal Reserve's contractual clearing balance program suggests that, on balance, the response of DIs to a DIF regime may indeed be larger than predicted by the model. Despite earning credit rates that are notably below the target funds rate, DIs voluntarily choose to hold substantial balances in that program, presumably to avoid the possibility of incurring inadvertent overdrafts.10 Moreover, the Bank of England expected that the response of banks to its voluntary reserve regime would be so large that the BOE itself imposed limits on the amount of balances that could earn interest. (The response of course would be more moderate if the BOE imposed a facility fee above zero.)
These considerations suggest that a central bank would likely have to be prepared to adjust the facility fee depending on the response of banks to the establishment of a DIF. Central banks may prefer to set a fee that is small enough to ensure a suitably elastic demand curve, but not so small that DIs engorge on balances to the point that overnight interbank trading dries up.
Caveats Regarding Differences between Large and Small DIs
Differences in the behavior of large and small DIs might lead to other complications in estimating reserve demand under a DIF regime. For instance, in the case of the Federal Reserve, smaller DIs evidently do not find it optimal to pay the informational and managerial costs needed to fine-tune the management of their balances at the central bank. In aggregate, however, these institutions currently hold the lion's share of excess reserves. This behavior suggests that, if such institutions participated in a DIF program, they might in aggregate hold substantial balances but not engage in much intertemporal arbitrage of market interest rates. This portion of the market would therefore presumably have a fairly inelastic demand function. By contrast, larger DIs currently hold a small portion of aggregate excess reserves at the Federal Reserve, but display considerable willingness to arbitrage deviations of market interest rates from the target rate.11 However, what matters for the implementation of policy is that the deep-pocket players have an elastic demand curve, reflecting a penchant to arbitrage rates. The inelastic demand for balances of smaller institutions would perhaps only serve to shift the aggregate demand curve to the right, without having much effect on its elasticity in the neighborhood of the target overnight rate.
Conclusion
This paper has discussed the idea of a facility that could be used for the implementation of monetary policy by central banks without either averaging or an interest rate corridor. Interest rate corridors have the advantage of allowing a central bank to know the aggregate quantity of balances demanded at its target interest rate, but only if the opportunity costs of positive account balances and overdrafts are equal at that rate, which may be difficult to achieve in practice, particularly for complex and heterogeneous financial sectors. Averaging facilities encourage depository institutions to arbitrage overnight interest rates to the expected rate at the end of the maintenance period, which helps smooth interest rates over the period. With averaging, however, interest rate volatility can be sizable on the last day of the maintenance period, and anticipation effects can induce market rates to move in advance of expected policy decisions. Moreover, averaging involves non-trivial administrative costs, particularly when associated with reserve requirements on DI deposit liabilities, and¯unless required balances are remunerated at a market rate¯financial sector inefficiencies associated with reserve avoidance behaviors.
The paper has described how a daily interest facility (DIF) could be used to implement monetary policy without incurring the drawbacks of rate corridors or averaging systems. DIs would set their own ceilings on DIF balances, subject to a small proportional fee, and the central bank would pay its target overnight interest rate, risk-adjusted, on DIF balances. No penalties would be associated with the facility, but account overdrafts would be made up by borrowing from the central bank at a penalty rate, and balances in excess of the ceiling would earn nothing or a significantly lower rate. Achieving symmetry in these opportunity costs would not be important. DIs would arbitrage market rates to the target rate earned on the DIF, and for that reason the demand curve for central bank balances would be rather elastic in the neighborhood of the central bank's target interest rate. Therefore, errors in estimating the position of the aggregate demand curve or in forecasting the supply of reserves from autonomous factors on the central bank's balance sheet would have only a small effect on the volatility of the overnight interest rate.
For comparison purposes, the elasticity predicted for such a facility was found to be comparable to estimates of the elasticity of demand for balances at the Federal Reserve with its current system of averaging of required reserve and contractual clearing balances. However, a DIF regime would avoid the problems of settlement day volatility, anticipation effects, reserve avoidance inefficiencies, and administrative reporting burdens associated with a system of reserve requirements. A DIF facility would also avoid the volatility of interest rates that can occur with interest rate corridors owing to shifts in the demand for reserves or errors in the central bank's forecasts of the supply of reserves through autonomous factors.
Nevertheless, as pointed out in the paper, idiosyncratic institutional features would need to be considered before a DIF facility could be recommended for a particular central bank. For instance, in the United States, the reserve management behavior of smaller DIs seems to differ substantially from that of the largest institutions. The latter typically manage their central bank balances actively to take advantage of intertemporal arbitrage opportunities and to minimize opportunity costs. Smaller institutions, however, devote fewer resources to reserve management and would likely continue to exhibit a fairly inelastic demand for balances, even with a DIF facility. In such a situation, a central bank would have to make a judgment as to whether the DIF facility would work as theory predicts based only on the active reserve management of the largest institutions.
Of course, in the United States, many types of innovations in the implementation of monetary policy, such as a DIF facility, a rate corridor, or a voluntary averaging system, could not be undertaken until passage of long-discussed legislative proposals to authorize the Federal Reserve to pay interest on the balances of DIs and to reduce reserve requirements below the minimum levels currently required by law. The Federal Reserve Board has itself supported such legislative proposals over the years because they could result in improved efficiencies in the financial system and because they would give the Federal Reserve increased flexibility to consider alternative policy implementation frameworks. Any framework that allowed the Federal Reserve to remove reserve requirements would entail substantial efficiencies for the banking sector, including the elimination of wasteful reserve avoidance activities by DIs and, potentially, a considerable reduction in the reporting burdens of banks and in the costs of processing of such data by the Federal Reserve.
Bank of England, 2005, "Reform of the Bank of England's Operations in the Sterling
Money Markets," April, available at:
www.bankofengland.co.uk/markets/money/smmreform050404.pdf.
Carpenter, S. and S. Demiralp, 2006a, forthcoming, "The Liquidity Effect in the Federal
Funds Market: Evidence from Daily Open Market Operations," Journal of Money,
Credit and Banking.
Carpenter, S. and S. Demiralp, 2006b, forthcoming, "Anticipation of Monetary Policy and
Open Market Operations," International Journal of Central Banking.
Clews, R., 2005, "Implementing Monetary Policy: Reforms to the Bank of England's
Operations in the Money Market," Bank of England Quarterly Bulletin,
summer, pages 211-220.
Federal Reserve Bank of New York, 2005, "Domestic Open Market Operations During
2005," available at www.newyorkfed.org/markets/omo/omo2005.pdf.
Freeman, S. and J. Haslag, 1996, "On the Optimality of Interest-Bearing Reserves in
Economies of Overlapping Generations" Economic Theory 7, pages 557-565.
Hamilton, J., 1996, "The Daily Market for Federal Funds," Journal of Political Economy
104: pages 26-56.
Hamilton, J., 1997, "Measuring the Liquidity Effect," American Economic Review 87:1,
March, pages 80-97.
Madigan, B. and W. Nelson, 2002, "Proposed Revision to the Federal Reserve's Discount
Window Lending Programs," Federal Reserve Bulletin, July, pages 313-319.
Whitesell, W., 2006, "Interest Rate Corridors and Reserves," Journal of Monetary
Economics, forthcoming.
Woodford, M., 2001, "Monetary Policy in the Information Economy," in Economic Policy
for the Information Economy, Federal Reserve Bank of Kansas City.
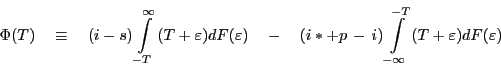
![\begin{displaymath} \mathop {\min _ }\limits_T \quad \Phi (T)\quad +\quad vM\quad -\quad (i\ast -s)\left\{ {\int\limits_{-T}^{M-T} {{\kern 1pt}(T+\varepsilon )\,dF(\varepsilon )} \quad +\quad M\left[ {1-F(M-T)} \right]} \right\}. \end{displaymath}](img11.gif)
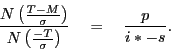
![\begin{displaymath} 0\quad <\quad \frac{\partial T}{\partial M}\quad \quad =\quad \quad \quad \quad \left[ {1\quad +\quad \frac{p{\kern 1pt}n\left( {\frac{-T}{\sigma }} \right)}{(i\ast -s){\kern 1pt}n\left( {\frac{M-T}{\sigma }} \right)}} \right]^{-1}\quad <\quad \quad 1, \end{displaymath}](img19.gif)
![\begin{displaymath} -1\quad <\quad \frac{\partial T}{\partial m}\quad \quad =\quad \quad \quad \quad -\left[ {1\quad +\quad \frac{(i\ast -s){\kern 1pt}n\left( {\frac{M-T}{\sigma }} \right)}{{\kern 1pt}pn\left( {\frac{-m-T}{\sigma }} \right)}} \right]^{-1}\quad <\quad \quad 0 \end{displaymath}](img33.gif)