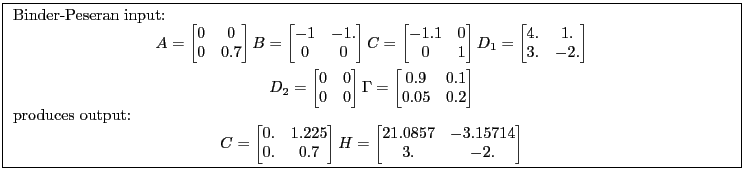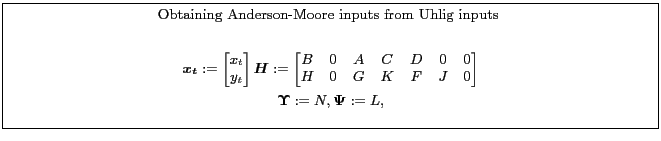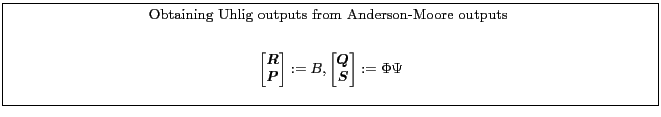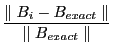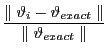Solving Linear Rational
Expectations Models:
A Horse Race
Keywords: Linear Rational Expectations, Blanchard-Kahn, Saddle Point Solution
Abstract:
1 Introduction and Summary
Since (Blanchard and Kahn, 1980) a number of alternative approaches for solving linear rational expectations models have emerged. This paper describes, compares and contrasts the techniques of (Anderson and Moore, 1983,1985; Anderson, 1997), (Binder and Pesaran, 1994), (King and Watson, 1998), (Klein, 1999), (Sims, 1996), and (Uhlig, 1999). All these authors provide MATLAB code implementing their algorithm.2
The paper compares the computational efficiency, functionality and accuracy of these MATLAB implementations. The paper uses numerical examples to characterize practical differences in employing the alternative procedures.
Economists use the output of these procedures for simulating models, estimating models, computing impulse response functions, calculating asymptotic covariance, solving infinite horizon linear quadratic control problems and constructing terminal constraints for nonlinear models. These applications benefit from the use of reliable, efficient and easy to use code.
A comparison of the algorithms reveals that:
- For models satisfying the Blanchard-Kahn conditions, the algorithms provide equivalent solutions.3
- The Anderson-Moore algorithm requires fewer floating point operations to achieve the same result. This computational advantage increases with the size of the model.
- While the Anderson-Moore, Sims and Binder-Pesaran approaches provide matrix output for accommodating arbitrary exogenous processes, the King-Watson and Uhlig implementations only provide solutions for VAR exogenous process.4Fortunately, there are straightforward formulae for augmenting the King-Watson Uhlig and Klein approaches with the matrices characterizing the impact of arbitrary shocks.
- The Anderson-Moore suite of programs provides a simple modeling language for developing models. In addition, the Anderson-Moore implementation requires no special treatment for models with multiple lags and leads. To use each of the other algorithms, one must cast the model in a form with at most one lead or lag. This can be a tedious and error prone task for models with more than a couple of equations.
- Using the Anderson-Moore algorithm to solve the quadratic matrix polynomial equation improves the performance of both Binder-Pesaran's and Uhlig's algorithms.
Section 2 states the problem and introduces notation. This paper divides the algorithms into three categories: eigensystem, QZ, and matrix polynomial methods. Section 3 describes the eigensystem methods. Section 4 describes applications of the QZ algorithm. Section 5 describes applications of the matrix polynomial approach. Section 6 compares the computational efficiency, functionality and accuracy of the algorithms. Section 7 concludes the paper. The appendices provide usage notes for each of the algorithms as well as information about how to compare inputs and outputs from each of the algorithms.
2 Problem Statement and Notation
These algorithms compute solutions for models of the form
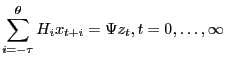 |
(1) |
with initial conditions, if any, given by constraints of the form |
|
| (2) | |
where both |
|
| (3) | |
Solutions can be cast in the form
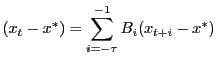 |
Given any algorithm that computes the ![]() , one can easily compute other quantities useful for characterizing the impact of exogenous variables. For models with
, one can easily compute other quantities useful for characterizing the impact of exogenous variables. For models with
![]() the formulae are especially simple.
the formulae are especially simple.
Let
We can write
and when |
|
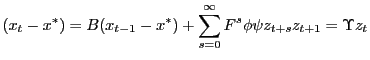 |
|
Consult (Anderson, 1997) for other useful formulae concerning rational expectations model solutions.
I downloaded the MATLAB code for each implementation in July, 1999. See the bibliography for the relevant URL's.
3.1 The Anderson-Moore Algorithm
(Anderson and Moore, 1985; Anderson, 1997) developed their algorithm in the mid 80's for solving rational expectations models that arise in large scale macro models. Appendix B.1 provides a synopsis of the model concepts and algorithm inputs and outputs. Appendix A presents pseudocode for the algorithm.
The algorithm determines whether equation 1 has a unique solution, an infinity of solutions or no solutions at all. The algorithm produces a matrix ![]() codifying
the linear constraints guaranteeing asymptotic convergence. The matrix
codifying
the linear constraints guaranteeing asymptotic convergence. The matrix ![]() provides a strategic point of departure for making many rational expectations computations.
provides a strategic point of departure for making many rational expectations computations.
The uniqueness of solutions to system 1 requires that the transition matrix characterizing the linear system have appropriate numbers of explosive and stable eigenvalues (Blanchard and Kahn, 1980), and that the asymptotic linear constraints are linearly independent of explicit and implicit initial conditions (Anderson and Moore, 1985).
The solution methodology entails
- Manipulating equation 1 to compute a state space transition matrix.
- Computing the eigenvalues and the invariant space associated with explosive eigenvalues
- Combining the constraints provided by:
- the initial conditions,
- auxiliary initial conditions identified in the computation of the transition matrix and
- the invariant space vectors
The first phase of the algorithm computes a transition matrix, ![]() , and auxiliary initial conditions,
, and auxiliary initial conditions, ![]() . The second phase combines left invariant space vectors associated with large eigenvalues of
. The second phase combines left invariant space vectors associated with large eigenvalues of ![]() with the auxiliary initial conditions to produce the matrix
with the auxiliary initial conditions to produce the matrix ![]() characterizing the saddle point solution. Provided the right hand half of
characterizing the saddle point solution. Provided the right hand half of ![]() is invertible,
the algorithm computes the matrix
is invertible,
the algorithm computes the matrix ![]() , an autoregressive representation of the unique saddle point solution.
, an autoregressive representation of the unique saddle point solution.
The Anderson-Moore methodology does not explicitly distinguish between predetermined and non-predetermined variables. The algorithm assumes that history fixes the values of all variables dated prior to time t and that these initial conditions, the saddle point property terminal conditions, and the model equations determine all subsequent variable values.
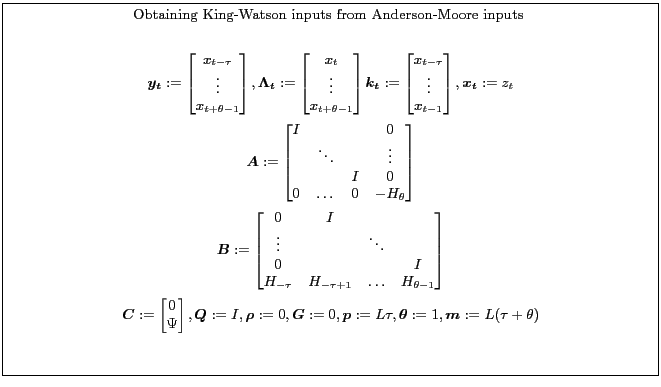
3.2 King & Watson's Canonical Variables/System Reduction Method
(King and Watson, 1998) describe another method for solving rational expectations models. Appendix B.2 provides a synopsis of the model concepts and algorithm inputs and outputs. The algorithm consists of two parts: system reduction for efficiency and canonical variables solution for solving the saddle point problem. Although their paper describes how to accommodate arbitrary exogenous shocks, the MATLAB function does not return the relevant matrices.
King-Watson provide a MATLAB function, resolkw, that computes solutions. The MATLAB function transforms the original system to facilitate the canonical variables calculations. The mdrkw program computes the solution assuming the exogenous variables follow a vector autoregressive process.
Given:
system reduction produces an equivalent model of the form |
|
Where
The mdrkw program takes the reduced system produced by redkw and the decomposition of its dynamic subsystem computed by dynkw and computes the rational expectations solution. The computation can use either eigenvalue-eigenvector decomposition or Schur decomposition.
Appendix B.2.1 shows one way to compute the King-Watson solution using the Anderson-Moore algorithm. Appendix B.2.2 shows one way to compute the Anderson-Moore solution using the King-Watson algorithm.
4 Applications of the QZ Algorithm
Several authors exploit the properties of the Generalized Schur Form (Golub and van Loan, 1989).
The algorithm uses the QZ decomposition to recast equation 5 in a canonical form that makes it possible to solve the transformed system "forward" for endogenous variables consistent with arbitrary values of the future exogenous variables.
4.1 Sims' QZ Method
(Sims, 1996) describes the QZ Method. His algorithm solves a linear rational expectations model of the form:
where
Here, as with all the algorithms except the Anderson-Moore algorithm, one must cast the model in a form with one lag and no leads. This can be problematic for models with more than a couple of equations.
Appendix B.3 summarizes the Sims' QZ method model concepts and algorithm inputs and outputs.
The ![]() designation of expectational errors identifies the "predetermined" variables. The Anderson-Moore technique does not explicitly require the identification of expectational errors.
In applying the Anderson-Moore technique, one chooses the time subscript of the variables that appear in the equations. All predetermined variables have historical values available through time
designation of expectational errors identifies the "predetermined" variables. The Anderson-Moore technique does not explicitly require the identification of expectational errors.
In applying the Anderson-Moore technique, one chooses the time subscript of the variables that appear in the equations. All predetermined variables have historical values available through time ![]() . The evolution of the solution path can have no effect on any variables dated
. The evolution of the solution path can have no effect on any variables dated ![]() or earlier. Future model values may influence time
or earlier. Future model values may influence time ![]() values of any variable.
values of any variable.
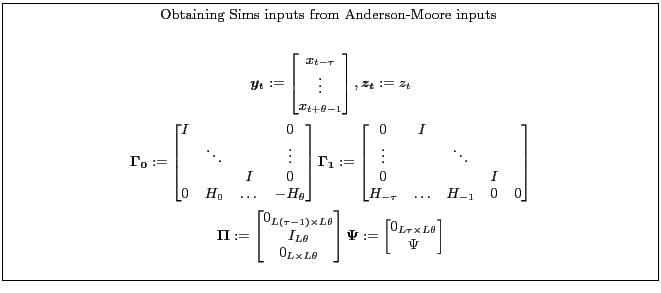
Appendix B.3.1 shows one way to transform the problem from Sims' form to Anderson-Moore form and how to reconcile the solutions. For the sake of comparison, the Anderson-Moore transformation adds ![]() variables and the same number of equations, setting future expectation errors to zero.
variables and the same number of equations, setting future expectation errors to zero.
Appendix B.3.2 shows one way to transform the problem from Anderson-Moore form to Sims form.
4.2 Klein's Approach
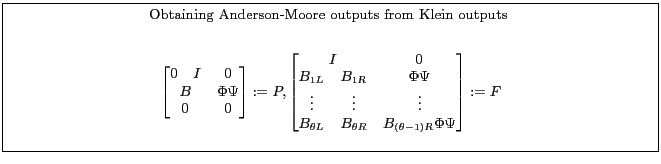
(Klein, 1999) describes another method. Appendix B.4 summarizes the model concepts and algorithm inputs and outputs.
The algorithm uses the Generalized Schur Decomposition to decouple backward and forward variables of the transformed system.
Although the MATLAB version does not provide solutions for autoregressive exogenous variables, one can solve the autoregressive exogenous variables problem by augmenting the system. The MATLAB program does not return matrices for computing the impact of arbitrary exogenous factors.
Appendix B.4.1 describes one way to recast a model from a form suitable for Klein into a form for the Anderson-Moore algorithm. Appendix B.4.2 describes one way to recast a model from a form suitable for the Anderson-Moore methodology into a form for the Klein Algorithm.
5 Applications of the Matrix Polynomial Approach
Several algorithms rely on determining a matrix ![]() satisfying
satisfying
They employ linear algebraic techniques to solve this quadratic equation. Generally there are many solutions.
When the homogeneous linear system has a unique saddle-path solution, the Anderson-Moore algorithm constructs the unique matrix ![]() that satisfies the quadratic matrix equation and
has all roots inside the unit circle.
that satisfies the quadratic matrix equation and
has all roots inside the unit circle.
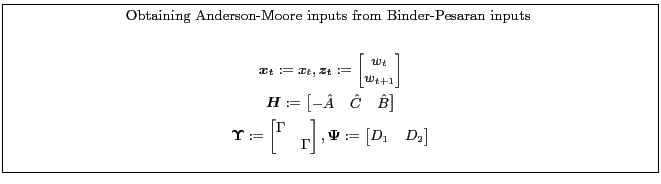
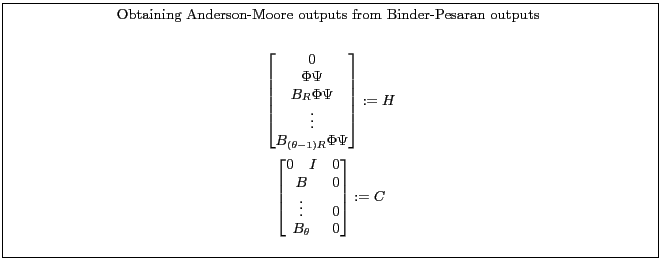
5.1 Binder & Pesaran's Method
(Binder and Pesaran, 1994) describe another method.
According to Binder & Pesaran(1994), under certain conditions, the unique stable solution, if it exists, is given by:
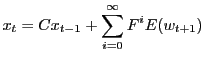 |
where
and
Their algorithm consists of a "recursive" application of the linear equations defining the relationships between C, H and F.
Appendix B.5.1 describes one way to recast a model from a form suitable for Binder-Pesaran into a form for the Anderson-Moore algorithm. Appendix B.5.2 describes one way to recast a model from a form suitable for the Anderson-Moore methodology into a form for the Binder-Pesaran Algorithm.
5.2 Uhlig's Technique
(Uhlig, 1999) describes another method. The algorithm uses generalized eigenvalue calculations to obtain a solution for the matrix polynomial equation.
One can view the Uhlig technique as preprocessing of the input matrices to reduce the dimension of the quadratic matrix polynomial. It turns out that once the simplification has been done, the Anderson-Moore algorithm computes the solution to the matrix polynomial more efficiently than the approach adopted in Uhlig's algorithm.
Uhlig's algorithm operates on matrices of the form:
 |
|
Uhlig in effect pre-multiplies the equations by the matrix |
|
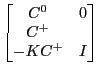 |
|
where |
|
to get |
|
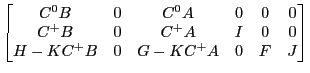 |
|
one can imagine leading the second block of equations by one period and using them to annihilate J to get |
|
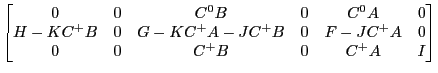 |
|
This step in effect decouples the second set of equations making it possible to investigate the asymptotic properties by focusing on a smaller system. |
|
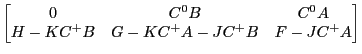 |
|
Uhlig's algorithm undertakes the solution of a quadratic equation like equation 6 with
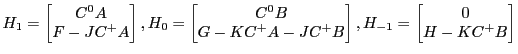 |
Appendix B.6.2 describes one way to recast a model from a form suitable for Uhlig into a form for the Anderson-Moore algorithm. Appendix B.6.1 describes one way to recast a model from a form suitable for the Anderson-Moore methodology into a form for the Uhlig Algorithm.
6 Comparisons
Section 2 identified
![]() and
and ![]() as potential outputs of a linear rational expectation
algorithm. Most of the implementations do not compute each of the potential outputs. Only Anderson-Moore and Binder-Pesaran provide all four outputs (See Table 6).
as potential outputs of a linear rational expectation
algorithm. Most of the implementations do not compute each of the potential outputs. Only Anderson-Moore and Binder-Pesaran provide all four outputs (See Table 6).
Generally, the implementations make restrictions on the form of the input. Most require the user to specify models with at most one lag or one lead. Only Anderson-Moore explicitly allows multiple lags and leads.
| Technique | Usage Notes | |||
|---|---|---|---|---|
| Anderson-Moore |  |
 |
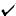 |
Allows multiple lags and leads. Has modeling language. |
| King & Watson | 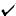 |
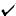 |
one lead, no lags | |
| Sims | 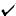 |
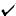 |
one lag, no leads | |
| Klein | 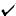 |
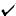 |
one lead, no lags | |
| Binder-Peseran | 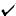 |
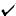 |
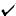 |
one lag, one lead; |
| Uhlig | 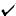 |
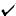 |
one lag, one lead; constraint involving choice of "jump" variables and rank condition on |
Note:
- The Klein and Uhlig procedures compute
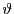 by augmenting linear system
by augmenting linear system - For the Uhlig procedure one must choose "jump" variables to guarantee that the
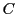 matrix has full rank.
matrix has full rank.
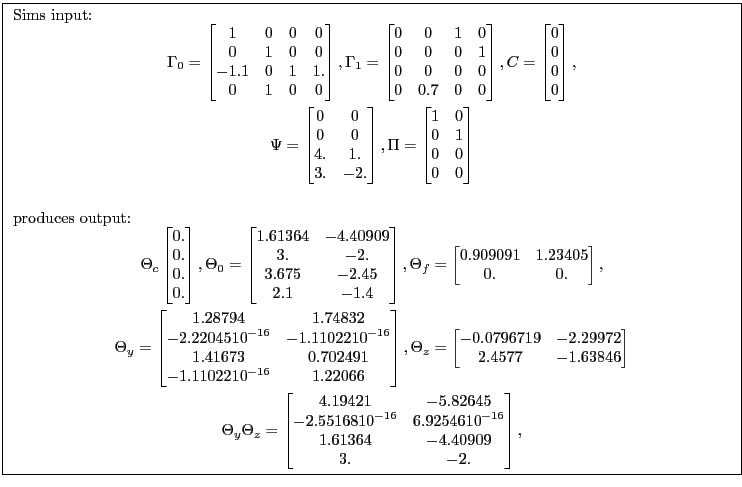
Each of the authors provides small illustrative models along with their MATLAB code. The next two sections present results from applying all the algorithms to each of the example models.
6.1 Computational Efficiency
Nearly all the algorithms successfully computed solutions for all the examples. Each of the algorithms, except Binder-Pesaran's, successfully computed solutions for all of Uhlig's examples. Uhlig's algorithm failed to provide a solution for the given parametrization of one of King's examples. However, Binder-Pesaran's and Uhlig's routines would likely solve alternative parametrization of the models that had convergence problems.
Tables 2-4 present the MATLAB-reported floating point operations (flops) counts for each of the algorithms applied to the example models.
The first column of each table identifies the example model. The second column provides the flops required by the Anderson-Moore algorithm to compute ![]() followed by the flops required to
compute
followed by the flops required to
compute ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Columns three through seven report the flops required by each algorithm divided by the flops required by the Anderson-Moore algorithm
for a given example model.
. Columns three through seven report the flops required by each algorithm divided by the flops required by the Anderson-Moore algorithm
for a given example model.
Note that the Anderson-Moore algorithm typically required a fraction of the number of flops required by the other algorithms. For example, King-Watson's algorithm required more than three times the flops required by the Anderson-Moore algorithm for the first Uhlig example. In the first row, one observes that Uhlig's algorithm required only 92% of the number of flops required by the Anderson-Moore algorithm, but this is the only instance where an alternative to the Anderson-Moore algorithm required fewer flops.
In general, Anderson-Moore provides solutions with the least computational effort. There were only a few cases where some alternative had approximately the same number of floating point operations. The efficiency advantage was especially pronounced for larger models. King-Watson generally used twice to three times the number of floating point operations. Sims generally used thirty times the number of floating point operations - never fewer than Anderson-Moore, King-Watson or Uhlig. It had about the same performance as Klein. Klein generally used thirty times the number of floating point operations. It never used fewer than Anderson-Moore, King-Watson or Uhlig. Binder-Pesaran was consistently the most computationally expensive algorithm. It generally used hundreds of times more floating point operations. In one case, it took as many as 100,000 times the number of floating point operations. Uhlig generally used about twice the flops of Anderson-Moore even for small models and many more flops for larger models.
Table 5 presents a comparison of the original Uhlig algorithm to a version using Anderson-Moore to solve the quadratic polynomial equation. Employing the Anderson-Moore algorithm speeds the computation. The difference was most dramatic for larger models.
6.2 Numerical Accuracy
Tables 6-11 presents the MATLAB relative errors. I have employed a symbolic algebra version of the Anderson-Moore algorithm to compute solutions to high precision5. Although ![]() and
and ![]() are relatively simple linear transformations of
are relatively simple linear transformations of ![]() , each of the authors uses radically different methods to compute these quantities. I then compare the matrices computed in
MATLAB by each algorithm to the high precision solution.
, each of the authors uses radically different methods to compute these quantities. I then compare the matrices computed in
MATLAB by each algorithm to the high precision solution.
Anderson-Moore always computed the correct solution and in almost every case produced the most accurate solution. Relative errors were on the order of ![]() . King-Watson always computed
the correct solution, but produced solutions with relative errors generally 3 times the size of the Anderson-Moore algorithm. Sims always computed correct solutions but produced solutions with relative errors generally 5 times the size of the Anderson-Moore algorithm. 6Sim's F calculation produced errors that were 20 times the size of the Anderson-Moore relative errors. Klein always computed the correct solution but produced solutions with relative errors generally 5 times
the size of the Anderson-Moore algorithm.
. King-Watson always computed
the correct solution, but produced solutions with relative errors generally 3 times the size of the Anderson-Moore algorithm. Sims always computed correct solutions but produced solutions with relative errors generally 5 times the size of the Anderson-Moore algorithm. 6Sim's F calculation produced errors that were 20 times the size of the Anderson-Moore relative errors. Klein always computed the correct solution but produced solutions with relative errors generally 5 times
the size of the Anderson-Moore algorithm.
Uhlig provides accurate solutions with relative errors about twice the size of the Anderson-Moore algorithm for each case for which it converges. It cannot provide a solution for King's example 3 for the particular parametrization I employed. I did not explore alternative parametrizations. For
the ![]() computation, the results were similar. The algorithm was unable to compute
computation, the results were similar. The algorithm was unable to compute ![]() for King example 3. Errors were generally 10 times the size of Anderson-Moore relative errors.
for King example 3. Errors were generally 10 times the size of Anderson-Moore relative errors.
Binder-Pesaran converges to an incorrect value for three of the Uhlig examples: example 3, 6 and example 7. In each case, the resulting matrix solves the quadratic matrix polynomial, but the particular solution has an eigenvalue greater than one in magnitude even though an alternative matrix
solution exists with eigenvalues less than unity. For Uhlig's example 3, the algorithm diverges and produces a matrix with NaN's. Even when the algorithm converges to approximate the correct solution, the errors are much larger than the other algorithms. One could tighten the convergence criterion
at the expense of increasing computational time, but the algorithm is already the slowest of the algorithms evaluated. Binder-Pesaran's algorithm does not converge for either of Sims' examples. The algorithm provides accurate answers for King & Watson's examples. Although the convergence
depends on the particular parametrization, I did not explore alternative parametrization when the algorithm's did not converge. The ![]() and
and ![]() results were similar to the
results were similar to the ![]() results. The algorithm was unable to compute
results. The algorithm was unable to compute ![]() for Uhlig 3 in addition to Uhlig 7. It computed the wrong value for Uhlig 6. It was unable to compute values for either of Sims's examples.
for Uhlig 3 in addition to Uhlig 7. It computed the wrong value for Uhlig 6. It was unable to compute values for either of Sims's examples.
7 Conclusions
A comparison of the algorithms reveals that:
- For models satisfying the Blanchard-Kahn conditions, the algorithms provide equivalent solutions.
- The Anderson-Moore algorithm proved to be the most accurate.
- Using the Anderson-Moore algorithm to solve the quadratic matrix polynomial equation improves the performance of both Binder-Pesaran's and Uhlig's algorithms.
- While the Anderson-Moore, Sims and Binder-Pesaran approaches provide matrix output for accommodating arbitrary exogenous processes, the King-Watson and Uhlig implementations only provide solutions for VAR exogenous process.7Fortunately, there are straightforward formulae for augmenting the King-Watson, Uhlig and Klein approaches with the matrices characterizing the impact of arbitrary shocks.
- The Anderson-Moore algorithm requires fewer floating point operations to achieve the same result. This computational advantage increases with the size of the model.
- The Anderson-Moore suite of programs provides a simple modeling language for developing models. In addition, the Anderson-Moore algorithm requires no special treatment for models with multiple lags and leads. To use each of the other algorithms, one must cast the model in a form with at most one lead or lag. This can be tedious and error prone task for models with more than a couple of equations.
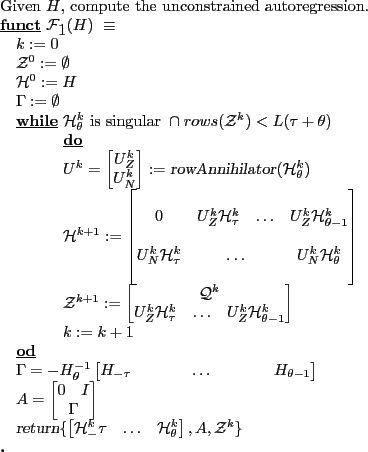
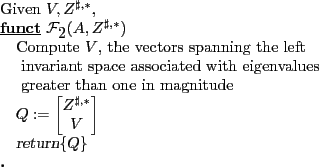
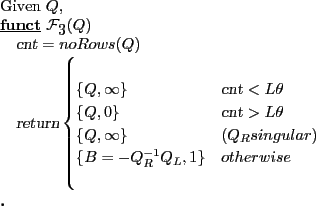
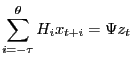
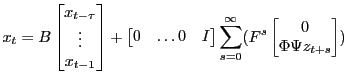
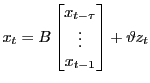

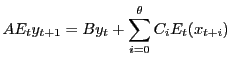
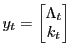
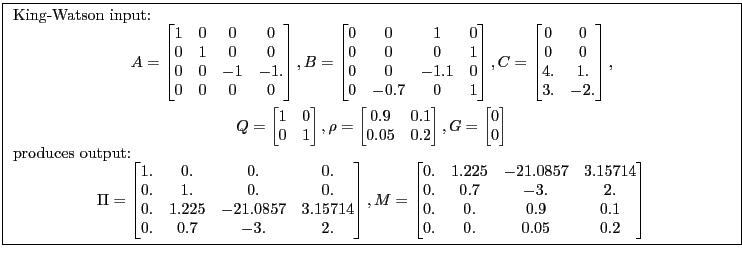
![\fbox{\parbox{0.9\textwidth}{\small \centerline{Obtaining Anderson-Moore inputs ... ...&0&0&0&\dots&0&0&0&0\ -G&0&0&0&&0&0&0&0 \end{matrix}\right ] \end{gather*} }}](img126.gif)
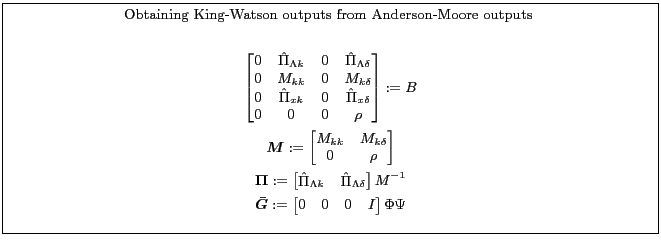



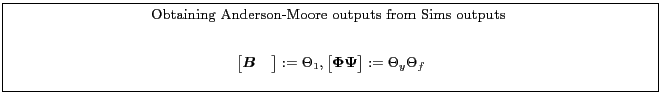
![\fbox{\parbox{0.9\textwidth}{\small \centerline{Obtaining Anderson-Moore inputs ... ...&0&0&0&\dots&0&0&0&0\ -G&0&0&0&&0&0&0&0 \end{matrix}\right ] \end{gather*} }}](img166.gif)