Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2006-37 Screen Reader version ^♣

Social Security's Delayed Retirement Credit and the Labor Supply of Older Men ¹

by Jonathan F. Pingle

Revised draft

August 2006

Keywords: Social security, labor supply, aging, retirement

Abstract:

This paper presents estimates of the impact of Social Security's Delayed Retirement Credit on the employment rates of older men. The credit raises lifetime social security benefit payments for recipients who delay receiving benefits after age 65 and offers a rare and important test of whether labor supply incentives built in to the program can promote work at older ages. The results suggest that the increased incentives raised employment among workers over age 65. In addition, the recent increases in social security's Normal Retirement Age also appear to be pushing up labor supply.

1. Introduction

Social security is one of the United States' largest social programs and a compelling subject of both voluminous economic research and extensive political debate. The program touches virtually every U.S. citizen, if not directly, then through taxes or spending. The aging of the baby boom cohort is poised to place considerable pressure on the program, as the ratio of workers paying for the program to recipients will shrink. At the same time, the labor supply of older workers is an important policy issue because of the financial relief their rising employment might bring to the program, and because of the persistent declines in aggregate labor supply stemming from population aging.

Faced with deficits and a looming funding dilemma for old age-programs, whether program incentives can influence older Americans' labor supply is among the most important economic policy questions facing the country. This paper tests whether increases in an incentive to delay receipt of social security benefits, the Delayed Retirement Credit (DRC), influences employment among older workers. The DRC raises monhtly social security benefits for individuals for each month that they delay their receipt of social security benefits after reaching their "Normal Retirement Age"--traditionally their 65th birthday.

Using data on older men from the Survey of Income and Program Participation (SIPP), the analysis in this paper tests whether the employment of older workers responded to increases in the DRC during the past 20 years instituted as part of the Social Security Amendments of 1983 (P.L. 98-21). The exogenous policy variation offers a rare and important chance to test how social security program incentives influence the decision to work among older Americans. Panel data regressions and difference-in-difference specifications estimate the influence of the policy changes on work behavior among 65 to 70 year old men and find significant correlation between the policy changes and work behavior of men past their 65th birthday. The results imply that policy initiatives can increase the share of older individuals who work, and more generally that older Americans respond to program incentives.

2. Policy description

Traditionally, people first qualified for social security benefits at age 62 and then qualified for full benefits at age 65--also called the Normal Retirement Age (NRA), the age at which one qualifies for their Primary Insurance Amount (PIA). The DRC was instituted in 1972 to provide a 1 percent bonus to a person's social security pension to compensate for each year past age 65 a person delayed receiving benefits, until age 70, in order to at least partially make up over time for the present value of the benefits not received. The DRC was increased from 1 percent to 3 percent in 1982. The credit is applied in monthly increments so that for each month past an eligible recipient's 65th birthday during which benefits are not received, there is an upward adjustment in the monthly Social Security payment amount the individual receives for the rest of their life. Lifetime benefits could be influenced by the DRC through two mechanisms (two ways in which an eligible recipient might not receive benefits after reaching their NRA): 1) because the person delayed applying for benefits, or 2) because of earnings. The reason earnings can cause the DRC to raise lifetime benefits is because the credit was applied to any social security payments lost by 65 to 69-year-olds because of the Retirement Earnings Test (RET). The RET reduced social security payments for workers earning more than a particular threshold. In 1991 this threshold, the Annual Exempt Amount (AEA), was $9,720 for workers age 65 to 69. At that time, for every $3 earned over that limit, social security benefits were reduced by $1.

Table 1 . Delayed Retirement Credit

Birth years	Benefit Increase for Each Month of Delay	Annualized Increase in Benefits
1918-1924	1/4 of 1 %	3 %
1925-1926	7/24 of 1 %	3.5 %
1927-1928	1/3 of 1 %	4 %
1929-1930	3/8 of 1 %	4.5 %
1931-1932	5/12 of 1%	5 %
1933-1934	11/24 of 1 %	5.5 %
1935-1936	1/2 of 1 %	6 %
1937-1938	13/24 of 1 %	6.5 %
1939-1940	7/12 of 1 %	7 %
1941-1942	5/8 of 1 %	7.5 %
1943-	2/3 of 1 %	8 %

In 1983, a commission on Social Security reform suggested increasing the DRC. Called the National Commission on Social Security Reform, it was formed as Congress and the Reagan administration became worried that the social security system, facing a financial crisis, might be insolvent by the middle of that decade. That fear, combined with the projected long-run deficits expected with the retirement of the baby boomers, prompted Congressional action to encourage workers to delay receiving benefits (Lilliard Richardson and Michael Munger, 1990). In addition to increasing the DRC, the 1983 amendments raised the NRA, or age at which an individual qualifies for full-benefits, from 65 gradually to 67. The legislation changed benefits for widows and widowers, and delayed the June 1983 cost-of-living increases. The amendments also changed the RET penalty for people turning age 65 in 1990 or later--reducing the penalty to social security payments from $1 of every $2 earned by people who were over the earned income limit, to $1 of every $3. In 1996, the exempt limit was raised by more than usual and then, in 2000, the RET was changed so that it only applied to people between age 62 and their NRA.

The new, higher levels of the DRC set out in the 1983 legislation were assigned by the year of an eligible worker's birth. Under the new policy, the DRC rose, from the 3 percent benefit for those born in 1924 or earlier, in half-percent increments every two birth years, until the credit reaches 8% for individuals born in 1943 or later. Thus, the DRC increased for workers born in 1925 or later, in effect starting in 1990 when that birth cohort turned 65. The levels of the credit assigned to each pair of birth years is shown in table 1. The gain can be substantial. Using the representative example on the SSA web site, someone born in 1941 who retires at their NRA would have a monthly benefit amount of $1,542. An 8 percent increase on that amount would be an extra $1,480 a year, and over 15 years (a little more than what a 65 year old can expect) that becomes an added $22,212 to lifetime income (without discounting), when the benefits forsaken (not received) totaled $18,509. Obviously a person's internal discount rate will influence whether this is a good deal or a bad one, but regardless of the actuarial fairness, an 8 percent DRC is a much, much, better deal than a 3 percent DRC. Plus, if the choice includes the tradeoff between an added year of labor earnings vs. an added year of leisure, the individual who delays retirement receives the income from the additional year of working.

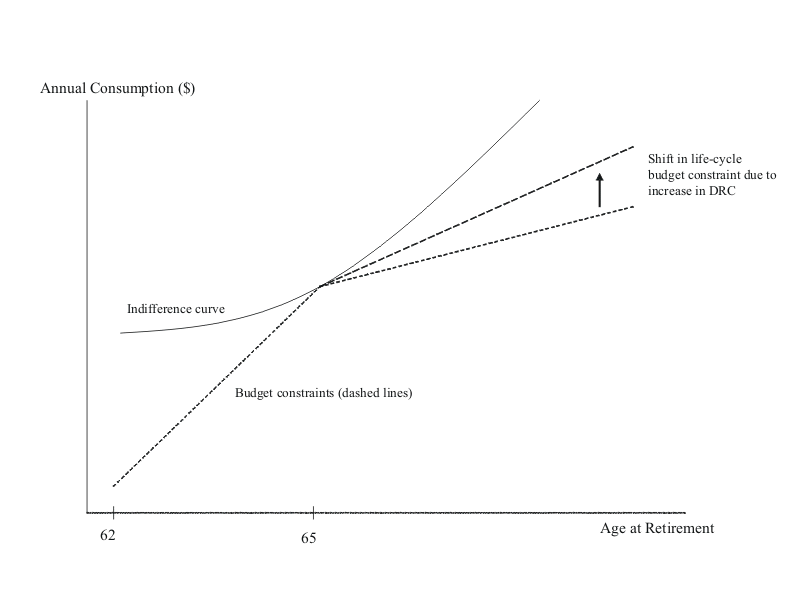
To see how the DRC influences labor supply (without the complexity of the life-cycle model incorporating the DRC suggested by Alan Gustman and Thomas Steinmeier (1991)), consider the decision problem graphed in figure 1 (this largely follows the discussion of Gary Burtless (1999) although similar expositions can be found elsewhere, including Olivia Mitchell and Gary Fields (1982)). A worker is considering when to stop working. The worker's preferences are defined over consumption and leisure. The trade-off the worker faces depends on the incentives in the social security system. Working an additional year adds another year of labor income to life-cycle income, but forsakes a year of social security benefits, which under the old DRC did not get completely made up later by increases to future benefits.

As noted by Burtless (1999), this produced a kink in the life-cycle budget constraint at age 65. Increases in the DRC will raise the slope of the life-cycle budget constraint after age 65 by increasing lifetime average annual income for people who work past age 65, as shown in the figure by the shift in the budget constraint. An indifference curve, as shown, displays a worker who would otherwise choose to retire at age 65, as many workers have done traditionally. If the budget constraint after age 65 shifts up enough--or the slope gets steep enough relative to the worker's marginal rate of substitution between average annual consumption and another year of leisure--the substitution effect will shift the worker off the kink at age 65 and prompt he or she to work more. If, before the policy changes, the worker would otherwise have chosen to retire sometime after age 65, the substitution effect of the increases in the DRC will be offset to some extent by an income effect.

Figure 1.

Because most workers leave the labor force before age 65, whether the DRC has any influence on behavior would seem to be a minor issue, and the policy has received little attention. Alternatively, the RET has been the subject of several papers--even though the changes in the two policies are nearly co-linear. For example, Leora Friedberg (1999) in a detailed and noteworthy study on the RET (using data before the 1983 amendment's changes took effect) avoided explicit modeling of the DRC. Noting the DRC would affect income lost to the RET, her specification tests hinted at little influence of the credit. More recently, David Loughran and Steven Haider (2005) argue the RET raised labor supply and influenced "claiming" behavior. Results of Bac Tran (2004) reach a similar conclusion, and he also notes that the RET incentives influenced only workers over 65 and not younger workers, which is evidence of a kink in the life-cycle budget constraint at age 65.

No paper before this one has estimated the actual influence of the DRC, but prior to the changes taking place predictions were in two camps--a big effect or no effect. Olivia Mitchell (1987) simulated responses of lower income workers and dual-earner couples and found little reaction to the DRC. Alternatively, Alan Gustman and Thomas Steinmeier (1985, 1991) predicted enormous response. Using a structural model of retirement, they predicted the overall response to the amendments would be very high, in particular that "the number of 66-year-olds who are working full-time would increase by about one-quarter, with similar if not larger figures applying to other age categories above age 65." They went on to say, "the principal element responsible for this increase in post-65-year-olds still working full time is not hard to spot - namely, the increase in the delayed retirement credit from 3% to 8%," (Gustman and Steinmeier, 1985).

They argue that this is because the credit restores some actuarial fairness to working past age 65. They note that with a 3% DRC the penalties from working past age 65 can be high since forgone social security benefits are not reimbursed fairly with future benefit level increases. However, after the DRC reaches 8% they note better than fair actuarial returns will be possible. Their model's outsized predictions stand in contrast to some economists who argue that social security plays only a small role in workers' labor supply decisions and that America's income growth and private pensions are more important influences (Alan Blinder, Roger Gordon and Donald Wise, 1981 and James Stock and David Wise, 1990). Alternatively, pretty convincing empirical evidence links the high rate of exit from the labor force at ages 62 and 65 to social security (David Blau, 1994 and John Rust and Christopher Phelan, 1997).

Whether or not social security incentives can influence the labor supply of older workers remains an important question, and the variation provided by the DRC offers a test of this hypothesis in what is close to a "natural experiment." In general, other studies exploiting "natural experiments" in changes to Social Security benefits have not uncovered much response. For example, Alan Krueger and Jorn-Steffen Pischke (1992) used the exogenous variation in a benefit "notch" in the mid-1970s--the 1977 amendments to the Social Security Act caused an unanticipated reduction in lifetime benefits for individuals born after 1916--and concluded that reducing benefits had no effect on retirement behavior. However, considering the relevance of the labor supply of older workers to policy makers, evaluating whether workers responded to the increases in the DRC is an important contribution to the literature on retirement programs and aggregate labor supply.

3. The labor supply of older men

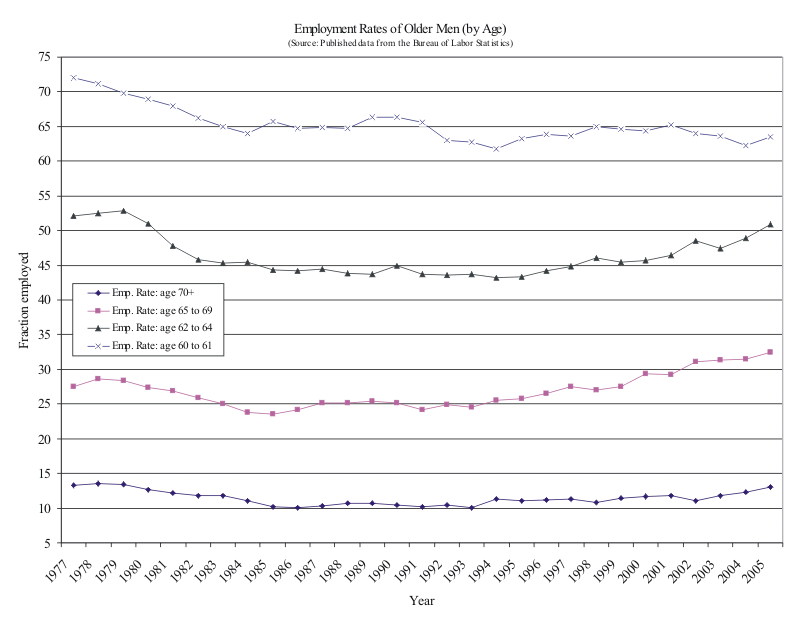
Figure 2.

The labor supply of older men has become a topic of interest among economists in its own right as population aging has begun to put substantial downward pressure on aggregate labor supply growth in the U.S. (Stephanie Aaronson, et.al., 2006). Reversing years of trend declines in work, the employment-to-population ratios and labor force participation rates of men over age 55 have risen in recent years. Figure 2 shows the employment-to-population ratios (referred to as employment rates throughout this paper) published by the Bureau of Labor Statistics for men ages 60 to 61, 62 to 64, 65 to 69 and age 70 and over. The corresponding time series are listed in table 2 (for readers interested in more exact comparisons). The published series are shown and are not adjusted for the Current Population Survey (CPS) 1994 redesign as suggested by Anne Polivka and Stephen Miller (1998). All four age groups were contained in wider age groups estimated to have had slightly elevated employment-to-population ratios as a result of the survey changes, however adjustments were not provided for these disaggregated series, only age 55 to 64 and age 65 and over. This should not invalidate comparisons of the differences in the changes over time between the age groups.

Table 2. Employment Rates of Older Men (Percent)

Year	Age 60 to 61	Age 62 to 64	Age 65 to 69	Age 70 Plus
2005	63.56	50.83	32.47	13.03
2004	62.24	48.92	31.41	12.33
2003	63.64	47.40	31.39	11.83
2002	63.97	48.48	31.11	11.07
2001	65.24	46.49	29.29	11.79
2000	64.36	45.70	29.33	11.63
1999	64.56	45.49	27.51	11.43
1998	64.97	46.00	27.07	10.80
1997	63.64	44.87	27.45	11.33
1996	63.85	44.20	26.47	11.19
1995	63.29	43.39	25.76	11.12
1994	61.81	43.18	25.58	11.32
1993	62.75	43.77	24.48	10.06
1992	63.01	43.60	24.91	10.43
1991	65.60	43.74	24.17	10.15
1990	66.34	44.89	25.17	10.44
1989	66.40	43.69	25.40	10.68
1988	64.76	43.81	25.13	10.67
1987	64.90	44.49	25.12	10.27
1986	64.77	44.26	24.12	10.13
1985	65.68	44.31	23.61	10.25
1984	64.04	45.46	23.78	11.06
1983	64.95	45.26	24.98	11.81
1982	66.26	45.78	25.86	11.81
1981	67.91	47.82	26.90	12.19
1980	68.92	51.04	27.44	12.69
1979	69.86	52.81	28.35	13.37
1978	71.13	52.46	28.59	13.58
1977	71.99	52.10	27.54	13.26

Note: Employment rates are annual averages of the published BLS monthly series on employment and population for each age group, i.e. the published employment to population ratios.

Of the groups shown in the table, the only age group not eligible for social security--age 60 to 61--is the only age group whose employment rate has fallen since 1990--by 2.8 percentage points or 4.4 percent. Among men age 62 to 64, the employment rate rose 5.9 percentage points, or 13.2 percent. The over age 70 men's employment rate rose by 2.6 percentage points, or 24.8 percent. Among the group most likely influenced by the DRC, men age 65 to 69, the employment rate rose by 7.3 percentage points, or 29 percent.

Whether this increase in labor supplied has been caused by longer life expectancies, cohort effects, higher levels of education, higher demand for older workers or the policy changes is not clear from the time series. However, the fact that the 60 to 61 year olds have had no increase in labor supply, while all the age groups influenced by social security have trended up since the policy changes is certainly suggestive. For example, if the increase was due to birth cohorts' progressively higher intrinsic labor market attachment, we would expect the 60 to 61 year olds' employment to turn up first and the age 70 and over employment to turn up last. In fact the post-1990 trough among the age 65 to 69 year olds in 1991 preceded the change of slope in the younger age groups. This pattern in the time series data would suggest that something influenced the age 65 to 69 year olds in a different way than the other age groups, which should not be the case if the influences were due to macroeconomic conditions, changes in life expectancy or cohort influences, each of which would suggest contemporaneous movements in all the series or a sequential timing of the changes in slope which is not apparent.

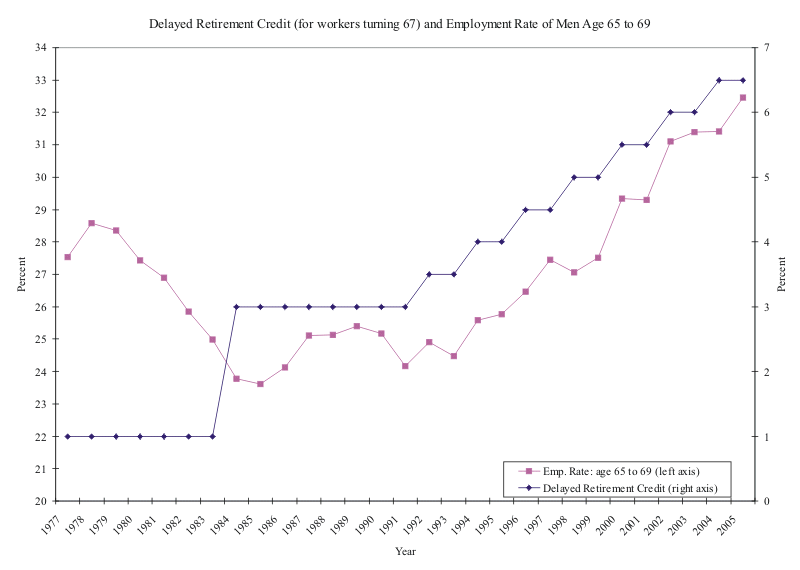
The correlation between the DRC and employment is clearly visible when the changes in the policy are plotted next to the time series of the employment rates of the age 65 to 69 year old men, as shown in figure 3--the value of the DRC is shown for the men turning age 67 in the corresponding year. Age 67 was chosen because it is the mid-point of the age 65 to 69 age range of the published BLS labor force series. The correlation between the two annual time series from 1977 to 2005 is 0.54. In addition, the employment rate does not reveal any discrete jump in 1990 that would be correlated with the changes in the RET that year. However, corresponding with the virtual repeal of the RET in 2000, there is a discrete increase in employment. On balance, though, the employment rates rise with the DRC, particularly after smoothing through the weak labor market of the early 1990s. For example, in even numbered years when entering 65-year-olds would have had a higher DRC than their predecessors, the employment rates rose in every year since 1990 except for 1990 and 1998, and the average increase in even-numbered years was 0.70 percentage points, as opposed to the average increase in odd-numbered years of 0.18 percentage points--so the correlation goes beyond the fact that both series are trending up.

Figure 3.

Another interesting feature of figure 3 (or complication depending on your point of view) is the possible influence of information on the employment rates. The changes in the DRC seem relatively benign in the early 1990s, which could be because the increases are offset by a weak cyclical recovery in the labor market. However, the pace of change appears to step-up after about 1995. This coincides with when the Social Security Administration (SSA) began sending out statements that showed individuals what their benefit payments would look like if they began receiving benefits at 65 as opposed to age 70. It could be that prior to that time, information problems and lack of knowledge of the program incentives might have limited the policy's take-up. Perhaps this is why the employment rates of both the 60 to 61 year olds and the 62 to 64 year olds reach their trough in 1994.

4. Data description

Despite the correlation found in the CPS data, the empirical analysis relies on pooled panels of data on individuals from eight of the 1985 to 2003 panels of the Survey of Income and Program Participation (SIPP). The SIPP includes the birth year information necessary to accurately assign levels of the DRC. Each panel consists of between 7 and 12 waves in which each household is interviewed every four months, following individuals if they move, and records their labor force status for each of the preceding four months. Only information from the month prior to the interview is used in the empirical analysis, mitigating the influence of potential recall error in the survey data.

Table 3. Sample means and variable descriptions

Variable	Mean	Std. Dev.	Description
age	66.3	4.22	Age
birth year	1919	4.29	Year of birth
birth month	6.50	3.45	Month of birth (range 1 to 12)
calendar year	1992	5.62	Calendar year of observation
working	0.40	0.49	= 1 if employed at all during month
black	0.09	0.28	= 1 if African American
widow	0.07	0.26	= 1 if widower
bachelor	0.13	0.33	= 1 if unmarried, not widower
high school graduate	0.47	0.50	= 1 if completed high school but no college
college graduate	0.18	0.39	= 1 if completed college
DRC	3.56	1.51	Delayed Retirement Credit (1 to 8 percent)
NRA	65.01	0.08	Normal Retirement Age (65 plus fraction of year)
GDP	3.36	2.93	Quarterly GDP growth at an annual percentage rate
social security	0.69	0.46	= 1 if receiving social security benefits
unemp	6.45	1.40	Quarterly U.S. break-adjusted unemployment rate
life expectancy at 65	15.64	0.64	life expectancy at age 65 for each calendar year
1993 panel	0.07	0.26	= 1 if in 1993 panel (covering 1993 to 1995)
n:	217,916		total observations, men age 60 to 74

Notes: The data covers 1983 to 2003 and utilizes the 1984, 1985, 1986, 1987, 1990, 1991, 1992, 1993, 1996 and 2001 panels, each of which last between 2 and 4 years.

Each individual was classified as "employed" if they reported that they had worked at some time during the month prior to the month of the interview. Rather than imperfectly approximate the labor force definition from the CPS by defining respondents as in or out of the labor force based on the SIPP job search information, an employment indicator is used as the dependent variable in the regressions. However, controls for fluctuations in aggregate labor demand intend to account for cyclical demand fluctuations in the labor market. The unemployment rate for 65 to 69 year olds has tighter bounds than the aggregate unemployment rate, rising from 3.3 percent in the strong labor market of 2000 to 4.4 percent in the weak labor market of 2003, when the aggregate unemployment rate rose from 4 to 6 percent. Considering the data and specifications, presumably the policy variables' coefficient estimates are safely interpreted as the effect on the labor supply of older men.

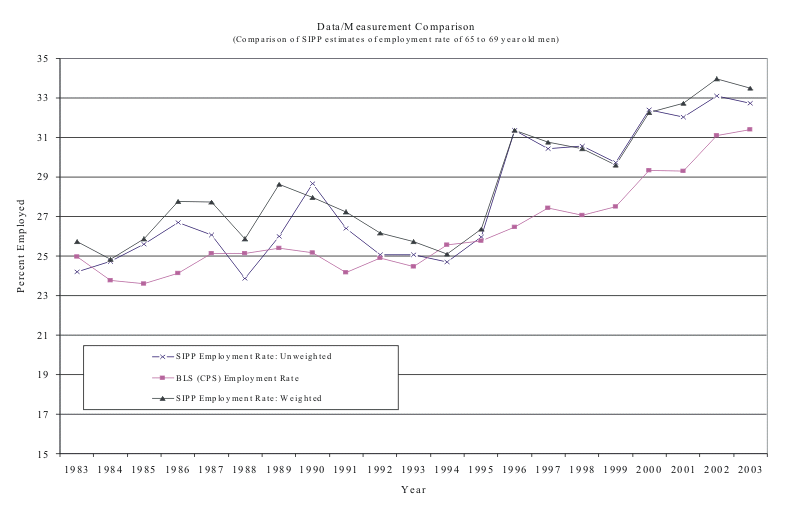
Figure 4.

The means and standard deviations of key variables are shown in table 3 with brief descriptions. The SIPP employment rates are comparable to the BLS employment rates, as shown in figure 4, although the SIPP estimates are noisier, which should be expected given the smaller sample size. The level of the employment rates run about two percentage points higher in the SIPP than in the CPS, which is probably due to the survey question on employment--the threshold for which is higher in the CPS. One cause for concern is that there is some evidence provided by Adam Looney (2005) that suggests the 1993 panel, which runs until 1995, did not adequately adjust the sample for the representation of low-income respondents. As a result, an indicator for the 1993 panel is included in specification tests shown later and identified by the overlap with the 1991 and 1992 panels. As shown in figure 4, the low levels of employment in 1993, 1994 and 1995 suggested by Looney (2005) exaggerate what would otherwise be a smaller increase from 1995 to 1996. Some of the noise in the SIPP data could also be due to mild seasonality from unbalanced panels that do not necessarily have equal representation of the months in each year. However, the month dummies in specification tests revealed little seasonality in the SIPP data, and the BLS finds so little seasonality in the employment of older men that they do not even publish seasonally adjusted series for men over age 55.

The reason the analysis does not go straight to the "gold standard" in macro labor--the CPS micro-data--is because neither the CPS's annual demographic supplement nor the basic monthly survey report birth year for survey respondents, information crucial for identification in this analysis. Finding birth years in the CPS would require matching the monthly surveys over a period of 20 years and observing when people's reported age changes value, when many cases would not be able to be matched, and age is often used as a qualifier for a match in the first place. Alternatively the SIPP staff can match birth years to administrative data, and the analysis does not need to rely on much survey response other than reported work.

The Health and Retirement Study (HRS and AHEAD), a panel data set of older Americans, was also considered and was used initially. However, the main HRS sample was born between 1931 and 1941. Data on the cohort born between 1924 and 1930 was not added until 1998, introducing two survey breaks timed with policy changes. Plus, employment data needed to be constructed from a retrospective summary, which required substantial assumptions and some faith in the accuracy of peoples' recall. The SIPP has a large sample (though smaller than the CPS), includes a long range of birth years, and had limited changes in the relevant survey question. None of the data's idiosyncrasies appear to be influencing the results, as comparisons of alternative specifications that used panel dummies, month dummies, weights and no weights, revealed.

5. Panel data regressions

The changes in the DRC are about as exogenous a policy change a researcher is likely to confront without a randomized trial. The policy is applied by birth year, hardly a characteristic an individual chooses, and social security enjoys nearly universal coverage outside of railroad workers and school teachers for these birth cohorts, who were not likely to choose careers because of foresight of the DRC changes. The policy changes were not likely influenced by the affected individuals, so there is no simultaneity to worry about. In addition, the policy has nonlinear variation, with a prolonged period at 3 percent and then the staggered two-year steps which separately identifies year and age fixed effects from the policy changes.

After considering duration models and estimation procedures in the treatment effects literature, the most appealing estimator is the linear panel data model. The data set is large, but without a long time series, and large N relative to T facilitates appealing to the asymptotic properties of the estimator. In addition, the panel nature of the data can not be fully exploited--although the policy varies by individual, it does not vary within an individual's observations which rules out differencing and fixed effects specifications. Alternatively, the employment rates are well-bounded, so a linear framework won't suffer from being near the 0-1 bounds imposed by the probability of being employed. The model relies on few assumptions for consistent estimates and can use the repeated observations of each person in each of the panels: simply,

$$y_{it} =\beta 'x_{it} +\varepsilon _{it}$$ (1)

Where is an indicator which equals one if the person was employed and zero otherwise; is a matrix of time varying characteristics; is a vector of coefficients, one of which is an estimate of the marginal effect of the policy; and is a mean-zero error term.

As noted by Jeffrey Wooldridge (2002), only two assumptions in the linear panel data model are sufficient to consistently estimate :

$$E(x_t ^\prime \varepsilon _t )=0,\mbox{ }t=1,...,T$$ (2)

and

$$rank(\sum\nolimits_{t=1}^T {E(x_t ^\prime x_t )} )=K$$ (3)

The first assumption is not violated by serial correlation or heteroskesdacity. It requires that the error term in each period is uncorrelated with that period's realizations of the variables in . The second assumption notes that none of the regressors can be linearly dependent ( is the number of independent variables, or columns of . Under only these two conditions, the linear panel data model estimates are consistent and asymptotically normal, although not necessarily efficient. In addition, the form of the dependent variable implies heteroskedasticity. For consistent estimates of the covariance matrix under very general assumptions including serial correlation and heteroskedasticity, a robust estimator of variance is used, producing valid t-statistics for testing (see Halbert White, 1980). Thus, the problem becomes specifying the variables in such that these assumptions are reasonable.

So, what unobserved characteristic in the error term would be correlated with the DRC? The RET is one possibility, but that can be controlled for with the discrete variation in the policy or with year indicators. Alternatively, the DRC is assigned by birth year, which could be correlated with age at a given point in time, life expectancy, health, education, the likelihood of military service, or disability. However, the diffusion of health care improvements and longer life expectancies are likely well captured by proxy, for example, a simple function of birth year, like a linear or quadratic trend, which can be separately identified from the DRC and added to the model. Education and age are observed and can be included in the model. Unobserved correlation with birth year aside, the model reasonably satisfies the assumptions for consistency.

The matrix includes age and year fixed effects. This means that RET indicators can not be separately identified from the year fixed effects, but the gain is that the nonparametric specification of time will control for any unobserved macro influences on the employment decision. Rather than specify age or year with a functional form assumption that risks being incorrect, the specifications are as general as possible in order capture any aggregate time series influence rather than limit the controls to only those influences we might specify in an equation, or model with a variable like the unemployment rate. Education indicators are included, plus an indicator for black, a variable for the NRA, the quarterly unemployment rate adjusted for all the CPS changes possible, the growth in quarterly GDP to control for robust aggregate demand, and specifications of birth cohort.

Although substantial effort will be made to control for unobserved birth year trends or influences, unobserved correlation with birth cohort visually does not appear to be playing a role in figure 2: if these birth cohorts were more likely to prolong their careers, then why don't these cohorts do so when they are 60 to 61, and why do the increases among 62 to 64 year olds lag by five years the increases among 65 to 69 year olds, a point noted in section 3? Alternatively, are people born in 1929 really so different from people born in 1930, or are people born in 1931 the same as people born in 1930 but a lot different from people born in 1932, and different in such a way that it is correlated with the staggered two-year step increases in the policy variable? In the end there is no way of knowing how different people of adjoining birth years might be and specification tests evaluate the results' sensitivity to unobserved trends correlated with birth year.

Despite the exogenous policy variation, panel attrition might be correlated with the likelihood of observing someone still working after age 65 because retirement might be correlated with moving or traveling and dropping out of the sample. In the SIPP data for men age 60 to 74, for most panels, about 10 percent of the initial sample is lost after the first year, which is not a large amount of attrition but enough that it could introduce non-random selection that could be correlated with employment. A two-step procedure suggested by Jerry Hausman and David Wise (1979) is used to correct for attrition. The model is comprised of two parts, an equation for employment and an attrition equation which is a probit for the probability of observing an individual at that interview date:

$$\Pr (d_{it} =1)=\Phi (\alpha 'R_{it} )$$ (4)

Note that is an indicator which equals 1 if the individual remains in the sample at time , and the matrix contains and parameterizations of the interview wave. Presumably, the wave of the observation is related to the probability of attrition and not a structural determinant of employment, thus providing exogenous identification of the attrition equations. Given we observe outcomes only if , estimating the policy effects conditional on remaining in the sample is based on the conditional densities and estimates of the conditional expectation of employment:

$$E(y_{it} \vert x_{it} ,d_{it} =1)=\beta 'x_{it} +\sigma _{t\varepsilon } \frac{\phi (\alpha 'R_{it} )}{\Phi (\alpha 'R_{it} )}$$ (5)

In the employment equation, conditional on being observed in the panel and not attriting, is the estimated covariance between and the error term in the probit equations for . The inverse Mill's ratios (the ratio of the normal distribution pdf to the cdf as shown in (4) and (5)) as outlined by Cheng Hsiao (1986). First, a probit equation is used to compute consistent estimates of the inverse Mill's ratios conditional on the wave of each interview, and then the structural equation estimates the coefficients and a for each of the interview periods. Bootstrapped standard errors and White-corrected covariance matrices produced very similar measures of precision for the coefficient of interest. To identify the probit equations for observability, survey respondents who attrit were assumed to acquire no more education than was observed at their last interview--presumably a safe assumption for over-65 men. Other than that, they were allowed to age so that the remaining variables assigned by time, year or age could be applied to the missing observations, and thus the values of are observed for attriters.

6. Results

The coefficient estimates from a group of baseline specifications of equation (1) are shown in Table 4. The sample is comprised of 65 to 69 year old men. The specification in the first column has no variable for birth year, the specification in the second column has quadratic polynomial of birth year, the specification in the third column contains a cubic polynomial of birth year, and the specification in the fourth column contains a sextic polynomial (the polynomials are actually Chebyshev polynomials). Results with a linear birth year trend are shown later, but produce similar results. An added specification (not shown) included indicator variables for each birth year, but constrained the coefficients of adjoining birth years for identification, producing a larger estimate of the policy effect than in the specifications shown in the table.² The fifth column shows the results of the specification shown in column 3 but with an estimated correction for attrition which altogether suggests attrition does not warrant further attention. The attrition probit results are not shown, nor are the correlation parameters, although they exhibited an interesting monotonic decline over the interview waves, suggesting that initial attrition is non-random, but later attrition becomes increasingly random.

For a range of specifications, the marginal effect of the policy was estimated to be between 0.010 and 0.020--suggesting that each percentage point increase in the DRC was raising the employment rate of men age 65 to 69 between 1 and 2 percentage points. On the low end of this bound, the specification in column 3 is used as a base of comparison because of the conservative estimates of the policy effect. The predicted values for this model fell well within the 0-1 bounds, ranging from 0.08 to 0.52, nicely avoiding the unappealing feature of the linear probability model--the possibility of predicted probabilities less than zero or greater than one. Judging from the sensitivity of the estimates in the table 4, the parameterization of birth year seems to be playing a small role, which requires further consideration, but does not undo the estimated treatment effect.

On balance, the remaining coefficient estimates are what one would expect. Being older implies less work, and having more education implies more work. The effects of the unemployment rate and GDP are estimated to be near zero--which would cause concern if not for the year indicators. The year indicators suggest a pattern of trend decline in male employment during the 1980s, but the pattern of the coefficients also reflects cyclical response, with relatively larger negative values for the weak labor markets of the early 1990s and 2002 and 2003. The NRA variable, the units of which are years, has an unexpected sign. However, when younger age groups are added the coefficient's sign changes as expected, which is noted below. Dropping the variable from the specifications because it is identified by a relatively small share of 65 to 69 year olds was one option, but since the DRC estimates are not sensitive to its inclusion, give or take 0.001, the NRA variable remained, rather than cover up an unappealing result by simply dropping it.

Table 4. Coefficient estimates: baseline specifications

Variable:	1 Coef.	1 t-stat	2 Coef.	2 t-stat	3 Coef.	3 t-stat	4 Coef.	4 t-stat	5 Coef.	5 t-stat
DRC	0.020	4.49	0.016	3.30	0.011	2.12	0.016	2.66	0.011	2.07
NRA	-0.148	-0.95	-0.125	-0.78	-0.272	-1.61	0.255	1.00	-0.267	-1.56
GDP	0.000	-0.22	0.000	-0.27	0.000	-0.20	0.000	-0.24	0.000	0.03
Unemp	0.003	0.44	0.004	0.57	0.004	0.48	0.003	0.45	0.007	0.69
black	-0.023	-4.33	-0.023	-4.32	-0.023	-4.34	-0.024	-4.37	-0.023	-3.86
1984 dummy	-0.011	-0.58	-0.013	-0.70	-0.017	-0.90	-0.022	-1.15	-0.010	-0.48
1985	-0.013	-0.66	-0.021	-1.04	-0.030	-1.44	-0.036	-1.74	-0.021	-0.69
1986	-0.008	-0.35	-0.021	-0.90	-0.032	-1.35	-0.036	-1.54	-0.020	-0.53
1987	-0.014	-0.53	-0.030	-1.09	-0.042	-1.52	-0.045	-1.64	-0.031	-0.70
1988	-0.038	-1.21	-0.059	-1.76	-0.073	-2.15	-0.074	-2.20	-0.058	-1.08
1989	-0.013	-0.35	-0.037	-0.94	-0.051	-1.30	-0.052	-1.33	-0.035	-0.65
1990	0.001	0.04	-0.031	-0.84	-0.044	-1.19	-0.045	-1.22	-0.036	-0.67
1991	-0.028	-1.16	-0.066	-2.01	-0.077	-2.33	-0.079	-2.37	-0.072	-1.46
1992	-0.043	-2.14	-0.086	-2.65	-0.095	-2.91	-0.097	-2.97	-0.093	-1.89
1993	-0.048	-2.02	-0.094	-2.57	-0.100	-2.74	-0.103	-2.79	-0.097	-1.74
1994	-0.055	-1.92	-0.104	-2.51	-0.108	-2.60	-0.110	-2.64	-0.101	-1.57
1995	-0.045	-1.36	-0.097	-2.10	-0.098	-2.13	-0.100	-2.16	-0.085	-1.21
1996	0.013	0.40	-0.042	-0.85	-0.041	-0.84	-0.041	-0.84	-0.040	-0.41
1997	-0.001	-0.01	-0.058	-1.10	-0.056	-1.06	-0.055	-1.05	-0.045	-0.43
1998	-0.006	-0.15	-0.066	-1.16	-0.063	-1.11	-0.063	-1.12	-0.050	-0.49
1999	-0.020	-0.46	-0.081	-1.36	-0.079	-1.32	-0.082	-1.37	-0.043	-0.43
2000	0.003	0.07	-0.060	-0.92	-0.058	-0.89	-0.063	-0.97	0.001	0.01
2001	-0.018	-0.43	-0.084	-1.32	-0.085	-1.33	-0.096	-1.51	-0.084	-0.57
2002	-0.018	-0.51	-0.087	-1.39	-0.092	-1.46	-0.102	-1.62	-0.086	-0.65
2003 dummy	-0.023	-0.67	-0.094	-1.46	-0.102	-1.59	-0.110	-1.70	-0.096	-0.80
high school	0.060	17.08	0.060	17.10	0.060	17.05	0.060	17.07	0.060	16.41
college grad	0.195	39.84	0.195	39.84	0.195	39.83	0.195	39.84	0.194	34.58
age 66	-0.031	-5.86	-0.028	-4.59	-0.028	-4.64	-0.029	-4.79	-0.027	-3.68
age 67	-0.044	-7.85	-0.037	-4.65	-0.037	-4.70	-0.039	-4.93	-0.036	-3.02
age 68	-0.064	-10.29	-0.053	-5.05	-0.054	-5.11	-0.055	-5.24	-0.051	-3.02
age 69	-0.080	-11.70	-0.065	-4.97	-0.066	-5.01	-0.066	-5.01	-0.062	-2.82
birth year			0.011	1.72	0.079	3.26	7.113	2.69	0.080	2.95
b. year^2			0.000	-1.14	-0.001	-3.00	-0.373	-2.66	-0.001	-2.85
b. year^3					0.000	2.87	0.010	2.65	0.000	2.74
b. year^4							0.000	-2.65
b. year^5							0.000	2.65
b. year^6							0.000	-2.66
constant	9.285	0.97	8.125	0.78	17.195	1.57	-44.485	-1.89	16.827	1.52
attrition adj.:									yes
n:	74,189		74,189		74,189		74,189		74,189

Note: All t-statistics based on robust estimates of covariance matrix, as noted in the text. Cohort indicators were pairs of birth years not collinear with the policy changes, the coefficients on which are not shown. Also not shown are the covariance estimates and first-stage estimates of the attrition-corrected estimates in column 5. Regression diagnostics are not shown, but all the R-squared values were 0.041 or 0.042, and the joint F-tests highly significant. Finally, the predicted values lie well-within the 0-1 bound, for the specification in column 3, the range of predicted probabilities is [0.079987,0.5163318].

Table 5. Coefficient estimates: DRC indicator variables

Variable:	1 Coef.	1 S. Er	2 Coef.	2 S. Er.	3 Coef.	3 S. Er.	4 Coef.	4 S. Er.
DRC 3	0.041	0.009	0.012	0.011	0.003	0.012	0.003	0.012
DRC 3.5 pct	0.057	0.013	0.033	0.015	0.031	0.015	0.031	0.015
DRC 4 pct	0.048	0.016	0.035	0.018	0.039	0.018	0.039	0.018
DRC 4.5 pct	0.089	0.020	0.094	0.023	0.101	0.023	0.101	0.023
DRC 5 pct	0.074	0.023	0.104	0.029	0.109	0.029	0.109	0.029
DRC 5.5 pct	0.081	0.027	0.141	0.037	0.139	0.037	0.139	0.037
DRC 6 pct	0.151	0.031	0.253	0.047	0.232	0.049	0.230	0.049
DRC 6.5 pct	0.086	0.035	0.225	0.058	0.183	0.064	0.178	0.064
NRA	0.082	0.171	0.239	0.177	0.127	0.188	0.136	0.189
GDP	0.000	0.001	0.000	0.001	0.000	0.001	0.000	0.001
Unemp	0.002	0.008	0.004	0.008	0.004	0.008	0.007	0.010
black	-0.024	0.005	-0.024	0.005	-0.024	0.005	-0.023	0.006
high school	0.060	0.003	0.060	0.003	0.060	0.003	0.060	0.004
college grad	0.195	0.005	0.195	0.005	0.195	0.005	0.194	0.006
age 66	-0.033	0.005	-0.030	0.006	-0.030	0.006	-0.029	0.007
age 67	-0.046	0.006	-0.040	0.008	-0.041	0.008	-0.039	0.012
age 68	-0.063	0.007	-0.055	0.011	-0.055	0.011	-0.052	0.017
age 69	-0.078	0.008	-0.065	0.013	-0.065	0.013	-0.061	0.022
birth year			0.047	0.011	0.127	0.043	0.132	0.043
b. year^2			0.000	0.000	-0.002	0.001	-0.002	0.001
b. year^3					0.000	0.000	0.000	0.000
n:	74,189		74,189		74,189		74,189

Note: Each specification includes year and race indicators as in table 4. Also, note that the DRC variables are indicators for each level of the Delayed Retirement Credit that appears in the sample. The 1 percent credit is the omitted category. White-adjusted standard errors are shown to facilitate comparison of the coefficients on the indicator variables--all the coefficients on the DRC indicators are statistically significant at the 5 percent level with the exception of the 3 percent DRC indicator in columns 2, 3 and 4.

Table 5 shows the results of specifications which break the policy variable up into indicator variables for each level of the policy (that appear in the data), with the original 1 percent level of the credit the omitted category. The specifications in the first three columns are all based on the specifications in table 4 (some coefficient estimates not shown), and include different polynomial specifications for birth year as noted. The fourth column corrects the estimates for attrition. Aside from the estimates of the 6.5 percent credit, all roughly follow the kind of sequential steps which would be implied by a rising incentive. All of the policy variables are significantly different from the 1 percent credit at the 5 percent level of significance, except for the 3 percent DRC coefficients in columns 2, 3 and 4. In columns 2 through 4, each successive indicator variable (up to 6 pct.) produces a higher estimate of the influence on labor supply, and a few of the estimates are significantly different from the adjoining levels of the credit. Admittedly, the estimates do not all rise by a uniform amount like the credit, but the confidence intervals would not rule this out.

As an experiment, comparing the employment rates of individuals on either side of the cut-offs, or policy changes, appears compelling. But of course that is what the DRC variable is doing when it enters the specifications as a single (linear) variable. It is just capturing the average effect of all the cutoffs we observe. By estimating the changes separately using the indicator variables as shown in table 5, it becomes clearer that the linear relationship between the DRC and the probability of employment is not an unreasonable functional form assumption, or an unreasonable way to summarize the effect of a number of discrete changes.

Table 6 organizes the results of a battery of alternative specifications. All specifications are based on the baseline specification shown in column 3 of table 4, which is among the most conservative estimates of the influence of the DRC. The first column of table 6 notes how the specification deviated from that baseline. The second column shows the corresponding coefficient estimate on the policy variable (DRC), and the third column shows the standard error. The fourth column shows the significance level of the t-statistic.

The first several rows note the influence of excluding birth year, and subsequently including up to a six-term (sextic) Chebyshev polynomial in birth year in the model. The DRC coefficient estimate remains significant at the 5 percent level for most parameterizations, but as the flexibility of the trend rises, it becomes increasingly collinear with the policy, although remains significant at about the 10 percent level of significance. A RESET specification test prefers a linear birth year trend which has a higher estimate of the policy effect to the more flexible specifications.³ However, in order to be cautious, and not be overly confident, the sensitivity to unobserved birth year trends is shown. There was no reduction in the estimated root mean square error of the regression when a fourth or fifth polynomial term is added (to five decimal places at least). Thus the cubic polynomial seems like a reasonable baseline, as good a fit to the actual data as the quartic or quintic polynomials. There was a reduction in root mean square error when adding a sixth polynomial term. At that point added polynomial terms increased the estimated policy effect. The most flexible parameterization of birth year shown, a six term Chebyshev polynomial, estimates that the DRC coefficient is 0.015 and significantly different from zero at the 1 percent level of significance. This suggests that, even after very flexible parameterization of unobserved birth year trends, the policy is estimated to have significantly influenced labor supply. Altogether, the policy estimates are robust, and estimated with reasonable precision for micro-data, with the evidence pointing toward a statistically significant effect of the policy, ranging upwards from 0.01. This assertion is further supported by using other age groups as control groups for the birth year trends, which also increases the statistical precision.

A number of other considerations are shown in table 6, including the addition of a 1993 panel indicator, with little influence on the coefficient of interest. The results of three probit specifications are shown also, to further alleviate concerns over the use of a linear probability model--the marginal effects and z-statistics from the probit equation with robust covariance matrix produce the same results as the linear probability models.

One criticism of employing birth year polynomials to control for omitted trends correlated with the policy might be that alternative causal explanations for the changes in labor supply are being ignored. For example, one candidate might be health and another longevity. To consider the influence of improving health, a vector of health variables was added to the model. They included five annual time series of death rates for men due to 1) heart disease, 2) cancer, 3) respiratory disease, 4) vascular disease, and 5) diabetes. However, as noted in the table, the addition of the health variables actually raises the coefficient estimate on the DRC variable. Adding life expectancy does little as well, and the coefficient on life expectancy and some of the health variables did not indicate that longer lives and better health are increasing labor supply. This is most likely a result of the fact that the health improvements and big gains to life expectancy in the 1980s corresponded to steady declines in labor supply among men this age. Similarly, (not shown) rising female labor supply among women in their 60s also corresponded to the long period of trend decline in male labor supply among 65 to 69 year old men in the years prior to 1990--suggesting that rising work among spouses, as a time series, would not explain the change in direction of employment rates among 65 to 69 year olds that can easily be seen in figure 3.

Table 6. Alternate specifications

Specification:	DRC Coefficient:	SE:	Prob t:
Baseline specification from column 3 in Table 4:	0.011	0.005	0.034
no birth year variable	0.020	0.004	0.000
birth year linear polynomial	0.017	0.005	0.000
birth year quadratic polynomial	0.016	0.005	0.001
birth year cubic polynomial	0.011	0.005	0.034
birth year quartic polynomial	0.009	0.005	0.105
birth year quintic polynomial	0.008	0.005	0.112
birth year sextic polynomial	0.015	0.006	0.009
Drop NRA	0.012	0.005	0.021
Add 1993 Panel Indicator	0.011	0.005	0.033
Drop GDP	0.011	0.005	0.034
Drop unemployment rate	0.011	0.005	0.035
Add bachelor indicator	0.011	0.005	0.030
Probit (marginal effect) with no birth year variable	0.021	0.005	0.000
Probit (marginal effect) with quadratic birth year	0.017	0.005	0.002
Probit (marginal effect) with cubic birth year	0.011	0.006	0.042
Add health variables, quadratic year, cubic birth year	0.013	0.005	0.014
Add life expectancy, quadratic year, cubic birth year	0.010	0.005	0.047
Add RET variables, quadratic year, no birth year:	0.018	0.004	0.000
Add RET variables, quadratic year, quad. birth year	0.014	0.005	0.002
Add RET variables, quadratic year, cubic birth year	0.009	0.005	0.080
Add RET variables, quadratic year, birth year indic.	0.023	0.010	0.019

Notes: Specifications are based on that shown in column 3 of table 4, with modifications as indicated. Prob t shows the significance level at which the t-test rejects that the coefficient is equal to zero.

The bottom four rows of table 6 show the results of four specifications that drop the year fixed effects, and replace them with a quadratic specification of calendar year, in order to identify RET policy indicators. These alternatives do not influence the DRC coefficient, but they do provide evidence that the RET, when the policy was in place for men age 65 to 69, lowered labor supply. The indicators included were a pre-1990 indicator, for the old penalty, a 1990-1996 indicator for the RET prior to a special increase in the earnings limit, and a 1997 to 1999 indicator for the policy's final years for this age group. The 2000 repeal and thereafter was the omitted category. Altogether the coefficient estimates on the three indicators suggest the RET lowered labor supply by a statistically significant amount--as much as 5 percentage points--which would suggest that the RET's removal is providing a sizeable boost to labor supply (more attention should be given to this topic). However, modeling the RET does not influence the estimates of the DRC's separately identified effect. Rather it seems likely both policies are playing a role in increasing labor supply, and this influence is confirmed below in difference-in-difference estimators.

7. Comparison group estimation (a.k.a. difference-in-difference estimators)

Control groups that might provide a faultless counterfactual are not readily apparent. However, the analysis can compare the employment behavior of the adjoining age groups to the employment behavior of the 65 to 69 year olds in order to exploit an added source of identification--and an alternative way to control for unobservable influences. The degree to which the labor supply increases among the 65 to 69 year olds are more correlated with the DRC than the labor supply increases among the adjoining age groups will separately identify the policy effect from some of the other influences that might be raising the labor supply of the successive pairs of birth cohorts. For example, to the extent better health, changing labor market structure, shifts in defined benefit to defined contribution plans or even spousal labor supply might be influencing the trend in male labor supply, the changes in employment among men age 60 to 64 and 70 to 74 can be used to control for the trends among men age 65 to 69. Thus, for the difference-in-difference estimators, the DRC variable can enter the model and control for general correlation between the DRC and outside influences while a separate variable, the interaction of DRC with an age 65 to 69 year old indicator, can identify the influence of the policy net of unobservable changes, trends or influences--whatever they might be--which are correlated with the DRC.

The results are shown in table 7. A sample of men age 60 to 74 from the SIPP was used, as described in table 3. Each specification shown contains year indicators. The first column shows the results of a specification with just the DRC variable in the equation, identified by all the age groups together. The second column shows the results of a specification that adds to that an interaction between the DRC and the age 65 to 69 year old age category. The corresponding coefficient estimates that, conditional on the influence of the DRC on all the age groups together, the DRC raised the employment rates of 65 to 69 year olds an additional 0.8 percentage point per unit change in the credit. The specification described in the third column adds a cubic birth year polynomial. The specification described in the fourth column includes interactions between the three stages of the RET and the 65 to 69 year old age category. The effect of the DRC gets larger when the RET controls are added to the specifications, although the RET coefficients are insignificant, unlike in the earlier specifications. This could be because of correlation with the year indicators, when in the earlier equations a polynomial for year was used to identify the indicators for each RET policy regime.

Table 7. Age category control groups

Variable:	1 Coef.	1 t-stat	2 Coef.	2 t-stat	3 Coef.	3 t-stat	4 Coef.	4 t-stat
DRC_65t69			0.008	5.00	0.006	3.34	0.010	2.45
DRC	0.011	4.32	0.008	2.89	0.011	3.81	0.005	1.65
RET_1_65t69							0.013	0.85
RET_2_65t69							0.000	0.05
RET_3_65t69							0.013	1.59
NRA	-0.014	-1.32	0.004	0.38	0.109	5.80	0.004	0.31
GDP	0.000	-0.10	0.000	-0.08	0.000	-0.35	0.000	-0.06
year indicators:	yes		yes		yes		yes
Unemp	0.000	-0.02	0.000	-0.02	0.001	0.22	0.000	-0.01
black	-0.036	-10.93	-0.035	-10.88	-0.035	-10.78	-0.035	-10.85
hs	0.065	30.75	0.065	30.79	0.065	30.90	0.065	30.74
col	0.187	66.91	0.187	66.92	0.187	66.88	0.187	66.91
age_61	-0.043	-8.22	-0.043	-8.25	-0.036	-6.71	-0.043	-8.33
age_62	-0.137	-25.36	-0.137	-25.41	-0.124	-19.57	-0.138	-25.34
age_63	-0.204	-36.48	-0.204	-36.56	-0.184	-24.49	-0.206	-36.07
age_64	-0.253	-44.24	-0.254	-44.35	-0.227	-25.66	-0.256	-43.20
age_65	-0.322	-54.95	-0.358	-38.05	-0.314	-24.13	-0.376	-13.06
age_66	-0.354	-57.91	-0.390	-41.55	-0.339	-23.98	-0.407	-14.39
age_67	-0.370	-57.31	-0.404	-43.04	-0.347	-22.56	-0.422	-15.20
age_68	-0.392	-57.05	-0.425	-44.81	-0.361	-21.55	-0.442	-16.27
age_69	-0.411	-56.55	-0.442	-46.04	-0.372	-20.47	-0.460	-17.19
age_70	-0.430	-56.75	-0.436	-56.75	-0.367	-19.81	-0.441	-50.29
age_71	-0.449	-57.60	-0.455	-57.59	-0.379	-18.78	-0.460	-50.75
age_72	-0.456	-56.56	-0.462	-56.56	-0.379	-17.31	-0.468	-49.60
age_73	-0.470	-56.12	-0.476	-56.10	-0.387	-16.38	-0.483	-48.87
age_74	-0.480	-54.53	-0.487	-54.48	-0.390	-15.41	-0.493	-47.17
constant	1.464	2.18	0.330	0.47	-6.464	-5.38	0.374	0.51

Notes: Sample size is 217,916. Specification in column 3 contains cubic polynomial in birth year. R-squared values are approximately 0.14. The DRC interactions represent the policy effect net of unobservable characteristics. The coefficients on the DRC interaction with the age 65 to 69 age group are all significant at the 0.02 percent level of significance.

In each of the specifications, the average effect of the DRC across all age groups is estimated by the DRC variable, and the added influence on the 65 to 69 year olds is estimated by the coefficient on the DRC interaction term. If other age groups are influenced by the policy, the coefficient on the interaction would under-estimate the policy effect, as some part of the policy effect would be reflected in the coefficient on the (non-interacted) DRC variable itself. However, using the other age groups as a control for unobserved economic trends that might be correlated with birth year and thus the DRC provides further evidence that the increases in employment are the result of the policy changes instead of an omitted variable that is trending or spuriously correlated with labor supply.

One final test is summarized in Table 8. To the extent that the DRC raised labor supply prior to 2000 by being applied to earnings reductions caused by the RET, then the higher levels of the DRC should raise the share of workers over the RET threshold. To test this, labor earnings data from the SIPP was used to classify whether or not an individual's monthly earnings when converted to an annual rate were above or below the RET threshold. Then, a series of specifications similar to those shown in table 4 were estimated, where the dependent variable equaled one if the individual had monthly labor earnings over what would be implied by the RET limit. This tests the influence of the DRC on this labor supply margin. Although not all of the estimates are significant, the results do not contradict the earlier findings.

Table 8. Marginal effect of DRC on RET eligibility

Specification:	DRC Coefficient:	SE:	Prob t:
no birth year variable	0.014	0.003	0.000
birth year linear polynomial	0.013	0.003	0.000
birth year quadratic polynomial	0.011	0.004	0.002
birth year cubic polynomial	0.009	0.004	0.021
no birth year variable, positive labor earnings	0.028	0.011	0.013
birth year linear polynomial, positive labor earnings	0.020	0.012	0.099
birth year quadratic polynomial, positive labor earnings	0.023	0.012	0.064
birth year cubic polynomial, positive labor earnings	0.018	0.013	0.184

Notes: Dependent variable in regressions was an indicator equal to 1 if the person's labor earnings for the month was on pace to be over the RET threshold. Total sample of men age 65 to 69 with useable income data consisted of 63,459 observations. Sample without labor earnings consisted of 14,350 observations. Time period was limited to 1983 to 1999, which is the sample period when the RET was applied to this age group.

Finally, a few points have not been discussed. For example, retirees have to file for Medicare when they turn 65, which might prompt many to start receiving social security benefits, even if they keep working. On one hand, some fraction of the treated group might not realize the treatment due to information problems or simply convenience (this is another reason to include age indicators), but on the other hand, anyone who had applied for social security at the same time as Medicare would have seen the DRC incentives through any reduction in earnings due to the RET. Also, after 2000, take-up of the DRC could only come through not receiving benefits entirely as the RET was no longer applied to 65 to 69 year olds. However, to the extent any year-specific aggregate influence would affect employment behavior, the year fixed effects in any of the regressions should capture the mean effect of being in that year on employment, and are more flexible than specifying other continuous variables. In addition, the RET indicators, which reflected the 2000 regime change, did not influence the estimates of the DRC, as shown in tables 6 and 7. Altogether, the policy estimates are very robust to a wide variety of alternative considerations and estimated with reasonable precision. Of course, after the empirical evaluation (using the SIPP data), the basic finding is depicted in figure 3 (using the BLS data)--there is an uncanny, striking correlation between the DRC and the labor supply behavior of men age 65 to 69--sufficiently striking and robust to suggest the policy is having the estimated effect.

8. Conclusion

Gustman and Steinmeier (1991) predicted the DRC changes would have a substantial impact on the labor supply of older individuals. The evidence described in this paper seems to confirm their prediction. The changes in the Delayed Retirement Credit are correlated with behavior in two data sets. The linear panel data regressions using the SIPP sample, which provides precise estimates of the policy effect, suggests that the order of magnitude of the policy effect is substantial--every percentage point increase in the DRC led to a percentage point increase in the employment rate of men age 65 to 70.

Of course, an even better test of the DRC will present itself when the DRC stops increasing, and finally reaches 8 percent. In the mean-time, the evidence is compelling that the regressions have identified what they were intended to identify. The correlation between the policy and the employment rates is found in the basic statistics in the CPS--including evidence that the increases in labor supply are more likely to be timed with the biennial increases in policy rather than with odd-numbered years. In the SIPP data the estimated policy effect was robust to a long list of considerations--none of which influenced in any meaningful way the estimated policy effect.

The results suggest the DRC does influence the labor supply of older workers. Incentives built into old age programs with the intent of influencing behavior can do so, despite some debate to the contrary. In addition, the social security incentives do have macro effects on aggregate labor supply. Even if people are not aware of DRC details or specifics, the actuarial fairness of giving up a year of social security benefits and remaining at work have improved dramatically due to the policy changes, and it seems likely people are aware of that basic concept. Prior to the increases, losing a year of social security benefits to stay and work later in life was perceptibly unfair for some, while every cohort since 1924 has seen improvement. The increasing DRC seems to have led at least some older men to work more than otherwise.

9. References

Aaronson, Stephanie, Bruce Fallick, Andrew Figura, Jonathan Pingle and William Wascher, (2006), "The Recent Declines in the Labor Force Participation Rate and its Implications for Potential Labor Supply," Brookings Papers on Macroeconomic Activity, 1, 2006.

Blau, David (1994): "The Labor Force Dynamics of Older Men," Econometrica, 62, 117-156.

Blinder, Alan, Roger Gordon and Donald Wise, (1981) "Rhetoric and Reality in Social Security Analysis - A Rejoinder," National Tax Journal, 34, 473- 478.

Burtless, Gary (1999): "An Economic View of Retirement," from Behavioral Dimensions of Retirement Economics, Henry Aaron, ed., 7-42, Washington: The Brookings Institution Press.

Diamond, Peter and Jonathan Gruber (1997): "Social Security and Retirement in the U.S." NBER, Working Paper, #6097.

Diamond, Peter and Jerry Hausman (1984): "The Retirement and Unemployment Behavior of Older Men," from Retirement and Economic Behavior," Henry Aaron and Gary Burtless ed., 97-134.

Friedberg, Leora (1999): "The Labor Supply Effects of the Social Security Earnings Test," The Review of Economics and Statistics, 82:1, 48-63.

Godfrey, Leslie G., and Christopher D. Orme (1994): "The Sensitivity of Some General Checks to Omitted Variables in the Linear Model," International Economic Review, 35:2, May, 489-506.

Gustman, Alan and Thomas Steinmeier (1985): "The 1983 Social Security Reforms and Labor Supply Adjustments of Older Individuals in the Long Run," Journal of Labor Economics, 3:2, 237-253.

Gustman, Alan and Thomas Steinmeier (1991): "Changing the Social Security Rules for Work After 65," Industrial and Labor Relations Review, 44:4, 733-745.

Hausman, Jerry A., and David A. Wise (1985): "Social Security, Health Status, and Retirement," in Pensions, Labor and Individual Choice, David Wise ed. 159-181, Chicago: University of Chicago Press.

Hausman, Jerry A., and David A. Wise (1979): "Attrition Bias in Experimental and Panel Data: The Gary Income Maintenance Experiment," Econometrica, 47:2, pp 455-473.

Hsiao, Cheng (1986): Analysis of Panel Data, Econometric Society Monographs, No. 11, Cambridge University Press.

Krueger, Alan B. and Jorn-Steffen Pischke (1992): "The Effect of Social Security on Labor Supply: A Cohort Analysis of the Notch Generation," Journal of Labor Economics, 10:4, 412-437.

Looney, Adam (2005). "The Effects of Welfare Reform and Related Policies on Single Mothers' Welfare Use and Employment," Finance and Economics Discussion Series, Board of Governors of the Federal Reserve System, 2005-45.

Loughran, David and Steven Haider (2005). "Do the Elderly Respond to Taxes on Earnings? Evidence from the Social Security Retirement Earnings Test," RAND Labor and Population Work Paper, WR-233, January.

Pagan, Adrian and Frank Vella (1989): "Diagnostic Tests for Models Based on Individual Data: A Survey," Journal of Applied Econometrics, 4, S29-S59.

Peters, Simon (2000): "On the use of the RESET test in micro-econometric models," Applied Economics Letters, 7, 361-365.

Polivka, Anne E., and Miller, Stephen M. (1998). The CPS After the Redesign: Refocusing the Economic Lens. In Labor Statistics Measurement Issues, NBER Studies in Income and Wealth, pp 249-286, Vol 60, University of Chicago Press.

Mitchell, Olivia S. (1987): "Social Security Reforms and Poverty Among Older Dual-Earner Couples," NBER Working Paper, #2382.

Mitchell, Olivia S. and Gary S. Fields (1982) "The Effects of Pensions and Earnings on Retirement: A Review Essay," in Research in Labor Economics, vol. 5, Ronald Ehrenberg, ed. 115-155, Connecticut: JAI Press.

Ramsey, James B. (1969): "Tests for Specification Errors in Classical Linear Least-Squares Regression Analysis," Journal of the Royal Statistical Society, Sr. B., 31:2, 350-371.

Richardson, Lilliard E. and Michael Munger (1990): "Shirking, Representation, and Congressional behavior: Voting on the 1983 amendments to the Social Security Act," Public Choice, 67, 11-33.

Rust, John and Christopher Phelan, "How Social Security and Medicare Affect Retirement Behavior in a World of Incomplete Markets," Econometrica, 65, 781-831.

Stock, James and David Wise (1990): "Pensions, the Option Value of Work, and Retirement," Econometrica, 58, 1151-1180.

Tran, Bac V. (2004), "The Impact of the Repeal of the Retirement Earnings Test on the Labor Supply of Older Workers," manuscript, October.

Wooldridge, Jeffrey M., (2002): Econometric Analysis of Cross Section and Panel Data, MIT Press, Cambridge.

Footnotes

1. The views expressed in this paper are solely those of the author and do not represent the views of the Federal Reserve System or its staff. Thanks to David Blau, William Grant, Tom Mroz, Melissa Banzhaf, Ben Piven and H. Wilbert van der Klaauw and two anonymous referees for suggestions on an earlier, related paper. Thanks to Stephanie Aaronson, Michael Kiley, Andreas Lehnert, Joseph Lupton, Louise Sheiner, Paul Smith, Bill Wascher and seminar participants at the Federal Reserve Board for helpful comments on this draft. Thanks to Blake Bailey and Leslie Carroll for expert research assistance. Any errors are mine. Contact information: Jonathan Pingle, Federal Reserve Board, 20^th and C Streets, Washington, D.C., 20551-0001, [email protected], (202) 452-3816. Return to Text

2. For example, the coefficient for 1924 was constrained to be equal to that of 1925 so as not to be co-linear with the DRC change between those two birth years, but the1925 indicator coefficient was not constrained to be equal to 1926. Return to Text

3. The RESET tests preferred not including a birth year variable in the models to even very flexible non-linear specifications of birth year. For more details on the tests see James Ramsey (1969), and in the case of discrete dependent variables see Simon Peters (2000) and Adrian Pagan and Frank Vella (1989). Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Home | Economic Research and Data
Accessibility | Contact us
Last update: November 9, 2006